六年级上册数学第一单元知识结构图
六年级数学知识结构图
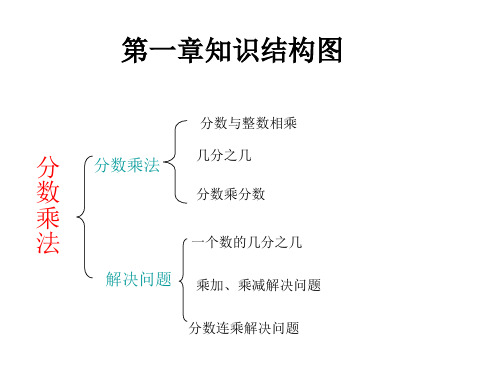
游戏规则的 公平性
可 能 性
西师大版六年级上
第八单元
放大
分数混和 运算 运算
图形的 变换 圆的认识
圆的 和 分
整
理
圆的
复
习
西南师大版六年级数学 第九单元
确定路线
结合律 交换律 分配律 应用
运算律 先乘除后加减 有括号先算括号 运算顺序 分 数 混 合 运 算
简单运算 数学应用
问题解决
西南师大版六年级数学 第六单元
应用 感知
认识
应用 必要性
产生和 意义
认识及 应用
负
产生和意义
数 的 初 步 认 识
西师大版六年级上
第七单元Biblioteka 可能不可能一定 应用
事件发生 的可能性
第一章知识结构图
分 数 乘 法
一
第二章知识结构图
圆的特征 圆的认识 画圆 设计图案
圆
概念 圆的 圆的 图 图 的 的 计 圆 计
第三章知识结构图
分 数 除 法
1”
第四章知识结构图
比 和 按 比 例 分 配
第五章知识结构图
图形的放大和缩小
图形运动和 位置确定
认识比例尺
比例尺
解决问题
确定位置
图形位置的确定
小学数学六年级上册各单元思维导图

小学数学六年级上册各单元思维导图第一部分:数的认识一、整数1. 自然数:0、1、2、3、4、5、6、7、8、9、10……2. 整数:自然数和它们的相反数3. 整数的分类:正整数、0、负整数二、分数1. 分数的意义:表示一个整体被平均分成若干份,其中的一份或几份2. 分数的表示:分子/分母3. 分数的分类:真分数、假分数、带分数三、小数1. 小数的意义:表示一个整体被平均分成若干份,其中的一份或几份,用小数点表示2. 小数的表示:整数部分和小数部分3. 小数的分类:有限小数、无限小数第二部分:数的运算一、加法1. 整数加法:相同符号的整数相加,异号整数相加2. 分数加法:同分母分数相加,异分母分数相加3. 小数加法:小数点对齐,逐位相加二、减法1. 整数减法:相同符号的整数相减,异号整数相减2. 分数减法:同分母分数相减,异分母分数相减3. 小数减法:小数点对齐,逐位相减三、乘法1. 整数乘法:相同符号的整数相乘,异号整数相乘2. 分数乘法:分子相乘,分母相乘3. 小数乘法:小数点对齐,逐位相乘四、除法1. 整数除法:相同符号的整数相除,异号整数相除2. 分数除法:分子相除,分母相除3. 小数除法:小数点对齐,逐位相除第三部分:数的性质一、数的性质1. 整数的性质:奇数、偶数、质数、合数2. 分数的性质:分子分母同乘(除)一个数,分数的值不变3. 小数的性质:小数点向左(右)移动一位,小数的值缩小(扩大)10倍二、数的运算定律1. 加法交换律:a + b = b + a2. 加法结合律:(a + b) + c = a + (b + c)3. 乘法交换律:a × b = b × a4. 乘法结合律:(a × b) × c = a × (b × c)5. 乘法分配律:a × (b + c) = a × b + a × c三、数的运算顺序1. 先算乘除,后算加减2. 同级运算,从左到右依次计算3. 括号内的运算优先级最高第四部分:数的应用一、整数应用1. 计算长度、面积、体积等2. 解决实际问题,如购物、分配、比较等二、分数应用1. 计算比例、比率等2. 解决实际问题,如分物品、分配资源等三、小数应用1. 计算长度、面积、体积等2. 解决实际问题,如购物、分配、比较等第五部分:几何图形一、平面图形1. 线段、射线、直线:线段是有限长的直线,射线有一个端点,直线无限长2. 角:由两条射线共同确定的图形,有一个顶点和两条边3. 三角形:由三条线段围成的图形,有三个角和三个边4. 四边形:由四条线段围成的图形,有四个角和四个边5. 圆:平面内到一个固定点距离相等的所有点组成的图形二、立体图形1. 长方体:由六个长方形围成的立体图形,有六个面、十二条边和八个顶点2. 正方体:由六个正方形围成的立体图形,有六个面、十二条边和八个顶点3. 圆柱:由两个底面和一个侧面围成的立体图形,底面是圆形4. 圆锥:由一个底面和一个侧面围成的立体图形,底面是圆形5. 球:由一个点向外无限延伸,到该点的距离相等的所有点组成的立体图形第六部分:几何图形的性质一、平面图形的性质1. 线段的性质:线段有长度,线段之间可以比较大小2. 角的性质:角有度数,角之间可以比较大小3. 三角形的性质:三角形的内角和为180度,等腰三角形的底角相等,直角三角形的勾股定理4. 四边形的性质:四边形的内角和为360度,矩形、正方形的对角线互相平分5. 圆的性质:圆的周长与直径的比例是圆周率,圆的面积与半径的平方成正比二、立体图形的性质1. 长方体的性质:长方体的体积等于长、宽、高的乘积2. 正方体的性质:正方体的体积等于边长的立方3. 圆柱的性质:圆柱的体积等于底面积乘以高4. 圆锥的性质:圆锥的体积等于底面积乘以高除以35. 球的性质:球的体积等于半径的立方乘以4/3π第七部分:几何图形的测量一、长度测量1. 线段长度:使用直尺或卷尺进行测量2. 角度测量:使用量角器进行测量二、面积测量1. 平面图形面积:根据公式计算,如长方形面积=长×宽,圆面积=πr²2. 立体图形表面积:根据公式计算,如长方体表面积=2(长×宽+长×高+宽×高)三、体积测量1. 立体图形体积:根据公式计算,如长方体体积=长×宽×高,圆柱体积=底面积×高2. 容器体积:使用量筒或量杯进行测量第八部分:数学应用与拓展一、数学在生活中的应用1. 购物:计算价格、找零等2. 测量:计算长度、面积、体积等3. 分配:分配物品、资源等二、数学在科学中的应用1. 物理学:计算速度、加速度、力等2. 化学:计算物质的量、浓度等3. 生物:计算种群数量、增长率等三、数学在艺术中的应用1. 音乐:计算音高、节奏等2. 绘画:计算比例、透视等3. 建筑设计:计算结构、空间等第九部分:数学问题解决策略一、问题解决步骤1. 理解问题:仔细阅读题目,明确已知条件和求解目标2. 制定计划:根据问题类型和条件,选择合适的解决方法3. 执行计划:按照计划进行计算和推导4. 检查结果:验证计算过程和结果的正确性二、常见问题解决方法1. 图形法:通过绘制图形,直观地表示问题条件,便于理解和解决2. 列表法:将问题条件列成表格,便于分析和比较3. 代数法:使用代数表达式和方程,进行符号运算和推导4. 逻辑推理法:根据已知条件和数学规律,进行逻辑推理和证明第十部分:数学思维培养一、培养逻辑思维能力1. 通过解决数学问题,锻炼逻辑推理和证明能力2. 学习数学定义、定理和公式,理解其背后的逻辑关系二、培养空间想象能力1. 学习几何知识,通过绘制图形和想象空间关系,培养空间想象力2. 参与数学建模活动,将实际问题转化为数学模型,提高空间想象能力三、培养数学建模能力1. 学习数学建模方法,将实际问题转化为数学问题2. 参与数学建模竞赛和活动,提高数学建模能力第十一部分:数学学习资源一、教材和辅导书1. 选择适合自己水平的教材和辅导书,进行系统学习2. 利用辅导书中的例题和习题,巩固所学知识二、在线资源和应用程序1. 利用在线教育平台和数学学习网站,获取丰富的学习资源2. 数学学习应用程序,进行互动式学习和练习三、数学竞赛和活动1. 参与数学竞赛,提高数学水平和竞争意识2. 参加数学讲座、研讨会等活动,拓宽数学视野。
人教版六上数学知识框架图
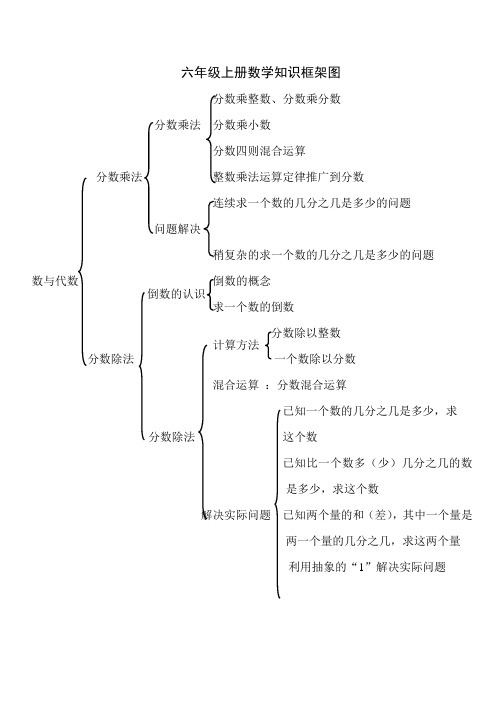
六年级上册数学知识框架图
分数乘整数、分数乘分数 分数乘法 分数乘小数
分数四则混合运算
分数乘法 整数乘法运算定律推广到分数
连续求一个数的几分之几是多少的问题
问题解决
稍复杂的求一个数的几分之几是多少的问题 数与代数 倒数的概念
求一个数的倒数
分数除以整数 分数除法 一个数除以分数
混合运算 :分数混合运算
已知一个数的几分之几是多少,求
分数除法 这个数
已知比一个数多(少)几分之几的数
是多少,求这个数
解决实际问题 已知两个量的和(差),其中一个量是
两一个量的几分之几,求这两个量
利用抽象的“1”解决实际问题
倒数的认识
计算方法
比的意义:求比值
比的基本性质比的基本性质
比
化简比
比的应用:按比分配
数与代数百分数的意义和读、写法
求百分率
百分数和分数、小数的互化
百分数求一个数的百分之几是多少
求一个数比另一个多(或少)百分之几
用百分数解决问题
求比一个数多(或少)百分之几的数是多少
根据平面示意图,用方向和距离描述某个点的位置位置与方向根据方向和距离的描述,在图上确定某个点的位置
描述简单的路线图
空间与几何圆的认识
圆的周长
圆基本应用
圆的面积圆环面积
解决实际问题
扇形
扇形统计图的认识统计与概率扇形统计图
选择合适的统计图
确定起跑线
综合实践活动
节约用水
数学广角数与形(找规律)。
数学六年级上册一单元的思维导

数学六年级上册一单元的思维导一、思维导图。
中心主题:分数乘法。
(一)分数乘整数。
1. 意义。
- 求几个相同分数的和的简便运算。
2. 计算方法。
- 用分子乘整数的积作分子,分母不变。
- 能约分的先约分再计算。
(二)分数乘分数。
1. 意义。
- 求一个分数的几分之几是多少。
2. 计算方法。
- 分子相乘的积作分子,分母相乘的积作分母。
- 能约分的先约分再计算。
(三)小数乘分数。
1. 计算方法。
- 把小数化成分数计算。
- 把分数化成小数计算(分数能化成有限小数时)- 直接约分计算(小数和分母能直接约分)(四)分数混合运算。
1. 运算顺序。
- 与整数混合运算顺序相同。
- 先乘除后加减,有括号先算括号里面的。
(五)解决问题。
1. 求一个数的几分之几是多少。
- 单位“1”的量×对应分率 = 对应量。
2. 连续求一个数的几分之几是多少。
- 用单位“1”的量依次乘对应的分率。
二、学习资料。
(一)分数乘整数。
1. 意义理解。
- 例如:(2)/(3)+(2)/(3)+(2)/(3),可以写成(2)/(3)×3,表示3个(2)/(3)相加。
这就是分数乘整数的意义,它是求几个相同分数的和的简便运算。
2. 计算示例。
- 计算(3)/(5)×4。
- 按照计算方法,用分子3乘整数4得到3×4 = 12作分子,分母5不变,结果是(12)/(5)。
如果能约分,比如计算(2)/(7)× 21,先约分,21和7约分,21变成3,7变成1,然后计算2×3 = 6,结果就是6。
(二)分数乘分数。
1. 意义理解。
- 例如:一张纸的(1)/(2)的(1)/(3)是多少。
就是求(1)/(2)的(1)/(3),用(1)/(2)×(1)/(3)表示。
这就是分数乘分数的意义,即求一个分数的几分之几是多少。
2. 计算示例。
- 计算(2)/(3)×(3)/(4)。
- 分子相乘2×3 = 6作分子,分母相乘3×4 = 12作分母,结果是(6)/(12),约分后为(1)/(2)。
六年级(上册)数学知识结构图

整数混合运算顺序: 先算乘除,后算加减; 同级运算从左往右按顺序计算; 带括号的先算小括号里面的,再算中括号里面的,然后算括号外面的。
乘法交换律: a × b = b × a 乘法结合律: ( a × b )×c = a × ( b × c ) 乘法分配律: ( a + b )×c = a c + b c (1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。
1、单位“1” 在分率句中“分数”的前面; 2、或在“占”、“是”、“比”“相当于”的后面。
、求一个数的几分之几是多少:用单位“1”的量×分数=具体量 2、求比一个数多(少)几分之几的数是多少: (1)单位“1”的量×(1+分数)=另一个部分量 (2)已知占单位“1”的几分之几的部分量+单位“1”的量-=要求的部分量1、八个方向:东、南、西、北、东北、东南、西北、西南。
其中,东对西、南对北、东北对西南、西北对东南。
2、地图一般按照“上北下南,左西右东”进行绘制的。
3、观测点不同,物体位置的描述方向也会有所不同。
1、“东偏南30°方向”就是以东为起始边,向南旋转30°的方向。
(“东偏南30°方向”也可以说成“南偏东60°方向”,但一般我们会选择角度更小的描述方法)2、物体的方向和距离是我们在描述物体具体位置时不可或缺的两个因素。
3、物体位置关系的相对性:方向相反,角度相同,距离相同。
角的画法:角的顶点对齐量角器圆心,起始边对齐量角器底边,根据量角器上的度数确定角度并打上点做好标记,连接点与顶点,擦除多余线条。
确定物体位置的方法: 1、先找观测点;2、再定方向(看方向夹角的度数);3、最后确定距离(看比例尺)。
(注:记得标注起点、终点、角度、距离)路线图的描述:每次描述都要说明起点、方向、距离和终点;语句可以用先、然后、接着、最后等词语进行连接。
人教版六年级数学上册 第一单元 分数乘法 思维导图(高清版)
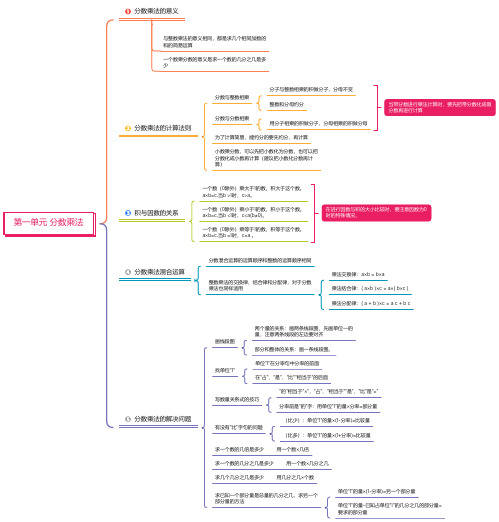
第一单元 分数乘法分数乘法的意义 分数乘法的计算法则 积与因数的关系 分数乘法混合运算 与整数乘法的意义相同,都是求几个相同加数的 和的简易运算 一个数乘分数的意义是求一个数的几分之几是多少 分数与整数相乘分数与分数相乘 分子与整数相乘的积做分子,分母不变 整数和分母约分 用分子相乘的积做分子,分母相乘的积做分母 为了计算简易,能约分的要先约分,再计算 小数乘分数,可以先把小数化为分数,也可以把 分数化成小数再计算(建议把小数化分数再计 算) 当带分数进行乘法计算时,要先把带分数化成假 分数再进行计算 一个数(0除外)乘大于1的数,积大于这个数。
a ×b=c,当b >1时,c>a 。
一个数(0除外)乘小于1的数,积小于这个数。
a ×b=c,当b <1时,c<a(b≠0)。
一个数(0除外)乘等于1的数,积等于这个数。
a ×b=c,当b =1时,c=a 。
在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
分数混合运算的运算顺序和整数的运算顺序相同整数乘法的交换律、结合律和分配律,对于分数 乘法也同样适用 乘法交换律:a×b = b×a乘法结合律:( a×b )×c = a×( b×c )乘法分配律:( a + b )×c = a c + b c分数乘法的解决问题 画线段图找单位“1”写数量关系式的技巧“的”相当于“×”,“占”、“相当于”“是”、“比”是“=”分率前是“的”字:用单位“1”的量×分率=部分量 两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐部分和整体的关系:画一条线段图。
单位“1”在分率句中分率的前面在“占”、“是”、“比”“相当于”的后面有没有“比”字句的问题(比少):单位“1”的量×(1-分率)=比较量(比多):单位“1”的量×(1+分率)=比较量求一个数的几倍是多少 求一个数的几分之几是多少 用一个数×几分之几求几个几分之几是多少 用几分之几×个数求已知一个部分量是总量的几分之几,求另一个 部分量的方法 单位“1”的量×(1-分率)=另一个部分量 单位“1”的量-已知占单位“1”的几分之几的部分量=要求的部分量 用一个数×几倍。
六年级数学上册知识结构网络图

例2
圆的认识和画法
例3
圆的对称特征
2.圆的周长
圆的周长计算公式
练习十五
例1
利用公式计算圆的周长
3.圆的面积
圆的面积计算公式
练习十六
例1
利用圆的面积计算公式求圆的面积
例2
利用圆的面积计算求环形面积
(三)统计与概率
统计(第六单元)
标 题
例 题 安 排
课后练习
统计
引入新知
练习二十五
条形统计图和扇形统计图
练习二十一
例3
求比一个数多(少)百分之几的数是多少
练习二十二
例4
折扣
练习二十三1~3
例5
纳税
练习二十三4、5
例6
利率
练习二十三6~9
(二)空间与图形
1.位置 (第一单元)
标 题
例 题 安 排
课后练习
位置
例1
引入新知
练习一
例2
用数对表示位置
2.圆(第四单元)
标 题
例 题 安 排
课后练习
1.认识圆
例1
想办法画圆,感受圆的曲线特征
练习十二
3.百分数 (第五单元)
标 题
例 题 安 排
课后练习
1.百分数的意义和写法
百分数的意义和写法
练习十八
2.百分数和分数、小数的互化
例1
小数化百分数
练习十九1、2、5、6
例2
百分数化小数
例3
百分数化分数
练习十九3~8
例4
分数化百分数
3.用百分数解决问题
例1
求常见的百分率
练习二十
例2
求一个数比另一个数多(少)百分之几
六年级数学知识结构图
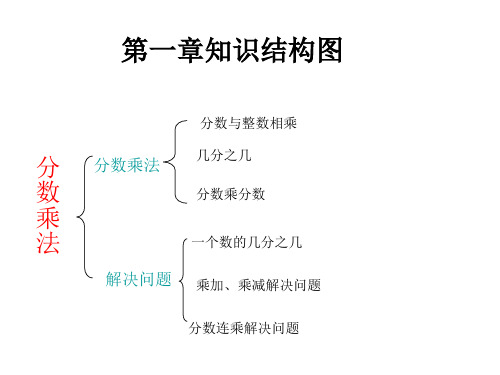
分数与整数相乘
分
分数乘法
几分之几
数
分数乘分数
乘
法
一个数的几分之几
解决问题 乘加、乘减解决问题
分数连乘解决问题
第二章知识结构图
圆
圆的认识
圆的周长 圆的面积
圆的特征 画圆
设计图案 概念 计算 圆周率
面积公式推导和计算
解决实际问题
组合图形的周长 组合图形的面积
第三章知识结构图
分数除法
倒数 分数除以整数
整数除以分数
分数除以分数
分
数
除
解决问题
认清单位”1” 的量
法
探索规律
发散思维 创造性思维
第四章知识结构图
前项
后项
比的意义
比号
比
比的意义 和性质
比值
和
基本性质
按 比
比的性质
例
化简
分
配
解决问题
按比例分配
第五章知识结构图
图形的放大和缩小
图形运动和
认识比例尺
位置确定
比例尺
解决问题
图形位置的确定
确定位置 确定路线
运算
分数混和 运算
应用
比和按比 例分配
六年级数学
整
理
复
习
第九单元
放大
图形的 变换
圆的认识
圆的周长 解决问题 圆的面积
交换律
结合律
分配律
应用
先乘除后加减 有括号先算括号
运算律
简单运算
数学应用
运算顺序
分 数 混 合 运 算
六年级数学
问题解决
第六单元
应用产生和 意义
六年级上册数学知识结构图

1、分数乘整数与整数乘法的意义相同。
都是求几个相同加数的和的简便运算。
(例如:65×5表示求5个65的和是多少? 1/3×5表示求5个1/3的和是多少?)2、一个数乘分数的意义是求一个数的几分之几是多少。
(例如:1/3×4/7表示求1/3的4/7是多少。
)、分数与整数相乘:分子与整数相乘的积做分子,分母不变。
(整数和分母约分)、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。
注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。
、为了计算简便,能约分的要先约分,再计算;也可以直接约分。
(交叉约分)分数化简约分的方法:分子分母同时除以它们的最大公因数。
、小数乘分数,可以先把小数化为分数再计算;也可以把分数化成小数再计算(建议把小数化分数再计算);也可以将小数与分母直接约分再计算。
1、一个数(0除外)乘大于1的数,积大于这个数。
、一个数(0除外)乘小于1的数(0除外),积小于这个数。
、一个数(0除外)乘1,积等于这个数。
整数混合运算顺序: 先算乘除,后算加减;同级运算从左往右按顺序计算;带括号的先算小括号里面的,再算中括号里面的,然后算括号外面的。
乘法交换律: a × b = b × a乘法结合律: ( a × b )×c = a × ( b × c )乘法分配律: ( a + b )×c = a c + b c(1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。
1、单位“1” 在分率句中“分数”的前面;2、或在“占”、“是”、“比”“相当于”的后面。
1、求一个数的几分之几是多少:用单位“1”的量×分数=具体量2、求比一个数多(少)几分之几的数是多少:(1)单位“1”的量×(1+分数)=另一个部分量(2)已知占单位“1”的几分之几的部分量+单位“1”的量-=要求的部分量1、 八个方向:东、南、西、北、东北、东南、西北、西南。
