数学中考每日一练
中考数学每日一练:含30度角的直角三角形练习题及答案_2020年填空题版

中考数学每日一练:含30度角的直角三角形练习题及答案_2020年填空题版答案答案答案答案2020年中考数学:图形的性质_三角形_含30度角的直角三角形练习题~~第1题~~(2020郑州.中考模拟) 如图,在Rt △ABC 中,∠ACB=90°,∠A =30°,AC =,分别以点A ,B 为圆心,AC ,BC的长为半径画弧,交AB 于点D ,E ,则图中阴影部分的面积是________.考点: 含30度角的直角三角形;几何图形的面积计算-割补法;扇形面积的计算;~~第2题~~(2020玉林.中考模拟) 如图所示,在四边形ABCD 中,AB ∥CD ,AD ⊥CD ,点E 、F 分别是AB ,BC 的中点,AB=4,E F=2,∠B=60°,则CD 的长为________.考点: 等边三角形的判定与性质;含30度角的直角三角形;~~第3题~~(2020乌鲁木齐.中考模拟) 如图,在矩形中,. 若将绕点旋转后,点落在延长线上的点 处,点 经过的路径为 ,则图中阴影部分的面积为________.考点: 三角形的面积;含30度角的直角三角形;勾股定理;扇形面积的计算;~~第4题~~(2019蒙自.中考模拟) 如图:∠DAE=∠ADE=15°,DE ∥AB ,DF ⊥AB ,若AE=8,则DF 等于________.考点: 角平分线的性质;含30度角的直角三角形;~~第5题~~(2019抚顺.中考真卷)如图,直线的解析式是,直线的解析式是 ,点在上,的横坐标为,作交于点 ,点在 上,以, 为邻边在直线,间作菱形,分别以点 ,为圆心,以为半径画弧得扇形和扇形 ,记扇形与扇形重叠部分的面积为;延长交于点,点在上,以,为邻边在, 间作菱形,分别以点,为圆心,以为半径画弧得扇形和扇形 ,记扇形 与扇形 重叠部分的面积为 按照此规律继续作下去,则 __.(用含有正整数 的式子表示)答案答案答案答案答案考点: 探索图形规律;等边三角形的判定与性质;含30度角的直角三角形;菱形的性质;扇形面积的计算;~~第6题~~(2019葫芦岛.中考真卷) 如图,河的两岸a ,b 互相平行,点A ,B ,C 是河岸b 上的三点,点P 是河岸a 上的一个建筑物,某人在河岸b 上的A 处测得∠PAB =30°,在B 处测得∠PBC =75°,若AB =80米,则河两岸之间的距离约为________米.( ≈1.73,结果精确到0.1米)考点: 等腰直角三角形;含30度角的直角三角形;~~第7题~~(2019丹东.中考真卷) 如图,在△ABC 中,∠C =90°,DE 是AB 的垂直平分线,AD 恰好平分∠BAC.若DE =1,则BC 的长是________.考点: 角平分线的性质;线段垂直平分线的性质;含30度角的直角三角形;~~第8题~~(2019朝阳.中考真卷) 如图,把三角形纸片折叠,使点A 、点C 都与点B 重合,折痕分别为EF,DG ,得到,,若 ,则FG 的长为________.考点: 含30度角的直角三角形;三角形中位线定理;翻折变换(折叠问题);~~第9题~~(2019宿迁.中考真卷) 如图,,若的顶点在射线上,且,点在射线上运动,当是锐角三角形时, 的取值范围是________.考点: 垂线段最短;含30度角的直角三角形;勾股定理;答案~~第10题~~(2019南京.中考真卷) 在△ABC 中,AB =4,∠C =60°,∠A >∠B ,则BC 的长的取值范围是________.考点: 等边三角形的性质;含30度角的直角三角形;圆周角定理;2020年中考数学:图形的性质_三角形_含30度角的直角三角形练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:。
中考数学每日一练:相反数及有理数的相反数练习题及答案_2020年填空题版

中考数学每日一练:相反数及有理数的相反数练习题及答案_2020年填空题版答案答案答案答案答案答案答案答案答案答案2020年中考数学:数与式_有理数_相反数及有理数的相反数练习题~~第1题~~(2020云南.中考模拟) 的相反数是________.考点: 相反数及有理数的相反数;~~第2题~~(2020遵化.中考模拟) 已知a 与b 的和为2,b 与c 互为相反数,若 =1,则a=________.考点: 相反数及有理数的相反数;绝对值及有理数的绝对值;~~第3题~~(2020广西壮族自治区.中考模拟) 的相反数的倒数是________考点: 相反数及有理数的相反数;有理数的倒数;二次根式的性质与化简;~~第4题~~(2019广州.中考模拟) 的相反数是________.考点: 相反数及有理数的相反数;~~第5题~~(2019泸西.中考模拟) ﹣4的绝对值是________.考点: 相反数及有理数的相反数;~~第6题~~(2019湖南.中考真卷) ﹣2019的相反数是________.考点: 相反数及有理数的相反数;~~第7题~~(2019南京.中考真卷) ﹣2的相反数是________; 的倒数是________.考点: 相反数及有理数的相反数;有理数的倒数;~~第8题~~(2019扬中.中考模拟) 如果5x+3与﹣2x+9是互为相反数,则x ﹣2的值是________.考点: 相反数及有理数的相反数;~~第9题~~(2019丹阳.中考模拟) 化简﹣(﹣ )的结果是________.考点: 相反数及有理数的相反数;~~第10题~~(2019南浔.中考模拟) 2019的相反数是________ 。
考点: 相反数及有理数的相反数;2020年中考数学:数与式_有理数_相反数及有理数的相反数练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:。
中考数学每日一练:二次函数y=ax^2+bx+c的性质练习题及答案_2020年压轴题版

中考数学每日一练:二次函数y=ax^2+bx+c 的性质练习题及答案_2020年压轴题版答案答案2020年中考数学:函数_二次函数_二次函数y=ax^2+bx+c 的性质练习题~~第1题~~(2020杭州.中考模拟) 如图,在平面直角坐标系中,平行四边形ABOC 如图放置,将此平行四边形绕点O 顺时针旋转90°得到平行四边形A ′B ′OC ′.抛物线y =﹣x +2x +3经过点A 、C 、A ′三点.(1) 求A 、A′、C 三点的坐标;(2) 求平行四边形ABOC 和平行四边形A′B′OC′重叠部分△C′OD 的面积;(3) 点M 是第一象限内抛物线上的一动点,问点M 在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M 的坐标.考点: 二次函数y=ax^2+bx+c 的性质;二次函数图象与坐标轴的交点问题;三角形的面积;平行四边形的性质;相似三角形的判定与性质;~~第2题~~(2020百色.中考模拟) 如图,在平面直角坐标系中,二次函数y =﹣x +bx+c 的图象与x 轴交于A 、B两点,A 点的坐标为(﹣3,0),B 点在原点的左侧,与y 轴交于点C (0,3),点P 是直线BC 上方的抛物线上一动点(1) 求这个二次函数的表达式;(2) 连接PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP′C (如图1所示),那么是否存在点P ,使四边形POP′C 为菱形?若存在,请此时点P 的坐标:若不存在,请说明理由;(3) 当点P 运动到什么位置时,四边形ABCP 的面积最大,并求出其最大值.考点: 二次函数y=ax^2+bx+c 的性质;待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;~~第3题~~(2020湖州.中考模拟) 如图, 已知抛物线的对称轴是直线x=3,且与x 轴相交于A ,B 两点(B 点在A 点右侧)与y 轴交于C 点 .22答案答案答案(1) 求抛物线的解析式和A 、B 两点的坐标;(2) 若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),则是否存在一点P ,使△PBC 的面积最大.若存在,请求出△PBC 的最大面积;若不存在,试说明理由;(3) 若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当MN=3时,求M 点的坐标.考点: 待定系数法求一次函数解析式;二次函数y=ax^2+bx+c 的性质;二次函数与一次函数的综合应用;二次函数的实际应用-动态几何问题;~~第4题~~(2020乌鲁木齐.中考模拟) 如图,直线y=x+2与抛物线y=ax +bx+6(a≠0)相交于A ()和B (4,6),点P 是线段AB上异于A 、B 的动点,过点P 作PC ⊥x 轴于点D ,交抛物线于点C.(1)求抛物线的解析式;(2) 当C 为抛物线顶点的时候,求的面积.(3) 是否存在质疑的点P ,使 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.考点: 二次函数y=ax^2+bx+c 的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式;~~第5题~~(2020长春.中考模拟) 在平面直角坐标系中,已知抛物线y=x -2mx-3m(1) 当m=1时,①抛物线的对称轴为直线①抛物线的对称轴为直线,,②抛物线上一点P 到x 轴的距离为4,求点P 的坐标③当n≤x≤ 时,函数值y 的取值范围是- ≤y≤2-n ,求n 的值(2) 设抛物线y=x -2mx-3m 在2m-1≤x≤2m+1上最低点的纵坐标为y ,直接写出y 与m 之间的函数关系式及m 的取值范围.考点: 二次函数y=ax^2 bx c 的图象;二次函数y=ax^2+bx+c 的性质;2020年中考数学:函数_二次函数_二次函数y=ax^2+bx+c 的性质练习题答案1.答案:222002.答案:3.答案:4.答案:5.答案:。
中考数学每日一练:二次函数的最值练习题及答案_2020年填空题版

中考数学每日一练:二次函数的最值练习题及答案_2020年填空题版答案答案答案答案答案答案答案答案2020年中考数学:函数_二次函数_二次函数的最值练习题~~第1题~~(2020农安.九上期中) 二次函数y=x ﹣2x ﹣5的最小值是________.考点: 二次函数的最值;~~第2题~~(2019哈尔滨.中考真卷) 二次函数y=-(x-6)+8的最大值是________。
考点: 二次函数的最值;~~第3题~~(2019哈尔滨.中考模拟) 二次函数y =﹣x ﹣2x+3的最大值是________.考点: 二次函数的最值;~~第4题~~(2019宿迁.中考模拟) 若min{a ,b ,c}表示a ,b ,c 三个数中的最小值,当y =min{x , x+2,8﹣x}(x≥0)时,则y 的最大值是________.考点: 比较一次函数值的大小;二次函数的最值;~~第5题~~(2019南京.中考模拟) 如图,矩形ABCD 中,AB =6,BC =8,E 为AB 的中点,P 为BC 上一动点,作PQ ⊥EP 交直线C D 于点Q ,设点P 每秒以1个单位长度的速度从点B 运动到点C停止,在此时间段内,点Q 运动的平均速度为每秒________个单位.考点: 二次函数的最值;矩形的性质;相似三角形的判定与性质;~~第6题~~(2019昆山.中考模拟)已知关于 的方程( 为实数)两非负实数根,则 的最小值是________.考点: 一元二次方程的根与系数的关系;二次函数的最值;~~第7题~~(2019浙江.中考模拟) 已知关于x 的代数式,当x =________时,代数式的最小值为________.考点: 配方法的应用;二次函数的最值;~~第8题~~(2019河南.中考模拟) 如图,扇形OAB 中,∠AOB=60°,扇形半径为4,点C 在上,CD ⊥OA ,垂足为点D ,当△OCD 的面积最大时,图中阴影部分的面积为________.考点: 二次函数的最值;三角形的面积;勾股定理;扇形面积的计算;2222答案答案~~第9题~~(2019潮南.中考模拟) 二次函数的最大值为________.考点: 二次函数的最值;~~第10题~~(2019乐山.中考真卷) 如图,点是双曲线 :()上的一点,过点 作 轴的垂线交直线: 于点,连结, .当点在曲线上运动,且点在 的上方时,△面积的最大值是________.考点: 一次函数图象与坐标轴交点问题;反比例函数的性质;反比例函数系数k 的几何意义;二次函数的最值;2020年中考数学:函数_二次函数_二次函数的最值练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:。
2020年中考数学复习每日一练 第二十七讲 《尺规作图》(包含答案)

2020年数学中考复习每日一练第二十七讲《尺规作图》一.选择题1.下列说法正确的是()A.用直尺和圆规作一条线段的垂直平分线的过程,是用“到线段两端距离相等的点在这条线段的垂直平分线上”B.用直尺和圆规作一个角的平分线的过程,是用“边角边”构造了全等三角形C.用直尺和圆规作一个角的平分线的过程,是用“到角的两边距离相等的点在这个角的平分线上”D.用直尺和圆规作一个角等于已知角的过程,是用“边角边”构造了全等三角形2.如图,仔细观察用直尺和圆规作出∠AOB的角平分线OE示意图,请你根据所学知识,说明画出的∠AOE=∠BOE的依据是()A.ASA B.SAS C.AAS D.SSS3.如图,在△ABC中,一位同学按以下步骤作图:(1)以点A为圆心,作与BC相交于C,E 两点的弧;(2)分别以点C和点E为圆心,适当长为半径作圆弧,两弧交于点P;(3)作射线AP,交BC于点D.则下列结论中错误的是()A.PE=PC B.ED=CD C.∠EAD=∠CAD D.∠BAE=∠CAD 4.如图,已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,下列画法中错误的是()A.B.C.D.5.如图,点C在∠AOB的OB边上,用尺规作出了∠BCD=∠AOB.以下是排乱的作图过程:则正确的作图顺序是()①以C为圆心,OE长为半径画,交OB于点M.②作射线CD,则∠BCD=∠AOB.③以M为圆心,EF长为半径画弧,交于点D.④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.A.①﹣②﹣③﹣④B.③﹣②﹣④﹣①C.④﹣①﹣③﹣②D.④﹣③﹣①﹣②6.作⊙O的内接正六边形ABCDEF,甲、乙两人的作法分别是:甲:第一步:在⊙O上任取一点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.第二步:依次连接这六个点.乙:第一步:任作一直径AD.第二步:分别作OA,OD的中垂线与⊙O相交,交点从点A 开始,依次为点B,C,E,F.第三步:依次连接这六个点.对于甲、乙两人的作法,可判断()A.甲正确,乙错误B.甲、乙均错误C.甲错误,乙正确D.甲、乙均正确7.如图,在∠AOB中,尺规作图如下:在射线OA、OB上,分别截取OD、OE,使OD=OE;分别以点D和点E为圆心、大于的长为半径作弧,两弧相交于点C;作射线OC,连结CE、CD.下列结论不一定成立的是()A.OE=EC B.CE=CD C.∠OEC=∠ODC D.∠ECO=∠DCO 8.如图,△ABC的周长为26cm,分别以A、B为圆心,以大于的长为半径画圆弧,两弧交于点D、E,直线DE与AB边交于点F,与AC边交于点G,连接BG,△GBC的周长为14cm,则BF的长为()A.6cm B.7cm C.8cm D.12cm9.下面是黑板上出示的尺规作图题,需要回答横线上符号代表的内容如图,已知∠AOB,求作:∠AOB的角平分线.作法如下:①以点O为圆心,适当长为半径画弧,交OA于点M,交☺于点N;②分别以点⊕为圆心,大于♡的长为半径画弧,两弧在⊗内部交于点C;③画射线OC,OC即为所求.()A.☺表示OA B.⊕表示M、C C.♡表示ON D.⊗表示∠AOB 10.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD,若BD=6,则CD的长为()A.2 B.4 C.6 D.3二.填空题11.如图,边长为2的正方形ABCD,以AB为直径作⊙O,CF与⊙O相切于点E,与AD交于点F,则△CDF的面积为.12.如图,用尺规作∠MON的平分线OP.由作图知△OAC≌△OBC,从而得OP平分∠MON,则此两个三角形全等的依据是.13.如图,已知线段AB,按下列要求自己完成画图并计算,延长线段AB到点C,使BC=2AB,取AC中点D;如果AB=6,则线段BD的长度为.14.如图,在边长是4×4,小正方形边长为1的正方形网格图中,线段AB的两个端点都在格点上,若以AB为斜边,则可以作出个格点直角三角形,并在答题卡的图中作出其中面积最大的格点直角三角形.15.小明分别以正六边形ABCDEF 的顶点B 、D 、F 为圆心,以BA 长为半径作圆弧,设计出如图所示的图案.若AB =1,则该图案外围轮廓的周长为 .16.如图,直线MN ∥PQ ,直线AB 分别与MN ,PQ 相交于点A 、B ,小宇同学利用尺规按以下步骤作图:①以点A 为圆心,以任意长为半径作弧交AN 于点C ,交AB 于点D ②分别以C ,D 为圆心,以大于, CD 长为半径作弧,两弧在∠NAB 内交于点E ;③作射线AE 交PQ 于点F ,若∠ABP =70°,则∠AFB = ,17.如图,在△ABC 中,∠C =90°,∠B =30°,以点A 为圆心,任意长为半径画弧,分别交AB ,AC 于点M 和N ,再分别以点M ,N 为圆心,大于MN 长的一半为半径画弧,两弧交于点P ,连结AP 并延长,交BC 于点D ,则下列说法中,正确的有 .(填写序号) ①AD 是∠BAC 的平分线;②∠ADC =60°;③点D 在AB 的中垂线上;④S △DAC :S △ABC =1:3.18.如图,已知钝角△ABC ,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C 为圆心,CA 为半径画弧①;步骤2:以B 为圆心,BA 为半径画弧②;步骤3:连接AD ,交BC 延长线于点H;下列结论:①BH垂直平分线段AD;②AC平分∠BAD;③S=BC•AH;④A H△ABC =DH.其中一定正确的有(只填序号)三.解答题19.已知,如图,∠MON.(1)用直尺和圆规画出∠MON的平分线OA(保留作图痕迹,不写作法,不用证明)(2)在射线OA上任意选取一点P,再在射线OM上选取一点B,要求∠OBP为钝角.①在射线ON上找到所有使得PD=PB的点D.②写出∠OBP与∠ODP之间的数量关系,并证明.20.如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注:此题作图不要求写出画法和结论)(1)作射线AC;(2)作直线BD与射线AC相交于点O;(3)分别连接AB、AD;(4)我们容易判断出线段AB、AD、BD的大小关系是AB+AD>BD,理由是.21.(1)如图1,在平行四边形ABCD中,点E1,E2是AB三等分点,点F1,F2是CD三等分点,E1F1,E2F2分别交AC于点G1,G2,求证:AG1=G1G2=G2C.(2)如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)22.如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B′处;将三角形NAE沿EN折叠,点A落在点A’处.(1)若∠MEB=30°,∠NEA=45°,用直尺、量角器画出射线EB′与EA′;(2)若∠MEB=30°,∠NEA=45°,求∠A'EB'的度数;(3)若∠MEB=α,∠NEA=β,用含α、β的代数式表示∠A'EB'的度数.23.七(1)班的学习小组学习“线段中点”内容时得到一个很有意思的结论,请跟随他们一起思考.(1)发现:如图1,线段AB=12,点C,E,F在线段AB上,当点E,F是线段AC和线段BC的中点时,线段EF的长为;若点C在线段AB的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段EF与线段AB之间的数量关系为.(2)应用:如图3,现有长为40米的拔河比赛专用绳AB左右两端各有一段(AC和BD)磨损了,磨损后的麻绳不再符合比赛要求,已知磨损的麻绳总长度不足20米.只利用麻绳AB和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳EF,学习小组应用“线段中点”的结论很快做出了符合要求的专用绳EF,请你尝试着“复原”他们的想法:①在图中标出点E点F的位置,并简述画图方法;②请说明①题中所标示E,F点的理由.24.LED显示屏是一种平板显示器,可以显示计算机生成的动态图文画面.如图①是平面显示的8X8正三角形网格的示意图,其中每个小正三角形的边长均为1,位于AD中的处的输入光点P按②的程序移动.(1)请在图①中画出光点P经过的路径;(2)求光点P经过的路径总长.参考答案一.选择题1.解:A.用直尺和圆规作一条线段的垂直平分线的过程,是用“到线段两端距离相等的点在这条线段的垂直平分线上“,所以A选项正确,符号题意;B.用直尺和圆规作一个角的平分线的过程,是用“边边边”构造了全等三角形,所以B选项错误,不符合题意;C.用直尺和圆规作一个角的平分线的过程,是用“是用“边边边”构造了全等三角形,所以C选项错误,不符合题意;D.用直尺和圆规作一个角等于已知角的过程,是用“边边边”构造了全等三角,所以D选项错误,不符合题意.故选:A.2.解:根据用直尺和圆规作出∠AOB的角平分线OE的过程可知:OD=OC,DE=CE,AE=AE,∴△ODE≌△OCE(SSS)∴∠AOE=∠BOE.故选:D.3.解:根据作图过程可知:AP是CE的垂直平分线,∴PE=PC,ED=CD,AE=AC,∴∠EAD=∠CAD.所以A、B、C选项都正确.故选:D.4.解:已知点A和直线MN,过点A用尺规作图画出直线MN的垂线,画法正确的是B、C、D选项,不符合题意.A选项错误,符合题意;故选:A.5.解:根据作一个角等于已知角的过程可知:④以O为圆心,任意长为半径画,分别交OA,OB于点E,F.①以C为圆心,OE长为半径画,交OB于点M.③以M为圆心,EF长为半径画弧,交于点D.②作射线CD,则∠BCD=∠AOB.故选:C.6.解:甲:由作图可知,AB=BO=AO,即△AOB为等边三角形,同理可得△BOC,△COD,△DOE,△EOF,△AOF均为等边三角形,故AB=BC=CD=DE=EF=FA,∠ABC=∠BCD=∠CDE=∠DEF=∠AFE=∠FAB=120°,所以六边形ABCDEF为正六边形;乙:由作图可得,BA=BO=AO,即△ABO为等边三角形,同理可得△AOF,△COD,△DOE均为等边三角形,故∠EOF=∠BOC=60°,而BO=CO=EO=FO,所以△BOC,△EOF均为等边三角形,所以AB=BC=CD=DE=EF=FA,∠ABC=∠BCD=∠CDE=∠DEF=∠AFE=∠FAB=120°,所以六边形ABCDEF为正六边形;因此,甲、乙两人的作法均正确,故选:D.7.解:根据作图过程可知:OE=OD,EC=DC,OC=OC∴△OEC≌△ODC(SSS)∴∠OEC=∠ODC∠ECO=∠DCO.所以B、C、D选项都成立.所以A选项不成立.故选:A.8.解:由画图可知:DE是AB的垂直平分线,∴AF=BF,AG=BG,∵△GBC的周长为14cm,即BC+BG+CG=14cm,∴BC+AC=14cm,∵△ABC的周长为26cm,即AB+BC+AC=26cm,∴AB=12cm,∴BF=6cm.故选:A.9.解:作法如下:①以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;②分别以点M、N为圆心,大于MN的长为半径画弧,两弧在∠AOB内部交于点C;③画射线OC,OC即为所求.故选:D.10.解:由作图过程可知:DN是AB的垂直平分线,∴AD=BD=6∵∠B=30°∴∠DAB=30°∴∠C=90°,∴∠CAB=60°∴∠CAD=30°∴CD=AD=3.故选:D.二.填空题(共8小题)11.解:∵⊙O与AD,CF,BC相切于点A,E,B,∴FA=FE,CE=CB=2,设AF=FE=x,在Rt△DFC中,∵DF2+CD2=CF2,∴(2﹣x)2+22=(2+x)2,解得x=,∴DF=,=•DC•DF=×2×=,∴S△CDF故答案为.12.解:由基本作图得OA=OB,AC=BC,而OC为公共边,所以利用“SSS”可判断△AOC≌△BOC,所以∠AOC=∠BOC.故答案为:SSS.13.解:如图,点C,D即为所求.∵BC=2AB,AB=6,∴BC=12,∴AC=AB+BC=6+12=18,∵AD=DC,∴AD=AC=9,∴BD=AD﹣AC=9﹣6=3,故答案为3.14.解:如图所示:线段AB的两个端点都在格点上,以AB为斜边,可以作出4个格点直角三角形,△ABC的面积最大.故答案为4.15.解:由题意可知:∵正六边形ABCDEF六个边相等都等于1,六个内角相等都等于120°,∴图案外围轮廓的周长为三个半径为1、圆心角为240度的弧长之和,即图案外围轮廓的周长为:3×=4π.故答案为4π.16.解:∵MN∥PQ,∴∠NAF=∠BFA,由题意得:AF平分∠NAB,∴∠NAF=∠BAF,∴∠BFA=∠BAF,∵∠ABP=∠BFA+∠BAF,∴∠ABP=2∠BFA=70°,∴∠AFB=70°÷2=35°,故答案为:35°.17.①证明:连接NP,MP,在△ANP与△AMP中,∵,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;②证明:∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.∵AD是∠BAC的平分线,∴∠1=∠2=∠CAB=30°,∴∠3=90°﹣∠2=60°,∠ADC=60°,故此选项正确;③证明:∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故此选项正确;④证明:∵在Rt△ACD中,∠2=30°,∴CD=AD,∴BC=BD+CD=AD+AD=AD,S△DAC=AC•CD=AC•AD,∴S△ABC=AC•BC=AC•AD=AC•AD,∴S△DAC :S△ABC=1:3,故此选项正确;故答案为:①②③④.18.解:连接CD,BD.由作图可知,AC=CD,BA=BD,∴BH垂直平分线段AD,故①④正确,∴S△ABC=•BC•AH,故③正确,无法判断②正确,故②错误,故答案为①③④三.解答题(共6小题)19.解:如图,(1)OA即为所求;(2)①点D1、D2即为所求;②∠OBP=∠OD1P,∠OBP+∠OD2P=180°.证明:分别作PE⊥AM于点E,PF⊥AM于点F ∵OA平分∠MON∴PE=PF∵PB=PD1∴Rt△BPE≌Rt△D1PF∴∠PBE=∠PD1F∴∠OBP=∠OD1P同理可证∠PBE=∠PD2F∵∠OBP+∠PBE=180°∴∠OBP+∠OD2P=180°.20.解:如图,(1)射线AC即为所求;(2)直线BD与射线AC相交于点O;(3)AB、AD即为所求;(4)线段AB、AD、BD的大小关系是AB+AD>BD,理由是:两点之间线段最短.故答案为:两点之间线段最短.21.(1)证明:如图1中,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,AD∥BC,∵DF1=CD,AE1=AB,∴DF1=AE1,∴四边形ADF1E1是平行四边形,∴AD∥E1F1,∴E1G1∥BC,∴==,同法可证:==,∴AG1=CG2=AC,∴AG1=G1G2=G2C.(2)如图,点P,Q即为所求.22.解:(1)图形如图1中所示:(2)与翻折可知:∠AEA′=2∠AEN=90°,∠BEB′=2∠BEM=60°,∴∠A′EB′=180°﹣90°﹣60°=30°.(3)当α+β≤90°时,∠A′EB′=180°﹣2(α+β),当α+β>90°时,∠A′EB′=2(α+β)﹣180°.23.解:(1)如图1中,∵EC=AC,CF=BC,∴EF=EC+CF=(AC+BC)=AB=6.如图2中,∵EC=AC,CF=BC,∴EF=EC﹣CF=(AC﹣BC)=AB.故答案为6, AB.(2)①如图3中,在CD上取得M,使得AC=CM,F为BM的中点,点E与C重合.②∵F为BM的中点,∴MF=FB,∵AB=AC+CM+MF+FM,CM=AC,∴AB=2CM+2MF=2(CM+MF)=2EF,∵AB=40m,∴EF=20m,∵AC+BD<20m,∵点E与C重合,EF=20m,∴CF=20m,∴点F落在线段CD上.24.解:(1)光点P经过的路径如图所示.(2)光点P经过的路径总长=2π×2=4π.。
中考数学每日一练:二次函数y=ax^2+bx+c的性质练习题及答案_2020年综合题版

得到平行四边形A′B′OC′.抛物线(1)求A、A′、C三点的坐标;关于的一元二次方程有两个不相等且非零的实数根,探究满足的步:设一元二次方程对应的二次函数为;第二步:借助二次函数图象,可以得到相应的一元二次方程中满足的条件,列表如下表。
满足的条件已知关于的方程,若方程的两根都是正数,求的取值范围一元二次方程根的判别式及应用;二次函数y=ax^2+bx+c答案答案答案(2020百色.中考模拟) 如图,在平面直角坐标系中,二次函数y =﹣x +bx+c 的图象与x 轴交于A 、B 两点,A 点的坐标为(﹣3,0),B 点在原点的左侧,与y 轴交于点C (0,3),点P 是直线BC 上方的抛物线上一动点(1) 求这个二次函数的表达式;(2) 连接PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP′C (如图1所示),那么是否存在点P ,使四边形POP′C 为菱形?若存在,请此时点P 的坐标:若不存在,请说明理由;(3) 当点P 运动到什么位置时,四边形ABCP 的面积最大,并求出其最大值.考点: 二次函数y=ax^2+bx+c 的性质;待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;~~第4题~~(2020湖州.中考模拟) 如图, 已知抛物线的对称轴是直线x=3,且与x 轴相交于A ,B 两点(B 点在A 点右侧)与y 轴交于C 点 .(1) 求抛物线的解析式和A 、B 两点的坐标;(2) 若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),则是否存在一点P ,使△PBC 的面积最大.若存在,请求出△PBC 的最大面积;若不存在,试说明理由;(3) 若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当MN=3时,求M 点的坐标.考点: 待定系数法求一次函数解析式;二次函数y=ax^2+bx+c 的性质;二次函数与一次函数的综合应用;二次函数的实际应用-动态几何问题;~~第5题~~(2020乌鲁木齐.中考模拟) 如图,直线y=x+2与抛物线y=ax +bx+6(a≠0)相交于A ()和B (4,6),点P 是线段AB 上异于A 、B 的动点,过点P 作PC ⊥x 轴于点D ,交抛物线于点C.(1) 求抛物线的解析式;(2) 当C 为抛物线顶点的时候,求的面积.(3) 是否存在质疑的点P ,使 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.考点: 二次函数y=ax^2+bx+c 的性质;二次函数图象上点的坐标特征;待定系数法求二次函数解析式;2020年中考数学:函数_二次函数_二次函数y=ax^2+bx+c 的性质练习题答案1.答案:222.答案:3.答案:4.答案:5.答案:。
中考数学每日一练:勾股定理练习题及答案_2020年压轴题版

是否存在最小值,若存在,求最小值:若不存在,请说明理由.
考点: 垂线段最短;勾股定理;圆周角定理;旋转的性质;
答案
~~第5题~~
(2019石景山.中考模拟) 如图矩形ABCO , 点A , C分别在y轴与x轴的正半轴上,O为坐标原点,B的坐标为(6,4) ,点D(1,0),点P为边AB上一个动点,过点D , P的圆⊙M与AB相切,⊙M交x轴于点E , 连接AM ,
.
(1) 求抛物线
的函数表达式;
(2) 如图2,当点N在线段 上时,求证:
;
(3) 当点N在线段 上时,直接写出此时直线 与抛物线交点的纵坐标;
(4) 设 的长度为n,直接写出在点M移动的过程中, 的取值范围.
考点: 二次函数y=ax^2+bx+c的性质;待定系数法求二次函数解析式;等边三角形的判定与性质;勾股定理;旋转的性质;
(1) 当P为AB的中点时,求DE的长及⊙M的半径; (2) 当AM⊥DP时,求点P的坐标与⊙M的半径; (3) 是否存在一点P使⊙M与矩形ABCO的另一条边也相切,若存在求出所有符合条件的点P的坐标.
考点: 等腰直角三角形;勾股定理;垂径定理的应用;数学思想;
答案
2020年 中 考 数 学 : 图 形 的 性 质 _三 角 形 _勾 股 定 理 练 习 题 答 案
的性质;
答案
~~第2题~~
(2020松江.中考模拟) 已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON , 垂足为点F. (1) 如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
图(1) (2) 如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
中考数学《统计》每日一练

1.下列说法正确的是()A.任意掷一枚质地均匀的骰子,掷出的点数一定是奇数B.“从一副扑克牌中任意抽取一张,抽到大王”是必然事件C.了解一批冰箱的使用寿命,采用抽样调查的方式D.若平均数相同的甲、乙两组数据,S甲2=3,S乙2=0.02,则甲组数据更稳定2.八年级二班在一次体重测量中,小明体重54.5kg,低于全班半数学生的体重,分析得到结论所用的统计量是()A.中位数B.众数C.平均数D.方差3.某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是()A.B.C.D.4.甲、乙两名队员参加射击训练,各自射击10次的成绩分别为:甲:7,5,8,7,6,7,8,6,7,9;乙:3,6,4,8,7,8,7,8,9,10.队员平均环中位数环众数环甲7b7乙a7.5c 根据以上信息,整理分析数据如下表:(1)填空:a=;b=;c=.(2)已知乙队员射击成绩的方差为4.2环2,请计算出甲队员射击成绩的方差,并判断哪个队员的射击成绩较稳定;(3)请根据所学统计量的意义,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?说明你的理由.1.在四张反面无差别的卡片上,其正面分别印有线段、等边三角形、平行四边形和正六边形.现将四张卡片的正面朝下放置,混合均匀后从中随机抽取两张,则抽到的卡片正面图形都是轴对称图形的概率为()A.B.C.D.2.对于一组数据1,1,3,1,4,下列结论不正确的是()A.平均数是2B.众数是1C.中位数是3D.方差是1.6 3.某市举办中学生科普知识竞赛,试卷满分为100分,规定85分及以上为合格,95分及以上为优秀.A,B两支代表队参加了这次科普知识竞赛,将两队的竞赛成绩制成统计图表(数据不完整).某市中学生科普知识竞赛A、B两队成绩条形统计图某市中学生科普知识竞赛A、B两队成绩统计表:组别平均分中位数众数方差合格率优秀率A队8890906170%30%B队87a b71c25%根据上述统计图表,解答下面的问题:(1)请直接写出统计表中a,b,c的值.(2)在这两支代表队中,小辉的成绩低于本队的平均分,但在本队里能位列中游,则小辉可能是哪一队的?请说明理由.(3)A、B两支代表队中,哪一队的成绩更好一些?请说明理由.1.某校举行学生会成员的竞选活动,对竞选者从民主测评和演讲两个方面进行考核,两项成绩均按百分制计,规定民主测评的成绩占40%,演讲的成绩占60%,小新同学的民主测评和演讲的成绩分别为80分和90分,则他的最终成绩是()A.83分B.84分C.85分D.86分2.连接正六边形不相邻的两个顶点,并将中间的六边形涂成黑色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在黑色区域的概率为()A.B.C.D.3.空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是;要反映2010~2018年泰安市学生数的变化情况,宜选用统计图.(从“条形图、扇形图、折线图”中选一个)4.某书店与一所中学建立帮扶关系,连续6个月向该中学赠送书籍的数量(单位:本)分别为:200,300,400,200,500,550,则这组数据的中位数是本.5.从﹣3、﹣1、1、2、﹣5中任取一个数作为a,则抛物线y=ax2+bx+c开口向上的概率是.6.甲、乙、丙三人各自随机选择到A,B两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.1.在一个不透明的袋中装有若干个材质、大小完全相同的红球,小明在袋中放入3个黑球(每个黑球除颜色外其余都与红球相同),摇匀后每次随机从袋中摸出一个球,记录颜色后放回袋中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.8左右,估计袋中红球有个.2.有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是.3.有六张正面分别写有数字﹣4,﹣3,0,2,3,4的卡片,六张卡片除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为n,则抽取的n既能使关于x的方程x2﹣2(n+1)x+n(n﹣3)=0有实数根,又能使以x为自变量的二次函数y=﹣x2+2nx+1当x>2时,y随x的增大而减小的概率为.4.一个不透明的袋子中装有4个只有颜色不同的小球,其中2个红球,2个白球,摇匀后从中一次性摸出两个小球.(1)请用列表格或画树状图的方法列出所有可能性;(2)若摸到两个小球的颜色相同,甲获胜;摸到两个小球颜色不同,乙获胜.这个游戏对甲、乙双方公平吗?请说明理由.1.如图,AD为△ABC的中线,点E,F分别为AD,AB的中点,连接EC,EF.现随机向△ABC内掷一枚小针,则针尖落在阴影区域的概率为.2.现有牌面编码为﹣1,1,2的三张卡片,背面向上,从中随机抽取一张卡片,记其数字为k,将抽到的卡片背面朝上,放回打乱后,再抽一张记其数字为m,则事件“关于a、b的方程组的解满足0≤a﹣b≤1,且二次函数y=x2﹣2x+m的图象与x轴恰有2个交点”成立的概率为.3.“赏中华诗词,寻文化基因,品文学之美”,某校对全体学生进行了古诗词知识测试,将成绩分为一般、良好、优秀三个等级,从中随机抽取部分学生的测试成绩,根据调查结果绘制成两幅不完整的统计图,根据图中信息,解答下列问题:(1)求本次抽样调查的人数;(2)在扇形统计图中,阴影部分对应的扇形圆心角的度数是;(3)将条形统计图补充完整;(4)该校共有1500名学生,根据抽样调查的结果,请你估计测试成绩达到优秀的学生人数.1.我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和.如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数k,此三角形的顺序旋转和与逆序旋转和的差小于4的概率是.2.某商场根据第二季度某品牌运动服装的S号、M号、L号、XL号、XXL号销售情况绘制了如图所示的不完整的两幅统计图.根据图中信息解答下列问题:(1)第二季度该品牌运动服装的销售总量是件,扇形统计图中XXL号服装销量占总量的百分比是,XL号所对应的圆心角度数是;(2)请补全条形统计图;(3)从M号、XL号运动服装中按照M号,XL号运动服装的销量比,分别取出一定数量的运动服,再取3件XXL号运动服装,将它们放在一起,现从这些运动服装中,随机取出1件,取得M号运动服装的概率为,求取出了M号、XL号运动服装各多少件?。
中考数学每日一练:一元一次不等式的应用练习题及答案_2020年综合题版

中考数学每日一练:一元一次不等式的应用练习题及答案_2020年综合题版答案答案答案答案2020年中考数学:方程与不等式_不等式与不等式组_一元一次不等式的应用练习题~~第1题~~(2020杭州.中考模拟) 某商店第一次用600元购进2B 铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的 倍,购进数量比第一次少了30支.(1) 求第一次每支铅笔的进价是多少元?(2) 若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?考点: 一元一次不等式的应用;~~第2题~~(2020湖州.中考模拟) 王老师从学校出发,到距学校 的某商场去给学生买奖品,他先步行了 后,换骑上了共享单车,到达商场时,全程总共刚好花了 .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).(1) 求王老师步行和骑共享单车的平均速度分别为多少?(2) 买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?考点: 一元一次不等式的应用;分式方程的实际应用;~~第3题~~(2020杭州.中考模拟) 六•一前夕,某幼儿园园长到厂家选购A 、B 两种品牌的儿童服装,每套A 品牌服装进价比B 品牌服装每套进价多25元,用2000元购进A 种服装数量是用750元购进B 种服装数量的2倍.(1) 求A 、B 两种品牌服装每套进价分别为多少元?(2) 该服装A 品牌每套售价为130元,B 品牌每套售价为95元,服装店老板决定,购进B 品牌服装的数量比购进A 品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A 品牌的服装多少套?考点: 一元一次不等式的应用;分式方程的实际应用;~~第4题~~(2020衢州.中考模拟) 某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.(1) 求出每天的销售利润y (元)与销售单价x (元)之间的函数关系式;(2) 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?(3) 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)考点: 一元一次不等式的应用;二次函数的实际应用-销售问题;~~第5题~~(2020玉林.中考模拟) 由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:品名价格甲种口罩乙种口罩进价(元/袋)2025售价(元/袋)2635答案(1) 求该网店购进甲、乙两种口罩各多少袋?(2) 该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?考点: 二元一次方程组的实际应用-销售问题;一元一次不等式的应用;2020年中考数学:方程与不等式_不等式与不等式组_一元一次不等式的应用练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
2020年数学中考复习每日一练 第二十四讲 《三角形》(包含答案)
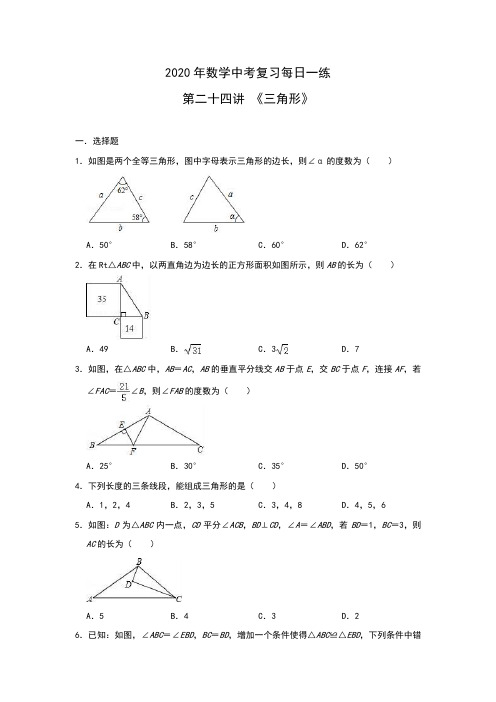
2020年数学中考复习每日一练第二十四讲《三角形》一.选择题1.如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数为()A.50°B.58°C.60°D.62°2.在Rt△ABC中,以两直角边为边长的正方形面积如图所示,则AB的长为()A.49 B.C.3D.73.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点E,交BC于点F,连接AF,若∠FAC=∠B,则∠FAB的度数为()A.25°B.30°C.35°D.50°4.下列长度的三条线段,能组成三角形的是()A.1,2,4 B.2,3,5 C.3,4,8 D.4,5,65.如图:D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若BD=1,BC=3,则AC的长为()A.5 B.4 C.3 D.26.已知:如图,∠ABC=∠EBD,BC=BD,增加一个条件使得△ABC≌△EBD,下列条件中错误的是()A.AC=ED B.BA=BE C.∠C=∠D D.∠A=∠E7.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=8cm,那么CE=()A.2cm B.3cm C.4cm D.5cm8.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是32,则图中阴影部分面积等于()A.16 B.8 C.4 D.29.如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边长是5,小正方形的边长是7,则大正方形的面积是()A.121 B.144 C.169 D.19610.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠A n﹣1BC与∠An﹣1CD的平分线交于点An,要使∠A n的度数为整数,则n的最大值为()A.4 B.5 C.6 D.711.如图,在Rt△ABC中,其中∠A=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=5,AD=2,则图中长度为的线段有()A.1条B.2条C.3条D.4条12.正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S2,…按此规律继续下去,则S5的值为()A.B.C.D.二.填空题13.如图,在△ABC中,∠A=150°,AB=20,AC=30,则△ABC的面积为.14.如图,在△ABC中,DH是AC的垂直平分线,交BC于点P,MN是AB的垂直平分线,交BC于点O,连接AP、AQ,已知∠BAC=72°,则∠PAQ=.15.在△ABC中,∠C=80°,∠A=40°,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧分别交于点E、F,作直线EF交AC于点D,则∠CBD的度数是.16.如图,在平面直角坐标系中,AD平分∠OAB,已知点D坐标为(0,﹣2),AB=10,则△ABD的面积为.17.如图,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角顶点C在边OA上,点D在边OB上,点F在边AB上,如果△CDF的面积是△AOB的面积的,OD=2,则△AOB 的面积为.18.如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=1,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第1个正方形的边长是,第2020个正方形的边长是.三.解答题19.在△ABC中,CF⊥AB于F,ED∥CF,∠1=∠2.(1)求证:FG∥BC;(2)若∠A=55°,∠1=30°,求∠FGC的度数20.如图,等边△ABC的边长为12,D为AB边上一动点,过点D作DE⊥BC于点E.过点E 作EF⊥AC于点F.(1)若AD=2,求AF的长;(2)当AD取何值时,DE=EF?21.(1)如图1,点D、E分别是等边△ABC边AC、AB上的点,连接BD、CE,若AE=CD,求证:BD=CE.(2)如图2,在(1)问的条件下,点H在BA的延长线上,连接CH交BD延长线于点F.若BF=BC,求证:EH=EC.22.已知,在△ABC中,∠BAC=120°,AB=AC,AD⊥BC,垂足为点G,且AD=AB,连接BD.(1)如图①,求证:△ABD是等边三角形;(2)如图①,若点E、F分别为AB,AC上的点,且∠EDF=60°,求证:BE=AF;(3)利用(1)(2)中的结论,思考并解答:如图②,H为AB上一点,连结DH,当∠HDF =30°时,线段BH,HF,AF之间有何数量关系,给出证明.23.如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E.F、G分别是OA、OB上的点,且PF=PG,DF=EG.(1)求证:OC是∠AOB的平分线.(2)若PF∥OB,且PF=8,∠AOB=30°,求PE的长.24.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,M在AC上,且AM=6cm,过点A作射线AN⊥AC(AN与BC在AC同侧),若动点P从点A出发,沿射线AN匀速运动,运动速度为1cm/s,设点P运动时间为t秒.(1)经过秒时,Rt△AMP是等腰直角三角形?(2)当PM⊥AB于点Q时,求此时t的值;(3)过点B作BD⊥AN于点D,已知BD=8cm,请问是否存在点P使△BMP是以BM为腰的等腰三角形?对存在的情况,请求出t的值,对不存在的情况,请说明理由.参考答案一.选择题1.解:∵两个三角形全等,∴∠α=180°﹣58°﹣62°=60°,故选:C.2.解:∵两个正方形的面积为35和14,∴AB2=AC2+BC2=35+14=49,则AB=7(负值舍去),故选:D.3.解:∵AB=AC,∴∠B=∠C,∵EF垂直平分AB,∴BF=AF,∴∠BAF=∠B=∠C,∵∠FAC=∠B,∴∠B+3∠B=180°,∴∠B=25°,∴∠FAB的度数为25°,故选:A.4.解:A、1+2<4,不能组成三角形;B、2+3=5,不能组成三角形;C、3+4<8,不能组成三角形;D、4+5>6,能够组成三角形.故选:D.5.解:延长BD交AC于E,如图,∵CD平分∠ACB,BD⊥CD,∴△BCD为等腰三角形,∴DE=BD=1,CE=CB=3,∵∠A=∠ABD,∴EA=EB=2,∴AC=AE+CE=2+3=5.故选:A.6.解:∵∠ABC=∠EBD,BC=BD,∴当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD;当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD;当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD.故选:A.7.解:∵BE平分∠ABC,ED⊥AB,EC⊥AC,∴ED=EC,在Rt△ADE中,∵∠A=30°,∴ED=AE=×8=4,∴CE=4cm.故选:C.8.解:∵D是BC的中点,∴S△ABD =S△ACD=S△ABC,∵E是AD的中点,∴S△BDE =S△ABD,S△CDE=S△ACD,∴S△BCE =S△ABC=×32=16,∵F是CE的中点,∴S△BEF =S△BCE=×16=8.答:图中阴影部分面积等于8.故选:B.9.解:∵直角三角形较短的直角边长是5,小正方形的边长是7,∴直角三角形的较长直角边=5+7=12,∴直角三角形斜边长=13,∴大正方形的边长是13,∴大正方形的面积是13×13=169.故选:C .10.解:由三角形的外角性质得,∠ACD =∠A +∠ABC ,∠A 1CD =∠A 1+∠A 1BC , ∵∠ABC 的平分线与∠ACD 的平分线交于点A 1, ∴∠A 1BC =∠ABC ,∠A 1CD =∠ACD ,∴∠A 1+∠A 1BC =(∠A +∠ABC )=∠A +∠A 1BC , ∵A 1B 、A 1C 分别平分∠ABC 和∠ACD ,∴∠ACD =2∠A 1CD ,∠ABC =2∠A 1BC ,而∠A 1CD =∠A 1+∠A 1BC ,∠ACD =∠ABC +∠A , ∴∠A =2∠A 1,∴∠A 1=∠A ,同理可得∠A 1=2∠A 2,∴∠A 2=∠A ,∴∠A =2n ∠A n ,∴∠A n =()n ∠A =, ∵∠A n 的度数为整数,∵n =6.故选:C .11.解:∵∠ABC 的平分线BD 交AC 于点D ,DE ⊥BC , ∴DE =DA =2,∵DE 是BC 的垂直平分线,∴DB =DC =5,BE =CE ,在Rt △ABD 中,AB ==; 在Rt △BDE 中,BD ==;∴CE =.故选:C .12.解:在图中标上字母E ,如图所示.∵正方形ABCD 的边长为1,△CDE 为等腰直角三角形,∴DE 2+CE 2=CD 2,DE =CE ,∴S 2+S 2=S 1.观察,发现规律:S 1=12=1,S 2=S 1=,S 3=S 2=,S 4=S 3=,…, ∴S n =()n ﹣1.当n =5时,S 5=()5﹣1=()4,故选:A .二.填空题(共6小题)13.解:过点B 作BD ⊥AC ,∵∠BAC =150°,∴∠BAD =30°,∴BD =AB ,∵AB =20,∴BD =10,∴S △ABC =AC •BD =×30×10=150.故答案为:150.14.解:∵DH 是AC 的垂直平分线,∴PA =PC ,∴∠PAC =∠C ,∵MN是AB的垂直平分线,∴QA=QB,∴∠QAB=∠B,∵∠B+∠C+∠BAC=180°,∴∠B+∠C=180°﹣72°=108°,∴∠PAC+∠QAB=∠B+∠C=108°,即∠ABC+∠PAQ=108°,∴∠PAQ=108°﹣72°=36°.故答案为72°.15.解:∠ABC=180°﹣∠A﹣∠C=60°,由作图可知,EF是线段AB的垂直平分线,∴DA=DB,∴∠ABD=∠A=40°,∴∠CB D=60°﹣40°=20°,故答案为:20°.16.解:如图,过点D作DE⊥AB于点E,,∵点D坐标为(0,﹣2),∴OD=2,∵AD是Rt△OAB的角平分线,OD⊥OA,DE⊥AB,∴DE=OD=2,∴S=AB•DE=×10×2=10.△ABD故答案为:10.17.解:过点F作FM⊥AO于点M,如图:则有:∠O=∠FMC=90°,∴∠1+∠2=90°,∵等腰直角△CDF,∴CF=CD,∠DCF=90°,∴∠2+∠3=90°,∴∠1=∠3,又∵∠O=∠FMC=90°,CF=CD,∴△DOC≌△CMF(AAS),∴CM=OD=2,MF=OC,∵∠AOB=90°,OA=OB,FM⊥AO,∴△AMF是等腰直角三角形,∴AM=MF=CO,设AM=MF=CO=x,则OA=OB=2x+2,CD=CF=,由△CDF的面积是△AOB的面积的,得:()2=(2x+2)2,解得:x=1.5,∴△AOB的面积=(2x+2)2=;故答案为:.18.解:∵OA=OB=1,∴△AOB是等腰直角三角形,∴第一个正方形的边长AB=,∠OAB=45°,∴∠DAE=180°﹣45°﹣90°=45°,∴△ADE是等腰直角三角形,∴AD=DE,∴第二个正方形的边长CE=CD+DE=2AB,…,后一个正方形的边长等于前一个正方形的边长的2倍,所以,第n个正方形的边长=2n﹣1AB=•2n﹣1,即第2020个正方形的边长是•22019.故答案为,•22019.三.解答题(共6小题)19.(1)证明:如图,∵DE∥FC,∴∠1=∠3.又∵∠1=∠2,∴∠2=∠3,∴FG∥BC;(2)解:∵∠1=∠2且∠1=30°,∴∠2=30°,∵CF⊥AB,∴∠AFG=90°﹣30°=60°,∴∠FGC=∠AFG+∠A=60°+55°=115°.20.解:(1)∵AB=12,AD=2∴BD=AB﹣AD=10在Rt△BDE中∠BDE=90°﹣∠B=30°∴BE=BD=5∴CE=BC﹣BE=7在Rt△CFE中∠CEF=90°﹣∠C=30°∴CF=CE=,∴AF=AC﹣FC=;(2)在△BDE和△EFC中,∴△BDE≌△CFE(AAS)∴BE=CF∴BE=CF=EC∴BE=BC=4,∴BD=2BE=8,∴AD=AB﹣BD=4,∴AD=4时,DE=EF.21.(1)证明:如图1中,∵△ABC是等边三角形,∴∠A=∠BCD=∠ABC=60°,AC=BC,∵AE=CD,∴△ACE≌△CBD(SAS),∴BD=EC.(2)①证明:如图2中,∵△ACE≌△CBD,∴∠ACE=∠CBD,∵∠ABC=∠ACB=60°,∴∠ABD=∠ECB,∵BF=BC,∴∠BFC=∠BCF,∴∠FBH+∠H=∠BCE+∠ECH,∴∠H=∠ECH,∴EH=EC.22.证明:(1)∵AB=AC,AD⊥BC,∴∠BA D=∠DAC=∠BAC,∵∠BAC=120°,∴∠BAD=∠DAC=×120°=60°,∵AD=AB,∴△ABD是等边三角形;(2)∵△ABD是等边三角形,∴∠ABD=∠ADB=60°=∠BAD=∠CAD,BD=AD=AB,∵∠EDF=60°,∴∠BDE=∠ADF,在△BDE与△ADF中,∴△BDE≌△ADF(ASA),∴BE=AF.(3)BH=HF+AF理由如下:如图②,连接BD,在BA上取一点E,连接DE,使∠EDH=30°.由(1)(2)可得,△BDE≌△ADF∴BE=AF,DE=DF在△EDH和△FDH中,∴△EDH≌△FDH(SAS)∴EH=HF,∴BH=HF+AF.23.解:(1)证明:在Rt△PFD和Rt△PGE中,,∴Rt△PFD≌Rt△PGE(HL),∴PD=PE,∵P是OC上一点,PD⊥OA,PE⊥OB,∴OC是∠AOB的平分线.(2)∵PF∥OB,∠AOB=30°,∴∠PFD=∠AOB=30°,在Rt△PDF中,.24.解:(1)当Rt△AMP是等腰直角三角形时,AP=AM=6cm,∴t=6÷1=6(s),故答案为:6.(2)当PM⊥AB时,∠PHA=90°,∴∠HPA+∠HAP=90°,又∠HAP+∠CAB=90°,∴∠APM=∠CAB,在△APM和△CAB中,,∴△APM≌△CAB(ASA),∴AP=CA=8,∴t=8,∴经过8秒时,PM⊥AB.(3)存在.理由:根据勾股定理得,BM==2,BP的最小值为8,∵2<8,∴BM≠BP,当MB=MP时,在Rt△BCM和Rt△MAP中,,∴Rt△BCM≌Rt△MAP(HL)∴AP=CM=2,则t=2,∴当△BMP是以BM为腰的等腰三角形时,t=2.。
2020年数学中考复习每日一练 第三十六讲 《概率》(包含答案)

2020年数学中考复习每日一练第三十六讲《概率》一.选择题1.下列说法正确的是()A.“概率为0.0001的事件”是不可能事件B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次C.“任意画出一个等边三角形,它是轴对称图形”是随机事件D.“任意画出一个平行四边行,它是中心对称图形”是必然事件2.掷一枚质地均匀硬币,前3次都是正面朝上,掷第4次时正面朝上的概率是()A.0 B.C.D.13.一个盒子装有红、黄、白球分别为2、3、5个,这些球除颜色外都相同,从袋中任抽一个球,则抽到黄球的概率是()A.B.C.D.4.一个不透明的袋子中装有20个红球和若干个白球,这些球除了颜色外都相同,若小英每次从袋子中随机摸出一个球,记下颜色后再放回,经过多次重复试验,小英发现摸到红球的频率逐渐稳定于0.4,则小英估计袋子中白球的个数约为()A.50 B.30 C.12 D.85.在一个10万人的小镇,随机调查了3000人,其中450人看某电视台的早间新闻,在该镇随便问一个人,他看该电视台早间新闻的概率大约是()A.0.0045 B.0.03 C.0.0345 D.0.156.下列说法正确的是()A.“打开电视机,正在播放动物世界”是必然事件B.在一只不透明的盒子里装有黑、白两种球(两种球除颜色外完全一样)共40个,小明做了50次试验,摸到黑球的概率是0.6,所以有24个黑球C.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次D.从一副去掉大、小王的扑克牌中随意抽5张,至少有2张花色相同7.设事件A:“a是实数,y=ax2+bx+c是y关于x的二次函数”,则事件A是()A.必然事件B.确定事件C.不可能事件D.随机事件8.一个盒子里有完全相同的三个小球,球上分别标上数字﹣1、1、2.随机摸出一个小球其数字记为p,不放回再随机摸出另一个小球其数字记为q,则p、q都是关于x的方程x2﹣x﹣2=0的实根的概率是()A.B.C.D.9.不透明的袋子中只有4个红球和2个绿球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是()A.3个球都是红球B.3个球都是绿球C.3个球中有红球D.3个球中有绿球10.有10名学生的身高如下(单位cm):160 170 166 165 170 152 159 175 158 160从中任选一名学生,身高不到161的概率是()A.B.C.D.二.填空题11.在一个不透明的袋子中有1个红球和3个白球,这些球除颜色外都相同,在袋子中再放入x个白球后,从袋子中随机摸出1个球,记录下颜色后放回袋子中并搅匀,经大量试验,发现摸到白球的频率稳定在0.95左右,则x=.12.从一副扑克牌中取出两张红桃和两张黑桃,将这四张扑克牌洗匀后背面朝上,从中随机摸出两张牌,那么摸到两张都是红牌的概率是.13.用如图所示的两个转盘(分别进行四等分和三等分),设计一个“配紫色”的游戏(红色与蓝色可配成紫色),则能配成紫色的概率为.14.如图所示的点阵中,相邻的四个点构成正方形,小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为.15.林业部门要考察某种幼树在一定条件下的移植成活率,如表是移植过程中的﹣组统计数据:移植棵数1000 2500 4000 8000 20000 30000 成活棵数865 2220 3500 7056 17580 26430 成活的频率0.865 0.888 0.875 0.882 0.879 0.881估计该种幼树在此条件下的移植成活的概率是.(结果精确到0.01)16.不透明的口袋里有除颜色外其它均相同的红、白、黑小球共计120个,玲玲通过多次摸球实验后发现,摸到红球和黑球的概率稳定在50%和30%,那么口袋中白球的个数极有可能是个.17.小红在地上画了半径为2m和3m的同心圆,如图,然后在一定距离外向圈内掷小石子,则掷中阴影部分的概率是.18.已知函数y=(3k+1)x+5(k为常数),若从﹣3≤k≤3中任取k值,则得到的函数是具有性质“y随x增加而减小”的一次函数的概率为.三.解答题19.一个不透明的袋子里装有黑白两种颜色的球共50只,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:(1)摸到黑球的频率会接近(精确到0.1),估计摸一次球能摸到黑球的概率是;袋中黑球的个数约为只;(2)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了个黑球.20.某超市抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和若两次所得的数字之和为8,则可获得50元代金券一张:若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张:其他情况都不中奖(1)请用列表或树状图的方法,把抽奖一次可能出现的结果表示出来;(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.21.为了“城市更美好、人民更幸福”,我市开展“三城联创”活动,环卫部门要求垃圾按A,B,C三类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收垃圾,甲、乙两人各投放一袋垃圾.(1)甲投放的垃圾恰好是C类的概率是;(2)用树状图或表格求甲、乙两人投放的垃圾是不同类别的概率.22.为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.(1)统计图中m=,n=;(2)若该校有1500名学生,请估计选择B基地的学生人数;(3)某班在选择B基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.23.2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,并根据调查结果绘制成了如下两幅不完整的统计图.根据图中信息解答下列问题:(1)扇形统计图中C部分所对应的扇形圆心角的度数为,并补全条形统计图;(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.参考答案一.选择题1.解:A、“概率为0.0001的事件”是随机事件,选项错误;B、任意掷一枚质地均匀的硬币10次,正面向上的可能是5次,选项错误.C、“任意画出一个等边三角形,它是轴对称图形”是必然事件,选项错误;D、“任意画出一个平行四边形,它是中心对称图形”是必然事件,选项正确;故选:D.2.解:掷一枚质地均匀的硬币,前3次都是正面朝上,则掷第4次时正面朝上的概率是;故选:B.3.解:∵布袋中装有红、黄、白球分别为2、3、5个,共10个球,从袋中任意摸出一个球共有10种结果,其中出现黄球的情况有3种可能,∴得到黄球的概率是:.故选:D.4.解:设袋中白球有x个,根据题意,得:=0.4,解得:x=30,经检验:x=30是分式方程的解,所以小英估计袋子中白球的个数约为30个,故选:B.5.解:∵随机调查了3000人,其中450人看某电视台的早间新闻,∴在该镇随便问一个人,他看该电视台早间新闻的概率大约是:=0.15;故选:D.6.解:A、“打开电视机,正在播放动物世界”是随机事件,故本选项错误;B、虽然摸到黑球的概率是0.6,但不一定就有24个黑球,故本选项错误;C、投掷一枚质地均匀的硬币1000次,正面朝上的次数不一定是500次,故本选项错误;D、从一副去掉大、小王的扑克牌中随意抽5张,至少有2张花色相同,故本选项正确;故选:D.7.解:a是实数,当a≠0时y=ax2+bx+c是y关于x的二次函数,否则不是,所以事件:“a是实数,y=ax2+bx+c是y关于x的二次函数”是随机事件,故选:D.8.解:画树状图得:∵方程x2﹣x﹣2=0的实根是﹣1和2,p、q是﹣1和2的情况有2种,共有6种情况,∴p、q都是关于x的方程x2﹣x﹣2=0的实根的概率是=.故选:A.9.解:A、3个球都是红球,是随机事件;B、3个球都是绿球,是不可能事件;C、3个球中有红球,是必然事件;D、3个球中有绿球,是随机事件;故选:B.10.解:在这10位同学的身高中,其身高超过161的有5位同学,∴从中任选一名学生,其身高超过161的概率是=;故选:D.二.填空题11.解:根据题意可得:=0.95,解得:x=16,经检验x=16是原方程的解,所有x的值为16;故答案为:16.12.解:根据题意画图如下:共有12中情况,从4张牌中任意摸出两张都是红牌有2种可能,所以两张都是红牌概率==,故答案为:.13.解:画树状图如下:由树状图知,共有12种等可能结果,其中能配成紫色的有3种结果,所以能配成紫色的概率为=,故答案为:.14.解:如图所示:根据题意可知四边形AEFB是正方形,直线MN把正方形AEFB平分分成两份,正方形CDEF 的面积与正方形ABFE的面积相同,所以小球只在矩形ABCD内自由滚动时,则小球停留在阴影区域的概率为.故答案为:.15.解:概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率∴这种幼树移植成活率的概率约为0.88.故答案为:0.88;16.解:设白球个数为:x个,∵摸到红球和黑球的概率稳定在50%和30%左右,∴口袋中得到白色球的概率为1﹣50%﹣30%=20%,∴=20%,解得:x=24,即白球的个数为24个,故答案为:24.17.解:∵S大圆=9πm2,S小圆=4πm2,S圆环=9π﹣4π=5πm2.∴掷中阴影部分的概率是=,故答案为:.18.解:当3k+1<0时,即k<﹣时,y随x增加而减小,又∵﹣3≤k≤3,∴﹣3≤k<,∴得到的函数具有“y随x增加而减小”的一次函数的概率为=,故答案为:.三.解答题19.解:(1)观察发现:随着实验次数的增加频率逐渐稳定到常数0.4附近,故摸到黑球的频率会接近0.4,∵摸到黑球的频率会接近0.4,∴黑球数应为球的总数的,∴估计袋中黑球的个数为50×=20只,故答案为:0.4,0.4,20;(2)设放入黑球x个,根据题意得:=0.6,解得x=25,经检验:x=25是原方程的根,故答案为:25;20.解:(1)列表得:1 2 3 41 2 3 4 52 3 4 5 63 4 5 6 74 5 6 7 8(2)由列表可知,所有可能出现的结果一共有16种,这些结果出现的可能性相同,其中两次所得数字之和为8、6、5的结果有8种,所以抽奖一次中奖的概率为:P ==.答:抽奖一次能中奖的概率为.21.解:(1)∵垃圾要按A,B,C三类分别装袋,甲投放了一袋垃圾,∴甲投放的垃圾恰好是C 类的概率为:,故答案为:;(2)A B C甲乙A(A,A)(A,B)(A,C)B(B,A)(B,B)(B,C)C(C,A)(C,B)(C,C)由表格可知,甲、乙两人投放的垃圾共有9 种结果,每种结果出现的可能性相同,其中甲、乙投放的垃圾恰是不同类别的有6 种,即(A,B),(A,C),(B,A),(B,C),(C,A),(C,B),∴P (甲、乙投放的垃圾是不同类别)=.22.解:(1)由题意可知:总人数=40÷20%=200(人)所以m=200×28%=56(人),n=×100%=15%,故答案为:56,15;(2)估计选择B基地的学生人数=(人)(3)根据题意列表如下:男1 男2 男3 男4 女1 女2 男1 (男1,男2)(男1,男3)(男1,男4)(男1,女1)(男1,女2)男2 (男2,男1)(男2,男3)(男2,男4)(男2,女1)(男2,女2)男3 (男3,男1)(男3,男2)(男3,男4)(男3,女1)(男3,女2)男4 (男4,男1)(男4,男2)(男4,男3)(男4,女1)(男4,女2)女1 (女1,男1)(女1,男2)(女1,男3)(女1,男4)(女1,女2)女2 (女2,男1)(女2,男2)(女2,男3)(女2,男4)(女2,女1)由上表可知,共有30种等可能的结果,其中“1男1女”的结果有16种.所以:P(1男1女)=23.解:(1)被调查的总人数为15÷25%=60(人),C类的总人数=60﹣25﹣15=20(人)所以扇形统计图中C部分所对应的扇形圆心角的度数为360°×=120°,补全条形统计图如图所示:故答案为:120°;(2)画树状图如下:共有12种可能的结果,恰好选到一男一女的结果有8个,∴P(选到一男一女)==.。
中考数学每日一练:解直角三角形练习题及答案_2020年填空题版

中考数学每日一练:解直角三角形练习题及答案_2020年填空题版答案答案答案答案答案答案2020年中考数学:图形的变换_锐角三角函数_解直角三角形练习题~~第1题~~(2020青浦.中考模拟) 在△ABC 中,∠C =90°,如果tan B =2,AB =4,那么BC =________.考点: 解直角三角形;~~第2题~~(2020湖州.中考模拟) 在△ABC 中,AC=6,点D 为直线AB 上一点,且AB=3BD,直线CD 与直线BC 所夹锐角的正切值为 ,并且CD ⊥AC ,则BC 的长为________.考点: 解直角三角形;~~第3题~~(2020上海.中考模拟) 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt △AB C 中,∠C=90°,若Rt △ABC 是“好玩三角形”,则tanA=________.考点: 解直角三角形;~~第4题~~(2020松江.中考模拟) 如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米.那么斜面AB 的坡度为________.考点: 解直角三角形;解直角三角形的应用﹣坡度坡角问题;~~第5题~~(2020上海.中考模拟) 如图,在四边形ABCD 中,∠B =∠D =90°,AB =3, BC=2,tanA =,则CD =________.考点: 锐角三角函数的定义;解直角三角形;~~第6题~~(2020虹口.中考模拟) 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果小正方形面积是49,直角三角形中较小锐角θ的正切为,那么大正方形的面积是________.考点: 锐角三角函数的定义;解直角三角形;~~第7题~~答案答案答案答案(2020上海.中考模拟) 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m ,已知木箱高BE=m ,斜面坡脚为30°,则木箱顶端E 距离地面AC 的高度EF 为________m 。
2020年中考数学复习每日一练 第十四讲 《坐标系的认识》(含答案)

2020年数学中考复习每日一练第十四讲《坐标系的认识》一.选择题1.若点M(a+3,2a﹣4)在x轴上,则点M的坐标为()A.(0,﹣10)B.(5,0)C.(10,0)D.(0,5)2.在平面直角坐标系中,点P的坐标是(2,3),则点P到y轴的距离是()A.2 B.3 C.D.43.下列数据不能确定物体位置的是()A.电影票5排8号B.北偏东30°C.希望路25号D.东经118°,北纬40°4.若点P(1﹣3m,2m)的横坐标与纵坐标互为相反数,则点P一定在()A.第一象限B.第二象限C.第三象限D.第四象限5.如图,若在象棋盘上建立平面直角坐标系,使棋子“车”的坐标为(﹣2,3),棋了“马”的坐标为(1,3),则棋子“炮”的坐标为()A.(3,2)B.(3,1)C.(2,2)D.(﹣2,2)6.平行于x轴的直线上的任意两点的坐标之间的关系是()A.横坐标相等B.纵坐标相等C.横坐标的绝对值相等D.纵坐标的绝对值相等7.在平面直角坐标系中,已知A(﹣2,0),B(2,0),则该平面直角坐标系中满足“△ABC 为∠C=90°且两条直角边长之比为1:2”的点C有()A.2个B.3个C.4个D.5个8.如图,是岑溪市几个地方的大致位置的示意图,如果用(0,0)表示孔庙的位置,用(1,5)表示东山公园的位置,那么体育场的位置可表示为()A.(﹣1,﹣1)B.(0, 1)C.(1,1)D.(﹣1,1)9.在平面直角坐标系中,点,点,则当AB取得最小值时, a 的值为()A.B.﹣3 C.0 D.10.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2020次运动后,动点P的坐标是()A.(2020,1)B.(2020,0)C.(2020,2)D.(2019,0)二.填空题11.如图,等边△OAB的边长为,则点B的坐标为.12.在平面直角坐标系中,点B在x轴上,位于原点右侧且距离原点1个单位长度,点B的坐标为 . 13.在平面直角坐标系xOy 中,点A 的坐标为(2,0),动点P 的坐标为(m , m ﹣4),若∠POA =45°,则m 的值为 .14.若点P (x ,y )在第四象限,且|x |=2,|y |=3,则x +y = .15.如图,在平面直角坐标系中,点M 的坐标为(3,0),⊙M 的半径为2,AB 为⊙M 的直径,其中点A 在第一象限,当OA =AB 时,点A 的坐标为 .16.如图,在平面直角坐标系中,点A 1,A 2,A 3…都在x 轴上,点B 1,B 2,B 3…都在第一象限的角平分线上,△B 1A 1A 2,△B 2A 2A 3,△B 3A 3A 4…都是等腰直角三角形,且OA 1=1,则点B 2020的坐标为 .17.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A 1B 1C 1D 1,A 2B 2C 2D 2,A 3B 3C 3D 3,……每个正方形四条边上的整点的个数.按此规律推算出正方形A 2019B 2019C 2019D 2019四条边上的整点共有 .三.解答题18.在平面直角坐标系中,已知点M (m ﹣1,2m +3)(1)若点M 在y 轴上,求m 的值.(2)若点M 在第一、三象限的角平分线上,求m 的值.19.平面直角坐标系中,我们把点P (x ,y )的横坐标与纵坐标的绝对值之和叫做点P (x ,y )的勾股值,记为:「P 」,即「P 」=|x |+|y |.(1)求点A (﹣1,3)的勾股值「A 」;(2)若点B 在第一象限且满足「B 」=3,求满足条件的所有B 点与坐标轴围成的图形的面积.20.如图所示,△ABC 在正方形网格中,若点A 的坐标为(0,3),按要求回答下列问题:(1)在图中建立正确的平面直角坐标系;(2)根据所建立的坐标系,写出点B 和点C 的坐标;(3)作出△ABC 关于x 轴的对称图形△A ′B ′C ′.(不用写作法)21.对于平面直角坐标系xOy 中的点P (a ,b ),若点P 1的坐标为(a +kb ,ka +b )(其中k 为常数,且k ≠0),则称点P 1为点P 的“k 属派生点”.例如,P (1,4)的“2属派生点”为P 1(1+2×4,2×1+4),即P 1(9,6).(1)点(﹣2,3)的“3属派生点”P 1的坐标为 (直接填空)(2)若点P 的 “5属派生点”P 1的坐标为(3,﹣9),则点P 坐标为 (直接填空);(3)若x 轴正半轴上一点P (a ,0)的“k 属派生点”为P 1,且线段PP 1的长度为线段OP 长度的2倍,则k = (直接填空);(4)在(3)的条件下,若点M 在y 轴上,连接MP 、MP 1,使MP 1平分∠PMO ,请直接写出点M 的纵坐标(用含a 的代数式表示).22.中国棋盘中蕴含着平面直角坐标系,如图所示是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形对角线走.例如:图中“马”所在位置可以直接走到点A、B处.(1)如果“相”位于点(4,2),“帅”位于点(0,0),则“马”所在点的坐标为,点D的坐标为.(2)若“马”的位置在C点,为了到达“D”点,请按“马”走的规则,写出一种你认为合理的行走路线,(在答题纸图中标出行走路线即可).23.材料一:中国象棋体现了我国古人的智慧和传统文化的精髓.中国象棋棋盘中蕴含着平面直角坐标系.如图是中国象棋棋盘的一半,棋子“马”走的规则是每步走“日”字形.例如:图中“马”所在的位置可以直接走到点A、B处;材料二:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位,用实数加法表示为3+(﹣2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.下面在图中的象棋棋盘上建立直角坐标系,设“帅”位于点(0,0),“相”位于点(4,2).请解决下列问题:(1)图中“马”所在的点的坐标为.(2)根据材料一和材料二,在整个直角坐标系中,不是棋子“马”的一步“平移量”的是.(可多选,填选项前的字母)A.{1,2}B.{﹣2,1}C.{1,﹣1}D.{﹣2,﹣1}E.{3,﹣1}(3)设“马”的初始位置如图中所示,如果现在命令“马“每一步只能向右和向上前进(例如图中的“马”只能走到点A、B处),在整个坐标系中,试问:①“马”能否走到点C?答:;(填“能”或“不能”)②“马”能否走到点(2018,2019)和点(2020,2021)?若能,则需要几步?为什么?若不能,请说明理由.参考答案一.选择题1.解:∵点M(a+3,2a﹣4)在x轴上,∴2a﹣4=0,解得:a=2,∴点M的坐标为:(5,0).故选:B.2.解:∵点P的坐标是(2,3),∴点P到y轴的距离是:2.故选:A.3.解:不能确定物体位置的是北偏东30°,故选:B.4.解:∵点P(1﹣3m,2m)的横坐标与纵坐标互为相反数,∴2m=﹣(1﹣3m),解得m=1,∴点P的坐标是(﹣2,2),∴点P在第二象限.故选:B.5.解:如图所示:棋子“炮”的坐标为(3,2).故选:A.6.解:平行于x轴的直线上的任意两点的坐标之间的关系是纵坐标相等.故选:B.7.解:如图所示,该平面直角坐标系中满足“△ABC为∠C=90°且两条直角边长之比为1:2”的点C有4个,故选:C.8.解:如图所示:体育场的位置可表示为(﹣1,﹣1).故选:A.9.解:∵点,点,∴AB==2,∴当AB取得最小值时,a的值为﹣,故选:A.10.解:点P坐标运动规律可以看做每运动四次一个循环,每个循环向右移动4个单位,则2020=505×4,所以,前505次循环运动点P共向右运动505×4=2020个单位,且在x轴上,故点P坐标为(2020,0).故选:B.二.填空题(共7小题)11.解:如图,作BH⊥OA于H.∵△OAB是等边三角形,BH⊥OA,∴OH=AH=,∠BOH=60°,∴BH=OH•tan60°=3,∴B(,3),故答案为(,3)12.解:∵点B在x轴上,位于原点右侧且距离原点1个单位长度,∴点B的坐标为:(1,0).故答案为:(1,0).13.解:∵在平面直角坐标系xOy中,点A的坐标为(2,0),∴点A在x轴的正半轴上,∵∠POA=45°,∴点P的坐标为(m, m﹣4)在第一象限或第四象限,∴m=m﹣4,或m=﹣(m﹣4),解得:m=﹣8(不合题意舍去),或m=,故答案为:.14.解:∵点P(x,y)在第四象限,且|x|=2,|y|=3,∴x=2,y=﹣3,x+y=2+(﹣3)=﹣1,故答案为:﹣1.15.解:过A作AC⊥OM于C,∴∠ACO=∠ACM=90°,∵点M的坐标为(3,0),∴OM=3,∵⊙M的半径为2,∴AM=2,OA=AB=4,∵OA2﹣OC2=AM2﹣CM2,∴42﹣OC2=22﹣(3﹣OC)2,解得:OC=,∴AC===,∴点A的坐标为(,),故答案为:(,).16.解:∵OA1=1,△OA1A2是等腰直角三角形,∴A1B1=1∴B1(1,1);△B1A1A2是等腰直角三角形∴A1A2=1∴A2B1=B1B2=,△B2B1A2是等腰直角三角形∴A2B2=2∴B2(2,2)同理可得A 3B2=B2B3=2∴A3B3=4,∴B3(22,22)…同理B4(23,23)…B n (2n ﹣1,2n ﹣1 )∴点B 2020的坐标为 (22019,22019).17.解:∵A 1B 1C 1D 1每条边上的整点共有:2×1+1=3个,A 2B 2C 2D 2每条边上的整点共有;2×2+1=5个,正方形A 3B 3C 3D 3每条边上的整点的个数有:2×3=1=7个,…∵A 1B 1C 1D 1四条边上的整点共有8个,即4+4×1=8,A 2B 2C 2D 2四条边上的整点共有16个,即4+4×3=16,正方形A 3B 3C 3D 3四条边上的整点的个数有4+4×5=24,…∴第n 个正方形上的整点个数是:4+4(2n ﹣1)=8n ,∴正方形A 2019B 2019C 2019D 2019四条边上的整点的个数=2019×8=16152,故答案为:16152.三.解答题(共6小题)18.解:(1)由题意得:m ﹣1=0,解得:m =1;(2)由题意得:m ﹣1=2m +3,解得:m =﹣4.19.解:(1)「A 」=|﹣1|+|3|=4,(2)设B (x ,y ),由「B 」=3且在第一象限知,x +y =3(x >0,y >0),即:y =﹣x +3(x >0,y >0).故所有点B 与坐标轴围成的图形如图所示的三角形,故其面积为×3×3=.20.解:(1)所建立的平面直角坐标系如下所示:(2)点B 和点C 的坐标分别为:B (﹣3,﹣1)C (1,1);(3)所作△A 'B 'C '如下图所示.21.解:(1)P 1(﹣2+3×3,﹣2×3+3),),即P 1(7,﹣3);故答案为(7,﹣3);(2)3=a +5b ,﹣9=5a +b ,∴a =﹣2,b =1,∴P (﹣2,1),故答案为(﹣2,1);(3)P (a ,0)的“k 属派生点”为P 1(a ,ka ),∴PP 1的长度为|ka |,OP 长度为a ,∵线段PP 1的长度为线段OP 长度的2倍,∴|ka |=2a ,∴k =±2, 故答案为±2;(4)∵k =±2,∴P1(a,±2a),当P1(a,2a)时,过点P1作P1B⊥MP,过点M作MC⊥P1P,∵MP1平分∠PMO,∴AP1=P1B=a,∵MC=a,∴△MCP≌△P1PB(AAS),∴MP=P1P=2a,∴PC=a,∴点M的纵坐标为±a.22.解:(1)由“相”位于点(4,2),“帅”位于点(0,0),∴“马”的坐标为(﹣3,0),D的坐标(3,1),故答案为(﹣3,0),(3,1);(2)如图所示:23.解:(1)由“帅”位于点(0,0),“相”位于点(4,2),∴“马”坐标为(﹣3,0);(2)由于马走“日”,因此马的平移向量左或右平移1,则相应的上或下平移2;平移向量左或右平移2,则相应的上或下平移1,∴A、B、D可以是“马”的一步“平移量”,故答案为C、E.(3)①马可以先走到A,再走到C;也可以先走到B,再走到C;故答案为能;②由题意可知“马”的走法只有两种平移量(2,1)或(1,2),设马沿着平移量(2,1)移动n次,沿着平移量(1,2)移动m次,则马沿着平移量(2n+m,2m+n)移动,如图马的初始位置是(﹣3,0),走到点(2018,2019)时,向右移动2021,马向上移动2019,∴2n+m=2021,2m+n=2019,∴m=(不合题意),∴马走不到(2018,2019);走到点(2020,2021)时,向右移动2023,马向上移动2021,∴2n+m=2023,2m+n=2021,∴m=673,n=675,∴能走到点(2020,2021),需要沿着平移量(2,1)移动675次,沿着平移量(1,2)移动673次.。
中考数学每日一练:三角形中位线定理练习题及答案_2020年综合题版

中考数学每日一练:三角形中位线定理练习题及答案_2020年综合题版答案答案2020年中考数学:图形的性质_三角形_三角形中位线定理练习题~~第1题~~(2020武汉.中考模拟) 已知平行四边形ABCD.(1) 如图1,将▱ABCD 绕点D 逆时针旋转一定角度得到▱A B C D ,延长B C ,分别与BC 、AD 的延长线交于点M 、N.①求证:∠BMB =∠ADA ;②求证:B N =AN+C M ;(2) 如图2,将线段AD 绕点D 逆时针旋转,使点A 的对应点A 落在BC 上,将线段CD 绕点D 逆时针旋转到C D 的位置,AC 与A D 交于点H.若H 为AC 的中点,∠ADC +∠A DC =180°,A B =nA C ,试用含n 的式子表示的值.考点: 全等三角形的判定与性质;三角形中位线定理;平行四边形的性质;旋转的性质;~~第2题~~(2020遵化.中考模拟) 如图,一次函数y =kx +b 与反比例函数y =.(其中mk≠0)图像交于A (-4,2),B (2,n)两点.(1) 求一次函数和反比例函数的表达式;(2) 求△ABO 的面积;(3) 请写出当一次函数值大于反比例函数值时x 的取值范围.考点: 偶次幂的非负性;立方根及开立方;常量、变量;一次函数的定义;反比例函数与一次函数的交点问题;线段的长短比较与计算;三角形的面积;勾股定理;三角形中位线定理;切线的判定与性质;相似三角形的性质;扇形统计图;~~第3题~~(2020遵化.中考模拟) 现有甲、乙、丙等多家食品公司在某市开设蛋糕店,该市蛋糕店数量的扇形统计图如图所示,其中统计图中没有标注相应公司数量的百分比.已知乙公司经营150家蛋糕店,请根据该统计图回答下列问题:(1) 求甲公司经营的蛋糕店数量和该市蛋糕店的总数.(2) 甲公司为了扩大市场占有率,决定在该市增设蛋糕店,在其余蛋糕店数量不变的情况下,若要使甲公司经营的蛋糕店数量达到全市的20%,求甲公司需要增设的蛋糕店数量.考点: 偶次幂的非负性;立方根及开立方;分式的通分;根据数量关系列出方程;常量、变量;一次函数的定义;线段的长短比较与计111111111111111111答案答案答案算;勾股定理;三角形中位线定理;切线的判定与性质;相似三角形的性质;扇形统计图;~~第4题~~(2020遵化.中考模拟) 图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B 可以上下调整高度,离地面CD 的距离BC =160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB =30cm.假设水柱AE 垂直AB 直线喷射,小华在离墙面距离CD =120cm 处淋浴.(1) 当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.(2) 如果小华要洗脚,需要调整水柱AE ,使点E 与点D 重合,调整的方式有两种:①其他条件不变,只要把活动调节点B 向下移动即可,移动的距离BF 与小华的身高DE 有什么数量关系?直接写出你的结论;②活动调节点B 不动,只要调整α的大小,在图3中,试求α的度数.(参考数据: ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)考点: 偶次幂的非负性;立方根及开立方;分式的通分;常量、变量;一次函数的定义;线段的长短比较与计算;勾股定理;三角形中位线定理;矩形的性质;切线的判定与性质;相似三角形的性质;特殊角的三角函数值;扇形统计图;~~第5题~~(2020遵化.中考模拟) 如图,直线OA 与反比例函数的图像交于点A (3,3),向下平移直线OA ,与反比例函数的图像交于点B (6,m )与y 轴交于点C ,(1) 求直线BC 的解析式;(2) 求经过A 、B 、C 三点的二次函数的解析式;(3) 设经过A 、B 、C 三点的二次函数图像的顶点为D ,对称轴与x 轴的交点为E.问:在二次函数的对称轴上是否存在一点P ,使以O 、E 、P 为顶点的三角形与△BCD 相似?若存在,请求出点P 的坐标;若不存在,请说明理由.考点: 一次函数的定义;反比例函数的图象;反比例函数的性质;线段的长短比较与计算;勾股定理;三角形中位线定理;相似三角形的性质;2020年中考数学:图形的性质_三角形_三角形中位线定理练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
初中数学中考每日一练试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √2B. πC. 2/3D. 无理数2. 已知 a > b > 0,则下列不等式中正确的是()A. a² > b²B. a³ > b³C. a² < b²D. a³ < b³3. 下列各式中,正确的是()A. (a+b)² = a² + 2ab + b²B. (a-b)² = a² - 2ab + b²C. (a+b)³ = a³ + 3a²b + 3ab² + b³D. (a-b)³ = a³ - 3a²b + 3ab² - b³4. 在△ABC中,∠A=45°,∠B=60°,则∠C的度数是()A. 75°B. 105°C. 135°D. 150°5. 下列各图中,是轴对称图形的是()A. ①B. ②C. ③D. ④6. 若a、b是方程2x²-5x+2=0的两个根,则a+b的值是()A. 2B. 3C. 4D. 57. 若x是方程3x²-2x-5=0的根,则3x³-2x²-5x的值是()A. 0B. 1C. 2D. 38. 已知a=√2+√3,b=√2-√3,则a²-b²的值是()A. 2B. 4C. 6D. 89. 下列各式中,正确的是()A. (a+b)(a-b) = a² - b²B. (a+b)(a+b) = a² + 2ab + b²C. (a-b)(a+b) = a² - 2ab + b²D. (a-b)(a-b) = a² + 2ab + b²10. 若x是方程2x²-5x+2=0的根,则方程2x²-5x+3=0的根是()A. x+1B. x-1C. 2xD. x/2二、填空题(每题5分,共30分)11. 若a、b是方程2x²-5x+2=0的两个根,则a+b的值是______。
中考数学每日一练:翻折变换(折叠问题)练习题及答案_2020年综合题版

(1) 如图1,若点A′恰好落在边AB上,且AN= AC,求AM的长; (2) 如图2,若点A′恰好落在边BC上,且A′N∥AC. ①试判断四边形AMA′N的形状并说明理由;
②求AM、MN的长;
(3) 如图3,设线段NM、BC的延长线交于点P,当
且
时,求CP的长.
考点: 菱形的判定;翻折变换(折叠问题);
(1) 用含a的代数式表示点C的坐标. (2) 如图1,若点D落在抛物线的对称轴上,且在x轴上方,求抛物线的解析式.
(3) 设
的面积为S1,
的面积为S2,若
,求a的值.
考点: 待定系数法求二次函数解析式;翻折变换(折叠问题);相似三角形的判年 中 考 数 学 : 图 形 的 变 换 _轴 对 称 变 换 _翻 折 变 换 ( 折 叠 问 题 ) 练 习 题 答 案
(1) 连结AF,若AF∥CE.证明:点E为AB的中点;
(2) 证明:GF=GD;
(3) 若AD=5,设EB=x,GD=y,求y与x的函数关系式.
考点: 正方形的性质;翻折变换(折叠问题);
答案
~~第3题~~ (2020绍兴.中考模拟) 如图,已知△ABC中,∠ACB=90°,AC=4,BC=3,点M、N分别是边AC、AB上的动点,连 接MN,将△AMN沿MN所在直线翻折,翻折后点A的对应点为A′.
第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3
第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的 虚线为折痕.
问题解决:
(1) 在图5中,∠BEC的度数是, 的值是;
(2) 在图5中,请判断四边形EMGF的形状,并说明理由;
中考数学每日一练:三角形的面积练习题及答案_2020年压轴题版

答案
2020年 中 考 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 的 面 积 练 习 题 答 案
1.答案:
2.答案:
3.答案:
4.答案:
5.答案:
(1) 当OM经过点A时, ①请直接填空:ON(可能,不可能)过D点:(图1仅供分析)
②如图2,在ON上截取OE=OA,过E点作EF垂直于直线BC,垂足为点F,作EH⊥CD于H,求证:四边形EFCH为正
方形;
③如图2,将②中的已知与结论互换,即在ON上取点E(E点在正方形ABCD外部),过E点作EF垂直于直线BC,垂 足为点F,作EH⊥CD于H,若四边形EFCH为正方形,那么OE与OA是否相等?请说明理由;
(2) 当点O在射线BC上且OM不过点A时,设OM交边AB于G,且OG=2.在ONO= S△OBG,连接GP,则当BO为何值时,四边形PKBG的面积最大?最大面积为多少?
考点: 三角形的面积;全等三角形的判定与性质;正方形的判定与性质;相似三角形的判定与性质;
中考数学每日一练:三角形的面积练习题及答案_2020年压轴题版
2020年 中 考 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 的 面 积 练 习 题
~~第1题~~
(2020杭州.中考模拟) 如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90° 得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.
(1) 求A、A′、C三点的坐标;
(2) 求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3) 点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M
中考数学每日一练:全等三角形的判定与性质练习题及答案_2020年解答题版

中考数学每日一练:全等三角形的判定与性质练习题及答案_2020年解答题版答案答案答案答案2020年中考数学:图形的性质_三角形_全等三角形的判定与性质练习题~~第1题~~(2020嘉兴.中考模拟) 如图,在▱ABCD 中,对角线 AC ,BD 相交于点 O ,过点 O 的一条直线分别交 AD ,BC于点 E ,F .求证:AE=CF .考点: 全等三角形的判定与性质;平行四边形的性质;~~第2题~~(2020温州.中考模拟) 如图,等腰直角△ABC 中,CA=CB ,点E 为△ABC 外一点,CE=CA ,且CD 平分∠ACB 交AE 于D ,且∠CDE=60°.(1) 求证:△CBE 为等边三角形;(2) 若AD=5,DE=7,求CD 的长.考点: 全等三角形的判定与性质;等边三角形的判定与性质;~~第3题~~(2019陕西.中考模拟) 如图,点B 、F 、C 、E 在一条直线上,FB=CE ,AB ∥ED ,AC ∥FD ,AD 交BE于O .求证:AD 与BE 互相平分.考点: 全等三角形的判定与性质;平行四边形的判定与性质;~~第4题~~(2019山西.中考真卷) (2019·山西) 已知:如图,点B ,D 在线段AE 上,AD=BE ,AC ∥EH,∠C=∠H.求证:BC=DH.考点:全等三角形的判定与性质;~~第5题~~(2019大连.中考真卷) 如图,点,在 上, , , ,求证: .考点:全等三角形的判定与性质;答案2020年中考数学:图形的性质_三角形_全等三角形的判定与性质练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
中考数学每日一练:三角形中位线定理练习题及答案_2020年单选题版

A . AE=EF B . AB=2DE C . △ADF和△ADE的面积相等 D . △ADE和△FDE的面积相等
考点: 等腰三角形的判定与性质;三角形中位线定理;翻折变换(折叠问题);
答案
~~第2题~~ (2020宿州.中考模拟) 若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
答案
~~第6题~~ (2019宝鸡.中考模拟) 如图,已知矩形ABCD中,R,P分别是DC、BC上的点,E,F分别是AP,RP的中点,当P在B C上从B向C移动而R不动时,那么下列结论成立的是( )
A . 线段EF的长逐渐增大 B . 线段EF的长逐渐减小 C . 线段EF的长不改变 D . 线段EF的长不能确定
答案
~~第5题~~ (2020长兴.中考模拟) 如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD 交AG于点F,已知AF=2,则线段AE的长是( )
A . 4 B . 6 C . 8 D . 10
考点: 三角形中位线定理;正方形的性质;相似三角形的性质;
答案
2020年 中 考 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 中 位 线 定 理 练 习 题 答 案
1.答 案 : C 2.答 案 : C 3.答 案 : B 4.答 案 : D 5.答 案 : B 6.答 案 : C 7.答 案 : C 8.答 案 : A 9.答 案 : A 10.答 案 : D
答案
~~第8题~~ (2019葫芦岛.中考真卷) 如图,正方形ABCD的对角线AC,BD相交于点O,点E在BD上由点B向点D运动(点E不与点 B重合),连接AE,将线段AE绕点A逆时针旋转90得到线段AF,连接BF交AO于点G.设BE的长为x,OG的长为y,下列图 象中大致反映y与x之间的函数关系的是( )
中考数学每日一练:二元一次方程组的实际应用-鸡兔同笼问题练习题及答案_2020年填空题版

答案
~~第6题~~
(2018大连.中考真卷) 《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3
匹小马能拉1片瓦,问有多少匹大马、多少匹小马?设有x匹大马,y匹小马,根据题意可列方程组为________.
考点: 二元一次方程组的实际应用-鸡兔同笼问题;
答案
~~第7题~~
中考数学每日一练:二元一次方程组的实际应用-鸡兔同笼问题练习题及答案 _2020年填空题版
2020年 中 考 数 学 : 方 程 与 不 等 式 _二 元 一 次 方 程 组 _二 元 一 次 方 程 组 的 实 际 应 用 -鸡 兔 同 笼 问 题 练 习 题
~~第1题~~ (2020长春.中考模拟) 《九章算术》是中国传统数学最重要的著作,方程术是《九章算术》最高的数学成就.《九章算 术》中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?译文:假设有5头牛、2只羊 ,值金10两;2头牛、5只羊,值金8两.问每头牛、每只羊各值金多少?若设每头牛值金x两,每只羊值金y两,可列方程 组为________.
考点: 二元一次方程组的实际应用-鸡兔同笼问题;
答案
~~第9题~~
(2018青岛.中考真卷) 5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,
采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为1
答案
~~第4题~~ (2019怀集.中考模拟) 《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直 金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值 金x两,每只羊值金y两,可列方程组为________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学中考每日一练
如图,已知抛物线y=ax2+bx+c过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
(1)求抛物线的解析式;
(2)设点M(1,m),当MB+MD的值最小时,求m的值;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E 作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.
【分析】(1)根据待定系数法,可得答案;
(2)利用轴对称求最短路径的知识,找到B点关于直线x=1的对称点B′,连接B'D,B'D与直线x=1的交点即是点M的位置,继而求出m的值.
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减去较小的纵坐标,可得PE的长,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;
(4)设出点E的,分情况讨论,①当点E在线段AC上时,点F在点E上方,②当点E在线段AC(或CA)延长线上时,点F在点E下方,根据平行四边形的性质,可得关于x的方程,继而求出点E的坐标.
【解答】解:(1)将A,B,C点的坐标代入解析式,得
,
解得,
抛物线的解析式为y=﹣x2﹣2x+3
(2)配方,得y=﹣(x+1)2+4,顶点D的坐标为(﹣1,4)
作B点关于直线x=1的对称点B′,如图1,则B′(4,3),由(1)得D(﹣1,4),
可求出直线DB′的函数关系式为y=﹣x+,
当M(1,m)在直线DN′上时,MN+MD的值最小,
则m=﹣×1+=.
(3)作PE⊥x轴交AC于E点,如图2,AC的解析式为y=x+3,设P(m,﹣m2﹣2m+3),E(m,m+3),PE=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m
S△APC=PE•|x A|=(﹣m2﹣3m)×3=﹣(m+)2+,
当m=﹣时,△APC的面积的最大值是;
(4)由(1)、(2)得D(﹣1,4),N(﹣1,2)
点E在直线AC上,设E(x,x+3),
①当点E在线段AC上时,点F在点E上方,则F(x,﹣x2﹣2x+3),
∵EF=DN
∴﹣x2﹣2x+3﹣(x+3)=4﹣2=2,
解得,x=﹣2或x=﹣1(舍去),
则点E的坐标为:(﹣2,1).
②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,﹣x2﹣2x+3),∵EF=DN,
∴(x+3)﹣(﹣x2﹣2x+3)=2,
解得x=或x=,
即点E的坐标为:(,)或(,)
综上可得满足条件的点E为E(﹣2,1)或:(,)或(,).
【点评】本题考查了二次函数的综合题,解(1)的关键是待定系数法,解(2)利用轴对称求最短路径;解(3)的关键是利用三角形的面积得出二次函数;解(4)的关键是平行四边形的性质得出关于x的方程,要分类讨论,以防遗漏.。
