2019年保定市定州市七年级上册期末数学试卷(有答案)
保定市人教版七年级上册数学期末试卷及答案-百度文库

保定市人教版七年级上册数学期末试卷及答案-百度文库一、选择题1.下列说法中正确的有()A.连接两点的线段叫做两点间的距离B.过一点有且只有一条直线与已知直线垂直C.对顶角相等D.线段AB的延长线与射线BA是同一条射线2.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x天,由题意得方程()A.410+415x-=1 B.410+415x+=1 C.410x++415=1 D.410x++15x=13.将图中的叶子平移后,可以得到的图案是()A.B.C.D.4.下列调查中,适宜采用全面调查的是()A.对现代大学生零用钱使用情况的调查B.对某班学生制作校服前身高的调查C.对温州市市民去年阅读量的调查D.对某品牌灯管寿命的调查5.如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2018个格子中的数为()4a b c﹣23…A.4 B.3 C.0 D.﹣26.下列日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上,老师测量某个同学的跳远成绩;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是( ) A .①④ B .②③ C .③D .④7.下列四个数中最小的数是( ) A .﹣1 B .0 C .2 D .﹣(﹣1) 8.若-4x 2y 和-23x m y n 是同类项,则m ,n 的值分别是( )A .m=2,n=1B .m=2,n=0C .m=4,n=1D .m=4,n=09.3的倒数是( ) A .3B .3-C .13D .13-10.下列变形中,不正确的是( ) A .若x=y ,则x+3=y+3 B .若-2x=-2y ,则x=y C .若x ym m=,则x y = D .若x y =,则x y m m= 11.已知105A ∠=︒,则A ∠的补角等于( ) A .105︒B .75︒C .115︒D .95︒12.如果2|2|(1)0a b ++-=,那么()2020a b +的值是( )A .2019-B .2019C .1-D .1二、填空题13.若代数式mx 2+5y 2﹣2x 2+3的值与字母x 的取值无关,则m 的值是__.14.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m 为________,第n 个正方形的中间数字为______.(用含n 的代数式表示)…………15.如图,是七(2)班全体学生的体有测试情况扇形统计图.若达到优秀的有25人,则不合格的学生有____人.16.因式分解:32x xy -= ▲ .17.已知a ,b 是正整数,且a 5b <<,则22a b -的最大值是______. 18.52.42°=_____°___′___″.19.中国古代数学著作《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有x 辆车,则可列方程_____.20.如图,将1~6这6个整数分别填入如图的圆圈中,使得每边上的三个数之和相等,则符合条件的x 为_____.21.若2a +1与212a +互为相反数,则a =_____. 22.-2的相反数是__.23.3.6=_____________________′ 24.材料:一般地,n 个相同因数a 相乘n a a a a⋅⋅⋅个:记为n a . 如328=,此时3叫做以2为底的8的对数,记为2log 8(即2log 83=);如45625=,此时4叫做以5为底的625的对数,记为5log 625(即5log 6254=),那么3log 9=_________.三、解答题25.滴滴快车是一种便捷的出行工具,其计价规则如图:(注:滴滴快车车费由里程费、时长费、远途费三部分构成,其中里程费按行车的具体时段标准和实际里程计算:时长费按具体时段标准和行车的实际时间计算,远途费的收取方式:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.3元)(1)小红早上7:00从家出发乘坐滴滴快车到学校,行驶里程2公里,用时8分钟,需付车费元,傍晚17:00放学乘坐滴滴快车到妈妈单位,行驶里程5公里,用时20分钟,需付车费元;(2)某人06:10出发,乘坐滴滴快车到某地,行驶里程20公里,用时40分钟,需付车费多少元?(3)某人普通时段乘坐演滴快车到某地,用时30分钟,共花车费39.8元,求他行驶的里程?26.(1)已知∠AOB=25°42′,则∠AOB的余角为,∠AOB的补角为;(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;(3)如图,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,且∠AOB=25°,则经过多少时间后,△AOB的面积第一次达到最大值.27.已知,,,A B C D四点如图所示,请按要求画图.(1)画直线AB;(2)若所画直线AB表示一条河流,点,C D分别表示河流两旁的两块稻田,要在河岸边某一位置开渠引水灌溉稻田,请在河流AB上确定点P,使得在点P处开渠到两块稻田,C D的距离之和最短,并说明理由.28.知图①,在数轴上有一条线段AB,点,A B表示的数分别是2-和11-.(1)线段AB=____________;(2)若M是线段AB的中点,则点M在数轴上对应的数为________;(3)若C为线段AB上一点.如图②,以点C为折点,将此数轴向右对折;如图③,点B落在点A的右边点B'处,若15AB B C''=,求点C在数轴上对应的数是多少?29.甲乙两站相距450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.(1)两车同时开出,相向而行,那么两车行驶多少小时相遇?(2)两车同时开出,同向而行,慢车在前,多少小时快车追上慢车?(3)快车先开30min,两车相向而行,慢车行驶多少小时两车相遇?30.设A=3a2+5ab+3,B=a2﹣ab.(1)化简;A﹣3B.(2)当a、b互为倒数时,求A﹣3B的值.四、压轴题31.(1)探究:哪些特殊的角可以用一副三角板画出?在①135︒,②120︒,③75︒,④25︒中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线EF,然后将一副三角板拼接在一起,其中45角(AOB∠)的顶点与60角(COD∠)的顶点互相重合,且边OA、OC都在直线EF上.固定三角板COD不动,将三角板AOB绕点O按顺时针方向旋转一个角度α,当边OB与射线OF第一次重合时停①当OB 平分EOD ∠时,求旋转角度α;②是否存在2BOC AOD ∠=∠?若存在,求旋转角度α;若不存在,请说明理由. 32.如图,己知数轴上点A 表示的数为8,B 是数轴上一点,且AB=22.动点P 从点A 出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)写出数轴上点B 表示的数____,点P 表示的数____(用含t 的代数式表示); (2)若动点Q 从点B 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P 、Q 同时出发,问点P 运动多少秒时追上点Q?(列一元一次方程解应用题)(3)若动点Q 从点B 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P 、Q 同时出发,问 秒时P 、Q 之间的距离恰好等于2(直接写出答案)(4)思考在点P 的运动过程中,若M 为AP 的中点,N 为PB 的中点.线段MN 的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN 的长.33.如图,P 是定长线段AB 上一点,C 、D 两点分别从P 、B 出发以1cm /s 、2cm /s 的速度沿直线AB 向左运动(C 在线段AP 上,D 在线段BP 上)(1)若C 、D 运动到任一时刻时,总有PD =2AC ,请说明P 点在线段AB 上的位置:(2)在(1)的条件下,Q 是直线AB 上一点,且AQ ﹣BQ =PQ ,求PQAB的值.(3)在(1)的条件下,若C 、D 运动5秒后,恰好有1CD AB 2=,此时C 点停止运动,D 点继续运动(D 点在线段PB 上),M 、N 分别是CD 、PD 的中点,下列结论:①PM ﹣PN 的值不变;②MNAB的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】分别利用直线的性质以及射线的定义和垂线定义分析得出即可.【详解】A.连接两点的线段的长度叫做两点间的距离,错误;B.在同一平面内,过一点有且只有一条直线与已知直线垂直,错误;C.对顶角相等,正确;D.线段AB的延长线与射线BA不是同一条射线,错误.故选C.【点睛】本题考查了直线的性质以及射线的定义和垂线的性质,正确把握相关定义和性质是解题的关键.2.B解析:B【解析】【分析】直接利用总工作量为1,分别表示出两人完成的工作量进而得出方程即可.【详解】设乙独做x天,由题意得方程:4 10+415x=1.故选B.【点睛】本题主要考查了由实际问题抽象出一元一次方程,正确表示出两人完成的工作量是解题的关键.3.A解析:A【解析】【分析】根据平移的特征分析各图特点,只要符合“图形的形状、大小和方向都不改变”即为正确答案.【详解】解:根据平移不改变图形的形状、大小和方向,将所示的图案通过平移后可以得到的图案是A,其它三项皆改变了方向,故错误.故选:A.【点睛】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状、大小和方向,学生易混淆图形的平移,旋转或翻转而误选.4.B解析:B【解析】【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【详解】解:A、对现代大学生零用钱使用情况的调查,工作量大,用抽样调查,故此选项错误;B、对某班学生制作校服前身高的调查,需要全面调查,故此选项正确;C、对温州市市民去年阅读量的调查,工作量大,用抽样调查,故此选项错误;D、对某品牌灯管寿命的调查,有破坏性,用抽样调查,故此选项错误.故选:B.【点睛】本题考查的是调查方法的选择,正确选择调查方式要根据全面调查和抽样调查的优缺点再结合实际情况去分析.5.D解析:D【解析】【分析】根据三个相邻格子的整数的和相等列式求出a、c的值,再根据第9个数是3可得b=3,然后找出格子中的数每3个为一个循环组依次循环,再用2018除以3,根据余数的情况确定与第几个数相同即可得解.【详解】解:∵任意三个相邻格子中所填整数之和都相等,∴4+a+b=a+b+c,解得c=4,a+b+c=b+c+(-2),解得a=-2,所以,数据从左到右依次为4、-2、b、4、-2、b,第9个数与第三个数相同,即b=3,所以,每3个数“4、-2、3”为一个循环组依次循环,∵2018÷3=672…2,∴第2018个格子中的整数与第2个格子中的数相同,为-2.故选D.【点睛】此题考查数字的变化规律,仔细观察排列规律求出a、b、c的值,从而得到其规律是解题的关键.6.A解析:A【解析】【分析】根据点到直线的距离,直线的性质,线段的性质,可得答案.【详解】①用两根钉子就可以把一根木条固定在墙上,利用了两点确定一条直线,故①正确;②把弯曲的公路改直,就能够缩短路程,利用“两点之间线段最短”,故②错误;③体育课上,老师测量某个同学的跳远成绩,利用了点到直线的距离,故③错误;④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙,利用了两点确定一条直线,故④正确.故选A.【点睛】本题考查了线段的性质,熟记性质并能灵活应用是解答本题的关键.7.A解析:A【解析】【分析】首先根据有理数大小比较的方法,把所给的四个数从大到小排列即可.【详解】解:﹣(﹣1)=1,∴﹣1<0<﹣(﹣1)<2,故选:A.【点睛】此题主要考查了有理数大小比较的方法,要熟练掌握正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小.8.A解析:A【解析】根据同类项的相同字母的指数相同可直接得出答案.解:由题意得:m=2,n=1.故选A.9.C解析:C 【解析】根据倒数的定义可知. 解:3的倒数是.主要考查倒数的定义,要求熟练掌握.需要注意的是:倒数的性质:负数的倒数还是负数,正数的倒数是正数,0没有倒数. 倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.10.D解析:D 【解析】 【分析】等式两边同时加减一个数,同时乘除一个不为0的数,等式依然成立,根据此性质判断即可. 【详解】A. x=y 两边同时加3,可得到x+3=y+3,故A 选项正确;B. -2x=-2y 两边同时除以-2,可得到x=y ,故B 选项正确;C. 等式x ym m=中,m ≠0,两边同时乘以m 得x y =,故C 选项正确; D. 当m=0时,x y =两边同除以m 无意义,则x ym m=不成立,故D 选项错误;故选:D . 【点睛】本题考查等式的变形,熟记等式的基本性质是解题的关键.11.B解析:B 【解析】 【分析】由题意直接根据互补两角之和为180°求解即可. 【详解】解:∵∠A=105°,∴∠A 的补角=180°-105°=75°. 故选:B . 【点睛】本题考查补角的知识,属于基础题,掌握互补两角之和为180°是关键.12.D解析:D 【解析】 【分析】根据非负数的性质可求得a ,b 的值,然后代入即可得出答案.【详解】解:因为2|2|(1)0a b ++-=,所以a +2=0,b -1=0,所以a =-2,b =1,所以()2020a b +=(-2+1)2020=(-1)2020=1.故选:D.【点睛】本题主要考查了非负数的性质——绝对值和偶次方,根据几个非负数的和为零,则这几个数均为零求出a ,b 的值是解决此题的关键. 二、填空题13.2【解析】解:mx2+5y2﹣2x2+3=(m ﹣2)x2+5y2+3,∵代数式mx2+5y2﹣2x2+3的值与字母x 的取值无关,则m ﹣2=0,解得m=2.故答案为2.点睛:本题主要考查合并同类解析:2【解析】解:mx 2+5y 2﹣2x 2+3=(m ﹣2)x 2+5y 2+3,∵代数式mx 2+5y 2﹣2x 2+3的值与字母x 的取值无关,则m ﹣2=0,解得m =2.故答案为2.点睛:本题主要考查合并同类项的法则.即系数相加作为系数,字母和字母的指数不变.与字母x 的取值无关,即含字母x 的系数为0.14.【解析】【分析】由前三个正方形可知:右上和右下两个数的和等于中间的数,根据这一个规律即可得出m 的值;首先求得第n 个的最小数为1+4(n-1)=4n-3,其它三个分别为4n-2,4n-1,4n ,解析:83n -【解析】【分析】由前三个正方形可知:右上和右下两个数的和等于中间的数,根据这一个规律即可得出m 的值;首先求得第n 个的最小数为1+4(n-1)=4n-3,其它三个分别为4n-2,4n-1,4n ,由以上规律即可求解.【详解】解:由题知:右上和右下两个数的和等于中间的数,∴第4个正方形中间的数字m=14+15=29;∵第n个的最小数为1+4(n-1)=4n-3,其它三个分别为4n-2,4n-1,4n,∴第n个正方形的中间数字:4n-2+4n-1=8n-3.故答案为:29;8n-3【点睛】本题主要考查的是图形的变化规律,通过观察、分析、归纳发现数字之间的运算规律是解题的关键.15.5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数,然后用总人数乘以不合格所占的百分比即可.【详解】解:∵学生总人数=25÷50%=50(人),∴不合格的学生人数=50×(1-5解析:5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数,然后用总人数乘以不合格所占的百分比即可.【详解】解:∵学生总人数=25÷50%=50(人),∴不合格的学生人数=50×(1-50%-40%)=5(人),故答案为:5.【点睛】本题考查了扇形统计图,熟知扇形统计图中各数据所表示的意义是解题关键.16.x(x﹣y)(x+y).【解析】【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方式或平方差式,若是就考虑用公式法继续分解因解析:x(x﹣y)(x+y).【解析】【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方式或平方差式,若是就考虑用公式法继续分解因式.【详解】x3﹣xy2=x(x2﹣y2)=x(x﹣y)(x+y),故答案为x(x﹣y)(x+y).17.-5【解析】【分析】根据题意确定出a的最大值,b的最小值,即可求出所求.【详解】解:,,,,则原式,故答案为【点睛】本题考查估算无理数的大小,熟练掌握估算的方法是解本题的关键.解析:-5【解析】【分析】根据题意确定出a的最大值,b的最小值,即可求出所求.【详解】<<,解:459∴<<,23=,∴=,b3a2=-=-,则原式495-故答案为5【点睛】本题考查估算无理数的大小,熟练掌握估算的方法是解本题的关键.18.52; 25; 12.【解析】【分析】将高级单位化为低级单位时,乘60,用0.42乘60,可得:0.42°=25.2′;用0.2乘60,可得:0.2′=12′′;据此求解即解析:52; 25; 12.【解析】【分析】将高级单位化为低级单位时,乘60,用0.42乘60,可得:0.42°=25.2′;用0.2乘60,可得:0.2′=12′′;据此求解即可.【详解】52.42°=52°25′12″.故答案为52、25、12.【点睛】此题主要考查了度分秒的换算,要熟练掌握,解答此题的关键是要明确:1度=60分,即1°=60′,1分=60秒,即1′=60″.19.3(x﹣2)=2x+9【解析】【分析】根据每三人乘一车,最终剩余2辆车,每2人共乘一车,最终剩余9个人无车可乘,进而表示出总人数得出等式即可.【详解】设有x辆车,则可列方程:3(x﹣2)解析:3(x﹣2)=2x+9【解析】【分析】根据每三人乘一车,最终剩余2辆车,每2人共乘一车,最终剩余9个人无车可乘,进而表示出总人数得出等式即可.【详解】设有x辆车,则可列方程:3(x﹣2)=2x+9.故答案是:3(x﹣2)=2x+9.【点睛】本题考查一元一次方程,解题的关键是读懂题意,掌握列一元一次方程.20.2【解析】【分析】直接利用有理数的加法运算法则得出符合题意的答案.【详解】解:如图所示:x的值为2.故答案为:2.【点睛】此题主要考查了有理数的加法,正确掌握相关运算法则是解题关键解析:2【解析】【分析】直接利用有理数的加法运算法则得出符合题意的答案.解:如图所示:x的值为2.故答案为:2.【点睛】此题主要考查了有理数的加法,正确掌握相关运算法则是解题关键.21.﹣1【解析】【分析】利用相反数的性质列出方程,求出方程的解即可得到a的值.【详解】根据题意得:去分母得:a+2+2a+1=0,移项合并得:3a=﹣3,解得:a=﹣1,故答案为:解析:﹣1【解析】【分析】利用相反数的性质列出方程,求出方程的解即可得到a的值.【详解】根据题意得:a2a110 22+++=去分母得:a+2+2a+1=0,移项合并得:3a=﹣3,解得:a=﹣1,故答案为:﹣1【点睛】本题考查了解一元一次方程的应用、解一元一次方程,掌握解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1,是解题的关键,此外还需注意移项要变号.22.2【解析】根据相反数的定义即可求解.【详解】-2的相反数是2,故填:2.【点睛】此题主要考查相反数,解题的关键是熟知相反数的定义.解析:2【解析】【分析】根据相反数的定义即可求解.【详解】-2的相反数是2,故填:2.【点睛】此题主要考查相反数,解题的关键是熟知相反数的定义.23.【解析】【分析】由题意直接根据角的度分秒的计算法则进行运算即可.【详解】解:=3°36′.故答案为:3; 36.【点睛】本题考查角的度分秒的运算,熟练掌握角的度分秒的解析:336【解析】【分析】由题意直接根据角的度分秒的计算法则进行运算即可.【详解】=︒+︒=︒+⨯=3°36′.解:3.630.63(0.660)'故答案为:3; 36.【点睛】本题考查角的度分秒的运算,熟练掌握角的度分秒的计算法则知道度分秒间的进率为60进行分析运算.24.2【解析】根据定义可得:因为,所以,故答案为:2.【解析】根据定义可得:因为239=,所以3log 92=,故答案为:2.三、解答题25.(1)10,20.5,(2)需付车费65元;(3)行驶的里程为13公里【解析】【分析】(1)根据计价规则,列式计算,即可得到答案,(2)根据计价规则,列式计算,即可得到答案,(3)若行驶的里程为10公里,计算所需要付的车费,得出行驶的里程大于10公里,设行驶的里程为x 公里,根据计价规则,列出关于x 的一元一次方程,解之即可.【详解】解:(1)根据题意得:2.5×2+0.45×8=7.6<10,即小红早上7:00从家出发乘坐滴滴快车到学校,行驶里程2公里,用时8分钟,需付车费10元,2.3×5+0.3×20+0.3×(20﹣10)=11.5+6+3=20.5(元),即傍晚17:00放学乘坐滴滴快车到妈妈单位,行驶里程5公里,用时20分钟,需付车费20.5元,故答案为:10,20.5,(2)20×2.4+40×0.35+(20﹣10)×0.3=48+14+3=65(元),答:需付车费65元,(3)若行驶的里程为10公里,需要付车费:2.3×10+0.3×30=29<39.8,即行驶的里程大于10公里,设行驶的里程为x 公里,根据题意得:2.3x+0.3×30+0.3(x ﹣10)=39.8,解得:x =13,答:行驶的里程为13公里.【点睛】本题考查了一元一次方程的应用和有理数的混合运算,解题的关键:(1)正确掌握有理数的混合运算法则,(2)正确掌握有理数的混合运算法则,(3)正确找出等量关系,列出一元一次方程.26.(1)64°18′,154°18′;(2)∠MON=2β+a;(3)150 11分【解析】【分析】(1)依据余角和补角的定义即可求出∠AOB的余角和补角;(2)依据角平分线的定义表示出∠AOM=∠BOM=12∠AOB=12α,∠CON=∠BON=12∠COB=12β,最后再依据∠MON与这些角的关系求解即可;(3)当OA⊥OB时面积最大,此时∠AOB=90°,根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.【详解】解:(1)∵∠AOB=25°42',∴∠AOB的余角=90°﹣25°42'=64°18′,∠AOB的补角=180°﹣25°42'=154°18′;故答案为:64°18′,154°18′;(2)①如图1:∵∠AOB=α,∠BOC=β∴∠AOC=∠AOB+∠BOC=90°+30°=120°∵OM平分∠AOB,ON平分∠BOC,∴∠AOM=∠BOM=12∠AOB=12α,∠CON=∠BON=12∠COB=12β,∴∠MON=∠BOM+∠CON=2β+a;②如图2,∠MON =∠BOM ﹣∠BON =a 2β-; ③如图3,∠MON =∠BON ﹣∠BOM =2βα-. ∴∠MON 为2β+a 或a 2β-或2βα-. (3)当OA ⊥OB 时,△AOB 的面积第一次达到最大值,此时∠AOB =90°,设经过x 分钟后,△AOB 的面积第一次达到最大值,根据题意得:6x+25﹣60x ×30=90, 解得x =15011. 【点睛】 此题考查了是角平分线的定义、角的和差、余角和补角的定义、三角形的面积以及角的计算以及钟面角,熟练掌握相关知识是解题的关键,解题时注意:分针60分钟转一圈,每分钟转动的角度为:360°÷60=6°;时针12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.27.(1)作图见解析;(2)作图见解析,理由:两点之间,线段最短.【解析】【分析】(1)根据直线的意义,画出直线AB即可.(2)根据两点之间线段最短,连接CD,与直线AB的交点即为所求.【详解】(1)直线AB为所求.(2)画线段CD交直线AB于点P,则点P为所求.理由:两点之间,线段最短.【点睛】本题考查了直线的画法和线段公理即两点之间线段最短,解决本题的关键是正确理解题意,熟练掌握线段公理.28.(1)9;(2)-6.5;(3)-6.【解析】【分析】(1)根据数轴上两点间的距离公式解决即可;(2)根据中点的性质,计算即可;(3)设AB'为x,根据题AB'与B'C的关系,将B'C用x表示出来,然后根据AC、AB、BC的关系,将AB用x表示出来,计算出x的值,即可求出AC的值,然后根据点A的坐标求出点C在数轴上的对应的数即可.【详解】(1)AB的长度为2(11)9---=.(2)M是线段AB的中点,所以M点在数轴上对应的点为2(11)6.52-+-=-.(3)设AB'=x,∵AB'=15B'C,则B'C=5x.∴由题意BC=B'C=5x,∴AC=B'C-AB'=4x,∴AB=AC+BC=AC+B'C=9x,即99x=,∴1x=,∴AC=4,又∵点A表示的数为-2,∴-2-4=-6,∴点C表示的数为-6.【点睛】本题考查了数轴上两点间的距离,中点的性质,线段折叠问题,解决本题的关键是正确理解题意,熟练掌握中点的性质,能够根据线段折叠找到线段之间的内在关系.29.(1)两车行驶3小时相遇;(2)行驶22.5小时快车追上慢车;(3)慢车行驶163 60小时两车相遇.【解析】【分析】(1)设两车行驶t1小时相遇,根据相遇时两车行驶路程之和为450km建立方程求解;(2)设t2小时快车追上慢车,快车比慢车多行驶450km建立方程求解;(3)设慢车行驶t3小时两车相遇,根据两车行驶路程之和为450km建立方程求解.【详解】解:(1)设两车行驶t1小时相遇,依题意得65t1+85t1=450解得:t1=3因此,那么两车行驶3小时相遇.(2)设t2小时快车追上慢车,依题意得 85t2-65t2=450解得:t2=22.5因此,行驶22.5小时快车追上慢车(3)设慢车行驶t3小时两车相遇,依题意得30分钟=0.5小时85×0.5+85t3+65t3=450解得:t3=163 60因此,慢车行驶16360小时两车相遇.【点睛】本题考查了一元一次方程的应用,熟练掌握行程问题中的等量关系是解题的关键.30.(1)8ab+3;(2)11【解析】【分析】(1)把A与B代入A﹣3B中,然后进行化简即可;(2)根据倒数的性质可得ab=1,然后代入计算即可.【详解】解:(1)∵A=3a2+5ab+3,B=a2﹣ab,∴A﹣3B=3a2+5ab+3﹣3a2+3ab=8ab+3;(2)由a,b互为倒数,得到ab=1,则A ﹣3B =8+3=11.【点睛】本题考查了整式的化简求值,灵活运用四则运算法则是解答本题的关键.四、压轴题31.(1)④;(2)①15α=︒;②当105α=,125α=时,存在2BOC AOD ∠=∠.【解析】【分析】(1)根据一副三角板中的特殊角,运用角的和与差的计算,只要是15°的倍数的角都可以画出来;(2)①根据已知条件得到∠EOD=180°-∠COD=180°-60°=120°,根据角平分线的定义得到∠EOB=12∠EOD=12×120°=60°,于是得到结论; ②当OA 在OD 的左侧时,当OA 在OD 的右侧时,根据角的和差列方程即可得到结论.【详解】解:(1)∵135°=90°+45°,120°=90°+30°,75°=30°+45°,∴只有25°不能写成90°、60°、45°、30°的和或差,故画不出;故选④;(2)①因为COD 60∠=,所以EOD 180COD 18060120∠∠=-=-=.因为OB 平分EOD ∠, 所以11EOB EOD 1206022∠∠==⨯=. 因为AOB 45∠=,所以αEOB AOB 604515∠∠=-=-=.②当OA 在OD 左侧时,则AOD 120α∠=-,BOC 135α∠=-.因为BOC 2AOD ∠∠=,所以()135α2120α-=-.解得α105=.当OA 在OD 右侧时,则AOD α120∠=-,BOC 135α∠=-.因为BOC 2AOD ∠∠=,所以()135α2α120-=-. 解得α125=.综合知,当α105=,α125=时,存在BOC 2AOD ∠∠=.【点睛】本题考查角的计算,角平分线的定义,正确的理解题意并分类讨论是解题关键.32.(1)-14,8-4t(2)点P运动11秒时追上点Q(3)103或4(4)线段MN的长度不发生变化,都等于11【解析】【分析】(1)根据AB长度即可求得BO长度,根据t即可求得AP长度,即可解题;(2)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可;(3)分①点P、Q相遇之前,②点P、Q相遇之后,根据P、Q之间的距离恰好等于2列出方程求解即可;(4)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.【详解】(1)∵点A表示的数为8,B在A点左边,AB=22,∴点B表示的数是8-22=-14,∵动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,∴点P表示的数是8-4t.故答案为-14,8-4t;(2)设点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,∵AC-BC=AB,∴4x-2x=22,解得:x=11,∴点P运动11秒时追上点Q;(3) ①点P、Q相遇之前,4t+2+2t =22,t=103,②点P、Q相遇之后,4t+2t -2=22,t=4,故答案为103或4(4)线段MN的长度不发生变化,都等于11;理由如下:①当点P在点A、B两点之间运动时:MN=MP+NP=12AP+12BP=12(AP+BP)=12AB=12×22=11②当点P运动到点B的左侧时:。
2019-2020学年保定市七年级(上)期末数学试卷(含答案)

2019-2020学年保定市七年级(上)期末数学试卷一、选择题(本题共12个小题,每小题3分,共36分)1.(3分)在﹣1,0,﹣2,1这四个数中,最小的数是()A.﹣2 B.﹣1 C.0 D.12.(3分)用四舍五入法将0.0257精确到0.001结果是()A.0.03 B.0.026 C.0.025 D.0.02573.(3分)下列计算正确的是()A.7a+a=7a2B.5y﹣3y=2C.3x2y﹣2yx2=x2y D.3a+2b=5ab4.(3分)如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于()A.49°07′B.54°53′C.55°53′D.53°7′5.(3分)将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是()A.B.C.D.6.(3分)如果2x与x﹣3的值互为相反数,那么x等于()A.﹣1 B.1 C.﹣3 D.37.(3分)如图,C、D是线段AB上的两点,且D是线段AC的中点.若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm8.(3分)如图,下列说法中错误的是()A.OA的方向是东北方向B.OB的方向是北偏西30°C.OC的方向是南偏西60°D.OD的方向是南偏东30°9.(3分)在解方程时,去分母正确的是()A.3(x﹣1)﹣2(2x+3)=6 B.3(x﹣1)﹣2(2x+3)=1 C.2(x﹣1)﹣2(2x+3)=6 D.3(x﹣1)﹣2(2x+3)=310.(3分)一个长方形的一边长为2a+3b,另一边长为a+b,则这个长方形的周长是()A.12a+16b B.6a+8b C.3a+4b D.2a2+5ab+3b211.(3分)已知关于x的方程2x+2m=5的解是x=﹣2,则m的值为()A.B.﹣ C.D.﹣12.(3分)某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108 B.54﹣x=20%(108+x)C.54+x=20%×162 D.108﹣x=20%(54+x)二、填空题(本大题共6个小题,每小题3分,共18分)13.(3分)比较大小:.14.(3分)如图是某几何体的展开图,那么这个几何体是.15.(3分)据测算,我国一年因土地沙漠化造成的经济损失约为54 750 000 000元,用科学记数法表示这一数据为元.16.(3分)一个角的余角比它的补角的一半还少20°,则这个角为.17.(3分)如果方程2x+1=3的解也是关于x的方程2﹣=0的解,那么k的值为.18.(3分)如图,对于大于或等于2的自然数n的平方进行如下“分裂”,分裂成n个连续奇数的和,则自然数92的分裂数中最大的数是.三、解答下列各题(本题有8个小题,共66分)19.(8分)计算:(1)﹣66×4+(﹣2.5)÷(﹣0.1)(2)(﹣2)3+(﹣3)×[(﹣4)2+2]+(﹣3)2÷(﹣2)20.(8分)先化简再求值(1)﹣9y+6x2+3(y﹣x2),其中x=2,y=﹣1.(2)2a2b﹣[2a2+2(a2b+2a2)],其中a=,b=1.21.(8分)解下列方程:(1)3(x﹣2)=x﹣(7﹣8x);(2)=2﹣.22.(6分)将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?23.(8分)已知:A﹣2B=7a2﹣7ab,且B=﹣4a2+6ab+7.(1)求A等于多少?(2)若|a+1|+(b﹣2)2=0,求A的值.24.(8分)已知数轴上两点A、B对应的数分别是6,﹣8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N 从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?25.(10分)已知∠AOB=60°,从点O引射线OC,使∠AOC=40°,作∠AOC的角平分线OD,(1)依题意画出图形;(2)求∠BOD的度数.26.(10分)延庆区某中学七年级(1)(2)两个班共104人,要去延庆地质博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如图:其中(1)班不足50人,经估算,如果两个班都以班为单位购票,一共应付1240元.(1)两个班各有多少学生?(2)如果两个班联合起来,作为一个团体购票,可以省多少钱?(3)如果七年级(1)班单独组织去博物馆参观,你认为如何购票最省钱?2019-2020学年保定市七年级(上)期末数学试卷参考答案与试题解析一、选择题(本题共12个小题,每小题3分,共36分)1.(3分)(2019秋•定州市期末)在﹣1,0,﹣2,1这四个数中,最小的数是()A.﹣2 B.﹣1 C.0 D.1【分析】根据正数大于0,0大于负数,正数大于负数直接进行比较大小,再找出最小的数.【解答】解:∵﹣2<﹣1<0<1,∴最小的数是﹣2.故选A.【点评】此题主要考查了有理数的比较大小,根据正数都大于0,负数都小于0,正数大于负数,两个负数绝对值大的反而小的原则解答.2.(3分)(2019秋•定州市期末)用四舍五入法将0.0257精确到0.001结果是()A.0.03 B.0.026 C.0.025 D.0.0257【分析】把万分位上的数字7进行四舍五入即可求解.【解答】解:0.0257≈0.026(精确到0.001).故选B.【点评】本题考查了近似数和有效数字:经过四舍五入得到的数为近似数;从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.3.(3分)(2019秋•曹县期末)下列计算正确的是()A.7a+a=7a2B.5y﹣3y=2C.3x2y﹣2yx2=x2y D.3a+2b=5ab【分析】根据合并同类项得法则依次判断即可.【解答】解:A、7a+a=8a,故本选项错误;B、5y﹣3y=2y,故本选项错误;C、3x2y﹣2yx2=x2y,故本选项正确;D、3a+2b=5ab,不是同类项,不能合并,故本选项错误;故选C.【点评】本题主要考查了合并同类项的法则,熟练掌握运算法则是解题的关键.4.(3分)(2019秋•定州市期末)如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于()A.49°07′B.54°53′C.55°53′D.53°7′【分析】根据∠AMC=52°48′,∠BMD=72°19°和∠CMD=180°﹣∠AMC﹣∠BMD,代入计算即可.【解答】解:∵∠AMC=52°48′,∠BMD=72°19°,∴∠CMD=180°﹣∠AMC﹣∠BMD=180°﹣52°48′﹣72°19°=54°53′;故选B.【点评】此题考查了角的计算,掌握平角的定义是本题的关键,是一道基础题.5.(3分)(2016•淮安校级二模)将一副三角板按如图所示位置摆放,其中∠α与∠β一定互余的是()A.B.C.D.【分析】根据图形,结合互余的定义判断即可.【解答】解:A、∠α与∠β不互余,故本选项错误;B、∠α与∠β不互余,故本选项错误;C、∠α与∠β互余,故本选项正确;D、∠α与∠β不互余,∠α和∠β互补,故本选项错误;故选C.【点评】本题考查了对余角和补角的应用,主要考查学生的观察图形的能力和理解能力.6.(3分)(2019秋•定州市期末)如果2x与x﹣3的值互为相反数,那么x等于()A.﹣1 B.1 C.﹣3 D.3【分析】根据题意得2x+x﹣3=0,然后解出x的值即可.【解答】解:∵2x与x﹣3的值互为相反数,∴2x+x﹣3=0,∴x=1.故选B.【点评】本题考查了解一元一次方程,相反数,解题的关键是明确两数互为相反数,它们的和为0.7.(3分)(2019秋•临城县期末)如图,C、D是线段AB上的两点,且D是线段AC的中点.若AB=10cm,BC=4cm,则AD的长为()A.2cm B.3cm C.4cm D.6cm【分析】利用已知得出AC的长,再利用中点的性质得出AD的长.【解答】解:∵AB=10cm,BC=4cm,∴AC=6cm,∵D是线段AC的中点,∴AD=3cm.故选:B.【点评】此题主要考查了两点间的距离,得出AC的长是解题关键.8.(3分)(2019秋•海拉尔区期末)如图,下列说法中错误的是()A.OA的方向是东北方向B.OB的方向是北偏西30°C.OC的方向是南偏西60°D.OD的方向是南偏东30°【分析】用方位角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方位角时,一般先叙述北或南,再叙述偏东或偏西,偏多少度(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南).依此判断即可.【解答】解:A、OA的方向是北偏东45度即东北方向,故正确;B、OB的方向是北偏西60°,故错误;C、OC的方向是南偏西60°,故正确;D、OD的方向是南偏东30°,故正确.故选B.【点评】此题主要考查了方向角的定义及表示方法,正确掌握方向角的定义是解题关键.9.(3分)(2019秋•定州市期末)在解方程时,去分母正确的是()A.3(x﹣1)﹣2(2x+3)=6 B.3(x﹣1)﹣2(2x+3)=1 C.2(x﹣1)﹣2(2x+3)=6 D.3(x﹣1)﹣2(2x+3)=3【分析】去分母的方法是:方程左右两边同时乘以各分母的最小公倍数,这一过程的依据是等式的基本性质,注意去分母时分数线起到括号的作用,容易出现的错误是:漏乘没有分母的项,以及去分母后忘记分数线的括号的作用,符号出现错误.【解答】解:方程左右两边同时乘以6得:3(x﹣1)﹣2(2x+3)=6.故选A.【点评】在去分母的过程中注意分数线起到括号的作用,并注意不能漏乘没有分母的项;注意只是去分母而不是解方程.10.(3分)(2019秋•定州市期末)一个长方形的一边长为2a+3b,另一边长为a+b,则这个长方形的周长是()A.12a+16b B.6a+8b C.3a+4b D.2a2+5ab+3b2【分析】根据题意列出关系式,去括号合并即可得到结果.【解答】解:根据题意得:2(2a+3b+a+b)=2(3a+4b)=6a+8b,故选B【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.11.(3分)(2019秋•定州市期末)已知关于x的方程2x+2m=5的解是x=﹣2,则m的值为()A.B.﹣ C.D.﹣【分析】把x=﹣2代入方程计算即可求出m的值.【解答】解:把x=﹣2代入方程得:﹣4+2m=5,解得:m=.故选C.【点评】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.12.(3分)(2015•杭州)某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程()A.54﹣x=20%×108 B.54﹣x=20%(108+x)C.54+x=20%×162 D.108﹣x=20%(54+x)【分析】设把x公顷旱地改为林地,根据旱地面积占林地面积的20%列出方程即可.【解答】解:设把x公顷旱地改为林地,根据题意可得方程:54﹣x=20%(108+x).故选B.【点评】本题考查一元一次方程的应用,关键是设出未知数以以改造后的旱地与林地的关系为等量关系列出方程.二、填空题(本大题共6个小题,每小题3分,共18分)13.(3分)(2019秋•定州市期末)比较大小:<.【分析】先比较出两个数的绝对值,再根据两个负数比较,绝对值大的反而小,即可得出答案.【解答】解:∵>,∴<.故答案为:<.【点评】此题考查了有理数的大小比较,掌握两个负数比较大小的方法即两个负数比较,绝对值大的反而小是本题的关键.14.(3分)(2019秋•定州市期末)如图是某几何体的展开图,那么这个几何体是圆柱.【分析】展开图为两个圆,一个长方形,易得是圆柱的展开图.【解答】解:这个几何体是圆柱,故答案为:圆柱【点评】此题主要考查圆柱的展开图,关键是根据圆柱的展开图为两个圆,一个长方形解答.15.(3分)(2019秋•定州市期末)据测算,我国一年因土地沙漠化造成的经济损失约为54 750 000 000元,用科学记数法表示这一数据为 5.475×1010元.【分析】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.【解答】解:将54 750 000 000用科学记数法表示为:5.475×1010.故答案为:5.475×1010.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.16.(3分)(2019秋•定州市期末)一个角的余角比它的补角的一半还少20°,则这个角为40°.【分析】设这个角为x,根据互为余角的两个角的和等于90°表示出它的余角,互为补角的两个角的和等于180°表示出它的补角,然后列出方程求解即可.【解答】解:设这个角为x,则它的余角为90°﹣x,它的补角为180°﹣x,由题意得,90°﹣x=(180°﹣x)﹣20°,解得x=40°,所以,这个角为40°.故答案为:40°.【点评】本题考查了余角和补角,熟记概念并列出方程是解题的关键.17.(3分)(2019秋•定州市期末)如果方程2x+1=3的解也是关于x的方程2﹣=0的解,那么k的值为7.【分析】解出一元一次方程的解后将其代入分式方程中即可求出k的值.【解答】解:∵2x+1=3,∴x=1,将x=1代入2﹣=0,∴2﹣=0,解得:k=7故答案为:7;【点评】本题考查一元一次方程的解,涉及方程的解的概念.18.(3分)(2019秋•相城区期末)如图,对于大于或等于2的自然数n的平方进行如下“分裂”,分裂成n个连续奇数的和,则自然数92的分裂数中最大的数是17.【分析】仔细观察可发现,前面是几的平方后面分的奇数的个数即为几,则92分出的奇数的个数为9个,找出9个连续的奇数即可得到最大的数的值.【解答】解:根据题意得,92分裂成的8个连续奇数分别为1,3,5,7,9,11,13,15,17,所以最大的数是17,故答案为:17.【点评】此题主要考查学生对规律型题的掌握情况,此题的关键是发现前面是几的平方分裂的奇数的个数即为几个.三、解答下列各题(本题有8个小题,共66分)19.(8分)(2019秋•定州市期末)计算:(1)﹣66×4+(﹣2.5)÷(﹣0.1)(2)(﹣2)3+(﹣3)×[(﹣4)2+2]+(﹣3)2÷(﹣2)【分析】(1)原式先计算乘除运算,再计算加减运算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣264+25=﹣239;(2)原式=﹣8﹣3×18﹣9÷2=﹣8﹣54﹣4.5=﹣66.5.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.20.(8分)(2019秋•定州市期末)先化简再求值(1)﹣9y+6x2+3(y﹣x2),其中x=2,y=﹣1.(2)2a2b﹣[2a2+2(a2b+2a2)],其中a=,b=1.【分析】(1)先去括号,再合并同类项,把已知数据代入化简后的整式,计算即可;(2)先去括号,再合并同类项,得到最简整式,把已知数据代入化简后的整式,计算即可.【解答】解:(1)﹣9y+6x2=﹣9y+6x2+3y﹣2x2=4x2﹣6y当x=2,y=﹣1时,原式=4×22﹣6×(﹣1)=22;(2)2a2b﹣[2a2+2(a2b+2ab2)]=2a2b﹣(2a2+2a2b+4ab2)=2a2b﹣2a2﹣2a2b﹣4ab2=﹣2a2﹣4ab2当a=,b=1时,原式=﹣2×()2﹣4××1=﹣.【点评】本题考查的是整式的加减,掌握去括号法则、合并同类项法则是解题的关键.21.(8分)(2019秋•定州市期末)解下列方程:(1)3(x﹣2)=x﹣(7﹣8x);(2)=2﹣.【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.【解答】解:(1)去括号得:3x﹣6=x﹣7+8x,移项合并得:6x=1,解得:x=;(2)去分母得:9y﹣6=24﹣20y+28,移项合并得:29y=58,解得:y=2.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.22.(6分)(2019秋•定州市期末)将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?【分析】30分=小时,可设甲、乙一起做还需x小时才能完成工作,等量关系为:甲小时的工作量+甲乙合作x小时的工作量=1,把相关数值代入求解即可.【解答】解:设甲、乙一起做还需x小时才能完成工作.根据题意,得×+(+)x=1,解这个方程,得x=,小时=2小时12分,答:甲、乙一起做还需2小时12分才能完成工作.【点评】考查用一元一次方程解决工程问题,得到工作量1的等量关系是解决本题的关键.23.(8分)(2019秋•定州市期末)已知:A﹣2B=7a2﹣7ab,且B=﹣4a2+6ab+7.(1)求A等于多少?(2)若|a+1|+(b﹣2)2=0,求A的值.【分析】(1)将B的代数式代入A﹣2B中化简,即可得出A的式子;(2)根据非负数的性质解出a、b的值,再代入(1)式中计算.【解答】解:(1)∵A﹣2B=A﹣2(﹣4a2+6ab+7)=7a2﹣7ab,∴A=(7a2﹣7ab)+2(﹣4a2+6ab+7)=﹣a2+5ab+14;(2)依题意得:a+1=0,b﹣2=0,a=﹣1,b=2.原式A=﹣(﹣1)2+5×(﹣1)×2+14=3.【点评】本题考查了非负数的性质和整式的化简,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.24.(8分)(2019秋•定州市期末)已知数轴上两点A、B对应的数分别是6,﹣8,M、N为数轴上两个动点,点M从A点出发向左运动,速度为每秒2个单位长度,与此同时,点N从B点出发向右运动,速度为M点的3倍,经过多长时间,点M与点N相距50个单位长度?这时点M、N所对应的数分别是多少?【分析】首先设经过x秒点M与点N相距50个单位,根据题意可得等量关系:点M的运动路程+N的运动路程=14=50,根据等量关系列出方程,再解,然后可得x的值,进而可得点M、N所对应的数.【解答】解:设经过x秒点M与点N相距50个单位.依题意可列方程为:2x+6x﹣14=50,解方程,得x=8.2x=16,16﹣6=10,即点M所对应的数是﹣10.6x=48,48﹣8=40,即点N所对应的数是40.答:经过8秒点M与点N相距50个单位,这时点M、N所对应的数分别是﹣10,40.【点评】此题主要考查了数轴,以及一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.25.(10分)(2019秋•定州市期末)已知∠AOB=60°,从点O引射线OC,使∠AOC=40°,作∠AOC的角平分线OD,(1)依题意画出图形;(2)求∠BOD的度数.【分析】(1)根据题意画出符合的两种情况;(2)根据角平分线定义求出∠AOD,即可求出答案.【解答】解:(1)分两种情况讨论:当∠AOC在∠AOB的外部时,如图1:;当∠AOC在∠AOB的内部时,如图2:;(2)如图1,∵射线OD平分∠AOC,∴∠AOD=∠AOC=20°,∴∠BOD=∠AOB+∠AOD=80°;如图2,∵射线OD平分∠AOC,∴∠COD=∠AOC=20°,∴∠BOD=∠AOB﹣∠AOC+∠COD=40°.【点评】本题考查了角的有关计算和角平分线定义的应用,能画出符合的两个图形是解此题的关键.26.(10分)(2019秋•定州市期末)延庆区某中学七年级(1)(2)两个班共104人,要去延庆地质博物馆进行社会大课堂活动,老师指派小明到网上查阅票价信息,小明查得票价如图:其中(1)班不足50人,经估算,如果两个班都以班为单位购票,一共应付1240元.(1)两个班各有多少学生?(2)如果两个班联合起来,作为一个团体购票,可以省多少钱?(3)如果七年级(1)班单独组织去博物馆参观,你认为如何购票最省钱?【分析】(1)设七年级(1)班x人,则七年级(2)班(104﹣x)人,根据两个班共付费1240元建立方程求出其解就可以;(2)先求出购团体票的费用,再用1240元﹣团体票的费用就是节约的钱;(3)先可以计算按照实际人数购票的费用,再计算购买51个人的票的费用,比较两个费用的大小就可以得出结论.【解答】解:(1)设七年级(1)班x人,则七年级(2)班(104﹣x)人,由题意可得:13x+11(104﹣x)=1240,解得x=48,则104﹣x=56.答:七年级(1)班48人,七年级(2)班56人;(2)1240﹣104×9=304(元);(3)七年级(1)班按照实际人数购票的费用为:48×13=624元,购51张票的费用为:51×11=561元.∵624>561,∴购买51张票划算些.【点评】本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,设计方案的运用,解答时找到等量关系建立方程求出各班人数是关键.。
保定市人教版七年级上册数学期末试卷及答案-百度文库

保定市人教版七年级上册数学期末试卷及答案-百度文库一、选择题1.下列判断正确的是( ) A .3a 2bc 与bca 2不是同类项B .225m n 的系数是2C .单项式﹣x 3yz 的次数是5D .3x 2﹣y +5xy 5是二次三项式2.如图,将线段AB 延长至点C ,使12BC AB =,D 为线段AC 的中点,若BD =2,则线段AB 的长为( )A .4B .6C .8D .123.已知a +b =7,ab =10,则代数式(5ab +4a +7b )+(3a –4ab )的值为( )A .49B .59C .77D .139 4.底面半径为r ,高为h 的圆柱的体积为2r h π,单项式2r h π的系数和次数分别是( ) A .π,3B .π,2C .1,4D .1,3 5.如图是小明制作的一张数字卡片,在此卡片上可以用一个正方形圈出44⨯个位置的16个数(如1,2,3,4,8,9,10,11,15,16,17,18,22,23,24,25).若用这样的正方形圈出这张数字卡片上的16个数,则圈出的16个数的和不可能为下列数中的( )A .208B .480C .496D .592 6.计算32a a ⋅的结果是( ) A .5a ;B .4a ;C .6a ;D .8a .7.下列方程变形正确的是( ) A .方程110.20.5x x --=化成1010101025x x--= B .方程 3﹣x=2﹣5(x ﹣1),去括号,得 3﹣x=2﹣5x ﹣1C .方程 3x ﹣2=2x+1 移项得 3x ﹣2x=1+2D .方程23t=32,未知数系数化为 1,得t=1 8.解方程121123x x +--=时,去分母得( ) A .2(x +1)=3(2x ﹣1)=6 B .3(x +1)﹣2(2x ﹣1)=1 C .3(x +1)﹣2(2x ﹣1)=6D .3(x +1)﹣2×2x ﹣1=69.如图是由下列哪个立体图形展开得到的?( )A .圆柱B .三棱锥C .三棱柱D .四棱柱10.不等式x ﹣2>0在数轴上表示正确的是( ) A . B . C .D .11.如果方程组223x y x y +=⎧⎨-=⎩的解为5x y =⎧⎨=⎩,那么“口”和“△”所表示的数分别是( )A .14,4B .11,1C .9,-1D .6,-4 12.如果代数式﹣3a 2m b 与ab 是同类项,那么m 的值是( )A .0B .1C .12D .313.已知a ﹣b=﹣1,则3b ﹣3a ﹣(a ﹣b )3的值是( ) A .﹣4 B .﹣2C .4D .214.如果韩江的水位升高0.6m 时水位变化记作0.6m +,那么水位下降0.8m 时水位变化记作( ) A .0m B .0.8m C .0.8m - D .0.5m - 15.如果一个有理数的绝对值是6,那么这个数一定是( )A .6B .6-C .6-或6D .无法确定二、填空题16.已知x =3是方程(1)21343x m x -++=的解,则m 的值为_____. 17.如图,线段AB 被点C ,D 分成2:4:7三部分,M ,N 分别是AC ,DB 的中点,若MN=17cm ,则BD=__________cm.18.已知|x |=3,y 2=4,且x <y ,那么x +y 的值是_____.19.将0.09493用四舍五入法取近似值精确到百分位,其结果是_____. 20.已知关于x 的一元一次方程320202020xx n +=+①与关于y 的一元一次方程3232020(32)2020y y n --=--②,若方程①的解为x =2020,那么方程②的解为_____. 21.一个商店把某件商品按进价提高20%作为定价,可是总卖不出去;后来按定价减价20%出售,很快卖掉,结果这次生意亏了4元.那么这件商品的进价是________元. 22.如图,这是一种数值转换机的运算程序,若第一次输入的数为7,则第2018次输出的数是_____;若第一次输入的数为x ,使第2次输出的数也是x ,则x =_____.23.在一样本容量为80的样本中,已知某组数据的频率为0.7,频数为_____.24.学校某兴趣活动小组现有男生30人,女生8人,还要录取女生多少人,才能使女生人数占该活动小组总人数的三分之一?设还要录取女生x 人,依题意列方程得_____. 25.化简:2x+1﹣(x+1)=_____.26.若2a +1与212a +互为相反数,则a =_____. 27.计算:3+2×(﹣4)=_____.28.若代数式x 2+3x ﹣5的值为2,则代数式2x 2+6x ﹣3的值为_____. 29.观察“田”字中各数之间的关系:则c 的值为____________________. 30.材料:一般地,n 个相同因数a 相乘n a a a a⋅⋅⋅个:记为n a . 如328=,此时3叫做以2为底的8的对数,记为2log 8(即2log 83=);如45625=,此时4叫做以5为底的625的对数,记为5log 625(即5log 6254=),那么3log 9=_________.三、压轴题31.已知长方形纸片ABCD ,点E 在边AB 上,点F 、G 在边CD 上,连接EF 、EG .将∠BEG 对折,点B 落在直线EG 上的点B ′处,得折痕EM ;将∠AEF 对折,点A 落在直线EF 上的点A ′处,得折痕EN .(1)如图1,若点F 与点G 重合,求∠MEN 的度数;(2)如图2,若点G 在点F 的右侧,且∠FEG =30°,求∠MEN 的度数; (3)若∠MEN =α,请直接用含α的式子表示∠FEG 的大小. 32.综合试一试(1)下列整数可写成三个非0整数的立方和:45=_____;2=______.(2)对于有理数a ,b ,规定一种运算:2a b a ab ⊗=-.如2121121⊗=-⨯=-,则计算()()532-⊗⊗-=⎡⎤⎣⎦______. (3)a 是不为1的有理数,我们把11a-称为a 的差倒数.如:2的差倒数是1112=--,1-的差倒数是()11112=--.已知12a =,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,……,以此类推,122500a a a ++⋅⋅⋅+=______.(4)10位裁判给一位运动员打分,每个人给的分数都是整数,去掉一个最高分,再去掉一个最低分,其余得分的平均数为该运动员的得分.若用四舍五入取近似值的方法精确到十分位,该运动员得9.4分,如果精确到百分位,该运动员得分应当是_____分. (5)在数1.2.3...2019前添加“+”,“-”并依次计算,所得结果可能的最小非负数是______(6)早上8点钟,甲、乙、丙三人从东往西直行,乙在甲前400米,丙在乙前400米,甲、乙、丙三人速度分别为120米/分钟、100米/分钟、90米/分钟,问:______分钟后甲和乙、丙的距离相等.33.已知:OC 平分AOB ∠,以O 为端点作射线OD ,OE 平分AOD ∠. (1)如图1,射线OD 在AOB ∠内部,BOD 82∠=︒,求COE ∠的度数. (2)若射线OD 绕点O 旋转,BOD α∠=,(α为大于AOB ∠的钝角),COE β∠=,其他条件不变,在这个过程中,探究α与β之间的数量关系是否发生变化,请补全图形并加以说明.34.已知,如图,A、B、C分别为数轴上的三点,A点对应的数为60,B点在A点的左侧,并且与A点的距离为30,C点在B点左侧,C点到A点距离是B点到A点距离的4倍.(1)求出数轴上B点对应的数及AC的距离.(2)点P从A点出发,以3单位/秒的速度向终点C运动,运动时间为t秒.①当P点在AB之间运动时,则BP=.(用含t的代数式表示)②P点自A点向C点运动过程中,何时P,A,B三点中其中一个点是另外两个点的中点?求出相应的时间t.③当P点运动到B点时,另一点Q以5单位/秒的速度从A点出发,也向C点运动,点Q到达C点后立即原速返回到A点,那么Q点在往返过程中与P点相遇几次?直.接.写.出.相遇时P点在数轴上对应的数35.如图,在平面直角坐标系中,点M的坐标为(2,8),点N的坐标为(2,6),将线段MN向右平移4个单位长度得到线段PQ(点P和点Q分别是点M和点N的对应点),连接MP、NQ,点K是线段MP的中点.(1)求点K的坐标;(2)若长方形PMNQ以每秒1个单位长度的速度向正下方运动,(点A、B、C、D、E分别是点M、N、Q、P、K的对应点),当BC与x轴重合时停止运动,连接OA、OE,设运动时间为t秒,请用含t的式子表示三角形OAE的面积S(不要求写出t的取值范围);(3)在(2)的条件下,连接OB、OD,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积?若存在,请求出t值;若不存在,请说明理由.36.射线OA、OB、OC、OD、OE有公共端点O.(1)若OA与OE在同一直线上(如图1),试写出图中小于平角的角;(2)若∠AOC=108°,∠COE=n°(0<n<72),OB平分∠AOE,OD平分∠COE(如图2),求∠BOD的度数;(3)如图3,若∠AOE=88°,∠BOD=30°,射OC绕点O在∠AOD内部旋转(不与OA、OD重合).探求:射线OC从OA转到OD的过程中,图中所有锐角的和的情况,并说明理由.37.从特殊到一般,类比等数学思想方法,在数学探究性学习中经常用到,如下是一个具体案例,请完善整个探究过程。
保定市七年级数学上册期末测试卷及答案

保定市七年级数学上册期末测试卷及答案一、选择题1.地球与月球的平均距离为384 000km ,将384 000这个数用科学记数法表示为( ) A .3.84×103B .3.84×104C .3.84×105D .3.84×1062.﹣3的相反数是( ) A .13-B .13C .3-D .33.如图是小明制作的一张数字卡片,在此卡片上可以用一个正方形圈出44⨯个位置的16个数(如1,2,3,4,8,9,10,11,15,16,17,18,22,23,24,25).若用这样的正方形圈出这张数字卡片上的16个数,则圈出的16个数的和不可能为下列数中的( )A .208B .480C .496D .5924.已知线段AB a ,,,C D E 分别是,,AB BC AD 的中点,分别以点,,C D E 为圆心,,,CB DB EA 为半径作圆得如图所示的图案,则图中三个阴影部分图形的周长之和为( )A .9a πB .8a πC .98a πD .94a π5.下列因式分解正确的是() A .21(1)(1)xx x +=+-B .()am an a m n +=-C .2244(2)m m m +-=-D .22(2)(1)a a a a --=-+6.已知关于x 的方程ax ﹣2=x 的解为x =﹣1,则a 的值为( ) A .1B .﹣1C .3D .﹣37.以下调查方式比较合理的是( )A .为了解一沓钞票中有没有假钞,采用抽样调查的方式B .为了解全区七年级学生节约用水的情况,采用抽样调查的方式C .为了解某省中学生爱好足球的情况,采用普查的方式D .为了解某市市民每天丢弃塑料袋数量的情况,采用普查的方式 8.下列各数中,绝对值最大的是( ) A .2B .﹣1C .0D .﹣39.下列式子中,是一元一次方程的是( ) A .3x+1=4x B .x+2>1 C .x 2-9=0 D .2x -3y=010.若OC 是∠AOB 内部的一条射线,则下列式子中,不能表示“OC 是∠AOB 的平分线”的是( ) A .∠AOC=∠BOC B .∠AOB=2∠BOC C .∠AOC=12∠AOB D .∠AOC+∠BOC=∠AOB11.当x=3,y=2时,代数式23x y的值是( ) A .43B .2C .0D .312.用代数式表示“a 的3倍与b 的差的平方”,正确的是( ) A .3(a ﹣b )2B .(3a ﹣b )2C .3a ﹣b 2D .(a ﹣3b )213.有理数a 、b 在数轴上的位置如图所示,则下列结论中正确的是( )A .a+b >0B .ab >0C .a ﹣b <oD .a÷b >014.如图,将长方形ABCD 绕CD 边旋转一周,得到的几何体是( )A .棱柱B .圆锥C .圆柱D .棱锥15.阅读:关于x 方程ax=b 在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x=ba;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x 的方程 3x •a= 2x ﹣ 16(x ﹣6)无解,则a 的值是( ) A .1 B .﹣1 C .±1 D .a≠1二、填空题16.将一根木条固定在墙上只用了两个钉子,这样做的依据是_______________. 17.若x =2是关于x 的方程5x +a =3(x +3)的解,则a 的值是_____.18.如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是_____.19.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m 为________,第n 个正方形的中间数字为______.(用含n 的代数式表示)…………20.根据下列图示的对话,则代数式2a +2b ﹣3c +2m 的值是_____.21.把5,5,35按从小到大的顺序排列为______.22.单项式22ab -的系数是________.23.9的算术平方根是________24.将一个含有30°角的直角三角板如图所示放置.其中,含30°角的顶点落在直线a 上,含90°角的顶点落在直线b 上.若//221a b ∠=∠,;,则1∠=__________°.25.若a a -=,则a 应满足的条件为______. 26.若a 、b 是互为倒数,则2ab ﹣5=_____.27.如图,已知OC 是∠AOB 内部的一条射线,∠AOC =30°,OE 是∠COB 的平分线.当∠BOE =40°时,则∠AOB 的度数是_____.28.下列是由一些火柴搭成的图案:图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第n 个图案用_____根火柴棒.29.当x= 时,多项式3(2-x )和2(3+x )的值相等.30.已知线段AB=8cm ,在直线AB 上画线段BC ,使它等于3cm ,则线段AC=______cm .三、压轴题31.已知120AOB ∠︒= (本题中的角均大于0︒且小于180︒)(1)如图1,在AOB ∠内部作COD ∠,若160AOD BOC ∠∠︒+=,求COD 的度数;(2)如图2,在AOB ∠内部作COD ∠,OE 在AOD ∠内,OF 在BOC ∠内,且3DOE AOE ∠∠=,3COF BOF ∠=∠,72EOF COD ∠=∠,求EOF ∠的度数;(3)射线OI 从OA 的位置出发绕点O 顺时针以每秒6︒的速度旋转,时间为t 秒(050t <<且30t ≠).射线OM 平分AOI ∠,射线ON 平分BOI ∠,射线OP 平分MON ∠.若3MOI POI ∠=∠,则t = 秒.32.如图,已知数轴上点A 表示的数为8,B 是数轴上位于点A 左侧一点,且AB =22,动点P 从A 点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t >0)秒.(1)出数轴上点B 表示的数 ;点P 表示的数 (用含t 的代数式表示) (2)动点Q 从点B 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P 、Q 同时出发,问多少秒时P 、Q 之间的距离恰好等于2?(3)动点Q 从点B 出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P 、Q 同时出发,问点P 运动多少秒时追上点Q ?(4)若M 为AP 的中点,N 为BP 的中点,在点P 运动的过程中,线段MN 的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN 的长.33.已知多项式3x 6﹣2x 2﹣4的常数项为a ,次数为b .(1)设a 与b 分别对应数轴上的点A 、点B ,请直接写出a = ,b = ,并在数轴上确定点A 、点B 的位置;(2)在(1)的条件下,点P 以每秒2个单位长度的速度从点A 向B 运动,运动时间为t 秒:①若PA ﹣PB =6,求t 的值,并写出此时点P 所表示的数;②若点P 从点A 出发,到达点B 后再以相同的速度返回点A ,在返回过程中,求当OP =3时,t 为何值?34.已知,如图,A 、B 、C 分别为数轴上的三点,A 点对应的数为60,B 点在A 点的左侧,并且与A 点的距离为30,C 点在B 点左侧,C 点到A 点距离是B 点到A 点距离的4倍.(1)求出数轴上B 点对应的数及AC 的距离.(2)点P 从A 点出发,以3单位/秒的速度向终点C 运动,运动时间为t 秒. ①当P 点在AB 之间运动时,则BP = .(用含t 的代数式表示)②P 点自A 点向C 点运动过程中,何时P ,A ,B 三点中其中一个点是另外两个点的中点?求出相应的时间t .③当P 点运动到B 点时,另一点Q 以5单位/秒的速度从A 点出发,也向C 点运动,点Q 到达C 点后立即原速返回到A 点,那么Q 点在往返过程中与P 点相遇几次?直.接.写.出.相遇时P 点在数轴上对应的数35.已知∠AOB 和∠AOC 是同一个平面内的两个角,OD 是∠BOC 的平分线. (1)若∠AOB=50°,∠AOC=70°,如图(1),图(2),求∠AOD 的度数;(2)若∠AOB=m 度,∠AOC=n 度,其中090090180m n m n <<,<<,< 且m n <,求∠AOD 的度数(结果用含m n 、的代数式表示),请画出图形,直接写出答案.36.如图,在平面直角坐标系中,点M的坐标为(2,8),点N的坐标为(2,6),将线段MN向右平移4个单位长度得到线段PQ(点P和点Q分别是点M和点N的对应点),连接MP、NQ,点K是线段MP的中点.(1)求点K的坐标;(2)若长方形PMNQ以每秒1个单位长度的速度向正下方运动,(点A、B、C、D、E分别是点M、N、Q、P、K的对应点),当BC与x轴重合时停止运动,连接OA、OE,设运动时间为t秒,请用含t的式子表示三角形OAE的面积S(不要求写出t的取值范围);(3)在(2)的条件下,连接OB、OD,问是否存在某一时刻t,使三角形OBD的面积等于三角形OAE的面积?若存在,请求出t值;若不存在,请说明理由.37.数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如:如图①,若点A,B在数轴上分别对应的数为a,b(a<b),则AB的长度可以表示为AB=b-a.请你用以上知识解决问题:如图②,一个点从数轴上的原点开始,先向左移动2个单位长度到达A点,再向右移动3个单位长度到达B点,然后向右移动5个单位长度到达C点.(1)请你在图②的数轴上表示出A,B,C三点的位置.(2)若点A以每秒1个单位长度的速度向左移动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动,设移动时间为t秒.①当t=2时,求AB和AC的长度;②试探究:在移动过程中,3AC-4AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.38.如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BO N= ;(直接写出结果)(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】试题分析:384 000=3.84×105.故选C.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.2.D解析:D【解析】【分析】相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.【详解】根据相反数的定义可得:-3的相反数是3.故选D. 【点睛】本题考查相反数,题目简单,熟记定义是关键.3.C解析:C 【解析】 【分析】由题意设第一列第一行的数为x ,依次表示每个数,并相加进行分析得出选项. 【详解】解:设第一列第一行的数为x ,第一行四个数分别为,1,2,3x x x x +++, 第二行四个数分别为7,8,9,10x x x x ++++, 第三行四个数分别为14,15,16,17x x x x ++++, 第四行四个数分别为21,22,23,24x x x x ++++,16个数相加得到16192x +,当相加数为208时x 为1,当相加数为480时x 为18,相加数为496时x 为19,相加数为592时x 为25,由数字卡片可知,x 为19时,不满足条件. 故选C. 【点睛】本题考查列代数式求解问题,理解题意设未知数并列出方程进行分析即可.4.D解析:D 【解析】 【分析】根据中点的定义及线段的和差关系可用a 表示出AC 、BD 、AD 的长,根据三个阴影部分图形的周长之和等于三个圆的周长之和即可得答案. 【详解】∵AB a ,C 、D 分别是AB 、BC 的中点, ∴AC=BC=12AB=12a ,BD=CD=12BC=14a , ∴AD=AC+BD=34a , ∴三个阴影部分图形的周长之和=aπ+12aπ+34aπ=94a π, 故选:D. 【点睛】本题考查线段中点的定义,线段上一点,到线段两端点距离相等的点是线段的中点;正确得出三个阴影部分图形的周长之和等于三个圆的周长之和是解题关键.5.D解析:D【解析】 【分析】分别利用公式法以及提取公因式法对各选项分解因式得出答案. 【详解】解:A 、21x +无法分解因式,故此选项错误; B 、()am an a m n +=+,故此选项错误; C 、244m m +-无法分解因式,故此选项错误; D 、22(2)(1)aa a a --=-+,正确;故选:D . 【点睛】此题主要考查了公式法以及提取公因式法分解因式,正确应用乘法公式是解题关键.6.B解析:B 【解析】 【分析】将1x =-代入2ax x -=,即可求a 的值. 【详解】解:将1x =-代入2ax x -=, 可得21a --=-, 解得1a =-, 故选:B . 【点睛】本题考查一元一次方程的解;熟练掌握一元一次方程的解与方程的关系是解题的关键.7.B解析:B 【解析】 【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现. 【详解】解:A .为了解一沓钞票中有没有假钞,采用全面调查的方式,故不符合题意; B .为了解全区七年级学生节约用水的情况,采用抽样调查的方式,故符合题意; C .为了解某省中学生爱好足球的情况,采用抽样调查的方式,故不符合题意; D .为了解某市市民每天丢弃塑料袋数量的情况,采用抽样调查的方式,故不符合题意; 故选:B . 【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.8.D解析:D【解析】试题分析:∵|2|=2,|﹣1|=1,|0|=0,|﹣3|=3,∴|﹣3|最大,故选D.考点:D.9.A解析:A【解析】A. 3x+1=4x是一元一次方程,故本选项正确;B. x+2>1是一元一次不等式,故本选项错误;C. x2−9=0是一元二次方程,故本选项错误;D. 2x−3y=0是二元一次方程,故本选项错误。
河北省定州市2019-2020学年七年级数学(上)期末试卷

定州2019—2020学年度七年级第一学期期末质量监测数 学本试卷满分为120分,考试时间为90分钟.一、选择题(本大题共12个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.18-的倒数是( )A.18B.18-C.118-D.1182.计算(2)3-⨯的结果是( )A.5-B.6-C.1D.63.下列各式中,运算正确的是( )A.224325a a a +=B.224a a a +=C.651a a -=D.22234a b ba a b -=-4.大量事实证明,环境污染治理刻不容缓,据统计,全球每分钟约有852.1万吨污水排入江河湖海,把852.1万用科学记数法表示为( )A.60.852110⨯B.7852110⨯C.68.52110⨯D.78.52110⨯5.下列说法不正确的是( )A.0是单项式B.单项式235x -的系数是35- C.单项式2a b 的次数为2D.多项式212xy x y -+是三次三项式6.如果2x =是方程25x a =-的解,那么a 的值为( )A.1B.2C.6D.12 7.如图,点C 在线段AB 上,点D 是AC 的中点,如果4CD =,14AB =,那么BC 长度为( )A.6B.5C.4D.6.58.如图所示,下列说法错误的是( )A.OA 的方向是西北方向B.OB 的方向是南偏西60︒C.OC 的方向是南偏东60︒D.OD 的方向是北偏东50︒9.一个两位数,它个位上的数与十位上的数的和等于9,设它个位上的数字为a ,则这个两位数可以表示为( )A.(9)a a -+B.(9)a a -C.10(9)a a +-D.10(9)a a -+10.表示,a b 两数的点在数轴上的位置如图所示,则下列判断不正确的是( )A.0a b +<B.a b a ->C.30b <D.0ab > 11.在如图所示的月历表中,任意框出表中竖列上的三个相邻的数,这三个数的和不可能是( )A.72B.65C.51D.2712.如图所示的运算程序中,若开始输入的x 值为5,则第1次输出的结果为8,第2次输出的结果为4,第3次输出的结果为2,…,第2019次输出的结果为( )A.1B.2C.4D.8二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)13.已知13517A '∠=︒,则A ∠的补角的度数是__________.14.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“我”字所在面相对的面上的汉字是__________.15.若代数式72x -和5x -互为相反数,则x 的值为__________.16.已知2|1|(3)0a b ++-=,则b a =__________.17.已知代数式2x y +的值是6,则代数式361x y ++的值是__________.18.父亲与小强下棋(假设没有平局),父亲胜一盘记2分,小强胜一盘记3分,下了10盘后,两人得分相等,则小强胜的盘数是__________. 三、解答下列各题(本题有8个小题,共66分)19.计算题(1)7(15)2(9)+--⨯-(2)23182(3)427⎛⎫-⨯+-⨯- ⎪⎝⎭20.解方程(1)37322x x +=-;(2)2157123y y ---=21.已知A 、B 是两个多项式,其中236B x x =-+-,A B +的和等于223x --.(1)求多项式A ;(2)当 1.5x =-时,求A 的值.22.一件夹克衫先按成本价提高60%标价,再将标价打7折出售,结果获利36元,这件夹克衫的成本价是多少元?23.把一根木棒MN (8个单位长度)放置在数轴上(M 在N 的左侧),它的两端点M 、N 落在数轴上的点所表示的数分别为m 、n ,木棒MN 的中点A 在数轴上所表示的数为a .(1)若2m =,求n 的值;(2)若3n =,求3()m a +的值.24.某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.(1)求钢笔和毛笔的单价各为多少元?(2)学校仍需要购买上面的两种笔共105支(每种笔的单价不变),陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么账肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的账算错了.25.如图,直线AB 、CD 相交于点O .已知105AOD ∠=︒,OE 把AOC ∠分成两个角,且:2:3AOE EOC ∠∠=.(1)求AOE ∠的度数;(2)若OF 是BOE ∠的平分线,那么OB 是DOF ∠的平分线吗?请说明理由.26.如图,数轴上有,A B 两点,18AB =,原点O 是线段AB 上的一点,且2OA OB =.(1)求出,A B 两点所表示的数;(2)若点C 是线段AO 上一点,且满足AC CO CB =+,求C 点所表示的数;(3)若点E 以每秒3个单位长度的速度从点A 沿数轴向右匀速运动,同时点F 以每秒1个单位长度的速度从点B 沿数轴向右匀速运动,并设运动时间为t 秒,问t 为多少时,E 、F 两点重合并求出此时点,E F 在数轴上所表示的数.参考答案见下一页定州2019—2020学年度七年级第一学期期末质量监测数 学一、选择题1—6: CBDCCA ; 7—12:AC DDBB.二、填空题13. 44°43′;14. 国;15. 4;16. -1;17.19;18. 4. 三、解答题19.解:(1)7+(-15)-2×(-9)=7+(-15)+18=10;(2)原式=﹣4×14+(﹣27)×(827-)=﹣1+8=720.解:(1)3x +7=32﹣2x ,移项得:3x +2x =32﹣7,合并得:5x =25,解得:x =5;(2)2157123y y ---=去分母得:3(2y ﹣1)﹣6=2(5y ﹣7),去括号得:6y ﹣3﹣6=10y ﹣14,移项:6y ﹣10y =﹣14+6+3,合并得:﹣4y =﹣5,系数化为1得:54y =21.解:根据题意得:()A A B B =+-2223(36)x x x =----+-222336x x x =--+-+23x x =-+;当 1.5x =-时,A=(-1.5)2-(-1.5)+393273424=++=22.解:设这件夹克衫的成本价是x元,依题意,得:0.7(1+0.6)x=x+36.解这个方程,0.12x=36x=300答:这件夹克衫的成本价是300元23.解:(1)因为,所以m=2或-2又因为M,N两点的距离为8,所以n的值为10或6;(2)因为n=3,M,N两点的距离为8,所以m=-5MN的中点A在数轴上所表示的数为a,所以a=-5+4=-1所以(m+a)3的值为(-5-1)3=-21624.解:(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.由题意得:30x+45(x+4)=1755解这个方程75x=1575x=21则x+4=25.答:钢笔的单价为21元,毛笔的单价为25元.(2)设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105﹣y)支. 根据题意,得21y+25(105﹣y)=2447.解这个方程-4y=-178y=44.5 (不符合题意).所以王老师肯定搞错了.25.解:(1)因为∠AOE:∠EOC=2:3.设∠AO E=2x,则∠EOC=3x,∠AOC=5x,由∠AOD=105°可得∠AOC=75°,即5x=75°,解得:x=15°,则2x=30°,即∠AOE=30°;(2)OB是∠DOF的平分线;理由如下:由∠AOE=30°,所以∠BOE=180°-∠AOE=150°,而OF平分∠BOE,所以∠BOF=∠BOE =75°,由∠AOD=105°可得∠BOD=75°,所以∠BOD=∠BOF,即OB是∠COF的角平分线.26.解:(1)由OA+OB=AB=18,且OA=2OB[来源:学科网ZXXK]所以OB=6,OA=12,A,B两点所表示的数分别是﹣12,6;(2)设OC=x,则AC=12﹣x,BC=6+x,因为AC=CO+CB,所以12﹣x=x+6+x,x=2,即OC=2,所以C点所表示的数是﹣2;(3)根据题意得:3t=18+t,解得t=9当t=9时,E、F两点重合,此时数轴上所表示的数为OB+9=6+9=15.。
七年级上册数学期末检测试卷(附答案和解释)

七年级上册数学期末检测试卷(附答案和解释)2019年七年级上册数学期末检测试卷(附答案和解释)距离期末考试越来越近了,期末考试考查的是整个学期的学习内容,内容很多。
各科都已经进入复习阶段,现在大家都在忙碌的复习阶段。
我们一起来看看这篇七年级上册数学期末检测试卷吧!一、选择题(每小题3分,共30分)1. 如果向东走80m记为+80m,那么向西走60m记为()A. ﹣60mB. |﹣60|mC. ﹣(﹣60)mD. m2. ﹣6的绝对值等于()A. 6B.C. ﹣D. ﹣63. 未来三年,国家将投入8 500亿元用于缓解群众看病难,看病贵问题.将8 500亿元用科学记数法表示为A. 0.85104亿元B. 8.5103亿元C. 8.5104亿元D. 85102亿元4. 当x=﹣2时,代数式x+1的值是()A. ﹣1B. ﹣3C. 1D. 35. 在解方程时,去分母正确的是()A. 3(x﹣1)﹣2(2x+3)=6B. 3(x﹣1)﹣2(2x+3)=1C. 2(x﹣1)﹣2(2x+3)=6 D. 3(x﹣1)﹣2(2x+3)=36. 中国古代问题:有甲、乙两个牧童,甲对乙说:把你的羊给我一只,我的羊数就是你的羊数的2倍.乙回答说:最18. 已知x=﹣2是方程3(x+a)=15的解,则a=.19. 如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则AOC+DOB=度.20. 如图,AOB中,OD是BOC的平分线,OE是AOC的平分线,若AOB=140,则EOD=度.三、计算题(每小题6分,共24分)21. (﹣18)2(1﹣)22. ﹣23+(﹣3)2﹣32(﹣2)2.23. 先化简,后求值:2(3x﹣4y)﹣5(x﹣2y)+10,其中x=2,y=﹣1.24. 解方程:四、解答题25. 用两架掘土机掘土,第一架掘土机比第二架掘土机每小时多掘土40m3,第一架工作16小时,第二架工作24小时,共掘土8640m3,问每架掘土机每小时可以掘土多少m3? 26. 如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.27. 海滨中学暑假将××部分学生到北京旅游,甲旅行社说:如果领队买全票一张,那么其他学生可以享受半价优惠.乙旅行社说:包括领队在内,全部按全票价的6折优惠.两家旅行社的全票价均为240元.(1)设学生数为x,甲旅行社收费为m,乙旅行社收费为n,列等式表示两家旅行社的收费情况.(2)当学生数是多少时,两家旅行社的收费一样多?参考答案与试题解析一、选择题(每小题3分,共30分)1. 如果向东走80m记为+80m,那么向西走60m记为()A. ﹣60mB. |﹣60|mC. ﹣(﹣60)mD. m考点:正数和负数.分析:在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解答:解:正和负相对,所以,如果向东走80m记为+80m,那么向西走60m记为﹣60m.2. ﹣6的绝对值等于()A. 6B.C. ﹣D. ﹣6考点:绝对值.专题:计算题.分析:根据绝对值的性质解答即可.解答:解:根据绝对值的性质,3. 未来三年,国家将投入8 500亿元用于缓解群众看病难,看病贵问题.将8 500亿元用科学记数法表示为A. 0.85104亿元B. 8.5103亿元C. 8.5104亿元D. 85102亿元考点:科学记数法表示较大的数.分析:科学记数法的表示形式为a10n的形式,其中110,n 为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值10时,n是正数;当原数的绝对值1时,n是负数.解答:解:按照科学记数法的形式8 500亿元应该写成8.5103亿元.4. 当x=﹣2时,代数式x+1的值是()A. ﹣1B. ﹣3C. 1D. 3考点:代数式求值.分析:把x=﹣2直接代入x+1计算.5. 在解方程时,去分母正确的是()A. 3(x﹣1)﹣2(2x+3)=6B. 3(x﹣1)﹣2(2x+3)=1C. 2(x﹣1)﹣2(2x+3)=6 D. 3(x﹣1)﹣2(2x+3)=3考点:解一元一次方程.专题:计算题.分析:去分母的方法是:方程左右两边同时乘以各分母的最小公倍数,这一过程的依据是等式的基本性质,注意去分母时分数线起到括号的作用,容易出现的错误是:漏乘没有分母的项,以及去分母后忘记分数线的括号的作用,符号出现错误.解答:解:方程左右两边同时乘以6得:3(x﹣1)﹣2(2x+3)=6.6. 中国古代问题:有甲、乙两个牧童,甲对乙说:把你的羊给我一只,我的羊数就是你的羊数的2倍.乙回答说:最好还是把你的羊给我一只,我们羊数就一样了.若设甲有x 只羊,则下列方程正确的是()A. x+1=2(x﹣2)B. x+3=2(x﹣1)C. x+1=2(x﹣3)D.考点:由实际问题抽象出一元一次方程.分析:根据甲的话可得乙羊数的关系式,根据乙的话得到等量关系即可.解答:解:∵甲对乙说:把你的羊给我1只,我的羊数就是你的羊数的两倍.甲有x只羊,乙有+1只,∵乙回答说:最好还是把你的羊给我1只,我们的羊数就一样了,7. 下列图形中,不是正方体的展开图的是()A. B. C. D.考点:几何体的展开图.专题:压轴题.分析:利用正方体及其表面展开图的特点解题.解答:解:A、B、C经过折叠均能围成正方体,D折叠后下边没有面,不能折成正方体,故选D.8. 已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有()①AP=BP; ②BP=AB; ③AB=2AP; ④AP+PB=AB.A. 1个B. 2个C. 3个D. 4个考点:两点间的距离.分析:根据题意画出图形,根据中点的特点即可得出结论. 解答:解:如图所示:①∵AP=BP,点P是线段AB的中点,故本小题正确;②∵BP=A B,AP=BP,即点P是线段AB的中点,故本小题正确;③∵AB=2AP,AB=AP+BP,AP=BP,即点P是线段AB的中点,故本小题正确;9. 一个多项式减去x2﹣2y2等于x2+y2,则这个多项式是()A. ﹣2x2+y2B. 2x2﹣y2C. x2﹣2y2D. ﹣x2+2y2考点:整式的加减.分析:被减式=差+减式.解答:解:多项式为:x2﹣2y2+(x2+y2)10. 如图,已知直线AB,CD相交于点O,OE平分COB,若EOB=55,则BOD的度数是()A. 35B. 55C. 70D. 110考点:角平分线的定义;余角和补角.分析:利用角平分线的定义和补角的定义求解.解答:解:OE平分COB,若EOB=55,二、填空题(共10个小题,每小题2分,共20分)11. 比较大小:﹣6﹣8(填、=或)考点:有理数大小比较.专题:计算题.分析:先计算|﹣6|=6,|﹣8|=8,根据负数的绝对值大的反而小,绝对值小的反而大即可得到﹣6与﹣8的大小.解答:解:∵|﹣6|=6,|﹣8|=8,12. 计算:|﹣3|﹣2= 1 .考点:有理数的减法;绝对值.分析:先根据绝对值定义去掉这个绝对值的符号再计算.13. 化简:2(x﹣3)﹣(﹣x+4)= 3x﹣10 .考点:整式的加减.分析:首先根据去括号法则去括号(注意括号前是负号时,去括号,括号里各项都要变号),再合并同类项(注意只把系数相加减,字母和字母的指数不变).解答:解:2(x﹣3)﹣(﹣x+4),14. 如果一个角的补角是150,那么这个角的余角是 60 度. 考点:余角和补角.专题:计算题.分析:本题考查互补和互余的概念,和为180度的两个角互为补角;和为90度的两个角互为余角.解答:解:根据定义一个角的补角是150,则这个角是180﹣150=30,15. 若x,y互为相反数,a、b互为倒数,则代数式的值为﹣3 .考点:代数式求值.分析:根据相反数的概念和倒数概念,可得x、y;a、b的等量关系,把所得的等量关系整体代入可求出代数式的值. 解答:解:∵x,y互为相反数,a、b互为倒数,16. 如果把6.48712保留三位有效数字可近似为 6.49 . 考点:近似数和有效数字.分析:一个近似数的有效数字是从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.近似数6.48712保留三位有效数字,精确到百分位.解答:解:6.48712保留三位有效数字可近似为:6.49.17. 若2x与2(1+x)互为相反数,则x的值为﹣ .考点:解一元一次方程.专题:计算题.分析:利用互为相反数两数之和为0列出方程,求出方程的解即可得到x的值.解答:解:根据题意得:2x+2(1+x)=0,去括号得:2x+2+2x=0,移项合并得:4x=﹣2,18. 已知x=﹣2是方程3(x+a)=15的解,则a= 7 .考点:一元一次方程的解.专题:计算题.分析:由x=﹣2是方程的解,将x=﹣2代入方程即可求出a 的值.解答:解:根据题意将x=﹣2代入方程得:3(﹣2+a)=15,19. 如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则AOC+DOB= 180 度.考点:角的计算.专题:计算题.分析:本题考查了角度的计算问题,因为本题中AOC始终在变化,因此可以采用设而不求的解题技巧进行求解.解答:解:设AOD=a,AOC=90+a,BOD=90﹣a,20. 如图,AOB中,OD是BOC的平分线,OE是AOC的平分线,若AOB=140,则EOD= 70 度.考点:角的计算;角平分线的定义.分析:由图形可知DOE=DOC+EOC,然后根据角平分线的性质,可推出DOC=BOC,EOC=AOC,由此可推出DOE=AOB,最后根据AOB的度数,即可求出结论.解答:解:∵OD是BOC的平分线,OE是AOC的平分线,DOC=BOC,EOC=AOC,DOE=DOC+EOC=AOB,三、计算题(每小题6分,共24分)21. (﹣18)2(1﹣)考点:有理数的除法;有理数的乘法.分析:根据除以一个数等于乘以这个数的倒数,可把除法转化成乘法,根据有理数的乘法运算,可得答案.22. ﹣23+(﹣3)2﹣32(﹣2)2.考点:有理数的乘方.分析:根据有理数的乘方的定义进行计算即可得解.解答:解:﹣23+(﹣3)2﹣32(﹣2)2=﹣8+9﹣9423. 先化简,后求值:2(3x﹣4y)﹣5(x﹣2y)+10,其中x=2,y=﹣1.考点:整式的加减化简求值.专题:计算题.分析:原式去括号合并得到最简结果,将x与y的值代入计算即可求出值.解答:解:原式=6x﹣8y﹣5x+10y+1024. 解方程:考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项、合并同类项,系数化为1,从而得到方程的解.解答:解:去分母得:2(x+3)=12﹣3(3﹣2x)去括号得:2x+6=12﹣9+6x移项得:2x﹣6x=12﹣9﹣6四、解答题25. 用两架掘土机掘土,第一架掘土机比第二架掘土机每小时多掘土40m3,第一架工作16小时,第二架工作24小时,共掘土8640m3,问每架掘土机每小时可以掘土多少m3?考点:一元一次方程的应用.专题:工程问题.分析:在工程问题中,注意公式:工作总量=工作效率工作时间.若设第一架掘土机每小时掘土xm3,那么,第二架掘土机每小时掘土(x﹣40)m3.第一架掘土机16小时掘土16xm3,第二架掘土机24小时掘土24(x﹣40)m3.解答:解:设第一架掘土机每小时掘土xm3,那么第二架掘土机每小时掘土(x﹣40)m3,依题意得:16x+24(x﹣40)=8640,解得:x=240,(x﹣40)=200m3.答:第一架掘土机每小时掘土240立方米,第二架掘土机每小时掘土200m3.26. 如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.考点:比较线段的长短.专题:计算题.分析:根据C点为线段AB的中点,D点为BC的中点,可知AC=CB=AB,CD=CB,AD=AC+CD,又AB=10cm,继而即可求出答案.解答:解:∵C点为线段AB的中点,D点为BC的中点,AB=10cm,27. 海滨中学暑假将××部分学生到北京旅游,甲旅行社说:如果领队买全票一张,那么其他学生可以享受半价优惠.乙旅行社说:包括领队在内,全部按全票价的6折优惠.两家旅行社的全票价均为240元.(1)设学生数为x,甲旅行社收费为m,乙旅行社收费为n,列等式表示两家旅行社的收费情况.(2)当学生数是多少时,两家旅行社的收费一样多?考点:一元一次方程的应用.分析: (1)根据甲乙两个旅行社的优惠情况,分别表示出示两家旅行社的收费情况即可;(2)令m=n,求出x的值.解答:解:(1)由题意得,甲旅行社收费为:m=240+120x,乙旅行社收费为:n=2400.6(x+1)=144x+144;(2)令m=n可得,240+120x=144x+144,解得:x=4,这篇七年级上册数学期末检测试卷的内容,希望会对各位同学带来很大的帮助。
2019年保定市定州市七年级上册期末数学试题(有答案)

河北省保定市定州市七年级(上)期末数学试卷一、选择题(本大题共12小题,共36.0分)1.-3的倒数是()A. 3B.C.D.2.在-3,-1,1,3四个数中,比-2小的数是()A. B. C. 1 D. 33.由四舍五入得到的近似数2.6万,精确到()A. 千位B. 万位C. 个位D. 十分位4.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为()A. B. C. D.5.在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是()A. 正方体B. 长方体C. 球D. 圆锥6.借助常用的直角三角尺,能画出一些度数的角,下列选项中不能画出角的是()A. B. C. D.7.下列判断正确的是()A. 与不是同类项B. 不是整式C. 单项式的系数是D. 是二三项式8.下列方程的变形,符合等式的性质的是()A. 由,得B. 由,得C. 由,得. 由,得9.如图,M,N是数轴上的两点,它们分别表示-4和2,P为数轴上另一点,PM=2PN,则点P表示的数是()A. 1B. 0C. 8D. 0或810.小明在解方程时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2y-=y-■怎么办呢?小明想了一想,便翻了书后的答案,此方程的解为y=-,很快补好了这个常数,你能补出这个常数吗?它应是()A. 1B. 2C. 3D. 411.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为()A. 1B. 5C.D.12.某项工程甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲、乙合作完成此项工程,若设甲一共做了天,则所列方程为()A. . . .、填空题(本大题共6小题,共18.0分)13.若2+1是-9的相反数,则=______.14. . °× =______度______分______秒.15.一个两位数,个位数字是a,十位数字比个位数字大2,则这个两位数是______.16.如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是______度.17.某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜______场比赛.18.如图,在每个“〇”中填入一个整数,使得其中任意四个相邻“〇”中所填整数之和都相等,可得d的值为______.三、计算题(本大题共3小题,共25.0分)19.计算题.(1)-6+3.6+4-5.6(2) ×(-)÷-(-12)÷(-4)(3)-12018+ ÷(-2)3-32×()220.(1)计算:-3(2a2-2ab)+4(a2+ab-6)(2)化简求值:12(2y-y2)+5(y2-2y)-22y,其中=,y=-5.21.解方程(1)3-7(-1)=3-2(+3)(2)=-1四、解答题(本大题共5小题,共41.0分)22.定义新运算:对于任意有理数a、b,都有a⊕b=a(a-b)+1,等式的右边是通常的有理数运算,例如2⊕5=2(2-5)+ = ×(-3)+1.(1)求(-2)⊕3.(2)若3⊕=-5,求的值.23.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=∠EOC,∠DOE= °,求∠EOC的度数.24.入冬以,某家电销售部以150元/台的价格购进一款烤火器,很快售完,又用相同的货款再次购进这款烤火器,因单价提高了30元,进货量比第一次少了10台.(1)家电销售部两次各购进烤火器多少台?(2)若以250元/台的售价卖完这两批烤火器,家电销售部共获利多少元?25.如图是2015年12月月历.(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为,则另三个数用含的式子表示出,从小到大依次是______,______,______.(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2=______.(3)当(1)中被框住的4个数之和等于76时,的值为多少?(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出的值;若不能,则说明理由.26.已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是______;(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.答案和解析1.【答案】C【解析】解:-3的倒数是-.故选:C.根据倒数的定义即可得出答案.此题主要考查了倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.【答案】A【解析】解:∵|-3|=3,|-2|=2,∴比-2小的数是:-3.故选:A.利用两个负数,绝对值大的其值反而小,进而得出答案.此题主要考查了有理数比较大小,正确把握两负数比较大小的方法是解题关键.3.【答案】A【解析】解:近似数2.6万精确到千位.故选:A.近似数2.6万精确到0.1万位.本题考查了近似数和有效数字:经过四舍五入得到的数称为近似数;从一个近似数左边第一个不为0的数数起到这个数完,所以这些数字都叫这个近似数的有效数字.4.【答案】C【解析】解:将9180 000用科学记数法表示为: . × 6.故选:C.科学记数法的表示形式为a× n的形式,其中 ≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查了科学记数法的表示方法.科学记数法的表示形式为a× n的形式,其中 ≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】B【解析】解:A、从左面看与从正面看都是正方形,即得到的平面图形相同;B、从左面看是小长方形,从正面看大长方形,得到的平面图形不相同;C、从左面看与从正面看都是圆,即得到的平面图形相同;D、从左面看与从正面看都是三角形,即得到的平面图形相同;本题是选择从左面看与从正面看所得到的平面图形不相同的,故选:B.主视图、左视图是分别从物体正面、左面看所得到的图形.根据主视图与左视图相同,可得答案.本题考查了简单几何体的三视图,非常简单,锻炼了学生的空间想象力和抽象思维能力.6.【答案】B【解析】解:A、利用 °和 °的角可以画出 °的角,故本选项错误;B、=,不合题意,即借助常用的直角三角尺,能画出一些度数的角,不能画出100度的角,故本选项正确;C、利用 °、 °和 °组合即可画出 °的角,故本选项错误;D、利用 °和 °组合即可画出 °的角,故本选项错误;故选:B.先分清一副三角尺,各个角的度数分别为多少,然后将各个角相加或相减即可得出答案.此题主要考查了用三角板直接画特殊角,关键掌握用三角板画出的角的规律:都是 °的倍数.7.【答案】C【解析】解:A、3a2b与ba2是同类项,故本选项错误;B、是整式,故本选项错误;C、单项式-3y2的系数是-1,故本选项正确;D、32-y+5y2是三次三项式,故本选项错误.故选:C.分别根据单项式、多项式、整式及同类项的定义判断各选项即可.本题考查单项式、多项式、整式及同类项的定义,注意掌握单项式是数或字母的积组成的式子;单项式和多项式统称为整式.8.【答案】C【解析】解:A、两边加不同的数,故A错误;B、两边除以不同的数,故B错误;C、两边都减同一个整式,故C正确;D、两边除以不同的数,故D错误;故选:C.根据等式的性质,可得答案.本题考查了等式的性质,熟记等式的性质是解题关键.9.【答案】D【解析】解:设点P表示的数是,∵PM=2PN,∴|+4|=2|-2|,解得:=0或8,故选:D.根据题意列方程即可得到结论.本题考查了数轴和一元一次方程的应用,主要利用了数轴上两点间的距离的表示方法,读懂题目信息,理解两点间的距离的表示方法是解题的关键.10.【答案】C【解析】解:设被污染的常数为,则:2y-=y-,∵此方程的解是y=-,∴将此解代入方程,方程成立∴ ×(-)-=×(-)-.解此一元一次方程可得:=3∴这个常数是3.故选:C.设这个常数为,已知此方程的解是y=-,将之代入二元一次方程2y-=y-,即可得这个常数的值.本题主要考查了一元一次方程的应用以及它的解的意义.知道一元一次方程的解,求方程中的常数项,可把方程的解代入方程求得常数项的值.(把■作为一个未知数看即可).11.【答案】B【解析】解:因为(b+c)-(a-d)=b+c-a+d=(b-a)+(c+d)=-(a-b)+(c+d)…(1),所以把a-b=-3、c+d=2代入(1)得:原式=-(-3)+2=5.故选:B.先把括号去掉,重新组合后再添括号.(1)括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“-”,去括号后,括号里的各项都改变符号.运用这一法则去括号;(2)添括号后,括号前是“+”,括号里的各项都不改变符号;添括号后,括号前是“-”,括号里的各项都改变符号.运用这一法则添括号.12.【答案】B【解析】解:设甲一共做了天,由题意得:+=1,故选:B.设甲一共做了天,则乙做了(-1)天,再根据工作效率×工作时间=工作量可得甲的工作量为,乙的工作量为,然后再根据甲的工作量+乙的工作量=1列出方程.此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,找出题目中等量关系,再列出方程.13.【答案】4【解析】解:∵2+1是-9的相反数,∴2+1=9.解得:=4.故答案为:4.先依据相反数的定义得到2+1=9,解关于的方程即可.本题主要考查的是相反数的定义、解一元一次方程,依据相反数的定义列出关于的方程是解题的关键.14.【答案】64 57 36【解析】解: . °× = 度 57分 36秒;故答案为:64;57;36.进行度、分、秒的转化运算,注意以60为进制.将度的小数部分化为分,将分的小数部分化为秒.此类题是进行度、分、秒的转化运算,相对比较简单,注意以60为进制即可.15.【答案】11a+20【解析】解:两位数,个位数字是a,十位数字比个位数字大2可表示为(a+2).∴这个两位数是10(a+2)+a=11a+20.两位数为: ×十位数字+个位数字.本题的关键是,两位数的表示方法:十位数字× +个位数字,要求掌握该方法.用字母表示数时,要注意写法:①在代数式中出现的乘号,通常简写做“•”或者省略不写,数字与数字相乘一般仍用“×”号;②在代数式中出现除法运算时,一般按照分数的写法写;③数字通常写在字母的前面;④带分数的要写成假分数的形式.16.【答案】135【解析】解:∵OB平分∠COD,∴∠COB=∠BOD= °,∵∠AOB= °,∴∠AOC= °,∴∠AOD= °.故答案为:135.本题是有公共定点的两个直角三角形问题,通过图形可知∠AOC+∠BOC= °,∠BOD+∠BOC= °,同时∠AOC+∠BOC+∠BOD+∠BOC= °,可以通过角平分线性质求解.本题是角的平分线与对顶角的性质的考查,角平分线的性质是将两个角分成相等的两个角.17.【答案】4【解析】解:8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了场,则3+(7-)=15,解得:=4.故答案是:4.8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了场,总分数为15即可列出方程,即可解题.本题考查了一元一次方程的应用,本题中根据题意找出总比赛场数为7是解题的关键.18.【答案】8【解析】解:∵a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,∴a+8+b-5=8+b-5+c①,8+b-5+c=b-5+c+d②,b-5+c+d=-5+c+d+4③,∴a-5=c-5,8+c=c+d,b-5=-5+4,∴b=4,d=8,a=c,故答案为8.由题意得a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,然后转化成方程组的形式,求得d的值即可.本题是一道找规律的题目,考查了有理数的加法和方程组的思想,是中档题难度不大.19.【答案】解:(1)-6+3.6+4-5.6=-11.6+7.6=-4;(2) ×(-)÷-(-12)÷(-4)=-8-3=-11;(3)-12018+ ÷(-2)3-32×()2=- + ÷(-8)- ×=-1-3-1=-5.【解析】(1)先同号相加,再异号相加即可求解;(2)先算乘除,后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;(3)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.20.【答案】解:(1)原式-6a2+6ab+4a2+4ab-24=-2a2+10ab-24;(2)原式=122y-4y2+5y2-52y-22y=52y+y2,当=,y=-5时,原式= ×()2×(-5)+× 2=-1+5=4.【解析】(1)去括号、合并同类项即可得;(2)原式去括号、合并同类项化简后,把,y的值代入计算可得.本题主要考查整式的加减-化简求值,解题的关键是掌握整式的加减运算顺序和运算法则.21.【答案】解:(1)去括号得:3-7+7=3-2-6,移项合并得:-2=-10,解得:=5;(2)去分母得:3-3=8-2-6,移项合并得:-11=-11,解得:=1.【解析】(1)方程去括号,移项合并,把系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.【答案】解:(1)(-2)⊕3=- ×(-2-3)+1=10+1=11;(2)3⊕=3(3-)+1=-5,9-3+1=-5,-3=-15,=5.【解析】(1)根据新运算得出原式=- ×(-2-3)+1,求出即可;(2)根据新运算得出3(3-)+1=-5,求出方程的解即可.本题考查了求代数式的值和有理数的混合运算,能读懂题意是解此题的关键.23.【答案】解:如图,设∠BOE=°,∵∠BOE=∠EOC,∴∠EOC= °,∵OD平分∠AOB,∴∠AOD=∠DOB= °-°,∵∠AOD+∠DOB+∠BOE+∠EOC= °,∴ °-+ °-+°+ °= °,∴=40,∴∠EOC= °.【解析】设∠BOE=°,则∠EOC= °,由∠DOE= °及OD平分∠AOB知∠AOD=∠DOB= °-°,根据∠AOD+∠DOB+∠BOE+∠EOC= °列出关于的方程,解之可得.本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.24.【答案】解:(1)设第一次购进烤火器台,则第二次购进烤火器(-10)台,根据题意得:150=180(-10),解得=60,-10=50.答:家电销售部第一次购进烤火器60台,第二次购进50台.(2)(250-150)× +(250-180)× = (元).答:以250元/台的售价卖完这两批烤火器,家电销售部共获利9500元.【解析】(1)设第一次购进烤火器台,则第二次购进烤火器(-10)台,根据第二次进货单价比第一次进货单价贵30元即可得出关于的一元一次方程,解之即可得出结论;(2)根据总利润=销售第一批烤火器的利润+销售第二批烤火器的利润即可求出家电销售部共获利多少元.本题考查了一元一次方程的应用,根据数量关系列出关于的一元一次方程是解题的关键.25.【答案】+1 +7 +8 128【解析】解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为,则另外三个数用含的式子从小到大依次表示+1;+7;+8;故答案为+1;+7;+8;(2)∵当四个数是1,2,8,9时最小,a1=1+2+8+9=20;当四个数是23,24,30,31时最大,a2=23+24+30+31=108,∴a1+a2=20+108=128.故答案为:128;(3)由题意得,++1++7++8=76,解得=15,答:当被框住的4个数之和等于76时,的值为15;(4)不能.由题意得,++1++7++8=92,解得=19,故由此框住的四个数应是19,20,26,27,但是19,20不在同行的相邻位置,所以不能框住4个数的和等于92.(1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其他三个数;(2)先求出四个数之和最小a1,和最大a2的值,再求和即可;(3)、(4)根据(1)中各数的表达式求出的值即可.本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.26.【答案】1【解析】解:(1)∵A,B表示的数分别为6,-4,∴AB=10,∵PA=PB,∴点P表示的数是1,故答案为:1;(2)设点P运动秒时,在点C处追上点R,则:AC=6 BC=4,AB=10,∵AC-BC=AB,∴6-4=10,解得,=5,∴点P运动5秒时,追上点R;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时(如图①):MN=MP+NP=AP+BP=(AP+BP)=AB=5.②当点P运动到点B左侧时(如图②),MN=PM-PN=AP-BP=(AP-BP)=AB=5;综上所述,线段MN的长度不发生变化,其长度为5.(1)由已知条件得到AB=10,由PA=PB,于是得到结论;(2)设点P运动秒时,在点C处追上点R,于是得到AC=6 BC=4,AB=10,根据AC-BC=AB,列方程即可得到结论;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时②当点P运动到点B左侧时,求得线段MN的长度不发生变化.此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.。
保定市人教版七年级上册数学期末试卷及答案-百度文库

保定市人教版七年级上册数学期末试卷及答案-百度文库一、选择题1.下列判断正确的是( ) A .3a 2bc 与bca 2不是同类项B .225m n 的系数是2C .单项式﹣x 3yz 的次数是5D .3x 2﹣y +5xy 5是二次三项式2.已知max{}2,,x x x 表示取三个数中最大的那个数,例如:当x =9时,max {}{}22,,max 9,9,9x x x ==81.当max {}21,,2x x x =时,则x 的值为( ) A .14-B .116C .14D .123.我国古代《易经》一书中记载了一种“结绳计数”的方法,一女子在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,下列图示中表示91颗的是( )A .B .C .D .4.下列每对数中,相等的一对是( ) A .(﹣1)3和﹣13 B .﹣(﹣1)2和12 C .(﹣1)4和﹣14D .﹣|﹣13|和﹣(﹣1)35.下列分式中,与2x yx y ---的值相等的是()A .2x y y x+-B .2x y x y+-C .2x y x y --D .2x y y x-+6.﹣2020的倒数是( ) A .﹣2020B .﹣12020C .2020D .12020 7.方程3x +2=8的解是( ) A .3 B .103C .2D .128.解方程121123x x +--=时,去分母得( )A .2(x +1)=3(2x ﹣1)=6B .3(x +1)﹣2(2x ﹣1)=1C .3(x +1)﹣2(2x ﹣1)=6D .3(x +1)﹣2×2x ﹣1=6 9.如果a ﹣3b =2,那么2a ﹣6b 的值是( ) A .4B .﹣4C .1D .﹣110.方程312x -=的解是( ) A .1x =B .1x =-C .13x =-D .13x =11.估算15在下列哪两个整数之间( ) A .1,2B .2,3C .3,4D .4,512.下列调查中,调查方式选择正确的是( ) A .为了了解1 000个灯泡的使用寿命,选择全面调查 B .为了了解某公园全年的游客流量, 选择抽样调查 C .为了了解生产的一批炮弹的杀伤半径,选择全面调查 D .为了了解一批袋装食品是否含有防腐剂,选择全面调查二、填空题13.已知|x |=3,y 2=4,且x <y ,那么x +y 的值是_____.14.如图,将一张长方形纸片分別沿着EP ,FP 对折,使点B 落在点B ,点C 落在点C ′.若点P ,B ′,C ′不在一条直线上,且两条折痕的夹角∠EPF =85°,则∠B ′PC ′=_____.15.如图,点B 在线段AC 上,且AB =5,BC =3,点D ,E 分别是AC ,AB 的中点,则线段ED 的长度为_____.16.已知m ﹣2n =2,则2(2n ﹣m )3﹣3m+6n =_____.17.如图,是七(2)班全体学生的体有测试情况扇形统计图.若达到优秀的有25人,则不合格的学生有____人.18.若a a -=,则a 应满足的条件为______.19.据科学家估计,地球的年龄大约是4600000000年,将4600000000用科学记数法表示 为_________.20.若a 、b 是互为倒数,则2ab ﹣5=_____.21.学校某兴趣活动小组现有男生30人,女生8人,还要录取女生多少人,才能使女生人数占该活动小组总人数的三分之一?设还要录取女生x 人,依题意列方程得_____. 22.某校全体同学的综合素质评价的等级统计如图所示,其中评价为C 等级所在扇形的圆心角是____度.23.已知代数式235x -与233x -互为相反数,则x 的值是_______. 24.若523m xy +与2n x y 的和仍为单项式,则n m =__________.三、压轴题25.阅读理解:如图①,若线段AB 在数轴上,A 、B 两点表示的数分别为a 和b (b a >),则线段AB 的长(点A 到点B 的距离)可表示为AB=b a -.请用上面材料中的知识解答下面的问题:如图②,一个点从数轴的原点开始,先向左移动2cm 到达P 点,再向右移动7cm 到达Q 点,用1个单位长度表示1cm .(1)请你在图②的数轴上表示出P ,Q 两点的位置;(2)若将图②中的点P 向左移动x cm ,点Q 向右移动3x cm ,则移动后点P 、点Q 表示的数分别为多少?并求此时线段PQ 的长.(用含x 的代数式表示);(3)若P 、Q 两点分别从第⑴问标出的位置开始,分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动,设运动时间为t (秒),当t 为多少时PQ=2cm ?26.已知数轴上,点A 和点B 分别位于原点O 两侧,AB=14,点A 对应的数为a ,点B 对应的数为b.(1) 若b =-4,则a 的值为__________. (2) 若OA =3OB ,求a 的值.(3) 点C 为数轴上一点,对应的数为c .若O 为AC 的中点,OB =3BC ,直接写出所有满足条件的c 的值.27.问题:将边长为的正三角形的三条边分别等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?如图①,连接边长为2的正三角形三条边的中点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,共有个;边长为2的正三角形一共有1个.探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有个;边长为2的正三角形共有个.探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)结论:将边长为的正三角形的三条边分别等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个. 28.(1)探究:哪些特殊的角可以用一副三角板画出?在①135︒,②120︒,③75︒,④25︒中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线EF ,然后将一副三角板拼接在一起,其中45角(AOB ∠)的顶点与60角(COD ∠)的顶点互相重合,且边OA 、OC 都在直线EF 上.固定三角板COD 不动,将三角板AOB 绕点O 按顺时针方向旋转一个角度α,当边OB 与射线OF 第一次重合时停止.①当OB 平分EOD ∠时,求旋转角度α;②是否存在2BOC AOD ∠=∠?若存在,求旋转角度α;若不存在,请说明理由. 29.已知,如图,A 、B 、C 分别为数轴上的三点,A 点对应的数为60,B 点在A 点的左侧,并且与A 点的距离为30,C 点在B 点左侧,C 点到A 点距离是B 点到A 点距离的4倍.(1)求出数轴上B 点对应的数及AC 的距离.(2)点P 从A 点出发,以3单位/秒的速度向终点C 运动,运动时间为t 秒. ①当P 点在AB 之间运动时,则BP = .(用含t 的代数式表示)②P 点自A 点向C 点运动过程中,何时P ,A ,B 三点中其中一个点是另外两个点的中点?求出相应的时间t .③当P 点运动到B 点时,另一点Q 以5单位/秒的速度从A 点出发,也向C 点运动,点Q 到达C 点后立即原速返回到A 点,那么Q 点在往返过程中与P 点相遇几次?直.接.写.出.相遇时P 点在数轴上对应的数30.如图,数轴上有A , B 两点,分别表示的数为a ,b ,且()225350a b ++-=.点P 从A 点出发以每秒13个单位长度的速度沿数轴向右匀速运动,当它到达B 点后立即以相同的速度返回往A 点运动,并持续在A ,B 两点间往返运动.在点P 出发的同时,点Q 从B 点出发以每秒2个单位长度向左匀速运动,当点Q 达到A 点时,点P ,Q 停止运动. (1)填空:a = ,b = ;(2)求运动了多长时间后,点P ,Q 第一次相遇,以及相遇点所表示的数; (3)求当点P ,Q 停止运动时,点P 所在的位置表示的数;(4)在整个运动过程中,点P 和点Q 一共相遇了几次.(直接写出答案)31.如图,己知数轴上点A 表示的数为8,B 是数轴上一点,且AB=22.动点P 从点A 出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)写出数轴上点B 表示的数____,点P 表示的数____(用含t 的代数式表示); (2)若动点Q 从点B 出发,以每秒2个单位长度的速度沿数轴向左匀速运动,若点P 、Q 同时出发,问点P 运动多少秒时追上点Q?(列一元一次方程解应用题)(3)若动点Q 从点B 出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若点P 、Q 同时出发,问 秒时P 、Q 之间的距离恰好等于2(直接写出答案)(4)思考在点P 的运动过程中,若M 为AP 的中点,N 为PB 的中点.线段MN 的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN 的长.32.如图,12cm AB =,点C 是线段AB 上的一点,2BC AC =.动点P 从点A 出发,以3cm /s 的速度向右运动,到达点B 后立即返回,以3cm /s 的速度向左运动;动点Q 从点C 出发,以1cm/s 的速度向右运动. 设它们同时出发,运动时间为s t . 当点P 与点Q 第二次重合时,P Q 、两点停止运动. (1)求AC ,BC ;(2)当t 为何值时,AP PQ =; (3)当t 为何值时,P 与Q 第一次相遇; (4)当t 为何值时,1cm PQ =.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】根据同类项的定义,单项式和多项式的定义解答. 【详解】A .3d 2bc 与bca 2所含有的字母以及相同字母的指数相同,是同类项,故本选项错误.B .225m n的系数是25,故本选项错误.C .单项式﹣x 3yz 的次数是5,故本选项正确.D .3x 2﹣y +5xy 5是六次三项式,故本选项错误. 故选C . 【点睛】本题考查了同类项,多项式以及单项式的概念及性质.需要学生对概念的记忆,属于基础题.2.C解析:C 【解析】 【分析】利用max}2,x x 的定义分情况讨论即可求解.【详解】解:当max }21,2x x =时,x ≥012,解得:x =14>x >x 2,符合题意;②x 2=12,解得:x =2x >x 2,不合题意;③x =12x >x 2,不合题意;故只有x =14时,max }21,2x x =. 故选:C . 【点睛】此题主要考查了新定义,正确理解题意分类讨论是解题关键.3.B解析:B 【解析】 【分析】由于从右到左依次排列的绳子上打结,满六进一,所以从右到左的数分别进行计算,然后把它们相加即可得出正确答案. 【详解】解:A 、5+3×6+1×6×6=59(颗),故本选项错误;B 、1+3×6+2×6×6=91(颗),故本选项正确;C 、2+3×6+1×6×6=56(颗),故本选项错误;D 、1+2×6+3×6×6=121(颗),故本选项错误; 故选:B . 【点睛】本题是以古代“结绳计数”为背景,按满六进一计数,运用了类比的方法,根据图中的数学列式计算;本题题型新颖,一方面让学生了解了古代的数学知识,另一方面也考查了学生的思维能力.4.A解析:A 【解析】 【分析】根据乘方和绝对值的性质对各个选项进行判断即可. 【详解】A.(﹣1)3=﹣1=﹣13,相等;B.﹣(﹣1)2=﹣1≠12=1,不相等;C.(﹣1)4=1≠﹣14=﹣1,不相等;D. ﹣|﹣13|=﹣1≠﹣(﹣1)3=1,不相等. 故选A.5.A解析:A 【解析】 【分析】根据分式的基本性质即可求出答案. 【详解】 解:原式=22x y x yx y y x++-=--, 故选:A . 【点睛】本题考查分式的基本性质,解题的关键熟练运用分式的基本性质,本题属于基础题型.6.B解析:B 【解析】 【分析】根据倒数的概念即可解答. 【详解】解:根据倒数的概念可得,﹣2020的倒数是12020-, 故选:B .本题考查了倒数的概念,熟练掌握是解题的关键.7.C解析:C 【解析】 【分析】移项、合并后,化系数为1,即可解方程. 【详解】解:移项、合并得,36x =, 化系数为1得:2x =, 故选:C . 【点睛】本题考查一元一次方程的解;熟练掌握一元一次方程的解法是解题的关键.8.C解析:C 【解析】 【分析】方程两边都乘以分母的最小公倍数即可. 【详解】解:方程两边同时乘以6,得:3(1)2(21)6x x +--=, 故选:C . 【点睛】本题主要考查了解一元一次方程的去分母,需要注意,不能漏乘,没有分母的也要乘以分母的最小公倍数.9.A解析:A 【解析】 【分析】将a ﹣3b =2整体代入即可求出所求的结果. 【详解】解:当a ﹣3b =2时, ∴2a ﹣6b =2(a ﹣3b ) =4, 故选:A . 【点睛】本题考查了代数式的求值,正确对代数式变形,利用添括号法则是关键.10.A【解析】试题分析:将原方程移项合并同类项得:3x=3,解得:x=1.故选A.考点:解一元一次方程.11.C解析:C【解析】【分析】.【详解】∵9<15<16,∴,故选C.【点睛】本题考查了无理数的估算,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.12.B解析:B【解析】选项A、C、D,了解1000个灯泡的使用寿命,了解生产的一批炮弹的杀伤半径,了解一批袋装食品是否含有防腐剂,都是具有破坏性的调查,无法进行普查,不适于全面调查,适用于抽样调查.选项B,了解某公园全年的游客流量,工作量大,时间长,需要用抽样调查.故选B.二、填空题13.﹣1或﹣5【解析】【分析】利用绝对值和乘方的知识确定x、y的值,然后计算即可解答.【详解】解:∵|x|=3,y2=4,∴x=±3,y=±2,∵x<y,∴x=﹣3,y=±2,当x=﹣解析:﹣1或﹣5【分析】利用绝对值和乘方的知识确定x、y的值,然后计算即可解答.【详解】解:∵|x|=3,y2=4,∴x=±3,y=±2,∵x<y,∴x=﹣3,y=±2,当x=﹣3,y=2时,x+y=﹣1,当x=﹣3,y=﹣2时,x+y=﹣5,所以,x+y的值是﹣1或﹣5.故答案为:﹣1或﹣5.【点睛】本题主要考查了有理数的乘方、绝对值的性质有理数的加法等知识,,解题的关键是确定x、y的值.14.10°.【解析】【分析】由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF,再根据角的和差关系,可得∠B′PE+∠C′PF=∠B′PC′+85°,再代入2∠B′PE+2∠C′PF-∠B′P解析:10°.【解析】【分析】由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF,再根据角的和差关系,可得∠B′PE+∠C′PF=∠B′PC′+85°,再代入2∠B′PE+2∠C′PF-∠B′PC′=180°计算即可.【详解】解:由对称性得:∠BPE=∠B′PE,∠CPF=∠C′PF,∴2∠B′PE+2∠C′PF﹣∠B′PC′=180°,即2(∠B′PE+∠C′PF)﹣∠B′PC′=180°,又∵∠EPF=∠B′PE+∠C′PF﹣∠B′PC′=85°,∴∠B′PE+∠C′PF=∠B′PC′+85°,∴2(∠B′PC′+85°)﹣∠B′PC′=180°,解得∠B′PC′=10°.故答案为:10°.【点睛】此题考查了角的计算,以及折叠的性质,熟练掌握折叠的性质是解本题的关键.15.5【解析】首先求出AC的长度是多少,根据点D是AC的中点,求出AD的长度是多少;然后求出AE的长度,即可求出线段ED的长度为多少.【详解】解:∵AB=5,BC=3,∴AC=5+3解析:5【解析】【分析】首先求出AC的长度是多少,根据点D是AC的中点,求出AD的长度是多少;然后求出AE的长度,即可求出线段ED的长度为多少.【详解】解:∵AB=5,BC=3,∴AC=5+3=8;∵点D是AC的中点,∴AD=8÷2=4;∵点E是AB的中点,∴AE=5÷2=2.5,∴ED=AD﹣AE=4﹣2.5=1.5.故答案为:1.5.【点睛】此题主要考查了两点间的距离,以及线段的中点的含义和应用,要熟练掌握.16.-22【解析】【分析】将m﹣2n=2代入原式=2[﹣(m﹣2n)]3﹣3(m﹣2n)计算可得.【详解】解:当m﹣2n=2时,原式=2[﹣(m﹣2n)]3﹣3(m﹣2n)=2×(﹣2)3解析:-22【解析】【分析】将m﹣2n=2代入原式=2[﹣(m﹣2n)]3﹣3(m﹣2n)计算可得.【详解】解:当m﹣2n=2时,原式=2[﹣(m﹣2n)]3﹣3(m﹣2n)=2×(﹣2)3﹣3×2=﹣16﹣6=﹣22,故答案为:﹣22.【点睛】本题主要考查代数式的求值,解题的关键是掌握整体代入思想的运用.17.5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数,然后用总人数乘以不合格所占的百分比即可.【详解】解:∵学生总人数=25÷50%=50(人),∴不合格的学生人数=50×(1-5解析:5【解析】【分析】根据达到优秀的人数和所占百分比求出总人数,然后用总人数乘以不合格所占的百分比即可.【详解】解:∵学生总人数=25÷50%=50(人),∴不合格的学生人数=50×(1-50%-40%)=5(人),故答案为:5.【点睛】本题考查了扇形统计图,熟知扇形统计图中各数据所表示的意义是解题关键.18.【解析】【分析】根据绝对值的定义和性质求解可得.【详解】解:,,故答案为.【点睛】本题考查绝对值,解题的关键是熟练掌握绝对值的定义和性质.解析:a0【解析】【分析】根据绝对值的定义和性质求解可得.【详解】-=,解:a a∴≥,a0≥.故答案为a0【点睛】本题考查绝对值,解题的关键是熟练掌握绝对值的定义和性质.19.6×【解析】试题解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.由于4 600 000 000有10位,所以可以确定n=10-1=9.所以,4 600 000 010解析:6×9【解析】试题解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.由于4 600 000 000有10位,所以可以确定n=10-1=9.所以,4 600 000 000=4.6×109.故答案为4.6×109.20.-3.【解析】【分析】根据互为倒数的两数之积为1,得到ab=1,再代入运算即可.【详解】解:∵a、b是互为倒数,∴ab=1,∴2ab﹣5=﹣3.故答案为﹣3.【点睛】本题考查了倒解析:-3.【解析】【分析】根据互为倒数的两数之积为1,得到ab=1,再代入运算即可.【详解】解:∵a、b是互为倒数,∴ab=1,∴2ab﹣5=﹣3.故答案为﹣3. 【点睛】本题考查了倒数的性质,掌握并灵活应用倒数的性质是解答本题的关键.21.8+x =(30+8+x ). 【解析】 【分析】设还要录取女生人,则女生总人数为人,数学活动小组总人数为人,根据女生人数占数学活动小组总人数的列方程. 【详解】解:设还要录取女生人,根据题意得:解析:8+x =13(30+8+x ). 【解析】 【分析】设还要录取女生x 人,则女生总人数为8x +人,数学活动小组总人数为308x ++人,根据女生人数占数学活动小组总人数的13列方程. 【详解】解:设还要录取女生x 人,根据题意得: 18(308)3x x +=++.故答案为:18(308)3x x +=++.【点睛】此题考查了由实际问题抽象出一元一次方程,关键是准确表示还要录取后女生的人数及总人数.22.72 【解析】 【分析】用360度乘以C 等级的百分比即可得. 【详解】观察可知C 等级所占的百分比为20%,所以C 等级所在扇形的圆心角为:360°×20%=72°, 故答案为:72. 【点睛】解析:72 【解析】 【分析】用360度乘以C 等级的百分比即可得. 【详解】观察可知C 等级所占的百分比为20%,所以C 等级所在扇形的圆心角为:360°×20%=72°, 故答案为:72. 【点睛】本题考查了扇形统计图,熟知扇形统计图中扇形圆心角度数的求解方法是解题的关键.23.【解析】 【分析】根据互为相反数的两个数之和为0,建立方程求解即可. 【详解】 ∵与互为相反数 ∴ 解得: 【点睛】本题考查了相反数的性质和解一元一次方程,熟记相反数的性质建立方程是解题的关键解析:278【解析】 【分析】 根据互为相反数的两个数之和为0,建立方程求解即可. 【详解】 ∵235x -与233x -互为相反数 ∴2323053-⎛⎫+-= ⎪⎝⎭x x 解得:278x = 【点睛】本题考查了相反数的性质和解一元一次方程,熟记相反数的性质建立方程是解题的关键.24.9 【解析】根据与的和仍为单项式,可知与是同类项,所以,解得,所以,故答案为:9.解析:9 【解析】 根据523m xy +与2n x y 的和仍为单项式,可知523m x y +与2n x y 是同类项,所以52m +=,解得m 3,n 2=-=,所以()239n m =-=,故答案为:9.三、压轴题25.(1)见详解;(2)2x --,53x +,47x +;(3)当运动时间为5秒或9秒时,PQ=2cm. 【解析】 【分析】(1)根据数轴的特点,所以可以求出点P ,Q 的位置; (2)根据向左移动用减法,向右移动用加法,即可得到答案;(3)根据题意,可分为两种情况进行分析:①点P 在点Q 的左边时;②点P 在点Q 的右边时;分别进行列式计算,即可得到答案. 【详解】解:(1)如图所示:.(2)由(1)可知,点P 为2-,点Q 为5;∴移动后的点P 为:2x --;移动后的点Q 为:53x +; ∴线段PQ 的长为:53(2)47x x x +---=+; (3)根据题意可知, 当PQ=2cm 时可分为两种情况: ①当点P 在点Q 的左边时,有(21)72t -=-,解得:5t =;②点P 在点Q 的右边时,有(21)72t -=+,解得:9t =;综上所述,当运动时间为5秒或9秒时,PQ=2cm. 【点睛】本题要是把方程和数轴结合起来,既要根据条件列出方程,又要把握数轴的特点.解题的关键是熟练掌握数轴上的动点运动问题,注意分类讨论进行解题. 26.(1)10;(2)212±;(3)288. 5±±,【解析】 【分析】(1)根据题意画出数轴,由已知条件得出AB=14,OB=4,则OA=10,得出a 的值为10. (2)分两种情况,点A 在原点的右侧时,设OB=m,列一元一次方程求解,进一步得出OA 的长度,从而得出a 的值.同理可求出当点A 在原点的左侧时,a 的值.(3)画数轴,结合数轴分四种情况讨论计算即可.【详解】(1)解:若b=-4,则a的值为 10(2)解:当A在原点O的右侧时(如图):设OB=m,列方程得:m+3m=14,解这个方程得,7m2 ,所以,OA=212,点A在原点O的右侧,a的值为212.当A在原点的左侧时(如图),a=-21 2综上,a的值为±212.(3)解:当点A在原点的右侧,点B在点C的左侧时(如图), c=-28 5.当点A在原点的右侧,点B在点C的右侧时(如图), c=-8.当点A在原点的左侧,点B在点C的右侧时,图略,c=28 5.当点A在原点的左侧,点B在点C的左侧时,图略,c=8.综上,点c的值为:±8,±28 5.【点睛】本题考查的知识点是通过画数轴,找出数轴上各线段间的数量关系并用一元一次方程来求解,需要注意的是分情况讨论时要考虑全面,此题充分锻炼了学生动手操作能力以及利用数行结合解决问题的能力.27.探究三:16,6;结论:n²,;应用:625,300.【解析】【分析】探究三:模仿探究一、二即可解决问题;结论:由探究一、二、三可得:将边长为的正三角形的三条边分别等分,连接各边对应的等分点,边长为1的正三角形共有个;边长为2的正三角形共有个;应用:根据结论即可解决问题. 【详解】 解:探究三:如图3,连接边长为4的正三角形三条边的对应四等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,第四层有7个,共有个;边长为2的正三角形有个.结论:连接边长为的正三角形三条边的对应等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,第四层有7个,……,第层有个,共有个;边长为2的正三角形,共有个.应用:边长为1的正三角形有=625(个),边长为2的正三角形有(个). 故答案为探究三:16,6;结论:n², ;应用:625,300.【点睛】本题考查规律型问题,解题的关键是理解题意,学会模仿例题解决问题.28.(1)④;(2)①15α=︒;②当105α=,125α=时,存在2BOC AOD ∠=∠. 【解析】 【分析】(1)根据一副三角板中的特殊角,运用角的和与差的计算,只要是15°的倍数的角都可以画出来;(2)①根据已知条件得到∠EOD=180°-∠COD=180°-60°=120°,根据角平分线的定义得到∠EOB=12∠EOD=12×120°=60°,于是得到结论; ②当OA 在OD 的左侧时,当OA 在OD 的右侧时,根据角的和差列方程即可得到结论. 【详解】解:(1)∵135°=90°+45°,120°=90°+30°,75°=30°+45°, ∴只有25°不能写成90°、60°、45°、30°的和或差,故画不出; 故选④;(2)①因为COD 60∠=,所以EOD 180COD 18060120∠∠=-=-=. 因为OB 平分EOD ∠, 所以11EOB EOD 1206022∠∠==⨯=. 因为AOB 45∠=,所以αEOB AOB 604515∠∠=-=-=.②当OA 在OD 左侧时,则AOD 120α∠=-,BOC 135α∠=-. 因为BOC 2AOD ∠∠=, 所以()135α2120α-=-. 解得α105=.当OA 在OD 右侧时,则AOD α120∠=-,BOC 135α∠=-. 因为BOC 2AOD ∠∠=, 所以()135α2α120-=-.解得α125=.综合知,当α105=,α125=时,存在BOC 2AOD ∠∠=. 【点睛】本题考查角的计算,角平分线的定义,正确的理解题意并分类讨论是解题关键. 29.(1)30,120(2)①30﹣3t②5或20③﹣15或﹣4834【解析】 【分析】(1)根据A 点对应的数为60,B 点在A 点的左侧,AB =30求出B 点对应的数;根据AC =4AB 求出AC 的距离;(2)①当P 点在AB 之间运动时,根据路程=速度×时间求出AP =3t ,根据BP =AB ﹣AP 求解;②分P 点是A 、B 两个点的中点;B 点是A 、P 两个点的中点两种情况讨论即可; ③根据P 、Q 两点的运动速度与方向可知Q 点在往返过程中与P 点相遇2次.设Q 点在往返过程中经过x 秒与P 点相遇.第一次相遇是点Q 从A 点出发,向C 点运动的途中.根据AQ ﹣BP =AB 列出方程;第二次相遇是点Q 到达C 点后返回到A 点的途中.根据CQ+BP =BC 列出方程,进而求出P 点在数轴上对应的数. 【详解】(1)∵A 点对应的数为60,B 点在A 点的左侧,并且与A 点的距离为30, ∴B 点对应的数为60﹣30=30;∵C 点到A 点距离是B 点到A 点距离的4倍, ∴AC=4AB =4×30=120; (2)①当P 点在AB 之间运动时, ∵AP=3t ,∴B P=AB﹣AP=30﹣3t.故答案为30﹣3t;②当P点是A、B两个点的中点时,AP=12AB=15,∴3t=15,解得t=5;当B点是A、P两个点的中点时,AP=2AB=60,∴3t=60,解得t=20.故所求时间t的值为5或20;③相遇2次.设Q点在往返过程中经过x秒与P点相遇.第一次相遇是点Q从A点出发,向C点运动的途中.∵AQ﹣BP=AB,∴5x﹣3x=30,解得x=15,此时P点在数轴上对应的数是:60﹣5×15=﹣15;第二次相遇是点Q到达C点后返回到A点的途中.∵CQ+BP=BC,∴5(x﹣24)+3x=90,解得x=1054,此时P点在数轴上对应的数是:30﹣3×1054=﹣4834.综上,相遇时P点在数轴上对应的数为﹣15或﹣4834.【点睛】本题考查了一元一次方程的应用,行程问题相等关系的应用,线段中点的定义,进行分类讨论是解题的关键.30.(1)25-,35(2)运动时间为4秒,相遇点表示的数字为27 ;(3)5;(4) 一共相遇了7次.【解析】【分析】(1)根据0+0式的定义即可解题;(2)设运动时间为x秒,表示出P,Q的运动路程,利用路程和等于AB长即可解题;(3)根据点Q达到A点时,点P,Q停止运动求出运动时间即可解题;(4)根据第三问点P运动了6个来回后,又运动了30个单位长度即可解题.【详解】解:(1)25-,35(2)设运动时间为x秒13x2x2535+=+解得x4=352427-⨯=答:运动时间为4秒,相遇点表示的数字为27(3)运动总时间:60÷2=30(秒),13×30÷60=6…30即点P运动了6个来回后,又运动了30个单位长度,∵25305-+=,∴点P所在的位置表示的数为5 .(4)由(3)得:点P运动了6个来回后,又运动了30个单位长度,∴点P和点Q一共相遇了6+1=7次.【点睛】本题考查了一元一次方程的实际应用,数轴的应用,难度较大,熟悉路程,时间,速度之间的关系是解题关键.31.(1)-14,8-4t(2)点P运动11秒时追上点Q(3)103或4(4)线段MN的长度不发生变化,都等于11【解析】【分析】(1)根据AB长度即可求得BO长度,根据t即可求得AP长度,即可解题;(2)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可;(3)分①点P、Q相遇之前,②点P、Q相遇之后,根据P、Q之间的距离恰好等于2列出方程求解即可;(4)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.【详解】(1)∵点A表示的数为8,B在A点左边,AB=22,∴点B表示的数是8-22=-14,∵动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,∴点P表示的数是8-4t.故答案为-14,8-4t;(2)设点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,∵AC-BC=AB,∴4x-2x=22,解得:x=11,∴点P运动11秒时追上点Q;(3) ①点P、Q相遇之前,4t+2+2t =22,t=103,②点P、Q相遇之后,4t+2t -2=22,t=4,故答案为103或4 (4)线段MN 的长度不发生变化,都等于11;理由如下:①当点P 在点A 、B 两点之间运动时:MN=MP+NP=12AP+12BP=12(AP+BP )=12AB=12×22=11 ②当点P 运动到点B 的左侧时:MN=MP ﹣NP=12AP ﹣12BP=12(AP ﹣BP )=12AB=11 ∴线段MN 的长度不发生变化,其值为11.【点睛】 本题考查了数轴一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.32.(1)AC=4cm, BC=8cm ;(2)当45t =时,AP PQ =;(3)当2t =时,P 与Q 第一次相遇;(4)35191cm.224t PQ =当为,,时, 【解析】【分析】(1)由于AB=12cm ,点C 是线段AB 上的一点,BC=2AC ,则AC+BC=3AC=AB=12cm ,依此即可求解;(2)分别表示出AP 、PQ ,然后根据等量关系AP=PQ 列出方程求解即可;(3)当P 与Q 第一次相遇时由AP AC CQ =+得到关于t 的方程,求解即可; (4)分相遇前、相遇后以及到达B 点返回后相距1cm 四种情况列出方程求解即可.【详解】(1)AC=4cm, BC=8cm.(2) 当AP PQ =时,AP 3t,PQ AC AP CQ 43t t ==-+=-+,即3t 43t t =-+,解得4t 5=. 所以当4t 5=时,AP PQ =. (3) 当P 与Q 第一次相遇时,AP AC CQ =+,即3t 4t =+,解得t 2=.所以当t 2=时,P 与Q 第一次相遇.(4)()()P,Q 1cm,4t 3t 13t 4t 1+-=-+=因为点相距的路程为所以或,。
保定市初一上学期数学期末试卷带答案

保定市初一上学期数学期末试卷带答案一、选择题1.在数3,﹣3,13,13-中,最小的数为( ) A .﹣3B .13C .13-D .32.地球与月球的平均距离为384 000km ,将384 000这个数用科学记数法表示为( ) A .3.84×103 B .3.84×104C .3.84×105D .3.84×1063.-2的倒数是( ) A .-2B .12- C .12D .24.如图是小明制作的一张数字卡片,在此卡片上可以用一个正方形圈出44⨯个位置的16个数(如1,2,3,4,8,9,10,11,15,16,17,18,22,23,24,25).若用这样的正方形圈出这张数字卡片上的16个数,则圈出的16个数的和不可能为下列数中的( )A .208B .480C .496D .5925.某班30位同学,在绿色护植活动中共种树72棵,已知女生每人种2棵,男生每人种3棵,设女生有x 人,则可列方程( ) A .23(30)72x x +-= B .32(30)72x x +-= C .23(72)30x x +-=D .32(72)30x x +-=6.一项工程,甲独做需10天完成,乙单独做需15天完成,两人合作4天后,剩下的部分由乙独做全部完成,设乙独做x 天,由题意得方程( ) A .410 +415x -=1 B .410 +415x +=1 C .410x + +415=1 D .410x + +15x=1 7.下列分式中,与2x yx y---的值相等的是() A .2x yy x +-B .2x yx y+-C .2x yx y--D .2x yy x-+ 8.已知点、、A B C 在一条直线上,线段5AB cm =,3BC cm =,那么线段AC 的长为( ) A .8cmB .2cmC .8cm 或2cmD .以上答案不对9.不等式x ﹣2>0在数轴上表示正确的是( ) A . B . C .D .10.如果方程组223x y x y +=⎧⎨-=⎩的解为5x y =⎧⎨=⎩,那么“口”和“△”所表示的数分别是( )A .14,4B .11,1C .9,-1D .6,-4 11.如果+5米表示一个物体向东运动5米,那么-3米表示( ).A .向西走3米B .向北走3米C .向东走3米D .向南走3米12.2019年3月15日,中山市统计局发布2018年统计数据,我市常住人口达3 310 000人.数据3 310 000用科学记数法表示为( ) A .3.31×105B .33.1×105C .3.31×106D .3.31×10713.如图,将长方形ABCD 绕CD 边旋转一周,得到的几何体是( )A .棱柱B .圆锥C .圆柱D .棱锥14.将方程212134x x -+=-去分母,得( ) A .4(21)3(2)x x -=+ B .4(21)12(2)x x -=-+C .(21)63(2)x x -=-+D .4(21)123(2)x x -=-+15.如图的几何体,从上向下看,看到的是( )A .B .C .D .二、填空题16.从一个n 边形的同一个顶点出发,分别连结这个顶点与其余各顶点,若把这个多边形分割为6个三角形,则n 的值是___________.17.若代数式mx 2+5y 2﹣2x 2+3的值与字母x 的取值无关,则m 的值是__.18.若212-my x 与5x 3y 2n 是同类项,则m +n =_____. 19.36.35︒=__________.(用度、分、秒表示)20.某农村西瓜论个出售,每个西瓜以下面的方式定价:当一个a 斤重的西瓜卖A 元,一个b 斤重的西瓜卖B 元时,一个()a b +斤重的西瓜定价为 36ab A B ⎛++⎫⎪⎝⎭元,已知一个12斤重的西瓜卖21元,则一个18斤重的西瓜卖_____元. 21.计算:()222a -=____;()2323x x ⋅-=_____.22.若a a -=,则a 应满足的条件为______.23.小马在解关于x 的一元一次方程3232a xx -=时,误将- 2x 看成了+2x ,得到的解为x =6,请你帮小马算一算,方程正确的解为x =_____.24.在数轴上,与表示-3的点的距离为4的点所表示的数为__________________. 25.将520000用科学记数法表示为_____.26.五边形从某一个顶点出发可以引_____条对角线. 27.4是_____的算术平方根.28.如图,在平面直角坐标系中,动点P 按图中箭头所示方向从原点出发,第1次运动到P 1(1,1),第2次接着运动到点P 2(2,0),第3次接着运动到点P 3(3,-2),…,按这的运动规律,点P 2019的坐标是_____.29.如图,点O 在直线AB 上,射线OD 平分∠AOC ,若∠AOD=20°,则∠COB 的度数为_____度.30.材料:一般地,n 个相同因数a 相乘n a a a a⋅⋅⋅个:记为n a . 如328=,此时3叫做以2为底的8的对数,记为2log 8(即2log 83=);如45625=,此时4叫做以5为底的625的对数,记为5log 625(即5log 6254=),那么3log 9=_________.三、压轴题31.如图1,O 为直线AB 上一点,过点O 作射线OC ,∠AOC =30°,将一直角三角板(其中∠P =30°)的直角顶点放在点O 处,一边OQ 在射线OA 上,另一边OP 与OC 都在直线AB 的上方.将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周. (1)如图2,经过t 秒后,OP 恰好平分∠BOC . ①求t 的值;②此时OQ 是否平分∠AOC ?请说明理由;(2)若在三角板转动的同时,射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC 平分∠POQ ?请说明理由;(3)在(2)问的基础上,经过多少秒OC 平分∠POB ?(直接写出结果).32.阅读理解:如图①,若线段AB 在数轴上,A 、B 两点表示的数分别为a 和b (b a >),则线段AB 的长(点A 到点B 的距离)可表示为AB=b a -.请用上面材料中的知识解答下面的问题:如图②,一个点从数轴的原点开始,先向左移动2cm 到达P 点,再向右移动7cm 到达Q 点,用1个单位长度表示1cm .(1)请你在图②的数轴上表示出P ,Q 两点的位置;(2)若将图②中的点P 向左移动x cm ,点Q 向右移动3x cm ,则移动后点P 、点Q 表示的数分别为多少?并求此时线段PQ 的长.(用含x 的代数式表示);(3)若P 、Q 两点分别从第⑴问标出的位置开始,分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动,设运动时间为t (秒),当t 为多少时PQ=2cm ? 33.已知AOD α∠=,OB 、OC 、OM 、ON 是AOD ∠内的射线.(1)如图1,当160α=︒,若OM 平分AOB ∠,ON 平分BOD ∠,求MON ∠的大小; (2)如图2,若OM 平分AOC ∠,ON 平分BOD ∠,20BOC ∠=︒,60MON ∠=︒,求α.34.观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,则以上三个等式两边分别相加得:1111111131122334223344++=-+-+-=⨯⨯⨯. ()1观察发现()1n n 1=+______;()1111122334n n 1+++⋯+=⨯⨯⨯+______.()2拓展应用有一个圆,第一次用一条直径将圆周分成两个半圆(如图1),在每个分点标上质数m ,记2个数的和为1a ;第二次再将两个半圆周都分成14圆周(如图2),在新产生的分点标上相邻的已标的两数之和的12,记4个数的和为2a ;第三次将四个14圆周分成18圆周(如图3),在新产生的分点标上相邻的已标的两数之和的13,记8个数的和为3a ;第四次将八个18圆周分成116圆周,在新产生的分点标上相邻的已标的两个数的和的14,记16个数的和为4a ;⋯⋯如此进行了n 次.n a =①______(用含m 、n 的代数式表示); ②当n a 6188=时,求123n1111a a a a +++⋯⋯+的值.35.如图1,线段AB 的长为a .(1)尺规作图:延长线段AB 到C ,使BC =2AB ;延长线段BA 到D ,使AD =AC .(先用尺规画图,再用签字笔把笔迹涂黑.)(2)在(1)的条件下,以线段AB 所在的直线画数轴,以点A 为原点,若点B 对应的数恰好为10,请在数轴上标出点C ,D 两点,并直接写出C ,D 两点表示的有理数,若点M 是BC 的中点,点N 是AD 的中点,请求线段MN 的长.(3)在(2)的条件下,现有甲、乙两个物体在数轴上进行匀速直线运动,甲从点D 处开始,在点C ,D 之间进行往返运动;乙从点N 开始,在N ,M 之间进行往返运动,甲、乙同时开始运动,当乙从M 点第一次回到点N 时,甲、乙同时停止运动,若甲的运动速度为每秒5个单位,乙的运动速度为每秒2个单位,请求出甲和乙在运动过程中,所有相遇点对应的有理数.36.如图,已知数轴上点A 表示的数为10,B 是数轴上位于点A 左侧一点,且AB=30,动点P 从点A 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为秒.(1)数轴上点B表示的数是________,点P表示的数是________(用含的代数式表示);(2)若M为线段AP的中点,N为线段BP的中点,在点P运动的过程中,线段MN的长度会发生变化吗?如果不变,请求出这个长度;如果会变化,请用含的代数式表示这个长度;(3)动点Q从点B处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?37.我国著名数学家华罗庚曾经说过,“数形结合百般好,隔裂分家万事非.”数形结合的思想方法在数学中应用极为广泛.观察下列按照一定规律堆砌的钢管的横截面图:用含n的式子表示第n个图的钢管总数.(分析思路)图形规律中暗含数字规律,我们可以采用分步的方法,从图形排列中找规律;把图形看成几个部分的组合,并保持结构,找到每一部分对应的数字规律,进而找到整个图形对应的数字规律.如:要解决上面问题,我们不妨先从特例入手: (统一用S表示钢管总数)(解决问题)(1)如图,如果把每个图形按照它的行来分割观察,你发现了这些钢管的堆砌规律了吗?像n=1、n=2的情形那样,在所给横线上,请用数学算式表达你发现的规律.S=1+2 S=2+3+4 _____________ ______________(2)其实,对同一个图形,我们的分析眼光可以是不同的.请你像(1)那样保持结构的、对每一个所给图形添加分割线,提供与(1)不同的分割方式;并在所给横线上,请用数学算式表达你发现的规律:_______ ____________ _______________ _______________(3)用含n的式子列式,并计算第n个图的钢管总数.38.问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s),甲乙两点之间距离为y(cm).(1)当甲追上乙时,x = .(2)请用含x的代数式表示y.当甲追上乙前,y= ;当甲追上乙后,甲到达C之前,y= ;当甲到达C之后,乙到达C之前,y= .问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.(2)若从4:00起计时,求几分钟后分针与时针第一次重合.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.【详解】解:∵3>13>13->﹣3,∴在数3,﹣3,13,13-中,最小的数为﹣3.故选:A.【点睛】此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.2.C解析:C【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】试题分析:384 000=3.84×105.故选C.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.B解析:B【解析】【分析】根据倒数的定义求解.【详解】-2的倒数是-1 2故选B【点睛】本题难度较低,主要考查学生对倒数相反数等知识点的掌握4.C解析:C【分析】由题意设第一列第一行的数为x ,依次表示每个数,并相加进行分析得出选项. 【详解】解:设第一列第一行的数为x ,第一行四个数分别为,1,2,3x x x x +++, 第二行四个数分别为7,8,9,10x x x x ++++, 第三行四个数分别为14,15,16,17x x x x ++++, 第四行四个数分别为21,22,23,24x x x x ++++,16个数相加得到16192x +,当相加数为208时x 为1,当相加数为480时x 为18,相加数为496时x 为19,相加数为592时x 为25,由数字卡片可知,x 为19时,不满足条件. 故选C. 【点睛】本题考查列代数式求解问题,理解题意设未知数并列出方程进行分析即可.5.A解析:A 【解析】 【分析】设女生x 人,男生就有(30-x )人,再表示出男、女生各种树的棵数,根据题中等量关系式:男生种树棵数+女生种树棵数=72棵,列方程解答即可. 【详解】 设女生x 人, ∵共有学生30名, ∴男生有(30-x )名,∵女生每人种2棵,男生每人种3棵, ∴女生种树2x 棵,男生植树3(30-x )棵, ∵共种树72棵, ∴2x+3(30-x)=72, 故选:A. 【点睛】本题考查一元一次方程的应用,正确找准数量间的相等关系是解题关键.6.B解析:B 【解析】 【分析】直接利用总工作量为1,分别表示出两人完成的工作量进而得出方程即可. 【详解】设乙独做x 天,由题意得方程:410+415x +=1.【点睛】本题主要考查了由实际问题抽象出一元一次方程,正确表示出两人完成的工作量是解题的关键.7.A解析:A 【解析】 【分析】根据分式的基本性质即可求出答案. 【详解】 解:原式=22x y x yx y y x++-=--, 故选:A . 【点睛】本题考查分式的基本性质,解题的关键熟练运用分式的基本性质,本题属于基础题型.8.C解析:C 【解析】 【分析】根据题意分两种情况讨论:①当点C 在线段AB 上时,②当点C 在线段AB 的延长线上时,分别根据线段的和差求出AC 的长度即可. 【详解】解:当点C 在线段AB 上时,如图,∵AC=AB−BC , 又∵AB=5,BC=3, ∴AC=5−3=2;②当点C 在线段AB 的延长线上时,如图,∵AC=AB+BC , 又∵AB=5,BC=3, ∴AC=5+3=8. 综上可得:AC=2或8. 故选C . 【点睛】本题考查两点间的距离,解答本题的关键是明确题意,利用分类讨论的数学思想解答.9.C解析:C【分析】先求出不等式的解集,再在数轴上表示出来,找出符合条件的选项即可.【详解】移项得,x>2,在数轴上表示为:故选:C.【点睛】本题考查的是在数轴上表示一元一次不等式的解集,解答此类题目的关键是熟知实心圆点与空心圆点的区别.10.B解析:B【解析】【分析】把5xy=⎧⎨=⎩x=5代入方程x-2y=3可求得y的值,然后把x、y的值代入2x+y=口即可求得答案.【详解】把x=5代入x-2y=3,得5-2y=3,解得:y=1,即△表示的数为1,把x=5,y=1代入2x+y=口,得10+1=口, 所以口=11,故选B.【点睛】本题考查了二元一次方程组的解,熟知二元一次方程组的解满足方程组中每一个方程是解题的关键.11.A解析:A【解析】∵+5米表示一个物体向东运动5米,∴-3米表示向西走3米,故选A.12.C解析:C【解析】【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.【详解】解:3310000=3.31×106.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.13.C解析:C【解析】【分析】根据面动成体可得长方形ABCD绕CD边旋转所得的几何体.【详解】解:将长方形ABCD绕CD边旋转一周,得到的几何体是圆柱,故选:C.【点睛】此题考查了平面图形与立体图形的联系,培养学生的观察能力和空间想象能力.14.D解析:D【解析】【分析】方程两边同乘12即可得答案.【详解】方程212134x x-+=-两边同时乘12得:4(21)123(2)x x-=-+故选:D.【点睛】本题考查一元一次方程去分母,找出分母的最小公倍数是解题的关键,注意不要漏乘.15.A解析:A【解析】【分析】根据已知图形和空间想象能力,从上面看图形,根据看的图形选出即可.【详解】从上面看是水平方向排列的两列,上一列是二个小正方形,下一列是右侧一个正方形,故A符合题意,故选:A.【点睛】本题考查了简单组合体的三视图的应用,主要培养学生的观察能力和空间想象能力.二、填空题16.8【解析】【分析】根据从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)的三角形作答.【详解】设多边形有n条边,则n−2=6,解得n=8.故答案为8.【点解析:8【解析】【分析】根据从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)的三角形作答.【详解】设多边形有n条边,则n−2=6,解得n=8.故答案为8.【点睛】此题考查多边形的对角线,解题关键在于掌握计算公式.17.2【解析】解:mx2+5y2﹣2x2+3=(m﹣2)x2+5y2+3,∵代数式mx2+5y2﹣2x2+3的值与字母x的取值无关,则m﹣2=0,解得m=2.故答案为2.点睛:本题主要考查合并同类解析:2【解析】解:mx2+5y2﹣2x2+3=(m﹣2)x2+5y2+3,∵代数式mx2+5y2﹣2x2+3的值与字母x的取值无关,则m﹣2=0,解得m=2.故答案为2.点睛:本题主要考查合并同类项的法则.即系数相加作为系数,字母和字母的指数不变.与字母x的取值无关,即含字母x的系数为0.18.4【解析】【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.【详解】解:根据题意得:2n=2,m=3,解得:n=1,m=3,则解析:4【解析】【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程,求出n,m的值,再代入代数式计算即可.【详解】解:根据题意得:2n=2,m=3,解得:n=1,m=3,则m+n=4.故答案是:4.【点睛】本题考查了利用同类项的定义求字母的值,熟练掌握同类项的定义是解答本题的关键,所含字母相同,并且相同字母的指数也相同的项,叫做同类项,根据相同字母的指数相同列方程(或方程组)求解即可.19.【解析】【分析】进行度、分、秒的转化运算,注意以60为进制,即1°=60′,1′=60″.【详解】解:36.35°=36°+0.35×60′=36°21′.故答案为:36°21′.【点解析:3621'o【解析】【分析】进行度、分、秒的转化运算,注意以60为进制,即1°=60′,1′=60″.【详解】解:36.35°=36°+0.35×60′=36°21′.故答案为:36°21′.【点睛】本题主要考查了度分秒的换算,相对比较简单,注意以60为进制,熟记1°=60′,1′=60″.20.33【解析】【分析】根据题意中的对应关系,由斤重的西瓜卖元,列方程求出6斤重的西瓜的定价;再根据“一个斤重的西瓜定价为元”可得出(12+6)斤重西瓜的定价.【详解】解:设6斤重的西瓜卖x 元解析:33【解析】【分析】根据题意中的对应关系,由12斤重的西瓜卖21元,列方程求出6斤重的西瓜的定价;再根据“一个()a b +斤重的西瓜定价为 36ab A B ⎛++⎫ ⎪⎝⎭元”可得出(12+6)斤重西瓜的定价. 【详解】解:设6斤重的西瓜卖x 元,则(6+6)斤重的西瓜的定价为:363(21)6x x x =+++元, 又12斤重的西瓜卖21元,∴2x+1=21,解得x=10.故6斤重的西瓜卖10元.又18=6+12,∴(6+12)斤重的西瓜定价为:6121021=3336⨯++(元). 故答案为:33.【点睛】本题主要考查求代数式的值以及一元一次方程的应用,关键是理解题意,找出等量关系. 21.【解析】【分析】根据幂的乘方与积的乘方、单项式乘法的运算方法,即可解答【详解】【点睛】此题考查幂的乘方与积的乘方、单项式乘法,掌握运算法则是解题关键 解析:44a 56x -【解析】【分析】根据幂的乘方与积的乘方、单项式乘法的运算方法,即可解答【详解】()222a-=44a()23⋅-=5x x23-6x【点睛】此题考查幂的乘方与积的乘方、单项式乘法,掌握运算法则是解题关键22.【解析】【分析】根据绝对值的定义和性质求解可得.【详解】解:,,故答案为.【点睛】本题考查绝对值,解题的关键是熟练掌握绝对值的定义和性质.≥解析:a0【解析】【分析】根据绝对值的定义和性质求解可得.【详解】-=,解:a a∴≥,a0≥.故答案为a0【点睛】本题考查绝对值,解题的关键是熟练掌握绝对值的定义和性质.23.3【解析】【分析】先根据题意得出a的值,再代入原方程求出x的值即可.【详解】∵方程的解为x=6,∴3a+12=36,解得a=8,∴原方程可化为24-2x=6x,解得x=3.故答案为3解析:3【解析】【分析】先根据题意得出a的值,再代入原方程求出x的值即可.【详解】∵方程3232a xx+=的解为x=6,∴3a+12=36,解得a=8,∴原方程可化为24-2x=6x,解得x=3.故答案为3【点睛】本题考查的是一元一次方程的解,熟知解一元一次方程的基本步骤是解答此题的关键.24.1或-7【解析】【分析】设这个数为x,利用数轴上两点间的距离公式可得|x-(-3)|=4,解出x即可. 【详解】设这个数为x,由题意得|x-(-3)|=4,所以x+3=4或x+3=-4,解解析:1或-7【解析】【分析】设这个数为x,利用数轴上两点间的距离公式可得|x-(-3)|=4,解出x即可.【详解】设这个数为x,由题意得|x-(-3)|=4,所以x+3=4或x+3=-4,解得x=1或-7.【点睛】本题考查数轴的应用,使用两点间的距离公式列出方程是解题的关键.25.2×105【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数解析:2×105【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:将520000用科学记数法表示为5.2×105.故答案为:5.2×105.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.26.2【解析】【分析】从n边形的一个顶点出发有(n−3)条对角线,代入求出即可.【详解】解:从五边形的一个顶点出发有5﹣3=2条对角线,故答案为2.【点睛】本题考查了多边形的对角线,熟记解析:2【解析】【分析】从n边形的一个顶点出发有(n−3)条对角线,代入求出即可.【详解】解:从五边形的一个顶点出发有5﹣3=2条对角线,故答案为2.【点睛】本题考查了多边形的对角线,熟记知识点(从n边形的一个顶点出发有(n−3)条对角线)是解此题的关键.27.【解析】试题解析:∵42=16,∴4是16的算术平方根.考点:算术平方根.解析:【解析】试题解析:∵42=16,∴4是16的算术平方根.考点:算术平方根.28.(2019,-2)【解析】【分析】观察不难发现,点的横坐标等于运动的次数,纵坐标每4次为一个循环组循环,用2019除以4,余数是几则与第几次的纵坐标相同,然后求解即可.【详解】∵第1次运动解析:(2019,-2)【解析】【分析】观察不难发现,点的横坐标等于运动的次数,纵坐标每4次为一个循环组循环,用2019除以4,余数是几则与第几次的纵坐标相同,然后求解即可.【详解】∵第1次运动到点(1,1),第2次运动到点(2,0),第3次接着运动到点(3,-2),第4次运动到点(4,0),第5次运动到点(5,1)…,∴运动后点的横坐标等于运动的次数,第2019次运动后点P的横坐标为2019,纵坐标以1、0、-2、0每4次为一个循环组循环,∵2019÷4=504…3,∴第2019次运动后动点P的纵坐标是第504个循环组的第3次运动,与第3次运动的点的纵坐标相同,为-2,∴点P(2019,-2),故答案为:(2019,-2).【点睛】本题是对点的坐标的规律的考查,根据图形观察出点的横坐标与纵坐标的变化规律是解题的关键.29.140【解析】【分析】【详解】解:∵OD平分∠AOC,∴∠AOC=2∠AOD=40°,∴∠COB=180°﹣∠COA=140°故答案为:140解析:140【解析】【分析】【详解】解:∵OD平分∠AOC,∴∠AOC=2∠AOD=40°,∴∠COB=180°﹣∠COA=140°故答案为:14030.2【解析】根据定义可得:因为,所以,故答案为:2.解析:2【解析】根据定义可得:因为239=,所以3log 92=,故答案为:2.三、压轴题31.(1)①5;②OQ 平分∠AOC ,理由详见解析;(2)5秒或65秒时OC 平分∠POQ ;(3)t =703秒. 【解析】【分析】(1)①由∠AOC =30°得到∠BOC =150°,借助角平分线定义求出∠POC 度数,根据角的和差关系求出∠COQ 度数,再算出旋转角∠AOQ 度数,最后除以旋转速度3即可求出t 值;②根据∠AOQ 和∠COQ 度数比较判断即可;(2)根据旋转的速度和起始位置,可知∠AOQ =3t ,∠AOC =30°+6t ,根据角平分线定义可知∠COQ =45°,利用∠AOQ 、∠AOC 、∠COQ 角之间的关系构造方程求出时间t ; (3)先证明∠AOQ 与∠POB 互余,从而用t 表示出∠POB =90°﹣3t ,根据角平分线定义再用t 表示∠BOC 度数;同时旋转后∠AOC =30°+6t ,则根据互补关系表示出∠BOC 度数,同理再把∠BOC 度数用新的式子表达出来.先后两个关于∠BOC 的式子相等,构造方程求解.【详解】(1)①∵∠AOC =30°,∴∠BOC =180°﹣30°=150°,∵OP 平分∠BOC ,∴∠COP =12∠BOC =75°, ∴∠COQ =90°﹣75°=15°,∴∠AOQ =∠AOC ﹣∠COQ =30°﹣15°=15°,t =15÷3=5;②是,理由如下:∵∠COQ =15°,∠AOQ =15°,∴OQ 平分∠AOC ;(2)∵OC 平分∠POQ ,∴∠COQ =12∠POQ =45°. 设∠AOQ =3t ,∠AOC =30°+6t ,由∠AOC ﹣∠AOQ =45°,可得30+6t ﹣3t =45,解得:t =5,当30+6t ﹣3t =225,也符合条件,解得:t =65,∴5秒或65秒时,OC 平分∠POQ ;(3)设经过t 秒后OC 平分∠POB ,∵OC 平分∠POB ,∴∠BOC =12∠BOP , ∵∠AOQ +∠BOP =90°,∴∠BOP =90°﹣3t ,又∠BOC =180°﹣∠AOC =180°﹣30°﹣6t ,∴180﹣30﹣6t =12(90﹣3t ), 解得t =703. 【点睛】本题主要考查一元一次方程的应用,根据角度的和差倍分关系,列出方程,是解题的关键.32.(1)见详解;(2)2x --,53x +,47x +;(3)当运动时间为5秒或9秒时,PQ=2cm.【解析】【分析】(1)根据数轴的特点,所以可以求出点P ,Q 的位置;(2)根据向左移动用减法,向右移动用加法,即可得到答案;(3)根据题意,可分为两种情况进行分析:①点P 在点Q 的左边时;②点P 在点Q 的右边时;分别进行列式计算,即可得到答案.【详解】解:(1)如图所示:.(2)由(1)可知,点P 为2-,点Q 为5;∴移动后的点P 为:2x --;移动后的点Q 为:53x +;∴线段PQ 的长为:53(2)47x x x +---=+;(3)根据题意可知,当PQ=2cm 时可分为两种情况:①当点P 在点Q 的左边时,有(21)72t -=-,解得:5t =;②点P在点Q的右边时,有(21)72t-=+,解得:9t=;综上所述,当运动时间为5秒或9秒时,PQ=2cm.【点睛】本题要是把方程和数轴结合起来,既要根据条件列出方程,又要把握数轴的特点.解题的关键是熟练掌握数轴上的动点运动问题,注意分类讨论进行解题.33.(1)80°;(2)140°【解析】【分析】(1)根据角平分线的定义得∠BOM=12∠AOB,∠BON=12∠BOD,再根据角的和差得∠AOD=∠AOB+∠BOD,∠MON=∠BOM+∠BON,结合三式求解;(2)根据角平分线的定义∠MOC=12∠AOC,∠BON=12∠BOD,再根据角的和差得∠AOD=∠AOC+∠BOD-∠BOC,∠MON=∠MOC+∠BON-∠BOC结合三式求解.【详解】解:(1)∵OM平分∠AOB,ON平分∠BOD,∴∠BOM=12∠AOB,∠BON=12∠BOD,∴∠MON=∠BOM+∠BON=12∠AOB+12∠BOD=12(∠AOB+∠BOD).∵∠AOD=∠AOB+∠BOD=α=160°,∴∠MON=12×160°=80°;(2)∵OM平分∠AOC,ON平分∠BOD,∴∠MOC=12∠AOC,∠BON=12∠BOD,∵∠MON=∠MOC+∠BON-∠BOC,∴∠MON=12∠AOC+12∠BOD -∠BOC=12(∠AOC+∠BOD )-∠BOC.∵∠AOD=∠AOB+∠BOD,∠AOC=∠AOB+∠BOC,∴∠MON=12(∠AOB+∠BOC+∠BOD )-∠BOC=12(∠AOD+∠BOC )-∠BOC,∵∠AOD=α,∠MON=60°,∠BOC=20°,∴60°=12(α+20°)-20°,∴α=140°.【点睛】本题考查了角的和差计算,角平分线的定义,明确角之间的关系是解答此题的关键.34.(1)11n n 1-+,n n 1+(2)①()()n 1n 2m 3++②75364 【解析】【分析】 ()1观察发现:先根据题中所给出的列子进行猜想,写出猜想结果即可;根据第一空中的猜想计算出结果;()2①由16a 2m m 3==,212a 4m m 3==,320a m 3=,430a 10m m 3==,找规律可得结论;②由()()n 1n 2m 22713173++=⨯⨯⨯⨯知()()m n 1n 22237131775152++=⨯⨯⨯⨯⨯=⨯⨯,据此可得m 7=,n 50=,再进一步求解可得.【详解】()1观察发现:()111n n 1n n 1=-++; ()1111122334n n 1+++⋯+⨯⨯⨯+, 1111111122334n n 1=-+-+-+⋯+-+, 11n 1=-+, n 11n 1+-=+, n n 1=+; 故答案为11n n 1-+,n n 1+. ()2拓展应用16a 2m m 3①==,212a 4m m 3==,320a m 3=,430a 10m m 3==, ⋯⋯()()n n 1n 2a m 3++∴=,故答案为()()n 1n 2m.3++ ()()n n 1n 2a m 61883②++==,且m 为质数, 对6188分解质因数可知61882271317=⨯⨯⨯⨯,()()n 1n 2m 22713173++∴=⨯⨯⨯⨯, ()()m n 1n 22237131775152∴++=⨯⨯⨯⨯⨯=⨯⨯,m 7∴=,n 50=,()()n 7a n 1n 23∴=++, ()()n 131a 7n 1n 2=⋅++, 123n1111a a a a ∴+++⋯+ ()()33336m 12m 20m n 1n 2m =+++⋯+++()()311172334n 1n 2⎡⎤=++⋯+⎢⎥⨯⨯++⎢⎥⎣⎦31131172n 27252⎛⎫⎛⎫=-=- ⎪ ⎪+⎝⎭⎝⎭ 75364=. 【点睛】 本题主要考查数字的变化规律,解题的关键是掌握并熟练运用所得规律:()111n n 1n n 1=-++. 35.(1)详见解析;(2)35;(3)﹣5、15、1123、﹣767. 【解析】【分析】(1)根据尺规作图的方法按要求做出即可;(2)根据中点的定义及线段长度的计算求出;(3)认真分析甲、乙物体运行的轨迹来判断它们相遇的可能性,分情况建立一元一次方程来计算相遇的时间,然后计算出位置.【详解】解:(1)如图所示;(2)根据(1)所作图的条件,如果以点A为原点,若点B对应的数恰好为10,则有点C对应的数为30,点D对应的数为﹣30,MN=|20﹣(﹣15)|=35(3)设乙从M点第一次回到点N时所用时间为t,则t=223522MN⨯==35(秒)那么甲在总的时间t内所运动的长度为s=5t=5×35=175可见,在乙运动的时间内,甲在C,D之间运动的情况为175÷60=2……55,也就是说甲在C,D之间运动一个来回还多出55长度单位.①设甲乙第一次相遇时的时间为t1,有5t1=2t1+15,t1=5(秒)而﹣30+5×5=﹣5,﹣15+2×5=﹣5这时甲和乙所对应的有理数为﹣5.②设甲乙第二次相遇时的时间经过的时间t2,有5t2+2t2=25+30+5+10,t2=10(秒)此时甲的位置:﹣15×5+60+30=15,乙的位置15×2﹣15=15这时甲和乙所对应的有理数为15.③设甲乙第三次相遇时的时间经过的时间t3,有5t3﹣2t3=20,t3=203(秒)此时甲的位置:30﹣(5×203﹣15)=1123,乙的位置:20﹣(2×203﹣5)=1123这时甲和乙所对应的有理数为112 3④从时间和甲运行的轨迹来看,他们可能第四次相遇.设第四次相遇时经过的时间为t4,有5t4﹣1123﹣30﹣15+2t4=1123,t4=91621(秒)此时甲的位置:5×91621﹣45﹣1123=﹣767,乙的位置:1123﹣2×91621=﹣767这时甲和乙所对应的有理数为﹣767.四次相遇所用时间为:5+10+203+91621=3137(秒),剩余运行时间为:35﹣3137=347(秒)当时间为35秒时,乙回到N点停止,甲在剩余的时间运行距离为5×347=5257⨯=1767.。
河北省保定市2019届数学七上期末试卷

河北省保定市2019届数学七上期末试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题1.下列说法,正确的是()A.若ac=bc,则a=bB.钟表上的时间是9点40分,此时时针与分针所成的夹角是50°C.一个圆被三条半径分成面积比2:3:4的三个扇形,则最小扇形的圆心角为90°D.30.15°=30°15′2.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )A.的B.中C.国D.梦3.如图所示,将一张长方形纸的一角斜折过去,使顶点A落在点A′处,BC为折痕,如果BD为∠A′BE 的平分线,则∠CBD等于( )A.80°B.90°C.100°D.70°4.如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以个单位长度/秒的速度绕正方形作逆时针运动,则它们第2017次相遇在()A.点AB.点BC.点CD.点D5.| x-2 |+3=4,下列说法正确的是( )A.解为3 B.解为1 C.其解为1或3 D.以上答案都不对6.学友书店推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元,但不超过200元,一律打9折;③一次性购书超过200元,一律打8折.如果小明同学一次性购书付款162元,那么他所购书的原价为( )A .180元B .202.5元C .180元或202.5元D .180元或200元7.下列计算正确的是( )A .4a ﹣2a =2B .2x 2+2x 2=4x 4C .﹣2x 2y ﹣3yx 2=﹣5x 2yD .2a 2b ﹣3a 2b =a 2b 8.我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在()(n a b n +为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按a 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则2019(1)x +展开式中含2018x 项的系数是( )A.2016B.2017C.2018D.2019 9.下列计算正确的是( ) A .x 2﹣2xy 2=﹣x 2yB .2a ﹣3b =﹣abC .a 2+a 3=a 5D .﹣3ab ﹣3ab =﹣6ab 10.若与互为相反数,则的值为( )A .-bB .C .-8D .811.1﹣2+3﹣4+5﹣6+…+2017﹣2018的结果不可能是( ) A.奇数 B.偶数 C.负数D.整数 12.a ,b ,c 三个数在数轴上的位置如图所示,则这三个数中绝对值最大的是( )A.aB.bC.cD.无法确定二、填空题13.111.已知∠1与∠2互余,∠2与∠3互补,若∠1=63°,则∠3=_____.14.已知线段AB=8cm ,在直线AB 上画线段BC ,使它等于3cm ,则线段AC=▲ cm .15.某超市在“五一”活动期间,推出如下购物优惠方案:①一次性购物在100元(不含100元)以内,不享受优惠; ②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠.小敏在该超市两次购物分别付款70元和288元,如果小敏把这两次购物改为一次性购物,则应付款_____元.16.如果x =23是关于x 的方程3x ﹣2m =4的解,则m 的值是_____. 17.23m x y -与35n x y 是同类项,则m n += 。
河北省保定市定州市2018-2019学年七年级(上)期末数学试卷 含解析
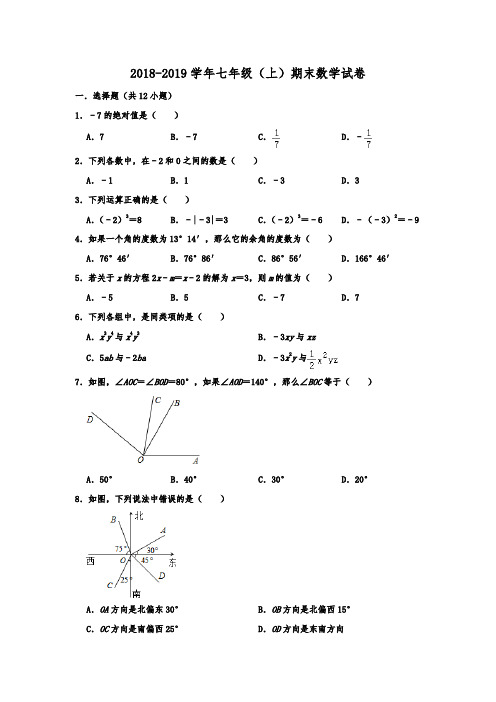
2018-2019学年七年级(上)期末数学试卷一.选择题(共12小题)1.﹣7的绝对值是()A.7 B.﹣7 C.D.﹣2.下列各数中,在﹣2和0之间的数是()A.﹣1 B.1 C.﹣3 D.33.下列运算正确的是()A.(﹣2)3=8 B.﹣|﹣3|=3 C.(﹣2)3=﹣6 D.﹣(﹣3)2=﹣9 4.如果一个角的度数为13°14′,那么它的余角的度数为()A.76°46′B.76°86′C.86°56′D.166°46′5.若关于x的方程2x﹣m=x﹣2的解为x=3,则m的值为()A.﹣5 B.5 C.﹣7 D.76.下列各组中,是同类项的是()A.x3y4与x4y3B.﹣3xy与xzC.5ab与﹣2ba D.﹣3x2y与7.如图,∠AOC=∠BOD=80°,如果∠AOD=140°,那么∠BOC等于()A.50°B.40°C.30°D.20°8.如图,下列说法中错误的是()A.OA方向是北偏东30°B.OB方向是北偏西15°C.OC方向是南偏西25°D.OD方向是东南方向9.已知a﹣2b=3,则3(a﹣b)﹣(a+b)的值为()A.3 B.6 C.﹣3 D.﹣610.如果线段AB=5cm,BC=4cm,且A、B、C在同一条直线上,那么A、C两点的距离是()A.1cm B.9cmC.1cm或9cm D.以上答案都不正确11.小明在文具用品商店买了3件甲种文具和2件乙种文具,一共花了23元,已知甲种文具比乙种文具单价少1元,如果设乙种文具单价为x元/件,那么下面所列方程正确的是()A.3(x﹣1)+2x=23 B.3x+2(x﹣1)=23C.3(x+1)+2x=23 D.3x+2(x+1)=2312.如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…则第8个图形中花盆的个数为()A.56 B.64 C.72 D.90二.填空题(共6小题)13.若式子3a﹣7与5﹣a的值互为相反数,则a的值为.14.我国高速公路发展迅速,据报道,到目前为止,全国高速公路总里程约为118000千米,用科学记数法表示为千米.15.如图,该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字是.16.如图所示,用含a、b字母的代数式表示图中阴影部分的面积为.17.某中学进行义务劳动,去甲处劳动的有30人,去乙处的有24人,从乙处调一部分人到甲处,使甲处的人数是乙处人数的2倍.若设从乙处调x人到甲处,则所列方程为.18.按下列程序输入一个数x,若输入的数x=0,则输出结果为.三.解答题(共8小题)19.计算题.(1)(﹣6)÷2×(﹣)(2)9+5×(﹣3)﹣(﹣2)2÷4(3)﹣14﹣(1﹣0.5)÷×[(﹣2)3﹣4]20.(1)化简x2﹣(2x2﹣4y)+2(x2﹣y);(2)先化简,再求值:(3x2﹣xy+y)﹣2(5xy﹣4x2+y),其中x=﹣2,y=.21.解方程(1)3(2x﹣1)=4x+3;(2).22.如图,平面上有射线AP和点B、点C,按下列语句要求画图:(1)连接AB;(2)用尺规在射线AP上截取AD=AB;(3)连接BC,并延长BC到E,使CE=BC;(4)连接DE.23.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON 的度数?24.有20袋胡萝卜,以每袋25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:与标准质量的差值(千克)﹣3 ﹣2 ﹣1.5 0 1 2.5袋数 1 8 2 3 2 4 (1)20袋胡萝卜中,最重的一袋比最轻的一袋重多少千克?(2)与标准重量比较,20袋胡萝卜总计超过或不足多少千克?(3)若胡萝卜每千克售价2.8元,则出售这20袋胡萝卜可卖多少元?25.某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:(1)如果购买乒乓球x(x不小于5)盒,则在甲店购买需付款元,在乙店购买需付款元.(用x的代数式表示)(2)当购买乒乓球多少盒时,在两店购买付款一样?(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?26.如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C 一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?参考答案与试题解析一.选择题(共12小题)1.﹣7的绝对值是()A.7 B.﹣7 C.D.﹣【分析】根据绝对值的性质解答,当a是负有理数时,a的绝对值是它的相反数﹣a.【解答】解:|﹣7|=7.故选:A.2.下列各数中,在﹣2和0之间的数是()A.﹣1 B.1 C.﹣3 D.3【分析】根据有理数的大小比较法则比较即可.【解答】解:A、﹣2<﹣1<0,故本选项正确;B、1>0,1不在﹣2和0之间,故本选项错误;C、﹣3<﹣2,﹣3不在﹣2和0之间,故本选项错误;D、3>0,3不在﹣2和0之间,故本选项错误;故选:A.3.下列运算正确的是()A.(﹣2)3=8 B.﹣|﹣3|=3 C.(﹣2)3=﹣6 D.﹣(﹣3)2=﹣9 【分析】根据乘方运算、绝对值及相反数的意义,逐个运算得结论.【解答】解:(﹣2)3=﹣8,故选项A、C错误;﹣|﹣3|=﹣3,故选项B错误;﹣(﹣3)2=﹣9,故选项D正确.故选:D.4.如果一个角的度数为13°14′,那么它的余角的度数为()A.76°46′B.76°86′C.86°56′D.166°46′【分析】本题考查角互余的概念:和为90度的两个角互为余角.【解答】解:根据定义的13°14′余角度数是90°﹣13°14′=76°46′.故选:A.5.若关于x的方程2x﹣m=x﹣2的解为x=3,则m的值为()A.﹣5 B.5 C.﹣7 D.7【分析】把x的值代入方程计算即可求出m的值.【解答】解:把x=3代入方程得:6﹣m=3﹣2,解得:m=5,故选:B.6.下列各组中,是同类项的是()A.x3y4与x4y3B.﹣3xy与xzC.5ab与﹣2ba D.﹣3x2y与【分析】根据同类项的定义逐个判断即可.【解答】解:A、不是同类项,故本选项错误;B、不是同类项,故本选项错误;C、是同类项,故本选项正确;D、不是同类项,故本选项错误;故选:C.7.如图,∠AOC=∠BOD=80°,如果∠AOD=140°,那么∠BOC等于()A.50°B.40°C.30°D.20°【分析】先求出∠COD的度数,然后根据∠BOC=∠BOD﹣∠COD,即可得出答案.【解答】解:∵∠AOC=80°,∠AOD=140°,∴∠COD=∠AOD﹣∠AOC=60°,∵∠BOD=80°,∴∠BOC=∠BOD﹣∠COD=80°﹣60°=20°.故选:D.8.如图,下列说法中错误的是()A.OA方向是北偏东30°B.OB方向是北偏西15°C.OC方向是南偏西25°D.OD方向是东南方向【分析】方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)多少度.根据定义就可以解决.【解答】解:A、OA方向是北偏东60°,此选项错误;B、OB方向是北偏西15°,此选项正确;C、OC方向是南偏西25°,此选项正确;D、OD方向是东南方向,此选项正确.错误的只有A.故选:A.9.已知a﹣2b=3,则3(a﹣b)﹣(a+b)的值为()A.3 B.6 C.﹣3 D.﹣6【分析】原式去括号合并整理后,将已知等式代入计算即可求出值.【解答】解:∵a﹣2b=3,∴原式=3a﹣3b﹣a﹣b=2a﹣4b=2(a﹣2b)=6,故选:B.10.如果线段AB=5cm,BC=4cm,且A、B、C在同一条直线上,那么A、C两点的距离是()A.1cm B.9cmC.1cm或9cm D.以上答案都不正确【分析】本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据正确画出的图形解题.当点C在AB之间时,AC=AB﹣BC;当点C在点B 的右侧时,AC=AB+BC.【解答】解:当点C在AB之间时,AC=AB﹣BC=5﹣4=1(cm);当点C在点B的右侧时,AC=AB+BC=5+4=9(cm).11.小明在文具用品商店买了3件甲种文具和2件乙种文具,一共花了23元,已知甲种文具比乙种文具单价少1元,如果设乙种文具单价为x元/件,那么下面所列方程正确的是()A.3(x﹣1)+2x=23 B.3x+2(x﹣1)=23C.3(x+1)+2x=23 D.3x+2(x+1)=23【分析】设乙种文具单价为x元/件,则甲种文具的单价为(x﹣1)元/件,根据“3件甲种文具和2件乙种文具,一共花了23元”列出方程即可得.【解答】解:设乙种文具单价为x元/件,则甲种文具的单价为(x﹣1)元/件,根据题意可得:3(x﹣1)+2x=23,故选:A.12.如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…则第8个图形中花盆的个数为()A.56 B.64 C.72 D.90【分析】由题意可知,三角形每条边上有3盆花,共计3×3﹣3盆花,正四边形每条边上有4盆花,共计4×4﹣4盆花,正五边形每条边上有5盆花,共计5×5﹣5盆花,…则正n变形每条边上有n盆花,共计n×n﹣n盆花,结合图形的个数解决问题.【解答】解:∵第一个图形:三角形每条边上有3盆花,共计32﹣3盆花,第二个图形:正四边形每条边上有4盆花,共计42﹣4盆花,第三个图形:正五边形每条边上有5盆花,共计52﹣5盆花,…第n个图形:正n+2边形每条边上有n盆花,共计(n+2)2﹣(n+2)盆花,则第8个图形中花盆的个数为(8+2)2﹣(8+2)=90盆.二.填空题(共6小题)13.若式子3a﹣7与5﹣a的值互为相反数,则a的值为 1 .【分析】利用互为相反数两数之和为0列出方程,求出方程的解即可得到a的值.【解答】解:根据题意得:3a﹣7+5﹣a=0,移项合并得:2a=2,解得:a=1.故答案为:114.我国高速公路发展迅速,据报道,到目前为止,全国高速公路总里程约为118000千米,用科学记数法表示为 1.18×105千米.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将118000用科学记数法表示为:1.18×105.故答案为:1.18×105.15.如图,该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字是着.【分析】正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答.【解答】解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以与“静”字相对的字是着.16.如图所示,用含a、b字母的代数式表示图中阴影部分的面积为.【分析】根据题意和图形可以用相应的代数式表示出阴影部分的面积.【解答】解:由图可得,阴影部分的面积是:(a+b)a﹣=,故答案为:.17.某中学进行义务劳动,去甲处劳动的有30人,去乙处的有24人,从乙处调一部分人到甲处,使甲处的人数是乙处人数的2倍.若设从乙处调x人到甲处,则所列方程为30+x =2(24﹣x).【分析】首先要根据题意找出存在的等量关系:2×(乙处原来的人数﹣调走的人数)=甲处原来的人数+调入的人数,根据此等量关系列出方程即可.【解答】解:设从乙处调x人到甲处,则甲处人数为(30+x)人,乙处人数为(24﹣x)人.由题意得30+x=2(24﹣x).故答案为:30+x=2(24﹣x).18.按下列程序输入一个数x,若输入的数x=0,则输出结果为 4 .【分析】根据运算程序算出第一、二次运算结果,由第二次运算结果为4>0即可得出结论.【解答】解:∵0×(﹣2)﹣4=﹣4,∴第一次运算结果为﹣4;∵(﹣4)×(﹣2)﹣4=4,∴第二次运算结果为4;∵4>0,∴输出结果为4.故答案为:4.三.解答题(共8小题)19.计算题.(1)(﹣6)÷2×(﹣)(2)9+5×(﹣3)﹣(﹣2)2÷4(3)﹣14﹣(1﹣0.5)÷×[(﹣2)3﹣4]【分析】(1)直接利用有理数的混合运算法则计算得出答案;(2)直接利用有理数的混合运算法则计算得出答案;(3)直接利用有理数的混合运算法则计算得出答案.【解答】解:(1)(﹣6)÷2×(﹣)=﹣3×(﹣)=;(2)9+5×(﹣3)﹣(﹣2)2÷4=9﹣15﹣1=﹣7;(3)﹣14﹣(1﹣0.5)÷×[(﹣2)3﹣4]=﹣1﹣×(﹣12)=﹣1+18=17.20.(1)化简x2﹣(2x2﹣4y)+2(x2﹣y);(2)先化简,再求值:(3x2﹣xy+y)﹣2(5xy﹣4x2+y),其中x=﹣2,y=.【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.【解答】解:(1)原式=x2﹣2x2+4y+2x2﹣2y=x2+2y;(2)原式=3x2﹣xy+y﹣10xy+8x2﹣2y=11x2﹣11xy﹣y,当x=﹣2,y=时,原式=44+﹣=51.21.解方程(1)3(2x﹣1)=4x+3;(2).【分析】(1)通过去括号、移项、合并同类项、系数化成1即可求解.(2)首先去分母,然后去括号、移项、合并同类项、系数化成1即可求解.【解答】(1)解:去括号,得6x﹣3=4x+3.移项、合并同类项,得 2 x=6.系数化为1,得x=3.(2)去分母,得3(x﹣3)﹣15=5(x﹣4).去括号,得3x﹣9﹣15=5x﹣20.移项、合并同类项,得﹣2x=4.系数化为1,得x=﹣2.22.如图,平面上有射线AP和点B、点C,按下列语句要求画图:(1)连接AB;(2)用尺规在射线AP上截取AD=AB;(3)连接BC,并延长BC到E,使CE=BC;(4)连接DE.【分析】(1)根据要求画出射线及直线即可;(2)射线AP上截取线段AD=AB即可;(3)延长线部分画虚线;(4)连接两点D、E.【解答】解:如图所示:(1)连接AB;(2)用尺规在射线AP上截取AD=AB;(3)连接BC,并延长BC到E,使CE=BC;(4)连接DE.23.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON 的度数?【分析】先根据角平分线定义得:∠AOM =×120°=60°,同理得:∠CON =∠BOC ==15°,最后利用角的差可得结论.【解答】解:∵∠AOB=90°,∠BOC=30°,∴∠AOC=90°+30°=120°,∵OM平分∠AOC,∴∠AOM =∠AOC =×120°=60°,∵ON平分∠BOC,∴∠CON =∠BOC ==15°,∴∠MON=∠AOC﹣∠AOM﹣∠CON=120°﹣60°﹣15°=45°.24.有20袋胡萝卜,以每袋25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:﹣3 ﹣2 ﹣1.5 0 1 2.5 与标准质量的差值(千克)袋数 1 8 2 3 2 4(1)20袋胡萝卜中,最重的一袋比最轻的一袋重多少千克?(2)与标准重量比较,20袋胡萝卜总计超过或不足多少千克?(3)若胡萝卜每千克售价2.8元,则出售这20袋胡萝卜可卖多少元?【分析】(1)最重的比最轻的多2.5﹣(﹣3)=5.5kg;(2)将表格中所有数相加,)﹣3×1+(﹣2)×8+(﹣1.5)×2+1×2+2.5×4=﹣10kg;(3)求出总的重量再乘以单价,即2.8×(25×20﹣10)=1372元.【解答】解:(1)最重的比最轻的多2.5﹣(﹣3)=5.5kg;(2)﹣3×1+(﹣2)×8+(﹣1.5)×2+1×2+2.5×4=﹣10kg,∴20袋胡萝卜总计不足10kg;(3)2.8×(25×20﹣10)=1372元,∴出售这20袋胡萝卜可卖1372元.25.某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:(1)如果购买乒乓球x(x不小于5)盒,则在甲店购买需付款(5x+125)元,在乙店购买需付款(4.5x+135)元.(用x的代数式表示)(2)当购买乒乓球多少盒时,在两店购买付款一样?(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?【分析】(1)根据实际付款数得到甲店购买需付款为=5(x﹣5)+30×5,乙店购买需付款为(5x+30×5)×0.9;(2)令甲乙的付款数相等得到5x+125=4.5x+135,然后解方程;(3)令甲乙的付款数都为450,然后解方程5x+125=450和4.5x+135=450,根据x的大小进行判断.【解答】解:(1)甲店购买需付款为=5(x﹣5)+30×5=(5x+125)元,乙店购买需付款为(5x+30×5)×0.9=(4.5x+135)元.故答案为(5x+125),(4.5x+135);(2)由(1)知:5x+125=4.5x+135,得x=20.答:当购买乒乓球20盒时,在两店购买付款一样;(3)去乙店购买.由5x+125=450,得x=65;由4.5x+135=450,得x=70所以去乙店购买.26.如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C 一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?【分析】(1)设点A的速度为每秒t个单位,则点B的速度为每秒4t个单位,由甲的路程+乙的路程=总路程建立方程求出其解即可;(2)设x秒时原点恰好在A、B的中间,根据两点离原点的距离相等建立方程求出其解即可;(3)先根据追击问题求出A、B相遇的时间就可以求出C行驶的路程.【解答】解:(1)设点A的速度为每秒t个单位,则点B的速度为每秒4t个单位,由题意,得3t+3×4t=15,解得:t=1,∴点A的速度为每秒1个单位长度,则点B的速度为每秒4个单位长度.如图:(2)设x秒时原点恰好在A、B的中间,由题意,得3+x=12﹣4x,解得:x=1.8.∴A、B运动1.8秒时,原点就在点A、点B的中间;(3)由题意,得B追上A的时间为:15÷(4﹣1)=5,∴C行驶的路程为:5×20=100单位长度.。
河北省保定市定州市2018-2019学年七年级(上)期末数学试卷

2018-2019学年七年级(上)期末数学试卷一.选择题(共12小题)1.﹣7的绝对值是()A.7 B.﹣7 C.D.﹣2.下列各数中,在﹣2和0之间的数是()A.﹣1 B.1 C.﹣3 D.33.下列运算正确的是()A.(﹣2)3=8 B.﹣|﹣3|=3 C.(﹣2)3=﹣6 D.﹣(﹣3)2=﹣9 4.如果一个角的度数为13°14′,那么它的余角的度数为()A.76°46′B.76°86′C.86°56′D.166°46′5.若关于x的方程2x﹣m=x﹣2的解为x=3,则m的值为()A.﹣5 B.5 C.﹣7 D.76.下列各组中,是同类项的是()A.x3y4与x4y3B.﹣3xy与xzC.5ab与﹣2ba D.﹣3x2y与7.如图,∠AOC=∠BOD=80°,如果∠AOD=140°,那么∠BOC等于()A.50°B.40°C.30°D.20°8.如图,下列说法中错误的是()A.OA方向是北偏东30°B.OB方向是北偏西15°C.OC方向是南偏西25°D.OD方向是东南方向9.已知a﹣2b=3,则3(a﹣b)﹣(a+b)的值为()A.3 B.6 C.﹣3 D.﹣610.如果线段AB=5cm,BC=4cm,且A、B、C在同一条直线上,那么A、C两点的距离是()A.1cm B.9cmC.1cm或9cm D.以上答案都不正确11.小明在文具用品商店买了3件甲种文具和2件乙种文具,一共花了23元,已知甲种文具比乙种文具单价少1元,如果设乙种文具单价为x元/件,那么下面所列方程正确的是()A.3(x﹣1)+2x=23 B.3x+2(x﹣1)=23C.3(x+1)+2x=23 D.3x+2(x+1)=2312.如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…则第8个图形中花盆的个数为()A.56 B.64 C.72 D.90二.填空题(共6小题)13.若式子3a﹣7与5﹣a的值互为相反数,则a的值为.14.我国高速公路发展迅速,据报道,到目前为止,全国高速公路总里程约为118000千米,用科学记数法表示为千米.15.如图,该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字是.16.如图所示,用含a、b字母的代数式表示图中阴影部分的面积为.17.某中学进行义务劳动,去甲处劳动的有30人,去乙处的有24人,从乙处调一部分人到甲处,使甲处的人数是乙处人数的2倍.若设从乙处调x人到甲处,则所列方程为.18.按下列程序输入一个数x,若输入的数x=0,则输出结果为.三.解答题(共8小题)19.计算题.(1)(﹣6)÷2×(﹣)(2)9+5×(﹣3)﹣(﹣2)2÷4(3)﹣14﹣(1﹣0.5)÷×[(﹣2)3﹣4]20.(1)化简x2﹣(2x2﹣4y)+2(x2﹣y);(2)先化简,再求值:(3x2﹣xy+y)﹣2(5xy﹣4x2+y),其中x=﹣2,y=.21.解方程(1)3(2x﹣1)=4x+3;(2).22.如图,平面上有射线AP和点B、点C,按下列语句要求画图:(1)连接AB;(2)用尺规在射线AP上截取AD=AB;(3)连接BC,并延长BC到E,使CE=BC;(4)连接DE.23.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数?24.有20袋胡萝卜,以每袋25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下: 与标准质量的差值(千克)﹣3 ﹣2 ﹣1.5 0 1 2.5袋数 1 8 2 3 2 4 (1)20袋胡萝卜中,最重的一袋比最轻的一袋重多少千克?(2)与标准重量比较,20袋胡萝卜总计超过或不足多少千克?(3)若胡萝卜每千克售价2.8元,则出售这20袋胡萝卜可卖多少元?25.某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:(1)如果购买乒乓球x (x 不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元.(用x 的代数式表示)(2)当购买乒乓球多少盒时,在两店购买付款一样?(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?26.如图,点A 从原点出发沿数轴向左运动,同时,点B 也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B 的速度是点A 的速度的4倍(速度单位:单位长度/秒).(1)求出点A 、点B 运动的速度,并在数轴上标出A 、B 两点从原点出发运动3秒时的位置;(2)若A 、B 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A 、点B 的正中间?(3)若A 、B 两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C 同时从B 点位置出发向A 点运动,当遇到A 点后,立即返回向B 点运动,遇到B 点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?。
2018-2019学年河北省保定市定州市七年级(上)期末数学试卷

8.下列方程的变形,符合等式的性质的是( )
A.由 ,得 B.由 ,得
C.由 ,得 D.由 ,得
9.如图,M,N是数轴上的两点,它们分别表示-4和2,P为数轴上另一点,PM=2PN,则点P表示的数是( )
A.1B.0C.8D.0或8
10.小明在解方程时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2y﹣ = y﹣■怎么办呢?小明想了一想,便翻了书后的答案,此方程的解为y=﹣ ,很快补好了这个常数,你能补出这个常数吗?它应是( )
第II卷(非选择题)分
二、填空题
13.若2x+1是﹣9的相反数,则x=______.
14.32.48°×2=__________度__________分__________秒.
15.一个两位数,个位数字是a,十位数字比个位数字大2,则这个两位数是_____.
16.如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是______度.
17.某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜______场比赛.
18.如图,在每个“〇”中填入一个整数,使得其中任意四个相邻“〇”中所填整数之和都相等,可得 的值为.
1.-3的倒数是( )
A.3B. C. D.
2.在-3,-1,1,3四个数中,比-2小的数是( )
A. B. C.1D.3
3.由四舍五入得到的近似数2.6万,精确到( )
A.千位B.万位C.个位D.十分位
4.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
保定市定州市七年级上册期末数学试卷(有答案)

2019-2020学年河北省保定市定州市七年级(上)期末数学试卷一、选择题(本大题共12小题,共36.0分)1. -3的倒数是( ) A. 3 B. −3 C. −13 D. 132. 在-3,-1,1,3四个数中,比-2小的数是( )A. −3B. −1C. 1D. 33. 由四舍五入得到的近似数2.6万,精确到( )A. 千位B. 万位C. 个位D. 十分位4. 2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )A. 9.18×104B. 9.18×105C. 9.18×106D. 9.18×1075. 在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是( )A. 正方体B. 长方体C. 球D. 圆锥6. 借助常用的直角三角尺,能画出一些度数的角,下列选项中不能画出角的是( )A. 15∘B. 100∘C. 165∘D. 135∘7. 下列判断正确的是( )A. 3a 2b 与ba 2不是同类项B. m 2n5不是整式C. 单项式−x 3y 2的系数是−1D. 3x 2−y +5xy 2是二次三项式 8. 下列方程的变形,符合等式的性质的是( )A. 由2x −3=1,得2x =1−3B. 由−2x =1,得x =−2C. 由8−x =x −5,得−x −x =−5−8D. 由2(x −3)=1,得2x −3=19. 如图,M ,N 是数轴上的两点,它们分别表示-4和2,P 为数轴上另一点,PM =2PN ,则点P 表示的数是( )A. 1B. 0C. 8D. 0或8 10. 小明在解方程时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2y -12=12y -■怎么办呢?小明想了一想,便翻了书后的答案,此方程的解为y =-53,很快补好了这个常数,你能补出这个常数吗?它应是( )A. 1B. 2C. 3D. 411. 已知a -b =-3,c +d =2,则(b +c )-(a -d )的值为( )A. 1B. 5C. −5D. −112. 某项工程甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲、乙合作完成此项工程,若设甲一共做了x 天,则所列方程为( )A. x 4+x+16=1B. x 4+x−16=1C. x+14+x 6=1D. x 4+14+x−16=1 二、填空题(本大题共6小题,共18.0分)13. 若2x +1是-9的相反数,则x =______.14. 32.48°×2=______度______分______秒. 15. 一个两位数,个位数字是a ,十位数字比个位数字大2,则这个两位数是______.16. 如图所示,两块三角板的直角顶点O 重叠在一起,且OB 恰好平分17. 某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜______场比赛.18. 如图,在每个“〇”中填入一个整数,使得其中任意四个相邻“〇”中所填整数之和都相等,可得d 的值为______.三、计算题(本大题共3小题,共25.0分)19. 计算题.(1)-6+3.6+4-5.6(2)42×(-23)÷72-(-12)÷(-4) (3)-12018+24÷(-2)3-32×(13)220. (1)计算:-3(2a 2-2ab )+4(a 2+ab -6) (2)化简求值:12(x 2y -13xy 2)+5(xy 2-x 2y )-2x 2y ,其中x =15,y =-5.21. 解方程(1)3x -7(x -1)=3-2(x +3)(2)1−x 2=4x−13-1四、解答题(本大题共5小题,共41.0分)22. 定义新运算:对于任意有理数a 、b ,都有a ⊕b =a (a -b )+1,等式的右边是通常的有理数运算,例如2⊕5=2(2-5)+1=2×(-3)+1.(1)求(-2)⊕3.(2)若3⊕x =-5,求x 的值.23.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE∠EOC,∠DOE=70°,求∠EOC的度数.在∠BOC内,∠BOE=1224.入冬以来,某家电销售部以150元/台的价格购进一款烤火器,很快售完,又用相同的货款再次购进这款烤火器,因单价提高了30元,进货量比第一次少了10台.(1)家电销售部两次各购进烤火器多少台?(2)若以250元/台的售价卖完这两批烤火器,家电销售部共获利多少元?25.如图是2015年12月月历.(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是______,______,______.(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2=______.(3)当(1)中被框住的4个数之和等于76时,x的值为多少?(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.26.已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是______;(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.答案和解析1.【答案】C【解析】解:-3的倒数是-.故选:C.根据倒数的定义即可得出答案.此题主要考查了倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.【答案】A【解析】解:∵|-3|=3,|-2|=2,∴比-2小的数是:-3.故选:A.利用两个负数,绝对值大的其值反而小,进而得出答案.此题主要考查了有理数比较大小,正确把握两负数比较大小的方法是解题关键.3.【答案】A【解析】解:近似数2.6万精确到千位.故选:A.近似数2.6万精确到0.1万位.本题考查了近似数和有效数字:经过四舍五入得到的数称为近似数;从一个近似数左边第一个不为0的数数起到这个数完,所以这些数字都叫这个近似数的有效数字.4.【答案】C【解析】解:将9180 000用科学记数法表示为:9.18×106.故选:C.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】B【解析】解:A、从左面看与从正面看都是正方形,即得到的平面图形相同;B、从左面看是小长方形,从正面看大长方形,得到的平面图形不相同;C、从左面看与从正面看都是圆,即得到的平面图形相同;D、从左面看与从正面看都是三角形,即得到的平面图形相同;本题是选择从左面看与从正面看所得到的平面图形不相同的,故选:B.主视图、左视图是分别从物体正面、左面看所得到的图形.根据主视图与左视图相同,可得答案.本题考查了简单几何体的三视图,非常简单,锻炼了学生的空间想象力和抽象思维能力.6.【答案】B【解析】解:A、利用45°和30°的角可以画出15°的角,故本选项错误;B、=,不合题意,即借助常用的直角三角尺,能画出一些度数的角,不能画出100度的角,故本选项正确;C、利用90°、45°和30°组合即可画出165°的角,故本选项错误;D、利用90°和45°组合即可画出165°的角,故本选项错误;故选:B.先分清一副三角尺,各个角的度数分别为多少,然后将各个角相加或相减即可得出答案.此题主要考查了用三角板直接画特殊角,关键掌握用三角板画出的角的规律:都是15°的倍数.7.【答案】C【解析】解:A、3a2b与ba2是同类项,故本选项错误;B、是整式,故本选项错误;C、单项式-x3y2的系数是-1,故本选项正确;D、3x2-y+5xy2是三次三项式,故本选项错误.故选:C.分别根据单项式、多项式、整式及同类项的定义判断各选项即可.本题考查单项式、多项式、整式及同类项的定义,注意掌握单项式是数或字母的积组成的式子;单项式和多项式统称为整式.8.【答案】C【解析】解:A、两边加不同的数,故A错误;B、两边除以不同的数,故B错误;C、两边都减同一个整式,故C正确;D、两边除以不同的数,故D错误;故选:C.根据等式的性质,可得答案.本题考查了等式的性质,熟记等式的性质是解题关键.9.【答案】D【解析】解:设点P表示的数是x,∵PM=2PN,∴|x+4|=2|x-2|,解得:x=0或8,故选:D.根据题意列方程即可得到结论.本题考查了数轴和一元一次方程的应用,主要利用了数轴上两点间的距离的表示方法,读懂题目信息,理解两点间的距离的表示方法是解题的关键.10.【答案】C【解析】解:设被污染的常数为x,则:2y-=y-x,∵此方程的解是y=-,∴将此解代入方程,方程成立∴2×(-)-=×(-)-x.解此一元一次方程可得:x=3故选:C.设这个常数为x,已知此方程的解是y=-,将之代入二元一次方程2y-=y-x,即可得这个常数的值.本题主要考查了一元一次方程的应用以及它的解的意义.知道一元一次方程的解,求方程中的常数项,可把方程的解代入方程求得常数项的值.(把■作为一个未知数来看即可).11.【答案】B【解析】解:因为(b+c)-(a-d)=b+c-a+d=(b-a)+(c+d)=-(a-b)+(c+d)…(1),所以把a-b=-3、c+d=2代入(1)得:原式=-(-3)+2=5.故选:B.先把括号去掉,重新组合后再添括号.(1)括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“-”,去括号后,括号里的各项都改变符号.运用这一法则去括号;(2)添括号后,括号前是“+”,括号里的各项都不改变符号;添括号后,括号前是“-”,括号里的各项都改变符号.运用这一法则添括号.12.【答案】B【解析】解:设甲一共做了x天,由题意得:+=1,故选:B.设甲一共做了x天,则乙做了(x-1)天,再根据工作效率×工作时间=工作量可得甲的工作量为,乙的工作量为,然后再根据甲的工作量+乙的工作量=1列出方程.此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,找出题目中等量关系,再列出方程.13.【答案】4【解析】解:∵2x+1是-9的相反数,∴2x+1=9.解得:x=4.故答案为:4.先依据相反数的定义得到2x+1=9,解关于x的方程即可.本题主要考查的是相反数的定义、解一元一次方程,依据相反数的定义列出关于x的方程是解题的关键.14.【答案】64 57 36【解析】解:32.48°×2=64度57分36秒;故答案为:64;57;36.进行度、分、秒的转化运算,注意以60为进制.将度的小数部分化为分,将分的小数部分化为秒.此类题是进行度、分、秒的转化运算,相对比较简单,注意以60为进制即可.15.【答案】11a+20【解析】解:两位数,个位数字是a,十位数字比个位数字大2可表示为(a+2).∴这个两位数是10(a+2)+a=11a+20.两位数为:10×十位数字+个位数字.本题的关键是,两位数的表示方法:十位数字×10+个位数字,要求掌握该方法.用字母表示数时,要注意写法:①在代数式中出现的乘号,通常简写做“•”或者省略不写,数字与数字相乘一般仍用“×”号;②在代数式中出现除法运算时,一般按照分数的写法来写;③数字通常写在字母的前面;④带分数的要写成假分数的形式.16.【答案】135【解析】解:∵OB平分∠COD,∴∠COB=∠BOD=45°,∵∠AOB=90°,∴∠AOC=45°,∴∠AOD=135°.故答案为:135.本题是有公共定点的两个直角三角形问题,通过图形可知∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,同时∠AOC+∠BOC+∠BOD+∠BOC=180°,可以通过角平分线性质求解.本题是角的平分线与对顶角的性质的考查,角平分线的性质是将两个角分成相等的两个角.17.【答案】4【解析】解:8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了x场,则3x+(7-x)=15,解得:x=4.故答案是:4.8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了x场,总分数为15即可列出方程,即可解题.本题考查了一元一次方程的应用,本题中根据题意找出总比赛场数为7是解题的关键.18.【答案】8【解析】解:∵a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,∴a+8+b-5=8+b-5+c①,8+b-5+c=b-5+c+d②,b-5+c+d=-5+c+d+4③,∴a-5=c-5,8+c=c+d,b-5=-5+4,∴b=4,d=8,a=c,故答案为8.由题意得a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,然后转化成方程组的形式,求得d的值即可.本题是一道找规律的题目,考查了有理数的加法和方程组的思想,是中档题难度不大.19.【答案】解:(1)-6+3.6+4-5.6=-4; (2)42×(-23)÷72-(-12)÷(-4) =-8-3=-11; (3)-12018+24÷(-2)3-32×(13)2=-1+24÷(-8)-9×19 =-1-3-1=-5.【解析】(1)先同号相加,再异号相加即可求解;(2)先算乘除,后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;(3)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.20.【答案】解:(1)原式-6a 2+6ab +4a 2+4ab -24=-2a 2+10ab -24;(2)原式=12x 2y -4xy 2+5xy 2-5x 2y -2x 2y=5x 2y +xy 2,当x =15,y =-5时,原式=5×(15)2×(-5)+15×52 =-1+5=4.【解析】(1)去括号、合并同类项即可得;(2)原式去括号、合并同类项化简后,把x ,y 的值代入计算可得.本题主要考查整式的加减-化简求值,解题的关键是掌握整式的加减运算顺序和运算法则.21.【答案】解:(1)去括号得:3x -7x +7=3-2x -6,移项合并得:-2x =-10,解得:x =5;(2)去分母得:3-3x =8x -2-6,移项合并得:-11x =-11,解得:x =1.【解析】(1)方程去括号,移项合并,把x 系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x 系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.【答案】解:(1)(-2)⊕3=-2×(-2-3)+1=10+1=11;(2)3⊕x =3(3-x )+1=-5,9-3x +1=-5,x =5.【解析】(1)根据新运算得出原式=-2×(-2-3)+1,求出即可;(2)根据新运算得出3(3-x )+1=-5,求出方程的解即可.本题考查了求代数式的值和有理数的混合运算,能读懂题意是解此题的关键.23.【答案】解:如图,设∠BOE =x °, ∵∠BOE =12∠EOC ,∴∠EOC =2x °,∵OD 平分∠AOB ,∴∠AOD =∠DOB =70°-x °,∵∠AOD +∠DOB +∠BOE +∠EOC =180°,∴70°-x +70°-x +x °+2x °=180°,∴x =40,∴∠EOC =80°.【解析】设∠BOE=x°,则∠EOC=2x°,由∠DOE=70°及OD 平分∠AOB 知∠AOD=∠DOB=70°-x°,根据∠AOD+∠DOB+∠BOE+∠EOC=180°列出关于x 的方程,解之可得. 本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.24.【答案】解:(1)设第一次购进烤火器x 台,则第二次购进烤火器(x -10)台,根据题意得:150x =180(x -10),解得x =60,x -10=50.答:家电销售部第一次购进烤火器60台,第二次购进50台.(2)(250-150)×60+(250-180)×50=9500(元). 答:以250元/台的售价卖完这两批烤火器,家电销售部共获利9500元.【解析】(1)设第一次购进烤火器x 台,则第二次购进烤火器(x-10)台,根据第二次进货单价比第一次进货单价贵30元即可得出关于x 的一元一次方程,解之即可得出结论;(2)根据总利润=销售第一批烤火器的利润+销售第二批烤火器的利润即可求出家电销售部共获利多少元.本题考查了一元一次方程的应用,根据数量关系列出关于x 的一元一次方程是解题的关键.25.【答案】x +1 x +7 x +8 128【解析】解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为x ,则另外三个数用含x 的式子从小到大依次表示x+1;x+7;x+8;故答案为x+1;x+7;x+8;(2)∵当四个数是1,2,8,9时最小,a 1=1+2+8+9=20;当四个数是23,24,30,31时最大,a 2=23+24+30+31=108,∴a 1+a 2=20+108=128.故答案为:128;(3)由题意得,x+x+1+x+7+x+8=76,解得x=15,答:当被框住的4个数之和等于76时,x的值为15;(4)不能.由题意得,x+x+1+x+7+x+8=92,解得x=19,故由此框住的四个数应是19,20,26,27,但是19,20不在同行的相邻位置,所以不能框住4个数的和等于92.(1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其他三个数;(2)先求出四个数之和最小a1,和最大a2的值,再求和即可;(3)、(4)根据(1)中各数的表达式求出x的值即可.本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.26.【答案】1【解析】解:(1)∵A,B表示的数分别为6,-4,∴AB=10,∵PA=PB,∴点P表示的数是1,故答案为:1;(2)设点P运动x秒时,在点C处追上点R,则:AC=6x BC=4x,AB=10,∵AC-BC=AB,∴6x-4x=10,解得,x=5,∴点P运动5秒时,追上点R;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时(如图①):MN=MP+NP=AP+BP=(AP+BP)=AB=5.②当点P运动到点B左侧时(如图②),MN=PM-PN=AP-BP=(AP-BP)=AB=5;综上所述,线段MN的长度不发生变化,其长度为5.(1)由已知条件得到AB=10,由PA=PB,于是得到结论;(2)设点P运动x秒时,在点C处追上点R,于是得到AC=6x BC=4x,AB=10,根据AC-BC=AB,列方程即可得到结论;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时②当点P运动到点B左侧时,求得线段MN的长度不发生变化.此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.11。
定州2019-2020学年度七年级数学上册期末

2019-2020学年河北省保定市定州市七年级(上)期末数学试卷一、选择题(本大题共12个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.﹣的绝对值是()A.﹣B.C.2 D.﹣22.用科学记数法表示8450亿为()A.0.845×104亿B.8.45×103亿C.8.45×104亿D.84.5×102亿3.单项式的次数是()A.2 B.3 C.5 D.64.下列计算正确的是()A.5a+2a=7a2B.5a﹣2b=3abC.5a﹣2a=3 D.﹣ab3+2ab3=ab35.如图所示的四条射线中,表示南偏西60°的是()A.射线OA B.射线OB C.射线OC D.射线OD6.将下列平面图形绕轴旋转一周,可得到圆锥的是()A.B.C.D.7.把弯曲的河道改直,这样能缩短航程,这样做的道理是()A.两点确定一条直线 B.两点之间线段最短C.线段有两个端点D.线段可以比较大小8.若2是关于x的方程x+a=﹣1的解,则a的值为()A.0 B.2 C.﹣2 D.﹣69.有理数a,b在数轴上的位置如图所示,则下列各式成立的是()A.b﹣a>0 B.﹣b>0 C.a>﹣b D.﹣ab<010.一张试卷只有25道选择题,做对一题得4分,做错1题倒扣1分,某学生做了全部试题共得70分,他做对了()道题.A.17 B.18 C.19 D.2011.元旦来临,各大商场都设计了促进消费增加利润的促销措施,“物美”商场把一类双肩背的书包按进价提高50%进行标价,然后再打出8折的优惠价,这样商场每卖出一个书包就可盈利8元,这种书包的进价是( )A.42元B.40元C.38元D.35元12.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n 的关系是( )A.M=mn B.M=n(m+1)C.M=mn+1 D.M=m(n+1)二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)13.计算:(﹣4)2015×(+0.25)2016=__________.14.在数轴上,若A点表示数﹣1,点B表示数2,A、B两点之间的距离为__________.15.若x=2是关于x的方程2x+3m﹣1=0的解,则m的值等于__________.16.当x=1时,代数式ax3+bx+4的值为5.则x=﹣1时,ax3+bx+4的值为__________.17.爷爷快八十大寿,小明想在日历上把这一天圈起来,但不知道是哪一天,于是便去问爸爸,爸爸笑着说,“在日历上,那一天的上下左右4个日期的和正好等于爷爷的年龄”.小明爷爷的生日是__________号.18.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m=__________,再将数对(m,1)放入其中后,得到的数是__________.三、解答下列各题(本题有7个小题,共66分)19.计算题.(1)计算:(﹣4)2×[(﹣)+(﹣)](2)计算:(﹣2)3﹣(1﹣0.5)××[2﹣(﹣4)2].20.先化简再求值(1)﹣2x2﹣[3y2﹣2(x2﹣y2)+6],其中x=﹣1,y=2.(2)x﹣2(x﹣y2)+(x+y2),其中x,y满足|x﹣6|+(y+2)2=0.21.解方程(1)3(y+1)=2y﹣1(2)2﹣=.22.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?23.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.24.已知线段AB=42,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=AC,求线段DE的长.25.在课间活动中,小英、小丽和小华在操场上画出A,B两个区域,一起玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.(1)沙包落在A区域和B区域所得分值分别是多少?(2)求出小华的四次总分.26.为了丰富学生的课外活动,学校决定购买一批体育活动用品,经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每幅球拍多50元,两个篮球与三幅球拍的费用相等,经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球超过80个,则购买羽毛球拍打八折.(1)求每个篮球和每幅羽毛球拍的价格是多少?(2)若学校购买100个篮球和a副羽毛球拍,请用含a的式子分别表示出到甲商店和乙商店购买体育活动用品所花的费用;(3)假如你是本次购买任务的负责人,你认为到哪家商店购买比较合算?2019-2020学年河北省保定市定州市七年级(上)期末数学试卷一、选择题(本大题共12个小题;每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算:(﹣1)+2的结果是( )A.﹣1 B.1 C.﹣3 D.3【考点】有理数的加法.【分析】异号两数相加,取绝对值较大加数的符号,再用较大绝对值减去较小绝对值.【解答】解:(﹣1)+2=+(2﹣1)=1.故选B.【点评】此题主要考查了有理数的加法,做题的关键是掌握好有理数的加法法则.2.下列运算正确的是( )A.x2+x2=x4B.3x3y2﹣2x3y2=1C.4x2y3+5x3y2=9x5y5D.5x2y4﹣3x2y4=2x2y4【考点】合并同类项.【分析】合并同类项,系数相加字母和字母的指数不变.【解答】解:A、x2+x2=2x2,本选项错误;B、3x3y2﹣2x3y2=x3y2,本选项错误;C、不是同类项,不能合并,本选项错误;D、5x2y4﹣3x2y4=2x2y4,故本选项正确.故选D.【点评】本题考查了合并同类项.合并”是指同类项的系数的相加,并把得到的结果作为新的系数,要保持同类项的字母和字母的指数不变.3.如图,OA⊥OB,若∠1=55°,则∠2的度数是( )A.35°B.40°C.45°D.60°【考点】余角和补角.【分析】根据两个角的和为90°,可得两角互余,可得答案.【解答】解:∵OA⊥OB,∴∠AOB=90°,即∠2+∠1=90°,∴∠2=35°,故选:A.【点评】本题考查了余角和补角,两个角的和为90°,这两个角互余.4.将260 000用科学记数法表示应为( )A.0.2×106B.26×104C.2.6×106D.2.6×105【考点】科学记数法—表示较大的数.【分析】确定a×10n(1≤|a|<10,n为整数)中n的值是易错点,由于260 000有6位,所以可以确定n=6﹣1=5.【解答】解:260 000=2.6×105.故选D.【点评】把一个数M记成a×10n(1≤a<10,n为整数)的形式,这种记数的方法叫做科学记数法.规律:(1)当M≥1时,n的值为a的整数位数减1;(2)当M<1时,n的值是第一个不是0的数字前0的个数,包括整数位上的0.5.一个数是10,另一个数比10的相反数小2,则这两个数的和为( )A.18 B.﹣2 C.﹣18 D.2【考点】有理数的减法;相反数;有理数的加法.【分析】先根据相反数的概念求出10的相反数,再根据有理数的减法求出比10的相反数小2,再把两数相加即可.【解答】解:∵10的相反数是﹣10,∴比10的相反数小2是﹣12,∴这两个数的和为10+(﹣12)=﹣2.故选B.【点评】解答此题的关键是熟知相反数的概念及有理数的加减法则.6.下列说法中正确的是( )A.两点之间的所有连线中,线段最短B.射线就是直线C.两条射线组成的图形叫做角D.小于平角的角可分为锐角和钝角两类【考点】直线、射线、线段;角的概念.【分析】根据线段、射线和角的概念,对选项一一分析,选择正确答案.【解答】解:A、两点之间的所有连线中,线段最短,选项正确;B、射线是直线的一部分,选项错误;C、有公共端点的两条射线组成的图形叫做角,选项错误;D、小于平角的角可分为锐角、钝角,还应包含直角,选项错误.故选A.【点评】考查线段、射线和角的概念.解题的关键是熟练运用这些概念.7.将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创“相对的字是( )A.文B.明C.城D.市【考点】专题:正方体相对两个面上的文字.【分析】根据正方体的平面展开图的特点,相对的两个面中间一定隔着一个小正方形,且没有公共的顶点,结合展开图很容易找到与“创”相对的字.【解答】解:结合展开图可知,与“创”相对的字是“明”.故选B.【点评】本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.8.下面四个立体图形,从正面、左面、上面观察都不可能看到长方形的是( ) A.B.C. D.【考点】简单几何体的三视图.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.依此找到从正面、左面、上面观察都不可能看到长方形的图形.【解答】解:A、主视图为长方形,左视图为长方形,俯视图为长方形,故本选项错误;B、主视图为长方形,左视图为长方形,俯视图为圆,故本选项错误;C、主视图为等腰三角形,左视图为等腰三角形,俯视图为圆,从正面、左面、上面观察都不可能看到长方形,故本选项正确;D、主视图为三角形,左视图为三角形,俯视图为有对角线的矩形,故本选项错误.故选:C.【点评】本题重点考查了三视图的定义以及考查学生的空间想象能力.9.丁丁比昕昕小,丁丁今年a岁,昕昕今年b岁,2年后丁丁比昕昕小( )岁.A.2 B.b﹣a C.a﹣b D.b﹣a+2【考点】列代数式.【分析】由于两个人的年龄差不变,2年后丁丁比昕昕小几岁,也就是现在的两个人的年龄差,由此列式即可.【解答】解:2年后丁丁比昕昕小(b﹣a)岁.故选:B.【点评】此题考查列代数式,利用年龄差不变是解决问题的关键.10.把方程3x+去分母正确的是( )A.18x+2(2x﹣1)=18﹣3(x+1)B.3x+(2x﹣1)=3﹣(x+1)C.18x+(2x﹣1)=18﹣(x+1)D.3x+2(2x﹣1)=3﹣3(x+1)【考点】解一元一次方程.【分析】同时乘以各分母的最小公倍数,去除分母可得出答案.【解答】解:去分母得:18x+2(2x﹣1)=18﹣3(x+1).故选:A.【点评】本题考查了解一元一次方程的步骤:去分母、去括号、移项、合并同类项和系数化为1,在去分母时一定要注意:不要漏乘方程的每一项.11.元旦来临,各大商场都设计了促进消费增加利润的促销措施,“物美”商场把一类双肩背的书包按进价提高50%进行标价,然后再打出8折的优惠价,这样商场每卖出一个书包就可盈利8元,这种书包的进价是( )A.42元B.40元C.38元D.35元【考点】一元一次方程的应用.【分析】设这种书包的进价为x元,根据等量关系:卖出一个书包就可盈利8元列出方程,求出方程的解即可得到结果.【解答】解:设这种书包的进价为x元,根据题意得:(1+50%)x×80%﹣x=8,解得:x=40,则这种书包的进价为40元.故选:B.【点评】此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.12.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n 的关系是( )A.M=mn B.M=n(m+1)C.M=mn+1 D.M=m(n+1)【考点】规律型:数字的变化类.【专题】规律型.【分析】根据数的特点,上边的数与比左边的数大1的数的积正好等于右边的数,然后写出M与m、n的关系即可.【解答】解:∵1×(2+1)=3,3×(4+1)=15,5×(6+1)=35,…,∴M=m(n+1).故选D.【点评】本题是对数字变化规律的考查,观察出上边的数与比左边的数大1的数的积正好等于右边的数是解题的关键.二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)13.计算:(﹣4)2015×(+0.25)2016=﹣0.25.【考点】有理数的乘方.【专题】计算题;实数.【分析】原式变形后,逆用积的乘方运算法则计算即可得到结果.【解答】解:原式=(﹣4×0.25)2015×0.25=﹣1×0.25=﹣0.25,故答案为:﹣0.25【点评】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.14.在数轴上,若A点表示数﹣1,点B表示数2,A、B两点之间的距离为3.【考点】数轴.【分析】用数轴上右边的点表示的数减去左边的点表示的数即可得到两点之间的距离.【解答】解:2﹣(﹣1)=3.故答案为:3【点评】本题主要考查了数轴,熟知数轴上两点间的距离公式是解答此题的关键.15.若x=2是关于x的方程2x+3m﹣1=0的解,则m的值等于﹣1.【考点】方程的解.【专题】计算题.【分析】使方程左右两边的值相等的未知数的值是该方程的解.将方程的解代入方程可得关于m的一元一次方程,从而可求出m的值.【解答】解:根据题意得:4+3m﹣1=0解得:m=﹣1,故答案为:﹣1.【点评】已知条件中涉及到方程的解,把方程的解代入原方程,转化为关于m字母系数的方程进行求解,注意细心.16.当x=1时,代数式ax3+bx+4的值为5.则x=﹣1时,ax3+bx+4的值为3.【考点】代数式求值.【专题】计算题.【分析】将x=1代入代数式使其值为5求出a+b的值,将x=﹣1代入代数式变形后,将a+b 的值代入计算即可求出值.【解答】解:当x=1时,代数式为a+b+4=5,即a+b=1,则x=﹣1时,代数式为﹣a﹣b+4=﹣(a+b)+4=﹣1+4=3.故答案为:3【点评】此题考查了代数式求值,利用了整体代入的思想,熟练掌握运算法则是解本题的关键.17.爷爷快八十大寿,小明想在日历上把这一天圈起来,但不知道是哪一天,于是便去问爸爸,爸爸笑着说,“在日历上,那一天的上下左右4个日期的和正好等于爷爷的年龄”.小明爷爷的生日是20号.【考点】一元一次方程的应用.【分析】要求小莉的爷爷的生日,就要明确日历上“上下左右4个日期”的排布方法.依此列方程求解.【解答】解:设那一天是x,则左日期=x﹣1,右日期=x+1,上日期=x﹣7,下日期=x+7,依题意得x﹣1+x+1+x﹣7+x+7=80解得:x=20故答案是:20.【点评】本题考查了一元一次方程的应用.此题关键是弄准日历的规律,知道左右上下的规律,然后依此列方程.18.数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m=8,再将数对(m,1)放入其中后,得到的数是66.【考点】有理数的混合运算.【专题】新定义.【分析】根据题中的新定义化简所求式子,计算即可得到结果.【解答】解:数对(﹣2,3)放入其中得到(﹣2)2+3+1=4+3+1=8;再将数对(8,1)放入其中得到82+1+1=64+1+1=66.故答案为:8;66.【点评】此题考查了有理数的混合运算,弄清题中的新定义是解本题的关键.三、解答下列各题(本题有7个小题,共66分)19.计算题.(1)计算:(﹣4)2×[(﹣)+(﹣)](2)计算:(﹣2)3﹣(1﹣0.5)××[2﹣(﹣4)2].【考点】有理数的混合运算.【专题】计算题;实数.【分析】(1)原式先计算乘方运算,再利用乘法分配律计算即可得到结果;(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.【解答】解:(1)原式=16×(﹣﹣)=﹣12﹣10=﹣22;(2)原式=﹣8﹣××(﹣14)=﹣8+=﹣5.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.20.先化简再求值(1)﹣2x2﹣[3y2﹣2(x2﹣y2)+6],其中x=﹣1,y=2.(2)x﹣2(x﹣y2)+(x+y2),其中x,y满足|x﹣6|+(y+2)2=0.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【专题】计算题;整式.【分析】(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;(2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.【解答】解:(1)原式=﹣2x2﹣y2+x2﹣y2﹣3=﹣x2﹣y2﹣3,当x=﹣1,y=﹣2时,原式=﹣1﹣10﹣3=﹣14;(2)原式=x﹣2x+y2+x+y2=y2,∵|x﹣6|+(y+2)2=0,∴x=6,y=﹣2,则原式=4.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.21.解方程(1)3(y+1)=2y﹣1(2)2﹣=.【考点】解一元一次方程.【专题】计算题;一次方程(组)及应用.【分析】(1)方程去括号,移项合并,把y系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去括号,得3y+3=2y﹣1,移项,得3y﹣2y=﹣1﹣3.合并同类项,得y=﹣4;(2)去分母得,12﹣2(2x+1)=3(1+x),去括号得,12﹣4x﹣2=3+3x,移项得,﹣4x﹣3x=3﹣12+2,合并同类项得,﹣7x=﹣7,系数化为1得,x=1.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?【考点】一元一次方程的应用.【专题】工程问题.【分析】30分=小时,可设甲、乙一起做还需x小时才能完成工作,等量关系为:甲小时的工作量+甲乙合作x小时的工作量=1,把相关数值代入求解即可.【解答】解:设甲、乙一起做还需x小时才能完成工作.根据题意,得×+(+)x=1,解这个方程,得x=,小时=2小时12分,答:甲、乙一起做还需2小时12分才能完成工作.【点评】考查用一元一次方程解决工程问题,得到工作量1的等量关系是解决本题的关键.23.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.【考点】对顶角、邻补角;角平分线的定义.【分析】根据角的和差,可得∠EOF的度数,根据角平分线的性质,可得∠AOC的度数,根据补角的性质,可得答案.【解答】解:由角的和差,得∠EOF=∠COE﹣COF=90°﹣28°=62°.由角平分线的性质,得∠AOF=∠EOF=62°.由角的和差,得∠AOC=∠AOF﹣∠COF=62°﹣28°=34°.由对顶角相等,得∠BOD=∠AOC=34°.【点评】本题考查了对顶角、邻补角,利用了角的和差,角平分线的性质,对顶角的性质.24.已知线段AB=42,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB 上,且CE=AC,求线段DE的长.【考点】两点间的距离.【分析】根据题意和中点的性质求出AC、BC的长以及CD、CE的长,分两种情况、结合图形计算即可.【解答】解:∵线段AB=42,点C为AB中点,∴AC=BC=AB=×42=21,∵点D为BC中点,∴CD=BD=BC=×21=10.5,∵CE=AC,∴CE=×21=7,如图1,DE=CD+CE=10.5+7=17.5;如图2,DE=CD﹣CE=10.5﹣7=3.5.综上所述,线段DE的长是17.5或3.5.【点评】本题考查的是两点间的距离的计算,掌握线段的中点的定义、正确运用数形结合思想是解题的关键.25.在课间活动中,小英、小丽和小华在操场上画出A,B两个区域,一起玩投包游戏,沙包落在A区域所得分值与落在B区域所得分值不同,当每人各投沙包四次时,其落点和四次总分如图所示.(1)沙包落在A区域和B区域所得分值分别是多少?(2)求出小华的四次总分.【考点】一元一次方程的应用.【分析】(1)设沙包落在A区域得分为x,则落在B区域得分为(33﹣3x),根据小丽得分列出方程2x+2(33﹣3x)=30,解方程求出x的值即可;(2)小华的总分=沙包落在A区域得分×1+沙包落在B区域得分×3,依此计算即可求解.【解答】解:(1)设沙包落在A区域得分为x,则落在B区域得分为(33﹣3x),由题意可列方程2x+2(33﹣3x)=30,解得x=9,33﹣3x=33﹣27=6.故沙包落在A区域得分为9分,落在B区域得分为6分.(2)小华四次总分为:9×1+6×3=9+18=27(分).故小华四次总分为27分.【点评】此题主要考查了一元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.26.为了丰富学生的课外活动,学校决定购买一批体育活动用品,经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每幅球拍多50元,两个篮球与三幅球拍的费用相等,经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球超过80个,则购买羽毛球拍打八折.(1)求每个篮球和每幅羽毛球拍的价格是多少?(2)若学校购买100个篮球和a副羽毛球拍,请用含a的式子分别表示出到甲商店和乙商店购买体育活动用品所花的费用;(3)假如你是本次购买任务的负责人,你认为到哪家商店购买比较合算?【考点】一元一次方程的应用.【分析】(1)设每个篮球的定价是x元,则每幅羽毛球拍是(x+50)元,根据两个篮球与三幅球拍的费用相等列出方程,解方程即可;(2)根据甲、乙两商店的优惠方案即可求解;(3)先求出到两家商店购买一样合算时篮球的个数,再根据题意即可求解.【解答】解:(1)设每个篮球的定价是x元,则每幅羽毛球拍是(x+50)元,根据题意得2(x+50)=3x,解得x=100,x+50=150.答:每副羽毛球拍150元,每个篮球100元.(2)到甲商店购买所花的费用为:150×100+100(a﹣)=100a+14000(元);到乙商店购买所花的费用为:150×100+0.8×100×a=80a+15000(元);(3)当在两家商店购买一样合算时,有100a+14000=80a+15000,解得a=50.所以购买的球拍数等于50副时,则在两家商店购买一样合算;购买的球拍数多于50个时,则到乙商店购买合算;购买的球拍数少于50个时,则到甲商店购买合算.【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.。
河北省保定市定州市2022—2023学年七年级上学期数学期末试卷 含答案

定州市2022-2023学年度第一学期期末教学质量检测七年级数学试题一、选择题(本大题共12小题,每小题3分,共36分)每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题中的括号内.1.《九章算术》中注有“今两算得失相反,要令正负以名之.”意思是:今有两数若其意义相反,则分别叫正数与负数.若收入150元记作150+,则80-元表示( )A .收入80元B .收入70元C .支出80元D .支出70元2.生活中的实物可以抽象出各种各样的几何图形,如图所示的不锈钢漏斗的形状类似于( )A .圆B .球C .圆柱D .圆锥3.以下说法中正确的是( )A .232x y 的次数是4B .23ab 与22a b -是同类项 C .1π2ab 的系数为12D .26m m +-的常数项为6 4.下列问题情境,不能用加法算式210-+表示的是( ) A .水位先下降2cm ,再上升10cm 后的水位变化情况B .某日最低气温为2-℃,温差为10℃,该日最高气温C .用10元纸币购买2元文具后找回的零钱D .数轴上表示2-与10的两个点之间的距离5.已知2x =-是方程240x m +-=的解,则m 的值是( )A .8B .8-C .6D .06.已知点M 在线段AB 上,点N 是线段MB 的中点,若6AN =,则AM AB +的值为( )A .10B .8C .12D .以上答案都不对7.若一个数的绝对值是25,则这个数是( ) A .25 B .25- C .25或25- D .52或52- 8.2022年10月1日早上6时许,北京天安门广场举行国庆升旗仪式.在严格落实北京市疫情防控政策要求和个人防护措施下,约218000名市民游客齐聚广场,共同见证五星红旗冉冉升起的庄严时刻,庆祝新中国73周年华诞,将218000用科学记数法表示为( )A .421.810⨯B .60.21810⨯C .52.1810⨯D .62.1810⨯9.下列图形中可以作为一个三棱柱的展开图的是( )A .B .C .D .10.如图,下列说法中不正确的是( )A .1∠与AOB ∠是同一个角 B .α∠与COB ∠是同一个角C .AOC ∠可以用O ∠来表示D .图中共有三个角:AOB ∠,BOC ∠,AOC ∠11.如图,数轴的单位长度为1,数轴上有A ,B ,C 三个点.若点A ,B 到原点的距离相等,则点C 表示的数是( )A .2B .1C .1-D .2-12.按如图所示的规律搭正方形:搭一个小正方形需要4根小棒,搭两个小正方形需要7根小棒,搭2020个这样的小正方形需要小棒( )根.A .8080B .6066C .6061D .6060二、填空题(本大题共6小题,每小题3分,共18分)把答案直接写在题中的横线上.13.多项式2835x x -+与多项式222253x mx x +-+相加后不含2x 项,则m 的值为___________.14.如图,在正方体表面展开图的每个面内都写有1个汉字,则该正方体中与“胜”相对的字是___________.15.若代数式2(3)x -的值与9x -的值互为相反数,x 的值为___________.16.如图,是一个公园的示意图,下列说法正确的是___________(填正确说法的序号).①孔雀馆在大门的北偏东50︒方向上; ②猴山在大门的正北方向;③狮子园在大门的南偏东30︒方向上; ④盆景园在大门的北偏东90︒方向上.17.20名同学在植树节这大共种了52棵树苗,其中男生每人种3棵,女生每人种2棵,设参加植树的男生x 人,则可列方程为___________.18.有一数值转换器,原理如图所示,若开始输入x 的值是1,可发现第一次输出的结果是4,第二次输出的结果是2,……,请你探索第2022次输出的结果是___________.三、解答题(本大题共7小题,共66分解答应写出文字说明、演算步骤或推理过程)19.(本题8分)计算:(1)517248612⎛⎫--+⨯ ⎪⎝⎭(2)2022211|2|(3)2---÷+- 20.(本题8分)先化简再求值.已知2|2|(1)0a b ++-=.求()()22422322a b ab ab a b ⎡⎤++---⎣⎦的值. 21.(本题8分)解方程:(1)45(21)x x -=+; (2)311510x x +=-. 22.(本题8分)如图,OB 是AOC ∠的平分线,OD 是COE ∠的平分线,15040AOE AOB ∠=︒∠=︒,.求A O D ∠的度数.23.(本题8分)某校新进了一批课桌椅,七年(2)班的学生利用活动课时间帮助学校搬运部分课桌椅,已知七年(2)班共有学生45人,其中男生的人数比女生人数的2倍少24人,要求每个学生搬运60张桌子或者搬运150张椅子.请解答下列问题:(1)七年(2)班有男生、女生各多少人?(2)一张桌子配两把椅子,为了使搬运的桌子和椅子刚好配套,应该分配多少个学生搬运桌子,多少个学生搬运椅子?24.一个两位数的个位上的数是a ,十位上的数是b .(1)列式表示这个两位数;(2)当2a b 时,若将a 与b 的位置对调,得到的新两位数比原数大18,求此时这个两位数.25.(本题8分)某校组织党史知识竞赛,共设50道选择题,各题分值相同,每题必答,答错扣分,下表记录的是其中3名参赛者的得分情况.(1)由表格知,答对一题得___________分,答错一题扣___________分;(2)某参赛者得73分,求该参赛者答对的题数;(3)参赛者的得分可能是90吗?请说明理由.26.(本题10分)某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价40元,乒乓球每盒10元,经洽谈后,甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需买球拍6副,乒乓球若干盒(不少于6盒).(1)设要买的乒乓球为x 盒,则到甲店购买需付___________元;到乙店购买需付___________元(用x 的代数式表示)(2)当购买20盒乒乓球时,到哪家商店购买比较合算?(3)当购买多少盒时,到两家商店购买一样?七年级数学参考答案一、选择题:1-6:CDADAC ; 7-12:CCBCCC .二、填空题:13.5-; 14.抗; 15.3-; 16.①②④; 17.32(20)52x x +-=; 18.1.三、解答题:19.(1)解:原式5172424248612=-⨯-⨯+⨯ 15414=--+5=- (2)解:原式2112(3)2=--÷+- 1229=--⨯+ 4=20.解:()()22422322a b ab ab a b ⎡⎤++---⎣⎦()22422324a b ab ab a b =++--+22422324a b ab ab a b =++-+-41ab =-,22|2|(1)0,|2|0,(1)0a b a b ++-=+≥-≥,2|2|(1)0a b ∴+=-=,20,10a b ∴+=-=,2,1a b ∴=-=,∴原式4(2)11819=⨯-⨯-=--=-.21.(1)解:原式去括号得,4105x x -=+,移项得,1054x x -=+,合并同类项得,99x -=,系数化1得,1x =-,∴原方程的解是:1x =-.(2)解:原式两边同时乘以10去分母得,23110x x =+-,移项得,239x x -=-,合并同类项得,9x -=-,系数化1得,9x =,∴原方程的解是:9x =.22.解:OB 是AOC ∠的平分线,40AOB ∠=︒,280AOC AOB ∴∠=∠=︒,70EOC AOE AOC ∴∠=∠-∠=︒.又OD 是COE ∠的平分线,1352EOD EOC ∴∠=∠=︒, 又150AOE ∠=︒, 15035115AOD AOE EOD ∴∠=∠-∠=︒-︒=︒.23.(1)解:设女生有x 人,则男生有(224)x -人,由题意得:22445x x -+=.解得23x =,452322-=.答:七年(2)班有男生22人、女生23人.(2)解:设分配y 名学生搬运桌子,则有(45)y -名学生搬运椅子, 由题意得:260150(45)y y ⨯=-解得25y =,452520-=.答:应该分配25名学生搬运桌子,名学生搬运椅子.24.解:(1)一个两位数的个位上的数是a ,十位上的数是b , ∴这个两位数为:10b a +,(2)当2a b =时,原来的两位数为1010212b a b b b +=+=,将a 与b 的位置对调,得到的新两位数为:102021a b b b b +=+=, 由题意得:211218b b -=,解得:2b =,所以原来的两位数为24,新两位数为42.25.(1)2,1:(2)设该参赛者答对的题数为x .依题意,2(50)73x x --=.这个方程,得41x =.所以,该参赛者答对的题数为41.(3)若某参赛者的得分为90,设其答对题数为m .则2(50)90m m --=,这个方程,得140/3m =.因为140/3不是整数,参赛者的得分不可能是90.26.(1)解:到甲店购买时,根据题意,因此赠送乒乓球6盒,超出6盒部分的乒乓球需付钱,所以到甲店购买需付40610(6)18010x x ⨯+-=+(元),到乙店购买时需付09(40610)09(24010)9216x x x ⨯+=+=+..(元),故到甲店购买需付18010x +(元),到乙店购买时需付9216x +(元).(2)当购买20盒乒乓球时,到甲店需付款:1801020380+⨯=(元),到乙店需付款:920216396⨯+=(元),380396<,∴到甲店合算;(3)设购买x 盒乒乓球时,两家优惠办法付款一样.由题意得:180109216x x +=+解得:36x =.答:购买36盒乒乓球时两种优惠办法付款一样.。
保定市人教版七年级上册数学期末试卷及答案-百度文库

保定市人教版七年级上册数学期末试卷及答案-百度文库一、选择题1.-2的倒数是( ) A .-2 B .12-C .12D .22.将方程3532x x --=去分母得( ) A .3352x x --= B .3352x x -+= C .6352x x -+= D .6352x x --=3.下列分式中,与2x yx y---的值相等的是() A .2x yy x +-B .2x yx y+-C .2x yx y--D .2x yy x-+ 4.已知:有公共端点的四条射线OA ,OB ,OC ,OD ,若点()1P O ,2P ,3P ⋯,如图所示排列,根据这个规律,点2014P 落在( )A .射线OA 上B .射线OB 上C .射线OC 上D .射线OD 上5.已知一个两位数,个位数字为b ,十位数字比个位数字大a ,若将十位数字和个位数字对调,得到一个新的两位数,则原两位数与新两位数之差为( ) A .9a 9b - B .9b 9a - C .9a D .9a - 6.下列各数中,有理数是( )A .2B .πC .3.14D .377.有理数a 、b 在数轴上的位置如图所示,则下列结论中正确的是( )A .a+b >0B .ab >0C .a ﹣b <oD .a÷b >0 8.单项式﹣6ab 的系数与次数分别为( )A .6,1B .﹣6,1C .6,2D .﹣6,2 9.观察一行数:﹣1,5,﹣7,17,﹣31,65,则按此规律排列的第10个数是( ) A .513B .﹣511C .﹣1023D .102510.如图的几何体,从上向下看,看到的是( )A .B .C .D .11.如图,两块直角三角板的直角顶点O 重叠在一起,且OB 恰好平分COD ∠,则AOD ∠的度数为( )A .100B .120C .135D .15012.把 1,3,5,7,9,⋯排成如图所示的数表,用十字形框中表内的五个数,当把十字形上下左右移动,保证每次十字形要框中五个数,则框中的五个数的和不可能是( )A .1685B .1795C .2265D .2125二、填空题13.在灯塔O 处观测到轮船A 位于北偏西54︒的方向,同时轮船B 在南偏东15︒的方向,那么AOB ∠的大小为______.14.甲乙两个足够大的油桶各装有一定量的油,先把甲桶中的油的一半给乙桶,然后把乙桶中的油倒出18给甲桶,若最终两个油桶装有的油体积相等,则原来甲桶中的油是乙桶中油的______倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省保定市定州市七年级(上)期末数学试卷一、选择题(本大题共12小题,共36.0分)1.-3的倒数是()A. 3B.C.D.2.在-3,-1,1,3四个数中,比-2小的数是()A. B. C. 1 D. 33.由四舍五入得到的近似数2.6万,精确到()A. 千位B. 万位C. 个位D. 十分位4.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为()A. B. C. D.5.在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是()A. 正方体B. 长方体C. 球D. 圆锥6.借助常用的直角三角尺,能画出一些度数的角,下列选项中不能画出角的是()A. B. C. D.7.下列判断正确的是()A. 与不是同类项B. 不是整式C. 单项式的系数是D. 是二三项式8.下列方程的变形,符合等式的性质的是()A. 由,得B. 由,得C. 由,得. 由,得9.如图,M,N是数轴上的两点,它们分别表示-4和2,P为数轴上另一点,PM=2PN,则点P表示的数是()A. 1B. 0C. 8D. 0或810.小明在解方程时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是2y-=y-■怎么办呢?小明想了一想,便翻了书后的答案,此方程的解为y=-,很快补好了这个常数,你能补出这个常数吗?它应是()A. 1B. 2C. 3D. 411.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为()A. 1B. 5C.D.12.某项工程甲单独做4天完成,乙单独做6天完成,若甲先做1天,然后甲、乙合作完成此项工程,若设甲一共做了天,则所列方程为()A. . . .、填空题(本大题共6小题,共18.0分)13.若2+1是-9的相反数,则=______.14.32.48°×2=______度______分______秒.15.一个两位数,个位数字是a,十位数字比个位数字大2,则这个两位数是______.16.如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数是______度.17.某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜______场比赛.18.如图,在每个“〇”中填入一个整数,使得其中任意四个相邻“〇”中所填整数之和都相等,可得d的值为______.三、计算题(本大题共3小题,共25.0分)19.计算题.(1)-6+3.6+4-5.6(2)42×(-)÷-(-12)÷(-4)(3)-12018+24÷(-2)3-32×()220.(1)计算:-3(2a2-2ab)+4(a2+ab-6)(2)化简求值:12(2y-y2)+5(y2-2y)-22y,其中=,y=-5.21.解方程(1)3-7(-1)=3-2(+3)(2)=-1四、解答题(本大题共5小题,共41.0分)22.定义新运算:对于任意有理数a、b,都有a⊕b=a(a-b)+1,等式的右边是通常的有理数运算,例如2⊕5=2(2-5)+1=2×(-3)+1.(1)求(-2)⊕3.(2)若3⊕=-5,求的值.23.如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=∠EOC,∠DOE=70°,求∠EOC的度数.24.入冬以,某家电销售部以150元/台的价格购进一款烤火器,很快售完,又用相同的货款再次购进这款烤火器,因单价提高了30元,进货量比第一次少了10台.(1)家电销售部两次各购进烤火器多少台?(2)若以250元/台的售价卖完这两批烤火器,家电销售部共获利多少元?25.如图是2015年12月月历.(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为,则另三个数用含的式子表示出,从小到大依次是______,______,______.(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2=______.(3)当(1)中被框住的4个数之和等于76时,的值为多少?(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出的值;若不能,则说明理由.26.已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是______;(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.答案和解析1.【答案】C【解析】解:-3的倒数是-.故选:C.根据倒数的定义即可得出答案.此题主要考查了倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.【答案】A【解析】解:∵|-3|=3,|-2|=2,∴比-2小的数是:-3.故选:A.利用两个负数,绝对值大的其值反而小,进而得出答案.此题主要考查了有理数比较大小,正确把握两负数比较大小的方法是解题关键.3.【答案】A【解析】解:近似数2.6万精确到千位.故选:A.近似数2.6万精确到0.1万位.本题考查了近似数和有效数字:经过四舍五入得到的数称为近似数;从一个近似数左边第一个不为0的数数起到这个数完,所以这些数字都叫这个近似数的有效数字.4.【答案】C【解析】解:将9180 000用科学记数法表示为:9.18×106.故选:C.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】B【解析】解:A、从左面看与从正面看都是正方形,即得到的平面图形相同;B、从左面看是小长方形,从正面看大长方形,得到的平面图形不相同;C、从左面看与从正面看都是圆,即得到的平面图形相同;D、从左面看与从正面看都是三角形,即得到的平面图形相同;本题是选择从左面看与从正面看所得到的平面图形不相同的,故选:B.主视图、左视图是分别从物体正面、左面看所得到的图形.根据主视图与左视图相同,可得答案.本题考查了简单几何体的三视图,非常简单,锻炼了学生的空间想象力和抽象思维能力.6.【答案】B【解析】解:A、利用45°和30°的角可以画出15°的角,故本选项错误;B、=,不合题意,即借助常用的直角三角尺,能画出一些度数的角,不能画出100度的角,故本选项正确;C、利用90°、45°和30°组合即可画出165°的角,故本选项错误;D、利用90°和45°组合即可画出165°的角,故本选项错误;故选:B.先分清一副三角尺,各个角的度数分别为多少,然后将各个角相加或相减即可得出答案.此题主要考查了用三角板直接画特殊角,关键掌握用三角板画出的角的规律:都是15°的倍数.7.【答案】C【解析】解:A、3a2b与ba2是同类项,故本选项错误;B、是整式,故本选项错误;C、单项式-3y2的系数是-1,故本选项正确;D、32-y+5y2是三次三项式,故本选项错误.故选:C.分别根据单项式、多项式、整式及同类项的定义判断各选项即可.本题考查单项式、多项式、整式及同类项的定义,注意掌握单项式是数或字母的积组成的式子;单项式和多项式统称为整式.8.【答案】C【解析】解:A、两边加不同的数,故A错误;B、两边除以不同的数,故B错误;C、两边都减同一个整式,故C正确;D、两边除以不同的数,故D错误;故选:C.根据等式的性质,可得答案.本题考查了等式的性质,熟记等式的性质是解题关键.9.【答案】D【解析】解:设点P表示的数是,∵PM=2PN,∴|+4|=2|-2|,解得:=0或8,故选:D.根据题意列方程即可得到结论.本题考查了数轴和一元一次方程的应用,主要利用了数轴上两点间的距离的表示方法,读懂题目信息,理解两点间的距离的表示方法是解题的关键.10.【答案】C【解析】解:设被污染的常数为,则:2y-=y-,∵此方程的解是y=-,∴将此解代入方程,方程成立∴2×(-)-=×(-)-.解此一元一次方程可得:=3∴这个常数是3.故选:C.设这个常数为,已知此方程的解是y=-,将之代入二元一次方程2y-=y-,即可得这个常数的值.本题主要考查了一元一次方程的应用以及它的解的意义.知道一元一次方程的解,求方程中的常数项,可把方程的解代入方程求得常数项的值.(把■作为一个未知数看即可).11.【答案】B【解析】解:因为(b+c)-(a-d)=b+c-a+d=(b-a)+(c+d)=-(a-b)+(c+d)…(1),所以把a-b=-3、c+d=2代入(1)得:原式=-(-3)+2=5.故选:B.先把括号去掉,重新组合后再添括号.(1)括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“-”,去括号后,括号里的各项都改变符号.运用这一法则去括号;(2)添括号后,括号前是“+”,括号里的各项都不改变符号;添括号后,括号前是“-”,括号里的各项都改变符号.运用这一法则添括号.12.【答案】B【解析】解:设甲一共做了天,由题意得:+=1,故选:B.设甲一共做了天,则乙做了(-1)天,再根据工作效率×工作时间=工作量可得甲的工作量为,乙的工作量为,然后再根据甲的工作量+乙的工作量=1列出方程.此题主要考查了由实际问题抽象出一元一次方程,关键是正确理解题意,找出题目中等量关系,再列出方程.13.【答案】4【解析】解:∵2+1是-9的相反数,∴2+1=9.解得:=4.故答案为:4.先依据相反数的定义得到2+1=9,解关于的方程即可.本题主要考查的是相反数的定义、解一元一次方程,依据相反数的定义列出关于的方程是解题的关键.14.【答案】64 57 36【解析】解:32.48°×2=64度57分36秒;故答案为:64;57;36.进行度、分、秒的转化运算,注意以60为进制.将度的小数部分化为分,将分的小数部分化为秒.此类题是进行度、分、秒的转化运算,相对比较简单,注意以60为进制即可.15.【答案】11a+20【解析】解:两位数,个位数字是a,十位数字比个位数字大2可表示为(a+2).∴这个两位数是10(a+2)+a=11a+20.两位数为:10×十位数字+个位数字.本题的关键是,两位数的表示方法:十位数字×10+个位数字,要求掌握该方法.用字母表示数时,要注意写法:①在代数式中出现的乘号,通常简写做“•”或者省略不写,数字与数字相乘一般仍用“×”号;②在代数式中出现除法运算时,一般按照分数的写法写;③数字通常写在字母的前面;④带分数的要写成假分数的形式.16.【答案】135【解析】解:∵OB平分∠COD,∴∠COB=∠BOD=45°,∵∠AOB=90°,∴∠AOC=45°,∴∠AOD=135°.故答案为:135.本题是有公共定点的两个直角三角形问题,通过图形可知∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,同时∠AOC+∠BOC+∠BOD+∠BOC=180°,可以通过角平分线性质求解.本题是角的平分线与对顶角的性质的考查,角平分线的性质是将两个角分成相等的两个角.17.【答案】4【解析】解:8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了场,则3+(7-)=15,解得:=4.故答案是:4.8个班进行友谊赛,也就是说每个班级要和其余7个班级比赛,根据总比赛场数为7,设赢了场,总分数为15即可列出方程,即可解题.本题考查了一元一次方程的应用,本题中根据题意找出总比赛场数为7是解题的关键.18.【答案】8【解析】解:∵a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,∴a+8+b-5=8+b-5+c①,8+b-5+c=b-5+c+d②,b-5+c+d=-5+c+d+4③,∴a-5=c-5,8+c=c+d,b-5=-5+4,∴b=4,d=8,a=c,故答案为8.由题意得a+8+b-5=8+b-5+c=b-5+c+d=-5+c+d+4,然后转化成方程组的形式,求得d的值即可.本题是一道找规律的题目,考查了有理数的加法和方程组的思想,是中档题难度不大.19.【答案】解:(1)-6+3.6+4-5.6=-11.6+7.6=-4;(2)42×(-)÷-(-12)÷(-4)=-8-3=-11;(3)-12018+24÷(-2)3-32×()2=-1+24÷(-8)-9×=-1-3-1=-5.【解析】(1)先同号相加,再异号相加即可求解;(2)先算乘除,后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;(3)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.20.【答案】解:(1)原式-6a2+6ab+4a2+4ab-24=-2a2+10ab-24;(2)原式=122y-4y2+5y2-52y-22y=52y+y2,当=,y=-5时,原式=5×()2×(-5)+×52=-1+5=4.【解析】(1)去括号、合并同类项即可得;(2)原式去括号、合并同类项化简后,把,y的值代入计算可得.本题主要考查整式的加减-化简求值,解题的关键是掌握整式的加减运算顺序和运算法则.21.【答案】解:(1)去括号得:3-7+7=3-2-6,移项合并得:-2=-10,解得:=5;(2)去分母得:3-3=8-2-6,移项合并得:-11=-11,解得:=1.【解析】(1)方程去括号,移项合并,把系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.【答案】解:(1)(-2)⊕3=-2×(-2-3)+1=10+1=11;(2)3⊕=3(3-)+1=-5,9-3+1=-5,-3=-15,=5.【解析】(1)根据新运算得出原式=-2×(-2-3)+1,求出即可;(2)根据新运算得出3(3-)+1=-5,求出方程的解即可.本题考查了求代数式的值和有理数的混合运算,能读懂题意是解此题的关键.23.【答案】解:如图,设∠BOE=°,∵∠BOE=∠EOC,∴∠EOC=2°,∵OD平分∠AOB,∴∠AOD=∠DOB=70°-°,∵∠AOD+∠DOB+∠BOE+∠EOC=180°,∴70°-+70°-+°+2°=180°,∴=40,∴∠EOC=80°.【解析】设∠BOE=°,则∠EOC=2°,由∠DOE=70°及OD平分∠AOB知∠AOD=∠DOB=70°-°,根据∠AOD+∠DOB+∠BOE+∠EOC=180°列出关于的方程,解之可得.本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.24.【答案】解:(1)设第一次购进烤火器台,则第二次购进烤火器(-10)台,根据题意得:150=180(-10),解得=60,-10=50.答:家电销售部第一次购进烤火器60台,第二次购进50台.(2)(250-150)×60+(250-180)×50=9500(元).答:以250元/台的售价卖完这两批烤火器,家电销售部共获利9500元.【解析】(1)设第一次购进烤火器台,则第二次购进烤火器(-10)台,根据第二次进货单价比第一次进货单价贵30元即可得出关于的一元一次方程,解之即可得出结论;(2)根据总利润=销售第一批烤火器的利润+销售第二批烤火器的利润即可求出家电销售部共获利多少元.本题考查了一元一次方程的应用,根据数量关系列出关于的一元一次方程是解题的关键.25.【答案】+1 +7 +8 128【解析】解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为,则另外三个数用含的式子从小到大依次表示+1;+7;+8;故答案为+1;+7;+8;(2)∵当四个数是1,2,8,9时最小,a1=1+2+8+9=20;当四个数是23,24,30,31时最大,a2=23+24+30+31=108,∴a1+a2=20+108=128.故答案为:128;(3)由题意得,++1++7++8=76,解得=15,答:当被框住的4个数之和等于76时,的值为15;(4)不能.由题意得,++1++7++8=92,解得=19,故由此框住的四个数应是19,20,26,27,但是19,20不在同行的相邻位置,所以不能框住4个数的和等于92.(1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其他三个数;(2)先求出四个数之和最小a1,和最大a2的值,再求和即可;(3)、(4)根据(1)中各数的表达式求出的值即可.本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.26.【答案】1【解析】解:(1)∵A,B表示的数分别为6,-4,∴AB=10,∵PA=PB,∴点P表示的数是1,故答案为:1;(2)设点P运动秒时,在点C处追上点R,则:AC=6 BC=4,AB=10,∵AC-BC=AB,∴6-4=10,解得,=5,∴点P运动5秒时,追上点R;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时(如图①):MN=MP+NP=AP+BP=(AP+BP)=AB=5.②当点P运动到点B左侧时(如图②),MN=PM-PN=AP-BP=(AP-BP)=AB=5;综上所述,线段MN的长度不发生变化,其长度为5.(1)由已知条件得到AB=10,由PA=PB,于是得到结论;(2)设点P运动秒时,在点C处追上点R,于是得到AC=6 BC=4,AB=10,根据AC-BC=AB,列方程即可得到结论;(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时②当点P运动到点B左侧时,求得线段MN的长度不发生变化.此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.。
