天津大学考研 811电路1996-2006十年试题超详细解答
天津大学信号与系统考研资料

天津大学信号与系统考研资料考研真题-考研资料-笔记讲义许多学生在考研复习的时候,都会遇到重点不明确,不知道从何复习的情况。
为此,天津考研网建议,考研复习中,专业的考研复习资料,是帮助考生能够快速掌握复习重点及方法必不可少的因素,然后就是真题和讲义,可以让同学了解历年考研的出题方向和大致范围。
天津考研网推出了天津大学信号与系统的考研复习资料及真题解析班,以下为详细介绍。
【适用对象】2014年报考天津大学且初试科目为815信号与系统的专业课基础不扎实、对院系内部信息了解甚少的同学,适合跨校考生使用【推荐理由】由本部签约的天津大学在读本硕博团队搜集整理精心编制成套,严格依照天津大学信号与系统最新考研大纲及考研参考书目整理,目前为市面上最全面的资料,作为基础强化及冲刺全程使用,分售400余元,全套购买享受大幅优惠并有赠品【包含资料】第一部分天津大学信号与系统考研真题及答案:1、天津大学815信号与系统1996-2012年考研真题(市场独家最全,全国独家推出,试卷均为原版,掌握最新试题动向先人一步),众所周知天大出题重复率高,一般多年的试题就是一个小题库,所以历年试题一定要仔细研究,通过多年试卷可总结出出题重点及思路;2、天津大学815信号与系统1996-2011年考研试题参考答案,解决学生答题后勘误的困惑,本套答案为签约团队独家主创,保证极高正确率,市面上的答案基本都有错误或模糊不清,请同学认真分辨市面一些低价劣质的资料,以免耽误考研;3、天津大学815信号与系统2006-2010年考研真题解析,由本院资深团队主创,视频格式,光盘发送,对考研真题进行了详细讲解并做深度分析,总结出题规律,进行必要的答题技巧点拨,同时在关键时刻做考点预测,全国独家研发;第二部分天津大学信号与系统高分学长全程复习资料:第一份笔记(初期使用,共47页)信号与系统课本重点整理这一份笔记是最开始看课本时用。
鉴于信号教材不一致,可能在符号书写上,知识点的梳理上,学校间可能不一样,因此出此笔记。
2007年天津大学电气考研专业课电路(811)试题
100 2 R( ) 25 R2 2 R 3
最后解得
R1 R2 R 300
X L X C X 100 3 173
2007-5 (16 分 ) 图示非正弦周期电流电路,已知, R1 40 , L1 10 ,
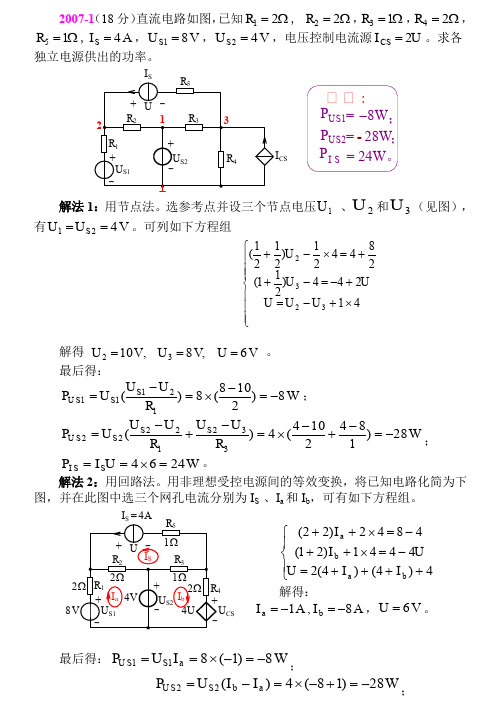
2007-1 (18 分) 直流电路如图, 已知 R1 2 , R2 2 , R4 2 , R3 1 , R5 1 , I S 4 A , U S1 8 V , U S 2 4 V ,电压控制电流源 I CS 2U 。求各 独立电源供出的功率。
IS + U R2 1 R1 + US1 + US2 R5 R3
( R2 X L - R1 X C )( R1 R2 ) - ( R1 R2 X L X C )( X L - X C ) ( R1 R2 ) 2 ( X L - X C ) 2
其虚部为
( R2 X L - R1 X C )( R1 R2 ) - ( R1 R2 X L X C )( X L - X C ) ( R1 R2 ) 2 ( X L - X C ) 2
由已知条件得知虚部为零,即
( R2 X L - R1 X C )( R1 R2 ) - ( R1 R2 X L X C )( X L - X C ) 0
即
( R2 X L - R1 X C )( R1 R2 ) ( R1 R2 X L X C )( X L - X C ) „„„(1)
Z j
( R1 j X L )( R2 - j X C ) ( R1 j X L ) ( R2 - j X C ) ( R1 R2 X L X C ) j( R2 X L - R1 X C ) ( R1 R2 ) j( X L - X C ) [( R1 R2 X L X C ) j( R2 X L - R1 X C )](( R1 R2 ) - j( X L - X C ) ( R1 R2 ) 2 ( X L - X C ) 2 ( R1 R2 X L X C )( R1 R2 ) ( R2 X L - R1 X C )( X L - X C ) ( R1 R2 ) 2 ( X L - X C ) 2
2009年天津大学电气考研专业课电路(811)试题

+
2 I USRຫໍສະໝຸດ U -R3 U S Ia
解法 1:用网孔法。设三个网孔电流分别为 IS 、Ia 和 Ib(见图) ,可有如 下方程组。
3I a 2 I b 6 I 1 4 I b 1 2 I a U 3 I Ib Ia U Ib 1
1 1
U 2060 Z1 1 j20 ; I 1 30 1 130 A 可得 200 V , I U
3
3
U 200 3 Z2 20 30 17.32 j10 。 I 3 130
2009-5 (16 分 ) 图示非正弦周期电流电路,已知, R 6 , 1 8 , C1
IU S I 6 U1 63 2 5 A , U I S U 1 R5 I S 3 2 1 1 V 。 R2 1 最后得:
IS S ; IS 。 2009-2 (14 分)直流电路如图,已知 R1 4 , R2 12 R3 6 ,
+ uS -
; 8 2 sin (2 t 143.1) V ( t 36.9 ) 1. uC2 (t ) 10 2 sin 2. I 2 . 236A; 3. P 30 W。
解:直流分量: I
( 0)
( 0) 0 ,U C 2 0。
答 答:
基波分量电路为下图。有 L
P U S U S I U S 6 5 30 W
P U I 11 1 W
R4 2 ,U S 16 V ,电流控制电压源 U CS 6 I 。求 RL 为多少时可获得最大 功率?并求此最大功率 Pmax 。
天津大学考研 811电路1996-2006十年试题超详细解答

PU S1 = U S1 (
PU S 2
U1 - U 3 U1 - U 2 20 - 8 20 - 19 + ) = 20 ´ ( ) = 62 W ; R3 R2 4 10 = -U S 2 I = -4 ´ 2 = -8 W
PU S1 = U S1 ( I - I 1 ) = 20 ´ (2 - ( -1 .1)) = 62 W PU S 2 = -U S 2 I = -4 ´ 2 = -8 W
;
;
PI S = I S ( R 2 ( I S + I 1 ) + R3 ( I S + I ) + R 4 I S ) = 1 ´ (10(1 - 1.1) + 4(1 + 2) + 3 ´ 1)) = 14 W 。
-5 = 3A 。 8 13
解:1. 将 R 左侧用戴维南等效电路替代后有左下图(a)电路。
图(a)
图(b)
由已知条件可有如下方程组 ì U OC ´3 =3 ï ï Rin + 3 í U ï OC ´ 6 = 4.8 ï î Rin + 6 解得 U OC = 12 V , Rin = 9W 。
(1) (1) 2 (1) IL = (I S ) R1 = 2 2 ´ 60 = 240 W 2 = 2A, P
二次谐波
Z L 2 // Z C = & =I & ( 2) I L2 S
(j 2wL2 )( - 1 2wC ) j120 ´ ( - j 30) = = - j 40W (j 2wL2 ) + ( - 1 2wC ) j120 - j 30 R1 - 1 2wC 60 - j 30 = 4.5 ´ R1 + R 2 (j 2wL2 ) + (- 1 2wC ) 60 + 30 j120 - j 30
天津大学811电路01年试题

2001-1直流电路如图(a ),试求电流1I 、2I 及各独立电源供出的功率。
(15分)I +--2+32ab1CCVS 22778+-0. 5I CCCS2ΩΩΩΩΩVV I 2I 1I +--2+321222178+-0. 5I 2ΩΩΩΩΩVV I 2I 1-+-7I 2I 2I 1-3I 2Ic(a)(b)答案:A 21=I ,A 5.22=I ,W 5.10V 7-=P ,W 32V 8-=P 。
解法1:将原电路等效化简为图(b)后用网孔法。
设三个网孔电流分别为I 、2I 和213I I -,可列如下方程组8212)3(95.02)3(2687242221121222+-=+-=-++-=+I I I I I I I I I I I 2(I -3I 2)2(I -3I )=1解得 A 21=I ,A 5.22=I ,A 5.1-=I 。
W 5.107V 7-==I P ; W 32)3(821V 8-=--=I I I P。
解法2:用节点法。
参考点和各独立节点见图(a),则有V 8=b U 可列如下方程组25.07125.032821)711(25.027212823121121ac c a c c a U U I I U I I I U U I U U -+==-=--++=--+(2121+U c 即05.0207565.342716155.03121121=+--=-=+--=--a c c a c c a U U I I U I I I U U I U U解得 V,14V,10==c a U U A 21=I ,A 5.22=I 。
W 5.10)27(7V 7-=--=a U P ; W 32)2828(8V 8-=-+-=ca U U P 。
2001-2图示电路,A N 为线性含源网络,电阻R 可调。
已知:∞=R 时,V 10=U 且有,A 31=I A 52=I ;当Ω=5R 时,R 获得最大功率,且有,A 41=I A 22=I 。
天津大学电气工程考研真题及学长谈做电气工程考研真题经验
天津大学电气工程考研真题及学长谈做电气工程考研真题经验相信大家都知道,真题是应该好好钻研的。
真题就是历年考题的原题,在真实性方面,它的作用是任何模拟试题都难以代替的,所以同学们复习真题的时候,一定要在“真”方面下功夫,细细品味。
接下来就和大家介绍一下天津大学电气工程考研真题的做题经验。
天津大学电气工程专业考研都会考到的专业课就是811电路。
专业目录:080800电气工程_01电力系统及其自动化、高电压与绝缘技术①101思想政治理论②201英语一或203日语③301数学一④811电路复试科目:电力系统基础_02电机与电器、电力电子与电力传动、电工理论与新技术①101思想政治理论②201英语一③301数学一④811电路复试科目:电气控制085207电气工程(专业学位)_01电力系统及其自动化、高电压与绝缘技术①101思想政治理论②201英语一或203日语③301数学一④811电路复试科目:电力系统基础_02电机与电器、电力电子与电力传动、电工理论与新技术①101思想政治理论②201英语一③301数学一④811电路复试科目:电气控制天津大学811电路2016及2015年考研大纲对比:天津大学811电路2016年考研大纲天津大学811电路2015年考研大纲一、考试的总体要求掌握电路的基本理论和分析计算电路的基本方法,灵活运用所学的电路理论及方法解决复杂的综合性电路问题。
二、考试的内容及比例1.基本概念:电压、电流及其参考方向,电阻、电容、电感、电压源和受控源等元件的特性及其电压电流关系,线性和非线性的概念,电功率和电能量,电路模型,基尔霍夫定律。
2.线性电阻电路的分析:简单电阻电路的计算,星角转换,非理想电源的模型及其等效转换,支路分析法,回路分析法,节点分析法,叠加定理,互易定理,替代定理,戴维南定理和诺顿定理,匹配的概念。
3.正弦交流电路的稳态分析:正弦量的基本概念,正弦量的相量、相量图、电路元件电压电流关系的相量形式、阻抗和导纳,基尔霍夫定律的相量形式,正弦电路的功率,功率因数,正弦电路的分析计算(复数运算、相量图分析),含互感电路的计算(互感电压、同名端、串联、并联、互感消去),谐振电路的特点及其分析计算,三相电路的连接方式,对称三相电路的电压、电流和功率的计算,非正弦周期电流电路的分析计算方法。
天津大学811电路05年试题

2005-1(18分)直流电路如图,已知Ω=41R , Ω=22R ,Ω=13R ,Ω=64R ,Ω=15R ,Ω=15R ,Ω=26R A 4S =I ,V 8S =U ,流控压源I U 4CS =,求各独立电源供出的功率。
R R R R -U S SI+1234I +-U R CS 5答案P U S =32W P I S =160W :;。
12I U S +-U I S-R 63 解:用节点法。
设参考点和三个独立节点电压1U 、2U 和3U如图,有V 82=U 。
可列如下方程组21)2141(==-+1U +11142)4(=+U I34-121U 4I U 3-2U 41-U 3×8-8化简为0.751U -U 3=80.25U -1=30.25-0.25U 8解得 A)8(V,16,V 1631===I U U 。
按非关联方向设独立电压源中的电流为S U I ,独立电流源两端电压为SI U (见图),可得A 4216811681821233252S -=-+-+=-+-+=R U U R U U R U I U ;` V 404616S 41S =⨯+=+=I R U U I 。
最后得:W 32)4(8S S S -=-⨯==U U I U P ;W 160404S S S =⨯==I I U I P 。
2005-2 (16分)图示S N 为含源线性电阻性网络。
已知当Ω=62R 时,V 62=U ,A 41-=I ;当Ω=152R 时,V 5.72=U ,A 71-=I 。
求(1) ?2=R 可获得最大功率,并求此最大功率P max 。
(2) ?2=R 可使01=I 。
N SI 1U 2+-R 1答案:R P =3Ωmax =6.75W ;。
R 2时P 2=(1)R =2.4Ω时(2)I 1=0R 22解:(1)将R 2左侧用戴维南等效电路替代后有下图(a )电路。
R +-i nR 2U OC +-U 2N SI 1U 2+-R 1(a) (b)由已知条件可有如下方程组⎪⎪⎩⎪⎪⎨⎧=⨯+=⨯+5.71515666in OC in OCR U R U解得 V 9OC =U ,Ω=3in R 。
天津大学自动控制理论考研真题-考研资料-笔记讲义

在天津大学自动控制理论复习中,资料、真题及讲义是必不可少的。
很多同学,特别是跨专业考生,在复习中没办法掌握重点,所以走了很多弯路。
而考研资料和讲义就可以让考生们在复习中迅速找到重点范围,掌握复习技巧。
另外、真题可以让考生掌握近几年的出题方向,测试自己的复习结果。
针对同学的复习情况,天津考研网独家推出了天津大学自动控制理论考研复习资料,以下为资料相关介绍。
【适用对象】2014年报考天津大学且初试科目为812自动控制理论(经典控制、现代控制)的专业课基础不扎实、对院系内部信息了解甚少的同学,适合跨校考生使用【推荐理由】由本部签约的天津大学在读本硕博团队搜集整理精心编制成套,严格依照天津大学最新考研大纲及考研参考书目整理,目前为市面上最全面的资料,作为基础强化及冲刺全程使用,分售500余元,全套购买享受大幅优惠并有赠品【使用方法】基础阶段使用课件及本科笔记配合指定教材复习,梳理知识点,切实感受天大课题氛围;强化阶段使用历年考研辅导班笔记总结分析总结天大授课重点;冲刺阶段使用历年试题等试题资料进行测试,通过试题答案可以检验做题效果,同时可以分析出题思路及重点。
【包含资料】第一部分天津大学自动控制理论考研真题及答案:1、天津大学812自动控制理论1991-2013年考研真题(市场独家最全,其中2012、2013年试题由本站特约考生团队回忆,并由签约研究生团队精确点评,全国独家推出,均为原版试卷,掌握最新试题动向先人一步),众所周知天大出题重复率高,一般多年的试题就是一个小题库,所以历年试题一定要仔细研究,通过多年试卷可总结出出题重点及思路;2、天津大学812自动控制理论1999-2012年考研试题参考答案,本套答案为签约团队独家主创,保证极高正确率,市面上的答案基本都有错误或模糊不清,请同学认真分辨市面一些低价劣质的资料,以免耽误考研。
尤其2006-2011年的答案均为出题老师判卷标准答案,内部获得,市场唯一推出;3、天津大学812自动控制理论2007-2011年考研真题解析,由本院资深团队主创,视频格式,光盘发送,对考研真题进行了详细讲解并做深度分析,总结出题规律,进行必要的答题技巧点拨,同时在关键时刻做考点预测,全国独家研发;第二部分天津大学自动控制理论核心资料:1、天津大学自动控制理论03-06、08(两套)、2011年、2013年考研辅导班笔记,03、04为最后两次校内主办,出题老师主讲,众所周知透题班,重要性可见一斑,2011年、2013年考研笔记为独家推出,历年对比参考,自己总结重点、趋势以推测今后出题思路,非常有效;3、天津大学自动控制理论本科笔记两套,重点突出,对比使用效果更好,跨校考生可侧面了解天大授课重点;4、天津大学现代控制理论课件,教师授课用,配合本科笔记感受天大授课课堂;5、天津大学自动控制理论简明教程,天津大学自动化学院内部本科上课讲义,不对外出售,由夏老师主编,书中有本科生上课勾画重点笔记,仅提供PDF电子版,现代控制部分用的不是这个讲义(用的是高教的教材);6、天津大学自动控制理论2007-2013年考研大纲,打印版,通过历年大纲对比可以更深入了解历年考试考点及参考书目变化情况从而预测趋势,独家提供;7、天津大学自动化专业复试资料,包括分数线、录取数据、复试笔记题、复试实验题、面试题,对于复试具有重要指导意义,独家资料;8、天津大学自动控制理论考研复习心得(初试+复试),由高分考生聚合多位同学经验执笔而成,对于自控考研具有重要参考价值,资料为打印版8页,包括:一、学院学科介绍、导师和招生情况介绍;二、试题风格的重大转变(较之以前的做出了整体分析)三、考试重点及复习方法(按章节顺序做出了具有针对性的分析,指出备考重点、难点。
天津大学2018年硕士研究生初试自命题科目大纲 - 811 电路、812 自动控制理论

811 电路
一、考试的总体要求
掌握电路的基本理论和分析计算电路的基本方法,灵活运用所学的电路理论及方法解决复杂的综合性电路问题。
二、考试的内容及比例
1.基本概念:电压、电流及其参考方向,电阻、电容、电感、电压源和受控源等元件的特性及其电压电流关系,线性和非线性的概念,电功率和电能量,电路模型,基尔霍夫定律。
2.线性电阻电路的分析:简单电阻电路的计算,星角转换,非理想电源的模型及其等效转换,支路分析法,回路分析法,节点分析法,叠加定理,互易定理,替代定理,戴维南定理和诺顿定理,匹配的概念。
3.正弦交流电路的稳态分析:正弦量的基本概念,正弦量的相量、相量图、电路元件电压电流关系的相量形式、阻抗和导纳,基尔霍夫定律的相量形式,正弦电路的功率,功率因数,正弦电路的分析计算(复数运算、相量图分析),含互感电路的计算(互感电压、同名端、串联、并联、互感消去),谐振电路的特点及其分析计算,三相电路的连接方式,对称三相电路的电压、电流和功率的计算,非正弦周期电流电路的分析计算方法。
4.线性动态电路的时域分析:一阶动态电路的动态过程,换路定则,一阶动态电路的分析计算(零输入响应,零状态响应和全响应,三要素法),阶跃函数和冲激函数,阶跃函数响应和冲激函数响应,二阶电路的时域分析。
5.线性电路的复频域分析:电路元件电压电流关系的复频域形式,复频域阻抗和复频域导。
2008年天津大学电气考研专业课电路(811)试题
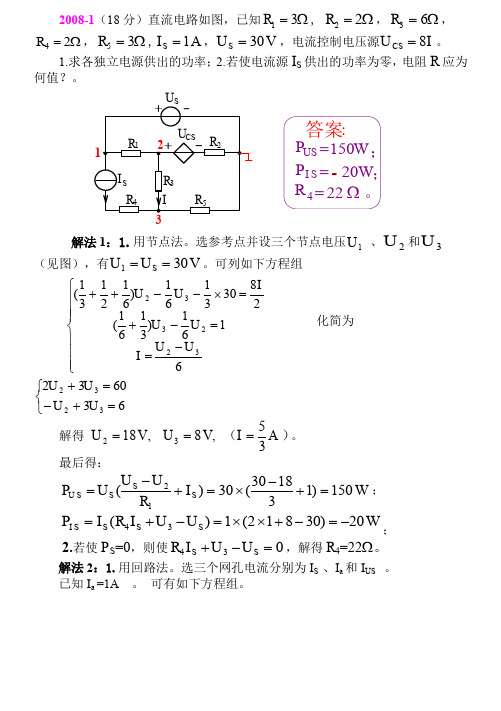
2.若使 PS=0,则使 R4 I S + U 3 - U S 0 ,解得 R4=22。
解法 2:1.用回路法。选三个网孔电流分别为 IS 、Ia 和 IUS 。 已知 Ia =1A 。 可有如下方程组。
-
UCS
答案: PUS =150W ; PI S = - 20W; R 4 = 22 。
+
化简为
5 。 A) 3
;
IU S UCS Ia R1 I S IS R4
得:
+
R3 I
PI S I S ( R4 I S + R5 I a - U S ) 8 1 (2 1 + 3 - 30) -20 W ; 3 2.若使 PS=0,则使 R4 I S + R5 I a - U S 0 ,解得 R4=22。
2008-3 (12 分)图(a)所示 N S 为线性含源电阻网络,RL=4。已知当 U S 12 V 时, I 1 3 A , I 2 2 A ;当 U S 10 V 时, I 1 2 A , I 2 1 A 。求: 1. U S 8 V 时, U 2 等于多少伏? 2. U S 8 V ,外接电路换接如图(b)所示, I S 3 A 时, I 1 等于多少安?
解得
a
+ I1 -6 + 1 -5 A I1 I1
2008-4 (10 分)图示正弦交流电路,已知电路的有功功率 P 240 W ,电流有 效值 I I 2 4 A ,I 1 无功功率 Q 。 i i1 i2 + C L u R 解:1. R
48 A 。1.求参数 R、XL 和 XC ;2.求电路的视在功率 S 和
天津大学811电路2006年真题

考试科目名称:电路考试科目代码:8112006-1(18分)直流电路如图,已知Ω=101R ,Ω=102R ,Ω=43R ,Ω=34R ,Ω=25R ,V 201S =U ,V 42S =U ,A 1S =I ,电流控制电压压源I U 4CS =。
求:各独立电源供出的功率。
考试科目名称:电路考试科目代码:8112006-2(15分)电路如图,已知Ω=41R ,Ω=62R ,Ω=43R ,Ω=14R ,Ω=25R ,Ω=46R ,V 30S =U ,电压控制电流源1CS 2U I =。
试用戴维南定理求图示电路中电流I 。
考试科目名称:电路考试科目代码:8112006-3(15分)图示N 为无源线性电阻网络,A 2S =I ,R 为可调电阻。
当Ω=3R 时,测得V 32=U ;当Ω=6R 时,测得V 8.42=U ;当∞=R 时,测得V 201=U 。
现A 4S =I 。
试求:1.R =?时,可获得最大功率,并求此最大功率P m a x ;2.此时I S 供出的功率。
考试科目名称:电路考试科目代码:811 2006-4(8分)对称三相星接电路如图,已知电源线电压U l=380V,三相功率P=3630W,负载(R - j X C)的功率因数cosϕ=0.5。
1.求电阻R和容抗X C;2.若图中m点发生断路,求U C N和U C P。
考试科目名称:电路考试科目代码:8112006-5(16分)非正弦电路如图,已知A 102sin 25.410sin 223i 33S t t ⨯++=,Ω=601R ,Ω=302R ,H 02.01=L ,H 06.02=L ,F 10614-⨯=C 。
1.求电感电流)(2t i L 及其有效值2L I ;2.求电路的有功功率P 。
考试科目名称:电路考试科目代码:8112006-6(16分)图示电路中,Ω=81R ,Ω=62R ,Ω=33R ,Ω=64R ,Ω=35R ,F 1.0=C ,H 5.0=L ,A 5S =I ,V 181S =U ,V 32S =U ,V 63S =U 。
天津大学811电路考研真题复习宝典

天津大学811电路考研真题复习宝典天津大学811电路考研真题复习宝典考研是一场刻苦攻坚战,如何在百万大军的战役中成为王者?如何在紧张繁忙的点滴时间高效复习?查漏补缺、实战演练是关键。
历年考研真题是首屈一指的考研复习法宝,但是绝大多数研友在网络上搜罗到的真题很多都很模糊,甚至有些真题是伪造的,真题答案也不详细,基于此天津考研网一直致力于为研友提供最全面、最详细、最权威的考研真题宝典。
以下复习方法摘自天津大学811电路考研真题复习宝典资料部分。
一、考研经验电路专业课复习时间安排因人而异,因为还有数学和英语要复习,我是在8月份开始复习的,以下是我的复习计划,供同学作为参考。
1、8月~9月两个月把电路课本复习两到三遍,电路课本一定要复习的扎实,这样在以后的考研过程中会容易得多。
在此期间,我也把天津考研网《考研红宝书》过了一遍,属于打基础阶段。
2、10月~11月一个月把天津考研网《考研红宝卷》认认真真的做一遍,做的过程中把自己认为有价值的题目勾出来并仔细品味,在过程中要打上自己的笔记,供后来复习参考。
3、12月~初试前在前面的三个月的扎实复习之后,就可以进行最重要的一环了:做真题。
可以参考天津考研网《天津大学811电路考研真题复习宝典》。
当自己的电路知识扎实之后才能研究真题,这样才有事半功倍的效果。
前面说了天大的电路总体是不容易的,天大电路共有十一题,平均一题用时13分钟,实际还是很难完成的,因为在试题中肯定会碰到20分钟都难以解决的题目,所以一再强调基础一定要打好,这样才能以不变应万变。
天大十一种题型如下:1.直流稳态分析2.戴维南定理求等效电路3.黑箱问题4.交流稳态分析5,非正弦稳态分析6,一阶电路7,二阶电路8,二端口9,网络分析10,状态方程11,均匀传输线这两年题型有小的变化,但根本上这11种题型不变,因为这十一种题型包含了电路中最重要的几乎全部知识点,再变化也不会离开这些知识点。
所以后来回归,参透真题是至关重要的,一定要记住在知识扎实之前不要碰真题,真题很珍惜,一定要等知识扎实之后集中歼灭真题并从中总结出自己的理解。
天津大学811电路2010年真题
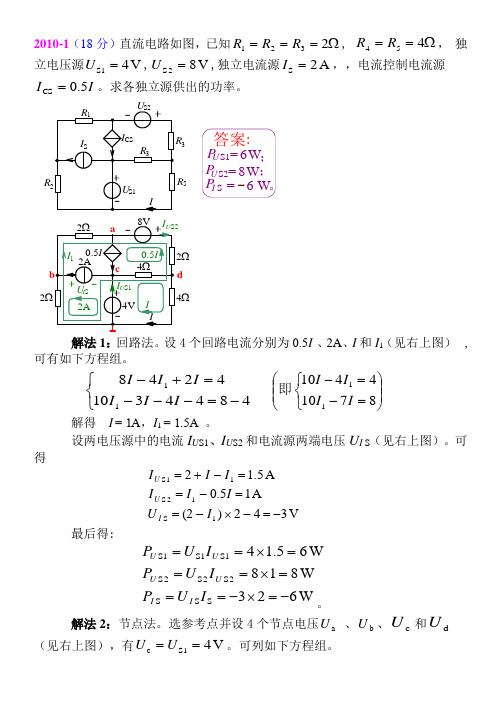
2010-1(18分)直流电路如图,已知Ω===2321R R R , Ω==454R R , 独立电压源V 41S =U ,V 82S =U ,独立电流源A 2S =I ,,电流控制电流源I I 5.0CS =。
求各独立源供出的功率。
-答案P U S1 =6W :;P I S =6W P U S2=8W ;R 532ΩΩ解法1:回路法。
设4个回路电流分别为0.5I 、2A 、I 和I 1(见右上图) ,可有如下方程组。
⎩⎨⎧-=---=+-4844310424811I I I I I I ⎪⎪⎭⎫ ⎝⎛⎩⎨⎧=-=-8710441011I I I I 即 解得 I = 1A ,I 1 = 1.5A 。
设两电压源中的电流I U S1、I U S2和电流源两端电压U I S (见右上图)。
可得A 5.1211S =-+=I I I U A 15.012S =-=I I I UV 342)(21S -=-⨯-=I U I最后得:W 65.141S 1S 1S =⨯==U U I U P W 8182S 2S 2S =⨯==U U I U P W 623S S S -=⨯-==I U P I I 。
解法2:节点法。
选参考点并设4个节点电压a U 、b U 、c U 和d U (见右上图),有V 41S c ==U U 。
可列如下方程组。
⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==--=---=--da d ab d b a 4141212215.042121U I U U U U I U U U 解得 A 1V 4V 1,V 2d b a ===-=I U U U ,,。
A 5.121121b 1S =+=+=U I I UA 15.02215.02a b 2S =-+=--=I U U I UV 3c b S -=-=U U U I最后得:W 65.141S 1S 1S =⨯==U U I U P W 8182S 2S 2S =⨯==U U I U P W 623S S S -=⨯-==I U P I I 。
(定稿)天津大学2010年《自动控制理论》考研试题与答案(附录)

天津大学2010年《自动控制理论》考研试题与答案一、选择题(每题6分,共30分)1.应用输入函数和系统脉冲响应函数的卷积运算,可以用来()。
A.计算线性定常系统对输入的影响B.计算定常系统对输入的相应,无论系统是线性的还是非线性的C.计算线性系统对输入的相应,无论系统是定常的还是时变的D.计算任意系统对任意输入的相应答案:A2.控制系统是稳定的,则()。
A.系统的控制误差渐近地趋于零B.系统去除扰动后控制误差会渐近地趋于零C.对给定的输入,系统不同初始条件下的响应渐近地趋于一致D.系统参数出现漂移时可以维持系统的控制性能答案:C3.在闭环系统的调试过程中,逐渐增大系统的开环增益,结果发现当快速性和稳定性达到设计要求时系统的控制精度欠佳,问应该采取下述那种措施?()A.采用滞后校正B.采用超前校正C.继续增加开环增益D.采用滞后-超前校正答案:A4.系统校正中控制器和被控对象间不稳定的零、极点间不能对消,是因为()。
A.零、极点对消会破坏系统的可控性和客观性B.参数变化可避免,严格对消没有实际意义C.零、极点对消往往导致复杂的控制器设计D.这样做会导致系统的不稳定答案:D5.被控对象是可控可观的,则()。
A.总能设计出控制器,使得闭环系统是稳定的B.可以构造状态观测器,使状态观测误差始终为零C.可以任意决定状态变量的收敛速度和观测误差的收敛速度D.应用状态反馈,可以任意配置系统的极点和零点答案:B二、(20分)质量弹簧系统如图所示,图中k为弹簧的弹力系数,f为阻尼器的摩擦系数,m为质量块的质量,F(t)为外力,以F(t)=0时重力作用下质量块的平衡位置为位移y的原点。
(1)试列写外力F(t)作为输入,位移y作为输出时系统的输入输出微分方程描述,给出系统的传递函数;(2)设系统在单位阶跃外力作用下,质量块的稳态位移为0.1,系统的无阻尼自然振荡频率n 10ω=,阻尼比0.5ζ=,求系统参数m、k、f;(3)求阶跃输入下系统的动态响应指标t r、t p、t s(按5%误差计算)和σ%。
2009年天津大学《电路(电路基础、网络分析)》考研真题

2009年天津大学《电路(电路基础、网络分析)》考研真题(总分:20.00,做题时间:90分钟)一、计算题(总题数:10,分数:20.00)1.直流电路如附图12—1所示,已知R 1=1Ω,R 2=1Ω,R 3=2Ω,R 4=1Ω,R 5=2Ω,I S=1A,U S=6V,电压控制电压源,电流控制电压源U CS2 =I。
求各独立源供出的功率。
(分数:2.00)__________________________________________________________________________________________ 正确答案:(正确答案:画出电路结构如附图12-2所示。
根据题意,列写节点电压方程,可得:所以:)解析:2.直流电路如附图12-3所示,已知R 1 =4Ω,R 2 =12Ω,R 3 =6Ω,R 4 =2Ω,U S =16V,电流控制电压源U CS =6I。
求R L为多少时可获得最大功率?并求此最大功率P max。
(分数:2.00)__________________________________________________________________________________________ 正确答案:(正确答案:先求解出R L两端的等效电路,然后根据最大功率计算原理求出结果。
当R L两端开路时,画出等效电路如附图12-4(a)所示,开路电压:当R L两端短路时,画出等效电路如附图12—4(b)所示,列写节点电压方程:因此有:当R L=R oc=8Ω时,得到最大功率:)解析:3.电路如附图12—5所示,已知N s为线性含源电阻网络,当R=18Ω时,I 1 =4A,I 2 =1A,I 3 =5A;当R=8Ω时,I 1 =3A,I 2 =2A,I 3 =10A。
求欲使I 1 =0,电阻R应为何值?此时I 2等于多少(分数:2.00)__________________________________________________________________________________________ 正确答案:(正确答案:将N S作戴维南等效,得到如附图12—6所示的等效电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 ´ 12 = 24 V 。 2 得当 R = Rin = 9W 时可获得最大功率,此最大功率为 ¢ = 根据齐次性原理当 I S = 4 A 时 U OC
2 U OC 24 2 = = 16 W 4 Rin 4 ´ 9 ¢ 2 = 12 V , I 2 = U 2 R = 12 9 = 4 3 A ,即所求为 2. 此时 U 2 = U OC 右上图(b)。将图(b)电阻支路用电流源替代后为左下图(c)。根据叠加定 理可有图(d)和图(e)。
( 或 o o & & & U CN = -U BC - 0.5U AB = -380Ð - 120 - 190Ð0 = 190 + j 329 - 190 = j 329 V ) & = -U & - RI & = -380Ð - 120 o - 10 ´ 9.5Ð60 o10 = 380Ð60 o - 95Ð60 o U
= -1 A = 1Ð180 o A ( 2) ( 2) 3 o iL 2 = 2 sin( 2 ´ 10 t + 180 ) A , I L 2 = 1 A R1 R2 60 ´ 30 ( 2) 2 ) = 405 W P (1) = ( I S = 4.5 2 ´ R1 + R2 60 + 30 最后得 i L 2 = 2 + 2 2 sin(10 3 t - 90 o ) + 2 sin( 2 ´ 10 3 t + 180 o ) A I L 2 = 2 2 + 2 2 + 12 = 3 A P = P ( 0 ) + P (1) + P (2 ) = 180 + 240 + 405 = 825 W 2006-6 (16 分) 图示电路中, R1 = 8W , R2 = 6W , R3 = 3W , R4 = 6W , R5 = 3W , C = 0.1 F , L = 0.5 H , I S = 5 A , U S1 = 18 V , U S 2 = 3 V ,
+
R1 C R2
S
IS uC
-
US1
+
US2
+
U ( ¥) =
I S + (U S 2 R 3 ) 5 + (3 3) = = 12 V , (1 R 2 ) + (1 R3 ) (1 6) + (1 3) u C (¥ ) = U (¥ ) - U S1 = 12 - 18 = -6 V U U 3 6 i L ( ¥ ) = S 2 + S 3 = + = 2 .5 A R4 R5 6 3 R R 6´3 , t RC = ( 2 3 + R1 )C = ( + 8) ´ 0.1 = 1s R2 + R3 6+3 L 0.5 1 t LC = = = s R2 R3 ( R2 + R) (6 ´ 3) (6 + 3) 4 最后得
N
电路N
+
U2 =U OC=12V 4A
+
U1
N
电路N
+
U 2 =12V 9
-
-
-
根据特勒根定理有
ˆ +U I ˆ ˆ U1I 1 2 2 = U 1 I1
解得
4 20(-4) + 12 ´ ˆ ˆ 3 = 32 V ˆ = U 1 I1 + U 2 I 2 = U 1 I1 -2
最后得
ˆ = 4 ´ 32 = 128 W PI S = I SU 1 2006-4 (8 分)对称三相星接电路如图,已知电源线电压 Ul =380V,三相 功率 P=3630W,负载(R - j XC)的功率因数 cosj=0.5 。1. 求电阻 R 和容抗 XC ;2. 若图中 m 点发生断路,求 UC N 和 UC P 。
PU S1 = U S1 ( I - I 1 ) = 20 ´ (2 - ( -1 .1)) = 62 W PU S 2 = -U S 2 I = -4 ´ 2 = -8 W
;
;
PI S = I S ( R 2 ( I S + I 1 ) + R3 ( I S + I ) + R 4 I S ) = 1 ´ (10(1 - 1.1) + 4(1 + 2) + 3 ´ 1)) = 14 W 。
i L (0 + ) = i L (0 - ) = i (0 - ) +
U S3 6 = 2 + = 4A R5 3 u C (0 + ) = u C (0 - ) = R 2 ( I S - i (0 - )) - U S 1 = 6 ´ (5 - 2) - 18 = 0 换路后为如下两一阶电路
U R3
最后得 I =
2006-3 (15 分)图示 N 为无源线性电阻网络, I S = 2 A ,R 为可调电阻。 当 R = 3W 时,测得 U 2 = 3 V ;当 R = 6W 时,测得 U 2 = 4.8 V ;当 R = ¥ 时,测 得 U 1 = 20 V 。现 I S = 4 A ,试求:1. R = ? 时,可获得最大功率,并求此最大功 率 Pm a x ;2. 此时 IS 供出的功率。
(1) (1) 2 (1) IL = (I S ) R1 = 2 2 ´ 60 = 240 W 2 = 2A, P
二次谐波
Z L 2 // Z C = & =I & ( 2) I L2 S
(j 2wL2 )( - 1 2wC ) j120 ´ ( - j 30) = = - j 40W (j 2wL2 ) + ( - 1 2wC ) j120 - j 30 R1 - 1 2wC 60 - j 30 = 4.5 ´ R1 + R 2 (j 2wL2 ) + (- 1 2wC ) 60 + 30 j120 - j 30
;
PI S = I S (U 2 - U 3 + R4 I S ) = 1 ´ (19 - 8 + 3 ´ 1) = 14 W 。
解法 2:用回路法。选三个网孔电流分别为 IS 、I 和 I1(见图),可有如下 方程组。 ì20 I 1 + 10 = -20 + 4 I í î 6 I + 4 = 20 - 4 解得 I = 2 A , I 1 = -1.1 A 。 最后得:
-5 = 3A 。 8 13
解:1. 将 R 左侧用戴维南等效电路替代后有左下图(a)电路。
图(a)
图(b)
由已知条件可有如下方程组 ì U OC ´3 =3 ï ï Rin + 3 í U ï OC ´ 6 = 4.8 ï î Rin + 6 解得 U OC = 12 V , Rin = 9W 。
(0) IL 2
解:直流分量 R1 60 ( 0) = IS =3 = 2A , R1 + R2 60 + 30
(0) 2 P (0) = ( I S )
R1 R2 60 ´ 30 = 32 = 180 W R1 + R2 60 + 30
基波分量
wL1 = 10 3 ´ 0.02 = 20W , wL 2 = 10 3 ´ 0.06 = 60W , 1 1 = = 60W 1 wC 3 -4 10 ´ ´ 10 6 (1) R1 I S 60 ´ 2 2 (1) m iL = sin(10 3 t - 90 o ) = sin(10 3 t - 90 o ) = 2 2 sin(10 3 t - 90 o ) A 2 wL2 60
U S 3 = 6 V 。开关 S 闭合前电路已达稳态,在 t=0 时 S 闭合。求 S 闭合后电容
电压 uC(t) 、电感电流 iL(t)和 R4 的电流 i (t)。
解:用三要素法有 I S R2 5´ 6 i (0 - ) = = = 2A , R 2 + R3 + R 4 6 + 3 + 6
Pmax =
图(c)
图(d)
图(e)
在图(d)电路中:由已知条件当 I S = 2 A , R = ¥ 时,测得 U 1 = 20 V 和齐
(1) ¢ = 24 V .。 次性原理可知 U 1(1) = 40 V ;由第一问得知 U 2 = U OC 图(d)和图(e)满足互易定理的第二种形式,根据互易定理的方向关系和 齐次性原理,在图(e)电路中有 1 (1) 4 3 U 1( 2 ) = -U 2 = -24 ´ = -8 V 4 3 由叠加原理得图(c)电路中的 U 1 为
1
4
+
2
R3
6
+ U1 + UOC
30V
4
图(a)
1 1 ì 1 1 1 ï( 4 + 4 + 6 )U 2 - 4 ´ 30 - 6 U O C = 0 解得 UOC = -5V。 í 1 1 1 2 ï ( + )U O C - U 2 = U OC 6 6 6 3 î 用开路短路法求入端电阻。将 R4 支路短路如上图(b),可得短路电流为 UOC 30 4 15 -5 8 = =- W ISC = ´ = A , 得 Rin = 4´ 6 4+6 8 I S C 15 8 3 +4 4+6 原电路等效为下图(c)
解: 1.
Il =
P 3U l cos j Z = Ul Il 3
= =
3630 3 ´ 380 ´ 0.5 220 = 20W 11
= 11 A
, j = arccos j = 60 o
可得
R = Z cos j = 20 ´ 0.5 = 10W X C = Z sin j = 20 ´ sin 60 = 10 3 = 17.32W
