2011年数学建模暑假培训第一次模拟题目(秦宣云)
2011年全国高中数学联赛一试模拟试题(1)及详细解答

2011年全国高中数学联赛一试模拟试题(1)一、填空题:(每题7分,共70分)1、方程6×(5a 2+b 2)=5c 2满足c ≤20的正整数解(a , b , c )的个数是__________个.2、过定点P (2, 1)作直线l 分别交x 轴正向和y 轴正向于A 、B ,使△AOB (O 为原点)的面积最小, 则l 的方程为_________________3、若方程cos 2x +3sin 2x =a +1在[0, π2]上有两个不同的实数解x ,则参数a 的取值范围是___________ 4、数列1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, …的第2011项是__________5、在1, 2, 3, 4, 5的排列a 1, a 2, a 3, a 4, a 5中,满足条件a 1<a 2, a 2>a 3, a 3<a 4, a 4>a 5的排列的个数是________6、[x ]表示不大于x 的最大整数,则方程 12·[x 2+x ]=19x +99的实数解x 是 . 7、设a 1=1,a n +1=2a n +n 2,则通项公式a n = .8、在△ABC 中,∠A =π3,sinB =513,则cosC = . 9、数(5+24)2012(n ∈N *)的个位数字是 .10、数799被2550除所得的余数是 .二、解答题:(20分+30分+30分,共80分)11.(20分) 已知△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,且(→AB )2=→AB ·→AC +→BA ·→BC +→CA ·→CB .(Ⅰ)判断△ABC 的形状,并求sinA +sinB 的取值范围;(Ⅱ)若不等式a 2(b +c )+b 2(c +a )+c 2(a +b )≥kabc ,对任意的满足题意的a ,b ,c 都成立,求k 的取值范围.12、(30分) △ABC 的内切圆分别切BC 、CA 、AB 三边于D 、E 、 F ,M求证:DM 平分∠BMC13、(30分) 给定无理数a 、b ,证明:满足方程 |x +ay +13|+|ax -y +a 3|=b 的整数x, y 至多只有一组。
数学建模模拟试题(一)

数学建模模拟试题(一)一、填空题(每题5分,共20分)1. 若,,x z z y ∝∝则y 与x 的函数关系是 .2. 在超级市场的收银台有两条队伍可选择,队1有1m 个顾客,每人都买了1n 件商品,队2有2m 个顾客,每人都买了2n 件商品,假设每个人付款需p 秒,而扫描每件商品需t 秒,则加入较快队1的条件是 .3. 马尔萨斯与罗捷斯蒂克两个人口增长模型的主要区别是假设了 .4. 在研究猪的身长与体重关系时,我们通过与已知其相关性质的的弹性梁作 的方法建立了模型.二、分析判断题(每小题15分,满分30分)1. 要为一所大学编制全校性选修课程表,有哪些因素应予以考虑?试至少列出5种.2. 一起交通事故发生3个小时后,警方测得司机血液中酒精的含量是),ml /mg (100/56 又过两个小时,含量降为),ml /mg (100/40试判断,当事故发生时,司机是否违反了酒精含量的规定(不超过80/100)ml /mg (.(提示:不妨设开始时刻为)(,0t C t =表示t 时刻血液中酒精的浓度,则依平衡原理,在时间间隔],[t t t ∆+内酒精浓度的改变量为t t kC t C t t C ∆-=-∆+)()()(其中0>k 为比例常数,负号则表示了浓度随时间的推移是递减的.)三、计算题(每题25分,满分50分)1. 一个毛纺厂使用羊毛、兔毛和某种纤维生产甲、乙两种混纺毛料,生产一个单位产品甲需要的三种原料依次为3、2、8个单位,产值为580元;生产一个单位产品乙需要的三种原料依次为2、3、5个单位,产值为680元,三种原料在计划期内的供给量依次为90、30和80单位.试建立线性规划模型以求一个生产方案,使得总产值达到最大,并由此回答:(1) 最优生产方案是否具有可选择余地?若有请至少给出两个,否则说明理由. (2) 原材料的利用情况.2. 三个砖厂321,,A A A 向三个工地321,,B B B 供应红砖.各砖厂的供应量与各工地的需求量以及各砖厂调运红砖到各工地的单价见表.试安排调运方案,使总费用最小?数学建模模拟试题(一)参考答案一、填空题(每题5分,共20分)1. k kx y ,=是比例常数;2. )()(2211t n p m t n p m +<+;3. 增长率是常数还是人口的递减函数;4. 类比.二、分析判断题(每小题15分,满分30分)1. 问题涉及到时间、地点和人员三大因素,故应该考虑到的因素至少有以下几个: (1)教师:是否连续上课,对时间的要求,对多媒体的要求和课程种类的限制等; (2)学生:是否连续上课,专业课课时与公共基础课是否冲突,选修人数等; (3)教室:教室的数量,教室的容纳量,是否具备必要的多媒体等条件;(每个因素3分) 2. 设)(t C 为t 时刻血液中酒精的浓度,则浓度递减率的模型应为,/kC C -=其通解是,e)0()(ktC t C -=而)0(C 就是所求量.由题设可知,40)5(,56)3(==C C 故有 56e )0(3=-kC 和 ,40e )0(5=-k C由此解得.94e 56)0(17.040/56e 32≈=⇒≈⇒=k k C k可见在事故发生时,司机血液中酒精的浓度已经超出了规定.三、计算题(每题25分,满分50分)1. 设21,x x 表示甲、乙两种产品的产量,则有 原材料限制条件: ,902321≤+x x ,303221≤+x x ,805821≤+x x 目标函数满足 ,680580m ax 21x x z += 合在一起便是所求线性规划模型:,680580m ax 21x x z +=⎪⎪⎩⎪⎪⎨⎧=≥≤+≤+≤+.2,1,0,8058,3032,9023212121j x x x x x x x j (1)使用图解法易得其最优生产方案只有一组(这是因为所有约束条件所在直线的斜率与目标函数直线的斜率均不相等),从而最优方案没有可选择余地.计算知:最优解为 ,)740,745(T*=X 目标值为 753300max =z (万元).(2)利用图解法求解中只用到了后两个约束条件,故羊毛有剩余量,将解代入可检验而知羊毛有7259单位的剩余量. 2. 本问题是一个产销平衡的运输问题,可以利用表上作业法直接求解,其次对方案进行最优性检验:λ11 = 10-4+6-7=5 > 0, λ12 = 6-4+6-5=3 > 0, λ31 = 8-7+5-3=3 > 0, λ33 = 9-3+5-6=5 > 0,故上述方案已是最优方案,即总运费最低的调运方案为:21503310223021160231701,,,,B A B A B A B A B A −→−−→−−→−−→−−→− 总费用为 2460150310630516071704=⨯+⨯+⨯+⨯+⨯(百元).数学建模模拟试题(二)一、填空题(每题5分,共20分)1. 设S 表示挣的钱数,x 表示花的钱数,则“钱越多花的也就越多”的数学模型可以简单表示为 .2. 假设,,21x C Y Y C S ∝∝则S 与x 的数学关系式为 ,其中21,C C 是常数.3. 在建立人口增长问题的罗捷斯蒂克模型时,假设人口增长率r 是人口数量)(t x 的递减函数,若最大人口数量记作,m x 为简化模型,采用的递减函数是 .4. 一次晚会花掉100元用于食品和饮料,其中食品至少要花掉40%,饮料起码要花30元,用f 和d 列出花在食品和饮料上的费用的数学模型是 .二、分析判断题(每题15分,满分30分)1. 作为经济模型的一部分,若产量的变化率与生产量和需求量之差成正比,且需求量中一部分是常数,另一部分与产量成正比,那么相应的微分方程模型是什么?.2. 考虑在一片面积为定数的草地上进行牛的养殖问题.为了获得最大经济效益,指出建立该问题数学模型应该考虑的相关因素至少5个.三、计算题(每题25分,满分50分)1. 设某小型工厂使用A ,B 两种原料生产甲、乙两种产品,按工艺,生产每件产品甲需要原料A ,B 依次为6、5个单位,生产每件产品乙需要原料A ,B 依次为2、10个单位,两种原料的供给量依次为18和40个单位,两种产品创造的产值分别为1万元和2万元,试建立其生产规划模型,并回答以下问题:(1)产值最大的生产方案是什么?最大产值是多少?方案是否有可选择余地?若有请至少再给出一个.(2)依你所给最优方案,说明原料的利用情况.2. 如图一是某村镇9个自然屯(用91,,v v 表示)间可架设有线电视线路的最短距离示意图,边旁数字为距离(单位:km ).若每km 的架设费用是定数20元/m ,试协助有线电视网络公司设计一个既使得各村屯都能看到有线电视又使架设费用最低的路线,并求出最小架设费用.数学建模模拟试题(二)参考答案一、填空题(每题5分,共20分) 1. 0,>=k kx S ;2. kx x C C k k S ==2121,其中2121C C k k k =;3. )1()(mx xr x r -=; 4. 30,4.0)/(,100≥≥+≤+d d f f f d .二、分析判断题(每题15分,满分30分)1. 令x 表示产量,y 表示需求量,则有)(d d x y k tx-=以及,bx a y +=其中k b a ,,均为常数.将后一式代入前一式即可得到d cx tx x b a k t x +=⇒-+=d d ))1((d d2. 饲料来源、公羊与母羊的比例、饲料冬储、繁殖问题、羊的养殖年限、出售时机、v 1 v 2 v 3 v 4 v 6 v 5 v 7v 9 v 8 3 4 6 2 5 4 11 3 6 4 2 8 7 5图一羊制品及其深加工等.三、计算题(每题25分,满分50分)1. 设生产甲、乙两种产品的数量依次为,,21x x z 表示总产值,则有模型如下:212m ax x x z +=⎪⎩⎪⎨⎧=≥≤+≤+.2,1,0401051826..2121j x x x x x t s j使用图解法易得其产值最大的生产方案将有无穷多组(这是因为第二个约束条件所在直线的斜率与目标函数直线的斜率相等),其中的两个方案可以选为该直线段上的两个端点:,)4,0(,)3,2(T 2T1==XX最大产值均为 8=z (万元)(2)按照上面的第一个解,原材料全部充分利用;而按照第二个解,原材料A 将有10个单位的剩余量,原材料B 将被充分利用(但产品甲不生产).2. 由题意可知,只需求出该网络图的最小树即可.利用破圈法容易得树形图(图二):故得架设路线为:总架线长度为27km ,故总架设费用为 5420100027=⨯⨯(万元)图二 v 1 v 2 v 3 v 4 v 6 v 5 v 8 v 7 v 9 4 32 43 42 5。
数学建模考试题(2011)

2011数学建模考试题(开卷)1.某饮料公司拥有甲、乙两家饮料厂,都能生产A、B两种牌号的饮料。
甲饮料厂生产A饮料的效率为8吨/小时,生产B饮料的效率为10吨/小时;乙饮料厂生产A饮料的效率为10吨/小时,生产B饮料的效率为4吨/小时。
甲饮料厂生产A饮料和B饮料的成本分别为1000元/吨和1100元/吨;乙饮料厂生产A饮料和B饮料的成本分别为850元/吨和1000元/吨。
现该公司接到一生产订单,要求生产A饮料1000吨,B饮料1600吨。
假设甲饮料厂的可用生产能力为200小时,乙饮料厂的生产能力为120小时。
(1)请你为该公司制定一个完成该生产订单的生产计划,使总的成本最小(要求建立相应的线性规划模型,并给出计算结果)。
(2)由于设备的限制,乙饮料厂如果生产某种牌号的饮料,则至少要生产该种牌号的饮料300吨。
此时上述生产计划应如何调整(给出简要计算步骤)?2.讨价还价中的数学。
在当前市场经济条件下,在商店,尤其是私营个体商店中的商品,所标价格a与其实际价值b之间,存在着相当大的差距。
对购物的消费者来说,总希望这个差距越小越好,即希望比值λ接近于1,而商家则希望λ>1。
这样,就存在两个问题:第一,商家应如何根据商品的实际价值(或保本价)b来确定其价格a才较为合理?第二,购物者根据商品定价,应如何与商家"讨价还价"?第一个问题,国家关于零售商品定价有相关规定,但在个体商家实际定价中,常用"黄金数"方法,即按实际价b定出的价格a,使b:a≈0.618。
虽然商品价值b位于商品价格a 的黄金分割点上,考虑到消费者讨价还价,应该说,这样定价还是较为合理的。
对消费者来说,如何"讨价还价"才算合理呢?一种常见的方法是"对半还价法":消费者第一次减去定价的一半,商家第一次讨价则加上二者差价的一半;消费者第二次还价要减去二者差价的一半;如此等等。
2011数学建模竞赛试题

数学建模竞赛试题1、磁盘的最大存储量现有一张半径为R 的磁盘,它的存储区是半径介于r 与R 之间的环形区域,试确定r ,使磁盘具有最大存储量。
2、新工人的学习曲线在电冰箱、电视机、汽车等行业中,装配工人的工作是一种重复性的熟练劳动。
在这些行业中,新工人的学习过程如下:刚开始时由于技术不熟练,生产单位产品需要较多的劳动时间,随着不断的工作,新工人的熟练程度逐步提高,生产单位产品所需的劳动时间越来越短;当工人达到完全熟练程度以后,生产单位产品所需要的劳动时间就会稳定在一个定值。
纺织厂招收一批新工人学习1511型织布机的操作。
观察工人的学习过程发现,当累计织完25匹布以后,工人织每匹布需要用16小时;当累计织完64匹布时,工人织每匹布用10小时.已知熟练工人织每匹布用8小时,是确定出新工人的学习曲线,并计算新工人用多少时间才能达到熟练工人的程度。
3、工人数量调整问题一工厂有x 名技术工人和y 名非技术工人,每天可生产的产品产量为2(,)f x y x y =现有16名技术工人和32名非技术工人,而厂长计划再雇佣一名技术工人。
试求厂长如何调整非技术工人的人数,可保持产品产量不变?4、乙酸回收的最好效果在,A B 两种物质的溶液中,我们想提取出物质A ,可以采取这样的方法:在,A B 的溶液中加入第三种物质C ,而C 与B 不互溶,利用A 在C 中的溶解度较大的特点,将A 提取出来。
这种方法就是化工中的萃取过程。
现有稀水溶液的乙酸,利用苯作为溶剂,设苯的总体积为m 。
进行3次萃取来回收乙酸.问每次应取多少苯量,方使从水溶液中萃取的乙酸最多?5、陈酒出售的最佳时机某酒厂有批新酿的好酒,如果现在就出售,可得总收入050R =万元,如果窖藏起来待来日(第n 年)按陈旧价格出售,第n 年末可得总收入为0R R =元。
而银行利率为0.05r =。
试分析这批好酒窖藏多少年后出售可使总收入的现值最大。
6、森林救火模型森林失火了!消防站接到报警后派多少消防队员前去救火呢?派的队员越多,森林的损失越小,但是救援的开支会越大。
2011年数学建模作业题目

数学建模题目1 授课教师评估问题大学要对每一位授课教师进行评估,评估主要由以下几个方面决定:学生对教师的评价;教师督导团(由专家组成)通过听课对教师的评价;教师所在院(系)对教师的评价;教务处平时对教师的情况掌握(如平时检查上课有无迟到早退现象、有无重大教学事故、有无违反教师职业道德的反映等)。
请你根据上述几方面的因素给出一个教师评价方案,并叙述其合理性。
2. 航空公司经营策略由于交通的多样化,航空公司日益受到来自铁路及公路的威胁,尤其对于短途客运。
请根据路途的远近为航空公司制定一个价格(优惠)计划,使航空公司效益最佳。
3. 旅游路线安排计划“五一”黄金周又到了,希望安排出外旅游。
你要考虑的因素很多。
首先,你得考虑时间有限(7天);其次要考虑费用问题:根据有限的费用安排你的交通方式。
当然,还要考虑出游的乐趣,希望多走几个景点。
还要考虑劳逸结合,如较远的地方如坐火车需乘坐卧铺,晚上休息。
如何安排你的假期。
假设一个景点一天的平均费用为100元,你手中恰有刚刚发下来的奖学金1000元。
4 校内通勤车运营方案校内通勤车由于存在等客问题,使得校内摩托车载人现象严重,影响校园内的安全。
为了彻底铲除校内摩托车,只靠保卫处严管远远不够,需从运营效益方面限制摩托车的收入,从而使其自行退出。
假设目前有校内通勤车10台,每台车可容纳7人;两轮摩托车20台,三轮摩托8台,分布于一道门、八公寓及老八饺子馆处。
如果在通勤高峰时(早晨7:00—8:00;中午12:00—12:30;晚4:00—6:00)通勤车等待的时间为3分钟,其它时间段通勤车等待的时间为10-20分钟。
请计算全天各类车的总的运客量,并根据这个运客量安排校内通勤车的数量、等车间隔时间,以使每辆摩托车的收入低于20元。
5.台球技术台球我们都打过至少是看过,一个漂亮的击球落袋使人赏心悦目。
虽然台球看起来很容易击打,但如果想打好台球却不是那么容易的。
这里边有经验的问题,也有技巧的问题。
数学建模题目20110606

2010级数学系数学建模作业题第1题计算平均学分绩点下面表格中是某同学所修各门课程的学分和成绩。
请编写一个Matlab程序,计算出这名同学的平均学分绩点。
第2题数据拟合问题混凝土的抗压强度随养护时间的延长而增加。
现将一批混凝土作成12个试块,记录了养护日期x(日)及抗压强度y(kg/cm2)的数据:(1) 分别用2,3,6次多项式拟合求出x与y的关系式,并画出散点图和拟合曲线图;(2) 若x与y之间满足关系式y = a + be mx + ce-mx,你能否求出参数a,b,c,m?并画图。
第3题工程承包问题某公司要把4个能源工程项目承包给4个互不相关的承包商,规定每个承包商只能且必须承包一个项目。
如果承包商对每个工程的报价如表所示,试在总费用最小的条件下确定各个项目的承包者。
要求:分别用匈牙利法和0-1规划(用Matlab)求解。
第4题线性规划(1) 某房地产公司有水泥100单位,木材160单位和玻璃400单位,用以建造A型和B型住宅。
建一栋A型住宅需要水泥、木材、玻璃分别为1,2,2单位,售价每栋100万元;建一栋B型住宅需要水泥、木材、玻璃分别为1,1,5单位,售价每栋150万元。
该公司如何安排两种住宅的建设,才能使总售价最大?要求:建立模型并用Matlab求解。
(2) 一贸易公司专门经营某商品的批发业务。
公司有库容5000单位的仓库。
1月1日,公司有库存1000单位,并有资金20000元,估计第1季度该商品价格如表所示。
如买进的商品当月到货,但需要下月才能卖出,且规定“货到付款”。
公司希望本季末库存为2000单位,问应采取什么样的买进卖出的策略可使3个月总的获利最大?要求:建立模型并用Matlab求解。
第5题图论(1) 用Matlab求下图中任意两点之间的最短路;(2) 分别用Kruskal算法和Prim算法求下图的最小生成树,并用Matlab验证。
数学建模第一次培训习题解答1

数学建模第一次作业院系:机电学院通信工程姓名:严宏海学号:20101003032数学建模习题11用给定的多项式,如y=x3-6x2+5x-3,产生一组数据(xi,yi,i=1,2,…,n),再在yi上添加随机干扰(可用rand产生(0,1)均匀分布随机数,或用rands产生N(0,1)分布随机数),然后用xi和添加了随机干扰的yi作的3次多项式拟合,与原系数比较。
分别作1、2、4、6次多项式拟合,比较结果,体会欠拟合、过拟合现象。
解:程序如下:x=1:0.5:10;y=x.^3-6*x.^2+5*x-3;y0=y+rand;f1=polyfit(x,y0,1)%输出多项式系数y1=polyval(f1,x);%计算各x点的拟合值plot(x,y,'+',x,y1)grid ontitle('一次拟合曲线');figure(2);f2=polyfit(x,y0,2)%2次多项式拟合y2=polyval(f2,x);plot(x,y,'+',x,y2);grid ontitle('二次拟合曲线');figure(3);f4=polyfit(x,y0,4)%4次多项式拟合y3=polyval(f4,x);plot(x,y,'+',x,y3)grid ontitle('四次拟合曲线');figure(4);f6=polyfit(x,y0,6)%6次多项式拟合y4=polyval(f6,x);plot(x,y,'+',x,y4)grid ontitle('六次拟合曲线');运行结果如下:依次为各个拟合曲线的系数(按降幂排列)f1 =43.2000 -149.0663f2 = 10.5000 -72.3000 89.8087f4 =0.0000 1.0000 -6.0000 5.0000 -2.5913f6 = 0.0000 -0.0000 0.0000 1.0000 -6.0000 5.0000-2.4199运行后,比较拟合后多项式和原式的系数,发现四次多项式系数与原系数比较接近,四次多项式的四次项系数很小。
数学建模模拟试题与答案

数学建模模拟试题及答案一、填空题(每题 5 分,共 20 分)1.若 y z, z x, 则 y 与x的函数关系是.2.在超级市场的收银台有两条队伍可选择,队 1 有m1个顾客,每人都买了n1件商品,队 2 有m2个顾客,每人都买了n2件商品,假设每个人付款需p 秒,而扫描每件商品需t 秒,则加入较快队 1 的条件是.3.马尔萨斯与罗捷斯蒂克两个人口增长模型的主要区别是假设了4.在研究猪的身长与体重关系时,我们通过与已知其相关性质的的弹性梁作的方法建立了模型 .二、分析判断题(每小题15 分,满分 30 分)1. 要为一所大学编制全校性选修课程表,有哪些因素应予以考虑?试至少列出 5 种.2.一起交通事故发生 3 个小时后,警方测得司机血液中酒精的含量是56 /100( mg / ml ), 又过两个小时,含量降为 40 / 100(mg / ml ), 试判断,当事故发生时,司机是否违反了酒精含量的规定(不超过80/100 (mg / ml ) .(提示:不妨设开始时刻为t0,C (t) 表示t时刻血液中酒精的浓度,则依平衡原理,在时间间隔 [ t,t t ] 内酒精浓度的改变量为C (t t ) C (t)kC(t)t其中 k0 为比例常数,负号则表示了浓度随时间的推移是递减的. )三、计算题(每题25 分,满分50 分)1.一个毛纺厂使用羊毛、兔毛和某种纤维生产甲、乙两种混纺毛料,生产一个单位产品甲需要的三种原料依次为3、2、8 个单位,产值为580 元;生产一个单位产品乙需要的三种原料依次为2、 3、5 个单位,产值为680 元,三种原料在计划期内的供给量依次为90、30 和 80 单位 . 试建立线性规划模型以求一个生产方案,使得总产值达到最大,并由此回答:(1)最优生产方案是否具有可选择余地?若有请至少给出两个,否则说明理由.( 2)原材料的利用情况.2.三个砖厂 A1 , A2 , A3向三个工地 B1 , B2 , B3供应红砖.各砖厂的供应量与各工地的需求量以及各砖厂调运红砖到各工地的单价见表. 试安排调运方案,使总费用最小?工地B1B2B3供应量 / 万块砖厂A11064170A2756200A3839150需求量 / 万块160180180数学建模模拟试题(一)参考答案一、填空题(每题 5 分,共 20 分)1.y kx, k 是比例常数;2.m1 ( p n1 t) m2 ( p n2t) ;3.增长率是常数还是人口的递减函数;4.类比 .二、分析判断题(每小题15 分,满分30 分)1.问题涉及到时间、地点和人员三大因素,故应该考虑到的因素至少有以下几个:(1)教师:是否连续上课,对时间的要求,对多媒体的要求和课程种类的限制等;( 2)学生:是否连续上课,专业课课时与公共基础课是否冲突,选修人数等;(3)教室:教室的数量,教室的容纳量,是否具备必要的多媒体等条件;(每个因素 3 分)2.设 C (t) 为t时刻血液中酒精的浓度,则浓度递减率的模型应为C /kC ,其通解是 C (t) C (0) e kt , 而 C (0)由题设可知 C(3)56,C(5) 40,就是所求量 .故有C (0)e 3 k56 和 C (0)e 5 k40,由此解得e2 k56 / 40k 0.17 C (0) 56e3 k94.可见在事故发生时,司机血液中酒精的浓度已经超出了规定.三、计算题(每题25 分,满分 50 分)1.设 x1 , x2表示甲、乙两种产品的产量,则有原材料限制条件:3x1 2 x290,2x13x230,8x15x280,目标函数满足max z 580x 1 680x 2 ,合在一起便是所求线性规划模型:max z 580x 1680x 2 , 3x 1 2x 2 90, 2x 1 3x 2 30, 8x 1 5x 2 80,x j 0, j1,2.( 1)使用图解法易得其最优生产方案只有一组(这是因为所有约束条件所在直线的斜率与目标函数直线的斜率均不相等),从而最优方案没有可选择余地 . 计算知:最优解为 X *( 45 , 40)T ,7 7 目标值为 max z 53300(万元) . 7( 2)利用图解法求解中只用到了后两个约束条件,故羊毛有剩余量,将解代入可检验而知羊毛有 592单位的剩余量 .72. 本问题是一个产销平衡的运输问题,可以利用表上作业法直接求解,首先确定初始方案:工地单价/ 百元B 1B 2B 3供应量 /万块170砖厂A 1 10160 630410 170 A 2 7 5150 6 200 A 38 3 9 150需求量 / 万块160180180其次对方案进行最优性检验:11= 10-4+6-7=5 > 0 , 12= 6-4+6-5=3 > 0,31= 8-7+5-3=3 > 0,33= 9-3+5-6=5 > 0,故上述方案已是最优方案,即总运费最低的调运方案为:1701603010B3,A3150B2A1B3,A2B1,A2B2,A2总费用为 4170 7 160530610 3 1502460 (百元).。
2011年数学建模模拟训练题(第一题)

2011年数学建模模拟训练题目第1题A 题 越野长跑团体赛记分规则的公平性越野长跑团体赛的记分规则是这样的:每个参赛团体由7名队员组成,取该团体跑在前面的5个队员在所有参赛选手中的排名顺序之和为该团体的得分,然后根据各参赛队得分(由小到大)的顺序决定比赛排名。
试回答以下问题:(1) 此规则是否存在不公平的地方?如果存在,举例说明。
(2)试讨论在不计时、仅考虑各位参赛选手的排序信息的前提下,公平的记分规则应满足哪些性质?(3)试根据(2)中的讨论,构造你们认为更合理的规则,对你们得到的结论需说明理由。
B 题 西瓜种植方案张三、李四和王五是自由市场上仅有的三个出售西瓜的农民,设三人种植西瓜的数量分别为z q 、l q 与w q (单位:个),成本分别为(单位:元/个)0.55,250000.50,25000z z z q C q ≤⎧=⎨>⎩ 0.55,200000.50,20000l l l q C q ≤⎧=⎨>⎩0.60,200000.50,20000w w w q C q ≤⎧=⎨>⎩西瓜的市场价格为375000250000,75000z l w z l w z l w q q q q q q p q q q ++⎧-++≤⎪=⎨⎪++>⎩, (1)张三、李四和王五同时播种,且三人对自己和对方的成本及市场需求具有完全信息,在互相不通种植信息的前提下求各自的决策,以及在此决策下各自的产量和收益。
(2)若李四和王五按上述决策执行,但张三没有按上述决策执行,而是等其它两方播种后,再决定播种数量。
那么,张三能否提高收益?其产量及收益分别是多少?(3)若李四与王五知道了张三的上述“计谋”,因此,根据他们自己的种植量l w q q +,就可以推算出张三的种植量,从而推算出市场价格以及自己的利润。
李四与王五为使他们的总利润最大,应该选择怎样的种植数量?同时,他们两人之间又应如何划分种植数量?收益各如何?(4)若三人决定合作,问应如何合作?各自的产量及收益分别是多少?。
2011年大学生数学建模竞赛试题(全套)

2011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?B题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能,需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
数模选拔题:2011年

A题教学楼的快速疏散问题近年来,诸如地震、火灾等突发事件时有发生。
虽然人们在很多情况下还不能准确预报这些突发事件,但当灾难发生时,尽可能减少伤亡人数是人们应对突发事件的首选。
在突发事件中,身处灾难环境的人员快速疏散可以有效减少伤亡人数。
本着居安思危的态度,假设某一天上午,学生正在主教学楼上课,突然该楼发生火灾,请你完成如下任务:1.用数学建模的方法,给出一种使学生快速疏散的方案;2.针对该教学楼,用你的方案给出其第二、三层学生快速撤离的具体方案和所用时间;3.建模研究你认为值得研究的其他相关问题;4.为学校管理层提供相关建议。
B题水资源短缺风险综合评价水资源,是指可供人类直接利用,能够不断更新的天然水体。
主要包括陆地上的地表水和地下水。
风险,是指某一特定危险情况发生的可能性和后果的组合。
水资源短缺风险,泛指在特定的时空环境条件下,由于来水和用水两方面存在不确定性,使区域水资源系统发生供水短缺的可能性以及由此产生的损失。
近年来,我国、特别是北方地区水资源短缺问题日趋严重,水资源成为焦点话题。
以北京市为例,北京是世界上水资源严重缺乏的大都市之一,其人均水资源占有量不足300m3,为全国人均的1/8,世界人均的1/30,属重度缺水地区,附表中所列的数据给出了1979年至2000年北京市水资源短缺的状况。
北京市水资源短缺已经成为影响和制约首都社会和经济发展的主要因素。
政府采取了一系列措施, 如南水北调工程建设, 建立污水处理厂,产业结构调整等。
但是,气候变化和经济社会不断发展,水资源短缺风险始终存在。
如何对水资源风险的主要因子进行识别,对风险造成的危害等级进行划分,对不同风险因子采取相应的有效措施规避风险或减少其造成的危害,这对社会经济的稳定、可持续发展战略的实施具有重要的意义。
《北京2009统计年鉴》及市政统计资料提供了北京市水资源的有关信息。
利用这些资料和你自己可获得的其他资料,讨论以下问题:1.评价判定北京市水资源短缺风险的主要风险因子是什么?影响水资源的因素很多,例如:气候条件、水利工程设施、工业污染、农业用水、管理制度,人口规模等。
2011年数学竞赛模拟训练试题(1)详细解答

2011年数学竞赛模拟训练试题(1)详细解答一、填空题:共64分,每小题8分.1.由10个元素组成的集合M = {1, 99,-1, 0, 25,-36,-91, 19,-2, 11},记M 的所有非空子集为i M ,i =1, 2,…,1023,每一个从中的所有元素之积为i m ,则10231ii m =∑= .2.如图1, ⊙O的半径为,D, B, C 为⊙O 上的三点,∠BOC=120°,DC=DB+1,则DB= .3.已知sin(20)cos(10)cos(10)x x x +=++- ,则tan x =.4.若实数,x y 满足22144x y -=,则21y x x -的取值范围是 . 5.所有能使2[]5n 为质数的正整数n 的倒数和为 .6.已知函数2()log (321)a f x ax x a =-++-对任意的(0,1]x ∈恒有意义,则实数a 的取值范围 .7.设三位数n abc =,若以,,a b c 为三条边的长可以构成一个等腰(含等边)三角形,这样的三位数n 有 个. 8,则它的表面积的最小值为 . 二、解答题:共56分,第9题16分,第10、11题各20分.9.在椭圆2214x y +=中,AB O 为坐标原点,求AOB ∆的面积S 的取值范围.10.设二次函数()y f x =的图象过点O (0,0),且满足231()62x f x x --≤≤+.数列{}n a 满足:111,()3n n a a f a +==. (l)确定()f x 的表达式; (2)证明:1n n a a +>;(3)证明:111330.5nn i ia +=≥--∑. 11.已知,,abc R +∈,且满足22()(4)kabc a b a b c a b c≥++++++,求 k 的最小值.参考答案1.-1.10231i i m =∑=(1+1)·(99+1)·(-1+1)·(0+1)·(25+1)·(-36+1)·(-91+1)·(19+1)·(-2 + 1)·(11+1)-1=-1.2.4.连接BC .在△ABC 中,由余弦定理可得BC ==设DB x =,则1DC x =+.在△DBC 中,由余弦定理可得222(1)2(1)cos60x x x x =++-+ ,解得4x =或5x =-(舍去).3sin cos 20cos sin 202cos cos10x x x +=,所以2cos10sin 20tan cos 20x -=. 又2cos10sin 202cos(3020)sin 20-=--2(cos30cos20sin30sin 20)sin 20=+-sin 20sin 20=+-= ,所以20tan cos 20x ==4.(-l, 1).令 2sec ,2tan ,(,)22x y ππθθθ==∈-,则222111cos sin 1(sin 1)(1,1)22y x x θθθ-=-=-+∈-. 5.3760.1,2,3n =时,2[]5n 都不是质数;n =4时,2[]5n =3是质数;n =5时,2[]5n =5是质数;n =6 时,2[]5n =7是质数.当8n ≥时,可设5n k r =±(其中k 丧为不小于2的正整数,r =0,1,或2),则 22222111(5)(2510)(52)5555n k r k kr r k k r r =±=±+=±+, 所以2[](52)5n k k r =±,因为2k ≥,所以522k r ±>, 所以2[](52)5n k k r =±不是质数.因此,能使2[]5n 为质数的正整数,只有4, 5, 6,它们的倒数和为1113745660++=.6.1[,1)(1,)2+∞ .显然0a >且1a ≠.由题意知23210ax x a -++->对一切(0,1]x ∈恒成立,即2312x a x ->-对一切(0,1]x ∈恒成立.令231()2x g x x -=-,则2'22326()(2)x x g x x -+-=-,显然,对一切(0,1]x ∈,'()0g x <,所以函数231()2x g x x -=-在(0,1]x ∈上单调递减,因此,当(0,1]x ∈时,(1)()(0)g g x g ≤<,即12()2g x -≤<.因此,12a ≥.综合可知:实数a 的取值范围是 1[,1)(1,)2+∞ .7.165.(2004年全国联赛题)解:a ,b ,c 要能构成三角形的边长,显然均不为0.即,,{1,2,...,9}a b c ∈.(1)若构成等边三角形,设这样的三位数的个数为1n ,由于三位数中三个数码都相同,所以,1199n C ==.(2)若构成等腰(非等边)三角形,设这样的三位数的个数为2n ,由于三位数中只有2个不同数码.设为a 、b ,注意到三角形腰与底可以置换,所以可取的数码组(a ,b )共有292C .但当大数为底时,设a>b ,必须满足2b a b <<.此时,不能构成三角形的数码是共20种情况.同时,每个数码组(a ,b )中的二个数码填上三个数位,有23C 种情况.故2399(220)6(10)156n C C C =-=-=。
2011数学建模培训题1

第一次数学建模课堂讨论题1.一家保姆服务公司专门向顾主提供保姆服务.根据估计,下一年的需求为:春季6000人日,夏季7500人日,秋季5500人日,冬季9000人日.公司新招聘的保姆必须经过5天的培训才能上岗,每个保姆每季度工作(新保姆包括培训)65天.保姆从该公司而不是从顾主那里得到报酬,每人每月工资800元.春季开始时公司拥有120名保姆,在每个季度结束后,将有%15的保姆自动离职.(1)如果公司不允许解雇保姆,请你为公司制定下一年的招聘计划.哪些季度需求的增加不影响招聘计划?可以增加多少?(2)如果公司在每个季度结束后允许解雇保姆,请为公司制定下一年的招聘计划.2.在甲乙双方的一场战争中,一部分甲方部队被乙方部队包围长达4个月.由于乙方封锁了所有水陆交通要道,被包围的甲方部队只能依靠空中交通维持供给.运送4个月的供给分别需要2次、3次、3次和4次飞行,每次飞行编队由50架飞机组成(每架飞机需要3名飞行员),可以运送10万吨物资.每架飞机每个月只能飞行一次,每名飞行员每个月也只能飞行一次.在执行完运输任务后的返回途中有%20的飞机会被乙方部队击落,相应的飞行员也因此牺牲或失踪.在第一个月开始时,甲方拥有110架飞机和330名熟练的飞行员.在每个月开始时,甲方可以招聘新飞行员和购买新飞机.新飞机必须经过一个月的检查后才可以投入使用,新飞行员必须在熟练飞行员的指导下经过一个月的训练才能投入飞行.每名熟练飞行员可以作为教练每个月指导20名飞行员(包括他自己在内)进行训练.每名飞行员在完成一个月的飞行任务后,必须有一个月的带薪假期,假期结束后才能再投入飞行.已知各项费用(单位略去)如下表所示,请你为甲方安排一个飞行计划.如果每名熟练飞行员可以作为教练每个月指导不超过20名飞行员(包括他自己在内)进行训练,模型和结果有哪些改变?。
2011年数学建模集训小题目

2011年数学建模集训小题目1.求下列积分的数值解(1)⎰+∞+-⋅23223x x x dx(2)σd y x D⎰⎰--221,}|),{(22x y x y x D ≤+=;(3)⎰⎰⎰Ω++++++dv z y x z y x z 1)1ln(2222222,{}2210|),,(y x z z y x --≤≤=Ω。
2.已知)s i n ()()c o s (),(2h t h t h t e h t f ht ++++=+,dt h t f h g ⎰=10),()(,画出]10,10[-∈h 时,)(h g 的图形。
3.画出由椭圆12222=+b y a x 所围成的图形绕x 轴旋转一周而成的旋转体(叫做旋转椭球体)的图形,并计算它的体积。
4.画出16)5(22=-+y x 绕x 轴一周所围成的图形,并求所产生的旋转体的体积。
5. 有一外表面母线为400130sin (25)130,[0,600]100x y ex x π-⎛⎫=++∈ ⎪⎝⎭的旋转体(绕x 轴旋转)工件,画出该工件并计算工件的体积。
6.画出下列曲面的图形(1)旋转单叶双曲面149222=-+z y x ; (2)旋转双叶双曲面149222=+-z y x ; (3)抛物柱面x y =2; (4)椭圆锥面22249z y x =+; (5)椭球面6649222=++z y x ; (6)马鞍面xy z =;(7)椭圆柱面14922=+y x 。
7.画出隐函数1cos sin =+y x 的图形。
8.(1)求函数xx y -+=12ln 的三阶导数;(2)求向量]425.00[=a 的一阶向前差分。
9.求解非线性方程组(1)⎪⎩⎪⎨⎧=-+=-+060622x y y x(2)⎩⎨⎧=+=++5ln 10tan 10cos sin y x y e y x10.求函数186)(23-++=x x x x f 的极值点,并画出函数的图形。
2011年全国高中数学联赛模拟卷第一试

2011年全国高中数学联赛模拟卷(5)第一试(考试时间:80分钟 满分:120分)姓名:_____________考试号:______________得分:____________一、填空题(本大题共8小题,每小题8分,共64分)__________1. 正八边形87654321A A A A A A A A 边长为1,任取两点j i A A ,则21A A A A j i ⋅最大值为__________2. 若ii ikk k kxa x x f C-==∑∑=--=20072007020072007)3()1()(,则∑=20071k ka=_________3. 若关于x 的方程0142)6(22222=+-+++-+-b a b a x b b a x 的两个实数根21,x x 满足,1021≤≤≤x x 则4422+++a b a 的最小值为______________, 最大值分别为____________4. 设P 双曲线x 2a 2-y 2b2=1右支上一动点,过P 向两条渐近线作垂线,垂足分别为点B A ,,若点B A ,始终在第一、第四象限内,则双曲线离心率e 的取值范围是___________. 5. 对于实数x ,[]x 表示不超过x 的最大整数。
对于某个整数k ,恰存在2008个正整数200821,,,n n n ,满足[][][]320083231n n n k ====,并且k 整除)2008,2,1( =i n i,则k =___________.6. A 、B 两队进行乒乓球团体对抗赛,每队各三名队员,每名队员出场一次。
A 队的三名队员是321,,A A A ,B 队三名队员是B 1, B 2, B 3,,且i A 对j B 的胜率为ii +j(1≤i , j ≤3),A 队得分期望的最大可能值是________.7. △ABC 的三边长分别为13, 14, 15, 有4个半径同为r 的圆O , O 1, O 2, O 3放在△ABC 内,并且⊙O 1与 边AB 、AC 相切,⊙O 2与边BA 、BC 相切,⊙O 3与边CB 、CA 相切,⊙O 与⊙O 1, O 2, O 3相切, 则r =_________. 8. 设,a b都是正整数,且(1001a +=,则ab 的个位数字是__________二、解答题(本大题共3小题,第9题16分,第10、11题20分,共56分)9.已知:实数),,2,1(n i a i =满足1(1,2,,)ia i n i≥=,证明:1212112(1)()()(12)2(1)!nn na a a a a na n n +++≥+++++10. 已知数列}{n a 由222*11112,,()3n nn a a a a a n N +-==++∈确定, 若对于任意*N n ∈,12111111nM a a a ++<+++恒成立。
2011年数学建模暑假培训第一次模拟题目(秦宣云)
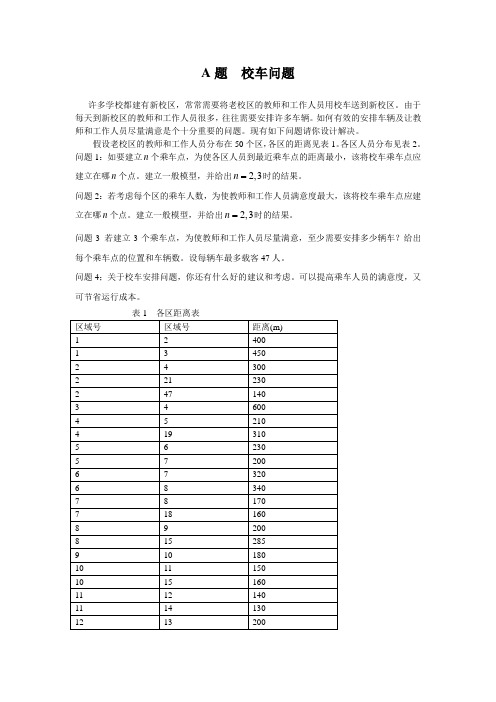
A题校车问题许多学校都建有新校区,常常需要将老校区的教师和工作人员用校车送到新校区。
由于每天到新校区的教师和工作人员很多,往往需要安排许多车辆。
如何有效的安排车辆及让教师和工作人员尽量满意是个十分重要的问题。
现有如下问题请你设计解决。
假设老校区的教师和工作人员分布在50个区,各区的距离见表1。
各区人员分布见表2。
问题1:如要建立n个乘车点,为使各区人员到最近乘车点的距离最小,该将校车乘车点应n=时的结果。
建立在哪n个点。
建立一般模型,并给出2,3问题2:若考虑每个区的乘车人数,为使教师和工作人员满意度最大,该将校车乘车点应建n=时的结果。
立在哪n个点。
建立一般模型,并给出2,3问题3 若建立3个乘车点,为使教师和工作人员尽量满意,至少需要安排多少辆车?给出每个乘车点的位置和车辆数。
设每辆车最多载客47人。
问题4;关于校车安排问题,你还有什么好的建议和考虑。
可以提高乘车人员的满意度,又可节省运行成本。
B题城市居民住房价格问题房价问题事关国计民生,对国家经济发展和社会稳定有重大影响,一直是各国政府大力关注的问题。
我国自从取消福利分房制度以来,随着房价的不断飙升,房价问题已经成为全民关注的焦点议题之一,从国家领导人、地方政府官员,到开发商、专家学者、普通百姓通过各种媒体表达各种观点,但对于房价是否合理、未来房价的走势等关键问题,至今尚未形成统一的认识。
请根据中国国情,收集建筑成本、居民收入等与房价密切相关的数据,选取我国具有代表性的几类城市对房价的合理性及房价的未来走势等问题进行定量分析;根据分析结果,进一步探讨使得房价合理的具体措施,以及可能对经济发展产生的影响,并进行定量分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A题校车问题
许多学校都建有新校区,常常需要将老校区的教师和工作人员用校车送到新校区。
由于每天到新校区的教师和工作人员很多,往往需要安排许多车辆。
如何有效的安排车辆及让教师和工作人员尽量满意是个十分重要的问题。
现有如下问题请你设计解决。
假设老校区的教师和工作人员分布在50个区,各区的距离见表1。
各区人员分布见表2。
问题1:如要建立n个乘车点,为使各区人员到最近乘车点的距离最小,该将校车乘车点应
n=时的结果。
建立在哪n个点。
建立一般模型,并给出2,3
问题2:若考虑每个区的乘车人数,为使教师和工作人员满意度最大,该将校车乘车点应建
n=时的结果。
立在哪n个点。
建立一般模型,并给出2,3
问题3 若建立3个乘车点,为使教师和工作人员尽量满意,至少需要安排多少辆车?给出每个乘车点的位置和车辆数。
设每辆车最多载客47人。
问题4;关于校车安排问题,你还有什么好的建议和考虑。
可以提高乘车人员的满意度,又可节省运行成本。
B题城市居民住房价格问题房价问题事关国计民生,对国家经济发展和社会稳定有重大影响,一直是各国政府大力关注的问题。
我国自从取消福利分房制度以来,随着房价的不断飙升,房价问题已经成为全民关注的焦点议题之一,从国家领导人、地方政府官员,到开发商、专家学者、普通百姓通过各种媒体表达各种观点,但对于房价是否合理、未来房价的走势等关键问题,至今尚未形成统一的认识。
请根据中国国情,收集建筑成本、居民收入等与房价密切相关的数据,选取我国具有代表性的几类城市对房价的合理性及房价的未来走势等问题进行定量分析;根据分析结果,进一步探讨使得房价合理的具体措施,以及可能对经济发展产生的影响,并进行定量分析。
