江苏省东台市五烈中学2012届高三上学期期中考试
2012学年第一学期期中考试高三(文科)数学试卷

2012学年第一学期期中考试高三(文科)数学试卷本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间为120分钟.第 Ⅰ 卷 (选择题 共50分)注意事项:用钢笔或圆珠笔将题目做在答题卷上,做在试题卷上无效.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则)(B A C U ⋂等于 (A){2,3} (B){1,4,5} (C){4,5} (D){1,5} 2. =︒330tan (A)3 (B)3- (C)33 (D)33- 3.函数f (x )=234lg(1)x x x -+++-的定义域是 (A )[-1,4](B )[1,4] (C )(1, 4] (D )(-1, 4]4. 若b a ,为实数,则“1≤+b a ”是“21≤a 且21≤b ”的 (A)必要而不充分条件 (B)充分而不必要条件 (C)充要条件 (D)既不充分也不必要条件5.o2o3-sin70=2-cos 10(A)12(B)22(C) 2(D) 326.函数13y x =的图像是7.在△ABC 中,点M 满足0=++MC MB MA ,若 0=++AM m AC AB ,则实数m 的值是 (A)3 (B)23 (C) 23- (D)3- 8.等差数列{}n a 的前n 项和为n S ,且224,6a S ==,则64n nS a +的最小值是 (A)7 (B)152(C) 8(D)172(A)(B) (C)(D)9. 若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥--≤--≤-+01033022y x y x y x ,则x y +的最小值是(A )0 (B )1-/(C )1 (D )210.函数()M f x 的定义域为R ,且定义如下: 1(),()0(),M x M f x x M ∈⎧=⎨∉⎩(其中M 为非空数集且R M ⊆),在实数集R 上有两个非空真子集A 、B 满足A B =∅,则函数()1()()()1A B A B f x F x f x f x +=++的值域为(A) ∅(B) {12}(C) {1} (D) {12,1} 第Ⅱ卷(非选择题共100分)注意事项:将卷Ⅱ的题目做在答题卷上,做在试题卷上无效.11.公差为1的等差数列{}n a 满足2469a a a ++=,则579a a a ++的值等于▲. 12.已知a 与b 为两个不共线的单位向量,若向量a +b 与向量k a -b 垂直,则实数k =▲.13.若sin α+cos α=12,则sin 2α=▲.14.在直角三角形ABC中,,1,==⊥AC AB AC AB DC BD 21=,则CD AD ⋅的值等于▲.15.函数()sin()f x A x ωϕ=+(A ,ω,ϕ是常数,0A >,0ω>)的部分图象如图所示,则(0)f 的值是▲.16. 类比等差数列求和公式的推导方法,解决下列问题:设()()sin sin 30x f x x =︒-,则()()()()()12293159f f f f f ︒+︒++︒+︒++︒=__ ▲___.17.等比数列{}n a 中,120121,9a a ==,函数122012()()()()2f x x x a x a x a =---+,则曲线()y f x = 在点(0,(0))f 处的切线方程为 __▲__ .三、解答题:本大题共5小题.共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,且满足sin 3cos b A a B =.(Ⅰ)求角B 的值; (Ⅱ)若25cos25A =,求sin C 的值. 19.(本题满分14分) 函数22x y -=和213y x =的图象如图所示,xy O 3π712π2-(第15题图)其中有且只有1x x =、2x 、3x 时,两函数数值相等,且1230x x x <<<,o 为坐标原点. (Ⅰ)请指出图中曲线1C 、2C 分别对应的函数; (Ⅱ)现给下列二个结论: ①当(,1)x ∈-∞-时,22x -<213x ; ②2(1,2)x ∈; 请你判定是否成立,并说明理由.20.(本题满分14分)已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ,0)0()2(==-f f ,)(x f 的最小值为1-.(Ⅰ)求函数)(x f 的解析式;(Ⅱ)设1)()()(+--=x f m x f x g ,若)(x g 在]1,1[-上是减函数,求实数m 的取值范围. 21.(本题满分15分)已知数列}{n a ,}{n b 满足:291=a ,n n n a a 2621⋅=-+, 12+-=n n n ab (*N n ∈).(Ⅰ)证明数列}{n b 为等比数列.并求数列}{n a ,}{n b 的通项公式; (Ⅱ)记数列}{n a ,}{n b 的前n 项和分别为n n T S ,,若对任意的∈n N*都有nn n b mT S ≤, 求实数m 的最小值.22.(本题满分15分)设1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点. (Ⅰ)若2,121=-=x x ,求函数)(x f 的解析式;(Ⅱ)若,22||||21=+x x 求实数b 的最大值;(Ⅲ)函数)()()(1x x a x f x g --'=若,,221a x x x x =<<且求函数)(x g 在),(21x x 内的最小值.(用a 表示)高三数学(文科)参考答案一.选择题:本大题共10小题,每小题5分,共50分.二.填空题:本大题共7小题,每小题4分,共28分.请将答案填在答题卡对应的位置上. 三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,且满足sin cos b A B =.第19题图(Ⅰ)求角B 的值; (Ⅱ)若25cos25A =,求sin C 的值. 解:(Ⅰ)由正弦定理BbA a sin sin =及已知条件sin 3cos b A a B =得…………………2分 B A A B cos sin 3sin sin =,………………………………………………………4分又因为0sin ≠A ,所以B B cos 3sin =,即3tan =B ,……………………6分又),0(π∈B ,所以3π=B ;…………………………………………………………7分(Ⅱ)因为25cos25A =,所以5312cos 2cos 2=-=A A ,………………………9分 又),0(π∈A ,所以54sin =A ,由(Ⅰ)知32π=+C A ,………………11分 所以10334sin 32cos cos 32sin )32sin(sin +=-=-=A A A C πππ.…………14分 19.函数22x y -=和213y x =的图象如图所示, 其中有且只有1x x =、2x 、3x 时,两函数数值相等,且1230x x x <<<,o 为坐标原点.(Ⅰ)请指出图中曲线1C 、2C 分别对应的函数; (Ⅱ)现给下列二个结论: ①当(,1)x ∈-∞-时,22x -<213x ; ②2(1,2)x ∈; 请你判定是否成立,并说明理由. 解:(Ⅰ)1C 为213y x =,………3分2C 为22x y -=; ………5分 (Ⅱ)结论①成立,理由如下:函数22x y -=在(,1]-∞-上是增函数,∴(,1)x ∈-∞-时,2121228x ---<=.…7分 又函数213y x =在(,1]-∞-上是减函数,∴(,1)x ∈-∞-时,22111(1)333x >⨯-=而1183<,所以当(,1)x ∈-∞-时,22123x x -<;……………10分结论②成立,理由如下: 构造函数221()23x f x x -=-, 则11(1)0,(2)063f f =>=-<∴()f x 在区间(1,2)内有零点.…14分20.已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ,第19题图0)0()2(==-f f ,)(x f 的最小值为1-.(Ⅰ)求函数)(x f 的解析式;(Ⅱ)设1)()()(+--=x f m x f x g ,若)(x g 在]1,1[-上是减函数,求实数m 的取值范围. 解:(Ⅰ)由题意设)2()(+=x ax x f ,…………………………………………2分 ∵ )(x f 的最小值为1-,∴ 0>a ,且1)1(-=-f ,∴ 1=a ,…………4分∴ x x x f 2)(2+= . ………………………………………………………7分 (Ⅱ)∵ 1)1(2)1()(2++--=x m x m x g ,………………………………8分 ① 当1=m 时,14)(+-=x x g 在[-1, 1]上是减函数,∴1=m 符合题意.……………………………………………………10分 ② 当1≠m 时,对称轴方程为:mmx -+=11, ⅰ)当01>-m ,即 1<m 时,抛物线开口向上,由111≥-+mm, 得 m m -≥+11 , ∴ 10<≤m ;……12分 ⅱ)当01<-m , 即 1>m 时,抛物线开口向下,由111-≤-+mm ,得 m m +-≥+11, ∴1>m .……13分 综上知,实数m 的取值范围为[)∞+,0.………………………14分21.已知数列}{n a ,}{n b 满足:291=a ,n n n a a 2621⋅=-+; 12+-=n n n ab (*N n ∈).(Ⅰ)证明数列}{n b 为等比数列.并求数列}{n a ,}{n b 的通项公式; (Ⅱ)记数列}{n a ,}{n b 的前n 项和分别为n n T S ,,若对任意的∈n N*都有nn n b mT S ≤, 求实数m 的最小值.解:(Ⅰ)由已知得1212)2(2+++-=-n n n n a a ,……………………………………2分所以n n b b 211=+, 因为211=b ,所以}{n b 为等比数列.………………………………………4分 所以n n b )21(=, ……………………………………………6分进而n n n a )21(21+=+. ……………………………………………7分(Ⅱ)1211422121)2121()222(2132+--=++++++++=++n n n n n nn T S 124+⋅=n (10)分则nn n m 21421)124(+=+⋅≥对任意的∈n N*成立. ……………………12分 所以数列}214{n +是递减数列,所以29)214(max =+n所以m 的最小值为29. ……………………………………………………15分22.设1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点. (Ⅰ)若2,121=-=x x ,求函数)(x f 的解析式; (Ⅱ)若,22||||21=+x x 求实数b 的最大值;(Ⅲ)函数)()()(1x x a x f x g --'=若,,221a x x x x =<<且求函数)(x g 在),(21x x 内的最小值.(用a 表示)解:).0(23)(22>-+='a a bx ax x f -------------------------------------------------------1分 (1)2,121=-=x x 是函数)(x f 的两个极值点,由⎪⎪⎩⎪⎪⎨⎧-=-=⨯--=+-332132212aa a ab 可得⎩⎨⎧-==9,6b a ------------------------------- ------------3分 x x x x f 3696)(23--=∴ -------------------------------------------------------------------4分(2)∵1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点,0)()(21='='∴x f x f ,∴21,x x 是方程02322=-+a bx ax 的两根,∵32124a b +=∆, ∴0>∆对一切R b a ∈>,0恒成立,而3,322121ax x a b x x -=⋅-=+,0>a ,021<⋅∴x x , ,3494)3(4)32(4)(||||||222212212121a a b a a b x x x x x x x x +=---=-+=-=+∴………6分由).6(3,22349422||||222221a a b a ab x x -=∴=+=+得………………7分 .60,0)6(3,022≤<≥-∴≥a a a b ………………………………………… 8分令.369)(),6(3)(22a a a h a a a h +-='-=则)(0)(,40a h a h a ∴>'<<时在(0,4)内是增函数; 0)(,64<'<<a h a 时∴h (a )在(4,6)内是减函数.∴4=a 时,)(a h 有极大值为96,(]6,0)(在a h ∴上的最大值是96,∴b 的最大值是.64…………………………………………………………………10分 (3)∵x 1、x 2是方程0)(='x f 的两根, )0(23)(22>-+='a a bx ax x f,31,,31221-=∴=-=⋅x a x a x x -------------------------------------------------11分∴)()()(1x x a x f x g --'=)31)(31(3)31())(31(3--+=+--+=a x x a x a a x x a ----------12分对称轴为2a x =,0>a ,),(),31(221x x a a =-∈∴ []12)23()312(3)312)(312(3)2()(22min+-=+-=--+==∴a a a a a a a a a g x g .-- ------15分。
江苏省盐城中学2012届高三上学期期中考试(数学)

江苏省盐城中学高三年级2011—2012学年度上学期期中考试数学试题(第Ⅰ卷)(2011.11)一、填空题(本大题共14小题,每小题5分,计70分)1.已知全集{1,2,3,4,5,6}U =,集合{1,3,5}A =,{1,2}B =,则()U A B =ð___▲____. 2.已知曲线x x y -=3在点),(00y x 处的切线平行于直线x y 2=,则=0x ___▲___.3.已知直线l 经过点(2,1)P ,且与直线2310x y ++=垂直,则l 的方程是____▲___.4.在等比数列{}n a 中,若12a =,98a =,则5a =___▲____.5.若变量,x y 满足条件30380x y x y -≤⎧⎨-+≥⎩,则z x y =+的最大值为___▲___.6.当(0,)2x π∈时,函数sin y x x =+的值域为___▲____.7.已知a b c ,,满足2a c b +=,且,||1,||2,a c a c ⊥==则||b = ▲ . 8.数列{}n a 满足*1111(),22n n a a n N a ++=∈=-,n S 是{}n a 的前n 项和,则2011S = _▲_ . 9.已知函数()(2)2a f x x x x =+>-的图像过点(3,7)A ,则此函数的最小值是 ▲__ . 10.当钝角ABC ∆的三边,,abc 是三个连续整数时,则ABC ∆外接圆的半径为__▲___.11.关于x 的方程3210ax x x -++=在(0,)+∞上有且仅有一个实数解,则a 的取值范围 为_ ▲ .12.如图,在ABC ∆和AEF ∆中,B 是EF 的中点,2AB EF ==,3CA CB ==,若 7AB AE AC AF ⋅+⋅=,则EF 与BC 的夹角的余弦值等于 ▲ _.13.已知0a b c >≥>,且22112444()a ac c ab a a b ++-+=-, 则a bc ++= ▲ . 14.已知数列{}n a 的各项均为正整数,对于⋅⋅⋅=,3,2,1n ,有11527,2n n n n n n k k a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数,, 若存在*m ∈N ,当n m >且n a 为奇数时,n a 恒为常数p ,则p 的值为___▲___.二、解答题(本大题共6小题,计90分.)15.(本题满分14分)已知函数()2sin()f x x ωϕ=+(0ω>,22ππϕ-<<)的图像如图所示,直线38x π=,78x π=是其两条对称轴.(1)求函数()f x 的解析式;(2)若6()5f α=,且388ππα<<,求()8f πα+的值.16.(本题满分14分)设函数2()2cos[(1)]ln f x x a k x π=-- (k ∈N *,a ∈R ).(1) 若2011k =,1a =,求函数()f x 的最小值;(2) 若k 是偶数,求函数()f x 的单调区间.17.(本题满分15分)ABC ∆中,A 、B 、C 所对的边为a 、b 、c .已知(2cos )m A A =,(cos ,2cos )n A A =-,1m n ⋅=-.(1)若a =2c =,求ABC ∆的面积S 的大小;(2)求2cos(60)b c a C -+的值.18.(本题满分15分)某厂家拟在2011年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x 万件与年促销费用0()m m ≥万元满足31k x m =-+(k 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2011年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2011年该产品的利润y 万元表示为年促销费用m 万元的函数;(2)该厂家2011年的促销费用投入多少万元时,厂家的利润最大?19.(本题满分16分)已知函数2()ln f x x a x =-,()2g x bx =-,其中a ,b R ∈且2ab =.函数()f x 在1[,1]4上是减函数,函数()g x 在1[,1]4上是增函数.(1)求函数()f x ,()g x 的表达式;(2)若不等式()()f x mg x ≥对1[,1]4x ∈恒成立,求实数m 的取值范围.(3)求函数1()()()2h x f x g x x =+-的最小值,并证明当*n N ∈,2n ≥时()()3f n g n +>.20.(本题满分16分) 设数列{}n a 、{}n b 满足14a =,252a =,12n n n a b a ++=,12n n n n n a b b a b +=+. (1)证明:2n a >,02n b <<(*n N ∈);(2)设32log 2n n n a c a +=-,求数列{}n c 的通项公式; (3)设数列{}n a 的前n 项和为n S ,数列{}n b 的前n 项和为n T ,数列{}n n a b 的前n 项和为{}n P ,求证:83n n n S T P +<+.()2n ≥江苏省盐城中学高三年级2011—2012学年度上学期期中考试数学附加题(第Ⅱ卷)(2011.11)一、选做题21.在A 、B 、c 、D 四小题中只能选做2题,每小题10分,共计20分.请在答题纸指定区域内 作答.解答应写出文字说明、证明过程或演算步骤.A .选修4—1:几何证明选讲如图,AB 是⊙O 的直径,点P 在AB 的延长线上,PC 与⊙O 相切于点C ,PC =AC =1.求⊙O 的半径.B .选修4—2:矩阵与变换已知二阶矩阵A =⎣⎢⎡⎦⎥⎤a b c d ,矩阵A 属于特征值λ1=-1的一个特征向量为α1=⎣⎢⎡⎦⎥⎤ 1-1,属于特征值λ2=4的一个特征向量为α2=⎣⎢⎡⎦⎥⎤32.求矩阵A .C .选修4-4:坐标系与参数方程已知⊙O 1和⊙O 2的极坐标方程分别是2cos ρθ=和2sin a ρθ=(a 是非零常数).(1) 将两圆的极坐标方程化为直角坐标方程;(2) 若两圆的圆心距为5,求a 的值.D .选修4—5:不等式选讲设对于任意实数x ,不等式|7||1|x x ++-≥m 恒成立.(1)求m 的取值范围;(2)当m 取最大值时,解关于x 的不等式:|3|2212x x m --≤-.二、必答题:本大题共2小题。
江苏省东台中学高三数学12月阶段性考试试题苏教版

江苏省东台中学2013届高三阶段性考试数 学 试 题2012-12-01时间∶120分钟,满分∶160分。
一、填空题:本大题共14小题,每小题5分,共70分。
请把答案填写在答卷纸相应位置.......上。
1. 已知集合{}{}3,2,0,3,2,1==B A ,则=B A ________. 2. 已知a 是实数,1a ii-+是纯虚数,则=a ___________. 3.如图是青年歌手电视大奖赛上某一位选手的得分茎叶图,若去掉一个最高分和一个最低分后,则剩下数据的方差2s =________.4. 设等差数列}{n a 的前n 项和为=+++==1413121184,20,8,a a a a S S S n 则若________.5. 已知,{1,2,3,4,5,6}a b ∈,直线12:210,:10,l x y l ax by --=+-=则直线12l l ⊥的概率为 . 6.已知直线,m l ,平面,αβ,且,m l αβ⊥⊂.下列命题中,其中正确命题的序号是 __. ①若//αβ,则m l ⊥; ②若αβ⊥,则//m l ;③若m l ⊥,则//αβ; ④若//m l ,则αβ⊥. 7. 已知双曲线C:)0,0(12222>>=-b a by a x 的右顶点、右焦点分别为A 、F,它的左准线与x 轴的交点为B ,若A 是线段BF 的中点,则双曲线C 的离心率为 .8. 已知222:450,:210(0)p x x q x x m m -->-+->>,若p 是q 的充分不必要条件,则m 的最大值为 .9.已知结论:“在三边长都相等的ABC ∆中,若D 是BC 的中点,G 是ABC ∆外接圆的圆心,则2AGGD=”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD 中,若M 是BCD ∆的三边中线的交点,O 为四面体ABCD 外接球的球心,则AOOM= ”. 10. 若直线2ax -by +2=0(a >0,b >0)被圆x 2+y 2+2x -4y +1=0截得的弦长为4,则ba 32+的最小值是________.11. 设x,y 满足约束条件⎪⎩⎪⎨⎧≤+≥≥123400y x y x ,则132+++x y x 的取值范围是______________.12.在平面直角坐标系xOy 中,已知A (0,-1),B (-3,-4)两点,若点C 在AOB ∠的平分线上,且10OC =C 的坐标是_________. 13. 数列{}n a 中,()()111,()211n n n na a a n N n na *+==∈++,则数列{}n a 的前2012项的和为_________.14. 已知函数201221122012)(+++++++-+-++-=x x x x x x x f()x ∈R ,且)()22(2a f a a f >++,则满足条件的实数a 的取值范围是_________.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内. 15.(本小题满分14分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c.已知(2cos )m A A =,(cos ,2cos )n A A =-,1m n ⋅=-.(1)若a =2c =,求ABC ∆的面积;(2)求2cos(60)b ca C -+的值.16.(本小题满分14分)在三棱柱111ABC A BC -中,AA ,1BC ⊥︒=∠601AC A ,11AA AC BC ===, 21=B A . (1)求证:平面1A BC ⊥平面11ACC A ;(2)如果D 为AB 的中点,求证:1BC ∥平面1ACD.17. (本小题满分14分)如图:某污水处理厂要在一个矩形污水处理池)(ABCD 的池底水平铺设污水净化管道FHE Rt ∆(,H 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H 是AB 的中点,F E ,分别落在线段AD BC ,上.已知20=AB 米,310=AD 米,记θ=∠BHE .(1)试将污水净化管道的长度L 表示为θ的函数,并写出定 义域;(2)问:当θ取何值时,污水净化效果最好?并求出此时 管道的长度.18. (本小题满分16分)如图,椭圆22221x y a b +=(0)a b >>过点3(1,)2P ,其左、右焦点分别为12,F F ,离心率12e =,,M N是椭圆右准线上的两个动点,且021=⋅N F M F . (1)求椭圆的方程; (2)求MN 的最小值;(3)以MN 为直径的圆C 是否过定点?请证明你的结论.19. (本小题满分16分)已知数列{a n }满足a 1=1,a 2=3,且a n +2=(1+2|cos n π2|)a n +|sinn π2|,n ∈N *.(1) 证明:数列{a 2n }(k ∈N *}为等比数列; (2) 求数列{a n }的通项公式; (3) 设b k =a 2k +(-1)k -1λ·221k a -(λ为非零整数),试确定λ的值,使得对任意k ∈N *都有b k+1>b k 成立.20. (本小题满分16分)已知函数1ln(1)()(0)x f x x x++=>.(1)试判断函数()f x 在(0,)+∞上单调性并证明你的结论; (2)若()1kf x x >+恒成立,求整数k 的最大值; (3)求证:23(112)(123)[1(1)]n n n e -+⨯+⨯++>江苏省东台中学2013届高三阶段性考试数学(附加题部分)试题时间∶30分钟,满分∶40分。
江苏省盐城市东台五烈镇中学高三物理模拟试卷带解析

江苏省盐城市东台五烈镇中学高三物理模拟试卷含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. 一根质量分布均匀的长绳AB,在恒定水平外力F的作用下,沿光滑水平面做直线运动,如图甲所示.绳内距A端x处的张力T与x的关系如图乙所示,由图可知A.水平外力F=6NB.绳子的质量m=3kgC.绳子的长度D.绳子的加速度参考答案:AC2. 下列现象中,能说明液体存在表面张力的有 _________.(A) 水黾可以停在水面上(B) 叶面上的露珠呈球形(C) 滴入水中的红墨水很快散开(D) 悬浮在水中的花粉做无规则运动参考答案:AB3. 氢原子核外电子分别在、的轨道上运动时,下列相关物理量的关系正确的有A.电子运动的向心力 B.电子的轨道半径C.电子运动的角速度 D.氢原子总能量参考答案:BD解析:量子数、对应的电子的轨道半径,B对;电子运动向心力,由此可知A、C都错;量子数越大,氢原子能级越高,D对。
4. 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B。
将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动。
导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g。
下列选项正确的是()A.P=2mgvsinθ B.P=3mgvsinθC.当导体棒速度达到时加速度大小为sinθD.在速度达到2v以后匀速运动的过程中,R上产生的焦耳热等于拉力所做的功参考答案:AC5. 如图所示,一质量为m的小球固定于轻质弹簧的一端,弹簧的劲度系数为k,另一端固定于O 点.将小球拉至A处,弹簧恰好无形变,由静止释放小球,当它运动到O点正下方B点时速度为v、,A、B两点间的高度差为h,不计空气阻力,则A.由A到B过程,小球机械能守恒B.由A到B过程,小球重力做的功等于mghC.小球到达B点时,受到的重力可能与弹力大小相等D.小球到达B点时,弹簧的弹性势能为参考答案:BD试题分析:A、小球从A到B的过程中,有重力做功,弹簧弹力做功,小球机械能不守恒,故A错误;B、重力做功只与初末位置的高度差有关,则由A至B重力做功为mgh,故B正确;C、小球到达B点时,具有向上的向心加速度,处于超重状态,弹力大于重力,故C错误;D、弹簧弹力做功量度弹性势能的变化,根据动能定理得:,所以小球到达位置B时弹簧的弹性势能为,故D正确;故选:BD。
江苏省盐城市东台中学高三数学上学期期中试卷苏教版

2012-2013学年江苏省盐城市东台中学高三(上)期中数学试卷一、填空题1.(5分)命题“∀x∈R,sinx≤1”是真命题(选填“真”,“假”)考点:全称命题.专题:计算题.分析:利用正弦函数的值域,直接判断全称命题的真假即可.解答:解:由正弦函数的值域可知:∀x∈R,sinx≤1,是正确命题.故答案为:真.点评:本题考查命题的真假判断,正弦函数的值域,考查基本知识的应用.2.(5分)已知复数,则复数z在复平面内对应的点位于第四象限.考点:复数代数形式的乘除运算;复数的代数表示法及其几何意义.专题:计算题.分析:利用复数的幂运算,求出分式中分子的值,然后利用复数的除法运算法则求解即可.解答:解:复数===,复数对应的点为().复数z在复平面内对应的点位于第四象限.故答案为:四.点评:本题考查复数的代数形式的混合计算,复数的幂运算,考查计算能力.3.(5分)集合A={1,log2x}中的实数x的取值范围为(0,2)∪(2,+∞).考点:对数函数的定义;集合的确定性、互异性、无序性.专题:计算题.分析:根据集合的互异性可得log2x≠1,再根据对数函数的定义进行求解;解答:解:∵集合A={1,log2x},∴,解得x∈(0,2)∪(2,+∞),故答案为:(0,2)∪(2,+∞);点评:此题主要考查集合的互异性以及对数成立的意义,是一道基础题;4.(5分)(2012•西城区二模)在△ABC中,,,,则B= .考点:正弦定理.专题:解三角形.分析:由三角形中大变对大角可得B<A,故B<.再由正弦定理解得 sinB=,由此求得B的值.解答:解:在△ABC中,,,,则由大变对大角可得B<A,故B<.再由正弦定理可得=,解得 sinB=,故B=,故答案为.点评:本题主要考查正弦定理的应用,及三角形中大边对大角,根据三角函数的值求角,属于中档题.5.(5分)在等比数列{a n}中,已知a1=1,a k=243,q=3,则数列{a n}的前k项的和S k= 364 .考点:等比数列的前n项和;等比数列的通项公式.专题:等差数列与等比数列.分析:已知首项和公比,可以求出等比数列的前n项和公式,再代入a k=243,根据等比数列前n项和公式进行求解;解答:解:等比数列前n项和为s n=,∵等比数列{a n}中,已知a1=1,a k=243,q=3,∴数列{a n}的前k项的和S k===364,故答案为:364;点评:此题主要考查等比数列前n项和公式,直接代入公式进行求解,会比较简单;6.(5分)函数f(x)=sinx+cosx的图象向左平移m(m>0)个单位后,与y=cosx﹣sinx 的图象重合,则实数m的最小值为.考点:函数y=Asin(ωx+φ)的图象变换;两角和与差的正弦函数.专题:计算题;三角函数的图像与性质.分析:化简两个函数的表达式为正弦函数的形式,按照平移的方法平移,即可得到m的最小值.解答:解:函数f(x)=sinx+cosx=sin(x+),y=cosx﹣sinx=sin(x+),所以函数至少向左平移个单位,即m的最小值为:.故答案为:,点评:本题考查两角和的正弦函数以及三角函数图象的平移,考查计算能力.7.(5分)设实数x,y满足约束条件,则目标函数z=2x+y的最大值为 6 .考点:简单线性规划.专题:计算题;不等式的解法及应用.分析:作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=2x+y 对应的直线进行平移,可得当x=2,y=2时,z=2x+y取得最大值为6.解答:.解:作出不等式组表示的平面区域,得到如图的△ABC及其内部,其中A(2,0),B(2,2),C(0,2)将直线l:z=2x+y进行平移,当l经过点B时,目标函数z达到最大值∴z最大值=2×2+2=6故答案为:6点评:本题给出二元一次不等式组,求目标函数z=2x+y的最大值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.8.(5分)(2013•镇江一模)已知,则cos(30°﹣2α)的值为.考点:二倍角的余弦;两角和与差的余弦函数.专题:三角函数的求值.分析:利用诱导公式求得sin(15°﹣α)=,再利用二倍角的余弦公式可得cos(30°﹣2α)=1﹣2sin2(15°﹣α),运算求得结果.解答:解:∵已知,∴sin(15°﹣α)=,则cos(30°﹣2α)=1﹣2sin2(15°﹣α)=,故答案为.点评:本题主要考查诱导公式,二倍角的余弦公式的应用,属于中档题.9.(5分)(2013•烟台一模)已知向量=(x﹣1,2),=(4,y),若⊥,则9x+3y的最小值为 6 .考点:基本不等式;数量积判断两个平面向量的垂直关系.专题:计算题;压轴题.分析:利用向量垂直的充要条件列出方程求出x,y满足的方程;利用基本不等式得到函数的最值,检验等号何时取得.解答:解:由已知⊥⇒=0⇒(x﹣1,2)•(4,y)=0⇒2x+y=2则9x+3y=,当且仅当32x=3y,即时取得等号.故答案为:6点评:本题考查向量垂直的充要条件:坐标交叉相乘相等、考查利用基本不等式求函数的最值需满足的条件:一正、二定、三相等.10.(5分)已知等比数列{a n}的各项均为不等于1的正数,数列{b n}满b n=lga n,b3=18,b6=12,则数列{b n}前n项和的最大值为132 .考点:等比数列的前n项和.专题:计算题.分析:由题意可知:lga3=b3,lga6=b6.再由b3,b6,用a1和q表示出a3和b6,进而求得q和a1,根据{a n}为正项等比数列推知{b n}为等差数列,进而得出数列b n的通项公式和前n 项和,可知S n的表达式为一元二次函数,根据其单调性进而求得S n的最大值.解答:解:由题意可知:lga3=b3,lga6=b6.又因为b3=18,b6=12,所以a1q2=1018,a1q5=1012,所以q3=10﹣6,即q=10﹣2,∴a1=1022.又因为数列{a n}为等比数列,所以数列{b n}是等差数列,并且且d=﹣2,b1=22,所以b n=22+(n﹣1)×(﹣2)=﹣2n+24.∴S n=22n+×(﹣2)=﹣n2+23n=+,又因为n∈N*,所以n=11或12时,数列{b n}前n项和的最大值为132.故答案为132.点评:本题主要考查了等比数列的性质.属基础题.11.(5分)已知奇函数f(x)=ax3+bx2+cx+d在点(1,f(1))处的切线方程为y=x+1,则这个函数的单调递增区间是.考点:利用导数研究曲线上某点切线方程;奇偶性与单调性的综合.专题:导数的概念及应用.分析:根据奇函数可求出b与d的值,然后根据在点(1,f(1))处的切线方程为y=x+1可求出a与c的值,最后根据f′(x)>0可求出函数的单调增区间.解答:解:因为f(x)=ax3+bx2+cx+d为奇函数,所以b=d=0所以f′(x)=3ax2+c由题意可知解得由f′(x)=x2+>0解得﹣<x<∴这个函数的单调递增区间是故答案为:点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数求函数的单调区间,同时考查了计算能力,属于基础题.12.(5分)设p:f(x)=x3+2x2+mx+1在(﹣∞,+∞)内单调递增;q:已知h(x)=x2,,若对任意x1∈[﹣1,3],总存在x2∈[0,2],使得h(x1)≥g(x2)成立,则p是q成立的充分不必要条件.考点:必要条件、充分条件与充要条件的判断.专题:计算题.分析:对于命题p,根据导数与函数单调性的关系,求出m的范围,命题q,利用转化的思想将问题转化为h(x)min≥g(x)min,从而求出m的范围,再根据充分必要条件的定义进行求解;解答:解:p:∀x∈R,f′(x)=3x2+4x+m≥0,⇒△=16﹣12m≤0,⇒m≥;q:h(x)=x2,,若对任意x1∈[﹣1,3],总存在x2∈[0,2],使得h(x1)≥g(x2)成∴h(x)min≥g(x)min⇒0≥﹣m⇒m≥故p⇒q反之不成立,∴p是q的充分不必要条件,故答案为:充分不必要;点评:此题主要考查利用导数研究函数的单调性以及函数的恒成立问题,其中用到了转化的思想,是一道中档题;13.(5分)设数列{a n}是首项为0的递增数列,,满足:对于任意的b∈[0,1),f n(x)=b总有两个不同的根,则{a n}的通项公式为.考点:数列与三角函数的综合.专题:计算题;等差数列与等比数列.分析:根据条件确定a n+1﹣a n=nπ,利用叠加可求得{a n}的通项公式.解答:解:∵a1=0,当n=1时,f1(x)=|sin(x﹣a1)|=|sinx|,x∈[0,a2],又∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a2=π∴f1(x)=sinx,x∈[0,π],a2=π又f2(x)=|sin(x﹣a2)|=|sin(x﹣π)|=|cos|,x∈[π,a3]∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a3=3π…(5分)又f3(x)=|sin(x﹣a3)|=|sin(x﹣3π)|=|sinπ|,x∈[3π,a4]∵对任意的b∈[0,1),f1(x)=b总有两个不同的根,∴a4=6π…(6分)由此可得a n+1﹣a n=nπ,∴a n=a1+(a2﹣a1)+…+(a n﹣a n﹣1)=0+π+…+(n﹣1)π=∴故答案为:点评:本题考查数列与三角函数的结合,考查学生分析解决问题的能力,具有一定的综合性,属于中档题.14.(5分)定义域为[a,b]的函数y=f(x)图象的两个端点为A、B,M(x,y)是f(x)图象上任意一点,其中x=λa+(1﹣λ)b∈[a,b],已知向量,若不等式恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数在[1,2]上“k阶线性近似”,则实数k的取值范围为.考点:平面向量的综合题.专题:综合题;压轴题;平面向量及应用.分析:先得出M、N横坐标相等,再将恒成立问题转化为求函数的最值问题.解答:解:由题意,M、N横坐标相等,恒成立,即,由N在AB线段上,得A(1,0),B(2,),∴直线AB方程为y=(x﹣1)∴=y1﹣y2=﹣(x﹣1)=﹣(+)≤(当且仅当x=时,取等号)∵x∈[1,2],∴x=时,∴故答案为:点评:本题考查向量知识的运用,考查基本不等式的运用,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.二、解答题15.(14分)已知函数(Ⅰ)求的值;(Ⅱ)求函数f(x)的最小正周期及单调递减区间.考点:两角和与差的正弦函数;三角函数中的恒等变换应用;复合三角函数的单调性.专题:计算题;三角函数的图像与性质.分析:(Ⅰ)通过二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求的值;(Ⅱ)直接利用正弦函数的周期的求法,以及三角函数的单调性直接求函数f(x)的单调递减区间.解答:(本小题满分13分)解:(Ⅰ)因为=2cos2x+sin2x…(2分)=1+cos2x+sin2x…(4分)=…(6分)所以…(7分)(Ⅱ)因为所以…(9分)又y=sinx的单调递减区间为,(k∈Z)…(10分)所以令…(11分)解得…(12分)所以函数f(x)的单调减区间为,(k∈Z)…(13分)点评:本题考查两角和的正弦函数与二倍角公式的应用,三角函数的周期的求法,单调区间的求法,考查计算能力.16.(14分)已知函数f(x)=ax2+2x+c,且f(x)>0的解集为.(1)求f(2)的取值范围;(2)在f(2)取得最小值时,若对于任意的x∈[2+∞),f(x)+2≥mf'(x)恒成立,求实数m的取值范围.考点:导数的加法与减法法则;二次函数的性质.专题:计算题;导数的概念及应用.分析:(1)根据已知函数f(x)=ax2+2x+c,且f(x)>0的解集为,可以函数开口向上,与x轴有一个交点,从而求解;(2)由(1)求出f(x)的解析式,对于任意的x∈[2+∞),f(x)+2≥mf'(x)恒成立,利用常数分离法,可以将问题转化为(x+2)+≥m在x∈[2+∞),恒成立,从而求出m的范围;解答:解:(1)由题意可得⇒ac=1⇒c>0所以f(2)=4a+4+c≥2+4=8当且仅当f(2)=4a+4+c≥2+4=8当且仅当4a=c即时“=”成立,故f(2)的取值范围为[8,+∞)(2)由(1)可得f(x)=x2+2x+2=(x+2)2,,∴f′(x)=x+2,因为对于任意的x∈[2+∞),f(x)+2≥mf'(x)恒成立,∴(x+2)+≥m在x∈[2+∞),恒成立,故[(x+2)+]min≥m即可,又函数y=(x+2)+在x∈[2+∞)上递增,所以[(x+2)+]min=,∴m≤;点评:此题主要考查二次函数的性质,以及解析式的求法,第二问利用了转化的思想,这是高考常考的热点问题,本题是一道中档题;17.(15分)已知数列{a n}的前n项和为S n,点在直线上,数列{b n}满足b n+2﹣2b n+1+b n=0(n∈N*),且b3=11,前9项和为153.(1)求数列{a n}、{b n}的通项公式;(2)求数列前n项的和.考点:数列递推式;数列的求和.专题:综合题;等差数列与等比数列.分析:(1)利用点在直线上,求得S n,再写一式,两式相减,可得数列{a n}的通项公式;确定数列{b n}是等差数列,利用b3=11,前9项和为153,即可求数列{b n}的通项公式;(2)利用错位相减法,可求数列前n项的和.解答:解:(1)由题意可知,∴n≥2时,a n=S n﹣S n﹣1=n+5n=1时,a1=S1=6也适合∴a n=n+5;∵b n+2﹣2b n+1+b n=0,∴b n+2﹣b n+1=b n+1﹣b n,∴{b n}是等差数列∵前9项和为153∴=9b5=153,∴b5=17∵b3=11,∴公差d==3∴b n=3n+2;(2)设数列前n项的和T n,则T n=26×5+27×8+…+2n+5•(3n+2)①∴2T n=27×5+28×8+…+2n+6•(3n+2)②①﹣②:﹣T n=26×5+3×(27+28+…+2n+5)﹣2n+6•(3n+2)=﹣26﹣(3n﹣1)•2n+6∴点评:本题考查数列的通项与求和,考查数列与函数的联系,正确运用求和公式是关键.18.(15分)两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065.(1)将y表示成x的函数;(11)讨论(1)中函数的单调性,并判断弧上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.考点:利用导数求闭区间上函数的最值;函数解析式的求解及常用方法.专题:计算题;应用题;压轴题;分类讨论.分析:(1)先利用AC⊥BC,求出BC2=400﹣x2,再利用圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,得到y和x之间的函数关系,最后利用垃圾处理厂建在的中点时,对城A和城B的总影响度为0.065求出k即可求出结果.(11)先求出导函数以及导数为0的根,进而求出其单调区间,找到函数的最小值即可.解答:解(1)由题意知AC⊥BC,BC2=400﹣x2,其中当时,y=0.065,所以k=9所以y表示成x的函数为(2),,令y'=0得18x4=8(400﹣x2)2,所以x2=160,即,当时,18x4<8(400﹣x2)2,即y'<0所以函数为单调减函数,当时,18x4>8(400﹣x2)2,即y'>0所以函数为单调增函数.所以当时,即当C点到城A的距离为时,函数有最小值.(注:该题可用基本不等式求最小值.)点评:本题主要考查函数在实际生活中的应用问题.涉及到函数解析式的求法以及利用导数研究函数的最值问题,属于中档题目,关键点在于把文字转化为数学符号.19.(16分)已知函数(其中e是自然对数的底数)(1)若f(x)是奇函数,求实数a的值;(2)若函数y=|f(x)|在[0,1]上单调递增,试求实数a的取值范围;(3)设函数,求证:对于任意的t>﹣2,总存在x0∈(﹣2,t),满足,并确定这样的x0的个数.考点:利用导数研究函数的单调性;函数奇偶性的判断;函数零点的判定定理.专题:导数的综合应用.分析:(1)利用f(0)=0即可求出a的值.(2)通过对a分类讨论和利用单调增函数的定义即可求出a的取值范围.(3)已知问题:对于任意的t>﹣2,总存在x0∈(﹣2,t),满足,等价于证明:对任意的t>﹣2,方程在区间(﹣2,t)内有实数解,通过对t分类讨论即可.解答:解:(1)∵函数f(x)是实数集R上的奇函数,∴f(0)=0,∴1+a=0,解得a=﹣1.∴f(x)=e x﹣e﹣x,经验证函数f(x)是R上的奇函数.故a=﹣1适合题意.(2)a=0时,y=e x在区间[0,1]上单调递增,适合题意;当a≠0时,令t=e x,∵x∈[0,1],∴t∈[1,e].且t=e x单调递增,故在t∈[1,e]时递增.当a>0时,函数y=在t∈[1,e]时单调递增,得,∴0<a≤1.当a<0时,在t∈[1,e]时单调递增恒成立,故∀t∈[1,e],.∴﹣1≤a<0.综上可知:﹣1≤a≤1.(3)∵f(x)+f′(x)==2e x,∴φ(x)=(x2﹣3x+3)e x,∴=x2﹣x.要证明:对于任意的t>﹣2,总存在x0∈(﹣2,t),满足.等价于证明:对任意的t>﹣2,方程在区间(﹣2,t)内有实数解.令g(x)=,则g(﹣2)=6﹣=﹣,g(t)=.所以①当t>4,或﹣2<t<1时,g(﹣2)g(t)<0,∴g(x)=0在(﹣2,t)内有解,且只有一解.②当1<t<4时,g(﹣2)>0,且g(t)>0,但g(0)=<0,∴g(x)=0在(﹣2,t)内有解,且由两解.③当t=1时,有且只有一个解x=0;当t=4时,有且只有一个解x=3.综上所述:对于任意的t>﹣2,总存在x0∈(﹣2,t),满足.且当t≥4或﹣2<≤1时,有唯一的x0适合题意;当1<t<4时,有两个不同的x0适合题意.点评:充分理解函数的单调性及分类讨论的思想方法是解题的关键.20.(16分)(2010•南通模拟)设数列{a n}是由正数组成的等比数列,公比为q,S n是其前n 项和.(1)证明;(2)设,记数列{b n}的前n项和为T n,试比较q2S n和T n的大小.考点:数列的应用;等比数列的性质.专题:计算题;证明题.分析:(1)由题设知当q=1时,S n•S n+2﹣S n+12=na1•(n+2)a1﹣(n+1)2a12=﹣a12<0;当q≠1时,S n•S n+2﹣S n+12==﹣a12q n<0.由此可知S n•S n+2﹣S n+12<0.所以.(2)方法一:由题意知T n=,T n﹣q2S n=≥2,所以T n>q2S.方法二:由题意知T n=,再由,利用均值不等式可知T n>q2S.解答:证明:(1)由题设知a1>0,q>0.(1分)(i)当q=1时,S n=na1,于是S n•S n+2﹣S n+12=na1•(n+2)a1﹣(n+1)2a12=﹣a12<0,(3分)(ii)当q≠1时,,于是S n•S n+2﹣S n+12==﹣a12q n<0.(7分)由(i)和(ii),得S n•S n+2﹣S n+12<0.所以S n•S n+2<S n+12,.(8分)(2)方法一:,(11分)T n=,T n﹣q2S n=,(13分)=≥2>0,(15分)所以T n>q2S.(16分)方法二:T n=,(11分)由,(13分)因为q>0,所以(当且仅当,即时取“=”号),因为,所以,即T n>q2S.(16分)点评:本题考查数列的性质和综合应用,难度较大,解题时要认真审题,仔细解答,注意公式的合理选用.。
江苏省东台市高三英语上学期期中试题牛津版

东台市2012年秋学期时堰中学高三年级期中联合考试英语试卷第一部分听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why does the man like his new room?A.It is near the friends’ flats.B. It is larger than the old one.C. It is close to the school.2. How much will the man pay for two general tickets and two student tickets?A. $40.B.$30 C.$20.3. What do we learn about Jack?A.He gave orders like a boss.B. He spoke to the bossC. He worked there as a boss.4. What does the woman suggest?A.The radio batteries have been replaced.B.They don’t really need to hear the radio.C.They should get a new radio.5. What do we learn about the woman?A.Sh e can’t afford any dictionary.B.She will plan for a good dictionary.C.She has a better dictionary.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
江苏省东台中学2012届高三第一次阶段性月考语文试题

江苏省东台中学2012届高三第一次阶段性练习语文命题顾权审核华林春2011.10.4一、语文文字运用(15分)1. 下列各组成语中,没有错误....的一组是(3分)A.甘拜下风自暴自弃一筹莫展味同嚼蜡B.义愤填膺嬉皮笑脸一枕黄梁天翻地覆C.不骄不躁沓无消息鼎力相助萎靡不振D.朝气蓬勃金榜题名涣然冰释走头无路2. 下列各句中,没有语病....的一句是(3分)()A.证监会和深交所从保护投资者特别是中小投资者利益为根本出发点,制定创业板相关规则,这是以中国资本市场是一个新兴加转轨、散户投资者为主的市场为根据的。
B.杭州湾跨海大桥建设有利于主动接轨上海,扩大开放,推动长江三角洲地区合作与交流,增强浙江省特别是宁波市和嘉兴市对内对外开放水平,提高综合实力和国际竞争力。
C.目前多所高水平大学自发联合起来在全国范围内实施的自主招生“联考”,在考试内容形式如何突出综合素质和能力的考查、如何突出不同高校学科特色、建立多元评价标准等方面,进行了有益探索。
D.江苏响水县陈家港、双港等镇区部分群众产生恐慌并连夜自发转移的原因是“陈家港化工园区大河化工厂要发生爆炸”的谣言所致。
3.阅读下面一段文字,给“宅经济”下一个定义,不超过40字。
(4分)所谓“宅经济”,是指一种新的经济模式,主要意思是在家中办公或者在家中从事商务工作。
在家中利用网络进行消费也是“宅经济”必不可少的一部分,如今,网购成了刺激“宅经济”的一个有效方式,而诸如此类的网络秒杀,亦将“宅经济”推向了一个新的高度4.艾佛山昨天发了一条关于“幸福”的微博,内容如下:在一片火红的夕阳下,遥远的小山包上,坐着两位老人,他们的脸上雕刻着岁月的痕迹,头发渲染了时间的颜色,可是他们的手却紧紧地握在了一起,互相依靠着,彼此会意地一笑。
你在生活中有类似的见闻吗?请你也写一条这样的微博。
要求:(1)字数不得少于60字;(2)要求有细节;(3)至少用到一种修辞手法。
(5分)1 / 15二、文言文阅读(19分)阅读下面的文言文,完成5-8题。
江苏省盐城市五烈中学高三生物月考试卷含解析

江苏省盐城市五烈中学高三生物月考试卷含解析一、选择题(本题共40小题,每小题1.5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 苹果含有微量元素锌,而锌是构成与记忆相关的蛋白质不可缺少的元素,儿童缺锌就会影响大脑的正常发育。
因此,苹果又被称为记忆之果。
这说明无机盐A.对维持酸碱平衡起重要作用 B.对维持细胞形态有重要作用C.对维持生物体生命活动有重要作用 D.对调节细胞内渗透压有重要作用参考答案:C2. 如图为某种植物幼苗(大小、长势相同)均分为甲、乙两组后,在两种不同浓度的KNO3溶液中培养时鲜重的变化情况(其他条件相同且不变),下列有关叙述,正确的是()A.6h时,甲组幼苗因根系开始吸收K+、NO3﹣,吸水能力增强,使鲜重逐渐提高B.由于根细胞失水,3h时,甲组植物细胞细胞液的浓度大于外界溶液浓度C.12h后,若继续培养,甲组幼苗的鲜重可能超过处理前,乙组幼苗将死亡D.该实验若把KNO3溶液改为蔗糖溶液,结果相同参考答案:C.A、实验开始时,甲组幼苗根系就已开始吸收K+、NO3﹣,而不是在6h时才开始吸收K+、NO3﹣,到6小时时细胞液浓度大于KNO3溶液浓度,从而使吸水能力增强,使鲜重逐渐提高,A错误;B、3h时,甲组幼苗鲜重仍然处于下降状态,即细胞仍在失水,因此甲组植物细胞细胞液的浓度小于外界溶液浓度,B错误;C、12h后,由于甲组根系不断通过主动运输吸收K+、NO3﹣,从而保持根细胞内外浓度差,使其吸水量大于蒸腾量而有可能超过处理前的鲜重量;乙组放在比根细胞液浓度大很多的KNO3溶液中,根细胞通过渗透作用和蒸腾作用不断大量失水造成严重萎蔫最后死亡,C正确;D、该实验若把KNO3溶液改为蔗糖溶液,则甲组幼苗不会发生质壁分离的自动复原,D错误.3. 关于细胞中元素与分子的叙述中,正确的是A. 微量元素不参与血红蛋白的构成B. 组成拟核与磷脂的元素种类不同C. DNA与三磷酸腺苷中的五碳糖不同D. T2噬菌体的遗传信息贮存在于脱氧核苷酸中参考答案:C组成血红蛋白的Fe属于微量元素,A错误;组成拟核和磷脂分子的组成元素都是C、H、O、N、P,B 错误;DNA中的五碳糖是脱氧核糖,三磷酸腺苷中的五碳糖是核糖,C正确;T2噬菌体的遗传信息贮存在于脱氧核糖核酸中,D错误。
江苏省盐城市东台五烈镇中学高三英语上学期期末试题含解析

江苏省盐城市东台五烈镇中学高三英语上学期期末试题含解析一、选择题1. Seeing the policemen coming, away immediately, leaving the things they’d just stolen.A. the thieves ranB. did the thieves runC. the thieves runD. ran the thieves 参考答案:D2. She had a feeling that she already knew _____ this conversation was going to lead.A. whereB. whenC. whyD. how参考答案:A3. Mr.Black can't help us, ____ he won't want to.Never hope for his help.A.other than B.rather thanC.more than D.or rather参考答案:D4. Investigators urged that safety procedures at the construction site ___________ as soon as possible.A. would improveB. were improvedC. improvedD. be improved参考答案:D【详解】考查虚拟语气。
句意:调查人员敦促建筑工地上的安全操作要尽早改善。
动词urge后的宾语从句要使用“should+动词原形”的虚拟语气,其中should可以省略。
本句主语safety procedures at the construction site与improve构成被动关系,要用被动语态,句中还省略了should。
故D项正确。
25. The two friends had a quarrel about money, but shortly afterwards they shook hands and ________.A. took upB. made upC. put upD. brought up参考答案:B略6. The government will come up with more volunteer projects just _______ the volunteer industry.A. to promoteB. to be promotedC. promotingD. being promoted参考答案:A7. —What a great cook your sister is!—Yeah! We ______ never have enough of her cookies.A.may B.must C.should D.can参考答案:D考查情态动词。
江苏省盐城市东台五烈镇中学高三英语联考试卷含解析

江苏省盐城市东台五烈镇中学高三英语联考试卷含解析一、选择题1. Unemployment in Japan is likely to remain high in 2013, and for the next few years.A.possibly B.necessarily C.gradually D.normally参考答案:A2. When you study the local map, you will find this town is .A. twice as a large town as thatB. twice the size that oneC. twice as larger as that oneD. twice as large a town as that one参考答案:D3. In our school there are some tall trees, some ________ more than forty meters.A.measured B.measure C.measuringD.to measure参考答案:C4. Messi’s talents _____ in comparison with other football players.A. stand outB. make outC. break outD. set out参考答案:A5.The old lady’s hand shook frequently . She explain ed to her doctor this shaking had begun half a year before , and ,only because of this , she had been forced to give up her job .A.when ; how B.how ; when C.how ; how D.why ; why参考答案:C解析:此题考查了疑问副词的用法。
江苏省东台市高三物理上学期期中考试试题新人教版
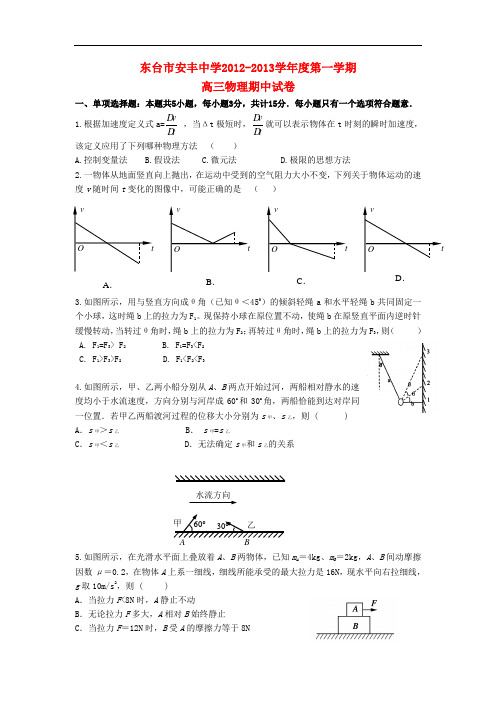
东台市安丰中学2012-2013学年度第一学期高三物理期中试卷一、单项选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意. 1.根据加速度定义式a=v t D D ,当Δt 极短时,v tD D 就可以表示物体在t 时刻的瞬时加速度,该定义应用了下列哪种物理方法 ( )A.控制变量法B.假设法C.微元法D.极限的思想方法2.一物体从地面竖直向上抛出,在运动中受到的空气阻力大小不变,下列关于物体运动的速度v 随时间t 变化的图像中,可能正确的是 ( )3.如图所示,用与竖直方向成θ角(已知θ<450)的倾斜轻绳a 和水平轻绳b 共同固定一个小球,这时绳b 上的拉力为F 1。
现保持小球在原位置不动,使绳b 在原竖直平面内逆时针缓慢转动,当转过θ角时,绳b 上的拉力为F 2;再转过θ角时,绳b 上的拉力为F 3,则( ) A. F 1=F 3> F 2 B. F 1=F 3<F 2 C. F 1>F 3>F 2 D. F 1<F 2<F 34.如图所示,甲、乙两小船分别从A 、B 两点开始过河,两船相对静水的速度均小于水流速度,方向分别与河岸成60o和30o角,两船恰能到达对岸同一位置.若甲乙两船渡河过程的位移大小分别为s 甲、s 乙,则 ( ) A .s 甲>s 乙 B . s 甲=s 乙C .s 甲<s 乙D .无法确定s 甲和s 乙的关系5.如图所示,在光滑水平面上叠放着A 、B 两物体,已知m A =4kg 、m B =2kg ,A 、B 间动摩擦因数μ=0.2,在物体A 上系一细线,细线所能承受的最大拉力是16N ,现水平向右拉细线,g 取10m/s 2,则 ( )A .当拉力F <8N 时,A 静止不动B .无论拉力F 多大,A 相对B 始终静止C .当拉力F =12N 时,B 受A 的摩擦力等于8NvtOvtOvtOvtOA .B .C .D .60o30o甲 乙 水流方向 BD .当拉力F >8N 时,A 相对B 滑动二、多项选择题:本题共4小题.每小题4分.共计16分.每小题有多个选项符合题意.全部选对的得4分。
江苏省东台中学2012届高三10月考英语试题

江苏省东台中学2012届⾼三10⽉考英语试题江苏省东台中学2012届⾼三10⽉考英语试题2012年10⽉05⽇本试题共分第⼀卷(选择题)和第⼆卷(⾮选择题)两部分。
共120分。
考试时间120分钟。
第⼀卷(三部分,共85分)第⼀部分:听⼒(共两节,满分20)第⼀节(共5⼩题;每⼩题1分,满分5分)听下⾯5 段对话。
每段对话后有⼀个⼩题,从题中所给的A,B,C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关⼩题和阅读下⼀⼩题。
每段对话仅读⼀遍。
1. Who reread these papers ?A. The manB. The womanC. Tom2. What does the man think of the woman?s story ?A. RidiculousB. Satisfying .C. Exciting3. Where most probably are the speakers ?A. At a post officeB. At a railway stationC. At a local hotel .4. What does the woman want the man to do ?A. Give up smoking .B. Go see a doctorC. Have one more cigarette5. What probably is the woman ?A. A shop assistantB. A tourist guideC. A bank clerk第⼆节(共15⼩题;每⼩题1分,满分15分)听下⾯5段对话或独⽩。
每段对话或独⽩后有⼏个⼩题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话或独⽩前,你都有时间阅读各个⼩题,每⼩题5秒钟;听完后,各⼩题将给出5秒的作答时间。
江苏省东台市五烈中学第一学期高三数学期末质量检测试卷

P 1P 2 III ⅢIVO 江苏省东台市五烈中学2007届第一学期高三数学期末质量检测试卷本试卷共有21道试题,满分150分。
考试时间120分钟。
一、选择题(本大题满分50分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得 4分,否则一律得零分。
( )1.若集合{}21,A m =,{}2,4B =,则“2m =”是“{}4A B =”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件( )2.已知向量的夹角为与则若c a c b a c b a ,25)(,5||),4,2(),2,1(=⋅+=--= A .30° B .60° C .120° D .150°( )3.已知定点A 、B 且|AB|=4,动点P 满足|PA|-|PB|=3,则|PA|的最小值是A .21 B .23 C .27D .5 ( )4.若{}n a 是等差数列,设公差d<0,20052006200520060,0a a a a +>⋅<.则前n 项和n S >0成立的最大自然数n 是(A )4009 (B )4010 (C )4011 (D )4012 ( )5.在北纬60°圈上有A 、B 两地,它们的纬度圈上的弧长等于2Rπ(R 是地球的半径).则A 、B 两地的球面距离为A.32R π B.2R π C. 3R π D.4Rπ( )6.有下列命题:(1)βαγβγα//,⇒⊥⊥;(2)γαγββα⊥⇒⊥⊥,; (3)1//αα,1//ββ,11βαβα⊥⇒⊥;(4)γβαγβγα⊥⇒=⊥⊥l l ,,;(5)如果在二面角111βα--l 与二面角222βα--l 中,已知:,,2121ββαα⊥⊥则二面角111βα--l 与二面角222βα--l 一定相等或互补.其中正确的有_____个A .1B .2C .3D .4( )7.在x y x y x y y x 2c o s,,lo g ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是 A .0 B .1 C .2 D .3( )8.如图,平面内的两条相交直线1OP 和2OP 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界).若12OP aOP bOP =+,且点P 落在第Ⅲ部分,则实数b a 、满足 A .0,0a b >> B .0,0a b ><C .0,0a b <>D .0,0a b << ( )9.下列四个函数中,图像如图所示的只能是A .lg y x x =+B .lg y x x =-C .lg y x x =-+D .lg y x x =--( )10.设b a 、是正实数,以下不等式2aba b>+,② a a b b >--,xyo③ 22243a b ab b +>-,④ 22ab ab+> 恒成立的序号为A .①、③B .①、④C .②、③D .②、④二、填空题(本大题满分30分)本大题共有6题,只要求直接填写结果,每题填对得4分,否则一律得零分。
江苏省东台市五烈中学2012届高三上学期第三次月考数学试卷

江苏省东台市五烈中学2012届高三上学期第三次月考数学试卷一、填空题:本大题共14小题,每小题5分,共70分.1.集合M={x|y=错误!},N={y|y=错误!},则M∩N=_______.2.若lg x+lg y=2,则错误!+错误!的最小值是.3.设复数z满足错误!=i,则|1+z|=________.4.等比数列{a n}中,a n>0,且a3·a6·a9=4,则log2a2+log2a4+log2a8+log2a10=______5.若错误!表示双曲线,则m的取值范围是_____________.6.若过正三角形ABC的顶点A任作一条直线l,则l与线段BC相交的概率为______.7.设f(x)=lg错误!是奇函数,则使f(x)<0成立的x的取值范围是__________.8.函数f(x)=cos x-sin x(x∈[-π,0])的单调递增区间为_______________.9.若正方形ABCD边长为1,点P在线段AC上运动,则错误!·(错误!+错误!)的取值范围是.10.已知函数f(x)在R上满足f(x)=2·f(2-x)-x2+8x-8,则f(2)=.11.已知直线x+y=a与圆x2+y2=4交于A、B两点,O是坐标原点,向量错误!、错误!满足|错误!+错误!|=|错误!-错误!|,则实数a的值是__________.12.函数y=错误!的图像上至少存在不同的三点到(1,0)的距离构成等比数列,则公比的取值范围_____________.13.函数y =-x 2+mx -1与以A (0,3)、B (3,0)为端点的线段(包含端点)有两个不同的公共点,则实数m 的取值范围是_____________.14. 已知F 1、F 2分别为双曲线x 2a 2-y 2b2=1错误!未找到引用源。
(a >0,b >0)的左、右焦点,若双曲线左支上存在一点P 使得 错误!=8a ,则双曲线的离心率的取值范围是 . 二、解答题15.(本小题满分14分)如图,在平面直角坐标系xOy 中,点A 在x 轴正半轴上,直线AB 的倾斜角为34,|OB |=2,设3,(,)24AOB。
江苏省盐城市东台五烈镇中学高三数学文上学期期末试卷含解析

江苏省盐城市东台五烈镇中学高三数学文上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 某几何体的三视图如图1所示,且该几何体的体积是,则正视图中的的值是()A.2 B.C. D. 3参考答案:C2. 设曲线在点处的切线的斜率为,则函数的部分图象可以为()参考答案:A略3. 设曲线C的方程为(x-2)2+(y+1)2=9,直线l的方程x-3y+2=0,则曲线上的点到直线l 的距离为的点的个数为()A、1B、2C、3D、4参考答案:4. 若正数满足,则的最小值是( )A. B. C. 5 D. 6参考答案:C由,可得,即,所以。
则,选C.5. 已知函数在曲线与直线的交点中,若相邻交点距离的最小值为,则的最小正周期为()A. B. C. D.参考答案:C∵,∴,∴或,则,又∵相邻交点距离的最小值为,∴,.6. 如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么( )A.S圆>S圆环B.S圆<S圆环C.S圆=S圆环D.不确定参考答案:C考点:旋转体(圆柱、圆锥、圆台).专题:计算题;空间位置关系与距离.分析:根据图形得出,S截面圆=π(R2﹣d2),r=d,S圆环=π(R2﹣d2),即可判断.解答:解:根据题意:①半球的截面圆:r=,S截面圆=π(R2﹣d2),②∵取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,∴r=d,S圆环=π(R2﹣d2),根据①②得出:S截面圆=S圆环,故选:C.点评:本题考查了球有关的截面问题,判断图形结构,求出半径即可,属于中档题.7. 一个几何体的三视图如图所示,则该几何体的体积为()A. B.C. D.参考答案:C8. 若x∈( e-1, 1) , a= l n x, b=2 l n x, c= l n 3x, 则()A.a<b<c B.c<a<b C.b<a<c D.b<c<a参考答案:C【知识点】对数与对数函数B7因为a=lnx在(0,+∞)上单调递增,故当x∈(e-1,1)时,a∈(-1,0),于是b-a=2lnx-lnx=lnx<0,从而b<a.又a-c=lnx-ln3x=a(1+a)(1-a)<0,从而a<c.综上所述,b<a<c.【思路点拨】根据函数的单调性,求a的范围,用比较法,比较a、b和a、c的大小.9. 已知m,n是两条不同的直线,是两个不同的平面,则下列四个命题中是真命题的是()A、B、C、D、参考答案:B10. 已知集合A={x||2x﹣1|≤3},B={x|log0.5x≥a},且B?A,则实数a的取值范围是()A.a≥﹣1 B.a≥1 C.a≤﹣1 D.a≤1参考答案:A略二、 填空题:本大题共7小题,每小题4分,共28分 11. 在中,角所对的边分别为且,,若,则的取值范围是 _____________.参考答案:由得,因为,所以由得.所以最大.因为,所以,即,所以,即,因为,所以,即,所以.因为,所以,所以,即,所以.,因为,所以,即,即,所以.即的取值范围是.【答案】 【解析】12. 如图所示一个几何体的三视图,则该几何体的体积为参考答案:【考点】由三视图求面积、体积. 【专题】空间位置关系与距离.【分析】由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,计算出底面面积和高,代入锥体体积公式,可得答案.【解答】解:由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥, 棱锥的底面面积S=×2×2=2, 棱锥的高h=2, 故棱锥的体积V==,故答案为:.【点评】本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.13. 函数的最大值是 。
江苏省东台市五烈镇中学-度第一学期高三数学期中考试卷 苏教版

东台市五烈镇中学2007~2008学年度第一学期期中考试高三年级数学试题 命题、校对人:黄明荣一、选择题:(5分×8=40分)1、设集合P ={1,2,3,4,5,6},Q ={x|2≤x ≤6},则P ∩Q 等于A 、{1}B 、{2,6}C 、{2,3,4,5}D 、{2,3,4,5,6} 2、设等差数列{a n }的前n 项和是S n ,且a 4+a 8=0,则A 、S 4<S 5B 、S 4=S 5C 、S 6<S 5D 、S 6=S 5 3、若P :x ≥2,Q :(x-2)1+x ≥0,则P 是Q 的 A 、充分而不必要条件 B 、必要而不充分条件 C 、定要条件 D 、既不充分也不必要条件 4、已知曲线y=42x 的一条切线的斜率为21,则切点的横坐标为A 、1B 、2C 、3D 、45、函数f(x)=sin (32x+2π)+sin 32x 的图象相邻的两条对称轴之间的距离是A 、3πB 、6πC 、23πD 、43πx+2y=52x+y ≤46、设变量x 、y 满足 则z=3x+4y 的最大值是x ≥0 y ≥0A 、9B 、10C 、11D 、127、设函数x 、y 满足log 2(x+y+3)= log 2x + log 2y,则x+y 的取值范围是 A 、(0,6) B 、[6,+ ∞) C 、[1+7,+∞) D 、(0,1+7)8、函数y=| log 2x|的定义域为[a ,b],值域为[0,2],则区间[a,b]的长度b-a 的最小值为 A 、3 B 、43 C 、2 D 、23二、填空(5分×8=40分)9、若sin θ+cos θ=51,则sin2θ=10、已知{a n }为等比数列,a 2a 4+2a 3a 5+a 4a 6=25,则a 3+a 5= 11、函数f(x)=3x-x 3(-3≤x ≤3)的最大值为 12、若a 、b ∈R +,且a+b=1,则ba 21+的最小值是 13、已知函数f(x)=2sin(wx+φ)对任意x 都是f(6π+x)= f(6π-x),则f(6π)= 14、在数列{a n }中,已知a 1=1,a n =a n-1+a n-2+…+a 2+a 1(n ∈N,n ≥2),这个数列的通项公式a n = 15、已知奇函数y=f(x)满足条件f(x+1)=f(x-1),且当x ∈[-1,0]时,f(x)=3x+94,则f(531log ) 的值是16、有以下四个命题: (1)y=sin 2x+x2sin 3的最小值是23(2)已知f(x)=1011--x x ,则f (4)>f (3)(3)y =log a (2+a x),(a >0,a ≠1)在R 上是增函数 (4)函数y =2sin (2x -6π)的图象的一个对称点是(12π,0) 其中真命题的序号是______________(把你认为正确命题的序号都填上)三、解答题(14分+16分+16分+16分+18分) 17、(14分)设函数f(x)=cos(2x+3π)+3sin2x+2a (1) 求函数f(x)的单凋递增区间 (2) 当0≤x ≤4π时,f(x)的最小值为0,求a 的值18、(16分)已知等差数列{a n}的前4项的和为10,且a2,a3,a7成等比数列(1)求通项公式a n(2)设b n=n a2,求数列{b n}的前n项的和S n19、(16分)设函数f(x)=2x3-3(a+1)x2+6x,a∈R(1)当a=1时,求证:f(x)为单凋增函数(2)当x∈[1,3]时,f(x)的最小值为4,求a的值20、(16分)设计一幅宣传画,要求画的面积为4840cm2,画面的宽与高的比为λ,画面的上、下各留8cm空白,左、右各留5cm空白,如果0<λ<1,怎样确定主画面的高与宽的尺寸,能使宣传画所用纸张面积最小,如果32≤λ≤43,结果又将如何?21、(18分)由原点O向三次曲线y=x3-3ax2+bx(a≠0)引切线,切于不同于点O的点P1(x1,y1),由P1引此曲线的切线,切于不同于P1的点P2(x2,y2),如此继续地作下去……,得到点列{(x n,y n)},试回答下列问题:(1)求x1(2)求x n与x n+1的关系(3)若a>0,求证:当n为正偶数时,x n<a;当n为正奇数时,x n>a[参考答案]一、D D A A C C B B 二、9、-252410、±5 11、2 12、3+22 13、±2 14、 1 n=12n-2n ≥215、-1 16、③④三、解答题(14分+16分+16分+16分+18分)17、(1)f(x)=cos2xcos 3π-sin2xsin 3π+3sin2x+2a=21cos2x+23sin2x+2a =cos(2x-3π)+2a (6分)由-π+2k π≤2x-3π≤2k π -3π+k π≤x ≤6π+ k π k ∈Z∴f(x)的单凋递增区间为[-3π+k π, 6π+ k π](k ∈Z)(10分)(2)由0≤x ≤4π 得-3π≤2x-3π≤6π∴21≤cos(2x-3π)≤1 由f(x)的最小值为0,得21+2a=0 a=-41(14分) 18、(1)设等差数列的公差为d;4a 1+6d=10(a 1+2d)2=(a 1+d)(a 1+6d) (4分)a 1=-2 a 1=25 解得d=3 d=0∴a n =3n-5 或a n=25(8分) (2)当a n =3n-5时,数列{b n }是首项为41, 公比为8的等比数列 ∴S n =281881)81(41-=--n n (12分)当a n =25时,b n =252∴S n=∙252n综上 s n =2818-n 或s n =∙252n (16分)19、(1)当a=1时,f(x)=2x 3-6x 2+6xf 1(x)=6x 2-12x+6=6(x-1)2≥0 ∴f(x)为单凋增函数(7分)(2)f 1(x)=6(x-1)(x-a)① 当a ≤1时,f(x)在区间[1,3]上是单凋增函数,最小值为f(1) f(1)=4,即2-3(a+1)+6a=4 得a=35>1(舍去) (10分)②当1<a<3时,f(x)在区间(1,a)上是减函数,在区间(a,3)上是增函数,故f(a)为最小值,f(a)=4,即a 3-3a 2+4=0解得a=-1(舍去),a=2 (13分)③当a ≥3,f(x)在区间(1,a)上是减函数,f(3)为最小值f(3)=4,即54-27(a+1)+18a=4得a=923<3(舍去) 综上所述 a=2 (16分)20、解:设画面高为xcm ,宽为λxcm ,则λx 2=4840所用纸张面积s(λ)=(x+16)( λx+10)= λx 2+(16λ+10)x+160=5000+44)58(10λλ+≥6760 (6分)其中等号当8λ=λ5,即λ=85时取得∴当λ=85时,S(λ)最小,此时画面的高x=λ4840=88cm,宽λx=55cm(8分)如果λ∈[43,32],则λ≠85此时考察正数s(λ)的单凋性 任取λ1,λ2∈[43,32],且λ1<λ2s(λ1)-s(λ2)=4410(1158λλ+-2258λλ-)=4410(21λλ-)(8-215λλ)其中∵21λλ>8532> ∴8-215λλ>0又21λλ-<0∴s(λ1)-s(λ2)<0 ∴s(λ1)<s(λ2) (14分) ∴s(λ)在[43,32]上为增函数,因此当λ=32时,s(λ)最小此时画面的高x=λ4840≈85.2cm ,宽λx=56.8cm (16分)21、(1)y=x 3-3ax 2+bx ①得y 1=3x 2-6ax+b过曲线①上点P (x 1,y 1)的切线l 1的方程是y-(x 13-3ax 12+bx 1)=(3x 12-6ax 1+b)(x-x 1), (x 1≠0)由它过原点,故有-x 13+3x 12-bx 1 = -x 1(3x 12-6ax 1+b)∴2x 13=3ax 12, (x 1≠0)∴x 1=23a(8分) (2)过曲线①上点P n+1(x n+1,y n+1)的①的切线l n+1的方程是:y-(x n+13-3ax n+12+bx n+1)=(3x 2n+1-6ax n+1+b)(x-x n+1) 由于l n+1过曲线①上点P n (x n ,y n )故 x n 3-3ax n 2+bx n -(x n+13-3ax n+12+bx n+1)=(3x n+12-6ax n+1+b)(x n -x n+1) ∵x n ≠x n +1,同除以x n -x n+1得 x n 2+x n x n+1+x n+12-3a(x n +x n+1)+b=3x n+12-6ax n+1+b x n 2+x n x n+1-2x n+12-3a(x n -x n+1)=0 以x n -x n+1除之 得 x n +2x n+1-3a=0 (13分) (3)由②得 x n+1=-21x n +23a ∴x n+1-a=21(x n -a) 故数列{x n -a}是以x 1-a=2a 为首项,比为-21的等比数列 ∴x n -a=2a (-21)n-1 ∴x n =[1-(-21)n]a ∴当n 为正偶数时 x n =[1-(-21)n ]a=[1-(21)n]a<a 当n 为正奇数时 x n =[1-(-21)n ]a=[1+(21)n]a>a (18分)注:各题用其他正确解法同样得分。
江苏省东台市五烈镇中学第一学期高三化学期中考试卷

东台市五烈镇中学2007~2008学年度第一学期期中考试高三年级化学试题命题人:奚太来本试卷分为第Ⅰ卷选择题和第Ⅱ卷(非选择题)两部分,共120分。
考试时间100分钟相对原子量:H-1 C-12 N-14 O-16 Al-27 S-32 Zn-65 Fe-56 Cu-64 Mg-24 Ag -108第I卷选择题(共48分)一、选择题(本题包括6小题,每小题3分,共18分。
每小题只有..1个.选项符合题意)1.据有关媒体报导,最近意大利一所大学的科学家使用普通的氧分子和带正电的氧离子制造出了一种新型氧分子,并用质谱仪探测到了它的存在。
这种新型氧分子是由4个氧原子构成的。
下列有关这种新型氧分子的叙述正确的是A.与168O互为同位素B.等质量时所含的O原子数比O3的多C.是除O2、O3外的又一种氧的同素异形体D.与同质量的O2具有相同的体积(同温同压)2.将表面已完全钝化的铝条,插入下列溶液中,不会发生反应的是A.稀硝酸B.硝酸铜C.稀盐酸D.氢氧化钠3.下列有关物质分类的说法正确的是A.O2和O3、H2和D2、H182O和H162O都互为同素异形体B.纯碱、烧碱、碱式碳酸铜都属于碱类物质C.煤、石油和天然气都属于化石能源D.CH2Cl2、CH4O、C2H4O2一定是纯净物4.某500mL溶液中含0.1molFe2+、0.2molFe3+,加入0.2mol铁粉,待Fe3+完全还原后,溶液中Fe2+的物质的量浓度为(假设反应前后体积不变)A.0.4mol·L-1B.0.6mol·L-1C.0.8mol·L-1D.1.0mol·L-15.Cu2S与一定浓度的HNO3反应,生成Cu(NO3)2、CuSO4、NO2、NO和H2O,当NO2和NO的物质的量之比为1∶1时,实际参加反应的Cu2S与HNO3的物质的量之比为A.1∶9 B.1∶7 C.1∶5 D.2∶96、下列离子方程式正确的是A.碳酸氢钠溶液与少量石灰水反应HCO-3+ Ca2+ + OH—= CaCO3↓+ H2OB.氯化铵与氢氧化钠两种浓溶液混合加热OH—+ NH+4△H2O + NH3↑C.氢氧化镁与稀硫酸反应H+ + OH—= H2OD.单质铜与稀硝酸反应Cu + 2 H++ 2NO-3= Cu2+ + 2NO↑+H2O二、选择题(本题包括10小题,每小题3分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省东台市五烈中学2012届高三上学期期中考试数学试卷一、填空题1.集合{}0,2A =,{}21,B a =,若{}0,1,2,4A B ⋃=,则实数a 的值为 . 2.已知角α的终边经过点(),6P x -,且3tan 5α=-,则x 的值为 .3.若复数12,1z a i z i =-=+(为虚数单位),且12z z ⋅为纯虚数,则实数a 的 值为 .4.某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为 . 5.“N M >”是“N M 22loglog >”成立的 条件;必要不充分6.盐城市教育局为了调查学生在盐城摸底考试中数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图),则10000人的数学成绩在[140,150]段的约是________人.7.函数)4(log 2x y -=的定义域是 . .8.函数2sin(2),,662y x x πππ⎡⎤=-∈⎢⎥⎣⎦的值域为 9.已知A B C △的面积是30,内角A B C 、、所对边分别为a b c 、、,1213cos A =,若1c b -=,则a 的值是 .510.函数)sin()(ϕω+=x x f )20,0,(πϕω≤≤>∈R x 的部分图象如图,则ϕ=________ 11.已知3sin(),45x π-=则sin 2x 的值为________.12.若点P 是曲线2ln y x x =-上一点,且在点P 处的切线与直线2y x =-平行,则点PBADCFE(第16题)的横坐标为________13.方程210x x =-的根)1,(+∈k k x ,k ∈Z ,则k = _ 14.若函数()23k k h x x x =-+在(1,)+∞上是增函数,则实数k 的取值范围是15.(本小题满分14分)已知函数()2cos 2cos 1f x x x x =+-()x ∈R . (Ⅰ)求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.(Ⅱ)若()065f x =,0,42x ππ⎡⎤∈⎢⎥⎣⎦.求0cos 2x 的值.16.(本小题满分14分)如图,四边形ABCD 为矩形,平面ABCD ⊥平面ABE ,BE =BC ,F 为CE 上的一点,且BF ⊥平面ACE . (1)求证:AE ⊥BE ; (2)求证:AE ∥平面BFD .17.(本小题满分14分)在△ABC 中,角A 、B 、C 所对应的边为c b a ,, (1)若,cos 2)6sin(A A =+π求A 的值; (2)若c b A 3,31cos ==,求C sin 的值.18.已知平面直角坐标系xOy 中,A (4+23,2),B (4,4),圆C 是△OAB 的外接圆. (1)求圆C 的方程;(2)若过点(2,6)的直线l 被圆C 所截得的弦长为43,求直线l 的方程.19.某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。
已知每投放质量为m 的药剂后,经过x 天该药剂在水中释放的浓度y (毫克/升)满足2(04)4(),()6(4)2xx y m f x f x x x ⎧+<≤⎪⎪==⎨⎪>⎪-⎩其中,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化。
(I )如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?(II )如果投放的药剂质量为m ,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定该投放的药剂质量m 的值。
20.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)已知函数()()323,f x ax bx x a b R =+-∈在点()()1,1f 处的切线方程为20y +=.⑴求函数()f x 的解析式;⑵若对于区间[]2,2-上任意两个自变量的值12,x x 都有()()12f x f x c -≤,求实数c 的最小值;⑶若过点()()2,2M m m ≠可作曲线()y f x =的三条切线,求实数m 的取值范围.江苏省东台市五烈中学2012届高三期中考试数学参考答案一、填空题 1. 2± 2. 10 3. 1- 4.145.必要不充分 6. 800 7.(,3]-∞8. [-2,-1] 9. 510. 4,4πϕπω==11.72512.1 13.2 14.[)2,-+∞ 二、解答题15.解:(Ⅰ)由()2cos 2cos 1f x x x x =+-得())()22sin cos 2cos 12cos 22sin 26fx x x x x x x π⎛⎫=+-=+=+ ⎪⎝⎭.所以函数的最小正周期为22T ππ==.因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以72,666x πππ⎡⎤+∈⎢⎥⎣⎦. 所以2,662x πππ⎡⎤+∈⎢⎥⎣⎦,即0,6x π⎡⎤∈⎢⎥⎣⎦时,函数()fx 为增函数,而在,62x ππ⎡⎤∈⎢⎥⎣⎦时,函数()f x 为减函数,所以2sin 262f ππ⎛⎫== ⎪⎝⎭为最大值,72sin 126f ππ⎛⎫===- ⎪⎝⎭为最小值.(Ⅱ)由(Ⅰ)知,()002sin 26f x x π⎛⎫=+⎪⎝⎭,又由已知()065f x =,则03s i n 265x π⎛⎫+= ⎪⎝⎭.因为0,42x ππ⎡⎤∈⎢⎥⎣⎦,则0272,636x πππ⎡⎤+∈⎢⎥⎣⎦,因此0cos 206x π⎛⎫+< ⎪⎝⎭, 所以04cos 265x π⎛⎫+=- ⎪⎝⎭,于是00cos 2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦, 00cos 2cos sin 2sin 6666x x ππππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭431525210=-⨯+⨯= 16.本小题满分14分)(1)证明:∵平面ABCD ⊥平面ABE ,平面ABCD ∩平面ABE =AB ,AD ⊥AB ,∴AD ⊥平面ABE ,∵AE ⊂平面ABE ∴AD ⊥AE . ∵AD ∥BC ,则BC ⊥AE . ……4分又BF ⊥平面ACE ,则BF ⊥AE .∵BC ∩BF =B ,∴AE ⊥平面BCE ,∴AE ⊥BE .…………7分 (2)设AC ∩BD =G ,连接FG ,易知G 是AC 的中点, ∵BF ⊥平面ACE ,则BF ⊥CE .而BC =BE ,∴F 是EC 中点.在△ACE 中,FG ∥AE ,…………11分 ∵AE ⊄平面BFD ,FG ⊂平面BFD ,∴ AE ∥平面BFD . …………14分 17.(1)sin()2cos ,sin ,cos 0,tan 063A A A A A A A A πππ+=∴=≠=<<∴=(2)在三角形中,22221cos ,3,2cos 8,3A b c a b c bc A c a ==∴=+-==G BAD C FE由正弦定理得:sin sin c AC=,而sin ,3A ==1sin 3C ∴=.(也可以先推出直角三角形)(也能根据余弦定理得到1cos ,0sin 33C C C π=<<⇒=)18.解:(1)设圆C 方程为x 2+y 2+Dx +Ey +F =0,则⎩⎨⎧F =04D +4E +F +32=0(4+23)D +2E +F +32+163=0解得D =-8,E =F =0.所以圆C :(x -4)2+y 2=16.(2)当斜率不存在时,l :x =2被圆截得弦长为43,符合题意; 当斜率存在时,设直线l :y -6=k (x -2),即kx -y +6-2k =0,因为被圆截得弦长为43,所以圆心到直线距离为2,所以|4k +6-2k |1+k2=2,解得k =-43,所以直线l :y -6=-43(x -2),即4x +3y -26=0.故所求直线l 为x =2,或4x +3y -26=0.19.解:(1)当m=4时,8(04)4()24(4)2x x y f x x x +<≤⎧⎪==⎨>⎪-⎩ -----------------2分当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化 ∴当04x <≤时,84y x =+≥,得4x = 当4x >时,2442y x =≥-,解得48x <≤故自来水达到有效净化一共可持续5天 -------------------6分 (2)为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化 即前4天和后3天的自来水达到最佳净化 ∴当04x <≤时,4(2)104x m ≤+≤在04x <≤恒成立,得168408m x m x ⎧≥⎪⎪+⎨⎪≤⎪+⎩在04x <≤恒成立,∴1023m ≤≤ ----------------------9分 当47x <≤时,64102m x ≤≤-在47x <≤恒成立,同理得103m =即投放的药剂质量m 的值为103------------------13分20.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)解:⑴()2323f x ax bx '=+-.…………………………………………………………2分根据题意,得()()12,10,f f =-⎧⎪⎨'=⎪⎩即32,3230,a b a b +-=-⎧⎨+-=⎩解得10a b =⎧⎨=⎩……………………3分所以()33f x x x =-.………………………………………………………………4分⑵令()0f x '=,即2330x -=.得1x =±.因为()12f -=,()12f =-,所以当[]2,2x ∈-时,()max 2f x =,()min 2f x =-.………………………………6分 则对于区间[]2,2-上任意两个自变量的值12,x x ,都有()()()()12max min 4f x f x f x f x -≤-=,所以4c ≥.所以c 的最小值为4.……………………………………………………………………8分 ⑶因为点()()2,2M m m ≠不在曲线()y f x =上,所以可设切点为()00,x y .则30003y x x =-.因为()20033f x x '=-,所以切线的斜率为2033x -.………………………………9分则2033x -=300032x x mx ---,………………………………………………………………11分即32002660x x m -++=.因为过点()()2,2M m m ≠可作曲线()y f x =的三条切线,所以方程32002660x x m -++=有三个不同的实数解.所以函数()32266g x x x m =-++有三个不同的零点.则()2612g x x x '=-.令()0g x '=,则0x =或2x =.则()()0022g g >⎧⎪⎨<⎪⎩ ,即6020m m +>⎧⎨-+<⎩,解得62m -<<.…………………………………16分。
