陕西省高三上学期数学期中考试试卷(I)卷

合集下载

陕西师范大学附属中学2022-2023学年高三上学期期中理科数学试题含解析

9.双曲线的左，右焦点分别是，过作倾斜角为的直线交双曲线的右支于点，若垂直于轴，则双曲线的离心率为（）
A. B. C.2D.
【答案】B
【解析】
【分析】将代入双曲线方程求出点的坐标，通过解直角三角形列出三参数，，的关系，求出离心率的值．
【详解】由于轴，且在第一象限，设
所以将代入双曲线的方程得即，
7.侏罗纪蜘蛛网是一种非常有规律的蜘蛛网，如图是由无数个正方形环绕而成的，且每一个正方形的四个顶点都恰好在它的外边最近一个正方形四条边的三等分点上，设外围第1个正方形的边长是m，侏罗纪蜘蛛网的长度(蜘蛛网中正方形的周长之和)为Sn，则（）
A.Sn无限大B.Sn<3(3＋ )m
C.Sn＝3(3＋ )mD.Sn可以取100m
17.已知中，角A，B，C的对边分别为a，b，c， .
（1）若，求的值；
（2）若的平分线交AB于点D，且，求的最小值；
【答案】（1）；（2）4
【解析】
【分析】（1）由，利用正弦定理将边转化为角得到，再根据，有，然后利用两角差的正弦公式展开求解.
（2）根据的平分线交AB于点D，且，由，可得，化简得到，则，再利用基本不等式求解.
【详解】设，，
则，，
如图所示，
连接交于点，连接、，
因为平面，平面，
所以，而，所以四边形是直角梯形，
则有，
，，
所以有，
故，
因为平面，平面，
所以，又因为为正方形，所以，
而平面，
所以平面，即平面，
,
所以，，
故答案为：③④.

2025届西安市高三数学上学期第一次质量检测考试卷附答案解析

2025届西安市高三数学上学期第一次质量检测考试卷本卷满分：150分考试时间：120分钟一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}(){}2210,1=-=-A x x B x log x x ，则A B ⋂=()A.{}10x x - B.{}10x x -< C.{}10x x -< D.{}10x x -<<2.“01a <<”是“函数()log (2)a f x a x =-在(,1)-∞上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.函数()()2sin x xf x x e e x-=-+-在区间[]2.8,2.8-的大致图像为()A. B. C. D.4.已知5log 2a =，2log b a =，1()2bc =，则()A.c b a >> B.c a b>> C.a b c>> D.b c a>>5.已知定义在R 上的函数()f x 满足3(2)()f x f x +=，且(2)1f =-，则(100)f =()A.3B.1C.1-D.3-6．已知函数1,0,()()12,0,x e x f x g x kx x x⎧-⎪==-⎨<⎪⎩ ，若关于x 的方程()()f x g x =有2个不相等的实数解，则实数k 的取值范围是()A.{}e B.[,)e +∞ C.1(,0){}8e -⋃ D.1(,){}8e -∞-⋃7.已知函数3()1f x x x =-+，则()A.()f x 有三个极值点B.()f x 有三个零点C.直线2y x =是曲线()y f x =的切线D.点(0,1)是曲线()y f x =的对称中心8.已知函数24,0(),0x x f x x log x x ⎧+>⎪=⎨⎪<⎩，2()g x x ax b =++，若方程()0g f x =⎡⎤⎣⎦有且仅有5个不相等的整数解，则其中最大整数解和最小整数解的和等于()A.28-B.28C.14- D.14二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.下列导数运算正确的是（）A.211(x x'=- B.()x xe e '--= C.21(tan )x cos x'=D.1(ln ||)x x'=10.甲乙丙等5人的身高互不相同，站成一排进行列队训练，则()A.甲乙不相邻的不同排法有48种B.甲乙中间恰排一个人的不同排法有36种C.甲乙不排在两端的不同排法有36种D.甲乙丙三人从左到右由高到矮的不同排法有20种11.已知0c b a <<<，则()A.ac b bc a+<+ B.333b c a +< C.a c ab c b+<+ D.>三、填空题：本题共3小题，每小题5分，共15分．12.某班的全体学生参加化学测试，成绩的频率分布直方图如图所示，数据的分组依次为[20,40),[40,60),[60,80),[80,100]，则该班学生化学测试成绩的第40百分位数为__________.13.若曲线x y e x =+在点(0,1)处的切线也是曲线ln(1)y x a =++的切线，则a =__________.14.5(1)(2)y x y x-+的展开式中，23x y 的系数为__________.四、解答题：本题共5小题，其中第15题13分，第16,17题15分，第18,19题17分，共77分．解答应写出文字说明、证明过程或演算步骤．15．已知函数3212()2.32a f x x x ax +=-+（1）若1a =，求函数()f x 的极值；（2）讨论函数()f x 的单调性.16．为践行“更快更高更强”的奥林匹克格言，落实全民健身国家战略.某校高三年级发起了“发扬奥林匹克精神，锻炼健康体魄”的年度主题活动，经过一段时间后，学生的身体素质明显提高.为了解活动效果，该年级对开展活动以来近6个月体重超重的人数进行了调查，调查结果统计如图，根据上面的散点图可以认为散点集中在曲线bx a y e +=的附近，请根据下表中的数据求出（1）该年级体重超重人数y 与月份x 之间的经验回归方程(系数a 和b 的最终结果精确到0.01)；（2）预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下.月份x 123456体重超标人数y987754483227ln z y= 4.58 4.37 3.98 3.87 3.46 3.29附：经验回归方程：ˆˆˆybx a =+中，1221ˆniii nii x ynx y b xnx ==-⋅=-∑∑，ˆˆay bx =-；参考数据：6123.52i i z ==∑，6177.72i ii x z==∑，62191i i x ==∑，ln10 2.30.≈17.已知函数()log (1)a f x x =+，()2log (2)(a g x x t t =+∈R )，0a >，且 1.a ≠（1）当01a <<且1t =-时，求不等式()()f x g x 的解集；（2）若函数()2()21f x F x a tx t =+-+在区间(1,2]-上有零点，求t 的取值范围．18.某企业对某品牌芯片开发了一条生产线进行试产.其芯片质量按等级划分为五个层级，分别对应如下五组质量指标值：[45,55),[55,65),[65,75),[75,85),[85,95].根据长期检测结果，得到芯片的质量指标值X 服从正态分布2(,)N μσ，并把质量指标值不小于80的产品称为A 等品，其它产品称为B 等品.现从该品牌芯片的生产线中随机抽取100件作为样本，统计得到如图所示的频率分布直方图.（1）根据长期检测结果，该芯片质量指标值的标准差s 的近似值为11，用样本平均数x 作为μ的近似值，用样本标准差s 作为σ的估计值.若从生产线中任取一件芯片，试估计该芯片为A 等品的概率(保留小数点后面两位有效数字);(①同一组中的数据用该组区间的中点值代表;②参考数据：若随机变量ξ服从正态分布2(,)N μσ，则()0.6827P μσξμσ-<<+≈，(22)0.9545P μσξμσ-<<+≈，(33)0.9973.)P μσξμσ-<<+≈（2）（ⅰ）从样本的质量指标值在[45,55)和[85,95]的芯片中随机抽取3件，记其中质量指标值在[85,95]的芯片件数为η，求η的分布列和数学期望；(ⅱ)该企业为节省检测成本，采用随机混装的方式将所有的芯片按100件一箱包装.已知一件A 等品芯片的利润是(124)m m <<元，一件B 等品芯片的利润是ln(25)m -元，根据(1)的计算结果，试求m 的值，使得每箱产品的利润最大.19.已知函数1()ln (1).x f x ae x a x -=+-+（1）当0=a 时，求函数()f x 的单调区间；（2）当1a =时，证明：函数()f x 在(0,)+∞上单调递增；（3）若1x =是函数()f x 的极大值点，求实数a 的取值范围.一.选择题（本题共8小题，每小题5分，共40分）二.选择题（本题共3小题，每小题6分，共18分）三、填空题：(本题共3小题，每小题5分，共15分.)12.6513.ln 214.40三、解答题：(本题共5小题，其中第15题13分，第16,17题15分，第18,19题17分，共77分)15.（本小题满分13分）解：(1)1a =时，3213()2,()(1)(2)32f x x x x f x x x '=-+=--，所以1x <或2x >时，()0f x '>；12x <<时，()0f x '<则()f x 在(1,2)上递减，在(,1),(2,)-∞+∞上递增，所以()f x 的极小值为2(2)3f =，极大值为5(1)6f =...............................5分陕西省西安中学高2025届高三第一次质量检测数学参考答案题号12345678答案CBABDCDA题号91011答案ACDBCDABD3212(2)()232a f x x x ax +=-+，则()()(2)f x x a x '=--，当2a =时，()0f x ' ，所以()f x 在(,)-∞+∞上递增，当2a >时，2x <或x a >时，()0f x '>；2x a <<时，()0f x '<,所以()f x 在(,2),(,)a -∞+∞上递增，在(2,)a 上递减，当2a <时，x a <或2x >时，()0f x '>；2a x <<时，()0f x '<所以()f x 在(,),(2,)a -∞+∞上递增；在(,2)a 上递减................................8分（2）令-+<=≈，所以，解得，由于，所以，所以从第十个月开始，该年级体重超标的人数降至10人以下................................5分17.（本小题满分15分）解：(1)1=- t 时，()()2log 1log 21a a x x +- ，又01a <<，21(21)210x x x ⎧+-∴⎨->⎩，2450151242x x x x ⎧-⎪∴∴<⎨>⎪⎩，∴解集为：15{|}24x x <；...............................6分(2)解法一：()222F x tx x t =+-+，由()0F x =得：22(2x t xx +=-≠-且12)x -< ，22(2)4(2)2x t x x +∴=-+-++，设2U x =+(14U < 且2U ≠，则212424U t U U U U=-=--+-+，令2()U U Uϕ=+，当1U <<时，()U ϕ4U <<时，()U ϕ单调递增，且9(1)3,(4).2ϕϕϕ===9()2U ϕ∴且() 4.U ϕ≠12402U U∴---< 或2044U U<--- ，t 的取值范围为：2t - 或224t +解法二：()222F x tx x t =+-+，若0t =，则()2F x x =+在(1,2]-上没有零点．下面就0t ≠时分三种情况讨论：①方程()0F x =在(1,2]-上有重根12x x =，则0∆=，解得：24t =，又1212x x t ==-(]1,2,∈-24t +∴=；②()F x 在(1,2]-上只有一个零点，且不是方程的重根，则有()()120F F -<，解得：2t <-或1t >，又经检验：2t =-或1t =时，()F x 在(1,2]-上都有零点；2t ∴- 或 1.t ③方程()0F x =在(1,2]-上有两个相异实根，则有0,01122(1)0(2)0t t F F >∆>⎧⎪⎪-<-<⎪⎨⎪->⎪>⎪⎩或0,01122(1)0(2)0t t F F <∆>⎧⎪⎪-<-<⎪⎨⎪-<⎪<⎪⎩，解得：214t +<<，综上可知：t 的取值范围为2t - 或224t +...............................15分18.（本小题满分17分）(1)(1)由题意，估计从该品牌芯片的生产线中随机抽取100件的平均数为：10(0.01500.025600.04700.015800.0190)69.x =⨯⨯+⨯+⨯+⨯+⨯=即69x μ≈=11s σ≈≈，所以X ∽2(69,11)N ，因为质量指标值X 近似服从正态分布2(69,11)N ，所以1(69116911)1()(80)22P X P X P X μσμσ--<<+--<<+== 10.68270.158650.162-≈=≈，所以从生产线中任取一件芯片，该芯片为A 等品的概率约为0.16................................5分(2)()(0.010.01)1010020i +⨯⨯=，所以所取样本的个数为20件，质量指标值在[85,95]的芯片件数为10件，故η可能取的值为0，1，2，3，相应的概率为：3010103202(0)19C C P C η===，21101032015(1)38C C P C η===，12101032015(2)38C C P C η===，0310103202(3)19C C P C η===，随机变量η的分布列为：η0123P21915381538219所以η的数学期望2151523()0123.193838192E η=⨯+⨯+⨯+⨯=...............................11分()ii 设每箱产品中A 等品有Y 件，则每箱产品中B 等品有(100)Y -件，设每箱产品的利润为Z 元，由题意知：(100)ln(25)(ln(25))100ln(25)Z mY Y m m m Y m =+--=--+-，由(1)知：每箱零件中A 等品的概率为0.16，所以Y ∽(100,0.16)B ，所以()1000.1616E Y =⨯=，所以()[(ln(25))100ln(25)]E Z E m m Y m =--+-(ln(25))()100ln(25)m m E Y m =--+-16(ln(25))100ln(25)m m m =--+-1684ln(25)m m =+-,令()1684ln(25)(124)f x x x x =+-<<84()16025f x x '=-=-得，794x =，又79(1,)4x ∈，()0f x '>，()f x 递增79;(,24)4x ∈，()0f x '<，()f x 递减，所以当79(1,24)4x =∈时，()f x 取得最大值.所以当794m =时，每箱产品利润最大................................17分19.（本小题满分17分）(1)解：当0=a 时，()ln =-f x x x ，且知11()1-'=-=xf x x x，在(0,1)上，()0'>f x >，()f x 在(0,1)上单调递增；在(1,)+∞上，()0'<f x ，()f x 在(1,)+∞上单调递减；所以函数()f x 的单调增区间为(0,1)，单调减区间为(1,)+∞..............................4分(2)证明：因为1a =，所以1()ln 2x f x e x x -=+-，且知11()2x f x e x-'=+-，要证函数()f x 单调递增，即证()0f x ' 在(0,)+∞上恒成立，设11()2x g x ex -=+-，0x >，则121()x g x e x-'=-，注意1x y e -=，21y x=-在(0,)+∞上均为增函数，故()g x '在(0,)+∞上单调递增，且(1)0g '=，于是()g x 在(0,1)上单调递减，在(1,)+∞上单调递增，()(1)0g x g = ，即()0f x ' ，因此函数()f x 在(0,)+∞上单调递增;...............................10分(3)由11()1x f x ae a x -'=+--，有(1)0f '=，令11()1x h x ae a x -=+--，有121()x h x ae x-'=-，①当0a 时，11()0x xh x aex -'=-<在(0,)+∞上恒成立，因此()f x '在(0,)+∞上单调递减，注意到(1)0f '=，故函数()f x 的增区间为(0,1)，减区间为(1,)+∞，此时1x =是函数()f x 的极大值点;②当0a >时，1x y ae -=与21y x=-在(0,)+∞上均为单调增函数，故()h x '在(0,)+∞上单调递增，注意到(1)1h a '=-，若(1)0h '<，即01a <<时，此时存在(1,)n ∈+∞，使()0h n '=，因此()f x '在(0,)n 上单调递减，在(,)n +∞上单调递增，又知(1)0f '=，则()f x 在(0,1)上单调递增，在(1,)n 上单调递减，此时1x =为函数()f x 的极大值点，若(1)0h '>，即1a >时，此时存在(0,1)m ∈，使()0h m '=，因此()f x '在(0,)m 上单调递减.在(,)m +∞上单调递增，又知(1)0f '=，则()f x 在(,1)m 上单调递减，在(1,)+∞上单调递增，此时1x =为函数()f x 的极小值点.当1a =时，由(1)可知()f x 单调递增，因此1x =非极大值点，综上所述，实数a 的取值范围为(,1).-∞..........................17分。

陕西省西安市高三数学上学期期中试题文新人教A版

陕西省西安市高三数学上学期期中试题文新人教A 版2012-2013学年度第一学期期中高三年级数学（文科）试题一．选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.)1．设集合}02|{2<-=x x x M ，},11|{≤≤-=x x N 则=N M （）A ．}10|{<<x xB ．}21|{<≤x xC ．}10|{≤<x xD ．}21|{<<x x2．若R a ∈，则“2=a ”是“0)2)(1(=--a a ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3．设n S 为等差数列}{n a 的前n 项和，公差2-=d ，若1110S S =，则=1a ( )A ．18B ．20C ．22D ．244．设复数z 满足2)1(=+z i ，其中i 为虚数单位，则=z （）A ．i +1B ．i -1C ．i 22+D ．i 22-5．函数233x x y +-=在点（1,2）处的切线方程为（）A ．13-=x yB ．53+-=x yC ．53+=x yD ．x y 2=6．在下列区间中，函数34)(-+=x e x f x 的零点所在的区间为（）A ．)0,41(-B ．)41,0(C ． )21,41(D ．)43,21( 7．如果函数)0(sin >=ωωx y 在区间]3,0[π上单调递增，在区间]2,3[ππ上单调递减，则ω的值是（）A ．32B ．3C ．2D ．23 8．若函数⎪⎩⎪⎨⎧<-≥-=2,1)21(,2,)2()(x x x a x f x 是R 上的单调递减函数，则实数a 的取值范围为（） A ．)2,(-∞ B ．]813,(-∞C ．)2,0(D ．)2,813[ 9．一个棱锥的三视图如右图所示，则它的体积为( ) A ．32 B ．1 C ． 13 D ．1210．在圆06222=--+y x y x 内，过点)1,0(E 的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为（）A ．25B ．210C ．215D ．220二．填空题（本大题共5小题，每小题5分，共25分）11．已知)3,(),1,0(),1,3(k c b a =-==，若b a 2-与c 共线，则=k ．12．设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≤+-≤-+≥043,041y x y x x 则目标函数y x z -=3的最大值为_______．13．某程序图如图所示，该程序运行后输出的结果是．14．若)2,0(πα∈，且412cos sin 2=+αα，则=αtan ______ __． 15．（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）A ．（几何证明选讲选做题）如图，点,,ABC 是圆O 上的点，且6,120BC BAC =∠=，则圆O 的面积等于．B .（不等式选讲选做题）若存在实数x 满足|3|||5x x m -+-<,则实数m 的取值范围为_________． C ．(极坐标与参数方程选讲选做题)设曲线C 的参数方程为23cos 13sin x y θθ=+⎧⎨=-+⎩（θ为参数），直线l 的方程为320x y -+=，则曲线C 上到直线l 距离为71010的点的个数有_________个．三．解答题（本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤）16．（本小题12分）已知)1cos ,cos 3(-=x x a ，)1cos ,(sin +=x x b ，函数)(21)(R x b a x f ∈+⋅= B A O（1）求函数)(x f 的周期；（2）函数)(x f 的图像可由函数x y sin =的图像经过怎样的变换得到？17．（本小题12分）如图，在四棱锥ABCD S -中，2==AB SA ，22SB SD ==，底面ABCD 是菱形，且60ABC ∠=︒，E 为CD 的中点．（1）求四棱锥ABCD S -的体积；（2）侧棱SB 上是否存在点F ，使得CF ∥平面SAE ？并证明你的结论．18．（本小题12分）某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：85987654322198653328698765叶茎6050分数组距0.040.0280.0160.008（1）求全班人数及分数在[)80,90之间的频数，并计算频率分布直方图中[)80,90 间的矩形的高；（2）若要从分数在[]80,100之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[]90,100之间的概率．19．（本小题12分）已知椭圆)0(1:2222>>=+b a b y a x E 的离心率为36，右焦点为)0,22(；斜率为1的直线l 与椭圆E 交于A 、B ，以AB 为底边作等腰三角形，顶点为)2,3(-P .(1)求椭圆E 的方程.(2)求PAB ∆的面积.20.（本小题13分）已知a 为实数，函数)()(23R x ax x x f ∈-=．（1）若5)1(='f ，求a 的值及曲线)(x f y =在))1(,1(f 处的切线方程；（2）求)(x f 在区间]2,0[上的最大值．21.（本小题14分）已知等差数列{}n a 中，公差0d >，其前n 项和为n S ，且满足2345a a ⋅=，1414a a +=．（1）求数列{}n a 的通项公式；（2）设n n n a b 2=（*n ∈N ），求数列{}n b 的前n 项和n T ；（3）设12)54(+⋅-=n n n F ，试比较n F 与n T 的大小．西安市第一中学2012-2013学年度第一学期期中高三年级数学（文科）试题参考答案及评分标准一．选择题：本大题共10小题，每小题5分，共50分．1-5 CABBA 6-10 CDBDB二．填空题：本大题共5小题，每小题5分，共25分．11. 1 12．4 13. 5 14．315. A π48 B )8,2(- C 2三．解答题：本大题共6小题，共75分．16．（1）由已知可得21)1)(cos 1(cos sin cos 3)(++-+⋅=x x x x x f ……（2分） 211cos sin cos 32+-+⋅=x x x 2122cos 12sin 23-++=x x ………………（4分） )62sin(2cos 212sin 23π+=+=x x x ………………（6分）所以函数)(x f 的最小正周期为π．……………………………（8分）（2)把x y sin =的图像上所有的点向左平移6π个单位，得到函数)6sin(π+=x y 的图像，再把)6sin(π+=x y 的图像上所有的点的横坐标变为原来的21（纵坐标不变），得到函数)62sin(π+=x y 的图像．……………………………（12分）或：把x y sin =的图像上所有的点的横坐标变为原来的21（纵坐标不变），得到函数x y 2sin =的图像．再把x y 2sin =的图像上所有的点向左平移12π个单位，得到得到函数)62sin(π+=x y 的图像．……………………………（12分）17．解:（1）,2===AD AB SA 22==SD SB ，则有222AB SA SB +=，222AD SA SD +=， AB SA ⊥∴，AD SA ⊥ 又A AD AB =⊥∴SA 底面ABCD ，………………………(2分) 13S ABCD ABCD V S SA -=⨯四边形14322sin 6023=⨯⨯⨯⨯= ……………(5分)（2）F 为侧棱SB 的中点时，//CF 平面SAE ． ………………(7分)证法一：设N 为SA 的中点，连FC NE NF ,,，则NF 是SAB ∆的中位线，AB NF //∴且AB NF 21=，又//CE 且AB CE 21=，NF CE //∴且NF CE =，∴四边形CENF 为平行四边形，NE CF //∴，⊂NE 平面SAE ，⊄CF 平面SAE ，//CF ∴平面SAE ． ………………(12分)证法二：设M 为AB 的中点，连FC MC MF ,,，则MF 是SAB ∆的中位线， SA MF //∴，⊂SA 平面SAE ，⊄MF 平面SAE ，//MF ∴平面SAE ．同理，由AE CM //，得//CM 平面SAE ．又M MC MF = ，∴平面//FMC 平面SAE ，又⊂CF 平面FMC ，//CF ∴平面SAE ． ……………………………(12分)18.（1）由茎叶图知，分数在[)50,60之间的频数为2，频率为0.008100.08⨯=，全班人数为2250.08=．所以分数在[)80,90之间的频数为25271024----= 频率分布直方图中[)80,90间的矩形的高为4100.01625÷=．……(6分) （2）将[)80,90之间的4个分数编号为1,2,3,4，[]90,100之间的2个分数编号为5,6，在[]80,100之间的试卷中任取两份的基本事件为：()1,2，()1,3，()1,4，()1,5，()1,6()2,3，()2,4，()2,5，()2,6，()3,4，()3,5，()3,6()4,5，()4,6. 共15个， ……………(9分)其中，至少有一个在[]90,100之间的基本事件有9个，故至少有一份分数在[]90,100之间的频率是90.615=．………(12分)19.解：（1）由已知得36,22==a cc ，解得32=a又4222=-=c a b ，所以椭圆E 的方程为141222=+y x …………（5分）设直线l 的方程为m x y += …………（6分）（2) 由⎪⎩⎪⎨⎧=++=141222y x mx y 得 01236422=-++m mx x ①设),(11y x A 、))(,(2122x x y x B <，线段AB 的中点为),(00y x C ，则 432210mx x x -=+=，400mm x y =+= …………（8分）因为AB 是等腰PAB ∆的底边，所以AB PC ⊥，所以143342-=+--=mmk PC 解得2=m …………（9分）此时，方程①为01242=+x x 解得0,321=-=x x所以2,121=-=y y则23||=AB …………（10分）这时，点)2,3(-P 到直线02:=+-y x AB 的距离为：2232|223|=+--=d ， …………（11分）所以PAB ∆的面积为292232321||21=⋅⋅=⋅=d AB S …………（12分）20.解：(1) 23)(ax x x f -=则ax x x f 23)(2-='523)1(=-='a f ， 1-=∴a又当1-=a 时，23)(x x x f +=，2)1(=f ，所以，曲线)(x f y =在点))1(,1(f 处的切线方程为)1(52-=-x y 即35-=x y ．…………………………………………（5分）13．令023)(2=-='ax x x f ，解得01=x ，322ax =，当032≤a，即0≤a 时，在)2,0(上0)(>'x f ，)(x f 在]2,0[上为增函数， a f x f 48)2()(max -==∴ 当232≥a，即3≥a 时，在)2,0(上0)(<'x f ，)(x f 在]2,0[上为减函数， 0)0()(max ==∴f x f 当2320<<a，即30<<a 时，在)32,0(a 上0)(<'x f ，在)2,32(a上0)(>'x f ，故)(x f 在]32,0[a 上为减函数，在]2,32[a上为增函数，故当)0()2(f f ≥即048≥-a 即20≤<a 时，a f x f 48)2()(max -== 当)0()2(f f <即048<-a 即32<<a 时，0)0()(max ==f x f 综上所述，⎩⎨⎧>≤-=2,02,48)(a a a x f ………………………………（13分）21.解：（1）由已知可得⎩⎨⎧=+=++143245)2)((111d a d a d a （0>d ）解得⎩⎨⎧==411d a34)1(41-=-+=∴n n a n …………………………………………（4分）或：由}{n a 为等差数列得：144132=+=+a a a a ，又4532=a a ，故2a 、3a 可以看作方程045142=+-x x 的两根，由0>d 得23a a > 5,923==∴a a 故1,42123=-==-=d a a a a d 34)1(41-=-+=∴n n a n …………………………………………（4分）（2) n n n n n a b 2)34(2⋅-==nn n n n T 2)34(2)74(2925211321⋅-+⋅-++⋅+⋅+⋅=∴- ① =n T 2 14322)34(2)74(292521+⋅-+⋅-++⋅+⋅+⋅n n n n ② ①-②得：1322)34()222(42+⋅--++++=-n n n n T 122)34(2122242+⋅---⋅-⋅+=n n n112)34(16242++⋅---⋅+=n n n142)74(1-⋅--=+n n142)74(1+⋅-=∴+n n n T ……………………………………（9分）（3）142142)74(2)54(211-=-⋅--⋅-=-+++n n n n n n n T F ∴当2≥n 时，14162242>=≥+n ，即01421>-+n 故n n T F > 当1=n 时，1482232<==+n ，即01421<-+n 故n n T F < 综上可得，当1=n 时，n n T F <；当2≥n 时，n n T F >．………（13分）。

陕西省高三上学期期中数学试卷(I)卷

陕西省高三上学期期中数学试卷（I）卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共15分)1. （1分） (2019高二下·江门月考) i为虚数单位，设复数z1 ， z2在复平面内对应的点关于原点对称，若z1=2﹣3i，则z2=________．2. （1分）(2018·新疆模拟) 一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图.为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在（元）月收入段应抽出________人.3. （1分） (2019高二上·田阳月考) 在区间上随机取一个数，则的概率是________.4. （2分）已知函数如图表示的是给定x的值，求其对应的函数值y的程序框图．①处应填写________；②处应填写________．5. （1分） (2016高一下·石门期末) 设函数f（x）=2x﹣cosx，{an}是公差为的等差数列，f（a1）+f （a2）+…+f（a5）=5π，则[f（a3）]2﹣a1a5=________．6. （1分）函数y=f（x）的图象是两条直线的一部分（如图所示），其定义域为[﹣1，0）∪（0，1]，则不等式f（x）﹣f（﹣x）＞﹣1的解集为________．7. （1分） (2017高二下·新乡期末) 已知函数y=sin（ωx+φ）（ω＞0，0＜φ≤ ）的部分图象如图所示，则cos（5ωφ）=________．8. （1分）在平行四边形ABCD中，AD=1，∠BAD=60°，=3．若•=﹣3，则的长为________9. （1分）(2017·江苏模拟) 已知sinα=3sin（α+ ），则tan（α+ ）=________．10. （1分） (2016高二上·长沙开学考) 若直线 =1（a＞0，b＞0）过点（1，1），则a+b的最小值等于________．11. （1分） (2016高二上·江北期中) 已知点P（x，y）在圆x2+y2=1上运动，则的最大值为________．12. （1分） (2018高二上·南京月考) 抛物线与过焦点的直线交于两点，为原点，则________.13. （1分） (2017高二下·濮阳期末) 数列{an}是首项为1的实数等比数列，Sn为数列{an}的前n项和，若28S3=S6 ，则数列{ }的前四项的和为________14. （1分）(2019·萍乡模拟) 设为整数，若对任意的，不等式恒成立，则的最大值是________．二、解答题 (共6题；共40分)15. （5分）在△ABC中，bsinA=acosB．（Ⅰ）求角B的大小；（Ⅱ）若b=3，sinC=2sinA，求a，c的值．16. （5分） (2017高二上·芜湖期末) 如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AA1=BC=2AC=2．（Ⅰ）若D为AA1中点，求证：平面B1CD⊥平面B1C1D；（Ⅱ）在AA1上是否存在一点D，使得二面角B1﹣CD﹣C1的大小为60°．17. （5分）(2016·城中模拟) 设椭圆C： =1的离心率e= ，动点P在椭圆C上，点P到椭圆C 的两个焦点的距离之和是4．（Ⅰ）求椭圆C的方程；（Ⅱ）若椭圆C1的方程为 =1（m＞n＞0），椭圆C2的方程为=λ（λ＞0，且λ≠1），则称椭圆C2是椭圆C1的λ倍相似椭圆．已知椭圆C2是椭圆C的3倍相似椭圆．若过椭圆C上动点P的切线l交椭圆C2于A，B两点，O为坐标原点，试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况．18. （10分） (2016高一下·福建期中) 如图，半径为4m的水轮绕着圆心O逆时针做匀速圆周运动，每分钟转动4圈，水轮圆心O距离水面2m，如果当水轮上点P从离开水面的时刻（P0）开始计算时间．（1）将点P距离水面的高度y（m）与时间t（s）满足的函数关系；（2）求点P第一次到达最高点需要的时间．19. （5分）(2017·自贡模拟) 已知数列{an}是公差为2的等差数列，数列{bn}满足，若n∈N*时，anbn+1﹣bn+1=nbn ．（Ⅰ）求{bn}的通项公式；（Ⅱ）设cn=anbn ，求{cn}的前n项和Sn ．20. （10分） (2018高二下·济宁期中) 设函数有两个零点，，且 .（1）求的求值范围；（2）求证： .三、附加题 (共4题；共40分)21. （5分）(2020·海安模拟) 在平面直角坐标系中，先对曲线作矩阵所对应的变换，再将所得曲线作矩阵所对的变换．若连续实施两次变换所对应的矩阵为，求的值．22. （10分）在极坐标系中，圆C的极坐标方程为，若以极点O为原点，极轴为x 轴的正半轴建立平面直角坐标系.（1）求圆C的一个参数方程；（2）在平面直角坐标系中，是圆C上的动点，试求的最大值，并求出此时点P的直角坐标.23. （10分）已知圆C：x2+y2﹣6y+8=0，O为原点．（1）求过点O的且与圆C相切的直线l的方程；（2）若P是圆C上的一动点，M是OP的中点，求点M的轨迹方程．24. （15分）已知：，设．（1）求n的值；（2）写出f（x）的展开式中所有的有理项；（3）求f（x）的展开式中系数最大的项．参考答案一、填空题 (共14题；共15分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题；共40分)15-1、17-1、18-1、18-2、19-1、20-1、20-2、三、附加题 (共4题；共40分)21-1、22-1、22-2、23-1、23-2、24-1、24-2、24-3、。

陕西省咸阳市高新一中2021届高三数学上学期期中质量检测试题文含解析

A.1B. C. D.2
【答案】B
【解析】
【分析】
由复数除法求得，再由模的运算求得模．
【详解】由题意，∴ ．
故选：B．
3.函数的定义域是（）
A. B. C. D.
【答案】Bቤተ መጻሕፍቲ ባይዱ
【解析】
【分析】
求出使函数式有意义的自变量的范围即可．
【详解】由题意，解得．
故选：B．
4.函数的一个零点落在下列哪个区间（）
（2）由（1）得bn＝1＋2(n－1)＝2n－1，即an＋1－an＝2n－1，进而利用累加求通项公式即可.
试题解析：
（1）证明由an＋2＝2an＋1－an＋2，得an＋2－an＋1＝an＋1－an＋2，即bn＋1＝bn＋2.
又b1＝a2－a1＝1，所以{bn}是首项为1，公差为2的等差数列．
（2）解由（1）得bn＝1＋2(n－1)＝2n－1，即an＋1－an＝2n－1.
故选：C.
【点睛】本题考查函数的图象、利用导数研究函数的单调性，识别函数图象问题，往往可根据特殊值或特殊自变量所在区间利用排除法解答，属于中档题.
12.已知函数的最小正周期为，且对，，恒成立，若函数在，上单调递减，则的最大值是
A. B. C. D.
【答案】B
【解析】
【分析】
利用函数的周期求出，对，，恒成立，推出函数的最小值，求出，然后求解函数的单调区间即可．
【详解】（1）由余弦定理可得，
的面积；
（2），
，
，
.
【点睛】本题考查余弦定理、三角恒等变换解三角形，熟记公式是解题的关键，考查计算求解能力，属于基础题.
20.数列满足，，．

陕西省西安中学高三(上)期中数学试卷含答案

∵ 퐴퐷 + 퐴퐸 = 푥퐴퐵 +푦퐴퐶，则푥 + 푦 = 2，
∵ 点 D，E 是线段 BC 上两个动点， ∴ 푥 > 0，푦 > 0．
∴
1 푥
+
4 푦
=
11 2(푥
+
4 푦)(푥
+ 푦)
=
12(5
+
푦 푥
+
4푦푥)
≥
12(5
∴ 푏4 = 푎3 + 푎5 = 2푎4 = 23，푎4 = 4，
又푏5 = 푎4 +2푎6 = 24，∴ 푎6 = 6 ，
∴ 푎6 = 푎4 +2푑，得푑 = 1，
第 8 页，共 19 页
푎6 = 푎1 +5푑 푎 = 1
，得
，
∴ 푎푛 = 푛．
1
∴ 푎2019 + 푏9 = 2019 + 28 = 2275，
푛
}的通项公式以及数列{푎푛}的通项公式即可计算出푎2019 + 푏9的值．
【解答】
解： ∵ 푏1 = 1，푏3 = 푏2 +2，{푏 }
∴ 푏1푞2 = 푏 1푞
+ 2，푞2 = 푞
是正项等比数列， + 2，푛 解得푞 = −1(舍)或푞
= 2，
∴ 푏푛 = 2푛−1，
∵ 数列{푎푛}是等差数列，푏4 = 푎3 + 푎5，푏5 = 푎4 +2푎6，
减函数，故正确．故选 D．
4.【答案】D
【解析】解：푎−2 = 0，即푎 = 2时，−4 < 0，恒成立；
{ 푎−2
≠ 0时，
푎−2 < 0 4(푎−2)2 + 16(푎−2) < 0，解得−2 < 푎

陕西省汉中市2023届高三上学期教学质量第一次检测理科数学试题(含答案解析)

（）
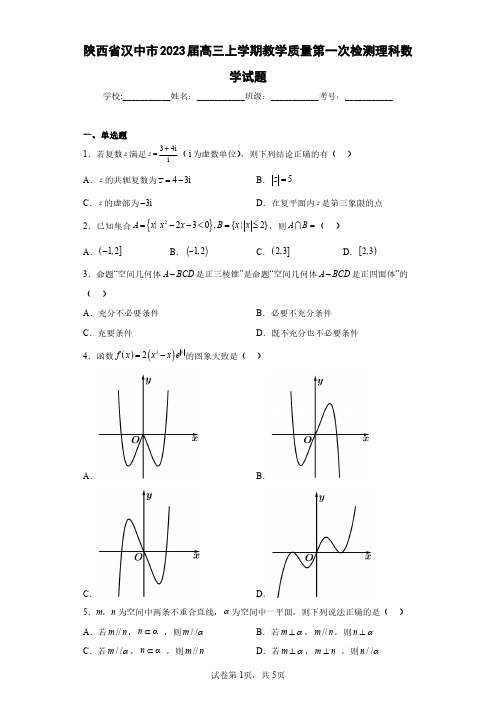
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
4．函数 f x 2 x3 x e x 的图象大致是（）
A．
B．
C．
D．
5．m，n 为空间中两条不重合直线，为空间中一平面，则下列说法正确的是（）
A．若 m // n ， n ，则 m / /
B．若 m ， m // n ，则 n
7．A 【分析】先将原函数用诱导公式变形为正弦函数表示，再根据“左加右减”的原则判断即可.
【详解】
y
cos
2x
3
cos
2x
5 6
2
sin
2x
5 6
sin
2
x
5 12
故可由
y
sin2x 的图象向左平移
5 12
个单位长度得到.
故选：A.
8．C
【分析】分别安排各场馆的志愿者，利用组合计数和乘法计数原理求解.
三、解答题
17．已知 a,b, c 分别为 ABC 内角 A, B,C 的对边，且 2b a cosC c cosA
(1)求角 C ； (2)若 c2 2ab,ABC 的面积为 3 ，求 a b 的值. 18．如图，多面体 ABCDEF 中，四边形 ABCD 为菱形， ABB FA 2ED 2 .
A．
1 3
B． 2 5
C．
1 2
D． 3 5
11．若双曲线
x2 a2
y2 b2
1(a
0, b
0)
的实轴的两个端点与抛物线
x2
8by
的焦点是一个直
角三角形的顶点，则该双曲线的离心率为（）

陕西省长安区高三数学上学期期中考试试题文新人教A版

陕西省长安区高三数学上学期期中考试试题文新人教A 版高三数学试题（文科）考试时间:100分钟试题分值:150分一、选择题（5×14=70分） 1. 复数22(1i)i 等于（） A.2 B.2- C.i 2- D.i 2 2.2.,a b 是平面α外的两条直线，若//,a α 则“//a b ”是“//b α” 的（）A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件3.已知}{n a 为等差数列，且1247-=-a a , 03=a ，则公差=d （）A.2-B.－12 C.12D.2 4.在右面的程序框图中，若5=x ，则输出的i 的值是（）A. 2B. 3C. 4D. 5 5.如图，一个体积为123的正三棱柱的三视图如图所示，则这个三棱柱的左视图的面积为（） A.36 B ．8 C ．38 D ．126.“1=m ”是“直线01)2(=+++my x m 与直线03)2()2(=-++-y m x m 相互垂直”的（） A ．充分必要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件7.()4cos ,0,5ααπ=∈，则tan α的值等于（） A.43 B.43C.43±D.34±8.一位母亲记录了她儿子3到9岁的身高，数据如下表：年龄3456789开始否输入 x是结束输出 i ?109>x23-=x x0=i1+=i i由此她建立了身高与年龄的回归模型x y 19.793.73+=，她用这个模型预测儿子10岁时的身高，则下列的叙述正确的是( )A.她儿子10岁时的身高一定是145.83㎝B.她儿子10岁时的身高在145.83㎝以上C.她儿子10岁时的身高在145.83㎝左右D.她儿子10岁时的身高在145.83㎝以下 9．把一个质地均匀的骰子掷两次，至少有一次骰子的点数为2的概率是（）A.21B.51 C.361 D.3611 10．三角形ABC 中角C 为钝角，则有（）A.sinA>cosBB. sinA<cosBC. sinA=cosBD. sinA 与cosB大小不确定11.已知互不相等的实数,,a b c 成等差数列,,,c a b 成等比数列,且310a b c ++=,则a =( )A ．4B ．2C ．－2D ．－4 12.曲线y=x 3+x-2在点P 0处的切线平行于直线y=4x ，则点P 0的坐标是（） A ．(0,1)B.(1,0)C.(-1,-4)或（1,0）D.(-1,-4)13.已知()⎩⎨⎧≤+>=0),1(02xx f x x x f ，则()()22-+f f 的值为A ．6B ．5C ．4D ．214.已知函数()f t 是奇函数且是R 上的增函数，若y x ,满足不等式22(2)(2)f x x f y y -≤--，则22x y + 的最大值是（）A B ．．8 D ．12二、填空题（6×5=30分）15.已知向量)2,4(=→a ，向量)3,(xb =→，且→→b a //，则=x . 16.不等式213x -<的解集为 .17.若实数,x y 满足不等式组⎪⎩⎪⎨⎧≥≤-+≥+-00101y y x y x ，则函数2z x y =+的最大值为 .18.直线1y x =-上的点到圆C ：224240x y x y ++-+=的最近距离为 . 19.已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边，若a =1，bA +C =2B ，则sin A =20.已知集合{}(,)1,,A x y y x x y ==-∈R ，{}(,)2,,B x y y ax x y ==+∈R ，若集合A B 有且只有一个元素，则实数a 的取值范围是 .三、解答题（本大题共4小题，满分50分） 21．（本小题满分12分）已知函数)2sin(sin 3sin )(2πωωω+⋅+=x x x x f （0>ω）的最小正周期为π．（Ⅰ）求ω的值；（Ⅱ）求函数)(x f 在区间]32,0[π上的取值范围．（Ⅲ）函数)(x f 的图象可由x y sin =的图象经过怎样的变化得到（注意文字表述）？ 22.（本小题满分12分）某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：（Ⅰ）求全班人数；（Ⅱ）求分数在)90,80[之间的人数；并计算频率分布直方图中)90,80[间的矩形的高；（Ⅲ）若要从分数在]100,80[之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在]100,90[之间的概率.PACBDO23. （本小题满分12分）在三棱锥P ABC -中，PAC∆和PBC ∆2AB =，,O D 分别是,AB PB 的中点．（Ⅰ）求证：OD ∥平面PAC ；（Ⅱ）求证：平面PAB ⊥平面ABC ；（Ⅲ）求三棱锥P ABC -的体积． 24．（本小题满分14分）已知函数321()(,3f x x x ax b a b =-+++∈R ). (Ⅰ) 若3=a ，试确定函数()f x 的单调区间；(Ⅱ) 若函数()f x 在其图象上任意一点00(,())x f x 处切线的斜率都小于22a ，求实数a的取值范围.长安一中2012—2013学年度第一学期期中质量检测高三数学试题答案（文科）一、选择题(5×14=70分)二、填空题(6×5=30分)15.6 16.(-1,2) 17.2 18.122-19. 1/2 20.(-∞,-1]∪[1,+∞)三、解答题（满分50分）21.解：（1）1cos211()cos cos2sin2222211cos sin2sin cos2sin226626xf x x x x xx x xωωωωωπππωωω-=+=-+⎛⎫⎛⎫=+-=+-⎪ ⎪⎝⎭⎝⎭212Tππωω==∴=1()sin(2)26f x xπω=+-（2）27023666x xππππ≤≤∴-≤-≤113sin(2)10sin(2)262623()0,2x xf xππωω∴-≤-≤≤+-≤⎡⎤∴∈⎢⎥⎣⎦（3）方法一：将siny x=的图象向右平移6π个单位得到sin()6y xπ=-，再将所得图像的横坐标压缩为原来的一半得到sin(2)6y x π=-，再将所得图像向上平移12个单位即得到1sin(2)62y x π=-+的图象。

陕西省西安市第一中学高三数学上学期期中试题理(含解析)

市一中大学区2021-2022度第一学期期中考试高三数学试题（理）一、选择题（本大题共12个小题，每小题5分，共60分．） 1．设集合{}|1A x x =>，集合{}2B a =+，若A B φ=，则实数a 的取值范围是（）．A ．(,1]-∞-B ．(,1)-∞-C ．[1,)-+∞D ．[1,)+∞【答案】A【解析】本题主要考查集合的运算．因为{}|1A x x =>且AB 为空集，所以21a +≤，即1a -≤，所以当1a -≤时，满足A 与B 的交集为空集的条件．故选A ．2．已知为i 虚数单位，若复数1i()1i a z a -=∈+R 的虚部为3-，则||z =（）． A ．5B 13C ．23D 10【答案】C 【解析】因为1i (1i)(1i)1(1)i 111i 2222ia a a a a a z -----+-+====-+，所以132a+-=-，所以5a =，所以23i z =--，所以22(2)(3)13z -+- 故选C ．3．已知命题:p x ∀∈R ，12(2)0x -<，则命题p ⌝为（）． A ．0x ∃∈R ，120(2)0x ->B ．x ∀∈R ，12(1)0x -> C ．x ∀∈R ，12(1)0x -≥D ．0x ∃∈R ，120(2)0x -≥【答案】C【解析】解：因为原命题为全称命题，所以原命题的否定是特称命题，即命题p x ⌝∀∈R ，20x >，的否定是：:p x ∃∈R ，20x ≤．故选C ．4．执行如图所示的算法框图，则输出的S 值是（）．是否S=4i=1i=9S=22Si =i +1输出S结束开始A ．1-B ．23C ．32D ．4 【答案】D【解析】i 1=，1S =-；i 2=，23S =；i 3=，32S =； i 4=，4S =；i 5=，1S =-；；i 8=，4S =；i 9=，结束循环，输出S 的值是4．故选D ．5．设55log 4log 2a =-，2ln ln33b =+，1lg5210c =，则a ，b ，c 的大小关系为（）．A ．a b c <<B ．b c a <<C ．c a b <<D ．b a c <<【答案】A 【解析】解：∵13log 20a =<，112211log log 132b =>=，0.30110122c ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭，∴a c b <<．故选A ．6．若函数()f x 满足1(1)()2f x f x +=，则()f x 的解析式在下列四式中只有可能是（）． A ．2x B ．12x +C ．2x -D ．12log x【答案】C【解析】本题主要考查函数的解析式．由已知该函数具有性质1(1)()2f x f x +=，将此运用到四个选项中： A 项，1(1)2x f x ++=，1()24xf x =，不符合题意，故A 项错误； B 项，3(1)2f x x +=+，11()224x f x =+，不符合题意，故B 项错误；C 项，(1)11(1)22()22x x f x f x -+-+==⨯=，符合题意，故C 项正确； D 项，12(1)log (1)f x x +=+，112211()log log 22f x x x ==D 项错误．故选C ．7．函数e x y x =和图象是（）．A ．xyOB ．yOx C ．yOx D ．yOx【答案】C 【解析】8．在区间[0,2]上随机取两个数x ，y ，则[0,2]xy ∈的概率是（）． A ．1ln 22- B ．32ln24- C ．1ln 22+ D ．12ln22+ 【答案】C【解析】本题主要考查微积分的基本定理和几何概型．由题意可将所求概率转化为图中阴影部分面积和正方形面积之比，故所求概率212222(ln )2d 11ln 2442x x S x P S +++====⎰阴影正方形．【注意有文字】故选C ．xy O412343219．设实数x ，y 满足22010210x y x y x y +-⎧⎪-+⎨⎪--⎩≤≥≤，则11y x --的最小值是（）．A ．5-B ．12-C ．12D ．5【答案】B【解析】(1,1)xyOy=x+44000x y x y -+⎧⎪⎨⎪⎩≥≤≥所表示的区域如图所示 11y z x -=-表示区域中的点到点(1,1)的斜率，故原点到点(1,1)的斜率最大．故选B ．10．若将函数π()2sin 23f x x ⎛⎫=+ ⎪⎝⎭的图象向右平移ϕ个单位，所得图象最新y 轴对称，则ϕ的最小正值是（）． A ．5π12B ．π3C ．2π3D ．5π6-【答案】A【解析】把该函数的图象右移ϕ个单位，所得图象对应的函数解析式为：π2sin 223y x ϕ⎛⎫=+- ⎪⎝⎭，又所得图象最新y 轴对称，则 π3π22πk ϕ-=+，k ∈Z ， ∴当1k =-时，ϕ有最小正值是 5π12．故选A ．11．设函数266,0()34,0x x x f x x x ⎧-+=⎨+<⎩≥，若互不相等的实数1x ，2x ，3x 满足123()()()f x f x f x ==，则123x x x ++的取值范围是（）．A ．11,63⎛⎤⎥⎝⎦B ．2026,33⎛⎫ ⎪⎝⎭C ．2026,33⎛⎤ ⎥⎝⎦D ．11,63⎛⎫ ⎪⎝⎭【答案】D【解析】解：函数266,0()34,0x x x f x x x ⎧-+=⎨+<⎩≥的图象，如图，xO y65432143211234564321不妨设123x x x <<，则2x ，3x 最新直线3x =对称，故236x x +=，且1x 满足1703x -<<；则123x x x ++的取值范围是：12376063x x x -+<++<+，即12311,63x x x ⎛⎫++∈ ⎪⎝⎭．故选D ．12．已知定义在(0,)+∞上的函数()f x ，满足（1）()0f x >；（2）()()2()f x f x f x '<<（其中()f x '是()f x 是导函数，e 是自然对数的底数），则(1)(2)f f 的范围为（）． A ．11,2e e 2⎛⎫⎪⎝⎭B ．211,e e ⎛⎫ ⎪⎝⎭C ．(e,2e)D ．3(e,e )【答案】B【解析】构造函数()()e x f x g x =，(0,)x ∈+∞，则2()e ()e ()()()(e )e x x x xfx f x f x f x g x ''--'==，由已知()()f x f x '<得()0g x '>在(0,)+∞上恒成立，则函数()g x 在(0,)+∞上递增，所以(1)(2)g g <，即2(1)(2)e ef f <，又因为()0f x >，所以根据2(1)(2)e ef f <有2(1)e (2)e f f <，即(1)1(2)e f f <，再构造函数2()()(e )x f x h x =，(0,)x ∈+∞，2242()(e )()2(e )()2()()(e )(e )x x x x fx f x f x f x g x ''⋅-'==，由已知()2()f x f x '<，所以()0h x '<在(0,)+∞，则函数()h x 在区间(0,)+∞上单调递减，所以(1)(2)h h >，即24(1)(2)e ef f <，又因为()0f x >，所以根据24(1)(2)e e f f <有24(1)e (2)e f f <，即2(1)1(2)e f f <，所以21(1)1e (2)e f f <<．故选B ．二、填空题（本大题共4小题，每小题5分，共20分）13．计算11130.7536170.027*********-⎛⎫+--= ⎪⎝⎭__________．【答案】31【解析】原式1133316412590.33625697295-⎛⎫⨯- ⎪-⎝⎭⎛⎫=-+-+- ⎪⎝⎭3109913643553=-+-+- 31=．14．已知423401234(23)x a a x a x a x a x =++++，则2202413()()a a a a a ++-+=__________．【答案】1【解析】令1x =，得401234(23)a a a a a =++++；令1x =-，得401234(23)a a a a a -=-+-+；两式相加得22024130123402413()()()()a a a a a a a a a a a a a a a ++-+=++++⋅++--444(23)(23)(1)1=⋅-=-=．15．一个类似杨辉三角形的数阵：则第九行的第二个数为__________．18221891177115653139【答案】见解析【解析】解：观察首尾两数都是1，3，5，7，可以知道第n 行的首尾两数均为21n -，设第(2)n n ≥行的第2个数构成数列{}n a ，则有323a a -=，435a a -=，547a a -=，，123n n a a n --=-，相加得232335(23)(2)(2)2n n a a n n n n +--=+++-=⨯-=-23(2)23n a n n n n =+-=-+．因此，本题正确答案是：223n n -+．16．某班班会，准备从包括甲、乙两人的七名同学中选派4名学生发言，要求甲、乙两人中至少有1人参加，则甲、乙都被选中且发言时不相邻的概率为__________．【答案】见解析【解析】解：22534475A A 1201A A 9401206==--．三、解答题：（共70分）17．（10分）已知函数2π()3cos sin 02222f x x x x ϕϕϕϕ⎛⎫⎛⎫⎛⎫⎛⎫=++++<< ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭的图像经过点π,13⎛⎫ ⎪⎝⎭．（1）求()f x ．（2）在ABC △中，A 、B 、C 的对边为a 、b 、c ，5a =25ABC S =△，角C 为锐角且π72126C f ⎛⎫-= ⎪⎝⎭，求C 边长．【答案】见解析．【解析】解：（1）∵2()3cos sin 222f x x x x ϕϕϕ⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭31cos(2))2x x ϕϕ-+=++ 311)cos(2)22x x ϕϕ=+-++ π1sin 262x ϕ⎛⎫=+-+ ⎪⎝⎭，∵图象经过点π,13⎛⎫⎪⎝⎭，∴ππ1sin 21362ϕ⎛⎫⋅+-+= ⎪⎝⎭，即π1sin 22ϕ⎛⎫+= ⎪⎝⎭，即1cos 2ϕ=，∵π02ϕ<<，∴π3ϕ=， ∴π1()sin 262f x x ⎛⎫=++ ⎪⎝⎭．（2）∵π17sin 21226C f C ⎛⎫-=+= ⎪⎝⎭，∴2sin 3C =， ∴45cos 19C =-， ∵112sin 525223ABC S ab C b ==⋅=△，∴6b =，∴22252cos 53625621c a b ab C =+-=+-=， ∴21c =18．（12分）已知ABC △中，D 是BC 上的点，AD 平分BAC ∠，ABD △面积是ADC △面积的2倍．（1）求sin sin BC∠∠．（2）若1AD =，2DC =BD 和AC 的长．【答案】见解析．【解析】（1）1sin 2ABD S AB AD BAD =⋅△∠，1sin 2ADC S AC AD CAD =⋅△∠，因为2ABD ADC S S =△△，BAD CAD =∠∠，所以2AB AC =，在ABC △中，由正弦定理得：sin sin AC AB B C =∠∠，所以sin 1sin 2B AC C AB ==∠∠．（2）设ADB θ=∠，则πADC θ=-∠．由（1）知12AC b AB c ==，所以2c b =①，由2CD =2BD = 在ACD △中，由余弦定理，2222121π)b θ=+-⨯-⎝⎭，即2322b θ=+②，在ABD △中，由余弦定理，21222c θ=+-，即2322c θ=-③，由①②③得1b =，故1AC =．19．（12分）私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：年龄（岁） [15,25)[25,35)[35,45)[45,55)[55,65)[65,75]频数 510151055赞成人数46 9 6 34（1（2）若从年龄在[15,25)，[25,35)的被调查者中各随机选取2人进行追踪调查，求恰有2人不赞成的概率．（3）在(2)在条件下，再记选中的4人中不．赞成．．“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．频率组距0.010.020.03【答案】见解析．【解析】（1）由表知年龄在[15,25)内的有5人，不赞成的有1人，年龄在[25,35) 内的有10人，不赞成的有4人，恰有2人不赞成的概率为：11122464442222510510C C C C C 424666622(2)C C C C 1025104522575P ξ==⋅+⋅=⋅+⋅==．（2） ξ的所有可能取值为：0，1，2，3，226422510C C 4515(0)C C 22575P ξ==⋅==， 21112646442222510510C C C C C 41562410234(1)C C C C 1045104522575P ξ⋅==⋅+⋅=⋅+⋅==， 124422510C C 46124(3)C C 104522575P ξ==⋅=⋅==，所以ξ的分布列是： ξ0 1 2 3 p1575 3475 2275 475 所以ξ的数学期望65E ξ=．20．（12分）已知在直角坐标系xOy 中，圆C 参数方程为32cos 42sin x y θθ=+⎧⎨=-+⎩（θ为参数）．（1）以原点为极点、x 轴正半轴为极轴建立极坐标系，求圆C 的极坐标方程．（2）已知(2,0)A -，(0,2)B ，圆C 上任意一点(,)M x y ，求ABM △面积的最大值．【答案】见解析．【解析】（1）圆C 的参数方程为32cos 42sin x y θθ=+⎧⎨=-+⎩（θ为参数），所以普通方程为22(3)(4)4x y -++=，所以圆C 的及坐标方程为26cos 8sin 210ρρθρθ-++=．（2）点(,)M x y 到直线:20AB x y -+=的距离2d =，ABM △的面积1π|||2cos 2sin 9|22924S AB d θθθ⎛⎫=⨯⨯=-+=-+ ⎪⎝⎭，所以ABM △的面积的最大值为922+21．（12分）已知函数()|3|f x x =+，()2|11|g x m x =--，若2()(4)f x g x +≥恒成立，实数m 的最大值为t ．（1）求实数t ．（2）已知实数x 、y 、z 满足22236(0)x y x a a 2++=>，且x y z ++的最大值是20t ，求a 的值．【答案】见解析．【解析】解：（1）根据题意可得(4)2|411|2|7|g x m x m x +=-+-=--，若2()(4)f x g x +≥恒成立， ∴2|3|2|7|x m x +--≥，即2(|3||7|)m x x ++-≤．而由绝对值三角不等式可得2(|3||7|)2|(3)(7)|20x x x x ++-+--=≥， ∴20m ≤，故m 的最大值20t =．（2）∵实数x 、y 、z 满足222236(0)x y z a a ++=>，由柯西不等式可得2222222[(2)(3)(6)]236236236x y z x y z ⎡⎤++⋅++⎢⎥⎢⎥⎣⎦≥， ∴21)a x y z ⨯++≥(， ∴x y z a ++再根据x y z ++的最大值是120t =， 1a ，∴1a =．22．（12分）已知二次函数2()1f x x ax m =+++，最新x 的不等式2()(21)1f x m x m <-+-的解集为(,1)m m +，(0)m ≠，设()()1f xg x x =-．（1）求a 的值．（2）()k k ∈R 如何取值时，函数()()ln(1)x g x k x ϕ=--存在极值点，并求出极值点．（3）若1m =，且0x >，求证：[(1)](1)22(*)n n n g x g x x +-+-∈N ≥．【答案】见解析．【解析】（1）因为最新x 的不等式2()(21)1f x m x m <-+-的解集为(,1)m m +，即不等式22(12)0x a m x m m ++-++<的解集为(,1)m m +，所以22(12)()(1)x a m x m m x m x m ++-++=---，所以222(12)(21)(1)x a m x m m x m x m m ++-++=-+++，所以12(21)a m m +-=-+，所以2a =-．（2）由（1）得2()21()(1)111f x x x m mg x x x x x -++===-+---，所以()()ln(1)(1)(1)1m x g x k x x k x x ϕ=--=-+---的定义域为(1,)+∞，所以222(2)1()1(1)1(1)m k x k x k m x x x x ϕ-++-+'=--=---，方程2(2)10x k x k m -++-+=（*）的判别式22(2)4(1)4k k m k m ∆=+---=+．①当0m >时，0∆>，方程（*）的两个实根为21241k k m x +-+=<，22241k k m x +++=>，则2(1,)x x ∈时，()0x ϕ'<；2(,)x x ∈+∞时，()0x ϕ'>，所以函数()x ϕ在2(1,)x 上单调递减，在2(,)x +∞上单调递增，所以函数()x ϕ有极小值点2x ． ②当0m <时，由0∆>，得2k m <--2k m >-2k m <-，则21241k k m x +-+<，22241k k m x +++=>，故(1,)x ∈+∞时，()0x ϕ'>，所以函数()x ϕ在(1,)+∞上单调递增．所以函数()x ϕ没有极值点，若2k m >-21241k k m x +-+=>，22241k k m x +++=>，则1(1,)x x ∈时，()0x ϕ'>；12(,)x x x ∈时，()0x ϕ'<；2(,)x x ∈+∞时，()0x ϕ'>，所以函数()x ϕ在1(1,)x 上单调递增，在12(,)x x 上单调递减，在2(,)x +∞上单调递增，所以函数()x ϕ有极小值点2x ，有极大值点1x ，综上所述，当0m >时，k 取任意实数，函数()x ϕ有极小值点2x ，当0m <时，2k m >-()x ϕ有极小值点2x ，有极大值点1x ，（其中2124k k m x +-+=2224k k m x +++=．（3）因为1m =，所以1()(1)1g x x x =-+-，所以1122122412211C C C C C n n n n n n n n n n n n x x x x x x x x------=+⋅+⋅=+++，令122412C C C n n n n n n n T x x x----=+++，则122412122412C C C C C C nn n n n n n n n n n n n n n T x x x x x x---------=+++=+++，因为0x >，所以1222441221212C ()C ()C ()2(C C C )n n n n n n n nn n n n n n T x x x x x x --------=++++++=+++12102(C C C +C C C C )2(22)n n n n n n n n n n n -=+++++-=-，所以22n T -≥，即[(1)](1)22n n n g x g x +-+-≥．。

陕西省2020年高三上学期期中数学试卷(理科)(I)卷

陕西省2020年高三上学期期中数学试卷（理科）（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）已知sinθ+cosθ=2sinα，sin2θ=2sin2β，则（）A . cosβ=2cosαB . cos2β=2cos2αC . cos2β+2cos2α=0D . cos2β=2cos2α2. （2分）(2020·汕头模拟) 已知集合A＝{x|1≤x≤4}，B＝{x| 0}，则A∩B＝（）A . {x|2≤x≤4}B . {x|2＜x≤4}C . {x|1≤x≤2}D . {x|1≤x＜2}3. （2分） (2019高一下·绍兴期末) 已知两个非零向量 , 满足 ,则（）A .B .C .D .4. （2分）tan19°+tan41°+ tan19°tan41°的值为（）A .B . 1C .D . ﹣5. （2分）下列命题中，真命题的个数有（）①；②；③“”是“”的充要条件；④是奇函数.A . 1个B . 2个C . 3个D . 4个6. （2分）已知中，内角所对边长分别为，若，则的面积等于（）A .B .C .D .7. （2分） (2017高三上·山西开学考) 函数f（x）=Asin（ωx+φ）的部分图象如图所示，若，且f（x1）=f（x2）（x1≠x2），则f（x1+x2）=（）A . 1B .C .D .8. （2分）(2019·淮南模拟) 函数的大致图象为A .B .C .D .9. （2分） (2017高一下·伊春期末) 方程根的个数为（）A . 0B . 1C . 2D . 310. （2分）已知函数f（x）=x3+bx的图象在点A（1，f（1））处的切线的斜率为4，则函数g（x）= sin2x+bcos2x 的最大值是（）A . 1B . 2C .D .11. （2分） (2020高三上·会昌月考) 已知实数满足，则对任意的正实数，的最小值为（）A .B . 8C .D . 1812. （2分）已知函数f(x)=sin(x+)cos(x+)，给出下列结论正确的是（）A . f（x）的最小正周期是2πB . f（x）的的一条对称轴是x=C . f（x）的的一条对称中心是（， 0）D . f（x-）是奇函数二、填空题 (共4题；共4分)13. （1分）定积分________14. （1分） (2016高一上·如东期中) 已知a=0.42 ， b=20.4 ， c=log0.42，则a，b，c的大小关系为________．（用“＜”连结）15. （1分）在△ABC中，若sin2A=sin2B，则该三角形是________ 三角形．16. （1分） (2018高一上·普兰期中) 若命题“ ”是真命题，则实数a的取值范围是 ________三、解答题 (共7题；共55分)17. （10分）已知函数f（x）=1﹣cos2（x﹣），g（x）=1+ sin2x．（1）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值；（2）求函数h（x）=f（x）+g（x）的单调递增区间．18. （5分）(2017·四川模拟) 如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．（Ⅰ）求证：AM⊥平面EBC；（Ⅱ）求二面角A﹣EB﹣C的大小．19. （5分）(2020·日照模拟) 在① 面积，② 这两个条件中任选一个，补充在下面问题中，求 .如图，在平面四边形中，，，，，求 .20. （10分） (2018高二上·思南月考) 已知椭圆C：＝1(a＞b＞0)的离心率为，短轴的一个端点到右焦点的距离为 .（1）求椭圆C的方程．（2）设斜率为1的直线经过左焦点与椭圆C交于A,B两点，求 .21. （5分） (2015高二下·霍邱期中) 已知函数f（x）=xlnx﹣x，求函数f（x）的单调区间和极值．22. （10分）(2020·长春模拟) 以直角坐标系的原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的参数方程为（t为参数）.（1）求曲线C的参数方程与直线l的普通方程；（2）设点过P为曲线C上的动点，点M和点N为直线l上的点，且满足为等边三角形，求边长的取值范围.23. （10分）已知f（x）=|x﹣1|+|x﹣a|（a∈R），g（x）=x+ +4（x＜0）（1）若a=3，求不等式f（x）≥4的解集；（2）对∀x1∈R，∀x2∈（﹣∞，0）有f（x1）≥g（x2）恒成立，求实数a的取值范围．。

陕西省西安中学高三(上)期中数学试卷(文科)

A．1：1： 3
B．2：2： 3
C．1：1：2
D．1：1：4
7．（5 分）下列函数中，最小正周期为 π 的奇函数是（）
휋 A．y＝sin（2x + 2）
휋 B．y＝cos（2x + 2）
C．y＝sin2x+cos2x
D．y＝sinx+cosx
1 8．（5 分）若 tanθ = 3，则 cos2θ＝（）
→
→
→→
4．（5 分）（2014•北京）已知向量a = （2，4），b = （﹣1，1），则 2a ‒ b = （）
A．（5，7）
B．（5，9）
C．（3，7）
D．（3，9）
【考点】9J：平面向量的坐标运算．【专题】5A：平面向量及应用．
【分析】直接利用平面向量的数乘及坐标减法运算得答案．
→
→
【解答】解：由a = （2，4），b = （﹣1，1），得：
휋
1
9．（5 分）（2016•新课标Ⅰ）将函数 y＝2sin（2x + 6）的图象向右平移4个周期后，所得图象对应的函数
5
2021-2021 学年陕西省西安中学高三（上）期中数学试卷（文科）
参考答案与试题解析
一、选择题：本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．（5 分）（2007•全国卷Ⅱ）cos330°＝（
1 A．2
1 B． - 2
） 3
C． 2
→→
→→
【解答】解：①若|a|＝|b|，但两向量方向不一定相同，则a = b不一定成立，故错误；
→→
②若 A，B，C，D 是不共线的四点，则AB = DC⇔AB＝DC 且 AB∥DC⇔四边形 ABCD 为平行四边形，

陕西省长安区高三数学上学期期中考试试题理新人教A版

陕西省长安区高三数学上学期期中考试试题理新人教A 版高三数学试题（理科）一、选择题：本大题共14题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若集合A=}40{，,B=}2{2a ，，则“2=a ”是“}4{=B A ”的（） A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既不充分也不必要条件2．已知sin sin cos ,cos sin cos x x αααα=+=，则cos2x =（）A.0B. 1C. -1D.不确定 3．已知函数22)(23+-=x x x f 则下列区间必存在零点的是（） A. (23,2--) B. ()1,23--C. (21,1--) D. (0,21-) 4．已知变量,x y 满足约束条件211y x y x y ≤⎧⎪+≥⎨⎪-≤⎩，则3z x y =+的最大值为（）A ．12B ．11C ．3D ．-1 5．等差数列{}n a 中，若75913a a =，则139S S = （）A ．913B ．139C ．1D ．26．在⊿ABC 中，若sin2A=sin2B,则⊿ABC 的形状是（）A ．等腰三角形B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形7．设l ，m ，n 表示三条直线，α，β，γ表示三个平面，给出下列四个命题： ①若l ⊥α，m ⊥α，则l ∥m ；②若m ⊂β，n 是l 在β内的射影，m ⊥l ，则m ⊥n ； ③若m ⊂α，m ∥n ，则n ∥α；④若α⊥γ，β⊥γ，则α∥β. 其中真命题为（）A.①②B.①②③C.②③④D.①③④8．定义在R 上的奇函数()f x 满足：对任意[)12,0,x x ∈+∞，且12x x ≠，都有1212()[()()]0x x f x f x -->，则（）A ．(3)(2)(1)f f f <-<B ．(1)(2)(3)f f f <-<C ．(2)(1)(3)f f f -<<D ．(3)(1)(2)f f f <<-9．如图为一个几何体的三视图，主视图和左视图均为矩形，俯视图中曲线部分为半圆，尺寸如图，则该几何体的全面积为（） A.3236++π B.2422++π C.3258++πD.2432++π10．将数列{}13n -按“第n 组有n 个数”的规则分组如下：（1），（3，9），（27，81，243），…，则第10组中的第一个数是：（）A ．443 B ．453 C ．463D ．47311．已知函数=)(x f ⎩⎨⎧<-≥-0,10,sin x e x x x x ，若)()2(2a f a f >-，则实数a 取值范围是（）A. (1,-∞-)),2(+∞B. (1,2-)C. (2,1-)D.(2,-∞-)+∞,1( ) 12．已知0ω>，函数()sin()4f x x πω=+在(,)2ππ上单调递减。

陕西省西安市雁塔区名校2022-2023学年高三上学期期中理科数学试题及答案解析

陕西省西安市雁塔区名校2022-2023学年高三上学期期中理科数学试题及答案解析一､选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知全集U ＝{x ∈Z|0<x <8}，集合M ＝{2,3,5}，N ＝{x |x 2－8x ＋12＝0}，则集合{1,4,7}为()A.M ∩(∁U N )B.∁U (M ∩N )C.∁U (M ∪N )D.(∁U M )∩N2.已知复数z 的共轭复数为z ，若(1i)2i -=z （i 为虚数单位），则z =（）A.IB.－1＋iC.－1－iD.－i3.设0a 为单位向量，下列命题中：①若a 为平面内的某个向量，则0||a a a =；②若a 与0a 平行，则0||a a a =；③若a与0a 平行且||1a = ，则0a a =，假命题的个数是（）A.0B.1C.2D.34.历史上第一个研究圆锥曲线的是梅纳库莫斯(公元前375年—325年)，大约100年后，阿波罗尼奥更详尽、系统地研究了圆锥曲线，并且他还进一步研究了这些圆锥曲线的光学性质，比如：从抛物线的焦点发出的光线或声波在经过抛物线反射后，反射光线平行于抛物线的对称轴；反之，平行于抛物线对称轴的光线，经抛物线反射后，反射光线经过抛物线的焦点.设抛物线C ：2y x =，一束平行于抛物线对称轴的光线经过()5,2A ，被抛物线反射后，又射到抛物线C 上的Q 点，则Q 点的坐标为（）A.11,42⎛⎫- ⎪⎝⎭B.11,84⎛⎫- ⎪⎝⎭C.11,164⎛⎫- ⎪⎝⎭D.11,648⎛⎫- ⎪⎝⎭5.设n S 为等差数列{}n a 的前n 项和．若525S =，348a a +=，则{}n a 的公差为（）A.2- B.1- C.1D.26.已知3sin()cos cos()sin 5βαβαββ---=，α为第三象限角，则cos 4πα⎛⎫+=⎪⎝⎭（）A.10-B.7210-C.210D.72107.侏罗纪蜘蛛网是一种非常有规律的蜘蛛网，如图是由无数个正方形环绕而成的，且每一个正方形的四个顶点都恰好在它的外边最近一个正方形四条边的三等分点上，设外围第1个正方形的边长是m ，侏罗纪蜘蛛网的长度(蜘蛛网中正方形的周长之和)为S n ，则（）A.S n 无限大B.S n <3(3＋5)mC.S n ＝3(3＋5)mD.S n 可以取100m8.已知函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><是奇函数，且()f x 的最小正周期为π，将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为()g x ．若24g π⎛⎫= ⎪⎝⎭，则38f π⎛⎫= ⎪⎝⎭（）A.2- B.2- C.2D.29.双曲线22221(0,0)x y a b a b-=>>的左，右焦点分别是12,F F ，过1F 作倾斜角为30 的直线交双曲线的右支于点M ，若2MF 垂直于x 轴，则双曲线的离心率为（）A.2B.3C.2D.510.已知函数()3log ,03πcos ,393x x f x x x ⎧<<⎪=⎨-≤≤⎪⎩，若存在实数1x ，2x ，3x ，4x ，当1234x x x x <<<时，满足()()()()1234f x f x f x f x ===，则1234x x x x ⋅⋅⋅的取值范围是（）A.297,4⎛⎫ ⎪⎝⎭B.13521,4⎛⎫⎪⎝⎭C.[)27,30 D.13527,4⎛⎫⎪⎝⎭11.已知在三棱锥S ABC -中，AB BC ⊥，2AB BC ==，22SA SC ==，二面角B AC S --的大小为23π，则三棱锥S ABC -的外接球的表面积为（）A1249π B.1054π C.1059π D.1049π12.函数()f x 满足()()1,,2x e f x f x x x ⎡⎫=+∈+∞⎢⎣'⎪⎭，()1f e =-，若存在[]2,1a ∈-，使得31232f a a e m ⎛⎫-≤--- ⎪⎝⎭成立，则m 的取值A.2,13⎡⎤⎢⎥⎣⎦B.2,3⎡⎫+∞⎪⎢⎣⎭C.[)1,+∞ D.12,23⎡⎤⎢⎥⎣⎦第II 卷（非选择题共90分）二､填空题（本大题共4小题，每小题5分，共20分，把答案填在答题纸中相成的横线上.）13.已知向量()()()2,1,1,,20a b k a a b ==-⋅-=，则k =___________.14.若不等式组0220x y x y y x y a-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩表示的平面区域是一个三角形，，则a 的取值范围是_____．15.已知2(1)n a +的展开式中各项系数之和等于2516(5x +的展开式的常数项，而2(1)na +的展开式中系数最大的项等于54，则正数a 的值为__________.16.如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，,2FB ED AB ED FB ==∥，记三棱锥E ACD -，F ABC -，F ACE -的体积分别为123,,V V V ，则下列四个结论：①322V V =；②31V V =；③312V V V =+；④3123V V =.其中正确结论的序号为__________.（写出所有正确结论的序号）三､解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤17.已知ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，120C ∠=︒.（1）若2a b =，求tan A 的值；（2）若ACB ∠的平分线交AB 于点D ，且1CD =，求a b +的最小值；18.为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后，发布了《个人所得税专项附加扣除暂行办法》，明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用，并公布了相应的定额扣除标准，决定自2019年1月1日起施行，某机关为了调查内部职员对新个税方案的满意程度与年龄的关系，通过问卷调查，整理数据得如下2×2列联表：（1）根据列联表,能否有99%的把握认为满意程度与年龄有关?（2）为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分x （单位：分）给予相应的住房补贴y （单位：元）,现有两种补贴方案，方案甲：1000700y x =+;方案乙：3000,055600,5109000,10x y x x <≤⎧⎪=<≤⎨⎪>⎩.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“A 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈，求恰好抽到3名“A 类员工”的概率．附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d=+++参考数据：()20P K k ≥0.500400.250.150.100.050.0250.010k 0.4550.7081323 2.072 2.706 3.841 5.024 6.63540岁及以下40岁以上合计基本满意153045很满意251035合计40408019.已知在四棱锥P ABCD -中，底面ABCD 是边长为4的正方形，PAD 是正三角形，CD ⊥平面PAD ，,,,E F G O 分别是,,,PC BC PD AD 的中点．（Ⅰ）求证：PO ⊥平面ABCD ；（Ⅱ）求平面EFG 与平面ABCD 所成锐二面角的大小．20.如图，经过点()2,3P ，且中心在坐标原点，焦点在x 轴上的椭圆C 的离心率为12.（1）求椭圆C 的方程；（2）若椭圆C 的弦,PA PB 所在直线交x 轴于点,C D ，且PC PD =.求证：直线AB 的斜率为定值.21.已知函数()()ln R xf x a x a=∈+，曲线()y f x =在点()()1,1f 处的切线与直线10x y ++=垂直.（1）试比较20232022与20222023的大小，并说明理由；（2）若函数()()g x f x k =-有两个不同的零点12,x x ，证明：212e x x ⋅>.请考生在第22､23题中任选一题做答，如果多做，则按所做的第一题记分，并请考生务必将答题卡中对所选试题的题号进行涂写.选修4-4：坐标系与参数方程选讲.22.在直角坐标系中，以原点为极点，x 轴的非负半轴为极轴，以相同的长度单位建立极坐标系.已知曲线C 的极坐标方程为22124cos ρθ=-，直线l 的参数方程为2525535x y ⎧=-⎪⎪⎨⎪=+⎪⎩（t 为参数）（1）求曲线C 的参数方程与直线l 的普通方程；（2）设点P 为曲线C 上的动点，点M 和点N 为直线l 上的点，且5MN =,求PMN 面积的取值范围选修4-5不等式选讲.23.设函数()211f x x x =++-.（1）当[)0,x ∈+∞，总有()f x ax b ≤+，求a b +的最小值t ；（2）若正数,m n 满足33165m n t +=，求证；4m n +≤.答案解析一､选择题1.C 【解析】由N 中方程解得：x =2或x =6,即N ={2,6}，∵全集U ={x ∈Z |0<x <8}={1,2,3,4,5,6,7},M ={2,3,5}，∴M ∪N ={2,3,5,6}，则M ∩(∁U N )={1,2,3,4,5,7};∁U (M ∩N )={1,3,4,5,6,7};∁U (M ∪N )={1,4,7};(∁U M )∩N ={2,6}.2.C 【解析】由已知可得2i 2i (1i)22i 1i 1i (1i)(1+i)2z ⋅+-+====-+--，则1i z =--.3.D 【解析】向量是既有大小又有方向的量，a与0||a a 的模相同，但方向不一定相同，故①是假命题；若a 与0a u u r 平行，则a 与0a uu r 的方向有两种情况：一是同向，二是反向，反向时0||a a a=-，故②③也是假命题．综上所述，假命题的个数是3．4.D 【解析】设从点()5,2A 沿平行于抛物线对称轴的方向射出的直线与抛物线交于点P ，易知2P y =，将(),P P x y 代入抛物线方程得4P x =，即()4,2P ，设焦点为F ，则1,04F ⎛⎫ ⎪⎝⎭，设()2,Q Q Q y y ，由P ，F ，Q 三点共线，有22011444Q Q y y --=--，化简得281520Q Q y y --=，解得18Q y =-或2Q y =(舍)，即11,648Q ⎛⎫- ⎪⎝⎭.5.A 【解析】依题意，可得()15355522522a a a S +⨯===，解得35a =，又348a a +=，所以43a =，所以公差43352d a a =-=-=-.6.A 【解析】∵3sin()cos cos()sin 5βαβαββ---=，所以3sin()5βαβ--=，即3sin 5α=-，由α为第三象限角知，4cos 5α=-，∴22432cos cos cos sin sin (cos sin )()444225510πππααααα⎛⎫+=-=-=-+=- ⎪⎝⎭.7.B【解析】由题意可得，外围第2个正方形的边长为2212()()33m m +＝53m ；外围第3个正方形的边长为221525()()3333m m ⨯+⨯＝59m ；……外围第n 个正方形的边长为15()3n -m .所以蜘蛛网的长度S n ＝4m 1555[1()39]3n -+++⋯+＝4m ×51()3513--<4m ×1513-＝3(3＋5)m .8.C 【解析】∵函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><是奇函数，且其最小正周期为π，∴0,2ϕω==，则()sin 2f x A x =，得()sin g x A x =．又sin 244g A ππ⎛⎫== ⎪⎝⎭，所以2A =，故()2sin 2f x x =，∴332sin 284f ππ⎛⎫== ⎪⎝⎭.9.B【解析】由于2MF x ⊥轴，且M 在第一象限，设(,)M x y 所以将x c =代入双曲线的方程得2222(),0,b b y y y a a =>∴=即2(,)b M c a，在△12MF F 中，2212tan 302b MF a F F c︒==，即22323c a ac -=,解得3==c e a.10.D【解析】作出函数()f x 的图象如图所示，可以发现3132log log x x =，即3132log log x x -=，∴()3132312log log log 0x x x x +=⋅=，121x x ⋅=.由余弦函数的图象可知，()f x 在[]3,9上的图象关于直线6x =对称，∴3412x x +=，且393,2x ⎛⎫∈ ⎪⎝⎭，因此1234x x x x ⋅⋅⋅变形为()()()223333331212636g x x x x x x =-=-+=--+，∴当33x =时，()3min 27g x =；当392x =时，()3max 1354g x =.∴1234x x x x ⋅⋅⋅的取值范围是13527,4⎛⎫⎪⎝⎭.11.D【解析】如图，取AC 的中点D ，连接BD ，SD ，∵2AB BC ==，SA SC ==，∴,BD AC SD AC ⊥⊥，∴SDB ∠为二面角B AC S --的平面角，∴23BDS π∠=，∵AB ⊥BC ，2AB BC ==，∴AC =BD CD ==∵SA SC ==SD ==，过点D 作与平面ABC 垂直的直线，则球心O 在该直线上，设球的半径为R ，连接OB ，OS ，可得222OD R=-，在△OSD 中，∠ODS ＝6π，利用余弦定理可得222322R R=-+-，解得R 2＝269，所以其外接球的表面积为210449R ππ=.12.A 【解析】由题意设()()x f x g x e =，则()()1()xf x f xg x e x-'='=，∴()ln g x x c =+（c 为常数）．∵()1f e =-，∴(1)(1)1f g c e==-=，∴()()(1ln )x x f x g x e e x =⋅=-+，∴1()(ln 1)xf x e x x =+-'．令1()ln 1h x x x =+-，则22111()x h x x x x-=-=，故当112x <<时，()0,()h x h x <'单调递减；当1x >时，()0,()h x h x >'单调递增．∴()(1)0h x h ≥=，从而当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时，()0f x '≥，∴()f x 在区间1,2⎡⎫+∞⎪⎢⎣⎭上单调递增．设[]3()32,2,1a a a e a ϕ=---∈-，则2()333(1)(1)a a a a ϕ'=-=+-，故()a ϕ在(2,1)--上单调递增，在(1,1)-上单调递减，所以max ()(1)a e ϕϕ=-=-．∴不等式31232f a a e m ⎛⎫-≤--- ⎪⎝⎭等价于12(1)f e f m ⎛⎫-≤-= ⎪⎝⎭，∴1211122m m ⎧-≤⎪⎪⎨⎪-≥⎪⎩，解得213m ≤≤，故m 的取值范围为2[,1]3．选A ．二､填空题13.12【解析】()()()24,21,5,2a b k k -=--=-，由()20a a b ⋅-=，得()()2,15,20k ⋅-=，1020k ∴+-=，解得12k =.14.4013a a <≤≥或【解析】如图，联立022x y x y -=⎧⎨+=⎩解得A 22,33⎛⎫⎪⎝⎭当x+y=a 过B （1，0）时，a=1；当x+y=a 过A 22,33⎛⎫⎪⎝⎭时，a=43∴若不等式组0220x y x y y x y a-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩表示的平面区域是一个三角形，则0＜a≤1或a≥43.故答案为0＜a≤1或a≥43.15.【解析】2516(5x +展开式的通项为:51051025221551616C ()()C 5,05,Z 5rrrr r r r r T x x x r r -----+⋅⋅⋅⋅≤==⋅≤∈，令51002r-=，解得4r =，故展开式的常数项为165165⨯=．由题意可得216n =，故有4n =．由于224(1)(1)n a a +=+展开式的系数最大的项等于244C 54a =，23a ∴=，解得a =．由于0a >，所以a =16.③④【解析】设22AB ED FB ===，DB ==，则1114222323V =⨯⨯⨯⨯=，2112221323V =⨯⨯⨯⨯=，如图所示，连接BD 交AC 于点M ，连接EM 、FM ，∵ED ⊥平面ABCD ，BD ⊂平面ABCD ，∴ED BD ⊥，而FB∥ED，∴四边形EDBF 是直角梯形，则有FM ==，EM ==3EF ==，∴有FM EM ⊥，故13222EMFS==，因为ED ⊥平面ABCD ，AC ⊂平面ABCD ，所以ED AC ⊥，又因为ABCD 为正方形，所以BD AC ⊥，而,,ED BD D ED BD =⊂ 平面EDBF ，所以AC ⊥平面EDBF ，即AC ⊥平面EMF ，311322332EMFV SAC =⨯=⨯⨯=,所以312V V V =+，3123V V =.三､解答题17.解：（1）解法一由2a b =及正弦定理，知sin 2sin A B =，即()sin 2sin 60A A =︒-，sin sin s A A A -=∴，3tan 2A ∴=.解法二22222212cos 42272c a b ab C b b b b b ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭，c ∴=，2222222c os b c a A bc +-===∴sin A ==∴sin tan cos 32A A A ∴==.（2）ACD BCDABC SSS+= ，111sin 60sin 60sin120222b a ab ∴︒+︒=︒，a b ab ∴+=，即111a b+=，()1124a b t a b a b a b b a ⎛⎫=+=++=+⎝∴+≥ ⎪⎭，当且仅当2a b ==时等号成立，a b ∴+的最小值为4.18.解：（1）根据列联表可以求得2K 的观测值：()22802530101580K 11.429354540407⨯-⨯==≈⨯⨯⨯.∵11.429 6.635>.∴有99%的把握认为满意程度与年龄有关（2）据题意，该8名员工的贡献积分及按甲、乙两种方案所获补贴情况为：积分23677111212方案甲24003100520059005900870094009400方案乙30003000560056005600900090009000由表可知，“A 类员工”有5名.设从这8名员工中随机抽取4名进行面谈，恰好抽到3名“A 类员工”的概率为P .则315348C C P C =37=19.解：（Ⅰ）因为PAD 是正三角形，O 是AD 的中点，所以PO AD ⊥，又因为CD ⊥平面PAD ，PO ⊂平面PAD ，所以PO CD ⊥，AD CD D = ，,AD CD ⊂平面ABCD ，所以PO ⊥面ABCD ；（Ⅱ）如图，以O 点为原点分别以,,OA OG OP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，则(0,0,0),(2,0,0),(2,4,0),(2,4,0),(2,0,0),(0,4,0),(0,0,O A B C D G P --，(1,(E F --，(0,2,0),(1,2,EF EG =-=，设平面EFG 的法向量为(,,),m x y z =因为00m EF m EG ⎧⋅=⎨⋅=⎩，所以2020y x y -=⎧⎪⎨+=⎪⎩，令1z =，则m =，又平面ABCD 的法向量(0,0,1)n =，设平面EFG 与平面ABCD 所成锐二面角为θ，所以||1cos 2||||m n m n θ⋅===.所以平面EFG 与平面ABCD 所成锐二面角为3π.20.解：（1）由题意可知：焦点在x 轴上，设椭圆的标准方程为：22221(0)x ya b a b+=>>，由椭圆的离心率12c e a ==，即2a c =，22223b a c c =-=，将(2,3)P 代入椭圆方程：2249143c c+=，解得：24c =，216a ∴=，212b =，∴椭圆的标准方程为：2211612x y+=；（2）由题意可知：直线PA 有斜率，且0k ≠，设直线PA 方程为()32y k x -=-，1(A x ，1)y ，2(B x ，2)y ，∴222311612y kx k x y =-+⎧⎪⎨+=⎪⎩，整理得：()()222(34)823423480k x k k x k +-+--=-，()()()22228234(34)42348016210k k k k k ∆⎡⎤---+-->⇒+>⎡⎤⎣⎣=⎦⎦，故12k ≠-由韦达定理可知：()()211222412382324343k k k k x x k k ---+=⇒=++，由PC PD =得：0PC PD k k +=,故直线PB 方程为()32y k x -=--()22224+12343k k x k -=+，因此()212212244348,4343k kx xxx k k -+-==++所以()()()()222121212121212443443224148243AB k k k k x k x k x x y y k k x x x x x x k ⎛⎫- ⎪-- ⎪+-----+--⎝⎭=====---+因此12AB k =，为定值.21.解：（1）由题可知：2ln ()()x a x xf x x x a +-'=+，()()2111af a ++'=，而直线10x y ++=的斜率1k =-，所以有21(1)1(1)af a +'==+，解得：1a =-或0a =，又因为函数()f x 在1x =处有意义，所以1a ≠-，故0a =，所以()ln x f x x =，()21ln xf x x-'=，(0,e)x ∈时，()0f x '>，(e,)x ∈+∞时，()0f x '<，∴()f x 在(0,e)上单调递增，在(e,)+∞上单调递减，∴(2022)(2023)f f >，即ln2022ln202320222023>，即2023ln 20222022ln 2023>，即有20232022ln 2022ln 2023>，∴2023202220222023>.（2）不妨设120x x >>，∴有12()()0g x g x ==，化简得1122ln 0,ln 0,x kx x kx -=-=即1212ln ln ()x x k x x +=+，1212ln ln ()x x k x x -=-，要证212e x x ⋅>，即证12ln ln 2x x +>，即证12()2k x x +>，因为1212ln ln x x k x x -=-，∴即证：121212ln ln 2x x x x x x ->-+，即1112212122222()ln 1x x x x xx x x x x -->=++，设12x t x =，因为120x x >>，所以1t >，即证22ln 1t t t ->+(1t >)设22()ln 1t h t t t -=-+(1t >)，则22214(1)()0(1)(1)t h t t t t t '-=-=>++，所以函数()h t 在(1,)+∞上单调递增，所以()(1)0h t h >=，即22ln 01t t t -->+，即22ln 1t t t ->+，即212e x x ⋅>.选修4-4：坐标系与参数方程选讲.22.解：（1）由22124cos ρθ=-得：2224cos 12ρρθ-=，又因为222cos sin x y x y ρθρθρ=⎧⎪=⎨⎪+=⎩，即得2224()12x y x +-=，化简得：22143x y +=，故曲线C的参数方程为：2cos x y θθ=⎧⎪⎨=⎪⎩（θ为参数），由2525535x y ⎧=-⎪⎪⎨⎪=+⎪⎩，消参可得：280x y +-=，直线l 的普通方程为：280x y +-=.（2）设(2cos )P θθ，则点P 到直线280x y +-=的距离d ==当sin(16πθ+=时，d 有最小值455，当sin(16+=-πθ时，d 有最大值1255，而5MN =，所以12PMNS MN d =⋅∈.故PMNS∈选修4-5不等式选讲.23.解：（1）记()()()()3,112,01a x x g x f x ax a x x ⎧-≥⎪=-=⎨-+≤<⎪⎩，当3a >时，3010a ,a -<-<，此时()g x 在[)0,x ∈+∞单调递减，故()()max02g xg ==，则()b g x ≥恒成立，故2b ≥，此时5a b +>，当13a <<时，3010a ,a ->-<，此时()g x 在[)0,1x ∈单调递减，在[)1,x ∞∈+单调递增，此时()g x 无最大值，不符合题意，当3a =时，此时()g x 在[)0,1x ∈单调递减，在[)1,x ∞∈+时，()0g x =，此时()()max02g xg ==，则()b g x ≥恒成立，故2b ≥，此时5a b +≥，当1a <时，3010a ,a ->->，此时()g x 在[)0,x ∈+∞单调递增，此时()g x 无最大值，不符合题意，当1a =时，在[)01x ∈，时，()2g x =，当[)1,x ∞∈+，()g x 单调递增，此时()g x 无最大值，不符合题意，综上可知：5a b +≥，故a b +的最小值为5，即5t =，（2）由（1）知5t =，所以3316=165m n t +=，又()()()()2333316163m n m n m n mn m n mn m n ⎡⎤+=++-=⇒+-=+⎣⎦，由于0,0m n >>，所以22m n mn +⎛⎫≤ ⎪⎝⎭，因此()()()3232163m n mn m n m n m n =+⎛⎫ ⎝≤⎪⎭+-++，即()()()33331616444m n m n m n m n +++-≤⇒≤⇒+≤，当且仅当=2m n =时，取等号.。

陕西省2021版高三上学期期中数学试卷A卷

陕西省2021版高三上学期期中数学试卷A卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共16分)1. （1分） (2020高一上·上海期中) 满足的集合有________个.2. （1分） (2019高二上·昌平月考) 把命题“ ”的否定写在横线上________.3. （1分）已知角α的终边经过点P（1，2），则tanα=________．4. （2分） (2020高三上·浙江月考) 已知函数（其中是自然对数的底数），则________；若与的图象有两个不同的公共点，则实数的取值范围是________.5. （1分）设f（x）=3x+3x﹣8，用二分法求方程3x+3x﹣8=0在x∈（1，2）内近似解的过程中，计算得到f（1）＜0，f（1.5）＞0，f（1.25）＜0，则方程的根落在区间________6. （1分） (2016高一上·云龙期中) 设定义在R上的奇函数f（x）在（0，+∞）上为增函数，且f（2）=0，则不等式f（x）＜0的解集为________．7. （1分）已知函数f（x）=cos2x+2sinx，x∈[0，α]的值域为[1， ]，其中α＞0，则角α的取值范围是________．8. （1分） (2018高二上·桂林期中) 在中，，点在边上，，则 ________．9. （1分） (2016高一下·安徽期中) 已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为________．10. （1分） (2016高二下·佛山期末) 已知向量夹角为45°，且，则=________．11. （1分） (2017高二下·新余期末) 已知函数f（x）=alnx﹣ x2+bx存在极小值，且对于b的所有可能取值，f（x）的极小值恒大于0，则a的最小值为________．12. （1分） (2019高二上·邗江期中) 已知数列1， ,9是等比数列，数列1, 9是等差数列，则 =________．13. （1分） (2019高一下·诸暨期中) 数列的通项公式，其前项和为，则等于________．14. （2分） (2019高二下·诸暨期中) 经过原点且与曲线相切的切线方程为________；点是曲线上任意一点，则点到直线的最小距离为________.二、解答题 (共6题；共60分)15. （5分）(2017·浙江模拟) 已知函数f（x）=cosx﹣8cos4 ．（Ⅰ）求该函数的最小正周期；（Ⅱ）求函数y=f（2x﹣）在x∈[﹣， ]上的值域．16. （10分） (2016高二上·湖州期中) 已知条件p：x2+12x+20≤0，条件q：1﹣m＜x＜1+m（m＞0）．（1）求条件p中x的取值范围；（2）若￢p是q的必要不充分条件，求m的取值范围．17. （10分）(2017·成都模拟) 在△ABC中，内角A，B，C的对边分别为a，b，c，已知向量与平行．（1）求的值；（2）若bcosC+ccosB=1，△ABC周长为5，求b的长．18. （10分） (2020高一上·南昌月考) 已知二次函数，且对任意实数均有成立.（1）求解析式；（2）若函数在上的最小值为求实数的值.19. （10分）设函数f（x）=（x﹣a）lnx+b．（1）当a=0时，讨论函数f（x）在[ ，+∞）上的零点个数；（2）当a＞1且函数f（x）在（1，e）上有极小值时，求实数a的取值范围．20. （15分） (2019高三上·吴中月考) 已知数列满足： .（1）若，求的值；（2）设，求证：数列从第2项起成等比数列；（3）若数列成等差数列，且，试判断数列是否成等差数列？并证明你的结论.参考答案一、填空题 (共14题；共16分)答案：1-1、考点：解析：答案：2-1、考点：解析：答案：3-1、考点：解析：答案：4-1、考点：解析：答案：5-1、考点：解析：答案：6-1、考点：解析：答案：7-1、考点：解析：答案：8-1、考点：解析：答案：9-1、考点：解析：答案：10-1、考点：解析：答案：11-1、考点：解析：答案：12-1、考点：解析：答案：13-1、考点：解析：答案：14-1、考点：解析：二、解答题 (共6题；共60分)答案：15-1、考点：解析：答案：16-1、答案：16-2、考点：解析：答案：17-1、答案：17-2、考点：解析：答案：18-1、答案：18-2、考点：解析：答案：19-1、答案：19-2、考点：解析：答案：20-1、答案：20-2、答案：20-3、考点：解析：。

2022-2023学年陕西省宝鸡市汉中市部分校联考高三上学期期中考试数学试题及答案

宝鸡中学等2020级高三11月月考试题数学（理科）第Ⅰ卷（选择题共60分）一．选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.若集合{}|24xA x =<，{}|13B x x =∈-<<N ，则A B = （）A .{}|12x x -<<B .{}01，C .{}1D .{}|13x x -<<2.若,R a b ∈且0ab ≠，则“1ab<”是“a b <”的（）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知复数2534z i =+，则复数z 的共轭复数为（）A .3+4iB .34i-C .34i--D .34i-+4.已知函数1,(1)()(2)3,(1)x a x f x a x a x -⎧<=⎨-+≥⎩在R 上单调递减，则a 的取值范围是（）A ．()0,1B ．3,14⎡⎫⎪⎢⎣⎭C ．30,4⎛⎤ ⎥⎝⎦D ．3,24⎡⎫⎪⎢⎣⎭5.已知n S 为等比数列{}n a 的前n 项和，若536412,24,a a a a -=-=则44S a =（）A .15B .14-C .158D .158-6.已知n S 为等差数列{}n a 的前n 项和，37a a ，是方程28+0x x m -=的两根，则9S =（）A .36B .40C .72D .807.已知向量=2tan ,(1,1)a b θ=- （，)，且//a b ，则tan(4πθ-的值为（）A .2B ．3-C ．3D ．13-8．若ln 2ln 3lg 2lg 5,,23a b c =⋅==，则a ，b ，c 的大小关系为（）A .b c a<<B .a b c <<C .b a c <<D .a c b<<9.已知π1sin 63α⎛⎫-= ⎪⎝⎭，则2πcos 23α⎛⎫+= ⎪⎝⎭（）A ．79B ．79-CD．10.已知函数()()2sin 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，其图象相邻的最高点之间的距离为π，将函数()y f x =的图象向左平移12π个单位长度后得到函数()g x 的图象，且()g x 为奇函数，则（）A ．()f x 的图象关于点,06π⎛⎫⎪⎝⎭对称B ．()f x 的图象关于点,06π⎛⎫- ⎪⎝⎭对称C ．()f x 在,63ππ⎛⎫- ⎪⎝⎭上单调递增D ．()f x 在2,36ππ⎛⎫-- ⎪⎝⎭上单调递增11.已知0,0a b >>，2a b +=，则下列结论中不正确的（）Ab 的最大值是94B ．122++a b的最小值是C ．sin 2+<a b D ．ln 1+>b a 12.已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别是12,F F ,斜率为12的直线l 经过左焦点1F 且交C 于,A B 两点(点A 在第一象限),设12AFF ∆的内切圆半径为112,r BFF ∆的内切圆半径为2r ,若123r r =,则椭圆的离心率e 的值为（）.A ．13B．4C ．12D．5第Ⅱ卷（非选择题共90分）二.填空题（本题共4小题,每小题5分，满分20分,把答案填在答题卡中对应题号后的横线上）13.式子π5πtantan 4125π1tan12+-的值为14.已知数列{}n a 中，1111,21)n n n n a a a n a na ++==+-（,则通项公式n a =_______．15.已知函数()2ln f x x =，直线l 的方程为2y x =+，则函数()f x 上的任意一点P 到直线l 的距离的最小值为16.如图所示，在三棱锥B ACD -,33ABC ABD DBC AB π∠=∠=∠==，2BC BD ==,则三棱锥B ACD -的外接球的表面积为三.解答题（本大题共6小题，满分70分，解答须写出文字说明，证题过程或演算步骤）17.(本题满分12分)设正项数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,且12b =,2724421,7n n n S a a S T a =++=+.(1)求数列{}{},n n a b 的通项公式;(2)求数列{}n n a b ⋅的前n 项和n M .18.(本题满分12分)已知向量1(2sin ),(sin ,sin )2a x xb x x == ，函数()f x a b=⋅ （1）求函数()f x 的单调增区间；（2）若函数()y f x k =-在区间π11,π612⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，求实数k 的取值范围．19.(本题满分12分)在《九章算术》中将四个面都是直角三角形的四面体称为鳖臑.在如图所示的四面体ABCD 中，AB BCD ⊥平面，平面ABC ACD ⊥平面.（1）判断该四面体是否为鳖臑，并说明理由；（2）若点E 是棱AD 的中点，AE AB BC ==，求二面角B CE D --的余弦值.20.(本题满分12分)已知双曲线22221(0)x y a a a-=>的右焦点为(2,0)F ,过右焦点F 作斜率为正的直线l ,直线l 交双曲线的右支于,P Q 两点,分别交两条渐近线于,A B 两点,点,A P 在第一象限,O 为坐标原点.(1)求直线l 斜率的取值范围;(2)设,,OAP OBP OPQ ∆∆∆的面积分别是,,OAP OBP OPQ S S S ∆∆∆,求OPQ OAP OBPS S S ∆∆∆⋅的范围.21．(本题满分12分)已知函数21()2f x lnx ax =-．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分22.(本题满分10分)在直角坐标系xoy 中，直线l 的参数方程为1(5x tt y t =+⎧⎨=+⎩为参数）.以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为23=2+cos2ρθ.（1）求直线l 的普通方程和曲线C 的直角坐标方程；（2）求C 的上的动点到l 的距离取值范围.23.(本题满分10分)已知函数()123f x x x =---.（1）求不等式1()1)2f x x ≥-（的解集；（2）若函数()f x 的最大值为m ，且2(0,0)a b m a b +=>>，求21a b+最小值.宝鸡中学2020级高三11月月考参考答案数学（理科）一．选择题B D A C C A C B B C D B二．填空题13.14.21nn -15.2ln 2)-16.192π三．解答题17.解：（1）由题意知，22-1-122112211-1111=21,=212)=2244=2+2++4n n n n n n n n n n n n n n n n n n n n n a a a a n a a a a a a a a a a a S S a a a a -------++++≥-+---可得（两式相减，得整理得即（）（）=2（）因为0n a >，所以1n n a a --=2令211111,4=211n a a a S =++=，得所以数列{}n a 是以1为首项，2为公差的等差数列所以1=+1)21n a a n d n -=-（717427+=49,7=62,S a a a T ==所以（）又21=2,4,2nn b b b ==所以（2）因为{}=,n n n n nc a b c n M 的前项和为则1231232341=123252(21)22=123252(21)2nn n n n M c c c c n M n +++++=⨯+⨯+⨯++-⋅⨯+⨯+⨯++-⋅ 两式相减，得12311=12222222(21)2=6(23)2n n n n M n n ++-⨯+⨯+⨯++⋅----- 所以1=6(23)2n n M n ++-18.解：2()1=2sin (sin )sin 21cos 2si 1(2n cos sin 22211cos 222221=sin 2)62sin )(sin ,sin )2a b f x x x x xx x x x x x xx x x x x π⋅==+⋅-=+=+=-++-⋅+（令222,26263k x k k x k πππππππππ-+<-<+-+<<+解得所以函数()f x 的单调增区间为)63k x k k Z ππππ⎛⎫-+<+∈ ⎪⎝⎭，（（2）由函数()y f x k =-在区间π11,π612⎡⎤-⎢⎥⎣⎦上有且仅有两个零点.即1sin(226k x π-=-在区间π11,π612⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，直线1g()sin(226y k x x π=-=-与的图像上有且仅有两个交点当π11,π612x ⎡⎤∈-⎢⎥⎣⎦，10522663x ππππ-≤-≤=由（1）函数g()sin(26x x π=-在区间π,63π⎡⎤-⎢⎥⎣⎦上单调递增，-1g()sin(2)16x x π≤=-≤在区间π5,36π⎡⎤⎢⎥⎣⎦上单调递减，-1g()sin(216x x π≤=-≤在区间511612ππ⎡⎤⎢⎥⎣⎦，上单调递增，1g()sin(262x x π-≤=-≤-所以111122k k <-<-=-或，即131222k k <<=-或19.解（1）该四面体是鳖臑理由如下：,,,AB BCDAB BC AB BD ABC ABD ⊥∴⊥⊥∴∆∆ 平面均为直角三角形如图,过点B 作BP AC P⊥于点,=ABC ACD ABC ACD AC⊥ 平面平面平面平面,BP ACD BP CD∴⊥∴⊥平面又,,,.,AB BCD AB CDAB BP B CD ABC CD AC CD BC ACD BCD BP CD∴⊥∴⊥=∴⊥∴⊥⊥∴∆∆∴⊥ 平面又平面均为直角三角形,,ABC ABD ACD BCD ∴∆∆∆∆，均为直角三角形故该四面体为鳖臑6分（2）以C 为坐标原点，CD CB ，所在直线分别为轴建立如图所示的空间直角坐标系C xyz -，设2,4,2,AB AD BC BD CD =====则(000),(0,2,0),(0,2,2),C B A D E ∴，，(0,2,0),CE CB CD ∴=== ，设平面CDE 的法向量为(,,)m x u z =，00,00CE m y z CD m ⎧⋅=++=⎪⎨⋅==⎪⎪⎩⎩，取(0,1,1)m =- 设平面BCE 的法向量为(,,)n a b c =，00,200CE n b c b CB m ⎧⋅=++=⎪⎨=⎪⋅=⎪⎩⎩，取(1,0,n = 3cos ,3m n m n m n⋅∴==-由图知二面角B CE D --为钝二面角，所以二面角B CE D --的余弦值为3-20.解：由题意可知：双曲线的方程为22122x y -=设直线l 的方程为112220),(,),(,)ty x t P x y Q x y =->（由方程组2222x y ty x ⎧-=⎨=-⎩得22120(1)4200t y ty y y ∆>⎧-++=⇒⎨<⎩所以01t <<，直线l 的斜率取值范围()1+∞，6分（2）由（1）双曲线的渐近线方程为y x =±，则点11(,)P x y 到两条渐近线的距离12,d d 满足121d d ⋅=又由2y x ty x =⎧⎨=-⎩得22,11A A x y t t ==--，同理2y x ty x =-⎧⎨=-⎩得22,11B B x y t t ==++所以121212211122241OAP OBP S S OA d OB d OA OB d d d t ∆∆⋅====-由2222x y ty x ⎧-=⎨=-⎩得22122122014(1)420121t t t y ty y y t y y t ⎧⎪<<⎪-⎪-++=⇒+=⎨-⎪⎪=⎪-⎩12122121OPQ OFP OFP S S S OF y y y y t ∆∆∆=+=-=-=-所以OPQ OAP OBPs S S ∆∆∆=⋅因为01t <<，所以)OPQ OAP OBPs S S ∆∆∆∈⋅12分21．解：（1）()f x 的定义域为(0,)+∞，且21()ax f x x-'=，当0a ≤时，()0f x '>，此时()f x 在(0,)+∞上单调递增；当0a >时，由()0f x '>解得0x a <<，由()0f x '<解得x a >，此时()f x在(0,a上单调递增，在(,)a+∞上单调递减；综上，当0a ≤时，()f x 在(0,)+∞上单调递增；当0a >时，()f x在a上单调递增，在()a+∞上单调递减；（2）由（1）知，当0a ≤时，()f x 在(0,)+∞上单调递增，函数()f x 至多一个零点，不合题意；当0a >时，()f x在上单调递增，在)+∞上单调递减，则211()1)22maxf x f a lna==⋅⋅=-+（，当1ae≥时，1()()(1)02maxf x f aa==-+≤，函数()f x至多有一个零点，不合题意；当10ae<<时，1()()1)02maxf x f lnaa==-+>（，由于1∈，且211(1)11022f ln a a=-⋅⋅=-<，由零点存在性定理可知，()f x在上存在唯一零点，由于2a>，且222122222()()02f ln a lna a a a a a a=-⋅⋅=-<-=（由于)lnx x<，由零点存在性定理可知，()f x在)+∞上存在唯一零点；综上，实数a的取值范围为1(0,e．22.解：因为直线直线l的参数方程为1(5x tty t=+⎧⎨=+⎩为参数）消去参数得直线l的普通方程为40x y-+=因为曲线C的极坐标方程为23=2+cos2ρθ，即222+cos2=3ρρθ所以曲线C的直角坐标方程22222(+)+=3x y x y-，即22+=13yx.（3）曲线C的参数方程为cos(xyααα=⎧⎪⎨=⎪⎩为参数）设曲线C上的动点(cos)Mαα,则曲线C上的动点M到直线l的距离d==因为[]2sin)2,26πα-∈-（所以曲线C上的动点到直线l的距离的最大值和最小值分别故曲线C上的动点到直线l距离取值范围为23.解：（1）由已知得2,13()=34,1232,2x x f x x x x x ⎧⎪-<⎪⎪-≤≤⎨⎪⎪-+>⎪⎩当1x <时，12(1)2x x -≥-，无解当312x ≤≤时，17334(1)252x x x -≥-<≤，，当32x >时，1352(1),223x x x -+≥-<≤综上所述，不等式的解集为7553⎡⎤⎢⎥⎣⎦，（2）由（1）可知max 31()(22f x f m===120,0)2a b m a b +==>>（2121222()(2)2(41104()10418b aa b a b a b a bb a a b ∴+=++=+++=++≥+⨯=当且仅当===6b a a b a b =，即时，成立故21a b∴+的最小值为18。