工期优化(例题)ppt课件
网络计划技术-工期优化例题(施工组织设计课件)

图4.67计算工期为159天,与合同工期146天相比尚需压缩 13天,考虑选择因素,选择③-④工作,因为有充足的资 源,且缩短工期对质量无太大的影响。由原62天压缩为52 天,即得网络计划图4.68。
第四章 网络计划技术-工期优化
图4.68计算工期为149天,与合同工期146天相比尚需压缩 3天,考虑选择因素,选择①-③工作,因为关键线路上可 压缩时间工作只剩①-③工作。由原52天压缩为49天,即得 网络计划图4.69。
第四章 网络计划技术
ቤተ መጻሕፍቲ ባይዱ
第四章 网络计划技术-工期优化
【例】 已知某网络计划初始方案如图4.65所示。图中箭 杆上数据为工作正常作业时间,括号内数据为工作最短 作业时间,假定合同工期为146天。
第四章 网络计划技术-工期优化
假设③-④工作有充足的资源,且缩短时间对质量无太 大的影响,④-⑥缩短时间所需费用最省,且资源充足。 ①-③工作缩短时间的有利因素不如③-④与④-⑥。
☆ 第三步,关键工作①-③可缩短12天,③-④可缩短 10天,④-⑥可缩短7天。共计可缩短时间29天。 ☆ 第四步,选择关键工作,考虑选择因素,由于④⑥缩短时间所需费用最省,且资源充足。优先考虑压 缩其工作时间,由原52天压缩为45天,即得网络计划 图4.67。
第四章 网络计划技术-工期优化
第四章 网络计划技术-工期优化
第四章 网络计划技术-工期优化
第一步,根据工作正常时间计算各个节点的最早和最迟时 间,并找出关键工作及关键线路。计算结果如图4.66所示。 图中①→③→④→⑥为关键线路。
第四章 网络计划技术-工期优化
☆ 第二步,计算需缩短的工期。根据图4.67计算工期 为166天,合同工期为146天,需要缩短时间为20天。
工期优化

定义:工期优化是指网络计划的计算工期不满 足要求工期时,需要通过压缩关键工作 的持续时间以满足要求工期目标的过程。
注意:
1.不改变逻辑关系,压缩关键工作; 2.不能将关键工作压缩成非关键工作; 3.多条关键线路,各条关键线路要同时 压缩,并且压缩相同时间; 4.经济合理;
优化步骤:
1.确定初始计算工期和关键线路; 2.计算应缩短的工期时间ΔT ΔT=Tc-Tr 其中 Tc—网络计划的计算日期 Tr—合同要求的工期
示例:
②
0.5 0.75 6(2) 3.0
④
9(5)
1.5 6(4) 1.25
⑤
2.0
①
5(1)
2(1)
0.4
7(5)
0.9
⑦ ⑥
4(1)
6(3)
③
1.0
5(2)
要求工期Tr=20,计算工期Tc1=26,ΔT=Tc1-Tr =26-20=6
若将工作1-3压缩至最短持续时间,则关键线路改变
5 11 17
第三次压缩:
关键线路未改变,工期仍未满足,继续压缩,对工作1-2 与1-3同时压缩,因为1-3工作最多只能压缩一天,所以同时压 缩1天。
4
②
0.5
0.75 6(2) 3.0
10
④
9(5) 7(5)
1.5 6(4) 1.25
16
⑤
2.0 20
①
4(1)
2(1)
0.4 3(3)
⑦
0.9
③
3
1.0 5(2)
③
3
1.0
⑥
19
4(1)
5(2)
要求工期Tr=20,计算工期Tc=23
网络计划优化工期

4
2(1) 2
1
7
32
4
6
6(5)
3(2)
1
3
5
6(3)
3(2)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作③-⑤,压缩2天,成为4天;
参考答案:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
6
3(2)
4(2)
4
2(1) 2
1
7
32
4
6
6(5)
1
3
5
3(3)
3(2)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第二次:选择工作③-④和③-⑤,同时压缩1天,③- ④成为2天,③-⑤成为3天 ;
工期变为12天,关键工作没有变化。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8
6
3(2)
4(2)
4
2(1) 2
3
20(15)
4 2
3
10(8) 30(18)
2
1
3
40(20)
3 60(30)
1
4
50(30)
5
2 30(20)
8 6
50(25)
(4)选择关键工作压缩时间,并重新计算工期Tc′; 第一次:选择工作①-③ ,压缩10天,成为40天;
工期变为150天,①-②和②-③也变为关键工作。
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160
6
4(2)
3
5
3(2)
工期优化(例题)

1
10 10
2
3 20(15)
2
3
40(20) 40 40
3 30(30)
70 70
5
8 50(25)
6 120 120
1 30(30)
4
70
70
2 30(20)
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 选择关键工作压缩作业时间,并重新计算工期T 第四次:选择工作① 同时压缩10 10天 第四次:选择工作①-③和②-③,同时压缩10天, 成为30 30天 成为20 20天 ①-③成为30天, ②-③ 成为20天;
4 2(1) 7 6(5)
2 6
2
8 3(2) 2 3(2) 1 4(3)
9 9
4
0 0
1
3
6 4(2) 3 3(2)
13 13
6
6 6
5
10 10
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 选择关键工作压缩作业时间,并重新计算工期T 第二次:选择工作③ 同时压缩1 第二次:选择工作③-④和③-⑤,同时压缩1天,③ 成为2 成为3 -④成为2天,③-⑤成为3天 ; 工期变为12 12天 关键工作没有变化。 工期变为12天,关键工作没有变化。
6 10
×
1
12
4
4 4
7 9
6 2 6
5
2
× 5
2
3
10
× 5
8
11
6
12
7
× 7
× 2
× 2
例题2 例题
请用关键节点法判断关键线路: 请用关键节点法判断关键线路:
流程优化ppt

技术咨询 销售部 建立合作 记录存档
流程优化的内容
流程优化涉及到工期优化、工艺优化、成本优化、 技术优化等优化指标。
根据需要,有的流程优化是对单个指标的优化, 有的流程优化是对多个指标的优化。对于一个特 定的流程,往往是以某个指标的优化为主,综合 考虑其他指标,如果片面地强调某一指标的优化, 可能会带来其他的指标的下降。因此,流程的优 化应在综合考虑各项指标的基础上,抓住主要矛 盾,突出重点指标的优化,综合权衡,以达到整 体优化的目的。
答案2:
①买电器元件
②焊底座 ③组装
④调试
⑤
做灯罩
通过分析各个环节之间的关系,在人手(2人)足够的情况 下,将串行环节改为并行环节,进行工期优化,周期变缩短 7小时。
综合案例;饮水设备公司加盟流程 图
煮 饭30 分 烧菜40分钟 吃饭20分钟
看报纸10分钟
还可以这么安排:
洗衣服(1小时)
烧菜(40分钟)
吃 饭
(20
煮饭(30分钟)
分 钟)
看报纸 (10分钟)
总结:把串行时序改为并行时序,从而节 约时间,提高经济效益的流程,把它称为 工期优化。
案例:
假设制作一只台灯的工序和所需时间如下
图:
①买电器元件
②焊底座 ③做灯罩 ④组装
⑤调试பைடு நூலகம்
⑥
2小时
2小时
4小时 2小时 1小时
这一流程的工期是否可以缩短?可以怎样 改进?改进之后可以带开什么问题?
答案1:
①买电器元件
② 组装
③调试
④
焊底座
做灯罩
通过分析各个环节之间的关系,在人手(3人)足够 的情况下,将串行环节改为并行环节,进行工期优化, 周期缩短7小时。
工期优化做法PPT

坚强保障
一次成优
3 装饰装修工程--塔吊、施工电梯拆除
沈阳腾越建筑工程有限公司
匠心引领 精益求精
吊篮外立面收口施工
坚强保障
一次成优
3 装饰装修工程--外立面收口施工
1.提前与安监站等沟通 吊篮安装、检测、验收、
使用、拆除手续,施工
人员提前进场布置,确 保安装人员具备特种作 业证件等要求。
沈阳腾越建筑工程有限公司
内墙抹灰工程插入
砌体结构施工至6层 时,抹灰工程开始 插入施工,此项穿 插应项目实际情况 需考虑砌体工程的 工艺间歇及分段主 体验收事宜。
坚强保障
一次成优
沈阳腾越建筑工程有限公司
匠心引领 精益求精
3 装饰装修工程--内墙抹灰工程
主体、砌体、抹灰工程同步施工
30F
.......... 12F 11F 10F 9F 8F 7F 6F 5F 4F 3F 2F 1F
沈阳腾越建筑工程有限公司
匠心引领 精益求精
3 装饰装修工程--室内装修工程
精装修一工序
烟道/吊洞 封堵
坚强保障
一次成优
防水施工
沉箱封板
工作面移 交
墙砖铺贴
墙面腻子
沈阳腾越建筑工程有限公司
匠心引领 精益求精
3 装饰装修工程--室内装修工程
精装修二工序 砂浆地坪 地砖铺贴
坚强保障
一次成优
墙面打磨 及油漆
坚强保障
一次成优
主体结构标准层工期
为4天/层(东北天气气候 即可满足),根据项目实 际情况对施工人数及人均 面积合理分配,悬挑层增 加2天,共五挑整体工期 增加10天。
沈阳腾越建筑工程有限公司
匠心引领 精益求精
工期优化例题
原网络计划计算工期为34d,需压缩8d。
8
5
2
10
5
6
12
6
Tc=34
1
11
4
10
3
18
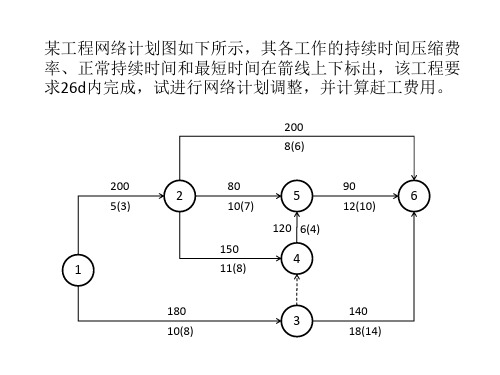
第一次计算: 将赶工费率最低的关键工作⑤→⑥缩短2d,④→⑤缩短2d, ②→④缩短2d,工期共缩短6d。关键线路变为两条:①→ ②→④→⑤→⑥,①→③→⑥。总工期为28d。 赶工费用为:150*2+120*2+90*2=720元
2
10
5
4
10
6
Tc=26
1
8
4
10
3
16
某工程网络计划图如下所示,其各工作的持续时间压缩费 率、正常持续时间和最短时间在箭线上下标出,该工程要 求26d内完成,试进行网络计划调整,并计算赶工费用。
200 8(6) 200 5(3) 80 10(7) 150 90 12(10)
2
5
120 6(4)
6
1
180 10(8)
11(8)
4
3
140 18(14)
第二次计算: 将关键工作②→④缩短1d,①→②缩短1d,同时③→⑥缩 短2d,工期共缩短2d。关键线路变为两条:①→②→④→ ⑤→⑥,①→③→⑥。总工期为26d。 赶工费用为:200*1+150*1+140*2=630元 总赶工费用为720+630=1350元
调整后的网络计划计算工期为26d。
8
4
工期成本优化

1
1320 5
1560 3
900(1530)
4
8(5)
5 T=12天
图4 第三次循环后网络图
第四次循环,从图4看出,关键线路有三条,同时压 缩3-5和4-5工作1天,直接费增加210+200=410元, 间接费减少165元,工程成本为9515元。压缩后的网络 图如图5。
950
2 1000(1160) 4 1200(1400)
所示。
费 用
总费用曲线
直接费曲线 间接费曲线
奖罚曲线 工期
图6 工期-成本曲线示例
练习1:已知某双代号网络计划中各项工作时
间,费用数据如表:试根据最优成本控制进
行优化。间接费6ห้องสมุดไป่ตู้千元/周.
工作 紧后工作 D(周) M(千元)
d
m(千元) 费率e
A
D,F
2
60
1
180
B
E,F
2
25
1
50
C
F
3
100
3
6(5)
3(2)
1
1320 5
1560 3
4
900(1530) 8(5)
5 T=12天
410
图4 第三次循环后网络图
950
1000(1160)
2
4
1400
3
6(5)
2
1
1320 5
1560 3
4
1110(1530) 7(5)
5 T=11天
图5 第四次循环后的网络图
(4)绘出工期-成本曲线,如图4-28。从图中看出工 程最低费用为9130元,对应最佳工期T=13天,相应的 网络图如图3。
网络计划优化案例-工期优化

网络计划优化案例-工期优化一、工期优化示例已知某工程双代号网络计划如图1所示,图中箭线下方括号外数字为工作的正常持续时间,括号内数字为最短持续时间;箭线上方括号内数字为优选系数,该系数综合考虑质量、安全和费用增加情况而确定。
选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。
若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和(组合优选系数)最小者应优先作为压缩对象。
现假设要求工期为15,试对其进行工期优化。
图1 初始网络计划(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图2所示。
此时关键线路为①—②—④—⑥。
(①,5)(②,11)(①,②,6)(④,11)图2 初始网络计划中的关键线路(2)由于此时关键工作为工作A、工作D和工作H,而其中工作A酌优选系数最小,故应将工作A作为优先压缩对象。
(3)将关键工作A的持续时间压缩至最短持续时间3,利用标号法确定新的计算工期和关键线路,如图3所示。
此时,关键工作A被压缩成非关键工作,故将其持续时间3延长为4,使之成为关键工作。
工作A恢复为关键工作之后,网络计划中出现两条关键线路,即:①—②—④—⑥和①—③—④—⑥,如图4所示。
(①,3)(③,10)(①,6)(④,10)图3 工作A压缩至最短时间时的关键线路(①,4)(②,③,10)(①,6)(④,10)图4 第一次压缩后的网络计划(4)由于此时计算工期为18,仍大于要求工期,故需继续压缩。
需要缩短的时间:△T=18 -15 = 3。
在图5所示网络计划中,有以下五个压缩方案:①同时压缩工作A和工作B,组合优选系数为:2+8=10;②同时压缩工作A和工作E,组合优选系数为:2+4=6;③同时压缩工作B和工作D,组合优选系数为:8+5=13;④同时压缩工作D和工作E,组合优选系数为:5+4=9;⑤压缩工作H,优选系数为10。
在上述压缩方案中,由于工作A和工作E的组合优选系数最小,故应选择同时压缩工作A和工作E的方案。
工程项目管理课件-工期优化

00 1
4 10(8)
10 10
2
3 20(15)
3 30(18)
2
3
40(20) 40 40
3 60(30)
100
5
100
8
6 150 150
50(25)
1 50(30)
2
4
30(20) 90 100
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第二次:选择工作③-⑤,压缩10天,成为50天; 工期变为140天,③-④和④-⑤也变为关键工作。
4
4(2)
15 15
6
1
3
5
6(3)
3(2)
12 12
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作③-⑤,压缩2天,成为4天;
工期变为13天,③-④和④-⑥也变为关键工作。
00 1
26
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 6
3(2)
99 6
4
4(2)
13 13
6
1
3
5
第七章自测题(一)
6.工期优化时,当出现多条关键线路时 A.压缩最原始的一条关键线路 B.要同时压缩多条关键线路
答案 B 7.当需要同时压缩多个关键工作的持续时间
时,应选择( )的组合进行压缩。 答案 优选系数之和最小
第七章自测题(一)
8.总时差和自由时差的关系是 A. TFi-j≥FFi-j B. TFi-j≤FFi-j
F(4)
H(2)
2. 计算工期大于要求工期的优化
方法:
压缩关键线路中关键工作的持续时间。
网络计划的工期成本优化PPT课件
31
从以上压缩过程得出结论,工程成本最低时的最优工期为10d 320
压缩次序 压缩工作
1
1-2
2
5-6
3
2-5
4
6-7
5
7-8
压缩时间
1d
1d 1d 2d
1d
直接费增加
0
40 50 120
70
间接费减少
100 100 100 200 100
总成本减少
100 60 50 80 30
内容小结
工期成本关系 工期成本优化的目的和基本思路 直接费率和间接费率的概念和组合
下节内容:网络计划的资源优化。
作业
请对下图中的双代号网络计划进行工期成本优化,间接 费率100元/天。
并首先选择关键线路上直接费率最小的工作或
工作组合。
3
C=3 4(2)
5
若要求工 期压缩2 天,该如 何压缩?
1
C=4 7(5)
2
7
4
C=4 5(4)
6
总结:工期成本优化的步骤
(1)确定关键线路,同时要确定各项工作的自由时差, 因此要绘制双代号时标网络计划;
(2)在不影响平行的非关键工作的前提下尽可能的压缩 直接费率最低的关键工作;
(3)当关键工作压缩到极限时,同时压缩平行的多条线 路上的直接费率最低的工作组合;
(4)在压缩工作的同时,计算直接费增加和间接费减少 的数值,得出总成本增减的数值,如果总成本减少,则 可以压缩,否则不能。
➢ 工程成本最低时的最优工期
例:对下图所示的网络计划,进行工期成本优化,寻求最
低工程成本下的最优工期。箭杆上方数据为该工作的直接
进度计划是否可以优化
网络计划的优化--工期优化 ppt课件

A(2) 5(3)
2
D(5) 6(4)
G(10)
4
8(6)
1
C(∞) 1 E(4)
4(3)
6
B(8) 6(4)
F(5) 3
2(1)
图例: 工作(优选系数)
正常时间(最短时间)
H(2)
5
4(2)
1、节点标号法快速计算工期、找关键线路
A(2) 5(3)
(①,5)
2
(②,11)
3
C2
10(6)
E 33
18(15)
4
15(15)
33
G
15(12)
14(12) 48
6
48
12(12) 47 47 45 45
D 22
8(5)
42 42
解(5) 压缩A,压缩天数⊿T= Min( 15-10,2,2, 19)=2天
28 28
30 30
ET LT 0
00
1
13 13
A
15 15
15(10) 13(10) 3
00 1
(8) 30
10
10(15)
60
(30)
50
50
160 160
(25)
6
20 (20)
(20)
30
3 50
5050(30)
5 110 130
30
解(3)继续压缩3-4工作⊿T= Min( 60-30,70) =30天
10 10 70 100 100 2 20(15) 4
00 1
(8) 30
6 (3)
8 (5)
4 67
33 5
网络优化-工期优化课件.

1 C(∞)
结论 选择压缩 工作A、E方 案,各压缩 至最短
选 择
A、B A、E B、D
D、E H
2+8=10 2+4=6 8+5=13
5+4=9
10
√
方
案
3
解决实际问题
工作A和工作E,组合优选系数为:6; 选压缩工作 A 和工作 E 方案,各压缩至最短,再确定计算工期和 关键线路。
E(4) 3
第二次优化 后网络图
A(2) 1
4 H(10) 8(6) 6 I(2) 4(2)
Tc=17周
1 C(∞)
G(5)
2(1)
5
第三次优化后同学们独立完成
3
解决实际问题
第三次优化 后网络图
2 A(2) 1 6 3 3 B(8) G(5) 2(1) 5
1 C(∞)
D(5) 6
E(4)
4 H(10) 6
1
6
1
C
E
4
I
5 4
8 4
3
3 2
G
2
D
6
?
5
H616源自1CE4
I Tc=19周
5
4
3
G
2
2
工期优化方法及步骤
承担某铁路桥梁施工单位按照合同要求为3-16m的简支T梁(
预制)、扩大基础编制了施工进度计划如下图所示;在即将开工 时接到甲方变更工期通知,要求在原来工期基础上压缩4周。
D(5) 优选系数:该系数是综合考虑质量要求、安全和费用增加情况 4 2 H(10) 而确定的。费用增加最小、资源供应有保证,对质量和安全影 A(2)
工期—费用优化例题

工期—费用优化例题
假设我们要建造一座简单的房子,建筑面积为100平方米,现在请你根据以下数据给出这个建筑项目的工期费用优化方案。
数据:
- 项目总工期:3个月
- 每个工人每天的工资:200元
- 建材费用:40万元
- 机械设备租赁费用:1万元/月
- 其他管理和运营费用:5万元/月
首先,我们需要计算出这个项目的总工资支出。
假设我们需要4名工人才能在规定的时间内完成这个项目,那么每个月的总工资支出就是:
4人 * 200元/人/天 * 30天/月 = 24,000元/月
如果我们的项目总工期为3个月,那么总工资支出就是:
24,000元/月 * 3个月 = 72,000元
接下来,我们需要计算建材费用和机械设备租赁费用。
假设建材费用和机械设备租赁费用在三个月内需要全部支付,那么总费用就是:
建材费用 + 机械设备租赁费用 = 40万元 + 1万元/月 * 3个月 = 43万元
最后,我们需要计算其他管理和运营费用,该部分费用也需要在三个月内支付。
那么总费用就是:
其他费用 = 5万元/月 * 3个月 = 15万元
因此,这个建筑项目的总费用是:
72,000元(总工资支出) + 43万元(建材费用和设备租赁费用) + 15万元(其他费用) = 515,000元
为了优化工期费用,我们可以考虑增加工人数量来缩短工期。
但是,增加工人数量的同时也会增加总工资支出。
因此,在确定工人数量时需要综合考虑项目时间和费用的平衡点,以达到合理的工期费用优化方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
00 1
26
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 6
3(2)
99 6
4
4(2)
13 13
6
1
3
5
4(3)
3(2)
10 10
14
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第二次:选择工作③-④和③-⑤,同时压缩1天,③ -④成为2天,③-⑤成为3天 ;
88 6
4
4(2)
12 12
6
3
5
3(2)
99
17
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第三次:选择工作①-③,压缩1天,成为5天 ; 工期变为11天,关键工作没有变化。
00 1
24
4
8
2
2(1)
3(2)
7
2
3
5(5) 5 5
2(2)
1 3(3)
77 6
4
4(2)
11 11
6
3
5
3(2)
8
5
例题2
请用关键节点法判断关键线路:
00
1 A(3)
B(3) 2 33
66
14 14
3
7
D(8)
G(4)
69
5 E(5)
6 11 14
18 18
9 I(2)
20 20
10
4
8
C(3)
F(4)
H(2)
69
11 16
6
例题2
请用破圈法判断关键线路:
1 A(3)
B(3)
2
×
C(3)
3 D(8)
×
5×
工期优化
1
补充:
• 破圈法判断关键线路:
从起点节点到终点节点进行观察,凡遇到 节点有两个及以上的内向箭线时,按线路 段工作时间长短,把较短线路流进的一个 箭头去掉(注意只去掉一个) ,便可把较 短路线断开。 能从起点顺箭头方向走到终点的所有路线, 便是关键线路。
2
例题1
请用破圈法判断关键线路:
1
×
5
7
2
×
12 3 10 4
7×
6
10
4
62
4
7
2
9 ×5 11 6 12
6
5
×2
×2
8
3
例题1
请用破圈法判断关键线路:
6
10
4
62
1
3 10
4
4
7
2
9
11 6 12
7
6
2
5
4
例题1
请用破圈法判断关键线路:
1 ×5
7
2
×
12 3 10 4
7×
6
10
4
62
4
7
2
9 ×5 11 6 12
6
5
×2
×2
E(5)
×
4×
F(4)
7 G(4)
×
6
9
10
I(2)
×
8×
H(2)
7
2. 计算工期大于要求工期的优化
方法:
压缩关键线路中关键工作的持续时间。
8
2. 计算工期大于要求工期的优化
注意:
• 在压缩过程中,一定要注意不能把关键 工作压缩成非关键工作。因此可能出现 多条关键线路,此时要同时压缩多条关 键线路。
00 1
4 10(8)
10 10
2
3 20(15)
3 30(18)
2
3
40(20) 40 40
3 60(30)
100
5
100
8
6 150 150
50(25)
1 50(30)
2
4
30(20) 90 100
4 10(8)
10 20
2
3 20(15)
3 30(18)
00 1
2
3
50(20) 50 50
3 60(30)
110
5
110
8
6 160 160
50(25)
1 50(30)
2
4
30(20) 100 110
21
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作①-③,压缩10天,成为40天;
88
18
例题:某工程双代号时标网络计划如图,要求
工期为110天,对其进行工期优化。
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160
3
20(15)
4 2
3
10(8) 30(18)
2
1
3
50(20)
3 60(30)
1 50(30)
8
5
6
50(25)
6
4
6
4(2)
3
5
3(2)
11
(1)计算并找出初始网络计划的关键线路、关键工作; (2)求出应压缩的时间 T Tc Tr 15 11 4天 (3)确定各关键工作能压缩的时间;
00 1
26
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 6
3(2)
9 11 6
4
4(2)
15 15
6
1
3
5
6(3)
3(2)
9
2. 计算工期大于要求工期的优化
再注意:
• 当需要同时压缩多个关键工作的持续时 间时,则优选系数之和最小者应优先选 择。
10
例题:
• 已知网络计划如下图,要求工期为11天,试 用非时标网络计划对其进行优化。
优选系数
1
正常 持续 时间
4
8
2
2(1)
3(2)
7
2
3
6(5)
3(2)
最短
1
持续 时间
6(3)
12 12
12
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作③-⑤,压缩2天,成为4天;
00 1
26
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 63(2)来自9 11 64
4(2)
15 15
6
1
3
5
6(3)
3(2)
12 12
13
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作③-⑤,压缩2天,成为4天;
00 1
26
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 6
3(2)
99 6
4
4(2)
13 13
6
1
3
5
4(3)
3(2)
10 10
15
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第二次:选择工作③-④和③-⑤,同时压缩1天,③ -④成为2天,③-⑤成为3天 ;
工期变为12天,关键工作没有变化。
4 2
30(20)
19
作业:某工程双代号网络计划如图,要求工期 为110天,试用非时标网络计划对其进行 工期优化。
优选系数
4 10(8)
3
2
20(15)
3 30(18)
2
1
50(20)
3
8
3
60(30)
4 50(25)
6
正常 持续 时间
最短 持续 时间
1
2
50(30)
5
30(20)
20
(1)计算并找出初始网络计划的关键线路、关键工作; (2)求出应压缩的时间 T Tc Tr 160 110 50天 (3)确定各关键工作能压缩的时间;
00 1
4 10(8)
10 20
2
3 20(15)
3 30(18)
2
3
50(20) 50 50
3 60(30)
110
5
110
8
6 160 160
50(25)
1 50(30)
2
4
30(20) 100 110
22
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第一次:选择工作①-③,压缩10天,成为40天; 工期变为150天,①-②和②-③也变为关键工作。
25
4
8
2
2(1)
3(2)
00 1
7
2
3
6(5) 6 6
2(2)
88 6
4
4(2)
12 12
6
1
3
5
3(3)
3(2)
99
16
(4)选择关键工作压缩作业时间,并重新计算工期Tc′ 第三次:选择工作①-③,压缩1天,成为5天 ;
00 1
25
4
8
2
2(1)
3(2)
7
2
3
6(5) 6 6
2(2)
1 3(3)
