二分图理论
分形几何理论在图像处理中的应用

分形几何理论在图像处理中的应用随着计算机技术的不断发展,图像处理已经成为了一个日益重要的领域。
分形几何理论作为一种新兴的数学理论,在图像处理中得到了广泛的应用。
本文将介绍分形几何理论在图像处理中的应用,并探讨其在该领域中所发挥的作用。
一、分形几何理论的基本概念和原理分形几何理论是由法国数学家Mandelbrot提出的,它对不规则、复杂的自然物体和现象进行了研究。
分形是指具有自相似性的图形或物体,即整体的一部分与整体的形状相似。
分形几何理论提供了一种描述和分析复杂系统的数学工具。
二、分形几何在图像压缩中的应用图像压缩是图像处理中的一个重要环节,它可以将原始图像的数据进行压缩存储,从而减少存储空间和传输带宽的占用。
分形几何理论可以通过对图像的分解和重构,实现对图像的压缩。
其基本思想是将图像分解为一系列的分形图元,并利用放缩变换对其进行重构,从而实现对图像的压缩和恢复。
三、分形几何在图像增强中的应用图像增强是将原始图像进行处理,以改善图像质量和显示效果的过程。
分形几何理论可以通过对图像的细节进行分解和合成,实现对图像的增强。
其基本思想是通过分形细节的提取和重构,对图像进行增强,使其更加清晰、细腻。
四、分形几何在图像分类与识别中的应用图像分类与识别是图像处理中的一个重要任务,它可以将图像按照其内容进行分类和识别。
分形几何理论可以通过对图像的分形维数和分形特征的提取,实现对图像的分类和识别。
其基本思想是通过分形维数的计算和分形特征的提取,对图像进行特征描述和匹配,从而实现对图像的分类和识别。
五、分形几何在图像生成中的应用图像生成是利用计算机生成新的图像,以满足特定需求的过程。
分形几何理论可以通过对图像的分解和合成,实现对图像的生成。
其基本思想是通过分形的自相似性和可变性,对图像的形状和颜色进行生成,从而实现对图像的创造和设计。
六、分形几何在图像编辑中的应用图像编辑是对原始图像进行修改和处理的过程,以改变图像的外观和内容。
分形几何学

分形几何学摘要:分形几何学作为当今活跃在科学领域和风靡世界的新理论与新学科,它也是一种方法论。
分形作为一门新兴的交叉学科满足了艺术多元化的需求。
分形图案将几何美学与视觉形态融为一体。
分形几何学利用其的自相似性,可以构造出千变万化而又具有任意高分辨率结构的艺术图案,被民众广泛关注。
分形几何学作为科学与艺术交融的载体,已成为当今世界科学文化发展的一大热点。
关键词:分形几何;科学与艺术;自相似中图分类号:g642.0 文献标志码:a 文章编号:1674-9324(2013)25-0133-02一、引言艺术是一种感悟,一如海德格尔所说的“朝向未来”,就艺术而言,无论视觉还是听觉,总包含着新的可能[1]。
法国著名文学家福楼拜早在19世纪中叶预言:“越往前走,艺术越要科学化,同时科学越要艺术化。
两者在山麓分手,回头又在山顶会合”,其实质已表明随着社会的发展和进步,科学与艺术逐步分化然后达到融合,分形艺术则是其最好的载体。
二、分形几何学分形(fractal)理论,是由美籍数学家、哈佛大学教授曼德勃罗特(mandelbrot)1975年提出的,它是20世纪70年代同混沌理论一起发展起来的非线性科学的重要组成部分。
自然界中不规则现象普遍存在,可以充分利用分形理论描述和解释自然界中不光滑、不规则的物体表面及形态,因此分形几何就是描述大自然的几何学。
它不同于传统的欧氏几何中以一维、二维、三维、四维对应的线、面、体和时空来描述物体的形状,分形理论用“分维”(fractal dimension)来描述大自然。
几何学中无法用语言表述的局部或整体概念由于分形的诞生从而得到了解决。
mandelbrot集合是向传统几何学的挑战。
mandelbrot集合其图形边界处具有无限复杂结构,其边界可以无限放大,假如计算机精度不受限制。
无论怎样放大其局部,它总是显示出曲折而且不光滑曲线,即连续不可微。
在生活中,微积分中抽象的光滑曲线实际上是不存在的。
图论1

d<u,v> + d<v,w> ≥ d<u,w> 《定义》:在简单有向图中,若图中任何一 定义》 对结点间,至少有一点到另一结点是可达 的,则称此图是单侧连通的;如果两结 点均是互相可达的,则称是强连通的。 如果在图中略去边的方向,将它看成无向 图后,图是连通的,则称此图为弱连通 的. 强连通⇒单侧连通⇒弱连通
(10)闭路(自回路): 闭路(自回路):图中起始且终止于同一结 闭路 ): 点的边 (闭路的箭头方向是没有意义的 )例:
(11)多重边(平行边): 多重边(平行边):二个结点之间 多重边 ): 方向相同的二条(多条)边 例:
多重图,非多重 《定义》:含有多重边的图称为多重图 定义》 多重图 图称为线图 线图。 线图 简单图: 简单图。 简单图:无自回路的线图称为简单图。由定义可 简单图 见,简单图是没有自回路和多重边的图。 例:
图论不断发展,它在解决运筹学,网络理 论,信息论,控制论,博奕论以及计算 机科学等各个领域的问题时,显示出越 来越大的效果。 对于这样一门应用广泛的学科,其包含的 内容是丰富的,本篇我们只准备介绍基 本的概念和定理,为今后有关学科及课 程的学习和研究提供方便。 第七章 图论
§1图的基本概念
1.基本名词和定义 1.基本名词和定义 定义》 《定义》一个图G是一个三元组<V(G),E(G), ΦG>, 其中V(G)为有限非空结点(或叫顶点)集合, E(G)是边的集合, ΦG是从边集E到结点偶对集 合上的函数。 (1). V(G) ={V1,V2,…,Vn}为有限非空集合, Vi称为结点,简称V是点集。 (2). E(G)={e1,…,em}为有限的边集合,ei称为边。 。 每个边ei都有V中的结点对与之相对应,称E为边集。 。 即每条边是连结V中的某两个点的。
二分图理论

*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图,本节先介绍二部图的基本概念和主要结论,然后介绍它的一个重要应用—匹配。
定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ,满足(1)12V V V =,12V V φ=;(2)(,)e u v E ∀=∈,均有1u V ∈,2v V ∈。
则称G 为二部图或偶图(Bipartite Graph 或Bigraph),1V 和2V 称为互补顶点子集,常记为12,,G V V E =。
如果1V 中每个顶点都与2V 中所有顶点邻接,则称G 为完全二部图或完全偶图(Complete Bipartite Graph),并记为,r s K ,其中12,r V s V ==。
由定义可知,二部图是无自回路的图。
图7-55中,(),(),(),(),()a b c d e 都是二部图,其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。
图7-55二部图示例显然,在完全二部图中,r s K 中,顶点数n r s =+,边数m rs =。
一个无向图如果能画成上面的样式,很容易判定它是二部图。
有些图虽然表面上不是上面的样式,但经过改画就能成为上面的样式,仍可判定它是一个二部图,如图7-56中()a 可改画成图()b ,图()c 可改画成图()d 。
可以看出,它们仍是二部图。
图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。
证明 先证必要性。
设G 是具有互补节点子集1V 和2V 的二部图。
121(,,,,)k v v v v 是G 中任一长度为k 的回路,不妨设11v V ∈,则211m v V +∈,22m v V ∈,所以k 必为偶数,不然,不存在边1(,)k v v 。
再证充分性。
设G 是连通图,否则对G 的每个连通分支进行证明。
图论-数学建模

山东建筑大学 贺长伟
1 引言
• 图论起源于18世纪。第一篇图论论文是瑞士数 学家欧拉于1736 年发表的“哥尼斯堡的七座 桥”。
• 图论中所谓的“图”是指某类具体事物和这些 事物之间的联系。如果我们用点表示这些具体事 物,用连接两点的线段(直的或曲的)表示两个 事物的特定的联系,就得到了描述这个“图”的 几何形象。图论为任何一个包含了一种二元关系 的离散系统提供了一个数学模型,借助于图论的 概念、理论和方法,可以对该模型求解。
元素(即中某两个元素的有序对) 记为
ak (v或i , v j )
ak vi,v j (k 1,2,, n)
当弧 ak 时viv,j 称为v尾i (tail), 为头(vhj ead).
• 2.3 完全图、二分图
• 每一对不同的顶点都有一条边相连的简单图称为
完全图(complete graph)。n个顶点的完全图记
vi (i 1,2称,为, n该) 图的一个顶点(vertex)或节点 (node); E(G) {e1,e称2 ,为,图em的} 边集 (edge set),E(G中) 的每一个元素 记ek 为
ek (v或i , v j ) ek viv j v ,jvi 被(称k 为1,2该,图,m的) 一条从 到 的边(edge) vi v j
• 例5 运输问题(transportation problem) 某种原材料有个产地,现在需要将原材料从产地运 往个使用这些原材料的工厂。假定个产地的产量 和家工厂的需要量已知,单位产品从任一产地到 任一工厂的运费已知,那么如何安排运输方案可 以使总运输成本最低?
• 上述问题有两个共同的特点:一是它们的目的都 是从若干可能的安排或方案中寻求某种意义下的 最优安排或方案,数学上把这种问题称为最优化 或优化(optimization)问题;二是它们都易于 用图形的形式直观地描述和表达,数学上把这种 与图相关的结构称为网络(network)。与图和 网络相关的最优化问题就是网络最优化或称网络 优化 (netwok optimization)问题。
二功分器的原理

张鹏,尉旭波 电子科技大学电科院,四川成都,610054
摘要: 本文首先简要介绍了功分器的基础理论,其次介绍了应用 Agilent 公司 ADS 软件对宽带功分器进行 设计仿真优化过程,并进行了矩量法仿真和电路仿真的对比,得到更接近实际的仿真结果。 关键词: 功分器 momentum 仿真
θ=
π⎡
⎢1 − 2⎣
*
f 2 / f1 − 1 ⎤ ⎥ f 2 / f1 + 1 ⎦
(2_3)
利用这些公式,结合阻抗变换节的形式,可
设计出特性优良的功率分配器。
三、利用 ADS 设计宽带功分器
设计一个 2 路 3 节分配器,其频带范围 为 0.8~2.7GHz,路间一致性小于 1°,隔离 大于 22 dB,驻波小于 1.3。那么,利用前述 公式并取阻抗变换比 R 恒为 2,即可求出变 换节阻抗 Zi 和隔离电阻 Ri(i=1,2,3,…,m), 求出 R1 为 100Ω,R2 为 240Ω,R3 为 300Ω。
layout生成的版图加上各个端口设置好参数进行仿真加上信号端口和内端口的电路图仿好以后生成s参数模型带回原理图中新的原理图进行仿真可以和原来的仿真结果进行对比输入输出端口s参数对比图图10隔离和插损对比图由以上对比仿真图来看除了输入驻波有所下降大概到了16db其他指标均有所提高可见该设计基本达到了所要求的指四结论图11功分器版图本设计的实际测试结果为相位路间一致性小于1隔离度大于22db插入损耗小于025db驻波最大为13测试的结果表明该宽频带功分器性能相当优良
二、功分器的原理:
威尔逊功分器的结构示意图如图 1 所示, 它是这样一种网络:当输出端口都匹配时, 它具有无耗的有用特性,只是耗散了反射功 率,当信号从端口 1 输入,从端口 2、端口 3 输出时为功率分配器。
二部图理论

基于二部图(Bipartite Network)的推荐算法不必考虑用户和项目的内容信息,它是一种结合物质扩散(Massive Diffusion)理论的推荐算法。
周涛[1]等人研究了一些物理学的知识,比如热传导理论以及物质扩散理论等,并将它们应用在推荐算法中,提出了这种基于二部图的推荐算法。
二部图是一种特殊的网络,它包含有两类不同类型节点,并且仅允许不同类型的节点之间可以有连线。
自然界许多问题可以利用二部图进行解决,比如性别关系、边着色问题等。
在二部图的应用中,同一类型节点之间的合作相互关系成为了研究领域的热点。
比如,可以利用由演员节点和演出剧目节点组成的二部图来研究演员之间在演出中的合作关系。
在一个具体的推荐系统中,可以把用户看作是一类节点,把项目看作是另一类节点。
通过由用户节点和项目节点组成的二部图,我们可以利用相邻的用户为目标用户推荐可能感兴趣的项目。
物质扩散类似于在复杂网络中的随机游走的概念。
它假设在一个系统中有着固定数量的“物质”在传递,并且在传递的过程中这些“物质”的总量始终保持守恒。
最后系统稳定状态的结果与节点的度数成正比。
在推荐系统中,我们认为目标用户所选择过的项目能够提供一定的推荐能力信息。
在操作过程中,首先为每个项目赋予初始资源1。
根据物质扩散的理论,物质的传递过程分两步走。
第一步,每个项目将自己的资源通过二部图的边均匀地分配给选择过该项目的每个用户,这样资源就从项目节点传递到了用户节点。
第二步,每个用户再将自己分配到的资源通过二部图的边平均分配给他选择过的项目,这样资源又传回到了项目节点。
虽然资源的总量在传递过程中是守恒的,但通过两次传递,每个项目所具有资源的分配状态发生了改变。
系统最后可以根据项目所拥有的资源的分布状态来计算它们之间的相似度,并确定最近邻集。
(引入具体的公式,并将改进的论文附上)文献[2]将物质扩散理论运用到了Item-based协同过滤推荐算法。
算法将选选项目的资源初始值都设为1,用稳定状态时两个项目的资源传递总量来表示它们之间的相似程度,最后利用这个相似度来计算目标用户的预测评分,并把评分较高的项目推荐给他。
江恩二分之一理论计算公式

江恩二分之一理论计算公式江恩二分之一理论
理论跌幅=明显高点-明显低点-明显低点(涨幅反之)------用股票的收盘价线来计算准确率更高
公式是:
最高收盘价-最低收盘价-最低收盘价=调整目标位。
(就是常说的颈线位理论)(图1)
算跌幅抄大底
计算方法是:(复权计算)(高点-低点-低点)的绝对值=理论最低点
⑴ 测算反弹的理论高度
方法是用最高点减去最低点再除以2,然后再加上最低点,即为最后的反弹理论高度。
其计算公式可表述为:X(理论涨幅)= D(最低点或最低价)+[H(最高点或最高价)—D(最低点或最低
价)]÷2。
⑵ 下跌低点的预测
其计算方法是用前期明显高点减前期明显反弹低点二次,负数为多少,就是它的理论跌幅的最低点或最低
价。
用公式表示为:X买入价=H前期高点-前期低点-前期低点
头碰脚跌,脚顶头涨。
(指上涨时碰到前期底点要回调,下跌时到了前期高点要涨)
江恩的二分之一理论:前期高点-(2 次)前期低点。
(就是常说的颈线位理论).。
二分图在足球机器人角色分配中的应用

m个 机器 人进 行 分 配工作 , 中 的角色 有 n个 , 其 这样 机 器人 构成 一
个 集 合设 为 (, 色构 成 的集 合 设为 V U和 V都 可 以看作 是一 个 ,角 ,
他 的队员 采取 相应 的辅助 角 色 。显然 , 是一种 静态 的方法 , 算 这 运
简单快 捷 。 ( 为 了保证 机 器人 执行 任务 的效 率 , 们对 每 个机 器 人 的任 3 ) 我
二分 图在足 球机器 人角色分配 中的应用
范 学 慧
( 州 建筑 业 技 术 学 院 , 徐 江 徐 州 2 】 1) 2 1 6
摘
要; 通过数学 的二 分图法来 计算足球机 器人_ 角色分配方 面的问题 , 存 利用 二分图匹配算法 对机 器人在场上 的角色重新 分配, 使机器 人
在 场 上 能 够 得 到 有 效 的 信 息 , 过 改 变 角 色 以达 到 最 佳 的 R 的 。 通
关键 词 : 分 图 ; 球 机 器 人 ; 色 分 雕 二 足 角
1 前 言 角色 的概 念和真 实人类 足球 比赛 中的概念 相似 , 它表 示一个 球
员在场上 的角色 , 如前锋 、 卫、 后 中锋 等 。每个角 色包 括 了这个角 色 的活动范 围 , 我们 需要给 各个球 员进 行分 配任 务 , 成不 同的角 色 。 完 目前 的角色 分配 的作 用是 把 队形 中的 角色和 实 际 的机 器 人 联系起 来 。角色 分配就 是为 已知队形 中的每个 角色选 择机器 人的过稗 。
配 为完 美 匹配 。
H l定理 : 于_ 部 图 G 存 在 一个 匹 配 肘, a l 对 二 , 使得 的 所 有顶
点 关于 饱 和 的 充要 条 件 是 : 于 的任 意 器 人 角 色 分 配
图像语义分析学习(一):图像语义分割的概念与原理以及常用的方法

图像语义分析学习(⼀):图像语义分割的概念与原理以及常⽤的⽅法1图像语义分割的概念1.1图像语义分割的概念与原理图像语义分割可以说是图像理解的基⽯性技术,在⾃动驾驶系统(具体为街景识别与理解)、⽆⼈机应⽤(着陆点判断)以及穿戴式设备应⽤中举⾜轻重。
我们都知道,图像是由许多像素(Pixel)组成,⽽「语义分割」顾名思义就是将像素按照图像中表达语义含义的不同进⾏分组(Grouping)/分割(Segmentation)。
图像语义分割的意思就是机器⾃动分割并识别出图像中的内容,⽐如给出⼀个⼈骑摩托车的照⽚,机器判断后应当能够⽣成右侧图,红⾊标注为⼈,绿⾊是车(⿊⾊表⽰back ground)。
2⽬前常⽤的算法2.1前 DL 时代的语义分割从最简单的像素级别“阈值法”(Thresholding methods)、基于像素聚类的分割⽅法(Clustering-based segmentation methods)到“图划分”的分割⽅法(Graph partitioning segmentation methods),在深度学习(Deep learning, DL)“⼀统江湖”之前,图像语义分割⽅⾯的⼯作可谓“百花齐放”。
在此,我们仅以“Normalized cut” [1]和“Grab cut” [2]这两个基于图划分的经典分割⽅法为例,介绍⼀下前DL时代语义分割⽅⾯的研究。
2.1.1Normalized Cut图像分割在Deeplearning技术快速发展之前,就已经有了很多做图像分割的技术,其中⽐较著名的是⼀种叫做“Normalized cut”的图划分⽅法,简称“N-cut ”。
Normalized cut (N-cut)⽅法是基于图划分(Graph partitioning)的语义分割⽅法中最著名的⽅法之⼀,于 2000 年 Jianbo Shi 和 Jitendra Malik 发表于相关领域顶级期刊 TPAMI。
二分图中存在哈密顿[k,k+1]因子的条件
![二分图中存在哈密顿[k,k+1]因子的条件](https://img.taocdn.com/s3/m/1658b15aad02de80d4d84019.png)
当且 仅 当 VS X , Y, kl +d — ( T 有 Sl G s T)
一
kl 三 , T l G , S) 三 . T l = kl +d 一 ( 一kl l = 三0 , 三0 S 定理 l 设 : 2 G=( , E) , X l , X Y, 中 } =
文献 [ ] k 2 G 为 顶 点数 为 的简 单 图 , 5设 ,
1 [ L
,
为偶 数 ;
5 为奇 数 ; k, 且 ( G)
J
,
二
则对 G 的 任 意 哈 密顿 圈 C, 有 [ , G k k+1 ]
因子包含 圈 C 但上述文献给 出的存在哈密顿 .
[, k k+1 因子 的度 条件 过 于严 格 , 且 近几 年 ] 并 来 在这 方面能 改进度条 件 的文献不 多见 . 本文针 对 均衡 二分 图 , 放宽 了度条件 , 过 限定 图 G 中 通
C. 若存在 V( 的不相交的子集 x, 使得 V G) y,
( =X 且 G 的所 有 边 均 一 个 顶 点 在 X G) U Y, 内, 另一 个顶点 在 y 内 , 称 G 为 二分 图 . 则 如果 l =l , Xl 则称 G 为均 衡二 分 图. 余 未 介绍 yl 其 的概念 与符号见 文献 [ ] 1. 因子理论一 直是 图论 的研 究重 点 , 方面 已 这 有 一些研 究成果 . 文献 [ ] G 为 阶图 , 2设 4
中图分类号 : O17 5 5 . 文献标识码 : A
本 文仅考 虑 简 单 有 限无 向 图. G 中顶 点 图 的个数 称为 阶 , 记作 l G) . G 的一 个 支 V( 1图 撑子 图 H 称为 G 的一个 [ , k k+1 因子 , 果对 ] 如 每个 3∈ V( 有 志 d ( ) k+l一 个 [ , g G) H , kk +1 因子是哈 密 顿 的如果 它 包 含 一个 哈 密 顿 圈 ]
轮廓分割原理

轮廓分割原理一、引言轮廓分割是图像处理和计算机视觉中的一项基本任务,它涉及到从数字图像中提取出感兴趣对象的边界。
这一过程对于后续的图像分析和理解至关重要,因为它可以帮助我们识别、定位和量化图像中的对象。
轮廓分割的原理和方法在许多领域都有广泛的应用,包括医学成像、遥感图像分析、工业检测、安全监控等。
二、轮廓分割的基本概念轮廓分割是指将图像分割成多个区域或对象,并识别出这些区域的边界。
在这个过程中,通常需要识别出图像中的不同特征,如颜色、纹理、亮度等,并将它们用于构建对象的轮廓。
轮廓分割的目标是尽可能地将图像中的每个独立对象与其周围环境区分开来,以便进行进一步的分析。
三、图像处理中的轮廓分割在图像处理中,轮廓分割通常涉及以下几个步骤:1. 预处理:包括去噪、增强对比度等,以改善图像质量。
2. 特征提取:识别图像中的关键特征,如边缘、角点等。
3. 分割算法应用:根据提取的特征应用不同的分割算法。
4. 后处理:对分割结果进行优化,如去除小的噪声区域、平滑边界等。
四、轮廓分割的算法与技术4.1 边缘检测边缘检测是一种基于图像亮度变化来检测对象边界的技术。
常用的边缘检测算子包括Sobel、Canny和Laplacian等。
这些算子通过计算图像中像素点的梯度强度和方向来识别边缘。
4.2 阈值分割阈值分割是一种简单有效的分割方法,它通过设定一个或多个灰度阈值将图像分为不同的区域。
当像素值高于(或低于)阈值时,该像素被归为对象区域;否则,被归为背景区域。
4.3 区域生长区域生长是一种基于区域相似性的分割方法。
它从一个或多个种子点开始,逐步将相邻的像素点合并到种子点所在的区域,直到满足一定的停止条件。
4.4 分水岭算法分水岭算法是一种基于拓扑理论的分割方法。
它将图像视为地形图,像素值代表高度,通过模拟水流的融合过程来确定区域的边界。
五、轮廓分割在不同领域的应用- 医学成像:用于病变组织的检测和分割,辅助医生进行诊断。
基于二分图理论的产业环境资源竞争网络模型研究——以广州开发区为例

目前解决 环境 外部 性 问题 主要 有两 种途 径 : 一 种 是依 据 科斯定 理建 立 的产权 制度 , 由环境 管理者 制 定 总排 污量
的上限 , 按 此上 限发布 排污 许可 证并将 其投 放 到排 污 者 中 进 行拍 卖交 易 ; 另 一 种 是 依 据 庇 古 定 理 建 立 的庇 古 税 方 法, 通 过对 分散 的排 污主体 征 收排污 费用来 进 行后 期 的污
模 可 以通过 二分 图理论 来简 化过程 和精 确联 系 。此外 , 由
理, 但 是这 种 “ 先 污染 、 后治理” 的 方 式 不仅 交 易 费 用 高 ,
而 且又 会衍生 出代 际不 公 平 等 问题 。虽 然 我 国在 积极 推
双模式 网络 向单模 式 网络 的转 化有 利 于 研 究产 业 竞 争 网 络 的网络特 征和演 化 规 律 。李 得荣 等 建 立 了零 部 件 企业 与产 品的二 分 网络 模 型 和根 据 产 品销 售 量 的加 权 二 分 网 络 模型 ; 后 锐 等 构 建 了 物 流 企业 竞 争关 系 复杂 网 络模 型 ; 吕康 娟 等建立并 验证 了基 于航运 企业 价值链 接 的世
反 映出来 。 ” 经 济主体 的经 济活 动所产 生 的外部性 , 易
导致 社 会 边 际 成 本 收 益 与 私 人 边 际 成 本 收 益 相 背 离 ,
从 而 出现 市 场 失 灵 和 资 源 配 置 失 当 。外 部 性 可 分 为 正 外 部性 与 负外 部 性 两 类 。 排 污 企 业 的 环 境 外 部 性 是 一 种 负外 部 性 , 即 该 外 部 性 的 影 响 能 够 对 承 受 者 造 成 某 种 损 害或 不 利 效 应 ( 外 部不 经济性 ) , 它 们 彼 此 之 间 存 在 着对 区域 环 境 资 源 和 纳 污 能 力 的 竞 争 关 系 。 如 何 将 这种关系进行 量化 分析 , 是 进 行 有 效 的 环 境 管 理 的 基
离散数学-图论

若图 G 是连通图,则 G 只有一个分图。
27
用第二章“关系”的概念解释分图的概念如下:
设有图 G = (V, E),其中 V 有 n 个结点。在 V 上定义一个二
元关系 ,当且仅当从 vi 到 vj 有路连接时,vi vj。 图 G 中结点之间的连接关系 是 V 上的一个等价关系。
要求的 V 到 V 的双射函数 h。
因为这两个图中边与结点的关联关系不相同。
例如,在 G 中度为 3 的 4 个结点构成一个长为 4 的环,而在
G 中度为 3 的 4 个结点没有构成长为 4 的环。
23
五、子图与分图
利用子集的概念可定义图 G 的子图。 定义8-7 设有图 G1 = (V1, E1) 和图 G2 = (V2, E2), (1) 若 V2 V1,E2 E1,则称 G2 是 G1 的子图,或称 G1 包含 G2,记作 G2 G1; (2) 若 G2 G1 但 G2 G1(即 V2 V1 或 E2 E1),则称 G2 是 G1 的真子图,记作 G2 G1; (3) 若 V2 = V1,E2 E1,则称 G2 是 G1 的生成子图。 显然,任一图 G 都是自己的子图。
8
例2 (a), (b) 分别给出了例 1 中图 G 的图解方法5
(a)
矩阵表示法
v1 v2 v3 v4 v5 (b)
用矩阵的方法也可以表示一个图。在 8.2 节中我们再专门讨论。
9
二、完全图与补图
v1
(n, m) 图
具有 n 个结点和 m 条边的图称为 (n, m) 图。
例1 设 V = {v1, v2, v3, v4, v5},
配第——克拉克定理

配第——克拉克定理配第——克拉克定理,是一种在计算机科学领域应用广泛的算法定理,可以用来判断无向图是否为二分图。
下面我们将分步骤来介绍这一定理的具体内容。
第一步,了解二分图首先,我们需要了解什么是二分图。
简单来说,二分图是指图中的所有顶点可以被分为两个不相交的子集,每个子集中的顶点之间没有边相连。
在实际应用中,二分图常常被用来表示一些具有互斥关系的问题,比如集合覆盖问题、染色问题等等。
第二步,理解配第算法接下来,我们需要理解配第算法。
配第算法,也称为匈牙利算法,是一种用来解决二分图匹配问题的算法。
在一个二分图中,我们需要找到一个子图,使其所有顶点都能够匹配到另一个子图的顶点。
为了实现这一目的,配第算法采用了一种贪心的思想。
具体来说,该算法从图中任选一个顶点(比如A),然后搜索与之相邻的点,如果找到了一个没有被匹配过的顶点(比如B),就将A和B匹配起来,并标记B 为已匹配。
接着,再找到图中与B相邻但未匹配的点,并将二者匹配起来。
如此循环查找直到无法再匹配为止。
第三步,介绍克拉克定理克拉克定理,也称为配第——克拉克定理,是判断一个无向图是否为二分图的定理。
克拉克定理的核心思想是:如果一个无向图中的每个点的度数都不超过二分图中最大的独立集大小(即子图中每个顶点都没有与自己相邻的点),那么它就是一个二分图。
这个定理的证明跟配第算法有关,通过一系列的推理可以证明,如果一个无向图不是二分图,那么存在一个奇环,且这个奇环大小不小于三。
接着,通过把奇环上的点分为两个集合,即黑白两个集合,就可以得到一个二分图。
第四步,实现配第——克拉克定理最后,我们需要介绍如何实现配第——克拉克定理。
实际上,这个定理的实现非常简单,只需要遍历图中的每个顶点,检查它的度数是否都不超过最大独立集的大小即可。
如果发现某个顶点的度数大于最大独立集的大小,那么这个图就不是一个二分图。
以上就是关于配第——克拉克定理的介绍,这个定理在计算机科学领域应用广泛,有着重要的理论和实际价值。
离散数学图论
1
2
3
(3)为(1)的生成子图,(2)为(1)的真子图。
补图
定义7 设图G=<V, E> ,若G是n阶无向图,则G的补图为: KnG。即为n阶完全无向图与G的差。若G是n阶有向图, 则G的补图为:n阶有向完全图与G的差。
(这一节介绍了图的一些基本概念,如图的定义,图 中顶点的度,图的所有顶点的度为边的2倍,且一个 图中有偶数个奇顶点,简单图等的定义,图的运算, 子图,补图的一些概念。要掌握这些简单的定义)
e3
d e2
d 1 1 1 0 0
c
e
0
0
0
0
0
有向图的矩阵表示
与无向图相对应,有向图也有类似的矩阵表示。 如右图:
称e关联于顶点a和b;称a和b是邻接的。 若边e对应的是无序偶{a,b},则称e为无向边。同样
称a,b是端点,称e关联于顶点a和b;称a和b是邻接 的。 每一条边都是有向边的图,称为有向图。每条边都 是无向边的图,称为无向图。
图中不与任何顶点邻接的点称为 孤立点。全都是孤 立点的图称为零图。关联于一个顶点的边称为自回路, 也称为自圈。
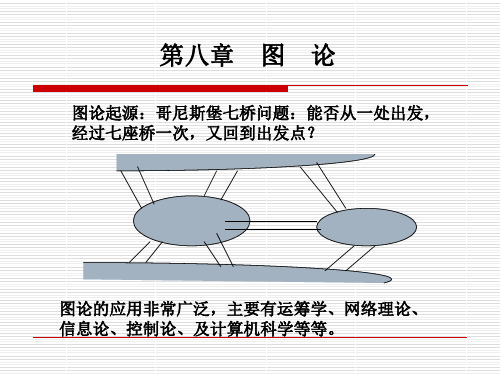
哥尼斯堡七桥问题
城的四个陆地部分分别表以A,B(大岛),C,D(小岛), 将陆地设想为图的顶点,把桥画成相应的边,
A
B
D
C
则问题等价于在图中从某一顶点出发找一条回径,通过它的每条 边一次且仅一次,并回到原顶点。
(你能否看出,此问题无解,即这样的走法不存在呢?)
主要内容
1.图的基本概念 2.路径与回路 3.图的矩阵表示 4.几种特殊的图 5.无向树, 有向树
定义5 在有向图G中,如果在任两个顶点中,存在从一个顶点到 另一个顶点的路径,则称图G为单向连通的。如果在G中,任 何两个顶点都互相可达,则称G为强连通的。如果它的基础图 (底图)是连通的,则称之为弱连通的。
证明白色路径定理

证明白色路径定理白色路径定理的证明可以通过归纳法来进行。
首先,我们来看一下什么是二分图。
二分图是一种特殊的图,其顶点集可以被分成两个互不相交的子集,使得每条边的两个端点在不同的子集中。
在一个二分图中,如果存在一条奇数长的路径,那么这个图一定存在偶数长的环,而实际上二分图是不可能存在奇数长的环的。
证明白色路径定理的基本思路是利用反证法。
假设存在一条从顶点u到顶点v的最短路径上经过了奇数条边。
我们将这条路径上经过的边全部重新染成红色,不在路径上的边则染成蓝色。
因为最短路径上经过了奇数条边,所以路径的起点和终点的连线是蓝色的。
接下来我们来证明这个情况下一定存在一个奇数长的环。
因为路径的起点和终点的连线是蓝色的,所以我们可以沿着蓝色的边从顶点u到达顶点v。
在顶点v处,我们发现了一条蓝色的边,这条边连接了顶点v和顶点w。
接着我们再沿着蓝色的边从顶点v到顶点w。
在顶点w处,我们又发现了一条蓝色的边,这条边连接了顶点w和顶点x。
我们一直重复这个过程,直到我们再次到达顶点u为止。
这样我们就得到了一条经过奇数个蓝色边的环。
由于我们假设了最短路径上经过了奇数条边,而我们通过反证得到了一条经过了奇数条蓝色边的环,这就产生了矛盾。
因此,我们的假设是错误的,最短路径一定不会经过奇数条边,也就证明了白色路径定理。
上面这一段是白色路径定理证明过程的基本思路,下面我们来进一步展开证明。
首先,我们需要介绍一些图论中使用到的概念和理论。
首先是二分图的概念。
二分图是一个图,其节点可以被分成两个互不相交的子集,使得每条边的两个端点在不同的子集中。
二分图在实际中有着广泛的应用,比如匹配问题、任务分配等。
二分图的性质非常重要,它为后续证明白色路径定理提供了重要的理论基础。
其次是路径的概念。
路径是指图中顶点的一个序列,这些顶点之间依次相连,且每两个相邻的顶点之间有一条边。
路径是图论中的基本概念之一,它在解决实际问题中的路径规划以及网络通信等方面有着重要的应用。
团队定向赛的技战术研究

团队定向赛的技战术研究定向越野团队赛的特征是团队协作,是所有定向越野项⽬中最具挑战性的项⽬。
定向越野团队赛中,队长起着⾄关重要的作⽤,需要总揽全局,明确分⼯;队员之间必须相互信任、相互协作,才能取得好的成绩。
定向越野团队赛起点准备阶段准备⼯作必须充分细致。
起点、场地和终点,不同阶段有不同的技战术要求。
(⼀)起点技战术要求1.划分地图,明确任务在团队赛中,遴选⼀个优秀的队长⾮常关键。
团队赛中队长最重要的任务是划分地图(习惯叫分图)、明确分⼯,就是将⽐赛地图上的⾃由点尽可能科学合理的分配给全队四名运动员。
这是整个团队能否取得好成绩的关键的第⼀步。
团队赛⽐赛⼀般有两种规定。
⼀种是分图时间计算在⽐赛时间内,就是团队所有队员统⼀打了起点开始计时后再拿地图,然后再进⾏分图;另⼀种是分图的时间不算在⽐赛时间内,就是在打起点正式开始⽐赛之前会给每个队三分钟准备时间,⽤于看图、分图。
(1)分图技术要求。
⾸先,所有队员拿到地图后迅速看图,注意了解地形和地物特征。
队长在看图、分析地图的同时,指定⼀个队员快速数清地图上有多少个必经点、多少个⾃由点,并告诉队长。
其次,队长在分图时要注意,第⼀,划分地图区域必须结合⾃⾝队员特点,尽量考虑每个队员的技术优势与不⾜。
如果队员技术⽔平相差不⼤,必须做到分点均匀,⼀般情况分为四个区域:起点附近作为⼀区,要求体能好、技术⽔平⼀般的队员;⼆区、三区要求技术⽔平好、体能也不错的队员;终点附近作为四区,适合体能差点、技术⽔平相对较弱的队员。
第⼆,如果队员中有新⼿,且技术与体能相对均较差时,除了⾸先考虑把终点附近区域的⾃由点分配给该队员外,还可以适当减少该队友的⾃由点任务,甚⾄为保险起见,有时可以让该队友只打必经点,⽽将所有⾃由点分为三个区域分配到其它三个队员。
这样,⼀⽅⾯可以避免因队友长时间找不到检查点⽽耽误时间,另⼀⽅⾯也便于最后团队实施帮助。
第三,队长在给其他队友划定区域时,必须要笔迹清晰、划闭合圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图7-55二部图示例显然,在完全二部图中中,顶点数,边数。
,r s K n r s =+m rs =一个无向图如果能画成上面的样式,很容易判定它是二部图。
有些图虽然表面上不是上面的样式,但经过改画就能成为上面的样式,仍可判定它是一个二部图,如图7-56可改画成图。
可以看出,它们仍是二部图。
)()d 图7-56二部图示例
()a()c()b 利用定理7.5.1可以很快地判断出图7-57中的、是二部图,而则不是二部图。
图7-57
即可。
给出匹配的基本概念和术语。
图7-59匹配问题示意图
设无向图,中有边集,且在中任意两条边都没有公,G V E =G M ⊆E M 共的端点,称边集为图的一个匹配(Matching)。
中一条边的两个端点,叫做在M G M 中不存在匹配,使得,则称为最大匹配(Maximum G 1M 1M M >M
4),(2,5),(3,6)}
图7-60
图7-61的一个匹配。
用(*)标记)a 3152{(,),(,)}M x y x y =V 的新标记过的节点,用()标记不通过中的边与邻接且未标记过的1x 1x M 1x ;类似地,用()标记。
2x 2y 的新标记过的节点, 用()标记通过中的边与1y 1y M 1y ;类似地,用()标记。
2y 5x 的新标记过的节点,因为不存在不通过中的边与邻接的3x M 3x 的节点;用()标记或,假定用()标记5x 3y 4y 5x y
图7-62这个问题即为:二部图是否存在―完全匹配。
当取12,,G V V E =1V ,根据霍尔定理,二部图没有―完全匹配,所以要使每()N A A <1V 个人都能分配到一项工作是不可能的。
基本原理
该算法是通过给每个顶点一个标号(叫做顶标)来把求最大权匹配的问题转化为求完备匹配的问题的。
设顶点Xi的顶标为A[ i ],顶点Yj的顶标为B[ j ],顶点Xi与Yj之间的边权为
w[i,j]。
在算法执行过程中的任一时刻,对于任一条边(i,j),A[ i ]+B[j]>=w[i,j]始终成立。
KM算法的正确性基于以下定理:
若由二分图中所有满足A[ i ]+B[j]=w[i,j]的边(i,j)构成的子图(称做相等子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配。
这个定理是显然的。
因为对于二分图的任意一个匹配,如果它包含于相等子图,那么它的边权和等于所有顶点的顶标和;如果它有的边不包含于相等子图,那么它的边权和小于所有顶点的顶标和。
所以相等子图的完备匹配一定是二分图的最大权匹配。
初始时为了使A[ i ]+B[j]>=w[i,j]恒成立,令A[ i ]为所有与顶点Xi关联的边的最大权,B[j]=0。
如果当前的相等子图没有完备匹配,就按下面的方法修改顶标以使扩大相等子图,直
到相等子图具有完备匹配为止。
我们求当前相等子图的完备匹配失败了,是因为对于某个X顶点,我们找不到一条从它
出发的交错路。
这时我们获得了一棵交错树,它的叶子结点全部是X顶点。
现在我们把交错
树中X顶点的顶标全都减小某个值d,Y顶点的顶标全都增加同一个值d,那么我们会发现:
1)两端都在交错树中的边(i,j),A[ i ]+B[j]的值没有变化。
也就是说,它原来属于相等子图,现在仍属于相等子图。
2)两端都不在交错树中的边(i,j),A[ i ]和B[j]都没有变化。
也就是说,它原来属于(或不属于)相等子图,现在仍属于(或不属于)相等子图。
3)X端不在交错树中,Y端在交错树中的边(i,j),它的A[ i ]+B[j]的值有所增大。
它原来不属于相等子图,现在仍不属于相等子图。
4)X端在交错树中,Y端不在交错树中的边(i,j),它的A[ i ]+B[j]的值有所减小。
也就说,它原来不属于相等子图,现在可能进入了相等子图,因而使相等子图得到了扩大。
现在的问题就是求d值了。
为了使A[ i ]+B[j]>=w[i,j]始终成立,且至少有一条边进入相等子图,d应该等于:
Min{A[ i ]+B[j]-w[i,j] | Xi在交错树中,Yi不在交错树中}。
改进
以上就是KM算法的基本思路。
但是朴素的实现方法,时间复杂度为O(n4)——需要找
O(n)次增广路,每次增广最多需要修改O(n)次顶标,每次修改顶标时由于要枚举边来求d值,复杂度为O(n2)。
实际上KM算法的复杂度是可以做到O(n3)的。
我们给每个Y顶点一个“松弛量”函数slack,每次开始找增广路时初始化为无穷大。
在寻找增广路的过程中,检查边(i,j)时,如果它不在相等子图中,则让slack[j]变成原值与A[ i ]+B[j]-w[i,j]的较小值。
这样,在修改顶标时,取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。
但还要注意一点:修改顶标后,要把所有的不在交错树中的Y顶点的slack值都减去d。
Kuhn-Munkras算法流程:
(1)初始化可行顶标的值
(2)用匈牙利算法寻找完备匹配
(3)若未找到完备匹配则修改可行顶标的值
(4)重复(2)(3)直到找到相等子图的完备匹配为止。
