数据结构课程设计AVL树实现及其分析实验报告
数据结构课程设计实践报告

数据结构课程设计实践报告数据结构课程设计实践报告1. 实验目的本次数据结构课程设计实践的目的是帮助学生掌握数据结构的基本概念,了解常见数据结构的实现原理,提高代码实现能力和问题解决能力。
2. 实验背景数据结构是计算机科学的基础课程,它是计算机科学的重要组成部分。
在计算机科学中,数据结构是针对计算机中的数据存储、管理和操作的方法论。
数据结构中的“数据”是指计算机中存储的各种信息,而“结构”则是指这些信息之间的相互关系。
常见的数据结构包括数组、链表、栈、队列、树和图等。
3. 实验内容本次数据结构课程设计实践包括以下内容:3.1 栈和队列实现一个基于栈和队列的计算器程序,能够进行加减乘除等基本运算和括号运算。
3.2 链表与树实现一个简单的文件系统,包括文件的创建、删除、移动、复制等操作,利用链表实现文件存储,利用树来实现文件目录结构。
3.3 图实现最短路径算法,并利用Graphviz工具将结果可视化展示出来。
4. 实验过程我们小组首先进行了团队分工,每个成员负责一个模块的代码实现,同时进行代码审查。
我们使用C++语言进行编码实现,采用面向对象设计思想,将每个数据结构封装成一个类,方便日后的调用和扩展。
在实现栈和队列的计算器程序时,我们使用了双栈法来进行括号运算的处理,使用队列来实现多项式的存储和输出。
在实现文件系统时,我们构建了一颗树形结构来表示文件的目录结构,同时在每个节点处保存了一个链表,来存储该目录下的文件信息,方便进行操作。
在实现最短路径算法时,我们采用了Dijkstra算法,并使用Graphviz 工具将结果可视化展示出来。
5. 实验结果我们小组经过不断尝试和调试,最终实现了所有要求的功能,并达到了预期的效果。
我们在实验过程中遇到的问题,如链表的指针操作、树的遍历方法以及Dijkstra算法的实现等,我们通过文献资料的查阅和团队讨论得以解决。
6. 实验总结通过本次数据结构课程设计实践,我们加深了对数据结构的理解和掌握,同时也提高了我们的编程能力和问题解决能力。
AVL树研究与实现

AVL树研究与实现摘要:计算机最广为人知的优点之一是其能储存大量的数据,如今随着时代的发展,储存容量更是犹如日进千里一般极速扩展,大容量的硬盘、u盘早已随处可见。
然而,要在巨大的数据中搜索出需要的内容却不是一件容易的事,由此,为了能减少在搜索储存数据上的开销,各种适应于不同访问搜索背景的数据结构应运而生。
树,便是计算机学科中最基本的数据结构之一,提供了快速的储存和访问性能。
该文探究了带有平衡条件的二叉查找树——avl树的原理,并对其使用c语言进行了实现。
关键词:数据结构;平衡二叉查找树;avl树中图分类号:tp311 文献标识码:a 文章编号:1009-3044(2013)07-1532-04对于大量的输入数据,普通的线性数据结构访问时间太慢,例如,对于一个有n个数据的线性数据结构,假设对每个数据的访问几率大致相同,每个数据每次访问有1/n的机会被访问,由于是线性数据,因此每个数据的访问花销可以经过一定的排列,最通常的是访问第一个数据花销1个单位时间,第二个2个单位时间,第三个3各单位时间……第n个n各单位时间,于是访问一次的平均花销为(n+[n2])/2n = (1+n)/ 2,用计算机专业的符号来说,其访问运行时间可以用o(n)来表示,即访问一次线性数据结构的花销在n这个数量级上。
使用树这一数据结构可将访问花销将至logn这个数量级上,也即o(logn),这里logn是以二为底的n的对数。
可以对比一下,若n=1267650600228229401496703205376,则logn=100。
数字越大,则o(n)与o(logn)相差越大。
一般来说,计算机学科中使用的最基本的树为二叉查找树,下图是一颗二叉树的简单示意图:图1 二叉树示意图二叉查找树则是在二叉树的基础上得来。
假设在一颗二叉树中,每个节点都有一个关键词值,并且关键词值都是互异且可以比较,若对于此二叉树中的每个节点,其左子树中所有节点的关键词值小于其本身关键词值,其右子树中所有关键词值大于其本身关键词值,则此二叉树为二叉查找树。
数据结构树的实验报告

数据结构树的实验报告数据结构树的实验报告一、引言数据结构是计算机科学中的重要概念,它可以帮助我们组织和管理数据,提高程序的效率和性能。
而树作为一种常见的数据结构,具有广泛的应用。
本实验旨在通过实践操作,深入理解树的基本概念、特性和操作。
二、实验目的1. 掌握树的基本概念和特性;2. 熟悉树的基本操作,如插入、删除、查找等;3. 理解树的遍历算法,包括前序、中序和后序遍历;4. 实现树的基本功能,并验证其正确性和效率。
三、实验过程1. 构建树的数据结构首先,我们需要定义树的数据结构。
树由节点组成,每个节点可以有零个或多个子节点。
我们可以使用面向对象的思想,创建一个节点类和树类。
节点类包含节点值和子节点列表的属性,以及插入、删除子节点等操作的方法。
树类则包含根节点的属性和遍历方法等。
2. 插入和删除节点在树中插入和删除节点是常见的操作。
插入节点时,我们需要找到合适的位置,并将新节点作为子节点添加到相应的位置。
删除节点时,我们需要考虑节点的子节点和兄弟节点的关系,并进行相应的调整。
通过实现这两个操作,我们可以更好地理解树的结构和特性。
3. 查找节点树中的节点可以通过值进行查找。
我们可以使用递归或迭代的方式,在树中进行深度优先或广度优先的搜索。
在查找过程中,我们需要注意节点的存在性和唯一性,以及查找算法的效率。
4. 树的遍历树的遍历是指按照一定的顺序访问树中的所有节点。
常见的遍历方式有前序、中序和后序遍历。
前序遍历先访问根节点,然后递归地访问左子树和右子树;中序遍历先递归地访问左子树,然后访问根节点,最后访问右子树;后序遍历先递归地访问左子树和右子树,最后访问根节点。
通过实现这三种遍历算法,我们可以更好地理解树的结构和遍历过程。
五、实验结果与分析通过实验,我们成功地实现了树的基本功能,并验证了其正确性和效率。
我们可以通过插入和删除节点操作,构建出不同形态的树,并进行查找和遍历操作。
在插入和删除节点时,树的结构会发生相应的变化,但其基本特性仍然保持不变。
数据结构与算法(5):AVL树

平衡⼆二叉树(AVL树,发明者的姓名缩写):⼀一种⾼高度平衡的排序⼆二叉树,其每⼀一个节点的左⼦子树和右⼦子树的⾼高度差最多等于1。
平衡⼆二叉树⾸首先必须是⼀一棵⼆二叉排序树!平衡因⼦子(Balance Factor):将⼆二叉树上节点的左⼦子树深度减去右⼦子树深度的值。
对于平衡⼆二叉树所有包括分⽀支节点和叶节点的平衡因⼦子只可能是-1,0和1,只要有⼀一个节点的因⼦子不不在这三个值之内,该⼆二叉树就是不不平衡的。
最⼩小不不平衡⼦子树:距离插⼊入结点最近的,且平衡因⼦子的绝对值⼤大于1的节点为根的⼦子树。
n个结点的AVL树最⼤大深度约1.44log2n。
查找、插⼊入和删除在平均和最坏情况下都是O(logn)。
增加和删除可能需要通过⼀一次或多次树旋转来重新平衡这个树。
这个⽅方案很好的解决了了⼆二叉查找树退化成链表的问题,把插⼊入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
但是频繁旋转会使插⼊入和删除牺牲掉O(logN)左右的时间,不不过相对⼆二叉查找树来说,时间上稳定了了很多。
可以采⽤用动态平衡技术保持⼀一个平衡⼆二叉树。
构造平衡⼆二叉树的时候,也可以采⽤用相同的⽅方法,默认初始时,是⼀一个空树,插⼊入节点时,通过动态平衡技术对⼆二叉树进⾏行行调整。
Adeleon-Velskii和Landis提出了了⼀一个动态地保持⼆二叉排序树平衡的⽅方法,其基本思想是:在构造⼆二叉排序树的过程中,每当插⼊入⼀一个结点时,⾸首先检查是否因插⼊入⽽而破坏了了树的平衡性,若是因插⼊入结点⽽而破坏了了树的平衡性,则找出其中最⼩小不不平衡树,在保持排序树特性的前提下,调整最⼩小不不平衡⼦子树各结点之间的连接关系,以达到新的平衡。
通常这样得到的平衡⼆二叉排序树简称为AVL树。
⾼高度差2。
容易易看出,这种不不平衡出现在下⾯面四种情况:为使树恢复平衡,我们把k2变成这棵树的根节点,因为k2⼤大于k1,把k2置于k1的右⼦子树上,⽽而原本在k1右⼦子树的Y⼤大于k1,⼩小于k2,就把Y置于k2的左⼦子树上,这样既满⾜足了了⼆二叉查找树的性质,⼜又满⾜足了了平衡⼆二叉树的性质。
数据结构中的红黑树与AVL树算法分析

数据结构中的红黑树与AVL树算法分析红黑树和AVL树都是常见的自平衡二叉搜索树数据结构,用于在动态插入、删除和查找操作中保持树的平衡。
本文将分析红黑树和AVL 树的算法,包括其定义、插入和删除操作、性能比较等方面。
一、红黑树1.定义红黑树是一种二叉搜索树,它满足以下性质:(1)每个节点要么是红色,要么是黑色。
(2)根节点是黑色。
(3)每个叶子节点(NIL节点,空节点)是黑色。
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)对于任意节点,从该节点到其子孙节点的所有路径上包含相同数目的黑色节点。
2.插入操作插入操作是红黑树中最复杂的操作之一,其大致步骤如下:(1)将新节点插入到树中,类似于二叉搜索树的插入。
(2)将插入的节点着为红色。
(3)根据红黑树的性质进行调整,以保持树的平衡。
具体调整的规则如下:a.如果插入的节点是根节点,将其变为黑色。
b.如果插入的节点的父节点是黑色,不需要调整。
c.如果插入的节点的父节点是红色:i.如果插入的节点的叔叔节点是红色,重新着色以保持红黑树的性质。
ii.如果插入的节点的叔叔节点是黑色,通过旋转操作来保持红黑树的性质。
3.删除操作删除操作也是红黑树中比较复杂的操作之一,其大致步骤如下:(1)找到要删除的节点,类似于二叉搜索树的查找。
(2)如果要删除的节点有两个子节点,则找到其后继节点(即右子树中最小的节点)来替代要删除的节点。
(3)如果要删除的节点为红色,则直接删除,不会违反红黑树的性质。
如果要删除的节点为黑色,则需要进行进一步的调整,以保持红黑树的性质。
(4)根据删除节点的颜色和兄弟节点的颜色进行调整,具体调整的规则如下:a.如果删除的节点是红色,直接删除,不需要调整。
b.如果删除的节点是黑色,将其替代节点的颜色设置为黑色,然后判断替代节点的兄弟节点的颜色:i.如果兄弟节点是红色,进行旋转和重新着色操作。
ii.如果兄弟节点是黑色,判断兄弟节点的子节点的颜色:1.如果兄弟节点的两个子节点都是黑色,重新着色并递归地将其父节点作为新的删除节点。
数据结构-树的实现实验报告

对某个具体的抽象数据类型,运用课程所学的知识和方法,设计合理的数据结构,并在此基础上实现该抽象数据类型的全部基本操作。通过本设计性实验,检验所学知识和能力,发现学习中存在的问题。进而达到熟练地运用本课程中的基础知识及技术的目的。
3.实验环境
1、硬件:PC机
2、软件:Microsoft Visual C++ 6.0
typedef struct LinkQueue
{
QueuePtr front,rear; /*队头、队尾指针*/
}LinkQueue;
/*******************************队列定义**************************************/
/*构造一个空队列*/
const char NIL=' ';
/*****************树的二叉链表孩子-兄弟-双亲存储表示***************************/
typedef struct CSnode
{
char data;
CSnode *firstchild,*nextsibling,*parent;
int InitQueue (LinkQueue &Q)
{
if(!(Q.front=Q.rear=new QNode))
exit(OVERFLOW);
Q.front->next=NULL;
return OK;
}
/*销毁队列Q*/
int DestroyQueue(LinkQueue &Q)
{
while(Q.front){
void Print(CSTree T,void (*visit)(CSTree));
数据结构实验报告

数据结构实验报告树是一种非线性的数据结构,它由节点和边组成,节点之间存在层次关系。
树的应用十分广泛,特别是在存储和检索数据上。
在本次实验中,我对树的应用进行了研究和实践,并撰写了本篇实验报告。
本次实验中,我首先学习了树的基本概念和相关术语。
树由根节点、子节点、叶节点以及它们之间的连接边组成。
每个节点可以有多个子节点,但只能有一个父节点(除了根节点)。
叶节点是没有子节点的节点。
这种层次结构使得树可以用来表示具有层次关系的数据,例如家谱、目录结构等。
接下来,我学习了树的不同种类和它们的特点。
最常见的树结构包括二叉树、二叉树(BST)、平衡二叉树、AVL树等。
二叉树是一种每个节点最多有两个子节点的树结构。
二叉树是二叉树的一种特殊形式,其中左子树的所有节点值都小于根节点的值,右子树的所有节点值都大于根节点的值。
平衡二叉树是一种高度平衡的二叉树,它的左右子树的高度差不超过1、AVL树是一种自平衡的二叉树,它通过旋转和重新平衡来保持树的平衡性。
为了更好地理解树的应用,我选择了二叉树(BST)作为本次实验的主要研究对象。
BST是一种高效的数据结构,可以用来存储一组有序的数据,并且支持快速的查找、插入和删除操作。
我首先实现了BST的基本操作,包括插入节点、删除节点和查找节点。
通过这些操作,我可以在BST中存储和检索数据。
在插入节点时,我按照BST的特性将节点插入到相应的位置,并保持树的有序性。
在删除节点时,我考虑了不同的情况,包括删除叶节点、删除只有一个子节点的节点以及删除有两个子节点的节点。
在查找节点时,我使用了递归的方式在树中查找节点的值。
接着,我实现了一些BST的扩展操作。
首先是中序遍历,它可以按照节点的值的升序输出BST中的所有节点。
其次是最小值和最大值的查找,它们分别返回BST中的最小值和最大值。
最后是查找一些节点的前驱和后继,前驱是小于该节点的最大节点,后继是大于该节点的最小节点。
这些扩展操作可以进一步提升BST的功能和灵活性。
AVL树研究与实现

语 言进 行 了 实现 。
关键 词 : 数据 结构 ; 平衡 二 叉 查 找树 ; A v L树 中 图分 类 号 : T P 3 l l 文 献 标 识码 : A 文章 编 号 : 1 0 0 9 — 3 O 4 4 ( 2 O 1 3 ) 0 7 — 1 5 3 2 — 0 4
ቤተ መጻሕፍቲ ባይዱ
d e r t O r e d u c e t h e d a t a s t o r a g e o v e r h e a d i n t h e s e a r c h , a l l k i n d s o f a d a p t a t i o n t O d i f e r e n t a c c e s s s e a r c h e me r g e a s t h e t i me s r e q u i r e
Re s e a r c h a n d I mp l e me n t a t i o n o f AVL Tr e e
XI E Che n
( Z h o n g s h a n Un i v e r s i t y , G u a n g z h o u 5 1 0 2 7 5 , Ch i n a )
Ab s t r a c t : On e o f t h e mo s t we l l k n o wn i s t h e a d v a n t a g e s o f c o mp u t e r c a n s t o r e l a r g e a mo u n t s o f d a t a , a n d n o w wi t h t h e d e v e l o p —
树的操作实验报告

实验名称:树的操作实验实验目的:1. 理解树的基本概念和操作。
2. 掌握树的创建、插入、删除、查找等基本操作。
3. 熟悉树在计算机科学中的应用。
实验环境:1. 操作系统:Windows 102. 编程语言:Java3. 开发工具:Eclipse实验内容:1. 树的基本概念2. 树的创建3. 树的插入4. 树的删除5. 树的查找6. 树的应用实验步骤:一、树的基本概念1. 树的定义:树是一种非线性数据结构,由若干节点组成,每个节点有一个唯一的父节点(根节点除外),除了根节点外,其他节点都有一个子节点。
2. 树的术语:- 节点:树中的数据元素。
- 父节点:节点的直接前驱节点。
- 子节点:节点的直接后继节点。
- 根节点:没有父节点的节点。
- 叶节点:没有子节点的节点。
- 节点的度:节点拥有的子节点个数。
- 树的深度:根节点到叶节点的最长路径长度。
二、树的创建1. 创建二叉树:```javapublic class BinaryTree {private TreeNode root;public BinaryTree() {root = null;}public void createTree(int[] data) {if (data == null || data.length == 0) {return;}root = new TreeNode(data[0]);int i = 1;Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();if (i < data.length && data[i] != 0) {node.left = new TreeNode(data[i]); queue.offer(node.left);i++;}if (i < data.length && data[i] != 0) { node.right = new TreeNode(data[i]); queue.offer(node.right);i++;}}}}```2. 创建二叉搜索树:```javapublic class BinarySearchTree {private TreeNode root;public BinarySearchTree() {root = null;}public void createTree(int[] data) {if (data == null || data.length == 0) {return;}for (int i = 0; i < data.length; i++) {root = insert(root, data[i]);}}private TreeNode insert(TreeNode node, int data) { if (node == null) {return new TreeNode(data);}if (data < node.data) {node.left = insert(node.left, data);} else if (data > node.data) {node.right = insert(node.right, data);}return node;}}```三、树的插入1. 在二叉树中插入节点:```javapublic void insert(TreeNode node, int data) {if (node == null) {return;}if (data < node.data) {insert(node.left, data);} else if (data > node.data) {insert(node.right, data);}}```2. 在二叉搜索树中插入节点:```javaprivate TreeNode insert(TreeNode node, int data) { if (node == null) {return new TreeNode(data);}if (data < node.data) {node.left = insert(node.left, data);} else if (data > node.data) {node.right = insert(node.right, data);}return node;}```四、树的删除1. 在二叉树中删除节点:```javapublic void delete(TreeNode node, int data) {if (node == null) {return;}if (data < node.data) {delete(node.left, data);} else if (data > node.data) {delete(node.right, data);} else {if (node.left == null && node.right == null) { node = null;} else if (node.left == null) {node = node.right;} else if (node.right == null) {node = node.left;} else {TreeNode minNode = findMin(node.right);node.data = minNode.data;delete(node.right, minNode.data);}}}```2. 在二叉搜索树中删除节点:```javaprivate TreeNode delete(TreeNode node, int data) {if (node == null) {return null;}if (data < node.data) {node.left = delete(node.left, data);} else if (data > node.data) {node.right = delete(node.right, data);} else {if (node.left == null && node.right == null) { node = null;} else if (node.left == null) {node = node.right;} else if (node.right == null) {node = node.left;} else {TreeNode minNode = findMin(node.right);node.data = minNode.data;node.right = delete(node.right, minNode.data); }}return node;}```五、树的查找1. 在二叉树中查找节点:```javapublic TreeNode search(TreeNode node, int data) {if (node == null) {return null;}if (data == node.data) {return node;} else if (data < node.data) {return search(node.left, data);} else {return search(node.right, data);}}```2. 在二叉搜索树中查找节点:```javapublic TreeNode search(TreeNode node, int data) {if (node == null) {return null;}if (data == node.data) {return node;} else if (data < node.data) {return search(node.left, data);} else {return search(node.right, data);}}```六、树的应用1. 堆排序:利用二叉堆的属性,实现高效排序。
数据结构树的实验报告

数据结构树的实验报告数据结构树的实验报告引言:数据结构是计算机科学中的重要基础,它涉及到如何组织和存储数据以便有效地使用。
树是一种常见的数据结构,它具有层次结构和分支特征,被广泛应用于各个领域。
本实验旨在通过实践操作和观察,深入理解树的特性和应用。
一、实验目的本实验的目的是通过实践操作,掌握树的基本概念、特性和常见操作。
具体目标包括:1. 了解树的基本概念和术语;2. 掌握树的构建和遍历方法;3. 理解树的应用场景和相关算法。
二、实验过程1. 树的构建在本实验中,我们使用Python编程语言实现了树的构建。
首先,我们定义了树的节点类,节点包含一个值和指向子节点的指针。
然后,我们通过递归的方式构建了一棵树,树的每个节点都可以有多个子节点。
2. 树的遍历树的遍历是指按照一定的顺序访问树的所有节点。
在本实验中,我们实现了树的三种遍历方式:前序遍历、中序遍历和后序遍历。
前序遍历是先访问根节点,然后依次递归遍历左子树和右子树;中序遍历是先递归遍历左子树,然后访问根节点,最后递归遍历右子树;后序遍历是先递归遍历左子树和右子树,最后访问根节点。
3. 树的应用树作为一种重要的数据结构,在实际应用中有着广泛的应用。
在本实验中,我们选择了两个常见的树的应用场景进行了实践操作。
(1)文件系统文件系统可以看作是一棵树,根目录为根节点,各级子目录和文件为子节点。
通过实践操作,我们可以模拟文件系统的创建、删除、查找等操作,加深对树的理解。
(2)家谱家谱也可以看作是一棵树,根节点为家族的祖先,各级子节点为后代。
通过实践操作,我们可以实现家谱的构建、查询和修改,了解家谱的组织和维护方式。
三、实验结果与分析通过实验操作,我们成功构建了树的数据结构,并实现了树的遍历和应用。
在文件系统的实践中,我们能够灵活地创建、删除和查找文件和目录,实现了对文件系统的基本操作。
在家谱的实践中,我们能够方便地构建和查询家族成员的关系,加深了对家谱的理解。
数据结构-树的实现实验报告

数据结构-树的实现实验报告数据结构-树的实现实验报告1-引言在计算机科学中,树是一种非常重要的数据结构,它可以用来模拟现实世界中的层次关系。
本实验旨在通过实现树的基本操作,加深对树数据结构的理解和掌握。
2-实验目的本实验的主要目标是:●理解树这种数据结构的基本概念和特点。
●学习树的常见操作,包括插入节点、删除节点、查找节点等。
●掌握树的遍历算法,包括前序遍历、中序遍历、后序遍历和层次遍历。
●实现树的基本操作,并验证其正确性。
3-实验设计3-1 树的定义首先,我们需要明确树的定义。
树是一种由节点和边组成的数据结构,具有以下特点:●每个节点都有零个或多个子节点。
●除了根节点外,每个节点都有且仅有一个父节点。
●没有父节点的节点称为根节点。
●没有子节点的节点称为叶子节点。
●在任意一棵树中,从根节点到任意一个节点都存在唯一一条路径。
3-2 树的实现我们可以通过链式存储结构来实现树。
每个节点包含一个数据域和一个指向子节点的指针域。
根据树的特点,我们可以定义一个树的节点类,如下所示:```javaclass TreeNode {Object data。
// 节点数据TreeNode parent。
// 父节点指针List<TreeNode> children。
// 子节点指针public TreeNode(Object data) {this(data, null, new ArrayList<>())。
}public TreeNode(Object data, TreeNode parent,List<TreeNode> children) {this-data = data。
this-parent = parent。
this-children = children。
}}```在树的实现中,我们还需要定义一些基本操作,包括插入节点、删除节点、查找节点等。
3-2-1 插入节点插入节点是将一个新节点插入到树中的指定位置。
大数据数据结构和算法_树2_AVL树部分

大数据数据结构和算法_树2_AVL树部分AVL树是一种自平衡二叉树,它的特点是每个节点的左子树和右子树的高度差不超过1、AVL树的平衡是通过旋转操作来实现的,这样可以保证树的高度始终在O(log n)的范围内。
AVL树的平衡是通过对节点进行四种旋转操作来实现的:LL、LR、RR、RL旋转。
LL旋转是指当一个节点的左子树的高度大于右子树的高度,并且左子树的左子树高度大于左子树的右子树高度时,需要进行LL旋转。
LL旋转是将当前节点的左子节点提升为根节点,然后将原根节点降为右子节点。
LR旋转是指当一个节点的左子树的高度大于右子树的高度,并且左子树的右子树高度大于左子树的左子树高度时,需要进行LR旋转。
LR旋转是先对当前节点的左子节点进行RR旋转,然后再对当前节点进行LL旋转。
RR旋转是指当一个节点的右子树的高度大于左子树的高度,并且右子树的右子树高度大于右子树的左子树高度时,需要进行RR旋转。
RR旋转是将当前节点的右子节点提升为根节点,然后将原根节点降为左子节点。
RL旋转是指当一个节点的右子树的高度大于左子树的高度,并且右子树的左子树高度大于右子树的右子树高度时,需要进行RL旋转。
RL旋转是先对当前节点的右子节点进行LL旋转,然后再对当前节点进行RR旋转。
AVL树的插入操作和二叉树的插入操作类似,都是先找到插入位置,然后将新节点插入到相应位置。
不同的是,在插入节点之后,需要向上回溯检查每个祖先节点的平衡因子。
如果一些祖先节点的平衡因子超过了1或者小于了-1,就需要进行相应的旋转操作,以恢复平衡。
AVL树的删除操作也和二叉树的删除操作类似,都是先找到要删除的节点,然后根据节点的情况进行删除。
删除节点之后,需要向上回溯检查每个祖先节点的平衡因子,进行相应的旋转操作以恢复平衡。
AVL树的优点是能够维护树的平衡性,使得在最坏情况下的、插入和删除操作的时间复杂度都是O(log n)。
然而,AVL树的缺点是在插入和删除操作中需要进行旋转操作,这会增加一定的时间开销。
实验报告

哈尔滨工业大学计算机科学与技术学院实验报告课程名称:数据结构与算法课程类型:必修实验项目名称:A VL树实验题目:A VL树班级:0836001学号:6080310126姓名:赵文博一、实验目的通过编写实现AVL树的各种功能,熟悉AVL树的原理与使用方法。
二、实验要求及实验环境要求:1.具有插入(建立)、删除和查找功能2.插入操作应包括四种类型的平衡化处理3.删除操作应包括四种类型的平衡化处理并且包括多次平衡化处理4.能体现操作前后二叉树的形态及其变化实验环境:IDE:Codeblocks 8.0.2系统:windows XP语言: C++三、设计思想所使用的变量与函数:struct node //A VL树中的节点{int height, data;node *left, *right;};node *root; //根节点int ret(node *po) //返回一个节点的height值,若节点为空返回0void rotateLL(node* &r) //LL旋转void rotateRR(node* &r) //RR旋转void rotateRL(node* &r) //RL旋转void rotateLR(node* &r) //LR旋转void insert(node* &p, int number) //插入这里未使用平衡因子,而是使用高度代替void rotateDelete(node* &p) //删除时的旋转void Delete(node* &p, int data) //删除元素int search(node* &p, int x) //查找元素void show(node* &p) //输出A VL树中的所有元素流程图:四、测试结果按如下顺序插入元素,不断的输出A VL树的结构:1 3 2 5 6 4 9 8 71:数据: [1] 左节点: NULL 右节点: NULL3:数据: [1] 左节点: NULL 右节点: [3]数据: [3] 左节点: NULL 右节点: NULL2:数据: [2] 左节点: [1] 右节点: [3]数据: [1] 左节点: NULL 右节点: NULL数据: [3] 左节点: NULL 右节点: NULL5:数据: [2] 左节点: [1] 右节点: [3]数据: [1] 左节点: NULL 右节点: NULL数据: [3] 左节点: NULL 右节点: [5]数据: [5] 左节点: NULL 右节点: NULL6:数据: [2] 左节点: [1] 右节点: [5]数据: [1] 左节点: NULL 右节点: NULL数据: [5] 左节点: [3] 右节点: [6]数据: [3] 左节点: NULL 右节点: NULL数据: [6] 左节点: NULL 右节点: NULL4:数据: [3] 左节点: [2] 右节点: [5]数据: [2] 左节点: [1] 右节点: NULL数据: [1] 左节点: NULL 右节点: NULL数据: [5] 左节点: [4] 右节点: [6]数据: [4] 左节点: NULL 右节点: NULL数据: [6] 左节点: NULL 右节点: NULL9:数据: [3] 左节点: [2] 右节点: [5]数据: [2] 左节点: [1] 右节点: NULL数据: [1] 左节点: NULL 右节点: NULL 数据: [5] 左节点: [4] 右节点: [6]数据: [4] 左节点: NULL 右节点: NULL 数据: [6] 左节点: NULL 右节点: [9]数据: [9] 左节点: NULL 右节点: NULL 8:数据: [3] 左节点: [2] 右节点: [5]数据: [2] 左节点: [1] 右节点: NULL数据: [1] 左节点: NULL 右节点: NULL 数据: [5] 左节点: [4] 右节点: [8]数据: [4] 左节点: NULL 右节点: NULL 数据: [8] 左节点: [6] 右节点: [9]数据: [6] 左节点: NULL 右节点: NULL 数据: [9] 左节点: NULL 右节点: NULL 7:数据: [3] 左节点: [2] 右节点: [6]数据: [2] 左节点: [1] 右节点: NULL数据: [1] 左节点: NULL 右节点: NULL 数据: [6] 左节点: [5] 右节点: [8]数据: [5] 左节点: [4] 右节点: NULL数据: [4] 左节点: NULL 右节点: NULL 数据: [8] 左节点: [7] 右节点: [9]数据: [7] 左节点: NULL 右节点: NULL 数据: [9] 左节点: NULL 右节点: NULL随后,删除1,7,31数据: [3] 左节点: [2] 右节点: [6]数据: [2] 左节点: NULL 右节点: NULL 数据: [6] 左节点: [5] 右节点: [8]数据: [5] 左节点: [4] 右节点: NULL数据: [4] 左节点: NULL 右节点: NULL 数据: [8] 左节点: [7] 右节点: [9]数据: [7] 左节点: NULL 右节点: NULL 数据: [9] 左节点: NULL 右节点: NULL 7:数据: [3] 左节点: [2] 右节点: [6]数据: [2] 左节点: NULL 右节点: NULL 数据: [6] 左节点: [5] 右节点: [8]数据: [5] 左节点: [4] 右节点: NULL数据: [4] 左节点: NULL 右节点: NULL数据: [8] 左节点: NULL 右节点: [9]数据: [9] 左节点: NULL 右节点: NULL3数据: [4] 左节点: [2] 右节点: [6]数据: [2] 左节点: NULL 右节点: NULL数据: [6] 左节点: [5] 右节点: [8]数据: [5] 左节点: NULL 右节点: NULL数据: [8] 左节点: NULL 右节点: [9]数据: [9] 左节点: NULL 右节点: NULL此时,查找元素2 5 102,5返回找到10返回未找到。
课题_一步一步写平衡二叉树(AVL树)

一步一步写平衡二叉树(AVL树)平衡二叉树(Balanced Binary Tree)是二叉查找树的一个进化体,也是第一个引入平衡概念的二叉树。
1962年,G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树,所以它又叫AVL树。
平衡二叉树要求对于每一个节点来说,它的左右子树的高度之差不能超过1,如果插入或者删除一个节点使得高度之差大于1,就要进行节点之间的旋转,将二叉树重新维持在一个平衡状态。
这个方案很好的解决了二叉查找树退化成链表的问题,把插入、查找、删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
平衡二叉树实现的大部分过程和二叉查找树是一样的(学平衡二叉树之前一定要会二叉查找树),区别就在于插入和删除之后要写一个旋转算法去维持平衡,维持平衡需要借助一个节点高度的属性。
我参考了机械工业出版社的《数据结构与算法分析- C语言描述》写了一个C++版的代码。
这本书的AVLTree讲的很好,不过没有很完整的去描述。
我会一步一步的讲解如何写平衡二叉树,重点是平衡二叉树的核心部分,也就是旋转算法。
第一步:节点信息相对于二叉查找树的节点来说,我们需要用一个属性表示二叉树的高度,目的是维护插入和删除过程中的旋转算法。
代码如下://AVL树节点信息template<class T>class TreeNode{public:TreeNode():lson(NULL),rson(NULL),freq(1),hgt(0){}T data;//值int hgt;//以此节点为根的树的高度unsigned int freq;//频率TreeNode* lson;//指向左儿子的地址TreeNode* rson;//指向右儿子的地址};第二步:平衡二叉树(AVL)类的声明声明中的旋转函数将在后边的步骤中详解。
java数据结构与算法之平衡二叉树(AVL树)的设计与实现分析

java数据结构与算法之平衡二叉树(A VL树)的设计与实现普通二叉查找树的问题在开篇,我们提到过,普通二叉树(二叉查找树)在操作的时间复杂度上不一定遵循O(㏒n),也有可能是O(n),这是为什么呢?在上一篇中,我们明明插入都按照一定规则比较的呀,其实那是因为我们在上篇测试时执行了随机插入的操作,如果此时利用上篇实现的二叉搜索树将一段已排序好的数据一个个插入后,就会发现如下情况了:从图中我们可以发现,把已排序的1-9数据进行正序和倒序插入后,树的结构已变成单向左子树或者右子树了,如果我们在往里插入已排序的数据,那么单向左子树或者右子树越来越长,此时已跟单链表没有什么区别了,因此对此结构的操作时间复杂度自然就由O(㏒n)变成O(n)了,这也就是普通二叉查找树不是严格意义上O(㏒n)的原因。
那么该如何解决这个问题呢?事实上一种解决的办法就是要有一个称为平衡的附加结构条件即:任何结点的深度不得过深,而这种数据结构就是我们本篇要分析的平衡二叉树(AVL),它本身也是一种二叉查找树,只不过不会出现前面我们分析的情形罢了,接下来我们就来分析一下这棵平衡二叉树。
平衡二叉树的定义通过上面的分析,我们明白的普通二叉查找树的不足,也知道了如何去解决这个缺点,即构建树时要求任何结点的深度不得过深(子树高度相差不超过1),而最终这棵树就是平衡二叉树(BalancedBinaryTree),它是G.M.Adelson-Velsky和ndis在1962年在论文中发表的,因此又叫AVL树。
这里我们还需要明确一个概念,AVL树只是实现平衡二叉树的一种方法,它还有很多的其他实现方法如红黑树、替罪羊树、Treap、伸展树等,后面我们还会分析其他树的实现。
ok~,接着来了解一下AVL树的特性:一棵AVL树是其每个结点的左子树和右子树的高度最多相差1的二叉查找树(空树的高度为-1),这个差值也称为平衡因子(其取值可以是1,0,-1,平衡因子是某个结点左右子树层数的差值,有的书上定义是左边减去右边,有的书上定义是右边减去左边,这样可能会有正负的区别,但是这个并不影响我们对平衡二叉树的讨论)。
数据结构:AVL树

数据结构:AVL树⼆叉查找树的⼀个局限性就是有可能退化成⼀个链表,这种情况下⼆叉查找树的效率就会急剧下降变成0(n)。
⽽AVL树可以很好地解决BST的这种困境。
本篇博客会介绍AVL树的基本特点和相关操作。
⽂章参考⾃博客:1. 什么是AVL树任何两个⼦树的⾼度差最⼤是1,这样的⼆叉树叫做AVL树。
先来确定⼏个概念:平衡因⼦:将⼆叉树上节点的左⼦树⾼度减去右⼦树⾼度的值称为该节点的平衡因⼦BF(Balance Factor)。
最⼩不平衡⼦树:距离插⼊节点最近的,且平衡因⼦的绝对值⼤于1的节点为根的⼦树。
左边⼆叉树的节点45的BF = 1,插⼊节点43后,节点45的BF=2。
节点45是距离插⼊点43最近的BF不在[-1,1]范围内的节点,因此以节点45为根的⼦树为最⼩不平衡⼦树。
2. 节点的实现public class AVLTreeNode<T extends Comparable> {// 存储的数据-⽤于排序T key;// 节点⾼度-⽤于计算⽗节点的BFint height;// 左⼉⼦ & 右⼉⼦AVLTreeNode<T> left;AVLTreeNode<T> right;public AVLTreeNode() {}public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {this.key = key;this.left = left;this.right = right;this.height = 0;}}节点的定义还是⽐较简单的,相对于之前的定义多了⼀个height属性⽤于计算⽗节点的BF。
树的定义public class AVLTree<T extends Comparable> {// 定义树的根节点AVLTreeNode<T> root;public AVLTree() {root = null;}}获取树的⾼度public int height() {return height(root);}private int height(AVLTreeNode<T> tree) {if (tree != null){return tree.height;}return 0;}本⽂章将空树的⾼度定义为0,⾼度以树的层次为准,根节点的⾼度为1,依次类推。
AVL树模拟用户登录系统的实验报告(附代码和详尽注释) (2)
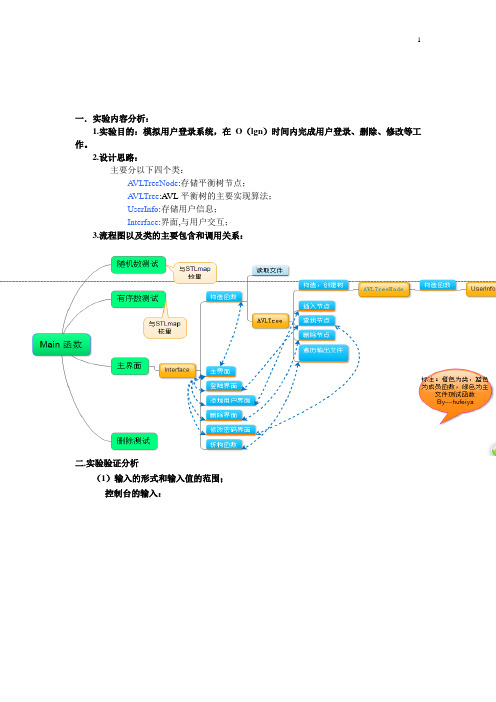
一.实验内容分析:1.实验目的:模拟用户登录系统,在O(lgn)时间内完成用户登录、删除、修改等工作。
2.设计思路:主要分以下四个类:A VLTreeNode:存储平衡树节点;A VLTree:A VL平衡树的主要实现算法;UserInfo:存储用户信息;Interface:界面,与用户交互;3.流程图以及类的主要包含和调用关系:二.实验验证分析(1)输入的形式和输入值的范围;控制台的输入:如图,输入为数字,超出范围将提示不正确并返回重新输入文件的输入:程序会找寻当前目录的database.data文件,并读入数据,如果未找到则自创此文件,创建空树(2)输出的形式;程序退出时析构函数保存文件到database.data并覆盖原文件。
(3)程序所能达到的功能;在O(lgn)时间内添加、查找、删除、修改用户信息。
(4)测试数据:本系统包含三个测试函数样例:1.顺序插入测试(分别在debug和release环境下和STL map比较速度)2.随机插入测试(分别在debug和release环境下和STL map比较速度)3.删除测试测试函数均在main文件里void randomTest();//随机数测试void orderTest();//顺序插入测试void deleteTest();//删除测试void main_interface();//主界面1,2均在debug模式下插入100W数据,在release模式下插入1000W数据。
顺序插入的实现是用整数1~n转换为string,位数不够的在前面补‘0’。
测试结果:1.debug下顺序插入测试:2.Release下顺序插入测试3.debug下随机插入测试4.release下随机插入测试实践证明map的红黑树在顺序插入测试时慢于我的avl树,但随机插入测试表现比A VL树要好。
3.删除数据的图形化表示(‘R’‘L’‘=’为平衡因子以检验正确性)下面删除3(树中无3):还是一样,下面删除2删除成功,下面删除7删除成功。
数据结构课程设计AVL树实现及其分析实验报告

算法与数据结构课程设计报告题目: A VLree的实现及分析班级: 12计算机1学号: ************: ***成绩:2013年12月31日一、AVLree的实现及分析AVL 树是平衡的二元查找树。
一株平衡的二元查找树就是指对其每一个节点,其左子树和右子树的高度只差不超过1.编写程序实现AVL树的判别;并实现AVL树的ADT,包括其上的基本操作;节点的加入和删除。
BSt和AVL的差别就在平衡性上,所以AVL的操作关键要考虑如何在保持二元查找树定义条件下对二元树进行平衡化。
(1)编写AVL树的判别程序,并判别一个人元查找数是否为AVL树。
二元查找树用其先序遍历结果表示,如:5,2,1,3,7,8.(2)实现AVL树的ADT,包括其上的基本操作:节点的加入和删除,另外包括将一般二元查找树转变为AVL树的操作。
二、设计思想(宋体,三号加粗)任意给定一组数据,设计一个算法,建立一棵平衡二叉树,对它进行查找、插入、删除等操作。
平衡二叉树ADT结构如下:typedef struct{Status key;}ElemType;typedef struct BSTNode{ElemType data;Status bf;struct BSTNode *lchild,*rchild;}BSTNode,*BSTree;给出一组数据,通过InsertAVL(BSTree &T, ElemType e, Status &taller)插入算法,构建平衡二叉树,若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个数据元素为e的新结点,并返回1,否则返回0。
若因插入而使二叉排序树失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。
在此算法中,利用到递归算法和LeftBalance(BSTree &T)左平衡处理,RightBalance(BSTree &T)右平衡处理。
有关AVL树的总结与感悟

有关AVL树的总结与感悟C/C++实现AVL树(二叉平衡搜索树)一开始以为很复杂很可怕,后来自己想了一下其实也没那么可怕,无非就是左右子树的顺序调换而已。
有关AVL的旋转的原理就不再说明,不懂自行百度查书了解旋转原理。
以下是部分代码实现AVL树首先是树的结构的构建struct tree{struct tree* ls; //左儿子struct tree* rs; //右儿子int siz,con,data,height; //大小,内容,数据,高度};typedef struct tree stu;typedef struct tree* ptr;下面是旋转的代码实现1.左单旋与右单旋什么时候单旋不再说明了,自行百度查书了解各种情况。
void left(ptr* now){ //左旋ptr tmp=(*now)->rs; //其实本质就是左右儿子的替换(*now)->rs=tmp->ls;tmp->ls=*now;tmp->siz=(*now)->siz;pushup(*now),pushup(tmp);*now=tmp;return;}void right(ptr* now){ //右旋ptr tmp=(*now)->ls;(*now)->ls=*now;tmp->siz=(*now)->siz;pushup(*now),pushup(tmp);*now=tmp;return;}2.插入、平衡、刷新过程平衡这一部分的代码是AVL的核心其实也就是比普通二叉搜索树多了一个平衡的操作而已写出二叉搜索树,再加上平衡操作就行了总的来说就是插入->平衡->刷新void ins(ptr* now,int num) //其实仔细分辨的话,也只是比二叉搜索树多了一些判断和平衡而已{if (*now==NULL){*now=(ptr)malloc(sizeof(stu));(*now)->siz=(*now)->con=1;(*now)->data=num,(*now)->height=0;(*now)->ls=(*now)->rs=NULL; return;}if ((*now)->data==num){(*now)->con++;pushup(*now); return;}if ((*now)->data>num) ins(&(*now)->ls,num);else ins(&(*now)->rs,num);pushup(*now); balance(now); return;}void balance(ptr *now) //进行平衡的操作对于不同情况的调用{if (*now==NULL) return;if (h((*now)->ls)-h((*now)->rs)==2){if (h((*now)->ls->ls)>h((*now)->ls->rs)) right(now);else left(&(*now)->ls),right(now); return;}if (h((*now)->rs)-h((*now)->ls)==2){if (h((*now)->rs->rs)>h((*now)->rs->ls)) left(now);else right(&(*now)->rs),left(now); return;}return;}void pushup(ptr now){ //进行重新刷新相当于树的重建过程if(now==NULL) return; //刷新当前树的高度,数据内容等now->height=1;now->siz=now->con;now->siz+=size(now->ls);now->siz+=size(now->rs);if(h(now->ls)>h(now->ls))now->height+=h(now->ls);else now->height+=h(now->rs);return;}3.删除节点后的平衡void del(ptr* now,int num){if (*now==NULL) return;if ((*now)->data==num){if ((*now)->con>1) (*now)->con--;else{ptr cng=*now;if ((*now)->ls==NULL) *now=(*now)->rs,free(cng);else if ((*now)->rs==NULL) *now=(*now)->ls,free(cng);else{cng=(*now)->rs;while (cng->ls) cng=cng->ls;(*now)->data=cng->data;(*now)->con=cng->con,cng->con=1;del(&(*now)->rs,cng->data);}}}else{if ((*now)->data>num) del(&(*now)->ls,num);else del(&(*now)->rs,num);}pushup(*now); balance(now); return;}4.打印AVL树的结点1.前序遍历void print(ptr p){printf("data:%d,con:%d,",p->data,p->con);printf("siz:%d,h:%d ",p->siz,p->height);return;}void printfst(ptr now){if (now){print(now);if (now->ls) printfst(now->ls);if (now->rs) printfst(now->rs);}else printf("NULL");return;}2.中序遍历void printmid(ptr now){if (now){if (now->ls) printmid(now->ls);print(now);if (now->rs) printmid(now->rs);}else printf("NULL");return;}3.后序遍历void printlst(ptr now){if (now){if (now->ls) printlst(now->ls);if (now->rs) printlst(now->rs);print(now);}else printf("NULL");return;}5.总结这个是链表实现的AVL树,后期会补充上数组实现AVL树,总的来说,并不算太难,比起复杂的图的递归,这个确实比较明确,就是旋转->平衡->刷新的过程。
数据结构中的平衡二叉树AVL树和红黑树的原理与实现

数据结构中的平衡二叉树AVL树和红黑树的原理与实现在计算机科学中,数据结构是指一种组织和存储数据的方式,同时也是一种操作数据的方法。
其中,平衡二叉树是一种常用的数据结构,在平衡二叉树中,每个节点的左子树和右子树的高度最多相差1。
然而,平衡二叉树在插入和删除节点时可能会出现树结构不平衡的问题,这就引出了AVL树和红黑树的概念。
一、AVL树的原理与实现AVL树是由G. M. Adelson-Velsky和E. M. Landis于1962年提出的一种自平衡二叉查找树。
它通过在每个节点中添加一个平衡因子来维持树的平衡性。
平衡因子可以是-1、0或1,对应于左子树比右子树高、左右子树高度相等以及右子树比左子树高的情况。
在插入或删除节点时,AVL树会通过旋转操作来调整树的结构,以保持平衡因子的平衡。
旋转操作有四种情况:左旋、右旋、先左旋后右旋和先右旋后左旋。
通过这些旋转操作,AVL树能够保持树的平衡性,从而提高查找、插入和删除操作的效率。
AVL树的实现需要考虑节点的旋转、平衡因子的更新以及树的遍历等问题。
在节点的插入和删除操作中,需要对节点进行平衡处理,并更新相应的平衡因子。
在树的遍历中,可以使用中序遍历、前序遍历或后序遍历等方式来访问树的节点。
二、红黑树的原理与实现红黑树是由Rudolf Bayer在1972年提出的一种平衡二叉查找树。
它通过在每个节点中添加一个额外的属性表示节点的颜色(红色或黑色)来保持树的平衡性。
红黑树具有以下性质:1. 每个节点要么是红色,要么是黑色。
2. 根节点是黑色。
3. 每个叶子节点(NIL节点)是黑色。
4. 如果一个节点是红色,则它的两个子节点都是黑色。
5. 对于每个节点,从该节点到其子孙节点的所有路径上包含相同数目的黑色节点。
通过这些性质,红黑树可以保持树的黑色平衡,在插入和删除节点时通过颜色变换和旋转操作来维持树的平衡性。
与AVL树相比,红黑树的调整操作较为简单,适用于动态插入和删除节点的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法与数据结构课程设计报告题目: A VLree的实现及分析班级: 12计算机1学号: ************: ***成绩:2013年12月31日一、AVLree的实现及分析AVL 树是平衡的二元查找树。
一株平衡的二元查找树就是指对其每一个节点,其左子树和右子树的高度只差不超过1.编写程序实现AVL树的判别;并实现AVL树的ADT,包括其上的基本操作;节点的加入和删除。
BSt和AVL的差别就在平衡性上,所以AVL的操作关键要考虑如何在保持二元查找树定义条件下对二元树进行平衡化。
(1)编写AVL树的判别程序,并判别一个人元查找数是否为AVL树。
二元查找树用其先序遍历结果表示,如:5,2,1,3,7,8.(2)实现AVL树的ADT,包括其上的基本操作:节点的加入和删除,另外包括将一般二元查找树转变为AVL树的操作。
二、设计思想(宋体,三号加粗)任意给定一组数据,设计一个算法,建立一棵平衡二叉树,对它进行查找、插入、删除等操作。
平衡二叉树ADT结构如下:typedef struct{Status key;}ElemType;typedef struct BSTNode{ElemType data;Status bf;struct BSTNode *lchild,*rchild;}BSTNode,*BSTree;给出一组数据,通过InsertAVL(BSTree &T, ElemType e, Status &taller)插入算法,构建平衡二叉树,若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个数据元素为e的新结点,并返回1,否则返回0。
若因插入而使二叉排序树失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。
在此算法中,利用到递归算法和LeftBalance(BSTree &T)左平衡处理,RightBalance(BSTree &T)右平衡处理。
进而实现构建平衡二叉树,使其左子树和右子树的高度之差不超过1.LeftBalance(BSTree &T)对以指针T所指结点为根的二叉树作左平衡旋转处理。
本算法结束时,指针T指向新的根结点。
RightBalance(BSTree &T)// 对以指针T所指结点为根的二叉树作右平衡旋转处理。
本算法结束时,指针T指向新的根结点。
R_Rotate(BSTree &p)对以*p为根的二叉排序树作右旋处理,处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点L_Rotate(BSTree &p)对以p↑为根的二叉排序树作左旋处理,处理之后p指向新的树根结点,即旋转处理之前的右子树的根结点和Delete(BSTree &p)key的数据元T所指二叉排序指向该数据元素结点,FALSE,指针f指向TAVL树,删除函数流程图:开始查找删除失败删除数据结束四、测试(宋体,三号加粗)创建AVL树,输入一组数据:按先序遍历输出:删除节点7;先序遍历结果:插入数据6后的先序遍历结果:然后退出子目录操作。
输入一组数据创建BST树,判断创建的BST是否为AVL树:创建的BST树不是AVL树,将BST转换为AVL树五、源程序(宋体,三号加粗)函数头代码#include "iostream.h" #include <stdio.h> #include <malloc.h>#define MAXNODE 100 #define TRUE 1 #define FALSE 0 #define OVERFLOW 1 #define LH +1 #define EH 0 #define RH -1typedef int Status; typedef char TElemType;typedef struct {Status key;}ElemType;typedef struct BSTNode { ElemType data; Status bf;struct BSTNode *lchild,*rchild;}BSTNode,*BSTree;Status SearchBST(BSTree T, Status key, BSTree f, BSTree &p) {// 算法9.5(b)// 在根指针T 所指二叉排序树中递归地查找其关键字等于key 的数据元素,// 若查找成功,则指针p 指向该数据元素结点,并返回TRUE ,// 否则指针p 指向查找路径上访问的最后一个结点并返回FALSE ,// 指针f 指向T 的双亲,其初始调用值为NULLif (!T) { p = f; return FALSE; } // 查找不成功else if (key==T->data.key) { p = T; return TRUE; } // 查找成功else if (key<T->data.key)return SearchBST(T->lchild, key, T, p); // 在左子树中继续查找 elsereturn SearchBST(T->rchild, key, T, p); // 在右子树中继续查找 } // SearchBSTStatus InsertBST(BSTree &T, ElemType e) { // 算法9.6 // 当二叉排序树T 中不存在关键字等于e.key 的数据元素时,// 插入e 并返回TRUE ,否则返回FALSE BSTree p,s;if (!SearchBST(T, e.key, NULL, p)) { // 查找不成功s = (BSTree)malloc(sizeof(BSTNode));s->data = e; s->lchild = s->rchild = NULL; if (!p) T = s; // 插入 s 为新的根结点 else if (e.key<p->data.key) p->lchild=s; // 插入s 为左孩子else p->rchild = s; // 插入 s 为右孩子 return TRUE;} else return FALSE; // 树中已有关键字相同的结点,不再插入 } // Insert BSTStatus CreateBST(BSTree &T)//将输入的一组数据,创建为二叉排序树 { Status num; ElemType e;cout<<"请输入二叉排序树结点数:"<<endl; cin>>num; while(num!=0) { cout<<"请输入结点值:"<<endl;cin>>e.key;InsertBST(T,e);//按二叉排序树插入方法; num--;}return 0;}Status max(Status lchild,Status rchild)//取较大的值返回{if(lchild>rchild)return lchild;elsereturn rchild;}Status Depth_bt(BSTree T)//求二叉树深度{if (T==NULL) return 0;return1+max(Depth_bt(T->lchild),Depth_bt(T->rchild));}Status Balance(BSTree T)//递归判断是不是平衡二叉树{Status bl,br;if (T==NULL) return 1;//空树输出是平衡二叉树bl=Depth_bt(T->lchild);//将左子树的深度赋值给bl br=Depth_bt(T->rchild);//将右子树的深度赋值给br if (bl-br>1||br-bl>1)return 0;//如果不满足平衡二叉树的定义返回错误信息return Balance(T->lchild)&&Balance(T->rchild);//递归调用}Status n=0;void N_PreOrderAVL(BSTree T)//先序遍历(根,左,右){if (T){cout<<" "<<T->data.key;n++;N_PreOrderAVL(T->lchild);N_PreOrderAVL(T->rchild);}}Status k_ey[40],k=0;void Key_PreOrderAVL(BSTree T)//先序遍历(根,左,右){if (T){if(k<n){k_ey[k]=T->data.key;k++;}Key_PreOrderAVL(T->lchild);Key_PreOrderAVL(T->rchild);}}int PreorderAVL(BSTree T){if (T){cout<<T->data.key<<" ";PreorderAVL(T->lchild);PreorderAVL(T->rchild);}return 1;}void R_Rotate(BSTree &p) { // 算法 9.9// 对以*p为根的二叉排序树作右旋处理,处理之后p指向新的树根结点,// 即旋转处理之前的左子树的根结点BSTree lc;lc = p->lchild; // lc指向*p的左子树根结点p->lchild = lc->rchild; // lc的右子树挂接为*p的左子树lc->rchild = p; p = lc; // p指向新的根结点} // R_Rotatevoid L_Rotate(BSTree &p) { // 算法 9.10// 对以p↑为根的二叉排序树作左旋处理,处理之后p指向新的树根结点,// 即旋转处理之前的右子树的根结点BSTree rc;rc = p->rchild; // rc指向*p的右子树根结点p->rchild = rc->lchild; // rc的左子树挂接为*p的右子树rc->lchild = p; p = rc; // p指向新的根结点} // L_Rotatevoid LeftBalance(BSTree &T) { // 算法 9.12// 对以指针T所指结点为根的二叉树作左平衡旋转处理。
