电路第八章剖析
电子技术基础——电路与模拟电子(第8章)

➢采用复合管
8.0 零点漂移
多级放大电路
输出 输入
第一级 放大电路
第二级
……
放大电路
功放级
第n级 放大电路
第 n-1 级 放大电路
耦合:即信号的传送。
耦合方式:阻容耦合;直接耦合;变压器耦合;光电耦合。
集成运算放大器主要采用直接耦合
多级放大电路对耦合电路要求:
1). 静态:保证各级Q点设置 2). 动态: 传送信号。
第一级反相比例
vO1
Rf 1 R1
vS1
第二级反相加法
vO
Rf 2 R2
vS2
Rf 2 R2
vO1
即
vO
Rf 2 R2
Rf 1 R1
vS1
Rf 2 R2
vS2
当 Rf 1 R1 ,Rf 2 R2 时
得 vO vS1 vS2
(减法运算)
4. 单运放的加减运算电路
R1
R5
ui1
ui2
R2
R3 ui3
重点难点
重点:集成运算放大器电路分析方法; 难点:理解差模信号和共模信号;
差放电路抑制共模信号的原理; 差放电路的分析;
集成电路的特点
➢电路结构与元件参数对称性好
➢电路中使用的二极管,多用作温度补偿元 件或电位集移成动电电路路:,将大二都极采管用、B三JT极的发射结 构成。 管、电阻等器件及导线共同 ➢(不Rb能)制代制 成作替作 特大,在定电大一的阻电块功。阻半能电恒导的阻流体电用源基子B代J片电T替的上路;体完。电阻 ➢不能制作大电容。电容用BJT结电容代替, 大电容只能外接;
通用型集成电路运算放大器F007
8.2.1 理想集成运放的电路模型
电路分析基础课件第8章耦合电感和变压器电路分析

耦合电感在电路中的应用
信号传输
耦合电感在电路中可以用于传输信号,由于其电磁耦 合的特性,信号可以在不同的电路之间传递。
滤波器
耦合电感可以组成各种滤波器,如高通、低通、带通 等,用于对信号进行筛选和过滤。
振荡器
在振荡电路中,耦合电感与电容配合使用,可以形成 振荡信号。
变压器在电路中的应用
电压转换
01
电路分析基础课件第8章耦合电感 和变压器电路分析
目 录
• 耦合电感电路分析 • 变压器电路分析 • 耦合电感和变压器在电路中的应用 • 习题与思考
01 耦合电感电路分析
耦合电感基本概念
耦合电感定义
由两个或多个线圈通过磁场相互耦合而构成的电路元件。
耦合系数
描述耦合电感线圈之间耦合程度的一个参数,其值在0到1之间 。
习题2
计算变压器初级和次级线圈的电压和电流, 以及变压器的变比。
习题3
分析一个具有变压器和耦合电感的电路,计 算各元件的电压和电流。
习题4
设计一个变压器,满足特定的电压和电流要 求,并计算所需的匝数和线径。
思考题
思考题1
如何理解耦合电感和变压器在 电路中的作用?
思考题2
如何分析具有耦合电感和变压 器的电路?
02
变压器在电力系统、电子设备和 工业自动化等领域有着广泛的应 用,是电力传输和分配的关键设 备之一。
变压器的工作原理
当交流电通过变压器的一次绕组时, 会在铁芯中产生交变磁场,这个磁场 会感应出电动势,从而在二次绕组中 产生电压和电流。
变压器的工作原理基于电磁感应定律 和全电流定律,通过改变绕组匝数实 现电压和电流的变换。
根据耦合系数和线圈的匝数比,可以确定电压和电流的幅值关系。
电路分析-第八章 线性动态电路的时域2006
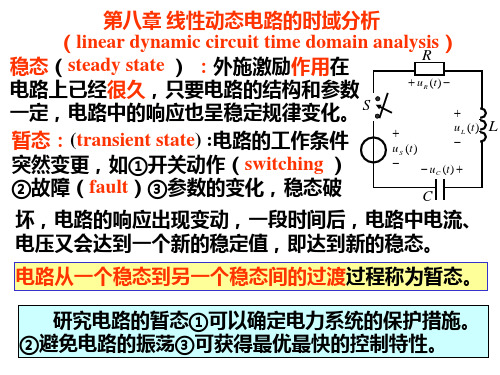
uR
P
0C
D
t
t
CD u
tg
u du dt
U0e
1
U
0e
t
R的单位为,L的单位为H ,则L / R的单位为s(秒)
令 L / R,具有时间的量纲。称为时间常数。
令p 1 , p具有频率的量纲。称为固有频率。
t
iL (t ) I0e (t 0),
一阶RC电路的零输入响应的求解步骤: ①求解电路换路前的状态; ②求解电路换路后初始值;(第一节)
③求时间常数:
RC, R为换路后从电容两个端纽看进去的等效电阻。
④代入(*)式
t
(*) rzi (t) r(0 )e (t 0)
二、一阶RL电路的零输入响应:
R0
iL(t)
电路换路前电路已达稳态:
t
)
R
uC (0 ) US , uR (0 ) 0,
i(0 ) 0
在t=0时,开关突然由a打向b,电容通过电阻R形成回
路放电,此时电路已没有外施激励源,响应由电容的初
始状态引起,即零输入响应。
由KVL得:
uC Ri 0
i C duC dt
RC
duC dt
uC
0(t
0)
是uc的一阶齐次微分方程,用分离变量法解之
uR (t)
uS (t)
uL (t) L
uC (t)
C
坏,电路的响应出现变动,一段时间后,电路中电流、
电压又会达到一个新的稳定值,即达到新的稳态。
电路从一个稳态到另一个稳态间的过渡过程称为暂态。
研究电路的暂态①可以确定电力系统的保护措施。 ②避免电路的振荡③可获得最优最快的控制特性。
《电路分析基础》第八章:阻抗和导纳

学 YR = 1 / R = G
YC = jω C
YL =
1 =−j 1
jω L
ωL
容纳: BC = ωC
感纳:
BL
=
−1
ωL
信息学院电子系
14
2 单口网络的阻抗和导纳
无源单口网络在正弦稳态时单口端钮的电压相量与电流相
中量之比为输入阻抗,阻抗的倒数为输入导纳
输入阻抗:Z
=
U I
(在关联参考方向下)
信息学院电子系
3
8.3 振幅相量
中1. 正弦稳态电路 国 ¾ 正弦波 u(t)= Umcos(ωt+θu) i(t)= Imcos(ωt+θi)
三特征: 振幅,角频率ω,初相角θ
海 + uR - + uL - iL 洋 iS
u
uS
uL
uR
o
ωt
大 ¾ 正弦稳态电路各电压电流响应与激励均为同频率正弦波。 学 ¾ 对于正弦稳态电路,只需确定初相位和振幅
Imcos(ωt+θi) =-CωUmsin(ωt+θu)
¾ 相量关系 =CωUmcos(ωt+θu+90º)
Re(Ime jωt ) = Re( jωCUme jωt )
Im = jωCUm
I = jωCU
Im∠θi =ωCUm∠(θu +90°)
电容 Im=ωCUm
I=ωCU
+ ... + + ... +
Z1n In Z2n In
= US11 = US22
⎪...
Zii:网孔i自阻抗
Zkj(k≠j):网孔k与j的互阻抗
第八章 正弦波振荡电路
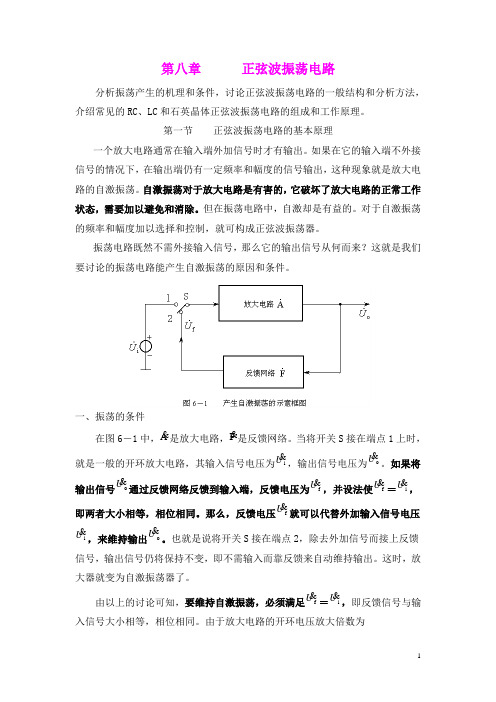
第八章 正弦波振荡电路分析振荡产生的机理和条件,讨论正弦波振荡电路的一般结构和分析方法,介绍常见的RC 、LC 和石英晶体正弦波振荡电路的组成和工作原理。
第一节 正弦波振荡电路的基本原理一个放大电路通常在输入端外加信号时才有输出。
如果在它的输入端不外接信号的情况下,在输出端仍有一定频率和幅度的信号输出,这种现象就是放大电路的自激振荡。
自激振荡对于放大电路是有害的,它破坏了放大电路的正常工作状态,需要加以避免和消除。
但在振荡电路中,自激却是有益的。
对于自激振荡的频率和幅度加以选择和控制,就可构成正弦波振荡器。
振荡电路既然不需外接输入信号,那么它的输出信号从何而来?这就是我们要讨论的振荡电路能产生自激振荡的原因和条件。
一、振荡的条件在图6-1中,A是放大电路,F 是反馈网络。
当将开关S 接在端点1上时,就是一般的开环放大电路,其输入信号电压为i U ,输出信号电压为o U 。
如果将输出信号o U 通过反馈网络反馈到输入端,反馈电压为f U ,并设法使f U=i U ,即两者大小相等,相位相同。
那么,反馈电压f U就可以代替外加输入信号电压i U ,来维持输出o U 。
也就是说将开关S 接在端点2,除去外加信号而接上反馈信号,输出信号仍将保持不变,即不需输入而靠反馈来自动维持输出。
这时,放大器就变为自激振荡器了。
由以上的讨论可知,要维持自激振荡,必须满足f U=i U ,即反馈信号与输入信号大小相等,相位相同。
由于放大电路的开环电压放大倍数为i o A U U = o f F U U =若i f U U =,则F A=o fi oU U U U =1(F A称为环路增益)。
因此,振荡电路维持自激振荡的条件是:F A=1 即F A=1称为幅值平衡条件。
其物理意义为:信号经放大电路和反馈网络构成的闭环回路后,幅值保持不变,既无增加也无衰减。
f a ϕϕ+=2n π(n =0,1,2……)称为相位平衡条件。
电路分析基础 第5版 第8章 电路的暂态分析

1/6/2022
3
8.1.2 换路定律
由于能量不能发生跃变,与能量有关的状态变
量iL和uC,在电路发生换路后的一瞬间,其数 值必定等于换路前一瞬间的原有值不变。即:
换路定律
iL (0) iL (0) uC (0) uC (0)
换路发生在t=0时刻,(0-)为换路前一瞬间,该时刻电路还 未换路;(0+)为换路后一瞬间,此时刻电路已经换路。(0-) 时刻、(0+)时刻 和0时刻的时间间隔趋近零但不等于零。
1/6/2022
RL一阶电路的零输入响应
图示电路在换路前已达稳态。t=0时开关闭合。
R
开关闭合将电流源短路,暂态过程在R和
+ uR -
Байду номын сангаас
iL
+
L构成的回路中进行。
对电路列KVL方程:
RiL
+
L
diL dt
=0
IS t=0 S
L uL
-
以iL为待求响应,可得上式的解:iL (t)
=
-Rt
iL (0+ )e L
工程实际一般认为:经历了3~5τ的时间过渡过程基本结束
1/6/2022
阅读理解
1. 时间常数τ是用来表征一阶电路过渡过程进行的快慢程度的 物理量。
2. 时间常数τ仅由电路参数决定,RC一阶电路中,τ=RC;RL 一阶电路中,τ=L/R。τ的大小反映了电路的特性,与换路情况 和外加电压无关。
3. 时间常数τ是已经完成了过渡过程63.2%所经过的时间。在 工程计算中,一般认为经历了3~5τ时间,过渡过程基本结束。
1. 一阶电路的零输入响应都是随时间按指数规律衰减到零 的,这实际上反映了在没有外激励(电源)的作用下,储能元 件的原始能量逐渐被电阻消耗掉的物理过程。
电工学第八章 基本放大电路

RL RC//RL
返回
(3)电压放大倍数的计算
•
•
Ui I b rbe
•
•
•
UoIcRL IbRL
式中 RL RC//RL 则放大电路的电压放大倍数
•
Au
U0
•
Ui
R' L rbe
输出端开路时(未接RL)
Au
RC rbe
结 论
❖ Au与β、rbe和并联电阻 有关;
❖负载电阻RL越小,放大倍数越小; ❖ 输入电压与输出电压相位相反。
返回
放大电路可分为静态和动态两种情况来分析。
动态:输入端加上输入信号时,放大电路的工作状态。
❖ 此时,电路中电流和电压值是直流和交流分量叠加。 ❖ iB、iC、iE、uBE和uCE,称为动态值(直流分量和交流 分量的叠加) ❖ 对放大电路的动态分析就是采用放大电路的交流通道, 确定电压放大倍数Au,输入电阻ri,输出电阻ro等。 ❖ 动态分析方法:微变等效电路法和图解法 直流通道——只考虑直流信号的分电路。 交流通道——只考虑交流信号的分电路。
步骤: ❖ 用估算法确定IB; ❖ 由输出特性曲线确定IC和UCE。
由 U CE U CC ICR C 得
IC=0时, UCEUCC
UCE=0时,I C
U CC RC
返回
(1)输入输出特性曲线
如下图所示,(IBQ,UBEQ) 和( ICQ,UCEQ )分别对 应于输入输出特性曲线上的一个点,称为静态工
0.0m 4 A40A
IC IB
3.750.04
1.5mA
U CE U CC ICR C
1 2 1.5 1 0 34 130
6V
返回
《电路理论》第八章 非正弦周期电流电路(第1-5节)课堂笔记及练习题

《电路理论》第八章非正弦周期电流电路(第1-5节)课堂笔记及练习题主题:第八章非正弦周期电流电路(第1-5节)学习时间: 2016年1月18日--1月24日内容:一、本周知识点及重难点分布表17-1 本周知识点要求掌握程度一览表序号学习知识点要求掌握程度本周难点了解熟悉理解掌握1 非正弦周期信号★2 非正弦周期信号的频谱★3 非正弦周期信号的有效值、平均值、平均功率★4 线性非周期电流电路的分析与计算★5 第八章小结★二、知识点详解【知识点1】非正弦周期信号1、非正弦周期信号的产生(1)电源电压不是理想的正弦交流量(2)电路中有几个不同频率的电源共同作用(3)电路中含有非线性元件2、常见的非正弦周期信号图17-1 非正弦电源电压信号如果上述激励和响应按一定规律周而复始地变化,称为非正弦周期电压和电流。
3、非正弦周期信号的表示既然两个不同频率的正弦信号叠加后得到一个非正弦周期变化的信号。
所以有:()()k k 0sin k f t A k t ωφ∞==+∑分析非正弦周期电流电路:利用傅里叶级数分解非正弦周期电压或电流;分别计算各频率正弦信号单独作用下的分量;根据叠加定理将分量相加得电路实际电压或电流。
【知识点2】非正弦周期信号的频谱1、周期函数的傅里叶级数周期为T 的时间函数()f t 展开:()()()01s 1s 2s 2s cos sin cos2sin 2f t a a t b t a t b t ωωωω=+++++()0k s k s 1cos sin k a a k t b k t ωω∞==++∑s 2T πω= 傅里叶系数()()()00k s 0k s 01d 2cos d 2sin d T T T a f t t T a f t k t t T b f t k t t T ωω⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩⎰⎰⎰ 01m s 12m s 20km s k 1()sin()sin(2)sin()k f t A A t A t A A k t ωφωφωφ∞==+++++=++∑其中:0k km k k km k km k k kcos sin arctan A aa Ab A A b a φφφ⎧=⎪=⎪⎪=⎨⎪=⎪⎪=⎩谐波分析:将周期函数()f t 分解为直流分量、基波分量和一系列不同频率的各次谐波分量之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 8. 1 复数
1. 复数的表示形式
F a jb 代数式
F | F | (cos j sin )
Im b
|F|
o
三角函数式
F | F | e jθ
指数式
F a Re
F | F | ejθ | F | θ
极坐标式
2. 复数运算 (1)加减运算——代数形式 A1±A2=(a1±a2)+j(b1±b2) (2) 乘除运算——指数形式或极坐标形式
如果F1=F2 则 a1=a2,且b1=b2
或 F1 F2 且θ1 θ2
作业:8-2 (1)、8-3、8-4
8.2 正弦量
1. 正弦量
i
T
波形
瞬时值表达式
0
t
i(t)=Imcos(w t+y)
正弦量为周期函数 f(t)=f ( t+kT )
周期T 和频率f
周期T :重复变化一次所需的时间。
单位:秒s
t
y
波形图
y y =0y =/2 y =-/2
一般 |y |
三、同频率正弦量的相位差 (phase difference)。
u, i
设 u(t)=Umsin(w t+y u)
u
i
i(t)=Imsin(w t+y i)
相位差
0
wt
yu yi
= (w t +y u) - (w t +y i)
= y u-y i
四. 有效值(effective value)
1. 定义
def
I
1 T i 2 (t )dt
T0
有效值也称方均根值(root-meen-square,简记为 rms。)
电压有效值
def
U
1 T u2 (t )dt
T0
2. 正弦电流、电压的有效值
设 i(t)=Imsin(w t + y )
def
复数 ejy = 1∠y 称为旋转因子
特
j
e2
cos
j sin
j
殊
2
2
旋 转
e j(
2
)
c
o
s
(
2
)
j
s i n (
2
)
j
因 子
e j( ) cos( ) j sin( ) 1
+j , –j , -1 都可以看成旋转因子。
3. 复数相等的运算
F1 a1 jb1 F1 θ1 F2 a2 jb2 F2 θ2
相量与正弦量不相等,但是一一对应
注意 统一采用cos函数表示正弦量
例 i 14.14sin(103t 60o)A 试用相量表示 i
解:统一采用cos函数表示正弦量 因此电流i的表达式应为
i 14.14cos(103t 60o 90o)A 14.14cos(103t 150o)A 14.14cos(103t 30o)A
i(t)=Imcos(w t +y )
i + u_
(1) 幅值 (amplitude) (振幅、 最大值) Im
(2) 角频率(angular frequency) w
(3) 初相位(initial phase angle) y
初相位 y
i i(t)=Imsin(w t+y)
i
Im
wt
00 0 0
Re[F(t)] 2Ucos(w t Ψ ) u(t)
结论
任意一个正弦时间函数都有唯一与其对应的
复数函数。
u
2Ucos(w t Ψ )
F(t)
j(w t Ψ )
2Ue
F (t) 2Uej(w tΨ ) F(t) 还可以写成 F (t) 2Ue jy ejwt
定义正弦量u对应的相量为
jy
U Ue
F(t) 则可以写成
F (t) 2Uejwt
u
2Ucos(w t Ψ )
jΨ
U Ue
相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相位
例1 i 141.4cos(314t 30o )A
u 311.1cos(314t 60o )V
试用相量表示 i, u .
解
•
I
10030
o
I
1 T i 2 (t )dt
T0
I
1 T
T 0
I
2 m
sin2
(
wt
y
)
dt
T sin2 ( wt y ) dt
T 1 cos 2(wt y ) 1
dt t
T
1 T
0
0
2
20 2
I
1 T
I
2 m
T 2
Im 2
0.707Im
Im 2I
注意:只适用正弦量
i(t ) Im sin(wt y ) 2I sin(wt y )
频率f :每秒重复变化的次数。 单位:赫(兹)Hz
正弦电流电路 激励和响应均为同频率的正弦量的线性电路
研究正弦电路的意义 1.正弦稳态电路在电力系统和电子技术领域 占有十分重要的地位。
特 ①正弦函数是周期函数,其加、减、求导、 点 积分运算后仍是同频率的正弦函数;
②正弦信号容易产生、传送和使用。
二. 正弦量的三要素:
A1 A2
A1 e jθ1 A 2 e jθ2
A A e j(θ1 θ2 ) 12
A1 A 2 A1 A 2 (ψ1 ψ2 )
A1 A2
A1 e jθ1 A 2 e jθ2
A e 1 j(θ1 θ2 ) A2
A1 A2
A1 A2
(ψ1 ψ2 )
3. 旋转因子
Aejy
A逆时针旋转一个角度y ,模不变
A,
•
U 220 60o V
例2
已知
•
I
50 15
A,
f 50Hz .
试写出电流的瞬时值表达式。
解
i 50 2cos(314t 15 ) A
任意一个正弦时间函数都有唯一与其对应的相量
jΨ
u 2Ucos(w t Ψ ) U Ue
正弦量u包含了三要素:U、 、w, 相量U包含了两个要素:U , 。
注意
① 工程上说的正弦电压、电流一般指有效值,如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。
②交流测量仪表的电压、电流读数一般为有效值。
③区分瞬时值、最大值、有效值的符号。
i, Im , I , u,Um ,U
掌握内容:
1.正弦量的初相位( y <π)
2.相位差的计算( | | )
一般 | |
>0, u 领先(超前)i ,或i 落后(滞后) u <0, i 领先(超前) u,或u 落后(滞后) i
特殊相位关系:
= 0, 同相:
u, i
u
i
0
wt
= ( 180o ) ,反相:
u, i
i
u
0
wt
u, i u i
0
= 9பைடு நூலகம்° 正交
u 领先 i 90°
wt
或 i 落后 u 90°
3.有效值的计算
8.3 相量法的基础
1. 问题的提出
u 2U cos(w t y )
+R
u
-
iL
L
+
u
-C
C
电路方程:
LC
d 2uC dt
RC
duC dt
uC
u(t)
数学运算较复杂
2. 正弦量的相量表示
F (t) 2Uej(w tΨ )
2Ucos(wt Ψ ) j 2Usin(wt Ψ )
