系数正则化论文：系数正则化分类学习回归学习梯度下降法偏方差再生核Hilbert空间

合集下载

机器学习中的回归模型优化方法

机器学习中的回归模型优化方法回归模型是机器学习领域中广泛应用的一种模型，用于预测数值型变量的值。

在实际应用中，我们常常面临着需要优化回归模型以提高预测精度和性能的需求。

本文将介绍机器学习中一些常见的回归模型优化方法，包括特征选择、正则化、模型融合和超参数调优等。

特征选择是回归模型优化的重要一环。

在特征选择过程中，我们会根据各种指标对特征进行评估和筛选，以选择最具有预测能力的特征子集。

常见的特征选择方法包括过滤法、包裹法和嵌入法。

过滤法通过计算特征与目标变量之间的相关性来进行筛选，常用的指标包括相关系数和卡方检验等。

包裹法通过将特征选择问题转化为一个搜索最优特征子集的问题，采用启发式搜索策略来进行特征选择。

嵌入法将特征选择问题融入到模型训练过程中，通过模型自身的特性选择最优特征子集。

正则化是回归模型优化的另一个重要手段。

正则化可以减小模型的复杂度，防止过拟合，提高模型的泛化能力。

常见的正则化方法包括L1正则化和L2正则化。

L1正则化通过在损失函数中加入L1范数惩罚项来促使模型系数稀疏化。

L2正则化通过在损失函数中加入L2范数惩罚项来限制模型系数的大小。

正则化参数可以通过交叉验证等方法来确定。

模型融合是一种通过结合多个回归模型来提高预测性能的方法。

常见的模型融合技术包括平均法、加权法和堆叠法等。

平均法通过对多个模型的预测结果进行平均来得到最终的预测结果。

加权法通过为每个模型分配不同的权重来结合多个模型的预测结果。

堆叠法将多个模型的预测结果作为新的特征输入到另一个模型中进行训练和预测。

超参数调优是回归模型优化的一个重要环节。

超参数是模型训练之前需要人为设定的参数，如学习率、正则化参数等。

超参数的选择直接影响模型的性能。

常见的超参数调优方法包括网格搜索、随机搜索和贝叶斯优化等。

网格搜索通过穷举搜索的方式在给定的超参数空间中寻找最优的超参数组合。

随机搜索通过随机采样的方式在超参数空间中搜索。

贝叶斯优化通过构建模型对超参数进行建模，并通过优化确定最优的超参数组合。

正则化技术在回归问题中的应用效果分析

正则化技术在回归问题中的应用效果分析引言：回归问题是机器学习中的一类重要问题，其目标是通过建立一个数学模型来预测一个或多个连续目标变量。

在实际应用中，为了提高回归模型的泛化能力以及防止过拟合，正则化技术被广泛应用。

本文将分析正则化技术在回归问题中的应用效果。

1. 正则化技术的概述正则化技术是一种通过对模型的复杂度进行惩罚来控制模型的泛化能力的方法。

常见的正则化技术包括L1正则化（Lasso）、L2正则化（Ridge）和弹性网络（Elastic Net）等。

它们通过引入正则化项来限制模型的参数大小，从而避免过度拟合和提高模型的泛化能力。

2. 正则化技术的优点2.1 控制过拟合风险：过拟合是指模型在训练集上表现良好，但在测试集或实际应用中表现不佳的现象。

正则化技术通过限制模型参数的大小，降低模型的复杂度，从而减少过拟合的风险。

2.2 特征选择：正则化技术可以通过L1正则化的方式自动选择特征，将不重要的特征的系数置为零，从而去除对模型的负面影响，提高模型的预测能力。

2.3 提高泛化能力：正则化技术通过限制模型参数的大小，降低模型的复杂度，从而使模型更加稳定和可靠，提高模型的泛化能力。

3. 正则化技术的应用效果分析3.1 L1正则化（Lasso）的应用效果L1正则化通过引入L1范数作为正则化项，可以将某些特征的系数置为零，从而实现特征选择。

L1正则化在具有大量特征的回归问题中表现出色，能够自动筛选出重要的特征，降低维度，提高模型预测能力。

然而，L1正则化在特征高度相关的情况下可能会选择出错误的特征，导致模型的预测能力下降。

3.2 L2正则化（Ridge）的应用效果L2正则化通过引入L2范数作为正则化项，可以限制模型参数的大小。

L2正则化在回归问题中可以有效防止过拟合，提高模型的泛化能力。

与L1正则化相比，L2正则化较为稳定，对异常值不敏感，但无法做到特征选择。

3.3 弹性网络（Elastic Net）的应用效果弹性网络是L1正则化和L2正则化的结合，通过引入L1范数和L2范数作为正则化项，兼具了L1正则化和L2正则化的优点。

正则化系数

正则化系数正则化系数是一种机器学习技术，用于减少模型复杂度和过拟合。

它是对模型参数的一种惩罚，使模型参数变得更小，而不会将模型的准确性降低太多。

在具体的应用中，我们经常使用正则化系数来减少模型的过拟合。

正则化系数的具体形式不是一成不变的，它有很多种，常见的有L1和L2正则化，还有Elastic Net正则化等。

L1正则化和L2正则化的区别主要在于它们的惩罚方式。

L1正则化通过加入绝对值惩罚来实现，而L2正则化则是通过优化器对参数更新过程中加入平方惩罚来实现的。

Elastic Net正则化是结合了L1正则化和L2正则化的一种形式，它通过综合使用L1正则化和L2正则化的惩罚方式来实现参数稀疏性。

当然，正则化系数也有它自己的困难，例如，使用正则化方法时，我们可能会发现它对模型的泛化能力影响不大，这是因为我们的正则化系数可能不够准确。

此外，当我们使用正则化方法时，模型的收敛速度也会变慢。

正则化系数的正确使用非常关键，只有选择合适的正则化系数，才能有效减少过拟合，提高模型的泛化能力。

在机器学习领域，我们会通过尝试不同的正则化系数，然后根据模型的表现来找出最合适的正则化系数。

虽然可以通过试验得出一个最佳的正则化系数，但是这也是需要考虑运行时间和计算资源的，因为大多数机器学习算法都需要合理的训练时间和计算资源。

因此，我们还可以借助一些其他的方法来调整正则化系数，例如比较网络深度，学习速率和正则化系数之间的关系，以获得最优的正则化系数。

总而言之，正则化系数是机器学习研究中非常重要的一块，它可以有效地减少过拟合，提高模型的泛化能力，而正确调整正则化系数也会是一项非常重要的任务。

如果正确使用正则化系数，那么就可以大大提高机器学习的性能。

梯度下降法的正则化和损失函数

梯度下降法的正则化和损失函数梯度下降法是机器学习中常用的最优化算法，其目标是通过更新模型参数来使代价函数（损失函数）最小化。

然而，当数据过拟合时，模型的泛化能力会变得很差，即该模型对新数据的预测能力非常差。

因此，这就需要我们进行正则化。

在本文中，我们将讨论如何使用梯度下降法来进行正则化，并如何改变损失函数以更好地反映模型的性能。

正规化正规化是一种减少模型复杂度的方法。

简而言之，它是通过添加额外的约束或惩罚项来减少模型的自由度。

最常见的正则化方法是L1和L2正则化。

L1正则化会向代价函数中添加一个惩罚项，该项通过对模型参数的绝对值之和进行惩罚来推动这些参数向零靠近。

这可以在某些情况下实现特征选择，因为它促使许多参数成为零。

L2正则化，则是通过向代价函数中添加一个惩罚项使模型的参数在方差上更加受限，从而减少模型的复杂度。

这可以通过限制参数的大小而实现。

考虑一个简单的线性回归问题，我们可以使用L2正则化来最小化代价函数。

假设我们有一个二维特征向量$x = [x_1, x_2]$和相应的标签向量$y$。

我们的目标是找到一个线性模型$y = wx + b$，其中$w$是一个权重向量，$b$是偏差。

我们的代价函数是：$J(w, b) = \frac{1}{2m}\sum_{i=1}^{m}(y^{(i)} - (w^T x^{(i)} + b))^2 + \frac{\lambda}{2}|w|^2$其中，$m$是训练示例的数量，$\lambda$是正则化参数。

第一个部分表示平方误差损失函数，第二个部分表示L2正则化项。

我们可以通过将损失函数和正则化项组合在一起来最小化代价函数。

梯度下降算法的目标是利用代价函数的梯度将目标向最小值移动。

具体来说，我们需要计算代价函数相对于每个权重和偏差的梯度，以便可以通过更新权重和偏差来最小化代价函数。

损失函数在机器学习中，损失函数用于衡量模型预测的质量。

通常，我们使用平均误差或均方误差来衡量模型的性能。

python 梯度下降法正则化

python 梯度下降法正则化梯度下降法及正则化是机器学习中常用的优化方法之一。

梯度下降法用于求解函数的最优解，而正则化则是对模型进行约束以解决过拟合问题。

本文将详细介绍梯度下降法和正则化的原理及实现方法，并展示其在模型训练中的重要性和应用场景。

一、梯度下降法梯度下降法是一种迭代优化算法，常用于求解无约束的多元函数最优化问题。

它的核心思想是通过不断迭代调整参数，使目标函数的值逐渐趋近最小值。

梯度下降法基于函数的一阶导数（梯度），根据梯度的负方向进行参数的更新。

下面是梯度下降法的具体步骤：1. 初始化参数：选取合适的初始参数向量。

2. 计算梯度：计算目标函数对参数的梯度，即目标函数在当前参数值处的导数。

3. 参数更新：根据梯度和学习率（步长），更新参数向量。

学习率决定了每次迭代参数更新的幅度。

4. 重复迭代：重复执行步骤2和步骤3，直到达到停止条件，如达到预定的迭代次数或目标函数的变化很小。

当目标函数是凸函数时，梯度下降法可以找到全局最优解；当目标函数是非凸函数时，梯度下降法只能找到局部最优解。

二、正则化在机器学习中，如果模型过于复杂，容易导致过拟合（即过度拟合训练数据，导致在新数据上的泛化能力下降）。

为了解决过拟合问题，可以引入正则化。

正则化是在目标函数中添加正则项，对模型的复杂度进行约束。

常见的正则化方法有L1正则化和L2正则化。

1. L1正则化：L1正则化是指在目标函数中添加参数向量的绝对值之和与一个正则化参数的乘积。

L1正则化可以使得模型参数稀疏化，即将某些参数变为0。

这样可以减少参数的个数，降低模型复杂度，提高泛化能力。

2. L2正则化：L2正则化是指在目标函数中添加参数向量的平方和与正则化参数的乘积。

L2正则化可以使得模型参数的取值受到约束，避免某些参数值过大。

L2正则化可以减小模型的方差，对离群点不敏感。

三、梯度下降法正则化将梯度下降法与正则化结合起来，可以进一步提高模型的性能。

在目标函数中同时加入正则项，既优化目标函数的值，又约束模型的复杂度。

深度学习模型的正则化方法与优化策略研究

深度学习模型的正则化方法与优化策略研究引言在近年来，深度学习技术在图像识别、自然语言处理和语音识别等领域取得了巨大成功。

然而，随着网络的深度增加和参数量的增加，深度学习模型容易出现过拟合以及训练过程中的收敛困难等问题。

为了解决这些问题，研究者们提出了许多正则化方法和优化策略。

本文将介绍深度学习模型的正则化方法与优化策略的研究进展，并对各种方法的优缺点进行综合分析。

一、正则化方法正则化是为了防止过拟合而采取的一种策略。

以下是几种常见的正则化方法：1. L1 和 L2 正则化L1 和 L2 正则化是最常见的正则化方法之一。

它们通过在损失函数中增加正则化项来约束模型的参数。

其中，L1 正则化使用参数的绝对值作为正则化项，它有助于产生稀疏的模型；而 L2 正则化使用参数的平方和作为正则化项，有助于减小参数的大小。

这两种方法在防止过拟合方面有着良好的效果。

2. DropoutDropout 是一种在训练过程中随机将部分神经元设置为0的方法。

通过随机丢弃神经元，Dropout 可以增强模型的泛化能力，减少模型对于某些特定神经元的依赖性。

然而，Dropout 会增加训练时间，并且在测试阶段需要对输出进行缩放。

3. 数据增强数据增强是利用已有的数据集生成更多的训练样本。

例如，对于图像识别任务，可以通过对图像进行平移、旋转、缩放等变换来生成新的样本。

数据增强可以有效提高模型的泛化能力，减轻过拟合问题。

四、优化策略优化策略是指在训练深度学习模型时调整模型参数的方法。

以下是几种常见的优化策略：1. 批量梯度下降法（Batch Gradient Descent）批量梯度下降法是最基本的优化算法之一，它通过在每一次迭代中使用所有训练样本来更新模型参数。

然而，批量梯度下降法的计算量较大，在处理大规模数据集时效率较低。

2. 随机梯度下降法（Stochastic Gradient Descent）随机梯度下降法是一种每次迭代仅使用一个样本来更新模型参数的方法。

正则化法和梯度下降法

正则化法和梯度下降法
正则化法和梯度下降法是机器学习中常用的两种方法，其主要目的是在训练模型时避免过拟合和提高准确度。

正则化法是通过在损失函数中添加一个正则化项，来惩罚模型的复杂度。

常见的正则化方法包括L1正则化和L2正则化。

L1正则化会让一部分参数变为0，从而实现特征的选择和降维；L2正则化则会让参数尽可能地趋近于0，从而避免过拟合。

正则化的系数越大，对模型复杂度的惩罚就越大。

梯度下降法则是一种优化算法，主要用于最小化损失函数。

其基本思想是通过迭代，不断调整模型参数，使得损失函数达到最小值。

梯度下降法分为批量梯度下降法、随机梯度下降法和小批量梯度下降法三种。

批量梯度下降法每次迭代需要计算所有样本的误差，计算量较大；随机梯度下降法则是每次迭代随机选择一个样本进行计算，计算速度快但容易陷入局部最优解；小批量梯度下降法则是在批量和随机之间取得平衡，每次迭代计算一部分样本的误差。

正则化法和梯度下降法常常同时使用，可以在保证模型准确率的同时，避免过拟合和提高泛化能力。

- 1 -。

《2024年具有L_q-正则项的稀疏线性判别分析及主成分分析》范文

《具有L_q-正则项的稀疏线性判别分析及主成分分析》篇一具有L_q-正则项的稀疏线性判别分析与主成分分析一、引言在数据分析和机器学习中，线性判别分析（LDA）和主成分分析（PCA）是两种重要的无监督学习方法。

这两种方法在许多领域如图像处理、生物信息学和自然语言处理中都有广泛的应用。

然而，传统的LDA和PCA方法在处理高维数据时可能会遇到一些问题，如过拟合和计算复杂性。

为了解决这些问题，我们引入了具有L_q-正则项的稀疏线性判别分析（Sparse LDA）和主成分分析（Sparse PCA）。

二、L_q-正则项与稀疏性L_q-正则项是一种在优化问题中常见的惩罚项，其目标是通过增加模型参数的稀疏性来防止过拟合。

在稀疏线性判别分析和主成分分析中，L_q-正则项被用来约束模型的系数，使得模型更加简洁，且只保留重要的特征。

三、具有L_q-正则项的稀疏线性判别分析具有L_q-正则项的稀疏线性判别分析是在传统线性判别分析的基础上引入了稀疏约束。

这种方法不仅可以有效避免过拟合问题，还能对数据的特征进行筛选和压缩。

我们首先构建一个包括类内散度矩阵和类间散度矩阵的目标函数，然后在其中加入L_q-正则项，形成具有稀疏约束的优化问题。

通过求解这个优化问题，我们可以得到稀疏的系数矩阵，该矩阵中的元素可以看作是各个特征的权重。

四、具有L_q-正则项的稀疏主成分分析与稀疏线性判别分析类似，具有L_q-正则项的稀疏主成分分析也是在传统主成分分析的基础上引入了稀疏约束。

我们首先计算数据的协方差矩阵或相关矩阵，然后通过求解一个包含L_q-正则项的优化问题来获得稀疏的主成分系数。

这种方法不仅能够帮助我们降维，还可以根据系数的权重来筛选出最重要的特征。

五、实验与结果我们使用一些公开的数据集来验证我们的方法。

首先，我们分别应用了传统的LDA和PCA方法，然后应用了具有L_q-正则项的稀疏LDA和Sparse PCA方法。

通过比较这些方法的性能，我们发现具有L_q-正则项的稀疏方法在处理高维数据时具有更好的效果，尤其是在防止过拟合和提高解释性方面。

机器学习-梯度下降、正则、交叉验证、特征选择、变量分类

best_feature, best_score while ( condition not meet):
for each feature fi in remaining_feature_set: best_feature_set <= best_feature_set + fi score = cal(data, best_feature_set) best_feature_set <= best_feature_set - fi if score > best_score: best_score = score best_feature = fi
属于中间折中的方案
还有哪些地方可以优化？？ LOGO do
直到收敛或者参数值变化很小
LOGO
正则
Bias variance trade-off LOGO 过拟合问题从这个角度能不能去解释为什么深度学习会有优势？
减少过拟合方法/模型复杂度 LOGO
1. 减少特征个数 2. 增加样本数量 3. 引入正则项
正则化是降低模型复杂度的一种方法 LOGO
惩罚参数
正则项
比如 L2，L1， L1+L2 正则
惩罚系数越大，模型复杂度越低；惩罚系数越小、模型复杂度越高
加LO入GO正则会降低bias, 假设逻辑回归，而且给定了所有可能的参数空间，那其实相当于从所有参数空间里选出最好的那一组参数。
第二步
训练集
测试集
第三步
for each \lambda in [0.001, 0.01, 0.1, 0.5, 1, 5, 10 ……] , we do 第4.1步
测试集测试集
训练模型
评估模型
得到一个准确率f_1

学习算法中的正则化方法

学习算法中的正则化方法在机器学习领域，正则化是一种常用的方法，用于控制模型的复杂度，防止过拟合。

正则化方法通过在损失函数中引入一个正则项，来约束模型的参数，从而达到降低模型复杂度的目的。

本文将介绍几种常见的正则化方法，并探讨它们的优缺点。

一、L1正则化L1正则化是一种常用的正则化方法，它通过在损失函数中添加参数的绝对值之和来约束模型的复杂度。

L1正则化可以使得模型的参数稀疏化，即将一些不重要的特征的权重降低甚至置零。

这种方法在特征选择和降维中非常有用。

然而，L1正则化也存在一些问题。

首先，由于L1正则化的非光滑性，优化过程可能会变得困难。

其次，当特征之间存在相关性时，L1正则化倾向于选择其中一个特征，而忽略其他相关特征。

因此，在处理高维数据时，需要谨慎使用L1正则化。

二、L2正则化L2正则化是另一种常见的正则化方法，它通过在损失函数中添加参数的平方和来约束模型的复杂度。

L2正则化可以使得模型的参数分布更加平滑，避免出现过大的权重。

这种方法在回归和分类问题中广泛应用。

与L1正则化相比，L2正则化具有一些优势。

首先，L2正则化的平滑性使得优化过程更加稳定，容易收敛。

其次，L2正则化可以保留更多的特征，而不像L1正则化那样容易将某些特征置零。

然而，L2正则化也有一个缺点，即它不能自动进行特征选择，可能会保留一些无关特征。

三、弹性网（Elastic Net）弹性网是L1正则化和L2正则化的一种结合，它在损失函数中同时引入了L1和L2正则项。

弹性网可以综合利用L1正则化和L2正则化的优点，既能够进行特征选择，又能够保留相关特征。

弹性网在处理高维数据时特别有用，可以有效地处理特征相关性和冗余性。

然而，弹性网的一个缺点是需要调节两个超参数，即L1正则化项的权重和L2正则化项的权重，这增加了模型的复杂度。

四、早停法（Early Stopping）早停法是一种简单而有效的正则化方法，它通过监控模型在验证集上的性能，来决定何时停止训练。

regularizer和normalization -回复

regularizer和normalization -回复Regularizer和Normalization是在机器学习和深度学习中经常使用的技术手段。

它们的目的都是为了提高模型的泛化能力和训练效果。

本文将以正则化（regularization）和归一化（normalization）为主题，分别进行详细的讲解和步骤回答。

一、正则化（Regularization）正则化是一种用于减小模型的复杂性，防止过拟合的技术手段。

在模型训练过程中，为了最小化训练数据的损失函数，模型会尽可能多地拟合训练样本，导致模型的复杂度过大，无法很好地适应未见过的数据。

正则化通过在损失函数中加入正则化项，约束模型的复杂度，从而使得模型更加简单。

常用的正则化方法有L1正则化和L2正则化。

L1正则化通过将模型参数的绝对值加权求和加入到损失函数中，使得模型参数尽可能稀疏化，即尽量将不重要的参数设为0；L2正则化通过将模型参数的平方和加权求和加入到损失函数中，使得模型参数尽量小，防止参数过大。

步骤回答：1. 初始化模型参数。

首先，需要初始化模型的权重和偏置，通常可以使用随机初始化的方法。

2. 定义损失函数。

为了最小化模型在训练集上的损失，需要定义一个损失函数。

常见的损失函数有平方损失、交叉熵损失等，可以根据具体的问题选择适合的损失函数。

3. 加入正则化项。

在定义损失函数的基础上，加入正则化项。

正则化项由模型参数的规则化项和系数组成，可以选择L1正则化项或L2正则化项。

加入正则化项后的损失函数可以表示为原始损失函数加上正则化项的加权和。

4. 设定超参数。

正则化项中的系数被称为超参数，需要根据经验或交叉验证来确定。

通常，超参数越大，模型的复杂度越小，正则化的效果越显著。

5. 优化算法。

为了最小化损失函数，需要选择一个优化算法。

常见的优化算法有梯度下降法、随机梯度下降法等。

优化算法的作用是通过更新模型的参数，使得损失函数不断减小。

6. 进行模型训练。

写给初学者的LASSO回归

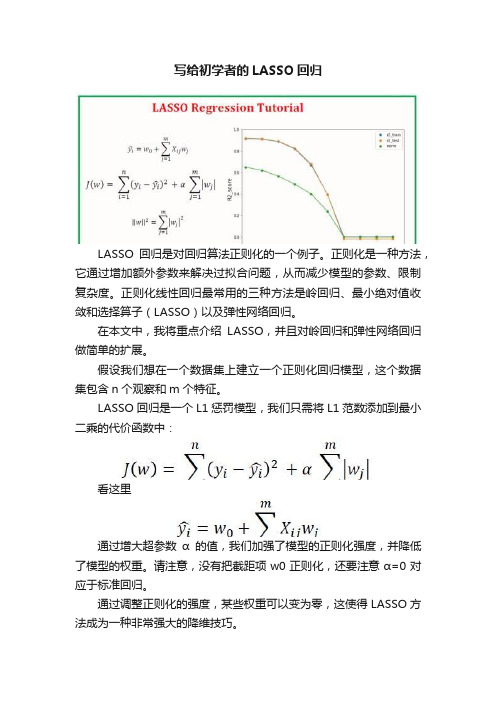
写给初学者的LASSO回归LASSO回归是对回归算法正则化的一个例子。

正则化是一种方法，它通过增加额外参数来解决过拟合问题，从而减少模型的参数、限制复杂度。

正则化线性回归最常用的三种方法是岭回归、最小绝对值收敛和选择算子（LASSO）以及弹性网络回归。

在本文中，我将重点介绍LASSO，并且对岭回归和弹性网络回归做简单的扩展。

假设我们想在一个数据集上建立一个正则化回归模型，这个数据集包含n个观察和m个特征。

LASSO回归是一个L1惩罚模型，我们只需将L1范数添加到最小二乘的代价函数中：看这里通过增大超参数α的值，我们加强了模型的正则化强度，并降低了模型的权重。

请注意，没有把截距项w0正则化，还要注意α=0对应于标准回归。

通过调整正则化的强度，某些权重可以变为零，这使得LASSO方法成为一种非常强大的降维技巧。

LASSO算法•对于给定的α，只需把代价函数最小化，即可找到权重或模型参数w。

•然后使用下面的等式计算w（不包括w0）的范数：案例研究：使用游轮数据集预测船员人数我们将使用邮轮数据集cruise_ship_info.csv来演示LASSO技术本案例已经发布在实验平台，请关注微信公众号：老齐教室。

并回复： #姓名+手机号+案例# 获取。

注意： # 必须要有。

1.导入必要的库import numpy as npimport pandas as pdimport matplotlib.pyplot as plt2.读取数据集并显示列df = pd.read_csv('cruise_ship_info.csv')df.head()3.选择重要的变量从《数据准备和特征工程》中的有关阐述可知，协方差矩阵图可用于特征选择和降维。

从前述数据集中发现，在6个预测特征（['age’, 'tonnage’, 'passengers’, 'length’, 'cabins’, 'passenger_density’] ）中，如果我们假设重要特征与目标变量的相关系数为0.6或更大，那么目标变量“crew”与4个预测变量“tonnage”, “passengers”, “length, and “cabins”的相关性很强。

线性回归中的L1与L2正则化

线性回归中的L1与L2正则化在这篇文章中，我将介绍一个与回归相关的常见技术面试问题，我自己也经常会提到这个问题:描述回归建模中的L1和L2正则化方法。

在处理复杂数据时，我们往往会创建复杂的模型。

太复杂并不总是好的。

过于复杂的模型就是我们所说的“过拟合”，它们在训练数据上表现很好，但在看不见的测试数据上却表现不佳。

有一种方法可以对损失函数的过拟合进行调整，那就是惩罚。

通过惩罚或“正则化”损失函数中的大系数，我们使一些(或所有)系数变小，从而使模型对数据中的噪声不敏感。

在回归中使用的两种流行的正则化形式是L1又名Lasso回归，和L2又名Ridge回归。

在线性回归中我们使用普通最小二乘(OLS)是用于拟合数据的:我们对残差(实际值与预测值之间的差异)进行平方，以得到均方误差(MSE)。

最小的平方误差，或最小的平方，是最适合的模型。

让我们来看看简单线性回归的成本函数:对于多元线性回归，成本函数应该是这样的，其中是预测因子或变量的数量。

因此，随着预测器()数量的增加，模型的复杂性也会增加。

为了缓解这种情况，我们在这个成本函数中添加了一些惩罚形式。

这将降低模型的复杂性，有助于防止过拟合，可能消除变量，甚至减少数据中的多重共线性。

L2 -岭回归L2或岭回归，将惩罚项添加到系数大小的平方。

是一个超参数，这意味着它的值是自由定义的。

你可以在成本函数的末端看到它。

加上惩罚，系数受到约束，惩罚系数大的代价函数。

L1 -Lasso回归L1或Lasso回归，几乎是一样的东西，除了一个重要的细节-系数的大小不是平方，它只是绝对值。

在这里，成本函数的最后是的绝对值，一些系数可以被精确地设置为零，而其他的系数则直接降低到零。

当一些系数变为零时，Lasso 回归的效果是特别有用的，因为它可以估算成本并同时选择系数。

还有最重要的一点，在进行任何一种类型的正则化之前，都应该将数据标准化到相同的规模，否则罚款将不公平地对待某些系数。

机器学习中的正则化与优化算法

机器学习中的正则化与优化算法在机器学习中，正则化与优化算法是两个非常重要的概念，它们广泛应用于各类算法模型中，如线性回归、逻辑回归、支持向量机等。

本文将分别介绍正则化和优化算法的基本概念及其在机器学习中的应用。

正则化正则化是一种在机器学习中广泛应用的技术，用于对过拟合进行控制。

所谓过拟合，是指模型过于复杂，表现出对于训练集的拟合能力非常好，但对于新样本的泛化能力却很差。

正则化通过限制模型参数的大小或者对模型参数进行约束，来使学习到的模型更简单，从而避免过拟合的问题。

在线性模型中，常用的正则化方法有L1正则化和L2正则化。

L1正则化（也称Lasso）通常会将一些参数缩小到0，从而起到特征筛选的作用。

而L2正则化（也称岭回归）则会使模型参数分散在各个维度上，从而减小模型的过拟合风险。

除了线性模型之外，正则化还可以应用于神经网络等复杂模型中，如Dropout、BatchNormalization等。

优化算法优化算法是机器学习算法中一个非常重要的概念，它的作用是通过对目标函数的优化，获得一个更优的模型参数组合。

机器学习算法通常需要优化的目标函数是非常复杂的，很难直接求解。

因此，常用的优化方法是通过迭代算法，通过一系列的步骤逐步寻找最优解。

在机器学习中，常见的优化算法有梯度下降、SGD、Adam等。

其中，梯度下降是最基本的优化算法，它通过计算函数的梯度，来确定函数的最小值。

当目标函数是凸函数时，梯度下降算法可以保证收敛到全局最优解。

而SGD则是一种更为高效的优化算法，它不需要计算全部训练数据的梯度，而是采用随机采样的方法，每次只计算一个样本的梯度。

Adam算法是近年来提出的一种非常有效的优化算法，它可以兼顾速度和准确性，具有较好的收敛性能。

与传统梯度下降算法相比，Adam算法在处理非凸函数时效果更好。

总结机器学习中的正则化与优化算法是非常重要的两个概念，在各类算法模型中都得到了广泛的应用。

正则化能够有效避免模型的过拟合问题，而优化算法则可以帮助我们获得更好的模型参数组合。

《正则化方法的有效应用》论文

《正则化方法的有效应用》论文
正则化方法是统计模型中常见的一类优化策略，它通过引入参数约束，来最小化模型的过拟合风险，以获得更稳定的模型性能。

在实际应用中，正则化方法已经成功应用于许多机器学习任务，如分类、回归、聚类等。

本文将简要介绍正则化方法的基本原理及其有效应用，为实际工作提供参考。

首先，我们介绍正则化方法的基本原理。

正则化是一种限制模型复杂度的有用技术。

它主要是在损失函数中引入一个正则化项，来控制模型参数的大小，从而降低模型的复杂度。

因此，正则化可以有效避免模型过拟合，提高模型的稳定性。

正则化技术可以分为L1正则化和L2正则化，其中L1正则化是一种
参数稀疏化技术，即参数向零的方向收敛，从而减少模型的参数量；L2正则化是一种参数衰减技术，它能使参数尽可能接
近于0，但不会降低模型的参数量。

其次，本文将介绍正则化方法的有效应用。

首先，正则化方法可以用于特征选择任务，通过L1正则化技术可以实现特征稀疏，有效地进行特征选择，提高模型的表现。

其次，正则化方法可以用于图像分类任务，以解决深度神经网络中参数过多而出现的过拟合问题，为图像分类提供更加稳定的性能。

最后，正则化方法可以用于性能优化任务，它能够实现训练时间缩短，获得更好的模型表现。

综上所述，正则化方法是一种有效的机器学习优化策略，它可以有效避免模型过拟合，为机器学习任务提供更稳定的模型性能。

此外，正则化方法在实际应用中也可以用于特征选择、图
像分类和性能优化等任务。

最后，本文只简要介绍了正则化方法的基本原理及其有效应用，希望能给读者提供参考。

梯度下降法、正则化与逻辑回归

梯度下降法、正则化与逻辑回归1.梯度下降法在介绍梯度下降法之前，先介绍下泰勒公式，泰勒公式的基本形式如下：f(x)=f(x0)+f′(x0)(x−x0)+1 2f″令x=w t+1，w t+1代表第t+1次参数向量的值；令x0=w t，代表第t次参数向量的值；其中w共有k个参数，w=[w1,w2,…,w k]；令x-x0=△w，取⼀阶泰勒公式，则：f({{\boldsymbol{w} }^{t+1}})\approx f({{\boldsymbol{w}}^{t}})+{{f}^{'}}({{\boldsymbol{w}}^{t}})\cdot \Delta \boldsymbol{w}由于是梯度下降，所以f({\boldsymbol{w}^{t + 1}}) \le f({\boldsymbol{w}^t})，所以\Delta \boldsymbol{w}=\text{-}\alpha \cdot {{f}^{'}}({{\boldsymbol{w}}^{t}})令函数f为损失函数J，则{{\boldsymbol{w}}^{t+1}}={{\boldsymbol{w}}^{t}}\text{-}\alpha \cdot {{J}^{'}}({{\boldsymbol{w}}^{t}})故第t+1次参数向量的值等于第t次参数向量的值减去损失函数偏导乘以学习率α。

2.正则化为了防⽌过拟合，⼀般采⽤正则化，正则化⼀般分为L1正则化和L2正则化，分别为：{J_1}(\boldsymbol{w}) = J(\boldsymbol{w}) + \lambda \sum\limits_{i = 1}^k {\left| {{w_i}} \right|}{J_2}(\boldsymbol{w}) = J(\boldsymbol{w}) + \frac{\lambda }{2}\sum\limits_{i = 1}^k {w_i^2}分别对w i求偏导，得w_i^{t + 1} = w_i^t - \alpha \frac{{\partial J(\boldsymbol{w})}}{{\partial w_i^t}} - \lambda \alpha {\mathop{\rm sgn}} (w_i^t) w_i^{t + 1} = w_i^t - \alpha \frac{{\partial J(\boldsymbol{w})}}{{\partial w_i^t}} - \lambda \alpha w_i^t最后，L1正则化：w_i^{t + 1} = w_i^t - \alpha (\frac{{\partial J(\boldsymbol{w})}}{{\partial w_i^t}} + \lambda {\mathop{\rm sgn}}(w_i^t))L2正则化：w_i^{t + 1} = (1 - \lambda \alpha )w_i^t - \alpha \frac{{\partial J(\boldsymbol{w})}}{{\partial w_i^t}}从以上公式可以发现L1正则化相对于L2正则化更容易产⽣数据稀疏性，并且两则都可以防⽌过拟合。

回归正则化方法

回归正则化方法
回归正则化方法是一种在机器学习算法中用于防止数据过拟合的技术。

该方法通过在模型中引入正则化项，对模型的复杂度进行约束，从而避免模型对训练数据的过度拟合。

在回归模型中，常见的正则化方法包括L1正则化（Lasso回归）和L2正则化（Ridge回归）。

L1正则化通过对模型参数的绝对值之和进行惩罚，使
得模型中的某些参数变为零，从而实现特征选择和模型简化。

L2正则化通
过对模型参数的平方和进行惩罚，使得模型参数变小，从而控制模型的复杂度。

除了L1和L2正则化，还有一些其他的正则化方法，如Elastic Net正则化、Group Lasso正则化等。

这些方法可以根据具体问题选择使用。

在实现上，回归正则化方法需要在训练模型时将正则化项加入到损失函数中，然后通过优化算法（如梯度下降法）最小化损失函数，得到正则化后的模型参数。

回归正则化的优点包括：
1. 防止过拟合：通过对模型复杂度的约束，回归正则化可以有效地避免模型对训练数据的过度拟合，提高模型的泛化能力。

2. 特征选择：L1正则化可以实现特征选择的功能，自动地识别出对模型预测最重要的特征。

3. 稀疏模型：L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，使得模型更加简洁易懂。

回归正则化的缺点包括：
1. 参数调优：需要手动调整正则化参数的大小，以获得最佳的模型效果。

2. 对异常值敏感：对于包含异常值的数据集，回归正则化可能会受到较大的影响。

机器学习算法的优化方法

机器学习算法的优化方法一、引言机器学习算法的优化是提高算法性能的关键，能够帮助我们更好地理解数据并做出准确的预测。

本文将介绍几种常见的机器学习算法优化方法，包括梯度下降法、正则化、特征选择和集成学习等。

二、梯度下降法梯度下降法是优化机器学习算法中常用的一种方法。

其基本思想是通过不断迭代来调整算法中的参数，使得目标函数的值达到最小化。

梯度下降法的核心是计算目标函数对于每个参数的梯度，然后按照梯度的反方向调整参数的取值，直到达到最小值。

梯度下降法有不同的变种，如批量梯度下降法、随机梯度下降法和小批量梯度下降法，根据问题的具体情况选择不同的方法进行优化。

三、正则化正则化是通过在目标函数中添加一个正则项，对模型进行约束，避免过拟合的一种优化方法。

常见的正则化方法有L1正则化和L2正则化。

L1正则化通过对参数的绝对值进行惩罚，使得参数更趋向于稀疏，从而实现特征选择和降维的目的；L2正则化通过对参数的平方进行惩罚，使得参数更趋向于0，从而抑制模型复杂度。

正则化可以在机器学习算法中有效地控制模型的复杂度，并改善预测性能。

四、特征选择特征选择是在机器学习算法中常用的一种优化方法，其目的是从原始数据中选择最相关和最有代表性的特征，以提高模型的预测性能和泛化能力。

特征选择可以通过多种方法实现，如过滤法、包裹法和嵌入法等。

过滤法通过对特征的相关性进行评估，并按照一定的标准筛选特征；包裹法将特征选择看作是一个搜索问题，并利用特定算法进行优化；嵌入法是将特征选择和模型训练过程结合起来，通过模型自身的优化来选择特征。

特征选择可以减少数据维度、降低计算复杂度，并提高模型的预测性能。

五、集成学习集成学习是将多个基分类器进行组合，以达到更好的分类性能的一种机器学习方法。

常见的集成学习方法包括Bagging、Boosting和随机森林等。

Bagging是通过对训练数据进行自助采样，并训练多个基分类器，最后通过投票方式进行分类；Boosting是通过迭代训练多个基分类器，每次训练都会调整样本权重以关注错误分类的样本；随机森林是通过建立多棵决策树并进行投票，从而实现分类。