陕西省吴起高级中学2018届高三下学期期中考试数学(理)

合集下载

【高考模拟】陕西省吴起高级中学2018届高三下学期期中考试英语(word版有答案)

吴起高级中学2018届高三第二学期中期考试英语试题第一卷（选择题共三部分）注意事项：请将答案正确填写在答题卡上。

第一部分听力（共两节，每小题1.5分，满分30 分）第一节听下面5段对话，每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What are the speakers doing ?A. Shopping in a supermarket.B. Doing some cooking.C. Having dinner.2. What seats are available?A. The window ones.B. The front row ones .C. The back row ones.3. What time is it now?A. 8:05p.m.B. 8:10p.m.C. 8:25p.m.4. How is the woman going into town?A. By car.B. By underground.C. By bus.5. What are the speakers talking about?A. Hobbies.B. School life.C. Future jobs.第二节听下面5段对话或独白，每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6至7题。

6. What does the woman think of her vacation ?A. Just so-so.B. Colourful.C. Tiring.7. What is the probable relationship between the speakers?A. Co-workers .B. Teacher and student.C. Travel agent and tourist.听第7段材料，回答第8至9题。

陕西省延安市吴起高级中学2018-2019学年高一上学期期中考试(基础卷)数学试题(精编含解析)

3.国内快递 1 000 g 以内的包裹的邮资标准如表：
关于原点对称。
0<x
500<x
1 000<x
运送距离 x(km)
…
≤500
≤1 000
≤1 500
邮资 y(元)
5.00
6.00
7.00
…
如果某人在西安要邮寄 800 g 的包裹到距西安 1 200 km 的某地，那么他应付的邮资是( ) A. 5.00 元 B. 6.00 元 C. 7.00 元 D. 无法确定【答案】C 【解析】【分析】由题目所给表格中，不同距离的邮费可以直接确定选项. 【详解】依题意，以下的公理到公理以内的邮资是元，故选 . 【点睛】本小题是图表分析题，可直接由图表中读出不同距离的邮资，由此可以确定正确选项，属于基础题.
4.已知
，则 m,n 的大小关系是( )
A. m>n B. m=n 【答案】A 【解析】
C. m<n
D. 不能确定
【分析】
利用函数
的单调性，结合
，可以比较出 m，n 的大小关系。
【详解】因为函数
在 R 上的单调递减，而
，所以 m>n.
故选 A.
【点睛】本题考查了指数函数单调性的运用，属于基础题。
5.设 f(x)是定义在 R 上的奇函数，若 f(-1)=3,则 f(1)等于( )
A. －1 B. －3 C. 1 D. 3
【答案】B
【解析】
【分析】利用奇函数的性质 f(-x)+ f(x)=0，可得到答案。【详解】由于 f(x)是定义在 R 上的奇函数，可得到 f(-1)+ f(1)=0，所以 f(1)=-3. 故选 B. 【点睛】本题考查了奇函数的性质，属于基础题。 6.已知 A＝B＝R，x∈A，y∈B，f：x→y＝x-2 是从 A 到 B 的映射，则 5 在 f 作用下的象是( ) A. 3 B. 4 C. 5 D. 6 【答案】A 【解析】【分析】利用映射的性质，将 x =5 代入 y＝x-2 可得到答案。【详解】由题意将 x =5 代入 y＝x-2 得到 y＝3，所以 5 在 f 作用下的象是 3. 故选 A. 【点睛】本题考查了映射的性质，属于基础题。

陕西省吴起高级中学2017_2018学年高二数学下学期期中试题能力卷

吴起高级中学2017-2018学年第二学期高二数学试题（文科能力卷）考试范围：选修4-4、4-5；考试时间：120分钟；注意事项：1．请答题前在答题卡上填写好自己的姓名、班级、考号等信息2．请将答案正确地填写在答题卡上第I 卷（选择题共60分）一、选择题：（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1、直角坐标系中，点)3,1(-的极坐标可以是( ) A.)65,2(π B. )611,2(π C. )34,2(π D. )35,2(π 2、将点M 的极坐标⎪⎭⎫ ⎝⎛310π，化成直角坐标是（）A.(5，B.()5 C.()5，5 D.()5-，-53、曲线的极坐标方程θρsin 4=化为直角坐标方程为（）A.4)2(22=++y xB.4)2(22=-+y xC.4)2(22=+-y xD.4)2(22=++y x 4、参数方程为参数）θθθ(2cos 1sin 22⎩⎨⎧+-=+=y x 化为普通方程是（） A. 042=+-y x B. 042=-+y xC. ]3,2[,042∈=+-x y xD. ]3,2[,042∈=-+x y x5、直线2cos303sin 30x t y t ⎧⎫=--⎨⎬=+⎩⎭（t 为参数）的倾斜角等于（） A. 30° B. 030- C.150° D.135°6、不等式3|2|<-x 的解集为（）A.)1,5(-B.),1()5,(+∞--∞C.)5,1(-D.),5()1,(+∞--∞7、已知d c b a >>,，则下列不等式中恒成立的是（）A. c b d a +>+B. bd ac >C.db c a > D. b c a d -<- 8、下列各式中最小值等于2的是（） A ．x y y x + B ．3422++x x C ．θθtan 1tan + D ．x x -+22 9、设M 11(,)ρθ，N 22(,)ρθ两点的极坐标同时满足下列关系：12120,0ρρθθ+=+=，则M ，N 两点的位置关系是（）A ．重合B ．关于极点对称C ．关于直线2πθ=对称 D ．关于极轴对称 10、如果R y x ∈,那么"0">xy 是|"|||||"y x y x +=+成立的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件11、如果关于x 的不等式a x x <-+-43的解集不是空集，则参数a 的取值范围是（）A. ()1,∞-B. ()+∞,1C. [)+∞,1D. (]1,∞-12、若直线y x b =-与曲线2cos ,sin x y θθ=+⎧⎨=⎩（[0,]θπ∈）有两个不同的公共点，则实数b 的取值范围为（）A.(2B.(+C. (,2(22,)-∞++∞ D.[12)-第II 卷（非选择题90分）二、填空题（本大题共4小题，每小题5分，共20分.每小题请填写最简结果。

2018届高三数学下学期期中试题理

吴起高级中学2017-2018学年第二学期高三中期数学(理科)试卷全卷满分150，考试时间120分钟一、选择题：本题共12小题，每小题5分，共60分．每小题只有一项是符合题目要求的．1.已知集合，，则( )A. B. C. D.2.复数的共轭复数是( )A. B. C. D.3.等差数列中，，则（）A．4 B．6 C．8 D．104.已知某学校有1680名学生，现在采用系统抽样的方法抽取84人，调查他们对学校食堂的满意程度，将1680人按1，2，3…，1680随机编号，则在抽取的84人中，编号落在内的人数为( )A.7B.5C.3D.45.已知向量满足则( )A .B .C .D .6.已知实数满足则的取值范围为（）A. B. C. D.7.《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题：“今有方物一束，外周一匝有四十枚，问积几何？”如右图是解决该问题的程序框图，若设每层外周枚数为，则输出的结果为（）A ．B ．C ．D ．8.一几何体被一个平面截去一部分后，剩余输出部分几何体的三视图如图所示，则剩余部分几何体的体积为（）A.B.C.第8题D.9.已知函数的最小正周期为，且其图像向左平移个单位后得到函数的图像，则函数的图像（）A ．关于直线对称B ．关于直线对称C ．关于点对称D ．关于点对称10.已知为圆：内任意一点，则点落在函数的图象与轴围成的封闭区域内的概率为（）A．0 B．1 C ．D ．11.已知抛物线与双曲线有相同的焦点F,点A是两曲线的交点,且AF ⊥轴,则双曲线的离心率为 ( )A. B. C. D.12.定义在上的可导函数，其导函数记为，满足，且当时，恒有．若，则实数的取值范围是（）A. B. C. D.二、填空题：本题共4小题，每小题5分，共20分．13．在△ABC中，AB ＝，∠A＝75°，∠B＝45°，则AC＝_______．14．已知，则的值是．15．有6名学生参加数学竞赛选拔赛，他们的编号分别是1——6号，得第一名者将参加全国数学竞赛.今有甲、乙、丙、丁四位老师在猜谁将得第一名，甲猜：不是1号就是2号；乙猜：3号不可能；丙猜：4号，5号，6号都不可能；丁猜：是4号，5号，6号中的某一个.以上只有一个人猜对，则他应该是_____________. 16．过球表面上一点引三条长度相等的弦，且两两夹角都为60°,若球半径为，求弦的长度_______．三、解答题:共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17.（本小题满分12分）在钝角中，角所对的边分别为且.（Ⅰ）求的值；（Ⅱ）求的取值范围．18. （本小题满分12分）某校为了解校园安全教育系列活动的成效，对全校学生进行了一次安全意识测试，根据测试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分.现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如图所示：（Ⅰ）求，，的值；（Ⅱ）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人中任选4人，记所选4人的量化总分为，求的分布列及数学期望；（Ⅲ）某评估机构以指标（，其中表示的方差）来评估该校安全教育活动的成效.若，则认定教育活动是有效的；否则认定教育活动无效，应调整安全教育方案.在（Ⅱ）的条件下，判断该校是否应调整安全教育方案？19. （本小题满分12分）如图，四棱锥的底面为平行四边形，.（Ⅰ）求证：;（Ⅱ）若,求二面角的正弦值.20. （本小题满分12分）已知椭圆的一个焦点为，左右顶点分别为，，经过点的直线与椭圆交于、两点.（Ⅰ）求椭圆方程；（Ⅱ）记与的面积分别为和，求的最大值.21. (本小题满分12分)设函数，．（Ⅰ）当时，求函数的最值；（Ⅱ）若函数有极值点，求的取值范围．（二）选考题：请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．(本小题满分10分)已知曲线的极坐标方程为，在以极点为直角坐标原点，极轴为轴的正半轴建立的平面直角坐标系中，直线的参数方程为（为参数）．（Ⅰ）写出直线的普通方程与曲线的直角坐标方程；（Ⅱ）在平面直角坐标系中，设曲线经过伸缩变换得到曲线，若为曲线上任意一点，求点到直线的最小距离．23．(本小题满分10分)已知．（Ⅰ）当时，求不等式的解集；（Ⅱ）若函数的值域为，且，求的取值范围．吴起高级中学2017-2018学年第二学期高三中期数学(理科)试题答案一、选择题13. 2 14.0 15. 丙 16.二、解答题17．【答案】（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）由得：（1分）又由正弦定理得，，（3分）所以（4分）又是钝角三角形，所以．（6分）（Ⅱ）由（Ⅰ）知（8分）又由，所以所以，（10分）又由于函数在上单调递增,所以的取值范围为. （12分）18.解：（I）样本容量，，，（II）从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈，其中“不合格”的学生数=，则“合格”的学生数=．由题意可得．则，，，，。

陕西省吴起高级中学高三物理下学期期中试题

陕西省吴起高级中学高三物理下学期期中试题吴起高级中学2017-2018学年第二学期中期考试高三理综试卷（考试时间：150分钟试卷满分：300分）可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一二、选择题：本题共8小题，每小题6分，共48分。

在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14．下列关于研究物理的思想方法的叙述中正确的是 ( )A ．理想化模型是把实际问题理想化，抓住主要因素，忽略次要因素，如：质点、合力、向心加速度B ．重心、交变电流的有效值等概念的建立都体现了等效替代的思想C ．根据速度定义式v ＝Δx Δt ，当Δt 足够小时，ΔxΔt 就可以表示物体在某时刻的瞬时速度，该定义应用了控制变量法D ．用比值法定义的物理量在物理学中占有相当大的比例，如：E ＝F q 、kdsC πε4=15．2017年8月我国自主设计的载人深潜器“深海勇士号”在南海进行下潜试验。

下图是它从水面开始下潜到返回水面的全过程的速度时间图像，则下列说法中正确的是( ) A ．本次实验过程中加速度最大值是0.025m/s 2B ．在0～1 min 和8～10min 的时间段内“深海勇士号” 处于超重状态C ．“深海勇士号”本次下潜的最大深度为360mD ．“深海勇士”在1～3min 的时间内处于静止状态 16．下列说法正确的是 ( )A ．一群处于n=5的激发态的氢原子向低能级跃迁时最多能辐射出10 种不同频率的光B ．卢瑟福在粒子散射实验中发现了电子，并提出了原子的核式结构学说C ．在光电效应实验中，用同种频率的光照射不同的金属表面，从金属表面逸出的光电子的最大初动能E k 越大，则这种金属的逸出功W 0越大D ．某放射性原子核经过2次α衰变和一次β衰变，核内中子减少了4个17．如图所示，A、B两个质量相同的小球在同一竖直线上，离地高度分别为2h和h，将两球水平抛出后，两球落地时的水平位移之比为1∶2，则下列说法正确的是( )A．A、B两球的初速度之比为1∶4B．A、B两球下落过程中的动能变化量之比为1∶2C．若两球同时抛出，则落地的时间差为2h gD．若两球同时落地，则两球抛出的时间差为(2－1)2h g18．如图，半圆形金属框竖直放在粗糙的水平地面上，套在其上的光滑小球P在水平外力F 的作用下处于静止状态，P与圆心O的连线与水平面的夹角为θ，现用力F拉动小球，使其缓慢上移到框架的最高点，在此过程中金属框架始终保持静止，下列说法中正确的是( )A．框架对小球的支持力先减小后增大B．水平拉力F 先增大后减小C．地面对框架的支持力先减小后增大D．地面对框架的摩擦力一直减小19．带电粒子以初速度v0从a点垂直y轴进入匀强磁场，如图所示。

陕西省吴起高级中学2018届高三下学期期中考试理科综合试题Word版含答案

吴起高级中学2017-2018学年第二学期中期考试高三理综试卷命题人：命题人：命题人：班级：姓名：考号：（考试时间：150分钟试卷满分：300分）可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.关于细胞中的化合物、结构和功能的叙述，正确的是( )A.生物细胞内核糖体的形成都与细胞核内的核仁有关B.纤维素是植物细胞壁的主要成分，它的基本组成单位是麦芽糖C.毛霉合成并分泌蛋白酶的过程与该菌的核糖体、内质网、高尔基体、线粒体有关D.合成固醇类激素的腺细胞中内质网和高尔基体一般不发达2.将芹菜叶片置于一定浓度的KNO3溶液中，鲜重变化与时间关系如图所示。

下列有关叙述正确的是( )NO-的跨膜运输方式与水的跨膜运输方式不同A．本实验可证明K+、3B．0～8 min内，芹菜叶肉细胞的相对表面积增大C．15 min后，芹菜叶肉细胞鲜重不再增加，说明细胞内外浓度相等D．芹菜叶肉细胞从8 min开始吸收无机盐离子，使细胞液浓度大于外界溶液浓度3.下列相关人和动植物的生命活动调节叙述正确的是( )A.人体细胞外液渗透压的90%以上来源于Na+和Cl-B.相邻的两个神经元之间可以通过突触直接接触C.温特在1928年通过对燕麦的实验证明了生长素的化学本质就是吲哚乙酸D.寒冷时，下丘脑会分泌较多的促甲状腺激素释放激素，直接促进甲状腺的活动来调节体温4．一个患某遗传病（由一对等位基因控制）的女性患者甲和一个表现正常的男性结婚后，生了一儿一女，且都患该遗传病。

下列有关叙述正确的是( )A．女性患者甲和该表现正常的男性都是纯合子B．该遗传病可能是伴X染色体隐性遗传病C．患该遗传病的子女一定可以从女性患者甲获得致病基因D．该遗传病在后代子女中的发病率相同5.下列关于实验的相关叙述中，错误的是( )A.双缩脲试剂A液、B液与斐林试剂甲液、乙液组成成分相同，但浓度和使用方法不相同B.在用绿叶中色素的提取液作为吸光度测定实验时，所设置的对照组应用蒸馏水作为对照溶液C.洋葱鳞片叶细胞在发生质壁分离复原时，细胞的吸水能力逐渐降低D.盐酸能够使染色质中的DNA与蛋白质分离，有利于DNA与染色剂结合6．下列关于生物学实验及研究方法的叙述，错误的是( )A．用样方法调查蚜虫的种群密度时，取样的关键是随机取样B．用标志重捕法调查某动物种群密度时，标志物部分脱落会使估算值偏大C．用血细胞计数板观察酵母菌种群数量的变化，应先在计数室上滴加菌液，再盖上盖玻片D．研究土壤中小动物类群丰富度常用取样器取样的方法进行采集、调查7.化学与生活密切相关，下列说法错误的是（）A“加铁酱油”可有效预防缺铁性贫血B维生素C具有还原性，在人体内起抗氧化作用C蛋白质水解产物氨基酸可以合成人体所需蛋白质D食品包装袋、食物保鲜膜等材料的主要成份是聚氯乙烯8.设N A为阿伏加德罗常数的数值，下列说法正确的是（）A．0.5mol/L亚硫酸溶液中含有的H+数小于N AB．0.1mol-CH3含有的电子数目为0.7 N AC．2.3g钠与足量的氧气充分反应，转移的电子数一定为0.1N AD．标准状况下，2.24 LCHCl3含有的共价键数目为0.4N A9.下图为海洋资源综合开发利用流程，有关说法中正确的是( )A．从海水中提取D2O是化学变化B．从海带中提取I2时可用乙醇进行萃取C．实验室用带玻璃塞的棕色瓶贮存液溴D．电解饱和MgCl2溶液时在阴极得到Mg10.茅台酒中存在少量具有凤梨香味的物质X ，其结构如图所示。

陕西省吴起高级中学2018届高三理综下学期期中试题2018052802153

吴起高级中学2017-2018学年第二学期中期考试高三理综试卷（考试时间：150分钟试卷满分：300分）可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

下列有关叙述正确的是( )A．本实验可证明K、NO的跨膜运输方式与水的跨膜运输方式不同3B．0～8 min内，芹菜叶肉细胞的相对表面积增大C．15 min后，芹菜叶肉细胞鲜重不再增加，说明细胞内外浓度相等D．芹菜叶肉细胞从8 min开始吸收无机盐离子，使细胞液浓度大于外界溶液浓度3.下列相关人和动植物的生命活动调节叙述正确的是( )A.人体细胞外液渗透压的90%以上来源于Na+和Cl-B.相邻的两个神经元之间可以通过突触直接接触C.温特在1928年通过对燕麦的实验证明了生长素的化学本质就是吲哚乙酸D.寒冷时，下丘脑会分泌较多的促甲状腺激素释放激素，直接促进甲状腺的活动来调节体温4．一个患某遗传病（由一对等位基因控制）的女性患者甲和一个表现正常的男性结婚后，生了一儿一女，且都患该遗传病。

下列有关叙述正确的是( )A．女性患者甲和该表现正常的男性都是纯合子B．该遗传病可能是伴X染色体隐性遗传病C．患该遗传病的子女一定可以从女性患者甲获得致病基因D．该遗传病在后代子女中的发病率相同5.下列关于实验的相关叙述中，错误的是( )A.双缩脲试剂A液、B液与斐林试剂甲液、乙液组成成分相同，但浓度和使用方法不相同B.在用绿叶中色素的提取液作为吸光度测定实验时，所设置的对照组应用蒸馏水作为对照溶液C.洋葱鳞片叶细胞在发生质壁分离复原时，细胞的吸水能力逐渐降低D.盐酸能够使染色质中的DNA与蛋白质分离，有利于DNA与染色剂结合6．下列关于生物学实验及研究方法的叙述，错误的是( )A．用样方法调查蚜虫的种群密度时，取样的关键是随机取样B．用标志重捕法调查某动物种群密度时，标志物部分脱落会使估算值偏大C．用血细胞计数板观察酵母菌种群数量的变化，应先在计数室上滴加菌液，再盖上盖玻片D．研究土壤中小动物类群丰富度常用取样器取样的方法进行采集、调查7.化学与生活密切相关，下列说法错误的是（）A“加铁酱油”可有效预防缺铁性贫血B维生素C具有还原性，在人体内起抗氧化作用C蛋白质水解产物氨基酸可以合成人体所需蛋白质D食品包装袋、食物保鲜膜等材料的主要成份是聚氯乙烯8.设N A为阿伏加德罗常数的数值，下列说法正确的是（）A．0.5mol/L亚硫酸溶液中含有的H+数小于N AB．0.1mol-CH3含有的电子数目为0.7 N AC．2.3g钠与足量的氧气充分反应，转移的电子数一定为0.1N AD．标准状况下，2.24 LCHCl3含有的共价键数目为0.4N A9.下图为海洋资源综合开发利用流程，有关说法中正确的是()A．从海水中提取D2O是化学变化B．从海带中提取I2时可用乙醇进行萃取C．实验室用带玻璃塞的棕色瓶贮存液溴D．电解饱和MgCl2溶液时在阴极得到Mg10.茅台酒中存在少量具有凤梨香味的物质X，其结构如图所示。

历史-陕西省吴起高级中学2018届高三下学期期中考试试题

陕西省吴起高级中学2018届高三下学期期中考试历史试题说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案涂到答题卡上，第Ⅱ卷可在各题后直接作答。

共300分，考试时间150分钟。

（只交答题卡）24.孔子说：“鸟兽不可与之同群，吾非斯人之徒与而谁与？天下有道，丘不与易也。

”这说明孔子（）A．主张实行礼治，反对法治B．对自身修养有极高的要求C．主张变法革新，积极入世D．人与自然之间要和谐相处25.宋代早市批售或零售“果子”竞争激烈，商贩用其特有的声韵叫卖，在勾栏瓦舍中的艺人听了相关的叫卖声而产生了“文八娘叫果子”的节目。

这反映出宋代（）A．商品经济发展影响文化创造B．商贩叫卖之语符合宋词韵律C．商业活动发展打破时空界限D．勾栏瓦舍成为主要休闲场所26.明朝皇帝每于郊祀上报皇天牧养有成时，都把全国的户口薄籍陈于祭台之上，即表示上天赐予他对人民、土地的所有权。

这一做法反映了（）A．明朝天人合一思想仍很盛行B．封建统治者对农业生产重视C．土地国有仍是主流土地制度D．明朝的人口户籍管理较严格27．清入关前，没有专门的饮食制度，仍“席地而坐，自割肉而食”，没有君臣之别。

入关后，明代宫廷饮食中的礼法、等级制度在清宫中重新得到体现。

这说明（）A．民族交融影响饮食习惯B．满族正统地位受到挑战C．经济发展促进礼仪变革D．传统习俗遭到全面摒弃28.张之洞认为，中国物产之盛甲于五洲，但因交通不便，工艰运贵，所以出产不多，销售不广一月，土货往往质粗价廉，只有经过机器、化学的加工，才能变粗为精，实现增值。

由材料可知，张之洞认识到（）A.经济对国家实力有重要影响B．中国处于商战劣势的根源C．大机器生产对商战的重要性D．专制政体导致了商战不利29．康有为断言：“政治之学最美者，莫如吾《六经》也。

尝考泰西所以强者，皆暗合吾经义者也。

”这表明康有为意在（）A．肯定中国传统文化的进步性B．复兴传统文化C．认同西方政治制度的优越性D．推动社会变革30．“九一八事变”后，《东三省各界联合会宣言》发表：“东北有三千余万民众，两百余万健儿，各输其财，各捐其躯，誓与日本帝国主义者作最后决斗。

陕西省延安市吴起县高三数学下学期第一次月考试题文

陕西省吴起高级中学2018届高三数学下学期第一次月考试题文考试说明：1．全卷满分150分，考试时间120分钟；2．所有题目的答案必须写在答题卡的规定位置上，否则无效。

第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．全集为实数集，，，则（）A. B.C.D.2．若1122aii i+=++，则a =（） A. 5i -- B. 5i -+ C. 5i - D. 5i + 3．函数sin 46y x π⎛⎫=-⎪⎝⎭的最小正周期为 A.8π B. 4π C. 2πD. π 4．如图，在四边形ABCD 中，设，，，则DC （）A.B.C.D.5．若双曲线2214x yk+=的离心率()1,2e ∈，则 k 的取值范围是（） A. (-∞, 0) B. (-3, 0) C. (-12, 0) D. (-60, -12) 6．一个几何体的三视图如下图所示，则该几何体的直观图可以是（）A. B. C. D.7．设点在不等式组表示的平面区域上，则的最小值为（）A. B. C. D.8．下列函数中，既是偶函数又在()0,+∞上单调递增的是（）A. 1y x =+B. 1y x =+C. 21y x =-+ D. 12xy ⎛⎫= ⎪⎝⎭9．甲、乙、丙三人参加某公司的面试，最终只有一人能够被该公司录用，得到面试结果以后甲说：丙被录用了；乙说：甲被录用了；丙说：我没被录用.若这三人中仅有一人说法错误，则下列结论正确的是（）A. 丙被录用了B. 乙被录用了C. 甲被录用了D. 无法确定谁被录用了 10．阅读程序框图，该算法的功能是输出（）A. 数列{}12n - 的前 4项的和B. 数列{}21n -的第4项 C. 数列{}2n 的前5项的和 D. 数列{}21n-的第5项11．鞋柜里有3双不同的鞋，从中取出一只左脚的，一只右脚的，恰好成双的概率为（）A.23 B. 13 C. 35 D. 2512．抛物线的焦点为，是上一点，若到的距离是到轴距离的两倍，且三角形的面积为（为坐标原点），则的值为A. B. C. D.第II 卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分）13．已知函数()2cos sin 2f x x x x π⎛⎫=-++ ⎪⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，函数()f x 的最小值与最大值之和为__________．14．已知函数()f x 是定义在R 上的奇函数，当(),0x ∈-∞时， ()322f x x x =+,则()2f =__________.15．长方体的长，宽，高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为__________.16．已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = ．三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演绎步骤） 17．(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ， 55,5,15n S a S ==. （1）求数列{}n a 的通项公式；（2）若11n n n b a a +=，求数列{}n b 的前100项和．18.(本小题满分12分)如图，在四棱锥P ABC D -中， PA ⊥底面A B C D ，,//,2AD AB AB DC AD DC AP ⊥===， 1AB =，点E 为棱PC 的中点.(1)证明： //BE 面APD ； (2)求三棱锥P BDE -的体积．19．(本小题满分12分)“中国人均读书4.3本（包括网络文学和教科书），比韩国的11本.法国的20本.日本的40本.犹太人的64本少得多，是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的，而且和其他国家相比，我国国民的阅读量如此之低，也和我国是传统的文明古国.礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段： [20,30）， [30,40）， [40,50）， [50,60）， [60,70）， []70,80后得到如图所示的频率分布直方图．问：（1）估计在40名读书者中年龄分布在[40,70）的人数；（2）求40名读书者年龄的平均数和中位数；（3）若从年龄在[20,40）的读书者中任取2名，求恰有1名读书者年龄在[30,40）的概率．20．(本小题满分12分)设动点()(),0P x y y ≥到定点()0,1F 的距离比它到x 轴的距离大1，记点P 的轨迹为曲线C . （1）求点P 的轨迹方程；（2）若圆心在曲线C 上的动圆M 过点()0,2A ，试证明圆M 与x 轴必相交，且截x 轴所得的弦长为定值.21．(本小题满分12分)已知函数()()2x f x x mx e =+(其中e 为自然对数的底数).（1）当2m =-时，求函数()f x 的单调递增区间；（2）若函数()f x 在区间[]1,3上单调递减，求m 的取值范围.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22．(本小题满分10分)在平面直角坐标系xoy 中，直线l的参数方程12 x ty =+⎧⎪⎨⎪⎩（t 为参数），以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为：4cos ρθ=．（1）把直线l 的参数方程化为极坐标方程，把曲线C 的极坐标方程化为普通方程；（2）求直线l 与曲线C 交点的极坐标（ρ≥0，0≤2θπ<）． 23．(本小题满分10分)已知01a b <<<，求证：（Ⅰ）1a b ab +<+；<参考答案一、选择题：1---5:ADCAC,6----10:BDBCD 11----12:BB 二、填空题：1312-、 14、12 15、14π 16、8 三、解答题：17解：（1）由及得，,解得，所以．（2），从而有：．故数列的前100项和为．18.证明：(1)取PD 中点F ，连接,AF EF ,E F 分别是,PC PD 的中点 ∴ 1//,2EF CD EF CD = 1//,2AB CD AB CD =∴ //,EF AB EF AB = ∴四边形ABEF 是平行四边形 ∴ //BE AF又,BE PAD AF PAD ⊄⊂面面∴ //BE PAD 面(2) 1112.2263P BDE B PDE B PDC P BDC BDC V V V V S PA ----∆=====.19、（1）由频率分布直方图知年龄在[40,70）的频率为（0．0200．0300．025）100．75，所以40名读书者中年龄分布在[40,70）的人数为400.75 30．（2）40名读书者的平均年龄为：250.05350.1450.2550.3650.25750.154⨯+⨯+⨯+⨯+⨯+⨯=，设中位数为x ，则()0.005100.010100.020100.030500.5x ⨯+⨯+⨯+⨯-=，解得： 55x =，即40名读者中年龄的中位数为55.（3）年龄在[)2030，的读书者有2人，记为：A 1 ,A 2.;年龄在[)3040，的读书者有4人，记为：B 1 ,B 2 ,B 3 ,B 4 .从这6名读者中随机抽取2人，所有可能的结果共有15中，分别是：{A 1 ,A 2}，{A 1 ,B 1}，{A 1 ,B 2}，{A 1 ,B 3}，{A 1 ,B 4}，{A 2 ,B 1}，{A 2 ,B 2}，{A 2 ,B 3}，{A 2 ,B 4}，{B 1 ,B 2}，{B 1 ,B 3}，{B 1 ,B 4}，{B 2 ,B 3}，{B 2 ,B 4}，{B 3 ,B 4}，又因为所抽取的2人恰有1人在 [)3040，的结果有8中，分别是：{A 1 ,B 1}，{A 1 ,B 2}，{A 1 ,B 3}，{A 1 ,B 4}，{A 2 ,B 1}，{A 2 ,B 2}，{A 2 ,B 3}，{A 2 ,B 4} 故所求概率8=15P .20、解：（1）依题意知，动点P 到定点F ()0,1的距离等于P 到直线1y =-的距离， ∴曲线C 是以原点为顶点， F ()0,1为焦点的抛物线．设曲线C 的方程为22x py =, 则12p=， ∴2p =，∴曲线C 方程是24x y = ．（2）设圆心为(),M a b ，则24a b =， ∵圆M 过A ()0,2，∴圆的方程为()()()22222x a y b a b -+-=+-，令0y =得22440x ax b -+-=．∵()()22244441616160a b a b ∆=--=-+=> ∴圆M 与x 轴必相交，设圆M 与x 轴的两交点分别为E ()1,0x ，G ()2,0x 则122x x a +=， 1244x x b ⋅=-，∴2||EG = ()()221212124x x x x x x -=+-⋅ 24161616a b =-+=，∴EG =4．故圆截x 轴所得的弦长为定值．21、解：(1)当m ＝－2时，f (x )＝(x 2－2x )e x， f ′(x )＝(2x －2)e x ＋(x 2－2x )e x ＝(x 2－2)e x ，令f ′(x )≥0，即x 2－2≥0，解得x ≤－或x ≥. 所以函数f (x )的单调递增区间是(－∞，－]和[，＋∞)(2)依题意，f ′(x )＝(2x ＋m )e x＋(x 2＋mx )e x＝[x 2＋(m ＋2)x ＋m ]e x，因为f ′(x )≤0对于x ∈[1,3]恒成立，所以x 2＋(m ＋2)x ＋m ≤0，即m ≤－＝－(x ＋1)＋令g (x )＝－(x ＋1)＋，则g ′(x )＝－1－()211x +<0恒成立，所以g (x )在区间[1,3]上单调递减，g (x )min ＝g (3)＝－，故m 的取值范围是.22.解：（1）直线l的参数方程122{ x ty =+=（t 为参数），消去参数t0y --=，把{x cos y sin ρθρθ==代入可得：cos sin 0θρθ--=，由曲线C 的极坐标方程为： 4cos ρθ=，变为24cos ρρθ=，化为2240x y x +-=. （2）联立220 40y x y x --=+-=，解得1{x y ==或3{x y ==，∴直线l 与曲线C 交点的极坐标（ρ≥0，0≤θ＜2π）为52,3π⎛⎫ ⎪⎝⎭，6π⎛⎫⎪⎝⎭． 23. 解（Ⅰ）∵（a ＋b ）－（1＋ab ）＝a ＋b －1－ab＝（a －1）＋b （1－a ）＝（a －1）（1－b ）， 0＜a ＜b ＜1，∴a－1＜0，1－b ＞0． ∴（a －1）（1－b ）＜0． ∴a＋b ＜1＋ab ．（Ⅱ）要证：< 只需证：只需证：22<，即11a b a b +++<+++ 从而只需证：<<只需证ab ＋a ＜ab ＋b ，即a ＜b ，显然成立， ∴原不等式成立．。

精品推荐2018届下学期陕西省吴起高级中学高三3月月考试卷数学(理)

2018届下学期陕西省吴起高级中学高三3月月考试卷理科数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1．设复数2z i =-+（i 是虚数单位），z 的共轭复数为z ，则()1z z +⋅等于（） AB．C．D2．已知集合{}|2 4 xA x =<， {}|21,B x x x N =-<-<∈，则A B ⋂=（） A ．{}1B ．{}|1 2 x x -<<C ．{}0,1D ．{}| 2 x x <3．中国古代数学著作《算法统综》中有这样一个问题：“三百七十八里关，初步健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔仔细算相还”．其大意为：“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地”．则该人第五天走的路程为（） A ．48里B ．24里C ．12里D ．6里4．如图，在边长为1的正方形网格中用粗线画出了某个多面体的三视图，则该多面体的体积为（）A ．15B ．13C ．12D ．95．若x ，y 满足约束条件1020220x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩,则z=x+2y 的最大值为（）A ．1B ．2C ．3D ．46．甲、乙、丙三人参加某公司的面试，最终只有一人能够被该公司录用，得到面试结果以后甲说：丙被录用了；乙说：甲被录用了；丙说：我没被录用．若这三人中仅有一人说法错误，则下列结论正确的是（）A ．丙被录用了B ．乙被录用了C ．甲被录用了D ．无法确定谁被录用了7．执行如图所示的程序框图，则输出的k 值为（）A ．9B ．10C ．11D ．128．25()xx y ++的展开式中，52x y 的系数为（）A ．10B ．20C ．30D ．609．已知双曲线()2222:10,0y x c a b a b-=>>的渐近线方程为34y x =±，且其焦点为()0,5,则双曲线C 的方程（）A ．221916x y -= B ．221169x y -= C ．221916y x -=D ．221169y x -=10．已知长方体ABCD —A 1B 1C 1D 1中，AB=BC=4，CC 1=2，则直线BC 1和平面DBB 1D 1所成角的正弦值为（） A．2B．2C．5D．1011．若2x =-是函数21()(1)e x f x x ax -=+-的极值点，则()f x 的极小值为（）此卷只装订不密封班级姓名准考证号考场号座位号A ．1-B ．32e --C ．35e -D ．112．已知定义在R 上的奇函数()f x 满足()()f x f x π+=-，当[0,]2x π∈时，()f x =则函数()()()1g x x f x π=--在区间3[,3]2ππ-上所有零点之和为（） A ．πB ．2πC ．3πD ．4π第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．已知随机变量ξ～(),B n p ，若3E ξ=，32D ξ=，则n =__________．14．当x =________时，函数()2cos sin 4f x x x x π⎛⎫=+≤ ⎪⎝⎭取最大值．15．设向量(3,3)a =，(1,1)b =-，若()()a b a b λλ+⊥-，则实数λ=________． 16．设S n 是数列{a n }的前项和，且11a =-，11n n n a S S ++=，则S n =________________．三、解答题（本题共6个小题，共70分．解答应写出必要的文字说明、证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．（本小题满分12分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ，其面积2sin S b A =．（1）求cb的值；（2）设内角A 的平分线AD 交BC 于D，AD =a =，求b ．18．（本小题满分12分）某种植园在芒果临近成熟时，随机从一些芒果树上摘下100个芒果，其质量分别在[100,150)， [150,200)，[200,250)，[250,300)，[300,350)， [350,400)（单位：克）中，经统计得频率分布直方图如图所示．（1）现按分层抽样从质量为[250,300)，[300,350)的芒果中随机抽取9个，再从这9个中随机抽取3个，记随机变量X 表示质量在[300,350)内的芒果个数，求X 的分布列及数学期望．（2）以各组数据的中间数代表这组数据的平均值，将频率视为概率，某经销商来收购芒果，该种植园中还未摘下的芒果大约还有10000个，经销商提出如下两种收购方案： A ：所有芒果以10元/千克收购；B ：对质量低于250克的芒果以2元/个收购，高于或等于250克的以3元/个收购．通过计算确定种植园选择哪种方案获利更多？19．（本小题满分12分）如图，四棱锥P ABCD -中，底面ABCD 为菱形，PA ⊥平面ABCD ，E 为PD 的中点．（1）证明：PB ∥平面AEC ；（2）设1,60PA ABC =∠=，三棱锥E ACD -的体积为8，求二面角D AE C --的余弦值．20．（本小题满分12分）已知椭圆E 的一个顶点为()0,1A -，焦点在x 轴上，若椭圆右焦点到直线0x y -+=的距离为3．（1）求椭圆E 的方程；（2）设直线():0l y kx m k =+≠与该椭圆交于不同的两点B ，C ，若坐标原点O 到直线l的距离为2，求△BOC 面积的最大值．21． (本小题满分12分) 已知函数()ln f x x =，21()2g x x bx =-（b 为常数）．（1）函数()f x 的图象在点))1(,1(f 处的切线与函数()g x 的图象相切，求实数b 的值；（2）若2b ≥，12,[1,2]x x ∀∈，且12x x ≠，都有1212|()()||()()|f x f x g x g x ->-成立，求实数b 的值．注意：请考生在22、23题两题中任选一道．．．．题作答，如果多做，则按所做的第一题计分． 22．（10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，以原点O 为极点，以x 轴正半轴为极轴，圆C的极坐标方程为π4ρθ⎛⎫=+ ⎪⎝⎭．（1）将圆C 的极坐标方程化为直角坐标方程；（2）过点P (2,0)作斜率为1直线l 与圆C 交于,A B 两点，试求11PA PB+的值．23．（10分）选修4-5：不等式选讲已知函数()|23||36|f x x x =-+-． (1)求()2f x <的解集；(2) 若()f x 的最小值为T ,正数,a b 满足12a b +=T ≤．第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1-6：DCCBBC7-12：BCCCAD第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．614．6π15．3 16．n1-三、解答题（本题共6个小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤，请把答案写在答题卷上）17．（1）21sin sin 2S bc A b A ==，可知2c b =，即2cb=．（6分）（2）由角平分线定理可知，3BD =，3CD =，在ABC △中，22cos B =ABD △中，2444cos b B+-=222444b +-1b =．（12分）18．（1）9个芒果中，质量在[250,300)和[300,350)内的分别有6个和3个．则X 的可能取值为0,1,2,3．363920(0)84C P X C ===，21633945(1)84C C P X C ===，12633918(2)84C C P X C ===，33391(3)84C P X C ===所以X 的分布列为X 的数学期望0123184848484EX =⨯+⨯+⨯+⨯=．（6分）（2）方案A ：(1250.0021750.0022250.0032750.0083250.0043750.001)5010000100.00125750⨯+⨯+⨯+⨯+⨯+⨯⨯⨯⨯⨯=元方案B ：低于250克：(0.0020.0020.003)501000027000++⨯⨯⨯=元高于或等于250克(0.0080.0040.001)5010000319500++⨯⨯⨯=元总计70001950026500+=元由2575026500<，故B 方案获利更多，应选B 方案．（12分） 19．（1）连接BD 交AC 于点O ，连接OE在PBD △中，////PE DE PB OE BO DO OE ACE PB ACE PB ACE =⎫⎫⇒⎬⎪=⎭⎪⎪⊂⇒⎬⎪⊄⎪⎪⎭平面平面平面，（2）24P ABCD P ACD E ACD V V V ---===，设菱形ABCD 的边长为a 211(2)133P ABCD ABCDV SPA -=⋅=⨯⨯=a = 取BC 中点M ，连接AM ．以点A 为原点，以AM 方向为x 轴，以AD 方向为y 轴，以AP 方向为z 轴，建立如图所示坐标系．D ，(0,0,0)A ，1)2E ，3(2C1(0,)2AE =，3(2AC =，1(1,n =，2(1,0,0)n =1212||cos ||||1n n n n θ⋅===⋅+即二面角D AE C --． 20．（1）2213x y +=；（221．（1）因为()ln f x x =，所以1'()f x x =，因此'(1)1f =，所以函数()f x 的图象在点(1,(1))f 处的切线方程为1y x =-，由21,1,2y x y x bx =-⎧⎪⎨=-⎪⎩得22(1)20x b x -++=．由24(1)80b ∆=+-=，得1b =-b ）（2）不妨设12x x >，因为函数()ln f x x =在区间[1,2]上是增函数，所以12()()f x f x >，函数()g x 图象的对称轴为x b =，且2b >．当2b ≥时，函数()g x 在区间[1,2]上是减函数，所以12()()g x g x <，所以1212|()()||()()|f x f x g x g x ->-，等价于1221()()()()f x f x g x g x ->-，即1122()()()()f x g x f x g x +>+，等价于()()()h x f x g x =+=21ln 2x x bx +-在区间[1,2]上是增函数，等价于1'()0h x x b x =+-≥在区间[1,2]上恒成立，等价于1b x x≤+在区间[1,2]上恒成立，所以2b ≤，又2b ≥，所以2b =．22．（1）由)4(24πθρ+=Cos 得：θθρSin Cos 44-=,θρθρρSin Cos 442-=∴即：04422=+-+y x y x ，∴C 的直角坐标方程为：()()82222=++-y x（2）设A ，B 两点对应的参数分别为21,t t ，直线t t y x ⎪⎪⎩⎪⎪⎨⎧=+=22222和圆的方程联立得,04222=-+t t 所以121240t t t t +=-=-<．所以261111212121=-=+=+t t t t t t PB PA ． 23．（1）()()()333263592233233623632322223362592x x x x x f x x x x x x x x x x x x x ≤≤≤≤⎧⎧⎛⎫⎛⎫-+- <-+ < ⎪ ⎪⎪⎪⎝⎭⎝⎭⎪⎪⎪⎪⎛⎫⎛⎫=-+-=-+- =-+ ⎨⎨ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎪⎪-+- >- >⎪⎪⎩⎩，由图像可知：()2f x <的解集为711,55⎛⎫⎪⎝⎭．（5分）（2）图像可知()f x 的最小值为1，12=，当且仅当a b =时，“=1T =．（10分）。

陕西省吴起高级中学2018-2019学年高二下学期期中考试数学(理)试题(能力卷)(含答案)

吴起高级中学2018-2019学年第二学期中期考试高二数学试题理科(能力卷）说明：1.全卷满分150分，时间120分钟；2.所有题的答案必须答在答题纸上，写在试卷上无效。

．．．．．．．．．．．．．．．．．．．．．．．第Ⅰ卷（选择题共60分）一．选择题（本大题共12小题，每小题5分，共60分） 1. 若复数z ＝a ＋i 的实部与虚部相等，则实数a ＝( ) A.－1 B.1 C.－2 D.2 2.20sin xdx π⎰＝( )A.1B.2C.－2D.0 3．设函数y ＝f(x)可导，则0(1)(1)limx f x f x→+-V V V 等于( )A.f ′(1)B.3f ′(1)C.13f′(1) D.以上都不对4. 已知复数z ＝i -3-，则复数z 在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 5．曲线1y x x=-在点(1,0)p 处的切线方程为( ) A ．210x y --= B ．220x y --= C ．220x y --= D ．1203x y --= 6. 已知7781n n n C C C +-=,则n 等于( )A.14B.12C.13D.157．设函数y ＝e xsin x ，则y ′等于( ) A ． e xcos x B ． e xsin xC ． e x sin xD ． e x(sin x ＋cos x )8. 6个人聚会，每两人握一次手，一共握多少次手？( ) A .14B .15C .30D .289．函数y ＝ln(2x ＋5)的导数为( ) A ．5x 22+ B ．ln(2x ＋5) C ．52+x e D.5x 21+f'的图象可能为( )10．若函数f(x)的图象如图所示，则导函数()x11. 某校为了提倡素质教育，丰富学生们的课外生活，分别成立绘画、象棋和篮球兴趣小组，现有甲、乙、丙、丁四名学生报名参加，每人仅参加一个兴趣小组，每个兴趣小组至少有一人报名，则不同的报名方法有( )A．12种 B．24种 C．36种D．72种12．设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图像如图所示，则下列结论中一定成立的是( )A．函数f(x)有极大值f(2)和极小值f(1)B．函数f(x)有极大值f(－2)和极小值f(1)C．函数f(x)有极大值f(2)和极小值f(－2)D．函数f(x)有极大值f(－2)和极小值f(2)第Ⅱ卷（非选择题共90分）二．填空题（本大题共4小题，每小题5分，共20分）13. 如图是由火柴棒拼成的图形，第n个图形由n个正方形组成.通过观察可以发现：第5个图形中有_______根火柴棒.14. 3个不同的球放入5个不同的盒子，每个盒子放球数量不限，共有放法. 15. 曲线y ＝x 2和曲线y ＝x 围成的图形的面积是________.16．要制作一个容积为4 m 3，高为1 m 的无盖长方体容器，已知底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是______元．三．解答题（本大题共6小题，共70分） 17. （本小题满分10分）（1）求函数y ＝e xx ＋1的导数．（2）计算复数z=3＋2i 2－3i －3－2i2＋3i 的值.18. （本小题满分12分）证明：2＋7<6＋ 319. （本小题满分12分）吴起高级中学第十五届校园科技文化艺术节需要抽调主持人，现有男主持人6名，女主持人4名，若选5人出来主持节目，在下列不同条件下，各有多少种抽调方法？ (1)男主持人3名，女主持人2名； (2)至少有1名女主持人． 20. （本小题满分12分）求函数32()31f x x x =-+，x ∈[－3,4]；单调区间及最值21.（本小题满分12分）将5个不同的元素a,b,c,d,e 排成一排.（1）a ，e 必须排在首位或末位，有多少种排法？（2）a ，e 既不在首位也不在末位，有多少种排法？（3）a 不排在首位，e 不排在末位，有多少种排法？22.（本小题满分12分）已知函数()ln()f x x x a =-+在x ＝1处取得极值． (1)求实数a 的值；(2)若关于x 的方程2()2f x x x b +=+在[12，2]上恰有两个不相等的实数根，求实数b 的取值范围．高二数学试题理科(能力卷）参考答案一、选择题B D AC B AD B A C C D 二、填空题13、16 14、125种 15、1616、160元三、解答题17、（1）y ′=2(1)xxe x (2) z=2i18、分析法证明19、解：(1)任选3名男运动员，方法数为C 36，再选2名女运动员，方法数为C 24，共有C 36·C 24＝120(种)方法． (2)法一：(直接法)至少1名女运动员包括以下几种情况：1女4男，2女3男，3女2男，4女1男，由分类加法计数原理可得总选法数为 C 14C 46＋C 24C 36＋C 34C 26＋C 44C 16＝246(种)．法二：(间接法)“至少有1名女运动员”的反面是“全是男运动员”，因此用间接法求解，不同选法有C 510－C 56＝246(种)．20、单调增区间（-3,0），（2,4）；单调减区间是（0,2）最大值是17，最小值是-53.21、见课本19页例题 (1)12种（2）36种（3）78种 22. 答案：(1)0 (2)54＋ln2≤b <2解析：(1)对f (x )求导，得f ′(x )＝1－1x ＋a. 由题意，得f ′(1)＝0，即1－11＋a ＝0，∴a ＝0.(2)由(1)得f (x )＝x －ln x .∴f (x )＋2x ＝x 2＋b ，即x 2－3x ＋ln x ＋b ＝0. 设g (x )＝x 2－3x ＋ln x ＋b (x >0)，则 g ′(x )＝2x －3＋1x ＝2x 2－3x ＋1x＝2x －1x －1x.令g ′(x )＝0，得x 1＝12，x 2＝1.当x 变化时，g ′(x )、g (x )的变化情况如下表：x (0，12)12 (12，1) 1 (1,2) 2 g ′(x ) ＋－＋＋g (x )极大值极小值b －2＋ln2∴当x ＝1时，g (x )的极小值为g (1)＝b －2. 又g (12)＝b －54－ln2，g (2)＝b －2＋ln2.∵方程f (x )＋2x ＝x 2＋b 在[12，2]上恰有两个不相等的实数根，∴⎩⎪⎨⎪⎧g 12≥0，g 1<0，g2≥0，即⎩⎪⎨⎪⎧b －54－ln2≥0，b －2<0，b －2＋ln2≥0，解得54＋ln2≤b <2.。

陕西省吴起高级中学高二数学下学期期中试题(基础卷)理

吴起高级中学2017-2018学年第二学期中期考试高二数学（理科基础卷）试题第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．函数2log y x=的导函数是（）A.1y x =B. ln2y x =C. 1ln2y x =D. 12ln y x =2．从10名学生中挑选出3名学生参加数学竞赛，不同的选法有（） A. 310A 种 B. 3！ C. 310C 种 D. 以上均不对 3）A. 综合法B. 分析法C. 反证法D. 数学归纳法 4．5名同学排成一排照相,不同的排法种数是( ) A.1 B.5 C.60 D.1205．412x x ⎛⎫+ ⎪⎝⎭的二项式系数之和为（）．A. 81B. 16C. 27D. 326．21．如图是函数()y f x =的导函数()'y f x =的图象，给出下列命题： ①-2是函数()y f x =的极值点； ②1是函数()y f x =的极值点；③()y f x =的图象在0x =处切线的斜率小于零； ④函数()y f x =在区间()2,2-上单调递增. 则正确命题的序号是（）A. ①③B. ②④C. ②③D. ①④ 7．5名运动员争夺3项比赛冠军，获得冠军的可能种数为： ( ) A ．53 B ．35 C ．35A D ．35C8．已知曲线22y x =上一点()1,2A ，则点A 处的切线斜率等于( )A. 2B. 4C. ()2662x x +∆+∆ D. 6 9．由曲线y ＝x 2与直线y ＝2x 所围成的平面图形的面积为( ) A.43 B. 2 C. 3 D. 3210．设函数()sin x f x x =，则2f π⎛⎫= ⎪⎝⎭'（） A. 2π-B. 2πC. 1D. ﹣1 11．已知函数33y x x =-，则它的单调递减区间是 ( ) A.(),0-∞ B.()0,+∞ C.()1,1- D.(),1-∞-,()1,+∞ 12．用数学归纳法证明()111112233411nn n n +++⋅⋅⋅+=⋅⋅⋅++()n N *∈时，由n k =到1n k =+，不等式左端应增加的式子为（）A.()11k k + B.()()()11112k k k k ++++C.()12k k + D.()()112k k ++第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．在10(x -的展开式中，6x 的系数是。

陕西省延安市吴起县高三数学下学期第一次月考试题文

第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．全集为实数集，，，则（）A. B.C.D.2．若1122aii i+=++，则a =（） A. 5i -- B. 5i -+ C. 5i - D. 5i + 3．函数sin 46y x π⎛⎫=-⎪⎝⎭的最小正周期为 A.8π B. 4π C. 2πD. π 4．如图，在四边形ABCD 中，设，，，则DC u u u v（）A.B.C.D.5．若双曲线2214x y k+=的离心率()1,2e ∈，则 k 的取值范围是（） A. (-∞, 0) B. (-3, 0) C. (-12, 0) D. (-60, -12) 6．一个几何体的三视图如下图所示，则该几何体的直观图可以是（）A. B. C. D.7．设点在不等式组表示的平面区域上，则的最小值为（）A. B. C. D.第4题图第6题图8．下列函数中，既是偶函数又在()0,+∞上单调递增的是（）A. 1y x =+B. 1y x =+C. 21y x =-+ D. 12xy ⎛⎫= ⎪⎝⎭9．甲、乙、丙三人参加某公司的面试，最终只有一人能够被该公司录用，得到面试结果以后甲说：丙被录用了；乙说：甲被录用了；丙说：我没被录用.若这三人中仅有一人说法错误，则下列结论正确的是（）A. 丙被录用了B. 乙被录用了C. 甲被录用了D. 无法确定谁被录用了 10．阅读程序框图，该算法的功能是输出（）A. 数列{}12n - 的前 4项的和B. 数列{}21n -的第4项 C. 数列{}2n 的前5项的和 D. 数列{}21n-的第5项11．鞋柜里有3双不同的鞋，从中取出一只左脚的，一只右脚的，恰好成双的概率为（）A.23 B. 13 C. 35 D. 2512．抛物线的焦点为，是上一点，若到的距离是到轴距离的两倍，且三角形的面积为（为坐标原点），则的值为A. B. C. D.第II 卷（非选择题共90分）二、填空题（本大题共4小题，每小题5分，共20分） 13．已知函数()2cos 3sin sin 2f x x x x π⎛⎫=-++⎪⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，函数()f x 的最小值与最大值之和为__________．14．已知函数()f x 是定义在R 上的奇函数，当(),0x ∈-∞时， ()322f x x x =+,则()2f =__________.15．长方体的长，宽，高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为__________.16．已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = ．三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演绎步骤） 17．(本小题满分12分)已知等差数列{}n a 的前n 项和为n S ， 55,5,15n S a S ==. （1）求数列{}n a 的通项公式；（2）若11n n n b a a +=，求数列{}n b 的前100项和．18.(本小题满分12分)如图，在四棱锥P ABCD -中， PA ⊥底面ABCD ，,//,2AD AB AB DC AD DC AP ⊥===， 1AB =，点E 为棱PC 的中点.(1)证明： //BE 面APD ； (2)求三棱锥P BDE -的体积．19．(本小题满分12分)“中国人均读书4.3本（包括网络文学和教科书），比韩国的11本.法国的20本.日本的40本.犹太人的64本少得多，是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的，而且和其他国家相比，我国国民的阅读量如此之低，也和我国是传统的文明古国.礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段： [20,30）， [30,40）， [40,50）， [50,60）， [60,70）， []70,80后得到如图所示的频率分布直方图．问：（1）估计在40名读书者中年龄分布在[40,70）的人数；（2）求40名读书者年龄的平均数和中位数；（3）若从年龄在[20,40）的读书者中任取2名，求恰有1名读书者年龄在[30,40）的概率．20．(本小题满分12分)设动点()(),0P x y y ≥到定点()0,1F 的距离比它到x 轴的距离大1，记点P 的轨迹为曲线C . （1）求点P 的轨迹方程；（2）若圆心在曲线C 上的动圆M 过点()0,2A ，试证明圆M 与x 轴必相交，且截x 轴所得的弦长为定值.21．(本小题满分12分)已知函数()()2x f x x mx e =+(其中e 为自然对数的底数).（1）当2m =-时，求函数()f x 的单调递增区间；（2）若函数()f x 在区间[]1,3上单调递减，求m 的取值范围.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22．(本小题满分10分)在平面直角坐标系xoy 中，直线l的参数方程12 x ty =+⎧⎪⎨⎪⎩（t 为参数），以坐标原点为极点， x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为：4cos ρθ=．（1）把直线l 的参数方程化为极坐标方程，把曲线C 的极坐标方程化为普通方程；（2）求直线l 与曲线C 交点的极坐标（ρ≥0，0≤2θπ<）． 23．(本小题满分10分)已知01a b <<<，求证：（Ⅰ）1a b ab +<+；<参考答案一、选择题：1---5:ADCAC,6----10:BDBCD 11----12:BB 二、填空题：1312-、 14、12 15、14π 16、8 三、解答题：17解：（1）由及得，,解得，所以．（2），从而有：．故数列的前100项和为．18.证明：(1)取PD 中点F ，连接,AF EFQ ,E F 分别是,PC PD 的中点 ∴ 1//,2EF CD EF CD = Q 1//,2AB CD AB CD =∴ //,EF AB EF AB = ∴四边形ABEF 是平行四边形 ∴ //BE AF又,BE PAD AF PAD ⊄⊂面面∴ //BE PAD 面(2) 1112.2263P BDE B PDE B PDC P BDC BDC V V V V S PA ----∆=====.19、（1）由频率分布直方图知年龄在[40,70）的频率为（0．0200．0300．025）100．75，所以40名读书者中年龄分布在[40,70）的人数为400.75 30．（2）40名读书者的平均年龄为：250.05350.1450.2550.3650.25750.154⨯+⨯+⨯+⨯+⨯+⨯=，设中位数为x ，则()0.005100.010100.020100.030500.5x ⨯+⨯+⨯+⨯-=，解得： 55x =，即40名读者中年龄的中位数为55.（3）年龄在[)2030，的读书者有2人，记为：A 1 ,A 2.;年龄在[)3040，的读书者有4人，记为：B 1 ,B 2 ,B 3 ,B 4 .从这6名读者中随机抽取2人，所有可能的结果共有15中，分别是：{A 1 ,A 2}，{A 1 ,B 1}，{A 1 ,B 2}，{A 1 ,B 3}，{A 1 ,B 4}，{A 2 ,B 1}，{A 2 ,B 2}，{A 2 ,B 3}，{A 2 ,B 4}，{B 1 ,B 2}，{B 1 ,B 3}，{B 1 ,B 4}，{B 2 ,B 3}，{B 2 ,B 4}，{B 3 ,B 4}，又因为所抽取的2人恰有1人在 [)3040，的结果有8中，分别是：{A 1 ,B 1}，{A 1 ,B 2}，{A 1 ,B 3}，{A 1 ,B 4}，{A 2 ,B 1}，{A 2 ,B 2}，{A 2 ,B 3}，{A 2 ,B 4} 故所求概率8=15P .20、解：（1）依题意知，动点P 到定点F ()0,1的距离等于P 到直线1y =-的距离， ∴曲线C 是以原点为顶点， F ()0,1为焦点的抛物线．设曲线C 的方程为22x py =, 则12p=， ∴2p =，∴曲线C 方程是24x y = ．（2）设圆心为(),M a b ，则24a b =， ∵圆M 过A ()0,2，∴圆的方程为()()()22222x a y b a b -+-=+-，令0y =得22440x ax b -+-=．∵()()22244441616160a b a b ∆=--=-+=> ∴圆M 与x 轴必相交，设圆M 与x 轴的两交点分别为E ()1,0x ，G ()2,0x 则122x x a +=， 1244x x b ⋅=-，∴2||EG = ()()221212124x x x x x x -=+-⋅ 24161616a b =-+=，∴EG =4．故圆截x 轴所得的弦长为定值．21、解：(1)当m ＝－2时，f (x )＝(x 2－2x )e x， f ′(x )＝(2x －2)e x ＋(x 2－2x )e x ＝(x 2－2)e x ，令f ′(x )≥0，即x 2－2≥0，解得x ≤－或x ≥. 所以函数f (x )的单调递增区间是(－∞，－]和[，＋∞)(2)依题意，f ′(x )＝(2x ＋m )e x＋(x 2＋mx )e x＝[x 2＋(m ＋2)x ＋m ]e x，因为f ′(x )≤0对于x ∈[1,3]恒成立，所以x 2＋(m ＋2)x ＋m ≤0，即m ≤－＝－(x ＋1)＋令g (x )＝－(x ＋1)＋，则g ′(x )＝－1－()211x +<0恒成立，所以g (x )在区间[1,3]上单调递减，g (x )min ＝g (3)＝－，故m 的取值范围是.22.解：（1）直线l 的参数方程122{ 3x ty =+=（t 为参数），消去参数t 330x y --=，把{x cos y sin ρθρθ==代入可得：3cos sin 230ρθρθ--=，由曲线C 的极坐标方程为： 4cos ρθ=，变为24cos ρρθ=，化为2240x y x +-=. （2）联立220 40y x y x --=+-=，解得1{x y ==或3{x y ==，∴直线l 与曲线C 交点的极坐标（ρ≥0，0≤θ＜2π）为52,3π⎛⎫ ⎪⎝⎭，6π⎛⎫⎪⎝⎭． 23. 解（Ⅰ）∵（a ＋b ）－（1＋ab ）＝a ＋b －1－ab＝（a －1）＋b （1－a ）＝（a －1）（1－b ）， 0＜a ＜b ＜1，∴a－1＜0，1－b ＞0． ∴（a －1）（1－b ）＜0． ∴a＋b ＜1＋ab ．（Ⅱ）要证：< 只需证：只需证：22<，即11a b a b +++<+++ 从而只需证：<<只需证ab ＋a ＜ab ＋b ，即a ＜b ，显然成立， ∴原不等式成立．。

陕西省延安市吴起高级中学2018届高三下学期期中考试物理试题

吴起高级中学2017-2018学年第二学期中期考试高三理综试卷（考试时间：150分钟试卷满分：300分）可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一二、选择题：本题共8小题，每小题6分，共48分。

在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14．下列关于研究物理的思想方法的叙述中正确的是 ( )A ．理想化模型是把实际问题理想化，抓住主要因素，忽略次要因素，如：质点、合力、向心加速度B ．重心、交变电流的有效值等概念的建立都体现了等效替代的思想C ．根据速度定义式v ＝Δx Δt ，当Δt 足够小时，ΔxΔt 就可以表示物体在某时刻的瞬时速度，该定义应用了控制变量法D ．用比值法定义的物理量在物理学中占有相当大的比例，如：E ＝Fq 、kds C πε4=15．2017年8月我国自主设计的载人深潜器“深海勇士号”在南海进行下潜试验。

下图是它从水面开始下潜到返回水面的全过程的速度时间图像，则下列说法中正确的是( )A ．本次实验过程中加速度最大值是0.025m/s 2B ．在0～1 min 和8～10min 的时间段内“深海勇士号” 处于超重状态C ．“深海勇士号”本次下潜的最大深度为360mD．“深海勇士”在1～3min的时间内处于静止状态16．下列说法正确的是( )A．一群处于n=5的激发态的氢原子向低能级跃迁时最多能辐射出10 种不同频率的光B．卢瑟福在粒子散射实验中发现了电子，并提出了原子的核式结构学说C．在光电效应实验中，用同种频率的光照射不同的金属表面，从金属表面逸出的光电子的最大初动能E k越大，则这种金属的逸出功W0越大D．某放射性原子核经过2次α衰变和一次β衰变，核内中子减少了4个17．如图所示，A、B两个质量相同的小球在同一竖直线上，离地高度分别为2h和h，将两球水平抛出后，两球落地时的水平位移之比为1∶2，则下列说法正确的是( )A．A、B两球的初速度之比为1∶4B．A、B两球下落过程中的动能变化量之比为1∶2C．若两球同时抛出，则落地的时间差为2h gD．若两球同时落地，则两球抛出的时间差为(2－1)2h g18．如图，半圆形金属框竖直放在粗糙的水平地面上，套在其上的光滑小球P在水平外力F 的作用下处于静止状态，P与圆心O的连线与水平面的夹角为θ，现用力F拉动小球，使其缓慢上移到框架的最高点，在此过程中金属框架始终保持静止，下列说法中正确的是( )A．框架对小球的支持力先减小后增大B．水平拉力F 先增大后减小C．地面对框架的支持力先减小后增大D．地面对框架的摩擦力一直减小19．带电粒子以初速度v0从a点垂直y轴进入匀强磁场，如图所示。

陕西省吴起高级中学2018届高三下学期期中考试 数学(理)

【高考模拟】陕西省吴起高级中学2018届高三下学期期中考试 英语(word版有答案)

陕西省延安市吴起高级中学2018-2019学年高一上学期期中考试(基础卷)数学试题(精编含解析)

陕西省吴起高级中学2017_2018学年高二数学下学期期中试题能力卷

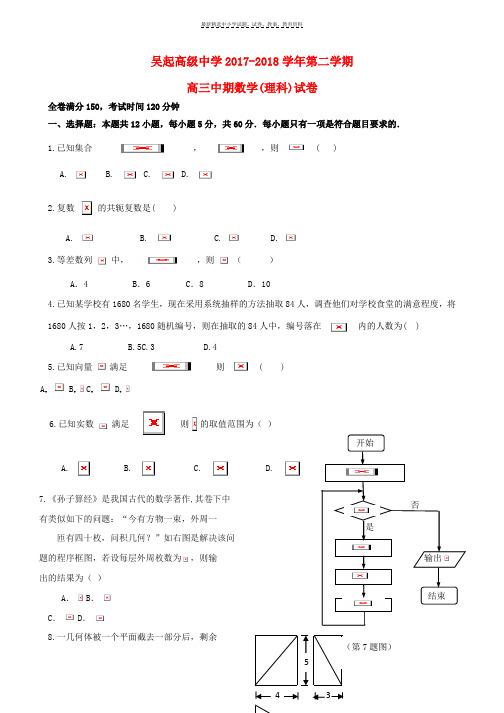
2018届高三数学下学期期中试题理

陕西省吴起高级中学高三物理下学期期中试题

陕西省吴起高级中学2018届高三下学期期中考试理科综合试题Word版含答案

陕西省吴起高级中学2018届高三理综下学期期中试题2018052802153

历史-陕西省吴起高级中学2018届高三下学期期中考试试题

陕西省延安市吴起县高三数学下学期第一次月考试题 文

精品推荐2018届下学期陕西省吴起高级中学高三3月月考试卷 数学(理)

陕西省吴起高级中学2018-2019学年高二下学期期中考试数学(理)试题(能力卷)(含答案)

陕西省吴起高级中学高二数学下学期期中试题(基础卷)理

陕西省延安市吴起县高三数学下学期第一次月考试题 文

陕西省延安市吴起高级中学2018届高三下学期期中考试物理试题

陕西省吴起高级中学2018届高三下学期期中考试数学(理)

【高考模拟】陕西省吴起高级中学2018届高三下学期期中考试英语(word版有答案)

陕西省延安市吴起县高三数学下学期第一次月考试题文

精品推荐2018届下学期陕西省吴起高级中学高三3月月考试卷数学(理)

陕西省延安市吴起县高三数学下学期第一次月考试题文