3第三章同步配套题解

合集下载

(完整word版)审计第三章同步练习题及答案解析

<<审计>> 第三章同步练习题（答案及解析在后面）（一）单项选择题1．A注册会计师担任某项审计业务的外勤负责人，如在执业过程中发现自己无法胜任，则应要求其所在会计师事务所（）。

A．聘请相关专家B．改派其他注册会计师C．终止该项审计业务约定D．出具无法表示意见的审计报告2．衡量注册会计师审计质量合格与否的标准是（）。

（教材P33第1段） A．独立审计准则B．注册会计师职业道德准则C．会计准则及国家其他有关财务会计制度D．审计质量控制准则3．下列没有违背注册会计师职业道德的相关规定的是（）。

A．注册会计师采用或有收费的方式向客户提供鉴证服务B．某项目经理6年对ABC公司审计，由于对ABC公司较熟悉，容易发现问题，故今年仍安排其负责该公司的年度会计报表审计工作C．注册会计师可以再聘请会计、审计专家协助其工作D．后任注册会计师发现前任注册会计师所审计的会计报表存在重大错报，首先应当提请审计客户告知前任注册会计师4．注册会计师对其助理人员应当（）。

（教材P37）A．进行监督和管理B．进行约束和指导C．进行指导和监督，并对其工作结果负责D．进行指导和监督，但不能对其工作结果负责5．会计师事务所和注册会计师不得对其能力进行广告宣传以招揽业务，下列陈述的原因中不正确的是（）。

（教材P55）A．广告可能导致同行之间的不正当竞争B．广告可以提高本会计师事务所的知名度C．广告可能损害专业服务的精神D．注册会计师的服务质量及能力无法由广告内容加以评估6．会计师事务所不得为同一家上市公司同时提供（）。

（教材P54） A．审计服务和纳税申报B．审计服务和代编会计报表C．审计服务和IT系统服务D．审计服务和法律服务7．会计师事务所的收费标准较为科学的是（）。

（教材P52） A．按照行业管理部门的规定B．按照被审计单位同行业的平均水平C．按照被审计单位资产规模大小以及按照审计工作量D．按照每一专业人员适当的小时费用率或日费用率为基础计算业务收费8．下列各项中，属于注册会计师违反职业道德规范行为的是（）。

第三章习题解答

第三章习题解答一、判断下列说法是否正确，凡对的在括号内打“√”，否则打“×”。

（1）现测得两个共射放大电路空载时的电压放大倍数均为－100，将它们连成两级放大电路，其电压放大倍数应为10000。

( )（2）阻容耦合多级放大电路各级的Q点相互独立，( )它只能放大交流信号。

( )（3）直接耦合多级放大电路各级的Q点相互影响，( )它只能放大直流信号。

( )（4）只有直接耦合放大电路中晶休管的参数才随温度而变化。

( )（5）互补输出级应采用共集或共漏接法。

( )二、现有基本放大电路：A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。

（1）要求输入电阻为1kΩ至2kΩ，电压放大倍数大于3000，第一级应采用，第二级应采用。

（2）要求输入电阻大于10MΩ，电压放大倍数大于300，第一级应采用，第二级应采用。

（3）要求输入电阻为100kΩ～200kΩ，电压放大倍数数值大于100，第一级应采用，第二级应采用。

（4）要求电压放大倍数的数值大于10，输入电阻大于10MΩ，输出电阻小于100Ω，第一级应采用，第二级应采用。

（5）设信号源为内阻很大的电压源，要求将输入电流转换成输出电压，且，输出电阻R o＜100，第一级应采用，第二级应采用。

三、选择合适答案填入空内。

（1）直接耦合放大电路存在零点漂移的原因是。

A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定（2）集成放大电路采用直接耦合方式的原因是。

A.便于设计B.放大交流信号C.不易制作大容量电容（3）选用差分放大电路的原因是。

A.克服温漂B. 提高输入电阻C.稳定放入倍数（4）差分放大电路的差模信号是两个输入端信号的，共模信号是两个输入端信号的。

A.差B.和C.平均值（5）用恒流源取代长尾式差分放大电路中的发射极电阻R e，将使电路的。

A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大（6）互补输出级采用共集形式是为了使。

3静力学第三章习题答案

第三章部分习题解答3-10 AB ,AC 和DE 三杆连接如图所示。

杆DE 上有一插销H 套在杆AC 的导槽内。

试求在水平杆DE 的一端有一铅垂力F 作用时，杆AB 所受的力。

设DE BC HE DH DB AD ===,,，杆重不计。

解：假设杆AB ，DE 长为2a 。

取整体为研究对象，受力如右图所示，列平衡方程：∑=0C M02=⋅a F By0=By F取杆DE 为研究对象，受力如图所示，列平衡方程：∑=0HM0=⋅-⋅a F a F DyF F Dy =∑=0B M 02=⋅-⋅a F a F DxF F Dx 2=取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0y F0=++By Dy Ay F F FF F Ay -=(与假设方向相反)∑=0A M02=⋅+⋅a F a F Bx DxF F Bx -=(与假设方向相反) ∑=0B M02=⋅-⋅-a F a F Dx AxF F Ax -=(与假设方向相反)3-12AD AC AB ,,和BC 四杆连接如图所示。

在水平杆AB 上作用有铅垂向下的力F 。

接触面和各铰链均为光滑的，杆重不计，试求证不论力F 的位置如何，杆AC 总是受到大小等于F 的压力。

解：取整体为研究对象，受力如图所示，列平衡方程：∑=0C M0=⋅-⋅x F b F DF bx F D =F CF C yF DF CxF CyF BxF ByF DxF DyF HyF BxF ByF DyF DxF Ax F Ay取杆AB 为研究对象，受力如图所示，列平衡方程：∑=0A M0=⋅-⋅x F b F BF bx F B =杆AB 为二力杆，假设其受压。

取杆AB 和AD 构成的组合体为研究对象，受力如图所示，列平衡方程：∑=0E M02)2(2)(=⋅--⋅+⋅+bF x b F b F F AC D B解得F F AC =，命题得证。

注意：销钉A 和C 联接三个物体。

大学物理第3章-刚体力学习题解答

大学物理第3章-刚体力学习题解答第3章刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。

求t 时刻的角速度和角加速度。

解：23212643ct bt ct bt a dt d dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ，车轮滚动半径为0.26m ，发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转？解：设车轮半径为R=0.26m ，发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。

显然，汽车前进的速度就是驱动轮边缘的线速度，909.0/2212Rn Rn v ππ==，所以：min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示，质量为m 的空心圆柱体，质量均匀分布，其内外半径为r 1和r 2，求对通过其中心轴的转动惯量。

解：设圆柱体长为h ，则半径为r ，厚为dr 的薄圆筒的质量dm 为：2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示，一半圆形细杆，半径为，质量为，求对过细杆二端轴的转动惯量。

解：如图所示，圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2，根据垂直轴定理z x y I I I =+和问题的对称性知：圆形细杆对过轴的转动惯量为12mR 2，由转动惯量的可加性可求得：半圆形细杆对过细杆二端轴的转动惯量为：214AA I mR '=3.18 在质量为M ，半径为R 的匀质圆盘上挖出半径为r 的两个圆孔，圆孔中心在半径R 的中点，求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。

第三章部分习题解答

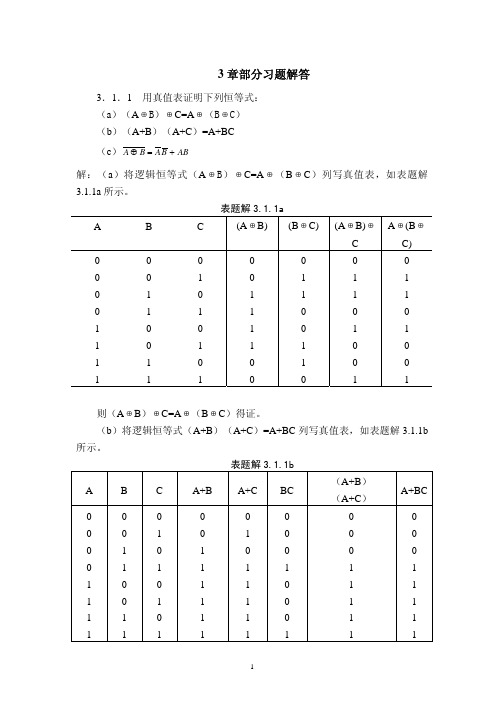
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路，如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3．4．7 某雷达站有 3 部雷达 A、B、C，其中 A 和 B 功率消耗相等，C 的功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电，发电机 X 的最大输出功率等于雷达 A 的功率消耗，发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一个逻辑电路，能够根据各雷达的启动和关闭信号，以最节约电能的方式启、停发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路，如图题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0

人教版物理八年级上册同步训练：第三章第一节温度(解析版)

人教版物理八年级上册同步训练：第三章第一节温度（解析版）人教版物理八年级上册第三章第一节温度同步训练一、单选题（共15题；共30分）1、如图所示，温度计的示数是（）A、65℃B、74℃C、66℃D、78℃2、下列图中温度计使用正确的是（）A、B、C、D、3、家庭用寒暑表的变化范围是（）A、0℃～100℃B、35℃～42℃C、﹣10℃～100℃D、﹣30℃～50℃4、下列温度值最接近实际的是（）A、健康成年人的体温是39℃B、让人感觉温暖而舒适的室内温度是25℃8、将两盆冰水混合物分别置于太阳下和冰箱冷冻室内，当这两个盆内都还有水和冰时，用温度计测量其温度（）A、放在太阳下的混合物其温度较高B、两盆冰水混合物温度相同C、放在太阳下的混合物其温度较低D、少条件不好判读温度的高低9、根据下表判断将水银温度计和酒精温度计相比较，使用水银温度计的优点是（）水银酒精沸点（℃）357 78.5熔点（℃）﹣38.8 ﹣117A、测量的范围更大B、能测量更高的温度C、测量的数值更精确D、以上三点都是它的优点10、体温计能精确到0.1℃，这是因为（）A、体温计玻璃泡内的水银比一般温度计多B、体温计测量范围小C、体温计短D、体温计玻璃泡的容积比玻璃管的容积大得多11、两支内径不同，下面玻璃泡内水银相等的合格的温度计同时插入一杯热水中，过一会儿则会看到（）A、两支温度计水银柱上升高度相同，示数不同B、内径细的温度计水银柱升得较高，示数相同C、内径粗的温度计升得高，示数较大D、内径粗的温度计水银柱升得低，示数较小12、在制作液体温度计时，为了提高温度计的灵敏度，下列措施可行的是（）A、玻璃管的内径做细一些B、玻璃管的内径做粗一些C、玻璃泡的容积做大一些D、玻璃泡的容积做小一些13、一把无刻度的温度计放在有刻度的尺旁，温度计在冰水混合物中水银柱面在6毫米处，温度计在一标准大气压下的沸水中水银柱在206毫米处，温度计中水银柱为100毫米处的温度是（）A、47℃B、48.5℃C、50℃D、100℃14、常用的液体温度计有酒精温度计、煤油温度计、水银温度计等，如果温度计中用“水”做测温物质，当被测物体的温度由0℃上升到10℃时，温度计的示数（）A、上升B、下降C、先上升后下降D、先下降后上升15、如图所示为体温计测得的温度，关于体温计的读数下列正确的是（）A、36.9℃B、37.0℃C、37.2℃D、37.6℃二、填空题（共5题；共7分）16、有一支温度计，其刻度是均匀的，但读数不准，在冰水混合物中读数为2℃，而在一标准大气压下沸水里读数为97℃，用这只温度计测一杯热水的读数为59℃，则这杯水的实际温度为________℃；当这只温度计的示数为________℃时，示数和当时的真实温度恰好相同．17、我国及世界上绝大多数国家日常生活中使用瑞典人摄尔修斯创立的摄氏温度（℃），美国等少数国家使用德国人华伦海特创立的华氏温度（单位符号°F）．下表为华氏温度T与摄氏温度t的对应关系，请你根据表格中的数据关系归纳出华氏温度T与摄氏温度t之间的关系式．T=________．t/℃ 10 15 20 25 30 35 40T/°F50 59 68 77 86 95 10418、如图所示，体温计的示数为________℃．19、（2019•赤峰）如图所示，温度计的示数为________℃（温度计的单位是摄氏度）．20、如图所示是人们常用的体温计，这种体温计是根据液体的________规律制成的，图中体温计的读数是________℃．三、计算题（共1题；共5分）21、一支刻度均匀的温度计放在冰水混合物中时，示数是2℃，放在一标准大气压下沸腾水中时温度为98℃，用它测量一杯水的温度为26℃，请你计算一下这杯水的实际温度是多少？四、综合题（共4题；共24分）22、小明通过学习得到下面几个结论，请帮他补充完整．(1)冰水混合物的温度是________．标准大气压下沸水的温度是________．(2)常用的液体温度计是根据________的规律制成的．温度计里的液体通常用________（列举两种）．(3)温度计上的字母“C”表示这个温度计采用________温度．人的正常体温约________，读作________．(4)实验室常用的温度计，它的下端是________，上面连着一根内径很细的________，当温度稍有变化时，细管内液面的位置就会有变化．23、如图所示的是意大利科学家伽利略根据气体热胀冷缩的性质制成的世界上第一支温度计．若图中的A处为第一天下午两点液面的位置，B处为第二天下午两点液面的位置．则：(1)哪天下午两点的气温高些？第________天下午．(2)这种温度计有什么不足之处？________．（答一条即可）．24、（2019•呼和浩特）小明同学设计的一个温度计，如图甲所示，瓶中装的是气体，瓶塞不漏气，弯管水平部分有一小段液柱．(1)这个温度计是根据________（选填“液体热胀冷缩”或“气体胀冷缩”）的规律制成的；(2)将此装置放在室内，当周围的温度降低时，液柱将向________（选填“左”或“右”）移动；(3)图乙是某患者测量体温时，体温计的示数图，此时患者的体温为________℃．25、两支温度计玻璃泡中所装的酒精一样多，但玻璃管内径粗细不同，经检测，温度计都合格．现将这两支温度计的玻璃泡同时插入同一杯热水中，(1)两支温度计的示数是否相同？(2)两支温度计的酒精升得是否一样高？若不一样高，哪支升得较高？答案解析部分一、单选题1、【答案】C【考点】温度计的使用及其读数【解析】【解答】解：由图知：温度计的最小刻度值是1℃，因此该温度计的示数是60℃+6℃=66℃；故C 正确．故选C．【分析】温度计在使用前要先观察其量程和分度值；温度计的示数在量程的范围内，分度值为1℃，注意液柱是在零刻度线的上方还是下方．可根据这两点读出此温度计的示数．2、【答案】D【考点】温度计的使用及其读数【解析】【解答】解： A、温度计的玻璃泡接触了烧杯底部．故A错误；B、温度计的玻璃泡接触了烧杯侧壁．故B错误；C、温度计的玻璃泡未与被测液体接触．故C错误；D、温度计的玻璃泡与被测液体充分接触，但没有接触容器底或容器壁．故D正确．故选D．【分析】使用温度计测量液体温度时，要使温度计的玻璃泡与被测液体充分接触，不要接触容器底或容器壁．3、【答案】D【考点】液体温度计的构造与工作原理【解析】【解答】解：A、我国北方广大地区在冬天的气温都低于0℃，故测量范围的最低温度应小于0℃，故A 是错误的； B、35℃～42℃是体温计的量程，无法用来测量冬天的环境范围，故B是错误的；C、在家庭中，无论南方和还是北方，夏天的最高温度一般为40℃左右，远远达不到100℃，故C是错误的；D、冬天，我国北方家庭里的温度一般不会低于﹣30℃；夏天，南方的气温一般不高于50℃，所以D是正确的．故选D．【分析】寒暑表是用来测量环境温度的，可以根据我国冬天和夏天温度来大致确定范围．4、【答案】B【考点】温度【解析】【解答】解：A、正常情况下，人的体温在37℃左右，变化幅度很小．此选项不符合实际； B、人体正常体温在37℃左右，感觉舒适的温度在25℃左右．此选项符合实际；C、人体正常体温在37℃左右，洗澡水的温度应该略高于体温，在40℃左右，不可能达到60℃．此选项不符合实际；D、晶体凝固点与物质种类有关，标准大气压下水的凝固点的0℃，盐水的凝固点要低一些．此选项不符合实际．故选B．【分析】此题考查我们对常见物体或环境温度的认识，结合对生活的了解和对温度单位摄氏度的认识，选出符合实际的选项．5、【答案】C【考点】体温计的使用及其读数【解析】【解答】解： A、体温计1℃之间有10个小格，每个小格为0.1℃，体温计的分度值是0.1℃，故A 错误；B、体温计的工作原理就是液体热胀冷缩的规律，故B错误；C、由于体温计的特殊结构（有缩口），它是能离开被测物体读数，故C正确；D、根据体温计的特点，使用前用力甩一下玻璃泡上方的水银才能回到玻璃泡中，不能进行连续测量，故D错误．故选C．【分析】体温计的分度值是0.1℃，根据分度值和液面位置可以读出温度值，由于体温计液泡上方有缩口，所以可以离开被测物体读数，温度计都是利用液体热胀冷缩的规律制成的；同时体温计在使用前要用力甩一下，将水银甩回玻璃泡中．6、【答案】D【考点】液体温度计的构造与工作原理【解析】【解答】解：不同的温度计测量的最低温度和最高温度如果相同，叫它们的测量范围相同，也就是量程相同，但它们的长度、细管内径、玻璃泡的体积、分度值等可以都不一定相同．故选D．【分析】温度计上标识的最高温度和最低温度，是此温度计的测量范围，也就是量程．【考点】摄氏温度及其计算【解析】【解答】解：甲放在空气中时，它所显示的是空气的温度；丙温度计置于有密闭盖子的水杯内，它显示的是杯中水的温度，因为是密闭的，因此它的温度等于外边空气的温度；乙温度计的液泡上包有含水的棉花团，棉花团中的水要蒸发，蒸发要吸热，因此该温度计的示数应该比外界空气的温度低．由此可以判断，乙温度计肯定不准确．故选B．【分析】放在空气中的温度计甲，测量的是空气的温度；丙温度计置于有密闭盖子的水杯内，不能蒸发；乙温度计的液泡上包有含水的棉花团，由于水的蒸发，蒸发吸热，所以乙温度计的示数应该是比较低的．8、【答案】B【考点】摄氏温度及其计算【解析】【解答】解：将两盆冰水混合物分别置于太阳下和冰箱冷冻室内，当这两个盆内都还有水和冰时，两盆内水的状态都是冰水混合物，而冰水混合物的温度是0℃，所以两盆内的温度相同．故选B．【分析】摄氏温度规定：1标准大气压下，冰水混合物的温度为0℃，沸水的温度为100℃．此题可以根据两容器中物质的状态来判断温度、得出结果．【考点】液体温度计的构造与工作原理【解析】【解答】解：A、水银的凝固点是﹣38.8℃、沸点是357℃；酒精的凝固点是﹣177℃沸点是78.5℃．故水银温度计的测量范围大； B、温度计能测量的最高温度取决于内部液体的沸点，水银的沸点高于酒精，故水银温度计能测量更高的温度；C、水银比酒精的比热容小、纯度高，故水银温度计测量的数值更精确；D、由分析可知，以上三点都是水银温度计的优点，故D 正确．故选D．【分析】液体温度计是利用液体热胀冷缩的性质制成的，其测量范围应在其凝固点和沸点之间．10、【答案】D【考点】液体温度计的构造与工作原理【解析】【解答】解：体温计和常用温度计相比，前者内径很细，而下端的玻璃泡则很大，使得有微小的温度变化，即吸引很少的热量，管中水银上升的高度会非常明显，所以可以测量的更为精密．故选D．【分析】体温计比常用的温度计测量精度高，即分度值小，只有0.1℃；而常用的温度计的分度值是1℃．可以从体温计的构造上进行分析．【考点】液体温度计的构造与工作原理【解析】【解答】解：同一杯热水说明最后温度计示数应该相同．玻璃泡中水银量相等，说明水银受热后膨胀程度相同，即增大的体积是相同的，内径的不同影响的是水银柱升高的高度．内径粗的温度计水银柱升得较低；内径细的温度计水银柱升得较高．故选B．【分析】本题温度计为合格的温度计，所以我们可以从题干中的两个关键词分析：①水银量相等；②同一杯热水．先得出结论，然后利用排除法选出正确答案．12、【答案】A【考点】液体温度计的构造与工作原理【解析】【解答】解：AB、玻璃泡中的液体升高相同的温度，体积膨胀相同，如果管越细，上升的刻度越多，越灵敏．所以内径要细一些．选项A正确，选项B错误；CD、玻璃泡容积越大，温度变化量相同时，液体总体积的变化量会更大，表现在毛细管中会更明显，灵敏度更高、准确程度更高，但玻璃管内径粗细不确定，灵敏程度不能确定．此两选项均错误．故选A．【分析】①液体温度计是根据液体的热胀冷缩性质制成的，玻璃泡中的液体遇热膨胀时，会在玻璃管中上升，升高相同的温度，体积膨胀相同，如果管越细，上升的刻度越多，越灵敏；②增大玻璃泡的容积，温度变化量相同时，液体总体积的变化量会更大，表现在毛细管中会更明显，会影响灵敏度．13、【答案】A【考点】液体温度计的构造与工作原理【解析】【解答】解：水银柱6mm时的温度是0℃，206mm 时的温度是100℃．所以1mm水银柱表示的温度= =0.5℃在液体中水银柱的长度上升了100mm﹣6mm=94mm，液体的温度=94mm×0.5℃/mm=47℃．故选A．【分析】冰水混合物的温度是0℃，一个标准大气压下沸水温度是100℃．此温度计上用200mm（206mm﹣6mm）表示，即1mm表示0.5℃，再根据温度计在液体中的实际长度100cm得出液体的温度．14、【答案】D【考点】液体温度计的构造与工作原理【解析】【解答】解：因为水的比热容较大，吸收相同的热量，水的温度变化小，用水做温度计灵敏度低；另外水还有反常膨胀，在0～4℃，当温度升高时，水体积缩小；因此制造温度计不用水．当被测物体的温度由0℃上升到10℃时，水在4℃的时候密度最大，故体积先减小，大于4℃再升高；故选：D【分析】常用温度计是利用液体热胀冷缩的原理制成的．水的比热容较大，相同质量的水和其它物质比较，吸收相同的热量水的温度变化小；水在0～4℃，当温度升高时体积缩小（反常膨胀）；据此回答．15、【答案】B【考点】体温计的使用及其读数【解析】【解答】解：由图知：体温计上1℃之间有10个小格，所以一个小格代表的温度是0.1℃，即此体温计的分度值为0.1℃；此时的温度为37℃．故选：B．【分析】使用体温计测量体温时，先要弄清楚体温计的量程和分度值，读数时视线与液柱最末端所对刻度相垂直．二、填空题16、【答案】60；40【考点】液体温度计的构造与工作原理【解析】【解答】解：用这只温度计测一杯热水的读数为59℃，则这杯水的实际温度为t=57× ≈60℃；示数和当时的真实温度t恰好相同时，t=（t﹣2）× ；所以t=40℃．故答案为：60；40．【分析】（1）我们知道在一标准大气压下冰水混合物的温度是0℃，沸水的温度是100℃．所以这支温度计上的示数2℃所对应的实际温度是0℃，示数97℃对应的实际温度是100℃．（2）由于2℃到97℃之间有95个格，那么用实际的100℃除以95个格就是这支温度计一个小格表示的温度值了，即；那么当示数为59℃时，从2℃到59℃之间有57个格，用57× 算出的就是实际的温度；示数和当时的真实温度恰好相同时对应的温度根据上述原理同样可求．17、【答案】（1.8°F/℃）t+32°F 【考点】摄氏温度及其计算【解析】【解答】解：设摄氏温度为t（℃）与华氏温度为T（°F）之间的函数关系式为T=kt+b，由题意得：50°F=10℃k+b﹣﹣﹣﹣①，59°F=15℃k+b﹣﹣﹣﹣②，由①②解得：k=1.8°F/℃；b=32°F；即T=（1.8°F/℃）t+32°F．故答案为：（1.8°F/℃）t+32°F．【分析】设摄氏温度为t（℃）与华氏温度为T（°F）之间的函数关系式为T=kt+b，由待定系数法求出其解．18、【答案】38.5【考点】体温计的使用及其读数【解析】【解答】解：图中体温计的分度值为0.1℃，其示数为38℃+0.1℃×5=38.5℃．故答案为：38.5．【分析】本题考查了体温计的使用方法．首先观察体温计的量程为35﹣42℃，最小分度值为0.1℃，由此可以读出体温计的示数．19、【答案】﹣9【考点】温度计的使用及其读数【解析】【解答】解：看图知，数值自下而上是变小的为零下多少摄氏度，比0℃低9格，即低9摄氏度，为﹣9℃．故答案为：﹣9．【分析】温度计的读数关键是区分零上多少摄氏度还是零下多少摄氏度，要点是看数值的变化情况，数值自下而上变大时是零上多少摄氏度，反之是零下多少摄氏度．20、【答案】热胀冷缩；37.8 【考点】体温计的使用及其读数【解析】【解答】解：（1）温度计、体温计都是利用液体的热胀冷缩的规律制成的．（2）由图可知，体温计的玻璃管中的液面对应的刻度比37℃多了8个小格，故示数为37℃+8×0.1℃=37.8℃．故答案为：热胀冷缩；37.8．【分析】（1）体温计是利用液体的热胀冷缩的原理制成的．（2）体温计的分度值为0.1℃，结合体温计中液面对应刻度，可以读取体温计的示数．三、计算题21、【答案】解：温度计上一个小格表示的实际温度为；温度计测量某种液体的温度为26℃时，这种液体的实际温度为×（26﹣2）=25℃．【考点】液体温度计的构造与工作原理【解析】【分析】冰水混合物的温度是0℃，标准大气压下沸水的温度是100℃；而此温度计测量冰水混合物体的温度是2℃，标准大气压沸水的温度是98℃，中间是98﹣2=96个小格，求出一个小格表示的温度；温度计插入水中显示温度是26℃，距离2℃有（26﹣4）个小格，求出这些小格表示的温度加上温度计显示为2℃时的实际温度0℃，就是水的实际温度．四、综合题22、【答案】（1）0；100（2）液体热胀冷缩；煤油（酒清、煤油等）（3）摄氏；37℃；三十七摄氏度（4）玻璃泡；玻璃管【考点】液体温度计的构造与工作原理【解析】【解答】解：（1）摄氏温度的规定：把一标准大气压下冰水混合物的温度规定为0度，把沸水的温度规定为100度，分别用0℃和100℃表示．（2）常用的液体温度计都是利用利用液体的热胀冷缩制成的，最常见的液体有水银（如体温计）、酒精、煤油（如寒暑表）等．故答案为：液体的热胀冷缩；水银（酒清、煤油等）．（3）温度计上的字母“℃”表示这个温度计采用摄氏温度，人的正常体温是37℃，读作三十七摄氏度；（4）在酒精温度计的下端做一个较大的玻璃泡，里面盛满酒精，是为了使酒精热胀冷缩的总体积变化量增大；内径的玻璃管做得非常细，是为了使体积的变化显示地更明显；温度升高，酒精体积增大时，管内酒精面的位置上升，温度降低，酒精体积收缩时，管内酒精面的位置下降．故答案为：（1）0；100；（2）液体热胀冷缩；煤油（酒清、煤油等）；（3）摄氏；37℃；三十七摄氏度；（4）玻璃泡；玻璃管．【分析】（1）物体的冷热程度叫温度．通常温度的单位叫摄氏度，摄氏单位是这样规定的：把标准大气压下，冰水混合物的温度规定为0度，把沸水的温度规定为100度．（2）常用的温度计都是液体温度计，其原理就是利用液体的热胀冷缩制成的．（3）温度计上的字母“℃”表示这个温度计采用摄氏温度，人的正常体温是37℃．（4）一般的液体都遵循热胀冷缩的规律，实验室温度计就是根据酒精的这一性质制成的．为了使酒精的热胀冷缩效果放大容易观察，我们在制作温度计时设计了相应的结构特点．23、【答案】（1）二（2）没有刻度值（或不便于携带等）【考点】液体温度计的构造与工作原理【解析】【解答】解：（1）气体温度计是利用气体的热胀冷缩性质制成的．液面在A处时，球形容器内的气体压强小，温度较低；液面在B处时，球形容器内的气体压强大，温度较高；（2）这种温度计没有刻度，不便于携带．故答案为：（1）二；（2）没有刻度值（或不便于携带等）．【分析】气体温度计的原理：气体的热胀冷缩性质．上方的球形容器是用来感知空气温度的，当空气温度降低时，球形容器中的气体受冷，体积减小，气体压强减小．据此答题．24、【答案】（1）气体热胀冷缩（2）左（3）39【考点】体温计的使用及其读数【解析】【解答】解：（1）这是个气体温度计，所以是根据气体的热胀冷缩来测量温度的；（2）温度升高时，瓶内气体就要膨胀，所以会把液柱向左推；（3）读图可知，体温计的测量范围是35℃～42℃，分度值是0.1℃，此时体温计示数是：39℃．故答案：（1）气体热胀冷缩；（2）左；（3）39．【分析】（1）通常用的液体温度计是根据液体的热胀冷缩原理制成的；（2）本题的温度计是利用空气的热胀冷缩原理，气体跟液体的差别在于会受到大气压的影响；（3）人的体温一般也不会超过35﹣﹣42℃的范围，体温计的测量范围是35℃～42℃，分度值是0.1℃，读数时要先明确分度值，再看液柱位置，然后读出温度值．25、【答案】（1）解：因为是放在同一杯热水中，因此两支温度计的示数应该是相同的（2）解：两支温度计的酒精升得不一样高；玻璃泡里装有的酒精体积相同，受到相同的热膨胀时，体积增加量相等，内径细的玻璃管，液柱上升得高．【考点】液体温度计的构造与工作原理【解析】【分析】温度计的玻璃泡里装有同样多的酒精，因此遇热膨胀时，膨胀的体积是相同的，但是，由于玻璃管的粗细不同，依据“体积=横截面积×高度”得出答案．。

高中化学选修3 第三章晶体结构与性质讲义及习题.含答案解析

高中化学选修三第三章晶体结构与性质一、晶体常识1、晶体与非晶体比较自范性：晶体的适宜的条件下能自发的呈现封闭的，规则的多面体外形。

对称性：晶面、顶点、晶棱等有规律的重复各向异性：沿晶格的不同方向，原子排列的周期性和疏密程度不尽相同，因此导致的在不同方向的物理化学特性也不尽相同。

2、获得晶体的三条途径①熔融态物质凝固。

②气态物质冷却不经液态直接凝固（凝华）。

③溶质从溶液中析出。

3、晶胞晶胞是描述晶体结构的基本单元。

晶胞在晶体中的排列呈“无隙并置”。

4、晶胞中微粒数的计算方法——均摊法某粒子为n个晶胞所共有，则该粒子有1/n属于这个晶胞。

中学常见的晶胞为立方晶胞。

立方晶胞中微粒数的计算方法如下：①晶胞顶角粒子为8个晶胞共用，每个晶胞占1/8②晶胞棱上粒子为4个晶胞共用，每个晶胞占1/4③晶胞面上粒子为2个晶胞共用，每个晶胞占1/2④晶胞内部粒子为1个晶胞独自占有，即为1注意：在使用“均摊法”计算晶胞中粒子个数时要注意晶胞的形状。

二、构成物质的四种晶体1、四种晶体的比较（1）不同类型晶体的熔、沸点高低一般规律：原子晶体＞离子晶体＞分子晶体。

金属晶体的熔、沸点差别很大，如钨、铂等熔、沸点很高，汞、铯等熔、沸点很低。

（2）原子晶体由共价键形成的原子晶体中，原子半径小的键长短，键能大，晶体的熔、沸点高。

如熔点：金刚石＞碳化硅＞硅（3）离子晶体一般地说，阴阳离子的电荷数越多，离子半径越小，则离子间的作用力就越强，相应的晶格能大，其晶体的熔、沸点就越高。

晶格能：1mol气态阳离子和1mol气态阴离子结合生成1mol离子晶体释放出的能量。

（4）分子晶体①分子间作用力越大，物质熔、沸点越高；具有氢键的分子晶体熔、沸点反常的高。

②组成和结构相似的分子晶体，相对分子质量越大，熔、沸点越高。

③组成和结构不相似的物质（相对分子质量接近），分子的极性越大，熔、沸点越高。

④同分异构体，支链越多，熔、沸点越低。

（5）金属晶体金属离子半径越小，离子电荷数越多，其金属键越强，金属熔、沸点就越高。

第三章习题解答及参考答案

(
)
①
2 式中 m 为整数。令 u = αr ，显然上式是 u 的周期函数，周期为 2π ，故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数：
其中，
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有：
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ；两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明，要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少？解：取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的空间频率成分不受到有限孔径的渐晕效应的影响，故透镜的口径 D 应满足条件：

医学高等数学习题解答(第3章)

第三章一元函数积分学习题题解(P108)一、判断题题解1. 错。

是原函数的全体，记作⎰+C dx x f )(。

2. 错。

)(x f 的任意两个原函数之差为常数。

3. 错。

是C x F +)(。

4. 正确。

5. 错。

被积函数在x =0处无界。

6. 正确。

x y sin ='，00='=x y7. 正确。

被积函数是奇函数，积分区间对称。

8. 正确。

二、选择题题解1. )()(x f x x x f -=--=-被积函数是奇函数，积分区间对称，定积分为零。

或⎰-11dx x x = ⎰⎰+--10212dx x dx x =130 133131x x +--=[]0)01(31)1(031=-+---。

(A )2.⎰+∞∞-+dx x 211=⎰∞-+0 211dx x +⎰+∞+0 211dx x =0 arctan ∞-x ++∞0arctan x =πππ=-+⎪⎭⎫ ⎝⎛--0220。

(A ) 3. 正确的是C 。

4.dx x f aa⎰-- )(xu dudx -=-=====令du u f aa⎰-- )(=dx x f aa⎰- )(。

(D )5. 令u ax b =-，du adx =-，du u f a dx ax b f ⎰⎰-=-)(1)(=C u F a +-)(1=C ax b F a+--)(1。

(B )6. 令xe x F -=)(，则xe xf --=)(，dx xe dx x xf x ⎰⎰--=)(=()⎰-x e xd =⎰---dx e xe x x =C x e x++-)1(。

(D )7.dt t x⎰+141u du u xut udu dt 21122⎰+========令=du u ux ⎰+1 121，∴⎪⎭⎫ ⎝⎛+⎰dt t dx d x 1 41=x x +121。

(D ) 或⎪⎭⎫ ⎝⎛+⎰dt t dx d x 1 41=)()(14'+x x =x x xx +=+12121128.⎰'''dx x f x f )()(=⎰'')()(x f d x f =[][]C x f x f d +'='⎰22)(21)(21，2)(x e x f -=，22)(x xe x f --=' []C x f +'∴2)(21 =()C xe x +--22221=C e x x +-2222。

线性代数(含全部课后题详细答案)3第三章矩阵习题解答.docx

习题三A 组1 •填空题.(1)设口 = (1,1,1), 6 = (-1,-1,-1),则ah x= _____________ , a vh= _________ro o>1 ](3)若么=(1, 2, 3), B — 1, —, — , A — a}d ,则 A n =I 2 3丿‘1 0⑷设A= 0 2J o解0.(5)设 a = (l, 0, -if ，矩阵 A=aa l \ 斤为正整数，贝 i\kE - A n解 k 2(k-2n ).(6)设昇为斤阶矩阵，且A =2,贝ij AA T= _________ , AA ： = _______2(2)设八1-3 2),B =-3丿1 -13 1 3>则AB = (0 0丿(—3 -3丿2 13232 3 1 1)0 ,正整数 /7 > 2 ,则 A n -2A ,l ~' =2“+i2".(cos& -sin&\(7)、sin& cos& 丿cos& sin&\、一sin& cos& 丿0 0、2 0 ,则(A*y =4 5,解討丫2(10)设矩阵/二,矩阵B满足BA = B + 2E,则B二，B<-1 2(2 0(11)设/，〃均为三阶矩阵，AB = 2A + B f B= 0 4,2 0‘0 0 P解0 1 0b o oj(12)设三阶矩阵/满足|力|二*, (3A)~l-2A* =1627(13)设/为加阶方阵,B为兀阶方阵,同=Q,\B\ = b, C =°, 则\c\ =(8)设…®?工0 ,则、\Z曾丿1)a n1%■■1 1■色丿丿a lP(9)设A= 22、0 ,贝=2丿/0、0 ,矩阵〃满足关系式ABA =2BA ^E,其屮才'为力的伴随矩阵，则|B | =解*•解0.解一3・是nxp 矩阵，C 是pxm 矩阵，加、n 、p 互不相等，则下列运算没有(B) ABC ；解D.(2)设/是mxn 矩阵(m n), B 是nxm 矩阵，则下列解(一l)〃5b ・(15)设4阶矩阵/的秩为1,则其伴随矩阵/的秩为 (14)设三阶矩阵/ =R(4)解1.(17)设矩阵力'a 、b\ a }b 2■ ■a 2b 2 ■ • ■a n b2,其中匕・工0, (Z=l,2,•••,/?),则力的秩，且7?(J) = 3,则丘=0、 -2i,则将/可以表示成以下三个初等矩阵的乘积(D) AC T .的运算结果是n 阶力•阵.(A) AB ；解B.(B) A YBT；(C) B r A T ；(D) (4B)T.(16 )设？1 = •咕、・仇・ a n b n)解2.选择题.(1)设/是mxn 矩阵,(3) 设力」是斤阶方阵，AB = O,贝I 」有 ________ • (A) A = B = Ox(B) A + B = O ； (C)同=0或|同=0；(D)同 + 圖=0・解C ・(4) 设力，〃都是斤阶矩阵，则必有 _______ . (A) \A + B\ = \^ + \B\； (B) AB = BA ； (C) \AB\ = \BA\ ；(D) (/1 + B)T M /T + BT ・解C ・(5) 设/,B 是斤阶方阵，下列结论正确的是 __________ ・ (A)若均可逆，则A^B 可逆； (B)若力，〃均可逆，则力〃可逆； (C)若A + B 可逆，则A-B 可逆；(D)若A + B 可逆，则4〃均可逆.解B.(6) 设斤阶方阵A,B,C 满足关系式 ABC = E ，则必有 ___________ ・ (A) ACB = E ； (B) CBA = E ；(C) BAC = E ；(D) BCA = E .解D.(7) 设昇，B,力 + B, /T+BT 均为斤阶可逆矩阵，贝等于 ________________________ (A)(B) A + B ；(C) (D) g + 3)".解C.(8) 设£B,C 均为兀阶矩阵，若B = E + MB , C = A^CA.则B-C 为 ________________ . (A) E\ (B) —E ； (C) ； (D) —A.. 解A.(9) 设矩阵A = (a i .} 满足才其中才是/的伴随矩阵，川为昇的转置矩阵.若\ "3x3。

人教新课标三年级数学上册讲练测(知识归纳+例题讲解+同步测试)第三章测量

做单位。
6、相邻两个质量单位进率是 1000。
1 吨=1000 千克 1000 千克= 1 吨 1 千克＝1000 克 1000 克＝1 千克
【例题精讲】
【例 1】60 厘米和 6 分米比，谁长？（）
A．60 厘米长
B．6 分米长
C．同样长
【分析】把 60 厘米化成用分米作单位的名数，再比较得解．
③ 进率是 1000： 1 千米=1000 米,
1 公里= =1000 米,
1000 米=1 千米,
1000 米 = 1 公里
5、当我们表示物体有多重时，通常要用到（质量单位）。在生活中，称比较轻的物品的质量，可以用（克）
做单位；称一般物品的质量，常用（千克）做单位；计量较重的或大宗物品的质量，通常用（吨）
【分析】低级单位厘米化高级单位米除以进率 100；低级单位克化高级单位千克除以进率 1000；低级单位米化高级单位千米除以进率 1000．【解答】解：120 厘米＝1.2 米 6500 克＝6.5 千克 9100 米＝9.1 千米成年大天鹅体长至少有 120 匣米，合 1.2 米；体重至少有 6500 克，合 6.5 千克．它是世界上飞得最高的鸟，每年飞越喜马拉雅山时，飞越高度达 9100 米，合 9.1 千米．故答案为：1.2，6.5，9.1．【点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位，其次记住单位间的进率；由高级单位化低级单位乘进率，由低级单位化高级单位除以进率．
2020-2021 学年三年级数学上册知识归纳+例题讲解+同步检测第三章测量
【知识点归纳】
1、在生活中，量比较短的物品，可以用（毫米、厘米、分米）做单位；量比较长的物体，常用（米）做单

2022年苏科版八年级物理上册第三章光现象同步练习试题(含答案解析版)

苏科版八年级物理上册第三章光现象同步练习考试时间：90分钟；命题人：物理教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 15分）一、单选题（5小题，每小题3分，共计15分）1、如图所示，是“探究光的反射定律”的实验，小王同学将一块平面镜放在水平桌面上，再把一块白色纸板A垂直放置在平面镜上，纸板A可以绕NO转动，让一束光贴着纸板A射向O点。

下列说法错误的是（）A．利用白纸板是为了显示光的传播路径B．图甲和丙，说明在反射现象中光路是可逆的C．当入射光垂直于平面镜入射时，入射角为90°D．图乙中，将纸板沿NO折叠后，反射光依然存在2、2000多年前，《墨经》中就记载了如图所示的小孔成像实验，小孔成像是下列哪种光现象形成的（）A．光的直线传播B．光的反射C．光的折射D．光的色散3、如图所示是小明探究光的反射定律的实验过程。

下列叙述正确的是（）A．图甲中若入射光绕O点顺时针转动，则反射光也绕O点顺时针转动B．图甲中若入射光沿NO方向入射，则反射角为90°C．图乙中反射光不存在D．甲、丙两图说明，在反射现象中光路是可逆的4、如题图所示，2022年北京冬奥会闭幕式上两个人在冰面上推着巨大的地球仪入场，在地球仪靠近光源的过程中，下列说法正确的是（）A．地球仪影子的形成与倒影的原理相同B．靠近光源过程中地球仪的影子变长C．靠近光源过程中地球仪的影子变短D．冰面发亮，是因为冰面也是光源5、对下列四幅图的描述选项正确的是（）A．平面镜成像，透过玻璃版看到的像是蜡烛的虚像B．小孔成像透过小孔只能成倒立缩小的实像C．发生漫反射时，有些光线不再遵循光的反射定律D．光的色散属于光的反射现象第Ⅱ卷（非选择题 85分）二、填空题（5小题，每小题4分，共计20分）1、在光学实验室内，将一辆玩具汽车放置在白色背景板前。

3 第三章圆锥曲线的方程新(定义)必刷必过题(解析版)

A ．123e e e >>B ．132e e e >>C ．213e e e >>D ．231e e e >>【答案】A【详解】由椭圆的短轴长与长轴长的比值为2b b =，离心率为2c c e ==A ．29011B ．29013C ．1311【答案】B【详解】依题意，以点2O 为原点，直线13O O 为x 轴建立平面直角坐标系，设双曲线C 的方程为2222x y a b -A．2213yx-=B．C．22139x y-=D．【详解】设双曲线的方程为：22221(0,0) x y a ba b-=>>A．2B．13 5C．74D．73【答案】B8．（2022·全国·高三专题练习（文））阿基米德不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．椭圆C的焦点在x轴上，且椭圆A ．10,2⎛⎫- ⎪⎝⎭B ．（0，－1【答案】A【详解】依题意()2,2A -在抛物线yA．2B．3【答案】A【详解】由题意可知21,23⎛⎫⎪⎪⎝⎭M，N经过M，N两点，1=【详解】|,||2CO a AO a==所以双曲线T 的方程为222213x y a a-=T 的方程为22214x y a -=,所以23a =的中点为G ,则3||32BG a ==||33||||2BG BD BD ===.所以||2BD =A ．22221212a ab b -<-A．曲线C的图象关于原点对称B．曲线C经过5个整点（横、纵坐标均为整数的点）C．曲线C上任意一点到坐标原点【答案】223144y x -=【详解】因为(22221y x a a b-=>所以下焦点的坐标为()0,c -，渐近线方程为【答案】22##122【详解】由椭圆的光学性质可知，13tan 4ABF ∠=，如图，所以1|3,||4,|AF k AB k BF ==|由椭圆的定义可知345k k ++可得2||633AF k k k =-=，在所以12||232F F c k ==，所以【答案】34【详解】设抛物线的方程为()220y px p =>，则f =设()00,A x y ，因为2π3θ=，所以0222p p AF x ⎛=+=- ⎝3y p =，所以232d y p ==，故其焦径比【答案】22【详解】设圆柱的底面半径为=2DE AB r ∴=．23．（2022·湖北·荆门市龙泉中学二模）历史上第一个研究圆锥曲线的是梅纳库莫斯（公元前375年-325年），大约还进一步研究了这些圆锥曲线的光学性质：如图甲，从椭圆的一个焦点出发的光线或声波，经椭圆反射后，反射光线经过椭圆的另一个焦点，相应切点的直线，如图乙，椭圆发出的光经椭圆两次反射后回到（1）椭圆C的离心率为__________．（2）点P是椭圆C上除顶点外的任意一点，椭圆在点P圆228x y+=上，则椭圆C的方程为__________．【答案】1##0.52216x y+=【答案】122【详解】若为圆，则ABP △为直角三角形，因为PQ AB ⊥，所以APQ PBQ ∽当为图形为椭圆时，如图建立平面直角坐标，设椭圆方程为则,,AQ m a BQ a m PQ n =+=-=，所以又22221m n a b +=，得22222b m n b a=-，即PQ【答案】25【详解】由图知，双曲线的渐近线的倾斜角为由上知双曲线为等轴双曲线，故设双曲线方程为故答案为：2；53.。

3第三章半导体中载流子的统计分布习题解答

第三章半导体中载流子的统计分布3-1、对于某n型半导体试证明其费米能级在其本征半导体的费米能级之上。

即EFnEFi。

证明设nn为n型半导体的电子浓度ni为本征半导体的电子浓度。

显然nn ni ininFFFccFccEETkEENTkEEN则即00expexp 即: 3-2、试分别定性定量说明1 在一定的温度下对本征材料而言材料的禁带宽度越窄载流子浓度越高2 对一定的材料当掺杂浓度一定时温度越高载流子浓度越高。

解1 在一定的温度下对本征材料而言材料的禁带宽度越窄则跃迁所需的能量越小所以受激发的载流子浓度随着禁带宽度的变窄而增加。

由公式TkEvcigeNNn02 也可知道温度不变而减少本征材料的禁带宽度上式中的指数项将因此而增加从而使得载流子浓度因此而增加。

2对一定的材料当掺杂浓度一定时温度越高受激发的载流子将因此而增加。

由公式可知这时两式中的指数项将因此而增加从而导致载流子浓度增加。

3-3、若两块Si样品中的电子浓度分别为2.25x1010cm-3和6.8x1016cm-3试分别求出其中的空穴的浓度和费米能级的相对位置并判断样品的导电类型。

假如再在其中都掺入浓度为2.25x1016cm-3的受主杂质这两块样品的导电类型又将怎样解由200inpn 得3316210022023101021001201103.3108.6105.1100.11025.2105.1cmnnpcmnnpii 可见TkEENpTkEENnVFVFcc0000expexp和型半导体本征半导体npnpn02020101 又因为TkEEvvFeNp00则eVEEpNTkEEeVEEpNTkEEvvnvFvvvvF331.0103.3101.1ln026.0ln234.0100.1101.1ln0 26.0ln319020210190101 假如再在其中都掺入浓度为2.25x1016cm-3的受主杂质那么将出现杂质补偿第一种半导体补偿后将变为p型半导体第二种半导体补偿后将近似为本征半导体。

[整理]3第三章微分中值定理与导数的应用习题解答23309

第三章微分中值定理与导数的应用答案§3.1 微分中值定理1．填空题（１）ππ-4 （２） 3 , )5,3(),3,2(),2,1(2．选择题（１） B （２） C （３） B3．证明：令x arc x x f cot arctan )(+=，则01111)(22=+-+='xx x f ，所以)(x f 为一常数．设c x f =)(，又因为(1)2f π=，故 )(2c o t a r c t a n ∞<<-∞=+x x arc x π．4．证明：由于)(x f 在],[21x x 上连续,在),(21x x 可导,且)()(21x f x f =，根据罗尔定理知，存在),(211x x ∈ξ，使0)(1='ξf ．同理存在),(322x x ∈ξ，使0)(2='ξf ．又)(x f '在],[21ξξ上符合罗尔定理的条件，故有),(31x x ∈ξ，使得0)(=''ξf ．5．证明：设621)(32x x x x f +++=，则031)2(,01)0(<-=->=f f ，根据零点存在定理至少存在一个)0,2(-∈ξ，使得0)(=ξf ．另一方面，假设有),(,21+∞-∞∈x x ，且21x x <，使0)()(21==x f x f ，根据罗尔定理，存在),(21x x ∈η使0)(='ηf ，即02112=++ηη，这与02112>++ηη矛盾．故方程062132=+++x x x 只有一个实根．6．证明：由于)(x f 在],[b a 内可导，从而)(x f 在闭区间],[b a 内连续，在开区间(,)a b 内可导．又因为()0,()0f a f c <>，根据零点存在定理，必存在点1(,)a c ξ∈，使得0)(1=ξf ．同理，存在点2(,)c b ξ∈，使得0)(2=ξf ．因此()f x 在[]21,ξξ上满足罗尔定理的条件，故存在),(b a ∈ξ，使0)(='ξf 成立．7.证明：只需令2)(x x g =，利用柯西中值定理即可证明.8．（１）证明：设t t t t f cos sin )(-=，函数)(t f 在区间],0[x 上满足拉格朗日中值定理的条件，且t t t f sin )(=', 故'()(0)()(0), 0f x f f x x ξξ-=-<<, 即0sin cos sin >=-ξξx x x x (π<<x 0)因此，当π<<x 0时，x xxcos sin >．（２）证明：设x x f ln )(=，则函数在区间[,]b a 上满足拉格朗日中值定理得条件，有'()()()(),f a f b f a b b a ξξ-=-<< 因为'1()f x x=，所以1ln ()a a b b ξ=-，又因为b a ξ<<，所以111a b ξ<<，从而 bba b a a b a -<<-ln ．§3.2 洛毕达法则1．填空题（１）35- （２） 0 （３）31 （４）1２．选择题（１） B （２） C3．（１）解： n n m m a x a x a x --→lim =nm n m a x a nm nx mx ---→=11lim．（２）解： 20222lim xx x x -+-→=x x x x 22ln 22ln 2lim 0-→-=2)2(ln 2)2(ln 2lim 220x x x -→+=2)2(ln ．（３）解：30tan sin lim x x x x -→＝32030)21(lim )1(cos tan lim x x x x x x x x -⋅=-→→＝21-．（４）解：20)(arcsin 1sin lim x x e x x --→＝201sin lim xx e x x --→＝212sin lim 2cos lim 00=+=-→→x e x x e x x x x ．（５）解： )ln 1()(x x x xx+='，x x x x x x ln 1lim1+--→＝x x x xx 11)ln 1(1lim 1+-+-→＝22111)ln 1(limxx x x x xx x --+-→2])ln 1([lim 1221=++=++→x x x x x x ．（６）解：2121lim )1(1lim )111(lim 22000==---=--→→→x xe x x e e x x x x x x x（７）解：1)1(lim 202000sin limcsc 1lim cot ln limln tan lim tan 0=====+→+→+→+→+----→x xxx xxxx xx x x x x e e ee x．（８）解： )31ln()21ln(lim x x x +++∞→=2ln 23ln(12)12lim ln(12)3lim 3lim1x x x x x x x x x →+∞→+∞→+∞+++== =xxx 212lim 2ln 3++∞→=2ln 3．（９）解：因为1lim1limln 1lim===∞→∞→∞→x x x x x x x eex ，所以nn n ∞→lim=1．§3.3 泰勒公式１．解： 10)1(,64)(3='+='f x x x f ，同理得24)1(,24)1(,18)1()4(=='''=''ff f ，且0)()5(=x f ．由泰勒公式得：43)(24++=x x x f =432)1()1(4)1(9)1(108-+-+-+-+x x x x ．2．解：因为)(!!2!112n nxx o n x x x e +++++= ，所以xe x xf 2)(==2222[1()]1!2!(2)!n n x x x x o x n --+++++-=)()!2(!2!1432n n x o n x x x x +-++++ ．3．解：设xx f 2)(=，则2ln 2)(xx f ='，2)2(ln 2)(xx f =''．2)2(ln )0(,2ln )0(,1)0(=''='=f f f ，故 )(!2)2(ln !12ln 12222x x x xο+++=，则 222)2(ln 2ln 1)(x x x p ++=为所求． 4．解：因为 ))1((3)1(2)1(1)11ln(332xo x x x x ++-=+，所以 )11ln(2x x x +-=)])1((3)1(2)1(1[3322x o x x x x x ++--=)1(3121x o x +-，故 21)]1(3121[lim )]11ln([lim 2=+-=+-∞→∞→x o x x x x x x ．5．证明：因为 0)(lim 20=→x x f x ，所以0)0(,0)0(,0)0(=''='=f f f ．由麦克劳林公式得：332!3)(!3)(!2)0()0()0()(x f x f x f x f f x f ξξ'''='''+''+'+= （ξ介于0与x 之间），因此 !3)()1(ξf f '''=，由于0)1(=f ，故0)(='''ξf ．§3.4函数的单调性与曲线的凹凸性1．填空题（１）),21()0,21(+∞- , )21,0()21,( --∞ （２）增加（３）0> （４）23-，29， )1,(-∞， ),1(∞．2．单项选择题（１）A （２） B （３） D （４）B 3．（１）解：1-='xe y ，当0>x 时，0>'y ,所以函数在区间),0[+∞为单调增加；当0<x 时，0<'y ，所以函数在区间]0,(-∞为单调减少．（２）解：)1(31031-='-x x y ，当1>x ，或0<x 时，0>'y ,所以函数在区间),1[]0,(+∞-∞ 为单调增加；当01x <<时，0<'y ，所以函数在区间]1,0[为单调减少．（３）解： 011111222>+=++++='xxx x x y ，故函数在),(+∞-∞单调增加．3．（１）证明：令xxx f +=1)(，则0)1(1)(2>+='x x f ， )(x f 在) , 0 [∞+内单调增加. 于是, 由 |||| ||b a b a +≤+, 就有 ) |||| () || (b a f b a f +≤+, 即||1||||1||||||1||||||1||||||1||||||1||b b a a b a b b a a b a b a b a b a +++≤+++++=+++≤+++（２）证明：设)1(2ln )1()(--+=x x x x f ， 11ln )('-+=xx x f ，由于当1x >时，211()0f x x x''=->, 因此)(x f '在),1[+∞单调递增, 当 1x >时, 0)1()(='>'f x f , 故)(x f 在),1[+∞单调递增, 当 1>x 时, 有0)1()(=>f x f .故当1>x 时,0)1(2ln )1()(>--+=x x x x f ,因此1)1(2ln +->x x x ．（３）证明：设6sin )(3x x x x f +-=, 021cos )(2=+-='x x x f ，当0>x ，()sin 0f x x x ''=->，所以)(x f '在),0[+∞单调递增, 当 0>x 时, 0)0()(='>'f x f , 故)(x f 在),0[+∞单调递增, 从而当 0>x 时, 有0)0()(=>f x f . 因此当 0>x 时，6sin 3x x x ->．4．解：设()sin ,2x x x k πϕ=-- 则()x ϕ在]2,0[π连续, 且k k -=-=)2(,)0(πϕϕ，由()1cos 02x x πϕ'=-=，得2arccos x π=为)2,0(π内的唯一驻点．()x ϕ在2[0,arccos ]π上单调减少，在2[arccos ,]2ππ上单调增加．故k ---=242arccos )2(arccos 2πππϕ为极小值，因此)(x ϕ在]2,0[π的最大值是k -,最小值是k ---242arccos 2ππ．（１）当,0≥k 或242arccos 2--<ππk 时,方程在)2,0(π内无实根；（２）当0242arccos 2<<--k ππ时,有两个实根；（３）当242arccos2--=ππk 时，有唯一实根．5．解： c bx ax y ++='232,b ax y 26+=''，所以2323(2)2(2)062010(2)(2)(2)44a b c a b a b c d a b c d ⎧-+-+=⎪+=⎪⎨+++=-⎪⎪-+-+-+=⎩解得 16,24,3,1=-=-==d c b a ．6．（１）解： 222)1(11-+-='x x y , 323)1(62-+=''x xx y , 令0=''y ,得0=x ，当1x =±时y ''不存在．当01<<-x 或1>x 时, 0>''y ,当1-<x 或10<<x 时, 0<''y ．故曲线12-+=x xx y 在)1,0()1,( --∞上是凸的, 在区间和),1()0,1(+∞- 上是凹的，曲线的拐点为)0,0(．（２）解：y '=，y ''=．当0=x 时，y y ''',不存在；当21-=x 时，0=''y ．故曲线在)21,(--∞上是凸的, 在),21(+∞-上是凹的，)23,21(3--是曲线的拐点,7．证明：令πx x x f -=2sin )(, 则π12cos 21)(-='x x f , 2sin 41)(x x f -=''．当π<<x 0时, 0)(<''x f , 故函数πxx x f -=2sin )(的图形在),0(π上是凸的, 从而曲线)(x f y =在线段AB （其中)(,()),0(,0(ππf B f A ）的上方，又0)()0(==πf f , 因此0)(>x f ,即πx x >2sin ．§3.5 函数的极值与最大值最小值1．填空题（１）1ln 2x =-（２） 322)21(=f ， (0)1f =-2．选择题（１） C （２） B （３）Ａ3．（１）解：由13()10f x x-'=-=，得1=x ．4''31(),(1)03f x x f -''=>，所以函数在1=x 点取得极小值．（２）解：定义域为),0(+∞，11ln 21, (1ln )x x xy ey xx x '==-，令0y '=得驻点x e =，当(0,)x e ∈时，0y '>，当(,)x e ∈+∞时，0y '<．因此ee e y 1)(=为极大值． 4．解：(3)23, (4)132y y -==．由266120y x x '=+-=，得1=x , 2-=x ．而34)2(,7)1(=-=y y , 所以最大值为132，最小值为7．5．解：设圆锥体的高为h , 底半径为r ,故圆锥体的体积为h r V 2 31π=，由于222)(R r R h =+-，因此)2( 31)(2h Rh h h V -=π )20(R h <<，由0)34( 31)(2=-='h Rh h V π，得34R h =，此时R r 322=．由于内接锥体体积的最大值一定存在,且在)2,0(R 的内部取得. 现在0)(='h V 在)2,0(R 内只有一个根,故当34Rh =, R r 322=时, 内接锥体体积的最大．6.解: 设AD x =, B 与C 间的运费为y , 则)100(340052x k x k y -++= （1000≤≤x ），其中k 是某一正数．由 0)34005(2=-+='xx k y , 得15=x .由于k y x 400|0==, k y x 380|15==, 2100511500|+==x y , 其中以k y x 380|15==为最小, 因此当AD =15=x km 时, 总运费为最省．7．解：问题转化为求过点C 的线段AB 的最大值. 设木料的长度为l , y CB x AC ==,，木料与河岸的夹角为t ，则l y x =+，且 t b y t a x sin ,cos ==, t b t a l s i n c o s += )2,0(π∈t ．则 ttb t t a l 22sin cos cos sin -='，由0='l 得3tan abt =, 此时233232)(b a l +=，故木料最长为233232)(b a l +=．§3.6 函数图形的描绘１．解：由 -∞=+-→231)1(limx x x ，所以1x =为曲线)(x f y =的铅直渐近线．因为 2)1(lim )(lim ,1)1(limlim 2322-=-+=-=+=∞→∞→∞→∞→x x x x y x x x y x x x x 所以2-=x y 为曲线)(x f y =的斜渐近线．2．解：函数的定义域为()(),11,-∞-+∞．()()()()()2342132, 211x x x y y x x -+-'''==--．令0='y ，得1 ,2-==x x ；令0=''y ，得2=x ．列表讨论如下：x(,1)-∞-1- (1,1)-(1,2)2 (2,)+∞y ' ＋ 0－＋ 0 ＋ y '' －－－－＋ ()x f y =⎛极大值83-⎫ ⎛拐点()3,2⎭由于()()21122lim lim 23=--=∞→∞→x x x x x f x x ， ()()11222lim 21lim 22=---=⎥⎦⎤⎢⎣⎡-∞→∞→x x x x x f x x ，所以，121+=x y 是曲线的斜渐近线．又因为()-∞=--→231122lim x x x ，所以1=x 是曲线的铅垂渐近线．当0=x 时1-=y ；当0=y 时32=x ．综合上述讨论，作出函数的图形如下3§3.7 曲率1．填空题:（１） __0__ （２） ___2____， 21（３） dx e x x 2)(cos 1++．2．解：由题设可知函数c bx ax y ++=2与xe y =在0=x 处由相同的函数值，一阶导数值，二阶导数值，故21,1,1===a b c ．3．解： x y x y sin ,cos -=''=', 曲线在一点处的曲率为332222|sin |sin (1cos )(2sin )x x K x x ==+-令 322()(2)xf x x =-, 25222(1)()(2)x f x x +'=-，当10≤≤x 时,0)(>'x f ,故)(x f 在]1,0[上单调增加, 因此)(x f 在]1,0[上的最大值是1)1(=f ,即)0(sin π<<=x x y 在点)1,2(π处的曲率半径最小, 其曲率半径为11==KR ．4．解：t b y t a x t b y t a x sin ,cos ;cos ,sin -=''-=''='-='因此曲率|||)cos sin (||)(||),0(2/322222/322a bt b t a ab y x y x y x k b =+='+''''-'''=，曲率半径||/1bak ==ρ．§3.7方程的近似解1.证明: 令055)(,15)(45>+='++=x x f x x x f ，函数)(x f 在)0,1(-单调递增．)(x f 在[1,0]-上连续，且01)0(,05)1(>=<-=-f f ,故方程0155=++x x 在区间)0,1(-内有唯一的实根．求近似值的过程略．第三章综合练习题1．填空题（１） 0 （２） )0,1(-， ),0(+∞ （３） 00==y x 和．（４） 1 ．2．（１）解：20)1ln(sin 1tan 1lim x x x x x x -++-+→＝xx x x x x x x sin 1tan 11])1[ln(sin tan lim 0+++⋅-+-→ ＝x x x x x x x tan lim )1ln(cos 1lim 2100→→⋅-+-＝x x x x -+-→)1ln(cos 1lim 210＝111sin lim 210-+→xx x ＝21)1(sin lim 210-=+-→x x x x ．（２）解：x e e x x x x a a x x 1sin )(1cos )1cos 11sin(lim 21-+-+∞→=xe e x x x x x a x 1sin )1(1cos )1cos 11sin (lim 212-+-∞→=x x e x x x a x 1)1(1cos 11sin lim 22+-∞→ =a x a e x x x x x x x e 2432223131sin 11cos 11cos 1lim 1-=-+-∞→．3．证明：令221)1ln()(x x x x f +-+=, 则 21()111x f x x x x'=-+=++, 当0>x 时, ()0f x '>，故)(x f 在),0[+∞单调增．当0>x 时，有()(0)0f x f >=，即)1ln(212x x x +<-．4．证明：设)(arctan )(x f x F =, 则)(1)()(2x f x f x F +'='，且2|)(|π≤x F ．由拉格朗日中值定理知, 存在),(0b a x ∈，使)()()(0x F a b a F b F '=--, 即 14422|)(||)(|)()()(1)(020<=+≤-+≤--=+'πππa b a F b F a b a F b F x f x f ．5．证明：设)(),(x g x f 分别在),(,21b a x x ∈取得最大值M ，则12()()f x g x M ==, 且12()()0f x g x ''==．令)()()(x g x f x F -=．当21x x =时, 0)()()(1===x F b F a F , 由罗尔定理知, 存在),(),,(1211b x x a ∈∈ξξ, 使 0)()(21='='ξξF F , 进一步由罗尔定理知, 存在),(21x x ∈ξ，使0)(=''ξF ，即)()(ξξg f ''=''当21x x ≠时, 0)()(11≥-=x g M x F ,0)()(22≤-=M x f x F ，由零点存在定理可知，存在],[211x x ∈ξ，使0)(1=ξF ．由于0)()(==b F a F ，由前面证明知, 存在),(b a ∈ξ，使0)(=''ξF ，即)()(ξξg f ''=''．6．证明：设11)(2-+=x kx x f ．当0=k ，显然112=x只有一个正的实根．下考虑0<k 时的情况．先证存在性：因为)(x f 在),0(+∞内连续，且+∞=→)(lim 0x f x ，-∞=+∞→)(lim x f x ，由零点存在定理知，至少存在一个),0(+∞∈ξ，使0)(=ξf ，即112=+xkx 至少有一个正的实根．再证唯一性：假设有12,0x x >，且21x x <，使0)()(21==x f x f ，根据罗尔定理，存在12(,)(0,)x x η∈⊂+∞，使0)(='ηf ，即023=-ηk ，从而023>=ηk ，这与0<k 矛盾．故方程112=+x kx 只有一个正的实根．7．解：因为12183)()(2++-='=t t t Q t x ,186)()(+-=''='t t Q t x , 令0)(='t x ,得3=t ．又当3t <时，()0x t '>．函数()x t 在[0,3]上单调增加；当3t >时，()0x t '<，函数()x t 在[3,)+∞上单调减少．故当3=t 时，)(t x 达到最大, 即上午11时这个工人的工作效率最高．。

人教版数学三年级上册第3单元《毫米、分米的认识》真题同步练习3(含解析)

人教版数学三年级上册第3单元《毫米、分米的认识》真题同步练习3（含解析）一、单选题1．（2020二上·沽源期末）下面用来计量物体长度的单位是（）。

A．时B．分C．厘米2．椅子高为（）A．59米B．59分米C．59厘米3．（2020三上·景县期中）下面不能测量出物体长度的是（）。

A．B．C．D．4．2米和800毫米加在一起是（）毫米。

A．2800B．20800C．800D．10005．（2020三上·昭通期中）一本书厚8毫米，5本同样的书厚4（）。

A．厘米B．分米C．毫米二、填空题6．钱市胡同是北京现存的最窄胡同，在商业区大栅栏附近，胡同长55 米，平均宽度仅7，两人对面走过都要侧身而行。

7．量出长方形每条边的长度。

8．填空（用分数表示）27秒=分5分米=米9．（2022三上·福清期中）量一量，填一填。

厘米毫米10．大约有个长；大约有个长．11．59厘米=分米109角=元12．一根蜡烛长1分米4厘米，点燃后还剩下9厘米，燃烧了厘米。

13．40毫米=厘米80厘米=分米20分米=米300厘米=米三、判断题14．判断对错（1）小明跑200米用了1分钟．（）（2）1枝铅笔长6分米．（）15．（2018三上·麒麟期末）长度单位间的进率都是10。

（）16．比1分米少5厘米的是95厘米。

（）17．（2019二上·叙州期末）在学生直尺上，从刻度1到刻度6的长度是5厘米。

（）18．图中，铅笔的长度是5厘米。

（）四、解答题19．量一量下面各线段的长度。

20．（2023二下·龙口月考）一枝铅笔用去50毫米，还剩13厘米，这枝铅笔原来长多少厘米？21．把下面的各数量按从小到大的顺序排列．21毫米4分米35厘米12毫米1米3厘米22．（2018三上·潘集期中）画一条比1分米短60毫米的线段．五、综合题23．（2021二上·菏泽期中）（1）这个回形针长厘米（2）蜡笔长厘米24．（2023三上·沁阳期末）（1）上边物体中厚度最接近1毫米的是。