【高中数学】湖南省衡阳市樟树中学2016-2017学年高二下学期第四次月考(理)

合集下载

【月考试卷】湖南省衡阳市2016-2017学年高二下学期第四次月考物理试题Word版含答案

樟树中学2018届高二下学期第四次月考物理试题考试范围：选修3-5、3-3(第一、二章) 考试时间：2017年5月18日本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,满分100分，考试用时100分钟。

一、单项选择题（本题共8小题，每小题3分，共24分）1. 容器中盛有冰水混合物，冰的质量和水的质量相等且保持不变，则容器内( )A．冰的分子平均动能大于水的分子平均动能B．水的分子平均动能大于冰的分子平均动能C．水的内能大于冰的内能D．冰的内能大于水的内能2．要估算出气体中分子间的平均距离，需要知道下列哪一组物理量（）A．阿伏伽德罗常数、该气体的质量和摩尔质量B．阿伏伽德罗常数、该气体的密度和摩尔质量C．阿伏伽德罗常数、该气体的质量和体积D．该气体的密度、体积和摩尔质量3．根据分子动理论，物质分子间距离为r0时分子所受到的引力与斥力相等，以下关于分子力和分子势能的说法正确的是（）A．分子间距离小于r0时，分子间距离减小，分子力减小B．分子间距离大于r0时，分子间距离增大，分子力一直增大C．当分子间距离为r0时，分子具有最大势能，距离增大或减小时势能都减小D．当分子间距离为r0时，分子具有最小势能，距离增大或减小时势能都增大4.关于分子热运动和布朗运动，下列说法正确的是（）A．布朗运动是指在显微镜中看到的液体分子的无规则运动B．布朗运动反映了液体分子在永不停息地做无规则运动C．悬浮微粒越大，同一时刻与它碰撞的液体分子越多，布朗运动越显著D．当物体温度达到0℃时，物体分子的热运动就会停止5．关于下列四幅图说法正确的是（）A．玻尔原子理论的基本假设认为，电子绕核运行轨道的半径是任意的B．光电效应产生的条件为：光强大于临界值C．电子束通过铝箔时的衍射图样证实了运动电子具有波动性D．发现少数α粒子发生了较大偏转，说明金原子质量大而且很坚硬6．近年来，数码相机几近家喻户晓，用来衡量数码相机性能的一个非常重要的指标就是像素，1像素可理解为光子打在光屏上的一个亮点，现知300万像素的数码相机拍出的照片比30万像素的数码相机拍出的等大的照片清晰得多，其原因可以理解为（）A．光是一种粒子，它和物质的作用是一份一份的B．光的波动性是大量光子之间的相互作用引起的C．大量光子表现光具有粒子性D．光具有波粒二象性，大量光子表现出光的波动性7．在匀强磁场中有一个原来静止的碳14原子核发生了某种衰变，已知放射出的粒子速度方向及反冲核的速度方向均与磁场方向垂直，它们在磁场中运动的径迹是两个相内切的圆，两圆的直径之比为7：1，如图所示．则碳14的衰变方程为（）A．C→e+ B B．C→He+BeC．C→e+N D．C→H+ B8．据央视报道，中科院等离子体物理研究所经过八年的艰苦努力，终于率先建成了世界上第一个全超导的托克马克试验装置并调试成功，这种装置被称为“人造太阳”（如图），它能够承受上亿摄氏度高温且能够控制等离子态的核子发生反应并稳定持续地输出能量，就像太阳一样为人类提供无限清洁的能源．在下列核反应方程中有可能是该装置内部所进行的核反应的是（）A．N+He→O+HB．H+H→He+nC．U→Th+HeD．U+n→Ba+Kr+3n二、多项选择题（本题共6小题，每小题4分，共24分.漏选得2分，错选不得分）9.在物理学的发展过程中，许多物理学家提出的理论和假设推动了人类历史的进步．下列表述符合物理学史实的是（）A．汤姆孙通过研究阴极射线实验，发现了电子并建立了原子的“枣糕”模型B．巴尔末根据氢原子光谱分析，总结出了氢原子光谱可见光区波长公式C．贝克勒尔通过对天然放射性的研究，发现原子核是由质子和中子组成的D．玻尔大胆提出假设，认为实物粒子也具有波动性10.量子理论是现代物理学两大支柱之一．量子理论的核心观念是“不连续”．关于量子理论，以下说法正确的是（）A．普朗克为解释黑体辐射，首先提出“能量子”的概念，他被称为“量子之父”B．爱因斯坦实际上是利用量子观念和能量守恒解释了光电效应C．康普顿效应证明光具有动量，也说明光是不连续的D．海森伯的不确定性关系告诉我们电子的位置是不能准确测量的11.下列说法正确的是（）A．一个处于n=3能级的氢原子向低能级跃迁时，能放出3种不同频率的光子B．每一种原子都有自己的特征谱线，因此可以用原子光谱来鉴别物质C．在原子核中，比结合能越大表示原子核中的核子结合得越牢固D．氡的半衰期为3.8天，若取100个氡原子核，经7.6天后剩下25个氡原子核12. 用原子级显微镜观察高真度的空间，结果发现有一对分子甲和乙环绕一个共同“中心”旋转，从而形成一个“双分子”体系，观测中同时发现此“中心”离乙分子较近，那么在上述“双分子”体系中（）A．甲、乙两分子之间一定只存在分子引力，不可能存在分子斥力B．甲分子的质量一定大于乙分子的质量C．甲分子旋转的速率一定大于乙分子的速率D．甲分子的动量大小和乙分子的动量大小一定相等13．在x坐标轴原点O固定一分子A，另一分子B从x坐标轴上距离原点0很远处静止释放并向A 运动，经过P点和Q点时分子速度相等，如图，则以下说法正确的是（）A．在P、Q两点分子的势能相等B．在P、Q两点分子间作用力相同C．分子B从Q运动到P点过程中分子力做功为零D．分子B从Q运动到P点过程中加速度一定是先增大后减小14. 2009年诺贝尔物理学奖得主威拉德．博伊尔和乔治．史密斯主要成就是发明了电荷耦合器件（CCD）图象传感器．他们的发明利用了爱因斯坦的光电效应原理．如图所示电路可研究光电效应规律，图中标有A和K的为光电管，其中A为阴极，K为阳极．理想电流计可检测通过光电管的电流，理想电压表用来指示光电管两端的电压．现接通电源，用光子能量为10.5eV的光照射阴极A，电流计中有示数，若将滑动变阻器的滑片P缓慢向右滑动，电流计的读数逐渐减小，当滑至某一位置时电流计的读数恰好为零，读出此时电压有的示数为6.0V；现保持滑片P位置不变，以下判断正确的是（）A．光电管阴极射出的光电子是具有瞬时性的B．光电管阴极材料的逸出功为4.5eVC．若增大入射光的强度，电流计的读数不为零D．若用光子能量为12eV的光照射阴极A，光电子的最大初动能一定变大三、实验题（共3题，第15、16题每题4分，第17题8分，共16分）15.甲同学用螺旋测微器测量一铜丝的直径，测微器的示数如左下图所示，该铜丝的直径为__________mm。

江西省樟树中学2016-2017学年高二上学期第四次月考数学(理)试题 Word版含答案

俯视图侧视图江西省樟树中学2018届高二（上）第四次月考理科数学试卷考试范围：已学内容考试时间：2016.12.11一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.若集合{}1 0 1 2A =-，，，，{}2 1 B y y x x A ==+∈，，则AB 中元素的个数是（）A ．4B ．6C ．7D ．8 2. 点()00,M x y 是圆()2220x y aa +=>外一点，则直线200x x y y a +=与该圆的位置关系是（）A ．相切 B ．相交 C ．相离 D ．相切或相交 3．已知函数f （x ）的值域是，则函数f （x ﹣2）的值域为（）A ．B ．C ．∪D ．4．设n S 是等差数列{}n a 的前n 项和，已知23a =，611a =，则7S 等于（）A ．13B ．35C ．49D ．635. 一个几何体的三视图如图所示，则该几何体的体积是（） A.64B.72C.80D. 1126．已知锐角ABC △的面积为4,3BC CA ==，则角C 的大小为（） A ．75° B．60° C．45° D．30° 7.下列命题中正确的是（） A ．若αβ>，则sin sin αβ>；B ．命题：“任意21,1x x >>都有”的否定是“存在21,1x x ≤≤使得”； C ．直线20ax y ++=与40ax y -+=垂直的充要条件为1a =±；D ．“若0xy =，则0x =或0y =”的逆否命题为“若0x ≠或0y ≠，则0xy ≠”8．某公司为确定明年投入某产品的广告支出，对近5年的广告支出m 与销售额y （单位：百万元）进行了初步统计，得到下列表格中的数据：y3040p5070m 2 4 5 6 8经测算，年广告支出m 与年销售额y 满足线性回归方程=6.5m+17.5，则p 的值为（）A ．45B ．50C ．55D ．609.已知0,0a b >>，若不等式3103m a b a b--≤+恒成立，则m 的最大值为（） A ． 4 B ．16 C ． 9 D ．310.已知关于x 的不等式c bx ax ++2＞0的解集为{1-x ＜x ＜}2，那么不等式c x b x a +-++)1()1(2＞ax 2的解集为（）A ．{0x ＜x ＜}3B ．{x x ＜0，或x ＞}3C ．{2-x ＜x ＜}1D ．{x x ＜2-，或x ＞}1 11.在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，6c b -=，2c b a +-=，且O 为此三角形的内心，则AO CB ⋅=（） A ．4B ．5C ．6D ．712. 已知22()log (0)1x g x x x =>+.若关于x 的方程2()()230g x m g x m +++= 有三个不同的实数解，则m 的取值范围是（）A ．(1,3) B. 1(,1)3 C.34(,]23-- D.4(,]3-∞-二、填空题、（每小题5分，共20分）13．某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生，为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为．14．棱长为2的正方体的顶点都在同一球面上，则该球的表面积为． 15.已知条件p ：0432≤--x x ，条件q ：09622≤-+-m x x 。

江西省樟树中学2016-2017学年高二下学期第二次月考数学理试题含答案

樟树中学2018届高二年级第二次月考数学理试卷考试范围：已学内容考试时间:2017年3月26日命题人：万浩春审题人:胡文斌一、选择题(本大题共12小题，每小题5分,共60分)1。

已知命题q p ,是简单命题，则“p ⌝是假命题”是“q p ∨是真命题”的条件A. 充分不必要B. 必要不充分 C 。

充要 D. 既不充分又不必要2.双曲线的顶点到渐进线的距离等于虚轴长的14，则此双曲线的离心率是 A ．2 B 。

32C ．3D.43。

设()ln f x x x =，若()02f x '=，则0x = ln 22A. 2e B 。

e C 。

D.ln 24.计算dx x )11(102⎰-+的结果为A 。

1B 。

4π C.21π+D 。

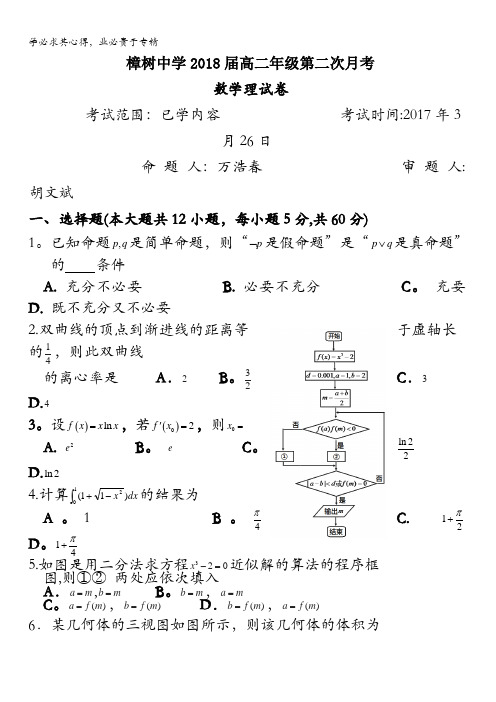
41π+5.如图是用二分法求方程320x -=近似解的算法的程序框图,则①② 两处应依次填入 A ．a m =,b m = B 。

b m =，a m =C 。

()a f m =，()b f m =D ．()b f m =，()a f m =6．某几何体的三视图如图所示，则该几何体的体积为D 。

5A 。

2 B.43 C 。

4 7。

M 是半径为R 的圆周上的一个定点,在圆周上等可能的任取一点N ，连接MN ，则弦MN 的长度超过2R的概率为A 。

15 B. 14 C 。

13 D 。

128。

设()(),f x g x 是定义域为R 的恒大于零的可导函数，且 ''()()()()0f x g x f x g x -<，则当a x b <<时，有A 。

()()()()f x g x f b g b ⋅>⋅ B. ()()()()f x g a f a g x ⋅>⋅ C. ()()()()f x g b f b g x ⋅>⋅ D 。

()()()()f x g x f a g a ⋅>⋅ 9 。

2016-2017学年湖南省衡阳市樟树中学高一(下)第四次月考数学试卷(文科)

2016-2017学年湖南省衡阳市樟树中学高一（下）第四次月考数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）直线x+y﹣1=0的倾斜角为（）A．30°B．60°C．120° D．150°2．（5分）在等差数列{a n}中，已知a4+a8=16，则a2+a6+a10=（）A．12 B．16 C．20 D．243．（5分）直线λ：2x﹣y+3=0与圆C：x2+（y﹣1）2=5的位置关系是（）A．相交B．相切C．相离D．不确定4．（5分）△ABC的内角A、B、C所对的边分别为a、b、c，若sinA=，b=sinB，则a等于（）A．3 B．C．D．5．（5分）已知函数f（x）是定义在R上的增函数，若f（a2﹣a）＞f（2a2﹣4a），则实数a的取值范围是（）A．（﹣∞，0）B．（0，3） C．（3，+∞）D．（﹣∞，0）∪（3，+∞）6．（5分）已知=（1，0），||=，|﹣|=||，则，的夹角是（）A．B．C．D．7．（5分）在△ABC中，角A、B、C所对的边分别为a，b，c，则直线xsinA+ay+c=0与直线bx﹣ysinB+sinC=0的位置关系是（）A．平行B．垂直C．重合D．相交但不垂直8．（5分）已知a=sin，b=cos，c=tan，则（）A．b＜a＜c B．c＜b＜a C．b＜c＜a D．a＜b＜c9．（5分）某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（）A．4πB．πC．πD．20π10．（5分）若函数f（x）=2x﹣a2﹣a在（﹣∞，1]上存在零点，则正实数a的取值范围是（）A．（0，1]B．[0，1]C．（0，2]D．[0，2]11．（5分）若将函数f（x）=1+sinωx（0＜ω＜4，ω∈Z）的图象向右平移个单位后，得到函数y=g（x）的图象，且y=g（x）的图象的一条对称轴方程为x=，则分f（x）的最小正周期为（）A．B．C． D．12．（5分）已知﹣＜α＜，且cos（α+）=，则sin（2α+）的值为（）A．B．C．D．二、填空题（本大题共4小题，每小题5分，共20分）.13．（5分）（）+log3+log3=．14．（5分）将函数f（x）=sinωx（其中ω＞0）的图象向右平移个单位长度，所得图象经过点（，0），则ω的最小值是．15．（5分）已知D是△ABC的边AB上一点，若=λ+λ2，其中0＜λ＜1，则λ的值为．16．（5分）在△ABC中，D为BC边上一点，若△ABD是等边三角形，且AC=4，则△ADC的面积的最大值为．三、解答题（本大题共6小题，共70分）17．（10分）已知函数f（x）=log3．（Ⅰ）求函数f（x）的定义域；（Ⅱ）判断函数f（x）的奇偶性；（Ⅲ）当x∈[﹣，]时，函数g（x）=f（x），求函数g（x）的值域．18．（12分）（1）已知0＜α＜β＜，sinα=，cos（α﹣β）=，求cosβ的值；（2）在△ABC中，sinA﹣cosA=，求cos2A的值．19．（12分）如图，要测底部不能到达的电视塔AB的高度，在C点测得塔顶A 的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，求电视塔AB的高度．20．（12分）已知圆C与x轴的交点分别为A（﹣1，0），B（3，0），且圆心在直线2x﹣y=0上．（I）求圆C的标准方程；（Ⅱ）求与圆C相切于点B（3，0）的切线方程；（Ⅲ）若圆C与直线y=x+m有公共点，求实数m的取值范围．21．（12分）已知向量=（sinx，﹣1），=（cosx，3）．（Ⅰ）当∥时，求的值；（Ⅱ）已知在锐角△ABC中，a，b，c分别为角A，B，C的对边，c=2asin（A+B），函数f（x）=（+）•，求f（B+）的取值范围．22．（12分）已知=（2sinx，sinx+cosx），=（cosx，sinx﹣cosx），函数f（x）=•．（Ⅰ）求函数f（x）的单调递减区间；（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，cosA=，若f（A）﹣m＞0恒成立，求实数m的取值范围．2016-2017学年湖南省衡阳市樟树中学高一（下）第四次月考数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）（2016秋•重庆期末）直线x+y﹣1=0的倾斜角为（）A．30°B．60°C．120° D．150°【分析】利用直线的倾斜角与斜率的关系即可得出．【解答】解：设直线x+y﹣1=0的倾斜角为α．直线x+y﹣1=0化为．∴tanα=﹣．∵α∈[0°，180°），∴α=150°．故选：D．【点评】本题考查了直线的倾斜角与斜率的关系，属于基础题．2．（5分）（2016春•中原区校级期末）在等差数列{a n}中，已知a4+a8=16，则a2+a6+a10=（）A．12 B．16 C．20 D．24【分析】由等差数列通项公式得a6=8，a2+a6+a10=3a6，由此能求出结果．【解答】解：∵在等差数列{a n}中，a4+a8=16，∴a4+a8=2a6=16，解得a6=8，∴a2+a6+a10=3a6=24．故选：D．【点评】本题考查等差数列的三项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．3．（5分）（2014•浦东新区校级模拟）直线λ：2x﹣y+3=0与圆C：x2+（y﹣1）2=5的位置关系是（）A．相交B．相切C．相离D．不确定【分析】求出圆心到直线的距离，与圆半径相比较，能求出结果．【解答】解：圆C：x2+（y﹣1）2=5的圆心C（0，1），半径r=，圆心C（0，1）到直线λ：2x﹣y+3=0的距离：d==＜r=，∴直线λ：2x﹣y+3=0与圆C：x2+（y﹣1）2=5相交．故选：A．【点评】本题考查直线与圆的位置关系的判断，是基础题，解题时要注意点到直线的距离公式的合理运用．4．（5分）（2012•包头三模）△ABC的内角A、B、C所对的边分别为a、b、c，若sinA=，b=sinB，则a等于（）A．3 B．C．D．【分析】根据正弦定理的式子，将题中数据直接代入，即可解出a 长，得到本题答案．【解答】解：∵△ABC中，sinA=，b=sinB，∴根据正弦定理，得解之得a=故选：D【点评】本题给出三角形中A的正弦和边角关系式，求a之长．着重考查了运用正弦定理解三角形的知识，属于基础题．5．（5分）（2017春•衡阳县校级月考）已知函数f（x）是定义在R上的增函数，若f（a2﹣a）＞f（2a2﹣4a），则实数a的取值范围是（）A．（﹣∞，0）B．（0，3） C．（3，+∞）D．（﹣∞，0）∪（3，+∞）【分析】因为f（x）为R上的增函数，所以f（a2﹣a）＞f（2a2﹣4a），等价于a2﹣a＞2a2﹣4a，即可求出实数a的取值范围．【解答】解：因为f（x）为R上的增函数，所以f（a2﹣a）＞f（2a2﹣4a），等价于a2﹣a＞2a2﹣4a，解得0＜a＜3，故选B．【点评】本题考查函数的单调性，考查学生解不等式的能力，属于中档题．6．（5分）（2017春•衡阳县校级月考）已知=（1，0），||=，|﹣|=||，则，的夹角是（）A．B．C．D．【分析】由条件利用两个向量的数量积的定义，求得cosθ的值，可得设与夹角θ的值．【解答】解：已知=（1，0），||=，|﹣|=||，设，的夹角为θ，θ∈[0，π]，则+﹣2=，∴=2•，∴2=2•1•cosθ，∴cosθ=，∴θ=，故选：C．【点评】本题主要考查两个向量的数量积的定义，属于基础题．7．（5分）（2017春•衡阳县校级月考）在△ABC中，角A、B、C所对的边分别为a，b，c，则直线xsinA+ay+c=0与直线bx﹣ysinB+sinC=0的位置关系是（）A．平行B．垂直C．重合D．相交但不垂直【分析】利用正弦定理和直线的斜率的关系判断两直线的位置关系．【解答】解：∵直线xsinA+ay+c=0的斜率k1=﹣，直线bx﹣ysinB+sinC=0的斜率k2=，∴k1k2=﹣=﹣1．∴直线xsinA+ay+c=0与直线bx﹣ysinB+sinC=0垂直．故选：B．【点评】本题考查两直线的位置关系的判断，是基础题，解题时要认真审题，注意正弦定理的合理运用．8．（5分）（2017•河北模拟）已知a=sin，b=cos，c=tan，则（）A．b＜a＜c B．c＜b＜a C．b＜c＜a D．a＜b＜c【分析】因为＜＜，所以cos＜sin，tan＞1，即可得出结论．【解答】解：因为＜＜，所以cos＜sin，tan＞1，所以b＜a＜c．故选A．【点评】本题考查三角函数值的大小比较，考查学生的计算能力，比较基础．9．（5分）（2017•惠州模拟）某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（）A．4πB．πC．πD．20π【分析】由三视图知，几何体是一个三棱柱，三棱柱的底面是边长为2的正三角形，侧棱长是2，根据三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径，求出半径即可求出球的表面积．【解答】解：由三视图知，几何体是一个三棱柱，三棱柱的底面是边长为2的正三角形，侧棱长是2，三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径，r==，球的表面积4πr2=4π×=π．故选：B．【点评】本题考查了由三视图求三棱柱的外接球的表面积，利用棱柱的几何特征求外接球的半径是解题的关键．10．（5分）（2017春•衡阳县校级月考）若函数f（x）=2x﹣a2﹣a在（﹣∞，1]上存在零点，则正实数a的取值范围是（）A．（0，1]B．[0，1]C．（0，2]D．[0，2]【分析】利用已知条件，求出2x的范围，得到不等式求解即可．【解答】解：在（﹣∞，1]上2x∈（0，2]．函数f（x）=2x﹣a2﹣a在（﹣∞，1]上存在零点，可得0＜a2+a≤2，解得a∈（0，1]．故选：A．【点评】本题考查函数的零点，以及不等式的解法，考查转化思想以及计算能力．11．（5分）（2017•河北模拟）若将函数f（x）=1+sinωx（0＜ω＜4，ω∈Z）的图象向右平移个单位后，得到函数y=g（x）的图象，且y=g（x）的图象的一条对称轴方程为x=，则分f（x）的最小正周期为（）A．B．C． D．【分析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数图象的对称性，求得ω的值，进而利用正弦函数的周期公式即可计算得解．【解答】解：将函数f（x）=1+sinωx的图象向右平移个单位后，得到的图象对应的解析式为：y=g（x）=sin[ω（x﹣）]+1=sin（ωx﹣）+1，∵y=g（x）的图象的一条对称轴方程为x=，∴ω﹣=kπ+，k∈Z，解得：ω=6k+3，k∈Z，∵0＜ω＜4，∴ω=3，可得：f（x）=1+sin3x，∴f（x）的最小正周期为T=．故选：C．【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数图象的对称性，三角函数周期公式的应用，考查了数形结合思想，属于基础题．12．（5分）（2017春•衡阳县校级月考）已知﹣＜α＜，且cos（α+）=，则sin（2α+）的值为（）A．B．C．D．【分析】利用“构造思想”，结合二倍角和和与差的公式即可求解．【解答】解：sin（2α+）=sin（α++α+）=2sin（）cos（），∵﹣＜α＜，∴0＜＜，∴0＜2α+＜，cos（α+）=，可得sin（）=，则sin（2）=2sin（）cos（）=，则cos（2）=，∴sin（2α+）=sin（2）==．故选：A．【点评】本题考查了“构造思想”，以及二倍角和和与差的公式的灵活运用．属于中档题．二、填空题（本大题共4小题，每小题5分，共20分）.13．（5分）（2014•安徽）（）+log3+log3=．【分析】直接利用对数运算法则以及有理指数幂的运算法则化简求解即可．【解答】解：（）+log3+log3=+log35﹣log34+log34﹣log35=．故答案为：．【点评】本题考查有理指数幂的运算法则以及对数运算法则的应用，考查计算能力．14．（5分）（2017•雁峰区校级二模）将函数f（x）=sinωx（其中ω＞0）的图象向右平移个单位长度，所得图象经过点（，0），则ω的最小值是2．【分析】首先利用三角函数的图象平移得到y=sinω（x﹣），代入点（，0）后得到sinω=0，由此可得ω的最小值．【解答】解：将函数y=sinωx（其中ω＞0）的图象向右平移个单位长度，所得图象对应的函数为y=sinω（x﹣）．再由所得图象经过点（，0），可得sinω（﹣）=sinω=0，∴ω=kπ，k∈z．故ω的最小值是2．故答案为：2．【点评】本题考查了三角函数的图象平移，考查了三角函数奇偶性的性质，是中档题．15．（5分）（2016•和平区四模）已知D是△ABC的边AB上一点，若=λ+λ2，其中0＜λ＜1，则λ的值为．【分析】根据D是△ABC的边AB上一点，设，（0＜k＜1），然后把用表示即可．【解答】解：∵D是△ABC的边AB上一点，设，（0＜k＜1）则，又，，∴2=，∴，∵=λ+λ2，∴，解得：或（舍），故答案为：．【点评】本题主要考查向量的共线和平面向量基本定理，属于基础题．16．（5分）（2015•泉州校级模拟）在△ABC中，D为BC边上一点，若△ABD是等边三角形，且AC=4，则△ADC的面积的最大值为．【分析】先利用余弦定理求得建立等式，利用基本不等式的性质确定AD•DC的最大值，进而根据三角形面积公式求得三角形面积的最大值．【解答】解：在△ACD中，cos∠ADC===﹣，整理得AD2+CD2=48﹣AD•DC≥2•AD•DC，∴AD•DC≤16，AD=CD时取等号，∴△ADC的面积S=AD•DC•sin∠ADC=AD•DC≤4，故答案为：【点评】本题主要考查了正弦定理的应用和余弦定理的应用．本题灵活运用了基本不等式的基本性质解决了三角形求最值的问题．三、解答题（本大题共6小题，共70分）17．（10分）（2014春•赤坎区校级期末）已知函数f（x）=log3．（Ⅰ）求函数f（x）的定义域；（Ⅱ）判断函数f（x）的奇偶性；（Ⅲ）当x∈[﹣，]时，函数g（x）=f（x），求函数g（x）的值域．【分析】（Ⅰ）根据对数式的真数部分大于0，构造关于x的不等式，解不等式可得函数f（x）的定义域；（II）根据函数的定义域关于原点对称，且f（﹣x）=﹣f（x），结合函数奇偶性的定义，可得结论；（III）当x∈[﹣，]时，先求出真数部分的取值范围，进而可得函数g（x）的值域．【解答】解：（I）要使函数f（x）=log3的解析式有意义，自变量x须满足：＞0，解得x∈（﹣1，1），故函数f（x）的定义域为（﹣1，1），（II）由（I）得函数的定义域关于原点对称，且f（﹣x）=log3=log3（）﹣1=﹣log3=﹣f（x）．故函数f（x）为奇函数，（III）当x∈[﹣，]时，令u=，则u′=﹣＜0，故u=在[﹣，]上为减函数，则u∈[，3]，又∵g（x）=f（x）=log3u为增函数，故g（x）∈[﹣1，1]，故函数g（x）的值域为[﹣1，1]．【点评】本题考查的知识点是对数函数的图象和性质，函数的定义域，值域，奇偶性，解分式不等式，是函数图象和性质的综合应用，难度中档．18．（12分）（2017春•衡阳县校级月考）（1）已知0＜α＜β＜，sinα=，cos（α﹣β）=，求cosβ的值；（2）在△ABC中，sinA﹣cosA=，求cos2A的值．【分析】（1）由条件利用同角三角函数的基本关系求得cosα 和sin（α﹣β）的值，再利用两角和差的余弦公式求得cosβ=cos[α﹣（α﹣β）]的值．（2）把sinA﹣cosA=①平方可得2sinAcosA=．从而求得sinA+cosA=的值，再利用二倍角的余弦公式求得cos2A=（sinA﹣cosA）（sinA+cosA）的值．【解答】解：（1）∵0＜α＜β＜，sinα=，cos（α﹣β）=，∴cosα=，sin（α﹣β）=﹣=﹣．∴cosβ=cos[α﹣（α﹣β）]=cosαcos（α﹣β）+sinαsin（α﹣β）=+×（﹣）=．（2）△ABC中，sinA﹣cosA=①，平方可得1﹣2sinAcosA=，2sinAcosA=．∴A为锐角．∴sinA+cosA===②．∴cos2A=cos2A﹣sin2A=﹣（sinA﹣cosA）（sinA+cosA）=．【点评】本题主要考查同角三角函数的基本关系、两角和差的余弦公式、二倍角的余弦公式的应用，属于基础题．19．（12分）（2013•榆阳区校级模拟）如图，要测底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD=120°，CD=40m，求电视塔AB的高度．【分析】设AB=xm，利用解直角三角形算出BD=m且BC=xm，然后在△DBC 中利用余弦定理，结合题中数据建立关于x的方程，解出x的值即可得到电视塔AB的高度．【解答】解：根据题意，设AB=xm，则Rt△ABD中，∠ADB=30°，可得BD==m，同理可得Rt△ABC中，BC=AB=xm，∵在△DBC中，∠BCD=120°，CD=40m，∴由余弦定理BD2=BC2+CD2﹣2BC•CD•cos∠DCB，得（）2=（40）2+x2﹣2•40•x•cos120°整理得：x2﹣20x﹣800=0，解之得x=40或x=﹣20（舍）即电视塔AB的高度为40米．【点评】本题给出实际应用问题，求电视塔AB的高度．着重考查了测量中的有关概念、解直角三角形和余弦定理等知识，属于中档题．20．（12分）（2015秋•大兴区期末）已知圆C与x轴的交点分别为A（﹣1，0），B（3，0），且圆心在直线2x﹣y=0上．（I）求圆C的标准方程；（Ⅱ）求与圆C相切于点B（3，0）的切线方程；（Ⅲ）若圆C与直线y=x+m有公共点，求实数m的取值范围．【分析】（I）设圆心C（a，2a），利用圆C与x轴的交点分别为A（﹣1，0），B （3，0），求出a，即可求圆C的标准方程；（Ⅱ）因为CB与切线垂直，所以k BC•k=﹣1，求出k，即可求与圆C相切于点B （3，0）的切线方程；（Ⅲ）若圆C与直线y=x+m有公共点，则圆C的圆心到直线的距离d≤r，即可求实数m的取值范围．【解答】解：（Ⅰ）因为圆C的圆心在直线2x﹣y=0上，所以设圆心C（a，2a）．…（1分）又因为圆C与x轴的交点分别为A（﹣1，0），B（3，0），所以a=1…（2分）故圆心C（1，2），半径为，…（4分）圆C的标准方程为（x﹣1）2+（y﹣2）2=8…（5分）（Ⅱ）因为CB与切线垂直，所以k BC•k=﹣1…（7分）因为，所以k=1…（8分）故与圆C相切于点B（3，0）的切线方程为：x﹣y﹣3=0…（10分）（Ⅲ）圆C与直线y=x+m有公共点，即圆C的圆心到直线的距离d≤r，…（11分）即，…（13分）解得﹣3≤m≤5所以圆C与直线y=x+m有公共点，则﹣3≤m≤5．…（14分）【点评】本题考查圆的方程，考查直线与圆的位置关系，考查学生的计算能力，属于中档题．21．（12分）（2012•绵阳三模）已知向量=（sinx，﹣1），=（cosx，3）．（Ⅰ）当∥时，求的值；（Ⅱ）已知在锐角△ABC中，a，b，c分别为角A，B，C的对边，c=2asin（A+B），函数f（x）=（+）•，求f（B+）的取值范围．【分析】（I）由∥，可得tanx=﹣，再由=，运算求得结果．（II）在△ABC中，由c=2asin（A+B）利用正弦定理求得sinA=，可解得A=．由△ABC为锐角三角形，得＜B＜，利用两个向量的数量积公式求得函数f（x）=sin（2x﹣）﹣．由此可得f（B+）=sin2B﹣，再根据B的范围求出sin2B的范围，即可求得f（B+）的取值范围．【解答】解：（I）由∥，可得3sinx=﹣cosx，于是tanx=﹣．∴===﹣．（II）∵在△ABC中，A+B=π﹣C，于是sin（A+B）=sinC，由c=2asin（A+B）利用正弦定理得：sinC=2sinAsinC，∴sinA=，可解得A=．…（6分）又△ABC为锐角三角形，于是＜B＜，∵函数f（x）=（+）•=（sinx+cosx，2）•（sinx，﹣1）=sin2x+sinxcosx﹣2=+﹣2=sin（2x﹣）﹣．∴f（B+）=sin[2（B+）﹣]﹣=sin2B﹣．…（10分）由＜B＜得＜2B＜π，∴0＜sin2B≤1，得﹣＜sin2B﹣≤﹣，即f（B+）的取值范围（﹣，﹣]．【点评】本题主要考查三角函数的恒等变换及化简求值，正弦定理，正弦函数的定义域和值域，两个向量的数量积公式的应用，属于中档题．22．（12分）（2017春•衡阳县校级月考）已知=（2sinx，sinx+cosx），=（cosx，sinx﹣cosx），函数f（x）=•．（Ⅰ）求函数f（x）的单调递减区间；（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，cosA=，若f（A）﹣m＞0恒成立，求实数m的取值范围．【分析】（Ⅰ）根据向量的数量积公式和三角函数的化简即可得到函数的解析式，再根据正弦函数的单调性即可求出答案减区间，（Ⅱ）由余弦定理或正弦定理求出即，即可求出m的取值范围．【解答】解：（Ⅰ）函数f（x）=•=2sinxcosx+（sinx+cosx）（sinx﹣cosx）=由2kπ+≤2x﹣≤2kπ+可得kπ+≤x≤kπ+．所以函数f（x）的单调减区间为，（Ⅱ）（法一）由．可得2b2﹣ac=b2+c2﹣a2即b2﹣c2+a2=ab．解得cosC=即C=因为，所以，，因为恒成立，则恒成立所以m≤﹣1．（法二）由可得2cosAsinc=2sinB﹣sinA=2sin（A+C）﹣sinA即2sinAcosC﹣sinA=0，解得，即因为，所以，因为恒成立，则恒成立即m≤﹣1．【点评】本题考查了向量的数量积的运算正弦函数的单调性，正弦定理和余弦定理，属于中档题参与本试卷答题和审题的老师有：沂蒙松；zlzhan；ywg2058；lcb001；caoqz；刘长柏；qiss；w3239003；左杰；sxs123；静静；wsj1012；豫汝王世崇；whgcn （排名不分先后）菁优网2017年7月19日。

湖南省衡阳市樟树中学2016-2017学年高二下学期第四次

樟树中学2018届高二年级下学期第四次月考数学（文科）试卷考试范围：高考范围考试时间 20170518一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.) 1.设集合{}{}{}1,2,3,4,5,A 2,3,4,1,4U B ===，则()U C A B = （） A ．{}1,4,5 B ．{}1,5 C ．{}1,4 D ．{}12.已知幂函数()af x x =的图像经过点⎛ ⎝⎭，则()4f 的值等于（）A ．16B ．116 C ．12D ．23.函数()()lg 2f x x =++的定义域为（） A ．()2,1- B ．[]2,1- C ．()2,-+∞ D ．(]2,1- 4．下列命题正确的个数为（）①“R x ∈∀都有02≥x ”的否定是“R x ∈∃0使得020≤x ” ②“3≠x ”是“3≠x ”成立的充分条件③命题“若21≤m ，则方程0222=++x mx 有实数根”的否命题 A.0 B.1C.2D.35．已知函数221,1(),1x x f x x ax x ⎧+<⎪=⎨+≥⎪⎩，若[](0)4f f a =，则实数a 等于（）A ．12B ．45C ．2D ．96．给定函数①y ＝x ) ，②y ＝log(x ＋1)，③y ＝|x －1|，④y ＝2x ＋1，其中在区间(0,1)上单调递减的函数的序号是( ) A ．①② B ．②③ C．③④D ．①④7．已知函数()f x 是定义在R 内的奇函数，且满足()()4f x f x +=，当()0,2x ∈时，()22f x x =，则()2015f =（）A ．-2B ．2C ．-98D ．988．函数f （x ）=lg （|x|﹣1）的大致图象是（）A ．B ．C ．D ．9．函数2log (2)a y x ax =-+在区间(,1]-∞上是减函数，则a 的取值范围是（） A ．[2,)+∞B ．[1,)+∞C ．[2,3) D.(2,3)10.某商店将进价为40元的商品按50元一件销售，一个月恰好卖500件，而价格每提高1元，就会少卖10个，商店为使该商品利润最大，应将每件商品定价为（） A ．50元 B ．60元 C ．70元 D ．100元11.已知()y f x =是奇函数，当()0,2x ∈时，()ln 1f x a x ax =-+，当()2,0x ∈-时，函数()f x 的最小值为1，则a =（） A ．-2 B ．2 C ．1± D ．112.设()f x 是定义在R 上的偶函数，任意实数x 都有(2)(2)f x f x -=+，且当[0,2]x ∈ 时，()22x f x =-，若函数-=)()(x f x g log a (x+1) (a ＞1)，在区间(-1,7)内恰有三个不同零点，则a 的取值范围是（）A ．),7()3,0(+∞B ．(3,7)C ．(2,7)D ．(2,3) l l第Ⅱ卷非选择题二、填空题（本小题共4小题，每题5分，满分20分，将答案填在答题纸上） 13．函数y ＝的定义域是___________.14.若函数(21)1()1ax f xx x++=++为奇函数，则a = ． 15.14．已知()f x 为偶函数，当0x ≤ 时，1()x f x e x --=-，则曲线()y f x =在(1,2)处的切线方程是___ __．16．已知定义在R 上的偶函数满足：(4)()(2)f x f x f +=+，且当[0,2]x ∈时，()y f x =单调递减，给出以下四个命题：①(2)0f =； ②4x =-为函数()y f x =图象的一条对称轴；③()y f x =在[8,10]单调递增；④若方程()f x m =在[6,2]--上的两根为1x 、2x ，则128.x x +=-以上命题中所有正确命题的序号为_______．三、解答题（本大题共6小题，共70分。

2016-2017年湖南省衡阳市樟树中学高二(下)第四次月考数学试卷(理科)(解析版)

2016-2017学年湖南省衡阳市樟树中学高二（下）第四次月考数学试卷（理科）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知复数（其中a∈R，i为虚数单位）是纯虚数，则a+i的模为（）A．B．C．D．2．（5分）用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（）A．假设三内角都不大于60度B．假设三内角都大于60度C．假设三内角至多有一个大于60度D．假设三内角至多有两个大于60度3．（5分）下列现象的相关程度最高的是（）A．某商店的职工人数与商品销售额之间的相关系数为0.87B．流通费用率与商业利润之间的相关系数为﹣0.94C．商品销售额与商业利润之间的相关系数为0.51D．商品销售额与流通费用率之间的相关系数为﹣0.814．（5分）若（x﹣2）5＝a5x5+a4x4+a3x3+a2x2+a1x+a0，则a1+a2+a3+a4+a5＝（）A．﹣1B．31C．﹣33D．﹣315．（5分）某校在高二年级开设选修课，其中数学选修课开了三个班．选课结束后，有四名选修英语的同学要求改修数学，但数学选修每班至多可再接收两名同学，那么安排好这四名同学的方案有（）A．72种B．54种C．36种D．18种6．（5分）f（x）＝ax3﹣x2+x﹣5在R上既有极大值也有极小值，则实数a的取值范围为（）A．a＞B．a≥C．a＜且a≠0D．a≤且a≠0 7．（5分）利用数学归纳法证明“（n+1）（n+2）…（n+n）＝2n×1×3×…×（2n﹣1），n∈N*”时，从“n＝k”变到“n＝k+1”时，左边应增乘的因式是（）A．2k+1B．C．D．8．（5分）函数f（x）＝x cos x的导函数f′（x）在区间[﹣π，π]上的图象大致是（）A．B．C．D．9．（5分）设X～N（1，δ2），其正态分布密度曲线如图所示，且P（X≥3）＝0.0228，那么向正方形OABC中随机投掷10000个点，则落入阴影部分的点的个数的估计值为（）附：（随机变量ξ服从正态分布N（μ，δ2），则P（μ﹣δ＜ξ＜μ+δ）＝68.26%，P（μ﹣2δ＜ξ＜μ+2δ）＝95.44%A．6038B．6587C．7028D．753910．（5分）已知抛物线C：y2＝4x的焦点为F，准线为l，过点F的直线交抛物线于A，B 两点（A在第一象限），过点A作准线l的垂线，垂足为E，若∠AFE＝60°，则△AFE 的面积为（）A．B．C．D．11．（5分）已知f′（x）是定义在（0，+∞）上的函数f（x）的导函数，若方程f′（x）＝0无解，且∀x∈（0，+∞），f[f（x）﹣log2016x]＝2017，设a＝f（20.5），b＝f（logπ3），c＝f（log43），则a，b，c的大小关系是（）A．b＞c＞a B．a＞c＞b C．c＞b＞a D．a＞b＞c12．（5分）已知p，q，r都是正实数，若q≤r（lnp﹣lnr），r﹣q≤p≤e（r+q），则的取值范围是（）A．（，e]B．（，1]C．（0，]D．（0，e]二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）已知f（x）＝，则．14．（5分）（x﹣）n的展开式中，所有二项式系数之和为512，则展开式中x3的系数为（用数字作答）．15．（5分）f（x）＝mx2+lnx﹣2x在定义域内单调递增，则实数m取值范围为．16．（5分）已知抛物线C1：y＝ax2（a＞0）的焦点F也是椭圆C2：+＝1（b＞0）的一个焦点，点M，P（，1）分别为曲线C1，C2上的点，则|MP|+|MF|的最小值为．三、解答题（共6个题，共70分，解答应写出必要的文字说明、证明过程或演算步骤）17．（10分）设a＞0，f（x）＝，令a1＝1，a n+1＝f（a n），n∈N*．（1）写出a2，a3，a4的值，并猜出数列{a n}的通项公式；（2）用数学归纳法证明你的结论．18．（12分）为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图：记成绩不低于70分者为“成绩优良”．（1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并大致判断哪种教学方式的教学效果更佳；（2）由以上统计数据填写下面2×2列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”？附：K2＝，（n＝a+b+c+d）独立性检验临界值表：19．（12分）某校高三年级有400人，在省标准化考试中，用简单随机抽样的方法抽取容量为50的样本，得到数学成绩的频率分布直方图（如图）．（1）求第四个小矩形的高；（2）估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有多少人？（3）样本中，已知成绩在[140，150]内的学生中有三名女生，现从成绩在[140，150]内的学生中选取3名学生进行学习经验推广交流，设有X名女生被选取，求X的分布列和数学期望．20．（12分）如图，在四棱锥P﹣ABCD中，P A⊥底面ABCD，∠DAB为直角，AB∥CD，AD＝CD＝2AB，E、F分别为PC、CD的中点．（Ⅰ）试证：AB⊥平面BEF；（Ⅱ）设P A＝k•AB，且二面角E﹣BD﹣C的平面角大于45°，求k的取值范围．21．（12分）已知椭圆C：+＝1（a＞b＞0）的短轴的一个顶点和两个焦点构成直角三角形，且该三角形的面积为1．（Ⅰ）求椭圆年C的方程；（Ⅱ）设F1，F2是椭圆C的左右焦点，若椭圆C的一个内接平行四边形的一组对边过点F1和F2，求这个平行四边形面积的最大值．22．（12分）已知函数f（x）＝lnx，g（x）＝（x﹣1）f′（x），其中f′（x）是f（x）的导函数．（Ⅰ）求曲线y＝f（x）在点（e，1）处的切线方程；（Ⅱ）若f（x）≥ag（x）在[3，+∞）上恒成立，求实数a的取值范围．2016-2017学年湖南省衡阳市樟树中学高二（下）第四次月考数学试卷（理科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知复数（其中a∈R，i为虚数单位）是纯虚数，则a+i的模为（）A．B．C．D．【解答】解：复数＝＝+i是纯虚数，∴＝0，≠0，∴a＝，则|a+i|＝＝＝．故选：C．2．（5分）用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（）A．假设三内角都不大于60度B．假设三内角都大于60度C．假设三内角至多有一个大于60度D．假设三内角至多有两个大于60度【解答】解：根据反证法的步骤，假设是对原命题结论的否定，“至少有一个”的否定：“一个也没有”；即“三内角都大于60度”．故选：B．3．（5分）下列现象的相关程度最高的是（）A．某商店的职工人数与商品销售额之间的相关系数为0.87B．流通费用率与商业利润之间的相关系数为﹣0.94C．商品销售额与商业利润之间的相关系数为0.51D．商品销售额与流通费用率之间的相关系数为﹣0.81【解答】解：两个变量之间的相关系数，r的绝对值越接近于1，表面两个变量的线性相关性越强，r的绝对值越接近于0，表示两个变量之间几乎不存在线性相关，故选：B．4．（5分）若（x﹣2）5＝a5x5+a4x4+a3x3+a2x2+a1x+a0，则a1+a2+a3+a4+a5＝（）A．﹣1B．31C．﹣33D．﹣31【解答】解：由（x﹣2）5＝a5x5+a4x4+a3x3+a2x2+a1x+a0，分别令x＝0，1，可得：（﹣2）5＝a0，（1﹣2）5＝a1+a2+a3+a4+a5+a0．则a1+a2+a3+a4+a5＝﹣1﹣（﹣32）＝31．故选：B．5．（5分）某校在高二年级开设选修课，其中数学选修课开了三个班．选课结束后，有四名选修英语的同学要求改修数学，但数学选修每班至多可再接收两名同学，那么安排好这四名同学的方案有（）A．72种B．54种C．36种D．18种【解答】解：由题意知有四名选修英语的同学要求改修数学，但数学选修每班至多可再接收两名同学，需要分类来解，将四名同学分成三组：1，1，2；和2，2两种情况分成1，1，2安排在三个数学班中：有＝36；分成两组2，2．安排在两个班里，有＝18．∴一共有36+18＝54种安排方案故选：B．6．（5分）f（x）＝ax3﹣x2+x﹣5在R上既有极大值也有极小值，则实数a的取值范围为（）A．a＞B．a≥C．a＜且a≠0D．a≤且a≠0【解答】解：求导函数：f′（x）＝3ax2﹣2x+1，∵函数f（x）＝ax3﹣x2+x﹣6既有极大值又有极小值，∴a≠0，且△＝4﹣12a＞0，∴a＜且a≠0．故选：C．7．（5分）利用数学归纳法证明“（n+1）（n+2）…（n+n）＝2n×1×3×…×（2n﹣1），n∈N*”时，从“n＝k”变到“n＝k+1”时，左边应增乘的因式是（）A．2k+1B．C．D．【解答】解：由题意，n＝k时，左边为（k+1）（k+2）…（k+k）；n＝k+1时，左边为（k+2）（k+3）…（k+1+k+1）；从而增加两项为（2k+1）（2k+2），且减少一项为（k+1），故选：C．8．（5分）函数f（x）＝x cos x的导函数f′（x）在区间[﹣π，π]上的图象大致是（）A．B．C．D．【解答】解：∵f（x）＝x cos x，∴f‘（x）＝x cos x＝cos x﹣x sin x，∵f‘（0）＝1，可排除C、D；又∵f‘（x）在x＝0处取最大值；故排除B故选：A．9．（5分）设X～N（1，δ2），其正态分布密度曲线如图所示，且P（X≥3）＝0.0228，那么向正方形OABC中随机投掷10000个点，则落入阴影部分的点的个数的估计值为（）附：（随机变量ξ服从正态分布N（μ，δ2），则P（μ﹣δ＜ξ＜μ+δ）＝68.26%，P（μ﹣2δ＜ξ＜μ+2δ）＝95.44%A．6038B．6587C．7028D．7539【解答】解：由题意P（0＜X≤1）＝1﹣×0.6826＝1﹣0.3413＝0.6587，则落入阴影部分点的个数的估计值为10000×0.6587＝6857，故选：B．10．（5分）已知抛物线C：y2＝4x的焦点为F，准线为l，过点F的直线交抛物线于A，B 两点（A在第一象限），过点A作准线l的垂线，垂足为E，若∠AFE＝60°，则△AFE 的面积为（）A．B．C．D．【解答】解：抛物线的焦点为F（1，0），准线方程为x＝﹣1．设E（﹣1，2a），则A（a2，2a），∴k AF＝，k EF＝﹣a，∴tan60°＝，∴a＝，∴A（3，2），∴△AFE的面积为＝4故选：A．11．（5分）已知f′（x）是定义在（0，+∞）上的函数f（x）的导函数，若方程f′（x）＝0无解，且∀x∈（0，+∞），f[f（x）﹣log2016x]＝2017，设a＝f（20.5），b＝f（logπ3），c＝f（log43），则a，b，c的大小关系是（）A．b＞c＞a B．a＞c＞b C．c＞b＞a D．a＞b＞c【解答】解：∵方程f′（x）＝0无解，∴f′（x）＞0或f′（x）＜0恒成立，∴f（x）是单调函数，由题意得∀x∈（0，+∞），f[f（x）﹣log2016x]＝2017，又f（x）是定义在（0，+∞）的单调函数，则f（x）﹣log2016x是定值，设t＝f（x）﹣log2016x，则f（x）＝t+log2016x，∴f（x）是增函数，又0＜log43＜logπ3＜1＜20.5∴a＞b＞c，故选：D．12．（5分）已知p，q，r都是正实数，若q≤r（lnp﹣lnr），r﹣q≤p≤e（r+q），则的取值范围是（）A．（，e]B．（，1]C．（0，]D．（0，e]【解答】解：p，q，r都是正实数，若q≤r（lnp﹣lnr），r﹣q≤p≤e（r+q），可得≤ln，1﹣≤≤e（1+），设＝y，＝x（x＞0，y＞0），则y≤lnx且1﹣y≤x≤e（1+y），作出y＝lnx和直线y＝1﹣x以及x﹣ey﹣e＝0在第一象限围成的图形（如图中斜线构成），则＝＝表示点（x，y）与原点的斜率．设过原点的直线的斜率为k，且与y＝lnx相切，切点为（m，lnm），由（lnx）′＝，可得k＝＝，解得m＝e，k＝，结合图象可得的范围为（0，]．故选：C．二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）已知f（x）＝，则+．【解答】解：dx+（x2﹣1）dx，由定积分的几何意义，可知dx表示以原点为圆心，以1为半径的圆的面积的一半，则＝×π＝，则（x2﹣1）dx＝（x3﹣x）＝（﹣2）﹣（﹣1）＝，∴dx+（x2﹣1）dx＝+，故答案为：+．14．（5分）（x﹣）n的展开式中，所有二项式系数之和为512，则展开式中x3的系数为126（用数字作答）．【解答】解：由题意2n＝512，则n＝9，通项公式为T r+1＝•（﹣1）r•，令9﹣r＝3，求得r＝4，可得该展开式中x3的系数＝126，故答案为：126．15．（5分）f（x）＝mx2+lnx﹣2x在定义域内单调递增，则实数m取值范围为[1，+∞）．【解答】解：f（x）＝mx2+lnx﹣2x的定义域为：x＞0．可得：f′（x）＝mx+﹣2，f（x）＝mx2+lnx﹣2x在定义域内单调递增，所以：mx+﹣2≥0，m≥＝1﹣（）2．因为1﹣（）2≤1，则实数m取值范围为：[1，+∞）．故答案为：[1，+∞）．16．（5分）已知抛物线C1：y＝ax2（a＞0）的焦点F也是椭圆C2：+＝1（b＞0）的一个焦点，点M，P（，1）分别为曲线C1，C2上的点，则|MP|+|MF|的最小值为2．【解答】解：P（，1）代入椭圆C2：+＝1，可得＝1，∴b＝，∴焦点F（0，1），∴抛物线C1：x2＝4y，准线方程为y＝﹣1．设点M在准线上的射影为D，则根据抛物线的定义可知|MF|＝|MD|∴要求|MP|+|MF|取得最小值，即求|MP|+|MD|取得最小，当D，M，P三点共线时|MP|+|MD|最小，为1﹣（﹣1）＝2．故答案为2．三、解答题（共6个题，共70分，解答应写出必要的文字说明、证明过程或演算步骤）17．（10分）设a＞0，f（x）＝，令a1＝1，a n+1＝f（a n），n∈N*．（1）写出a2，a3，a4的值，并猜出数列{a n}的通项公式；（2）用数学归纳法证明你的结论．【解答】解：（1）由a n+1＝f（a n）＝，因为a1＝1，所以a2＝＝，，，猜想．（2）证明：①易知，n＝1时，猜想正确；②假设n＝k（k∈N*）时，a k＝成立，则这说明，n＝k+1时成立．由①②知，对于任何n∈N*，都有．18．（12分）为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图：记成绩不低于70分者为“成绩优良”．（1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并大致判断哪种教学方式的教学效果更佳；（2）由以上统计数据填写下面2×2列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”？附：K2＝，（n＝a+b+c+d）独立性检验临界值表：【解答】解：（1）甲班样本化学成绩前十的平均分为；…（2分）乙班样本化学成绩前十的平均分为．…（4分）甲班样本化学成绩前十的平均分远低于乙班样本化学成绩前十的平均分，大致可以判断“高效课堂”教学方式的教学效果更佳．…（6分）（2）…（8分）根据2×2列联表中的数据，得K2的观测值为，…（10分）∴能在犯错概率不超过0.05的前提下认为“成绩优良与教学方式有关”．…（12分）19．（12分）某校高三年级有400人，在省标准化考试中，用简单随机抽样的方法抽取容量为50的样本，得到数学成绩的频率分布直方图（如图）．（1）求第四个小矩形的高；（2）估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有多少人？（3）样本中，已知成绩在[140，150]内的学生中有三名女生，现从成绩在[140，150]内的学生中选取3名学生进行学习经验推广交流，设有X名女生被选取，求X的分布列和数学期望．【解答】解：（1）由频率分布直方图可知，第四个小矩形的高为：[1﹣（0.01+0.020+0.030+0.012）×10]÷10＝0.028．（3分）（2）∵样本中，数学成绩在120分以上的频率为：1﹣（0.01+0.020）×10＝0.7，（4分）∴通过样本估计总体（即将频率看作概率），可估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有400×0.7＝280（人）．（6分）（3）由频率分布直方图可知，样本中成绩在[140，150]内的学生共有0.012×10×50＝6（人）．于是，由题设知这6人恰好是3男3女．（7分）∴X的所有可能取值为0、1、2、3，P（X＝0）＝＝，P（X＝1）＝＝，P（X＝2）＝＝，P（X＝3）＝＝．（10分）∴X的分布列为：∴X的数学期望为：EX＝＝．（12分）20．（12分）如图，在四棱锥P﹣ABCD中，P A⊥底面ABCD，∠DAB为直角，AB∥CD，AD＝CD＝2AB，E、F分别为PC、CD的中点．（Ⅰ）试证：AB⊥平面BEF；（Ⅱ）设P A＝k•AB，且二面角E﹣BD﹣C的平面角大于45°，求k的取值范围．【解答】解：（Ⅰ）证：由已知DF∥AB且∠DAB为直角，故ABFD是矩形，从而AB⊥BF．又P A⊥底面ABCD，所以平面P AD⊥平面ABCD，因为AB⊥AD，故AB⊥平面P AD，所以AB⊥PD，在△PDC内，E、F分别是PC、CD的中点，EF∥PD，所以AB⊥EF．由此得AB⊥平面BEF．（6分）（Ⅱ）以A为原点，以AB、AD、AP为OX、OY、OZ正向建立空间直角坐标系，设AB的长为1，则＝（﹣1，2，0），＝（0，1）设平面CDB的法向量为，平面EDB的法向量为，则∴，取y＝1，可得设二面角E﹣BD﹣C的大小为θ，则cosθ＝|cos＜m1，m2＞|═化简得，则．（12分）21．（12分）已知椭圆C：+＝1（a＞b＞0）的短轴的一个顶点和两个焦点构成直角三角形，且该三角形的面积为1．（Ⅰ）求椭圆年C的方程；（Ⅱ）设F1，F2是椭圆C的左右焦点，若椭圆C的一个内接平行四边形的一组对边过点F1和F2，求这个平行四边形面积的最大值．【解答】解：（1）由勾股定理可知：丨PF1丨+丨PF2丨＝丨F1F2丨，即2a2＝4c2，则a＝c，b2＝a2﹣c2＝c2，S＝丨F1F2丨×丨OP丨＝×2c×b＝1，即b＝c＝1，∴a＝，∴椭圆的标准方程为：；（2）设过椭圆右焦点F2的直线l：x＝ty+1与椭圆交于A，B两点，则，整理得：（t2+2）y2+2ty﹣1＝0，由韦达定理，得：y1+y2＝﹣，y1y2＝﹣，∴|y1﹣y2|＝＝＝，＝+＝，丨OF丨•|y1﹣y2|＝，∴S椭圆C的内接平行四边形面积为S＝4S△OAB＝，令m＝≥1，则S＝f（m）＝＝，注意到S＝f（m）在[1，+∞）上单调递减，∴S max＝f（1）＝4，当且仅当m＝1，即t＝0时等号成立．故这个平行四边形面积的最大值为4．22．（12分）已知函数f（x）＝lnx，g（x）＝（x﹣1）f′（x），其中f′（x）是f（x）的导函数．（Ⅰ）求曲线y＝f（x）在点（e，1）处的切线方程；（Ⅱ）若f（x）≥ag（x）在[3，+∞）上恒成立，求实数a的取值范围．【解答】解：（Ⅰ）∵f（x）＝lnx，∴f′（x）＝，则f′（e）＝．又f（e）＝lne＝1，∴求曲线y＝f（x）在点（e，1）处的切线方程为y﹣1＝，即x﹣ey＝0；（Ⅱ）g（x）＝（x﹣1）f′（x）＝，f（x）≥ag（x）在[3，+∞）上恒成立，即lnx≥a（1﹣）在[3，+∞）上恒成立，也就是a≤在[3，+∞）上恒成立，令h（x）＝（x≥3），h′（x）＝＝．令t（x）＝x﹣lnx﹣1，则t′（x）＝1﹣＝＞0，∴t（x）在[3，+∞）上单调递增，又t（3）＝2﹣ln3＞0，∴h′（x）＞0在[3，+∞）上恒成立，即．∴a≤．∴实数a的取值范围是（﹣∞，]．。

【数学】湖南省衡阳市樟树中学2016-2017学年高二下学期第四次月考(理)

湖南省衡阳市樟树中学2016-2017学年高二下学期第四次月考（理）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1（其中a R ∈， i 为虚数单位）是纯虚数，则a i +的模为（）A.B. C. 5D.2、用反证法证明命题“三角形的内角中至少有一个不大于60度”时，反设正确的是（） A ．假设三内角都不大于60度 B ．假设三内角至多有两个大于60度 C ．假设三内角至多有一个大于60度 D ．假设三内角都大于60度3、下列现象的线性相关程度最高的是( )A ．某商店的职工人数与商品销售额之间的相关系数为0.87B ．流通费用率与商业利润率之间的相关系数为－0.94C ．商品销售额与商业利润率之间的相关系数为0.51D ．商品销售额与流通费用率之间的相关系数为0.814、若()554325432102X a X a X a X a X a X a -=+++++，则12345a a a a a ++++=（）A ．1-B ．31 C.33- D ．31-5、学校在高二年级开设选修课程，其中数学开设了三个不同的班，选课结束后，有四名选修英语的同学要求改修数学，但数学选修班每班至多可接收两名同学，那么安排好这四名同学的方案有（）A. 72种B. 54种C. 36种D. 18种 6、()325f x ax x x =-+-在R 上既有极大值也有极小值，则实数a 的取值范围为（）A 、13a >B 、13a ≥C 、13a <且0a ≠D 、13a ≤且0a ≠7、利用数学归纳法证明“()()()()1221321n n n n n n +++=⨯⨯⨯⨯-， *n N ∈”时，从“n k =”变到“1n k =+”时，左边应增乘的因式是（）A. 21k +B. C.8、函数()cos f x x x=的导函数()'f x 在区间[],ππ-上的图象大致是（）9、设()21,XN δ，其正态分布密度曲线如右图所示，且()30.0228P X ≥=，那么向正方形OABC 中随机投掷10000个点，则落入阴影部分的点的个数的估计值为（）附：（随机变量ξ服从正态分布()21,Nδ，则A ．6038B ．6587C ．7028D ．753910、已知抛物线2:4C y x =的焦点为F ，准线为l ，过点F 的直线交抛物线于,A B 两点（A在第一象限），过点A 作准线l 的垂线，垂足为E ，若60AFE ∠=︒，则AFE ∆的面积为（）B.C.D. 11、已知()f x 是定义在()0,+∞上的单调函数，且()0,x ∀∈+∞，()2016log 2017f f x x ⎡⎤-=⎣⎦，设()0.52a f =， ()log 3b f π=， ()4log 3c f =，则a ，b ，c 的大小关系是（） A. b c a >> B. a c b >> C. c b a >> D. a b c >>12、已知p,q,r 都是正实数，若q≤r(lnp -lnr),r-q≤p≤e(r+q),则的取值范围是（）二、填空题（本大题共4小题，每小题5分，共20分）qp].(0,D e ]1.(,A e e1.(0,C e ⎤⎥⎦]1.(,1B e13，则()21f x dx -=⎰．14512，则展开式中3x的系数为．（用数字作答）15、函数y＝的定义域是___________.16、已知抛物线1C：2y ax=（0a>）的焦点F也是椭圆2C：（0b>）的一个焦点，点M分别为曲线1C，2C__________．三、解答题（共6个题，共70分，解答应写出必要的文字说明、证明过程或演算步骤）17、（本小题满分10分）设0a>，，令11a=，()1n na f a+=，*n N∈. （1）写出234,,a a a的值，并猜出数列{}na的通项公式；（2）用数学归纳法证明你的结论.18、（本小题12分）为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如右图：记成绩不低于70分者为“成绩优良”.（1）分别计算甲、乙两班20个样本中，化学分数前十的平均分，并大致判断哪种教学方式的教学效果更佳；（2）由以上统计数据填写下面22⨯列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”？19、（本小题满分12分)某校高三年级有400人，在省普通高中学业水平考试中，用简单随机抽样的方法抽取容量为50的样本，得到数学成绩的频率分布直方图（右图）（1）求第四个小矩形的高；（2）估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有多少人；（3）样本中，已知成绩在[140,150]内的学生中有三名女生，现从成绩在[140,150]内的学生中选取3名学生进行学习经验推广交流，设有X 名女生被选取，求X 的分布列和数学期望.20、(本小题满分12分）如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，DAB ∠为直角，//AB CD ，2AD CD AB ==，E ，F 分别为PC ，CD 的中点．（1）证明：AB ⊥平面BEF ；（2）设PA k AB =⋅，若平面EBD 与平面BDC 的夹角等于45︒，求k 的值．21、（本小题满分12分）已知椭圆C ：点构成直角三角形，且该三角形的面积为1. （1）求椭圆C 的方程；（2）设1F ，2F 是椭圆C 的左、右焦点，若椭圆C 的一个内接平行四边形的一组对边过点1F 和2F ，求这个平行四边形面积的最大值．22、已知函数()lnf x x=，()()()1'g x x f x=-，其中()'f x是()f x的导函数．（1）求曲线()y f x=在点(),1e处的切线方程；（2）若()()f x ag x≥在[)3,+∞上恒成立，求实数a的取值范围．参考答案一、选择题：1-12、BDBBB CCABA DC二、填空题：1314、126 15、(0,1] 16、2三、解答题：17、解：（1）因为11a=，(4分)（2）证明：①易知，1n =时，猜想正确；②假设()*n k k N=∈时，这说明，1n k =+时成立.由①②知，对于任何*n N ∈，都有(10分)18、解：（1）甲班样本化学成绩前十的平均分为乙班样本化学成绩前十的平均分为甲班样本化学成绩前十的平均分远低于乙班样本化学成绩前十的平均分，大致可以判断“高效课堂”教学方式的教学效果更佳. （6分）（2）根据22⨯列联表中的数据，2K 的观测值为∴能在犯错概率不超过0.05的前提下认为“成绩优良与教学方式有关”.（12分） 19、解：（1）由频率分布直方图可知，第四个小矩形的高为[1(0.010.0200.0300.012)10]100.028-+++⨯÷=；（3分）（2）因为样本中，数学成绩在120分以上的频率为1(0.010.020)100.7-+⨯=，（4分）所以通过样本估计总体（即将频率看作概率），可估计该校高三年级在这次考试中数学成绩在120分以上的学生大约有4000.7280⨯=（人）；（6分）（3）由频率分布直方图可知，样本中成绩在[140,150]内的学生共有0.01210506⨯⨯=（人）.于是，由题设知这6人恰好是3男3女.（7分）因为X 的所有可能取值为0、1、2、3，（8分）（10分）所以X 的分布列为：所以X 的数学期望为（12分）20、（1）证明：由已知//DF AB ，且DAB ∠为直角，故ABFD 是矩形，从而AB ⊥BF ，又PA ⊥底面ABCD ，所以平面PAD ⊥平面ABCD ，因为AB AD ⊥，故AB ⊥平面PAD ，所以AB ⊥PD ，在△PDC 内，E 、F 分别是PC 、CD 的中点，//EF PD ，所以AB ⊥EF ，由此得AB ⊥平面BEF ．（6分）（2）解：以A 为原点，以AB 、AD 、AP 为OX 、OY 、OZ 正向建立空间直角坐标系，设AB 的长为1，则(1,0,0)B ，(2,2,0)C ，(0,2,0)D ，(0,0,)P k ，则(1,2,0)BD =-，(0,1,BE = 设平面CDB 的法向量为1(0,0,1)n =，平面EDB 的法向量为2(,,)n x y z =，则220,0,n BD n BE ⎧⋅=⎪⎨⋅=⎪⎩所以取1y =，可得(2,1,n =由二面角E BD C --的大小为45︒，12,||||nn n n n n ⋅<>==⋅（12分）21、解：（Ⅰ）依题意222,{1,,a b c bc b c =+==解得即椭圆C 的方程为（4分）（Ⅱ）设过椭圆右焦点2F 的直线l ：1x ty =+与椭圆交于A ，B 两点，则221,{22,x ty x y =++=整理得()222210t y ty ++-=，（6分）椭圆C 的内接平行四边形面积为（9分），注意到()S f m =在[)1,+∞上单调递减，所以()max 1s f ==，当且仅当1m =，即0t =时等号成立，故这个平行四边形的面积最大值为．（ 12分）22、解：（1）函数()f x 的定义域为()0,+∞，且，即x ey-=．（4分）（2）()lnf x x=，，∴()()f x ag x≥在[)3,+∞上恒成立，在[)3,+∞上恒成立，即令()ln1x x xϕ=--，，当1x>时，()'0xϕ>，∴()xϕ在()1,+∞上单调递增．∴()()10xϕϕ>=，∴ln10x x-->（1x>），∴()'0h x>，∴()h x在()1,+∞上单调递增，当然在[)3,+∞上也单调递增，（12分)。

湖南省衡阳市樟树中学2016-2017学年高二下学期第四次月考英语---精校解析Word版

樟树中学2018届高二下学期第四次月考英语试卷考试范围：必修1----选修8 unit2第一部分听力(共两节，满分30分)第一节（共5小题; 每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。

听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

第二部分阅读理解（共两节，满分40分）第一节（共15小题：每小题2分，满分30分）阅读下列短文，从每题所给的四个选项（A、B、C和D）中，选出最佳选项，并在答题卡上将该项涂黑。

AHere are the responses from parents to the posts(帖子)about toys.●Michele ManhireMy son Aaron is 8. It’s been 8 birthdays and 9 Christmases of “What can we get, Aaron?” without proper toys along the way. He is just simply particular about toys.I can honestly tell you, I am printing this list, and heading to a couple of stores (some online) that I can get some of these items! Maybe this won’t be such a depressing Christmas.●VeraDo you have any yam balls (纱球)I bought a giant one for my classroom but ended up keeping it for my own kids. They’re strong enough to throw but soft enough to use as a doll bed.●NatalieExcellent post! Thank you so much for putting this together. I have been looking through special needs toy lists to find one that I thought would be most helpful to my followers. This post agrees to our personal experience most closely. I have sharedit with many other groups and the feedback has been wonderful.●MeaganThis is a great list. My son loved his egg chair and empty bottles are always a win. He also loves to turn a globe and look at wonder tubes. Wonder tubes are about $ 6 on Amazon. This year one of his gifts is a gel (凝胶）filled medicine ball.1. What are the four posts responding to?A. A game listB. A party listC. A toy listD. A food list2. What is Michele’s problem?A. She has no money for toys.B. She can’t find good toys for herself.C. Her son has a special taste for gifts.D. Her son missed too many birthdays.3. Who suggests a good toy which can be used as a bed for dolls?A. Michele Manhire.B. Natalie.C. Meagan.D. Vera.【答案】1. C 2. C 3. D【解析】本文主要向我们介绍了四位家长对于有关玩具帖子的各自回应。

江西省樟树市高二数学下学期周练试题(2)(一部)文

江西省樟树市2016-2017学年高二数学下学期周练试题（2）（一部）文一．选择题（本大题共12小题，每小题5分，共60分,在每小题给出的四个选项中，只有一项是符合题目要求的） 1.已知复数z 满足2z i i ⋅=-（i 为虚数单位)，则z 在复平面内对应的点所在的象限是 A 。

第一象限 B 。

第二象限 C. 第三象限 D 。

第四象限2．设f 0(x )＝sinx ，f 1（x ）＝f 0′(x ），f 2(x )＝f 1′(x ），…,f n ＋1(x ）＝f n ′（x ），n ∈N ，则f 2006（x )＝( ）A ．sinxB ．－sinxC ．cos xD ．－cosx3.已知,αβ表示两个不同的平面,m 为平面α内的一条直线,则“m β⊥”是“αβ⊥”的 A. 充分不必要条件 B. 必要不充分条件 C 。

充要条件 D 。

既不充分也不必要条件4.一个几何体的三视图如图1，则该几何体的体积为 A. π B 。

2π C. 3π D 。

6π5.一程序框图如图2所示,如果输出的函数值在区间[]1,2内,那么输入实数x 的取值范围是A. (),0-∞ B 。

[]1,0- C. [)1,+∞D .[]0,16。

已知点P 是抛物线y 2=2x 上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为（ ) A ．172 B ．3 C 5 D ．927、若实数,x y 满足|3|1x y -≤≤，则2x yz x y+=+的最小值为（） A 。

53B.2 C 。

35D 。

128.正项等比数列{n a }中，存在两项m a ,n a , 14m n a a a ⋅=，且6542a a a =+，则14m n+的最小值是( ） A ．32 B ．2 C ．73 D ．2569.直线3y x =-与椭圆()2222:10x y C a b a b+=>>交于A B 、两点,以线段AB 为直径的圆恰好经过椭圆的右焦点，则椭圆C 的离心率为( ） A ．32 B ．423- C ．312- D ．31- 10、已知函数2()(1)x f x e x =-+(e 为自然对数的底）,则()f x 的大致图象是（ )11、设函数()33sin ,f x x x x x R =++∈，若当02πθ<<时，不等式()()sin 10f m f m θ+->恒成立，则实数m 的取值范围是（）A ．(],1-∞B ．[)1,+∞C ．1,12⎛⎫⎪⎝⎭D ．1,12⎛⎤⎥⎝⎦12、已知函数2()|ln |1||f x x x =-+与()2g x x =，则它们所有交点的横坐标之和为（） A ．0 B ．2 C ．4 D ．8二、填空题（本大题共4小题，每小题5分,共20分）13、若复数z 满足()12i z i +=（i 为虚数单位)，则复数z =_____________．14、若1132x <<是不等式m ﹣1＜x ＜m+1成立的一个充分非必要条件，则实数m 的取值范围是．15、平面直角坐标系xOy 中，已知(1,0)A ，(0,1)B ，点C 在第一象限内，6AOC π∠=，且2OC =，若OC OA OB λμ=+,则λμ+的值是．16、已知函数()()3211232f x x ax bx c a b c R =+++∈，，,且函数()f x 在区间()01，内取得极大值，在区间()12，内取得极小值，则()223z a b =++的取值范围为。

江西省樟树中学2016-2017学年高二数学上学期第四次月考试题文

江西省樟树中学2018届高二第四次月考数学(文)试卷一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.) 1.设，若B A ⊆,则a 的取值范围是 ( )A ．B ．C ．D ．2.已知命题p ：∀x ∈R ，cos x ≤1，则( )A ．非p ：∃x ∈R ，cos x ≥1B ．非p ：∀x ∈R ，cos x ≥1C ．非p ：∃x ∈R ，cos x >1D ．非p ：∀x ∈R ，cos x >1 3.有一个几何体的三视图及其尺寸如图(单位：cm)，则该几何体的表面积和体积分别为( ) A ． 24π cm 2,12π cm 3B ． 15π cm 2,12π cm 3C ． 24π cm 2,36π cm 3D ．以上都不正确4.已知点P (x ，y )的坐标满足条件则x 2＋y 2的最大值为( ) A.10 B.8 C.16 D.10 5.阅读右面的程序框图，则输出的S 等于( ) A.14 B.20 C.30 D.556.已知x 、y 的取值如右表所示：如果y 与x 呈线性相关，且线性回归方程为213+=∧bx y ，则b ＝( )A. －12B. 13C. 12 D. 17.已知向量b a ,,12==,且)25()(-⊥+,则b a 与的夹角为（）第5题图A ．3π B ．4π C ．2π D ．6π 8.设点A 为抛物线y 2＝4x 上一点，点B (1,0)，且|AB |＝1，则A 的横坐标的值为( ) A.－2 B.0 C.－2或0 D.－2或29.在区间[－1,1]上任取两数x 和y ，组成有序实数对(x ，y )，记事件A 为 “x 2＋y 2<1”，则P (A )等于( ) A ．4π B ． 2πC ． πD ． 2π 10.已知点(m ，n )在椭圆8x 2＋3y 2＝24上，则2m ＋4的取值范围是( ) A ． [4－23，4＋23] B ． [4－3，4＋3] C ． [4－22，4＋22] D ． [4－2，4＋2]11.已知数列{}n a 满足11=a ，且对任意的*∈N n m ,，都有mn a a a n m n m ++=+，则=++++20163211111a a a a （） A ．20164032B ．20184034C ．20184032D ．2017403212.设正实数x ， y ，z 满足x 2－3xy ＋4y 2－z ＝0，则当zxy取得最大值时,z y x 212-+的最大值为( )A.0B.1C.49D.3 二、填空题（本大题共4小题，每小题5分，共20分） 13.设f (x )＝则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛21f f ＝___________．14.已知P 是△ABC 的边BC 上的任一点，且满足R y x y x ∈+=,,,则yx 41+的最小值是______．15.已知1tan 2sin )(++=x b x a x f ,且4)2(=-f ，那么=+)2(πf 16.对于顶点在原点的抛物线，给出下列条件： ①焦点在y 轴上； ②焦点在x 轴上；③抛物线上横坐标为1的点到焦点的距离等于6；④抛物线的通径的长为5；⑤由原点向过焦点的某条直线作垂线，垂足坐标为(2,1)．能使这条抛物线方程为y 2＝10x 的条件是________(要求填写合适条件的序号)．三、解答题（本大题共6小题，共70分。

江西省樟树市2016-2017学年高二数学下学期第一次月考试题理

江西省樟树市2016-2017学年高二数学下学期第一次月考试题理一．选择题（本大题共12小题，每小题5分，共60分）1. 已知R N ⋂C R M=( )A ．（1,2）B ．[0,2]C ．∅D ．[1,2] 2. 某个命题与正整数n 有关，如果()*n k k N =∈时命题成立，那么可推得当1n k =+时该命题也成立，现已知7n =时，该命题不成立，那么可以推得（）A ．6n =时该命题不成立B ．6n =时该命题成立C ．8n =时该命题不成立D ．8n =时该命题成立3. 设a ，b 是向量，则“||||a b =”是“||||a b a b +=-”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4. 已知,,a b c 是互不相等的非零实数，若用反证法证明三个方程22220,20,20ax bx c bx cx a cx ax c ++=++=++=至少有一个方程有两个相异实根，反证假设应为：（）A ．三个方程中至多有一个方程有两个相异实根B ．三个方程都有两个相异实根C ．三个方程都没有两个相异实根D ．三个方程都没有实根5. 已知函数f （x ）=x 2+bx 的图象在点A （1，f （1））处的切线l 与直线3x ﹣y+2=0平行，n 项和为T n ，则T 2014的值为（）由上表求得回归方程9.49.1y x ∧=+，当广告费用为3万元时销售额为（）A ．39万元B ．38万元C ．38.5万元D ．37.3万元7.若长方体1111ABCD A B C D -中，1AB =，11,B C C D 分别与底面ABCD 所成的角为45，60，则长方体1111ABCD A B C D -的外接球的体积为（）A ． C D 8. 已知等差数列{}n a 的公差0d ≠，且1a ，3a ，13a 成等比数列，若11a =，n S 为数列{}n a 的前n项和，则2163n n S a ++的最小值为（）A ．4 B ．3 C．2 D ．2 9.已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（） A. B. C. D.10.在闭区间]6,4[-上随机取出一个数x ，执行右上图程序框图，则输出x 不小于39的概率为（）A ．51 B.52 C.53 D.54 11. 下列命题中，正确命题的个数是（） ①命题“∃x ∈R ，使得x 3+1＜0”的否定是““∀x ∈R ，都有x 3+1＞0”． ②双曲线22221(0,0)x y a b a b-=>>中，F 为右焦点，A 为左顶点，点B （0，b ）且=0，则此双曲线的离心率为．③在△ABC 中，若角A 、B 、C 的对边为a 、b 、c ，若cos2B+cosB+cos （A ﹣C ）=1，则a 、c 、b 成等比数列．④已知向量,a b 是夹角为120°的单位向量，则向量2λa b a b +-与垂直的充要条件是λ=．A ．1 个B ．2 个C ．3 个D ．4 个12. 已知椭圆()2222:10x y C a b a b+=>>，四个顶点构成的四边形的面积为12，直线l 与椭圆C 交于,A B 两点，且线段AB 的中点为()2,1M -，则直线l 的斜率为（）A ．13B ．32C ．12D ．1 二．填空题（本大题共有4个小题，每题5分，共20分）13. 在ABC ∆中，6,5,4===c b a ，则=C A sin 2sin ．14. 若,,a b c 为直角三角形的三边，其中c 为斜边，则222a b c +=，称这个定理为勾股定理，现将这一定理推广到立体几何中：在四面体O ABC -中，90AOB BOC COA ∠=∠=∠=，S 为顶点O 所对面的面积，123,,S S S 分别为侧面,,OAB OAC OBC ∆∆∆的面积，则123,,,S S S S 满足的关系式为 .15. 设M 是△ABC 内一点，且23AB AC ⋅=30BAC ∠=︒，定义()(,,)f M m n p =，其中m ，n ，p 分别是△MBC ，△MCA ，△MAB 的面积，若1()(,,)2f M x y =，则14x y+的最小值是 16. 已知函数()2log ,0416,42x x f x x x ⎧<<⎪=⎨-+≥⎪⎩，若方程()0f x k +=有三个不同的解,,a b c ，且a b c <<，则ab c +的取值范围是 .三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.)17、（本小题满分10分）设：p 实数x 满足0)3)((<--a x a x ，其中0>a .：q 实数x 满足⎪⎩⎪⎨⎧>+-<+-015808622x x x x . （1）若1=a 且q p ∧为真，求实数x 的取值范围；（2）若p 是q 的必要不充分条件，求实数a 的取值范围.18、（本小题满分12分）某学校高三年级800名学生在一次百米测试中，成绩全部在12秒到17秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[12，13），第二组[13，14），…，第五组[16，17]，如图是根据上述分组得到的频率分布直方图．（1）若成绩小于13秒被认为优秀，求该样本在这次百米测试中成绩优秀的人数；（2）请估计本年级800名学生中，成绩属于第三组的人数；（3）若样本中第一组只有一名女生，第五组只有一名男生，现从第一、第五组中各抽取1名学生组成一个实验组，求所抽取的2名同学中恰好为一名男生和一名女生的概率．19.已知向量(sin ,1)m x =-，向量1(3cos ,)2n x =-，函数()()f x m n m =+⋅.(1)求()f x 的解析式及单调增区间；(2)已知a ，b ，c 分别为ABC D 内角A ，B ，C 的对边，A 为锐角，a =4c =，且()f A 恰是()f x 在⎥⎦⎤⎢⎣⎡2,0π上的最大值，求A ，b 和ABC ∆的面积S . 20. 对于数列{}{}n n a b 、， n S 为数列{}n a 的前n 项和，且1111(1),1,32,n n n n n S n S a n a b b b n N +++-+=++===+∈（1）求数列{}{}n n a b 、的通项公式；（2）令()()21n n n a n c n b +=+，求数列{}n c 的前n 项和n T21. （本小题满分12分）在等腰Rt ABC ∆中，90BAC ∠=︒，腰长为2，D 、E 分别是边AB 、BC 的中点，将BDE ∆沿DE 翻折，得到四棱锥B ADEC-，且F 为棱BC 中点，BA =．（1）求证：EF ⊥平面BAC ；（2）在线段AD 上是否存在一点Q ，使得//AF 平面BEQ？若存在，求二面角Q BE A --的余弦值，若不存在，请说明理由．22. （本小题满分12分）已知圆221:(1)4M x y ++=，圆2249:(1)4N x y -+=，动圆D 与圆M 外切并与圆N 内切，圆心D 的轨迹为曲线E .（1）求曲线E 的方程；（2）若双曲线C 的右焦点即为曲线E 的右顶点，直线y =为C 的一条渐近线.①.求双曲线C 的方程；②.过点)4,0(P 的直线l ，交双曲线C 于B A ,两点，交x 轴于Q 点（Q 点与C 的顶点不重合），当12=PQ QA QB λλ=，且3821-=+λλ时，求Q 点的坐标.江西省樟树中学2018届高二下学期第一次月考数学试卷一．选择题（60分）一、填空题（20分）13.___________________ 14.____________________15.___________________ 16._____________________三．解答题樟树2018届高二下学期第一次月考数学试卷参考答案1.D,2.A,3.D, 4C, 5.D, 6.A, 7.A, 8.A, 9.C, 10.A, 11.B, 12.C. 13.1, 14. 2322212S S S S ++= 15.18, 16. ()9,13 17. 解：依题意知：a x a p 3:<<⎩⎨⎧>--<--0)5)(3(0)4)(2(:x x x x q ，所以⎩⎨⎧<><<3542x x x 或，即32<<x . （1）当1=a 时，31:<<x p 要使q p ∧为真，则须满足⎩⎨⎧<<<<3231x x ，解得：32<<x ；（2） p 是q 的必要不充分条件∴)3,()3,2(a a ⊂⎩⎨⎧≥≤∴332a a ，解得：21≤≤a .18. (1) 21()()sin 1cos 2f x m n m x x x =+⋅=+++1cos 211122cos 22222x x x x -=+++=-+sin(2)26x π=-+ ………………3分因为2ω=，所以22T ππ== 单调递增区间为,63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦…6分(2) 由(1)知：()sin(2)26f A A π=-+ 当[0,]2x π∈时,52666x πππ-≤-≤ 由正弦函数图象可知,当262x ππ-=时()f x 取得最大值3。

江西省樟树中学高二上学期第四次月考数学(理)试题

江西省樟树中学2019届高二年级第四次月考数学试卷（理）考试范围：考到选修2－1，以选修2－1为主考试时间：12月29日一、选择题（本大题共12小题，每小题5分，共60分） 1.设命题为则p ,2,:2⌝>∈∃n n N n p （）A.nn N n 2,2>∈∀ B.nn N n 2,2≤∈∃ C.nn N n 2,2≤∈∀ D.nn N n 2,2=∈∃ 2.“1a =”是“方程22220x y x y a +-++=表示圆”的（） A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件3.某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人，现用分层抽样方法抽取一个容量为30的样本，则各职称中抽取的人数分别为 ( ) A ．5，10，15 B ．3，9，18 C ．5，9，16 D ．3，10，174．双曲线22221(0,0)x y a b a b-=>>的离心率为2，则它的渐近线方程是( )A ．3y x =±B ．y =C ．y =D ．32y x =±5. 如图所示，在两个圆盘中，指针在本圆盘每个数所在区域的机会均等，那么两个指针同时落在奇数所在区域的概率是（）A ．49B ．29C ．23D ． 136.已知a ＞0，b ＞0，若不等式212ma b a b+≥+恒成立，则m 的最大值等于（）A ．10B ．9C ．8D ．77.某产品的广告费用x 与销售额y 的统计数据如表：根据上表可得回归方程y b x a ∧∧=+中的b ∧为9.4，据此模型预报广告费用为6万元时销售额为（）A ．63.6万元B ．67.7万元C ．65.5万元D ．72.0万元 8.如图程序框图的功能（）A ．求满足1+2+…+n ＞2004的最小整数B ．求满足1+2+…+n ﹣1＞2004的最小整数C ．求满足1+2+…+n ＜2004的最大整数D ．求满足1+2+…+n ﹣1＜2004的最大整数9.“珠算之父”程大位是我国明代伟大是数学家，他的应用数学巨著《算法统综》的问世，标志着我国的算法由筹算到珠算转变的完成．程大位在《算法统综》中常以诗歌的形式呈现数学问题，其中有一首“竹筒容米”问题：“家有九节竹一茎，为因盛米不均平，下头三节三升九，上梢四节贮三升，唯有中间两节竹，要将米数次第盛，若有先生能算法，也教算得到天明．”（[注释]三升九：3.9升．次第盛：盛米容积依次相差同一数量．）用你所学的数学知识求得中间两节的容积为（） A ．1.9升 B ．2.1升C ．2.2升D ．2.3升10.若点O 和点F 分别为椭圆13422=+y x 的中心和左焦点，点P 为椭圆上的任意一点，则∙的最大值为（）A ． 4B ． 5 C. 6 D ．711.如图，过抛物线22(0)y px p =>的焦点F 的直线交抛物线于点A B 、，交其准线l 于点C ，若点F 是AC 的中点，且4AF =，则线段AB 的长为（）A.5B. 6C.163D. 20312.已知双曲线E:22221(0,0)x y a b a b-=>>的右顶点为A ，抛物线2:8C y ax =的焦点为F ，若在双曲线E 的渐近线上存在点P 使得PA FP ⊥，则双曲线E 的离心率的取值范围为（） A. (1,2)B. C. (2,)+∞D. )+∞二、填空题（本大题共4小题，共20分）13. 若变量,x y 满足约束条件1211x y x y y +≥-⎧⎪-≤⎨⎪≤⎩，则3z x y =-的最大值为________.14．点P (4，－2)与圆x 2＋y 2＝4上任一点连线的中点的轨迹方程是________.15．已知球面上四点A,B,C,D ，DA ⊥平面ABC ，AB ⊥BC ，则该球体积等于______.16．已知12,F F 是椭圆和双曲线的公共焦点，P 是它们的一个公共点，且321π=∠PF F ，椭圆的离心率为1e ，双曲线的离心率2e ，则=+222131e e ．三、解答题（本大题共6小题，共70分）17.（本小题满分10分）求倾斜角是直线1y =+的倾斜角的14，且分别满足下列条件的直线方程： (1)经过点1)-； (2)在y 轴上的截距是5-.18．（本小题满分12分）为调查学生每周平均体育运动时间的情况，某校收集到高三（1）班20位学生的样本数据（单位：小时），将他们的每周平均体育运动时间分为6组：[0，2），[2，4），[4，6），[6，8），[8，10），[10，12]加以统计，得到如图所示的频率分布直方图．（1）根据频率分布直方图，求出该班学生的每周平均体育运动时间的平均数的估计值；（2）若在该班每周平均体育运动时间低于4小时的学生中任意抽取2人，求抽取到运动时间低于2小时的学生的概率．19.（本小题满分12分）在ABC ∆中，内角A,B,C 的对边分别为c b a ,,，已知b ac B C A -=-2cos cos 2cos .（1）求ACsin sin ；（2）若2,41cos ==b B ，求ABC ∆的面积S .20.（本小题满分12分）如图，四边形ABCD 与BDEF 均为菱形，∠DAB=∠DBF=60°，且FA=FC ．（1）求证：AC⊥平面BDEF ；（2）求二面角A ﹣FC ﹣B 的余弦值．21.本小题满分12分）等差数列{}n a 前n 项和为n S ，已知37a =，5726a a +=. （1）求n a 及n S ；（2）令1n n b S =（*n N ∈），数列{}n b 的前n 项和n T ，证明34n T <.22.（本小题满分12分）已知21F ,F 是椭圆 12222=+by a x 的左、右焦点，O 为坐标原点，点)22P(-1,在椭圆上，线段2PF 与y 轴的交点M 满足0PM 2=+M F . （1）求椭圆的标准方程；（2）圆O 是以21F F 为直径的圆，一直线m kx y l +=:与圆O 相切，并与椭圆交于不同的两点B A ,，当λ=∙，且满足4332≤≤λ时，求OAB ∆的面积S 的取值范围.樟树中学2019届高二年级第四次月考数学（理科）答案一、选择题（本大题共12小题，每小题5分，共60分）15.412. 2 13.(x－2)2＋(y＋1)2＝1 14.217. ∵直线的方程为y＝－x＋1，∴k＝－，倾斜角α＝120°，倾斜角为30°，即斜率为.(1)∵直线经过点(，－1)，所求直线方程为y＋1＝(x－)，即x－3y－6＝0.(2)∵直线在y轴上的截距为－5，∴由斜截式知所求直线方程为y＝x－5，即x－3y－15＝0.18. （1）解：根据频率分布直方图，各组的频率分别为：0.05，0.2，0.3，0.25，0.15，0.05，各组的中点分别为：1，3，5，7，9，11，该班学生的每周平均体育运动时间的平均数的估计值为0.05×1+0.2×3+0.3×5+0.25×7+0.15×9+0.05×11=4.45…（6分）（2）依题意可知，平均运动时间低于4小时的学生中，在[0，2）的人数有0.05×20=1，记为1，在[2，4）的人数有0.2×20=4，记为2，3，4，5，从这5人中随机抽取2人的可能情况有10种，分别为：（1，2），（1，3），（1，4），（1，5），（2，3），（2，4），（2，5），（3，4），（3，5），（4，5）；）其中，运动时间低于2小时的学生的可能情况有4种，分别为：（1，2），（1，3），（1，4），（1，5）；故所求概率12分20 Ⅰ）证明：设AC与BD相交于点O，连接FO．因为四边形ABCD为菱形，所以AC⊥BD，且O为AC中点．又 FA=FC，所以AC⊥FO．因为FO∩BD=O，所以AC⊥平面BDEF．……6分（Ⅱ）解：因为四边形BDEF为菱形，且∠DBF=60°，所以△DBF为等边三角形．因为O为BD中点，所以FO⊥BD，故FO⊥平面ABCD．由OA，OB，OF两两垂直，建立如图所示的空间直角坐标系O﹣xyz．设AB=2．因为四边形ABCD为菱形，∠DAB=60°，则BD=2，所以OB=1，．所以．所以，．设平面BFC的法向量为=（x，y，z），则有，取x=1，得．∵平面AFC的法向量为=（0，1，0）．由二面角A ﹣FC ﹣B 是锐角，得|cos ＜，＞|==．所以二面角A ﹣FC ﹣B 的余弦值为．19（Ⅰ）由正弦定理得2sin ,a R A =2sin ,b R B =2sin ,c R C =所以c o s A -2c o s C 2c -a =c o s B b =2sin sin sin C A B-, 即sin cos 2sin cos 2sin cos sin cos B A B C C B A B -=-,即有sin()2sin()A B B C +=+,即sin 2sin C A =,所以sin sin CA=2. （3）（Ⅱ）由（Ⅰ）知:sin sin c Ca A ==2,即c=2a,又因为2b =,所以由余弦定理得：（4）2222cos b c a ac B =+-，即222124224a a a a =+-⨯⨯,解得1a =,所以c=2,又因为cosB=14，所以ABC ∆的面积为11sin 1222ac B =⨯⨯⨯.21. 解（1）解：（1）设数列{}n a 的公差为d ，则由题知576226a a a +== 613a ∴= 316127513a a d a a d =+=⎧⎨=+=⎩ 132a d =⎧⇒⎨=⎩ 32(1)21n a n n ∴=+-=+1()(2)2n n n a a S n n +==+ （2）则11111()(2)22n n b S n n n n ===-++ 那么 123111111n n nT S S S S S -=+++++ 111111111111111111()()()()()()21322423524621122n n n n =-+-+-+-++-+--++ 1111(1)2212n n =+--++32342(1)(2)nn n +=-++2302(1)(2)n n n +>++34n T ∴<…12分 22、（1）因为，所以是线段的中点，所以是的中位线，又所以,所以，又因为，解得，所以椭圆的标准方程为. （2）因为直线与相切，所以，即联立得.设因为直线与椭圆交于不同的两点、，所以，，又因为，所以解得.设，则单调递增，所以，即。

江西省樟树市2016_2017学年高二数学下学期第一次月考试题文

2710xy江西省樟树2018届高二（下）第一次月考数学(文)试卷一．选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1.若集合{}|6M x N x =∈<，{}|(2)(9)0N x x x =--<，则M N 等于（）A ．{}3,4,5B ．{}|26x x <<C ．{}|35x x ≤≤D ．{}2,3,4,52．某高中共有学生900人，其中高一年级240人，高二年级260人，为做某项调查，拟采用分层抽样抽取容量为45的样本，则在高三年级抽取的人数是（） A ．25 B ．24 C ．22 D ．20 3.若,m n N *∈则a b >是()()0m m n n a b a b -⋅->成立的（）A.充分非必要条件B.必要非充分条件C.充分必要条件D.即非充分又非必要条件4．已知函数(4)2()22()2x f x x f x e x f x x ->⎧⎪=-≤≤⎨⎪-<-⎩，则(2017)f -= ( )A ．1B ．eC ．1eD ．2e5.阅读如下程序框图，如果输出，那么空白的判断框中应填入的条件是（）A ．B ．C ．D ．6．已知关于x 的不等式x 2﹣2x ﹣3＞0和x 2+bx+c ≤0的解集分别为A ，B ，若A ∪B=R ， A∩B=（3，4]，则b+c=（）A ．7B ．﹣7C ．12D ．﹣12 7.某几何体的三视图如图所示，当xy 最大时，该几何体的体积为（） A ．72 B ． 47 C ．87 D ．1677题图8.已知向量(3,2)a =-，(,1)b x y =-且a ∥b ，若,x y 均为正数，则32xy+的最小值是（）A ．24B ．8C ．83 D ．539．若函数f （x ）=x 3﹣3x 在（a ，6﹣a 2）上有最大值，则实数a 的取值范围是（） A ．（﹣，﹣1） B ．（﹣，﹣1]C ．（﹣，﹣2）D ．（﹣，﹣2]10.已知双曲线）＞，＞00(1:2222b a by a x C =-的左焦点为F N M c 、),0,(-在双曲线C 上，O 是坐标原点，若四边形OFMN 为平行四边形，且四边形OFMN 的面积为cb 2，则双曲线C 的离心率为（）A.2 .2 C 2 D.3211．已知偶函数f （x ）的定义域为R ，且f （1+x ）=f （1﹣x ），又当x∈[0，1]时，f （x ）=x ，函数g （x ）=，则函数h （x ）=f （x ）﹣g （x ）在区间[﹣4，4]上的零点个数为（） A ．8 B ．6C ．9D ．712．已知函数32()f x ax bx cx d =+++的图象如图所示，则21++a b 的取值范围是（）A ．)21,23(-B ．)21,52(-C ．)23,21(-D ．)25,23(-二．填空题（本大题共4小题，每小题5分，共20分） 13．已知命题21:02p x x >--，则p ⌝对应的x 集合为___________．14. 若方程210x mx --=有两根，其中一根大于2，另一根小于2的充要条件是______． 15．把半径为2的圆分成相等的四弧，再将四弧围成星形放在半径为2 的圆内，现在往该圆内任投一点，此点落在星形内的概率为．16.若函数423()x x f x k x-=-有3个零点，则实数k 的取值范围是．三．解答题：（本大题共6题，共70分，17题10分，其余5题各12分.解答应写出文字说明，证明过程或演算步骤）17. 已知a ,b ,c 分别为ABC ∆三个内角A ,B ,C 的对边，3sin cos c a C c A =-. （1）求A ；-11xy212题图15题图（2）若2a=,ABC∆的面积为3，求b,c.18.已知函数)2ln()(,ln)(2axxxgxaxxf+-=-=，（1）若0=a，求)()()(F xgxfx+=的零点；（2）设命题)(:xfP在⎥⎦⎤⎢⎣⎡2141，单调递减，)(:xgq的定义域为R，若qp∧为真命题，求a的范围。

湖南省衡阳市樟树中学2016-2017学年高一下学期第四次月考数学(理)试题Word版含答案

江西省樟树中学2019届高一下学期第四次月考理科数学试卷考试范围：必修一、二、四，必修五部分考试时间：2017.5.26一、选择题：本大题共12小题，每小题5分，共60分。

每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知直线l20y -+=，则直线l 的倾斜角为 A ．30 B ．60 C ．120 D ．150 2. 设α为钝角，3sin 5α=，则sin2α= A ．1225- B ．1225C ．2425-D ．24253.已知(sin ,1)a α=，(2,4cos )b α=-，若a 与b 垂直，则tan α= A ．2- B ．2 C ．2± D4. 在ABC ∆中，已知122,3,sin ,13b a A ===则sin B = A.813B.913C.1013D. 11135. 已知圆O ：221x y +=，一只蚂蚁从点1,22A ⎛- ⎝⎭出发，沿圆周爬行（逆时针或顺时针），当它爬行到点()1,0B -时，蚂蚁爬行的最短路程为 A.76π B.56π C.43π D.23π6. 已知数列{}n a 是首项为1，公差为d （*N d ∈）的等差数列，若81是该数列中的一项，则公差d 不可能是A.5B. 4C. 3D. 2 7. 一个机器零件的三视图如右图所示，其中俯视图是一个半圆内切于边长为2的正方形，则该机器零件的体积为A. 883π+B.483π+ C. 283π+ D. 83π+8. 下列函数中，最小正周期为π且一条对称轴为8x π=的函数是A.sin(2)2y x π=+ B.x x y cos sin += C.cos(2)2y x π=+ D.x x y 2cos 2sin +=9.10. 已知,,a b c 分别是ABC ∆中角,,A B C 的对边长，b 和c 是关于x 的方程2925cos 0x x A -+=的两个根()b c >，且18(sin sin sin )(sin sin sin )sin sin 5B C A B C A B C +++-=，则ABC ∆的形状为 A ．等腰三角形B ．锐角三角形C ．直角三角形D ．钝角三角形11. 如果函数()f x 对任意的实数x ，存在常数M ，使得不等式()f x M x ≤恒成立，那么就称函数()f x 为有界泛函．给出下面三个函数：①()1f x =；②2()f x x =；③2()1xf x x x =++．其中属于有界泛函的是A ．①B ．②C.③D ．①②③12.已知函数21,0()21,0x x x f x x x ⎧++≥=⎨+<⎩，若(sin sin sin 1)1f αβγ++-=-(cos cos cos 1)3f αβγ+++=，则cos()cos()αββγ-+-的值为A ．2B ．1C ．﹣2D ．﹣1二、填空题：（本大题共4小题，每小题5分，共20分. ） 13. 已知O 的方程224x y +=，则过点P 且与圆O 相切的切线方程为 .14．已知3()sin f x x a x b =++为奇函数（,a b 为常数）且3()128f ππ=+,则a = ．15. 在ABC ∆中，若120,5,7A AB BC ∠===则ABC ∆的面积S = ．16. 已知单位向量12,e e →→的夹角为3π，如果12(cos )2sin (cos 1)a e e ααα→→→=++其中R α∈，则a →在1e →上的投影的最大值是．三.解答题：(本题共6小题，共70分解答应写出必要计算过程，推理步骤和文字说明) 17.（本题满分10分）已知{}n a 是等差数列，其中1425,16a a == （1）求{}n a 的通项；（2）数列{}n a 中共有几项大于0.18. （本题满分12分）如图，在四棱锥中ABCD P -，底面ABCD 为正方形，PC PA =，若M ，N 分别为PB ，AD 的中点.求证：（1）PDC MN 平面//；（2）AC PD ⊥.19．（本题满分12分）已知02παβπ<<<<，4tan ,cos()3αβα=-=（1）求sin α的值；（2）求β的值.20.（本题满分12分）已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边，cos sin 0a C C b c --=（1）求角A ; （2）若2a =， ABC ∆,b c 两边.21．（本题满分12分）已知(2cos ,2sin ),(sin(),cos())66a x xb x x ππ→→==--，函数()cos ,,f x a b →→=(,a b →→表示两向量的夹角)（1）求函数()f x 零点；（2）若()f x 的三内角,,A B C 的对边分别是,,a b c 且()1f A =，求b ca+的取值范围．22.（本题满分12分）已知向量13log ,1()m x f x →⎛⎫=- ⎪⎝⎭，()31,2log n x →=+,且向量m →∥n →.（1）求函数)(x f y =的解析式及函数))32(cos(π-=x f y 的定义域；（2）若函数2sin cos )(2+--=θθθa g ,存在R a ∈, 对任意⎥⎦⎤⎢⎣⎡∈3,2711x ,总存在唯一⎥⎦⎤⎢⎣⎡-∈2,20ππθ,使得)()(01θg x f =成立, 求实数a 的取值范围.高一下学期第4次月考理科数学答案一.选择题（本大题共12小题，每小题5分，共60分。

2023-2024学年湖南省衡阳市衡阳县四中高二(上)期中数学试卷(A卷)【答案版】

2023-2024学年湖南省衡阳市衡阳县四中高二（上）期中数学试卷（A卷）一、选择题（本题共8小题，每题5分，共40分）1．与向量a →=（1，﹣3，2）平行的一个向量的坐标是（） A ．（13，1，1）B ．（﹣1，﹣3，2）C ．（−12，32，﹣1）D ．（√2，﹣3，﹣2√2）2．若直线ax ﹣4y +2＝0与直线2x +5y +c ＝0垂直，垂足为（1，b ），则a +b +c ＝（） A ．﹣6B ．4C ．﹣10D ．﹣43．过点A （11，2）作圆（x +1）2+（y ﹣2）2＝169的弦，其中弦长为整数的弦共有（） A ．16条B ．17条C ．32条D ．34条4．攒尖是古代中国建筑中屋顶的一种结构形式．如图，在重檐四角攒尖中，它的上层轮廓可近似看作一个正四棱锥，若此正四棱锥的侧面积是底面积的√2倍，则侧面与底面所成角的大小为（）A ．30°B ．45°C ．60°D ．15°5．已知正四棱柱ABCD ﹣A 1B 1C 1D 1的底面边长为2，侧棱长为4，E 为CD 1的中点，则点A 1到平面BDE 的距离为（） A ．32B ．2C ．94D ．836．已知椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)，焦距为2c ，以点O 为圆心，b 为半径作圆O ，若过点P(√155a ，√155a)作圆O 的两条切线，切点分别为A ，B ，且|AB|=4√33c ，则椭圆C 的离心率为（） A ．√22B ．√55C ．√33D ．127．数学上有很多著名的猜想，角谷猜想就是其中之一，它是指对于任意一个正整数，如果是奇数，则乘3加1．如果是偶数，则除以2，得到的结果再按照上述规则重复处理，最终总能够得到1．对任意正整数a 0，记按照上述规则实施第n 次运算的结果为a n （n ∈N ），则使a 7＝1的a 0所有可能取值的个数为（） A ．3B ．4C ．5D ．68．已知S n 为等差数列{a n }的前n 项和，若a 1+a 3＝6，S 5＝S 3+11，则S n +8a n −1的最小值为（） A ．112B ．285C ．173D ．132二、多项选择题（本题共4小题，每题5分，共20分；漏选记2分，错选记0分） 9．设r ＞0，圆（x ﹣1）2+（y +3）2＝r 2与圆x 2+y 2＝16的位置关系不可能是（） A ．外离B ．外切C ．相交D ．内切10．对于数列{a n }，若存在正整数k （k ≥2），使得a k ＜a k ﹣1，a k ＜a k +1，则称a k 是数列{a n }的“谷值”，k 是数列{a n }的“谷值点”，在数列{a n }中，若a n =|n +9n−8|，下列数不能作为数列{a n }的“谷值点”的是（） A ．3B ．2C ．7D ．511．给定两个不共线的空间向量a →与b →，定义叉乘运算：a →×b →．规定：①a →×b →为同时与a →，b →垂直的向量；②a →，b →，a →×b →三个向量构成右手系（如图1）；③|a →×b →|=|a →||b →|sin ＜a →，b →＞．如图2，在长方体ABCD ﹣A 1B 1C 1D 1中，AB ＝AD ＝2，AA 1＝4，则下列结论正确的是（）A ．AB →×AD →=AA 1→B ．AB →×AD →=AD →×AB →C ．(AB →+AD →)×AA 1→=AB →×AA 1→+AD →×AA 1→D ．长方体ABCD ﹣A 1B 1C 1D 1的体积V =(AB →×AD →)⋅CC 1→12．抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出．已知抛物线y 2＝4x 的焦点为F ，一束平行于x 轴的光线l 1从点M （3，1）射入，经过抛物线上的点P （x 1，y 1）反射后，再经抛物线上另一点Q （x 2，y 2）反射后，沿直线l 2射出，则下列结论中正确的是（） A ．x 1x 2＝1 B ．k PQ =−43C ．|PQ |=254D ．l 1与l 2之间的距离为4三、填空题（本题共4小题，每题5分，共20分）13．已知空间向量a →，b →，|a →|＝2，|b →|=√2，a →•b →=−2，则＜a →，b →＞= ．14．已知圆C 1经过点C （4，7）且圆心在y 轴上，圆C 2：x 2+（y ﹣1）2＝4内切于圆C 1，圆C 1与x 轴分别交于A ，B 两点（点A 在点B 左侧），则直线AC 截圆C 2所得的弦长为． 15．已知椭圆的方程为x 2a 2+y 2＝1（a ＞1），上顶点为A ，左顶点为B ，设P 是椭圆上的任一点，则△P AB的最大值为√2+1，若已知M （−√3，0），N （√3，0），点Q 为椭圆上的任意一点，则1|QN|+4|QM|的最小值为．16．如图，圆锥的底面直径AB ＝2，高OC =√2，D 为底面圆周上的一点，∠AOD ＝120°，则直线AD 与BC 所成角的大小为．四、解答题（本题共6小题，共70分）17．（10分）如图，在平行四边形OABC 中，A （3，0），C （1，3）．（1）求AB 所在直线的方程；（2）过点C 作CD ⊥AB 于点D ，求CD 所在直线的方程．18．（12分）已知等差数列{a n }，a 6＝5，a 3+a 8＝5．（1）求{a n }的通项公式；（2）求数列{a n }的前n 项和为S n ．19．（12分）已知圆C ：x 2+y 2﹣8y +12＝0，直线l ：ax +y +2a ＝0，（1）当a 为何值时，直线l 与圆C 相切．（2）当直线l 与圆C 相交于A 、B 两点，且|AB |＝2√2时，求直线l 的方程． 20．（12分）已知抛物线y 2＝﹣x 与直线y ＝k （x +1）相交于A 、B 两点．（1）求证：OA ⊥OB ；（2）当△OAB 的面积等于√10时，求k 的值．21．（12分）某商品的包装纸如图1，其中菱形ABCD 的边长为3，且∠ABC ＝60°，AE ＝AF =√3，BE ＝DF ＝2√3．将包装纸各三角形沿菱形的边进行翻折后，点E ，F ，M ，N 汇聚为一点P ，恰好形成如图2的四棱锥形的包裹．（Ⅰ）证明：P A ⊥底面ABCD ；（Ⅱ）设点T 为BC 上的点，且二面角B ﹣P A ﹣T 的正弦值为√2114，试求PC 与平面P AT 所成角的正弦值.22．（12分）已知椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)经过点（√2，1），离心率为√22．（1）求椭圆C 的方程；（2）设直线l ：y ＝kx +t （t ≠0）与椭圆C 相交于A ，B 两点，若以OA ，OB 为邻边的平行四边形OAPB 的顶点P 在椭圆C 上，求证：平行四边形OAPB 的面积为定值．2023-2024学年湖南省衡阳市衡阳县四中高二（上）期中数学试卷（A卷）参考答案与试题解析一、选择题（本题共8小题，每题5分，共40分）1．与向量a →=（1，﹣3，2）平行的一个向量的坐标是（） A ．（13，1，1）B ．（﹣1，﹣3，2）C ．（−12，32，﹣1）D ．（√2，﹣3，﹣2√2）解：对于C 中的向量：（−12，32，﹣1）=−12（1，﹣3，2）=−12a →，因此与向量a →=（1，﹣3，2）平行的一个向量的坐标是(−12，32，−1)．故选：C ．2．若直线ax ﹣4y +2＝0与直线2x +5y +c ＝0垂直，垂足为（1，b ），则a +b +c ＝（） A ．﹣6B ．4C ．﹣10D ．﹣4解：∵直线ax ﹣4y +2＝0与直线2x +5y +c ＝0垂直， ∴2a ﹣20＝0，解得a ＝10，∵垂足为（1，b ），∴{10×1−4×b +2=02×1+5×b +c =0，解得b ＝3，c ＝﹣17，故a +b +c ＝﹣4．故选：D ．3．过点A （11，2）作圆（x +1）2+（y ﹣2）2＝169的弦，其中弦长为整数的弦共有（） A ．16条B ．17条C ．32条D ．34条解：圆的标准方程是：（x +1）2+（y ﹣2）2＝132，圆心（﹣1，2），半径r ＝13，过点A （11，2）的最短的弦长是以A （11，2）为中点的弦，为10，有1条，最长的弦长是过点A （11，2）的直径，为26，有1条，还有长度为11，12，…，25的各2条，所以共有弦长为整数的2+2×15＝32条．故选：C ．4．攒尖是古代中国建筑中屋顶的一种结构形式．如图，在重檐四角攒尖中，它的上层轮廓可近似看作一个正四棱锥，若此正四棱锥的侧面积是底面积的√2倍，则侧面与底面所成角的大小为（）A ．30°B ．45°C ．60°D ．15°解：如图，设正四棱锥为P ﹣ABCD ，连接AC ，BD 交于点O ，连接PO ，则PO ⊥底面ABCD ，作OE ⊥CD 于E ，连接PE ，CD ⊂底面ABCD ，则PO ⊥CD ，而OE ∩PO ＝O ，OE ，PO ⊂平面POE ，故CD ⊥平面POE ，PE ⊂平面POE ，故CD ⊥PE ，故∠PEO 即为平面PCD 与底面ABCD 所成角，也即正四棱锥P ﹣ABCD 的侧面与底面所成角，因为正四棱锥的侧面积是底面积的√2倍，故4S △PCD =√2×4S △OCD ，即S △PCD =√2S △OCD ，所以12CD ×PE =√22CD ×OE ，即OE PE =√22，在Rt △POE 中，cos ∠PEO =OE PE =√22，则∠PEO ＝45°，即正四棱锥的侧面与底面所成角的大小为45°．故选：B ．5．已知正四棱柱ABCD ﹣A 1B 1C 1D 1的底面边长为2，侧棱长为4，E 为CD 1的中点，则点A 1到平面BDE 的距离为（） A ．32B ．2C ．94D ．83解：正四棱柱ABCD ﹣A 1B 1C 1D 1的底面边长为2，侧棱长为4，E 为CD 1的中点，如图，以D 为原点，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系，则D （0，0，0），A 1（2，0，4），B （2，2，0），E （0，1，2），所以DA 1→⬚=(2，0，4)，DB →=(2，2，0)，DE →=(0，1，2)，设平面BDE 的法向量为n →=(x ，y ，z)，则{n →⋅DB →=2x +2y =0n →⋅DE →=y +2z =0，令y ＝﹣1，则x =1，z =12，即n →=(1，−1，12)，则点A 1到平面BDE 的距离d =|DA 1→⋅n →||n →|=2+4×12√1+1+14=83．故选：D ． 6．已知椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)，焦距为2c ，以点O 为圆心，b 为半径作圆O ，若过点P(√155a ，√155a)作圆O 的两条切线，切点分别为A ，B ，且|AB|=4√33c ，则椭圆C 的离心率为（） A ．√22B ．√55C ．√33D ．12解：由椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)，焦距为2c ，以点O 为圆心，b 为半径作圆O ，若过点P(√155a ，√155a)作圆O 的两条切线，切点分别为A ，B ，且|AB|=4√33c ， OP =√(155a)2+(155a)2=√305a ，AH =2√33c ，OA ＝b ，故AP =√OP 2−OA 2=√65a 2−(a 2−c 2)=√15a 2+c 2，在Rt △AOP 中，由AH ⊥OP ，有OA •AP ＝AH •OP ，故b √15a 2+c 2=2√33c ×√305a ，得：b√a 2+5c 2=2√2ac ，有（a 2﹣c 2）（a 2+5c 2）＝8a 2c 2，化为：5c 4+4a 2c 2﹣a 4＝0，有5e 4+4e 2﹣1＝0，得（5e 2﹣1）（e 2+1）＝0，解得e =√55．故选：B ．7．数学上有很多著名的猜想，角谷猜想就是其中之一，它是指对于任意一个正整数，如果是奇数，则乘3加1．如果是偶数，则除以2，得到的结果再按照上述规则重复处理，最终总能够得到1．对任意正整数a 0，记按照上述规则实施第n 次运算的结果为a n （n ∈N ），则使a 7＝1的a 0所有可能取值的个数为（） A ．3B ．4C ．5D ．6解：由题意知∀n ∈N *，a n ={3a n−1+1，a n−1为奇数a n−12，a n−1为偶数，由a 7＝1，得a 6＝2，∴a 5＝4，∴a 4＝1或a 4＝8．①当a 4＝1时，a 3＝2，∴a 2＝4，∴a 1＝1或a 1＝8，∴a 0＝2或a 0＝16． ②若a 4＝8，则a 3＝16，∴a 2＝5或a 2＝32，当a 2＝5时，a 1＝10，此时，a 0＝3或a 0＝20，当a 2＝32时，a 1＝64，此时，a 0＝21或a 0＝128，综上，满足条件的a 0的值共有6个．故选：D ．8．已知S n 为等差数列{a n }的前n 项和，若a 1+a 3＝6，S 5＝S 3+11，则S n +8a n −1的最小值为（） A ．112B ．285C ．173D ．132解：设{a n }的公差d ，由a 1+a 3＝6，S 5＝S 3+11，得{2a 1+2d =65a 1+10d =3a 1+3d +11，解得{a 1=2d =1，所以a n =n +1，S n =n(n+3)2，则S n +8a n −1=n 22+3n2+8n=n 2+32+8n≥2√n 2×8n+32=112，当且仅当n ＝4时等号成立．故选：A ．二、多项选择题（本题共4小题，每题5分，共20分；漏选记2分，错选记0分）9．设r ＞0，圆（x ﹣1）2+（y +3）2＝r 2与圆x 2+y 2＝16的位置关系不可能是（） A ．外离B ．外切C ．相交D ．内切解：圆（x ﹣1）2+（y +3）2＝r 2的圆心为（1，﹣3），半径为r ，圆x 2+y 2＝16的圆心为（0，0），半径为4，所以两圆心之间的距离d =√10，因为4+r ＞√10，所以两圆的位置关系不可能是外离和外切．故选：AB ．10．对于数列{a n }，若存在正整数k （k ≥2），使得a k ＜a k ﹣1，a k ＜a k +1，则称a k 是数列{a n }的“谷值”，k 是数列{a n }的“谷值点”，在数列{a n }中，若a n =|n +9n−8|，下列数不能作为数列{a n }的“谷值点”的是（） A ．3B ．2C ．7D ．5解：由a n =|n +9n−8|，则a 1＝2，a 2=32，a 3＝2，a 4=74，a 5=65，a 6=12，a 7=27，a 8=98，所以n ＝2，7是数列{a n }的“谷值点” 当n ＝3，5不是数列{a n }的“谷值点”，故选：AD ．11．给定两个不共线的空间向量a →与b →，定义叉乘运算：a →×b →．规定：①a →×b →为同时与a →，b →垂直的向量；②a →，b →，a →×b →三个向量构成右手系（如图1）；③|a →×b →|=|a →||b →|sin ＜a →，b →＞．如图2，在长方体ABCD ﹣A 1B 1C 1D 1中，AB ＝AD ＝2，AA 1＝4，则下列结论正确的是（）A ．AB →×AD →=AA 1→B ．AB →×AD →=AD →×AB →C ．(AB →+AD →)×AA 1→=AB →×AA 1→+AD →×AA 1→D ．长方体ABCD ﹣A 1B 1C 1D 1的体积V =(AB →×AD →)⋅CC 1→解：∵|AB →×AD →|=|AB →||AD →|sin90°=2×2×1=4，且AA 1→分别与AB →、AD →垂直，∴AB →×AD →=AA 1→，故A 正确；由题意，AB →×AD →=AA 1→，AD →×AB →=A 1A →，故B 错误；∵AB →+AD →=AC →，∴|(AB →+AD →)×AA 1→|=|AC →×AA 1→|=2√2×4×1=8√2，且(AB →+AD →)×AA 1→与DB →共线同向，∵|AB →×AA 1→|=2×4×1=8，AB →×AA 1→与DA →共线同向，|AD →×AA 1→|=2×4×1=8，AD →×AA 1→与DC →共线同向，∴|AB →×AA 1→+AD →×AA 1→|=8√2，且AB →×AA 1→+AD →×AA 1→与DB →共线同向，故C 正确； (AB →×AD →)⋅CC 1→=|AB →||AD →|×|CC 1→|×sin90°×cos0°=2×2×4＝16，故D 成立．故选：ACD ．12．抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出．已知抛物线y 2＝4x 的焦点为F ，一束平行于x 轴的光线l 1从点M （3，1）射入，经过抛物线上的点P （x 1，y 1）反射后，再经抛物线上另一点Q （x 2，y 2）反射后，沿直线l 2射出，则下列结论中正确的是（） A ．x 1x 2＝1B ．k PQ =−43C ．|PQ |=254D ．l 1与l 2之间的距离为4解：如图所示，由抛物线的光学性质可知，直线PQ 过焦点F （1，0），∴x 1x 2=p 24=1，即选项A 正确；由题意可得，点P 的坐标为(14，1)，点Q 的坐标为（4，﹣4）， ∴k PQ =−4−14−14=−43，即选项B 正确；由抛物线的定义可知，|PQ |=x 1+x 2+p =14+4+2=254，即选项C 正确； ∵l 1与l 2平行，∴l 1与l 2之间的距离d ＝|y 1﹣y 2|＝5，即选项D 错误；故选：ABC ．三、填空题（本题共4小题，每题5分，共20分）13．已知空间向量a →，b →，|a →|＝2，|b →|=√2，a →•b →=−2，则＜a →，b →＞= 3π4．解：cos ＜a →，b →＞=a →⋅b→|a →||b →|=−22×2=−√22，∵0≤＜a →，b →＞≤π，则＜a →，b →＞=3π4．故答案为：3π4．14．已知圆C 1经过点C （4，7）且圆心在y 轴上，圆C 2：x 2+（y ﹣1）2＝4内切于圆C 1，圆C 1与x 轴分别交于A ，B 两点（点A 在点B 左侧），则直线AC 截圆C 2所得的弦长为 2√2 ．解：设圆C 1的圆心为C 1（0，m ）．因为圆C 2：x 2+(y −1)2=4内切于圆C 1，所以圆C 1的半径r 1＝|m ﹣1|+2，又r 1=|CC 1|=√(4−0)2+(7−m)2，所以√(4−0)2+(7−m)2=|m −1|+2，化简得12m +4|m ﹣1|﹣60＝0，当m ≥1时，12m +4（m ﹣1）﹣60＝0，解得m ＝4，当m ＜1时，12m +4（1﹣m ）﹣60＝0，解得m ＝7（舍去），所以圆C 1的半径r 1＝|m ﹣1|+2＝5，所以圆C 1的方程为x 2+（y ﹣4）2＝25，当y ＝0时，x ＝3或x ＝﹣3，所以圆C 1与x 轴交于A （﹣3，0），B （3，0）两点，所以k AC =74−(−3)=1，所以直线AC 的方程为x ﹣y +3＝0，圆心C 2（0，1）到直线AC 的距离为d =2=√2，所以直线AC 截圆C 2所得的弦长为2√r 22−d 2=2√4−(√2)2=2√2．故答案为：2√2． 15．已知椭圆的方程为x 2a 2+y 2＝1（a ＞1），上顶点为A ，左顶点为B ，设P 是椭圆上的任一点，则△P AB的最大值为√2+1，若已知M （−√3，0），N （√3，0），点Q 为椭圆上的任意一点，则1|QN|+4|QM|的最小值为94．解：由椭圆的知识可知A （0，1），B （﹣a ，0），故直线AB 的方程为−x a+y =1，即x ﹣ay +a ＝0，设P （a cos θ，sin θ），可得P 到直线AB 的距离d =√2asin(θ+π4)+a|√1+a 2，∴当θ＝135°时，d 取最大值为√2+1)a √1+a 2，此时△P AB 的面积S 取最大值为：12×√1+a 2×√2+1)a √1+a 2=√2+1，∴a ＝2， ∴椭圆的方程为x 24+y 2=1，∴M （−√3，0），N （√3，0）为焦点， ∴|QN |+|QM |＝2a ＝4， ∴1|QN|+4|QM|=14×（1|QN|+4|QM|）（|QN |+|QM |）=14×（5+4|QN||QM|+|QM||QN|）≥14×（5+4）=94，当且仅当|QM |＝2|QN |时，取等号， ∴1|QN|+4|QM|的最小值为94．故答案为：94．16．如图，圆锥的底面直径AB ＝2，高OC =√2，D 为底面圆周上的一点，∠AOD ＝120°，则直线AD 与BC 所成角的大小为 60° ．解：取AB ⌢的中点E ，连接OE ，以O 为原点，OE →，OB →，OC →的方向分别为x ，y ，z 轴的正方向，建立空间直角坐标系，如图，依题意，A(0，−1，0)，B(0，1，0)，C(0，0，√2)，D(√32，12，0)，则AD →=(√32，32，0)，BC →=(0，−1，√2)，设直线AD 与BC 所成的角为θ，0＜θ＜π2，则cosθ=|cos〈AD →，BC →〉|=|AD →⋅BC →||AD →||BC →|=32√3×√3=12，解得θ＝60°，所以直线AD 与BC 所成的角为60°．故答案为：60°．四、解答题（本题共6小题，共70分）17．（10分）如图，在平行四边形OABC 中，A （3，0），C （1，3）．（1）求AB 所在直线的方程；（2）过点C 作CD ⊥AB 于点D ，求CD 所在直线的方程．解：（1）因为A （3，0），C （1，3），所以k OC ＝3，在平行四边形OABC 中，AB ∥OC ，所以AB 的斜率等于直线OC 的斜率，所以直线AB 的方程为y ﹣0＝3（x ﹣3），即3x ﹣y ﹣9＝0；（2）因为CD ⊥AB ，设直线CD 的方程为x +3y +c ＝0，将点C 的坐标代入可得：1+3×3+c ＝0，可得c ＝﹣10，所以直线CD 的方程为：x +3y ﹣10＝0．18．（12分）已知等差数列{a n }，a 6＝5，a 3+a 8＝5．（1）求{a n }的通项公式；（2）求数列{a n }的前n 项和为S n ．解：（1）由已知得{a 6=a 1+5d =5a 3+a 8=a 1+2d +a 1+7d =5，解得{a 1=−20d =5，∴{a n }的通项公式为a n ＝﹣20+（n ﹣1）×5，即a n ＝5n ﹣25；（2）由（1）得数列{a n }的前n 项和S n =n(−20+5n−25)2=52n(n −9)．19．（12分）已知圆C ：x 2+y 2﹣8y +12＝0，直线l ：ax +y +2a ＝0，（1）当a 为何值时，直线l 与圆C 相切．（2）当直线l 与圆C 相交于A 、B 两点，且|AB |＝2√2时，求直线l 的方程．（12分）解：（1）设圆心到直线的距离为d ，圆C ：x 2+y 2﹣8y +12＝0的圆心C （0，4）半径r =12√64−48=2， ∵直线l ：ax +y +2a ＝0与圆相切， ∴d =|4+2a|√a 2+1=2，解得a =−34．（2）∵圆心到直线的距离d =|4+2a|√a 2+1，直线l 与圆C 相交于A 、B 两点，且|AB |＝2√2时，d =√r 2−(|AB|2)2=√2， ∴d =√a 2+1=√2，解得a ＝﹣7或a ＝﹣1．∴所求直线为7x ﹣y +14＝0或x ﹣y +2＝0．20．（12分）已知抛物线y 2＝﹣x 与直线y ＝k （x +1）相交于A 、B 两点．（1）求证：OA ⊥OB ；（2）当△OAB 的面积等于√10时，求k 的值．解：（1）由方程y 2＝﹣x ，y ＝k （x +1）消去x 后，整理得ky 2+y ﹣k ＝0．设A （x 1，y 1）、B （x 2，y 2），由韦达定理y 1•y 2＝﹣1．∵A 、B 在抛物线y 2＝﹣x 上，∴y 12＝﹣x 1，y 22＝﹣x 2，y 12•y 22＝x 1x 2．∵k OA •k OB =y 1x 1•y 2x 2=y 1y 2x 1x 2=1y 1y 2=−1，∴OA ⊥OB ．（2）设直线与x 轴交于N ，又显然k ≠0， ∴令y ＝0，则x ＝﹣1，即N （﹣1，0）．∵S △OAB ＝S △OAN +S △OBN =12|ON ||y 1|+12|ON ||y 2|=12|ON |•|y 1﹣y 2|，∴S △OAB =12•1•√(y 1+y 2)2−4y 1y 2=12√(1k)2+4．∵S △OAB =√10， ∴√10=12√1k2+4．解得k ＝±16．21．（12分）某商品的包装纸如图1，其中菱形ABCD 的边长为3，且∠ABC ＝60°，AE ＝AF =√3，BE ＝DF ＝2√3．将包装纸各三角形沿菱形的边进行翻折后，点E ，F ，M ，N 汇聚为一点P ，恰好形成如图2的四棱锥形的包裹．（Ⅰ）证明：P A ⊥底面ABCD ；（Ⅱ）设点T 为BC 上的点，且二面角B ﹣P A ﹣T 的正弦值为√2114，试求PC 与平面P AT 所成角的正弦值.解：（I ）由菱形ABCD 的边长为3，AE ＝AF =√3，BE ＝DF ＝2√3，可得BE 2＝AB 2+AE 2，即有AB ⊥AE ，同理DF 2＝AD 2+AF 2，即有AD ⊥AF ，在翻折的过程中，垂直关系保持不变可得P A ⊥AB ，P A ⊥AD ，AB ∩AD ＝A ，所以P A ⊥底面ABCD ；（II ）如图，以点A 为原点，AB 为x 轴，过点A 作AB 的垂线为y 轴，AP 为z 轴建立空间直角坐标系，由第（I ）问可得P A ⊥底面ABCD ，则P A ⊥AB ，P A ⊥AT ，则∠BAT 为二面角B ﹣P A ﹣T 的平面角，由题意可得sin ∠BAT =√2114，考虑△BAT ，∠ABT ＝60°，可得sin ∠ATB ＝sin （∠ABT +60°）=3√2114，利用正弦定理ABsin∠ATB=BT Sin∠BTA，可得BT ＝1，所以点T 的坐标为（52，√32，0），点P （0，0，√3），A （0，0，0），C （32，3√32，0），设面P AT 的一个法向为量m →=（x ，y ，z ），则有{m →⋅AP →=0m →⋅AT →=0，即{√3z =05x +√3y =0，令x ＝3，则有m →=（3，﹣5√3，0），PC →=（32，3√32，−√3），所以cos ＜m →，PC →＞=m →⋅PC→|⬚||⬚|=−3√714，所以PC 与面P AT 所成角的正弦值为3√714．22．（12分）已知椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)经过点（√2，1），离心率为√22．（1）求椭圆C 的方程；（2）设直线l ：y ＝kx +t （t ≠0）与椭圆C 相交于A ，B 两点，若以OA ，OB 为邻边的平行四边形OAPB 的顶点P 在椭圆C 上，求证：平行四边形OAPB 的面积为定值．（1）解：由题意， {2a 2+1b 2=1c a =√22a 2=b 2+c 2，解得a 2＝4，b 2＝2．∴椭圆方程为x 24+y 22=1；（2）证明：联立{y =kx +tx 24+y 22=1，得（2k 2+1）x 2+4ktx +2（t 2﹣2）＝0． ∴Δ＝（4kt ）2﹣8（2k 2+1）（t 2﹣2）＝8[2（2k 2+1）﹣t 2]＞0．设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=−4kt2k 2+1，x 1x 2=2(t 2−2)2k 2+1．∴y 1+y 2=k(x 1+x 2)+2t =2t 2k 2+1．∵四边形OAPB 是平行四边形，∴OP →=OA →+OB →=(x 1+x 2，y 1+y 2)=(−4kt 2k 2+1，2t 2k 2+1)，则P （−4kt 2k 2+1，2t 2k 2+1）．又∵点P 在椭圆上，∴4k 2t 2(2k 2+1)2+2t 2(2k 2+1)2=1，即t 2=2k 2+12．∵|AB |=√1+k 2|x 1−x 2|=√1+k 2√(x 1+x 2)2−4x 1x 2=2√2√1+k2√2(2k 2+1)−t 22k 2+1=√3√2√2k+1．又点O 到直线l 的距离d =|t|√1+k．∴平行四边形OAPB 的面积S =2S △OAB =|AB|⋅d =√3|t|√2k+1=√6√2√2k+1=√6．即平行四边形OAPB 的面积为定值√6．。