动态规划习题
动态规划练习试题和解答
动态规划练习题[题1] 多米诺骨牌（DOMINO）问题描述：有一种多米诺骨牌是平面的，其正面被分成上下两部分，每一部分的表面或者为空，或者被标上1至6个点。
现有一行排列在桌面上：顶行骨牌的点数之和为6+1+1+1=9；底行骨牌点数之和为1+5+3+2=11。
顶行和底行的差值是2。
这个差值是两行点数之和的差的绝对值。
每个多米诺骨牌都可以上下倒置转换，即上部变为下部，下部变为上部。
现在的任务是，以最少的翻转次数，使得顶行和底行之间的差值最小。
对于上面这个例子，我们只需翻转最后一个骨牌，就可以使得顶行和底行的差值为0，所以例子的答案为1。
输入格式：文件的第一行是一个整数n（1〈=n〈=1000〉，表示有n个多米诺骨牌在桌面上排成一行。
接下来共有n行，每行包含两个整数a、b（0〈=a、b〈=6，中间用空格分开〉。
第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数（0表示空）。
输出格式：只有一个整数在文件的第一行。
这个整数表示翻动骨牌的最少次数，从而使得顶行和底行的差值最小。
[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出：3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿（BOOKS）问题描述：假设有M本书（编号为1，2，…M），想将每本复制一份，M本书的页数可能不同（分别是P1，P2，…PM）。
动态规划练习例题
动态规划方法总结
动态规划算法的设计步骤
– – – – – – – 将问题表示成多步判断 确定是否满足优化原则——必要条件 确定子问题的重叠性——估计算法效率 列出关于优化函数的递推方程(或不等式)和边界条件 自底向上计算子问题的优化函数值----非递归的算法 备忘录方法记录中间结果 标记函数追踪问题的解
• S(i)表示结束于位置i的最大子区间和 • max{S(i)}即为所求最大子区间和 • 考虑如何递推求解并反算问题解
最大子矩阵
• 已知矩阵的大小定义为矩阵中所有元素的 和。给定一个矩阵，找到最大的非空(大小 至少是1 * 1)子矩阵。 • 例如这个矩阵的最大子矩阵大小为15。
0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2
动态规划练习例题在棋盘上移动在一个nn的棋盘上棋子可以向上方右上方或左上方移动每次从x方格移动到y方格将获得pxy元钱pxy不一定是正数现求一个获得钱最多的从底边到顶边的一种移动棋子的方案
动态规划练习例题
在棋盘上移动
• 在一个n×n的棋盘上，棋子可以向上方、 右上方或左上方移动，每次从x方格移动到y 方格将获得p(x,y)元钱， p(x,y)不一定是正 数，现求一个获得钱最多的从底边到顶边 的一种移动棋子的方案。
解题思路
Qx, y 1 Q x, y max Qx 1, y 1 Q x 1, y 1 y 1 px, y 1, x, y y 1 px 1, y 1, x, y y 1且x 1 px 1, y 1, x, y y 1且x 字符串X=x1,x2,…xm和Y=y1,y2,…yn 使用一系列编辑操作将字符串X转变成Y。允许使 用插入，删除，修改三种操作，每种操作都有 一定的代价，求一个总代价最小的操作序列。 – 设从字符X中删除符号xi的代价为D(xi) – 将符号yj插入X的代价为I(yj) – 将X中的符号xi修改成yj的代价为C(xi,yj)
动态规划典型例题
1、单调递增最长子序列描述求一个字符串的最长递增子序列的长度如：dabdbf最长递增子序列就是abdf，长度为4输入第一行一个整数0<n<20,表示有n个字符串要处理随后的n行，每行有一个字符串，该字符串的长度不会超过10000 输出输出字符串的最长递增子序列的长度样例输入3aaaababcabklmncdefg样例输出1372、最长公共子序列描述如题，需要写一个程序，得出最长公共子序列。
tip：最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。
其定义是，一个序列S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。
输入第一行给出一个整数N(0<N<100)表示待测数据组数接下来每组数据两行，分别为待测的两组字符串。
每个字符串长度不大于1000.输出每组测试数据输出一个整数，表示最长公共子序列长度。
每组结果占一行。
样例输入2asdfadfsd123abcabc123abc样例输出363、括号匹配时间限制：1000 ms | 内存限制：65535 KB描述给你一个字符串，里面只包含"(",")","[","]"四种符号，请问你需要至少添加多少个括号才能使这些括号匹配起来。
如：[]是匹配的([])[]是匹配的((]是不匹配的([)]是不匹配的输入第一行输入一个正整数N，表示测试数据组数(N<=10)每组测试数据都只有一行，是一个字符串S，S中只包含以上所说的四种字符，S的长度不超过100输出对于每组测试数据都输出一个正整数，表示最少需要添加的括号的数量。
每组测试输出占一行样例输入4[]([])[]((]([)]样例输出324、完全背包描述直接说题意，完全背包定义有N种物品和一个容量为V的背包，每种物品都有无限件可用。
动态规划典型例题
1、单调递增最长子序列描述求一个字符串的最长递增子序列的长度如：dabdbf最长递增子序列就是abdf，长度为4输入第一行一个整数0<n<20,表示有n个字符串要处理随后的n行，每行有一个字符串，该字符串的长度不会超过10000 输出输出字符串的最长递增子序列的长度样例输入3aaaababcabklmncdefg样例输出1372、最长公共子序列描述如题，需要写一个程序，得出最长公共子序列。
tip：最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。
其定义是，一个序列S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。
输入第一行给出一个整数N(0<N<100)表示待测数据组数接下来每组数据两行，分别为待测的两组字符串。
每个字符串长度不大于1000.输出每组测试数据输出一个整数，表示最长公共子序列长度。
每组结果占一行。
样例输入2asdfadfsd123abcabc123abc样例输出363、括号匹配时间限制：1000 ms | 内存限制：65535 KB描述给你一个字符串，里面只包含"(",")","[","]"四种符号，请问你需要至少添加多少个括号才能使这些括号匹配起来。
如：[]是匹配的([])[]是匹配的((]是不匹配的([)]是不匹配的输入第一行输入一个正整数N，表示测试数据组数(N<=10)每组测试数据都只有一行，是一个字符串S，S中只包含以上所说的四种字符，S的长度不超过100输出对于每组测试数据都输出一个正整数，表示最少需要添加的括号的数量。
每组测试输出占一行样例输入4[]([])[]((]([)]样例输出324、完全背包描述直接说题意，完全背包定义有N种物品和一个容量为V的背包，每种物品都有无限件可用。
动态规划 练习题
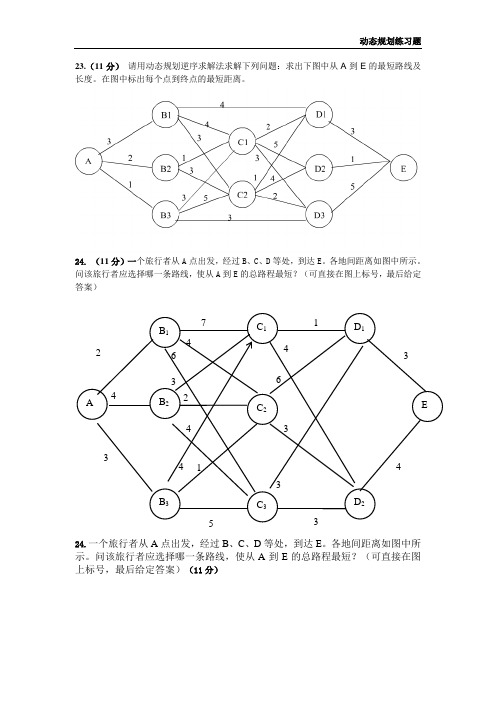
23.（11分）请用动态规划逆序求解法求解下列问题：求出下图中从A到E的最短路线及长度。
在图中标出每个点到终点的最短距离。
24. （11分）一个旅行者从A点出发，经过B、C、D等处，到达E。
各地间距离如图中所示。
问该旅行者应选择哪一条路线，使从A到E的总路程最短？（可直接在图上标号，最后给定答案）
24.一个旅行者从A点出发，经过B、C、D等处，到达E。
各地间距离如图中所示。
问该旅行者应选择哪一条路线，使从A到E的总路程最短？（可直接在图上标号，最后给定答案）（11分）
解：此为动态规划之“最短路问题”，可用逆向追踪“图上标号法”解决如下：
最佳策略为：A →B 2→C 1→D 1→E 或A →B 3→C 1→D 1→E 此时从A 到E 的总路程的最短距离都是11
23. 请用动态规划逆序求解法求解下列问题：
各点标号依次为：A:8, B1：7，B2:6, B3:8, C1：5， C2：4，D1：3，D2：1，D3：5.
25. 某厂生产C B A ,,三种产品，其所需劳动力、材料等有关数据见下表。
要求：建立模型，并用单纯形法计算，确定获利最大的产品生产计划。
解：（1）设C B A ,,
各生产321,,x x x 件。
有
32143min x x x z ++=
st.⎪⎩⎪
⎨⎧=≥≤++≤++)3,2,1(,03054345
536321321j x x x x x x x j
（4分）
获利最大的生产计划是C B A ,,各生产5件、0件、3件，最大利润为273453=⨯+⨯=z 元。
（15分）。
运筹学 动态规划-作业及答案
1
第五章 动态规划作业题及答案
1．用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2．用动态规划法求解资源分配问题
有资金4万元，投资A 、B 、C 三个项目，每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益（万吨）和投入资金（万元）的关系见下表：
用动态规划法求解对三个项目的最优投资分配，使总投资效益最大。
3．用动态规划法求解生产库存问题
一个工厂生产某种产品，1～7月份生产成本和产品需求量的变化情况如下表：
为了调节生产生产和需求，工厂设有一个产品仓库，库容量H=9。
已知期初库存量为2，要求期末（七月低）库存量为0。
每个月生产的产品在月末入库，月初根据当月需求发货。
求七个月的生产量，能满足各月的需求，并使生产成本最低。
4．用动态规划法求解背包问题
第i 种每件价值c 1=65，c 2=85，c 3=40元; 第i 种物品每件重量为:w 1=2，w 2=3，w 3=1公斤;现有一只可装载重量为5公斤的背包，求各种物品应各取多少件放入背包，使背包中物品的价值最高。
动态规划题目
动态规划总结1.POJ 1160Post OfficeTime Limit: 1000MS Memory Limit: 10000KTotal Submissions: 17936 Accepted: 9655DescriptionThere is a straight highway with villages alongside the highway. The highway is represented as an integer axis, and the position of each village is identified with a single integer coordinate. There are no two villages in the same position. The distance between two positions is the absolute value of the difference of their integer coordinates.Post offices will be built in some, but not necessarily all of the villages. A village and the post office in it have the same position. For building the post offices, their positions should be chosen so that the total sum of all distances between each village and its nearest post office is minimum.You are to write a program which, given the positions of the villages and the number of post offices, computes the leastpossible sum of all distances between each village and its nearest post office.IntputYour program is to read from standard input. The first line contains two integers: the first is the number of villages V, 1 <= V <= 300, and the second is the number of post offices P, 1 <= P <= 30, P <= V. The second line contains V integers in increasing order. These V integers are the positions of the villages. For each position X it holds that 1 <= X <= 10000. outputThe first line contains one integer S, which is the sum of all distances between each village and its nearest post office. Sample input10 51 2 3 6 7 9 11 22 44 50Sample output9题目大意：用数轴描述一条高速公路，有V个村庄，每一个村庄坐落在数轴的某个点上，需要选择P个村庄在其中建立邮局，要求每个村庄到最近邮局的距离和最小。
动态规划模拟试卷及答案
动态规划模拟试卷及答案模拟试卷——第三章动态规划一、填空题（每小题4分，共20分）1、动态规划算法的基本要素是（）和（）。
2、（）是动态规划法的变形。
3、（）是最大子段和问题想二维的推广。
4、矩阵连乘问题的算法可由（）设计实现。
5、动态规划算法中，通常不同子问题的个数随问题大小呈（）增长。
二、简答题（每小题6分，共30分）1、写出设计动态规划算法的主要步骤。
2、简述什么是备忘录方法。
3、简述备忘录法与动态规划法的异同。
4、简述动态规划算法的基本思想。
5. 写出最长公共子序列问题具有的性质。
三、综合题（每小题25分，共50分）1、用动态规划算法实现最长公共子序列问题。
2、用动态规划算法实现下列问题：设A和B是两个字符串。
我们要用最少的字符操作将字符串A转换为字符串B，这里所说的字符操作包括：（1）删除一个字符；（2）插入一个字符；（3）将一个字符改为另一个字符。
将字符串A变换为字符串B所用的最少字符操作数称为字符串A 到B的编辑距离，记为d（A,B）。
试设计一个有效算法，对任给的两个字符串A和B，计算出它们的编辑距离d（A,B）。
答案一、填空题1、最优子结构、子问题重叠2、备忘录方法3、最大子矩阵的问题4、动态规划法5、多项式二、简答题1、（1）找出最优解的性质，并刻画其结构特征；（2）递归地定义最优解；（3）以自底向上的方法计算出最优值；（4）根据计算最优值时得到的信息，构造最优解。
2、备忘录方法是动态规划算法的变形。
备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免了相同子问题的重复求解。
3、与动态规划算法一样，备忘录方法用表格保存已解决的子问题的答案，在下次需要解此子问题时，只要简单地查看该子问题的解答，而不必重新计算。
与动态规划算法不同的是，备忘录方法的递归方式是自顶向下的，而动态规划算法则是自底向上递归的。
4、动态规划算法的基本思想是将待求解问题分解成若干子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 1 4 s1 ，故 f1 ( s1 ) s1 4 64 1 1 由于 s1=c，∴ x1* c ， f1 (c ) c 4 4 64 2 1 1 由 s2 =s1－x1＊，∴ x2* s2 c , f 2 ( s2 ) c 3 3 2 16 1 1 由 s3 =s2－x2＊，∴ x3* s3 c ， f3 ( s3 ) c 4 4 1 1 1 因此最优解为： x1* c ， x2* c ， x3* c ， 4 2 4 1 4 最大值为： max z f1 (c) c 64
u3* (C3 ) D1
2)当 k=2 时：s2 的取值为 B1、B2、B3，从 B1 出发到 E 有三条路，分别是经 过 C1、C2、C3 到 E，则有：
d ( B1 , C1 ) f 3 (C1 ) 6 7 f 2 ( B1 ) d ( B1 , C2 ) f3 (C2 ) 4 5 9, d ( B , C ) f (C ) 5 5 1 3 3 3
回
于是得到从 A 到 E 的最短距离 17，为了找出最短路线，按计算的顺序逆推 去 ， 可 得 到 最 优 策 略 为 ：
p1,4 ( A) {u1* ( A) B1 , u2* ( B1 ) C2 , u3* (C2 ) D2 , u4* ( D2 ) E} ，最短路线是 A→B1→
例 1：最短路线问题 某工厂需要把一批货物从城市 A 运到城市 E，中间可经过 B1 、B2、B3、C1、 C2 、C3、D1 、D2 等城市，各城市之间的交通线和距离如下图所示，问应该选择一 条什么路线，使得从 A 到 E 的距离最短？ 6 B1 C1 3 8 4 5 D1 5 6 4A B2 9 8 C2 7 2 6 D3 3 6 7 1 8 3 C B3 3 7 下面利用动态规划的逆推归纳法，将例 1 从最后一个城市 E 逐步推算到第 一个城市 A，在此 f k ( sk ) 表示第 k 阶段从城市 sk 到城市 E 最短路。 1)当 k=4 时：要求 f 4 ( s4 ) ，由于第 4 阶段只有两个城市 D1、D2（即 s4 的取 值为 D1、D2） ，从 D1 到 E 只有一条路，故 f 4 ( D1 ) d ( D1 , E ) 4, u4* ( D1 ) E ，同 理 f 4 ( D2 ) d ( D2 , E ) 3, u4* ( D2 ) E 。 2)当 k=3 时：s3 的取值为 C1、C2、C3，从 C1 出发到 E 有两条路，一条是经 过 D1 到 E，另一条是经过 D2 到 E ，显然：
u2* ( B1 ) C2
同理
d ( B2 , C1 ) f3 (C1 ) 8 7 f 2 ( B2 ) d ( B2 , C2 ) f3 (C2 ) 7 5 11, d ( B , C ) f (C ) 6 5 2 3 3 3 d ( B3 , C1 ) f3 (C1 ) 7 7 f 2 ( B3 ) d ( B3 , C2 ) f 3 (C2 ) 8 5 12, d ( B3, C ) f (C ) 7 5 3 3 3
d (C2 , D1 ) f 4 ( D1 ) 6 4 f3 (C2 ) 5, d (C2 , D2 ) f 4 ( D2 ) 2 3 d (C3 , D1 ) f 4 ( D1 ) 1 4 f3 (C3 ) 5, d (C3 , D2 ) f 4 ( D2 ) 3 3 u3* (C2 ) D2
max z 4 x12 x2 2 2 x3 2 12
例 4：用顺推解法求解下面问题: 3 x1 2 x2 x3 9 x1 , x2 , x3 0 解: 按问题的变量个数划分阶段,把它看作一个三阶段决策问题。 设状态变量为 s0，s1，s2，s3。并记 s3≤9； 令变量 x1，x2，x3 为决策变量； 最优值函数 f k(sk)表示为第 k 阶段末的结束状态为 sk， 从第 1 阶段到第 k 阶 段所得到的最大值。 设: 3x1=s1, s1+2x2=s2, s2+ x3=s3≤9 则有：x1=s1／3,0≤x2≤s2／2 , 0≤x3≤s3≤9 即状态转移方程为： s1=s2－2x2, s2=s3－x3 由顺推解法， f1 ( s1 ) max(4 x12 )
x1 s2
f 2 ( s3 ) max[ x1 x2 2 ] max [ x2 2 f1 (s2 )]
x1 , x2 0 x2 s3
max [ x2 2 ( s3 x2 )]
0 x2 s3
4 3 s3 27
最优解 x2*
2 s3 。 3
f3 ( s4 ) max[ x1 x2 2 x3 ] max [ x3 f 2 (s3 )]
由
dh2 14 16 8 x2 s2 0 ,得 x2 s2 (它不在决策集内) 7 dx2 9 9
s 4 2 1 s2 , h2 ( 2 ) s2 2 9 2 4 4 2 ∴最大值点为 x2=0。故得到 f 2 ( s2 ) s2 及最优解 x2* 0 。 9
则最大值在端点上，∵ h2 (0)
由
dh3 44 8 2 x3 s3 0 ,得 x3 s3 11 dx3 9 9
dh3 2 44 0 ，故该点为极小值点。 dx32 9
4 2 s3 12, h2 ( s3 ) 2s32 12 9
又
而 h3 (0)
∴最大值点为 x3=s3。故得到 f3 ( s3 ) 2 s3 2 12 及最优解 x3* s3 。 由于 s3 不知道，故须在对 s3 求一次极值，即
C2→D2→E。
max z x1 x2 2 x3
例 3：逆推解法求解下面问题: x1 x2 x3 c
x1 , x2 , x3 0
解: 按问题的变量个数划分阶段,把它看作一个三阶段决策问题。设状态变 量为 s1，s2，s3，s4。并记 s1＝c；令变量 x1，x2，x3 为决策变量；各阶段指标按 乘积方式结合。 即令: v1 ( s1 , x1 ) x1 , v2 ( s2 , x2 ) x2 2 , v3 ( s3 , x3 ) x3 令最优值函数 f k(sk)表示为第 k 阶段的初始状态为 sk 时， 从第 k 阶段到第 3 阶段所得到的最大值。 设: s3= x3, s3+ x2=s2, s2+ x1=s1=c 则有：x3=s3, 0≤x2≤s2, 0≤x1≤s1=c 即状态转移方程为： s3=s2－x2, s2 =s1－x1 由逆推解法，
x1 s1 3
4 2 s1 , 即最优解 x1＊=s1／3, 9
f 2 ( s2 ) max[4 x12 x2 2 ] max [ x2 2 f1 ( s1 )]
x1 , x2 0 x2 s2 2
4 max [ x2 2 ( s2 2 x2 ) 2 ] max h2 ( s2 , x2 ) s s 9 0 x2 2 0 x2 2 2 2
E
d (C1 , D1 ) f 4 ( D1 ) 3 4 f 3 (C1 ) min min 7, d ( C , D ) f ( D ) 5 3 1 2 4 2
u3* (C1 ) D1
即从 C1 出发到 E 的最短路为 7，相应决策为 u3* (C1 ) D1 ，最短路线是 C1 →D1→E。 同理
f3 ( s3 ) max[4 x12 x2 2 2 x32 12] max [2 x3 2 12 f 2 ( s2 )]
x1 , x2 , x3 0 x3 s3
4 max [2 x32 12 ( s3 x3 )2 ] max h3 ( s3 , x3 ) 0 x3 s3 0 x3 s3 9
x1 , x2 , x3 0 x3 s4
max [ x3
0 x3 s4
4 1 4 (s4 x3 )3 ] s4 27 64
最优解 x3*
1 s4 4
1 1 由于 s4=c，∴ x3* c ， f3 (c) c 4 4 64 2 1 1 由 s3=s4－x3＊，∴ x2* s3 c , f 2 ( s2 ) c 3 2 16 1 1 由 s2=s3－x2＊，∴ x1* s2 c ， f3 ( s3 ) c 4 4 1 1 1 因此最优解为： x1* c ， x2* c ， x2* c ， 4 2 4 1 最大值为： max z c 4 64
0 x2 s2 0 x2 s2
由
dh2 2 2 x2 s2 3 x2 2 0 ,得 x2 s2 和 x2 0 （舍去） 3 dx2
d 2 h2 d 2 h2 2 ，而 2 s 6 x | 2 s2 0 ，故 x2 s2 为极大值点。 2 2 2 2 x 2s 3 dx2 dx2 2 3 2
u2* ( B2 ) C3
u2* ( B3 ) C3
2)当 k=1 时：s1 的只有一个取值为 A. 从 A 出发到 E 有三条路，分别是经 过 B1、B2、B3 到 E，则有：
d ( A, B1 ) f 2 ( B1 ) 8 9 f1 ( A) min d ( A, B2 ) f 2 ( B2 ) min 9 11 17, d ( A, B ) f ( B ) 6 12 3 2 3 u1* ( A) B1
4 2 2 s2 即最优解 x2* s2 。 27 3
0 x1 s1
又
所以 f 2 ( s2 )