专题4立体几何(含答案)
《立体几何》微专题4 空间中常见的组合体

四、典型例题 例 1 如图所示,平行四边形 ABCD 中,AB=2BD=2,且 AB⊥BD.将其沿 BD 折成直二面 角,所得的四面体 A-BCD 的外接球表面积为( )
A
B
D
B
D
C
A1
B1
D1
B1
D1
C1
类型 1
A
B
D
D
C
B
A1
B1
D1
M
B1
D1
C1
特征: 三棱锥中交于同一顶点的三条棱两两垂直. 类型 2
A
B
D
D
C
B
A1
B1
D1
B1
D1
C1
特征: 三棱锥的四个面都为直角三角形. 类型 3
2
A
B
D
B
D
C
A1
B1
D1
M
B1
D1
C1
特征: 三棱锥中的对棱相等. 类型 4
用以及利用重要截面“降维”处理,以供参考.
二、知识梳理
1.判断下列说法是否正确,正确的打“√”,错的打“×”.
(1)在空间中,到定点的距离等于定长的所有点的集合叫球面.( √ )
(2)用一个平面去截球面,所得图形均为圆面.( × )
(3)球的小圆的圆心与球心的连线垂直于这个小圆所在平面.( √ )
(4)经过球面上不同的两点只能作一个大圆.( × )
④若直棱柱的所有顶点都在同一个球面上,则该球的球心 O 是直棱柱的两个底面外接圆圆
心的连线的中点.半径的求解往往通过抓含球心的截面,将空间问题平面化,从而得解.
【多面体的内切球问题】
方法提炼:
1.利用等体积法求内切球半径;2.抓含球心与切点的截面.
第8章立体几何专题4 垂直的证明-人教A版(2019)高中数学必修(第二册)常考题型专题练习

垂直的证明【方法总结】1、证明线面垂直的方法:①利用线面垂直定义:如果一条直线垂直于平面内任一条直线,则这条直线垂直于该平面;②用线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,则这条直线与平面垂直;③用线面垂直性质:两条平行线中的一条垂直于一个平面,则另一条也必垂直于这个平面.2、证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.3、证明面面垂直一般要先找到两个面的交线,然后再在两个面内找能与交线垂直的直线,最后通过证明线面垂直证明面面垂直。
【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中,PA ⊥底面ABCD ,//AB CD ,AB BC ⊥,1AB BC ==,2DC =,点E 在PB 上求证:CA ⊥平面PAD ;【答案】(1)证明见解析;(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ,又PA ⊥底面ABCD ,AC ⊂面ABCD ,所以AC ⊥PA ,因为PA 、AD ⊂面PAD ,且PA ∩AD =A ,所以AC ⊥平面PAD .例2、如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;解析:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .例3、如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点求证:AC ⊥平面BEF ;【解析】(1)在三棱柱111ABC A B C -中,∵1CC ⊥平面ABC ,∴四边形11A ACC 为矩形.又E ,F 分别为AC ,11A C 的中点,∴AC ⊥EF .∵AB BC =.∴AC ⊥BE ,∴AC ⊥平面BEF .例4、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,CD ⊥AD ,BC ∥AD ,12BC CD AD ==.(Ⅰ)求证:BD ⊥平面PAB ;【解析】因为PA ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥PA .所以222AD AB BD =+,所以BD AB ⊥.因为PA AB A = ,所以BD ⊥平面PAB .【巩固练习】1、如图,在三棱柱ABC-A 1B 1C 1中,AB=AC,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.证明:A 1D⊥平面A 1BC;【答案】见解析【解析】证明:设E 为BC 的中点,连接A 1E,AE.由题意得A 1E⊥平面ABC,所以A 1E⊥AE.因为AB=AC,所以AE⊥BC.故AE⊥平面A 1BC.连接DE,由D,E 分别为B 1C 1,BC 的中点,得DE∥B 1B 且DE=B 1B,从而DE∥A 1A 且DE =A 1A,所以AA 1DE 为平行四边形.于是A 1D∥AE.因为AE⊥平面A 1BC,所以A 1D⊥平面A 1BC.2.(2019·上海格致中学高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .(1)证明:PA ∥平面EDB ;(2)证明:PB ⊥平面EFD .【答案】(1)详见解析;(2)详见解析.【解析】(1)设AC 与BD 相交于O ,连接OE ,由于O 是AC 中点,E 是PC 中点,所所以PA ∥平面EDB .(2)由于PD ⊥底面ABCD ,所以PD BC ⊥,由于,BC CD PD CD D ⊥⋂=,所以BC ⊥平面PCD ,所以BC DE ⊥.由于DP DC =且E 是PC 中点,所以DE PC ⊥,而PC BC C ⋂=,所以DE ⊥平面PBC ,所以DE PB ⊥.依题意EF PB ⊥,DE EF E = ,所以PB ⊥平面EFD .3.(2019·江苏高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AC ,BD 相交于点O ,OP OC =,E 为PC 的中点,PA PD ⊥.(1)求证://PA 平面BDE ;(2)求证:PA ⊥平面PCD【答案】(1)详见解析(2)详见解析【解析】(1)连结OE .因为四边形ABCD 是平行四边形,AC ,BD 相交于点O ,所以O 为AC 的中点.因为E 为PC 的中点,所以//OE PA .因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以//PA 平面BDE .(2)因为OP OC =,E 为PC 的中点,所以OE PC ⊥.由(1)知,//OE PA ,所以PA PC ⊥.因为PA PD ⊥,PC ,PD ⊂平面PCD ,PC PD P ⋂=,所以PA ⊥平面PCD .考向二面面垂直例1、如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,且AB =,1BC =,E ,F 分别是AB ,PC 的中点,PA DE ⊥.(1)求证://EF 平面PAD ;(2)求证:平面PAC ⊥平面PDE .【答案】(1)详见解析(2)详见解析【解析】证明:(1)取PD 中点G ,连AG ,FG ,F ,G 分别是PC ,PD 的中点又E 为AB 中点//AE FG ∴,AE FG=四边形AEFG 为平行四边形//EF AG ∴,又EF ⊄平面PAD ,AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥,PA AC A= DE ⊥平面PAC ,又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直,M 是 CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为 CD上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .例3、如图,在梯形ABCD 中,AB ∥CD ,AD=DC=CB=a ,∠ABC=3π,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形,AE=AD ,点M 在线段EF 上。
2022版优化方案高考数学(浙江版·文科)二轮专题复习练习:专题4 立体几何第1讲 Word版含答案

[A卷]1.(2021·宁波市高三模拟) 用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是()解析:选B.由题意知,用平行于水平面的平面去截球所得的底面圆是看不见的,所以在俯视图中该部分应当是虚线圆,结合选项可知选B.2.下列命题中,错误的是()A.圆柱的轴截面是过母线的截面中面积最大的一个B.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台C.圆台的全部平行于底面的截面都是圆D.圆锥全部的轴截面都是全等的等腰三角形解析:选B.依据棱台的定义,用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台.3.(2021·台州市高三调考)一个空间几何体的三视图如图所示,其体积为()A.16B.32C.48 D.96解析:选A.由题意作出直观图P-ABCD如图所示,则该几何体是一个四棱锥,底面是一个直角梯形,其面积为12×(2+4)×4=12,高为4,因此其体积V=13×12×4=16.4.(2021·高考全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1 B.2C.4 D.8解析:选B.如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=12×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,所以(5π+4)r2=16+20π,所以r2=4,r=2,故选B.5.如图是一个体积为10的空间几何体的三视图,则图中x的值为()A.2 B.3C.4 D.5解析:选A.依据给定的三视图可知,该几何体对应的直观图是一个长方体和四棱锥的组合体,所以几何体的体积V=3×2×1+13×3×2×x=10,解得x=2.故选A.6. 如图,水平放置的三棱柱的侧棱长为1,且侧棱AA1⊥平面A1B1C1,正视图是边长为1的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为()A.2 3 B. 3C.32D.1解析:选C.由直观图、正视图以及俯视图可知,侧视图是宽为32,长为1的长方形,所以面积S=32×1=32.故选C.7.一平面截一球得到直径为2 5 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是() A.12πcm3B.36πcm3C.646πcm3D.108πcm3解析:选B.由于球心和截面圆心的连线垂直于截面,由勾股定理得,球半径R=22+(5)2=3,故球的体积为43πR3=36π(cm3).8.(2021·石家庄市第一次模拟)一个几何体的三视图如图所示,则该几何体的体积是()A.64B.72C.80D.112解析:选B.由三视图可知该几何体是一个组合体,下面是一个棱长为4的正方体;上面是一个三棱锥,三棱锥的高为3.故所求体积为43+13×12×4×4×3=72.9.已知某组合体的正视图与侧视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是________(把正确的图的序号都填上).解析:几何体由四棱锥与四棱柱组成时,得①正确;几何体由四棱锥与圆柱组成时,得②正确;几何体由圆锥与圆柱组成时,得③正确;几何体由圆锥与四棱柱组成时,得④正确.答案:①②③④10.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长是10 cm,则圆锥的母线长为________ cm.解析:作出圆锥的轴截面如图,设SA=y,O′A′=x,利用平行线截线段成比例,得SA′∶SA=O′A′∶OA,则(y-10)∶y=x∶4x,解得y=403.所以圆锥的母线长为403cm.答案:40311.(2022·高考课标全国卷Ⅱ改编)正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为 3,D为BC中点,则三棱锥AB1DC1的体积为________.解析:由题意可知AD⊥BC,由面面垂直的性质定理可得AD⊥平面DB1C1,又AD=2sin 60°=3,所以V AB1DC1=13AD·S△B1DC1=13×3×12×2×3=1,故选C.答案:112.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积为________,体积为________.解析:由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为22+12=5,所以S 侧=4×⎝⎛⎭⎫12×2×5=45,V=13×22×2=83.答案:458313.(2021·南昌市第一次模拟)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,点P 是平面A 1B 1C 1D 1内一点,则三棱锥P -BCD 的正视图与侧视图的面积之比为________.解析:依据题意,三棱锥P -BCD 的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高,故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1. 答案:1∶114.如图是某空间几何体的三视图,则该几何体的体积为________.解析:由三视图可知,该几何体是棱长为2,2,1的长方体挖去一个半径为1的半球,所以长方体的体积为2×2×1=4,半球的体积为12×43π×13=2π3,所以该几何体的体积是4-2π3.答案:4-2π315.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1EDF的体积为________.解析:由于B 1C ∥平面ADD 1A 1,所以F 到平面ADD 1A 1的距离d 为定值1,△D 1DE 的面积为12D 1D ·AD =12,所以V D 1EDF =V F D 1DE =13S △D 1DE ·d =13×12×1=16.答案:16[B 卷]1.一个锥体的正视图和侧视图如图所示,下面选项中,不行能是该锥体的俯视图的是( )解析:选C.依据三视图中“正俯长一样,侧俯宽一样,正侧高一样”的规律,C 选项的侧视图宽为32,不符合题意,故选C.2.(2021·邢台市摸底考试)已知一个几何体的三视图是三个全等的边长为1的正方形,如图所示,则该几何体的体积为( )A.16 B.13 C.23D .56解析:选D.依题意得,题中的几何体是从棱长为1的正方体ABCD -A ′B ′C ′D ′中截去三棱锥A ′ABD 后剩余的部分,因此该几何体的体积等于13-13×⎝⎛⎭⎫12×12×1=56,故选D. 3.(2022·高考湖南卷)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A .1B .2C .3D .4解析:选B.由三视图可知该几何体是一个直三棱柱,如图所示.由题意知,当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆相同时,该球的半径最大,故其半径r =12×(6+8-10)=2.因此选B.4.(2021·高考山东卷)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B .4π3 C.5π3D .2π 解析:选C.过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V 圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C.5.(2021·郑州市第一次质量猜测)某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为( )A .32B .327C .64D .647解析:选C.依题意,题中的几何体是三棱锥P -ABC (如图所示), 其中底面ABC 是直角三角形,AB ⊥BC ,P A ⊥平面ABC , BC =27,P A 2+y 2=102,(27)2+P A 2=x 2,因此xy =x 102-[x 2-(27)2]=x128-x 2≤x 2+(128-x 2)2=64,当且仅当x 2=128-x 2,即x =8时取等号,因此xy 的最大值是64,故选C.6.(2021·山西省第三次四校联考)在半径为10的球面上有A ,B ,C 三点,假如AB =83,∠ACB =60°,则球心O 到平面ABC 的距离为( )A .2B .4C .6D .8解析:选C.设A ,B ,C 三点所在圆的半径为r ,圆心为P .由于∠ACB =60°,所以∠APB =120°.在等腰三角形ABP 中,AP =43sin 60°=8,所以r =8,所以球心O 到平面ABC 的距离为102-82=6,故选C.7.如图是一个几何体的三视图,则该几何体的表面积是( )A .5+ 3B .5+2 3C .4+2 2D .4+2 3解析:选A.该几何体的直观图如图.表面积S =1×1+12×1×1×2+2×12×(1+2)×1+12×6×2=5+3,所以选A.8.在三棱锥P -ABC 中,P A ⊥平面ABC ,AC ⊥BC ,D 为侧棱PC 上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )A .AD ⊥平面PBC ,且三棱锥D -ABC 的体积为83B .BD ⊥平面P AC ,且三棱锥D -ABC 的体积为83C .AD ⊥平面PBC ,且三棱锥D -ABC 的体积为163D .BD ⊥平面P AC ,且三棱锥D -ABC 的体积为163解析:选C.由正视图可知,P A =AC ,且点D 为线段PC 的中点,所以AD ⊥PC .由侧视图可知,BC =4.由于P A ⊥平面ABC ,所以P A ⊥BC .又由于BC ⊥AC ,且AC ∩P A =A ,所以BC ⊥平面P AC ,所以BC ⊥AD .又由于AD ⊥PC ,且PC ∩BC =C ,所以可得AD ⊥平面PBC ,V D ABC =13×12×P A ×S △ABC =163.9.某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为________.解析:侧视图由一个矩形和一个等腰三角形构成,矩形的长为3,宽为2,面积为3×2=6.等腰三角形的底边为3,高为3,其面积为12×3×3=32,所以侧视图的面积为6+32=152.答案:15210.(2021·洛阳市高三班级统考)如图是某几何体的三视图,则该几何体的外接球的表面积为( )解析:由三视图知,该几何体可以由一个长方体截去一个角后得到,该长方体的长、宽、高分别为5、4、3,所以其外接球半径R 满足2R =42+32+52=52,所以该几何体的外接球的表面积为S =4πR 2=4π×⎝⎛⎭⎫5222=50π.答案:50π 11.(2021·绍兴市高三诊断性测试)若某几何体的三视图如图所示,则该几何体的体积为________,最长的侧棱长为________.解析:依据三视图及有关数据还原该几何体,得该几何体是底面为直角梯形的四棱锥P -ABCD ,如图,过点P 作PH ⊥AD 于点H ,连接CH .底面面积S 1=(1+2)×12=32,V =13×32×1=12,最长的侧棱长为PB = 3.答案:12312.设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________. 解析:设两个圆柱的底面半径和高分别为r 1,r 2和h 1,h 2,由S 1S 2=94,得πr 21πr 22=94,则r 1r 2=32.由圆柱的侧面积相等,得2πr 1h 1=2πr 2h 2,即r 1h 1=r 2h 2,则h 1h 2=23,所以V 1V 2=πr 21h 1πr 22h 2=32.答案:3213.(2021·洛阳市统考)已知点A ,B ,C ,D 均在球O 上,AB =BC =6,AC =23,若三棱锥D -ABC 体积的最大值为3,则球O 的表面积为________.解析:由题意可得,∠ABC =π2,△ABC 的外接圆半径r =3,当三棱锥的体积最大时,V D ABC =13S △ABC ·h (h为D 到底面ABC 的距离),即3=13×12×6×6h ⇒h =3,即R +R 2-r 2=3(R 为外接球半径),解得R =2,所以球O 的表面积为4π×22=16π.答案:16π 14.(2021·杭州市联谊学校高三其次次联考)一个等腰直角三角形的三个顶点分别在正三棱柱ABC -A 1B 1C 1的三条侧棱上,已知正三棱柱的底面边长为2,则该三角形的斜边长为________.解析:如图,在正三棱柱ABC -A 1B 1C 1中,△ABC 为正三角形,边长为2,△DEF 为等腰直角三角形,DF 为斜边,设DF 的长为x ,则DE =EF =22x ,作DG ⊥BB 1,GH ⊥CC 1,EI ⊥CC 1,垂足分别为G ,H ,I ,则EG =DE 2-DG 2=x 22-4,FI =EF 2-EI 2=x 22-4,FH =FI +HI =FI +EG=2x 22-4.连接DH ,在Rt △DHF 中,DF 2=DH 2+FH 2,即x 2=4+⎝⎛⎭⎫2x 22-42,解得x =23,即该三角形的斜边长为2 3.答案:2 3 15.(2021·浙江省名校新高考联盟第一次联考)如图,ABEDFC 为多面体,平面ABED 与平面ACFD 垂直,点O 在线段AD 上,OA =1,OD =2,△OAB ,△OAC ,△ODE ,△ODF 都是正三角形,则BC =________,四棱锥F-OBED的体积为________.解析:取AO的中点M,连接CM,BM,由△OAB,△OAC是正三角形,OA=1,可知CM⊥AO,BM⊥AO,且BM=CM=32,又平面ABED⊥平面ACFD,所以CM⊥平面ABED,所以CM⊥BM,故BC=62.过点F作FQ⊥OD于点Q,由于平面ABED⊥平面ACFD,所以FQ⊥平面ABED,FQ就是四棱锥F-OBED的高.易知FQ=3,又S△OBE=12×1×2×32=32,S△OED=12×2×2×32=3,所以S四边形OBED=32+3=332,故V四棱锥F-OBED=13×332×3=32.答案:6232。
高三数学一轮专题4 高考中的立体几何问题(含解析)北师

专题四 高考中的立体几何问题1.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面PAD ;(2)若PA =AB =1,AD =3,CD =2,∠CDA =45°,求四棱锥P -ABCD 的体积.[解析] (1)∵PA ⊥底面ABCD ,CE 平面ABCD∴CE ⊥PA ,又∵AB ⊥AD ,CE ∥AB .∴CE ⊥AD .又∵PA ∩AD =A ,∴CE ⊥平面PAD .(2)由(1)可知CE ⊥AD .在Rt △ECD 中,DE =CD·cos45°=1,CE =CD·sin45°=1.又∵AB =CE =1,AB ∥CE ,所以四边形ABCE 为矩形.∴S 四边形ABCD =S 矩形ABCE +S △CDE =AB·AE +12CE·DE=1×2+12×1×1=52.又PA ⊥底面ABCD ,PA =1所以V 四棱锥p -ABCD =13S 四边形ABCD×PA =13×52×1=56.2.(2015·潍坊模拟)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E 、F 分别是AP 、AD 的中点.求证:(1)直线EF ∥平面PCD ;(2)平面BEF ⊥平面PAD .[证明] (1)在△PAD 中,因为E 、F 分别为AP 、AD 的中点,所以EF ∥PD .又因为E F ⃘平面PCD ,PD 平面PCD .所以直线EF ∥平面PCD .(2)连结BD .因为AB =AD ,∠BAD =60°,所以△ABD 为正三角形.因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF平面ABCD,平面PAD∩平面ABCD=AD,所以BF⊥平面PAD.又因为BF平面BEF,所以平面BEF⊥平面PAD.3.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD、PC的中点,求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.[解析](1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,所以PA⊥底面ABCD.(2)因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE.所以四边形ABED为平行四边形.所以BE∥AD.又因为B E⃘平面PAD,AD平面PAD,所以BE ∥平面PAD .(3)因为AB ⊥AD ,而且四边形ABED 为平行四边形,所以BE ⊥CD ,AD ⊥CD .由(1)知PA ⊥底面ABCD .所以PA ⊥CD .所以CD ⊥平面PAD .所以CD ⊥PD .因为E 和F 分别是CD 和PC 的中点,所以PD ∥EF.所以CD ⊥EF ,又因为CD ⊥BE ,BE ∩EF =E ,所以CD ⊥平面BEF.所以平面BEF ⊥平面PCD .4.如图,在几何体P -ABCD 中,四边形ABCD 为矩形,PA ⊥平面ABCD ,AB =PA =2.(1)当AD =2时,求证:平面PBD ⊥平面PAC ;(2)若PC 与AD 所成的角为45°,求几何求P -ABCD 的体积.[解析] (1)证明:当AD =2时,四边形ABCD 是正方形,则BD ⊥AC .∵PA ⊥平面ABCD ,BD 平面ABCD ,∴PA ⊥BD .又∵PA ∩AC =A ,∴BD ⊥平面PAC .∵BD 平面PBD ,∴平面PBD ⊥平面PAC .(2)解:PC 与AD 成45°角,AD ∥BC ,则∠PCB =45°.∵BC ⊥AB ,BC ⊥PA ,AB ∩PA =A ,∴BC ⊥平面PAB ,PB 平面PAB .∴BC ⊥PB .∴∠CPB =90°-45°=45°.∴BC =PB =2 2.∴几何体P -ABCD 的体积为13×(2×22)×2=823.1.(2014·四川高考)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC ⊥BC ,证明:直线BC ⊥平面ACC1A1;(2)设D ,E 分别是线段BC ,CC1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A1MC ?请证明你的结论.[解析] (1)因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB ,AA1⊥AC .因为AB ,AC 为平面ABC 内两条相交直线,所以AA1⊥平面ABC .因为直线BC 平面ABC ,所以AA1⊥BC .又由已知,AC ⊥BC ,AA1,AC 为平面ACC1A1内两条相交直线,所以BC ⊥平面ACC1A1.(2)取线段AB 的中点M ,连接A1M ,MC ,A1C ,AC1,设O 为A1C ,AC1的交点. 由已知,O 为AC1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC1的中位线,所以,MD 綊12AC ,OE 綊12AC ,因此MD綊OE.连接OM,从而四边形MDEO为平行四边形,则DE∥MO.因为直线D E⃘平面A1MC,MO平面A1MC.所以直线DE∥平面A1MC.即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.2.如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.[解析](1)∵DD1⊥平面ABCD,BD平面ABCD∴DD1⊥BD,又∵AB=2AD且∠BAD=60°∴由余弦定理得BD2=AB2+AD2-2AB·ADcos∠BAD即BD=3AD,∴AD2+BD2=AB2,∴BD⊥AD又∵AD∩DD1=D∴BD⊥平面ADD1A1,又∵AA1平面ADD1A1,∴BD⊥AA1(2)连接AC,交BD于M,连接A1M,A1C1,∵底面ABCD 是平行四边形,∴AM =CM =12AC又∵AB =2AD =2A1B1∴A1G 綊CM ,即四边形A1MCC1是平行四边形;∴CC1∥AM1,又∵CC 1⃘平面A1BD ,A1M 平面A1BD∴CC1∥平面A1BD .3.(文)(2015·临沂模拟)如图,在边长为3的正三角形ABC 中,G ,F 为边AC 的三等分点,E ,P 分别是AB ,BC 边上的点,满足AE =CP =1,今将△BEP ,△CFP 分别沿EP ,FP 向上折起,使边BP 与边CP 所在的直线重合,B ,C 折后的对应点分别记为B1,C1.(1)求证:C1F ∥平面B1GE ;(2)求证:PF ⊥平面B1EF.[解析] (1)取EP 的中点D ,连接FD ,C1D .因为BC =3,CP =1,所以折起后C1为B1P 的中点.所以在△B1EP 中,DC1∥EB1.又因为AB =BC =AC =3,AE =CP =1,所以EP AC =EB AB ,所以EP =2且EP ∥GF.因为G ,F 为AC 的三等分点,所以GF =1.又因为ED =12EP =1,所以GF =ED ,所以四边形GEDF 为平行四边形.所以FD ∥GE.又因为DC1∩FD =D ,GE ∩B1E =E ,所以平面DFC1∥平面B1GE.又因为C1F 平面DFC1, 所以C1F ∥平面B1GE.(2)连接EF ,B1F ,由已知得∠EPF =60°,且FP =1,EP =2,由余弦定理,得EF2=12+22-2×1×2×cos60°=3,所以FP2+EF2=EP2,可得PF ⊥EF.因为B1C1=PC1=1,C1F =1,得FC1=B1C1=PC1,所以△PB1F 的中线C1F =12PB1,可得△PB1F 是直角三角形,即B1F ⊥PF.因为EF ∩B1F =F ,EF ,B1F 平面B1EF ,所以PF ⊥平面B1EF.(理)(2014·浙江高考)如图,在四棱锥A -BCDE 中,平面ABC ⊥平面BCDE ,∠CDE =∠BED =90°,AB =CD =2,DE =BE =1,AC = 2.(1)证明:DE ⊥平面ACD ;(2)求二面角B -AD -E 的大小.[解析] (1)在平面四边形BCDE 中,BC =2,在三角形ABC 中,AB=2,BC =2,AC = 2.根据勾股定理逆定理.∴AC ⊥BC .∵平面ABC ⊥平面BCOE ,而平面ABC ∩平面BCDE =BCAC ⊥BC ,∴AC ⊥平面BCDE ,∴AC ⊥DE ,又∵AC ⊥DE ,DE ⊥DC ,∴DE ⊥平面ACD .(2)由(1)知分别以CD →、CA →为x 轴、z 轴正方向.以过C 平行DE →为y 轴正向建立坐标系.则B(1,1,0),A(0,0,2),D(2,0,0),E(2,1,0)∴AB →=(1,1,-2),AD →=(2,0,-2),DE →=(0,1,0)设平面ABD 法向量n1=(x1,y1,z1),由n1·DE →=n1·AD →=0,解得n1=(1,1,2)设平面ADE 法向量n2=(x2,y2,z2),则n2·AE →=n2·AD →=0,解得:n2=(1,0,2)设平面ABD 与平面ADE 夹角为θ,cosθ=|cos 〈n1,n2〉|=1+0+22×3=32π∴平面ABD与平面ADE的二面角平面角为6.。
微专题4:+立体几何中的探索问题+2022-2023学年高一下学期数学人教A版(2019)必修第二册

解:AD 上存在一点 P,AP=λPD,使得 CP
∥平面 ABEF,此时λ=3. 2
理由如下: 当λ=32时,AP=32PD,可知AADP=35,如图,过点 P 作 MP∥FD 交 AF 于点 M,连接 EM,PC,则有MFDP=AADP=35, 又 BE=1,可得 FD=5,故 MP=3, 又 EC=3,MP∥FD∥EC,故有 MP 綊 EC, 故四边形 MPCE 为平行四边形,所以 CP∥ME,
变式:如图,直三棱柱 ABC A1B1C1中,D,E分别是棱BC , AB的中点,点F在棱 CC1 上,已知AB=AC,AA1 3 , BC=CF=2.
(1)求证: C1E//平面ADF; (2)在棱 BB1 上是否存在点M,使平面 CAM 平面ADF ,若存在,试求出BM的值; 若不存在,请说明理由.
又BM=1,BC=2,CD=1,FC=2, Rt△CBM≌Rt△FCD
故 CM DF
DF . AD=D DF,AD
易证CM ,又
,
平面ADF,
故CM 平面ADF .
CAM
又 平面 CAM ,故平面
平面ADF.
翻折中的位置关系探索问题
例 3:如图,四边形 ABCD 中,AB⊥AD,AD∥BC,AD=6, BC=4,E,F 分别在 BC,AD 上,EF∥AB.现将四边形 ABCD 沿 EF 折起,使平面 ABEF⊥平面 EFDC.
证明如下:因为AB=AC, AD 平面ABC,故 AD BC.
在直三棱柱 ABC
中, A1B1C1
BB1
平面
ABC
《创新设计》2022高考数学(浙江专用理科)二轮专题精练:专题四 立体几何4-2 Word版含解析

第2讲空间中的平行与垂直(建议用时:60分钟)一、选择题1.在下列命题中,不是公理的是().A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.假如一条直线上的两点在一个平面内,那么这条直线上全部的点都在此平面内D.假如两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线解析选项A是面面平行的性质定理.答案 A2.(2022·辽宁卷)已知m,n表示两条不同直线,α表示平面.下列说法正确的是().A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α解析法一若m∥α,n∥α,则m,n可能平行、相交或异面,A错;若m⊥α,n⊂α,则m⊥n,由于直线与平面垂直时,它垂直于平面内任始终线,B正确;若m⊥α,m⊥n,则n∥α或n⊂α,C错;若m∥α,m⊥n,则n与α可能相交,可能平行,也可能n⊂α,D错;法二如图,在正方体ABCD-A′B′C′D′中,用平面ABCD表示α.A项中,若m为A′B′,n为B′C′,满足m∥α,n∥α,但m与n是相交直线,故A错.B项中,m⊥α,n⊂α,∴m⊥n,这是线面垂直的性质,故B正确.C项中,若m为AA′,n为AB,满足m⊥α,m⊥n,但n⊂α,故C错.D项中,若m为A′B′,n为B′C′,满足m∥α,m⊥n,但n∥α,故D错.答案 B3.(2021·丽水模拟)已知两条直线a,b与两个平面α,β,b⊥α,则下列命题中正确的是().①若a∥α,则a⊥b;②若a⊥b,则a∥α;③若b⊥β,则α∥β;④若α⊥β,则b∥β.A.①③B.②④C.①④D.②③解析过直线a作平面γ使α∩γ=c,则a∥c,再依据b⊥α可得b⊥c,从而b⊥a,命题①是真命题;下面考虑命题③,由b⊥α,b⊥β,可得α∥β,命题③为真命题.故正确选项为A.答案 A4.已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中确定能推出m⊥β的是().A.α⊥β,且m⊂αB.m∥n,且n⊥βC.α⊥β,且m∥αD.m⊥n,且n∥β解析依据定理、性质、结论逐个推断.由于α⊥β,m⊂α⇒可能平行、相交、m在β面内,故A错误;由线面垂直的性质定理可知B正确;若α⊥β,m∥α,则m,β的位置关系也不确定,故C错误;若m⊥n,n∥β,则m,β的位置关系也不确定,故D错误.答案 B5.已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有().A.1 B.2 C.3 D.4解析①中m,n可能异面或相交,故不正确;②由于m∥α,n⊥β且α⊥β成立时,m,n 两直线的关系可能是相交、平行、异面,故不正确;③由于m⊥α,α∥β可得出m⊥β,再由n∥β可得出m⊥n,故正确;④分别垂直于两个垂直平面的两条直线确定垂直,正确.故选B.答案 B6.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则().A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l解析假设α∥β,由m⊥平面α,n⊥平面β,则m∥n,这与已知m,n为异面直线冲突,那么α与β相交,设交线为l1,则l1⊥m,l1⊥n,在直线m上任取一点作n1平行于n,那么l1和l都垂直于直线m与n1所确定的平面,所以l1∥l.答案 D7.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H 必在().A.直线AB上B.直线BC上C.直线AC上D.△ABC的内部解析∵AC⊥AB,AC⊥BC1,AB∩BC1=B,∴AC⊥平面ABC1.又AC⊂平面ABC,∴平面ABC1⊥平面ABC,∴C1在面ABC上的射影H必在两平面交线AB上,故选A.答案 A二、填空题8.设α和β为两个不重合的平面,给出下列四个命题:①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;②若α外一条直线l与α内的一条直线平行,则l和α平行;③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.其中为真命题的是________(写出全部真命题的序号).解析由①知α内两条相交直线分别平行于平面β,则两条相交直线确定的平面α平行于平面β,故①为真命题;由线面平行的判定定理知,②为真命题;对于③,如图,α∩β=l,a ⊂α,a⊥l,但不愿定有α⊥β,故③为假命题;对于④,直线l与平面α垂直的充分必要条件是l与α内的两条相交直线垂直,故④为假命题.综上所述,真命题的序号为①②.答案①②9.(2021·金华调研)下列四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出直线AB∥平面MNP的图形的序号是________(写出全部符合要求的图形序号).。
高考总复习二轮数学精品课件 专题4 立体几何 素养提升微专题(五) 截面问题

①当 t=0 时,点 P 与点 B 重合,=(-1,1,0), =(1,1,0),1 =(0,0,1),所以 ·
=0, ·1 =0,所以 BD⊥AC,BD⊥AA1,又 AC∩AA1=A,所以 BD⊥平面
AA1C1C,此时平面 α 即为平面 AA1C1C,截面面积 S=AA1·
易错警示在判断截面形状时,如果对截面与几何体的各个面是否存在交线,
交线是什么形状,交线的位置等情况分析不清,那么容易导致判断错误,因
此要结合空间中线面平行、面面平行的判定定理和性质定理等进行分析
判断.
角度二 确定截面的个数
[例2]已知四棱锥P-ABCD的底面不是平行四边形,用平面α去截此四棱锥,
∴四边形 AEGD1 是梯形,且为平面 AED1 截正方体 ABCD-A1B1C1D1 的截面.
又 D1G=AE= 13,在等腰梯形 AEGD1 中,过 G 作 GH⊥AD1,
∴GH= 1 2 -1 2 = 11,
∴截面面积
1
1
S=2 ·(EG+AD1)·
GH=2 ·(
2+3 2)· 11=2 22.
2
32
5
,A1C1=2
2
2,
[例 3—3]已知正四面体 ABCD 的棱长为 2,平面 α 与棱 AB,CD 均平行,则平
面 α 截该正四面体所得截面面积的最大值为( A )
A.1
B. 2
C. 3
D.2
解析 如图,取CD的中点O,连接OA,OB.
因为△ACD为等边三角形,O为CD的中点,
所以OA⊥CD.
同理OB⊥CD.
又OA∩OB=O,
所以CD⊥平面AOB.
专题04 立体几何(解析版)

专题04 立体几何1.【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D【答案】D【解析】解法一:,PA PB PC ABC ==Q △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥I 平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分,2R ==即344π33R V R =∴=π==,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC Q △为边长为2的等边三角形,CF ∴=又90CEF ∠=︒,12CE AE PA x ∴===, AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯,作PD AC ⊥于D ,PA PC =Q ,D \为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,22121222x x x ∴+=∴==,,,PA PB PC ∴===又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==2R ∴=,34433V R ∴=π==,故选D.【名师点睛】本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决. 2.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线 D .α,β垂直于同一平面【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,a b a b αβ⊂⊂∥,则αβ∥”此类的错误.3.【2019年高考全国Ⅲ卷理数】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线 【答案】B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,Q 平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知12EO ON EN ===,,5,22MF BF BM ==∴=BM EN ∴≠,故选B .【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.4.【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm ),则该柱体的体积(单位:cm 3)是A .158B .162C .182D .324【答案】B【解析】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯= ⎪⎝⎭.故故B.【名师点睛】本题首先根据三视图,还原得到几何体——棱柱,根据题目给定的数据,计算几何体的体积,常规题目.难度不大,注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算.5.【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P –AC –B 的平面角为γ,则 A .β<γ,α<γB .β<α,β<γC .β<α,γ<αD .α<β,γ<β【答案】B【解析】如图,G 为AC 中点,连接VG ,V 在底面ABC 的投影为O ,则P 在底面的投影D 在线段AO 上,过D 作DE 垂直于AC 于E ,连接PE ,BD ,易得PE VG ∥,过P 作PF AC ∥交VG 于F ,连接BF ,过D 作DH AC ∥,交BG 于H ,则,,BPF PBD PED αβγ=∠=∠=∠,结合△PFB ,△BDH ,△PDB 均为直角三角形,可得cos cos PF EG DH BDPB PB PB PBαβ===<=,即αβ>; 在Rt △PED 中,tan tan PD PDED BDγβ=>=,即γβ>,综上所述,答案为B.【名师点睛】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.常规解法下易出现的错误有,不能正确作图得出各种角,未能想到利用“特殊位置法”,寻求简便解法.6.【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得,214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形, ∵四棱锥O −EFGH 的高为3cm , ∴3112312cm 3O EFGH V -=⨯⨯=. 又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=, 所以该模型体积为3214412132cm O EFGH V V V -=-=-=,其质量为0.9132118.8g ⨯=.【名师点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质量即可.7.【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【答案】40【解析】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体,则几何体的体积()3142424402V =-⨯+⨯⨯=. 【名师点睛】本题首先根据三视图,还原得到几何体,再根据题目给定的数据,计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.8.【2019年高考北京卷理数】已知l ,m 是平面α外的两条不同直线.给出下列三个论断:①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________. 【答案】如果l ⊥α,m ∥α,则l ⊥m .【解析】将所给论断,分别作为条件、结论,得到如下三个命题: (1)如果l ⊥α,m ∥α,则l ⊥m ,正确;(2)如果l ⊥α,l ⊥m ,则m ∥α,不正确,有可能m 在平面α内; (3)如果l ⊥m ,m ∥α,则l ⊥α,不正确,有可能l 与α斜交、l ∥α. 故答案为:如果l ⊥α,m ∥α,则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断,分别作为条件、结论加以分析即可.9.【2019底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________. 【答案】π42=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,圆柱的底面半径为12, 故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭. 【名师点睛】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.10.【2019年高考江苏卷】如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E −BCD的体积是 ▲ .【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120,所以1120AB BC CC ⋅⋅=, 因为E 为1CC 的中点,所以112CE CC =, 由长方体的性质知1CC ⊥底面ABCD ,所以CE 是三棱锥E BCD -的底面BCD 上的高, 所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. 【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.11.【2019年高考全国Ⅰ卷理数】如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A−MA 1−N 的正弦值.【答案】(1)见解析;(2)5. 【解析】(1)连结B 1C ,ME . 因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C . 又因为N 为A 1D 的中点,所以ND =12A 1D . 由题设知A 1B 1=P DC ,可得B 1C =P A 1D ,故ME =P ND , 因此四边形MNDE 为平行四边形,MN ∥ED . 又MN ⊄平面EDC 1,所以MN ∥平面C 1DE . (2)由已知可得DE ⊥DA .以D 为坐标原点,DA uuu r的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz ,则(2,0,0)A ,A 1(2,0,4),2)M ,(1,0,2)N ,1(0,0,4)A A =-u u u r,1(12)A M =--u u u u r,1(1,0,2)A N =--u u u u r,(0,MN =u u u u r.设(,,)x y z =m 为平面A 1MA 的法向量,则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r m m ,所以2040x z z ⎧-+-=⎪⎨-=⎪⎩,.可取=m .设(,,)p q r =n 为平面A 1MN 的法向量,则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u ur ,.n n所以020p r ⎧=⎪⎨--=⎪⎩,.可取(2,0,1)=-n .于是cos ,||5⋅〈〉===‖m n m n m n , 所以二面角1A MA N --【名师点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系,从而通过求解法向量夹角的余弦值来得到二面角的正弦值,属于常规题型.12.【2019年高考全国Ⅱ卷理数】如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B –EC –C 1的正弦值. 【答案】(1)证明见解析;(2【解析】(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A , 故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知Rt ABE △≌11Rt A B E △,所以45AEB ∠=︒, 故AE AB =,12AA AB =.以D 为坐标原点,DA u u u r的方向为x 轴正方向,||DA uuu r 为单位长,建立如图所示的空间直角坐标系D –xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E (1,0,1),(1,0,0)CB =u u u r ,(1,1,1)CE =-u u u r,1(0,0,2)CC =u u u u r.设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u ur n n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩u u u u ru u ur m m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =(1,1,0). 于是1cos ,||||2⋅<>==-n m n m n m .所以,二面角1B EC C --的正弦值为2. 【名师点睛】本题考查了利用线面垂直的性质定理证明线线垂直以及线面垂直的判定,考查了利用空间向量求二角角的余弦值,以及同角的三角函数关系,考查了数学运算能力.13.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2. (1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B −CG −A 的大小.【答案】(1)见解析;(2)30o .【解析】(1)由已知得AD P BE ,CG P BE ,所以AD P CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,所以EH ⊥平面ABC . 由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EH.以H 为坐标原点,HC u u u r的方向为x 轴的正方向,建立如图所示的空间直角坐标系H –xyz ,则A (–1,1,0),C (1,0,0),G (2,0),CG u u u r =(1,0),AC u u u r=(2,–1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n即0,20.x x y ⎧+=⎪⎨-=⎪⎩ 所以可取n =(3,6,又平面BCGE 的法向量可取为m =(0,1,0),所以cos ,||||2⋅〈〉==n m n m n m . 因此二面角B –CG –A 的大小为30°.【名师点睛】本题是很新颖的立体几何考题,首先是多面体折叠问题,考查考生在折叠过程中哪些量是不变的,再者折叠后的多面体不是直棱柱,最后通过建系的向量解法将求二面角转化为求二面角的平面角问题,突出考查考生的空间想象能力.14.【2019年高考北京卷理数】如图,在四棱锥P –ABCD 中,PA ⊥平面ABCD ,AD ⊥CD ,AD ∥BC ,PA =AD =CD =2,BC =3.E 为PD 的中点,点F 在PC 上,且13PF PC =. (1)求证:CD ⊥平面PAD ; (2)求二面角F –AE –P 的余弦值; (3)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.【答案】(1)见解析;(2)(3)见解析. 【解析】(1)因为PA ⊥平面ABCD ,所以PA ⊥CD . 又因为AD ⊥CD ,所以CD ⊥平面PAD . (2)过A 作AD 的垂线交BC 于点M .因为PA ⊥平面ABCD ,所以PA ⊥AM ,PA ⊥AD .如图建立空间直角坐标系A −xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0),P (0,0,2).因为E 为PD 的中点,所以E (0,1,1).所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-=u u u r u u u r u u u r.所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .设平面AEF 的法向量为n =(x ,y ,z ),则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩令z =1,则1,1y x =-=-.于是=(1,1,1)--n .又因为平面PAD 的法向量为p =(1,0,0),所以cos ,||⋅〈〉==‖n p n p n p . 由题知,二面角F −AE −P为锐角,所以其余弦值为3.(3)直线AG 在平面AEF 内.因为点G 在PB 上,且2,(2,1,2)3PG PB PB ==--u u ur ,所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .由(2)知,平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++=u u u r n .所以直线AG 在平面AEF 内.【名师点睛】(1)由题意利用线面垂直的判定定理即可证得题中的结论;(2)建立空间直角坐标系,结合两个半平面的法向量即可求得二面角F −AE −P 的余弦值;(3)首先求得点G 的坐标,然后结合平面AEF 的法向量和直线AG 的方向向量即可判断直线是否在平面内.15.【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,1,2AD AB AB AD AE BC ⊥====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值; (3)若二面角E BD F --的余弦值为13,求线段CF 的长.【答案】(1)见解析;(2)49;(3)87. 【解析】依题意,可以建立以A 为原点,分别以AB AD AE u u u r u u u r u u u r,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>>,则()1,2,F h .(1)依题意,(1,0,0)AB =u u u r 是平面ADE 的法向量,又(0,2,)BF h =u u u r,可得0BF AB ⋅=u u u r u u u r ,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE .(2)依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--u u u r u u u r u u u r.设(,,)x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =, 可得(2,2,1)=n .因此有4cos ,9||||CE CE CE ⋅==-u u u ru u u r u u u r n n n .所以,直线CE 与平面BDE 所成角的正弦值为49. (3)设(,,)x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rm m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =,可得21,1,h ⎛⎫=-⎪⎝⎭m .由题意,有||1cos ,||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意.所以,线段CF 的长为87.【名师点睛】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.16.【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1; (2)BE ⊥C 1E .【答案】(1)见解析;(2)见解析.【解析】(1)因为D ,E 分别为BC ,AC 的中点, 所以ED ∥AB .在直三棱柱ABC−A 1B 1C 1中,AB ∥A 1B 1, 所以A 1B 1∥ED .又因为ED ⊂平面DEC 1,A 1B 1⊄平面DEC 1,所以A 1B 1∥平面DEC 1.(2)因为AB =BC ,E 为AC 的中点,所以BE ⊥AC . 因为三棱柱ABC−A 1B 1C 1是直棱柱,所以CC 1⊥平面ABC . 又因为BE ⊂平面ABC ,所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,C 1C ∩AC =C , 所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BE ⊥C 1E .【名师点睛】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力和推理论证能力.17.【2019年高考浙江卷】(本小题满分15分)如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是AC ,A 1B 1的中点. (1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.【答案】(1)见解析;(2)35. 【解析】方法一:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC . 又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1, 平面A 1ACC 1∩平面ABC =AC , 所以,A 1E ⊥平面ABC ,则A 1E ⊥BC . 又因为A 1F ∥AB ,∠ABC =90°,故BC ⊥A 1F . 所以BC ⊥平面A 1EF .因此EF ⊥BC .(2)取BC 中点G ,连接EG ,GF ,则EGFA 1是平行四边形. 由于A 1E ⊥平面ABC ,故A 1E ⊥EG ,所以平行四边形EGFA 1为矩形. 由(1)得BC ⊥平面EGFA 1,则平面A 1BC ⊥平面EGFA 1, 所以EF 在平面A 1BC 上的射影在直线A 1G 上.连接A 1G 交EF 于O ,则∠EOG 是直线EF 与平面A 1BC 所成的角(或其补角).不妨设AC =4,则在Rt △A 1EG 中,A 1E ,EG由于O 为A 1G 的中点,故12A G EO OG ===所以2223cos 25EO OG EG EOG EO OG +-∠==⋅.因此,直线EF 与平面A 1BC 所成角的余弦值是35. 方法二:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC . 又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1, 平面A 1ACC 1∩平面ABC =AC ,所以,A 1E ⊥平面ABC .如图,以点E 为原点,分别以射线EC ,EA 1为y ,z 轴的正半轴,建立空间直角坐标系E –xyz .不妨设AC =4,则A 1(0,0,B1,0),1B,3,22F ,C (0,2,0).因此,3(,22EF =u u u r,(BC =u u u r .由0EF BC ⋅=u u u r u u u r得EF BC ⊥. (2)设直线EF 与平面A 1BC 所成角为θ. 由(1)可得1=(10)=(02BC A C -u u u r u u u u r,,,. 设平面A 1BC 的法向量为n ()x y z =,,, 由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩u u u rn n,得00y y ⎧+=⎪⎨=⎪⎩, 取n (11)=,故||4sin |cos |=5|||EF EF EF θ⋅==⋅u u u ru u u r u u u r ,n n n |, 因此,直线EF 与平面A 1BC 所成的角的余弦值为35. 【名师点睛】本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力.18.【云南省昆明市2019届高三高考5月模拟数学试题】已知直线l ⊥平面α,直线m ∥平面β,若αβ⊥,则下列结论正确的是 A .l β∥或l β⊄ B .//l m C .m α⊥ D .l m ⊥【答案】A【解析】对于A ,直线l ⊥平面α,αβ⊥,则l β∥或l β⊂,A 正确;对于B ,直线l ⊥平面α,直线m ∥平面β,且αβ⊥,则//l m 或l 与m 相交或l 与m 异面,∴B 错误;对于C ,直线m ∥平面β,且αβ⊥,则m α⊥或m 与α相交或m α⊂或m α∥,∴C 错误; 对于D ,直线l ⊥平面α,直线m ∥平面β,且αβ⊥,则//l m 或l 与m 相交或l 与m 异面,∴D 错误. 故选A .【名师点睛】本题考查了空间平面与平面关系的判定及直线与直线关系的确定问题,也考查了几何符号语言的应用问题,是基础题.19.【陕西省2019届高三年级第三次联考数学试题】已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为A.4B .34 C.4D .54【答案】B【解析】如图,设BC 的中点为D ,连接1A D 、AD 、1A B , 易知1A AB ∠即为异面直线AB 与1CC 所成的角(或其补角). 设三棱柱111ABC A B C -的侧棱与底面边长均为1,则AD =112A D =,1A B =由余弦定理,得2221111cos 2A A AB A B A AB A A AB+-∠=⋅111322114+-==⨯⨯. 故应选B.【名师点睛】本题主要考查了异面直线所成角的求解,通过平移找到所成角是解这类问题的关键,若平移不好作,可采用建系,利用空间向量的运算求解,属于基础题.解答本题时,易知1A AB ∠即为异面直线AB 与1CC 所成的角(或其补角),进而通过计算1ABA △的各边长,利用余弦定理求解即可. 20.【四川省宜宾市2019届高三第三次诊断性考试数学试题】如图,边长为2的正方形ABCD 中,,E F 分别是,BC CD 的中点,现在沿,AE AF 及EF 把这个正方形折成一个四面体,使,,B C D 三点重合,重合后的点记为P ,则四面体P AEF -的高为A .13B .23C .34D .1【答案】B【解析】如图,由题意可知PA PE PF ,,两两垂直,∴PA ⊥平面PEF , ∴11111123323PEF A PEF V S PA -=⋅=⨯⨯⨯⨯=△, 设P 到平面AEF 的距离为h ,又2111321212112222AEF S =-⨯⨯-⨯⨯-⨯⨯=△, ∴13322P AEF hV h -=⨯⨯=,∴123h =,故23h =, 故选B .【名师点睛】本题考查了平面几何的折叠问题,空间几何体的体积计算,属于中档题.折叠后,利用A PEF P AEF V V --=即可求得P 到平面AEF 的距离.21.【广东省深圳市高级中学2019届高三适应性考试(6月)数学试题】在三棱锥P ABC -中,平面PAB ⊥平面ABC ,ABC △是边长为6的等边三角形,PAB △是以AB 为斜边的等腰直角三角形,则该三棱锥外接球的表面积为_______. 【答案】48π【解析】如图,在等边三角形ABC 中,取AB 的中点F ,设等边三角形ABC 的中心为O ,连接PF ,CF ,OP .由6AB =,得23AO BO CO CF OF ===== PAB Q △是以AB 为斜边的等腰角三角形,PF AB ∴⊥,又平面PAB ⊥平面ABC ,PF ∴⊥平面ABC ,PF OF ∴⊥,OP ==则O 为棱锥P ABC -的外接球球心,外接球半径R OC ==∴该三棱锥外接球的表面积为(24π48π⨯=,故答案为48π.【名师点睛】本题主要考查四面体外接球表面积,考查空间想象能力,是中档题. 要求外接球的表面积和体积,关键是求出球的半径.求外接球半径的常见方法有:①若三条棱两两垂直,则用22224R a b c =++(,,a b c 为三条棱的长);②若SA ⊥面ABC (SA a =),则22244R r a =+(r 为ABC △外接圆半径);③可以转化为长方体的外接球;④特殊几何体可以直接找出球心和半径. 22.【2019北京市通州区三模数学试题】如图,在四棱柱1111ABCD A B C D -中,侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB =,12,AC AA AD CD ===E 为线段1AA 上的点,且12AE =.(1)求证:BE ⊥平面1ACB ;(2)求二面角11D AC B --的余弦值;(3)判断棱11A B 上是否存在点F ,使得直线DF ∥平面1ACB ,若存在,求线段1A F 的长;若不存在,说明理由.【答案】(1)见解析;(2;(3)见解析. 【解析】(1)因为1A A ABCD ⊥底面, 所以1A A AC ⊥. 又因为AB AC ⊥, 所以AC ⊥平面11ABB A , 又因为BE ⊂平面11ABB A , 所以AC ⊥BE . 因为112AE ABAB BB ==,∠EAB =∠ABB 1=90°, 所以1Rt Rt ABE BB A △∽△. 所以1ABE AB B ∠=∠. 因为1190BAB AB B ∠+∠=︒, 所以190BAB ABE ∠+∠=︒. 所以BE ⊥1AB . 又1AC AB A =I , 所以BE ⊥平面1ACB .(2)如图,以A 为原点建立空间直角坐标系,依题意可得111(0,0,0),(0,1,0),(2,0,0),(1,2,0),(0,0,2),(0,1,2),(2,0,2),A B C D A B C -11(1,2,2),(0,0,)2D E -.由(1)知,1(0,1,)2EB u u u r =-为平面1ACB 的一个法向量,设(,,)x y z =n 为平面1ACD 的法向量.因为1(1,2,2),(2,0,0)AD AC u u u u r u u u r=-=,则10,0,AD AC ⎧⋅=⎪⎨⋅=⎪⎩u u u u u u u r r n n 即220,20,x y z x -+=⎧⎨=⎩不妨设1z =,可得(0,1,1)=n .因此cos ,||||EB EB EB u u u r u u u r u u u r n n n ×<>=. 因为二面角11D AC B --为锐角, 所以二面角11D AC B --. (3)设1A F a =,则(0,,2)F a ,(1,2,2)DF a u u u r=-+.1(1,2,2)(0,1,)2102DF EB a a u u u r u u u r ?-+?=+-=,所以1a =-(舍).即直线DF 的方向向量与平面1ACB 的法向量不垂直, 所以,棱11A B 上不存在点F ,使直线DF ∥平面1ACB .【名师点睛】本题主要考查线面垂直与平行、以及二面角的问题,熟记线面垂直的判定定理以及空间向量的方法求二面角即可,属于常考题型.(1)根据线面垂直的判定定理,直接证明,即可得出结论成立;(2)以A 为原点建立空间直角坐标系,由(1)得到1(0,1,)2EB u u u r =-为平面1ACB 的一个法向量,再求出平面1ACD 的一个法向量,求两向量夹角的余弦值,即可得出结果; (3)先设1A F a =,用向量的方法,由0DF EBu u u r u u u r?求出a 的值,结合题意,即可判断出结论.【扫描二维码关注更多精彩★玩转高中数学研讨】。
《创新设计》2022高考数学(浙江专用理科)二轮专题精练:专题四 立体几何4-3 Word版含解析

第3讲 立体几何中的向量方法(建议用时:60分钟) 一、选择题1.已知平面ABC ,点M 是空间任意一点,点M 满足条件OM→=34OA →+18OB →+18OC →,则直线AM( ).A .与平面ABC 平行B .是平面ABC 的斜线 C .是平面ABC 的垂线D .在平面ABC 内解析 由已知得M ,A ,B ,C 四点共面,所以AM 在平面ABC 内,选D. 答案 D2.如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是 ( ).A .相交B .平行C .垂直D .不能确定解析 MN →=MB →+BC →+CN →=23A 1B →+BC →+23CA → =23(A 1B 1→+B 1B →)+BC →+23(CD →+DA →) =23B 1B →+BC →+23DA →, 又CD →是平面BB 1C 1C 的一个法向量,且MN →·CD →=23B 1B →+BC →+23DA →·CD →=0,∴MN →⊥CD →,又MN ⊄面BB 1C 1C ,∴MN ∥平面BB 1C 1C . 答案 B3.如图,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是 ( ).A .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角解析 选项A 正确,由于SD 垂直于底面ABCD ,而AC ⊂平面ABCD ,所以AC ⊥SD ;再由四边形ABCD 为正方形,所以AC ⊥BD ;而BD 与SD 相交,所以,AC ⊥平面SBD ,AC ⊥SB . 选项B 正确,由于AB ∥CD ,而CD ⊂平面SCD ,AB ⊄平面SCD ,所以AB ∥平面SCD . 选项C 正确,设AC 与BD 的交点为O ,易知SA 与平面SBD 所成的角就是∠ASO ,SC 与平面SBD 所成的角就是∠CSO ,易知这两个角相等.选项D 错误,AB 与SC 所成的角等于∠SCD ,而DC 与SA 所成的角是∠SAB ,这两个角不相等. 答案 D4.已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与侧面ACC 1A 1所成角的正弦等于 ( ).A.64B.104C.22D.32解析 如图所示建立空间直角坐标系,设正三棱柱的棱长为2,O (0,0,0),B (3,0,0),A (0,-1,0),B 1(3,0,2),则AB 1→=(3,1,2),则BO →=(-3,0,0)为侧面ACC 1A 1的法向量,由sin θ=|AB 1→·BO →||AB1→||BO →|=64.答案 A5.(2022·新课标全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为 ( ). A.110 B.25 C.3010D.22解析 法一 由于∠BCA =90°,三棱柱为直三棱柱,且BC =CA =CC 1,可将三棱柱补成正方体.建立如图(1)所示空间直角坐标系.设正方体棱长为2,则可得A (0,0,0),B (2,2,0),M (1,1,2),N (0,1,2),∴BM→=(1,1,2)-(2,2,0)=(-1,-1,2),AN →=(0,1,2).∴cos 〈BM →,AN →〉=BM →·AN →|BM →||AN →|=-1+4(-1)2+(-1)2+22×02+12+22=36×5=3010. 法二 如图(2),取BC 的中点D ,连接MN ,ND ,AD ,由于MN 綉12B 1C 1綉BD ,因此有ND 綉BM ,则ND 与NA 所成角即为异面直线BM 与AN 所成角.设BC =2,则BM =ND =6,AN =5,AD =5,因此cos ∠AND =ND 2+NA 2-AD 22ND ·NA =3010.答案 C6.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB→的值为( ).A .0B .1C .0或1D .任意实数 解析 AP→可为下列7个向量:AB →,AC →,AD →,AA 1→,AB 1→,AC 1→,AD 1→. 其中一个与AB →重合,AP →·AB →=|AB →|2=1; AD →,AD 1→,AA 1→与AB →垂直, 这时AP →·AB→=0; AC →,AB 1→与AB →的夹角为45°, 这时AP →·AB→=2×1×cos π4=1, 最终AC 1→·AB →=3×1×cos ∠BAC 1=3×13=1,故选C. 答案 C7.(2021·浙江卷)如图,已知△ABC ,D 是AB 的中点,沿直线CD 将△ACD 翻折成△A ′CD ,。
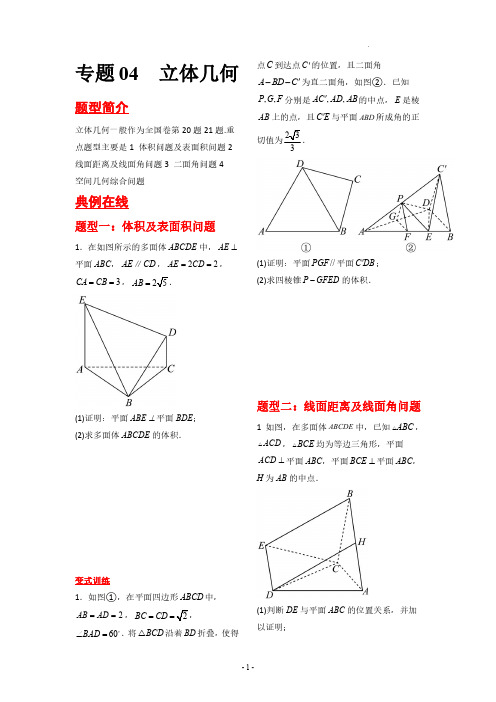
专题04 立体几何-【李金柱梳理】冲刺2023年高考数学大题突破+限时集训(新高考专用)(原卷版)
专题04立体几何题型简介立体几何一般作为全国卷第20题21题.重点题型主要是1体积问题及表面积问题2线面距离及线面角问题3二面角问题4空间几何综合问题典例在线题型一:体积及表面积问题1.在如图所示的多面体ABCDE 中,⊥AE 平面ABC ,AE CD ∥,22AE CD ==,3CA CB ==,25AB =(1)证明:平面ABE ⊥平面BDE ;(2)求多面体ABCDE 的体积.变式训练1.如图①,在平面四边形ABCD 中,2AB AD ==,2BC CD ==60BAD ∠= .将BCD △沿着BD 折叠,使得点C 到达点C '的位置,且二面角A BD C '--为直二面角,如图②.已知,,P G F 分别是,,AC AD AB '的中点,E 是棱AB 上的点,且C E '与平面ABD 所成角的正233(1)证明:平面//PGF 平面C DB ';(2)求四棱锥P GFED -的体积.题型二:线面距离及线面角问题1如图,在多面体ABCDE 中,已知ABC ,ACD ,BCE 均为等边三角形,平面ACD ⊥平面ABC ,平面BCE ⊥平面ABC ,H 为AB的中点.(1)判断DE 与平面ABC 的位置关系,并加以证明;(2)求直线DH 与平面ACE 所成角的正弦值.变式训练1如图,PD 垂直于梯形ABCD 所在平面,90ADC BAD ∠=∠=,F 为PA 的中点,2PD =112AB AD CD ===,四边形PDCE 为矩形.(1)求证://AC 平面DEF ;(2)求平面ABCD 与平面BCP 的夹角的大小;(3)求点F 到平面BCP 的距离.题型三:二面角问题1如图,四棱锥P -ABCD 中,已知AD BC ∥,BC =2AD ,AD =DC ,∠BCD =60°,CD ⊥PD ,PB ⊥BD.(1)证明:PB ⊥AB ;(2)设E 是PC 的中点,直线AE 与平面ABCD 所成角等于45°,求二面角B -PC -D 的余弦值.变式训练1如图,在四棱锥S ABCD -中,底面ABCD 为梯形,AB CD ∥,2AB CD =,AD SD =,SAB △为正三角形,SC BC ⊥,CB CS =.(1)求证:平面SAB ⊥平面SBC ;(2)求二面角C SA D --的余弦值.题型四:空间几何综合问题1.如图所示,正方形ABCD 所在平面与梯形ABMN 所在平面垂直,AN BM ∥,2AN AB BC ===,4BM =,23CN =(1)证明:BM ⊥平面ABCD ;(2)在线段CM (不含端点)上是否存在一点E ,使得二面角E BN M --33若存在,求出的CEEM值;若不存在,请说明理由.变式训练1如图,在四棱锥E -ABCD 中,平面ADE ⊥平面ABCD ,O 、M 分别为线段AD 、DE 的中点,四边形BCDO 是边长为1的正方形,AE =DE ,AE ⊥DE.(1)求证:CM //平面ABE ;(2)求直线CM 与BD 所成角的余弦值;(3)点N 在直线AD 上,若平面BMN ⊥平面ABE ,求线段AN 的长.模拟尝试1.(2023·山东·潍坊一中校联考模拟预测)如图,在四棱锥P ABCD -中,PAD 为等边三角形,M 为PA 的中点,PD AB ⊥,平面PAD ⊥平面ABCD .(1)证明:平面MCD ⊥平面PAB ;(2)若//AD BC ,2AD BC =,2CD AB =,求平面MCD 与平面PBC 夹角的余弦值.2.(2023·山东·日照一中校考模拟预测)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为22(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AAAB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C--的正弦值.3.(2023·吉林·长春十一高校联考模拟预测)如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 为线段AB 的中点,4CB =,43AB =118AC =,三棱锥1A A DC -的体积为8.(1)证明:1A D ⊥平面11B C D ;(2)求平面1ACD 与平面1A BC 夹角的余弦值.4.(2022·江苏南京·南京师大附中校考模拟预测)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60ADC ∠=︒,PAD 为等边三角形,O 为线段AD 的中点,且平面PAD ⊥平面ABCD ,M 是线段PC 上的点.(1)求证:OM BC ⊥;(2)若直线AM 与平面PAB 的夹角的正弦值为1010,求四棱锥M ABCD -的体积.5.(2023·河北衡水·衡水市第二中学校考模拟预测)如图,直四棱柱1111ABCD A B C D -中,16AA =E 是1AA 的中点,底面ABCD 是平行四边形,若1A C ⊥平面1BDC.(1)若1AB AA =,证明:底面ABCD 是正方形(2)若60BAD ∠=︒,求二面角1B BE D --的余弦值6.(2022·河北衡水·河北衡水中学校考模拟预测)直四棱柱1111ABCD A B C D -被平面α所截,所得的一部分如图所示,EF DC =.(1)证明://ED 平面ACF ;(2)若1242DC AD A E ===,3ADC π∠=,平面EFCD 与平面ABCD 所成角的正切值433,求点E 到平面ACF 的距离.真题再练1.(2021·全国·统考高考真题)如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,1PD DC ==,M 为BC 的中点,且PB AM ⊥.(1)求BC ;(2)求二面角A PM B --的正弦值.2.(2021·全国·统考高考真题)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,D 为棱11A B 上的点.11BF A B ⊥(1)证明:BF DE ⊥;(2)当1B D 为何值时,面11BB C C 与面DFE 所成的二面角的正弦值最小?3.(2021·全国·统考高考真题)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.4.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.5.(2022·全国·统考高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD 是边长为8(单位:cm )的正方形,,,,EAB FBC GCD HDA 均为正三角形,且它们所在的平面都与平面ABCD 垂直.(1)证明://EF 平面ABCD ;(2)求该包装盒的容积(不计包装盒材料的厚度).6.(2022·全国·统考高考真题)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为22(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C--的正弦值.7.(2022·全国·统考高考真题)如图,PO 是三棱锥-P ABC 的高,PA PB =,AB AC ⊥,E 是PB的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B --的正弦值.8.(2022·北京·统考高考真题)如图,在三棱柱111ABC A B C -中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N 分别为11A B ,AC的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值.条件①:AB MN ⊥;条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.9.(2022·天津·统考高考真题)直三棱柱111ABC A B C -中,112,,AA AB AC AA AB AC AB ===⊥⊥,D为11A B 的中点,E 为1AA 的中点,F 为CD 的中点.(1)求证://EF 平面ABC ;(2)求直线BE 与平面1CC D 所成角的正弦值;(3)求平面1ACD 与平面1CC D 所成二面角的余弦值.。
专题04 立体几何-【李金柱梳理】冲刺2023年高考数学大题突破+限时集训(新高考专用)解析版1

专题04立体几何题型简介立体几何一般作为全国卷第20题21题.重点题型主要是1体积问题及表面积问题2线面距离及线面角问题3二面角问题4空间几何综合问题典例在线题型一:体积及表面积问题1.在如图所示的多面体ABCDE 中,⊥AE 平面ABC ,AE CD ∥,22AE CD ==,3CA CB ==,25AB =.(1)证明:平面ABE ⊥平面BDE ;(2)求多面体ABCDE 的体积.【答案】(1)证明见解析(2)25解(1)证明:设AB ,BE 的中点分别为F ,G ,连接CF ,FG ,DG ,则FG AE ∥,且12FG AE =,又CD AE ∥,且12CD AE =,所以FG CD ∥,且FG CD =,所以四边形CFGD 为平行四边形,所以∥CF DG .因为⊥AE 平面ABC ,CF ⊂平面ABC ,所以AE CF ⊥,所以AE DG ⊥,因为CA CB =,F 为AB 的中点,所以CF AB ⊥,所以DG AB ⊥,又AB ,AE ⊂平面ABE ,且AB AE A = ,所以DG ⊥平面ABE ,又DG ⊂平面BDE ,所以平面ABE ⊥平面BDE .(2)由(1)得CF AB ⊥,CF AE ⊥,且AB ,AE ⊂平面ABE ,AB AE A = ,所以CF ⊥平面ABE ,又因为3CA CB ==,25AB =,F 为AB 的中点,所以2CF =.因为CD AE ∥,AE ⊂平面ABE ,CD ⊄平面ABE ,所以CD ∥平面ABE ,所以点D 到平面ABE 的距离等于点C 到平面ABE 的距离CF .因为⊥AE 平面ABC ,AC ,BC ⊂平面ABC ,所以AE AC ⊥,AE BC ⊥,又CD AE ∥,所以CD AC ⊥,CD BC ⊥,又AC ,BC ⊂平面ABC ,且AC BC C = ,所以CD ⊥平面ABC ,连接AD ,多面体ABCDE 的体积V 等于三棱锥D ABC -的体积与三棱锥D ABE -的体积之和,而11252521323D ABC V -=⨯⨯⨯⨯=,11452522323D ABE V -=⨯⨯⨯⨯=,所以多面体ABCDE 的体积25452533V =+=.变式训练1.如图①,在平面四边形ABCD 中,2AB AD ==,2BC CD ==,60BAD ∠=.将BCD △沿着BD 折叠,使得点C 到达点C '的位置,且二面角A BD C '--为直二面角,如图②.已知,,P G F 分别是,,AC AD AB'的中点,E 是棱AB 上的点,且C E '与平面ABD 所成角的正切值为3.(1)证明:平面//PGF 平面C DB ';(2)求四棱锥P GFED -的体积.【答案】(1)证明见解析解(1),,P G F 分别为,,AC AD AB '的中点,//PG C D '∴,//PF BC ',,PG PF ⊄ 平面C DB ',,C D BC ''⊂平面C DB ',//PG ∴平面C DB ',//PF 平面C DB ',又PG PF P ⋂=,,PG PF ⊂平面PGF ,∴平面//PGF 平面C DB '.(2)取BD 的中点M ,连接,C M EM ',2AB AD == ,60BAD ∠= ,ABD ∴ 为等边三角形,2BD ∴=,又BC C D ''==222BC C D BD ''∴+=,C DB '∴ 为等腰直角三角形,112C M BD '∴==,C M BD '⊥; 二面角A BD C '--是直二面角,即平面C DB '⊥平面ABD ,平面C DB '⋂平面ABD BD =,C M '⊂平面C DB ',C M '∴⊥平面ABD ,C EM '∴∠即为C E '与平面ABD所成角,1tan 3C M C EM EM EM ''∴∠===,解得:2EM =;在EMB △中,由余弦定理得:2222cos60EM BM BE BM BE =+-⋅ ,即2314BE BE =+-,解得:12BE =,E ∴为线段AB 上靠近点B 的四等分点,111442ABD AGF BDE ABD ABD ABD ABDGFED S S S S S S S S ∴=--=--=四边形211222=⨯⨯⨯111113232P GFED GFED V S C M -'∴=⨯⨯=⨯=四棱锥四边形题型二:线面距离及线面角问题.如图,在多面体ABCDE 中,已知ABC ,ACD ,BCE 均为等边三角形,平面ACD ⊥平面ABC ,平面BCE ⊥平面ABC ,H 为AB的中点.(1)判断DE 与平面ABC 的位置关系,并加以证明;(2)求直线DH 与平面ACE 所成角的正弦值.【答案】(1)DE ∥平面ABC ,证明见解析;(2)155【详解】(1)DE ∥平面ABC ,理由如下:分别取,AC BC 的中点,O P ,连接,,DO EP OP ,因为AD CD =,所以DO AC ⊥,又平面ACD ⊥平面ABC ,平面ACD 平面ABC AC =,DO ⊂平面ACD ,所以DO ⊥平面ABC ,同理EP ⊥平面ABC ,所以EP DO ∥,又因为,ACD BCE 是全等的正三角形,所以EP DO =,所以四边形DOPE 是平行四边形,所以DE OP ∥,因为ED ⊄平面ABC ,OP ⊂平面ABC ,所以ED ∥平面ABC ;(2)连接BO ,则易知BO ⊥平面ACD ,以O 为坐标原点,分别以,,OD OA OB的方向为,,x y z 轴的正方向,建立如图所示的空间直角坐标系O xyz -,令2AC =.则()()())13130,0,0,0,1,0,0,1,0,3,0,0,0,,,0,,2222O A C DH P ⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,13,3,,22DE OP E ⎫=∴-⎪⎪⎭所以()33130,2,0,3,,3,2222AC AE DH ⎛=-=-= ⎭⎝⎭ ,设平面ACE 的法向量为(),,m x y z =,所以·0·0m AC m AE ⎧=⎪⎨=⎪⎩ ,所以20333022y y z -=⎧⎪⎨-+=⎪⎩则0y =,取2z =,1x ∴=-,则()1,0,2m =-,所以2315cos ,525DH m DH m DH m ===,设直线DH 与平面ACE 所成的角为θ,则15sin cos ,5DH m θ==.变式训练1如图,PD 垂直于梯形ABCD 所在平面,90ADC BAD ∠=∠=,F 为PA 的中点,2PD =112AB ADCD ===,四边形PDCE 为矩形.(1)求证://AC 平面DEF ;(2)求平面ABCD 与平面BCP 的夹角的大小;(3)求点F 到平面BCP 的距离.【答案】(1)证明见解析(2)45 (3)14【详解】(1)设CP DE G = ,连接FG,四边形PDCE 为矩形,G ∴为PC 中点,又F 为PA 中点,//AC FG ∴,又FG ⊂平面DEF ,AC ⊄平面DEF ,//AC ∴平面DEF .(2)以D 为坐标原点,,,DA DC DP正方向为,,x y z 轴,可建立如图所示空间直角坐标系,则()1,1,0B ,()0,2,0C,(P ,()1,1,0BC ∴=-,(0,CP =-,设平面BCP 的法向量(),,n x y z =,020BC n x y CP n y ⎧⋅=-+=⎪∴⎨⋅=-+=⎪⎩,令1y =,解得:1x =,z =,(n ∴=;z 轴⊥平面ABCD ,∴平面ABCD 的一个法向量()0,0,1m =,cos ,2m n m n m n⋅∴<>==⋅ ,则平面ABCD 与平面BCP的夹角为45 .(3)由(2)知:1,0,22F ⎛ ⎝⎭,(P,1,0,22PF ⎛⎫∴= ⎪ ⎪⎝⎭,由平面BCP的法向量(n =,∴点F 到平面BCP 的距离11224PF nd n⋅=== .题型三:二面角问题1如图,四棱锥P -ABCD 中,已知AD BC ∥,BC =2AD ,AD =DC ,∠BCD =60°,CD ⊥PD ,PB ⊥BD .(1)证明:PB ⊥AB ;(2)设E 是PC 的中点,直线AE 与平面ABCD 所成角等于【答案】(1)证明见解析(2)77解(1)连结BD ,在BDC 中,因为BC=2DC ,∠BCD=60°,由余弦定理()22222cos603BD DC DC DC DC +-⋅⋅︒.因为222BD CD BC +=,所以CD ⊥BD ,又CD ⊥PD ,BD PD D = ,,BD PD ⊂平面PDB ,所以CD ⊥平面PDB ,由于PB ⊂平面PDB ,所以CD ⊥PB .因为PB ⊥BD ,CD BD D =I ,,CD BD ⊂平面ABCD ,所以PB ⊥平面ABCD ,由于AB ⊂平面ABCD ,因此PB ⊥AB .(2)解法1:以B 为坐标原点,BC的方向为x 轴正方向,||DC为单位长度,建立如图所示的空间直角坐标系A-xyz ,由(1)可知y 轴在平面ABCD 内.则(0,0,0)B ,1322A ⎛⎫⎪ ⎪⎝⎭,(2,0,0)C ,3322D ⎛⎫ ⎪⎝⎭,13,22DC ⎛⎫= ⎪⎝⎭ .设(0,0,)(0)P t t >,则(2,0,)PC t =- ,1,0,2t E ⎛⎫ ⎪⎝⎭,13,222t AE ⎛⎫= ⎪⎝⎭ .因为平面ABCD 的法向量为(0,0,1)m =,所以2cos ,||||4AE m AE m AE m t 〈〉==⋅+⋅由AE 与平面ABCD 所成角等于45°,2sin 454t =+,解得t=2.设平面DPC 的法向量1(,,)n x y z =,则110,0.n PC n DC ⎧⋅=⎪⎨⋅=⎪⎩即220,130.22x z x -=⎧⎪⎨=⎪⎩所以可取1(3,1,3)n =.因为平面BPC 的法向量为2(0,1,0)n = ,于是1212127cos ,7n n n n n n 〈〉=⋅=.因为二面角B-PC-D 是锐二面角,所以其余弦值为77.解法2:取BC 中点为F ,连结EF ,AF ,则EF PB ∥,且AF=DC .由(1)可知EF ⊥平面ABCD ,∠EAF 是AE 与平面ABCD 所成角,所以∠EAF=45°,所以EF=AF=DC ,于是PB=2EF=2DC .以B 为坐标原点,BC的方向为x 轴正方向,||DC 为单位长度,建立如图所示的空间直角坐标系A-xyz ,由(1)可知y 轴在平面ABCD 内.则(0,0,0)B ,(2,0,0)C ,332D ⎛⎫ ⎪⎝⎭,(0,0,2)P ,(2,0,2)PC =-,13,22DC ⎛⎫= ⎪⎝⎭ .设平面DPC 的法向量(,,)m x y z =,则0,0.m PC m DC ⎧⋅=⎪⎨⋅=⎪⎩即可得220,130.22x z x y -=⎧⎪⎨-=⎪⎩所以可取(3,1,3)m = .因为平面BPC 的法向量(0,1,0)n = ,于是7cos ,7||||m n m n m n ⋅〈〉==⋅.因为二面角B-PC-D 是锐二面角,所以其余弦值为77.解法3:取BC 中点为F ,连结EF ,AF ,则//EF PB ,且AF=DC .由(1)可知EF ⊥平面ABCD ,∠EAF 是AE 与平面ABCD 所成角,故∠EAF=45°,因此EF=AF=DC ,于是PB=2EF=2DC=BC ,可得22PC DC =.连结BE ,则BE ⊥PC .过E 在平面PDC 内作EG ⊥PC ,交PD 于点G ,则∠BEG 是二面角B-PC-D 的平面角.因为PB ⊥BC ,所以2BE DC ,7PD DC =.因为CD ⊥PD ,由PEG PDC △∽△可得147EG =.由PC ⊥平面BEG ,BG ⊂平面BEG ,所以PC ⊥BG ,而CD ⊥BG ,,,PC CD C PC CD ⋂=⊂平面PDC ,故BG ⊥平面PDC ,由于GE Ì平面PDC ,所以BG ⊥GE ,所以由余弦定理得7cos 7GE BEG BE ∠==.因此二面角B PCD --的余弦值为77.变式训练1如图,在四棱锥S ABCD -中,底面ABCD 为梯形,AB CD ∥,2AB CD =,AD SD =,SAB △为正三角形,SC BC ⊥,CB CS =.(1)求证:平面SAB ⊥平面SBC ;(2)求二面角C SA D --的余弦值.【答案】(1)证明见解析(2)277解(1)分别取BS ,AS 的中点O ,E ,连接OE ,OC ,ED ,则//OE AB 且12OE AB =.因为//AB CD ,2AB CD =,所以//,OE CD OE CD =,所以四边形OCDE 为平行四边形,则//CO DE .因为AD SD =,故DE SA ⊥,故CO SA ⊥.因为CB CS =,故CO SB ⊥.因为SA SB S =I ,SA ,SB ⊂平面SAB ,所以CO ⊥平面SAB.因为CO ⊂平面SBC ,所以平面SAB ⊥平面SBC.(2)连接AO ,因为△SAB 为正三角形,所以AO SB ⊥,因为平面SAB ⊥平面SBC ,平面SAB 平面SBC SB =,AO ⊂面SAB ,所以AO ⊥平面SBC ,OC 、OS 在面SBC 内,又CO SB ⊥,故OA ,OS ,OC 两两垂直,故以O 为坐标原点,OC ,OS ,OA 所在直线分别为x ,y ,z 轴建立空间直角坐标系,如图所示.设2BC SC ==,则22AB SB ==,6OA =,2OC =,所以()0,0,6A ,()2,0,0C,()0,2,0S ,262,,22D ⎛⎫ ⎪ ⎪⎝⎭,(难点:点D 的坐标不易直接看出,可先求出点E 的坐标,利用CO DE =求解点D 的坐标)所以()0,2,6AS =- ,262,,22SD ⎛⎫=- ⎪ ⎪⎝⎭ ,()2,2,0CS =-.设面SAD 的法向量为()111,,m x y z =,由11111260262022m AS y z m SD x y z ⎧⋅=-=⎪⎨⋅=-+=⎪⎩,令11z =,得()0,3,1m =.设面SAC 的法向量为()222,,x n y z =,则2222260220n AS y z n CS x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ ,令23y =,得()3,3,1n = .则427cos ,727m n m n m n ⋅===⨯⋅,显然二面角C SAD --为锐二面角,所以二面角C SA D --的余弦值为277.题型四:空间几何综合问题1.如图所示,正方形ABCD 所在平面与梯形ABMN 所在平面垂直,AN BM ∥,2AN AB BC ===,4BM =,CN =(1)证明:BM ⊥平面ABCD ;(2)在线段CM (不含端点)上是否存在一点E ,使得二面角E BN M --的余弦值为3.若存在,求出的CE EM 值;若不存在,请说明理由.【答案】(1)见解析(2)存在,12CE EM =【详解】(1)证明:正方形ABCD 中,BC AB ⊥,平面ABCD ⊥平面ABMN ,平面ABCD ⋂平面ABMN AB =,BC ⊂平面ABCD ,BC ∴⊥平面ABMN ,又BM ⊂平面ABMN ,BC ∴⊥BM ,且BC BN ⊥,又2,BC ==BN ∴=2AB AN == ,222BN AB AN ∴=+,AN AB ∴⊥,又//AN BM ,BM AB ∴⊥,又,,BC BA B BA BC =⊂ 平面ABCD ,∴BM ⊥平面ABCD ;(2)解:如图,以B 为坐标原点,,,BA BM BC 所在直线分别为,,x y z 轴建立空间直角坐标系,则()()()0,0,0,2,0,0,0,0,2B A C ,()()()2,0,2,2,2,0,0,4,0D N M ,设点(),,E a b c ,()01CE CM λλ=<<,()(),,20,4,2a b c λ∴-=-,()04,0,4,2222a b E c λλλλ=⎧⎪∴=∴-⎨⎪=-⎩,()()2,2,0,0,4,22BN BE λλ∴==-,设平面BEN 的法向量为(),,m x y z = ,()2204220BN m x y BE m y z λλ⎧⋅=+=⎪∴⎨⋅=+-=⎪⎩,令221,1,,1,1,11x y z m λλλλ⎛⎫=∴=-=∴=- ⎪--⎝⎭ ,显然,平面BMN 的法向量为()0,0,2BC =,cos ,3BC m BC m BC m⋅∴==,==,即=即23210λλ+-=,解得13λ=或1-(舍),所以存在一点E,且12CE EM =.变式训练1如图,在四棱锥E -ABCD 中,平面ADE ⊥平面ABCD ,O 、M 分别为线段AD 、DE 的中点,四边形BCDO 是边长为1的正方形,AE =DE ,AE ⊥DE.(1)求证:CM //平面ABE ;(2)求直线CM 与BD 所成角的余弦值;(3)点N 在直线AD 上,若平面BMN ⊥平面ABE ,求线段AN 的长.【答案】(1)证明见解析(2)6(3)53【详解】(1)证明:取AE 的中点P ,连接BP 、MP ,如图所示.∵M 、P 分别为ED 、AE 的中点,∴PM //AD ,且PM=12AD.又四边形BCDO 是边长为1的正方形,∴BC //OD ,且BC=OD ,又O 为AD 的中点,∴BC //AD ,且BC=12AD ,即PM //BC ,且PM=BC ,∴四边形BCMP 为平行四边形,∴CM //PB ,又CM ⊄平面ABE ,PB ⊂平面ABE ,∴CM //平面ABE.(2)(2)连接EO ,∵AE=DE ,O 为AD 中点,∴EO ⊥AD.∵EO ⊂平面ADE ,且平面ADE ⊥平面ABCD ,平面ADE∩平面ABCD=AD ,∴EO ⊥平面ABCD.又OB ⊂平面ABCD ,OD ⊂平面ABCD ,∴EO ⊥OB ,EO ⊥OD ,以O 为原点,OB 、OD 、OE 所在直线分别为x 轴,y 轴,z轴建立空间直角坐标系,如图所示,则(0A ,1-,0),C (1,1,0),B (1,0,0),D (0,1,0),(0E ,0,1),M 11(0,,22∴11(1,,),22CM BD=-- =(-1,1,0).设直线CM 与BD 所成角为θ,则cosθ=1||2||||CM BD CM BD ⋅=,∴直线CM 与BD所成角的余弦值为6.(3)设ON →=λOD →,则N (0,λ,0),∴NB →=(1,-λ,0),11(1,,)22MB =-- ,设平面BMN 的法向量为n →=(a ,b ,c),则0,0,n MB n NB ⎧⋅=⎨⋅=⎩ 即220220a b c a b λ⎧--=⎪⎨⎪-=⎩,令a=λ,则b=1,c=2λ-1,∴n →=(λ,1,2λ-1),设面ABE 的法向量为(,,)m x y z =,(1,1,0),(0,1,1)AB AE ==由00AB m x y AE m y z ⎧⋅=+=⎨⋅=+=⎩,可取(1,1,1)m =- .∵平面BMN ⊥平面ABE ,∴0m n →→⋅=,即λ-1+2λ-1=0,解得λ=23,53AN ∴=.模拟尝试一、解答题1.(2023·山东·潍坊一中校联考模拟预测)如图,在四棱锥P ABCD -中,PAD 为等边三角形,M 为PA 的中点,PD AB ⊥,平面PAD ⊥平面ABCD.(1)证明:平面MCD ⊥平面PAB ;(2)若//AD BC ,2AD BC =,2CD AB =,求平面MCD 与平面PBC 夹角的余弦值.【答案】(1)证明见解析;.【详解】(1)设AD 的中点为E ,连接PE ,因为PAD 为等边三角形,所以PE AD ⊥,又因为平面PAD ⊥平面ABCD ,平面PAD ⋂平面ABCD AD =,且PE ⊂平面PAD ,所以PE ⊥平面ABCD ,因为AB ⊂平面ABCD ,所以PE AB ⊥,又PD AB ⊥,,PD PE P PD PE =⊂ ,平面PAD ,所以AB ⊥平面PAD ,又因为MD ⊂平面PAD ,所以AB MD ⊥,因为在等边三角形PAD 中,M 为PA 的中点,所以MD AP ⊥,因为AB AP A =I ,,AB AP ⊂平面PAB ,所以MD ⊥平面PAB ,因为MD ⊂平面MCD ,所以平面MCD ⊥平面PAB ;(2)连接CE ,由(1)知,AB ⊥平面PAD ,因为AD ⊂平面PAD ,所以AB AD ⊥,因为//AD BC ,2AD BC =,2CD AB =,所以四边形ABCE 为矩形,即CE AD ⊥,BC AE DE ==,22CD AB CE ==,所以30∠=︒CDE ,设BC a =,2AD a =,tan 60PE AE =⋅︒,tan 303AB CE DE ==⋅︒=,以E 为原点,分别以EC 、ED 、EP 所在直线为x 、y 、z轴建立空间直角坐标系,所以()0,,0A a -,()P,C ⎫⎪⎪⎝⎭,,0B a ⎫-⎪⎪⎝⎭,()0,,0D a,0,2a M ⎛- ⎝⎭,所以,,322a MC ⎛⎫=- ⎪ ⎪⎝⎭,30,,22a MD ⎛⎫=- ⎪ ⎪⎝⎭,,,3PB a ⎛⎫=- ⎪ ⎪⎝⎭,,0,3PC ⎛⎫= ⎪ ⎪⎝⎭,设平面MCD 和平面PBC 的法向量分别为()1111,,n x y z =,()2222,,n x y z =,则111111102302a n MC y a n MD y ⎧⋅=+-=⎪⎪⎨⎪⋅=-=⎪⎩,222222200n PB ay n PC ⎧⋅=--=⎪⎪⎨⎪⋅=-=⎪⎩,即1111x z ⎧=⎪⎨=⎪⎩,22203y x z =⎧⎨=⎩,取11y =,21z =,则1n = ,()23,0,1n =,所以121212cos ,35n n n n n n ⋅==⋅,所以平面MCD 与平面PBC.2.(2023·山东·日照一中校考模拟预测)如图,直三棱柱111ABC A B C -的体积为4,1A BC的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.【答案】【详解】(1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h ,则1111111111433333A A BC A A ABC A ABC A B BC C C B V S h h V S A A V ---=⋅===⋅== ,解得h =所以点A 到平面1A BC;(2)取1A B 的中点E,连接AE,如图,因为1AA AB =,所以1AE A B ⊥,又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =,且AE ⊂平面11ABB A ,所以⊥AE 平面1A BC ,在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥,又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A ,所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得2AE =,所以12AA AB ==,12A B =以2BC =,则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1AC 的中点()1,1,1D ,则()1,1,1BD = ,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩,可取()1,0,1m =- ,设平面BDC 的一个法向量(),,n a b c =,则20n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩,可取()0,1,1n =-r,则1cos ,222m n m n m n ⋅==⨯⋅,所以二面角A BD C --213122⎛⎫-= ⎪⎝⎭3.(2023·吉林·长春十一高校联考模拟预测)如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 为线段AB 的中点,4CB =,43AB =118AC =,三棱锥1A A DC -的体积为8.(1)证明:1A D ⊥平面11B C D ;(2)求平面1ACD 与平面1A BC 夹角的余弦值.【答案】(1)见解析65555【详解】(1)证明:因为1AA ⊥平面ABC ,CB ⊂平面ABC ,所以1AA BC ⊥,在三棱柱111ABC A B C -中,四边形11AAC C 为平行四边形,则118AC AC ==,因为43AB =4CB =,所以222AB CB AC +=,所以CB AB ⊥,又因为1AB AA A ⋂=,1AA ⊂平面11ABB A ,AB ⊂平面11ABB A ,所以CB ⊥平面11ABB A ,因为11//CB C B ,所以11C B ⊥平面11ABB A ,又1A D ⊂平面11ABB A ,所以111C B A D ⊥.1832ABC S AB BC =⋅=△,D 为AB 的中点,则132ACD ABC S S ==△△因为1AA ⊥平面ABC ,1111113833A A CD A ACD ACD V V S AA AA --==⋅=⨯= ,所以123AA =11A DB △中,1126A D B D ==1143A B =2221111A D B D A B +=,所以11A D B D ⊥,1111C B BD B ⋂=,111,C B B D ⊂平面11B C D ,所以1A D ⊥平面11B C D ;(2)因为1BB ⊥平面ABC ,BC AB ⊥,以点B 为坐标原点,BA 、1BB 、BC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()0,0,4C 、()3,0,0D 、()143,3,0A 、()10,23,0B ,设平面1DAC 的法向量为()111,,m x y z =,()123,3,0DA = ,()23,0,4DC =-,则11111330340m DA x y m DC x z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩ ,取12x =,可得(2,3m =-,设平面1A CB 的法向量为()222,,x n y z =,()13,3,0BA = ,()0,0,4BC =,则1222433040n BA x y n BC z ⎧⋅=+=⎪⎨⋅==⎪⎩ ,取21x =,可得()1,2,0n =- ,所以,6655cos ,55115m n m n m n ⋅===⋅⨯,所以平面1DAC 与平面1ACB 夹角的余弦值为65555.4.(2022·江苏南京·南京师大附中校考模拟预测)如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60ADC ∠=︒,PAD 为等边三角形,O 为线段AD 的中点,且平面PAD ⊥平面ABCD ,M 是线段PC 上的点.(1)求证:OM BC ⊥;(2)若直线AM 与平面PAB 的夹角的正弦值为1010,求四棱锥M ABCD -的体积.【答案】(1)证明见解析;(2)43【详解】(1)因为PAD 为等边三角形,O 为线段AD 的中点,所以PO AD ⊥;因为平面PAD ⊥平面ABCD ,所以PO ⊥平面ABCD ;又BC ⊂平面ABCD ,所以PO BC ⊥;在OCD 中,1,2,60OD CD ADC ==∠=︒,由余弦定理可得OC =因为222OC OD CD +=,所以CO AD ⊥;因为//AD BC ,所以CO BC ⊥,所以BC ⊥平面POC ;因为OM ⊂平面POC ,所以OM BC ⊥.(2)由(1)得,,OP OC OD 两两垂直,以O 为坐标原点,建系如图,则()())0,1,0,0,0,,2,0,A P BC -;)(1,0,,0,1,AB PC AP =-=-=;设PM PC λ=,则)AM AP PM =+= ;设平面PAB 的一个法向量为(),,n x y z =,则00n AB n AP ⎧⋅=⎨⋅=⎩,0y y -==⎪⎩,令y =则()1n =- .因为直线AM 与平面PAB所以n AM n AM ⋅==,解得13λ=或23λ=-(舍),即有13PM PC =,M 是靠近P 的三等分点,所以四棱锥M ABCD -的高等于OP 的23.四棱锥M ABCD -的体积为114222sin 603233V ︒=⨯⨯⨯⨯⨯⨯=.5.(2023·河北衡水·衡水市第二中学校考模拟预测)如图,直四棱柱1111ABCD A B C D -中,1AA =,E 是1AA 的中点,底面ABCD 是平行四边形,若1A C ⊥平面1BDC.(1)若1AB AA =,证明:底面ABCD 是正方形(2)若60BAD ∠=︒,求二面角1B BE D --的余弦值【答案】(1)证明见解析;(2)【详解】(1)如图,连接1,AC CD ,1A C ⊥平面1BDC ,BD ⊂平面1BDC ,1C D ⊂平面1BDC ,则1AC BD ⊥,11AC C D ⊥,直棱柱中1AA ⊥底面ABCD ,BD ⊂平面ABCD ,1AA BD ⊥,111AA A C A = ,11,AA A C ⊂平面1ACA ,则BD ⊥平面1ACA ,又AC ⊂平面1ACA ,所以BD AC ⊥,所以平行四边形ABCD 是菱形,1AA AB =,则直棱柱的侧面11ABB A 是正方形,因此侧面11CDD C 也是正方形,所以11CD C D ⊥,11A C CD C = ,11,AC CD ⊂平面11ACD ,所以1C D ⊥平面11ACD ,又11A D ⊂平面11ACD ,所以111C D A D ⊥,直棱柱中易知111DD A D ⊥,而111DD CD D = ,11,DD CD ⊂平面11CC D D ,所以11A D ⊥平面11CC D D ,11C D ⊂平面11CC D D ,所以1111A D C D ⊥,因此底面1111D C B A 是矩形,即四边形ABCD是矩形,所以四边形ABCD 是正方形;(2)由(1)知底面ABCD 是菱形,因此AC BD ⊥,设AC BD O ⋂=,分别以,OA OB 为,x y 轴,过O 与1AA 平行的直线为z 轴建立空间直角坐标系,如图,设2AB a =,则3OA a =,OB a =,1(36)A a ,(3,0,0)C a -,(0,,0)B a ,1(36)C a -,1(23,0,6)AC a =-- ,1(3,6)BC a a =-- ,由(1)知211660AC BC a ⋅=-= ,1a =(负值舍去),6(3,0,2E ,(0,1,0)B ,(0,1,0)D -,16)B ,6(3,)2BE =- ,(0,2,0)DB = ,16)BB = ,设平面1B BE 的一个法向量是111(,,)m x y z =,则11111606302m BB m BE y z ⎧⋅=⎪⎨⋅=-=⎪⎩,取11x =得3,0)m = ,设平面BED 的一个法向量是222(,,)n x y z =,则2222630220n BE x y n DB y ⎧⋅=-+=⎪⎨⎪⋅==⎩,取21x =,得(1,0,2)n = ,3cos ,623m n m n m n ⋅==⨯,所以二面角1B BE D--的余弦值为366.(2022·河北衡水·河北衡水中学校考模拟预测)直四棱柱1111ABCD A B C D -被平面α所截,所得的一部分如图所示,EF DC =.(1)证明://ED 平面ACF ;(2)若1242DC AD A E ===,3ADC π∠=,平面EFCD与平面ABCD 433,求点E 到平面ACF 的距离.【答案】(1)详见解析;(2255.【详解】(1)依题:平面α与两平行平面ABCD ,1111D C B A 的交线分别为EF ,DC ,故有//EF DC ,又EF DC =,故有平行四边形EFCD ,∴//ED FC ,ED ⊄面ACF ,FC ⊂面ACF ,∴//ED 平面ACF .(2)ADC △中,由余弦定理可得3AC =得AC AD ⊥,又1AA ⊥平面ABCD ,故而1AA ,AC ,AD 两两垂直,如图建系.【法一求EH 】取AD 中点H ,由1//AH A E ,1AH A E =得平行四边形1A AHE ,∴1//AA HE ,HE ⊥平面ACD ,作HI DC ⊥,(连EI ),又HE CD ⊥,∴CD ⊥平面EHI ,得CD EI ⊥,又HI DC ⊥,∴EIH ∠为所求二面角的平面角.易求3HI =4tan 33EH EIH HI ∠==,1EH =.【法二求EH 】面ABCD 的法向量显然为()0,0,1n =,设面EFCD 的法向量为(),,k x y z = ,1,0,2E h ⎛⎫⎪⎝⎭,00k DC k DE ⎧⋅=⎨⋅=⎩,令3x =33,1,2k h ⎫=⎪⎪⎭,依题:3119n k h n k⋅=⇒= .由//ED 平面ACF ,点E 到平面ACF 的距离转化为D 到平面ACF 的距离d ,()1,0,0D ,()3,0C ,13,12DC EF F ⎛⎫=⇒- ⎪⎝⎭ ,设平面ACF 的法向量为(),,m x y z = ,00m AC m m AF ⎧⋅=⇒⎨⋅=⎩可为()2,0,1,255m AD d m⋅== .真题再练1.(2021·全国·统考高考真题)如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,1PD DC ==,M 为BC 的中点,且PB AM ⊥.(1)求BC ;(2)求二面角A PM B --的正弦值.【答案】(12(2)7014【详解】(1)[方法一]:空间坐标系+空间向量法PD ⊥ 平面ABCD ,四边形ABCD 为矩形,不妨以点D 为坐标原点,DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系D xyz -,设2BC a =,则()0,0,0D 、()0,0,1P 、()2,1,0B a 、(),1,0M a 、()2,0,0A a ,则()2,1,1PB a =- ,(),1,0AM a =-,PB AM ⊥ ,则2210PB AM a ⋅=-+= ,解得22a =22BC a ==[方法二]【最优解】:几何法+相似三角形法如图,连结BD .因为PD ⊥底面ABCD ,且AM ⊂底面ABCD ,所以PD AM ⊥.又因为PB AM ⊥,PB PD P = ,所以AM ⊥平面PBD .又BD ⊂平面PBD ,所以AM BD ⊥.从而90ADB DAM ∠+∠=︒.因为90∠+∠=︒MAB DAM ,所以∠=∠MAB ADB .所以 ∽ADB BAM ,于是=AD BAAB BM.所以2112BC =.所以BC =[方法三]:几何法+三角形面积法如图,联结BD 交AM 于点N.由[方法二]知⊥AM DB .在矩形ABCD 中,有 ∽DAN BMN ,所以2==AN DAMN BM,即23AN AM =.令2(0)=>BC t t ,因为M 为BC 的中点,则BM t =,=DB,=AM 由1122=⋅=⋅ DAB S DA AB DB AN,得=t 212t =,所以2==BC t (2)[方法一]【最优解】:空间坐标系+空间向量法设平面PAM 的法向量为()111,,m x y z =,则,1,02AM ⎛⎫=- ⎪ ⎪⎝⎭,()AP = ,由1111020m AM x y mAP z ⎧⋅=+=⎪⎨⎪⋅=+=⎩,取1x =)m =,设平面PBM 的法向量为()222,,n x y z =,,0,02BM ⎛⎫=- ⎪ ⎪⎝⎭,()1,1BP =- ,由222200n BM n BP y z ⎧⋅==⎪⎨⎪⋅=-+=⎩,取21y =,可得()0,1,1n =,cos ,14m n m n m n ⋅==⋅,所以,sin ,m n = 因此,二面角A PM B --14.[方法二]:构造长方体法+等体积法如图,构造长方体1111ABCD A B C D -,联结11,AB A B ,交点记为H ,由于11AB A B ⊥,1AB BC ⊥,所以AH ⊥平面11A BCD .过H 作1D M 的垂线,垂足记为G .联结AG ,由三垂线定理可知1⊥AG D M ,故AGH ∠为二面角A PM B --的平面角.易证四边形11A BCD 是边长为2的正方形,联结1D H ,HM .111111111,2D HM D HM D A H HBM MCD A BCD S D M HG S S S S S =⋅=--- 正方形,由等积法解得31010=HG .在Rt AHG 中,2310,210==AH HG ,由勾股定理求得355=AG .所以,70sin 14AH AGH AG ∠==,即二面角A PM B --的正弦值为7014.2.(2021·全国·统考高考真题)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,D 为棱11A B 上的点.11BF A B ⊥(1)证明:BF DE ⊥;(2)当1B D 为何值时,面11BB C C 与面DFE 所成的二面角的正弦值最小?【答案】(1)证明见解析;(2)112B D =【详解】(1)[方法一]:几何法因为1111,//BF AB AB AB ⊥,所以BF AB ⊥.又因为1AB BB ⊥,1BF BB B ⋂=,所以AB ⊥平面11BCC B .又因为2AB BC ==,构造正方体1111ABCG A B C G -,如图所示,过E 作AB 的平行线分别与AG BC ,交于其中点,M N ,连接11,AM BN ,因为E ,F 分别为AC 和1CC 的中点,所以N 是BC 的中点,易证1Rt Rt BCF B BN ≅ ,则1CBF BBN ∠=∠.又因为1190BBN BNB ∠+∠=︒,所以1190CBF BNB BF BN ∠+∠=︒⊥,.又因为111111,BF AB BN AB B ⊥= ,所以BF ⊥平面11A MNB .又因为ED ⊂平面11A MNB ,所以BF DE ⊥.[方法二]【最优解】:向量法因为三棱柱111ABC A B C -是直三棱柱,1BB ∴⊥底面ABC ,1B B AB ∴⊥11//A B AB ,11BF A B ⊥,BF AB ∴⊥,又1BB BF B ⋂=,AB ∴⊥平面11BCC B .所以1,,BA BC BB 两两垂直.以B 为坐标原点,分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系,如图.()()()0,0,0,2,0,0,0,2,0,B AC ∴()()()1110,0,2,2,0,2,0,2,2B A C ,()()1,1,0,0,2,1E F .由题设(),0,2D a (02a ≤≤).因为()()0,2,1,1,1,2BF DE a ==--,所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=,所以BF DE ⊥.[方法三]:因为11BF A B ⊥,11//A B AB ,所以BF AB ⊥,故110BF A B ⋅= ,0BF AB ⋅=,所以()11BF ED BF EB BB B D ⋅=⋅++ ()11=BF B D BF EB BB ⋅+⋅+ 1BF EB BF BB =⋅+⋅ 11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=52520255-⨯⨯⨯,所以BF ED ⊥.(2)[方法一]【最优解】:向量法设平面DFE 的法向量为(),,m x y z = ,因为()()1,1,1,1,1,2EF DE a =-=--,所以00m EF m DE ⎧⋅=⎨⋅=⎩,即()0120x y z a x y z -++=⎧⎨-+-=⎩.令2z a =-,则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =,设平面11BCC B 与平面DEF 的二面角的平面角为θ,则cos m BA m BA θ⋅=⋅ 222214a a =⨯-+22214a a =-+当12a =时,2224a a -+取最小值为272,此时cos θ=.所以()minsin θ=,此时112B D =.[方法二]:几何法如图所示,延长EF 交11A C 的延长线于点S ,联结DS 交11B C 于点T ,则平面DFE 平面11B BCC FT =.作1BH FT ⊥,垂足为H ,因为1DB ⊥平面11BB C C ,联结DH ,则1D H B ∠为平面11BB C C 与平面DFE 所成二面角的平面角.设1,B D t =[0,2],t ∈1B T s =,过1C 作111//CG AB 交DS 于点G .由111113C S C G SA A D ==得11(2)3C G t =-.又1111B D BT C G C T=,即12(2)3t s s t =--,所以31t s t =+.又111B H BT C F FT=,即11B H =1B H =所以DH ===则11sin B D DHB DH∠===所以,当12t =时,()1min sin 3DHB ∠=.[方法三]:投影法如图,联结1,FB FN,DEF 在平面11BB C C 的投影为1BN F ,记面11BB C C 与面DFE 所成的二面角的平面角为θ,则1cos B NF DEFS S θ=.设1(02)BD t t =≤≤,在1Rt DB F中,DF ==在Rt ECF中,EF 过D 作1B N 的平行线交EN 于点Q .在Rt DEQ △中,DE ==在DEF 中,由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅=sin DFE ∠=1sin 2DFE S DF EF DFE =⋅∠ =13,2B NF S = 1cos B NF DFES S θ==sin θ当12t =,即112B D =,面11BBC C 与面DFE所成的二面角的正弦值最小,最小值为3.(2021·全国·统考高考真题)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,ABAD =,O 为BD 的中点.(1)证明:OA CD ⊥;(2)若OCD 是边长为1的等边三角形,点E 在棱AD 上,2DE EA =,且二面角E BC D --的大小为45︒,求三棱锥A BCD -的体积.【答案】(1)证明见解析;(2)6.(2)方法二:利用几何关系找到二面角的平面角,然后结合相关的几何特征计算三棱锥的体积即可.【详解】(1)因为AB AD =,O 是BD 中点,所以OA BD ⊥,因为OA ⊂平面ABD ,平面ABD ⊥平面BCD ,且平面ABD ⋂平面BCD BD =,所以OA ⊥平面BCD .因为CD ⊂平面BCD ,所以OA CD ⊥.(2)[方法一]:通性通法—坐标法如图所示,以O 为坐标原点,OA 为z 轴,OD 为y 轴,垂直OD 且过O 的直线为x 轴,建立空间直角坐标系O xyz-,则1,0),(0,1,0),(0,1,0)2C D B -,设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,0)3322EB m BC =--= ,设(),,n x y z =r为平面EBC 的法向量,则由00EB n EC n ⎧⋅=⎨⋅=⎩ 可求得平面EBC 的一个法向量为2(3,1,)n m=--.又平面BCD 的一个法向量为()0,0,OA m =,所以222cos ,244n OA m m -=⋅+,解得1m =.又点C 到平面ABD 321133213226A BCD C ABD V V --==⨯⨯⨯=所以三棱锥A BCD -36.[方法二]【最优解】:作出二面角的平面角如图所示,作EG BD ⊥,垂足为点G .作GF BC ⊥,垂足为点F ,连结EF ,则OA EG ∥.因为OA ⊥平面BCD ,所以EG ⊥平面BCD ,EFG ∠为二面角E BC D --的平面角.因为45EFG ∠=︒,所以EG FG =.由已知得1OB OD ==,故1OB OC ==.又30OBC OCB ∠=∠=︒,所以3BC =.因为24222,,,,133333GD GB FG CD EG OA ======,111122(11)13332A BCD BCD BOC V S O S OA A -==⨯⨯=⨯⨯⨯⨯⨯ .[方法三]:三面角公式考虑三面角B EDC -,记EBD ∠为α,EBC ∠为β,30DBC ∠=︒,记二面角E BC D --为θ.据题意,得45θ=︒.对β使用三面角的余弦公式,可得cos cos cos30βα=⋅︒,化简可得cos 2βα=.①使用三面角的正弦公式,可得sin sin sin αβθ=,化简可得sin βα=.②将①②两式平方后相加,可得223cos 2sin 14αα+=,由此得221sin cos 4αα=,从而可得1tan 2α=±.如图可知π(0,)2α∈,即有1tan 2α=,根据三角形相似知,点G 为OD 的三等分点,即可得43BG =,结合α的正切值,可得2,13EG OA ==从而可得三棱锥A BCD -的体积为6.4.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【答案】(1)证明过程见解析(2)CF 与平面ABD 所成的角的437【详解】(1)因为AD CD =,E 为AC 的中点,所以AC DE ⊥;在ABD △和CBD △中,因为,,B A C D CD ADB DB DB D ∠=∠==,所以ABD CBD ≌△△,所以AB CB =,又因为E 为AC 的中点,所以AC BE ⊥;又因为,DE BE ⊂平面BED ,DE BE E ⋂=,所以AC ⊥平面BED ,因为AC ⊂平面ACD ,所以平面BED ⊥平面ACD .(2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED ,所以AC EF ⊥,所以1=2AFC S AC EF ⋅△,当EF BD ⊥时,EF 最小,即AFC △的面积最小.因为ABD CBD ≌△△,所以2CB AB ==,又因为60ACB ∠=︒,所以ABC 是等边三角形,因为E 为AC 的中点,所以1AE EC ==,3BE =因为AD CD ⊥,所以112DE AC ==,在DEB 中,222DE BE BD +=,所以BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz -,则()()()1,0,0,3,0,0,0,1A B D ,所以()()1,0,1,3,0AD AB =-=-,设平面ABD 的一个法向量为(),,n x y z =,则00n AD x z n AB x ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩,取y =()n = ,又因为()31,0,0,,4C F ⎛⎫- ⎪ ⎪⎝⎭,所以34CF ⎛⎫= ⎪ ⎪⎝⎭ ,所以cos ,7n CF n CF n CF⋅==,设CF 与平面ABD 所成的角的正弦值为02πθθ⎛⎫≤≤ ⎪⎝⎭,所以sin cos ,n CF θ== 所以CF 与平面ABD所成的角的正弦值为7.5.(2022·全国·统考高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD 是边长为8(单位:cm )的正方形,,,,EAB FBC GCD HDA 均为正三角形,且它们所在的平面都与平面ABCD垂直.(1)证明://EF 平面ABCD ;(2)求该包装盒的容积(不计包装盒材料的厚度).【答案】(1)证明见解析;【详解】(1)如图所示:分别取,AB BC 的中点,M N ,连接MN ,因为,EAB FBC为全等的正三角形,所以,EM AB FN BC ⊥⊥,EM FN =,又平面EAB ⊥平面ABCD ,平面EAB ⋂平面ABCD AB =,EM ⊂平面EAB ,所以EM ⊥平面ABCD ,同理可得FN ⊥平面ABCD ,根据线面垂直的性质定理可知//EM FN ,而EM FN =,所以四边形EMNF 为平行四边形,所以//EF MN ,又EF ⊄平面ABCD ,MN ⊂平面ABCD ,所以//EF 平面ABCD .(2)[方法一]:分割法一如图所示:分别取,AD DC 中点,K L ,由(1)知,//EF MN 且EF MN =,同理有,//,HE KM HE KM =,//,HG KL HG KL =,//,GF LN GF LN =,由平面知识可知,BD MN ⊥,MN MK ⊥,KM MN NL LK ===,所以该几何体的体积等于长方体KMNL EFGH -的体积加上四棱锥B MNFE -体积的4倍.因为MN NL LK KM ====,8sin 60EM == 点B 到平面MNFE 的距离即为点B 到直线MN 的距离d,d =(21343V =⨯+⨯⨯==.[方法二]:分割法二如图所示:连接AC,BD,交于O ,连接OE,OF,OG,OH.则该几何体的体积等于四棱锥O-EFGH 的体积加上三棱锥A-OEH 的4倍,再加上三棱锥E-OAB 的四倍.容易求得,OE=OF=OG=OH=8,取EH 的中点P ,连接AP,OP.则EH 垂直平面APO.由图可知,三角形APO,四棱锥O-EFGH 与三棱锥E-OAB 的高均为EM 的长.所以该几何体的体积(21111144444433232V =⋅+⋅⋅⋅⋅6.(2022·全国·统考高考真题)如图,直三棱柱111ABC A B C -的体积为4,1A BC的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.【答案】2.【详解】(1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h ,则111111111143333A A BC A A ABC A ABC A B BC C C B V S h V S A A V ---=⋅===⋅==,解得h =所以点A 到平面1A BC;(2)取1A B 的中点E,连接AE,如图,因为1AA AB =,所以1AE A B ⊥,又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =,且AE ⊂平面11ABB A ,所以⊥AE 平面1A BC ,在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥,又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A ,所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB ==,1A B =以2BC =,则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1AC 的中点()1,1,1D ,则()1,1,1BD = ,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩,可取()1,0,1m =- ,设平面BDC 的一个法向量(),,n a b c = ,则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩,可取()0,1,1n =-r,则1cos ,2m n m n m n ⋅==⋅,所以二面角A BD C --2=.7.(2022·全国·统考高考真题)如图,PO 是三棱锥-P ABC 的高,PA PB =,AB AC ⊥,E 是PB的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B --的正弦值.【答案】(1)证明见解析(2)1113【详解】(1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥-P ABC 的高,所以PO ⊥平面ABC ,,AO BO ⊂平面ABC ,所以PO AO ⊥、PO BO ⊥,又PA PB =,所以POA POB ≅△△,即OA OB =,所以OAB OBA ∠=∠,又AB AC ⊥,即90BAC ∠=︒,所以90OAB OAD ∠+∠=︒,90OBA ODA ∠+∠=︒,所以ODA OAD∠=∠所以AO DO =,即AO DO OB ==,所以O 为BD 的中点,又E 为PB 的中点,所以//OE PD ,又OE ⊄平面PAC ,PD ⊂平面PAC ,所以//OE 平面PAC(2)解:过点A 作//Az OP ,如图建立空间直角坐标系,因为3PO =,5AP =,所以224OA AP PO =-=,又30OBA OBC ∠=∠=︒,所以28BD OA ==,则4=AD ,43AB =所以12AC =,所以()23,2,0O ,()43,0,0B ,()23,2,3P ,()0,12,0C ,所以333,1,2E ⎛⎫ ⎪⎝⎭,则333,1,2AE ⎛⎫= ⎪⎝⎭ ,()3,0,0AB =,()0,12,0AC = ,设平面AEB 的法向量为(),,n x y z =,则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩,令2z =,则=3y -,0x =,所以()0,3,2n =-;设平面AEC 的法向量为(),,m a b c =,则33302120m AE a b c m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩,令a 6c =-,0b =,所以)6m =-;所以cos ,n m n m n m⋅==设二面角C AE B --的大小为θ,则cos cos ,=n m θ=所以11sin 13θ==,即二面角C AE B --的正弦值为1113.8.(2022·北京·统考高考真题)如图,在三棱柱111ABC A B C -中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N 分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值.条件①:AB MN ⊥;条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.【答案】(1)见解析(2)见解析【详解】(1)取AB 的中点为K ,连接,MK NK ,由三棱柱111ABC A B C -可得四边形11ABB A 为平行四边形,而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B ,而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B ,而,,NK MK K NK MK =⊂ 平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B ,(2)因为侧面11BCC B 为正方形,故1CB BB ⊥,而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A ,平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A ,因为//NK BC ,故NK ⊥平面11ABB A ,因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N = ,故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥,所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M ,故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩ ,从而020x y y z +=⎧⎨+=⎩,取1z =-,则()2,2,1n =--,设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯ .若选②,因为//NK BC ,故NK ⊥平面11ABB A ,而KM ⊂平面MKN ,故NK KM ⊥,而11,1B M BK NK ===,故1B M NK =,而12B B MK ==,MB MN =,故1BB M MKN ≅ ,所以190BB M MKN ∠=∠=︒,故111A B BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M ,故()()()0,2,0,1,1,0,0,1,2BA BN BM === ,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =-,则()2,2,1n =--,设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯.9.(2022·天津·统考高考真题)直三棱柱111ABC A B C -中,112,,AA AB AC AA AB AC AB ===⊥⊥,D 为11A B 的中点,。
专题4:立体几何(理科)

专题四:立体几何【一、基础知识归类:】1、三视图画法规则:高平齐:主视图与左视图的高要保持平齐 长对正:主视图与俯视图的长应对正 宽相等:俯视图与左视图的宽度应相等2、空间几何体三视图:正视图(从前向后的正投影);侧视图(从左向右的正投影); 俯视图(从上向下正投影).3、空间几何体的直观图——斜二测画法特点:①斜二测坐标系的y 轴与x 轴正方向成 45角; ②原来与x 轴平行的线段仍然与x 平行,长度不变; ③原来与y 轴平行的线段仍然与y 平行,长度为原来的一半. 常用结论:平面图形面积与其斜二侧直观图面积之比为22:1. 4、特殊几何体表面积公式(c 为底面周长,h 为高,'h 为斜高,l 为母线):ch S =直棱柱侧面积 rh S π2=圆柱侧 '21ch S =正棱锥侧面积 rl S π=圆锥侧面积 ')(2121h c c S +=正棱台侧面积 l R r S π)(+=圆台侧面积 ()l r r S +=π2圆柱表 ()l r r S +=π圆锥表()22R Rl rl r S +++=π圆台表 S 球面=24R π5、柱体、锥体、台体和球的体积公式:V Sh =柱 2V Sh r h π==圆柱 13V S h =锥 h r V 231π=圆锥'1()3V S S h =台'2211()()33V S S h r rR R h π=++=++圆台V 球=343R π 6、空间线面的位置关系①直线与直线:相交、平行、异面(不同在任何一个平面内的两条直线); ②直线与平面:属于a ⊂α、相交a∩α=A 、平行a ∥α;③ 平面与平面:平行—没有公共点:α∥β、相交—有一条公共直线:α∩β=b . 7、垂直和平行证明问题的解决方法须熟练掌握两类相互转化关系: 1.平行转化2.垂直转化同时注意结合运用中位线定理、勾股定理、等腰(等边)三角形“三线合一”; 平行四边形两组对边分别平行且相等,对角线互相平分; 菱形对边平行且四边相等,对角线互相垂直平分并平分对角; 矩形对边平行且相等,四个角为直角,以及对角线互相平分且相等;正方形对边平行且四边相等,四个角为直角,对角线互相垂直平分且相等并平分对角; 梯形上底和下底平行; 圆直径对应圆周角为直角、垂径定理、过切点的半径垂直于切线等. 8、立体几何中体积的求法:直接法、割补法、等积转化等方法. 9、(1)求异面直线所成的角θ∈(0,2π]. ①平移转化法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线;或过空间任一点分别作两异面直线的平行线,这样就作出了两异面直线所成的角θ,构造一个含θ的三角形,解三角形即可.②空间向量法:232221232221332211||||,cos bb b a a a b a b a b a b a ba b a ++⋅++++=⋅⋅>=<.(2)求直线与平面所成的角θ∈0,2π⎡⎤⎢⎥⎣⎦. ①一般先确定直线与平面的交点(斜足),然后在直线上取一点(除斜足外)作平面的垂线,再连接垂足和斜足(即得直接在平面内的射影),最后解由垂线、斜线、射影所组成的直角三角形,求出直线与平面所成的角.②法向量求直线与平面所成的角:要求直线a 与平面α所成的角θ,先求这个平面α的法向量与直线a的夹角的余弦a ,易知θ=a 2-π.(3)求二面角θ∈(0,π).1)直接法求二面角通常有:①根据定义作二面角的平面角;②垂面法作二面角的平面角; ③利用三垂线定理及其逆定理作二面角的平面角;无棱二面角先作出棱后同上进行. 2)间接法主要是投影法:即在一个平面α上的图形面积为S ,它在另一个平面β上的 投影面积为S′,这两个平面的夹角为θ,则S ′=S cos θ.3)法向量求二面角:如图,有两个平面α与β,分别作这两个平面的法向量1n 与2n ,则平面α与β所成的角跟法向量1n 与2n 所成的角2n 相等或互补,所以首先必须判断二面角是锐角还是钝角. 10.空间求距离(1)用法向量求异面直线间的距离:如右图所示,a 、b 是两异面直线,是a 和b的法向量,点E ∈a ,F ∈b ,则异面直线a 与b之间的距离是d=.(2)求点到平面的距离:①法向量:如右图所示,已知AB 是平面α的一条斜线,n 为平面α的法向量,则 A 到平面α的距离为d =;②等体积法:即求棱锥的高.(3)用法向量求直线到平面间的距离:首先必须确定直线与平面平行,然后将直线到平面的距离问题转化成直线上一点到平面的距离问题.(4)用法向量求两平行平面间的距离:首先必须确定两个平面是否平行,这时可以在一个平面上任取一点,将两平面间的距离问题转化成点到平面的距离问题.【二、专题练习:】一、选择题(本大题共12小题,每小题5分,总分60分)1.(2009天津重点学校二模) 如图,直三棱柱的主视图面积为2a 2,则左视图的面积为( )A .2a 2B .a 2C .23a D .243a2.(2009枣庄市二模)一个几何体的三视图如图所示, 则这个几何体的体积等于( ) A .361a B .321a C .332a D .365a 3.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( ) A .38π B .328π C .π28 D .332π 4.如图,正四棱柱1111D C B A ABCD -中,AB AA 21=, 则异面直线11AD B A 与所成角的余弦值为( )aaaA .51 B .52C .53D .545.给定空间中的直线l 及平面α,条件“直线l 与平面α内无 数条直线都垂直”是“直线l 与平面α垂直”的( )条件A .充要B .充分非必要C .必要非充分D .既非充分又非必要 6.一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )为( )A .48+B .48+C .36+D .36+7.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1, 则BC 1与平面BB 1D 1D 所成角的余弦值为( )B.C.D.8.如图,在四面体ABCD 中,截面PQMN 是正方形, 则在下列命题中,错误..的为( ) A . AC BD ⊥B . AC ∥截面PQMNC . AC BD =D . 异面直线PM 与BD 所成的角为459.(2009泰安一模)一个几何体的三视图如图所示,则这个几何体的体积等于( )A .4B .6C .8D .1210.设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是( ) A .βαβα⊥⊥,//,b a B .βαβα//,,⊥⊥b aC .βαβα//,,⊥⊂b aD .βαβα⊥⊂,//,b a11.如图,1111ABCD A BC D -为正方体,下面结论错误..的是( ) (A )//BD 平面11CB D (B )1AC BD ⊥(C )1AC ⊥平面11CB D(D )异面直线AD 与1CB 所成的角为60︒12.正六棱锥P -ABCDEF 中,G 为PB 的中点,则三棱锥D -GAC 与三棱锥P -GAC 体积之比为( ) A .1:1 B .1:2 C .2:1 D .3:2二、填空题(本大题共4小题,每小题4分,总分16分)13.如果一个水平放置的图形的斜二测直观图是一个底面为045,腰和上底均为1的等腰梯形,那么原平面图形的面积是 .14.在半径为13的球面上有A , B , C 三点,AB=6,BC=8,CA=10,则球心到平面ABC 的距离为 . 15.图2中实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD 是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是14,则此长方体的体积是 .16.如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D ,作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .三、解答题(本大题共6小题,总分74分)17.如图,四棱锥P —ABCD 的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点. (Ⅰ)证明PA//平面BDE ;A(Ⅱ)求二面角B —DE —C 的平面角的余弦值;(Ⅲ)在棱PB 上是否存在点F ,使PB ⊥平面DEF ?证明你的结论.18.(2009东莞一模)如图,在长方体1,1,11111>==-AB AA AD D C B A ABCD 中,点E 在棱AB 上移动,小蚂蚁从点A 沿长方体的表面爬到点C 1,所爬的最短路程为22. (1)求证:D 1E ⊥A 1D ; (2)求AB 的长度;(3)在线段AB 上是否存在点E ,使得二面角41π的大小为D EC D --.若存在,确定点E 的位置;若不存在,请说明理由.19.(2009番禺一模)如图,在四棱锥P ABCD-中,底面形,侧面PAD ⊥底面ABCD,且PA P D ==,若E 、F分别为线段PC 、BD 的中点. (1)求证:直线EF // 平面PAD ; (2)求证:平面PDC ⊥平面PAD ; (3)求二面角B PD C --的正切值.20.(广东省湛江二中2010届高三第四次月考)如图,在四棱锥P-ABCD 中,底面ABCD 是正方形,PA ⊥底面ABCD ,垂足为A ,PA=AB ,点M 在棱PD 上,PB ∥平面ACM . (1)试确定点M 的位置;(2)计算直线PB 与平面MAC 的距离;(3)设点E 在棱PC 上,当点E 在何处时,使得AE ⊥平面PBD ?21.(2009汕头一模)如图,己知∆BCD 中,∠BCD = 900,BC =CD =1,AB ⊥平面BCD ,∠ADB =600,E 、F 分别是AC 、AD 上的动点,且(01)AE AFAC ADλλ==<<. (1)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;D(2)若平面BEF 与平面BCD 所成的二面角的大小为60°,求λ的值.22.如图,四面体ABCD 中,O 是BD 的中点,ABD ∆和BCD ∆均为等边三角形,2,AB AC = (I )求证:AO ⊥平面BCD ;(Ⅱ)求二面角A BC D --的余弦值; (Ⅲ)求O 点到平面ACD 的距离.【参考答案】一、选择题 1.C 2.D3.答案:B 解析:截面面积为π⇒截面圆半径为1,又与球心距离为1⇒的体积公式知3433R V π==球,故B 为正确答案. 4.D5.答案:C 解析:直线与平面α内的无数条平行直线垂直,但该直线未必与平面α垂直,即充分性不成立. 6.答案:A 解析:棱锥的直观图如右,则有PO =4,OD =3,由勾股定理,得PD =5,AB =62,全面积为:21×6×6+2×21×6×5+21×62×4=48+122,故选A . 7.【解析】选D. 连11AC 与11B D 交于O 点,再连BO ,则1OBC ∠为BC 1与平面BB 1D 1D 所成的角.111cos OC OBC BC ∠=,1OC =1BC =1cos OBC ∴∠=.8—9:D A10.答案:C 解析:由b β⊥,α∥β得b α⊥,又a α⊂,可知b a ⊥,故a b ⊥的一个充分条件是C . 11.【解析】选D .显然异面直线AD 与1CB 所成的角为45︒.12.【解析】选C .由于G 是PB 的中点,故P -GAC 的体积等于B -GAC 的体积 在底面正六边形ABCDER 中 BH =ABtan30°=而BD故DH =2BH 于是V D -GAC =2V B -GAC =2V P -GAC .二、填空题13.恢复后的原图形为一直角梯形1(11)222S =+⨯=+ 14.答案:12解析:由ABC ∆的三边大小易知此三角形是直角三角形,所以过,,A B C 三点小圆的直径即为10,也即半径是5,设球心到小圆的距离是d ,则由222513d +=,可得12d =.15.【解析】向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是14,设长方体的高为x ,则()()42122214x x x +=++,所以3x =,所以长方体的体积为3.16.【解析】此题的破解可采用二个极端位置法,即对于F 位于DC 的中点时,1t =,随着F 点到C 点时,因,,CB AB CB DK CB ⊥⊥∴⊥平面A D B ,即有CB BD ⊥,对于2,1,CD BC BD ==∴,又1,2AD AB ==,因此有AD BD ⊥,则有12t =,因此t 的取值范围是1,12⎛⎫⎪⎝⎭.三、解答题17.【解析】(Ⅰ)以D 为坐标原点,分别以DA 、DC 、DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,设PD=DC=2,则A (2,0,0),P (0,0,2),E (0,1,1),B (2,2,0), )0,2,2(),1,1,0(),2,0,2(==-=设 1(,,)n x y z =是平面BDE 的一个法向量,则由 111001,(1,1,1).2200n DE y z y n x y n DB ⎧⋅=+=⎧⎪=-=-⎨⎨+=⋅=⎩⎪⎩得取得∵11220,,//.PA n PA n PA BDE PA BDE ⋅=-=∴⊥⊄∴,又平面平面 (Ⅱ)由(Ⅰ)知1(1,1,1)n =-是平面BDE 的一个法向量, 又2(2,0,0)n DA ==是平面DEC 的一个法向量.设二面角B —DE —C 的平面角为θ,由图可知12,n n θ=<>∴121212cos cos ,||||3n n n n n n θ⋅=<>===⋅⨯故二面角B —DE —C 的余弦值为33(Ⅲ)∵)1,1,0(),2,2,2(=-= ∴.,0220DE PB DE PB ⊥∴=-+=⋅ 假设棱PB 上存在点F ,使PB ⊥平面DEF ,设)10(<<=λλ, 则)22,2,2(),2,2,2(λλλλλλ-=+=-=PF DP DF PF ,由0)22(244022=--+=⋅λλλλ得∴PB PF 31)1,0(31=∈=,此时λ即在棱PB 上存在点F ,31=PF PB ,使得PB ⊥平面DEF18.解一:(1)证明:连结AD 1,由长方体的性质可知:AE ⊥平面AD 1,∴AD 1是ED 1在 平面AD 1内的射影。
江苏名校备战高考12讲专题04 立体几何(学生版)

专题04 立体几何 一、单选题1. 【江苏省南通市2020-2021学年高三上学期12月月考模拟】在三棱锥P ABC -中,PA ⊥平面ABC ,23BAC π∠=,3AP =,23AB =,Q 是边BC 上的一动点,且直线PQ 与平面ABC 所成角的最大值为3π,则三棱锥P ABC -的外接球的表面积为( )A .50πB .55πC .57πD .108π2. 【江苏省南通市2020-2021学年高三上学期期中】把与直线l 垂直的向量称为直线l 的法向量.设(,)e A B =是直线l 的一个方向向量,那么(,)n B A =- 就是直线l 的一个法向量.借助直线的法向量,我们可以方便地计算点到直线的距离.已知P 是直线l 外一点,n 是直线l 的一个法向量,在直线l 上任取一点Q ,那么PQ 在法向量n 上的投影向量为()cos n PQ n θ⋅(θ为向量n 与PQ 的夹角),其模就是点P 到直线l 的距离d ,即PQ n d n ⋅=.据此,请解决下面的问题:已知点A (-4,0),B (2,-1),C (-1,3),则点A 到直线BC 的距离是( ) A .215 B .7 C .275 D .83. 【江苏省南通市2021届高三下学期3月模拟】一个正三棱锥(底面积是正三角形,顶点在底面上的射影为底面三角形的中心)的四个顶点都在半径为1的球面上,球心在三棱锥的底面所在平面上,则该正三棱锥的体积是A .334B .33C .34D .3124. 【江苏省南通市海安高级中学2020-2021学年高三上学期12月测试】三棱锥A BCD -中,60ABC CBD DBA ∠=∠=∠=︒,2BC BD ==,ACD △的面积为11,则此三棱锥外接球的体积为( )A .16πB .4πC .163πD .323π 5. 【江苏省南通市海安市实验中学2020-2021学年高三上学期第三次学情检测】如图所示,在正方体1111ABCD A B C D -中,E ,F 分别是11AB BC ,的中点,则异面直线EF 与1C D 所成的角为( )A .30B .45︒C .60︒D .90︒6. 【江苏省南通市如皋市2020-2021学年高三上学期10月第一次教学质量调研】在三棱锥P ABC -中,PA ⊥面ABC ,ABC 是边长为2的正三角形,且3PA =,则二面角P BC A --的大小为( ) A .30 B .45︒ C .60︒ D .无法确定7. 【江苏省南通市如皋市2020-2021学年高三上学期教学质量调研(三)】直三棱柱111ABC A B C -中,侧棱14BB =,2AB =,3AC BC ==,则点C 到平面11A BC 的距离为( )A .22211B .42211C .62211D .1222118. 【江苏省南通市如皋市2020-2021学年高三上学期期中】正三棱锥S ABC -中,2SA =,22AB =,则该棱锥外接球的表面积为( )A .43πB .4πC .12πD .6π9. 【江苏省南通市如皋市2021届高三下学期4月第二次适应性考试】如图,在边长为2的正方形ABCD 中,点M 、N 分别是边CD 、BC 的中点,将ADM △沿AM 翻折到PAM △,在ADM △翻折到PAM △的过程中,tan PND ∠的最大值为( )A .54B .255C .55D .2310. 【江苏省南通市通州区、启东市2020-2021学年高三上学期期末】攒尖是古代中国建筑中屋顶的一种结构形式依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑如图所示,某园林建筑为六角攒尖,它的主要部分的轮廓可近似看作一个正六棱锥,设正六棱锥的侧面等腰三角形的顶角为2θ,则侧棱与底面内切圆半径的比为( )A .33sin θB .33cos θC .12sin θD .12cos θ11. 【江苏省镇江市、南通市如皋2020-2021学年高三上学期教学质量调研(二)】正三棱锥S ABC -中,2SA =,22AB =,则该棱锥外接球的表面积为( )A .43πB .4πC .12πD .6π12. 【江苏省如东高级中学、丹阳高级中学、如皋中学2020-2021学年高三上学期12月三校联考】棱长为6的正四面体ABCD 与正三棱锥E BCD -的底面重合,若由它们构成的多面体ABCDE 的顶点均在一球的球面上,则正三棱锥E BCD -的体积为( )A .92B .242C .362D .722二、多选题1. 【江苏省南通,徐州,淮安,泰州,宿迁,镇江,连云港等七市2021届高三下学期2月第一次调研】已知m ,n 是两条不重合的直线,α,β是两个不重合的平面,则( )A .若//m α,//n α,则//m nB .若//m α,m β⊥,则αβ⊥C .若//αβ,m α⊥,n β⊥,则//m nD .若αβ⊥,//m α,βn//,则m n ⊥ 2. 【江苏省南通市2020-2021学年高三上学期12月月考模拟】已知边长为2的等边ABC ,点D 、E 分别是边AC 、AB 上的点,满足//DE BC 且ADAC λ=(()0,1λ∈),将ADE 沿直线DE 折到A DE '的位置,在翻折过程中,下列结论成立的是( )A .在边A E '上存在点F ,使得在翻折过程中,满足//BF 平面ACD 'B .存在102λ∈⎛⎫ ⎪⎝⎭,,使得在翻折过程中的某个位置,满足平面A BC '⊥平面BCDE C .若12λ=,当二面角A DE B '--等于60°时,72A B '= D .在翻折过程中,四棱锥A BCDE '-体积的最大值记为()f λ,()f λ的最大值为2393. 【江苏省南通市2020-2021学年高三上学期期中】如图,四棱锥P ABCD -中,平面PAD ⊥底面ABCD ,PAD △是等边三角形,底面ABCD 是菱形,且60BAD ∠=︒,M 为棱PD 的中点,N 为菱形ABCD 的中心,下列结论正确的有( )A .直线PB 与平面AMC 平行B .直线PB 与直线AD 垂直C .线段AM 与线段CM 长度相等D .PB 与AM 所成角的余弦值为24 4. 【江苏省南通市2021届高三下学期3月模拟】已知菱形ABCD 中,∠BAD =60°,AC 与BD 相交于点O .将∠ABD 沿BD 折起,使顶点A 至点M ,在折起的过程中,下列结论正确的是( ) A .BD ∠CMB .存在一个位置,使∠CDM 为等边三角形C .DM 与BC 不可能垂直D .直线DM 与平面BCD 所成的角的最大值为60°5. 【江苏省南通市海安市2020-2021学年高三上学期阶段质量检测(一)】如图所示,在长方体1111ABCD A B C D -,若AB BC =,E 、F 分别是1AB 、1BC 的中点,则下列结论中成立的是( )A .EF 与1BB 垂直B .EF ⊥平面11BDD BC .EF 与1CD 所成的角为45︒ D .//EF 平面1111D C B A6. 【江苏省南通市海安市2020-2021学年高三上学期期末】在棱长为2的正四面体ABCD 中,点E ,F ,G 分别为棱BC ,CD ,DA 的中点,则( )A .//AC 平面EFGB .过点E ,F ,G 的截面的面积为12C .AD 与BC 的公垂线段的长为2D .CD 与平面GBC 所成角的大小小于..二面角G BC D --的大小 7. 【江苏省南通市启东市2020-2021学年高三上学期期中】已知正方体1111ABCD A B C D -的棱长为4,点M ,N 分别是棱11A D ,CD 的中点,点P 在四边形ABCD 内,点Q 在线段BN 上,若25PM =,则( ) A .点P 的轨迹的长度为2π B .线段MP 的轨迹与平面11ADC B 的交线为圆弧C .PQ 长度的最小值为65105-D .PQ 长度的最大值为252+ 8. 【江苏省南通市如东县2020-2021学年高三上学期期末】如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段11B D 上一动点(包括端点),则以下结论正确的有( )A .三棱锥1P A BD -的体积为定值13B .过点P 平行于平面1A BD 的平面被正方体1111ABCD A BCD -截得的多边形的面积为32C .直线1PA 与平面1A BD 所成角的正弦值的范围为36,33⎡⎤⎢⎥⎣⎦ D .当点P 与1B 重合时,三棱锥1P A BD -的外接球的体积为32π 9. 【江苏省南通市如皋市2020-2021学年高三上学期10月第一次教学质量调研】设α,β是两个相交平面,则下列说法正确的是( )A .若直线m α⊥,则在平面β内一定存在无数条直线与直线m 垂直B .若直线m α⊥,则在平面β内一定不存在与直线m 平行的直线C .若直线m α⊂,则在平面β内一定存在与直线m 垂直的直线D .若直线m α⊂,则在平面β内一定不存在与直线m 平行的直线10. 【江苏省南通市如皋市2020-2021学年高三上学期期末】如图,在边长为2的正方形ABCD 中,点M 是边CD 的中点,将ADM △沿AM 翻折到PAM △,连结PB ,PC ,在ADM △翻折到PAM △的过程中,下列说法正确的是( )A .四棱锥P ABCM -的体积的最大值为255B .当面PAM ⊥平面ABCM 时,二面角PAB C 的正切值为54C .存在某一翻折位置,使得AM PB ⊥D .棱PB 的中点为N ,则CN 的长为定值 11. 【江苏省南通市如皋市2020-2021学年高三上学期期中】在正方体1111ABCD A B C D -中,若E ,F 分别为1B B ,11B C 的中点,则( )A .直线1//A E 平面1ACDB .直线1B D ⊥平面1ACDC .平面1//A EF 平面1ACD D .平面11A B CD ⊥平面1ACD 12. 【江苏省南通市如皋市2021届高三下学期4月第二次适应性考试】在四面体ABCD 中,ABC 是边长为2的正三角形.60ADB ∠=︒,二面角D AB C --的大小为60︒,则下列说法正确的是( )A .AB CD ⊥B .四面体ABCD 的体积V 的最大值为32 C .棱CD 的长的最小值为3D .四面体ABCD 的体积最大时,四面体ABCD 的外接球的表面积为529π 13. 【江苏省镇江市、南通市如皋2020-2021学年高三上学期教学质量调研(二)】在正方体1111ABCD A B C D -中,若E ,F 分别为1B B ,11B C 的中点,则( )A .直线1//A E 平面1ACDB .直线1B D ⊥平面1ACDC .平面1//A EF 平面1ACD D .平面11A B CD ⊥平面1ACD14. 【江苏省如东高级中学、丹阳高级中学、如皋中学2020-2021学年高三上学期12月三校联考】如图,正方体1111ABCD A B C D -的棱长为1,E 为1BA 的中点( )A .直线1EC 与直线AD 是异面直线B .在直线11AC 上存在点F ,使EF ⊥平面1ACDC .直线1BA 与平面1ACD 所成角是6π D .点B 到平面1ACD 的距离是22 15. 【江苏省南通市学科基地2020-2021学年高三上学期第一次联考】如图,在半圆柱中,AB 为上底面直径,DC 为下底面直径,AD ,BC 为母线,AB =AD =2,点F 在AB 上,点G 在DC 上,BF =DG =1,P 为DC 的中点.则( )A .BF ∠PGB .异面直线AF 与CG 所成角为60°C .三棱锥P —ACG 的体积为32D .直线AP 与平面ADG 所成角的正弦值为1510 16. 【江苏省南通市通州区2020-2021学年高三上学期第三次调研考试】下列命题中正确的是( ) A .,,,A B M N 是空间中的四点,若,,BA BM BN 不能构成空间基底,则,,,A B M N 共面B .已知{},,a b c 为空间的一个基底,若m a c =+,则{},,a b m 也是空间的基底C .若直线l 的方向向量为(1,0,3)e =,平面α的法向量为2(2,0,)3n =-,则直线//l αD .若直线l 的方向向量为(1,0,3)e =,平面α的法向量为(2,0,2)n =-,则直线l 与平面α所成角的正弦值为55三、填空题1. 【江苏省南通,徐州,淮安,泰州,宿迁,镇江,连云港等七市2021届高三下学期2月第一次调研】已知在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切.过直线12O O 的平面截圆柱得到四边形ABCD ,其面积为8.若P 为圆柱底面圆弧CD 的中点,则平面PAB 与球O 的交线长为___________.2. .【江苏省南通市2020-2021学年高三上学期期中】如图所示,在边长为2的菱形ABCD 中,60BCD ∠=︒,现将ABD △沿对角线BD 折起,得到三棱锥P BCD -.则当二面角P BD C --的大小为23π时,三棱锥P BCD -的外接球的表面积为______.3. 【江苏省南通市海安高级中学2020-2021学年高三上学期1月调研】在三棱锥P ABC -中,ABC 与PBC 均为边长为1的等边三角形,,,,P A B C ,四点在球O 的球面上,当三棱锥P ABC -的体积最大时,则球O 的表面积为______.4. 【江苏省南通市海安高级中学2020-2021学年高三上学期12月测试】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角三角形的四面体称为鳖臑.如图,四面体P ABC -为鳖臑,PA ⊥平面ABC ,AB BC ⊥,且1==PA AB ,2BC =,则二面角A PC B --的正弦值为______.5. .【江苏省南通市海安高级中学2020-2021学年高三上学期期中】已知三棱锥P ABC -中,PA ,PB ,PC 两两垂直,且1PA PB PC ===,以P 为球心,22为半径的球面与该三棱锥表面的交线的长度之和为______. 6. 【江苏省南通市海安市2020-2021学年高三上学期阶段质量检测(一)】如图,某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体,该正三棱锥的底面三角形内接于半球底面大圆,顶点在半球面上,则被挖去的正三棱锥体积为_______.7. 【江苏省南通市海安市2020-2021学年高三上学期期末】已知某空心圆锥的母线长为5cm ,高为4cm ,记该圆锥内半径最大的球为球O ,则球O 与圆锥侧面的交线的长为________cm .8. 【江苏省南通市海安市实验中学2020-2021学年高三上学期第三次学情检测】某同学在参加《通用技术》实践课时,制作了一个实心..工艺品(如图所示).该工艺品可以看成一是个球体被一个棱长为8的正方体的6个面所截后剩余的部分(球心与正方体的中心重合).若其中一个截面圆的周长为6π,则该球的半径为___;现给出定义:球面被平面所截得的一部分叫做球冠.截得的圆叫做球冠的底,垂直于截面的直径被截得的一段叫做球冠的高.如果球面的半径是R ,球冠的高是h ,那么球冠的表面积计算公式是2S Rh π= . 由此可知,该实心..工艺品的表面积是____.9. 【江苏省南通市启东市2020-2021学年高三上学期期中】在我国古代数学名著《九章算术》中,把两底面为直角三角形的直棱柱称为“堑堵”,已知三棱柱111ABC A B C -是一个“堑堵”,其中12AB BB ==,1BC =,5AC =,则这个“堑堵”的外接球的表面积为________.10. 【江苏省南通市如皋市2020-2021学年高三上学期10月第一次教学质量调研】在梯形ABCD 中,//AD BC ,AB BC ⊥,222AD AB BC ===,将ABC 沿对角线AC 翻折到AMC ,连结MD .当三棱锥M ACD -的体积最大时,该三棱锥的外接球的表面积为__________.11. 【江苏省南通市如皋市2020-2021学年高三上学期教学质量调研(三)】如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,三角形PAD 为正三角形,且平面PAD ⊥平面ABCD ,则四棱锥P ABCD -外接球的表面积为_________.12. 【江苏省南通市通州高级中学2020-2021学年高三上学期第五次阶段性测试】我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童ABCD EFGH -有外接球,且26,22,15,5AB AD EH EF ====,平面EFGH 与平面ABCD 的距离为1则,该刍童外接球的体积为______.13. 【江苏省如东高级中学、丹阳高级中学、如皋中学2020-2021学年高三上学期12月三校联考】如图,三棱锥P ABC -中,1BC =,2AC =,3PC =,PA AB =,PA AC ⊥,PB BC ⊥.点Q 在棱PB 上且1BQ =,则直线CQ 与平面ABC 所成的角是__________.14. 【江苏省南通市学科基地2020-2021学年高三上学期第一次联考】某公司周年庆典活动中,制作的“水晶球”工艺品如图所示,底座是用一边长为2m 的正方形钢板,按各边中点连线垂直折起四个小三角形制成,再将一个水晶玻璃球放入其中.若水晶球最高点到底座底面的距离为(2+1)m ,则水晶球的表面积为_______m 2.15. 【江苏省南通市通州区2020-2021学年高三上学期第三次调研考试】正方体1111ABCD A B C D -的棱长为1,E ,F 分别为BC ,1CC 的中点.则平面AEF 截正方体所得的截面面积为______;以点E 为球心,以104为半径的球面与对角面11ACC A 的交线长为______.四、解答题1. 【江苏省南通,徐州,淮安,泰州,宿迁,镇江,连云港等七市2021届高三下学期2月第一次调研】如图,在正六边形ABCDEF 中,将ABF 沿直线BF 翻折至A BF '△,使得平面A BF '⊥平面BCDEF ,O ,H 分别为BF 和A C '的中点.(1)证明://OH 平面A EF ';(2)求平面A BC '与平面A DE 所成锐二面角的余弦值.2. 【江苏省南通市2020-2021学年高三上学期12月月考模拟】如图,在四棱锥P ABCD -中,PD ⊥底面ABCD ,//AD BC ,90ABC ∠=︒,45BCD ∠=︒,2BC AD =.(1)求证:BD PC ⊥;(2)若PC BC =,求平面PAD 和平面PBC 所成的角(锐角)的余弦值.3. 【江苏省南通市2020-2021学年高三上学期期末模拟】如图,在四棱锥P -ABCD 中,23,AD =3,AB =3,AP =//AD BC ,AD ⊥平面PAB ,90APB ︒∠=,点E 满足2133PE PA PB =+.(1)证明:PE DC ⊥; (2)求二面角A -PD -E 的余弦值.4. 【江苏省南通市2020-2021学年高三上学期期中】已知四棱锥P ABCD ,底面ABCD 为菱形,PD =PB ,H 为PC 上的点,过AH 的平面分别交PB ,PD 于点M ,N ,且BD ∠平面AMHN .(1)证明:MN ∠PC ;(2)当H 为PC 的中点,PA =PC =3AB ,PA 与平面ABCD 所成的角为60°,求AD 与平面AMHN 所成角的正弦值.5. 【江苏省南通市海安高级中学2020-2021学年高三上学期1月调研】如图,平面ABCD ⊥平面DBNM ,且菱形ABCD 与菱形DBNM 全等,且MDB DAB ∠=∠,G 为MC 中点.(1)求证:平面//GBD 平面AMN .(2)求直线AD 与平面AMN 的所成角的正弦值.6. 【江苏省南通市海安高级中学2020-2021学年高三上学期12月测试】如图,在三棱锥P ABC -中,2AB BC ==,2PA PB PC AC ====.(1)证明:平面PAC ⊥平面ABC ;(2)点M 在棱BC 上,且PC 与平面PAM 所成角的正弦值为34,求BM . 7. 【江苏省南通市海安高级中学2020-2021学年高三上学期期中】如图,四棱锥P ABCD -的底面为直角梯形,//AB CD ,AD CD ⊥,1AB AD ==,2CD =,PD ⊥平面ABCD .(1)求证:BC ⊥平面PBD ;(2)已知2PD =,点E 为棱PB 的中点,求直线AE 与平面DCE 所成角的正弦值.8. 【江苏省南通市海安市2020-2021学年高三上学期阶段质量检测(一)】如图,四边形ABCD 与BDEF 均为菱形,FA FC =,且60DAB DBF ∠=∠=︒.(1)求证:AC ⊥平面BDEF ;(2)求直线AD 与平面AEF 所成角的正弦值.9. 【江苏省南通市海安市2020-2021学年高三上学期期末】如图,在四棱锥A BCDE -中,//BC DE ,22BC DE ==,BC CD ⊥,F 为AB 的中点,BC EF ⊥.(1)求证:AC BC ⊥;(2)若AD CD =,2AC =,求直线AE 与平面BDE 所成角的正弦值的最大值.10. 【江苏省南通市海安市实验中学2020-2021学年高三上学期第三次学情检测】如图,四边形ABCD 与BDEF 均为菱形,FA FC =,2AB =,且60DAB DBF ∠=∠=.(1)求证:AC BF ⊥;(2)求二面角E AF B --的余弦值.11. 【江苏省南通市启东市2020-2021学年高三上学期期中】如图,在正三棱柱111ABC A B C -中,233AB =,12A A =,D ,E ,F 分别为线段AC ,1A A ,1C B 的中点.(1)证明://EF 平面ABC ;(2)求直线1C B 与平面BDE 所成角的正弦值.12. 【江苏省南通市启东市2020-2021学年高三上学期期中】如图所示的某种容器的体积为318dm π,它是由半球和圆柱两部分连接而成,半球的半径与圆柱的底面半径都为dm r ,圆柱的高为dm h .已知顶部半球面的造价为3a 元2/dm ,圆柱的侧面造价为a 元2/dm ,圆柱底面的造价为23a 元2/dm .(1)将圆柱的高h 表示为底面半径r 的函数,并求出定义域;(2)当容器造价最低时,圆柱的底面半径r 为多少?13. 【江苏省南通市如东县2020-2021学年高三上学期期末】如图,几何体为圆柱Ω的一半,四边形ABCD为圆柱Ω的轴截面,点E 为圆弧AB 上异于A ,B 的点,点F 为线段ED 上的动点.(1)求证:BE AF ⊥;(2)若2AB =,1AD =,30ABE ∠=︒,且直线CA 与平面ABF 所成角的正弦值为1510,求EF ED 的值. 14. 【江苏省南通市如皋市2020-2021学年高三上学期10月第一次教学质量调研】如图,在六面体1111ABCD A B C D -中,11//AA CC ,底面ABCD 是菱形,且1A D ⊥平面1AA C .(1)求证:平面1AB C ⊥平面1A DB ;(2)求证:11//BB DD .15. 【江苏省南通市如皋市2020-2021学年高三上学期教学质量调研(三)】如图,已知五面体ABCDEF 中,CDEF 为正方形,且平面CDEF ⊥平面ABCD ,120ADC BCD ∠=∠=.(1)证明:ABCD 为等腰梯形;(2)若AD DE =,求二面角F BD C --的余弦值.16. 【江苏省南通市如皋市2020-2021学年高三上学期期末】如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AC ,BD 相交于点N ,2DN NB =,已知3PA AC AD ===,33BD =30ADB ∠=︒.(1)求证:AC ⊥平面PAD ;(2)设棱PD 的中点为M ,求平面PAB 与平面MAC 所成二面角的正弦值.17. 【江苏省南通市如皋市2020-2021学年高三上学期期中】如图,在三棱柱111ABC A B C -中,底面ABC 是边长为2正三角形,侧面11ACC A 是菱形,且平面11ACC A ⊥平面ABC ,E ,F 分别是棱11A C ,BC 的中点,12C G GC =.(1)证明://EF 平面11ABB A ;(2)若①三棱锥1C ABC -的体积为1;②1C C 与底面所成的角为60︒;③异面直线1BB 与AE 所成的角为30.请选择一个条件求平面EFG 与平面11ACC A 所成的二面角(锐角)的余弦值.18. 【江苏省南通市如皋市2021届高三下学期4月第二次适应性考试】如图,在多面体ABCDEF 中,底面ABCD 是边长为2的的菱形,60BAD ∠=,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,3BF =,G 和H 分别是CE 和CF 的中点.(∠)求证:平面//BDGH 平面AEF ;(∠)求二面角H BD C --的大小.19. 【江苏省南通市通州高级中学2020-2021学年高三上学期第五次阶段性测试】如图所示,该几何体是由一个直三棱柱ADE BCF 和一个正四棱锥P ABCD -组合而成,AD AF ⊥,2AE AD ==.(∠)证明:平面PAD ⊥平面ABFE ;(∠)求正四棱锥P ABCD -的高h ,使得二面角C AF P --的余弦值是223. 20. 【江苏省南通市通州区、启东市2020-2021学年高三上学期期末】如图,在四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥平面ABCD ,E 是PD 上的点.(1)当E 是PD 的中点时,求证://PB 平面AEC ;(2)设1==PA AB ,3PC =,若直线PC 与平面AEC 所成角的正弦值为13,求PE 的长. 21. 【江苏省南通市通州区2020-2021学年高三上学期第三次调研考试】如图,在四棱锥P ABCD -中,四边形ABCD 是等腰梯形,//,2,4AB DC BC CD AB ===.M N ,分别是,AB AD 的中点,且PD NC ⊥,平面PAD ⊥平面ABCD .(1)证明:PD ⊥平面ABCD ;(2)已知三棱锥D PAB -的体积为23,求二面角C PN M --的大小. 22. 【江苏省南通市学科基地2020-2021学年高三上学期第一次联考】如图,已知多面体ABCDEF 的底面ABCD 是边长为2的正方体,FA ∠底面ABCD ,AF =2,且DE =AF λ(0<λ<1).(1)求证:CE ∠平面ABF ;(2)若二面角B —CF —E 的大小为56π,求λ的值. 23. 【江苏省如东高级中学、丹阳高级中学、如皋中学2020-2021学年高三上学期12月三校联考】如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 为梯形,//BC AD ,AB AD ⊥,E 为侧棱PA 上一点,且2AE PE =,3AP =,2AB BC ==,4=AD .(1)证明://PC 平面BDE . (2)求平面PCD 与平面BDE 所成锐二面角的余弦值.24. 【江苏省镇江市、南通市如皋2020-2021学年高三上学期教学质量调研(二)】如图,在三棱柱111ABC A B C -中,底面ABC 是边长为2正三角形,侧面11ACC A 是菱形,且平面11ACC A ⊥平面ABC ,E ,F 分别是棱11A C ,BC 的中点,12C G GC =.(1)证明://EF 平面11ABB A ;(2)若①三棱锥1C ABC -的体积为1;②1C C 与底面所成的角为60︒;③异面直线1BB 与AE 所成的角为30.ACC A所成的二面角(锐角)的余弦值.请选择一个条件求平面EFG与平面11。
专题提升卷04 立体几何中组合体问题(解析版)

高一下学期期中复习备考精准测试卷---第二篇 专题提升卷 专题4 立体几何中的组合体问题类型一 组合体的表面积与体积【典型例题】早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把sin 36︒按35计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于___________.【答案】36π【分析】可得正二十面体的外接球即为上方正五棱锥的外接球,设外接球半径为R ,正五边形的外接圆半径为r ,正二十面体的棱长为l ,可得56l r =,11R =,即可表示出外接球的表面积和正二十面体的表面积,得出答案.【详解】由图知正二十面体的外接球即为上方正五棱锥的外接球,设外接球半径为R ,正五边形的外接圆半径为r ,正二十面体的棱长为l ,则3sin 3652lr =︒=,得56lr =,所以正五棱锥的顶点到底面的距离是h ===,所以222()R r R h =+-,即22256l R R ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪⎝⎭⎝⎭,解得R =.所以该正二十面体的外接球表面积为22236441111S R l πππ⎛⎫==⨯= ⎪ ⎪⎝⎭球,而该正二十面体的表面积是2 120sin 602S l l =⨯⨯⨯⨯︒=正二十面体,所以该正二十面体的表面积与该正二十面体的外.【变式训练】已知一个圆锥的底面半径与高均为2,且在这个圆锥中有一个内接圆柱.当此圆柱的侧面积最大时,此圆柱的体积等于___________. 【答案】π【分析】先画出几何体的轴截面图,设圆柱的底面半径为r ,则圆柱的侧面积为222(2)2(2)2[(1)1]S r r r r r πππ=-=--=---,从而可求出1r =时,S 取得最大值,进而可求出圆柱的体积【详解】该几何体的轴截面如图所示,则2OA OB OC ===,设圆柱的底面半径为r ,则,2OD ME AM r OM r ====-,所以圆柱的侧面积为222(2)2(2)2[(1)1]S r r r r r πππ=-=--=---, 所以当1r =时,S 取得最大值2π,此时圆柱的体积为211V ππ=⨯⨯=。
专题4.4 立体几何中最值问题(解析版)

一.方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目,而几何问题中的最值与范围类问题,既可以考查学生的空间想象能力,又考查运用运动变化观点处理问题的能力,因此,将是有中等难度的考题.此类问题,可以充分考查图形推理与代数推理,同时往往也需要将问题进行等价转化,比如求一些最值时,向平面几何问题转化,这些常规的降维操作需要备考时加强关注与训练.立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;三是将几何体平面化,如利用展开图,在平面几何图中直观求解.二.解题策略类型一距离最值问题【例1】【河南省焦作市2019届高三三模】在棱长为4的正方体ABCD﹣A1B1C1D1中,点E、F分别在棱AA1和AB上,且C1E⊥EF,则|AF|的最大值为()A.B.1 C.D.2【答案】B【解析】以AB,AD,AA1所在直线为x,y,z轴,建立空间直角坐标系如图所示,则C1(4,4,4),设E(0,0,z),z∈[0,4],F(x,0,0),x∈[0,4],则|AF|=x.=(4,4,4﹣z),=(x,0,﹣z).因为C1E⊥EF,所以,即:z2+4x﹣4z=0,x=z﹣.当z=2时,x取得最大值为1.|AF|的最大值为1.故选:B.【指点迷津】建立空间直角坐标系,求出坐标,利用C 1E⊥EF,求出|AF|满足的关系式,然后求出最大值即可.利用向量法得到|AF|的关系式是解题的关键,故选D.【举一反三】1、【江西省吉安市2019届高三上学期期末】若某几何体的三视图如图所示,则该几何体的最长棱的棱长为A.B.C.D.【答案】A【解析】解:根据三视图知,该几何体是一个正四棱锥,画出图形如图所示;则,,底面CDEB,结合图形中的数据,求得,在中,由勾股定理得,同理求得,.故选:A .2、【河南省顶级名校2019届高三第四次联合测评】在侧棱长为的正三棱锥中,侧棱OA ,OB ,OC 两两垂直,现有一小球P 在该几何体内,则小球P 最大的半径为 A . B . C .D .【答案】B 【解析】当小球与三个侧面,,及底面都相切时,小球的体积最大此时小球的半径最大,即该小球为正三棱锥的内切球设其半径为由题可知因此本题正确选项:3、如右图所示,在棱长为2的正方体1111ABCD A B C D 中, E 为棱1CC 的中点,点,P Q 分别为面1111A B C D和线段1B C 上的动点,则PEQ ∆周长的最小值为_______.【解析】将面1111A B C D 与面11BB C C 折成一个平面,设E 关于11B C 的对称点为M ,E 关于1B C 对称点为N,则PEQ ∆周长的最小值为MN ==类型二 面积的最值问题【例2】【河南省郑州市2019年高三第二次质量检测】在长方体中,,,分别是棱的中点,是底面内一动点,若直线与平面没有公共点,则三角形面积的最小值为( )A .B .C .D .【答案】C 【解析】补全截面EFG 为截面EFGHQR 如图,其中H 、Q 、R 分别为、的中点,易证平面ACD 1∥平面EFGHQR ,∵直线D 1P 与平面EFG 不存在公共点, ∴D 1P∥面ACD 1,∴D 1P 面ACD 1,∴P ∈AC ,∴过P 作AC 的垂线,垂足为K ,则BK=,此时BP 最短,△PBB 1的面积最小,∴三角形面积的最小值为,故选:C.【指点迷津】截面问题,往往涉及线面平行,面面平行定义的应用等,考查空间想象能力、逻辑思维能力及计算求解能力.解题的关键是注意明确截面形状,确定几何量.本题由直线与平面没有公共点可知线面平行,补全所给截面后,易得两个平行截面,从而确定点P所在线段,得解.【举一反三】1、【湖南省衡阳市2019届高三二模】如图,直角三角形,,,将绕边旋转至位置,若二面角的大小为,则四面体的外接球的表面积的最小值为()A.B.C.D.【答案】B【解析】如图,,,分别为,,的中点,作面,作面,连,,易知点即为四面体的外接球心,,,.设,,则,,,.【处理一】消元化为二次函数..【处理二】柯西不等式..所以.2、如图,在正四棱柱1111D C B A ABCD -中,2,11==AA AB ,点P 是平面1111D C B A 内的一个动点,则三棱锥ABC P -的正视图与俯视图的面积之比的最大值为( )A .1B .2C .21D .41 【答案】BABC P -的正视图与俯视图的面积之比的最大值为2;故选B .3、【福建省2019届高三模拟】若某几何体的三视图如图所示,则该几何体的所有侧面和底面中,面积的最大值为( )A .2B .C .3D .【答案】C【解析】由三视图可得,该几何体的直观图如图所示,其中,为的中点,平面,,.所以,,.又因为,,所以,故,所以.故选C.类型三体积的最值问题【例3】如图,已知平面平面,,、是直线上的两点,、是平面内的两点,且,,,,,是平面上的一动点,且有,则四棱锥体积的最大值是()A. B. C. D.【答案】A【指点迷津】本题主要考查面面垂直的性质,棱锥的体积公式以及求最值问题. 求最值的常见方法有①配方法:若函数为一元二次函数,常采用配方法求函数求值域,其关键在于正确化成完全平方式,并且一定要先确定其定义域;②换元法;③不等式法;④单调性法;⑤图像法,本题首先根据线面关系将体积最值转化为函数求最值问题,然后应用方法①解答的. 【举一反三】1、已知AD 与BC 是四面体ABCD 中相互垂直的棱,若6AD BC ==,且60ABD ACD ∠=∠=,则四面体ABCD 的体积的最大值是A. B. C. 18 D. 36 【答案】A2、如图,已知平面l αβ=,A 、B 是l 上的两个点,C 、D 在平面β内,且,,DA CB αα⊥⊥4AD =,6,8AB BC ==,在平面α上有一个动点P ,使得APD BPC ∠=∠,则P ABCD -体积的最大值是( )A. B.16 C.48 D.144 【答案】C 【解析】,,DA DA βααβ⊂⊥∴⊥面.,,DA CB αα⊥⊥PAD ∴∆和PBC ∆均为直角三角形.,APD BPC PAD ∠=∠∴∆∽PBC ∆.4,8,2AD BC PB PA ==∴=.学科&网过P 作PM AB ⊥,垂足为M .则PM β⊥.令AM t =,()t R ∈.则2222PA AM PB BM -=-,即()222246PA t PA t -=--,2124,PA t PM ∴=-∴=底面四边形ABCD 为直角梯形面积为()1486362S =+⨯=.学科&网136483P ABCD V -∴=⨯=.故C 正确.3.【河南省八市重点高中联盟“领军考试”2019届高三第三次测评】已知一个高为l 的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,内有 一个体积为的球,则的最大值为( ) A . B .C .D .【答案】A 【解析】依题意,当球与三棱锥的四个面都相切时,球的体积最大, 该三棱锥侧面的斜高为,,,所以三棱锥的表面积为,设三棱锥的内切球半径为, 则三棱锥的体积,所以,所以,所以,故选A.类型四 角的最值问题【例4】如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E 、F 分别为AB 、BC 的中点.设异面直线EM 与AF 所成的角为θ,则θcos 的最大值为.【答案】25【解析】建立坐标系如图所示.设1AB =,则11(1,,0),(,0,0)22AF E =.设(0,,1)(01)M y y ≤≤,则1(,,1)2EM y =-,由于异面直线所成角的范围为(0,]2π,所以cos θ==.2281145y y +=-+,令81,19y t t +=≤≤,则281161814552y y t t+=≥++-,当1t =时取等号.所以2cos 5θ==≤=,当0y =时,取得最大值.C【指点迷津】空间的角的问题,只要便于建立坐标系均可建立坐标系,然后利用公式求解.解本题要注意,空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.当点M 在点P 处时,EM 与AF 所成角为直角,此时余弦值为0(最小),当点M 向左移动时,.EM 与AF 所成角逐渐变小,点M 到达点Q 时,角最小,余弦值最大. 【举一反三】1、矩形ABCD 中,,,将△ABC 与△ADC 沿AC 所在的直线进行随意翻折,在翻折过程中直线AD 与直线BC 成的角范围(包含初始状态)为( )A.B.C.D.【答案】C2、在正方体1111D C B A ABCD -中,O 是BD 中点,点P 在线段11D B 上,直线OP 与平面BD A 1所成的角为α,则αsin 的取值范围是( ) A .]33,32[B .]21,31[C .]33,43[D .]31,41[ 【答案】A3.【云南省昆明市云南师范大学附属中学2019届高三上学期第四次月考】如图,在正方体中,点P为AD的中点,点Q为上的动点,给出下列说法:可能与平面平行;与BC所成的最大角为;与PQ一定垂直;与所成的最大角的正切值为;.其中正确的有______写出所有正确命题的序号【答案】【解析】解:由在棱长为1的正方体中点P为AD的中点,点Q为上的动点,知:在中,当Q为的中点时,,由线面平行的判定定理可得PQ与平面平行,故正确;在中,当Q为的中点时,,,,可得,故错误;在中,由,可得平面,即有,故正确;在中,如图,点M为中点,PQ与所成的角即为PQ与所成的角,当Q与,或重合时,PQ与所成的角最大,其正切值为,故正确;在中,当Q 为的中点时,PQ 的长取得最小值,且长为,故正确.故答案为:.4、在正四面体P ABC -中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN AB λ=,设异面直线NM 与AC 所成角为α,当1233λ≤≤时,则cos α的取值范围是__________.【答案】,3838⎡⎢⎣⎦ 【解析】设P 到平面ABC 的射影为点O ,取BC 中点D ,以O 为原点,在平面ABC 中,以过O 作DB 的平行线为x 轴,以OD 为y 轴,以OP 为z 轴,建立空间直角坐标系,如图,设正四面体P −ABC的棱长为则()()(((0,4,0,,,,A B C P M --,由AN AB λ=,得(),64,0N λ-,∴((),56,NM AC λ=--→-=-,∵异面直线NM 与AC 所成角为α, 1233λ≤≤,∴2NM AC cos NM AC α⋅==⋅,设32t λ-=,则5733t 剟∴222111124626()41t cos t t t tα==-+-⋅+,∵1313375t <剟cos α.∴cos α的取值范围是⎣⎦.三.强化训练一、选择题1、【甘肃省2019届高三第一次高考诊断】四棱锥的顶点均在一个半径为3的球面上,若正方形的边长为4,则四棱锥的体积最大值为()A.B.C.D.【答案】D【解析】设正方形的中心为,当在于球心的连线上时,四棱锥高最高,由于底面面积固定,则高最高时,四棱锥体积取得最大值.设高为,,球的半径为,故,解得.故四棱锥的体积的最大值为.故选D.2.【广东省东莞市2019届高三第二次调研】已知一个四棱锥的正主视图和俯视图如图所示,其中,则该四棱锥的高的最大值为A.B.C.4 D.2【答案】A【解析】解:如图所示,由题意知,平面平面ABCD,设点P到AD的距离为x,当x最大时,四棱锥的高最大,因为,所以点P的轨迹为一个椭圆,由椭圆的性质得,当时,x取得最大值,即该四棱锥的高的最大值为.故选:A.3.【四川省教考联盟2019届高三第三次诊断】已知四棱锥的底面四边形的外接圆半径为3,且此外接圆圆心到点距离为2,则此四棱锥体积的最大值为()A.12 B.6 C.32 D.24【答案】A【解析】由锥体的体积公式v=,可知,当s和h都最大时,体积最大.由题得顶点P到底面ABCD的距离h≤2.当点P在底面上的射影恰好为圆心O时,即PO⊥底面ABCD时,PO最大=2,即,此时,即四边形ABCD为圆内接正方形时,四边形ABCD的面积最大,所以此时四边形ABCD的面积的最大值=,所以.故选:A4.【安徽省蚌埠市2019届高三第一次检查】某三棱锥的三视图如图所示,网格纸上小正方形的边长为1,三棱锥表面上的点M在俯视图上的对应点为A,三棱锥表面上的点N在左视图上的对应点为B,则线段MN的长度的最大值为A .B .C .D .【答案】D 【解析】由三视图可知,该三棱锥的底面是直角三角形, 一条侧棱与底面垂直(平面),为几何体的直观图如图,在上,重合,当与重合时, 线段的长度的最大值为.故选D .5.如图,在矩形ABCD 中, 2,1AB AD ==,点E 为CD 的中点, F 为线段CE (端点除外)上一动点现将DAF ∆沿AF 折起,使得平面ABD ⊥平面ABC 设直线FD 与平面ABCF 所成角为θ,则sin θ的最大值为( )A.13 B. 4 C. 12 D. 23【答案】C 【解析】如图:在矩形中,过点作的垂线交于点,交于点设,6.【2019年4月2019届高三第二次全国大联考】已知正四面体的表面积为,点在内(不含边界). 若,且,则实数的取值范围为( ) A . B . C .D .【答案】A 【解析】 设正四面体的棱长为则,解得则正四面体的高为记点到平面、、的距离分别为则因为,所以,则故又,故即实数的取值范围为本题正确选项:二、填空题7.【山东省青岛市2019届高三3月一模】在四棱锥中,底面是边长为2的正方形,面,且,若在这个四棱锥内有一个球,则此球的最大表面积为__________.【答案】【解析】在这个四棱锥内有一个球,则此球的最大表面积时,对应的球应该是内切球,此时球的半径最大,设内切球的球心为O半径为R,连接球心和ABCD四个点,构成五个小棱锥,根据体积分割得到,五个小棱锥的体积之和即为大棱锥的体积,,根据AB垂直于AD,PD垂直于AB 可得到AB垂直于面PDA,故得到AB垂直于PA,同理得到BC垂直于PC,表面积为:,此时球的表面积为:.故答案为:.8.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知正四棱柱和半径为的半球O,底面ABCD在半球O底面所在平面上,,,,四点均在球面上,则该正四棱柱的体积的最大值为______.【答案】4【解析】设正四棱柱的高为h,底面棱长为a,则正四棱柱的底面外接圆直径为,所以,.由勾股定理得,即,得,其中,所以,正四棱柱的体积为,其中,构造函数,其中,则,令,得.当时,;当时,.所以,函数在处取得极大值,亦即最大值,则.因此,该正四棱柱的体积的最大值为4.9.【陕西省西安地区陕师大附中、西安高级中学、高新一中、铁一中学、西工大附中等八校2019届高三3月联考】如图,已知圆柱和半径为的半球O,圆柱的下底面在半球O底面所在平面上,圆柱的上底面内接于球O,则该圆柱的体积的最大值为_____.【答案】2π【解析】解:设圆柱的底面圆半径为r,高为h;则h2+r2=R2=3;所以圆柱的体积为V=πr2h=π(3﹣h2)h=π(3h﹣h3);则V′(h)=π(3﹣3h2),令V′(h)=0,解得h=1;所以h∈(0,1)时,V′(h)>0,V(h)单调递增;h∈(1,)时,V′(h)<0,V(h)单调递减;所以h=1时,V(h)取得最大值为V(1)=2π.故答案为:2π.10.【江西省上饶市2019届高三二模】一个棱长为的正方体形状的铁盒内放置一个正四面体,且能使该正四面体在铁盒内任意转动,则该正四面体的体积的最大值是_____.【答案】【解析】由题该正四面体在铁盒内任意转动,故其能在正方体的内切球内任意转动,内切球半径为6,设正四面体棱长为a, 将此正四面体镶嵌在棱长为x的正方体内,如图所示:则x=,外接球的球心和正方体体心O重合,∴外接球的球半径为:=6,a=4又正四面体的高为∴该正四面体的体积为故答案为11.【河北省衡水市第二中学2019届高三上期中】已知体积为的正四棱锥外接球的球心为,其中在四棱锥内部.设球的半径为,球心到底面的距离为.过的中点作球的截面,则所得截面圆面积的最小值是___________.【答案】【解析】如图取底面的中心为,连接平面,且球心在上,由条件知,,连接,,则,于是底面的边长为.又,故四棱锥的高是,所以,即,从而,,于是,过的中点的最小截面圆是以点为圆心的截面圆,该截面圆的半径是,故所求面积为.12.【江西省临川第一中学等九校2019届高三3月联考】如图所示,三棱锥的顶点,,,都在同一球面上,过球心且,是边长为2等边三角形,点、分别为线段,上的动点(不含端点),且,则三棱锥体积的最大值为__________.【答案】【解析】过球心,又是边长为的等边三角形,,,三角形是等腰直角三角形,,,又因为,在平面内,由线面垂直的判定定理可得平面,即平面,设,,则三棱锥体积,当且仅当,即时取等号,故答案为.13.【安徽省蚌埠市2019届高三下学期第二次检查】正三棱锥中,,点在棱上,且.正三棱锥的外接球为球,过点作球的截面,截球所得截面面积的最小值为__________.【答案】【解析】因为,所以,所以,同理,故可把正三棱锥补成正方体(如图所示),其外接球即为球,直径为正方体的体对角线,故,设的中点为,连接,则且,所以,当平面时,平面截球的截面面积最小,此时截面为圆面,其半径为,故截面的面积为.填.14.【江西师范大学附属中学2019高三上学期期末】若一个四棱锥的底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球的体积最小时,它的高为_________.【答案】【解析】设四棱锥底面边长为a,高为h,底面对角线交于O,由条件四棱锥P-ABCD为正四棱锥,其外接球的球心M在高PO上,设外接球半径为R,在直角三角形MAO中,,又该四棱锥的体积为9,所以所以,,,时,时,所以时R极小即R最小,此时体积最小.故答案为3.15.【江西省上饶市2019届高三二模】已知正方体的棱长为,平面与对角线垂直且与每个面均有交点,若截此正方体所得的截面面积为,周长为,则的最大值为______.【答案】【解析】因为平面与对角线垂直,所以平面与对角面平行,作出图象,为六边形,设则,所以,由对称性得平面过对角线中点时截面面积取最大值为,则的最大值为.16.【河南省洛阳市2019届高三第二次统考】正四面体中,是的中点,是棱上一动点,的最小值为,则该四面体内切球的体积为_____.【答案】【解析】如下图,正方体中作出一个正四面体将正三角形和正三角形沿边展开后使它们在同一平面内,如下图:要使得最小,则三点共线,即:,设正四面体的边长为,在三角形中,由余弦定理可得:,解得:,所以正方体的边长为2,正四面体的体积为:,设四正面体内切球的半径为,由等体积法可得:,整理得:,解得:,所以该四面体内切球的体积为.17.【2019届湘赣十四校高三联考第二次考试】如图,正三棱锥的高,底面边长为4,,分别在和上,且,当三棱锥体积最大时,三棱锥的内切球的半径为________.【答案】【解析】设,,当时,取得最大值,此时为中点,经过点,且,,所以可求,,因此易求,,,,又∵,∴.。
高考专题突破四 高考中的立体几何问题

高考专题突破四 高考中的立体几何问题【考点自测】1.在正三棱柱ABC -A 1B 1C 1中,D 为BC 的中点,E 为A 1C 1的中点,则DE 与平面A 1B 1BA 的位置关系为________. 答案 平行解析 如图取B 1C 1的中点为F ,连结EF ,DF ,则EF ∥A 1B 1,DF ∥B 1B , 且EF ∩DF =F ,A 1B 1∩B 1B =B 1, ∴平面EFD ∥平面A 1B 1BA , ∴DE ∥平面A 1B 1BA .2.设x ,y ,z 是空间中不同的直线或平面,对下列四种情形:①x ,y ,z 均为直线;②x ,y 是直线,z 是平面;③z 是直线,x ,y 是平面;④x ,y ,z 均为平面.其中使“x ⊥z 且y ⊥z ⇒x ∥y ”为真命题的是________.(填序号) 答案 ②③解析 由正方体模型可知①④为假命题;由线面垂直的性质定理可知②③为真命题. 3.一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________. 答案 12解析 设六棱锥的高为h ,则V =13Sh ,所以13×34×4×6h =23,解得h =1.设六棱锥的斜高为h ′,则h 2+(3)2=h ′2,故h ′=2. 所以该六棱锥的侧面积为12×2×2×6=12.4.设α,β,γ是三个平面,a ,b 是两条不同的直线,有下列三个条件:①a ∥γ,b ⊂β;②a ∥γ,b ∥β;③b ∥β,a ⊂γ.如果命题“α∩β=a ,b ⊂γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________.(把所有正确的序号填上)答案①或③解析由线面平行的性质定理可知,①正确;当b∥β,a⊂γ时,a和b在同一平面内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.5.如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①BD⊥AC;②△BAC是等边三角形;③三棱锥D-ABC是正三棱锥;④平面ADC⊥平面ABC.其中正确的是________.(填序号)答案①②③解析由题意知,BD⊥平面ADC,故BD⊥AC,①正确;AD为等腰直角三角形斜边BC上的高,平面ABD⊥平面ACD,所以AB=AC=BC,△BAC是等边三角形,②正确;易知DA=DB=DC,又由②知③正确;由①知④错.题型一求空间几何体的表面积与体积例1 如图,在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AC⊥BC,AC=BC=CC1=2,点D为AB 的中点.(1)证明:AC1∥平面B1CD;(2)求三棱锥A1—CDB1的体积.(1)证明连结BC1交B1C于点O,连结OD.在三棱柱ABC —A 1B 1C 1中,四边形BCC 1B 1是平行四边形, ∴点O 是BC 1的中点.∵点D 为AB 的中点,∴OD ∥AC 1. 又OD ⊂平面B 1CD ,AC 1⊄平面B 1CD , ∴AC 1∥平面B 1CD .(2)解 ∵AC =BC ,AD =BD ,∴CD ⊥AB . 在三棱柱ABC —A 1B 1C 1中,由AA 1⊥平面ABC ,得平面ABB 1A 1⊥平面ABC . 又平面ABB 1A 1∩平面ABC =AB ,CD ⊂平面ABC , ∴CD ⊥平面ABB 1A 1, ∵AC ⊥BC ,AC =BC =2, ∴AB =A 1B 1=22,CD =2,1111——A CDB C A DB V V =三棱锥三棱锥=13×12×2×22×2=43. 思维升华 (1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.跟踪训练1 如图,在三棱柱ABC -A 1B 1C 1中,底面是边长为a 的正三角形,AA 1与AC ,AB 所成的角均为60°,且A 1A =AB ,求该三棱柱的侧面积和体积.解 作A 1O ⊥底面ABC 于点O ,∵AA 1与AC ,AB 所成的角均为60°, 且A 1A =AB ,∴O 是△ABC 的中心, ∴AO =23×32a =33a .又A 1O =A 1A 2-AO 2=63a , S △ABC =34a 2,A 1O ⊥AD , ∴V =Sh =34a 2×63a =24a 3. 又O 是△ABC 的中心,∴AO ⊥BC ,A 1O ⊥BC , 从而BC ⊥平面A 1AO .∵A 1A ⊂平面A 1AO ,∴BC ⊥A 1A , 又A 1A ∥B 1B ,故BC ⊥B 1B , ∴侧面BCC 1B 1是矩形.11112222sin 60A ABB BCC B S S S a a ∴⨯⨯︒=+=+侧=(1+3)a 2.题型二 空间点、线、面的位置关系例2 (2017·江苏)如图,在三棱锥A-BCD 中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E ,F (E 与A ,D 不重合)分别在棱AD ,BD 上,且EF ⊥AD .求证:(1)EF ∥平面ABC ; (2)AD ⊥AC .证明 (1)在平面ABD 内,因为AB ⊥AD ,EF ⊥AD , 则AB ∥EF .又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC.又因为AC⊂平面ABC,所以AD⊥AC.思维升华 (1)平行问题的转化利用线线平行、线面平行、面面平行的相互转化解决平行关系的判定问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而应用性质定理时,其顺序正好相反.在实际的解题过程中,判定定理和性质定理一般要相互结合,灵活运用.(2)垂直问题的转化在空间垂直关系中,线面垂直是核心,已知线面垂直,既为证明线线垂直提供依据,又可为利用判定定理证明面面垂直作好铺垫.应用面面垂直的性质定理时,一般作辅助线,基本作法是过其中一个平面内一点作交线的垂线,从而把面面垂直问题转化为线面垂直问题,进而可转化为线线垂直问题.跟踪训练2 (2013·江苏)如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.证明(1)由AS=AB,AF⊥SB知F为SB的中点,则EF∥AB,FG∥BC,又EF∩FG=F,AB∩BC=B,因此平面EFG∥平面ABC.(2)由平面SAB⊥平面SBC,平面SAB∩平面SBC=SB,AF⊂平面SAB,AF⊥SB,所以AF⊥平面SBC,则AF⊥BC.又BC⊥AB,AF∩AB=A,AF,AB⊂平面SAB,则BC⊥平面SAB,又SA⊂平面SAB,因此BC⊥SA.题型三平面图形的翻折问题例3 五边形ANB1C1C是由一个梯形ANB1B与一个矩形BB1C1C组成的,如图甲所示,B为AC的中点,AC=CC1=2AN=8.沿虚线BB1将五边形ANB1C1C折成直二面角A—BB1—C,如图乙所示.(1)求证:平面BNC⊥平面C1B1N;(2)求图乙中的多面体的体积.(1)证明四边形BB1C1C为矩形,故B1C1⊥BB1,又由于二面角A—BB1—C为直二面角,故B1C1⊥平面BB1A,又BN⊂平面BB1A,故B1C1⊥BN,由线段AC=CC1=2AN=8知,BB21=NB21+BN2,即BN⊥NB1,又B1C1∩NB1=B1,B1C1,NB1⊂平面NB1C1,所以BN⊥平面C1B1N,因为BN⊂平面BNC,所以平面BNC⊥平面C1B1N.(2)解连结CN,过N作NM⊥BB1,垂足为M,V 三棱锥C —ABN =13×BC ·S △ABN=13×4×12×4×4=323, 又B 1C 1⊥平面ABB 1N , 所以平面CBB 1C 1⊥平面ABB 1N , 且平面CBB 1C 1∩ABB 1N =BB 1,NM ⊥BB 1,NM ⊂平面ABB 1N ,所以NM ⊥平面B 1C 1CB ,1111—1·3B C CB N B C CB V NM S =⨯矩形四棱锥=13×4×4×8=1283, 则此几何体的体积11——N B C CB C ABN V V V 四棱=+锥三棱锥=323+1283=1603.思维升华 平面图形的翻折问题,关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.跟踪训练3 为了迎接某节日,商场进行促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片ABCD 剪去四个全等的等腰三角形△SEE ′,△SFF ′,△SGG ′,△SHH ′,再将剩下的阴影部分折成一个四棱锥形状的包装盒S —EFGH ,其中A ,B ,C ,D 重合于点O ,E 与E ′重合,F 与F ′重合,G 与G ′重合,H 与H ′重合(如图所示).(1)求证:平面SEG ⊥平面SFH ;(2)已知AE =52,过O 作OM ⊥SH 交SH 于点M ,求cos ∠EMO 的值.(1)证明 ∵折后A ,B ,C ,D 重合于一点O ,∴拼接成底面EFGH 的四个直角三角形必为全等的等腰直角三角形, ∴底面EFGH 是正方形,故EG ⊥FH . 连结SO .∵在原平面图形中,△SEE ′≌△SGG ′, ∴SE =SG ,∴EG ⊥SO ,∵EG ⊥FH ,EG ⊥SO ,FH ∩SO =O ,FH ,SO ⊂平面SFH ,∴EG ⊥平面SFH , 又∵EG ⊂平面SEG , ∴平面SEG ⊥平面SFH .(2)解 由题意,当AE =52时,OE =52,Rt △SHO 中,SO =5,SH =552,∴OM =SO ·OHSH= 5. 由(1)知,EO ⊥平面SHF , 又∵OM ⊂平面SHF ,∴EO ⊥OM . 在Rt △EMO 中,EM =EO 2+OM 2=352,∴cos ∠EMO =OM EM =23.题型四 立体几何中的存在性问题例4 如图,在四棱锥P —ABCD 中,△PAD 为正三角形,平面PAD ⊥平面ABCD ,AB ∥CD ,AB ⊥AD ,CD =2AB =2AD =4.(1)求证:平面PCD ⊥平面PAD ; (2)求三棱锥P —ABC 的体积;(3)在棱PC 上是否存在点E ,使得BE ∥平面PAD ?若存在,请确定点E 的位置并证明;若不存在,请说明理由.(1)证明 因为AB ∥CD ,AB ⊥AD ,所以CD ⊥AD . 因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,CD ⊂平面ABCD , 所以CD ⊥平面PAD . 因为CD ⊂平面PCD , 所以平面PCD ⊥平面PAD . (2)解 取AD 的中点O ,连结PO . 因为△PAD 为正三角形,所以PO ⊥AD .因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PO ⊂平面PAD , 所以PO ⊥平面ABCD , 所以PO 为三棱锥P —ABC 的高.因为△PAD 为正三角形,CD =2AB =2AD =4, 所以PO = 3.所以V 三棱锥P —ABC =13S △ABC ·PO=13×12×2×2×3=233. (3)解 在棱PC 上存在点E ,当E 为PC 的中点时,BE ∥平面PAD . 分别取CP ,CD 的中点E ,F ,连结BE ,BF ,EF , 所以EF ∥PD .因为AB ∥CD ,CD =2AB , 所以AB ∥FD ,AB =FD ,所以四边形ABFD 为平行四边形, 所以BF ∥AD .因为BF ∩EF =F ,AD ∩PD =D , 所以平面BEF ∥平面PAD . 因为BE ⊂平面BEF , 所以BE ∥平面PAD .思维升华 对于线面关系中的存在性问题,首先假设存在,然后在该假设条件下,利用线面关系的相关定理、性质进行推理论证,寻找假设满足的条件,若满足则肯定假设,若得出矛盾的结论则否定假设.跟踪训练4 (2017·江苏无锡天一中学模拟)如图所示,在正方体ABCD -A 1B 1C 1D 1中,E 是棱DD 1的中点.(1)证明:平面ADC 1B 1⊥平面A 1BE ;(2)在棱C 1D 1上是否存在一点F ,使B 1F ∥平面A 1BE ?证明你的结论. (1)证明 如图,因为ABCD -A 1B 1C 1D 1为正方体, 所以B 1C 1⊥平面ABB 1A 1.因为A 1B ⊂平面ABB 1A 1,所以B 1C 1⊥A 1B .又因为A 1B ⊥AB 1,B 1C 1∩AB 1=B 1,AB 1,B 1C 1⊂平面ADC 1B 1,所以A 1B ⊥平面ADC 1B 1. 因为A 1B ⊂平面A 1BE , 所以平面ADC 1B 1⊥平面A 1BE .(2)解 当点F 为C 1D 1的中点时,可使B 1F ∥平面A 1BE .证明如下: 设A 1B ∩AB 1=O , 连结EO ,EF ,B 1F .易知EF ∥C 1D ,且EF =12C 1D ,B 1O ∥C 1D 且B 1O =12C 1D ,所以EF ∥B 1O 且EF =B 1O ,所以四边形B 1OEF 为平行四边形. 所以B 1F ∥OE .又因为B 1F ⊄平面A 1BE ,OE ⊂平面A 1BE . 所以B 1F ∥平面A 1BE .1.(2017·江苏新海中学期中)将斜边长为4的等腰直角三角形绕其斜边所在直线旋转一周,则所形成的几何体的体积是________. 答案16π3解析 等腰直角三角形的斜边长为4,斜边的高为2. ∴旋转后的几何体为两个大小相等的圆锥的组合体. 圆锥的底面半径为2,高为2.∴几何体的体积V =2×13×π×4×2=16π3.2.若α,β,γ是三个不同的平面,m ,n 是两条不同的直线,且α∩γ=m ,β∩γ=n .命题甲:m ∥n ;命题乙:α∥β.则甲是乙成立的________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”) 答案 必要不充分解析 若α与β平行,则必有m ∥n ,反之,当m ∥n 时,α与β可能相交,如三棱柱中侧棱平行,侧面不平行.3.如图所示,已知平面α∩平面β=l ,α⊥β.A ,B 是直线l 上的两点,C ,D 是平面β内的两点,且AD ⊥l ,CB ⊥l ,DA =4,AB =6,CB =8.P 是平面α上的一动点,且有∠APD =∠BPC ,则四棱锥P -ABCD 体积的最大值是________.答案 48解析 由题意知,△PAD ,△PBC 是直角三角形, 又∠APD =∠BPC ,所以△PAD ∽△PBC . 因为DA =4,CB =8,所以PB =2PA . 作PM ⊥AB 于点M ,由题意知,PM ⊥平面β.令BM =t ,则AM =|6-t |,PA 2-(6-t )2=4PA 2-t 2,所以PA 2=4t -12.所以PM =-t 2+16t -48,即为四棱锥P -ABCD 的高, 又底面ABCD 为直角梯形,S =12×(4+8)×6=36,所以V =13×36×-t 2+16t -48=12-(t -8)2+16≤12×4=48.4.如图梯形ABCD 中,AD ∥BC ,∠ABC =90°,AD ∶BC ∶AB =2∶3∶4,E ,F 分别是AB ,CD 的中点,将四边形ADFE 沿直线EF 进行翻折,给出四个结论:①DF ⊥BC ; ②BD ⊥FC ;③平面DBF ⊥平面BFC ; ④平面DCF ⊥平面BFC .在翻折过程中,可能成立的结论是________.(填写结论序号) 答案 ②③解析 因为BC ∥AD ,AD 与DF 相交不垂直,所以BC 与DF 不垂直,则①错误;设点D 在平面BCF 上的射影为点P ,当BP ⊥CF 时就有BD ⊥FC ,而AD ∶BC ∶AB =2∶3∶4,可使条件满足,所以②正确;当点P 落在BF 上时,DP ⊂平面BDF ,从而平面BDF ⊥平面BCF ,所以③正确;因为点D 的投影不可能在FC 上,所以平面DCF ⊥平面BFC 不成立,即④错误. 5.下列三个命题都缺少一个条件P ,补上这个条件使其构成真命题(其中l ,m 为直线,α,β为平面),则条件P 为________.①⎭⎪⎬⎪⎫m ⊂α,l ∥m ,P ⇒l ∥α;②⎭⎪⎬⎪⎫l ∥m ,m ∥α,P⇒l ∥α;③⎭⎪⎬⎪⎫l ⊥β,α⊥β,P⇒l ∥α. 答案 l ⊄α解析 根据直线与平面平行的判定定理可得①所缺条件为l ⊄α,可推②③同样可补此条件. 6.如图,在三棱锥S —ABC 中,SA =SB ,AC =BC ,O 为AB 的中点,SO ⊥平面ABC ,AB =4,OC =2,N 是SA 的中点,CN 与SO 所成的角为α,且tan α=2.(1)证明:OC ⊥ON ; (2)求三棱锥S —ABC 的体积.(1)证明 ∵AC =BC ,O 为AB 的中点, ∴OC ⊥AB ,又SO ⊥平面ABC ,OC ⊂平面ABC , ∴OC ⊥SO ,又AB ∩SO =O ,AB ,SO ⊂平面SAB , ∴OC ⊥平面SAB ,又∵ON ⊂平面SAB , ∴OC ⊥ON .(2)解 设OA 的中点为M ,连结MN ,MC ,则MN ∥SO ,故∠CNM 即为CN 与SO 所成的角α, 又MC ⊥MN 且tan α=2, ∴MC =2MN =SO , 又MC =OC 2+OM 2=22+12=5, 即SO =5,∴三棱锥S —ABC 的体积V =13Sh =13·12·2·4·5=453. 7.如图1,在矩形ABCD 中,AB =4,AD =2,E 是CD 的中点,将△ADE 沿AE 折起,得到如图2所示的四棱锥D 1—ABCE ,其中平面D 1AE ⊥平面ABCE .(1)证明:BE ⊥平面D 1AE ;(2)设F 为CD 1的中点,在线段AB 上是否存在一点M ,使得MF ∥平面D 1AE ,若存在,求出AM AB的值;若不存在,请说明理由. (1)证明 连结BE ,∵ABCD 为矩形且AD =DE =EC =BC =2, ∴∠AEB =90°,即BE ⊥AE , 又平面D 1AE ⊥平面ABCE ,平面D 1AE ∩平面ABCE =AE ,BE ⊂平面ABCE , ∴BE ⊥平面D 1AE .(2)解 AM =14AB ,取D 1E 的中点L ,连结AL ,FL ,∵FL ∥EC ,EC ∥AB ,∴FL ∥AB 且FL =14AB ,∴M ,F ,L ,A 四点共面, 若MF ∥平面AD 1E ,则MF ∥AL .∴AMFL 为平行四边形,∴AM =FL =14AB .故线段AB 上存在满足题意的点M ,且AM AB =14.8.如图,在四棱锥P —ABCD 中,ABCD 是正方形,PD ⊥平面ABCD .PD =AB =2,E ,F ,G 分别是PC ,PD ,BC 的中点.(1)求证:平面PAB ∥平面EFG ;(2)在线段PB 上确定一点Q ,使PC ⊥平面ADQ ,并给出证明. (1)证明 ∵在△PCD 中,E ,F 分别是PC ,PD 的中点, ∴EF ∥CD ,又∵四边形ABCD 为正方形, ∴AB ∥CD ,∴EF ∥AB ,∵EF ⊄平面PAB ,AB ⊂平面PAB , ∴EF ∥平面PAB .同理EG ∥平面PAB , ∵EF ,EG 是平面EFG 内两条相交直线, ∴平面PAB ∥平面EFG .(2)解 当Q 为线段PB 的中点时,PC ⊥平面ADQ .取PB 的中点Q ,连结DE ,EQ ,AQ ,DQ , ∵EQ ∥BC ∥AD ,且AD ≠QE ,∴四边形ADEQ为梯形,由PD⊥平面ABCD,AD⊂平面ABCD,得AD⊥PD,∵AD⊥CD,PD∩CD=D,PD,CD⊂平面PCD,∴AD⊥平面PDC,又PC⊂平面PDC,∴AD⊥PC.∵△PDC为等腰直角三角形,E为斜边中点,∴DE⊥PC,∵AD,DE是平面ADQ内的两条相交直线,∴PC⊥平面ADQ.9.(2018届镇江中学检测)如图,正三棱柱A1B1C1-ABC中,点D,E分别是A1C,AB的中点.(1)求证:ED∥平面BB1C1C;(2)若AB=2BB1,求证:A1B⊥平面B1CE.证明(1)连结AC1,BC1,因为四边形AA1C1C是矩形,D是A1C的中点,所以D是AC1的中点.在△ABC1中,因为D,E分别是AC1,AB的中点,所以DE∥BC1,因为DE⊄平面BB1C1C,BC1⊂平面BB1C1C,所以ED∥平面BB1C1C.(2)因为△ABC是正三角形,E是AB的中点,所以CE⊥AB.又因为在正三棱柱A1B1C1-ABC中,平面ABC⊥平面ABB1A1,交线为AB,CE⊂平面ABC,所以CE⊥平面ABB1A1,又A1B⊂平面ABB1A1,从而CE⊥A1B.因为A 1B 1B 1B =AB B 1B =2,B 1B BE =B 1B12AB=2, 所以A 1B 1B 1B =B 1B BE, 又∠A 1B 1B =∠B 1BE =90°, 所以Rt △A 1B 1B ∽Rt △B 1BE , 所以∠A 1BB 1=∠BEB 1, 又∠BEB 1+∠BB 1E =90°, 所以∠A 1BB 1+∠BB 1E =90°, 所以A 1B ⊥B 1E ,又因为CE ,B 1E ⊂平面B 1CE ,CE ∩B 1E =E , 所以A 1B ⊥平面B 1CE .。
2022年高考数学备考中等生百日捷进提升系列 专题04立体几何解答题(理)(综合提升篇)解析版

2021中等生百日综合提升篇专题四 立体几何解答题(理)空间向量运算与利用向量证明平行、垂直的位置关系【背一背重点学问】1.用向量证明线面平行的方法主要有:①证明直线的方向向量与平面的法向量垂直;②证明可在平面内找到一个向量与直线的方向向量是共线向量;③利用共面对量定理,即证明直线的方向向量可用平面内两个不共线向量线性表示.2.面面平行:①证明两个平面的法向量平行;②转化为线面平行,线线平行.3.用向量证明线面垂直的方法有:①证明直线的方向向量与平行的法向量平行;②利用线面垂直的判定定理,转化为线线垂直.4.面面垂直的证明发法:①两个平面的法向量垂直;②转化为线面垂直,线线垂直. 【讲一讲提高技能】 必备技能:1.用向量证明空间中的平行关系①设直线1l 和2l 的方向向量分别为1v 和2v ,则1l ∥2l (或1l 与2l 重合)⇔ 1v ∥2v .②设直线l 的方向向量为v ,与平面α共面的两个不共线向量1v 和2v ,则l ∥α或l ⊂α⇔存在两个实数,x y ,使12v xv yv =+.③设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u . ④设平面α和β的法向量分别为1u ,2u ,则α∥β⇔1u ∥2u . 2.用向量证明空间中的垂直关系①设直线l 1和l 2的方向向量分别为1v 和2v ,则l 1⊥l 2⇔1v ⊥2v ⇔1v .2v =0. ②设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u ③设平面α和β的法向量分别为1u 和2u ,则α⊥β⇔1u ⊥2u ⇔1u ·2u =0. 典型例题:例1如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,//AB CD ,090ADC ∠=,1PD AD AB ===,2DC =.(1)求证:BC ⊥平面PBD ; (2)求二面角A PB C --的大小. 【答案】(1)证明见解析;(2)56π. 【解析】例2如图,正方形CD AB 和四边形C F A E 所在平面相互垂直,C C E ⊥A ,F//C E A ,2AB =,C F 1E =E =.(1)求证:F//A 平面D B E ; (2)求证:CF ⊥平面D B E ; (3)求二面角D A-BE-的大小.【答案】(1)证明见解析;(2)证明见解析;(3)6π. 【解析】(2)证明:由于正方形CD AB 和四边形C F A E 所在的平面相互垂直,且C C E ⊥A , 所以C E ⊥平面CD AB .如图,以C 为原点,建立空间直角坐标系C xyz -. 则()C 0,0,0,)2,2,0A,()2,0B ,()D2,0,0,()0,0,1E ,22F ,22⎛⎫⎪ ⎪⎝⎭.22CF 2⎛⎫= ⎪ ⎪⎝⎭,()0,2,1BE =-,()D 2,0,1E =-.CF 0110⋅BE =-+=,CF D 1010⋅E =-++=,所以CF ⊥BE ,CF D ⊥E ,又D BE E =E ,所以CF ⊥平面D B E .(3)由(2)知,22CF ,22⎛⎫= ⎪ ⎪⎝⎭是平面D B E 的一个法向量.设平面ABE 的法向量(),,n x y z =,则0n ⋅BA =,0n ⋅BE =,即()()()(),,2,0,00,,0,2,10x y z x y z ⎧⋅=⎪⎨⋅-=⎪⎩,得0x =,且2z y =.令1y =,则2z =,()0,1,2n =.从而CF 3cos ,CF 2CFn n n ⋅==. 故二面角D A-BE-为锐角,故二面角D A-BE-的大小为6π. 【练一练提升力量】1已知在四棱锥P ABCD -中,底面ABCD 是矩形,且2AD =,1AB =,PA ⊥平面ABCD ,E 、F 分别是线段AB 、BC 的中点. (1)证明:PF FD ⊥(2)在线段PA 上是否存在点G ,使得EG ∥平面PFD ,若存在,确定点G 的位置;若不存在,说明理由. (3)若PB 与平面ABCD 所成的角为45,求二面角A PD F --的余弦值【解析】(Ⅱ)设平面PFD 的法向量为(),,n x y z =,由0n PF n DF ⎧⋅=⎪⎨⋅=⎪⎩,得00x y tz x y +-=⎧⎨-=⎩,令1z =,得:2t x y ==.∴,,122t t n ⎛⎫= ⎪⎝⎭.设G 点坐标为(0,0,)m ()0m t ≤≤,1,0,02E ⎛⎫⎪⎝⎭,则1(,0,)2EG m =-,要使EG ∥平面PFD ,只需0EG n =,即1()0102224t t tm m -⨯+⨯+⨯=-=,得14m t =,从而满足14AG AP =的点G 即为所求.2. 如图,四棱锥ABCD P -的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,DC PD =,E 是PC 的中点. (Ⅰ)证明:PA //平面BDE ;(Ⅱ)求二面角C DE B --的平面角的余弦值;(Ⅲ)在棱PB 上是否存在点F ,使PB ⊥平面DEF ?证明你的结论.【解析】法二:(I )连接AC ,AC 交BD 于O ,连接OE .在PAC ∆中,OE 为中位线,∴OE //PAPA BDE ⊄又平面,∴PA //平面BDE .利用空间向量求空间角 【背一背重点学问】1.求两条异面直线所成的角,设b a ,分别是直线21,l l 的方向向量,则21,l l 所成角为θ,b a ,的夹角为><b a ,,则ba b a b a ⋅>=<=,cos cos θ2.求直线与平面所成的角,设直线l 的方向向量为a ,平面α的法向量为n ,直线l 与平面α所成的角为θ,ba n a n a ⋅=><=,cos sin θ.3. 设n m ,是二面角βα-l -的法向量,则n m ,的夹角大小就是二面角的平面角的大小,nm n m n m ⋅>=<=,cos cos θ,再依据平面是锐角还是钝角,最终确定二面角的平面角的大小.【讲一讲提高技能】 1.必备技能: 用法向量求角(1)用法向量求二面角如图,有两个平面α与β,分别作这两个平面的法向量1n 与2n ,则平面α与β所成的角跟法向量1n 与2n 所成的角2n 相等或互补,所以首先必需推断二面角是锐角还是钝角.(2)法向量求直线与平面所成的角要求直线a 与平面α所成的角θ,先求这个平面α的法向量n 与直线a 的夹角的余弦a n ,cos ,易知θ=a n ,或者a n ,2-π.2.典型例题:例1如图,在四棱锥P ABCD -中,底面ABCD 是菱形,且60DAB ∠=︒.点E 是棱PC 的中点,平面ABE 与棱PD 交于点F .F BD CP EA(1)求证://AB EF ;(2)若PA PD AD ==,且平面PAD ⊥平面ABCD ,求平面PAF 与平面AFE 所成的锐二面角的余弦值. 【答案】(1)详见解析;(2)1313. 【解析】试题分析:(1)首先证明//AB 面PCD ,再利用线面平行的性质即可得证;(2)建立空间直角坐标系,求得两个平面的法向量后即可求解.zyG AEP CDBF例2如图,四棱锥ABCD P -中,底面是以O 为中心的菱形,⊥PO 底面ABCD , 3,2π=∠=BAD AB ,M 为BC 上一点,且AP MP BM ⊥=,21. αβ1n(Ⅰ)求PO 的长;(Ⅱ)求二面角C PM A --的正弦值.分析:(Ⅰ)连结AC 、BD ,由于是菱形ABCD 的中心,ACBD O =,以O 为坐标原点,,,OA OB OP 的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系,依据题设条件写出,,O A M 的坐标,并设出点P 的坐标()0,0,a ,依据空间两点间的距离公式和勾股定理列方程解出a 的值得到PO 的长;.(Ⅱ)设平面APM 的法向量为()1111,,n x y z =,平面PMC 的法向量为()2222,,n x y z =,首先利用向量的数量积列方程求出向量12,n n 的坐标,再利用向量的夹角公式求出12cos ,n n <>,进而求出二面角C PM A --的正弦值. 【解析】从而33,,044OM OB BM ⎛⎫=+=- ⎪ ⎪⎝⎭,即33,,0.44M ⎛⎫- ⎪ ⎪⎝⎭设()0,0,,0,P a a >,则()333,0,,,,.44AP a MP a ⎛⎫=-=-⎪ ⎪⎝⎭由于MP AP ⊥, 故0,MP AP ⋅=即2304a -+=,所以33,22a a ==-(舍去),即32PO =.【练一练提升力量】1. 如图,在长方体1111ABCD A B C D -中,11,2AD AA AB ===,点E 在棱AB 上移动.(Ⅰ)证明:11D E A D ⊥;(Ⅱ)当E 为AB 的中点时,求点E 到面1ACD 的距离; (Ⅲ)AE 等于何值时,二面角1D EC D --的大小为4π.【解析】2. 如图,四棱锥P —ABCD 中,PAB ∆为边长为2的正三角形,底面ABCD 为菱形,且平面PAB ⊥平面ABCD ,AB PC ⊥,E 为PD 点上一点,满足ED PE 21=(1)证明:平面ACE ⊥平面ABCD ;(2)求直线PD 与平面ACE 所成角正弦值的大小.【解析】E BACPABCDA 1B 1C 1D 1E解答题(共10题)1.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,AB AP =,E 为棱PD 的中点.(1)证明:AE CD ⊥;(2)求直线AE 与平面PBD 所成角的正弦值;(3)若F 为AB 中点,棱PC 上是否存在一点M ,使得FM AC ⊥,若存在,求出PMMC的值,若不存在,说明理由.【答案】(1)详见解析;(2)63;(3)13PM MC =.【解析】6cos ,3AE EF <>=所以,直线EF 与平面PBD 所成角的正弦值为63;(3)向量(2,2,2)CP =--,(2,2,0)AC =,(2,0,0)AB =.由点M 在棱PC 上,设(01)CM CP λλ=≤≤,故(12,22,2)FM FC CM λλλ=+=--,由FM AC ⊥,得0FM AC ⋅=, 因此(12)2(22)20λλ-⨯+-⨯=,解得34λ=,所以13PM MC =.2. 如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱AA 1⊥底面ABCD ,AB ∥DC ,11AA =,3AB k =, 456(0)AD k BC k DC k k ===>,,.(Ⅰ)求证:CD ⊥平面ADD 1A 1;(Ⅱ)若直线AA 1与平面AB 1C 所成角的正弦值为67,求k 的值. 【解析】(Ⅱ)以D 为原点,DA ,DC ,1DD 的方向为x ,y ,z 轴的正方向建立如图所示的空间直角坐标系,3. 如图,在直三棱柱111ABC A B C -中,平面1A BC ⊥ 侧面11A ABB 且12AA AB ==.(Ⅰ)求证:AB BC ⊥;(Ⅱ)若直线AC 与平面1A BC 所成的角为6π,求锐二面角1A A C B --的大小. 【解析】(1)证明:如图,取1A B 的中点D ,连接AD ,因1AA AB =,则1AD AB ⊥ ,由平面1A BC ⊥侧面11A ABB ,且平面1A BC 侧面11A ABB 1A B =,得1AD A BC ⊥平面,又BC ⊂平面1A BC , 所以AD BC ⊥. 由于三棱柱111ABC A B C —是直三棱柱,则1AA ABC ⊥底面,所以1AA BC ⊥. 又1=AA AD A ,从而BC ⊥侧面11A ABB ,又AB ⊂侧面11A ABB ,故AB BC ⊥.解法二(向量法):由(1)知AB BC ⊥且1BB ABC ⊥底面,所以以点B 为原点,以1BC BA BB 、、所在直线分别为,,x y z 轴建立空间直角坐标系B xyz -,如图所示,且设BC a =,则(0,2,0)A ,(0,0,0)B ,(,0,0)C a ,1(0,2,2)A ,(,0,0)BC a =,1(0,2,2)BA =,(,2,0)AC a =-,1(0,0,2)AA = 设平面1A BC 的一个法向量1(,,)n x y z =,由1BC n ⊥, 11BAn ⊥ 得: 0220xa y z =⎧⎨+=⎩令1y = ,得 0,1x z ==-,则1(0,1,1)n =- 设直线AC 与1A BC 平面所成的角为θ,则6πθ=得12121sin6242AC n AC n a π-===+,解得2a =,即(2,2,0)AC =- 又设平面1A AC 的一个法向量为2n ,同理可得2(1,1,0)n =,设锐二面角1A A C B --的大小为α,则1212121cos cos ,2n n n n n n α=<>==,且(0,)2πα∈,得 3πα=∴ 锐二面角1A A C B --的大小为3π. 4. 在三棱柱111C B A ABC -中,侧面11A ABB 为矩形,2=AB ,221=AA ,D 是1AA 的中点,BD 与1AB 交于点O ,且CO ⊥平面11A ABB .(1)证明:1AB BC ⊥;(2)若OA OC =,求直线CD CD 与平面ABC 所成角的正弦值. 【答案】(1)证明见解析;(2)515. 【解析】又BC ⊂平面CBD ,∴BC AB ⊥1.5. 如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,BC =CD =2,AC =4,∠ACB =∠ACD =3π,F 为PC 的中点,AF ⊥PB.(1)求PA 的长;(2)求二面角B -AF -D 的正弦值. 【解析】(2)由(1)知()03,3,-=AD ,()03,3,=AB ,()320,,=AF .设平面FAD FAD 的法向量为()1111,z y x n =,平面FAB 的法向量为()2222,z y x n =.由0,011=⋅=⋅AF n AD n 得,⎪⎩⎪⎨⎧=+=+032033-1111z y y x 因此可取()2,3,31-=n .由0,022=⋅=⋅AF n AB n 得⎪⎩⎪⎨⎧=+=+0320332222z y y x 故可取()2,3,32-=n .从而法向量21,n n 的夹角的余弦值为81,cos 212121=⋅>=<n n n n n n .故二面角D AF B --正弦值为873. 6. 如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,60ABC ∠=E 、F 分别是PB 、CD 的中点,且4PB PC PD ===.(1)求证:PA ABCD ⊥平面;(2)求证://EF 平面PAD ; (3)求二面角A PB C --的余弦值.ADBCPE FBCADP EFN GH M【解析】(3)取AB 的中点,G 过G 作GH PB ⊥于点,H 连结,.HC GC 则,CG AB ⊥又,,CG PA PAAB A CG ⊥=∴⊥平面.PAB ,HC PB ∴⊥ GHC ∴∠是二面角A PB C --的平面角.在Rt PAB ∆中,2,4,2 3.AB PB PA ==∴= 又Rt BHG ∆∽Rt BAP ∆,3,2HG BG HG PA PB ∴=∴=.在Rt HGC ∆中,可求得153,,2GC HC =∴=5cos 5GHC ∴∠=, 故二面角A PB C --的余弦值为5.57. 直三棱柱111ABC A B C -中,11AA AB AC ===,,E F 分别是1,CC BC 的中点,11AE A B ⊥,D 为棱11A B 上的点.(1)证明:AC AB ⊥ ; (2)证明:DF AE ⊥;(3)是否存在一点D ,使得平面DEF 与平面ABC 所成锐二面角的余弦值为1414?若存在,说明点D 的位置,若不存在,说明理由.【答案】(1)证明见解析;(2)存在,点D 为11A B 中点. 【解析】试题解析:(1)证明:∵11AE A B ⊥,11//,A B AB AE AB ∴⊥,又∵11,AA AB AA AE A ⊥=∴AB ⊥面11A ACC .又∵AC ⊂面11A ACC ,∴AB AC ⊥,以A 为原点建立如图所示的空间直角坐标系A xyz -,则有()()()111110,0,0,0,1,,,,0,0,0,1,1,0,1222A E F A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,设()111,,,D x y z A D A B λ=且()0,1λ∈,即(),,1(1,0,0)x y z λ-=,则11(,0,1),,,122D DF λλ⎛⎫∴=--⎪⎝⎭,∵1110,1,,0222AE DF AE ⎛⎫=∴⋅=-= ⎪⎝⎭,所以DF AE ⊥;8. 如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC ,∠ABC =90°,P A ⊥平面ABCD ,P A =3,AD =2,AB =23,BC =6. (1)求证:BD ⊥平面P AC ; (2)求二面角P -BD -A 的大小.【解析】9. 如图1,直角梯形ABCD 中,AD ∥,BC 90ABC ∠=,BC AB AD 21==,E 是底边BC 上的一点,且BE EC 3=.现将CDE ∆沿DE 折起到DE C 1∆的位置,得到如图2所示的四棱锥,1ABED C -且AB A C =1.ABCDE 图1BE ADMC 1图2(1)求证:⊥A C 1平面ABED ;(2)若M 是棱E C 1的中点,求直线BM 与平面DE C 1所成角的正弦值. 【答案】(1)见解析;(2)49. 【解析】(2)由(1)知:⊥A C 1平面ABED 且AD AB ⊥,分别以1AC AD AB 、、为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系,如图:z xB EAD MC 1y则)0,1,0(),0,21,1(),1,0,0(),0,0,1(1D E C B10.在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,△PAD 是等边三角形,底面ABCD 是边长为2的菱形,∠BAD =60°,E 是AD 的中点,F 是PC 的中点.(1)求证:BE ⊥平面PAD ; (2)求证:EF ∥平面PAB ;(3)求直线EF 与平面PBE 所成角的余弦值. 【解析】(2)取PB 中点为H ,连接AH FH ,,则⎪⎪⎭⎫⎝⎛23,230,H ,⎪⎪⎭⎫ ⎝⎛-=23,231,EF ,()⎪⎪⎭⎫⎝⎛-=-⎪⎪⎭⎫ ⎝⎛=23,23100123,230,,,,AH , AH EF //∴, 又⊄EF 平面PAB ,⊂AH 平面PAB ,//EF ∴平面PAB .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题4:立体几何[典型例题]例1. 一个几何体是由圆柱11ADD A 和三棱锥E ABC -组合而成,点A 、B 、C 在圆O 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图所示,其中EA ABC ⊥平面,AB AC ⊥,AB AC =,2AE =.(Ⅰ)求证:AC BD ⊥;(Ⅱ)求二面角A BD C --的平面角的大小.方法1:(1)证明:因为EA ABC ⊥平面,C AABC ⊂平面,所以EA AC ⊥,即E D A C ⊥.又因为AC AB ⊥,AB ED A = ,所以AC ⊥平面EBD .因为B D ⊂平面,所以A C ⊥.………………………………………………………………4分(2)解:因为点A 、B 、C 在圆O 的圆周上,且AB AC ⊥,所以BC 为圆O 的直径.设圆O 的半径为r ,圆柱高为h ,根据正(主)视图、侧(左)视图的面积可得,12210,2122212.2rh r rh r ⎧+⨯=⎪⎪⎨⎪+⨯⨯=⎪⎩…………………………………………6分 解得2,2.r h =⎧⎨=⎩所以4BC =,AB AC ==.………………………………………………………………………7分过点C 作CH BD ⊥于点H ,连接AH ,由(1)知,AC BD ⊥,AC CH C = ,所以BD ⊥平面ACH . 因为AH ⊂平面ACH ,所以BD AH ⊥.所以A H ∠为二面角A BD C --的平面角.…………………………………………………………9分由(1)知,AC ⊥平面ABD ,AH ⊂平面ABD ,AODE正(主)视图E A侧(左)视图A 1D 1A D 1A 1EBCO DAD 1A 1EBCOD所以AC AH ⊥,即△CAH 为直角三角形. 在Rt △BAD中,AB =2AD =,则BD =由AB AD BD AH ⨯=⨯,解得3AH =. 因为t a ACAHC AH∠==…………………………………………………………………………13分所以AHC ∠60=. 所以二面角A BD C--的平面角大小为60 .………………………………………………………14分方法2:(1)证明:因为点A 、B 、C 在圆O 的圆周上,且AB AC ⊥,所以BC 为圆O 的直径.设圆O 的半径为r ,圆柱高为h ,根据正(主)视图、侧(左)视图的面积可得,12210,2122212.2rh r rh r ⎧+⨯=⎪⎪⎨⎪+⨯⨯=⎪⎩…………………………………………2分 解得2,2.r h =⎧⎨=⎩所以4BC =,AB AC ==.………………………………………………………………………3分以点D 为原点,1DD 、DE 所在的射线分别为x 轴、z 轴建立如图的空间直角坐标系D xyz -,则()0,0,0D ,()14,0,0D ,()0,0,2A ,()2,2,2B ,()2,2,2C -,()2,2,0AC =- ,()2,2,2DB =.………………………5分因为()()2,2,02,2,20AC DB =-=, 所以AC DB ⊥ .所以AC BD ⊥.…………………………………………………9分 (2)解:设(),,x y z =n 是平面BCD 的法向量,因为()0,4,0BC =-,AD 1A 1EBCOD所以0,0.BC DB ⎧=⎪⎨=⎪⎩n n 即40,2220.y x y z -=⎧⎨++=⎩ 取1z =-,则()1,0,1=-n 是平面B C 的一个法向量.……………………………………………11分由(1)知,AC BD ⊥,又AC AB ⊥,AB BD B = ,所以AC ⊥平面ABD .所以()2,2,0AC =-是平面ABD的一个法向量.……………………………………………………12分因为1cos ,2AC AC AC ⋅===⋅n n n , 所以,60AC =n .而,ACn 等于二面角A BD C --的平面角,所以二面角A BD C--的平面角大小为60 .………………………………………………………14分方法3:(1)证明:因为EA ABC ⊥平面,C A ABC ⊂平面,所以EA AC ⊥,即ED A C ⊥.又因为AC AB ⊥,AB ED A = ,所以AC ⊥平面EBD . 因为BD EBD ⊂平面,所以A ⊥.…………………………………………………………………………………………4分(2)解:因为点A 、B 、C 在圆O 的圆周上,且AB AC ⊥,所以BC 为圆O 的直径.设圆O 的半径为r ,圆柱高为h ,根据正(主)视图、侧(左)视图的面积可得,12210,2122212.2rh r rh r ⎧+⨯=⎪⎪⎨⎪+⨯⨯=⎪⎩…………………………………………6分 解得2,2.r h =⎧⎨=⎩所以4BC =,AB AC ==.………………………………………………………………………7分以点D 为原点,1DD 、DE 所在的射线分别为x 轴、z 轴建立如图的空间直角坐标系D xyz -,则()0,0,0D ,()14,0,0D ,()0,0,2A ,()2,2,2B ,()2,2,2C -,AD 1A 1EBCODBED CBA()0,4,0BC =- ,()2,2,2DB =.…………………………9分设(),,x y z =n 是平面BCD 的法向量,则0,0.BC DB ⎧=⎪⎨=⎪⎩n n 即40,2220.y x y z -=⎧⎨++=⎩取1z =-,则()1,0,1=-n 是平面BCD 的一个法向量.………11分 由(1)知,AC BD ⊥,又AC AB ⊥,AB BD B = , 所以AC ⊥平面ABD . 所以()2,2,0AC =-是平面ABD的一个法向量.……………………………………………………12分因为1cos ,2AC AC AC ⋅===⋅n n n , 所以,60AC =n .而,ACn 等于二面角A BD C --的平面角,所以二面角A BD C--的平面角大小为60 .………………………………………………………14分例2. 如图,ABC ∆是以C 为直角的等腰直角三角形,直角边长为8,BC //DE ,3:5EC :AE =,沿DE 将三角形ADE 折起使得点A 在平面BCED 上的射影是点C , M C=32AC . (Ⅰ)在BD 上确定点N 的位置,使得ADE //MN 平面; (Ⅱ)在(Ⅰ)的条件下,求CN 与平面ABD 所成角的正弦值.解:(Ⅰ)由已知, 点A 在平面BCED 上的射影是点C , 则可知BCED AC 平面⊥,而CE BC ⊥如图建立空间直 角坐标系,则可知各点的坐标为C(0,0,0),A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0)----------------------- 2分由MC=32AC ,可知点M 的坐标为(0,0,38),设点N 则可知y=8-x ,即点N 的坐标为(x,8-x,0) 设平面ADE 的法向量为)z ,y ,x (n 1=,由题意可知⎩⎨⎧=⋅=⋅0n 0DE n 11,而)0,5,0(DE -=,)4,0,3(AE -=可得⎩⎨⎧=-=0z 4x 30y ,取x=4,则z=3,可得)3,0,4(n 1=要使ADE //MN 平面等价于0MN n 1=⋅即0383)x 8(0x 4=⋅+-+解之可得2x =,即可知点N 的坐标为(2,6,0),点N 为BD 的三等分点.------7分 (Ⅱ)由(Ⅰ)可知)0,6,2(CN =,设平面ADB 的法向量为)z ,y ,x (n 2=,由题意可知⎩⎨⎧=⋅=⋅0n 0DB n 11,而)0,3,3(-=,)4,8,0(-=可得⎩⎨⎧=-=+-0z 4Y 80y 3X 3,取x=1,则y=1,z=2可得)2,1,1(n 2= ------------------------------------------------11分 设CN 与平面ABD 所成角为θ,sin =θ15152---------------14分例3. 如图,在四棱锥P -ABCD 中,底面ABCD 为直角梯形,AD //BC ,∠ADC =90°,平面P AD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,P A =PD=2,BC =12AD =1,CD (Ⅰ)求证:平面PQB ⊥平面P AD ;(Ⅱ)若二面角M -BQ -C 为30°,设PM=tMC ,试确定t 的值解:(1)∵AD // BC ,BC =12AD ,Q 为AD 的中点, ∴四边形BCDQ 为平行四边形,∴CD // BQ . ∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD .又∵平面P AD ⊥平面ABCD 且平面P AD ∩平面ABCD=AD ,∴BQ ⊥平面P AD . ∵BQ ⊂平面PQB ,∴平面PQB ⊥平面P AD . ……………………7分 另证:AD // BC ,BC =12AD ,Q 为AD 的中点, ∴ 四边形BCDQ 为平行四边形, ∴CD // BQ .∵ ∠ADC =90° ∴∠AQB =90°. ∵P A =PD , ∴PQ ⊥AD .∵ PQ ∩BQ =Q , ∴AD ⊥平面PBQ . ∵ AD ⊂平面P AD , ∴平面PQB ⊥平面P AD .……7分(2)∵P A =PD ,Q 为AD 的中点, ∴PQ ⊥AD .∵平面P AD ⊥平面ABCD ,且平面P AD ∩平面ABCD=AD , ∴PQ ⊥平面ABCD .如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n =;(0,0,0)Q,P,B,(1C -.设(,,)M x y z,则(,,PM x y z =,(1,)MC x y z =---,∵t =,∴(1))(x t x y t y z t z =--⎧⎪=⎨⎪=-⎩),∴11t x t y t z ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪⎩ ……………………12分在平面MBQ中,QB =,(1t QM t =-+ , ∴ 平面MBQ法向量为)m t =.∵二面角M -BQ -C 为30°,c o s 30n m n m ︒⋅===∴ 3t =. ……………………14分 注:此小题若用几何法做也相应给分。
例4.如图,在边长为4的菱形ABCD 中,60DAB ∠=。
点E 、F 分别在边CD 、CB 上,点E 与点C 、D 不重合,EF AC ⊥,EF AC O = 。
