2018年高考上海卷(理)
(完整)2018年上海高考化学试题及答案wod版,推荐文档

2018年全国普通高等学校招生统一考试上海化学试卷考生注意:1.本试卷满分150分,考试时间120分钟。
2.本考试设试卷和答题纸两部分,试卷包括试卷和答题要求;所有答案必须凃或写在答题纸上;做在试卷上一律不得分。
3.答题前,考试务必将答题纸上用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号,并将核后的条形码贴在指定位置上,在答题纸反面清楚地填写姓名。
4.答题纸与试卷在试卷编号上是一一对应的,答题时应特别注意,不能错位。
相对原子质量:H-1 C-12 O-8 Na-23 S-32 Ca-40 Fe-56 Ni-59 Cu-64Br-80 Ba-137一、选择题<本题共10分,每小题2分,每题只有一个正确选项)1.2018年4月24日,东航首次成功进行了由地沟油生产的生物航空燃油的验证飞行。
能区别地沟油<加工过的餐饮废弃油)与矿物油<汽油、煤油、柴油等)的方法是A.点燃,能燃烧的是矿物油B.测定沸点,有固定沸点的是矿物油C.加入水中,浮在水面上的是地沟油D.加入足量氢氧化钠溶液共热,不分层的是地沟油【答案】D【解读】地沟油的主要成分是油脂,在氢氧化钠溶液可水解而不分层,矿物油的主要成分是烃的混合物,不溶于水,氢氧化钠溶液,他们都能燃烧,密度比水小、没有固定的沸点,因此,选D2.氰酸铵<NH4OCN)与尿素[CO(NH2>2]A.都是共价化合物B.都是离子化合物C.互为同分异构体D.互为同素异形体【答案】C【解读】氰酸铵是离子化合物,尿素是共价化合物,他们的分子式相同,结构不同,是同分异构体的关系,因此选C3.230Th和232Th是钍的两种同位素,232Th可以转化成233U。
下列有关Th的说法正确的是A. Th 元素的质量数是232B. Th 元素的相对原子质量是231C. 232Th 转换成233U是化学变化D. 230Th和232Th的化学性质相同【答案】D【解读】232Th 230Th的质量分别是232,230 A项错误,元素的相对原子质量是由各种同位素的相对原子质量取得的平均值,B项错误同位素的物理性质可以不同,但化学性质几乎相同,D项正确,化学变化是生成新物质的变化,原子不变,而C项的原子发生变化错误。
2018年上海高考物理试题以及答案详细解析版

2018 年高考真题—物理学科<上海卷)解读版本试卷共7 页,满分l50 分,考试时间l20 分钟。
全卷包括六大题,第一、二大题为单项选择题,第三大题为多项选择题,第四大题为填空题,第五大题为实验题,第六大题为计算题。
考生注意:1、答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号,并将核对后的条形码贴在指定位置上,在答题纸反面清楚地填写姓名。
9Lnt6hCeiT2、第一、第二和第三大题的作答必须用28 铅笔涂在答题纸上相应区域内与试卷题号对应的位置,需要更改时,必须将原选项用橡皮擦去,重新选择。
第四、第五和第六大题的作答必须用黑色的钢笔或圆珠笔写在答题纸上与试卷题号对应的位置(作图可用铅笔>。
9Lnt6hCeiT3、第30、31、32、33 题要求写出必要的文字说明、方程式和重要的演算步骤。
只写出最后答案,而未写出主要演算过程的,不能得分。
有关物理量的数值计算问题,答案中必须明确写出数值和单位。
9Lnt6hCeiT一.单项选择题(共16 分,每小题 2 分。
每小题只有一个正确选项。
>1.电磁波与机械波具有的共同性质是(A>都是横波(B>都能传输能量(C>都能在真空中传播(D>都具有恒定的波速答案:B解读:电磁波与机械波具有的共同性质是都能传输能量,选项 B 正确。
2.当用一束紫外线照射锌板时,产生了光电效应,这时(A>锌板带负电(B>有正离子从锌板逸出(C>有电子从锌板逸出(D>锌板会吸附空气中的正离子答案:C解读:当用一束紫外线照射锌板时,产生了光电效应,有电子从锌板逸出,锌板带正电,选项 C 正确ABD错误。
3.白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的(A>传播速度不同(B>强度不同(C>振动方向不同(D>频率不同答案:D解读:白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的频率不同。
【精校解析版】2018年全国统一高考(新课标Ⅱ卷)物理试题及答案解析

2018年全国统一高考(新课标Ⅱ)物理试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I卷(选择题)一、单选题1.如图,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有某一速度,木箱获得的动能一定( )A.等于拉力所做的功B.小于拉力所做的功C.等于克服摩擦力所做的功D.大于克服摩擦力所做的功2.高空坠物极易对行人造成伤害。
若一个50 g的鸡蛋从一居民楼的25层坠下,与地面的撞击时间约为2 ms,则该鸡蛋对地面产生的冲击力约为()A.10 N B.102 N C.103 N D.104 N3.2018年2月,我国500 m口径射电望远镜(天眼)发现毫秒脉冲星“J0318+0253”,其自转周期T=5.19 ms,假设星体为质量均匀分布的球体,已知万有引力常量为6.67×10-11N·m2/kg2。
以周期T稳定自转的星体的密度最小值约为()A.5×109kg/m3B.5×1012kg/m3C.5×1015kg/m3D.5×1018kg/m34.用波长为300nm的光照射锌板,电子逸出锌板表面的最大初动能为1.28×10-19J.已知普朗克常量为6.63×10-34J·s,真空中的光速为3.00×108m·s-1,能使锌产生光电效应的单色光的最低频率约为()A.1×1014Hz B.8×1014HzC.2×1015Hz D.8×1015Hz5.如图,在同一平面内有两根平行长导轨,导轨间存在依次相邻的矩形匀强磁场区域,区域宽度均为l ,磁感应强度大小相等、方向交替向上向下。
2018年全国高考理综1卷(化学试题部分)答案与分析
2018年全国高考理综(Ⅰ)卷化学试题部分参考答案一、选择题:每小题6分,在每小题给出的四个选项中,只有一选项是符合题目要求的。
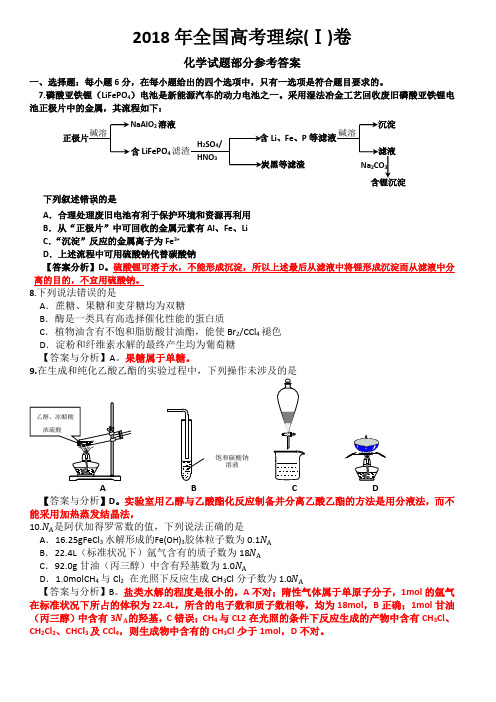
7.磷酸亚铁锂(LiFePO 4)电池是新能源汽车的动力电池之一。
采用湿法冶金工艺回收废旧磷酸亚铁锂电池正极片中的金属,其流程如下:下列叙述错误..的是 A .合理处理废旧电池有利于保护环境和资源再利用 B .从“正极片”中可回收的金属元素有Al 、Fe 、Li C .“沉淀”反应的金属离子为Fe 3+ D .上述流程中可用硫酸钠代替碳酸钠【答案分析】D 。
硫酸锂可溶于水,不能形成沉淀,所以上述最后从滤液中将锂形成沉淀而从滤液中分离的目的,不宜用硫酸钠。
8.下列说法错误的是A .蔗糖、果糖和麦芽糖均为双糖B .酶是一类具有高选择催化性能的蛋白质C .植物油含有不饱和脂肪酸甘油酯,能使Br 2/CCl 4褪色D .淀粉和纤维素水解的最终产生均为葡萄糖 【答案与分析】A 。
果糖属于单糖。
9.A B C D【答案与分析】D 。
实验室用乙醇与乙酸酯化反应制备并分离乙酸乙酯的方法是用分液法,而不能采用加热蒸发结晶法,10.N A 是阿伏加得罗常数的值,下列说法正确的是A .16.25gFeCl 3水解形成的Fe(OH)3胶体粒子数为0.1N AB .22.4L (标准状况下)氩气含有的质子数为18N AC .92.0g 甘油(丙三醇)中含有羟基数为1.0N AD .1.0molCH 4与Cl 2 在光照下反应生成CH 3Cl 分子数为1.0N A【答案与分析】B 。
盐类水解的程度是很小的,A 不对;隋性气体属于单原子分子,1mol 的氩气在标准状况下所占的体积为22.4L ,所含的电子数和质子数相等,均为18mol ,B 正确;1mol 甘油(丙三醇)中含有3N A 的羟基,C 错误;CH 4与CL2在光照的条件下反应生成的产物中含有CH 3Cl 、CH 2Cl 2、CHCl 3及CCl 4,则生成物中含有的CH 3Cl 少于1mol ,D 不对。
2018年上海高考物理试题以及答案详细解析版(可编辑修改word版)

2018年高考真题—物理学科<上海卷)解读版本试卷共7页,满分l50分,考试时间l20分钟。
全卷包括六大题,第一、二大题为单项选择题,第三大题为多项选择题,第四大题为填空题,第五大题为实验题,第六大题为计算题。
考生注意:1、答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号,并将核对后的条形码贴在指定位置上,在答题纸反面清楚地填写姓名。
2、第一、第二和第三大题的作答必须用28铅笔涂在答题纸上相应区域内与试卷题号对应的位置,需要更改时,必须将原选项用橡皮擦去,重新选择。
第四、第五和第六大题的作答必须用黑色的钢笔或圆珠笔写在答题纸上与试卷题号对应的位置(作图可用铅笔> 。
3、第30、31、32、33题要求写出必要的文字说明、方程式和重要的演算步骤。
只写出最后答案,而未写出主要演算过程的,不能得分。
有关物理量的数值计算问题,答案中必须明确写出数值和单位。
一.单项选择题(共16分,每小题2分。
每小题只有一个正确选项。
>1.电磁波与机械波具有的共同性质是(A>都是横波(B>都能传输能量(C>都能在真空中传播(D>都具有恒定的波速答案:B解读:电磁波与机械波具有的共同性质是都能传输能量,选项B正确。
2.当用一束紫外线照射锌板时,产生了光电效应,这时(A>锌板带负电(B>有正离子从锌板逸出(C>有电子从锌板逸出(D>锌板会吸附空气中的正离子答案:C解读:当用一束紫外线照射锌板时,产生了光电效应,有电子从锌板逸出,锌板带正电,选项C正确ABD错误。
3.白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的(A>传播速度不同(B>强度不同(C>振动方向不同(D>频率不同答案:D解读:白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的频率不同。
4.做简谐振动的物体,当它每次经过同一位置时,可能不同的物理量是(A>位移(B>速度(C>加速度(D>回复力答案:B解读:做简谐振动的物体,当它每次经过同一位置时,位移相同,加速度相同,位移相同,可能不同的物理量是速度,选项B正确。
2018年上海市普通高中学业水平等级性考试(高考)物理试卷(含答案)

3
B. 运动员具有动能和重力势能,撑杆具有弹性势能和动能 C. 运动员和撑杆都只具有弹性势能 D. 运动员和撑杆都只具有动能 【答案】B 【详解】运动员放手瞬间,对于运动员来说,具有水平方向的速度,故运动具有动能,以地面为零势能面, 运动员具有重力势能;对于撑杆而言,撑杆有形变,故有弹性势能,与运动员分离的瞬间,上端跟运动员 具有相同的速度,故有动能;故 B 正确,ACD 错误; 故选 B。 12.一个学生设计实验,闭合电路观察电流表有无变化,判断电源有无内阻。则以下说法正确的是( ) A. 不能通过该实验证明是否是恒压电源 B. 能,若电流不变则有内阻 C. 能,若电流不变则无内阻 D. 能,电流变大,则有内阻 【答案】C
B. 波长不变 D. 波速不变
【详解】绳波在同一绳中传播,波速不变。当人的手频率加快时,波的频率增大,由 v = f 分析知此波的
波长变小。故 ABC 错误,D 正确。
故选 D。
6.有些物理量是过程量,有的是状态量,下面哪个是过程量( )
A. 热量
B. 内能
C. 压强
D. 体积
【答案】A
【详解】A.热量是某一过程中物体吸收或放出的能量,是过程量,故 A 正确;
. 的 【答案】A
【详解】设这三个力大小均为 F ,则 F1 和 F2 的合力大小为:
F合 = 2F F 故三个力一定不会平衡,故 BCD 错误,A 正确。 故选 A。 10.沿 x 轴方向,电场为正,则正电荷从 x1 运动到 x2,电势能的变化是( ) A 电势能一直增大
B. 电势能先增大再减小 C. 电势能先减小再增大 D. 电势能先减小再增大再减小 【答案】C
【详解】沿 x 轴正方向,电场强度为正,依据 E 与 x 图象,可知,从 x1 运动到 x2 ,电场线先向右,再向左,
2018年上海高考物理试题以与答案详细解析版

2018 年高考真题—物理学科 <上海卷)解读版本试卷共 7 页,满分 l50 分,考试时间 l20 分钟。
全卷包括六大题,第一、二大题为单项选择题,第三大题为多项选择题,第四大题为填空题,第五大题为实验题,第六大题为计算题。
考生注意:1、答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号,并将核对后的条形码贴在指定位置上,在答题纸反面清楚地填写姓名。
9Lnt6hCeiT2、第一、第二和第三大题的作答必须用 28 铅笔涂在答题纸上相应区域内与试卷题号对应的位置,需要更改时,必须将原选项用橡皮擦去,重新选择。
第四、第五和第六大题的作答必须用黑色的钢笔或圆珠笔写在答题纸上与试卷题号对应的位置(作图可用铅笔>。
9Lnt6hCeiT3、第 30、31、 32、 33 题要求写出必要的文字说明、方程式和重要的演算步骤。
只写出最后答案,而未写出主要演算过程的,不能得分。
有关物理量的数值计算问题,答案中必须明确写出数值和单位。
9Lnt6hCeiT一.单项选择题(共 16 分,每小题 2 分。
每小题只有一个正确选项。
>1.电磁波与机械波具有的共同性质是(A>都是横波(B>都能传输能量(C>都能在真空中传播(D>都具有恒定的波速答案: B解读:电磁波与机械波具有的共同性质是都能传输能量,选项 B 正确。
2.当用一束紫外线照射锌板时,产生了光电效应,这时(A>锌板带负电(B>有正离子从锌板逸出(C>有电子从锌板逸出(D>锌板会吸附空气中的正离子答案: C解读:当用一束紫外线照射锌板时,产生了光电效应,有电子从锌板逸出,锌板带正电,选项 C 正确 ABD 错误。
3.白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的(A>传播速度不同(B>强度不同(C>振动方向不同(D>频率不同答案: D解读:白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的频率不同。
2018年上海高考数学真题及答案

2018年上海市高考数学试卷参考答案与试题解析一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸的相应位置直接填写结果.1.(4分)(2018?上海)行列式的值为18.【考点】OM:二阶行列式的定义.【专题】11 :计算题;49 :综合法;5R :矩阵和变换.【分析】直接利用行列式的定义,计算求解即可.【解答】解:行列式=4×5﹣2×1=18.故答案为:18.【点评】本题考查行列式的定义,运算法则的应用,是基本知识的考查.2.(4分)(2018?上海)双曲线﹣y2=1的渐近线方程为±.【考点】KC:双曲线的性质.【专题】11 :计算题.【分析】先确定双曲线的焦点所在坐标轴,再确定双曲线的实轴长和虚轴长,最后确定双曲线的渐近线方程.【解答】解:∵双曲线的a=2,b=1,焦点在x轴上而双曲线的渐近线方程为y=±∴双曲线的渐近线方程为y=±故答案为:y=±【点评】本题考察了双曲线的标准方程,双曲线的几何意义,特别是双曲线的渐近线方程,解题时要注意先定位,再定量的解题思想3.(4分)(2018?上海)在(1+x)7的二项展开式中,x2项的系数为21(结果用数值表示).【考点】DA:二项式定理.【专题】38 :对应思想;4O:定义法;5P :二项式定理.【分析】利用二项式展开式的通项公式求得展开式中x2的系数.【解答】解:二项式(1+x)7展开式的通项公式为T r+1=?x r,令r=2,得展开式中x2的系数为=21.故答案为:21.【点评】本题考查了二项展开式的通项公式的应用问题,是基础题.4.(4分)(2018?上海)设常数a∈R,函数f(x)=1og2(x+a).若f(x)的反函数的图象经过点(3,1),则a=7.【考点】4R:反函数.【专题】11 :计算题;33 :函数思想;4O:定义法;51 :函数的性质及应用.【分析】由反函数的性质得函数f(x)=1og2(x+a)的图象经过点(1,3),由此能求出a.【解答】解:∵常数a∈R,函数f(x)=1og2(x+a).f(x)的反函数的图象经过点(3,1),∴函数f(x)=1og2(x+a)的图象经过点(1,3),∴log2(1+a)=3,解得a=7.故答案为:7.【点评】本题考查实数值的求法,考查函数的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.5.(4分)(2018?上海)已知复数z满足(1+i)z=1﹣7i(i是虚数单位),则|z|= 5.【考点】A8:复数的模.【专题】38 :对应思想;4A :数学模型法;5N :数系的扩充和复数.【分析】把已知等式变形,然后利用复数代数形式的乘除运算化简,再由复数求模公式计算得答案.【解答】解:由(1+i)z=1﹣7i,得,则|z|=.故答案为:5.【点评】本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.6.(4分)(2018?上海)记等差数列{a n}的前n项和为S n,若a3=0,a6+a7=14,则S7=14.【考点】85:等差数列的前n项和.【专题】11 :计算题;34 :方程思想;4O:定义法;54 :等差数列与等比数列.【分析】利用等差数列通项公式列出方程组,求出a1=﹣4,d=2,由此能求出S7.【解答】解:∵等差数列{a n}的前n项和为S n,a3=0,a6+a7=14,∴,解得a1=﹣4,d=2,∴S7=7a1+=﹣28+42=14.故答案为:14.【点评】本题考查等差数列的前7项和的求法,考查等差数列的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.7.(5分)(2018?上海)已知α∈{﹣2,﹣1,﹣,1,2,3},若幂函数f (x)=xα为奇函数,且在(0,+∞)上递减,则α=﹣1.【考点】4U:幂函数的概念、解析式、定义域、值域.【专题】11 :计算题;34 :方程思想;4O:定义法;51 :函数的性质及应用.【分析】由幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,得到a是奇数,且a<0,由此能求出a的值.【解答】解:∵α∈{﹣2,﹣1,,1,2,3},幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,∴a是奇数,且a<0,∴a=﹣1.故答案为:﹣1.【点评】本题考查实数值的求法,考查幂函数的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.8.(5分)(2018?上海)在平面直角坐标系中,已知点A(﹣1,0)、B(2,0),E、F是y轴上的两个动点,且||=2,则的最小值为﹣3.【考点】9O:平面向量数量积的性质及其运算.【专题】11 :计算题;35 :转化思想;41 :向量法;5A :平面向量及应用.【分析】据题意可设E(0,a),F(0,b),从而得出|a﹣b|=2,即a=b+2,或b=a+2,并可求得,将a=b+2带入上式即可求出的最小值,同理将b=a+2带入,也可求出的最小值.【解答】解:根据题意,设E(0,a),F(0,b);∴;∴a=b+2,或b=a+2;且;∴;当a=b+2时,;∵b2+2b﹣2的最小值为;∴的最小值为﹣3,同理求出b=a+2时,的最小值为﹣3.故答案为:﹣3.【点评】考查根据点的坐标求两点间的距离,根据点的坐标求向量的坐标,以及向量坐标的数量积运算,二次函数求最值的公式.9.(5分)(2018?上海)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是(结果用最简分数表示).【考点】CB:古典概型及其概率计算公式.【专题】11 :计算题;34 :方程思想;49 :综合法;5I :概率与统计.【分析】求出所有事件的总数,求出三个砝码的总质量为9克的事件总数,然后求解概率即可.【解答】解:编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,3个数中含有1个2;2个2,没有2,3种情况,所有的事件总数为:=10,这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两个,所以:这三个砝码的总质量为9克的概率是:=,故答案为:.【点评】本题考查古典概型的概率的求法,是基本知识的考查.10.(5分)(2018?上海)设等比数列{a n}的通项公式为a n=q n﹣1(n∈N*),前n 项和为S n.若=,则q=3.【考点】8J:数列的极限.【专题】11 :计算题;34 :方程思想;35 :转化思想;49 :综合法;55 :点列、递归数列与数学归纳法.【分析】利用等比数列的通项公式求出首项,通过数列的极限,列出方程,求解公比即可.【解答】解:等比数列{a n}的通项公式为a=q n﹣1(n∈N*),可得a1=1,因为=,所以数列的公比不是1,,a n+1=q n.可得====,可得q=3.故答案为:3.【点评】本题考查数列的极限的运算法则的应用,等比数列求和以及等比数列的简单性质的应用,是基本知识的考查.11.(5分)(2018?上海)已知常数a>0,函数f(x)=的图象经过点P(p,),Q(q,).若2p+q=36pq,则a=6.【考点】3A:函数的图象与图象的变换.【专题】35 :转化思想;51 :函数的性质及应用.【分析】直接利用函数的关系式,利用恒等变换求出相应的a值.【解答】解:函数f(x)=的图象经过点P(p,),Q(q,).则:,整理得:=1,解得:2p+q=a2pq,由于:2p+q=36pq,所以:a2=36,由于a>0,故:a=6.故答案为:6【点评】本题考查的知识要点:函数的性质的应用,代数式的变换问题的应用.12.(5分)(2018?上海)已知实数x1、x2、y1、y2满足:x12+y12=1,x22+y22=1,x1x2+y1y2=,则+的最大值为+.【考点】7F:基本不等式及其应用;IT:点到直线的距离公式.【专题】35 :转化思想;48 :分析法;59 :不等式的解法及应用.【分析】设A(x1,y1),B(x2,y2),=(x1,y1),=(x2,y2),由圆的方程和向量数量积的定义、坐标表示,可得三角形OAB为等边三角形,AB=1,+的几何意义为点A,B两点到直线x+y﹣1=0的距离d1与d2之和,由两平行线的距离可得所求最大值.【解答】解:设A(x1,y1),B(x2,y2),=(x1,y1),=(x2,y2),由x12+y12=1,x22+y22=1,x1x2+y1y2=,可得A,B两点在圆x2+y2=1上,且?=1×1×cos∠AOB=,即有∠AOB=60°,即三角形OAB为等边三角形,AB=1,+的几何意义为点A,B两点到直线x+y﹣1=0的距离d1与d2之和,显然A,B在第三象限,AB所在直线与直线x+y=1平行,可设AB:x+y+t=0,(t>0),由圆心O到直线AB的距离d=,可得2=1,解得t=,即有两平行线的距离为=,即+的最大值为+,故答案为:+.【点评】本题考查向量数量积的坐标表示和定义,以及圆的方程和运用,考查点与圆的位置关系,运用点到直线的距离公式是解题的关键,属于难题.二、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确选项.考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.13.(5分)(2018?上海)设P是椭圆=1上的动点,则P到该椭圆的两个焦点的距离之和为()A.2 B.2 C.2 D.4【考点】K4:椭圆的性质.【专题】11 :计算题;49 :综合法;5D :圆锥曲线的定义、性质与方程.【分析】判断椭圆长轴(焦点坐标)所在的轴,求出a,接利用椭圆的定义,转化求解即可.【解答】解:椭圆=1的焦点坐标在x轴,a=,P是椭圆=1上的动点,由椭圆的定义可知:则P到该椭圆的两个焦点的距离之和为2a=2.故选:C.【点评】本题考查椭圆的简单性质的应用,椭圆的定义的应用,是基本知识的考查.>1”是“<1”的()14.(5分)(2018?上海)已知a∈R,则“aA.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分又非必要条件【考点】29:充分条件、必要条件、充要条件.【专题】11 :计算题;34 :方程思想;4O:定义法;5L :简易逻辑.【分析】“a>1”?“”,“”?“a>1或a<0”,由此能求出结果.【解答】解:a∈R,则“a>1”?“”,“”?“a>1或a<0”,∴“a>1”是“”的充分非必要条件.故选:A.【点评】本题考查充分条件、必要条件的判断,考查不等式的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.15.(5分)(2018?上海)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设AA1是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以AA1为底面矩形的一边,则这样的阳马的个数是()A.4 B.8 C.12 D.16【考点】D8:排列、组合的实际应用.【专题】11 :计算题;38 :对应思想;4R:转化法;5O :排列组合.【分析】根据新定义和正六边形的性质可得答案.【解答】解:根据正六边形的性质,则D1﹣A1ABB1,D1﹣A1AFF1满足题意,而C1,E1,C,D,E,和D1一样,有2×6=12,当A1ACC1为底面矩形,有2个满足题意,当A1AEE1为底面矩形,有2个满足题意,故有12+2+2=16故选:D.【点评】本题考查了新定义,以及排除组合的问题,考查了棱柱的特征,属于中档题.16.(5分)(2018?上海)设D是含数1的有限实数集,f(x)是定义在D上的函数,若f(x)的图象绕原点逆时针旋转后与原图象重合,则在以下各项中,f(1)的可能取值只能是()A.B.C.D.0【考点】3A:函数的图象与图象的变换.【专题】35 :转化思想;51 :函数的性质及应用;56 :三角函数的求值.【分析】直接利用定义函数的应用求出结果.【解答】解:由题意得到:问题相当于圆上由12个点为一组,每次绕原点逆时针旋转个单位后与下一个点会重合.我们可以通过代入和赋值的方法当f(1)=,,0时,此时得到的圆心角为,,0,然而此时x=0或者x=1时,都有2个y与之对应,而我们知道函数的定义就是要求一个x只能对应一个y,因此只有当x=,此时旋转,此时满足一个x只会对应一个y,因此答案就选:B.故选:B.【点评】本题考查的知识要点:定义性函数的应用.三、解答题(本大题共有5题,满分76分)解答下列各题必须在答题纸的相应位置写出必要的步骤.17.(14分)(2018?上海)已知圆锥的顶点为P,底面圆心为O,半径为2.(1)设圆锥的母线长为4,求圆锥的体积;(2)设PO=4,OA、OB是底面半径,且∠AOB=90°,M为线段AB的中点,如图.求异面直线PM与OB所成的角的大小.【考点】LM:异面直线及其所成的角;L5:旋转体(圆柱、圆锥、圆台);LF:棱柱、棱锥、棱台的体积.【专题】11 :计算题;31 :数形结合;41 :向量法;5F :空间位置关系与距离;5G :空间角.【分析】(1)由圆锥的顶点为P,底面圆心为O,半径为2,圆锥的母线长为4能求出圆锥的体积.(2)以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出异面直线PM与OB所成的角.【解答】解:(1)∵圆锥的顶点为P,底面圆心为O,半径为2,圆锥的母线长为4,∴圆锥的体积V===.(2)∵PO=4,OA,OB是底面半径,且∠AOB=90°,M为线段AB的中点,∴以O为原点,OA为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,P(0,0,4),A(2,0,0),B(0,2,0),M(1,1,0),O(0,0,0),=(1,1,﹣4),=(0,2,0),设异面直线PM与OB所成的角为θ,则cosθ===.∴θ=arccos.∴异面直线PM与OB所成的角的为arccos.【点评】本题考查圆锥的体积的求法,考查异面直线所成角的正切值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.18.(14分)(2018?上海)设常数a∈R,函数f(x)=asin2x+2cos2x.(1)若f(x)为偶函数,求a的值;(2)若f()=+1,求方程f(x)=1﹣在区间[﹣π,π]上的解.【考点】GP:两角和与差的三角函数;GS:二倍角的三角函数.【专题】11 :计算题;38 :对应思想;4R:转化法;58 :解三角形.【分析】(1)根据函数的奇偶性和三角形的函数的性质即可求出,(2)先求出a的值,再根据三角形函数的性质即可求出.【解答】解:(1)∵f(x)=asin2x+2cos2x,∴f(﹣x)=﹣asin2x+2cos2x,∵f(x)为偶函数,∴f(﹣x)=f(x),∴﹣asin2x+2cos2x=asin2x+2cos2x,∴2asin2x=0,∴a=0;(2)∵f()=+1,∴asin+2cos2()=a+1=+1,∴a=,∴f(x)=sin2x+2cos2x=sin2x+cos2x+1=2sin(2x+)+1,∵f(x)=1﹣,∴2sin(2x+)+1=1﹣,∴sin(2x+)=﹣,∴2x+=﹣+2kπ,或2x+=π+2kπ,k∈Z,∴x=﹣π+kπ,或x=π+kπ,k∈Z,∵x∈[﹣π,π],∴x=或x=或x=﹣或x=﹣【点评】本题考查了三角函数的化简和求值,以及三角函数的性质,属于基础题.19.(14分)(2018?上海)某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族S中的成员仅以自驾或公交方式通勤.分析显示:当S中x%(0<x<100)的成员自驾时,自驾群体的人均通勤时间为f(x)=(单位:分钟),而公交群体的人均通勤时间不受x影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)当x在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族S的人均通勤时间g(x)的表达式;讨论g(x)的单调性,并说明其实际意义.【考点】5B:分段函数的应用.【专题】12 :应用题;33 :函数思想;4C :分类法;51 :函数的性质及应用.【分析】(1)由题意知求出f(x)>40时x的取值范围即可;(2)分段求出g(x)的解析式,判断g(x)的单调性,再说明其实际意义.【解答】解;(1)由题意知,当30<x<100时,f(x)=2x+﹣90>40,即x2﹣65x+900>0,解得x<20或x>45,∴x∈(45,100)时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;(2)当0<x≤30时,g(x)=30?x%+40(1﹣x%)=40﹣;当30<x<100时,g(x)=(2x+﹣90)?x%+40(1﹣x%)=﹣x+58;∴g(x)=;当0<x<32.5时,g(x)单调递减;当32.5<x<100时,g(x)单调递增;说明该地上班族S中有小于32.5%的人自驾时,人均通勤时间是递减的;有大于32.5%的人自驾时,人均通勤时间是递增的;当自驾人数为32.5%时,人均通勤时间最少.【点评】本题考查了分段函数的应用问题,也考查了分类讨论与分析问题、解决问题的能力.20.(16分)(2018?上海)设常数t>2.在平面直角坐标系xOy中,已知点F(2,0),直线l:x=t,曲线Γ:y2=8x(0≤x≤t,y≥0).l与x轴交于点A、与Γ交于点B.P、Q分别是曲线Γ与线段AB上的动点.(1)用t表示点B到点F的距离;(2)设t=3,|FQ|=2,线段OQ的中点在直线FP上,求△AQP的面积;(3)设t=8,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在Γ上?若存在,求点P的坐标;若不存在,说明理由.【考点】KN:直线与抛物线的位置关系.【专题】35 :转化思想;4R:转化法;5D :圆锥曲线的定义、性质与方程.【分析】(1)方法一:设B点坐标,根据两点之间的距离公式,即可求得|BF|;方法二:根据抛物线的定义,即可求得|BF|;(2)根据抛物线的性质,求得Q点坐标,即可求得OD的中点坐标,即可求得直线PF的方程,代入抛物线方程,即可求得P点坐标,即可求得△AQP的面积;(3)设P及E点坐标,根据直线k PF?k FQ=﹣1,求得直线QF的方程,求得Q点坐标,根据+=,求得E点坐标,则()2=8(+6),即可求得P点坐标.【解答】解:(1)方法一:由题意可知:设B(t,2t),则|BF|==t+2,∴|BF|=t+2;方法二:由题意可知:设B(t,2t),由抛物线的性质可知:|BF|=t+=t+2,∴|BF|=t+2;(2)F(2,0),|FQ|=2,t=3,则|FA|=1,∴|AQ|=,∴Q(3,),设OQ的中点D,D(,),k QF==﹣,则直线PF方程:y=﹣(x﹣2),联立,整理得:3x2﹣20x+12=0,解得:x=,x=6(舍去),∴△AQP的面积S=××=;(3)存在,设P(,y),E(,m),则k PF==,k FQ=,直线QF方程为y=(x﹣2),∴y Q=(8﹣2)=,Q(8,),根据+=,则E(+6,),∴()2=8(+6),解得:y2=,∴存在以FP、FQ为邻边的矩形FPEQ,使得点E在Γ上,且P(,).【点评】本题考查抛物线的性质,直线与抛物线的位置关系,考查转化思想,计算能力,属于中档题.21.(18分)(2018?上海)给定无穷数列{a n},若无穷数列{b n}满足:对任意n ∈N*,都有|b n﹣a n|≤1,则称{b n}与{a n}“接近”.(1)设{a n}是首项为1,公比为的等比数列,b n=a n+1+1,n∈N*,判断数列{b n}是否与{a n}接近,并说明理由;(2)设数列{a n}的前四项为:a1=1,a2=2,a3=4,a4=8,{b n}是一个与{a n}接近的数列,记集合M={x|x=b i,i=1,2,3,4},求M中元素的个数m;(3)已知{a n}是公差为d的等差数列,若存在数列{b n}满足:{b n}与{a n}接近,且在b2﹣b1,b3﹣b2,…,b201﹣b200中至少有100个为正数,求d的取值范围.【考点】8M:等差数列与等比数列的综合.【专题】34 :方程思想;48 :分析法;54 :等差数列与等比数列.【分析】(1)运用等比数列的通项公式和新定义“接近”,即可判断;(2)由新定义可得a n﹣1≤b n≤a n+1,求得b i,i=1,2,3,4的范围,即可得到所求个数;(3)运用等差数列的通项公式可得a n,讨论公差d>0,d=0,﹣2<d<0,d≤﹣2,结合新定义“接近”,推理和运算,即可得到所求范围.【解答】解:(1)数列{b n}与{a n}接近.理由:{a n}是首项为1,公比为的等比数列,可得a n=,b n=a n+1+1=+1,则|b n﹣a n|=|+1﹣|=1﹣<1,n∈N*,可得数列{b n}与{a n}接近;(2){b n}是一个与{a n}接近的数列,可得a n﹣1≤b n≤a n+1,数列{a n}的前四项为:a1=1,a2=2,a3=4,a4=8,可得b1∈[0,2],b2∈[1,3],b3∈[3,5],b4∈[7,9],可能b1与b2相等,b2与b3相等,但b1与b3不相等,b4与b3不相等,集合M={x|x=b i,i=1,2,3,4},M中元素的个数m=3或4;(3){a n}是公差为d的等差数列,若存在数列{b n}满足:{b n}与{a n}接近,可得a n=a1+(n﹣1)d,①若d>0,取b n=a n,可得b n+1﹣b n=a n+1﹣a n=d>0,则b2﹣b1,b3﹣b2,…,b201﹣b200中有200个正数,符合题意;②若d=0,取b n=a1﹣,则|b n﹣a n|=|a1﹣﹣a1|=<1,n∈N*,可得b n+1﹣b n=﹣>0,则b2﹣b1,b3﹣b2,…,b201﹣b200中有200个正数,符合题意;③若﹣2<d<0,可令b2n﹣1=a2n﹣1﹣1,b2n=a2n+1,则b2n﹣b2n﹣1=a2n+1﹣(a2n﹣1﹣1)=2+d>0,则b2﹣b1,b3﹣b2,…,b201﹣b200中恰有100个正数,符合题意;④若d≤﹣2,若存在数列{b n}满足:{b n}与{a n}接近,即为a n﹣1≤b n≤a n+1,a n+1﹣1≤b n+1≤a n+1+1,可得b n+1﹣b n≤a n+1+1﹣(a n﹣1)=2+d≤0,b2﹣b1,b3﹣b2,…,b201﹣b200中无正数,不符合题意.综上可得,d的范围是(﹣2,+∞).【点评】本题考查新定义“接近”的理解和运用,考查等差数列和等比数列的定义和通项公式的运用,考查分类讨论思想方法,以及运算能力和推理能力,属于难题.感恩和爱是亲姐妹。
【真题】2018年上海市高考数学试题含答案解析

2018年高考数学真题试卷(上海卷) 一、填空题1.(2018•上海)行列式4125的值为 。
【答案】18 【解析】【解答】4125=45-21=18 【分析】a cb d=ad-bc 交叉相乘再相减。
【题型】填空题 【考查类型】中考真题 【试题级别】高三 【试题地区】上海【试题】2018年高考数学真题试卷(上海卷)2.(2018•上海)双曲线2214x y -=的渐近线方程为 。
【答案】12y x =±【解析】【解答】2214x y -=,a=2,b=1。
故渐近线方程为12y x =± 【分析】渐近线方程公式。
注意易错点焦点在轴上,渐近线直线方程为22221x y ba -=时,by x a=±。
【题型】填空题 【考查类型】中考真题 【试题级别】高三 【试题地区】上海【试题】2018年高考数学真题试卷(上海卷)3.(2018•上海)在(1+)7的二项展开式中,²项的系数为 。
(结果用数值表示) 【答案】21【解析】【解答】(1+)7中有T r+1=7r rC x ,故当r=2时,27C =762⨯=21【分析】注意二项式系数,与各项系数之间差别。
考点公式()na b +第r+1项为T r+1=r n r rn C ab-。
【题型】填空题 【考查类型】中考真题 【试题级别】高三 【试题地区】上海【试题】2018年高考数学真题试卷(上海卷)4.(2018•上海)设常数a R ∈,函数2()log ()f x x a =+,若f x ()的反函数的图像经过点31(,),则a= 。
【答案】7【解析】【解答】f x ()的反函数的图像经过点31(,),故()f x 过点3(1,),则()13f =,()2log 1a +=3,1+a=23所以a=23-1,故a=7.【分析】原函数()f x 与反函数图像关于y=对称,如:原函数上任意点()00,x y ,则反函数上点为()00,y x【题型】填空题 【考查类型】中考真题 【试题级别】高三 【试题地区】上海【试题】2018年高考数学真题试卷(上海卷)5.(2018•上海)已知复数满足117i z i +=-()(i 是虚数单位),则∣∣= 。
2018年全国卷高考真题(理科)

伪满时期的哈尔滨市立医院,如今仍是医院。后来得知赵一曼女士曾在这里 住过院,我便翻阅了她的一些资料。 赵一曼女士, 是一个略显瘦秀且成熟的女性。在她身上弥漫着拔俗的文人气 质和职业军人的冷峻。在任何地方,你都能看出她有别于他人的风度。 赵一曼女士率领的抗联活动在小兴安岭的崇山峻岭中, 那儿能够听到来自坡 镇的钟 声,冬夜里,钟声会传得很远很远。钟声里,抗联的兵士在森林里烤火,烤野味 儿,或者唱着“火烤胸前暖,风吹背后寒......战士们哟”......这些都给躺在 病床上的赵一曼女士留下清晰回忆。 赵一曼女士单独一间病房,由警察昼夜看守。 白色的小柜上有一个玻璃花瓶,里面插着丁香花。赵一曼女士喜欢丁香花。 这束丁香花,是女护士韩勇义折来摆放在那里的。听说,丁香花现在已经成为这 座城市的“市花”了。 她是在山区中了日军的子弹后被捕的。滨江省警务厅的大野泰治对赵一曼女 士进行了严刑拷问,始终没有得到有价值的回答,他觉得很没面子。 大野泰治在向上司呈送的审讯报告上写道: 赵一曼是中国共产党珠河县委委员,在该党工作上有与赵尚志同等的权 力。她是北满共产党的重要干部,通过对此人的严厉审讯,有可能澄清中共与苏 联的关系。 1936 年初,起一曼女士以假名“王氏”被送到医院监禁治疗。 《滨江省警务厅关于赵一曼的情况》扼要地介绍了赵一曼女士从市立医院逃 走和被害的情况。 赵一曼女士是在 6 月 28 日逃走的。夜里,看守董宪勋在他叔叔的协助下, 将赵一曼抬出医院的后门。一辆雇好的出租车已等在那里。几个人上了车, 车立刻就开走了。出租车开到文庙屠宰场的后面,韩勇义早就等候在那里, 扶着赵一曼女士上了雇好的轿子,大家立刻向宾县方向逃去。 赵一曼女士住院期间, 发现警士董宪勋似乎可以争取。经过一段时间的观 察、分析,她觉得有把握去试一试。 她躺在病床上,和蔼地问董警士:“董先生,您一个月的薪俸是多少?” 董警士显得有些忸怩,“十多块钱吧……” 赵一曼女士遺憾地笑了,说:“真没有想到,薪俸会这样少。” 董警士更加忸怩了。 赵一曼女士神情端庄地说:“七尺男儿,为着区区十几块钱,甘为日本人役 使,不是太愚蠢了吗?” 董警士无法再正视这位成熟女性的眼睛了,只是哆哆嗦嗦给自己点了一颗
【数学】2018高考真题——上海卷(解析版)

2018年上海市高考数学试卷
一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸的相应位置直接填写结果.
1.行列式的值为.
【答案】18
【解析】行列式=4×5﹣2×1=18.
故答案为:18.
2.双曲线﹣y2=1的渐近线方程为.
【答案】y=±
【解析】∵双曲线的a=2,b=1,焦点在x轴上
而双曲线的渐近线方程为y=±,
∴双曲线的渐近线方程为y=±,
故答案为:y=±.
3.在(1+x)7的二项展开式中,x2项的系数为(结果用数值表示).
【答案】21
【解析】二项式(1+x)7展开式的通项公式为T r+1=•x r,
令r=2,得展开式中x2的系数为=21.
故答案为:21.
4.设常数a∈R,函数f(x)=log2(x+a).若f(x)的反函数的图象经过点(3,1),则a =.
【答案】7
【解析】∵常数a∈R,函数f(x)=log2(x+a).
f(x)的反函数的图象经过点(3,1),。
2018年全国高考地理试题及答案-上海

2018年全国普通高等学校招生统一考试<上海卷)地理一、选择题<共50分,每小题2分。
每小题只有一个正确答案)<一)“我在仰望,月亮之上;有多少梦想,在自由地飞翔”。
21世纪人类将进入开发月球资源,探索太空的新时代,人类的美好愿望准将变为现实。
Iiiss40C7o1.月球的表面形态给人类深刻印象。
下列因素中,影响月表形态形成的主要因素是A.太阳的能量 B.地球的引力 C.陨石的撞击 D.太阳风侵袭Iiiss40C7o2.若科学家在未来的月球表面实验室进行科学实验,其利用的月球表面特殊条件是①弱重力②超高温③低辐射④高真空A.①② B.③④ C.②③ D.①④3.月球和地球距太阳的距离差别不大,但表面环境迥然不同。
其主要原因是二者的A.质量差异 B.形态差异 C.自转差异 D.公转差异Iiiss40C7o<二)2018年5月,印度第一大信息软件服务企业印孚瑟斯技术公司在沪投资一亿多美元,建设软件园区,拓展在华业务。
Iiiss40C7o4.上海吸引印孚瑟斯技术公司在沪拓展业务的主要区位优势是A.劳动力价格低廉 B.人才技术力量雄厚 C.接近原料产地 D.产品运输便利5.印孚瑟斯技术公司在沪拓展业务对上海经济、社会发展的积极意义是①填补信息软件业空白②有效利用大批闲置土地③提高信息行业的集聚程度④促进现代服务业发展A.①② B.②③ C.③④D.①④<三)人口迁移有着各种各样的原因,对社会、经济、生态、文化产生一定的影响。
6.在以下人口迁移的事例中,由生态问题引发的是①三峡库区移民前往东部沿海②宁夏西部农民迁出干旱地区③东部知识青年迁入西部边疆④陕西南部农民搬离多灾山区A.①② B.①③ C.③④D.②④7.一般而言,有组织的大规模移民过程中,需要考虑的主要因素是迁入区的Iiiss40C7oA.人口密度 B.人口容量 C.人口构成 D.人口素质Iiiss40C7o8.20世纪60年代末,一批京津沪知识青年来到北大荒。
2018年上海高考物理试题以及答案详细解析版

2018 年高考真题—物理学科 <上海卷)解读版本试卷共 7 页,满分 l50 分,考试时间 l20 分钟。
全卷包括六大题,第一、二大题为单项选择题,第三大题为多项选择题,第四大题为填空题,第五大题为实验题,第六大题为计算题。
考生注意:1、答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号,并将核对后的条形码贴在指定位置上,在答题纸反面清楚地填写姓名。
9Lnt6hCeiT2、第一、第二和第三大题的作答必须用 28 铅笔涂在答题纸上相应区域内与试卷题号对应的位置,需要更改时,必须将原选项用橡皮擦去,重新选择。
第四、第五和第六大题的作答必须用黑色的钢笔或圆珠笔写在答题纸上与试卷题号对应的位置(作图可用铅笔>。
9Lnt6hCeiT3、第 30、31、 32、 33 题要求写出必要的文字说明、方程式和重要的演算步骤。
只写出最后答案,而未写出主要演算过程的,不能得分。
有关物理量的数值计算问题,答案中必须明确写出数值和单位。
9Lnt6hCeiT一.单项选择题(共 16 分,每小题 2 分。
每小题只有一个正确选项。
>1.电磁波与机械波具有的共同性质是(A>都是横波(B>都能传输能量(C>都能在真空中传播(D>都具有恒定的波速答案: B解读:电磁波与机械波具有的共同性质是都能传输能量,选项 B 正确。
2.当用一束紫外线照射锌板时,产生了光电效应,这时(A>锌板带负电(B>有正离子从锌板逸出(C>有电子从锌板逸出(D>锌板会吸附空气中的正离子答案: C解读:当用一束紫外线照射锌板时,产生了光电效应,有电子从锌板逸出,锌板带正电,选项 C 正确 ABD 错误。
3.白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的(A>传播速度不同(B>强度不同(C>振动方向不同(D>频率不同答案: D解读:白光通过双缝后产生的干涉条纹是彩色的,其原因是不同色光的频率不同。
【高三物理试题精选】上海市2018年高考物理试卷

上海市2018年高考物理试卷
3W的连续激光。
已知可见光波长的数量级为10-7m,普朗克常量h=663×10-34J s,该激光器发出的
(A)是紫外线
(B)是红外线
(C)光子能量约为13×10-18J
(D)光子数约为每秒38×1016个
18.两个共点力Fl、F2大小不同,它们的合力大小为F,则
(A)F1、F2同时增大一倍,F也增大一倍
(B)F1、F2同时增加10N,F也增加10N
(C)F1增加10N,F2减少10N,F一定不变
(D)若F1、F2中的一个增大,F不一定增大
19.如图,轰炸机沿水平方向匀速飞行,到达坡底端正上方时释放一颗炸弹,并垂直击中坡上的目标A。
已知A点高度为h,坡倾角为θ,由此可算出
(A)轰炸机的飞行高度
(B)轰炸机的飞行速度
(C)炸弹的飞行时间
(D)炸弹投出时的动能
20.右图为在平静海面上,两艘拖船A、B拖着驳船C运动的示意图。
A、B的速度分别沿着缆绳CA、CB方向,A、B、C不在一条直线上。
由于缆绳不可伸长,因此C的速度在CA、CB方向的投影分别与A、B的速度相等,由此可知C的
(A)速度大小可以介于A、B的速度大小之间
(B)速度大小一定不小于A、B的速度大小
(C)速度方向可能在CA和CB的夹角范围外
(D)速度方向一定在CA和CB的夹角范围内
四.填空题(共20分,每小题4分。
)
本大题中第22题为分叉题,分A、B两类,考生可任选一类答题。
上海2018年高考数学 第16题优美解 精品

2018年高考数学(上海)第16题(理)试题优美解
试题(上海、 理科16)
在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是( )
A .锐角三角形
B .直角三角形
C .钝角三角形
D .不能确定
解析 由正弦定理,得,sin 2,sin 2,sin 2C R
c B R b A R a ===代入得到222a b c +<, 由余弦定理的推理得222
cos 02a b c C ab
+-=<,所以C 为钝角,所以该三角形为钝角三角形.故选择C
试题或解法赏析.
本题主要考查正弦定理及其推理、余弦定理的运用.主要抓住所给式子的结构来选择定理,如果出现了角度的正弦值就选择正弦定理,如果出现角度的余弦值就选择余弦定理.本题属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年上海市秋季高考理科数学一、填空题 1.计算:20lim______313n n n →∞+=+2.设m R ∈,222(1)i m m m +-+-是纯虚数,其中i 是虚数单位,则________m = 3.若2211x xx y y y=--,则______x y +=4.已知△ABC 的内角A 、B 、C 所对应边分别为a 、b 、c ,若22232330a ab b c ++-=,则角C 的大小是_______________(结果用反三角函数值表示)5.设常数a R ∈,若52a x x ⎛⎫+ ⎪⎝⎭的二项展开式中7x 项的系数为10-,则______a =6.方程1313313x x -+=-的实数解为________ 7.在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为__________8.盒子中装有编号为1,2,3,4,5,6,7,8,9的九个球,从中任意取出两个,则这两个球的编号之积为偶数的概率是___________(结果用最简分数表示)9.设AB 是椭圆Γ的长轴,点C 在Γ上,且4CBA π∠=,若AB=4,BC =Γ的两个焦点之间的距离为________[来源:学科网ZXXK]10.设非零常数d 是等差数列12319,,,,x x x x 的公差,随机变量ξ等可能地取值12319,,,,x x x x ,则方差_______D ξ= 11.若12cos cos sin sin ,sin 2sin 223x y x y x y +=+=,则sin()________x y += 12.设a 为实常数,()y f x =是定义在R 上的奇函数,当0x <时,2()97a f x x x=++,若()1f x a ≥+对一切0x ≥成立,则a 的取值范围为________13.在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y =和1y =-围成的封闭图形记为D ,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48π,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________[来源:学科网ZXXK][来源:学科网]14.对区间I 上有定义的函数()g x ,记(){|(),}g I y y g x x I ==∈,已知定义域为[0,3]的函数()y f x =有反函数1()y f x -=,且11([0,1))[1,2),((2,4])[0,1)f f --==,若方程()0f x x -=有解0x ,则0_____x =二、选择题15.设常数a R ∈,集合{|(1)()0},{|1}A x x x a B x x a =--≥=≥-,若A B R ⋃=,则a 的取值范围为( ) (A) (,2)-∞(B) (,2]-∞(C) (2,)+∞(D) [2,)+∞16.钱大姐常说“便宜没好货”,她这句话的意思是:“不便宜”是“好货”的()(A)充分条件 (B)必要条件 (C)充分必要条件 (D)既非充分也非必要条件17.在数列{}n a 中,21n n a =-,若一个7行12列的矩阵的第i 行第j 列的元素,i j i j i j a a a a a =⋅++,(1,2,,7;1,2,,12i j == )则该矩阵元素能取到的不同数值的个数为( )(A)18 (B)28 (C)48 (D)6318.在边长为1的正六边形ABCDEF 中,记以A 为起点,其余顶点为终点的向量分别为12345,,,,a a a a a ;以D 为起点,其余顶点为终点的向量分别为12345,,,,d d d d d.若,m M 分别为()()i j k r s t a a a d d d ++⋅++ 的最小值、最大值,其中{,,}ij k⊆,{,,}{1,2,3,4,5}r s t ⊆,则,m M 满足( ). (A) 0,0m M => (B) 0,0m M <>(C) 0,0m M <=(D) 0,0m M <<三、解答题19.(本题满分12分)如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C ,并求直线BC 1到平面D 1AC 的距离.C 11A[来源:]20.(6分+8分)甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求110x ≤≤),每小时可获得利润是3100(51)x x+-元.(1)要使生产该产品2小时获得的利润不低于3000元,求x 的取值范围;(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.21.(6分+8分)已知函数()2sin()f x x ω=,其中常数0ω>; (1)若()y f x =在2[,]43ππ-上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图像,区间[,]a b (,a b R ∈且a b <)满足:()y g x =在[,]a b 上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值.22.(3分+5分+8分)如图,已知曲线221:12x C y -=,曲线2:||||1C y x =+,P 是平面上一点,若存在过点P 的直线与12,C C 都有公共点,则称P 为“C 1—C 2型点”.(1)在正确证明1C 的左焦点是“C 1—C 2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);(2)设直线y kx =与2C 有公共点,求证||1k >,进而证明原点不是“C 1—C 2型点”; (3)求证:圆2212x y +=内的点都不是“C 1—C 2型点”.[来源:学.科.网]23.(3 分+6分+9分)给定常数0c >,定义函数()2|4|||f x x c x c =++-+,数列123,,,a a a 满足*1(),n n a f a n N +=∈.[来源:](1)若12a c =--,求2a 及3a ;(2)求证:对任意*1,n n n N a a c +∈-≥,;(3)是否存在1a ,使得12,,,n a a a 成等差数列?若存在,求出所有这样的1a ,若不存在,说明理由.参考答案一、选择题1.13. 2. 2m =-.3.0x y +=. 4.1arccos 3C π=- 5.2a =- 6.3log 4x =.7. 8.1318.9.10.|D d ξ=.11.2sin()3x y +=. 12.87a ≤-. 13.2216ππ+. 14.02x =.15.B .16.B .[来源:] 17.A . 18.D .19.因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C ;直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1ADC ∆中,11AC DC AD ==132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.20.(1)根据题意,33200(51)30005140x x x x+-≥⇒--≥ 又110x ≤≤,可解得310x ≤≤(2)设利润为y 元,则4290031161100(51)910[3()]612y x x x x =⋅+-=⨯--+ 故6x =时,max 457500y =元.21.(1)因为0ω>,根据题意有34202432ππωωππω⎧-≥-⎪⎪⇒<≤⎨⎪≤⎪⎩ (2) ()2sin(2)f x x =,()2sin(2())12sin(2)163g x x x ππ=++=++[来源:学#科#网Z#X#X#K]1()0sin(2)323g x x x k πππ=⇒+=-⇒=-或7,12x k k Z ππ=-∈,即()g x 的零点相离间隔依次为3π和23π,故若()y g x =在[,]a b 上至少含有30个零点,则b a -的最小值为2431415333πππ⨯+⨯=.22.:(1)C 1的左焦点为(F ,过F的直线x =C 1交于(2±,与C 2交于(1))±,故C 1的左焦点为“C 1-C 2型点”,且直线可以为x = (2)直线y kx =与C 2有交点,则(||1)||1||||1y kxk x y x =⎧⇒-=⎨=+⎩,若方程组有解,则必须||1k >;[来源:学§科§网Z §X §X §K] 直线y kx =与C 2有交点,则2222(12)222y kx k x x y =⎧⇒-=⎨-=⎩,若方程组有解,则必须212k < 故直线y kx =至多与曲线C 1和C 2中的一条有交点,即原点不是“C 1-C 2型点”。
(3)显然过圆2212x y +=内一点的直线l 若与曲线C 1有交点,则斜率必存在; 根据对称性,不妨设直线l 斜率存在且与曲线C 2交于点(,1)(0)t t t +≥,则:(1)()(1)0l y t k x t kx y t kt =+=-⇒-++-=直线l 与圆2212x y +=<化简得,221(1)(1)2t tk k +-<+。
① 若直线l 与曲线C 1有交点,则2222211()2(1)(1)10212y kx kt t k x k t kt x t kt x y =-++⎧⎪⇒-++-++-+=⎨-=⎪⎩ 22222214(1)4()[(1)1]0(1)2(1)2k t kt k t kt t kt k ∆=+---+-+≥⇒+-≥-化简得,22(1)2(1)t kt k +-≥-。
②由①②得,222212(1)(1)(1)12k t tk k k -≤+-<+⇒< 但此时,因为2210,[1(1)]1,(1)12t t k k ≥+-≥+<,即①式不成立;当212k =时,①式也不成立综上,直线l 若与圆2212x y +=内有交点,则不可能同时与曲线C 1和C 2有交点,即圆2212x y +=内的点都不是“C 1-C 2型点” .23.:(1)因为0c >,1(2)a c =-+,故2111()2|4|||2a f a a c a c ==++-+=,3122()2|4|||10a f a a c a c c ==++-+=+(2)要证明原命题,只需证明()f x x c ≥+对任意x R ∈都成立,()2|4|||f x x c x c x c x c ≥+⇔++-+≥+即只需证明2|4|||+x c x c x c ++≥++若0x c +≤,显然有2|4|||+=0x c x c x c ++≥++成立;若0x c +>,则2|4|||+4x c x c x c x c x c ++≥++⇔++>+显然成立 综上,()f x x c ≥+恒成立,即对任意的*n N ∈,1n n a a c +-≥(3)由(2)知,若{}n a 为等差数列,则公差0d c ≥>,故n 无限增大时,总有0n a > 此时,1()2(4)()8n n n n n a f a a c a c a c +==++-+=++[来源:Z 。
