北京市示范高中新高一分班数学考试讲义9-创新问题专题+新定义问题1
2020中考数学复习(北京)重点专题九 新定义问题

解:由题意知,点A坐标为(6,0),点B坐标为(0,2 3), 则在Rt△AOB中,OB=2 3 ,OA=6,∴∠OAB=30°. 如解图①,当⊙C与线段AB相切时, 即有一个公共点P,则CP=2, ∴在Rt△ACP中,AC=4, ∴此时点C坐标为(2,0);
例1题解图①
专题九 新定义问题
如解图②,当⊙C的横坐标2<xC≤4时,⊙C与线段AB有两个公共点; 如解图③,当⊙C的横坐标4<xC≤8时,⊙C与线段AB有一个公共点. 综上所述,当⊙C与线段AB有公共点时,xC的取值范围是2≤xC≤8.
直线l与⊙O相离
直线l与⊙O相切
直线l与⊙O相交
专题九 新定义问题
【作法提示】如解图:
第2题解图
专题九 新定义问题 典例精讲
例1 直线l:y=- 3 x+2 3 与x轴交于点A,与y轴交于点B,⊙C的圆心在x轴
3 上,半径为2,若⊙C与线段AB有公共点,求圆心C的横坐标xC的取值范围.
例1题图
专题九 新定义问题
专题九 新定义问题(必考)
【专题解读】本题是一道创设情境、引入新的数学概念的探索性问题,从 运动与变化的角度观察图形、分析问题,发现问题间的区别和联系,创造 性地解决问题,主要考查数形结合、类比与归纳的数学思想方法,考查抽 象概括能力、发现问题并解决问题的能力,考查创新意识.在解题过程中, 要重视分析动点轨迹及临界状态.
拓展2解图①
专题九 新定义问题
当圆心C在点A右侧时,如解图②,同理可得点C坐标为(3,0).
拓展2解图②
综上所述,圆心C的横坐标xC的取值范围为-9≤xC≤3.
拓展1解图
专题九 新定义问题
拓展2 直线l:y= 3 x+ 3 与x轴交于点A,与y轴交于点B,⊙C的圆心在x
新定义问题(讲义及答案)

新定义问题(讲义)➢ 知识点睛1. 新定义问题是一类以未接触过的概念为载体,要求学生现学现用,侧重考查观察、尝试、分析、理解、应用等能力的问题.2. 新定义问题的一般处理思路:提取概念中的关键词,理解新定义的实质,与已学知识结合, 在新定义的框架下解决问题.➢ 精讲精练1. 已知实数 a ,b ,定义运算“ * ”如下:a * b =⎧⎪b (a ≤b ) ,则 7 *( 2 * 3) 的值为a 2 -b 2(a > b ) .2. 在平面直角坐标系中,将点(-b ,-a )称为点(a ,b )的“关联点”(例如点(-2,-1)是点(1,2)的“关联点”).如果一个点和它的“关联点”在同一象限内,那么这个点在第 ______ 象限.3. 在平面直角坐标系中,对于点 P (x ,y )和 Q (x ,y′),给出如下 定义:若 ⎧ y (x ≥0) y' = ⎨- y (x < 0 ,则称点 Q 为点 P 的“可控变点”,⎩)例如:点(1,2)的“可控变点”为点(1,2),点(-1,3)的“可控变点”为点(-1,-3).结合定义,请回答下列问题: (1)点(-3,-4)的“可控变点”为 ;(2)若点 N (m ,2)是函数 y =x -1 图象上点 M 的“可控变点”,求点 M 的坐标.4.定义:直线y=m x+n 与直线y=nx+m互为“友好直线”,如:直线y=2x+1 与直线y=x+2 互为“友好直线”.(1)点A(a,2)在直线y=-x+1 的“友好直线”上,则a= ;(2)直线y=4x+3 上的一点B(b,c)又是它的“友好直线”上的点,求点B 的坐标;(3)若点C(5,6)在直线l:y=mx+n 上,点D(1,-2)在直线l 的“友好直线”上,求直线l 的解析式.5.在平面直角坐标系中,点P 到x 轴的距离为d1,到y 轴的距离为d2,给出下列定义:若d1≥d2,则称d1 为点P 的最大距离;若d1<d2,则称d2 为点P 的最大距离.例如:点P(-1,2)到x 轴的距离为2,到y 轴的距离为1,因为2>1,所以点P 的最大距离为2.根据以上定义解答下列问题:(1)点A(5,-6)的“最大距离”为;(2)若点B(a,4)的“最大距离”为7,则a 的值为;(3)若点C 在直线y=-2x+3 上,且点C 的“最大距离”为5,求点C 的坐标.6.定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x =a +c,y =b +d,那么称点T 3 3是点A,B 的融合点.例如:A(-1,8),B(4,-2),当点T(x,y)满足x =-1+ 4= 1 ,3y =8 + (-2)= 2 时,点T(1,2)是点A,B 的融合点.3(1)已知点A(-1,5),B(7,7),C(2,4),请说明其中一个点是另外两个点的融合点.(2)已知点D(3,0),点E(t,2t+3)(t 为任意数),点T是点D,E 的融合点.①用含t 的式子表示点T 的坐标;②若直线ET 交x 轴于点H,当△DTH 是以DH 为直角边的直角三角形时,则点E 的坐标为.1 = 3 x +17. 小明根据学习函数的经验,对函数 y =|x +1|-2 的图象、性质进行了探究.小明的探究过程如下: (1)列表:=.(2) 描点并画出该函数的图象. (3) 根据函数图象可得:①该函数的最小值为 ;②观察函数 y =|x +1|-2 的图象,写出该图象的两条性质:,.(4) 结合函数图象,解决问题:①函数图象与 x 轴有 个交点,所以对应方程|x +1|-2=0有个解;②已知函数 y = 1x +1的图象如图所示,结合你所画的函数图3象,直接写出方程 x +1 - 2 = 1x +1的解: .3⎪⎩ ⎪⎩8. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 y = ⎧⎪ x (x ≤1)的图象与性质.(1)列表:⎨-2x + 3(x > 1)=.(2) 描点并画出该函数的图象. (3) 根据函数图象可得:点 A ( 1 ,y 1),B ( 2,y 2),C (x 1,-2),D (x 2, - 3 )在函数图象2 3 2上,则 y 1 y 2,x 1 x 2.(填“>”,“=”或“<”)(4) 结合函数图象,解决问题:①当函数值 y = 5时,自变量 x 的值为;2②若一次函数 y =kx +1(k 为常数且 k ≠0)的图象与分段函数y = ⎧⎪ x (x ≤1) 的图象只有 1 个交点,则 k 的取值范围是 ⎨-2x + 3(x > 1).3 【参考答案】 ➢ 精讲精练1. 2.2. 二或第四.3. (1)(-3,4);(2)点 M 的坐标为(3,2)或(-1,-2). 4. (1)3;(2)B (1,7);(3)直线 l 的解析式为 y = 2x - 4 . 5. (1)6;(2)±7 ;(3)点 C 的坐标为(-1,5)或(4,-5). 6. (1)点 C 是 A ,B 的融合点;(2)①T ⎛ t +1 2 t +1⎫;②(6,15)或( 3 ,6)., ⎪ ⎝ 3 ⎭ 2 7. (1)2;(2) 图略;(3) ①-2;②该函数的图象是轴对称图形;当 x <-1 时,y 随 x 的增大而减小,当 x >-1 时,y 随 x 的增大而增大; (4)①两、两;② x 1 = 3,x 2 = -3 . 8. (1)1;(2)图略;(3)<,>; (4)① - 5;②k >0 或 k ≤-2.2。
北京市中考数学复习专题:新定义阅读理解问题

新定义阅读理解问题新定义学习型阅读理解题,是指题目中首先给出一个新定义(新概念或新公式),通过阅读题目提供的材料,理解新定义,再通过对新定义的理解来解决题目提出的问题。
其主要目的是通过对新定义的理解与运用来考查学生的自学能力,便于学生养成良好的学习习惯。
解决此类题的关键是(1)深刻理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论;(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”; 归纳“举例”提供的做题方法;归纳“举例”提供的分类情况;(3)依据新定义,运用类比、归纳、联想、分类讨论以及数形结合的数学思想方法解决题目中需要解决的问题。
一、基础练习部分★例1:【——海淀期末】对于正整数n ,定义210()=()10,,≥n n F n f n n ⎧<⎨⎩,其中f(n )表示n 的首位数字、末位数字的平方和.例如:F(6)=62=36,F(123)=f(123)=12+32=10.规定F 1(n )=F(n ),F k +1(n )=F(F K (n ))(K 为正整数).例如:F 1(123)=F(123)=10,F 2(123)=F(F 1(123))=F(10)=1.(1)求:F 2(4)= ,F(4)= ;(2)若F 3m (4)=89,则正整数m 的最小值是 . 答案:(1)37,26;(2)6. 练习①: 【通州一模】定义一种对正整数n 的“F 运算”:①当n 为奇数时,结果为31n +;②当n 为偶数时,结果为k n 2(其中k 是使得k n 2为奇数的正整数),并且运算重复进行.例如,取6n =,则:12363105F F F −−−→−−−→−−−→① ②②第次第次第次……,若1n =,则第2次“F 运算”的结果是 ;若13n =,则第次“F 运算”的结果是 . 答案:1,4练习②:【门头沟二模】我们知道,一元二次方程x 2=-1没有实数根,即不存在一个实数的平方等于-1,若我们规定一个新数“i ”,使其满足i 2=-1 (即方程x 2=-1有一个根为i ),并且进一步规定: 一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有i 1=i ,i 2=-1,i 3= i 2·i =(-1)(-1)·i =-i , i 4=( i 2)2=(-1) 2=1,从而对任意正整数n ,则i 6=______________;由于i 4n+1=i 4n ﹒i=(i 4)n ﹒i=i,同理可得i 4n+2=﹣1, i 4n+3=﹣i , i 4n =1那么i + i 2+ i 3+ i 4+…+ i+ i 的值为_____ 答案:-1,i★例2:【宣武一模】任何一个正整数n 都可以进行这样的分解:n =p ×q (p 、q 是正整数,且p ≤q ), 如果p ×q 在n 的所有这种分解中两因数之差的绝对值最小,我们就称p ×q 是n 的最佳分解,并规定:()p F n q =.例如18可以分解成1×18、2×9或3×6,这时就有31(18)62F ==.给出下列关于F(n )的说法:(1)1(2)2F =;(2)3(24)8F =;(3)(27)3F =;(4)若n 是一个完全平方数,则F(n )=1.其中正确说法的个数是 ( )A.1 B.2 C.3D.4 答案:B 练习①:【北京中考】在右表中,我们把第i 行第j 列的数记为a i ,j (其中i ,j 都是不大于5的正整数),对于表中的每个数a i ,j ,规定如下:当i ≥j 时,a i ,j =1;当i <j 时,a i ,j =0.例如:当i =2,j=1时,a i ,j =a 2,1=1.按此规定,a 1,3= ;表中的25个数中,共有 个1;计算a 1,1•a i ,1+a 1,2•a i ,2+a 1,3•a i ,3+a 1,4•a i ,4+a 1,5•a i ,5的值为 .答案:0;15;1. 练习②:【海淀二模】某种数字化的信息传输中,先将信息转化为数学0和1组成的数字串,并对数字串进行了加密后再传输.现采用一种简单的加密方法:将原有的每个1都变成10,原有的每个0变成01.我们用A 0表示没有经过加密的数字串.这样对A 0进行一次加密就得到一个新的数字串A 1,对A 1再进行一次加密又得到一个新的数学串A 2,依此类推,…,例如:A 0:10,则A 1:1001.若已知A 2:100101101001,则A 0: ,若数字串A 0共有4个数字,则数字串A 2中相邻两个数字相等的数对至少..有 对. 答案:101 ,4练习③:【燕山一模】若将代数式中的任意两个字母互相替换,代数式不变,则称这个代数式为完全对称式.如在代数式a +b +c 中,把a 和b 互相替换,得b +a +c ;把a 和c 互相替换,得c +b +a ;把b 和c ……;a +b +c 就是完全对称式.下列三个代数式:① (a -b )2;② ab +bc +ca ;③ a 2b +b 2c +c 2a .其中为完全对称式的是A .① ②B .② ③C .① ③D .①②③ 答案:A练习④:【西城一模】在平面直角坐标系中,对于平面内任一点P (a ,b )若规定以下两种变换: ①f (a ,b )= (-a ,-b ).如f (1,2)= (-1,-2);②g (a ,b )= (b ,a ).如g (1,3)= (3,1)按照以上变换,那么f (g (a ,b ))等于A .(-b ,-a )B .(a ,b )C .(b ,a )D .(-a ,-b ) 答案:A★例3:【昌平二模】请阅读下列材料:我们规定一种运算:,例如:. 按照这种运算的规定,请解答下列问题:(1)直接写出 的计算结果;(2)若,直接写出和的值.(3)当取何值时, ; 答案:(1)3.5; (2)x=8,y=2. (3) ;a b ad bc c d=-2325341012245=⨯-⨯=-=-1220.5--0.517830.51x y xy --==--x y x 0.5012x xx -=15x -±=a 1,1 a 1,2 a 1,3 a 1,4 a 1,5 a 2,1 a 2,2 a 2,3 a 2,4 a 2,5 a 3,1 a 3,2a 3,3 a 3,4 a 3,5 a 4,1 a 4,2a 4,3 a 4,4 a 4,5 a 5,1 a 5,2 a 5,3 a 5,4 a 5,5变式练习:【宣武一模】对于实数d c b a ,,,规定一种运算:c a bc ad d b -=,如21=-20()21-⨯ 220-=⨯-,那么)3(2x -2554=-时,=x ( ).(A )413- (B )427 (C )423- (D )43- 答案:(D)练习:①【北京中考(课标卷)】用“☆”定义新运算: 对于任意实数a 、b , 都有a ☆b =b 2+1。
北京初中数学新定义问题题型解析

北京初中数学新定义问题题型解析第一篇嘿,亲爱的小伙伴们!今天咱们来聊聊北京初中数学里那个让人又爱又恨的新定义问题题型。
你说这新定义问题啊,就像是个神秘的小怪兽,乍一看可把咱弄迷糊了。
但别怕,咱们一起来揭开它的面纱。
比如说,它会给你一个全新的概念,以前从来没见过的那种。
这时候可别慌,静下心来,仔细读题,把题目里给的条件和信息都理清楚。
就像拼图一样,一块一块地找线索。
有时候呢,新定义问题会和图形结合起来。
这时候,咱们得瞪大眼睛,看清图形中的各种关系。
可别被那些弯弯绕绕的线条给绕晕了,要找到关键的点和线。
还有啊,做新定义问题一定要大胆尝试。
别害怕出错,反正就试着按照题目给的定义去操作,说不定就柳暗花明啦!总之呢,新定义问题虽然有点难搞,但只要咱们有耐心,有勇气,就一定能把它拿下!加油哦小伙伴们!第二篇宝子们,咱们今天好好唠唠北京初中数学的新定义问题题型。
这新定义问题啊,就像是个藏着宝藏的迷宫。
刚进去的时候,感觉晕头转向的,不知道往哪儿走。
但是咱别慌!先把题目给的新定义反反复复多看几遍,理解清楚到底是咋回事。
有时候可能得自己在草稿纸上画画写写,把那个新的概念给琢磨透。
比如说,它可能会让你根据一个新的运算规则来计算,这时候你就得灵活点儿,别死脑筋,按照它说的来就行。
还有那种给了新的图形定义的,你就得发挥你的想象力,把那个图形在脑子里构建出来。
看看它有啥特点,和咱们学过的旧知识能不能联系起来。
做新定义问题,心态也很重要哦!别一看是新的就害怕,要相信自己的能力。
就算一开始做错了,也没关系,从错误中吸取教训,下次就能做得更好啦!反正记住啦,遇到新定义问题,勇敢地冲上去,用咱们聪明的小脑瓜把它攻克!宝子们,加油加油!。
北京一中新生必备初中数学分班真题解析全攻略

北京一中新生必备初中数学分班真题解析全攻略为了使北京一中学生在初中数学学习中有更好的起步,每年都会进行分班测试。
这次我们来为大家详细分析一下分班测试中常见的数学题目及解题技巧。
一、整数中因数性质的应用整数因数是指一个整数能够除尽这个数的整数,这个数称为这个整数的因数。
本题中,首先让我们来了解一下整数因数的性质。
1.若正整数的因数为奇数个,则这个整数为完全平方数。
2.若正整数的因数为偶数个,则这个整数不是完全平方数。
3.一个正整数,能被表示为 $a^2\times b$ 的形式,则这个数的因数个数为 $(2+1)\times(1+1)$,即因数为十二个。
有了这些背景知识后,我们再来看一道分班测试经常考察的题目:将一个自然数各位数字从左到右顺次排列成一个数,又得到了一个新的自然数。
证明这两个自然数的差为 9 的倍数。
这道题目中,我们需要注意到“排列成一个数”这个关键词,它暗示我们需要把数字相加得出一个新的自然数然后计算两个自然数的差值。
考虑这个新的自然数与原自然数的差,它们的差值就是新自然数的每一位数字减去原自然数的对应位数字。
而对于这种数字差定为9倍数的问题,则是因为差为9,说明相邻的两个数字的差为9,此时每一个数字可以看成是由某个倍数加上9的形式得到的,因此差为9的倍数。
二、分式运算与股票投资问题分式运算是初中数学中相对比较难的一块内容,其应用范围也非常广泛。
在很多实际问题中,例如股票投资问题中都需要用到分式运算的知识,因此这里向大家介绍一下分式运算的基本应用。
1. 加、减分式的通分:求得加、减分式的公分母后,分子之和(或差)除以公分母即可得到加、减分式的结果。
2. 乘、除分式的化简:求得乘、除分式的公因数或公倍数后,将分子、分母分别乘、除公因/倍数即可化简分式。
3. 分式的倒数:将分式的分子与分母对调得到分式的倒数,即$a/b$ 的倒数为 $b/a$。
4. 分式的代数式:将分式的分子和分母用代数式表示,使其最终为一个分式。
北京数学中考一模新定义创新题带答案

西城29、给出如下规定:两个图形1G 和2G ,点P 为1G 上任一点,点Q 为2G 上任一点,如果线段PQ 的长度存在最小值,就称该最小值为两个图形1G 和2G 之间的距离.在平面直角坐标系xOy 中,O 为坐标原点.(1)点A 的坐标为A (1,0)则点B (2,3)和射线OA 之间的距离为__________, 点C (-2,3)和射线OA 之间的距离为_________; (2)如果直线y=x 和双曲线xky =之间的距离为2,那么k =_______;(可在图1中进行研究) (3)点E 的坐标为(1,3),将射线OE 绕原点O 逆时针旋转 60,得到射线OF ,在坐标平面所有和射线OE ,OF 之间的距离相等的点所组成的图形记为图形M .①请在图2中画出图形M ,并描述图形M 的组成部分;(若涉及平面中某个区域时可以用阴影表示)②将射线OE,OF 组成的图形记为图形W ,抛物线22-=x y 与图形M 的公共部分记为图形N ,请直接写出图形W 和图形N 之间的距离.解析: 29.解:(1)3,13(每空各1分) (2)-1;(3)①如图9,过点O 分别作射线OE,OF 的垂线OG 、OH ,则图形M 为:y 轴正半轴,GOH ∠的边及其容的所有点(图中的阴影部分).说明:(画图2分,描述1分)(图形M 也可以描述为:y 轴正半轴,直线x y 33=下方与直线x y 33-=下方重叠的部分(含边界)) ②34东城29.定义符号{}min a b ,的含义为:当a b ≥时, {}min a b b =,;当a b <时,{}min a b a =,.如:{}min 122-=-,,{}min 121-=-,. (1)求{}2min x -1,-2;(2)已知2min{2,3}3x x k -+-=-, 数k 的取值围;(3) 已知当23x -≤≤时,22min{215,(1)}215x x m x x x --+=--.直接写出实数m 的取值围.解析:29.解:(1)∵20x ≥, ∴2x -1≥-1.∴2-x -1>2.∴{}2min 2x =--1,-2.┉┉2分 (2) ∵()2211x x k x k -+=-+-2,∴()2111x k k -+--≥.∵2min{2,3}3x x k -+-=-, ∴13k --≥.∴2k -≥.┉┉5分(3)37m -≤≤. ┉┉8分29.定义:对于平面直角坐标系xOy 中的线段PQ 和点M ,在△MPQ 中,当PQ 边上的高为2时,称M 为PQ 的“等高点”,称此时MP +MQ 为PQ 的“等高距离”. (1)若P (1,2),Q (4,2) .①在点A (1,0),B (25,4),C (0,3)中,PQ 的“等高点”是;②若M (t ,0)为PQ 的“等高点”,求PQ 的“等高距离”的最小值及此时t 的值.(2)若P (0,0),PQ =2,当PQ 的“等高点”在y 轴正半轴上且“等高距离”最小时,直接写出点Q 的坐标.解析:29. 解:(1)A 、B ……………………………………………………………………………2分(2)如图,作点P 关于x 轴的对称点P ′,连接P ′Q ,P ′Q 与x 轴的交点即为“等高点”M ,此时“等高距离”最小,最小值为线段P ′Q 的长. ………………………3分 ∵P (1,2), ∴ P ′(1,-2).设直线P ′Q 的表达式为b kx y +=, 根据题意,有⎩⎨⎧=+-=+242b k b k ,解得⎪⎩⎪⎨⎧-==31034b k .∴直线P ′Q 的表达式为31034-=x y .……………4分 当0=y 时,解得25=x . 即25=t .………………………………………………………………………5分 根据题意,可知PP ′=4,P Q =3, P Q ⊥PP ′, ∴5''22=+=PQ PP Q P .∴“等高距离”最小值为5.…………………………………………………6分 (3)Q (554,552)或Q (554-,552). ………………………………8分海淀29.在平面直角坐标系xOy 中,对于点(,)P a b 和点(,)Q a b ',给出如下定义:若,1,1≥b a b b a ⎧'=⎨-<⎩,则称点Q 为点P 的限变点.例如:点()2,3的限变点的坐标是()2,3,点()2,5-的限变点的坐标是()2,5--. (1)①点)的限变点的坐标是___________;②在点()2,1A --,()1,2B -中有一个点是函数2y x=图象上某一个点的限变点, 这个点是_______________(2)若点P 在函数3(2,2)y x x k k =-+->-≤≤的图象上,其限变点Q 的纵坐标b '的取值围是52≤≤b '-,求k 的取值围;(3)若点P 在关于x 的二次函数222y x tx t t =-++的图象上,其限变点Q 的纵坐标b '的取值围是≥b m '或b n '<,其中m n >.令s m n =-,求s 关于t 的函数解析式及s 的取值围. 解析:29.(本小题满分8分)解:(1)①;………………………………1分②点B .………………………………2分(2)依题意,3(2)y x x =-+-≥图象上的点P 的限变点必在函数3,13,21x x y x x -+⎧=⎨--<⎩≥≤的图象上.2≤b '∴,即当1x =时,b '取最大值2.当2b '=-时,23x -=-+.5x ∴=.………………………………………3分当5b '=-时,53x -=-或53x -=-+.2x ∴=-或8x =.………………………………4分52≤≤b '-,由图象可知,k 的取值围是58≤≤k .……………………………………………5分(3)2222()y x tx t t x t t =-++=-+,∴顶点坐标为(,)t t .……………………………………6分若1t <,b '的取值围是≥b m '或≤b n ',与题意不符. 若1≥t ,当1≥x 时,y 的最小值为t ,即m t =; 当1x <时,y 的值小于2[(1)]t t --+,即2[(1)]n t t =--+.22(1)1s m n t t t t ∴=-=+-+=+.∴s 关于t 的函数解析式为 211)s t t =+≥ ( .……………………………7分当t=1时,s 取最小值2.∴s 的取值围是s ≥2. ………………………………………………………8分丰台29. 设点Q 到图形W 上每一个点的距离的最小值称为点Q 到图形W 的距离.例如正方形ABCD 满足A (1,0),B (2,0),C (2,1),D (1,1),那么点O (0,0)到正方形ABCD 的距离为1.(1)如果⊙P 是以(3,4)为圆心,1为半径的圆,那么点O (0,0)到⊙P 的距离为; (2)①求点(3,0)M 到直线21y x =+的距离;②如果点(0,)N a 到直线21y x =+的距离为3,那么a 的值是; (3)如果点(0,)G b 到抛物线2y x =的距离为3,请直接写出b 的值. 解析:29. (1)4;.…….2分(2)①直线21y x =+记为l ,过点M 作MH l ⊥,垂足为点H,.…….3分∵EOF MHE ∆∆∽∴MH MEOF EF =,即72152MH =.∴755MH =.∴点M 到直线21y x =+的距离为755..…….4分 ②135a =±..…….6分(3)3b =-或374b =..…….8分通州29.如图,在平面直角坐标系中,已知点A (2,3)、B (6,3),连结AB . 若对于平面一点P ,线段AB 上都存在点Q ,使得PQ ≤1,则称点P 是线段AB 的“邻近点”. (1)判断点D 719(,)55,是否线段AB 的“邻近点”(填“是”或“否”); (2)若点H (m ,n )在一次函数1-=x y 的图象上,且是线段AB 的“邻近点”,求m 的取值围.(3)若一次函数y x b =+的图象上至少存在一个邻近点,直接写出b 的取值围.解析:29.(1)点D是线段AB的“邻近点”;…………………..(2分)(2)∵点H(m,n)是线段AB的“邻近点”,点H(m,n)在直线y=x-1上,∴n=m-1; ………………………………………..(3分)直线y=x-1与线段AB交于(4,3)①当m≥4时,有n=m-1≥3,又AB∥x轴,∴此时点H(m,n)到线段AB的距离是n-3,∴0≤n-3≤1,∴4 ≤m≤5,…………………………………..(4分)②当m≤4时,有n=m-1 ∴n≤3,又AB∥x轴,∴此时点H(m,n)到线段AB的距离是3-n,∴0≤3-n≤1,∴ 3≤m≤4,………………………………………..(5分)综上所述,3≤m≤5; ………………………………………..(6分)(3) 3212b--≤≤+………………………………………..(8分)房山29.【探究】如图1,点()N m,n 是抛物线21114y x =-上的任意一点,l 是过点()02,-且与x 轴平行的直线,过点N 作直线NH ⊥l ,垂足为H .①计算: m=0时,NH=; m =4时,NO =.②猜想: m 取任意值时,NONH (填“>”、“=”或“<”).【定义】我们定义:平面到一个定点F 和一条直线l (点F 不在直线l 上)距离相等的点的集合叫做抛物线,其中点F 叫做抛物线的“焦点”,直线l 叫做抛物线的“准线”.如图1中的点O 即为抛物线1y 的“焦点”,直线l :2y =-即为抛物线1y 的“准线”.可以发现“焦点”F 在抛物线的对称轴上.【应用】(1)如图2,“焦点”为F (-4,-1)、“准线”为l 的抛物线()221+44y x k =+与y 轴交于点N (0,2),点M 为直线FN 与抛物线的另一交点.MQ ⊥l 于点Q ,直线l 交y 轴于点H .①直接写出抛物线y 2的“准线”l :; ②计算求值:1MQ +1NH=;(2)如图3,在平面直角坐标系xOy 中,以原点O 为圆心,半径为1的⊙O 与x 轴分别交于A 、B 两点(A 在B 的左侧),直线y = 33x +n 与⊙O 只有一个公共点F ,求以F 为“焦点”、图2图3图1解析: 29. 解:【探究】① 1 ; 5 ; ……………2分② = . …………………3分【应用】(1)①3y =-;……………………4分② 1 . ……………………5分(2)如图3,设直线y n =+与x 轴相交于点C .由题意可知直线CF 切⊙O 于F ,连接OF .∴∠OFC =90° ∴∠COF=60° 又∵OF =1, ∴OC =2 ∴()20C ±,∴“焦点”112F ,⎛ ⎝⎭、212F ⎛- ⎝⎭.………6分∴抛物线3y的顶点为1122,⎛⎛- ⎝⎭⎝⎭或.①当“焦点”为112F ,⎛ ⎝⎭,顶点为12,⎛ ⎝⎭,()20C , 时,易得直线CF 1:y x = 过点A 作AM ⊥x 轴,交直线CF 1于点M.∴1MA MF =∴(1M -,在抛物线3y 上.设抛物线2312y a x ⎛⎫=- ⎪⎝⎭,将M 点坐标代入可求得:a = ∴22312y x ⎫=-=⎪⎝⎭7分 ②当“焦点”为212F ⎛ ⎝⎭,顶点为12⎛- ⎝⎭,()20C -,时,由中心对称性可得:2231+2y x x x ⎫=⎪⎝⎭8分综上所述:抛物线23y x =23y x =+.怀柔29. 对某种几何图形给出如下定义: 符合一定条件的动点所形成的图形,叫做符合这个条件的点的轨迹.例如,平面到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.(1)如图1,在△ABC 中,AB=AC ,∠BAC=90°,A(0,2),B 是x 轴上一动点,当点B 在x轴上运动时,点C 在坐标系中运动,点C G.则直线DE(2)当△ABC 是等边三角形时,在(1)的条件下,动点C 形成的轨迹也是一条直线.①当点B 运动到如图2的位置时,AC ∥x 轴,则C 点的坐标是.②在备用图中画出动点C 形成直线的示意图,并求出这条直线的表达式.③设②中这条直线分别与x,y 轴交于E,F 两点,当点C 在线段EF 上运动时,点H 在线段OF 上运动,(不与O 、F 重合),且CH=CE,则CE 的取值围是. 解析:29. 解:(1)x=2. …………………………1分.(2)①C 点坐标为:23()…………………………3分. ②由①C 点坐标为: 2)再求得其它一个点C,1),或(0,-2)等代入表达式y=kx+b,解得b=-2k ⎧⎪⎨=⎪⎩∴直线的表达式是2y =-.………………………5分.动点C 运动形成直线如图所示. ……………6分.EC <…………………………8分.门头沟29.如图,在平面直角坐标系xOy 中,抛物线y =ax 2+bx +c (a >0)的顶点为M ,直线y =m与x 轴平行,且与抛物线交于点A 和点B ,如果△AMB 为等腰直角三角形,我们把抛物线上A 、B 两点之间部分与线段AB 围成的图形称为该抛物线的准蝶形,顶点M 称为碟顶,线段AB 的长称为碟宽.AABBMMOxyy=m准蝶形AMB(1)抛物线212y x =的碟宽为,抛物线y =ax 2(a >0)的碟宽为. (2)如果抛物线y =a (x -1)2-6a (a >0)的碟宽为6,那么a =.(3)将抛物线y n =a n x 2+b n x +(a n >0)的准蝶形记为F n (n =1,2,3,…),我们定义F 1,F 2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.如果F n与F n-1的相似比为12,且F n的碟顶是F n-1的碟宽的中点,现在将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.①求抛物线y2的表达式;②请判断F1,F2,…,F n的碟宽的右端点是否在一条直线上?如果是,直接写出该直线的表达式;如果不是,说明理由.解析:29.(本小题满分8分)解:(1)4,2a;………………………………………………………………………2分(2)13;…………………………………………………………………………3分(3)①∵F1的碟宽︰F2的碟宽=2:1,∴12222:1a a=.∵a1=13,∴a2=23.………………………………………………………………4分又∵由题意得F2的碟顶坐标为(1,1),…………………………5分∴()222113y x=-+.……………………………………………………6分②F1,F2,…,F n的碟宽的右端点在一条直线上;……………………7分其解析式为y=-x+5.……………………………………………………8分石景山29.在平面直角坐标系xOy 中,点A 在直线l 上,以A 为圆心,OA 为半径的圆与y 轴的另一个交点为E .给出如下定义:若线段OE ,⊙A 和直线l 上分别存在点B ,点C 和点D ,使得四边形ABCD 是矩形(点,,,A B C D 顺时针排列),则称矩形ABCD 为直线l 的“理想矩形”.例如,下图中的矩形ABCD 为直线l 的“理想矩形”.(1)若点(1,2)A -,四边形ABCD 为直线1x =-的“理想矩形”,则点D 的坐标为 ; (2)若点(3,4)A ,求直线1y kx =+(0)k ≠的“理想矩形”的面积; (3)若点(1,3)A -,直线l 的“理想矩形”面积的最大值为,此时点D 的坐标为.解析:29.解:(1)()1,0D -.(2)连结,AO AC ,过点A 作AF y ⊥则5AC AO ==备用图3145EF AE =∠=︒∴=∴∴在Rt AEB ∆中,由勾股定理AB =∴在Rt ∆中,由勾股定理得,BC =∴所求“理想矩形”ABCD面积为AB BC ⨯=……………………………………………………5分(3)“理想矩形”面积的最大值是5.………………………………6分()()1,23,2D ---或. ………………………………8分延庆29. 对于平面直角坐标系xOy 中的点P 和线段AB ,给出如下定义:在线段AB 外有一点P ,如果在线段AB 上存在两点C 、D ,使得∠CPD =90°,那么就把点P 叫做线段AB 的悬垂点. (1)已知点A (2,0),O (0,0)①若1(1,)2C ,D (1,1),E (1,2),在点C ,D ,E 中,线段AO 的悬垂点是______;②如果点P (m ,n )在直线1y x =-上,且是线段AO 的悬垂点,求m 的取值围;(2)如下图是帽形M (半圆与一条直径组成,点M 是半圆的圆心),且圆M 的半径是1,若帽形部的所有点是某一条线段的悬垂点,求此线段长的取值围.解析: 29.(1)线段AO 的悬垂点是C ,D ;(2)以点D 为圆心,以1为半径做圆,设1y x =-与⊙D 交于点B ,C与x 轴,y 轴的交点坐标为(1,0),(0,-1) ∴∠ODB=45° ∴DE=BE在Rt △DBE 中,由勾股定理得:DE=22∴2211122m m -≤≤+≠ (3)设这条线段的长为a①当2a <时,如图1,凡是⊙D 外的点不满足条件; ②当2a =时,如图2,所有的点均满足条件; ③当2a >时,如图3,所有的点均满足条件; 综上所述:2a ≥-----------2分-----------6分-----------4分 -----------3分-----------8分燕山29.在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P 为和谐点.例如点(1,1),(31-,31-),(2-,2-),…,都是和谐点.(1)分别判断函数12+-=x y 和12+=x y 的图象上是否存在和谐点,若存在,求出其和谐点的坐标;(2)若二次函数)0(42≠++=a c x ax y 的图象上有且只有一个和谐点(23,23),且当m x ≤≤0时,函数)0(4342≠-++=a c x ax y 的最小值为-3,最大值为1,求m 的取值围.(3)直线2:+=kx y l 经过和谐点P ,与x 轴交于点D ,与反比例函数xny G =:的图象交于M ,N 两点(点M 在点N 的左侧),若点P 的横坐标为1,且23<+DN DM ,请直接写出n 的取值围.解析:29.解:(1)令x x =+-12,解得31=x ,∴函数12+-=x y 的图象上有一个和谐点(31,31); ………………………2分 yxO11图1图2图32令x x =12+,即012=+-x x ,∵根的判别式Δ=114)1(2⨯⨯--=-3<0,∴方程012=+-x x 无实数根,∴函数12+=x y 的图象上不存在和谐点. ………………………3分(2)令x c x ax =++42,即032=c x ax ++,由题意,Δ=ac 432-=0,即94=ac ,又方程的根为2323=-a , 解得1-=a ,49-=c . ………………………4分∴函数4342-++=c x ax y ,即342-+-=x x y ,如图,该函数图象顶点为(2,1),与y 轴交点为(0,-3), 由对称性,该函数图象也经过点(4,-3). ………………………5分由于函数图象在对称轴2=x 左侧y 随x 的增大而增大,在对称轴右侧y 随x 的增大而减小,且当m x ≤≤0时,函数342-+-=x x y 的最小值为-3,最大值为1,∴42≤≤m . ………………………6分 (3)045<<n -,或10<<n . ………………………8分。
中考数学 新定义题型专题01 数与式中的新定义问题(老师版)

专题01 数与式中的新定义问题一、考情分析"新定义"型问题是指在问题中定义了初中数学中没有学过的一些概念、新运算、新符号,要求学生读懂题意并结合已有知识进行理解,而后根据新定义进行运算、推理、迁移的一种题型。
它一般分为三种类型: (1)定义新运算;(2)定义初、高中知识衔接"新知识"; (3)定义新概念。
这类试题考查考生对"新定义"的理解和认识,以及灵活运用知识的能力,解题时需要将"新定义"的知识与已学知识联系起来,利用已有的知识经验来解决问题.利用的数学思想:(1)转化的思想,把未知的问题转化为学过的知识解决。
(2)对全新的概念,需要灵活的迁移运用。
二、精选考题1.定义新运算:对于任意实数a 、b ,都有13a b a b =-⊗,则12x x -⊗⊗的值为 1 . 【解答】解:13a b a b =-⊗, 12131(132)x x x x ∴-=---⊗⊗131132x x =--+1=.故答案为:1.2.定义新运算:对于任意实数a ,b ,都有a ⊕(1)b a b b =+-,等式右边是通常的加法、减法及乘法运算,比如:3⊕23(21)2927=⨯+-=-=. (1)2⊕(3)-= 1- .(2)若2-⊕x 等于5-,则x = . 【解答】解:(1)原式2(31)(3)=⨯-+-- 2(2)3=⨯-+ 43=-+1=-.故答案为:1-.(2)由题意可知:2(1)5x x -+-=-, 225x x ∴---=-, 33x ∴-=-, 1x ∴=,故答案为:1.3.对于任意实数a ,b ,定义关于“⊗”的一种运算如下:2a b a b =+⊗.例如3523511=⨯+=⊗;4(3)24(3)5-=⨯+-=⊗.若()2x y -=⊗,且21y x =-⊗,则20202020x y +=20203. 【解答】解:()2x y -=⊗,2()2x y ∴+-=①. 21y x =-⊗,41y x ∴+=-②.①+②得:331x y +=. 13x y ∴+=. 2020202020202020()3x y x y ∴+=+=. 故答案为:20203. 4.对于非零的两个实数m ,n ,定义一种新运算“&”,规定2&m n m n =-,若2&(3)7-=,则(3)&(2)--的值为 11 . 【解答】解:(3)&(2)--2(3)(2)=--- 92=+11=,故答案为:11.5.有一种用“☆”定义的新运算,对于任意实数a ,b ,都有a ☆221b b a =++.例如7☆24427131=+⨯+=.(1)已知m -☆3的结果是4-,则m = 7 .(2)将两个实数2n 和2n -用这种新定义“☆”加以运算,结果为9,则n 的值是多少? 【解答】解:(1)根据题意可得:m -☆233214m =-+=-, 解得:7m =; 故答案为:7;(2)根据题意可得:2n ☆(2)9n -=, 即2(2)419n n -++=, 解得:2n =或2-,(2)n -☆2242(2)19n n n =+-+=,解得:2n =-或32, 则2n =-或32或2. 6.规定:符号[]x 叫做取整符号,它表示不超过x 的最大整数,例如:[5]5=,[2.6]2=,[0.2]0=.现在有一列非负数1a ,2a ,3a ,⋯,已知110a =,当2n 时,11215([][])55n n n n a a ---=+--,则2022a 的值为 11 . 【解答】解:110a =, 21115([]0)115a a ∴=+--=,322115([][])1255a a =+--=,433215([][])1355a a =+--=,544315([][])1455a a =+--=,65415([1][])105a a =+--=,⋯1a ∴,2a ,3a ,⋯,每5个结果循环一次,202254042÷=⋯,2022211a a ∴==,故答案为:11.7.有一种用“☆”定义的新运算:对于任意实数a ,b 都有a ☆2b b a =+.例如7☆244723=+=.(1)已知m ☆2的结果是6,则m 的值是多少?(2)将两个实数n 和2n +用这种新定义“☆”加以运算,结果为4,则n 的值是多少? 【解答】解:(1)根据题中的新定义得:m ☆246m =+=, 解得:2m =;(2)根据题意得:n ☆(2)4n +=,即2(2)4n n ++=, 解得:0n =或5n =-; (2)n +☆224n n n =++=,解得:2n =-或1n =, 则0n =或5-或2-或1.8.请你阅读如图框内老师的新定义运算规定,然后解答下列各小题. (1)若x ⊕1y =,x ⊕22y =-,分别求出x 和y 的值; (2)若x 满足x ⊕20,且3x ⊕(8)0->,求x 的取值范围.【解答】解:(1)根据题意得4314322x y x y -=⎧⎨-⨯=-⎩,解得11x y =⎧⎨=⎩;(2)根据题意得4320433(8)0x x -⨯⎧⎨⨯-⨯->⎩,解得322x-<. 故x 的取值范围是322x-<. 9.用※定义一种新运算:对于任意实数m 和n ,规定m ※23n m n mn n =--,如:1※221212326=⨯-⨯-⨯=-.则(2)-( )A .B .-C .D .【解答】解:原式2(2)(2)=--==故选:A .10.定义:如果一个数的平方等于1-,记为21i =-,这个数i 叫做虚数单位,把形如(a bi a +,b 为实数)的数叫做复数,其中a 叫这个复数的实部,b 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(3)(53)(35)(13)82i i i i -++=++-+=+;2(1)(3)1333(13)142i i i i i i i +⨯-=⨯-+⨯-=+-++=+. 根据以上信息,完成下列问题: (1)填空:3i = i - ,4i = ; (2)计算:(2)(34)i i +⨯-; (3)计算:2342022i i i i i ++++⋯+.【解答】解:(1)321i i i i i =⋅=-⋅=-,4221(1)1i i i =⋅=-⋅-=, 故答案为:i -,1; (2)(2)(34)i i +⨯-; 6834i i =-++105i =-;(3)2342022i i i i i ++++⋯+ 111i i i =--++⋯+-1i =-.11.阅读理解:定义:如果一个数的平方等于1-,记为21i =-,这个数i 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为(a bi a +,b 为实数),a 叫这个复数的实部,b 叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似. 例如计算:2(1)(23)13234i i i i i i +⨯-=-+-=-. (1)填空:3i = i - ,4i = ; (2)(7)(7)i i +-; (3)计算:2(2)i +;(4化简成a bi +的形式. 【解答】解:(1)21i =-,32(1)i i i i i ∴=⋅=-⋅=-, 4222()(1)1i i ==-=, 3i i ∴=-,41i =,故答案为:i -,1; (2)(7)(7)i i +- 249i =- 49(1)=-- 50=;(3)2(2)i + 244i i =++ 34i =+;(4=====∴= 12.先阅读下列材料,再解答后面的问题:材料:一般地,若(0n a b a =>且1a ≠,0)b >,则n 叫做以a 为底b 的对数,记为log a b (即log )a b n =.如4381=,则4叫做以3为底81的对数,记为3log 81(即3log 814)=.问题:(1)计算:2log 16= 4 ,2331(log 9)813log += .(2)5log 5、5log 25、5log 125之间满足怎样的关系式,请说明理由. (3)由(2)的结果,你能归纳出一个一般性的结论吗? log log a a M N += (0a >,且1a ≠,0M >,0)N >.根据幂的运算法则:n m n m a a a +⋅=以及对数的含义证明上述结论. 【解答】解:(1)4216=, 2log 164∴=,239=,4381=, 3log 92∴=,8143log =,2331(log 9)813log ∴+21243=+⨯443=+ 163=, 故答案为:4;163; (2)555log 5log 25log 125+=,理由如下: 根据题意,5log 51=,5log 252=,5log 1253=, 555log 5log 25log 125∴+=;(3)log log log ()a a a M N MN +=,证明如下:设1log a M b =,2log a N b = 则1b a M =,2b a N =,∴1212b b b b MN a a a +=⋅=,又n m n m a a a +⋅=,∴1212b b b b a a a +⋅=,即log log log ()a a a M N MN +=, 故答案为:log ()a MN .13.定义:如果4(0,1)a N a a =>≠,那么x 叫做以a 为底N 的对数,记作log a x N =.例如:因为2749=,所以7log 492=;因为3125s =,所以log 1253S =.则下列说法中正确的有()个.①6log 636=;②3log 814=;③若4log (14)4a +=,则50a =;④222log 128log 16log 8=+; A .4B .3C .2D .1【解答】解:166=, 6log 61∴=,故①不符合题意;4381=,3log 814∴=,故②符合题意;44256=, 14256a ∴+=,242a ∴=,故③不符合题意;72128=, 2log 1287∴=,4216=, 2log 164∴=,328=, 2log 83∴=,743=+,222log 128log 16log 8∴=+,故④符合题意;综上所述,符合题意的有2个, 故选:C .14.对a ,b ,c ,d 定义一种新运算:a c ad bcb d =-,如232413514=⨯-⨯=,计算2x yx x y=+ 22x xy + .【解答】解:原式2()x x y xy =+-222x xy xy =+- 22x xy =+,故答案为:22x xy +.15.阅读材料:对于任何有理数,我们规定符号a b c d 的意义是:a bad bc c d=-.例如:14232=⨯-⨯=-.按照这个规定,解决下列问题: (1)请你计算3574-的值. (2)求当3x =,1y =-时,2222332x xy yx xy y+--+的值.(3)如果2157353x x -=--,求x 的值.【解答】解:(1)原式345(7)=⨯-⨯- 1235=+47=;(2)原式222(32)3(2)x xy y x xy y =-+-+-22642633x xy y x xy y =-+--+ 75xy y =-+;当3x =,1y =-时, 原式73(1)5(1)=-⨯⨯-+⨯- 216=-16=;(3)(3)(21)5(35)7x x ----=, 6315257x x -+-+=, 6257153x x -+=+-, 1919x =, 1x =.16.材料1:对于一个四位自然数M ,如果M 满足各数位上的数字均不为0,它的百位上的数字比千位上的数字大1,个位上的数字比十位上的数字大1,则称M 为“满天星数”.对于一个“满天星数” M ,同时将M 的个位数字交换到十位、十位数字交换到百位、百位数字交换到个位,得到一个新的四位数N ,规定:()9M NF M -=. 例如:2378M =,因为321-=,871-=,所以2378是“满天星数”;将M 的个位数字8交换到十位,将十位数字7交换到百位,将百位数字3交换到个位,得到2783N =,23782783(2378)459F -==-.材料2:对于任意四位自然数100010010(abcd a b c d a =+++、b 、c 、d 是整数且19a ,0b ,c ,9)d ,规定:()G abcd c d a b =⋅-⋅.根据以上材料,解决下列问题:(1)请判断2467、3489是不是“满天星数”,请说明理由;如果是,请求出对应的()F M 的值;(2)已知P 、Q 是“满天星数”,其中P 的千位数字为(m m 是整数且17)m ,个位数字为7;Q 的百位数字为5,十位数字为(s s 是整数且28)s .若()()G P G Q +能被11整除且s m >,求()F P 的值.【解答】解:(1)2467不是“满天星数”,3489是“满天星数”,理由如下: 2467的百位数字为4,千位数字为2,4221∴-=≠,2467∴不是“满天星数”.3489的千位数字为3,百位数字为4,十位数字为8,个位数字为9,431∴-=,981-=,3489M ∴=是“满天星数”, 3894N ∴=,34893894(3489)459F -∴==-. (2)由题意可得:(1)67P m m =+,45(1)Q s s =+,则1000100(1)6071100167P m m m =++++=+,4000500101450111Q s s s =++++=+. 2()67(1)42G P m m m m ∴=⨯-+=--,2()(1)2020G Q s s s s =+-=+-,2222()()422022G P G Q m m s s s s m m ∴+=--++-=+--+.()()G P G Q +能被11整除且s m >,∴只要22()()()(1)s s m m s m s m s m s m s m +--=+-+-=-++能被11整除.28s ,17m ,s 、m 均为整数,s m >,4116s m ∴++,111s m ∴++=即10s m +=.∴876234s s s m m m ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩或或. 2367P ∴=或3467或4567.23672673(2367)349F -∴==-,34673674(3467)239F -==-,45674675(4567)129F -==-. 17.在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数-- “好数”.定义:对于三位自然数n ,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n 为“好数”.例如:426是“好数”,因为4,2,6都不为0,且426+=,6能被6整除;643不是“好数”,因为6410+=,10不能被3整除.问百位数字比十位数字大5的所有“好数”有 7 个.【解答】解:611,617,721,723,729,831,941共7个,理由:设十位数数字为a ,则百位数字为5(04a a +<的整数),525a a a ∴++=+,当1a =时,257a +=,7∴能被1,7整除,∴满足条件的三位数有611,617,当2a =时,259a +=,9∴能被1,3,9整除,∴满足条件的三位数有721,723,729,当3a =时,2511a +=,11∴能被1整除,∴满足条件的三位数有831,当4a =时,2513a +=,13∴能被1整除,∴满足条件的三位数有941,即满足条件的三位自然数为611,617,721,723,729,831,941共7个.故答案为:7.18.阅读下列材料,解决问题.【材料1】对于任意一个多位数,如果它的各位数字之和除以一个正整数n 所得的余数与它自身除以这个正整数n 所得的余数相同,我们就称这个多位数是n 的“余同数”.例如:对于多位数2714,271439042÷=⋯,且(2714)342+++÷=⋯,则2714是3的“余同数”.【材料2】对于任意两个多位数A ,B ,若A 除以正整数n 所得的余数与B 除以正整数n 所得的余数相同,则A 与B 的差一定能被n 整除.(1)判断3142是否是5的“余同数”,并说明理由;(2)若一个三位数是7的“余同数”,它的百位数字与十位数字之和小于9,个位数字比百位数字大1,求所有符合条件的三位数.【解答】解:(1)不是,理由如下:31425628......2÷=,(3142)52+++÷=,3142∴不是5的同余数;(2)设这个三位数为10010a b c ++,则9a b +<,1c a =+,这个三位数是7的“余同数”,10010()a b c a b c ∴++-++能被7整除,10010()7a b c a b c ++-++ 100107a b c a b c ++---= 9997a b += 2147a b a b +=++, ∴27a b +是整数, 又18a ,09b ,9a b +<,1218a b ∴+<,27a b ∴+=或214a b +=,∴708a b c =⎧⎪=⎨⎪=⎩或516a b c =⎧⎪=⎨⎪=⎩或324a b c =⎧⎪=⎨⎪=⎩或132a b c =⎧⎪=⎨⎪=⎩或263a b c =⎧⎪=⎨⎪=⎩,综上,这个三位数为708或516或324或132或263.19.新定义题:小明在课外阅读中对有关“自定义型题”有了一定的了解,他也尝试着自定义了“颠倒数”的概念:从左到右写下一个自然数,再把它按从右到左的顺序写一遍,如果两数位数相同,这样就得到了这个数的“颠倒数”,如286的颠倒数是682.请你探究,解决下列问题:(1)请直接写出2022的“颠倒数”为 2202 .(2)能否找到一个数字填入空格,使由“颠倒数”构成的等式126⨯□=□621⨯成立? 请你用下列步骤探究“□”所表示的数字.①设这个数字为x ,将自然数“6□”和“□6”转化为用含x 的代数式表示分别为 和 ;②列出关于x 的满足条件的方程,并求出x 的值;③经检验,所求x 的值符合题意吗? (填“符合”或“不符合” )【解答】解:(1)由“颠倒数”的定义可得:2022的“颠倒数”为2202,故答案为:2202,;(2)①设这个数字为x ,自然数“6□”用含x 的代数式表示为:61060x x ⨯+=+,自然数“□6”用含x 的代数式表示为:106x +,故答案为:60x +,106x +;②由题意得:12(60)21(106)x x +=+,解得:3x =,x ∴的值为3;③检验:1263756⨯=,3621756⨯=,12633621∴⨯=⨯,3x ∴=符合题意,故答案为:符合.20.我们规定用(,)a b 表示一对数对,给出如下定义:记m=0,0)n a b =>>,将(,)m n 与(,)n m 称为数对(,)a b 的一对“对称数对”.例如:(4,1)的一对“对称数对”为1(2,1)与1(1,)2. (1)数对(25,4)的一对“对称数对”是 1(,2)5 和 ; (2)若数对(3,)y 的一对“对称数对”的两个数对相同,求y 的值;(3)若数对(,2)x 的一对“对称数对”的一个数对是1),求x 的值;(4)若数对(,)a b 的一对“对称数对”的一个数对是,求ab 的值.【解答】解:(1)由题意知:1,25m n ====, ∴数对(25,4)的一对“对称数对”是1(,2)5和1(2,)5, 故答案为:1(,2)5;1(2,)5.(2)数对(3,)y 的一对“对称数对”的两个数对相同,∴=,∴= ∴13y =.(3)数对(,2)x的一对“对称数对”是和,∴=,∴1=,1x∴=.(4)数对(,)a b的一对“对称数对”是和,∴====或,∴11327273a ab b⎧⎧==⎪⎪⎨⎨⎪⎪==⎩⎩或,∴199ab=或.21.若一个三位正整数m abc=(各个数位上的数字均不为0)满足9a b c++=,则称这个三位正整数为“长久数”.对于一个“长久数”m,将它的百位数字和个位数字交换以后得到新数n,记()9m nF m+=.如:216m=满足2169++=,则216为“长久数”,那么612n=,所以216612(216)929F+==.(1)求(234)F、(522)F的值;(2)对于任意一个“长久数”m,若()F m能被5整除,求所有满足条件的“长久数”.【解答】解:(1)当234m=时,2349++=,m是长久数,432n∴=,234432(234)749F+∴==.当522m=时,5229++=,m是长久数,225n∴=,522225(522)839F+∴==.(2)由题意得:10010m a b c=++,10010n c b a=++.1001010010()9a b c c b aF m+++++∴=101101209a c b ++= 101()209a cb ++=. 9a bc ++=,101(9)20()9b b F m -+∴= 901819b -= 1019b =-.又a 、b 、c 均为不为0的正整数,1b ∴=,2,3,⋯⋯,7. ∴当1b =时,()1019192F m =-⨯=,不能被5整除,舍去;当2b =时,()1019283F m =-⨯=,不能被5整除,舍去;当3b =时,()1019374F m =-⨯=,不能被5整除,舍去;当4b =时,()1019465F m =-⨯=,能被5整除,此时5a c +=,∴12344321a a a a c c c c ====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩或或或. 144m ∴=或243或342或441.当5b =时,()1019556F m =-⨯=,不能被5整除,舍去;当6b =时,()1019647F m =-⨯=,不能被5整除,舍去;当7b =时,()1019738F m =-⨯=,不能被5整除,舍去.综上所述,所有满足条件的“长久数”有144或243或342或441.22.对于一个四位自然数N ,如果N 满足各数位上的数字不全相同且均不为0,它的千位数字减去个位数字之差等于百位数字减去十位数字之差,那么称这个数N 为“差同数”.对于一个“差同数” N ,将它的千位和个位构成的两位数减去百位和十位构成的两位数所得差记为s ,将它的千位和十位构成的两位数减去百位和个位构成的两位数所得差记为t ,规定:2()29s t F N +=.例如:7513N =,因为7351-=-,故:7513是一个“差同数”.所以:735122715318s t =-==-=,则:2236(7513)229F +==. (1)请判断2586、8734是否是“差同数”.如果是,请求出()F N 的值;(2)若自然数P ,Q 都是“差同数”,其中100010616P x y =++,1003042(19Q m n x =++,08y ,19m ,07n ,x ,y ,m ,n 都是整数),规定:()()F P k F Q =,当3()()F P F Q -能被11整除时,求k 的最小值.【解答】解:(1)对于2586,其各数位上的数字不全相同且均不为0,2658-≠-, 2586∴不是“差同数”, 对于8734,其各数位上的数字不全相同且均不为0,8473-=-,8734∴是“差同数”, 847311s ∴=-=,83749t =-=,1129(8734)129F +⨯∴==, 2586∴不是“差同数”,8734是“差同数”, (8734)1F =; (2)100010616100060010(1)6P x y x y =++=++++,P ∴的千位数字为x ,百位数字为6,十位数字为(1)y +,个位数字为6, 又自然数P 是差同数,66(1)x y ∴-=-+即11x y +=,(106)(61)1055p S x y x y ∴=+-+=--,(101)661065p t x y x y =++-=+-,10552(1065)()629y x y F P x --++-∴==-, 10030423000100402Q m n m n =++=++++,Q ∴的千位数字为3,百位数字为m ,十位数字为4,个位数字为(2)n +, 又自然数Q 是差同数,3(2)4n m ∴-+=-,即5m n +=,302(104)1028Q s n m n m ∴=++-+=-+,34(102)3210Q t m n m n =-++=--,10282(3210)()329n m m n F Q m -++--∴==-, 3()()3(6)(3)321F P F Q x m x m ∴-=---=+-,19x ,08y ,且11x y +=,39x ∴,19m ,07n ,且5m n +=,15m ∴,1132111x m ∴-+-,又321x m +-能被11整除,32111x m ∴+-=±或0,①当32111x m +-=-时,3x =,1m =,8y =,4n =, 此时,()363()312F P k F Q -===--; ②当32111x m +-=时,9x =,5m =,2y =,0n =, 此时,()963()352F P k F Q -===--; ③当3210x m +-=时,6x =,3m =,此时,()0F Q =,k ∴值不存在,综上,k 的最小值为32-.23.对于实数P ,我们规定:用的最小整数.2=,2=,现在对72进行如下操作: {}{}{}727299332===第一次第二次第三次,即对72只需进行3次操作后变为2.类比上述操作:对36只需进行 3 次操作后变为2;如果只需进行3次操作后变为2的所有正整数中最大的数为 .【解答】解:由题意得:现在对36进行如下操作: {}{}{}363666332===第一次第二次第三次,∴对36只需进行3次操作后变为2;现在对256进行如下操作: {}{}{}2562561616442===第一次第二次第三次,如果只需进行3次操作后变为2的所有正整数中最大的数为:256;故答案为:3,256.24.如果一个三位数满足各数位上的数字都不为0,且百位数字比十位数字大1,则称这个数为“阶梯数”.若s ,t 都是“阶梯数”,将组成s 的各数位上的数字中最大数字作为十位数字,组成t 的各数位上的数字中最小数字作为个位数字,得到一个新两位数m 叫做s ,t 的“萌数”,将组成s 的各数位上的数字中最小数字作为十位数字,组成t 的各数位上的数字中最大数字作为个位数字,得到一个新两位数n 叫做s ,t 的“曲数”,记(,)2F s t m n =+.例如:因为211-=,615-=,所以211和654都是“阶梯数”;211和654的“萌数” 24m =,“曲数” 16n =,(211,654)2241664F =⨯+=.(1)判断435 是 (填“是”或“否” )为“阶梯数”;(2)若(1)6s a a =-,(1)5t b b =+(其中25a <,69b <,且a ,b 都是整数),且(,)167F s t =,求满足条件的s 、t 的值;(3)若p 、q 都是“阶梯数”,其中100103p x y =++,20010q a b =++(其中23x ,18y ,28b 且a ,b ,x ,y 都是整数),当(F p ,132)(F q +,824)157=时,求(,)F p q 的值. 【解答】解:(1)435中,百位4比十位3大1,符号阶梯数定义.故答案为:是.(2)s 和t 的萌数为65,曲数为(1)(1)a b -+,(F s ∴,)265(1)(1)167t a b =⨯+-+=,解得4a =,6b =.436s ∴=,765b =.(3)p 、q 都是阶梯数,1y x ∴=-,1a =,又23x ,28b ,10010(1)3213p x x ∴=+-+=或323,212q =、213、214、215、216、217、218. (F p ∴、132)31210(1)3x =⨯+-+,(F q ,824)(102)218b =+⨯+,由(F p 、132)(F q +,824)157=,得102080x b +=,其中x 为偶数,2x ∴=,3b =,即213p =,213q =.(F p 、)2311375q =⨯+=.25.一个多位自然数分解为末三位与末三位以前的数,让末三位数减去末三位以前的数,所得的差能被13整除,则原多位数一定能被13整除.(1)判断266357 能 (选填“能”或“不能” )被13整除;(2)证明:任意一个多位自然数都满足上述规律;(3)将一个多位自然数分解为个位与个位之前的数,若让个位之前的数加上个位数的k 倍(k 为正整数),所得之和能被13整除,且原多位自然数也能被13整除,求当150k 时,所有满足条件的k 的值.【解答】(1)解:266357能被13整除;理由如下:266357的末三位数为357,末三位以前的数为266,35726691∴-=,91137÷=,266357∴能被13整除,故答案为:能;(2)证明:设这个多位数的末三位数为a ,末三位以前的数为b ,则这个多位数可表示为1000b a +,根据题意得:13(a b n n -=为整数),13a n b ∴=+,则1000100013100113b a b n b b n +=++=+,100113b n +可以被13整除,1000b a ∴+可以被13整除,∴任意一个三位以上的自然数都满足这个规律,即任意一个多位自然数都满足上述规律;(3)解:设个位之前及个位数分别为m 、n (出现的字母均为自然数),依题意不妨设13m kn t +=,则原多位数为10m n +,依题意不妨设1013m n s +=, 联立可得:3110(101)101313n k s t k t kn +=--=-+, 则31k +为13倍数,分别将1k =、2、3、4、550⋯代入可知,4k ∴=或17k =或30k =或43k =.26.一个三位自然数a ,满足各数位上的数字之和不超过10,并且个位数字与百位数字不同,我们称这个数为“完美数”.将a 的个位数字与百位数字交换得到一个新数a ',记G (a )11a a '-=.例如,当125a =时,521a '=,125521(125)3611G -==-;当370a =时,73a '=,37073(370)2711G -==. (1)判断236 不是 (选填“是”或“不是” )完美数,计算(321)G = ;(2)已知两个“完美数” m ,n ,满足10010m a b =++,100(09n c d b a =+<,09c ,09d ,a ,b ,c ,d 为整数),若()G m 能被7整除,且()()9(2)G m G n d +=+,求m n -的最小值.【解答】解:(1)2361110++=>,236∴不是完美数, 根据题意,321123(321)1811G -==; 故答案为:不是;18.(2)10010m a b =++,10010m b a '∴=++,100n c d =+,100n d c '∴=+,()()9(2)112m m n n G m G n d -'-'∴+=+=+, 22a b c d ∴-+=+,设()7G m x =,x 为整数, ∴9999711a b x -=,即9()7a b x -=, 09b a <,∴满足条件的a 只有7或8或9,当9a =时,m 不是完美数,故舍去,当8a =时,1b =,这个数是811,是完美数,此时,8122c d -+=+,即25c d =-,09c ,09d ,3d ∴=,1c =时,301n =,则510m n -=;4d =,3c =时,403n =,则811403408m n -=-=;5d =,5c =时,505n =,则811505306m n -=-=;6d =,7c =(舍去), ∴共有三种情况,最小的为306;当7a =时,0b =,这个数是710,是完美数,此时,7022c d -+=+,即25c d =-,09c ,09d ,3d ∴=,1c =时,301n =,则710301409m n -=-=;4d =,3c =时,403n =,则710403302m n -=-=;5d =,5c =时,505n =,则710505205m n -=-=;6d =,7c =(舍去), ∴共有三种情况,最小的为205;综上,m n -的最小值为205.27.阅读材料:我们知道,任意一个正整数k 都可以进行这样的分解:(k m n m =⨯,n 是正整数,且)m n ,在k 的所有这种分解中,如果m ,n 两因数之差的绝对值最小,我们就称m n⨯是k 的最佳分解,并规定:()m f k n=.例如:18可以分解成118⨯,29⨯或36⨯,因为1819263->->-,所以36⨯是18的最佳分解,所以31(18)62f ==. (1)计算:f (6)=23 ,f (4)= ,2()f x = .(其中x 为正整数) (2)若21010(2)1011f x x +=,其中x 是正整数,求x 的值. (3)若2(9)1f x -=,其中x 是正整数,求x 的值.【解答】解:(1)6的最佳分解为23⨯,所以f (6)23=;4的最佳分解为22⨯,所以f (4)1=;2x 的最佳分解为x x ⋅,所以2()1f x =. 故答案为:23;1;1. (2)22x x +的最佳分解为:(2)x x +, ∴2(2)2x f x x x +=+, 又21010(2)1011f x x +=, 所以101021011x x =+, 解得2020x =,经检验,2020x =符合题意.(3)由2(9)1f x -=,可设229(x t t -=为正整数),即2(3)(3)x x t +-=,33x t x ∴-<<+,有以下几种情况:①当2t x =-时,229(2)x x -=-,解得134x =(舍去); ②当1t x =-时,229(1)x x -=-,解得5x =;③当t x =时,229x x -=,无解;④当1t x =+时,229(1)x x -=+,解得5x =-;⑤当2t x =+时,229(2)x x -=+,解得134x =-; 综上所述,5x =.28.阅读下列材料:材料一:对于一个百位数字不为0的四位自然数M ,以它的百位数字作为十位,十位数字作为个位,得到一个两位数m ,若m 等于M 的千位数字与个位数字的平方差,则称数M 为“平方差数”.例如:7136是“平方差数”,因为227613-=,所以7136是“平方差数”;又如:4251不是“平方差数”,因为22411525-=≠,所以4251不是“平方差数”.材料二:我们有时可以利用分解因数的方法解决求整数解的问题,例如:若p ,q 为两个正整数()18p q pq >=,则p ,q 为18的正因数,又因为18可以分解为181⨯或92⨯或63⨯,所以方程18pq =的正整数解为181p q =⎧⎨=⎩或92p q =⎧⎨=⎩或63p q =⎧⎨=⎩. 根据上述材料解决问题:(1)判断9810,6361是否是“平方差数”?并说明理由;(2)若一个四位“平方差数” M ,将它的千位数字、个位数字及m 相加,其和为30,求所有满足条件的“平方差数” M .【解答】解:(1)9810是“平方差数”,229081-=,9810∴是“平方差数”; 6361不是“平方差数”,22613536-=≠,6361∴不是“平方差数”. (2)设M 的千位数字为a ,个位数字为b ,则22m a b =-,由题意得2230a b a b ++-=,即()(1)30a b a b +-+=.a b +>,11a b -+>且均为30的正因数,∴将30分解为215⨯或310⨯或56⨯.①()(1)215a b a b +-+=⨯,解得87a b =⎧⎨=⎩,即8157M =; ②()(1)310a b a b +-+=⨯,解得64a b =⎧⎨=⎩,即6204M =; ③()(1)56a b a b +-+=⨯,解得50a b =⎧⎨=⎩,即5250M =; 解得51a b =⎧⎨=⎩,即5241M =.8157∴=或6204或5250或5241.M29.【阅读】在数轴上,若点A表示数a,点B表示数b,则点A与点B之间的距离为AB a b=-.||例如:两点A,B表示的数分别为3,1AB=--=.-,那么|3(1)|4(1)若|3|2x-=,则x的值为1或5.(2)当x=(x是整数)时,式子|1||2|3-++=成立.x x(3)在数轴上,点A表示数a,点P表示数p.我们定义:当||1-=时,点P叫点A的1倍伴随点,p a当||2-=时,点P叫点A的2倍伴随点,p a⋯当||-=时,点P叫点A的n倍伴随点.p a n试探究下列问题:若点M是点A的1倍伴随点,点N是点B的2倍伴随点,是否存在这样的点A和点B,使得点M恰与点N重合,若存在,求出线段AB的长;若不存在,请说明理由.【解答】解:(1)|3|2x-=,表示到表示数x的点到表示数3的点的距离为2,当表示数x的点在表示数3的点的左侧时,321x=-=;当表示数x的点在表示数3的点的右侧时,325x=+=;故答案为:1或5;(2)|1||2|3-++=表示的是表示数x的点到表示数1的点的距离和表示数2x x-的点的距离之和,分下列三种情况:①当表示数x的点在2-到1之间时,如图1,此时|1||2|3-++=成立;x x满足条件的x的整数为2-,1-,0,1;②当表示数x的点在2-左侧时,如图2,此时|1||2|3-++>,不存在这样的点;x x③表示数x的点在1右侧时,如图3,此时|1||2|3-++>,不存在这样的点;x x故答案为:2-或1-或0或1;(3)存在,理由如下:设点M 所表示的数位m ,点A 所表示的数为a ,点B 所表示的数为b ,点M 和N 重合,∴点N 所表示的数为n ,点M 是点A 的1倍伴随点,点N 是点B 的2倍伴随点,||1m a ∴-=,||2m b -=,12m a b ∴=±=±,当12a b +=+时,1a b -=,此时1AB =;当12a b +=-时,3a b -=-,此时3AB =;当12a b -=+时,3a b -=,此时3AB =;当12a b -=-时,1a b -=-,此时1AB =;综上,存在,此时AB 的长为1或3.30.如果一个自然数M 能分解成A B ⨯,其中A 和B 都是两位数,且A 与B 的十位数字之和为10,个位数字之和为9,则称M 为“十全九美数”,把M 分解成A B ⨯的过程称为“全美分解”,例如:28384366=⨯,4610+=,369+=,2838∴是“十全九美数“;3912317=⨯,2110+≠,391∴不是“十全九美数”. (1)判断2100和168是否是“十全九美数”?并说明理由;(2)若自然数M 是“十全九美数“,“全美分解”为A B ⨯,将A 的十位数字与个位数字的差,与B 的十位数字与个位数字的和求和记为()S M ;将A 的十位数字与个位数字的和,与B 的十位数字与个位数字的差求差记为()T M .当()()S M T M 能被5整除时,求出所有满足条件的自然数M . 【解答】解:(1)2100是“十全九美数”,168不是“十全九美数”,理由如下: 21002584=⨯,2810+=,549+=,2100∴是“十全九美数”;1681412=⨯,10l l +≠,168∴不是“十全九美数“;(2)设A 的十位数字为m ,个位数字为n ,则10A m n =+, M 是“十全九美数”, M A B =⨯, B ∴的十位数字为10m -,个位数字为9n -,则10(10)910910B m n m n =-+-=--, 由题知:()109192S M m n m n n =-+-+-=-,()[10(9)]21T M m n m n m =+----=-, 根据题意,令()1925(()21S M n k k T M m -==-为整数), 由题意知:19m ,09n ,且都为整数,119219n ∴-,12117m -,当k l =时,192521n m -=-, ∴1925211n m -=⎧⎨-=⎩或19210212n m -=⎧⎨-=⎩或19215213n m -=⎧⎨-=⎩, 解得17m n =⎧⎨=⎩或3292m n ⎧=⎪⎪⎨⎪=⎪⎩(舍去)或22m n =⎧⎨=⎩; 17921564M A B ∴=⨯=⨯=或22871914M A B =⨯=⨯=;当2k =时,1921021n m -=-, ∴19210211n m -=⎧⎨-=⎩, 解得192m n =⎧⎪⎨=⎪⎩(舍去); 当3k =时,1921521n m -=-, ∴19215211n m -=⎧⎨-=⎩, 解得12m n =⎧⎨=⎩; 12971164M A B ∴=⨯=⨯=,综上,满足“十全九美数”条件的M 有:1564或1914或1164.31.一个自然数能分解成A B ⨯,其中A ,B 均为两位数,A 的十位数字比B 的十位数字大1,且A ,B 的个位数字之和为10,则称这个自然数为“分解数”.例如:48197961=⨯,7比6大1,1910+=,4819∴是“分解数”;又如:14964434=⨯,4比3大1,4410+≠,1496∴不是“分解数”.(1)判断325,851是否是“分解数”,并说明理由;(2)自然数M A B =⨯为“分解数”,若A 的十位数字与B 的个位数字的和为()P M ,A 的个位数字与B 的十位数字的和()F M ,令()()()P M G M F M =,当()G M 为整数时,则称M 为“整分解数”.若B 的十位数字能被2整除,求所有满足条件的“整分解数” M .【解答】解:(1)3252513=⨯,2比1大1,5310+≠,325∴不是“分解数”; 68513723=⨯,3比2大l ,7310+=,851∴是“分解数”. (2)令10B x y =+,10(1)10A x y =++-,(8l x <<,19y ,且x ,y 为整数), ()1P M x y =++,()10F m x y =-+,1()10x y G M x y ++∴=-+,2x 为整数, 2x ∴=,4,6,8,当2x =时,315()11212y G M y y +==-+-+-+,为整数, 12y ∴-+的值为3或5,解得9y =或7,13129899M ∴=⨯=,23327891M =⨯=;当4x =或6x =时,不存在()G M 为整数,∴舍去;当8x =时,927()11818y G M y y +==-+-+-+为整数, 189y ∴-+=,解得9y =,391898099M ∴=⨯=.综上所述,M 的值为899,891,8099.32.对于任意一个四位数N ,如果N 满足各个位上的数字互不相同,且个位数字不为0,N的百位上的数字与十位上的数字之差是千位上的数字与个位上的数字之差的2倍,则称这个四位数N 为“双减数”.对于一个“双减数” N abcd =,将它的千位和百位构成的两位数为ab ,个位和十位构成的两位数为dc ,规定;()12ab dc F N -=. 例如:7028N =.因为2(78)02⨯-=-,故7028是一个“双减数”,则7082(7028)112F -==-. (1)判断9527,6713是否是“双减数”,并说明理由,如果是,并求出()F N 的值;(2)若自然数A 为“双减数”, F (A )是3的倍数,且A 各个数位上的数字之和能被13整除,求A 的值.【解答】解:(1)9527:523-=,972-=,不满足“双减数”的定义,故9527不是双减数;6713:716-=,633-=,满足623=⨯,且满足各个位上的数字互不相同,且个位数字不为0,故6713是双减数;6731(6713)312F -==. 9527∴不是双减数,6713是双减数,(6713)3F =.(2)设A abcd =,由题意可知,F (A )是3的倍数,且A 各个数位上的数字之和能被13整除且百位数与十位数之差是千位数与个位数之差的两倍.()312ab dc F A k -∴==. 13a b c d n +++=②(n 为正整数,能被13整除说明是13的倍数), 2()b c a d -=-③,由③式可得知,ab dc -的结果中,个位数是十位数的两倍,而且()312ab dc F A k -==①. ∴36ab dc k -=,(说明ab dc -是36的倍数), 根据“双减数“各位数不重复与0d ≠的性质,ab 最大为98,dc 最小为10,ab dc ∴-最大为88, ∴36ab dc -=或36-或72(舍去)或72-(舍去),(根据“双减数“百位上的数字与十位上的数字之差是千位上的数字与个位上的数字之差的2倍排除),3a d ∴-=,6b c -=或3a d -=-,6b c -=-,即3a d =+④,6b c =+⑤或3a d =-⑥,6b c =-⑦,将④⑤代入②可得,(3)(6)13d c c d n ++-++=, 将⑥⑦代入②可得,(3)(6)13d c c d n -+-++=, 同理,根据“双减数“的性质可得a b c d +++的最大值为987630+++=,最小值为01236+++=,630a b c d ∴+++,a b c d ∴+++是13的倍数,a b c d ∴+++只能取13或26.Ⅰ、当13a b c d +++=时,可得2d c +=或11d c +=;当2d c +=时,d 与c 的值可能为20d c =⎧⎨=⎩,02d c =⎧⎨=⎩(舍去),11d c =⎧⎨=⎩(舍去),(根据双减数个位数不能为0,且每位数不相等排除), 即20d c =⎧⎨=⎩; 当11d c +=时,2a b +=,则20a b =⎧⎨=⎩,02a b =⎧⎨=⎩(舍去),11a b =⎧⎨=⎩(舍去), 即20a b =⎧⎨=⎩,此时,6c =,5d =. Ⅱ、当26a b c d +++=时,可得2()17d c +=,2()35d c +=. 172d c +=(舍去)或352d c +=(由于d ,c 不为整数,与题意不符,故舍去), 3235a d ∴=+=+=,66b c =+=5602A ∴=或2065.33.对于一个四位自然数(R abcd a =,b ,c ,d 不全相同且均不为0),如果a d b c -=-,那么称这个数R 为“天平数”,对于一个“天平数” R ,将它的千位和个位构成的两位数减去百位和十位构成的两位数所得差记为s ,将它的千位和十位构成的两位数减去百位和个位构成的两位数所得差记为t ,规定:()10s t f R +=;例如:8734R =,因为8473-=-,故:8734是一个“天平数”.所以:847311s =-=,83749t =-=,则:119()210f R +==. (1)请判断7513是否是“天平数”,如果是,请求出()f R 的值;如果不是,请说明理由;(2)若自然数M ,N 都是“天平数”,其中1007051M x y =++,100010512(19N m n x =++,08y ,19m ,08n ,x ,y ,m ,n 都是整数),规定:()()f M k f N =,当()()4f N f M -=时,求k 的值. 【解答】解:(1)是,且(7513)4f =,理由如下:7351-=-,7513∴是一个“天平数”. 735122s ∴=-=,715318t =-=,2218(7513)410f +∴==; (2)1007051700010050(1)M x y x y =++=++++,M ∴的前位数字是7,百位数字是x ,十位数字是5,个位数字是1y +, M 是“天平数”, 7(1)5y x ∴-+=-,即11x y +=,(701)(105)6610Ms y x x y ∴=++-+=-+,75(101)7410Mt x y x y =-++=--,66107410()1421010s t x y x y f M x +-++--∴===-, 100010512100050010(1)2N m n m n =++=++++,N ∴的前位数字是m ,百位数字是5,十位数字是(1)n +,个位数字是2, N 是“天平数”, 25(1)m n ∴-=+,即6m n +=,(102)(501)1049Ns m n m n ∴=+-++=--,(101)521051Nt m n m n =++-=+-,10491051()2101010s t m n m n f N m +--++-∴===-, 19x ,08y 且11x y +=,39x ∴,19m ,08n ,且6m n +=,16m ∴,()()(210)(142)22244f N f M m x x m -=---=+-=,14x m ∴+=,14x m ∴=-,56m ∴, 此时,()142721()21055f M x m k f N m m m --====----, 当5m =时,k 值不存在;当6m =时,1k =-,综上,k 的值为1-.34.如果一个自然数M 的个位数字不为0,且能分解成A B ⨯,其中A 与B 都是两位数,A 与B 的十位数字相同,个位数字之和为8,则称数M 为“团圆数”,并把数M 分解成M A B =⨯的过程,称为“欢乐分解”.例如:5722226=⨯,22和26的十位数字相同,个位数字之和为8,572∴是“团圆数”. 又如:2341813=⨯,18和13的十位数字相同,但个位数字之和不等于8,234∴不是“团圆数”.(1)最小的“团圆数”是 187 ;(2)判断195,621是否是“团圆数”?并说明理由;(3)把一个“团圆数” M 进行“欢乐分解”,即M A B =⨯,A 与B 之和记为()P M ,A 与B 差的绝对值记为()Q M ,令()()()P M G M Q M =,当()G M 能被8整除时,求出所有满足条件的M 的值. 【解答】解:(1)由题意可知,最小的“团圆数”十位数字是1,个位数字分别为1和7, ∴最小的“团圆数”是1117187⨯=,故答案为:187;(2)1951315=⨯,且358+=,195∴是“团圆数”, 6212327=⨯,378+≠,621∴不是“团圆数”; (3)设10A a b =+,则108B a b =+-,208A B a ∴+=+,|||28|A B b -=-,()()()||P M A B G M Q M A B +==-能被8整除, ∴2088|28|a kb +=-,k 为整数, 52(|4|)4a b k ∴+=-,52a ∴+是4的倍数,∴满足条件的a 有2,6,若2a =,则488|28|k b =-,k 为整数, ∴3|4|k b =-, |4|b ∴-是3的因数,43b ∴-=-,1-,1,3,∴满足条件的b 有1,3,5,7,21A ∴=,27B =或23A =,25B =或25A =,23B =或27A =,21B =,567A B ∴⨯=或575,若6a =,则1288|28|k b =-,k 为整数, ∴8|4|k b =-, |4|b ∴-是8的因数,48b ∴-=-,4-,2-,1-,1,2,4,8,∴满足条件的b 有2,3,5,6,62A ∴=,66B =或63A =,65B =或65A =,63B =或66A =,62B =,62664092A B ∴⨯=⨯=或4095,综上,M 的值为567或575或4092或4095.35.对于任意一个四位数m ,若m 满足各数位上的数字都不为0,且千位与百位上的数字不相等,十位与个位上的数字不相等,那么称这个数为“智慧数”.将一个“智慧数” m 的任意一个数位上的数字去掉后可以得到四个新三位数,把这四个新三位数的和与3的商记为()F m .例如“智慧数” 1234m =,去掉千位上的数字得到234,去掉百位上的数字得到134,去掉十位上的数字得到124,去掉个位上的数字得到123.这四个新三位数的和为234134124123615+++=,6153205÷=,所以(1234)205F =.(1)计算:(2131)F = 262 ;(5876)F = ;(2)若“智想数” 780010(15n x y x =++,19y ,x ,y 都是正整数),()F n 也是“智慧数”,且()F n 能被12整除,求满足条件的n 的值.【解答】解:(1)(2131)(213211231131)3262F =+++÷=;(5876)(587586576876)3875F =+++÷=;故答案为:262;875;(2) “智慧树” 78001071000810010n x y x y =++=⨯+⨯++, ∴数n 的千位上的数为7,百位上的数为8,十位上的数为x ,个位上的数为y , ()(7807807001080010)310207F n x y x y x y x y ∴=+++++++++÷=++, 15x ,19y ,()F n 也是“智慧数”,且()F n 能被12整除, ∴可设()1020712F n x y k =++=,即()F n 是3的倍数,也是4的倍数, ()743403402333F n x y x y k x ++∴==+=++,且()3F n 是4的倍数, 当1x =时,y 可取2,5,8,此时()3433F n =(舍)或344或345(舍),此时()1032F n =,符合定义,7815n =;当2x =时,y 可取1,4,7,此时()3453F n =(舍)或346(舍)或347(舍),无符合题意的n ;当3x =时,()340733F n y =++,y 可取3,6,9,此时()3483F n =或349(舍)或350(舍),此时()7833F n =,不符合题意;当4x =时,y 可取2,5,8,此时()3503F n =(舍)或351(舍)或352,此时()1056F n =,7848n =, 当5x =时,y 可取1,4,7,此时()3523F n =或353(舍)或354(舍),此时()1056F n =,7851n =, 综上,符合题意的点n 值为7815或7848或7851.。
完整版)北京中考数学新定义题目汇总

完整版)北京中考数学新定义题目汇总28.对于平面内的圆C和圆C外一点Q,定义如下:若过点Q的直线与圆C存在公共点,记为点A、B,设$k=\frac{AQ+BQ}{CQ}$,则称点A(或点B)是圆C的“k相关依附点”。
特别地,当点A和点B重合时,规定$AQ=BQ$,$k=\frac{2AQ^2}{CQ^2}$。
已知在平面直角坐标系$xOy$中,$Q(-1,0)$,$C(1,0)$,圆C的半径为$r$。
1) 当$r=2$时。
①若$A_1(0,1)$是圆C的“k相关依附点”,则$k$的值为$\frac{3}{2}$。
② $A_2(3,0)$是否为圆C的“2相关依附点”:否。
2) 若圆C上存在“k相关依附点”点M。
①当$r=1$,直线QM与圆C相切时,$k$的值为$2$。
②当$k=3$时,$r$的取值范围为$[\sqrt{\frac{3}{2}},2]$。
3) 若存在$r$的值使得直线$y=-3x+b$与圆C有公共点,且公共点是圆C的“3相关依附点”,则$b$的取值范围为$[-2\sqrt{2},2\sqrt{2}]$。
28.在平面直角坐标系$xOy$中,点M的坐标为$(x_1,y_1)$,点N的坐标为$(x_2,y_2)$,且$x_1\neq x_2$,$y_1\neq y_2$,以MN为边构造菱形,若该菱形的两条对角线分别平行于$x$轴,$y$轴,则称该菱形为边的“坐标菱形”。
1) 已知点$A(2,0)$,$B(0,23)$,则以AB为边的“坐标菱形”的最小内角为$60^\circ$。
2) 若点$C(1,2)$,点$D$在直线$y=5$上,以CD为边的“坐标菱形”为正方形,则直线$CD$的表达式为$y=5$。
3) 圆O的半径为2,点$P(m,1)$。
若在圆O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,则$m$的取值范围为$[-1,3]$。
28.对于平面上两点A、B,定义如下:以点A或B为圆心,AB长为半径的圆称为点A、B的“确定圆”。
2019-2020学年度北师大实验中学新高一入学分班考试数学试题-含详细解析

6.
A. 乙盒中黑球不多于丙盒中黑球
B. 乙盒中红球与丙盒中黑球一样多
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
某学校运动会的立定跳远和 30 秒跳绳两个单项比赛分成预赛和决赛两个阶段,表中为 10 名学生的预赛成
绩,其中有三个数据模糊.
学生序号
1
2
“割圆术”相似,数学家阿尔⋅卡西的方法是:当正整数 n 充分大时,计算单位圆的内接正 6n 边形的周长和外切
正 6n 边形(各边均与圆相切的正 6n 边形)的周长,将它们的算术平均数作为2的近似值.按照阿尔⋅卡西的方
法,的近似值的表达式是(
A. 3(sin
C. 3(sin
3.
30°
60°
19.某学习小组由学生和教师组成,人员构成同时满足以下三个条件:
()男学生人数多于女学生人数;
()女学生人数多于教师人数;
()教师人数的两倍多于男学生人数.
①若教师人数为 4,则女学生人数的最大值为______.
②该小组人数的最小值为______.
第 5 页,共 23 页
20.某网店统计了连续三天售出商品的种类情况:第一天售出 19 种商品,第二天售出 13 种商品,第三天售出 18 种
A. 中位数
B. 平均数
C. 方差
D. 极差
11. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说,你们四人中有 2 位优秀,2 位良好,我
现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩,看后甲对大家说:我还是不知道我的成绩,
根据以上信息,则(
)
A. 乙可以知道两人的成绩
中考数学:新定义创新型综合压轴问题真题+模拟(原卷版北京专用)

中考数学新定义创新型综合压轴问题【方法归纳】新定义"型问题是指在问题中定义了初中数学中没有学过的一些概念、新运算、新符号,要求学生读懂题意并结合已有知识进行理解,而后根据新定义进行运算、推理、迁移的一种题型。
它一般分为三种类型:(1)定义新运算;(2)定义初、高中知识衔接"新知识";(3)定义新概念.这类试题考查考生对"新定义"的理解和认识,以及灵活运用知识的能力,解题时需要将"新定义"的知识与已学知识联系起来,利用已有的知识经验来解决问题。
解决此类题的关键是(1)深刻理解“新定义”——明确“新定义”的条件、原理、方法、步骤和结论;(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”;归纳“举例”提供的做题方法;归纳“举例”提供的分类情况;(3)依据新定义,运用类比、归纳、联想、分类讨论以及数形结合的数学思想方法解决题目中需要解决的问题。
北京中考最后一题的新定义主要涉及函数与圆的有关新定义问题,属于函数的范畴,已经考过“对应点”、“关联线段”、“平移距离”“闭距离”、“相关矩形”、“反称点”、“有界函数”、“关联点”等新定义。
在平时的教学过程中要从细节中挖掘出数学的本质特征,引领学生找到解决问题的思想方法。
解答这类问题的关键是要读懂题目提供的新知识,理解其本质,把它与已学的知识联系起来,把新的问题转化为已学的知识进行解决。
【典例剖析】【例1】(2022·北京·中考真题)在平面直角坐标系xOy中,已知点M(a,b),N.对于点P给出如下定义:将点P向右(a≥0)或向左(a<0)平移|a|个单位长度,再向上(b≥0)或向下(b<0)平移|b|个单位长度,得到点P′关于点N的对称点为Q,称点Q为点P的“对应点”.(1)如图,点M(1,1),点N在线段OM的延长线上,若点P(−2,0),点Q为点P的“对应点”.①在图中画出点Q;OM;②连接PQ,交线段ON于点T.求证:NT=12(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t(1<t<1),若P为⊙O外2一点,点Q为点P的“对应点”,连接PQ.当点M在⊙O上运动时直接写出PQ长的最大值与最小值的差(用含t的式子表示)【例2】(2021·北京·中考真题)在平面直角坐标系xOy中,⊙O的半径为1,对于点A和线段BC,给出如下定义:若将线段BC绕点A旋转可以得到⊙O的弦B′C′(B′,C′分别是B,C的对应点),则称线段BC是⊙O的以点A为中心的“关联线段”.(1)如图,点A,B1,C1,B2,C2,B3,的横、纵坐标都是整数.在线段B1C1,B2C2,B3C3中,⊙O 的以点A为中心的“关联线段”是______________;(2)△ABC是边长为1的等边三角形,点A(0,t),其中t≠0.若BC是⊙O的以点A为中心的“关联线段”,求t的值;(3)在△ABC中,AB=1,AC=2.若BC是⊙O的以点A为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC长.【真题再现】1.(2020·北京·中考真题)在平面直角坐标系xOy中,⊙O的半径为1,A,B为⊙O外两点,AB=1.给出如下定义:平移线段AB,得到⊙O的弦A′B′(A′,B′分别为点A,B的对应点),线段AA′长度的最小值称为线段AB到⊙O的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为1的弦P 1P 2和P 3P 4,则这两条弦的位置关系是 ;在点P 1,P 2,P 3,P 4中,连接点A 与点 的线段的长度等于线段AB 到⊙O 的“平移距离”;(2)若点A ,B 都在直线y =√3x +2√3上,记线段AB 到⊙O 的“平移距离”为d 1,求d 1的最小值;(3)若点A 的坐标为(2,32),记线段AB 到⊙O 的“平移距离”为d 2,直接写出d 2的取值范围.2(2019·北京·中考真题)在△ABC 中,D ,E 分别是△ABC 两边的中点,如果DE⌢上的所有点都在△ABC 的内部或边上,则称DE⌢为△ABC 的中内弧.例如,下图中DE ⌢是△ABC 的一条中内弧.(1)如图,在Rt △ABC 中,AB =AC =2√2,D ,E 分别是AB ,AC 的中点.画出△ABC 的最长的中内弧DE⌢,并直接写出此时DE ⌢的长;(2)在平面直角坐标系中,已知点A(0,2),B(0,0),C(4t,0)(t >0),在△ABC 中,D ,E 分别是AB ,AC 的中点.①若t =12,求△ABC 的中内弧DE⌢所在圆的圆心P 的纵坐标的取值范围;②若在△ABC 中存在一条中内弧DE⌢,使得DE ⌢所在圆的圆心P 在△ABC 的内部或边上,直接写出t 的取值范围.3.(2018·北京·中考真题)对于平面直角坐标系xOy 中的图形M ,N ,给出如下定义:P 为图形M 上任意一点,Q 为图形N 上任意一点,如果P ,Q 两点间的距离有最小值,那么称这个最小值为图形M ,N 间的“闭距离”,记作d (M ,N ).已知点A (−2,6),B (−2,−2),C (6,−2).(1)求d (点O ,△ABC );(2)记函数y =kx (−1≤x ≤1,k ≠0)的图象为图形G ,若d (G ,△ABC )=1,直接写出k 的取值范围;(3)⊙T 的圆心为T (t ,0),半径为1.若d (⊙T ,△ABC )=1,直接写出t 的取值范围. 4.(2017·北京·中考真题)在平面直角坐标系xOy 中的点P 和图形M ,给出如下的定义:若在图形M 存在一点Q ,使得P 、Q 两点间的距离小于或等于1,则称P 为图形M 的关联点.(1)当⊙O 的半径为2时,①在点P 1(12,0),P 2(12,√32),P 3(52,0) 中,⊙O 的关联点是_______________. ②点P 在直线y=-x 上,若P 为⊙O 的关联点,求点P 的横坐标的取值范围.(2)⊙C 的圆心在x 轴上,半径为2,直线y=-x+1与x 轴、y 轴交于点A 、B .若线段AB 上的所有点都是⊙C 的关联点,直接写出圆心C 的横坐标的取值范围.5.(2016·北京·中考真题)在平面直角坐标系xOy 中,点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2),且x 1≠x 2,y 1≠y 2,若P ,Q 为某个矩形的两个顶点,且该矩形的边均与,Q 的“相关矩形”.下图为点P ,Q 的“相关矩形”的示意图.(1)已知点A 的坐标为(1,0).①若点B 的坐标为(3,1)求点A ,B 的“相关矩形”的面积;②点C 在直线x=3上,若点A ,C 的“相关矩形”为正方形,求直线AC 的表达式;(2)⊙O 的半径为,点M 的坐标为(m ,3).若在⊙O 上存在一点N ,使得点M ,N 的“相关矩形”为正方形,求m 的取值范围.6.(2015·北京·中考真题)在平面直角坐标系xOy 中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.(1)当⊙O的半径为1时.,0),T(1,√3)关于⊙O的反称点是否存在?若存在,求①分别判断点M(2,1),N(32其坐标;②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;x+2√3与x轴、y轴分别交于点A,B,若(2)⊙C的圆心在x轴上,半径为1,直线y=﹣√33线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.7.(2014·北京·中考真题)对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足−M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(x>0)和y=x+1(−4<x≤2)是不是有界函数?若是有界函数,(1)分别判断函数y=1x求其边界值;(2)若函数y=−x+1(a⩽x⩽b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x2(−1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值≤t≤1?是t,当m在什么范围时,满足348.(2013·北京·中考真题)对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若⊙C 上存在两个点A ,B ,使得∠APB=60°,则称P 为⊙C 的关联点.已知点D (,),E (0,-2),F (,0)(1)当⊙O 的半径为1时,①在点D ,E ,F 中,⊙O 的关联点是 ;②过点F 作直线交y 轴正半轴于点G ,使∠GFO=30°,若直线上的点P (m ,n )是⊙O 的关联点,求m 的取值范围;(2)若线段EF 上的所有点都是某个圆的关联点,求这个圆的半径r 的取值范围.【模拟精练】一、解答题1.(2022·北京朝阳二模)在平面直角坐标系xOy 中,⊙O 的半径为1,AB =1,且A ,B 两点中至少有一点在⊙O 外.给出如下定义:平移线段AB ,得到线段A ′B ′(A ′,B ′分别为点A ,B 的对应点),若线段A ′B ′上所有的点都在⊙O 的内部或⊙O 上,则线段AA ′长度的最小值称为线段AB 到⊙O 的“平移距离”.(1)如图1,点A 1,B 1的坐标分别为(-3,0),(-2,0),线段A 1B 1到⊙O 的“平移距离”为___,点A 2,B 2的坐标分别为(-12,√3),(12,√3),线段A 2B 2到⊙O 的“平移距离”为___;(2)若点A,B都在直线y=√3x+2√3上,记线段AB到⊙O的“平移距离”为d,求d的最小值;(3)如图2,若点A坐标为(1,√3),线段AB到⊙O的“平移距离”为1,画图并说明所有满足条件的点B形成的图形(不需证明).2.(2022·北京北京·二模)在平面直角坐标系xOy中,⊙O的半径为1.对于线段PQ给出如下定义:若线段PQ与⊙O有两个交点M,N,且PM=MN=NQ,则称线段PQ是⊙O的“倍弦线”.(1)如图,点A,B,C,D的横、纵坐标都是整数.在线段AB,AD,CB,CD中,⊙O的“倍弦线”是_____________;(2)⊙O的“倍弦线”PQ与直线x=2交于点E,求点E纵坐标y E的取值范围;(3)若⊙O的“倍弦线”PQ过点(1,0),直线y=x+b与线段PQ有公共点,直接写出b的取值范围.3.(2022·北京大兴·二模)在平面直角坐标系xOy中,对于点P和直线y=1,给出如下定义:若点P在直线y=1上,且以点P为顶点的角是45°,则称点P为直线y=1的“关联点”.(1)若在直线x=1上存在直线y=1的“关联点”P.则点P的坐标为_____;(2)过点P(2,1)作两条射线,一条射线垂直于x轴,垂足为A;另一条射线、交x轴于点B,若点P为直线y=1的“关联点”.求点B的坐标;(3)以点O为圆心,1为半径作圆,若在⊙O上存在点N,使得∠OPN的顶点P为直线y=1的“关联点”.则点P的横坐标a的取值范围是________.4.(2022·北京东城·二模)在平面直角坐标系xOy中,对于图形G及过定点P(3,0)的直线l,有如下定义:过图形G上任意一点Q作QH⊥l于点H,若QH+PH有最大值,那么称这个最大值为图形G关于直线l的最佳射影距离,记作d(G,l),此时点Q称为图形G关于直线l的最佳射影点.(1)如图1,已知A(2,2),B(3,3),写出线段AB关于x轴的最佳射影距离d(AB,x轴)=____________;(2)已知点C(3,2),⊙C的半径为√2,求⊙C关于x轴的最佳射影距离d(⊙C,x轴),并写出此时⊙C关于x轴的最佳射影点Q的坐标;(3)直接写出点D(0,√3)关于直线l的最佳射影距离d(点D,l)的最大值.5.(2022·北京·清华附中一模)在平面直角坐标系xOy中,对于两个点P,Q和图形W,如果在图形W上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.(1)如图1,已知点A(0,3),B(2,3);①设点O与线段AB上一点的距离为d,则d的最小值是______,最大值是______;,0),P2(1,4),P3(−3,0)这三个点中,与点O是线段AB的一对平衡点的是______.②在P1(32(2)如图2,已知⊙O的半径为1,点D的坐标为(5,0).若点E(x,2)在第一象限,且点D 与点E是⊙O的一对平衡点,求x的取值范围;(3)如图3,已知点H(−3,0),以点O为圆心,OH长为半径画弧交x的正半轴于点K.点C(a,b)(其中b≥0)是坐标平面内一个动点,且OC=5,⊙C是以点C为圆心,半径为2的圆,若HK上的任意两个点都是⊙C的一对平衡点,直接写出b的取值范围.6.(2022·北京丰台·一模)在平面直角坐标系xOy中,⊙O的半径为1,T(0,t)为y轴上一点,P为平面上一点.给出如下定义:若在⊙O上存在一点Q,使得△TQP是等腰直角三角形,且∠TQP=90°,则称点P为⊙O的“等直点”,△TQP为⊙O的“等直三角形”.如图,点A,B,C,D的横、纵坐标都是整数.(1)当t=2时,在点A,B,C,D中,⊙O的“等直点”是;(2)当t=3时,若△TQP是⊙O“等直三角形”,且点P,Q都在第一象限,求CP的值.OQ 7.(2022·北京市第一六一中学分校一模)在平面直角坐标系xOy中,对于点P和图形W,如果线段OP与图形W无公共点,则称点P为关于图形W的“阳光点”;如果线段OP与图形W有公共点,则称点P为关于图形W的“阴影点”.(1)如图1,已知点A(1,3),B(1,1),连接AB.①在P1(1,4),P2(1,2),P3(2,3),P4(2,1)这四个点中,关于线段AB的“阳光点”是;②线段A1B1∥AB,A1B1上的所有点都是关于线段AB的“阴影点”,且当线段A1B1向上或向下平移时,都会有A1B1上的点成为关于线段AB的“阳光点”,若,A1B1的长为4,且点A1在B1的上方,则点A1的坐标为.(2)如图2,已知点C(1,√3),⊙C与y轴相切于点D,若⊙E的半径为3,圆心E在直线2l:y=−√3x+4√3上,且⊙E的所有点都是关于⊙C的“阴影点”,求点E的横坐标的取值范围;(3)如图3,⊙M的半径为3,点M到原点的距离为5,点N是⊙M上到原点距离最近的点,点Q和T是坐标平面的两个动点,且⊙M上的所有点都是关于△NQT的“阴影点”直接写出△NQT的周长的最小值.8.(2022·北京市第五中学分校模拟预测)定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的“冰雪距离”,已知O(0,0),A(1,√2),B (m,n),C(m,n+2)是平面直角坐标系中四点.(1)根据上述定义,完成下面的问题:①当m=2√2,n=√2时,如图1,线段BC与线段OA的“冰雪距离”是;②当m=2√2时,线段BC与线段OA的“冰雪距离”是√2,则n的取值范围是;(2)如图2,若点B落在圆心为A,半径为√2的圆上,当n≥√2时,线段BC与线段OA的“冰雪距离”记为d,结合图象,求d的最小值;(3)当m的值变化时,动线段BC与线段OA的“冰雪距离”始终为√2,线段BC的中点为M.直接写出点M随线段BC运动所走过的路径长.9.(2022·北京市师达中学模拟预测)如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少..一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是;(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2√3)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.10.(2021·北京朝阳·二模)在平面直角坐标系xOy中,对于图形Q和∠P,给出如下定义:若图形Q上的所有的点都在∠P的内部或∠P的边上,则∠P的最小值称为点P对图形Q的可视度.如图1,∠AOB的度数为点O对线段AB的可视度.(1)已知点N(2,0),在点M1(0,2√3),M2(1,√3),M3(2,3)中,对线段ON的可视度为360º的点是______.(2)如图2,已知点A(-2,2),B(-2,-2),C(2,-2),D(2,2),E(0,4).①直接写出点E对四边形ABCD的可视度为______°;②已知点F(a,4),若点F对四边形ABCD的可视度为45°,求a的值.11.(2022·北京四中模拟预测)在平面内,对点组A1,A2,...,An和点P给出如下定义:点P与点A1,A2,...,An的距离分别记作d1,d2,...,dn,数组d1,d2,...,dn的中位数称为点P对点组A1,A2,...,An的中位距离.例如,对点组A1(0,0),A2(0,3),A3(4,1)和点P(4,3),有d1=5,d2=4,d3=2,故点P对点组A1,A2,A3的中位距离为4.(1)设Z1(0,0),Z2(4,0),Z304),Y(0,3),直接写出点Y对点组Z1,Z2,Z3的中位距离;(2)设C1(0,0),C2(8,0),C3(6,6),则点Q1(7,3),Q2(3,3),Q3(4,0),Q4(4,2)中,对点组C1,C2,C3的中位距离最小的点是,该点对点组C1,C2,C3的中位距离为;(3)设M(1,0),N(0,√3),T1(t,0),T2(t+2,0),T3(t,2),若线段MN上任意一点对点组T1,T2,T3的中位距离都不超过2,直接写出实数t的取值范围.12.(2020·北京·人大附中模拟预测)在平面直角坐标系xOy中,对于平面中的点P,Q和图形M,若图形M上存在一点C,使∠PQC=90°,则称点Q为点P关于图形M的“折转点”,称△PCQ为点P关于图形M的“折转三角形”(1)已知点A(4,0),B(2,0)①在点Q1(2,2),Q2(1,−√3),Q3(4,−1)中,点O关于点A的“折转点”是______;②点D在直线y=−x上,若点D是点O关于线段AB的“折转点”,求点D的横坐标x D的取值范围;(2)⊙T的圆心为(t,0),半径为3,直线y=x+2与x,y轴分别交于E,F两点,点P为⊙T 上一点,若线段EF上存在点P关于⊙T的“折转点”,且对应的“折转三角形”是底边长为2的等腰三角形,直接写出t的取值范围.13.(2020·北京市陈经纶中学分校三模)平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的对于图形W1和图形W2,若图形W1和图形W2分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形W1和图形W2是“中心轴对称”的.特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的.(1)如图1,在正方形ABCD中,点A(1,0),点C(2,1),①下列四个点P1(0,1),P2(2,2),P3(−12,0),P4(−12,−√32)中,与点A是“中心轴对称”的是________;②点E在射线OB上,若点E与正方形ABC D是“中心轴对称”的,求点E的横坐标x E的取值范围;(2)四边形GHJK的四个顶点的坐标分别为G(−2,2),H(2,2),J(2,−2),K(−2,−2),一次函数y=√3x+b图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.14.(2022·北京房山·二模)对于平面直角坐标系xOy中的图形G和点Q,给出如下定义:将图形G绕点Q顺时针旋转90°得到图形N,图形N称为图形G关于点Q的“垂直图形”,例如,图1中线段OD为线段OC关于点O的“垂直图形”.(1)线段MN关于点M(1,1)的“垂直图形”为线段MP.①若点N的坐标为(1,2),则点P的坐标为__________;②若点P的坐标为(4,1),则点N的坐标为__________;(2)E(−3,3),F(−2,3),H(a,0).线段EF关于点H的“垂直图形”记为E′F′,点E的对应点为E′,点的对应点为F′.①求点E′的坐标(用含a的式子表示);②若⊙O的半径为2,E′F′上任意一点都在⊙O内部或圆上,直接写出满足条件的EE′的长度的最大值.15.(2022·北京丰台·xOy中,⊙O的半径为1,A为任意一点,B 为⊙O上任意一点,给出如下定义:记A,B两点间的距离的最小值为p(规定:点A在⊙O上时,p=0),最大值为q,那么把p+q的值称为点A与⊙O的“关联距离”,记作d(A,2⊙O)(1)如图,点D,E,F的横、纵坐标都是整数①d(D,⊙O)=__________;②若点M在线段EF上,求d(M,⊙O)的取值范围;(2)若点N在直线y=√3x+2√3上,直接写出d(N,⊙O)的取值范围;(3)正方形的边长为m,若点P在该正方形的边上运动时,满足d(P,⊙O)的最小值为1,最大值为√10,直接写出m的最小值和最大值.16.(2022·北京平谷·二模)对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q间的“非常距离”,记作d(P,Q).已知点A(−2,2),B(2,2),连接AB.(1)d(点O,AB)=;(2)⊙O半径为r,若d(⊙O,AB)=0,直接写出r的取值范围;(3)⊙O半径为r,若将点A绕点B逆时针旋转α°(0°<α<180°),得到点A′.①当α=30°时d(⊙O,A′)=0,求出此时r的值;②对于取定的r值,若存在两个α使d(⊙O,A′)=0,直接写出r的范围.17.(2022·北京密云·二模)对于平面直角坐标系xOy中的点P(2,3)与图形T,给出如下定义:在点P与图形T上各点连接的所有线段中,线段长度的最大值与最小值的差,称为图形T关于点P的“宽距”.(1)如图,⊙O的半径为2,且与x轴分别交于A,B两点.①线段AB关于点P的“宽距”为______;⊙O关于点P的“宽距”为______.②点M(m,0)为x轴正半轴上的一点,当线段AM关于点P的“宽距”为2时,求m的取值范围.(2)已知一次函数y=x+1的图象分别与x轴、y轴交于D、E两点,⊙C的圆心在x轴上,且⊙C的半径为1.若线段DE上的任意一点K都能使得⊙C关于点K的“宽距”为2,直接写出圆心C的横坐标x C的取值范围.18.(2022·北京门头沟·二模)我们规定:如图,点H在直线MN上,点P和点P′均在直线MN的上方,如果HP=HP′,∠PHM=∠P′HN,点P′就是点P关于直线MN的“反射点”,其中点H为“V点”,射线HP与射线HP′组成的图形为“V形”.在平面直角坐标系xOy中,(1)如果点P(0,3) ,H(1.5,0),那么点P关于x轴的反射点P′的坐标为;(2)已知点A(0,a) ,过点A作平行于x轴的直线l.①如果点B(5,3) 关于直线l的反射点B′和“V点”都在直线y=−x+4上,求点B′的坐标和a的值;②⊙W是以(3,2) 为圆心,1为半径的圆,如果某点关于直线l的反射点和“V点”都在直线y=−x+4上,且形成的“V形”恰好与⊙W有且只有两个交点,求a的取值范围.19.(2022·北京东城·一模)对于平面直角坐标系xOy中的点C及图形G,有如下定义:若图形G上存在A,B两点,使得△ABC为等腰直角三角形,且∠ABC=90°,则称点C为图形G的“友好点”.(1)已知点O(0,0),M(4,0),在点C1(0,4),C2(1,4),C3(2,−1)中,线段OM的“友好点”是_______;(2)直线y=−x+b分别交x轴、y轴于P,Q两点,若点C(2,1)为线段PQ的“友好点”,求b 的取值范围;(3)已知直线y=x+d(d>0)分别交x轴、y轴于E,F两点,若线段EF上的所有点都是半径为2的⊙O的“友好点”,直接写出d的取值范围.20.(2022·北京顺义·二模)在平面直角坐标系xOy中,对于点R和线段PQ,给出如下定义:M为线段PQ上任意一点,如果R,M两点间的距离的最小值恰好等于线段PQ的长,则称点R为线段PQ的“等距点”.(1)已知点A(5,0).①在点B1(−3,4),B2(1,5),B3(4,−3),B4(3,6)中,线段OA的“等距点”是______;②若点C在直线y=2x+5上,并且点C是线段OA的“等距点”,求点C的坐标;(2)已知点D(1,0),点E(0,−1),图形W是以点T(t,0)为圆心,1为半径的⊙T位于x轴及x 轴上方的部分.若图形W上存在线段DE的“等距点”,直接写出t的取值范围.21.(2022·北京市十一学校模拟预测)在平面直角坐标系xOy中,给出如下定义:点P为图形G上任意一点,将点P到原点O的最大距离与最小距离之差定义为图形G的“全距”.特别地,点P到原点O的最大距离与最小距离相等时,规定图形G的“全距”为0.(1)已知,点A(−4√2,2),B(2√2,2).①原点O到线段AB上一点的最大距离为_______,最小距离为_______;②当点C的坐标为(0,m)时,且△ABC的“全距”为4,求m的取值范围;(2)已知OM=7,等边△DEF的三个顶点均在半径为3的⊙M上.求△DEF的“全距”d的取值范围.22.(2022·北京房山·二模)对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M、N 可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系(1)如图1,点C(√3,0),D(0,−1),E(0,1),点P在线段CE上运动(点P可以与点C,E重合),连接OP,DP.①线段OP的最小值为__________,最大值为__________;线段DP的取值范围是__________;②在点O,点D中,点__________与线段EC满足限距关系;(2)在(1)的条件下,如图2,⊙O的半径为1,线段FG与x轴、y轴正半轴分别交于点F,G,且FG∥EC,若线段FG与⊙O满足限距关系,求点F横坐标的取值范围;(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,2为半径作圆得到⊙H和⊙K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.23.(2022·北京昌平·二模)在平面直角坐标系xOy中,⊙O的半径为1,对于△ABC和直线l给出如下定义:若△ABC的一条边关于直线l的对称线段PQ是⊙O的弦,则称△ABC是⊙O 的关于直线l的“关联三角形”“关联轴”.(1)如图1,若△ABC是⊙O的关于直线l的“关联三角形”,请画出△ABC与⊙O的“关联轴”(至少画两条);(2)若△ABC中,点A坐标为(2,3),点B坐标为(4,1),点C在直线y=−x+3的图像上,存在“关联轴l”使△ABC是⊙O的关联三角形,求点C横坐标的取值范围;(3)已知A(√3,1),将点A向上平移2个单位得到点M,以M为圆心MA为半径画圆,B,C为⊙M 上的两点,且AB=2(点B在点A右侧),若△ABC与⊙O的关联轴至少有两条,直接写出OC 的最小值和最大值,以及OC最大时AC的长.24.(2022·北京市十一学校二模)对于平面直角坐标系xOy中的图形W,给出如下定义:点P是图形W上任意一点,若存在点Q,使得∠OQP是直角,则称点Q是图形W的“直角点”.(1)已知点A(6,8),在点Q1(5,0),Q2(−2,4),Q3(9,5)中,________是点A的“直角点”;(2)已知点B(-4,4),C(3,4),若点Q是线段BC的“直角点”,求点Q的横坐标n的取值范围;(3)在(2)的条件下,已知点D(m-1,0),E(m,0),以线段DE为边在x轴上方作正方形DEFG.若正方形DEFG上的所有点均为线段BC的“直角点”,求m的取值范围.25.(2022·北京通州·一模)在平面直角坐标系xOy中,给出如下定义:点P为图形G上任意―点,将点P到原点O的最大距离与最小距离之差定义为图形G的“全距”.特别地,点P 到原点O的最大距离与最小距离相等时,规定图形G的“全距”为0.(1)如图,点A(−√3,1),B(√3,1).①原点O到线段AB上一点的最大距离为______,最小距离为______;②当点C的坐标为(0,m)时,且△ABC的“全距”为1,求m的取值范围;(2)已知OM=2,等边△DEF的三个顶点均在半径为1的⊙M上.请直接写出△DEF的“全距”d 的取值范围.26.(2022·北京石景山·一模)在平面直角坐标系xOy中,点P不在坐标轴上,点P关于x 轴的对称点为P1,点P关于y轴的对称点为P2,称△P1PP2为点P的“关联三角形”.(1)已知点A(1,2),求点A的“关联三角形”的面积;(2)如图,已知点B(m,n),⊙T的圆心为T(2,2),半径为2.若点B的“关联三角形”与⊙T 有公共点,直接写出m的取值范围;(3)已知⊙O的半径为r,OP=2r,若点P的“关联三角形”与⊙O有四个公共点,直接写出∠PP1P2的取值范围.27.(2022·北京一七一中一模)已知平面直角坐标系xOy中,对于线段MN及P、Q,若∠MPN= 45°且线段MN关于点P的中心对称线段M′N′恰好经过点Q,则称Q是点P的线段MN−45°对经点.(1)设点A(0,2),①Q1(4,0),Q2(2,2),Q3(2+√7,1),其中为某点P的线段OA−45°对经点的是___________.②选出①中一个符合题意的点Q,则此时所对应的对称中心P的坐标为.③已知B(0,1),设⊙B的半径是r,若⊙B上存在某点P的线段OA−45°对经点,求r的取值范围.(2)已知C(0,t),D(0,−t)(t>0),若点Q(4,0)同时是相异两点P1,P2的线段CD−45°对经点,直接写出t的取值范围.28.(2022·北京大兴·一模)在平面直角坐标系xOy中,⊙O的半径为1,已知点A,过点A 作直线MN.对于点A和直线MN,给出如下定义:若将直线MN绕点A顺时针旋转,直线MN与⊙O有两个交点时,则称MN是⊙O的“双关联直线”,与⊙O有一个交点P时,则称MN是⊙O的“单关联直线”,AP⊙O的“单关联线段”.(1)如图1,A(0,4),当MN与y轴重合时,设MN与⊙O交于C,D两点.则MN是⊙O的“______的值为______;关联直线”(填“双”或“单”);ACAD(2)如图2,点A为直线y=−3x+4上一动点,AP是⊙O的“单关联线段”.①求OA的最小值;②直接写出△APO面积的最小值.29.(2022·北京市燕山教研中心一模)对于平面直角坐标系xOy中的线段PQ,给出如下定义:若存在△PQR使得S△PQR=PQ2,则称△PQR为线段PQ的“等幂三角形”,点R称为线段PQ 的“等幂点”.(1)已知A(2,0).①在点P1(2,4),P2(1,2),P3(−4,1),P4(1,−4)中,线段OA的“等幂点”是____________;②若存在等腰△OAB是线段OA的“等幂三角形”,求点B的坐标;(2)已知点C的坐标为C(2,−1),点D在直线y=x−3上,记图形M为以点T(1,0)为圆心,2为半径的⊙T位于x轴上方的部分.若图形M上存在点E,使得线段CD的“等幂三角形”△CDE 为锐角三角形,直接写出点D的横坐标x D的取值范围.30.(2022·北京平谷·一模)在平面直角坐标系xOy中,⊙O的半径为r,对于平面上任一点P,我们定义:若在⊙O上存在一点A,使得点P关于点A的对称点点B在⊙O内,我们就称点P为⊙O的友好点.(1)如图1,若r为1.①已知点P1(0,0),P2(﹣1,1),P3(2,0)中,是⊙O的友好点的是;②若点P(t,0)为⊙O的友好点,求t的取值范围;(2)已知M(0,3),N(3,0),线段MN上所有的点都是⊙O的友好点,求r取值范围.。
2024年北京初三九年级上学期数学期末考《新定义》
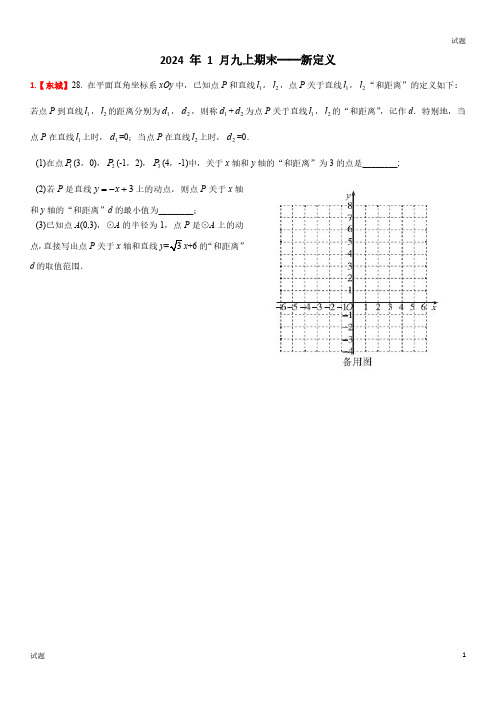
2024年1月九上期末——新定义1.【东城】28.在平面直角坐标系xOy 中,已知点P 和直线1l ,2l ,点P 关于直线1l ,2l “和距离”的定义如下:若点P 到直线1l ,2l 的距离分别为1d ,2d ,则称1d +2d 为点P 关于直线1l ,2l 的“和距离”,记作d .特别地,当点P 在直线1l 上时,1d =0;当点P 在直线2l 上时,2d =0.(1)在点1P (3,0),2P (-1,2),3P (4,-1)中,关于x 轴和y 轴的“和距离”为3的点是________;(2)若P 是直线3y x =-+上的动点,则点P 关于x 轴和y 轴的“和距离”d 的最小值为________;(3)已知点A (0,3),⊙A 的半径为1,点P 是⊙A 上的动点,直接写出点P 关于x 轴和直线y =3x +6的“和距离”d 的取值范围.2.【西城】28.如图,在平面直角坐标系xOy 中,点()1,0S -,()1,0T .对于一个角α(0180α︒<≤︒),将一个图形先绕点S 顺时针旋转α,再绕点T 逆时针旋转α,称为一次“α对称旋转”.备用图(1)点R 在线段ST 上,则在点()1,1A -,()3,2B -,()2,2C -,()0,2D -中,有可能是由点R 经过一次“90°对称旋转”后得到的点是________;(2)x 轴上的一点P 经过一次“α对称旋转”得到点Q .①当60α=︒时,PQ =________;②当30α=︒时,若QT x ⊥轴,求点P 的坐标;(3)以点O 为圆心作半径为1的圆.若在O 上存在点M ,使得点M 经过一次“α对称旋转”后得到的点在x 轴上,直接写出α的取值范围.3.【海淀】28.在平面直角坐标系xOy 中,将中心为T 的正方形记作正方形T ,对于正方形T 和点P (不与O 重合)给出如下定义:若正方形T 的边上存在点Q ,使得直线OP 与以TQ 为半径的T 相切于点P ,则称点P 为正方形T 的“伴随切点”.(1)如图、正方形T 的顶点分别为点O ,()2,2A ,()4,0B ,()2,2C -.①在点()12,1P ,()21,1P ,()31,1P -中,正方形T 的“伴随切点”是________;②若直线y x b =+上存在正方形T 的“伴随切点”,求b 的取值范围;(2)已知点(),1T t t +,正方形T 的边长为2.若存在正方形T 的两个“伴随切点”M ,N ,使得OMN △为等边三角形,直接写出t 的取值范围.4.【朝阳】28.在平面直角坐标系xOy 中,已知A (t -2,0),B (t +2,0).对于点P 给出如下定义:若∠APB=45°,则称P 为线段AB 的“等直点”.(1)当t =0时,①在点),(22201+P ,),(042-P ,)-,(2223-P ,),(524P 中,线段AB 的“等直点”是________;②点Q 在直线y =x 上,若点Q 为线段AB 的“等直点”,直接写出点Q 的横坐标.(2)当直线t x y +=上存在线段AB 的两个“等直点”时,直接写出t 取值范围.5.【石景山】28.在平面直角坐标系xOy 中,⊙O 的半径为1.对于⊙O 的弦AB 和点C 给出如下定义:若点C 在弦AB 的垂直平分线上,且点C 关于直线AB 的对称点在⊙O 上,则称点C 是弦AB 的“关联点”.(1)如图,点13(22A ,,13(22B -,.在点1(00)C ,,2(10)C ,,3(11)C ,,4(20)C ,中,弦AB 的“关联点”是;(2)若点1(0)2C ,是弦AB 的“关联点”,直接写出AB 的长;(3)已知点(02)M ,,(0)15N ,.对于线段MN 上一点S ,存在⊙O 的弦PQ ,使得点S 是弦PQ 的“关联点”.记PQ 的长为t ,当点S 在线段MN 上运动时,直接写出t 的取值范围.6.【丰台】28.在平面直角坐标系xOy中,⊙O的半径为1,对于线段AB和x轴上的点P,给出如下定义:将线段AB绕点P旋转180°可以得到⊙O的弦A'B'(A',B'分别为A,B的对应点),则称线段AB为⊙O以点P 为中心的“关联线段”.(1)如图,已知点A(-2,-1),B(-2,0),C(-2,1),D(-1,1),在线段AC,BD,CD中,⊙O以点P 为中心的“关联线段”是;x的取值范围;(2)已知点E(-4,1),线段EF是⊙O以点P为中心的“关联线段”,求点F的横坐标F (3)已知点E(m,1),若直线y=-x+2m上存在点F,使得线段EF是⊙O以点P为中心的“关联线段”,直接写出m的取值范围.备用图7.【昌平】28.对于在平面直角坐标系xOy 中⊙T 和⊙T 外的点P ,给出如下定义:已知⊙T 的半径为1,若⊙T 上存在点Q ,满足PQ ≤2,则称点P 为⊙T 的关联点.(1)如图1,若点T 的坐标为(0,0),28题图1①在点1P (3,0),2P (3,-2),3P (-2,2)中,是⊙T 的关联点的是____________;②直线2y x b =+分别交x 轴,y 轴于点A ,B ,若线段AB 存在⊙T 的关联点,求b 的取值范围;(2)已知点C (0,D (1,0),T (m ,1),△COD 上的每一个点都是⊙T 的关联点,直接写出m 的取值范围.28题图28.【通州】28.在平面直角坐标系xOy 中,O 的半径为1.给出如下定义:过O 外一点P 做直线与O 交于点M 、N ,若M 为线段PN 的中点,则称线段PN 是O 的“外倍线”。
北京市2021年中考数学总复习题型突破(07)新定义问题课件

P(x1,y1),Q(x2,y2),那么“中立点”M 的坐标为
1 + 2 1 + 2
,
2
2
.
已知,点 A(-3,0),B(0,4),C(4,0).
(2)已知点 G(3,0),☉G 的半径为 2.如果直线 y=-x+1 上存在点 K 可以成为
P 为☉C 的“特征点”.
(2)☉C 的圆心在 x 轴上,半径为 1,直线 y=x+1 与 x 轴,y 轴分别交于点 M,N,
若线段 MN 上的所有点都不是☉C 的“特征点”,直接写出点 C 的横坐标的
取值范围.
(2)x> 3或 x<-3.
图Z7-1
类型1 点与图形关系类〔针对2021 29题〕
2.[2018·延庆一模] 平面直角坐标系 xOy 中,点 A(x1,y1)与
2
2
1
1
∴将 - 2 ,- 2 代入双曲线表达式中,得 k=xy=2.∵点 P 位于☉O 内部,∴0<k<2.
类型1 点与图形关系类〔针对2021 29题〕
3.[2018·房山一模] 在平面直角坐标系 xOy 中,当图形 W 上的点 P 的横坐标和纵坐标相等时,则称点 P
为图形 W 的“梦之点”.
(3)若二次函数 y=ax2-ax+1 的图象上存在两个“梦之点”A(x1,y1),B(x2,y2),且|x1-x2|=2,求二次函数图象的顶
点坐标.
(3)由“梦之点”定义可得:A(x1,x1),B(x2,x2).则 x=ax2-ax+1.
新定义(解析)

解答下列问题: (1) 在平面直角坐标系中画出有向线段 (有向线段与 轴的长度单位相同), 与 轴的正
半轴的夹角是 ,且
.
(2) 若 的终点 坐标为
,求它的模及它与 轴的正半轴的夹角 的度数.
答案
(1) 画图见解析. (2) 的度数为 .
解析 (1) 如图所示,有向线段 即为所求.
(2) ∵
,
∴
,
∵
,
,
∴ 与 轴正半轴夹角为 ,
∴ 的度数为 .
考点 三角形 > 锐角三角函数及解直角三角形 > 锐角三角函数
三、圆
5 2017~2018学年北京东城区东直门中学初三上学期期中第28题8分
对于平面直角坐标系 中的某点 和⊙ ,给出如下定义:若⊙ 上存在两个点 , ,使得
,则称点 为⊙ 的“凤尾点”,
度为
.
(1) 回答下列问题:
1 如图 ,在平面直角坐标系 中,图形 为以 为圆心, 为半径的圆,直接写出
以下各点到图形 的距离跨度:
的距离跨度
;
的距离跨度
;
的距离跨度
.
图
2 根据①中的结果,猜想到图形 的距离跨度为 的所有的点组成的图形的形状是
. (2) 如图 ,在平面直角坐标系
中,图形 为以
为圆心, 为半径的圆,直线
即恰好 、 点为圆 的关联时,则
,
此时, ,
故若线段 上的所有点都是某个圆的凤尾点,这个圆的半径 的取值范围为 .
考点 三角形 > 直角三角形 > 直角三角形的性质 > 30°所对的直角边是斜边的一半
6 2017~2018学年北京东城区北京五中分校初三上学期期中第27题
专题1.1 集合中的新定义问题(解析版).

专题1.1集合中的新定义问题集合新定义问题的类型:(1)新定义性质,(2)新定义运算.解决集合新定义问题的着手点:(1)正确理解新定义:剥去新定义、新法则、新运算的外表,转化为我们熟悉的集合知识.(2)合理利用集合性质:运用集合的性质(如元素的性质、集合的运算性质等)是破解新定义型集合问题的关键.(3)对于选择题,可结合选项,通过验证、排除、对比、特值法等进行求解或排除错误选项,当不满足新定义的要求时,只需通过举反例来说明.1.若对任意x A ∈,有1A x ∈,就称A 是具有“伙伴关系”的集合,集合{1M =-,0,13,12,1,2,3,4}的所有非空子集中,具有“伙伴关系”的集合的个数为()A .15B .16C .82D .52【解答】解:具有伙伴关系的元素组有1-,1,12、2,13、3共四组,它们中任一组、二组、三组、四组均可组成非空伙伴关系集合,由组合数公式可得其个数依次为1234444415C C C C +++=故选:A .2.设A 是整数集的一个非空子集,对于k A ∈,如果1k A -∉且1k A +∉,那么k 是A 的一个“孤立元”,给定{1A =,2,3,4,5},则A 的所有子集中,只有一个“孤立元”的集合共有()A .10个B .11个C .12个D .13个【解答】解:“孤立元“是1的集合:{1};{1,3,4};{1,4,5};{1,3,4,5};“孤立元“是2的集合:{2};{2,4,5};“孤立元“是3的集合:{3};“孤立元“是4的集合:{4};{1,2,4};“孤立元“是5的集合:{5};{1,2,5};{2,3,5};{1,2,3,5}.共有13个;故选:D .3.对于任意两个正整数m ,n ,定义某种运算“※”如下:当m ,n 都为正偶数或正奇数时,m ※n m n =+;当m ,n 中一个为正偶数,另一个为正奇数时,m ※n mn =.则在此定义下,集合{(,)|M a b a =※12b =,*a N ∈,*}b N ∈中的元素个数是()A .10个B .15个C .16个D .18个【解答】解:a ※12b =,a 、*b N ∈,若a 和b 一奇一偶,则12ab =,满足此条件的有11234⨯=⨯,故点(,)a b 有4个;若a 和b 同奇偶,则12a b +=,满足此条件的有11121039485766+=+=+=+=+=+共6组,故点(,)a b 有26111⨯-=个,所以满足条件的个数为41115+=个.故选:B .4.对于任意两个正整数m ,n ,定义某种运算“※”如下:当m ,n 都为正偶数或都为正奇数时,m ※n m n =+;当m ,n 中一个为正偶数,另一个为正奇数时,m ※n mn =,则在此定义下,集合{(,)|M a b a =※8}b =中的元素个数是()A .10B .9C .8D .7【解答】解:由定义知,当a ,b 都为正偶数或都为正奇数时,a ※8b a b =+=,故(,)a b 是(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1);当a ,b 中一个为正偶数,另一个为正奇数时,a ※8b ab ==,故(,)a b 是(1,8),(8,1);故共9个元素,故选:B .5.集合{0S =,1,2,3,4,5},A 是S 的一个子集,当x A ∈时,若有1x A -∉,且1x A +∉,则称x 为A 的一个“孤立元素”,那么S 中无“孤立元素”的非空子集有()个.A .16B .17C .18D .20【解答】解:当x A ∈时,若有1x A -∉,且1x A +∉,则称x 为A 的一个“孤立元素”,∴单元素集合都含孤立元素,S 中无“孤立元素”的2个元素的子集A 为{0,1},{1,2},{2,3},{3,4},{4,5},共5个S 中无“孤立元素”的3个元素的子集A 为{0,1,2},{1,2,3},{2,3,4},{3,4,5},共4个S 中无“孤立元素”的4个元素的子集A 为{0,1,2,3},{0,1,3,4},{0,1,4,5}},{1,2,3,4},{1,2,4,5},{2,3,4,5}共6个S 中无“孤立元素”的5个元素的子集A 为{0,1,2,3,4},{1,2,3,4,5},{0,1,2,4,5},{0,1,3,4,5},共4个S 中无“孤立元素”的6个元素的子集A 为{0,1,2,3,4,5},共1个故S 中无“孤立元素”的非空子集有20个故选:D .6.用C (A )表示非空集合A 中的元素个数,定义()()()()()()()(),*,C A C B C A C B A B C B C A C A C B -⎧⎪=⎨-<⎪⎩当当 ,若{1A =,2},2{||1|1}B x x ax =++=,且*1A B =,由a 的所有可能值构成的集合是S ,那么()C S 等于()A .4B .3C .2D .1【解答】解:22|1|111x ax x ax ++=⇔++=或211x ax ++=-,即20x ax +=①或220x ax ++=②,{1A =,2},且*1A B =,∴集合B 要么是单元素集合,要么是三元素集合,1︒集合B 是单元素集合,则方程①有两相等实根,②无实数根,0a ∴=;2︒集合B 是三元素集合,则方程①有两不相等实根,②有两个相等且异于①的实数根,即280a a ≠⎧⎨=-=⎩,解得a =±综上所述0a =或a =±()3C S ∴=.故选:B .7.在整数集Z 中,被5所除得余数为k 的所有整数组成一个“类”,记为[]k ,即[]{5|}k n k n Z =+∈,0k =,1,2,3,4;给出四个结论:(1)2015[0]∈;(2)3[3]-∈;(3)[0][1][2][3][4]Z =;(4)“整数a ,b 属于同一“类”的充要条件是“[0]a b -∈”.其中正确结论的个数是()A .1个B .2个C .3个D .4个【解答】解:201554030÷=⋯,2015[0]∴∈,故(1)正确;35(1)2-=⨯-+,3[3]∴-∉,故(2)错误;整数集中的数被5除的数可以且只可以分成五类,故[0][1][2][3][4]Z =,故(3)正确;整数a ,b 属于同一“类”,∴整数a ,b 被5除的余数相同,从而a b -被5除的余数为0,反之也成立,故“整数a ,b 属于同一“类”的充要条件是“[0]a b -∈”.故(4)正确.故选:C .8.设S 为复数集C 的非空子集.若对任意x ,y S ∈,都有x y +,x y -,xy S ∈,则称S 为封闭集.下列命题:①集合{|(S a bi a =+,b 为整数,i 为虚数单位)}为封闭集;②若S 为封闭集,则一定有0S ∈;③封闭集一定是无限集;④若S 为封闭集,则满足S T C ⊆⊆的任意集合T 也是封闭集.其中真命题是.(写出所有真命题的序号)【解答】解:取集合{|(S a bi a =+,b 为整数,i 为虚数单位)}中任意两个元素m ni +和(p qi m+、n 、p 、)q Z ∈,则()()()()m ni p qi m p n q i S +++=+++∈;()()()()m ni p qi m p n q i S +-+=-+-∈;()()()()m ni p qi mp nq mq np i S +⋅+=-++∈;满足集合{|(S a bi a =+,b 为整数,i 为虚数单位)}为封闭集;①正确.当S 为封闭集时,因为x y S -∈,取x y =,得0S ∈,②正确对于集合{0}S =,显然满足所有条件,但S 是有限集,③错误取{0}S =,{0T =,1},满足S T C ⊆⊆,但由于011-=-不属于T ,故T 不是封闭集,④错误.9.若集合{1n U =,2,3,,}n ,2n ,*n N ∈,A ,n B U ⊆,且满足集合A 中最大的数大于集合B 中最大的数,则称有序集合对(,)A B 为“兄弟集合对”.当3n =时,这样的“兄弟集合对”有对;当3n 时,这样的“兄弟集合对”有对(用含有n 的表达式作答).【解答】解:当3n =时,{1n U =,2,3},A 中的最大元素为2,则B 是{1}的非空子集,有1211-=个,此时A 有2个;A 中的最大元素为3,则B 是{1,2}的非空子集,有2213-=个,此时A 有4个;共有这样的“兄弟集合对”432114⨯+⨯=个,当3n 时,{1n U =,2,3,,}n ,当A 的最大元素为n ,此时A 有12n -个,B 是{1=,2,3,,1}n -的非空子集,有121n --个;当A 的最大元素为1n -,A 有22n -个,B 是{1=,2,3,,2}n -的非空子集,有221n --个;⋅⋅⋅当A 的最大元素为3,A 有22个,B 是{1=,2}的非空子集,有221-个;当A 的最大元素为2,A 有12个,B 是{1}=的非空子集,有121-个;故11223322112(21)2(21)2(21)2(21)2(21)n n n n n n -------+-+-+⋅⋅⋅+-+-22124222212122222222n n n n ----⨯⨯=-+-+⋅⋅⋅+-+-123211231_)44444(2222n n n n ----=+++⋅⋅⋅++-+++⋅⋅⋅+114(14)2(12)1412n n ----=---124233n n =⨯-+.故答案为:14;124233n n ⨯-+.10.设Q 是有理数,集合{|,,0}X x x a a b Q x ==+∈≠,在下列集合中:①|}x X ∈;②2|x X x ⎧⎫∈⎨⎬⎩⎭;③121{|x x x +,2}x X ∈;④121{|x x x ,2}x X ∈;与X 相等的集合的序号是【解答】解:设①②③④对应的集合分别为A ,B ,C ,D ,则对于①:x X ∀∈,设,x a a b Q =+∈,则x b =,而b X +,从而x A ∈,故X A ⊆2b X =+,故A X ⊆,从而A X =;对于②:x X ∀∈,设,x a a b Q =+∈,令,x m n Q =∈,则可得2(2am bn an bm +++,从而22am bn +=,0an bm +=,解得2222a m a b =-,222bn a b=--,且m ,n Q ∈,从而x B ∈,故X B ⊆,反过来,22222a X x a b ==-,故B X ⊆,从而B X =;对于③:取1211x x ==--,则120x x X +=∉,从而C 不是X 的子集,故C X ≠;对于④:x X ∀∈,设,x a a b Q =+∈,则1(x a =⨯+,取121,x x a ==+,则x D ∈,即X D ⊆,反过来1x ,2x X ∈时,12x x X ∈,故D X ⊆,故D X =.综上,①②④正确,故答案为①②④.11.设集合1{A r =,2r ,,}{1n r ⊆,2,3,,37},且A 中任意两数之和不能被5整除,则n 的最大值为【解答】解:设{5B =,10,15,20,25,30,35},则card (B )7=;可将A 集合分为4组:1{1A =,6,11,16,21,26,31,36},则1()8card A =;2{2A =,7,12,17,22,27,32,37},则2()8card A =;3{3A =,8,13,18,23,28,33},则3()7card A =;4{4A =,9,14,19,24,29,34},则4()7card A =.因为A 中的任何两个数之和不能被5整除,所以1A 和4A ,2A 和3A 中不能同时取数,且B 中最多取1个,所以最多的取法是取12A A 和B 中的一个元素,故card (A )88117max =++=,故n 的最大值为17,故答案为:17.12.若使集合2(){|(6)(4)0A k x kx k x =--- ,}x Z ∈中元素个数最少,则实数k 的取值范围是(3,2)--,设B Z ⊆,对B 中的每一个元素x ,至少存在一个()A k ,有()x A k ∈,则B =.【解答】解:集合2{|(6)(4)0A x kx k x =--- ,}x Z ∈,方程2(6)(4)0kx k x ---=,0k ≠解得:16x k k=+,24x =,2(6)(4)0kx k x ∴--- ,x Z∈当0k =时,(A =-∞,4];当0k >时,64k k <+,(A =-∞,64][k k+,)+∞;当0k <时,64k k +<,6[A k k=+,4];∴当0k 时,集合A 的元素的个数无限;当0k <时,64k k +<,6[A k k =+,4],集合A 的元素的个数有限,令函数6()g k k k=+,(0)k <则有:()g k - ,对于集合A ,[0,4]满足条件的元素只有0,1,2,3,4,只需6[k k+,0]包含的整数最小,题意要求x Z ∈,故只需65k k +>-,且64k k+- ,解得:32k -<<-,根据对()A k 的讨论,所以B Z =,故答案为:32k -<<-,B Z =.13.非空集合G 关于运算⊕满足:(1)对任意a ,b G ∈,都有a b G +∈;(2)存在e G ∈使得对于一切a G ∈都有a e e a a ==⊕⊕,则称G 是关于运算⊕的融洽集,现有下列集合与运算:①G 是非负整数集,⊕:实数的加法;②G 是偶数集,⊕:实数的乘法;③G 是所有二次三项式构成的集合,⊕:多项式的乘法;④{|G x x a ==+,a ,}b Q ∈,⊕:实数的乘法;其中属于融洽集的是(请填写编号)【解答】解:①对于任意非负整数a ,b 知道:a b +仍为非负整数,所以a b G ∈⊕;取0e =,及任意非负整数a ,则00a a a +=+=,因此G 对于⊕为整数的加法运算来说是“融洽集”;②对于任意偶数a ,b 知道:a b +仍为偶数,故有a b G +∈;但是不存在e G ∈,使对一切a G ∈都有a e e a a ==⊕⊕,故②的G 不是“融洽集”.③对于{G =二次三项式},若a 、b G ∈时,a ,b 的两个同类项系数,则其积不再为二次三项式,故G 不是和谐集,故③不正确;④{|G x x a ==+,a ,}b Q ∈,设1x a =+,2x c =+,则设12()(x x a c b d +=+++G ,取1e =,11a a a ⨯=⨯=,因此G 对于⊕实数的乘法运算来说是“融洽集”,故④中的G 是“融洽集”.故答案为①④.14.设集合A R ∈,如果0x R ∈满足:对任意0a >,都存在x A ∈,使得00||x x a <-<,那么称0x 为集合A 的一个聚点,则在下列集合中:①{|0}x Z x ∈≠;②{|0}x R x ∈≠;③1{|x x n =,*}n N ∈;④{|1nx x n =+,*}n N ∈其中以0为聚点的集合的序号是.【解答】解:(1)对于某个0a >,比如0.5a =,此时对任意的{|0}x x Z x ∈∈≠,都有0||0x x -=或者0||1x x - ,也就是说不可能00||0.5x x <-<,从而0不是{|0}x Z x ∈≠的聚点;(2)集合{|0}x R x ∈≠,对任意的a ,都存在2ax =(实际上任意比a 小得数都可以),使得0||2ax a <=<,0∴是集合{|0}x R x ∈≠的聚点;(3)集合1{|x x n =,*}n N ∈中的元素是极限为0的数列,对于任意的0a >,存在1n a>,使10||x a n<=<,0∴是集合1{|x x n=,*}n N ∈的聚点;(4)中,集合{|1nx x n =+,*}n N ∈中的元素是极限为1的数列,除了第一项0之外,其余的都至少比0大12,∴在12a <的时候,不存在满足得0||x a <<的x ,0∴不是集合{|1nx x n =+,*}n N ∈的聚点;故答案为:②③.15.在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[]k ,即[]{5|}k n k n Z =+∈,0k =,1,2,3,4.给出如下四个结论:①2017[2]∈;②3[3]-∈;③[0][1][2][3][4]Z =;④“整数a ,b 属于同一‘类’”的充要条件是“[0]a b -∈”.其中正确的结论序号有.【解答】解:①201754032÷=⋯,2017[2]∴∈,故①正确;②35(1)2-=⨯-+,3[3]∴-∉,故②错误;③整数集中的数被5除的数可以且只可以分成五类,[0][1][2][3][4]Z ∴=,故③正确;④整数a ,b 属于同一“类”,∴整数a ,b 被5除的余数相同,从而a b -被5除的余数为0,反之也成立,故“整数a ,b 属于同一“类”的充要条件是“[0]a b -∈”.故④正确.故答案为:①③④.17.设n 是正整数,集合{1M =,2,⋯,2}n .求最小的正整数k ,使得对于M 的任何一个k 元子集,其中必有4个互不相同的元素之和等于41n +.【解答】解:考虑M 的2n +元子集{1P n =-,n ,1n +,⋯,2}n ,P 中任何4个不同元素之和不小于11242n n n n n -+++++=+,所以3k n + ,将M 的元配对为n 对,(,21)i B i n i =+-,1i n ,对M 的任一3n +元子集A ,必有三对1i B ,2i B ,3i B ,同属于(1A i ,2i ,3i 两两不同)又将M 的元配为1n -对,(,2)i C i n i =-,11i n - ,对M 的任一3n +元子集A ,必有一对4i C 同属于A ,这一对4i C 必与1i B ,2i B ,3i B 中至少一个无公共元素,这4个元素互不相同,且和为21241n n n ++=+,故最小的正整数3k n =+.故答案为:41n +.18.定义集合运算:{|A B z z xy ==⊗,x A ∈,}y B ∈,设{1A =,2},{2B =,4},则集合A B ⊗的所有元素之和为.【解答】解:有题意:{|A B z z xy ==⊗,x A ∈,}y B ∈,设{1A =,2},{2B =,4},那么:当1x =时:2y =或4,可得:2z 、4,当2x =时:2y =或4,可得:4z 、8,故得z 的所有元素:2、4、8,即集合A B ⊗的所有元素为:2、4、8,元素之和为:24814++=.故答案为:14.19.如果具有下述性质的x 都是集合M 中的元素,其中:,)x a a b Q =+∈,则下列元素中属于集合M 的元素的是(填序号).①0x =,②x =③3x =-,④x⑤x =+.【解答】解:①000x ==+,其中0a =,0b Q =∈,∴①满足条件.②01x ==+,其中0a =,1b Q =∈,∴②满足条件.③3x =-,其中3a Q =∈,但2b Q π=-∉,∴③不满足条件.④3x ===+,其中3a =,2b Q =∈,∴④满足条件⑤22440x =-+=+.其中4a =,0b Q =∈,∴⑤满足条件.故答案为:①②④⑤.20.如果非空数集A 满足:①0A ∉;②若x A ∀∈,有1A x∈,那么称A 是“互倒集”.给出以下数集:①2{|10}x R x ax ∈++=;②2{|610}x x x -+ ;③2{|y y x=,[1x ∈,4]};其中“互倒集”的是.(请在横线上写出所有正确答案的序号)【解答】解:对于①2{|10}x R x ax ∈++=,当3a =时,2{|10}x R x ax ∈++==∅,故不是互倒集;对于②2{|610}x x x -+ ;△364320=-=>,2{|610}x x x ∴-+ 是非空数集,且20{|610}x x x ∉-+ ,若21{|610}x x x x ∈-+ ,即211610x x -+ ,则221121116111(610x x x x x -+-+= ,故211{|610}x x x x ∈-+ ,故是互倒集;对于③2{|y y x =,[1x ∈,14]}[2=,2],若11[2x ∈,2],易知111[2x ∈,2],故是互倒集;故答案为:②③.。
2020北京市中考数学专题复习---新定义问题

2020北京市中考数学专题复习---新定义问题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN二、重难专题突破专题九新定义问题(必考)类型一新定义点与函数问题(8年4考:2017.29、2015.29、2014.25、2013.25)1. (2019房山区一模)在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C的关联整点.(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是;(2)若直线y=-x+4上存在⊙O的关联整点,且不超过7个,求r的取值范围;(3)⊙C的圆心在x轴上,半径为2,若直线y=-x+4上存在⊙C的关联整点.求圆心C的横坐标t的取值范围.第1题图2. (2019丰台区二模)对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若⊙C 上存在两个点A ,B ,使得点P 在射线BC 上,且∠APB =14∠ACB (0°<∠ACB <180°),则称P 为⊙C 的依附点.(1)当⊙O 的半径为1时,①已知点D (-1,0),E (0,-2),F (2.5,0),在点D ,E ,F 中,⊙O 的依附点是 ;②点T 在直线y =-x 上,若T 为⊙O 的依附点,求点T 的横坐标t 的取值范围;(2)⊙C 的圆心在x 轴上,半径为2,直线y =-x +2与x 轴、y 轴分别交于点M ,N .若线段MN 上的所有点都是⊙C 的依附点,直接写出圆心C 的横坐标m 的取值范围.3. (2019西城区一模)在平面直角坐标系xOy中,对于两个点P,Q和图形W,如果在图形W上存在点M,N(M,N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.第3题图①(1)如图①,已知点A (0,3),B (2,3).①设点O 与线段AB 上一点的距离为d ,则d 的最小值是 ,最大值是 ;②在P 1(32,0),P 2(1,4),P 3(-3,0)这三个点中,与点O 是线段AB 的一对平衡点的是 ; (2)如图②,已知⊙O 的半径为1,点D 的坐标为(5,0).若点E (x ,2)在第一象限,且点D 与点E 是⊙O 的一对平衡点,求x 的取值范围;(3)如图③,已知点H (-3,0),以点O 为圆心,OH 长为半径画弧交x 轴的正半轴于点K .点C (a ,b )(其中b ≥0)是坐标平面内一个动点,且OC =5,⊙C 是以点C 为圆心,半径为2的圆.若HK ︵上的任意两个点都是⊙C 的一对平衡点,直接写出b 的取值范围.第3题图② 第3题图③4. (2019朝阳区二模)M (-1,-12),N (1,-12)是平面直角坐标系xOy 中的两点,若平面内直线MN 上方的点P 满足:45°≤∠MPN ≤90°,则称点P 为线段MN 的可视点.(1)在点A 1(0,12),A 2(12,0),A 3(0,2),A 4(2,2)中,线段MN 的可视点为 ; (2)若点B 是直线y =x +12上线段MN 的可视点,求点B 的横坐标t 的取值范围; (3)直线y =x +b (b ≠0)与x 轴交于点C ,与y 轴交于点D ,若线段CD 上存在线段MN 的可视点,直接写出b 的取值范围.第4题图类型二 新定义距离与函数问题(8年2考:2018.28、2012.25)1. (2012北京)在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|;若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|.例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图①中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点).第1题图①(1)已知点A (-12,0),B 为y 轴上的一个动点, ①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标;②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直线y =34x +3上的一个动点, ①如图②,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标; ②如图③,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 和点C 的坐标.第1题图2. (2019东城区一模)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.第2题图(1)已知点A的坐标为(-3,1),①在点E(0,3),F(3,-3),G(2,-5)中,为点A的“等距点”的是;②若点B在直线y=x+6上,且A,B两点为“等距点”,则点B的坐标为;(2)直线l:y=kx-3(k>0)与x轴交于点C,与y轴交于点D,①若T1(-1,t1),T2(4,t2)是直线l上的两点,且T1与T2为“等距点”,求k的值;②当k=1时,半径为r的⊙O上存在一点M,线段CD上存在一点N,使得M,N两点为“等距点”,直接写出r的取值范围.备用图3.(2018北京)对于平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q 为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“闭距离”,记作d(M,N).已知点A(-2,6),B(-2,-2),C(6,-2).(1)求d(点O,△ABC);(2)记函数y=kx(-1≤x≤1,k≠0)的图象为图形G.若d(G,△ABC)=1,直接写出k的取值范围;(3)⊙T的圆心为T(t,0),半径为1.若d(⊙T,△ABC)=1,直接写出t的取值范围.4.(2019石景山一模)在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).(1)已知点E(0,4),①直接写出d(点E)的值;②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;(2)⊙T的圆心为T(t,3),半径为1,若d(⊙T)<6,直接写出t的取值范围.类型三新定义图形与函数问题(仅2016.29考查)1.(2019石景山区二模)对于平面直角坐标系xOy中的点P,Q,给出如下定义:若P,Q为某个三角形的顶点,且边PQ上的高h,满足h=PQ,则称该三角形为点P,Q的“生成三角形”.(1)已知点A(4,0).①若以线段OA为底的某等腰三角形恰好是点O,A的“生成三角形”,求该三角形的腰长;②若Rt△ABC是点A,B的“生成三角形”,且点B在x轴上,点C在直线y=2x-5上,则点B的坐标为;(2)⊙T的圆心为点T(2,0),半径为2,点M的坐标为(2,6),N为直线y=x+4上一点,若存在Rt△MND,是点M,N的“生成三角形”,且边ND与⊙T有公共点,直接写出点N的横坐标x N的取值范围.2.(2018平谷区一模)在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.(1)已知点A(2,0),B(0,23),则以AB为边“坐标菱形”的最小内角为°;(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD表达式;(3)⊙O的半径为2,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.图①图②第2题图类型四 新定义几何问题(2019.28新考查)1. (2019北京)在△ABC 中,D ,E 分别是△ABC 两边的中点,如果DE ︵上的所有点都在△ABC 的内部或边上,则称DE ︵为△ABC 的中内弧.例如,如图①中DE ︵是△ABC 的一条中内弧.第1题图① 第1题图②(1)如图②,在Rt △ABC 中,AB =AC =22,D ,E 分别是AB ,AC 的中点,画出△ABC 的最长的中内弧DE ︵,并直接写出此时DE ︵的长;(2)在平面直角坐标系中,已知点A (0,2),B (0,0),C (4t ,0)(t >0).在△ABC 中,D ,E 分别是AB ,AC 的中点.①若t =12,求△ABC 的中内弧DE ︵所在圆的圆心P 的纵坐标的取值范围; ②若在△ABC 中存在一条中内弧DE ︵,使得DE ︵所在圆的圆心P 在△ABC 的内部或边上,直接写出t 的取值范围.2.P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把P A·PB的值称为点P关于⊙O的“幂值”.第2题图(1)⊙O的半径为6,OP=4.①如图,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为;②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙O的“幂值”的取值范围;(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围;(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,已知点M(t,0),N(0,-t),若在直线MN 上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出t的取值范围.参考答案类型一新定义点与函数问题1. 解:(1)E,F;【解法提示】∵D(2,-2),E(-1,0),F(0,2),O(0,0),∴OD=22+22=22>2,OE=1<2,OF=2,∴E,F为⊙O的关联整点;(2)如解图①,当⊙O与直线y=-x+4相切时,切点为G(2,2),则r=OG=22+22=22.当⊙O过点Q(-2,6)时,则r=OQ=22+62=210,结合图象,当直线y=-x+4上存在⊙O的关联整点,且不超过7个时,r的取值范围为22≤r<210;第1题解图①(3)如解图②,当⊙C过点M(3,1)时,CM=2,ME=1,则CE=3,此时点C的横坐标t=3-3,当⊙C′过点N(5,-1)时,则FC′=3,此时点C′的横坐标t=5+3,结合函数图象,圆心C的横坐标t的取值范围为3-3≤t≤5+3.第1题解图②2. 解:(1)①E、F;【解法提示】如解图①,根据P为⊙O的依附点,可知:当r<OP<3r(r为⊙O的半径)时,点P为⊙O的依附点.第2题解图①∵D(-1,0),E(0,-2),F(2.5,0),∴OD=1,OE=2,OF=2.5,∴1<OE<3,1<OF<3,∴点E,F是⊙O的依附点,故答案为:E、F;②如解图②,第2题解图②当点T 在第四象限,OT ′=1时,作T ′N ⊥x 轴于点N ,易知N (22,0),OT =3时,作TM ⊥x 轴于点M ,易知M (322 ,0),∴满足条件的点T 的横坐标t 的取值范围为22 <t <322. 当点T 在第二象限时,同理可得满足条件的t 的取值范围为-322 <t <-22, 综上所述,满足条件的t 的值的范围为22 <t <322 或-322 <t <-22. (2)4<m <42 或-4<m <2-22 .【解法提示】如解图③,当点C 在点M 的右侧时,第2题解图③由题意M (2,0),N (0,2),当CN =6时,OC =CN 2-ON 2 =42 ,此时C (42 ,0),当CM =2时,此时C (4,0),∴满足条件的m 的值的范围为4<m <42 .如解图④,当点C 在点M 的左侧时,第2题解图④当⊙C 与直线MN 相切时,易知C ′(2-22 ,0),当CM =6时,C (-4,0),∴满足条件的m 的值的范围为-4<m <2-22 ,综上所述,满足条件的m 的值的范围为:4<m <42 或-4<m <2-22 . 3. 解:(1)① 3,13 ;【解法提示】d 的最小值=OA =3,d 的最大值=OB =22+32 =13 . ②P 1;【解法提示】由题图①可知,P 1到线段AB 的最小距离=OA =3,最大距离=P 1A =(32)2+32 =352,则线段AB 上存在点M ,N ,使得P 1M =ON ;P 2到线段AB 的最大距离=12+12 =2 ,∵2 <3,∴P 2不符合题意;P 3到线段AB 的最小距离=32+32 =32 ,∵32 >13 ,∴P 3不符合题意.(2)第3题解图①由题意得,点D 到⊙O 的最近距离是4,最远距离是6,点D 与点E 是⊙O 的一对平衡点,此时需要满足E 1到⊙O 的最大距离是4,即OE 1=3,根据OE 1=3解出此时x =5 ;同理当E 2到圆O 的最小距离是6,即OE 2=7, 根据OE 2=7,解得此时x =35 , ∴5 ≤x ≤35 ; (3)4143≤b ≤5.【解法提示】点C 在以O 为圆心,半径为5的上半圆上运动,以C 为圆心,半径为2的圆刚好与弧HK 相切,此时要想弧HK 上的任意两点都是⊙C 的平衡点,需要满足CK ≤6,如解图②,当CK =6,此时a =-13 ,b =4143 ,同理,当CH =6时,a =13 ,b =4143 .在两者中间时,如解图③所示,此时a =0,b =5,∴4143≤b ≤5.第3题解图②第3题解图③4. 解:(1)A 1,A 3;【解法提示】如解图①,以MN 为直径的半圆交y 轴于点E ,以E 为圆心,EM 长为半径的⊙E 交y 轴于点F ,∵MN 是⊙G 的直径,M (-1,-12 ),N (1,-12 ),∴∠MA 1N =90°,MN ⊥EG ,EG =1,MN =2.∴EF =EM =2 ,∴∠MFN =12 ∠MEN =45°,∵45°≤∠MPN ≤90°,∴点P 应落在⊙E 内部,且落在⊙G 外部(包含边界),且不与点M 、N 重合.∴线段MN 的可视点为A 1,A 3.第4题解图①(2)如解图②,以(0,-12 )为圆心,MN 为直径作⊙G ,以(0,12 )为圆心,2 为半径作⊙E ,两圆在直线MN 上方的部分与直线y =x +12分别交于点E ,F .如解图②,过点F 作FQ ⊥x 轴于点Q ,过点E 作EH ⊥FQ 于点H ,∵FQ ⊥x 轴, ∴FQ ∥y 轴,∴∠EFH =∠MEG =45°. ∵∠EHF =90°,EF =2 , ∴EH =FH =1. ∵E (0,12 ),∴F (1,32).只有当点B 在线段EF 上时,满足45°≤∠MBN ≤90°,点B 是线段MN 的可视点. ∴点B 的横坐标t 的取值范围是0≤t ≤1;第4题解图②(3)-32 <b ≤-32 或12 ≤b ≤52;【解法提示】如解图③,⊙G 与x 轴交于点H ,与y 轴交于点E ,连接GH ,OG =12 ,GH =1,∴OH =GH 2-OG 2 =12-(12)2 =32,∴H (32 ,0),E (0,12). 当直线y =x +b (b ≠0)与x 轴交于点C ,与y 轴交于点D ,若线段CD 上存在线段MN 的可视点, ①当直线y =x +b 与y 轴交点在y 负半轴上,将H (32 ,0)代入y =x +b 得32 +b =0,解得b 1=-32, 将N (1,-12 )代入y =x +b 得1+b =-12 ,解得b 2=-32 ,∴-32 <b ≤-32;②当直线y =x +b 与y 轴交点在y 正半轴上, 将 E (0,12 )代入得b =12,当直线y =x +b 与⊙E 相切于T 时交y 轴于Q ,连接ET ,则ET ⊥TQ , ∵∠EQT =45°, ∴TQ =ET =EM =2 ,∴EQ =ET 2+TQ 2 =(2)2+(2)2 =2. ∴OQ =OE +EQ =12 +2=52 .∴12 ≤b ≤52. 综上所述:-32 <b ≤-32 或12 ≤b ≤52.第4题解图③类型二 新定义距离与函数问题1. 解:(1)①B (0,2)或B (0,-2)(写出一个答案即可); ②12; (2)①设C 点坐标为(m ,34m +3),D (0,1);于是当非常距离最小时有|m |=|34 m +3-1|,解得 m 1=-87 ,m 2=8(舍去),于是点C 的坐标为(-87 ,157);②平移直线y =34 x +3与⊙O 相切,切点为点E ,与x 轴、y 轴交点分别为点A 、B ,由切线的性质可知点E 即为最接近直线y =34x +3的点,亦为题中所求的点.第1题解图如解图,过点E 作EF ⊥x 轴于点F . 设点E 的坐标为E (x 0,y 0),x 0<0; 易知:Rt △EFO ∽ Rt △AOB , ∴FO EF =OB AO =34 ,即-x 0y 0 =34, 又∵点E 为⊙O 上的点,∴可得方程组:⎩⎪⎨⎪⎧x 20 +y 20 =1,4x 0+3y 0=0,解得:x 0=-35 ,y 0=45 ,∴点E 的坐标为(-35 ,45).设点C 的坐标为C (a ,34 a +3),由①可知:当|-35 -a |=|(34 a +3)-45 |时有最小值,∴a =-85 或325(舍去),∴点C 的坐标为C (-85 ,95 ),此时最小值为-35 -(-85 )=1.2. 解:(1)①E ,F ;【解法提示】点A 到x ,y 轴的距离中的最大值等于3,点E 到x ,y 轴的距离中的最大值等于3,点F 到x ,y 轴的距离中的最大值等于3,点G 到x ,y 轴的距离中的最大值等于5;∴点E ,F 是点A 的“等距点”.②(-3,3);【解法提示】∵点A 到x ,y 轴的距离中的最大值等于3,A ,B 两点为“等距点”,∴点B 到x ,y 轴的距离中的最大值等于3,∵点B 在直线y =x +6上,∴设B (a ,a +6),当a =3时,a +6=9,不符合题意,当a +6=3时,a =-3,符合题意,∴B (-3,3).(2)①∵T 1(-1,t 1),T 2(4,t 2)是直线l 上的两点, ∴t 1=-k -3,t 2=4k -3. ∵k >0,∴|-k -3|=k +3>3,4k -3>-3, 依题意可得:当-3<4k -3<4时,k +3=4,解得k =1; 当4k -3≥4时,k +3=4k -3,解得k =2. 综上所述,k 的值为1或2; ②32≤r ≤32 . 【解法提示】当k =1时,y =x -3,则点C 的坐标为(3,0),点D 的坐标为(0,-3);如解图,过点O 作OE ⊥CD 于点E ,过点E 作EF ⊥x 轴于点F ,∵CD =32+32 =32 ,∴OE =CE =322 .∴EF =22×322 =32 .则线段CD 上的点到x ,y 轴的距离中的最小值等于32 ,∴半径r 的最小值为32;线段CD 到x ,y 轴的距离中的最大值等于3,∴半径为r 的⊙O 上存在一点M ,使得点M 到x ,y 轴的距离中的最大值等于3,如解图,过点G (3,3)作x 轴的垂线,垂足为点C ,连接OG ,则OG =32+32 =32 ,∴⊙O 的半径r 的最大值为32 ;综上所述,r 的取值范围是32≤r ≤32 .第2题解图3. 解:(1)如解图①,d (点O ,△ABC )=2; (2)-1≤k ≤1且k ≠0;【解法提示】如解图①,y =kx (k ≠0)经过原点,在-1≤x ≤1范围内,函数图象为线段.第3题解图①当y =kx (-1≤x ≤1,k ≠0)经过(1,-1)时,k =-1, 此时d (G ,△ABC )=1,当y =kx (-1≤x ≤1,k ≠0)经过(-1,-1)时,k =1, 此时d (G ,△ABC )=1, ∴-1≤k ≤1, ∵k ≠0,∴-1≤k≤1且k≠0.(3)如解图②,⊙T与△ABC的位置关系分三种情况:①⊙T在△ABC的左侧时,d(⊙T,△ABC)=1,此时,t=-4;②⊙T在△ABC的内部时,d(⊙T,△ABC)=1,此时,0≤t≤4-22;③⊙T在△ABC的右侧时,d(⊙T,△ABC)=1,此时,t=4+22;综上,t=-4或0≤t≤4-22或t=4+22.第3题解图②4. 解:(1)①5;【解法提示】∵正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0),点E(0,4)在y轴上,∴点E到正方形ABCD边上C点间的距离有最大值,EC=5,即d(点E)的值为5.②如解图①所示:∵d(点E)=5,∴d(线段EF)的最小值是5,∴符合题意的点F满足d(点F)≤5,当d(点F)=5时,BF1=DF2=5,∴点F1的坐标为(4,0),点F2的坐标为(-4,0),将点F1的坐标代入y=kx+4得:0=4k+4,解得:k=-1,将点F2的坐标代入y=kx+4得:0=-4k+4,解得:k=1,∴k=-1或k=1.∴当d(线段EF)取最小值时,EF1直线y=kx+4中k≤-1,EF2直线y=kx+4中k≥1,∴当d(线段EF)取最小值时,k的取值范围为:k≤-1或k≥1;(2)t的取值范围为-3<t<3.【解法提示】⊙T的圆心为T(t,3),半径为1,当d(⊙T)=6时,如解图②所示:CM=CN=6,OH=3,∴T1C=TC=5,CH=OC+OH=1+3=4,∴T1H=T1C2-CH2=52-42=3,TH=TC2-CH2=52-42=3,∴d(⊙T)<6,t的取值范围为-3<t<3.图①图②第4题解图类型三 新定义图形与函数问题1. 解:(1)①如解图①,不妨设满足条件的三角形为等腰△OAR ,则OR =AR .过点R 作RH ⊥OA 于点H ,∴OH =HA =12OA =2,∵以线段OA 为底的等腰△OAR 恰好是点O ,A 的“生成三角形”, ∴RH =OA =4.∴OR =OH 2+RH 2 =25 . 即该三角形的腰长为25 ;第1题解图①②(1,0),(3,0)或(7,0)【解法提示】如解图②所示:若A 为直角顶点时,点B 的坐标为(1,0)或(7,0); 若B 为直角顶点时,点B 的坐标为(1,0)或(3,0). 综上,点B 的坐标为(1,0),(3,0)或(7,0).第1题解图②(2)如解图③可得:若N 为直角顶点:-1-2 ≤x N ≤0;第1题解图③如解图④可得:若M 为直角顶点:-6≤x N ≤-2;第1题解图④综上,点N 的横坐标x N 的取值范围为:-6≤x N ≤0. 2. 解:(1)60;【解法提示】如解图①所示,∵点A (2,0),B (0,23 ), ∵OA =2,OB =23 ,在Rt △AOB 中,由勾股定理得:AB =22+(23)2 =4, ∵OA =12 AB ,∠AOB =90°,∴∠ABO =30°, ∵四边形ABCD 是菱形,∴∠ABC=2∠ABO=60°,∵AB∥CD,∴∠DCB=180°-60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°;第2题解图①(2)如解图②,第2题解图②∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.过点C作CE⊥DE于点E.∴D(4,5)或(-2,5).∴直线CD的表达式为:y=x+1或y=-x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如解图③,第2题解图③∵⊙O的半径为2,且△OQ′D是等腰直角三角形,∴OD=2 OQ′=2,∴BD=3-2=1,∵△P′DB是等腰直角三角形,∴P′B=BD=1,∴P′(3,1),同理可得:OA=2,∴AB=3+2=5,∵△ABP是等腰直角三角形,∴PB=5,∴P(3,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;②先作直线y=-x,再作圆的两条切线,且平行于直线y=-x,如解图④,∵⊙O的半径为2,且△OQ′D是等腰直角三角形,∴OD=2 OQ′=2,∴BD=3-2=1,∵△P′DB是等腰直角三角形,∴P′B=BD=1,∴P′(3,-1),同理可得:OA=2,∴AB=3+2=5,∵△ABP是等腰直角三角形,∴PB=5,∴P(3,-5),∴当-5≤m≤-1时,以QP为边的“坐标菱形”为正方形;综上所述,m的取值范围是1≤m≤5或-5≤m≤-1.第2题解图④类型四 新定义几何问题1. 解:(1)画出DE ︵如解图①所示,DE ︵与BC 相切时,△ABC 的中内弧最长.此时DE ︵的长为以DE 长为直径的半圆.∵在Rt △ABC 中,AB =AC =22,∴BC =2AB =2·22=4.∵D 、E 分别为AB 、AC 的中点,∴DE =12BC =12×4=2.∴lDE ︵=180π360×2=π;第1题解图①(2)①当t =12时,C (2,0).连接DE ,当DE ︵在DE 的下方时,点P 的纵坐标最小时点P 为DE 的中点,如解图②所示.∵A (0,2),∴BA =2.∵点D 是BA 的中点,∴BD =1.∵点D 、E 分别为AB 、AC 的中点,∴DE =12BC =12×2=1.∴⊙P 的半径PD =12.∵12<1,∴DE ︵是△ABC 的中内弧.∴y P ≥1.第1题解图②第1题解图③当DE ︵在DE 的上方时,点P 的纵坐标最大时,⊙P 与AC 相切于点E .如解图③所示,作DE 的垂直平分线FG 交DE 于点F ,交x 轴于点G ,则四边形DBGF 是矩形,圆心P 在FG 上.∵C (2,0),A (0,2),∴BC =BA =2.∴Rt △ABC 是等腰直角三角形.∴∠ACB =45°.∵点D 、E 分别为AB 、AC 的中点,∴DE ∥BC .∴∠AED =∠ACB .∴∠AED =45°.连接PE ,∵⊙P 与AC 相切于点E ,∴PE ⊥AC .∴∠PEA =90°.∴∠PEF =∠PEA -∠AED =45°.∵PF ⊥DE ,∴∠FPE =45°.∴∠PEF =∠FPE .∴PF =EF .∵FG 平分DE ,∴DF =EF =12DE =12×1=12.∴PF =12.∵FG =BD =1,∴PG =FG -PF =1-12=12.∴P (12,12).∴y P ≤12.综上,圆心P 的纵坐标y P 的取值范围为y P ≥1或y P ≤12 ;②0<t ≤2 .【解法提示】ⅰ. 当P 在DE 上方时,如解图④所示,圆心P 在边AC 上且DE ︵与边BC 相切于点F 时,符合题意.∵C (4t ,0),∴BC =4t .∵D 、E 分别为AB 、AC 的中点,∴DE ∥BC ,DE =12 BC =12 ×4t =2t .连接PF .∵⊙P 与BC 相切于点F ,∴PF ⊥BC .∵DE ∥BC ,∴DE ⊥PF .∴DG =12 DE =12 ×2t =t .∵PF ⊥BC ,∴PF ∥y 轴.∴△EPG ∽△EAD .∴PG AD =EG ED =12 .∴PG =12 AD =12 ×1=12.又∵GF =BD =1,∴PF =PG +GF =12 +1=32 .∴DP =32 .在Rt △PDG 中,由勾股定理得DP 2=DG 2+GP 2,即(32 )2=t 2+(12 )2.解得t =±2 .∵t >0,∴t =2 .∴t 的取值范围是0<t ≤2 .第1题解图④ⅱ. 当P 在DE 下方时,如解图⑤.⊙P 与AC 相切于点E 为临界状态,过P 作PM ⊥DE 于点M ,DE 为△ABC 的中内弧,只需PM ≤1即可.此时易得△EMP ∽△ABC ,∴PM CB =EM AB ,即PM 4t =t2 .得PM =2t 2,故0<t ≤22.第1题解图⑤综上,t 的取值范围为0<t ≤2 .2. 解:(1)①20;【解法提示】如解图①所示:连接OA、OB、OP.∵OA=OB,P为AB的中点,∴OP⊥AB.∵在Rt△PBO中,由勾股定理得:PB=OB2-OP2=62-42=25,∴P A=PB=25.∴⊙O的“幂值”=25×25=20.第2题解图①②当弦AB的位置改变时,点P关于⊙O的“幂值”为定值.证明:如解图②,AB为⊙O中过点P的任意一条弦,且不与OP垂直.过点P作⊙O的弦A′B′⊥OP,连接AA′、BB′,OA′.第2题解图②∵在⊙O中,∠AA′P=∠B′BP,∠AP A′=∠BPB′,∴△AP A′∽△B′PB.∴P APB′=P A′PB.∴P A·PB=P A′·PB′=20.∴当弦AB的位置改变时,点P关于⊙O的“幂值”为定值.(2)r2-d2;【解法提示】如解图③所示,连接OP,过点P作AB⊥OP,交圆O与A、B两点,连接OA,OB.第2题解图③∵AO=OB,PO⊥AB,∴AP=PB.∴点P关于⊙O的“幂值”=AP·PB=P A2.在Rt△APO中,AP2=OA2-OP2=r2-d2.∴点P关于⊙O的“幂值”=r2-d2.(3)1-6≤t≤6+1.【解法提示】如解图④所示:过点C作CP⊥AB交AB于点P.第2题解图④∵点P关于⊙C的“幂值”为6,若⊙O半径为r,CP=d,则由(2)可知r2-d2=6.∴d2=3,即d=3.如解图⑤,以点C为圆心,3为半径作辅助圆⊙C′,∵点P在直线MN上,∴当直线MN与⊙C′相交即可满足条件.当点M在x轴正半轴时,直线MN与⊙C′相切如解图⑤,∵M(t,0)、N(0,-t),∴ON=OM=t,∵OM=ON,∴∠OMN=45°.∴在直角三角形CPM中,PM=CP=3.则CM=CP2+PM2=6,∴OM=6+1.∴t=6+1.同理当点M在x轴负半轴时,解得t=1-6,结合函数图象,t的取值范围为1-6≤t≤6+1.第2题解图⑤。
高中数学新定义型问题(解析版)

新定义型问题1(新高考北京卷)生物丰富度指数d =S -1ln N是河流水质的一个评价指标,其中S ,N 分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d 越大,水质越好.如果某河流治理前后的生物种类数S 没有变化,生物个体总数由N 1变为N 2,生物丰富度指数由2.1提高到3.15,则()A.3N 2=2N 1B.2N 2=3N 1C.N 22=N 31 D.N 32=N 21【答案】D【分析】根据题意分析可得S -1ln N 1=2.1,S -1ln N 2=3.15,消去S 即可求解.【详解】由题意得S -1ln N 1=2.1,S -1ln N 2=3.15,则2.1ln N 1=3.15ln N 2,即2ln N 1=3ln N 2,所以N 32=N 21.故选:D .2(新高考上海卷)定义一个集合Ω,集合中的元素是空间内的点集,任取P 1,P 2,P 3∈Ω,存在不全为0的实数λ1,λ2,λ3,使得λ1OP 1+λ2OP 2 +λ3OP 3 =0.已知(1,0,0)∈Ω,则(0,0,1)∉Ω的充分条件是()A.0,0,0 ∈Ω B.-1,0,0 ∈ΩC.0,1,0 ∈ΩD.0,0,-1 ∈Ω【答案】C【分析】首先分析出三个向量共面,显然当1,0,0 ,0,0,1 ,0,1,0 ∈Ω时,三个向量构成空间的一个基底,则即可分析出正确答案.【详解】由题意知这三个向量OP 1,OP 2 ,OP 3 共面,即这三个向量不能构成空间的一个基底,对A ,由空间直角坐标系易知0,0,0 ,(1,0,0),(0,0,1)三个向量共面,则当-1,0,0 ,(1,0,0)∈Ω无法推出(0,0,1)∉Ω,故A 错误;对B ,由空间直角坐标系易知-1,0,0 ,(1,0,0),(0,0,1)三个向量共面,则当0,0,0 ,(1,0,0)∈Ω无法推出(0,0,1)∉Ω,故A 错误;对C , 由空间直角坐标系易知1,0,0 ,0,0,1 ,0,1,0 三个向量不共面,可构成空间的一个基底,则由1,0,0 ,0,1,0 ∈Ω能推出0,0,1 ∉Ω,对D ,由空间直角坐标系易知1,0,0 ,0,0,1 ,0,0,-1 三个向量共面,则当0,0,-1 (1,0,0)∈Ω无法推出(0,0,1)∉Ω,故D 错误.故选:C .3(新高考上海卷)已知函数f (x )的定义域为R ,定义集合M =x 0x 0∈R ,x ∈-∞,x 0 ,f x <f x 0 ,在使得M =-1,1 的所有f x 中,下列成立的是()A.存在f x 是偶函数B.存在f x 在x =2处取最大值C.存在f x 是严格增函数D.存在f x 在x =-1处取到极小值【答案】B【分析】对于ACD 利用反证法并结合函数奇偶性、单调性以及极小值的概念即可判断,对于B ,构造函数f x =-2,x <-1x ,-1≤x ≤11,x >1即可判断.【详解】对于A ,若存在 y =f (x ) 是偶函数, 取 x 0=1∈[-1,1],则对于任意 x ∈(-∞,1),f (x )<f (1), 而 f (-1)=f (1), 矛盾, 故 A 错误;对于B ,可构造函数f x =-2,x <-1,x ,-1≤x ≤1,1,x >1,满足集合M =-1,1 ,当x <-1时,则f x =-2,当-1≤x ≤1时,f x ∈-1,1 ,当x >1时,f x =1,则该函数f x 的最大值是f 2 ,则B 正确;对C ,假设存在f x ,使得f x 严格递增,则M =R ,与已知M =-1,1 矛盾,则C 错误;对D ,假设存在f x ,使得f x 在x =-1处取极小值,则在-1的左侧附近存在n ,使得f n >f -1 ,这与已知集合M 的定义矛盾,故D 错误;故选:B .4(新高考上海卷)无穷等比数列a n 满足首项a 1>0,q >1,记I n =x -y x ,y ∈a 1,a 2 ∪a n ,a n +1 ,若对任意正整数n 集合I n 是闭区间,则q 的取值范围是.【答案】q ≥2【分析】当n ≥2时,不妨设x ≥y ,则x -y ∈0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n ,结合I n 为闭区间可得q -2≥-1qn -2对任意的n ≥2恒成立,故可求q 的取值范围.【详解】由题设有a n =a 1q n -1,因为a 1>0,q >1,故a n +1>a n ,故a n ,a n +1 =a 1q n -1,a 1q n ,当n =1时,x ,y ∈a 1,a 2 ,故x -y ∈a 1-a 2,a 2-a 1 ,此时I 1为闭区间,当n ≥2时,不妨设x ≥y ,若x ,y ∈a 1,a 2 ,则x -y ∈0,a 2-a 1 ,若y ∈a 1,a 2 ,x ∈a n ,a n +1 ,则x -y ∈a n -a 2,a n +1-a 1 ,若x ,y ∈a n ,a n +1 ,则x -y ∈0,a n +1-a n ,综上,x -y ∈0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n ,又I n 为闭区间等价于0,a 2-a 1 ∪a n -a 2,a n +1-a 1 ∪0,a n +1-a n 为闭区间,而a n +1-a 1>a n +1-a n >a 2-a 1,故a n +1-a n ≥a n -a 2对任意n ≥2恒成立,故a n +1-2a n +a 2≥0即a 1q n -1q -2 +a 2≥0,故q n -2q -2 +1≥0,故q -2≥-1qn -2对任意的n ≥2恒成立,因q >1,故当n →+∞时,-1qn -2→0,故q -2≥0即q ≥2.故答案为:q ≥2.【点睛】思路点睛:与等比数列性质有关的不等式恒成立,可利用基本量法把恒成立为转为关于与公比有关的不等式恒成立,必要时可利用参变分离来处理.5(新课标全国Ⅰ卷)设m 为正整数,数列a 1,a 2,...,a 4m +2是公差不为0的等差数列,若从中删去两项a i 和a j i <j 后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列a 1,a 2,...,a 4m +2是i ,j -可分数列.(1)写出所有的i ,j ,1≤i <j ≤6,使数列a 1,a 2,...,a 6是i ,j -可分数列;(2)当m ≥3时,证明:数列a 1,a 2,...,a 4m +2是2,13 -可分数列;(3)从1,2,...,4m +2中一次任取两个数i 和j i <j ,记数列a 1,a 2,...,a 4m +2是i ,j -可分数列的概率为P m ,证明:P m >18.【答案】(1)1,2 ,1,6 ,5,6 (2)证明见解析(3)证明见解析【分析】(1)直接根据i ,j -可分数列的定义即可;(2)根据i ,j -可分数列的定义即可验证结论;(3)证明使得原数列是i ,j -可分数列的i ,j 至少有m +1 2-m 个,再使用概率的定义.【详解】(1)首先,我们设数列a 1,a 2,...,a 4m +2的公差为d ,则d ≠0.由于一个数列同时加上一个数或者乘以一个非零数后是等差数列,当且仅当该数列是等差数列,故我们可以对该数列进行适当的变形a k =a k -a 1d+1k =1,2,...,4m +2 ,得到新数列a k =k k =1,2,...,4m +2 ,然后对a 1,a 2,...,a 4m +2进行相应的讨论即可.换言之,我们可以不妨设a k =k k =1,2,...,4m +2 ,此后的讨论均建立在该假设下进行.回到原题,第1小问相当于从1,2,3,4,5,6中取出两个数i 和j i <j ,使得剩下四个数是等差数列.那么剩下四个数只可能是1,2,3,4,或2,3,4,5,或3,4,5,6.所以所有可能的i ,j 就是1,2 ,1,6 ,5,6 .(2)由于从数列1,2,...,4m +2中取出2和13后,剩余的4m 个数可以分为以下两个部分,共m 组,使得每组成等差数列:①1,4,7,10 ,3,6,9,12 ,5,8,11,14 ,共3组;②15,16,17,18 ,19,20,21,22 ,...,4m -1,4m ,4m +1,4m +2 ,共m -3组.(如果m -3=0,则忽略②)故数列1,2,...,4m +2是2,13 -可分数列.(3)定义集合A =4k +1 k =0,1,2,...,m =1,5,9,13,...,4m +1 ,B =4k +2 k =0,1,2,...,m =2,6,10,14,...,4m+2.下面证明,对1≤i<j≤4m+2,如果下面两个命题同时成立,则数列1,2,...,4m+2一定是i,j-可分数列:命题1:i∈A,j∈B或i∈B,j∈A;命题2:j-i≠3.我们分两种情况证明这个结论.第一种情况:如果i∈A,j∈B,且j-i≠3.此时设i=4k1+1,j=4k2+2,k1,k2∈0,1,2,...,m.则由i<j可知4k1+1<4k2+2,即k2-k1>-14,故k2≥k1.此时,由于从数列1,2,...,4m+2中取出i=4k1+1和j=4k2+2后,剩余的4m个数可以分为以下三个部分,共m组,使得每组成等差数列:①1,2,3,4,5,6,7,8,...,4k1-3,4k1-2,4k1-1,4k1,共k1组;②4k1+2,4k1+3,4k1+4,4k1+5,4k1+6,4k1+7,4k1+8,4k1+9,...,4k2-2,4k2-1,4k2,4k2+1,共k2-k1组;③4k2+3,4k2+4,4k2+5,4k2+6,4k2+7,4k2+8,4k2+9,4k2+10,...,4m-1,4m,4m+1,4m+2,共m-k2组.(如果某一部分的组数为0,则忽略之)故此时数列1,2,...,4m+2是i,j-可分数列.第二种情况:如果i∈B,j∈A,且j-i≠3.此时设i=4k1+2,j=4k2+1,k1,k2∈0,1,2,...,m.则由i<j可知4k1+2<4k2+1,即k2-k1>14,故k2>k1.由于j-i≠3,故4k2+1-4k1+2≠3,从而k2-k1≠1,这就意味着k2-k1≥2.此时,由于从数列1,2,...,4m+2中取出i=4k1+2和j=4k2+1后,剩余的4m个数可以分为以下四个部分,共m组,使得每组成等差数列:①1,2,3,4,5,6,7,8,...,4k1-3,4k1-2,4k1-1,4k1,共k1组;②4k1+1,3k1+k2+1,2k1+2k2+1,k1+3k2+1,3k1+k2+2,2k1+2k2+2,k1+3k2+2,4k2+2,共2组;③全体4k1+p,3k1+k2+p,2k1+2k2+p,k1+3k2+p,其中p=3,4,...,k2-k1,共k2-k1-2组;④4k2+3,4k2+4,4k2+5,4k2+6,4k2+7,4k2+8,4k2+9,4k2+10,...,4m-1,4m,4m+1,4m+2,共m-k2组.(如果某一部分的组数为0,则忽略之)这里对②和③进行一下解释:将③中的每一组作为一个横排,排成一个包含k2-k1-2个行,4个列的数表以后,4个列分别是下面这些数:4k1+3,4k1+4,...,3k1+k2,3k1+k2+3,3k1+k2+4,...,2k1+2k2,2k1+2k2+3,2k1+2k2+3,...,k1+3k2,k1+3k2+3,k1+3k2+4,...,4k2.可以看出每列都是连续的若干个整数,它们再取并以后,将取遍4k1+1,4k1+2,...,4k2+2中除开五个集合4k1+1,4k1+2,3k1+k2+1,3k1+k2+2,2k1+2k2+1,2k1+2k2+2,k1+3k2+1,k1+3k2+2,4k2+1,4k2+2中的十个元素以外的所有数.而这十个数中,除开已经去掉的4k1+2和4k2+1以外,剩余的八个数恰好就是②中出现的八个数.这就说明我们给出的分组方式满足要求,故此时数列1,2,...,4m+2是i,j-可分数列.至此,我们证明了:对1≤i<j≤4m+2,如果前述命题1和命题2同时成立,则数列1,2,...,4m+2一定是i,j-可分数列.然后我们来考虑这样的i,j的个数.首先,由于A∩B=∅,A和B各有m+1个元素,故满足命题1的i,j总共有m+12个;而如果j-i=3,假设i∈A,j∈B,则可设i=4k1+1,j=4k2+2,代入得4k2+2-4k1+1=3.但这导致k2-k1=12,矛盾,所以i∈B,j∈A.设i=4k1+2,j=4k2+1,k1,k2∈0,1,2,...,m,则4k2+1-4k1+2=3,即k2-k1=1.所以可能的k1,k2恰好就是0,1,1,2,...,m-1,m,对应的i,j分别是2,5,6,9,..., 4m-2,4m+1,总共m个.所以这m+12个满足命题1的i,j中,不满足命题2的恰好有m个.这就得到同时满足命题1和命题2的i,j的个数为m+12-m.当我们从1,2,...,4m+2中一次任取两个数i和j i<j时,总的选取方式的个数等于4m+24m+12=2m+14m+1.而根据之前的结论,使得数列a1,a2,...,a4m+2是i,j-可分数列的i,j至少有m+12-m个.所以数列a1,a2,...,a4m+2是i,j-可分数列的概率P m一定满足P m≥m+12-m2m+14m+1=m2+m+12m+14m+1>m2+m+142m+14m+2=m+12222m+12m+1=18.这就证明了结论.【点睛】关键点点睛:本题的关键在于对新定义数列的理解,只有理解了定义,方可使用定义验证或探究结论.6(新课标全国Ⅱ卷)已知双曲线C:x2-y2=m m>0,点P15,4在C上,k为常数,0<k<1.按照如下方式依次构造点P n n=2,3,...,过P n-1作斜率为k的直线与C的左支交于点Q n-1,令P n为Q n-1关于y轴的对称点,记P n的坐标为x n,y n.(1)若k=12,求x2,y2;(2)证明:数列x n-y n是公比为1+k1-k的等比数列;(3)设S n为△P n P n+1P n+2的面积,证明:对任意的正整数n,S n=S n+1.【答案】(1)x2=3,y2=0(2)证明见解析(3)证明见解析【分析】(1)直接根据题目中的构造方式计算出P2的坐标即可;(2)根据等比数列的定义即可验证结论;(3)思路一:使用平面向量数量积和等比数列工具,证明S n的取值为与n无关的定值即可.思路二:使用等差数列工具,证明S n的取值为与n无关的定值即可.【详解】(1)由已知有m=52-42=9,故C的方程为x2-y2=9.当k=12时,过P15,4且斜率为12的直线为y=x+32,与x2-y2=9联立得到x2-x+322=9.解得x=-3或x=5,所以该直线与C的不同于P1的交点为Q1-3,0,该点显然在C的左支上.故P23,0,从而x2=3,y2=0.(2)由于过P n x n,y n且斜率为k的直线为y=k x-x n+y n,与x2-y2=9联立,得到方程x2-k x-x n+y n2=9.展开即得1-k2x2-2k y n-kx nx-y n-kx n2-9=0,由于P n x n,y n已经是直线y=k x-x n+y n和x2 -y2=9的公共点,故方程必有一根x=x n.从而根据韦达定理,另一根x=2k y n-kx n1-k2-x n=2ky n-x n-k2x n1-k2,相应的y=k x-x n+y n=y n+k2y n-2kx n1-k2.所以该直线与C的不同于P n的交点为Q n2ky n-x n-k2x n1-k2,y n+k2y n-2kx n1-k2,而注意到Q n的横坐标亦可通过韦达定理表示为-y n-kx n2-91-k2x n,故Q n一定在C的左支上.所以P n+1x n+k2x n-2ky n1-k2,y n+k2y n-2kx n1-k2.这就得到x n+1=x n+k2x n-2ky n1-k2,y n+1=y n+k2y n-2kx n1-k2.所以x n+1-y n+1=x n+k2x n-2ky n1-k2-y n+k2y n-2kx n1-k2=x n+k2x n+2kx n1-k2-y n+k2y n+2ky n1-k2=1+k2+2k1-k2x n-y n=1+k1-kx n-y n.再由x 21-y 21=9,就知道x 1-y 1≠0,所以数列x n -y n 是公比为1+k1-k 的等比数列.(3)方法一:先证明一个结论:对平面上三个点U ,V ,W ,若UV =a ,b ,UW=c ,d ,则S △UVW =12ad -bc .(若U ,V ,W 在同一条直线上,约定S △UVW =0)证明:S △UVW =12UV⋅UW sin UV ,UW =12UV ⋅UW 1-cos 2UV ,UW=12UV⋅UW 1-UV ⋅UWUV ⋅UW 2=12UV 2⋅UW 2-UV ⋅UW 2=12a 2+b 2c 2+d 2-ac +bd2=12a 2c 2+a 2d 2+b 2c 2+b 2d 2-a 2c 2-b 2d 2-2abcd =12a 2d 2+b 2c 2-2abcd =12ad -bc2=12ad -bc .证毕,回到原题.由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2,y n +1=y n +k 2y n -2kx n 1-k 2,故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k 2x n +y n=1-k1+k x n +y n .再由x 21-y 21=9,就知道x 1+y 1≠0,所以数列x n +y n 是公比为1-k 1+k 的等比数列.所以对任意的正整数m ,都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n=921-k 1+k m -1+k 1-k m .而又有P n +1P n =-x n +1-x n ,-y n +1-y n ,P n +1P n +2=x n +2-x n +1,y n +2-y n +1 ,故利用前面已经证明的结论即得S n =S △P n P n +1P n +2=12-x n +1-x n y n +2-y n +1 +y n +1-y n x n +2-x n +1 =12x n +1-x n y n +2-y n +1 -y n +1-y n x n +2-x n +1 =12x n +1y n +2-y n +1x n +2 +x n y n +1-y n x n +1 -x n y n +2-y n x n +2=12921-k 1+k -1+k 1-k +921-k 1+k -1+k 1-k -921-k 1+k 2-1+k 1-k 2.这就表明Sn 的取值是与n 无关的定值,所以S n =S n +1.方法二:由于上一小问已经得到x n +1=x n +k 2x n -2ky n 1-k 2,y n +1=y n +k 2y n -2kx n1-k 2,故x n +1+y n +1=x n +k 2x n -2ky n 1-k 2+y n +k 2y n -2kx n 1-k 2=1+k 2-2k 1-k2x n +y n =1-k1+k x n +y n .再由x 21-y 21=9,就知道x 1+y 1≠0,所以数列x n +y n 是公比为1-k 1+k 的等比数列.所以对任意的正整数m ,都有x n y n +m -y n x n +m=12x n x n +m -y n y n +m +x n y n +m -y n x n +m -12x n x n +m -y n y n +m -x n y n +m -y n x n +m =12x n -y n x n +m +y n +m -12x n +y n x n +m -y n +m =121-k 1+k m x n -y n x n +y n-121+k 1-k mx n +y n x n -y n =121-k 1+k m -1+k 1-k m x 2n -y 2n =921-k 1+k m -1+k 1-k m .这就得到x n +2y n +3-y n +2x n +3=921-k 1+k -1+k1-k=x n y n +1-y n x n +1,以及x n +1y n +3-y n +1x n +3=921-k 1+k 2-1+k 1-k 2=x n y n +2-y n x n +2.两式相减,即得x n +2y n +3-y n +2x n +3 -x n +1y n +3-y n +1x n +3 =x n y n +1-y n x n +1 -x n y n +2-y n x n +2 .移项得到x n +2y n +3-y n x n +2-x n +1y n +3+y n x n +1=y n +2x n +3-x n y n +2-y n +1x n +3+x n y n +1.故y n +3-y n x n +2-x n +1 =y n +2-y n +1 x n +3-x n .而P n P n +3 =x n +3-x n ,y n +3-y n ,P n +1P n +2 =x n +2-x n +1,y n +2-y n +1 .所以P n P n +3 和P n +1P n +2平行,这就得到S △P n P n +1P n +2=S △P n +1P n +2P n +3,即S n =S n +1.【点睛】关键点点睛:本题的关键在于将解析几何和数列知识的结合,需要综合运用多方面知识方可得解.7(新高考北京卷)设集合M =i ,j ,s ,t i ∈1,2 ,j ∈3,4 ,s ∈5,6 ,t ∈7,8 ,2i +j +s +t .对于给定有穷数列A :a n 1≤n ≤8 ,及序列Ω:ω1,ω2,...,ωs ,ωk =i k ,j k ,s k ,t k ∈M ,定义变换T :将数列A 的第i 1,j 1,s 1,t 1项加1,得到数列T 1A ;将数列T 1A 的第i 2,j 2,s 2,t 2列加1,得到数列T 2T 1A ⋯;重复上述操作,得到数列T s ...T 2T 1A ,记为ΩA .(1)给定数列A :1,3,2,4,6,3,1,9和序列Ω:1,3,5,7 ,2,4,6,8 ,1,3,5,7 ,写出ΩA ;(2)是否存在序列Ω,使得ΩA 为a 1+2,a 2+6,a 3+4,a 4+2,a 5+8,a 6+2,a 7+4,a 8+4,若存在,写出一个符合条件的Ω;若不存在,请说明理由;(3)若数列A 的各项均为正整数,且a 1+a 3+a 5+a 7为偶数,证明:“存在序列Ω,使得ΩA 为常数列”的充要条件为“a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8”.【答案】(1)ΩA :3,4,4,5,8,4,3,10(2)不存在符合条件的Ω,理由见解析(3)证明见解析【分析】(1)直接按照ΩA 的定义写出ΩA 即可;(2)利用反证法,假设存在符合条件的Ω,由此列出方程组,进一步说明方程组无解即可;(3)分充分性和必要性两方面论证.【详解】(1)由题意得ΩA :3,4,4,5,8,4,3,10;(2)假设存在符合条件的Ω,可知ΩA 的第1,2项之和为a 1+a 2+s ,第3,4项之和为a 3+a 4+s ,则a 1+2 +a 2+6 =a 1+a 2+sa 3+4 +a 4+2 =a 3+a 4+s,而该方程组无解,故假设不成立,故不存在符合条件的Ω;(3)我们设序列T k ...T 2T 1A 为a k ,n 1≤n ≤8 ,特别规定a 0,n =a n 1≤n ≤8 .必要性:若存在序列Ω:ω1,ω2,...,ωs ,使得ΩA 为常数列.则a s ,1=a s ,2=a s ,3=a s ,4=a s ,5=a s ,6=a s ,7=a s ,8,所以a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8.根据T k ...T 2T 1A 的定义,显然有a k ,2j -1+a k ,2j =a k -1,2j -1+a k -1,2j ,这里j =1,2,3,4,k =1,2,....所以不断使用该式就得到,a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8,必要性得证.充分性:若a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8.由已知,a 1+a 3+a 5+a 7为偶数,而a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8,所以a 2+a 4+a 6+a 8=4a 1+a 2 -a 1+a 3+a 5+a 7 也是偶数.我们设T s ...T 2T 1A 是通过合法的序列Ω的变换能得到的所有可能的数列ΩA 中,使得a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 最小的一个.上面已经证明a k ,2j -1+a k ,2j =a k -1,2j -1+a k -1,2j ,这里j =1,2,3,4,k =1,2,....从而由a 1+a 2=a 3+a 4=a 5+a 6=a 7+a 8可得a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8.同时,由于i k +j k +s k +t k 总是偶数,所以a k ,1+a k ,3+a k ,5+a k ,7和a k ,2+a k ,4+a k ,6+a k ,8的奇偶性保持不变,从而a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数.下面证明不存在j =1,2,3,4使得a s ,2j -1-a s ,2j ≥2.假设存在,根据对称性,不妨设j =1,a s ,2j -1-a s ,2j ≥2,即a s ,1-a s ,2≥2.情况1:若a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 =0,则由a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数,知a s ,1-a s ,2≥4.对该数列连续作四次变换2,3,5,8 ,2,4,6,8 ,2,3,6,7 ,2,4,5,7 后,新的a s +4,1-a s +4,2 +a s +4,3-a s +4,4 +a s +4,5-a s +4,6 +a s +4,7-a s +4,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 减少4,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾;情况2:若a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 >0,不妨设a s ,3-a s ,4 >0.情况2-1:如果a s ,3-a s ,4≥1,则对该数列连续作两次变换2,4,5,7 ,2,4,6,8 后,新的a s +2,1-a s +2,2 +a s +2,3-a s +2,4 +a s +2,5-a s +2,6 +a s +2,7-a s +2,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 至少减少2,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾;情况2-2:如果a s ,4-a s ,3≥1,则对该数列连续作两次变换2,3,5,8 ,2,3,6,7 后,新的a s +2,1-a s +2,2 +a s +2,3-a s +2,4 +a s +2,5-a s +2,6 +a s +2,7-a s +2,8 相比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 至少减少2,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾.这就说明无论如何都会导致矛盾,所以对任意的j =1,2,3,4都有a s ,2j -1-a s ,2j ≤1.假设存在j =1,2,3,4使得a s ,2j -1-a s ,2j =1,则a s ,2j -1+a s ,2j 是奇数,所以a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8都是奇数,设为2N +1.则此时对任意j =1,2,3,4,由a s ,2j -1-a s ,2j ≤1可知必有a s ,2j -1,a s ,2j =N ,N +1 .而a s ,1+a s ,3+a s ,5+a s ,7和a s ,2+a s ,4+a s ,6+a s ,8都是偶数,故集合m a s ,m =N 中的四个元素i ,j ,s ,t 之和为偶数,对该数列进行一次变换i ,j ,s ,t ,则该数列成为常数列,新的a s +1,1-a s +1,2 +a s +1,3-a s +1,4 +a s +1,5-a s +1,6 +a s +1,7-a s +1,8 等于零,比原来的a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 更小,这与a s ,1-a s ,2 +a s ,3-a s ,4 +a s ,5-a s ,6 +a s ,7-a s ,8 的最小性矛盾.综上,只可能a s ,2j -1-a s ,2j =0j =1,2,3,4 ,而a s ,1+a s ,2=a s ,3+a s ,4=a s ,5+a s ,6=a s ,7+a s ,8,故a s ,n =ΩA 是常数列,充分性得证.【点睛】关键点点睛:本题第三问的关键在于对新定义的理解,以及对其本质的分析.8(新高考上海卷)对于一个函数f x 和一个点M a ,b ,令s x =(x -a )2+f x -b 2,若P x 0,f x 0 是s x 取到最小值的点,则称P 是M 在f x 的“最近点”.(1)对于f (x )=1x(x >0),求证:对于点M 0,0 ,存在点P ,使得点P 是M 在f x 的“最近点”;(2)对于f x =e x ,M 1,0 ,请判断是否存在一个点P ,它是M 在f x 的“最近点”,且直线MP 与y =f (x )在点P 处的切线垂直;(3)已知y =f (x )在定义域R 上存在导函数f (x ),且函数g (x )在定义域R 上恒正,设点M 1t -1,f t -g t ,M 2t +1,f t +g t .若对任意的t ∈R ,存在点P 同时是M 1,M 2在f x 的“最近点”,试判断f x 的单调性.【答案】(1)证明见解析(2)存在,P 0,1 (3)严格单调递减【分析】(1)代入M (0,0),利用基本不等式即可;(2)由题得s x =(x -1)2+e 2x ,利用导函数得到其最小值,则得到P ,再证明直线MP 与切线垂直即可;(3)根据题意得到s 1 x 0 =s 2 x 0 =0,对两等式化简得f x 0 =-1g (t ),再利用“最近点”的定义得到不等式组,即可证明x 0=t ,最后得到函数单调性.【详解】(1)当M (0,0)时,s x =(x -0)2+1x -02=x 2+1x2≥2x 2⋅1x 2=2,当且仅当x2=1x2即x=1时取等号,故对于点M0,0,存在点P1,1,使得该点是M0,0在f x 的“最近点”.(2)由题设可得s x =(x-1)2+e x-02=(x-1)2+e2x,则s x =2x-1+2e2x,因为y=2x-1,y=2e2x均为R上单调递增函数,则s x =2x-1+2e2x在R上为严格增函数,而s 0 =0,故当x<0时,s x <0,当x>0时,s x >0,故s x min=s0 =2,此时P0,1,而f x =e x,k=f 0 =1,故f x 在点P处的切线方程为y=x+1.而k MP=0-11-0=-1,故k MP⋅k=-1,故直线MP与y=f x 在点P处的切线垂直.(3)设s1x =(x-t+1)2+f x -f t +g t2,s2x =(x-t-1)2+f x -f t -g t2,而s 1x =2(x-t+1)+2f x -f t +g tf x ,s 2x =2(x-t-1)+2f x -f t -g tf x ,若对任意的t∈R,存在点P同时是M1,M2在f x 的“最近点”,设P x0,y0,则x0既是s1x 的最小值点,也是s2x 的最小值点,因为两函数的定义域均为R,则x0也是两函数的极小值点,则存在x0,使得s1 x0=s2 x0=0,即s1 x0=2x0-t+1+2f x0f x0-f(t)+g(t)=0①s2 x0=2x0-t-1+2f x0f x0-f(t)-g(t)=0②由①②相等得4+4g(t)⋅f x0=0,即1+f x0g(t)=0,即f x0=-1g(t),又因为函数g(x)在定义域R上恒正,则f x0=-1g(t)<0恒成立,接下来证明x0=t,因为x0既是s1x 的最小值点,也是s2x 的最小值点,则s1x0≤s(t),s2x0≤s(t),即x0-t+12+f x0-f t +g t2≤1+g t2,③x0-t-12+f x0-f t -g t2≤1+g t2,④③+④得2x0-t2+2+2f x0-f(t)2+2g2(t)≤2+2g2(t)即x0-t2+f x0-f t2≤0,因为x0-t2≥0,f x0-f t2≥0则x0-t=0f x0-f t =0,解得x=t,则f t =-1g(t)<0恒成立,因为t的任意性,则f x 严格单调递减.【点睛】关键点点睛:本题第三问的关键是结合最值点和极小值的定义得到f x 0 =-1g (t ),再利用最值点定义得到x 0=t 即可.一、单选题1(2024·湖南怀化·二模)给定整数n ≥3,有n 个实数元素的集合S ,定义其相伴数集T =a -b a ,b ∈S ,a ≠b ,如果min T =1,则称集合S 为一个n 元规范数集.(注:min X 表示数集X 中的最小数).对于集合M =-0.1,-1.1,2,2.5 、N =-1.5,-0.5,0.5,1.5 ,则()A.M 是规范数集,N 不是规范数集B.M 是规范数集,N 是规范数集C.M 不是规范数集,N 是规范数集D.M 不是规范数集,N 不是规范数集【答案】C【分析】利用规范数集的定义,逐项判断即可得解.【详解】集合M =-0.1,-1.1,2,2.5 中,2∈M ,2.5∈M ,则|2-2.5|=0.5<1,即M 的相伴数集中的最小数不是1,因此M 不是规范数集;集合N =-1.5,-0.5,0.5,1.5 ,|-1.5-(-0.5)|=1,|-0.5-0.5|=1,|0.5-1.5|=1,|-1.5-0.5|=|-0.5-1.5|=2,|-1.5-1.5|=3,即N 的相伴数集中的最小数是1,因此N 是规范数集.故选:C2(2024·四川绵阳·模拟预测)一般地,任意给定一个角α∈R ,它的终边OP 与单位圆的交点P 的坐标,无论是横坐标x 还是纵坐标y ,都是唯一确定的,所以点P 的横坐标x 、纵坐标y 都是关于角α的函数.下面给出这些函数的定义:①把点P 的纵坐标y 叫作α的正弦函数,记作sin α,即sin α=y ;②把点P 的横坐标x 叫作α的余弦函数,记作cos α,即cos α=x ;③把点P 的纵坐标y 的倒数叫作α的余割函数,记作csc α,即csc α=1y ;④把点P 的横坐标x 的倒数叫作α的正割函数,记作sec α,即sec α=1x.下列结论错误的是()A.sin α⋅csc α=1B.sec2π3=-2C.函数f x =sec x 的定义域为x x ≠k π,k ∈Z D.sec 2α+sin 2α+csc 2α+cos 2α≥5【答案】C【分析】根据定义可判断A ;利用定义转化为余弦求解可判断B ;转化为余弦表示,根据分母不为0求解可判断C ;转化为正弦和余弦,利用平方关系和二倍角公式化简,由正弦函数性质可判断D .【详解】由题知,csc α=1sin α,sec α=1cos α,对于A ,sin α⋅csc α=y ⋅1y=1,A 正确;对于B ,sec2π3=1x =1cos 2π3=1cos π-π3 =1-cos π3=-2,B 正确;对于C ,函数f x =sec x =1cos x ,由cos x ≠0得x ≠k π+π2,k ∈Z所以f x 的定义域为x x ≠k π+π2,k ∈Z ,C 错误;对于D ,sec 2α+sin 2α+csc 2α+cos 2α=1+1cos 2α+1sin 2α=1+1sin 2αcos 2α=1+4sin 22α≥5,当sin2α=±1时,等号成立,D 正确.故选:C .3(2024·河北邯郸·二模)对任意两个非零的平面向量a 和b ,定义:a ⊕b =a ⋅ba 2+b2,a ⊙b=a ⋅bb2.若平面向量a ,b 满足a >b >0,且a ⊕b 和a ⊙b 都在集合n 4|n ∈Z ,0<n ≤4 中,则a ⊕b +a ⊙b =()A.1B.32C.1或74D.1或54【答案】D【分析】根据a >b >0,得到a 2+b 2>2a b ,再利用题设中的定义及向量夹角的范围,得到a ⊕b <12,a ⊙b >12,再结合条件,即可求出结果.【详解】因为n 4|n ∈Z ,0<n ≤4=14,12,34,1,设向量a 和b 的夹角为θ,因为a >b >0,所以a 2+b 2>2a b,得到a⊕b =a ⋅b a 2+b 2=a b cos θa 2+b 2<a b cos θ2a ⋅b=cos θ2,又θ∈0,π ,所以cos θ2≤12,又a ⊕b 在集合n 4|n ∈Z ,0<n ≤4 中,所以cos θ2>14,即cos θ>12,得到a ⊕b =14,又因为a ⊙b =a ⋅b b 2=a ⋅b cos θb 2=a b cos θ>cos θ>12,所以a ⊙b =34或1,所以a ⊕b +a ⊙b =1或54,故选:D .4(2024·上海杨浦·二模)平面上的向量a 、b 满足:a =3,b =4,a ⊥b.定义该平面上的向量集合A ={x ||x +a |<|x +b |,x ⋅a >x ⋅b}.给出如下两个结论:①对任意c ∈A ,存在该平面的向量d ∈A ,满足c -d=0.5②对任意c ∈A ,存在该平面向量d ∉A ,满足c -d =0.5则下面判断正确的为()A.①正确,②错误B.①错误,②正确C.①正确,②正确D.①错误,②错误【答案】C【分析】根据给定条件,令a =(3,0),b =(0,4),设x =(m ,n ),利用向量模及数量积的坐标表示探求m ,n 的关系,再借助平行线间距离分析判断得解.【详解】由|a |=3,|b |=4,a ⊥b ,不妨令a =(3,0),b =(0,4),设x=(m ,n ),|x +a |<|x +b |,得|x +a |2<|x +b |2,而x +a =(m +3,n ),x +b =(m ,n +4),则(m +3)2+n 2<m 2+(n +4)2,整理得6m -8n -7<0,由x ⋅a >x ⋅b,得3m -4n >0,平行直线6m -8n -7=0和3m -4n =0间的距离为d =0-(-7)62+82=0.7,到直线6m -8n -7=0和直线3m -4n =0距离相等的点到这两条直线的距离为0.35,如图,阴影部分表示的区域为集合A ,因此无论d 是否属于A ,都有c -d=0.5,所以命题①②都正确.故选:C【点睛】思路点睛:已知几个向量的模,探求向量问题,可以在平面直角坐标系中,借助向量的坐标表示,利用代数方法解决.5(2024·甘肃兰州·一模)球面上两点间距离的定义为:经过球面上两点的大圆在这两点间劣弧的长度(大圆就是经过球心的平面截球面所得的圆).设地球的半径为R ,若甲地位于北纬45°东经120°,乙地位于北纬45°西经60°,则甲、乙两地的球面距离为()A.2π6R B.2π3R C.π2R D.2π2R 【答案】C【分析】分析甲、乙两地的球心角,即可得解.【详解】甲、乙两地在北纬45°线上,所对圆心角为120°+60°=180°,即甲、乙两地在北纬45°线所在小圆的直径的两端,且小圆的半径r =R sin45°=22R ,则R 2+R 2=2R 2,所以甲、乙两地的球心角为π2,故甲、乙两地的球面距离为π2R .故选:C .二、多选题6(2024·安徽芜湖·二模)在平面直角坐标系xOy 中,角θ以坐标原点O 为顶点,以x 轴的非负半轴为始边,其终边经过点M a ,b ,OM =m m ≠0 ,定义f θ =b +a m ,g θ =b -am,则()A.f π6 +g π6 =1 B.f θ +f 2θ ≥0C.若f θg θ=2,则sin2θ=35 D.f θ g θ 是周期函数【答案】ACD【分析】根据题意分别求出cos θ=a m ,sin θ=b m ,则f θ =2sin θ+π4 ,g θ =2sin θ-π4,从而可对A 判断求解,利用换元法令t =sin θ+cos θ=2sin θ+π4 ∈-2,2 可对B 判断求解,由f θ g θ=tan θ+1tan θ-1=2求出tan θ=3,并结合sin2θ==2tan θtan 2θ+1从而可对C 判断求解,由f θ g θ =-cos2θ可对D 判断求解.【详解】由题意得M a ,b 在角θ的终边上,且OM =m ,所以cos θ=a m ,sin θ=b m,则f θ =b +a m =sin θ+cos θ=2sin θ+π4 ,g θ =b -a m =sin θ-cos θ=2sin θ-π4,对A :f π6+g π6 =sin π6+cos π6+sin π6-cos π6=1,故A 正确;对B :f θ +f 2θ =sin θ+cos θ+sin θ+cos θ 2,令t =sin θ+cos θ=2sin θ+π4∈-2,2 ,所以f θ +f 2θ =t +t 2=t +122-14≥-14,故B 错误;对C :f θ g θ =sin θ+cos θsin θ-cos θ=tan θ+1tan θ-1=2,解得tan θ=3,又由sin2θ=2sin θcos θ=2sin θcos θsin 2θ+cos 2θ=2tan θtan 2θ+1=2×332+1=35,故C 正确;对D :f θ g θ =sin θ+cos θ sin θ-cos θ =sin 2θ-cos 2θ=-cos2θ,因为y =cos2θ为周期函数,故D 正确.故选:ACD .7(2024·全国·模拟预测)已知函数f x 和实数m ,n ,则下列说法正确的是()A.定义在R 上的函数f x 恒有f x =f m -nx ,则当n =1时,函数的图象有对称轴B.定义在R 上的函数f x 恒有f x =f m -nx ,则当n =-1时,函数具有周期性C.若m =1,n =2,f x =-3x 2+2x ,x ≤13f m -nx ,x >13,则∀t ∈-∞,13 ,f t >f 23-t 恒成立D.若m =4,n =1,f x =ln x -a ,x ∈0,2 f m -nx ,x ∈2,4,且f x 的4个不同的零点分别为x 1,x 2,x 3x 4,且x 1<x 2<x 3<x 4,则x 1x 2+x 3x 4-4x 3+x 4 =-14【答案】ACD【分析】根据函数的对称性和周期性可分别判断AB ;求出x >13时的解析式,然后根据自变量范围代入相应表达式解不等式即可判断C ;将问题转化为直线y =a 与函数g x =ln x ,x ∈0,2ln 4-x ,x ∈2,4 有四个交点,结合图象求得四根的关系即可判断D .【详解】对于A ,若n =1,则f x =f m -x ,所以函数f x 的图象的对称轴为直线x =m2,故A 正确.对于B ,当n =-1时,f x =f m +x .若m =0,则f x =f x ,函数不具有周期性,故B 错误.对于C ,若m =1,n =2,则f x =-3x 2+2x ,x ≤13f 1-2x ,x >13,当x >13时,1-2x <13,则f x =-31-2x 2+21-2x =-34x 2-4x +1 +21-2x =-12x 2+8x -1,即当x >13时,f x =-12x 2+8x -1.当t ∈-∞,13 时,23-t ∈13,+∞ ,所以f t -f 23-t=-3t 2+2t --1223-t 2+823-t -1 =9t 2-6t +1=3t -1 2>0,所以f t >f 23-t恒成立,C 正确.对于D ,当x ∈2,4 时,4-x ∈0,2 ,则f x =ln x -a ,x ∈0,2ln 4-x -a ,x ∈2,4 ,令g x =ln x ,x ∈0,2ln 4-x ,x ∈2,4,作出函数g x 的图象和直线y =a ,如图.要使f x 有4个不同的零点,则函数g x 的图象与直线y =a 有4个不同的交点.又x 1<x 2<x 3<x 4,则-ln x 1=ln x 2=ln 4-x 3 =-ln 4-x 4 ,所以ln x 1+ln x 2=0,ln 4-x 3 +ln 4-x 4 =0, 所以x 1x 2=1,4-x 3 4-x 4 =1,则16-4x 3+x 4 +x 3x 4=1,所以x 1x 2+x 3x 4-4x 3+x 4 =-14,D 正确.故选:ACD .【点睛】思路点睛:关于函数零点个数的有关问题,一般转化为两个函数图象交点问题,利用函数图象分析求解即可.8(2024·浙江绍兴·模拟预测)对于任意的两点A x 1,y 1 ,B x 2,y 2 ,定义A ,B 间的折线距离d AB =x 1-x 2 +y 1-y 2 ,反折线距离l AB =x 1-y 2 +x 2-y 1 ,O 表示坐标原点. 下列说法正确的是()A.d AB +d BC ≥d AC .B.若d AB <l AB ,则y 1-x 1 y 2-x 2 ≥0.C.若AB 斜率为k ,d AB =1+k1+k2AB .D.若存在四个点P x ,y 使得d OP =1,且x 2+y -r 2=r 2r >0 ,则r 的取值范围2-1,12 .【答案】ABD【分析】对于A ,直接使用绝对值不等式即可证明;对于B ,在使用绝对值不等式的同时考虑到绝对值不等式取等的条件(即a +b =a +b ,a +b ≥a -b ,ab ≥0两两等价,对两个不等式两边同时平方即得结论),即可判断;对于C ,举出一个反例即可否定;对于D ,先将问题转化为方程组的解的个数问题,然后利用解析几何工具直观理解,猜出答案,最后再严格论证结果即可.【详解】对于A ,设C x 3,y 3 ,我们有d AB +d BC =x 1-x 2 +y 1-y 2 +x 2-x 3 +y 2-y 3 =x 1-x 2 +x 2-x 3 +y 1-y 2 +y 2-y 3 ≥x 1-x 2 +x 2-x 3 +y 1-y 2 +y 2-y 3 =x 1-x 3 +y 1-y 3 =d AC ,故A 正确;对于B ,若d AB <l AB ,则l AB >d AB =x 1-x 2 +y 1-y 2 ≥x 1-x 2 +y 1-y 2 =x 1-y 2 +y 1-x 2 ,这意味着x 1-y 2 +y 1-x 2 =x 1-y 2 +x 2-y 1 =l AB >x 1-y 2 +y 1-x 2 .从而由x 1-y 2 +y 1-x 2 >x 1-y 2 +y 1-x 2 ,知x 1-y 2 y 1-x 2 <0,即y 2-x 1 y 1-x 2 >0,所以y 2-x 1 +y 1-x 2 =y 2-x 1 +y 1-x 2 .故y 1-x 1 +y 2-x 2 =y 2-x 1 +y 1-x 2 =y 2-x 1 +y 1-x 2 =l AB .而d AB =x 1-x 2 +y 1-y 2 ≥y 1-y 2 -x 1-x 2 =y 1-x 1 -y 2-x 2 .故y 1-x 1 +y 2-x 2 =l AB >d AB ≥y 1-x 1 -y 2-x 2 .从而由y 1-x 1 +y 2-x 2 >y 1-x 1 -y 2-x 2 ,知y 1-x 1 y 2-x 2 ≥0,故B 正确;对于C ,考虑A 1,0 ,B 0,1 ,此时k =-1,所以1+k1+k 2AB =0.但d AB =1-0 +0-1 =2>0,故C 错误;对于D ,条件等价于关于x ,y 的方程组x +y =1x 2+y -r 2=r2,即x +y =1x 2+y 2=2ry 有四个解.如下图所示,该方程组可以直观地理解为正方形x +y =1和圆x 2+y 2=2ry 有四个公共点,直观的理解即为圆x 2+y 2=2ry 与矩形上方的两条边所在的直线均相交,且交点都在边的内部,而当r =2-1时,圆与上方的两条边相切,当r =12时,圆与上方的边的交点恰落在端点上,故可猜测取值范围是2-1,12,下面再使用二次方程工具严格证明此结论(也可以使用距离公式等其它方法证明).若x ,y 满足原方程组,则y =x 2+y 22r>0,故x +y =1.而r 2=x 2+y -r 2=x 2+1-x -r 2=2x 2-21-r x +1-r 2,故2x 2-21-r x +1-2r =0,同时还有x =1-y ≤1.由于当x 确定后,y 只有唯一可能的取值1-x ,而方程组有四个解,所以使得相应的y 存在的x 至少有四个.根据前面的讨论,这样的x 必满足2x 2-21-r x +1-2r =0,且x ≤1,所以方程2x 2-21-r x +1-2r =0必定在-1,1 上有四个解.这表明关于t 的方程2t 2-21-r t +1-2r =0在0,1 上一定有两个解,所以首先有判别式为正数,结合Δ=41-r 2-81-2r =41-2r +r 2-2+4r =4r 2+2r -1 ,就有r >2-1.同时,由于两根都在0,1 内,故两根乘积为正数,故1-2r >0,即r <12.这就证明了2-1<r <12.最后,当2-1<r <12时,原方程组的确存在四组不同的解:x =1-r +r 2+2r -12y =1+r -r 2+2r -12,x =-1-r +r 2+2r -12y =1+r -r 2+2r -12,x =1-r -r 2+2r -12y =1+r +r 2+2r -12,x =-1-r -r 2+2r -12y =1+r +r 2+2r -12.所以r 的取值范围是2-1,12,D 正确.故选:ABD .三、填空题9(2024·湖南长沙·三模)已知函数y =f x ,任取t ∈R ,定义集合A t ={y ∣y =f x ,点P t ,f t 、Q x ,f x 满足PQ ≤2 . 设M t ,m t 分别表示集合A t 中元素的最大值和最小值,记h t =M t -m t ,试解答以下问题:(1)若函数f x =x 2,则h 0 =;(2)若函数f x =sin π2x ,则h t 的最小正周期为.【答案】12【分析】(1)把t =0代入,然后计算A t 的最大值和最小值即可.(2)先表示出P t ,sin π2t 、Q x ,sin π2x ,然后根据P 的位置分类分析M t ,m t 的值.【详解】对于 1 ,因为函数 f x =x 2,当 t =0 时,P 0,0 、Q x ,x 2 且 x -0 2+x 2-0 2≤2,即 x 2+x 4≤2,令 x 2=m ,即 m 2+m ≤2,解得 0≤m ≤1,所以 M t =1,m t =0,所以 h 0 =1-0=1 ;对于 2 ,如图所示,若函数 f x =sin π2x ,此时,函数的最小正周期为 2ππ2=4,点 P t ,sin π2t 、Q x ,sin π2x ,当点 P 在 A 点时,点 Q 在曲线 OAB 上,M t =1,m t =0,h t =M t -m t =1;当点 P 在曲线上从 A 接近 B 时,h t 逐渐增大,当点 P 在 B 点时,M t =1,m t =-1h t =M t -m t =2;当点 P 在曲线上从 B 接近 C 时,h t 逐渐减小,当点 P 在 C 点时,M t =1,m t =0,h t =M t -m t =1;当点 P 在曲线上从 C 接近 D 时,h t 逐渐增大,当点 P 在 D 点时,M t =1,m t =-1,h t =M t -m t =2;当点 P 在曲线上从 D 接近 E 时,h t 逐渐减小,当点 P 在 E 点时,M t =1,m t =0,h t =M t -m t =1;依此类推,发现 h t 的最小正周期为 2 ,故答案为:(1)1;(2)2.10(2024·四川成都·模拟预测)定义在封闭的平面区域D 内任意两点的距离的最大值称为平面区域D 的“直径”.如图,已知锐角三角形的三个顶点A ,B ,C 在半径为1的圆上,角的对边分别为a ,b ,c ,A =π3.分别以△ABC 各边为直径向外作三个半圆,这三个半圆和△ABC 构成平面区域D ,则平面区域D 的“直径”的取值范围是.【答案】3+32,332【分析】(1)根据给定条件,利用正弦定理边化角,结合和角的正弦公式求出A ;(2)利用向量线性运算,结合向量的三角不等式求出区域D 的“直径”关系式,再利用三角恒等变换结合正弦函数性质求出范围即得.【详解】如图,F ,G 是AC ,BC 的中点,E ,F ,G ,H 四点共线,设P ,Q 分别为BC 、AC 上任意一点,PQ =PG +GF +FQ,PQ =PG +GF +FQ ≤PG +GF +FQ=HG +GF +FE =HE =a +b +c2,即PQ 的长小于等于△ABC 周长的一半,当PQ 与HE 重合时取等,同理,三个半圆上任意两点的距离最大值等于△ABC 周长的一半,因此区域D 的“直径”为△ABC 的周长l 的一半,由正弦定理得:a =2sinπ3=3,b =2sin B ,c =2sin C ,则l =3+2sin B +2sin 2π3-B =3+3sin B +3cos B =3+23sin B +π6.由△ABC 为锐角三角形,得0<B <π20<2π3-B <π2 ,即π6<B <π2,则π3<B +π6<2π3,32<sin B +π6≤1,于是3+3<l ≤33,所以平面区域D 的“直径”的取值范围是3+32,332.故答案为:3+32,332.11(2024·广东佛山·二模)近年,我国短板农机装备取得突破,科技和装备支撑稳步增强,现代农业建设扎实推进.农用机械中常见有控制设备周期性开闭的装置.如图所示,单位圆O 绕圆心做逆时针匀速圆周运动,角速度大小为2πrad /s ,圆上两点A ,B 始终满足∠AOB =2π3,随着圆O 的旋转,A ,B 两点的位置关系呈现周期性变化.现定义:A ,B 两点的竖直距离为A ,B 两点相对于水平面的高度差的绝对值.假设运动开始时刻,即t =0秒时,点A 位于圆心正下方:则t =秒时,A ,B 两点的竖直距离第一次为0;A ,B 两点的竖直距离关于时间t 的函数解析式为f t =.【答案】133sin 2πt +π3【分析】以O 为原点,以OA 所在直线为y 轴建立平面直角坐标系,利用三角函数定义表示点A ,B 的坐标,由已知结合和角的正弦公式化简即得.【详解】以O 为原点,以OA 所在直线为y 轴,建立平面直角坐标系,由于角速ω=2πrad /s ,设点A cos 2πt -π2 ,sin 2πt -π2 ,圆上两点A 、B 始终保持∠AOB =2π3,则B cos 2πt +π6 ,sin 2πt +π6,要使A 、B 两点的竖直距高为0,则sin 2πt -π2 =sin 2πt +π6 ,第一次为0时,4πt -π3=π,解得t =13,f (t )=sin 2πt +π6 -sin 2πt -π2=32sin2πt +12cos2πt +cos2πt=32sin2πt +32cos2πt=3sin 2πt +π3.故答案为:13;3sin 2πt +π3【点睛】关键点点睛:涉及三角函数实际应用问题,探求动点坐标,找出该点所在射线为终边对应的角是关键,特别注意,始边是x 轴非负半轴.12(2024·山东枣庄·模拟预测)设A x 1,y 1 ,B x 2,y 2 为平面上两点,定义d (A ,B )=x 1-x 2 +y 1-y 2 、已知点P 为抛物线C :x 2=2py (p >0)上一动点,点Q (3,0),d (P ,Q )的最小值为2,则p =;若斜率为32的直线l 过点Q ,点M 是直线l 上一动点,则d (P ,M )的最小值为.【答案】 232【分析】利用定义结合二次函数求最值计算即可得第一空,过P 作PN ⎳x 并构造直角三角形,根据d (P ,M )。
2019-2020学年北京人大附中高一分班考数学试题含解析

2019年人大附中新高一分班考试数学试题真题一、选择题(本大题共17小题,共34分)1. 小雨利用几何画板探究函数()a y x b x c =--图象,在他输λ一组,,a b c 的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )A. 0,0,0a b c >>= B. 0,0,0a b c <>=C. 0,0,0a b c >== D. 0,0,0a b c <=>【答案】B 2. 大于1的正整数m 的三次幂可“分裂”成若干个连续奇数的和,如33235,37911=+=++,3413151719,=+++⋯若3m 分裂后,其中有一个奇数是103,则m 的值是( )A. 9B. 10C. 11D. 12【答案】B3. 如图,AB 是半圆O 直径,按以下步骤作图:(1)分别以,A B 为圆心,大于AO 长为半径作弧,两弧交于点P ,连接OP 与半圆交于点C ;(2)分别以,A C 为圆心,大于12AC 长为半径作弧,两弧交于点Q ,连接OQ 与半圆交于点D ;(3)连接,,,AD BD BC BD 与OC 交于点E .根据以上作图过程及所作图形,下列结论:①BD 平分ABC ∠;②//BC OD ;③CE OE =;④2AD OD CE =⋅;所有正确结论的序号是( )的A. ①②B. ①④C. ②③D. ①②④【答案】D 4. 图1的摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,9号车厢才会运行到最高点?( )A. 10B. 20C. 152D. 452【答案】B 5. 某旅行团到森林游乐区参观,如表为两种参观方式与所需的缆车费用.已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘览车,回程有10人搭乘缆车.若他们缆车费用的总花费为4100元,则此旅行团共有多少人?( )参观方式缆车费用去程及回程均搭乘缆车300元单程搭乘缆车,单程步行200元A. 16B. 19C. 22D. 25【答案】A 6. 如图,坐标平面上有一顶点为A 的抛物线,此拋物线与方程式2y 的图形交于B C 、两点,ABC 为正三角形.若A 点坐标为()3,0-,则此拋物线与y 轴的交点坐标为何?( )A. 90,2⎛⎫ ⎪⎝⎭ B. 270,2⎛⎫ ⎪⎝⎭ C. ()0,9 D. ()0,19【答案】B7. 如图的七边形ABCDEFG 中,,AB ED 的延长线相交于O 点.若图中1,2,3,4∠∠∠∠的外角的角度和为220 ,则BOD ∠的度数为何?( )A. 40B. 45C. 50D. 60【答案】A 8. 如图,菱形ABCD 的边长为10,圆O 分别与AB AD 、相切于、E F 两点,且与BG 相切于G 点.若5AO =,且圆O 的半径为3,则BG 的长度为( )A. 4B. 5C. 6D. 7【答案】C9. 桌面上有甲、乙、丙三个杯子,三杯内原本均装有一些水.先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的2倍多40毫升;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的3倍少180毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升?( )A. 80B. 110C. 140D. 220【答案】B10. 如图,坐标平面上,二次函数24y x x k =-+-的图形与x 轴交于、A B 两点,与y 轴交于C 点,其顶点为D ,且0k >.若ABC 与ABD △的面积比为1:4,则k 值为何?( )A. 1B. 12C. 43D. 45【答案】D 11. 如图的ABC 中有一正方形DEFG ,其中D 在AC 上,、E F 在AB 上,直线AG 分别交DE BC 、于M N 、两点.若90,4,3,1B AB BC EF ∠==== ,则BN 的长度为何?( )A. 43 B. 32 C. 85 D. 127【答案】D12. 图(一)、图(二)分别为甲、乙两班学生参加投篮测验的投进球数直方图.若甲、乙两班学生的投进球数的众数分别为a b 、;中位数分别为c d 、,则下列关于a b c d 、、、的大小关系,何者正确?( )A. ,a b c d>> B. ,a b c d ><C. ,a b c d<> D. ,a b c d<<【答案】A 13. 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )A. 12 B. 35 C. 2 D. 4-【答案】D14. 如图的矩形ABCD 中,E 点在CD 上,且AE AC <.若P Q 、两点分别在AD AE 、上,:4:1AP PD =,:4:1AQ QE =,直线PQ 交AC 于R 点,且Q R 、两点到CD 的距离分别为q r 、,则下列关系何者正确?( )A. ,q r QE RC <=B. ,q r QE RC<<C. ,q r QE RC== D. ,q r QE RC=<【答案】D 15. 下表为小洁打算在某电信公司购买一支MAT 手机与搭配一个号码的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费,若小洁每个月的通话费均为x 元,x 为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x 至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )甲方案乙方案号码的月租费(元)400600MAT 手机价格(元)1500013000注意事项:以上方案两年内不可变更月租费A. 500B. 516C. 517D. 600【答案】C 16. 如图的矩形ABCD 中,E 为AB 的中点,有一圆过,,C D E 三点,且此圆分别与,AD BC 相交于,P Q 两点.甲、乙两人想找到此圆的圆心O ,其作法如下:(甲)作DEC ∠的角平分线L ,作DE 的中垂线,交L 于O 点,则O 即为所求;(乙)连接,PC QD ,两线段交于一点O ,则O 即为所求.对于甲、乙两人的作法,下列判䉼何者正确?( )A. 两人皆正确B. 两人皆错误C 甲正确,乙错误D. 甲错误,乙正确【答案】A17. 如图,正六边形ABCDEF 中,P Q 、两点分别为,ACF CEF △△的内心.若2AF =,则PQ 的长度为何?( ).A. 1B. 2C. 2- D. 4-【答案】C 二、填空题(本大题共3小题,共9分)18. 如图,正方形ABCD 的边长是3,,P Q 分别在,AB BC 的延长线上,BP CQ =,连接,AQ DP 交于点O ,并分别与,CD BC 交于点,F E ,连接AE .下列结论:①AQ DP⊥②2OA OE OP=⋅③AOD OECFS S = 四边形④当1BP =时,1an 136t OAE ∠=其中正确结论的序号是__________.【答案】①③④19. 在等边ABC 中,M N P 、、分别是边AB BC CA 、、上的点(不与端点重合),对于任意等边ABC ,下面四个结论中:①存在无数个MNP △是等腰三角形;②存在无数个MNP △是等边三角形;③存在无数个MNP △是等腰直角三角形;④存在一个MNP △在所有MNP △中面积最小.所有正确结论的序号是__________.【答案】①②③20. 如图,在Rt ABC 中,90C = ∠,记,x AC y BC AC ==-,在平面直角坐标系xOy 中,定义(),x y 为这个直角三角形的坐标,Rt ABC 为点(),x y 对应的直角三角形.有下列结论:①在x 轴正半轴上的任意点(),x y对应的直角三角形均满足AB =;②在函数2019(0)y x x=>的图象上存在两点边,P Q ,使得它们对应的直角三角形相似;③对于函2(2020)1(0)y x x =-->图象上的任意一点P ,都存在该函数图象上的另一点Q ,使得这两个点对应的直角三角形相似;④在函数22020(0)y x x =-+>的图象上存在无数对点,(P Q P 与Q 不重合),使得它们对应的直角三角形全等.所有正确结论的序号是__________.【答案】①③④三、解答题(本大题共9小题,第21-26题每题6分,第27-29题,每题7分,共57分)21. 如图,AM 是ABC 的中线,D 是线段AM 上一点(不与点A 重合)//DE AB 交AC 于点,//F CE AM ,连结AE.的(1)如图1,当点D 与M 重合时,求证:四边形ABDE 是平行四边形;(2)如图2,当点D 不与M 重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,延长BD 交AC 于点H ,若BH AC ⊥,且BH AM =.①求CAM ∠的度数;②当4FH DM ==时,求DH 的长.【答案】(1)证明见解析;(2)成立,理由见解析;(3)①30°;②22. 对于平面直角坐标系xOy 中的点P 和M ,给出如下定义:若M 上存在两个点,A B ,使AB =2PM ,则称点P 为 的“美好点”.(1)当 M 半径为2,点M 和点O 重合时.①点()()()1232,0,1,1,2,2P P P -中, O 的“美好点"是__________.②若直线2y x b =+上存在点P 为 O 的“美好点”,求b 的取值范围;(2)点M 为直线y x =上一动点,以2为半径作M ,点P 为直线4y =上一动点,点P 为 M 的“美好点”,求点M 的横坐标m 的取值范围.【答案】(1)①P 1和P 2;②b (2)2≤m ≤6.23. 如图,在平面直角坐标系xOy 中,过T e 外一点P 引它的两条切线,切点分别为,M N ,若60≤ 180MPN ∠< ,则称P 为T e 的环绕点.(1)当 O 半径为1时,①在()()()1231,0,1,1,0,2P P P 中,O 的环绕点是__________.②直线2y x b =+与x 轴交于点A ,与y 轴交于点B ,若线段AB 上存在 的环绕点,求b 的取值范围;(2)T e 的半径为1,圆心为()0,t ,以(0)m m ⎛⎫> ⎪ ⎪⎝⎭为半径的所有圆构成图形H ,若在图形H 上存在T e 的环绕点,直接写出t 的取值范围.【答案】(1)①P 1,P 3;②1b ≤<或1b ≤-<;(2)-2<t ≤4.24. 在平面直角坐标系xOy 中,我们称横从坐标都是整数的点为整点,若坐标系内两个整点(),A p q 、()(),B m n m n ≤满足关于x 的多项式2x px q ++能够因式分解为()()x m x n ++,则称点B 是A 的分解点.例如()3,2A 、()1,2B 满足()()23212x x x x ++=++,所以B 是A 的分解点.(1)在点()15,6A 、()20,3A 、()32,0A -中,请找出不存在分解点的点__________;(2)点P 、Q 在纵轴上(P 在Q 的上方),点R 在横轴上,且点P 、Q 、R 都存在分解点,若PQR 面积为6,请直接写出满足条件的PQR 的个数及每个三角形的顶点坐标;(3)已知点D 在第一象限内,D 是C 的分解点,请探究OCD 是否可能是等腰三角形?若可能请求出所有满足条件的点D 的坐标;若不可能,请说明理由.【答案】(1)2A ;(2)答案见解析;(3)OCD 不可能为等腰三角形,理由见解析.25. 已知关于x 的一元二次方程2104x bx c ++=(1)21c b =-时,求证:方程一定有两个实数根.(2)有甲、乙两个不透明的布袋,甲袋中装有3个除数字外完全相同的小球,分别标有数字1,2,3,乙袋中装有4个除数字外完全相同的小球,分别标有数字1,2,3,4,从甲袋中随机抽取一个小球,记录标有的数字为b ,从乙袋中随机抽取一个小球,记录标有的数字为c ,利用列表法或者树状图,求b c 、的值使方程2104x bx c ++=两个相等的实数根的概率.【答案】(1)证明见解析;(2)16.26. 如图,在平面直角坐标系xOy 中,直线():10l y kx k =-≠与函数(0)m y x x=>的图象交于点()3,2A .(1)求,k m 的值;(2)将直线l 沿y 轴向上平移(0)t t >个单位后,所得直线与x 轴,y 轴分别交于点,P Q ,与函数y =(0)m x x>的图象交于点C .①当2t =时,求线段QC 的长.②若23QC PQ<<,结合函数图象,直接写出t 的取值范围.【答案】(1)1,6k m ==;(2)①;②12t <<.27. 在平面直角坐标系xOy 中,拋物线2224y x ax a a =-+-+顶点为A ,点,B C 为直线3y =上的两个动点(点B 在点C 的左侧),且3BC =.(1)求点A 的坐标(用含a 的代数式表示);(2)若ABC 是以BC 为直角边的等腰直角三角形,求拋物线的解析式;(3)过点A 作x 轴的垂线,交直线3y =于点D ,点D 恰好是线段BC 三等分点且满足3BC BD =,若抛物线与线段BC 只有一个公共点,结合函数的图象,直接写出a 的取值范围.【答案】(1)(),4A a a -;(2)2(2)6y x =++或2(4)y x =-;(3)1a =或25a <≤.28. 如图,在Rt ABC 中,90ACB ∠= ,点C 关于直线AB 的对称点为D ,连接,BD CD ,过点B 作//BE AC 交直线AD 于点E .(1)依题意补全图形;(2)找出一个图中与CDB △相似的三角形,并证明;(3)延长BD 交直线AC 于点F ,过点F 作FH //AE 交直线BE 于点H ,请补全图形,猜想,,BC CF BH 之间的数量关系并证明.【答案】(1)答案见解析;(2)与CDB △相似的三角形是ABE △,证明见解析;(3)作图见解析;22BH FC BC CF ⋅=+,证明见解析.29. 新定义:在平面直角坐标系xOy 中,若几何图形G 与A 有公共点,则称几何图形G 的叫A 的关联图形,特别地,若A 的关联图形G 为直线,则称该直线为A 的关联直线.如图,M ∠为A 的关联图形,的直线l 为A 的关联直线.(1)已知 O 是以原点为圆心,2为半径的圆,下列图形:①直线22y x =+;②直线3y x =-+;③双曲线2y x=,是O 关联图形的是__________(请直接写出正确的序号);(2)如图1,T e 的圆心为()1,0T ,半径为1,直线:l y x b =-+与x 轴交于点N ,若直线l 是T e 的关联直线,求点N 的横坐标的取值范围;(3)如图2,已知点()0,2B 、()2,0C 、()0,2D -,I 经过点C ,I 的关联直线HB 经过点B ,与I 的一个交点为P ;I 的关联直线HD 经过点D ,与I 的一个交点为Q ;直线HB 、HD 交于点H ,若线段PQ 在直线6x =上且恰为I 的直径,请直接写出点H 横坐标h 的取值范围.【答案】(1)①③;(2)11b +≤≤;(3)60h -≤<或02h <≤.的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲:创新问题和新定义问题
1. (2015江淮名校一模)把几个数用大括号围起来,中间用逗号断开,如:{1,2,3}、{-2,7,8,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当实数a是集合的元素时,实数8-a也必是这个集合的元素,这样的集合我们称为好的集合.下列集合为好的集合的是( )
A. {1,2}
B. {1,4,7}
C. {1,7,8}
D. {-2,6}
2. (2015钦州)对于任意的正数m、n,定义运算※为:m※n
=
)
)
m n
m n
≥
<
.计算(3※2)×(8※12)的结
果为( )
A. 2-
4 B. 2
D. 20
3. (2015成都)如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”. 以下关于倍根方程的说法,正确的是.(写出所有正确说法的序号)
①方程x2-x-2=0是倍根方程;
②若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
③若点(p,q)在反比例函数y=2
x
的图象上,则关于x的方程px2+3x+q=0是倍根方程;
④若方程ax2+bx+c=0是倍根方程,且相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,则方程
ax2+bx+c=0的一个根为5 4 .
4. 我们用[x]表示不大于x的最大整数,例如[1.5]=1,[-2.5]=-3.请解决下列问题: (1)[π]= ,[-π]= .(其中π为圆周率);
(2)已知x、y满足方程组
[][] 1
2[]3[]4
x y
x y
+=
⎧
⎨
+=
⎩
,求x、y的取值范围;
(3)当-1≤x≤2时,求函数y=[x]2-2[x]+3的最大值与最小值.
5. 在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),(2,2),…,都是“梦之点”.显然“梦之点”有无数个.
(1)若点P(m,5)是反比例函数y=n
x
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)一次函数y=2kx-1(k为常数,k≠0)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由;
(3)若二次函数y=ax2+bx+1(a,b为常数,a≠0)的图象上有且只有一个“梦之点”A(c,c),令t=b2+4a,当-2<b<2时,求t的取值范围.
6. 如图①,在矩形ABCD中,将矩形折叠,使点B落在边AD(含端点)上,落点记为E,这时折痕与边BC或边CD(含端点)交于点F.然后再展开铺平,则以B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.
(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”一定是一个三角形;
(2)如图②,在矩形ABCD中,AB=2,BC=4.当它的“折痕△BEF”的顶点E位于边AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;
(3)如图③,在矩形ABCD中,AB=2,BC=4.该矩形是否存在面积最大的“折痕△BEF”?若存在,说明理由,并求出此时点E的坐标;若不存在,为什么?
一、选择题
1.[2015·德州] 一组数1,1,2,x ,5,y ,…,满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y 表示的数为( )
A .8
B .9
C .13
D .15
2.[2015·永州] 定义[x]为不超过x 的最大整数,如[3.6]=3,[0.6]=0,[-3.6]=-4.对于任意实数x ,下列式子中错误的是( )
A .[x]=x(x 为整数)
B .0≤x -[x]<1
C .[x +y]≤[x]+[y]
D .[n +x]=n +[x](n 为整数)
3.[2015·资阳] 如图K 35-1,AD ,BC 是⊙O 的两条互相垂直的直径,点P 从点O 出发,沿O →C →D →O 的路线匀速运动,设∠APB =y(单位:度),那么y 与点P 运动的时间x(单位:秒)的关系图象是( )
图K 35-1 图K 35-2
4.[2015·重庆] 如图K 35-3,在平面直角坐标系中,菱形ABOC 的顶点O 在坐标原点,边BO 在x 轴的负半
轴上,∠BOC =60°,顶点C 的坐标为(m ,3 3),反比例函数y =k x
的图象与菱形对角线AO 交于点D ,连接BD ,当BD ⊥x 轴时,k 的值是( )
A .6 3
B .-6 3
C .12 3
D .-12 3
图K 35-4 图K 35-3
5.[2014·湖州] 如图K 35-4,已知正方形ABCD ,E 是边AB 的中点,O 是线段AE 上的一个动点(不与点A ,E 重合),以点O 为圆心,OB 为半径的圆与边AD 相交于点M ,过点M 作⊙O 的切线交DC 于点N ,连接OM ,ON ,BM ,BN.记△MNO ,△AOM ,△DMN 的面积分别为S 1,S 2,S 3,则下列结论不一定成立的是( )
A .S 1>S 2+S 3
B .△AOM ∽△DMN
C .∠MBN =45°
D .MN =AM +CN
二、填空题
6.[2015·东莞] 观察下列一组数:13,25,37,49,511
,…,根据该组数的排列规律,可推出第10个数是________. 7.定义一种新运算:a ⊗b =b 2-ab ,如:1⊗2=22-1×2=2,则(-1⊗2)⊗3=________.
8.定义⎪⎪⎪⎪⎪⎪a
b c d 为二阶行列式,规定它的运算法则为⎪⎪⎪⎪⎪⎪
a b c d =ad -bc ,那么当x =1时,二阶行列式⎪⎪⎪⎪⎪⎪x +1 10 x -1的值为________.
9.[2015·益阳] 如图K 35-5是用长度相等的小棒按一定规律摆成的一组图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n 个图案中有________根小棒.
图K 35-5 图K 35-6
10.我们经常运用数形结合的思想方法,把数量关系和几何图形巧妙地结合起来,以解决一些数学问题.如图
11.[2015·达州] 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图K35-7的方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…,点A1,A2,A3,…在直线y=x+1上,点C1,C2,C3,…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1,S2,S3,…,S n,则S n的值为________.(用含n的代数式表示,n为正整数)
图K35-7 图K35-8 图K35-9 12.[2014·龙东] 如图K35-8,等腰直角三角形ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+2;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+2;…,按此规律继续旋转,直至得到点P2014为止,则AP2014=________.
13.[2015·资阳] 已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A,B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线所对应的函数解析式为____________.
14.[2015·深圳] 如图K35-9,Rt△ABC的直角边BC在x轴负半轴上,斜边AC上的中线BD的反向延长线
交y轴正半轴于点E,双曲线y=k
x(x<0)的图象经过点A,若S△BEC=8,则k等于________.
15.[2015·日照] 如图K35-10,在平面直角坐标系中,四边形ODEF和四边形ABCD都是正方形,点F在x
轴的正半轴上,点C在边DE上,反比例函数y=k
x(k≠0,x>0)的图象过点B,E,若AB=2,则k的值为________.
图K35-10 图K35-11
16.[2015·宜宾] 如图K35-11,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于
点E,F,连接BD,DP,BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②FP
PH=3
5;③DP
2=PH·PB;④
S△BPD S正方形ABCD =
3-1
4.其中正确的是________(写出所有正确结论的序号).。
