8577 合并顺序表
节点坐标表

-42 -272 139 144 146 173 265 263 597 521 79 3 -54 41 42 419 539 544 176 211 215 267 263 257 257 249 249 563 563 209 209 210 211 580 579 606 606 597 524 468 469 80 418 472 470 541
33 33 34 34 35 35 36 36 37 37 38 38 39 39 40 40 41 41 42 42 43 43 44 44 45 45 46 46 47 47 48 48 49 49 50 50 51 51 52 52 53 53 54 54 55 55 56
I[34] J[35] I[35] J[36] I[36] J[37] I[37] J[38] I[38] J[39] I[39] J[10] I[41] J[40] I[42] J[41] I[43] J[42] I[45] J[44] I[47] J[46] I[49] J[48] I[50] J[49] I[51] J[50] I[53] J[52] I[54] J[43] I[44] J[54] I[55] J[45] I[56] J[55] I[57] J[56] I[58] J[57] I[59] J[58] I[60] J[59] I[61]
56 57 57 58 58 59 59 60 60 61 61 62 62 63 63 64 64 65 65 66 66 67 67
J[60] I[46] J[61] I[62] J[47] I[48] J[62] I[63] J[51] I[52] J[63] I[64] J[53] I[65] J[64] I[66] J[65] I[67] J[66] I[68] J[67] I[10] J[68]
禾驮乡核查底册

编制
国税
地税
质检
其他
名录
组机构代码
1
1
1
1 1
665414515 GS7346651
编制
国税
地税
质检
其他
名录 1
组织机构代码 01533462B 015334628 43880066x
1 1 1 1
1
1
43880066X
1 1 1 1 1
GS7347005 GS734703X GS7347048 GS7340276
联系方式
质:15809461688; 地:15809461688; 质:15809461688; 国:15809461688; 工:15809461688; 工:15809461688; 工:15809461688 工:甘肃省定西市岷 县禾驮乡卓洛村;工:甘肃 工:15593278188; 省定西市岷 县禾驮乡卓洛村;工:甘肃省定西市 工:15593278188; 岷 县禾驮乡卓洛村 工:15593278188 统:禾驮 统:7722184 工:13993247218; 编:岷县禾驮乡禾驮村 工:13993247218; 工:13993247218 统:禾驮;质:甘肃省定西市岷县禾驮乡禾驮村; 工:13993277287; 工:13830236936; 编:岷县禾驮乡禾驮村 工:13830236936; 工:13830236936
乔成福 占建平 乔爱民 刘光祖 卢兴广
621126 621126205211 621126 621126205211 621126
详细名称
法定代表人 行政区划代码
岷县新安粮油有限责任公司 西江供电所
韩李安 马军军
621126205211 621126205211
电话电缆色谱排列顺序

电话电缆色谱排列顺序5种主色:白色、红色、黑色、黄色、紫色5种次色:兰色、桔色、绿色、棕色、灰色100对电话电缆色谱线序表说明:100对的电话电缆里有4种标识线,第一的25对是用“白兰"标识线缠着的!!第二的25对是用“白桔"标识线缠着的!第三的25对是用“白绿"标识线缠着的!第四的25对是用“白棕"标识线缠着的!(注意:用“白兰"标识线缠着)1对—白兰 2对—白桔 3对—白绿 4对—白棕 5对—白灰6对—红兰 7对—红桔 8对—红绿 9对—红棕 10对—红灰11对—黑兰 12对—黑桔 13对—黑绿 14对—黑棕 15对—黑灰16对—黄兰 17对—黄桔 18对—黄绿 19对—黄棕 20对—黄灰21对—紫兰 22对—紫桔 23对—紫绿 24对—紫棕 25对—紫灰(注意:用“白桔"标识线缠着)26对—白兰 27对—白桔 28对—白绿 29对—白棕 30对—白灰31对—红兰 32对—红桔 33对—红绿 34对—红棕 35对—红灰36对—黑兰 37对—黑桔 38对—黑绿 39对—黑棕 40对—黑灰41对—黄兰 42对—黄桔 43对—黄绿 44对—黄棕 45对—黄灰46对—紫兰 47对—紫桔 48对—紫绿 49对—紫棕 50对—紫灰(注意:用“白绿"标识线缠着)51对—白兰 52对—白桔 53对—白绿 54对—白棕 55对—白灰56对—红兰 57对—红桔 58对—红绿 59对—红棕 60对—红灰61对—黑兰 62对—黑桔 63对—黑绿 64对—黑棕 65对—黑灰66对—黄兰 67对—黄桔 68对—黄绿 69对—黄棕 70对—黄灰71对—紫兰 72对—紫桔 73对—紫绿 74对—紫棕 75对—紫灰(注意:用“白棕"标识线缠着)76对—白兰 77对—白桔 78对—白绿 79对—白棕 80对—白灰81对—红兰 82对—红桔 83对—红绿 84对—红棕 85对—红灰86对—黑兰 87对—黑桔 88对—黑绿 89对—黑棕 90对—黑灰91对—黄兰 92对—黄桔 93对—黄绿 94对—黄棕 95对—黄灰96对—紫兰 97对—紫桔 98对—紫绿 99对—紫棕 100对—紫灰。
[计算机软件产品开发文件编制指南]GB8567-88
![[计算机软件产品开发文件编制指南]GB8567-88](https://img.taocdn.com/s3/m/f66c638e04a1b0717fd5ddf5.png)
引言1 目的一项计算机软件的筹划、研制及实现,构成一个软件开发项目。
一个软件开发项目的进行,一般需要在人力和自动化资源等方面作重大的投资。
为了保证项目开发的成功,最经济地花费这些投资,并且便于运行和维护,在开发工作的每一阶段,都需要编制二定的文件。
这些文件连同计算机程序及数据一起,构成为计算机软件。
文件是计算机软件中不可缺少的组成部分,它的作用是:a.作为开发人员在一定阶段内的工作成果和结束标志;b.向管理人员提供软件开发过程中的进展和情况,把软件开发过程中的一些“不可见的”事物转换成“可见的”文字资料。
以便管理人员在各个阶段检查开发计划的实施进展,使之能够判断原定目标是否已达到,还将继续耗用资源的种类和数量;C.记录开发过程中的技术信息,便于协调以后的软件开发、使用和修改;d.提供对软件的有关运行、维护和培训的信息,便于管理人员、开发人员、操作人员和用户之间相互了解彼此的工作;e.向潜在用户报导软件的功能和性能,使他们能判定该软件能否服务于自己的需要。
换言之,本指南认为:文件的编制必须适应计算机软件整个生存周期的需要。
计算机软件所包含的文件有两类:一类是开发过程中填写的各种图表,可称之为工作表格;另一类则是应编制的技术资料或技术管理资料,可称之为文件。
本指南规定软件文件的编制形式,并提供对这些规定的解释。
本指南的目的是使得所编制的软件文件确实能够起到软件文件应该发挥的作用。
2 范围本指南是一份指导性文件。
本指甫建议,在一项计算机软件的开发过程中,一般地说,应该产生十四种文件。
这十四种文件是:可行性研究报告;项目开发计划;软件需求说明书;数据要求说明书;概要设计说明书;详细设计说明书;数据库设计说明书;用户手册;操作手册;模块开发卷宗;测试计划;测试分析报告;开发进度月报;项目开发总结报告。
本指南将给出开发过程中建议产生的这十四种文件的编制指导,同时,本指南也是这十四种文件的编写质量的检验准则。
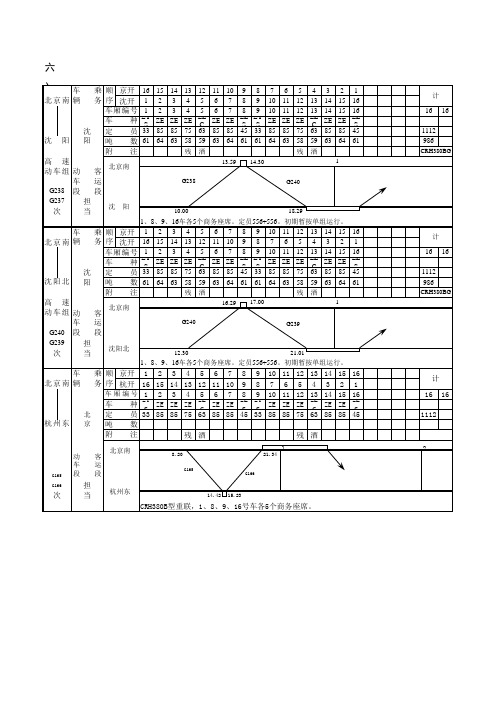
中国铁路2015年下半年运行图直通旅客列车编组调整表
担 当
邵阳
15.15 15.35
统型CRH380B重联,1、8、9、16车各5个商务座席 乘 顺 南开 务 序 深开 车 定 吨 附
客 运 段 8 1 车厢编号 1 7 2 2 6 3 3 5 4 4 4 5 5 3 6 6 2 7 7 1 8 8
计 8 556 0
2
21.23
16
深圳北
种 ZYS ZE ZE ZE ZEC ZE ZE ZES 员 33 85 85 75 63 85 85 45 数 注 残 酒
11 6 6 ZE 85 63
10 9 8 7 8 9 7 8 9 ZE ZES ZYS 85 45 33 64 61 61
13.59 14.30
7 10 10 ZE 85 64
6 11 11 ZE 85 63
5 12 12 ZE 75 58 残
4 13 13 ZEC 63 59 酒
3 14 14 ZE 85 63
1
14.41 14.08
郑州东调向,CRH380A型,1、8车各5个特等座。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ZYS ZY SW ZY ZE ZE ZE ZE CA ZE ZE ZE ZE ZE ZE ZYS
16 1 16 ZES 45 61
计 16 1112 986
CRH380BG
16
附 高 速 动车组 动 车 G240 段
G239
注
残 酒
16.29 17.00
残
酒
[小学奥数专题15】7-5_组合_题库学生版

组合知识框架图7 计数综合7-5 组合7-5-1组合及其应用7-5-2排除法7-5-3插板法教学目标1.使学生正确理解组合的意义;正确区分排列、组合问题;2.了解组合数的意义,能根据具体的问题,写出符合要求的组合;3.掌握组合的计算公式以及组合数与排列数之间的关系;4.会分析与数字有关的计数问题,以及与其他专题的综合运用,培养学生的抽象能力和逻辑思维能力;通过本讲的学习,对组合的一些计数问题进行归纳总结,重点掌握组合的联系和区别,并掌握一些组合技巧,如排除法、插板法等.知识要点一、组合问题日常生活中有很多“分组”问题.如在体育比赛中,把参赛队分为几个组,从全班同学中选出几人参加某项活动等等.这种“分组”问题,就是我们将要讨论的组合问题,这里,我们将着重研究有多少种分组方法的问题.一般地,从个不同元素中取出个()元素组成一组不计较组内各元素的次序,叫做从个不同元素中取出个元素的一个组合.从排列和组合的定义可以知道,排列与元素的顺序有关,而组合与顺序无关.如果两个组合中的元素完全相同,那么不管元素的顺序如何,都是相同的组合,只有当两个组合中的元素不完全相同时,才是不同的组合.从个不同元素中取出个元素()的所有组合的个数,叫做从个不同元素中取出个不同元素的组合数.记作.一般地,求从个不同元素中取出的个元素的排列数可分成以下两步:第一步:从个不同元素中取出个元素组成一组,共有种方法; 第二步:将每一个组合中的个元素进行全排列,共有种排法.根据乘法原理,得到.因此,组合数.这个公式就是组合数公式.二、组合数的重要性质一般地,组合数有下面的重要性质:()这个公式的直观意义是:表示从个元素中取出个元素组成一组的所有分组方法.表示从个元素中取出()个元素组成一组的所有分组方法.显然,从个元素中选出个元素的分组方法恰是从个元素中选个元素剩下的()个元素的分组方法.例如,从人中选人开会的方法和从人中选出人不去开会的方法是一样多的,即.规定,.例题精讲模块一、组合及其应用【例 1】 计算:⑴ ,;⑵ ,.(2级)【例 2】 计算:⑴ ;⑵ ;⑶ .(2级)【巩固】 计算:⑴ ;⑵ ;⑶ .(2级)【例3】 6个朋友聚会,每两人握手一次,一共握手多少次?(2级)【巩固】 某班毕业生中有名同学相见了,他们互相都握了一次手,问这次聚会大家一共握了多少次手?(2级)【例4】 (难度等级 ※※)学校开设门任意选修课,要求每个学生从中选学门,共有多少种不同的选法?(4级)【例5】 某校举行排球单循环赛,有个队参加.问:共需要进行多少场比赛?(2级)【巩固】 芳草地小学举行足球单循环赛,有个队参加.问:共需要进行多少场比赛?(2级)【例6】 一批象棋棋手进行循环赛,每人都与其他所有的人赛一场,根据积分决出冠军,循环赛共要进行78场,那么共有多少人参加循环赛?(4级)【例7】 某校举行男生乒乓球比赛,比赛分成3个阶段进行,第一阶段:将参加比赛的48名选手分成8个小组,每组6人,分别进行单循环赛;第二阶段:将8个小组产生的前2名共16人再分成个小组,每组人,分别进行单循环赛;第三阶段:由4个小组产生的个第名进行场半决赛和场决赛,确定至名的名次.问:整个赛程一共需要进行多少场比赛?(4级)【例8】 从分别写有、、、、的五张卡片中任取两张,做成一道两个一位数的乘法题,问:⑴ 有多少个不同的乘积?2 有多少个不同的乘法算式?(6级)【巩固】 9、8、7、6、5、4、3、2、1、0这10个数字中划去7个数字,一共有多少种方法?(4级)【巩固】 从分别写有、、、、、、、的八张卡片中任取两张,做成一道两个一位数的加法题,有多少种不同的和?(4级)【例在中任意取出两个不同的数相加,其和是偶数的共有多9】 少种不同的取法?(6级)【巩固】 从、、……、、这个数中,选取两个不同的数,使其和为偶数的选法总数是多少?(6级)【例10】 一个盒子装有个编号依次为,,,,的球,从中摸出个球,使它们的编号之和为奇数,则不同的摸法种数是多少?(6级)【例11】 用2个1,2个2,2个3可以组成多少个互不相同的六位数?用个,个,个可以组成多少个互不相同的六位数?(6级)【例12】 从,,,,中任取三个数字,从,,,中任取两个数字,组成没有重复数字的五位数,一共可以组成多少个数?(6级)【例13】 从、、、、、、这七个数字中,任取3个组成三位数,共可组成多少个不同的三位数?(这里每个数字只允许用次,比如100、210就是可以组成的,而211就是不可以组成的).(2008年“陈省身杯”国际青少年数学邀请赛五年级)(4级)【例14】 用2个1,2个2,2个3可以组成多少个互不相同的六位数?用2个0,2个1,2个2可以组成多少个互不相同的六位数?(6级)【巩固】用两个3,一个2,一个1,可以组成多少个不重复的4位数?(6级)【例15】 工厂某日生产的10件产品中有2件次品,从这10件产品中任意抽出3件进行检查,问:(1)一共有多少种不同的抽法?(2)抽出的3件中恰好有一件是次品的抽法有多少种?(3)抽出的3件中至少有一件是次品的抽法有多少种?(6级)【例16】 200件产品中有5件是次品,现从中任意抽取4件,按下列条件,各有多少种不同的抽法(只要求列式)?⑴都不是次品;⑵至少有1件次品;⑶不都是次品.(6级)【例17】 在一个圆周上有个点,以这些点为端点或顶点,可以画出多少不同的:1 直线段;⑵ 三角形;⑶ 四边形.(6级)【巩固】 平面内有10个点,以其中每2个点为端点的线段共有多少条?(4级)【巩固】 在正七边形中,以七边形的三个顶点为顶点的三角形共有多少个?(4级)【例18】 平面内有个点,其中点共线,此外再无三点共线.⑴ 可确定多少个三角形?⑵ 可确定多少条射线?(6级)【巩固】 如图,问:⑴ 图中,共有多少条线段?⑵ 图中,共有多少个角?(4级) 图 图【例19】 某班要在名同学中选出名同学去参加夏令营,问共有多少种选法?如果在人中选人站成一排,有多少种站法?(6级)【巩固】 学校新修建的一条道路上有盏路灯,为了节省用电而又不影响正常的照明,可以熄灭其中盏灯,但两端的灯不能熄灭,也不能熄灭相邻的盏灯,那么熄灯的方法共有多少种?(6级)【例20】 将三盘同样的红花和四盘同样的黄花摆放成一排,要求三盘红花互不相邻,共有__________种不同的方法.(2007年“希望杯”第一试)(4级)【例21】 在一次合唱比赛中,有身高互不相同的8个人要站成两排,每排4个人,且前后对齐.而且第二排的每个人都要比他身前的那个人高,这样才不会被挡住.一共有多少种不同的排队方法?(4级)【例22】 在一次考试的选做题部分,要求在第一题的个小题中选做个小题,在第二题的个小题中选做个小题,在第三题的个小题中选做个小题,有多少种不同的选法?(6级)【例23】 某年级个班的数学课,分配给甲、乙、丙三名数学老师任教,每人教两个班,分派的方法有多少种?(6级)【例24】 (2007年“迎春杯”高年级初赛)将19枚棋子放入的方格网内,每个方格至多只放一枚棋子,且每行每列的棋子个数均为奇数个,那么共有________种不同的放法.(4级)【例25】 甲射击员在练习射击,前方有三种不同类型的气球,共3串,有一串是红气球3个,有一串是黄气球2个,有一串是绿气球4个,而且每次射击必须射最下面的气球,问有多少种不同的射法?(6级)【例26】 有8个队参加比赛,采用如下图所示的淘汰制方式.问在比赛前抽签时,可以得到多少种实质不同的比赛安排表?(6级)【例27】 某池塘中有三只游船,船可乘坐人,船可乘坐人,船可乘坐人,今有个成人和个儿童要分乘这些游船,为安全起见,有儿童乘坐的游船上必须至少有个成人陪同,那么他们人乘坐这三支游船的所有安全乘船方法共有多少种?(6级)【例28】 有蓝色旗面,黄色旗面,红色旗面.这些旗的模样、大小都相同.现在把这些旗挂在一个旗杆上做成各种信号,如果按挂旗的面数及从上到下颜色的顺序区分信号,那么利用这些旗能表示多少种不同信号? (4级)【例29】 从名男生,名女生中选出人参加游泳比赛.在下列条件下,分别有多少种选法?⑴恰有名女生入选;⑵至少有两名女生入选;⑶某两名女生,某两名男生必须入选;⑷某两名女生,某两名男生不能同时入选;⑸某两名女生,某两名男生最多入选两人.(6级)【例30】 从名男生,名女生中选出名代表.⑴ 不同的选法共有多少种?⑵ “至少有一名女生”的不同选法共有多少种?⑶ “代表中男、女生都要有”的不同选法共有多少种?(6级)【巩固】 在6名内科医生和4名外科医生中,内科主任和外科主任各一名,现要组成5人医疗小组送医下乡,按照下列条件各有多少种选派方法?⑴ 有3名内科医生和2名外科医生;⑵ 既有内科医生,又有外科医生;⑶ 至少有一名主任参加;⑷ 既有主任,又有外科医生.(8级)【例31】 在10名学生中,有5人会装电脑,有3人会安装音响设备,其余2人既会安装电脑,又会安装音响设备,今选派由人组成的安装小组,组内安装电脑要人,安装音响设备要人,共有多少种不同的选人方案?(8级)【例32】 有11名外语翻译人员,其中名是英语翻译员,名是日语翻译员,另外两名英语、日语都精通.从中找出人,使他们组成两个翻译小组,其中人翻译英文,另人翻译日文,这两个小组能同时工作.问这样的分配名单共可以开出多少张?(8级)【巩固】 某旅社有导游人,其中人只会英语,人只会日语,其余个既会英语又会日语.现要从中选人,其中人做英语导游,另外人做日语导游.则不同的选择方法有多少种?(8级)板块二、排除法对于某些有特殊要求的计数,当限制条件较多时,可以先计算所有可能的情况,再从中排除掉那些不符合要求的情况.【例33】 如图所示,在半圆弧及其直径上共有9个点,以这些点为顶点可画出多少个三角形?(6级)【例34】 如图,正方形的边界上共有7个点、、、、、、、其中、、分别在边、、上.以这7个点中的4个点为顶点组成的不同的四边形的个数是_____ 个.(小学数学奥林匹克决赛) (6级)【巩固】 图中正方形的四边共有8个点,其中任意4点不在一条直线上,那么可组成多少个四边形?(4级)【例35】 如图,有个点,取不同的三个点就可以组合一个三角形,问总共可以组成____个三角形.(4级)【例36】 在的所有自然数中,百位数与个位数不相同的自然数有多少个?(4级)【例37】 1到1999的自然数中,有多少个与5678相加时,至少发生一次进位?(6级)【巩固】 所有三位数中,与456相加产生进位的数有多少个?(6级)【巩固】从1到2004这2004个正整数中,共有几个数与四位数8866相加时,至少发生一次进位?(6级)【例38】 在三位数中,至少出现一个6的偶数有多少个?(6级)【例39】 由0,1,2,3,4,5组成的没有重复数字的六位数中,百位不是2的奇数有 个.(6级)【例40】 从三个0、四个1,五个2中挑选出五个数字,能组成多少个不同的五位数?(6级)【例41】 个人围成一圈,从中选出两个不相邻的人,共有多少种不同选法?(6级)【例42】 一栋12层楼房备有电梯,第二层至第六层电梯不停.在一楼有3人进了电梯,其中至少有一个要上12楼,则他们到各层的可能情况共有多少种?(6级)【例43】 8个人站队,冬冬必须站在小悦和阿奇的中间(不一定相邻),小慧和大智不能相邻,小光和大亮必须相邻,满足要求的站法一共有多少种?(6级)【例44】 若一个自然数中至少有两个数字,且每个数字小于其右边的所有数字,则称这个数是“上升的”.问一共有多少“上升的”自然数?(6级)【例45】 6人同时被邀请参加一项活动.必须有人去,去几个人自行决定,共有多少种不同的去法?(6级)【例46】 由数字1,2,3组成五位数,要求这五位数中1,2,3至少各出现一次,那么这样的五位数共有________个.(2007年“迎春杯”高年级组决赛) (6级)【例47】 5条直线两两相交,没有两条直线平行,没有任何三条直线通过同一个点,以这5条直线的交点为顶点能构成几个三角形?(构成的三角形的边不一定在这5条直线上) (8级)【例48】 正方体的顶点(8个),各边的中点(12个),各面的中心(6个),正方体的中心(1个),共27个点,以这27个点中的其中3点一共能构成多少个三角形?(6级)【例49】 用A、B、C、D、E、F六种染料去染图中的两个调色盘,要求每个调色盘里的六种颜色不能相同,且相邻四种颜色在两个调色盘里不能重复,那么共有多少种不同的染色方案(旋转算不同的方法)(6级)【解析】【解析】板块三、插板法插板法一般用来解决求分解一定数量的无差别物体的方法的总数,使用插板法一般有三个要求:①所要分解的物体一般是相同的:②所要分解的物体必须全部分完:③参与分物体的组至少都分到1个物体,不能有没分到物体的组出现.在有些题目中,已知条件与上面的三个要求并不一定完全相符,对此应当对已知条件进行适当的变形,使得它与一般的要求相符,再适用插板法.使用插板法一般有如下三种类型:⑴ 个人分个东西,要求每个人至少有一个.这个时候我们只需要把所有的东西排成一排,在其中的个空隙中放上个插板,所以分法的数目为.⑵ 个人分个东西,要求每个人至少有个.这个时候,我们先发给每个人个,还剩下个东西,这个时候,我们把剩下的东西按照类型⑴来处理就可以了.所以分法的数目为.⑶ 个人分个东西,允许有人没有分到.这个时候,我们不妨先借来个东西,每个人多发1个,这样就和类型⑴一样了,不过这时候物品总数变成了个,因此分法的数目为.【例50】 有10粒糖,分三天吃完,每天至少吃一粒,共有多少种不同的吃法?(4级)【巩固】小红有10块糖,每天至少吃1块,7天吃完,她共有多少种不同的吃法?(6级)【巩固】(2008年西城实验考题)有12块糖,小光要6天吃完,每天至少要吃一块,问共有 种吃法.(6级)【巩固】(2009年十三分小升初入学测试题)把5件相同的礼物全部分给3个小朋友,要使每个小朋友都分到礼物,则分礼物的不同方法一共有 种.(6级)【巩固】把7支完全相同的铅笔分给甲、乙、丙3个人,每人至少1支,问有多少种方法?(6级)【巩固】学校合唱团要从个班中补充名同学,每个班至少名,共有多少种抽调方法?(6级)【例51】 10只无差别的橘子放到3个不同的盘子里,允许有的盘子空着.请问一共有多少种不同的放法?(6级)【例52】 把20个苹果分给3个小朋友,每人最少分3个,可以有多少种不同的分法?(6级)【巩固】 如果把20支铅笔,分给甲、乙、丙三人,每人至少3支,可以有多少种不同的分法?(6级)【巩固】三所学校组织一次联欢晚会,共演出14个节目,如果每校至少演出3个节目,那么这三所学校演出节目数的不同情况共有多少种?(6级)【例53】 (1)小明有10块糖,每天至少吃1块,8天吃完,共有多少种不同吃法?(2)小明有10块糖,每天至少吃1块,8天或8天之内吃完,共有多少种吃法? (6级)【巩固】(难度等级 ※※※※)有10粒糖,每天至少吃一粒,吃完为止,共有多少种不同的吃法?(6级)【例54】 马路上有编号为,,,…,的十只路灯,为节约用电又能看清路面,可以把其中的三只灯关掉,但又不能同时关掉相邻的两只,在两端的灯也不能关掉的情况下,求满足条件的关灯方法有多少种?(6级)【例55】 在四位数中,各位数字之和是4的四位数有多少?(6级)【巩固】大于2000小于3000的四位数中数字和等于9的数共有多少个?(6级)【例56】 兔妈妈摘了15个相同的磨菇,分装在3个相同的筐子里,如果不允许有空筐,共有多少种不同的装法?如果分装在3个不同的筐子里,不允许有空筐,又有多少种不同的装法?(8级)。
夏国涛 数字编码表 最新记忆宫殿

1铅笔26河流51工人76汽油01
2鸭子27耳机52碗77七七事
变
卢沟桥
02
3耳朵28恶霸53午餐屋山、
乌纱
78青蛙03 4旗子29阿娇阿胶54武士79汽球04
5秤勾30山洞55火车80巴黎铁
塔
05
6哨子31鲨鱼山药、
起重机
56蜗牛81白蚁06 7镰刀32扇儿57武器82靶儿07
数字编码表
8葫芦33蝴蝶58同城网83猪芭蕉扇08
9球拍34山寺59武警84巴士84
消毒液
09 10棒球35烟60榴莲85白虎0 11筷子36山鹿61儿童86八路
12婴儿37山鸡62牛儿87白旗兔
13医生38孕妇63硫酸88阿里
巴巴
马云
爸爸
14钥匙39三舅64律师89白酒斑鸠
15鹦鹉40司令65锣鼓90酒瓶精灵、
邓小平
16杨柳41中学司仪66溜溜球91球衣17仪器42杮儿67油漆92球18泥巴43石山68喇叭93旧伞
19药酒44蛇69八卦94教师(黑板)
20耳洞
(耳环)
45
师傅
(唐僧)
70麒麟95酒壶救护车
21鳄鱼46石榴71起义蜥蜴96酒楼旧炉22鸳鸯47司机72企鹅97酒器
23乔丹48扫巴73花旗参98酒吧
24耳屎49石臼74骑士9999朵玫瑰
25二胡50五菱75起舞00眼镜
灵药铃儿灵山零食灵符领路邦德
篱笆灵柩鸡蛋。
7位t码与5位b码对应编码

7位t码与5位b码对应编码
要将7位的t码与5位的b码进行对应编码,我们需要确定一个具体的编码规则或映射关系。
在没有具体规定的情况下,我可以提供一种可能的编码方式,但请注意这只是一种示例。
假设我们使用十进制数字作为编码方式,将t码的7位转换成5位的b码。
首先,我们需要确定t码和b码的取值范围。
对于7位的t码,每一位可以取0-9的十个数字,因此总共有10^7=10,000,000种不同的组合。
对于5位的b码,每一位也可以取0-9的十个数字,因此总共有10^5=100,000种不同的组合。
由于t码的取值范围大于b码,因此我们无法将每一个t码都对应一个唯一的b码。
但我们可以采用某种规则进行映射。
一种可能的映射方式是将t码的每一位进行压缩,将7位的t 码转换成5位的b码。
具体步骤如下:
1. 将t码的第1、2位合并,作为b码的第1位。
2. 将t码的第3、4位合并,作为b码的第2位。
3. 将t码的第5、6位合并,作为b码的第3位。
4. 将t码的第7位作为b码的第4位。
5. b码的第5位可以留空或者根据需要进行其他规定。
这样,我们可以将10,000,000种不同的7位t码映射到100,000种不同的5位b码上。
需要注意的是,以上只是一种可能的编码方式,实际应用中可能会有不同的规则或映射方式。
具体的编码方式需要根据实际需求和约束来确定。
2到7的合成

2到7的合成2到7的合成在数学中,合成是指将两个或多个数相乘的操作。
而在生活中,合成也可以指两个或多个事物的结合,产生新的效果或结果。
2和7是两个不同的数字,它们各自具有独特的特点和意义。
然而,当我们将它们进行合成时,会发现一些有趣和有意义的事情。
首先,让我们来看看2和7在数学上的合成。
当我们将2乘以7时,得到的结果是14。
这个结果是一个全新的数字,它不再是2或7本身。
这种合成可以被视为两个数字相互作用、相互影响的结果。
类似地,在生活中,我们也可以将不同事物进行合成。
例如,在音乐中,不同乐器的声音可以通过合奏产生出更加丰富和动听的音乐效果。
当各种声音相互融合时,会创造出一种独特而美妙的和谐。
此外,在科学领域中也存在着许多有趣的合成现象。
例如,在化学实验中,通过将不同元素进行化学反应,可以创造出新的化合物。
这些化合物可能具有完全不同于原始元素的性质和用途。
在人际关系中,合成也是非常重要的。
当不同的个体相互合作、相互支持时,可以创造出更加强大和有力的团队。
每个人都有自己独特的技能和才能,当这些才能相互结合时,可以产生出更大的成果和效益。
总之,2到7的合成不仅仅是数学上的概念,它也存在于我们生活的方方面面。
通过将不同事物进行合成,我们可以创造出新的结果、新的体验和新的可能性。
这种合成不仅丰富了我们的生活,也推动了社会和科学的发展。
让我们珍惜并善于利用这种合成力量,创造出更加美好和有意义的未来。
数据结构825和857

数据结构825和857
“825”是密码学和网络安全。
信息安全,简称信安,意为保护信息及信息系统免受未经授权的进入、使用、披露、破坏、修改、检视、记录及销毁。
涉及计算机科学、网络技术、通信技术、密码技术、信息安全技术等多种综合性技术。
主要包括以下五方面的内容,即需保证信息的保密性、真实性、完整性、未授权拷贝和所寄生系统的安全性。
网络环境下的信息安全体系是保证信息安全的关键,包括计算机安全操作系统、各种安全协议、安全机制(数字签名、消息认证、数据加密等),直至安全系统,不受偶然的或者恶意的原因而遭到破坏、更改、泄露,系统连续可靠正常地运行,信息服务不中断,最终实现业务连续性。
857(十进制)=1101011001(二进制)
二进制,是计算技术中广泛采用的一种数制。
计算方法:二进制数据是用0和1两个数码来表示的数。
它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。
当前的计算机系统使用的基本上是二进制系统,数据在计算机中主要是以补码的形式存储的。
计算机中的二进制则是一个非常微小的开关,用“开”来表示1,“关”来表示0。
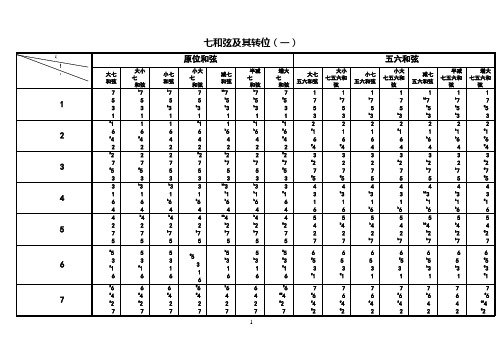
七和弦原位及转位总结图表
称
类
根
型
音
1
2
3
4
5
6
7
大七 和弦
7 5 3 1 #1 6 #4 2 #2 7 #5 3 3 1 6 4 4 2 7 5
#5 3 #1 6
#6 #4 #2 7
大小 七 和弦
b7 5 3 1 1 6 #4 2 2 7 #5 3 b3 1 6 4 b4 2 7 5
5 3 #1 6
6 #4 #2 7
小七 和弦
七和弦及其转位(二)
三四和弦
二和弦
小七 和弦
b3 1 b7 5 4 2 1 6 5 3 2 7 b6 4 b3 1 b7 5 b4 2 1 6 5 3
小大 七 和弦
b3 1 7 5 4 2 #1 6 5 3 #2 7 b6 4 3 1 b7 5 4 2 1 6 #5 3
减七 和弦
b3 1 bb7 b5 4 2 1 b6 5 3 b2 b7 b6 4 bb3 b1 b7 5 bb4 b2 1 6 b5 b3
1 b7 5 b3 2 1 6 4 3 2 7 5 4 b3 1 b6 5 b4 2 b7
小大 七五六和
弦 1 7 5 b3 2 #1 6 4 3 #2 7 5 4 3 1 b6 5 4 2 b7
减七 五六和弦
1 bb7 b5 b3
2 1 b6 4 3 b2 b7 5 4 bb3 b1 b6 5 bb4 b2 b7
bb7 b5 b3 1 1 b6 4 2 b2 b7 5 3 bb3 b1 b6 4 bb4 b2 b7 5
b5 b3 1 6
b6 4 2 7
半减 七 和弦
b7 b5 b3 1 b1 b6 4 2 2 b7 5 3 b3 b1 b6 4 b4 b2 b7 5
《四则运算》4

西宁
格尔木
拉萨
814 + 1142 = 1956(千米) 答:西宁到拉萨的铁路长1956千米。 把两个数合并成一个数的运算,叫做加法。
2、一列火车从西宁经过格尔木开往拉萨。西宁到格尔 木的铁路长814km,格尔木到拉萨的铁路长1142km。 西宁到拉萨的铁路长多少千米?
814km
1142km
手法 诗歌主要运用“兴”的表现手法,使得感情的抒发舒缓,诗歌韵味悠长;诗中多用重章叠句的形式加强抒情效果,再加上双声、叠韵词语如“参差”“窈窕”的使用,增强了诗歌音调的和谐
850-239 =611
239+611= 850
850-611= 239
说一说
今天的学习,你是否重新认识了加、减法 之间的关系呢?说说你的新收获吧!
西宁
814 km
?km
格尔木
拉萨
1956 - 814 = 1142(千米) 答:格尔木到拉萨的铁路长1142千米。
3、西宁到拉萨的铁路全长1956km,其中格尔木到拉萨 长1142km。西宁到格尔木的铁路长多少千米?
?km
1142km
西宁
格尔木
拉萨
西宁到拉萨的铁路长1956km
问题:求西宁到格尔木的铁路长多少千米,用什 么方法?你是怎么想的?
1956-1142=814(千米)
(1)814+1142=1956 (2)1956-814=1142 (3)1956-1142=814
问题:用你自己的话说一说,你认为什么是减法?
已知两个数的和与其中的一个加数,求另一 个加数的运算,叫做减法。在减法中,已知的和 叫做被减数。
1. 加法各部分间的关系
江城子·
白雪歌送
西宁到拉萨的铁路长多少km?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
int *elem,length,listsize;
}SqList;
int InitList_Sq(SqList &L)
{
L.elem=(ElemType*)malloc(LIST_INIT_SIZE*sizeof(ElemType));
L.length=0;
L.listsize=LIST_INIT_SIZE;
}
while(j<=Lb_len)
{
GetElem(Lb,j++,bj);
ListInsert_Sq(Lc,++k,bj);
}
Load_Sq(Lc);
}
int main()
{
int an,bn,i,e;
SqList La,Lb,Lc;
InitList_Sq(La);
{
ListInsert_Sq(Lc,++k,ai);
i++;
}
else
{
ListInsert_Sq(Lc,++k,bj);
j++;
}
}
while(i<=La_len)
{
GetElem(La,i++,ai);
ListInsert_Sq(Lc,++k,ai);
return OK;
}
int Load_Sq(SqList &L)
{
int i;
for(i=0;i<L.length;i++)
printf("%d ",L.elem[i]);
printf("\n");
return OK;
}
int ListLength(SqList L)
}
L.elem=newbase;
L.listsize+=LISTINCREMENT;
}
q=&(L.elem[i-1]);
for(p=&(L.elem[L.length-1]);p>=q;p--)
*(p+1)=*p;
*q=e;
L.length++;
return OK;
{
return L.length;
}
int GetElem(SqList L,int i,ElemType &e)
{
e=L.elem[i-1];
return OK;
}
int ListInsert_Sq(SqList &L,int i,int e)
{
if(i<1||i>L.length+1)
for(i=1;i<=an;i++)
{
scanf("%d",&e);
ListInsert_Sq(Lb,i,e);
}
printf("List B:");
Load_Sq(Lb);
printf("List C:");
MergeList(La,Lb,Lc);
return 0;
k=0;
InitList_Sq(Lc);
La_len=ListLength(La);
Lb_len=ListLength(Lb);
while((i<=La_len)&&(j<=Lb_len))
{
GetElem(La,i,ai);
GetElem(Lb,j,bj);
if(ai<=bj)
#include<stdio.h>
#include<malloc.h>
#define OK 1
#define ERROR 0
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
#define ElemType int
typedef struct
scanf("%d",&an);
for(i=1;i<=an;i++)
{
scanf("%d",&e);
ListInsert_Sq(La,i,e);
}
printf("List A:");
Load_Sq(La);
InitList_Sq(Lb);
scanf("%d",&bn);
return Eቤተ መጻሕፍቲ ባይዱROR;
ElemType *p,*q,*newbase;
if(L.listsize<=L.length)
{
newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
}
void MergeList(SqList La,SqList Lb,SqList &Lc)
//已知线性表La和Lb中的数据元素按值非递减排列
//归并La和Lb得到新的线性表Lc,Lc的数据元素也按值非递减排列
{
int i,j,k,La_len,Lb_len,ai,bj;
i=j=1;
