三角形的重心PPT课件
《三角形的四心》课件

三角形的中线和垂线
中线
探讨三角形中线的定义和 性质。
垂线
探索三角形垂线的概念以 及与三角形边的关系。
垂线定理
研究垂心以及和垂线定理 的应用。
三角形的重心和质心
1
重心
了解三角形的重心是如何定义的,并探索其性质。
2
质心
讨论质心和质心定理在实际问题中的应用。
3
重心与重心定理
研究重心与重心定理对三角形的性质的关系。
1角平分线的应用2源自讨论角平分线在实际问题中的应用。
3
定理介绍
了解角平分线定理的表述及其重要 性。
常见三角形中心位置关系
探索内心、外心、重心、垂心在三 角形中的相对位置关系。
勾股定理与三角形
勾股定理
学习勾股定理的表述和证明方法。
勾股定理的应用
探讨勾股定理在解决实际问题中的应用。
闵可夫斯基不等式
介绍闵可夫斯基不等式,了解其应用和重要性。
带权重心的应用
1 带权重心的定义
研究带权重心的概念及其性质。
2 带权重心的应用
探索带权重心在解决实际问题中的应用。
三角形的性质及应用
三角形的性质
总结三角形的各种性质 和特点。
三角形的应用
讨论三角形在几何学和 实际生活中的广泛应用。
例题和练习
通过例题和练习来巩固 学习的知识。
总结和展望
回顾三角形的各个重要概念和定理,展望将来继续研究和探索三角形的更多 奥秘。
三角形的外心及外心定理
外心的定义
介绍三角形的外心及其相关 定理。
外心定理
了解外心定理在三角形中的 应用。
外心与周长关系
探索外心与三角形周长的关 联。
三角形的重心课件

三角形的重心课件关键信息项:1、课件的使用目的:____________________________2、课件的版权归属:____________________________3、课件的更新与维护责任:____________________________4、课件的适用范围:____________________________5、课件的使用期限:____________________________6、对课件内容的保密要求:____________________________7、违反协议的责任与处罚:____________________________11 协议的背景和目的本协议旨在规范关于三角形的重心课件的使用、传播、更新和维护等相关事宜,以确保该课件能够有效地服务于其预期的教育目的,并保障相关各方的合法权益。
111 三角形的重心课件的定义本协议中所提及的三角形的重心课件,是指一套专门用于讲解三角形重心相关知识的多媒体教学材料,包括但不限于演示文稿、动画、视频、练习题等。
12 协议的适用范围本协议适用于所有获得、使用或传播三角形的重心课件的个人和机构。
21 课件的使用目的该课件仅用于教育和学习目的,不得用于任何商业盈利活动。
使用者可以将其用于课堂教学、自主学习、辅导教学等与教育相关的活动。
211 禁止的使用方式使用者不得对课件进行修改、篡改、反编译或以其他方式破坏其完整性和功能性,不得将其用于非法、有害、淫秽或违背社会公德的目的。
22 课件的版权归属三角形的重心课件的版权归创作者所有,未经版权所有者的明确书面授权,任何人不得擅自复制、分发、传播或对其进行二次创作。
221 授权使用范围版权所有者授予使用者在一定范围内非独家的使用权利,但使用者必须遵守本协议的各项规定。
31 课件的更新与维护责任版权所有者有责任对课件进行必要的更新和维护,以确保其内容的准确性和时效性。
但在合理的范围内,使用者也有义务向版权所有者反馈发现的错误或需要改进的地方。
三角形的重心 ppt课件

3
3
3
重心与一边中点的连线的长
重心与一顶点的连线的长
对应中线长
三角形的重心
尝试练习
分析各部分的面积
分析各部分的长度 A
F
E
O
BD
C
三角形的重心
尝试练习
分析各部分的面积 分析各部分的长度 A
E O
BD
C
三角形的重心
求线段长 课堂检测
如图,在Rt△ABC中,∠A=30°,点 D是斜边AB的中点,当G是Rt△ABC的重 心,GE⊥AC于点E,若BC=6cm,则 GE= cm。
A
三角形的重心
B DG
EC
三角形的重心
今日作业 求面积
在△ABC中,中线AD、BE相交
于点O,若△BOD的面积等于5,求
△ABC的面积。
A
选作
E O
B D பைடு நூலகம்证:顺次连结矩形四边中点所得的三角四形的边重心形是菱形
C
§23.4.2 三角形的重心
三角形的重心
请同学们画出 一个三角形的三条中线
第1、2、3竖排画锐角三角形 第4、5竖排画直角三角形 第6、7、8竖排画钝角三角形
三角形的重心
导入 三条中线相交于几个点?
我们把这个点叫三角形的重心
三角形的重心
学习目 标 1.理解三角形的重心的含义
2.理解掌握三角形重心的性质
3.运用三角形重心的性质解决问题
三角形的重心
试一试
已知:△ABC中,D、E分别是边 BC、AB的中点,AD、CE相交于G。
GE GD1
CE 求AD 证3 :GE GD 1 CE AD 3
A E
G
B
三角形的重心

三角形的重心在我们的数学世界中,三角形是一个极其基础且重要的图形。
而三角形的重心,作为三角形的一个重要特性,有着独特的性质和广泛的应用。
首先,让我们来明确一下,什么是三角形的重心。
简单来说,三角形的重心就是三角形三条中线的交点。
那什么又是中线呢?连接三角形顶点和它对边中点的线段就叫做中线。
为了更直观地理解三角形的重心,我们不妨动手做一个小实验。
拿一张稍硬的纸,画出一个三角形,然后找出三条边的中点,连接顶点和中点画出中线。
这时,你会发现这三条中线相交于一点,这个点就是三角形的重心。
三角形的重心有一些非常有趣的性质。
其中一个重要的性质是,重心到三角形顶点的距离与重心到对边中点的距离之比为2:1。
这意味着,如果我们把重心和顶点相连,并延长这条线,使其与对边相交,那么重心到顶点的距离是重心到对边中点距离的两倍。
比如说,在三角形 ABC 中,G 是重心,连接 AG 并延长交 BC 于 D。
那么就有 AG = 2GD。
同样的道理,BG = 2GE,CG = 2GF,其中 E、F 分别是 AC、AB 的中点。
为什么会有这样的比例关系呢?我们可以通过一些简单的几何证明来理解。
以证明 AG = 2GD 为例。
连接 BE,因为 E 是 AC 的中点,所以三角形 ABE 和三角形 CBE 的面积相等。
又因为三角形 AGB 和三角形 BGD 分别以 AG 和 GD 为底时,高相同,且三角形 ABE 的面积是三角形 AGB 面积的两倍,三角形 CBE 的面积是三角形 BGD 面积的两倍,所以 AG = 2GD。
三角形重心的另一个重要性质是,它是三角形的几何中心。
这意味着,如果我们把三角形看成是一块均匀的薄板,那么重心就是薄板的平衡点。
也就是说,如果用一个支点支撑在重心的位置,三角形薄板能够保持平衡。
这个性质在实际生活中有很多应用。
比如在建筑设计中,为了保证建筑物的结构稳定,工程师们需要考虑重心的位置。
如果建筑物的重心不在合理的位置,就可能会出现倾斜、倒塌等危险情况。
第八讲 三角形的重心

第八讲三角形的重心-CAL-FENGHAI.-(YICAI)-Company One1第八讲 三角形的重心、垂心、外心和内心初中阶段我们已经学习了关于三角形的边和角的许多性质,也涉及三角形边上中线、高线、垂直平分线以及内角平分线的一些性质。
例如,线段(如三角形的一边)的垂直平分线上的点和这条线段两站点的距离相等。
反之,和一条线段两个端点距离相等的点在这线段的垂直平分线上;角(如三角形的一个内角)的平分线上的点到这个角的两边的距离相等。
反之,到一个角的两边距离相等的点在这个角的平分线上,诸如此类。
涉及一个三角形的三条中线、三条高线、三条边的垂直平分线以及三个内角平分线的性质及相互关系是中学平面几何的重要内容。
在高中学习中,会涉及三角形三条中线交点、三条高线交点、三条边的垂直平分线交点以及三个内角平分线交点,即三角形的几个“巧合点”。
本节将对这些知识作较系统的阐述。
一、三角形的重心如图8-1,在△ABC 中,AD 、BD 是两条中线,记它们的交点为G ,连接DE 、DE 是三角形的中位线。
∴DE ∥AB ,且.21AB DE ∴∠GAB=∠GDE ,∠GBA=∠GED.∴△AGB ∽△DGE ,且相似比为2:1.∴AG=2GD ,BG=2GE. 于是得到关于三角形中线的一个重要性质:三角形的两条中线的交点把这两条中线都分成2:1的两段。
现在再研究第三条中线与其他两条中线交点有什么特殊性质。
图8-1图8-2如图8-2,设△ABC 的两条中线AD 、BE 交于G ,中线CF 、BE 交于G ′.由已知的三角形中线的性质,则有BG=2GE ,且BG ′=2G ′E ,CG ′=2G ′F.∴G ′与G 重合,则三角形的三条中线相交于一点,且该点把三角形的各中线分成长度比为2:1的两段,这个交点称为三角形的重心。
三角形的重心必在三角形的内部。
今后我们也常说:三角形的重心把中线分成2:1的两段。
例1 如图8-3,已知E 、F 分别是平行四边形ABCD 边AD 、CD 的中点,BE 和BF 分别交对角线AC 于M 、N ,求证:AM=MN=NC 。
三角形的重心性质

三角形的重心性质目录1. 三角形的重心性质1.1 重心的定义1.2 重心的位置1.2.1 等边三角形的重心1.2.2 直角三角形的重心1.3 重心和质心的区别1.3.1 定义区别1.3.2 几何性质区别2. 重心与三角形内部区域的关系2.1 重心到顶点的距离比2.2 重心将三角形分割的性质2.2.1 重心将三角形分割成三等面积的三角形2.2.2 重心将三角形分割成六等面积的三角形2.2.3 重心将三角形分割成三个面积比为1:2的三角形三角形的重心性质1.1 重心的定义三角形的重心是指三条中线的交点,即由三条中线交汇形成的点称为三角形的重心。
1.2 重心的位置1.2.1 等边三角形的重心在等边三角形中,三角形的重心和质心重合,且重心距离任何一个顶点和中心的距离都相等。
1.2.2 直角三角形的重心对于直角三角形,重心位于斜边上离直角边的邻边的1/3处。
1.3 重心和质心的区别1.3.1 定义区别重心是在三角形内部的点,是由三条中线交汇形成的点;而质心是三角形的三条边上的距离各角相等的点。
1.3.2 几何性质区别重心是三角形的一个几何中心,质心是三角形的一个几何参数。
重心与三角形内部区域的关系2.1 重心到顶点的距离比三角形的重心到各个顶点的距离比为2:1,即重心到顶点的距离是中位线长度的两倍。
2.2 重心将三角形分割的性质2.2.1 重心将三角形分割成三等面积的三角形三角形的重心将三角形分割成三个面积相等的三角形。
2.2.2 重心将三角形分割成六等面积的三角形三角形的重心将三角形分割成六个面积相等的三角形。
2.2.3 重心将三角形分割成三个面积比为1:2的三角形三角形的重心将三角形分割成三个面积比为1:2的三角形,其中比重心到顶点的距离2/3的那一个三角形面积为整个三角形面积的1/4,另外两个的面积之和为3/4。
第八讲--三角形的重心

第八讲 三角形的重心、垂心、外心和内心初中阶段我们已经学习了关于三角形的边和角的许多性质,也涉及三角形边上中线、高线、垂直平分线以及内角平分线的一些性质。
例如,线段(如三角形的一边)的垂直平分线上的点和这条线段两站点的距离相等。
反之,和一条线段两个端点距离相等的点在这线段的垂直平分线上;角(如三角形的一个内角)的平分线上的点到这个角的两边的距离相等。
反之,到一个角的两边距离相等的点在这个角的平分线上,诸如此类。
涉及一个三角形的三条中线、三条高线、三条边的垂直平分线以及三个内角平分线的性质及相互关系是中学平面几何的重要内容。
在高中学习中,会涉及三角形三条中线交点、三条高线交点、三条边的垂直平分线交点以及三个内角平分线交点,即三角形的几个“巧合点”。
本节将对这些知识作较系统的阐述。
一、三角形的重心如图8-1,在△ABC 中,AD 、BD 是两条中线,记它们的交点为G ,连接DE 、DE 是三角形的中位线。
∴DE ∥AB ,且.21AB DE ∴∠GAB=∠GDE ,∠GBA=∠GED.∴△AGB ∽△DGE ,且相似比为2:1.∴AG=2GD ,BG=2GE. 于是得到关于三角形中线的一个重要性质:三角形的两条中线的交点把这两条中线都分成2:1的两段。
现在再研究第三条中线与其他两条中线交点有什么特殊性质。
图8-1 图8-2如图8-2,设△ABC 的两条中线AD 、BE 交于G ,中线CF 、BE 交于G ′.由已知的三角形中线的性质,则有BG=2GE ,且BG ′=2G ′E ,CG ′=2G ′F.∴G ′与G 重合,则三角形的三条中线相交于一点,且该点把三角形的各中线分成长度比为2:1的两段,这个交点称为三角形的重心。
三角形的重心必在三角形的内部。
今后我们也常说:三角形的重心把中线分成2:1的两段。
例1 如图8-3,已知E 、F 分别是平行四边形ABCD 边AD 、CD 的中点,BE 和BF 分别交对角线AC 于M 、N ,求证:AM=MN=NC 。
三角形的重心PPT课件

A
精选ppt
B
DG
E
C 9
精选ppt
10
今日作业 求面积
在△ABC中,中线AD、BE相交
于点O,若△BOD的面积等于5,求
△ABC的面积。
A
选作
E O
B D 求证:顺次连结矩形四边中点所得的精四选p边pt 形是菱形
C
11
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
§23.4.2 三角形的重心
设计者 刘书山
精选ppt
1
请同学们画出 一个三角形的三条中线
第1、2、3竖排画锐角三角形
第4、5竖排画直角三角形
第6、7、8竖排画钝角三角形
精选ppt
2
导入 三条中线相交于几个点?
我们把这个点叫三角形的重心
精选ppt
3
学习目标 1.理解三角形的重心的含义
2.理解掌握三角形重心的性质 3.运用三角形重心的性质解决问题
精选ppt
4
试一试
已知:△ABC中,D、E分别是边 BC、AB的中点,AD、CE相交于G。
GE GD1
CE 求AD 证3 :GE GD 1 CE AD 3
A E
G
B
精选ppt
D
C 5
归纳
1
重心与一边中点的连线的长是对应中线长的 3
1重心与一顶点的连1 线边中点的连线的长
重心与一顶点的连线的长
对应中线长
精选ppt
6
尝试练习
分析各部分的面积
分析各部分的长度 A
F
E
O
BD
C
精选ppt
7
尝试练习
三角形的重心、垂心、内心、外心

一、三角形重心定理二、三角形外心定理三、三角形垂心定理四、三角形内心定理五、三角形旁心定理有关三角形五心的诗歌三角形五心定理三角形的重心,外心,垂心,内心和旁心称之为三角形的五心。
三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。
2、重心和三角形任意两个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A 为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
外心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
三角形的重心与外心

三角形的重心与外心三角形是几何学中最基本的图形之一,由三条线段组成的闭合图形。
在三角形中,有两个特殊的点,即重心和外心。
本文将介绍三角形的重心和外心的定义、性质以及它们在三角形中的重要作用。
一、重心重心是指三角形的三个顶点的垂直平分线的交点,它在三角形内部且到三角形的三条边的距离相等。
重心通常用字母G来表示。
重心有以下性质:1. 重心将每个垂直平分线分成两个部分,其中一部分的长度是另一部分的两倍。
2. 重心到三角形的顶点的距离与重心到对边的距离成正比,即重心到顶点的距离等于重心到对边的距离的两倍。
3. 重心是三角形中心的共点,包括重心、内心、外心和垂心。
二、外心外心是指三角形三个顶点的垂直平分线的延长线的交点,它在三角形外部且到三角形的每条边的距离相等。
外心通常用字母O来表示。
外心有以下性质:1. 外心到三角形的每个顶点距离相等,即外心到顶点的距离等于外心到各边的距离。
2. 外心是三角形外接圆的圆心,外接圆是将三角形三个顶点作为圆上的点的圆,且外切于三角形的每条边。
3. 与重心不同,外心不在三角形内部,而是在三角形的外部。
三、重心和外心的作用重心和外心在三角形的研究和应用中具有重要的作用。
1. 重心的作用:重心在计算三角形的重要参数时起着关键作用,比如重心是三角形的中位线、高线、角平分线的交点,它将三角形划分为等面积的三个小三角形。
这些特点让重心在计算三角形的面积、质心、惯性矩等物理量时非常有用。
2. 外心的作用:外心在解决三角形相关问题时发挥着重要作用。
比如外心是三角形三条垂直平分线的交点,通过外心可以构造三角形的外接圆,并且外心到三个顶点的距离相等,这使得外心在三角形的外界接触领域中具有重要意义。
此外,外心还是求解三角形的外接圆半径、角平分线、旁切圆等问题的关键。
综上所述,重心和外心是三角形中两个重要的点。
它们在三角形的性质和计算中起着关键作用。
重心可以帮助计算三角形的重要参数,而外心可以帮助解决与三角形相关的几何问题。
高考复习三角形的四心重心内心外心垂心PPT课件
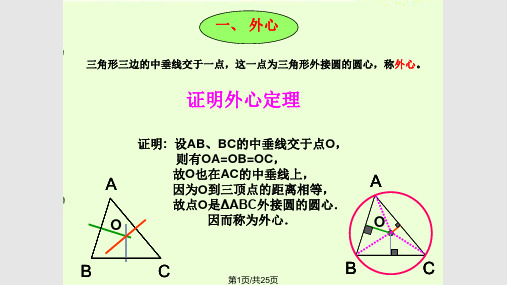
OE
C
OD与OE共线且2|OD || OE |, SCOE 2SCOD ,
SAOC
2SCOE
2
2 3
SCDE
2
2 3
1 4
SABC
1 3
SABC
第22页/共25页
思考: 如图,设点O在 ABC 内部,且有OA 2OB 3OC 0,
则 ABC 的面积与 AOC 的面积的比为_____3______.
例2.证明:三角形重心与顶点的距离等于它到对边中点距离的两倍.
另证: 连结EF,则EF为ABC的中位线,EF//BC, 且EF:BC=1:2,由平行线分线段成比例
得 FG:GC=1:2,同样可得 EG:GB=1:2, DG:GA=1:2. A
F E
G
B
D
C
第13页/共25页
重心
四、内心
三角形三内角平分线交于一点,这一点为三角形内切圆的圆心,称内心。
| AB | cos B | AC | cosC
则P的轨迹一定通过△ABC的 _______
解: ∵ BC ( AB AC ) BC AB BC AC
| AB | cos B | AC | cosC | AB | cos B | AC | cosC
| BC | | AB | cos( B) | BC | | AC | cosC | BC | | BC | 0
垂心
同理可得O在CB边的高线上.
5. P是△ABC所在平面上一点,若
PA PB PB PC PC PA, 则P是△ABC的( D )
A.外心 B.内心 第C8.页/重共2心5页 D.垂心
三、重心
三角形三边中线交于一点,这一点叫三角形的重心。
第三节三角形的重心

§3 三角形的重心基础知识性质1 三角形的重心是三角形三条中线的交点.性质2 设G 为ABC ∆的重心,连AG 并延长交BC 于D , 则D 为BC 的中点,AG :GD 2=:1, 且()22224121BC AC AB AD -+=. 性质3 设G 为ABC ∆的重心,过G 作DE ∥BC 交AB 于D , 交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F , 过G 作KH ∥AB 交AC 于K ,交BC 于H ,则 (1)32===AB KH CA FP BC DE ; (2)2=++ABKH CA FP BC DE . 性质4 设G 为ABC ∆的重心,P 为ABC ∆内任一点,则 (1)22222223PG CG BG AG CP BP AP +++=++; (2)()22222231CA BC AB GC GB GA ++=++. 注 三角形中的莱布尼兹公式:()2222222313CA BC AB PG CP BP AP +++=++ 性质5 设G 为ABC ∆内一点,G 为ABC ∆的重心的充要条件是下列条件之一:(了解必要性即可) (1)ABC GAB GCA GBC S S S S ∆∆∆∆===31; (2)当点G 在三边BC 、CA 、AB 上的射影分别为D 、E 、F 时,GF GE GD ⋅⋅值最大; (3)当AG 、BG 、CG 的延长线交三边于D 、E 、F 时,CEG BDG AFG S S S ∆∆∆==; (4)过G 的直线交AB 于P ,交AC 于Q 时,3=+AQACAP AB ; (5)222222333GC AB GB CA GA BC +=+=+.性质6 设P 是锐角ABC ∆内一点,射线AP 、BP 、CP 分别交边BC 、CA 、AB 于点D 、E 、F ,则P 为ABC ∆重心的 充分必要条件是DEF ∆∽ABC ∆.例题讲解例1 过ABC ∆的重心G 任作一条直线把这个三角形分成两部分.试证:这两部分面积之差不大于整个三角形面积的91.例2 在ABC ∆中,G 为重心,P 为形内一点,直线PG. 求证:3=''+''+''GC PC G B P B G A P A .例3 如图,M 、N 、P 分别为正ABC ∆、正DCE ∆、正BEF ∆的重心.求证:MNP ∆为正三角形.例4 设O 为ABC ∆的外心,AC AB=,D 是AB 的中点,G 是ACD ∆的重心.求证:CD OG ⊥.ABCBCBCEBF例1 过ABC 的重心G 任作一条直线把这个三角形分成两部分.试证:这两部分面积之差不大于整个三角形面积的91. 证明:如图,作三角形三边的两个三等分点,过三等分点作边的平行线,分该三角形为9个等面积的小三角形。
知识卡片-三角形的重心

三角形的重心
能量储备
(一)定义:三角形三条中线的交点叫做三角形的重心.
(二)性质:1.重心到顶点的距离与重心到对边中点的距离之比为2:1;
2.重心和三角形3个顶点组成的3个三角形面积相等.
(三)特殊三角形的重心
1.等腰三角形的重心在底边的高或中线或定角的角平分线上.
2.等边三角形的重心是三边的高或中线或三个角的角平分线交点.
通关宝典
★基础方法点
1.利用三角形重心的性质求面积
例1:如图,在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,求△ABC 的面积.
解:因为O是△ABC的重心,所以AO∶OD=2∶1 ,所以S△AOB∶S△BOD=2∶1
即S△AOB=2 S△BOD=10
所以S△ABD= S△AOB+ S△BOD=10+5=15 又AD是△ABC的中线
所以S△ABC=2 S△ABD=30.
★★易混易误点
蓄势待发
考前攻略
考查三角形的重心,主要以选择题形式考查,难度适中..
完胜关卡。
三角形的五心-第3讲重心与垂心学生版

第三讲三角形的重心与垂心一、基础知识1.重心的定义:三角形的三中线(或二中线)的交点叫做三角形的重心.2.重心的性质1)三角形的重心必在三角形的內部;2)三角形的重心到顶点的距离等于过这顶点的中线长的三分之二;3)三角形三中线分原三角形为六个等面积的三角形;4)三角形重心到三顶点的连线分原三角形为三个等面积的三角形;5)到三角形的三个顶点距离的平方和最小的点是这个三角形的重心;3.垂心的定义:三角形的三条高线的交点叫做三角形的垂心.4.垂心的性质1)锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部;2)垂心会在三角形内部产生很多相似直角三角形;同时会出现四点共圆问题;二、例题部分第一部分重心例1. 如图,已知△ABC与△CDA全等,点G、H分别是△ABC、△CDA的重心,则△AGH 的面积与△ABC的面积的比为 ( )A.4:9 B.2:3 C.1:3 D.1:6例2. 在△ABC中,BC=3,AC=4,BC和AC的中线AE、BD互相垂直,则AB等于 ( )A.36 B.5 C.22 D.7例3. 在直角三角形ABC 中. ∠A=90,G 为重心,且GA=2,则22GB GC += .例4. 设M 是△ABC 的重心,过M 的线段交AB ,AC 于P 、Q ,且AP PB =m ,AQ QC =n ,则11m n + =( )A .2B .1C .12D .13第二部分 垂心例5. (2000年,四川省中考题)如图,已知△ABC 的内切圆0与各边相切于D 、E 、F ,那么点0是△DEF的 ( )A .三条中线的交点B .三条高的交点C .三条角平分线的交点D .三条边的垂直平分线的交点例6. 如图,△ABC 中,高BD 、CE 相交于点F , ∠A=45,△ DEF 的面积为S ,则△BFC 的面积为 .例7. 如图,已知H 是△ABC 的垂心,△ABC 外接圆的半径为R ,那么sin BH BCH∠= .例8. 如图,已知⊙0中,直径AB 与弦CD 垂直,垂足为E ,CH 切⊙0于点C ,且与AB 的延长线交于H ,P 是CD 延长线上一点,PA 交⊙0于F ,AD 平分∠HAP 并交HP 于M .求证:(1)点D 是△AHP 的垂心;(2)AH :AB=AE :AF .第三部分 综合题目例9. (1998年,全国竞赛试题)如图,已知P 为ABCD 内一点,O 为AC 与BD 的交点,M 、N 分别为PB 、PC 的中点,Q 为AN 与DM 的交点,求证:(1)P 、Q 、O 三点在一条直线上;(2)PQ=20Q .例10. 如图,设G 为△ABC 的重心,P 为△ABC 内部的任意一点,直线PG 交BC 、CA 、AB 或其延长线于A '、B '、C '.求证:3A P B P C P A G B G C G'''++='''.三、课后练习1. ABC的中线AD、BE相交于O,F、G分别是OB、OA的中点,则四边形DEGF是( )A.梯形 B.正方形 C.平分四边形 D.菱形2. 在△ABC中,BC=a,AC=b,AB=c,∠C=90,CD和BE是△ABC的两条中线,且CD⊥BE,那么a:b:c=( )A.1:2:3 B.3:2:1 C..3:2:1 D.1:2:33.如图,AD是△ABC的高,G是三角形垂心,∠C=60,则∠BGD= .4. 如图,已知点P是△ABC的垂心,PD⊥AC,垂足D.延长PC交AB于E,连结DE,若BC=2DE,则tanA= .5.在△ABC中,∠A是锐角,0是垂心,AO=BC,则∠0BC+∠0CB=.。
三角形重心

三角形重心重心是三角形三边中线的交点,三线交一可用燕尾定理证明。
证明过程又是塞瓦定理的特例。
:△ ABC 中,D 为 BC 中点, E 为 AC 中点, AD 与 BE 交于 O,CO 延长线交 AB于 F。
求证: F 为 AB 中点。
证明:依照燕尾定理, S△AOB=S △AOC,又 S△AOB=S △BOC,∴S△AOC=S △BOC,再应用从中点得 AF=BF ,命题得证。
重心的几条性质及证明方法:1、重心到极点的距离与重心到对边中点的距离之比为 2:1。
2、重心和三角形 3 个极点组成的 3 个三角形面积相等。
证明方法:在▲ABC 内,三边为 a,b,c,点 O 是该三角形的重心, AOA1 、BOB1 、COC1 分别为 a、b、c 边上的中线依照重心性质知, OA1=1/3AA1 ,OB1=1/3BB1 ,OC1=1/3CC1 过 O,A 分别作 a 边上高 h1,h 可知 h1=1/3h 那么,S( ▲BOC)=1/2 × h1a=1/2 × 1/3ha=1/3S( ▲;A同BC) 理可证 S(▲AOC)=1/3S(▲ABC) ,S(▲AOB)=1/3S(▲ABC) 所以,S( ▲BOC)=S(▲AOC)=S(▲AOB)3、重心到三角形 3 个极点距离的和最小。
(等边三角形〕证明方法:设三角形三个极点为 (x1,y1),(x2,y2),(x3,y3) 平面上任意一点为〔 x,y〕那么该点到三顶点距离和为: (x1-x)^2+(y1-y)^2+(x2-x)^2+(y2-y)^2+(x3-x)^2+(y3-y)^2=3x^2-2x(x1+x2+x3)+3y^2-2y(y1+y2+y3)+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2=3(x-1/3*(x1+x2+x3))^2+3(y-1/3(y1+y2+y3))^2+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2显然当 x=(x1+x2+x3)/3,y=(y1+y2+y3)/3 〔重心坐标〕时上式获取最小值x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2 最后得出结论4、在平面直角坐标系中,重心的坐标是极点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3) ;空间直角坐标系——横坐标: (X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:〔 z1+z2+z3〕/35、三角形内到三边距离之积最大的点。
三角形的重心

三角形的重心关键信息项:1、三角形的定义和性质三角形的边、角关系三角形的分类(按角、按边)2、重心的定义和特征重心的位置确定方法重心与三角形各边的关系3、重心的计算方法通过坐标计算通过几何图形计算4、重心的应用领域物理学中的应用工程学中的应用数学解题中的应用11 三角形的定义和性质三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形,在数学、建筑学有应用。
三角形具有稳定性,这一特性使其在建筑和工程结构中得到广泛应用。
三角形的内角和为 180 度,这是三角形的基本性质之一。
根据三角形内角的大小,可将三角形分为锐角三角形(三个内角都小于 90 度)、直角三角形(有一个内角等于 90 度)和钝角三角形(有一个内角大于 90 度)。
按边的长度关系,三角形又可分为等边三角形(三条边长度相等)、等腰三角形(至少有两条边长度相等)和不等边三角形(三条边长度都不相等)。
111 三角形边与角的关系三角形的任意两边之和大于第三边,任意两边之差小于第三边。
这一关系对于判断三条线段能否构成三角形非常重要。
在一个三角形中,大角对大边,大边对大角。
即较大的内角所对的边较长,较长的边所对的内角较大。
112 三角形的面积公式三角形的面积可以通过多种方法计算,常见的公式有:面积=底×高÷2。
12 重心的定义和特征三角形的重心是三角形三条中线的交点。
中线是连接三角形顶点和它对边中点的线段。
重心到三角形顶点的距离与到对边中点的距离之比为 2:1。
也就是说,重心将每条中线分为 2:1 的两段。
121 重心的位置确定方法可以通过作图法来确定三角形的重心。
首先,画出三角形的三条中线,它们的交点就是重心。
也可以通过计算的方法来确定重心的位置,如果已知三角形三个顶点的坐标,那么重心的坐标可以通过以下公式计算:重心横坐标=(顶点 1 横坐标+顶点 2 横坐标+顶点 3 横坐标)÷ 3;重心纵坐标=(顶点 1 纵坐标+顶点 2 纵坐标+顶点 3 纵坐标)÷ 3 。
关于三角形重心的知识点

关于三角形重心的知识点
嘿,你知道三角形的重心吗?这可太神奇啦!就好像是三角形的“心脏”一样呢!比如说,你看那个三脚架,它能稳稳地立在那里,为啥呀?就是因为它的重心在那呀!
咱来仔细说说,三角形的重心呢,就是三条中线的交点。
哎呀,想象一下,这就像是三角形里有一个特别重要的点,把三角形给“抓”住了!比如咱在生活中玩跷跷板,跷跷板能平衡就是因为找到了重心呀,是不是很有意思?
嘿,你再想想,如果一个三角形摇摇晃晃的,那不就是重心没找好嘛!就好比你走路不稳,那就是没找到平衡的那个点呀。
那怎么找这个神奇的重心呢?嘿,很简单呀,把三条边的中点都找到,然后把它们连起来,那个交点就是啦!
三角形的重心有好多特点呢!它到三角形顶点的距离是中线长的三分之二。
哇塞,这多酷呀!就好像在一个团队里,有个人有着特别重要的地位和作用。
我觉着呀,了解三角形的重心真的很重要,它能帮我们解决好多问题呢,在生活中也有很多应用呀!你觉得呢?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
且
OAOBO ,C N A N B N C , 0
P A P B P B P C P C P A ,则O,N,P依次是△ABC的
A.重心 外心 垂心 B.重心 外心 内心
C.外心
重心 垂心
A
D.外心 重心 内心
解析:
AA
答案:(C)
P NO
B
C
BB
CC
2021/3/7
CHENLI
16
【课后思考】:1.设G为△ABC的重心, M、N分别为AB、CA的中点, 求证:四边形GMAN和△GBC的面积相等.
O
2021/3/7
B
CHENLI
C
12
(2) O为垂心(三条垂线的交点)
OO A B OO B C OO CA
A
O
B
C
2021/3/7
CHENLI
13
(3) O为外心(中垂线交点,外接圆圆心)
2
2
2
OAOBOC
A
O
B
C
2021/3/7
CHENLI
14
(4) O为内心(角平分线交点,内切圆圆心) A
A OE
D
C
(3)中线AD上的点P满足:
APABAC
2021/3/7
CHENLI
8
重心性质5
设直线l过重心O,交AB、AC于点M、N,
AMxAB ,AN yAC,xy 0,
则 1 1 .3
xy
A
连接AO,因为M、O、N三点共线
O N 所以 AOAM1-AN
M
xAB1-yAC
B
C AO1AB1AC
点D、E分别是BC、 AC的中点.
O E 连接AD,BE,交于点O,
B
D
C O点即为△ABC的重心.
2021/3/7
CHENLI
3
重心性质1
重心分中线之比为2:1. 即 AO:OD=2:1
A
E
O
H
B
D
C
取EC中点H,连接DH
可证 AO:OD= 2:1
2021/3/7
CHENLI
4
重心性质2
三角形的三中线必然交于一点. 此点恰是重心.
33
11
2021/3/7
可得
3 x yCHENLI
9
它的逆命题也成立!
设直线l交AB、AC于点M、N,
且满足
AB AC 3 AM AN
A
则直线l必过△ABC的重心
N
M
B
C
2021/3/7
CHENLI
10
【友情链接】
1. (2010年湖北卷)已知△ABC和点M满足 M AM BM C0,若存在实数m使得
2021/3/7
CHENLI
20
A
连接CO并延长,交AB于F
F O E过点D作DG//CF ,交AB于G G
B
D
C
根据性质1,可以证明
AF:FG=2:1 FG:GB=1:1
2021/3/7
故F为AB中CHEN点LI .
5
重心性质3
SAOBSBO CSAOC
A
F
OE
B
D
C
分别延长中线,可交对边的中点.
易知:S△AOB= 2S△BOD= S△BOC
ABACmAM成立,则 m(C )
A.2 B.2
3
C.3
D.6
解析: A M
AM1AB1AC 33
B
C
2021/3/7
CHENLI
11
【补充内容】
三角形“五心”向量形式的充要条件: 设O为△ABC所在平面内一点,角A,B,C
所对的边长分别为,b,c,则
(1) O为重心 (三条中线的交点) A
OA O B O C0
aOA bO B cO C 0
(5) O为∠A旁心
B
M
F
E
K I
DH
C
(旁切圆圆心,∠A平分线与两外角平分线交点)
A
aO AbO BcOC
BD
C
F
☺(1)(2)(3)常考;
E Ia
202☺1/3/7(4)(5)只作了解CHENL.I
15
【友情链接】
2.(2009•宁夏海南卷)已知O,N,P在△ABC所在平面内,
A
M
N
G
B
C
提示: 连GA △AMG的面积=△GBM的面积, △GAN的面积=△GNC的面积,
2021/3/7
CHENLI
17
【课后思考】 2.已知A,B,C三点不共线,且点O满足
OAO BOC 0,下列结论正确的是( )
A. OA1AB2BC
33
C. OA-1AB-2BC
33
B. OA2AB1BC
A
F OE
B
D
C
三角形的重心
高中数学 毛 维
播种行为,收获习惯!
2021/3/7
CHENLI
1
主要内容:
• 一、 三角形重心的定义 • 二、 重心的五个重要性质 • 三、 三角形的五“心”简介
2021/3/7
CHENLI
2
重心的定义
三角形的三条中线交于一点,这点称为三 角形的重心.
A
如图所示:在△ABC中,
33
D. OA-2AB-1BC
33
提示: AO1AB1AC
33
A C A B B C
2021/3/7
CHENLI
18
小结
1.重心的定义 2.重心五个性质及其变化形式
3.“五心”的认识及其向量 的基本形式
4. 友情链接高考试题
天聪 才明 出由 于于 勤积 奋累 。,
2021/3/7
CHENLI
19
2021/3/7
CHENLI
6
重心性质4
如果O为△ABC的重心,那么 O AO BOC 0 A
O
O
B
D
B
D
C
C
P
由中线向量的性质: O BOC OP 2OD
∵ O A2O D?0
∴ 2021/3/7 O AO BOCC HE0 NLI
7
重心向量常见变化形式:
(1)AO BO CO 0 F
(2) AO1AB1AC 33 B
