用Matlab实现击实试验数据处理
MATLAB数据处理和分析教程

MATLAB数据处理和分析教程第一章:介绍与基础知识MATLAB(Matrix Laboratory)是一种高效的数值计算和科学数据分析软件,被广泛应用于各个领域的科学研究和工程实践中。
本教程将带领读者逐步了解MATLAB中的数据处理和分析方法。
在开始学习之前,我们先来了解一些MATLAB的基础知识。
1.1 MATLAB的安装和环境设置首先,需要下载并安装MATLAB软件。
在安装完成后,我们可以进行一些基本的环境设置,如设置工作目录、添加搜索路径等。
1.2 MATLAB的基本操作了解MATLAB的基本操作是使用它进行数据处理和分析的基础。
包括变量的定义和使用、矩阵的创建和运算、函数的调用和编写等。
第二章:数据导入和导出在进行数据处理和分析之前,我们需要将数据导入到MATLAB中,并将分析结果导出。
本章介绍了MATLAB中常用的数据导入和导出方法。
2.1 导入各种格式的数据文件MATLAB支持导入各种常见的数据文件格式,包括文本文件(如.csv、.txt)、Excel文件(.xls、.xlsx)、图像文件等。
本节将介绍如何导入这些文件,并将其转换为MATLAB中的矩阵或向量。
2.2 导出数据与导入数据相反,我们有时候需要将处理结果导出到外部文件中。
MATLAB提供了多种导出格式,包括文本文件、Excel文件、图像文件等。
本节将详细介绍这些导出方法的使用。
第三章:数据预处理在进行数据分析之前,通常需要对数据进行预处理,以提高数据的质量和准确性。
本章将介绍MATLAB中的常用数据预处理方法。
3.1 数据清洗数据中常常包含有噪声、缺失值、异常值等,需要通过数据清洗来进行处理。
本节将介绍如何使用MATLAB来进行数据清洗,包括去除噪声、插补缺失值、筛选异常值等。
3.2 数据转换与归一化有时候,我们需要对数据进行转换或归一化,以满足分析的需求。
例如,对数转换、指数转换、归一化等。
本节将详细介绍MATLAB中常用的数据转换和归一化方法。
使用Matlab进行模拟物理与实验数据处理

使用Matlab进行模拟物理与实验数据处理引言近年来,随着计算机技术的迅猛发展,越来越多的科学家和研究人员开始使用计算机模拟和实验数据处理的方法来解决各种物理问题。
其中,Matlab作为一种高效、灵活的科学计算工具,被广泛应用于物理领域。
本文将介绍如何使用Matlab进行模拟物理和实验数据处理。
一、Matlab概述Matlab是一种基于矩阵和向量运算的高级编程语言,专门用于科学计算和数据可视化。
它提供了丰富的内置函数和工具箱,可以方便地进行数值计算、符号计算和图形绘制等操作。
Matlab还支持面向对象编程和并行计算,使得处理大规模物理问题更加高效和便捷。
二、模拟物理1. 数值模拟Matlab提供了一系列的数值模拟工具,可以用来解决常微分方程、偏微分方程、边值问题等各种物理模型。
通过定义自定义函数和调用内置的求解器,可以轻松地实现各种数值求解算法。
例如,可以使用欧拉法、龙格-库塔法等经典算法对运动方程进行数值积分,得到粒子的轨迹。
此外,还可以利用有限元方法对结构力学、电磁场等问题进行数值求解。
2. 模型建立Matlab的强大矩阵和向量运算能力为物理模型的建立提供了很大的便利。
结合图形绘制工具箱,可以利用Matlab绘制出需要建模的物体的几何结构和其他参数。
然后,可以使用线性代数或者非线性优化等方法,通过数值迭代的方式求解模型的参数。
例如,在光学领域,可以利用矢量计算来模拟和优化光波的传播和调控。
三、实验数据处理1. 数据导入与预处理Matlab提供了灵活的数据导入和预处理工具,可以方便地处理各种类型的实验数据。
通过读取不同格式的文件,如文本、Excel、MAT等,可以将实验数据导入到Matlab工作空间中。
之后,可以使用Matlab的矩阵和向量运算功能对数据进行预处理,如去除异常值、平滑信号、插值数据等。
2. 数据分析与可视化Matlab内置了大量的数据分析函数和工具箱,可以对实验数据进行统计分析、频域分析、时频分析等。
用matlab处理大学简单实验报告数据方法

MATLAB实验报告数据处理1、均值数学定义:Matlab函数:mean>>X=[1,2,3]>>mean(X)=2如果X是一个矩阵,则其均值是一个向量组。
mean(X,1)为列向量的均值,mean (X,2)为行向量的均值。
>>X=[123456]>>mean(X,1)=[2.5,3.5,4.5]>>mean(X,2)=[25]若要求整个矩阵的均值,则为mean(mean(X))。
>>mean(mean(X))=3.5也可使用mean2函数:>>mean2(X)=3.5median,求一组数据的中值,用法与mean相同。
>>X=[1,2,9]>>mean(X)=4>>median(X)=22、方差数学定义:均方差:Matlab函数:var要注意的是var函数所采用公式中,分母不是,而是。
这是因为var函数实际上求的并不是方差,而是误差理论中“有限次测量数据的标准偏差的估计值”。
>>X=[1,2,3,4]>>var(X)=1.6667>>sum((X(1,:)-mean(X)).^2)/length(X)=1.2500>>sum((X(1,:)-mean(X)).^2)/(length(X)-1)=1.6667var没有求矩阵的方差功能,可使用std先求均方差,再平方得到方差。
std,均方差,std(X,0,1)求列向量方差,std(X,0,2)求行向量方差。
>>X=[1234]>>std(X,0,1)=1.41421.4142>>std(X,0,2)=0.70710.7071若要求整个矩阵所有元素的均方差,则要使用std2函数:>>std2(X)=1.29104、协方差矩阵A=[61.45,55.9,61.95,59,58.14,53.61,55.48,54.21,61.52,54.92]; B=[40.36,39.8,49.2,48,51.5,49.39,51.13,58.06,61,62.35];C=[8.61,8.91,10.43,13.32,13.48,15.75,18.14,19.95,21.95,23.53]; D=[14.31,14.72,15.28,15.91,14.67,15,15.86,15.16,13.72,12.94];E=[7.67,7.75,8.15,9.24,10.68,10.58,10.31,10,8.91,8.51];>>q=[A',B',C',D',E'];>>w=cov(q)w=10.3710-4.7446-6.6023-0.1873-1.8881-4.744659.150338.7606-3.07433.0982-6.602338.760628.6966-2.01992.4166-0.1873-3.0743-2.01990.84740.3936-1.88813.09822.41660.39361.3412。
Matlab实验仿真实验数据
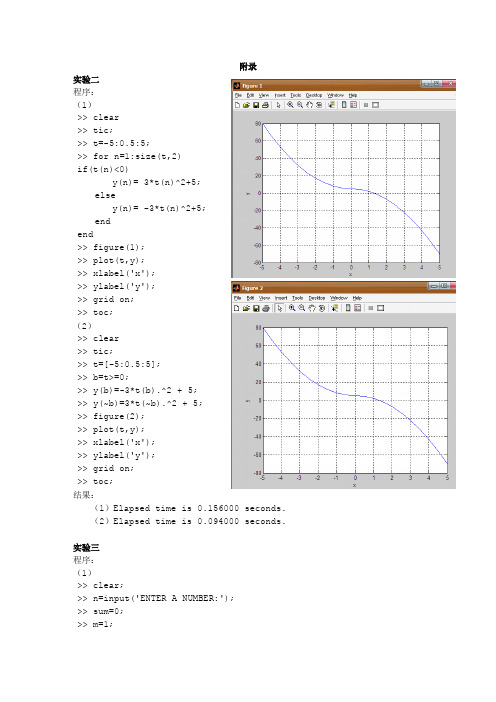
附录实验二程序:(1)>> clear>> tic;>> t=-5:0.5:5;>> for n=1:size(t,2)if(t(n)<0)y(n)= 3*t(n)^2+5;elsey(n)= -3*t(n)^2+5;endend>> figure(1);>> plot(t,y);>> xlabel('x');>> ylabel('y');>> grid on;>> toc;(2)>> clear>> tic;>> t=[-5:0.5:5];>> b=t>=0;>> y(b)=-3*t(b).^2 + 5;>> y(~b)=3*t(~b).^2 + 5;>> figure(2);>> plot(t,y);>> xlabel('x');>> ylabel('y');>> grid on;>> toc;结果:(1)Elapsed time is 0.156000 seconds.(2)Elapsed time is 0.094000 seconds.实验三程序:(1)>> clear;>> n=input('ENTER A NUMBER:');>> sum=0;>> m=1;>> while m<nsum=sum+m;m=m+2;end>> fprintf('The result of all odd numbers within a given number is:%d\n',sum);(2)创建Fib.m文件% 函数功能: 计算斐波那契数列的第 n 个斐波那契数% 文件名: Fib.m% 含有 n 个数的斐波那契数列的定义如下:% f(1) = 1% f(2) = 2% f(n) = f(n-1) + f(n-2)function y=Fib(n);a(1)=1;a(2)=1;i=2;while i<=na(i+1)=a(i-1)+a(i);i=i+1;end;y=a(i);结果:(1)ENTER A NUMBER:6The result of all odd numbers within a given number is:9(2)>> Fib(7)ans =21实验四(1)程序:创建myfun.m文件% 函数功能: 计算x的双曲正弦、双曲余弦和双曲正切,并画出对应的图象。
基于MATLAB实验数据的几种处理方法

模式识别与仿真技术Pattern Recognition and Simulation《自动化技术与应用》2005年第24卷第1期基于MAT LAB实验数据的几种处理方法吴晓光,徐精彩,李树刚,李 华(西安科技大学,陕西 西安 710054)摘要:本文从M AT LAB的工程计算与数据处理能力出发,着重讨论如何运用M AT LAB实现实验数据处理的方法,包括数据拟合、数值插值、数值微商和数值积分,并通过实际应用得出M AT LAB是具有强大数据计算和分析功能的软件,同时将使用者从繁琐的底层编程中解放出来,大大提高工作效率。
关键词:数据处理;M AT LAB;曲线拟合中图分类号:TP27412 文献标识码:B 文章编号:100327241(2005)0120025203Matla b-bas e d Proces sin g Met h o ds of Exp eri m e ntal DataWU Xiao-guang,XU Jing-cai,LI Shu-gang,LI H ua(X i’an University of Science&T echnology,X i’an710054,China)Abstract:Because of the high capability of the engineering calculation and data processing of M AT LAB,the data processing methods suck as data fit2 ting,data interpretation,differential and integral for the experimental data by using M AT LAB are all presented in the paper.K ey w ords:Data processing;M AT LAB;Curve fitting1 引言数据处理是一项复杂、繁琐的事情,随着计算机技术的迅速发展,美国Mathw orks公司于1967年推出了Matrix Laboratory(缩写为M AT LAB)软件包,集应用程序和图形于同一环境[1]。
MATLAB数据处理与分析实战

MATLAB数据处理与分析实战在科学研究和工程领域中,数据处理和分析是重要的环节。
而MATLAB作为一款功能强大的数据处理和分析工具,在学术界和工业界得到广泛应用。
本文将介绍MATLAB在数据处理和分析方面的实战经验,并探讨一些应用案例。
一、数据预处理数据预处理是数据分析的第一步,它包括数据清洗、数据转换和数据集成等过程。
对于大规模和复杂的数据集,预处理的重要性不言而喻。
MATLAB提供了丰富的函数和工具箱,可以帮助我们进行高效的数据预处理。
首先,我们需要对原始数据进行清洗。
在MATLAB中,一般使用数据筛选、数据去重和数据异常值检测等函数来实现数据清洗的过程。
例如,通过使用“find”函数可以筛选出满足某个条件的数据;使用“unique”函数可以去除重复的数据;使用“isoutlier”函数可以检测异常值。
其次,我们需要对原始数据进行转换。
转换包括数据标准化、数据离散化和数据归一化等过程。
MATLAB中提供了许多函数和工具箱来实现这些转换操作。
例如,使用“zscore”函数可以进行标准化处理;使用“quantize”函数可以进行离散化处理;使用“normalize”函数可以进行归一化处理。
最后,我们需要将预处理好的数据进行集成。
数据集成包括数据合并、数据连接和数据汇总等过程。
MATLAB提供了一系列的函数和工具箱来实现这些集成操作。
例如,使用“vertcat”函数可以垂直合并数据;使用“horzcat”函数可以水平合并数据;使用“groupsummary”函数可以进行数据分组汇总。
二、数据可视化数据可视化是数据分析的重要方式之一,通过直观的图表展示,我们可以更好地理解数据结构和趋势。
MATLAB提供了丰富的绘图函数和工具箱,可以帮助我们实现各种类型的数据可视化。
在MATLAB中,我们可以使用“plot”函数来绘制二维折线图,使用“scatter”函数来绘制二维散点图,使用“bar”函数来绘制柱状图,使用“pie”函数来绘制饼图。
matlab实验报告1

matlab实验报告1MATLAB实验报告1摘要:本实验使用MATLAB软件进行了一系列的实验,主要包括数据处理、图像处理和信号处理。
通过实验,我们掌握了MATLAB软件在科学计算和工程领域的应用,深入了解了MATLAB在数据处理、图像处理和信号处理方面的强大功能。
一、数据处理实验在数据处理实验中,我们使用MATLAB对一组实验数据进行了分析和处理。
首先,我们导入了实验数据并进行了数据清洗和预处理,然后利用MATLAB的统计分析工具对数据进行了描述性统计分析,包括均值、方差、标准差等指标的计算。
接着,我们利用MATLAB的绘图工具绘制了数据的直方图和散点图,直观地展现了数据的分布规律和相关性。
二、图像处理实验在图像处理实验中,我们使用MATLAB对一幅图像进行了处理和分析。
首先,我们读取了图像并进行了灰度化处理,然后利用MATLAB的图像滤波工具对图像进行了平滑和锐化处理,最后利用MATLAB的图像分割工具对图像进行了分割和特征提取。
通过实验,我们深入了解了MATLAB在图像处理领域的应用,掌握了图像处理的基本原理和方法。
三、信号处理实验在信号处理实验中,我们使用MATLAB对一组信号进行了处理和分析。
首先,我们生成了一组模拟信号并进行了频域分析,利用MATLAB的信号滤波工具对信号进行了滤波处理,然后利用MATLAB的频谱分析工具对信号的频谱特性进行了分析。
通过实验,我们深入了解了MATLAB在信号处理领域的应用,掌握了信号处理的基本原理和方法。
综上所述,本实验通过对MATLAB软件的应用实验,使我们对MATLAB在数据处理、图像处理和信号处理方面的功能有了更深入的了解,为我们今后在科学计算和工程领域的应用奠定了良好的基础。
MATLAB软件的强大功能和广泛应用前景,将为我们的学习和科研工作提供有力的支持和帮助。
Matlab中的现场数据采集与实时处理

Matlab中的现场数据采集与实时处理现场数据采集和实时处理在许多科学研究和工程项目中扮演着至关重要的角色。
无论是环境监测、运动分析还是生物医学研究,实时数据采集和处理对于获得准确的结果和及时的决策至关重要。
而Matlab作为一种功能强大且广泛应用的科学计算软件包,提供了丰富的工具和功能,使得现场数据采集和实时处理变得更加高效和简便。
一、数据采集现场数据采集是实时数据处理的前提。
Matlab提供了各种数据采集接口和工具,可以与各种传感器、设备和数据源进行无缝集成。
通过使用Matlab的数据采集工具箱,用户可以轻松连接各种硬件设备,如传感器和数据采集卡。
此外,Matlab还支持多种数据传输方式,包括串口通信、网络通信和无线通信等。
在进行数据采集之前,必须对采集参数进行设置和优化。
Matlab提供了丰富的数据预处理工具,可进行采样率控制、滤波和去噪等操作。
通过使用Matlab的信号处理工具箱,用户可以对采集的数据进行频谱分析、时频分析和特征提取等操作,从而对信号进行处理和优化。
二、实时处理实时处理是现场数据采集的关键环节。
Matlab提供了多种实时处理工具和算法,可以对采集的数据进行实时分析、处理和可视化。
通过使用Matlab的实时工具箱,用户可以轻松构建实时数据处理系统。
该工具箱包括各种实时算法和滤波器,可以实时处理和分析采集的数据。
Matlab的并行计算功能也可以加速实时数据处理。
并行计算可以利用多核处理器或分布式计算机群集来并行计算任务,提高处理速度和效率。
在实时数据处理任务中,通过使用Matlab的并行计算功能,用户可以同时处理多个数据流,从而实现高效的数据处理和分析。
三、数据可视化数据可视化是实时数据处理的重要环节。
Matlab提供了强大的数据可视化工具和函数,可以将采集的数据以直观的方式展示出来。
通过使用Matlab的图形和可视化工具箱,用户可以创建各种静态和动态图形,如折线图、散点图、柱状图和动画图等。
如何使用MATLAB进行数据处理和模拟实验

如何使用MATLAB进行数据处理和模拟实验第一章:MATLAB简介MATLAB是一种强大的数值计算软件,广泛应用于科学与工程领域。
它具备丰富的数学和统计函数库,可以进行各种数据处理和模拟实验。
在本章中,我们将简要介绍MATLAB的基本特点和使用方法。
1.1 MATLAB的特点MATLAB具备以下特点:(1)矩阵计算:MATLAB内置了矩阵运算功能,使得数据处理更加简便和高效。
(2)图形显示:MATLAB可以生成高质量的二维和三维图形,方便数据可视化。
(3)函数丰富:MATLAB内置了大量的数学和统计函数,能够满足各种数值计算需求。
(4)易于学习:MATLAB的语法简单易懂,上手较容易,适合初学者。
1.2 MATLAB的安装和启动要使用MATLAB进行数据处理和模拟实验,首先需要安装MATLAB软件。
(1)从MathWorks官方网站下载MATLAB安装程序。
(2)运行安装程序,并按照提示进行安装。
(3)安装完成后,通过启动菜单或桌面图标启动MATLAB。
1.3 MATLAB的基本语法MATLAB的语法类似于其他编程语言,主要包括变量定义、函数调用、循环和条件判断等基本操作。
(1)变量定义:使用等号将数值或表达式赋给变量,例如:x = 2.5。
(2)函数调用:通过函数名和参数调用函数,例如:y =sin(x)。
(3)循环:使用for或while循环重复执行一段代码,例如:for i = 1:10。
(4)条件判断:使用if语句根据条件执行不同的代码块,例如:if x > 0。
第二章:数据处理数据处理是指从原始数据中提取、转换和整理信息的过程。
在MATLAB中,通过使用各种数据处理函数和工具箱可以实现对数据的各种操作。
2.1 数据导入和导出MATLAB支持多种数据格式的导入和导出,包括文本文件、Excel文件、图像文件等。
通过导入数据,可以将数据加载到MATLAB工作空间中进行处理。
(1)导入文本文件:使用readtable函数可以将文本文件中的数据读取为一个表格变量。
matlab实验报告

matlab实验报告Matlab实验报告实验题目:利用Matlab进行数据处理与分析实验目的:通过使用Matlab进行数据处理与分析的实践,掌握Matlab的基本操作和数据处理的方法。
实验内容:1. 数据读取:从文件中读取原始数据,并进行初步的观察和分析。
2. 数据清洗:对原始数据进行清洗,包括去除空值、异常值等。
3. 数据可视化:利用Matlab的绘图函数,将数据可视化呈现,以方便对数据进行进一步的分析和理解。
4. 数据分析:对清洗后的数据进行统计分析,包括求平均值、方差、相关系数等。
5. 模型建立:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
6. 结果验证:利用实验数据和模型进行实验结果的对比,验证模型的准确性和可靠性。
实验步骤:1. 准备实验数据:从实验样本中获得原始数据,并将其存储为文本文件。
2. 使用Matlab导入数据:使用Matlab的数据导入函数,将文本文件中的数据导入到Matlab的工作空间中。
3. 数据分析与处理:使用Matlab的数据处理函数,对导入的数据进行清洗和处理,去除异常值和空值,并进行初步的数据观察和分析。
4. 数据可视化:利用Matlab的绘图函数,绘制数据的直方图、散点图、折线图等,以展示数据的分布和趋势。
5. 数据统计分析:使用Matlab的统计分析函数,对处理后的数据进行统计分析,包括计算平均值、方差、相关系数等。
6. 模型建立与验证:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
7. 结果对比和讨论:将实验结果与模型预测结果进行对比,并进行结果的讨论和分析。
8. 实验结论:总结实验结果并给出结论。
实验结果:根据实验数据的分析和处理,得出如下结论:1. 数据呈现正态分布,符合正态性假设。
2. 数据之间存在显著的正相关关系,相关系数为0.8,结果具有统计学意义。
3. 建立的数学模型与实验数据拟合良好,模型预测结果与实验结果吻合度高。
Matlab在实验数据处理中的应用

表 达式 ( ) 中 、 4 式 的值分 别 为 :
㈣
图形处理等多 种功 能于一体 的科 学计算 软件r , 1 它 ]
只需使用简单 的编 程 , 就能完 成复杂 计算 。本 文 即 以波尔共振这一基 本 的本科 物理实验 为例 , 论述 基
一 aca r tn () 6
表 达式 ( )和 ( )分 别 为 波尔 共 振 系统 摆 轮 5 6
定 状 态 时 的表 达 式 为 :
0 = Oc s a + ) to ( . # (泛 , 由于计算 过程较 但
繁琐 , 在实验 教学 中往 往 不作 要 求 。实 际上 , 果 如 教师 能使 学 生 掌握 Mal t b这一 数 学 工具 , 能 轻 a 就 松解决这个 矛盾 。Mal t b是集数值计算 、 a 符号计算 、
基础 。 目前 , 实验 课 时缩 减等 因素影 响 , 师 通 受 教
常更关 注学生 的实验方法和过程 , 而对数据 处理 环 节重视 不够 。这 主要 是 因为数 据 处理 往往 涉 及 复 杂 的计 算 , 需花 费较 多 时 间, 在实 验 时间 不宽 裕 的 情况 下 , 只能有 所侧 重 。例 如 , 小二 乘 法虽 然 在 最
收稿 日期 :2 1 - 0 —2 . 01 3 5 作 者 简介 : 林 (9 5 )男 , 北 省 武 汉 市 人 , 验 师 , 究 方 向 : 验技 术 和 电 子信 息 。 黄 17一 , 湖 实 研 实
89
第 2 4卷第 3 期
2 1 年 6月 01
高等 函授学 报( 自然科 学版 )
数 nif t 或 l cr e i) 再 根 据 表 达 式 ( )采 ln i( s u v ft , q 3
如何利用Matlab进行数据分析和处理

如何利用Matlab进行数据分析和处理一、引言数据分析和处理是现代科学研究和工程实践中不可或缺的一部分。
而Matlab作为一款功能强大的计算软件,提供了丰富的工具和函数,可以帮助研究者和工程师进行高效的数据分析和处理。
本文将介绍如何利用Matlab进行数据分析和处理的方法和技巧。
二、数据导入和预处理在进行数据分析和处理之前,首先需要将数据导入到Matlab中,并进行必要的预处理。
在Matlab中,可以使用多种方式导入数据,如读取文本文件、Excel文件或者直接从数据库中读取数据。
一般可以使用readtable或csvread等函数进行读取。
导入数据后,可能需要进行缺失值处理、数据清洗或者数据转换等预处理操作,以保证数据的完整性和准确性。
三、数据可视化数据可视化是数据分析的重要一环,能够帮助我们更好地理解和分析数据。
Matlab提供了丰富的可视化函数和工具包,可以绘制各种类型的图表,如散点图、直方图、折线图等。
通过调整图表的样式、颜色和坐标轴等参数,可以使图表更加清晰明了。
此外,Matlab还支持交互式可视化,可以通过鼠标操作进行多维数据的探索和交互式分析。
四、数据分析和模型建立在进行数据分析时,可能需要对数据进行一定的统计学分析,如计算均值、标准差、相关系数等。
此外,Matlab还支持各种常见的数据分析方法和技术,如线性回归、逻辑回归、聚类分析、主成分分析等。
通过调用相关函数,可以快速进行各种分析操作,并得到分析结果。
若需要建立模型进行预测和预测,可以使用Matlab中的机器学习和深度学习工具箱,灵活选择和使用各种算法和模型。
五、数据处理和特征提取在实际的数据分析和处理中,往往需要对数据进行进一步处理和特征提取,以发现数据中隐藏的信息。
Matlab提供了一系列的数据处理和特征提取函数,如滤波、傅里叶变换、小波变换等。
这些函数可以帮助我们处理信号数据、图像数据和时间序列数据,从中提取出关键特征,并用于后续的分析和建模。
使用Matlab进行数据处理的基本流程

使用Matlab进行数据处理的基本流程数据处理是科学研究和工程实践中必不可少的一环,而Matlab作为一种强大的数值计算与数据分析工具,在数据处理方面具有广泛的应用。
本文将介绍使用Matlab进行数据处理的基本流程,旨在帮助读者快速上手并运用Matlab解决实际问题。
一、准备阶段在使用Matlab进行数据处理之前,我们首先需要明确数据处理的目的和所需数据的来源。
例如,我们可能需要对实验数据进行统计分析、进行图像处理、处理传感器采集的数据等等。
此外,还要准备好Matlab的安装包并安装在计算机上。
二、导入数据在Matlab中,我们可以使用多种方式导入数据。
常见的方法包括读取文本文件、导入Excel或者CSV文件和直接从其他数据源(如数据库)中获取数据等。
对于文本文件,可以使用"readtable"函数进行读取并生成表格数据;对于Excel或者CSV文件,可以使用"readmatrix"或者"readcell"函数进行读取。
需要注意的是,在导入数据之前,要确保数据的格式和结构是符合Matlab的要求的。
三、数据预处理在进行后续的数据处理之前,通常需要对原始数据进行清洗和预处理。
这包括处理缺失值、处理异常值、去除重复数据、标准化数据等等。
Matlab提供了众多的函数和工具箱,例如"nanmean"可以用于计算均值并自动忽略缺失值,"isoutlier"可以用于检测异常值等。
根据具体的需求,选择合适的方法进行数据预处理,以确保数据的质量和准确性。
四、数据分析与可视化在数据预处理完成后,我们可以进行数据分析和可视化工作。
Matlab中提供了丰富的函数和工具箱,可用于进行统计分析、回归分析、聚类分析等等。
例如,我们可以使用"histogram"函数绘制直方图来观察数据的分布特征,使用"scatter"函数绘制散点图来观察变量之间的关系,使用"boxplot"函数进行箱线图分析等。
利用MATLAB进行实验数据处理

2.多项式插值和拟合:
设 a = x0 < x1 < ⋯ < xn = b ,已知有 n +1对节点 (xi , yi ) , i = 0,1, 2⋯, n ,其中 xi 互不相 同,这些节点 (xi , yi ) , i = 0,1, 2⋯, n 可以看成是由某个函数 y = f (x) 产生的。 f 的解析表达
2
利用 MATLAB 进行实验数据处理
最小误差平方和,且所用的曲线限定为多项式时,这种拟合方法相当简捷,称为多项式拟合(也 称曲线拟合)。这在分析实验数据,将实验数据做解析描述时非常有用。
拟合和插值有许多相似之处,但是这两者最大的区别在于拟合要找出一个曲线方程式,而 插值仅是要求出插值数值即可。
下面以一维插值为例进行讨论。一维插值在 MATLAB 中可用多项式插值函数 interp1 来实 现,多项式拟合用 polyfit 来实现。
%计算在这些 x 点的多项式值
plot(xcurve,p3curve,'--',xcurve,p4curve,'-.',xcurve,p5curve,'-',x,y,'.')
>> lx=[-1,1.5];ly=[0,0];hold on;
plot(lx,ly,'--',lx,ly-1.3,'-.',lx,ly-2.6,'-');
p=polyfit(x,y,n)
[p,s]=polyfit(x,y,n)
其中,x,y 为已知的数据组,n 为要拟合的多项式的阶次,向量 p 为返回的要拟合的多项式
基于MATLAB实验数据的几种处理方法

基于MATLAB实验数据的几种处理方法1.数据可视化:MATLAB提供了丰富的绘图函数和工具箱,可以通过绘制柱状图、折线图、散点图等可视化方式来展示实验数据的分布和趋势。
通过数据可视化,可以更直观地观察数据的特征,发现异常值或者趋势,并作为后续数据处理的依据。
2.数据预处理:对实验数据进行预处理可提高后续分析的准确性。
常见的数据预处理方法有:数据清洗(去除异常值、重复值、缺失值)、数据平滑(滤波处理,如移动平均、中值滤波)、数据标准化(归一化、标准化)等。
可以使用MATLAB的内置函数或者工具箱来实现这些数据预处理方法。
3.拟合与回归分析:通过拟合与回归分析,可以建立实验数据的数学模型,用于预测和估计。
MATLAB提供了各种拟合函数和回归分析工具,如线性回归、非线性回归、多项式拟合等。
这些方法可以帮助我们找到最佳的拟合曲线或者回归方程,用于预测未来的数据或者进行参数估计。
4. 数据聚类与分类:聚类与分类是将数据集划分为不同的类别或者簇群,利用相似性或距离度量确定数据之间的关系。
MATLAB提供了多种聚类和分类算法,如K-means聚类、层次聚类、支持向量机(SVM)等。
通过聚类与分类,我们可以发现数据内在的结构与规律,对数据进行分类,提取关键特征。
5.数据频谱分析:频谱分析是研究信号在频域上的特性,对于周期性信号或者周期性成分较强的信号,频谱分析可以揭示其频率分量和相应的能量分布。
MATLAB提供了多种频谱分析方法,如傅里叶变换、功率谱估计等。
通过频谱分析,我们可以对实验数据进行频域特征提取,提供有关信号周期性、频率成分等信息。
6.时间序列分析:时间序列分析是研究时序数据之间的相关性和趋势性的方法。
MATLAB提供了时间序列分析的函数和工具箱,如自相关函数(ACF)、偏自相关函数(PACF)、平稳性检验、ARMA模型等。
通过时间序列分析,可以建立模型预测未来的数据,或者研究数据随时间的变化规律。
Matlab在物理实验数据处理中的应用指南

Matlab在物理实验数据处理中的应用指南引言物理实验是科学研究的重要组成部分,而数据处理则是物理实验中不可或缺的环节。
随着计算机科学的迅速发展,Matlab成为了一种广泛应用于数据分析和处理的工具。
本文将探讨Matlab在物理实验数据处理中的应用指南,介绍如何使用Matlab进行数据处理,展示其在物理实验中的重要作用。
不但要学会如何通过Matlab处理数据,更要了解其背后的原理,以提高数据分析的准确性和可靠性。
第一部分:准备数据在使用Matlab处理实验数据之前,首先需要准备好原始数据。
通常,实验数据以文本文件的形式存储,可以通过Excel等软件导出。
在导出数据之后,需要对数据进行预处理,如去除异常值、填补缺失数据等。
Matlab提供了一系列强大的函数,如importdata、readtable和xlsread,可以用于读取各种类型的数据文件,方便快捷地将数据载入到Matlab工作环境中。
第二部分:数据可视化数据可视化是数据处理的重要环节,能够直观地展示数据的分布和趋势。
Matlab提供了丰富的绘图函数,如plot、scatter和histogram,可以方便地绘制二维和多维数据图形。
通过选择合适的绘图方式和参数设置,可以用直线、曲线、散点图、柱状图等形式展示数据的规律。
此外,Matlab还支持绘制动态图像和三维图形,更加生动地展示实验结果。
第三部分:数据处理与分析Matlab具备强大的数值计算和数据处理能力,可以对物理实验数据进行各种精确的计算和分析。
例如,可以使用Matlab进行数据平滑、拟合、差分、积分等操作,进一步深入研究数据的特征和规律。
Matlab还提供了大量的统计分析函数,如均值、标准差、方差、相关系数等,可供用户快速计算和分析数据的统计特性。
此外,Matlab还支持矩阵运算和线性代数,可用于解析物理模型和求解数学方程。
第四部分:数据模型与拟合在物理实验中,常常需要建立数据模型和进行曲线拟合。
基于Matlab的击实试验数值分析方法

基于Matlab的击实试验数值分析方法
张平;宋仲明
【期刊名称】《交通标准化》
【年(卷),期】2006(000)002
【摘要】对于公路填方路基工程,路基压实是数据的拟合曲线,并将其应用到Matlab中,可以极大地提高工作效率和减少人为误差,具有一定的推广应用价值.【总页数】3页(P145-147)
【作者】张平;宋仲明
【作者单位】中南大学,湖南,长沙,410083;岳阳路桥总公司,湖南,岳阳,414000【正文语种】中文
【中图分类】U416.1
【相关文献】
1.确定标准击实试验极值的一种数值分析方法 [J], 王驰;许民哲
2.击实试验数据的数值分析方法研究 [J], 毛生华
3.基于Matlab的击实试验数值分析方法 [J], 张平;宋仲明
4.基于 MATLAB 的土工击实试验数据处理的探讨 [J], 白宏光
5.击实试验数据的数值分析方法 [J], 俞文生;蒲华;
因版权原因,仅展示原文概要,查看原文内容请购买。
MATLAB数据处理实验方案

MATLAB实验报告subplot(1,2,2),surfl(peaks,[15,10]),shading interp6、动画绘制实验:Getframe方法n=100;M = moviein(n);x=(1:360)/180*pi;set(gcf,'doublebuffer','on')for k=1:n;plot(x,sin(x)*k*0.03);ylim([-3,3]);M(k) = getframe(gcf);endclose allaxis off;set(gca,'position',[0.03 0.01 0.775 0.815])movie(M,0,30)实验记录1.离散数据可视化实验:2.二维曲线绘制实验:1)Plot方法用于绘制图像2)Subplot绘制子表3)Axis函数表示坐标的范围4)Set设置坐标轴系统5)Legend用于添加图例或者图表的声明6)xlabel、ylabel、zlabel、用于标示各个坐标轴的名称7)Title设置图表的标题8)Text添加文本,注释坐标系中一点9)grid on10)Hold指令的基本格式11)双坐标轴3、三维曲线绘制实验1)plot3函数2)Mesh绘制曲面3)Surf函数的使用方法4)Fplot函数的使用方法4、统计图绘制实验:1)面域图(area)2)直方图(bar、barh、bar3、bar3h)3)Pie指令4)散点图(scatter、scatter3、plotmatrix)5、三维图形编辑(精细控制)实验:1)View的用法2)Rotate的用法3)Colordef指令的使用4)Colormap方法5)Shading方法6)Light方法7)Lighting命令8)Material指令9)Surfl指令6、制作动画实验总结1、Matlab绘图的基本步骤:1)准备图标的数据。
用户需要确定图标的绘制范围,制定对应的自变量,最后计算相应的函数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质量重要指标压实度控制的关键。
2 Mal t b实现击实试验数据处理原理 a
基于上述情况, 提出以下数据处理方法。假定给定的实验数
1 击实试验数据处理方法
目 击实试验数据处理方法有图解法 、 前, 三点书解法、 数值解 据 ( y ) i= l 2 … , 。 于各实验 数据 精度不 同引 入权 函 X ,i( , , ) 由 法 、 拟合法 , 曲线 下面分别详细介绍其基本原理 。
1 一 一 2
第二、 三个土样按 2%递增分别加水拌和后击实则相应的变换密
度 , =I , P / 1 .2 ,3 P / 1 .4 , ( , ) II D l2 2 ( +0 0 )P 3( +0 0 )按 0 P1 , D ID
咛 ( =1 妒 ( =l— , ( =( 一0 ) , ) , I o ) z)  ̄ k ( ( ) =2 3 … , , , , m)
(, )( ,' 三点用合抛物线拟合 , 0 l , p3 D 2 0 ) 求出抛物线的顶点即为最 大干密度 和最优含水量与填 料含水 量的差值 2 , 为施工 现场
提供快速压实控制方法L 。
则(= 笛 ( , 据初, , ) 将 的值 长 值 数 步终
并用 p t ) l ( 语句可显示出所需的数值和击实曲线。 o
,,一
、
_- 的极值点 , ,T ’) ( 再用 N w o 迭代 格式 + = 一 et n I
一
, 给定
个初值, 反复迭代求解, 即可求出满足精度要求 的最佳含水量
>>smsXyA=[nss e x )X, . . ]a A\y y ; o e(i ( ) z X . x 3 ; . 2 - ;
1 1 图解 法 .
数叫 , 差 , ) 限 使∑ () 小。 空 基H中 2 i ( 误 z 最 在 间 构 ̄ E -
即 pn I … }构成一组线形 无关 的 o 2 图解法是一种常用方法, 根据击实试验得到的数据组在厘米 交函数族 , H =sa { , , , , 。, ( t )+ a ( )+ a 9( )+ … + O l x 1 2 2x 纸上取点绘制曲线 , 曲线 的峰值点 即为所求 的最大 干密 度 , 相对 近似 函数。 )=  ̄ 伽( a ( ( = 12… , , : )m ,, ) 则 应的含水量为最优含水量。此法具有快速简便特点 , 但结果误差
13 数 值 解法 .
・
3 Mal t b实现数据处理的实例 a
为展示 Maa 数据 处理的方便 , tb l 文中采用文献 [] 3 的数据 , 见 数值解法是用函数 ‘ ) , 在 十1 ( 互异节点 0 , , , 2…, I 表1 。为说明方便设 叫 ) , ( =1正交函数族选 m: , ( ) , 3 o工 =1 上的函数数值 f x ), I, , )求出关于节点 ( o, ( )…,( , 的k 妒( = ( = , ( = , l ) , ) 3 ) 则用 Ma s 处理数据的源 t1 l . 0 阶差商 , k阶差商可求 出 以 , I , , 为插 值节 点的 由 o I … 2
维普资讯
2006 年 4 月
第3 2卷 第 8期
山 西 建 筑
S HANXI ARaHI TEC I E T 瓜
Vo . 2 No 8 I3 .
A t 20 p. 06
・8 ・ 1
文章确号 : 0 . 2 10 60 4 8 - 1 96 5 20 }8 ) 1 2 0 8 0 0
关键词 : 击实试验 , 最佳含水量 , 最大干 密度 , 数据处理 , tb Maa l 中圈分类号 : U4 2 3 T 7 . 文献标识码 : A
在道路、 堤坝、 机场、 房屋建筑等土木工程施工中, 经常要根 分布得累计分布函数的概率 P求出拟合多项式, 即曲线与数据点 据现行的技术规范来对填筑的材料进行压实 , 以改善土的性质, 的加权残差为最小和残差分步累积分布函数的概率 P较小来表 提高填料的强度 , 保证工程质量 。压 实度是评 价施工质最 的一个 示确定多项式模型的拟合曲线, 可用 M tb aa 实现多项式曲线… 。 l 1
用 Malb实 现 击 实 试 验 数 据 处 理 t a
何建平 张 伟 姜 兵
摘 要: 分析四种击实试验数据处理方法的优劣, 在此基础上提出了用 M tb al 实现数据处理的方法, a 并用实例说明用 Maa 实现 数据处理 的方法简便, tb l 易操作 , 精度高适宜推广应用。
语句 如下 :
次插值 多项式 , 以此作 为击实 曲线 的函数表达 式 , 用 =0 出 求
(Ⅵ
裹 1 实验数据 I古水量 I 1. I 1. l l. l l. I 1 . l 1 35 57 77 96 6 I干密度 I l 2 I L 7 I l85 185 I 1 7 l 。 6 7 6 2 l .1 . 0 7 7
较大[ 。
ak :
12 三点 数 解 法 .
三点数解法来 自于 D / 1920 碾压 土石坝施工 规范 中 LT 52. 1 0 的三点击实验数解法 。 基本 原理 是第一 个土 样含水 量保 持不 变 ,
=
∑Yk f ∑ ( 忌 ,…,) i( ) tX/ p =1 , , 2 ∑f Ix /  ̄ 2 ∑ 一 =l , , , k ) - 2 ) x ( ,…, ) 2 , I
