中考数学压轴题 (203)
2023届中考数学压轴题含答案解析

2023年中考数学压轴题
1.如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),
B(0,2),二次函数y=1
2
x2+bx﹣2的图象经过C点.
(1)求二次函数的解析式;
(2)平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;
(3)将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P 点坐标;若不存在,请说明理由.
解:(1)过点C作KC⊥x轴交于点K,
∵∠BAO+∠CAK=90°,∠BAO+∠CAK=90°,
∴∠CAK=∠OBA,
又∠AOB=∠AKC=90°,AB=AC,
∴△ABO≌△CAK(AAS),
∴OB=AK=2,AO=CK=1,故点C的坐标为(3,1),
将点C的坐标代入二次函数表达式得:1=1
2
×9+3b﹣2,
第1页共12页。
2023年九年级数学中考专题:二次函数与圆综合压轴题(含简单答案)

2023年九年级数学中考专题:二次函数与圆综合压轴题1.如图1,在平面直角坐标系中,O为坐标原点,已知抛物线与x轴交于,两点,与y轴交于点C.(1)求抛物线解析式;(2)如图2,M是抛物线顶点,的外接圆与x轴的另一交点为D,与y轴的另一交点为E.①求;②若点N是第一象限内抛物线上的一个动点,在射线上是否存在点P,使得与相似?如果存在,请求出点P的坐标;(3)点Q是拋物线对称轴上一动点,若为锐角,且,请直接写出点Q 纵坐标的取值范围.2.【概念学习】在平面直角坐标系中,对于已知的点和图形,给出如下定义:如果图形上存在一点,使得当时,,则称点为图形的一个“垂近点”.(1)【初步理解】若图形为线段,,,在点、、、中,是线段的“垂近点”的为________;(2)【知识应用】若图形为以坐标原点为圆心,2为半径的圆,直线与轴交于点、与轴交于点,如果线段上的点都是的“垂近点”,求的取值范围;(3)若图形为抛物线,以点为中心,半径为的四边形,轴,轴,如果正四边形上存在“垂近点”,直接写出的取值范围.3.在平面直角坐标系xOy中,已知抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y 轴交于C点,D为抛物线顶点.(1)连接AD,交y轴于点E,P是抛物线上的一个动点.①如图一,点P是第一象限的抛物线上的一点,连接PD交x轴于F,连接,若,求点P的坐标.②如图二,点P在第四象限的抛物线上,连接AP、BE交于点G,若,则w 有最大值还是最小值?w的最值是多少?(2)如图三,点P是第四象限抛物线上的一点,过A、B、P三点作圆N,过点作轴,垂足为I,交圆N于点M,点在运动过程中,线段是否变化?若有变化,求出MI的取值范围;若不变,求出其定值.(3)点Q是抛物线对称轴上一动点,连接OQ、AQ,设AOQ外接圆圆心为H,当的值最大时,请直接写出点H的坐标.4.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx-4(a≠0)经过点A(-2,0)和点B(4,0).(1)求这条抛物线所对应的函数表达式;(2)点P为抛物线上第一象限内一点,若S△ABC=2S△PBC,求点P的坐标;(3)如图2,点D是第二象限内抛物线上一点,过点D作DF⊥x轴,垂足为F,△ABD 的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.5.如图,抛物线经过点,,直线AC的解析式为,且与y轴相交于点C,若点E是直线AB上的一个动点,过点E作轴交AC于点F.(1)求抛物线的解析式;(2)点H是y轴上一动点,连结EH,HF,当点E运动到什么位置时,四边形EAFH 是矩形?求出此时点E,H的坐标;(3)在(2)的前提下,以点E为圆心,EH长为半径作圆,点M为上以动点,求的最小值.6.已知二次函数的图象经过点A(2,0),B(,0),C(0,4),点为二次函数第二象限内抛物线上一动点,轴于点,交直线于点,以为直径的圆⊙M与交于点.(1)求这个二次函数的关系式;(2)当三角形周长最大时.求此时点点坐标及三角形的周长;(3)在(2)的条件下,点N为⊙M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.7.如图,在平面直角坐标系中,抛物线,y与轴交于A、B两点,与轴交于点C.(1)求点A、B、C的坐标;(2)如图1,连接BC,点D是抛物线上一点,若∠DCB=∠ABC,求点D的坐标;(3)如图2,若点P在以点O为圆心,OA长为半径作的圆上,连接BP、CP,请你直接写出CP+BP的最小值.8.如图,在平面直角坐标系中,半径为1的圆的圆心在坐标原点,且与两坐标轴分别交于、、、四点,点坐标为.抛物线与轴交于点,与直线交于点、,且、分别与圆相切于点和点.(1)求抛物线的解析式.(2)过点作圆的切线交的延长线于点,判断点是否在抛物线上,说明理由.(3)抛物线对称轴交轴于点,连接并延长交于点,求点的坐标.9.如图,在平面直角坐标系中,抛物线交y轴于点,交x轴于两点.(1)求此抛物线的解析式;(2)已知点P是抛物线上的一个动点,且位于A、C两点之间,问:当点P运动到什么位置时,的面积最大?并求出此时P点的坐标和的最大面积;(3)过点B作线段的垂线交抛物线于点D,如果以点C为圆心的圆与直线相切,请判断抛物线的对称轴l与有怎样的位置关系,并给出证明.10.如图,直线与x轴交于点B,与y轴交于点C,抛物线经过B、C两点,且与x轴交于另一点A.(1)求抛物线的解析式.(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC 于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.11.直角坐标系xOy中,有反比例函数上的一动点P,以点P为圆心的圆始终与y轴相切,设切点为A(1)如图1,⊙P运动到与x轴相切时,求OP2的值.(2)设圆P运动时与x轴相交,交点为B、C,如图2,当四边形ABCP是菱形时,①求出A、B、C三点的坐标.②设一抛物线过A、B、C三点,在该抛物线上是否存在点Q,使△QBP的面积是菱形ABCP 面积的?若存在,求出所有满足条件的Q点的坐标;若不存在,说明理由.12.已知:如图,在平面直角坐标系xOy中,以点P(2,)为圆心的圆与y轴相切于点A,与x轴相交于B、C两点(点B在点C的左边).(1)求经过A、B、C三点的抛物线的解析式;(2)在(1)中的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的.如果存在,请直接写出所有满足条件的M点的坐标;如果若不存在,请说明理由;(3)如果一个动点D自点P出发,先到达y轴上的某点,再到达x轴上某点,最后运动到(1)中抛物线的顶点Q处,求使点D运动的总路径最短的路径的长.13.已知,如图,二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),B(3,0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.(1)求这个二次函数关系式.(2)当△EFR周长最大时.①求此时点E点坐标及△EFR周长.②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.14.如图所示,对称轴为直线的抛物线与轴交于、两点,与轴交于点,点在抛物线对称轴上并且位于轴的下方,以点为圆心作过、两点的圆,恰好使得弧的长为周长的.(1)求该抛物线的解析式;(2)求的半径和圆心的坐标,并判断抛物线的顶点与的位置关系;(3)在抛物线上是否存在一点,使得?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.15.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P 点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.16.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E四点,B 为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.17.已知一次函数:与轴交于点,与轴交于点.抛物线(、为常数)过定点,连接,点为线段上一动点.(1)求出点的坐标;(2)过作于点,于点,设点横坐标为,长度为,试求关于的函数解析式;(3)①当,时,该抛物线上存在唯一的点使,求此时抛物线的解析式;②过点作交线段于点,连接并延长交的外接圆于点,当点在上移动时,求的最大值.18.已知抛物线经过,,三个点.(1)求抛物线的解析式;(2)如图1,作的外接圆,为上方半圆上一点,当时,求的长;(3)如图2,直线与抛物线交于,两点,与轴交于点,作轴的平行线,分别与线段、抛物线交于,两点(点与点,不重合),点为射线上一点,当与相似时,求的最大面积.参考答案:1.(1)(2)①;②存在,或或或(3)或2.(1),;(2);(3)或时,正方形上存在抛物线的“垂近点”.3.(1)①,②w有最小值,w的最值是(2)不变,(3)或4.(1);(2);(3)为定值.5.(1);(2),;(3)6.(1);(2)F(,4),△EFD的周长为;(3).7.(1),,;(2),;(3)8.(1);(2)点在抛物线上;(3)9.(1);(2),;(3)相交,10.(1)y=x2﹣x﹣2;(2)m=2时,DE有最大值,此时P;(3),或E或11.(1)16;(2)①A(0,),B(2,0),C(6,0);②存在,满足条件的Q点有(0,),(14,),(8,)和(6,0).12.(1).(2)存在,点M的坐标为(0,),(3,0),(4,),(7,).(3).13.(1)y=﹣x2+2x+3;(2)①E(,),周长为+;②HQ的最大值大为:+.14.(1)(2)2,,点在上(3)存在,,,15.(1)抛物线解析式为y=x2﹣x+5(2)圆心P点的坐标为(,)(3)①四边形OEAF的面积是定值,这个定值为;②当△OEF的面积取得最小值时,E点坐标为(,)16.(1)y=﹣x2+x+2;(2)M(,);(3)四边形CFEH是矩形.17.(1);(2)();(3)①;②18.(1);(2);(3).。
安徽省2023中考数学题型3填空压轴题习题

题型三填空压轴题高分帮类型1多空类1.如图,在直角三角形纸片ABC中,∠ACB=90°,点D,E分别是BC,AC上的点(不含端点),折叠△DCE使得直角顶点C落在斜边AB上的点F处,且△BDF是直角三角形.(1)四边形DCEF的形状是正方形;.(2)若AB=10,AC=6,则CD的长为2472.如图(1),在△ABC中,AB=AC,∠BAC=90°,AF在∠BAC内部,且AF=AB.分别对折∠BAF,∠CAF,使得AB,AC与AF重合,如图(2)(BD<CE).(1)△DEF的形状是直角三角形;(2)若AB=6√2,DE=5,则AD的长为3√5.3.在矩形纸片ABCD中,AB=6,BC=8,E为边CD上一点.如图(1),将△BCE沿BE所在直线折叠,点C恰好落在AD 边上的点F处;将纸片展开,如图(2),沿着CF所在直线折叠△CDF得到△CD'F,折痕CF与BE交于点M.(1)点D' 是BF上的一点;(填“是”或“不是”)(2)若点N是AF的中点,连接MN,则MN= 5.4.如图(1),四边形ABCD是正方形,点E是边AD上的点,将△CDE沿着直线CE折叠,使得点D落在AC上,对应点为点F.(1)CCCC = √2+1 ;(2)如图(2),点G 是BC 上的点,将△ABG 沿着直线AG 折叠,使得点B 落在AC 上,对应点为H ,连接FG ,EH ,则C 正方形CCCC C 四边形CCCC=4+3√22.5.在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图(1)~(4)的过程折叠、展开.(1) (2) (3) (4)(1)在图(4)中,四边形ABCD 是 菱 形;(2)若四边形ABCD 的面积为S ,则正方形纸片的面积为 (√2+1)S . 类型2 几何多解类 1.点、线位置不确定类多解题6.[2020亳州二模]如图,在△ABC 中,∠C=90°,AC=8,BC=16,点D ,E 分别在边BC ,AB 上,沿DE 将△ABC 折叠,使点B 与点A 重合,连接AD ,点P 在线段AD 上,当点P 到△ABC 的直角边距离等于5时,AP 的长为253或154.7.[2019宣城二模]在正方形ABCD 中,AB=6,连接AC ,BD ,P 是正方形边或对角线上一点,若PD=2AP ,则AP 的长为 2,2√3或√14-√2 .8.[2020安庆模拟]已知在△ABC 中,∠ABC=90°,AB=9,BC=12.点Q 是线段AC 上的一个动点,过点Q 作AC 的垂线交射线AB 于点P.连接BQ ,当△PQB 为等腰三角形时,AP 的长为 5或18 . 2.图形形状不确定类多解题9.如图,已知在等腰三角形ABC 中,AB=AC=√5,BC=4,点D 从点A 出发,以每秒√5个单位长度的速度向点B 运动,同时点E 从点B 出发,以每秒4个单位长度的速度向点C 运动,在DE 的右侧作∠DEF=∠B ,交直线AC 于点F ,连接DF.设运动时间为t 秒,则当△ADF 是一个以AD 为腰的等腰三角形时,t 的值为521,511或12.10.[2019合肥包河区一模]如图,在矩形ABCD 中,AD=4,AC=8,点E 是AB 的中点,点F 是对角线AC 上一点,△GEF 与△AEF 关于直线EF 对称,EG 交AC 于点H.当△CGH 中有一个内角为90°时,CG 的长为 2√7或4 .11.如图,在正方形ABCD 中,AB=3,点E 在AD 边上,且AE=2.点P 是射线BC 上一动点,连接BE ,PE ,过点P 作PF ⊥BE 于点F.当△PEF 与△ABE 相似时,BP 的长为 2或134 .3.操作过程不确定类多解题12.如图是一张有一个角为30°,最小边长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,则所得四边形的周长为 8+4√3或16 .13.在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线剪去两个三角形,剩下的部分是如图所示的四边形,经测量这个四边形的相邻两边长分别为10cm,6cm,一条对角线的长为8cm,则原三角形纸片的周长是 48或(32+8√13) cm.类型3 函数多解类14.在抛物线y=ax 2+bx+c 中,当-3≤x ≤3时,-3≤y ≤3,且该抛物线经过点(3,-3),(-3,3),则a 的取值范围为-16≤a<0或0<a ≤16 .15.[2020合肥48中一模]在平面直角坐标系中,点O 为坐标原点,抛物线y=-x 2-2x+c 与y 轴交于点P ,以OP 为一边向左作正方形OPBC ,点A 为抛物线的顶点,当△ABP 是锐角三角形时,c 的取值范围是 1<c<2或-2<c<-1 .16.[2020合肥瑶海区二模]如果二次函数y=x 2+b (b 为常数)与正比例函数y=2x 的图象在-1≤x ≤2时有且只有一个交点,那么常数b 的值应为 b=1或-3≤b<0 .17.如图,直线y=x 与抛物线 y=x 2-x-3交于A ,B 两点(点A 在点B 的左侧),点P 是抛物线上的一个动点,过点P 作PQ ⊥x 轴交直线y=x 于点Q ,设点P 的横坐标为m ,则线段PQ 的长度随着m 的增大而减小时,m 的取值范围是 m<-1或1<m<3(等号写不写均可) .18.如图,若双曲线L :y=CC (x<0)与抛物线G :y=-34x (x+4)所围成的区域(不含边界)内整点(点的横、纵坐标都是整数)的个数是3,则k 的取值范围是 -3<k ≤-2 .参考答案题型三 填空压轴题1.(1)正方形 (2)247(1)易知∠B<90°.由折叠可知∠DFE=90°,∴∠BFD=90°-∠AFE<90°,∴∠BDF=90°,∴∠CDF=180°-∠BDF=90°,∴四边形DCEF 是矩形.又DC=DF ,∴四边形DCEF 是正方形.(2)如图,∵四边形DCEF 是正方形,∴EF ∥BC ,EC ∥FD ,∴∠AEF=∠C=∠FDB ,∠AFE=∠B ,∴△AEF ∽△FDB ,∴CC CC =CCCC,∴AE ·DB=EF ·FD.易得BC=8.设CD=x ,则CE=EF=DF=CD=x ,∴BD=8-x ,AE=6-x ,∴(6-x )·(8-x )=x 2,解得x=247,即CD=247.2.(1)直角三角形 (2)3√5 (1)由折叠可知∠AFD=∠B ,∠AFE=∠C.∵∠BAC=90°,∴∠B+∠C=90°,∴∠AFD+∠AFE=90°,故△DEF 是直角三角形.(2)如图,过点A 作AG ⊥BC ,垂足为点G.∵AB=AC=6√2,∠BAC=90°,∴BC=√CC 2+CC 2=12.∵AB=AC ,AG ⊥BC ,∴AG=BG=CG=6.设BD=x ,则DF=x ,EF=EC=12-DE-BD=12-5-x=7-x.在Rt△DEF 中,DE 2=DF 2+EF 2,即25=x 2+(7-x )2,解得x=3或4.∵BD<CE ,∴BD=3,∴DG=3,∴AD=√32+62=3√5.3.(1)是 (2)5 (1)由折叠的性质可知BC=BF ,∠DFC=∠D'FC ,∴∠BFC=∠BCF.∵AD ∥BC ,∴∠DFC=∠BCF ,∴∠D'FC=∠BFC ,∴点D'是BF 上的点.(2)连接AC.由折叠的性质可知,BE 垂直平分线段CF ,∴点M 是FC 的中点.又点N 是AF 的中点,∴MN 是△ACF 的中位线,∴MN=12AC.∵四边形ABCD 是矩形,∴∠ABC=90°,∴AC=√CC 2+CC 2=√62+82=10,∴MN=12AC=5.4.(1)√2+1 (2)4+3√22(1)由题意可知△AEF 是等腰直角三角形,且AF=EF.设EF=m ,则DE=m ,AE=√2EF=√2m ,∴CD=AD=m+√2m=(1+√2)m ,∴CC CC =(1+√2)CC=√2+1.(2)易知△CHG 是等腰直角三角形,且CH=GH.由折叠和正方形的性质可知∠DCE=∠BAG=22.5°.又∵CD=AB ,∠D=∠B=90°,∴△DCE ≌△BAG ,∴DE=BG ,∴EF=DE=BG=GH.易知∠GHF=∠EFH=90°,∴EF ∥GH ,∴四边形EFGH 是平行四边形,∴S 四边形EFGH =EF×FH.CH=HG=EF=AF=m ,AC=√2CD=√2(m+√2m ).S 正方形ABCD =CD 2=(1+√2)2m 2,S 四边形EFGH=EF (AC-AF-CH )=m [√2(m+√2m )-2m ]=√2m2,∴C 正方形CCCC C 四边形CCCC=√2)2√2=√2√2=4+3√22.5.(1)菱 (2)(√2+1)S (1)如图,由折叠可知,∠MAD=∠DAC=12∠MAC ,∠CAB=∠NAB=12∠CAN ,∠DCA=∠MCD=12∠ACM ,∠ACB=∠NCB=12∠ACN.∵四边形AMCN 是正方形,∴∠MAC=∠MCA=∠NAC=∠NCA ,∴∠DAC=∠BAC=∠BCA=∠DCA ,∴AD ∥BC ,AB ∥DC ,∴四边形ABCD 为平行四边形.∵∠DAC=∠DCA ,∴AD=CD ,∴四边形ABCD 为菱形.(2)连接MN 交AC 于点O ,过点B 作BP ⊥AN 于点P ,易知MN 经过点B ,D ,△BPN 是等腰直角三角形,则OB=BP ,BN=√2BP.设OB=BP=a ,则BD=2a ,BN=√2a ,∴C△CCC C △CCC=CC CC =√2C +C C =√2+1.根据正方形和菱形的对称性,可知C 正方形CCCC C 四边形CCCC =2C △CCC2C △CCC=√2+1,∴S 正方形AMCN=(√2+1)S.6.253或154 设BD=x ,则AD=BD=x ,CD=16-x.在Rt△ACD 中,由勾股定理,得AD 2=AC 2+CD 2,即x 2=82+(16-x )2,解得x=10,∴BD=10,CD=6.分以下两种情况讨论.(1)当点P 到AC 边的距离等于5时,过点P 作PF ⊥AC 于点F ,如图(1),则PF=5,PF ∥CD ,∴△APF ∽△ADC ,∴CC CC =CC CC ,即CC 10=56,∴AP=253.(2)当点P 到BC 边的距离等于5时,过点P 作PG ⊥BC 于点G ,如图(2),则PG=5,PG ∥AC ,∴△DPG ∽△DAC ,∴CC CC =CCCC ,即CC 10=58,∴DP=254,∴AP=10-254=154.综上所述,AP 的长为253或154.7.2,2√3或√14-√2 当点P 是AD 上的点时,如图(1),∵PD=2AP ,∴AP=13AD=13AB=2.当点P 是AB 上的点时,如图(2),∵PD=2AP ,∠DAP=90°,∴∠ADP=30°,∴AP=√33AD=√33×6=2√3.如图(3),当点P 是AC 上的点时,过点P 作AD 的垂线,垂足为点E.设AP=x ,则PD=2x ,AE=PE=√22x ,∴DE=6-√22x.在Rt△DEP 中,由勾股定理,得PD 2=DE 2+PE 2,即(2x )2=(6-√22x )2+(√22x )2,解得x=√14-√2(负值已舍去),故AP=√14-√2.当点P 是CD ,BD 或BC 上的点时,都不能满足PD=2AP.综上所述,AP 的长为2,2√3或√14-√2.8.5或18 在Rt△ABC 中,AB=9,BC=12,由勾股定理,得AC=15.分以下2种情况讨论.①当点P 在线段AB 上时,如图(1).∵∠QPB=∠A+∠AQP=∠A+90°,∴∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PQ=PB=9-PA.易证△AQP ∽△ABC ,∴CC CC =CCCC ,即CC 15=9−CC 12,∴AP=5.②当点P 在线段AB 的延长线上时,如图(2),易知∠QBP为钝角,∴当△PQB 为等腰三角形时,只可能是PB=BQ ,∴∠BQP=∠P.又∵∠BQP+∠AQB=90°,∠A+∠P=90°,∴∠AQB=∠A ,∴BQ=AB=9,∴BP=9,∴AP=18.综上所述,当△PQB 为等腰三角形时,AP 的长为5或18.9.521,511或12根据题意可得AD=√5t ,BE=4t ,则BD=√5-√5t ,CE=4-4t.易证△BDE ∽△CEF ,∴CC CC =CCCC,∴BD ·CF=BE ·CE.分以下三种情况讨论.①如图(1),当点F 在线段AC 上,且AF=AD=√5t 时,CF=BD=√5-√5t ,∴(√5-√5t )2=4t (4-4t ),解得t=521(不合题意的解已舍去).②如图(2),当点F在CA 的延长线上,且AF=AD=√5t 时,CF=√5+√5t ,∴(√5-√5t )(√5+√5t )=4t (4-4t ),解得t=511(不合题意的解已舍去).③如图(3),当点F 在CA 的延长线上,且DF=AD=√5t 时,过点B 作BM ⊥AC ,垂足为点M.设AM=x ,由勾股定理可得AB 2-AM 2=BC 2-CM 2,即(√5)2-x 2=42-(√5+x )2,解得x=3√55.取AF 的中点H ,连接DH ,则∠HDA=∠MBA ,∴sin∠HDA=sin∠MBA ,即CC CC =CC CC ,∴√5C =3√55√5,解得AH=3√55t ,∴AF=6√55t ,∴(√5-√5t )(√5+6√55t )=4t (4-4t ),解得t=12(不合题意的解已舍去).综上所述,t 的值为521,511或12.图(1) 图(2) 图(3)10.2√7或4 在矩形ABCD 中,AB=CD=√CC 2-CC 2=4√3,tan∠BAC=CC CC =4√3=√33,∴∠BAC=30°.如图(1),当∠CHG=90°时,EH=12AE=√3,AH=√3EH=3,∴CH=8-3=5,GH=EG-EH=√3,∴CG=√CC 2+CC 2=√52+(√3)2=2√7.如图(2),当∠CGH=90°时,连接CE ,∵BE=AE=GE ,CE=CE ,∴Rt△CEG ≌Rt△CEB ,∴CG=BC=4.由题意可知,点G 在以点E 为圆心,EA 为半径的圆上运动,∴∠GCH<90°,故∠GCH ≠90°.图(1) 图(2)11.2或134 在△PEF 与△ABE 中,∠A=∠EFP=90°,∴当△PEF 与△ABE 相似时,分两种情况讨论.(1)如图(1),当△PEF ∽△EBA 时,∠PEF=∠EBA ,∴AB ∥EP.易得四边形ABPE 是矩形,∴BP=AE=2.(2)如图(2),当△PEF ∽△BEA 时,∠PEF=∠BEA.∵AD ∥BC ,∴∠EBP=∠BEA ,∴∠PEF=∠EBP ,∴BP=EP ,∴点F 是BE 的中点.由勾股定理可求得BE=√CC 2+CC 2=√32+22=√13,∴EF=12BE=√132.∵△PEF ∽△BEA ,∴CC CC =CC CC,即√1322=√13,∴EP=134,∴BP=EP=134.综上可知,BP 的长为2或134.图(1) 图(2)12.8+4√3或16 如图,由题意可得AB=4.∵∠C=30°,∴BC=8,AC=4√3.根据题意易知CD=AD=2√3,CF=BF=4,DF=2.剪开后有如图(1)、图(2)、图(3)3种拼接方式.图(1)中所得四边形ABED 为矩形,其周长为2+2+4+2√3+2√3=8+4√3;图(2)中所得四边形为平行四边形,其周长为4+4+4+4=16;图(3)中所得四边形为等腰梯形,其周长为2+4+2+4+4=16.综上,所得四边形的周长为8+4√3或16.13.48或(32+8√13) 原三角形纸片有如图(1)、图(2)两种可能.如图(1),原三角形纸片的三边长分别为20,16,12,故其周长为48cm;如图(2),∵BD=6,BC=8,CD=10,∴BD 2+BC 2=CD 2,∴∠CBD=90°.易知AC ∥BD ,∴∠BCA=90°,∴AB=√CC 2+CC 2=4√13,故原三角形纸片的三边长分别为20,12,8√13,故其周长为(32+8√13)cm.综上所述,原三角形纸片的周长是48cm 或(32+8√13)cm.14.-16≤a<0或0<a ≤16由于y=ax 2+bx+c 经过(3,-3),(-3,3),则9a+3b+c=-3①,9a-3b+c=3②,①-②,得6b=-6,∴b=-1,∴抛物线y=ax 2+bx+c 的对称轴为直线x=12C .当a<0时,抛物线的开口向下,当x=12C ≤-3时符合题意,解得-16≤a<0;当a>0时,抛物线的开口向上,当x=12C≥3时符合题意,解得0<a ≤16.综上所述,a 的取值范围为-16≤a<0或0<a ≤16.15.1<c<2或-2<c<-1 根据抛物线的顶点坐标公式可得A (-1,c+1).分两种情况讨论.①当c>0时,如图(1),此时B (-c ,c ),P (0,c ),∴AP 2=(-1-0)2+(c+1-c )2=2,AB 2=[-1-(-c )]2+(c+1-c )2=c 2-2c+2.易知当0<c<1时,∠ABP 为钝角;当c=1时,∠ABP 为直角;当c>1时,随着c 的增大,∠ABP 逐渐减小,∠BAP 逐渐增大,当∠BAP 增加到90°时,AB 2+AP 2=BP 2,即c 2-2c+2+2=c 2,解得c=2.故△ABP 是锐角三角形时,1<c<2.②当c<0时,如图(2),此时B (c ,c ),P (0,c ),∴AP 2=(-1-0)2+(c+1-c )2=2,AB 2=(-1-c )2+(c+1-c )2=c 2+2c+2.易知当-1<c<0时,∠ABP 为钝角;当c=-1时,∠ABP 为直角;当c<-1时,随着c 的减小,∠ABP 逐渐减小,∠BAP 逐渐增大,当∠BAP 增加到90°时,AB 2+AP 2=BP 2,即c 2+2c+2+2=c 2,解得c=-2.故△ABP 是锐角三角形时,-2<c<-1.综上所述,c 的取值范围为1<c<2或-2<c<-1.16.b=1或-3≤b<0 对于y=2x ,当x=-1时,y=-2,当x=2时,y=4.令x 2+b=2x ,移项,得x 2-2x+b=0,当Δ=4-4b=0时,解得b=1,此时抛物线与正比例函数y=2x 的图象的交点为(1,2),-1<1<2,故b=1符合题意,此时函数图象如图(1)所示.随着b 的减小,抛物线向下平移,当抛物线经过点(2,4)时,易得b=0,函数图象如图(2)所示,易知当0≤b<1时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时有两个交点.当抛物线过点(-1,-2)时,b=-3,函数图象如图(3)所示,易知当-3≤b<0时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时有一个交点.随着抛物线继续向下平移,易知当b<-3时,抛物线与正比例函数y=2x 的图象在-1≤x ≤2时无交点.综上所述,b=1或-3≤b<0.图(1) 图(2) 图(3)17.m<-1或1<m<3(等号写不写均可) 令x=x 2-x-3,解得x 1=-1,x 2=3,∴A (-1,-1),B (3,3).易得P (m ,m 2-m-3),Q (m ,m ).当m<-1或m>3时,PQ=m 2-m-3-m=m 2-2m+1-4=(m-1)2-4,∴当m<-1时,PQ 的长度随m 的增大而减小;当-1<m<3时,PQ=m-(m 2-m-3)=-m 2+2m+3=-(m-1)2+4,∴当1<m<3时,PQ 的长度随m 的增大而减小.综上可知,m 的取值范围为m<-1或1<m<3.18.-3<k ≤-2 ∵y=-34x (x+4)=-34(x+2)2+3,∴抛物线G 的顶点坐标为(-2,3).对于y=-34x (x+4),当x=-1时,y=94;当x=-3时,y=94;当x=-4或x=0时,y=0,∴抛物线与x 轴围成的区域(不含边界)内包含的整点有(-3,2),(-3,1),(-2,2),(-2,1),(-1,2),(-1,1),共6个.分析题意可知,符合要求的整点一定是(-3,2),(-2,2),(-3,1),故当双曲线y=CC 经过(-2,1)和(-1,2)两点时,k 取最大值,为-2;当双曲线y=CC 经过点(-3,1)时,符合条件的整点只有(-3,2)和(-2,2).综上可知,k 的取值范围为-3<k ≤-2.。
2023年九年级数学中考专题:几何探究压轴题

2023年九年级数学中考专题:几何探究压轴题一、解答题1.如图,在ABC 中,4AC =,3BC =,90ACB ∠=︒,D 是边AC 上一动点(不与点A 、C 重合),CE BD ⊥,垂足为E ,交边AB 于点F .(1)当点D 是边AC 中点时,求DE ,EC 的值;(2)设CD x =,AF y =,求y 关于x 的函数关系式,并写出定义域;(3)当EFD △与EFB △相似时,求线段CD 的长.2.【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,点C 把线段AB 分成两部分,如果BC AC AC AB=,那么称点C 为线段AB 的黄金分割点.(1)【问题发现】如图1,点C 为线段AB 的黄金分割点,且AC BC >,若2AB =,请直接写出CB 的值是__________.(2)【问题探究】如图2,在Rt ABC △中,90C ∠=︒,2AC =,1BC =,在BA 上截取BD BC =,再在AC 上截取AE AD =,则AE AC的值为__________. (3)【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE 得折痕MN ,连接EN ,将AE 折叠到EN 上,点A 对应点H ,得折痕CE ,试说明:C 是AB 的黄金分割点.3.定义:若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形,我们称这条线段为该三角形的智慧线,这个三角形叫做智慧三角形.(1)如图1,在智慧三角形ABC 中,AD BC ⊥,AD 为该三角形的智慧线,1CD =,则BD 长为_____,B ∠的度数为_____.(2)如图2,ABC 为等腰直角三角形,90BAC ∠︒=,2AB =,F 是斜边BC 延长线上一点,连接AF ,以AF为直角边作等腰直角三角形AFE (点A ,F ,E 按顺时针排列),90EAF ∠=︒, CF =AE 交BC 于点D ,连接EC ,EB .当2BDE BCE ∠=∠时,求线段ED 的长;(3)如图3,ABC 中,5AB AC ==,BC =BCD △是智慧三角形,且AC 为智慧线,求BCD △的面积.4.【问题提出】如图1,在等边三角形ABC 内部有一点P ,3PA=,4PB =,5PC =,求APB ∠的度数.(1)【尝试解决】将APC △绕点A 逆时针旋转60︒,得到AP B '△,连接PP ',则APP '为等边三角形. ∵3P P PA '==,4PB =,5P B PC '==,∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为.(2)【类比探究】如图2,在等边三角形ABC 外部有一点P ,若∠BP A =30°,求证222PA PB PC +=.(3)【联想拓展】如图3,在ABC 中,90BAC ∠︒=,AB AC =.点P 在直线BC 上方且45APB ∠︒=,PC BC ==求PA 的长.5.已知正方形 ABCD 和正方形 CEFG ,连接 AF 交 BC 于点 O ,点 P 是 AF 的中点,过点 P 作 PH DG ⊥ 于 H ,2CD =,1CG =.(1)如图1,点 D ,C ,G 在同一直线上,点 E 在 BC 边上,求 PH 的长;(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<.①如图2,当点E 落在AF 上时,求CO 的长;②如图3,当DG =PH 的长.6.在ABC ∆中,点E 为AC 边上一动点,以CE 为边在CE 上方作等边CEN .(1)如图1,EN 与AB 交于点P ,连接PC ,若tan A =,1AE =,5CN =,求PC 的长: (2)如图2.当N 与B 重合时,在BC 上取一点D ,过点D 作DF AC ∥,连接BF ,EF ,过C 作CH EF ⊥交EF 于点H ,若30FBC DFE ︒∠-∠=,求证:CH BF +=;(3)如图3,若BC AB ⊥,且4AB BC ==,过点B 作BQ AC ∥,I 为射线.BQ 上一动点,取AC 中点M ,连接MI ,过点B 作BK MI ⊥交M 于点K ,连接NK ,直接写出NK 的最小值.7.问题情境:如图1,在Rt △ABC 和Rt △BEF 中,∠ACB =∠EFB =90°,AC =3,BC =4,且M ,N 分别为AE ,CF 的中点.(1)猜想证明:如图2,将Rt △BEF 绕点B 按逆时针方向旋转90°,其他条件不变.试判断54AM CN =是否成立?若成立,请写出证明过程;若不成立,请说明理由.(2)解决问题:如图3,将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F ',连接AE ',CF ,并分别取它们的中点P ,H ,连接CP ,FP ,PH .①试判断CP 与FP 之间的数量关系,并说明理由.②若AB =2BE ',BC =2BF ,请直接写出PH 的长.8.【方法尝试】(1)如图1,矩形ABFC 是矩形ADGE 以点A 为旋转中心,按逆时针方向旋转90︒所得的图形,CB ED 、分别是它们的对角线.则CB 与ED 数量关系________,位置关系________.【类比迁移】(2)如图2,在Rt ABC 和Rt ADE △中,90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====.将DAE 绕点A 在平面内逆时针旋转,设旋转角BAE ∠为()0360αα︒<︒,连接,CE BD .请判断线段CE 和BD 的数量关系和位置关系,并说明理由;【拓展延伸】(3)如图3,在Rt ABC 中,90,6ACB AB ∠=︒=,过点A 作AP BC ∥,在射线AP 上取一点D ,连结CD,使得3tan4ACD∠=,请求写出线段BD的最大值.9.如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.10.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(1)猜测探究:在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度,得到线段AN,连接NB.①如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;②如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(2)拓展应用:如图3,在△A 1B 1C 1中,A 1B 1=8,∠A 1B 1C 1=60°,∠B 1A 1C 1=75°,P 是B 1C 1上的任意点,连接A 1P ,将A 1P 绕点A 1按顺时针方向旋转75°,得到线段A 1Q ,连接B 1Q .求线段B 1Q 长度的最小值. 11.如图,在Rt ABC △中,90BAC ∠=︒,AB AC =,D 为AC 边上一点,连接BD ,作AP BD ⊥于点P ,过点C 作CE AC ⊥交AP 延长线于点E .(1)如图1,求证:AD CE =;(2)如图2,以AD ,BD 为邻边作ADBF ,连接EF 交BC 于点G ,连接AG ,①求证:AG EF ⊥;②若点D 为AC 中点,EF 、AB 交于点H ,求BH AB的值. 12.如图1,在ABC 中,90ACB ∠=︒,D 为AC 边上的一点,过点D 作DE AB ⊥,垂足为E ,连接BD ,P 为BD 中点,连接PC ,PE .(1)求证:PC PE =;(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置,其他条件不变,(1)中的结论是否成立?若成立,请证明:若不成立,请说明理由;(3)若10AB =,6AD =,30BAC DAE ∠=∠=︒,在平面内,将Rt ADE △绕点A 旋转一周,当A ,C ,E 三点共线时,请直接写出PCE 的面积.13.如图1,在直角坐标系中,点()2,0A ,点()0,2C ,点D ,点E 分别为OA ,OC 的中点,ODE 绕原点O 顺时针旋转α角(090α︒<<︒)得11OD E ,射线1CD ,1AE 相交于点F .(1)求证:11OCD OAE △≌△;(2)如图2,在ODE 旋转过程中,当点1D 恰好落在线段CE 上时,求AF 的长;(3)如图3,在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中,求点F 的运动路线长.14.已知ABC 为等边三角形,边长为4,点D 、E 分别是BC 、AC 边上一点,连接AD 、BE .AE CD =.(1)如图1,若2AE =,求BE 的长度;(2)如图2,点F 为AD 延长线上一点,连接BF 、CF ,AD 、BE 相交于点G ,连接CG ,已知60,∠=︒=EBF CE CG ,求证:2+=BF GE CF ;(3)如图3,点P 是ABC 内部一动点,顺次连接PA PB PC 、、++的最小值.15.【问题提出】(1)如图1,在ABC 中,90C ∠=︒,BD 平分ABC ∠交AC 于点D ,设CD 的长为m ,点D 到边AB 的距离为n ,则m _______n ;(填“>”“<”或“=”)【问题探究】(2)如图2,在梯形ABCD 中,90A ∠=︒,AD BC ∥,(201AB =,BD 为对角线,且45BDC ∠=︒,求BCD △面积的最小值;【问题解决】(3)某景点有一个形状为菱形ABCD 的草坪,如图3,AB ==60B ∠︒,现欲将该草坪扩建为BEF △,使得点E 、F 分别在BA 、BC 的延长线上,且边EF 经过点D ,为了节省成本,要求扩建后的草坪面积(BEF △的面积)尽可能小,问BEF △的面积是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.16.综合与实践:数学课外小组研究了两个问题,请你帮助解答.问题一:如图1,在矩形ABCD 中,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为矩形,连接CG .问题二:数学小组对图形的旋转进行了拓展研究,如图4,在平行四边形ABCD 中,=60B ∠︒,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为平行四边形,连接CG .数学小组发现DF 与CG 仍然存在着特定的数量关系.(1)请直接写出CG 的长是______.如图2,当矩形AEGF 绕点A 旋转(如顺时针旋转)至点G 落在边AB 上时,DF =______,CG =______,DF 与CG 之间的数量关系是______.(2)当矩形AEGF 绕点A 旋转至如图3的位置时,(1)中DF 与CG 之间的数量关系是否还成立?并说明理由.(3)如图5,当平行四边形ABCD 绕点A 旋转(如顺时针旋转),其它条件不变时,数学小组发现DF 与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系是______.17.如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,连接BO 并延长交边AD 或边CD 于点E .(1)如图1,当点E 在AD 上时,连接CE ,求证:四边形ABCE 是矩形.(2)如图2,当点E 在CD 上时,当AC =4,BC =3时,求DAC S △与OBC S的比值.(3)若DE =2,OE =3,直接写出CD 的长.18.已知在正方形ABCD 中,E 是BC 边上一动点,作点B 关于AE 的对称点F ,BF 交AE 于点G ,连结DF .(1)如图1,求DFB ∠的度数;(2)如图2,过点D 作DM BF ⊥交BF 的延长线于点M ,连结,CM CF .若DF CM =,试探究四边形DFCM 的形状,并说明理由;(3)如图3,连结BD ,在AG 上截取=GT GB ,点P ,Q 分别是,AD BD 上的动点.若正方形ABCD 的面积为32,直接写出PTQ 周长的最小值.。
2023年九年级中考数学:二次函数综合题压轴题(特殊四边形问题)(含答案)
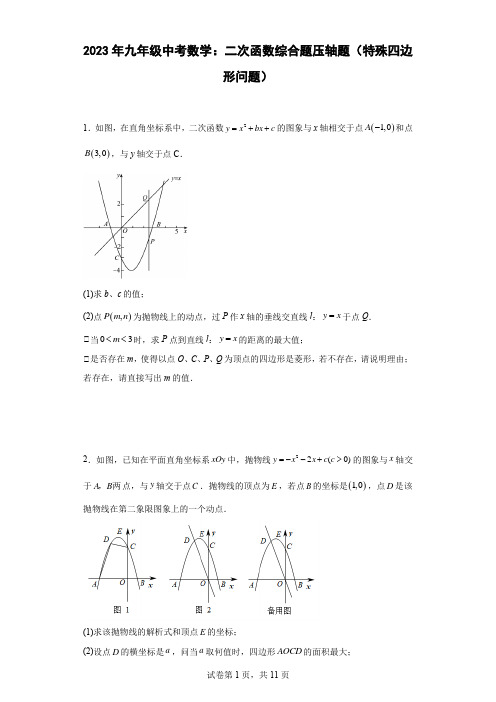
(1)求该抛物线的解析式和顶点 的坐标;
(2)设点 的横坐标是 ,问当 取何值时,四边形 的面积最大;
(3)如图,若直线 的解析式是 ,点 和点 分别在抛物线上和直线 上,问:是否存在以点 为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点 的坐标
3.综合与探究
如图,在平面直角坐标系中,抛物线 与 轴交于 、 两点,与 轴交于点 ,点 为抛物线顶点.
(1)求抛物线解析式;
(2)点 在此抛物线的对称轴上,当 最大时,点 的坐标为_____,此时 的面积为_____;
(3)点 在抛物线上,平面内存在点 使四边形 为菱形时,请直接写出点 的坐标.
4.如图,在平面直角坐标系中,抛物线 和直线 交于 、 两点,直线 交 轴于点 .
20.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上, , ,抛物线 经过点B,且与x轴交于点 和点E.
(1)求抛物线的表达式:
(2)若P是第一象限抛物线上的一个动点,连接CP,PE,当四边形OCPE的面积最大时,求点P的坐标,此时四边形OCPE的最大面积是多少;
(3)若N是抛物线对称轴上一点,在平面内是否存在一点M,使以点C,D,M,N为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,说明理由.
(1)求点 的坐标与 的值;
(2)当点 恰好是 的中点时,求点 的坐标;
(3)连结 ,作点 关于直线 的对称点 ,当点 落在线段 上时,则点 的坐标为______ 直接写出答案
6.已知抛物线 与x轴有公共点.
2024杭州中考数学压轴题

中考数学试卷一、单项选择题(共12分)1.如图图形中是中心对称图形的为()A.B. C. D.2.如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()A.4对 B.3对C.2对D.1对3.在正方形网格中,△ABC的位置如图所示,则tanB的值为()A.1B.√22C.√3D.√334.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3D.x1=0,x2=35.一个由相同正方体堆积而成的几何体如图所示,从正面看,这个几何体的形状是()。
A.B.C.D.6.如图,实数a,b,c,d在数轴上表示如下,则最小的实数为()A.aB.bC.cD.d二、填空题(共24分)7.把一张半径为2cm,圆心角为120°的扇形纸片卷成一个圆锥的侧面,那么这个圆锥的底面积是。
8.已知方程x2+mx﹣6=0的一个根为﹣2,则另一个根是。
9.如图,正方形ABCD的面积为4,点E,F,G,H分别为边AB,BC,CD,AD的中点,则四边形EFGH的面积为____.三、解答题(共20分)10.如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E。
(1)求证:△ADE∽△MAB;(2)求DE的长。
11.已知△ABC和△DEF中,有ABDE =BCEF=CAFD=23,且△DEF和△ABC的周长之差为15厘米,求△ABC和△DEF的周长。
16.某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件。
(1)当每件的销售价为52元时,该纪念品每天的销售数量为件;(2)当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润。
12.如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,AB=7,AD=5,DE=10,求BC的长.13.如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30∘方向,同时测得岛礁P正东方向上的避风港M在北偏东60∘方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达多少?(结果保留根号)14.如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E。
压轴题27选择压轴题(几何篇)-2023年中考数学压轴题专项训练(全国通用)(原卷版)

2023年中考数学压轴题专项训练压轴题27选择压轴题(几何篇)一.选择题(共40小题)1.(2023•朝阳区校级三模)如图,AB是⊙O的直径,将OB绕着点O逆时针旋转40°得到OC,P是⊙O 上一点,且与点C在AB的异侧,连结P A、PC、AC,若P A=PC,则∠P AB的大小是()A.20°B.35°C.40°D.70°2.(2023•河北区二模)如图,在平面直角坐标系中,菱形OABC的顶点A在x轴上,且∠COA=45°,OA =4,则点B的坐标为()A.(4+2√2,2√2)B.(2√2,2√2)C.(2+2√2,2)D.(√2,2)3.(2023•奉贤区二模)如图,矩形ABCD中,AB=1,∠ABD=60°,点O在对角线BD上,圆O经过点C.如果矩形ABCD有2个顶点在圆O内,那么圆O的半径长r的取值范围是()A.0<r≤1B.1<r≤√3C.1<r≤2D.√3<r≤24.(2023•广灵县模拟)如图,在Rt△ABC中,∠C=90°,BC=3,AC=6,点O,D,E是AB边上的点,以点O为圆心,DE长为直径的半圆O与AC相切于点M,与BC相切于点N,则图中阴影部分的面积为()A .5B .9﹣2πC .9﹣πD .5﹣π5.(2023•普陀区二模)如图,△ABC 中,∠BAC =60°,BO 、CO 分别平分∠ABC 、∠ACB ,AO =2,下面结论中不一定正确的是( )A .∠BOC =120°B .∠BAO =30°C .OB =3D .点O 到直线BC 的距离是16.(2023•瓯海区模拟)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形EFGH ,连结DH 并延长交AB 于点K ,若DF 平分∠CDK ,则DH HK =( )A .2√33B .65C .√5−1D .4√577.(2023•花溪区模拟)勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题的最重要工具也是数形结合的组带之一,如图,秋千静止时,踏板离地的垂直高度BE =1m ,将它往前推6m 至C 处时(即水平距离CD =6m ),踏板离地的垂直高度CF =4m ,它的绳索始终拉直,则绳索AC 的长是( )A .152mB .92mC .6mD .212m8.(2023•承德一模)如图,在菱形ABCD 中,AC 、BD (AC >BD )相交于点O ,E 、F 分别为OA 和OC 上的点(不与点A 、O 、C 重合).其中AE =OF .过点E 作GH ⊥AC ,分别交AD 、AB 于点G 、H ;过点F 作IJ ⊥AC 分别交CD 、CB 于点J 、I ;连接GJ 、HI ,甲、乙、丙三个同学给出了三个结论:甲:随着AE 长度的变化,GH +IJ =BD 始终成立.乙:随着AE 长度的变化,四边形GHIJ 可能为正方形.丙:随着AE 长度的变化,四边形GHIJ 的面积始终不变,都是菱形ABCD 面积的一半.下列选项正确的是( )A .甲、乙、丙都对B .甲、乙对,丙不对C .甲、丙对,乙不对D .甲不对,乙、丙对 9.(2023•石家庄二模)如图,在平行四边形ABCD 中,对角线AC ,BD 交于点O ,E ,F 分别是OB 与OD 的中点,依连接点A ,E ,C ,F ,A ,当四边形AECF 是矩形时,与线段BE 相等的线段有( )A .4条B .5条C .6条D .7条10.(2023•青山区二模)如图,边长为2的正方形ABCD 的对角线AC 与BD 相交于点O ,E 是BC 边上一点,F 是BD 上一点,连接DE ,EF .若△DEF 与△DEC 关于直线DE 对称,则OF 的长为( )A .√22B .2√2−2C .2−√2D .√2−111.(2023•柳城县一模)七巧板是我国古代劳动人民的发明之一,被誉为“东方魔板”,它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.(清)陆以活《冷庐杂识》卷中写道:近又有七巧图,其式五,其数七,其变化之式多至千余,体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图,是一个用七巧板拼成的装饰图,放入长方形ABCD 内,装饰图中的三角形顶点E ,F 分别在边AB ,BC 上,三角形①的边GD 在边AD 上,则BF BE 的值为( )A .1+√22B .√22C .2+√24D .2+√2212.(2023•泉州模拟)如图,在矩形ABCD 中,AB =2,BC =4,将△ABC 沿BC 的方向平移至△A 'B 'C ',使得A ′E =A ′F ,其中E 是A ′B ′与AC 的交点,F 是A ′C ′与CD 的交点,则CC ′的长为( )A .52−√52B .112−√5C .5−√5D .92−√5 13.(2023•定远县二模)如图,在Rt △ABC 中,∠BAC =90°,AB =3,BC =5,点P 为BC 边上任意一点,连接P A ,以P A ,PC 为邻边作平行四边形P AQC ,连接PQ ,则PQ 长度的最小值为( )A .3B .2.5C .2.4D .214.(2023•烟台一模)如图,在矩形ABCD 中,AB =12,AD =10,点E 在AD 上,点F 在BC 上,且AE =CF ,连结CE ,DF ,则CE +DF 的最小值为( )A .26B .25C .24D .2215.(2023•郯城县一模)如图,在Rt △ABC 中,∠BAC =90°,AB =6,BC =10,点P 为BC 边上任意一点,连接P A ,以P A ,PC 为邻边作平行四边形P AQC ,连接PQ ,则PQ 长度的最小值为( )A .4.8B .5C .2.4D .416.(2023•白云区一模)如图,正方形ABCD 的面积为3,点E 在边CD 上,且CE =1,∠ABE 的平分线交AD 于点F ,点M ,N 分别是BE ,BF 的中点,则下列结论错误的是( )A .FD =√2MNB .△DEF 是等腰直角三角形C .BN =1D .tan ∠FBE =√317.(2023•九龙坡区校级模拟)如图,在正方形ABCD 中,O 为AC 、BD 的交点,△DCE 为直角三角形,∠CED =90°,OE =3√2,若CE •DE =6,则正方形的面积为( )A .20B .22C .24D .2618.(2023•杭州一模)如图,有两张矩形纸片ABCD 和EFGH ,AB =EF =2cm ,BC =FG =8cm .把纸片ABCD 交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且B 点D 与点G 重合,当两张纸片交叉所成的角α最小时,tan α等于( )A .14B .815C .12D .81719.(2023•高明区二模)矩形ABCD 和直角三角形EFG 的位置如图所示,点A 在EG 上,点D 在EF 上,若∠2=55°,则∠1等于( )A.155°B.135°C.125°D.105°20.(2023•余姚市一模)如图,由两个正三角形组成的菱形内放入标记为①,②,③,④的四种不同大小的小正三角形5个,其中编号①的有2个.设未被覆盖的浅色阴影部分的周长为C1,深色阴影部分的周长为C2,若要求出C1﹣C2的值,只需知道其中两个小正三角形的边长,则这两个小三角形的编号为()A.①②B.②③C.①③D.②④21.(2023•衡水二模)如图,点P是正方形ABCD的边BC上一点,点M是对角线BD上一点,连接PM 并延长交BA的延长线于点Q,交AD于点G,取PQ的中点N.连接AN.若AQ=PC,有下面两个结论:①DM=DG,②AN⊥BD,则这两个结论中,正确的是()A.①对B.②对C.①②都对D.①②都不对22.(2023•新乡二模)如图,在矩形ABCD中,点B(0,4),点C(2,0),BC=2CD,先将矩形ABCD 沿y轴向下平移至点B与点O重合,再将平移后的矩形ABCD绕点O逆时针旋转90°得到矩形EOMN,则点D的对应点N的坐标为()A.(3,3)B.(4,4)C.(3,4)D.(4,3)23.(2023•荆门一模)如图,菱形ABCD各边的中点分别是E、F、G、H,若EH=2EF,则下列结论错误的是()A.EH⊥EF B.EH=AC C.∠B=60°D.AB=√5EF24.(2023•中原区校级二模)如图,在Rt△ABO中,AB=OB,顶点A的坐标为(2,0),以AB为边向△ABO的外侧作正方形ABCD,将组成的图形绕点O逆时针旋转,每次旋转45°,则第98次旋转结束时,点D的坐标为()A.(1,﹣3)B.(﹣1,3)C.(﹣1,2+√2)D.(1,3)25.(2023•中原区模拟)如图,▱ABCD的边BC在x轴的负半轴上,点B与原点O重合,DE⊥AB,交BA 的延长线于点E,已知∠ABC=60°,AB=4,BC=6,则点E的坐标为()A.(﹣2,﹣,2√3)B.(﹣3,3√3)C.(−72,72√3)D.(−52√3,52)26.(2023•武邑县二模)如图,N是正六边形ABCDEF对角线CF上一点,延长FE,CD相交于点M,若S△ABN=2,则S五边形ABCMF=()A.10B.12C.14D.1627.(2023•承德一模)如图,正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分,则该三部分的面积比为()A.1:2:3B.2:2:4C.1:2:4D.2:3:528.(2023•罗湖区二模)如图,AB为圆O的直径,C为圆O上一点,过点C作圆O的切线交AB的延长线于点D,DB=13AD,连接AC,若AB=8,则AC的长度为()A.2√3B.2√5C.4√3D.4√529.(2023•杭州一模)如图,过⊙O外一点A作⊙O的切线AD,点D是切点,连结OA交⊙O于点B,点C是⊙O上不与点B,D重合的点.若∠A=α°,则∠C的度数为()A.(45−12α)°B.12α°C.2α°D.(45+12α)°30.(2023•西宁一模)如图,扇形纸片AOB的半径为3,沿AB所在直线折叠扇形纸片,圆心D恰好落在AB̂上的点C处,则阴影部分的面积是()A.3π−9√32B.3π−3√32C.2π−3√32D.2π−9√3231.(2023•太原一模)如图,在扇形纸片OAB 中,∠AOB =105°,OA =6、点C 是半径OA 上的点、沿直线BC 折叠△OBC 得到△DBC ,点O 的对应点D 落在AB̂上,图中阴影部分的面积为( )A .9π−92B .9π−182C .9π﹣18D .12π﹣1832.(2023•西山区校级模拟)如图,分别以等边△ABC 的三个顶点为圆心,边长为半径画弧,得到的封闭图形是莱洛三角形,若AB 为6,则图中阴影部分的面积为( )A .18π−27√3B .6π−9√3C .12π−9√3D .18π−18√333.(2023•莆田模拟)如图,在⊙O 中,∠AOB =120°,点C 在AB̂上,连接AC ,BC ,过点B 作BD ⊥AC 的延长线于点D ,当点C 从点A 运动到点B 的过程中,∠CBD 的度数( )A .先增大后减小B .先减小后增大C .保持不变D .一直减小 34.(2023•蚌埠二模)如图是某芯片公司的图标示意图,其设计灵感源于传统照相机快门的机械结构,圆O 中的阴影部分是一个正六边形,其中心与圆心O 重合,且AB =BC ,则阴影部分面积与圆的面积之比为( )A .3√38πB .√32πC .√3πD .2√39π35.(2023•鄞州区校级模拟)如图,AB 为⊙O 的直径,将弧BC 沿BC 翻折,翻折后的弧交AB 于D .若BC =4√5,sin ∠ABC =√55,则图中阴影部分的面积为( )A .256πB .253πC .8D .1036.(2023•九龙坡区模拟)如图,在⊙O 中,AB 是圆的直径,过点B 作⊙O 的切线BC ,连接AC 交⊙O 于点D ,点E 为弧AD 中点,连接AE ,若AE =AO ,AB =6,则CD 的长为( )A .2B .3√32C .√3D .3√337.(2023•宁德模拟)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以等边三角形ABC 的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”.若等边三角形ABC 的边长为2,则该“莱洛三角形”的周长等于( )A .2πB .2π−√3C .23πD .2π+√338.(2023•虹口区二模)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AB =5,BC =12.分别以点O 、D 为圆心画圆,如果⊙O 与直线AD 相交、与直线CD 相离,且⊙D 与⊙O 内切,那么⊙D 的半径长r 的取值范围是( )A .12<r <4B .52<r <6C .9<r <252D .9<r <1339.(2023•苏州一模)东南环立交是苏州中心城区城市快速内环道路系统的重要节点,也是江苏省最大规模的城市立交.左图是该立交桥的部分道路示意图(道路宽度忽略不计),A 为立交桥入口,D 、G 为出口,其中直行道为AB 、CD 、FG ,且AB =CD =FG ;弯道是以点O 为圆心的一段弧,且BC 、CE 、EF 所在的圆心角均为90°.甲、乙两车由A 口同时驶入立交桥,均以16m /s 的速度行驶,从不同出口驶出,其间两车到点O 的距离y (m )与时间x (s )的对应关系如右图所示.结合题目信息,下列说法错误的是( )A .该段立交桥总长为672mB .从G 口出比从D 口出多行驶192mC .甲车在立交桥上共行驶22sD .甲车从G 口出,乙车从D 口出40.(2023•滨城区一模)如图,点A ,B 是半径为2的⊙O 上的两点,且AB =2√3,则下列说法正确的是( )A .圆心O 到AB 的距离为√3B .在圆上取异于A ,B 的一点C ,则△ABC 面积的最大值为3√3C .以AB 为边向上作正方形,与⊙O 的公共部分的面积为3+√34πD .取AB 的中点C ,当AB 绕点O 旋转一周时,点C 运动的路线长为3π。
几何最值问题-2023年中考数学压轴题专项训练(全国通用)(解析版)

12023年中考数学压轴题专项训练1.几何最值问题一、压轴题速练1一、单选题1(2023·山东烟台·模拟预测)如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD +PE 的最小值为()A.8 B.45 C.10 D.45-2【答案】A【分析】根据∠BEC =90°得到点的运动轨迹,利用“将军饮马”模型将PE 进行转化即可求解.【详解】解:如图,设点O 为BC 的中点,由题意可知,点E 在以BC 为直径的半圆O 上运动,作半圆O 关于AB 的对称图形(半圆O '),点E 的对称点为E 1,连接O 'E 1,则PE =PE 1,∴当点D 、P 、E 1、O '共线时,PD +PE 的值最小,最小值为DE 1的长,如图所示,在Rt △DCO '中,CD =8,CO '=6,∴DO '=82+62=10,又∵O 'E 1=2,∴DE 1=DO '-O 'E 1=8,即PD +PE 的最小值为8,故选:A .【点睛】本题考查线段和最短问题、轴对称的性质、勾股定理及圆周角定理,利用“将军饮马”模型将PE 进行转化时解题的关键.2(2023·安徽黄山·校考模拟预测)如图,在平面直角坐标系中,二次函数y =32x 2-32x -3的图象与x 轴交于点A ,C 两点,与y 轴交于点B ,对称轴与x 轴交于点D ,若P 为y 轴上的一个动点,连接PD ,则12PB +PD 的最小值为()2A.334B.32C.3D.543【答案】A【分析】作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,可求得∠ABO =30°,从而得出PE =12PB ,进而得出PD +12PB =PD +EP ,进一步得出结果.【详解】解:如图,作射线BA ,作PE ⊥BA 于E ,作DF ⊥BA 于F ,交y 轴于P ,抛物线的对称轴为直线x =--322×32=12,∴OD =12,当x =0时,y =-3,∴OB =3,当y =0时,32x 2-32x -3=0,∴x 1=-1,x 2=2,∴A (-1,0),∴OA =1,∵tan ∠ABO =OA OB =13=33,∴∠ABO =30°,∴PE =12PB ,∴12PB +PD =PD +PE ≥DF ,当点P 在P 时,PD +PE 最小,最大值等于DF ,在Rt △ADF 中,∠DAF =90°-∠ABO =60°,AD =OD +PA =12+1=32,∴DF =AD ⋅sin ∠DAE =32×32-334,∴12PB +PD 最小=DF =334,故选:A .【点睛】本题以二次函数为背景,考查了二次函数与一元二次方程之间的关系,解直角三角形等知识,解决问题的关键是用三角函数构造12PB .3(2023秋·浙江金华·九年级统考期末)如图,正方形ABCD 的边长为4,点E 是正方形ABCD 内的动点,点P 是BC 边上的动点,且∠EAB =∠EBC .连结AE ,BE ,PD ,PE ,则PD +PE 的最小值为()3A.213-2B.45-2C.43-2D.215-2【答案】A【分析】先证明∠AEB =90°,即可得点E 在以AB 为直径的半圆上移动,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,问题随之得解.【详解】解:∵四边形ABCD 是正方形,∴∠ABC =90°,∴∠ABE +∠EBC =90°,∵∠EAB =∠EBC ,∴∠EAB +∠EBA =90°,∴∠AEB =90°,∴点E 在以AB 为直径的半圆上移动,如图,设AB 的中点为O ,作正方形ABCD 关于直线BC 对称的正方形CFGB ,则点D 的对应点是F ,连接FO 交BC 于P ,交半圆O 于E ,根据对称性有:PD =PF ,则有:PE +PD =PE +PF ,则线段EF 的长即为PE +PD 的长度最小值,E∵∠G =90°,FG =BG =AB =4,∴OG =6,OA =OB =OE =2,∴OF =FG 2+OG 2=213,∴EF =OF -OE =213-2,故PE +PD 的长度最小值为213-2,故选:A .【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理,正确的作出辅助线,得出点E 的运动路线是解题的关键.4(2022秋·安徽池州·九年级统考期末)如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD 的最小值为()4 A.154 B.245 C.5 D.203【答案】B【分析】作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,点P 即为所求作的点,此时PB +PD 有最小值,连接AB ,根据对称性的性质,可知:BP =B P ,△ABC ≅△AB C ,根据S △ABB =S △ABC +S △AB C =2S △ABC ,即可求出PB +PD 的最小值.【详解】解:如下图,作点B 关于AC 的对称点B ,过点B 作B D ⊥AB 于点D ,交AC 于点P ,连接AB ,点P 即为所求作的点,此时PB +PD 有最小值,根据对称性的性质,可知:BP =B P ,在Rt △ABC 中,∠ACB =90°,AC =4,BC =3,∴AB =AC 2+BC 2=5,根据对称性的性质,可知:△ABC ≅△AB C ,∴S △ABB =S △ABC +S △ABC =2S △ABC ,即12×AB ⋅B D =2×12BC ⋅AC ,∴5B D =24,∴B D =245,故选:B .【点睛】本题考查了轴对称一最短路线问题,解题的关键是掌握轴对称的性质.5(2023秋·甘肃定西·八年级校考期末)如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB 的度数是()A.118°B.125°C.136°D.124°【答案】D【分析】先在BC 上截取BE =BQ ,连接PE ,证明△PBQ ≌△PBE SAS ,得出PE =PQ ,说明AP +PQ =AP +PE ,找出当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ 最小,过点A 作AE ⊥BC 于点E ,交BD 于点P ,根据三角形外角的性质可得答案.【详解】解:在BC 上截取BE =BQ ,连接PE ,如图:∵BD 平分∠ABC ,∠ABC =68°,∴∠ABD =∠CBD =12∠ABC =34°,∵BP =BP ,∴△PBQ ≌△PBE SAS ,∴PE =PQ ,∴AP +PQ =AP +PE ,∴当A 、P 、E 在同一直线上,且AE ⊥BC 时,AP +PE 最小,即AP +PQ最小,过点A作AE ⊥BC 于点E ,交BD 于点P ,如图:∵∠AEB =90°,∠CBD =34°,∴∠APB =∠AEB +∠CBD =124°.故选:D .5【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,垂线段最短,三角形内角和定理与三角形的外角的性质,解题的关键是找出使AP +PQ 最小时点P 的位置.6(2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末)如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA +PE 的最小值为()A.5B.42C.210D.10【答案】A【分析】连接EC 交BD 于P 点,根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长,求出EC 的长即可.【详解】连接EC ,交BD 于P 点∵四边形ABCD 为正方形∴A 点和C 点关于BD 对称∴PA =PC∴PA +PE =PC +PE =EC根据“两点之间线段最短”,可知PA +PE 的最小值即为线段EC 的长.∵AE =1,DE =3∴AD =4∴DC =4∴CE =DE 2+CD 2=32+42=5∴PA +PE 的最小值为5故选:A【点睛】本题主要考查了正方形的性质和两点之间线段最短,这是一个将军饮马模型.熟练掌握正方形的性质并且能够识别出将军饮马模型是解题的关键.7(2023春·湖南张家界·八年级统考期中)如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.5【答案】D【分析】由正方形的对称性可知点B 与D 关于直线AC 对称,连接BM 交AC 于N ′,N ′即为所求在Rt △BCM 中利用勾股定理即可求出BM 的长即可.【详解】∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,6连接BD ,BM 交AC 于N ′,连接DN ′,∴当B 、N 、M 共线时,DN +MN 有最小值,则BM 的长即为DN +MN 的最小值,∴AC 是线段BD 的垂直平分线,又∵CD =4,DM =1∴CM =CD -DM =4-1=3,在Rt △BCM 中,BM =CM 2+BC 2=32+42=5故DN +MN 的最小值是5.故选:D .【点睛】本题考查的是轴对称-最短路线问题及正方形的性质,先作出D 关于直线AC 的对称点,由轴对称及正方形的性质判断出D 的对称点是点B 是解答此题的关键.8(2022秋·浙江杭州·九年级杭州外国语学校校考开学考试)如图,在平面直角坐标系中,二次函数y =-x 2+bx +3的图像与x 轴交于A 、C 两点,与x 轴交于点C (3,0),若P 是x 轴上一动点,点D 的坐标为(0,-1),连接PD ,则2PD +PC 的最小值是()A.4B.2+22C.22D.32+232【答案】A【分析】过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H ,根据2PD +PC =2PD +22PC =2PD +PJ ,求出DP +PJ 的最小值即可解决问题.【详解】解:连接BC ,过点P 作PJ ⊥BC 于J ,过点D 作DH ⊥BC 于H .∵二次函数y =-x 2+bx +3的图像与x 轴交于点C (3,0),∴b =2,∴二次函数的解析式为y =-x 2+2x +3,令y =0,-x 2+2x +3=0,解得x =-1或3,∴A (-1,0),令x =0,y =3,∴B (0,3),∴OB =OC =3,∵∠BOC =90°,∴∠OBC =∠OCB =45°,∵D(0,-1),∴OD =1,BD =4,∵DH ⊥BC ,∴∠DHB =90°,设DH =x ,则BH =x ,∵DH 2+BH 2=BD 2,7∴x =22,∴DH =22,∵PJ ⊥CB ,∴∠PJC =90°,∴PJ =22PC ,∴2PD +PC =2PD +22PC =2PD +PJ ,∵DP +PJ ≥DH ,∴DP +PJ ≥22,∴DP +PJ 的最小值为22,∴2PD +PC 的最小值为4.故选:A .【点睛】本题考查了二次函数的相关性质,以及等腰直角三角形的判定和性质,垂线段最短等知识,得到∠OBC =∠OCB =45°,PJ =22PC 是解题的关键.9(2022·山东泰安·统考中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52 B.125 C.13-32 D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的圆上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的圆上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.810(2022·河南·校联考三模)如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()A.42,35B.22,35C.35,22D.35,42【答案】A【分析】根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,从而确定正方形的边长为6,根据将军饮马河原理,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,利用相似三角形,计算AG 的长即为横坐标.【详解】如图,根据图像,当P 与C 重合时,PB +PE =9即CB +CE =9,∵点E 是BC 的中点,∴BC =6,连接DE 交AC 于点G ,当点P 与点G 重合时,PE +PB 最小,且为DE 的长即点M 的纵坐标,∵四边形ABCD 是正方形,AB =6,∴CE ∥AD ,AC =62+62=62,DE =62+32=35,∴△CGE ∽△AGD ,∴CG AG =CE AD =12,∴AC AG=32,∴AG =42,故点M 的坐标为(42,35),故A 正确.故选:A .【点睛】本题考查了正方形的性质,三角形相似的判定和性质,函数图像信息的获取,将军饮马河原理,熟练掌握正方形的性质,灵活运用三角形相似,构造将军饮马河模型求解是解题的关键.2二、填空题11(2023春·江苏宿迁·九年级校联考阶段练习)如图,矩形ABCD ,AB =4,BC =8,E 为AB 中点,F 为直线BC 上动点,B 、G 关于EF 对称,连接AG ,点P 为平面上的动点,满足∠APB =12∠AGB ,则DP 的最小值.【答案】210-22【分析】由题意可知,∠AGB =90°,可得∠APB =12∠AGB =45°,可知点P 在以AB 为弦,圆周角∠APB =45°的9圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧),设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,可知△AOB 为等腰直角三角形,求得OA =22AB =22=OP ,AQ =OQ =22OA =2,QD =AD -AQ =6,OD =OQ 2+QD 2=210,再由三角形三边关系可得:DP ≥OD -OP =210-22,当点P 在线段OD 上时去等号,即可求得DP 的最小值.【详解】解:∵B 、G 关于EF 对称,∴BH =GH ,且EF ⊥BG∵E 为AB 中点,则EH 为△ABG 的中位线,∴EH ∥AG ,∴∠AGB =90°,∵∠APB =12∠AGB ,即∠APB =12∠AGB =45°,∴点P 在以AB 为弦,圆周角∠APB =45°的圆上,(要使DP 最小,则点P 要靠近蒂点D ,即点P 在AB 的右侧)设圆心为O ,连接OA ,OB ,OE ,OP ,OD ,过点O 作OQ ⊥AD ,则OA =OB =OP ,∵∠APB =45°,∴∠AOB =90°,则△AOB 为等腰直角三角形,∴OA =22AB =22=OP ,又∵E 为AB 中点,∴OE ⊥AB ,OE =12AB =AE =BE ,又∵四边形ABCD 是矩形,∴∠BAD =90°,AD =BC =8,∴四边形AEOQ 是正方形,∴AQ =OQ =22OA =2,QD =AD -AQ =6,∴OD =OQ 2+QD 2=210,由三角形三边关系可得:DP ≥OD-OP =210-22,当点P 在线段OD 上时去等号,∴DP 的最小值为210-22,故答案为:210-22.【点睛】本题考查轴对称的性质,矩形的性质,隐形圆,三角形三边关系,正方形的判定及性质,等腰直角三角形的判定及性质,根据∠APB =12∠AGB =45°得知点P 在以AB 为弦,圆周角∠APB =45°的圆上是解决问题的关键.12(2023春·江苏连云港·八年级期中)如图,在边长为8的正方形ABCD 中,点G 是BC 边的中点,E 、F 分别是AD 和CD 边上的点,则四边形BEFG 周长的最小值为.【答案】2410【分析】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G ,根据两点之间线段最短即可解决问题.【详解】作点G 关于CD 的对称点G ,作点B 关于AD 的对称点B ,连接B G∵EB =EB ,FG =FG ,∴BE +EF +FG +BG =B E +EF +FG +BG ,∵EB +EF +FG ≥B G ,∴四边形BEFG 的周长的最小值=BG +B G ,∵正方形ABCD 的边长为8∴BG =4,BB =16,BG =12,∴B G =162+122=20,∴四边形BEFG 的周长的最小值为=4+20=24.故答案为:24.【点睛】本题考查轴对称求线段和的最短问题,正方形的性质,勾股定理,解题的关键是学会利用轴对称解决最短问题.13(2022·湖南湘潭·校考模拟预测)如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.【答案】50【分析】作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,根据菱形的性质和勾股定理求出BC 长,即可得出答案.【详解】解:作M 关于BD 的对称点Q ,连接NQ ,交BD 于P ,连接MP ,当P 点与P 重合时,MP +NP =MP +NP =NQ 的值最小,∵四边形ABCD 是菱形,∴AC ⊥BD ,∠QBP =∠MBP ,即Q 在AB 上,∵MQ ⊥BD ,∴AC ∥MQ ,∴M 为BC 中点,∴Q 为AB 中点,∵N 为CD 中点,四边形ABCD 是菱形,∴BQ ∥CD ,BQ =CN ,∴四边形BQNC 是平行四边形,∴NQ =BC ,设AC 与BD 的交点为点O ,∵四边形ABCD 是菱形,∴AC ⊥BD,OC =12AC =30米,OB =12BD =40米,∴BC =OB 2+OC 2=50米,∴PM +PN 的最小值是50米.故答案为:50.11【点睛】本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P 的位置.14(2023春·江苏·九年级校考阶段练习)如图,正方形ABCD 的边长为4,⊙B 的半径为2,P 为⊙B 上的动点,则2PC -PD 的最大值是.【答案】2【分析】解法1,如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,连接PM 、DM ,推得2PC -PD=2PC -22PD =2PC -PM ,因为PC -PM ≤MC ,求出MC 即可求出答案.解法2:如图:连接BD 、BP 、PC ,在BD 上做点M ,使BM BP =24,连接MP ,证明△BMP ∼△BPD ,在BC 上做点N ,使BN BP=12,连接NP ,证明△BNP ∼△BPC ,接着推导出2PC -PD =22MN ,最后证明△BMN ∼△BCD ,即可求解.【详解】解法1如图:以PD 为斜边构造等腰直角三角形△PDM ,连接MC ,BD ,∴∠PDM =45,DM =PM =22PD ,∵四边形ABCD 正方形∴∠BDC =45°,DB DC=2又∵∠PDM =∠PDB +MDB ,∠BDC =∠MDB +MDC∴∠PDB =∠MDC在△BPD 与△MPC 中∠PDB =∠MDC ,DB DC=DP DM =2∴△BPD ∼△MPC∴PB MC=2∵BP =2∴MC =2∵2PC -PD =2PC-22PD =2PC -PM ∵PC -PM ≤MC ∴2PC -PD =2PC -PM ≤2MC =2故答案为:2.解法2如图:连接BD 、BP 、PC根据题意正方形ABCD 的边长为4,⊙B 的半径为2∴BP =2,BD =BC 2+CD 2=42+42=42∵BP BD =242=2412在BD 上做点M ,使BM BP=24,则BM =22,连接MP 在△BMP 与△BPD 中∠MBP =∠PBD ,BP BD =BM BP∴△BMP ∼△BPD∴PM PD =24,则PD =22PM ∵BP BC =24=12在BC 上做点N ,使BN BP=12,则BN =1,连接NP 在△BNP 与△BPC 中∠NBP =∠PBC ,BN BP =BP PC∴△BNP ∼△BPC∴PN PC=12,则PC =2PN ∴如图所示连接NM ∴2PC -PD =2×2PN -22PM =22PN -PM ∵PN -PM ≤NM ∴2PC -PD =22PN -PM ≤22NM在△BMN 与△BCD 中∠NBM=∠DBC ,BM BC =224=28,BN BD =142=28∴BM BC=BN BD ∴△BMN ∼△BCD∴MN CD=28∵CD =4∴MN =22∴22MN =22×22=2∴2PC -PD ≤22NM =2故答案为:2.【点睛】本题考查正方形的性质,相似三角形,勾股定理等知识,难度较大,熟悉以上知识点运用是解题关键.15(2023秋·广东广州·九年级统考期末)如图,四边形ABCD 中,AB ∥CD ,AC ⊥BC ,∠DAB =60°,AD =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则△MBC 面积的最小值为.【答案】63-4【分析】取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则OM +ME ≥OF ,通过计算得出当O ,M ,E 三点共线时,ME 有最小值,求出最小值即可.【详解】解:如图,取AD 的中点O ,连接OM ,过点M 作ME ⊥BC 交BC 的延长线于点E ,过点O 作OF ⊥BC 于F ,交CD 于G ,则13OM +ME ≥OF ,∵AB ∥CD ,∠DAB =60°,AD =CD =4,∴∠ADC =120°,∵AD =CD ,∴∠DAC =30°,∴∠CAB =30°,∵AC ⊥BC ,∴∠ACB =90°∴∠B =90°-30°=60°,∴∠B =∠DAB ,∴四边形ABCD 为等腰梯形,∴BC =AD =4,∵∠AMD =90°,AD =4,OA =OD ,∴OM =12AD =2,∴点M 在以点O 为圆心,2为半径的圆上,∵AB ∥CD ,∴∠GCF =∠B =60°,∴∠DGO =∠CGF =30°,∵OF ⊥BC ,AC ⊥BC ,∴∠DOG =∠DAC =30°=∠DGO ,∴DG =DO =2,∴OG =2OD ⋅cos30°=23,GF =3,OF =33,∴ME ≥OF -OM =33-2,∴当O ,M ,E 三点共线时,ME 有最小值33-2,∴△MBC 面积的最小值为=12×4×33-2 =63-4.【点睛】本题考查了解直角三角形、隐圆、直角三角形的性质等知识点,点M 位置的确定是解题关键.16(2023春·全国·八年级专题练习)如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .【答案】5【分析】如图所示,作点P 关于BD 的对称点P ,且点P 在BC 上,则PM +QM =P M+QM ,当P ,M ,Q 在同一条直线上时,有最小值,证明四边形PP QA 是平行四边形,P Q =AP =AB -BP ,由此即可求解.【详解】解:如图所示,作点P 关于BD 的对称点P ,∵△ABC 是等边三角形,BD ⊥AC ,∴∠ABD =∠DBC =12∠ABC =12×60°=30°,14∴点P 在BC 上,∴P M =PM ,则PM +QM =P M +QM ,当P ,M ,Q 在同一条直线上时,有最小值,∵点P 关于BD 的对称点P ,∠ABD =∠DBC =30°,∴PP ⊥BM ,BP =BP =1cm ,∴∠BP P =60°,∴△BPP 是等边三角形,即∠BP P =∠C =60°,∴PP ∥AC ,且PP =AQ =1cm ,∴四边形PP QA 是平行四边形,∴P Q =AP =AB -BP ,在Rt △ABD 中,∠ABD =30°,AD =3,∴AB =2AD =2×3=6,∴AP =P Q =P M +QM =PM +QM =AB -BP =6-1=5,故答案为:5.【点睛】本题主要考查动点与等边三角形,对称-最短路径,平行四边形的判定和性质的综合,理解并掌握等边三角形得性质,对称-最短路径的计算方法,平行四边形的判定和性质是解题的关键.17(2022秋·山东菏泽·九年级校考阶段练习)如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.【答案】3【分析】作F 点关于BD 的对称点F ,连接EF 交BD 于点P ,则PF =PF ,由两点之间线段最短可知当E 、P 、F 在一条直线上时,EP +FP 有最小值,然后求得EF 的长度即可.【详解】解:作F 点关于BD 的对称点F ,则PF =PF ,连接EF '交BD 于点P .∴EP +FP =EP +F P .由两点之间线段最短可知:当E 、P 、F '在一条直线上时,EP +FP 的值最小,此时EP +FP =EP +F P =EF .∵四边形ABCD 为菱形,周长为12,∴AB =BC =CD =DA =3,AB ∥CD ,∵AF =2,AE =1,∴DF =AE =1,∴四边形AEF D 是平行四边形,∴EF =AD =3.∴EP +FP 的最小值为3.故答案为:3.【点睛】本题主要考查的是菱形的性质、轴对称--路径最短问题,明确当E 、P 、F 在一条直线上时EP +FP 有最小值是解题的关键.18(2023春·上海·八年级专题练习)如图,直线y =x +4与x 轴,y 轴分别交于A和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD 的值最小时,点P 的坐标为.15【答案】(-1,0)【分析】直线y =x +4与x 轴,y 轴分别交于A 和B ,可求出点A ,B 的坐标,点C 、D 分别为线段AB 、OB 的中点,可求出点C 、D 的坐标,作点C 关于x 轴的对称点C ,连接C D 与x 轴的交点就是所求点P 的坐标.【详解】解:直线y =x +4与x 轴,y 轴分别交于A 和B ,∴当y =0,x =-4,即A (-4,0);当x =0,y =4,即B (0,4),∵点C 、D 分别为线段AB 、OB 的中点,∴C (-2,2),D (0,2),如图所示,过点C 关于x 轴的对称点C,∴C (-2,-2),∴直线C D 的解析式为:y =2x +2,当y =0,x =-1,即P (-1,0),故答案为:(-1,0).【点睛】本题主要考查一次函数与最短线段的综合,掌握对称中最短线段的解题方法是解题的关键.19(2023秋·黑龙江鸡西·九年级统考期末)如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.【答案】32+10【分析】根据“将军饮马”模型,先求出A 1,0 ,B 3,0 ,C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,从而C △MAC =CA +CM +MA =CA +CM +MB ,AC =OA 2+OC 2=10,则△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,从而得到CB =OC 2+OB 2=32,即可得到答案.【详解】解:∵抛物线y =x 2-4x +3与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,16∴当y =0时,0=x 2-4x +3解得x =1或x =3,即A 1,0 ,B 3,0 ;当x =0时,y =3,即C 0,3 ,由二次函数对称性,A ,B 关于对称轴对称,即MA =MB ,∴C △MAC =CA +CM +MA =CA +CM +MB ,∵AC =OA 2+OC 2=10,∴△MAC 周长的最小值就是CM +MB 的最小值,根据两点之间线段最短即可得到CM +MB 的最小值为C ,M ,B 三点共线时线段CB 长,∵CB =OC 2+OB 2=32,∴△MAC 周长的最小值为CA +CB =32+10,故答案为:32+10.【点睛】本题考查动点最值问题与二次函数综合,涉及“将军饮马”模型求最值、二次函数图像与性质、解一元二次方程、勾股定理求线段长等知识,熟练掌握动点最值的常见模型是解决问题的关键.20(2023秋·浙江温州·九年级校考期末)如图所示,∠ACB =60°,半径为2的圆O 内切于∠ACB.P 为圆O 上一动点,过点P 作PM 、PN 分别垂直于∠ACB 的两边,垂足为M 、N ,则PM +2PN 的取值范围为.【答案】6-23≤PM +2PN ≤6+23【分析】根据题意,本题属于动点最值问题-“阿氏圆”模型,首先作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示,通过代换,将PM +2PN 转化为PN +12PM =PN +HP =NH ,得到当MP 与⊙O 相切时,MF 取得最大值和最小值,分两种情况,作出图形,数形结合解直角三角形即可得到相应最值,进而得到取值范围.【详解】解:作MH ⊥NP 于H ,作MF ⊥BC 于F ,如图所示:∵PM ⊥AC ,PN ⊥CB ,∴∠PMC =∠PNC =90°,∴∠MPN =360°-∠PMC -∠PNC -∠C =120°,∴∠MPH =180°-∠MPN =60°,∴HP =PM ⋅cos ∠MPH =PM ⋅cos60°=12PM ,∴PN +12PM =PN +HP =NH ,∵MF =NH ,∴当MP 与⊙O 相切时,MF 取得最大和最小,①连接OP ,OG ,OC ,如图1所示:可得:四边形OPMG 是正方形,∴MG =OP =2,在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG +GM =2+23,在Rt △CMF 中,MF =CM ⋅sin60°=3+3,∴HN =MF =3+3,即PM +2PN =212PM +PN =2HN =6+23;②连接OP ,OG ,OC ,如图2所示:可得:四边形OPMG 是正方形,17∴MG =OP =2,由上同理可知:在Rt △COG 中,CG =OG ⋅tan60°=23,∴CM =CG -GM =23-2,在Rt △CMF 中,MF =CM ⋅sin60°=3-3,∴HN =MF =3-3,即PM +2PN =212PM +PN =2HN =6-23,∴6-23≤PM +2PN ≤6+23.故答案为:6-23≤PM +2PN ≤6+23.【点睛】本题考查动点最值模型-“阿氏圆”,难度较大,掌握解决动点最值问题的方法,熟记相关几何知识,尤其是圆的相关知识是解决问题的关键.3三、解答题21(2022春·江苏·九年级专题练习)综合与探究如图,已知抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,交y 轴于点C .(1)求抛物线的解析式,连接BC ,并求出直线BC 的解析式;(2)请在抛物线的对称轴上找一点P ,使AP +PC 的值最小,此时点P 的坐标是;(3)点Q 在第一象限的抛物线上,连接CQ ,BQ ,求出△BCQ 面积的最大值.【答案】(1)y =-x 2+3x +4;y =-x +4(2)32,52(3)8【分析】(1)将A -1,0 ,B 4,0 两点,代入抛物线解析式,可得到抛物线解析式,从而得到C 0,4 ,再设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入,即可求解;(2)连接BC ,PB ,根据题意可得A 、B 关于抛物线的对称轴直线x =32对称,从而得到当P 在直线AB 上三点共线时,AP +CP 的值最小,把x =32代入直线BC 的解析式,即可求解;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,可得QD =-d 2+4d ,从而得到S ΔBCQ =12OB ×QD =-2d -2 2+8,即可求解;【详解】(1)解:(1)∵抛物线y =ax 2+bx +4经过A -1,0 ,B 4,0 两点,∴a -b +4=016a +4b +4=0,解得:a =-1b =3 ,18∴抛物线的解析式为y =-x 2+3x +4;∵抛物线与y 轴的交点为C ,∴C 0,4 ,设直线BC 的解析式为y =kx +b k ≠0 ,把点B 、C 的坐标代入得:4k +b =0b =4 ,解得:k =-1b =4 ,∴直线BC 的解析式为y =-x +4;(2)如图,连接BC ,PB ,∵y =-x 2+3x +4=-x -32 2+74,∴抛物线的对称轴为直线x =32,根据题意得:A 、B 关于抛物线的对称轴直线x =32对称,∴AP =BP ,∴AP +CP =BP +CP ≥BC ,即当P 在直线AB 上时,AP +CP 的值最小,∴当x =32时,y =-32+4=52,∴P 32,52 ,故答案是:32,52 ;(3)过Q 作QD ⊥x 轴,交BC 于D ,设Q d ,-d 2+3d +4 ,其中0≤d ≤4,则D d ,-d +4 ,∴QD =-d 2+3d +4 --d +4 =-d 2+4d ,∵B 4,0 ,∴OB =4,∴S ΔBCQ =12OB ×QD =-2d 2+8d =-2d -2 2+8,当d =2时,S ΔBCQ 取最大值,最大值为8,∴△BCQ 的最大面积为8;【点睛】本题主要考查了二次函数的图像和性质,利用数形结合思想和分类讨论思想是解题的关键.22(2023秋·江苏淮安·八年级统考期末)如图1,直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,过点B 的直线交x 轴负半轴于点C -3,0 .(1)请直接写出直线BC 的关系式:(2)在直线BC 上是否存在点D,使得S △ABD =S △AOD 若存在,求出点D 坐标:若不存请说明理由;(3)如图2,D 11,0 ,P 为x 轴正半轴上的一动点,以P 为直角顶点、BP 为腰在第一象限内作等腰直角三角形△BPQ ,连接QA ,QD .请直接写出QB -QD 的最大值:.19【答案】(1)y =2x +6(2)当D 185,665 或D -185,-65时,S △ABD =S △AOD (3)37【分析】(1)根据直线AB 与y 轴的交点,可求出点B 的坐标,再用待定系数法即可求解;(2)设D (a ,2a +6),分别用含a 的式子表示出出S △AOD ,S △ABD ,由此即可求解;(3)△BPQ 是等腰直角三角形,设P (m ,0)(m >0),可表示出QB ,再证Rt △BOP ≌Rt △PTQ (AAS ),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值,可求得点R 的坐标,根据勾股定理即可求解.【详解】(1)解:∵直线AB :y =-x +6分别与x ,y 轴交于A ,B 两点,令x =0,则y =6,∴B (0,6),且C -3,0 ,设直线BC 的解析式为y =kx +b ,∴b =6-3k +b =0,解得,k =2b =6 ,∴直线BC 的解析式为y =2x +6,故答案为:y =2x +6.(2)解:由(1)可知直线BC 的解析式为y =2x +6,直线AB 的解析式为y =-x +6,∴A (6,0),B (0,6),C (-3,0),∴OA =6,BO =6,OC =3,如图所示,点D 在直线BC 上,过点D 作DE ⊥x 轴于E ,∴设D (a ,2a +6),E (a ,0),∴S △ABC =12AC ·OB =12×(6+3)×6=27,S △ADC =12AC ·DE =12×(6+3)×a =92a ,S △AOD =12OA ·DE =12×6×a =3a ,∴S △ABD =S △ABC -S △ADC =27-92a ,若S △ABD =S △AOD ,则27-92a =3a ,当a >0时,27-92a =3a ,解得,a =185,即D 185,665 ;当a <0时,27+92a =-3a ,解得,a =-185,即D -185,-65 ;综上所述,当D 185,665 或D -185,-65时,S △ABD =S △AOD .(3)解:已知A (6,0),B (0,6),D (11,0),设P (m ,0)(m >0),∴在Rt △BOP 中,OB =6,OP =m ,∵△BPQ 是等腰直角三角形,∠BPQ =90°,∴BP =QP ;如图所示,过点Q 作QT ⊥x 轴于T ,20在Rt △BOP ,Rt △PTQ 中,∠BOP =∠PTQ =90°,∠BPO +∠QPA =∠QPA +∠PQT =90°,∴∠BPO =∠PQT ,∴∠BPO =∠PQT∠BOP =∠PTQ BP =QP,∴Rt △BOP ≌Rt △PTQ (AAS ),∴OP =TQ =m ,OB =PT =6,∴AT =OP +PT -OA =m +6-6=m ,∴AT =QT ,且QT ⊥x 轴,∴△ATQ 是等腰直角三角形,∠QAT =45°,则点Q 的轨迹在射线AQ 上,如图所示,作点D 关于直线AQ 的对称点R,连接QR ,BR ,AR ,A (6,0),B (0,6),D (11,0),∵△ATQ 是等腰直角三角形,即∠QAT =45°,根据对称性质,∴∠QAR =45°,∴RA ⊥x 轴,且△DQA ≌△RQA ,∴AR =AD =11-6=5,则R (6,5),如图所示,当点B ,R ,Q 在一条直线上时,QB -QD 的值最大,最大值为BR 的值;∴由勾股定理得:BR =62+(6-5)2=37,故答案为:37.【点睛】本题主要考查一次函数,几何的综合,掌握待定系数法求解析式,将军饮马问题,等腰直角三角形的性质,勾股定理是解题的关键.23(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)△ABC 中,∠B =60°.(1)如图1,若AC >BC ,CD 平分∠ACB 交AB 于点D ,且AD =3BD .证明:∠A =30°;(2)如图2,若AC <BC ,取AC 中点E ,将CE 绕点C 逆时针旋转60°至CF ,连接BF 并延长至G ,使BF =FG ,猜想线段AB 、BC 、CG 之间存在的数量关系,并证明你的猜想;(3)如图3,若AC =BC ,P 为平面内一点,将△ABP 沿直线AB 翻折至△ABQ ,当3AQ +2BQ +13CQ 取得最小值时,直接写出BPCQ的值.【答案】(1)见解析(2)BC =AB +CG ,理由见解析(3)213+33913【分析】(1)过点D 分别作BC ,AC 的垂线,垂足为E ,F ,易得DE =DF ,由∠B =60°,可得DE =DF =32BD ,由AD =3BD ,求得sin A =DE AD=12,可证得∠A =30°;(2)延长BA ,使得BH =BC ,连接EH ,CH ,易证△BCH 为等边三角形,进而可证△BCF ≌△HCE SAS ,可得BF =HE ,∠BFC =∠HEC ,可知∠AEH =∠CFG ,易证得△AEH ≌△CFG SAS ,可得AH =CG ,由BC =BH =AB +AH =AB +CG 可得结论;(3)由题意可知△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,可得CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,可知△ACQ ∽△MCN ,可得MN =32AQ ,由3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM 可知点Q ,N 都在线段BM 上时,3AQ +2BQ+13CQ 有最小值,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,可得CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,可证△CBR ∽△MBT ,得BR CR =BT MT ,设BC =a 由等边三角形的性质,可得CM =32a ,进而可得CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,结合BR CR=BTMT 可得:BQ +213CQ 313CQ =a +334a 34a ,可得BQ CQ =213+33913,由翻折可知,BP =BQ ,可求得BP CQ的值.【详解】(1)证明:过点D 分别作BC ,AC 的垂线,垂足为E ,F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,∴DE =DF ,又∵∠B =60°,∴DE =BD ⋅sin60°=32BD ,则DE =DF =32BD ,又∵AD =3BD ,∴sin A =DE AD =32BD3BD=12,∴∠A =30°;(2)BC =AB +CG ,理由如下:延长BA ,使得BH =BC ,连接EH ,CH ,∵∠ABC =60°,BH =BC ,∴△BCH 为等边三角形,∴CB =CH ,∠BCH =60°,∵CE 绕点C 逆时针旋转60°至CF ,∴CE =CF ,∠ECF =60°,则∠BCH -∠ACB =∠ECF -∠ACB ,∴∠ECH =∠FCB ,∴△BCF ≌△HCE SAS ,∴BF =HE ,∠BFC =∠HEC ,则∠AEH =∠CFG ,∵BF =FG ,∴BF =HE =FG ,又∵E 为AC 中点,∴AE =CE =CF ,∴△AEH ≌△CFG SAS ,∴AH =CG ,∴BC =BH =AB +AH =AB +CG ;(3)∵∠ABC =60°,AC =BC ,∴△ABC 是等边三角形,如图,作CM ⊥CA ,且CM =32CA ,作CN ⊥CQ ,且CN =32CQ ,则CM CA=CN CQ =32,QN =CQ 2+CN 2=132CQ ,∴sin ∠CQN =CN QN =313,cos ∠CQN =CQ QN =213,则∠ACM =∠QCN =90°,∴∠ACM -∠ACN =∠QCN -∠ACN ,则∠ACQ =∠MCN∴△ACQ ∽△MCN ,∴MN AQ =CM CA=32,即:MN =32AQ ,∴3AQ +2BQ +13CQ =232AQ +BQ +132CQ =2MN +BQ +QN ≥2BM即:点Q ,N 都在线段BM 上时,3AQ +2BQ +13CQ 有最小值,如下图,过点C 作CR ⊥BM ,过点M 作MT ⊥BC 交BC 延长线于T ,则∠BRC =∠BTM =90°,CR =CQ ⋅sin ∠CQN =313CQ ,QR =CQ ⋅cos ∠CQN =213CQ ,又∵∠CBR =∠MBT ,∴△CBR ∽△MBT ,∴BR CR=BT MT ,∵△ABC 是等边三角形,设BC =a ∴∠ACB =60°,AC =BC =a ,则CM =32a ,∵∠ACM =90°,∴∠MCT =30°,则CT =CM ⋅cos30°=334a ,MT =CM ⋅sin30°=34a ,则由BR CR=BT MT 可得:BQ +213CQ 313CQ =a +334a34a ,整理得:133BQ CQ +23=4+333,得BQ CQ=213+33913,由翻折可知,BP =BQ ,∴BP CQ =BQ CQ=213+33913.【点睛】本题属于几何综合,考查了解直角三角形,等边三角形的判定及性质,全等三角形的判定及性质,相似三角形的判定及性质,旋转的性质以及费马点问题,掌握费马点问题的解决方法,添加辅助线构造全等三角形和相似三角形是解决问题的关键.24(2023春·江苏·八年级专题练习)定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB 、AC 上,AD =AE ,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .(1)观察猜想线段PM 与PN 填(“是”或“不是”)“等垂线段”.(2)△ADE 绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.(3)拓展延伸把△ADE 绕点A 在平面内自由旋转,若DE =2,BC =4,请直接写出PM 与PN 的积的最大值.。
2023年九年级数学中考专题:二次函数综合压轴题(含简单答案)
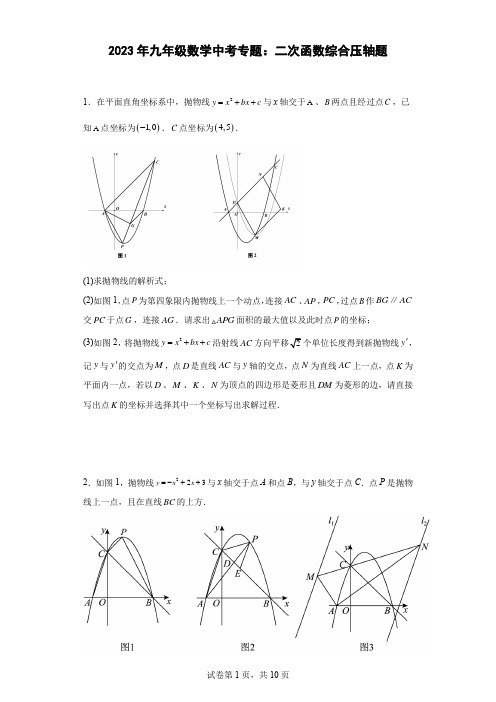
2023年九年级数学中考专题:二次函数综合压轴题1.在平面直角坐标系中,抛物线2y x bx c =++与x 轴交于A 、B 两点且经过点C ,已知A 点坐标为()1,0-.C 点坐标为()4,5.(1)求抛物线的解析式;(2)如图1,点P 为第四象限内抛物线上一个动点,连接AC 、AP ,PC ,过点B 作BG AC ∥交PC 于点G ,连接AG .请求出APG 面积的最大值以及此时点P 的坐标;(3)如图2,将抛物线2y x bx c =++沿射线AC y ',记y 与y '的交点为M ,点D 是直线AC 与y 轴的交点,点N 为直线AC 上一点,点K 为平面内一点,若以D 、M 、K 、N 为顶点的四边形是菱形且DM 为菱形的边,请直接写出点K 的坐标并选择其中一个坐标写出求解过程.2.如图1,抛物线223y x x =-++与x 轴交于点A 和点B ,与y 轴交于点C .点P 是抛物线上一点,且在直线BC 的上方.(1)直接写出点A 的坐标为 ,点B 的坐标为 ; (2)当点P 的坐标为()1,4时,求四边形BOCP 的面积;(3)如图2,AP 交BC 于点D .PE AC ∥交BC 于点E ,记,,DEP CPD CDA 的面积分别为123,,S S S ,判断1223S S S S +是否存在最大值.若存在,求出最大值;若不存在,请说明理由.(4)如图3,点C 在线段MN 上,满足90MAN ∠=︒,2CN CM =,直线1l 过点M ,直线2l 过点N ,且12l AC l ∥∥,求直线1l 与2l 之间的最大距离.3.如图,抛物线212y x bx c =-++与x 轴交于点A ,点B ,与y 轴交于点C .抛物线的对称轴为直线1x=-,点C 坐标为()04,.(1)求抛物线表达式;(2)在抛物线上是否存在点P ,使ABP BCO ∠=∠,如果存在,求出点P 坐标;如果不存在,请说明理由;(3)在(2)的条件下,若点P 在x 轴上方,点M 是直线BP 上方抛物线上的一个动点,求点M 到直线BP 的最大距离.4.如图1,在平面直角坐标系xOy 中,抛物线223y x x =-++与x 轴分别交于点A 和点B ,与y 轴交于点C ,连接BC .(1)求点B 和点C 的坐标;(2)如图2,点P 是该抛物线上一个动点,并沿抛物线从点B 运动至点A ,连接PO 、PB ,并以PO 、PB 为边作POQB .①当POQB 的面积为9时,求点P 的坐标;①在整个运动过程中,求点Q 与线段BC 的最大距离.5.如图,已知抛物线2=++30y ax bx a ≠()经过点10A (),和点30B (),,与y 轴相交于点C .(1)求此抛物线的解析式.(2)若点P 是直线BC 下方的抛物线上一动点(不与点B 、C 重合),过点P 作y 轴的平行线交直线BC 于点D ,设点P 的横坐标为m . ①用含有m 的代数式表示线段PD 的长;①连接PB ,PC ,求PBC 的面积最大时点P 的坐标.6.如图,抛物线212y x bx c =++与x 轴交于点()1,0A -和点B ,与y 轴交于点()0,2C -,(1)求抛物线的解析式;(2)点P 在第四象限的抛物线上,设ABC 的面积为1S ,PBC 的面积为2S ,当2S =451S 时,求点P 的坐标;(3)点M 在抛物线上,当2MAB ACO ∠∠=时,求点M 的横坐标.7.如图,已知抛物线2y ax c =+交x 轴于点()10A -,和点B ,交y 轴于点()01C -,.(1)求此抛物线的解析式.(2)过点A 作AP CB ∥交抛物线于点P ,求四边形ACBP 的面积.(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG x ⊥轴于点G ,使以A 、M 、G 三点为顶点的三角形与ACP △相似.若存在,请求出M 点的坐标;否则,请说明理由.8.如图1,直线25y x =-+与x 轴、y 轴分别交于点A 、点B ,抛物线2L y x bx c =-++:(1)①点A 的坐标为__________,点B 的坐标为__________;①求L 的解析式; (2)当点P 到AB 距离最大时,求出点P 的坐标;(3)尺规作图:在图2中作出经过C 、D 两点且圆心在抛物线对称轴上的圆,并结合图像直接写出该圆与抛物线的交点P 的坐标.9.在平面直角坐标系中,抛物线(1)(3)y a x x =+-(0)a ≠与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点(0,3)C ,点D 为抛物线的顶点,点P 是抛物线的对称轴上一点.(1)求抛物线的解析式及点D 的坐标;(2)如图①连接PB ,PD ,求PB 的最小值; (3)如图①,连接CP ,PB ,BC ,若135CPB ∠=︒,求点P 的坐标.的左边),与y 轴交于点C .点P ,Q 为抛物线上两动点.(1)若点P 坐标为(1,3),求抛物线的表达式;(2)如图①,连接BC ,在(1)的条件下,是否存在点Q ,使得BCQ ABC ∠=∠.若存在,请求出点Q 的坐标,若不存在,请说明理由;(3)若点P 为抛物线顶点,连接OP ,当a 的值从3-变化到1-的过程中,求线段OP 扫过的面积.11.如图,已知二次函数2y ax 2x c =++的图象经过点()0,3C ,与x 轴分别交于点()1,0A -和点B ,点P 是直线BC 上方的抛物线上一动点.(1)求二次函数的表达式; (2)求BC 所在直线的函数解析式;(3)过点P 作PM y ∥轴交直线BC 于点M ,求线段PM 长度的最大值.12.如图,在平面直角坐标系中,点O 为坐标原点,抛物线22y ax x c =-+与x 轴交于点A (1,0),点B (﹣3,0),与y 轴交于点C ,连接BC ,点P 在第二象限的抛物线上,连接PC 、PO ,线段PO 交线段BC 于点E .(1)求抛物线的表达式;(2)设:PCE 的面积为1S ,OCP △的面积为2S ,当1225S S =时,求点P 的坐标; (3)设:点C 关于抛物线对称轴的对称点为点N ,连接BN ,点H 在x 轴上,当HCB NBC ∠=∠时,①直接写出所有满足条件的所有点H 的坐标;①当点H 在线段AB 上时,点Q 是线段BH 外一点,1QH =,连接AQ ,将线段AQ 绕着点Q 逆时针旋转90︒得到线段QM ,连接MH ,直接写出线段MH 的取值范围.13.如图,直线1112y x =+与抛物线221482y x x =-+交于B 、C 两点(B 在C 的左侧)(1)求B 、C 两点的坐标;(2)直接写出12y y <时,x 的取值范围; (3)抛物线的顶点为A ,求ABC 的面积.14.如图,二次函数2y ax bx c =++的图象交x 轴于()1,0A -,()2,0B ,交y 轴于()0,2C -.(1)求二次函数的解析式;(2)点P 在该二次函数图象的对称轴上,且使PB PC -最大,求点P 的坐标; (3)若点M 为该二次函数图象在第四象限内一个动点,当点M 运动到何处时,四边形ACMB 的面积最大?求出此时点M 的坐标及四边形ACMB 面积的最大值.15.如图,直线1112y x =+与抛物线221482y x x =-+交于B 、C 两点(B 在C 的左侧).(1)求B 、C 两点的坐标;(2)直接写出12y y <时,x 的取值范围; (3)抛物线的顶点为A ,求ABC 的面积.16.如图,在平面直角坐标系中,二次函数2y x bx c =++的图像与x 轴交于()1,0A -,(1)求这个二次函数的解析式;(2)是否存在点P ,使POC △是以OC 为底边的等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)动点P 运动到什么位置时,PBC 面积最大,求出此时P 点坐标和PBC 的最大面积.17.如图1,在平面直角坐标系中,抛物线212y x bx c =-++的顶点为()2,8D ,与x 轴交于两点A ,B (A 在B 的左侧),与y 轴交于点C .(1)求抛物线的函数表达式;(2)如图2,连接AD BC ,,点P 是线段BC 上方抛物线上的一个动点,过点P 作PQ AD ∥交CB 于点Q ,求PQ 的最大值及此时点P 的坐标;(3)将该抛物线关于直线1x =对称得到新抛物线1y ,点E 是原抛物线y 和新抛物线1y 的交点,F 是原抛物线对称轴上一点,G 为新抛物线上一点,若以E 、F 、A 、G 为顶点的四边形是是平行四边形,请直接写出点F 的坐标.18.如图,在平面直角坐标系xOy 中,抛物线22y ax bx =++与x 轴相交于()()4010A C -,,,两点,于y 轴相交于点B .(1)求抛物线的解析式;(2)若P 为线段AB 的中点,连接OP ,求三角形PAO 的面积;(3)在(2)的条件下,点M 是抛物线第二象限上一点,若2APM ABO ∠∠=,求点M 的横坐标.参考答案:1.(1)2=23y x x --(2)当32t =时,APG 面积的最大,最大值为458;点P 的坐标为31524⎛⎫ ⎪⎝⎭,-(3)(23-或(23-.2.(1)()1,0-;()3,0 (2)152(3)存在,983.(1)2142y x x =--+ (2)532P ⎛⎫- ⎪⎝⎭,或752P ⎛⎫-- ⎪⎝⎭,(3)MN4.(1)(3,0)B ;(0,3)C(2)点P 的坐标为(0,3)或(2,3);点Q 与线段BC .5.(1)2=4+3y x x -(2)①2+3m m -;①3122⎛⎫- ⎪⎝⎭,6.(1)213222y x x =-- (2)P 的坐标为()2,3-(3)点M 的横坐标为203或437.(1)21y x =-(2)4(3)存在点M ,使以A 、M 、G 三点为顶点的三角形与PCA 相似,M 点的坐标为()23-,,4739⎛⎫ ⎪⎝⎭,,()415,8.(1)①5,02⎛⎫ ⎪⎝⎭,()0,5;①23522y x x =-++ (2)733416P ⎛⎫ ⎪⎝⎭, (3)39,44P ⎛⎫ ⎪⎝⎭9.(1)223y x x =-++,(1,4)D(2)(3)P 或(1,3P10.(1)233322y x x =-++; (2)存在;()1,3Q ;339(,)525Q -; (3)3411.(1)223y x x =-++(2)3y x =-+ (3)9412.(1)223y x x =--+;(2)()1,4-或()2,3-;(3)①()1,0-或()9,0-;①22MH ≤≤13.(1)()2,2B ,97,2C ⎛⎫ ⎪⎝⎭(2)2x <或7x > (3)15214.(1)2y x x 2=-- (2)1,32⎛⎫- ⎪⎝⎭(3)1,2,415.(1)(2,2)B ,9(7,)2C ; (2)7x >或2x <; (3)152.16.(1)234y x x =--(2)2-) (3)当P 点坐标为()26-,时,PBC 的最大面积为817.(1)21262y x x =-++(2)PQ =153,2P ⎛⎫ ⎪⎝⎭ (3)()2,4或()2,15或()2,12-.18.(1)213222y x x =--+ (2)2(3)7-。
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)(含简单答案)
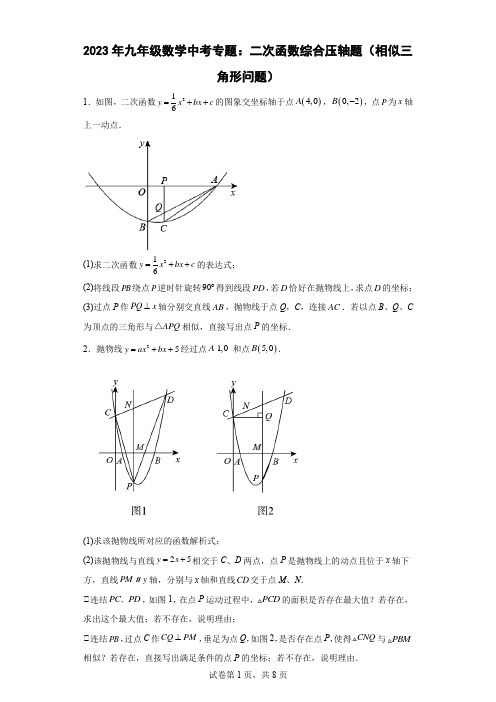
2023年九年级数学中考专题:二次函数综合压轴题(相似三角形问题)1.如图,二次函数216y x bx c =++的图象交坐标轴于点()4,0A ,()0,2B -,点P 为x 轴上一动点.(1)求二次函数216y x bx c =++的表达式; (2)将线段PB 绕点P 逆时针旋转90︒得到线段PD ,若D 恰好在抛物线上,求点D 的坐标; (3)过点P 作PQ x ⊥轴分别交直线AB ,抛物线于点Q ,C ,连接AC .若以点B 、Q 、C 为顶点的三角形与APQ △相似,直接写出点P 的坐标. 2.抛物线25y ax bx =++经过点1,0A 和点()5,0B .(1)求该抛物线所对应的函数解析式;(2)该抛物线与直线25y x =+相交于C 、D 两点,点P 是抛物线上的动点且位于x 轴下方,直线PM y ∥轴,分别与x 轴和直线CD 交于点M 、N .①连结PC PD 、,如图1,在点P 运动过程中,PCD 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;①连结PB ,过点C 作CQ PM ⊥,垂足为点Q ,如图2,是否存在点P ,使得CNQ 与PBM 相似?若存在,直接写出满足条件的点P 的坐标;若不存在,说明理由.3.已知抛物线24y ax ax b =-+与x 轴交于A ,B 两点,(A 在B 的左侧),与y 轴交于C ,若OB OC =,且03C (,).(1)求抛物线的解析式;(2)设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标; (3)在抛物线上是否存在一点M ,过M 作MN x ⊥轴于N ,以A 、M 、N 为顶点的三角形与AOC ∆相似,若存在,求出所有符合条件的M 点坐标,若不存在,请说明理由. 4.如图.在平面直角坐标系中.抛物线212y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点C .点A 的坐标为()1,0-,点C 的坐标为()0,2-.已知点(),0E m 是线段AB 上的动点(点E 不与点A ,B 重合).过点E 作PE x ⊥轴交抛物线于点P ,交BC 于点F .(1)求该抛物线的表达式;(2)若:1:2EF PF =,请求出m 的值;(3)是否存在这样的m ,使得BEP △与ABC 相似?若存在,求出此时m 的值;若不存在,请说明理由;(4)当点E 运动到抛物线对称轴上时,点M 是x 轴上一动点,点N 是抛物线上的动点,在运动过程中,是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,请直接写出点M 的坐标.5.如图,二次函数212y x bx c =-++图像交x 轴于点A ,B (A 在B 的左侧),与y 轴交于点(0,3)C ,CD y ⊥轴,交抛物线于另一点D ,且5CD =,P 为抛物线上一点,PE y轴,与x 轴交于E ,与BC ,CD 分别交于点F ,G .(1)求二次函数解析式;(2)当P 在CD 上方时,是否存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,若存在,求出CPG △与FBE 的相似比,若不存在,说明理由.(3)点D 关于直线PC 的对称点为D ,当点D 落在抛物线的对称轴上时,此时点P 的坐标为________.6.如图,抛物线22y ax bx =++与x 轴交于点A ,B ,与y 轴交于点C ,已知A ,B 两点坐标分别是(1,0)A ,(4,0)B -,连接,AC BC .(1)求抛物线的表达式;(2)将ABC ∆沿BC 所在直线折叠,得到DBC ∆,点A 的对应点D 是否落在抛物线的对称轴上?若点D 在对称轴上,请求出点D 的坐标;若点D 不在对称轴上,请说明理由;(3)若点P 是抛物线位于第二象限图象上的一动点,连接AP 交BC 于点Q ,连接BP ,BPQ ∆的面积记为1S ,ABQ ∆的面积记为2S ,求12S S 的值最大时点P 的坐标. 7.已知,二次函数23y ax bx =+-的图象与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于C 点,点A 的坐标为()1,0-,且OB OC =.(1)求二次函数的解析式;(2)当04x ≤≤时,求二次函数的最大值和最小值分别为多少?(3)设点C '与点C 关于该抛物线的对称轴对称.在y 轴上是否存在点P ,使PCC '△与POB 相似,且PC 与PO 是对应边?若存在,求出点P 的坐标;若不存在,请说明理由.8.已知菱形OABC 的边长为5,且点(34)A ,,点E 是线段BC 的中点,过点A ,E 的抛物线2y ax bx c =++与边AB 交于点D ,(1)求点E 的坐标;(2)连接DE ,将BDE △沿着DE 翻折痕.①当B 点的对应点B '恰好落在线段AC 上时,求点D 的坐标;①连接OB ,BB ',若BB D '△与BOC 相似,请直接写出此时抛物线二次项系数=a ______. 9.如图,抛物线22(0)y ax x c a =-+≠与x 轴交于A 、()3,0B 两点,与y 轴交于点()0,3C -,抛物线的顶点为D .(1)求抛物线的解析式;(2)已知点M 是x 轴上的动点,过点M 作x 轴的垂线交抛物线于点G ,是否存在这样的点M ,使得以点A 、M 、G 为顶点的三角形与BCD △相似,若存在,请求出点M 的坐标;若不存在,请说明理由.(3)在直线BC 下方抛物线上一点P ,作PQ 垂直BC 于点Q ,连接CP ,当CPQ 中有一个角等于ACO ∠时,求点P 的坐标.10.如图,抛物线顶点D 在x 轴上,且经过(0,3)-和(4,3)-两点,抛物线与直线l 交于A 、B 两点.(1)直接写出抛物线解析式和D 点坐标;(2)如图1,若()03A ,-,且 94ABDS =,求直线l 解析式; (3)如图2,若90ADB ∠=︒,求证:直线l 经过定点,并求出定点坐标.11.如图1,已知抛物线2=23y x x --与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接BC ,点P 是线段BC 下方抛物线上一动点,过点P 作∥PE BC ,交x 轴于点E ,连接OP 交BC 于点F .(1)直接写出点A ,B ,C 的坐标以及抛物线的对称轴; (2)当点P 在线段BC 下方抛物线上运动时,求BFPE取到最小值时点P 的坐标; (3)当点P 在y 轴右边抛物线上运动时,过点P 作PE 的垂线交抛物线对称轴于点G ,是否存在点P ,使以P 、E 、G 为顶点的三角形与①AOC 相似?若存在,来出点P 的坐标;若不存在,请说明理由.12.如图,抛物线212ax ax b =-+y 经过()1,0A -,32,2C ⎛⎫⎪⎝⎭两点,与x 轴交于另一点B .(1)求此抛物线的解析式;(2)若抛物线的顶点为M ,点P 为线段OB 上一动点(不与点B 重合),点Q 在线段MB 上移动,且2PM MQ MB =⋅,设线段OP x =,2MQ y =,求2y 与x 的函数关系式,并直接写出自变量x 的取值范围;并直接写出PM APPQ BQ-的值;(3)在同一平面直角坐标系中,两条直线x m =,x n =分别与抛物线交于点E ,G ,与(2)中的函数图象交于点F ,.H 问四边形EFHG 能否为平行四边形?若能,求m ,n 之间的数量关系;若不能,请说明理由.13.已知抛物线213222y x x =-++交x 轴于A 、B 两点,A 在B 的左边,交y 轴于点C .(1)求抛物线顶点的坐标;(2)如图1,若10,2E ⎛⎫- ⎪⎝⎭,P 在抛物线上且在直线AE 上方,PQ AE ⊥于O ,求PQ 的最大值;(3)如图2,点(),3D a (32a <)在抛物线上,过A 作直线交抛物线于第四象限另一点F ,点M 在x 轴上,以M 、B 、D 为顶角的三角形与AFB △相似,求点M 的坐标. 14.如图,抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ,与y 轴交于点C ,联结AC 、BC .(1)求该抛物线的表达式及顶点D 的坐标;(2)如果点P 在抛物线上,CB 平分ACP ∠,求点P 的坐标:(3)如果点Q 在抛物线的对称轴上,DBQ 与ABC 相似.求点Q 的坐标.15.如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45︒得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式; (2)当点D 在第二象限且34DE EO =时,求点D 的坐标; (3)当ODF △为直角三角形时,请直接写出点D 的坐标.16.如图①,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,3),顶点为D (4,-1),对称轴与直线BC 交于点E ,与x 轴交于点F .(1)求二次函数的解析式;(2)点M 在第一象限抛物线的对称轴上,若点C 在BM 的垂直平分线上,求点M 的坐标; (3)如图①,过点E 作对称轴的垂线在对称轴的右侧与抛物线交于点H ,x 轴上方的对称轴上是否存在一点P ,使以E ,H ,P 为顶点的三角形与EFB △相似,若存在,求出P点坐标;若不存在,请说明理由.17.如图,在平面直角坐标系xOy 中,已知抛物线2y ax x c =++经过()2,0A -,()0,4B 两点,直线3x =与x 轴交于点C .(1)求a ,c 的值;(2)经过点O 的直线分别与线段AB ,直线3x =交于点D ,E ,且BDO △与OCE △的面积相等,求直线DE 的解析式;(3)P 是抛物线上位于第一象限的一个动点,在线段OC 和直线3x =上是否分别存在点F ,G ,使B ,F ,G ,P 为顶点的四边形是以BF 为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.18.如图1,抛物线2y ax bx c =++与x 轴交于A ,B (点A 在点B 左侧),与y 轴负半轴交于C ,且满足2OA OB OC ===.(1)求抛物线的解析式;(2)如图2,D 为y 轴负半轴上一点,过D 作直线l 垂直于直线BC ,直线l 交抛物线于E ,F 两点(点E 在点F 右侧),若3DF DE =,求D 点坐标; (3)如图3,点M 为抛物线第二象限部分上一点,点M ,N 关于y 轴对称,连接MB ,P 为线段MB 上一点(不与M 、B 重合),过P 点作直线x t =(t 为常数)交x 轴于S ,交直线NB 于Q ,求QS PS -的值(用含t 的代数式表示).参考答案:1.(1)211266y x x =-- (2)()3,1D -或()8,10D -(3)点P 的坐标为()011-,或()10,.2.(1)265y x x =-+ (2)37,24⎛⎫- ⎪⎝⎭或()3,4-3.(1)243y x x =-+ (2)()2,2P 或()2,2-(3)存在符合条件的M 点,且坐标为:110(3M ,7)9-,()26,15M ,38(3M ,5)9-4.(1)213222y x x =--; (2)2m =;(3)存在,m 的值为0或3;(4)存在,M 点的坐标为()7,0或()1,0M 或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭.5.(1)215322y x x =-++;(2)存在点P ,使得以C ,P ,G 为顶点的三角形与FBE 相似,CPG △与FBE 的相似比为2或25;(3)P 点横坐标55.6.(1)213222y x x =--+(2)点D 不在抛物线的对称轴上, (3)(2,3)-7.(1)2=23y x x --(2)函数的最大值为5,最小值为4- (3)存在,(0,9)P -或9(0,)5P -8.(1)13(2)2E , (2)①11(4)2D ,或23(4)6D ,;①47-9.(1)2=23y x x --(2)()0,0,()6,0,8,03⎛⎫ ⎪⎝⎭,10,03⎛⎫⎪⎝⎭(3)57,24⎛⎫- ⎪⎝⎭或者315,24⎛⎫- ⎪⎝⎭10.(1)()2324y x =--,()2,0D (2)334y x =-或1534y x =- (3)证明见解析,定点坐标为423⎛⎫- ⎪⎝⎭,11.(1)A (﹣1,0),B (3,0),C (0,﹣3),对称轴为直线x =1(2)当t =32时,BF PE 最小,最小值为47,此时P (32,﹣154).(3)存在,点P 的坐标为(2,﹣3)12.(1)211322y x x =-++(2)22150322y x x x =-+≤<(),PM AP PQ BQ -的值为0 (3)m 、n 之间的数量关系是2(1)m n m +=≠13.(1)(32,258)答案第3页,共3页(3)(2,0)或(-5,0)或13,07⎛⎫ ⎪⎝⎭或2205⎛⎫- ⎪⎝⎭,14.(1)2=+43y x x --,(21)D , (2)111639⎛⎫ ⎪⎝⎭,- (3)(2,−2)或12,3⎛⎫ ⎪⎝⎭15.(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)(3,4)-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭16.(1)21234y x x =-+(2)(4,3(3)存在P 1)或(4,1),使以E ,H ,P 为顶点的三角形与EFB △相似,17.(1)12a =-,4c = (2)23y x =- (3)存在这样的点F ,点F 的坐标为(2,0)或18.(1)2122y x =- (2)()0,1D -或190,8D ⎛⎫- ⎪⎝⎭, (3)24QS PS t -=-+。
2023中考数学真题汇编13 二次函数解答压轴题(含答案与解析)

2023中考数学真题汇编·13二次函数解答压轴题一、解答题1.(2023·浙江绍兴)已知二次函数2y x bx c .(1)当4,3b c 时,①求该函数图象的顶点坐标.②当13x 时,求y 的取值范围.(2)当0x 时,y 的最大值为2;当0x 时,y 的最大值为3,求二次函数的表达式.2.(2023·浙江)已知点 ,0m 和 3,0m 在二次函数23,(y ax bx a b 是常数,0)a 的图像上.(1)当1m 时,求a 和b 的值;(2)若二次函数的图像经过点 ,3A n 且点A 不在坐标轴上,当21m 时,求n 的取值范围;(3)求证:240b a .3.(2023·上海)在平面直角坐标系xOy 中,已知直线364y x 与x 轴交于点A ,y 轴交于点B ,点C 在线段AB 上,以点C 为顶点的抛物线M :2y ax bx c 经过点B .(1)求点A ,B 的坐标;(2)求b ,c 的值;(3)平移抛物线M 至N ,点C ,B 分别平移至点P ,D ,联结CD ,且CD x ∥轴,如果点P 在x 轴上,且新抛物线过点B ,求抛物线N 的函数解析式.4.(2023·浙江嘉兴)在二次函数223(0)y x tx t 中,(1)若它的图象过点(2,1),则t 的值为多少?(2)当03x 时,y 的最小值为2 ,求出t 的值:(3)如果(2,),(4,),(,)A m a B b C m a 都在这个二次函数的图象上,且3a b ,求m 的取值范围.5.(2023·浙江杭州)设二次函数21y ax bx ,(0a ,b 是实数).已知函数值y 和自变量x 的部分对应取值如下表所示:x …1 0123…y …m 1n1p …(1)若4m ,求二次函数的表达式;(2)写出一个符合条件的x 的取值范围,使得y 随x 的增大而减小.(3)若在m 、n 、p 这三个实数中,只有一个是正数,求a 的取值范围.6.(2023·湖南常德)如图,二次函数的图象与x 轴交于 1,0A , 5,0B 两点,与y 轴交于点C ,顶点为D .O 为坐标原点,1tan 5ACO .(1)求二次函数的表达式;(2)求四边形ACDB 的面积;(3)P 是抛物线上的一点,且在第一象限内,若ACO PBC ,求P 点的坐标.7.(2023·天津)已知抛物线2y x bx c (b ,c 为常数,1c )的顶点为P ,与x 轴相交于A ,B 两点(点A 在点B 的左侧),与y 轴相交于点C ,抛物线上的点M 的横坐标为m ,且2b c m ,过点M 作MN AC ,垂足为N .(1)若2,3b c .①求点P 和点A 的坐标;②当MN M 的坐标;(2)若点A 的坐标为 ,0c ,且MP AC ∥,当3AN MN 时,求点M 的坐标.8.(2023·山东烟台)如图,抛物线25y ax bx 与x 轴交于,A B 两点,与y 轴交于点,4C AB .抛物线的对称轴3x 与经过点A 的直线1y kx 交于点D ,与x 轴交于点E .(1)求直线AD 及抛物线的表达式;(2)在抛物线上是否存在点M ,使得ADM △是以AD 为直角边的直角三角形?若存在,求出所有点M 的坐标;若不存在,请说明理由;(3)以点B 为圆心,画半径为2的圆,点P 为B 上一个动点,请求出12PC PA 的最小值.9.(2023·江苏苏州)如图,二次函数268y x x 的图像与x 轴分别交于点,A B (点A 在点B 的左侧),直线l 是对称轴.点P 在函数图像上,其横坐标大于4,连接,PA PB ,过点P 作PM l ,垂足为M ,以点M 为圆心,作半径为r 的圆,PT 与M 相切,切点为T .(1)求点,A B 的坐标;(2)若以M 的切线长PT 为边长的正方形的面积与PAB 的面积相等,且M 不经过点 3,2,求PM 长的取值范围.10.(2023·山东东营)如图,抛物线过点 0,0O , 10,0E ,矩形ABCD 的边AB 在线段OE 上(点B 在点A 的左侧),点C ,D 在抛物线上,设 ,0B t ,当2t 时,4BC .(1)求抛物线的函数表达式;(2)当t 为何值时,矩形ABCD 的周长有最大值?最大值是多少?(3)保持2t 时的矩形ABCD 不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点G ,H ,且直线GH 平分矩形ABCD 的面积时,求抛物线平移的距离.11.(2023·四川自贡)如图,抛物线2443y x bx 与x 轴交于(3,0)A ,B 两点,与y 轴交于点C .(1)求抛物线解析式及B ,C 两点坐标;(2)以A ,B ,C ,D 为顶点的四边形是平行四边形,求点D 坐标;(3)该抛物线对称轴上是否存在点E ,使得45ACE ,若存在,求出点E 的坐标;若不存在,请说明理由.12.(2023·山东枣庄)如图,抛物线2y x bx c 经过(1,0),(0,3)A C 两点,并交x 轴于另一点B ,点M是抛物线的顶点,直线AM 与轴交于点D .(1)求该抛物线的表达式;(2)若点H 是x 轴上一动点,分别连接MH ,DH ,求MH DH 的最小值;(3)若点P 是抛物线上一动点,问在对称轴上是否存在点Q ,使得以D ,M ,P ,Q 为顶点的四边形是平行四边形?若存在,请直接..写出所有满足条件的点Q 的坐标;若不存在,请说明理由.13.(2023·四川达州)如图,抛物线2y ax bx c 过点 1,0,3,,00,3A B C .(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.14.(2023·四川泸州)如图,在平面直角坐标系xOy 中,已知抛物线2y ax 2x c 与坐标轴分别相交于点A ,B , 0,6C 三点,其对称轴为2x .(1)求该抛物线的解析式;(2)点F 是该抛物线上位于第一象限的一个动点,直线AF 分别与y 轴,直线BC 交于点D ,E .①当CD CE 时,求CD 的长;②若CAD ,CDE ,CEF △的面积分别为1S ,2S ,3S ,且满足1322S S S ,求点F 的坐标.15.(2023·全国)如图,在平面直角坐标系中,抛物线22y x x c 经过点(0,1)A .点P ,Q 在此抛物线上,其横坐标分别为,2(0)m m m ,连接AP ,AQ .(1)求此抛物线的解析式.(2)当点Q 与此抛物线的顶点重合时,求m 的值.(3)当PAQ 的边与x 轴平行时,求点P 与点Q 的纵坐标的差.(4)设此抛物线在点A 与点P 之间部分(包括点A 和点P )的最高点与最低点的纵坐标的差为1h ,在点A 与点Q 之间部分(包括点A 和点Q )的最高点与最低点的纵坐标的差为2h .当21h h m 时,直接写出m 的值.16.(2023·四川成都)如图,在平面直角坐标系xOy 中,已知抛物线2y ax c 经过点3(4,)P ,与y 轴交于点(0,1)A ,直线(0)y kx k 与抛物线交于B ,C 两点.(1)求抛物线的函数表达式;(2)若ABP 是以AB 为腰的等腰三角形,求点B 的坐标;(3)过点(0,)M m 作y 轴的垂线,交直线AB 于点D ,交直线AC 于点E .试探究:是否存在常数m ,使得OD OE 始终成立?若存在,求出m 的值;若不存在,请说明理由.17.(2023·四川遂宁)在平面直角坐标系中,O 为坐标原点,抛物线214y x bx c 经过点(0O ,0),对称轴过点(2B ,0),直线l 过点 2,2C ,且垂直于y 轴.过点B 的直线1l 交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当:3:5BM MQ 时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线1l 下方的抛物线上一动点,连接PQ 、PO ,其中PO 交1l 于点E ,设OQE 的面积为1S ,PQE 的面积为2S .求21S S 的最大值.18.(2023·四川眉山)在平面直角坐标系中,已知抛物线2y ax bx c 与x 轴交于点 3,0,1,0A B 两点,与y 轴交于点 0,3C ,点P是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PD DB的值最大时,求点P 的坐标及PD DB 的最大值;(3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将PCM △沿直线PC 翻折,当点M 的对应点'M 恰好落在y 轴上时,请直接写出此时点M 的坐标.19.(2023·湖南郴州)已知抛物线24y ax bx 与x 轴相交于点()1,0A , 4,0B ,与y 轴相交于点C.(1)求抛物线的表达式;(2)如图1,点P 是抛物线的对称轴l 上的一个动点,当PAC △的周长最小时,求PA PC 的值;(3)如图2,取线段OC 的中点D ,在抛物线上是否存在点Q ,使1tan 2QDB?若存在,求出点Q 的坐标;若不存在,请说明理由.20.(2023·甘肃武威)如图1,抛物线2y x bx 与x 轴交于点A ,与直线y x 交于点 4,4B ,点 0,4C 在y 轴上.点P 从点B 出发,沿线段BO 方向匀速运动,运动到点O 时停止.(1)求抛物线2y x bx 的表达式;(2)当22BP 时,请在图1中过点P 作PD OA 交抛物线于点D ,连接PC ,OD ,判断四边形OCPD 的形状,并说明理由.(3)如图2,点P 从点B 开始运动时,点Q 从点O 同时出发,以与点P 相同的速度沿x 轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接BQ ,PC ,求CP BQ 的最小值.21.(2023·山东聊城)如图①,抛物线29y ax bx 与x 轴交于点 30A ,, 6,0B ,与y 轴交于点C ,连接AC ,BC .点P 是x 轴上任意一点.(1)求抛物线的表达式;(2)点Q 在抛物线上,若以点A ,C ,P ,Q 为顶点,AC 为一边的四边形为平行四边形时,求点Q 的坐标;(3)如图②,当点 ,0P m 从点A 出发沿x 轴向点B 运动时(点P 与点A ,B 不重合),自点P 分别作∥PE BC ,交AC 于点E ,作PD BC ,垂足为点D .当m 为何值时,PED V 面积最大,并求出最大值.22.(2023·江苏连云港)如图,在平面直角坐标系xOy 中,抛物线21:23L y x x 的顶点为P .直线l 过点 0,3M m m ,且平行于x 轴,与抛物线1L 交于A B 、两点(B 在A 的右侧).将抛物线1L 沿直线l 翻折得到抛物线2L ,抛物线2L 交y 轴于点C ,顶点为D .(1)当1m 时,求点D 的坐标;(2)连接BC CD DB 、、,若BCD △为直角三角形,求此时2L 所对应的函数表达式;(3)在(2)的条件下,若BCD △的面积为3,E F 、两点分别在边BC CD 、上运动,且EF CD ,以EF 为一边作正方形EFGH ,连接CG ,写出CG 长度的最小值,并简要说明理由.23.(2023·湖南怀化)如图一所示,在平面直角坐标系中,抛物线28y ax bx 与x 轴交于(4,0)(2,0)A B 、两点,与y 轴交于点C .(1)求抛物线的函数表达式及顶点坐标;(2)点P 为第三象限内抛物线上一点,作直线AC ,连接PA 、PC ,求PAC △面积的最大值及此时点P 的坐标;(3)设直线135:4l y kx k 交抛物线于点M 、N ,求证:无论k 为何值,平行于x 轴的直线237:4l y 上总存在一点E ,使得MEN 为直角.24.(2023·吉林长春)在平面直角坐标系中,点O 为坐标原点,抛物线22y x bx (b 是常数)经过点(2,2).点A 的坐标为(,0)m ,点B 在该抛物线上,横坐标为1m .其中0m .(1)求该抛物线对应的函数表达式及顶点坐标;(2)当点B在x轴上时,求点A的坐标;(3)该抛物线与x轴的左交点为P,当抛物线在点P和点B之间的部分(包括P、B两点)的最高点与最低点的纵坐标之差为2m时,求m的值.轴于点C,连结AC、BO.若四边形AOBC的边和抛物线有(4)当点B在x轴上方时,过点B作BC y两个交点(不包括四边形AOBC的顶点),设这两个交点分别为点E、点F,线段BO的中点为D.当以点C、E、O、D(或以点C、F、O、D)为顶点的四边形的面积是四边形AOBC面积的一半时,直接写出所有满足条件的m的值.【参考答案与解析】1.【答案】(1)解:①当4,3b c 时,2243(2)7y x x x ,∴顶点坐标为 2,7.②∵顶点坐标为 2,7.抛物线开口向下,当12x 时,y 随x 增大而增大,当23x 时,y 随x 增大而减小,∴当2x 时,y 有最大值7.又 2132∴当=1x 时取得最小值,最小值=2y ;∴当13x 时,27y ≤≤.(2)∵0x 时,y 的最大值为2;0x 时,y 的最大值为3,∴抛物线的对称轴2bx在y 轴的右侧,∴0b ,∵抛物线开口向下,0x 时,y 的最大值为2,∴2c ,又∵241341c b ,∴2b ,∵0b ,∴2b ,∴二次函数的表达式为222y x x .【分析】(1)①将4,3b c 代入解析式,化为顶点式,即可求解;②已知顶点 2,7,根据二次函数的增减性,得出当2x 时,y 有最大值7,当=1x 时取得最小值,即可求解;(2)根据题意0x 时,y 的最大值为2;0x 时,y 的最大值为3,得出抛物线的对称轴2bx在y 轴的右侧,即0b ,由抛物线开口向下,0x 时,y 的最大值为2,可知2c ,根据顶点坐标的纵坐标为3,求出2b ,即可得解.2.【答案】(1)解:当1m 时,图像过点 1,0和 3,0 ,∴030933a b a b,解得12a b ,∴223y x x ,∴1,2a b .(2)解:∵函数图像过点 ,0m 和 3,0m ,∴函数图像的对称轴为直线x m .∵图像过点 ,3,0,3n ,∴根据图像的对称性得2n m .∵21m ,∴42n .(3)解:∵图像过点 ,0m 和 3,0m ,∴根据图像的对称性得2bm a.∴2b am ,顶点坐标为2,3m am bm .将点 ,0m 和 3,0m 分别代人表达式可得22030933am bm am bm ①②①3 ②得212120am ,∴21am .∴222232334am bm am am am .∴21244a b a.∴21216a b a .∴240b a .【分析】(1)由1m 可得图像过点 1,0和 3,0 ,然后代入解析式解方程组即可解答;(2)先确定函数图像的对称轴为直线x m ,则抛物线过点 ,3,0,3n ,即2n m ,然后再结合21m 即可解答;(3)根据图像的对称性得2bm a,即2b am ,顶点坐标为 2,3m am bm ;将点 ,0m 和 3,0m 分别代入表达式并进行运算可得21am ;则222232334am bm am am am ,进而得到21244a b a,然后化简变形即可证明结论.3.【答案】(1)解:∵直线364y x与x 轴交于点A ,y 轴交于点B ,当0x 时,代入得:6y ,故 0,6B ,当0y 时,代入得:8x ,故 8,0A ,(2)设3,64C m m,则可设抛物线的解析式为: 2364y a x m m ,∵抛物线M 经过点B ,将 0,6B 代入得:23664am m ,∵0m ,∴34am ,即34m a,∴将34m a 代入 2364y a x m m ,整理得:2362y ax x ,故32b,6c ;(3)如图:∵CD x ∥轴,点P 在x 轴上,∴设 ,0P p ,3,64C m m,∵点C ,B 分别平移至点P ,D ,∴点B ,点C 向下平移的距离相同,∴3366644m m,解得:4m ,由(2)知34m a,∴316a,∴抛物线N 的函数解析式为: 2316y x p ,将 0,6B 代入可得:p∴抛物线N 的函数解析式为: 2316y x 或 2316y x .【分析】(1)根据题意,分别将0x ,0y 代入直线364y x即可求得;(2)设3,64C m m,得到抛物线的顶点式为 2364y a x m m ,将 0,6B 代入可求得34m a ,进而可得到抛物线解析式为2362y ax x ,即可求得b ,c ;(3)根据题意,设 ,0P p ,3,64C m m,根据平移的性质可得点B ,点C 向下平移的距离相同,即列式求得4m ,316a ,然后得到抛物线N 解析式为: 2316y x p ,将 0,6B 代入可得p得到答案.4.【答案】(1)将(2,1)代入223y x tx 中,得1443t ,解得,32t ;(2)抛物线对称轴为x t .若03t ,当x t 时,函数值最小,22232t t ,解得t 0t ∵,t 若3t ,当3x 时,函数值最小,2963t ,解得73t (不合题意,舍去)综上所述t (3)(2,),(,)A m a C m a ∵关于对称轴对称,2,12m mt m t,且A 在对称轴左侧,C 在对称轴右侧∵抛物线与y 轴交点为(0,3),抛物线对称轴为直线x t , 此交点关于对称轴的对称点为(23)2,m 3,3a b ∵且0t 422m ,解得3m .当A ,B 都在对称轴左边时,a b∵42m ,解得6m ,6m 当A ,B 分别在对称轴两侧时a b B ∵到对称轴的距离大于A 到对称轴的距离4(1)1(2)m m m ,解得4m 34m 综上所述34m 或6m .【分析】(1)将坐标代入解析式,求解待定参数值;(2)确定抛物线的对称轴,对待定参数分类讨论,分03t ,当x t 时,函数值最小,以及3t ,当3x 时,函数值最小,求得相应的t 值即可得;(3)由(2,),(,)A m a C m a 关于对称轴对称得1m t ,且A 在对称轴左侧,C 在对称轴右侧;确定抛物线与y 轴交点(0,3),此交点关于对称轴的对称点为(23)2,m ,结合已知确定出3m ;再分类讨论:A ,B 都在对称轴左边时,A ,B 分别在对称轴两侧时,分别列出不等式进行求解即可.5.【答案】(1)解:把 1,4 , 2,1代入21y ax bx ,得144211a b a b ,解得:12a b ,∴221y xx .(2)解:∵ 0,1, 2,1在21y ax bx 图象上,∴抛物线的对称轴为直线0212x ,∴当0a 时,则1x 时,y 随x 的增大而减小,当a<0时,则1x 时,y 随x 的增大而减小.(3)解:把 2,1代入21y ax bx ,得1421a b ,∴2b a∴22121y ax bx ax ax 把 1,m 代入221y ax ax 得,2131m a a a ,把 1,n 代入221y ax ax 得,211n a a a ,把 3,p 代入221y ax ax 得,96131p a a a ,∴m p ,∵m 、n 、p 这三个实数中,只有一个是正数,∴10310a a,解得:13a .【分析】(1)用待定系数法求解即可.(2)利用抛物线的对称性质求得抛物线的对称轴为直线1x ;再根据抛物线的增减性求解即可.(3)先把 2,1代入21y ax bx ,得2b a ,从而得221y ax ax ,再求出31m a ,1n a ,31p a ,从而得m p ,然后m 、n 、p 这三个实数中,只有一个是正数,得10310a a,求解即可.6.【答案】(1)∵二次函数的图象与x 轴交于 1,0,5,0A B 两点.∴设二次函数的表达式为 15y a x x ∵11,tan 5AO ACO,∴5OC ,即C 的坐标为 0,5,则 50105a ,得1a ∴二次函数的表达式为 15y x x ;(2) 215(2)9y x x x ,∴顶点的坐标为2,9过D 作DN AB 于N ,作DM OC 于M ,四边形ACDB 的面积AOC CDM DNB OMDN S S S S △△△矩形 111152929552930222;(3)如图,P 是抛物线上的一点,且在第一象限,当ACO PBC 时,连接PB ,过C 作CE BC 交BP 于E ,过E 作EF OC 于F ,∵5OC OB ,则OCB 为等腰直角三角形,45OCB .由勾股定理得:52CB ∵ACO PBC ,∴tan tan ACO PBC ,即1552CE CB ∴2CE 由CH BC ,得90BCE ,∴180180904545ECF BCE OCB .∴EFC 是等腰直角三角形,∴1FC FE ,∴E 的坐标为 1,6所以过B E 、的直线的解析式为31522y x令 3152215y x y x x ,解得50x y ,或12274x y所以BE 直线与抛物线的两个交点为 1275,0,,24B P ,即所求P 的坐标为127,24P【分析】(1)用两点式设出二次函数的解析式,然后求得C 点的坐标,并将其代入二次函数的解析式,求得a 的值,再将a 代入解析式中即可.(2)先将二次函数变形为顶点式,求得顶点坐标,然后利用矩形、三角形的面积公式即可求得答案.(3)根据各点的坐标的关系及同角三角函数相等的结论可以求得相关联的函数解析式,最后联立一次函数与二次函数的解析式,求得点P 的坐标.7.【答案】(1)解:①由2,3b c ,得抛物线的解析式为223y x x .∵2223(1)4y x x x =--+=-++,∴点P 的坐标为 1,4 .当0y 时,2x 2x 30 .解得123,1x x .又点A 在点B 的左侧,∴点A 的坐标为 3,0 .②过点M 作ME x 轴于点E ,与直线AC 相交于点F .∵点 30A ,,点 0,3C ,∴OA OC .可得Rt AOC 中,45OAC .∴Rt AEF 中,EF AE .∵抛物线223y x x 上的点M 的横坐标为m ,其中3<1m ,∴设点 2,23M m m m ,点 ,0E m .得 33EF AE m m .即点 ,3F m m .∴222333FM m m m m m .Rt FMN 中,可得45MFN .∴2FM MN .又2MN 得2FM .即232m m .解得122,1m m (舍).∴点M 的坐标为 2,3 .(2)∵点 ,0A c 在抛物线2y x bx c 上,其中1c ,∴20c bc c .得1b c .∴抛物线的解析式为 21y x c x c .得点2,1M m m c m c ,其中12cc m.∵ 2221(1)124c c y x c x c x,∴顶点P 的坐标为21(1),24c c,对称轴为直线1:2cl x .过点M 作MQ l 于点Q ,则90MQP ,点 21,12c Q m c m c.由MP AC ∥,得45PMQ .于是MQ QP .∴ 221(1)124c c m m c m c .即2(2)1c m .解得1221,21c m c m (舍).同(Ⅰ),过点M 作ME x 轴于点E ,与直线AC 相交于点F ,则点 ,0E m ,点 ,1F m m ,点 2,1M m m .∵332292AN MN AF FN MN FM221221192m m m即22100m m .解得125,22m m (舍).∴点M 的坐标为521,24.【分析】(1)①待定系数法求解析式,然后化为顶点式,即可求得P 的坐标,令0y ,解方程,即可求得A 的坐标;②过点M 作ME x 轴于点E ,与直线AC 相交于点F .得出OA OC .可得Rt AOC 中,45OAC .Rt AEF 中,EF AE .设点 2,23M m m m ,点 ,0E m .根据MN求解;(2)根据题意得出抛物线的解析式为 21y x c x c .得点2,1M m m c m c ,其中12cc m .则顶点P 的坐标为21(1),24c c,对称轴为直线1:2c l x .过点M 作MQ l 于点Q ,则90MQP ,点 21,12c Q m c m c.由MP AC ∥,得45PMQ .于是MQ QP .得出1221,21c m c m (舍).,同(Ⅰ),过点M 作ME x 轴于点E ,与直线AC 相交于点F ,则点 ,0E m ,点 ,1F m m ,点 2,1M m m .根据已知条件式,建立方程,解方程即可求解.8.【答案】(1)解:∵抛物线的对称轴3x ,4AB ,∴ 1,0,5,0A B ,将()1,0A 代入直线1y kx ,得10k ,解得1k ,∴直线AD 的解析式为1y x ;将 1,0,5,0A B 代入25y ax bx ,得5025550a b a b ,解得16a b ,∴抛物线的解析式为265y x x ;(2)存在点M ,∵直线AD 的解析式为1y x ,抛物线对称轴3x 与x 轴交于点E .∴当3x 时,12y x ,∴ 3,2D ,①当90DAM 时,设直线AM 的解析式为y x c ,将点A 坐标代入,得10c ,解得1c ,∴直线AM 的解析式为1y x ,解方程组2165y x y x x,得10x y 或43x y ,∴点M 的坐标为 4,3 ;②当90ADM 时,设直线DM 的解析式为y x d ,将 3,2D 代入,得32d ,解得5d ,∴直线DM 的解析式为5y x ,解方程组2565y x y x x ,解得05x y 或5x y ,∴点M 的坐标为 0,5或5,0综上,点M 的坐标为 4,3 或 0,5或 5,0;(3)如图,在AB 上取点F ,使1BF ,连接CF ,∵2PB ,∴12BF PB ,∵2142PB AB ,∴BF PBPB AB,又∵PBF ABP ,∴PBF ABP ∽,∴12PF BF PA PB ,即12PF PA ,∴12PC PA PC PF CF,∴当点C 、P 、F 三点共线时,12PC PA 的值最小,即为线段CF 的长,∵5,1514OC OF OB ,∴CF ∴12PC PA【分析】(1)根据对称轴3x ,4AB ,得到点A 及B 的坐标,再利用待定系数法求解析式即可;(2)先求出点D 的坐标,再分两种情况:①当90DAM 时,求出直线AM 的解析式为1y x ,解方程组2165y x y x x ,即可得到点M 的坐标;②当90ADM 时,求出直线DM 的解析式为5y x ,解方程组2565y x y x x,即可得到点M 的坐标;(3)在AB 上取点F ,使1BF ,连接CF ,证得BF PBPB AB,又PBF ABP ,得到PBF ABP ∽,推出12PF PA ,进而得到当点C 、P 、F 三点共线时,12PC PA 的值最小,即为线段CF 的长,利用勾股定理求出CF 即可.9.【答案】(1)解:令0y ,则有:2680x x ,解得:2x 或4x ,∴ 2,0,4,0A B .(2)解:∵抛物线过 2,0,4,0A B ∴抛物线的对称轴为3x ,设 2,68P m m m ,∵PM l ,∴ 23,68M m m ,如图:连接MT ,则MT PT ,∴ 222223PT PM MT m r ,∴切线PT 为边长的正方形的面积为 223m r ,过点P 作PH x 轴,垂足为H ,则:21682PAB S AB PH m m ,∴ 222368m r m m ∵0r ,∴1r ,假设M 过点 3,2N ,则有以下两种情况:①如图1:当点M 在点N 的上方,即3,3M ∴2683m m ,解得:5m 或1m ,∵4m ,∴5m ;②如图2:当点M 在点N 的上方,即3,1M ∴2681m m ,解得:32m ∵4m ,∴32m 综上,32PM m 2∴当M 不经过点 3,2时,12PM 22PM 或2PM .【分析】(1)令0y 求得点,A B 的横坐标即可解答;(2)由题意可得抛物线的对称轴为3x ,设 2,68P m m m ,则 23,68M m m ;如图连接MT ,则MT PT ,进而可得切线长PT 为边长的正方形的面积为 223m r ;过点P 作PH x 轴,垂足为H ,可得21682PAB S AB PH m m;由题意可得 222368m r m m ,解得1r ;然后再分当点M 在点N 的上方和下方两种情况解答即可.10.【答案】(1)解:设抛物线的函数表达式为 100y ax x a .∵当2t 时,4BC ,∴点C 的坐标为 2,4 .将点C 坐标代入表达式,得 22104a ,解得14a .∴抛物线的函数表达式为21542y x x.(2)解:由抛物线的对称性得:AE OB t ,∴102AB t .当x t 时,21542BC t t .∴矩形ABCD 的周长为2152210242AB BC t t t21202t t 2141122t .∵102,∴当1t 时,矩形ABCD 的周长有最大值,最大值为412.(3)解:连接AC ,BD 相交于点P ,连接OC ,取OC 的中点Q ,连接PQ .∵直线GH 平分矩形ABCD 的面积,∴直线GH 过点P ..由平移的性质可知,四边形OCHG 是平行四边形,∴PQ CH .∵四边形ABCD 是矩形,∴P 是AC 的中点.∴12PQ OA .当2t 时,点A 的坐标为 8,0,∴142CH OA .∴抛物线平移的距离是4.【分析】(1)设抛物线的函数表达式为 100y ax x a ,求出点C 的坐标,将点C 的坐标代入即可求出该抛物线的函数表达式;(2)由抛物线的对称性得AE OB t ,则102AB t ,再得出21542BC t t ,根据矩形的周长公式,列出矩形周长的表达式,并将其化为顶点式,即可求解;(3)连接A C ,BD 相交于点P ,连接OC ,取OC 的中点Q ,连接PQ ,根据矩形的性质和平移的性质推出四边形OCHG 是平行四边形,则PQ CH ,12PQ OA .求出2t 时,点A 的坐标为 8,0,则142CH OA,即可得出结论.11.【答案】(1)解:∵抛物线2443y x bx 与x 轴交于(3,0)A ,∴ 2433403b 解得:83b ,∴抛物线解析式为248433y x x ,当0x 时,4y ,∴ 0,4C ,当0y 时,2480433x x ,解得:123,1x x ,∴10B ,(2)∵ 3,0A , 10B ,, 0,4C ,设 ,D m n ,∵以A ,B ,C ,D 为顶点的四边形是平行四边形当AB 为对角线时,031400,2222m n ,解得:2,4m n ,∴ 2,4D ;当AC 为对角线时,301400,2222m n,解得:4,4m n ,∴ 4,4D 当BC 为对角线时,301040,2222m n,解得:4,4m n ,∴ 44D ,综上所述,以A ,B ,C ,D 为顶点的四边形是平行四边形, 2,4D 或 4,4D 或 44D ,(3)解:如图所示,作AG CE 交于点G ,F 为AC 的中点,连接,GO GF ,∵45ACE ,∴AGC 是等腰直角三角形,∴,,,A O C G 在F 上,∵ 3,0A , 0,4C ,∴3,22F,5AC ,1522GF AC∵45AOG ACG ,∴G 在y x 上,设 ,G t t ,则 222235222GF t t,解得:12702t t ,(舍去),∴点7722G ,设直线CG 的解析式为4y kx ,∴77422k ,解得:17k .,∴直线CG 的解析式147y x ∵ 3,0A , 10B ,,∴抛物线对称轴为直线3112x,当=1x 时, 12714=77 ,∴271,7E.【分析】(1)将点0()3,A ﹣代入抛物线解析式,待定系数法求解析式,进而分别令,0x y ,即可求得,B C 两点的坐标;(2)分三种情况讨论,当AB ,,AC BC 为对角线时,根据中点坐标即可求解;(3)根据题意,作出图形,作AG CE 交于点G ,F 为AC 的中点,连接,GO GF ,则,,,A O C G 在F 上,根据等弧所对的圆周角相等,得出G 在y x 上,进而勾股定理,根据52FG 建立方程,求得点G 的坐标,进而得出CG 的解析式,即可求解.12.【答案】(1)解:∵抛物线2y x bx c 经过(1,0),(0,3)A C 两点,∴103b c c,解得:23b c ,∴223y x x ;(2)∵ 222314y x x x ,∴ 1,4M ,设直线)0:(A y k M x m k ,则:04k m k m ,解得:22k m,∴22:A y M x ,当0x 时,2y ,∴ 0,2D ;作点D 关于x 轴的对称点D ¢,连接D M ,则: 0,2D ,MH DH MH D H D M ,∴当,,M H D 三点共线时,MH DH 有最小值为D M 的长,∵ 0,2D , 1,4M ,∴ 2214237D M ,即:MH DH 37;(3)解:存在;∵ 222314y x x x ,∴对称轴为直线1x ,设 ,P p t , 1,Q n ,当以D ,M ,P ,Q 为顶点的四边形是平行四边形时:①DM 为对角线时:10142p t n,∴06p t n,当0p 时,3t ,∴3n ,∴ 1,3Q ;②当DP 为对角线时:01124p t n,∴224p t n,当2p 时,222233t ,∴1n ,∴ 1,1Q ;③当MP 为对角线时:10142p t n,∴02p n t,当0p 时,3t ,∴3n ,∴ 1,5Q ;综上:当以D ,M ,P ,Q 为顶点的四边形是平行四边形时, 1,3Q 或 1,1Q 或 1,5Q .【分析】(1)待定系数法求出函数解析式即可;(2)作点D 关于x 轴的对称点D ¢,连接D M ,D M 与x 轴的交点即为点H ,进而得到MH DH 的最小值为D M 的长,利用两点间距离公式进行求解即可;(3)分DM ,DP ,MP 分别为对角线,三种情况进行讨论求解即可.13.【答案】(1)解:将点 1,0,3,,00,3A B C 代入解析式得:09303a b c a b c c ,解得:123a b c,∴抛物线的解析式为223y x x ;(2)设直线BC 的解析式为y kx b ,将点B 、C 代入得:303k b b ,解得:13k b,∴直线BC 的解析式为3y x ,∵ 3,0B ,∴3OB ,设点 2,23(03)P x x x x ,过点P 作PD x 轴于点D ,交BC 于点E ,如图所示:∴ ,3E x x ,∴ 222333PE x x x x x ,∴22211393327332222228PBC S PE OB x x x x x,∴当32x时,PBC 的最大面积为278,2915233344x x ,∴315,24P(3)存在, 2,2N 或17或 4,17或 143 ,2,143 ,证明如下:∵ 3,0,0,3B C ,∵抛物线的解析式为223y x x ,∴对称轴为:1x ,设点 1,,M t N x y ,,若BC 为菱形的边长,菱形BCMN ,则22BC CM ,即 221813t ,解得:1173t ,2173t ,∵31003xt y,∴4,3x y t ,∴ 117N , 24,17N ;若BC 为菱形的边长,菱形BCNM ,则22BC BM ,即 221831t ,解得:114t 214t ,∵30103x y t,∴2,3x y t ,∴ 3143N ,42,143N ;综上可得:17或 4,17 或 143 ,2,143 .【分析】(1)利用待定系数法代入求解即可;(2)利用待定系数法先确定直线BC 的解析式为3y x ,设点 2,23(03)P x x x x ,过点P 作PD x 轴于点D ,交BC 于点E ,得出23PE x x ,然后得出三角形面积的函数即可得出结果;(3)分两种情况进行分析:若BC 为菱形的边长,利用菱形的性质求解即可.14.【答案】(1)解:根据抛物线的对称轴为2x ,得222a,解得12a ,将 0,6C 代入抛物线可得6c , 抛物线的解析式为21262y x x ;(2)解:当0y 时,得210262x x ,解得16x ,22x , 2,0A , 6,0B ,设CB 的解析式为y kx b ,将 0,6C , 6,0B 代入y kx b ,得606b k b ,解得16k b,CB 的解析式为6y x ,设CD a ,则 0,6D a ,设AD 的解析式为11y k x b ,将 0,6D a , 2,0A 代入11y k x b ,得111602a b k b ,解得11626a k b a,AB 的解析式为662a y x a ,联立方程6662y x ay x a ,解得284888a x aa y a,根据CD CE,得a18a28a ,经检验,18a28a 是方程的解,∵点F 是该抛物线上位于第一象限的一个动点,D 在y 轴正半轴,6a,8a 即CD的长为8 ;②解:如图,过,E F 分别作AB 的垂线段,交AB 于点,G H ,过点D 作EG 的垂线段,交EG 于点I,1322S S S ∵,2AD EF DE ,13DE AF,设21,262F h h h,则2AH h ,,EG AB FH AB ∵,EG FH ∥,DEI AFB ,DI EG ∵,90DIE ,DEI AFB △∽△,112333DI AB h ,即点D 的横坐标为1233h ,21122363EI FH h h ,设AF 的解析式为22y k x b ,将 2,0A ,21,262F h h h,代入得22222021262k b h h k h b,解得221326k h b h ,AF 的解析式为1362y h x h, 0,6D h ,即6DO h ,90DOG ∵, 四边形DOGI 是矩形,6IG DO h ,211863EG EI IG h h ,即21211,83363E h h,将21211,83363E h h h代入6y x ,得21112866333h h h ,解得14h ,240h (舍去), 4,6F .【分析】(1)根据抛物线对称轴为2x ,可得222a ,求得12a ,再将 0,6C 代入抛物线,根据待定系数法求得c ,即可解答;(2)①求出点B ,点A 的坐标,即可得到直线BC 的解析式为6y x ,设CD a ,则 0,6D a ,求得AD 的解析式,列方程求出点E 的坐标,最后根据CD CE 列方程,即可求出CD 的长;②过,E F 分别作AB 的垂线段,交AB 于点,G H ,过点D 作EG 的垂线段,交EG 于点I ,根据1322S S S ,可得2AD EF DE ,即13DE AF ,证明DEI AFB △∽△,设21,262F h h h,得到直线AF 的解析式,求出点D 的坐标,即可得到点E 的坐标,将点E 的坐标代入6y x 解方程,即可解答.15.【答案】(1)解:∵抛物线22y x x c 经过点(0,1)A .∴1c ∴抛物线解析式为221y x x ;(2)解:∵221y x x 212x ,顶点坐标为 1,2,∵点Q 与此抛物线的顶点重合,点Q 的横坐标为2m ∴21m ,解得:12m ;(3)①AQ x ∥轴时,点,A Q 关于对称轴1x 对称,22Q x m ,∴1m ,则212112 ,222211 ,∴ 1,2P ,Q2,1∴点P 与点Q 的纵坐标的差为211 ;②当AP x ∥轴时,则A P ,关于直线1x 对称,∴2P x m ,24Q x m 则242417 ∴ 2,1P , 4,7Q ;∴点P 与点Q 的纵坐标的差为 178 ;综上所述,点P 与点Q 的纵坐标的差为1或8;(4)①如图所示,当P Q ,都在对称轴1x 的左侧时,则021m ∴102m∵ 2,21P m m m ,22,2221Q m m m 即22,441Q m m m ∴ 21211P A h y y m m 22m m ;222441144Q A h y y m m m m∵21h h m ∴22442m m m m m 解得:13m 或0m (舍去);②当,P Q 在对称轴两侧或其中一点在对称轴上时,则211m m ,,即112m ,则2122,211h m m h ,∴212m m m ,解得:m (舍去)或352(舍去);③当点P 在1x 的右侧且在直线0y 上方时,即12m ,1211h , 2222441441h m m m m ∴24411m m m 解得:54m或0m (舍去);④当P 在直线1y 上或下方时,即2m,,22122121h m m m m , 2222441441h m m m m ,2244121m m m m m 解得:1m (舍去)或0m (舍去)综上所述,13m 或54m.【分析】(1)待定系数法求解析式即可求解;(2)化为顶点式,求得顶点坐标,进而根据点Q 的横坐标为2m ,即可求解;(3)分AQ x ∥轴时,AP x ∥轴时分别根据抛物线的对称性求得Q 的横坐标与P 的横坐标,进而代入抛物线解析式,求得纵坐标,即可求解;(4)分四种情况讨论,①如图所示,当,P Q 都在对称轴1x 的左侧时,当,P Q 在对称轴两侧时,当点P 在1x 的右侧时,当P 的纵坐标小于1时,分别求得12,h h ,根据21h h m 建立方程,解方程即可求解.16.【答案】(1)解:∵抛物线2y ax c 经过点3(4,)P ,与y 轴交于点(0,1)A ,∴1631a c c,解得141a c,∴抛物线的函数表达式为2114y x ;(2)解:设21,14B t t,根据题意,ABP 是以AB 为腰的等腰三角形,有两种情况:当AB AP 时,点B 和点P 关于y 轴对称,∵ 4,3P ,∴ 4,3B ;当AB BP 时,则22AB BP ,∴ 2222221101141344t t t,整理,得24160t t ,解得12t 22t ,当2t 时,2114t 212154,则 25B ,当2t 2114t 21215425B ,综上,满足题意的点B 的坐标为(4,3) 或(25 或(25 ;(3)解:存在常数m ,使得OD OE .根据题意,画出图形如下图,设抛物线2114y x 与直线(0)y kx k 的交点坐标为 ,B a ka , ,C b kb ,由2114y x kx 得2440x kx ,∴4a b k ,4ab ;设直线AB 的表达式为y px q ,则1ap q ka q ,解得11ka p a q,∴直线AB 的表达式为11ka y x a ,令y m ,由11ka y x m a得 11a m x ka ,∴ 1,1a m D m ka,同理,可得直线AC 的表达式为11kb y x b,则 1,1b m E m kb,过E 作EQ x 轴于Q ,过D 作DN x 轴于N ,则90EQO OND ,EQ ND m , 11b m QO kb,11a m ON ka,若OD OE ,则90EOD ,∴90QEO QOE DON QOE ,∴QEO DON ,∴EQO OND ∽,∴EQ QOON ND,则1111b m m kb a m mka,整理,得 22111m ka kb ab m ,即 22211m abk k a b ab m ,将4a b k ,4ab 代入,得222244141m k k m ,即 2241m m ,则 21m m 或 21m m ,解得12m ,223m,综上,存在常数m ,使得OD OE ,m 的值为2或23.【分析】(1)利用待定系数法求解即可;(2)设21,14B t t,分AB AP 和AB BP 两种情况,分别根据等腰三角形性质和两点坐标距离公式列方程求解即可;(3)先根据题意画出图形,设抛物线2114y x 与直线(0)y kx k 的交点坐标为 ,B a ka , ,C b kb ,联立抛物线和直线解析式,根据根与系数关系得到4a b k ,4ab ,利用待定系数法分别求得直线AB 、AC 的表达式为得到 1,1a m D m ka , 1,1b m E m kb,过E 作EQ x 轴于Q ,过D 作DN x 轴于N ,证明EQO OND ∽得到1111b m mkb a m mka,整理可得到 2241m m ,进而求解即可.。
2023届中考数学压轴难题含答案解析

2023年中考数学压轴题
1.如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,B,C在第一象限,
反比例函数y=k
x(k≠0)的图象经过点C,交AB于D,已知OC=12,OA=4√3,∠AOC
=60°
(1)求反比例函数y=k
x(k≠0)的函数表达式;
(2)连结CD,求△BCD的面积;
(3)P是线段OC上的一个动点,以AP为一边,在AP的右上方作正方形APEF,在点P的运动过程中,是否存在一点P使顶点E落在▱OABC的边所在的直线上,若存在,请求出此时OP的长,若不存在,请说明理由.
解:(1)如图1,过点C作CG⊥x轴于点G
∴∠OGC=90°
∵OC=12,∠AOC=60°
∴cos∠AOC=OG
OC
=12,sin∠AOC=CG
OC
=√32
∴OG=1
2OC=6,CG=
√3
2OC=6√3
∴C(6,6√3)
∵反比例函数y=k
x(k≠0)的图象经过点C
∴6√3=k
6解得:k=36√3
∴反比例函数的函数表达式为y=36√3 x
(2)如图2,过点D作DH⊥BC于点H
∵OA=4√3,点A在x轴上
∴A(4√3,0)
第1页共11页。
2023年九年级中考数学:二次函数综合题压轴题(特殊三角形问题)(含答案)

(2)求该二次函数的表达式;
(3)如果点p在坐标轴上,且 是等腰三角形,直接写出p点坐标.
14.如图,在平面直角坐标系中,抛物线 与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接 .
(1)求线段AC的长;
(2)若点Р为该抛物线对称轴上的一个动点,当 时,求点P的坐标;
(2)点F的坐标为:F1(2 ,3 )或F2(﹣1,4);
(3)
20.(1) ;
(3)
(2)
(3)点P的坐标为 或 或 或
5.(1)抛物线解析式为 ;
(2)点 运动到 时,四边形CDBF的面积最大,最大面积为
(3)存在,点P 或 或 或
6.(1)
(2)
(3) 或 或 或
7.(1)
(2)点E的坐标为 或 或(
8.(1) ;
(2)存在,点P的坐标为( ,0)或(4+2 ,0)或(4﹣2 ,0)或(﹣4,0);
(1)求该抛物线对应的函数表达式;
(2)x轴上是否存在一点P,使△PBC为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由;
(3)当点P在线段OB上运动时,试探究:当m为何值时,四边形CQMD是平行四边形?请说明理由.
9.如图,在平面直角坐标系中,二次函数 的图象与 轴交于 、 两点,与 轴交于 , 点在原点的左侧, 点的坐标为 .点 是抛物线上一个动点,且在直线 的上方.
(2)点E是第一象限内抛物线的一个动点,其横坐标为m,直线 交y轴于点F.
①用m的代数式表示直线 的截距;
②在 的面积与 的面积相等的条件下探究:在y轴右侧存在这样一条直线,满足:以该直线上的任意一点及点C、F三点为顶点的三角形的面积都等于 面积,试用规范、准确的数学语言表达符合条件的直线.
中考数学28道压轴题含答案解析

中考数学选填压轴题练习一.根的判别式(共1小题)1.(2023•广州)已知关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,则的化简结果是()A.﹣1B.1C.﹣1﹣2k D.2k﹣3【分析】首先根据关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,得判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,由此可得k≤1,据此可对进行化简.【解答】解:∵关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,∴判别式Δ=[﹣(2k﹣2)]2﹣4×1×(k2﹣1)≥0,整理得:﹣8k+8≥0,∴k≤1,∴k﹣1≤0,2﹣k>0,∴=﹣(k﹣1)﹣(2﹣k)=﹣1.故选:A.二.函数的图象(共1小题)2.(2023•温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.【问题】路线①③⑥⑦⑧各路段路程之和为()A.4200米B.4800米C.5200米D.5400米【分析】设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.【解答】解:由图象可知:小州游玩行走的时间为75+10﹣40=45(分钟),小温游玩行走的时间为205﹣100=105(分钟),设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米由图象可得:,解得:x+y+z=2700,∴游玩行走的速度为:(2700﹣2100)÷10=60 (米/分),由于游玩行走速度恒定,则小温游路线①④⑤⑥⑦⑧的路程为:3x+3y=105×60=6300,∴x+y=2100,∴路线①③⑥⑦⑧各路段路程之和为:2x+2y+z=x+y+z+x+y=2700+2100=4800(米).故选:B.三.动点问题的函数图象(共1小题)3.(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.D.【分析】如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=,易知∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,可知AO=OB=,过点O作OD⊥AB,解直角三角形可得AD=AO•cos30°,进而得出等边三角形ABC的边长.【解答】解:如图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,\结合图象可知,当点P在AO上运动时,,∴PB=PC,,又∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∴△APB≌△APC(SSS),∴∠BAO=∠CAO=30°,当点P在OB上运动时,可知点P到达点B时的路程为,∴OB=,即AO=OB=,∴∠BAO=∠ABO=30°,过点O作OD⊥AB,垂足为D,∴AD=BD,则AD=AO•cos30°=3,∴AB=AD+BD=6,即等边三角形ABC的边长为6.故选:A.四.反比例函数系数k的几何意义(共1小题)4.(2023•宁波)如图,点A,B分别在函数y=(a>0)图象的两支上(A在第一象限),连结AB交x 轴于点C.点D,E在函数y=(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若AC =2BC,△ABE的面积为9,四边形ABDE的面积为14,则a﹣b的值为12,a的值为9.【分析】依据题意,设A(m,),再由AE∥x轴,BD∥y轴,AC=2BC,可得B(﹣2m,﹣),D (﹣2m,﹣),E(,),再结合△ABE的面积为9,四边形ABDE的面积为14,即可得解.【解答】解:设A(m,),∵AE∥x轴,且点E在函数y=上,∴E(,).∵AC=2BC,且点B在函数y=上,∴B(﹣2m,﹣).∵BD∥y轴,点D在函数y=上,∴D(﹣2m,﹣).∵△ABE的面积为9,∴S△ABE=AE×(+)=(m﹣)(+)=m••==9.∴a﹣b=12.∵△ABE的面积为9,四边形ABDE的面积为14,∴S△BDE=DB•(+2m)=(﹣+)()m=(a﹣b)••()•m=3()=5.∴a=﹣3b.又a﹣b=12.∴a=9.故答案为:12,9.五.反比例函数图象上点的坐标特征(共2小题)5.(2023•德州)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(6,3),D是OA的中点,AC,BD交于点E,函数的图象过点B.E.且经过平移后可得到一个反比例函数的图象,则该反比例函数的解析式()A.y=﹣B.C.D.【分析】先根据函数图象经过点B和点E,求出a和b,再由所得函数解析式即可解决问题.【解答】解:由题知,A(6,0),B(6,3),C(0,3),令直线AC的函数表达式为y1=k1x+b1,则,解得,所以.又因为点D为OA的中点,所以D(3,0),同理可得,直线BD的函数解析式为y2=x﹣3,由得,x=4,则y=4﹣3=1,所以点E坐标为(4,1).将B,E两点坐标代入函数解析式得,,解得.所以,则,将此函数图象向左平移3个单位长度,再向下平移4个单位长度,所得图象的函数解析式为:.故选:D.6.如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.(1)k=;(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2﹣BD2的值为4.【分析】(1)根据直角三角形的性质,求出A、B两点坐标,作出辅助线,证得△OPC≌△APC(HL),利用勾股定理及待定系数法求函数解析式即可解答.(2)求出AC、BD的解析式,再联立方程组,求得点D的坐标,分两种情况讨论即可求解.【解答】解:(1)在Rt△OAB中,AB=2,∠AOB=30°,∴,∴,∵C是OB的中点,∴OC=BC=AC=2,如图,过点C作CP⊥OA于P,∴△OPC≌△APC(HL),∴,在Rt△OPC中,PC=,∴C(,1).∵反比例函数y=(k>0)的图象经过斜边OB的中点C,∴,解得k=.故答案为:.(2)设直线AC的解析式为y=k1x+b(k≠0),则,解得,∴AC的解析式为y=﹣x+2,∵AC∥BD,∴直线BD的解析式为y=﹣x+4,∵点D既在反比例函数图象上,又在直线BD上,∴联立得,解得,,当D的坐标为(2+3,)时,BD2==9+3=12,∴OB2﹣BD2=16﹣12=4;当D的坐标为(2﹣3,)时,BD2=+=9+3=12,∴OB2﹣BD2=16﹣12=4;综上,OB2﹣BD2=4.故答案为:4.六.反比例函数与一次函数的交点问题(共1小题)7.(2023•湖州)已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t,p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠﹣2),点C(t,m)和点D(t+2,n)在函数的图象上.当p﹣m与q﹣n的积为负数时,t的取值范围是()A.或B.或C.﹣3<t<﹣2或﹣1<t<0D.﹣3<t<﹣2或0<t<1【分析】将交点的横坐标1代入两个函数,令二者函数值相等,得k1=k2.令k1=k2=k,代入两个函数表达式,并分别将点A、B的坐标和点C、D的坐标代入对应函数,进而分别求出p﹣m与q﹣n的表达式,代入解不等式(p﹣m)(q﹣n)<0并求出t的取值范围即可.【解答】解:∵y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,∴k1=k2.令k1=k2=k(k>0),则y=k1x=kx,=.将点A(t,p)和点B(t+2,q)代入y=kx,得;将点C(t,m)和点D(t+2,n)代入y=,得.∴p﹣m=kt﹣=k(t﹣),q﹣n=k(t+2)﹣=k(t+2﹣),∴(p﹣m)(q﹣n)=k2(t﹣)(t+2﹣)<0,∴(t﹣)(t+2﹣)<0.∵(t﹣)(t+2﹣)=•=<0,∴<0,∴t(t﹣1)(t+2)(t+3)<0.①当t<﹣3时,t(t﹣1)(t+2)(t+3)>0,∴t<﹣3不符合要求,应舍去.②当﹣3<t<﹣2时,t(t﹣1)(t+2)(t+3)<0,∴﹣3<t<﹣2符合要求.③当﹣2<t<0时,t(t﹣1)(t+2)(t+3)>0,∴﹣2<t<0不符合要求,应舍去.④当0<t<1时,t(t﹣1)(t+2)(t+3)<0,∴0<t<1符合要求.⑤当t>1时,t(t﹣1)(t+2)(t+3)>0,∴t>1不符合要求,应舍去.综上,t的取值范围是﹣3<t<﹣2或0<t<1.故选:D.七.二次函数图象与系数的关系(共3小题)8.(2023•乐至县)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).现有以下结论:①abc<0;②5a+c=0;③对于任意实数m,都有2b+bm≤4a﹣am2;④若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,则y1<y2,其中正确的结论是()A.①②B.②③④C.①②④D.①②③④【分析】根据题意和函数图象,利用二次函数的性质,可以判断各个小题中的结论是否正确,从而可以解答本题.【解答】解:由图象可得,a>0,b>0,c<0,∴abc<0,故①正确,∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).∴﹣=﹣2,a+b+c=0,∴b=4a,∴a+b+c=a+4a+c=0,故5a+c=0,故②正确,∵当x=﹣2时,y=4a﹣2b+c取得最小值,∴am2+bm+c≥4a﹣2b+c,即2b+bm≥4a﹣am2(m为任意实数),故③错误,∵抛物线开口向上,对称轴为直线x=﹣2,若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,∴y1<y2,故④正确;故选:C.9.(2023•丹东)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为A(﹣3,0),与y轴交于点C,点D是抛物线的顶点,对称轴为直线x=﹣1,其部分图象如图所示,则以下4个结论:①abc>0;②E(x1,y1),F(x2,y2)是抛物线y=ax2+bx(a≠0)上的两个点,若x1<x2,且x1+x2<﹣2,则y1<y2;③在x轴上有一动点P,当PC+PD的值最小时,则点P的坐标为;④若关于x的方程ax2+b(x﹣2)+c =﹣4(a≠0)无实数根,则b的取值范围是b<1.其中正确的结论有()A.1个B.2个C.3个D.4个【分析】根据所给函数图象可得出a,b,c的正负,再结合抛物线的对称性和增减性即可解决问题.【解答】解:根据所给函数图象可知,a>0,b>0,c<0,所以abc<0,故①错误.因为抛物线y=ax2+bx的图象可由抛物线y=ax2+bx+c的图象沿y轴向上平移|c|个单位长度得到,所以抛物线y=ax2+bx的增减性与抛物线y=ax2+bx+c的增减性一致.则当x<﹣1时,y随x的增大而减小,又x1<x2,且x1+x2<﹣2,若x2<﹣1,则E,F两点都在对称轴的左侧,此时y1>y2.故②错误.作点C关于x轴的对称点C′,连接C′D与x轴交于点P,连接PC,此时PC+PD的值最小.将A(﹣3,0)代入二次函数解析式得,9a﹣3b+c=0,又,即b=2a,所以9a﹣6a+c=0,则c=﹣3a.又抛物线与y轴的交点坐标为C(0,c),则点C坐标为(0,﹣3a),所以点C′坐标为(0,3a).又当x=﹣1时,y=﹣4a,即D(﹣1,﹣4a).设直线C′D的函数表达式为y=kx+3a,将点D坐标代入得,﹣k+3a=﹣4a,则k=7a,所以直线C′D的函数表达式为y=7ax+3a.将y=0代入得,x=.所以点P的坐标为(,0).故③正确.将方程ax2+b(x﹣2)+c=﹣4整理得,ax2+bx+c=2b﹣4,因为方程没有实数根,所以抛物线y=ax2+bx+c与直线y=2b﹣4没有公共点,所以2b﹣4<﹣4a,则2b﹣4<﹣2b,解得b<1,又b>0,所以0<b<1.故④错误.所以正确的有③.故选:A.10.(2023•河北)已知二次函数y=﹣x2+m2x和y=x2﹣m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.m2C.4D.2m2【分析】求出三个交点的坐标,再构建方程求解.【解答】解:令y=0,则﹣x2+m2x=0和x2﹣m2=0,∴x=0或x=m2或x=﹣m或x=m,∵这四个交点中每相邻两点间的距离都相等,若m>0,则m2=2m,∴m=2,若m<0时,则m2=﹣2m,∴m=﹣2.∵抛物线y=x2﹣m2的对称轴为直线x=0,抛物线y=﹣x2+m2x的对称轴为直线x=,∴这两个函数图象对称轴之间的距离==2.故选:A.八.二次函数图象上点的坐标特征(共1小题)11.(2023•广东)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac 的值为()A.﹣1B.﹣2C.﹣3D.﹣4【分析】过A作AH⊥x轴于H,根据正方形的性质得到∠AOB=45°,得到AH=OH,利用待定系数法求得a、c的值,即可求得结论.【解答】解:过A作AH⊥x轴于H,∵四边形ABCO是正方形,∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m),则B(0,2m),∴,解得am=﹣1,m=,∴ac的值为﹣2,故选:B.九.二次函数与不等式(组)(共1小题)12.(2023•西宁)直线y1=ax+b和抛物线(a,b是常数,且a≠0)在同一平面直角坐标系中,直线y1=ax+b经过点(﹣4,0).下列结论:①抛物线的对称轴是直线x=﹣2;②抛物线与x轴一定有两个交点;③关于x的方程ax2+bx=ax+b有两个根x1=﹣4,x2=1;④若a >0,当x<﹣4或x>1时,y1>y2.其中正确的结论是()A.①②③④B.①②③C.②③D.①④【分析】根据直线y1=ax+b经过点(﹣4,0).得到b=4a,于是得到=ax2+4ax,求得抛物线的对称轴是直线x=﹣﹣=2;故①正确;根据Δ=16a2>0,得到抛物线与x轴一定有两个交点,故②正确;把b=4a,代入ax2+bx=ax+b得到x2+3x﹣4=0,求得x1=﹣4,x2=1;故③正确;根据a>0,得到抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,于是得到结论.【解答】解:∵直线y1=ax+b经过点(﹣4,0).∴﹣4a+b=0,∴b=4a,∴=ax2+4ax,∴抛物线的对称轴是直线x=﹣﹣=2;故①正确;∵=ax2+4ax,∴Δ=16a2>0,∴抛物线与x轴一定有两个交点,故②正确;∵b=4a,∴方程ax2+bx=ax+b为ax2+4ax=ax+4a得,整理得x2+3x﹣4=0,解得x1=﹣4,x2=1;故③正确;∵a>0,抛物线的开口向上,直线y1=ax+b和抛物线交点横坐标为﹣4,1,∴当x<﹣4或x>1时,y1<y2.故④错误,故选:B.一十.三角形中位线定理(共1小题)13.(2023•广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是 1.2.若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是3≤S≤4.【分析】依据题意,根据三角形中位线定理可得DE=AM=1.2;设AM=x,从而DE=x,由DE∥AM,且DE=AM,又FG∥AM,FG=AM,进而DE∥FG,DE=FG,从而四边形DEFG是平行四边形,结合题意可得DE边上的高为(4﹣x),故四边形DEFG面积S=4x﹣x2,进而利用二次函数的性质可得S的取值范围.【解答】解:由题意,点D,E分别是AB,MB的中点,∴DE是三角形ABM的中位线.∴DE=AM=1.2.如图,设AM=x,∴DE=AM=x.由题意得,DE∥AM,且DE=AM,又FG∥AM,FG=AM,∴DE∥FG,DE=FG.∴四边形DEFG是平行四边形.由题意,GF到AC的距离是x,BC==8,∴DE边上的高为(4﹣x).∴四边形DEFG面积S=2x﹣x2,=﹣(x﹣4)2+4.∵2.4<x≤6,∴3≤S≤4.故答案为:1.2;3≤S≤4.一十一.矩形的性质(共2小题)14.(2023•宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连结AE,AD,设△AED,△ABE,△ACD的面积分别为S,S1,S2,若要求出S﹣S1﹣S2的值,只需知道()A.△ABE的面积B.△ACD的面积C.△ABC的面积D.矩形BCDE的面积【分析】作AG⊥ED于点G,交BC于点F,可证明四边形BFGE是矩形,AF⊥BC,可推导出S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,所以只需知道S△ABC,就可求出S﹣S1﹣S2的值,于是得到问题的答案.【解答】解:作AG⊥ED于点G,交BC于点F,∵四边形BCDE是矩形,∴∠FBE=∠BEG=∠FGE=90°,BC∥ED,BC=ED,BE=CD,∴四边形BFGE是矩形,∠AFB=∠FGE=90°,∴FG=BE=CD,AF⊥BC,∴S﹣S1﹣S2=ED•AG﹣BE•EG﹣CD•DG=ED•AG﹣FG•ED=BC•AF=S△ABC,∴只需知道S△ABC,就可求出S﹣S1﹣S2的值,故选:C.15.(2023•河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为2或1+.【分析】以点D,M,N为顶点的三角形是直角三角形时,分两种情况:如图1,当∠MND=90°时,如图2,当∠NMD=90°时,根据矩形的性质和等腰直角三角形的性质即可得到结论.【解答】解:以点D,M,N为顶点的三角形是直角三角形时,分两种情况:①如图1,当∠MND=90°时,则MN⊥AD,∵四边形ABCD是矩形,∴∠A=90°,∴MN∥AB,∵M为对角线BD的中点,∴AN=DN,∵AN=AB=1,∴AD=2AN=2;如图2,当∠NMD=90°时,则MN⊥BD,∵M为对角线BD的中点,∴BM=DM,∴MN垂直平分BD,∴BN=DN,∵∠A=90°,AB=AN=1,∴BN=AB=,∴AD=AN+DN=1+,综上所述,AD的长为2或1+.故答案为:2或1+.一十二.正方形的性质(共2小题)16.如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为()A.B.C.D.【分析】由正方形ABCD的边长为4及BG=3CG,可求出BG的长,进而求出AG的长,证△ADE∽△GAB,利用相似三角形对应边成比例可求得AE、DE的长,证△ABF≌△DAE,得AF=DE,根据线段的和差求得EF的长即可.【解答】解:∵四边形ABCD是正方形,AB=4,∴BC=CD=DA=AB=4,∠BAD=∠ABC=90°,AD∥BC,∴∠DAE=∠AGB,∵BG=3CG,∴BG=3,∴在Rt△ABG中,AB2+BG2=AG2,∴AG=,∵DE⊥AG,∴∠DEA=∠DEF=∠ABC=90°,∴△ADE∽△GAB,∴AD:GA=AE:GB=DE:AB,∴4:5=AE:3=DE:4,∴AE=,DE=,又∵BF∥DE,∴∠AFB=∠DEF=90°,又∵AB=AD,∠DAE=∠ABF(同角的余角相等),∴△ABF≌△DAE,∴AF=DE=,∴EF=AF﹣AE=,∴tan∠EDF=,故选:A.17.(2023•湖州)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.(1)若EF=3cm,AE+FC=11cm,则BE的长是4cm.(2)若,则tan∠DAH的值是3.【分析】(1)将AE和FC用BE表示出来,再代入AE+FC=11cm,即可求出BE的长;(2)由已知条件可以证明∠DAH=∠CDG,从而得到tan∠DAH=tan∠CDG,设AH=x,DG=5k,GH =4k,用x和k的式子表示出CG,再利用tan∠DAH=tan∠CDG列方程,解出x,从而求出tan∠DAH 的值.【解答】解:(1)∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∵AE+FC=11cm,∴BE+BF=11cm,即BE+BE+EF=11cm,即2BE+EF=11cm,∵EF=3cm,∴2BE+3cm=11cm,∴BE=4cm,故答案为:4;(2)设AH=x,∵,∴可设DG=5k,GH=4k,∵四边形EFGH是正方形,∴HE=EF=FG=GH=4k,∵Rt△ABE和Rt△BCF都是等腰直角三角形,∴AE=BE,BF=CF,∠ABE=∠CBF=45°,∴CG=CF+GF=BF+4k=BE+8k=AH+12k=x+12k,∠ABC=∠ABE+∠CBF=45°+45°=90°,∵四边形ABCD对角互补,∴∠ADC=90°,∴∠ADH+∠CDG=90°,∵四边形EFGH是正方形,∴∠AHD=∠CGD=90°,∴∠ADH+∠DAH=90°,∴∠DAH=∠CDG,∴tan∠DAH=tan∠CDG,∴,即,整理得:x2+12kx﹣45k2=0,解得x1=3k,x2=﹣15k(舍去),∴tan∠DAH===3.故答案为:3.一十三.正多边形和圆(共1小题)18.(2023•河北)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:(1)∠α=30度;(2)中间正六边形的中心到直线l的距离为2(结果保留根号).【分析】(1)作图后,结合正多边形的外角的求法即可得到结论;(2)把问题转化为图形问题,首先作出图形,标出相应的字母,把正六边形的中心到直线l的距离转化为求ON=OM+BE,再根据正六边形的性质以及三角函数的定义,分别求出OM,BE即可.【解答】解:(1)作图如图所示,∵多边形是正六边形,∴∠ACB=60°,∵BC∥直线l,∴∠ABC=90°,∴α=30°;故答案为:30°;(2)取中间正六边形的中心为O,作图如图所示,由题意得,AG∥BF,AB∥GF,BF⊥AB,∴四边形ABFG为矩形,∴AB=GF,∵∠BAC=∠FGH,∠ABC=∠GFH=90°,∴△ABC≌△GFH(SAS),∴BC=FH,在Rt△PDE中,DE=1,PE=,由图1知AG=BF=2PE=2,OM=PE=,∵,∴,∴,∵,∴,∴.∴中间正六边形的中心到直线l的距离为2,故答案为:2.一十四.扇形面积的计算(共1小题)19.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为5.若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为.【分析】根据不共线三点确定一个圆,根据对称性得出圆心的位置,进而垂径定理、勾股定理求得r,连接OE,取ED的中点T,连接OT,在Rt△OET中,根据勾股定理即可求解.【解答】解:如图所示,依题意,GH=2=GQ,∵过左侧的三个端点Q,K,L作圆,QH=HL=4,又NK⊥QL,∴O在KN上,连接OQ,则OQ为半径,∵OH=r﹣KH=r﹣2,在Rt△OHQ中,OH2+QH2=QO2,∴(r﹣2)2+42=r2,解得:r=5;连接OE,取ED的中点T,连接OT,交AB于点S,连接PB,AM,过点O作OU⊥AM于点U.连接OA.由△OUN∽△NPM,可得==,∴OU=.MN=2,∴NU=,∴AU==,∴AN=AU﹣NU=2,∴AN=MN,∵AB∥PN,∴AB⊥OT,∴AS=SB,∴NS∥BM,∴NS∥MP,∴M,P,B共线,又NB=NA,∴∠ABM=90°,∵MN=NB,NP⊥MP,∴MP=PB=2,∴NS=MB=2,∵KH+HN=2+4=6,∴ON=6﹣5=1,∴OS=3,∵,设EF=ST=a,则,在Rt△OET中,OE2=OT2+TE2,即,整理得5a2+12a﹣32=0,即(a+4)(5a﹣8)=0,解得:或a=﹣4,∴题字区域的面积为.故答案为:.一十五.轴对称-最短路线问题(共1小题)20.(2023•安徽)如图,E是线段AB上一点,△ADE和△BCE是位于直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,则下列结论错误的是()A.P A+PB的最小值为3B.PE+PF的最小值为2C.△CDE周长的最小值为6D.四边形ABCD面积的最小值为3【分析】延长AD,BC交于M,过P作直线l∥AB,由△ADE和△BCE是等边三角形,可得四边形DECM 是平行四边形,而P为CD中点,知P为EM中点,故P在直线l上运动,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB=P A'+PB最小,即可得P A+PB 最小值A'B==2,判断选项A错误;由PM=PE,即可得当M,P,F共线时,PE+PF 最小,最小值为MF的长度,此时PE+PF的最小值为2,判断选项B正确;过D作DK⊥AB于K,过C作CT⊥AB于T,由△ADE和△BCE是等边三角形,得KT=KE+TE=AB=2,有CD≥2,故△CDE周长的最小值为6,判断选项C正确;设AE=2m,可得S四边形ABCD=(m﹣1)2+3,即知四边形ABCD面积的最小值为3,判断选项D正确.【解答】解:延长AD,BC交于M,过P作直线l∥AB,如图:∵△ADE和△BCE是等边三角形,∴∠DEA=∠MBA=60°,∠CEB=∠MAB=60°,∴DE∥BM,CE∥AM,∴四边形DECM是平行四边形,∵P为CD中点,∴P为EM中点,∵E在线段AB上运动,∴P在直线l上运动,由AB=4知等边三角形ABM的高为2,∴M到直线l的距离,P到直线AB的距离都为,作A关于直线l的对称点A',连接A'B,当P运动到A'B与直线l的交点,即A',P,B共线时,P A+PB =P A'+PB最小,此时P A+PB最小值A'B===2,故选项A错误,符合题意;∵PM=PE,∴PE+PF=PM+PF,∴当M,P,F共线时,PE+PF最小,最小值为MF的长度,∵F为AB的中点,∴MF⊥AB,∴MF为等边三角形ABM的高,∴PE+PF的最小值为2,故选项B正确,不符合题意;过D作DK⊥AB于K,过C作CT⊥AB于T,如图,∵△ADE和△BCE是等边三角形,∴KE=AE,TE=BE,∴KT=KE+TE=AB=2,∴CD≥2,∴DE+CE+CD≥AE+BE+2,即DE+CE+CD≥AB+2,∴DE+CE+CD≥6,∴△CDE周长的最小值为6,故选项C正确,不符合题意;设AE=2m,则BE=4﹣2m,∴AK=KE=m,BT=ET=2﹣m,DK=AK=m,CT=BT=2﹣m,∴S△ADK=m•m=m2,S△BCT=(2﹣m)(2﹣m)=m2﹣2m+2,S梯形DKTC =(m+2﹣m)•2=2,∴S四边形ABCD=m2+m2﹣2m+2+2=m2﹣2m+4=(m﹣1)2+3,∴当m=1时,四边形ABCD面积的最小值为3,故选项D正确,不符合题意;故选:A.一十六.翻折变换(折叠问题)(共2小题)21.(2023•乐至县)如图,在平面直角坐标系xOy中,边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动,将△ABC沿BC所在直线翻折得到△DBC,则OD的最大值为+1.【分析】过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,在Rt△ABO 中利用斜边中线性质求出OE,根据OE+DE≥OD确定当D、O、E三点共线时OD最大,最大值为OD =OE+DE.【解答】解:如图,过点D作DF⊥AB,交AB延长线于点F,取AB的中点E,连接DE,OE,OD,∵等边三角形ABC的边长为2,∴AB=2,∠ABC=60°,由翻折可知:∠DBC=∠ABC=60°,DB=AB=2,∴∠DBF=60°,∵DF⊥AB,∴∠DFB=90°,∴∠BDF=30°,∴BF=BD=1,∴DF=BF=,∵E是AB的中点,∴AE=BE=OE=AB=1,∴EF=BE+BF=2,∴DE===,∴OD≤DE+OE=+1,∴当D、E、O三点共线时OD最大,最大值为+1.故答案为:+1.22.(2023•南京)如图,在菱形纸片ABCD中,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB′⊥AD,垂足为F.若CF=4cm,FB′=1cm,则BE=cm.【分析】作EH⊥BC于点H,由CF=4cm,FB′=1cm,求得B′C=5cm,由折叠得BC=B′C=5cm,由菱形的性质得BC∥AD,DC=BC=5cm,∠B=∠D,因为CB′⊥AD于点F,所以∠BCB′=∠CFD =90°,则∠BCE=∠B′CE=45°,DF==3cm,所以∠HEC=∠BCE=45°,则CH=EH,由=sin B=sin D=,=cos B=cos D=,得CH=EH=BE,BH=BE,于是得BE+BE =5,则BE=cm.【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,∵CF=4cm,FB′=1cm,∴B′C=CF+FB′=4+1=5(cm),由折叠得BC=B′C=5cm,∠BCE=∠B′CE,∵四边形ABCD是菱形,∴BC∥AD,DC=BC=5cm,∠B=∠D,∵CB′⊥AD于点F,∴∠BCB′=∠CFD=90°,∴∠BCE=∠B′CE=∠BCB′=×90°=45°,DF===3(cm),∴∠HEC=∠BCE=45°,∴CH=EH,∵=sin B=sin D==,=cos B=cos D==,∴CH=EH=BE,BH=BE,∴BE+BE=5,∴BE=cm,故答案为:.一十七.旋转的性质(共1小题)23.(2023•西宁)如图,在矩形ABCD中,点P在BC边上,连接P A,将P A绕点P顺时针旋转90°得到P A′,连接CA′,若AD=9,AB=5,CA′=2,则BP=2.【分析】过A′点作A′H⊥BC于H点,如图,根据旋转的性质得到P A=P A′,再证明△ABP≌△PHA′得到PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=4﹣x,然后在Rt△A′CH中利用勾股定理得到x2+(4﹣x)2=(2)2,于是解方程求出x即可.【解答】解:过A′点作A′H⊥BC于H点,如图,∵四边形ABCD为矩形,∴BC=AD=9,∠B=90°,∵将P A绕点P顺时针旋转90°得到P A′,∴P A=P A′,∵∠P AB+∠APB=90°,∠APB+∠A′PH=90°,∴∠P AB=∠A′PH,在△ABP和△PHA′中,,∴△ABP≌△PHA′(AAS),∴PB=A′H,PH=AB=5,设PB=x,则A′H=x,CH=9﹣x﹣5=4﹣x,在Rt△A′CH中,x2+(4﹣x)2=(2)2,解得x1=x2=2,即BP的长为2.故答案为:2.一十八.相似三角形的判定与性质(共2小题)24.(2023•杭州)如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设=k,若AD=DF,则=(结果用含k的代数式表示).【分析】方法一:先根据轴对称的性质和已知条件证明DE∥AC,再证△BDE∽△BAC,推出EC=k•AB,通过证明△ABC∽△ECF,推出CF=k2•AB,即可求出的值.方法二:证明AD=DF=BD,可得BF⊥AC,设AB=AC=1,BC=k,CF=x,则AF=1﹣x,利用勾股定理列方程求出x的值,进而可以解决问题.【解答】解:方法一:∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB,∵AD=DF,∴∠A=∠DF A,∵点B和点F关于直线DE对称,∴∠BDE=∠FDE,∵∠BDE+∠FDE=∠BDF=∠A+∠DF A,∴∠FDE=∠DF A,∴DE∥AC,∴∠C=∠DEB,∠DEF=∠EFC,∵点B和点F关于直线DE对称,∴∠DEB=∠DEF,∴∠C=∠EFC,∵AB=AC,∴∠C=∠B,∵∠ACB=∠EFC,∴△ABC∽△ECF,∴=,∵DE∥AC,∴∠BDE=∠A,∠BED=∠C,∴△BDE∽△BAC,∴==,∴EC=BC,∵=k,∴BC=k•AB,∴EC=k•AB,∴=,∴CF=k2•AB,∴====.方法二:如图,连接BF,∵点B和点F关于直线DE对称,∴DB=DF,∵AD=DF,∴AD=DB=DF,∴BF⊥AC,设AB=AC=1,则BC=k,设CF=x,则AF=1﹣x,由勾股定理得,AB2﹣AF2=BC2﹣CF2,∴12﹣(1﹣x)2=k2﹣x2,∴x=,∴AF=1﹣x=,∴=.故答案为:.25.(2023•广东)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为15.【分析】根据相似三角形的性质,利用相似比求出梯形的上底和下底,用面积公式计算即可.【解答】解:如图,∵BF∥DE,∴△ABF∽△ADE,∴=,∵AB=4,AD=4+6+10=20,DE=10,∴=,∴BF=2,∴GF=6﹣2=4,∵CK∥DE,∴△ACK∽△ADE,∴=,∵AC=4+6=10,AD=20,DE=10,∴=,∴CK=5,∴HK=6﹣5=1,∴阴影梯形的面积=(HK+GF)•GH=(1+4)×6=15.故答案为:15.一十九.相似三角形的应用(共1小题)26.(2023•南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB 的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是()A.36cm B.40cm C.42cm D.45cm【分析】过点B作BC⊥AH,垂足为C,再证明A字模型相似△AOH∽△ABC,从而可得=,过点A作AD⊥BH,垂足为D,然后证明A字模型相似△ABD∽△OBH,从而可得=,最后进行计算即可解答.【解答】解:如图:过点B作BC⊥AH,垂足为C,∵OH⊥AC,BC⊥AC,∴∠AHO=∠ACB=90°,∵∠BAC=∠OAH,∴△AOH∽△ABC,∴=,∴=,如图:过点A作AD⊥BH,垂足为D,∵OH⊥BD,AD⊥BD,∴∠OHB=∠ADB=90°,∵∠ABD=∠OBH,∴△ABD∽△OBH,∴=,∴=,∴+=+,∴+=,∴+=1,解得:OH=36,∴跷跷板AB的支撑点O到地面的高度OH是36cm,故选:A.二十.解直角三角形(共1小题)27.(2023•丹东)如图,在平面直角坐标系中,点O是坐标原点,已知点A(3,0),B(0,4),点C在x 轴负半轴上,连接AB,BC,若tan∠ABC=2,以BC为边作等边三角形BCD,则点C的坐标为(﹣2,0);点D的坐标为(﹣1﹣2,2+)或(﹣1+2,2﹣).【分析】过点C作CE⊥AB于E,先求处AB=5,再设BE=t,由tan∠ABC=2得CE=2t,进而得BC =,由三角形的面积公式得S△ABC=AC•OB=AB•CE,即5×2t=4×(3+OC),则OC=﹣3,然后在Rt△BOC中由勾股定理得,由此解出t1=2,t2=10(不合题意,舍去),此时OC=﹣3=2,故此可得点C的坐标;设点D的坐标为(m,n),由两点间的距离公式得:BC2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,由△BCD为等边三角形得,整理:,②﹣①整理得m=3﹣2n,将m=3﹣2n代入①整理得n2﹣4n+1=0,解得n=,进而再求出m即可得点D的坐标.【解答】解:过点C作CE⊥AB于E,如图:∵点A(3,0),B(0,4),由两点间的距离公式得:AB==5,设BE=t,∵tan∠ABC=2,在Rt△BCE中,tan∠ABC=,∴=2,∴CE=2t,由勾股定理得:BC==t,∵CE⊥AB,OB⊥AC,AC=OC+OA=3+OC,∴S△ABC=AC•OB=AB•CE,即:5×2t=4×(3+OC),∴OC=﹣3,在Rt△BOC中,由勾股定理得:BC2﹣OB2=OC2,即,整理得:t2﹣12t+20=0,解得:t1=2,t2=10(不合题意,舍去),∴t=2,此时OC=﹣3=2,∴点C的坐标为(﹣2,0),设点D的坐标为(m,n),由两点间的距离公式得:BC2=(﹣2﹣0)2+(0﹣4)2=20,BD2=(m﹣0)2+(n﹣4)2,CD2=(m+2)2+(n﹣0)2,∵△BCD为等边三角形,∵BD=CD=BC,∴,整理得:,②﹣①得:4m+8n=12,∴m=3﹣2n,将m=3﹣2n代入①得:(3﹣2n)2+n2﹣8n=4,整理得:n2﹣4n+1=0,解得:n=,当n=时,m=3﹣2n=,当n=时,m=3﹣2n=,∴点D的坐标为或.故答案为:(﹣2,0);或.二十一.解直角三角形的应用(共1小题)28.(2023•杭州)第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连接BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1:n,tanα=tan2β,则n=()A.5B.4C.3D.2【分析】设AE=a,DE=b,则BF=a,AF=b,解直角三角形可得,化简可得(b﹣a)2=ab,a2+b2=3ab,结合勾股定理及正方形的面积公式可求得S正方形EFGH;S正方形ABCD=1:3,进而可求解n的值.【解答】解:设AE=a,DE=b,则BF=a,AF=b,∵tanα=,tanβ=,tanα=tan2β,∴,∴(b﹣a)2=ab,∴a2+b2=3ab,∵a2+b2=AD2=S正方形ABCD,(b﹣a)2=S正方形EFGH,∴S正方形EFGH:S正方形ABCD=ab:3ab=1:3,∵S正方形EFGH:S正方形ABCD=1:n,∴n=3.故选:C.。
安徽中考压轴题数学2023

安徽中考压轴题数学2023安徽中考压轴题数学2023【引言】数学,作为一门精密严谨的学科,一直是中学教育中必不可少的一部分。
每年的中考都有着一道难度较高的压轴题,今年的安徽中考也不例外。
以下将为大家介绍2023安徽中考数学压轴题。
【题目】某班级有96名学生,其中60%是男生。
其中,35%的男生身高在160cm以上,而女生中,超过160cm的比例是25%。
请回答以下问题:1. 这个班级的男生有多少人?2. 这个班级的女生有多少人?3. 身高在160cm以上的男生有多少人?4. 这个班级中身高在160cm以上的女生有多少人?5. 这个班级男生与女生的身高在160cm以上的比例分别是多少?【解答】1. 这个班级的男生人数:根据题意可得,班级中男生占比60%,因此男生人数为96 × 0.6 = 57.6,即约58人。
2. 这个班级的女生人数:根据题意可得,班级中女生占比40%,因此女生人数为96 × 0.4 = 38.4,即约38人。
3. 身高在160cm以上的男生人数:根据题意可得,男生中身高在160cm以上的人占比35%,因此身高在160cm以上的男生人数为58 × 0.35 = 20.3,即约20人。
4. 这个班级中身高在160cm以上的女生人数:根据题意可得,女生中身高在160cm以上的人占比25%,因此身高在160cm以上的女生人数为38 × 0.25 = 9.5,即约9人。
5. 这个班级男生与女生的身高在160cm以上的比例:男生身高在160cm以上的人数为20人,女生身高在160cm以上的人数为9人,因此男生与女生的身高在160cm以上的比例为20:9。
【结语】本文展示了2023年安徽中考数学压轴题。
通过解答这道题目,学生们可以运用百分数的知识来分析和计算数据。
数学作为一门能力型科目,注重培养学生的分析、计算和推理能力,通过解题训练,学生可以提高自己的数学素养。
2023年中考数学专题复习:二次函数综合压轴题(动点问题)

2023年中考数学专题复习:二次函数综合压轴题(动点问题)1.抛物线2y x bx c =-++与x 轴交于点()10A -,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式;(2)点D 为第一象限内抛物线上的一动点,作DE x ⊥轴于点E ,交BC 于点F ,过点F 作BC 的垂线与抛物线的对称轴、x 轴、y 轴分别交于点G ,N ,H ,设点D 的横坐标为m .①当DF HF +取最大值时,求点F 的坐标;②连接EG ,若45GEH ∠=︒,求m 的值.2.如图,已知抛物线2y x bx c =-++与x 轴交于()1,0A -,()5,0B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上存在一点P ,使得PA PC +的值最小,求此时点P 的坐标;(3)点D 是第一象限内抛物线上的一个动点(不与点C 、B 重合),过点D 作DF x ⊥轴于点F ,交直线BC 于点E ,连接BD ,直线BC 把BDF V 的面积分成两部分,若:3:2BDE BEF S S =V V ,请求出点D 的坐标.3.如图1,对于平面内小于等于90︒的MON ∠,我们给出如下定义:若点P 在MON ∠的内部或边上,作PE OM ⊥于点E ,PF ON ⊥于点F ,则将PE PF +称为点P 与MON ∠的“点角距”,记作(),d MON P ∠.如图2,在平面直角坐标系xOy 中,x 、y 正半轴所组成的角为xOy ∠.(1)已知点()5,0A 、点()3,2B ,则(),d xOy A ∠=______ ,(),d xOy B ∠=______.(2)若点P 为xOy ∠内部或边上的动点,且满足(),5d xOy P ∠=,在图2中画出点P 运动所形成的图形.(3)如图3,在平面直角坐标系xOy 中,抛物线212y x mx n =-++经过()5,0A 与点()3,4D 两点,点Q 是A 、D 两点之间的抛物线上的动点(点Q 可与A 、D 两点重合),求当(),d xOD Q ∠取最大值时点Q 的坐标.4.如图,抛物线2134y ax bx =++与x 轴交于点()30A -,和点B ,点D 是抛物线1y 的顶点,过点D 作x 轴的垂线,垂足为点()10C -,.(1)求抛物线1y 所对应的函数表达式;(2)如图1,点M 是抛物线1y 上一点,且位于x 轴上方,横坐标为m ,连接MC ,若MCB DAC ∠=∠,求m 的值;(3)如图2,将抛物线1y 平移后得到顶点为B 的抛物线2y .点P 为抛物线1y 上的一个动点,过点P 作y 轴的平行线,交抛物线2y 于点Q ,过点Q 作x 轴的平行线,交抛物线2y 于点R .当以点P ,Q ,R 为顶点的三角形与ACD V 全等时,请直接写出点P 的坐标.5.如图,抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点,与y 轴交于点()0,6C ,顶点为D ,且()1,8D .(1)求抛物线的解析式;(2)若在线段BC 上存在一点M ,过点O 作OH OM ⊥交BC 的延长线于H ,且MO HO =,求点M 的坐标;(3)点P 是y 轴上一动点,点Q 是在对称轴上一动点,是否存在点P ,Q ,使得以点P ,Q ,C ,D 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.6.如图,已知二次函数24y x bx =+-的图像经过点()3,4A -,与x 轴负半轴交于点B ,与y 轴交于点C ,连接AB ,BC .(1)填空:b =______;(2)点P 是直线AB 下方抛物线上一个动点,过点P 作PT x ⊥轴,垂足为T ,PT 交AB 于点Q ,求线段PQ 的最大值;(3)点D 是y 轴正半轴上一点,若∠=∠BDC ABC ,求点D 的坐标.7.如图,抛物线2y x bx c =++(b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,()1,0A ,4AB =(1)求该抛物线的解析式;(2)点P 为线段AB 上的动点,过P 作PQ BC ∥交AC 于点Q ,求CPQ V 面积的最大值,并求此时P 点坐标;(3)如图,设抛物线与y 轴交于点D ,平行于BD 的直线MN 交抛物线于点M ,N ,作直线MB ND 、交于点G ,问点G 是否在某一定直线上运动,若在求此直线的解析式,若不在说明理由.8.如图,已知抛物线23y ax bx =+-的图象与x 轴交于点A ()10,和B ()30,,与y 轴交于点C ,D 是抛物线的顶点,对称轴与x 轴交于E .(1)求抛物线的解析式;(2)如图1,在抛物线的对称轴DE 上求作一点M ,使A M C V 的周长最小,M 的坐标__________周长的最小值______.(3)如图2,点P 是x 轴上的动点,过P 点作x 轴的垂线分别交抛物线和直线BC 于F 、G .设点P 的横坐标为m .是否存在点P ,使FG 最长?若存在,求出m 的值;若不存在,请说明理由.9.如图1,抛物线()230y ax bx a =+->交x 轴于点A ,B (点A 在点B 左侧),交y 轴于点C ,且3O B O C O A ==,点D 为抛物线上第四象限的动点.(1)求抛物线的解析式.(2)如图1,直线AD 交BC 于点P ,连接AC BD ,,若ACP △和BDP △的面积分别为1S 和2S ,当12S S -的值最小时,求直线AD 的解析式.(3)如图2,直线BD 交抛物线的对称轴于点N ,过点B 作AD 的平行线交抛物线的对称轴于点M ,当点D 运动时,线段MN 的长度是否会改变?若不变,求出其值;若变化,求出其变化的范围.10.已知抛物线23y ax bx =++(0a ≠)交x 轴于()0A 1,和()30B -,,交y 轴于C .(1)求抛物线的解析式;(2)若M 为抛物线上第二象限内一点,求使MBC V 面积最大时点M 的坐标;(3)若F 是对称轴上一动点,Q 是抛物线上一动点,是否存在F 、Q ,使以B 、C 、F 、Q 为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标.11.如图,在平面直角坐标系中,二次函数的图象交坐标轴于()20A -,,()40B ,,()08C ,三点,点P 是直线BC 上方抛物线上的一个动点.(1)求这个二次函数的解析式;(2)动点P 运动到什么位置时,PBC V 的面积最大,求此时P 点坐标及PBC V 面积的最大值;(3)在y 轴上是否存在点Q ,使以O ,B ,Q 为顶点的三角形与AOC V 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.12.如图,抛物线2y x bx c =++与x 轴交于()1,0A -,()3,0B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)若点E 是线段BC 上的一个动点,平行于y 轴的直线EF 交抛物线于点F ,求FBC V 面积的最大值;(3)设点P 是(1)中抛物线上的一个动点,是否存在满足6PAB S =△的点P ?如果存在,请求出点P 的坐标;若不存在,请说明理由.13.如图,抛物线2y ax bx =+经过()()3,0,2,10A B -两点.(1)求抛物线的解析式;(2)点P 是直线AB 下方抛物线上的一个动点,求PAB V 面积的最大值;(3)点M 是直线AB 上的一个动点,将点M 向左平移3个单位长度得到点N ,设点M 的横坐标为m ,若线段MN 与抛物线只有一个公共点,请直接写出m 的取值范围.14.如图,在平面直角坐标系中,直线122y x =-与x 轴交于点A ,与y 轴交于点C ,抛物线212y x bx c =++经过A ,C 两点,与x 轴的另一交点为点B ,点P 为抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当ACP △的面积与ABC V 的面积相等时,求点P 的坐标;(3)是否存在点P ,使得ACP ABC BAC ∠=∠-∠,若存在,请直接写出点P 的横坐标;若不存在,请说明理由.15.如图,已知拋物线2y ax bx c =++与x 轴交于点()1,0A ,()3,0B -,与y 轴交于点()0,3C -.点P 是抛物线上一动点,且在直线BC 的下方,过点P 作PD x ⊥轴,垂足为D ,交直线BC 于点E .(1)求抛物线的函数解析式;(2)连接CP ,若45CPD ∠=︒,求点P 的坐标;(3)连接BP ,求四边形OBPC 面积的最大值.16.如图,在平面直角坐标系中,抛物线28y x bx =-++与x 轴交于点A ,B ,与y 轴交于点C ,直线y x t =-过点B ,与y 轴交于点D ,点C 与点D 关于x 轴对称.点P 是线段OB 上一动点,过点P 作x 轴的垂线交抛物线于点M ,交直线BD 于点N .(1)求抛物线的解析式;(2)当MDB △的面积最大时,求点P 的坐标;(3)在(2)的条件下,在y 轴上是否存在点Q ,使得以Q ,M ,N ,D 为顶点的四边形是平行四边形,若存在,求出点Q 的坐标;若不存在;说明理由17.如图,抛物线21262y x x =--与x 轴相交于点A 、点B ,与y 轴相交于点C .(1)请直接写出点A ,B ,C 的坐标;(2)若点P 是抛物线BC 段上的一点,当PBC V 的面积最大时求出点P 的坐标,并求出PBC V 面积的最大值.(3)点F 是抛物线上的动点,作FE AC ∥交x 轴于点E ,是否存在点F ,使得以A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F 的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,抛物线21=2y x bx c ++经过点()4,0A -,点M 为抛物线的顶点,点B 在y 轴上,直线AB 与抛物线在第一象限交于点()2,6C .(1)求抛物线的解析式;(2)连接OC ,点Q 是直线AC 上不与A 、B 重合的点,若2OAQ OAC S S =V V ,请求出点Q 的坐标;(3)在x 轴上有一动点H ,平面内是否存在一点N ,使以点A 、H 、C 、N 为顶点的四边形是菱形?若存在,直接写出点N 的坐标,若不存在,请说明理由.参考答案:1.(1)223y x x =-++(2)①点F 的坐标为⎝⎭;②1或952.(1)245y x x =-++(2)()2,3P (3)335,24D ⎛⎫ ⎪⎝⎭3.(1)5,5 (3)54,2⎛⎫ ⎪⎝⎭4.(1)21113424y x x =--+(2)2-(3)304⎛⎫ ⎪⎝⎭,或524⎛⎫- ⎪⎝⎭,5.(1)2246y x x =-++ (2)126,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭6.(1)3-(2)PQ 的最大值是4 (3)50,3⎛⎫ ⎪⎝⎭7.(1)223y x x =+-(2)CPQ V 面积的最大值为2,此时P 点坐标为()1,0-(3)在,3y x =--8.(1)2=+43y x x --(2)()21-,(3)存在,m 的值为329.(1)2=23y x x --(2)22y x =--(3)不变,值为810.(1)223y x x =--+ (2)31524⎛⎫- ⎪⎝⎭, (3)存在,点Q 的坐标为()23-,或()45-,-或()25,-11.(1)228y x x =-++(2)当P 点坐标为()28,时,PBC V 的最大面积为8; (3)存在,点Q 的坐标为()016,或()016-,或()01,或()01-,.12.(1)2=23y x x -- (2)278(3)存在,点P 的坐标为()1或()1或()0,3-或()2,3-13.(1)23y x x =-(2)PAB S V 最大值为1258(3)23m -≤<或34m <<或338m =14.(1)抛物线的函数表达式为213222y x x =-- (2)点P 的坐标为(5,3)P(3)存在,点P 的横坐标为2911或7.15.(1)223y x x =+- (2)(14)--, (3)63816.(1)278y x x =-++(2)()3,0(3)存在,()0,17Q 或()0,33-17.(1)()2,0A -,()6,0B ,()0,6C - (2)点P 的坐标为153,2⎛⎫- ⎪⎝⎭时,PBC S V 有最大值272(3)存在,点F 的坐标为()4,6-或()2+或()2-18.(1)21=22y x x + (2)()8,12或()16,12--(3)()2N +或()2N -或()2,6N -或()4,6-。
2023年九年级数学中考专题:二次函数综合压轴题(特殊四边形问题)(含简单答案)

(1)求抛物线的函数表达式.
(2)当 的面积等于 的面积的 时,求m的值.
(3)当 时,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形?若存在,请直接写出点M的的坐标;若不存在,请说明理由.
(3)点 的坐标为 , ,
5.(1) ,
(2)2
(3) 或 或
6.(1)
(2)
(3)矩形的周长
7.(1) , ;
(2)存在, 或 ;
(3) 或 或 或 .
8.(1) ,
(2)当 时,
(3)存在, 或 或
9.(1)
(2) 的面积最大值为4
(3)四边形 能构成菱形,点 的坐标为 或
10.(1)
(2)
(3)存在, 或 或
15.如图所示,在矩形 中,把点 沿 对折,使点 落在 上的 点.已知 .
(1)求 点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与抛物线仅一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过 ,且直线 是该抛物线的切线.求抛物线的解析式.并验证点 是否在该抛物线上.
(3)在(2)的条件下,若点 是位于该二次函数对称轴右侧图象上不与顶点重合的任意一点,试比较 与 的大小(不必证明),并写出此时点 的横坐标 的取值范围.
11.(1) ;
(2) ;
(3) 、 、 .
12.(1)
(2)
(3)M的坐标为 或 或 或
13.(1)
(2)13.5
(3)存在, , 或
14.(1)
(2)点 的坐标为 或 或 或
2024安徽中考数学压轴题

选择题在直角坐标系中,点A(3,4)关于x轴对称的点的坐标是:A. (-3, -4)B. (3, -4)(正确答案)C. (-3, 4)D. (4, 3)已知二次函数y = ax2 + bx + c的图像经过点(1,0),(0,3),且对称轴为直线x = 1,则a的值为:A. 1B. -1C. 3(正确答案)D. -3下列四边形中,不一定是平行四边形的是:A. 两组对边分别平行的四边形B. 两组对角分别相等的四边形C. 一组对边平行且相等的四边形D. 对角线互相平分的四边形但不等长(正确答案)若圆O的半径为5,圆心O到直线l的距离为3,则直线l与圆O的位置关系是:A. 相离B. 相切C. 相交(正确答案)D. 无法确定已知三角形ABC的三边长为a, b, c,且满足a2 + b2 + c2 = ab + bc + ca,则三角形ABC是:A. 直角三角形(正确答案)B. 等腰三角形C. 等边三角形D. 锐角三角形函数y = (x - 1)/(x2 - 1)的自变量x的取值范围是:A. x ≠ 1B. x ≠ -1C. x ≠ ±1(正确答案)D. x为任意实数在平行四边形ABCD中,AB = 5,AD = 8,∠BAD的平分线交BC于点E,则DE的长为:A. 3B. 5(正确答案)C. 6D. 8已知关于x的一元二次方程x2 - (2k + 1)x + 4(k - 1/2) = 0有两个相等的实数根,则k的值为:A. 1B. 2C. 3(正确答案)D. 4下列说法中,正确的是:A. 无限小数都是无理数B. 有理数都是有限小数C. 无理数都是无限不循环小数(正确答案)D. 数轴上的点都能表示无理数。
2023中考数学压轴题20题精选

2023中考数学压轴题20题精选数学作为一门重要的学科,对于学生的综合素质培养起着至关重要的作用。
中考数学压轴题是对学生数学知识的综合考察,也是对学生数学思维能力和解题能力的一次全面检验。
下面,我将为大家精选出2023中考数学压轴题的20道题目。
1. 已知正方形ABCD的边长为2cm,点E是边AB的中点,连接DE并延长交边BC于点F,求EF的长度。
2. 若a:b=3:4,b:c=5:6,求a:b:c的比值。
3. 一辆汽车以每小时60公里的速度行驶,行驶了4小时后,又以每小时80公里的速度行驶,问这辆汽车行驶了多少公里?4. 一块长方形的面积是24平方米,宽是3米,求其长度。
5. 一条铁路上有两个车站A、B,A、B之间的距离是120公里,一辆火车从A站开往B站,速度是每小时80公里,另一辆火车从B站开往A站,速度是每小时60公里,两辆火车同时出发,问两辆火车相遇需要多长时间?6. 一辆汽车以每小时50公里的速度行驶,行驶了2小时后,又以每小时60公里的速度行驶,问这辆汽车行驶了多少公里?7. 一块长方形的周长是20米,宽是3米,求其面积。
8. 一条铁路上有两个车站A、B,A、B之间的距离是180公里,一辆火车从A站开往B站,速度是每小时60公里,另一辆火车从B站开往A站,速度是每小时80公里,两辆火车同时出发,问两辆火车相遇需要多长时间?9. 一辆汽车以每小时40公里的速度行驶,行驶了3小时后,又以每小时50公里的速度行驶,问这辆汽车行驶了多少公里?10. 一块长方形的周长是16米,宽是4米,求其面积。
11. 一条铁路上有两个车站A、B,A、B之间的距离是150公里,一辆火车从A站开往B站,速度是每小时70公里,另一辆火车从B 站开往A站,速度是每小时90公里,两辆火车同时出发,问两辆火车相遇需要多长时间?12. 一辆汽车以每小时30公里的速度行驶,行驶了4小时后,又以每小时40公里的速度行驶,问这辆汽车行驶了多少公里?13. 一块长方形的面积是36平方米,宽是6米,求其长度。
