山东省青岛市2008年初级中学学业水平考试数学试卷
2008年初中毕业、升学统一考试数学模拟试题以及参考答案

2008年初中毕业、升学统一考试数学模拟试题 08.6.1(考试时间:120分钟 满分:150分)请注意:1.本试卷分选择题和非选择题两个部分。
2.考生答卷前,必须将自己的姓名、考试号、座位号用黑色或蓝色钢笔或圆珠笔填写在试卷和答题卡的相应位置,再用2B 铅笔将考试号、科目填涂在答题卡上相应的小框内。
第一部分 选择题(共36分)请注意:考生必须将所选答案的字母标号用2B 铅笔填涂在答题卡相应的题号内,答在试卷上无效。
一、选择题 1.2的绝对值是 A. 2B. -2C. 0.5D. -0.52.下列计算中,正确的是A .2a 3-3a =-a ;B .(-ab )2=-a 2b 2;C .a 2·a -3=a -1;D .-2a 3÷(-2a )=-a 2.3.为迎接2008年北京奥运会修建的鸟巢,将用于国际、国内体育比赛和文化、娱乐活动,鸟巢的建筑面积约为258000 平方米,将258000用科学记数法表示应为 A .62.5810⨯B .52.610⨯C .42.5810⨯D .52.5810⨯4.小明从正面观察下图所示的两个物体,看到的是5.右图可以看作是一个等腰直角三角形旋转若干次 而生成的则每次旋转的度数可以是A. 90°B. 60°C. 45°D. 30°6.在直角坐标系中,⊙O 的圆心在原点,半径为3,⊙A 的圆心A 的坐标为(3-,1),半径为1,那么⊙O 与⊙A 的位置关系是B A CDA .内含B 内切C 相交D 外切7. 如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪下,则右图展开得到 的图形的面积是A .34 B.12 C . 38D .3168.如图是一个电脑桌面背景图,左右 两个“京”字图的面积比约是A .2∶1B .4∶1C .8∶1D .16∶19.下列事件的概率是1的是A. 任意两个偶数的和是4的倍数 B. 任意两个奇数的和是2的倍数 C. 任意两个质数的和是2的倍数 D. 任意两个整数的和是2的倍数 10.如果不等式组212x m x m >+⎧⎨>+⎩,的解集是1x >-,那么m 的值是A.3 B.1 C.1- D.3-11.匀速向一个容器注满水,容器水面的高度变化过程如左图所示:则这个容器可能是A .B .C .D . 12.从A 点出发的一条光线在直线AD 与CD 之间反射了n 次以后,垂直地射到B 点(该点可能在AD 上,也 可能在CD 上),然后按原路返回点A ,如图所示是n =3时的光路图,若∠CDA =8°,则n 的最大值是沿虚线剪开635412A. 10B. 11C. 12D. 14 二.填空题 (每题3分,共24分)13.为支援南方雪灾地区,某校团委举行了“雪灾无情人有情”的捐资活动,其中6个班同学的人均捐款数分别为:6元、4.6元、4.1元、3.8元、4.8元、5.2元.则这组数据的中位数是 元.14.如图,一扇窗户打开后,用窗钩BC 可将其固定,•这里所运用的几何原理是__________.第14题 第18题 第20题15.已知一段公路在斜坡上,坡度i=1:3,若汽车在斜坡上行驶100米,则汽车升高_______________米. 16.时钟的时针长6㎝,经过80分钟时针扫过的面积为 ㎝2 (结果保留π) . 17.下表所描述的是1y 与2y 分别与x 的函数关系:若两个函数的图象只有一个交点,则交点坐标是_________.18. 一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的21的概率是___________.19.晓莹按如图所示的程序输入一个数x ,最后从输出端得到的数为16,则晓莹输入的最大的负数为 .20.如图所示,已知反比例函数y =1x的图象上有一点P ,过点P 分别作x 轴和y 轴的垂 线,垂足分别为A 、B ,使四边形OAPB 为正方形,又在反比例函数的图象上有一点P 1,过点P 1分别作BP 和y 轴的垂线。
二○一○年山东省青岛市初级中学学业水平考试数学试卷

二○一○年山东省青岛市初级中学学业水平考试数 学 试 题(考试时间:120分钟;满分:120分)亲爱的同学,欢迎你参加本次考试,祝你答题成功!1.请务必在指定位置填写座号,并将密封线内的项目填写清楚.2.本试题共有24道题.其中1—8题为选择题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—14题为填空题,请将做出的答案填写在第14题后面给出表格的相应位置上;15—24题,请在试题给出的本题位置上做答. 3分)3.由四舍五入法得到的近似数8.8×103,下列说法中正确的是( ).A .精确到十分位,有2个有效数字B .精确到个位,有2个有效数字C .精确到百位,有2个有效数字D .精确到千位,有4个有效数字 4.下列图形中,中心对称图形有( ).第2题图A .1个B .2个C .3个D .4个5.某外贸公司要出口一批规格为150g 的苹果,现有两个厂家提供货源,它们的价格相同,苹果的品质也相近. 质检员分别从甲、乙两厂的产品中随机抽取了50个苹果称重,并将所得数据处理后,制成如下表格. 根据表中信息判断,下列说法错误的是( ).A .本次的调查方式是抽样调查B .甲、乙两厂被抽取苹果的平均质量相同C .被抽取的这100个苹果的质量是本次调查的样本D .甲厂苹果的质量比乙厂苹果的质量波动大6.如图,在Rt △ABC 中,∠C = 90°,∠B = 30°,BC = 4 cm ,以点C 为圆心,以2 cm 的长为半径作圆,则⊙C 与AB 的位置关系是( ).7C ). 8请将1—8各小题所选答案的标号填写在下表的相应位置上:10.如图,点A 、B 、C 在⊙O 上,若∠BAC = 24°,则∠BOC = °. 11.某市为治理污水,需要铺设一段全长为300 m 的污水排放管道.铺设120 m 后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.求原计划每天铺设管道的长度.如果设原计划每天铺设m x 管道,那么根据题意,可得方程 .12.一个口袋中装有10个红球和若干个黄球.在不允许将球倒出来数的前提下,为估计口袋中黄球的个数,小明采用了如下的方法:每次先从口袋中摸出10个球,求出其中红球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程20次,得到红球数与10的比值的平均数为0.4.根据上述数据,估计口袋中大约有 个黄球. 13.把一张矩形纸片(矩形ABCD )按如图方式折叠,使顶点B 和点D 重合,折痕为EF .若14三、作图题(本题满分4分)用圆规、直尺作图,不写作法,但要保留作图痕迹. 15.如图,有一块三角形材料(△ABC ),请你画出一个圆,使其与△ABC 的各边都相切.解: OABC第10题图·结论: 四、解答题(本题满分74分,共有9道小题) 16.(本小题满分8分,每题4分)(1)解方程组:34194x y x y +=⎧⎨-=⎩; (26分)配餐公司为某学校提供A 、B 、C 三类午餐供师生选择,三类午餐每份的价格分别是:A餐5元,B 餐6元,C 餐8元.为做好下阶段的营销工作,配餐公司根据该校上周A 、B 、C 三类午餐购买情况,将所得的数据处理后,制成统计表(如下左图);根据以往销售量与平均每份利润之间的关系,制成统计图(如下右图).以往销售量与平均每份利润之间的关系统计图请根据以上信息,解答下列问题:(1)该校师生上周购买午餐费用的众数是元;(2)配餐公司上周在该校销售B餐每份的利润大约是元;(3)请你计算配餐公司上周在该校销售午餐约盈利多少元?解:(3)18.(本小题满分6分)Array“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.(1)写出转动一次转盘获得45元购书券的概率;(2)转转盘和直接获得购书券,你认为哪种方式对读者更合第18题图算?请说明理由.解:(1)(2)19.(本小题满分6分)小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD 的长度.(结果保留整数)(参考数据:o o o o 337sin37tan37sin 48tan485410≈≈≈,,,解:8分)若单独租用35座客车若干辆,则刚好坐满;45个空座位.55座客车的租金为每辆400元.根据租车4辆(可以坐不满).请你计算第19题图(2)(本小题满分8分)分别在BC和CD上,AE = AF.,使OM = OA,连接EM、FM.判断四边形AEMF(2)A DB EFOCM 第21题图22.(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:10500=-+.y x(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)解:(1)(2)(3)23.(本小题满分10分)问题再现现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题.今天我们把正多边形....的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究.我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如右图中,用正方形镶嵌平面,可以发现在一个顶点O 周围围绕着4个正方形的内角.试想:如果用正六边形来镶嵌平面,在一个顶点周围应该围绕着 个从平面图形的镶嵌中可以发现,解决具体地说,就是个正方形和y 个正八边形的内角可以拼成一38y +=,12x y =⎧⎨=⎩ .结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.验证2:O结论2:.上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案.问题拓广请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.猜想3: .验证3:于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:(1)当t为何值时,点A在线段PQ的垂直平分线上?(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)解:(1)(2)(3)真情提示:亲爱的同学,请认真检查,不要漏题哟!A C图(3)(用圆珠笔或钢笔画图)二○一○年山东省青岛市初级中学学业水平考试数学试题参考答案及评分标准三、作图题(本题满分4分)15.正确画出两条角平分线,确定圆心;········2分确定半径;········3分正确画出圆并写出结论.········4分四、解答题(本题满分74分,共有9道小题)16.(本小题满分8分)(1)34194x yx y+=⎧⎨-=⎩解:②×4得:4416x y-=,③①+③得:7x = 35,解得:x = 5.·········4分········4分17解:(1)6元;········2分(2)3元;········4分(3)1.5×1000+3×1700+3×400 = 1500+5100+1200 = 7800(元).答:配餐公司上周在该校销售午餐约盈利7800元.········6分18.(本小题满分6分)解:(1)P(获得45元购书券)=112;········2分②①(2)12345302515121212⨯+⨯+⨯=(元). ∵15元>10元,∴转转盘对读者更合算.········ 6分19.(本小题满分6分) 解:设CD = x . 在Rt △ACD 中,tan37ADCD ︒=, 则34AD x =, ∴34AD x =.在Rt △BCD 中,tan48° = BDCD, 则1110BD x=, ∴1110BD x =. (4)分43米. ………………… 6分20175人. ········· 3分 4y -)辆,由题意得:3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤, ······· 6分 解这个不等式组,得111244y ≤≤.∵y 取正整数,∴y = 2.∴4-y = 4-2 = 2.∴320×2+400×2 = 1440(元).所以本次社会实践活动所需车辆的租金为1440元. ········ 8分21.(本小题满分8分)证明:(1)∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°. ∵AE = AF ,∴Rt Rt ABE ADF △≌△. ∴BE =DF . ········ 4分 (2)四边形AEMF 是菱形.∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC .∵BE =DF ,∴BC -BE = DC -DF . 即CE CF =.∴OE OF =.∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.分22.(本小题满分10分)解:(1)由题意,得:w = (x -20)·y=(x -20)·(10500x -+) 21070010000x x =-+-352b x a=-=.答:当销售单价定为35元时,每月可获得最大利润. ········ 3分(2)由题意,得:210700100002000x x -+-=解这个方程得:x 1 = 30,x 2 = 40.答:李明想要每月获得2000元的利润,销售单价应定为30元或40元. (6)分(3)法一:∵10a =-<0, ∴抛物线开口向下. ∴当30≤x ≤40时,w ≥2000. ∵x ≤32, ∴当30≤x ≤32时,w ≥2000. 设成本为P (元),由题意,得: 20(10500)P x =-+20010000x =-+∵200k =-<0,∴P 随x 的增大而减小.∴当x = 32时,P 最小=3600. 答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.········· 10分23.(本小题满分10分)解:3个; ········ 1分验证2:在镶嵌平面时,设围绕某一点有a 个正三角形和b 个正六边形的内角可以拼成一个周角.根据题意,可得方程:法二:∵10a =-<0, ∴抛物线开口向下.∴当30≤x ≤40时,w ≥2000. ∵x ≤32, ∴30≤x ≤32时,w ≥2000. ∵10500y x =-+,100k =-<, ∴y 随x 的增大而减小. ∴当x = 32时,y 最小=180.∵当进价一定时,销售量越小,成本越小,∴201803600⨯=(元).60120360a b+=.整理得:26a b+=,可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩.·······3分结论2:镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌.····5分猜想3:是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌?········6分验证3:在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意,可得方程:6090120360m n c++=,整理得:23412m n c++=,可以找到惟一一组适合方程的正整数解为121mnc=⎧⎪=⎨⎪=⎩. ········8分结论3:镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. (说明:本题答案不惟一,符合要求即可.)······· 10分24.(本小题满分12分)解:(1)∵点A在线段PQ的垂直平分线上,∴AP = AQ.∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,∴∠EQC = 45°.∴∠DEF =∠EQC.∴CE = CQ.由题意知:CE = t,BP =2 t,∴CQ = t.∴AQ = 8-t.在Rt△ABC中,由勾股定理得:AB = 10 cm .则AP = 10-2 t.∴10-2 t = 8-t.解得:t = 2.答:当t = 2 s时,点A在线段PQ的垂直平分线上. ····· 4分(2)过P作PM BE⊥,交BE于M,∴90BMP∠=︒.在Rt△ABC和Rt△BPM中,sinAC PMBAB BP==,∴8210PMt= . ∴PM =85t.∵BC = 6 cm ,CE = t , ∴ BE = 6-t .∴y = S △ABC -S △BPE =12BC AC ⋅-12BE PM ⋅= 1682⨯⨯-()186t t 25⨯-⨯=24242455t t -+ = ()2484355t -+. ∵405a =>,∴抛物线开口向上.∴当t = 3时,y 最小=845.答:当t = 3s 时,四边形APEC 的面积最小,最小面积为845cm 2. ···· 8分(3)假设存在某一时刻t ,使点P 、Q 、F 三点在同一条直线上.过P 作PN AC ⊥,交AC 于N , ∴90ANP ACB PNQ ∠=∠=∠=︒.∵PAN BAC ∠=∠,∴△PAN ∽△BAC .∴PN AP AN BC AB AC==. ∴1026108PN t AN -==. ∴665PN t =-,885AN t =-. ∵NQ = AQ -AN ,∴NQ = 8-t -(885t -) = 35t .在同一条直线上, . .. 12分图(3)。
2008年山东省青岛市初级中学学业水平考试

2008年山东省青岛市初级中学学业水平考试英语试题(考试时间:120分钟,满分:105分)第一卷(共60分)第一部分听力测试(25分)I.听句子,选择最佳答语。
每个句子读一遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)1.A.I got it for my birthday.B.It cost me two hundred yuan.C.Thanks a lot.2.A.Sorry , he isn’t in.B.It’s OK. C.I’m not sure.3.A.No ,thanks. B.It’s my pleasure.C.Never mind.4.A.No, I don’t agree with you.B.But there is enough space.C.Sorry, I didn’t see the sign.5.A.I did some chores.B.I felt sick and stayed in bed.C.It was pretty good .I had fun.II.听对话和问题,选择正确答案。
对话和问题读两遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)6.7.8.A.$ 5.90. B.$ 50. C.$ 9.50.9.A.Get a pen for himself.B.Borrow a pen from Susan.C.Give his pen to Susan.10.A.There is a little time left.B.The traffic is heavy.C.She is late.III.听对话,回答问题。
对话读两遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)听第一段对话,回答11—12小题。
11.Where may this conversation take place?A.In a bank. B.In a shop. C.At a restaurant.12.What does the man want?A.A pair of shoes. B.Some tasty fruit. C.Some sports wear.听第二段对话。
2008年山东省中考数学试题

2008年山东省中考数学试题注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷4页为选择题,36分;第Ⅱ卷8页为非选择题,84分;全卷共12页,满分120分.考试时间为120分钟.2.答Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目和试卷类型涂写在答题卡上,并在本页正上方空白处写上姓名和准考证号.考试结束,试题和答题卡一并收回.3.第Ⅰ卷每题选出答案后,必须用2B 铅笔把答题卡上对应题目的答案标号(A B C D)涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.第Ⅰ卷 (选择题 共36分)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分. 1.下列运算中,正确的是A .235a a a +=B .3412a a a ⋅=C .236a a a =÷ D .43a a a -=2.右图是北京奥运会自行车比赛项目标志,图中两车轮所在圆的位置关系是A .内含B .相交C .相切D .外离3.如图,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线 剪去∠C ,则∠1+∠2等于A .315° B.270° C .180° D.135°4.如图,点A 的坐标为(1,0),点B 在直线y x =-上运动,当线段AB 最短时,点B 的坐标为A .(0,0)B .(12,-12) C .(22,-22) D .(-12,12) 5.小华五次跳远的成绩如下(单位:m ):3.9,4.1, 3.9,3.8,4.2.关于这组数据, 下列说法错误的是A .极差是0.4B .众数是3.9C .中位数是3.98D .平均数是3.98第2题图第3题图第4题图6.如图,已知⊙O 的半径为5,弦AB =6,M 是AB 上任意一点,则线段OM 的长可能是A .2.5B .3.5C .4.5D .5.57.下列四副图案中,不是轴对称图形的是8.已知代数式2346x x -+的值为9,则2463x x -+的值为A .18B .12 C.9 D .79.一个正方体的表面展开图如图所示,每一个面上都写有一个整数, 并且相对两个面上所写的两个整数之和都相等,那么A .a =1,b =5B .a =5,b =1C .a =11,b =5D .a =5,b =1110.国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,我市就“你每天在校体育活动时间是多少”的问题随机调查了某区300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:0.5h t <; B组:0.5h 1h t <≤; C组:1h 1.5h t <≤;D组: 1.5h t ≥.根据上述信息,你认为本次调查数据的中位数落在 A .B 组 B .C 组 C .D 组 D .A 组11.如图,扇形OAB 是圆锥的侧面展开图,若小正方形方格的边长为1 cm ,则这个圆锥的底面半径为 A .22cm B .2cmC .22cm D .21cm12.如图,两个高度相等且底面直径之比为1∶2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙 杯,则乙杯中的液面与图中点P 的距离是 A .43cm B .6cmA. B. C. D.ABOM第6题图第9题图AOB第11题图A B C D 组别人数第10题图第12题图C .8cmD .10cm2008年山东省枣庄市中考数学试题第Ⅱ卷 (非选择题 共84分)注意事项:1.第Ⅱ卷共8页,用钢笔或圆珠笔(蓝色或黑色)直接写在试卷上. 2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共6小题,共24分.只要求填写最后结果,每小题填对得4分.13.如图,在△ABC 中,AB =2,AC =2,以A 为圆心,1为半径的圆与边BC 相切,则BAC ∠的度数是 .14.函数y =211x x +-中,自变量x 的取值范围是 . 15.已知二次函数c bx ax y ++=21(0≠a )与一次函数)0(2≠+=k m kx y 的图象相交于点A (-2,4),B (8,2)(如图所示),则能使21y y >成立的x 的取值范围是 . 16.已知x 1、x 2是方程x 2-3x -2=0的两个实根,则(x 1-2) (x 2-2)= .17.将边长分别为2、3、5的三个正方形按如图方式排列,则图中阴影部分的面积为 . 、18.在实数的原有运算法则中,我们补充新运算法则 “ * ” 如下:当a ≥b 时,2*a b b =;当a < b 时,*a b a =.则当x = 2时,(1*)(3*)x x x - =__________.(“ · ” 和 “ – ”仍为实数运算中的乘号和减号)三、解答题:本大题共7小题,共60分.解答时,要写出必要的文字说明、证明过程或演算步骤. 19.(本题满分7分)先化简,再求值:22212221x x x x x x --+--+÷x ,其中x=23.ABC第13题图第15题图第17题B ′ ABCE Oxy20.(本题满分7分)一口袋中装有四根长度分别为1cm ,3cm ,4cm 和5cm 的细木棒,小明手中有一根长度为3cm 的细木棒,现随机从袋内取出两根细木棒与小明手中的细木棒放在一起,回答下列问题: (1)求这三根细木棒能构成三角形的概率; (2)求这三根细木棒能构成直角三角形的概率; (3)求这三根细木棒能构成等腰三角形的概率.21.(本题满分8分)某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案: (1)甲队单独完成这项工程刚好如期完成; (2)乙队单独完成这项工程要比规定日期多用6天;(3)若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.22.(本题满分8分)如图,在直角坐标系中放入一个边长OC 为9的矩形纸片ABCO .将纸片翻折后,点B 恰好落在x 轴上,记为B ′,折痕为CE ,已知tan ∠OB ′C =34. (1)求B ′ 点的坐标;(2)求折痕CE 所在直线的解析式.23.(本题满分10分)已知:如图,在半径为4的⊙O 中,AB ,CD 是两条直径,M 为OB 的中点,CM 的延长线交⊙O 于点E ,且EM >MC .连结DE ,DE =15.(1) 求证:AM MB EM MC ⋅=⋅; (2) 求EM 的长;(3)求sin ∠EOB 的值.A BCEDOM24.(本题满分10分)在直角坐标平面中,O 为坐标原点,二次函数2(1)4y x k x =-+-+的图象与y 轴交于点A ,与x 轴的负半轴交于点B ,且6OAB S ∆=.(1)求点A 与点B 的坐标; (2)求此二次函数的解析式;(3)如果点P 在x 轴上,且△ABP 是等腰三角形,求点P 的坐标.25.(本题满分10分)把一副三角板如图甲放置,其中90ACB DEC == ∠∠,45A = ∠,30D = ∠,斜边6cm AB =,7cm DC =.把三角板DCE 绕点C 顺时针旋转15°得到△D 1CE 1(如图乙).这时AB 与CD 1相交于点O ,与D 1E 1相交于点F . (1)求1OFE ∠的度数; (2)求线段AD 1的长;(3)若把三角形D 1CE 1绕着点C 顺时针再旋转30°得△D 2CE 2,这时点B 在△D 2CE 2的内部、外部、还是边上?说明理由.(甲)ACE DB B(乙)AE 1CD 1OF2008年山东省枣庄市中考数学试题参考答案及评分意见评卷说明:1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步所应得的累计分数.本答案中每小题只给出一种解法,考生的其他解法,请参照评分意见进行评分.3.如果考生在解答的中间过程出现计算..错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半,若出现较严重的逻辑错误,后续部分就不给分. 一、选择题:(本大题共12小题,每小题3分,共36分)二、填空题:(本大题共6小题,每小题4分,共24分)13.105° 14.x ≥-12 且x ≠115.x <-2或x >8 16.-4 17.15418.-2三、解答题:(本大题共7小题,共60分) 19.(本题满分7分)解:原式=()()()()x x x x x x x 1221112⨯--+-+-…………………………………………2分=11-+x x +1 =12-x x . …………………………………………………………………5分 当x =23时,原式=223213⨯-=-4.……………………………………………………7分 20.(本题满分7分)解:用枚举法或列表法,可求出从四根细木棒中取两根细木棒的所有可能情况共有6种.枚举法:(1,3)、(1,4)、(1,5)、(3,4)、(3,5)、(4,5)共有6种.…4分 (1)P (构成三角形)=4263=; …………………………………………………5分 题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案DDBBCCADABCB(2)P (构成直角三角形)=16; …………………………………………………6分 (3)P (构成等腰三角形)=36=12. ……………………………………………7分21.(本题满分8分)解:设规定日期为x 天.由题意,得163=++x x x . …………………………………… 3分 解之,得 x =6.经检验,x =6是原方程的根. ……………………………………5分 显然,方案(2)不符合要求; 方案(1):1.2×6=7.2(万元); 方案(3):1.2×3+0.5×6=6.6(万元). 因为7.2>6.6,所以在不耽误工期的前提下,选第三种施工方案最节省工程款. ………………8分 22.(本题满分8分)解:(1)在Rt △B ′OC 中,tan ∠OB ′C =34,OC =9, ∴934OB ='. ………………………………………………………………………2分 解得OB ′=12,即点B ′ 的坐标为(12,0). ………………………………………3分 (2)将纸片翻折后,点B 恰好落在x 轴上的B ′ 点,CE 为折痕, ∴ △CBE ≌△CB ′E ,故BE =B ′E ,CB ′=CB =OA .由勾股定理,得 CB ′=22OB OC '+=15. … …………………………………4分 设AE =a ,则EB ′=EB =9-a ,AB ′=AO -OB ′=15-12=3. 由勾股定理,得 a 2+32=(9-a )2,解得a =4.∴点E 的坐标为(15,4),点C 的坐标为(0,9). ·········· 5分 设直线CE 的解析式为y =kx +b ,根据题意,得 9,415.b k b =⎧⎨=+⎩ …………… 6分解得9,1.3b k =⎧⎪⎨=-⎪⎩∴CE 所在直线的解析式为 y =-13x +9. …………………8分23.(本题满分10分)解:⑴ 连接AC ,EB ,则∠CAM =∠BEM . ……………1分A BCEDO MF又∠AMC =∠EMB , ∴△AMC ∽△EMB . ∴EM MBAM MC=,即AM MB EM MC ⋅=⋅.………3分 (2) ∵DC 为⊙O 的直径,∴∠DEC =90°,EC =22228(15)7.DC DE -=-= ………………………4分∵OA =OB =4,M 为OB 的中点,∴AM =6,BM =2. …………………………………5分 设EM =x ,则CM =7-x .代入(1),得 62(7)x x ⨯=-.解得x 1=3,x 2=4.但EM >MC ,∴EM=4. …………………………………………7分 (3) 由(2)知,OE =EM =4.作EF ⊥OB 于F ,则OF =MF =41OB =1. ………………8分在Rt △EOF 中,EF =,15142222=-=-OF OE …………………………9分∴sin ∠EOB =415=OE EF . ……………………………………………………………10分 24.(本题满分10分)解:(1)由解析式可知,点A 的坐标为(0,4). …………………………………1分 ∵1462OAB S BO ∆=⨯⨯=,∴BO =3. ∴点B 的坐标为(-3,0). ………………………………………………………2分 (2)把点B 的坐标(-3,0)代入4)1(2+-+-=x k x y ,得2(3)(1)(3)40k --+-⨯-+=. 解得351-=-k . …………………4分∴所求二次函数的解析式为4352+--=x x y . …………………………………5分 (3)因为△ABP 是等腰三角形,所以①当AB =AP 时,点P 的坐标为(3,0). …………………………………………6分 ②当AB =BP 时,点P 的坐标为(2,0)或(-8,0). …………………………8分 ③当AP =BP 时,设点P 的坐标为(x ,0).根据题意,得3422+=+x x .解得 67=x .∴点P 的坐标为(67,0). ……………………………………10分综上所述,点P 的坐标为(3,0)、(2,0)、(-8,0)、(67,0).25.(本题满分10分)54123 OFB1ECA 1D解:(1)如图所示,315∠=,190E ∠= ,∴1275∠=∠=. ………………………………1分 又45B ∠=,∴114575120OFE B ∠=∠+∠=+= . ………3分 (2)1120OFE ∠= ,∴∠D 1FO =60°.1130CD E ∠= ,∴490∠= .··················· 4分 又AC BC = ,6AB =,∴3OA OB ==.90ACB ∠= ,∴116322CO AB ==⨯=. ·············· 5分 又17CD = ,∴11734OD CD OC =-=-=.在1Rt AD O △中,222211345AD OA OD =+=+=. ········· 6分 (3)点B 在22D CE △内部. ···················· 7分 理由如下:设BC (或延长线)交22D E 于点P ,则2153045PCE ∠=+= . 在2Rt PCE △中,27222CP CE ==, ………… ········ 9分 72322CB =<,即CB CP <,∴点B 在22D CE △内部. ……………10分声明:本资料由 考试吧( ) 收集整理,转载请注明出自 服务:面向较高学历人群,提供计算机类,外语类,学历类,资格类,会计类,工程类,医学类等七大类考试的全套考试信息服务及考前培训.。
山东青岛2008年初级中学学业水平考试
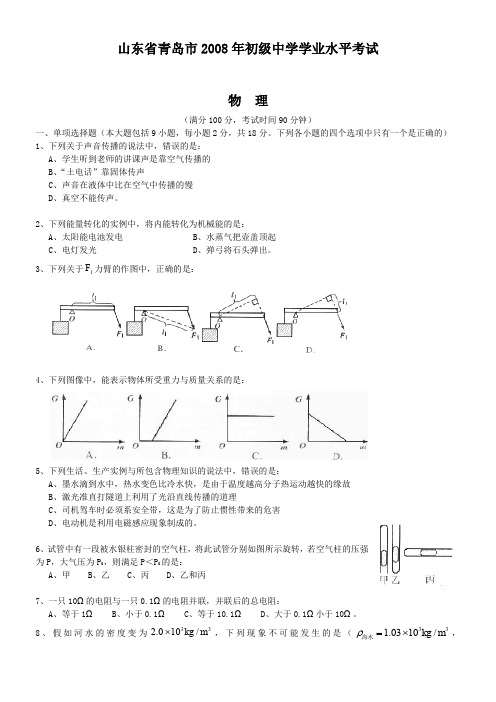
山东省青岛市2008年初级中学学业水平考试物 理(满分100分,考试时间90分钟)一、单项选择题(本大题包括9小题,每小题2分,共18分。
下列各小题的四个选项中只有一个是正确的) 1、下列关于声音传播的说法中,错误的是: A 、学生听到老师的讲课声是靠空气传播的 B 、“土电话”靠固体传声C 、声音在液体中比在空气中传播的慢D 、真空不能传声。
2、下列能量转化的实例中,将内能转化为机械能的是:A 、太阳能电池发电B 、水蒸气把壶盖顶起C 、电灯发光D 、弹弓将石头弹出。
3、下列关于1F 力臂的作图中,正确的是:4、下列图像中,能表示物体所受重力与质量关系的是:5、下列生活、生产实例与所包含物理知识的说法中,错误的是:A 、墨水滴到水中,热水变色比冷水快,是由于温度越高分子热运动越快的缘故B 、激光准直打隧道上利用了光沿直线传播的道理C 、司机驾车时必须系安全带,这是为了防止惯性带来的危害D 、电动机是利用电磁感应现象制成的。
6、试管中有一段被水银柱密封的空气柱,将此试管分别如图所示旋转,若空气柱的压强为P ,大气压为P 0,则满足P <P 0的是:A 、甲B 、乙C 、丙D 、乙和丙7、一只10Ω的电阻与一只0.1Ω的电阻并联,并联后的总电阻:A 、等于1ΩB 、小于0.1ΩC 、等于10.1ΩD 、大于0.1Ω小于10Ω。
8、假如河水的密度变为332.010/kg m ⨯,下列现象不可能发生的是(331.0310/kg m ρ=⨯海水,337.910/kg m ρ=⨯铁)A 、船从河中驶入海是将沉下一些B 、提起同体积的河水用力较小C 、潜水员在河底会受到更大的压强D 、实心铁球在河水中仍然下沉。
9、下列关于科学方法的说法中,错误的是:A 、为研究光现象,引入“光线”描述光的传播路径和方向,这是模型法B 、噪声对人的身心健康会造成危害,科学家却能利用噪声来除草,这是缺点利用法C 、根据加快蒸发的方法,想到减慢蒸发的方法,这是逆向思维法D 、制作滑动变阻器时,发现导线太长而采取缠绕的方式,这是换元法二、不定项选择题(本大题包括4小题,共12分。
2008年初中毕业学业考试数学试题

2008年初中毕业学业考试数学试题(考试形式:闭卷;全卷共五大题25小题;卷面分数:120分;考试时限:120分钟) 考生注意:1.本试卷分为两卷,解答第Ⅰ卷(1~2页)时请将解答结果填写在第Ⅱ卷(3~8页)上指定的位置,否则答案无效,交卷时只交第Ⅱ卷. 2.答卷时允许使用科学计算器. 以下公式供参考:二次函数y =ax 2+bx +c (a ≠0)图象的顶点坐标是)442(2ab ac a b ,第Ⅰ卷 (选择题、填空题 共45分)一、选择题.(本大题共10小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将符合要求的选项前面的字母代号填写在第Ⅱ卷上指定的位置.01.实数a 、b 在数轴上的位置如图所示,则( ) A .b > 0 B .0> a C .b >a D .a>b02.如图是一个物体的三视图,则该物体的形状是( ) A .圆锥 B .圆柱C .三棱锥D .三棱柱03.下列四个数据中,是近似数的是( )A .三班有50人参加今年中考B .全市今年初中毕业学生有6321人C .我在初中学习了6本数学书D .玉泉铁塔高16.945米 04.在下列的计算中,正确的是( )A .2x +3y =5xyB .(a +2)(a -2)=a 2+4C .a 2•ab =a 3bD .(x -3)2=x 2+6x +905.如图,在△ABC 中,点D 、E 、F 分别是三边的中点,那么平移△ADE 可以得到( )A .△DBF 和△DEFB .△DBF 和△ABC C .△DEF 和△CEFD .△DBF 和△EFC06.据预报,2007年“五一”下雨的概率为80%,则下列理解正确的是( )A .“五一”80%的地区会下雨B .“五一”80%的时间会下雨C .“五一”一定会下雨D .“五一”下雨的可能性很大07.木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB 和CD ),这样做的根据是( )A .矩形的对称性B .矩形的四个角都是直角C .三角形的稳定性D .两点之间线段最短第9题图 A C 第7题图 B D第1题图F第5题图E C D B A第2题图 主视图 左视图 俯视图08.某皮鞋店在近一周内各种皮鞋的售出情况记录如下表,该店老板决定下周要多进一些40码皮鞋,其决策的依据是一周内所销售皮鞋数量的( )A .平均数B .众数C .中位数D .方差09.如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB =8cm ,OC =5 cm ,则OD 的长是( ) A .3 cm B .2.5 cm C .2 cm D .1 cm 10.学校升旗仪式上,匀速上升国旗的高度与时间的关系可以用图象近似地刻画,其图象是( )二、填空题.(本大题共5小题,每小题3分,共15分) 请将下列各题的答案填写在第Ⅱ卷上指定的位置. 11.巴黎与北京两地的时差是-7小时(带正号的数表示同一时间比北京早的时间数).2007年“中法文化交流之春”活动内容中的“城堡文化艺术展”将于5月26日在北京时间9:00开幕,那么实况转播开幕式从法国巴黎时间 开始.12.如图,AB 是⊙O 的切线,OB =2OA ,则∠B 的度数是__________.13.为测量校园平地上一棵大树的高度,学校数学兴趣小组做了如下的探索.他们根据光的反射原理,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面镜子放在离树底B 有9米的点E 处,然后沿着直线BE 后退到点D ,这时恰好在镜子里看到树梢顶点A ,再用皮尺量得DE =0.9米,若观察者目高CD =1.65米,则树的高度AB 约为________米.14.为了迎接国家普及九年级义务教育验收,某学校对家长进行了教育教学工作满意度地调查,随机调查了25名家长,调查的结果如右表.根据表中给出的信息,请你估计一下本校800名家长中对学校教育教学工作不.满意的有 人. 15.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成.依此规律,第n个图案中白色正方形的个数为 .…第1个第2个第3个第15题图A B O第12题图第13题图2007年初中毕业学业考试数学训练题(一)第Ⅱ卷 (解答题 共75分)一、选择题答题栏.(请将第Ⅰ卷中选择题的答案填写在下表中)二、填空题答题栏.(请将第Ⅰ卷中填空题的答案填写在下表中)三、解答题.(本大题共4小题,每小题6分,共24分) 16.先化简(1+1x -1)÷xx 2-1,再选择一个恰当的x 的值代入并求值.17.如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O .(1)用尺规作出OC 、OB 中点,分别为E 、F (保留作图痕迹,不写作法与证明); (2)连结AE 、DF ,求证AE=DF .18.2007年3月12日植树节,某中学教师参加义务植树活动,准备种植一批树苗.活动采用分工负责制,若每位教师种植10棵树苗,则还剩88棵;若每位教师种植12棵树苗,则有—名教师种植的树种苗不到4棵,求准备种植树苗的棵数与参加植树的教师人数.ABOCD第17题图19.如图,电路图上有A 、B 、C 、D 四个开关和一个小灯泡,闭合开关D 或同时闭合开关A 、B 、C 都可使小灯泡发光.(1)任意闭合其中一个开关,则小灯泡发光的概率等于 ;(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.四、解答题.(本大题共3小题,每小题7分,共21分)20.如图,已知△ABC 内接于⊙O ,点D 在OC 的延长线上,∠B=∠D=30°.(1)AD 是⊙O 的切线吗?说明理由; (2)若OD ⊥AB ,BC =5,求AD 的长.O 第20题图●B CDA第19题图21.心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x (分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分).(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知——自主探索,合作交流——总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不底于40.请问这样的课堂学习安排是否合理?并说明理由.22.如图,是学校背后山坡上一棵原航空标志的古柏树AB的示意图,在一个晴天里,数学教师带领学生进行测量树高的活动.通过分组活动,得到以下数据:一是测得太阳光线AC与垂线AB的夹角∠CAB为150;二是测得树在斜坡上影子BC的长为10m;三是测得影子BC与水平线的夹角∠BCD为300;请你帮助计算出树的高度AB (精确到0.1m).第23题图五、解答题.(本大题共3小题,每小题10分,共30分)23.如图,在△ABC 中,AB =4,AC =6,D 是BC 上的一个动点,过D 作DE ∥AC 交AB 于E ,DF ∥AB 交AC 于F .(1)△BDE 和△DCF 有怎样特殊的关系,为什么? (2)当D 运动到什么位置时,四边形AEDF 是菱形;(3)存在长与宽的比为2:1的矩形AEDF 吗?若不存在,说明理由;若存在,求出其面积.AB C FD E 第23题图24.在农村合作医疗卫生体系建设中,国家每年安排2亿元资金用于医疗系统设备更新.2006年初我国有7.46亿农村人口,其中参加农村合作医疗试点的人数为4.1亿,国家按照人均10元标准补助给农民所在的医疗机构,这样使农村合作医疗试点范围在年底达到1451个县(市、区),占全国总数的50.7%;2007年国家加大资金投入,预算投入的总资金比2006年投入总资金的2倍还多14.4亿元,使参加农村合作医疗人数的增长率比农民的人均补助标准年增长率多10个百分点,参加农村合作医疗的人数达到当年全部农村人口的87.5 %,试点县(市、区)扩大到80%.(1)2007年将有多少个县(市、区)参加农村合作医疗试点?(2)2007年参加农村合作医疗试点的人数比2006年增长了百分之几?(3)若农村人口自然增长率及国家给农民的人均医疗补助的增长率不变,那么到2008年解决全部农村人口的合作医疗问题国家财政应支出多少亿元?(结果保留整数)25.如图,已知矩形ABCO在坐标系的第一象限,它的长AO是宽OC的3倍,且有两边在坐标轴上.将△ACO沿对角线AC翻折得△ACP,P点落在经过矩形ABCO四个顶点的⊙E上,⊙E 的半径为R.(1)用R的式子表示点B的坐标;(2)若抛物线y=ax2+3x+c经过P、A两点,请你判断点C是否在此抛物线上;(3)若(2)中的抛物线的顶点为Q,该抛物线与x轴的另一个交点为M,那么直线OB将△AMQ 的面积分为两个部分的比值k是否是一个定值?如果不是,请说明理由;如果是,请求出其比值k.第25题图。
2008年山东省青岛市初级中学学业水平考试

2008年山东省青岛市初级中学学业水平考试历史试题第一卷(共60分)一、单项选择题1每个民族都有自己的传说时代。
他是我国传说时代的一位代表人物,在他的身上集中了古人的各种优点、诸多创造,他带领中华民族从野蛮走向文明,被后人尊称为“人文初祖”。
他是()A黄帝 B 尧 C 舜 D 启3、“泰山不让砾石故能成其大,汪海不辞小流固能成其深”。
在用人问题上,只有树立正确的人才观,以宏阔的胸襟接待天下之士,才能发现成就伟业的有用人才。
春秋时期,齐桓公发现的有用人才是()A 伊尹 B 管仲 C 伍子胥 D 商鞅5、我们生活的齐鲁大地是思想家的摇篮。
在中国古代思想史上,大师级的人物层次不穷,涌现出孔子、孟子、墨子等春秋战国时期独领风骚的伟大思想家。
孔子的思想精华是对世界文明的贡献,也为现代精神文明建设提供了充分的养分。
以下属于孔子思想观点的是()A仁B法治C兼爱、非攻 D 无为而治6、随着世界中医热潮的不断兴起,中医被越来越多的海内外人士所尊崇。
医圣祠作为一座历史的丰碑,铭刻着人类与自然疾病作斗争的拼搏精神。
医圣张仲景的医学思想已成为加强中国同世界各国联系的桥梁。
张仲景的著作是()A 《伤寒杂病论》B 《唐本草》C 《千金方》D 《本草纲目》8、“海内存知己,天涯若比邻”。
在日本的唐招提寺内,有一座和尚坐像,被日本人民视为国宝。
他是中日两国人民友好往来的历史见证。
2008年5月,中共中央总书记胡锦涛出访日本,并亲临唐招提寺,你知道寺内的和尚是谁吗?()A 晁衡B玄奘C鉴真D僧一行10、有人说他是“世界征服者”;有人说他是“千年风云第一人”;有人则说他是世界历史上取得最伟大成功的人物,他开创了有史以来版图最大的帝国,对人类社会的发展产生过巨大的影响。
他就是“一代天骄”()A阿保机B阿骨打C成吉思汗 D 忽必烈13、“粤海硝烟扬我威,但悲港岛易英徽。
百年国耻今昭雪,只缘华夏已腾飞”。
这是我国著名外交官凌青的一首诗。
青岛市初级中学学业水平考试数学试题(课标版,含答案)

数学试题(课标版)(考试时间:120分钟 满分:120分)一 •选择题(本题满分 21分,共有7道小题,每小题3分) 下列每小题都给出标号为 A 、B 、C 、D 的四个结论, 得分;不选、选错或选出的标号超过一个的不得分.1 • 2的算术平方根是( 6.如图,在△ ABC 中,BC = 4,以点A 为圆心、2为半径的O A 与BC 相切于点D ,交 AB 于E ,交AC 于F ,点P 是O A 上的一点,且/ EPF = 40°,则图中阴影部分的面积是 ()•48^48A • 4— nB • 4— nC • 8 — nD . 8— n99997 •某商店的老板销售一种商品,他要以不低于进价20%的价格才能出售,但为了获得更多利润,他以高出进价 80%的价格标价.若你想买下标价为360元的这种商品,最多降价(),商店老板才能出售.其中只有一个是正确的•每小题选对 A • 、.2 B • -2 C • ± .2 D . 22 •右边几何体的主视图是(A .B .3. 某课外兴趣小组为了解所在地区老年人的健康状况, 认为抽样比较合理的是()•A .在公园调查了 1000名老年人的健康状况B .在医院调查了 1000名老年人的健康状况C .调查了 10名老年邻居的健康状况D .利用派出所的户籍网随机调查了该地区 10%的老年人的健康状况4. 点P 1 (X 1, y 1),点P 2 (X 2, y 2)是一次函数 y = — 4x + 3图象上的两个点,且 X 1< X 2, 则y 1与y 2的大小关系是( )•A . y 1 > y 2B . y 1 > y 2 > 0C • y 1< y 25. 已知△ ABC 在直角坐标系中的位置如图所示,如果△ 那么点A 的对应点A'的坐标为().A . (— 4, 2)B . ( — 4, — 2)C . (4, — 2)分别作了四种不同的抽样调查.你D • y i = y 2A'B'C'与厶ABC 关于y 轴对称,)•)D • (4, 2) 6题图炉A . 80 元B . 100 元C . 120 元二.填空题(本题满分 21分,共有7道小题,每小题 &如图,O O 的直径 AB = 8cm , C 为0 O 上的一点,9 .分解因式: 4 a 3 — 4 a 2 + a = ________ .10.如图,在△ ABC 中,AB = AC ,/ A = 50°, BD 为/ ABC 的平分线,则/ BDC =三.作图题(本题满分 6分) 用圆规、直尺作图,不写作法,但要保留作图痕迹.15. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面 的半径,下图是水平放置的破裂管道有水部分的截面.(1) 请你补全这个输水管道的圆形截面; (2) 若这个输水管道有水部分的水面宽 圆形截面的半径.D . 160元3分)/ BAC = 30°,贝U BC =I (A )与可变电阻 R (Q)之间的 函数关系如图所示,当用电器的电流为10A 时,用电器的可变电阻为 _________ Q .12.一个口袋中有12个白球和若干个黑球, 在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程5次,得到的白球数与 10的比值分别为:0.4, 0.1, 0.2, 0.1 , 0.2.根据上述数据,小亮可估计口袋中大约有 ____________ 个黑球.13.如图,P 是正三角形 ABC 内的一点,且 PA = 6, PB = 8,■'PC = 10.若将△ PAC 绕点A 逆时针旋转后,得到△ P'AB ,贝U 点P 与点P'之间的距离为 , / APB = °14.如图,下列几何体是由棱长为 1的小立方体按 一定规律在地面上摆成的,若将露出的表面都涂上颜色 (底面不涂色),则第n 个几何体中只有两个面小立方体共有 个.图①*图②屮涂色的图③2四•解答题(本题满分72分,共有9道小题)16. (本小题满分6分)2 -X 1解分式方程: ---- ——=1。
山东省青岛市初级中学学业水平考试数学试题、答案(word)

山东省青岛市初级中学学业水平考试数学试题(考试时间:120 分钟;满分:120 分)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!1.请务必在指定地点填写座号,并将密封线内的项目填写清楚.2.本试题共有24 道题.此中1- 8 题为选择题.请将所选答案的标号填写在第8 题后边给出表格的相应地点上;9- 14 题为填空题,请将做出的答案填写在第14 题后边给出表格的相应地点上;15- 24 题请在试题给出的此题地点上做答.一、选择题(此题满分24 分,共有8 道小题,每题 3 分)以下每题都给出标号为A、 B、 C、 D 的四个结论,此中只有一个是正确的.每题选对得分;不选、选错或选出的标号超出一个的不得分.请将1- 8 各小题所选答案的标号填写在第 8 小题后边给出表格的相应地点上.1.以下四个数中,其相反数是正整数的是()A . 31C.21 B.D.3 22.以下图的几何体是由一些小立方块搭成的,则这个几何体的俯视图是()A .B.C. D .第 2题图3.在等边三角形、平行四边形、矩形、等腰梯形和圆中,既是轴对称图形又是中心对称图形的有()A.1 种B.2 种C.3种D.4 种4.在一个不透明的袋子里装有两个红球和两个黄球,它们除颜色外都同样.随机从中摸出一球,记下颜色后放回袋中,充足摇匀后,再随机摸出一球,两次都摸到黄球的概率是()1B.1 1 1A .3 C.D.2 4 65.以下图,数轴上点P 所表示的可能是()A . 6 B.10 C.15 D.31PO1 0 123 4第 5题图第6题图6.一根水平搁置的圆柱形输水管道横截面以下图,此中有水部分水面宽0.8 米,最深处水深 0.2 米,则此输水管道的直径是()A.0.4 米B.0.5 米C. 0.8 米D.1 米7.一块蓄电池的电压为定值,使用此蓄电池为电源时,电流I (A )与电阻 R (Ω)之间 的函数关系以下图, 假如以此蓄电池为电源的用电器限制电流不得超出10A ,那么此用电 器的可变电阻应( )A .不小于 4.8ΩB .不大于 4.8ΩC .不小于 14ΩD .不大于 14ΩI /AyA6O8 R/ΩOx第7题图第8题图8.一艘轮船从港口 O 出发,以 15 海里 /时的速度沿北偏东 60°的方向航行 4 小时后到达 A处,此时观察到其正西方向 50 海里处有一座小岛 B .若以港口 O 为坐标原点, 正东方向为 x 轴的正方向, 正北方向为 y 轴的正方向, 1 海里为 1 个单位长度成立平面直角坐标系 (如图),则小岛 B 所在地点的坐标是( )A . (303 50,30) B . (30,30 3 50) C . (30 3,30) D . (30,30 3)二、填空题(此题满分 18 分,共有 6 道小题,每题3 分)请将 9- 14 各小题的答案填写在第 14 小题后边给出表格的相应地点上9.我国首个火星探测器“萤火一号”已经过研制阶段的查核和考证,并将于今年下半年发射升空, 估计历经约 10 个月,行程约 380 000 000 公里到达火星轨道并定位. 将 380 000 000 公里用科学记数法可表示为公里.10.在第 29 届奥林匹克运动会上,青岛姑娘张娟娟为中国代表团夺得了历史上首枚奥运会射箭金牌,为祖国争得了荣誉. 下表记录了她在备战奥运会时期的一次训练成绩 (单位:环): 序号1 2 3 4 5 6 7 8 9 10 11 12 成绩9910981010987109依据表中的数据可得: 张娟娟此次训练成绩的中位数是环,众数是环.11.如图, AB 为 ⊙O 的直径, CD 为 ⊙O 的弦,ACD 42°,则 BAD °.12.某公司 2006 年的产值为 500 万元, 2008 年的产值为 720 万元,则该公司产值的年均匀 增添率为 . 13.如图.边长为1 的两个正方形相互重合,按住此中一个不动,将另一个绕极点A 顺时针旋转45°.,则这两个正方形重叠部分的面积是DDC BDE6cmABAB COCA1cmB3cm第 11题图第 13题图第 14题图14.如图,长方体的底面边长分别为 1cm 和 3cm ,高为 6cm .假如用一根细线从点 A 开始经过 4 个侧面环绕一圈到达点 B ,那么所用细线最短需要 cm ;假如从点 A 开始经过 4 个侧面环绕 n 圈到达点 B ,那么所用细线最短需要cm .三、作图题(此题满分 4 分)用圆规、直尺作图,不写作法,但要保存作图印迹.15.为美化校园,学校准备在以下图的三角形(△ ABC)空地上修筑一个面积最大的圆形花坛,请在图中画出这个圆形花坛.解:AB C结论:四、解答题(此题满分74 分,共有9 道小题)16.(本小题满分8 分,每题4 分)(1)化简:x 1x2 1 ( 2)解不等式组:x x23x 2 x 2,11≤ 73x x.2 217.(本小题满分 6 分)某中学为认识该校学生的课余活动状况,采纳抽样检查的方式,从运动、娱乐、阅读和其余四个方面检查了若干名学生的兴趣喜好状况,并依据检查结果制作了以下两幅统计图.人数/人5040 其余40阅读30 25 运动20 15 娱乐10 40%运动娱乐阅读其余项目人数统计图散布统计图依据图中供给的信息解答以下问题:(1)补全人数统计图;(2)若该校共有 1500 名学生,请你估计该校在课余时间喜爱阅读的人数;(3)联合上述信息,说说你对该校学生课余活动的建议和建议(字数不超出30 字).在“六·一”小孩节到临之际,某妇女小孩用品商场为吸引顾客,建立了一个能够自由转动 的转盘(如图,转盘被均匀分红20 份),并规定:顾客每购物满100 元,就能获取一次转动转盘的时机.假如转盘停止后,指针正好瞄准红色、黄色、绿色地区,那么顾客就能够分别获取 80 元、 50 元、 20 元的购物券,凭购物券能够在该商场持续购物.假如顾客不肯意转转盘,那么可直接获取15元的购物券.转转盘和直接获取购物券,你以为哪一种方式对顾客更合算?请说明原因.红 黄绿绿 绿黄绿黄绿第 18题图19.(本小题满分 6 分)在一次数学活动课上,老师率领同学们去丈量一座古塔 CD 的高度.他们第一从 A 处布置测倾器, 测得塔顶 C 的仰角CFE21°50 米到达 B 处,此时测得仰,而后往塔的方向行进 角 CGE37°1.5 米,请你依据以上数据计算出古塔CD 的高度.,已知测倾器高 (参照数据: °≈ 3 ,°≈ 3 , °≈ 9 , °≈ 3 )sin 37 tan37 sin21 tan2154 25 8 CFGEABD第 19题图20.(本小题满分 8 分)北京奥运会开幕前, 某体育用品商场展望某品牌运动服能够热销, 就用 32000 元购进了一批这类运动服, 上市后很快畅销, 商场又用 68000 元购进第二批这类运动服, 所购数目是第一批购进数目的 2 倍,但每套进价多了10元. (1)该商场两次共购进这类运动服多少套?(2)假如这两批运动服每套的售价同样,且所有售完后总收益率不低于 20%,那么每套售价起码是多少元?(收益率收益 100% )成本已知:如图,在ABCD 中,AE是BC边上的高,将△ ABE 沿 BC 方向平移,使点 E 与点 C 重合,得△GFC.(1)求证:BEDG;(2)若B ,当 AB 与 BC 知足什么数目关系时,四边形ABFG 是菱形?证明你的60°结论.A GDB E F C第21题图22.(本小题满分10 分)某水产品养殖公司为指导该公司某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了检查.检查发现这类水产品的每千克售价y1(元)与销售月份 x (月)知足关系式 y 3x 36 ,而其每千克成本y2(元)与销售月份 x(月)知足的函数关系以下图.8(1)试确立b、c的值;y (元)与销售月份x(月)之间的函数关系式;(2)求出这类水产品每千克的收益(3)“五·一”以前,几月份销售这类水产品每千克的收益最大?最大收益是多少?y2(元)y2 1x2 bx c 82524O 1 2 3 4 5 6 7 8 910 11 12 x(月)第22题图23.(本小题满分10 分)我们在解决数学识题时,常常采纳“转变”(或“化归”)的思想方法,把待解决的问题,经过某种转变过程,归纳到一类已解决或比较简单解决的问题.比如,在学习了一元一次方程的解法此后,进一步研究二元一次方程组的解法时,我们往常采纳“消元”的方法,把二元一次方程组转变为一元一次方程;再比如,在学习了三角形内角和定理此后,进一步研究多边形的内角和问题时,我们往常借助增添协助线,把多边形转变为三角形,进而解决问题.问题提出:怎样把一个正方形切割成n (n≥9)个小正方形?为解决上边问题,我们先来研究两种简单的“基本切割法”.基本切割法1:如图①,把一个正方形切割成 4 个小正方形,即在本来 1 个正方形的基础上增添了 3 个正方形.基本切割法2:如图②,把一个正方形切割成 6 个小正方形,即在本来 1 个正方形的基础上增添了 5 个正方形.图①图②图③图④图⑤图⑥问题解决:有了上述两种“基本切割法”后,我们就能够把一个正方形切割成n (n≥9 )个小正方形.(1)把一个正方形切割成9 个小正方形.一种方法:如图③,把图①中的随意 1 个小正方形按“基本切割法2”进行切割,便可增添5 个小正方形,进而切割成 4 5 9(个)小正方形.另一种方法:如图④,把图②中的随意 1 个小正方形按“基本切割法1”进行切割,便可增加 3 个小正方形,进而切割成 6 3 9 (个)小正方形.(2)把一个正方形切割成10 个小正方形.方法:如图⑤,把图①中的随意 2 个小正方形按“基本切割法 1”进行切割,便可增添 3 2 个小正方形,进而切割成 4 3 2 10 (个)小正方形.(3)请你参照上述切割方法,把图⑥给出的正方形切割成 11 个小正方形(用钢笔或圆珠笔划出草图即可,不用说明切割方法)(4)把一个正方形切割成n(n≥9)个小正方形.方法:经过“基本切割法 1”、“基本切割法 2”或其组合把一个正方形切割成9 个、10 个和 11 个小正方形,再在此基础上每使用 1 次“基本切割法 1”,便可增添 3 个小正方形,进而把一个正方形切割成 12 个、 13 个、 14 个小正方形,挨次类推,即可把一个正方形切割成 n (n≥9)个小正方形.从上边的分法能够看出,解决问题的重点就是找到两种基本切割法,而后经过这两种基安分割法或其组合把正方形切割成n (n≥9)个小正方形.类比应用:模仿上边的方法,我们能够把一个正三角形切割成n (n≥9)个小正三角形.(1)基本切割法1:把一个正三角形切割成 4 个小正三角形(请你在图 a 中画出草图).(2)基本切割法 2:把一个正三角形切割成 6 个小正三角形(请你在图 b 中画出草图).(3)分别把图 c、图 d 和图 e 中的正三角形切割成 9 个、 10 个和 11 个小正三角形(用钢笔或圆珠笔划出草图即可,不用说明切割方法)图 a图b图c图d图 e(4)请你写出把一个正三角形切割成n(n≥9)个小正三角形的切割方法(只写出切割方法,不用绘图).24.(本小题满分 12 分)如图,在梯形 ABCD 中,AD∥BC,AD 6cm,CD 4cm , BC BD 10cm ,点 P 由 B 出发沿 BD 方向匀速运动,速度为 1cm/s;同时,线段 EF 由 DC 出发沿DA 方向匀速运动,速度为 1cm/s,交BD于 Q,连结 PE .若设运动时间为t (s)( 0 t 5 ).解答以下问题:(1)当t为什么值时,PE∥AB?(2)设△PEQ的面积为y( cm2),求y与t之间的函数关系式;( 3)能否存在某一时辰t,使△2 △?若存在,求出此时t的值;若不存在,SPEQ 25 S BCD说明原因.(4)连结PF,在上述运动过程中,五边形PFCDE 的面积能否发生变化?说明原因.A E DQPB CF第 24题图山东省青岛市初级中学学业水平考试数学试题参照答案及评分标准说明:1.假如考生的解法与本解法不一样,可参照本评分标准拟订相应评分细则.2.当考生的解答在某一步出现错误,影响了后继部分时,假如这一步此后的解答未改变这道题的内容和难度,可视影响程度决定后边部分的给分.但不得超事后边部分应给分数的一半,假如这一步此后的解答有较严重的错误,就不给分.3.为阅卷方便,本解答中的计算步骤写得较为详尽,但同意考生在解答过程中,合理省略非重点性的计算步骤.4.解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(此题满分24 分,共有8 道小题,每题 3 分)题号 1 2 3 4 5 6 7 8答案 C D B C B D A A 二、填空题(此题满分18 分,共有 6 道小题,每题 3 分)题号9 10 11答案 3.8 108 9 9 48题号12 13 14答案20% 2 1 10 2 9 16n2(或36 64n2)三、作图题(此题满分 4 分)15.正确画出两条角均分线,确立圆心;······························2 分确立半径;················································3 分正确画出图并写出结论.······································4分四、解答题(此题满分74 分,共有9 道小题)16.(本小题满分8 分)x 1 x2(1)解:原式x (x 1)(x 1)x .········································4 分x 13x 2 x 2 ①(2)1 ≤7 3 ②x 1 x2 2解:解不等式①得x 2 ,解不等式②得x ≤ 4 .因此原不等式组的解集为2 x ≤ 4 .·······························4分17.(本小题满分 6 分)解:( 1)正确补全统计图;·······································2 分(2) 300 人. ···············································4 分(3)合理即可. ·············································6 分18.(本小题满分 6 分)解: 80 1 50 3 205 16.5(元), ························4 分 20 20 20∵ 16.5元 5元∴选择转转盘对顾客更合算.······································6 分19.(本小题满分 6 分)解:由题意知 CD ⊥ AD , EF ∥ AD ,C∴CEF 90°,设 CE x ,在 Rt △CEF 中,tan CFE CE ,则 EFCEx 8x ;EF tan CFEtan21° 3在 Rt △CEG 中,FGEtan CGE CE,GEA B则 GECE xD4 x ; ········4 分第 19 题图tan CGE tan37° 3∵ EF FG EG ,∴8x 50 4x . 3 3x 37. 5,∴ CD CE ED 37.5 1.5 39 (米).答:古塔的高度约是 39 米. ·······································6 分 20.(本小题满分 8 分)解:( 1)设商场第一次购进x 套运动服,由题意得:68000 32000 10, ··········································3 分2xx解这个方程,得 x 200 .经查验, x 200 是所列方程的根. 2x x 2 200 200 600 . 因此商场两次共购进这类运动服 600 套. ······························5 分 (2)设每套运动服的售价为y 元,由题意得:600y32000 68000≥ 20% , 32000 68000解这个不等式,得 y ≥ 200 , 因此每套运动服的售价起码是200 元. ································8 分21.(本小题满分 8 分)证明:( 1)∵四边形 ABCD 是平行四边形, ∴ AB CD .∵ AE 是 BC 边上的高,且 CG 是由 AE 沿 BC 方向平移而成. ∴ CG ⊥ AD .∴ AEBCGD 90°.∵ AE CG ,∴ Rt △ ABE ≌ Rt △CDG .∴ BE DG . ···············································4 分(2)当 BC 3AB 时,四边形 ABFC 是菱形.2∵ AB ∥GF , AG ∥ BF ,∴四边形 ABFG 是平行四边形. AG∵ Rt △ ABE中,B 60°D,∴BAE 30°,∴ BE1AB .2 BC∵ BECF ,BCEF 3AB ,2第 21题图∴ EF 1AB .2∴ AB BF .∴四边形 ABFG 是菱形.······································8 分22.(本小题满分 10 分) 解:( 1)由题意:25 1 32 3b c8 24 1 42 4b c8b17解得8················································4 分c1292(2) yy 1 y 23x 3 61 x2 1 5x 2 9 1 88821 23 1xx6 ; ······································6 分8 22(3) y1 x 23 x 6 182 21( x 212x36) 4 1 6 18 221(x 6 2) 1 18∵ a1,8∴抛物线张口向下.在对称轴 x6 左边 y 随 x 的增大而增大.由题意 x 5 ,因此在 4 月份销售这类水产品每千克的收益最大.··············9 分最大收益1(4 6)211 10182(元). ······························10 分23.(本小满分 10 分) 解:把一个正方形切割成11 个小正方形:图⑥ (2)分把一个正三角形切割成 4 个小正三角形:图 a·······························3 分把一个正三角形切割成6 个小正三角形:图 b ································5 分把一个正三角形切割成 9 个、 10 个和 11 个小正三角形:图 c图 d 图 e····················8 分把一个正三角形切割成 n ( n ≥ 9 )个小正三角形的切割方法: 经过“基本切割法 1”、“基 本切割法 2”或其组合,把一个正三角形切割成 9 个、 10 个和 11 个小正三角形,再在此基 础上每使用 1 次“基本切割法 1”,便可增添3 个小正三角形,进而把一个正三角形切割成12 个、 13 个、 14 个小正三角形,挨次类推,即可把一个正三角形切割成 n ( n ≥ 9 )个小正三角形. ··················································10 分24.(本小题满分 12 分) 解:( 1)∵ PE ∥ AB∴ DE DP .AEDDA DB而 DE t ,DP 10 t ,Q∴t 10 tPN M6,10BFC15∴ t .4 ∴当 t15(s), PE ∥ AB . ··········2 分4( 2)∵ EF 平行且等于 CD ,∴四边形 CDEF 是平行四边形.∴DEQ C , DQE BDC .∵ BC BD 10,∴ DEQCDQEBDC . ∴△DEQ ∽△ BCD . ∴ DEEQ .BC CD t EQ10.4∴ EQ2t .5 过B 作BM ⊥CD ,交CD 于M ,过 P 作PN ⊥EF ,交 EF 于N .BM10222100496 4 6 .∵ EDDQBP t ,∴ PQ 10 2t .又△PNQ ∽△BMD ,PQ PN ,BD BM10 2tPN ,104 6PN4 6 1t5S △ PEQ1EQ PN1 2 t 4 6 1 t 4 6 t 2 4 6t . ··············6 分2 2 55 25 5(3) S △ BCD 1 1 4 6 8 6 .CD BM 42 2 2 若S △ PEQ S △ BCD , 25则有4 6 t 2 4 6 t 28 6 ,25525解得 t 1 1, t 2 4 . ·············································9 分(4)在△PDE和△FBP中,DE BP t,PD BF 10 t,△ PDE ≌△ FBP PDE FBP ,∴S五边形PFCDE S△PDE S四边形 PFCDS△FBP S四边形PFCDS△ BCD 8 6 .∴在运动过程中,五边形PFCDE 的面积不变.························12 分。
2008青岛中考数学及答案.
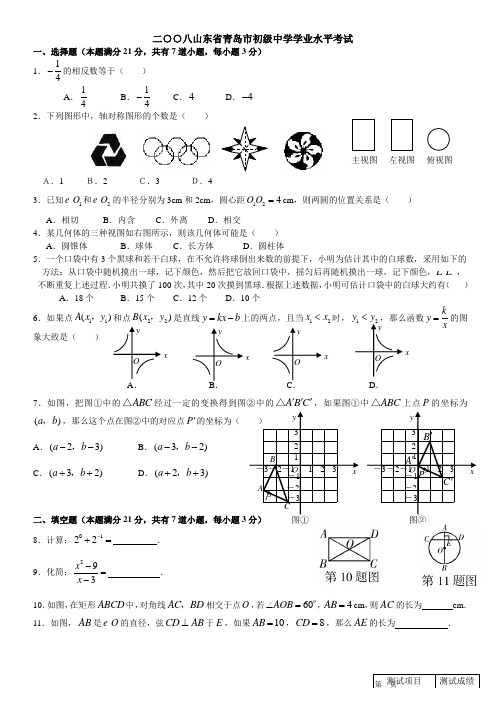
二○○八山东省青岛市初级中学学业水平考试一、选择题(本题满分21分,共有7道小题,每小题3分)1.14-的相反数等于( ) A .14 B .14-C .4D .4-2.下列图形中,轴对称图形的个数是( )A.1 B.2 C.3 D.43.已知1O 和2O 的半径分别为3cm 和2cm ,圆心距124O O =cm ,则两圆的位置关系是( )A .相切B .内含C .外离D .相交4.某几何体的三种视图如右图所示,则该几何体可能是( ) A .圆锥体 B .球体 C .长方体D .圆柱体5.一个口袋中有3个黑球和若干白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用如下的 方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色, , 不断重复上述过程.小明共摸了100次,其中20次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( ) A .18个 B .15个 C .12个 D .10个 6.如果点11()A x y ,和点22()B x y ,是直线y kx b =-上的两点,且当12x x <时,12y y <,那么函数ky x =的图象大致是( )7.如图,把图①中的ABC △经过一定的变换得到图②中的A B C '''△,如果图①中ABC △上点P 的坐标为()a b ,,那么这个点在图②中的对应点P '的坐标为( )A .(23)a b --,B .(32)a b --,C .(32)a b ++,D .(23)a b ++,二、填空题(本题满分21分,共有7道小题,每小题3分) 8.计算:0122-+= .9.化简:293x x -=- .10.如图,在矩形ABCD 中,对角线AC BD ,相交于点O ,若60AOB ∠=,4AB =cm ,则AC 的长为 cm . 11.如图,AB 是O 的直径,弦CD AB ⊥于E ,如果10AB =,8CD =,那么AE 的长为 .主视图 左视图 俯视图y x O yx O y x O y x O A . B . C . D .32 1 -1 O -2 -3-3 -2 -1 1 2 3x y 图①32 1-1 O -2 -3-3 -2 -1 1 2 3xy 图②P ABCA 'B 'C 'P '12.为了帮助四川地震灾区重建家园,某学校号召师生自愿捐款.第一次捐款总额为20000元,第二次捐款总额为 56000元,已知第二次捐款人数是第一次的2倍,而且人均捐款额比第一次多20元.求第一次捐款的人数是多少?若设第一次捐款的人数为x ,则根据题意可列方程为 .13.某市广播电视局欲招聘播音员一名,对A B ,两名候选人进行了两项素质测试,两 人的两项测试成绩如右表所示.根据实际需要,广播电视局将面试、综合知识测试 的得分按3:2的比例计算两人的总成绩,那么 (填A 或B )将被录用.14.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF 长为10cm .母线()OE OF 长为10cm .在母线OF 上的点A 处有一块爆米花残渣,且2FA =cm ,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点.则此蚂蚁爬行的最短距离为 cm .三、作图题(本题满分6分)(用圆规、直尺作图,不写作法,但要保留作图痕迹)15.如图,AB AC ,表示两条相交的公路,现要在BAC ∠的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处A 点的距离为1000米.(1)若要以1:50000的比例尺画设计图,求物流中心到公路交叉处A 点的图上距离; (2)在图中画出物流中心的位置P .四、解答题(本题满分72分,共有9道小题) 16.(本小题满分6分) 用配方法解一元二次方程:2220x x --=.17.(本小题满分6分)某市为调查学生的视力变化情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下: 解答下列问题:(1)该市共抽取了多少名九年级学生?(2)若该市共有8万名九年级学生,请你估计该市九年级视力不良(4.9以下)的学生大约有多少人? (3)根据统计图提供的信息,谈谈自己的感想(不超过30字).18.(本小题满分6分)小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?A B面试90 95 综合知识测试 85 80AFEO第14题图A CB1cm人数 时间(年) 800 5003002006 2007 2008 被抽取学生视力在4.9以下 的人数变化情况统计图 A 40% B30%C 20%D 10% A :4.9以下B :4.9-5.1C :5.1-5.2D :5.2以上 (每组数据只含最低值不含最高值) 被抽取学生2008年的视 力分布情况统计图 红 黄 蓝 红白蓝19.(本小题满分6分)在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图 如图所示,其中,AB 表示窗户,且2AB =米,BCD 表示直角遮阳蓬,已知当地一 年中在午时的太阳光与水平线CD 的最小夹角α为18.6,最大夹角β为64.5.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD 的长是多少米?(结果保留两个 有效数字)(参考数据:sin18.60.32=,tan18.60.34=,sin 64.50.90=,tan 64.5 2.1=)20.(本小题满分8分)2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A 种船票600元/张,B 种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A ,B 两种船票共15张,要求A 种船票的数量不少于B 种船票数量的一半.若设购买A 种船票x 张,请你解答下列问题: (1)共有几种符合题意的购票方案?写出解答过程; (2)根据计算判断:哪种购票方案更省钱?21.(本小题满分8分) 已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE CG =, 连接BG 并延长交DE 于F . (1)求证:BCG DCE △≌△;(2)将DCE △绕点D 顺时针旋转90得到DAE '△,判断四边形E BGD '是什么特殊四边形?并说明理由. 22.(本小题满分10分)某服装公司试销一种成本为每件50元的T 恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y (件)与销售单价x (元)的关系可以近似的看作一次函数(如图). (1)求y 与x 之间的函数关系式;(2)设公司获得的总利润(总利润=总销售额-总成本)为P 元,求P 与x 之间的函数关系式,并写出自变量x 的取值范围;根据题意判断:当x 取何值时,P 的值最大?最大值是多少? 23.(本小题满分10分)实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生? 建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型: 在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球? 为了找到解决问题的办法,我们可把上述问题简单化: (1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球? 假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:134+=(如图①); (2)若要确保从口袋中摸出的小球至少有3个是同色的呢?我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是:1327+⨯=(如图②)(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?ADCBβα400 30060 70 O y (件)x (元) A B CD EF E 'G我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是:13310+⨯=(如图③):(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:13(101)28+⨯-=(如图⑩)模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ; (2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ; (3)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是 . 模型拓展二:在不透明口袋中装有m 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球: (1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 . (2)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是 . 问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型; (2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生. 24.(本小题满分12分)已知:如图①,在Rt ACB △中,90C ∠=,4cm AC =,3cm BC =,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为(s)t (02t <<),解答下列问题: (1)当t 为何值时,PQ BC ∥?(2)设AQP △的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使线段PQ 恰好把Rt ACB △的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把PQC △沿QC 翻折,得到四边形PQP C ',那么是否存在某一时刻t ,使四边形PQP C '为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.红黄 红 红或黄或白图② 黄白 白红 黄 白红或黄或白 图红红 红或黄或白图③ 红白 白 白黄黄黄红 红红或黄或白图⑩红白 白 白 黄 黄黄白… 红黄9个 9个9个 ...A Q C PB 图①AQCPB 图②二○○八年山东省青岛市初级中学学业水平考试一、选择题(本题满分21分,共有7道小题,每小题3分)题号 1 2 3 4 5 6 7 答案ABDDCBC二、填空题(本题满分21分,共有7道小题,每小题3分) 题号 89 10 11 1213 14答案23 x +3822020000256000=-xx B 412三、作图题(本题满分6分)15.解:(1)1000米=100000厘米,100000÷50000=2(厘米);2′ (2) 略6′ 四、解答题(本题满分72分,共有9道小题)16.(本小题满分6分)311+=x , 312-=x . 6′17.(本小题满分6分)解:(1)800÷40% = 2000(人)2′(2)80000×40% = 32000(人);4′(3)合理即可 6′ 18.(本小题满分6分)解:2′ ∴P (配成紫色)=92,P (配不成紫色)=97.∴小刚得分:92192=⨯, 小明得分:97197=⨯,∵ 9792≠ , ∴游戏对双方不公平. 4修改规则的方法不惟一.(如改为:若配成紫色时小刚得7分,否则小明得2分.)6′ 19.(本小题满分6分)解:设CD 为x ,在Rt △BCD 中, 6.18==∠αBDC , ∵CDBCBDC =∠tan ,∴x BDC CD BC 34.0tan =∠⋅=.2′在Rt △ACD中, 5.64==∠βADC , ∵CDACADC =∠tan ,∴x ADC CD AC 1.2tan =∠⋅= 4′ ∵BC AC AB -=,∴x x 34.01.22-=. 5 1.14x ≈答:CD 长约为1.14米. 6′ 20.(本小题满分8分)解:(1)设A 种票x 张,则B 种票)15(x -张,根据题意得:152600120(15)5000x x x x -⎧⎪⎨⎪+-⎩≥,≤ 3′解得: 5≤x ≤320.∴满足条件的x 为5或6. ∴共有两种购买方案:方案一:A 种票5张, B 种票10张, 方案二:A 种票6张, B 种票9张. 6′ (2)方案一购票费用: 600×5+120×10=4200(元),方案二购票费用: 600×6+120×9=4680(元),∵4200<4680,∴ 方案一更省钱. ·················· 8′21.(本小题满分8分) 证明:(1) ∵四边形ABCD 是正方形,∴BC=CD ,∠BCD=90°.∵∠BCD +∠DCE=180°,∴∠BCD=∠DCE=90°.又∵CG=CE ,∴△BCG ≌△DCE . 4′(2)∵△DCE 绕D 顺时针旋转90︒得到△DAE ′, ∴CE=AE ′.∵CE=CG ,∴CG=AE ′.∵四边形ABCD 是正方形,∴BE ′∥DG ,AB=CD .∴AB -AE ′ =CD -CG , 即BE ′ =DG . ∴四边形DE ′ BG 是平行四边形. 8′ 22.(本小题满分10分)解:(1)设b kx y x y +=的函数关系式为:与,∵函数图象经过点(60,400)和(70,红 白 蓝 红(红,红) (红,白) (红,蓝) 黄(黄,红) (黄,白) (黄,蓝) 蓝(蓝,红)(蓝,白) (蓝,蓝)300),∴⎩⎨⎧+=+=b k bk 7030060400, 解得⎩⎨⎧=-=100010b k .∴100010+-=x y . 4′(2))100010)(50(+--=x x P 500001500102-+-=x x P 6′自变量取值范围:50≤x ≤70. 7′ ∵752015002=--=-a b ,10-=a <0. ∴函数500001500102-+-=x x P 图象开口向下,对称轴是直线x=75. ∵50≤x ≤70,此时y 随x 的增大而增大,∴当70=x 时,6000=最大值P . 10′23.(本小题满分10分)模型拓展一:(1)1+5=6 1′ (2)1+5×9=46 2′(3)1+5(n -1) 3′ 模型拓展二:(1)1+m 4′ (2)1+m(n -1) 5′问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球? 8′ (2)1+18×(10-1) =163 10′ 24.(本小题满分12分)解:(1)在Rt △ABC 中,522=+=AC BC AB ,由题意知:AP = 5-t ,AQ = 2t ,若PQ ∥BC ,则△APQ ∽△ABC ,∴=AC AQ AB AP ,∴5542tt -=,∴710=t .3′ (2)过点P 作PH ⊥AC 于H . ∵△APH ∽△ABC ,∴=BCPHAB AP , ∴=3PH 55t -,∴t PH 533-=,∴t t t t PH AQ y 353)533(221212+-=-⨯⨯=⨯⨯=. ···································· 6′(3)若PQ 把△ABC 周长平分,则AP+AQ=BP+BC+CQ .∴)24(32)5(t t t t -++=+-, 解得:1=t . 若PQ 把△ABC 面积平分,则ABC APQ S S ∆∆=21, 即-253t +3t =3.∵ t =1代入上面方程不成立,∴不存在这一时刻t ,使线段PQ 把Rt △ACB 的周长和面积同时平分. ············ 9′ (4)过点P 作PM ⊥AC 于M,PN ⊥BC 于N ,若四边形PQP ′ C 是菱形,那么PQ =PC .∵PM ⊥AC 于M , ∴QM=CM .∵PN ⊥BC 于N ,易知△PBN ∽△ABC . ∴ABBP AC PN =, ∴54t PN =,∴54t PN =, ∴54tCM QM ==, ∴425454=++t t t ,解得:910=t . ∴当910=t 时,四边形PQP ′ C 是菱形.此时37533=-=t PM , 9854==t CM ,在Rt △PMC 中,9505816494922=+=+=CM PM PC , ∴菱形PQP ′ C 边长为9505. 12′图①BA Q P CHP ′B A QPC图②MN。
初中数学中考真题精编-山东省2008试题及答案

更多内容见微信公众号或小编微信空间绝密★启用前 试卷类型:A山东省二○○八年中等学校招生考试数 学 试 题注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷4页为选择题,24分;第Ⅱ卷8页为非选择题,96分;全卷共12页,满分120分,考试时间为120分钟.2.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束,试题和答题卡一并收回.3.第Ⅰ卷每题选出答案后,必须用2B 铅笔把答题卡上对应题目的答案标号【ABCD 】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.4.考试时,不允许使用科学计算器.第Ⅰ卷(选择题 共24分)一、选择题:本大题共8小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分.1.只用下列图形不能镶嵌的是 A .三角形B .四边形C .正五边形D .正六边形2.下列计算结果正确的是 A .4332222y x xy y x -=⋅- B .2253xy y x -=y x 22- C .xy y x y x 4728324=÷ D .49)23)(23(2-=---a a a3.在平面直角坐标系中,若点P (m -3,m +1)在第二象限,则m 的取值范围为A .-1<m <3B .m >3C .m <-1D .m >-14.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开,得到的图形是5.若关于x 的一元二次方程0235)1(22=+-++-m m x x m 的常数项为0,则m 的值等于A .1B .2C .1或2D .06.如图1,在矩形ABCD 中,动点P 从点B 出发,沿BC ,CD ,DA 运动至点A 停止.设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△ABC 的面积是A .B .C .D .A .10B .16C .18D .20 7.若A (1,413y -),B (2,45y -),C (3,41y )为二次函数245y x x =+-的图象上的三点,则1,y 2,y 3y 的大小关系是A .123y y y <<B .213y y y <<C .312y y y <<D .132y y y <<8.如图所示,AB 是⊙O 的直径,AD =DE ,AE 与BD 交于点C ,则图中与∠BCE 相等的角有A .2个B .3个C .4个D .5 个yx图 1 OA BDC P4 9图 2BEDA CO绝密★启用前 试卷类型:A山东省二○○八年中等学校招生考试数 学 试 题第Ⅱ卷(非选择题 共96分)注意事项:1.第Ⅱ卷共8页,用钢笔或圆珠笔直接写在试卷上. 2.答卷前将密封线内的项目填写清楚. 题号 二 三总分 17 18 19 20 21 22 23 得分二、填空题:本大题共8小题,每小题填对得4分,共32分.只要求填写最后结果.9.在2008年北京奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.581亿帕的钢材.4.581亿帕用科学计数法表示为__________帕(保留两位有效数字).10.如图,已知AB ∥CD ,BE 平分∠ABC , ∠CDE =150°,则∠C =__________.11.分解因式:ab b a 8)2(2+- =____________.12.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形, 俯视图是一个圆,那么这个几何体的侧面积是 .得 分评 卷 人ABCDE13.某书店把一本新书按标价的九折出售,仍可获利20%.若该书的进价为21元,则标价为 .14.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:所剪次数12 3 4 … n 正三角形个数 471013…a n则a n = (用含n 的代数式表示).15.“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等).任取一个两位数,是 “上升数”的概率是 .16.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:① AD =BE ; ② PQ ∥AE ; ③ AP =BQ ; ④ DE =DP ; ⑤ ∠AOB =60°.恒成立的有______________(把你认为正确的序号都填上).三、解答题:本大题共7小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤.17.(本题满分6分)先化简,再求值:11a b a b ⎛⎫- ⎪-+⎝⎭÷222b a ab b-+,其中21+=a ,21-=b .得 分评 卷 人ABCE DO P Q得分评卷人18.(本题满分8分)振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3︰4︰5︰8︰6,又知此次调查中捐款25元和30元的学生一共42人.(1)他们一共调查了多少人?(2)这组数据的众数、中位数各是多少?(3)若该校共有1560名学生,估计全校学生捐款多少元?人数10 15 20 25 30 捐款数/元得分评卷人19.(本题满分8分)为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”.该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?20.(本题满分10分)在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.得分评卷人A CBD E21. (本题满分10分)如图,AC 是某市环城路的一段,AE ,BF ,CD 都是南北方向的街道,其与环城路AC 的交叉路口分别是A ,B ,C .经测量花卉世界D 位于点A 的北偏东45°方向、点B 的北偏东30°方向上,AB =2km ,∠DAC =15°.(1)求B ,D 之间的距离; (2)求C ,D 之间的距离.得 分评 卷 人A BC中山路文化路D 和平路45° 15°30°环城路EF22.(本题满分10分)(1)探究新知:如图1,已知△ABC 与△ABD 的面积相等, 试判断AB 与CD 的位置关系,并说明理由.(2)结论应用:① 如图2,点M ,N 在反比例函数xky (k >0)的图象上,过点M 作ME ⊥y轴,过点N 作NF ⊥x 轴,垂足分别为E ,F .试证明:MN ∥EF .② 若①中的其他条件不变,只改变点M ,N 的位置如图3所示,请判断 MN 与EF 是否平行.得 分评 卷 人OyNM图 2 EFxN xOyDM图 3NABDC图 123.(本题满分12分)在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切?(3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?得 分 评 卷 人ABCMND 图 2OABCMNP图 1O ABCMN P 图 3O山东省二○○八年中等学校招生考试数学试题参考解答及评分意见评卷说明:1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种解法,对考生的其他解法,请参照评分意见进行评分.3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.一、选择题(本大题共8小题,每小题3分,共24分)题号 1 2 3 4 5 67 8 答案 C C A C B A BD二、填空题 (本大题共5小题,每小题4分,共20分)9.8106.4⨯;10.120°;11.2)2(b a +;12.2π;13.28元;14.13+n ;15.5216.①②③⑤. 三、解答题 (本大题共7小题,共64分): 17.(本题满分6分)解:原式=222))(()()(b ab a bb a b a b a b a +-÷+---+ ……………………………2分 =b b a b a b a b 2)())((2-⋅+- …………………………………………3分=ba b a +-)(2. (4)分当21+=a ,21-=b 时,原式=222222=⨯. …………………………………………………6分 18.(本题满分8分)解:(1)设捐款30元的有6x 人,则8x +6x =42.∴ x =3. ..................................................................2分 ∴ 捐款人数共有:3x +4x +5x +8x +6x =78(人). ........................3分 (2)由图象可知:众数为25(元);由于本组数据的个数为78,按大小顺序排列处于中间位置的两个数都是25(元),故中位数为25(元). (6)分(3) 全校共捐款:(9×10+12×15+15×20+24×25+18×30)×781560=34200(元).……………8分 19.(本题满分8分)解:设生产奥运会标志x 套,生产奥运会吉祥物y 套.根据题意,得⎩⎨⎧=+=+②00300103①0020054.y x ,y x ……………………………………………2分①×2-②得:5x =10000.∴ x =2000. ………………………………………………………………6分 把x =2000代入①得:5y =12000.∴ y =2400.答:该厂能生产奥运会标志2000套,生产奥运会吉祥物2400套. (8)分20.(本题满分10分)证明: 过点C 作CF ⊥AB ,垂足为F .……………… 1分 ∵ 在梯形ABCD 中,AB ∥CD ,∠A =90°, ∴ ∠D =∠A =∠CF A =90°. ∴四边形AFCD 是矩形.AD=CF , BF=AB -AF=1.……………………………… 3分 在R t △BCF 中, CF 2=BC 2-BF 2=8,∴ CF=22.∴ AD=CF=22.………………………………………………………………5分∵ E 是AD 中点, ∴ DE=AE=21AD=2.…………………………………………………… 6分在R t △ABE 和 R t △DEC 中, EB 2=AE 2+AB 2=6, EC 2= DE 2+CD 2=3, EB 2+ EC 2=9=BC 2.∴ ∠CEB =90°. (9)ACBDE F分∴ EB ⊥EC . …………………………………………………………………… 10分21.(本题满分10分)解:(1)如图,由题意得,∠EAD =45°,∠FBD =30°. ∴ ∠EAC =∠EAD +∠DAC =45°+15°=60°. ∵ AE ∥BF ∥CD , ∴ ∠FBC =∠EAC =60°.∴ ∠DBC =30°. …………………………2分 又∵ ∠DBC =∠DAB +∠ADB , ∴ ∠ADB =15°.∴ ∠DAB =∠ADB . ∴ BD =AB =2.即B ,D 之间的距离为2km .… …………………………………………………5分(2)过B 作BO ⊥DC ,交其延长线于点O , 在Rt △DBO 中,BD =2,∠DBO =60°.∴DO =2×sin60°=2×323=,BO =2×cos60°=1.………………………………8分 在Rt △CBO 中,∠CBO =30°,CO =BO tan30°=33, ∴ CD =DO -CO =332333=-(km ). 即C ,D 之间的距离为332km . (1)分22.(本题满分10分)(1)证明:分别过点C ,D ,作CG ⊥AB ,DH ⊥AB , 垂足为G ,H ,则∠CGA =∠DHB =90°.……1分∴ CG ∥DH .∵ △ABC 与△ABD 的面积相等,∴ CG =DH . …………………………2分 ∴ 四边形CGHD 为平行四边形.∴ AB ∥CD . ……………………………3分OA BC中山路文化路D 和平路45° 15°30°环城路EF AB DC图 1 G Hy ME(2)①证明:连结MF ,NE . …………………4分设点M 的坐标为(x 1,y 1),点N 的坐标为(x 2,y 2). ∵ 点M ,N 在反比例函数xky =(k >0)的图象上, ∴ k y x =11,k y x =22. ∵ ME ⊥y 轴,NF ⊥x 轴, ∴ OE =y 1,OF =x 2. ∴ S △EFM =k y x 212111=⋅, ………………5分 S △EFN =k y x 212122=⋅. ………………6分 ∴S △EFM =S △EFN . ……………… 7分 由(1)中的结论可知:MN ∥EF . ………8分 ② MN ∥EF . …………………10分(若学生使用其他方法,只要解法正确,皆给分.) 23.(本题满分12分)解:(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C . ∴ △AMN ∽ △ABC .∴ AM AN AB AC=,即43x AN=.∴ AN =43x . ……………2分 ∴ S =2133248MNP AMNS S x x x ∆∆==⋅⋅=.(0<x <4) ………………3分(2)如图2,设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN . 在Rt △ABC 中,BC =22AB AC +=5. 由(1)知 △AMN ∽ △ABC .∴ AM MN AB BC =,即45x MN=.∴ 54MN x =,xOyDNM图 3EFABCMND 图 2OQABC MNP图 1O∴ 58OD x =. …………………5分 过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==. 在Rt △BMQ 与Rt △BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA . ∴ BM QM BC AC=.∴ 55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线BC 相切. (7)分(3)随点M 的运动,当P 点落在直线BC 上时,连结AP ,则O 点为AP的中点.∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC . ∴ △AMO ∽ △ABP .∴ 12AM AO AB AP ==. AM =MB =2.故以下分两种情况讨论:① 当0<x ≤2时,2Δ83x S y PMN ==.∴ 当x =2时,2332.82y =⨯=最大 …………………………………………8分② 当2<x <4时,设PM ,PN 分别交BC 于E ,F . ∵ 四边形AMPN 是矩形, ∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x .∴ ()424PF x x x =--=-.ABCMNP 图 4OE FABCMNP 图 3O又△PEF ∽ △ACB .∴ 2PEF ABCS PF AB S ∆∆⎛⎫= ⎪⎝⎭. ∴ ()2322PEF S x ∆=-.……………………………………………………… 9分MNP PEFy S S ∆∆=-=()222339266828x x x x --=-+-.……………………10分当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭.∴ 当83x =时,满足2<x <4,2y =最大. (11)分综上所述,当83x =时,y 值最大,最大值是2. ……………………………12分。
08nian会考081]
![08nian会考081]](https://img.taocdn.com/s3/m/c4d5de190b4e767f5acfcead.png)
地理试题第1页(共14页)二○○八年山东省青岛市初级中学学业水平考试地 理 试 题友情提示:嘿!亲爱的同学,你好!经过两年的学习,相信你一定具备了相当强的地理学习水平和能力。
展示自己的时候到了,只要你仔细审题、冷静思考、沉着应答,肯定会有出色的表现。
相信自己,你会成功!来,做一个深呼吸,开始吧。
加油啊!1.本试题分第I 卷和第II 卷两部分。
第I 卷6页为选择题40分;第II 卷8页为非选择题60分;共100分。
考试时间为90分钟。
2.答第I 卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。
考试结束,试题和答题卡一并收回。
3.第I 卷每题选出答案后,都必须用2B 铅笔把答题卡上对应题目的答案标号(ABCD )涂黑,如需改动,必须先用橡皮擦干净,再改涂其他答案。
第Ⅰ卷(选择题 共40分)一、单项选择题(下列各题的四个选项中,只有一个是符合题意要求的;每题1分,共40分) 1.世界四大洋中,在图1上看不到...的是 A. 大西洋 B. 印度洋 C. 北冰洋 D. 太平洋 2.图2景观最常见于A. 美国B. 荷兰C. 巴西D. 埃及 读图3,完成3—5题。
3.D 点的经纬度是A .70°S ,60°W B. 70°S ,90°W图2图1150°120°图3地理试题第2页(共14页)C .70°N ,60°E D. 70°N ,90°E 4.若B 点是16点,则C 点是A. 12点B. 14点 C .18点 D. 20点 5.有关图中四个点的说法,正确的是A .A 点位于南半球B .B 点处于高纬度C .C 点处于北寒带D .D 点位于在西半球 读图4,完成6—8题。
6.图中①②两洲的洲界是A .苏伊士运河 B. 巴拿马运河 C .白令海峡 D. 乌拉尔山 7.关于两洲洲界的说法,正确的是A .国际日期变更线经过该地 B. 本初子午线经过该地 C .沟通了太平洋和大西洋 D. 沟通了大西洋和印度洋 8.①②两洲的北部都临A. 太平洋B. 印度洋 C .大西洋 D. 北冰洋 读图5,完成9—10题。
青岛中考真题集合2000-2008年

2008年山东省青岛市初级中学学业水平考试英语试题(考试时间:120分钟,满分:105分)第一卷(共60分)第一部分听力测试(25分)I.听句子,选择最佳答语。
每个句子读一遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)1.A.I got it for my birthday.B.It cost me two hundred yuan.C.Thanks a lot.2.A.Sorry , he isn’t in.B.It’s OK.C.I’m not sure.3.A.No ,thanks. B.It’s my pleasure.C.Never mind.4.A.No, I don’t agree with you.B.But there is enough space.C.Sorry, I didn’t see the sign.5.A.I did some chores.B.I felt sick and stayed in bed.C.It was pretty good .I had fun.II.听对话和问题,选择正确答案。
对话和问题读两遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)6.7.8.A.$ 5.90. B.$ 50. C.$ 9.50.9.A.Get a pen for himself.B.Borrow a pen from Susan.C.Give his pen to Susan.10.A.There is a little time left.B.The traffic is heavy.C.She is late.III.听对话,回答问题。
对话读两遍。
你将有10秒钟的时间完成有关小题和阅读下一小题。
(共5小题,每小题1分,共5分)听第一段对话,回答11—12小题。
11.Where may this conversation take place?A.In a bank. B.In a shop. C.At a restaurant.12.What does the man want?A.A pair of shoes. B.Some tasty fruit. C.Some sports wear.听第二段对话。
山东省青岛市2008年初级中学学业水平考试物理试卷

山东省青岛市2008年初级中学学业水平考试物理(满分100分,考试时间90分钟)一、单项选择题(本大题包括9小题,每小题2分,共18分。
下列各小题的四个选项中只有一个是正确的)1、下列关于声音传播的说法中,错误的是:A、学生听到老师的讲课声是靠空气传播的B、“土电话”靠固体传声C、声音在液体中比在空气中传播的慢D、真空不能传声。
2、下列能量转化的实例中,将内能转化为机械能的是:A、太阳能电池发电B、水蒸气把壶盖顶起C、电灯发光D、弹弓将石头弹出。
F力臂的作图中,正确的是:3、下列关于14、下列图像中,能表示物体所受重力与质量关系的是:5、下列生活、生产实例与所包含物理知识的说法中,错误的是:A、墨水滴到水中,热水变色比冷水快,是由于温度越高分子热运动越快的缘故B、激光准直打隧道上利用了光沿直线传播的道理C、司机驾车时必须系安全带,这是为了防止惯性带来的危害D、电动机是利用电磁感应现象制成的。
6、试管中有一段被水银柱密封的空气柱,将此试管分别如图所示旋转,若空气柱的压强为P,大气压为P0,则满足P<P0的是:A、甲B、乙C、丙D、乙和丙7、一只10Ω的电阻与一只0.1Ω的电阻并联,并联后的总电阻:A、等于1ΩB、小于0.1ΩC、等于10.1ΩD、大于0.1Ω小于10Ω。
8、假如河水的密度变为332.010/kg m ⨯,下列现象不可能发生的是(331.0310/kg m ρ=⨯海水,337.910/kg m ρ=⨯铁)A 、船从河中驶入海是将沉下一些B 、提起同体积的河水用力较小C 、潜水员在河底会受到更大的压强D 、实心铁球在河水中仍然下沉。
9、下列关于科学方法的说法中,错误的是:A 、为研究光现象,引入“光线”描述光的传播路径和方向,这是模型法B 、噪声对人的身心健康会造成危害,科学家却能利用噪声来除草,这是缺点利用法C 、根据加快蒸发的方法,想到减慢蒸发的方法,这是逆向思维法D 、制作滑动变阻器时,发现导线太长而采取缠绕的方式,这是换元法二、不定项选择题(本大题包括4小题,共12分。
2008年山东省青岛市初级中学学业水平考试

二○○八山东省青岛市初级中学学业水平考试数学试题(考试时间:120分钟;满分120分)总体评析2008年山东省青岛市的中考试题秉承2007年该市试卷风格,低档题大都源于教材,又不拘泥于教材,淡化知识的记忆和重现,突出能力立意,注重联系实际;中、高档题主要依据教材、复习指导改编或自编而成,突出了对重要数学知识和思想方法综合运用的考查,需要考生把握知识内在联系,不仅能深刻领会各知识点的意义,而且能通过对问题的分析揭示出这种联系,从整体的角度探索、解决问题一、重视能力与创新关注整合与衔接今年中考数学命题注重对“三基”———这份试卷的选择题和填空题注重对基础知识、基本技能和基本思想方法的考查,关注学生基本数学素养的发展,充分体现新课程理念;注重数学核心内容和重要数学思想方法的考查,二、关注学生获取数学知识的思维方法和探究过程;注重考查学生的“数感、符号感、空间观念、统计观念、数学应用意识、推理能力”,关注社会热点,不回避社会热点问题,第12题就出现了关于四川汶川地震的问题关注生活实际,第13题出现了招聘播音员的问题,第19题出现“遮阳蓬”问题,第20题出现了设计方案的问题。
在第23题的阅读理解题中渗透归纳思想,加强了学科知识高初中知识的衔接,并且关注学生获取数学信息、认识数学对象的基本过程与方法,促进教师教学方式的变革和学生学习方式的转变;第24题是一道动态几何问题,拓宽探索空间,发展学生的可持续发展能力。
难度信息本卷难度适中易错题 5、14难度系数 070 较难题 23、24一、选择题(本题满分21分,共有7道小题,每小题3分)114-的相反数等于()A 14B14-C4D4-【参考答案】A【解析】本题主要考查学生对双基的掌握情况,一个具体的实数,我们只需改变前面的性质符号,就会得到原数的相反数一个正数的相反数是负数,0的相反数是0,一个负数的相反数是正数2下列图形中,轴对称图形的个数是()A 1 B2 C 3 D 4【参考答案】B【解析】本题考查学生对轴对称概念的理解,判断一个图形是不是轴对称图形的关键是能不能找到一条直线,沿这条直线对折,直线两旁的部分能够重合3已知1O 和2O 的半径分别为3cm 和2cm ,圆心距124O O =cm ,则两圆的位置关系是( )A 相切B 内含C 外离D 相交 【参考答案】D【解析】本题考查两圆的位置关系,两圆的位置关系取决于两圆的圆心距设两圆半径分别为R 、r ,两圆的圆心距为d ,则当d >R +r 时,两圆外离;当d =R +r 时,两圆外切;当R -r <d <R +r 时,两圆相交;当d =R -r 时,两圆内切;当d <R -r 时,两圆内含 4某几何体的三种视图如右图所示,则该几何体可能是( ) A 圆锥体 B 球体 C 长方体 D 圆柱体【参考答案】D【解析】主视图:从正面看到的视图;俯视图:从上面看到的图形;左视图:从左边看到的视图。
山东省2008-2017数学学业水平考试真题

山东省2008年普通高中学生学业水平考试数学试题第Ⅰ卷(选择题 共45分)一、选择题(本答题共15个小题,每小题3分,共45分,在每小题给出的四个选项中,只有一个符合题目要求)1.若全集U={1.,2,3,4},集合M={1,2},N={2,3},则集合C U (M N)= ( ) A.{1,2,3} B.{2} C.{1,3,4} D.{4}2.若一个几何体的三视图都是三角形,则这个集合体是 ( ) A. 圆锥 B.四棱锥 C.三棱锥 D.三棱台3.若点P(-1,2)在角θ的终边上,则tan θ等于 ( ) A. -2 B. 55-C. 21-D. 5524.下列函数中,定义域为R 的是 ( ) A. y=x B. y=log 2X C. y=x 3 D. y=x15.设a >1,函数f (x )=a |x|的图像大致是 ( )6.为了得到函数y=sin (2x-3π)(X ∈R )的图像,只需把函数 y=sin2x 的图像上所有的点 ( )A.向右平移3π个单位长度B.向右平移6π个单位长度 C.向左平移3π个单位长度 D.向左平移6π个单位长度7.若一个菱长为a 的正方形的个顶点都在半径为R 的球面上,则a 与R 的关系是 ( )A. R=aB. R=a 23C. R=2aD. R=a 3 8.从1,2,3,4,5这五个数字中任取两数,则所取两数均为偶数,则所取两数均为偶数的概率是 ( ) A.101 B. 51 C. 52 D. 539.若点A (-2,-3)、B (0,y )、C (2,5)共线,则y 的值等于 ( )A. -4B. -1C. 1D. 410.在数列{a n }中,a n+1=2a n ,a 1=3,则a 6为 ( )A. 24B. 48C. 96D. 19211.在知点P (5a+1,12a )在圆(x-1)2+y 2=1的内部,则实数a 的取值范围是 ( )A. -1<a <1B. a <131C.51-<a <51D. 131-<a <13112.设a ,b ,c ,d ∈R ,给出下列命题: ①若ac >bc ,则a >b ; ②若a >b ,c >d ,则a+b >b+d ; ③若a >b ,c >d ,则ac >bd ; ④若ac 2>bc 2,则a >b ;其中真命题的序号是 ( ) A. ①② B. ②④ C. ①②④ D. ②③④13.已知某学校高二年级的一班和二班分别有m 人和n 人(m ≠n )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省青岛市2008年初级中学学业水平考试数 学(满分120分,考试时间120分钟)一、选择题(本题满分21分,共有7道小题,每小题3分)1.14-的相反数等于( ) A .14 B .14- C .4 D .4-2.下列图形中,轴对称图形的个数是( )A .1B .2C .3D .43.已知1O 和2O 的半径分别为3cm 和2cm ,圆心距124O O =cm ,则两圆的位置关系是( ) A .相切 B .内含 C .外离 D .相交4.某几何体的三种视图如右图所示,则该几何体可能是( ) A .圆锥体 B .球体 C .长方体 D .圆柱体5.一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,……,不断重复上述过程.小明共摸了100次,其中20次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( )A .18个B .15个C .12个D .10个6.如果点11()A x y ,和点22()B x y ,是直线y kx b =-上的两点,且当12x x <时,12y y <,那么函数k y x=的图象大致是( )7.如图,把图①中的ABC △经过一定的变换得到图②中的A B C '''△,如果图①中ABC △上点P 的坐标为()a b ,,那么这个点在图②中的对应点P '的坐标为( )A .(23)a b --,B .(32)a b --,C .(32)a b ++,D .(23)a b ++,二、填空题(本题满分21分,共有7道小题,每小题3分)请将8—14各小题的答案填写在第14小题后面表格的相应位置上. 8.计算:0122-+=________.9.化简:293x x -=-________________. 10.如图,在矩形ABCD 中,对角线AC BD ,相交于点O ,若60AOB ∠=,4AB =cm ,则AC 的长为________cm .11.如图,AB 是O 的直径,弦CD AB ⊥于E ,如果10AB =,8CD =,那么AE 的长为_____________.12.为了帮助四川地震灾区重建家园,某学校号召师生自愿捐款.第一次捐款总额为20000元,第二次捐款总额为56000元,已知第二次捐款人数是第一次的2倍,而且人均捐款额比第一次多20元.求第一次捐款的人数是多少?若设第一次捐款的人数为x ,则根据题意可列方程为 .13.某市广播电视局欲招聘播音员一名,对A B ,两名候选人进行了两项素质测试,两人的两项测试成绩如右表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么 (填A 或B )将被录用.14.如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF 长为10cm .母线()OE OF 长为10cm .在母线OF 上的点A 处有一块爆米花残渣,且2FA =cm ,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点.则此蚂蚁爬行的最短距离为 cm .三、作图题(本题满分6分,用圆规、直尺作图,不写作法,但要保留作图痕迹)15.如图,AB AC ,表示两条相交的公路,现要在BAC ∠的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处A 点的距离为1000米.(1)若要以1:50000的比例尺画设计图,求物流中心到公路交叉处A 点的图上距离; (2)在图中画出物流中心的位置P .四、解答题(本题满分72分,共有9道小题) 16.(本小题满分6分) 用配方法解一元二次方程:2220x x --=.17.(本小题满分6分)某市为调查学生的视力变化情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下:解答下列问题:(1)该市共抽取了多少名九年级学生?(2)若该市共有8万名九年级学生,请你估计该市九年级视力不良(4.9以下)的学生大约有多少人? (3)根据统计图提供的信息,谈谈自己的感想(不超过30字). 18.(本小题满分6分)小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?19.(本小题满分6分)在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB 表示窗户,且2AB =米,BCD 表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD 的最小夹角α为18.6 ,最大夹角β为64.5 .请你根据以上数据,帮助小明同学计算出遮阳蓬中CD 的长是多少米?(结果保留两个有效数字) (参考数据:sin18.60.32=,tan18.60.34=,sin 64.50.90=,tan 64.5 2.1=)20.(本小题满分8分)2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A 种船票600元/张,B 种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A ,B 两种船票共15张,要求A 种船票的数量不少于B 种船票数量的一半.若设购买A 种船票x 张,请你解答下列问题:(1)共有几种符合题意的购票方案?写出解答过程; (2)根据计算判断:哪种购票方案更省钱? 21.(本小题满分8分)已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使C E C G =,连接BG 并延长交DE 于F .(1)求证:BCG DCE △≌△;(2)将DCE △绕点D 顺时针旋转90得到DAE '△, 判断四边形E BGD '是什么特殊四边形?并说明理由.22.(本小题满分10分)某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).(1)求y与x之间的函数关系式;(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大?最大值是多少?23.(本小题满分10分)实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?为了找到解决问题的办法,我们可把上述问题简单化:(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相+=(如同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:134图①);(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的+⨯=(如图②)个数是:1327(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的+⨯=(如图③):个数是:13310……(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:13(101)28+⨯-=(如图⑩)模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________; (2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是________; (3)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是________. 模型拓展二:在不透明口袋中装有m 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球: (1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是________. (2)若要确保摸出的小球至少有n 个同色(20n <),则最少需摸出小球的个数是________. 问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型; (2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生. 24.(本小题满分12分)已知:如图①,在Rt ACB △中,90C ∠=,4cm AC =,3cm BC =,点P 由B 出发沿BA 方向向点A匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为(s)t (02t <<),解答下列问题: (1)当t 为何值时,PQ BC ∥?(2)设AQP △的面积为y (2cm ),求y 与t 之间的函数关系式;(3)是否存在某一时刻t ,使线段PQ 恰好把Rt ACB △的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把PQC △沿QC 翻折,得到四边形PQP C ',那么是否存在某一时刻t ,使四边形PQP C '为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.参考答案 一、选择题三、作图题15.解:(1)1000米=100000厘米,100000÷50000=2(厘米);(2)略.16.解: 222x x -=,22121x x -+=+,2(1)3x -=, 1x -=∴ 11x = 21x =.17.解:(1)800÷40% = 2000(人);(2)80000×40% = 32000(人); (3)合理即可.18.解:∴ P(配成紫色)=29,P(配不成紫色)=79. ∴小刚得分:22199⨯=,小明得分:77199⨯=,∵ 2799≠ , ∴ 游戏对双方不公平.修改规则的方法不惟一.(如改为:若配成紫色时小刚得7分,否则小明得2分.)19.解:设CD 为x ,在Rt△BCD 中,18.6BDC α∠==o, ∵ tan BCBDC CD∠=, ∴ tan 0.34BC CD BDC x =⋅∠=. 在Rt△ACD 中,64.5ADC β∠==o, ∵ tan ACADC CD∠=, ∴ tan 2.1AC CD ADC x =⋅∠=. ∵ AB AC BC =-, ∴ 2 2.10.34x x =-. 1.14x ≈.答:CD 长约为1.14米.20.解:(1)设A 种票x 张,则B 种票(15-x)张,根据题意得:152600120(15)5000x x x x -⎧⎪⎨⎪+-⎩≥,≤ 解得: 5≤x ≤320. ∴ 满足条件的x 为5或6. ∴ 共有两种购买方案:方案一:A 种票5张, B 种票10张, 方案二:A 种票6张, B 种票9张.(2)方案一购票费用: 600×5+120×10=4200(元), 方案二购票费用: 600×6+120×9=4680(元), ∵ 4200<4680, ∴ 方案一更省钱.21.证明:(1)∵ 四边形ABCD 是正方形,∴ BC=CD ,∠BCD=90°. ∵ ∠BCD +∠DCE=180°, ∴ ∠BCD=∠DCE=90°. 又∵ CG=CE ,∴ △BCG≌△DCE.(2)∵△DCE 绕D 顺时针旋转90︒得到△DAE′,∴ CE=AE ′. ∵ CE=CG , ∴ CG=AE ′.∵ 四边形ABCD 是正方形, ∴ BE ′∥DG,AB=CD . ∴ AB -AE ′ =CD -CG , 即BE ′=DG .∴ 四边形DE ′BG 是平行四边形.22.解:(1)设b kx y x y +=的函数关系式为:与,∵ 函数图象经过点(60,400)和(70,300),∴ 4006030070k bk b =+⎧⎨=+⎩, 解得101000k b =-⎧⎨=⎩.∴ 101000y x =-+. (2)(50)(101000)P x x =--+210150050000P x x =-+-自变量取值范围:50≤x ≤70. ∵ 150075220b a -=-=-,10a =-<0. ∴ 函数210150050000P x x =-+-图象开口向下,对称轴是直线x=75. ∵ 50≤x ≤70,此时y 随x 的增大而增大, ∴ 当70x =时,6000P =最大值.23.模型拓展一:(1)1+5=6(2)1+5×9=46 (3)1+5(n -1)模型拓展二:(1)1+m(2)1+m(n -1)问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?(2)1+18×(10-1) =16324.解:(1)在Rt△ABC 中,5AB ==,由题意知:5,2AP t AQ t =-=, 若PQ∥BC,则△APQ ∽△ABC,∴ AQ APAC AB =, ∴ 2545t t -=, ∴ 107t =.(2)过点P 作PH⊥AC 于H . ∵△APH ∽△ABC,∴ PH APBC AB =, ∴ 535PH t-=, ∴ 335PH t =-,∴ 211332(3)32255y AQ PH t t t t =⨯⨯=⨯⨯-=-+. (3)若PQ 把△ABC 周长平分,则AP+AQ=BP+BC+CQ .∴ (5)23(42)t t t t -+=++-, 解得: 1t =.若PQ 把△ABC 面积平分, 则12APQ ABC S S ∆∆=, 即23335t t -+=. ∵ t=1代入上面方程不成立,∴ 不存在这一时刻t ,使线段PQ 把Rt△ACB 的周长和面积同时平分. (4)过点P 作PM⊥AC 于M,PN⊥BC 于N ,若四边形PQP C '是菱形,那么PQ =PC .∵ PM⊥AC 于M , ∴ QM=CM .∵ PN⊥BC 于N ,易知△PBN∽△ABC. ∴PN BPAC AB=, ∴ 45PN t =, ∴ 45tPN =, ∴ 45t QM CM ==, ∴442455t t t ++=,北京四中网校 ▪ 11 ▪地址:北京市西城区新德街20号四层 邮编:100088 电话:82025511 传真:82079687 解得:109t =. ∴ 当109t =时,四边形PQP C '是菱形. 此时37353PM t =-=, 4859CM t ==, 在Rt△PMC中,PC ===, ∴ 菱形PQP C '.。
