高频电子线路(第二章 选频网络)-2
高频电子线路 张肃文 第五版 课后答案

第二章选频网络注意:①有部分答案有差异;②3-1题是2-1题;③只有计算题答案和部分问答题;④答案不齐全。
(pF)).(L C H)(.QR L ΩR Δf f Q (kHz)Δf MHz:f ..159101*********11591014321010010100101010121010990101211362620603670036700=××××===×××====××===×−×==−−ωµω, .C L ωC L ) (, .C L ωC L ) ( , .C L ωC L ) :(22021101220211012202110111311211123======−ωωωR R C L R )LCωL(jωR )LC ωLR(jωC L R C jωR L jωR )C jωL)(R jω(R :Z =+=−+−++=+++++=−2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C LpF - C C CpFC C C:=×+××××=′+==+=×+=+=×+−−ω。
L C C ’()()()()mV V Q V V mA .R V I μH ..C L ..R C :Q -Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=××====×===××××===××××××==−ωω()()()()()()Ωj ..j .C j R Z Ω.....Q L Q L R pF C pF .L C C C C .V V Q μH .C :L X X X X X X X S C 7967471020010143217471747100102531014321052102531014322001001025310143211100101025310100101432116312606666000626200122620−=××××−=−==××××−××××=−==→=××××==+⋅====××××==−−−−−−ωωωωω()()().21kΩ0.5R,R , 0.5Q Q , f 22f 2Δ320105105552310023100101501052220105010514321173000.70.7660036700012620电阻所以应并上=′=′∆×=′=××−××===××===×××××==−−.f Δf Q ξΔf f Q μH ..C ω :L .∑===−g QCωΔf f C πf C πΔf :..070007022483()()()()()()()()MHz ...Q f Δf .....L ωR Q kΩ..R C C C C R R R kΩ..C LQ R MHz ....LC πf pF .C C C C C C C :C L .L P i P i 4812281064122281080106411432108858855202020209201092010202010801006411031810801432121318202020202020593607066302211021261201260102102=×===××××××===×⎠⎞⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++==×+××===××××===++++=++++=−−∑∑−−−−)))RZ 30Z 20Z 1123f1f1f1===−解:)()()()())()()()()()()))())()()()()()()Ω.j .j ..Z M Z j ..j C L j R Z pF .L C kHz .R ρf Q f Δf .R R L Q kΩC R R L Z Ω..R M Z μH ..ηR M pF .L C C μH .ρL L :f .f f f P 8437680100201018310143210020101771014321101591014322011771015910950143211522810201022224252020101591014323251015920201015920201018310143221831014322011591015910143211159101432101133266222011126662*********2322022361100706611101112611112662201160116261201216301121−=+××××==+=⎟⎠⎞⎜⎝⎛××××−××××+=⎟⎟⎠⎞⎜⎜⎝⎛′−+==×××××=′=′=××====+××××=+==××+×=+==××××===×××===××××====××===−−−−−−−−−−ωωωωωωωωω()100101410222002010159105010159153367.00111236=×=∆==→=∴=Ω=××××==−−−f f Q M R R C R L R f P ∵解:)()()()()()()()))013.02001122211222005101001032510102402051010010205101011632207.067101671012671120126722011=×−×+=⋅−+=∆=××===×==Ω=+××=+=Ω=×==−−−−−Q f f R L Q R M k R RL R R M R :f ab f ηηωωηωω5.75.22303021103001010112118.111020*********.325.22115.2225.111030010101121117323320012302332=−=′−=→=⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛∆+==××××××===′→=⎟⎟⎠⎞⎜⎜⎝⎛××′+=⎟⎟⎠⎞⎜⎜⎝⎛∆′+=−−Q Q Q Q f f Q I I C Q R Q Q f f Q I I :ω()⎩⎨⎧==→⎪⎪⎩⎪⎪⎨⎧+==−μL μH L CL L ω C L ω :12537511218321212第三章高频小信号放大器5102501050501501 ,5012.1102501020501501 ,20491025010501501 ,154266200266200266200=⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛×××+=⎟⎟⎠⎞⎜⎜⎝⎛+===⎟⎟⎠⎞⎜⎜⎝⎛××+=⎟⎟⎠⎞⎜⎜⎝⎛+==−TT T f f ββMHz f f f ββMHz f f f ββMHz f βββ当当解:当()()()()()()()()()()()()()()()()()()()()mS j .j .j b a jb a g r C j b a jb a C j g g r C j g y mS j .j b a jb a g y mS j .j .j b a jb a C j g y mS .j ..j .j b a jb a C j g y ..r ωC b .g r a pF ..πf g C mS ..r βg mS .βI g m b b c b c b c b m b b c b ce oe m fe c b c b re e b e b ieb b e b e b b b T m eb eb m E e b 68.0049.01011.01107.377011031014321733.3327.371011.01107.37187.00187.01011.0110310143241189501011.01102410143210754.010701024101432110754070112410250143210737273710754050754015026112674223127222222322221272222127322127363300+=⎟⎠⎞⎜⎝⎛+−×××+××××≈⎟⎠⎞⎜⎝⎛+−+≈+−+++=−=+−××=+−=−−=+−×××××−≈+−+−=+=+−×××××+×=+−+=≈×××××==≈××+=+==××××===××===+×=+=−−−′′′′′′−−′′−−′′−′′−′′−′−′′ωωωωω解:()()()()4124142701010042104010041704070121101241104221104210124212422124284−−=⎟⎟⎠⎞⎜⎜⎝⎛−⎟⎟⎠⎞⎜⎜⎝⎛−==⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎟⎟⎠⎞⎜⎜⎝⎛⋅⎟⎟⎠⎞⎜⎜⎝⎛−==⎟⎟⎠⎞⎜⎜⎝⎛+=⎠⎞⎜⎜⎝⎛−m mm m ...r m .m.m vo v m .m.mvo v Δf Δf K Q f Δf f ΔfQ A A Q f Δf f Δf Q A A 故得令得解:令()()()()()()()()()1103101045952110830081020010286021830082501020025010237952258854tan 2tan 431100316116570316107102316104107102105228113151********5228104525025052281028604110200411023723710410010710211250205250205943326662262621222206070666022632162626222166001345213231>>××+×+×××=+′++=××+×=+=′−=−−=+==⎟⎠⎞⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛−==×===××××××======××××===××+××+×=++==×××××========−−−−−−−−−−−−−−−−−∑−...y y ξg g g g S μS ....p g p g g ..ξ..Q Q K MH ...Q f Δf ..π.L ωg Q ..A A ....g y p p A μS ..g p g p g g μS ..πL Q ωg .N N p .N N p refe L oe ie s ie p L oo re fe L Z L .ΣL vo po Σfe vo ie oe p p ϕϕ解:()()()()()()()()()()()()()()()()()()()()7221698266804238225025668042479479610444454782122259044546104422610441222565197445412212243822502578213445410158010410710143222782115802438303015801503008203010037010370104107101432100111104444447070707041707041704147044436260070222122222156600..-.A A ..A A ....f ΔΔf A A kHz ...Δf f ΔkHz .Δf f ΔkHz ..Δf Δf ..A A kHz ....f Lg ωΔf .....g y p p A mS .......g p g p R g g mS ...L ωQ g vo vo vo vo ..vo vo ......vo vo .fe vo ie oe p p ==′−==′=′=×=′=′=−=−′=−=′=×−=⋅−=====×××××××===+××===×+×++=+++==××××××==−−−∑∑∑−解:()()()()不能满足解:9.1K 522106250110511432121625011830500114r0.1122620221<=×××××===×+=+=−−∑∑μH ....C πf L pF ..C p C C oe ()74.73.05.24.364.265.2144220=×+==−refeS vo C y A ω解:()()()()()()()163910601046522260104910100410465274104921040574513114910010100010465210620574513491001010001046521020100440574513100010044100012051373118607311873118118101000104652111741030706123121206321123320202236123601012222236112563423612231201.K kH .Q f Δf πg C ωQ ..g y p p A μS π...Q C ωg p g μS πQ C ωg g pF ..C p C C pF C C C .L L L L μH πC ωL .r Z L .L fe vo i o i o ==××===×××××===×××××===∴=××××+××⎟⎠⎞⎜⎝⎛=+==××××+×=+==×⎟⎠⎞⎜⎝⎛+=+==+=+==×+×+=++==××××==−−−−−−−−−−,则。
通信电子线路2 选频网络

w wC wL
1 1 1 2 2 2 CQ 2Vsm sin 2 t CQ 2Vsm cos 2 t CQ 2Vsm 2 2 2
说明:回路中储存的能量保持不变,只是在电感与电容之间相 互转换。
2)一个周期的wR
1V 1 1V 1 1 1V 1V 1 2 sm wR PR T I 02 R T sm T sm 2 sm 2 R 2f 0 2 R 0 2 2 R 2 R f0
2.2.3 2.2.4
信号源内阻和负载电阻的影响 低Q值的并联谐振回路
1.电路结构 并联LC谐振回路
L R
串联LC谐振回路
C L
C iS RS
RS uS R
iS RS C
Rp
L
Rp
L CR
证明:
Z 1 CR 1 j C L L
L
Is
R
C
1 CR 1 Y j C Z L L
Vi RP
2
pCRP RP
C L
I i2 0C 1 I i2 R 0 RC
1 L R C
pL 1 1 L p RC R R C
L L Is
Rs
C R
Rs + Vs _
R C
4 回路阻抗频率特性
1 Z p ( R jL) // jC L RC 1 1 j (L ) C
1 LC
最小
ZR VS 4. 谐振电流 I0 R 5. 谐振电容 VL0 VC 0 jQVs
1 1 L 储能 2 0 RC R C 耗能
6. 回路的品质因数 7. 通频带
高频电子线路 第2章-高频电路基础

1 1 L= 2 = ω0 C (2π ) 2 f 02C
以兆赫兹(MHz)为单位 C以皮法 为单位, 以皮法(pF)为单位 L以 为单位, 将f0以兆赫兹 为单位 为单位 以 微亨( )为单位, 上式可变为一实用计算公式: 微亨(µH)为单位, 上式可变为一实用计算公式:
1 2 1 25330 6 L = ( ) 2 × 10 = 2 2π f 0 C f0 C
(3) 求满足 求满足0.5 MHz带宽的并联电阻。 设回路上并联 带宽的并联电阻。 带宽的并联电阻 电阻为R 并联后的总电阻为R 电阻为 1, 并联后的总电阻为 1∥R0, 总的回路有载品 f0 质因数为Q 由带宽公式, 质因数为 L。 由带宽公式 有 Q =
L
B
此时要求的带宽B=0.5 MHz, 故 QL = 20 此时要求的带宽 回路总电阻为
主要包括电台、工业、空间电磁、天电等 主要包括电台、工业、空间电磁、
内部产生的一般称为噪声
人为:接地 回路耦合等 人为 接地,回路耦合等 接地 系统内:电阻 电子器件等的热噪声等 系统内 电阻,电子器件等的热噪声等 电阻
电子噪声:电子线路中普遍存在。 电子噪声:电子线路中普遍存在。指电子线路中的随 机起伏的电信号,与电子扰动有关。 机起伏的电信号,与电子扰动有关。 当噪声,干扰与信号可比拟时 称信号被噪声淹没 当噪声 干扰与信号可比拟时,称信号被噪声淹没 干扰与信号可比拟时 称信号被噪声淹没.
ωM M = 对于互感耦合: 对于互感耦合 k = 2 L1L2 ω L1L2
通常情况: 通常情况
M L1 = L2 = L 则 k = L
CC k= 对于电容耦合: 对于电容耦合 (C1 + CC )(C2 + CC )
(完整版)高频电子线路(知识点整理)

127.02ωωω-=∆高频电子线路重点第二章 选频网络一. 基本概念所谓选频(滤波),就是选出需要的频率分量和滤除不需要的频率分量。
电抗(X)=容抗( )+感抗(wL) 阻抗=电阻(R)+j 电抗 阻抗的模把阻抗看成虚数求模 二.串联谐振电路 1.谐振时,(电抗) ,电容、电感消失了,相角等于0,谐振频率: ,此时|Z|最小=R ,电流最大2.当w<w 0时,电流超前电压,相角小于0,X<0阻抗是容性;当w>w 0时,电压超前电流,相角大于0,X>0阻抗是感性;3.回路的品质因素数 (除R ),增大回路电阻,品质因数下降,谐振时,电感和电容两端的电位差大小等于外加电压的Q 倍,相位相反4.回路电流与谐振时回路电流之比 (幅频),品质因数越高,谐振时的电流越大,比值越大,曲线越尖,选频作用越明显,选择性越好5.失谐△w=w (再加电压的频率)-w 0(回路谐振频率),当w 和w 0很相近时, ,ξ=X/R=Q ×2△w/w 0是广义失谐,回路电流与谐振时回路电流之比6.当外加电压不变,w=w 1=w 2时,其值为1/√2,w 2-w 1为通频带,w 2,w 1为边界频率/半功率点,广义失谐为±17. ,品质因数越高,选择性越好,通频带越窄 8.通频带绝对值 通频带相对值 9.相位特性Q 越大,相位曲线在w 0处越陡峭10.能量关系电抗元件电感和电容不消耗外加电动势的能量,消耗能量的只有损耗电阻。
回路总瞬时储能 回路一个周期的损耗 , 表示回路或线圈中的损耗。
就能量关系而言,所谓“谐振”,是指:回路中储存的能量是不变的,只是在电感与电容之间相互转换;外加电动势只提供回路电阻所消耗的能量,以维持回路的等幅振荡,而且谐振回路中电流最大。
11. 电源内阻与负载电阻的影响Q L 三. 并联谐振回路 1.一般无特殊说明都考虑wL>>R ,Z 反之w p =√[1/LC-(R/L)2]=1/√RC ·√1-Q2 2.Y(导纳)= 电导(G)= 电纳(B)= . 与串联不同 )1(CL ωω-010=-=C L X ωωLC 10=ωCR R L Q 001ωω==)(j 0)()(j 11ωψωωωωωe N Q =-+=Q702ωω=∆⋅21)(2=+=ξξN Q f f 0702=∆⋅Qf f 1207.0=∆ξωωωωψ arctan arctan 00-=⎪⎪⎭⎫⎝⎛-⋅-=Q ⎪⎭⎫ ⎝⎛-+≈C L R C L ωω1j ⎪⎭⎫ ⎝⎛-+=C CR ω1j ⎪⎭⎫ ⎝⎛-+L C LCRωω1j LCR ⎪⎭⎫ ⎝⎛-L C ωω1C ω1-+ –CV sLRI s C L R22222221cos 21sin 21sm sm sm V CQ t V CQ t V CQ w w w C L 22=+=+=ωω2sm 02sm 21π2121π2CQV R V w R⋅=⋅⋅=ωQCQV V CQ w w w R C L ⋅=⋅=+π2121π2212sm sm每周期耗能回路储能π2 =Q 所以RR R R Q LS 0=3.谐振时,回路谐振电阻R p= =Q p w p L=Q p/w p C4.品质因数(乘R p)5.当w<w p时,B>0导纳是感性;当w>w p时,B<0导纳是容性(看电纳)电感和电容支路的电流等于外加电流的Q倍,相位相反并联电阻减小品质因数下降通频带加宽,选择性变坏6.信号源内阻和负载电阻的影响由此看出,考虑信号源内阻及负载电阻后,品质因数下降,并联谐振回路的选择性变坏,通频带加宽。
高频电子线路02选频网络

f0
2
1 LC
谐振频率
➢Q值(品质因数)的定义: Q 2 WS WR
即在一个周期内,电路储存的电磁能量与损耗能量的比值的2π倍。 在谐振状态下:Ws不随时间变化,即谐振电路不与外界交换无功功 率,就是在谐振状态下稳定的储存在电路中的电磁能,这些能量是在 谐振电路开始接通时经历的暂态过程中由外电路输入给它的。达到稳 定的振荡以后,为了维持振荡,外电路需要不断的输入有功功率,以 补偿R的损失,但在谐振状态下,无需供给无功功率,由此可见,Q 值反映了一个谐振电路储能的效率。
BBWW0.07.7==f22 -f1f=
f0f= Q0
f0 Q
➢ Q值与频率带宽的关系
BW0.7
=2f=
f0 Q
对固定频率的谐振电路,回路Q值越高,通频带越
窄,二者矛盾。
(Q值越大,谐振电路的选择性越好)
?
思考题与习题20、21
由Q值的定义推导LC串联谐振电路Q值表达式。
➢ 2.1.3 相频特性
L C 高Q
Is
Is
损
耗 电
R
阻
L Rp C
p
1 LC
Rp
2 P
L2
R
Qp2 R
L CR
对于高Q值并联谐振回路,其谐振频率与串联谐
振回路相近,谐振阻抗可以通过串联支路的串并联互
换得到。
思考题与习题20.21
1. 能量关系
串联单振荡回路由电感线圈(包括其损耗电阻)和电容
器构成,电抗元件电感和电容不消耗外加电动势的能量,消耗
能量的只有损耗电阻。
L
R
+
Vs –
C
思考题与习题20.21
第二章 选频网络

第二章:选频网络
1.选频网络的作用:滤波
高频放大电路的负载
阻抗变换
相移;
2.选频网络分为:振荡电路、滤波器(LC集中滤波器、石英晶体滤波器、陶瓷滤波器、声表面波滤波器);
3.串联谐振回路:(谐振时,回路阻抗等于R,达到最小,回路电流则达到最大。
L与C两端的电压降将等于信号源电压V s的Q倍,因而称为电压谐振)
R
w0=f0=
品质因数:Q=wL
R 回路通频带:2∆f0.7=f0
Q
✓串联谐振回路适用于信号源内阻低的情况,信号源内阻越大,回路品质因数Q越低,谐振曲线越钝,选择性也就越差。
✓谐振时,电感、电容没有消失!
4.并联谐振回路(通常,损耗电阻R在工作频段内满足:R<<wL 或高Q)
w p=f p=
品质因数: Q=1
WCR
✓谐振时,Z p为纯电阻,且等于电感之路(或电容支路)电抗的Q p倍,因而此时并联谐振回路阻抗为最大值,而在偏离谐振点时,回路等效阻抗为感性(低于谐振频率时)或为容性(高于谐振频率时);
习题整理:
题1:
题2.
题3.。
高频电路原理与应用第2章选频网络

3
优化方法
使用优化方法来改善选频网络的性能,以提高电路的选择精度和信号质量。
选频网络的实验与应用案例
实验设计和测量方法
介绍选频网络实验的设计和测量方法,以验证电 路的性能和应用的可行性。
应用案例
展示选频网络在实际应用中的案例,如电视机、 无线电和雷达等。
2 音频处理和放大
选频网络常用于音频处理 和音频放大系统中,以选 择特定频率的声音。
3 高频信传输
选频网络在高频信号传输 系统中用于选择特定频率 的信号进行传输。
选频网络的性能分析和优化
1
带宽和增益分析
对选频网络的带宽和增益进行分析,以确保所选择的频率范围和信号增益符合要 求。
2
噪声和失真分析
分析选频网络的噪声和失真,确保在传输和处理过程中不会引入额外的干扰或失 真。
常见的选频网络电路
LC选频网络
LC选频网络使用电感器和电容器 来选择特定频率的信号。
RC选频网络
RC选频网络使用电阻和电容器 来选择特定频率的信号。
滤波器和共振器
滤波器和共振器是常见的选频网 络电路,用于消除不需要的频率 或增强特定频率。
选频网络的应用
1 无线通信系统
选频网络在无线通信系统 中用于选择特定频率的信 号进行传输。
高频电路原理与应用第2 章选频网络
本章将介绍选频网络在高频电路中的重要性和应用。探讨不同类型的选频网 络,以及如何进行设计和优化。
选频网络的概述
作用
选频网络用于在高频电路中选择特定频率的信号。
组成部分
选频网络由基本元件,如电容器和电感器,以及其他辅助元件组成。
基本原理和设计
选频网络的设计涉及基本元件和参数的选择,以及特定应用的设计方法。
高频电子线路 第二章 选频网络

Chapter 2 选频网络§2.1 概述 §2.2 串联谐振回路12.1 概述一.选频的基本概念 二.选频网络的分类振荡回路(由L、C组成)单振荡回路 耦合振荡回路各种滤波器LC集中滤波器 石英晶体滤波器 陶瓷滤波器 声表面波滤波器2三.选频网络的的元器件选频网络中的元件主要是电阻(器)、电容(器) 和电感(器), 它们都属于无源的线性元件。
1.电阻器一个电阻R的高频等效电路如图所示,其中CR为分布电容, LR为引线电感,R为电阻。
CR LR R电阻的高频等效电路32. 电感线圈的高频特性电感+损耗电阻r+分布电容(忽略)L r 1 L r 2电感线圈的串联等效电路 在两种形式中,电 感值近似不变,串 联电阻与并联电阻 的乘积等于感抗的 平方。
1’ LP R 2’电感线圈并联等效电路43. 电容器的高频特征R C Cpr电容器的串、并联等效电路两种形式中电容值近似不变,串联电阻 和并联电阻的乘积等于容抗的平方。
52.2 串联谐振回路串联谐振回路是指电感、电容、信号源三 者串联形成的电路。
6一. 谐振及谐振条件我们称当ω = ω0 时发生了串联谐振,谐振角频率ω0为:1 LCω0 =当回路谐振时的感抗或容抗,称之为特性阻抗, 用ρ表示。
X L0 = X C01 = ω0 L = = L =ρ C ω0C7二. 谐振特性回路阻抗的模|Zs|和幅角随φ变化的曲线分别如图所示 |Zs| φπ/ 2 r O ω0 O -π / 2 ω ω0 ω因此串联谐振时,电感L和电容C上的电压达到最大值且 为输入信号电压的Q倍,故串联谐振也称为电压谐振。
8三. 幅值特性谐振电流:发生串联谐振时因阻抗最小,流过电路的电流最 大,称为谐振电流,其值为.Vs I0 = R非谐振点处电流称为失谐处电流 I9谐振曲线:串联谐振回路中电流幅值与外加电动势频率之间 的关系曲线称为谐振曲线。
可用|N(f)|表示谐振曲线的函数。
高频电子线路张肃文第五版一二章总结
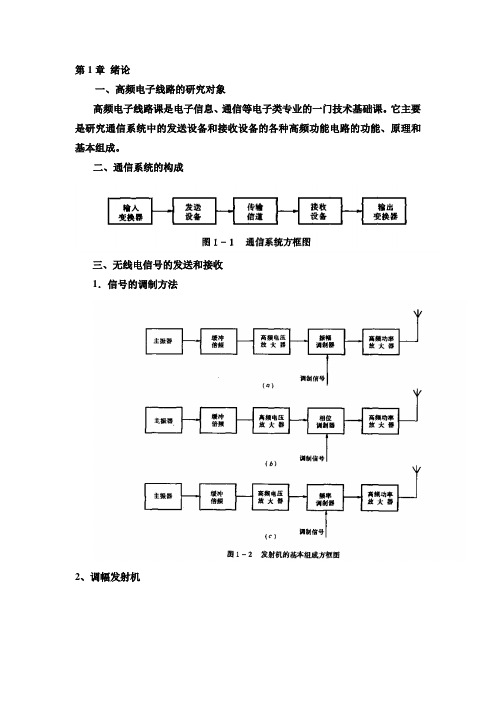
l.为什么在无线电通信中要便用“载波”发射,其作用是什么?
答:由于需要传送的信息转变成电信号后,其占有的频率成分基本上是低频范围。将这些低频范围的电信号直接发肘出去,有两个下可克服的缺点,一是选择性,相互干扰,下能实现多路通信。二是电信号频率低,天线发射无线尺寸太大。为此采用对载波进行调制的发送方式就能较好地解决这两个缺点,选用高频载频作为运载信息的信号,由于频率高,天线尺寸小。另外,不同的电台采用不同的载频,就很容易实现多路通信。
2 a图只要L1C1或L2C2之一为并联则为并联,二者为容性则为串联;
B图L1C1与L2C2只能呈现感性才能谐振,为并联谐振;
C图L1C1与L2C2只能呈现感性才能谐振,为串联谐振。
3注意利用 但不要使用
4根据 的比值选取合适的电容器。
2画出无线通信收发信机的原理框图,并说出各部分的功用。
答:
上图是一个语音无线电广播通信系统的基本组成框图,它由发射部分、接收部分以及无线信道三大部分组成。发射部分由话筒、音频放大器、调制器、变频器(不一定必须)、功率放大器和发射天线组成。
低频音频信号经放大后,首先进行调制后变成一个高频已调波,然后可通过变频,达到所需的发射频率,经高频功率放大后,由天线发射出去。接收设备由接收天线、高频小信号放大器、混频器、中频放大器、解调器、音频放大器、扬声器等组成。由天线接收来的信号,经放大后,再经过混频器,变成一中频已调波,然后检波,恢复出原来的信息,经低频功放放大后,驱动扬声器。
1.接入系数
电感抽头接入法、电容抽头部分接入法
2.电压源、电流源、电阻、电容、电感的折合
四、耦合回路
1.耦合系数
2.反射阻抗与等效阻抗
3.耦合回路的频率特性
高频电子系统课件-选频网络

当
时
而
通频带与回路的品质因数Q成反比,两者存在矛盾
第2章 选频网络
通用谐振曲线
I (η ) I0
0.707
Q=0.5
Q=1
Q=10
0
1 1 2
Q越大,谐振曲线越尖。当稍微偏离谐振点时,曲线就
急剧下降,电路对非谐振频率下的电流具有较强的抑
制能力,所以选择性好。
第2章 选频网络
2.1.5 相频特性曲线
例2.3如图,设给定串联谐振回路的f0=1MHz,Q0=50,若输出电流 超前信号源电 压相位45°,试求: 1) 此时信号源频率f是多少?输出电流 相对于谐振时衰减了多少分贝? 2) 现要在回路中的再串联一个元件,使 回路处于谐振状态,应该加入何种元 件, 并定性分析元件参数的求法。
第2章 选频网络
2.2 并联谐振回路
电感L、电容C和外加信号源组成的并联谐振回路。r是电感L的 损耗电阻,电容的损耗一般可以忽略。 适用于信号源内阻和负载较大的电路。
R
C L
+
•
IS
•
U
G
CL
_
由于外加信号源内阻很大,为了分析方便,采用恒流源。
第2章 选频网络 1. 回路阻抗
L 当线圈Q值很高时,即: R
1
时,可近似为:
R2
b
b
电感抽头式并联谐振回路
第2章 选频网络
抽头式并联电路的等效互换(续)
令
p L1 L1
L1 L2 L
称为接入系数
则
Zab
( p L1 )2
R1 R2
( p pL)2
R1 R2
( p L)2
R1 R2
p2
高频电子电路第2章_选频网络

L Is
损 耗 电 阻
C
R
要研究并联振荡回路的选频特性,可以考察其阻 抗随频率变化的规律。
32
一、并联振荡回路特性
回路的总阻抗
1 1 R j wL R jwL jw C j wC Z Is 1 1 R jw L R j wL wC L jw C 1 C 1 1 CR j wC R j wL L wL wC
27
回路总的瞬时储能
1 1 1 2 2 2 2 2 2 2 w wL wC CQ Vsm sin w t CQ Vsm cos w t CQ 2Vsm 2 2 2
图 3.1.9 串联谐振回路中的能量关系
28
就能量关系而言,所谓“谐振”,是指:回路中 储存的能量是不变的,只是在电感与电容之间相互转 换;外加电动势只提供回路电阻所消耗的能量,以维 持回路的等幅振荡,而且谐振回路中电流最大。
R
8
电抗
感性
wL
x = w L- 1 wC
L + – Vs
R
X
O
w0
- 1 wC
w
容性
C
阻抗 Z R jX R j(wL
1 ) wC
2. 阻抗性质随频率变化的规律: 1) w < w0时, X <0呈容性; 2) w = w0时, X =0呈纯阻性; 3) w > w0时, X >0呈感性。
1 2
1
Q
2w
w0
w0 f0 2w07 或 2f 0 .7 Q Q
20
1 1 w2,1 w0 ( 2Q 1 2Q )
高频电子线路(第五版)_第二章_选频网络

V V0
1 p 1 jQp p
第二节
V V0
1 p 1 jQp p
失谐 量
广义失谐量
当ω与ω0很接近时
0 0 0 2 2 0 0 0 0
第一节
I 1 I0 1 ξ2
谐振特性方程式
ξ 当谐振时: 0
为了衡量谐振回路的选择性,引入通频带的 概念。
回路外加电压的幅值不变时,改变频率,回 路电流 I 下降到Io 的0.707时所对应的频率范围 称为谐振回路的通频带,用B表示:
B 2 0.7 2 1或B 2f 0.7 f 2 f1
第一节
I 1 1 当 时 2 Io 2 1 ξ
第一节
一、串联谐振回路的基本原理
1 jC
2
Z s R jX R jL
R j (L
1
C
) | Z s | e
j
| Z s |
R X
2
2
R (L
1
1 ωL X ωC arctan arctan R R
C
)
2
+ -
L
Vs
R
0 2 1 Q ( ) 0
2
I/I0
Q1> Q2
第一节
由图可知,回路的品质 因数越高,谐振曲线越尖 锐,回路的选择性越好。
表示频率偏置谐振的程度
Q2 Q1 ω0 ω
0
0 f 2Q 令 :ξ Q 2Q 0 f0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L1
去掉抽头后电阻变大
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
5、抽头式电路中电流源的等效变换
a
Vbc 根据前面的电压关系的 结论 p Vac
L2
IS
b
C
L1
c a
Vbc I S Z bc p Z ac Vac I S
Vbc I S 2 带入上式得p p Vac I S
阻抗的关系
Z bc 2 p Z ac
电压的关系
抽头处看进去的阻抗和电压都比较小
Vbc p Vac
电阻去抽头
电流源去抽头
电容去抽头
1 Ri 2 Ri p
变大
pIS IS
变小
Ci p 2Ci
变小
•高频电子技术•
习题:
教材P85(四版)习题3.9 教材P55(五版)习题2.9 注意:
并联电路的广义形式:
•高频电子技术•
Zp
( p L)2 R1 R2
1 或Z p (R1 R2) ( pC )2
这时,如果R1,R2都不大的情况下, 可以认为R1,R2都集中在电感之路。 且Q p =
pL
R1 +R2
, 这一概念在实际中很
有用。
第二章 选频网络
•高频电子技术•
请同学们回忆 一下并联谐振 回路中的Q值:
Rp Q Rp pC pL Rp 恰好可以表示为 XP
倒数 代入
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
1、并联等效成串联(结论)
得到 RP RS 1 Q2 Q2 XS XP 2 1 Q
由于高频电路中 , 通常Q 1, 所以
§2.3.2 抽头式电路的阻抗变换
为什么会存在“抽头式”电路?
–
–
1、减小信号源内阻和负载对回路的影响; 2、可调抽头还可以实现阻抗匹配功能。 按被抽头的元件分:电感抽头和电容抽头 按抽头在整个电路中位置分:源端抽头和负载端抽 头
常见的抽头电路(电路图见下页):
–
–
§2.3.2 抽头式电路的阻抗变换
RP Q 2 RS XP XS
这个结论用语言表达就是: 谐振电路中的串联支路等效成并联支路时,电抗 部分基本不变,电阻部分变为原来的Q2倍
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
注意:利用上述结论回顾和理解并联谐振回路知识
C
L
r
iS RS C
iS
RS
Rp
L
L Rp Cr
( p L)2 r
L 1 253 106 15.9() 12 C 100 100 10
1 R 15.9() 6 12 Q00C 100 2 10 100 10
253H 15.9
L R
1
解:再看第二次谐振, 11端接Z X。
?
+
1MHz 0.1V
ZX
注意:谐振频率 0没有改变。
所谓等效就是指电路工作在某一频率时,不管其内 部的电路形式如何,从外部看去其阻抗是相等的。 主要是为了使电路的分析更加方便。例如:
为什么要进行等效变换?
–
等效
导纳直接相加,计算得以简化!
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
1、并联等效成串联
A
注:图中电抗带颜色,纯电阻不带颜色
A
XS
0 V
jQ I I Lp p S
jQ I I Cp p S
IS
L
Ik
C
Rp
I k:通常被称作谐振环路 电流
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
3、抽头式电路中电压的关系(续)
a
L2
b
Vbc jL1 I k Vac j ( L1 L2 ) I k
2.5V
1
CX 同时L也没变根据0 L
可知C总还是100pF
C2 200pF
可见Z X中一定含有电容
1 0C总
C X C2 由C X 与C2串联后仍为 100pF( 100pF) 可以推出C X 200pF C X C2 V C总 2.5 又 C总两端的电压为2.5V Q2 25 0.1 VS
R
+
1MHz 0.1V
1
1 0 L 0C1 1 1 L 2 0 C1 (2 106 ) 2 1001012
V C1 VS
C1 100pF
又 V C1 Q0 V S Q0
253 (H)
10 100 0.1
1 L 1 而 Q0 R R C Q0 1
1 1 2 Q L Q Q p p p pr 2 r ( pC ) pC
电抗部分(在图中为L)等效后不变 上图中的r其实就是Rs ; 图中RP , 它约为Q 2 倍的Rs (即r) 可见RP 和r是有很大差别的,验证了我们学过的知识
•高频电子技术•
3.并联谐振回路其他形式
为了简化这 些表达式, 提出了接入 系数p的概 念
r
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
2、抽头系数(接入系数)p的严格定义
抽头式电路中,抽头所夹的那个元件的阻抗, 与它所在的那个支路的整个阻抗之比,称为抽 头系数或接入系数,通常记为p 例如:a p L1 Z L1 L1 p Z L1串L 2 p ( L1 L2 ) L1 L2 L
RP RS 2 Q XS XP
这个结论用语言表达就是: 谐振电路中的并联支路等效成串联支路时,电抗 部分基本不变,电阻部分变为原来的1/Q2
§2.3.1 串、并联阻抗等效变换
•高频电子技术•
2、串联等效成并联
采用上面相同的方法进行分析(推导从略) 得出的结论是相同的 用公式表达为
习题详解:习题2.5
1 1 解:Q0 212 6 12 0C0 R 2 3.14 1.5 10 100 10 5 1 1 L0 2 113 H 6 2 12 0 C0 (2 3.14 1.5 10 ) 100 10
Vsm 1mV 谐振时回路电流:I 0 0.2mA R 5 VL 0m VC 0m Q0Vsm =212mV
–
请同学们在Ci的两端再并联一个电阻Rp(其值可以 通过Qp求出);
习题详解:习题2.9(3.9四版)
1
Ci
5 pF
5k
Ri
Rp
0.8H
C2 20 pF
L
C1 20 pF
2
RO 5k
CO 20 pF
Rp是L的内阻等效到 1、 2 两端的电阻,所以题面 没画出来。
方法一:将 CO看成从C1C2抽头出来的元件,等效 到12两端。
Z X由RX 47.7和CX 200pF串联而成
1 Z X RX j 0 C X
由于Q公式有好几个,所以解法也 有很多种,但结果应当是一样的。
1 47.7 j (47.7 j 796 ( ) ) 6 12 2 10 20010
第二章 选频网络
从而可近似认为 I L1 I L2 I k
注:高频电路通常工作于谐振状态或接近于谐振状态
§2.2.1 并联谐振回路基本原理
•高频电子技术•
并联谐振时各支路的电流
Qp Rp I I R p S S I j I Lp S j p L G jpL jpL pL j C I V S p 0 Rp j C jRp CI I Cp I S p p S 1 G j pC
r
注意:电感、电容串并联时 值的大小的计算!
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
引入抽头时阻抗的变化
b
由于L2与C串联后这个支路 ,
L2
在谐振频率 p下呈容性, 所以在 p下可将其看作一个电容 C
Zbc
c
L1
C’ C
Z bc
2 p 1
L
p 1
2
L
r
Z bc L1 2 r 所以 ( ) 2 Z ac L1 L2 p ( L1 L2 )
•高频电子技术•
§2.3 串、并联电路及抽头式电路的等效变换
本节主要内容: – §2.3.1 串、并联阻抗等效变换 – §2.3.2 抽头式电路的等效变换
学习这一节的目的在于 为学习“高频小信号放大器”打好基础
第二章 选频网络
•高频电子技术•
§2.3.1 串、并联阻抗等效变换
什么是“等效”?
–
XP
RP 等效 RS
B
B
根据等效的要求 , 两个电路从 AB两点看去 ,阻抗应该相等
显然串联电路的阻抗为 RS jX S 2 2 RP ( jX P ) XP RP 而并联电路的阻抗为 2 RP j 2 XP 2 2 RP jX P RP X P RP X P
§2.3.1 串、并联阻抗等效变换
2
b
L1
c
C
Z bc 带入上页, 可得 p2 Z ac
抽头处看进去的阻抗较小
§2.3.2 抽头式电路的阻抗变换
•高频电子技术•
关于电容抽头时p的公式
根据接入系数 p的严格定义
C2
a
L C1
p
抽头所夹元件阻抗 抽头所在支路总阻抗
b
1 jC1 1 1 jC1 jC2
Hale Waihona Puke C2 C1 C2•高频电子技术•
