第十一章第2课时知能演练轻松闯关
Section Ⅱ 知能演练轻松闯关(5)

Ⅰ.品句填词1.She quit(停止) her job and continued to receive education.2.I will visit Li Yan, a volunteer(志愿者) for the 2022 Beijing Winter Olympic Games.3.We had a heated debate(辩论) on whether or not to accept the offer.4.I asked for a(n)__extra(额外的) day to finish the work because it can't be finished in a day.5.I can't find suitable(合适的) words to express my thanks.6.As we all know, Li Jian, a famous singer, graduated(毕业于) from Tsinghua University.7.After your final topic__(主题,话题) is chosen, you cannot change it.8.Usually, each book has its contents(目录) in the front of it.9.Her fluent(流畅的) ballet movements surprised all the students present at the party.10.The new government's first challenge(挑战) is the economy.Ⅱ.完成句子1.为了赶上一早的航班,我们提前订了出租车,而且起床很早。
To catch the early flight, we ordered a taxi__in__advance and got up very early.2.首先,因为我擅长英语口语,所以我认为我适合这项工作。
第十一章第1课时知能演练轻松闯关
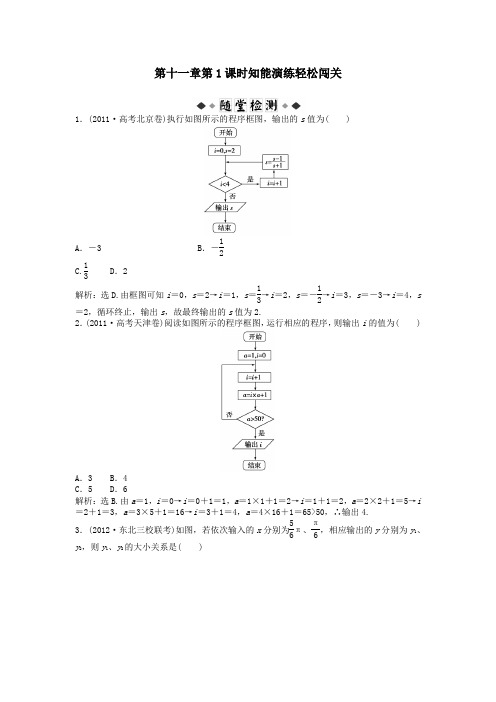
第十一章第1课时知能演练轻松闯关1.(2011·高考北京卷)执行如图所示的程序框图,输出的s 值为( )A .-3B .-12C.13D .2 解析:选D.由框图可知i =0,s =2→i =1,s =13→i =2,s =-12→i =3,s =-3→i =4,s=2,循环终止,输出s ,故最终输出的s 值为2. 2.(2011·高考天津卷)阅读如图所示的程序框图,运行相应的程序,则输出i 的值为( )A .3B .4C .5D .6解析:选B.由a =1,i =0→i =0+1=1,a =1×1+1=2→i =1+1=2,a =2×2+1=5→i =2+1=3,a =3×5+1=16→i =3+1=4,a =4×16+1=65>50,∴输出4.3.(2012·东北三校联考)如图,若依次输入的x 分别为56π、π6,相应输出的y 分别为y 1、y 2,则y 1、y 2的大小关系是( )A .y 1=y 2B .y 1>y 2C .y 1<y 2D .无法确定解析:选C.由程序框图可知,当输入的x 为5π6时,sin 5π6>cos 5π6成立,所以输出的y 1=sin 5π6=12;当输入的x 为π6时,sin π6>cos π6不成立,所以输出的y 2=cos π6=32,所以y 1<y 2.4.执行如图所示的程序框图,若输出的S =88,则判断框内应填入的条件是( )A .k >7B .k >6C .k >5D .k >4 解析:选C.第一次循环k =1+1=2,S =2×0+2=2; 第二次循环k =2+1=3,S =2×2+3=7; 第三次循环k =3+1=4,S =2×7+4=18; 第四次循环k =4+1=5,S =2×18+5=41; 第五次循环k =5+1=6,S =2×41+6=88,满足条件则输出S 的值,而此时k =6,故判断框内应填入的条件应是k >5,故选C.一、选择题1.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( ) A .一个算法只能含有一种逻辑结构B .一个算法最多可以包含两种逻辑结构C .一个算法必须含有上述三种逻辑结构D .一个算法可以含有上述三种逻辑结构中的任一种解析:选D.在一个算法中,可出现顺序结构、条件结构、循环结构三种结构中的任一种. 2.已知一个算法: (1)m =a .(2)如果b <m ,则m =b ,输出m ;否则执行第3步. (3)如果c <m ,则m =c ,输出m .如果a =3,b =6,c =2,那么执行这个算法的结果是( ) A .3 B .6 C .2 D .m解析:选C.当a =3,b =6,c =2时,依据算法设计,执行后,m =a =3<b =6,c =2<a =3=m ,∴c =2=m ,即输出m 的值为2,故选C.3.执行如图所示的程序框图,若输出的b 的值为16,则图中判断框内①处应填( )A .5B .4C .3D .2解析:选C. ①a =1,b =1,b =2,a =2; ②a =2,b =2,b =22=4,a =3; ③a =3,b =4,b =24=16,a =4. ∵输出b 的值为16, ∴退出循环,则a ≤3.4.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )A .f (x )=x 2B .f (x )=1xC .f (x )=ln x +2x -6D .f (x )=sin x解析:选D.本题的程序框图的功能是判断函数是否是奇函数且是否存在零点,满足既是奇函数又存在零点的函数是选项D.5.如果执行如图的程序框图,若输入n =6,m =4,那么输出的p 等于( )A .720B .360C .240D .120解析:选B.程序运行如下:n =6,m =4,k =1,p =1,p =p (n -m +k )=6-4+1=3,k <m ;k =1+1=2,p =p (n -m +k )=3×(6-4+2)=12,k <m ;k =2+1=3,p =p (n -m +k )=12×(6-4+3)=60,k <m ;k =3+1=4,p =p (n -m +k )=60×(6-4+4)=360,k =m ,所以输出p ,p =360,故选B. 二、填空题6.某算法的程序框图如图所示,则输出量y 与输入实数x 满足的关系式是________.解析:由题意知,程序框图表达的是一个分段函数y =⎩⎪⎨⎪⎧2x,x ≤1x -2,x >1.答案:y =⎩⎪⎨⎪⎧2x ,x ≤1x -2,x >17.(2010·高考安徽卷)如图所示,程序框图(算法流程图)的输出值x =________.解析:程序运行如下:x =1,x =2,x =4,x =5,x =6,x =8,x =9,x =10,x =12,输出12.答案:128.(2010·高考湖南卷)如图是求12+22+32+…+1002的值的程序框图,则正整数n =________.解析:第一次判断执行后,i =2,s =12;第二次判断执行后,i =3,s =12+22,而题目要求计算12+22+…+1002,故n =100. 答案:100 三、解答题9.已知某算法的程序框图如图所示,将输出的(x ,y )值依次记为(x 1,y 1)、(x 2,y 2)、…、(x n ,y n )、….若程序运行中输出的一个数组是(x ,-8),求x 的值.解:开始n =1,x =1,y =0→n =3,x =3,y =-2→n =5,x =9,y =-4→n =7,x =27,y =-6→n =9,x =81,y =-8,则x =81.10.某居民区的物业管理部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费只需画出程序框图即可. 解:依题意得,费用y 与人数n 之间的关系为:y =⎩⎪⎨⎪⎧5 n ≤35+1.2n -3 n >3.程序框图如图所示:11.已知数列{a n }的各项均为正数,观察程序框图,若k =5,k =10时,分别有S =511和S=1021.(1)试求数列{a n }的通项公式;(2)令b n =2a n ,求b 1+b 2+…+b m 的值.解:由框图可知S =1a 1a 2+1a 2a 3+…+1a k a k +1.由题知{a n }为等差数列,公差为d ,则有1a k a k +1=1d ⎝⎛⎭⎫1a k -1a k +1.∴S =1d ⎝⎛⎭⎫1a 1-1a 2+1a 2-1a 3+…+1a k -1a k +1=1d ⎝⎛⎭⎫1a 1-1a k +1.(1)由题意可知,k =5时,S =511;k =10时,S =1021. 即⎩⎪⎨⎪⎧1d 1a 1-1a 6=5111d 1a 1-1a 11=1021.解得⎩⎪⎨⎪⎧a 1=1d =2或⎩⎪⎨⎪⎧a 1=-1d =-2(舍去).故a n =a 1+(n -1)d =2n -1.(2)由(1)可得:b n =2a n =22n -1, ∴b 1+b 2+…+b m =21+23+…+22m -1=21-4m 1-4=23(4m -1).。
人教版化学必修1:第一章 第二节 第2课时 知能演练轻松闯关

1.下列说法不.正确的是()A.1 mol H2的质量只有在标准状况下才约为2 gB.在标准状况下,1 mol任何气体的体积都约为22.4 LC.273 ℃,1.01×105Pa状况下,1 mol气体体积大于22.4 LD.标准状况下,0.5 mol O2和0.5 mol N2组成的混合气体体积约为22.4 L解析:选A。
气体的质量只与气体的摩尔质量和气体的物质的量有关,与气体的温度、压强无关,1 mol H2的质量为2 g是不变的,A选项不正确;B选项正确;C选项中273 ℃高于0 ℃,温度升高,气体分子间的距离增大,气体的体积增大,C选项正确;无论是混合气体还是纯净的气体,在标准状况下,1 mol任何气体的体积都约为22.4 L,D选项正确。
2.相等物质的量的CO和CO2的下列比较中正确的是()①所含的分子数目之比为1∶1②所含的O原子数目之比为1∶2③所含的原子总数目之比为2∶3④所含的C原子数目之比为1∶1⑤所含的电子数目之比为7∶11A.①和④B.②和③C.④和⑤D.①②③④⑤解析:选D。
CO和CO2的物质的量相同,则含有的CO和CO2的分子数目也相同,则①正确。
又因CO和CO2分子中的O原子数分别为1和2,则物质的量相同的CO和CO2,所含的O原子数目之比1∶2,②正确。
CO和CO2的分子中原子总数之比为2∶3,所以,③也正确。
物质的量相同的CO和CO2,C原子数目之比也是1∶1,选项④也正确。
CO和CO2分子中电子总数分别为14和22,即物质的量相同的CO和CO2电子总数之比为14∶22=7∶11,选项⑤也正确。
所以,本题的正确答案应为D。
3.(2012·武汉高一质检)已知同温同压下,气体的密度与它的摩尔质量成正比。
一只气球若放在空气(空气平均摩尔质量为29 g/mol)中可静止不动,那么在相同条件下该气球放在下列气体中会下沉的是()A.O2B.Cl2C.CO2D.CH4解析:选D。
人教版B数学选修1-2:3.1.2第二课时知能演练轻松闯关

1.当0<m <1时,z =(m +1)+(m -1)i 对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选D.z =(m +1)+(m -1)i 对应的点为(m +1,m -1),∵0<m <1,∴1<m +1<2,-1<m -1<0,∴点(m +1,m -1)位于第四象限.2.若z 1=(x -2)+y i 与z 2=3x +i(x ,y ∈R)互为共轭复数,则z 1对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选C.∵z 1与z 2互为共轭复数,∴⎩⎪⎨⎪⎧x -2=3x ,y =-1,∴z 1=-3-i.3.若复数cos θ+isin θ和sin θ+icos θ相等,则θ=__________.解析:由题意知sin θ=cos θ,即tan θ=1,∴θ=k π+π4k ∈Z.答案:k π+π4k ∈Z)4.复数z =3a -6i 的模为40,则实数a 的值为__________.解析:由|z |=(3a )2+(-6)2=40得a =±23.答案:±23[A 级 基础达标]1.在复平面内,复数z =sin2+icos2对应的点位于( )A .第一象限B .第二象限C .第三角限D .第四象限解析:选D.∵π2<2<π,∴sin2>0,cos2<0.∴复数z 在复平面内对应的点(sin2,cos2)位于第四象限.2.已知复数z 对应的点在第二象限,它的模是3,实部是-5,则z 是( )A .-5+2iB .-5-2iC.5+2iD.5-2i解析:选A.设z =x +y i(x ,y ∈R),则x =-5,由|z |=3得(-5)2+y 2=9,即y =±2,又因为复数z 对应的点在第二象限,所以y =2.3.若a ,b ∈R ,复数(a 2-3a +2)+(b -1)i =0,则实数对(a ,b )表示的点的坐标为() A .(1,-1) B .(2,1)C .(1,1)或(2,1)D .(-1,-1)解析:选C.由题意知⎩⎪⎨⎪⎧a 2-3a +2=0b -1=0, 解得⎩⎪⎨⎪⎧a =1b =1或⎩⎪⎨⎪⎧a =2b =1,故(a ,b )表示点(1,1)或(2,1). 4.在复平面内,表示复数z =(m -3)+2m i 的点在直线y =x 上,则实数m 的值为__________. 解析:由题意得(m -3,2m )在直线y =x 上,则有2m =m -3,解得m =9.答案:95.已知复数a +i ,2-i 在复平面内对应的点分别为A ,B ,若直线AB 的斜率为-1,则a =__________.解析:易知A (a ,1),B (2,-1),故k AB =-1-12-a=-1⇒a =0. 答案:06.实数m 取什么值时,复数z =m (m -1)+(m -1)i(1)表示复数z 的点位于第一象限;(2)表示复数z 的点位于直线y =2x 上?解:(1)由表示复数z 的点位于第一象限,可得⎩⎪⎨⎪⎧m (m -1)>0,m -1>0,解得m >1,即当m >1时,表示复数z 的点位于第一象限,故m 的取值范围是(1,+∞);(2)由表示复数z 的点位于直线y =2x 上,可得m -1=2m (m -1),解得m =1或m =12即当m =1或m =12时,表示复数z 的点位于直线y =2x 上. [B 级 能力提升]7.在复平面内,O 为原点,向量OA →对应的复数为-1-2i ,点A 关于直线y =-x 的对称点为B ,则向量OB →对应的复数为( )A .-2-iB .2+iC .1+2iD .-1+2i解析:选B.点A (-1,-2)关于直线y =-x 的对称点为B (2,1),则向量OB →对应的复数为2+i.8.复数1+cos α+isin α(π<α<2π)的模为( )A .2cos α2B .-2cos α2C .2sin α2D .-2sin α2解析:选B.(1+cos α)2+sin 2α=2+2cos α=2|cos α2|. ∵α∈(π,2π),∴α2∈(π2,π), ∴上式=-2cos α2. 9.以非零实数a 、纯虚数b i(b ∈R)和复数a +b i 对应的点为顶点所构成的三角形必是__________.解析:在复平面作出各点如图.故△ABC 为直角三角形.答案:直角三角形10.已知复数z =(m 2-3m )+(m 2-m -6)i ,求当实数m 为何值时,复数z 是:①实数;②z =4+6i ;③对应的点在第三象限.解:∵z =(m 2-3m )+(m 2-m -6)i ,①令m 2-m -6=0⇒m =3或m =-2,即m =3或m =-2时,z 为实数.②⎩⎪⎨⎪⎧m 2-3m =4m 2-m -6=6⇒m =4; ③若z 所对应点在第三象限,则⎩⎪⎨⎪⎧m 2-3m <0m 2-m -6<0⇒ 0<m <3.11.(创新题)已知复数z =(2x +a )+(2-x +a )i(x ,a ∈R),当x 在(-∞,+∞)内变化时,求|z |的最小值g (a ).解:|z |2=(2x +a )2+(2-x +a )2=22x +2-2x +2a (2x +2-x )+2a 2.令t =2x +2-x ,则t ≥2且22x +2-2x =t 2-2.从而|z |2=t 2+2at +2a 2-2=(t +a )2+a 2-2,当-a ≥2,即a ≤-2时,g (a )=a 2-2;当-a <2,即a >-2时,g (a )=(a +2)2+a 2-2=2|a +1|.。
湘教版数学选修2-26.2.1知能演练轻松闯关.docx

1.(2012·渝北调研)已知a >b >0,则证明a -b <a -b 可选择的方法,以下最合理的是( )A .综合法B .分析法C .类比法D .归纳法解析:选B.首先,排除C 、D.然后,比较综合法、分析法. 我们选择分析法,欲证:a -b <a -b ,只需证:a <b +a -b ,即证:a <b +(a -b )+2b (a -b ),只需证:0<2b (a -b ),显然成立,原不等式得证.2.在不等边三角形中,a 为最大边,要想得到∠A 为钝角的结论,则三边a ,b ,c 应满足的条件为( )A .a 2<b 2+c 2B .a 2=b 2+c 2C .a 2>b 2+c 2D .a 2≤b 2+c 2解析:选C.若∠A 为钝角,则由余弦定理得cos A =b 2+c 2-a 22bc<0,即b 2+c 2<a 2. 3.(2011·高考天津卷)已知a =log 23.6,b =log 43.2,c =log 43.6,则( )A .a >b >cB .a >c >bC .b >a >cD .c >a >b解析:选B.∵2<3.6<4,∴log 23.6>1>log 43.6.又∵log 43.6>log 43.2,∴a >c >b .4.设a =2,b =7-3,c =6-2,则a 、b 、c 的大小关系为________.解析:∵b =47+3,c =46+2, 显然b <c .而a 2=2,∴c 2=(6-2)2=8-212=8-48<8-36=2=a 2,∴a >c ,∴a >c >b .答案:a >c >b一、选择题1.下列表述:①综合法是由因导果法;②综合法是顺推法;③分析法是执果索因法;④分析法是逆推法.其中正确的语句有( )A .4个B .3个C .2个D .1个解析:选A.①②③④正确.2.(2011·高考北京卷)如果log 12x <log 12y <0,那么( )A .y <x <1B .x <y <1C .1<x <yD .1<y <x 解析:选D.不等式转化为⎩⎪⎨⎪⎧log 12x <log 12y log 12y <0,⇒1<y <x .3.某同学证明不等式7-1>11-5的过程如下: 要证7-1>11-5,只需证7+5>11+1,即证7+27×5+5>11+211+1,即证35>11,即证35>11.因为35>11成立,所以原不等式成立.这位同学使用的证明方法是( )A .综合法B .分析法C .综合法,分析法结合使用D .其他证法解析:选B.根据分析法的思维特点可判定出来.4.(2012·江北检测)已知函数f (x )=⎝⎛⎭⎫12x ,A =f ⎝⎛⎭⎫a +b 2,B =f (ab ),C =f ⎝⎛⎭⎫2ab a +b (a >0,b >0),则A ,B ,C 的大小关系为( )A .A ≤B ≤C B .A ≤C ≤BC .B ≤C ≤AD .C ≤B ≤A解析:选A.由于a +b 2≥ab ≥2ab a +b, 又函数f (x )=⎝⎛⎭⎫12x 在R 上为减函数,故f ⎝⎛⎭⎫a +b 2≤f (ab )≤f ⎝⎛⎭⎫2ab a +b . 5.(2012·南川检测)已知A ,B 为△ABC 的两个内角,则A >B 是sin A >sin B 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:选C.A >B ⇔a >b ⇔2R sin A >2R sin B ⇔sin A >sin B .6.若P =a +a +7,Q =a +3+a +4(a ≥0),则P ,Q 的大小关系为( )A .P >QB .P =QC .P <QD .由a 的取值确定解析:选C.由于P >0,Q >0,所以要比较P 与Q 的大小,只须比较P 2与Q 2的大小. Q 2-P 2=(a +3+a +4)2-(a +a +7)2=2a 2+7a +12-2a 2+7a .∵a 2+7a +12>a 2+7a ,∴a 2+7a +12>a 2+7a ,∴2a 2+7a +12>2a 2+7a ,∴Q 2>P 2,∴Q >P .二、填空题7.将下面用分析法证明a 2+b 22≥ab 的步骤补充完整:要证a 2+b 22≥ab ,只需证a 2+b 2≥2ab ,也就是证____________,即证______________,由于______________显然成立,因此原不等式成立.答案:a 2+b 2-2ab ≥0 (a -b )2≥0 (a -b )2≥08.(2011·高考天津卷)已知log 2a +log 2b ≥1,则3a +9b 的最小值为________.解析:由log 2a +log 2b ≥1得log 2(ab )≥1,即ab ≥2,∴3a +9b =3a +32b ≥2×3a +2b 2(当且仅当3a =32b ,即a =2b 时“=”号成立).又∵a +2b ≥22ab ≥4(当且仅当a =2b 时“=”成立),∴3a +9b ≥2×32=18.即当a =2b 时,3a +9b 有最小值18. 答案:189.已知x ,y ∈R +,当x 2+y 2=________时,有x 1-y 2+y 1-x 2=1.解析:要使x 1-y 2+y 1-x 2=1,只需x 2(1-y 2)=1+y 2(1-x 2)-2y 1-x 2, 即2y 1-x 2=1-x 2+y 2.只需使(1-x 2-y )2=0,即1-x 2=y ,∴x 2+y 2=1.答案:1三、解答题10.已知a >b >c ,且a +b +c =0,求证:b 2-ac a< 3. 证明:∵a >b >c ,且a +b +c =0,∴a >0,c <0,要证原不等式成立,只要证b 2-ac <3a ,即证b 2-ac <3a 2,也即证(a +c )2-ac <3a 2,即(a -c )(2a +c )>0,∵a -c >0,2a +c =(a +c )+a=a -b >0.∴(a -c )(2a +c )>0成立,故原不等式成立.11.如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,P A =AB =BC ,E 是PC 的中点.(1)证明:CD ⊥AE ;(2)证明:PD ⊥平面ABE .证明:(1)在四棱锥P -ABCD 中,∵P A ⊥底面ABCD ,CD ⊂平面ABCD ,故P A ⊥CD .∵AC ⊥CD ,P A ∩AC =A ,∴CD ⊥平面P AC .而AE ⊂平面P AC ,∴CD ⊥AE .(2)由P A =AB =BC ,∠ABC =60°,可得AC =P A ,∵E 是PC 的中点,∴AE ⊥PC .由(1)知,AE ⊥CD ,且PC ∩CD =C ,∴AE ⊥平面PCD .而PD ⊂平面PCD ,∴AE ⊥PD .∵P A ⊥底面ABCD ,PD 在底面ABCD 内的射影是AD ,AB ⊥AD ,∴AB ⊥PD ,又∵AB ∩AE =A ,综上得PD ⊥平面ABE .12.(创新题)已知非向零量a ⊥b ,求证:|a |+|b ||a -b |≤ 2. 证明:∵a ⊥b ,∴a ·b =0.要证|a |+|b ||a -b |≤2,只需证|a |+|b |≤2|a -b |, 平方得|a |2+|b |2+2|a ||b |≤2(|a |2+|b |2-2a ·b ),只需证|a |2+|b |2-2|a ||b |≥0,即(|a |-|b |)2≥0,显然成立.故原不等式得证.。
苏教版化学必修1:专题3 第一单元 第二课时 知能演练轻松闯关

1.下列各组物质中,在高温引燃的条件下,不.能发生化学反应的是( ) A .Al 粉和Fe 3O 4粉末混合 B .V 2O 5粉末和Al 粉混合 C .Al 粉和MgO 粉末混合 D .C 粉和CuO 粉末混合解析:选C 。
Al 粉和Fe 3O 4、V 2O 5在高温时均可发生铝热反应,而Al 粉和MgO 粉在高温时不发生化学反应,因为Mg 比Al 活泼。
C 粉和CuO 粉末在高温也发生化学反应 2CuO +C=====高温2Cu +CO 2↑。
2.等质量的同种镁铝合金分别与下列4种过量的溶液充分反应,放出氢气最多的是( )A .2 mol·L -1 H 2SO 4溶液B .18 mol·L -1 H 2SO 4溶液C .6 mol·L -1 KOH 溶液D .3 mol·L -1 HNO 3溶液解析:选A 。
镁、铝与稀H 2SO 4均可反应放出H 2;在KOH 溶液中只有铝与KOH 反应放出H 2;镁与浓H 2SO 4反应不生成H 2,Al 在浓H 2SO 4中钝化;Mg 、Al 与HNO 3作用都不生成H 2。
3.若在加入铝粉能放出氢气的溶液中,分别加入下列各组离子,一定能大量共存的是( )A .NH +4、SO 2-4、CO 2-3、K +B .Na +、Ba 2+、Ca 2+、HCO -3C .Mg 2+、Ag +、K +、Cl -D .K +、Cl -、Na +、SO 2-4解析:选D 。
铝与酸、强碱反应都放出氢气,则加入铝粉能放出氢气的溶液中可能含H +,也可能含OH -。
分别加入各组离子,一定能大量共存,是指各组离子应与H +和OH -都能共存。
A 项中,NH +4与OH -生成NH 3·H 2O ,CO 2-3与H +生成H 2CO 3;B 项中,HCO -3与H +、OH -都能发生反应;C 项,Mg 2+与OH -不能共存,Ag +与Cl -不能共存;D 项中,各离子与H +和OH -都不发生反应,符合要求。
第十章第1课时知能演练轻松闯关

【优化方案】2021-2021学年高中数学 4.4知能演练轻松闯关 湘教版选修2-2(1)

【优化方案】2021-2021学年高中数学 知能演练轻松闯关 湘教版选修2-21.用边长为48 cm 的正方形铁皮做一个无盖的铁盒,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能够焊成一个铁盒.那么所做的铁盒容积最大时,在四角截去的正方形的边长为( ) A .6 cm B .8 cmC .10 cmD .12 cm解析:选B.设截去小正方形的边长为x cm ,铁盒的容积为V cm 3.因此V =x (48-2x )2(0<x <24),V ′=12(x -8)(x -24).令V ′=0,则x =8∈(0,24),且此是所做铁盒的容积最大.2.(2021·渝北检测)某产品的销售收入y 1(万元)是产量x (千台)的函数:y 1=17x 2(x >0);生产本钱y 2(万元)是产量x (千台)的函数:y 2=2x 3-x 2(x >0),为使利润最大,那么应生产( )A .6千台B .7千台C .8千台D .9千台解析:选A.设利润为y (万元),则y =y 1-y 2=17x 2-(2x 3-x 2)=-2x 3+18x 2(x >0),∴y ′=-6x 2+36x =-6x ·(x -6).令y ′=0,解得x =0或x =6,经查验知x =6既是函数的极大值点又是函数的最大值点.应选A. 3.炼油厂某分厂将原油精炼为汽油,需对原油进行冷却和加热,若是第x 小时,原油温度(单位:℃)为f (x )=13x 3-x 2+8(0≤x ≤5),那么,原油温度的瞬时转变率的最小值是( ) A .8 C .-1D .-8解析:选C.原油温度的瞬时转变率为f ′(x )=x 2-2x =(x -1)2-1(0≤x ≤5),因此当x =1时,原油温度的瞬时转变率取得最小值-1.4.(2021·梁平质检)某车间靠墙壁要盖一间地面为长方形的小屋,现有存砖只够砌20 m 长的墙壁,那么应围成长为________m ,宽为____________m 的长方形才能使小屋占地面积最大.解析:设长为x m ,宽为y m ,面积为S m 2,则x +2y =20,即y =10-x2,S =x ·y =x (10-x 2)=10x -x 22.S ′=10-x ,因此当x =10时,小屋占地面积最大,因此x =10,y =5. 答案:10 5 一、选择题1.某商品一件的本钱为30元,在某段时刻内,假设以每件x 元出售,可卖出(200-x )件,当每件商品的定价为________元时,利润最大.( ) A .105 B .110 C .115D .120解析:选C.利润为S (x )=(x -30)(200-x )=-x 2+230x -6000,S ′(x )=-2x +230,由S ′(x )=0得x =115,这时利润最大为7225元.2.设底为等边三角形的直棱柱的体积为V ,那么其表面积最小时,底面边长为( )D .23V解析:选C.设该直棱柱的底面边长为x ,高为h ,表面积为S ,则V =34x 2·h ,h =4V 3x 2,表面积S =32x 2+3·x ·4V 3x 2,S ′=3x +-12V 3x2,令S ′=0,得x =34V .应选C.3.(2021·南开调研)已知某生产厂家的年利润y (单元:万元)与年产量x (单位:万件)的函数关系式为y =-13x 3+81x -234,那么使该生产厂家获取最大年利润的年产量为( )A .13万件B .11万件C .9万件D .7万件解析:选C.因为y ′=-x 2+81,因此当x >9时,y ′<0;当x ∈(0,9)时,y ′>0,因此函数y =-13x 3+81x -234在(9,+∞)上单调递减,在(0,9)上单调递增,因此x =9是函数的极大值点,又因为函数在(0,+∞)上只有一个极大值点,因此函数在x =9处取得最大值. 4.某公司生产一种产品,固定本钱为20000元,每生产一单位的产品,本钱增加100元,假设总收入R 与年产量x (0≤x ≤390)的关系是R (x )=-x 3900+400x ,0≤x ≤390,那么当总利润最大时,每一年生产的产品单位数是( ) A .150 B .200 C .250D .300解析:选D.由题意可得总利润P (x )=-x 3900+300x -20000,0≤x ≤390.由P ′(x )=-x 2300+300,令P ′(x )=0,得x =300.当0≤x <300时,P ′(x )>0,当300<x ≤390时,P ′(x )<0,因此当x =300时,P (x )最大.5.假设一球的半径为r ,那么内接于球的圆柱的侧面积最大为( ) A .2πr 2 B .πr 2 C .4πr 2πr 2解析:选A.如图,设内接圆柱的底面半径为R ,母线长为l , 则R =r cos θ,l =2r sin θ. ∴S 侧=2πR ·l =2πr cos θ×2r sin θ =4πr 2sin θcos θ.∴由S ′=4πr 2(cos 2θ-sin 2θ)=0,得θ=π4.∴当θ=π4,即R =22r 时,S 侧最大,且S 侧最大值为2πr 2.6.(2021·涪陵调研)某工厂要围建一个面积为512平方米的矩形堆料场,一边能够利用原有的墙壁,其他三边需要砌新的墙壁,当砌壁所用的材料最省时,堆料场的长和宽别离为( ) A .32米,16米 B .30米,15米 C .40米,20米 D .36米,18米解析:选A.要求材料最省确实是要求新砌的墙壁总长度最短,如下图,设场地宽为x 米,那么长为512x米,因此新墙总长度L =2x +512x(x >0),则L ′=2-512x2.令L ′=0,得x =±16.∵x >0,∴x =16.当x =16时,L 极小值=L min =64, ∴堆料场的长为51216=32(米).二、填空题7.用总长为14.8 m 的钢条制作一个长方体容器的框架,假设所制作容器的底面的一边比高长0.5 m ,那么当高为______ m 时,容器的容积最大.解析:由题意直接列出函数表达式,再用导数求最值,设高为x m , 则V =x (x +-2x ), 令V ′=-6x 2++=0, 即解15x 2-11x -4=0, 得x =1,x =-415(舍去).答案:18.把长60 cm的铁丝围成矩形,当长为________cm,宽为________cm时,矩形面积最大.解析:设长为x cm ,那么宽为(30-x ) cm , 因此面积S =x (30-x )=-x 2+30x . 由S ′=-2x +30=0,得x =15. 答案:15 159.(2021·沙坪坝质检)做一个容积为256 dm 3的方底无盖水箱,它的高为______dm 时最省料.解析:设底面边长为x dm ,那么高为h =256x2dm ,其表面积为S =x 2+4×256x 2×x =x 2+256×4x, S ′=2x -256×4x2,令S ′=0,则x =8, 那么高h =25664=4 (dm).答案:4 三、解答题10.(创新题)已知矩形的两个极点A 、D 位于x 轴上,另两个极点B 、C 位于抛物线y =4-x 2在x 轴上方的曲线上,求那个矩形的面积最大时的边长.解:设矩形边长AD =2x , 则AB =4-x 2,∴矩形面积为S =2x (4-x 2)=8x -2x 3(0<x <2). ∴S ′=8-6x 2.令S ′=0,解之得x 1=233,x 2=-233(舍去).当0<x <233时,S ′>0;当233<x <2时,S ′<0.当x =233时,S 取最大值为3239. 即矩形的边长别离是433、83时,矩形的面积最大.11.(2020·高考福建卷)某商场销售某种商品的体会说明,该商品每日的销售量y (单位:千克)与销售价钱x (单位:元/千克)知足关系式y =ax -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价钱为5元/千克时,每日可售出该商品11千克. (1)求a 的值;(2)假设该商品的本钱为3元/千克,试确信销售价钱x 的值,使商场每日销售该商品所取得的利润最大.解:(1)因为x =5时,y =11,因此a2+10=11,因此a =2.(2)由(1)可知,该商品每日的销售量y =2x -3+10(x -6)2,因此商场每日销售该商品所取得的利润f (x )=(x -3)⎣⎢⎡⎦⎥⎤2x -3+10(x -6)2=2+10(x -3)(x -6)2,3<x <6.从而,f ′(x )=10[(x -6)2+2(x -3)(x -6)]=30(x -4)(x -6).于是,当x 转变时,f ′(x ),f (x )的转变情形如下表:x (3,4) 4 (4,6) f ′(x ) + 0 - f (x )单调递增极大值42单调递减由上表可得,x =4是函数f (x )在区间(3,6)内的极大值点,也是最大值点.因此,当x =4时,函数f (x )取得最大值,且最大值等于42.即当销售价钱为4元/千克时,商场每日销售该商品所取得的利润最大. 12.(2020·高考山东卷)某企业拟建如下图的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两头均为半球形,依照设计要求容器的容积为80π3立方米,且l ≥2r .假设该容器的建造费用仅与其表面积有关.已知圆柱形部份每平方米建造费用为3千元,半球形部份每平方米建造费用为c (c >3)千元.设该容器的建造费用为y 千元.(1)写出y 关于r 的函数表达式,并求该函数的概念域;(2)求该容器的建造费用最小时的r .解:(1)设容器的容积为V ,由题意知V =πr 2l +43πr 3,又V =80π3, 故l =V -43πr 3πr 2=803r 2-43r =43⎝ ⎛⎭⎪⎫20r 2-r . 由于l ≥2r ,因此0<r ≤2.因此建造费用y =2πrl ×3+4πr 2c=2πr ×43⎝ ⎛⎭⎪⎫20r 2-r ×3+4πr 2c , 因此y =4π(c -2)r 2+160πr,0<r ≤2. (2)由(1)得y ′=8π(c -2)r -160πr 2 =8π(c -2)r 2⎝ ⎛⎭⎪⎫r 3-20c -2,0<r ≤2. 由于c >3,因此c -2>0.当r 3-20c -2=0时,r = 320c -2.令 320c -2=m ,则m >0,因此y ′=8π(c -2)r2(r -m )(r 2+rm +m 2). ①当0<m <2,即c >92时, 当r =m 时,y ′=0;当r ∈(0,m )时,y ′<0;当r ∈(m ,2)时,y ′>0,因此r =m 是函数y 的极小值点,也是最小值点.②当m ≥2,即3<c ≤92时, 当r ∈(0,2)时,y ′<0,函数单调递减, 因此r =2是函数y 的最小值点.综上所述,当3<c ≤92时,建造费用最小时r =2; 当c >92时,建造费用最小时r = 320c -2.。
教科物理必修1:第二章2知能演练轻松闯关

1.关于力,下列说法中错误的是()A.因为力是物体对物体的作用,所以,只有相互接触的物体间才有力的作用B.力不一定都有受力物体C.不接触的物体间也可以产生力的作用D.物体间的两个力总是同时产生的解析:选AB.不接触的物体间也可以产生力的作用,选项A错误;一个力一定涉及受力物体和施力物体,选项B错误;由力的产生条件知,选项C正确;物体间力的作用总是同时产生的,没有时间上的先后,选项D正确.2.下列关于力的作用效果的叙述正确的是()A.物体的运动状态发生改变必定是物体受到力的作用B.物体的运动状态没有发生改变,物体也可能受到力的作用C.力的作用效果不仅取决于力的大小和方向,还与力的作用点有关D.力作用在物体上,必定同时出现形变和运动状态的改变解析:选ABC.因为力是改变物体运动状态的原因,故物体的运动状态发生改变时,必定受到力的作用,故选项A正确;由于力的作用效果是使物体发生形变或改变物体的运动状态,两者可同时发生,也可不同时发生,故选项B正确;这里力可能只是使物体发生了形变.力的效果取决于力的三要素,故选项C正确;由以上分析知选项D错误.3.(2012·广安中学高一检测)下列关于力的叙述正确的是()A.所有物体间力的作用都是相互的B.施力物体必定也是受力物体C.汽车发动机运转产生了牵引力,可见,有的力不是别的物体施加的D.宇宙飞船在太空飞行,调节它飞行姿态的力是由飞船自身施加的解析:选AB.根据力的相互作用的特点,选项A、B正确;任何物体运动状态的改变都是靠外力的作用,内力不能改变自身的运动状态,选项C、D错误.4.关于物体重心的说法,正确的是()A.物体的重心一定在物体上B.质量分布均匀、形状规则的物体的重心一定在物体上C.只有形状规则的物体用悬线悬挂时,悬线方向才通过重心D.任何物体用细线悬挂时,悬线方向都通过重心答案:D5.图2-1-6(2012·成都龙泉中学高一检测)如图2-1-6所示,绳对物体竖直向上的拉力大小为150 N,试用力的图示法表示出该拉力.解析:画力的图示要严格按照以下步骤进行:(1)选定标度.(2)从作用点沿力的方向画一线段,线段长短按选定的标度和力的大小画.线段上加刻度,如图甲所示,从O点竖直向上画一段3倍于标度的线段;(3)在线段终点上加箭头表示力的方向.为了简便,也可以照图乙那样不画物体,而用质点来表示物体,画出力F的图示.答案:见解析一、选择题1.对于被运动员踢出的在水平草地上运动的足球,下列说法中正确的是()A.足球受到踢力B.足球受到沿运动方向的动力C.足球受到地面对它的阻力D.足球没有受到任何力的作用解析:选C.运动员踢球的力只有脚与球接触的时候才存在,球离开脚后,脚踢球的力也就没有了,因此A项错误.说足球受到沿运动方向的动力,但由于找不到施力物体,因此这个动力也就不存在,所以B项错.在草地上运动的足球受到重力、地面对它的支持力和地面对它的阻力,所以C项正确,D项错误.2.图2-1-7在世界壮汉大赛上有拉汽车前进的一项比赛,如图2-1-7是某壮汉正通过绳索拉汽车运动.则汽车所受拉力的施力物体和受力物体分别是()A.壮汉、汽车B.壮汉、绳索C.绳索、汽车D.汽车、绳索解析:选C.要研究的是汽车,直接对汽车产生拉力的是绳索而不是壮汉,汽车所受拉力是绳索和汽车之间的相互作用,故其施力物体是绳索,受力物体是汽车.3.下列说法中正确的是()A.自由下落的石块的速度越来越大,说明石块所受重力越来越大B.在空中飞行的物体不受重力作用C.一抛出的石块轨迹是曲线,说明石块所受的重力方向始终在改变D.将一石块竖直向上抛出,在先上升后下降的整个过程中,石块所受重力的大小与方向都不变解析:选D.物体的重力大小G=mg,g的值与物体运动的速度大小和方向无关,重力的方向总是竖直向下的,与物体的运动状态也无关,因此,A、B、C均错误,D正确.4.(2012·河北衡水中学高一检测)关于物体的重心,下列说法中正确的是()A.物体升高或降低时,重心在物体上的位置也相应升高或降低B.物体改变形状时,重心位置一定发生变化C. 物体的重心可能位于物体之外D.重心是物体内最重的一点解析:选C.对于一个确定的物体,其重心位置相对物体是固定不变的,不随物体上、下运动而变化,选项A错误;一条粗细均匀的绳子组成正方形时其重心为几何中心,组成圆形时其重心仍为几何中心,位置可能不变,选项B错误;重心可能在物体外,选项C正确;重心是物体所受重力的等效作用点,但并非物体的全部重力都集中于那一点,也不是物体内最重的点,选项D错误.5.如图2-1-8所示,走钢丝是一项传统的杂技项目,常常给观众带来惊险、刺激的感觉.走钢丝的过程中,演员往往手拿一根很长的铁棍.关于铁棍的作用,下列说法正确的是( )图2-1-8 A .为了增大演员与钢丝间的压力B .为了增大演员与钢丝间的摩擦力C .为了调节演员自身重心的位置D .为了增加观众的观赏性解析:选C.杂技演员手拿一长铁棍,主要是为了调节自身重心的位置,以便时时保持平衡,好安全走过钢丝.6.一人用斜向下的力推小车前进,力的大小为40 N ,方向与水平方向成30°,则下面画出的推小车的力的图示,如图2-1-9所示,正确的是( )图2-1-9解析:选D.力的图示法是用一条有向线段来表示力:有向线段的长短表示力的大小,有向线段的方向表示力的方向,箭尾画在作用点上.A 图中没有反映出力的大小,B 图中力的作用点画错,没在小车上,C 图中力的方向画反了,D 图中力的大小、方向、作用点均是正确的.7.月球表面的自由落体加速度是地球表面自由落体加速度的16,将一物体在地球表面上放在水中,恰好有一半浸在水中.若将该物体在月球表面上放在水中,则该物体将( )A .下沉B .漂浮,但浸没在水中的体积为该物体体积的1/30C .漂浮,浸没在水中的体积仍为该物体体积的一半D .悬浮在水中答案:C8.一人站在体重计上称体重,保持立正姿势称的体重为G ,当其缓慢地把一条腿伸出台面,体重计指针稳定后读数为G ′,则( )A .G >G ′B .G <G ′C .G =G ′D .无法判定解析:选C.人对体重计台面的压力大小依然等于人的重力,所以体重计读数G =G ′,C 项对.9.如果地面上一切物体受到的重力都消失了,则不可能出现的现象是( )A .江河的水不会流动B .鸡毛和铁球都可以悬浮在空中C .天不会下雨D .一切物体的质量都变为零解析:选D.江河的水从高处向低处流动,鸡毛、铁球下落,雨滴下落,靠的都是重力作用,如果没有了重力,这些现象都不会发生,因此,A 、B 、C 都会出现,所以不选A 、B 、C ;质量是物质的一种属性,不随重力的改变而改变,所以不可能出现的现象是选项D.10.关于重力的大小,下面说法中正确的是( )A .悬挂在竖直绳子上的物体静止时,绳子对物体的拉力大小等于物体重力的大小B .静止放在水平面上的物体对水平面的压力大小等于该物体重力的大小C .在天空中飞行的飞机不会掉下来,说明飞机所受的重力等于零D .浮于水面的物体,由于水的浮力作用,物体的重力将变小解析:选AB.A 项对,物体静止时,处于二力平衡状态,绳对物体的拉力和物体的重力是一对平衡力,所以相等.B 项对,物体对水平面的压力和水平面对物体的支持力是一对相互作用力,大小相等,当物体静止时,水平面对物体的支持力和物体的重力是一对平衡力,也相等,所以静止在水平面上的物体对水平面的压力大小等于该物体重力的大小.C 、D 项错,物体所受重力的大小跟物体的运动状态以及物体是否受其他作用力无关,只与物体的质量以及所处位置的g 值有关.二、非选择题11.(改编题)据报道,我国将在2017年左右实现载人登月,届时我国宇航员将登临月球,假设质量为60 kg 的宇航员乘太空船登上了月球.已知月球表面的重力加速度g ′=1.6 N/kg ,而地球表面的重力加速度g =9.8 N/kg ,则该宇航员:(1)在月球上的质量为多少,所受重力大小为多少;(2)在地球上的质量为多少,所受重力大小为多少.解析:(1)质量是物质的多少,与物体所处的环境无关,宇航员在月球上的质量为60 kg ,所受重力大小G ′=mg ′=60 kg ×1.6 N/kg =96 N.(2)宇航员在地球上的质量为60 kg ,所受重力大小G =mg =60 kg ×9.8 N/kg =588 N.答案:(1)60 kg 96 N (2)60 kg 588 N 12.图2-1-10如图2-1-10所示,把一边长为a 的匀质立方体,绕AB 棱翻转至对角面ABCD 处于竖直位置时,其重心位置升高多少?解析:如图所示,立方体在两位置时重心离地面的高度分别为a 2和22a ,所以重心位置升高为22a -a 2=2-12a .答案:2-12a s。
专题四第2讲知能演练轻松闯关

1.(2012·山西四校联考)如图,四棱锥S -ABCD 的底面是正方形,SD ⊥平面ABCD ,SD =AD =a ,点E 是SD 上的点,且DE =λa (0<λ≤1).(1)求证:对任意的λ∈(0,1],都有AC ⊥BE ; (2)若二面角C -AE -D 的大小为60°,求λ的值. 解:(1)证明:如图,建立空间直角坐标系D -xyz ,则A (a,0,0),B (a ,a,0),C (0,a,0),D (0,0,0),E (0,0,λa ),∴AC →=(-a ,a,0),BE →=(-a ,-a ,λa ), ∴AC →·BE →=0对任意λ∈(0,1]都成立, 即对任意的λ∈(0,1],都有AC ⊥BE .(2)显然n =(0,1,0)是平面ADE 的一个法向量, 设平面ACE 的法向量为m =(x ,y ,z ), ∵AC →=(-a ,a,0),AE →=(-a,0,λa ),∴⎩⎪⎨⎪⎧m ·AC →=0m ·AE →=0,即⎩⎪⎨⎪⎧ -ax +ay =0-ax +λaz =0,∴⎩⎪⎨⎪⎧x -y =0x -λz =0,令z =1,则x =y =λ,∴m =(λ,λ,1),∵二面角C -AE -D 的大小为60°,∴cos 〈n ,m 〉=n·m |n ||m |=λ1+2λ2=12,∵λ∈(0,1],∴λ=22.2.(2012·长春调研)如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC ,∠ABC =90°,PD ⊥平面ABCD ,AD =1,AB =3,BC =4. (1)求证:BD ⊥PC ;(2)求直线AB 与平面PDC 所成的角的大小;(3)设点E 在棱PC 上,PE →=λPC →,若DE ∥平面P AB ,求λ的值.解:如图,在平面ABCD 内过点D 作直线DF ∥AB ,交BC 于点F ,以D 为坐标原点,DA 、DF 、DP 所在的直线分别为x 、y 、z 轴建立空间直角坐标系D -xyz ,则A (1,0,0),B (1,3,0),D (0,0,0),C (-3,3,0).(1)证明:设PD =a ,则P (0,0,a ),BD →=(-1,-3,0),PC →=(-3,3,-a ), ∵BD →·PC →=3-3=0, ∴BD ⊥PC .(2)由(1)及PD ⊥平面ABCD 易知BD ⊥平面PDC ,则DB →就是平面PDC 的一个法向量. AB →=(0,3,0),DB →=(1,3,0). 设AB 与平面PDC 所成的角的大小为θ,则sin θ=|DB →·AB →||DB →|·|AB →|=323=32.∵0°<θ<90°,∴θ=60°,即直线AB 与平面PDC 所成的角的大小为60°.(3)由题意知,AB →=(0,3,0),DP →=(0,0,a ),P A →=(1,0,-a ),PC →=(-3,3,-a ), ∵PE →=λPC →,∴PE →=(-3λ,3λ,-aλ), DE →=DP →+PE →=(0,0,a )+(-3λ,3λ,-aλ) =(-3λ,3λ,a -aλ).设n =(x ,y ,z )为平面P AB 的法向量,则⎩⎪⎨⎪⎧AB →·n =0P A →·n =0,即⎩⎨⎧3y =0x -az =0.令z =1,得x =a ,∴n =(a,0,1).∵DE ∥平面P AB ,∴DE →·n =0,∴-3aλ+a -aλ=0,即a (1-4λ)=0,∵a ≠0,∴λ=14.3.(2012·郑州质量预测)如图,在四棱锥S -ABCD 中,AB ⊥AD ,AB ∥CD ,CD =3AB =3,平面SAD ⊥平面ABCD ,E 是线段AD 上一点,AE =ED =3,SE ⊥AD . (1)证明:平面SBE ⊥平面SEC ;(2)若SE =1,求直线CE 与平面SBC 所成角的正弦值.解:(1)证明:∵平面SAD ⊥平面ABCD ,平面SAD ∩平面ABCD =AD ,SE ⊂平面SAD ,SE ⊥AD ,∴SE ⊥平面ABCD ,∵BE ⊂平面ABCD ,∴SE ⊥BE .∵AB ⊥AD ,AB ∥CD ,CD =3AB =3,AE =ED =3, ∴∠AEB =30°,∠CED =60°.∴∠BEC =90°,即BE ⊥CE .又SE ∩CE =E ,∴BE ⊥平面SEC , ∵BE ⊂平面SBE ,∴平面SBE ⊥平面SEC .(2)由(1)知,直线ES ,EB ,EC 两两垂直.如图,以E 为原点,EB 为x 轴,EC 为y 轴,ES 为z 轴,建立空间直角坐标系. 则E (0,0,0),C (0,23,0),S (0,0,1),B (2,0,0), ∴CE →=(0,-23,0),CB →=(2,-23,0),CS →=(0,-23,1). 设平面SBC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·CB →=0n ·CS →=0,即⎩⎨⎧2x -23y =0-23y +z =0,令y =1,得x =3,z =2 3.∴平面SBC 的一个法向量为n =(3,1,23). 设直线CE 与平面SBC 所成角的大小为θ,则sin θ=|n ·CE →|n |·|CE →||=14,∴直线CE 与平面SBC 所成角的正弦值为14.4.(2012·高考江西卷)在三棱柱ABC -A 1B 1C 1中,已知AB =AC =AA 1=5,BC =4,点A 1在底面ABC 的投影是线段BC 的中点O .(1)证明在侧棱AA 1上存在一点E ,使得OE ⊥平面BB 1C 1C ,并求出AE 的长; (2)求平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值.解:(1)证明:连接AO ,在△AOA 1中,作OE ⊥AA 1于点E .因为AA 1∥BB 1,得OE ⊥BB 1. 因为A 1O ⊥平面ABC ,所以A 1O ⊥BC . 因为AB =AC ,OB =OC ,得AO ⊥BC ,所以BC ⊥平面AA 1O ,所以BC ⊥OE , 所以OE ⊥平面BB 1C 1C .又AO = AB 2-BO 2=1,AA 1=5,得AE =AO 2AA 1=55.(2)如图,分别以OA ,OB ,OA 1所在直线为x ,y ,z 轴,建立空间直角坐标系,则A (1,0,0),B (0,2,0),C (0,-2,0),A 1(0,0,2),B 1(-1,2,2),由AE →=15AA 1→得点E 的坐标是(45,0,25),由(1)得平面BB 1C 1C 的法向量是OE →=(45,0,25),设平面A 1B 1C 的法向量n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·A 1B 1→=0,n ·A 1C →=0,得⎩⎪⎨⎪⎧-x +2y =0,y +z =0.令y =1,得x =2,z =-1,即n =(2,1,-1),所以cos 〈OE →,n 〉=OE →·n |OE →|·|n |=3010,即平面A 1B 1C 与平面BB 1C 1C 夹角的余弦值是3010.5.(2012·山西适应性考试)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,P A ⊥平面ABCD ,P A =AB ,M ,N 分别是线段PB ,AC 上的动点,且不与端点重合,PM =AN . (1)求证:MN ∥平面P AD ;(2)当MN 的长最小时,求二面角A -MN -B 的余弦值.解:(1)证明:过M 作BA 的平行线交P A 于点E ,过N 作BA 的平行线交AD 于F 点,连接EF ,设PM =AN =a ,因为ME ∥NF ,ME =NF =22a , 所以四边形MEFN 为平行四边形, 所以MN ∥EF .又因为EF ⊂平面P AD ,MN ⊄平面P AD , 所以MN ∥平面P AD .(2)由(1)知MN =EF ,在Rt △EAF 中,设AF =x ,则可求得EA =1-x .所以MN 2=EF 2=AF 2+EA 2=x 2+(1-x )2≥12,当且仅当x =12时取等号,此时MN 的长最小,且M ,N 分别为PB ,AC 的中点.如图,以A 为坐标原点,射线AB 为x 轴的正半轴建立空间直角坐标系A -xyz ,则A (0,0,0),M (12,0,12),N (12,12,0),B (1,0,0),所以AM →=(12,0,12),AN →=(12,12,0),BM →=(-12,0,12),BN →=(-12,12,0). 设平面AMN 的法向量m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·AM →=0m ·AN →=0,即⎩⎨⎧12x +12z =012x +12y =0,令x =1,可取m =(1,-1,-1).设平面BMN 的法向量为n =(x 1,y 1,z 1),则⎩⎪⎨⎪⎧n ·BM →=0n ·BN →=0,即⎩⎨⎧-12x 1+12z 1=0-12x 1+12y 1=0,令x 1=1,则可取n =(1,1,1).所以cos 〈m ,n 〉=m·n |m |·|n |=-13,故二面角A -MN -B 的余弦值为-13.6.(2012·西城区期末考试)如图,在直三棱柱ABC -A 1B 1C 1中,AB =BC =2AA 1,∠ABC =90°,D 是BC 的中点. (1)求证:A 1B ∥平面ADC 1;(2)求二面角C 1-AD -C 的余弦值;(3)试问线段A 1B 1上是否存在点E ,使AE 与DC 1成60°角?若存在,确定E 点位置;若不存在,说明理由.解:(1)证明:连接A 1C ,交AC 1于点O ,连接OD .由ABC -A 1B 1C 1是直三棱柱,得四边形ACC 1A 1为矩形,O 为A 1C 的中点. 又D 为BC 的中点,所以OD 为△A 1BC 的中位线, 所以A 1B ∥OD ,因为OD ⊂平面ADC 1,A 1B ⊄平面ADC 1, 所以A 1B ∥平面ADC 1.(2)由ABC -A 1B 1C 1是直三棱柱,且∠ABC =90°,得BA 、BC 、BB 1两两垂直.以BC 、BA 、BB 1所在直线分别为x 、y 、z 轴,建立如图所示的空间直角坐标系B -xyz . 设BA =2,则B (0,0,0),C (2,0,0),A (0,2,0),C 1(2,0,1),D (1,0,0),所以AD →=(1,-2,0),AC 1→=(2,-2,1).设平面ADC 1的法向量为n =(x ,y ,z ),则有⎩⎪⎨⎪⎧n ·AD →=0,n ·AC 1→=0.所以⎩⎪⎨⎪⎧x -2y =0,2x -2y +z =0,取y =1,得n =(2,1,-2).易知平面ADC 的一个法向量为v =(0,0,1).所以cos 〈n ,v 〉=n ·v |n |·|v |=-23.因为二面角C 1-AD -C 是锐二面角,所以二面角C 1-AD -C 的余弦值为23.(3)假设存在满足条件的点E .因为点E 在线段A 1B 1上,A 1(0,2,1),B 1(0,0,1), 故可设E (0,λ,1),其中0≤λ≤2.所以AE →=(0,λ-2,1),DC 1→=(1,0,1). 因为AE 与DC 1成60°角,所以|cos 〈AE →,DC 1→〉|=|AE →·DC 1→|AE →|·|DC 1→||=12.即|1(λ-2)2+1·2|=12,解得λ=1或λ=3(舍去). 所以当点E 为线段A 1B 1的中点时,AE 与DC 1成60°角.。
课时知能演练轻闯关

课时知能演练轻闯关————————————————————————————————作者:————————————————————————————————日期:第二章第9课时知能演练轻松闯关1.《优化方案》系列丛书第三年的销量比第一年的销量增长了44%,若每年的平均增长率相同(设为x ),则以下结论正确的是( ) A .x >22% B .x <22% C .x =22%D .x 的大小由第一年的销量确定解析:选B.(1+x )2=1+44%,解得x =20%<22%.故选B.2.(2011·高考北京卷)根据统计,一名工人组装第x 件某产品所用的时间(单位:分钟)为f (x )=⎩⎪⎨⎪⎧c x ,x <A ,cA ,x ≥A(A ,c 为常数).已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么c 和A 的值分别是( )A .75,25B .75,16C .60,25D .60,16解析:选D.由函数解析式可以看出,组装第A 件产品所需时间为cA=15,故组装第4件产品所需时间为c4=30,解得c =60,将c =60代入cA=15得A =16.3.(2012·荆州调研)将甲桶中的a 升水缓慢注入空桶乙中,t 分钟后甲桶中剩余的水符合指数衰减曲线y =a e nt.若5分钟后甲桶和乙桶的水量相等,又过了m 分钟后甲桶中的水只有a8升,则m 的值为________.解析:令18a =a e nt ,即18=e nt ,因为12=e 5n ,故18=e 15n,比较知t =15,m =15-5=10.答案:104.小王每月除去所有日常开支,大约结余a 元.小王决定采用零存整取的方式把余钱积蓄起来,每月初存入银行a 元,存期1年(存12次),到期取出本和息.假设一年期零存整取的月利率为r ,每期存款按单利计息.那么,小王的存款到期利息为________元.解析:依题意得,小王存款到期利息为12ar +11ar +10ar +…+3ar +2ar +ar =12×12+12ar =78ar 元.答案:78ar一、选择题1.某种商品2011年提价25%,2012年欲恢复成原价,则应降价( ) A .30% B .25% C .20% D .15% 解析:选C.设2011年提价前的价格为a,2012年要恢复成原价应降价x .于是有a (1+25%)(1-x )=a ,解得x =20%,即应降价20%.2.(2012·海口市调研)若一根蜡烛长20 cm ,点燃后每小时燃烧5 cm ,则燃烧剩下的高度h (cm)与燃烧时间t (小时)的函数关系用图象表示为( )解析:选B.根据题意得解析式为h =20-5t (0≤t ≤4),其图象为B.3.如图,正方形ABCD 的顶点A ⎝ ⎛⎭⎪⎫0,22,B ⎝ ⎛⎭⎪⎫22,0,顶点C 、D 位于第一象限,直线l :x=t (0≤t ≤2)将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为f (t ),则函数s =f (t )的图象大致是( )解析:选C.直线l :x =t (0≤t ≤2)从左向右移动的过程中,直线l 左侧阴影部分的面积f (t )的改变量开始逐渐增大,当t =22时,面积f (t )的改变量最大,而后面积f (t )的改变量逐渐减小.故选C.4.在某种新型材料的研制中,实验人员获得了下列一组实验数据,现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )x 1.95 3.00 3.94 5.10 6.12 y 0.97 1.59 1.98 2.35 2.61A.y =2xB .y =log 2xC .y =12(x 2-1) D .y =2.16cos x解析:选B.通过检验可知,y =log 2x 较为接近,故选B.5.(2010·高考陕西卷)某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )A .y =[x 10]B .y =[x +310]C .y =[x +410]D .y =[x +510]解析:选B.由题意,当x =17时,A 选项错误,当x =16时,[x +410]=2,[x +510]=2,所以C 、D 选项错误,故选B. 二、填空题6.某电脑公司2011年的各项经营收入中,经营电脑配件的收入为400万元,占全年经营总收入的40%.该公司预计2013年经营总收入要达到1690万元,且计划从2011年到2013年,每年经营总收入的年增长率相同,2012年预计经营总收入为________万元.解析:设增长率为x ,则有40040%×(1+x )2=1690,1+x =1310,因此2012年预计经营总收入为40040%×1310=1300(万元). 答案:13007.某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣,如果顾客购物总金额超过800元,则超过800元部分享受一定的折扣优惠,按下表折扣分别累计计算.可以享受折扣优惠金额 折扣率 不超过500元的部分 5% 超过500元的部分 10%某人在此商场购物总金额为x 元,可以获得的折扣金额为y 元,则y 关于x 的解析式为 y =⎩⎪⎨⎪⎧0,0<x ≤800,5%x -800,800<x ≤1300,10%x -1300+25,x >1300.若y =30元,则他购物实际所付金额为________元. 解析:若x =1300元,则y =5%(1300-800)=25(元)<30(元), 因此x >1300.∴10%(x -1300)+25=30,得x =1350(元). 答案:13508.铁道机车运行1 h 所需的成本由两部分组成:固定部分m 元,变动部分(元)与运行速度x (km/h)的平方成正比,比例系数为k (k >0).如果机车从甲站匀速开往乙站,甲、乙两站间的距离为500 km ,则机车从甲站运行到乙站的总成本y (元)与机车运行速度x 之间的函数关系为________.解析:∵1 h 的成本为(m +kx 2),甲、乙两站间需运行500x (h),∴y =500x(m +kx 2)=500⎝ ⎛⎭⎪⎫m x +kx .答案:y =500⎝ ⎛⎭⎪⎫mx+kx三、解答题9.我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动x 小时的收费为f (x )元(15≤x ≤40),在乙家租一张球台开展活动x 小时的收费为g (x )元(15≤x ≤40).试求f (x )和g (x ); (2)小张选择哪家比较合算?为什么? 解:(1)f (x )=5x (15≤x ≤40),g (x )=⎩⎪⎨⎪⎧90,15≤x ≤302x +30,30<x ≤40.(2)由f (x )=g (x )得,⎩⎪⎨⎪⎧15≤x ≤305x =90,或⎩⎪⎨⎪⎧30<x ≤405x =2x +30,即x =18或x =10(舍). 当15≤x <18时,f (x )-g (x )=5x -90<0, ∴f (x )<g (x ),即选甲家;当x =18时,f (x )=g (x ),即可以选甲家,也可以选乙家; 当18<x ≤30时,f (x )-g (x )=5x -90>0, ∴f (x )>g (x ),即选乙家;当30<x ≤40时,f (x )-g (x )=5x -(2x +30)=3x -30>0, ∴f (x )>g (x ),即选乙家. 综上所述,当15≤x <18时,选甲家;当x =18时,可以选甲家,也可以选乙家;当18<x ≤40时,选乙家.10.某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至x 元,则本年度新增用电量y (亿千瓦时)与(x -0.4)元成反比例.又当x =0.65时,y =0.8. (1)求y 与x 之间的函数关系式;(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价-成本价)] 解:(1)∵y 与(x -0.4)成反比例,∴设y =kx -0.4(k ≠0).把x =0.65,y =0.8代入上式, 得0.8=k0.65-0.4,k =0.2.∴y =0.2x -0.4=15x -2,即y 与x 之间的函数关系式为y =15x -2. (2)根据题意,得⎝⎛⎭⎪⎫1+15x -2·(x -0.3)=1×(0.8-0.3)×(1+20%). 整理,得x 2-1.1x +0.3=0,解得x 1=0.5,x 2=0.6. 经检验x 1=0.5,x 2=0.6都是所列方程的根. ∵x 的取值范围是0.55~0.75,故x =0.5不符合题意,应舍去.∴x =0.6.∴当电价调至0.6元时,本年度电力部门的收益将比上年度增加20%.11.某跨国饮料公司在对全世界所有人均GDP(即人均纯收入)在0.5千美元~8千美元的地区销售该公司A 饮料的情况的调查中发现:人均GDP 处在中等的地区对该饮料的销售量最多,然后向两边递减.(1)下列几个模拟函数中(x 表示人均GDP ,单位:千美元,y 表示年人均A 饮料的销量,单位:升),用哪个模拟函数来描述人均A 饮料销量与地区的人均GDP 关系更合适?说明理由.①y =ax 2+bx ,②y =kx +b ,③y =log a x +b ,④y =a x+b ;(2)若人均GDP 为1千美元时,年人均A 饮料的销量为2升,人均GDP 为4千美元时,年人均A 饮料的销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,年人均A 饮料的销量最多是多少?解:(1)用函数①y =ax 2+bx 来描述人均A 饮料销量与地区的人均GDP 的关系更合适.因为函数y =kx +b ,y =log a x +b ,y =a x+b 在其定义域内都是单调函数,不具备先递增后递减的特征.(2)依题意知,函数图象过点(1,2)和(4,5),则有⎩⎪⎨⎪⎧a +b =216a +4b =5,解得⎩⎪⎨⎪⎧a =-14b =94,∴y =-14x 2+94x (0.5≤x ≤8),∵y =-14x 2+94x=-14(x -92)2+8116≤8116,∴在各地区中,当x =92时,年人均A 饮料销量最多是8116升.。
Section Ⅱ 知能演练轻松闯关(4)

Ⅰ.品句填词1.If we leave now, I can catch the earlier flight(航班).2.Australia is home to many unique(独特的) animals, such as kangaroos and koala bears.3.I__recognised(辨认出) his voice the moment I picked up the phone.4.I drove along the__narrow(狭窄的) road half an hour until I reached the village.5.As the idea of low-carbon life is now widely accepted, more and more people travel by public transport(交通).6.For a long distance, air travel is the fastest way to get to your destination(目的地).7.Let me see your passport and visa(签证) please.8.Both English and French are official(官方的) languages in Canada.9.This suitcase is full.I can't pack(捆扎) any more clothes in.10.Your local library will be a useful source(来源) of information.Ⅱ.完成句子1.我跟大多数同学已经失去了联系。
I've lost__contact__with most of my classmates.2.是我母亲在我遇到困难时给予我鼓励。
Section Ⅲ 知能演练轻松闯关(2)

Ⅰ.单句语法填空1.There was a time when Anne was so crazy about everything to do with nature.2.I will never forget the days when I was in the summer camp.3.He is a teacher of rich experience, from whom we can learn a lot.4.The reason why he was late was that something was wrong with his bike on the way.5.The film in which he played the leading role was a great success.6.After graduation, he returned to the city where he grew up.7.I wanted to find someone with whom I could share my travel experience.8.We visited the house where the famous scientist once lived.9.The car whose window got broken in the accident belongs to Mr. Brown.10.This is the primary school where both my brother and I stayed for six years.11.It was a period when they met very frequently.12.When I arrived, my friend took me to see the house where I would be staying.13.We have come to a point where everyone has different opinions and it is difficult to reach an agreement.14.Bob is now in a position where he has no more money to pay his rent.15.One of the reasons why he was refused in the interview was that his spoken English was terrible.Ⅱ.语法与写作——将下列句子合并升级为定语从句1.The university is big and beautiful.My brother studies in the university.The university where/in__which__my__brother__studies__is__big__and__beautiful.2.The party turned out to be quite successful.We sang the beautiful song Fore v er Young at the party.The party where/at which we sang the beautiful song Fore v er Young turned out to be quite successful.3.Do you know the lady? Our English teacher is taking a photo of her.Do__you__know__the__lady__whom__our__English__teacher__is__taking__a __photo__of?4.Rose knew the year.The Red Cross was founded in the year.Rose__knew__the__year__when/in__which__the__Red__Cross__was__founde d.5.Paul looked so excited today.His friends didn't know the real reason.Paul's__friends__didn't__know__the__real__reason__why/for__which__he__lo oked__so__excited__today.6.We paid a visit to the coffee shop last summer.A writer wrote his famous book in the coffee shop.Last__summer__we__paid__a__visit__to__the__coffee__shop__where/in__whi ch__a__writer__wrote__his__famous__book.7.We'll go to meet the famous singer.We often talked about the famous singer.We'll go to meet the famous singer whom__we__often__talked__about.8.She has three sons.All of her sons are abroad now.She has three sons, all__of__whom are abroad now.9.There are sixty students in our class.Thirty of the students in our class are boys.There are sixty students in our class, thirty__of__whom are boys.10.He wrote many children's books.Nearly half of the children's books were published in the 1990s.He wrote many children's books, nearly half__of__which were published in the 1990s.Ⅰ.单句语法填空1.I still remember the moment when we first met.2.My hometown that/which I spent most of my childhood has taken on a new look.3.She is a very kind lady, who looks after my little brother.4.The Smiths have two children, both of whom work in New York.5.This is the most interesting novel__that__ I have ever read.6.The reason why he gave up his wellpaid job isn't known to us.7.I'll never forget the time that/which we spent together in the army camp.8.I'll never forget the moment when we first met.9.The number of the people that/who come to visit the city each year has risen to one million.10.They have reached the stage where they are going to get married.Ⅱ.阅读理解AAs everyone knows, English is very important today. It hasbeen used everywhere in the world. It has become the mostcommon language on the Internet and for international trade. Ifwe can speak English well, we will have more chances tosucceed. Because more and more people have taken notice of it,the number of the people who learn English has increased at ahigh speed.But for myself, I learn English not only because of its importance and its usefulness, but also because of my love for it.When I learn English, I can feel a different way of thinking which gives me more room to touch the world. When I read English novels, I can feel the pleasure from the book which is different from reading the translation.When I speak English, I can feel the confidence from my words. When I write English, I can see the beauty which is not the same as our Chinese...I love English, because it gives me a colorful dream. I hope I can travel around the world one day. With my good English, I can make friends with many people from different countries and see many places of great interests. I dream that I can go to London, because it is the birthplace of English. I also want to use my good English to introduce our great places to the people who speak English. I hope that they can love our country like us. I know, Rome was not built in a day. I believe that after continuous hard study, one day I can speak English very well.If you want to be loved, you should learn to love and be lovable. So I believe, as I love English, it will love me, too.I am sure that I will realize my dream one day!【解题导语】作者介绍了英语对自己而言很重要,并说明了自己学习英语的原因。
Section Ⅱ 知能演练轻松闯关(3)

Ⅰ.品句填词1.Olympic athletes(运动员) train hard so that they can get good grades at the final competition.2.Learning to play the piano isn't easy at the beginning and takes effort and determination(决心).3.Many old legends(传说) were handed down from generation to generation.4.When he was only a boy, he was expected to become a world champion(冠军).5.The captain(队长) of this football team scored two wonderful goals early in the game.6.As far as I'm concerned, students should place their study, fitness/health(健康) and safety before the other things.7.To begin with, a new stadium(体育场) has been built,which has become the new landmark in our school.8.Since the purpose of this event(比赛项目) is to help more people learn about the traditional Chinese culture, all the students are welcome to take part.9.I am lucky enough to be chosen as one of the hosts(主持人).10.If you study English hard, you will master(掌握) the language.Ⅱ.完成句子1.举办奥运会不仅承担巨大的责任,同时也享有极大的荣誉。
第一章1.3.第1课时知能演练轻松闯关

1.cos(-420°)的值等于( )A.32B .-32 C.12 D .-12 解析:选C.cos(-420°)=cos(360°+60°)=cos 60°=12. 2.sin 2(2π-α)+cos(π+α)·cos(π-α)+1的值是( )A .1B .2C .0D .2sin 2α解析:选B.原式=sin 2α+cos α·cos α+1=1+1=2.3.已知cos α=35,则sin(3π+α)·cos(2π-α)·tan(π-α)等于( ) A .±35 B .±45C.925D.1625解析:选D.原式=sin(π+α)·cos(-α)·tan(π-α)=(-sin α)·cos α·(-tan α)=sin 2α,由cos α=35,得sin 2α=1-cos 2α=1625. 4.已知角α和β的终边关于x 轴对称,则下列各式中正确的是( )A .sin α=sin βB .sin(α-2π)=sin βC .cos α=cos βD .cos(2π-α)=-cos β解析:选C.由α和β的终边关于x 轴对称,故β=-α+2k π(k ∈Z ),故cos α=cos β.5.下列三角函数:①sin(n π+4π3);②cos(2n π+π6);③sin(2n π+π3); ④cos[(2n +1)π-π6];⑤sin[(2n +1)π-π3](n ∈Z ). 其中与sin π3数值相同的是( ) A .①② B .②③④C .②③⑤D .①③⑤解析:选C.①sin(n π+4π3)=⎩⎨⎧sin π3(n 为奇数)-sin π3(n 为偶数); ②cos(2n π+π6)=cos π6=sin π3;③sin(2n π+π3)=sin π3;④cos[(2n +1)π-π6]=cos 5π6=-sin π3; ⑤sin[(2n +1)π-π3]=sin π3.故②③⑤正确. 6.sin(-17π6)的值为________.解析:sin(-17π6)=-sin 17π6=-sin(5π6+2π)=-sin 5π6=-sin(π-π6) =-sin π6=-12. 答案:-127.化简:cos (-α)tan (7π+α)sin (π+α)=________. 解析:原式=cos αtan α-sin α=-sin αsin α=-1. 答案:-18.若cos(π6-α)=33,则cos(α+5π6)=________. 解析:cos(α+5π6)=cos[π-(π6-α)]=-cos(π6-α) =-33. 答案:-339.求下列各式的值: (1)sin π4cos 19π6tan 21π4; (2)sin 420°cos 330°+sin(-690°)cos(-660°).解:(1)原式=sin π4cos(2π+7π6)tan(5π+π4) =22cos 7π6tan π4=22cos(π+π6)=22(-cos π6) =-22×32=-64. (2)原式=sin(360°+60°)cos(360°-30°)+sin(-2×360°+30°)cos(-2×360°+60°)=sin 60°cos 30°+sin 30°cos 60°=32×32+12×12=1. 10.求sin(2n π+2π3)cos(n π+4π3)(n ∈Z )的值. 解:①当n 为奇数时,原式=sin 2π3(-cos 4π3) =sin(π-π3)[-cos(π+π3)] =sin π3cos π3=32×12=34. ②当n 为偶数时,原式=sin 2π3cos 4π3=sin(π-π3)cos(π+π3) =sin π3(-cos π3)=32×(-12)=-34.1.给出下列各函数值:①sin(-1 000°);②cos(-2 200°);③tan(-10);④sin 7π10cosπtan 17π9.其中符号为负的是( )A .①B .②C .③D .④解析:选C.sin(-1 000°)=sin 80°>0;cos(-2 200°)=cos(-40°)=cos 40°>0;tan(-10)=tan(3π-10)<0; sin 7π10cosπtan 17π9=-sin 7π10tan 17π9,sin 7π10>0,tan 17π9<0. ∴原式>0. 2.3sin(-1 200°)tan 19π6=________. 解析:原式=-3sin(4×360°-240°)tan(3π+π6) =-3sin(-240°)tan π6=3×33sin(180°+60°) =-3×33sin 60°=-32. 答案:-323.化简:(1)cos π5+cos 2π5+cos 3π5+cos 4π5; (2)tan 10°+tan 170°+sin 1 866°-sin(-606°).解:(1)原式=(cos π5+cos 4π5)+(cos 2π5+cos 3π5) =[cos π5+cos(π-π5)]+[cos 2π5+cos(π-2π5)] =(cos π5-cos π5)+(cos 2π5-cos 2π5)=0. (2)原式=tan 10°+tan(180°-10°)+sin 1 866°-sin(-606°)=tan 10°-tan 10°+sin (5×360°+66°)-sin[(-2)×360°+114°]=tan 10°-tan 10°+sin 66°-sin 66°=0.4.设f (x )=a sin(πx +α)+b cos(πx +β)+7,α,β均为实数,若f (2 013)=6,求f (2 014)的值.解:∵f (2 013)=a sin(2 013π+α)+b cos(2 013π+β)+7=-a sin α-b cos β+7,∴-a sin α-b cos β+7=6,∴a sin α+b cos β=1,又∵f (2 014)=a sin(2 014π+α)+b cos(2 014π+β)+7=a sin α+b cos β+7,∴f (2 014)=1+7=8.。
【教育资料】2.5第二课时知能演练轻松闯关学习专用

1.已知数列{a n }的前n 项和S n =1-5+9-13+17-21+…+(-1)n -1(4n -3),则S 15=( )A .-29B .29C .30D .-30 解析:选B.S 15=1-5+9-13+…+57=-4×7+57=29.2.数列{a n }的通项公式是a n =1n +n +1,若前n 项和为10,则项数为( ) A .11 B .99C .120D .121解析:选C.∵a n =1n +n +1=n +1-n , ∴S n =a 1+a 2+…+a n =2-1+3-2+…+n +1-n=n +1-1=10, ∴n +1=121,∴n =120.3.(2019·滨州调研)数列9,99,999,9 999,…,的前n 项和等于( )A .10n -1 B.10(10n -1)9-n C.109(10n -1) D.109(10n -1)+n 解析:选B.a n =10n -1,∴S n =a 1+a 2+…+a n=(10-1)+(102-1)+…+(10n -1)=(10+102+…+10n )-n =10(10n -1)9-n . 4.数列1,11+2,11+2+3,…,11+2+…+n的前n 项和为( ) A.2n 2n +1 B.2n n +1C.n +2n +1D.n 2n +1解析:选B.该数列的通项为a n =2n (n +1),分裂为两项差的形式为a n =2(1n -1n +1),令n =1,2,3,…,则S n =2(1-12+12-13+13-14+…+1n -1n +1), ∴S n =2(1-1n +1)=2n n +1. 5.已知数列{a n }={12,13+23,14+24+34,15+25+35+45,…},那么数列{b n }={1a n a n +1}前n 项的和为( )A .4(1-1n +1) B .4(12-1n +1) C .1-1n +1 D.12-1n +1解析:选A.∵a n =1+2+3+…+n n +1=n (n +1)2n +1=n 2, ∴b n =1a n a n +1=4n (n +1)=4(1n -1n +1). ∴S n =4(1-12+12-13+13-14+…+1n -1n +1) =4(1-1n +1). 6.等差数列18,15,12,…,前n 项和的最大值为________.解析:由已知得a 1=18,d =-3,∴a n =a 1+(n -1)d =18-3(n -1)=21-3n .∴当n =7时,a 7=0.∴S n 最大值为S 6=S 7=18×7+7×62×(-3)=63. 答案:637.已知数列{a n }中,a n =⎩⎪⎨⎪⎧2n -1 (n 为正奇数),2n -1 (n 为正偶数),则a 9=________(用数字作答),设数列{a n }的前n 项和为S n ,则S 9=________(用数字作答). 解析:a 9=29-1=256.S 9=(a 1+a 3+a 5+a 7+a 9)+(a 2+a 4+a 6+a 8)=1-451-4+4×(3+15)2=377. 答案:256 3778.数列22,422,623,…,2n 2n ,…,前n 项的和为________. 解析:由题可知,{2n 2n }的通项是等差数列{2n }的通项与等比数列{12n }的通项之积. 设S n =22+422+623+…+2n 2n ,① 12S n =222+423+624+…+2n 2n +1,② ①-②得(1-12)S n =22+222+223+224+…+22n -2n 2n +1 =2-12n -1-2n 2n +1 ∴S n =4-n +22n -1. 答案:4-n +22n -1 9.已知数列{a n }是首项a 1=4、公比q ≠1的等比数列,S n 是其前n 项和,且4a 1,a 5,-2a 3成等差数列.(1)求公比q 的值;(2)设A n =S 1+S 2+S 3+…+S n ,求A n .解:(1)由已知2a 5=4a 1-2a 3,即2a 1·q 4=4a 1-2a 1·q 2,∵a 1≠0,整理得,q 4+q 2-2=0,解得q 2=1,即q =1或q =-1.又q ≠1,∴q =-1.(2)S n =4[1-(-1)n ]1-(-1)=2-2(-1)n , ∴A n =S 1+S 2+…+S n =2n -2·-1[1-(-1)n ]1-(-1)=2n +1-(-1)n .10.(2019·日照高二检测)等差数列{a n }中,a 1=3,公差d =2,S n 为前n 项和,求1S 1+1S 2+…+1S n. 解:∵等差数列{a n }的首项a 1=3,公差d =2,∴前n 项和S n =na 1+n (n -1)2d =3n +n (n -1)2×2 =n 2+2n (n ∈N *),∴1S n =1n 2+2n =1n (n +2)=12(1n -1n +2), ∴1S 1+1S 2+…+1S n=12[(1-13)+(12-14)+(13-15)+…+(1n -1-1n +1)+(1n -1n +2)]=12(1+12-1n +1-1n +2)=34-2n +32(n +1)(n +2). 1.在数列{a n }中,a 1=2,na n +1=(n +1)a n +2(n ∈N *),则a 10等于( )A .34B .36C .38D .40解析:选C.由na n +1=(n +1)a n +2,得(n -1)a n =na n -1+2.则有a n n -a n -1n -1=2n (n -1)=2(1n -1-1n),∴a n -1n -1-a n -2n -2=2(1n -2-1n -1),…, a 22-a 11=2(11-12),累加,得a n n -a 1=2(1-1n).∴a n =2n +2n (1-1n)=4n -2.∴a 10=38.2.(2019·临沂质检)已知a n =n +13n ,则数列{a n }的前n 项和S n =__________. 解析:S n =(1+2+…+n )+(13+132+…+13n )=12(n 2+n +1-13n ). 答案:12(n 2+n +1-13n ) 3.(2019·兖州高二检测)设数列{a n }为等差数列,前n 项和为S n ,已知a 2=2,S 5=15,(1)求{a n }的通项公式;(2)若b n =a n 2n ,求数列{b n }的前n 项和T n .解:(1)由⎩⎪⎨⎪⎧ a 2=2S 5=15⇒⎩⎪⎨⎪⎧a 1+d =25a 1+10d =15⇒a 1=1,d =1,∴a n =n . (2)b n =a n 2n =n 2n , T n =12+222+323+…+n 2n ,① 12T n =122+223+324+…+n 2n +1,②①-②得12T n =12+122+123+…+12n -n 2n +1, 12T n =12[1-(12)n ]1-12-n 2n +1=1-12n -n 2n +1, T n =2-12n -1-n 2n .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.x =5
y =6PRINT x +y =11
END
上面程序运行时输出的结果是( )
A .x +y =11
B .11
C .x +y
D .出错信息
解析:选A.这是个简单的程序,只有赋值语句和输出语句,输出语句有运算功能可知选A.
2.下面程序输出的结果是( ) S =1
i =1
WHILE S<=2012
i =i +2S =S*i
WEND
PRINT i
END
A .满足1×3×5×…×n >2012的最小整数n
B .1+3+5+…+2012
C .求方程1×3×5×…×n =2012中的n 值
D .1×3×5×…×2012
解析:选 A.从所给的程序来看是循环语句,而输出的是i ,且S ≤2012,故输出的是满足1×3×5×…×n >2012的最小整数n .
3.下面是一个用基本语句编写的程序,阅读后解决所给出的问题: (1)该算法程序的功能是什么?
(2)画出该程序相应的程序框图.
解:(1)由算法程序可知,该算法程序的功能是计算分段函数
f (x)=⎩
⎪⎨⎪⎧
x 2-2x (x ≥2)x +5 (x <2)的函数值. (2)程序框图:
一、选择题
1.下列赋值语句正确的是( )
A .a -b =2
B .5=a
C .a =b =4
D .a =a +2
解析:选D .根据赋值语句的格式要求知A 、B 、C 均不正确,只有D 正确,故选D .
2.当a =3时,下面的程序段输出的结果是(
)
A .3
B .6
C .9
D .10
解析:选B.根据条件3<10,故y =2×3=6.
3.(2011·高考福建卷改编)运行如图所示的程序,输出的结果是( ) a =1
b =2
a =a +
b PRINT a
END
A .2
B .3
C .5
D .6
解析:选B.a =1,b =2.
a =a +
b =1+2=3.
所以输出的结果是3.
4.下列程序的功能是:判断任意输入的数x 是否是正数,若是,输出它的平方值;若不是,
则填入的条件应该是( )
A .x>0
B .x<0
C .x>=0
D .x<=0
解析:选D.因为条件满足则执行y =-x ,条件不满足则执行y =x*x ,由程序功能知条件应为x<=0.
5.在十进制中,2012=2×100+1×101+0×102+2×103,那么在五进制中数码2012折合成十进制数为( )
A .30
B .257
C .603
D .2012
解析:选B.2012(5)=2×50+1×51+0×52+2×53
=2+5+0+250=257.
二、填空题
6.给出一个算法:
INPUT x
IF x<=0 THEN
f(x)=4*x
ELSE
f(x)=2^ x
END IF
PRINT f(x)
根据以上算法,可求得f (-1)+f (2) =_____________.
解析:f (x )=⎩
⎪⎨⎪⎧
4x ,x ≤0,2x ,x >0, ∴f (-1)+f (2)=-4+22=0.
答案:0
7.已知f (x )=x 4+4x 3+6x 2+4x +1,则f (9)=________.
解析:f (x )=(((x +4)x +6)x +4)x +1
v 0=1,v 1=9+4=13,
v 2=13×9+6=123,
v 3=123×9+4=1111,
v 4=1111×9+1=10000,
∴f (9)=10000.
答案:10000 8.为了在运行下面的程序之后得到结果y =16,则键盘输入的x 应该是________. INPUT x
IF x<0 THEN
y =(x +1)*(x +1)
ELSE
y =(x -1)*(x -1)END IF
PRINT y
END
解析:由程序可得:当x <0时y =(x +1)2.
∴若y =16,则(x +1)2=16.∴x +1=±4.
∴x =-5或3(舍去),∴x =-5.
当x ≥0时y =(x -1)2.若y =16,则(x -1)2=16,
∴x -1=±4.∴x =5或-3(舍去).
∴x =5.综上所述:x =±5.
答案:±5
三、解答题
9.根据如图所示的框图写出程序语句.
解: i =1
S =1
WHILE i<=50
S =S +i i =i +2
WEND
PRINT S
END 10.根据下面的程序写出相应的算法功能,并画出相应的程序框图. S =0
i =1
WHILE i<=999
S =S +i^2i
=i +2
WEND
PRINT S
END
解:其程序的算法功能是求和.
12+32+52+ (9992)
其程序框图如图.
11.已知程序框图如图所示,求输出的S 值.
解:由题意,
S =1×2+2×22+3×23+…+9×29+10×210, 两边同乘以2,得
2S =1×22+2×23+…+8×29+9×210+10×211 ∴-S =2+22+23+…+29+210-10×211
∴S =10×211-2(1-210
)1-2
=10×211-211+2
=9×211+2=9×2048+2
=18434.。
