高二理科数学函数高考模拟卷2
高三第二次模拟数学试题(理科2)

高三第二次模拟数学试题(理科2)一、选择题:1.若集合{}{}2||,0A x x x B x x x ===+≥,则AB = ( B )A .[1,0]-B .[0,)+∞C . [1,)+∞D .(,1]-∞- 2.设m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:①//////αββγαγ⎫⇒⎬⎭ ② //m m αββα⊥⎫⇒⊥⎬⎭③//m m ααββ⊥⎫⇒⊥⎬⎭ ④////m n m n αα⎫⇒⎬⊂⎭, 其中为真命题的是 ( C )A . ①④B . ②③C . ①③D .②④3.“2ω=”是“函数sin()y x ωϕ=+的最小正周期为π”的 ( A ) A .充分非必要条件 B .必要非充分条件 C .充分必要条件 D .既不充分也不必要条件 4.将圆122=+y x 按向量a ()1,2-=平移后,恰好与直线0=+-b y x 相切,则实数b 的值为 ( B )A 23±B 23±-C 22±D 22±-5.在三角形ABC 中,120=A ,5=AB ,7=BC ,则CBsin sin 的值为 ( D ) A58 B 85 C 35 D 53 6.函数(),,0)(0,sin xy x xππ=∈-的图象可能是下列图象中的 ( C )yxOπ -π 12 (A ) O1yxπ-π2 (B ) 12 y xOπ -π (C ) yxOπ -π12(D )7.以椭圆的右焦点2F 为圆心作一个圆,使此圆过椭圆中心O 并交椭圆于点M ,N ,若过椭圆左焦点1F 的直线MF 1是圆2F 的切线,则椭圆的右准线与圆2F ( A ) A .相交 B .相离 C .相切 D .位置关系随率心率改变8.函数,,y kx b k b =+其中(0k ≠)是常数,其图象是一条直线,称那个函数为线性函数.关于非线性可....导.函数()x f ,在点0x 邻近一点x 的函数值()x f ,能够用如下方法求其近似代替值:()()()()000'≈+-f x f x f x x x .利用这一方法,9983.m =的近似代替值 ( A )(A )大于m (B )小于m (C )等于m (D )与m 的大小关系无法确定 二、填空题:9. 若 12z a i =+, 234z i =-,且12z z +为纯虚数,则实数a 的值为 -310.一个与球心距离为2的平面截球所得的圆面面积为π,则球的表面积为 20π11.已知向量AB =(4, 0),AC =(2, 2),则= (-2,2) ;AC 与的夹角的大小为 90°12.已知函数()()21,02log (2),0xx f x x x ⎧≤⎪=⎨⎪+>⎩,若()0x f ≥2,则0x 的取值范畴是13.有如此一种数学游戏:在33⨯的表格中,要求每个格子中都填上1、2、3三个数字中的某一个数字,且每一行和每一列都不能显现重复的数字,则此游戏共有 12 种不同的填法 14.数列{ a n },{ b n }(1,2,3,n =⋅⋅⋅)由下列条件所确定: (ⅰ)a 1<0, b 1>0 ;(ⅱ)k ≥2时,a k 与b k 满足如下条件:当110k k a b --+时,a k = a k-1, b k =112k k a b --+; 当11<0k k a b --+时,a k =112k k a b --+, b k =b k-1. 那么,当a 1=-5,b 1=5时, { a n }的通项公式为 5 , n=1,,n2;n a -⎧=⎨⎩当b 1> b 2>…>b n (n ≥2)时,用a 1,b 1表示{ b k }的通项公式为b k = (k =2,3…,n ). (1)215() 2n --;(2)11111()()2k k b a b a -=+-三、解答题: 15.(本小题12分)已知α为钝角,且1tan()47πα+=- 求: (Ⅰ)tan α;(Ⅱ)cos 21)sin 24απαα+--.解: (Ⅰ)由已知:tan 11tan()41tan 7πααα++==-- …………………2分得4tan 3α=- …………………5分(Ⅱ)cos 21)sin 24απαα+--22cos sin cos sin 2αααα=+- 22cos sin cos 2sin cos ααααα=+- …………………8分 ∵(,)2παπ∈且4tan 3α=-∴34sin ,cos 55αα==- …………………10分∴22cos sin cos 2sin cos ααααα+- 9225=43432()5555⨯--⨯⨯- 1829=…………………12分 16.(本小题13分)某公司有10万元资金用于投资,假如投资甲项目,依照市场分析明白:一年后可能获利10﹪,可能缺失10﹪,可能不赔不赚,这三种情形发生的概率分别为21,41,41;假如投资乙项目,一年后可能获利20﹪,也可能缺失20﹪,这两种情形发生的概率分别为)(和1 =+βαβα.(Ⅰ)假如把10万元投资甲项目,用ξ表示投资收益(收益=回收资金-投资资金),求ξ的概率分布及ξE ;(Ⅱ)若把10万元投资投资乙项目的平均收益不低于投资甲项目的平均收益,求α的取值范畴.解:(Ⅰ)依题意,ξ的可能取值为1,0,-1 …………1分ξ的分布列为…………4分ξE =2141-=41…………6分 (Ⅱ)设η表示10万元投资乙项目的收益,则η的分布列为…………8分2422-=-=αβαηE …………10分依题意要求14249116αα-≥≥…………13分 注:只写出916α≥扣1分 17.(本小题13分)如图,在四棱锥P-ABCD 中,平面P AD ⊥平面ABCD , 90ABC BCD ∠=∠=︒,12PA PD DC CB AB ====,E 是BD 的中点.(Ⅰ)求证:EC//平面APD ;(Ⅱ)求BP 与平面ABCD 所成角的正切值; (Ⅲ) 求二面角P-AB-D 的大小. 解法一:(Ⅰ)如图,取PA 中点F ,连结EF 、FD ,∵E 是BP 的中点,∵EF//AB 且12EF AB =,又∵1 ,2DC AB DC AB =∴EF //DC ∴四边形EFDC 是平行四边形,故得EC//F D …………2分 又∵EC ⊄平面PAD ,FD ⊂平面PAD∴EC//平面ADE …………4分 (Ⅱ)取AD 中点H ,连结PH ,因为PA=PD ,因此PH ⊥AD∵平面P AD ⊥平面ABCD 于AD ∴PH ⊥面ABCD∴HB 是PB 在平面ABCD 内的射影PABCDE∴∠PBH 是PB 与平面ABCD 所成角 …………6分 ∵四边形ABCD 中,90ABC BCD ∠=∠=︒ ∴四边形ABCD 是直角梯形12DC CB AB ==设AB=2a,则BD ,在ABD ∆中,易得45DBA ∠=︒,AD ∴=PH ===,又∵22224BD AD a AB +==,∴ABD ∆是等腰直角三角形,90ADB ∠=︒∴HB == ∴在Rt PHB ∆中,tan PH PBH HB ∠=== …………10分 (Ⅲ)在平面ABCD 内过点H 作AB 的垂线交AB 于G 点,连结PG ,则HG 是PG 在平面ABCD 上的射影,故PG ⊥AB ,因此∠PGH 是二面角P-AB-D 的平面角,由AB=2a …………11分HA =,又45HAB ∠=︒∴12HG a = 在Rt PHG ∆中,2tan 12PHPGH HG a ∠=== 13分 ∴二面角P-AB-D的大小为 …………14分解法二:(Ⅰ)同解法一 4分(Ⅱ)设AB=2a ,同解法一中的(Ⅱ)可得 90ADB ∠=︒如图,以D 点为原点,DA 所在直线为x 轴,DB 所在直线为y 轴,过D 点且垂直于平面ABCD 的直线为z 轴建立空间直角坐标系. …………5分则,0)B,(,0,)22P ,则(,)PB =-,平面ABCD 的一个法向量为m =(0,0,1), …………7分因此,2cos ,||||PB m PB m PB m ⋅<>===⋅PABCDE FHG可得PB 与平面ABCD因此 PB 与平面ABCD所成角的正切值为5…………10分(Ⅲ)易知,0,0)A,则(,0)AB =-,设平面PAB 的一个法向量为000(,,)n x y z =,则0000000000000y x n AB z x n PB ⎧=⎧=⋅=⎧⎪⎪⇔⇔⎨⎨⎨=⋅=+=⎩⎪⎪⎩⎩,令01x =,可得(1,1,1)n =……12分得cos ,m n <>==, 因此二面角P-AB-D 的大小为…………14分18.(本小题13分) 已知:()212,n n n f x a x a x a x =+++ ()1(1)n n f n -=- ,1,2,3,n =⋅⋅⋅.(I )求1a 、2a 、3a ; (II )求数列{}n a 的通项公式; (II )求证:131<⎪⎭⎫⎝⎛n f解:(I )由已知()1111-=-=-a f ,因此11=a 1分()21212=+-=-a a f ,因此32=a()313213-=-+-=-a a a f ,因此53=a 3分(II )()()()11111(1)11(1)1(1)(1)n n n n n n n a f f n na n n+++++-⋅=---=-⋅+--⋅∴=++即121n a n +=+因此关于任意的 3,2,1=n , 12-=n a n 7分(III )()()nn x n x x x x f 125332-++++=∴()nn n f ⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛3112315313313132 ①()14323112315313313131+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⋅n n n f ②①─②,得()2312111111222213333333nn n f n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭9分()11211931122212113333313n n nn n -+⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭-⎢⎥⎛⎫⎛⎫⎣⎦=+--=- ⎪⎪⎝⎭⎝⎭- ∴11133n nn f -⎛⎫=-⎪⎝⎭, 12分 又n =1,2,3…,故⎪⎭⎫ ⎝⎛31n f < 1 13分 19.(本小题14分)如图, ()A m 和(,)B n 两点分别在射线OS 、OT 上移动,且12OA OB ⋅=-,O 为坐标原点,动点P满足OP OA OB =+.(Ⅰ)求m n ⋅的值;(Ⅱ)求P 点的轨迹C 的方程,并说明它表示如何样的曲线?(Ⅲ)若直线l 过点E (2,0)交(Ⅱ)中曲线C 于M 、N 两点,且3ME EN =,求l 的方程. 解:(Ⅰ)由已知得()(,) 11 22OA OB m n mn ⋅=⋅=-=-分14mn ∴⋅=…………4分(Ⅱ)设P 点坐标为(x ,y )(x >0),由OP OA OB =+得(,)()(,)x y m n =+())m n m n =+- …………5分∴)x m ny m n =+⎧⎪⎨=-⎪⎩ 消去m ,n 可得2243y x mn -=,又因14mn = 8分∴ P 点的轨迹方程为221(0)3y x x -=>它表示以坐标原点为中心,焦点在x 轴上,且实轴长为2,焦距为4的双曲线2213y x -=的右支 …………9分(Ⅲ)设直线l 的方程为2x ty =+,将其代入C 的方程得 223(2)3ty y +-=即 22(31)1290t y ty -++=易知2(31)0t -≠(否则,直线l的斜率为又22214436(31)36(1)0t t t ∆=--=+>设1122(,),(,)M x y N x y ,则121222129,3131t y y y y t t -+==--∵ l 与C 的两个交点,M N 在y 轴的右侧12122121222222(2)(2)2()491224313134031x x ty ty t y y t y y t t t t t t t =++=+++-=⋅+⋅+--+=->- ∴ 2310t -<,即2103t <<又由 120x x +>同理可得 2103t << …………11分由3ME EN =得1122(2,)3(2,)x y x y --=-∴121223(2)3x x y y -=-⎧⎨-=⎩由122222123231t y y y y y t +=-+=-=--得 22631t y t =-由21222229(3)331y y y y y t =-=-=-得222331y t =-- 消去2y 得 2222363(31)31t t t =--- 解之得:2115t = ,满足2103t << …………13分故所求直线l 0y --=0y +-= …………14分 20.(本小题14分)设关于x 的方程210x mx --=有两个实根α、β,且α<β.定义函数22().1x mf x x -=+ (Ⅰ)求()()f f αα+ββ的值;(Ⅱ)判定()f x 在区间(,)αβ上的单调性,并加以证明; (Ⅲ)若,λμ为正实数,证明不等式:|()()|||.f f λα+μβμα+λβ-<α-βλ+μλ+μ(Ⅰ)解:∵,αβ是方程210x mx --=的两个实根∴1mαβαβ+=⎧⎨⋅=-⎩∴222()21()()1m f ααβαβααααβααααβ-+--====-+- 同理1()f ββ=∴()()2f f ααββ+= …………3分(Ⅱ)∵22()1x m f x x -=+ ∴2222222(1)(2)22(1)()(1)(1)x x m x x mx f x x x +--⋅--'==-++ …………4分当(,)x αβ∈时,21()()0x mx x x --=-α-β< …………5分而()0f x '>∴()f x 在(,)αβ上为增函数 …………7分 (Ⅲ)∵,R λμ+∈且αβ<∴()()0λαμβλμαμβαλαμβαλμλμλμ+-+-+-==>+++()()0λαμβλμβλαβλαμββλμλμλμ+-+-+-==<+++∴λαμβαβλμ+<<+ …………9分由(Ⅱ)可知()()()f f f λαμβαβλμ+<<+同理可得()()()f f f μαλβαβλμ+<<+ …………10分∴()()()()()()f f f f f f λαμβμαλβαββαλμλμ++-<-<-++∴()()()()f f f f λαμβμαλβαβλμλμ++-<-++ …………12分又由(Ⅰ)知11(),(),1f f αβαβαβ===-∴11()()||||f f βααβαβαβαβ--=-==- 因此 |()()|||.f f λα+μβμα+λβ-<α-βλ+μλ+μ…………14分。
湖南省郴州市高考数学二模试卷(理科)含答案解析

湖南省郴州市高考数学二模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分,每小题给出四个选项,只有一个选项符合题目要求.1.若复数z满足zi=1﹣i,则z的共轭复数是()A.﹣1﹣i B.1﹣i C.﹣1+i D.1+i2.若A={x|x2+2x﹣8<0},B={x|x<1},则图中阴影部分表示的集合为()A.(﹣4,1]B.(1,2)C.[1,2)D.(﹣4,1)3.如图所示,程序框图(算法流程图)的输出结果是()A.B. C.D.4.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取()A.55人,80人,45人B.40人,100人,40人C.60人,60人,60人D.50人,100人,30人5.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是()A.若α⊥β,m⊂α,n⊂β,则m⊥n B.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β6.直线与圆O:x2+y2=4交于A、B两点,则=()A.2 B.﹣2 C.4 D.﹣47.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为()A.150 B.180 C.240 D.5408.如图,椭圆+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为()A.0 B.C.D.﹣9.在区间[﹣1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率()A. B. C. D.10.设点P是曲线C:y=x3﹣x+上的任意一点,曲线C在P点处的切线的倾斜角为α,则角α的取值范围是()A.[π,π)B.(,π]C.[0,)∪[π,π)D.[0,)∪[π,π)11.已知倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是()A.B. C.2 D.12.已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导数f′(x)在R上的恒有f′(x)<(x∈R),则不等式f(x2)<+的解集为()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣2,2) C.(﹣∞,﹣)∪(,+∞)D.(﹣,)二、填空题:本大题共4小题,每小题5分,共25分.13.已知四边形ABCD满足|AB|=|AD|,|CD|=且∠BAD=60°,﹣=,那么四边形ABCD的面积为.14.记不等式组所表示的平面区域为D.若直线y=a(x+1)与D有公共点,则a的取值范围是.15.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是.16.已知函数f(x)=asinx+bcosx(其中ab≠0)且对任意的x∈R,有f(x)≤f(),给出以下命题:①a=b;②f(x+)为偶函数;③函数y=f(x)的图象关于点(,0)对称;④函数y=f′(x)的图象可由函数y=f(x)的图象向左平移得到;⑤函数f(x)在y轴右侧的图象与直线y=的交点按横坐标从小到大依次为P1,P2,P3,P4,…,则|P2P4|=2π.其中正确命题的序号是.(将所有正确命题的序号都填上)三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤. 17.已知函数f(x)=sin2x﹣cos2x﹣,x∈R.(1)求函数f(x)的最小正周期及单调递增区间;(2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=,f(C)=0,sinB=2sinA,求△ABC的面积S.18.已知数列{a n}满足a1=3,且对任意的正整数m,n都有a n+m=a n•a m,若数列{b n}满足b n=n﹣1+log3a n,{b n}的前n项和为B n.(Ⅰ)求a n和B n;(Ⅱ)令c n=a n•b n,d n=,数列{c n}的前n项和为S n,数列{d n}的前n项和为T n,分别求S n和T n.19.如图,四棱锥P﹣ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.(Ⅰ)求证:BC⊥PC;(Ⅱ)线段PC上是否存在点M,使得二面角P﹣AD﹣M的平面角余弦值为?若存在,求出的值;若不存在,说明理由.20.已知函数(1)若x=1是函数f(x)的极大值点,求函数f(x)的单调递减区间;(2)若恒成立,求实数ab的最大值.21.已知椭圆Γ的中心在原点,焦点F1,F2在x轴上,离心率等于,它的一个顶点恰好是抛物线y=x2的焦点.(1)求椭圆Γ的标准方程;(Ⅱ)Q为椭圆Γ的左顶点,直线l经过点(﹣,0)与椭圆Γ交于A,B两点.(1)若直线l垂直于x轴,求∠AQB的大小;(2)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.22.已知a为实数,函数f(x)=alnx+x2﹣4x.(Ⅰ)是否存在实数a,使得f(x)在x=1处取极值?证明你的结论;(Ⅱ)若函数f(x)在[2,3]上存在单调递增区间,求实数a的取值范围;(Ⅲ)设g(x)=(a﹣2)x,若存在x0∈[,e],使得f(x0)≤g(x0)成立,求实数a 的取值范围.湖南省郴州市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,每小题给出四个选项,只有一个选项符合题目要求.1.若复数z满足zi=1﹣i,则z的共轭复数是()A.﹣1﹣i B.1﹣i C.﹣1+i D.1+i【考点】复数代数形式的乘除运算.【分析】由复数z满足zi=1﹣i,可得z,从而求出即可.【解答】解:∵复数z满足zi=1﹣i,∴z===﹣1﹣i,故=﹣1+i,故选:C.2.若A={x|x2+2x﹣8<0},B={x|x<1},则图中阴影部分表示的集合为()A.(﹣4,1]B.(1,2)C.[1,2)D.(﹣4,1)【考点】Venn图表达集合的关系及运算.【分析】先观察Venn图,由图可知阴影部分表示的集合为(C R B)∩A,根据集合的运算求解即可.【解答】解:A={x|x2+2x﹣8<0}=(﹣4,2),∵B={x|x<1},∴C R B=[1,+∞),∴(C R B)∩A=[1,2).故选:C.3.如图所示,程序框图(算法流程图)的输出结果是()A.B. C.D.【考点】程序框图.【分析】模拟程序图框的运行过程,得出当n=8时,不再运行循环体,直接输出S值.【解答】解:模拟程序图框的运行过程,得;该程序运行后输出的是计算S=++=.故选:D.4.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取()A.55人,80人,45人B.40人,100人,40人C.60人,60人,60人D.50人,100人,30人【考点】分层抽样方法.【分析】先根据总体数和抽取的样本,求出每个个体被抽到的概率,用每一个层次的数量乘以每个个体被抽到的概率就等于每一个层次的值.【解答】解:每个个体被抽到的概率为=,∴专科生被抽的人数是×1500=50,本科生要抽取×3000=100,研究生要抽取×900=30,故选:D.5.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是()A.若α⊥β,m⊂α,n⊂β,则m⊥n B.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β【考点】空间中直线与平面之间的位置关系;命题的真假判断与应用;平面与平面之间的位置关系.【分析】由α⊥β,m⊂α,n⊂β,可推得m⊥n,m∥n,或m,n异面;由α∥β,m⊂α,n ⊂β,可得m∥n,或m,n异面;由m⊥n,m⊂α,n⊂β,可得α与β可能相交或平行;由m⊥α,m∥n,则n⊥α,再由n∥β可得α⊥β.【解答】解:选项A,若α⊥β,m⊂α,n⊂β,则可能m⊥n,m∥n,或m,n异面,故A 错误;选项B,若α∥β,m⊂α,n⊂β,则m∥n,或m,n异面,故B错误;选项C,若m⊥n,m⊂α,n⊂β,则α与β可能相交,也可能平行,故C错误;选项D,若m⊥α,m∥n,则n⊥α,再由n∥β可得α⊥β,故D正确.故选D.6.直线与圆O:x2+y2=4交于A、B两点,则=()A.2 B.﹣2 C.4 D.﹣4【考点】平面向量数量积的运算;直线与圆相交的性质.【分析】先求圆心到直线的距离,再求弦心距所在直线与AO的夹角,然后求数量积.【解答】解:圆O:x2+y2=4的圆心是(0,0),由此知圆心到直线的距离是=<2所以直线与圆相交故AB=2=2=r,所以∠AOB=所以=2×2×cos=2故选A7.某班5位同学分别选择参加数学、物理、化学这3个学科的兴趣小组,每人限选一门学科,则每个兴趣小组都至少有1人参加的不同选择方法种数为()A.150 B.180 C.240 D.540【考点】计数原理的应用.【分析】根据题意,分析有将5位同学分成满足题意的3组有1,1,3与2,2,1两种,分别计算可得分成1、1、3与分成2、2、1时的分组情况种数,进而相加可得答案.【解答】解:将5位同学分成满足题意的3组有1,1,3与2,2,1两种,分成1、1、3时,有C53•A33=60种,分成2、2、1时,有=90种,所以共有60+90=150种,故选:A.8.如图,椭圆+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为()A.0 B.C.D.﹣【考点】椭圆的简单性质.【分析】由OF1⊥B1B2,OF2⊥B1B2,可得∠F1OF2为二面角F1﹣B1B2﹣F2的平面角,即为120°,求得椭圆的a,b,c,运用向量的夹角公式可得cos<,>=,计算即可得到所求异面直线所成的角的余弦值.【解答】解:由OF1⊥B1B2,OF2⊥B1B2,可得∠F1OF2为二面角F1﹣B1B2﹣F2的平面角,即为120°,椭圆+y2=1中a=,b=1.c=,可得B1F2=B2F1==,=+, =+,•=•+•+•+•=﹣1+0+0+••(﹣)=﹣2,即有cos<,>===﹣,可得异面直线F1B2与B1F2所成角的余弦值为.故选:C.9.在区间[﹣1,1]上任取两数m和n,则关于x的方程x2+mx+n=0的两根都是负数的概率()A. B. C. D.【考点】几何概型.【分析】根据几何概型的概率公式,利用积分求出对应区域的面积进行求解即可.【解答】解:∵区间[﹣1,1]上任取两数m和n,∴,对应的区域为正方形,面积S=2×2=4,若方程x2+mx+n=0的两根都是负数,则,即,作出不等式组对应的平面区域如图:则对应的面积S=∫dm=m3|=,则对应的概率P==,故选:A.10.设点P是曲线C:y=x3﹣x+上的任意一点,曲线C在P点处的切线的倾斜角为α,则角α的取值范围是()A.[π,π)B.(,π]C.[0,)∪[π,π)D.[0,)∪[π,π)【考点】利用导数研究曲线上某点切线方程.【分析】求函数的导数,利用导数的几何意义求出切线斜率的取值范围,结合正切函数的图象和性质进行求解即可.【解答】解:函数的导数f′(x)=3x2﹣,则f′(x)=3x2﹣≥﹣,即tanα≥﹣,则0≤α<或π≤α<π,故角α的取值范围是[0,)∪[π,π),故选:D11.已知倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,M(4,2)是弦AB的中点,则双曲线C的离心率是()A.B. C.2 D.【考点】双曲线的简单性质.【分析】设A(x1,y1),B(x2,y2),根据AB的中点P的坐标,表示出斜率,从而得到关于a、b的关系式,再求离心率.【解答】解:∵倾斜角为的直线与双曲线C:﹣=1(a>0,b>0)相交于A,B两点,∴直线的斜率k=tan=,设A(x1,y1),B(x2,y2),则﹣=1,①;﹣=1,②,①﹣②得=,则k==•∵M(4,2)是AB的中点,∴x1+x2=8,y1+y2=4,∵直线l的斜率为,∴=•,即=,则b2=a2,c2=a2+b2=(1+)a2,∴e2=1+==()2.则e=故选:D.12.已知定义在R上的函数f(x)满足f(2)=1,且f(x)的导数f′(x)在R上的恒有f′(x)<(x∈R),则不等式f(x2)<+的解集为()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣2,2) C.(﹣∞,﹣)∪(,+∞)D.(﹣,)【考点】利用导数研究函数的单调性;不等式的综合.【分析】由f′(x)<,构造辅助函数g(x)=f(x)﹣x,求导,利用导数判断函数单调递减,根据f(2)=1,求得g(2)=,根据f(x2)<+,将其转换成g(x2)<g (2),根据函数单调性即可求得不等的解集.【解答】解:f′(x)<(x∈R),f′(x)﹣<0,设g(x)=f(x)﹣x,g′(x)=f′(x)﹣<0,∴g(x)是R上的减函数,g(2)=g(2)﹣=,∴f(x2)<+,g(x2)=f(x2)﹣<=g(2),∴x2>2,解得:x>或x<﹣,∴原不等式的解集为(﹣∞,﹣)∪(,+∞).故答案选:C.二、填空题:本大题共4小题,每小题5分,共25分.13.已知四边形ABCD满足|AB|=|AD|,|CD|=且∠BAD=60°,﹣=,那么四边形ABCD的面积为.【考点】向量的线性运算性质及几何意义.【分析】由题意作图辅助,从而可判断四边形为直角梯形,从而求其面积.【解答】解:由题意作图如右图,∵﹣==,∴BC∥AD且|BC|=|AD|,又∵|AB|=|AD|,且∠BAD=60°,∴|AE|=|AB|=|AD|,∴|BC|=|DE|,∴BCDE是平行四边形,∴CD∥BE,∴DC⊥AD,∵|CD|=,∴|AB|=|AD|=2,∴S==,故答案为:.14.记不等式组所表示的平面区域为D.若直线y=a(x+1)与D有公共点,则a的取值范围是[,4].【考点】简单线性规划.【分析】本题考查的知识点是简单线性规划的应用,我们要先画出满足约束条件的平面区域,然后分析平面区域里各个角点,然后将其代入y=a(x+1)中,求出y=a(x+1)对应的a的端点值即可.【解答】解:满足约束条件的平面区域如图示:因为y=a(x+1)过定点(﹣1,0).所以当y=a(x+1)过点B(0,4)时,得到a=4,当y=a(x+1)过点A(1,1)时,对应a=.又因为直线y=a(x+1)与平面区域D有公共点.所以≤a≤4.故答案为:[,4]15.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是16π.【考点】由三视图求面积、体积.【分析】由三视图知,几何体是一个三棱柱,三棱柱的底面是边长为3的正三角形,侧棱长是2,根据三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径,求出半径即可求出球的表面积.【解答】解:由三视图知,几何体是一个三棱柱ABC﹣A1B1C1,三棱柱的底面是边长为3的正三角形ABC,侧棱长是2,三棱柱的两个底面的中心连接的线段MN的中点O与三棱柱的顶点A的连线AO就是外接球的半径,∵△ABC是边长为3的等边三角形,MN=2,∴AM=,OM=1,∴这个球的半径r==2,∴这个球的表面积S=4π×22=16π,故答案为:16π.16.已知函数f(x)=asinx+bcosx(其中ab≠0)且对任意的x∈R,有f(x)≤f(),给出以下命题:①a=b;②f(x+)为偶函数;③函数y=f(x)的图象关于点(,0)对称;④函数y=f′(x)的图象可由函数y=f(x)的图象向左平移得到;⑤函数f(x)在y轴右侧的图象与直线y=的交点按横坐标从小到大依次为P1,P2,P3,P4,…,则|P2P4|=2π.其中正确命题的序号是①②④⑤.(将所有正确命题的序号都填上)【考点】命题的真假判断与应用.【分析】由三角函数的最大值相等列式判断①;利用辅助角公式化简代值判断②;求出得值判断③;求导后利用函数的图象平移判断④;由函数图象平移周期不变判断⑤【解答】解:①f(x)=asinx+bcosx=,∵对任意的x∈R,有f(x)≤f(),∴,则2a2+2b2=(a+b)2,∴(a﹣b)2=0,则a=b,故①正确;②∵f(x)=asinx+bcosx=a(sinx+cosx)=,∴f(x+)=,∴f(x+)为偶函数,故②正确;③∵=≠0,故③错误;④y=f′(x)=acosx﹣asinx==,而f(x+)==,故④正确;⑤由f(x)的周期为2π,而f(x)=是把向左平移个单位得到的,∴|P2P4|=2π,故⑤正确.故答案为:①②④⑤.三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.17.已知函数f(x)=sin2x﹣cos2x﹣,x∈R.(1)求函数f(x)的最小正周期及单调递增区间;(2)设△ABC的内角A,B,C的对边分别为a,b,c,且c=,f(C)=0,sinB=2sinA,求△ABC的面积S.【考点】三角函数中的恒等变换应用;正弦函数的图象.【分析】(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2x﹣)﹣1,由周期公式可求最小正周期,由2k,k∈Z 可解得单调递增区间.(2)由f(C)=sin(2C﹣)﹣1=0,可得sin(2C﹣)=1,解得C的范围利用正弦函数的图象和性质即可求得C的值,由sinB=2sinA,利用正弦定理,余弦定理即可解得a,b,根据三角形面积公式即可得解.【解答】解:(1)∵f(x)=sin2x﹣cos2x﹣=sin2x﹣=sin(2x﹣)﹣1,…∴最小正周期T=,.由2k,k∈Z 得k,k∈Z,∴f(x)的最小正周期为π,单调递增区间为[k,k](k∈Z).…(2)f(C)=sin(2C﹣)﹣1=0,则sin(2C﹣)=1,∵0<C<π,∴0<2C<2π,∴﹣,∴2C﹣=,∴C=,…∵sinB=2sinA,由正弦定理,得,①由余弦定理,得c2=a2+b2﹣2abcos,即a2+b2﹣ab=3,②由①②解得a=1,b=2.∴S△ABC==.…18.已知数列{a n}满足a1=3,且对任意的正整数m,n都有a n+m=a n•a m,若数列{b n}满足b n=n﹣1+log3a n,{b n}的前n项和为B n.(Ⅰ)求a n和B n;(Ⅱ)令c n=a n•b n,d n=,数列{c n}的前n项和为S n,数列{d n}的前n项和为T n,分别求S n和T n.【考点】数列的求和;数列递推式.【分析】(I)对任意的正整数m,n都有a n+m=a n•a m,可得a n+1=a n•a1=3a n,利用等比数列的通项公式可得a n.可得b n,即可得出{b n}的前n项和为B n.(II)c n=(2n﹣1)•3n.利用“错位相减法”与等比数列的前n项和公式可得S n.d n===,利用“裂项求和”即可得出.【解答】解:(I)∵对任意的正整数m,n都有a n+m=a n•a m,∴a n+1=a n•a1=3a n,∴数列{a n}是等比数列,公比为3,首项为3,∴a n=3n.∴b n=n﹣1+log3a n=n﹣1+n=2n﹣1,∴{b n}的前n项和为B n==n2.(II)c n=a n•b n,=(2n﹣1)•3n.∴数列{c n}的前n项和为S n=3+3×32+5×33+…+(2n﹣1)•3n,∴3S n=32+3×33+…+(2n﹣3)•3n+(2n﹣1)•3n+1,∴﹣2S n=3+2(32+33+…+3n)﹣(2n﹣1)•3n+1=﹣3﹣(2n﹣1)•3n+1=(2﹣2n)•3n+1﹣6,∴S n=(n﹣1)•3n+1+3.d n===,当n=1时,d1=;当n≥2时,T n=+++…++=﹣﹣.当n=1时也成立,∴T n=﹣﹣.19.如图,四棱锥P﹣ABCD的底面ABCD是菱形,且∠ABC=60°,侧面PAD是边长为2的正三角形且与底面ABCD垂直.(Ⅰ)求证:BC⊥PC;(Ⅱ)线段PC上是否存在点M,使得二面角P﹣AD﹣M的平面角余弦值为?若存在,求出的值;若不存在,说明理由.【考点】二面角的平面角及求法;空间中直线与直线之间的位置关系.【分析】(Ⅰ)取AD中点O,连结OP,OC,以O为原点,OC为x轴,OD为y轴,OP 为z轴,建立空间直角坐标系,利用向量法能证明BC⊥PC.(Ⅱ)设M(a,b,c),由=λ可得点M的坐标为M(λ,0,﹣λ),求出平面AMD的法向量和平面PAD的法向量,由此利用向量法能求出结果.【解答】(Ⅰ)证明:取AD中点O,连结OP,OC,∵侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,∴△ADC是等边三角形,PO、AD、CO两两垂直,以O为原点,OC为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,由题意得P(0,0,),C(,0,0),B(,﹣2,0),=(0,﹣2,0),=(﹣,0,),∴=0,∴CB⊥CP.(Ⅱ)解:假设存在符合要求的点M,令=λ(0≤λ≤1),则=λ=λ(,0,﹣),可得M(λ,0,﹣λ),∴=(λ,1,﹣λ),=(λ,﹣1,﹣λ),设平面MAD的法向量为=(x,y,z),则,令z=λ,得=(λ﹣1,0,λ),显然平面PAD的一个法向量为=(,0,0),∵二面角P﹣AD﹣M的平面角余弦值为,∴|=,∴λ=或λ=﹣1(舍去)∴线段PC上存在点M, =时,使得二面角P﹣AD﹣M的平面角余弦值为.20.已知函数(1)若x=1是函数f(x)的极大值点,求函数f(x)的单调递减区间;(2)若恒成立,求实数ab的最大值.【考点】利用导数求闭区间上函数的最值;函数在某点取得极值的条件.【分析】(1)求导数,利用x=1是函数f(x)的极大值点,确定a的范围,即可得到函数f(x)的单调递减区间;(2)构造函数,确定函数的单调性,可得函数的最值,即可得到结论.【解答】解:(1)求导数可得,f′(x)=∵x=1是函数f(x)的极大值点,∴0<a<1∴函数f(x)的单调递减区间为(0,a),(1,+∞);(2)∵恒成立,∴alnx﹣x+b≤0恒成立,令g(x)=alnx﹣x+b,则g′(x)=∴g(x)在(0,a)上单调递增,在(a,+∞)上单调递减∴g(x)max=g(a)=alna﹣a+b≤0∴b≤a﹣lna,∴ab≤a2﹣a2lna令h(x)=x2﹣x2lnx(x>0),则h′(x)=x(1﹣2lnx)∴h(x)在(0,)上单调递增,在(,+∞)上单调递减∴h(x)max=h()=,∴ab≤即ab的最大值为.21.已知椭圆Γ的中心在原点,焦点F1,F2在x轴上,离心率等于,它的一个顶点恰好是抛物线y=x2的焦点.(1)求椭圆Γ的标准方程;(Ⅱ)Q为椭圆Γ的左顶点,直线l经过点(﹣,0)与椭圆Γ交于A,B两点.(1)若直线l垂直于x轴,求∠AQB的大小;(2)若直线l与x轴不垂直,是否存在直线l使得△QAB为等腰三角形?如果存在,求出直线l的方程;如果不存在,请说明理由.【考点】抛物线的简单性质.【分析】(I)设椭圆的标准方程为:,根据条件列方程组解出a,b即可;(II)(1)把x=﹣代入椭圆方程解出A,B坐标,根据三角形的边长即可求出∠AQB;(2)设AB斜率为k,联立方程组求出A,B坐标的关系,通过计算=0得出,则当△QAB为等腰直角三角形时,取AB中点N,则QN⊥AB,计算QN的斜率判断是否为﹣即可得出结论.【解答】解:(I)设椭圆的标准方程为:,(a>b>0).抛物线y=x2的焦点为(0,1),∴,解得a2=4,∴椭圆Γ的标准方程为+y2=1.(II)Q(﹣2,0),设A(x1,y1),B(x2,y2),(1)当直线l垂直于x轴时,直线l的方程为x=﹣.则直线l与x轴交于M(﹣,0).联立方程组,解得或.不妨设A在第二象限,则A(﹣,),B(﹣,﹣).∴|QM|=|AM|=.∴∠AQM=45°,∴∠AQB=2∠AQM=90°.(2)当直线l与x轴不垂直时,设直线l方程为y=k(x+)(k≠0).联立方程组,消元得(25+100k2)x2+240k2x+144k2﹣100=0.∴x1+x2=,x1x2=.y1y2=k2(x1+)(x2+)=﹣•+.∵=(x1+2,y1),=(x2+2,y2),∴=x1x2+2(x1+x2)+4+y1y2=﹣+4+﹣•+=0.∴QA⊥QB,即△QAB是直角三角形.假设存在直线l使得△QAB是等腰直角三角形,则|QA|=|QB|.取AB的中点N,连结QN,则QN⊥AB.又x N=(x1+x2)=﹣=﹣,y N=k(x N+)=.∴k QN=,∴k QN•k AB=≠﹣1.∴QN与AB不垂直,矛盾.∴直线l与x轴不垂直,不存在直线l使得△QAB为等腰三角形.22.已知a为实数,函数f(x)=alnx+x2﹣4x.(Ⅰ)是否存在实数a,使得f(x)在x=1处取极值?证明你的结论;(Ⅱ)若函数f(x)在[2,3]上存在单调递增区间,求实数a的取值范围;(Ⅲ)设g(x)=(a﹣2)x,若存在x0∈[,e],使得f(x0)≤g(x0)成立,求实数a的取值范围.【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求得函数的定义域,求导,假设存在实数a,使f(x)在x=1处取极值,则f′(1)=0,解出a的值,根据x=1的左右单调性是否相同,即可判断x=1是不是极值点;(Ⅱ)先求出f(x)的导数,将问题转化成,a≥2﹣2(x﹣1)2,在x∈[2,3]有解,构造辅助函数,利用函数的求得φ(x)=2﹣2(x﹣1)2的最小值,即可求得a的取值范围.(Ⅲ)在[1,e]上存在一点x0,使得f(x0)<g(x0)成立,即在[,e],上存在一点x0,使得G(x0)<0,即函数G(x)在[,e],上的最小值小于零.对G(x)求导.求出G(x)的最小值,即可a的取值范围.【解答】解:(Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=+2x﹣4=,假设存在实数a,使得f(x)下x=1处取极值,则f′(1)=0,∴a=2,此时,f(x)=,∴当0<x<1时,f′(x)>0,f(x)单调递增,当x>1时,f′(x)>0,f(x)单调递增,∴x=1不是f(x)的极值点,故不存在实数a,使得f(x)=1处取极值.(Ⅱ)f′(x)==(x>0),问题等价于,存在x∈[2,3],使得f′(x)≥0,即a≥2﹣2(x﹣1)2,在x∈[2,3]有解,∴φ(x)=2﹣2(x﹣1)2,在[2,3]上递减,∴φmin=φ(3)=﹣6,∴a>﹣6;(Ⅲ)记F(x)=x﹣lnx,∴F′(x)=(x>0),∴当0<x<1,F′(x)<0,F(x)单调递减;当x>1时,F′(x)>0,F(x)单调递增;∴F(x)≥F(1)=1>0,即x>lnx,(x>0),由f(x0)≤g(x0)得:(x0﹣lnx0)a≥x02﹣2x0,∴a≥,记G(x)=,x∈[,e],G′(x)==,x∈[,e],∴2﹣2lnx=2(1﹣lnx)≥0,∴x﹣2lnx+2>0,∴x∈(,e)时,G′(x)<0,G(x)递减,x∈(1,e)时,G′(x)>0,G(x)递增,∴a≥G(x)min=G(1)=﹣1,故实数a的取值范围为[﹣1,+∞).8月1日。
(新课标)高考数学模拟系列(二)试题 理 新人教A版

12023年高考模拟系列试卷(二) 数学试题【新课标版】(理科)1.本试卷分第一卷(阅读题)和第二卷(表达题)两局部。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试完毕后,将本试卷和答题卡一并交回。
第一卷(选择题,共60分)一、此题共12小题,每题5分,共60分,在每题给出的四个选项中只有一个选项是符合题目要求的1、设集合{}21,M x x x =-≤∈R ,{}21,02N y y x x ==-+≤≤,那么()RM N ⋂等于( )A .RB .{}|1x x R x ∈≠且C .{}1D .∅2、在复平面内,复数2013ii 1iz =+-表示的点所在的象限是( ) A .第一象限 B .第二象限C .第三象限D .第四象限3、假设sin601233,log cos60,log tan 30a b c ===,那么( )A .a b c >>B .b c a >>C .c b a >>D .b a c >>4、设数列{}n a 是公差不为零的等差数列,它的前n 项和为n S ,且1S 、2S 、4S 成等比数列,那么41a a 等于( ) A .6B .7C .4D .35、已知点()1,0A -和圆222x y +=上一动点P ,动点M 满足2MA AP =,那么点M 的轨迹方程是( )A .()2231x y -+=B .223()12x y -+=C .2231()22x y -+= D .223122x y ⎛⎫+-= ⎪⎝⎭6、命题“存在,αβ∈R ,使22sin()sin()sin sin αβαβαβ+-≥-”的否认为( )A .任意,αβ∈R ,使22sin()sin()sin sin αβαβαβ+-≥- B .任意,αβ∈R ,使22sin()sin()sin sin αβαβαβ+-<- C .存在,αβ∈R ,使22sin()sin()sin sin αβαβαβ+-<- D .存在,αβ∈R ,使22sin()sin()sin sin αβαβαβ+-≤- 7、设a b <,函数()()2y x a x b =--的图象可能是( )28、程序框图如下:如果上述程序运行的结果S 的值比2023小,假设使输出的S 最大,那么判断框中应填入( ) A .10k ≤ B .10k ≥ C .9k ≤ D .9k ≥9、图为一个空间几何体的三视图,其中俯视图是下边一个等边三角形,其内切圆的半径是1,正视图和侧视图是上边两个图形,数据如图,那么此几何体的体积是( )A .1533π+B .21533π+C .3033π+D .43033π+ 10、在9212x x ⎛⎫- ⎪⎝⎭的展开式中,常数项为( )A .5376-B .5376C .84-D .8411、如果点P 在平面区域220140x y x x y -+≤⎧⎪≥-⎨⎪+-≤⎩上,点Q 在曲线(x -1)2+(y -1)2=1上,那么|PQ |的最小值为( )A .5-1B .355 C .3515- D .523-1 12、已知椭圆C :22221(0)x ya b a b+=>>的左右焦点为12,F F ,过2F 的直线与圆222()()x a y b b -+-=相切于点A ,并与椭圆C 交与不同的两点P ,Q ,如图,假设A 为线段PQ 的靠近P 的三等分点,那么椭圆的离心率为 ( )3A .23B .33C .53D .73第二卷(非选择题,共90分)二、填空题:本大题共4小题,每题4分,共16分,把答案填在题中横线上 13、由曲线23y x =-和直线2y x =所围成的面积为 。
高考模拟理科数学试卷二卷

一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列各数中,有最小正整数根的是()A. 2.3B. 2.7C. 2.9D. 3.12. 若函数f(x) = ax^2 + bx + c的图象开口向上,且f(1) = 3,f(2) = 5,则a 的取值范围是()A. a > 0B. a < 0C. a ≥ 0D. a ≤ 03. 已知等差数列{an}的前n项和为Sn,若S3 = 9,S6 = 27,则S9 =()A. 36B. 45C. 54D. 634. 在△ABC中,∠A = 60°,∠B = 45°,则sinC的值为()A. √3/2B. √2/2C. 1/2D. 1/√25. 若复数z满足|z - 1| = |z + 1|,则复数z的实部为()B. 1C. -1D. 无法确定6. 已知函数f(x) = log2(3 - 2x),则f(x)的定义域为()A. (-∞, 3/2]B. (-∞, 3/2)C. [3/2, +∞)D. [3/2, +∞)7. 已知向量a = (2, -3),向量b = (1, 2),则向量a与向量b的夹角θ的余弦值为()A. 1/5B. 2/5C. 3/5D. 4/58. 下列不等式中,正确的是()A. |x| > 0B. |x| < 0C. |x| ≥ 0D. |x| ≤ 09. 若等比数列{an}的前n项和为Sn,且S4 = 80,S8 = 640,则公比q为()A. 1/2B. 2C. 1/410. 在△ABC中,若a^2 + b^2 = c^2,则△ABC是()A. 直角三角形B. 钝角三角形C. 锐角三角形D. 等腰三角形11. 已知函数f(x) = x^3 - 3x,则f(x)的单调递增区间为()A. (-∞, -1)和(1, +∞)B. (-∞, -1)和(1, 0)C. (-∞, 0)和(0, +∞)D. (-∞, 0)和(0, 1)12. 若复数z满足|z - 1| = |z + 1|,则复数z在复平面上的轨迹是()A. 一条直线B. 一条射线C. 一个圆D. 一个点二、填空题(本大题共6小题,每小题5分,共30分。
2022年全国卷Ⅰ高考数学理科模拟试题卷含答案(2)
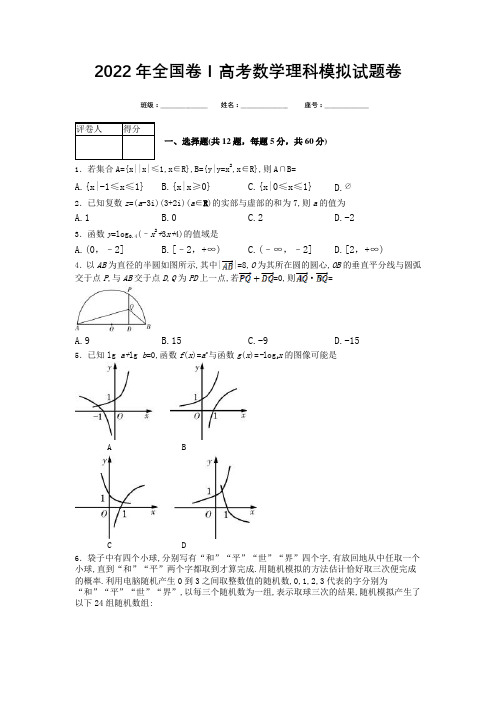
2022年全国卷Ⅰ高考数学理科模拟试题卷班级:_________________ 姓名:_________________ 座号:________________评卷人得分一、选择题(共12题,每题5分,共60分)1.若集合A={x||x|≤1,x∈R},B={y|y=x2,x∈R},则A∩B=A.{x|-1≤x≤1}B.{x|x≥0}C.{x|0≤x≤1}D.2.已知复数z=(a-3i)(3+2i)(a∈R)的实部与虚部的和为7,则a的值为A.1B.0C.2D.-23.函数y=log0.4(–x2+3x+4)的值域是A.(0,–2]B.[–2,+∞)C.(–∞,–2]D.[2,+∞)4.以AB为直径的半圆如图所示,其中||=8,O为其所在圆的圆心,OB的垂直平分线与圆弧交于点P,与AB交于点D,Q为PD上一点,若=0,则·=A.9B.15C.-9D.-155.已知lg a+lg b=0,函数f(x)=a x与函数g(x)=-log b x的图像可能是A BC D6.袋子中有四个小球,分别写有“和”“平”“世”“界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到才算完成.用随机模拟的方法估计恰好取三次便完成的概率.利用电脑随机产生0到3之间取整数值的随机数,0,1,2,3代表的字分别为“和”“平”“世”“界”,以每三个随机数为一组,表示取球三次的结果,随机模拟产生了以下24组随机数组:由此可以估计,恰好取三次便完成的概率为A. B. C. D.7.在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=,D,E分别是AC1和BB1的中点,则直线DE 与平面BB1C1C所成的角为A.30°B.45°C.60°D.90°8.执行如图所示的程序框图,若输入的k=,则输出的S=A. B. C. D.9.已知等差数列的前项和分别为,若,则的值是A. B. C. D.10.若x1,x2∈R,则的最小值是A.1B.2C.3D.411.已知直线l过点(1,0),且倾斜角为直线l0:x-2y-2=0的倾斜角的2倍,则直线l的方程为A.4x-3y-3=0B.3x-4y-3=0C.3x-4y-4=0D.4x-3y-4=012.若a,b是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是A.若a⊥b,b⊥α,α⊥β,则a⊥βB.若α⊥β,a⊥α,b∥β,则a⊥bC.若a∥α,a∥β,α∩β=b,则a∥bD.若a∥b,a⊥α,b∥β,则α∥β第II卷(非选择题)请点击修改第II卷的文字说明评卷人得分二、填空题(共4题,每题5分,共20分)13.曲线y=在点(-1,-3)处的切线方程为.14.已知{a n}是递增的等差数列,其前n项和为S n,且S2=S7,写出一个满足条件的数列{a n}的通项公式a n= .15.已知数列{a n}的前n项和为S n,a n+2S n=3n,数列{b n}满足(3a n+2-a n+1)(n∈N*),则数列{b n}的前10项和为.16.已知双曲线C:=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线上.若△PF1F2为直角三角形,且tan∠PF1F2=,则双曲线的离心率为.评卷人得分三、解答题(共7题,共70分)17.在△ABC中,角A,B,C的对边分别为a,b,c,且sin(+C)=.(1)求角A;(2)若a=4,△ABC的周长为9,求△ABC的面积.18.如图,已知四棱柱ABCD-A1B1C1D1的底面是菱形,BB1⊥底面ABCD,E是棱CC1的中点.(1)求证:AC∥平面B1DE;(2)求证:平面BDD1B1⊥平面B1D E.19.2020年12月10日,首届全国职业技能大赛在广州广交会展馆拉开帷幕,活动为期4天,2 557名参赛选手围绕86个比赛项目展开激烈角逐.大赛组委会秘书长、人社部职业能力建设司司长张立新表示,这次大赛是新中国成立以来规格最高、项目最多、规模最大、水平最高的综合性国家职业技能赛事.为了准备下一届比赛,甲、乙两支代表队各自安排了10名选手参与选拔活动,他们在活动中取得的成绩(单位:分,满分100分)如下:甲代表队:95 95 79 93 86 94 97 88 81 89乙代表队:88 83 95 84 86 97 81 82 85 99(1)分别求甲、乙两支代表队成绩的平均值,并据此判断哪支代表队的成绩更好;(2)甲、乙两支代表队的总负责人计划从这两支队伍得分超过90分的选手中随机选择4名参加强化训练,记参加强化训练的选手来自甲代表队的人数为X,求X的分布列和数学期望.20.已知椭圆的右焦点为,过且与轴垂直的弦长为3.(1)求椭圆的标准方程;(2)过作直线与椭圆交于两点,问在轴上是否存在点,使为定值,若存在,请求出点坐标,若不存在,请说明理由.21.已知函数f(x)=(x-2)e x-x2+ax,a∈R.(1)讨论函数f(x)的单调性;(2)若不等式f(x)+(x+1)e x+x2-2ax+a>0恒成立,求a的取值范围.请考生在第 22、23 三题中任选二道做答,注意:只能做所选定的题目。
高三数学模拟试卷二答案

一、选择题1. 答案:D解析:由题意可知,函数f(x)的周期为T=π,且f(0)=0,f(π)=1。
因此,f(π/2)的值应等于f(π/2-π)的值,即f(-π/2)。
由周期性,f(-π/2)=f(π/2),故f(π/2)=0。
选项D正确。
2. 答案:A解析:设a、b为等差数列的前两项,公差为d。
根据等差数列的性质,有a+b=2a+d。
由题意可知,a+b=2,解得a=1,d=1。
因此,该等差数列的前两项为1和2,所以a^2+b^2=1^2+2^2=5。
选项A正确。
3. 答案:C解析:设函数f(x)在区间[0,2]上的最大值为M,最小值为m。
由题意可知,f(0)=0,f(2)=2。
因为函数在[0,2]上连续,所以根据极值定理,函数在[0,2]上存在最大值和最小值。
又因为f(0)=f(2),所以最大值和最小值相等,即M=m=0。
选项C正确。
4. 答案:B解析:设a、b为等比数列的前两项,公比为q。
根据等比数列的性质,有ab=q^2。
由题意可知,a+b=1,ab=1/2。
将ab=1/2代入ab=q^2中,得到q^2=1/2。
解得q=√2或q=-√2。
因为a、b为正数,所以q=√2。
选项B正确。
5. 答案:D解析:由题意可知,函数f(x)在区间[0,1]上单调递增,在区间[1,2]上单调递减。
因此,函数在x=1处取得极大值。
又因为f(0)=f(2),所以函数在x=0和x=2处取得相同的函数值。
选项D正确。
二、填空题6. 答案:3解析:设等差数列的前两项为a、b,公差为d。
由题意可知,a+b=10,ab=21。
根据等差数列的性质,有a+b=2a+d,解得a=5,d=5。
因此,等差数列的第三项为a+2d=5+25=15。
7. 答案:-4解析:设函数f(x)在x=1处的导数为f'(1)。
由题意可知,f'(1)=2。
因此,函数在x=1处的切线方程为y=2x-1。
8. 答案:√2解析:设函数f(x)在x=0处的导数为f'(0)。
(完整)2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)

2019届全国高考高三模拟考试卷数学(理)试题(二)(解析版)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2019·南昌一模]已知复数()i2ia z a +=∈R 的实部等于虚部,则a =( ) A .12-B .12C .1-D .12.[2019·梅州质检]已知集合{}31,A x x n n ==-∈N ,{}6,8,10,12,14B =,则集合A B I 中元素的个数为( ) A .2B .3C .4D .53.[2019·菏泽一模]已知向量()1,1=-a ,()2,3=-b ,且()m ⊥+a a b ,则m =( ) A .25B .25-C .0D .154.[2019·台州期末]已知圆C :()()22128x y -+-=,则过点()3,0P 的圆C 的切线方程为( ) A .30x y +-=B .30x y --=C .230x y --=D .230x y +-=5.[2019·东北三校]中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取礼物都满意,则选法有( ) A .30种B .50种C .60种D .90种6.[2019·汕尾质检]边长为1的等腰直角三角形,俯视图是扇形,则该几何体的体积为( )A .π9B .π3C .π6D .π187.[2019合肥质检]将函数()π2sin 16f x x ⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是( ) A .函数()g x 的图象关于点π,012⎛⎫- ⎪⎝⎭对称B .函数()g x 的周期是π2C .函数()g x 在π0,6⎛⎫⎪⎝⎭上单调递增D .函数()g x 在π0,6⎛⎫⎪⎝⎭上最大值是18.[2019·临沂质检]执行如图所示的程序框图,输出的值为( )A .0B .12C .1D .1-9.[2019·重庆一中]2sin80cos70cos20︒︒-=︒( )A .3B .1C 3D .210.[2019·揭阳一模]函数()f x 在[)0,+∞单调递减,且为偶函数.若()21f =-,则满足()31f x -≥-的x 的取值范围是( ) A .[]1,5B .[]1,3C .[]3,5D .[]2,2-11.[2019·陕西联考]已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为2F ,若C 的左支上存在点M ,使得直线0bx ay -=是线段2MF 的垂直平分线,则C 的离心率为( )AB .2CD .512.[2019·临川一中]若函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,其坐标满足条件:1212x x y y +0,则称()f x 为“柯西函数”,则下列函数:①()()10f x x x x=+>;②()()ln 0e f x x x =<<;③()cos f x x =;④()21f x x =-.其中为“柯西函数”的个数为( ) A .1 B .2 C .3 D .4二、填空题:本大题共4小题,每小题5分,共20分.13.[2019·江门一模]已知a 、b 、c 是锐角ABC △内角A 、B 、C 的对边,S 是ABC △的面积,若8a =,5b =,S =,则c =_________.14.[2019·景山中学]已知a ,b 表示直线,α,β,γ表示不重合平面. ①若a αβ=I ,b α⊂,a b ⊥,则αβ⊥;②若a α⊂,a 垂直于β内任意一条直线,则αβ⊥; ③若αβ⊥,a αβ=I ,b αγ=I ,则a b ⊥;④若a α⊥,b β⊥,a b ∥,则αβ∥.上述命题中,正确命题的序号是__________.15.[2019·林芝二中]某传媒大学的甲、乙、丙、丁四位同学分别从影视配音、广播电视、公共演讲、播音主持四门课程中选修一门,且这四位同学选修的课程互不相同.下面是关于他们选课的一些信息:①甲同学和丙同学均不选播音主持,也不选广播电视;②乙同学不选广播电视,也不选公共演讲;③如果甲同学不选公共演讲,那么丁同学就不选广播电视.若这些信息都是正确的,依据以上信息可推断丙同学选修的课程是_______(填影视配音、广播电视、公共演讲、播音主持)16.[2019·河南联考]若一直线与曲线eln y x =和曲线2y mx =相切于同一点P ,则实数m =________.三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(12分)[2019·长郡中学]设正项数列{}n a 的前n 项和为n S n a 与1n a +的等比中项,其中*n ∈N .(1)求数列{}n a 的通项公式;(2)设()11211n n n n n a b a a +++=-⋅,记数列{}n b 的前n 项和为n T ,求证:21n T <.18.(12分)[2019·维吾尔一模]港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件.从某企业生产的桥梁构件中抽取100件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[)55,65,[)65,75,[]75,85内的频率之比为4:2:1.(1)求这些桥梁构件质量指标值落在区间[]75,85内的频率;(2)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取3件,记这3件桥梁构件中质量指标值位于区间[)45,75内的桥梁构件件数为X ,求X 的分布列与数学期望.19.(12分)[2019·淄博模拟]如图,在四棱锥P ABCD -中,AB CD ∥,1AB =,3CD =,2AP =,23DP =,60PAD ∠=︒,AB ⊥平面PAD ,点M 在棱PC 上.(1)求证:平面PAB ⊥平面PCD ;(2)若直线PA ∥平面MBD ,求此时直线BP 与平面MBD 所成角的正弦值.20.(12分)[2019·泰安期末]已知椭圆()22122:10x y C a b a b+=>>的离心率为2,抛物线22:4C y x =-的准线被椭圆1C 截得的线段长为2.(1)求椭圆1C 的方程;(2)如图,点A 、F 分别是椭圆1C 的左顶点、左焦点直线l 与椭圆1C 交于不同的两点M 、N (M 、N 都在x 轴上方).且AFM OFN ∠=∠.证明:直线l 过定点,并求出该定点的坐标.21.(12分)[2019·衡水中学]已知函数()23ln f x x ax x =+-,a ∈R . (1)当13a =-时,求函数()f x 的单调区间;(2)令函数()()2x x f x ϕ'=,若函数()x ϕ的最小值为32-,求实数a 的值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.(10分)【选修4-4:坐标系与参数方程】[2019·揭阳一模]以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为22cos 2a ρθ=(a ∈R ,a 为常数)),过点()2,1P 、倾斜角为30︒的直线l 的参数方程满足32x t =+,(t 为参数).(1)求曲线C 的普通方程和直线l 的参数方程;(2)若直线l 与曲线C 相交于A 、B 两点(点P 在A 、B 之间),且2PA PB ⋅=,求a 和PA PB -的值.23.(10分)【选修4-5:不等式选讲】[2019·汕尾质检]已知()221f x x x =++-的最小值为t .求t 的值;若实数a ,b 满足2222a b t +=,求221112a b +++的最小值.2019届高三第三次模拟考试卷理 科 数 学(二)答 案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】C 【解析】∵()2i i i 1i 2i 2i 22a a a z -++===--的实部等于虚部,∴122a=-,即1a =-.故选C . 2.【答案】A【解析】由题意,集合{}31,A x x n n ==-∈N ,{}6,8,10,12,14B =, ∴{}8,14A B =I ,∴集合A B I 中元素的个数为2.故选A . 3.【答案】A【解析】()()()1,12,312,31m m m m m +=-+-=--a b ,结合向量垂直判定,建立方程,可得12310m m --+=,解得25m =,故选A . 4.【答案】B【解析】根据题意,圆C :()()22128x y -+-=,P 的坐标为()3,0, 则有()()2231028-+-=,则P 在圆C 上,此时20113CP K -==--,则切线的斜率1k =, 则切线的方程为3y x =-,即30x y --=,故选B . 5.【答案】B【解析】若同学甲选牛,那么同学乙只能选狗和羊中的一种,丙同学可以从剩下的10中任意选,∴共有11210C C 20⋅=,若同学甲选马,那么同学乙能选牛、狗和羊中的一种,丙同学可以从剩下的10中任意选,∴共有11310C C 30⋅=,∴共有203050+=种.故选B . 6.【答案】A【解析】 侧视图是直角边长为1的等腰直角三角形,圆锥的高为1,底面半径为1, 俯视图是扇形,圆心角为2π3,几何体的体积为112ππ113239⨯⨯⨯⨯=.故选A .7.【答案】C【解析】将函数()f x 横坐标缩短到原来的12后,得到()π2sin 216g x x ⎛⎫=+- ⎪⎝⎭,当π12x =-时,π112f ⎛⎫-=- ⎪⎝⎭,即函数()g x 的图象关于点π,112⎛⎫-- ⎪⎝⎭对称,故选项A 错误;周期2ππ2T ==,故选项B 错误; 当π0,6x ⎛⎫∈ ⎪⎝⎭时,πππ2662x ⎛⎫+∈ ⎪⎝⎭,,∴函数()g x 在π0,6⎛⎫⎪⎝⎭上单调递增,故选项C 正确;∵函数()g x 在π0,6⎛⎫ ⎪⎝⎭上单调递增,∴()π16g x g ⎛⎫<= ⎪⎝⎭,即函数()g x 在π0,6⎛⎫⎪⎝⎭上没有最大值,故选项D 错误.故选C .8.【答案】A【解析】第一次循环,1k =,cos01S ==,112k =+=,4k >不成立; 第二次循环,2k =,π131cos 1322S =+=+=,213k =+=,4k >不成立; 第三次循环,3k =,32π31cos 12322S =+=-=,314k =+=,4k >不成立; 第四次循环,4k =,1cos π110S =+=-=,415k =+=,4k >成立, 退出循环,输出0S =,故选A . 9.【答案】C 【解析】∵()2sin 6020cos702sin80cos70cos20cos20︒+︒︒-︒-︒=︒︒2sin 60cos202cos60sin 20cos70cos20︒︒+︒︒-︒=︒2sin 60cos20sin 20cos70cos20︒︒+︒-︒=︒2sin 60cos202sin 603cos20︒︒==︒=︒.故选C .10.【答案】A【解析】∵函数()f x 为偶函数,∴()()312f x f -≥-=等价于()()32f x f -≥, ∵函数()f x 在[)0,+∞单调递减,∴32x -≤,232x -≤-≤,15x ≤≤,故选A . 11.【答案】C【解析】()2,0F c ,直线0bx ay -=是线段2MF 的垂直平分线, 可得2F 到渐近线的距离为222F P b b a ==+,即有22OP c b a =-=,由OP 为12MF F △的中位线,可得122MF OP a ==,22MF b =,可得212MF MF a -=,即为222b a a -=,即2b a =,可得221145c b e a a==+=+=.故选C .12.【答案】B【解析】由柯西不等式得:对任意实数1x ,1y ,2x ,2y ,2222121211220x x y y x y x y +-+⋅+≤恒成立, (当且仅当1221x y x y =取等号)若函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,其坐标满足条件:222212121122x x y y x y x y +-+⋅+的最大值为0,则函数()f x 在其图象上存在不同的两点()11,A x y ,()22,B x y ,使得OA u u u r,OB u u u r 共线,即存在过原点的直线y kx =与()y f x =的图象有两个不同的交点: 对于①,方程()10kx x x x=+>,即()211k x -=,不可能有两个正根,故不存在; 对于②,,由图可知不存在;对于③,,由图可知存在;对于④,,由图可知存在,∴“柯西函数”的个数为2,故选B .二、填空题:本大题共4小题,每小题5分,共20分. 13.【答案】7【解析】根据三角形面积公式得到1sin sin 2S ab C C =⨯⇒=∵三角形为锐角三角形,故得到角C 为π3,再由余弦定理得到222π1cos 7322a b c c ab+-==⇒=.故答案为7.14.【答案】②④【解析】对于①,根据线面垂直的判定定理,需要一条直线垂直于两条相交的直线,故不正确, 对于②,a α⊂,a 垂直于β内任意一条直线,满足线面垂直的定理,即可得到αβ⊥, 又a α⊂,则αβ⊥,故正确,对于③,αβ⊥,a αβ=I ,b αγ=I ,则a b ⊥或a b ∥,或相交,故不正确, 对于④,可以证明αβ∥,故正确. 故答案为②④. 15.【答案】影视配音【解析】由①知甲和丙均不选播音主持,也不选广播电视; 由②知乙不选广播电视,也不选公共演讲;由③知如果甲不选公共演讲,那么丁就不选广播电视,综上得甲、乙、丙均不选广播电视,故丁选广播电视,从而甲选公共演讲,丙选影视配音, 故答案为影视配音. 16.【答案】12【解析】曲线eln y x =的导数为e'y x=,曲线2y mx =的导数为2y mx '=,由e2mx x =,0x >且0m >,得x =e 2⎫⎪⎪⎭,代入eln y x =得e 2=,解得12m =,故答案为12.三、解答题:本大题共6大题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1)n a n =;(2)见解析.【解析】(1)∵2n S 是n a 与1n a +的等比中项,∴()221n n n n n S a a a a =+=+, 当1n =时,21112a a a =+,∴11a =.当2n ≥时,22111222n n n n n n n a S S a a a a ---=-=+--,整理得()()1110n n n n a a a a --+--=. 又0n a >,∴()112n n a a n --=≥,即数列{}n a 是首项为1,公差为1的等差数列. ∴()()1111n a a n d n n =+-=+-=. (2)()()()1121111111n n n n b n n n n +++⎛⎫=-⋅=-+ ⎪++⎝⎭,∴21232111111111122334212221n n T b b b b n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++=+-+++-++-+ ⎪ ⎪ ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭L L11121n =-<+. 18.【答案】(1)0.05;(2)见解析.【解析】(1)设区间[]75,85内的频率为x ,则区间[)55,65,[)65,75内的频率分别为4x 和2x . 依题意得()0.0040.0120.0190.0310421x x x +++⨯+++=,解得0.05x =. ∴这些桥梁构件质量指标值落在区间[]75,85内的频率为0.05.(2)从该企业生产的该种桥梁构件中随机抽取3件,相当于进行了3次独立重复实验, ∴X 服从二项分布(),B n p ,其中3n =.由(1)得,区间[]45,75内的频率为0.30.20.10.6++=, 将频率视为概率得0.6p =.∵X 的所有可能取值为0,1,2,3,且()00330C 0.60.40.064P X ==⨯⨯=,()11231C 0.60.40.288P X ==⨯⨯=,()22132C 0.60.40.432P X ==⨯⨯=,()33033C 0.60.40.216P X ==⨯⨯=.∴X 的分布列为:X P0.0640.2880.4320.216X 服从二项分布(),B n p ,∴X 的数学期望为30.6 1.8EX =⨯=.19.【答案】(1)见解析;(2219565【解析】(1)∵AB ⊥平面PAD ,∴AB DP ⊥,又∵23DP=,2AP=,60PAD∠=︒,由sin sinPD PAPAD PDA=∠∠,可得1sin2PDA∠=,∴30PDA∠=︒,90APD∠=︒,即DP AP⊥,∵AB AP A=I,∴DP⊥平面PAB,∵DP⊂平面PCD,∴平面PAB⊥平面PCD;(2)以点A为坐标原点,AD所在的直线为y轴,AB所在的直线为z轴,如图所示,建立空间直角坐标系,其中()0,0,0A,()0,0,1B,()0,4,3C,()0,4,0D,)3,1,0P.从而()0,4,1BD=-u u u r,)3,1,0AP=u u u r,()3,3,3PC=-u u u r,设PM PCλ=u u u u r u u u r,从而得()33,31,3Mλλλ+,()33,31,31BMλλλ=+-u u u u r,设平面MBD的法向量为(),,x y z=n,若直线PA∥平面MBD,满足BMBDAP⎧⋅=⎪⎪⋅=⎨⎪⋅=⎪⎩u u u u ru u u ru u u rnnn,即)()()31313104030x y zy zx yλλλ-+++-=-=⎨+=,得14λ=,取()3,3,12=--n,且()3,1,1BP=-u u u r,直线BP与平面MBD所成角的正弦值等于33122sin195651565BPBPθ⋅-+===⨯⋅u u u ru u u rnn20.【答案】(1)2212xy+=;(2)直线l过定点()2,0.【解析】(1)由题意可知,抛物线2C的准线方程为1x=,又椭圆1C2,∴点2⎛⎝⎭在椭圆上,∴221112a b+=,①又2cea==,∴222212a bea-==,∴222a b=,②,由①②联立,解得22a=,21b=,∴椭圆1C的标准方程为2212xy+=.(2)设直线:l y kx m =+,设()11,M x y ,()22,N x y ,把直线l 代入椭圆方程,整理可得()222214220k x km m +++-=,()()222222164212216880k m k m k m ∆=-+-=-+>,即22210k m -+>,∴122421kmx x k +=-+,21222221m x x k -=+,∵111FM y k x =+,221FN yk x =+,M 、N 都在x 轴上方,且AFM OFN ∠=∠,∴FM FN k k =-,∴121211y yx x =-++,即()()()()122111kx m x kx m x ++=-++, 整理可得()()1212220kx x k m x x m ++++=,∴()2222242202121m km k k m m k k -⎛⎫⋅++-+= ⎪++⎝⎭,即22224444420km k k m km k m m ---++=,整理可得2m k =, ∴直线l 为()22y kx k k x =+=+,∴直线l 过定点()2,0. 21.【答案】(1)见解析;(2)56-.【解析】(1)13a =-时,()2ln f x x x x =--,则()()()221121x x x x f x x x +---'==, 令()'0f x =,解得12x =-或1x =,而0x >,故1x =,则当()0,1x ∈时,()0f x '<,即()f x 在区间内递减, 当()1,x ∈+∞时,()0f x '>,即()f x 在区间内递增. (2)由()23ln f x x ax x =+-,()123f x x a x'=+-, 则()()23223x x f x x ax x ϕ'==+-,故()2661x x ax ϕ'=+-, 又()()264610a ∆=-⨯⨯->,故方程()0x ϕ'=有2个不同的实根,不妨记为1x ,2x ,且12x x <, 又∵12106x x =-<,故120x x <<,当()20,x x ∈时,()0x ϕ'<,()x ϕ递减, 当()2,x x ∈+∞时,()0x ϕ'>,()x ϕ递增, 故()()322222min 23x x x ax x ϕϕ==+-,①又()20x ϕ'=,∴2226610x ax +-=,即222166x a x -=,②将222166x a x -=代入式,得2222222222222233316112323622x x x x x x x x x x x -+⋅⋅-=+--=--, 由题意得3221322x x --=-,即322230x x +-=,即()()222212230x x x -++=,解得21x =, 将21x =代入式中,得56a =-.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.【答案】(1)222x y a -=,3212x t y =+=+⎧⎪⎪⎨⎪⎪⎩(t 为参数);(2)2a =±,432. 【解析】(1)由22cos 2a ρθ=得()2222cos sin a ρθθ-=,又cos x ρθ=,sin y ρθ=,得222x y a -=,∴C 的普通方程为222x y a -=, ∵过点()2,1P 、倾斜角为30︒的直线l 的普通方程为)321y x =-+, 由32x =得112y t =+,∴直线l 的参数方程为3212x t y =+=+⎧⎪⎪⎨⎪⎪⎩(t 为参数). (2)将3212x t y ==+⎧⎪⎪⎨⎪⎪⎩代入222x y a -=,得()()222231230t t a ++-=, 依题意知()()222231830a ∆⎡⎤=-->⎣⎦,则上方程的根1t 、2t 就是交点A 、对应的参数,∵()21223t t a ⋅=-,由参数t 的几何意义知1212PA PB t t t t ⋅=⋅=⋅,得122t t ⋅=, ∵点P 在A 、B 之间,∴120t t ⋅<,∴122t t ⋅=-,即()2232a -=-,解得24a =(满足0∆>),∴2a =±, ∵1212PA PB t t t t -=-=+,又()122231t t +=-, ∴432PA PB -=. 23.【答案】(1)2;(2)1.【解析】(1)()31,12213,1131,1x x f x x x x x x x +≥⎧⎪=++-=+-<<⎨⎪--≤-⎩,故当1x =-时,函数()f x 有最小值2,∴2t =. (2)由(1)可知22222a b +=,故22124a b +++=,∴2222222222212111112121121244b a a b a b a b a b +++++++⎛⎫+++=+⋅=≥ ⎪++++⎝⎭, 当且仅当22122a b +=+=,即21a =,20b =时等号成立,故221112a b +++的最小值为1.。
2020届高三第二次模拟考试卷 理科数学(二) 解析版

12020届高三第二次模拟考试卷理 科 数 学(二)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|1}A x x =<,2{|log 1}B x x =<,则( )A .{|1}AB x x =<U B .{|2}A B x x =<UC .{|1}A B x x =<ID .{|2}A B x x =<I【答案】B【解析】{|1}A x x =<,{|02}B x x =<<,{|01}A B x x =<<I ,{|2}A B x x =<U . 2.i 是虚数单位,4i1iz =-,则||z =( ) A .2 B .22C .4D .42【答案】B【解析】由题意得4i 4i(1i)2i(1i)22i 1i (1i)(1i)z +===+=-+--+,∴22||(2)222z =-+=. 故选B .3.已知某公司按照工作年限发放年终奖金并且进行年终表彰.若该公司有工作10年以上的员工100人,工作510:年的员工400人,工作05:年的员工200人,现按照工作年限进行分层抽样,在公司的所有员工中抽取28人作为员工代表上台接受表彰,则工作510:年的员工代表有( ) A .8人 B .16人C .4人D .24人【答案】B【解析】依题意知,该公司的所有员工中工作10年以上、工作510:年、工作05:年的员工人数比例为1:4:2,所以工作510:年的员工代表有428167⨯=. 4.已知向量||2=a ,||1=b ,(2)2⋅-=a a b ,则a 与b 的夹角为( ) A .30︒ B .60︒ C .90︒ D .150︒【答案】B【解析】∵2(2)2422⋅-=-⋅=-⋅=a a b a a b a b ,∴1⋅=a b . 设a 与b 的夹角为θ,则1cos ||||2θ⋅==a b a b ,又0180θ︒≤≤︒,∴60θ=︒,即a 与b 的夹角为60︒.5.长方体1111ABCD A B C D -,1AB =,2AD =,13AA =,则异面直线11A B 与1AC 所成角的 余弦值为( ) A .1414B .8314C .1313D .13【答案】A【解析】∵1111C D A B ∥,∴异面直线11A B 与1AC 所成的角即为11C D 与1AC 所成的角11AC D ∠, 在11AC D Rt △中,111C D =,222112314AC =++=, ∴11111114cos 1414C D AC D AC ∠===,故选A . 6.执行下图的程序框图,若输出的结果为10,则判断框中的条件是( )A .4?i <B .5?i <C .6?i <D .7?i <【答案】B此卷只装订不密封班级 姓名 准考证号 考场号 座位号。
新课标高考理科数学模拟试题含答案

新课标高考理科数学模拟试题含答案The following text is amended on 12 November 2020.2017年普通高等学校招生全国统一考试理科数学模拟试卷(一)第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知命题:p x ∀∈R ,sin x ≤1,则( )A .:p x ⌝∃∈R ,sin x ≥1B .:p x ⌝∀∈R ,sin x ≥1C .:p x ⌝∃∈R ,sin x >1 不能D .:p x ⌝∀∈R ,sin x >12.已知平面向量a =(1,1),b (1,-1),则向量1322-=a b ( )A .(-2,-1)B .(-2,1)C .(-1,0)D .(-1,2)3.函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区间ππ2⎡⎤-⎢⎥⎣⎦,的简图是( )4.已知{a n }是等差数列,a 10=10,其前10项和S 10=70,则其公差d =( )A .23-B .13-C .13D .235.如果执行右面的程序框图,那么输出的S=( )A .2450B .2500 y x11-2π-3π-O6ππyx11-2π-3π-O 6ππy x11-2π-3πO 6π-πy xπ2π-6π-1O1-3π A.B.C .D .6.已知抛物线22(0)y px p =>的焦点为F ,点P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3)在抛物线上,且2x 2=x 1+x 3, 则有( )A .123FP FP FP +=B .222123FP FP FP += C .2132FP FP FP =+ D .2213FPFP FP =· 7.已知x >0,y >0,x ,a ,b ,y 成等差数列,x ,c ,d ,y 成等比数列,则2()a b cd+的最小值是( )A .0B .1C .2D .48.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )A .34000cm 3 B .38000cm 3C .2000cm 3D .4000cm 3 9.若cos 22π2sin 4αα=-⎛⎫- ⎪⎝⎭,则cos sin αα+的值为( ) A .7.12- C .12D 7 10.曲线12e x y =在点(4,e 2)处的切线与坐标轴所围三角形的面积为( )A .29e 2年B .4e 2, C .2e 2 D .e 2s 1,s 2,s 3分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )甲的成绩 环数7 8 9 10 频数 5 5 5 5 乙的成绩 环数7 8 9 1频数 6 4 4 6 丙的成绩 环数7 8 9 1频数4 6 6 412.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等。
2023届陕西省咸阳市高考模拟检测(二模)理科数学试题及答案

注意事项z 威阳市2023年高考模拟检测〈二)数学〈理科〉试题l.本试题共4页,满分150分,时间120分钟2.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上.3.回答选择题时,逃出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题不回收.第I卷〈选择题共60分〉一、选择题z本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.I.己知复数z满足iz+l =i,那么lz l=人l B ..Ji C.Ji2已失u综合M=lx l v=.J x-U, N={x l主主<0�,那么M N=l 1· J I I x'+ l IA.{xll运x�2}B.{xix注1} c. {xll白<2}D.2D.{xll<x<2}3.某商场要将单价分别为36元/kg,48元/kg,72元/kg的3种糖果按3:2: l的比例混合销售,其中混合糖果中每一颗糖果的质量都相等.那么该商场对混合糖果比较合理的定价应为A.52元/kgB.50元/kg c.48元/kg D.46元/kg4.已知I'll,n是两条不同的直线,α,p是两个不同的平面,有以下四个命题:①若ml/n, nl>α,则,n//α@若m..lα,m..lβ,则αIIβ其中正确的命题是A.②③B.②④5. 函数J(x)=丘:的大致图像为lx lxA. B.x②若ml>α,m..lβ,则αiβ④若αiβ,ml>α,nl>β,则m..lnc.①③ D.①②1’c. D.π6.已失11函数f(x)=4sin(缸’-ψ),当x=一时,f(x)取得最小值,则|叫的最小值是3 x1πSπ丁πB. -C .- D.-63667.数列{α,,)的前,1项和为S ,,,对一切正整数n ,点(n ,乱)在函数f(x)=x 2+2x 的图像上,b =2( n εN *且应1),则数列队}的前,1项和为已=F,+在二A.在Ml -石;;=-IB.在Z三-1c.在二-石�A.JrD.d古3-./38.已知直角三角形ABC ,ζC=90°,AC=4, BC =3,现将该三角形沿斜边AB 旋转一周,则旋转形成的儿何体的体积为48万24万A 12πB 16πc -一-D.-一一539.巴塞尔问题是一个著名的级数问题,这个问题首先白皮耶特罗·门戈利在1644年提出,由莱昂II合德·账;J11π24立在1735年解诀.欧位通过推导得出:l+-+-++一+=一.某同学为了验证15,役的结论,设计4 9n26J II 了如阁的第法,计算1+-+-++一一一的值来估算,则判断框槟入的是4 9 20232 A.n>2023B.n 注2023c.n运2023D.n<202310.2022年卡珞尔世界杯足球赛落幕,这是历史上首次在卡塔尔和中东国家境内举行、也是第二次在亚洲举行的世界杯足球赛.有甲,乙,丙,丁四个人相互之间进行传球,从叩开始传球,甲等可能地把球传给乙,两,丁中的任何-个人,以此类推,贝I]经过三次传球后己只接到-次球的概率为A .-27l-QJnpc 立27D.162711.己叫线C:兰卡(α>0,b>O).c 叫线的半焦距则当取得最大酬,双曲线2α+3bc的离心$为、/13A.-一一2.J3D.___:____223e=2.718 ...,对任意xe(-1,叫,不等式扩注ae[2+ln (创刊)]恒成立,Y!瞧B亟c主12.己知实数a>O,数。
2023年贵州省天之王教育高考数学模拟试卷(二)(理科)+答案解析(附后)

2023年贵州省天之王教育高考数学模拟试卷(二)(理科)1. 已知集合,,则( )A. B. C. D.2. 若复数在复平面内对应的点位于第一象限,则实数a的取值范围是( )A. B. C. D.3. 已知在平行四边形ABCD中,E,F分别是边CD,BC的中点,则( )A. B. C. D.4. 若,则( )A. B. C. D.5. 设,,,则a,b,c的大小关系是( )A. B. C. D.6. 已知偶函数在上单调递增,则的解集是( )A. B. C. D.7. 如图,在直三棱柱中,,,,则异面直线BD与AE所成角的余弦值为( )A. B. C. D.8. 数学竞赛小组有4位同学,指导老师布置了4道综合题,要求每位同学只做其中1道题,则“每位同学所做题目各不相同”的概率为( )A. B. C. D.9. 一个空间几何体的三视图如图所示,则该几何体的体积是( )A. B. C. D.10. 函数在上零点的个数为( )A. 3B. 4C. 5D. 611. 已知抛物线C:的焦点为F,过F的直线l与抛物线C交于A,B两点,若,则( )A. 9B. 7C. 6D. 512. 如图,为了在两座山之间的一条河流上面修建一座桥,勘测部门使用无人机测量得到如下数据:无人机P距离水平地面的高度为h,A,B两点的俯角分别为,则下列求A,B 两点间的距离的表达式中,错误的是( )A. B.C. D.13. 半径为2且与x轴y轴都相切的圆的标准方程为______ 写出一个符合题意的方程即可14. 若实数x,y满足则的最小值是______ .15. 若不等式对任意恒成立,则实数a的取值范围是______ .16. 双曲线的右焦点为F,过点F的直线与双曲线C的右支交于A,B两点,点A关于原点O的对称点为P,,且,则双曲线C 的离心率为______ .17. 已知在等差数列中,,求数列的通项公式;设是数列的前n项和,求18. 近年我国新能源产业的发展取得了有目共睹的巨大成果年国务院在正式发布的《新能源汽车产业发展规划年》中提出,到2025年,新能源汽车新车销售量达到汽车新车销售总量的左右.力争经过15年的持续努力,使纯电动汽车成为新销售车辆的主流.在此大背景下,某市新能源汽车保有量持续增加,有关部门将该市从2018年到2022年新能源汽车保有量单位:万辆作了统计,得到y与年份代码如代表2018年的统计表如下所示.t12345y46请通过计算相关系数r说明y与t具有较强的线性相关性;若,则变量间具有较强的线性相关性求出线性回归方程,并预测2023年新能源汽车的保有量.参考公式:相关系数;回归方程中斜率和截距的最小二乘估计公式分别为,参考数据:,,,19. 在三棱台中,平面ABC,,,,M为AC的中点.证明:平面;求平面与平面所成锐二面角的余弦值.20. 已知椭圆的一个焦点为,且点F到C的左、右顶点的距离之积为求椭圆C的标准方程;过点F作斜率乘积为的两条直线,,与C交于A,B两点,与C交于D,E 两点,线段AB,DE的中点分别为M,证明:直线MN与x轴交于定点,并求出定点坐标.21. 已知函数,,若曲线与曲线在上有一个公共点P,且存在以P为切点的公共切线,求a的值;若曲线与曲线在上有两个公共点,求a的取值范围.22. 在平面直角坐标系xOy中,直线l的参数方程为为参数以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为求圆C的普通方程与直线l的直角坐标方程;已知点,直线l与圆C交于A,B两点,求的值.23. 已知函数若对,恒成立,求实数k的取值范围;当时,记的最小值为m,且正数a,b满足,求的最小值.答案和解析1.【答案】A【解析】解:集合,,则故选:求出集合A,利用交集定义能求出本题考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.2.【答案】C【解析】解:若复数在复平面内对应的点位于第一象限,则,解得,故实数a的取值范围是故选:根据已知条件,结合复数的几何意义,即可求解.本题主要考查复数的几何意义,属于基础题.3.【答案】D【解析】解:在平行四边形ABCD中,E,F分别是边CD,BC的中点,,错误,D正确.故选:利用平面向量的线性运算,平面向量基本定理求解即可.本题考查平面向量的线性运算,平面向量基本定理,属于基础题.4.【答案】D【解析】解:若,则故选:由已知结合二倍角的正切公式即可求解.本题主要考查了二倍角的正切公式,属于基础题.5.【答案】B【解析】解:,,故故选:由已知先分别确定a,b,c的范围即可比较a,b,c的大小.本题主要考查了函数的单调性在函数值大小比较中的应用,属于基础题.6.【答案】D【解析】解:因为偶函数在上单调递增,故函数在上单调递减,由可得,解得故选:由已知结合函数的奇偶性及单调性即可求解不等式.本题主要考查了函数的单调性及奇偶性在不等式求解中的应用,属于基础题.7.【答案】C【解析】解:如图,连接BF,,或其补角为异面直线BD与AE所成的角,根据题意知,,,且,,,且,在中,根据余弦定理得:故选:可连接BF,从而可得出或其补角为异面直线BD与AE所成的角,然后根据三棱柱为直三棱柱可得出,,然后可求出BD和EF,DF的值,然后根据余弦定理即可求出的值.本题考查了直三棱柱的定义,勾股定理,余弦定理,异面直线所成角的定义,考查了计算能力,属于基础题.8.【答案】B【解析】解:数学竞赛小组有4位同学,指导老师布置了4道综合题,要求每位同学只做其中1道题,基本事件总数,“每位同学所做题目各不相同”包含的基本事件个数,则“每位同学所做题目各不相同”的概率为故选:基本事件总数,“每位同学所做题目各不相同”包含的基本事件个数,由此能求出“每位同学所做题目各不相同”的概率.本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,是基础题.9.【答案】D【解析】解:由三视图知,该几何体是上底面直径为2,下底面直径为4,高为3的圆台,截去部分的组合体,则该几何体的体积是故选:由三视图知该几何体是圆台,截去部分的剩余组合体,由此求出该几何体的体积.本题考查了空间几何体三视图应用问题,是基础题.10.【答案】C【解析】解:函数,可得,可得或,,可得,或,,因为,所以,,可得,0,;,,可得,,故函数在上零点的个数为5,故选:通过求解三角方程,推出x的解,结合x的范围,求解方程解的个数,可得结论.本题主要考查函数的零点的定义,正弦函数的图象,属于中档题.11.【答案】A【解析】解:由题意直线l的斜率必存在,抛物线C:的焦点为,设直线l:,则,得,设,,则,,又,则,,,故选:由题意直线l的斜率必存在,设直线l:,直线与抛物线联立后利用韦达定理得到,,,代入弦长公式即可求解.本题考查了直线与抛物线的综合应用,属于中档题.12.【答案】C【解析】解:如图所示:设点P在AB上的射影为C,设,A,B两点的俯角分别为,故,,所以,故,故A正确;由于,故B正确;在中,由于,,,利用余弦定理:,整理得:,故C错误,D正确.故选:直接利用解三角形知识中的三角函数关系式的变换及余弦定理判断A、B、C、D的结论.本题考查的知识要点:三角函数的关系式的变换,余弦定理,主要考查学生的理解能力和计算能力,属于中档题.13.【答案】【解析】解:半径为2且与x轴y轴都相切的一个圆的标准方程为故答案为:由已知可得圆的圆心坐标与半径,则圆的标准方程可求.本题考查圆的标准方程,是基础题.14.【答案】1【解析】解:由约束条件作出可行域,如图所示:由可得,,由图可知,当直线平移到与直线重合时,在y轴上的截距最小,此时z的值最小,所以z的最小值为故答案为:作出不等式组对应的平面区域,由可得,利用数形结合即可得到结论.本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.15.【答案】【解析】解:因为,所以,令,则,故不等式对任意恒成立,可以转化为:对任意恒成立,即在上恒成立,令,则,故时,,函数递减,时,,函数递增,所以:实数a的取值范围是:故答案为:根据已知条件转化为对任意恒成立,进而转化求解的最大值即可.本题考查了导数的综合应用及恒成立问题,属于中档题.16.【答案】【解析】解:设左焦点为,,易知四边形为矩形,设AB直线的倾斜角为,则根据双曲线倾斜角的焦半径公式可得:,又,,,又,,,,,又,在中,由勾股定理可得:,,故答案为:设左焦点为,则易知四边形为矩形,设AB直线的倾斜角为,则根据双曲线倾斜角的焦半径公式可得,又,从而可得,,再在中,由勾股定理,即可求解.本题考查双曲线的几何性质,双曲线倾斜角的焦半径公式的应用,勾股定理的应用,化归转化思想,属中档题.17.【答案】解:由题意,设等差数列的公差为d,则,化简整理,得,解得,,由题意及可得,当,即时,解得,当,即时,解得,则,【解析】先设等差数列的公差为d,再根据题干已知条件列出关于首项与公差d的方程组,解出与d的值,即可计算出等差数列的通项公式;先根据第题的结果将等差数列的通项公式与0比较大小,判断数列各项的正负性,在求数列的前30项和时先逐项代入,然后根据分组求和法,以及等差数列的求和公式即可推导出数列的前30项和.本题主要考查等差数列的基本运算,以及绝对值数列的求和问题.考查了方程思想,整体思想,转化与化归思想,不等式的运算,差数列求和公式的运用,以及逻辑推理能力和数学运算能力,属中档题.18.【答案】解:,,,,与t具有较强的线性相关性;,,,关于t的线性回归方程为,取,可得预测2023年新能源汽车的保有量为万辆.【解析】由已知结合相关系数公式求得r值,结合题意得结论;求出线性回归方程,取求得的值即可.本题考查相关系数与线性回归方程的求法,考查运算求解能力,是基础题.19.【答案】证明:平面ABC,平面,平面平面ABC,,M为AC的中点,,平面平面,平面,平面,,,由三棱台可得,又,M为AC的中点,,四边形是正方形,,又,平面;解:由题意可得AC,BM,两两垂直,以M为坐标原点,MA,MB,为坐标轴建立空间直角坐标系,设,则,,,,,则,,,,设平面的一个法向量为,,令,则,平面的一个法向量为,设平面的一个法向量为,,令,则,平面的一个法向量为,,平面与平面所成锐二面角的余弦值为【解析】由已知可证平面,进而再证四边形是正方形,进而可证平面;以M为坐标原点,MA,MB,为坐标轴建立空间直角坐标系,求得平面与平面的一个法向量,可求平面与平面所成锐二面角的余弦值.本题考查线面垂直的证明,考查面面角的求法,属中档题.20.【答案】解:由题意,且,即,可得,所以椭圆的标准方程为:;证明:由题意可得直线,互相垂直,且斜率存在又不为0,设直线的方程为,设,,联立,整理可得:,可得,,所以AB的中点,同理可得,即,当时,M,N的横坐标相同,则M,N的横坐标为,这时直线MN与x轴的交点为,当时,则直线MN的斜率,所以直线MN的方程为:,令,因为,可得,综上所述:可证得直线MN恒过定点【解析】由椭圆的焦点可知c的值,再由焦点到左右顶点的距离之积可得b的值,进而求出a 的值,求出椭圆的方程;由题意可得直线,互相垂直,且斜率存在又不为0,设直线的方程,与椭圆的方程联立,可得两根之和,求出AB的中点M的坐标,同理可得N的坐标,当M,N的横坐标相等时,可得它们的横坐标,即求出与x轴的坐标,当M,N的横坐标不相等时,求出直线MN的方程,令,可得直线MN与x轴的交点为定值,即证得结论成立.本题考查椭圆方程的求法及直线与椭圆的综合应用,直线恒过定点的求法,属于中档题.21.【答案】解:设,则,所以,所以存在,使得,因为,存在以点P为切点的公切线,所以,又,,所以,所以,由可得或,当时,,当时,代入,可得,所以,所以,所以,若,则,所以,令,,,令得,所以在上,单调递减,在上,单调递增,所以,所以方程,无解,所以舍去,所以,因为曲线与曲线在上有两个公共点,所以方程在上有两个根,即在上有两个根,设,,则有两个零点,函数,,令,则,令,,则有两个零点,,当时,令,得,所以只有一个零点,不合题意,当时,,当时,,单调递增,当时,,单调递减,所以在处取得极小值也是最小值,所以,要使得有两个零点,则,所以,所以,当时,令得,,所以当时,,单调递增,当时,,单调递减,当时,,单调递增,,,所以,所以,由知方程无解,当时,,所以在上单调递增,所以至多有一个零点,当时,,所以,所以,所以无解,综上所述,a 的取值范围为【解析】设,则,即存在,使得,由,存在以点P 为切点的公切线,得,则,解方程组,即可得出答案.因为曲线与曲线在上有两个公共点,则在上有两个根,设,,则有两个零点,进而可得答案.本题考查导数的综合应用,解题中需要理清思路,属于难题.22.【答案】解:圆C 的极坐标方程为,根据,转换为直角坐标方程为:,由消去t 得直线l 的直角坐标方程为:;将直线l 的参数方程为参数代入圆的直角坐标方程,整理得,设,是方程的两根,由韦达定理可知,,,,设,【解析】将代入圆的极坐标方程即可得出圆的普通方程为:,由直线的参数方程消去t即可得出直线的直角坐标方程;将直线的参数方程代入到圆的普通方程可得出,然后根据韦达定理可得出,然后设,然后根据两点间距离公式即可求出的值.本题考查了圆的极坐标方程和普通方程的转化,两点间的距离公式,韦达定理,考查了计算能力,属于中档题.23.【答案】解:对,恒成立,即,所以或,解得或,所以实数k的取值范围是;当时,,所以的最小值为,所以,所以,当且仅当,即,时取“=”,所以的最小值是【解析】利用绝对值不等式求出函数,再列不等式求出实数k的取值范围;求出时的最小值,代入利用基本不等式求解即可.本题考查了基本不等式与绝对值不等式的应用问题,是中档题.。
高三第二次模拟考试数学(理)试题及答案

呼伦贝尔市高考模拟统一考试(二)数 学 (理工类)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,本卷满分150分,考试时间120分钟.2.答卷前,考生务必将自己的姓名、考生号、座位号,填写在答题卡内的相关空格上.3.第Ⅰ卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.4.第Ⅱ卷每题的答案填写在答题卡相应题号下的空格内.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知,则QP ⋂( )A. B. C. D. 2.已知复数33iiz +-=,则z 的虚部为( ) A.3- B.3 C.i 3 D.i 3-3.已知倾斜角为α的直线l 与直线x -2y+2=0平行,则tan 2α的值为( ) A .45B .34C .23D .434.“a=1”是“(1+ax )6的展开式的各项系数之和为64”的( )A . 必要不充分条件B . 充分不必要条件C . 充要条件D . 既不充分也不必要条件 5.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )A .()cos f x x =B .C .()lg f x x =D .()2x x e e f x --={}{}1,0,2,sin ,P Q y y R θθ=-==∈∅{}0{}1,0-{}1,0,2-1()f x x=俯视正视侧视364 26.一个几何体的三视图如图所示,则该几何体的体积为( ) A .12 B . 24 C .40 D .727.如图所示,点)0,1(A ,B 是曲线132+=x y 上一点,向矩形OABC 内随机投一点,则该点落在图中阴影内的概率为( ) A.21 B.31C.41D.528.已知矩形ABCD ,F E 、分别是BC 、AD 的中点,且22BC AB ==,现沿EF 将平面ABEF 折起,使平面ABEF ⊥平面EFDC ,则三棱锥A FEC -的外接球的体积为( )D.9.已知不等式组210,2,10x y x x y -+⎧⎪⎨⎪+-⎩≥≤≥表示的平面区域为D ,D 上的点,则实数m 的取值范围是( )D.[2,1]-10.函数的最小正周期是,若其图象向右平移3π个单位后得到的函数为奇函数,则函数的图象( )A .关于点)0,6(π对称B .关于对称C .关于点对称D .关于对称 11. 已知双曲线c :,以右焦点F 为圆心,|OF|为半径的圆交双曲线两渐近线于点M 、N (异于原点O ),若|MN|=,则双曲线C 的离心率 是( )A .B .C . 2D .12.已知函数f (x )=x 2+bx+c ,(b ,c ∈R ),集合A={x 丨f (x )=0},B={x|f (f (x ))=0},若存在x 0∈B ,x 0∉A 则实数b 的取值范围是( ) A . 0≤b≤4 B . b ≤0或 b≥4 C . 0≤b<4 D . b <0或b≥4第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分。
全国100所名校2020年最新高考模拟示范卷(二)数学理科试题+答案+详解MNJ.Y

全国100所名校最新高考模拟示范卷·数学卷(二)(120分钟 150分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{0,1,2,3}, {2,3,4,5}A B ==,则A B =U ( ) A.{}1,2,3,4,5B.{}0,1,4,5C.{}2,3D.{}0,1,2,3,4,52.i 是虚数单位,2z i =-,则z =( )A.B.2C.3.已知向量()1,2a =r ,(1,)b λ=-r ,若a b r r∥,则实数λ等于( )A.-1B.1C.-2D.24.“22x -<≤”是“22x -≤≤”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件D 既不充分也不必要条件5.双曲线22221x y a b -= (0a >,0b >)的离心率为53,则该双曲线的渐近线方程为( ) A.45y x =±B.54y x =±C.43y x =±D.34y x =±6.第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )A.第一场得分的中位数为52B.第二场得分的平均数为193C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等7.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若5b =,22625c c a ---,则cos A =( )A.45 B.35C.310D.258.函数1())1x xe f x x e-=+的图象大致为( )A BC D9.某几何体的三视图如图所示,三个视图中的曲线都是圆弧,则该几何体的体积为( )A.152πB.12πC.112π D.212π10.图为祖冲之之子祖晒“开立圆术”中设计的立体模型.祖晒提出“祖氏原理”,他将牟合方盖的体积化成立方体与一个相当于四棱锥的体积之差,从而求出牟合方盖的体积等于323d (d 为球的直径),并得到球的体积为316V d π=,这种算法比外国人早了一千多年.人们还用过一些类似的近似公式,根据3.1415926π=⋅⋅⋅,判断下列公式中最精确的一个是( )A.d ≈B.d ≈C.d ≈D.d ≈11.已知32cos cos 2αβ-=,2sin sin 2αβ+=,则cos()αβ+等于( ) A.12 B.12-C.14D.14-12.已知A B C ,,为椭圆2214x y +=上三个不同的点,若坐标原点O 为ABC △的重心,则ABC △的面积为( )A.B.2C.2D.二、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.设()f x 是定义在R 上的函数,若()()g x f x x =+是偶函数,且()24g -=-,则()2f =___________.14.已知数列()*(}n f a n ∈N 是等差数列,其前n 项和为n S ,若66nS =,则4a =___________.15.已知函数()sin()(0)f x x ωϕω=+>,点2,03π⎛⎫ ⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是函数()f x 图象上相邻的两个对称中心,则ω=___________.16.在正三棱柱111ABC A B C -中,12AB AA ==,E F ,分别为111AB AC ,的中点,平面a 过点1C ,且平面a ∥平面11A B C ,平面a I 平面111A B C l =,则异面直线EF 与l 所成角的余弦值为___________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.从中国教育在线官方公布的考研动机调查来看,本科生扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力;通过考研选择真正感兴趣的专业;为了获得学历;继续深造;随大流;有名校情结如图是2015~2019年全国硕士研究生报考人数趋势图(单位:万人)的折线图.(1)求y 关于t 的线性回归方程;(2)根据(1)中的回归方程,预测2021年全国硕士研究生报考人数. 参考数据:()()51311iii t t y y =--=∑.回归方程$$y abt =+$中斜率和截距的最小二乘估计公式分别:()()()121ii i ni i tty y b t t ∞==--=-∑∑,$a y bt=-$. 18.已知数列{}n a 的前n 项和为n S ,()()21112,4,314,(1)log n n nn n n n S aS a b a -++==-=-⋅.(1)求数列{}n a 的通项公式; (2)求数列{}n b 的前2n 项和2n T .19.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 为直角梯形,AB AD ⊥ ,BC AD ∥,2222AD BC PA AB ====,点E F G ,,分别为线段AD DC PB ,,的中点.(1)证明:直线AG ∥平面PEF.(2)求多面体 ACCPEF 的体积.20.已知函数2()e ,x f x ax x a =--∈R ,()g x 为函数()f x 的导函数.(1)若函数()gx 的最小值为0,求实数a 的值;(2)若0x ∀>,2()(1)(1)1f x a x a x --++…恒成立,求实数a 的取值范围.21.已知点()(),80Pt t <是抛物线2(:20)C x py p =>上一点,点F 为抛物线C 的焦点,||10PF =.(1)求直线PF 的方程; (2)若直线l 过点()0,4,与抛物线相交于M N ,两点,且曲线C 在点M 与点N 处的切线分别为m n ,,直线m n ,相交于点G ,求||PG 的最小值.(二)选考题:共10分请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分. 22.[选修4-4:坐标系与参数方程]在直角坐标系xOy 中,曲线C 的参数方程为2cos 2sin x ay α=⎧⎨=⎩(a 为参数),在以坐标原点为极点,,x 轴的正半轴为极轴的极坐标系中,直线l 的极坐标方程为sin 3m πρθ⎛⎫-= ⎪⎝⎭. (1)若直线l 与曲线C 至多只有一个公共点,求实数m 的取值范围;(2)若直线l 与曲线C 相交于A B ,两点,且A B ,的中点为P ,求点P 的轨迹方程. 23.[选修4-5:不等式选讲] 已知a b ,为正实数,222a b +=. (1)证明:2a b ab +≥. (2)证明:442a b +….2020年普通高等学校招生全国统一考试数学模拟测试参考答案1.D 本题考查集合的运算因为{0,1,2,3}, {2,3,4,5}A B ==,所以{}0,12,3,4,5A B =U .2C 本题考查复数的模.因为2z i =-,所以||z ==3.C 本题考查向量的平行.因为a b r r∥,所以20λ--=,解得2λ=-.4.A 本题考查充分、必要条件“22x -<≤”是“22x -≤≤”的充分不必要条件.5.C 本题考查双曲线的渐近线.22225161199b e a =-=-=,即43b a =,故双线的渐近线方程为43y x =±. 6.C 本题考查茎叶图.由茎叶图可知第一场得分的中位数为52,众数为0,极差为19,第二场得分的众数为 0,平均数为193,极差为2,所以选项C 的说法是错误的. 7.B 本题考查解三角形.因为225625b c c a =⋅---,所以2226b c a c +-=,所以62cos c bc A =⋅, 所以3cos 5A =. 8.B 本题考查函数的图象.因为()()f x f x -=,所以()f x 为偶函数,排除CD 项,又因为)1(1)ln 101cf e-=>+,所以排除A 项.9.A 本題考查三视图.根据三视图可知,该几何体是由14个圆锥和18个球组成的, 如图所示,其中球的半径为3,圆锥的底面半径也为3,高为4,故该几何体的体积为2311119153433438322x ππππ⨯⨯⨯+⨯⨯-+=.10.C 本题考查数学史与立体几何.由316V xd =,解得36V x d =,选项A 化简得3916V d ≈, 所以69 3.37516π⨯≈=;选项B 化简得212V d ≈,所以632π≈=;选项C 化简得3157300V d ≈, 所以6157 3.14300π⨯≈=;选项D 化简得2815V d ≈,所以683.215π⨯≈=;所以选项C 的 公式最精确.11.A 本题考查三角恒等变换.因为32cos cos 2αβ-=,2sin sin αβ+-,所以2294cos 4cos cos cos 4ααββ-+=,2234sin 4sin sin sin 4ααββ++=, 两式相加得54(cos cos sin sin )3αβαβ--=,解得1cos()2αβ+=. 12.B 本题考查直线与椭圆的位置关系.不妨设直线AB 的方程为y kx m =+代人椭圆方程得()()222148410k xkmx m +++-=.设()11,Ax y ,()22,B x y ,则122814kmx x k +=-+,()21224114m x x k-=+. 设()33,Cx y ,因为O 为ABC △的重心,所以()2122814kmxx x k=-+=+, ()()2121222214my y y k x x m k =-+=-++=-⎡⎤⎣⎦+,代入椭圆方程得22441m k -+,12|||AB x x -, 点O 到直线AB的距离d -,所以OMB △的面积111||||22S AB d m =⨯⨯-⨯因为22441m k -+,所以1S =, 因为O 为ABC △的重心,所以ABC △的面积132S S ==. (另解:不妨设()2,0A,因为O 为ABC △的重心,所以BC 横坐标为1-,可得||BC =ABC△的面积为1322S =⨯=.) 13.6本题考查函数的性质,由题知,(2)(2)2(2)4g f g -+--=-,解得()26f =-.14.6本题考查等差数列基本量的求解设等差数列{}n a 的公差为d ,因为66n S =,所以41166a =,解得a6.15.2本题考查三角函数的性质因为点2,03π⎛⎫ ⎪⎝⎭和7,06π⎛⎫⎪⎝⎭是函数()f x 图象上相邻的两个对称中心,所以是72632wππππ=--,解得2ω=.16.4本题考在异面直线所成角.因为平面a ∥平面11A B C , 平面a I 平面111A B C l =,平面11A B C I 平面11111A B C A B =,所以11l A B ∥,取11A B ,11B C 的中点分别为H G ,,连接EH BG GH GF AC ,,,,,如图所示,则11GF A B ∥, 所以GF l ∥所以异面直线EF 与所成的角为GFE ∠或其补角,又因为AB =12AA =,所以14AC =,1EH =,HP GP ==所以2EG EF -=,所以22cos 24GF GFE RP ∠==.【解题方法】本题以三棱柱为载体,综合考查异面直线所成角的概念.解答的基本方法是通过平移直线,把异面直线平移到两条相交直线上,明确异面直线所成角的概念,应用三角函数知识求解,充分利用图形特征,则可事半功倍.例如本题利用图形易得11D A B ∥,这是本题的题眼. 17.解:本题考查线性回归方程. (1)由题中数据计算得1(12345)35t =++++=, ()2223215(2)(1)01210i i i a t =---+-+++=∑,由参考数据知,()()51311iii t t y y =--=∑,所以()()()532131131.110iiiii tty y b tt=--=-=-∑∑,$214.2-31.13120.9ay bt --=⨯=$, 故所求回归方程为31.1120.9yt =+.(2)将2021年对应的7t =代人回归方程得31.17120.9338.6y =⨯+=, 所以预测2021年全国硕士研究生报考人数约为338.6万人. 18.解:本题考查数列通项公式及前n 项和 (1)因为()1311n nn S a+=-,所以当2n ≥时,所以()1314n n n S a +--,所以()11314(14)nn n n n a aa ++-=--,整理得()()11440nn n aa +--=,所以14,(2)n n a a n +=>,当1n =时,()12314nS a--,14a =,所以216a =,所以24a a =,所以数列{}n a 是首项和公比均为4的等比数列,所以1444n n a +=⨯=,即4n n a =.(2)由(1)知4n na =,所以()()221121222(1)log 4(1)log 24(1)n n n n n n b n +++=-⋅--⋅--⋅22222241234(21)(2)4[37(41)]4(21)n T n n n n n ⎡⎤=-+-++--=-----=-⋅+⎣⎦L L ,故数列{}n b 的前2n 项和24(21)n T n n =-+.【名师点睛】等差数列、等比数列的通项公式及前n 项和问题,是高考的常考内容,解题过程中要注意应用函数与方程思想,构建方程(或方程组)求基本量,例如此题,从已知出发,构建1,a d 的方程组求数列通项公式,利用前后项合并,构造等差数列,求数列的前n 项和. 19.解:本题考查线面平行及多面体的体积.(1)证明:因为2BC AD AD BC E =∥,,为线段AD 的中点,所以BC AE ∥,连接EC ,因为AB AD ⊥,所以四边形ABCE 为矩形,连接BE 交AC 于点O ,连GO ,因为G 为线段PB 的中点,所以OG PE ∥,因为GO ⊄平面PEF ,PBC 平面PEF , 所以GO ∥平面PEF ,由题易知,AC ∥平面PEF , 又因为GC ⊂平面GAC ,AC ⊂平面GAC .AC GO O =I ,所以平面PEF ∥平面GAC ,又因为AGC 平面GMC ,所以直线AC ∥平面PEF .(2)因为22 2 AD BC PA ===,1AB =,所以四棱锥P ABCD -的体积111(12)11322S =⨯⨯+⨯⨯=,三棱锥G ABC -的体联11111132212S =⨯⨯⨯⨯=,棱锥P DEF -的体积 11111132212S =⨯⨯⨯⨯=,故所求多面体AGCPEF 的体积为1111212123--=.20.解:本题考查函数最值及恒成立求参数范围. (1)()21x f x e ax '=--,所以()21xg x eax =--,()2x g x e a '=-,①当0a ≤时,()0g x '>,所以()21x g x e ax =--在R 上单词递增,不合题意;②当0a >时,(,ln 2)x a ∈-∞,()0g x '<,(ln 2,)x a ∈+∞,()0g x '>, 所以函数()gx 在区间(,ln 2)a -∞上单调递减,在区间(ln 2,)a +∞上单调递增,()(ln 2)2(1ln 2)10g x g a a a ----…,令()ln 1x x x x μ'---,则()ln x x μ'=-,所以()x μ在区间()0,1上单调递增,在区间(1,)+∞上单调递减,所以()()10x μμ≤=,所以由2(1ln 2)10a a --=,解得12a =, 即实数a 的值为12. (2)因为0x ∀>,2()(1)(1)1f x a x a x >--++恒成立,所以210x e x ax -+-≥,即21x e x a x ---<对任意0x >恒成立,令21()x e x x xϕ---,则()2(1)1()x x e x x x ϕ---'=,由(1)知,10x e x --≥,当且仅当0x =时,等号成立,所以函数()x ϕ在区间()0,1上单调递减,在区间(1,)+∞上单词递增,所以()(1)2x e ϕϕ=-…,所以2a e -≤-,即2a e ≥-. 所以实数a 的取值范围为[2,)e -+∞. 21.解:本题考查抛物线的性质. (1)因为||10PF =,所以8102p+-,解得4p =,所以()0,2F , 因为288t =⨯,且0t <,所以8t =-,所以()8,8P -,故直线PF 的方程为822(0)80y x ------, 化简得3480x y +-=.(2)由(1)知,抛物线方程为28x y =,点()0,2F .设()()1122,,,Mx y N x y ,又因为14y x '=, 所以直线m 的方程为()11114y y x x x -=- 整理得1114y x x y =-, 同理可得直线n 的方程为1214y x x y =-,设()33,G x y , 联立311332321414y x x y y x x y⎧--⎪⎪⎨⎪=-⎪⎩,得直线l 的方程为3314y xx y =-,又因为直线l 过点()0,4,所以4y =-,即点G 在定直线4y =-上,所以PG 的最小值为()8412--=.【解题思路】解决直线与抛物线的综合问题时,需要注意:(1)观察、应用题设中的每一个条件,明确确定直线、抛物线的条件;(2)强化有关直线与抛物线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.22.解:本题考查坐标与参数方程: (1)由题知,曲线C 的直角坐标方程为224x y +=,直线l20y m -+=,因为直线l 与曲线C||2m =≥, 所以实数m 的取值范围为(,2][2,)-∞-+∞U . (2)设()()1122,,,,(,)Ax y B x y P u v ,由(1)知,(2,2)m ∈-,由22204y m x y -+=+=⎪⎩,解得224440x m ++-=,所以122u x x -+-=,)121224v y y x x m m -+++=,所以2u =-,即u =,故点P的轨迹方程为0(11)x y +=-<<.23.解:本题考查不等式证明.(1)因为222a b +=所以1ab ≤,所以1ab ≤≤,2a b +≤,所以2a b ab +≤, 即2a b ab +≥,当且仅当a b =时等号成立, (2)()244222222242a b a b a b a b +-+-=-, 由(1)知1ab ≤,所以221a b ≤,所以2242422a b -≥--,即442a b +≥,当且仅当a b =时等号成立.。
【冲锋号考场模拟】赢战2023年高考数学模拟仿真卷 02卷(理科)(全国卷专用)(解析版)

【冲锋号·考场模拟】赢战2023年高考数学模拟仿真卷02卷(理科)(全国卷专用)(解析版)(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.4.测试范围:高考全部内容5.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|2A x x x =<+,{}1,0,1,2,3B =-,则A B = ()A .{}1,0,1-B .{}0,1,2C .{}0,1D .{}1,2【答案】C【分析】解不等式得到{}|12A x x =-<<,求出交集.【详解】22x x <+,即220x x --<,解得:12x -<<,故{}|12A x x =-<<,所以{}{}{}1,0,1,1|122,30,A x B x =--<=< .故选:C 2.若复数z 满足2iz+为纯虚数,且1z =,则z 的虚部为()A .5±B C .D①命题“x ∃∈R ,210x x ++≥”的否定是“x ∀∈R ,210x x ++<”;②0a b +=的充要条件是1ba=-;③若函数()y f x =为奇函数,则()0f x =;④0ab ≥是222a b ab +≥的必要条件.A .1个B .2个C .3个D .4个能是()A .1()f x x=-B .2()f x x =-C .()e e x x f x -=+D .1()ln1x f x x-=+111中,11分別是1111的中点,1,则1BD 与1AF 所成角的正弦值是()A 10B .12C .10D .3015位女生中安排3人到三个场馆做志愿者,每个场馆各位男生入选,则不同安排方法有()种.A .16B .20C .96D .120【答案】C【分析】分一男两女与两男一女两类讨论.【详解】若选一男两女共有:123243C C A 72=;若选两男一女共有:213243C C A 24=;因此共有96种,故选:C7.函数()()f x x ωϕ=+其中π0,||2ωϕ><,的图象的一部分如图所示,()g x x ω=,要想得到()g x 的图象,只需将()f x 的图象()A .向右平移π4个单位长度B .向右平移2个单位长度C .向左平移π4个单位长度D .向左平移2个单位长度中,每场比赛甲队获胜的概率为23,乙队获胜的概率为13,则在这场“五局三胜制”的排球赛中乙队获胜的概率为()A.1481B.13C.1781D.1681的锐角组成的对称多边形纹样,具有组合性强、结构稳定等特点.有的八角星纹中间镂空出一个正方形,有的由八个菱形组成,内部呈现米字形线条.八角星纹目前仍流行在中国南方的挑花和织锦中.在图2所示的八角星纹中,各个最小的三角形均为全等的等腰直角三角形,中间的四边形是边长为2的正方形,在图2的基础上连接线段,得到角α,β,如图3所示,则αβ+=()A.30°B.45°C.60°D.75°【答案】B则Rt ABC △中,2BC =,AC 在Rt DEF△中,2EF =,DE =所以()tan tan tan 1tan tan αβαβαβ++=-(),0,45αβ∈10.函数()e e cos 2x xf x x -=-在区间ππ,22⎡⎤-⎢⎥⎣⎦大致图像可能为()A .B .C .D .【答案】B【分析】利用定义判断()f x 的奇偶性,再结合函数值的符号分析判断,即可得答案.【详解】∵()()()()()()e e cos 2e e cos 2e e e e cos 20x x x xx x x x f x f x x x x ----+-=-+--=-+-=,即()()f x f x =--,11.若双曲线()2210,0x y a b a b-=>>的渐近线与圆C :22420x y x +-+=相交,则此双曲线的离心率的取值范围是()A .(B .()1,2C .)2D .)+∞12A .2121e e ln ln x xx x ->-B .2121e e ln ln x xx x -<-C .1221e e x xx x >D .1221e e x xx x <13.双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ,已知焦距为8,离心率为2,过右焦点2F 作垂直于x 轴的直线l 与双曲线C 的右支交于,A B 两点,则||AB =_____.故||6(6)12AB =--=,故答案为:12.14.已知O 为坐标原点,且(1,),(4,4)A m B m -,若,,O A B 三点共线,则实数m =_____.【答案】45##0.8的面积为___________.绕AD 顺时针旋转π2,则线段AP 扫过的区域面积为____________.故答案为:5π4.三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.某商场计划按月订购一种酸奶,每天进货量相同,进货成本每瓶8元,售价每瓶10元,未售出的酸奶降价处理,以每瓶4元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为600瓶;如果最高气温位于区间[20,25),需求量为400瓶;如果最高气温低于20,需求量为300瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数117382275以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)估计六月份这种酸奶一天的需求量不超过400瓶的概率,并求出前三年六月份这种酸奶每天平均的需求量;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为550瓶时,写出Y的所有可能值,并估计Y大于零的概率.38;②7;③2,4,5成等比数列.从中任选1个,补充到下面的问题中并解答问题:设数列{}n a 的前n 项和为n S ,已知()*12N n n n S S a n +=++∈,.(1)求数列{}n a 的通项公式;(2)n S 的最小值并指明相应的n 的值.【答案】(1)212n a n =-;(2)n =5或者6时,n S 取到最小值30-.【分析】(1)由已知可得12n n a a +-=,则{}n a 是公差为2的等差数列,若选①,则由382a a +=-列方程可求出1a ,从而可求出通项公式;若选②,则由728S =-列方程可求出1a ,从而可求111的底面为正三角形,1,点D ,E 分别在AB ,1BB 上,且AD DB =,113BE EB =.(1)证明:平面1A DC ⊥平面EDC ;(2)求二面角1A EC D --的余弦值.由题意得()1,0,0B ,()1,0,0C -,(A 因为AD DB =,113BE EB =,所以D 所以113,,222DE ⎛⎫=- ⎪ ⎪⎝⎭ ,3,0,2DC ⎛=- ⎝)AD DB =,113BE EB =,所以1,0,2D ⎛⎝12,,02CE ⎫ ⎪⎭=⎛⎝,()11,2,3CA = ,1DA 设平面1A EC 的法向量为(),,n x y z =,20.已知椭圆C :221x y a b+=()0a b >>的下顶点为点D ,右焦点为()21,0F .延长2DF 交椭圆C 于点E ,且满足223DF F E =.(1)试求椭圆C 的标准方程;(2)A ,B 分别是椭圆长轴的左右两个端点,M ,N 是椭圆上与A ,B 均不重合的相异两点,设直线AM ,AN 的斜率分别是1k ,2k .若直线MN 过点2⎫⎪⎪⎝⎭,则12k k ⋅是否为定值,若是求出定值,若不是请说明理由.联立222212x my x y ⎧=+⎪⎪⎨⎪+=⎪⎩,消去x ,得则12222m y y m +=-+,122y y =-y y,ln x a a g x =+(0a >,是自然对数的底数).(1)若直线y kx =与曲线()y f x =,()y g x =都相切,求a 的值;(2)若()()f x g x ≥恒成立,求实数a 的取值范围.按所做的第一题计分.选修4-4:坐标系与参数方程22.在平面直角坐标系中,曲线1C 的参数方程为3cos 2sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以O 为极点,x轴的正半轴为极轴建立极坐标系,曲线2C 是圆心在极轴上且经过极点的圆,射线6πθ=与曲线2C交于点6D π⎛⎫ ⎪⎝⎭.(1)求曲线1C ,2C 的普通方程;(2)()1,A ρθ,2,2B πρθ⎛⎫- ⎪⎝⎭是曲线1C 上的两点,求221211ρρ+的值.选修4-5:不等式选讲23.(1)已知0a >,0b >,412a b+=,求a b +的最小值;(2)已知a ,b ,c ,为任意实数,求证:222a b c ab bc ca ++≥++.。
高二理科数学高考模拟卷(二)

高二理科数学高考模拟卷(二)函数的概念与基本初等函数完成日期:03月08日一.选择题(共12小题)1.下列函数是偶函数的是()A.B.C.D.2.已知函数f(x)满足f(x+1)的定义域是[0,31),则f(2x)的定义域是()A.[1,32)B.[﹣1,30)C.[0,5)D.(﹣∞,log230)3.已知定义在R上的偶函数f(x)满足f(x+3)=f(x),且当x∈[0,1]时,,则f(18)+f(﹣28)=()A.B.C.D.4.已知定义在R上的奇函数f(x),满足f(x+4)=f(x)恒成立,且f(1)=1,则f(3)+f(4)+f(5)的值为()A.﹣1B.1C.2D.05.已知a=70.6,b=log76,c=log0.67,则()A.a>c>b B.a>b>c C.c>a>b D.b>a>c6.若函数f(x)=(m2﹣2m﹣2)x m﹣1是幂函数,且y=f(x)在(0,+∞)上单调递增,则f(2)=()A.B.C.2D.47.已知函数.在下列区间中,包含f(x)零点的区间是()A.(0,1)B.(1,3)C.(3,5)D.(5,7)8.已知函数f(x)=,则f[f(3)]等于()A.﹣27B.C.3D.99.已知函数y=f(x)的图象是连续不断的,且有如下对应值表:x12345y﹣2﹣0.310.430.89 1.21则函数f(x)一定存在零点的区间是()A.(1,2)B.(2,3)C.(3,4)D.(4,5)10.已知函数,若f(ln2)=a,则的值为()A.a B.﹣a C.2﹣a D.11.已知函数f(x)=a x﹣1+log b x﹣1(a>0且a≠1,b>0且b≠1),则f(x)的图象过定点()A.(0,1)B.(1,1)C.(1,0)D.(0,0)12.函数则关于x的方程[f(x)]2+2f(x)﹣3=0的根的个数是()A.5B.6C.7D.8二.填空题(共4小题)13.函数f(x)为R上的奇函数,在(﹣∞,0)上是增函数,f(5)=0,则xf(x)>0的解集是.14.已知a>0,且a≠1,函数,若f[f(0)]=2,则a=.15.已知函数f(x)是定义在(﹣2,2)上的奇函数且是减函数,若f(m﹣1)+f(1﹣2m)≥0,则实数m的取值范围是.16.已知函数,若f(a2)>f(2a+3),则实数a的取值范围是.三.解答题(共6小题)17.已知函数,若函数g(x)=2x+a的图象过点(0,4).(1)求实数a的值;(2)求函数f(x)的值域.18.设二次函数f(x)=ax2+bx+c在[﹣2,2]上的最大值和最小值分别是M和m,集合A={x|f(x)=x}.(1)若A={1,2},且f(0)=2,求f(x)的解析式;(2)若A={2},且a≥1,记g(a)=M+m,求g(a)的最小值.19.已知函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f(xy)=f(x)+f(y),当x>1时,f(x)>0.(1)判断f(x)的单调性并加以证明;(2)若f(4)=2,解不等式f(x)>f(2x﹣1)+1.20.已知函数f(x)=x2﹣mx+1(m∈R).(1)若函数f(x)在x∈[﹣1,1]上是单调函数,求实数m的取值范围;(2)若函数f(x)在x∈[1,2]上有最大值为3,求实数m的值.21.已知a∈R,函数f(x)=log2(+a).(1)当a=﹣5时,解关于x的不等式f(x)>0;(2)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差都不超过1,求实数a 的取值范围.22.已知幂函数.(1)求f(x)的解析式;(2)(i)若f(x)图象不经过坐标原点,直接写出函数f(x)的单调区间.(ii)若f(x)图象经过坐标原点,解不等式f(2﹣x)>f(x).。
湖北省高考数学二模试卷(理科)

湖北省高考数学二模试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)复数()A .B .C .D .2. (2分) (2017高二下·汪清期末) 已知集合()A . {2}B . {2,3}C . {1,,3 }D . {1,2,3,4,5}3. (2分)为非零向量。
“”是“函数为一次函数”的()A . 充分而不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件4. (2分)已知k<﹣4,则函数y=cos2x+k(cosx﹣1)的最小值是()A . 1B . -1C . 2k+1D . ﹣2k+15. (2分)某三棱锥的三视图如所示,该三棱锥的体积为()A . 20B .C . 56D . 606. (2分) (2016高二上·临川期中) 已知点P是抛物线x= y2上的一个动点,则点P到点A(0,2)的距离与点P到y轴的距离之和的最小值为()A . 2B .C .D .7. (2分)(2017·枣庄模拟) 已知a∈R,则“a<0”是“函数f(x)=|x(ax+1)|在(﹣∞,0)上是减函数”的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要8. (2分) (2019高一下·黑龙江月考) 设直线与函数的图像分别交于点,则当达到最小时的值为()A . 1B .C .D .9. (2分) (2016高二上·会宁期中) 设a=lge,b=(lge)2 , c=lg ,则()A . a>b>cB . c>a>bC . a>c>bD . c>b>a10. (2分) (2019高一下·中山月考) 函数为奇函数,该函数的部分图像如图所示,、分别为最高点与最低点,并且,则该函数图象的一条对称轴为()A .B .C .D .11. (2分)设椭圆+=1和x轴正半轴交点为A,和y轴正半轴的交点为B,P为第一象限内椭圆上的点,那么四边形OAPB面积最大值为()A . aB . aC . aD . 2a12. (2分) (2016高一上·黑龙江期中) 设函数f(x)= ,若关于x的方程f2(x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , h(x)=lg|x﹣4|,则h(x1+x2+x3+x4+x5)等于()A . 3B . lg12C . lg20D . 4lg2二、填空题 (共4题;共5分)13. (1分)电视中某一娱乐性节目有一种猜价格的游戏,在限定时间内(如15秒)猜出某一种商品的售价,就把该商品奖给选手,每次选手给出报价,主持人告诉说高了低了,以猜对或到时为止游戏结束.如猜一种品牌的电风扇,过程如下:游戏参与者开始报价500元,主持人说高了,300元,高了,260元,低了,280元,低了,290元,高了,285元,低了,288元,你猜对了!恭喜!请问游戏参与者用的数学知识是________(只写出一个正确答案).14. (1分)(2018高二下·张家口期末) 已知随机变量,且,,则 ________.15. (1分) (2016高二上·南昌开学考) 如图,在边长为1的正方形中随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为________.16. (2分)若如图为某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧视图、俯视图,则其正视图的面积为________ ,三棱锥D﹣BCE的体积为________三、解答题 (共7题;共60分)17. (10分)(2013·江西理) 正项数列{an}的前n项和Sn满足:Sn2(1)求数列{an}的通项公式an;(2)令b ,数列{bn}的前n项和为Tn .证明:对于任意n∈N* ,都有.18. (10分)(2016·南平模拟) 某研究性学习小组为了解学生每周用于体育锻炼时间的情况,在甲、乙两所学校随机抽取了各50名学生,做问卷调查,并作出如下频率分布直方图:(1)根据直方图计算:两所学校被抽取到的学生每周用于体育锻炼时间的平均数;(2)在这100名学生中,要从每周用于体育锻炼时间不低于10小时的学生中选出3人,该3人中来自乙学校的学生数记为X,求X的分布列和数学期望.19. (10分)如图,已知是平行四边形所在平面外一点,分别是的中点.(1)求证:平面;(2)若,,求异面直线与所成的角的大小.20. (5分) (2018高二上·西城期末) 已知椭圆的一个焦点为,离心率为 . 点为圆上任意一点,为坐标原点.(Ⅰ)求椭圆的标准方程;(Ⅱ)记线段与椭圆交点为,求的取值范围;(Ⅲ)设直线经过点且与椭圆相切,与圆相交于另一点,点关于原点的对称点为,试判断直线与椭圆的位置关系,并证明你的结论.21. (10分)(2017·盘山模拟) 设,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直.(1)求a的值;(2)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围.22. (10分) (2019高三上·江西月考) 在平面直角坐标中,直线的参数方程为,( 为参数) .以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为 .(1)若,试判断直线与曲线的位置关系;(2)当时,直线与曲线的交点为,若点的极坐标为,求的面积.23. (5分) (2020高二上·黄陵期中) 设x,y都是正数,且,求的最小值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共60分) 17-1、17-2、18-1、18-2、19-1、19-2、21-1、21-2、22-1、22-2、23-1、。
高考数学高三模拟考试试卷压轴题高考数学全真模拟试卷理科二

高考数学高三模拟考试试卷压轴题高考数学全真模拟试卷(理科)(二)一、选择题(共12小题,每小题5分,满分60分)1.(5分)(•陕西二模)设集合M={x|},函数f(x)=ln(1﹣)的定义域为N,则M∩N为()A.[,1] B.[,1)C.(0,] D.(0,)2.(5分)(•陕西二模)已知命题p:∃x∈R,log3x≥0,则()A.¬p:∀x∈R,log3x≤0 B.¬p:∃x∈R,log3x≤0C.¬p:∀x∈R,log3x<0 D.¬p:∃x∈R,log3x<03.(5分)(•陕西二模)若tanα=,则sin4α﹣cos4α的值为()A.﹣B.﹣C.D.4.(5分)(•新课标Ⅱ)等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=()A.B.C.D.5.(5分)(•陕西二模)某几何体的三视图如图所示,则此几何体的体积是()A.28π B.32π C.36π D.40π6.(5分)(•陕西二模)将除颜色外完全相同的一个白球、一个黄球、两个红球分给三个小朋友,且每个小朋友至少分得一个球的分法有()种.A.15 B.18 C.21 D.247.(5分)(•新课标I)已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=|x0|,则x0=()A.1 B.2 C.4 D.88.(5分)(•陕西模拟)如果执行如图的框图,输入N=5,则输出的数等于()A.B.C.D.9.(5分)(•陕西二模)曲线y=e在点(6,e2)处的切线与坐标轴所围成的三角形的面积为()A.B.3e2 C.6e2 D.9e210.(5分)(•陕西二模)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,且f(α)=1,α∈(0,),则cos(2)=()A.B.C.﹣D.11.(5分)(•陕西二模)若f(x)是定义在(﹣∞,+∞)上的偶函数,∀x1,x2∈[0,+∞)(x1≠x2),有,则()A.f(3)<f(1)<f(﹣2)B.f(1)<f(﹣1)<f(3)C.f(﹣2)<f(1)<f (3)D.f(3)<f(﹣2)<f(1)12.(5分)(•陕西二模)若直线l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0的四个交点把圆C分成的四条弧长相等,则m=()A.0或1 B.0或﹣1 C.1或﹣1 D.0二、填空题(共4小题,每小题5分,满分20分)13.(5分)(•陕西二模)(x+cosx)dx=.14.(5分)(•陕西二模)已知单位向量,的夹角为60°,则向量与的夹角为.15.(5分)(•陕西二模)不等式a2+8b2≥λb(a+b)对于任意的a,b∈R恒成立,则实数λ的取值范围为.16.(5分)(•陕西二模)已知F是双曲线C:x2﹣=1的右焦点,若P是C的左支上一点,A(0,6)是y轴上一点,则△APF面积的最小值为.三、解答题(共5小题,满分60分)17.(12分)(•陕西二模)在△ABC中,角A、B、C所对的边分别为a,b,c.已知a+c=3,b=3.(I)求cosB的最小值;(Ⅱ)若=3,求A的大小.18.(12分)(•陕西二模)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手大多在以下两个年龄段:21~30,31~40(单位:岁),统计这两个年龄段选手答对歌曲名称与否的人数如图所示.(1)写出2×2列联表,并判断是否有90%的把握认为答对歌曲名称与否和年龄有关,说明你的理由.(下面的临界值表供参考)P(K2≥k0) 0.1 0.05 0.01 0.005k0 2.706 3.841 6.635 7.879(2)在统计过的参考选手中按年龄段分层选取9名选手,并抽取3名幸运选手,求3名幸运选手中在21~30岁年龄段的人数的分布列和数学期望.(参考公式:K2=,其中n=a+b+c+d)19.(12分)(•陕西二模)如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11.(1)求二面角B﹣AD﹣C的平面角的余弦值;(2)在四面体A﹣BCD的棱AD上是否存在点P,使得•=0?若存在,请指出点P的位置;若不存在,请给出证明.20.(12分)(•陕西二模)设O是坐标原点,椭圆C:x2+3y2=6的左右焦点分别为F1,F2,且P,Q是椭圆C上不同的两点,(I)若直线PQ过椭圆C的右焦点F2,且倾斜角为30°,求证:|F1P|、|PQ|、|QF1|成等差数列;(Ⅱ)若P,Q两点使得直线OP,PQ,QO的斜率均存在.且成等比数列.求直线PQ的斜率.21.(12分)(•陕西二模)设函数f(x)=ex﹣lnx.(1)求证:函数f(x)有且只有一个极值点x0;(2)求函数f(x)的极值点x0的近似值x′,使得|x′﹣x0|<0.1;(3)求证:f(x)>2.3对x∈(0,+∞)恒成立.(参考数据:e≈2.718,ln2≈0.693,ln3≈1.099,ln5≈1.609,ln7≈1.946).[选修41:几何证明选讲]22.(10分)(•陕西二模)如图,已知AB为⊙O的直径,C,F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.求证:DE2=DA•DB.[选修44:坐标系与参数方程]23.(•陕西二模)在平面直角坐标系xOy中,已知圆C1:x2+y2=4,圆C2:(x﹣2)2+y2=4.(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别求圆C1与圆C2的极坐标方程及两圆交点的极坐标;(Ⅱ)求圆C1与圆C2的公共弦的参数方程.[选修45:不等式选讲]24.(•陕西二模)已知函数f(x)=|x+1|﹣2|x|.(1)求不等式f(x)≤﹣6的解集;(2)若存在实数x满足f(x)=log2a,求实数a的取值范围.高考数学全真模拟试卷(理科)(二)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(•陕西二模)设集合M={x|},函数f(x)=ln(1﹣)的定义域为N,则M∩N为()A.[,1] B.[,1)C.(0,] D.(0,)【解答】解:集合M={x|}=[,3),函数f(x)=ln(1﹣)=[0,1),则M∩N=[,1),故选:B.2.(5分)(•陕西二模)已知命题p:∃x∈R,log3x≥0,则()A.¬p:∀x∈R,log3x≤0 B.¬p:∃x∈R,log3x≤0C.¬p:∀x∈R,log3x<0 D.¬p:∃x∈R,log3x<0【解答】解:命题p:∃x∈R,log3x≥0,则¬p:∀x∈R,log3x<0.故选:C.3.(5分)(•陕西二模)若tanα=,则sin4α﹣cos4α的值为()A.﹣B.﹣C.D.【解答】解:∵tan,则sin4α﹣cos4α=(sin2α+cos2α)•(sin2α﹣cos2α)=sin2α﹣cos2α===﹣,故选:B.4.(5分)(•新课标Ⅱ)等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=()A.B.C.D.【解答】解:设等比数列{an}的公比为q,∵S3=a2+10a1,a5=9,∴,解得.∴.故选C.5.(5分)(•陕西二模)某几何体的三视图如图所示,则此几何体的体积是()A.28π B.32π C.36π D.40π【解答】解:图为三视图复原的几何体是一圆台和一个圆柱的组合体,圆柱的底面半径为2,高为2,体积为:22π•2=8π.圆台的底面半径为4,上底面半径为2,高为3,体积为:=28π,几何体的体积为:36π.故选:C.6.(5分)(•陕西二模)将除颜色外完全相同的一个白球、一个黄球、两个红球分给三个小朋友,且每个小朋友至少分得一个球的分法有()种.A.15 B.18 C.21 D.24【解答】解:把4个小球分成(2,1,1)组,其中2个小球分给同一个小朋友的有4种方法(红红,红黄,红白,白黄),若(红红,红黄,红白)分给其中一个小朋友,则剩下的两个球分给2个小朋友,共有3×3×A22=18种,若(白黄两个小球)分给其中一个小朋友,剩下的两个红色小球只有1种分法,故有3×1=3种,根据分类计数原理可得,共有18+3=21种.故选:C.7.(5分)(•新课标I)已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=|x0|,则x0=()A.1 B.2 C.4 D.8【解答】解:抛物线C:y2=x的焦点为F,∵A(x0,y0)是C上一点,AF=|x0|,∴=x0+,解得x0=1.故选:A.8.(5分)(•陕西模拟)如果执行如图的框图,输入N=5,则输出的数等于()A.B.C.D.【解答】解:经过第一次循环得到 S=,满足进入循环的条件,k=2,经过第二次循环得到S=+=,满足进入循环的条件,k=3,经过第三次循环得到S=+=,满足进入循环的条件,k=4,经过第四次循环得到S=+=,满足进入循环的条件,k=5,经过第五次循环得到S=+=,不满足进入循环的条件,执行输出,故输出结果为:,故选:D9.(5分)(•陕西二模)曲线y=e在点(6,e2)处的切线与坐标轴所围成的三角形的面积为()A.B.3e2 C.6e2 D.9e2【解答】解:y=e的导数为y′=e,可得在点(6,e2)处的切线斜率为e2,即有在点(6,e2)处的切线方程为y﹣e2=e2(x﹣6),即为y=e2x﹣e2,令x=0,可得y=﹣e2;令y=0,可得x=3.即有切线与坐标轴所围成的三角形的面积为•3•e2=e2.故选:A.10.(5分)(•陕西二模)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,且f(α)=1,α∈(0,),则cos(2)=()A.B.C.﹣D.【解答】解:由图象可得A=3,=4(﹣),解得ω=2,故f(x)=3sin(2x+φ),代入点(,﹣3)可得3sin(+φ)=﹣3,故sin(+φ)=﹣1,+φ=2kπ﹣,∴φ=2kπ﹣,k∈Z结合0<φ<π可得当k=1时,φ=,故f(x)=3sin(2x+),∵f(α)=3sin(2α+)=1,∴sin(2α+)=,∵α∈(0,),∴2α+∈(,),∴cos(2)=﹣=﹣,故选:C.11.(5分)(•陕西二模)若f(x)是定义在(﹣∞,+∞)上的偶函数,∀x1,x2∈[0,+∞)(x1≠x2),有,则()A.f(3)<f(1)<f(﹣2)B.f(1)<f(﹣1)<f(3)C.f(﹣2)<f(1)<f (3)D.f(3)<f(﹣2)<f(1)【解答】解:∵∀x1,x2∈[0,+∞)(x1≠x2),有,∴当x≥0时函数f(x)为减函数,∵f(x)是定义在(﹣∞,+∞)上的偶函数,∴f(3)<f(2)<f(1),即f(3)<f(﹣2)<f(1),故选:D12.(5分)(•陕西二模)若直线l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0的四个交点把圆C分成的四条弧长相等,则m=()A.0或1 B.0或﹣1 C.1或﹣1 D.0【解答】解:∵l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0,∴直线l1∥l2,且l1、l2把⊙C分成的四条弧长相等,画出图形,如图所示.又⊙C可化为(x﹣m)2+(y﹣n)2=m2+n2,当m=0,n=1时,圆心为(0,1),半径r=1,此时l1、l2与⊙C的四个交点(0,0),(1,1),(0,2),(﹣1,1)把⊙C分成的四条弧长相等;当m=﹣1,n=0时,圆心为(﹣1,0),半径r=1,此时l1、l2与⊙C的四个交点(0,0),(﹣1,1),(﹣2,0),(﹣1,﹣1)也把⊙C 分成的四条弧长相等;故选:B.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(•陕西二模)(x+cosx)dx=.【解答】解:(x2+sinx)|=故答案为:.14.(5分)(•陕西二模)已知单位向量,的夹角为60°,则向量与的夹角为.【解答】解:∵单位向量,的夹角为60°,∴|+|===,||==,(+)()=﹣•﹣2+=﹣﹣2+1=﹣,设向量与的夹角为θ,则cosθ==﹣,故θ=,故答案为:.15.(5分)(•陕西二模)不等式a2+8b2≥λb(a+b)对于任意的a,b∈R恒成立,则实数λ的取值范围为[﹣8,4].【解答】解:∵a2+8b2≥λb(a+b)对于任意的a,b∈R恒成∴a2+8b2﹣λb(a+b)≥0对于任意的a,b∈R恒成即a2﹣(λb)a+(8﹣λ)b2≥0恒成立,由二次不等式的性质可得,△=λ2+4(λ﹣8)=λ2+4λ﹣32≤0∴(λ+8)(λ﹣4)≤0解不等式可得,﹣8≤λ≤4故答案为:[﹣8,4]16.(5分)(•陕西二模)已知F是双曲线C:x2﹣=1的右焦点,若P是C的左支上一点,A(0,6)是y轴上一点,则△APF面积的最小值为6+9.【解答】解:双曲线C:x2﹣=1的右焦点为(3,0),由A(0,6),可得直线AF的方程为y=﹣2x+6,|AF|==15,设直线y=﹣2x+t与双曲线相切,且切点为左支上一点,联立,可得16x2﹣4tx+t2+8=0,由判别式为0,即有96t2﹣4×16(t2+8)=0,解得t=﹣4(4舍去),可得P到直线AF的距离为d==,即有△APF的面积的最小值为d•|AF|=××15=6+9.故答案为:6+9.三、解答题(共5小题,满分60分)17.(12分)(•陕西二模)在△ABC中,角A、B、C所对的边分别为a,b,c.已知a+c=3,b=3.(I)求cosB的最小值;(Ⅱ)若=3,求A的大小.【解答】解:(I)在△ABC中,由余弦定理得cosB===.∵ac≤()2=.∴当ac=时,cosB取得最小值.(II)由余弦定理得b2=a2+c2﹣2accosB.∵=accosB=3.∴9=a2+c2﹣6,∴a2+c2=15.又∵a+c=3,∴ac=6.∴a=2,c=或a=,c=2.∴cosB=,sinB=.由正弦定理得,∴sinA==1或.∴A=或A=.18.(12分)(•陕西二模)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手大多在以下两个年龄段:21~30,31~40(单位:岁),统计这两个年龄段选手答对歌曲名称与否的人数如图所示.(1)写出2×2列联表,并判断是否有90%的把握认为答对歌曲名称与否和年龄有关,说明你的理由.(下面的临界值表供参考)P(K2≥k0) 0.1 0.05 0.01 0.005k0 2.706 3.841 6.635 7.879(2)在统计过的参考选手中按年龄段分层选取9名选手,并抽取3名幸运选手,求3名幸运选手中在21~30岁年龄段的人数的分布列和数学期望.(参考公式:K2=,其中n=a+b+c+d)【解答】解:(1)2×2列联表正确错误合计21~30 10 30 4031~40 10 70 80合计20 100 120∴K2==3>2.706有90%的把握认为猜对歌曲名称与否和年龄有关.﹣﹣﹣﹣﹣﹣(4分)(2)按照分层抽样方法可知:21~30(岁)抽取3人,31~40(岁)抽取6人.设3名选手中在21~30岁之间的人数为ξ,可能取值为0,1,2,3﹣﹣﹣﹣(5分)P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==.﹣﹣﹣﹣﹣(10分)ξD的分布列ξ0 1 2 3P﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)E(ξ)=0×+1×+2×+3×=1﹣﹣﹣﹣﹣﹣(12分)19.(12分)(•陕西二模)如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11.(1)求二面角B﹣AD﹣C的平面角的余弦值;(2)在四面体A﹣BCD的棱AD上是否存在点P,使得•=0?若存在,请指出点P的位置;若不存在,请给出证明.【解答】解:(1)由已知AD⊥BD,AD⊥CD,故二面角B﹣AD﹣C的平面角为∠BDC,在图①,设BD=x,AD=h,则CD=14﹣x,在△ABD与△ACD中,分别用勾股定理得x2+h2=152,(14﹣x)2+h2=132,得x=9,h=12,从而AD=12,BD=9,CD=5,在图②的△BCD中,由余弦定理得BC2=BD2+CD2﹣2BD•CDcos∠BDC,即112=92+52﹣2×9×5cos∠BDC,则cos∠BDC=﹣,即二面角B﹣AD﹣C的平面角的余弦值是﹣.(2)假设在四面体A﹣BCD的棱AD上存在点P,使得,则0==(+)•(+)=2+•+•+•=2+0+0+9×5×(﹣)=2﹣,则||=<12,符号题意,即在棱AD上存在点P,使得,此时||=.20.(12分)(•陕西二模)设O是坐标原点,椭圆C:x2+3y2=6的左右焦点分别为F1,F2,且P,Q是椭圆C上不同的两点,(I)若直线PQ过椭圆C的右焦点F2,且倾斜角为30°,求证:|F1P|、|PQ|、|QF1|成等差数列;(Ⅱ)若P,Q两点使得直线OP,PQ,QO的斜率均存在.且成等比数列.求直线PQ的斜率.【解答】解:(I)证明:x2+3y2=6即为+=1,即有a=,b=,c==2,由直线PQ过椭圆C的右焦点F2(2,0),且倾斜角为30°,可得直线PQ的方程为y=(x﹣2),代入椭圆方程可得,x2﹣2x﹣1=0,即有x1+x2=2,x1x2=﹣1,由弦长公式可得|PQ|=•=•=,由椭圆的定义可得|F1P|+|PQ|+|QF1|=4a=4,可得|F1P|+|QF1|=4﹣==2|PQ|,则有|F1P|、|PQ|、|QF1|成等差数列;(Ⅱ)设直线PQ的方程为y=kx+m,代入椭圆方程x2+3y2=6,消去y得:(1+3k2)x2+6kmx+3(m2﹣2)=0,则△=36k2m2﹣12(1+3k2)(m2﹣2)=12(6k2﹣m2+2)>0,x1+x2=﹣,x1x2=,故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,∵直线OP、PQ、OQ的斜率依次成等比数列,∴•==k2,即km(x1+x2)+m2=0,即有﹣+m2=0,由于m≠0,故k2=,∴直线PQ的斜率k为±.21.(12分)(•陕西二模)设函数f(x)=ex﹣lnx.(1)求证:函数f(x)有且只有一个极值点x0;(2)求函数f(x)的极值点x0的近似值x′,使得|x′﹣x0|<0.1;(3)求证:f(x)>2.3对x∈(0,+∞)恒成立.(参考数据:e≈2.718,ln2≈0.693,ln3≈1.099,ln5≈1.609,ln7≈1.946).【解答】(1)证明:f(x)的定义域是(0,+∞),f′(x)=ex﹣,∵函数y=ex和y=﹣在(0,+∞)均递增,∴f′(x)在(0,+∞)递增,而f′()=﹣2<0,f′(1)=e﹣1>0,∴f′(x)在(,1)上存在零点,记x0,且f′(x)在x0左右两侧的函数值异号,综上,f′(x)有且只有一个零点x0,即函数f(x)有且只有一个极值点x0;(2)解:∵ln=ln5﹣ln3≈0.51<⇒>,且f′(x)在[,]上的图象连续,f′()<0,f′()=﹣>0,∴f′(x)的零点x0∈(,),即f(x)的极值点x0∈(,),即x0∈(0.5,0.6),∴x0的近似值x′可以取x′=0.55,此时的x′满足|x′﹣x0|<0.6﹣.05=0.1;(3)证明:∵ln=ln7﹣2ln2≈0.56<⇒>,且f′(x)在[,]上图象连续,f′()<0,f′()=﹣>0,∴f′(x)的零点x0∈(,),f(x)的极值点x0∈(,)⇒x0<,由(1)知:f′(x0)=﹣=0,且f(x)的最小值是f(x0)=﹣lnx0=﹣lnx0,∵函数g(x)=﹣lnx在(0,+∞)递减,且x0<,∴g(x0)>g()=1.75﹣(2ln2﹣ln7)≈2.31>2.3,∴f(x)≥f(x0)=﹣lnx0>2.3对x∈(0,+∞)恒成立.[选修41:几何证明选讲]22.(10分)(•陕西二模)如图,已知AB为⊙O的直径,C,F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.求证:DE2=DA•DB.【解答】证明:连接OF.因为DF切⊙O于F,所以∠OFD=90°.所以∠OFC+∠CFD=90°.因为OC=OF,所以∠OCF=∠OFC.因为CO⊥AB于O,所以∠OCF+∠CEO=90°.(5分)所以∠CFD=∠CEO=∠DEF,所以DF=DE.因为DF是⊙O的切线,所以DF2=DB•DA.所以DE2=DB•DA.(10分)[选修45:不等式选讲]24.(•陕西二模)已知函数f(x)=|x+1|﹣2|x|.(1)求不等式f(x)≤﹣6的解集;(2)若存在实数x满足f(x)=log2a,求实数a的取值范围.【解答】解:(1)x≥0时,f(x)=x+1﹣2x=﹣x+1≤﹣6,解得:x≥7,﹣1<x<0时,f(x)=x+1+2x≤﹣6,无解,x≤﹣1时,f(x)=﹣x﹣1+2x≤﹣6,解得:x≤﹣7,故不等式的解集是{x|x≥7或x≤﹣7};(2)x≥0时,f(x)=﹣x+1≤1,﹣1<x<0时,f(x)=3x+1,﹣2<f(x)<1,x≤﹣1时,f(x)=x﹣1≤﹣2,故f(x)的最大值是1,若存在实数x满足f(x)=log2a,只需≤1即可,解得:0<a≤2.[选修44:坐标系与参数方程]23.(•陕西二模)在平面直角坐标系xOy中,已知圆C1:x2+y2=4,圆C2:(x﹣2)2+y2=4.(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别求圆C1与圆C2的极坐标方程及两圆交点的极坐标;(Ⅱ)求圆C1与圆C2的公共弦的参数方程.【解答】解:(Ⅰ)在平面直角坐标系xOy中,已知圆C1:x2+y2=4,转化成极坐标方程为:ρ=2.圆C2:(x﹣2)2+y2=4.转化成极坐标方程为:ρ=4cosθ,所以:解得:ρ=2,,(k∈Z).交点坐标为:(2,2kπ+),(2,2k).(Ⅱ)已知圆C1:x2+y2=4①圆C2:(x﹣2)2+y2=4②所以:①﹣②得:x=1,y=,即(1,﹣),(1,).所以公共弦的参数方程为:.高考理科数学试题及答案(考试时间:120分钟试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二理科数学函数高考模拟卷2
一.选择题(共12小题)
1.下列函数是偶函数的是()
A.B.C.D.
2.已知函数f(x)满足f(x+1)的定义域是[0,31),则f(2x)的定义域是()
A.[1,32)B.[﹣1,30)C.[0,5)D.(﹣∞,log230)
3.已知定义在R上的偶函数f(x)满足f(x+3)=f(x),且当x∈[0,1]时,,则f(18)+f(﹣28)=()
A.B.C.D.
4.已知定义在R上的奇函数f(x),满足f(x+4)=f(x)恒成立,且f(1)=1,则f(3)+f(4)+f(5)的值为()
A.﹣1B.1C.2D.0
5.已知a=70.6,b=log76,c=log0.67,则()
A.a>c>b B.a>b>c C.c>a>b D.b>a>c
6.若函数f(x)=(m2﹣2m﹣2)x m﹣1是幂函数,且y=f(x)在(0,+∞)上单调递增,则f(2)=()A.B.C.2D.4
7.已知函数.在下列区间中,包含f(x)零点的区间是()
A.(0,1)B.(1,3)C.(3,5)D.(5,7)
8.已知函数f(x)=,则f[f(3)]等于()
A.﹣27B.C.3D.9
9.已知函数y=f(x)的图象是连续不断的,且有如下对应值表:
x12345
y﹣2﹣0.310.430.89 1.21
则函数f(x)一定存在零点的区间是()
A.(1,2)B.(2,3)C.(3,4)D.(4,5)
10.已知函数,若f(ln2)=a,则的值为()A.a B.﹣a C.2﹣a D.
11.已知函数f(x)=a x﹣1+log b x﹣1(a>0且a≠1,b>0且b≠1),则f(x)的图象过定点()A.(0,1)B.(1,1)C.(1,0)D.(0,0)
12.函数则关于x的方程[f(x)]2+2f(x)﹣3=0的根的个数是()
A.5B.6C.7D.8
二.填空题(共4小题)
13.函数f(x)为R上的奇函数,在(﹣∞,0)上是增函数,f(5)=0,则xf(x)>0的解集是.14.已知a>0,且a≠1,函数,若f[f(0)]=2,则a=.
15.已知函数f(x)是定义在(﹣2,2)上的奇函数且是减函数,若f(m﹣1)+f(1﹣2m)≥0,则实数m的取值范围是.
16.已知函数,若f(a2)>f(2a+3),则实数a的取值范围是.
三.解答题(共6小题)
17.已知函数,若函数g(x)=2x+a的图象过点(0,4).
(1)求实数a的值;
(2)求函数f(x)的值域.
18.设二次函数f(x)=ax2+bx+c在[﹣2,2]上的最大值和最小值分别是M和m,集合A={x|f(x)=x}.
(1)若A={1,2},且f(0)=2,求f(x)的解析式;
(2)若A={2},且a≥1,记g(a)=M+m,求g(a)的最小值.
19.已知函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f(xy)=f(x)+f(y),当x>1时,f(x)>0.
(1)判断f(x)的单调性并加以证明;
(2)若f(4)=2,解不等式f(x)>f(2x﹣1)+1.
20.已知函数f(x)=x2﹣mx+1(m∈R).
(1)若函数f(x)在x∈[﹣1,1]上是单调函数,求实数m的取值范围;
(2)若函数f(x)在x∈[1,2]上有最大值为3,求实数m的值.
21.已知a∈R,函数f(x)=log2(+a).
(1)当a=﹣5时,解关于x的不等式f(x)>0;
(2)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差都不超过1,求实数a 的取值范围.
22.已知幂函数.
(1)求f(x)的解析式;
(2)(i)若f(x)图象不经过坐标原点,直接写出函数f(x)的单调区间.
(ii)若f(x)图象经过坐标原点,解不等式f(2﹣x)>f(x).。
