2011年本区重点校初一下数学期中考试压轴题
2010-2011学年度第二学期期中考试七年级数学试卷

第14题图2010-2011学年度第二学期期中考试七年级数学试卷班级_______ 姓名____________ 成绩____________一、选择题:(每题3分,共30分)1、下列各点中,在第四象限的点是( )A .(2,3)B .(2,-3)C .(-2,3)D .(-2, -3)2、已知坐标平面内点M(a , b)在第三象限,那么点N(b, -a )在( )A .第一象限B .第二象限C .第三象限D .第四象限3、在第二象限的N 点,到x 轴和y 轴的距离分别 8和5,那么点N 的坐标为( )A . (-5,8)B .(-8,5)C .(5,-8)D .(8,-5)4、下列线段长度一定可以组成三角形的是( )A . 3cm 、3cm 、6cmB . 2cm 、3cm 、6cmC . 5cm 、8cm 、12cmD . 4cm 、7cm 、11cm5、如果一个三角形的三个内角的度数之比为2:2:4,那么这个三角形是( )A .锐角三角形 B. 直角三角形C .钝角三角形 D. 锐角三角形或直角三角形6、下列正多边形中,能铺满地面的是( ) A .正五边形 B .正六边形 C .正八边形 D.正十边形7、如图,在△ABC 中,∠ABC=48°,∠A=70°,BD 是∠ABC 的平分线,则∠BDC 等于( )A. 26°B.96°C.52°D.94° 8、已知一个多边形的内角和为540°,则这个多边形为( )A .三角形B .四边形C .五边形D .六边形9、一个三角形的两边长分别为5cm 和3cm ,第三边也是整数,且周长是偶数,则第三边长是( )A. 2cm 或4cmB. 4cm 或6cmC. 4cmD. 2cm 或6cm10、如图,BE 是∠ABD 的平分线,CF 是∠ACD 的平分线,BE 与CF 交于点G ,若=120°,∠BGC =100°,BDC ∠则∠A 等于( )A. 80°B. 75°C. 70°D. 60°二、填空题:(每题3分,共24分)11、不等式≤的正整数解是________________.75-x ()13+x 12、若m>n ,则-3m -3n (用“>”,“<”或其它不等号)13、在平面直角坐标系内,把点P(-1,3)向下平移1个单位长度,再向右平移2个单位长度后,所到达的位置点P的坐标为_________________.'14、如图所示,AD=BC, 请你添加一个条件使得△ABD ≌△CDB ,可添条件是 (添一个即DA第7题图第10题第17题图(第18题)321可).15、若是二元一次方程的一个解,则 .⎩⎨⎧-==32y x 0=-y kx =k 16、在△ABC 中,∠A=125°,∠B=15°,则∠C=_______.17、如图,P 为△ABC 中BC 边的延长线上一点,∠A =50°,∠B =70°,则∠ACP= ____°.18、如图,将三角尺的直角顶点放在直尺的一边上,∠1=,∠2=,则∠3= .30︒50︒19、如图,把一副常用三角板如图所示拼在一起,延长ED 交AC 于F ,那么图中∠AFE 是 度.三、解答题:(第20—23题,每小题4分;第24—26题,每小题5分;第27—28题,每小题6分;共43分)20、解方程组: 21、解方程组:⎩⎨⎧-==-22534x y y x ⎩⎨⎧-=--=+935524y x y x22、解不等式 , 并把解集在数轴上表示出来.第19题图1213<--x x班级_______ 姓名____________23、求不等式组的整数解. ()()⎪⎩⎪⎨⎧-<-+<-22531413x x x x24、如图,中: ABC △,,(23)A -,(31)B -,(12)C -,(1)将向右平移个单位长度,ABC △4画出平移后的;并写出 111A B C △的顶点坐标.111A B C △ 解:(2)的面积是 .ABC △25、一个多边形的内角和是它外角和的3倍,求这个多边形的边数.26、已知:如图,点A 、C 、B 、D 在同一直线上,AM =CN ,BM =DN ,AC =BD.求证:AM ∥CN .证明:∵AC =BD∴AC+CB =BD+CB即AB=CD在△ABM 与△CDN 中( ) ∵ ( ) ( ) ∴△ABM ≌△CDN( )∴∠A =∠1( )∴AM ∥CN( )27、已知:如图,已知△ABC 中,AD 是BC 边上的高,AE 是∠BAC 的平分线,若∠B = 65°,∠C = 45°,求:∠DAE 的度数.28、某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:(1)春游学生共多少人?原计划租45座客车多少辆?(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算?A B C D E⎪⎩⎪⎨⎧===,,,CD AB DN BM CNAM。
2010-2011七年级数学下期中考试试题

义兴小学2011年春季七年级(下)中期考试数学试卷(一)(满分:150分,完卷时间:120分钟)一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填在题后的括号中.1.点P(-3,2)所在的象限是 ( ) A.第—象限内 B.第二象限内 C.第三象限内 D.第四象限内2.下列命题中是真命题的是( )A.同位角都相等B.内错角都相等C.同旁内角都互补D.对顶角都相等3.下列图中,正确画出AC 边上的高的是( ) A . B . C . D . 4.如图,直线a b ∥,∠1=400,则∠2=( ) A .400 B .600 C .1000 D .14005.将一直角三角形与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°④∠4+∠5=180°,其中正确的个数是( ) A .1 B . 2 C . 3 D .46.下列各组数中不可能是一个三角形的边长的是( ) A . 5,12,13 B . 5,7,7 C . 5,7,12 D . 101,102,1037.用一批完全相同的正多边形地砖铺地面,不能进行镶嵌的是( ) A .正三角形 B .正四边形 C .正六边形 D .正八边形8.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A=120°,第※※※※※※※※※※※※※※※※※※※※※密 封 线内 不 要答 题 ※※※※※※※※※※※班别: 姓名:座号:____ B A E A B E A B B ca b21 第4题图 第5题图二次拐的角∠B 是150°,第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 是( ) A.120° B.130° C.140° D.150°9.如图,一块实验田的形状是三角形(设其为△ABC ),管理员从BC 边上的一点D 出发,沿DC →CA →AB →BD 的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体( )A.转过90°B.转过180°C.转过270°D.转过360° 10.如图,AB ∥CD ∥EF ,则下列各式中正确的是( ) A.∠1+∠3=180° B.∠1+∠2=∠3C.∠2+∠3+∠1=180°D.∠2+∠3-∠1=180° 二、填空题:(本大题6个小题,每小题4分,共24分)在每小题中,请将正确答案直接填在题后的横线上. 11. 点P(05,-)在___________上.(填“x 轴”或“y 轴”). 12.如图,已知直线AB CD ,相交于点O ,OE AB ⊥,28EOC ∠=,则AOD ∠=度.13. 把一副常用三角板如图所示拼在一起,延长ED 交AC 于F .那么图中∠AFE 的度 数为是 度.14.如图,直角ΔDEF 是由直角ΔABC 平移得到的,如果AB=6cm ,BE=5 cm ,DG=2 cm ,28EBDA O C第12题图第13题图第14题图G BACD 第9题图第8题图第10题图 B E FA231那么图中阴影部分四边形 DGCF的面积是_____________cm2.15.已知点A(―2 ,―1)、B(3 ,―1)、C(―1 ,2)、D(4 ,2),则线段AB 与线段CD的关系是______________ .16.正方形网格中,每个小格的顶点叫做格点.当所做正方形边上的点刚好在格点上的点称为整点.如图中1111A B C D四条边上的整点共有8个;2222A B C D四条边上的整点共有16个.请你观察图中正方形3333A B C D四条边上的整点的个数…按此规律,推算出正方形10101010A B C D四条边上的整点共有__________个.三、解答题:(本大题4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤.17. 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1 ,2),(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C',则A'B'C'的三个顶点坐标分别是A'(,)、B'(,)、C'(,)(3)△ABC的面积为____________.18.如图,已知∠1+∠2=180°∠3=∠B,则∠EDG与∠DGB相等吗?下面是王冠同学的部分推导过程,请你帮他在括号内填上推导依据或内容。
2011-2012学年第二学期期中考试七年级数学试卷

2011-2012学年武汉市第二学期期中考试七年级数学试卷本试卷由选择题和非选择题两部分组成,共25题,考试时间120分钟,共120分。
第一卷(选择题部分)一、选择题(每小题3分,共36分)1.点P(-1,2)位于平面直角坐标系的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.如图所示,由AB//CD,可以得到()A ∠1=∠2B ∠2=∠3C ∠1=∠4D ∠3=∠43.将点(1, 1 )向右平移两个单位长度,再向上平移3个单位长度,则对应点的坐标为()A ( 3, 4 )B ( 4,3 )C (-1,-2)D (-2,-1)4.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ;②∠3=∠4③∠2+∠4=90°④∠4+∠5=180°,期中结论正确的个数有()A 4个B 3个C 2个D 1个第四题图第二题图DBCA B5,如图所示,已知AB//CD直线PQ分别交AB,CD与点E,F,EG平分∠PED,交AB于点G,若∠QED=40°,则∠EGB的度数是()A 80°B 100°C 110°D 120°6.如图所示,已知∠1=∠2=∠3=55°,则∠4的度数是()A 110°B 115°C 120°D 125°7.如图所示,点E在AD的延长线上,下列条件中能判断AB//CD的是()A ∠3=∠4B ∠1=∠2 C ∠D=∠DCE D ∠D+∠ACD=180°第七题图AE第八题图A第六题图8.如图所示,AB//CD ,∠A=45°,∠C=∠E ,则∠C 的度数为( ) A 20° B 22.5° C 25° D 27.5°9. 在正三角形,正方形,正五边形,正六边形中不能单独镶嵌平面的是( ) A 正三角形 B 正方形 C 正五边形 D 正六边形10.如图所示,小李从O 点出发,前进5米后向右转20°,再前进5米后又向右转20°,……,这样一直走下去,他第一次回到出发点O 时一共走了( )A 60米B 100米C 90米D 120米11.如图,已知O 点是四边形ABCD 内一点,∠ABO=∠BAO ,∠CBO=∠BCO , ∠ABC=∠ADC=70°,则∠DAO+∠DCO 的度数是( )A 150°B 140°C 110°D 70°AC12.如图,在△ABC 中,∠ABC 的平分线与△ABC 的外角∠ACD 的平分线相交于点P ,O 是BP上一点,且CO 平分∠ACB ,OH ⊥BC 于点H ,以下结论:①OC ⊥PC; ②∠BOC=90°+21∠A③∠P=21∠A ; ④∠COH=∠ABP+∠P ,期中正确结论的个数有( )第十二题图OPA BC DHA 1个B 2个C 3个D 4个第二卷(非选择题部分)二、 填空题(每小题3分,共12分)13. 如图所示,AB//CD ,∠ABE=66°,∠D=54°,则∠E 的度数为14. 如图,A ,B 的坐标为(2 ,0),(0 ,1)若将线段AB 平移至A 1B 1,则a+b 的值为第十三题图Ab )15,如图所示,已知a//b ,∠1=70°,∠2=40°,则∠3的度数是 16,如图所示,在△ABC 中,∠A=α,∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1,∠A 1BC 与∠A 1CD 的平分线相交与点A 2,得∠A 2;。
2011(下)初一期中数学考试.doc
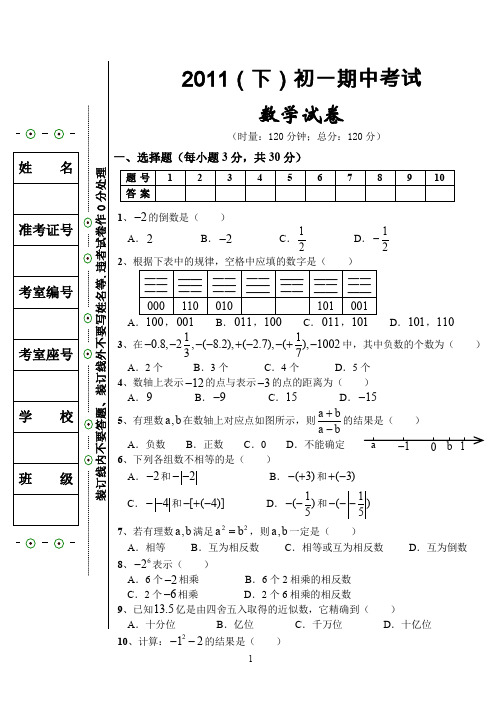
2011(下)初一期中考试数学试卷(时量:120分钟;总分:120分)一、选择题(每小题3分,共30分)1、2-的倒数是( )A .2B .2-C .12 D .12- 2A .,B .,C .,D .101,1103、在110.8,2,(8.2),( 2.7),(),100237----+--+-中,其中负数的个数为( )A .2个B .3个C .4个D .5个4、数轴上表示12-的点与表示3-的点的距离为( ) A .9 B .9- C .15 D .15-5、有理数,a b 在数轴上对应点如图所示,则a ba b+-的结果是( ) A .负数 B .正数 C .0 D .不能确定 6、下列各组数不相等的是( )A .2-和2--B .(3)-+和(3)+-C .4--和[(4)]-+-D .1()5--和1()5---7、若有理数,a b 满足22a b =,则,a b 一定是( )A .相等B .互为相反数C .相等或互为相反数D .互为倒数 8、62-表示( )A .6个2-相乘B .6个2相乘的相反数C .2个6-相乘D .2个6相乘的相反数9、已知13.5亿是由四舍五入取得的近似数,它精确到( )A .十分位B .亿位C .千万位D .十亿位 10、计算:212--的结果是( )A .4-B .3-C .1-D .0二、填空题(每小题3分,共18分)11、根据你所发现的规律,在横线上填上适当的数:1,4,9,_______。
12、3-的相反数是__________;5-的绝对值是__________。
13、若,a b 互为相反数,则2102a b ++=________;若,x y 互为倒数,则3xy-=_________。
14、若340x y -++=,则xy=_________。
15、0.03054保留3个有效数字约为__________;7508000-用科学记数法表示为____________。
期中解答题压轴必刷常考题七年级数学下学期期中期末满分必刷常考压轴题人教版

解答题压轴必刷常考题【压轴题题必考】1.(安溪)如图,将一条数轴在原点O和点B处各折一下,AO∥BC,得到一条“折线数轴”.图中点A表示﹣20,点B表示20,点C表示36.动点M从点A出发,以2个单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点N从点C出发,以1个单位/秒的速度沿着“折线数轴”的负方向运动,从点B运动到点O期间的速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.(1)填空:点A和点C在数轴上相距56个单位长度;(2)当t为何值时,点M与点N相遇?(3)当t为何值时,M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等.【答案】(1)56 (2)t=(3)t的值为4或13或22或34【解答】解:(1)∵点A表示﹣20,点C表示36,∴点A和点C在数轴上相距36﹣(﹣20)=56(个单位长度),故答案为:56;(2)由题意知,N从C到B需16s,M从A到O需10s,∴M、N在OB段相遇,根据题意得:20+(t﹣10)+16+2(t﹣16)=56,解得t=,答:t为时,点M与点N相遇;(3)分四种情况:①当点M在AO上,点N在CB上时,OM=20﹣2t,BN=16﹣t,∴20﹣2t=16﹣t,解得t=4,②当M在OB上,N在CB上时,OM=t﹣10,BN=16﹣t,∴t﹣10=16﹣t,解得t=13,③当M在OB上,N在OB上时,OM=t﹣10,BN=2(t﹣16),∴t﹣10=2(t﹣16),解得t=22,④当M在BC上,N在OA上时,20+2(t﹣30)=20+(t﹣26),解得t=34,综上所述,t的值为4或13或22或34时,M、O两点在数轴上相距的长度与N、B两点在数轴上相距的长度相等.2.(朝阳)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.(1)若∠1=25°,则∠2的度数为;(2)直接写出∠1与∠3的数量关系:;(3)直接写出∠2与∠ACB的数量关系:;(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值.【答案】(1)65°(2)∠1=∠3;(3)∠2+∠ACB=180°(4)30°或45°或120°或135°或165°.【解答】解:(1)∵∠1=25°,∠ACD=90°,∴∠2=∠ACD﹣∠1=65°,故答案为:65°;(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,∴∠1+∠2=∠2+∠3,∴∠1=∠3,故答案为:∠1=∠3;(3)∵∠ACD=∠BCE=90°,∴∠ACB+∠2=∠1+∠2+∠3+∠2=∠ACD+∠BCE=180°,即∠2+∠ACB=180°,故答案为:∠2+∠ACB=180°;(4)存在,①当BC∥AD时,∵BC∥AD,∴∠BCD=∠D=30°,∴∠ACB=90°+30°=120°,∴∠ACE=∠ACB﹣∠BCE=120°﹣90°=30°;②当BE∥AC时,如图,∵BE∥AC,∴∠ACE=∠E=45°;③当AD∥CE时,如图,∵AD∥CE,∴∠DCE=∠D=30°,∴∠ACE=90°+30°=120°;④当BE∥CD时,如图,∵BE∥CD,∴∠DCE=∠E=45°,∴∠ACE=∠ACD+∠DCE=135°;⑤当BE∥AD时,如图,过点C作CF∥AD,∵BE∥AD,CF∥AD,∴BE∥AD∥CF,∴∠ECF=∠E=45°,∠DCF=∠D=30°,∴∠DCE=30°+45°=75°,∴∠ACE=90°+75°=165°.综上所述:当∠ACE=30°或45°或120°或135°或165°时,有一组边互相平行.故答案为:30°或45°或120°或135°或165°.3.(淇县)如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.解:猜想∠BPD+∠B+∠D=360°理由:过点P作EF∥AB,∴∠B+∠BPE=180°(两直线平行,同旁内角互补)∵AB∥CD,EF∥AB,∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)∴∠EPD+∠D=180°(两直线平行,同旁内角互补)∴∠B+∠BPE+∠EPD+∠D=360°∴∠B+∠BPD+∠D=360°(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.【答案】(1)∠BPD=∠B+∠D(2)∠BPD=∠B﹣∠D.【解答】解:(1)∠BPD=∠B+∠D.理由:如图2,过点P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠1=∠B,∠2=∠D,∴∠BPD=∠1+∠2=∠B+∠D;(2)如图(3):∠BPD=∠D﹣∠B.理由:∵AB∥CD,∴∠1=∠D,∵∠1=∠B+∠P,∴∠D=∠B+∠P,即∠BPD=∠D﹣∠B;如图(4):∠BPD=∠B﹣∠D.理由:∵AB∥CD,∴∠1=∠B,∵∠1=∠D+∠P,∴∠B=∠D+∠P,即∠BPD=∠B﹣∠D.4.(西乡塘)如图,已知DC∥FP,∠1=∠2,∠DEF=30°,∠AGF=70°,FH平分∠EFG.(1)求证:DC∥AB;(2)求∠PFH的度数.【答案】(1)略(2)∠PFH的度数为20°【解答】解:(1)∵DC∥FP,∴∠C=∠2,又∵∠1=∠2,∴∠C=∠1,∴DC∥AB;(2)∵DC∥FP,DC∥AB,∠DEF=30°,∴∠DEF=∠EFP=30°,AB∥FP,又∵∠AGF=70°,∴∠AGF=∠GFP=70°,∴∠GFE=∠GFP+∠EFP=70°+30°=100°,又∵FH平分∠EFG,∴∠GFH=∠GFE=50°,∴∠PFH=∠GFP﹣∠GFH=70°﹣50°=20°.答:∠PFH的度数为20°.5.(海勃湾)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN 上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ 平分∠EPK,求∠HPQ的度数.【答案】(1)AB∥CD(2)PF∥GH(3)∠HPQ的度数为45°【解答】解:(1)AB∥CD,理由如下:∵∠1与∠2互补,∴∠1+∠2=180°,又∵∠1=∠AEF,∠2=∠,∴∠AEF+∠CFE=180°,∴AB∥CD;(2)由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.又∵∠BEF与∠EFD的角平分线交于点P,∴,∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,∴PF∥GH;(3)∵∠PHK=∠HPK,∴∠PKG=2∠HPK.又∵GH⊥EG,∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK.∴∠EPK=180°﹣∠KPG=90°+2∠HPK.∵PQ平分∠EPK,∴.∴∠HPQ=∠QPK﹣∠HPK=45°.答:∠HPQ的度数为45°.6.(黔江)(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由;(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=60°,∠ABC=40°,求∠BED的度数;(3)如图3,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=α,∠ABC=β,请你求出∠BED的度数(用含α,β的式子表示).【答案】(1)成立(2)∠BED=50°(3)【解答】解:(1)成立,理由:如图1中,作EF//AB,则有EF//CD,∴∠1=∠BAE,∠2=∠DCE∴∠AEC=∠1+∠2=∠BAE+∠DCE;(2)如图2,过点E作EH//AB,∵AB//CD,∠F AD=60°,∴∠F AD=∠ADC=60°,∵DE平分∠ADC,∠ADC=60°,∴,∵BE平分∠ABC,∠ABC=40°,∴,∵AB//CD,∴AB//CD//EH,∴∠ABE=∠BEH=20°,∠CDE=∠DEH=30°,∴∠BED=∠BEH+∠DEH=50°.(3)如图3,过点E作EG//AB,∵BE平分∠ABC,DE平分∠ADC,∠ABC=β,∠ADC=∠F AD=α,∴,,∵AB//CD,∴AB//CD//EG,∴,,∴.7.(拱墅)小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由.(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠F AD=50°,∠ABC=40°,求∠BED的度数.【答案】(1)∠AEC=∠BAE+∠DCE.(2)∠BED=45°【解答】解:(1)∠AEC=∠BAE+∠DCE成立,理由:过点E作EF∥AB,如图,∵EF∥AB,∴∠A=∠AEF.∵EF∥AB,AB∥CD,∴FE∥CD.∴∠C=∠CEF.∵∠AEC=∠AEF+∠CEF,∴∠AEC=∠BAE+∠DCE.(2)过点E作EH∥AB,如图,由(1)的结论可得:∠BED=∠ABE+∠EDC,∵BE平分∠ABC,∠ABC=40°,∴∠ABE=∠ABC=20°.∵∠F AD=50°,AB∥CD,∴∠ADC=∠F AD=50°.∵DE平分∠ADC,∴∠EDC=∠ADC=25°.∴∠BED=20°+25°=45°.8.(宜兴)如图①,已知PQ∥MN,且∠BAM=2∠BAN.(1)填空:∠PBA=°;(2)如图(1)所示,射线AM绕点A开始顺时针旋转至AN便立即按原速度回转至AM 位置,射线BP绕点B开始顺时针旋转至BQ便立即按原速度回转至BP位置.若AM转动的速度是每秒2度,BP转动的速度是每秒1度,若射线BP先转动30秒,射线AM才开始转动,在射线BP到达BQ之前,射线AM转动几秒,两射线互相平行?(3)如图(2),若两射线分别绕点A,B顺时针方向同时转动,速度同题(2),在射线AM到达AN之前,若两射线交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.【答案】(1)120(2)AM转动30秒或110秒(3)∠BAC=2∠BCD【解答】解:(1)∵∠BAM=2∠BAN,∠BAM+∠BAN=180°,∴∠BAM=120°.∵PQ∥MN,∴∠PBA=∠BAM=120°.故答案为:120;(2)设射线AM转动t秒,两射线互相平行,当0<t<90时,如图,AM′和BP′为经过t秒后AM,BP旋转的位置,则∠MAM′=2t°,∠PBP′=(t+30)°,∵PQ∥MN,∴∠BM′A=∠MAM′=2t°,∵AM′∥BP′,∴∠AM′B=∠PBP′.∴2t=t+30.解得:t=30;当90<t<150时,如图,AM′和BP′为经过t秒后AM,BP旋转的位置,则∠MAM′=(360﹣2t)°,∠PBP′=(t+30)°,∵PQ∥MN,∴∠BM′A=∠MAM′=2t°,∵AM′∥BP′,∴∠AM′B=∠PBP′.∴360﹣2t=t+30.解得:t=110.综上所述,当射线AM转动30秒或110秒时,两射线互相平行.(3)∠BAC与∠BCD的数量关系不会发生变化,∠BAC=2∠BCD.理由:设射线AM,BP转动时间为m秒,∴∠BAC=(2m﹣120)°,∠ABC=(120﹣t)°,∴∠ACB=180°﹣(2m﹣120)°﹣(120﹣m)°=(180﹣m)°.∵∠ACD=120°,∴∠BCD=120°﹣(180﹣m)°=(m﹣60)°.∵2m﹣120=2(m﹣60),∴∠BAC=2∠BCD.∴∠BAC与∠BCD的数量关系不会发生变化,∠BAC=2∠BCD.9.(仁寿)如图①.已知AM∥CN,点B为平面内一点,AB⊥BC于点B,过点B作BD⊥AM于点D,设∠BCN=α.(1)若α=30°,求∠ABD的度数;(2)如图②,若点E、F在DM上,连接BE、BF、CF,使得BE平分∠ABD、BF平分∠DBC,求∠EBF的度数;(3)如图③,在(2)问的条件下,若CF平分∠BCH,且∠BFC=3∠BCN,求∠EBC 的度数.【答案】(1)30°(2)45°(3)97.5°.【解答】解:(1)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α=30°,∴∠HBC=90°﹣∠BCN=60°.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=30°;(2)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α,∴∠HBC=90°﹣α.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=α.∵BE平分∠ABD,∴∠DBE=∠ABE=α.∵∠HBC=90°﹣α,∴∠DBC=180°﹣∠HBC=90°+α.∵BF平分∠DBC,∴∠DBF=∠CBF=∠DBC=45°+α.∴∠EBF=∠DBF﹣∠DBE=45°+α﹣α=45°;(3)∵∠BCN=α,∴∠HCB=180°﹣∠BCN=180°﹣α.∵CF平分∠BCH,∴∠BCF=∠HCF=∠HCB=90°﹣α.∵AM∥CN,∴∠DFC=∠HCF=90°﹣α.∵∠BFC=3∠BCN,∴∠BFC=3α.∴∠DFB=∠DFC﹣∠BFC=90°﹣α.由(2)知:∠DBF=45°+α.∵BD⊥AM,∴∠D=90°.∴∠DBF+∠DFB=90°.∴45°+α+90°﹣α=90°.解得:α=15°.∴∠FBC=∠DBF=45°+α=52.5°.∴∠EBC=∠FBC+∠EBF=52.5°+45°=97.5°.10.(邵东)点A、B在数轴上分别表示实数a、b,A、B两点之间的距离记作AB.当A、B 两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=|b|=|a﹣b|.当A、B两点都不在原点时:(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB﹣OA=|b|﹣|a|=b﹣a=|b﹣a|=|a﹣b|(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB﹣OA=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA =|b|+|a|=a+(﹣b)=|a﹣b|回答下列问题:(1)综上所述,数轴上A、B两点之间的距离AB=.(2)数轴上表示2和﹣4A和B之间的距离AB=.(3)数轴上表示x和﹣2的两点A和B之间的距离AB=| ,如果AB=2,则x的值为.(4)若代数式|x+2|+|x﹣3|有最小值,则最小值为.【答案】(1)AB=|a﹣b|(2)6 (3)0或﹣4 (4)5【解答】解:(1)综上所述,数轴上A、B两点之间的距离AB=|a﹣b|;(2)数轴上表示2和﹣4的两点A和B之间的距离AB=2﹣(﹣4)=2+4=6;(3)数轴上表示x和﹣2的两点A和B之间的距离AB=|x+2|,如果AB=2,则x的值为0或﹣4;(4)若代数式|x+2|+|x﹣3|有最小值,则最小值为5.故答案为:(1)|a﹣b|;(2)6;(3)|x+2|;0或﹣4;(4)511.(广安)点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,例如:数轴上表示﹣1与﹣2的两点间的距离=|﹣1﹣(﹣2)|=﹣1+2=1;而|x+2|=|x﹣(﹣2)|,所以|x+2|表示x与﹣2两点间的距离.利用数形结合思想回答下列问题:(1)数轴上表示﹣2和5两点之间的距离.(2)若数轴上表示点x的数满足|x﹣1|=3,那么x=.(3)若数轴上表示点x的数满足﹣4<x<2,则|x﹣2|+|x+4|=.【答案】(1)76(2)﹣2或4(3)6【解答】解:(1)根据题意知数轴上表示﹣2和5两点之间的距离为5﹣(﹣2)=7,故答案为:7;(2)∵|x﹣1|=3,即在数轴上到表示1和x的点的距离为3,∴x=﹣2或x=4,故答案为:﹣2或4;(3)∵|x﹣2|+|x+4|表示在数轴上表示x的点到﹣4和2的点的距离之和,且x位于﹣4到2之间,∴|x﹣2|+|x+4|=2﹣x+x+4=6,故答案为:6.12.(兴宁)如图,在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是3个单位长度,长方形ABCD的长AD是6个单位长度,长方形EFGH的长EH是10个单位长度,点E在数轴上表示的数是5.且E、D两点之间的距离为14.(1)填空:点H在数轴上表示的数是,点A在数轴上表示的数是.(2)若线段AD的中点为M,线段EH上一点N,EN=EH,M以每秒4个单位的速度向右匀速运动,N以每秒3个单位的速度向左运动,设运动时间为x秒,原点为O.当OM=2ON时,求x的值.(3)若长方形ABCD以每秒2个单位的速度向右匀速运动,长方形EFGH固定不动,设长方形ABCD运动的时间为t(t>0)秒,两个长方形重叠部分的面积为S,当S=12时,求此时t的值.【答案】(1)15;﹣15(2)或.(3)t的值为9或13.【解答】解:(1)由题意可得,点H在数轴上表示的数为:5+10=15;点A在数轴上表示的数为:5﹣14﹣6=﹣15.故答案为:15;﹣15.(2)∵点M是线段AD的中点,∴点M表示的数为5﹣14﹣=﹣12,又∵EN=EH,∴点N在数轴上表示的数为:5+(15﹣5)=,由题意可得,x秒时,点M在数轴上表示的数为:﹣12+4x,点N在数轴上表示的数为:﹣3x,∴OM=|4x﹣12|,ON=|3x﹣|,∵OM=2ON,∴|4x﹣12|=2|3x﹣|∴4x﹣12=2(3x﹣)或4x﹣12=﹣2(3x﹣),解得x=或x=.故答案为:或.(3)当CD与EF重合时,所用时间为=7秒,由题意得:AD与EH重合的部分为=4,如图1所示,设长方形ABCD从EF运动到AD与EH重叠部分为4时,所用的时间为t1秒,∴t1==2,∴第一次重叠面积为12时,时间t为2+7=9(秒);当AD与EH重叠部分为4时,如图2所示,设长方形ABCD从EF运动到AD与EH重叠部分为4时,所用的时间为t2秒,∴t2==6,∴第二次重叠面积S=12时,时间t为6+7=13(秒);∴当长方形ABCD与长方形EFGH重叠部分的面积为12时,t的值为9或13.13.(宣化)如图,一只蚂蚁从点A沿数轴向右爬了2个单位长度到达点B,点A表示﹣,设点B所表示的数为m.(1)实数m的值是;(2)求|m+1|+|m﹣1|的值;(3)在数轴上还有C、D两点分别表示实数c和d,且有|2c+d|与互为相反数,求2c﹣3d的平方根.【答案】(1)2﹣(2)2 (3)±4.【解答】解:(1)m=﹣+2=2﹣;(2)∵m=2﹣,则m+1>0,m﹣1<0,∴|m+1|+|m﹣1|=m+1+1﹣m=2;答:|m+1|+|m﹣1|的值为2.(3)∵|2c+d|与互为相反数,∴|2c+d|+=0,∴|2c+d|=0,且=0,解得:c=﹣2,d=4,或c=2,d=﹣4,①当c=﹣2,d=4时,所以2c﹣3d=﹣16,无平方根.②当c=2,d=﹣4时,∴2c﹣3d=16,∴2c﹣3d的平方根为±4,答:2c﹣3d的平方根为±4.14.(锦江)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;如图3,当点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;如图4,当点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|.回答下列问题:(1)数轴上表示1和6的两点之间的距离是数轴上表示2和﹣3的两点之间的距离是.(2)数轴上若点A表示的数是x,点B表示的数是﹣4,则点A和B之间的距离是,若|AB|=3,那么x为.(3)当x是时,代数式|x+2|+|x﹣1|=7.(4)若点A表示的数﹣1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q 同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒个单位长度,求运动几秒后,B、P、Q三点中,有一点恰好是另两点所连线段的中点?(请写出必要的求解过程).【答案】(1)5,5(2)﹣1或﹣7 (3)﹣4或3 (4)运动或或5秒【解答】解:(1)数轴上表示1和6的两点之间的距离是|6﹣1|=5,数轴上表示2和﹣3的两点之间的距离是|2﹣(﹣3)|=5.(2)数轴上若点A表示的数是x,点B表示的数是﹣4,则点A和B之间的距离是|x+4|,若|AB|=3,则|x+4|=3,解得x=﹣1或﹣7.(3)当x>1时,|x+2|+|x﹣1|=x+2+x﹣1=7,2x=6,x=3,当x<﹣2时,|x+2|+|x﹣1|=﹣x﹣2+1﹣x=7,﹣2x=8,x=﹣4,当﹣2≤x≤1时,|x+2|+|x﹣1|=x+2+1﹣x=3≠7,∴当x=﹣4或3时,代数式|x+2|+|x﹣1|=7.(4)设运动t秒后,有一点恰好是另两点所连线段的中点,由题意,得①点B为线段PQ中点时,,解得,②点P为线段BQ中点时,,解得,③点Q为线段BP中点时,,解得t=5.答:运动或或5秒后,B、P、Q三点中,有一点恰好是另两点所连线段的中点.15.(宣化)阅读下面的文字,解答问题.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能完全地写出来,于是小明用﹣1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,用这个数减去其整数部分,差就是小数部分.请解答下列问题:(1)求出+2的整数部分和小数部分;(2)已知:10+=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.【答案】(1)3,﹣1 (2)﹣14【解答】解:(1)∵1<<2,∴3<+2<4,∴+2的整数部分是1+2=3,+2的小数部分是﹣1;(2)∵2<<3,∴12<10+<13,∴10+的整数部分是12,10+的小数部分是10+﹣12=﹣2,即x=12,y=﹣2,∴x﹣y=12﹣(﹣2)=12﹣+2=14﹣,则x﹣y的相反数是﹣14.16.(靖江)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶派生点”(其中a为常数,且a≠0).例如:点P(1,4)的“2阶派生点”为点Q(2×1+4,1+2×4),即点Q(6,9).(1)若点P的坐标为(﹣1,5),则它的“3阶派生点”的坐标为;(2)若点P的“5阶派生点”的坐标为(﹣9,3),求点P的坐标;(3)若点P(c+1,2c﹣1)先向左平移2个单位长度,再向上平移1个单位长度后得到了点P1.点P1的“﹣4阶派生点”P2位于坐标轴上,求点P2的坐标.【答案】(1)(2,14)(2)(﹣2,1);(3)(0,﹣15)或(,0).【解答】解:(1)3×(﹣1)+5=2;﹣1+3×5=14,∴点P的坐标为(﹣1,5),则它的“3级派生点”的坐标为(2,14).故答案为:(2,14);(2)设点P的坐标为(a,b),由题意可知,解得:,∴点P的坐标为(﹣2,1);(3)由题意,P1(c﹣1,2c),∴P1的“﹣4阶派生点“P2为:(﹣4(c﹣1)+2c,c﹣1﹣8c),即(﹣2c+4,﹣7c﹣1),∵P2在坐标轴上,∴﹣2c+4=0或﹣7c﹣1=0,∴c=2或c=﹣,∴P2(0,﹣15)或(,0).17.(黄山)在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x、y轴的距离中的最大值,则称P,Q两点为“等距点”.下图中的P,Q两点即为“等距点”.(1)已知点A的坐标为(﹣3,1),①在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是;②若点B的坐标为B(m,m+6),且A,B两点为“等距点”,则点B的坐标为;(2)若T1(﹣1,﹣k﹣3),T2(4,4k﹣3)两点为“等距点”,求k的值.【答案】(1)①E、F;②(﹣3,3);(2)1或2【解答】解:(1)①∵点A(﹣3,1)到x、y轴的距离中最大值为3,∴与A点是“等距点”的点是E、F.②当点B坐标中到x、y轴距离其中至少有一个为3的点有(3,9)、(﹣3,3)、(﹣9,﹣3),这些点中与A符合“等距点”的是(﹣3,3).故答案为①E、F;②(﹣3,3);(2)T1(﹣1,﹣k﹣3),T2(4,4k﹣3)两点为“等距点”,①若|4k﹣3|≤4时,则4=﹣k﹣3或﹣4=﹣k﹣3解得k=﹣7(舍去)或k=1.②若|4k﹣3|>4时,则|4k﹣3|=|﹣k﹣3|解得k=2或k=0(舍去).根据“等距点”的定义知,k=1或k=2符合题意.即k的值是1或2.18.(延长)在平面直角坐标系中,O为坐标原点,过点A(8,6)分别作x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).(1)直接写出点B和点C的坐标B(,)、C(,);(2)当点P运动时,用含t的式子表示线段AP的长,并写出t的取值范围;(3)点D(2,0),连接PD、AD,在(2)条件下是否存在这样的t值,使S△APD=S,若存在,请求出t值,若不存在,请说明理由.四边形ABOC【答案】(1)0、6,8、0 (2)AP=8﹣2t(0≤t<4);AP=2t﹣8(4≤t≤7).(3)当t为3秒和5秒时S△APD=S四边形ABOC【解答】解:(1)B(0,6),C(8,0),故答案为:0、6,8、0;(2)当点P在线段BA上时,由A(8,6),B(0,6),C(8,0)可得:AB=8,AC=6∵AP=AB﹣BP,BP=2t,∴AP=8﹣2t(0≤t<4);当点P在线段AC上时,∵AP=点P走过的路程﹣AB=2t﹣8(4≤t≤7).(3)存在两个符合条件的t值,当点P在线段BA上时∵S△APD=AP•AC S四边形ABOC=AB•AC∴(8﹣2t)×6=×8×6,解得:t=3<4,当点P在线段AC上时,∵S△APD=AP•CD CD=8﹣2=6∴(2t﹣8)×6=×8×6,解得:t=5<7,综上所述:当t为3秒和5秒时S△APD=S四边形ABOC,19.(齐齐哈尔)如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3(1)写出点A、B、C的坐标.(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.【答案】(1)A(﹣2,0),B(2,0),C(2,3);(2)90°(3)45°【解答】解:(1)依题意得:A(﹣2,0),B(2,0),C(2,3);(2)∵BD∥AC,∴∠ABD=∠BAC,∴CAB+∠BDO=∠ABD+∠BDO=90°;(3):∵BD∥AC,∴∠ABD=∠BAC,∵AE,DE分别平分∠CAB,∠ODB,∴∠CAE+∠BDE=(∠BAC+∠BDO)=(∠ABD+∠BDO)=×90°=45°,过点E作EF∥AC,则∠CAE=∠AEF,∠BDE=∠DEF,∴∠AED=∠AEF+∠DEF=∠CAE+∠BDE=45°.20.(随县)如图,在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.【答案】(1)6(2)P(﹣8,1)【解答】解:(1)∵B(4,0),C(4,3),∴BC=3,∴S△ABC=×3×4=6;(2)∵A(0,2)(4,0),∴OA=2,OB=4,∴S四边形ABOP=S△AOB+S△AOP=×4×2+×2(﹣m)=4﹣m,又∵S四边形ABOP=2S△ABC=12,∴4﹣m=12,解得:m=﹣8,∴P(﹣8,1).。
(2稿)2011学年初一年级第二学期数学期中试卷

2011学年初一年级第二学期数学期中试卷一、填空:(每题2分,共32 分)1、的平方根是2、每年4月22日是世界地球日,它的主题始终是“只有一个地球”,现在地球的海洋面积361745300平方公里,请把此数取近似值,并用科学记数法表示为(精确到千万位)3、把方根化成幂的形式:=4、如果,那么整数a=5、若等式成立,则a的取值范围是 。
6、数轴上与表示的点相距个单位长度的点表示的数是______________。
7、已知则=8、如图,已知∠1=74°,∠2=106°,若∠4=78°,则∠3= °。
9、如图,AB∥CD, ∠1=(2x+33)°, ∠2=(3x+17)°,则∠2-∠1=°。
一9 一1010、运动会上,甲、乙两名同学测得小明的跳远成绩分别为PA=5.51米,PB=5.13米,则小明的真实成绩为 米。
11、将两个直角三角形的直角顶点重合为如图所示的形状,且满足OD∥AB,若∠AOC=27°则∠B=___ °12、如图, AB∥CD∥EF,又AF∥CG,那么图中与∠A相等的角有个。
一11 一12 一1313、如图已知AB∥CD,∠B=17°,∠ECF=112°则∠BEC= °。
14、若时,化简=15、已知2.006≈1.4162≈1.2613,20.06≈4.4792≈2.7173,则≈(保留两个有效数字)16、如图由16个边长为1的小正方形组成,图中阴影部分的面积是正方形,则此正方形的边长为 .二、选择题:(每题2分,共14分)1、下列语句正确的是( )A、负数没有方根B、不带根号的数一定是有理数C、数轴上的每一个点都有一个有理数与它对应D、是2的一个平方根2、下列实数中,(两个2之间依次多一个1)其中无理数个数是 ( )A、2个B、3个C、4个D、5个3、如图,已知∠1=∠2=∠3=∠4,那么下列说法错误的是( )A、∠5与∠6相等B、∠6与∠7互补C、∠7与∠8互补D、∠5与∠8互补二3 二4二54、如图,在图中与∠1构成同位角的个数 ( )A. 5个B.4个C.3个D.2个5、如图,AB∥CD,BE、CE分别平分∠ABC、∠BCD,则∠AEB+∠CED的度数为( )A. 70°B.80°C. 90°D.100°6、下列语句中,错误的是 ( )A.在同一平面内,不相交的两条线段是平行线B.在同一平面内,过一点与已知直线垂直的直线有且只有一条C.过直线外一点,有且只有一条直线与已知直线平行D.同一个角的两个位置不同的邻补角是对顶角。
期中模拟测试卷(二)七年级数学下学期期中期末满分必刷常考压轴题人教版

七年级下册期中模拟测试(二)数学学科(考试时间:120分钟满分:120分)注意:本试卷分试题卷和答题卡(卷)两部分,答案一律填写在答题卡(卷)上,在试题卷上作答无效.一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)1.的算术平方根为()A.B.C.D.﹣【答案】C【解答】解:的算术平方根为.故选:C.2.在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是()A.B.C.D.【答案】D【解答】解:观察图形可知图案D通过平移后可以得到.故选:D.3.下列坐标中,是第二象限的坐标是()A.(1,﹣5)B.(﹣2,4)C.(﹣1,﹣5)D.(5,7)【答案】B【解答】解:A、(1,﹣5)在第四象限,故本选项不合题意;B、(﹣2,4)在第二象限,故本选项符合题意;C、(﹣1,﹣5)在第三象限,故本选项不合题意;D、(5,7)在第一象限,故本选项不合题意;故选:B.4.下列图形中,∠1与∠2是同位角的是()A.B.C.D.【答案】B【解答】解:A选项,∠1与∠2是对顶角,不是同位角,故该选项不符合题意;B选项,∠1与∠2是同位角,故该选项符合题意;C选项,∠1与∠2是内错角,不是同位角,故该选项不符合题意;D选项,∠1与∠2是同旁内角,不是同位角,故该选项不符合题意;故选:B.5.若点P在x轴的下方,y轴的左方,且到每条坐标轴的距离都是4,则点P的坐标为()A.(4,4)B.(﹣4,4)C.(﹣4,﹣4)D.(4,﹣4)【答案】C【解答】解:∵点P在x轴的下方y轴的左方,∴点P在第三象限,∵点P到每条坐标轴的距离都是4,∴点P的坐标为(﹣4,﹣4).故选:C.6.如图,把河AB中的水引到C,拟修水渠中最短的是()A.CM B.CN C.CP D.CQ【答案】C【解答】解:如图,CP⊥AB,垂足为P,在P处开水渠,则水渠最短.因为直线外一点与直线上各点连线的所有线段中,垂线段最短.故选:C.7.如图,下列条件:①∠1=∠3;②∠DAB=∠BCD;③∠ADC+∠BCD=180°;④∠2=∠4,其中能判定AB∥CD的有()A.1个B.2个C.4个D.3个【答案】A【解答】解:①由∠1=∠3可判定AD∥BC,不符合题意;②由∠DAB=∠BCD不能判定AB∥CD,不符合题意;③由∠ADC+∠BCD=180°可判定AD∥BC,不符合题意;④由∠2=∠4可判定AB∥CD,符合题意.故选:A.8.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,那么(10,20)表示的位置是()A.点A B.点B C.点C D.点D【答案】B【解答】解:根据如图所建的坐标系,易知(10,20)表示的位置是点B,故选:B.9.下列说法中,正确的是()①两点之间的所有连线中,线段最短;②过一点有且只有一条直线与已知直线垂直;③平行于同一直线的两条直线互相平行;④直线外一点到这条直线的垂线段叫做点到直线的距离.A.①②B.①③C.①④D.②③【答案】B【解答】解:①两点之间的所有连线中,线段最短,说法正确;②在同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;③平行于同一直线的两条直线互相平行,说法正确;④直线外一点到这条直线的垂线段的长度叫做点到直线的距离,说法错误.故选:B.10.如图,将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠ABC+∠ACB=120°,则∠ABD+∠ACD的值为()A.60°B.50°C.40°D.30°【答案】D【解答】解:在△ABC中,∠ABC+∠ACB=120°,在△DBC中,∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,∴∠ABD+∠ACD=120°﹣90°=30°.故选:D.11.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是()A.纸带①的边线平行,纸带②的边线不平行B.纸带①、②的边线都平行C.纸带①的边线不平行,纸带②的边线平行D.纸带①、②的边线都不平行【答案】C【解答】解:如图①所示:∵∠1=∠2=50°,∴∠3=∠2=50°,∴∠4=∠5=180°﹣50°﹣50°=80°,∴∠2≠∠4,∴纸带①的边线不平行;如图②所示:∵GD与GC重合,HF与HE重合,∴∠CGH=∠DGH=90°,∠EHG=∠FHG=90°,∴∠CGH+∠EHG=180°,∴纸带②的边线平行.故选:C.12.如图,点A(1,0)第一次跳动至点A1(﹣1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是()A.(50,51)B.(51,50)C.(49,50)D.(50,49)【答案】B【解答】解:观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),…第2n次跳动至点的坐标是(n+1,n),∴第100次跳动至点的坐标是(51,50).故选:B二、填空题(本大题共6小题,每小题3分,共18分)13.5的平方根是.【答案】±【解答】解:∵(±)2=5,∴5的平方根是±.故答案为:±.14.如图,AB、CD相交于点O,OE是∠AOC的平分线,∠BOD=70°,∠EOF=65°,则∠AOF的度数为°.【答案】30【解答】解:∵∠BOD=70°,∴∠AOC=∠BOD=70°,∵OE是∠AOC的平分线,∴∠AOE=∠AOC=70°=35°,∵∠EOF=65°,∴∠AOF=65°﹣35°=30°,故答案为:30.15.已知≈4.496,≈14.22,则≈.【答案】44.96【解答】解:==10≈10×4.496=44.96,故答案为:44.96.16.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,则∠1+∠2=.【答案】45°【解答】解:如图,过点A作l∥m,则∠1=∠3.又∵m∥n,∴l∥n,∴∠4=∠2,∴∠1+∠2=∠3+∠4=45°.故答案是:45°.17.如图所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条”之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为m2.【答案】540【解答】解:如图,把两条”之”字路平移到长方形地块ABCD的最上边和最左边,则余下部分EFGH是矩形.∵CF=32﹣2=30(米),CG=20﹣2=18(米),∴矩形EFCG的面积=30×18=540(平方米).答:绿化的面积为540m2.故答案为:540.18.在平面直角坐标系中,点P位于原点,第1秒钟向右移动1个单位,第2秒钟向上移动2个单位,第3秒钟向左移动3个单位,第4秒钟向下移动4个单位,第5秒钟向右移动5个单位,…依此类推,经过2021秒钟后,点P的坐标是.【答案】(1011,﹣1010)【解答】解:观察图形可知经过2017秒钟后,点P在第四象限的直线y=﹣x+1上,∵2021÷4=505余1,∴P2021的横坐标为1+2×505=1011,∴y=﹣1011+1=﹣1010,∴P(1011,﹣1010).故答案为(1011,﹣1010)三、解答题(本大题共8小题,共66分.解答题应写出文字说明,证明过程或演算步骤.)19.计算:+﹣(﹣1).【答案】1﹣【解答】解:+﹣(﹣1)=3﹣3﹣+1=1﹣20.已知正数m的两个不同平方根分别是2a﹣7和a+4,又b﹣7的立方根为﹣2.(1)求a和正数m及b的值;(2)求3a+2b的算术平方根.【答案】(1)a=1,m=25,b=﹣1 (2)1【解答】解:(1)∵正数m的两个不同平方根分别是2a﹣7和a+4,∴(2a﹣7)+(a+4)=0,∴a=1,2a﹣7=﹣5,∴m=25,∵b﹣7的立方根为﹣2,∴b﹣7=﹣8,∴b=﹣1,∴a=1,m=25,b=﹣1;(2)由(1)有a=1,b=﹣1,∴3a+2b=3×1+2×(﹣1)=1,∴3a+2b的算术平方根为1.21.补全下列题目的解题过程.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.证明:∵∠1=∠2(已知),且∠2=∠3,∠1=∠4(),∴∠3=∠4(等量代换),∴DB∥(),∴∠C=∠ABD(),∵∠C=∠D(已知),∴∠D=∠ABD(),∴DF∥AC().【答案】对顶角相等;CE;内错角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.【解答】证明:∵∠1=∠2(已知),且∠2=∠3,∠1=∠4(对顶角相等),∴∠3=∠4(等量代换),∴DB∥CE(内错角相等,两直线平行),∴∠C=∠ABD(两直线平行,同位角相等),∵∠C=∠D(已知),∴∠D=∠ABD(等量代换),∴DF∥A C(内错角相等,两直线平行),故答案为:对顶角相等;CE;内错角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行.22.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).(1)点A的坐标是点B的坐标是.(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;(3)求三角形ABC的面积.【答案】(1)(2,﹣1);(4,3)(2)略(3)5【解答】解:(1)A(2,﹣1),B(4,3);故答案为(2,﹣1);(4,3);(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);(3)三角形ABC的面积=3×4﹣×3×1﹣×3×1﹣×2×4=5.23.已知点P(2m﹣4,m+4),解答下列问题:(1)若点P在y轴上,则点P的坐标为;(2)若点P的纵坐标比横坐标大7,求出点P坐标;(3)若点P在过A(2,3)点且与x轴平行的直线上,则AP的长为多少?【答案】(1)(0,6)(2) (﹣2,5)(3)8【解答】解:(1)令2m﹣4=0,解得m=2,所以P点的坐标为(0,6),故答案为:(0,6);(2)令m+4﹣(2m﹣4)=7,解得m=1,所以P点的坐标为(﹣2,5);(3)∵点P在过A(2,3)点且与x轴平行的直线上,∴m+4=3,解得m=﹣1.∴P点的坐标为(﹣6,3),∴AP=2+6=8.24.点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,例如:数轴上表示﹣1与﹣2的两点间的距离=|﹣1﹣(﹣2)|=﹣1+2=1;而|x+2|=|x﹣(﹣2)|,所以|x+2|表示x与﹣2两点间的距离.利用数形结合思想回答下列问题:(1)数轴上表示﹣2和5两点之间的距离.(2)若数轴上表示点x的数满足|x﹣1|=3,那么x=.(3)若数轴上表示点x的数满足﹣4<x<2,则|x﹣2|+|x+4|=.【答案】(1)76(2)﹣2或4(3)6【解答】解:(1)根据题意知数轴上表示﹣2和5两点之间的距离为5﹣(﹣2)=7,故答案为:7;(2)∵|x﹣1|=3,即在数轴上到表示1和x的点的距离为3,∴x=﹣2或x=4,故答案为:﹣2或4;(3)∵|x﹣2|+|x+4|表示在数轴上表示x的点到﹣4和2的点的距离之和,且x位于﹣4到2之间,∴|x﹣2|+|x+4|=2﹣x+x+4=6,故答案为:6.25如图①.已知AM∥CN,点B为平面内一点,AB⊥BC于点B,过点B作BD⊥AM于点D,设∠BCN=α.(1)若α=30°,求∠ABD的度数;(2)如图②,若点E、F在DM上,连接BE、BF、CF,使得BE平分∠ABD、BF平分∠DBC,求∠EBF的度数;(3)如图③,在(2)问的条件下,若CF平分∠BCH,且∠BFC=3∠BCN,求∠EBC 的度数.【答案】(1)30°(2)45°(3)97.5°.【解答】解:(1)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α=30°,∴∠HBC=90°﹣∠BCN=60°.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=30°;(2)延长DB,交NC于点H,如图,∵AM∥CN,BD⊥AM,∴DH⊥NC.∴∠BHC=90°.∵∠BCN=α,∴∠HBC=90°﹣α.∵AB⊥BC,∴∠ABC=90°.∴∠ABD=180°﹣∠ABC﹣∠HBC=α.∵BE平分∠ABD,∴∠DBE=∠ABE=α.∵∠HBC=90°﹣α,∴∠DBC=180°﹣∠HBC=90°+α.∵BF平分∠DBC,∴∠DBF=∠CBF=∠DBC=45°+α.∴∠EBF=∠DBF﹣∠DBE=45°+α﹣α=45°;(3)∵∠BCN=α,∴∠HCB=180°﹣∠BCN=180°﹣α.∵CF平分∠BCH,∴∠BCF=∠HCF=∠HCB=90°﹣α.∵AM∥CN,∴∠DFC=∠HCF=90°﹣α.∵∠BFC=3∠BCN,∴∠BFC=3α.∴∠DFB=∠DFC﹣∠BFC=90°﹣α.由(2)知:∠DBF=45°+α.∵BD⊥AM,∴∠D=90°.∴∠DBF+∠DFB=90°.∴45°+α+90°﹣α=90°.解得:α=15°.∴∠FBC=∠DBF=45°+α=52.5°.∴∠EBC=∠FBC+∠EBF=52.5°+45°=97.5°.26.如图1,在平面直角坐标系中,点A,B的坐标分别是(﹣2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度,得到A,B的对应点C,D.连接AC、BD、CD.(1)写出点C,D的坐标并求出四边形ABDC的面积.(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.(3)如图2,点F是直线BD上一个动点,连接FC、FO,当点F在直线BD上运动时,请直接写出∠OFC与∠FCD,∠FOB的数量关系.【答案】(1) 12(2)存在(3)当点F在线段BD上,∠OFC=∠FOB+∠FCD;;当点F在线段BD的延长线上,∠OFC=∠FOB﹣∠FCD.【解答】解:(1)∵点A,B的坐标分别是(﹣2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度得到A,B的对应点C,D,∴点C的坐标为(0,2),点D的坐标为(6,2);四边形ABDC的面积=2×(4+2)=12;(2)存在.设点E的坐标为(x,0),∵△DEC的面积是△DEB面积的2倍,∴×6×2=2××|4﹣x|×2,解得x=1或x=7,∴点E的坐标为(1,0)和(7,0);(3)当点F在线段BD上,作FM∥AB,如图1,∵MF∥AB,∴∠2=∠FOB,∵CD∥AB,∴CD∥MF,∴∠1=∠FCD,∴∠OFC=∠1+∠2=∠FOB+∠FCD;当点F在线段DB的延长线上,作FN∥AB,如图2,∵FN∥AB,∴∠NFO=∠FOB,∵CD∥AB,∴CD∥FN,∴∠NFC=∠FCD,∴∠OFC=∠NFC﹣∠NFO=∠FCD﹣∠FOB;同样得到当点F在线段BD的延长线上,得到∠OFC=∠FOB﹣∠FCD.。
2010-2011年度第二学期期中考试七年级数学试卷有答案

七年级数学试卷一、细心选一选(每小题3分,共30分) 1.计算:–2 a 2+ a 2的结果是( )A .–3 a 2B .–a 2C .–3 a 4D .–a 4 2.下列说法中,正确的是( )A .同位角相等B .内错角相等C .对顶角相等D .同旁内角互补 3.下列式子中一定成立的是( )A 、(a - b )2 = a 2 - b 2B 、(a + b)2 = a 2 + b 2C 、(a - b)2 = a 2 -2ab + b 2D 、(-a - b)2 = a 2 -2ab + b 24.小明和三名女生、四名男生一起玩丢手帕游戏,小明随意将手帕丢在一名同学的后面,那么这名同学是女生的概率为( ) A 、73 B 、83 C 、74D 、无法确定 5.计算 (–a )6÷(–a )3的结果是( ) A .a 3B.–a 2C.–a 3D. a 26.梵帝冈是世界上最小的国家,它的面积仅有244.0千米,相当于天安门广场的面积。
请你估计一下,梵帝冈的百万分之一大约相当于( )(A )一间教室地面的面积 (B )一个操场的面积 (C )一只铅笔盒盒面的面积 (D )一张课桌面的面积 7.若)3)((++x m x 展开式中不含x 的一次项,则m 的值为( )A 3B –3C 0D –6 8.如图, 下列判断中错误的是 ( )A.∠A +∠ADC =180°→AB ∥CDB. AD ∥BC →∠3=∠4C. AB ∥CD →∠ABC +∠C =180°D. ∠1=∠2→AD ∥BC9.如果两条平行线被第三条直线所截, 那么一组同位角的平分线( ) A. 互相平行 B. 互相垂直 C. 交角是锐角 D. 交角是钝角 10.设a m=8,a n=16,则anm +=( )A .24 B.32 C.64 D.128二、耐心填一填(每小题3分,共24分)11.某种细菌的直径约为0.02微米,用科学计数法表示该细菌的直径约为 米A BDC123412.如右图,是一把剪刀,若,9021︒=∠+∠,则=∠2 13.若=+==+2255b a ,,ab b a 则 ,14.当右图中的∠1和∠2满足__________时,能使OA ⊥OB . (只需填上一个条件即可) 15.计算:21--(-21+23)0= 16. 2001年3月,国家统计局公布我国总人口为129533万 人,如果以亿为单位,保留三位有效数字,可以写成约 亿人。
七年级期中数学试卷压轴题

一、(本题满分20分)已知二次函数y=ax^2+bx+c的图象开口向上,且顶点坐标为(1,-2),且过点(2,4)。
(1)求该二次函数的解析式;(4分)(2)若点A在抛物线上,且点A的横坐标为3,求点A的纵坐标;(4分)(3)若直线y=kx+b与抛物线y=ax^2+bx+c有两个交点,且交点横坐标分别为1和3,求直线y=kx+b的解析式。
(12分)二、(本题满分20分)在平面直角坐标系中,点A(-2,3)和点B(2,-1)在直线y=kx+b上。
(1)求直线y=kx+b的解析式;(4分)(2)若点C(x,y)在直线y=kx+b上,且满足x+y=5,求点C的坐标;(4分)(3)若点D(x,y)在直线y=kx+b上,且满足x-y=4,求点D的坐标。
(12分)三、(本题满分20分)在△ABC中,AB=AC,∠B=60°,BC=4。
(1)求△ABC的面积;(4分)(2)若点D在BC边上,且BD=2,求△BCD的面积;(4分)(3)若点E在AC边上,且AE=2AC,求△AEC的面积。
(12分)四、(本题满分20分)某市为了改善城市交通状况,计划在市区内修建一条长为8km的公路。
已知该公路横跨一座山,山高h米(h>0),公路的设计坡度为1:10。
(1)求该公路的坡长L(单位:米);(4分)(2)若该公路的实际坡长比设计坡长长100米,求实际坡度;(4分)(3)若该公路的实际坡度比设计坡度大1%,求实际坡长。
(12分)答案:一、(1)由题意得,顶点坐标为(1,-2),代入二次函数的顶点式得:y=a(x-1)^2-2又过点(2,4),代入得:4=a(2-1)^2-2解得:a=6所以二次函数的解析式为y=6(x-1)^2-2。
(2)将x=3代入解析式得:y=6(3-1)^2-2=16所以点A的纵坐标为16。
(3)设直线y=kx+b与抛物线y=ax^2+bx+c有两个交点,横坐标分别为1和3,则:a(1)^2+b(1)+c=k(1)+ba(3)^2+b(3)+c=k(3)+b解得:a=1,b=0,c=0所以直线y=kx+b的解析式为y=kx。
2010—2011学年度第二学期七年级数学期中试题(卷)

与很多的竞技项目不一样,高尔夫与其说是一场与他人的抗衡,更像是一次自己与自己的较量,它需要足够的耐心和专注,锻炼一个人独立思虑的能力,培育一个人踊跃进步的心态。
有人形容高尔夫的18 洞就仿佛人生,阻碍重重,崎岖不停。
但是一旦踏上了球场,你就一定集中注意力,独立面对照赛中可能出现的各样困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
2010—2011 学年度第二学期七年级期中试题(卷)数学题号 A 卷 B 卷二三四共计29 30313233共计一得分评卷人得分A 卷(100 分)一、认真选,必定准。
(共30分,每题 3 分)1、已知同一平面内的三条直线l1,l 2, l 3,假如 l1⊥ l2, l2⊥ l 3那么 l1与 l3 的地点关系是();A 、订交B、垂直C、平行 D 、以上全不是A2、如图 1,已知 AB ⊥ CD 于 O,图中∠ 1 与∠ 2 的关系是();A 、相等B、互余C、互补 D 、没法确立EC 1D3、同一平面内的三条直线,其交点个数可能是()个;O2A、0,1B、0, 1,3 FC、 1, 2,3D、0, 1,2,3 B4、如图 2, AB ∥ CD ,AC ⊥ BC ,图中与∠ CAB 互余的角有(图 1 )个;A 、 1B 、 2C、 3 D 、 45、一辆汽车在笔挺的公路行驶,两次拐弯后,仍在本来的方向 A B上平行行驶,那么两次拐弯的角度可能是()A、先左转60 o,后右转 40oB、先左转60o,后右转 30oCDC、先左转60o,后右转 60oD、先左转60o,后右转 120o 图 26、点 P( -2, -3)在()A、第一象限B、第二象限C、第三象限D、第四象限7、把一个图形整体沿某一个方向挪动,会获得一个新图形,新图形与原图形的关系是()得分A、形状同样,大小不一样B、大小同样,形状不一样评卷人C、形状、大小都同样D、形状、大小都不一样8、一个三角形中,它的两边长分别是8和13,则第三边a的长可能是()A 、 4 B、 5 C、 20 D、 219、在△ ABC 中,∠ A=1∠B=1∠C,则△ ABC 是()2 3A 、锐角三角形B 、直角三角形 C、钝角三角形 D 、没法确立10、若一个多边形的每一个外角为20o,则这个多边形的边数是()A 、 9 B、 10 C、 17 D、 18二、专心填,我会填。
2010-2011年初一下期中考试数学试卷(新课标人教版 七年级下 数学试卷)

2010-2011第二学期期中考试初一数学试卷命题人:崔恒往 校对人: (考试时间:100分钟 总分:100分)一、 细心选一选(每小题2分,共20分)1.下列图形中,不能..通过其中一个四边形平移得到的是 ( )2.若∠1与∠2是内错角,∠1=40°,则 ( ) A .∠2=40° B.∠2=140° C.∠2=40°或∠2=140° D.∠2的大小不确定 3.下列运算正确的是 ( )A.632a a a =∙ B.632)(a a -=- C.22)(ab ab = D.236a a a =÷ 4.下列各式从左到右的变形,是因式分解的是:( )A 、x x x x x 6)3)(3(692+-+=+- B 、()()103252-+=-+x x x xC 、()224168-=+-x x x D 、623ab a b =⋅5.下列各式能用平方差公式进行计算的是A.)3(3+--x x )( B.)2)(2(b a b a -+ C.)1)(1(---a a D.2)3(-x 6.如图,不能判断1l ∥2l 的条件是 A .∠1=∠3B .∠2=∠3C .∠4=∠5D .∠2+∠4=180°7.在下列各组线段中,不能构成三角形的是( )A 、5,7,10B 、7,10,13C 、5,7,13D 、5,10,13 8.已知2294y mxy x ++是关于,x y 的完全平方式,则m 的值为( ) A 、±72 B 、6± C 、12 D 、 12± 9.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°, ∠3=20°,则∠2=( ) A .50°B .30°C .20°D .15°A B C D215341l2l(第6题图)12 3 第9题10.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 的外部时,则与和之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是A .212∠-∠=∠AB .)21(23∠-∠=∠AC .2123∠-∠=∠AD .21∠-∠=∠A用心填一填(每小题3分,共24分) 11. 若0.0000102=1.02n 10⨯,则n=_______ .12.已知一个多边形的每一个外角都是400,则这个多边形的边数为 。
2010—2011学年度下学期部分学校七年级期中联合考试数学试题(含答案及评分标准)

C B AE D 第题3123A B CD31425第题4EMAC D B 第题10AB D GC EF 第题122010—2011学年度下学期部分学校七年级期中联合考试数学试卷本试卷满分120分,考试时间120分钟*祝考生考试顺利*一、选择题(本大题共12个小题,每小题3分,共36分)在每小题给出的四个选项中,只有一个是正确的。
1、点P (-4,3)在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2、下列线段中,不能构成三角形的三条线段的是( ) A .4cm,6cm,8cm B . a+1,a+2,a+3(a >0)C . 3x,5x,2x+1(x >1)D . 三线段的比为2:4:7 3、如图,AB ∥ED ,∠1+∠2+∠3等于( ) A 180º B 270º C 360º D 540º4、如图,点E 是四边形ABCD 的BC 边延长线上的一点,下列条件: ①∠B+∠BCD=180º②∠1=∠2③∠3=∠4④∠B=∠5,其中判断AB//CD 的条件是( )A ①②③④B ①③④C ②③④D ①②③5、能进行密铺的正多边形是( )A 正三边形B 正五边形C 正八边形D 正n 边形6、将点A (3,2)向下平移2个单位长度后,再向左平移4个单位长度后的点为( ) A (-1,0) B (5,6) C (8,-4) D (1,2)7、能把三角形分成两个面积相等的三角形的是( ) A 中线 B 高 C 角平分线 D 以上都不是8、点P (x+3,2-x ),无论x 为何数时,点P 一定不在( )A 第一象限B 第二象限C 第三象限D 第四象限9、一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( )A 直角三角形B 等腰三角形C 锐角三角形D 钝角三角形 10、如图,AB ∥CD ,∠A=35º,∠C=75º,那么∠M=( )A 35ºB 40ºC 45ºD 75º11、若一个多边形的内角和等于720º,则这个多边形的边数是( ) A 5 B 6 C 7 D 812、如图,△ABC 中,∠BAC=90º,AD ⊥BC ,∠ABC 的平分线BE 交AD 于点F ,AG 平分∠DAC ,给出下列结论:①∠BAD=∠C ②∠AEF=∠AFE ③∠EBC=∠C ④AG ⊥EF ,其中正确的结论是( ) A ②③④ B ①③④ C ①②④ D ①②③BG D A CF E第题18AEBF DCG231第题19二、填空(本大题共4小题,每小题3分,共计12分) 13、已知点M (x+1,x-1)在y 轴上,则点M 的坐标是14、三角形两边长分别是2cm ,7cm ,当周长为偶数时,第三边长15、已知点A (2a+3b,-2)和B (8,3a+2b )关于x 轴对称,那么a+b=16、一个角的余角和它的补角的比是3:7,则这个角是三、解答题(本大题共8题,共计72分) 17、(本题6分)如图,O 为直线AB 上一点,∠AOC=31∠BOC ,OC 是∠AOD 的平分线. (1)求∠COD 的度数(2)试判断OD 与AB 的位置关系18、(本题6分)已知:如图,∠B=∠ADE ,∠EDC=∠GFB ,FG ⊥AB.求证:CD ⊥AB.19、(本题7分)如图:AD ⊥BC ,EF ⊥BC ,∠1=∠2.求证:AB ∥DG . OABCD第题1720、(本题7分)如图,在平面直角坐标系中,△AOB的坐标分别为A(3,1),O(0,0),B(-2,-3).求△AOB的面积21、(本题8分)在等腰三角形中,一腰上的中线把它的周长分成15cm和6cm两部分,求此等腰三角形各边的长。
2011~2012学年度第二学期七年级数学期中试卷

A C DB A2011~2012学年度第二学期七年级数学期中试卷(时间:120分钟 满分:150分)一、选择题:(每小题3分,共36分 )1.点P (1,-5)所在的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限2.下列图中,哪个可以通过左边图形平移得到 ( )3. 下列长度的三条线段能组成三角形的是 ( ) A.1,2,3 B.1,7,6 C.2,3,6 D.6,8,104.下面四个图形中,∠1与∠2是对顶角的图形 ( )A 、1个B 、2个C 、3个D 、4个 5.如图,下列条件中,能判断直线1l //2l 的是( )A .32∠=∠B .31∠=∠C . 18054=∠+∠D .42∠=∠6. 如图,在△ABC 中,BD 平分∠ABC ,且∠ABC =70°, 则∠DBC 的度数是 ( )A .110°B .70°C .140°D .35°7. 下列图形中有稳定性的是 ( ) A .正方形 B .长方形 C .平行四边形 D .直角三角形 8.三角形的一个外角小于与它相邻的内角,则这个三角形是 ( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定9.下列图形中,正确画出AC 边上的高的是 ( ).10.一个多边形的内角和等于它的外角和,这个多边形是 ( )A.三角形B.四边形C.五边形D.六边形11.下面各语句中,正确的是 ( )A .同位角相等 B.垂直于同一条直线的两条直线平行C .若a∥b,c∥b ,则a∥c D.12. 如图,已知∠1=∠2,∠BCA=∠DAC ,则下列结论(1)AB//CD ;(2)AD//BC ;(3)∠B=∠D ;(4)∠DAB=∠DCB 。
其中正确的有( ) A.1个 B.2个 C.3个 D.4个 二.填空题:(每小题3分,共36分)13、如图,直线AB 、CD 相交于点O ,若∠AOC =100°,则∠14、如果用(7,8)表示七年级八班,那么八年级七班可表示成 。
2011年七年级下数学期中试卷
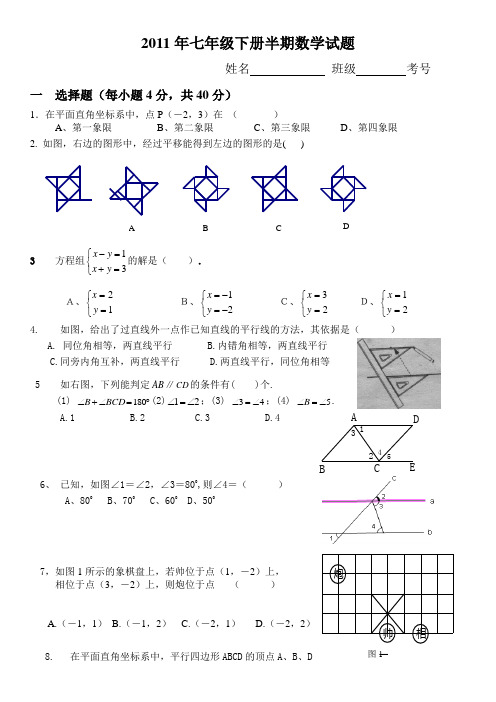
54D3E21C B A2011年七年级下册半期数学试题姓名 班级 考号一 选择题(每小题4分,共40分)1.在平面直角坐标系中,点P (-2,3)在 ( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限 2. 如图,右边的图形中,经过平移能得到左边的图形的是( )3 方程组13x y x y -=⎧⎨+=⎩的解是( ).A、21x y =⎧⎨=⎩ B、12x y =-⎧⎨=-⎩ C、32x y =⎧⎨=⎩ D、12x y =⎧⎨=⎩4. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )A. 同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.两直线平行,同位角相等 5 如右图,下列能判定AB ∥CD 的条件有( )个.(1) ︒=∠+∠180BCD B (2)21∠=∠;(3) 43∠=∠;(4) 5∠=∠B . A.1 B.2 C.3 D.46、 已知,如图∠1=∠2,∠3=800,则∠4=( )A 、800B 、700C 、600D 、5007,如图1所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点 ( )A.(-1,1)B.(-1,2)C.(-2,1)D.(-2,2)8. 在平面直角坐标系中,平行四边形ABCD 的顶点A 、B 、D_ A_ B_ C_ D图3相帅炮图1的坐标分别是(0,0),(5,0),(2,3),则顶点C 的坐标是( )A.(3,7);B.(5,3)C.(7,3);D.(8,2)9,若方程组322,23x y a x y a+=+⎧⎨+=⎩的解x 与y 的和是2,则a 的值是( )A.4 B . .-4 C.0 D.任意数10、已知:正方形ABCD 的面积为64,被分成四个相同的长方形和一个面积为4的小正方形,则a,b 的长分别是 ( )A 、a=3, b=5B 、a=5, b=3C 、a=6.5, b=1.5D 、a=1.5, b=6.5二 填空题(每小题4分,共32分)11 命题“对项角相等”中的题设是_______ ________,结论是__________ ________12 将一张长方形纸片按如图所示折叠, 如果641=∠,那么2∠等于 .13 写出一个以⎩⎨⎧=-=21y x 为解二元一次方程组为__ ___ __14如图所示,直线AB ∥CD ,∠B=23°,∠D =42°,则∠E =_______.15若532y xa b +与2244x y a b --是同类项,则___,___.x y ==16如图所示,如果OBC ∆的面积为12,那么点C 的纵坐标 为__________ 17 甲乙两人同时解方程组⎩⎨⎧-=-=+232y cx by ax ,正确解得⎩⎨⎧-==11y x 乙因抄错了c,得⎩⎨⎧-==62y x 则a=_ ____,b=__ _ __, c=18.已知关于x,y 的二元一次方程y=kx+b 的解为⎩⎨⎧==43y x 和⎩⎨⎧=-=21y x 则k=__ _ __,b=__ _ __三 解答题19解方程组(12分) ⎩⎨⎧=+=-82302y x y x (2).⎪⎩⎪⎨⎧+=-=-1)1(33132y x y x20、(本题10分)如图,EF//AD ,1∠=2∠.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.(14题图)yx()6,0B O C【第16题图】b a BD A C解:∵EF//AD ,(已知)∴2∠=__ ___. (_____________________________). 又∵1∠=2∠, (________________________). ∴1∠=3∠, (________________________).∴AB//___ ___, (_______________ _____________) ∴∠DGA+∠BAC=180°. (_______________ _____________)21(本题12分)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,⊿ABC 的顶点在格点上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年本区重点校初一下数学期中考试压轴题30.探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的ABC∆中,AB、BC是两腰,所以BCABAC∠=∠.利用这条性质,解决下面的问题:已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为α.如下图:. . .. . .正五边形正六边形正八边形. . .. . .=α=α=α;当正多边形的边数是n时,则=α.30.解:72°;60°; 45°;=αn︒360.(每空各1分,共4分)31.如图,长方形OABC中,O为平面直角坐标系的原点,A、C两点的坐标分别为(3,0),(0,5),点B在第一象限内.(1)如图1,写出点B的坐标();(2)如图2,若过点C的直线CD交AB于点D,且把长方形OABC的周长..分为3:1两部分,则点D的坐标();(3)如图3,将(2)中的线段CD向下平移,得到C'D',使C'D'平分长方形OABC的面积,则此时点D'的坐标是().31.解:B(3,5);D(3,4);D/(3,2). (每空各1分,共3分)32. 如图①,ABC△为等边三角形,面积为S.111D E F,,分别是ABC△三边上的点,且11112AD BE CF AB===,连结111111D E E F F D,,,可得111D E F△.(1)用S表示11AD F△的面积1S= ,111D E F△的面积'1S= ;(1分)(2)当222D E F,,分别是等边ABC△三边上的点,且22213AD BE CF AB===时,如图②图①D 2E 2F 2F 1E 1D 1ABCCBA图②,则22AD F △的面积2S =___________,222D E F △的面积2S '=____________(2分) (3)按照上述思路探索下去,当n n n D E F ,,分别是等边ABC △三边上的点,且11n n n AD BE CF AB n ===+时(n 为正整数),n n AD F △的面积n S = , n n n D E F △的面积n S '= .(2分)32.如图,△ABC 中,点D 在AB 上,AD =31AB .点E 在BC 上,BE =41BC .点F 在AC上,CF =51CA .已知阴影部分(即△DEF )的面积是25cm 2.则△ABC 的面积为_______ cm 2.(写出简要推理) 解:S -1354⨯S - 1435⨯S - 1243⨯S = 25 ∴2560S = 25 ∴S = 6030.如图1,等腰直角三角形纸片ABC 中,AB =AC =12,∠BAC =90°,D 是AB边上一点,作DE ∥BC 交AC 于点E ,作DF ⊥BC 于F ,作EG ⊥BC 于G . 沿DE 折叠纸片,点A 落在点A '处,如图2; 沿DF 折叠纸片,点B 落在点B '处,如图3; 沿EG 折叠纸片,点C 落在点C ′处,如图4.BCEC图4图1图2图3B CAB CA备用图备用图若点A ′、B ′、C ′在矩形..DFGE ....内或在其边上,且互不重合............,则存在△A B C '''.按上述操作方法,折一折、画一画(可以利用备用图),然后解答下面问题: (1)△A B C '''的形状是 ;(2)设AD 的长为x ,B A ''的长为y ,请用含x 的代数式表示y : ,其中x 的取值范围是 ;(3)探究△A B C '''的面积有最小值还是最大值?这个值是多少? _________________________________________________(4) 若(3)中△A B C '''的面积有最值,请写出满足要求的点'A 的面积坐标系。
(以三角形CBA 为坐标三角形)_______________【说明:面积坐标系也叫重心坐标系。
在平面上,任意取定一个三角形CBA (称为坐标三角形),面上建立了一个面积坐标系(如图5)。
这个平面上任意一点M 用它的面积坐标来表示。
所谓任一点M 面积坐标是指有序数组()321,,S S S 其中1S ,2S ,3S 分别是M B C ∆,MCA ∆,MAB∆的有向面积(顶点按逆时针方向排列的三角形的面积为正,针方向排列的三角形的 面积为负。
图5中MBC ∆的面积1S 是正,MCA ∆的面积2S 是正,MAB ∆的面积3S 是负)显然平面上任一点都有确定的面积坐标系与之对应。
如果坐标三角形CBA 的面积是S ,则有321S S S S ++=。
】30.(4分)如图,△ADE 和△ABC 中,∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF .(1)求∠ECF+∠DAC+∠ECA 的度数;(2) 判断ED 与FC 的位置关系,并对你的结论加以证明.FEDCBA图5解:(1)∵∠ECF=∠ECB+∠BCF ,∠BAD=∠BCF ∴∠ECF+∠DAC+∠ECA=∠ECB+∠BCF+∠DAC+∠ECA=(∠BAD+∠DAC )+(∠ECB+∠ECA )=∠BAC+∠BCA又∵∠BAC=∠BCA∴∠ECF+∠DAC+∠ECA=45°=45°+45°=90° (2)ED ∥BC ,证明如下:由△AEC ,得:∠AEC+∠EAC+∠ECA=180°,∵∠EAD=∠AED =45°,∠AEC=∠AED+∠DEC ,∠EAC=∠EAD+∠DAC , ∴∠DEC+∠DAC+∠ECA=180°-90°=90°,又由(1)知∠ECF+∠DAC+∠ECA=45°=45°+45°=90°, ∴∠DEC=∠ECF , ∴ED ∥BC.1.三个同学对问题“若方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩,求方程组111222325325a x b y c a x b y c +=⎧⎨+=⎩的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是: . 1.510x y =⎧⎨=⎩分析:由方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩,得1112223434a b c a b c +=⎧⎨+=⎩,上式可写成111222352105352105a b c a b c ⨯+⨯=⎧⎨⨯+⨯=⎩,与111222325325a x b y c a x b y c +=⎧⎨+=⎩比较,即可得结果。
2.一个凸十一边形,它由若干个边长为1的正三角形和正方形镶嵌而成,求这个十一边形各内角的度数.2、各内角的度数分别是:120°(1个),150°(10个)分析:正三角形的每个内角是60°,正方形的每个内角是90°. 凸十一边形有11个内角,由60°和90°可能组成的角有60°、90°、120°和150°,又150°×10+120°=(11-2)×180°。
(1) 若11个角都是150°,150°×11>(11-2)×180°;(2) 若其中有少于10个角的度数为150°,则此时正十一边形的内角和小于150°×10+120°;(3) 若有10个角的度数为150°,但另一个角的度数不是120°,则它肯定是60°或90°,此时正十一边形的内角和小于150°×10+120°。
综上所述,正十一边形有1个角的度数是120°,10个角的度数是150°.29、(本题4分)如图△ABC 中,内角∠A 和外角∠CBE 和∠BCF 的角平分线交于点P, AP交BC于D.过B作BG⊥AP于G(1) 若∠GBP=45º,求证:AC⊥BC;(2) 在图上作出△PDC在PC边的高DH,并探究∠A PB和∠HDC的数量关系,并说明理由;29。
(1)略;(2)相等。
(2+1+1)。
