可视的复分析
多层次信息的可视化和可视性分析

多层次信息的可视化和可视性分析信息可视化从来不是新话题,但总是在继续发展与改进。
多层次信息可视化作为信息可视化的一种新形式,引起了越来越多人的关注。
通过多层次信息可视化,我们可以更直观地认识信息世界,更高效地获取所需信息,因此,在必要时,把信息可视化成多层次的形式,能够更好地满足信息用户的需求。
1. 什么是多层次信息可视化?一般情况下,我们面对的信息都是多层次的。
这些层次可能是基于数据的属性,时间、分类、以及诸如地理位置等因素。
而多层次信息可视化就是指将这些完整数据的每一层次进行分层设计,并有效地对其进行可视化的过程。
基于多层次的思路和可视化技术,我们可以将复杂的信息进行排列组合,有效提取信息的关键因素。
2. 多层次信息可视化的应用场景2.1. 复杂系统和大型项目管理在大型项目中,多层次信息可视化将有着巨大的作用。
因为大型项目中涉及的信息种类繁多、信息量庞大。
多层次信息可视化可以将这些繁杂的信息呈现为多个层次,利用可视化手段,更容易理解真实的信息和情况。
2.2. 地图信息可视化多层次信息可视化在地图应用领域中也有很大的应用。
例如,我们可以将大量的地图信息按照不同层次进行可视化。
比如,我们可以将市级地图与县级地图、乡镇地图、村庄地图进行层次划分,可以更加清晰地了解某一地方的细节。
它还可以为交通出行指引、城市规划等提供更全面的信息支持。
3. 多层次信息可视化的可视性分析多层次信息可视化的目的之一就是更好的展示信息。
可视性分析是指对信息展现进行评判及改进的过程。
为了更好地为用户服务,我们需要针对不同用户的需求,对可视化方式进行优化。
3.1. 满足用户需求一个好的可视化设计要能够满足用户的需求。
在设计过程中,需要牢记用户的目标,从而设计合理的可视化方案。
例如,在地图信息可视化中,有些用户关注的是地图中某一区域的具体信息,而有些用户则关心整个地区的比较。
3.2. 实用性与可读性可视化还要具有实用性与可读性。
空间可视分析

2、以 V 到 P 的投影直线为 X 轴, V 的投影点为原点,求出视线在 X-Z 坐标 系的直线方程:
H[k]
z[m0 ][n0 ቤተ መጻሕፍቲ ባይዱ k
z[m1][n1] k
z[m0 ][n0 ]
(0 < k < K)
K 为 V 到 P 投影直线上离散点数量。
3、比较数组H[k]与数组z[k]中对应元素的值如果 " k, k∈[ 1, K - 1] ,且存在
z[ k ] > H[ k ] ,则 V 与 P 不可见;否则可见。
点对线的可视性
• 点对线的通视,实际上就是求点的视域。应该注意的是,对于视域之外的任 何一个地形表面上的点都是不可见的,但在视域线内的点可能可见,也可能 不可见。基于格网 DEM 点对线的通视算法如下:
1、设 P 点为一沿着 DEM 数据边缘顺时针移动的点,与计算点对点的通视 相仿,求出视点到 P 点投影直线上点集{ x , y} ,并求出相应的地形剖面{ x ,
点对区域通视
点对区域的通视算法是点对点算法的扩展。与点到线通视问题相同, P 点沿数据边缘顺时针移动。逐点检查视点至 P 点的直线上的点是否通视。 一个改进的算法思路是,视点到 P 点的视线遮挡点,最有可能是地形剖面线上 高程最大的点,因此,可以将剖面线上的点按高程值进行排序,按降序依次检 查排序后每个点是否通视,只要有一个点不满足通视条件,其余点不再检查。 点对区域的通视实质仍是点对点的通视,只是增加了排序过程。
CAD中的数据可视化和可视分析方法

CAD中的数据可视化和可视分析方法CAD(计算机辅助设计)是一种通过计算机软件辅助进行设计和绘图的工具。
在CAD中,数据可视化和可视分析是非常重要的方法,它们能够帮助我们更好地理解和分析设计数据。
本文将为大家介绍CAD中的数据可视化和可视分析方法。
在CAD中,数据可视化是将设计数据以图形或图表等形式呈现出来,以便更直观地观察和理解。
在进行数据可视化时,我们可以使用各种颜色、线条、填充等图形元素来表示不同的数据属性。
例如,我们可以使用不同的颜色来表示不同的材料属性,使用不同的线条来表示不同的尺寸属性。
在CAD中,我们可以使用不同的数据可视化方法来展示不同的数据。
其中之一是2D数据可视化,它将设计数据以平面的方式进行呈现。
通过使用2D数据可视化,我们可以更方便地查看和编辑设计数据。
例如,在CAD中,我们可以通过选择特定的视图来查看不同的设计图层,以便更好地理解设计数据。
另一个数据可视化方法是3D数据可视化,它将设计数据以三维的方式进行呈现。
通过使用3D数据可视化,我们可以更直观地观察和理解设计数据。
例如,在CAD中,我们可以将设计数据转换为三维模型,然后通过旋转、缩放等操作来查看和分析设计数据。
这种方法非常有利于我们对设计数据的全面理解。
在CAD中,可视分析是一种通过可视化方法对设计数据进行分析的技术。
通过使用可视分析,我们可以更好地理解设计数据的特征和规律。
例如,在CAD中,我们可以使用可视分析方法来分析设计数据的尺寸、形状、位置等属性。
通过对这些属性进行可视分析,我们可以提前发现设计中的问题,并及时进行调整和优化。
在可视分析中,我们还可以使用一些辅助工具来增强分析效果。
例如,我们可以使用剖面分析工具来观察设计数据的截面。
通过将设计数据切割为平面,我们可以更清楚地观察设计数据的内部结构和特征。
这种方法非常有用,特别是对于一些复杂的设计数据。
此外,在CAD中,我们还可以使用动画和交互式操作等技术来辅助数据可视化和可视分析。
26369983_齐民友:为推动中国的数学学科进步贡献一生

特写人物一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一具有远见的数学家齐民友1930年2月出生于安徽省芜湖市,从1948年考入武汉大学数学系后,一辈子都在珞珈山上度过。
可视化分析

4.4.1 可视化技术
定义: 所谓可视化(Visualization)是利用计算机图形学和图像处理技术,把数据转变 成图形或图像在屏幕上显示出来,再进行交互处理的理论、方法和技术目前,可 视化技术根据所处理数据的抽象层次划分是比较通俗易懂的,其划分方法主要有: 科学计算可视化、数据可视化、信息可视化和知识可视化
Gephi是基于JVM的复杂网络分析软件,是对各种网络和复杂系统进行可视化分 析的工具。它在生成可视化图形的同时也会对数据进行清洗和分类
划分方法
信息可视化
指用计算机支撑的、交互性的、对抽象数 据的可视表示法,用来增强人们对抽象信 息的认知,信息可视化技术存在时间比较 短,有着非常广泛的应用前景,比如高空 飞行和治安管理。
知识可视化
对基于领域内容的结构进行的可视化,简 单来说,就是把个体知识用图解的方式表 示出来,生成能够直接对人的感官起作用 的知识外在表现形式,进而促进知识的传 播和创新
大数据可视化工具
1、入门级工具
Excel是对数据进行快速分析的理想工具,同时也能创建供内部使用的数据图。 虽然它在颜色、线条和样式上可选择的范围有限,但是作为一个入门级工具已 经足够了。 CSV(逗号分隔值)和JSON(JavaScript对象注释)是常见的数据格式,所有数 据可视化工具基本都支持至少CSV、JSON两种的中一种格式。我们需要清楚它 们的结构,这样才能理解怎么从这些文件导入或者导出数据。
可视化技术划分方法
科学计算可视化
利用计算机图形图像处理技术,把 科学计算过程中产生的数据和计算 结果转变为图形或图像在屏幕上显 示出来并进行交互处理的理论、方 法和技术
数据可视化
对大型数据库或数据仓库中数据的可视 化。它可以把数据及其结构关系用更为 直观的方式展现出来,是可视化技术在 非空间数据领域的应用
如何做好数据可视化分析?
如何做好数据可视化分析?数据可视化是利用计算机图形学和图像处理技术,将数据转换成图形或图像在屏幕上显示出来,并进行交互处理的理论、方法和技术。
数据可视化的实质是借助图形化手段,清晰有效的传达与沟通信息,使通过数据表达的内容更容易被理解。
那么,怎样来分析大量、复杂和多维的数据呢?答案是要提供直观的、可交互的和反应灵敏的可视化环境。
因此,数据可视化的主要特点是:⚫交互性。
用户可以方便的以交互的方式管理和开发数据。
⚫多维性。
可以看到表示对象或事件的数据的多个属性或变量,而数据可以按其每一维的值,将其分类、排序、组合和显示。
⚫可视性。
数据可以用图像、曲线、二维图形、三维体和动画来显示,并可对其模式和相互关系进行可视化分析。
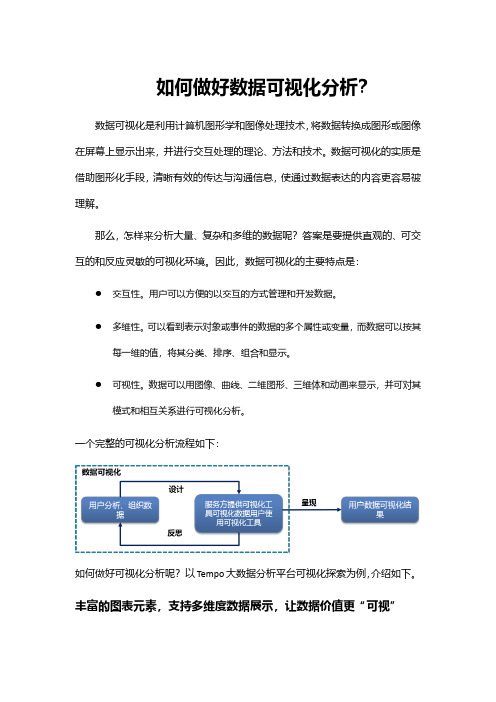
一个完整的可视化分析流程如下:如何做好可视化分析呢?以Tempo大数据分析平台可视化探索为例,介绍如下。
丰富的图表元素,支持多维度数据展示,让数据价值更“可视”把数据转化成有效的可视化形式(任何种类的图表)是让数据发挥作用的第一步,因此图表是可视化的核心。
要达到合适的数据用合适的图表展示,我们需要掌握图表的特性,可视化图表按其特性可分为分布类、流程类、占比类、区间类、关联类、趋势类、时间类和地图类,可视化图表众多,常用的包括柱图、线图、条图、地图、雷达图、矩形树图、气泡图、饼图、环图、仪表盘等。
示例如下:多样的图表交互,提升分析交互性,让数据逻辑更清晰。
可视化分析可以对以多维形式组织起来的数据进行联动、钻取、维度切换、链接等各种分析操作,以便剖析数据,使分析者、决策者能从多个角度、多个侧面观察数据库中的数据,从而深入了解包含在数据中的信息和内涵。
钻取钻取包括上卷与下钻。
上卷是通过在维级别中上升或通过消除某个或某些维来观察更概括的数据。
下钻是通过在维级别中下降或通过引入某个或某些维来更细致的观察数据。
唯独切换用于实现跨层级的数据钻取。
联动可视化设计不一定需要将所有信息同时展示,而是通过筛选随时调取感兴趣的数据绘图,此时,就需要图表联动功能。
多维数据的可视分析方法与工具研究

多维数据的可视分析方法与工具研究随着科技的快速发展,大数据已成为当今社会中一个重要的资源。
然而,对于大量和复杂的数据进行有效的分析和理解却是一项挑战。
传统的数据分析方法往往难以准确地捕捉多个维度之间的关系和趋势。
为了解决这个问题,多维数据的可视分析方法和工具应运而生。
多维数据的可视分析是指利用图形、图像和视觉元素来表示和分析多维数据集合的方法。
它能够帮助用户发现数据中的隐藏模式、趋势和异常,并提供直观的方式来解释、理解和传达数据的内在结构。
在本文中,将介绍多维数据的可视分析方法与工具的研究现状和发展趋势。
首先,为了实现多维数据的可视分析,需要选择合适的可视化方法和工具。
传统的可视化方法如柱状图、折线图、饼图等仅适用于简单的单一维度数据。
对于多维数据,需要采用更高级的可视化方法。
例如,散点矩阵图能够同时显示多个维度之间的关系,帮助用户发现变量之间的相关性。
雷达图则能够将多个维度的数据绘制在同一个图形上,直观地比较不同维度的重要性和偏好。
其次,研究人员还开发了许多专门用于多维数据可视分析的工具。
其中一些工具提供了灵活的交互功能,例如可缩放和平移视图、联动操作和过滤器。
这些交互功能使用户能够根据自己的需求动态地探索数据,发现感兴趣的模式和关系。
另一些工具则提供了高级的分析功能,如聚类分析、分级标记和可视化查询。
这些工具使用户能够进行更深入的数据分析,揭示数据中的复杂关系和规律。
此外,研究人员还提出了一些新颖的多维数据可视分析方法。
例如,基于视觉噪声的分析方法可以帮助用户识别可能的数据异常和错误。
这种方法通过在可视化中添加噪声或扰动,使用户能够更容易地察觉数据中的异常点。
另一个例子是基于用户感知的可视分析方法,通过考虑用户感知和认知的特点,优化可视化设计和交互方式,提高用户对多维数据的理解和解释能力。
未来,多维数据的可视分析将面临一些挑战和机遇。
首先,随着数据规模的增加,如何高效地处理和呈现大规模多维数据将是一个重要的研究方向。
复分析可视化方法英文版课程设计

Complex Analysis Visualization Method: Course Design(English Version)IntroductionComplex analysis, also known as the theory of functions of a complex variable, is the study of complex valued functions of a complex variable. It is an important field in mathematics with many applications inscience and engineering. Visualizing complex analysis concepts can help students to understand the material better. This course design ms to introduce students to visualization methods for complex analysis.Course ObjectiveThe objective of this course is to provide students with an understanding of complex analysis concepts through visualization methods. Students will learn how to visualize complex functions, conformal mappings, complex exponentials, and other related concepts.Course Outline1. Introduction to Complex AnalysisThe first section of the course will introduce students to the basic concepts of complex analysis, such as complex numbers, the complex plane, and the Cauchy-Riemann equations. Students will also learn about complex functions, their properties, and their graphical representation.2. Visualizing Complex FunctionsIn this section, students will learn how to visualize complex functions using color contour maps, level curves, and 3D plots. Some examples of complex functions that will be visualized include the exponential function, the logarithmic function, and the complex sine and cosine functions.3. Conformal MappingThis section will focus on conformal mapping, which is a type of mapping that preserves angles. Students will learn about the properties of conformal mapping and how it can be used to visualize complex functions. Some examples of conformal mappings that will be covered include the stereographic projection, the Mercator projection, and the conformal map of the unit disk to the upper half-plane.4. Complex ExponentialsIn this section, students will learn about complex exponentials, which are functions of the form e^z where z is a complex number. Students will learn how to visualize complex exponentials using contour plots and 3D plots. Some applications of complex exponentials in physics and engineering will also be covered.5. Advanced VisualizationsThe final section of the course will cover advanced visualization techniques for complex analysis concepts. Students will learn how to visualize the Dirichlet problem, the Laplace equation, and other advanced topics in complex analysis.PrerequisiteThis course requires students to have a strong understanding of calculus, including complex numbers and basic differential equations.ConclusionVisualization is an important tool for learning complex analysis concepts. This course will introduce students to visualization methods for complex analysis and provide them with a deeper understanding of the subject. With hands-on exercises and examples, students will be able to apply the skills learned in this course to real-world problems.。
信息可视化与可视分析

信息可视化与可视分析信息可视化与可视分析是一门涉及信息可视化和可视分析的学科,旨在使用视觉表达和交互技术以更直观、有效地理解和分析数据。
本文将介绍信息可视化和可视分析的基本概念、原则以及应用领域。
一、信息可视化和可视分析的基本概念信息可视化是通过图形、图像等视觉表达方式将抽象的数据或信息转化为可视化形式的过程。
通过视觉化的方式,人们能够更快速、直观地理解和发现数据中的模式、趋势和关联。
可视分析则是在信息可视化的基础上,引入交互技术,使用户能够主动参与到数据的探索和分析中,从而获得更深入的洞察和认识。
二、信息可视化和可视分析的原则1. 设计原则:信息可视化和可视分析的设计应注重简洁明了、直观易懂的原则,以确保用户能够准确地理解和解读所呈现的信息。
2. 数据映射原则:信息可视化需要将数据映射到合适的视觉属性上,例如颜色、形状、大小等,以帮助用户发现和分析数据之间的关系。
3. 交互设计原则:可视分析强调用户与数据之间的交互,因此交互设计应考虑用户的需求和行为习惯,提供灵活、高效的操作方式,使用户能够自由探索数据。
4. 多样性原则:信息可视化和可视分析技术提供了丰富多样的图表和可视化形式,如折线图、散点图、热力图等,应根据数据特点和分析目的选择最适合的可视化形式。
三、信息可视化和可视分析的应用领域1. 商业分析:信息可视化和可视分析在商业领域广泛应用,如销售数据分析、市场调研、客户行为分析等。
通过可视化呈现,企业能够更好地了解市场趋势、优化业务决策。
2. 医疗健康:可视化和可视分析在医疗健康领域用于疾病监测、病人管理、医疗决策等。
例如,通过可视化展示,医生能够更好地诊断和治疗病情。
3. 地理信息系统:信息可视化和可视分析在地理信息系统中广泛应用,用于地图制作、土地利用规划、交通管理等。
通过地理信息可视化,我们能够更好地理解地理空间数据。
4. 社交媒体分析:随着社交媒体的普及,信息可视化和可视分析技术也被应用于社交媒体数据的分析和挖掘,如舆情分析、社交网络分析等。
复分析可视化方法

复分析可视化方法复分析是一种数学分析方法,它可以帮助我们更好地理解复变函数的性质和行为。
而可视化方法则是一种直观展示数据和结果的手段。
将这两者结合起来,可以为我们提供更直观、更深入的理解。
本文将介绍复分析可视化方法的基本原理和应用,以及如何利用这些方法来更好地理解复变函数的性质。
首先,我们来看一下复分析可视化方法的基本原理。
复分析是研究复变函数的性质和行为的一门学科,它涉及到复平面上的函数、积分、级数等概念。
而可视化方法则是利用图形、动画等手段将抽象的数学概念直观地展现出来。
将这两者结合起来,就可以通过图形、动画等形式直观地展示复变函数的性质,帮助我们更好地理解和掌握这些概念。
其次,我们来看一下复分析可视化方法的应用。
在实际研究和教学中,复分析可视化方法可以被广泛应用。
比如,在研究复变函数的性质和行为时,我们可以利用图形和动画来展示函数的零点、极点、奇点等特性,帮助我们更好地理解函数的性质。
在教学中,我们可以利用可视化方法来展示复变函数的性质和行为,让学生们通过直观的图形和动画来理解抽象的数学概念,提高他们的学习兴趣和学习效果。
最后,我们来看一下如何利用复分析可视化方法来更好地理解复变函数的性质。
首先,我们可以利用复平面上的图形来展示函数的零点、极点、奇点等特性。
通过这些图形,我们可以直观地看出函数在不同点的性态,帮助我们更好地理解函数的性质。
其次,我们可以利用动画来展示函数在复平面上的变化过程,帮助我们更好地理解函数的行为。
通过这些图形和动画,我们可以直观地感受到函数在复平面上的变化,从而更好地理解函数的性质。
综上所述,复分析可视化方法是一种重要的数学分析方法,它可以帮助我们更好地理解复变函数的性质和行为。
通过图形、动画等形式的展示,我们可以直观地感受到函数在复平面上的性态和行为,从而更好地掌握和应用这些数学概念。
因此,在实际研究和教学中,我们应该充分利用复分析可视化方法,提高我们对复变函数的理解和掌握水平。
素数定理复分析证明

素数定理复分析证明证明素数定理是数论中最重要也是最引人关注的概念。
几个世纪以来,许多数学家和理论物理学家都在致力于从它的定义及其后的一系列后果中寻求更深层的智慧。
自古以来,人们就发现,在整数集合N中,有一些整数比其他整数更容易受到其他整数整除,这就是素数(也叫质数)。
而定理是把素数分解成乘积的形式,称为素数定理。
素数定理的发现可追溯到古希腊拉普拉斯的著作。
古希腊时期的数学家认为,数字可以表示一切,并且用它来解决不断出现的种种问题。
他们认为,如果一个数字可以分解成仅由素数的乘积,那么它必定是一个质数,而不可能是合数。
然而,他们无法证明这一点,因此只能依赖观察和推测,而无法得出一个必然的结论,直到17世纪,贝尔才在欧洲发表了他的素数定理,证实了这一猜想。
贝尔是第一个证明素数定理的人,也是第一个提出素数定理的人。
他的证明是从古代任意数字的分解开始的。
素数定理的定义是此数字被素数乘积表示,并且乘积的唯一表示是其中一种乘积形式。
贝尔利用古希腊时期的知识,以及拉普拉斯提出的数学结论,推出了一系列完美的数学证明,从而证实了素数定理。
贝尔把它称为“可视论”,用来证明数学真理,而不是为了提出一种具体的定理。
贝尔的这一巨大成就在未来的几个世纪中都被公认,并被用来证明其他重要的数论定理,如欧拉定理、哥德巴赫猜想等。
贝尔的证明具有非常强大的数学智慧,但他的证明确实存在一定的缺陷。
如今,理论物理学家和数学家们正在精心研究素数定理,期望发现更多的有价值的信息,以及更有效的证明方法。
复分析是一种以极其精密的计算来证明素数定理的方法。
它通过建立数学模型,然后数学模型得出的恒等式来证明素数定理。
复分析的核心在于建立一系列的调和函数,将原始的素数分解函数转化为一系列的不相同的调和函数,然后再求出最终的定结论。
而且,这种方法证明素数定理的过程不受数字大小的限制,因此可用于对超大数字的证明。
复分析的精确性和准确性也使它成为证明素数定理的理想方法。
信息科学中的数据可视化与可视分析研究

信息科学中的数据可视化与可视分析研究近年来,随着信息科学的迅猛发展,数据的规模和复杂性也呈现出爆炸式增长。
在庞大的数据海洋中,如何从海量数据中提取有用的信息成为了学术界和工业界共同面临的挑战。
数据可视化与可视分析作为一项重要的技术手段,在这个领域中发挥着举足轻重的作用。
本文将探讨数据可视化与可视分析的研究进展与应用前景。
首先,我们需要明确数据可视化与可视分析的概念。
数据可视化是指将抽象的数据通过各种图形、图表等可视化手段呈现出来,以便用户能够直观地理解和分析数据。
而可视分析则是在数据可视化的基础上,结合交互技术、统计方法等,对数据进行更深入的挖掘和分析,以发现数据中的潜在规律和价值。
在数据可视化与可视分析的研究中,最基础的问题就是如何选择合适的图形来呈现数据。
不同图形具有不同的用途,比如折线图适用于呈现数据随时间变化的趋势,散点图则适合用于显示数据之间的关联关系等。
因此,选择合适的图形不仅需要考虑数据的特点,还要考虑用户的需求和认知。
研究者们通过探索人类视觉系统的特性,设计出了一系列适用于不同情境的图形,从而提高了数据可视化的效果。
此外,交互性是数据可视化与可视分析研究中的另一个重要方面。
传统的数据可视化通常是静态的,用户无法主动地与数据进行交互,限制了数据的探索与分析。
为了解决这一问题,研究者们提出了一系列交互式数据可视化技术,如拖拽、缩放、过滤等。
这些技术可以帮助用户更加直观地感知数据的变化,从而提高数据的理解和分析效率。
此外,近年来,人工智能技术的快速发展也为数据可视化与可视分析研究带来了巨大的机遇。
以机器学习为代表的人工智能技术可以帮助我们处理和分析海量的数据,在数据可视化中发挥着重要作用。
比如,利用机器学习算法可以对海量数据进行聚类分析,将相似的数据点聚集在一起,从而提供更直观的展示效果。
同时,人工智能技术还可以通过分析用户的交互行为,提供更个性化的数据可视化服务。
然而,数据可视化与可视分析研究依然面临一些挑战。
软件工程中的数据可视化与可视分析

软件工程中的数据可视化与可视分析随着信息时代的到来,数据的规模和复杂性不断增加,如何从海量数据中提取有用的信息成为了一项重要的任务。
在软件工程领域,数据可视化和可视分析成为了解决这一问题的有效工具。
本文将探讨软件工程中的数据可视化与可视分析的意义、方法和应用。
一、数据可视化的意义数据可视化是将抽象的数据转化为图形、图表等可视化形式的过程。
它能够帮助人们更直观地理解数据,并从中发现隐藏的模式和规律。
在软件工程中,数据可视化具有以下几个重要意义。
首先,数据可视化可以帮助软件工程师更好地理解软件系统的结构和行为。
通过将软件系统的各个组件、模块以及其之间的关系以图形的方式展示出来,软件工程师可以更清晰地把握系统的整体架构,从而更好地进行软件开发和维护。
其次,数据可视化可以帮助软件工程师发现软件系统中的潜在问题和风险。
通过对软件系统中的各种指标和指标之间的关系进行可视化分析,软件工程师可以及时发现系统中的异常情况和潜在问题,并采取相应的措施进行修复和优化。
最后,数据可视化可以帮助软件工程师更好地与非技术人员进行沟通和交流。
通过将软件系统的数据以可视化形式展示给非技术人员,软件工程师可以更直观地向他们解释系统的运行情况和性能指标,从而促进各方之间的合作和理解。
二、数据可视化的方法在软件工程中,数据可视化的方法有很多种。
常见的方法包括折线图、柱状图、散点图、饼图等。
不同的方法适用于不同类型的数据和不同的分析目的。
折线图适用于展示数据随时间变化的趋势。
通过将时间作为横轴,数据值作为纵轴,可以清晰地展示数据的波动情况,帮助软件工程师发现数据的周期性变化和趋势。
柱状图适用于比较不同组之间的差异。
通过将不同组的数据以柱状图的形式展示出来,可以直观地比较它们之间的差异,帮助软件工程师找出问题所在并采取相应的措施。
散点图适用于展示两个变量之间的关系。
通过将两个变量的取值分别作为横轴和纵轴,可以清晰地展示它们之间的相关性和趋势,帮助软件工程师发现变量之间的关系和影响因素。
可视分析系统的设计与实现

可视分析系统的设计与实现1可视分析系统可视分析系统是一种专业用来收集、处理、分析大量数据并转化为可视化形式的分析模式。
其可视化数据形式可以方便解释和理解,通过图表、报表等形式更好地宣传和展现分析结果。
可视分析系统有助于高效、准确地分析数据,可以收集数据、分类、分析、过滤、聚合等操作,从而辅助数据决策。
2设计原则设计可视分析系统,应根据用户需求和要求,选择合适的视觉元素和算法实现,进行良好的设计,方能使系统更加友好、美观。
设计可视分析系统应当满足下述基本原则:(1)易用性:完成数据的可视分析时应尽量简化步骤,让操作尽量简单有效,以降低学习陡度和操作复杂性;(2)语义性:通过可视化,可以用分清的简单的、容易理解的语义表达来解释得出的分析结论;(3)动态性:根据用户的不同需求更改可视化内容,对分析结果进行调整,灵活性强,数据可以实时显示;(4)系统性:可视化中要尽量展示出丰富的数据和形式,使其整体系统性更强。
3实施过程实施可视分析系统实际上是一个阶段性的系统实施过程,包括需求分析、技术分析、性能测试、系统实施等具体步骤。
首先在需求分析阶段,需要了解用户的具体需求,如使用的计算机硬件、软件、数据库以及工具特性等,以便确定系统的功能需求和性能要求。
然后在技术分析阶段,需要采用进行软硬件安装、部署脚本开发、系统构建,运行测试等步骤,以确保系统能够满足用户的功能需求和性能要求。
最后在性能测试和系统实施阶段,分别要进行系统的性能测试,以及系统的实施部署,确保可视分析系统能够正常运行,满足用户的使用需求。
4结论可视分析系统的设计与实现是极具挑战性又具有重要意义的一项工作。
实施可视分析系统,通常需要经过从用户需求、技术分析到性能测试等一系列步骤,从而才能实现可视化分析数据的有效管理,完成更加高效和准确的分析工作。
数学中的复分析理论研究

数学中的复分析理论研究复分析理论是数学中的一个重要分支,它是对复数域的函数和序列进行研究的一门学科。
在复分析理论中,最基本的概念就是解析函数。
解析函数指的是在某一区域内光滑无穷次可微的函数。
这些函数由于具有出色的性质,如洛朗展开式、柯西积分公式等,因此被广泛应用于物理、工程、计算机科学等领域。
下面就让我们深入了解一下复分析理论的研究。
一、基本概念1.1 复数与复平面复数是由实数构成的有序对,记作(z1, z2)或z1+i*z2,其中i为虚数单位。
复平面是以复数为点的平面。
一个复数可以表示为z=x+iy,其中x,y为实数。
复平面上,当一般情况下,点(z1, z2)表示为(x, y),其中x为点在实轴上的坐标,y为点在虚轴上的坐标。
1.2 解析函数解析函数是指在复平面上某一区域内无穷次可微的函数。
解析函数在平面上的性质非常出色,如说可通过洛朗展开式来表示,且具有高度的可微性,因此被广泛地应用。
1.3 洛朗展开式洛朗展开式是解析函数在一个除去有限个泊松点的区域内的展开式,它表现为一个经过逆泊松变换的傅立叶级数形式。
洛朗展开式在复分析的研究中十分常见,因为它可以表示出复数函数在任一点处的全局性。
1.4 柯西积分公式柯西积分公式也是解析函数的一个重要性质。
柯西积分公式说明了解析函数的积分在包含解析函数的区域D内沿一个任意简单闭曲线的积分值,关于积分曲线不变,只取决于积分起点和终点。
因此柯西积分公式是解析函数处理问题的一个重要工具。
二、复分析中的特殊函数2.1 Gamma函数Gamma函数是复分析中一种特殊的函数,它可视为阶乘函数的推广。
Gamma函数在解析函数中具有着重要的地位,它可以用来推导Laplace变换的性质,也是指数函数及超几何函数等的重要组成部分。
2.2 Zeta函数Zeta函数是复分析中常见的一个特殊函数,它是Riemann Zeta 函数在整数集合上推广而来。
该函数在数论中扮演了非常重要的角色,它们是数论中许多问题的解决基础。
空间可视分析

(0 < k < K)
点对线的可视性
• 点对线的通视,实际上就是求点的视域。应该注意的是,对于视域之外的任 何一个地形表面上的点都是不可见的,但在视域线内的点可能可见,也可能 不可见。基于格网 DEM 点对线的通视算法如下: 1、设 P 点为一沿着 DEM 数据边缘顺时针移动的点,与计算点对点的通视 相仿,求出视点到 P 点投影直线上点集{ x , y} ,并求出相应的地形剖面{ x , y, z ( x , y ) } ; 2、计算视点至每个 Pk∈{ x , y , z ( x , y )} , k = 1 ,2 ,…, K - 1,与 Z 轴的 夹角β k ; k k arctan[ ] Z pk Z vp 3、求得 α= min[β k ] ,α对应的点就为视点视域线的一个点; 4 、移动 P 点,重复以上过程,直至 P 点回到初始位置,算法结束。
式中: S为不可视部分的长度;V为可视部分的长度; H 为建筑物高度; T 为建筑物所在 位置的地面高程; h和t为中间障碍物的高度和地面高程; t w 地面高程。
与可视性分析相关的应用问题
1、观察点问题
比较典型的观察点问题是在地形环境中选择数量最少的观察点,使得地形环境中 的每一个点,至少有一个观察点与之可视,如配置哨位问题、 设置炮兵观察哨、 配置 雷达站等问题。作为这类问题的延伸的一种常见问题,就是对于给定的观察点数据(甚 至给定观察点高程) ,确定地形环境中可视的最大范围。实际上可能出现两种情况:第 一,观察者从某一地点可以看到的范围;第二,观察者不仅想知道从某点看到的范围,而 且也要确定从另一个观察者的视点能看到多少,或者相互看到多少。 另一类问题就是与单个观察点相关的问题,如确定能够通视整个地形环境的高程 值最小的观察点问题,或者给定高程,查找能够通视整个地形环境的观察点。这方面的 例子如森林火塔的定位、 电视塔的定位、 旅游塔的定位等。
轨迹数据可视分析研究

轨迹数据可视分析研究轨迹数据可视分析研究是一个涉及多个领域的综合性研究课题。
在本文中,我们将对轨迹数据可视分析的相关研究进行概述,包括轨迹数据的采集与处理、可视化方法以及应用领域等方面。
一、轨迹数据的采集与处理轨迹数据的采集是进行可视分析的前提。
采集的方法包括全球定位系统(GPS)、移动通信网络、传感器网络等多种手段。
在处理轨迹数据时,通常需要进行数据清洗、格式转换等预处理工作,以便为后续的可视化分析提供准确的基础。
二、轨迹数据可视化方法研究1. 轨迹线可视化:将轨迹数据转化为轨迹线,在地图上以线的形式呈现。
这种方法可以清晰地展示物体的运动路径和方向变化。
2. 轨迹点可视化:将轨迹数据转化为一系列的点,在地图上以点的形式呈现。
这种方法可以突出每个点的特征信息,适用于需要关注单个物体运动的情况。
3. 热力图可视化:将轨迹数据转化为热力图,用颜色深浅表示物体运动密度或频率。
这种方法可以直观地展示物体在空间中的分布情况,适用于关注群体行为的分析。
此外,还有一些特殊的可视化方法,如粒子轨迹图、流场图等,适用于特定领域的轨迹数据可视分析。
三、轨迹数据可视分析的应用领域1. 交通领域:用于交通流量分析、车辆轨迹跟踪、交通事件检测等。
通过可视化分析,可以直观地展示交通状况、预测未来交通趋势,为交通规划和管理提供决策支持。
2. 生物医学领域:用于动物行为分析、疾病传播追踪等。
通过可视化分析,可以深入探究动物行为模式、疾病传播路径等,为动物生态学和公共卫生领域提供科学依据。
3. 社会经济领域:用于人口流动分析、消费行为分析等。
通过可视化分析,可以揭示人口分布规律、消费习惯变化等社会经济现象,为社会学和经济学的相关研究提供有力支持。
四、研究现状与展望目前,轨迹数据可视分析研究已经取得了一定的成果。
在学术界,越来越多的学者关注这一领域,发表了大量的研究论文和报告。
在实际应用方面,轨迹数据可视分析也已经在多个领域得到广泛应用,并取得了显著成效。
可视思维方法论

可视思维方法论随着信息技术的发展和普及,可视化已经成为了人们获取和表达信息的重要方式之一。
可视思维方法论就是一种利用可视化工具和技术来辅助思考、问题解决和决策制定的方法论。
它将复杂的概念、关系和数据通过图表、图像、动画等形式进行可视化展示,使人们能够更直观、更全面地理解和分析问题。
可视思维方法论的基本原理是利用人类视觉系统对图像和模式的敏感性和记忆能力,将抽象的概念和关系转化为具体的可视化图形,从而帮助人们更好地理解和记忆信息。
通过可视化,人们可以将复杂的问题转化为简单的图形,以便更好地进行思考和分析。
可视思维方法论的应用范围非常广泛。
在教育领域,可视化工具可以帮助学生更好地理解和记忆知识点,激发他们的学习兴趣和创造力。
在商业领域,可视化工具可以帮助企业分析市场趋势、制定营销策略和监控业务运营。
在科学研究领域,可视化工具可以帮助科学家更好地理解和展示实验结果,从而推动科学发展。
可视思维方法论的核心工具是数据可视化。
数据可视化通过图表、图像、动画等形式将数据转化为可视化图形,使人们能够更直观地理解数据的含义和趋势。
常见的数据可视化工具包括条形图、饼图、折线图、散点图等。
通过这些工具,人们可以更直观地看到数据之间的关系和趋势,从而更好地进行数据分析和决策制定。
除了数据可视化,可视思维方法论还包括思维导图、概念图、流程图等可视化工具。
思维导图通过图形化地展示思维过程和思维关系,帮助人们更好地组织和表达思维。
概念图通过图形化地展示概念和关系,帮助人们更好地理解和记忆知识。
流程图通过图形化地展示流程和步骤,帮助人们更好地理解和分析工作流程。
在应用可视思维方法论时,需要注意以下几点。
首先,要选择合适的可视化工具和技术,以确保能够清晰地表达信息和思维。
其次,要注意信息的层次结构和逻辑关系,以确保可视化能够准确地反映问题的本质和关键点。
最后,要注重创意和美感,以提高可视化的吸引力和影响力。
可视思维方法论是一种利用可视化工具和技术来辅助思考、问题解决和决策制定的方法论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可视的复分析(译后记)译 后 记在译完这本书后.觉得有一些想法愿与读者分享.翻译过程中看到几位过去并不相识的读者对本书的评论和一些刊物上的书评,还有读过部分译稿的读者的意见.几乎一致的看法是,这本书有很高的独创性:在一门有近两百年历史的基础分支学科里,而且是已经有了数十部公认的名著的分支学科里,能够写出如此不同凡响的著作,实在难得.但是应该承认,本书仍然是一本基本的教科书.因为一方面它的基本内容确实属于复分析的传统领域;另一方面,它所要求于读者的预备知识也仅限于“比较认真地”读过微积分与线性代数(当然,“比较认真地”也是说起来容易做起来难).那么,还有什么可以向读者说一说的呢?Ⅰ这本书标题就标明可视化.可视化当然属于当前最热门的时尚“品牌”,而且完全是由信息技术派生出来的.那么,本书的要点是否教读者如何使用计算机之类?否.本书确实强调计算机的作用,甚至许多习题需要用计算机来完成.但是正如作者指出的那样,应该如象物理学家对待实验室那样对待计算机:用它来发现或验证新思想,解决新问题.作者认为,他的这本书出生于“牛顿的《原理》一书的创世纪中.”他从牛顿那里学到了方法,甚至学到了技巧.这就是强调问题的几何本质,或者说,强调从事物的几何与物理侧面来直观地理解事物.著名数学家克莱因(即爱尔朗根纲领的提出者)在他的名著《高观点下的初等数学》(此书中译本即将由复旦大学出版社重印出版)一书的第1卷关于“数学的现代发展及一般结构”的一节中指出,数学的发展和教学有三种进程,即进程A,进程B 和进程C.进程A 的特点是强调概念的明确性,逻辑上的无懈可击,方法的单纯性,逐步演绎,环环相扣,绝无不必要的引申,总之,使数学成为严整的体系.其陈述方式则是:定义,定理,证明,推论等等,每句话,每个式子都要有根据.进程B,这是克莱因特别推崇的进程,则强调数学概念的生成和发展,强调各个分支的相互联系,强调逻辑推理后面的直觉和物理内涵.其陈述方式则主张夹叙夹议,娓娓道来,生动活泼,发人深省.已故的吴大任教授,在为《高观点下的初等数学》中译本写的序言中说,克莱因的思想可以用“融合”二字来概括:数学与物理学的融合,数学各分支的融合,逻辑推理与直觉的融合,还有数学的逻辑展开与历史发展的融合.克莱因还以欧拉公式 为例详细讨论了两种进程A 和B 的比较.他尖锐地批评了当时(指19世纪末年的)德国数学教学.实际上他的批评对我们今天的教学cos sin ixe x i =+x也完全适用:这个是怎样来的?何以以它为底的对数称为自然对数?其“自然”何在?欧拉公式难道是天上掉下来的吗?我自己就遇到过类似的问题:幂级数e 0()!nix n ix e n ∞==∑的每一项都没有周期,为什么加起来以后就出现了周期?总之,学生们在逻辑上接受了某个结论,不等于“实际上”理解了这个结论.这就是过分强调进程A 在教学上带来的副作用.本书作者强调自己是认真研究了牛顿的《原理》以后才理解了,必须从数学问题的直觉的经验的侧面去“体会”数学,才能有真正的掌握,才能“悟”其真谛.因此,他用了极大的精力去探求复分析的许多我们已经非常熟悉的结论的几何内涵和处理方法,包括对上述欧拉公式的理解.所以,读后确有耳目一新之感.把克莱因的说法与作者的说法比较,这本书可以说是作者按照进程B 帮助读者教或学复分析的一个努力,而作者取得的成功是有目共睹的.进程C 是另外一回事,这里不去讨论.如果要比较进程A 和B 的优劣,您会得到进程B 远优于进程A 的结论.本书作者当然是这样看的.但是,克莱因尽管充分评价进程B,而且自己一直身体力行,却没有说孰高孰低.他认为,这两种进程都是数学发展所必需,互相切磋,又互相补充.克莱因说得很对,在教学与研究中,采取哪一种进程,视各人的学识素养与爱好而定,也视整个数学发展的需要而定.为什么牛顿特别倾向几何学?至少部分地是由于在牛顿的时代几何学最为成熟,而且是人们(不止是牛顿)解决科学问题的最有力的工具.牛顿以及他的同时代的大科学家(还应加上伽利略)都是欧氏几何的高手.他的《原理》一书可以说是充满了求解 “几何难题”的例子,以致微积分的基本思想:略去高阶无穷小,也时常隐藏在几何难题后面,所以读起来很难得其三昧.说个笑话:如果您不能放开慧眼,从几何与物理角度审视问题,就难以看穿大千世界,但是,如果您这样做了,立定足跟,循此渐进,自然能进入牛顿的不二法门.就是一种几何化的物理科学.本书作者是这样在做,值得我们效法.这当然有很大的难度.所以牛顿以后,如欧拉,拉格朗日以至拉普拉斯,就以分析的方法来处理同样的问题.欧拉说过,完全几何的方法,时常难以解决力学问题,或者只能部分地解决;而拉普拉斯的名著《天体力学》则把天体运动的研究完全归结为研究微分方程.再考虑到微积分的基础经过两百多年的锤炼,借助εδ−语言得到了较完美的解决,进程A 就占据了统治地位.当然,从几何和物理侧面考察问题的方法,也就退居后台了.19世纪的数学发展,风向似乎又有了改变.这里起了决定作用的有高斯,特别是黎曼(他是本书特别推崇的大师).“回到牛顿”可能是20世纪才有的口号,但是潮流的改变在当时已经十分明显.不妨说,这是本书的一条主线.但是,作者并没有简单地着力于几个几何难题(但是看来本书作者对几何难题情有独钟,所以本书中有不少很有趣的几何题),所谓强调几何和物理实质,其具体内容读者能在书中看到.这里需要特别强调的是,计算机的出现不仅对于研究工作的影响已经有目共睹,它为数学教学开辟了多么广阔的前景远非我们今天敢于估计的.作者以《可视化》作为本书标题,不但是由于数学的本质就有可视化这一侧面,而且由于今天的信息技术的现状使我们能够在前人无法想象的程度上揭示这个侧面.当然,任何事物都有两个方面.强调了几何直觉一面,就有可能对于数学严格性有所忽视.作者并没有回避这一点.他明白地宣称,他总是把“洞察力”置于严格性之前.为了得到更−语言,而深刻的洞察,宁可以(在某种程度上)牺牲严格性为代价.全书基本上没有用εδ且非常自由地把小量与无穷小量混起来用.作者常用“最终相等”之类的说法,时常把相差高阶无穷小就说成是相等.当然作者明白地说,这些说法都有确切的数学含义,但是他并不引述任何一本数学书,而是引证了一位大物理学家S. Chandrasekhar的Newton’s Principia for the Common Readers一书.(在这部关于复分析的近600页的大书里,竟然完全没有维尔斯特拉斯的名字,这恐怕只能以作者是“性情中人”来解释了).当然读者会问,这样作利弊如何,是有利于学生更深刻地理解数学概念,方法,理论的实质,还是实际上在鼓励一种大而化之的空疏作风?这当然要看教学的实际情况而定.但是,问题并不如此简单.例如在第5章里,作者实际上宣布了,一个解析函数序列,只要收敛,必可逐项求导.这当然是错了,但是即如哥西这样的大师,也犯过类似错误.正是阿贝尔以至维尔斯特拉斯等人按照进程A 的要求正确地处理了这个问题,否则就不会有今天的复分析.至于译者,在大多数问题上是尊重了原作者的处理,但在这类问题上,就不能简单地,客气地说原书错了,只好写一个比较长的脚注.这里并不是讨论数学方法论或教学论的合适地方,但是应该指出,并非所有数学概念,方法和理论都可以或者适合于可视化.进程B和进程A相辅相成甚至相反相成.能不能说,进程B帮助我们放开慧眼,而进程A则让我们立定足跟?对于译者,本书的启示在于,数学书没有一个至高无上不得违抗的写法,现今最流行的不一定是最好的,更不一定是最适合您的.这就给学数学和教数学留下了广阔的创造空间.Ⅱ一个数学分支被认为是基本的分支,一门课程被认为是基础课,有两个原因:1.它从其他分支吸取营养;2.它又影响其他分支的发展或其他课程的教学.数学,和其他极为广博的科学一样,虽然是一座高耸入云的伟大建筑,必然有一些最为基础,影响又最为深远的思想,方法等等,可以说是其精华.基础课的教学有一个无可推卸的责任,就是把这些精华交给学生.为此,按当前流行的做法,就是开许多课程,各司其职,分兵把关.姑不论多数学校有没有可能开这么多课程,即令开设了,也一定会助长各门课程孤立分离,看不到数学作为一个整体是如何在发展,有什么真正关键的问题.这也是进程A 带来的副作用.因此,解决之道,在于从进程B 找出路.正如吴大任先生给克莱因的思想所作的概括:在融合二字上下功夫.下面看一下本书是怎样处理这个问题的.作者按照复分析发展的内在要求,也按照自己的科学兴趣,选择了三个问题,使读者能从数学发展的整体来看待复分析,引导读者走向更广阔的科学天地.A. 几何学和非欧几何什么是几何学?克莱因在他的爱尔朗根纲领里作了回答:几何学所研究的就是几何图形在某类运动所成的群下面的不变性质.这本是每一个想学数学的大学生都应该了解的.遗憾的是,绝大多数大学生也就只是知道这一句话而已.似乎多数大学里也找不到一门课认真地解释这个极其重要的思想.(但是有不少大学为文科学生开设的“数学与文化”之类的课程里却简单地介绍了一下).原因可能在于,现在我国多数大学数学系里,几何教学很不恰当地被削弱了,而一门几何课要能够包含认真地介绍爱尔朗根纲领,必定有相当份量,对教学两方面都是不轻的负担.请看本书是如何解决这个问题的.“怎样来描述运动?”对于实轴的情况,运动简单地就是x ax b +a ,其中都是实数,而且,a b 0a ≠.对于2维欧氏平面,本书指出,只要进入复域,就立刻可见运动就是z az b +a ,其中都是复数,而且.作者这样讲,本是为了克服一个大家都知道是历史的虚构的说法:“复数出现于需要求解二次方程”,(但是这样讲最“方便”).复数的出现深刻地适合了描述空间本性的需要,而非简单地来自什么“实际需要”.作者还指出,物理学中有许多类似情况是复数的用武之地.例如(下面的例子是译者在教学中遇到过的,而不一定就是作者心目中所想的,因为作者的兴趣明显地在于理论物理等方面)我们在工科数学中都会讲如何用复数讲交变电流以及振动现象,表面上看,这也是一种“方便”,其实,稍想一下,就会发现,并不是电流,电压等等取了虚数值,而是实数现在已经不足以描述它们.需要平面向量,而平面向量就是复数.这里的情况和2维欧氏平面的运动需用复数来描述是一样的.读者自然会问,是否有一种“空间复数”足以描述3维欧氏空间的运动?从作者的分析看到,这是不可能的.怪就怪在,到了4维欧氏空间,却又可能了,这就是四元数.对大学生讲四元数,“离经叛道”,匪,a b 0a ≠210x +=夷所思.然而,作者非常顺畅地引导读者和他一同在这条思想的小道上漫游,真可谓“花径不曾缘客扫,蓬门今始为君开.”关键在于,放开慧眼,得到了一个深刻的洞察:数学为的是更加深刻地描述大自然.当然,这样作要有本事,具体说来就是要比较认真地读过线性代数.其实,所用的线性代数知识有限,并无“超纲”之嫌,很容易懂.问题仍然在于,大学生们是否想过“线性代数还可以这样读?”那么很好,这本书这样告诉您了,帮助您放开慧眼.再转到非欧几何.这时我们遇到的情况也与以上说到的相仿:可能大多数学生知道的仅限于:几何学中有一桩公案:过直线外一点对此直线是否可以做出恰好一条(或多于一条或少于一条)平行线,或者三角形三内角之和(,).π=><但是,每一个学数学的学生都应该知道:在高斯,特别是黎曼以后,问题的症结就变得很明显了:“现实的物理空间是什么样的空间?是否欧氏空间?”这个问题在黎曼手上成了一个微分几何问题.于是出现了内蕴几何与外在几何的区别和联系,出现了空间的度量问题,曲率问题等等.贝尔特拉米发现曲率为的常负曲率曲面—伪球面上的几何就是双曲几何,即罗巴切夫斯基的非欧几何,他还做出了几个不同的映伪球面为平面的映射(本书就说是几种不同的地图),得到了罗巴切夫斯基的非欧几何的几种不同的“模型”.那么,非欧几何也是几何,则按照克莱因的观点应该有相应的运动群.而庞加莱发现这些运动全是默比乌斯变换1−.az b z cz d++a 于是非欧几何与复分析的深刻内在联系浮出了水面.在讲复分析的同时也讲非欧几何就是题中之义了.在我国,在上世纪50年代,翻译过一本前苏联的教材:普里瓦洛夫《复变函数引论》,认真地,但只是用小字介绍了默比乌斯变换,并且兼及罗巴切夫斯基度量.后来大概再也没有我国的教材涉足于此.于是学生们对非欧几何的了解,最多也就是当作一桩公案,或者还知道一点公理系统的相容性独立性.对于它在现时数学的发展中的地位作用就不明白了.总之,我们交臂失去了一个让学生接触一项数学的精华的机会.本书则可以说是“借题发挥”,简单地然而负责地介绍了有关的知识,使得大学生在低年级就能不太困难地接触内蕴几何的许多基本思想,直到高斯的“绝妙定理”(Theorema Egregium ),而且告诉学生们,如果想在这条微分几何的路上走下去,他可以读些什么.作者认为这是复分析的意义最为重大的一部分,这当然是由于他是Penrose 的学生,走的是Penrose 的路子.在此愿请读者去找一下华罗庚先生的《从单位圆谈起》一书.华先生也是沿着自己的学术道路(例如多复变函数论,矩阵几何等等)也介绍了许多关于非欧几何的知识,读后必可大获教益.B. 拓扑学与复分析拓扑学与复分析有深刻的内在联系,这本是众所周知的事情.可以沿着多种不同的途径来揭示二者的联系.例如,把积分回路看成某个同调类的元,被积式(一个微分形式)则看成上同调类的元,积分则是二者的对偶.由此再进一步就达到了de Rham 理论.许多书都是这样作的,只是走多远各有不同.例如Ahlfors 的名著《复分析》就给出了十分清晰简明的初步介绍.本书则由分析学的另一个基本问题开始,就是方程()0g x =的解的存在问题.先看特别简单的1维问题.这时假定在()g x []0,1上连续.如果记()(),g x f x x =−问题就归结为求映射()f x (()f x 也在[]0,1上连续)的不动点:即求一个x 使得().f x x =一个非常本质的假设是:设f 作为一个映射,映[]0,1到其自身.如果0x =或1x =已经是不动点,自然无话可说了.如果不然,则00(0)1,()0x f f x x =<<−>,同理1()0.x f x x =−<由连续函数的介值定理知道,一定存在至少一个[]00,1x ∈使得0()0f x x =,即为所求的不动点.这个定理是极端重要的.如果()0g x =是一个代数方程,在最简单的次数不高于4时,可以用根式和其他代数式把解写出来.5次以至更高次的代数方程的解用根式来表示的问题,引申到群论的发现.这是另外一个故事了.如果就根的存在问题而言,第一个正确的证明应该归功于高斯(1799).高斯前后给出过好几个证明,最后才明确了必须在复平面上才能解决问题.复平面的提出者之一Argand 也是就这个问题提出就是旋转i /2.π看起来高斯本人对这个定理十分看重,所以才称之为代数的基本定理,高斯的证明本质上是一个拓扑证明,而且就是依赖于上述的连续函数的介值定理.但是高斯并未认识到这是一个有待证明的严重的定理,是波尔察诺指出了高斯的毛病.其实波尔察诺是想用我们现在使用的实数完备性的结果来证明,但他也不知道实数完备性理论一直到19世纪末年才完全地确立.那么,看起来需要的是在2维平面(即复平面)上建立上述的不动点定理.回到本书,作者不是简单地说代数的基本定理是复分析的某个具体结果的推论(是偶然的推论吗?),而是进一步看出复分析的这么大一块都具有拓扑学的本质.由幅角原理,鲁歇定理而到代数的基本定理,只不过是“这一大块”出其余绪而已.这样我们又一次看到,得到了新的洞察,引导我们走向广阔的新天地.复变量的解析函数,作为从一个2维空间(平面)到另一个2维空间(平面)的映射,只不过是很大一类映射的特例.因此在本书的这一部分里,作者总是把解析映射和更一般的非解析映射对照,力图把解析映射的拓扑特性说明白.例如上面讲的不动点定理,在2维情况下就是:如果由z w z 平面到平面的连续映射(不一定解析)w ()z w f z =a 把单位圆盘||映到另一个单位圆盘||1z ≤1w ≤,则它必有至少一个不动点.这就是著名的布劳威尔不动点定理的2维情况.1维情况的证明是很容易的(如果您认为连续函数的介值定理也算很容易的定理的话),2维情况的证明也不算难.但是更高维数的情况又如何?对于维空间的单位球体,它仍然是对的.但是其证明就需要全新的概念和方法.这就是环绕数,映射度等等.作者由此而进到霍普夫定理,奇点的指数,欧拉示性数,庞加莱—霍普夫定理等等,直到发现连中学生都知道的欧拉公式n 2V E F −+=其实是一只微笑着的大恐龙!这块新天地有自己的尊神,例如庞加莱.我想借此机会请读者们,特别是大学生,看一篇文章:辛布洛特,不动点定理,见齐民友等译《现代世界中的数学》,上海教育出版社,2004年242-251页,可能有助于体会这个新世界是多么美丽而有趣.C. 黎曼的思想1851年,黎曼发表了以高斯为评阅人(supervisor, examiner)的著名博士论文,题为《单复变量函数的一般理论基础》(Grundlagen f ür eine allgemeine Theorie der Funktionen einer veränderlichen complexen Grösse ).高斯通常很少称赞他的同时代人,但是对于黎曼他却热情地称赞说:“黎曼先生提交的这篇论文令人信服地证实了他在这篇论文处理的主题上深刻而彻底的研究,表现了一种创造的,富有活力的,真正的数学才智,一种光辉的富有成果的独创性”.黎曼的基本思想可以说是把函数概念从某种固定的代数形式(例如幂级数)下解放出来,而放在几何与物理学的基础上.为此,他使用了(宁可说是创造了)许多今天看来极其重要的概念和方法.他对解析函数的研究基本上是从哥西—黎曼方程出发,即设(),f z u iv =+而是一对共轭调和函数.,u v ()f z 是一个共形映射,而为了确定它,需要在某个(或某些)边值条件下求u 和(或)例如在条件.v boundary u φ=(已知函数)下求黎曼指出,为此只需求一个适合上述条件的函数u 使得所谓能量泛函(这个名词来自u 在物理上表示例如静电场的能量).u 22()xy I u u u dxdy ⎡⎤=+⎣⎦∫∫达到最小值.黎曼把这个方法称为狄里希莱原理.这并非由于狄里希莱发现了这个方法,事实上,William Thomson (即凯尔文勋爵—Lord Kelvin,这是他的贵族封号,而不是人名,但是人们时常弄混了),Kirchhoff, Stokes 以及高斯本人都使用了它.黎曼是因为这是狄里希莱教他的,所以这样称呼.黎曼用这个方法证明了共形映射的基本定理.尤其值得注意的是黎曼是把复变量的解析函数作为静电场来处理的,而由把静电场看成一种理想流体的流场.所以,在物理上成立的,黎曼就认为在数学上也成立.他至少是把这样的方法看成探索数学真理的手段.这是十分值得注意的,而本书,特别是在最后三章里充分发挥了这一点.黎曼在这篇博士论文提出了现在以他命名的几何对象—黎曼曲面.现在的教本里通常要么根本不提黎曼曲面,要么就把它说成是一个奇怪的崂山道士可以钻过来钻过去的虚构的“曲面”—一切都是为了“方便”的权宜之计.这就离黎曼的思想相距太远了.对于黎曼,黎曼曲面是具有深刻几何(准确些说,是拓扑)内涵的数学对象,而一个解析函数的本性,可以说是由它的黎曼曲面决定的.后来由于克莱因,庞加莱等人的功绩,直到外尔(Hermann Weyl)1913年发表《黎曼曲面的思想》(Die Idee der Riemannsche Fläche )这部名著,才明确了黎曼曲面是一个微分流形.由于微分流形的概念,再加上黎曼提出的许多新的拓扑概念或思想,说黎曼是拓扑学的奠基人之一绝不过分.黎曼的这些贡献对20世纪(以及21世纪)的数学发展影响如何深远,绝非这里能够讨论的.我们只能就本书的写法,介绍一点情况,以供本书的读者参考而已.如上所述,不妨认为黎曼的函数论是进程B 的代表,那么,另一位大师维尔斯特拉斯的函数论则可以说是进程A 的代表.尽管黎曼和维尔斯特拉斯互相很熟悉,他们的研究工作互相借鉴也很多,可是在函数论的发展方向上,二人却是针锋相对:维尔斯特拉斯认为研究解析函数必须依托其具体的表示—幂级数.从一个幂级数开始,作一切可能的解析拓展所得的总体,维尔斯特拉斯称之为一个analytic configuration.他认为如黎曼曲面那样的东西是“超验的”,即人类经验无法接受与理解的.也是靠不住的.维尔斯特拉斯指出黎曼的狄里希莱原理是错误的.因为对于所有“可容许”的函数上面的能量泛函所以集合,u ()0,I u ≥{()}I u 下有界,所以有下确界.但是,下确界不一定是最小值.维尔斯特拉斯还举出了一个反例说明,一个有下确界的泛函可以根本达不到下确界,因此没有最小值.这个批评确实是击中了要害.但是据说当时的数学家们反而有一种如释重负的感觉,因为黎曼的基本思想虽有极大的说服力(是不是可以说是“诱惑力”?),可是黎曼的文章又太难懂,其中甚至找不到一个具体例子.有人说这就是“雄鹰不去抓苍蝇”!有了维尔斯特拉斯,似乎就用不着再去跟黎曼较劲了.但是数学家是不会放弃这样精彩的几何与物理直觉的.经过好几十年的努力,直到1901-1902才由希尔伯特“挽救”了狄里希莱原理,由此发展起来的理论对于当代的数学物理等等,是极为重要的.不过要掌握它,必须要有进程A 的良好训练.经过希尔伯特“挽救”的狄里希莱原理也部分地失去了原来数学与物理学融合的风韵.这个“故事”是否能够说明,进程A 和进程B 甚至可以是相反相成的呢?现在回到本书.作者感到遗憾地说,由于篇幅的限制,他不可能比较完全地介绍黎曼曲。
