6杨永利无序分类资料的统计推断4.4
最新研究生统计学讲义第6讲第7章分类资料统计描述与推断PPT课件

二项分布变量的标准差用相对数(率)表示时,称为
率的标准误,总体率的标准误记为σp,样本率的标准 误记为Sp,计算公式为:
p
(1)
n
Sp p(1p)/n (9.8)
二、 Poisson分布 Poisson分布(Poisson distribution)是一种重要的离散 型分布。适用条件:① 两分类的资料;② 所考察的事 件发生率π(一般用大样本率p来估计π)很小,n很大, nπ(或np)为一不大的常数;③ 事件的发生是独立的, 如各病人的患病与否与他人无关。如人群中,对某种 物质中过敏的人数,遗传缺陷、癌症等非传染性疾病 的发病例数;又如大量产品中不合格品出现的次数; 用显微镜观察片子上每一格子内的细菌数;细胞发生 某种变化或细菌死亡的数目等等,都服从或近似服从 Poisson分布。Poisson分布可视为二项分布的特例。 Poisson分布常用于研究单位容积(或面积、时间)内稀 有事件发生数的规律。
神外
291
53
0.75
23.3
18.21
合计
2126
227
—
100.0
10.7
表 7-1的①~③栏,表9-3第①、②列,都是将分类资料的观察结果,按照 分析的要求,分类汇总统计观察单位数(频数),列出的分类资料频数分布 表。表9-2中第②、③两栏及表9-3第②列的数据都是绝对数。绝对数说明 实际发生的绝对水平,是统计分析的基础。但仅使用绝对数,不能进行比 较分析研究
(2) 进行率的对比分析时,应注意资料有可比性。除 了被研究的因素之外,其余可能影响指标的重要因素 应控制在“齐同对比”的条件下。若两组分类资料的 诊断标准或疗效判断标准不一致,则组间缺乏可比性 ;若两组资料内部构成(如病人的性别、年龄、病程 及病情等)缺乏齐同性,则两个总率也不能直接进行 比较。如果需要直接比较总率,为了消除某一混杂因 素(如年龄,职业,病性等)对观察结果的影响,可作 率的标准化处理。
第七讲 无序分类资料的统计分析

无序分类资料的统计分析分类资料又称为定性资料,其取值是定性的,表现为互不相容的类别或属性。
按类别间的关系,又分为有序分类资料(即等级资料)和无序分类资料。
Stata用于处理分类资料的命令为:tabulate var1 var2 [fw=频数变量] [,选择项] 其中,var1,var2分别表示行变量和列变量[fw=频数变量]只在变量以频数形式存放时选用选择项常用的有:chi2 /*(Pearson) x2检验lrchi2 /*似然比x2检验exact /*Fisher的确切概率cell /*打印每个格子的频数占总频数的百分比column /*打印每个格子的频数占相应列合计的百分比row /*打印每个格子的频数占相应行合计的百分比nofreq /*不打印频数以上命令可以同时选用。
分类资料的一个特点是重复数较多,一般将数据整理成频数表,但收集数据时都是未整理的原始形式,stata对这两种形式的资料都可以进行分析,所得结果相同,只是命令稍有区别。
一、两独立样本四格表资料(一)X2检验(n>=40且各个格子的理论数T>=5)例11-2 某研究小组为研究慢支口服液II号对慢性支气管炎治疗效果,以口服消咳喘为对照进行了临床试验,试验组120人、对照组117人(两组受试者病程、病情等均衡),疗程2周,疗效见表11-3。
问慢支口服液II号与消咳喘治疗慢性支气管炎的疗效是否相同?表11-3 试验组与对照组疗效组别有效无效合计有效率(%)试验组116 4 120 96.67对照组82 35 117 70.09合计198 39 237 83.541.建立检验假设,确定检验水准0H :21ππ=,即两种药物治疗慢性支气管炎的疗效相同 1H :21ππ≠,即两种药物治疗慢性支气管炎的疗效不同05.0=α结果:Pearson chi2(1) = 30.4463 Pr = 0.000,05.0<P ,按α=0.05水准拒绝0H ,差别有统计学意义,可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
SPSS 无序分类变量的统计推断 卡方检验

5.分层卡方检验 6.SPSS 软件部分
6.1.‘统计量’子对话框界面说明
打开方式:点击工具栏‘分析’->‘描述’-》 ‘交叉表’ ,点击选项‘统计 量’ 。项。
‘卡方’复选框:进行卡方检验。
‘Kappa’复选框:计算 Kappa 值,即内部一致性系数。原假设 H0 是无一 致性;Kappa≥0.75 表明两者一致性较好,介于 0.4 至 0.75 表明一致性一般,小 于 0.4 表明两者一致性较差。 ‘风险’复选框:计算 OR 值(比数比)和 RR 值(相对危险度) ,这些指 标用于反映交叉表的行、列变量之间的关联强度。 ‘McNemar’复选框:进行 McNemar 检验,即常用的配对卡方检验。 ‘Cochran’s and Mantel-Haenszel 统计量’复选框:为两个二分类变量进 行分层卡方检验,即层间的独立性检验和同质性(齐性)检验,同时可进行分层 因素的调整。
4.一致性检验与配对卡方检验
你得首先理解配对设计,这里略。
4.1.Kappa 一致性检验
Pearson 卡方检验并不适用于配对设计的数据, 它无法明确说明结果的一致 程度。 更准确地说, Pearson 卡方只能告诉用户两种测量结果之间是否存在关联, 但不能判断其是否具有一致性。
4.2.配对卡方检验
3.1.相对危险度
RR 值是一个概率的壁纸,是指实验组人群反应阳性概率与对照组人群反应 阳性概率的壁纸。RR=1,表明实验因子与反应阳性无关联。
3.2.优势比
OR 值是一个比值的比,是反应阳性人群中实验因素有无的比例与反应阴性 人群中实验因素有无的比例之比。OR=1,表明实验因素与反应阳性无关联。 由于优势比是两个比值的比值,因此它不太好解释,而解释相对危险度则要 容易得多, 因此在大多数情况下人们希望能够按照相对危险度的含义来解释优势 比。 当所关注的事件发生概率比较小时(<0.1), 优势比可作为相对危险度的近似。
无序分类资料统计分析

验只能说明效应指标定性反应类别的构成 比是否相同,而各组效应的比较宜采用秩 和检验
注意的问题
3.行列表卡方检验的适用条件
–理论频数不宜太小,一般认为不宜有1/5以上 格子的理论频数小于5或有一个格子的理论频 数小于1 –不太理想的办法
• 与邻近行或列中的实际频数合并 • 删去理论频数太小的格子所对应的行或列
一、两独立样本四格表资料卡方检验
例11-2 某研究小组为研究慢支口服液II号对慢性支气管炎治疗效果,以口服消咳喘为对 照进行了临床试验,试验组120人、对照组117人(两组受试者病程、病情等均衡),疗程 2周,两组治疗后有效的患者分别为116人、82人。问慢支口服液II号与消咳喘治疗慢性支 气管炎的疗效是否相同?
组别 正常胃粘膜 不典型增生 胃癌组织 合计 观测例数 25 25 50 100 阳性例数 7(15.250) 11(15.250) 43(30.500) 61 阴性例数 18(9.750) 14(9.750) 7(19.500) 39 阳性率(%) 28.0 44.0 86.0 61.0
注 :括号内为理论频数
组别 中西医结合组 西医组 有效 92(88.973) 85(88.027) 无效 2(5.027) 8(4.973) 合计 94 93 有效率(%) 97.87 91.40
注 :括号内为理论频数
连续性校正公式:
( A − T − 0.5) 2 T
χ2 = ∑
;
n 2 ( ad − bc − ) n 2 χ2 = (a + b)(c + d )(a + c)(b + d )
–本例即28、8、22、14保持不变的条件下,若 H0成立,计算出现各种四格表的概率
8 第十一章 无序分类变量描述与推断

率的标准误
(standard error of rate)
样本率的标准差叫做率的标准误,以
p
(1 )
n
表示。它是描述率的抽样误差
大小的指标,反映含量相同的样本率的离散
趋势或变异程度。σp越大,说明样本率p的 波动范围越大或率的抽样误差越大。实际应
用中, π常属未知,无法计算σp,故常以
sp
动态数列的分析指标
一、绝对增长量 1、累计增长量:固定某年为基数,各年与之相减; 2、逐年增长量:以前一年为基数,相邻的后一年与 之相减。
二、发展速度和增长速度 1、定基比:固定某年为基数,各年与之相比; 2、环比:以前一年为基数,相邻的后一年与之相比。 增长速度=发展速度-1(或100%)。
三、平均发展速度和平均增长速度 1、平均发展速度(环比发展速度的几何均数)= n√an / a0 。 2、平均增长速度=平均发展速度-1(或100%)。
实际发生的例数与可能发生该现象的 总数之比,用以说明某现象发生的强 度或频率,故又称频率指标。根据不 同需要选用适当的比例基数。
某现象实际发生的例数
率=
× 比例基数
可能发生某现象的总数
率的特点
1、真正的率:分子是分母的一部分,其数值在0到1之间 变动,它们是概率的估计值,符合二项分布,可以计 算可信区间和进行差别的假设检验;
在某一时点(或某短时期内),平均每 百(或千、万、十万等)受检查人数中 发现正患病的人数,常用于估计某病对 居民危害的严重程度。其与发病率的主 要区别在于它是从时点断面来观察疾病 的频率。
正患疾病的病例数
患病率=
× 比例基数
受检查人数
死亡率
(death rate,mortality rate)
第十七章分类资料的统计推断

H0 :1=2,… H1 :12,… =0.05
(2)求检验统计量值
c2
a
ad bc n /
bc da
22 n
cb
d
251 7 27 60 / 22 60
32 28528
2.89 (2 1)(2 1) 1
(3) 确定P 值,作出推断结论
2 0.05,1
3.84
P>0.05….
• n ≥ 40,且Tmin ≥ 5时,用2检验基本公式和专用公式
• n≥ 40,但1≤Tmin<5时,用2检验校正公式 • n<40,或Tmin<1时,或P≈α用四格表Fisher确切概率法
校正公式:
2 c
( A T 0.5)2 T
( ad bc n)2 n
2 c
(a
b)(c
d )(a
阴性
b d
b+d
合计
a+b
c+d a+b + c+d
2
(ad bc)2 n
, 1
(a b)(c d )(a c)(b d )
为了不计算理论频数T, 可由基本公式推导出,直接由各 格子的实际频数(a、b、c、d)计算卡方值的公式:
基本公式abc
❖(3) 确定P 值,作出推断结论
查2界值表:
2 0.05,1
3.84
2 0.025,1
5.02
2 0.01,1
6.63
故P < 0.01,按=0.05的检验水准,拒绝 H0,接受H1,差别有统计学意义,可认为 女生的患病率高于男性。
二、四格表资料2检验的专用公式
组别 A组 B组
分类资料的统计描述

结果:城区肺癌死亡率为郊区的194.1%或1.94倍
三、应用相对数时的注意事项 1.计算相对数时,分母不宜过少
如:用某药治疗某病患者,5例中有3例治愈,计算治愈率为 3/5×100%=60.0%,如果有4例治愈,则其治愈率为80%。显然,这个结果 是不稳定的。 在分母例数很少的情况下,个别的偶然因素会导致结果的变化,只有分 母例数较大时,计算的相对数才比较稳定。在例数较少时,通常直接用绝对 数表示。如果要用相对数表示,则需列出其总体率的臵信区间。 又如:某医生用组织埋藏法治疗了2例视网膜炎患者,1例有效, 即报道有效率为50%。这显然是不可靠的,不能正确反映事实真相。
例: 某地2003-2005年不同性别新生儿数见下表,
试计算该地不同年份新生儿性别比。
表 表11-5 3-5 年 份 2003 2004 2005 某地 2003-2005 年新生儿性别比 新生儿数 90919 109671 125513 男性 48636 58908 66814 女性 42283 50763 58699 性别比
3.关于“死亡率”与“病死率”
这是 2 个不同含义的指标, 在进行人群研究时, 它们的 分子可能相同, 但分母不同。死亡率的分母是同期人口数, 是观察人群中某病的死亡频率, 反映了观察人口因某病的死 亡水平, 是一个人口学指标, 一般以 10 万分率表示; 而病 死率的分母是患某病的患者总数, 是某病患者中因该病而死
下面各率中那个率最能反映疾病对人群的威胁程度
发病率 n年生存率 生存率
患病率
治愈率 有效率 死亡率 病死率
?
感染率
两分类资料的统计描述与推断

频数分布表包括两列,一列表示类别, 另一列表示该类别出现的频数。通过 频数分布表,可以直观地了解各类别 的数量分布情况,为后续的统计分析 提供基础数据。
比例与百分比
总结词
比例和百分比是用来描述两分类资料中各类别的相对大小。
详细描述
比例是各类别的数量与总数量的比值,而百分比则是比例乘以100。通过比例和 百分比,可以了解各类别的相对大小,进一步分析各类别的权重和影响。
详细描述
在两分类资料中,中位数通常用于描述某一类别的中间状态或中心趋势。例如,在一组 关于消费者年龄的数据中,中位数可以表示消费者的平均年龄或年龄分布的中心趋势。
算术平均数
总结词
算术平均数是所有数值的和除以数值的 个数。
VS
详细描述
在两分类资料中,算术平均数可以用于描 述某一类别的平均水平或中心趋势。例如 ,在一组关于消费者购买力的数据中,算 术平均数可以表示消费者的平均购买力水 平。
概率与概率分布
概率
描述随机事件发生的可能性大小。
概率分布
描述随机变量取值可能性的分布情况。
随机抽样与抽样分布
随机抽样
从总体中按照随机原则抽取一部分观察单位进行研究 。
抽样分布
由样本数据推导出的统计量值的分布。
统计量与参数
统计量
基于样本数据计算出的量值,用于描 述样本数据的特征。
参数
描述总体特性的量值,通常通过总体 数据计算得出。
03
CHAPTER
两分类资料的离散程度描述
异众比率
异众比率
异众比率是用于描述分类数据中非众数频数 的相对重要性。其计算公式为异众比率=非 众数频数/总频数。异众比率越大,说明非 众数频数所占比重越大,数据的离散程度越 大。
12无序分类资料的统计分析
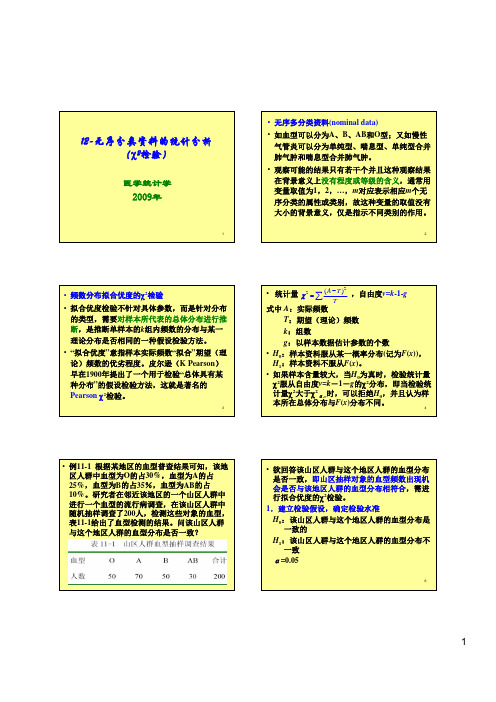
与这个地区人群的血型分布是否一致?53.计算χ统计量及自由度22()20.38A T Tχ−==∑10与消咳喘治疗慢性支气管炎的疗效是否相同?11数据,其余数据均由此派生。
13•一般地,R 行C 列的理论频数n :总频数n R :第R 行频数合计n C :第C 列频数合计•两个独立样本率的比较可用基本公式•亦可用上述基本公式的展开式n n n T CR =∑−=TT A 22)(χ)1(22−=∑CR n n A n χ14•四格表专用公式•在此,式(11-1)、(11-3)及(11-4)等价。
•由于受到“行频数合计等于n ,且列频数合计等于n ”条件的约束,自由度为•对于两独立样本四格表资料,自由度22()()()()()ad bc na b c d a c b d χ−=++++)(列数)行数11(−×−=ν11212(=−×−=)()ν151.建立检验假设,确定检验水准H 0:π1=π2,即两种药物治疗慢性支气管炎的疗效相同H 1:π1≠π2,即两种药物治疗慢性支气管炎的疗效不同α=0.05162.求检验统计量χ2值和自由度v•首先,计算a 、b 、c 、d 对应的理论频数。
•当然,在计算T 11基础上,其余三个理论数也可以按以下方式计算。
253.100237/19812011=×=T 747.19237/3912012=×=T 747.97237/19811721=×=T 253.19237/3911722=×=T 747.19253.10012012=−=T 747.97253.10019821=−=T 253.19747.9711722=−=T 17然后,计算检验统计量χ2值和自由度v•四个表专用公式:45.30 253.19)253.1935(747.97)747.9782(747.19)747.194(253.100)253.100116( )(222222=−+−+−+−=−=∑TT A χ1ν=×(2-1)(2-1)=222()()()()()(11635482)23730.44631(1164)(8235)(11682)(435)ad bc na b c d a c b d −=++++×−××==+×+×+×+χ183.确定P 值,下结论•查附表8,χ20.05,1=3.84,χ2=30.45>χ20.05,1,P<0.05,按α=0.05水准拒绝H 0,差别有统计学意义,可认为慢支口服液II 号治疗慢性支气管炎有效率高于消咳喘。
阅读经典__统计系推荐读物

一、书目1、《应用统计学》胡健颖,北京大学出版社,1997年;2、《应用经济统计学》李心愉编著,北京大学出版社,1999年;3、《统计学的世界-第五版》[美]戴维*S*穆尔中信出版社,2003年;4、《管理统计学-MBA系列教材》缪柏其中国科学技术大学出版社,2002年;5、《数据挖掘》[美] MicchaelJ·A·Berry等袁卫等译中国人民大学出版社,2004年;6、《统计分析与SPSS的应用》贾俊平等中国人民大学出版社,2003年;7、《市场调查方法与技术》简明金勇进蒋妍,中国人民大学出版社,2002年;8、《抽样调查理论与方法》胡健颖孙山泽主编,北京大学出版社,1990年;9、《抽样技术》金勇进等中国人民大学出版社,2002年;10、《SAS 8.X经济统计》樊欣北京希望电子出版社,2003年;11、《Statistics for Business and Economics(第7版)》David R Anderson等,机械工业出版社;12、《Business Statistics by Example》[美]Terry Sincich著清华大学出版社,2001年;13、《金融统计分析》张彦云,中国金融出版社,2002年;14、《多云统计分析》于秀林等,中国统计出版社,1999年;15、《统计学案例集》董逢谷等,上海财经大学出版社,2002年;16、《实验设计分析》[美]Douglas C·Montgomery, 汪仁官等译,中国统计出版,199 8年;17、《探索性数据分析》[美]Dvid C·Hoaglin等,陈忠琏等译,中国统计出版社,19 98年;18、统计学(第二版)D.Freedman等著,魏宗舒等译,中国统计出版社,1997年;19、《数理统计引论》,陈希孺著,科学出版社,1981年;20、《高等数理统计》,峁诗松, 王静龙,高等教育出版社,2003年;二、导读1、《应用统计学》胡健颖,北京大学出版社,1997年《应用统计学》全面介绍了统计学的概念、理论和方法(覆盖了在我国称为经济统计和数理统计的各部分)。
无序分类变量的统计推断ppt课件

bc
121
υ=(2-1)(2-1)=1
本例χ2=7.69>3.84,P<0.05 。可以为两种方法 检出阳性率不同,ITA 的检出率高于LAT 。
SPSS操作
data weight case weight case by : freq
OK
Analyze descriptive row: ITA columns: LAT
无序分类变量的统计推断
北京大学医学部 流行病学与统计学系
李凯
第一节 率的抽样误差与 总体率的估计
一、率规范误
率的抽样误差用率的规范差,又称率的规 范误 p来描画
P
(1 )
n
率的规范误的sPp估计值p(1(n1np) )
二、总体率可信区间估计
1.查表法 当n较小,比如n 50,特别是p 很接近0或100%时,可以经过查 相应统计用表,确定百分率的可 信区间。
患病人数 12 12 29 35
88
未患人数 699 666 665 717
2747
合计 711 678 694 752
2835
患病率(%) 1.69 1.77 4.18 4.65
3.10
H0:π1=π2=π3 H1:四个季节呼吸道感染率不一样或不全一样 α=0.05
2 2835( 122 6992
crosstables
SPSS结果〔例3〕
SPSS结果〔例3〕
本例χ2=17.427>5.99,P=0.001<0.05, 不同 季节上呼吸道疾病感染率不同
练习:例4 SPSS操作及结果解释
三、配对四格表的χ2检验
例5 某医生对55例类风湿关节炎患 者,分别采用免疫比浊法〔ITA〕和 乳胶凝集实验法〔LAT〕检测类风湿 因子〔 FR 〕,结果见下表。问两种 方法检测效果有无差别?
[管理学]第一章-绪论
![[管理学]第一章-绪论](https://img.taocdn.com/s3/m/3bd185ee1b37f111f18583d049649b6649d70945.png)
你的回报期望:收回0.8元钱!是你投资 数的40%。但最大可能是收回1元钱, 机率大约为50%。
《统计学》第一章 绪论
如果你花2000元钱购买1000张奖券:
他们强调统计学是研究社会现象的科学,包括统 计资料的搜集、整理和分析研究,目的是要揭示现象 内部的联系。
(三)统计学的现代期(20世纪初至今)
统计学的主流从描述统计学转向推断统计学。20 世纪30年代R·费希尔的推断统计理论标志着现代数 理统计学的确立。
20世纪60年代以后统计学发展有三个明显的趋势:
平又如何? 记者去各店配镜时的环境是否相同?
《统计学》第一章 绪论
统计学的解释: 要从整体的角度来观察评价事物,个别
的情况不能成为对总体进行判断的依据; 样本容量对推断结果有影响; 样本所反映的差异要经过显著性检验。
《统计学》第一章 绪论
第二个例子:购买彩票
设某体育彩票发行量为500万张,总价 值1000万元。总奖数为250万个,其中大 奖1个,奖金额为34万元;一等奖9个, 各奖10000元;二等奖90个,各奖1000元; 三等奖9900个,各奖100元;末奖249万 个,各奖1元。总奖金额为400万元。
统计 是“认识社会的最有力的武器之一”
——列宁
统计学
Statistics
《统计学原理》第一章 绪论
参考书目 STAT
1.《统计学》黄良文主编,中国统计出版社; 2. 《统计学原理》杨坚白、莫曰达等编写,上海人 民出版社出版; 3.《现代统计分析方法与应用》何晓群编著,中国 人民大学出版社; 4. 《统计学中的计算机应用》童忠勇编,中国统计 出版社出版。
分类资料的推断与x2检验统计学课件

3
联系
两者都是用于检验变量之间关系的统计方法,但 所针对的变量类型不同,一个是连续变量,一个 是分类变量。
X2检验与回归分析的比较
回归分析
主要用于研究一个或多个自 变量对因变量的影响,并估 计自变量对因变量的预测值
。
X2检验
主要用于检验分类变量之间 的关系,不涉及预测值的估
分类资料的常见类型
总结词
分类资料的常见类型包括计数资料、等级资料和属性 资料等。
详细描述
计数资料是指对某一事件或现象发生的次数进行计数的 数据类型,例如某地区的人口数量、某时间段内交通事 故发生的次数等。等级资料是指将观察对象按照某种属 性或特征进行等级划分的数据类型,例如按照病情严重 程度将病人分为轻症、中症和重症等。属性资料是指对 个体或单位按照某种属性或特征进行分类的数据类型, 例如性别、婚姻状况、血型等。
数据整理
对数据进行整理,确保数据符合X2检验的要 求。
实际案例分析:拟合优度检验
建立期望频数
根据理论分布,建立期望频数。
计算实际频数和期望频数
统计实际频数和期望频数,并计算X2值。
判断显著性
根据X2值和自由度,判断显著性水平。
结论推断
根据显著性水平,得出结论并解释结果。
04
X2检验的优缺点与注意事 项
贝叶斯推断
贝叶斯推断是一种基于概率的统计方法,它能够将先验信息与样本数据相结合,进行更准确的推断。近年来,贝叶斯 方法在分类资料推断中得到了广泛应用,如贝叶斯分类器、高斯过程回归等。
集成学习方法
集成学习是一种通过结合多个学习器来提高预测性能的方法。在分类资料推断中,集成学习方法如 bagging、boosting等被广泛应用于提高模型的稳定性和预测精度。
7杨永利-非参数检验

1) 建立检验假设 H 0 :接受不同剂量(4 种)激素的大白鼠耻 骨间隙宽度的增加量总体分布相同 H 1 :接受不同剂量(4 种)激素的大白鼠耻 骨间隙宽度的增加量总体分布不全相同 α =0.05 2) 编秩 将各组数据混合,由小到大编秩,若有相等 数值则取平均秩次。
2012-3-1 30
7
非参数统计方法的主要优点
适用范围广,对变量的类型和分布无特殊要求 对变量的类型和分布无特殊要求。 ①适用范围广 对变量的类型和分布无特殊要求 不论样本资料所来自的总体分布形式如何,甚至 是未知的,都能适用;适合于对某些难以准确测 定指标的分析,如疾病的疗效(无效、显效、痊 愈);自感健康状况(无、轻、中、重);对卫 生服务的满意度(非常满意、比较满意、不满 意)。 ②对样本量无严格要求。 对样本量无严格要求。
2012-3-1
41
配对符号秩和检验步骤 1 建立假设,确定检验水准
H0:两种方法测得尿汞值含量差值的总体中位数为零,即Md=0 H1:两种方法测得尿汞值含量差值的总体中位数不等于零,即Md≠0 α=0.05
(P190)
2012-3-1 34
【例12-3】 试根据表12-4 的资料,检验针刺 不同穴位的镇痛效果有无差别?
表12-4 针刺不同穴位的镇痛效果
2012-3-1
35
2012-3-1
36
2012-3-1
37
第四节 配对设计定量资
料的秩和检验
(P130)
2012-3-1 38
留取12名在医用仪表厂工作的工人尿液,分成两份, 一份用离子交换法,另一份用蒸馏法测得尿汞值如 下,问两种方法测得尿汞值平均含量有无差别?
2012-3-1
7.分类变量资料统计推断

四个格子数a,b,c,d中a和d对χ2值影响较小,因此只通过对b 和c有无差异来进行两法检出率的比较。
b+c>40时
(b c) bc
2
2
b+c<40时,须校正
2 c
( b c 1) bc
2
,
1
1.建立假设、确定检验水准α。
H0:B=C,即两种方法的总体检测结果相同
2检验的校正公式 三、四格表资料
校正公式:
( A T 0.5) T
2 c
2
n 2 ( ad bc ) n 2 2 c (a b)(c d )(a c)(b d )
三、四格表资料2检验的校正公式
例2 某研究所研制出甲乙两种隔离服,用于某传染病的临 床防护。现在某医院随机抽取11名医生穿甲隔离服,30名医生 乙隔离服,在其他防护措施相同的条件下,观察一段时间后,
pearson列联系数(C)=0.1887,可认为2种试剂的检验结
果虽有关系,但关系不太密切。
Pearson列联系数(C )
2 2 n
差别性检验:McNemar检验
甲试剂 + + 合计 80(a) 31(c) 111 乙试剂 10(b) 11(d) 21 90 42 132 合计
(b c) 2 2 10.76 bc
H1:B≠C,即两种方法的总体检测结果不相同 α=0.05
2.计算检验统计量。
(b c)2 2 10.76 bc
3.确定P值,下结论。
1
P<0.005,按=0.05检验水准,拒绝H0,接受H1,可以认为
两种方法的检测结果不同,乙试剂的阳性检测率较高。
高中数学 第一章 统计案例 1.2 回归分析 统计思维漫谈素材 新人教B版选修12

统计思维漫谈开展《统计思维》研究已经很早,那是在1983年;到现在一直在研究。
因此,可以说是执著探索近30载,我们还将继续探索下去。
当然更加希望同学们和我一起探索这个问题。
统计思维作为一个影响较大的概念提出在我的视野在是19世纪逐步形成的。
当时的代表人物主要有社会评论家H.G 韦尔斯,后来被学者们逐渐完善,比如台湾学者的黄文璋,中国学者尹俊峰、曾五一等等。
(H.G.韦尔斯(1866~1946)Herbert George Wells 是英国著名作家,20世纪初英国现实主义小说三杰之一,也是社会评论家).西方学者H.G韦尔斯也说过,统计思维如同读写能力一样,总有一天会成为讲求效率的公民所必需的本领。
由于上述特点,决定了对任何现象的分析和判断以及对未来的预测,对离不开统计信息,都要借助于统计思维的工具。
《统计思维》的内容:什么叫统计思维;统计思维的特征;数量性、总结性(总体性)、实践性。
个体到一般、定量化分析统计思维的意义;推断学科发展、完善教学技术、理清知识体系(课程体系)统计思维对于认识论的促进作用;实事求是认识,精确管理认识,质与量的统一与互变的认识。
统计思维的培养渠道和模式;从基础方法学起。
统计思维的技术辅助意义等等统计思维的社会经济意义;统计思维的规律等等。
目地:1.打造一批文章出来,影响统计学科建设2.提高教学效果和质量;3.完善教学方式探索研究生教学改革。
4.出一本专著《统计思维论》1.《统计思维与确定性思维的差异》,孟雨薇:统计思维于确定性思维是数学中常用的两种思维方式,在两种方式对于解决数学问题具有独特作用,他们自己存在着显著差异。
统计思维是一种模糊数。
2.《统计思维与典型案例的分析》统计思维统计是研究如何合理收集、整理、分析数据的学科,它可以为人们制定决策提供依据.统计思维:统计思维是在抽取数据、从数据中提取信息、论证结论可靠性等的过程中表现出来的一种思维模式.统计思维是如何刺激偶然到必然的兴奋、合理收集、整理、分析数据的学科,它可以为人们制定决策提供依据.统计思维是研究从个别表现到一般特征的认识事物整体状况和发展过程的一种思维模式. –陈正伟统计思维与确定性思维1)确定性思维——结果的确定性统计思维——结果的随机性2)在学习统计的过程中,仍然要使用研究确定性现象的数学手段进行抽象概括、运算求解、推理论证等.统计思维与典型案例1)必修3中的典型案例:“一个著名的案例”、“城市居民月用水量”、“人体的脂肪百分比与年龄之间的关系”2)选修2—3中的典型案例:“人的体重与身高的关系”、“新药是否有效”、“肺癌与吸烟有关吗” 、“水果的分类”3.马鞍山市统计局创新统计思维提升统计能力---统计工作方法、思路。
8.无序分类资料的统计推断—X2检验

8 无序分类资料的统计推断—— χ2检验χ2检验(chi-square test )是一种用途较广的假设检验方法,这里仅介绍它在分类变量资料中的应用,检验两个或两个以上的样本率或构成比之间的差异是否有统计意义。
8.1 四格表资料的χ2检验四格表即2 ⨯ 2列联表,其自由度df =1,又分为一般与配对两种情形,本节介绍一般四格表的χ2检验,主要是用来推断两个总体率或构成比之间有无差别。
一般四格表,①在总频数n ≥40且所有理论频数≥5时,用Pearson χ2统计量;②在总频数n ≥40且有理论频数<5但≥1时,用校正χ2统计量;③在总频数n <40或有理论频数<1时,用Fisher 精确概率法检验。
计数资料的数据格式有两种,一种是频数表格式,如表8-1;一种是原始记录格式,如前面第4章统计描述中的表4-3,这两种格式在SPSS 操作时有所不同。
例8-1 欲研究内科治疗对某病急性期和慢性期的治疗效果有无不同,某医生收集了182例采用内科疗法的该病患者的资料,数据见表8-1。
请分析不同病期的总体有效率有无差别?表8-1 两种类型疾病的治疗效果组别 有效 无效 合计 有效率(%)急性期 69 37 106 65.1 慢性期 30 46 76 39.5 合计998318254.4解 这是一般四格表,012:H ππ=,即急性期和慢性期的总体有效率相同。
建立3列4行的数据文件,如图8-1,其中行变量r 表示组别(值标签:1=“急性期”、2=“慢性期”),列变量c 表示疗效(值标签:1=“有效”、2=“无效”),freq 表示频数。
1.指定频数变量 选择菜单Data →Weight cases ,弹出Weight cases 对话框,见图8-2;选中Weight cases by ;在左边框中选中频数freq ,并将其送入Frequency 框中;单击OK 。
图8-1 例8.1数据文件 图8-2 Weight cases 对话框2.进行χ2检验 选择菜单Analyze → Descriptive Statistics → Crosstabs (交叉表),弹出Crosstabs 主对话框;将组别r 送入行变量Row(s)框,将疗效c 送入列变量Column(s)框,如图8-3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.建立检验假设,确定检验水准
H0 :该山区人群与这个地区人群的血型分布是一致的
H1 :该山区人群与这个地区人群的血型分布不一致
α=0.05
2.求出H0为真时各组的理论频数
3.计算χ2统计量及自由度 ν=4-1=3
表8
Χ2界值表(部分)
第二节 四格表资料的χ2检验
[ 典型案例 ]
例1 在某山区小学随机抽取男生80人,其 中肺吸虫感染23人;随机抽取女生85人, 其中肺吸虫感染13人。问该山区小学男生
表5
类型 一般胃溃疡 老年胃溃疡 合计
两种类型胃溃疡病内科疗法治疗结果
治愈 63 31 94 未愈 17 68 85 合计 80 99 179 治愈率(%) 78.8 31.3 52.5
H0: π 1=π 2 H1: π 1≠π 2 α =0.05
n=179,最小理论值为:T12=(80×85)/179=37.99, 大于 5,故不需校正。
ν =(行数-1) (列数-1)
图2 x2分布的临界值示意图
二、四格表资料的χ2检验的基本步骤
H0: π1=π2 H1: π1≠π2 α=0.05 n=165>40,最小理论值为T11=(80×36)/165=17.45>5 ( A T )2 2 T
(23 17 .45) 2 (57 62 .55) 2 (13 18 .55) 2 (72 66 .45) 2 17 .45 62 .55 18 .55 66 .45 4.38
4、无效假设下频数的重新分配-理论频数:
TRC n R nC n
式中 TRC 表示 R 行(row)C 列(column)的理论频数,nR 为相应 行的合计,nC 为相应列的合计,n 为总例数。
表1 性别 男生 女生 合计
某山区小学男生和女生的肺吸虫感染率 未感染人数 57(62.55) 72(66.45) 129 合计 80 85 165 感染率(%) 28.75 15.29 21.82
根据专用公式求χ2值
(ad bc) 2 n 2 (a b)( c d )( a c)(b d ) (23 72 57 13) 165 80 85 36 129 4.37 结果与基本公式相同
2
[ 电脑实验 ]
例1 数 据 录 入
SPSS运算过程 此步骤的目的是 对频数进行加权
感染人数 23(17.45) 13(18.55) 36
23 57 13 72
a c
b d
2 检验的基本思想: 5、 如果两个率不同只是抽样误差 所致,那未实际频数与理论频数之差就不会很大,即
( A T )2 T
2
(式中 A 代表实际频数;T 代表理论频数)
2 的值不会太大。如实际频数与理论频数相差过大,即
SPSS运算过程
SPSS结果输出
性 别 * 感 染 状 况 Crosstabulation Count 感 染 状况 1 性别 Total 1 2 23 13 36 2 57 72 129 Total 80 85 165
Chi-Square Tests Value 4.374b 3.621 4.411 4.348 165 df 1 1 1 1 Asymp. Sig. (2-sided) .036 .057 .036 .037 Exact Sig. (2-sided) Exact Sig. (1-sided)
7.81 12.59
6
9 12 ¿ ·Ö ¨½ µ
15
18
二、拟和优度检验
概念:根据样本的频率分布检验其 总体分布是否等于某给定的理论分
布或检验一个因素多项分类的实际
观察数与某理论频数是否有差别。
步骤:
建立假设,确定检验水准
计算检验统计量 确定p值
P≤α
作推断结论
P>α
拒绝H0,接受H1
不拒绝H0
(ad bc) 2 n 2 (a b)(c d )( a c)(b d ) (63 68 17 31) 2 179 39.93 80 99 94 85
υ=1,查附表10,χ2界值表得:P<0.05。
按α=0.05水准拒绝H0,接受H1,可认为
当 b + c ≤40 时,应作连续性校正,公式为
2
( b c 1) 2 bc
式中 b 与 c 分别代表两种方法处理结果不同部分的实际 频数。
例 3 某研究者用甲、 乙两种试剂检验 132 份血清, 结果见表 6,问(1)两种检验结果有无差别(2)两 种试剂有无联系。
表 6 两种试剂检测结果 甲试剂 + - 合计 乙试剂 + 80(a) 31(c) 111 - 10(b) 11(d) 21 合计 90 42 132
Pearson Chi-Square Continuity Correction a Likelihood Ratio Fisher's Exact Test Linear-by-Linear Association N of Valid Cases
.040
.028
a. Computed only for a 2x2 table b. 0 cells (.0%) have expected count less than 5. The minimum expected count is 17.45.
一、χ2分布(chi-square distribution)
χ2分布是一种连续型随机变量的概率分布
如果Z服从标准正态分布,那么Z2服从自由 度为1的χ2分布 设有k个相互独立的标准正态分布随机变量 Z1,Z2,……Zν ,Z12+Z22 + ……+ Zν 2服 从自由度为ν的χ2分布
0.5 0.4 0.3
=2.75
υ =1,查附表 10,χ 2 界值表得: P>0.05。按α =0.05 水准不拒绝 H0,可认为两疗法治愈率的差异无统计学意义。
练习题
某医院用内科疗法治疗一般胃溃疡患 者80例,治愈63例,治愈率为78.8%; 治疗65岁以上胃溃疡患者99例,治愈31 例,治愈率为31.3%。试将上述资料整 理成四格表,并比较内科疗法对2组胃溃 疡病人的治愈率有无不同?
公式
实际频数
2
理论频数
2
(A T) (T 5) T
校正公式
2
( A T 0.5) T
2
(T 5)
根据某地区的血型普查结果可知,该地区 人群中血型为O 的占30%,血型为A 的占 25%,血型为B 的占35%,血型为AB 的 占10%。研究者在邻近该地区的一个山区 人群中进行一个血型的流行病调查,在该 山区人群中随机抽样调查了200 人,检测 这些对象的血型,问该山区人群与这个地 区人群的血型分布是否一致?
[ 统计报告 ]
表3 性别 男生 女生 合计 某山区小学男生和女生的肺吸虫感染率 未感染人数 57 72 129 合计 80 85 165 感染率(%) 28.75 15.29 21.82 感染人数 23 13 36
χ 2=4.374,P=0.036。说明男女生 感染率不同,男性高于女性。
2 检验的校正: 三、四格表
例如,两个医生分别检查n个病人,检验的结果如下:
原始数据 Id A B 1 + + 2 + …… j - + …… n 配对四格表 B + -
A
+
-
a
c
b
d
问题:两个医生的检验结果一致吗?
2 检验 (二)配对四格表资料的
b+c>40 时,直接计算
2
2
(b c) 2 bc
ν =1
无序分类资料的统计分析
【教学内容】
第一节 χ2 分布和拟合优度检验
第二节 四格表资料的χ2检验
第三节 行×列表资料的χ2检验
【教学目的和要求】
①了解四格表的概念及四格表中4个基本数据的 含义;了解配对四格表的概念以及配对四格表 与一般四格表在设计上的不同。 ②熟悉χ2检验的基本思想。 ③掌握四格表资料χ2检验的基本公式及各公式的 适用条件;配对四格表检验的基本公式及各公 式的适用条件;掌握四格表的确切概率法的适 用条件。
T ( ad bc n / 2) 2 n
(a b)(c d )( a c)(b d )
(3)T<1或n<40或A=0时,需改用四格表 资料的确切概率法。
(a b)!(c d )!(a c)!(b d )! p a!b!c!d!n!
例2 某医师用甲、乙两疗法治疗小儿单纯 性消化不良,结果如表4。试比较两种疗法结 果有无差别?
f ( ) 2( / 2) 2
2
1
2
( / 21)
e
2 / 2
Ý ß ×·
×Ó ¶ £ 1 Ô É È ½
0.2 0.1 0.0 0 3
3.84
×Ó ¶ £ 2 Ô É È ½ ×Ó ¶ £ 3 Ô É È ½ ×Ó ¶ £ 6 Ô É È ½
P=0.05的临界值
a c
b d
[ 案例分析 ]
资料类型:四格表资料(定性资料) 设计类型:两样本率的比较,目的是推 断两样本所来自的总体率是否相等,即
π1= π2 。
分析方法:两样本率比较χ2检验
一、χ2检验的基本思想
1、 实际频数(actual frequency) 。 2、 两个样本率不相同的原因有两种可能: 一种是抽样误差所致;另一种是总体率确 有所不同。 3、 通过假设检验对两种原因进行判断: 为 了判别这两种情况,先作出“无效假设” , 即假设这两个率相同,差别仅是抽样误差 所致。
