江苏省高考数学模拟试题专题精练:与几何相关的应用题
江苏省苏州市2024年数学(高考)统编版真题(预测卷)模拟试卷

江苏省苏州市2024年数学(高考)统编版真题(预测卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题若复数,且,则实数()A.或3B.或C.3D.第(2)题集合,,则()A.B.C.D.第(3)题已知对任意实数,有,且时,,则时A.B.C.D.第(4)题已知变量满足约束条件则的最大值为()A.B.C.D.第(5)题已知(),(),(),则()A.B.C.D.第(6)题已知集合,则()A.B.C.D.第(7)题设球的半径是1,,,是球面上三点,已知到,两点的球面距离都是,且二面角的大小是,则从点沿球面经,两点再回到点的最短距离是( )A.B.C.D.第(8)题组合数恒等于()A.B.C.D.二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题函数的部分图像如图所示,则下列说法中正确的有()A.f(x)的周期为πB .f(x)的单调递减区间是(k∈Z)C .f(x)的图像的对称轴方程为(k∈Z)D.f(2020)+f(2021)=0第(2)题圆锥内半径最大的球称为该圆锥的内切球,若圆锥的顶点和底面的圆周都在同一个球面上,则称该球为圆锥的外接球.如图,圆锥的内切球和外接球的球心重合,且圆锥的底面直径为6,则()A.设圆锥的轴截面三角形为,则其为等边三角形B.设内切球的半径为,外接球的半径为,则C.设圆锥的体积为,内切球的体积为,则D.设是圆锥底面圆上的两点,且,则平面截内切球所得截面的面积为第(3)题已知,,则下列说法正确的是()A.若,两圆的公切线过点B.若,两圆的相交弦长为C.若两圆的一个交点为,分别过点的两圆的切线相互垂直,则D.若时,两圆的位置关系为内含三、填空(本题包含3个小题,每小题5分,共15分。
2022年江苏省高考数学模拟应用题选编一-图文

2022年江苏省高考数学模拟应用题选编一-图文1、(江苏省如皋市2022届高三下学期语数英联考)如图,矩形公园ABCD中:OA2km,OC1km,公园的左下角阴影部分为以O为圆心,半径为1km的1圆面的人4工湖。
现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点。
(1)试求观光道路EF长度的最大值;(2)公园计划在道路EF右侧种植草坪,试求草坪ABFE面积S的最大值。
2.(江苏省张家港市崇真中学2022届高三上学期寒假自主学习检测)梯形ABCD顶点B、C在以AD为直径的圆上,AD=2米,(1)如图1,若电热丝由AB,BC,CD这三部分组成,在AB,CD上每米可辐射1单位热量,在BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大,并求总热量的最大值;⌒⌒⌒⌒(2)如图2,若电热丝由弧AB,CD和弦BC这三部分组成,在弧AB,CD上每米可辐射1单位热量,在弦BC上每米可辐射2单位热量,请设计BC的长度,使得电热丝辐射的总热量最大.图1第2题图图23、(江苏省淮阴中学、南师附中、海门中学、天一中学2022届高三下学期期初考试)如图,在某商业区周边有两条公路l1,l2,在点O处交汇,该商业区为圆心角,半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分布交31于A,B,要求AB与扇形弧相切,切点T不在l1,l2上..(1)设OAakm,OBbkm,,试用a,b表示新建公路AB的长度,求出a,b 满足的关系式,并写出a,b的范围;(2)设AOT,试用表示新建公路AB的长度,并且确定A,B的位置,使得新建公路AB的长度最短.4、(江苏省联盟大联考2022届高三2月联考数学试题)某校园内有一块三角2,绿地内种植有3一呈扇形AMN的花卉景观,扇形AMN的两边分别落在AE和AF上,圆弧MN与形绿地AEF(如图1),其中AE20m,AF10m,EAFEF相切于点P.(1)求扇形花卉景观的面积;(2)学校计划2022年年整治校园环境,为美观起见,设计在原有绿地基础上2,并种植两块面积相同3的扇形花卉景观,两扇形的边都分别落在平行四边形ABCD的边上,圆弧都与扩建成平行四边形ABCD(如图2),其中BADBD相切,若扇形的半径为8m,求平行四边形ABCD绿地占地面积的最小值.5、(江苏省如皋市2022-2022学年度高三第二学期期初高三数学试卷)如图2所示,某工厂要设计一个三角形原料,其中AB3AC.(1)若BC2,求ABC的面积的最大值;(2)若ABC的面积为1,问BAC为何值时BC取得最小值.6、(江苏省中华中学、溧水高级中学、省句中、省扬中、镇江一中、省镇中2022届高三下学期六校联考试卷)某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.3(1)若漏斗的半径为2R,求圆形铁皮的半径R;(2)这张圆形铁皮的半径R至少是多少?7、(江苏盐城中学2022年高三开学检测)悦达集团开发一种新产品,为便于运输,现欲在大丰寻找一个工厂代理加工生产该新产品,为保护核心技术,核心配件只能从集团购买且由集团统一配送,该厂每天需要此核心为200个,配件的价格为1.8元/个,每次购买需支付运费238元。
江苏数学高考模拟试题

江苏数学高考模拟试题一、选择题1. 设直线L的方程为:y = 2x + 3,则直线L与x轴、y轴交点的坐标分别为:A. (3,0)、(0,3)B. (-3,0)、(0,-3)C. (-3,0)、(0,3)D. (3,0)、(0,-3)2. 若函数f(x) = 3x^2 + 4x + 5,求f(2)的值为:A. 13B. 19C. 25D. 293. 已知等差数列的前5项和为35,前10项和为100,求此等差数列的首项和公差。
A. 首项为3,公差为4B. 首项为2,公差为3C. 首项为4,公差为5D. 首项为1,公差为24. 若集合A = {1, 2, 3, 4, 5},则集合A的子集个数为:A. 15B. 16C. 17D. 185. 一个边长为3cm的正方形,其内切于这个正方形的圆的面积等于:A. 7.07 cm²B. 7.85 cm²C. 8.48 cm²D. 9.42 cm²6. 已知函数y = ax^2 + bx + c,且f(1) = 2, f(2) = 4, f(3) = 6,则a、b、c的值分别为:A. a = 1, b = 1, c = 0B. a = 3, b = 6, c = -3C. a = 2, b = 3, c = -4D. a = 4, b = -2, c = 07. 已知平面直角坐标系中有点A(1,2)、B(4,5),则线段AB的中点坐标为:A. (2.5,3.5)B. (2.5,3)C. (3,3.5)D. (3,3)8. 若P(A) = 0.4,P(B) = 0.3,P(A∪B) = 0.5,求P(A∩B)的值为:A. 0.1B. 0.2C. 0.3D. 0.49. 要将6件物品分成2组,每组3件,求总共有多少种分法。
A. 10B. 12C. 15D. 2010. 已知二次函数y = 2x^2 + 4x + 3的顶点坐标为:(-1,1),则二次函数的对称轴方程为:A. x = 1B. x = 0C. x = -1D. x = -2答案及解析:1. A。
高考数学 2024年江苏省南京市高考数学全真模拟试卷

2024年江苏省南京市高考数学全真模拟试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.A .(4,+∞)B .[4,+∞)C .(-∞,0)∪[4,+∞)D .(-∞,0]∪(4,+∞)1.(5分)已知全集U =R ,集合A ={x |log 2x ⩽2},则∁U A =( )A .1B .C .2D .22.(5分)已知复数z =,则|z |=( )+iM 6√21-iM 3√2A .B .-C .D .-3.(5分)已知sin (-α)+sinα=,则sin (2α+)=( )π313π679798989A .134B .135C .136D .1374.(5分)已知数列{a n }和数列{b n }的通项公式分别为a n =3n +1和b n =5n +1,若它们的公共项从小到大依次排列构成新数列{cn },则满足不等式c n ≤2024的最大的整数n =( )A .=,<B .Z 甲=Z 乙,>C .>,>D .Z 甲<Z 乙,>5.(5分)甲、乙两名运动员在一次射击训练中各射靶20次,命中环数的频率分布条形图如图.设甲、乙命中环数的众数分别为Z 甲,Z 乙,方差分别为,,则( )s 甲2s 乙2Z 甲Z 乙s 甲2s 乙2s 甲2s 乙2Z 甲Z 乙s 甲2s 乙2s 甲2s 乙2A .若m ⊂α,n ⊂α,l ⊥m ,l ⊥n ,则l ⊥α6.(5分)设α是空间中的一个平面,l ,m ,n 是三条不同的直线,则( )二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分对的得部分分,有选错的得0分.B .若l ∥m ,m ∥n ,l ⊥α,则n ⊥αC .若l ∥m ,m ⊥α,n ⊥α,则l ⊥nD .若m ⊂α,n ⊥α,l ⊥n ,则l ∥mA .(0,e )B .(e ,+∞)C .(0,2e )D .(2e ,+∞)7.(5分)若函数f (x )=-有两个零点,则实数m 的取值范围为( )lnx x xmA .B .C .D .28.(5分)已知A 为双曲线E :-=1(a >0,b >0)的右顶点,O 为坐标原点,B ,C 为双曲线E 上两点,且AB +AC =2AO ,直线AB ,AC 的斜率分别为4和,则双曲线E 的离心率为( )x 2a 2y 2b 2→→→12M 3M 52M 62A .拿走x 3,这组数据的方差变大B .拿走x 2,x 4,这组数据的方差变大C .拿走x 2,x 3,x 4,这组数据的方差减小D .拿走x 1,x 2,x 4,x 5,这组数据的方差减小9.(6分)设一组样本数据x 1,x 2,x 3,x 4,x 5满足x i <x i +1(i =1,2,3,4),则( )A .正四面体P -ABC 的外接球表面积为4πB .正四面体P -ABC 内任意一点到四个面的距离之和为定值C .正四面体P -ABC 的相邻两个面所成二面角的正弦值为D .正四面体S -EFG 在正四面体P -ABC 的内部,且可以任意转动,则正四面体S -EFG 的体积最大值为10.(6分)已知正四面体P -ABC 的棱长为,则( )√213181A .函数f (x )的单调递减区间为(0,1)∪(1,e )B .f (π)<f (2)11.(6分)对于函数f (x )=,下列说法正确的是( )xlnx三、填空题:本题共3小题,每小题5分,共15分.四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、明过程或演算步骤.C .若方程|f (|x |)|=k 有6个不等实数根,则k >eD .对任意正实数x 1,x 2,且x 1≠x 2,若f (x 1)=f (x 2),则>x 1x 2e 212.(5分)已知向量a =(2-t ,-3),b =(-1,2+t ),若a ⊥b ,则t =.→→→→13.(5分)设(2-x =+(x -1)+(x -1+⋯+(x -1,若a 5+a 6=0,则n =.)na 0a 1a 2)2a n )n14.(5分)已知△ABC 的三内角A ,B ,C 满足16sinCcos (A -B )+8sin 2C =3π,则△ABC 的面积与△ABC 外接圆的面积之比为.15.(13分)设△ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,且向量m =(a ,b ),n =(-cosA ,sinB )满足m ∥n .(1)求A ;(2)若a =,b =3,求BC 边上的高h .→→M 3→→M 1316.(15分)已知数列{a n }满足=,+=2.(1)证明数列{}是等差数列,并求{a n }的通项公式;(2)若数列{b n }满足,b n =(a n -1)(a n +1-1),求{b n }的前n 项和S n .a 132a n +11a n 1-1a n 17.(15分)某公司为了解旗下的某产品的客户反馈情况,随机抽选了250名客户体验该产品并进行评价,评价结果为“喜欢”和“不喜欢”,整理得到如下列联表:不喜欢喜欢合计男50100150女5050100合计100150250(1)是否有99%的把握认为客户对该产品评价结果与性别因素有关系?(2)公司为进一步了解客户对产品的反馈,现从评价结果为“喜欢”的客户中,按性别用分层抽样的方法选取6人,收集对该产品改进建议.若在这6人中随机抽取2人,求所抽取的2人中至少有1名女性的概率.附:=,P (K 2≥k )0.100.050.0100.001K 2n (ad -bc )2(a +b )(c +d )(a +c )(b +d )k 2.706 3.841 6.63510.82818.(17分)如图,在三棱台ABC -A 1B 1C 1中,AC 1与A 1C 相交于点D ,BB 1⊥平面ABC ,AB =6,BC =4,BB 1=2,=,AE =2EB ,且DE ∥平面BCC 1B 1.(1)求线段AC 的长;(2)求三棱锥C -A 1B 1C 1的体积.A 1C 1M 13→→19.(17分)已知椭圆C :+=1(a >0,b >0)的左、右焦点分别为F 1、F 2,离心率为,经过点F 1且倾斜角为θ(0<θ<)的直线l 与椭圆交于A 、B 两点(其中点A 在x 轴上方),△ABF 2的周长为8.(1)求椭圆C 的标准方程;(2)如图,将平面xOy 沿x 轴折叠,使y 轴正半轴和x 轴所确定的半平面(平面AF 1F 2)与y 轴负半轴和x 轴所确定的半平面(平面BF 1F 2)互相垂直.(i )若θ=,求异面直线AF 1和BF 2所成角的余弦值;(ii )是否存在θ(0<θ<),使得△ABF 2折叠后的周长与折叠前的周长之比为?若存在,求tanθ的值;若不存在,请说明理由.x 2a 2y 2b 212π2π3π21516。
2021年江苏高考练习解析几何50题

2021年江苏高考练习解析几何50题1. 有如下结论:“圆_2?y2?r2上一点P(_0,y0)处的切线方程为22_y_0y?y0y?r2”,类比也有结论:“椭圆2?2?1(a?b?0)上一点P(_0,y0)处的切ab_0_y0y_2?y2?1的右准线l上任意一点M引椭圆C的线方程为2?2?1”,过椭圆C:4ab两条切线,切点为 A、B.(1)求证:直线AB恒过一定点;(2)当点M在的纵坐标为1时,求△ABM的面积_1_43,t)(t?R),A(_1,y1),B(_2,y2),则MA的方程为?y1y?1 1.解:(1)设M(343_1?ty1?1 ①……………………3分∵点M在MA上∴33_2?ty2?1②…………………………5分同理可得33_?ty?1,即_?3(1?ty)…………6分由①②知AB的方程为3易知右焦点F(3,0)满足③式,故AB恒过椭圆C的右焦点F(3,0)……8分_2?y2?1,化简得7y?6y?1?0 (2)把AB的方程_?3(1?y)代入436?2816?……………………12分∴|AB|?1?3?7743|3?23又M到AB的距离d?31?3|∴△ABM的面积S?1163?|AB|?d? (15)分 2211aa_2y22. 在平面直角坐标系_Oy中,椭圆C:2?2?1(a?b?0)过点A(,),B(3,1). ab22(1)求椭圆C的方程;(2)已知点P(_0,y0)在椭圆C上,F为椭圆的左焦点,直线l的方程为_0_?3y0y?6?0.①求证:直线l与椭圆C有唯一的公共点;②若点F关于直线l的对称点为Q,求证:当点P在椭圆C上运动时,直线PQ 恒过定点,并求出此定点的坐标.232y2_3. 如图,在平面直角坐标系_Oy中,椭圆2?2?1(a?b?0)的右焦点为F(1, 0),离心率为2.2ab分别过O,F的两条弦AB,CD相交于点E(异于A,C两点),且OE?EF.(1)求椭圆的方程;(2)求证:直线AC,BD的斜率之和为定值.(1)解:由题意,得c?1,e?c?2,故a?2,a2 从而b2?a2?c2?1,所以椭圆的方程为_?y2?1. 2 (2)证明:设直线AB的方程为y?k_,②2y C A E O F D _ B (第18题)① ………5分直线CD的方程为y??k(_?1),③ ………7分由①②得,点A,B的横坐标为?22k?12,2k2?2(k2?1) 由①③得,点C,D的横坐标为,………9分2k2?1 k_2),C(_3, k(1?_3)),D(_4, k(1?_4)), k_1),B(_2,记A(_1,则直线AC,BD的斜率之和为k_1?k(1?_3)k_2?k(1?_4) ?_1?_3_2?_4(_1?_3?1)(_2?_4)?(_1?_3)(_2?_4?1)(_1?_3)(_2?_4)2(_1_2?_3_4)?(_1?_2)?(_3?_4) ………13分(_1?_3)(_2?_4) ?k? ?k?22(k2?1)???24k2?2???0?222k?1 2k?12k?1 ?? ?k?(_1?_3)(_2?_4) ?0.………16分44. 椭圆C的右焦点为F,右准线为l,离心率为个公共点是B,D.3,点A在椭圆上,以F为圆心,FA为半径的圆与l的两2(1)若?FBD是边长为2的等边三角形,求圆的方程;(2)若A,F,B三点在同一条直线m上,且原点到直线m的距离为2,求椭圆方程.解:设椭圆的半长轴是a,半短轴是b,半焦距离是c,由椭圆C的离心率为3,可得椭圆C方程是2_2y2?2?1,······························ 2分 24bb(只要是一个字母,其它形式同样得分,)焦点F(3b,0),准线_?4b,设点A(_0,y0), 3(1)?FBD是边长为2的等边三角形,则圆半径为2,且F到直线l的距离是3,ba2b2b?3,b?3, FM??c??又F到直线l的距离是,所以,cc33所以c?33 22所以,圆的方程是(_?33)?y?4。
江苏省高三下学期模拟考试(理科)数学试卷-附带答案解析

江苏省高三下学期模拟考试(理科)数学试卷-附带答案解析班级:___________姓名:___________考号:___________一、单选题1.已知集合{}{}22,0,1,2,3A x x x B =-≥=,则()RBA =( )A .{0}B .{}0,1C .{}1,2D .{}0,1,22.设复数z 的共轭复数为z ,若()()1i i z z -=∈C ,则z 对应的点位于复平面内的( ) A .第一象限 B .第二象限 C .第三象限D .第四象限3.在ABC ∆中点N 满足2AN NC =,记BN a =,NC b =那么BA =( ) A .2a b -B .2a b +C .a b -D .a b +4.将正弦曲线向右平移π4个单位长度,再将图象上各点的纵坐标伸长到原来的2倍(横坐标不变),得到下列哪个函数的图象( ) A .π2sin()4x + B .π2sin()4y x =- C .1πsin()24y x =+D .1πsin()24y x =-5.已知正项等差数列{}n a 的前n 项和为()*n S n N ∈,若28793a a a --=,则158S a -的值为( )A .3B .14C .28D .426.如图,一个底面半径为2a 的圆锥,其内部有一个底面半径为a 的内接圆柱,3a ,则该圆锥的体积为( ).A 3a B 3a C .3a D .3a7.已知函数f (x )满足f (2x )=log 2x ,则f (16)=( ) A .﹣1 B .1C .2D .48.记i A d 为点i A 到平面α的距离,给定四面体1234A A A A -,则满足()122,3,4i A A d d i ==的平面α的个数为( ) A .1B .2C .5D .8二、多选题9.已知正四棱锥的侧面积为 )A B .侧棱与底面所成的角为60︒ C .棱锥的每一个侧面都是等边三角形D .棱锥的内切球的表面积为(8π- 10.已知,,0x y x y ∈<<R 且,则( ) A .sin sin x y <B <C .21x y -<D .11x y x y <++ 11.已知椭圆()2222:10x y C a b a b +=>>的离心率为12,左,右焦点分别为1F 和2F ,P 为椭圆上一点(异于左,右顶点),且12PF F △的周长为6,则下列结论正确的是( )A .椭圆C 的焦距为1B .椭圆C 的短轴长为C .12PF F △D .椭圆C 上存在点P ,使得1290F PF ∠=12.以下命题正确的是( )A .设()f x 与()g x 是定义在R 上的两个函数,若()()()()1212f x f x g x g x +≥+恒成立,且()f x 为奇函数,则()g x 也是奇函数B .若对任意1x ,2x ∈R 都有()()()()1212f x f x g x g x ->-成立,且函数()f x 在R 上单调递增,则()()f xg x +在R 上也单调递增C .已知0a >,1a ≠函数(),1,,1,x a x f x a x x ⎧≤=⎨->⎩若函数()f x 在[]0,2上的最大值比最小值多52,则实数a 的取值集合为12⎧⎫⎨⎬⎩⎭三、填空题13.若(6x 的展开式中4x 的系数为30,则=a ______.14.点P 为抛物线y 2=x 上的动点,过点P 作圆M :(x -3) 2+y 2=1的一条切线,切点为A ,则PA ·PM 的最小值为________.15.若直线y x m =+与曲线2y ax =和ln y x =均相切,则=a __________.16.设点O 是面积为4的ABC 内部一点,且有340OA OB OC ++=,则BOC 的面积为__________.四、解答题17.在凸四边形ABCD 中(1)若=45ABC ∠︒,求CD ;(2)若BCD ∠的角平分线交对角线BD 于点E ,求BC CE CD ++的最大值. 18.如图,在直三棱柱111ABC A B C 中(1)求证:平面1A BC ⊥平面11ABB A ; (2)若AC 与平面1A BC 所成的角为π6,点E 为线段1A C 的中点,求平面AEB 与平面CEB 夹角的大小. 19.古人云:“腹有诗书气自华.”现在校园读书活动热潮正在兴起,某校为统计学生一周课外读书的时间,从全校学生中随机抽取200名学生,获得了他们一周课外读书时间(单位:h )的数据如表所示:(1)求,a b 的值;如果按读书时间0,6],6,12],1(((2,18]分组,用分层抽样的方法从这200名学生中抽取20人,再从这20人中随机选取3人,求恰有2人一周课外读书时间在(12,18]内的概率.(2)若将样本频率视为概率,从该校学生中随机选取3人,记X 为一周课外读书时间在(12,18]内的人数,求X 的分布列和数学期望,并估计该校一周人均课外读书的时间. 20.已知数列{}n a ,{}n b 满足1n n n b a a +=-,其中*N n ∈.(1)若12a =和2nn b =.①求证:{}n a 为等比数列; ②试求数列{}n n a ⋅的前n 项和.(2)若2n n b a +=,数列{}n a 的前6291项之和为1926,前77项之和等于77,试求前2024项之和是多少? 21.已知点A 是抛物线x 2=2py (p >0)上的动点,过点M (-1,2)的直线AM 与抛物线交于另一点B . (1)当A 的坐标为(-2,1)时,求点B 的坐标;(2)已知点P (0,2),若M 为线段AB 的中点,求PAB 面积的最大值.22.记()f x ',()g x '分别为函数()f x ,()g x 的导函数.若存在0x R ∈,满足()()00f x g x =,且()()00f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.已知()ln f x x ax =+和()2g x bx =.(1)若1b =,()f x 和()g x 存在“S 点”,求a 的值;(2)对任意0a >,是否存在实数0b >,使得()ln f x x ax =+,()2g x bx =存在“S 点”?请说明理由.参考答案与解析1.B【分析】求出A 及其补集,通过交集运算求得结果.【详解】集合{}{221A x x x x x =-≥=≤-或2}x ≥R {|12}A x x ∴=-<<又{}0,1,2,3B = 所以()RBA ={}0,1故选:B . 2.C【分析】利用复数除法运算求得z ,从而求得z ,进而确定正确答案. 【详解】依题意()()()i 1i i 1i 11i 1i 1i 1i 222z +-+====-+--+ 所以11i 22z =--,对应点为11,22⎛⎫-- ⎪⎝⎭,在第三象限.故选:C 3.A【分析】根据向量的线性运算将BA 分解为BA BN NA =+,再转化为a ,b 表示即可. 【详解】22BA BN NA BN NC a b =+=-=-. 故选:A. 4.B【解析】左右平移变换是横坐标x 改变,原则简记为 “左加右减”;伸缩变换是相应变量乘以对应倍数即可.【详解】sin y x =向右平移π4个单位长度得sin(4)πy x =-,再将图象上各点的纵坐标伸长到原来的2倍(横坐标不变)得π2sin()4y x =-. 故选:B.【点睛】本题考查图象的平移和伸缩变化,要牢记每一种变换对解析式系数的影响,方可解决此类题. 5.D【分析】根据等差数列的性质得7982a a a +=,则可由已知等式求8a 的值,从而利用求和公式和等差数列性质求158S a -得值.【详解】解:正项等差数列{}n a ,则0n a >若28793a a a --=,则28798323a a a a =++=+,解得83a =或81a =-(舍)则()115815888815215144222a a a S a aa a +⨯⨯-=-=-==. 故选:D. 6.B【分析】作出该几何体的轴截面,求出内接圆柱的高,利用三角形相似求出圆锥的高,即可求的其体积. 【详解】作出该几何体的轴截面如图示:AB 为圆锥的高设内接圆柱的高为h ,而2,BC a BD r a ===3a ,即23πa h a =则h =由于AB ED ∥,故CAB CED △∽△,则h DCAB BC=即22a aa-=,故AB =所以圆锥体积为231π(2)3V a a =⨯⨯=故选:B 7.C【分析】根据16=24,代入求解即可.【详解】∵函数f (x )满足f (2x )=log 2x ,且f (16)=f (24) ∴f (16)=f (24)=log 24=2 故选:C . 8.D【分析】分类讨论,当平面α与平面234A A A 平行时,分析可得2个,当平面α经过234A A A △的中位线时分析可得6个,从而得解.【详解】到点23,A A 和4A 的距离相等的平面α有两种类型,与平面234A A A 平行或者经过234A A A △的某一条中位线.当平面α与平面234A A A 平行时,如下图1设121314,,A A A A A A 的三等分点分别为234,B B B ,(靠近1A ) 对于平面234B B B ,利用三角形相似可知1212222A A d A B d A B ==,平面234B B B 符合题意. 在线段1i A A 的延长线上取i C 使得()12,3,4i i i A A AC i == 对于平面234C C C ,利用三角形相似可知1212222A A d AC d A C ==,平面234C C C 符合题意 即平面α与平面234A A A 平行时,满足条件的平面有2个; 设232434,,A A A A A A 的中点分别为,,E F G 当平面α经过234A A A △的中位线EF 时 如下图2:对于平面2B EF ,2B 在线段12A A 上且12222A B A B =利用三角形相似可知1212222AAd A Bd A B==又34//EF A A,EF⊂平面2B EF,34A A⊄平面2B EF,可得34A A//平面2B EF且E、F分别为2324,A A A A的中点则到平面2B EF的距离相等因此平面2B EF符合题意.如下图3:对于平面34B B FE,3B在线段13A A上,4B在线段41A A上且131433442A B A BA B A B==,利用三角形相似可知1313332AAd A Bd A B==又34//EF A A,EF⊂平面34B B FE,34A A⊄平面34B B FE,可得34A A∥平面34B B FE且E、F分别为2324,A A A A的中点则到平面34B B FE的距离相等因此平面34B B FE符合题意.对于中位线EG GF、,也有类似结论,即平面α经过234A A A△的某条中位线时,满足条件的平面有6个综上所述,符合题意的平面共有8个. 故选:D .【点睛】难点点睛:本题判断满足条件的平面的个数时,难点在于要发挥空间想象能力,明确满足条件的平面的位置,作图分析,说明平面所处的位置是怎样的,加以说明,解决问题. 9.ACD【分析】设底面边长为2a ,侧棱长为b ,求出棱锥体积,通过构造函数,求导可知当1a =,及2b =时棱锥体积最大,然后再逐项判断即可.【详解】设底面边长为2a ,侧棱长为b ,则14242a S =⨯⨯=侧面即=而21(2)3V a =⨯=故243a V ==设26()3(0f a a a a =-<<,则()()()542666161(1)()'1a a a a a f a a a a =-=-=++-易知函数()f a 在()0,1单调递增,在单调递减∴当1a =时,()f a 取得最大值,此时棱锥的体积最大,且2b = ∴底面边长为2,侧棱长为A 正确;侧棱与底面所成的角为PBO ∠,而sin OP PBO PB ∠=45PBO ∠=︒,选项B 错误; 由于底面边长与侧棱长均为2,故侧面为等边三角形,选项C 正确;设内切球的半径为r ,由于P ABCD V -=1442242S ⎛=+⨯⨯⨯=+ ⎝⎭表∴3V r S ===表∴4(8S ππ==-内,选项D 正确.故选:ACD .10.BCD【分析】取特殊值可说明A 错;根据指数函数以及幂函数的单调性,可判断B,C 的对错;利用作差法可判断D 的对错.【详解】对于A ,取2,33x y ππ==满足,,0x y x y ∈<<R 且,但sin sin x y =,故A 错;对于B ,12y x =是定义域上的增函数,故,,0x y x y ∈<<R 且B 正确; 对于C, 0x y -<,故0221x y -<=,故C 正确; 对于D ,011(1)(1)x y x y x y x y --=<++++故11x y x y <++,故D 正确 故选:BCD. 11.BC 【分析】根据12e =,226a c +=解得,,a b c 可判断AB ;设()00,P x y ,由1212012PF F S F F y =知当P 点为椭圆的上顶点或下顶点时面积最大,求出面积的最大值可判断C ;假设椭圆C 上存在点P ,设12,PF m PF n ==,求出m n +、mn ,,m n 可看作方程2460x x -+=,求出判别式∆可判断D. 【详解】由已知得12c e a ==,226a c +=解得2,1a c == 2223b a c =-= 对于A ,椭圆C 的焦距为22c =,故A 错误;对于B ,椭圆C 的短轴长为2b =B 正确; 对于C ,设()00,P x y ,12120012==PF F SF F y c y 当P 点为椭圆的上顶点或下顶点时面积的最大,此时0==y b 12PF F △C 正确;对于D ,假设椭圆C 上存在点P ,使得1290F PF ∠=,设12,PF m PF n == 所以24m n a +==,22216244m n mn c +=-==和6mn =所以,m n 是方程2460x x -+=,其判别式16240∆=-<,所以方程无解,故假设不成立,故D 错误. 故选:BC. 12.ABD【分析】A 选项,利用赋值法及()f x 的奇偶性推导出()g x 的奇偶性;B 选项,利用定义法和()f x 在R 上单调递增证明出结论;C 选项,对a 分类讨论,由单调性求出最值,列出方程,求出a 的值;D 选项,由函数的对称性求解.【详解】令21x x =-,则()()()()1111f x f x g x g x +-≥+-,因为()f x 为奇函数,所以()()()()1111f x f x g x g x -≥+-恒成立,即()()110g x g x ≥+-,所以()()110g x g x +-=,即()()11g x g x -=-,所以则()g x 也是奇函数,A 正确;设12x x <,因为()f x 在R 上单调递增,所以()()12f x f x <,因为()()()()1212f x f x g x g x ->-恒成立,所以()()()()()()121221f x f x g x g x f x f x -<-<-,从而()()()()11220f x g x f x g x +-+<⎡⎤⎡⎤⎣⎦⎣⎦ 令()()()h x f x g x =+,则()()()()()()1211220h x h x f x g x f x g x -=+--<,所以()()12h x h x <,故()()()h x f x g x =+在R 上也单调递增,B 正确;当1a >时,(),1,,1,x a x f x a x x ⎧≤=⎨->⎩在[]0,2上的最大值为()1f a =,最小值为()01f =或()22f a =-,当512a -=时,解得:72a =此时()3212f =>,满足题意;当()522a a --=时,522=无解,舍去; 当01a <<时,在[]0,1x ∈上,()xf x a =是减函数,(]1,2x ∈上,()f x x a =-+是减函数,因为()011f a =>-+,所以函数最大值为()01f =,而()()2211f a a f =-+<-+=,所以函数的最小值为()22f a =-+,因此()5122a --+=,解得:()10,12a =∈符合题意; 综上:实数a 的取值集合为1,272⎧⎫⎨⎬⎩⎭,C 错误;由()()2f x f x -+=可得:()f x 关于()0,1中心对称,()1x g x x+=也关于()0,1中心对称,从而()f x 与()g x 的图象的交点关于()0,1中心对称,从而1280x x x ++⋅⋅+=⋅与128248y y y ++⋅⋅⋅+=⨯=,D 正确. 故选:ABD【点睛】抽象函数的对称性有以下结论:若()()f a x f b x c -++=,则()f x 关于,22a b c +⎛⎫⎪⎝⎭中心对称; 若()()f a x f b x -=+,则()f x 关于2a bx +=对称.13.2【分析】利用二项展开式的通项公式,列式求a .【详解】二项展开式的通项公式616rr rr T C x-+=⋅⋅当2r =时,4x 的系数是2630C a ⋅=解得:2a = 故答案为:214.74【分析】求出22||||1PA PM PA PM ⋅==-,设点2(,)P y y ,化简表达式,利用二次函数的性质,求解最小值即可.【详解】解:由已知易得22||||1PA PM PA PM ⋅==-设点2(,)P y y ,则()22224222577||13158()244PM y y y y y -=-+-=-+=-+当252y =时,2||1PA PM PM ⋅=-取得最小值74. 故答案为:7415.14##0.25【分析】先根据直线和ln y x =相切求出m ,再利用直线和2y ax =相切求出a . 【详解】设直线y x m =+与ln y x =相切于点()00,ln x x 1y x'= 因为直线y x m =+与ln y x =相切,所以011x =,且00ln x x m =+; 解得01,1x m ==-;因为直线1y x =-与曲线2y ax =相切联立得210ax x -+=,0a ≠且140a ∆=-=,即14a =. 故答案为:1416.12##0.5【分析】根据340OA OB OC ++=确定点O 的位置,然后将面积比转化为边长比即可.【详解】340OA OB OC ++= 371747OA OB OC ∴=-+;设17OA OD -=;则:3477OD OB OC =+,即B,C,D 三点共线;所以||18||BOC ABCS OD AD S==; 11482BOCS∴=⨯=;故答案为:12 17.; .【分析】(1)运用差角公式求得sin DBC ∠,再运用正弦定理求得CD 即可.(2)运用余弦定理及基本不等式求得BC CD +的范围,由等面积法求得CE ,将问题转化为求关于BC CD +的二次型函数在区间上的最值. 【详解】(1)连接BD ,如图所以35,sin5BD ABD=∠=4cos5ABD∠=所以43sin sin(45)()55DBC ABD∠=︒-∠-BCD△中sin sinCD BDDBC DCB=∠∠;∴sinsinBDCD DBCDCB=⋅∠==∠(2)BCD△中2222cos120BD BC CD BC CD=+-⋅⋅︒∴2222()325()()()44BC CDBC CD BC CD BC CD BC CD+=+-⋅≥+-=+,当且仅当BC CD=时取等号∴2100()3BC CD+≤,即:0BC CD<+∵BCD BCE CDES S S=+△△△∴111sin120sin60sin60222BC CD BC CE CD CE⋅⋅︒=⋅⋅︒+⋅⋅︒∴BC CD BC CE CD CE⋅=⋅+⋅∴2()25BC CD BC CDCEBC CD BC CD⋅+-==++∴2()25BC CDCE CD BC BC CDBC CD+-++=+++令t BC CD=+∴225252tCE CD BC t tt t-++=+=-0t<∵252y tt=-在(上单调递增∴当t y取得最大值为2.∴BC CE CD++.18.(1)证明见解析;(2)π3.【分析】(1)根据线面垂直的判定定理可得BC ⊥平面11ABB A ,再由面面垂直的判定定理得证; (2)利用线面角求出边长,再建立空间直角坐标系,利用向量法求夹角. 【详解】(1)在直三棱柱111ABC A B C 中1A A BC ⊥ 又AB BC ⊥,1A AAB A =和1,A A AB ⊂平面11ABB A所以BC ⊥平面11ABB A ,又BC ⊂平面1A BC 所以平面1A BC ⊥平面11ABB A . (2)设11A BAB M =,连接CM ,如图则1A B 中点为M ,且1AM A B ⊥∵平面1A BC ⊥平面11ABB A 且交线为1A B ,AM ⊂平面11ABB A ∴AM ⊥平面1A BC所以直线AC 与平面1A BC 所成的角为π6ACM ∠=又12AA AB ==,则2AM AC BC = 以B 为原点,1,,BA BC BB 分别为x ,y ,z 轴正方向建立坐标系 则(2,0,0),(0,2,0),(1,1,1)A C E 设平面AEB 的法向量为(,,)n x y z =20n BA x n BE x y z ⎧⋅==⎪⎨⋅=++=⎪⎩,令1y =,则0,1x z ==-,故(0,1,1)n =- 设平面CEB 的法向量为()111,,m x y z =111120m BC y m BE x y z ⎧⋅==⎪⎨⋅=++=⎪⎩,令11x =,则10y =,11z =-故(1,0,1)m =- 设平面AEB 与平面CEB 的夹角为θ ∴1cos 2||||n m n m θ⋅==⋅,又π02θ<≤ π3θ∴=.19.(1)1224,a b ==;读书时间在(12,18]内的概率为91190; (2)分布列见解析,()E X =3920;该校一周人均课外读书的时间为12.32h.【分析】(1)由频数÷总数=频率可得,a b 的值;由分层抽样可知20人中在]((0,6],6,12中的有7人,在(12,18]中的有13人,据此可得答案;(2)由题可得X 的可能取值为0,1,2,3,且13~3,20X B ⎛⎫⎪⎝⎭,由此可得分布列及期望;结合表格数据可估计该校一周人均课外读书的时间.【详解】(1)由频数÷总数=频率可得2000.0612,2000.1224a b =⨯==⨯=. 由题意知,从样本中抽取20人,抽取比例为110,所以从(](](]0,6,6,12,12,18三组中抽取的人数分别为2,5,13,从这20人中随机抽取3人,恰有2人一周课外读书时间在(]12,18内的概率12713320C C 91C 190P ==.(2)由题意得,总人数为200,一周课外读书时间在(]12,18内的人数为130,因此从该校任取1人,一周课外读书时间落在区间(]12,18内的概率是1320. X 的可能取值为0,1,2,3,且13~3,20X B ⎛⎫ ⎪⎝⎭,所以33137()C (0,1,2,3)2020kkk P X k k -⎛⎫⎛⋅⎫=== ⎪⎪⎝⎭⎝⎭所以X 的分布列为数学期望1339()32020E X =⨯=. 该校一周人均课外读书时间的估计值为10.0230.0350.0570.0690.07110.1213⨯+⨯+⨯+⨯+⨯+⨯+⨯0.25150.23170.1712.32(h)+⨯+⨯=.20.(1)①证明见解析;②1(1)22+=-⋅+n n S n(2)20241849=T【分析】(1)①,利用累加法求解n a 即可;②由①得2n n a =,令2nn n c na n ==⋅,{}n c 的前n 项和为n S ,利用错位相减法求解数列的和即可;(2)推出数列{}n a 是一个周期为6的周期数列,然后求解数列{}n a 的任意连续6项之和为0,然后利用其周期和相关值求出12,a a ,则得到答案.【详解】(1)①证明:12nn n a a +-=,当2n ≥时累加得()()()112211n n n n n a a a a a a a a ---=-+-++-+1212222n n --=++++()12122212n n --=+=-11222n n n n a a ++∴== ()2n ≥ 又211212,2,4,2a a b a a ===∴=所以{}n a 为首项为2,公比为2的等比数列.②由①得2n n a =,令2nn n c na n ==⋅,{}n c 的前n 项和为n S则2311231122232(1)22n nn n n S c c c c c n n --=+++⋯++=⋅+⋅+⋅+⋯+-⋅+⋅,A23412122232(1)22n n n S n n +=⋅+⋅+⋅+⋯+-⋅+⋅,BA B -得23122222n n n S n +-=+++⋯+-⋅()211121222(1)2212n n n n n -++-=+-⋅=-⋅--1(1)22n n S n +∴=-⋅+(2)若21n n n n b a a a ++==-,则32163n n n n n n n a a a a a a a +++++=-=-⇒=-= 所以数列{}n a 是周期为6的周期数列,设1a m = 2a t =1234560a a a a a a ∴+++++=设数列{}n a 的前n 项和为n T ,则60n T =. 所以629110486332221926963T T T a a ⨯+====⇒= 7712655377T T T a ⨯+====,所以123886a a a =-=所以2024337622128869631849T T T a a ⨯+===+=+=. 21.(1)()6,9 (2)2【分析】(1)将A 的坐标代入抛物线方程可得抛物线的方程为:24x y = 再根据直线AM 的方程,联立抛物线方程可得B 的坐标;(2)设直线AB 的方程:()21y k x -=+ 联立抛物线的方程,结合韦达定理与M 为线段AB 的中点可得1pk =-再代入PAB 的面积可得S =进而根据二次函数的最值求解即可 (1)当A 的坐标为()2,1-时,则2221p =⋅,所以24p = 所以抛物线的方程为:24x y = 由题意可得直线AM 的方程为:()211212y x --=+-+,即3y x代入抛物线的方程可得24120x x --=解得2x =-(舍)或6 所以,B 的坐标为()6,9 (2)法一:设直线AB 的方程:()21y k x -=+ 即2y kx k =++设直线AB 与y 轴的交点为Q ,()11,A x y 和()22,B x y由222y kx k x py=++⎧⎨=⎩ 可得22240x pkx pk p ---=,122x x pk +=和1224x x pk p =-- 因为M 为线段AB 的中点,所以1212x x pk +==- 令0x =,2y k =+即()0,2Q k +,所以PQ k = 则PAB 的面积12111222S PQ x x k k =⋅-=⋅=⋅12k =⋅把1pk =-代入上式,S当2k =时,则max 2S =,所以PAB 的面积的最大值为2.(2)法二:222y kx k x py =++⎧⎨=⎩可得22240x pkx pk p ---=,122x x pk +=,1224x x pk p =-- 因为M 为线段AB 的中点,所以1212x x pk +==- 设点P 到直线AB 的距离为d,则d =AB ==1122S AB d k =⋅=⋅把1pk =-代入上式 S所以,当2k =时,ABC 的面积的最大值为2 22.(1)1(2)存在,理由见解析【分析】(1)设“S 点”为0x ,然后可得200000ln 12x ax x a x x ⎧+=⎪⎨+=⎪⎩,然后解出即可;(2)假设对任意0a >,存在实数0b >,使得()y f x =与()y g x =有“S 点”, 设为1x ,然后可得2111ln x ax bx +=,1112a bx x +=,消去b 得1112ln 0x ax -=>,然后可得10x <消去a 得1211ln x b x -=,然后证明对任意0a >,方程1112ln x ax -=在(有解即可. 【详解】所以200000ln 12x ax x a x x ⎧+=⎪⎨+=⎪⎩,消去a 得200ln 1x x +=记()2ln h x x x =+,显然()h x 在()0,+∞上是增函数,而()11h =因此200ln 1x x +=只有一个解01x =,所以211a =-=.(2)假设对任意0a >,存在实数0b >,使得()y f x =与()y g x =有“S 点” 设为1x ()2g x bx '= 所以2111ln x ax bx +=①,1112a bx x +=②,由②得21112ax bx +=③ ①③消去b 得1112ln 0x ax -=>,11ln 2x <和10x < ①③消去a 得1211ln x b x -=,在10x <<1211ln 0x b x -=> 下面证明对任意0a >,方程1112ln x ax -=在(有解设()(0l 1n 2x H x ax x =--<<,函数()H x在定义域(上是减函数0x →时 ()H x →+∞0H=-<,图像连续不断,所以存在10x <使得()10H x =.综上,任意0a >,存在实数1211ln 0x b x -=>,使得()y f x =与()y g x =有“S 点”。
江苏高三高中数学高考模拟带答案解析

江苏高三高中数学高考模拟班级:___________ 姓名:___________ 分数:___________一、填空题1.若复数满足(是虚数单位),则.2.已知全集,集合,,则中最大的元素是.3.直线与直线平行的充要条件是.4.设等比数列的前项和为,若,则数列的公比是.5.如图,沿田字型的路线从往走,且只能向右或向下走,随机地选一种走法,则经过点的概率是.6.实数满足,则的值为.7.与抛物线有且仅有一个公共点,并且过点的直线方程为.8.空间三条直线中,任何两条不共面,且两两互相垂直,另一条直线与这三条直线所成的角均为,则.9.将函数的图象向左平移至少个单位,可得一个偶函数的图象.10.将一个长和宽分别为的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则的取值范围是.11.在中,角所对边分别是,若,则.12.已知函数是定义在上的增函数,函数的图象关于对称.若对任意的,不等式恒成立,则当时,的取值范围是.13.已知中,,为的外心,若点在所在的平面上,,且,则边上的高的最大值为.14.各项为正数的数列,其前项的和为,且,若,且数列的前项的和为,则.二、解答题1.设函数,其中,若,且图象的一条对称轴离一个对称中心的最近距离是.(1)求函数的解析式;(2)若是的三个内角,且,求的取值范围2.在所有棱长都相等的斜三棱柱中,已知,,且,连接.(1)求证:平面;(2)求证:四边形为正方形.3.如图1,、是某地一个湖泊的两条互相垂直的湖堤,线段和曲线段分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥上某点分别修建与、平行的栈桥、,且以、为边建一个跨越水面的三角形观光平台.建立如图2所示的直角坐标系,测得线段的方程是,曲线段的方程是,设点的坐标为,记(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).(1)求的取值范围;(2)试写出三角形观光平台面积关于的函数解析式,并求出该面积的最小值.4.已知椭圆的右焦点为,点在圆上任意一点(点第一象限内),过点作圆的切线交椭圆于两点、.(1)证明:;(2)若椭圆离心率为,求线段长度的最大值.5.已知函数().(1)若,在上是单调增函数,求的取值范围;(2)若,求方程在上解的个数.6.已知数列单调递增,且各项非负,对于正整数,若任意的,(≤≤≤),仍是中的项,则称数列为“项可减数列”.(1)已知数列是首项为2,公比为2的等比数列,且数列是“项可减数列”,试确定的最大值;(2)求证:若数列是“项可减数列”,则其前项的和;(3)已知是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,并说明理由.7.已知矩阵,向量.求向量,使得.8.在直角坐标系中,直线的参数方程为(为参数),若以直角坐标系的点为极点,为极轴,且长度单位相同,建立极坐标系,得曲线的极坐标方程为.(1)求直线的倾斜角;(2)若直线与曲线交于两点,求9.学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设为选出的人中既会唱歌又会跳舞的人数,且.(1)求文娱队的队员人数;(2)写出的概率分布列并计算10.在数列和中,,,,其中且,.设,,试问在区间上是否存在实数使得.若存在,求出的一切可能的取值及相应的集合;若不存在,试说明理由.江苏高三高中数学高考模拟答案及解析一、填空题1.若复数满足(是虚数单位),则.【答案】.【解析】.2.已知全集,集合,,则中最大的元素是.【答案】3【解析】,,,.所以最大元素为3.3.直线与直线平行的充要条件是.【答案】-2.【解析】,当a=2时,两直线重合;当a=-2时,两直线平行4.设等比数列的前项和为,若,则数列的公比是.【答案】.【解析】当q=1时,.当时,,所以.5.如图,沿田字型的路线从往走,且只能向右或向下走,随机地选一种走法,则经过点的概率是.【答案】.【解析】从A到N共需要走四步,两横步,两纵步.共有,其中经过点C的走法有横竖横竖,横竖竖横,竖横横竖,竖横竖横共4种方法.所以所求事件的概率为.6.实数满足,则的值为.【答案】8.【解析】,7.与抛物线有且仅有一个公共点,并且过点的直线方程为.【答案】或y="1."【解析】设此直线方程为,它与抛物线方程联立消经得,,k=0时,符合要求,此时直线方程为y=1.当时,.所以直线方程为,即.所以所求直线方程为或y=1.8.空间三条直线中,任何两条不共面,且两两互相垂直,另一条直线与这三条直线所成的角均为,则.【答案】.【解析】在空间取一点分别作三条直线的平行线,然后构造一个正方体如右图所示,则直线OD所OA、OB、OC所成的角相等均为,则.9.将函数的图象向左平移至少个单位,可得一个偶函数的图象.【答案】.【解析】,设向左至少平移m(m>0)个单位,得到一个偶函数的图像,则平移后的函数解析式为,的最小值为10.将一个长和宽分别为的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则的取值范围是.【答案】.【解析】设正方形的边长为x,则,则此长方体的外接球直径最小时,其外接球的体积存在最小值.由于当时,2R才存在最小值,因为0<a<b,所以,所以11.在中,角所对边分别是,若,则.【答案】.【解析】,.12.已知函数是定义在上的增函数,函数的图象关于对称.若对任意的,不等式恒成立,则当时,的取值范围是.【答案】.【解析】的图象关于对称,所以的图像关于原点对称,所以y=f(x)是奇函数,并且是R上的增函数,所以所以,即,则当x>3时,由于点(3,2)到原点的距离为,半圆上的点到原点的最大距离为圆心(3,4)到原点的距离加上半径,即5+2=7,所以13.已知中,,为的外心,若点在所在的平面上,,且,则边上的高的最大值为.【答案】.【解析】取AC的中点为D,设的外接圆半径为R,则,设的夹角为,则.又因为所以所以R的最小值为,所以h的最大值为.14.各项为正数的数列,其前项的和为,且,若,且数列的前项的和为,则.【答案】.【解析】,数列是首项为,公差为的等差数列,所以,所以,.所以,所以二、解答题1.设函数,其中,若,且图象的一条对称轴离一个对称中心的最近距离是.(1)求函数的解析式;(2)若是的三个内角,且,求的取值范围【答案】(1).(2).【解析】(1)根据,可得,进而可确定.由题意知,进而可确定,所以解析式确定.(2) 根据,可确定,然后,再利用三角函数的性质求值域即可.(1)由条件,,……………………3分又图象的一条对称轴离一个对称中心的最近距离是,所以周期为,,.(2)由,知,是的内角,,,,从而.……………………………9分由,…………12分,,即.2.在所有棱长都相等的斜三棱柱中,已知,,且,连接.(1)求证:平面;(2)求证:四边形为正方形.【答案】(1)略(2)略【解析】(1)证明本小题的关键是证明,,再证,问题得证.(2)证明本小题的关键是证明:,进而关键是证明,从而说明其是矩形,又因为此四边形本身是菱形,所以所证四边形是正方形.问题得证(1)证明:因为是菱形,所以又,,所以因为,所以…………………4分因为,所以由,所以………………………8分(2)证明:因为,所以,……………………………10分又因为,所以,所以所以四边形为正方形3.如图1,、是某地一个湖泊的两条互相垂直的湖堤,线段和曲线段分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥上某点分别修建与、平行的栈桥、,且以、为边建一个跨越水面的三角形观光平台.建立如图2所示的直角坐标系,测得线段的方程是,曲线段的方程是,设点的坐标为,记(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).(1)求的取值范围;(2)试写出三角形观光平台面积关于的函数解析式,并求出该面积的最小值.【答案】(1)(2)225【解析】(1)先确定z关于x的函数关系式,因而要求y与x的等式关系消y.,然后要注意x 的取值范围.(2) ,,利用导数研究单调性再求其最值.(1),………………………2分由题知,在曲线段上,∴且,∴,………………………4分……………………7分(2)……10分时,,∴在上单调递减,∴4.已知椭圆的右焦点为,点在圆上任意一点(点第一象限内),过点作圆的切线交椭圆于两点、.(1)证明:;(2)若椭圆离心率为,求线段长度的最大值.【答案】(1)略(2)2表示出来.相加即【解析】(1) 设,先利用焦半径公式表示,然后再想法求出|PQ|,也用x1可.(2)根据离心率可求出a值,进而椭圆方程确定,然后设直线的方程为,由直线QR与圆O相切,进而得到,然后直线与椭圆方程联立,消y之后,表示出,则,,,因而确定当且仅当时,取最大值2.(1)设,得,…………………3分由是圆的切线,,注意到,,……………6分所以.……………7分(2)由题意,,.…………………………9分方法一:设直线的方程为,点在第一象限,.由直线与圆相切,.…………………………11分由,消得,设,则.由(1)知,,…14分,.当且仅当时,取最大值2,此时直线的方程为,过焦点.方法二:设,则直线的方程为.……11分由,消得,则,,,由(1)知,,……14分,,当且仅当时,取最大值2,此时,直线过焦点.方法三:由(1)同理可求,则,………11分,当且仅当直线过焦点时等号成立,从而.5.已知函数().(1)若,在上是单调增函数,求的取值范围;(2)若,求方程在上解的个数.【答案】(1).(2)当a≥3时,≥0,∴g(x)=0在上有惟一解.当时,<0,∴g(x)=0在上无解.【解析】(1)然后分别研究时,恒成立且时,恒成立时b的取值范围即可.(2) 构造函数,即分别研究和上的单调性,极值和最值.做出草图,数形结合解决即可(1)…………………2分①当时,,.由条件,得恒成立,即恒成立,∴.……………………4分②当时,,.由条件,得恒成立,即恒成立,∴b≥-2.综合①,②得b的取值范围是.……………6分(2)令,即………………8分当时,,.∵,∴.则.即,∴在(0,)上是递增函数.………………………10分当时,,.∴在(,+∞)上是递增函数.又因为函数在有意义,∴在(0,+∞)上是递增函数.………12分∵,而,∴,则.∵a≥2,∴,……14分当a≥3时,≥0,∴g(x)=0在上有惟一解.当时,<0,∴g(x)=0在上无解6.已知数列单调递增,且各项非负,对于正整数,若任意的,(≤≤≤),仍是中的项,则称数列为“项可减数列”.(1)已知数列是首项为2,公比为2的等比数列,且数列是“项可减数列”,试确定的最大值;(2)求证:若数列是“项可减数列”,则其前项的和;(3)已知是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,并说明理由.【答案】(1)2 (2).(3)(2)的逆命题为:已知数列为各项非负的递增数列,若其前项的和满足,则该数列一定是“项可减数列”,该逆命题为真命题.【解析】(1)根据题意可知,易得,即数列一定是“2项可减数列”.(2)因为数列是“项可减数列”,所以必定是数列中的项.而是递增数列,故,所以必有,,是解决本小题的关键.(3) 的逆命题为:已知数列为各项非负的递增数列,若其前项的和满足,则该数列一定是“项可减数列”,该逆命题为真命题.证明要注意利用≤≤,求出的通项公式.(1)设,则,易得,即数列一定是“2项可减数列”,但因为,所以的最大值为2.………………5分(2)因为数列是“项可减数列”,所以必定是数列中的项,………………………7分而是递增数列,故,所以必有,,则,所以,即.又由定义知,数列也是“项可减数列”,所以.……………………………10分(3)(2)的逆命题为:已知数列为各项非负的递增数列,若其前项的和满足,则该数列一定是“项可减数列”,该逆命题为真命题.……………………12分理由如下:因为≤≤,所以当≥时,,两式相减,得,即()则当时,有()由()-(),得,又,所以,故数列是首项为0的递增等差数列.设公差为,则,对于任意的≤≤≤,,因为≤,所以仍是中的项,故数列是“项可减数列”.7.已知矩阵,向量.求向量,使得.【答案】【解析】设出,根据=,得到方程组求解即可.,………………………4分设,则=……………8分,.8.在直角坐标系中,直线的参数方程为(为参数),若以直角坐标系的点为极点,为极轴,且长度单位相同,建立极坐标系,得曲线的极坐标方程为.(1)求直线的倾斜角;(2)若直线与曲线交于两点,求【答案】(1)(2)【解析】(1)可以先求出直线l的普通方程,即,所以斜率为,倾斜角为.(2)先求出曲线C的普通方程为,再求出圆心到直线l的距离d,进而利用即可求值.(1)设直线的倾斜角为,则且,,即直线的倾斜角为…………………………5分(2)的直角坐标方程为,的直角坐标方程为,所以圆心到直线的距离,9.学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设为选出的人中既会唱歌又会跳舞的人数,且.(1)求文娱队的队员人数;(2)写出的概率分布列并计算【答案】(1)2(2) 的概率分布列为:∴.【解析】(1)设既会唱歌又会跳舞的有人,则文娱队中共有()人,只会一项的人数是()人,再利用,∴,即,可解出x的值.(2)分别求出对应的概率,列出分布列,根据期望公式求期望即可.设既会唱歌又会跳舞的有人,则文娱队中共有()人,只会一项的人数是()人.………………2分(1)∵,∴,即.∴,解得.故文娱队共有5人.………………………5分(2),,………………………7分的概率分布列为:∴.10.在数列和中,,,,其中且,.设,,试问在区间上是否存在实数使得.若存在,求出的一切可能的取值及相应的集合;若不存在,试说明理由.【答案】在区间上存在实数,使成立,当时,;当时,【解析】设存在实数,使,设,则,且,设,,则,所以,因为,且,所以能被整除.然后分三种情况讨论(1) ;(2) ;(3) 进行研究.设存在实数,使,设,则,且,设,,则,所以,因为,且,所以能被整除…………………………4分(1)当时,因为,,所以;…………………………5分(2)当时,,由于,所以,,所以,当且仅当时,能被整除. …………………………7分(3)当时,,由于,所以,所以,当且仅当,即时,能被整除.………………9分综上,在区间上存在实数,使成立,当时,;当时,.。
苏教版高中数学立体几何与应用题

应用题专题训练:17.如图,已知矩形油画的长为a ,宽为b .在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x ,上下两边金箔的宽为y ,壁画的总面积为.S (1)用x ,y ,a ,b 表示S ;(2)若S 为定值,为节约金箔用量,应使四个矩形木雕的总面积最大.求四个矩形木雕总面积的最大值及对应的x ,y 的值. (X=2abs ab b -,y=2abs aba-时,面积有最大值ab+S-2abs )17.(本小题满分14分)某公司为了应对金融危机,决定适当进行裁员.已知这家公司现有职工m 2人(50060<<m ,且m 为10的整数倍),每人每年可创利100千元.据测算,在经营条件不变的前提下,若裁员人数不超过现有人数的%20,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的%20,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的%75.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.( I )设公司裁员人数为x ,写出公司获得的经济效益y (元)关于x 的函数(经济效益=在职人员创利总额—被裁员工生活费);( II)为了获得最大的经济效益,该公司应裁员多少人?(1)解:设公司裁员人数为x,获得的经济效益为y 元, 则由题意得当()()1022100205x m y m x x x <≤⨯=-+-时。
()()212210022054m x m y m x x x ≤≤⨯=-+-当时,① ②(2)由①得对称轴 600,x m =->当060100m <-≤,即60100m <≤时,60x m =-时,y取最大值21803600y m m =++,当100500m <<时,25x m =时,y 取最大值221615225y m m =+ 由②得对称轴30-=m x ,160500,302m m m ∴-><<23314022m x y y m m ∴==+当时,取得最大值()22231601000.56036000.56054000.5120540018000m y y m m m ≤-=+-=+->⨯-=>当<时,2323100500434312120,60m 5005050m y y m m m m y <<⎛⎫-=-=-><< ⎪⎝⎭当时,即当时,最大 即当公司应裁员数为m 21,即原有人数的41时,获得的经济效益最大。
江苏省盐城中学2023届高三全仿真模拟考试数学试题(含答案解析)

江苏省盐城中学2023届高三全仿真模拟考试数学试题学校:___________姓名:___________班级:___________考号:___________A .()2π123+7.已知0ε>,,x A .cos cos x y ≤二、多选题9.2022年11月,国内猪肉、鸡蛋、鲜果、禽肉、粮食、食用油、鲜菜价格同比(与去年同期相比)的变化情况如下图所示,则下列说法错误的是()A.猪肉、鸡蛋、鲜果、禽肉、粮食、食用油这6种食品中,食用油价格同比涨幅最小三、填空题四、双空题五、填空题六、解答题(1)证明:F为PD的中点;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线角的正弦值.条件①:三角形BCF的面积为-的体积为条件②:三棱锥P BCF注:如果选择条件①和条件②分别解答,按第一个解答计分19.深受广大球迷喜爱的某支欧洲足球队,在对球员的使用上总是进行数据分析,为了考查甲球员对球队的贡献,现作如下数据统计:球队胜球队负甲参加22b(1)求 BC的长度;(2)为满足市民健康生活需要,提升城市品位,改善人居环境,现计划新建健康步道--(B,D在AC两侧),其中AD,CDA D C参考答案:故选:AC.11.ABC【分析】分点A在圆外,圆内(非原点)【详解】当点A在圆外,如下图所示:设=,则连接AQ,则PQ AQ为焦点的双曲线;+=当点A在圆内(非原点),如下图所示,此时QA OQ则此时Q轨迹为以,O A为焦点的椭圆;OQ=当A在坐标原点,如下图所示,此时B,Q重合,则2半径为2的圆;当A 在圆上,由垂径定理,可知Q 点与O 重合,此时Q 的轨迹为点O .故选:ABC 12.BC【分析】对于A ,由题意,作图,根据对称性以及公共点所在区间,可得答案;对于B ,由题意,作图,可得函数在3x x =处相切,可得方程,结合三角恒等式,可得答案;对于C ,根据函数与方程的关系,两函数作差构造新函数,利用导数研究其零点个数,可得答案;对于D ,利用三角函数的值域与周期性,可得答案.【详解】对于A ,当4n =时,如下图,则10x =,4π2πx <<,所以142πx x +<,又()f x 图像关于πx =对称,结合图像有32ππx x ->-,即有32142πx x x x +>>+,故A 错误;对于B ,当3n =时,如下图,易知在3x x =,且()3π,2πx ∈,()f x 与()g x 图像相切,由当(),2x ∈ππ时,()sin f x x =-,则()cos f x x '=-,()g x k '=,所以1n =时,1k ≥,故C 正确;对于D ,当22023πk =时,由2023π2023π()22f g ⎛= ⎝()f x 与()g x 的图像在y 轴右侧的前1012个周期中,每个周期均有公共点,故D 错误.故选:BC.【点睛】关键点晴:对于选项A 和D ,处理的关键在于,借助函数图像的对称性和周期性解决问题;对于选项B 和D 13.10【分析】求数据中的四分位数得5n =,利用二项式展开式通项求常数项即可【详解】由题设675% 4.5⨯=,则5n =,所以,5212x x ⎛⎫+ ⎪⎝⎭展开式通项为2515C (2)(r r r T x -+=当4r =,则4552C 10T ==,即常数项为10.故答案为:1014.23--/32--因为菱形的四条边相等,对角线互相垂直ABC -中,面ADC 与面ABC 的面积是确定的,所以要使三棱锥表面积最大,则需与面DAB 最大即可,而且DCB DAB S S = ;sin DCB DC BC ∠⋅⋅,当π2DCB ∠=时,DBC S △取得最大值向平面ABC 作垂线,设AC 的中点为E 垂足为D ¢,因为2DB =,32EB ED ==,所以由余弦定理知cos BED ∠所以22sin 3DED '∠=,易得63DD '=.所以1361823433612D ABC V -=⨯⨯==.因为12ABD BDC S S == ,34ABC ADC S S ==设内切球的半径为r ,则根据等体积法,有:1113222323412r r ⎛⎫⎛⎫⨯⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭,即323612r r +=,解之得2423r =+,所以其内切球的表面积为224π4π42S r ⎛== +⎝故答案为:()1483π-17.(1)2352n a n n =-+选①,则1102BCF S CF BC =⋅= ,故选②,由1132P BCF B PCF V V BC --==⋅此时,3(0,,1)2E ,(2,3,0)B ,则EB 又(0,1,0)m =是面PAD 的一个法向量,若直线所以32sin ||||||9414EB m EB m θ⋅===++ 19.(1)8b c ==,20d e ==,n =(2)①0.68;②317;③乙球员担当中锋【分析】(1)利用给定的数表求值即可,再计算(2)①利用全概率公式计算即可;②利用条件概率公式计算即可;③利用条件概率公式计算,再比较大小即可判断作答.【详解】(1)由列联表中的数据,222cos 16122BC AC AB AC AB BAC =+-⋅⋅∠=+-所以 12π1π2BC =⨯⨯⨯=,即 BC的长度为(πkm (2)①方案一:因为3tan tan tan tan αβαβ--则()tan tan 31tan tan αβαβ+=--,所以(tan αβ+又()0,παβ+∈,所以2π3αβ+=,记AD a =,CD b =,则在ACD 中,由余弦定理可得即2216a b ab +-=,从而()221631632a b a b ab +⎛⎫+=+≤+ ⎪⎝⎭,所以(14时,等号成立;所以新建健康步道A D C --的最长路程为(8km 即新建的健康步道A D C --的路程最多可比原有健康步道②方案二:因为()π2sin sin 3cos 3βαβ⎛⎫-=-- ⎪⎝⎭即ππ2sin 2sin 33βαβ⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭,又CDA 为锐角三角形,π02β<<,π02α<<则πππ336β-<-<,5πππ663αβ-<--<,所以22.(1)23b a =--;4a <-,()f x 的单调递增区间为为[1,3]a --;当4a >-时,()f x 的单调递增区间为[3,1]a --;(2)221111e e a -+<<+.。
江苏省各地2019届高考模拟考试数学试题分类汇编:立体几何(含答案)

第 1 页 共 10 页 江苏省各地2019届高考模拟考试数学试题分类汇编:立体几何一、填空题1、(南京市、盐城市2019届高三第二次模拟)已知正四棱锥P ABCD -的所有棱长都相等,高为2,则该正四棱锥的表面积为 .2、(南京市2019届高三第三次模拟)有一个体积为2的长方体,它的长、宽、高依次为a ,b ,1.现将它的长增加1,宽增加2,且体积不变,则所得新长方体高的最大值为 .3、(南通、如皋市2019届高三下学期语数英学科模拟(二))已知一个圆锥的底面半径为3cm ,侧面积为6πcm 2,则该圆锥的体积是__cm 3。
4、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第一次模拟(2月)) 已知正四棱柱的底面边长是3 cm ,侧面的对角线长是35cm ,则这个正四棱柱的体积为 cm 3.5、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第二次模拟) 设P ,A ,B ,C 为球O 表面上的四个点,PA ,PB ,PC 两两垂直,且PA = 2 m ,PB = 3 m , PC = 4 m ,则球O 的表面积为 m 2.6、(七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第二次模拟(5月)) 已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =3 cm ,BC =1 cm ,CD =2 cm .将此直角梯形 绕AB 边所在的直线旋转一周,由此形成的几何体的体积为 cm 3.7、(苏锡常镇四市2019届高三教学情况调查(一))已知圆柱的轴截面的对角线长为2,则这个圆柱的侧面积的最大值为8、(盐城市2019届高三第三次模拟)如图所示,三棱柱ABC-A 1B 1C 1的体积为6,O 为四边形BCC 1B 1的中心,则四面体A 1B 1OB 的体积为____.9、(江苏省2019年百校大联考)如图所示的四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 是矩形,2AB =,3AD =,点E 为棱CD 上一点,若三棱锥E PAB -的体积为4,则PA 的长为 .。
江苏省2022届高三数学下学期模拟模拟试题分类汇编几何证明选讲
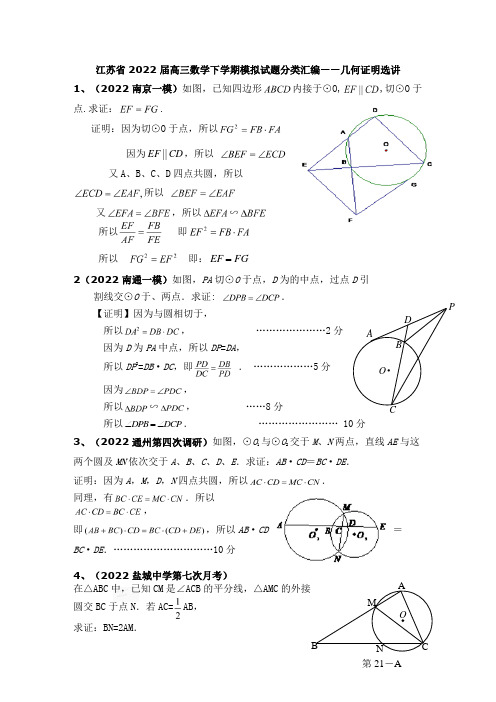
PADB CO ·江苏省2022届高三数学下学期模拟试题分类汇编——几何证明选讲 1、(2022南京一模)如图,已知四边形内接于⊙O,,切⊙O 于点.求证:.证明:因为切⊙O 于点,所以 因为CD EF ||,所以又A 、B 、C 、D 四点共圆,所以所以又,所以∽所以 即所以即:FG EF =2(2022南通一模)如图,PA 切⊙O 于点,D 为的中点,过点D 引割线交⊙O 于、两点.求证: .【证明】因为与圆相切于, 所以, …………………2分因为D 为PA 中点,所以DP =DA ,所以DP 2=DB ·DC ,即 . ………………5分因为,所以∽, ……8分所以DPB DCP ∠=∠. …………………… 10分3、(2022通州第四次调研)如图,⊙O 1与⊙O 2交于M 、N 两点,直线AE 与这两个圆及MN 依次交于A 、B 、C 、D 、E .求证:AB ·CD =BC ·DE . 证明:因为A ,M ,D ,N 四点共圆,所以.同理,有.所以,即,所以AB ·CD=BC ·DE .…………………………10分4、(2022盐城中学第七次月考)在△ABC 中,已知CM 是∠ACB 的平分线,△A MC 的外接 圆交BC 于点N .若AC=AB ,求证:BN=2AM .ABCMN 第21-A 题O证明:如图,在△ABC中,因为CM是∠ACM的平分线,所以.又已知,所以…①…………………… 4分又因为BA与BC是圆O过同一点B的弦,所以,即……②………………………………8分由①、②可知,,所以BN=2AM.………………………………10分5、(2022江苏百校高三样本分析考试)如图,在Rt△ABC 中,∠=,BE平分∠ABC交AC于点E,点D在AB 上,.C90(1)求证:AC是△BDE的外接圆的切线;(2)若,求EC的长.解(1)取BD的中点O,连接OE.∵BE平分∠ABC,∴∠CBE=∠OBE.又∵OB=OE,∴∠OBE=∠BEO,∴∠CBE=∠BEO,∴BC∥OE. (3)分∵∠C=90°,∴OE⊥AC,∴AC是△BDE的外接圆的切线. (5)分(2)设⊙O的半径为r,则在△AOE中,,即,解得, ………………………7分∴OA=2OE,∴∠A=30°,∠AOE=60°.∴∠CBE=∠OBE=30°.∴EC=.………………………10分内容总结(1)10分。
【创新设计】江苏高考数学理二轮专题复习演练6.3解析几何的综合应用(含答案解析)

第3讲 解析几何的综合应用1.(2013·济南3月模拟)若双曲线x 2a 2-y 2b 2=1(a >0,b >0)与直线y =3x 无交点,则离心率e 的取值范围是 ________.解析 因为双曲线的渐近线为y =±ba x ,要使直线y =3x 与双曲线无交点,则直线y =3x 应在两渐近线之间,所以有ba ≤3,即b ≤3a ,所以b 2≤3a 2, ∴c 2-a 2≤3a 2,则c 2≤4a 2,故1<e ≤2. 答案 (1,2]2.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为 ________. 解析 设C :x 2a 2-y 2a 2=1.∵抛物线y 2=16x 的准线为x =-4,联立x 2a 2-y 2a 2=1和x =-4得A (-4,16-a 2),B (-4,-16-a 2),∴|AB |=216-a 2=43,∴a =2,∴2a =4.∴C 的实轴长为4. 答案 43.(2013·四川改编)从椭圆x 2a 2+y 2b 2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x 轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是 ________.解析 由题意可设P (-c ,y 0)(c 为半焦距),k OP =-y 0c ,k AB =-ba ,由于OP ∥AB ,∴-y 0c =-b a ,y 0=bc a ,把P ⎝ ⎛⎭⎪⎫-c ,bc a 代入椭圆方程得(-c )2a 2+⎝ ⎛⎭⎪⎫bc a 2b 2=1,因而⎝ ⎛⎭⎪⎫c a 2=12,∴e =c a =22.答案 224.在抛物线y =2x 2上有一点P ,它到A (1,3)的距离与它到焦点的距离之和最小,则点P 的坐标是 ________.解析 显然点A 在抛物线y =2x 2内部,如图,过点A 作准线l 的垂线AH ,垂足为H ,交抛物线于P .由抛物线定义,|PF |=|PH |, ∴(|P A |+|PF |)min =|PH |+|P A |=|AH |, 将x =1代入y =2x 2,得y =2, ∴点P 的坐标为(1,2). 答案 (1,2)5.(2013·潍坊质检)已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2.若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为 ________.解析 ∵双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2, ∴c a =a 2+b 2a=2,∴b =3a , ∴双曲线的渐近线方程为3x ±y =0,∴抛物线C 2:x 2=2py (p >0)的焦点⎝ ⎛⎭⎪⎫0,p 2到双曲线的渐近线的距离为⎪⎪⎪⎪⎪⎪3×0±p 22=2,∴p =8. ∴所求的抛物线方程为x 2=16y .答案 x 2=16y6.椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别是A 、B ,左、右焦点分别是F 1、F 2.若|AF 1|,|F 1F 2|,|F 1B |成等比数列,则此椭圆的离心率为________.解析 由题意知|AF 1|=a -c ,|F 1F 2|=2c ,|F 1B |=a +c ,且三者成等比数列,则|F 1F 2|2=|AF 1|·|F 1B |,即4c 2=a 2-c 2,a 2=5c 2,所以e 2=15,所以e =55. 答案 557.(2013·浙江)设F 为抛物线C :y 2=4x 的焦点,过点P (-1,0)的直线l 交抛物线C 于A 、B 两点,点Q 为线段AB 的中点,若|FQ |=2,则直线l 的斜率等于________.解析 设直线l 的方程为y =k (x +1),A (x 1,y 1)、B (x 2,y 2)、Q (x 0,y 0). 解方程组⎩⎪⎨⎪⎧y =k (x +1),y 2=4x .化简得:k 2x 2+(2k 2-4)x +k 2=0, ∴x 1+x 2=4-2k 2k 2, y 1+y 2=k (x 1+x 2+2)=4k , ∴x 0=2-k 2k 2,y 0=2k , 由(x 0-1)2+(y 0-0)2=2得:⎝ ⎛⎭⎪⎫2-2k 2k 22+⎝ ⎛⎭⎪⎫2k 2=4.∴k =±1. 答案 ±18.已知椭圆x 24+y 2b 2=1(0<b <2)与y 轴交于A ,B 两点,点F 为该椭圆的一个焦点,则△ABF 面积的最大值为________. 解析 不妨设点F 的坐标为(4-b 2,0),而|AB |=2b , ∴S △ABF =12×2b ×4-b 2=b4-b 2=b 2(4-b )2≤b 2+4-b 22=2(当且仅当b 2=4-b 2.即b =2时取等号).故△ABF 面积的最大值为2. 答案 29.已知抛物线C 的顶点为O (0,0),焦点为F (0,1).(1)求抛物线C 的方程;(2)过点F 作直线交抛物线C 于A ,B 两点.若直线AO 、BO 分别交直线l :y =x -2于M 、N 两点,求|MN |的最小值.解 (1)由题意可设抛物线C 的方程为x 2=2py (p >0),则p2=1,所以抛物线C 的方程为x 2=4y . (2)设A (x 1,y 1),B (x 2,y 2),直线AB 的方程为y =kx +1. 由⎩⎨⎧y =kx +1,x 2=4y 消去y ,整理得x 2-4kx -4=0, 所以x 1+x 2=4k ,x 1x 2=-4. 从而|x 1-x 2|=4k 2+1. 又y =y 1x 1x ,且y =x -2,解得点M 的横坐标x M =2x 1x 1-y 1=2x 1x 1-x 124=84-x 1. 同理点N 的横坐标x N =84-x 2. 所以|MN |=2|x M -x N | =2⎪⎪⎪⎪⎪⎪84-x 1-84-x 2=82⎪⎪⎪⎪⎪⎪x 1-x 2x 1x 2-4(x 1+x 2)+16 =82·k 2+1|4k -3|,令4k -3=t ,t ≠0,则k =t +34. 当t >0时,|MN |=2225t 2+6t +1>2 2. 当t <0时,|MN |=22⎝ ⎛⎭⎪⎫5t +352+1625≥852. 综上所述,当t =-253,即k =-43时, |MN |取到最小值, 且|MN |的最小值是85 2.10.(2013·北京)已知A ,B ,C 是椭圆W :x 24+y 2=1上的三个点,O 是坐标原点.(1)当点B 是W 的右顶点,且四边形OABC 为菱形时,求此菱形的面积; (2)当点B 不是W 的顶点时,判断四边形OABC 是否可能为菱形,并说明理由.解 (1)椭圆W :x 24+y 2=1的右顶点B 的坐标为(2,0). 因为四边形OABC 为菱形,所以AC 与OB 相互垂直平分. 所以可设A (1,m ),代入椭圆方程得14+m 2=1, 即m =±32.所以菱形OABC 的面积是12|OB |·|AC |=12×2×2|m |= 3. (2)假设四边形OABC 为菱形.因为点B 不是W 的顶点,且直线AC 不过原点,所以可设AC 的方程为y =kx +m (k ≠0,m ≠0),由⎩⎨⎧x 2+4y 2=4,y =kx +m ,消y 并整理得(1+4k 2)x 2+8kmx +4m 2-4=0. 设A (x 1,y 1),C (x 2,y 2),则x 1+x 22=-4km 1+4k 2,y 1+y 22=k ·x 1+x 22+m =m1+4k 2. 所以AC 的中点为M ⎝ ⎛⎭⎪⎫-4km 1+4k 2,m 1+4k 2. 因为M 为AC 和OB 的交点,所以直线OB 的斜率为-14k . 因为k ·⎝ ⎛⎭⎪⎫-14k ≠-1,所以AC 与OB 不垂直. 所以四边形OABC 不是菱形,与假设矛盾.所以当点B 不是W 的顶点时,四边形OABC 不可能是菱形. 11.(2013·浙江)如图,点P (0,-1)是椭圆C 1:x 2a 2+y 2b2=1(a >b >0)的一个顶点,C 1的长轴是圆C 2:x 2+ y 2=4的直径.l 1,l 2是过点P 且互相垂直的两条直 线,其中l 1交圆C 2于A ,B 两点,l 2交椭圆C 1于 另一点D .(1)求椭圆C 1的方程;(2)求当△ABD 的面积取最大值时,直线l 1的方程. 解 (1)由题意得⎩⎨⎧b =1,a =2.所以椭圆C 的方程为x 24+y 2=1. (2)设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0). 由题意知直线l 1的斜率存在,不妨设其为k , 则直线l 1的方程为y =kx -1. 又圆C 2:x 2+y 2=4, 故点O 到直线l 1的距离 d =1k 2+1,所以|AB |=24-d 2=24k 2+3k 2+1. 又l 2⊥l 1,故直线l 2的方程为x +ky +k =0. 由⎩⎨⎧x +ky +k =0,x 2+4y 2=4. 消去y ,整理得(4+k 2)x 2+8kx =0, 故x 0=-8k 4+k 2.所以|PD |=8k 2+14+k 2.设△ABD 的面积为S ,则 S =12·|AB |·|PD |=84k 2+34+k 2,所以S =324k 2+3+134k 2+3≤3224k 2+3·134k 2+3=161313,当且仅当k =±102时取等号.所以所求直线l 1的方程为y =±102x -1.。
江苏省各地2020年高考模考试题汇编第3部分立体几何旧人教版

2020 年江苏各地高考模考试题汇编第 3 部分立体几何旧人教版(江苏最后 1 卷)给出以下四个命题:( 1)假如平面与平面订交,那么平面内全部的直线都与平面订交( 2)假如平面⊥平面,那么平面内全部直线都垂直于平面( 3)假如平面⊥平面,那么平面内与它们的交线不垂直的直线与平面也不垂直( 4)假如平面不垂直于平面,那么平面内必定不存在直线垂直于平面真命题的序号是▲.(写出全部真命题的序号)...【答案】( 3)( 4)(南师大信息卷)在棱长为 1 的正方体ABCD A1B1C1D1中,若点P是棱上一点,则知足PA PC1 2 的点 P 的个数为 6 .提示:点 P 在以AC1为焦点的椭圆上, P 分别在 AB 、 AD 、AA1、 C1B1、 C1D1、 C1C 上.或许,若 P 在 AB 上,设 AP x ,有 PA PC1x(1 x)2( 2)22, x 1 .2故 AB 上有一点 P ( AB 的中点)知足条件.同理在 AD 、AA1、C1B1、C1D1、C1C上各有一点知足条件.又若点 P 在BB1上上,则 PA PC11BP2 1 B1P22.故 BB1上不存在知足条件的点P ,同理DD1上不存在知足条件的点P .(南通三模)已知正方体C1的棱长为 18 2 ,以 C1各个面的中心为极点的凸多面体为C2,以 C2各个面的中心为极点的凸多面体为C3,以 C3各个面的中心为极点的凸多面体为C4,依此类推。
记凸多面体C n的棱长为 a n,则 a6=▲ .分析:考察推理方法以及几何体中元素的关系理解应用。
正方体C1的棱长为a1A1B118 2 ,由C1各个面的中心为极点的几何体为正八面体 C2,其棱长a2A2 B22A1 B1 18 ,由 C 2各个面的中心为极点的几何体为正方体C3,其棱长2B2B2A2A3A2B3A2A3B3A1B1B2a3 A3 B32A2 B2 6 2 ,这样类推:获得a46, a5 2 2, a62。
江苏省13市高三第一次模拟考试数学试题分类汇编(新高考):立体几何

江苏省13市高三第一次模拟考试数学试题分类汇编立体几何(地区名后面,题号1-8为单选,9-12为多选)1.(2021·扬州·一模)13.已知一个圆锥的侧面积为6π,它的侧面展开图是一个半圆,则此圆锥的体积为.2.(2021·扬州·一模)12.我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相切的称为棱切球,设下列“等长正棱柱(锥)”的棱长都为1,则下列说法中正确的有()AB.正四面体的棱切球的表面积为2πC.等长正六棱柱的棱切球的体积为4 3πD.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为7 12π3.(2021·盐城、南京·一模)8.已知点A,B,C,D在球O的表面上,AB⊥平面BCD,BC⊥CD,若AB=2,BC=4,AC与平面ABD,则球O表面上的动点P到平面ACD距离的最大值为A.2 B.3 C.4 D.54.(2021·无锡·一模)15.我国南北朝时代的祖暅提出“幂势既同,则积不容异”,即祖暅原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等(如图1).在xOy平面上,将双曲线的一支2214xy-=及其渐近线12y x=和直线y=0,y= 2围成的封闭图形记为D,如图2中阴影部分.记D绕y轴旋转一周所得的几何体为Ω,利用祖暅原理试求Ω的体积为________.图1 图25. (2021·苏州·一模)16.如图,已知球O 的半径为√5,圆O 1,O 2为球O 的两个半径均为2的截面圆,圆面O 、圆面O 1、圆面O 2两两垂直,点A ,B 分别为圆O 与圆O 1,O 2的交点,P ,Q 两点分别从A ,B 同时出发,按箭头方向沿圆周O 1,O 2以每秒π6弧度的角速度运动,直到两点回到起始位置时停止运动,则其运动过程中线段PQ 长度的最大值为 ;研究发现线段PQ 长度最大的时刻有两个,则这两个时刻的时间差为秒.(本小题第一空2分,第二空3分)6. (2021·无锡·一模)11.如图,正四棱锥S -BCDE 底面边长与侧棱长均为a ,正三棱锥A -SBE 底面边长与侧棱长均为a ,则下列说法正确的是( )A .AS ⊥CDB .正四棱锥S -BCDE 的外接球半径为22aC .正四棱锥S -BCDE 的内切球半径为212a⎛⎫- ⎪ ⎪⎝⎭ D .由正四棱锥S -BCDE 与正三棱锥A -SBE 拼成的多面体是一个三棱柱7. (2021·苏州·一模)12.在长方体ABCD —A 1B 1C 1D 1中,已知AA 1=AB =2AD =2,E ,F 分别为BB 1,D 1C 1的中点,则A .EF ⊥ECB .BD ∥平面AEFC .三棱锥C 1—CEF 外接球的表面积为5πD.平面A1BCD1被三棱锥C1—CEF外接球截得的截面圆面积为9π88.(2021·苏州·一模)8.我国南北朝时期的数学家祖暅在计算球的体积时,提出了一个原理(祖暅原理):“幂势既同,则积不容异”.这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形,模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为A.23B.43C.π3D.2π39.(2021·南通、徐州、宿迁、淮安、泰州、镇江·一模)16.已知在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切.过直线O1O2的平面截圆柱得到四边形ABCD,其面积为8.若P为圆柱底面圆弧CD的中点,则平面PAB与球O的交线长为.10.(2021·南通、徐州、宿迁、淮安、泰州、镇江·一模)9.已知m,n是两条不重合的直线,α,β是两个不重合的平面,则A.若m∥α,n∥α,则m∥nB.若m∥α,m⊥β,则α⊥βC.若α∥β,m⊥α,n⊥β,则m∥nD.若α⊥β,m∥α,n∥β,则m⊥n11.(2021·连云港·一模)11.如图,直三棱柱ABC—A1B1C1中,AC=BC=1,AA1=2,D是棱AA1的中点,DC1⊥BD.则A.直线DC1与BC所成角为90°B.三棱锥D—BCC1的体积为1 3C.二面角A1—BD—C1的大小为60°D.直三棱柱ABC—A1B1C1外接球的表面积为6π12.(2021·常州·一模)13.圆柱上、下底面的圆周都在一个体积为5003π的球面上,圆柱底面直径为8,则该圆柱的表面积为.13.(2021·南通、徐州、宿迁、淮安、泰州、镇江·一模)20.(本小题满分12分)如图,在正六边形ABCDEF中,将△ABF沿直线BF翻折至△A′BF,使得平面A′BF⊥平面BCDEF,O,H分别为BF和A′C的中点.(1)证明:OH∥平面A′EF;(2)求平面A′BC与平面A′DE所成锐二面角的余弦值.14.(2021·苏州·一模)21.(本小题满分12分)如图,四棱锥P—ABCD的底面ABCD是边长为2的正方形,PA=PB=3.(1)证明:∠PAD=∠PBC;(2)当直线PA与平面PCD所成角的正弦值最大时,求此时二面角P—AB—C的大小.15. (2021·连云港·一模)20.(本小题满分12分)如图,在三棱锥P —ABC 中,AB =BC =BAC =4,PA =PB =PC =4. (1)证明:平面PAC ⊥平面ABC ;(2)若点M 在棱BC 上,PC 与平面PAM CM 的长.16. (2021·常州·一模)20.(本小题满分12分)如图,在四棱锥P —ABCD 中,底面四边形ABCD 是矩形,AB =AP =2BC ,平面PAB ⊥平面ABCD ,二面角P —BC —A 的大小为45°.(1)求证:PA ⊥平面ABCD ;(2)求直线PB 与平面PAC 所成的角的正弦值.17.(2021·无锡·一模)19.(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠BAD=120°,AB=AD=2,点M在线段PD上,且DM=2MP,PB∥平面MAC.(1)求证:平面MAC⊥平面PAD;(2)若PA=3,求平面PAB和平面MAC所成锐二面角的余弦值.18.(2021·盐城、南京·一模)19.(本小题满分12分)如图,在五面体ABCDEF中,四边形ABEF为正方形,平面ABEF⊥平面CDFE,CD∥EF,DF⊥EF,EF=2CD=2.(1)若DF=2,求二面角A-CE-F的正弦值;(2)若平面ACF⊥平面BCE,求DF的长.19.(2021·扬州·一模)19.(本小题满分12分)如图,在三棱锥A-BCD中,△ABD与△B C D都为等边三角形,平面ABD⊥平面BCD,M,O分别为AB,BD的中点,AO∩DM =G,N在棱CD上且满足2CN=ND,连接MC,GN.(1)证明:GN∥平面ABC;(2)求直线AC和平面GND所成角的正弦值.。
江苏省高考模拟应用题大全数学试卷(四)
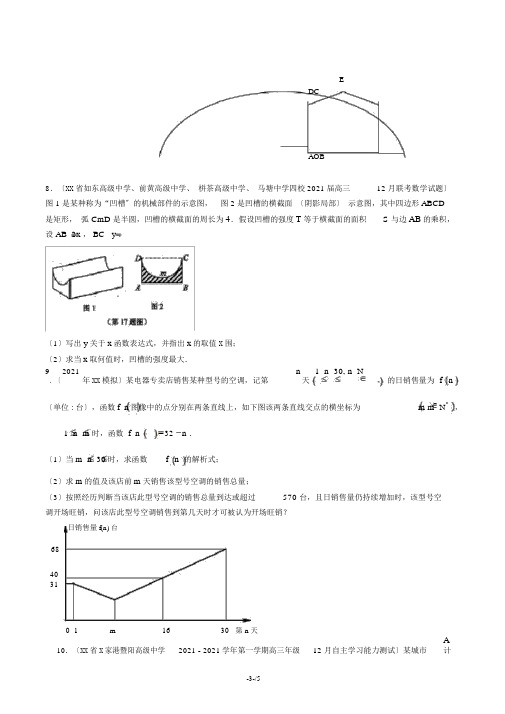
EDCAO B8.〔XX省如东高级中学、前黄高级中学、栟茶高级中学、马塘中学四校2021届高三12 月联考数学试题〕图 1 是某种称为“凹槽〞的机械部件的示意图,图 2 是凹槽的横截面〔阴影局部〕示意图,其中四边形ABCD 是矩形,弧 CmD 是半圆,凹槽的横截面的周长为4.假设凹槽的强度T等于横截面的面积S 与边AB的乘积,设 AB 2x , BC y .〔1〕写出y关于x函数表达式,并指出x的取值X围;〔2〕求当x取何值时,凹槽的强度最大.92021年XX模拟〕某电器专卖店销售某种型号的空调,记第n天1 n 30, n N*的日销售量为f n.〔〔单位 : 台〕,函数f n图像中的点分别在两条直线上,如下图该两条直线交点的横坐标为m m N*,1 n m 时,函数 f n32n .〔1〕当m n 30时,求函数f n 的解析式;〔2〕求m的值及该店前m天销售该型号空调的销售总量;〔3〕按照经历判断当该店此型号空调的销售总量到达或超过570 台,且日销售量仍持续增加时,该型号空调开场旺销,问该店此型号空调销售到第几天时才可被认为开场旺销?日销售量f(n) 台6840310 1m1630 第 n天A划每天从蔬菜基地B 处给本市供给蔬菜,为此,准备从主干道AD 的C处〔不在端点A 、 D 处〕做一条道路 CB ,主干道AD的长为 60 千米,设计路线如下图,测得蔬菜基地B 在城市 A 的东偏北60处, AB长为 60 千米,设BCD,运输汽车在主干道AD 上的平均车速为60 千米/小时,在道路 CB 上的平均车速为 20千米/小时.⑴求运输汽车从城市A 到蔬菜基地 B 处所用的时间t 关于的函数关系式t( ) ,并指出其定义域;⑵求运输汽车从城市A 到蔬菜基地 B 处所用的时间t 的最小11.【2021XX 4 月质检】某公司生产一种产品,第一年投入资金1000 万元,出售产品收入40 万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80 万元,同时,当预计投入的资金低于20 万元时,就按 20 万元投入,且当年出售产品收入与上一年相等.〔1〕求第n年的预计投入资金与出售产品的收入;〔2〕预计从哪一年起该公司开场盈利?〔注:盈利是指总收入大于总投入〕12.〔2021XX模拟〕如图,欲在一四边形花坛ABCD 内挖一个等腰三角形的水池AQR AQ A R ,四边形 ABCD 中,△ABD 是等腰直角三角形,AB AD 6 2 米,△ BCD 是等腰三角形,CB CD ,角C 的大小为 arctan 24,要求△ AQR 的三个顶点在花坛的边缘上,设水池底边QR 到点A的距离为 h 米,水7池的面积为 S 平方米.(1〕试将S表示成关于h的函数;(2〕当h为多少米时,S能取到最大值?求出最大值 .13.〔XX省启东中学2021届高三上学期第一次月考数学〔理〕试卷〕如图,某城市设立以城中心O 为圆心、 r 公里为半径圆形保护区,从保护区边缘起,在城中心O 正东方向上一条高速公路PB 、西南方向上有一条一级公路QC ,现要在保护区边缘 PQ 弧上选择一点A作为出口,建一条连接两条公路且与圆 O 相切直道BC .通往一级公路道路 AC 每公里造价为 a 万元,通往高速公路的道路AB每公里造价为 m2 a 万元,...划每天从蔬菜基地B 处给本市供给蔬菜,为此,准备从主干道AD 的C处〔不在端点A 、 D 处〕做一条道路 CB ,主干道AD的长为 60 千米,设计路线如下图,测得蔬菜基地B 在城市 A 的东偏北60处, AB长为 60 千米,设BCD,运输汽车在主干道AD 上的平均车速为60 千米/小时,在道路 CB 上的平均车速为 20千米/小时.⑴求运输汽车从城市A 到蔬菜基地 B 处所用的时间t 关于的函数关系式t( ) ,并指出其定义域;⑵求运输汽车从城市A 到蔬菜基地 B 处所用的时间t 的最小11.【2021XX 4 月质检】某公司生产一种产品,第一年投入资金1000 万元,出售产品收入40 万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80 万元,同时,当预计投入的资金低于20 万元时,就按 20 万元投入,且当年出售产品收入与上一年相等.〔1〕求第n年的预计投入资金与出售产品的收入;〔2〕预计从哪一年起该公司开场盈利?〔注:盈利是指总收入大于总投入〕12.〔2021XX模拟〕如图,欲在一四边形花坛ABCD 内挖一个等腰三角形的水池AQR AQ A R ,四边形 ABCD 中,△ABD 是等腰直角三角形,AB AD 6 2 米,△ BCD 是等腰三角形,CB CD ,角C 的大小为 arctan 24,要求△ AQR 的三个顶点在花坛的边缘上,设水池底边QR 到点A的距离为 h 米,水7池的面积为 S 平方米.(1〕试将S表示成关于h的函数;(2〕当h为多少米时,S能取到最大值?求出最大值 .13.〔XX省启东中学2021届高三上学期第一次月考数学〔理〕试卷〕如图,某城市设立以城中心O 为圆心、 r 公里为半径圆形保护区,从保护区边缘起,在城中心O 正东方向上一条高速公路PB 、西南方向上有一条一级公路QC ,现要在保护区边缘 PQ 弧上选择一点A作为出口,建一条连接两条公路且与圆 O 相切直道BC .通往一级公路道路 AC 每公里造价为 a 万元,通往高速公路的道路AB每公里造价为 m2 a 万元,。
江苏省高考数学提分专练:第19题 空间几何(解答题)

江苏省高考数学提分专练:第19题空间几何(解答题)姓名:________ 班级:________ 成绩:________一、真题演练 (共6题;共45分)1. (10分) (2016高二上·绍兴期中) 一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为a的正方形.(1)请在指定的框内画出多面体的俯视图;(2)若多面体底面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;(3)求该多面体的表面积.2. (10分)(2017·重庆模拟) 在斜三棱柱ABC﹣A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.(1)证明:平面A′DE⊥平面BCC′B′;(2)求二面角D﹣B′C﹣B的正弦值.3. (5分) (2017高一下·汽开区期末) 如图,在四棱锥P−ABCD中,AB∥CD ,且∠BAP=∠CDP =90°.(1) .证明:平面PAB⊥平面PAD;(2) .若PA=PD=AB=DC, ∠APD =90°,且四棱锥P−ABCD的体积为 ,求该四棱锥的侧面积.4. (5分) (2017高一上·福州期末) 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:(1)直线EF∥平面PCD;(2)平面BEF⊥平面PAD.5. (10分) (2016高二上·中江期中) 如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD 且PD=AD=2EC=2.(I)求证:AC⊥平面PDB;(II)求四棱锥B﹣CEPD的体积;(III)求该组合体的表面积.6. (5分)如图,四边形是正方形,△ 与△ 均是以为直角顶点的等腰直角三角形,点是的中点,点是边上的任意一点.(1)求证:;(2)求二面角的平面角的正弦值.二、模拟实训 (共9题;共90分)7. (10分)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,E在B1D1上,且ED1=2B1D,AC与BD交于点O.(Ⅰ)求证:AC⊥平面BDD1B1;(Ⅱ)求三棱锥O﹣CED1的体积.8. (10分) (2020高二上·舟山期末) 如图,在四棱锥中,四边形为平行四边形,为边长为2的等边三角形,O为的中点,平面 .(1)求证:;(2)当四边形为菱形时,求与平面所成角大小的正弦值.9. (10分) (2017高二下·新乡期末) 如图,在四面体P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= .(1)求证:PA⊥BD;(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.10. (10分)(2020·安徽模拟) 如图所示,在多面体中,平面,,点M在上,点N是的中点,且,且 .(Ⅰ)证明:平面;(Ⅱ)求二面角的余弦值.11. (10分)(2017·和平模拟) 如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB∥DC,DA⊥AB,AB=AP=2,DA=DC=1,E为PC上一点,且PE= PC.(Ⅰ)求PE的长;(Ⅱ)求证:AE⊥平面PBC;(Ⅲ)求二面角B﹣AE﹣D的度数.12. (10分) (2019高二上·西安月考) 如图,在四棱锥中,平面,底面是菱形,AB=2,.(Ⅰ)求证:平面PAC;(Ⅱ)若,求与所成角的余弦值;13. (10分) (2018高三上·赣州期中) 如图,已知多面体中,为菱形,,平面,,, .(1)求证:平面平面;(2)求二面角的余弦值.14. (10分)如图,正三棱柱ABC﹣A1B1C1中,底面边长为.(1)设侧棱长为1,求证:AB1⊥BC1;(2)设AB1与BC1的夹角为,求侧棱的长.15. (10分)如图,在三棱锥P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N 点在PB上,且4PN=PB.(Ⅰ)证明:平面PCE⊥平面PAB;(Ⅱ)证明:MN∥平面PAC.参考答案一、真题演练 (共6题;共45分)答案:1-1、答案:1-2、答案:1-3、考点:解析:答案:2-1、答案:2-2、考点:解析:答案:3-1、答案:3-2、考点:解析:答案:4-1、答案:4-2、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:二、模拟实训 (共9题;共90分)答案:7-1、考点:解析:答案:8-1、答案:8-2、考点:解析:答案:9-1、答案:9-2、考点:解析:答案:10-1、略考点:解析:答案:11-1、略考点:解析:答案:12-1、考点:解析:答案:13-1、答案:13-2、略考点:解析:答案:14-1、答案:14-2、考点:解析:答案:15-1、考点:解析:第21 页共21 页。
江苏省高考文科数学三轮复习练习:小题专题练四 解析几何立体几何 含解析

小题专题练(四) 解析几何、立体几何(建议用时:50分钟)1.抛物线y 2=4x 的准线方程为________.2.已知双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a =________. 3.一个六棱锥的体积为23,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.4.(2019·连云港调研)已知圆C :(x -3)2+(y -5)2=5,直线l 过圆心且交圆C 于A ,B 两点,交y 轴于P 点,若2P A →=PB →,则直线l 的斜率k =________.5.如图,60°的二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB ,已知AB =4,AC =6,BD =8,则CD 的长为________.6.已知圆C 1:(x -2)2+(y -3)2=1,圆C 2:(x -3)2+(y -4)2=9,M ,N 分别是圆C 1,C 2上的动点,P 为x 轴上的动点,则|PM |+|PN |的最小值为________.7.(2019·徐州调研)在三棱柱ABC -A 1B 1C 1中,侧棱AA 1与侧面BCC 1B 1的距离为2,侧面BCC 1B 1的面积为4,则此三棱柱ABC -A 1B 1C 1的体积为________.8.已知圆C 1:x 2+(y -2)2=4,抛物线C 2:y 2=2px (p >0),C 1与C 2相交于A ,B 两点,|AB |=855,则抛物线C 2的方程为____________. 9.如图,在直角梯形ABCD 中,BC ⊥DC ,AE ⊥DC ,M ,N 分别是AD ,BE 的中点,将△ADE 沿AE 折起,则下列说法正确的是________.(填上所有正确说法的序号)①不论D 折至何位置(不在平面ABC 内)都有MN ∥平面DEC ;②不论D 折至何位置都有MN ⊥AE ;③不论D 折至何位置(不在平面ABC 内)都有MN ∥AB ;④在折起过程中,一定存在某个位置,使EC ⊥AD .10.已知O 为坐标原点,过双曲线x 2-y 2b 2=1(b >0)上的点P (1,0)作两条渐近线的平行线,分别交两渐近线于A ,B 两点,若平行四边形OBP A 的面积为1,则双曲线的离心率为________.11.(2019·盐城模拟)已知圆C :(x -3)2+(y -4)2=1和两点A (-m ,0)、B (m ,0)(m >0),若圆上存在一点P ,使得∠APB =90°,则m 的最小值为________.12.已知半径为1的球O 中内接一个圆柱,当圆柱的侧面积最大时,球的体积与圆柱的体积的比值为________.13.(2019·宿迁质检)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左右焦点为F 1,F 2,若椭圆C 上恰好有6个不同的点P ,使得△F 1F 2P 为等腰三角形,则椭圆C 的离心率的取值范围是________.14.如图,椭圆C :x 2a 2+y 24=1(a >2),圆O :x 2+y 2=a 2+4,椭圆C 的左、右焦点分别为F 1,F 2,过椭圆上一点P 和原点O 作直线l 交圆O于M ,N 两点,若|PF 1|·|PF 2|=6,则|PM |·|PN |的值为________.小题专题练(四)1.解析:易知抛物线y 2=4x 的准线方程为x =-p 2=-1. 答案:x =-12.解析:因为c 2=a 2+3,所以e =c a =a 2+3a 2=2,得a 2=1,所以a =1. 答案:13.解析:设该六棱锥的高是h .根据体积公式得,V =13×12×2×3×6×h =23,解得h =1,则侧面三角形的高为1+(3)2=2,所以侧面积S =12×2×2×6=12. 答案:124.解析:依题意得,点A 是线段PB 的中点,|PC |=|P A |+|AC |=3 5.过圆心C (3,5)作y 轴的垂线,垂足为C 1,则|CC 1|=3,|PC 1|=(35)2-32=6.记直线l 的倾斜角为θ,则有|tan θ|=|PC 1||CC 1|=2,即k =±2. 答案:±25.解析:因为60°的二面角的棱上有A ,B 两点,AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB ,所以CD →=CA →+AB →+BD →,CA →·AB →=0,AB →·BD →=0,因为AB =4,AC =6,BD =8,所以|AB →|=4,|AC →|=6,|BD →|=8,所以CD →2=(CA →+AB →+BD →)2=CA →2+AB →2+BD →2+2CA →·BD →=36+16+64+2×6×8×cos 120°=68,所以CD 的长为217.答案:2176.解析:圆C 1关于x 轴对称的圆C ′1的圆心为C ′1(2,-3),半径不变,圆C 2的圆心为(3,4),半径r =3,|PM |+|PN |的最小值为圆C ′1和圆C 2的圆心距减去两圆的半径,所以|PM |+|PN |的最小值为(3-2)2+(4+3)2-1-3=52-4.答案:52-47.解析:补形法将三棱柱补成四棱柱,如图所示.记A 1到平面BCC 1B 1的距离为d ,则d =2.则V 三棱柱=12V 四棱柱=12S 四边形BCC 1B 1·d =12×4×2=4. 答案:48.解析:由题意,知圆C 1与抛物线C 2的其中一个交点为原点,不妨记为B ,设A (m ,n ).因为|AB |=855,所以⎩⎪⎨⎪⎧m 2+n 2=855,m 2+(n -2)2=4,解得⎩⎨⎧m =85,n =165,即A ⎝⎛⎭⎫85,165.将点A 的坐标代入抛物线方程得⎝⎛⎭⎫1652=2p ×85,所以p =165,所以抛物线C 2的方程为y 2=325x . 答案:y 2=325x 9.解析:如图,设Q ,P 分别为CE ,DE 的中点,可得四边形MNQP是矩形,所以①②正确;不论D 折至何位置(不在平面ABC 内)都有MN与AB 是异面直线,不可能MN ∥AB ,所以③错;当平面ADE ⊥平面ABCD时,可得EC ⊥平面ADE ,故EC ⊥AD ,④正确.故填①②④.答案:①②④10.解析:依题意,双曲线的渐近线方程为y =±bx ,则过点P 且与渐近线平行的直线方程为y =±b (x -1),联立⎩⎪⎨⎪⎧y =bx y =-b (x -1)得|y |=b 2,所以平行四边形OBP A 的面积S ▱OBP A =2S △OBP =2×⎝⎛⎭⎫12×1×|y |=b 2=1,所以b =2,所以双曲线的离心率e =c a =1+221= 5. 答案: 511.解析:显然AB =2m ,因为∠APB =90°,所以OP =12AB =m ,所以要求m 的最小值即求圆C 上点P 到原点O 的最小距离,因为OC =5,所以OP min =OC -r =4,即m 的最小值为4. 答案:4 12.解析:如图所示,设圆柱的底面半径为r ,则圆柱的侧面积为S =2πr ×21-r 2=4πr 1-r 2≤4π×r 2+(1-r 2)2=2π(当且仅当r 2=1-r 2,即r =22时取等号).所以当r =22时,V 球V 圆柱=4π3×13π⎝⎛⎭⎫222×2=423. 答案:42313.解析:6个不同的点有两个为短轴的两个端点,另外4个分别在第一、二、三、四象限,且上下对称、左右对称.不妨设P 在第一象限,PF 1>PF 2,当PF 1=F 1F 2=2c 时,PF 2=2a -PF 1=2a -2c ,即2c >2a -2c ,解得e =c a >12,又因为e <1,所以 12<e <1;当PF 2=F 1F 2=2c 时,PF 1=2a -PF 2=2a -2c ,即2a -2c >2c 且2c >a -c ,解得13<e <12, 综上可得13<e <12或12<e <1. 答案:⎝⎛⎭⎫13,12∪⎝⎛⎭⎫12,114.解析:由已知|PM |·|PN |=(R -|OP |)(R +|OP |)=R 2-|OP |2=a 2+4-|OP |2,|OP |2=|OP →|2=14(PF 1→+PF 2→)2=14(|PF 1→|2+|PF 2→|2+2|PF 1→|·|PF 2→|cos ∠F 1PF 2)=12(|PF 1→|2+|PF 2→|2)-14(|PF 1→|2+|PF 2→|2-2|PF 1→||PF 2→|cos ∠F 1PF 2)=12[(2a )2-2|PF 1||PF 2|]-14×(2c )2=a 2-2,所以|PM |·|PN |=(a 2+4)-(a 2-2)=6.答案:6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与几何相关的应用题
1.若曲线y=x3+ax在原点处的切线方程是2x-y=0,则实数a= .
2.在平面直角坐标系xOy中,抛物线y2=8x上横坐标为1的点到抛物线焦点的距离为.
3.已知向量a=(3,1),b=-,若a+λb与a垂直,则λ等于.
4.若实数x,y满足-则x2+(y+1)2的最大值与最小值的差为.
5.(2018苏锡常镇四市高三调研)若正四棱锥的底面边长为2cm,侧面积为8cm2,则它的体积为
cm3.
6.函数f(x)=Asin(2x+φ)(A,φ∈R)的部分图象如图所示,则f(0)= .
7.(2018盐城田家炳中学第一学期期末)已知椭圆+=1的左、右焦点分别为F1,F2,点P在椭圆上,若PF1=4,则点P到右准线的距离是.
8.设等比数列{a n}的前n项和为S n,已知a1=2017,且a n+2a n+1+a n+2= (n∈N*),则S2018= .
9.(2018南通高三第一次调研)如图,在三棱锥P-ABC 中 AB⊥PC CA=CB M 是AB 的中点,点N 在棱PC 上,点D 是BN 的中点. 求证:( )MD∥平面PAC; (2)平面ABN⊥平面PMC.
10.(2018常州教育学会学业水平检测)已知△ABC 中,a,b,c 分别为三个内角A,B,C 所对的边, bsinC=ccosB+c. (1)求角B; (2)若b 2
=ac,求
n +
n
的值.
答案精解精析
1.答案 2
解析因为y'=3x2+a,所以在原点处的导数即为在该点外的切线的斜率,即a=2.
2.答案 3
解析抛物线y2=8x的准线方程为x=-2,所以该抛物线上横坐标为1的点到准线的距离为3,等于到焦点的距离,即到焦点的距离为3.
3.答案 4
解析由条件可得a+λb=-,所以(a+λb)⊥ ⇒3(3-λ)+1+λ=0⇒λ=4.
4.答案 3
解析不等式组对应的平面区域如图,由图可知,当(x,y)为(0,1)时,x2+(y+1)2取得最大值4,当(x,y)为(0,0)时,x2+(y+1)2取得最小值1,故最大值与最小值的差是3.
5.答案
解析由题意得正四棱锥斜高为2cm,从而得正四棱锥的高为cm,所以体积为× ×=cm3.
6.答案-1
解析由图象可知,A=2,
且sin=1,解得φ的一个值为-,即函数解析式可以是f(x)=2sin-,故
f(0)=2sin-=-1.
7.答案
解析由题意及PF1=4,知PF2=6,又离心率e=,所以点P到右准线的距离==.
8.答案0
解析因为{a n}是等比数列,a n+2a n+1+a n+2=0,所以a n+2a n q+a n q2=0,即q2+2q+1=0,解得q=-1,
所以S2018=-(- )
=0.
-(- )
9.证明(1)在△ABN中,M是AB的中点,D是BN的中点,
所以MD∥AN.
又因为AN ⊂平面PAC,MD ⊄平面PAC,所以MD∥平面PAC. (2)在△ABC 中,CA=CB,M 是AB 的中点,所以AB⊥MC
又因为AB⊥PC PC ⊂平面PMC,MC ⊂平面PMC PC∩MC=C 所以AB⊥平面PMC.又因为AB ⊂平面ABN,所以平面ABN⊥平面PMC.
10.解析 (1) bsinC=cosB+c 由正弦定理得 sinBsinC=cosBsinC+sinC,因为0<C<π,所以sinC>0,所以 sinB-cosB=1,所以sin - = ,由0<B<π,得- <B- <
,所以B-
=
,
所以B=
.
(2)因为b 2
=ac,由正弦定理得sin 2
B=sinAsinC,
n +
n = n +
n =
n n
n n
= n( ) n n =
n( - )
n n = n
n n
, 所以
n +
n = n
n B =
n =
=
.。
