2020届江苏高考数学应用题专题复习
2020年江苏卷数学高考题及答案
高考数学试卷1．已知集合{1,0,1,2},{0,2,3}A B =-=，则A B =_____. 【答案】{}0,2 【解析】 【分析】根据集合的交集即可计算. 【详解】∵{}1,0,1,2A =-,{}0,2,3B = ∴{}0,2A B = 故答案为：{}0,2. 【点睛】本题考查了交集及其运算，是基础题型．2．已知i 是虚数单位，则复数(1i)(2i)z =+-的实部是_____. 【答案】3 【解析】 【分析】根据复数的运算法则，化简即可求得实部的值. 【详解】∵复数()()12z i i =+- ∴2223z i i i i =-+-=+ ∴复数的实部为3. 故答案为：3.本题考查复数的基本概念，是基础题．3．已知一组数据4,2,3,5,6a a -的平均数为4，则a 的值是_____. 【答案】2 【解析】 【分析】根据平均数的公式进行求解即可． 【详解】∵数据4,2,3,5,6a a -的平均数为4 ∴4235620a a ++-++=，即2a =. 故答案为：2. 【点睛】本题主要考查平均数的计算和应用，比较基础．4．将一颗质地均匀的正方体骰子先后抛掷2次，观察向上的点数，则点数和为5的概率是_____. 【答案】19【解析】 【分析】分别求出基本事件总数，点数和为5的种数，再根据概率公式解答即可． 【详解】根据题意可得基本事件数总为6636⨯=个.点数和为5的基本事件有()1,4，()4,1，()2,3，()3,2共4个. ∴出现向上的点数和为5的概率为41369P ==.故答案为：19. 【点睛】本题考查概率的求法，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题．5．如图是一个算法流程图，若输出y 的值为2-，则输入x 的值是_____.【答案】3- 【解析】 【分析】根据指数函数的性质，判断出1y x =+，由此求得x 的值. 【详解】由于20x >，所以12y x =+=-，解得3x =-. 故答案为：3- 【点睛】本小题主要考查根据程序框图输出结果求输入值，考查指数函数的性质，属于基础题.6．在平面直角坐标系xOy 中，若双曲线22x a﹣25y =1(a ＞0)的一条【答案】32【解析】 【分析】根据渐近线方程求得a ，由此求得c ，进而求得双曲线的离心率. 【详解】双曲线22215x y a -=，故b =由于双曲线的一条渐近线方程为y x =，即2b a a =⇒=，所以3c ===，所以双曲线的离心率为32c a =.故答案为：32【点睛】本小题主要考查双曲线的渐近线，考查双曲线离心率的求法，属于基础题.7．已知y =f (x )是奇函数，当x ≥0时，()23f x x = ，则f (-8)的值是____. 【答案】4- 【解析】 【分析】先求(8)f ，再根据奇函数求(8)f - 【详解】23(8)84f ==，因为()f x 为奇函数，所以(8)(8)4f f -=-=-故答案为：4- 【点睛】本题考查根据奇函数性质求函数值，考查基本分析求解能力，属8．已知2sin ()4πα+ =23，则sin 2α的值是____.【答案】13【解析】 【分析】直接按照两角和正弦公式展开，再平方即得结果. 【详解】221sin ()()(1sin 2)4222παααα+=+=+121(1sin 2)sin 2233αα∴+=∴= 故答案为：13【点睛】本题考查两角和正弦公式、二倍角正弦公式，考查基本分析求解能力，属基础题.9．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是____cm.【答案】2π【解析】 【分析】先求正六棱柱体积，再求圆柱体积，相减得结果.正六棱柱体积为2624⨯⨯ 圆柱体积为21()222ππ⋅=所求几何体体积为2π故答案为： 2π【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题. 10．将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是____. 【答案】524x π=- 【解析】 【分析】先根据图象变换得解析式，再求对称轴方程，最后确定结果. 【详解】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=-故答案为：524x π=-【点睛】本题考查三角函数图象变换、正弦函数对称轴，考查基本分析求解能力，属基础题.11．设{a n }是公差为d 的等差数列，{b n }是公比为q 的等比数列．已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-∈N ，则d +q 的值是_______． 【答案】4 【解析】 【分析】结合等差数列和等比数列前n 项和公式的特点，分别求得{}{},n n a b 的公差和公比，由此求得d q +. 【详解】设等差数列{}n a 的公差为d ，等比数列{}n b 的公比为q ，根据题意1q ≠.等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -⎛⎫=+=+- ⎪⎝⎭， 等比数列{}n b 的前n 项和公式为()1111111n n n b q b bQ q qq q-==-+---， 依题意n n n S P Q =+，即22111212211nn b b d d n n n a n q q q ⎛⎫-+-=+--+ ⎪--⎝⎭， 通过对比系数可知111212211dd a q b q⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒112021d a q b =⎧⎪=⎪⎨=⎪⎪=⎩，故4d q +=. 故答案为：4 【点睛】本小题主要考查等差数列和等比数列的前n 项和公式，属于中档题.12．已知22451(,)x y y x y R +=∈，则22x y +的最小值是_______． 【答案】4【解析】 【分析】根据题设条件可得42215y x y -=，可得4222222114+555y y x y y y y -+=+=，利用基本不等式即可求解. 【详解】∵22451x y y += ∴0y ≠且42215y x y -=∴42222221144+5555y y x y y y y -+=+=≥，当且仅当221455y y =，即2231,102x y ==时取等号. ∴22x y +的最小值为45.故答案为：45. 【点睛】本题考查了基本不等式在求最值中的应用.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用≥或≤时等号能否同时成立）.13．在△ABC 中，43=90AB AC BAC ==︒，，∠，D 在边BC 上，延长AD到P ，使得AP =9，若3()2PA mPB m PC =+-（m 为常数），则CD 的长度是________．【答案】185【解析】 【分析】根据题设条件可设()0PA PD λλ=>，结合32PA mPB m PC⎛⎫=+- ⎪⎝⎭与,,B D C 三点共线，可求得λ，再根据勾股定理求出BC ，然后根据余弦定理即可求解. 【详解】∵,,A D P 三点共线， ∴可设()0PA PD λλ=>，∵32PA mPB m PC⎛⎫=+- ⎪⎝⎭，∴32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭，即32m m PD PB PC λλ⎛⎫- ⎪⎝⎭=+， 若0m ≠且32m ≠，则,,B D C 三点共线， ∴321m m λλ⎛⎫-⎪⎝⎭+=，即32λ=， ∵9AP =，∴3AD =， ∵4AB =,3AC =,90BAC ∠=︒， ∴5BC =，设CD x =，CDA θ∠=，则5BD x =-，BDA πθ∠=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅，()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-，∵()cos cos 0θπθ+-=，∴()()2570665x x x --+=-，解得185x =，∴CD 的长度为185. 当0m =时， 32PA PC =，,C D 重合，此时CD 的长度为0， 当32m =时，32PA PB =，,B D 重合，此时12PA =，不合题意，舍去. 故答案为：0或185.【点睛】本题考查了平面向量知识的应用、余弦定理的应用以及求解运算能力，解答本题的关键是设出()0PA PD λλ=>．14．在平面直角坐标系xOy 中，已知0)P ，A ，B 是圆C ：221()362x y +-=上的两个动点，满足PA PB =，则△PAB 面积的最大值是__________．【答案】【解析】 【分析】根据条件得PC AB ⊥,再用圆心到直线距离表示三角形PAB 面积，最后利用导数求最大值. 【详解】设圆心C 到直线AB 距离为d ，则||1AB PC ==所以11)2PABSd ≤⋅+= 令222(36)(1)(06)2(1)(236)04y d d d y d d d d '=-+≤<∴=+--+=∴=（负值舍去）当04d ≤<时，0y '>；当46d ≤<时，0y '≤，因此当4d =时，y 取最大值，即PABS取最大值为故答案为：【点睛】本题考查垂径定理、利用导数求最值，考查综合分析求解能力，属中档题.15．在三棱柱ABC -A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．（1）求证：EF ∥平面AB 1C 1； （2）求证：平面AB 1C ⊥平面ABB 1．【答案】（1）证明详见解析；（2）证明详见解析. 【解析】 【分析】（1）通过证明1//EF AB ，来证得//EF 平面11AB C .（2）通过证明AB ⊥平面1AB C ，来证得平面1AB C ⊥平面1ABB . 【详解】（1）由于,E F 分别是1,AC B C 的中点，所以1//EF AB .由于EF ⊂/平面11AB C ,1AB ⊂平面11AB C ，所以//EF 平面11AB C . （2）由于1B C ⊥平面ABC ，AB 平面ABC ，所以1B C AB ⊥. 由于1,AB AC AC B C C ⊥⋂=，所以AB ⊥平面1AB C , 由于AB 平面1ABB ，所以平面1AB C ⊥平面1ABB .【点睛】本小题主要考查线面平行的证明，考查面面垂直的证明，属于中档题.16．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知3,45a c B ===︒．（1）求sin C 的值； （2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值．【答案】（1）sin C =；（2）2tan 11DAC ∠=.【解析】 【分析】（1）利用余弦定理求得b ，利用正弦定理求得sin C .（2）根据cos ADC ∠的值，求得sin ADC ∠的值，由（1）求得cos C 的值，从而求得sin ,cos DAC DAC ∠∠的值，进而求得tan DAC ∠的值. 【详解】（1）由余弦定理得2222cos 922352b ac ac B =+-=+-⨯=，所以b =由正弦定理得sin sin sin sin 5c b c B C C B b =⇒==. （2）由于4cos 5ADC ∠=-，,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以3sin 5ADC ∠==.由于,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以0,2C π⎛⎫∈ ⎪⎝⎭，所以cos 5C ==. 所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅34555525⎛⎫=⨯+-⨯= ⎪⎝⎭.由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭，所以cos DAC ∠==所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查三角恒等变换，属于中档题.17．某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O 在水平线MN 上、桥AB 与MN 平行，OO '为铅垂线(O '在AB 上).经测量，左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO '的距离a (米)之间满足关系式21140h a =；右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO '的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO '的距离为40米.（1）求桥AB 的长度；（2）计划在谷底两侧建造平行于OO '的桥墩CD 和EF ，且CE 为80米，其中C ，E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E '为多少米时，桥墩CD 与EF 的总造价最低?【答案】（1）120米（2）20O E '=米 【解析】 【分析】（1）根据A,B 高度一致列方程求得结果；（2）根据题意列总造价的函数关系式，利用导数求最值，即得结果. 【详解】（1）由题意得2311||40640||8040800O A O A ''=-⨯+⨯∴= ||||||8040120AB O A O B ''∴=+=+=米（2）设总造价为()f x 万元，21||8016040O O '=⨯=，设||O E x '=， 32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<< 3221336()(160),()()0208008080080f x k x x f x k x x x '∴=+-∴=-=∴=(0舍去)当020x <<时，()0f x '<；当2040x <<时，()0f x '>，因此当20x时，()f x 取最小值，答：当20O E '=米时，桥墩CD 与EF 的总造价最低. 【点睛】本题考查实际成本问题、利用导数求最值，考查基本分析求解能力，属中档题.18．在平面直角坐标系xOy 中，已知椭圆22:143x y E +=的左、右焦点分别为F 1，F 2，点A 在椭圆E 上且在第一象限内，AF 2⊥F 1F 2，直线AF 1与椭圆E 相交于另一点B ．（1）求△AF 1F 2的周长；（2）在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP QP ⋅的最小值；（3）设点M 在椭圆E 上，记△OAB 与△MAB 的面积分别为S 1，S 2，若S 2=3S 1，求点M 的坐标．【答案】（1）6；（2）-4；（3）()2,0M 或212,77⎛⎫-- ⎪⎝⎭.【解析】 【分析】（1）根据椭圆定义可得124AF AF +=，从而可求出12AF F △的周长； （2）设()0,0P x ，根据点A 在椭圆E 上，且在第一象限，212AF F F ⊥，求出31,2A ⎛⎫ ⎪⎝⎭，根据准线方程得Q 点坐标，再根据向量坐标公式，结合二次函数性质即可出最小值；（3）设出设()11,M x y ，点M 到直线AB 的距离为d ，由点O 到直线AB 的距离与213S S =，可推出95d =，根据点到直线的距离公式，以及()11,M x y 满足椭圆方程，解方程组即可求得坐标. 【详解】（1）∵椭圆E 的方程为22143x y +=∴()11,0F -,()21,0F由椭圆定义可得：124AF AF +=. ∴12AF F △的周长为426+=（2）设()0,0P x ，根据题意可得01x ≠.∵点A 在椭圆E 上，且在第一象限，212AF F F ⊥ ∴31,2A ⎛⎫⎪⎝⎭∵准线方程为4x = ∴()4,Q Q y∴()()()()200000,04,4244Q OP QP x x y x x x ⋅=⋅--=-=--≥-，当且仅当02x =时取等号.∴OP QP ⋅的最小值为4-.（3）设()11,M x y ，点M 到直线AB 的距离为d . ∵31,2A ⎛⎫ ⎪⎝⎭，()11,0F -∴直线1AF 的方程为()314y x =+ ∵点O 到直线AB 的距离为35，213S S =∴2113133252S S AB AB d ==⨯⨯⨯=⋅ ∴95d =∴113439x y -+=①∵2211143x y +=② ∴联立①②解得1120x y =⎧⎨=⎩，1127127x y ⎧=-⎪⎪⎨⎪=-⎪⎩. ∴()2,0M 或212,77⎛⎫-- ⎪⎝⎭.【点睛】本题考查了椭圆的定义，直线与椭圆相交问题、点到直线距离公式的运用，熟悉运用公式以及根据213S S =推出95d =是解答本题的关键.19．已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+∈R 在区间D 上恒有()()()f x h x g x ≥≥．（1）若()()222 2()f x x x g x x x D =+=-+=∞-∞+，，，，求h (x )的表达式；（2）若2 1 ln ,()()()(0) x x g k x h kx k D f x x x =-+==-=+∞，，，，求k 的取值范围；（3）若()422242() 2() (48 () 4 3 02 f x x x g x x h x t t x t t t =-=-=--+<，，，[], D m n =⊆⎡⎣，求证：n m -【答案】（1）()2h x x =；（2）[]0,3k ∈；（3）证明详见解析 【解析】 【分析】（1）求得()f x 与()g x 的公共点，并求得过该点的公切线方程，由此求得()h x 的表达式.（2）先由()()0h x g x -≥，求得k 的一个取值范围，再由()()0f x h x -≥，求得k 的另一个取值范围，从而求得k 的取值范围.（3）先由()()f x h x ≥，求得t 的取值范围，由方程()()0g x h x -=的两个根，求得n m -的表达式，利用导数证得不等式成立. 【详解】（1）由题设有2222x x kx b x x -+≤+≤+对任意的x ∈R 恒成立. 令0x =，则00b ≤≤，所以0b =.因此22kx x x ≤+即()220x k x +-≥对任意的x ∈R 恒成立，所以()220k ∆=-≤，因此2k =. 故()2h x x =.（2）令()()()()()1ln 0F x h x g x k x x x =-=-->，()01F =. 又()1x F x k x-'=⋅. 若k 0<，则()F x 在0,1上递增，在1,上递减，则()()10F x F ≤=，即()()0h x g x -≤，不符合题意.当0k =时，()()()()()0,F x h x g x h x g x =-==，符合题意.当0k >时， ()F x 在0,1上递减，在1,上递增，则()()10F x F ≥=，即()()0h x g x -≥，符合题意. 综上所述，0k ≥.由()()()21f x h x x x kx k -=-+--()()2110x k x k =-+++≥当102k x +=<，即1k <-时，()211y x k x k =-+++在0,为增函数，因为()()0010f h k -=+<，故存在()00,x ∈+∞，使()()0f x h x -<，不符合题意.当102k x +==，即1k =-时，()()20f x h x x -=≥，符合题意. 当102k x +=>，即1k >-时，则需()()21410k k ∆=+-+≤，解得13k -<≤.综上所述，k 的取值范围是[]0,3k ∈.（3）因为()423422243248x x t t x t t x -≥--+≥-对任意[,][x m n ∈⊂恒成立，()423422432x x t t x t t -≥--+对任意[,][x m n ∈⊂恒成立，等价于()222()2320x t x tx t -++-≥对任意[,][x m n ∈⊂恒成立.故222320x tx t ++-≥对任意[,][x m n ∈⊂恒成立. 令22()232M x x tx t =++-，当201t <<，2880,11t t ∆=-+>-<-<，此时1n m t -+<<， 当212t ≤≤，2880t ∆=-+≤，但()234248432x t t x t t -≥--+对任意的[,][x m n ∈⊂恒成立.等价于()()()2322443420x t t x t t --++-≤对任意的[,][x m n ∈⊂恒成立.()()()2322443420x t t x t t --++-=的两根为12,x x ，则4231212328,4t t x x t t x x --+=-⋅=，所以12=n m x x --=.令[]2,1,2t λλ=∈，则n m -=. 构造函数()[]()325381,2P λλλλλ=-++∈，()()()23103331P λλλλλ'=-+=--，所以[]1,2λ∈时，()0P λ'<，()P λ递减，()()max 17P P λ==.所以()max n m -=n m -≤【点睛】本小题主要考查利用的导数求切线方程，考查利用导数研究不等式恒成立问题，考查利用导数证明不等式，考查分类讨论的数学思想方法，属于难题.20．已知数列{}*()∈n a n N 的首项a 1=1，前n 项和为S n ．设λ与k是常数，若对一切正整数n ，均有11111k k k n n n S S a λ++-=成立，则称此数列为“λ–k ”数列．（1）若等差数列{}n a 是“λ–1”数列，求λ的值；（2）若数列{}n a 是“2”数列，且a n ＞0，求数列{}n a 的通项公式；（3）对于给定的λ，是否存在三个不同的数列{}n a 为“λ–3”数列，且a n ≥0?若存在，求λ的取值范围；若不存在，说明理由， 【答案】（1）1（2）21,134,2n n n a n -=⎧=⎨⋅≥⎩（3）01λ<< 【解析】【分析】（1）根据定义得+11n n n S S a λ+-=，再根据和项与通项关系化简得11n n a a λ++=，最后根据数列不为零数列得结果；（2）根据定义得111222+1+1)n nn n S S S S -=-，根据平方差公式化简得+1=4n n S S ，求得n S ，即得n a ；（3）根据定义得111333+11n n n S S a λ+-=，利用立方差公式化简得两个方程，再根据方程解的个数确定参数满足的条件，解得结果 【详解】（1）+111111101n n n n n n S S a a a a a λλλ++++-=∴==∴≡∴=/（2）11221100n n n n n a S S S S ++>∴>∴->111222+1+1)n nn n S S S S -=- 1111112222222+1+1+11()()()3n n n n n n S S S S S S ∴-=-+1111111222222+1+1+1+11()=2=443n n nn n n n n n n S S S S S S S S S -∴-=+∴∴∴= 111S a ==，14n n S -= 1224434,2n n n n a n ---∴=-=⋅≥21,134,2n n n a n -=⎧∴=⎨⋅≥⎩（3）假设存在三个不同的数列{}n a 为"3"λ-数列.111113333333+11+1+1()()n n n n n n n S S a S S S S λλ+-=∴-=- 1133+1n n S S ∴=或11221123333333+1+1+1()()n n n n n n S S S S S S λ-=+++1n n S S ∴=或22113333333+1+1(1)(1)(2)0n n n n SS S S λλλ-+-++=∵对于给定的λ，存在三个不同的数列{}n a 为"3"λ-数列，且0n a ≥1,10,2n n a n =⎧∴=⎨≥⎩或()22113333333+1+1(1)(1)(2)01n n n n S S S S λλλλ-+-++=≠有两个不等的正根.()22113333333+1+1(1)(1)(2)01n n n n S S SS λλλλ-+-++=≠可转化为()2133333+1+12133(1)(2)(1)01n n nnS S S S λλλλ-++-+=≠，不妨设()1310n n S x x S +⎛⎫=> ⎪⎝⎭，则()3233(1)(2)(1)01x x λλλλ-+++-=≠有两个不等正根，设()()3233(1)(2)(1)01f x x x λλλλ=-+++-=≠.① 当1λ<时，32323(2)4(1)004λλλ∆=+-->⇒<<，即01λ<<，此时()3010f λ=-<，33(2)02(1)x λλ+=->-对，满足题意. ② 当1λ>时，32323(2)4(1)004λλλ∆=+-->⇒<<，即1λ<<()3010f λ=->，33(2)02(1)x λλ+=-<-对，此情况有两个不等负根，不满足题意舍去. 综上，01λ<< 【点睛】本题考查数列新定义、由和项求通项、一元二次方程实根分步，考查综合分析求解能力，属难题.21．平面上点(2,1)A -在矩阵11ab ⎡⎤=⎢⎥-⎣⎦M 对应的变换作用下得到点(3,4)B -．（1）求实数a ，b 的值； （2）求矩阵M 的逆矩阵1M -．【答案】（1）22a b =⎧⎨=⎩；（2）121 5512 55M -⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦.【解析】 【分析】（1）根据变换写出具体的矩阵关系式，然后进行矩阵的计算可得出实数,a b 的值；（2）设出逆矩阵，由定义得到方程，即可求解. 【详解】（1）∵平面上点()2,1A -在矩阵 11 a M b ⎡⎤=⎢⎥-⎣⎦对应的变换作用下得到点()3,4B -∴ 1 2 31 14a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦ ∴21324a b -=⎧⎨--=-⎩，解得22a b =⎧⎨=⎩（2）设1 m n M c d -⎡⎤=⎢⎥⎣⎦，则12 2 1 0=2 20 1m c n d MM m c n d -++⎡⎤⎡⎤=⎢⎥⎢⎥-+-+⎣⎦⎣⎦∴21202021m c n d m c n d +=⎧⎪+=⎪⎨-+=⎪⎪-+=⎩，解得25151525m n c d ⎧=⎪⎪⎪=-⎪⎨⎪=⎪⎪⎪=⎩∴121 5512 55M -⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦【点睛】本题考查矩阵变换的应用，考查逆矩阵的求法，解题时要认真审题，属于基础题．22．在极坐标系中，已知点1π(,)3A ρ在直线:cos 2l ρθ=上，点2π(,)6B ρ在圆:4sin C ρθ=上（其中0ρ≥，02θπ≤<）． （1）求1ρ，2ρ的值（2）求出直线l 与圆C 的公共点的极坐标． 【答案】（1）1242ρρ==，（2）)4π【解析】 【分析】(1)将A,B 点坐标代入即得结果；（2）联立直线与圆极坐标方程，解得结果. 【详解】（1）以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系，11cos2,43πρρ=∴=，因为点B为直线6πθ=上，故其直角坐标方程为y =， 又4sin ρθ=对应的圆的直角坐标方程为：2240x y y+-=，由2240y x x y y ⎧=⎪⎨⎪+-=⎩解得00x y==⎧⎨⎩或1x y ⎧=⎪⎨=⎪⎩对应的点为())0,0,，故对应的极径为20ρ=或22ρ=. （2）cos 2,4sin ,4sin cos 2,sin 21ρθρθθθθ==∴=∴=，5[0,2),,44ππθπθ∈∴=，当4πθ=时ρ=当54πθ=时0ρ=-<，舍；即所求交点坐标为当),4π【点睛】本题考查极坐标方程及其交点，考查基本分析求解能力，属基础题.23．设x ∈R ，解不等式2|1|||4x x ++≤．【答案】22,3⎡⎤-⎢⎥⎣⎦【解析】 【分析】根据绝对值定义化为三个方程组，解得结果 【详解】1224x x x <-⎧⎨---≤⎩或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩21x ∴-≤<-或10x -≤≤或203x <≤ 所以解集为22,3⎡⎤-⎢⎥⎣⎦【点睛】本题考查分类讨论解含绝对值不等式，考查基本分析求解能力，属基础题.24．在三棱锥A —BCD 中，已知CB =CD ,BD =2，O 为BD 的中点，AO ⊥平面BCD ，AO =2，E 为AC 的中点．（1）求直线AB 与DE 所成角的余弦值；（2）若点F 在BC 上，满足BF =14BC ，设二面角F —DE —C 的大小为θ，求sin θ的值．【答案】（1）15（2）13【解析】 【分析】（1）建立空间直角坐标系，利用向量数量积求直线向量夹角，即得结果；（2）先求两个平面法向量，根据向量数量积求法向量夹角，最后根据二面角与向量夹角关系得结果. 【详解】（1）连,CO BC CD BO OD CO BD ==∴⊥ 以,,OB OC OA 为,,x y z 轴建立空间直角坐标系，则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -∴(1,0,2),(1,1,1)cos ,AB DE AB DE ∴=-=∴<>==从而直线AB 与DE 所成角的余弦值为15（2）设平面DEC 一个法向量为1(,,),n x y z =11200(1,2,0),00x y n DC DC x y z n DE ⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩令112,1(2,1,1)y x z n =∴=-=∴=- 设平面DEF 一个法向量为2111(,,),n x y z =11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩令111272,5(2,7,5)y x z n =-∴==∴=-12cos ,n n ∴<>==因此sin θ== 【点睛】本题考查利用向量求线线角与二面角，考查基本分析求解能力，属中档题.25．甲口袋中装有2个黑球和1个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放入另一口袋，重复n 次这样的操作，记甲口袋中黑球个数为X n ，恰有2个黑球的概率为p n ，恰有1个黑球的概率为q n ． （1）求p 1·q 1和p 2·q 2； （2）求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示) ．【答案】（1）112212716,,332727p q p q ====；；（2）()111222+33n n n n p q p q --+=+ 【解析】 【分析】（1）直接根据操作，根据古典概型概率公式可得结果；（2）根据操作，依次求n n p q ，，即得递推关系，构造等比数列求得2n n p q +，最后根据数学期望公式求结果. 【详解】（1）11131232,333333p q ⨯⨯====⨯⨯， 211131211227++3333333927p p q ⨯⨯=⨯⨯=⨯⨯=⨯⨯，211231122222516+0+3333333927q p q ⨯⨯+⨯=⨯⨯+=⨯⨯=⨯⨯.（2）1111131212++333339n n n n n p p q p q ----⨯⨯=⨯⨯=⨯⨯， 111112*********+(1)+33333393n n n n n n q p q p q q -----⨯⨯+⨯⨯=⨯⨯+--⨯=-⨯⨯⨯，因此112122+333n n n n p q p q --+=+， 从而11111212(2+),21(2+1)333n n n n n n n n p q p q p q p q ----+=+∴+-=-，即1111121(2+1),2133n n n n n n p q p q p q -+-=-∴+=+.又n X 的分布列为故1()213n n n nE X p q =+=+. 【点睛】本题考查古典概型概率、概率中递推关系、构造法求数列通项、数学期望公式，考查综合分析求解能力，属难题.。
2020年江苏省高考数学专项训练-真题解析-专题20 计数原理与二项式定理-2020年江苏省高考数学命题规律大揭秘
高考冲刺 提分必备2020年江苏省高考数学专项训练-真题解析专题20 计数原理与二项式定理【真题感悟】1、【2019年江苏，22】设2*012(1),4,n n n x a a x a x a x n n +=++++∈N L ….已知23242a a a =. （1）求n 的值；（2）设(1n a +=+*,a b ∈N ，求223a b -的值. 【答案】（1）5n =； （2）-32. 【解析】（1）因为0122(1)C C C C 4n n nn n n n x x x x n +=++++≥L ，，所以2323(1)(1)(2)C ,C 26n nn n n n n a a ---====， 44(1)(2)(3)C 24nn n n n a ---==． 因为23242a a a =，所以2(1)(2)(1)(1)(2)(3)[]26224n n n n n n n n n ------=⨯⨯，解得5n =．（2）由（1）知，5n =．5(1(1n +=+02233445555555C C C C C C =++++a =+解法一：因为*,a b ∈N ，所以024135555555C 3C 9C 76,C 3C 9C 44a b =++==++=，从而222237634432a b -=-⨯=-． 解法二：50122334455555555(1C C (C (C (C (C (=+++++02233445555555C C C C C C =--+-．因为*,a b ∈N ，所以5(1a =-．因此225553((1(1(2)32a b a a -=+-=+⨯=-=-．2、【2018江苏，理23】设*n ∈N ，对1，2，···，n 的一个排列12n i i i L ，如果当s <t 时，有s t i i >，则称(,)s t i i 是排列12n i i i L 的一个逆序，排列12n i i i L 的所有逆序的总个数称为其逆序数．例如：对1，2，3的一个排列231，只有两个逆序(2，1)，(3，1)，则排列231的逆序数为2．记()n f k 为1，2，···，n 的所有排列中逆序数为k 的全部排列的个数． （1）求34(2),(2)f f 的值；（2）求(2)(5)n f n ≥的表达式(用n 表示)．【答案】（1）34(2)2,(2)5f f ==（2）222n n --【解析】解：（1）记()abc τ为排列abc 的逆序数，对1，2，3的所有排列，有(123)=0(132)=1(213)=1(231)=2(312)=2(321)=3ττττττ，，，，，，所以333(0)1(1)(2)2f f f ===，．对1，2，3，4的排列，利用已有的1，2，3的排列，将数字4添加进去，4在新排列中的位置只能是最后三个位置．因此，4333(2)(2)(1)(0)5f f f f =++=．（2）对一般的n （n ≥4）的情形，逆序数为0的排列只有一个：12…n ，所以(0)1n f =．逆序数为1的排列只能是将排列12…n 中的任意相邻两个数字调换位置得到的排列，所以(1)1n f n =-．为计算1(2)n f +，当1，2，…，n 的排列及其逆序数确定后，将n +1添加进原排列，n +1在新排列中的位置只能是最后三个位置．因此，1(2)(2)(1)(0)(2)n n n n n f f f f f n +=++=+． 当n ≥5时，112544(2)[(2)(2)][(2)(2)][(2)(2)](2)n n n n n f f f f f f f f ---=-+-++-+…242(1)(2)4(2)2n n n n f --=-+-+⋯++=，因此，n ≥5时，(2)n f =222n n --．3. 【2017江苏，23】已知一个口袋有m 个白球,n 个黑球(,*,2m n n ∈N ≥),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出，并放入如图所示的编号为1,2,3,,m n +L 的抽屉内，其中第k 次取出的球放入编号为k 的抽屉(1,2,3,,)k m n =+L .（1）试求编号为2的抽屉内放的是黑球的概率p ;（2）随机变量X 表示最后一个取出的黑球所在抽屉编号的倒数,()E X 是X 的数学期望,证明:()()(1)nE X m n n <+-【答案】（1）nm n+（2）见解析 【解析】解:(1) 编号为2的抽屉内放的是黑球的概率p 为:11C C n m n n m n n p m n-+-+==+. (2) 随机变量 X 的概率分布为:随机变量 X 的期望为：11C 111(1)!()C C (1)!()!n m nm nk n nk n k n m nm n k E X k k n k n -++-==++-=⋅=⋅--∑∑. 所以1(2)!1(2)!()C (1)!()!(1)C (2)!()!m nm nn n k n k nm nm nk k E X n k n n n k n ++==++--<=-----∑∑ 222121(1C C C )(1)C n n n n n m n nm nn ----+-+=++++-L 12221121(C C C C )(1)C n n n n n n n m n nm nn ------+-+=++++-L12221(C C C )(1)C n n n n n m n nm nn ---+-+=+++-L 12221(C C )(1)C n n m n m n nm nn --+-+-+==+-L 11C (1)C ()(1)n m n nm n n n m n n -+-+==-+- ()()(1)nE X m n n <+-.4. 【2016江苏，23】（1）求3467–47C C 的值； （2）设m ，n ∈N *，n ≥m ，求证：（m +1）C m m +（m +2）+1C m m +（m +3）+2C m m +L +n –1C m n +（n +1）C m n =（m +1）+2+2C m n .【答案】（1）0（2）详见解析 【解析】解：（1）3467654765474740.321C C 4321⨯⨯⨯⨯⨯-=⨯-⨯=⨯⨯⨯⨯⨯（2）当n m =时，结论显然成立，当n m >时11(1)!(1)!(1)(1)(1),1,2,,.!()!(1)![(1)(1)]C !C m m k k k k k k m m k m m n m k m m k m +++⋅++==+=+=++-++-+L又因为122112C C C ,m m m k k k +++++++=所以2221C C C (1)(1)(),1,+2,.m m m k k k k m k m m n +++++=+-=+L ，因此12122222222232432122(1)(2)(3)(1)(1)[(2)(3)(1)](1)(1)[()(C C C C C C C C CCCCC)(CCC )](1).m m m mm m m n m m m m m m m n m m m m m m m m m m m m n n m n m m m n m m m n m m m ++++++++++++++++++++++++++++=++++++++=+++-+-++-=+L L L5. 【2012江苏，23】设集合P n ＝{1,2，…，n }，n ∈N *.记f (n )为同时满足下列条件的集合A 的个数： ①AP n ；②若x ∈A ，则2x A ；③若x ∈P n A ，则2xP n A ．(1)求f (4)；(2)求f (n )的解析式(用n 表示)．【答案】(1)4．(2) 2122,()2,.nn n f n n +⎧⎪=⎨⎪⎩为偶数，为奇数 【解析】解：(1)当n ＝4时，符合条件的集合A 为：{2}，{1,4}，{2,3}，{1,3,4}，故f(4)＝4.(2)任取偶数x ∈Pn ，将x 除以2，若商仍为偶数，再除以2，…，经过k 次以后，商必为奇数，此时记商为m ，于是x ＝m·2k ，其中m 为奇数，k ∈N*. 由条件知，若m ∈A ，则x ∈Ak 为偶数；若m A ，则x ∈Ak 为奇数．于是x 是否属于A 由m 是否属于A 确定．设Qn 是Pn 中所有奇数的集合，因此f(n)等于Qn 的子集个数． 当n 为偶数(或奇数)时，Pn 中奇数的个数是2n (或12n +)． 所以2122,()2,.nn n f n n +⎧⎪=⎨⎪⎩为偶数，为奇数.【考纲要求】1.加法原理与乘法原理2.排列组合3.二项式定理以上考查要求均为理解.【考向分析】计数原理与二项式定理均是以解答题的形式进行考查，涉及到分类讨论的思想，着重考查学生运算能力和逻辑思维能力，本章知识点常与概率等知识一起考查，难度中等偏上.【高考预测】组合式的证明是考查的一个方向【迎考策略】1.在应用通项公式时，要注意以下几点：①它表示二项展开式的任意项，只要n 与r 确定，该项就随之确定； ②1r T +是展开式中的第1r +项，而不是第r 项；③公式中，a ，b 的指数和为n 且a ，b 不能随便颠倒位置；④对二项式()na b -展开式的通项公式要特别注意符号问题．⑤在二项式定理的应用中，“赋值思想”是一种重要方法，是处理组合数问题、系数问题的经典方法． 2. 二项定理问题的处理方法和技巧:⑴运用二项式定理一定要牢记通项1r n r rr n T C a b -+=，注意()n a b +与()nb a +虽然相同，但具体到它们展开式的某一项时是不同的，一定要注意顺序问题，另外二项展开式的二项式系数与该项的(字母)系数是两个不同的概念，前者只指rn C ，而后者是字母外的部分．前者只与n 和r 有关，恒为正，后者还与a ，b 有关，可正可负．⑵ 对于二项式系数问题，应注意以下几点：①求二项式所有项的系数和，可采用“特殊值取代法”，通常令字母变量的值为1； ②关于组合恒等式的证明，常采用“构造法”——构造函数或构造同一问题的两种算法； ③证明不等式时，应注意运用放缩法.⑶ 求二项展开式中指定的项，通常是先根据已知条件求r ，再求1r T +，有时还需先求n ，再求r ，才能求出1r T +.⑷ 有些三项展开式问题可以变形为二项式问题加以解决；有时也可以通过组合解决，但要注意分类清楚，不重不漏.⑸ 对于二项式系数问题，首先要熟记二项式系数的性质，其次要掌握赋值法，赋值法是解决二项式系数问题的一个重要手段.⑹ 近似计算要首先观察精确度，然后选取展开式中若干项.⑺ 用二项式定理证明整除问题，一般将被除式变为有关除式的二项式的形式再展开，常采用“配凑法”“消去法”配合整除的有关知识来解决.多项式乘法的进位规则:在求系数过程中,尽量先化简，降底数的运算级别,尽量化成加减运算，在运算过程可以适当注意令值法的运用，例如求常数项，可令0x =.在二项式的展开式中，要注意项的系数和二项式系数的区别.3. 排列组合在二项展开式中的应用：()na b +展开式可以由次数、项数和系数来确定．(1)次数的确定：从n 个相同的a b +中各取一个(a 或b )乘起来，可以构成展开式中的一项，展开式中项的形式是p qma b ，其中,,p q N p q n ∈+=.(2)项数的确定：满足条件,,p q N p q n ∈+=的(),p q 共1n +组． 即将()na b +展开共2n项，合并同类项后共1n +项．(3)系数的确定：展开式中含p q a b (p q n +=)项的系数为pn C (即p 个a ，q 个b 的排列数)因此()na b +展开式中的通项是：1r n r rr n T C a b -+= (0,1,2,3,,r n =L )()()011*nn n r n r r n n n n n n a b C a C a b C a b C b n N --+=+++++∈L L 这种方法比数学归纳法推导二项式定理更具一般性和创造性，不仅可二项展开，也可三项展开，四项展开等．4. 求几个二项式积的展开式中某项的系数或特定项时，一般要根据这几个二项式的结构特征进行分类搭配，分类时一般以一个二项式逐项分类，分析其他二项式应满足的条件，然后再求解结果．5. “赋值法”普遍适用于恒等式，是一种重要的方法，对形如()nax b +、()2nax bx c++ (,,a b c R ∈)的式子求其展开式的各项系数之和，常用赋值法，只需令1x =即可；对形如()nax by + (,a b R ∈)的式子求其展开式各项系数之和，只需令1x y ==即可．“赋值法”是求二项展开式系数问题常用的方法，注意取值要有利于问题的解决，可以取一个值或几个值，也可以取几组值，解题易出现漏项等情况，应引起注意．例：若()2012nn f x a a x a x a x =++++L ，则()f x 展开式中各项系数之和为()1f ，奇数项系数之和为()()024112f f a a +-+++=L ，偶数项系数之和为()()135112f f a a --+++=L ，令0x =，可得()00a f =．6. 求展开式系数最大项：如求()nax b + (,a b R ∈)的展开式系数最大的项，一般是采用待定系数法，设展开式各项系数分别为1231,,,,n A A A A +L ，且第k 项系数最大，应用11k k kk A A A A -+≥⎧⎨≥⎩从而解出k 来，即得．7. (1)利用二项式定理解决整除问题时，关键是进行合理地变形构造二项式，应注意：要证明一个式子能被另一个式子整除，只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可． (2)求余数问题时，应明确被除式()f x 与除式()g x (()0g x ≠)，商式()q x 与余式的关系及余式的范围．(3)展开式中常数项、有理项的特征是通项中未知数的指数分别为零和整数．解决这类问题时，先要合并通项中同一字母的指数，再根据上述特征进行分析．(4)有关求二项展开式中的项、系数、参数值或取值范围等，一般要利用通项公式，运用方程思想进行求值，通过解不等式(组)求取值范围．8.组合数的性质不仅有课本上介绍的111C C C m m m k k k ++++=、C =C m k m k k-，更有11C C k k n n k n --=，现在又有11(1)C (1)C ,,1,,m m k k k m k m m n +++=+=+L ，这些性质不需记忆，但需会推导，更需会应用.【强化演练】1．【2019年高考全国Ⅲ卷理数】（1+2x 2 ）（1+x ）4的展开式中x 3的系数为A ．12B ．16C ．20D ．24【答案】A【解析】由题意得x 3的系数为3144C 2C 4812+=+=，故选A ．2．【2019年高考浙江卷理数】在二项式9(2)x +的展开式中，常数项是__________；系数为有理数的项的个数是__________．【答案】162 5【解析】由题意，9(2)x +的通项为919C (2)(0,1,29)rr r r T x r -+==L ，当0r =时，可得常数项为0919C (2)162T ==；若展开式的系数为有理数，则1,3,5,7,9r =，有246810T , T , T , T , T 共5个项．故答案为：162，5． 3．已知函数．（1）当时，若，求实数的值； （2）若，求证：．【答案】（1）。
2020届江苏省高考数学应用题模拟试题选编(含解析)(2020年7月整理).pdf
2020届江苏高考应用题模拟试题选编（十）
1、（江苏省如皋市 2019—2020 学年高三年级第二学期语数英学科模拟（二）数学试题） 现有一块废弃的半圆形钢板，其右下角一小部分因生锈无法使用，其形状如图所示，已知该
钢板的圆心为 O，线段 AOB 为其下沿，且 OA＝2m，OB＝ 2 m．现欲从中截取一个四边
学）疫情期间B，某小区超市平A 面图如图所示，由矩形 OABC
与
扇形 OCD 组成（，第江苏6 题省）南京市十校 2020 届高三下学期 5 月调研试题数学含 OA＝30 米，
AB＝50 米，∠COD＝ ，经营者决定在 O 点处安装一个监控摄像头，摄像头的监控视角 6
∠EOF＝ ，摄像头监控区域为图中阴影部分，要求点 E 在弧 CD 上，点 F 在线段 AB 上．设 3
3、（江苏省2020年高考数学全真模拟试卷(六 (南通教研室)）为了打击海盗犯罪,甲、乙、
丙三国海军进行联合军事演习,分别派出一艘军舰A,B,C.演习要求: 任何时刻军舰A,B,C均
不得在同一条直线上.
(1) 如图 1, 若演习过程中,A,B 间的距离始终保持 3 n mile, B,C 间的距离始终保持
场，半圆 的直径 在一条东西走向的公路上， A
，半圆边界上点 处是娱乐休闲
B
A
B
区域，且圆心在正北方向.
（图 1）
（图 2）
（图 3）
（1）若在圆心 北偏西某一方向的圆周上设立另一个休闲点 ，问当点 在何处时，四边形
（第 8 题）
3
学海无涯
观赏区域
的面积最大？
（2）若计划修建一条从点 出发，经过点 到达点 处的栈道（其中点 在半径 上， 为
江苏省2020届高考数学二轮复习 专题十五 附加题23题 苏教版
江苏省2020届高考数学（苏教版）二轮复习专题15 附加题23题1江苏高考考试说明中附加题圆锥曲线与方程中抛物线为B级要求，2020年、2020年高考中均没有考查，预测2020年高考中可能会考查；2江苏高考考试说明附加题中对空间向量与立体几何是B级要求，2020年、2020年、2020年高考没有考查，2020年高考考查空间角的概念，求线段的长.预测2020年高考会考查.[典例1]在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A(2,2)，其焦点F在x轴上．(1)求抛物线C的标准方程；(2)求过焦点F，且与直线OA垂直的直线的方程；(3)设过点M(m,0)(m>0)的直线交抛物线C于D，E两点，ME＝2DM，记D和E两点间的距离为f(m)，求f(m)关于m的表达式．[解] (1)由题意，可设抛物线C的标准方程为y2＝2px.因为点A(2,2)在抛物线C上，所以p＝1.因此，抛物线C的标准方程为y2＝2x.(2)由(1)可得焦点F 的坐标是⎝ ⎛⎭⎪⎫12，0，又直线OA 的斜率为22＝1，故与直线OA 垂直的直线的斜率为－1.因此，所求直线的方程是x ＋y －12＝0.(3)法一：设点D 和E 的坐标分别为(x 1， y 1)和(x 2，y 2)，直线DE 的方程是y ＝k (x －m )，k ≠0.将x ＝yk＋m 代入y 2＝2x ，有ky 2－2y －2km ＝0， 解得y 1,2＝1±1＋2mk2k.由ME ＝2DM ，知1＋1＋2mk 2＝2(1＋2mk 2－1)， 化简得k 2＝4m，因此DE 2＝(x 1－x 2)2＋(y 1－y 2)2＝⎝ ⎛⎭⎪⎫1＋1k 2(y 1－y 2)2＝⎝ ⎛⎭⎪⎫1＋1k 241＋2mk 2k 2＝94(m 2＋4m )． 所以f (m )＝32m 2＋4m (m >0)．法二：设D ⎝ ⎛⎭⎪⎫s 22，s ，E ⎝ ⎛⎭⎪⎫t 22，t ， 由点M (m,0)及ME u u u r ＝2DM u u u u r得12t 2－m ＝2⎝ ⎛⎭⎪⎫m －s 22，t －0＝2(0－s )． 因此t ＝－2s ，m ＝s 2，所以f (m )＝DE ＝⎝⎛⎭⎪⎫2s 2－s 222＋－2s －s2＝32m 2＋4m (m >0)．本小题主要考查直线、抛物线方程及两点间的距离公式等基本知识，考查运算求解能力． [演练1](2020·徐州信息卷)过直线x ＝－2上的动点P 作抛物线y 2＝4x 的两条切线PA ，PB ，其中A ，B 为切点．(1)若切线PA ，PB 的斜率分别为k 1，k 2，求证：k 1k 2为定值； (2)求证：直线AB 恒过定点．证明：(1)不妨设A (t 21，2t 1)(t 1>0)，B (t 22，2t 2)(t 2<0)，P (－2，m )． 因为y 2＝4x ，所以当y >0时，y ＝2x ，y ′＝1x，所以k 1＝1t 1.同理k 2＝1t 2.由k 1＝2t 1－m t 21＋2＝1t 1，得t 21－mt 1－2＝0.同理t 22－mt 2－2＝0.所以t 1，t 2是方程t 2－mt －2＝0的两个实数根． 所以t 1t 2＝－2. 所以k 1k 2＝1t 1t 2＝－12为定值． (2)直线AB 的方程为y －2t 1＝2t 2－t 1t 22－t 21(x －t 21)， 即y ＝2t 1＋t 2x ＋2t 1－2t 21t 1＋t 2，即y ＝2t 1＋t 2x ＋2t 1t 2t 1＋t 2，由于t 1t 2＝－2， 所以直线方程化为y ＝2t 1＋t 2(x －2)， 所以直线AB 恒过定点(2,0)．[典例2](2020·泰州期末)如图，在三棱锥P —ABC 中，平面ABC ⊥平面APC ，AB ＝BC ＝AP ＝PC ＝2，∠ABC ＝∠APC ＝90°.(1)求直线PA 与平面PBC 所成角的正弦值；(2)若动点M 在底面三角形ABC 上，二面角M －PA －C 的余弦值为31111，求BM 的最小值．[解] (1)取AC 中点O ， ∵AB ＝BC ，∴OB ⊥OC . ∵平面ABC ⊥平面APC ， 平面ABC ∩平面APC ＝AC ， ∴OB ⊥平面PAC . ∴OB ⊥OP .以O 为坐标原点，OB ，OC ，OP 分别为x ，y ，z 轴建立如图所示空间直角坐标系． ∵AB ＝BC ＝PA ＝2，∴OB ＝OC ＝OP ＝1.从而O (0,0,0)，B (1,0,0)，A (0，－1,0)，C (0,1,0)，P (0,0，1)，∴BC u u u r＝(－1,1,0)，PB u u u r ＝(1,0，－1)，AP u u u r ＝(0,1,1)．设平面PBC 的法向量n 1＝(x ，y ，z )，由BC u u u r ·n 1＝0，PB u u u r ·n 1＝0得方程组⎩⎪⎨⎪⎧－x ＋y ＝0，x －z ＝0.取n 1＝(1,1,1)，∴cos 〈AP u u u r ，n 1〉＝AP u u u r·n 1| AP u u u r ||n 1|＝63. 设PA 与平面PBC 所成角为θ，则sin θ＝|cos 〈AD u u u r ，n 1〉|＝63.∴直线PA 与平面PBC 所成角的正弦值为63. (2)由题意平面PAC 的法向量n 2＝(1,0,0)． 设平面PAM 的法向量为n 3＝(x ，y ，z )，M (m ，n,0)．∵AP u u u r ＝(0,1,1)，AM u u u u r＝(m ，n ＋1,0)，又∵AP u u u r ·n 3＝0，AM u u u u r·n 3＝0，∴⎩⎪⎨⎪⎧y ＋z ＝0，mx ＋n ＋1y ＝0，取n 3＝⎝⎛⎭⎪⎫n ＋1m ，－1，1.∴cos 〈n 2，n 3〉＝n 2·n 3|n 2||n 3|＝n ＋1m ⎝ ⎛⎭⎪⎫n ＋1m 2＋2＝31111.∴⎝⎛⎭⎪⎫n ＋1m 2＝9.∴n ＋1＝3m 或n ＋1＝－3m (舍去)．∴AM u u u u r＝(m,3m,0)． 又AB u u u r＝(1,1,0)，∴cos 〈AM u u u u r ，AB u u u r 〉＝⎪⎪⎪⎪⎪⎪m ，3m ，0·1，1，010m 2·2＝255. 则sin 〈AM u u u u r ，AB u u u r 〉＝53，∴d ＝AB ·55＝105. ∴B 点到AM 的最小值为垂直距离d ＝105.考查空间向量在立体几何中的应用，求出平面的法向量是解题的关键． [演练2](2020·苏北四市二模)在棱长为2的正方体ABCD —A 1B 1C 1D 1中，E 为棱AB 的中点，点P 在平面A 1B 1C 1D 1中，D 1P ⊥平面PCE .(1)试求：线段D 1P 的长；(2)直线DE 与平面PCE 所成角的正弦值．解：(1)建立如图所示的空间直角坐标系，则D 1(0,0,2)，E (2,1,0)，C (0,2,0)．设P (x ，y,2)，则1D P u u u u r＝(x ，y,0)， EP u u u r＝(x －2，y －1,2)， EC u u u r＝(－2,1,0)．因为D 1P ⊥平面PCE ，所以D 1P ⊥EP .D 1P ⊥EC .所以1D P u u u u r ·EP u u u r ＝0，1D P u u u u r ·EC u u u r＝0，故⎩⎪⎨⎪⎧x x －2＋y y －1＝0，－2x ＋y ＝0.解得⎩⎪⎨⎪⎧x ＝0，y ＝0(舍去)或⎩⎪⎨⎪⎧x ＝45，y ＝85.即P ⎝ ⎛⎭⎪⎫45，85，2，所以1D P u u u u r ＝⎝ ⎛⎭⎪⎫45，85，0，所以D 1P ＝1625＋6425＝455.(2)由(1)知，DE u u u r＝(2,1,0)，1D P u u u u r ＝⎝ ⎛⎭⎪⎫45，85，0，1D P u u u u r ⊥平面PEC ，设DE 与平面PEC 所成角为θ，1D P u u u u r 与DE u u u r 所成角为α，则sin θ＝|cos α|＝⎪⎪⎪⎪⎪⎪⎪⎪1D P u u u u r ·DE u u u r | 1D P u u u u r ||DE u u u r |＝1655·8025＝45. 所以直线DE 与平面PEC 所成角的正弦值为45.[专题技法归纳](1)抛物线与直线的位置关系中重点考查顶点在原点的抛物线与过焦点的直线的位置关系，熟练掌握抛物线的几何性质，利用几何性质解决问题较为简单；(2)空间向量与立体几何主要考查向量的坐标表示、向量运算、平面的法向量、空间角及距离的计算．对于点的位置的探索问题，可以利用向量共线定理设元确定．1.(2020·苏北四市三模)在三棱锥S —ABC 中，底面是边长为23的正三角形，点S 在底面ABC 上的射影O 恰是BC 的中点，侧棱SA 和底面成45°角．(1) 若D 为侧棱SA 上一点，当SD DA为何值时，BD ⊥AC ； (2) 求二面角S —AC —B 的余弦值大小．解：以O 点为原点，OC 为x 轴，OA 为y 轴，OS 为z 轴建立空间直角坐标系．因为△ABC 是边长为23的正三角形，又SA 与底面所成角为45°，所以∠SAO ＝45°.所以SO ＝AO ＝3.所以O (0,0,0)，C (3，0,0)，A (0,3,0)，S (0,0,3)，B (－3，0，0)．(1)设AD ＝a ，则D ⎝⎛⎭⎪⎫0，3－22a ，22a ，所以BD u u u r ＝⎝⎛⎭⎪⎫3，3－22a ，22a ，AC u u u r ＝(3，－3,0)．若BD ⊥AC ，则BD u u u r ·AC u u u r ＝3－3⎝⎛⎭⎪⎫3－22a ＝0，解得a ＝22，而AS ＝32，所以SD ＝ 2.所以SD DA ＝222＝12.(2)因为AS u u u r ＝(0，－3,3)，BC u u u r＝(23，0,0)．设平面ACS 的法向量为n 1＝(x ，y ，z )，则⎩⎨⎧n 1·AC u u u r＝x ，y ，z ·3，－3，0＝3x －3y ＝0，n 1·AS u u u r＝x ，y ，z ·0，－3，3＝－3y ＋3z ＝0，令z ＝1，则x ＝3，y ＝1，所以n 1＝(3，1,1)． 而平面ABC 的法向量为n 2＝(0,0,1)， 所以cos 〈n 1，n 2〉＝3×0＋1×0＋1×112＋12＋32·1＝15，显然所求二面角的平面角为锐角，故所求二面角的余弦值的大小为55. 2.(2020·镇江5月)在正方体ABCD －A 1B 1C 1D 1中，O 是AC 的中点，E 是线段D 1O 上一点，且D 1E ＝λEO .(1)若λ＝1，求异面直线DE 与CD 1所成角的余弦值； (2)若平面CDE ⊥平面CD 1O ，求λ的值．解：(1)不妨设正方体的棱长为1，以DA u u u r ，DC u u u r ，1DD u u u ur 为单位正交基底建立如图所示的空间直角坐标系D －xyz .则A (1,0,0)，O ⎝ ⎛⎭⎪⎫12，12，0，C (0,1,0)，D 1(0,0,1)，E ⎝ ⎛⎭⎪⎫14，14，12， 于是DE u u u r ＝⎝ ⎛⎭⎪⎫14，14，12，1CD u u u u r＝(0，－1,1)．由cos 〈DE u u u r ，1CD u u u u r 〉＝DE u u u r ·1CD u u u u r| DE u u ur |·| 1CD u u u u r |＝36. 所以异面直线AE 与CD 1所成角的余弦值为36. (2)设平面CD 1O 的向量为m ＝(x 1，y 1，z 1)，由m ·CO u u u r ＝0，m ·1CD u u u u r＝0，得⎩⎪⎨⎪⎧12x 1－12y 1＝0，－y 1＋z 1＝0，取x 1＝1，得y 1＝z 1＝1，即m ＝(1,1,1)． 由D 1E ＝λEO ，则E ⎝⎛⎭⎪⎫λ21＋λ，λ21＋λ，11＋λ，DE u u u r ＝⎝ ⎛⎭⎪⎫λ21＋λ，λ21＋λ，11＋λ.又设平面CDE 的法向量为n ＝(x 2，y 2，z 2)，由n ·CD u u u r＝0，n ·DE u u u r ＝0.得⎩⎪⎨⎪⎧y 2＝0，λx 221＋λ＋λy 221＋λ＋z 21＋λ＝0，取x 2＝2，得z 2＝－λ，即n ＝(－2,0，λ)．因为平面CDE ⊥平面CD 1O ，所以m ·n ＝0，得λ＝2.3.(2020·南通密卷)如图，已知三棱柱ABC －A 1B 1C 1的侧棱与底面垂直，AA 1＝AB ＝AC ＝1，AB ⊥AC ，M 是CC 1的中点，N 是BC 的中点，点P 在直线A 1B 1上，且满足1A P u u u r ＝λ11A B u u u u r.(1)当λ取何值时，直线PN 与平面ABC 所成的角θ最大？(2)若平面PMN 与平面ABC 所成的二面角为45°，试确定点P 的位置． 解：(1)以AB ，AC ，AA 1分别为x ，y ，z 轴，建立空间直角坐标系A —xyz ，则N ⎝ ⎛⎭⎪⎫12，12，0，P (λ，0,1)，则PN u u u r ＝⎝ ⎛⎭⎪⎫12－λ，12，－1， 平面ABC 的一个法向量为n ＝(0,0,1)，则sin θ＝|cos 〈PN u u u r ，n 〉|＝|PN u u u r·n || PN u u u r ||n |＝1⎝ ⎛⎭⎪⎫λ－122＋54.于是问题转化为二次函数求最值，而θ∈⎣⎢⎡⎦⎥⎤0，π2，当θ最大时，sin θ最大，所以当λ＝12时，sin θ最大，θ也最大．(2)已知给出了平面PMN 与平面ABC 所成的二面角为45°，即可得到平面ABC 的一个法向量为n ＝1AA u u u r ＝(0,0,1)，设平面PMN 的一个法向量为m ＝(x ，y ，z )，MP u u u r ＝⎝⎛⎭⎪⎫λ，－1，12.由⎩⎨⎧m ·NP u u u r＝0，m ·MP u u u r＝0，得⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫λ－12x －12y ＋z ＝0，λx －y ＋12z ＝0，解得⎩⎪⎨⎪⎧y ＝2λ＋13x ，z ＝21－λ3x .令x ＝3，得m ＝(3,2λ＋1,2(1－λ))，于是由 |cos 〈m ，n 〉|＝|m ·n ||m ||n|＝|21－λ|9＋2λ＋12＋41－λ2＝22，解得λ＝－12， 故点P 在B 1A 1的延长线上，且|A 1P |＝12.4．(2020·泰州期末)对称轴为坐标轴，顶点在坐标原点的抛物线C 经过两点A (a,2a )，B (4a,4a )(其中a 为正常数)．(1)求抛物线C 的方程；(2)设动点T (m,0)(m >a )，直线AT ，BT 与抛物线C 的另一个交点分别为A 1，B 1，当m 变化时，记所有直线A 1B 1组成的集合为M ，求证：集合M 中的任意两条直线都相交且交点都不在坐标轴上．解：(1)当抛物线焦点在x 轴上时， 设抛物线方程y 2＝2px ，∵⎩⎪⎨⎪⎧ 4a 2＝2pa ，16a 2＝8pa ，∴p ＝2a .∴y 2＝4ax .当抛物线焦点在y 轴上时，设抛物线方程x 2＝2py ，∵⎩⎪⎨⎪⎧16a 2＝8pa ，a 2＝4pa ，方程无解，∴抛物线不存在．综上抛物线C 的方程为y 2＝4ax .(2)设A 1(as 2,2as )，B 1(at 2,2at )，T (m,0)(m >a )． ∵k TA ＝kTA 1，∴2a a －m ＝2asas 2－m， ∴as 2＋(m －a )s －m ＝0.∵(as ＋m )(s －1)＝0，∴s ＝－m a ，∴A 1⎝ ⎛⎭⎪⎫m 2a ，－2m .∵k TB ＝kTB 1，∴4a 4a －m ＝2atat 2－m.∵2at 2＋(m －4a )t －2m ＝0，∴(2at ＋m )(t －2)＝0.∴t ＝－m 2a .∴B 1⎝ ⎛⎭⎪⎫m 24a ，－m .∴直线A 1B 1的方程为y ＋2m ＝－2m ＋m m 2a －m 24a⎝ ⎛⎭⎪⎫x －m 2a .∵直线的斜率为－4a3m 在(a ，＋∞)单调，∴集合M 中的直线必定相交．∵直线的横截距为－m 22a 在(a ，＋∞)单调，纵截距为－2m 3在(a ，＋∞)单调， ∴任意两条直线都相交且交点都不在坐标轴上． 5．(2020·常州)已知斜率为k (k ≠0)的直线l 过抛物线C ：y 2＝4x 的焦点F 且交抛物线于A ，B 两点．设线段AB 的中点为M .(1)求点M 的轨迹方程；(2)若－2<k <－1时，点M 到直线l ′：3x ＋4y －m ＝0(m 为常数，m <13)的距离总不小于15，求m 的取值范围．解：(1)焦点F (1,0)，直线AB 方程为y ＝k (x －1)，因为k ≠0，所以x ＝yk＋1. 由⎩⎪⎨⎪⎧ x ＝y k＋1，y 2＝4x 得y 2－4ky －4＝0. 设A (x 1，y 1)，B (x 2，y 2)，M (x 0，y 0)，显然Δ>0恒成立，则y 0＝y 1＋y 22＝2k . 又x 0＝y 0k ＋1，消去k ，得y 20＝2(x 0－1)，所以点M 的轨迹方程为y 2＝2(x －1)．(2)由(1)知，点M ⎝ ⎛⎭⎪⎫2k 2＋1，2k . 因为m <13，所以d ＝15⎪⎪⎪⎪⎪⎪6k 2＋8k －m ＋3＝15⎝ ⎛⎭⎪⎫6k 2＋8k －m ＋3. 由题意，得15⎝ ⎛⎭⎪⎫6k 2＋8k －m ＋3≥15，m ≤6k 2＋8k ＋2对－2<k <－1恒成立． 因为－2<k <－1时，6k 2＋8k ＋2的最小值是－23， 所以m ≤－23. 6．(2020·南通密卷)在平面直角坐标系xOy 中，已知焦点为F 的抛物线x 2＝4y 上有两个动点A ，B ，且满足AF u u u r ＝λFB u u u r ， 过A ，B 两点分别作抛物线的切线，设两切线的交点为M .(1)求：OA u u u r ·OB u u u r 的值；(2)证明：FM u u u u r ·AB u u u r 为定值．解：(1)设A ⎝ ⎛⎭⎪⎫x 1，x 214，B ⎝ ⎛⎭⎪⎫x 2，x 224，∵焦点F (0,1)，∴AF u u u r ＝⎝ ⎛⎭⎪⎫－x 1，1－x 214，FB u u u r ＝⎝ ⎛⎭⎪⎫x 2，x 224－1. ∵AF u u u r ＝λFB u u u r ，∴⎩⎪⎨⎪⎧ －x 1＝λx 2，1－x 214＝λ⎝ ⎛⎭⎪⎫x 224－1，消λ，得x 1⎝ ⎛⎭⎪⎫x 224－1＋x 2⎝ ⎛⎭⎪⎫1－x 214＝0. 化简整理得(x 1－x 2)⎝ ⎛⎭⎪⎫x 1x 24＋1＝0. ∵x 1≠x 2，∴x 1x 2＝－4.∴y 1y 2＝x 214·x 224＝1. ∴OA u u u r ·OB u u u r ＝x 1x 2＋y 1y 2＝－3.(2)证明：抛物线方程为y ＝14x 2，∴y ′＝12x . ∴过抛物线A ，B 两点的切线方程分别为y ＝12x 1(x －x 1)＋x 214和y ＝12x 2(x －x 2)＋x 224， 即y ＝12x 1x －x 214和y ＝12x 2x －x 224. 联立解出两切线交点M 的坐标为⎝ ⎛⎭⎪⎫x 1＋x 22，－1. ∴FM u u u u r ·AB u u u r ＝⎝ ⎛⎭⎪⎫x 1＋x 22，－2·⎝⎛⎭⎪⎫x 2－x 1，x 22－x 214 ＝x 22－x 212－x 22－x 212＝0(定值).7.(2020·淮阴联考)在平面直角坐标系xOy 中，已知点A (－1,1)，P是动点，且三角形POA 的三边所在直线的斜率满足k OP ＋k OA ＝k PA .(1)求点P 的轨迹C 的方程；(2)若Q 是轨迹C 上异于点P 的一个点，且PQ u u u r ＝λOA u u u r ，直线OP 与QA 交于点M ，问：是否存在点P 使得△PQA 和△PAM 的面积满足S △PQA ＝2S△PAM ？若存在，求出点P 的坐标；若不存在，说明理由．解：(1)设点P (x ，y )为所求轨迹上的任意一点，则由k OP ＋k OA ＝k PA得，y x ＋1－1＝y －1x ＋1，整理得轨迹C 的方程为y ＝x 2(x ≠0且x ≠－1)． (2)设P (x 1，x 21)，Q (x 2，x 22)， 由PQ u u u r ＝λOA u u u r 可知直线PQ ∥OA ，则k PQ ＝k OA ，故x 22－x 21x 2－x 1＝1－0－1－0，即x 2＝－x 1－1. 直线OP 方程为y ＝x 1x .①直线QA 的斜率为－x 1－12－1－x 1－1＋1＝－x 1－2， ∴直线QA 方程为y －1＝(－x 1－2)(x ＋1)，即y ＝－(x 1＋2)x －x 1－1.②联立①②，得x ＝－12，∴点M 的横坐标为定值－12. 由S △PQA ＝2S △PAM ，得到QA ＝2AM ，因为PQ ∥OA ，所以OP ＝2OM ， 由PO u u u r ＝2 OM u u u u r ，得x 1＝1，∴P 的坐标为(1,1)．∴存在点P 满足S △PQA ＝2S △PAM ，P 的坐标为(1,1)．8.(2020·徐州一模)如图，过抛物线C ：y 2＝4x 上一点P (1，－2)作倾斜角互补的两条直线，分别与抛物线交于点A (x 1，y 1)，B (x 2，y 2)．(1)求y 1＋y 2的值；(2)若y 1≥0，y 2≥0，求△PAB 面积的最大值．解：(1)因为A (x 1，y 1)，B (x 2，y 2)在抛物线C ： y 2＝4x 上，所以A ⎝ ⎛⎭⎪⎫y 214，y 1，B ⎝ ⎛⎭⎪⎫y 224，y 2， k PA ＝y 1＋2y 214－1＝4y 1＋2y 21－4＝4y 1－2， 同理k PB ＝4y 2－2，依题有k PA ＝－k PB ， 所以4y 1－2＝－4y 2－2，即y 1＋y 2＝4. (2)由(1)知k AB ＝y 2－y 1y 224－y 214＝1，设AB 的方程为 y －y 1＝x －y 214，即x －y ＋y 1－y 214＝0， P 到AB 的距离为d ＝⎪⎪⎪⎪⎪⎪3＋y 1－y 2142，AB ＝2⎪⎪⎪⎪⎪⎪y 214－y 224＝2|y 1－y 2|＝22|2－y 1|， 所以S △PAB ＝12×⎪⎪⎪⎪⎪⎪3＋y 1－y 2142×22|2－y 1|＝14|y 21－4y 1－12||y 1－2| ＝14|(y 1－2)2－16||y 1－2|， 令y 1－2＝t ，由y 1＋y 2＝4，y 1≥0，y 2≥0，可知－2≤t ≤2.S △PAB ＝14|t 3－16t |， 因为S △PAB ＝14|t 3－16t |为偶函数，只考虑0≤t ≤2的情况， 记f (t )＝|t 3－16t |＝16t －t 3，f ′(t )＝16－3t 2>0，故f (t )在[0,2]是单调增函数，故f (t )的最大值为f (2)＝24，故S △PAB 的最大值为6.。
2020年高考江苏版高考数学 3.3 导数在实际问题中的应用及综合应用
当 θ∈ 6,2 时, f '(θ)<0,所以 f(θ)为减函数,
π
因此,当 θ=6时, f(θ)取到最大值.
π
答:当 θ=6时,能使甲、乙两种蔬菜的年总产值最大. 名师点睛 (1)用 θ 表示 OE 和 EC,就能求出矩形 ABCD 及三角形 CPD 的面积,求定义域时抓住 N、G 关于 OK 对称得到∠GOK 的正弦值,从而求得 sin θ 的范围. (2)先构造函数,再用导数求最值,求导时,交代 θ 的范围,判断 f '(θ)的符号,再确定 f(θ)的单调性,就 能得到最大值,从而解决问题. 2.(2016 江苏,17,14 分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥 P-A1B1C1D1,下 部的形状是正四棱柱 ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高 O1O 是正四棱锥的高 PO1 的 4 倍. (1)若 AB=6 m,PO1=2 m,则仓库的容积是多少? (2)若正四棱锥的侧棱长为 6 m,则当 PO1 为多少时,仓库的容积最大?
3
∴长方体体积的最大值为36立方分米.
备战 2020 高考
过专题 【五年高考】 A 组 自主命题·江苏卷题组
1.(2018 江苏,17,14 分)某农场有一块农田,如图所示,它的边界由圆 O 的一段圆弧 MPN(P 为此圆弧的中点) 和线段 MN 构成.已知圆 O 的半径为 40 米,点 P 到 MN 的距离为 50 米.现规划在此农田上修建两个温室大棚, 大棚Ⅰ内的地块形状为矩形 ABCD,大棚Ⅱ内的地块形状为△CDP,要求 A,B 均在线段 MN 上,C,D 均在圆弧上. 设 OC 与 MN 所成的角为 θ. (1)用 θ 分别表示矩形 ABCD 和△CDP 的面积,并确定 sin θ 的取值范围; (2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为 4∶3. 求当 θ 为何值时,能使甲、乙两种蔬菜的年总产值最大.
2020届江苏高考数学应用题精选试题(一)
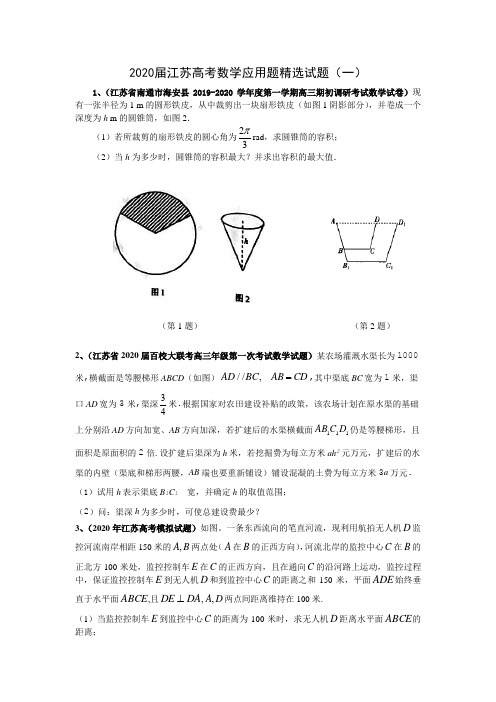
2020届江苏高考数学应用题精选试题（一）1、（江苏省南通市海安县2019-2020学年度第一学期高三期初调研考试数学试卷）现有一张半径为1 m 的圆形铁皮，从中裁剪出一块扇形铁皮（如图1阴影部分），并卷成一个深度为h m 的圆锥筒，如图2．（1）若所裁剪的扇形铁皮的圆心角为23πrad ，求圆锥筒的容积； （2）当h 为多少时，圆锥筒的容积最大？并求出容积的最大值．（第1题） （第2题）2、（江苏省2020届百校大联考高三年级第一次考试数学试题）某农场灌溉水渠长为1000米,横截面是等腰梯形ABCD （如图）//,AD BC AB CD =,其中渠底BC 宽为1米，渠口AD 宽为3米,渠深43米.根据国家对农田建设补贴的政策，该农场计划在原水渠的基础上分别沿AD 方向加宽、AB 方向加深，若扩建后的水渠横截面111AB C D 仍是等腰梯形，且面积是原面积的2倍.设扩建后渠深为h 米，若挖掘费为每立方米ah 2元万元，扩建后的水渠的内壁（渠底和梯形两腰，AB 端也要重新铺设）铺设混凝的土费为每立方米3a 万元.（1）试用h 表示渠底B 1C 1宽，并确定h 的取值范围；（2）问：渠深h 为多少时，可使总建设费最少？3、（2020年江苏高考模拟试题）如图。
一条东西流向的笔直河流，现利用航拍无人机D 监控河流南岸相距150米的B A ,两点处（A 在B 的正西方向），河流北岸的监控中心C 在B 的正北方100米处，监控控制车E 在C 的正西方向，且在通向C 的沿河路上运动，监控过程中，保证监控控制车E 到无人机D 和到监控中心C 的距离之和150米，平面ADE 始终垂直于水平面ABCE ,且DA DE ⊥,D A ,两点间距离维持在100米.（1）当监控控制车E 到监控中心C 的距离为100米时，求无人机D 距离水平面ABCE 的距离；（2）若记无人机D 看A 处的俯角（)θ=∠DAE ,监控过程中，四棱锥D —ABCE 内部区域的体积为监控影响区域V ,请将V 表示为关于θ的函数，并求出监控影响区域的最大值.(第3题) (第4题)4（江苏省海门市（海门中学）2020届高三第一次教学质量调研数学）场计划设计建造一条2000米长的水渠，其横断面如图所示其中，底部是半径为1米的圆 弧AB,上部是有一定倾角的线段AD 与BC,渠深MN 为23米，且圆弧的圆心为O 在MN 上，AD 丄OA , BC 丄OB , AD = BC , AB//DC .据测算，水渠底部曲面每平方米的造价为35百元，上部矩形壁面每平方米的造价为1百元，其他费用忽略不计.设20,πθθ<<=∠BON（1） 试用θ表示水渠建造的总费用)(θf （单位:百元）：（2） 试确定θ的值，使得建造总费用最低.5、（江苏省“百校大联考”高三年级第二次考试数学）如图，在矩形纸片ABCD 中，cm AB 6=，cm AD 12=，在线段AB 上取一点M ，沿着过M 点的直线将矩形右下角折起，使得右下角顶点B 恰好落在矩形的左边AD 边上．设折痕所在直线与BC 交于N 点,记折痕MN 的长度为l ，翻折角BNM ∠为θ．（1）探求l 与θ的函数关系，推导出用θ表示l 的函数表达式；（2）设BM 的长为xcm ，求x 的取值范围；（3）确定点M 在何处时，翻折后重叠部分的图形面积最小．6、（2020届江苏省启东中学高三年级第一学期期初考试）启东市政府拟在蝶湖建一个旅游观光项目，设计方案如下：如图所示的圆O 是圆形湖的边界，沿线段DA CD BC AB ,,,建一个观景长廊，其中D C B A ,,, 是观景长廊的四个出入口且都在圆O 上，已知：12=BC百米，8=AB 百米,在湖中P 处和湖边D 处各建一个观景亭，且它们关于直线AC 对称,在湖面建一条观景桥APC 观景亭的大小、观景长廊、观景桥的宽度均忽略不计，设α=∠ABC ．（1）若观景长廊4=AD 百米，AB CD =，求由观景长廊所围成的四边形ABCD 内的湖面面积；（2）当060=α时，求三角形区域ADC 内的湖面面积的最大值；（3）若8=CD 百米且规划建亭点P 在三角形ABC 区域内（不包括边界），试判断四边形ABCP 内湖面面积是否有最大值？若有，求出最大值，并写出此时α的值；若没有，请说明理由．(第5题) （第6题）7、（江苏省泰州中学、江都中学、宜兴中学2020届高三10月月考数学试题）某同学大学毕业后，决定利用所学专业进行自主创业，经过市场调 查，生产一小型电子产品需投入固定成本2万元，每生产x 万件，需另投入流动成本()C x 万元，当年产量小于7万件时，21()23C x x x =+（万元）：当年产量不小于7万件时，3()6ln 17e C x x x x =++-（万元）.己知每件产品售价为6元，若该同学生产的产品当年全部售完.（1）写出年利润()P x （万元）关于年产量x （万件）的函数解析式；（注；年利润=年销售收人-固定成本-流动成本（2）当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润是多少？（取320e ≈〉8、（江苏省如皋市2019-2020学年度高三年级第一学期教学质量调研（一））某市在精准扶贫和生态文明建设的专项工作中，为改善农村生态环境，建设美丽乡村，开展农村生活用水排污管道“村村通”。
江苏专用2020年高考数学一轮复习考点数学归纳法必刷题含解析(1).doc
课时训练(九)平面直角坐标系与函数(限时:30分钟)|夯实基础|1.[2019·株洲]在平面直角坐标系中,点A(2,-3)位于()A.第一象限B.第二象限C.第三象限D.第四象限2.[2019·杭州]在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则 ()A.m=3,n=2B.m=-3,n=2C.m=2,n=3D.m=-2,n=33.[2018·扬州] 在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M 的坐标是()A.(3,-4)B.(4,-3)C.(-4,3)D.(-3,4)4.[2019·枣庄]在平面直角坐标系中,将点A(1,-2)先向上平移3个单位长度,再向左平移2个单位长度,得到点A',则点A'的坐标是()A.(-1,1)B.(-1,-2)C.(-1,2)D.(1,2)5.[2019·安顺]在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在 ()A.第一象限B.第二象限C.第三象限D.第四象限6.[2019·金华]如图K9-1是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是()图K9-1A.在南偏东75°方向处B.在5 km处C.在南偏东15°方向5 km处D.在南偏东75°方向5 km处7.[2019·随州]第一次“龟兔赛跑”,兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是()图K9-28.[2019·荆州]在平面直角坐标系中,点A的坐标为(1,√3),以原点为中心,将点A顺时针旋转30°得到点A',则点A'的坐标为()A.(√3,1)B.(√3,-1)C.(2,1)D.(0,2)9.[2019·安顺]函数y=√x-2中自变量x的取值范围为.10.[2019·泸州]在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值是.11.[2019·福建] 在平面直角坐标系xOy中,▱OABC的三个顶点分别为O(0,0),A(3,0),B(4,2),则其第四个顶点C的坐标是.12.已知点A(a,-5),B(8,b),根据下列要求,确定a,b的值.(1)A,B两点关于y轴对称;(2)A,B两点关于原点对称;(3)AB∥x轴;(4)A,B两点在第一、三象限的角平分线上.13.[2019·桂林]如图K9-3,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐标为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.图K9-314.[2018·舟山] 小红帮弟弟荡秋千(如图K9-4①),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图②所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:①当t=0.7 s时,h的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多长时间?图K9-4|拓展提升|15.如图K9-5所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…,组成一条平滑的曲线,点P从原点O出发沿这条曲线向右运动,速度为每秒π个单位长度,则第2019秒时,点P的坐标是()2图K9-5A.(2018,0)B.(2019,1)C.(2019,-1)D.(2020,0)16.从某容器口以均匀地速度注入酒精,若液面高度h随时间t的变化情况如图K9-6所示,则对应容器的形状为()图K9-6图K9-7【参考答案】1.D2.B[解析]点A与点B关于y轴对称,则横坐标互为相反数,纵坐标相同,故选B.3.C[解析]平面直角坐标系中,点M在第二象限内,所以横坐标为负,纵坐标为正.由点M到x轴的距离为3,得纵坐标为3;由到y轴的距离为4,得横坐标为-4,所以M点的坐标为(-4,3),故选C.4.A[解析]根据平面直角坐标系中点的平移与坐标的关系,向上平移3个单位长度,则点A的纵坐标加3,向左平移2个单位长度,则点A的横坐标减去2,则A'(1-2,-2+3),即A'(-1,1),故选A.5.D[解析]m2是非负数,m2+1一定是正数,所以点P(-3,m2+1)在第二象限.关于原点对称的两个点横、纵坐标都互为相反数.由此得点P关于原点的对称点在第四象限.6.D[解析]目标A的位置在南偏东75°方向5 km处,故选D.7.B[解析]根据题意可知兔子先让乌龟跑了一段距离,但是比乌龟晚到终点,故选项B正确.8.A[解析]如图,作AE⊥y轴于E,A'F⊥x轴于F.∴∠AEO=∠OFA'=90°,∠AOE=∠AOA'=∠A'OF=30°,∴∠OAE=∠A'.∵OA=OA',∴△AOE≌△A'OF,∴OF=OE=√3,A'F=AE=1,∴A'(√3,1).故选A.9.x≥210.411.(1,2)[解析]如图,过C,B分别作x轴的垂线,垂足分别为D,E,可证△OCD≌△ABE,∴CD=BE=2,OD=AE=1,∴C(1,2).12.解:(1)当点A ,B 关于y 轴对称时, 有{x A =−x B ,y A =y B ,∴{a =−8,b =−5.(2)当点A ,B 关于原点对称时, 有{x A =−x B ,y A =−y B,∴{a =−8,b =5.(3)当AB ∥x 轴时,有{x A ≠x B ,y A =y B,∴{a ≠8,b =−5.(4)当A ,B 两点位于第一、三象限的角平分线上时,有x A =y A 且x B =y B ,即a=-5,b=8. 13.解:(1)如图,△A 1B 1C 1为所作三角形. (2)平面直角坐标系如图.(3)点A 1的坐标为(2,6).14.解:(1)∵对于每一个摆动时间t ,都有一个唯一的h 的值与其对应,∴变量h 是关于t 的函数. (2)①h=0.5 m,它的实际意义是秋千摆动0.7 s 时,离地面的高度为0.5 m . ②2.8 s .15.C [解析]点P 运动一个半圆用时为2π2÷π2=2(秒). ∵2019=1009×2+1,∴2019秒时,P 在第1010个半圆的中点处, ∴此时点P 坐标为(2019,-1). 故选C . 16.C。
江苏省2020届高考数学二轮复习 专题8 向量与复数
江苏省2020届高考数学（苏教版）二轮复习专题8 向量与复数回顾2020～2020年的考题，2020年第5题，2020年第2题、第15题，2020年第15题，2020年第10题，2020年第9题、第15题分别考查了向量的线性运算、坐标运算或数量积运算，属于中低档题；2020年第3题，2020年第1题，2020年第2题，2020年第3题，2020年第3题分别考察了复数的概念与四则运算，属容易题.预测在2020年的高考题中：1复数题依然是必考题，而且考查相对简单，在前3题； 2向量问题多以填空题的形式考查，也可能在解答题中以条件的形式出现.重点考查数量积的运算及应用.1．(2020·江苏高考)设a ，b ∈R ，a ＋b i ＝11－7i1－2i (i 为虚数单位)，则a ＋b ＝________.解析：∵a ＋b i ＝11－7i1＋2i5＝25＋15i5＝5＋3i ， ∴a ＝5，b ＝3，故a ＋b ＝8. 答案：82.设E ，F 分别是Rt△ABC 的斜边BC 上的两个三等分点，已知AB＝3，AC ＝6，则AE u u u r ·AF u u u r＝________.解析：AE u u u r ·AF u u u r ＝()AB u u u r ＋BE u u u r·()AC u u u r ＋CF uuu r ＝⎝ ⎛⎭⎪⎫AB uu u r ＋13 BC uuu r ·⎝ ⎛⎭⎪⎫AC u u u r －13 BC uuu r ＝AB u u u r ·AC u u u r －19|BC uuu r |2＋13BC uuu r ·(AC u u u r －AB u u u r)＝29|BC uuur |2＝29×45＝10. 答案：103．(2020·江苏高考)已知e 1，e 2是夹角为23π的两个单位向量，a ＝e 1－2e 2，b ＝k e 1＋e 2.若a ·b ＝0，则实数k 的值为____．解析：由题意知：a ·b ＝(e 1－2e 2)·(k e 1＋e 2)＝0， 即k e 21＋e 1e 2－2k e 1e 2－2e 22＝0，即k ＋cos 2π3－2k cos 2π3－2＝0，化简可求得k ＝54.答案：544．(2020·扬州质检)设OA u u u r ＝(1，－2)，OB uuu r ＝(a ，－1)，OC u u u r＝(－b,0)，a >0，b >0，O 为坐标原点，若A ，B ，C 三点共线，则1a ＋2b的最小值为________．解析：AB u u u r ＝OB uuur －OA u u u r ＝(a －1,1)，AC u u u r ＝(－b －1,2)．∵A ，B ，C 三点共线，∴AB u u u r ∥AC u u ur .∴2(a －1)＋(b ＋1)＝0. ∴2a ＋b ＝1.∴1a ＋2b ＝2a ＋b a ＋4a ＋2b b ＝4＋b a ＋4a b≥4＋2b a ·4ab＝8. 答案：85.如图，设点P 是三角形ABC 内一点(不包括边界)，且AP u u u r ＝m AB u u u r＋n AC u u u r ，m ，n ∈R ，则m 2＋(n －2)2的取值范围为________．解析：因为点P 是三角形ABC 内一点(不包括边界)，所以0<m ，n <1,0<m ＋n <1，根据线性规划的知识，作出如图阴影部分，m 2＋(n －2)2表示点P (0,2)到阴影内点的距离的平方，显然到点A (0,1)的距离最近，为1；到点B (1,0)的距离最远，这时m 2＋(n －2)2＝5，故所求取值范围为(1,5)．答案：(1,5)[典例1]若z 是实系数方程x 2＋2x ＋p ＝0的一个虚根，且|z |＝2，则p ＝________. [解析] 设z ＝a ＋b i(a ，b ∈R ，b ≠0)， 则a 2＋b 2＝4，且(a ＋b i)2＋2(a ＋b i)＋p ＝0，得⎩⎪⎨⎪⎧a 2＋b 2＝4，a 2－b 2＋2a ＋p ＝0，2ab ＋2b ＝0，解得p ＝4.[答案] 4利用复数相等的充要条件，将复数问题实数化是处理复数问题的基本策略． [演练1]设关于x 的方程x 2－(tan θ＋i)x －(2＋i)＝0有实根，求锐角θ及这个实根． 解：设实数根为a ，则a 2－(tan θ＋i)a －(2＋i)＝0，即a 2－a tan θ－2－(a ＋1)i ＝0.∵a ，tan θ∈R ，∴⎩⎪⎨⎪⎧a 2－a tan θ－2＝0，a ＋1＝0.∴a ＝－1且tan θ＝1. 又0<θ<π2，∴θ＝π4.[典例2]如图，在△ABC 和△AEF 中，B 是EF 的中点，AB ＝EF ＝1，CA ＝CB＝2，若AB u u u r ·AE u u u r ＋AC u u u r ·AF u u u r ＝2，则EF u u u r 与BC uuur 的夹角θ等于________．[解析] 因为△ABC 中，CA ＝CB ＝2，AB ＝1，所以cos ∠CAB ＝12·ABAC＝14，所以AC u u u r ·AB u u u r ＝12.又因为AB u u u r ·AE u u u r ＋AC u u u r ·AF u u u r＝2，所以AB u u u r ·(AB u u u r ＋BE u u u r )＋AC u u u r ·(AB u u u r ＋BF u u u r)＝2，即1＋AB u u u r ·BE u u u r ＋12＋AC u u u r ·BF u u u r＝2，所以AB u u u r ·BE u u u r ＋AC u u u r ·BF u u u r ＝12.因为BE u u u r ＝－BF u u u r ，所以－AB u u u r ·BF u u u r ＋AC u u u r ·BF u u u r ＝12，即BF u u u r (AC u u u r －AB u u u r )＝12，所以BF u u u r ·BC uuur ＝12，所以cos θ＝12，故θ＝π3.[答案]π3本题中△ABC 为确定的三角形，所以以AC u u u r ，AB u u u r 为基底，通过BF u u u r ，BC uuur 与基底的关系，进行计算．这类问题比较难建立未知向量与基底向量之间的关系，本题中关键是利用条件AB u u u r ·AE u u u r ＋AC u u u r ·AF u u u r＝2进行转化．另外本题也可以以B 为原点建立直角坐标系，用坐标进行研究．[演练2](2020·江苏高考)如图，在矩形ABCD 中，AB ＝2，BC ＝2，点E 为BC 的中点，点F 在边CD 上，若AB u u u r ·AF u u u r ＝2，则AE u u u r ·BF u u u r的值是________．解析：以A 为坐标原点，AB ，AD 所在的直线分别为x 轴，y 轴建立直角坐标系，则B (2，0)，E (2，1)，D (0,2)，C (2，2)．设F (x,2)(0≤x ≤2)，由AB u u u r ·AF u u u r＝2⇒2x ＝2⇒x ＝1，所以F (1,2)，AE u u u r ·BF u u u r＝(2，1)·(1－2，2)＝ 2.答案： 2 [典例3]如图，在正方形ABCD 中，E 为AB 的中点，P 为以A 为圆心、AB 为半径的圆弧上的任意一点，设向量AC u u u r ＝λDE u u u r ＋μAP u u u r，则λ＋μ的最小值为________．[解析] 以A 为原点，AB u u u r 为x 轴正方向，AD u u u r为y 轴正方向，建立直角坐标系．设AB ＝1，P (cos θ，sin θ)，θ∈⎣⎢⎡⎦⎥⎤0，π2，则AC u u u r ＝(1,1)，DE u u u r ＝⎝ ⎛⎭⎪⎫12，－1，AP u u u r ＝(cos θ，sin θ)，由题意得⎩⎪⎨⎪⎧1＝12λ＋μcos θ，1＝－λ＋μsin θ，解得μ＝32cos θ＋sin θ.又λ＝μsin θ－1，所以λ＋μ＝μ(sin θ＋1)－1＝31＋sin θ2cos θ＋sin θ－1.设y ＝1＋sin θ2cos θ＋sin θ，则y ′＝cos θ2cos θ＋sin θ－1＋sin θcos θ－2sin θ2cos θ＋sin θ2＝2＋2sin θ－cos θ2cos θ＋sin θ2，因为y ′＝2＋2sin θ－cos θ2cos θ＋sin θ2>0，所以y ＝1＋sin θ2cos θ＋sin θ在⎣⎢⎡⎦⎥⎤0，π2递增．所以(λ＋μ)min ＝12.[答案] 12解决本题的关键是将点P 坐标设为三角函数，从而引入三角函数来表示参数λ，μ.难点是对所得函数的进一步研究，通过导数确定函数的单调性，从而求得最小值．[演练3]设e 1，e 2是夹角为60°的两个单位向量，已知OM u u u u r ＝e 1，ON u u u r＝e 2，OP uuu r ＝x ·OM u u u u r ＋y ·ON u u u r(x ，y 为实数)．若△PMN 是以M 为直角顶点的直角三角形，则x －y 取值的集合为________．解析：由题意得|OM u u u u r |＝|ON u u u r |＝1，OM u u u u r ·ON u u u r ＝12，又因为△PMN 是以M 为直角顶点的直角三角形，所以有MP u u u r ·MN u u u ur ＝0，即(OP uuu r －OM u u u u r )·(ON u u u r －OM u u u u r)＝0，所以((x －1) OM u u u u r ＋y ON u u u r )·(ON u u u r －OM u u u u r)＝0，得(1－x )＋y ＋12(x －1－y )＝0，所以－12(x －y )＝－12，即x －y ＝1，故x －y 取值的集合为{1}． 答案：{1}[专题技法归纳](1)向量的数量积问题主要涉及向量的模、夹角、坐标这三个基本方面，有关向量数量积的运算都是这三个方面的运算．(2)处理向量问题，一般有两个途径，一是建立直角坐标系用坐标运算研究向量间的问题，二是用基底表示后直接运算．(3)平面向量的线性运算中应注意以下几个关键要素： ①基底向量的建立；②未知向量与基底向量的关系； ③向量条件的几何意义； ④参数取值范围的几何解法．1．(2020·南通第一次调研)若复数z 满足(1＋2i)z ＝－3＋4i(i 是虚数单位)，则z ＝________.解析：z ＝－3＋4i 1＋2i ＝－3＋4i1－2i5＝5＋10i5＝1＋2i. 答案：1＋2i2．定义：复数b ＋a i 是z ＝a ＋b i(a ，b ∈R )的转置复数，记为z ′＝b ＋a i ；复数a －b i 是z ＝a ＋b i(a ，b ∈R )的共轭复数，记为z ＝a －b i.给出下列三个命题：①z ′＝i·z ；②z ′＋z ′＝0；③z 1′·z 2′＝z 1·z 2.其中真命题的个数为________．解析：i·z ＝i(a －b i)＝b ＋a i ＝z ′，①正确；z ′＋z ′＝(a －b i)′＋b ＋a i ＝－b ＋a i ＋b －a i ＝0，②正确；z 1′·z 2′＝(a 1＋b 1i)′(a 2＋b 2i)′＝(b 1＋a 1i)(b 2＋a 2i)＝(b 1b 2－a 1a 2)＋(b 1a 2＋a 1b 2)i ，z1·z2＝a 1＋b 1i ·a 2＋b 2i ＝a 1a 2－b 1b 2＋a 1b 2＋b 1a 2i ＝(a 1a 2－b 1b 2)－(a 1b 2＋a 2b 1)i ，∴z 1′·z 2′≠z 1·z 2，③错，因此真命题个数是2.答案：23．在△ABC 中，角A 、B 、C 所对的边长分别为a 、b 、c ，设向量x ＝(sin B ，sin C )，向量y ＝(cos B ，cos C )，向量z ＝(cos B ，－cos C )，若z ∥(x ＋y )，则tan B ＋tan C 的值为________．解析：x ＋y ＝(sin B ＋cos B ，sin C ＋cos C )， 由z ∥(x ＋y )，得cos C (sin B ＋cos B )＋cos B (sin C ＋cos C )＝0， 即sin B cos C ＋cos B sin C ＝－2cos B cos C . 所以sin B cos C ＋cos B sin C cos B cos C ＝tan B ＋tan C ＝－2.答案：－24．平面内两个非零向量α，β，满足|β|＝1，且α与β－α夹角为135°，则|α|的取值范围________．解析：如图所示，在△OAB 中，设∠OBA ＝θ， 所以OB sin 45°＝OAsin θ，即|α|＝OA ＝2sin θ，又θ∈⎝ ⎛⎭⎪⎫0，34π，故|α|∈(0， 2 ]．答案：(0， 2 ]5．等边三角形ABC 中，P 在线段AB 上，且AP u u u r ＝λAB u u u r ，若CP u u u r ·AB u u u r ＝PA u u u r ·PB u u u r，则实数λ的值是________．解析：P 在线段AB 上，所以0≤λ≤1，不妨设等边三角形ABC 边长为1，∵CP u u u r ·AB u u u r＝PA u u u r ·PB u u u r ，∴(CA u u u r ＋AP u u u r )·AB u u u r ＝PA u u u r ·(AB u u u r －AP u u u r)，从而有CA u u u r ·AB u u u r ＋AP u u u r ·AB u u u r ＝PA u u u r ·AB u u u r －PA u u u r ·AP u u u r ，∴－12＋2λ＝λ2，解得λ＝1±22.又0≤λ≤1，∴λ＝1－22. 答案：1－226.如图放置的边长为1的正方形ABCD 的顶点A 、D 分别在x 轴、y 轴正半轴上(含原点)滑动，则OB uuu r ·OC u u u r的最大值是________．解析：设∠OAD ＝θ，则OA ＝AD ·cos θ＝cos θ， 点B 的坐标为(cos θ＋cos(90°－θ)，sin(90°－θ))， 即B (cos θ＋sin θ，cos θ)， 同理可求得C (sin θ，sin θ＋cos θ)，所以OB uuu r ·OC u u u r＝(cos θ＋sin θ，cos θ)·(sin θ，sin θ＋cos θ)＝1＋sin 2θ.所以(OB uuu r ·OC u u u r)max ＝2.答案：27．等腰直角三角形ABC 中，∠A ＝90°，AB ＝2，AD 是BC 边上的高，P 为AD 的中点，点M 、N 分别为AB 边和AC 边上的点，且M 、N 关于直线AD 对称，当PM u u u u r ·PN u u u r ＝－12时，AMMB＝________.解析：由等腰直角三角形ABC 中，∠A ＝90°，AB ＝2，AD 是BC 边上的高，P 为AD 的中点知，AD ＝1，AP ＝12.由PM u u u u r ·PN u u u r ＝－12知(PA u u u r ＋AM u u u u r )·(PA u u u r ＋AN u u u r )＝－12，即P PA u u u r 2＋(AM u u u u r ＋AN u u u r )·PA u u u r ＋AM u u u u r ·AN u u u r ＝－12.又M 、N 关于直线AD 对称，得|AM u u u u r |×12×cos 135°＋|AN u u u r |×12×cos 135°＝－34，故|AM u u u u r |＝324，所以AM MB＝3.答案：38.在平面直角坐标系xOy 中，设A 、B 、C 是圆x 2＋y 2＝1上相异三点，若存在正实数λ，μ，使得OC u u u r ＝λOA u u u r ＋μOB uuu r ，则λ2＋(μ－3)2的取值范围是________．解析：设OA u u u r 与OB uuu r 的夹角为θ，则由OC u u u r ＝λOA u u u r ＋μOB uuu r 得λ2＋2λμcos θ＋u 2＝1，从而由正实数λ，μ及|cos θ|<1，得－1<1－λ2－μ22λμ<1，所以λ＋μ>1，且|λ－μ|<1，作出如图所示的可行域，则λ2＋(μ－3)2表示区域内任一点到点(0,3)的距离的平方，而当点(0,3)到直线λ－μ＋1＝0的距离d 为最小值时，d 2＝2，所以λ2＋(μ－3)2的取值范围为(2，＋∞)．答案：(2，＋∞)9．(1)设向量a ＝(cos α，sin α)，b ＝(cos β，sin β)，其中0<α<β<π，若|2a ＋b |＝|a －2b |，则β－α＝________.(2)在△ABC 中，AB ＝1，AC ＝2，O 为△ABC 外接圆的圆心，则AO u u u r ·BC uuu r＝________.解析：(1)由|2a ＋b |＝|a －2b |得3a 2＋8a ·b －3b 2＝0，即a ·b ＝0，从而cos(β－α)＝0.又0<α<β<π，故0<β－α<π，所以β－α＝π2.(2)法一：AO u u u r ·BC uuu r ＝AO u u u r ·(OC u u u r －OB uuu r) ＝AO u u u r ·OC u u u r －AO u u u r ·OB uuu r ，又|AB u u u r|＝|OB uuu r －OA u u u r |，|AC u u u r |＝|OC u u u r －OA u u u r |，所以⎩⎨⎧|OB uuu r －OA u u u r |2＝OB uuu r 2－2OB uuu r ·OA u u u r ＋OA u u u r 2＝1，| OC u u u r －OA u u u r |2＝OC u u u r 2－2OC u u u r ·OA u u u r ＋OA u u u r 2＝4，即AO u u u r ·OC u u u r －AO u u u r ·OB uuu r ＝32，故AO u u u r ·BC uuu r ＝32.法二：过O 作OD 垂直于BC ，垂足为D ，因为O 是三角形ABC 的外接圆圆心，所以D 为线段BC 的中点，所以AO u u u r ＝AD u u u r ＋DO u u u r ，则AO u u u r ·BC uuu r ＝(AD u u u r ＋DO u u u r)·BC uuu r ＝AD u u u r ·BC uuu r ＝12(AB u u ur ＋AC u u u r )·(AC u u u r －AB u u u r )＝12|AC u u u r |2－12|AB u u u r |2＝32. 答案：(1)π2 (2)3210．在平面直角坐标系xOy 中，点A (－1，－2)，B (2,3)，C (－2，－1)．(1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长；(2)设实数t 满足(AB u u u r －t OC u u u r )·OC u u u r ＝0，求t 的值．解：(1)由题设知AB u u u r ＝(3,5)，AC u u u r ＝(－1,1)，则AB u u u r ＋AC u u u r ＝(2,6)，AB u u u r －AC u u u r ＝(4,4)．所以|AB u u u r ＋AC u u u r |＝210，|AB u u u r －AC u u u r |＝4 2.故所求的两条对角线长分别为42，210.(2)由题设知OC u u u r ＝(－2，－1)，AB u u u r － t OC u u u r ＝(3＋2t,5＋t )，由(AB u u u r －t OC u u u r )·OCu u u r ＝0，得(3＋2t,5＋t )·(－2，－1)＝0，从而5t ＝－11，所以t ＝－115. 11．已知点A (2,0)，B (0,2)，点C (x ，y )在以原点为圆心的单位圆上．(1)若|OA u u u r ＋OC u u u r |＝7(O 为坐标原点)，求向量OB uuu r 与OC u u u r 的夹角θ；(2)若AC u u u r ⊥BC uuu r ，求点C 的坐标．解：(1)由OA u u u r ＝(2,0)，OC u u u r ＝(x ，y )，得OA u u u r ＋OC u u u r ＝(2＋x ，y )．由|OA u u u r ＋OC u u u r |＝7，得(2＋x )2＋y 2＝7，所以⎩⎪⎨⎪⎧ x 2＋y 2＝1，2＋x 2＋y 2＝7，解得x ＝12，y ＝±32. cos θ＝OB uuu r ·OC u u u r | OB uuu r |·|OC u u u r |＝2y 2x 2＋y2＝y ＝±32， 所以OB uuu r 与OC u u u r 的夹角为30°或150°.(2) AC u u u r ＝(x －2，y )，BC uuu r ＝(x ，y －2)，由AC u u u r ⊥BC uuu r 得，AC u u u r ·BC uuu r ＝0，则x 2－2x ＋y 2－2y ＝0.由⎩⎪⎨⎪⎧ x 2＋y 2＝1，x 2＋y 2－2x －2y ＝0，解得⎩⎪⎨⎪⎧ x ＝1－74，y ＝1＋74，或⎩⎪⎨⎪⎧ x ＝1＋74，y ＝1－74，所以点C 的坐标为⎝ ⎛⎭⎪⎫1－74，1＋74或⎝ ⎛⎭⎪⎫1＋74，1－74. 12.已知点P 是圆x 2＋y 2＝1上的一个动点，过点P 作PQ ⊥x 轴于点Q ，设OM u u u u r ＝OP uuu r ＋OQ uuu r .(1)求点M 的轨迹方程；(2)求向量OP uuu r 和OM u u u u r 夹角最大时的余弦值，并求此时P 点的坐标． 解：(1)设P (x 0，y 0)，M (x ，y )，则OP uuu r ＝(x 0，y 0)，OQ uuu r ＝(x 0,0)，OM u u u u r ＝OP uuu r ＋OQ uuu r ＝(2x 0，y 0)．∴⎩⎪⎨⎪⎧ x ＝2x 0，y ＝y 0⇒⎩⎪⎨⎪⎧ x 0＝12x ，y 0＝y .∵x 20＋y 20＝1，∴x 24＋y 2＝1. 故点M 的轨迹方程为x 24＋y 2＝1. (2)设向量OP uuu r 与OM u u u u r 的夹角为α，则cos α＝OP uuu r ·OM u u u u r |OP uuu r |·|OM u u u u r |＝2x 20＋y 204x 20＋y 20＝ x 20＋123x 20＋1， 令t ＝3x 20＋1，则cos α＝13 t ＋22t ＝13t ＋4t ＋4≥223， 当且仅当t ＝2时，等号成立，即α最大．∴OP uuu r 与OM u u u u r 夹角最大时的余弦值为223，此时P 点坐标为⎝ ⎛⎭⎪⎫±33，±63.。
2020年江苏省高考数学专项训练-真题解析-专题22 抛物线-2020年江苏省高考数学命题规律大揭秘(原卷版)
高考冲刺 提分必备2020年江苏省高考数学专项训练-真题解析专题22 抛物线【真题感悟】1、【2016江苏，22】如图，在平面直角坐标系xOy 中，已知直线l ：x y 2=0，抛物线C ：y 2=2px （p ＞0）.（1）若直线l 过抛物线C 的焦点，求抛物线C 的方程； （2）已知抛物线C 上存在关于直线l 对称的相异两点P 和Q. ①求证：线段PQ 的中点坐标为；②求p 的取值范围.2、【2009江苏，22】（本题满分10分）在平面直角坐标系xoy 中，抛物线C 的顶点在原点，经过点A （2，2），其焦点F 在x 轴上。
（1）求抛物线C 的标准方程；（2）求过点F ，且与直线OA 垂直的直线的方程；（3）设过点(),0(0)M m m >的直线交抛物线C 于D 、E 两点，ME =2DM ，记D 和E 两点间的距离为()f m ，求()f m 关于m 的表达式。
【考纲要求】1．掌握抛物线的定义、几何图形、标准方程及简单性质． 2．了解抛物线的简单应用．【考向分析】抛物线的定义、标准方程及性质是高考考查的重点，直线与抛物线的位置关系是考查的热点．【高考预测】抛物线好多年未考，需注意。
考查方向为直线与抛物线的位置关系，尤其相切是考查重点.【迎考策略】1、“看到准线想到焦点，看到焦点想到准线”，许多抛物线问题均可根据定义获得简捷、直观的求解．“由数想形，由形想数，数形结合”是灵活解题的一条捷径． 2.(1)解决焦点弦问题时，要注意以下几点： ①设抛物线上的点为(x 1，y 1)，(x 2，y 2)；②因为(x 1，y 1)，(x 2，y 2)在抛物线上，故满足y 12＝2px 1，y 22＝2px 2； ③利用y 12y 22＝4p 2x 1x 2可以整体得到y 1y 2或x 1x 2.(2)利用抛物线的定义把过焦点的弦分成两个焦半径的和，转化为到准线的距离，再求解．【强化演练】1．【2019年高考全国Ⅰ卷理数】已知抛物线C ：y 2=3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P ．（1）若|AF |+|BF |=4，求l 的方程；（2）若3AP PB =u u u r u u u r，求|AB |．2．【2019年高考全国Ⅲ卷理数】已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点： （2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积. 3．【2019年高考北京卷理数】已知抛物线C ：x 2=−2py 经过点（2，−1）．（1）求抛物线C 的方程及其准线方程；（2）设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y =−1分别交直线OM ，ON 于点A 和点B ．求证：以AB 为直径的圆经过y 轴上的两个定点．4．【2019年高考浙江卷】如图，已知点(10)F ，为抛物线22(0)y px p =>的焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 的右侧．记,AFG CQG △△的面积分别为12,S S ．（1）求p 的值及抛物线的准线方程； （2）求12S S 的最小值及此时点G 的坐标．5．设顶点在原点，焦点在x 轴上的拋物线过点()2,4P ，过P 作抛物线的动弦PB PA ,，并设它们的斜率分别为DC .（1）求拋物线的方程；（2）若0=+PB PA k k ，求证：直线AB 的斜率为定值，并求出其值； （3）若1PA PB k k =，求证：直线AB 恒过定点，并求出其坐标. 6．已知抛物线C ：22(0)y px p =>的焦点为F ，过F 且斜率为43的直线l 与抛物线C 交于A ，B 两点，B 在x 轴的上方，且点B 的横坐标为4.（1）求抛物线C 的标准方程；（2）设点P 为抛物线C 上异于A ，B 的点，直线PA 与PB 分别交抛物线C 的准线于E ，G 两点，x 轴与准线的交点为H ，求证：HG HE ⋅为定值，并求出定值. 7. 在平面直角坐标系中，抛物线的焦点为，点是抛物线上一点，且．（1）求的值； （2）若为抛物线上异于的两点，且．记点到直线的距离分别为，求的值．8．如图，O 为坐标原点，点F 为抛物线C 1： 22(0)x py p =>的焦点，且抛物线C 1上点M 处的切线与圆C 2： 221x y +=相切于点Q ．（Ⅰ）当直线MQ 的方程为20x y -=时，求抛物线C 1的方程； （Ⅱ）当正数p 变化时，记S 1 ，S 2分别为△FMQ ，△FOQ 的面积，求12S S 的最小值． 9．在平面直角坐标系xOy 中，点()1,0F ，直线1x =-与动直线y n =的交点为M ，线段MF 的中垂线与动直线y n =的交点为P ． （1）求动点P 的轨迹E 的方程；（2）过动点M 作曲线E 的两条切线，切点分别为A ， B ，求证： AMB ∠的大小为定值．10．已知点，直线 ，点是上的动点，过点垂直于轴的直线与线段的垂直平分线相交于点．（1）求点的轨迹方程； （2）若，直线与点的轨迹交于两点，试问的轨迹上是否存在两点，使得四点共圆？若存在，求出圆的方程；若不存在，请说明理由．11．已知抛物线方程24y x =，F 为焦点，P 为抛物线准线上一点，Q 为线段PF 与抛物线的交点，定义:()PFd P FQ=. （1）当8(1)3P --，时，求()d P ； （2）证明:存在常数a ，使得2()d P PF a =+.（3）123,,P P P 为抛物线准线上三点，且1223PP P P =，判断13()()d P d P +与22()d P 的关系. 12．已知直线上有一动点，过点作直线垂直于轴，动点在上，且满足（为坐标原点），记点的轨迹为曲线. （1）求曲线的方程； （2）已知定点，，为曲线上一点，直线交曲线于另一点，且点在线段上，直线交曲线于另一点，求的内切圆半径的取值范围． 13．如图，在平面直角坐标系中，已知直线：，抛物线：（）．（1）若直线过抛物线的焦点，求抛物线的方程；（2）已知抛物线上存在关于直线对称的相异两点和．①求证：线段PQ的中点坐标为；②求的取值范围．14．在平面直角坐标系中，已知点F为抛物线的焦点，点A在抛物线E上，点B在x轴上，且是边长为2的等边三角形。
江苏省2020届高三数学高考一轮复习应用题专题
应用题专题一.知识归纳：1.应用题的背景丰富，题目灵活多变，但应用题的解答却是一个程序化的过程：（1）审题（2）建模（3）运算.2.要做好高考应用题，需注意以下三个方面：（1）文字关：即阅读理解题意，罗列题目的条件，分清题目中的已知量、未知量、常量、变量、新词汇，分析题目所求，思考可能采用的方法——审题.（2）建模关：建立数学模型主要包括代数建模、几何建模.代数建模主要利用函数、数列、不等式进行建模，其难度主要在阅读题意，建立等式或不等式关系上；几何建模主要是利用解析几何知识，建立直角坐标系，使实际问题几何化，解决实际问题.（3）运算关：考查学生运算的稳定度，精确度.3.应用题在考查知识上主要有：①函数、基本不等式的应用题，数学模型主要有一次函数、反比例函数、二次函数、分段函数、以及形如y =ax +b x的函数等. ②数列、不等式应用题，常用的数学模型有构造等差、等比数列的模型，然后应用数列求和或特殊数列求和求解；构造数列通项的递推公式或Sn 的递推公式，利用待定系数法或an 与Sn 的关系求解，注意n 的范围问题等.③三角、向量应用题，引入角作为参变量，构造三角形，借助正弦定理、余弦定理、三角函数公式、三角函数的最值、向量、不等式、图象的对称及平移等知识，求解实际问题，对于参变量的角要注意角的范围.④解析几何应用题，命题点主要为有线性规划应用题及椭圆应用题、双曲线应用题、抛物线应用题等，利用线性规划求最优解、使用导数与切线的关系或利用圆锥曲线的定义或性质等求解问题.4.数学应用题的解题程序5.注意事项：①建立数学模型重在审题！审题时一要身临其境要慢！要“品”！②要抓自变量，找等量关系！③自变量要考虑实际范围④抓重点：等量关系是关键；破难点：变量思想是主线二.例题讲解【例1】在某次水下科研考察活动中，需要潜水员潜入水深为60米的水底进行作业，根据以往经验，潜水员下潜的平均速度为ν(米/单位时间)，每单位时间的用氧量为(v 10)3+1(升)，在水底作业10个单位时间，每单位时间用氧量为0.9(升)，返回水面的平均速度为v 2(米/单位时间)，每单位时间用氧量为1.5(升)，记该潜水员在此次考察活动中的总用氧量y(升)．(1)求y 关于ν的函数关系式；(2)若c ≤ν≤15(c >0)，求当下潜速度取什么值时，总用氧量最少【例2】某企业为了减少噪声对附近居民的干扰，计划新增一道“隔音墙”，从上往下看，“隔音墙”可以看成曲线，在平面直角坐标系xOy中，“隔音墙”的一部分所在曲线的方程f(x)=ln x+ax∈[1,2]为(单位：千米).已知居民区都在x轴的下方，这部分曲线上任意两点x+1连线的斜率都小于−1时“隔音墙”的隔音效果最佳．(1)当a=9时，求“隔音墙”所在曲线f(x)上的点到x轴最近距离；2(2)当实数a在什么范围时，“隔音墙”的隔音效果最佳？【例3】某工厂生产某种黑色水笔，每百支水笔的成本为30元，并且每百支水笔的加工费为m 元(其中m为常数，且3⩽m⩽6).设该工厂黑色水笔的出厂价为x元/百支(35⩽x⩽40)，根据市场调查，日销售量与e x成反比例，当每百支水笔的出厂价为40元时，日销售量为10万支．(1)当每百支水笔的日售价为多少元时，该工厂的利润y最大，并求y的最大值．(2)已知工厂日利润达到1000元才能保证工厂的盈利．若该工厂在出厂价规定的范围内，总能盈利，则每百支水笔的加工费m最多为多少元？(精确到0.1元)【例4】为了在雨季来之前处理好受污染的化工原料，某公司拟建造如图所示的蓄水池密封存放.该蓄水池下方是高为h的圆柱体，上方是半径为r的半球体(中空).设计要求：蓄水池总体积m3，且ℎ≥2r.经测算，上方半球形部分每平方米建造费用为c(c为常数且c>3)千元，下为64π3方圆柱体的侧面和下底面部分平均每平方米建造费用为3千元，设该蓄水池的总建造费用为y千元．(1)求y关于r的函数解析式，并指出该函数的定义域；(2)当该蓄水池的总建造费用y最小时，求半径r的值．【例5】为建设美丽乡村，政府欲将一块长12百米，宽5百米的矩形空地ABCD建成生态休闲园，园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴，AB的垂直平分线为y轴，建(x>0)模型．园区服务立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数y=x+1x百米．中心P在x轴正半轴上，PO=43(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM，求OM的最短长度；(2)若在线段DE上设置一园区出口Q，试确定Q的位置，使通道PQ最短．【例6】金镶玉奖牌是中国文化与体育精神完美结合的载体．现有一矩形玉片BCEF，CE为36毫米，BC为32毫米，G为EF的中点．现要开槽镶嵌金丝，将其加工为镶金工艺品，如图，金丝部分为优弧PQ⌢和线段MP，NQ，MN，其中优弧PQ⌢所在圆的圆心为O，圆O与矩形的边FB，BC，CE分别相切于点A、H、D，M、N在线段EF上(M在N的左侧)，MP，NQ分别与圆O相切于点P，Q，且FM=NE.若优弧PQ⌢部分镶嵌的金丝每毫米造价为3a元(a>0)，线段MP，NQ，MN部分镶嵌的金丝每毫米造价为2a元．记锐角∠POG=α，镶嵌金丝总造价为W 元．(1)试表示出关于α的函数W(α)，并写出cosα的范围；(2)当M，N位于什么位置时，镶嵌金丝的总造价最低？【例7】某单位将举办庆典活动，要在广场上竖立一形状为等腰梯形的彩门BADC(如图)，设计要求彩门的面积为S(单位：m2)，高为ℎ(单位：m)(S，h为常数)，彩门的下底BC固定在广场地面上，上底和两腰由不锈钢支架构成，设腰和下底的夹角为α，不锈钢支架的长度和记为l．(1)请将l表示成关于α的函数l=f(α)；(2)问当α为何值时l最小⊕并求最小值．【例8】某农场灌溉水渠长为1000m，横截面是等腰梯形ABCD(如图)，AD//BC,AB=CD，m.根据国家对农田建设补贴的政策，该农其中渠底BC宽为1m，渠口AD宽为3m，渠深34场计划在原水渠的基础上分别沿AD方向加宽、AB方向加深，若扩建后的水渠横截面A1B1C1D1仍是等腰梯形，且面积是原面积的2倍.设扩建后渠深为hm，若挖掘费为aℎ2元/m3，扩建后的水渠的内壁AB1，C1D1和渠底B1C1铺设混凝土费为3a元/m2．(1)试用h表示渠底B1C1的宽，并确定h的取值范围；(2)问：渠深h为多少时，可使总建设费最少？(注：总建设费为挖掘费与铺设混凝土费之和)【例9】为了丰富学生活动，在体育课上，体育教师设计了—个游戏，让甲、乙、丙三人各抓住橡皮带的一端，甲站在直角△ABC斜边AC的中点F处，乙站在B处．丙站在C处．游戏开始，甲不动，乙、丙分别以v(m/s)和v2(m/s)的速度同时出发，匀速跑向终点A和B.运动过程中绷紧的橡皮带围成一个如图所示的△DEF(规定：只要有一人跑到终点，游戏就结束，且0<v≤3(m/s)).已知AB长为40m，BC长为80m，记经过t(s)后△DEF的面积为S(m2).(1)求S关于t的函数表达式，并求出t的取值范围；(2)当游戏进行到10s时，体育教师宣布停止，求此时S(m2)的最小值．【例10】如图1，一艺术拱门由两部分组成，下部为矩形ABCD，AB，AD的长分别为2√3m和4m，上部是圆心为O的劣弧CD，∠COD=2π．3(1)求图1中拱门最高点到地面的距离；(2)现欲以点B为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2、图3、图4所示.设BC与地面水平线l所成的角为θ.记拱门上的点到地面的最大距离为h，试用θ的函数表示h，并求出h的最大值．【例11】市民小张计划贷款60万元用于购买一套商品住房，银行给小张提供了两种贷款方式．①等额本金：每月的还款额呈递减趋势，且从第二个还款月开始，每月还款额与上月还款额的差均相同；②等额本息：每个月的还款额均相同．银行规定，在贷款到账日的次月当天开始首次还款(若2019年7月7日贷款到账，则2019年8月7日首次还款)．已知小张该笔贷款年限为20年，月利率为0.004．(1)若小张采取等额本金的还款方式，现已得知第一个还款月应还4900元，最后一个还款月应还2510元，试计算小张该笔贷款的总利息；(2)若小张采取等额本息的还款方式，银行规定，每月还款额不得超过家庭平均月收入的一半，已知小张家庭平均月收入为1万元，判断小张该笔贷款是否能够获批(不考虑其他因素)；(3)对比两种还款方式，从经济利益的角度来考虑，小张应选择哪种还款方式．参考数据：1.004240≈2.61．三.课后练习1.某中学新校区内有一块以O为圆心，R(单位：米)为半径的半圆形荒地(如图)，学校计划对其开发利用，其中弓形BCD区域(阴影部分)用于种植观赏植物，△OBD区域用于种植花卉出售，其余区域用于种植草皮出售.已知种植观赏植物的成本是每平方米20元，种植花卉的利润是每平方米80元，种植草皮的利润是每平方米30元．(1)设∠BOD=θ(单位：弧度)，用θ表示弓形BCD的面积S弓=f(θ)．(2)如果该校邀请你规划这块土地，如何设计的大小才能使总利润最大？并求出该最大值．2.某市每年春节前后，由于大量的烟花炮竹的燃放，空气污染较为严重．该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现，每天空气污染的指数f(t)随时刻t(时)t+1)−a|+3a+2，t∈[0,24]，其中a为空气治理调变化的规律满足表达式f(t)=|lg(38节参数，且a∈(0,1)．(1)令x=lg(3t+1)，求x的取值范围；8(2)若规定每天中f(t)的最大值作为当天的空气污染指数，要使该市每天的空气污染指数不超过5，试求调节参数a的取值范围．3.如图，某城市有一块半径为40m的半圆形绿化区域(以O为圆心，AB为直径)，现计划对其进行改建．在AB的延长线上取点D，OD=80m，在半圆上选定一点C，改建后的绿化区域由扇形区域AOC和三角形区域COD组成，其面积为S m2.设∠AOC=x rad．(1)写出S关于x的函数关系式S(x)，并指出x的取值范围；(2)试问∠AOC多大时，改建后的绿化区域面积S取得最大值．4.某校在圆心角为直角，半径为1km的扇形区域内进行野外生存训练.如图所示，在相距1km的A，B两个位置分别为300，100名学生，在道路OB上设置集合地点D，要求所有学生沿最短路径到D点集合，记所有学生进行的总路程为S(km)．(1)设∠ADO=θ，写出S关于θ的函数表达式；(2)当S最小时，集合地点D离点A多远？。
江苏省2020届高考数学二轮复习 专题七 三角恒等变换与解三角形 苏教版
江苏省2020届高考数学（苏教版）二轮复习专题7 三角恒等变换与解三角形回顾2020～2020年的考题，在填空题中主要考查了三角公式的运用、正、余弦定理的运用.在解答题中有2020、2020年主要考查了三角化简求值，2020年考查了向量与三角化简的综合问题，2020年考查角的恒等变换及正、余弦定理.在近五年的应用题考查中，有两年考查了与三角函数有关的应用题.,在近四年的考查中，同角三角函数关系与诱导公式没有两角和与差的公式考查力度大，但作为三角化简的基本功还是要掌握的.预测在2020年的高考题中：1填空题依然是考查简单的三角函数化简、解三角形，随着题目设置的顺序，难度不一.2在解答题中，三角函数的化简、三角函数的性质与解三角形和平面向量的交汇问题仍是考查的重点.1．(2020·南京名校4月阶段性考试)若sin α＋cos αsin α－cos α＝3，tan(α－β)＝2，则tan(β－2α)＝________.解析：由题意得tan α＋1tan α－1＝3.所以tan α＝2.又tan(α－β)＝2，所以tan(β－α)＝－2. 所以(β－2α)＝tan[(β－α)－α]＝tan β－α－tan α1＋tan β－αtan α＝43.答案：432.1＋cos 20°2sin 20°－sin 10°(tan －15°－tan 5°)＝________.解析：原式＝2cos 210°4sin 10°cos 10°－sin 10°⎝ ⎛⎭⎪⎫cos 5°sin 5°－sin 5°cos 5°＝cos 10°2sin 10°－2cos 10°＝cos 10°－2sin 20°2sin 10°＝cos 10°－2sin 30°－10°2sin 10°＝cos 10°－2sin 30° cos 10°＋2cos 30° sin 10°2sin 10°＝cos 30°＝32. 答案：323．在锐角△ABC 中，BC ＝1，B ＝2A ，则ACcos A 的值等于________，AC 的取值范围为________．解析：设A ＝θ，则B ＝2θ.由正弦定理得AC sin 2θ＝BCsin θ，∴AC2cos θ＝1⇒ACcos θ＝2. 由锐角△ABC 得0°<2θ<90°⇒0°<θ<45°，又0°<180°－3θ<90°⇒30°<θ<60°，故30°<θ<45°⇒22<cos θ<32， ∴AC ＝2cos θ∈(2，3)． 答案：2 (2，3)4．(2020·西安名校三检)在△ABC 中，已知a ，b ，c 分别为∠A ，∠B ，∠C 所对的边，S 为△ABC 的面积．若向量p ＝(4，a 2＋b 2－c 2)，q ＝(3，S )，满足p ∥q ，则∠C ＝________.解析：由p ∥q ⇒4S －3(a 2＋b 2－c 2)＝0，又4S ＝4×12ab sin ∠C ＝3(a 2＋b 2－c 2)，可得sin ∠C ＝3×a 2＋b 2－c 22ab ＝3cos ∠C ，即tan ∠C ＝3，故∠C ＝π3.答案：π35．在△ABC 中，A 为最小角，C 为最大角，已知cos(2A ＋C )＝－43， sin B ＝45，则cos 2(B＋C )＝________.解析：∵A 为最小角，∴2A ＋C ＝A ＋A ＋C <A ＋B ＋C ＝180°. ∵cos(2A ＋C )＝－45，∴sin(2A ＋C )＝35.∵C 为最大角，∴B 为锐角． 又sin B ＝45，故cos B ＝35.即sin(A ＋C )＝45，cos(A ＋C )＝－35.∵cos(B ＋C )＝－cos A ＝－cos[(2A ＋C )－(A ＋C )]＝－2425，∴cos 2(B ＋C )＝2cos 2(B ＋C )－1＝527625.答案：527625[典例1]已知π2<β<α<3π4，cos(α－β)＝1213，sin(α＋β)＝－35.(1)用α＋β，α－β表示2α；(2)求sin 2α，cos 2α的值． [解] (1)2α＝(α－β)＋(α＋β)．(2)因为π2<β<α<3π4，所以0<α－β<π4，π<α＋β<3π2.又因为cos(α－β)＝1213，sin(α＋β)＝－35，所以sin(α－β)＝1－cos 2α－β＝513，cos(α＋β)＝－1－sin 2α＋β＝－45. 所以sin 2α＝sin[(α－β)＋(α＋β)]＝sin(α－β)cos(α＋β)＋cos(α－β)sin(α＋β) ＝513×⎝ ⎛⎭⎪⎫－45＋1213×⎝ ⎛⎭⎪⎫－35＝－5665， cos 2α＝cos[(α－β)＋(α＋β)]＝cos(α－β)cos(α＋β)－sin(α－β)sin(α＋β) ＝1213×⎝ ⎛⎭⎪⎫－45－513×⎝ ⎛⎭⎪⎫－35＝－3365.三角函数式的化简、求值，常从角的差异入手，寻求条件与结论之间的关系，通过三角恒等变换消除差异，使问题获解．[演练1]已知sin ⎝ ⎛⎭⎪⎫x ＋π6＝14，则sin ⎝ ⎛⎭⎪⎫56π－x ＋sin 2⎝ ⎛⎭⎪⎫11π6－x 的值为________．解析：sin ⎝ ⎛⎭⎪⎫56π－x ＋sin 2⎝ ⎛⎭⎪⎫11π6－x ＝sin ⎣⎢⎡⎦⎥⎤π－⎝ ⎛⎭⎪⎫π6＋x ＋sin 2⎣⎢⎡⎦⎥⎤2π－⎝ ⎛⎭⎪⎫x ＋π6＝sin ⎝ ⎛⎭⎪⎫x ＋π6＋sin 2⎝⎛⎭⎪⎫x ＋π6＝516.答案：516[典例2](2020·南通第一次调研)在斜三角形ABC 中，角A ，B ，C 的对边分别为a ，b ，c . (1)若2sin A cos C ＝sin B ，求a c的值； (2)若sin(2A ＋B )＝3sin B ，求tan Atan C 的值．[解] (1)由正弦定理得sin A sin B ＝ab.从而2sin A cos C ＝sin B 可化为2a cos C ＝b .由余弦定理得2a ×a 2＋b 2－c 22ab＝b .整理得a ＝c ，即ac＝1.(2)在斜三角形ABC 中，A ＋B ＋C ＝π，所以sin(2A ＋B )＝3sin B 可化为sin[π＋(A －C )]＝3sin[π－(A ＋C )]， 即－sin(A －C )＝3sin(A ＋C )．故－sin A cos C ＋cos A sin C ＝3(sin A cos C ＋cos A sin C )． 整理得4sin A cos C ＝－2cos A sin C ， 因为△ABC 是斜三角形，所以cos A cos C ≠0， 所以tan A tan C ＝－12.解三角形常用的工具是正弦定理和余弦定理，要熟悉它们的使用的条件，合理选用．解三角形常与三角恒等变换、三角求值综合考查，要注意三角形中角的限制条件．[演练2]在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，若1＋tan A tan B ＝2cb ，则角A 的大小为________．解析：由1＋tan A tan B ＝2c b ，得sin A ＋B cos A sin B ＝2sin Csin B ，即cos A ＝12，故A ＝π3.答案：π3[典例3](2020·安徽高考)设△ABC 的内角A ，B ，C 所对的边为a ，b ，c ；则下列命题正确的是________．①若ab >c 2，则C <π3；②若a ＋b >2c ，则C <π3；③若a 3＋b 3＝c 3，则C <π2；④若(a ＋b )c <2ab ，则C >π2；⑤若(a 2＋b 2)c 2<2a 2b 2，则C >π3. [解析] ①ab >c 2⇒cos C ＝a 2＋b 2－c 22ab >2ab －ab 2ab ＝12⇒C <π3；②a ＋b >2c ⇒cos C ＝a 2＋b 2－c 22ab >4a 2＋b 2－a ＋b28ab≥12⇒C <π3； ③当C ≥π2时，c 2≥a 2＋b 2⇒c 3≥a 2c ＋b 2c >a 3＋b 3与a 3＋b 3＝c 3矛盾；④取a ＝b ＝2，c ＝1满足(a ＋b )c <2ab 得C <π2；⑤取a ＝b ＝2，c ＝1满足(a 2＋b 2)c 2<2a 2b 2得C <π3.[答案] ①②③利用正、余弦定理可实现三角形中的边角转化，常用方法是：①化边为角结合内角和定理求解；②化角为边结合勾股定理、三边关系求解．[演练3]在△ABC 中，sin A ＝sin B ＋sin Ccos B ＋cos C ，判断这个三角形的形状．解：应用正弦定理、余弦定理，可得a ＝b ＋c c 2＋a 2－b 22ca ＋a 2＋b 2－c22ab，所以b (a 2－b 2)＋c (a 2－c 2)＝bc (b ＋c )．所以(b ＋c )a 2＝(b 3＋c 3)＋bc (b ＋c )． 所以a 2＝b 2－bc ＋c 2＋bc .所以a 2＝b 2＋c 2. 所以△ABC 是直角三角形．[专题技法归纳](1)在三角化简、求值、证明中，表达式往往出现较多的相异角，可根据角与角之间的和差、倍半、互补、互余的关系，运用角的变换，沟通条件与结论中的角，使问题获解．如角的变形：15°＝45°－30°＝60°－45°＝30°2，α＝(α＋β)－β＝⎝ ⎛⎭⎪⎫α2＋β－⎝⎛⎭⎪⎫β－α2，2α＝(α＋β)＋(α－β)＝⎝⎛⎭⎪⎫π4＋α－⎝ ⎛⎭⎪⎫π4－α.特别地，π4＋α与π4－α为互余角，它们之间可以互相转化，在三角变形中使用频率高．(2)两定理的形式、内容、证法及变形应用必须引起足够的重视，通过向量的数量积把三角形和三角函数联系起来，用向量方法证明两定理，突出了向量的工具性，是向量知识应用的实例．另外，利用正弦定理解三角形时可能出现一解、两解或无解的情况，这时应结合“三角形中大边对大角”定理及几何作图来帮助理解．1．(2020·连云港调研)在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若a 2＝b 2＋bc ，sin C ＝2sin B ，则A ＝________.解析：由sin C ＝2sin B ，得c ＝2b .又a 2＝b 2＋bc ，所以cos A ＝b 2＋c 2－a 22bc ＝c 2－bc 2bc ＝4b 2－2b 24b2＝12，所以A ＝π3. 答案：π32．设α∈⎝⎛⎭⎪⎫π4，3π4，β∈⎝ ⎛⎭⎪⎫0，π4，cos ⎝ ⎛⎭⎪⎫α－π4＝35，sin ⎝ ⎛⎭⎪⎫3π4＋β＝513，则sin(α＋β)＝________.解析：α∈⎝⎛⎭⎪⎫π4，3π4，α－π4∈⎝ ⎛⎭⎪⎫0，π2，又cos ⎝⎛⎭⎪⎫α－π4＝35，∴sin ⎝ ⎛⎭⎪⎫α－π4＝45.∵β∈⎝ ⎛⎭⎪⎫0，π4，∴3π4＋β∈⎝ ⎛⎭⎪⎫3π4，π，sin ⎝ ⎛⎭⎪⎫3π4＋β＝513，∴cos ⎝⎛⎭⎪⎫3π4＋β＝－1213.∴sin(α＋β)＝sin ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π4＋⎝ ⎛⎭⎪⎫3π4＋β－π2 ＝－cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α－π4＋⎝ ⎛⎭⎪⎫3π4＋β＝－cos ⎝ ⎛⎭⎪⎫α－π4·cos ⎝ ⎛⎭⎪⎫3π4＋β＋sin ⎝ ⎛⎭⎪⎫α－π4·sin ⎝ ⎛⎭⎪⎫3π4＋β＝－35×⎝ ⎛⎭⎪⎫－1213＋45×513＝5665. 即sin(α＋β)＝5665.答案：56653．已知sin α＝35，α∈⎝ ⎛⎭⎪⎫π2，π，tan(π－β)＝12，则tan(α－2β)＝________. 解析：∵sin α＝35，α∈⎝ ⎛⎭⎪⎫π2，π，∴cos α＝－45. 则tan α＝－34.由tan(π－β)＝12，可得tan β＝－12，tan 2β＝2tan β1－tan 2β＝2×⎝ ⎛⎭⎪⎫－121－⎝ ⎛⎭⎪⎫－122＝－43. tan(α－2β)＝tan α－tan 2β1＋tan α·tan 2β＝－34－⎝ ⎛⎭⎪⎫－431＋⎝ ⎛⎭⎪⎫－34×⎝ ⎛⎭⎪⎫－43＝724.答案：7244.如图，l 1、l 2、l 3是同一平面内的三条平行直线，l 1与l 2间的距离是1，l 2与l 3间的距离是2，正三角形ABC 的三顶点分别在l 1、l 2、l 3上，则△ABC 的边长是________．解析：因为l 1、l 2、l 3是同一平面内的三条平行直线，l 1与l 2间的距离是1，l 2与l 3间的距离是2，所以过A 作l 2的垂线，交l 2、l 3分别于点D 、E ，如图，则∠BAD ＝∠BAC ＋∠CAE ，即∠BAD ＝60°＋∠CAE ，记正三角形ABC 的边长为a ，两边取余弦得1a ＝cos 60°·cos ∠CAE －sin 60°sin ∠CAE ，即1a ＝12×3a －32×a 2－32a 整理得，3a 2－9＝1，解之得，a ＝2213.答案：22135．已知α∈⎝ ⎛⎭⎪⎫0，π4，β∈(0，π)，且tan(α－β)＝12，tan β＝－17，则2α－β的值是________．解析：tan α＝tan[(α－β)＋β]＝tan α－β＋tan β1－tan α－βtan β＝13，tan(2α－β)＝tan α－β＋tan α1－tan α－βtan α＝1.∵tan β＝－17，∴β∈⎝ ⎛⎭⎪⎫3π4，π， ∴2α－β∈⎝ ⎛⎭⎪⎫－π，－π4.∴2α－β＝－3π4.答案：－3π46．在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，如果a ，b ，c 成等差数列，B ＝30°，△ABC 的面积为32，那么b ＝________.解析：∵2b ＝a ＋c ，∴a 2＋c 2＝(a ＋c )2－2ac ＝4b 2－2ac .在△ABC 中，B ＝30°，△ABC 的面积32，所以12ac sin B ＝32，即ac ＝6，于是a 2＋c 2＝4b 2－12，由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝32，即4b 2－12－b 212＝32，解得b 2＝4＋23，于是b ＝1＋ 3. 答案：1＋ 37．△ABC 中，A ，B ，C 所对的边分别为a ，b ，c ，tan C ＝sin A ＋sin B cos A ＋cos B，sin(B －A )＝cosC ．则B ＝________.解析：因为tan C ＝sin A ＋sin B cos A ＋cos B ，即sin C cos C ＝sin A ＋sin Bcos A ＋cos B ，所以sin C cos A ＋sin C cos B ＝cos C sin A ＋cos C sin B ， 即sin C cos A －cos C sin A ＝cos C sin B －sin C cos B ， 得sin(C －A )＝sin(B －C )，所以C －A ＝B －C 或C －A ＝π－(B －C )(不成立)． 即2C ＝A ＋B ，得C ＝π3，所以B ＋A ＝2π3.又因为sin(B －A )＝cos C ＝12，则B －A ＝π6或B －A ＝5π6(舍去)，得A ＝π4，B ＝5π12.答案：5π12 8．已知圆内接四边形ABCD 的边长分别为AB ＝2，BC ＝6，CD ＝DA ＝4，则四边形ABCD 的面积为________．解析：如图：连结BD ，则有四边形ABCD 的面积S ＝S △ABD ＋S △CDB ＝12·AB ·AD sin A ＋12·BC ·CD ·sin C .∵A ＋C ＝180°，∴sin A ＝sin C .故S ＝12(AB ·AD ＋BC ·CD )sin A ＝12(2×4＋6×4)·sin A ＝16sin A .由余弦定理，在△ABD 中，BD 2＝AB 2＋AD 2－2AB ·AD ·cos A ＝20－16cos A ，在△CDB 中，BD 2＝CB 2＋CD 2－2CB ·CD ·cos C ＝52－48cos C ，∴20－16cos A ＝52－48cos C ．∵cos C ＝－cos A ，∴64cos A ＝－32，cos A ＝－12. 又0°<A <180°，∴A ＝120°，故S ＝16sin 120°＝8 3.答案：839．在正三角形ABC 的边AB 、AC 上分别取D 、E 两点，使沿线段DE 折叠三角形时，顶点A 正好落在边BC 上，在这种情况下，若要使AD 最小，则AD ∶AB ＝________.解析：按题意，设折叠后A 点落在边BC 上改称P 点，显然A 、P 两点关于折线DE 对称，又设∠BAP ＝θ，∴∠DPA ＝θ，∠BDP ＝2θ，再设AB ＝a ，AD ＝x ，∴DP ＝x .在△ABC 中，∠APB ＝180°－∠ABP －∠BAP ＝120°－θ，由正弦定理知：BP sin ∠BAP ＝AB sin ∠APB. ∴BP ＝a sin θsin 120°－θ.在△PBD 中，DP sin ∠DBP ＝BP sin ∠BDP， 所以BP ＝x ·sin 2θsin 60°，从而a sin θsin 120°－θ＝x sin 2θsin 60°， ∴x ＝a sin θ·sin 60°sin 2θ·sin 120°－θ＝3a 2sin 60°＋2θ＋3. ∵0°≤θ≤60°，∴60°≤60°＋2θ≤180°.∴当60°＋2θ＝90°，即θ＝15°时，sin(60°＋2θ)＝1，此时x 取得最小值3a 2＋3＝(23－3)a ，即AD 最小， ∴AD ∶DB ＝23－3. 答案：23－3 10．(2020·江苏高考)设α为锐角，若cos ⎝ ⎛⎭⎪⎫α＋π6＝45，则sin ⎝⎛⎭⎪⎫2α＋π12的值为________． 解析：因为α为锐角，cos ⎝ ⎛⎭⎪⎫α＋π6＝45，所以sin ⎝ ⎛⎭⎪⎫α＋π6＝35，sin 2⎝⎛⎭⎪⎫α＋π6＝2425，cos 2⎝ ⎛⎭⎪⎫α＋π6＝725，所以sin ⎝ ⎛⎭⎪⎫2α＋π12＝sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫α＋π6－π4＝22×1725＝17250. 答案：1725011．已知△ABC 的三个内角A 、B 、C 满足A ＋C ＝2B .1cos A ＋1cos C ＝－2cos B ，求cos A －C 2的值． 解：由题设条件知B ＝60°，A ＋C ＝120°设α＝A －C2，则A －C ＝2α，可得A ＝60°＋α，C ＝60°－α，所以1cos A ＋1cos C ＝1cos 60°＋α＋1cos60°－α ＝112cos α－32sin α＋112cos α＋32sin α ＝cos α14cos 2α－34sin 2α＝cos αcos 2α－34， 依题设条件有cos αcos 2α－34＝－2cos B ， 又cos B ＝12，∴cos αcos 2α－34＝－2 2. 整理得42cos 2α＋2cos α－32＝0，即(2cos α－2)(22cos α＋3)＝0.∵22cos α＋3≠0，∴2cos α－2＝0.从而得cos A －C2＝22.12.(2020·苏锡调研)如图，在四边形ABCD 中，已知AB ＝13，AC ＝10，AD ＝5，CD ＝65，AB u u u r ·AC u u u r ＝50. (1)求cos ∠BAC 的值； (2)求sin ∠CAD 的值；(3)求△BAD 的面积．解：(1)因为AB u u u r ·AC u u u r ＝| AB u u u r || AC u u u r |cos ∠BAC ，所以cos ∠BAC ＝AB u u u r ·AC u u u r | AB u u u r || AC u u u r |＝5013×10＝513. (2)在△ADC 中，AC ＝10，AD ＝5，CD ＝65，由余弦定理得cos ∠CAD ＝AC 2＋AD 2－CD 22AC ·AD ＝102＋52－6522×10×5＝35. 因为∠CAD ∈(0，π)，所以sin ∠CAD ＝ 1－cos 2∠CAD ＝ 1－⎝ ⎛⎭⎪⎫352＝45. (3)由(1)知，cos ∠BAC ＝AB u u u r ·AC u u u r | AB u u u r || AC u u u r |＝513. 因为∠BAC ∈(0，π)，所以sin ∠BAC ＝1－cos 2∠BAC＝ 1－⎝ ⎛⎭⎪⎫5132＝1213. 从而sin ∠BAD ＝sin(∠BAC ＋∠CAD )＝sin ∠BAC ·cos ∠CAD ＋cos ∠BAC sin ∠CAD＝1213×35＋513×45＝5665. 所以S △BAD ＝12AB ·AD ·sin ∠BAD ＝12×13×5×5665＝28.。
精品解析：2020年江苏省高考数学试卷(解析版)
2020年高三全国统一考试（江苏卷）数学Ⅰ一、耐心填空题：（本大题共14小题，每小题5分，共计70分．）1.已知集合{1,0,1,2},{0,2,3}A B =-=，则A B =_____.【答案】{}0,2【解析】【分析】根据集合的交集即可计算.【详解】∵{}1,0,1,2A =-,{}0,2,3B =∴{}0,2A B =故答案为：{}0,2.【点睛】本题考查了交集及其运算，是基础题型．2.已知i 是虚数单位，则复数(1i)(2i)z =+-的实部是_____.【答案】3【解析】【分析】根据复数的运算法则，化简即可求得实部的值.【详解】∵复数()()12z i i =+-∴2223z i i i i =-+-=+∴复数的实部为3.故答案为：3.【点睛】本题考查复数的基本概念，是基础题．3.已知一组数据4,2,3,5,6a a -的平均数为4，则a 的值是_____.【答案】2【解析】【分析】根据平均数的公式进行求解即可．【详解】∵数据4,2,3,5,6a a -的平均数为4∴4235620a a ++-++=，即2a =.故答案为：2.【点睛】本题主要考查平均数的计算和应用，比较基础．4.将一颗质地均匀的正方体骰子先后抛掷2次，观察向上的点数，则点数和为5的概率是_____. 【答案】19【解析】【分析】分别求出基本事件总数，点数和为5的种数，再根据概率公式解答即可．【详解】根据题意可得基本事件数总为6636⨯=个.点数和为5的基本事件有()1,4，()4,1，()2,3，()3,2共4个.∴出现向上的点数和为5的概率为41369P ==. 故答案为：19. 【点睛】本题考查概率的求法，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题． 5.如图是一个算法流程图，若输出y 的值为2-，则输入x 的值是_____.【答案】3-【解析】【分析】根据指数函数的性质，判断出1y x =+，由此求得x 的值.【详解】由于20x >，所以12y x =+=-，解得3x =-.故答案为：3-【点睛】本小题主要考查根据程序框图输出结果求输入值，考查指数函数的性质，属于基础题.6.在平面直角坐标系xOy 中，若双曲线22x a ﹣25y =1(a ＞0)的一条渐近线方程为y=2x ，则该双曲线的离心率是____. 【答案】32【解析】【分析】根据渐近线方程求得a ，由此求得c ，进而求得双曲线的离心率.【详解】双曲线22215x y a -=，故b =由于双曲线的一条渐近线方程为y x =，即2b a a =⇒=，所以3c =，所以双曲线的离心率为32c a =. 故答案为：32【点睛】本小题主要考查双曲线的渐近线，考查双曲线离心率的求法，属于基础题. 7.已知y =f (x )是奇函数，当x ≥0时，( f 的值是____.【答案】4-【解析】【分析】先求(8)f ，再根据奇函数求(8)f -【详解】23(8)84f ==，因为()f x 为奇函数，所以(8)(8)4f f -=-=-故答案为：4-【点睛】本题考查根据奇函数性质求函数值，考查基本分析求解能力，属基础题.8.已知2sin ()4πα+ =23，则sin 2α的值是____. 【答案】13【解析】 【分析】 直接按照两角和正弦公式展开，再平方即得结果.【详解】221sin ()(cos )(1sin 2)4222παααα+=+=+121(1sin 2)sin 2233αα∴+=∴= 故答案为：13【点睛】本题考查两角和正弦公式、二倍角正弦公式，考查基本分析求解能力，属基础题.9.如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是____cm.【答案】1232π【解析】 【分析】 先求正六棱柱体积，再求圆柱体积，相减得结果. 【详解】正六棱柱体积为23622=1234⨯⨯⨯ 圆柱体积为21()222ππ⋅= 所求几何体体积为1232π-故答案为： 1232π【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题.10.将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是____.【答案】524x π=-【解析】【分析】先根据图象变换得解析式，再求对称轴方程，最后确定结果.【详解】3sin[2()]3sin(2)6412y x x πππ=-+=-72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈ 当1k =-时524x π=-故答案为：524x π=- 【点睛】本题考查三角函数图象变换、正弦函数对称轴，考查基本分析求解能力，属基础题.11.设{a n }是公差为d 的等差数列，{b n }是公比为q 的等比数列．已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-∈N ，则d +q 的值是_______．【答案】4【解析】【分析】结合等差数列和等比数列前n 项和公式的特点，分别求得{}{},n n a b 的公差和公比，由此求得d q +.【详解】设等差数列{n a 1q ≠.等差数列{}n a 的前n 等比数列{}n b 的前n 项和公式为依题意n n n S P Q =+，即通过对比系数可知111212211d d a q b q⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒112021d a q b =⎧⎪=⎪⎨=⎪⎪=⎩，故4d q +=. 故答案为：4【点睛】本小题主要考查等差数列和等比数列的前n 项和公式，属于中档题.12.已知22451(,)x y y x y R +=∈，则22xy +的最小值是_______． 【答案】45【解析】【分析】根据题设条件可得42215yxy-=，可得4222222114+555y yx y yy y-+=+=，利用基本不等式即可求解.【详解】∵22451x y y+=∴0y ≠且42215yxy-=∴422222222114144+2555555y y yx y yy y y-+=+=≥⋅=，当且仅当221455yy=，即2231,102x y==时取等号.∴22x y+的最小值为45.故答案为：45.【点睛】本题考查了基本不等式在求最值中的应用.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用≥或≤时等号能否同时成立）.13.在△ABC中，43=90AB AC BAC==︒，，∠，D在边BC上，延长AD到P，使得AP=9，若3()2PA mPB m PC=+-（m为常数），则CD的长度是________．【答案】185【解析】【分析】根据题设条件可设()0PA PDλλ=>，结合32PA mPB m PC⎛⎫=+-⎪⎝⎭与,,B D C三点共线，可求得λ，再根据勾股定理求出BC，然后根据余弦定理即可求解.【详解】∵,,A D P三点共线，∴可设()0PA PDλλ=>，∵32PA mPB m PC⎛⎫=+-⎪⎝⎭，∴32PD mPB m PCλ⎛⎫=+-⎪⎝⎭，即32mmPD PB PCλλ⎛⎫-⎪⎝⎭=+，若0m ≠且32m ≠，则,,B D C 三点共线， ∴321m m λλ⎛⎫- ⎪⎝⎭+=，即32λ=， ∵9AP =，∴3AD =，∵4AB =,3AC =,90BAC ∠=︒，∴5BC =，设CD x =，CDA θ∠=，则5BD x =-，BDA πθ∠=-. ∴根据余弦定理可得222cos 26AD CD AC x AD CD θ+-==⋅，()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-， ∵()cos cos 0θπθ+-=， ∴()()2570665x x x --+=-，解得185x =， ∴CD 5当m =32PA PC =，,C D 重合，此时CD 的长度为0， 当m =时，32PA PB =，,B D 重合，此时12PA =，不合题意，舍去. 【点睛】本题考查了平面向量知识的应用、余弦定理的应用以及求解运算能力，解答本题的关键是设出()0PA PD λλ=>．14.在平面直角坐标系xOy 中，已知0)P ，A ，B 是圆C ：221()362x y+-=上的两个动点，满足PA PB =，则△P AB 面积的最大值是__________．【答案】【解析】【分析】根据条件得PC AB ⊥,再用圆心到直线距离表示三角形PAB 面积，最后利用导数求最大值.【详解】PA PB PC AB =∴⊥设圆心C 到直线AB 距离为d ，则||1AB PC ==所以2221236(1)(36)(1)2PAB S d d d d ≤⋅-+=-+ 令222(36)(1)(06)2(1)(236)04y d d d y d d d d '=-+≤<∴=+--+=∴=（负值舍去）当04d ≤<时，0y '>；当46d ≤<时，0y '≤，因此当4d =时，y 取最大值，即PAB S取最大值为105，故答案为：105【点睛】本题考查垂径定理、利用导数求最值，考查综合分析求解能力，属中档题. 二、精心解答题：(本大题共6小题，共计90分，)15.在三棱柱ABC -A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．（1）求证：EF ∥平面AB 1C 1；（2）求证：平面AB 1C ⊥平面ABB 1．【答案】（1）证明详见解析；（2）证明详见解析.【解析】【分析】（1）通过证明1//EF AB ，来证得//EF 平面11AB C .（2）通过证明AB ⊥平面1AB C ，来证得平面1AB C ⊥平面1ABB .【详解】（1）由于,E F 分别是1,AC B C 的中点，所以1//EF AB .由于EF ⊂/平面11AB C ,1AB ⊂平面11AB C ，所以//EF 平面11AB C .（2）由于1B C ⊥平面ABC ，AB 平面ABC ，所以1B C AB ⊥.由于1,AB AC AC B C C ⊥⋂=，所以AB ⊥平面1AB C ,由于AB 平面1ABB ，所以平面1AB C ⊥平面1ABB .【点睛】本小题主要考查线面平行的证明，考查面面垂直的证明，属于中档题.16.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知3,2,45a c B ===︒．（1）求sin C 的值；（2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值． 【答案】（1）5sin C =；（2）2tan 11DAC ∠=. 【解析】【分析】 （1）利用余弦定理求得b ，利用正弦定理求得sin C .（2）根据cos ADC ∠的值，求得sin ADC ∠的值，由（1）求得cos C 的值，从而求得sin ,cos DAC DAC ∠∠的值，进而求得tan DAC ∠的值.【详解】（1）由余弦定理得22222cos 9223252b ac ac B =+-=+-⨯=，所以5b =由正弦定理得sin 5sin sin sin 5c b c B C C B b =⇒==. （2）由于4cos 5ADC ∠=-，,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以23sin 1cos 5ADC ADC ∠=-∠=.2020年高考（江苏卷） 由于,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以0,2C π⎛⎫∈ ⎪⎝⎭，所以225cos 1sin 5C C =-=.所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅3254525555525⎛⎫=⨯+-⨯= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭，所以2115cos 1sin 25DAC DAC ∠=-∠=. 所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查三角恒等变换，属于中档题.17.某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O 在水平线MN 上、桥AB 与MN 平行，OO '为铅垂线(O '在AB 上).经测量，左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO '的距离a (米)之间满足关系式21140h a =；右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO '的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO '的距离为40米.（1）求桥AB 的长度；（2）计划在谷底两侧建造平行于OO '的桥墩CD 和EF ，且CE 为80米，其中C ，E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E '为多少米时，桥墩CD 与EF 的总造价最低?【答案】（1）120米（2）20O E '=米【解析】【分析】（1）根据A,B 高度一致列方程求得结果；（2）根据题意列总造价的函数关系式，利用导数求最值，即得结果. 【详解】（1）由题意得2311||40640||8040800O A O A ''=-⨯+⨯∴= ||||||8040120AB O A O B ''∴=+=+=米（2）设总造价为()f x 万元，21||8016040O O '=⨯=，设||O E x '=， 32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<<3221336()(160),()()0208008080080f x k x x f x k x x x '∴=+-∴=-=∴=(0舍去)当020x <<时，()0f x '<；当2040x <<时，()0f x '>，因此当20x 时，()f x 取最小值，答：当20O E '=米时，桥墩CD 与EF 的总造价最低.【点睛】本题考查实际成本问题、利用导数求最值，考查基本分析求解能力，属中档题.18.在平面直角坐标系xOy 中，已知椭圆22:143x y E +=的左、右焦点分别为F 1，F 2，点A 在椭圆E 上且在第一象限内，AF 2⊥F 1F 2，直线AF 1与椭圆E 相交于另一点B ．（1）求△AF 1F 2的周长；（2）在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP QP ⋅的最小值； （3）设点M 在椭圆E 上，记△OAB 与△MAB 的面积分别为S 1，S 2，若S 2=3S 1，求点M 的坐标． 【答案】（1）6；（2）-4；（3）()2,0M 或212,77⎛⎫-- ⎪⎝⎭. 【解析】 【分析】（1）根据椭圆定义可得124AF AF +=，从而可求出12AF F △的周长；（2）设()0,0P x ，根据点A 在椭圆E 上，且在第一象限，212AF F F ⊥，求出31,2A ⎛⎫⎪⎝⎭，根据准线方程得Q 点坐标，再根据向量坐标公式，结合二次函数性质即可出最小值；（3）设出设()11,M x y ，点M 到直线AB 的距离为d ，由点O 到直线AB 的距离与213S S =，可推出95d =，根据点到直线的距离公式，以及()11,M x y 满足椭圆方程，解方程组即可求得坐标.【详解】（1）∵椭圆E 的方程为22143x y +=∴()11,0F -,()21,0F 由椭圆定义可得：124AF AF +=. ∴12AF F △的周长为426+=（2，根据题意可得01x ≠.∵点A 上，且在第一象限，212AF F F ⊥ ∴A ⎛ ⎝∴(Q Q ∴()()()()200000,04,4244Q OP QP x x y x x x ⋅=⋅--=-=--≥-，当且仅当02x =时取等号.∴OP QP ⋅的最小值为4-.（3）设()11,M x y ，点M 到直线AB 的距离为d .∵31,2A ⎛⎫ ⎪⎝⎭，()11,0F - ∴直线1AF 的方程为()314y x =+ ∵点O 到直线AB 的距离为35，213S S =∴2113133252S S AB AB d ==⨯⨯⨯=⋅∴95d =∴113439x y -+=①∵2211143x y +=②∴联立①②解得1120x y =⎧⎨=⎩，1127127x y ⎧=-⎪⎪⎨⎪=-⎪⎩. ∴()2,0M 或212,77⎛⎫-- ⎪⎝⎭. 【点睛】本题考查了椭圆的定义，直线与椭圆相交问题、点到直线距离公式的运用，熟悉运用公式以及根据2S =是解答本题的关键. 19.(),()f x y g x ==与()(,)h x kx b k b =+∈R()f x ．（1()22()g x x x D =-+=∞-∞+，，，求h (x )的表达式；（2 ln ,()()(0) g k x h kx k D x x ==-=+∞，，，，求（3()2242() (48 () 4 3 2g x x h x t t x t t =-=--+， ，求证：n m -【答案】（1）()2h x x =；（2）[]0,3k ∈；（3）证明详见解析 【解析】 【分析】（1）求得()f x 与()g x 的公共点，并求得过该点的公切线方程，由此求得()h x 的表达式.（2）先由()()0h x g x -≥，求得k 的一个取值范围，再由()()0f x h x -≥，求得k 的另一个取值范围，从而求得k 的取值范围.（3）先由()()f x h x ≥，求得t 的取值范围，由方程()()0g x h x -=的两个根，求得n m -的表达式，利用导数证得不等式成立.【详解】（1）由题设有2222x x kx b x x -+≤+≤+对任意的x ∈R 恒成立.令0x =，则00b ≤≤，所以0b =.因此22kx x x ≤+即()220x k x +-≥对任意的x ∈R 恒成立，所以()220k ∆=-≤，因此2k =. 故()2h x x =.（2）令()()()()()1ln 0F x h x g x k x x x =-=-->，()01F =. 又()1x F x k x-'=⋅. 若k 0<，则()F x 在0,1上递增，在1,上递减，则()()10F x F ≤=，即()()0h x g x -≤，不符合题意.当0k =时，()()()()()0,F x h x g x h x g x =-==，符合题意. 当0k >时， ()F x 在0,1上递减，在1,上递增，则()()10F x F ≥=，即(h ，符合题意. 由(()1f x kx k +--()()2110x k x k =-+++≥当x =1<-时，()211y x k x k =-+++在0,为增函数，因为10+<，故存在()00,x ∈+∞，使()()0f x h x -<，不符合题意. 当102k x +==，即1k =-时，()()20f x h x x -=≥，符合题意. 当102k x +=>，即1k >-时，则需()()21410kk ∆=+-+≤，解得13k -<≤. 综上所述，k 的取值范围是[]0,3k ∈.（3）因为()423422243248x x t t x t tx -≥--+≥-对任意[,][x m n ∈⊂恒成立，()423422432x x tt x t t -≥--+对任意[,][x m n ∈⊂恒成立，等价于()222()2320x t xtx t -++-≥对任意[,][x m n ∈⊂恒成立.故222320x tx t ++-≥对任意[,][x m n ∈⊂恒成立 令22()232M x x tx t =++-，当201t <<，2880,11t t ∆=-+>-<-<，此时1n m t -≤<<， 当212t ≤≤，2880t ∆=-+≤，但()234248432x t t x t t -≥--+对任意的[,][x m n ∈⊂恒成立.等价于()()()2322443420x t t x t t --++-≤对任意的[,][x m n ∈⊂恒成立.()()()2322443420x t t x t t --++-=的两根为12,x x ，则4231212328,4t t x x t t x x --+=-⋅=，所以12=n m x x --==.令[]2,1,2t λλ=∈，则n m -=[])51,2∈，()()()23103331P λλλλλ'=-+=--，所以λλ递减，()()max 17P P λ==. 所以(【点睛】本小题主要考查利用的导数求切线方程，考查利用导数研究不等式恒成立问题，考查利用导数证明不等式，考查分类讨论的数学思想方法，属于难题.20.已知数列{}*()∈n a n N 的首项a 1=1，前n 项和为S n ．设λ与k 是常数，若对一切正整数n ，均有11111k k kn n n S S a λ++-=成立，则称此数列为“λ–k ”数列．（1）若等差数列{}n a 是“λ–1”数列，求λ的值；（2）若数列{}n a 是2-”数列，且a n ＞0，求数列{}n a 的通项公式；（3）对于给定的λ，是否存在三个不同的数列{}n a 为“λ–3”数列，且a n ≥0?若存在，求λ的取值范围；若不存在，说明理由， 【答案】（1）1（2）21,134,2n n n a n -=⎧=⎨⋅≥⎩（3）01λ<<【解析】 【分析】（1）根据定义得+11n n n S S a λ+-=，再根据和项与通项关系化简得11n n a a λ++=，最后根据数列不为零数列得结果；（2）根据定义得111222+1+1()3n n n n S S S S -=-，根据平方差公式化简得+1=4n n S S ，求得n S ，即得n a ； （3）根据定义得111333+11n n n SS a λ+-=，利用立方差公式化简得两个方程，再根据方程解的个数确定参数满足的条件，解得结果【详解】（1）+111111101n n n n n n S S a a a a a λλλ++++-=∴==∴≡∴=/（2）11221100n n n n n a S S S S ++>∴>∴->111222)n n S S -(n n S S ∴1124n n n n S S S -∴∴= 11S a ==4n -1224434,2n n n n a n ---∴=-=⋅≥21,134,2n n n a n -=⎧∴=⎨⋅≥⎩（3）假设存在三个不同的数列{}n a 为"3"λ-数列.111113333333+11+1+1()()n n n n n n n S S a S S S S λλ+-=∴-=- 1133+1n nS S ∴=或11221123333333+1+1+1()()n n n n n n SS S S S S λ-=+++1n n S S ∴=或22113333333+1+1(1)(1)(2)0n n n n S S S S λλλ-+-++=∵对于给定的λ，存在三个不同的数列{}n a 为"3"λ-数列，且0n a ≥1,10,2n n a n =⎧∴=⎨≥⎩或()22113333333+1+1(1)(1)(2)01n n n nS S S S λλλλ-+-++=≠有两个不等的正根.()22113333333+1+1(1)(1)(2)01n n n n S S SS λλλλ-+-++=≠可转化为()2133333+1+12133(1)(2)(1)01n n nnS S S S λλλλ-++-+=≠，不妨设()1310n n S x x S +⎛⎫=> ⎪⎝⎭，则()3233(1)(2)(1)01x x λλλλ-+++-=≠有两个不等正根，设()()3233(1)(2)(1)01f x x x λλλλ=-+++-=≠.① 当1λ<时，32323(2)4(1)004λλλ∆=+-->⇒<<，即01λ<<，此时()3010f λ=-<，33(2)02(1)x λλ+=->-对，满足题意.② 当1λ>时，32323(2)4(1)004λλλ∆=+-->⇒<<，即1λ<<()3010f λ=->，33(2)02(1)x λλ+=-<-对，此情况有两个不等负根，不满足题意舍去.综上，01λ<<【点睛】本题考查数列新定义、由和项求通项、一元二次方程实根分步，考查综合分析求解能力，属难题.数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题，请选定其中两小题，并在相应的答题区域内作答．．．．．．．．．．．．．．．．．．．．．．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤． A ．[选修4-2：矩阵与变换]21.平面上点(2,1)A -在矩阵11a b ⎡⎤=⎢⎥-⎣⎦M 对应的变换作用下得到点(3,4)B -． （1）求实数a ，b 的值； （2）求矩阵M 的逆矩阵1M -．【答案】（1）22a b =⎧⎨=⎩；（2）121 5512 55M -⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦. 【解析】 【分析】（1）根据变换写出具体的矩阵关系式，然后进行矩阵的计算可得出实数,a b 的值； （2）设出逆矩阵，由定义得到方程，即可求解.【详解】（1）∵平面上点()2,1A -在矩阵 11 a M b ⎡⎤=⎢⎥-⎣⎦对应的变换作用下得到点()3,4B -∴ 1 2 31 14a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦∴21324a b -=⎧⎨--=-⎩，解得22a b =⎧⎨=⎩（2）设1m n Mc d -⎡⎤=⎢⎥⎣⎦，则12 2 1 0=2 20 1m c n d MM m c n d -++⎡⎤⎡⎤=⎢⎥⎢⎥-+-+⎣⎦⎣⎦∴21202021m c n d m c n d +=⎧⎪+=⎪⎨-+=⎪⎪-+=⎩，解得251515m n c ⎧=⎪⎪⎪=-⎪⎨⎪=⎪∴1M -【点睛】本题考查矩阵变换的应用，考查逆矩阵的求法，解题时要认真审题，属于基础题．B ．[选修4-4：坐标系与参数方程]22.在极坐标系中，已知点1π(,)3A ρ在直线:cos 2l ρθ=上，点2π(,)6B ρ在圆:4sinC ρθ=上（其中0ρ≥，02θπ≤<）． （1）求1ρ，2ρ的值（2）求出直线l 与圆C 的公共点的极坐标． 【答案】（1）1242ρρ==，（2）)4π【解析】 【分析】(1)将A,B 点坐标代入即得结果；（2）联立直线与圆极坐标方程，解得结果. 【详解】（1）以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系，11cos2,43πρρ=∴=，因为点B 为直线6πθ=上，故其直角坐标方程为3y x =， 又4sin ρθ=对应的圆的直角坐标方程为：2240x y y +-=，由22340y x x y y ⎧=⎪⎨⎪+-=⎩解得00x y ==⎧⎨⎩或1x y ⎧=⎪⎨=⎪⎩ 对应的点为())0,0,，故对应的极径为20ρ=或22ρ=.（2）cos 2,4sin ,4sin cos 2,sin 21ρθρθθθθ==∴=∴=，5[0,2),,44ππθπθ∈∴=， 当4πθ=时ρ= 当5πθ=时0ρ=-<，舍；即所求交点坐标为当),4π【点睛】本题考查极坐标方程及其交点，考查基本分析求解能力，属基础题.C ．[：不等式选讲]23.设x 2|1|||4x x ++≤． 【分析】根据绝对值定义化为三个方程组，解得结果 【详解】1224x x x <-⎧⎨---≤⎩或10224x x x -≤≤⎧⎨+-≤⎩或0224x x x >⎧⎨++≤⎩21x ∴-≤<-或10x -≤≤或203x <≤所以解集为22,3⎡⎤-⎢⎥⎣⎦【点睛】本题考查分类讨论解含绝对值不等式，考查基本分析求解能力，属基础题.【必做题】第24题、第25题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．24.在三棱锥A —BCD 中，已知CB =CD=5,BD =2，O 为BD 的中点，AO ⊥平面BCD ，AO =2，E 为AC 的中点．（1）求直线AB 与DE 所成角的余弦值； （2）若点F 在BC 上，满足BF =14BC ，设二面角F —DE —C 的大小为θ，求sin θ的值． 【答案】（1）15（2）239 【解析】 【分析】（1）建立空间直角坐标系，利用向量数量积求直线向量夹角，即得结果；（2）先求两个平面法向量，根据向量数量积求法向量夹角，最后根据二面角与向量夹角关系得结果.详解】（1）连,COBC CD BO OD CO BD ==∴⊥以,,OB OC OA 为,,x y z 轴建立空间直角坐标系，则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -∴15(1,0,2),(1,1,1)cos ,1553AB DE AB DE ∴=-=∴<>==-2020年高考（江苏卷）从而直线AB 与DE所成角的余弦值为15（2）设平面DEC 一个法向量为1(,,),n x y z =11200(1,2,0),00x y n DC DC x y z n DE ⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩ 令112,1(2,1,1)y x z n =∴=-=∴=-设平面DEF 一个法向量为2111(,,),n x y z =11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩ 令111272,5(2,7,5)y x z n =-∴==∴=-cos ∴因此【点睛】本题考查利用向量求线线角与二面角，考查基本分析求解能力，属中档题.25.个白球，乙口袋中装有3个白球．现从甲、乙两口袋中各任取一个球交换放次这样的操作，记甲口袋中黑球个数为X n ，恰有2个黑球的概率为p n ，恰有1个黑球的概率为q n ．（1）求p 1·q 1和p 2·q 2； （2）求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示) ．【答案】（1）112212716,,332727p q p q ====；；（2）()111222+33n n n n p q p q --+=+ 【解析】【分析】（1）直接根据操作，根据古典概型概率公式可得结果；（2）根据操作，依次求n n p q ，，即得递推关系，构造等比数列求得2n n p q +，最后根据数学期望公式求结果.【详解】（1）11131232,333333p q ⨯⨯====⨯⨯，2020年高考（江苏卷）211131211227++3333333927p p q ⨯⨯=⨯⨯=⨯⨯=⨯⨯， 211231122222516+0+3333333927q p q ⨯⨯+⨯=⨯⨯+=⨯⨯=⨯⨯. （2）1111131212++333339n n n n n p p q p q ----⨯⨯=⨯⨯=⨯⨯， 111112*********+(1)+33333393n n n n n n q p q p q q -----⨯⨯+⨯⨯=⨯⨯+--⨯=-⨯⨯⨯， 因此112122+333n n n n p q p q --+=+， 从而11111212(2+),21(2+1)333n n n n n n n n p q p q p q p q ----+=+∴+-=-， 即1111121(2+1),2133n n n n n n p q p q p q -+-=-∴+=+. 又n X 的分布列为。
2020年全国高考数学-江苏卷解析(Word域、极致精编版)
2020年普通高等学校招生全国统一考试——江苏数学Ⅰ参考公式：柱体的体积V ＝Sh ，其中S 是柱体的底面积，h 是柱体的高． 一、填空题：本大题共14小题，每小题5分，共计70分．1．已知集合A ＝{－1，0，1，2}，B ＝{0，2，3}，则A ∩B ＝▲________． 答案：{0，2}2．已知i 是虚数单位，则复数z ＝(1＋i )(2－i )的实部是▲________． 答案：3解析：因为复数z ＝(1＋i )(2－i )＝2－i ＋2i －i 2＝3＋i ，所以复数的实部为3．3．已知一组数据4，2a ，3－a ，5，6的平均数为4，则a 的值是▲________． 答案：2解析：由题得4＋2a ＋3－a ＋5＋6＝20，解得a ＝2．4．将一颗质地均匀的正方体骰子先后抛掷2次，观察向上的点数，则点数和为5的概率是▲________． 答案：19解析：基本事件总数为6×6＝36个，点数和为5的基本事件有(1，4)，(4，1)，(2，3)，(3，2)，共4个，所以概率为436＝19．5．如图是一个算法流程图，若输出y 的值为－2，则输入x 的值是▲________． 答案：－3解析：由于2x ＞0，所以y ＝x ＋1＝－2，得x ＝－3．6．在平面直角坐标系xOy 中，若双曲线x 2a 2－y 25＝1(a ＞0)的一条渐近线方程为y ＝52x ，则该双曲线的离心率是▲________． 答案：32解析：由题得5a ＝52，得a ＝2，所以c ＝a 2＋b 2＝3，所以双曲线的离心率为c a ＝32．7．已知y ＝f (x )是奇函数，当x ≥0时，f (x )＝x 23，则f (－8)的值是▲________．答案：－4解析：f (－8)＝－f (8)＝－823＝－4．8．已知sin 2(π4＋α)＝23，则sin2α的值是▲________．答案：13解析：因为sin 2(π4＋α)＝(22cos α＋22sin α)2＝12(1＋sin2α)＝23，所以sin2α＝13．9．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm ，高为2cm ，内孔半轻为0.5cm ，则此六角螺帽毛坯的体积是▲________cm ． 答案：123－π2解析：正六棱柱体积为6×34×22×2＝123，圆柱体积为π(12)2·2＝π2，所求几何体体积为123－π2．10．将函数y ＝3sin(2x ＋π4)的图象向右平移π6个单位长度，则平移后的图象中与y 轴最近的对称轴的方程是▲________． 答案：x ＝－5π24解析：平移得y ＝3sin[2(x －π6)＋π4]＝3sin(2x －π12)，令2x －π12＝π2＋k π，得x ＝7π24＋k π2(k ∈Z )．当k ＝－1时，x ＝－5π24是与y 轴最近的对称轴．11．设{a n }是公差为d 的等差数列，{b n }是公比为q 的等比数列．已知数列{a n ＋b n }的前n 项和S n ＝n 2－n ＋2n －1(n ∈N *)，则d ＋q 的值是▲________． 答案：4解析：易知等差数列{a n }的前n 项和为n 2－n ，故d ＝2．等比数列{b n }的前n 项和为2n －1，故q ＝2． 故d ＋q ＝4．12．已知5x 2y 2＋y 4＝1(x ，y ∈R )，则x 2＋y 2的最小值是▲________． 答案：45解析：因为5x 2y 2＋y 4＝1，所以y ≠0且x 2＝1－y 45y2．于是x 2＋y 2＝1－y 45y 2＋y 2＝15y 2＋4y 25≥215y 2·4y 25＝45，当且仅当15y 2＝4y 25，即x 2＝310，y 2＝12时取等号．所以x 2＋y 2的最小值为45．法二：4＝(5x 2＋y 2)4y 2≤(5x 2＋y 2＋4y 22)2＝25(x 2＋y 2)24，得x 2＋y 2≥45．13．在△ABC 中，AB ＝4，AC ＝3，∠BAC ＝90º，D 在边BC 上，延长AD 到P ，使得AP ＝9．若P A →＝m PB →＋(32－m )PC →(m 为常数)，则CD 的长度是▲________．答案：0或185解析：设P A →＝λPD →(λ＞0)，因为P A →＝m PB →＋(32－m )PC →，所以λPD →＝m PB →＋(32－m )PC →，即PD →＝mλPB →＋(32－m )λPC →．因为B ，D ，C 三点共线，所以m λ＋(32－m )λ＝1，故λ＝32．因为AP ＝9，所以AD ＝3，因此△ACD 为等腰三角形或C ，D 重合．若△ACD 为等腰三角形，作AE ⊥BC 于E ，故E 为CD 中点，由等面积法得AE ＝125，由勾股定理得CE ＝DE ＝95，所以CD ＝185．若C ，D 重合，则CD ＝0． 所以，CD 的长度为0或185．14．在平面直角坐标系xOy 中，已知P (32，0)，A ，B 是圆C ：x 2＋(y －12)2＝36上的两个动点，满足P A ＝PB ，则△P AB 面积的最大值是▲________． 答案：10 5解析：因为P A ＝PB ，易得PC ⊥AB ．设圆心C 到直线AB 距离为d ，则|AB |＝236－d 2，|PC |＝34＋14＝1，S △P AB ＝12·AB ·d P －AB ≤12·236－d 2·max{d －1，1－d ，d ＋1}＝12·236－d 2·(d ＋1)＝(36－d 2)(d ＋1)2． 令y ＝(36－d 2)(d ＋1)2(0≤d ＜6)，由y'＝2(d ＋1)(－2d 2－d ＋36)＝0，得d ＝4． 当0≤d ＜4时，y'＞0，y (x )递增；当4＜d ＜6时，y'＜0，y (x )递减． 因此当d ＝4时，y max ＝500，故(S △P AB )max ＝105．二、解答题：本大题共6小题，共计90分，请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．15．在三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．(1)求证：EF ∥平面AB 1C 1； (2)求证：平面AB 1C ⊥平面ABB 1．解析：(1)因为E ，F 分别是AC ，B 1C 的中点，所以EF ∥AB 1．又EF ⊄平面AB 1C 1，AB 1⊂平面AB 1C 1，所以EF ∥平面AB 1C 1． (2)因为B 1C ⊥平面ABC ，AB ⊂平面ABC ，所以B 1C ⊥AB ．又AB ⊥AC ，AC ∩B 1C ＝C ，所以AB ⊥平面AB 1C ． 因为AB ⊂平面ABB 1，所以平面AB 1C ⊥平面ABB 1．16．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知a ＝3，c ＝2，B ＝45º．(1)求sin C 的值；(2)在边BC 上取一点D ，使得cos ∠ADC ＝－45，求tan ∠DAC 的值．解析：(1)由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝9＋2－2×3×2×22＝5，所以b ＝5．由正弦定理得c sin C ＝b sin B ，故sin C ＝c sin B b ＝55．(2)由于cos ∠ADC ＝－45，∠ADC ∈(π2，π)，所以sin ∠ADC ＝1－cos 2∠ADC ＝35．易知C ∈(0，π2)，所以cos C ＝1－sin 2C ＝255．所以sin ∠DAC ＝sin(π－∠DAC )＝sin(∠ADC ＋∠C )＝sin ∠ADC ·cos C ＋cos ∠ADC ·sin C ＝35×255＋(－45)×55＝2525． 因为∠DAC ∈(0，π2)，所以cos ∠DAC ＝1－sin 2∠DAC ＝11525．于是，tan ∠DAC ＝sin ∠DAC cos ∠DAC ＝211．17．某地准备在山谷中建一座桥梁，桥址位置的竖直截面图如图所示：谷底O 在水平线MN 上、桥AB 与MN 平行，OO'为铅垂线(O'在AB 上)．经测量，左侧曲线AO 上任一点D 到MN 的距离h 1(米)与D 到OO'的距离a (米)之间满足关系式h 1＝140a 2；右侧曲线BO 上任一点F 到MN 的距离h 2(米)与F 到OO'的距离b (米)之间满足关系式h 2＝－1800b 3＋6b ．已知点B 到OO'的距离为40米．(1)求桥AB 的长度；(2)计划在谷底两侧建造平行于OO'的桥墩CD 和EF ，且CE 为80米，其中C ，E 在AB 上(不包括端点)．桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k＞0)．问O'E 为多少米时，桥墩CD 与EF 的总造价最低?解析：(1)当b ＝40时，OO'＝－1800×403＋6×40＝160，又140|O'A |2＝OO'＝160，所以|O'A |＝80．所以|AB |＝|O'A |＋|O'B |＝80＋40＝120米． (2)设|O'E |＝x ，总造价为f (x )万元．f (x )＝k (160＋1800x 3－6x )＋32k [160－140(80－x )2]＝k (160＋1800x 3－380x 2)(0＜x ＜40)，由f'(x )＝k (3800x 2－680x )＝0，得x ＝20(0舍去)．当0＜x ＜20时，f'(x )＜0，f (x )递减；当20＜x ＜40时，f'(x )＞0，f (x )递增．因此当x ＝20时，f (x )取最小值．答：当O'E ＝20米时，桥墩CD 与EF 的总造价最低．18．在平面直角坐标系xOy 中，已知椭圆E ：x 24＋y 23＝1的左、右焦点分别为F 1，F 2，点A 在椭圆E 上且在第一象限内，AF 2⊥F 1F 2，直线AF 1与椭圆E 相交于另一点B ．(1)求△AF 1F 2的周长；(2)在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP →·QP →的最小值；(3)设点M 在椭圆E 上，记△OAB 与△MAB 的面积分别为S 1，S 2，若S 2＝3S 1，求点M 的坐标．解析：(1)因为椭圆E 的方程为x 24＋y 23＝1，所以a ＝2，c ＝1，所以△AF 1F 2的周长为2a ＋2c ＝6．(2)设P (x 0，0)，x 0≠1，Q (4，y Q )．易得A (1，32)．所以OP →·QP →＝(x 0，0)·(x 0－4，－y Q )＝(x 0－4)x 0＝(x 0－2)2－4≥－4，当且仅当x 0＝2时取等号． 所以OP →·QP →的最小值为－4．(3)设M (x 1，y 1)，点M 到直线AB 的距离为d ．因为A (1，32)，F 1(－1，0)，所以直线AF 1的方程为y ＝34(x ＋1)，即3x －4y ＋3＝0，因此点O到直线AB 的距离为35．因为S 2＝3S 1，12|AB |·d M －AB ＝3×12×|AB |×35，所以d M －AB ＝95＝|3x 1－4y 1＋3|5，得3x 1－4y 1＋12＝0或3x 1－4y 1－6＝0．由⎩⎪⎨⎪⎧3x 1－4y1＋12＝0，x 124＋y 123＝1，得7x 2＋24x ＋32＝0，此方程无解；由⎩⎪⎨⎪⎧3x 1－4y 1－6＝0，x 124＋y 123＝1，得7x 2－12x －4＝0，解得M (2，0)或(－27，－127)．19．已知关于x 的函数y ＝f (x )，y ＝g (x )与h (x )＝kx ＋b (k ，b ∈R )在区间D 上恒有f (x )≥h (x )≥g (x )．(1)若f (x )＝x 2＋2x ，g (x )＝－x 2＋2x ，D ＝(－∞，＋∞)，求h (x )的表达式； (2)若f (x )＝x 2－x ＋1，g (x )＝k ln x ，h (x )＝kx －k ，D ＝(0，＋∞)，求k 的取值范围；(3)若f (x )＝x 4－2x 2，g (x )＝4x 2－8，h (x )＝4(t 3－t )x －3t 4＋2t 2(0＜|t |≤2)，D ＝[m ，n ]⊆[－2，2]，求证：n －m ≤7．解析：(1)由题得－x 2＋2x ≤kx ＋b ≤x 2＋2x 对任意的x ∈R 恒成立．令x ＝0，则0≤b ≤0，所以b ＝0．由kx ≤x 2＋2x ，即x 2＋(2－k )x ≥0对任意的x ∈R 恒成立，所以Δ＝(2－k )2≤0，因此k ＝2． 此时也满足－x 2＋2x ≤2x 对任意的x ∈R 恒成立． 所以h (x )＝2x ．(2)令F (x )＝h (x )－g (x )＝k (x －1－ln x )(x ＞0)，则F (1)＝0，由题得F (x )≥F (1)恒成立．易得F'(x )＝k ·x －1x．若k ＜0，则F (x )在(0，1)上递增，在(1，＋∞)上递减，则F (x )≤F (1)＝0，不合题意． 当k ＝0时，F (x )＝F (1)＝0，h (x )＝g (x )，符合题意．当k ＞0时，F (x )在(0，1)上递减，在(1，＋∞)上递增，则F (x )≥F (1)＝0，符合题意． 综上，k ≥0．又f (x )－h (x )＝x 2－x ＋1－(kx －k )＝x 2－(k ＋1)x ＋(k ＋1)≥0．当x ＝k ＋12＜0，即k ＜－1时，y ＝x 2－(k ＋1)x ＋k ＋1在(0，＋∞)为增函数，因为y (0)＝k ＋1＜0，不合题意．当x ＝k ＋12＝0，即k ＝－1时，f (x )－h (x )＝x 2≥0，符合题意．当x ＝k ＋12＞0，即k ＞－1时，应有Δ＝(k ＋1)2－4(k ＋1)≤0，解得－1＜k ≤3．综上，k 的取值范围是k ∈[0，3]．(3)由题得x 4－2x 2≥4(t 3－t )x －3t 4＋2t 2≥4x 2－8对任意x ∈[m ，n ]⊆[－2，2]恒成立．x 4－2x 2≥4(t 3－t )x －3t 4＋2t 2对任意x ∈[m ，n ]⊆[－2，2]恒成立， 等价于(x －t )2(x 2＋2tx ＋3t 2－2)≥0对任意x ∈[m ，n ]⊆[－2，2]恒成立， 故x 2＋2tx ＋3t 2－2≥0对任意x ∈[m ，n ]⊆[－2，2]恒成立．令M (x )＝x 2＋2tx ＋3t 2－2．当Δ＝－8t 2＋8＞0，即0＜t 2＜1时，对称轴x ＝－t ∈(－1，1)，记M (x )的两个零点为x 1＜x 2，此时n －m ≤max{2－x 2，x 1－(－2)}≤max{2－(－t )，(－t )－(－2)}＝max{2±t }≤2＋|t |＜2＋1＜7．当Δ＝－8t 2＋8≤0，即1≤t 2≤2时，M (x )≥0对x ∈R 恒成立． 而4x 2－8≤4(t 3－t )x －3t 4＋2t 2对任意的x ∈[m ，n ]⊆[－2，2]恒成立， 等价于4x 2－4(t 3－t )x ＋(3t 2＋4)(t 2－2)≤0对任意的x ∈[m ，n ]⊆[－2，2]恒成立．记4x 2－4(t 3－t )x ＋(3t 2＋4)(t 2－2)＝0的两根为x 1，x 2，则x 1＋x 2＝t 3－t ，x 1·x 2＝3t 4－2t 2－84，所以n －m ＝|x 1－x 2|＝(x 1＋x 2)2－4x 1x 2＝t 6－5t 4＋3t 2＋8．令λ＝t 2∈[1，2]，则n －m ＝λ3－5λ2＋3λ＋8．记P (λ)＝λ3－5λ2＋3λ＋8，λ∈[1，2]，P'(λ)＝3λ2－10λ＋3＝(λ－3)(3λ－1)，所以当λ∈[1，2]时，P'(λ)＜0，P (λ)递减，所以P (λ)max ＝P (1)＝7．所以(n －m )max ＝7，即n －m ≤7．20．已知数列{a n }(n ∈N *)的首项a 1＝1，前n 项和为S n ．设λ与k 是常数，若对一切正整数n ，均有Sn ＋11k －S n 1k＝λa n ＋11k 成立，则称此数列为“λ－k ”数列．(1)若等差数列{a n }是“λ－1”数列，求λ的值； (2)若数列{a n }是“33－2”数列，且a n ＞0，求数列{a n }的通项公式； (3)对于给定的λ，是否存在三个不同的数列{a n }为“λ－3”数列，且a n ≥0?若存在，求λ的取值范围；若不存在，说明理由．解析：(1)若等差数列{a n }是“λ－1”数列，则S n ＋1－S n ＝λa n ＋1，即a n ＋1＝λa n ＋1．因为a n 不恒为0，所以λ＝1． (2)因为S n ＋112－S n 12＝33a n ＋112，所以(S n ＋112－S n 12)2＝13(S n ＋1－S n )＝13(S n ＋112－S n 12)(S n ＋112＋S n 12)． 因为a n ＞0，所以S n ＋1＞S n ，因此S n ＋112－S n 12＞0，于是S n ＋112－S n 12＝13(S n ＋112＋S n 12)，即S n ＋112＝2S n 12，所以S n ＋1＝4S n ．因为S 1＝a 1＝1，所以S n ＝4n －1，a n ＝4n －1－4n －2＝3·4n －2，n ≥2．所以a n ＝⎩⎨⎧1，n ＝1，3·4n －2，n ≥2．(3)假设存在三个不同的数列{a n }为“λ－3”数列，且a n ≥0．由S n ＋113－S n 13＝λa n ＋113，得(S n ＋113－S n 13)3＝λ3(S n ＋1－S n )，所以S n ＋113＝S n 13或(S n ＋113－S n 13)2＝λ3(S n ＋123＋S n 23＋S n ＋113S n 13)，即S n ＋1＝S n 或(λ3－1)Sn ＋123＋(λ3－1)S n 23＋(λ3＋2)S n ＋113S n 13＝0．由S n ＋1＝S n ，得a n ＝⎩⎨⎧1，n ＝1，0，n ≥2．因为存在三个不同的数列{a n }为“λ－3”数列，且a n ≥0，所以(λ3－1)S n ＋123＋(λ3－1)S n 23＋(λ3＋2)S n ＋113S n 13＝0(λ≠1)有两个不等的正根．(λ3－1)S n ＋123＋(λ3－1)S n 23＋(λ3＋2)S n ＋113S n 13＝0(λ≠1)可转化为(λ3－1)S n ＋123S n 23＋(λ3－1)＋(λ3＋2)S n ＋113S n 13＝0(λ≠1)，不妨设(S n ＋1S n )13＝x (x ＞0)，则(λ3－1)x 2＋(λ3＋2)x ＋(λ3－1)＝0(λ≠1)有两个不等正根，设f (x )＝(λ3－1)x 2＋(λ3＋2)x ＋(λ3－1)＝0(λ≠1)．①当λ＜1时，令Δ＝(λ3＋2)2－4(λ3－1)2＞0，得0＜λ3＜4，故0＜λ＜1，此时f (0)＝λ3－1＜0，对称轴x ＝－(λ3＋2)2(λ3－1)＞0，满足题意．②当λ＞1时，令Δ＝(λ3＋2)2－4(λ3－1)2＞0，得0＜λ3＜4，故1＜λ＜34，此时f (0)＝λ3－1＞0，对称轴x ＝－(λ3＋2)2(λ3－1)＜0，此情况有两个不等负根，不满足题意，舍去．综上，0＜λ＜1．数学Ⅱ(附加题)[选做题]本题包括A 、B 、C 三小题，请选定其中两小题．．．．．．．．，．并在相应的答题区域内作答．．．．．．．．．．．．．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤． A ．[选修4－2：矩阵与变换] 21．平面上点A (2，－1)在矩阵M ＝⎣⎡⎦⎤a 1 －1b 对应的变换作用下得到点B (3，－4)．(1)求实数a ，b 的值； (2)求矩阵M 的逆矩阵M －1．解析：(1)由题得⎣⎡⎦⎤ a 1 －1 b ⎣⎡⎦⎤2－1＝⎣⎡⎦⎤ 3－4，所以⎩⎨⎧2a －1＝3，－2－b ＝－4，解得a ＝2，b ＝2．(2)设M －1＝⎣⎡⎦⎤m n c d ，则MM －1＝⎣⎡⎦⎤2m ＋c 2n ＋d －m ＋2c －n ＋2d ＝⎣⎡⎦⎤1 00 1，所以⎩⎨⎧2m ＋c ＝1，2n ＋d ＝0，－m ＋2c ＝0，－n ＋2d ＝1，解得m ＝25，n ＝－15，c ＝15，d ＝25，所以M －1＝⎣⎢⎡⎦⎥⎤25 －1515 25．B ．[选修4－4：坐标系与参数方程]22．在极坐标系中，已知点A (ρ1，π3)在直线l ：ρcos θ＝2上，点B (ρ2，π6)在圆C ：ρ＝4sin θ上(其中ρ≥0，0≤θ＜2π)．(1)求ρ1，ρ2的值；(2)求出直线l 与圆C 的公共点的极坐标．解析：(1)以极点为原点，极轴为x 轴的正半轴，建立平面直角坐标系。
2020届江苏高考数学应用题精选试题(三)
2020届江苏高考数学应用题精选试题（三）1、（江苏省南京师大附中2020届高三年级模拟考试数学试题）某人利用一根原木制作一件手工作品，该作品由一个球体和一个正四棱柱组成. 假定原木为圆柱体（如图1）,底面半径为r ，高为h ，制作要求如下：首先需将原木切割为两部分（分别为第Ⅰ圆柱和第Ⅱ圆柱），要求切面与原木的上下底面平行（不考虑损耗）.然后将第Ⅰ圆柱切割为一个球体，要求体积最大，将第Ⅱ圆柱切割为一个正四棱柱，要求正四棱柱的上下底面分别为第Ⅱ圆柱上下底面圆的内接正方形.（1）当8,2==h r 时，若第Ⅰ圆柱和第Ⅱ圆柱的体积相等，求该手工作品的体积；（2）对于给定的r 和h （h ＞r 2），求手工作品体积的最大值.（第1题） （第3题）2、（江苏省南通市通州区2020届高三第二次调研抽测数学试题）中国高铁的快速发展给群众出行带来巨大便利，极大促进了区域经济社会发展.己知某条高铁线路通车后， 发车时间间隔t （单位：分钟）满足525,t t N *≤≤∈.经测算，高铁的载客量与发车时间间隔r 相关：当2025t ≤≤时高铁为满载状态，载客量为1000人；当520t ≤≤时，载客量会在满载基础上减少，减少的人数与()220t -成正比，且发车时间为5分钟时的载客量为100人.记发车间隔时间为t 分钟时，高铁载客量为()P t .（1） 求()P t 的表达式；（2） 若该线路发车时间间隔t 分钟时的净收入()2()4065020004t Q t P t t t =-+-（元），当发车时间间隔为多少时，单位时间的净收益()Q t t最大.3、（江苏省无锡市普通高中2019-2020学年上学期高三期中调研考试）为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端，甲站在直角ABC ∆斜边AC 的中点F 处，乙站在B 处，丙站在C 处游戏开始，甲不动，乙、丙分别以v (m/s)和v 2(m/s)的速度同时出发，匀速跑向终点A 和B .运动过程中绷紧的橡皮带围成一个如图所示的.(规定:只要有一人跑到终点游戏就结束，且(m/s))。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高三数学应用题专题
1. 经销商用一辆J 型卡车将某种水果从果园运送(满载)到相距400 km 的水果批发市场．据测算，J 型卡车满载行驶时，每100 km 所消耗的燃油量u(L)与速度v(km/h)的关系近似地满
足u ＝⎩
⎨⎧100v ＋23，0<v ≤50，v 2500
＋20，v>50.除燃油费外，人工工资、车损等其他费用平均每小时为300元．已知燃油价格为每升(L)7.5元．
(1) 设运送这车水果的费用为y(元)(不计返程费用)，将y 表示成速度v 的函数关系式；
(2) 卡车应该以怎样的速度行驶，才能使运送这车水果的费用最少？
2. 某城市受雾霾影响严重，现欲在该城市中心P 的两侧建造A ，B 两个空气净化站（A ，P ，
B 三点共线），A ，B 两站对该城市的净化度分别为1a a -，，其中(01)a ∈，．已知对该城市总净化效果为A ，B 两站对该城市的净化效果之和，且每站净化效果与净化度成正比，与中心P 到净化站距离成反比．若1AB =，且当
34AP =时，A 站对该城市的净化效果为3a ，B 站对
该城市的净化效果为1a -．
（1）设AP x =，(01)x ∈，，求A ，B 两站对该城市的总净化效果()f x ； （2）无论A ，B 两站建在何处，若要求A ，B 两站对该城市的总净化效果至少达到2
5，求a 的取值集合．
3. 如图,直线1l 是某海岸线，2l 是位于近海的虚拟线，12l l ⊥于点P,点A,C 在2l 上，AC 的中点为O ，且km AC PA 2==.
（1）原计划开发一片以AC 为一条对角线,周长为8 km 的平行四边形水域ABCD,建深水养殖场.求深水养殖场的最大面积;
（2）现因资金充裕,计划扩大开发规模,开发如图五边形水域QABCD,建养殖场,其中ABCD 是周长为8 km 的平行四边形,点Q 在1l 上,且在点P 的上方,AD OQ ⊥, ︒≤∠90OCD . 养殖场分两个区域,四边形QAOD 区域内养殖浅水产品,其他区域内养
殖深水产品,要求养殖浅水产品区域的面积最大.求点Q 与点P
的距离.
4. 如图(1)是某水上乐园拟开发水滑梯项目的效果图，考虑到空间和安全方面的原因，初步设计方案如下:如图(2)，自直立于水面的空中平台CP 的上端点P 处分别向水池内的三个不同方向建水滑道PA,PM,PB ，水滑道的下端点B,M,A 在同一条直线上，CM = 10m,∠
BCA=120°，CM 平分∠BCA ，假设水滑梯的滑道可以看成线段，B,M,A 均在过C 且与PC 垂直的平面内，为了滑梯的安全性，设计要求ACB PCA PCB S S S ∆∆∆≤+2.
(1)求滑梯的高PC 的最大值;
(2)现在开发商考虑把该水滑梯项目设计成室内游玩项目，且为保证该项目的趣味性，设计∠PBC=30°，求该滑梯装置(即图(2)中的几何体)的体积最小值.
.
5.如图，已知，两镇分别位于东西湖岸的处和湖中小岛的处，点在的
正西方向km 处，经测量，．现计划铺设一条电缆联通，两镇．有两种方案供选择：①沿线段在水下铺设；②在湖岸上设立一中转站，先沿线段在地下铺设，再沿线段在水下铺设．预算地下、水下的电缆修建费用分别为2万、4万．
（1）求，两镇间的距离；
（2）应该选择哪种方案，使总修建费用较低？
A B MN A B C A 13tan 4BAN ∠=
π4
BCN ∠=A B AB MN P AP PB /km /km A B C A P B (第17题)。