计量经济学(庞浩)第二版第十一章练习题与参考解答
(2020年7月整理)庞皓版计量经济学课后习题答案.doc
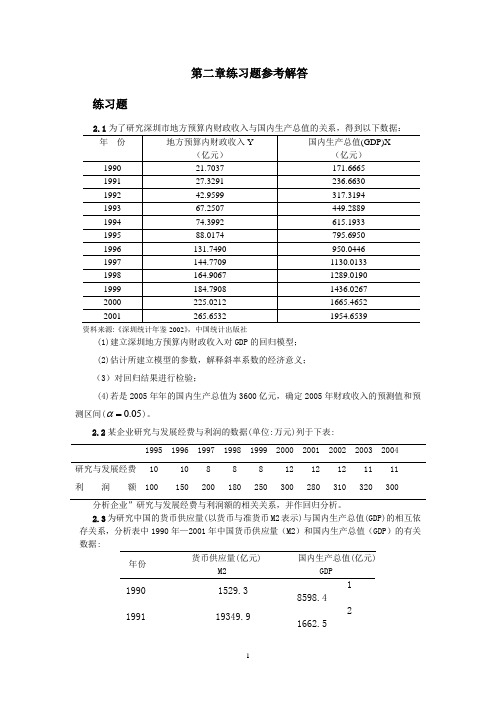
第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验;(4)若是2005年年的国内生产总值为3600亿元,确定2005年财政收入的预测值和预测区间(0.05α=)。
2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2001年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.2 26651.91993 34879.8 34560.51994 46923.5 46670.01995 60750.5 57494.91996 76094.9 66850.51997 90995.3 73142.71998 104498.5 76967.21999 119897.9 80579.42000 134610.3 88228.12001158301.994346.4资料来源:《中国统计年鉴2002》,第51页、第662页,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明分析结果的经济意义。
2.4表中是16支公益股票某年的每股帐面价值和当年红利:根据上表资料:(1)建立每股帐面价值和当年红利的回归方程; (2)解释回归系数的经济意义;(3)若序号为6的公司的股票每股帐面价值增加1元,估计当年红利可能为多少?2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street 1。
计量经济学第二版课后习题1-14章中文版答案汇总

第四章习题 1.(1)22ˆ=TSR estScore T =520.4-5.82×22=392.36 (2)ΔTestScore=-5.82×(23-19)=-23.28即平均测试成绩所减少的分数回归预测值为23.28。
(3)core est S T =βˆ0 +βˆ1×CS =520.4-5.82×1.4=395.85 (4)SER 2=∑=-n i u n 1ˆ21i 2=11.5 ∴SSR=∑=ni u1ˆi2=SER 2×(n-2)=11.5×(100-2)=12960.5R 2=T SS ESS =1-T SSSSR =0.08∴TSS=SSR ÷(1-R 2)=12960.5÷(1-0.08)=14087.5=21)(Y ∑=-ni iY∴s Y 2=1-n 121)(Y ∑=-ni iY =14087.5÷(100-1)≈140.30∴s Y ≈11.93 2. (1)①70ˆ=Height eight W =-99.41+3.94×70=176.39 ②65ˆ=Height eight W =-99.41+3.94×65=156.69 ③74ˆ=Height eight W=-99.41+3.94×74=192.15(2)ΔWeight=3.94×1.5=5.91(3)1inch=2.54cm,1lb=0.4536kg①eight Wˆ(kg)=-99.41×0.4536+54.24536.0×94.3Height(cm)=-45.092+0.7036×Height(cm)②R 2无量纲,与计量单位无关,所以仍为0.81③SER=10.2×0.4536=4.6267kg 3.(1)①系数696.7为回归截距,决定回归线的总体水平②系数9.6为回归系数,体现年龄对周收入的影响程度,每增加1岁周收入平均增加$9.6 (2)SER=624.1美元,其度量单位为美元。
计量经济学(庞皓)第二版课后思考题答案

计量经济学(庞皓)第二版课后思考题答案思考题答案第一章绪论思考题1.1怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作用?答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
我们只要坚持以科学的经济理论为指导,紧密结合中国经济的实际,就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥重要作用。
1.2理论计量经济学和应用计量经济学的区别和联系是什么?答:计量经济学不仅要寻求经济计量分析的方法,而且要对实际经济问题加以研究,分为理论计量经济学和应用计量经济学两个方面。
理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3怎样理解计量经济学与理论经济学、经济统计学的关系?答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
计量经济学-庞皓-第二版-思考题-答案

第一章 绪论 思考题1.1答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
1.2答:理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
区别:经济统计学主要用统计指标和统计分析方法对经济现象进行描述和计量;计量经济学主要利用数理统计方法对经济变量间的关系进行计量。
1.4答:解释变量是变动的原因,被解释变量是变动的结果。
被解释变量是模型要分析研究的对象。
解释变量是说明被解释变量变动主要原因的变量。
1.5一个完整的计量经济模型应包括哪些基本要素?你能举一个例子吗?答:一个完整的计量经济模型应包括三个基本要素:经济变量、参数和随机误差项。
计量经济学庞皓课后思考题答案

计量经济学庞皓课后思考题答案第⼀章绪论思考题1.1 怎样理解产⽣于西⽅国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作⽤?答:计量经济学的产⽣源于对经济问题的定量研究,这是社会经济发展到⼀定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在⼀起的,它反映了社会化⼤⽣产对各种经济因素和经济活动进⾏数量分析的客观要求。
经济学从定性研究向定量分析的发展,济学逐步向更加精密、更加科学发展的表现。
我们只要坚持以科学的经济理论为指导,结合中国经济的实际,就能够使计量经济学的理论与⽅法在中国的经济理论研究和现代化建设中发挥重要作⽤。
1.2 理论计量经济学和应⽤计量经济学的区别和联系是什么?答:计量经济学不仅要寻求经济计量分析的⽅法,⽽且要对实际经济问题加以研究,论计量经济学和应⽤计量经济学两个⽅⾯。
理论计量经济学是以计量经济学理论与⽅法技术为研究内容,⽬的在于为应⽤计量经济学提供⽅法论。
所谓计量经济学理论与⽅法技术的研究,实质上是指研究如何运⽤、改造和发展数理统计⽅法,使之成为适合测定随机经济关系的特殊⽅法。
应⽤计量经济学是在⼀定的经济理论的指导下,以反映经济事实的统计数据为依据,计量经济⽅法技术研究计量经济模型的实⽤化或探索实证经济规律、济⾏为以及对经济政策作定量评价。
1.3 怎样理解计量经济学与理论经济学、经济统计学的关系?答: 1、计量经济学与经济学的关系。
联系:计量经济学研究的主体的数量规律;计量经济学必须以经济学提供的理论原则和经济运⾏规律为依据;析的结果:对经济理论确定的原则加以验证、充实、并不对经济关系提供数量上的具体度量;理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
计量经济学(庞皓)课后思考题答案

思考题答案第一章绪论思考题1.1怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作用?答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
我们只要坚持以科学的经济理论为指导,紧密结合中国经济的实际,就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥重要作用。
1.2理论计量经济学和应用计量经济学的区别和联系是什么?答:计量经济学不仅要寻求经济计量分析的方法,而且要对实际经济问题加以研究,分为理论计量经济学和应用计量经济学两个方面。
理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3怎样理解计量经济学与理论经济学、经济统计学的关系?答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
计量经济学庞皓课后思考题答案

思考题答案第一章绪论思考题1、1怎样理解产生于西方国家的il鱼经济学能够在中国的经济理论研究与现代化建设中发挥重要作用?答:计量经济学的产生源于对经济问题的左疑研究,这就是社会经济发展到一泄阶段的客观需要。
il鱼经济学的发展就是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素与经济活动进行数呈:分析的客观要求。
经济学从左性研究向定量分析的发展,就是经济学逐步向更加精密、更加科学发展的表现。
我们只要坚持以科学的经济理论为指导, 紧密结合中国经济的实际,就能够使计量经济学的理论与方法在中国的经济理论研究与现代化建设中发挥重要作用。
1、2理论计量经济学与应用计量经济学的区别与联系就是什么?答:il慢经济学不仅要寻求经济计量分析的方法,而且要对实际经济问题加以研究,分为理论计量经济学与应用计量经济学两个方而。
理论计量经济学就是以计量经济学理论与方法技术为研究内容,目的在于为应用计疑经济学提供方法论。
所谓il涅经济学理论与方法技术的研究,实质上就是指研究如何运用、改造与发展数理统计方法,使之成为适合测泄随机经济关系的特殊方法。
应用汁量经济学就是在一左的经济理论的指导下,以反映经济事实的统讣数据为依据,用计量经济方法技术研究讣疑经济模型的实用化或探索实证经济规律、分析经济现象与预测经济行为以及对经济政策作定量评价。
1、3怎样理解计鱼经济学与理论经济学、经济统计学的关系?答:1、计虽经济学与经济学的关系。
联系:计量经济学研究的主体一经济现象与经济关系的数量规律;讣量经济学必须以经济学提供的理论原则与经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出立量的估计,对经济理论提岀经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统il•提供的数拯就是il鱼经济学据以估汁参数、验证经济理论的基本依拯;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统讣数据。
计量经济学庞皓课后思考题答案

答:定义关系是指根据定义而表达的恒等式,是由经济理论或客观存在的经济关系决定的恒等关系。国民经济中许多平衡关系都可以建立恒等关系,这样的模型称为定义方程式。在联立方程组模型中经常利用定义方程式。但是,定义方程式的恒等关系中没有随机误差项和需要估计的参数,所以一般不宜用于建立单一方程模型。
1.12为什么计量经济模型可以用于政策评价?其前提条件是什么?
答:所谓政策评价,是利用计量经济模型对各种可供选择的政策方案的实施后果进行模拟运算,从而对各种政策方案作出评价。前提是,我们是把计量经济模型当作经济运行的实验室,去模拟所研究的经济体计量经济模型体系,分析整个经济体系对各种假设的政策条件的反映。在实际的政策评价时,经常把模型中的某些变量或参数视为可用政策调整的政策变量,然后分析政策变量的变动对被解释变量的影响。
1.4在计量经济模型中被解释变量和解释变量的作用有什么不同?
答:在计量经济模型中,解释变量是变动的原因,被解释变量是变动的结果。被解释变量是模型要分析研究的对象。解释变量是说明被解释变量变动主要原因的变量。
1.5一个完整的计量经济模型应包括哪些基本要素?你能举一个例子吗?
答:一个完整的计量经济模型应包括三个基本要素:经济变量、参数和随机误差项。
2.9为什么对被解释变量个别值的预测区间会比对被解释变量平均值的预测区间更宽?
答:预测被解释变量平均值仅存在抽样误差,而对被解释变量个别值的预测,不仅存在抽样误差,而且要受随机扰动项的影响。所以对个别值的预测区间比对平均值的预测区间更宽。
2.10如果有人利用中国1978~2000年的样本估计的计量经济模型直接预测“中国综合经济水平将在2050年达到美国2002年的水平”,你如何评论这种预测?
计量经济学(庞皓)课后思考题规范标准答案

2.4为什么在对参数作最小二乘估计之前,要对模型提出古典假设?
答:在对参数作最小二乘估计之前,要对模型提出古典假设。因为模型中有随机扰动,估计的参数是随机变量,只有对随机扰动的分布作出假定,才能确定所估计参数的分布性质,也才可能进行假设检验和区间估计。只有具备一定的假定条件,所作出的估计才具有较好的统计性质。
在简单线性回归中,可决系数越大,说明在总变差中由模型作出了解释的部分占的比重越大,X对Y的解释能力越强,模型拟合优度越好。对参数的t检验是判断解释变量X是否是被解释变量Y的显著影响因素。二者的目的作用是一致的。
2.7有人说:“得到参数区间估计的上下限后,说明参数的真实值落入这个区间的概率为 。”如何评论这种说法?
一般来说参数是未知的,又是不可直接观测的。由于随机误差项的存在,参数也不能通过变量值去精确计算。只能通过变量样本观测值选择适当方法去估计。
1.10你能分别举出三个时间序列数据、截面数据、面板数据、虚拟变量数据的实际例子,并分别说明这些数据的来源吗?
答:时间序列数据:中国1981年至2010年国内生产总值,可从中国统计年鉴查得数据。
最新整理计量经济学(庞皓)第二版课后思考题答案

1 。”如何评论这种说法?
答:这种说法是错误的。 区间是随机的, 只是说明在重复抽样中, 像这样的区间可构造许多
次,从长远看平均地说,这些区间中将有 1 的概率包含着参数的真实值。参数的真实值
虽然未知, 却是一个固定的值, 不是随机变量。 所以应理解为区间包含参数真实值的概率是
1 ,而不能认为参数的真实值落入这个区间的概率为
验证经济理论的基本依据; 经济现
象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
区别:经济统计学主要用统计指标和统计分析方法对经济现象进行描述和计量;
计量经济学
主要利用数理统计方法对经济变量间的关系进行计量。
1.4 在计量经济模型中被解释变量和解释变量的作用有什么不同? 答:在计量经济模型中, 解释变量是变动的原因, 被解释变量是变动的结果。被解释变量是 模型要分析研究的对象。解释变量是说明被解释变量变动主要原因的变量。
经济计量分
析的结果:对经济理论确定的原则加以验证、充实、完善。区别:经济理论重在定性分析
,
并不对经济关系提供数量上的具体度量; 理论提出经验的内容。
计量经济学对经济关系要作出定ቤተ መጻሕፍቲ ባይዱ的估计,
对经济
2、计量经济学与经济统计学的关系。联系:经济统计侧重于对社会经济现象的描述性
计量; 经济统计提供的数据是计量经济学据以估计参数、
答:可决系数是回归平方和占总离差平方和的比重, 即由样本回归作出解释的离差平方和在
总离差平方和中占的比重, 如果样本回归线对样本观测值拟合程度好, 各样本观测点与回归
线靠得越近, 由样本回归作出解释的离差平方和在总离差平方和中占的比重也将越大,
反之
拟合程度越差, 这部分所占比重就越小。 所以可决系数可以作为综合度量回归模型对样本观
计量经济学(庞浩)第二版课后习题答案(全)
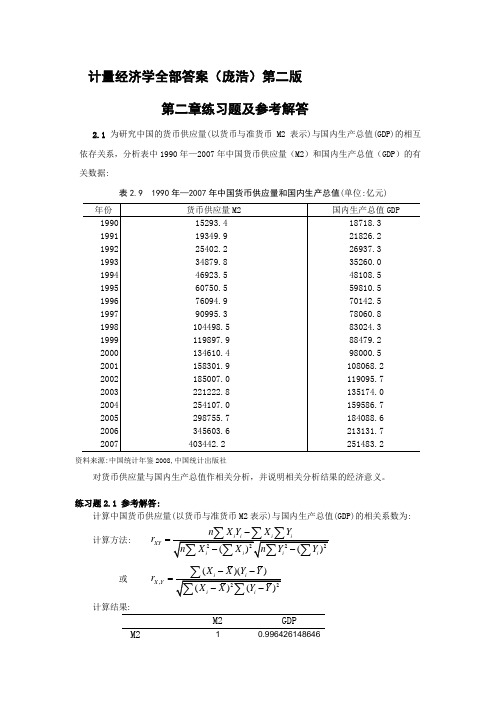
计量经济学全部答案(庞浩)第二版第二章练习题及参考解答2.1 为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2007年中国货币供应量(M2)和国内生产总值(GDP )的有关数据:表2.9 1990年—2007年中国货币供应量和国内生产总值(单位:亿元)资料来源:中国统计年鉴2008,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明相关分析结果的经济意义。
练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或 ,()()X Y X X Y Y r --=计算结果:M2GDPM210.996426148646GDP 0.996426148646 1经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
2.2 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据表2.10 美国软饮料公司广告费用与销售数量品牌名称广告费用X(百万美元) 销售数量Y(百万箱) Coca-Cola Classic 131.3 1929.2Pepsi-Cola 92.4 1384.6Diet-Coke 60.4 811.4Sprite 55.7 541.5Dr.Pepper 40.2 546.9Moutain Dew 29.0 535.67-Up 11.6 219.5 资料来源:(美) Anderson D R等. 商务与经济统计.机械工业出版社.1998. 405绘制美国软饮料公司广告费用与销售数量的相关图, 并计算相关系数,分析其相关程度。
能否在此基础上建立回归模型作回归分析?练习题2.2参考解答美国软饮料公司的广告费用X与销售数量Y的散点图为说明美国软饮料公司的广告费用X与销售数量Y正线性相关。
计量经济学(庞浩)第二版第十一章练习题及参考解答(优选.)

计量经济学(庞浩)第二版第十一章练习题及参考解答11.1 考虑以下凯恩斯收入决定模型:βββββ-=++=+++=++1011120212212t t tt t t t t t t tC Y u I Y Y u Y C I G其中,C =消费支出,I =投资指出,Y =收入,G =政府支出;t G 和1t Y -是前定变量。
(1)导出模型的简化型方程并判定上述方程中哪些是可识别的(恰好或过度)。
(2)你将用什么方法估计过度可识别方程和恰好可识别方程中的参数。
练习题11.1参考解答:1011120212212112122112102012221112111211121112110111121(1)11111t t t t t t t t t tt t t t tt t t t t t t tY C I G Y u Y Y u G Y Y Y G u u u u Y Y G Y G v βββββββββββββββββββπππ----=++=+++++++=++++++++=+++--------=+++ 1020122210111111211121112111211011211110201122111211121111211111211121101021112011()1111(1)()11()111t t t t t tt t t t tu u C Y G u Y u u G u βββββββββββββββββββββββββββββββββββββ--++=+++++----------++=++----++++-----+=-1121211112211112111211121112120211222111t tt t t t t tu u u Y G Y G v ββββββββββββπππ--+-+++-------=+++ 1020122220211112111211121112122122011212110202122211112111211121211222*********1()1111(1)()111()11t t t t t t tt t t t t u u I Y G Y u Y G u u Y βββββββββββββββββββββββββββββββββββ----++=++++--------++--++=+++------++++----2202011202110212021222111121112111212112112221112111213031132311111t t t t t t t t t tu Y G u u u Y Y G v ββββββββββββββββββββββββπππ-----++=+++------+-++----=+++101111212021122230311323t t t t t t t t tt t tY Y G v C Y G v I Y G v πππππππππ---=+++=+++=+++ 由模型的结构型,M=3,K=2。
计量经济学课后思考题答案庞皓版

计量经济学课后思考题答案庞皓版第一章绪论思考题1.1怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化建设中发挥重要作用?答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
我们只要坚持以科学的经济理论为指导,紧密结合中国经济的实际,就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥重要作用。
1.2理论计量经济学和应用计量经济学的区别和联系是什么?答:计量经济学不仅要寻求经济计量分析的方法,而且要对实际经济问题加以研究,分为理论计量经济学和应用计量经济学两个方面。
理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3怎样理解计量经济学与理论经济学、经济统计学的关系?答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
计量经济学-庞皓-第二版-思考题-答案

第一章 绪论 思考题1.1答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定阶段的客观需要。
计量经济学的发展是与现代科学技术成就结合在一起的,它反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。
经济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展的表现。
1.2答:理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用计量经济学提供方法论。
所谓计量经济学理论与方法技术的研究,实质上是指研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的特殊方法。
应用计量经济学是在一定的经济理论的指导下,以反映经济事实的统计数据为依据,用计量经济方法技术研究计量经济模型的实用化或探索实证经济规律、分析经济现象和预测经济行为以及对经济政策作定量评价。
1.3答:1、计量经济学与经济学的关系。
联系:计量经济学研究的主体—经济现象和经济关系的数量规律;计量经济学必须以经济学提供的理论原则和经济运行规律为依据;经济计量分析的结果:对经济理论确定的原则加以验证、充实、完善。
区别:经济理论重在定性分析,并不对经济关系提供数量上的具体度量;计量经济学对经济关系要作出定量的估计,对经济理论提出经验的内容。
2、计量经济学与经济统计学的关系。
联系:经济统计侧重于对社会经济现象的描述性计量;经济统计提供的数据是计量经济学据以估计参数、验证经济理论的基本依据;经济现象不能作实验,只能被动地观测客观经济现象变动的既成事实,只能依赖于经济统计数据。
区别:经济统计学主要用统计指标和统计分析方法对经济现象进行描述和计量;计量经济学主要利用数理统计方法对经济变量间的关系进行计量。
1.4答:解释变量是变动的原因,被解释变量是变动的结果。
被解释变量是模型要分析研究的对象。
解释变量是说明被解释变量变动主要原因的变量。
1.5一个完整的计量经济模型应包括哪些基本要素?你能举一个例子吗?答:一个完整的计量经济模型应包括三个基本要素:经济变量、参数和随机误差项。
《计量经济学教程(第二版)》习题解答课后习题答案

《计量经济学(第二版)》习题解答第一章1.1 计量经济学的研究任务是什么?计量经济模型研究的经济关系有哪两个基本特征? 答:(1)利用计量经济模型定量分析经济变量之间的随机因果关系。
(2)随机关系、因果关系。
1.2 试述计量经济学与经济学和统计学的关系。
答:(1)计量经济学与经济学:经济学为计量经济研究提供理论依据,计量经济学是对经济理论的具体应用,同时可以实证和发展经济理论。
(2)统计数据是建立和评价计量经济模型的事实依据,计量经济研究是对统计数据资源的深层开发和利用。
1.3 试分别举出三个时间序列数据和横截面数据。
1.4 试解释单方程模型和联立方程模型的概念,并举例说明两者之间的联系与区别。
1.5 试结合一个具体经济问题说明计量经济研究的步骤。
1.6 计量经济模型主要有哪些用途?试举例说明。
1.7 下列设定的计量经济模型是否合理,为什么?(1)ε++=∑=31i iiGDP b a GDPε++=3bGDP a GDP其中,GDP i (i =1,2,3)是第i 产业的国内生产总值。
答:第1个方程是一个统计定义方程,不是随机方程;第2个方程是一个相关关系,而不是因果关系,因为不能用分量来解释总量的变化。
(2)ε++=21bS a S其中,S 1、S 2分别为农村居民和城镇居民年末储蓄存款余额。
答:是一个相关关系,而不是因果关系。
(3)ε+++=t t t L b I b a Y 21其中,Y 、I 、L 分别是建筑业产值、建筑业固定资产投资和职工人数。
答:解释变量I 不合理,根据生产函数要求,资本变量应该是总资本,而固定资产投资只能反映当年的新增资本。
(4)ε++=t t bP a Y其中,Y 、P 分别是居民耐用消费品支出和耐用消费品物价指数。
答:模型设定中缺失了对居民耐用消费品支出有重要影响的其他解释变量。
按照所设定的模型,实际上假定这些其他变量的影响是一个常量,居民耐用消费品支出主要取决于耐用消费品价格的变化;所以,模型的经济意义不合理,估计参数时可能会夸大价格因素的影响。
计量经济学(庞浩)第二版课后习题答案

2.7 设销售收入X 为解释变量,销售成本Y 为被解释变量。
现已根据某百货公司某年12个月的有关资料计算出以下数据:(单位:万元) 2()425053.73tXX -=∑ 647.88X = 2()262855.25tY Y -=∑ 549.8Y =()()334229.09tt XX Y Y --=∑(1) 拟合简单线性回归方程,并对方程中回归系数的经济意义作出解释。
(2) 计算可决系数和回归估计的标准误差。
(3) 对2β进行显著水平为5%的显著性检验。
(4) 假定下年1月销售收入为800万元,利用拟合的回归方程预测其销售成本,并给出置信度为95%的预测区间。
练习题2.7参考解答:(1)建立回归模型: i i i u X Y ++=21ββ用OLS 法估计参数: 222()()334229.09ˆ0.7863()425053.73i i i i i iX X Y Y x y X X x β--====-∑∑∑∑ 12ˆˆ549.80.7863647.8866.2872Y X ββ=-=-⨯= 估计结果为: ˆ66.28720.7863i iY X =+ 说明该百货公司销售收入每增加1元,平均说来销售成本将增加0.7863元。
(2)计算可决系数和回归估计的标准误差 可决系数为:22222222222ˆˆˆ()0.7863425053.73262796.990.999778262855.25262855.25i i iiiiy x x Ry yyββ===⨯===∑∑∑∑∑∑由 2221i ie ry=-∑∑ 可得222(1)i i e R y =-∑∑222(1)(10.999778)262855.2558.3539ii eR y =-=-⨯=∑∑回归估计的标准误差: ˆ 2.4157σ===(3) 对2β进行显著水平为5%的显著性检验*222^^22ˆˆ~(2)ˆˆ()()t t n SE SE βββββ-==-^22.4157ˆ()0.0037651.9614SE β====*2^2ˆ0.7863212.51350.0037ˆ()t SE ββ===查表得 0.05α=时,0.025(122) 2.228t -=<*212.5135t = 表明2β显著不为0,销售收入对销售成本有显著影响.(4) 假定下年1月销售收入为800万元,利用拟合的回归方程预测其销售成本,并给出置信度为95%的预测区间。
计量经济学(庞浩)第二版课后习题答案

计量经济学(庞浩)第二版课后习题答案表明2β显著不为0,销售收入对销售成本有显著影响.(4) 假定下年1月销售收入为800万元,利用拟合的回归方程预测其销售成本,并给出置信度为95%的预测区间。
ˆ66.28720.786366.28720.7863800695.3272i iY X =+=+⨯=万元预测区间为: 21ˆˆF FYY t n ασ=695.3272 2.228 2.4157695.3272 1.9978F Y =⨯=。
第三章练习题参考解答练习题3.1为研究中国各地区入境旅游状况,建立了各省市旅游外汇收入(Y ,百万美元)、旅行社职工人数(X1,人)、国际旅游人数(X2,万人次)的模型,用某年31个省市的截面数据估计结果如下:ii i X X Y 215452.11179.00263.151ˆ++-= t=(-3.066806) (6.652983) (3.378064)R 2=0.934331 92964.02=R F=191.1894 n=31(1) 从经济意义上考察估计模型的合理性。
(2) 在5%显著性水平上,分别检验参数21,ββ的显著性。
(3) 在5%显著性水平上,检验模型的整体显著性。
3.2根据下列数据试估计偏回归系数、标准误差,以及可决系数与修正的可决系数:367.693Y =, 1402.760X =, 28.0X =,15n =, 2()66042.269i Y Y -=∑,211()84855.096i X X -=∑, 222()280.000i X X -=∑,11()()74778.346i i Y Y X X --=∑,22()()4250.900i i Y Y XX --=∑, 1122()()4796.000i i X X X X --=∑练习题参考解答练习题3.1参考解答有模型估计结果可看出:旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。
平均说来,旅行社职工人数增加1人,旅游外汇收入将增加0.1179百万美元;国际旅游人数增加1万人次,旅游外汇收入增加1.5452百万美元。
计量经济学(庞浩)第二版第十一章练习题及参考解答

计量经济学(庞浩)第二版第十一章练习题及参考解答10201222202111121112111211121221220112121102021222111121112111212112221112111211()1111(1)()111()11t t t t t t tt t t t t u u I Y G Y u Y G u u Y βββββββββββββββββββββββββββββββββββ----++=++++--------++--++=+++------++++----2202011202110212021222111121112111212112112221112111213031132311111t t t t t t t t t tu Y G u u u Y Y G v ββββββββββββββββββββββββπππ-----++=+++------+-++----=+++101111212021122230311323t t t t t t t t tt t tY Y G v C Y G v I Y G v πππππππππ---=+++=+++=+++由模型的结构型,M=3,K=2。
下面只对结构型模型中的第一个方程和第二个方程判断其识别性。
首先,用阶条件判断。
第一个方程,已知112,0m k==,因为112021211K k m -=-=>-=-=所以该方程有可能为过度识别。
第二个方程,已知222,1mk ==,因为222111211K k m -=-==-=-=所以该方程有可能恰好识别。
第三个方程为定义式,故可不判断其识别性。
其次,用秩条件判断。
写出结构型方程组的参数矩阵10112011221000010011101βββββ--⎛⎫ ⎪--- ⎪ ⎪--⎝⎭对于第一个方程,划去该方程所在的行和该方程中非零系数所在的列,得()22010101B β-⎛⎫Γ=⎪-⎝⎭由上述矩阵可得到三个非零行列式,根据阶条件,该方程为过度识别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学(庞浩)第二版第十一章练习题及参考解答11.1 考虑以下凯恩斯收入决定模型:βββββ-=++=+++=++1011120212212t t tt t t t t t t tC Y u I Y Y u Y C I G其中,C =消费支出,I =投资指出,Y =收入,G =政府支出;t G 和1t Y -是前定变量。
(1)导出模型的简化型方程并判定上述方程中哪些是可识别的(恰好或过度)。
(2)你将用什么方法估计过度可识别方程和恰好可识别方程中的参数。
练习题11.1参考解答:1011120212212112122112102012221112111211121112110111121(1)11111t t t t t t t t t tt t t t tt t t t t t t tY C I G Y u Y Y u G Y Y Y G u u u u Y Y G Y G v βββββββββββββββββββπππ----=++=+++++++=++++++++=+++--------=+++ 1020122210111111211121112111211011211110201122111211121111211111211121101021112011()1111(1)()11()111t t t t t tt t t t tu u C Y G u Y u u G u βββββββββββββββββββββββββββββββββββββ--++=+++++----------++=++----++++-----+=-1121211112211112111211121112120211222111t tt t t t t tu u u Y G Y G v ββββββββββββπππ--+-+++-------=+++ 1020122220211112111211121112122122011212110202122211112111211121211222*********1()1111(1)()111()11t t t t t t tt t t t t u u I Y G Y u Y G u u Y βββββββββββββββββββββββββββββββββββ----++=++++--------++--++=+++------++++----2202011202110212021222111121112111212112112221112111213031132311111t t t t t t t t t tu Y G u u u Y Y G v ββββββββββββββββββββββββπππ-----++=+++------+-++----=+++101111212021122230311323t t t t t t t t tt t tY Y G v C Y G v I Y G v πππππππππ---=+++=+++=+++ 由模型的结构型,M=3,K=2。
下面只对结构型模型中的第一个方程和第二个方程判断其识别性。
首先,用阶条件判断。
第一个方程,已知112,0m k ==,因为112021211K k m -=-=>-=-=所以该方程有可能为过度识别。
第二个方程,已知222,1m k ==,因为222111211K k m -=-==-=-=所以该方程有可能恰好识别。
第三个方程为定义式,故可不判断其识别性。
其次,用秩条件判断。
写出结构型方程组的参数矩阵10112011221000010011101βββββ--⎛⎫ ⎪--- ⎪ ⎪--⎝⎭ 对于第一个方程,划去该方程所在的行和该方程中非零系数所在的列,得()22010101B β-⎛⎫Γ=⎪-⎝⎭由上述矩阵可得到三个非零行列式,根据阶条件,该方程为过度识别。
事实上,所得到的矩阵的秩为2,则表明该方程是可识别,再结合阶条件,所以该方程为过度识别。
同理,可判断第二个方程为恰好识别。
(2)根据上述判断的结果,第一个方程可用两段最小二乘法估计参数;第二个方程可用间接最小二乘法估计参数。
11.2 考虑如下结果:OLS: -=+++10.2760.2580.046 4.959ˆt t t tP W P V 2R =0.924 OLS: -=+-++12.6930.2320.5440.2470.064ˆt t t tt W X M M P 2R =0.982 TSLS: -=+++10.2720.2570.046 4.966ˆt t tt P W P V 2R =0.920TSLS: -=+-++12.6860.2330.5440.2460.064ˆt t t t t W X M M P 2R =0.981 其中t W 、t P 、t M 和t X 分别是收益,价格,进口价格以及劳动生产力的百分率变化(所有百分率变化,均相对于上一年而言),而t V 代表未填补的职位空缺率(相对于职工总人数的百分率)。
试根据上述资料对“由于OLS 和TSLS 结果基本相同,故TSLS 是无意义的。
”这一说法加以评论。
练习题11.2参考解答:从两种方法估计的结果看,尽管系数的估计值非常接近,但不能说用TSLS 方法估计得到的估计值无意义。
原因是用TSLS 方法能保证参数的估计是一致的,而用OLS 方法估计得到的参数估计值在统计上是有偏且非一致。
因此,从这个意义上说,运用TSLS 方法得到的参数估计值可靠、可信。
11.3 考虑如下的货币供求模型:货币需求: t t t t dt u P R Y M 13210++++=ββββ 货币供给: t t st u Y M 210++=αα其中,M=货币,Y =收入,R =利率,P =价格,t t u u 21,为误差项;Y 、R 和P 是前定变量。
(1) 需求函数可识别吗? (2) 供给函数可识别吗?(3) 你会用什么方法去估计可识别的方程中的参数?为什么?(4) 假设我们把供给函数加以修改,多加进两个解释变量1t Y - 和1t M -,会出现什么识别问题?你还会用你在(3)中用的方法吗?为什么?练习题11.3参考解答:(1)首先,用阶条件判断如下:根据模型可知2,3M K ==,对于需求函数,有11331110K k m -=-=-=-=所以,该方程有可能是恰好识别。
其次,用秩条件判断。
将结构型模型转化为简化型模型后,写出其系数的矩阵为012301100100ββββαα----⎛⎫ ⎪--⎝⎭对于需求函数,划掉第一行和第一行里零所对应的非零元素以外的元素,得到一个非零元素,即1,按照秩条件原理,说明该方程为恰好识别。
(2)根据识别的原理,对于供给函数,运用阶条件有223121110K k m -=-=>-=-=所以,该方程有可能是过度识别。
对于供给函数,按秩条件原理,可得三个非零元素,按照秩条件的原理,说明该方程为过度识别。
(3)对于货币需求函数在过度识别的情况下,可考虑用间接最小二乘法估计参数;对于货币供给函数为恰好识别的情况下,可考虑用两段最小二乘法估计参数。
(4)在货币供给函数里再引进变量1t Y - 和1t M -,使得函数变为过度识别的情况,这时对参数的估计就只能用两段最小二乘法。
11.4 考虑以下模型:βββαα=+++=++0121012t t t t t t tR M Y u Y R u其中t M (货币供给)是外生变量;t R 为利率,t Y 为GDP ,它们为内生变量。
(1)请说出此模型的合理性。
(2)这些方程可识别吗? 假使把上述模型改变如下:ββββαα-=++++=++012311012t t t t t t t tR M Y Y u Y R u判断此方程组是否可识别,其中1-t Y 为滞后内生变量。
练习题11.4参考解答:(1)在上述第二个函数显然不正确,因为,按照经济学原理,GDP 应该受到投入要素的影响,而不是货币的价值利率的影响。
(2)根据识别的意义,可知上述模型中第一个方程,包含了模型中的全体变量,所以为不可识别;根据识别的阶条件,已知2,1M K ==,对于第一个方程,有111101211K k m -=-=<-=-=则表明该方程为不可识别。
第二个方程除了t R 和t Y 外,还有第一个方程没有包含的变量t M ,所以该方程为可识别。
从而整个方程组为不可识别。
(3)将模型变为上述第二种形式,从结构的形式看与第一种情况一致,所以方程组的识别情况没有变化,仍然为不可识别。
11.5 设我国的关于价格、消费、工资模型设定为tt t t t tt t t tt t u C W I P u W I C u I W 343212321121++++=+++=++=γγγγβββαα其中,I 为固定资产投资,W 为国有企业职工年平均工资,C 为居民消费水平指数,P 为价格指数,C 、P 均以上一年为100%,样本数据见下表11.6。
表11.6 样本数据(1)该方程组是否可识别?(2)选用适当的方法估计模型的未知参数?。
练习题11.5参考解答:(1)由于该方程组为递归模型,而递归模型并非真正意义下的联立方程组模型。
因而淡化它的识别性判断。
事实上,该方程组模型中除第一个方程为恰好识别外,其余两个方程均是不可识别。
(2)直接利用OLS进行估计,结果如下ˆ2498.5620.183545t tW I =+ ˆ109.52450.000180.000918t t tC I W =+- ˆ224.12550.0009310.0053760.95397t t t tP I W C =+--11.6 表中给出了四川省宏观经济统计资料,试判断模型的识别性,再用TSLS 法估计如下宏观经济模型tt t t t t t t t tt t X G I C Y u Y Y I u Y C +++=+++=++=-21210110βββαα其中,t t t Y I C ,,分别表示消费,投资和收入;t t t X G Y ,,1-分别表示收入的滞后一期,政府支出和净出口。
表11.7 四川省宏观经济统计资料 (单位:亿元)练习题11.6参考解答:(1)依题意,方程组中的内生变量个数M=3,外生变量的个数为K=3。
根据阶条件,对于第一个方程,有K-k 1=3-0>m 1-1=2-1所以,该方程可能为过度识别。
对于第二个方程,有K-k 2=3-1> m 2-1=2-1所以,该方程仍可能为过度识别。
第三个方程是定义方程,所以不需对其识别性进行判别。
将结构型模型转化为标准型,并写出其系数的矩阵形式010121000001000111011ααβββ--⎛⎫ ⎪--- ⎪ ⎪----⎝⎭按照秩条件,对于第二个方程,可的如下矩阵21001011β-⎛⎫⎪---⎝⎭由此可得到三个非零二阶行列式,即表明该方程是过度识别。
