二进制十进制算法
信息技术二进制十进制十六进制算法

信息技术二进制十进制十六进制算法信息技术中,二进制、十进制和十六进制是最常用的数制。
在计算机科学和计算机编程中,对于数据的存储、处理和表示而言,这三种数制起着重要的作用。
首先,二进制是一种由0和1组成的数制。
这是因为计算机中的信息通过电压的高低来表示,高电压为1,低电压为0。
二进制的每一位被称为一个比特(bit),8个比特组成一个字节(byte)。
二进制中的数字转换为十进制可以通过不断将二进制的每一位乘以相应的权值并求和得到。
例如,二进制数1101可以转换为十进制数的计算过程如下:1×2³+1×2²+0×2¹+1×2⁰=8+4+0+1=13其次,十进制是我们最为熟悉的数制,由0到9这10个数字组成。
十进制中的每一位权值为10的幂。
例如,十进制数253可以转换为二进制数的计算过程如下:2³×2+5×10²+3×10¹=8×2+5×100+3×10=16+500+30=546最后,十六进制是一种由0到9和字母A到F(代表10到15)这16个字符组成的数制。
十六进制中的每一位权值为16的幂。
它在计算机科学中被广泛应用,因为它可以简洁地表示二进制数。
十六进制中的A对应的十进制数为10,B对应的是11,C对应的是12,以此类推。
例如,十六进制数3A对应的十进制数的计算过程如下:3×16¹+10×16⁰=48+10=581.将二进制数按照4位分组:110110112.将每一组转换为十六进制数:DB3.得到十六进制数DB反过来,十六进制转换为二进制可以通过将每一位十六进制数转换为4位的二进制数。
例如,十六进制数7F可以通过如下的算法转换为二进制数的过程:1.将每一位十六进制数转换为4位的二进制数:01111111在信息技术中,二进制、十进制和十六进制算法是非常重要的基础知识。
十进制数字与二进制数字的转换方法

十进制数字与二进制数字的转换方法
十进制和二进制是两种不同的进制系统。
十进制以10为基数,每个数位可以取0到9的10个数字;二进制以2为基数,每个数位只能取0或1两个数字。
一、十进制转二进制
方法一:除2取余法
1.将十进制数不断除以2,取余数。
2.将余数从下往上逆序排列,即得到二进制数。
方法二:快速转换法
1.找到最大的2的幂,使其小于或等于十进制数。
2.将该2的幂的系数记为1,其余2的幂的系数记为0。
3.将十进制数减去最大的2的幂,得到余数。
4.继续步骤1-3,直到余数为0。
5.将各2的幂的系数按位排列,即得到二进制数。
二、二进制转十进制
方法一:按权展开法
1.将二进制数的每一位乘以2的相应次幂。
2.将各乘积相加,得到十进制数。
方法二:快速转换法
1.将二进制数从左往右逐位读取。
2.若当前位为1,则将该位的权值累加到十进制数中。
3.继续步骤1-2,直到读取完所有位。
总结:十进制和二进制的转换方法有多种,可以根据实际情况选择合适的方法进行转换。
二进制八进制十进制十六进制之间的转换算法

二进制八进制十进制十六进制之间的转换算法二进制、八进制、十进制和十六进制是计算机中常用的数字表示方法。
它们之间的转换可以通过一些算法来实现。
下面将介绍这些算法,并给出详细的解释。
1.二进制转八进制:将二进制数从右往左每3位一组进行分组,不足3位的可以在左侧补0。
然后将每组的二进制数转换为对应的八进制数。
如:分组:11010110转换为八进制数:3262.二进制转十进制:二进制数转换为十进制数可以使用加权的方式计算。
从最右边的位开始,每一位的值乘以2的对应次幂(从0开始),然后将所有结果相加。
如:二进制数:1101转换为十进制数:(1*2^3)+(1*2^2)+(0*2^1)+(1*2^0)=133.二进制转十六进制:将二进制数从右往左每4位一组进行分组,不足4位的可以在左侧补0。
然后将每组的二进制数转换为对应的十六进制数。
如:分组:110110101转换为十六进制数:DA14.八进制转二进制:将八进制数的每一位转换为对应的3位二进制数。
如:八进制数:326转换为二进制数:0110101105.八进制转十进制:八进制数转换为十进制数可以使用加权的方式计算。
从最右边的位开始,每一位的值乘以8的对应次幂(从0开始),然后将所有结果相加。
如:八进制数:326转换为十进制数:(3*8^2)+(2*8^1)+(6*8^0)=2146.八进制转十六进制:先将八进制数转换为二进制数,然后将二进制数转换为十六进制数。
如:八进制数:326转换为二进制数:011010110转换为十六进制数:DA67.十进制转二进制:十进制数转换为二进制数可以使用除2取模的方式计算。
将十进制数一直除以2,直到商为0为止,然后将每一步的余数倒序排列即可。
如:十进制数:13转换为二进制数:11018.十进制转八进制:十进制数转换为八进制数可以使用除8取模的方式计算。
将十进制数一直除以8,直到商为0为止,然后将每一步的余数倒序排列即可。
如:十进制数:214转换为八进制数:3269.十进制转十六进制:十进制数转换为十六进制数也可以使用除法和取模的方式计算。
信息技术二进制十进制十六进制算法

信息技术二进制十进制十六进制算法随着信息技术的快速发展,计算机已经成为人们日常生活中不可或缺的一部分。
而计算机中最基本的运算方式就是二进制、十进制和十六进制。
这三种进制方式在计算机中广泛应用,因此了解它们的运算方法对于学习计算机编程和理解计算机原理非常重要。
一、二进制二进制是基于二个数字0和1的一种进制方式。
在计算机中,所有数据都以二进制形式存储和处理。
例如,一个字节(Byte)由8个二进制位组成,每个二进制位的值为0或1,它们依次表示2的0次方、2的1次方、2的2次方……2的7次方,即从右到左的位数分别为1、2、4、8、16、32、64、128。
因此,一个字节的取值范围为0~255。
二进制的运算方法与十进制基本相同,只是数字只有0和1两种情况。
例如,二进制数1101表示十进制数13,它的运算方法如下: 1. 二进制加法二进制加法的规则与十进制加法相同,只是进位的条件是1+1=10。
例如,将二进制数1101和1011相加,得到的结果为:1101+ 1011------110002. 二进制减法二进制减法的规则与十进制减法相同,只是借位的条件是0-1=1,而不是10-1=9。
例如,将二进制数1101减去1011,得到的结果为: 1101- 1011------103. 二进制乘法二进制乘法的规则也与十进制乘法相同,只是乘数和被乘数都是0或1。
例如,将二进制数1101乘以1011,得到的结果为:1101x 1011------1000011101------1110114. 二进制除法二进制除法的规则与十进制除法相同,只是被除数和除数都是0或1。
例如,将二进制数1101除以101,得到的结果为:1--------101|1101101----11101----10因此,二进制数1101除以101的商为1,余数为10。
二、十进制十进制是基于十个数字0~9的一种进制方式。
在人类社会中,十进制是最常见的进制方式。
二进制和十进制转换

二进制和十进制转换?十进制与二进制转换之相互算法十进制转二进制:用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如302302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110二进制转十进制从最后一位开始算,依次列为第0、1、2...位第n位的数(0或1)乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.-----------------------二进制中最后一个数字是一,转换成十进制则是基数。
一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
2.十进制小数转换为二进制小数十进制小数转换成二进制小数采用"乘2取整,顺序排列"法。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
信息技术二进制十进制十六进制算法

信息技术二进制十进制十六进制算法在计算机科学中,二进制、十进制和十六进制是三种最重要的数字系统。
它们在信息技术中的应用非常广泛,特别是在编程和数据处理领域。
本文将介绍二进制、十进制和十六进制的原理和相互转换的算法。
一、二进制二进制是一种基于2的计数系统,也就是说,所有数字都只有两个可能的值:0和1。
因为计算机中的所有数据都是二进制形式的,因此二进制对于计算机而言非常重要。
例如,计算器、手机、电脑中的所有数据都是以二进制形式存储的。
1.1二进制的原理二进制的原理很简单,它的计数方法只有两个数字(0和1),当它们用完后,数字将从0重新开始,并把前一个数字的位置加1。
如果我们将二进制转换为十进制,每个数字的值将乘以2的幂。
第一个位置的权值为1,第二个为2,第三个为4,第四个为8,以此类推。
例如,二进制数1101的十进制值是1x2的3次方+1x2的2次方+0x2的1次方+1x2的0次方=8+4+0+1=13。
1.2二进制的应用二进制在计算机科学等领域有着广泛的应用。
计算机中的所有数据(指数据类型)都以二进制形式存储。
位(bit)是计算机中最小的数据单位,它只有两种状态:0或1。
一个字节(byte)由8个位(bit)组成,可以存储256个不同的整数值(0-255)。
计算机中的所有指令都是由一组数字串组成的,这些数字串代表各种二进制操作码。
1.3二进制转换二进制转换指的是将二进制数转换为十进制或十六进制。
在计算机科学中,常常需要将二进制转换为其他数字系统,因为比如网络协议、CPU指令、内存地址等都以不同的数字格式表示。
二进制转十进制的方法很简单,只要将二进制数的每一位按照权值系数加权求和即可。
例如,二进制数1101的十进制值是1x2的3次方+1x2的2次方+0x2的1次方+1x2的0次方=8+4+0+1=13。
二进制转换为十六进制需要先将二进制数划分成4位一组,然后将每一组转换为相应的十六进制数即可。
例如,二进制数10101010可以分成两组:1010和1010。
二进制转十进制,十进制转二进制的算法
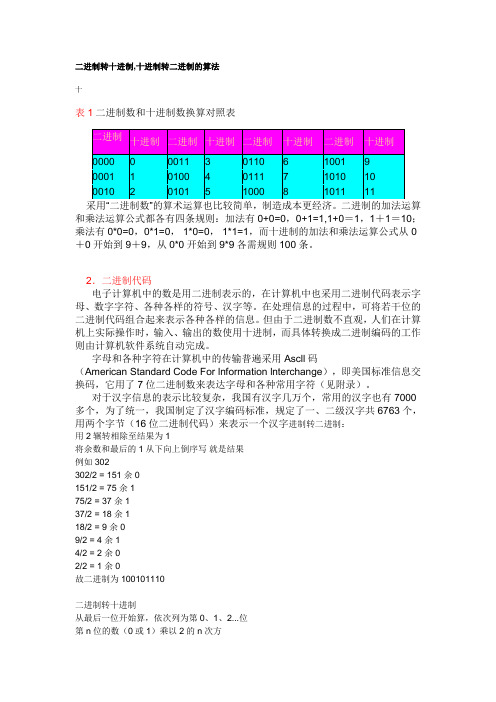
二进制转十进制,十进制转二进制的算法十表1二进制数和十进制数换算对照表得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方=01乘2的3次方=80乘2的4次方=01乘2的5次方=321乘2的6次方=640乘2的7次方=0然后:1+2+0+8+0+32+64+0=107.二进制01101011=十进制107.一、二进制数转换成十进制数由二进制数转换成十进制数的基本做法是,把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。
这种做法称为"按权相加"法。
二、十进制数转换为二进制数十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
2.十进制小数转换为二进制小数十进制小数转换成二进制小数采用"乘2取整,顺序排列"法。
具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
回答者:HackerKinsn - 试用期一级 2-24 13:311.二进制与十进制的转换(1)二进制转十进制<BR>方法:"按权展开求和"例:(1011.01)2 =(1×23+0×22+1×21+1×20+0×2-1+1×2-2)10=(8+0+2+1+0+0.25)10=(11.25)10(2)十进制转二进制·十进制整数转二进制数:"除以2取余,逆序输出"例:(89)10=(1011001)22 892 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)·十进制小数转二进制数:"乘以2取整,顺序输出"例:(0.625)10= (0.101)20.625X 21.25X 20.5X 21.02.八进制与二进制的转换例:将八进制的37.416转换成二进制数:37 . 4 1 6011 111 .100 001 110即:(37.416)8 =(11111.10000111)2例:将二进制的10110.0011 转换成八进制:0 1 0 1 1 0 . 0 0 1 1 0 02 6 . 1 4即:(10110.011)2 =(26.14)83.十六进制与二进制的转换<BR>例:将十六进制数5DF.9 转换成二进制:5 D F . 90101 1101 1111.1001即:(5DF.9)16 =(10111011111.1001)2例:将二进制数1100001.111 转换成十六进制:0110 0001 . 11106 1 . E即:(1100001.111)2 =(61.E)16。
二进制转十进制,十进制转二进制的算法

12M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
十进制整数转换为二进制整数采用"除2取余,逆序排列"法。具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
2.十进制小数转换为二进制小数
字母和各种字符在计算机中的传输普遍采用Ascll码(American Standard Code For lnformation lnterchange),即美国标准信息交换码,它用了7位二进制数来表达字母和各种常用字符(见附录)。
对于汉字信息的表示比较复杂,我国有汉字几万个,常用的汉字也有7000多个,为了统一,我国制定了汉字编码标准,规定了一、二级汉字共6763个,用两个字节(16位二进制代码)来表示一个汉字进制转二进制:
2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
2 1 …… 0
0 …… 1
·十进制小数转二进制数:"乘以2取整,顺序输出"
例:
(0.625)10= (0.101)2
0.625
2进制8进制10进制及16进制算法分析详解

十进制整数转换为二进制整数采用"除2取余,逆序排列"法。具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
9/2 = 4 余1
4/2 = 2 余0
2/2 = 1 余0
故二进制为100101110
二进制转十进制
从最后一位开始算,依次列为第0、1、2...位
第n位的数(0或1)乘以2的n次方
得到的结果相加就是答案
例如:01101011.转十进制:
6 1 . E
即:(1100001.111)2 =(61.E)16
=(11.25)10
(2)十进制转二进制
· 十进制整数转二进制数:"除以2取余,逆序输出"
例: (89)10=(1011001)2
2 89
2 44 …… 1
2 22 …… 0
2 11 …… 0
2 5 …… 1
2 2 …… 1
回答者:HackerKinsn - 试用期 一级 2-24 13:31
1.二进制与十进制的转换
(1)二进制转十进制
办法:"按权展开求和"
例:
(1011.01)2 =(1×23+0×22+1×21+1×20+0×2-1+1×2-2)10
=(8+0+2+1+0+0.25)10
二进制转十进制,十进制转二进制的算法
十进制转二进制:
用2辗转相除至结果为1
将余数和最后的1从下向上倒序写 就是结果
二进制八进制十进制十六进制之间的转换算法

二进制,八进制,十进制,十六进制之间的转换算法一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,()2分析:第一步,将168除以2,商84,余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即(2)小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。
例2,将0.45转换为二进制(保留到小数点第四位)大家从上面步骤可以看出,当第五次做乘法时候,得到的结果是0.4,那么小数部分继续乘以2,得0.8,0.8又乘以2的,到1.6这样一直乘下去,最后不可能得到小数部分为零,因此,这个时候只好学习十进制的方法进行四舍五入了,但是二进制只有0和1两个,于是就出现0舍1入。
二进制转化为十进制最容易懂的方法

二进制转化为十进制最容易懂的方法1、二进制转换为十进制:如果按照传统的方法,算2的乘方与二进制每一位的积,这样容易理解,但是在编程过程中,求2的乘法用到的pow函数是一个double类型的函数,而我们经常用到的是int类型的数,在处理数据类型的时候会很麻烦,更甚者会出错。
所以我们换另一种方法,即不用pow函数,用一个初值为1的变量,将这个变量与每一位二进制从后往前相乘,相乘一次后这个变量就乘2。
即我们换了一种方法来求2的乘方。
代码如下://res为最终的结果,A数组储存二进制的每一位int res=0,temp=1;for(int i=A.length-1;i>=0;i--){res+=A[i]*temp;temp*=2;}2、十进制转换为二进制:传统的方法,将这个数不断地取余2,再除以2,直到这个数变成0。
这种方法会改变这个数的值,而且效率比较低。
我们可以用位运算,首先了解两个位运算符:&和<<其中&运算符表示将两个数的二进制按位做与运算,例如5&7,其中5的二进制是101,7的二进制是111,&运算符将他们的二进制按位与,得到的结果即101,即5&7=5。
<<运算符是移位运算符,即将一个数的二进制向左移位,右边补0,例如5<<3,5的二进制是101,将101向左移3位,末尾补0,结果为101000。
即5<<3=40。
也可以理解为5<<3=5×(2^3)。
而将一个十进制数转换为二进制,假设这个数的二进制有5位,那么我们可以用这个数与10000,1000,100,10,1这5个二进制数分别做&运算,求出这个数的二进制的每一位是1还是0。
例如求40的二进制。
假设我们知道40的二进制有6位,那就让他与100000,10000,1000,100,10,1这6个数分别作&运算: 101000&100000=1,即40的二进制的第一位是1101000&010000=0,即40的二进制的第二位是0101000&001000=1,即40的二进制的第三位是1101000&000100=0,即40的二进制的第四位是0101000&000010=0,即40的二进制的第五位是0101000&000001=0,即40的二进制的第六位是0这样就把40的二进制的每一位取出来了,那么我们接下来就是要生成100000,10000,1000,100,10,1这几个数,这里就可以用到<<运算符了,100000=1<<5,10000=1<<4,1000=1<<3,100=1<<2,10=1<<1,1=1<<0。
二进制八进制十进制十六进制之间的转换算法

二进制八进制十进制十六进制之间的转换算法二进制、八进制、十进制和十六进制都是常见的数字系统。
在计算机科学和电子工程中,经常需要进行不同进制之间的转换。
以下是二进制、八进制、十进制和十六进制之间的转换算法。
1.二进制转换为八进制、十进制和十六进制:-二进制转十进制:将二进制数从右往左,每一位乘以2的幂次方,幂次方从0开始递增。
将各位的乘积相加得到十进制数。
例如,将二进制数1101转换为十进制数:(1x2^3)+(1x2^2)+(0x2^1)+(1x2^0)=132.八进制转换为二进制、十进制和十六进制:-八进制转十进制:将八进制数从右往左,每一位乘以8的幂次方,幂次方从0开始递增。
将各位的乘积相加得到十进制数。
例如,将八进制数137转换为十进制数:(1x8^2)+(3x8^1)+(7x8^0)=95-八进制转十六进制:先将八进制数转换为二进制数,然后将二进制数按照从右往左的顺序每四位一组,转换成对应的十六进制数。
如果二进制数位数不是四的倍数,则在左边补0。
然后将十六进制数按照从左到右的顺序排列。
例如,将八进制数362转换为十六进制数:(011)(110)(010),即1D23.十进制转换为二进制、八进制和十六进制:-十进制转八进制:将十进制数除以8,将余数从右往左排列,直到商为0。
例如,将十进制数125转换为八进制数:175-十进制转十六进制:将十进制数除以16,将余数从右往左排列,直到商为0。
对于10以上的余数,分别用A、B、C、D、E、F表示,分别对应10、11、12、13、14、15、例如,将十进制数255转换为十六进制数:FF。
4.十六进制转换为二进制、八进制和十进制:-十六进制转二进制:将十六进制数中的每一位转换为对应的四位二进制数。
例如,将十六进制数3F转换为二进制数:(0011)(1111)。
-十六进制转八进制:先将十六进制数转换为二进制数,然后将二进制数按照从右往左的顺序每三位一组,转换成对应的八进制数。
二进制八进制十进制十六进制四种算法之间的互相转换

二进制八进制十进制十六进制四种算法之间的互相转换1.二进制转十进制:二进制数是基于2的数制系统,只包含0和1两个数字。
转换二进制数到十进制数非常简单,只需要将二进制数中的每个数字乘以2的幂次方,然后将结果相加即可。
例如,二进制数"1010"转换为十进制数的计算方法如下:1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=102.八进制转十进制:八进制数是基于8的数制系统,只包含0到7的数字。
转换八进制数到十进制数也非常简单,只需要将八进制数中的每个数字乘以8的幂次方,然后将结果相加即可。
例如,八进制数"753"转换为十进制数的计算方法如下:7*8^2+5*8^1+3*8^0=7*64+5*8+3=448+40+3=4913.十六进制转十进制:十六进制数是基于16的数制系统,包含0到9的数字和A到F的字母。
转换十六进制数到十进制数也非常简单,只需要将每个十六进制数字乘以16的幂次方,然后将结果相加即可。
其中字母A到F分别表示10到15、例如,十六进制数"3AF"转换为十进制数的计算方法如下:3*16^2+10*16^1+15*16^0=3*256+10*16+15=768+160+15=9434.十进制转二进制:十进制数是我们日常生活中最常用的数制系统,包含数字0到9、转换十进制数到二进制数可以使用除2取余法。
具体步骤是:将十进制数除以2,直到商为0,然后将每次的余数倒序排列起来作为二进制数的结果。
例如,将十进制数10转换为二进制数的步骤如下:10/2=5余05/2=2余12/2=1余01/2=0余1倒序排列余数得到二进制数"1010"。
5.十进制转八进制:将十进制数转换为八进制数也可以使用除8取余法。
具体步骤与转换为二进制数相似,只需要将除数改为8即可。
例如,将十进制数25转换为八进制数的步骤如下:25/8=3余13/8=0余3倒序排列余数得到八进制数"31"。
二进制转十进制快速计算

如:255=(11111111)B
255/2=127=====余1
127/2=63======余1
63/2=31=======余1
31/2=15=======余1
15/2=7========余1
7/2=3=========余1
3/2=1=========余1
1/2=0=========余1
789=1100010101
789/2=394.5 =1第10位
394/2=197 =0第9位
197/2=98.5 =1第8位
98/2=49 =0第7位
49/2=24.5 =1第6位
24/2=12 =0第5位
12/2=6 =0第4位
6/2=3 =0第3位
3/2=1.5 =1第2位
1/2=0.5 =1第1位
部分0
0.8*2=1.6========取出整数
部分1
0.6*2=1.2========取出整数
部分1
0.2*2=0.4========取出整数
部分0
原理:假设一个十进制数的小数
部分能写成二进制数小数0.ab的形
式,那么该二进制小数转化为十进制
数就是a/2&#化成十进制
1101(2)
=1*2^0+0*2^1+1*2^2+1*2^3=1+0+4+8=13
转化成十进制要从右到左用二进
制的每个数去乘以2的相应次方
不过次方要从0开始
相反用十进制的数除以2每除
一下将余数就记在旁边
最后按余数从下向上排列就可得
到1101或者用下面这种方法:
13=8+4+0+1=8+4+1(算出等
计算机基础二进制与十进制的转换

计算机基础二进制与十进制的转换计算机基础:二进制与十进制的转换在计算机科学与技术领域中,二进制(Binary)和十进制(Decimal)是最基本且广泛应用的数制系统。
二进制由0和1组成,而十进制由0到9的十个数字组成。
在计算机中,数据以二进制形式存储和运算。
因此,了解和掌握二进制与十进制之间的转换方法对于理解计算机工作原理以及进行编程和算法相关的工作至关重要。
一、二进制与十进制的基本概念1. 二进制(Binary)二进制是计算机中最基础的数制系统,使用0和1两个数码来表示数值。
它是一种离散的数制,其中每位数的权值均为2的幂次。
例如,二进制数1101表示的是:1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 13。
2. 十进制(Decimal)十进制是我们日常生活中最常用的数制系统,也被称为“人类数制”。
它由0到9这十个基数数字组成,每一位的权值均为10的幂次。
例如,十进制数482表示的是:4 × 10² + 8 × 10¹ + 2 × 10⁰ = 482。
二、二进制转十进制的方法在计算机编程中,我们常需要将二进制数转换为十进制数,以便更好地理解和处理数据。
下面介绍两种常用的转换方法:逐位相加法和权重法。
1. 逐位相加法逐位相加法是一种直观易懂的转换方法。
我们可以将二进制数的每一位对应到十进制数的每一位,然后按照权值加和的方式计算。
例如,将二进制数1101转换为十进制数,按照逐位相加法进行计算:1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 8 + 4 + 0 + 1 = 132. 权重法权重法是一种更为快速的转换方法。
每一位的权重可以通过计算2的幂次得到,然后与对应的二进制位相乘并求和即可得到十进制数。
二进制与十进制的转换

我们常用的数是十进位制的数,而计算机程序使用的是只有数码0和1的二进位制这两者可以互相转换:
如将1101换成十进位制数应为:1*2^0+0*2^1+1*2^2+1*2^3=1+0+4+8=13也就是十进制要从右到左用二进制的每个数去乘以2的相应次方不过次方要从0开始。
十进制转二进制采用“除2取余”,逆序排列"法。
具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为0时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
如:25/2=12 (1)
12/2=6 0
6/2=3 0
3/2=1 (1)
1/2=0 (1)
由此可见得出25转换成二进位制数位11001我们可以通过windows自带的计算器实验一下:
单击查看,科学型,输入选十进制输入25
在上图箭头处改为二进制,得出二进制结果11001
怎么样,学会了吗?。
各种进制的算法范文

各种进制的算法范文进制是一种计数系统,用于表示数字和数值。
在计算机科学中,常用的进制有二进制(基数为2)、八进制(基数为8)、十进制(基数为10)、十六进制(基数为16)等。
不同进制对应不同的符号集,以及不同的计数规则。
下面将介绍各种进制的算法。
1.二进制算法:二进制是最基本的进制,仅包含两个数字0和1、二进制的表达方式非常简洁,并且在计算机中被广泛应用。
二进制算法是计算机内部运算的基础,例如加法、减法、乘法、除法等。
-加法算法:对于两个二进制数的相加,从右至左逐位相加,若两个位数相加结果为2,则将其写成0并将进位标记为1;若两个位数相加结果为3,则将其写成1并将进位标记为1、然后继续向左进行相加直至最高位,最后若有进位则写成新的位数。
-减法算法:对于两个二进制数的相减,从右至左逐位相减,若两个位数相减结果为负数,则从较高位借位1,被减位加2、直到最高位。
-乘法算法:对于两个二进制数的相乘,采用类似于十进制乘法的竖式计算。
从被乘数的最低位开始,逐位与乘数进行乘法运算,并将结果相加。
2.八进制算法:八进制是一种基数为8的进制方式,使用8个数字(0-7)。
在计算机科学中,八进制主要用于表示字节和内存地址。
八进制的运算与二进制类似,但每个八进制位代表3个二进制位。
-加法算法:对于两个八进制数的相加,从右至左逐位相加,若两个位数相加结果为8,则将其写成0并将进位标记为1;若两个位数相加结果为9,则将其写成1并将进位标记为1、然后继续向左进行相加直至最高位,最后若有进位则写成新的位数。
-减法算法:对于两个八进制数的相减,从右至左逐位相减,若两个位数相减结果为负数,则从较高位借位1,被减位加8、直到最高位。
3.十进制算法:十进制是最常用的进制方式,基数为10,使用0-9这10个数字。
十进制运算是人类日常生活和大部分计算机系统中最常见的运算方式。
-加法算法:从右至左逐位相加,若两个位数相加结果大于10,则将结果写成个位数并将进位标记为1、然后继续向左进行相加直至最高位,最后若有进位则写成新的位数。
二进制转十进制十进制转二进制的算法

二进制转十进制十进制转二进制的算法1. 初始化结果变量result为0。
2. 从二进制数的最右边开始,将每一位上的数字依次与2的幂次方相乘,并将结果累加到result中。
3.将二进制数向左移动一位,即除以24.重复步骤2和步骤3,直到二进制数变为0时结束。
5. 返回结果变量result,即为转换后的十进制数。
例如,将二进制数1101转换为十进制数的步骤如下:初始result = 01. 取最右边一位1,1 * 2^0 = 1,result = 12. 将1101向左移动,变为110,result = 13. 取最右边一位0,0 * 2^1 = 0,result = 14. 将110向左移动,变为11,result = 15. 取最右边一位1,1 * 2^2 = 4,result = 56. 将11向左移动,变为1,result = 57. 取最右边一位1,1 * 2^3 = 8,result = 138. 将1向左移动,变为0,result = 13最终结果为十进制数13十进制转二进制算法介绍:十进制转二进制是将一个十进制数转换成对应的二进制数的过程。
转换的算法如下:1. 初始化结果变量result为一个空字符串。
2.将十进制数除以2,得到商和余数。
3.将余数加到结果变量的最左边。
4.当商为0时结束,返回结果变量。
例如,将十进制数13转换为二进制数的步骤如下:初始result = ""1.商为6,余数为12. 商为3,余数为0,result = "01"3. 商为1,余数为1,result = "101"4. 商为0,结束,返回result为"101"最终结果为二进制数101算法复杂度分析:二进制转十进制和十进制转二进制的算法都属于线性时间复杂度的算法,时间复杂度为O(n),其中n为二进制或十进制数的位数。
这是因为需要将每一位进行相应的计算和处理。
二进制转十进制算法步骤

二进制转十进制算法步骤一、引言二进制(Binary)和十进制(Decimal)是计算机领域中常用的数制系统。
二进制由0和1组成,而十进制由0至9这十个数字组成。
在计算机中,二进制常用于表示数据和进行计算,而在人类的日常生活中,十进制更为常见。
因此,当需要将二进制数转换为十进制数时,我们需要使用二进制转十进制算法。
本文将介绍二进制转十进制的算法步骤。
二、算法步骤1. 确定二进制数的位数首先,我们需要确定给定的二进制数的位数。
位数是指二进制数中的数字个数。
例如,二进制数1101有4位。
2. 确定权重在十进制数中,每个数字的权重与其位置相关。
同样地,在二进制数中,每个数字的权重也与其位置相关。
权重的计算方式是从右往左,每个数字的权重是2的n次方,其中n为该数字的位置(从0开始计数)。
例如,对于二进制数1101,从右往左的权重分别为2^0、2^1、2^2和2^3。
3. 计算十进制值接下来,我们需要根据二进制数的每一位和对应的权重,计算出十进制数的值。
具体步骤如下:- 从最右边的位开始,将每个位上的数字与对应的权重相乘。
- 将所有乘积相加,得到最终的十进制值。
4. 举例演示让我们通过一个示例来演示上述算法步骤。
假设我们要将二进制数1101转换为十进制数。
- 首先,确定二进制数的位数,即4位。
- 确定权重,从右往左依次为2^0、2^1、2^2和2^3,即1、2、4和8。
- 计算十进制值,将每个位上的数字与对应的权重相乘并相加:1 * 1 + 1 *2 + 0 * 4 + 1 * 8 = 1 + 2 + 0 + 8 = 11因此,二进制数1101转换为十进制数为11。
5. 算法复杂度分析二进制转十进制的算法复杂度较低。
由于我们只需对每个位上的数字进行乘法和加法运算,因此时间复杂度为O(n),其中n为二进制数的位数。
由于每个位上的数字和权重都是常数,空间复杂度为O(1)。
6. 结语二进制转十进制是计算机领域中常见的数值转换操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在一种数制中,只能使用一组固定的数字符号来表示数目的大小,具体使用多少个数字符号来表示数目的大小,就称为该数制的基数。
例如:1.十进制(Decimal)基数是10,它有10个数字符号,即0,l,2,3,4,5,6,7,8,9。
其中最大数码是基数减1,即9,最小数码是0。
2.二进制(Binary)基数是2,它只有两个数字符号,即0和1。
这就是说,如果在给定的数中,除0和1外还有其它数,例如 1012,它就决不会是一个二进制数。
3.八进制(Octal)基数是8,它有8个数字符号,即0,l,2,3,4,5,6,7。
最大的也是基数减1,即7,最小的是0。
4.十六进制(Hexadecilnal)基数是16,它有16个数字符号,除了十进制中的10个数可用外,还使用了6个英文字母。
它的16个数字依次是0,l,2,3,4,5,6,7,8,9,A,B,C,D,E,F。
其中A至F分别代表十进制数的10至15,最大的数字也是基数减1。
既然有不同的进制,那么在给出一个数时,需指明是什么数制里的数。
例如:(1010)2,(1010)8,(1010)10,(1010)16所代表的数值就不同。
除了用下标表示外,还可用后缀字母来表示数制。
例如 ZA4EH,FEEDH,BADH(最后的字母 H表示是十六进制数),与(ZA4E)16,(FEED)16,(BAD)16的意义相同。
进制和位权在数制中,还有一个规则,这就是,N进制必须是逢N进一。
对于多位数,处在某一位上的“l”所表示的数值的大小,称为该位的位权。
例如十进制第2位的位权为10,第3位的位权为100;而二进制第2位的位权为2,第3位的位权为4,对于 N进制数,整数部分第 i位的位权为Ni-1,而小数部分第j位的位权为N-j。
l.十进制数的特点是逢十进一。
例如:(1010)10 =1× 103+0× 102+1× 101+0× 1002.二进制数的特点是逢二进一。
例如:(1010)2 =l× 23+0 × 22+l× 21+0 × 20=(10)10 3.八进制数的特点是逢八进一。
例如:(1010)8 =l× 83+0 × 82+l× 81+0 × 80=(520)10 4.十六进制数的特点是逢十六进一。
例如:(BAD)16 =11× 162+10×l61+13×160=(2989)10一、二进制的算术运算1.运算法则(1)、加法法则0+0=00+1=11+0=11+1=10 进位为11+1+1=10+1=11 进位为1实例将两个二进制数1011和1010相加解:相加过程如下10 1 1被加数加数10 1 0进位 1 1─────1 0 1 0 1(2)、二进制减法法则0 - 0 = 0 1 - 0 = 1 1 - 1 = 00 - 1 = 1 有借位,借1当(10)2 0 - 1 - 1 = 0 有借位 1 - 1 - 1 = 1 有借位 注:(10)2表示为二进制中的2实例:从(110000)2中减去(10111)2解释分析:①我们用在某位上方有标记1表示该位被借位。
具体过程为从被减数的右边第一位开始减去减数,在本例中,由于0减1而向右数第二位借位,第二位为0不够借转而向右数第三位,以此类推,最后从右数第五位借得1相减过程如下:借 位 1 1 1 1 1 ②该1拿到右数第四位上做为(10)2(联想在十进制中从千位借位拿到百位上做10用),而右数第四位上借得的(10)2又须借给右数第三位一个1(记住,该位上还剩一个1),以此类推,最后右数第五位上值为0(由于被借位),右数第四位、第三位、第二位均借得1 被减数 1 1 0 0 0 0减 数 1 0 1 1 1 ───────────③右数第一位借得(10)2,用(10)减1得1,右数第二位上已借得1,用该1减去减数1则得数的右数第二位为0,同理可得其它各位的值分别为0,0,1(从右往左)。
结 果 1 1 0 0 1 ④最后还剩两位,由于右数第五位的数已被借去,则需从高位借1,(高位为1,借位后为0),借位后当(10)2用,(10)2减1为1。
因此得结果为(11001)2(2)、二进制乘法法则 实例:1110 X 01100 X 0 = 0 被乘数1 11 0乘 数 X 0 11 01 X 0 = 0 ─────────────0 0 01X 1 = 11 1 11 1 100 X 1 = 0 + 0 0 0 0─────────────积 1 0 1 0 1 0 0 (3)、二进制除法法则实例:(1001110)2÷(110)商 1 1 0 1被除数1 10 √1 0 0 1 1 1 0- 1 1 0--------0 1 1 1- 1 1 0--------1 1 0- 1 1 0--------结果为:1101二、数制转换1.十进制数到二进制数的转换(1)、整数部分除2取余法(余数为0为止),最后将所取余数按逆序排列。
实例:将十进制数23转换为二进制数2|232|11余数 12| 5余数 12| 2余数 12|1余数 0余数 1结果为 (23)10 = (10111)2(2)、小数部分乘2取整法(如果小数部分是5的倍数,则以最后小数部分为0为止,否则以约定的精确度为准,最后将所取整数按顺序排列。
实例1:将十进制数0.25转换为二进制数0.2 5X2──────0.5 0 ...取整数位0X2──────1.0 0 ...取整数位1结果为 (0.25)10 = (0.01)2实例2:将十进制数125.24转换为二进制数(取四位小数) 整数部分转换小数部分转换 2|1 2 50.2 42| 6 2...1 X2 2|3 1...0 ──────2|1 5...1 0.4 8 02| 7 ...1 X22| 3...1 ──────2|1...1 0.9 6 00 ...1 X2──────1.9 2 (1)X2──────1.8 4 (1)结果为 (125.24)10 = (1111101.0011)22.二进制数到十进制数的转换基本原理:将二进制数从小数点开始,往左从0开始对各位进行正序编号,往右序号则分别为-1,-2,-3,...直到最末位,然后分别将各位上的数乘以2的k次幂所得的值进行求和,其中k的值为各个位所对应的上述编号。
实例:将二进制数1101.101转换为十进制数编号: 3 2 1 0 -1 -2 -31 1 0 1 . 1 0 1 = 1×23 + 1×22 + 0×21 + 1×20 + 1×2-1 + 0×2-2 + 1×2-3 = 8 +4 + 1 + 0.5 + 0.125 = 13.625结果为 (1 1 0 1.1 0 1)2 = (13.625)103.二进制数到十六进制数的转换基本原理:由于十六进制数基数是2的四次幂,所以一个二进制转换为十六进制,如果是整数,只要从它的低位到高位每4位组成一组,然后将每组二进制数所对应的数用十六进制表示出来。
如果有小数部分,则从小数点开始,分别向左右两边按照述方法进行分组计算。
实例:将二进制数111010111100010111转换为十六进制数二进制数11 1010 1111 0001 0111十六进制数3 A F 1 7结果为 (111010111100010111)2 = (3AF17)163.十六进制转换为二进制基本原理:十六进制数转换为二进制,只要从它的低位开始将每位上的数用二进制表示出来。
如果有小数部分,则从小数点开始,分别向左右两边按照述方法进行转换。
实例:将二进制数6FBE4转换为十六进制数十六进制数 6 F B E 4二进制数110 1111 1011 1110 0100结果为 (6FBE4)16 = (1101111101111100100)24.十进制转换为十六进制仿照十进制转换为二进制,可采用“除16取余法,乘16取整法”。
5.十六进制转换为十进制仿照二进制转换为十进制将其按权展开求和即可,例如:(32CF.4B)16=3 ×163+2 ×162+12×161+15×160+4 × 16-1+11×16-2 = 12288+512+192+15+0.25+0.04296875=(13007.29296875)10三.基本逻辑运算1."与"运算(AND)"与"运算又称逻辑乘,用符号"."或"∧"来表示。
运算规则如下:0∧0 = 0 0∧1 = 0 1∧0 = 0 1∧1 = 1即当两个参与运算的数中有一个数为0,则运算结果为0,都为1结果为12."或"运算(OR)"或"运算又称逻辑加,用符号"+"或"∨"表示。
运算规则如下:0∨0 = 0 0∨1 = 1 1∨0 = 1 1∨1 = 1即当两个参与运算的数中有一个数为1,则运算结果为1,都为0结果为0 3."非"运算(NOT)如果变量为A,则它的非运算结果用 A 表示。
运算规则如下:0 = 1 1 = 04."异或"运算(XOR)"异或"运算用符号"-∨"来表示。
其运算规则如下:- 0∨0 = 0 - 0∨1 = 1 - 1∨0 = 1 - 1∨1 = 0 即当两个参与运算的数取值相异时,运算结果为1,否则为0.计算机的应用一、科学计算科学计算是计算机最早的应用领域,如航空航天、气象、军事等,都离不开准确的计算。
二、数据处理计算机可对大量的数据进行分类、综合、排序、分析、整理、统计等加工处理,并可要求输出结果。
如人事管理、卫星图片分析、金融管理、仓库管理、图书和资料检索等。
三、实时控制在工业、科学和军事方面,利用计算机能够按照预定的方案进行自动控制,完成一些人工无法亲自操作的工作,如汽车生产流水线等。
四、计算机辅助工程利用计算机辅助系统可以帮助我们快速的设计出各种模型,图案,例如飞机、船舶、建筑、集成电路等工程的设计和制造。
当前计算机在辅助教学领域也得到了广泛的发展。
五、人工智能利用计算机模拟人的智能去处理某些事情,完成某项工作。
例如,医疗诊断专家系统可以模拟医生看病;人机对弈。
二、计算机软件系统计算机软件系统包括系统软件和应用软件两大类。
