921399-数据统计分析-第11章聚类分析
聚类分析数据

聚类分析数据聚类分析是一种数据挖掘技术,用于将相似的数据对象归类到同一个簇中。
通过对数据进行聚类分析,可以发现数据中的隐藏模式、结构和关系,帮助我们更好地理解数据。
本文将介绍聚类分析的基本概念、常用方法和步骤,并通过一个示例来演示如何进行聚类分析。
1. 聚类分析的基本概念聚类分析是一种无监督学习方法,不需要事先标记好的训练数据。
它根据数据样本之间的相似性,将它们划分为不同的簇。
聚类分析的目标是使同一簇内的数据对象相似度较高,而不同簇之间的相似度较低。
2. 聚类分析的常用方法聚类分析有多种方法,常见的包括层次聚类和K均值聚类。
2.1 层次聚类层次聚类是一种自底向上的聚类方法,它从每个数据对象作为一个簇开始,逐步合并最相似的簇,直到所有数据对象都被合并为一个簇或达到预设的簇数目。
2.2 K均值聚类K均值聚类是一种迭代的聚类方法,它将数据对象划分为K个簇,每个簇由一个质心代表。
初始时,随机选择K个质心,然后迭代地将每个数据对象分配到最近的质心所在的簇,再更新质心的位置,直到质心的位置不再变化或达到预设的迭代次数。
3. 聚类分析的步骤聚类分析通常包括以下步骤:3.1 数据准备首先,需要收集和整理要进行聚类分析的数据。
数据可以是数值型、分类型或混合型的。
确保数据的质量和完整性,处理缺失值和异常值。
3.2 特征选择根据分析目标和数据特点,选择合适的特征作为聚类分析的输入。
特征应该具有代表性,能够区分不同的数据对象。
3.3 数据标准化对于具有不同量纲的特征,需要进行数据标准化,以消除量纲影响。
常用的标准化方法包括最小-最大标准化和Z-score标准化。
3.4 选择聚类方法和参数根据数据的特点和分析目标,选择合适的聚类方法和参数。
不同的聚类方法适用于不同类型的数据和分析需求。
3.5 执行聚类分析根据选择的聚类方法和参数,执行聚类分析。
对于层次聚类,可以使用聚类树或热图来可视化聚类结果。
对于K均值聚类,可以绘制簇内离散度图或簇间离散度图来评估聚类的质量。
聚类分析简介
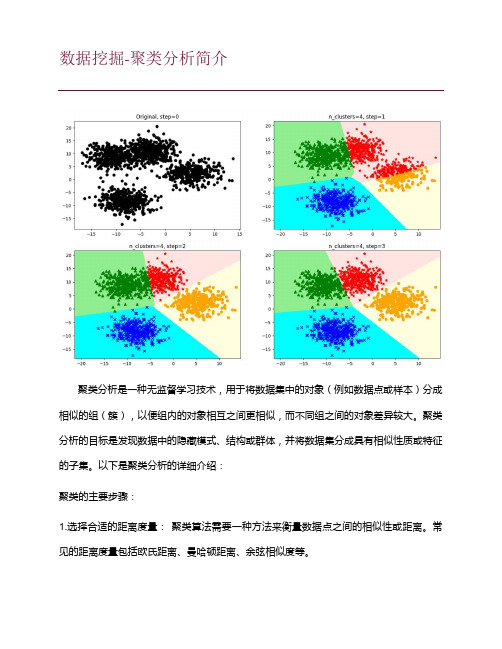
数据挖掘-聚类分析简介聚类分析是一种无监督学习技术,用于将数据集中的对象(例如数据点或样本)分成相似的组(簇),以便组内的对象相互之间更相似,而不同组之间的对象差异较大。
聚类分析的目标是发现数据中的隐藏模式、结构或群体,并将数据集分成具有相似性质或特征的子集。
以下是聚类分析的详细介绍:聚类的主要步骤:1.选择合适的距离度量:聚类算法需要一种方法来衡量数据点之间的相似性或距离。
常见的距离度量包括欧氏距离、曼哈顿距离、余弦相似度等。
2.选择聚类算法:选择适合数据和问题的聚类算法。
常见的聚类算法包括K均值聚类、层次聚类、DBSCAN(基于密度的聚类)、高斯混合模型等。
3.初始化:对于迭代型聚类算法(例如K均值),需要初始化聚类中心或其他参数。
初始值的选择可以影响聚类结果。
4.分配数据点到簇:根据数据点之间的相似性,将每个数据点分配到一个簇中。
不同的算法使用不同的分配策略。
5.更新簇的代表:对于迭代聚类算法,计算每个簇的新代表,通常是簇内所有数据点的平均值。
6.重复迭代:重复步骤4和步骤5,直到满足停止条件,例如簇中心不再改变或达到最大迭代次数。
7.评估聚类结果:使用合适的评估指标来评估聚类的质量。
常用的指标包括轮廓系数、Davies-Bouldin指数、互信息等。
常见的聚类算法:1.K均值聚类(K-Means Clustering):K均值是一种迭代型聚类算法,通过指定簇的数量K来将数据分成K个簇。
它以簇的中心点(均值)作为代表。
2.层次聚类(Hierarchical Clustering):层次聚类是一种层次化的聚类方法,可以创建层次化的聚类结构。
它可以是自底向上的凝聚聚类或自顶向下的分裂聚类。
3.DBSCAN(Density-Based Spatial Clustering of Applications with Noise): DBSCAN 是一种基于密度的聚类算法,能够识别不规则形状的簇,并能处理噪声数据。
聚类分析数据

聚类分析数据聚类分析是一种数据分析方法,它将相似的数据点分组为具有共同特征的簇。
通过聚类分析,我们可以发现数据中的潜在模式、结构和关联性,从而帮助我们理解数据集的特征和性质。
本文将详细介绍聚类分析的基本概念、常用方法和应用场景。
一、概念介绍聚类分析是一种无监督学习方法,它不需要事先标记好的训练样本。
聚类分析的目标是将数据点划分为不同的簇,使得同一簇内的数据点相似度较高,而不同簇之间的相似度较低。
聚类分析的结果通常以可视化的方式展示,例如散点图或热力图。
二、常用方法1. K-means聚类K-means聚类是最常用的聚类算法之一。
它将数据点分为K个簇,其中K是用户事先指定的。
算法的核心思想是通过迭代优化来找到使得簇内差异最小化的簇中心。
K-means聚类的步骤包括初始化簇中心、分配数据点到最近的簇、更新簇中心,重复执行这些步骤直到满足停止准则。
2. 层次聚类层次聚类是一种基于距离的聚类方法,它将数据点逐步合并成越来越大的簇。
层次聚类可以分为凝聚式和分裂式两种。
凝聚式层次聚类从每个数据点作为一个簇开始,然后逐渐合并最相似的簇,直到达到指定的簇数目。
分裂式层次聚类从所有数据点作为一个簇开始,然后逐渐分裂成更小的簇,直到达到指定的簇数目。
3. 密度聚类密度聚类是一种基于密度的聚类方法,它将数据点分为高密度区域和低密度区域。
密度聚类的核心思想是通过计算每个数据点的密度来确定簇的边界。
常用的密度聚类算法包括DBSCAN和OPTICS。
三、应用场景聚类分析在各个领域都有广泛的应用,下面介绍几个常见的应用场景。
1. 市场细分聚类分析可以帮助企业将市场细分为不同的消费者群体。
通过对消费者的购买行为、偏好和特征进行聚类分析,企业可以更好地了解不同群体的需求,从而制定个性化的营销策略。
2. 社交网络分析聚类分析可以帮助研究人员发现社交网络中的社区结构。
通过对社交网络中的节点(用户)进行聚类分析,可以揭示出节点之间的紧密关系和群体特征,从而更好地理解社交网络的组织结构和信息传播模式。
聚类分析方法

聚类分析方法聚类分析是一种常用的数据分析方法,它可以将数据集中的对象按照其相似性进行分组,形成若干个簇。
通过聚类分析,我们可以发现数据中的内在结构,帮助我们更好地理解数据集的特点和规律。
在实际应用中,聚类分析被广泛应用于市场分割、社交网络分析、图像处理等领域。
本文将介绍聚类分析的基本原理、常用方法和应用场景,希望能够帮助读者更好地理解和应用聚类分析。
聚类分析的基本原理是将数据集中的对象划分为若干个簇,使得同一簇内的对象相似度较高,不同簇之间的对象相似度较低。
在进行聚类分析时,我们需要选择合适的相似性度量方法和聚类算法。
常用的相似性度量方法包括欧氏距离、曼哈顿距离、余弦相似度等,而常用的聚类算法包括K均值聚类、层次聚类、DBSCAN等。
不同的相似性度量方法和聚类算法适用于不同的数据类型和应用场景,选择合适的方法对于聚类分析的效果至关重要。
K均值聚类是一种常用的聚类算法,它通过不断迭代更新簇中心的方式,将数据集中的对象划分为K个簇。
K均值聚类的优点是简单、易于理解和实现,但是它对初始簇中心的选择较为敏感,容易收敛到局部最优解。
层次聚类是另一种常用的聚类算法,它通过逐步合并或分裂簇的方式,构建一棵层次化的聚类树。
层次聚类的优点是不需要事先确定簇的个数,但是它对大数据集的处理效率较低。
DBSCAN是一种基于密度的聚类算法,它能够发现任意形状的簇,并且对噪声数据具有较强的鲁棒性。
不同的聚类算法适用于不同的数据特点和应用场景,我们需要根据具体情况选择合适的算法进行聚类分析。
聚类分析在实际应用中有着广泛的应用场景。
在市场分割中,我们可以利用聚类分析将顾客分为不同的群体,从而制定针对性的营销策略。
在社交网络分析中,我们可以利用聚类分析发现社交网络中的社区结构,从而发现潜在的影响力人物。
在图像处理中,我们可以利用聚类分析对图像进行分割和特征提取,从而实现图像内容的理解和识别。
聚类分析在各个领域都有着重要的应用,它为我们理解和利用数据提供了有力的工具。
聚类分析数据

聚类分析数据聚类分析是一种无监督学习方法,用于将相似的数据点分组成不同的类别或簇。
它是数据挖掘和统计分析中常用的技术,能够帮助我们发现数据中的隐藏模式和结构。
在进行聚类分析之前,首先需要明确的是要分析的数据集。
假设我们有一份销售数据集,其中包含了不同产品的销售额和销售量。
我们希望通过聚类分析来探索这些产品之间的关系和相似性。
首先,我们需要对数据进行预处理。
这包括数据清洗、缺失值处理和数据标准化等步骤。
例如,我们可以删除缺失值较多的样本,使用均值或中位数填充缺失值,并对数据进行标准化,以消除不同特征之间的尺度差异。
接下来,我们选择合适的聚类算法。
常见的聚类算法包括K均值聚类、层次聚类和DBSCAN等。
在本次分析中,我们选择使用K均值聚类算法进行分析。
K均值聚类算法是一种基于距离的聚类方法,通过将数据点分配到K个簇中,使得同一簇内的数据点之间的距离最小化,不同簇之间的距离最大化。
对于我们的销售数据集,我们可以选择将产品分为不同的簇,每个簇代表一类相似的产品。
在进行K均值聚类之前,我们需要确定簇的数量K。
一种常用的方法是通过绘制“肘部曲线”来选择最合适的K值。
肘部曲线显示了不同K值下聚类的误差平方和(SSE)的变化情况。
我们选择使得SSE开始显著下降的K值作为最终的簇数。
接下来,我们使用K均值聚类算法对数据进行聚类。
该算法的基本步骤如下:1. 随机选择K个初始聚类中心。
2. 将每个数据点分配到距离最近的聚类中心所在的簇。
3. 更新每个簇的聚类中心,即计算簇内所有数据点的均值。
4. 重复步骤2和3,直到聚类中心不再变化或达到最大迭代次数。
在完成聚类之后,我们可以对结果进行评估和解释。
常用的评估指标包括簇内平方和(WCSS)和轮廓系数等。
WCSS表示簇内数据点与其聚类中心的距离之和,越小表示聚类效果越好。
轮廓系数则度量了数据点在自己所属的簇内的紧密度与与其他簇的分离度,取值范围在-1到1之间,越接近1表示聚类效果越好。
聚类分析_精品文档

1聚类分析内涵1.1聚类分析定义聚类分析(Cluste.Analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术.也叫分类分析(classificatio.analysis)或数值分类(numerica.taxonomy), 它是研究(样品或指标)分类问题的一种多元统计方法, 所谓类, 通俗地说, 就是指相似元素的集合。
聚类分析有关变量类型:定类变量,定量(离散和连续)变量聚类分析的原则是同一类中的个体有较大的相似性, 不同类中的个体差异很大。
1.2聚类分析分类聚类分析的功能是建立一种分类方法, 它将一批样品或变量, 按照它们在性质上的亲疏、相似程度进行分类.聚类分析的内容十分丰富, 按其聚类的方法可分为以下几种:(1)系统聚类法: 开始每个对象自成一类, 然后每次将最相似的两类合并, 合并后重新计算新类与其他类的距离或相近性测度. 这一过程一直继续直到所有对象归为一类为止. 并类的过程可用一张谱系聚类图描述.(2)调优法(动态聚类法): 首先对n个对象初步分类, 然后根据分类的损失函数尽可能小的原则对其进行调整, 直到分类合理为止.(3)最优分割法(有序样品聚类法): 开始将所有样品看成一类, 然后根据某种最优准则将它们分割为二类、三类, 一直分割到所需的K类为止. 这种方法适用于有序样品的分类问题, 也称为有序样品的聚类法.(4)模糊聚类法: 利用模糊集理论来处理分类问题, 它对经济领域中具有模糊特征的两态数据或多态数据具有明显的分类效果.(5)图论聚类法: 利用图论中最小支撑树的概念来处理分类问题, 创造了独具风格的方法.(6)聚类预报法:利用聚类方法处理预报问题, 在多元统计分析中, 可用来作预报的方法很多, 如回归分析和判别分析. 但对一些异常数据, 如气象中的灾害性天气的预报, 使用回归分析或判别分析处理的效果都不好, 而聚类预报弥补了这一不足, 这是一个值得重视的方法。
聚类分析数据

聚类分析数据引言概述:聚类分析是一种数据分析方法,通过将数据分成不同的群组或者类别,匡助我们理解数据之间的关系和模式。
在各个领域,聚类分析都被广泛应用,例如市场营销、社交网络分析和医学研究等。
本文将详细介绍聚类分析的原理和应用,以及使用聚类分析来解决实际问题的方法。
一、聚类分析的原理1.1 聚类分析的定义和目标聚类分析是一种无监督学习方法,它通过将相似的数据点归为一类,将不相似的数据点分为不同的类别。
其目标是在数据中发现隐藏的模式和结构。
1.2 聚类算法的类型聚类算法有多种类型,常见的包括层次聚类、K均值聚类和密度聚类等。
层次聚类通过不断合并或者分割数据点来构建聚类树。
K均值聚类将数据点分为K个簇,通过最小化簇内的平方误差来优化聚类结果。
密度聚类根据数据点的密度来划分簇。
1.3 聚类分析的评估指标评估聚类结果的指标包括轮廓系数、Davies-Bouldin指数和互信息等。
轮廓系数衡量了数据点在自己所在簇和其他簇之间的距离。
Davies-Bouldin指数衡量了簇的密切度和分离度。
互信息衡量了聚类结果与真实类别之间的一致性。
二、聚类分析的应用2.1 市场营销中的聚类分析聚类分析可以匡助市场营销人员理解消费者的行为和需求。
通过将消费者分为不同的群组,可以定制个性化的营销策略。
例如,可以将消费者分为高价值客户、潜在客户和流失客户等,针对不同群组制定不同的促销活动。
2.2 社交网络分析中的聚类分析在社交网络中,聚类分析可以匡助我们发现社区结构和关键人物。
通过将用户分为不同的社区,可以了解社交网络中的群组和交互模式。
例如,可以将社交网络中的用户分为朋友圈、兴趣群体和影响力人物等,进一步分析他们之间的关系和行为。
2.3 医学研究中的聚类分析聚类分析在医学研究中被广泛应用,例如疾病分类和药物研发等。
通过将患者分为不同的簇,可以发现不同疾病的特征和治疗方法。
同时,聚类分析还可以匡助筛选候选药物和预测药物的疗效。
聚类分析方法

聚类分析方法
聚类分析是一种常用的数据挖掘方法,它可以将相似的数据点分组在一起。
在聚类分析中,数据被分为多个类别,每个类别都包含具有类似特征的数据点。
聚类分析方法有很多种,其中一种是K均值聚类。
K均值聚
类的目标是将数据点分为K个簇,使得每个数据点都属于与
其最近的质心所代表的簇。
首先,在聚类分析中,需要先选择一个初始的簇质心,然后迭代地将每个数据点分配到与其最近的质心所代表的簇中,然后更新簇质心的位置,直到达到收敛。
另一种常见的聚类分析方法是层次聚类。
层次聚类将数据点逐渐合并成一个个的簇,直到所有数据点都属于同一个簇。
层次聚类可以根据不同的相似性度量来合并簇,例如单链接、完全链接或平均链接等。
另外,谱聚类是一种基于图论的聚类方法,它利用数据点之间的相似性构建一个相似度矩阵,并将其转化为一个图。
然后,通过计算图的特征向量来对数据进行聚类分析。
聚类分析方法还有很多其他的变体和扩展,例如密度聚类、模糊聚类和网格聚类等。
这些方法可以根据具体的问题和数据类型来选择和应用。
总的来说,聚类分析方法是一种无监督学习的方法,可以用于发现数据中的内在结构和模式。
它在很多领域都有广泛的应用,
如市场分析、社交网络分析和生物信息学等。
通过应用聚类分析方法,可以帮助我们更好地理解和分析数据。
聚类分析数据

聚类分析数据聚类分析是一种常用的数据分析方法,它能够将相似的数据点聚集在一起,形成具有相似特征的群组。
通过对数据进行聚类分析,我们可以发现数据中的潜在模式和结构,从而更好地理解数据集的特点和规律。
在进行聚类分析之前,需要明确以下几个步骤:1. 数据收集和准备:首先,我们需要收集相关的数据,并对数据进行清洗和预处理。
清洗数据包括处理缺失值、异常值和重复值等,确保数据的质量和准确性。
预处理数据包括特征选择、特征缩放和特征转换等,以便于后续的聚类分析。
2. 特征选择:在进行聚类分析之前,需要选择合适的特征用于聚类。
特征选择的目标是选择那些能够最好地区分不同类别的特征。
可以使用统计方法、领域知识或者特征工程技术来进行特征选择。
3. 聚类算法选择:聚类算法是进行聚类分析的核心方法,常用的聚类算法包括K均值聚类、层次聚类、DBSCAN等。
在选择聚类算法时,需要考虑数据的特点、聚类的目标和算法的适用性。
不同的聚类算法有不同的假设和参数设置,需要根据实际情况进行选择。
4. 聚类分析:在进行聚类分析时,首先需要确定聚类的数量。
可以使用肘部法则、轮廓系数等方法来确定最优的聚类数量。
然后,使用选择的聚类算法对数据进行聚类,将数据点划分到不同的簇中。
聚类结果可以通过可视化方法进行展示,如散点图、簇状图等。
5. 结果评估:在完成聚类分析后,需要对聚类结果进行评估。
常用的评估指标包括簇内相似性、簇间距离和轮廓系数等。
评估结果可以帮助我们判断聚类的效果和质量,进而进行后续的分析和决策。
聚类分析可以应用于各个领域,如市场营销、客户分群、图像分析等。
通过对数据进行聚类分析,我们可以发现数据中的规律和潜在关系,为决策提供有力的支持。
然而,在进行聚类分析时需要注意以下几点:1. 数据质量:聚类分析的结果受到数据质量的影响,因此需要确保数据的准确性和完整性。
在进行聚类分析之前,需要对数据进行清洗和预处理,以排除无效数据对结果的影响。
2. 特征选择:特征选择是聚类分析的关键步骤,选择合适的特征能够提高聚类的效果。
聚类分析

聚类分析1聚类分析的概念聚类分析是一组将研究对象认为相对同质的群组的统计分析技术,即依据研究对象在特征上的“亲疏”程度,在没有先验知识的情况下自动进行分类的方法,其中:类内个体具有较高的相似性,类间的差异性较大,其目的是为了将相近事物归入类,减少研究对象的数目。
聚类分析起源于分类学,在考古的分类学中,人们主要依靠经验和专业知识来实现分类。
随着生产技术和科学的发展,人类的认识不断加深,分类越来越细,要求也越来越高,有时光凭经验和专业知识是不能进行确切分类的,往往需要定性和定量分析结合起来去分类,于是数学工具逐渐被引进分类学中,形成了数值分类学。
后来随着多元分析的引进,聚类分析又逐渐从数值分类学中分离出来而形成一个相对独立的分支。
从统计学的观点看,聚类分析是通过数据建模简化数据的一种方法。
传统的统计聚类分析方法包括系统聚类法、分解法、加入法、动态聚类法、有序样品聚类、有重叠聚类和模糊聚类等。
采用k-均值、k-中心点等算法的聚类分析工具已被加入到许多著名的统计分析软件包中,如SPSS、MATLAB等。
2.聚类分析的主要步骤(1)数据处理数据预处理包括选择数量,类型和特征的标度,它依靠特征选择和特征抽取,特征选择选择重要的特征,特征抽取把输入的特征转化为一个新的显著特征,它们经常被用来获取一个合适的特征集来为避免“维数灾”进行聚类,数据预处理还包括将孤立点移出数据,孤立点是不依附于一般数据行为或模型的数据,因此孤立点经常会导致有偏差的聚类结果,因此为了得到正确的聚类,我们必须将它们剔除。
(2)为衡量数据点间的相似度定义一个距离常用来衡量数据点间的相似度的距离有海明距离、欧式距离、切比雪夫距离过程一直进行下去,每个样品总能聚到合适的类中。
有时为了直观反映系统聚类过程,可以把整个分类系统画成一张谱系图,因此系统聚类也称为谱系分析。
(2)系统聚类过程:○1假设总共有n 个样品,首先将每个样品独自聚成一类,共有n 类;然后根据所确定的样品“距离”公式,形成初始距离阵。
聚类分析数据

聚类分析数据聚类分析是一种数据挖掘技术,用于将一组数据划分为不同的类别或群组。
它可以帮助我们发现数据中的模式、关系和趋势,从而更好地理解数据和做出决策。
在本文中,我们将介绍聚类分析的基本概念、流程和常用的聚类算法,并通过一个实际案例来演示如何应用聚类分析来解决问题。
一、聚类分析的基本概念聚类分析是一种无监督学习方法,它不需要预先标记的训练数据,而是根据数据之间的相似性将其划分为不同的类别。
在聚类分析中,我们通常使用距离或相似度作为衡量数据之间关系的指标。
常用的聚类算法包括K均值聚类、层次聚类和密度聚类等。
其中,K均值聚类是最常用的一种方法,它将数据划分为K个不重叠的类别,使得同一类别内的数据之间的距离最小化。
二、聚类分析的流程聚类分析的流程包括数据准备、特征选择、相似度计算、聚类算法选择和结果评估等步骤。
1. 数据准备:首先,我们需要收集和整理待分析的数据。
数据可以来自各种来源,如数据库、文本文件或实验观测。
确保数据的完整性和准确性非常重要。
2. 特征选择:根据分析目的和数据特点,选择合适的特征进行聚类分析。
特征应具有区分度和代表性,能够区分不同类别的数据。
3. 相似度计算:计算数据之间的相似度或距离。
常用的相似度计算方法包括欧氏距离、曼哈顿距离和余弦相似度等。
相似度计算的选择取决于数据的类型和特征的性质。
4. 聚类算法选择:根据数据的特点和分析目的,选择合适的聚类算法。
常用的聚类算法有K均值聚类、层次聚类和密度聚类等。
不同的算法适用于不同的数据类型和聚类目标。
5. 结果评估:评估聚类结果的质量和稳定性。
常用的评估指标包括轮廓系数、Davies-Bouldin指数和Calinski-Harabasz指数等。
评估结果可以帮助我们判断聚类的效果和调整参数。
三、聚类分析的应用案例为了更好地理解聚类分析的应用,我们以一个电商公司为例,通过对用户购买行为进行聚类分析,帮助公司制定个性化的营销策略。
1. 数据准备:收集用户的购买记录和个人信息,如购买时间、购买金额、购买商品类别、用户地理位置等。
聚类分析数据

聚类分析数据聚类分析是一种数据分析方法,用于将相似的数据点分组或聚集在一起。
它可以帮助我们发现数据中的模式和结构,并从中提取有用的信息。
在本文中,我们将介绍聚类分析的标准格式,并通过一个示例来说明如何应用聚类分析来解决实际问题。
一、引言聚类分析是一种无监督学习方法,它不需要事先标记的训练数据。
它通过对数据进行相似性度量和数据点聚类来发现数据中的隐藏模式。
聚类分析广泛应用于各个领域,如市场分析、社交网络分析、图像处理等。
二、数据准备在进行聚类分析之前,我们需要准备一组数据。
这些数据可以是数值型数据、文本数据或其他类型的数据。
在本例中,我们将使用一个虚拟的销售数据集作为示例。
该数据集包含了不同产品的销售量和价格。
三、相似性度量在聚类分析中,我们需要定义一种相似性度量来衡量数据点之间的相似程度。
常用的相似性度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。
在本例中,我们将使用欧氏距离来度量数据点之间的相似性。
四、聚类算法聚类算法是实现聚类分析的关键步骤。
常用的聚类算法包括K-means算法、层次聚类算法、DBSCAN算法等。
在本例中,我们将使用K-means算法来进行聚类分析。
K-means算法是一种迭代的聚类算法,它将数据点划分为K个簇,使得每个数据点都属于与其最近的簇。
算法的具体步骤如下:1. 随机选择K个初始聚类中心。
2. 将每个数据点分配到与其最近的聚类中心。
3. 更新聚类中心为每个聚类的平均值。
4. 重复步骤2和步骤3,直到聚类中心不再改变或达到最大迭代次数。
五、聚类结果解释在完成聚类分析后,我们需要解释聚类结果。
通常我们可以通过可视化方法来展示聚类结果。
在本例中,我们将使用散点图来展示不同簇的数据点,并通过不同颜色的标记来表示不同的聚类。
六、实例分析现在我们将通过一个实例来演示如何应用聚类分析来解决实际问题。
假设我们有一个电商平台的销售数据,包含了不同产品的销售量和价格。
我们希望通过聚类分析来发现潜在的销售模式。
聚类分析数据

聚类分析数据聚类分析是一种数据挖掘技术,旨在将一组相似的数据对象分组为具有相似特征的簇。
它是一种无监督学习方法,不需要预先定义类别或标签,而是根据数据对象之间的相似性进行自动分类。
为了进行聚类分析,我们需要准备一组数据集。
假设我们有一个关于顾客购买行为的数据集,其中包含每个顾客的购买金额、购买频率和购买种类等信息。
我们的目标是根据这些特征将顾客分为不同的群组,以便更好地了解他们的购买偏好和行为模式。
首先,我们需要对数据进行预处理。
这包括数据清洗、缺失值处理和特征选择等步骤。
我们可以使用数据清洗技术来删除重复值、处理异常值和填充缺失值。
然后,我们可以使用特征选择方法来选择最具代表性的特征,以减少数据维度和提高聚类效果。
接下来,我们可以选择适当的聚类算法来对数据进行分组。
常用的聚类算法包括K均值聚类、层次聚类和密度聚类等。
K均值聚类是一种基于距离的聚类方法,它将数据分成K个簇,使得簇内的数据对象之间的距离最小化。
层次聚类是一种自底向上或自顶向下的聚类方法,它通过计算数据对象之间的相似性来构建聚类树。
密度聚类是一种基于密度的聚类方法,它将数据分成高密度区域和低密度区域。
在选择聚类算法之后,我们需要确定合适的聚类数目。
这可以通过评估聚类结果的质量来实现。
常用的评估指标包括轮廓系数、Davies-Bouldin指数和Calinski-Harabasz指数等。
这些指标可以帮助我们确定最佳的聚类数目,以使得簇内的相似性最大化,簇间的差异性最大化。
完成聚类分析后,我们可以对每个簇进行进一步的分析和解释。
我们可以计算每个簇的平均值、方差和频率等统计指标,以了解每个簇的特征。
此外,我们还可以使用可视化技术来展示聚类结果。
常用的可视化方法包括散点图、热力图和雷达图等,它们可以帮助我们更直观地理解不同簇之间的差异和相似性。
最后,我们可以根据聚类结果采取相应的行动。
例如,我们可以根据不同簇的特征来制定个性化的营销策略,以满足不同顾客群体的需求。
聚类分析法

聚类分析法聚类分析是一种常用的数据分析方法,主要用于将相似的样本归类到同一类别中。
它是数据挖掘和机器学习领域中非常重要的一项技术,被广泛应用于各个领域,如市场研究、医学诊断、社交网络分析等。
本文将介绍聚类分析的基本概念、方法和应用,并分析其优势和局限性。
聚类分析是一种无监督学习方法,它不依赖于事先标定好的训练数据集。
通过对给定的数据进行聚类,我们可以发现数据中隐藏的模式、结构和规律。
聚类分析的基本思想是通过计算样本之间的相似度或距离,将相似的样本归为一类,从而实现对数据的分类。
在聚类分析中,相似度或距离的度量是一个关键问题,常用的度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。
聚类分析的方法主要有层次聚类和划分聚类两种。
层次聚类是将样本逐步合并或分割成不同的类别,形成层次化的分类结果。
划分聚类是将所有的样本划分为K个不相交的类别,每个类别之间是互不重叠的。
这两种方法各有优劣,选择何种方法取决于具体的问题和数据特点。
聚类分析的应用非常广泛。
在市场研究中,聚类分析可以将消费者按照其购买行为、兴趣偏好等特征划分为不同的群体,为企业提供有针对性的营销策略。
在医学诊断中,聚类分析可以将病人按照其病情特征进行分类,帮助医生进行准确的诊断和治疗。
在社交网络分析中,聚类分析可以将社交网络中的用户划分为不同的社区,研究社交网络的结构和特征。
然而,聚类分析也存在一些局限性和挑战。
首先,聚类算法的结果很大程度上依赖于选择的相似度或距离度量方法,不同的度量方法可能导致不同的聚类结果。
其次,聚类算法对初始的聚类中心的选择非常敏感,不同的初始选择可能会得到不同的聚类结果。
此外,聚类算法还面临维度灾难的问题,当数据的维度很大时,聚类算法的计算复杂度会急剧增加。
在实际应用中,我们还可以将聚类分析与其他数据挖掘方法相结合,以获得更好的分析结果。
比如,我们可以将聚类分析与关联规则挖掘结合起来,通过挖掘不同类别之间的关联规则,深入分析不同类别之间的关系。
MBA统计学聚类分析

7
D0
(d ij )
1
9
0 6 3
0 8
0
8 5 7 4 0
步骤: 阶段
D0 D1 D2 D3 D4
最短距离法 最长距离法
bk第k阶段类的集合 Dk
Dk
12345
0
0
1;3245
1
1
1;32;45
3
3
1;32;4;5
4
5
1;3;2;4;5
6
9
注:最短和最长距离法结果一样一般不一定一样
就可以得到最后的三类的中心以及每类有多少点
Final Cluster Centers
CALORIE
203.10 1.65
13.05 3.15
33.71 4.16
10.06 2.69
107.34 3.49 8.76 2.94
Number of Cases in each Cluster
Cluster 1 2 3
在饮料数据中;每种饮料都有四个变 量值 这就是四维空间点的问题了
两个距离概念
按照远近程度来聚类需要明确两 个概念:一个是点和点之间的距 离;一个是类和类之间的距离
点间距离有很多定义方式 最简单 的是歐氏距离
当然还有一些和距离相反但起同 样作用的概念;比如相似性等;两点 越相似度越大;就相当于距离越短
方法
ai i=p;q
最短距离 ½
最长距离 ½
b
g
0
1/2
0
1/2
重心
ni/nr
apaq
0
类平均Βιβλιοθήκη ni/nr00
离差平方和ni+nk/ nr+nk
聚类分析方法

聚类分析方法聚类分析是一种常用的数据分析方法,它可以帮助我们将数据集中的对象按照它们的相似性进行分组。
通过聚类分析,我们可以发现数据中的内在结构和规律,从而更好地理解数据。
在本文中,我们将介绍聚类分析的基本概念、常见的聚类方法以及聚类分析的应用场景。
首先,让我们来了解一下聚类分析的基本概念。
聚类分析是一种无监督学习方法,它不需要预先标记的训练数据,而是根据数据对象之间的相似性来进行分组。
在聚类分析中,我们通常会使用距离或相似度作为衡量对象之间关系的指标。
常见的距离指标包括欧氏距离、曼哈顿距离和余弦相似度等。
通过计算对象之间的距离或相似度,我们可以将它们划分到不同的类别中,从而实现数据的聚类。
接下来,让我们来介绍一些常见的聚类方法。
最常用的聚类方法包括层次聚类、K均值聚类和密度聚类。
层次聚类是一种基于对象之间相似性构建层次结构的方法,它可以分为凝聚式层次聚类和分裂式层次聚类。
K均值聚类是一种迭代的聚类方法,它将数据对象划分为K个类别,并通过迭代优化来找到最优的聚类中心。
密度聚类是一种基于数据密度的聚类方法,它可以发现任意形状的聚类簇,并对噪声数据具有较强的鲁棒性。
最后,让我们来看一些聚类分析的应用场景。
聚类分析可以应用于各个领域,例如市场营销、生物信息学、社交网络分析等。
在市场营销中,我们可以利用聚类分析来识别不同的消费群体,并针对不同群体制定个性化的营销策略。
在生物信息学中,聚类分析可以帮助我们发现基因表达数据中的基因模式,并识别相关的生物过程。
在社交网络分析中,我们可以利用聚类分析来发现社交网络中的社区结构,并识别影响力较大的节点。
总之,聚类分析是一种非常有用的数据分析方法,它可以帮助我们发现数据中的内在结构和规律。
通过本文的介绍,相信大家对聚类分析有了更深入的了解,希望能够在实际应用中发挥其价值,为各行各业的发展提供有力支持。
聚类分析数据

聚类分析数据聚类分析是一种数据分析方法,用于将相似的数据对象分组到同一类别中。
它是一种无监督学习方法,不需要预先定义类别或者标签。
聚类分析可以匡助我们发现数据中的潜在模式和结构,从而更好地理解数据。
在聚类分析中,我们使用各种算法来计算数据对象之间的相似性或者距离。
常用的聚类算法包括K均值聚类、层次聚类和DBSCAN等。
这些算法根据不同的原理和假设,将数据对象划分为不同的簇。
聚类分析的步骤通常包括以下几个方面:1. 数据准备:首先,我们需要采集和整理待分析的数据。
这些数据可以是数值型、文本型或者混合型的。
我们需要对数据进行清洗、预处理和特征选择等操作,以便使数据适合聚类分析。
2. 特征选择:在进行聚类分析之前,我们需要选择适当的特征来描述数据对象。
特征应该具有区分性和代表性,能够有效地区分不同的数据对象。
常用的特征选择方法包括主成份分析(PCA)和信息增益等。
3. 距离度量:在聚类分析中,我们需要计算数据对象之间的相似性或者距离。
常用的距离度量方法包括欧氏距离、曼哈顿距离和余弦相似度等。
选择合适的距离度量方法可以影响聚类结果的准确性。
4. 聚类算法选择:根据数据的性质和需求,选择合适的聚类算法进行分析。
不同的聚类算法有不同的假设和约束条件,适合于不同类型的数据和问题。
常用的聚类算法包括K均值聚类、层次聚类和DBSCAN等。
5. 聚类结果评估:在完成聚类分析后,我们需要评估聚类结果的质量和有效性。
常用的评估指标包括轮廓系数、Davies-Bouldin指数和Calinski-Harabasz指数等。
这些指标可以匡助我们判断聚类结果的密切度和分离度。
6. 结果解释和应用:最后,我们需要解释和应用聚类分析的结果。
通过对聚类结果的解释,我们可以发现数据中的模式和结构,从而获得对数据的更深刻理解。
聚类分析的应用包括市场细分、社交网络分析和基因表达分析等。
综上所述,聚类分析是一种重要的数据分析方法,可以匡助我们发现数据中的潜在模式和结构。
聚类分析数据

聚类分析数据聚类分析是一种数据挖掘技术,用于将一组数据分成不同的组或类别,使得同一类别内的数据相似度较高,不同类别间的数据相似度较低。
聚类分析可以帮助我们发现数据中的隐藏模式和结构,从而更好地理解数据和做出决策。
在进行聚类分析之前,我们需要明确以下几个步骤:1. 数据收集:首先,我们需要收集相应的数据。
数据可以来自于各种渠道,如数据库、文件、传感器等。
收集到的数据应该能够反映我们所关注的问题或目标。
2. 数据预处理:在进行聚类分析之前,我们需要对数据进行预处理,以确保数据的质量和可用性。
预处理包括数据清洗、数据变换和数据规范化等步骤。
数据清洗可以去除异常值和缺失值,数据变换可以将数据转换为适合聚类分析的形式,数据规范化可以将数据缩放到相同的范围内。
3. 特征选择:在进行聚类分析之前,我们需要选择合适的特征或变量。
特征选择可以帮助我们减少数据维度,提高聚类分析的效果。
选择合适的特征需要考虑特征的相关性、重要性和可解释性等因素。
4. 聚类算法选择:选择合适的聚类算法是进行聚类分析的关键步骤。
常用的聚类算法包括K均值聚类、层次聚类和密度聚类等。
不同的聚类算法适用于不同的数据类型和问题场景。
我们可以根据数据的特点和需求选择合适的聚类算法。
5. 聚类分析:在选择了合适的聚类算法之后,我们可以开始进行聚类分析。
聚类分析的目标是将数据分成不同的组或类别,使得同一类别内的数据相似度较高,不同类别间的数据相似度较低。
聚类分析可以通过计算样本之间的距离或相似度来实现。
聚类分析的结果可以通过可视化或统计指标来展示。
6. 结果解释和应用:最后,我们需要对聚类分析的结果进行解释和应用。
我们可以通过可视化、统计分析和模型评估等方法来解释聚类分析的结果。
聚类分析的结果可以帮助我们发现数据中的隐藏模式和结构,从而更好地理解数据和做出决策。
总结起来,聚类分析是一种数据挖掘技术,用于将一组数据分成不同的组或类别。
在进行聚类分析之前,我们需要进行数据收集、数据预处理、特征选择、聚类算法选择、聚类分析和结果解释和应用等步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③在图11.2中单击“Plots”按钮,进入对话框,如图11.2示。
选择“Variable Importance Plot”中“Rank Variable”的“by variable”,以便显示在两步聚类中各个变量重要性的图形, 再选择“Continue”按钮,回到原来菜单。
④在图11.2中单击“Output”按钮,进入对话框,如图11.3所 示。
数据统计分析 ——聚类分析和判别分析
Data Statistics & Analysis
黄润龙Biblioteka 2011年3月学习目标解释聚类分析的基本概念
熟悉系统聚类分析方法 分析“Classify”菜单,阐述聚类分析与判别 分析的基本原理和基本操作。用实例说明5 种方法的具体实现过程,解释其主要功能、 背景知识及其主要选择项。
聚类分析又称群分析,它是研究(样品或指标)分类 问题的一种多元统计方法,所谓类,通俗地说,就是指 相似元素的集合。
若对某些大城市的物价指数进行考察,而物价指数很多, 有农用生产物价指数、服务项目价指数、食品消费物价 指数、建材零售价格指数等等。由于要考察的物价指数 很多,通常先对这些物价指数进行分类。总之,需要分 类的问题很多,因此聚类分析这个有用的数学工具越来 越受到人们的重视,它在许多领域中都得到了广泛的应 用。
第11章 聚类分析和判别分析
11.1 聚类分析和判别分析过程综述 11.2 两步聚类
11.3 快速聚类 11.4 分层聚类分析 11.5 分类树 11.6 判别分析
11.1聚类分析和判别分析过程综述
11.1.1 聚类分析 11.1.2 判别分析
11.1.3 Classify的功能
11.1.1 聚类分析
a.“Statistics”复选项提供了3个选项,以便在“Output”窗口给 出各个类别的描述统计量、各类别中的成员数以及所选的 信息标准值。默认为前2个输出。
b.对于“Working Data File”项,打“√”选择“Create cluster membership variable”。该选项会在“Data View”中生成说明 每个样本所属的类别的变量,如果不选择此项,就无法知 道各个样本分到了哪个类别中。
2、变量(Variables)聚类 变量聚类在统计学中又称为R型聚类,是对变量(Variables) 进行聚类。反映同一事物特点的变量有很多,而我们是用各 种变量来对事物进行研究的,由于对客观事物的认识是有限 的,往往难以找出彼此独立的有代表性的变量,而影响对问 题的进一步认识和研究,如在回归分析中由于自变量的共线 性导致偏回归系数不能真正反映自变量对因变量的影响,因 此可以先对变量进行聚类,找出彼此独立且有代表性的自变 量。在生产活动中不乏其例,制衣业制定衣服型号就是根据 人体各部分尺寸数据找出最能反映人体特征的指标如身长、 胸围,裤长、腰围作为上衣和裤子的代表性指标。
1、个案(Cases)聚类 个案聚类在统计学中又称为Q型聚类,用SPSS的术语来说就 是对样本即个案(cases)进行聚类,它是根据每个样本的多 项观测量,将它们归为不同的类别。例如在高等学校的分类 研究中,根据考核高校的指标(学校规模、师生比例、教学 水平、科研水平等),将指标相近的划分到一起,最终得到 重点院校、普通院校、需整改院校等。
11.3.2 快速聚类的应用实例
【例11-2】某公司集团为研究下属不同企业的经营特点调查了20个企业, 请专家为每个企业的盈利能力、领导才干、组织文化和员工发展4项指标进 行打分评价。要求将这20个企业按照各自的特点分成4种类型。 1)基本操作步骤 ① 在Data Editor窗口中输入5个变量20个样本,建立数据文件。 ② 依次单击“Analyze”→“Classify”→“K-Means Cluster”命令,打开“KMeans Cluster Analysis”主对话框,如图11.7所示。 a.“Variables”用于确定进行快速聚类的变量,本题选入“盈利能力”、“领 导才干”、“组织文化”和“员工发展”4个变量。 图11.7 “K-Means Cluster Analysis”主对话框 b.“Label Cases by”用于确定标签变量,该变量的取值将在分析结果中取代 样本号出现,本例将“企业”选入。 c.“Number of Clusters”应输入准备分类的数字(如4)表示将个案分成4类, 系统默认分为2类,本例填入4类。 d.“Method”单选框是选择聚类方法,系统默认在初始类中心的基础上不断 迭代和更换中心位置,从而将Cases(个案)分配到最近的类别中去。也可 以更改为只使用初始类中心对Cases进行分类,这样可以节省运算时间。 e.“Cluster Centers”复选项可展开、定义类中心坐标。“Read initial”选项用 于指定数据文件中的观察值为初始类中心坐标;“Write final”选项用于将分 析结果中的类中心坐标数据存入指定文件。
聚类分析
值得提出的是将聚类分析和其它方法联合起来使用, 如判别分析、主成分分析、回归分析等往往效果更好。
聚类分析内容非常丰富,有系统聚类法、有序样品 聚类法、动态聚类法、模糊聚类法、图论聚类法、聚类 预报法等。本章主要介绍常用的系统聚类法。
11.1.2 判别分析
判别分析是根据表明事物特点的变量值和它们所属的类来求出判别函 数,根据判别函数对未知所属类别的事物进行分类的一种分析方法。 在自然科学和社会科学领域中都会遇到判断问题,如植物学家对植物 进行分类,需要判断其属于哪一门、目、纲、类、属;又如经济学家 根据人均GDP、人均消费水平等多项指标来判断一个国家的经济发展 属于哪种类型;在医疗诊断上,根据病人的各项检查指标判断病情或 病因等。这些都是判别分析研究的范畴。 判别分析是在研究对象分类已知的情况下,根据样本数据推导出一个 或一组判别函数,同时指定一种判别规则,用于确定待判别样本的所 属类别,使错判率最小。判别分析的关键是判别函数,依照判别函数 就可以将研究对象进行归类。例如,根据啤酒中含有的酒精成分、钠 成分、所含“卡路里”对啤酒进行分类,得出各类酒的分类标准,当 新产品问世时,根据相应指标,就很容易将各种酒进行归类处理。又 如,银行为了对贷款进行管理,需要预测哪些类型的客户可能会按时 归还贷款。已知过去几年中,1000个客户的贷款归还信誉度,据此可 以将客户分成两组:可靠客户和不可靠客户。再通过收集客户的一些 资料,如年龄、工资收入、教育程度、存款等将这些资料作为自变量。 通过判别分析,建立判别函数。那么,如果有150个新的客户提交贷款 请求,就可以利用创建好的判别函数,对新的客户进行分析,从而判 断新的客户是属于可靠客户类,还是不可靠客户类。
11.2 两步聚类
11.2.1 两步聚类的概念 两步聚类分析(Two-Step Cluster Analysis)能 够同时根据连续变量(continuous variables)和 分类变量(categorical variables)进行聚类,适 用于数据量很大的数据集,并且它可以自动确定 类的数目。 “两步聚类”将整个过程分为两步:第一步, 把数据行,即Cases预聚类(pre-cluster)形成许 多子类(sub-cluster);第二步,将这些子类用 分层聚类的方法再聚类。在确定最终的类别数量 以及各类别中的成员数量时,采用的是BIC(the Bayesian Information Criterion)或AIC(the Akaike Information Criterion)信息标准。
在SPSS中快速个案聚类由K-Means Cluster过程实现,使用K均值 分类法对样本进行聚类,K是我们指定的聚类数目。分析步骤如下: ①指定聚类数目K,以便将所有样本聚为K类,K的最小值为2, 最大值不超过Cases数目; ②按某种原则选择(或人为指定)K行Cases作为聚类的聚心,它 们将作为各类的初始聚心;快速聚类也可以处理初始聚心未知的 情况,但在初始聚心已知的情况下,该方法能取到更好的效果。 ③按照个案“离初始聚心的距离最小为先聚”的原则将其余观测 值(Cases)向凝聚点凝集,这样得到一个初始分类方案,形成第 一次迭代的子类。 ④计算出每类中所有变量的中心位置(用均值表示),作为第二 次迭代的聚心,使用计算出的中心位置重新进行聚类,因此在该 方法中,各观测的分类情况会在运算过程中不断改变,分类完毕 后再次计算各类的中心位置。如此反复循环,直至达到指定的迭 代次数或达到迭代终止的条件(收敛)为止。 ⑤最终将几个子类合并生成单一聚类解,并且根据研究对象的背 景知识对“类”作出合理解释。 在分析时可以人为指定初始中心位置,或将曾做过的聚类分析结 果作为初始位置引入分析,这在有前人工作可借鉴时显得尤其有 效率。
11.1.3 Classify的功能
SPSS的“Classify”菜单中提供了5种分类分析。 ① 两步聚类(TwoStep Cluster)提供了可以同时 根据连续变量和分类变量进行聚类的功能。 ② 快速聚类(K-Means Cluster),又称为逐步聚 类法,主要用于对大样本的Q型聚类。 ③ 分层聚类(Hierarchical Cluster),又称系统 聚类,提供了全面而强大的聚类分析功能,用于Q 型和R型聚类。 ④ 分类树(Trees)提供了构建树形分析的结构 框架。 ⑤ 判别分析(Discriminant)提供了全面的判别 分析功能。
11.2.2 两步聚类的应用实例
【例11-1】SPSS自备模拟数据库“tree_car.sav”中包含着3110个样本数据, 其中变量有汽车价格(car)与购买者的年龄(age)、性别(gender)、 收入水平(inccat)、受教育水平(ed)和婚姻状态(marital)。请根据 提供的资料对样本进行分类。 1)基本操作步骤 ① 在“Data Editor”中调入数据文件(“tree_car.sav”)。 ② 选择“Analyze”→“Classify”→“TwoStep Cluster命令,打开“TwoStep Cluster Analysis”主对话框,如图11.1所示。 a.“Categorical Variables”选择用于进行聚类的分类变量。这里将性别 (gender)、收入水平(inccat)和受教育水平(ed)选入。 b.“Continuous Variables”选择用于进行聚类的定比或定距变量。这里我们 将汽车价格(car)和购买者的年龄(age)选入。 c.“Distance Measure”选项提供了在计算距离时的两种方法。此例由于有 分类变量,因此只能用“Log-likelihood”。 d.“Count of continuous Variables”中记录了选择需要进行标准化的连续变 量的数目。 e.“Number of Cluster”选项区提供了两种确定分类组数的方法,一种是由 SPSS自动提供,这里需要给出最大的分类组数;另一种是人为确定分类 组数,这里需要给出最终的分类组数。 f.“Clustering Critertion”选项区提供了两种在聚类时用到的信息标准: BIC和AIC。
