2007-2015山东卷高考数学文科专题真题-立体几何’

合集下载

(2007—2015)9年山东高考数学分类汇总(文)

A ．[1,2 ）
B ．[1,2]
C．（ 2,3]
D ．[2,3]
6. (2012 山东卷文 (2) ) 已知全集 U {0,1,2,3,4} ，集合 A { 1,2,3 } ， B {2,4} ，则 (eU A) B 为
(A){1,2,4} (B){2,3,4}
(C){0,2,4} (D){0,2,3,4}
的值为
2. (2009 山东卷文 ) 已知定义在 R 上的奇函数 f ( x) ，满足 f ( x 4) f ( x) ,且在区间 [0,2] 上是增函数 ,
则(
).
A. f ( 25) f (11) f (80)
B.
f (80) f (11) f ( 25)
C. f (11) f (80) f ( 25)
（2007— 2015） 9 年山东高考数学分类汇总（文）
集合
1. (07 山东 ) 命题“对任意的 x R, x3 x 2 1 0 ”的否定是（）
A. 不存在 x R, x3 x2 1 0 B. 存在 x R, x3 x 2 1 0
C. 存在 x R, x3 x 2 1 0 D. 对任意的 x R, x 3 x2 1 0
9.
（ 2015?山东 8）若函数 f ( x)
2x 2x
1 是奇函数，则使 a
f （x） >3 成立的 x 的取值范围为 ( )
（ A） (
) (B)(
) （ C）（ 0,1 ）（D）（ 1， + ）
三、图象
π 1. （ 08 山东卷 3）函ห้องสมุดไป่ตู้ y＝lncos x(- ＜ x＜ ) 的图象是
2
2. （ 08 山东卷 1）满足 M ｛ a1, a 2, a 3, a 4｝, 且 M∩｛ a1 ,a 2, a 3｝ ={ a 1， a2} 的集合 M的个数是

2007年高考“立体几何”题--(文科)高考数学试题全解

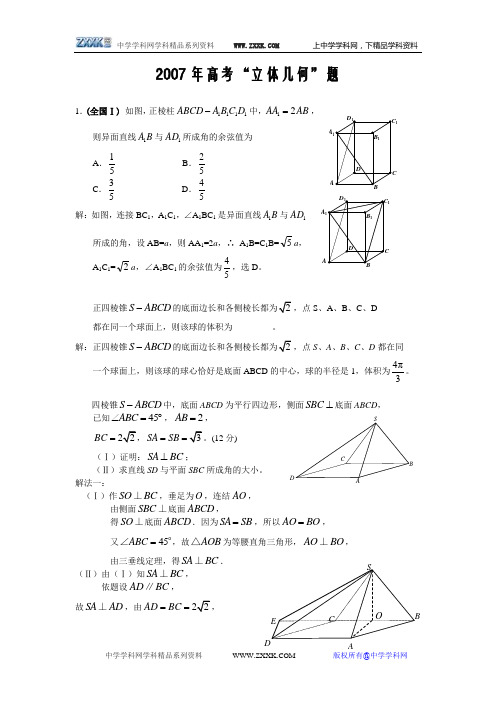
2007年高考“立体几何”题1．(全国Ⅰ) 如图，正棱柱1111ABCD A BC D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为A ．15 B ．25 C ．35 D ．45解：如图，连接BC 1，A 1C 1，∠A 1BC 1是异面直线1A B 与1AD所成的角，设AB=a ，则AA 1=2a ，∴ A 1B=C 1B=5a ， A 1C 1=2a ，∠A 1BC 1的余弦值为45，选D 。

正四棱锥S ABCD -S 、A 、B 、C 、D 都在同一个球面上，则该球的体积为_________。

解：正四棱锥S ABCD -S 、A 、B 、C 、D 都在同一个球面上，则该球的球心恰好是底面ABCD 的中心，球的半径是1，体积为4π3。

四棱锥S ABCD -中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD ，已知45ABC ∠=︒，2AB =，BC =SA SB =(12分)（Ⅰ）证明：SA BC ⊥；（Ⅱ）求直线SD 与平面SBC 所成角的大小。

解法一：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥底面ABCD ．因为SA SB =，所以AO BO =，又45ABC =∠，故AOB △为等腰直角三角形，AO BO ⊥，由三垂线定理，得SA BC ⊥．（Ⅱ）由（Ⅰ）知SA BC ⊥，依题设AD BC ∥，故SA AD ⊥，由AD BC ==，1A1A DCSDCASO ESA =SD ==又sin 45AO AB ==DE BC ⊥，垂足为E ，则DE ⊥平面SBC ，连结SE ．ESD ∠为直线SD 与平面SBC 所成的角．sin ED AO ESD SD SD ====∠ 所以，直线SD 与平面SBC所成的角为arcsin11．解法二：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥平面ABCD ．因为SA SB =，所以AO BO =．又45ABC =∠，AOB △为等腰直角三角形，AO OB ⊥．如图，以O 为坐标原点，OA 为x 轴正向，建立直角坐标系O xyz -，因为2AO BO AB ===，1SO =，又BC =0)A ，，(0B，(0C ． (001)S ，，，1)SA =- ，，(0CB =，0SA CB =，所以SA BC ⊥．（Ⅱ）1)SD SA AD SA CB =+=-=--，0)OA =，. OA 与SD的夹角记为α，SD 与平面ABC 所成的角记为β，因为OA为平面SBC 的法向量，所以α与β互余．cos OA SD OA SDα==sin β= 所以，直线SD 与平面SBC所成的角为arcsin 11．2．(全国II) 已知三棱锥的侧棱长是底面边长的2倍，则侧棱与底面所成角的余弦值等于 ABC．2D解：已知三棱锥的侧棱长的底面边长的2倍，设底面边长为1，侧棱长为2，连接顶点与底面中心，则侧棱在底面上的射影长为33，所以侧棱与底面A 。

2007年高考“立体几何”题

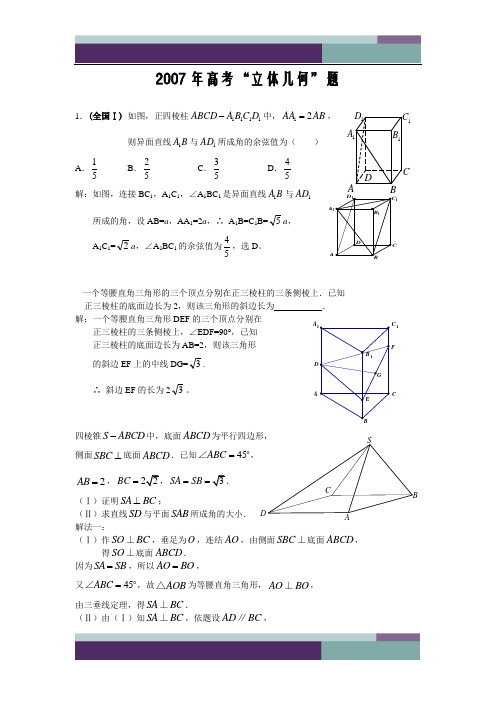
2007年高考“立体几何”题1．(全国Ⅰ) 如图，正四棱柱1111ABCD A BC D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为（）A ．15B ．25C ．35D ．45解：如图，连接BC 1，A 1C 1，∠A 1BC 1是异面直线1A B 与1AD所成的角，设AB=a ，AA 1=2a ，∴ A 1B=C 1B=5a ， A 1C 1=2a ，∠A 1BC 1的余弦值为45，选D 。

一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上．已知正三棱柱的底面边长为2，则该三角形的斜边长为．解：一个等腰直角三角形DEF 的三个顶点分别在正三棱柱的三条侧棱上，∠EDF=90°，已知正三棱柱的底面边长为AB=2，则该三角形的斜边EF 上的中线DG=3. ∴ 斜边EF 的长为23。

四棱锥S ABCD -中，底面ABCD 为平行四边形，侧面SBC ⊥底面ABCD ．已知45ABC =∠，2AB =，BC =SA SB ==（Ⅰ）证明SA BC ⊥；（Ⅱ）求直线SD 与平面SAB 所成角的大小．解法一：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥底面ABCD ．因为SA SB =，所以AO BO =，又45ABC =∠，故AOB △为等腰直角三角形，AO BO ⊥，由三垂线定理，得SA BC ⊥．（Ⅱ）由（Ⅰ）知SA BC ⊥，依题设AD BC ∥，1A AB1B1A1D1C C DC 1A CFAD BCS故SA AD ⊥，由AD BC ==，SA =AO ，得1SO =，SD =．SAB △的面积211122S ABSA ⎛=-= ⎝连结DB ，得DAB △的面积21sin13522S AB AD == 设D 到平面SAB 的距离为h ，由于D SAB S ABD V V --=，得121133h S SO S =，解得h = 设SD 与平面SAB 所成角为α，则sin 11h SD α===．所以，直线SD 与平面SBC 所成的我为．解法二：（Ⅰ）作SO BC ⊥，垂足为O ，连结AO ，由侧面SBC ⊥底面ABCD ，得SO ⊥平面ABCD ．因为SA SB =，所以AO BO =．又45ABC =∠，AOB △为等腰直角三角形，AO OB ⊥．如图，以O 为坐标原点，OA 为x 0)A ，，(0B ，(0C ，(001)S ，，，(2，(0CB =，0SA CB =，所以SA BC ⊥．（Ⅱ）取AB 中点E ，0E ⎫⎪⎪⎝⎭，连结SE ，取SE 中点G ，连结OG ，12G ⎫⎪⎪⎝⎭，． 12OG ⎫=⎪⎪⎝⎭，，1SE ⎫=⎪⎪⎝⎭，(AB =． 0SE OG =，0AB OG =，OG 与平面SAB 内两条相交直线SE ，AB 垂直．所以OG ⊥平面SAB ，OG 与DS 的夹角记为α，SD 与平面SAB 所成的角记为β，OD BCAS则α与β互余．D，(DS =． 22cos 11OG DS OG DSα==，sin 11β=所以，直线SD 与平面SAB 所成的角为arcsin 11．2．(全国II) 已知正三棱柱111ABC A B C -的侧棱长与底面边长相等，则1AB 与侧面11ACC A 所成角的正弦值等于（）ABC ．2D 解：已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，取A 1C 1的中点D 1，连接BD 1，AD 1，∠B 1AD 1是AB 1与侧面ACC 1A 1所成的角，11sin 4B AD ∠==，选A 。

数学高考真题-2015年山东卷文科

2015年普通高等学校招生全国统一考试（山东卷）数学（文科）本试卷分第I 卷和第II 卷两部分，满分150分.考试用时120分钟.第I 卷一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知集合{}24A x x =<< ，()(){}130B x x x =--< ，则A B =I ( ) A.()1,3 B.()1,4 C.()2,3 D.()2,4 2、若复数z 满足1zi i=- ，其中i 为虚数单位，则z = ( ) A.1i - B.1i + C.1i -- D.1i -+ 3、设0.61.50.60.6,0.6, 1.5a b c === ，则,,a b c 的大小关系是 ( )A.a b c <<B.a c b <<C.b a c <<D.b c a << 4、要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭的图象，只需将函数sin 4y x =的图象 ( ) A.向左平移12π个单位 B.向右12π平移个单位 C.向左平移3π个单位 D.向右平移3π个单位5、设m R ∈ ，命题“若0m > ，则方程20x x m +-= 有实根”的逆否命题是 ( ) A.若方程20x x m +-=有实根，则0m > B. 若方程20x x m +-=有实根，则0m ≤C.若方程20x x m +-=没有实根，则0m >D.若方程20x x m +-=没有实根，则0m ≤6、为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图。

考虑以下结论：①甲地该月14时的平均气温低于乙地该月14时的平均气温； ②甲地该月14时的平均气温高于乙地该月14时的平均气温；③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差； ④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差. 其中根据茎叶图能得到的统计结论的编号为 ( )A. ①③B. ①④C. ②③D. ②④ 7、在区间[]0,2上随机地取一个数x ，则事件“1211log 12x ⎛⎫-≤+≤ ⎪⎝⎭”发生的概率为 ( ) A.34 B.23 C.13 D.148、若函数()212x x f x a+=- 是奇函数，则使()3f x > 成立的x 的取值范围为 ( )A.(),1-∞-B.()1,0-C.()0,1D.()1,+∞9. 已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为 ( ) A.223π B.423πC.22πD.42π 10.设函数()3,1,2,1,xx b x f x x -<⎧=⎨≥⎩ 若546f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，则b =** B. C. D.第II 卷二、填空题（本大题共5小题，每小题5分，共25分。

2015年高考试题汇编数学文-立体几何

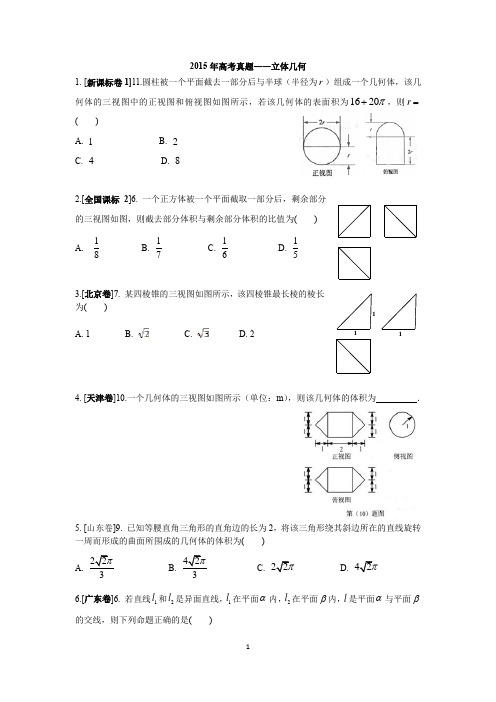
2015年高考真题――立体几何1. [新课标卷1]11.圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( )A. 1B. 2C. 4D. 82.[全国课标2]6. 一个正方体被一个平面截取一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为( ) A.B. C. D.3.[北京卷]7. 某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为( ) A. 1B.C.D. 24. [天津卷]10.一个几何体的三视图如图所示（单位：m ），则该几何体的体积为．5. [山东卷]9. 已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.B.C.D. 6.[广东卷]6. 若直线1l 和2l 是异面直线，1l 在平面α内，2l 在平面β内，l 是平面α与平面β的交线，则下列命题正确的是( )81716151111A ．l 至少与1l ，2l 中的一条相交B ．l 与1l ，2l 都相交C ．l 至多与1l ，2l 中的一条相交D ．l 与1l ，2l 都不相交 7. [重庆卷]5. 某几何体的三视图如图所示，则该几何体的体积为( ) A.123π+ B. 136π C. 73π D. 52π8.[安徽卷]9. 一个四面体的三视图如图所示，则该四面体的表面积是( )A.1B.1+C.2D.9.[江苏卷]9.现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2、高为8的圆柱各一个. 若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为 .10.[浙江卷]2.某几何体的三视图如图所示（单位：cm ），则该几何体的体积是( )A ．83cmB ．123cmC ．3233cm D ．4033cm11.[湖南卷]10.某工作的三视图如图3所示，现将该工作通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工作的一个面内，则原工件材料的利用率为（材料利用率=新工件的体积/原工件的体积）( )A.89πB.827πC.21)πD.21)π221112212.[陕西卷]5. 一个几何体的三视图如图所示，则该几何体的表面积为( )A.3πB. 4πC. 2π＋4D. 3π＋313.[湖北卷]5．12,l l 表示空间中的两条直线，若p ：12,l l 是异面直线；q ：12,l l 不相交，则( ) A ．p 是q 的充分条件，但不是q 的必要条件 B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D ．p 既不是q 的充分条件，也不是q 的必要条件14.[新课标1]18.（本小题满分12分）如图四边形ABCD 为菱形，G 为AC 与BD 交点，BE ABCD ⊥平面，(I)证明：平面AEC ⊥平面BED ；(II)若120ABC ∠=，,AE EC ⊥ 三棱锥E ACD -.15.[全国课标2]19.（本小题满分12分）如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8,点E ，分别在A 1B 1, D 1C 1上，A 1E= D 1F=4.过点E,F 的平面α与此长方体的面相交，交线围成一个正方形. (I)在图中画出这个正方形（不必说明画法和理由） (II)求平面α把该长方体分成的两部分体积的比值.22FD C 1A 1C如图，在三棱锥E-ABC 中，平面EAB ⊥平面ABC ，三角形EAB 为等边三角形，AC ⊥ BC,且AC=BC=,O,M 分别为AB,V A 的中点.(I)求证:VB//平面MOC.(II)求证：平面MOC ⊥平面 V AB (III)求三棱锥V-ABC 的体积.17. [天津卷]17.（满分13分）如图，已知1AA ⊥平面ABC ，11,BB AA AB=AC=3，1BC AA =，1BB =点E ，F 分别是BC ，1AC 的中点，（I ）求证：EF 平面11A B BA ；（II ）求证：平面1AEA ⊥平面1BCB 。

2007年高考数学试题汇编——立体几何(三)

2007 年高考数学试题汇编——立体几何（三）28．（全国Ⅱ ?理 ?19 题）如图，在四棱锥 S-ABCD 中，底面 ABCD 为正方形，侧棱SD⊥底面 ABCD ， E、 F 分别是 AB 、 SC 的中点。

(Ⅰ )求证： EF∥平面 SAD ； (Ⅱ )设 SD = 2CD ，求二面角 A － EF－D 的大小；【解答】解法一：（1）作交于点，则为的中点．连接故，又为平行四边形．，，又平面平面．因此平面（ 2）不如设取中点，连接．，则，则．为等腰直角三角形．又平面，因此，而，因此面．取中点，连接，则．连接，则．故为二面角的平面角．因此二面角的大小为．解法二：（ 1）如图，成立空间直角坐标系．设，则，．取的中点，则．平面平面，因此平面．（ 2）不如设，则．中点又，，因此向量和的夹角等于二面角的平面角．．因此二面角的大小为．29．（北京 ?理 ?16 题）如图，在中，，斜边．能够经过以直线为轴旋转获得，且二面角是直二面角．动点的斜边上．（I ）求证：平面平面；（II ）当为的中点时，求异面直线与所成角的大小；（III ）求与平面所成角的最大值．【解答】解法一：（ I）由题意，，，是二面角是直二面角，又二面角是直二面角，，又，平面，又平面．平面平面．（ II ）作，垂足为，连接（如图），则，是异面直线与所成的角．在中，，，．又．在中，．异面直线与所成角的大小为．（III ）由（ I ）知，平面，是与平面所成的角，且．当最小时，最大，这时，，垂足为，，，与平面所成角的最大值为．解法二：（I ）同解法一．（ II ）成立空间直角坐标系，如图，则，，，，，，．异面直线与所成角的大小为．（III ）同解法一30．（安徽 ?理?17 题）如图，在六面体 ABCD － A1B1C1D1 中，四边形 ABCD 是边长为 2 的正方形，四边形 A1B1C1D1 是边长为 1 的正方形， DD 1⊥平面 A1B1C1D1， DD1⊥平面 ABCD ， DD 1＝ 2。

2015年山东省高考数学试卷(文科)答案与解析

2015年山东省高考数学试卷（文科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）（2015•山东）已知集合A={x|2＜x＜4}，B={x|（x﹣1）（x﹣3）＜0}，则A∩B=2．（5分）（2015•山东）若复数z满足=i，其中i为虚数单位，则z=（）=i=i0.6 1.50.64．（5分）（2015•山东）要得到函数y=sin（4x﹣）的图象，只需将函数y=sin4x的图象向左平移向右平移单位向左平移向右平移单位﹣﹣﹣的图象向右平移5．（5分）（2015•山东）当m∈N*，命题“若m＞0，则方程x2+x﹣m=0有实根”的逆否命题6．（5分）（2015•山东）为比较甲，乙两地某月14时的气温，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图，考虑以下结论：①甲地该月14时的平均气温低于乙地该月14时的平均气温；②甲地该月14时的平均气温高于乙地该月14时的平均气温；③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差；④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差．其中根据茎叶图能得到的统计结论的编号为（）时的平均气温：时的平均气温：时温度的方差为：=[时温度的方差为：=[＞，7．（5分）（2015•山东）在区间[0，2]上随机地取一个数x，则事件“﹣1≤log（x+）≤1”Blog（）∴解可得，﹣≤，P=8．（5分）（2015•山东）若函数f（x）=是奇函数，则使f（x）＞3成立的x的取值=整理可得，＞∴整理可得，9．（5分）（2015•山东）已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在Bπ×π×π×（×=10．（5分）（2015•山东）设函数f（x）=，若f（f（））=4，则b=（），若）），可得b=，可得（舍去）二、填空题（共5小题，每小题5分，满分25分）11．（5分）（2015•山东）执行如图的程序框图，若输入的x的值为1，则输出的y的值是13．12．（5分）（2015•山东）若x，y满足约束条件，则z=x+3y的最大值为7．解：作出不等式组13．（5分）（2015•山东）过点P（1，）作圆x2+y2=1的两条切线，切点分别为A，B，则=．PA=∴=故答案为：14．（5分）（2015•山东）定义运算“⊗”x⊗y=（x，y∈R，xy≠0）．当x＞0，y＞0时，x⊗y+（2y）⊗x的最小值为．x=x==2=∴，故答案为：15．（5分）（2015•山东）过双曲线C：（a＞0，b＞0）的右焦点作一条与其渐近线平行的直线，交C于点P．若点P的横坐标为2a，则C的离心率为2+．±b（∴=2+．三、解答题（共6小题，满分75分）16．（12分）（2015•山东）某中学调查了某班全部45名同学参加书法社团和演讲社团的情（Ⅱ）在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5，3名女同学B1，B2，B3．现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率．=这是一个古典概型，∴17．（12分）（2015•山东）△ABC中，角A，B，C所对的边分别为a，b，c，已知cosB=，sin（A+B）=，ac=2，求sinA和c的值．cosB=，，所以sinB=sinAcosB+cosAsinB=，所以cosA=，结合平方关系得6sinA=a=2ac=218．（12分）（2015•山东）如图，三棱台DEF﹣ABC中，AB=2DE，G，H分别为AC，BC 的中点．（1）求证：BD∥平面FGH；（2）若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH．∴∴19．（12分）（2015•山东）已知数列{a n}是首项为正数的等差数列，数列{}的前n 项和为．（1）求数列{a n}的通项公式；（2）设b n=（a n+1）•2，求数列{b n}的前n项和T n．分离分母，并项相加并利用数列{，=[﹣[﹣﹣+] [﹣，{项和为，∴2=，．20．（13分）（2015•山东）设函数f（x）=（x+a）lnx，g（x）=．已知曲线y=f（x）在点（1，f（x））处的切线与直线2x﹣y=0平行．（Ⅰ）求a的值；（Ⅱ）是否存在自然数k，使得方程f（x）=g（x）在（k，k+1）内存在唯一的根？如果存在，求出k；如果不存在，请说明理由；（Ⅲ）设函数m（x）=min{f（x），g（x）}（min{p，q}表示p，q中的较小值），求m（x）的最大值．，=lnx+1+，﹣==，﹣＜﹣==21．（14分）（2015•山东）平面直角坐标系xOy中，已知椭圆C：=1（a＞b＞0）的离心率为，且点（，）在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）设椭圆E：=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E 与A，B两点，射线PO交椭圆E于点Q．（Ⅰ）求的值；（Ⅱ）求△ABQ面积的最大值．、及的方程为：+、，利用+及=+y+=1，∵=1，及，即（）=2，=，=|m|t==2=，，．。

2015年高考数学（文科）真题分类汇编G单元立体几何

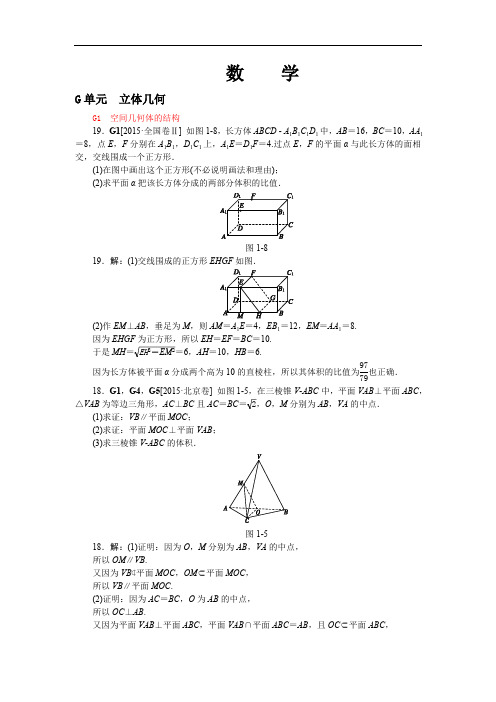
数学G 单元立体几何G1 空间几何体的结构19．G1[2015·全国卷Ⅱ] 如图18，长方体ABCD A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值．图1819．解：(1)交线围成的正方形EHGF 如图．(2)作EM ⊥AB ，垂足为M ，则AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8.因为EHGF 为正方形，所以EH ＝EF ＝BC ＝10.于是MH ＝＝6，AH ＝10，HB ＝6.EH 2－EM 2因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为也正确．977918．G1，G4，G5[2015·北京卷] 如图15，在三棱锥V ABC 中，平面VAB ⊥平面ABC ，△VAB 为等边三角形，AC ⊥BC 且AC ＝BC ＝，O ，M 分别为AB ，VA 的中点．2(1)求证：VB ∥平面MOC ；(2)求证：平面MOC ⊥平面VAB ；(3)求三棱锥V ABC 的体积．图1518．解：(1)证明：因为O ，M 分别为AB ，VA 的中点，所以OM ∥VB .又因为VB ⊄平面MOC ，OM ⊂平面MOC ，所以VB ∥平面MOC .(2)证明：因为AC ＝BC ，O 为AB 的中点，所以OC ⊥AB .又因为平面VAB ⊥平面ABC ，平面VAB ∩平面ABC ＝AB ，且OC ⊂平面ABC ，所以OC ⊥平面VAB .又因为OC ⊂平面MOC ，所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中，AC ＝BC ＝，2所以AB ＝2，OC ＝1.所以等边三角形VAB 的面积S △VAB ＝.3又因为OC ⊥平面VAB ，所以三棱锥C VAB 的体积等于OC ·S △VAB ＝.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等，所以三棱锥V ABC 的体积为.3318．G1、G5[2015·湖南卷] 如图14，直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形，E ，F 分别是BC ，CC 1的中点．(1)证明：平面AEF ⊥平面B 1BCC 1；(2)若直线A 1C 与平面A 1ABB 1所成的角为45°，求三棱锥F AEC 的体积．18．解：(1)证明：如图，因为三棱柱ABC A 1B 1C 1是直三棱柱，所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点，所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ，所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ，连接A 1D 因为△ABC 是正三角形，所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱，所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1，于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角．由题设，∠CA 1D ＝45°，所以A 1D ＝CD ＝AB ＝.323在Rt △AA 1D 中，AA 1＝＝＝，所以FC ＝AA 1＝.A 1D 2－AD 23－121222故三棱锥F AEC 的体积V ＝S △AEC ·FC ＝××＝.131********9．G1[2015·山东卷] 已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.B.22π342π3C ．2πD ．4π229．B [解析] 由条件知该直角三角形的斜边长为2，斜边上的高为，故围成的几22何体的体积为2××π×()2×＝.132242π318．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．(1)请将字母F ，G ，H 标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG 与平面ACH 的位置关系，并证明你的结论；(3)证明：直线DF图1218．解：(1)点F ，G ，H 的位置如图所示．(2)平面BEG ∥平面ACH .证明如下：因为ABCD EFGH 为正方体，所以BC ∥FG ，BC ＝FG ，又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH ，于是BCHE 为平行四边形，所以BE ∥CH .又CH ⊂平面ACH ，BE ⊄平面ACH ，所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG ＝B ，所以平面BEG ∥平面ACH .(3)证明：连接FH .因为ABCD EFGH 为正方体，所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ，所以DH ⊥EG ，又EG ⊥FH ，EG ∩FH ＝O ，所以EG ⊥平面BFHD .又DF ⊂平面BFHD ，所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG ＝G ，所以DF ⊥平面BEG .10．G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位：m)，则该几何体的体积为________m 3.图1310.π　[解析] 根据三视图可知，该几何体是圆柱与两个圆锥的组合体，其体积V ＝π83×12×2＋2××π×12×1＝π(m 3)．1383G2 空间几何体的三视图和直观图9．G2[2015·安徽卷] 一个四面体的三视图如图12所示，则该四面体的表面积是( )A ．1＋B ．1＋232C ．2＋D ．2329．C [解析] 四面体的直观图如图所示，设O 是AC 的中点，则OP ＝OB ＝1，因此PB＝，于是S △PAB ＝S △PBC ＝×()2＝，S △PAC ＝S △ABC ＝×2×1＝1，故四面体的表面积23423212S ＝2×1＋2×＝2＋.32311．G2[2015·全国卷Ⅰ] 圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图14所示．若该几何体的表面积为16＋20π，则r ＝( )图14A ．1B ．2C ．4D ．811．B [解析] 由三视图可知，此组合体的前半部分是一个底面半径为r ，高为2r 的半圆柱(水平放置)，后半部分是一个半径为r 的半球，其中半圆柱的一个底面与半球的半个圆面重合，所以此几何体的表面积为2r ·2r ＋πr 2＋πr 2＋πr ·2r ＋2πr 2＝4r 2＋5πr 2＝16＋121220π，解得r ＝2.6．G2[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后，剩余部分的三视图如图12，则截去部分体积与剩余部分体积的比值为( )图12A. B.1817C. D.16156．D [解析] 由剩余部分的三视图可知，正方体被截去一个三棱锥，剩余部分如图所示，设正方体的棱长为a ，则被截去的三棱锥的体积为×a 2×a ＝a 3，而正方体的体积为131216a 3，所以截去部分体积与剩余部分体积的比值为.157．G2[2015·北京卷] 某四棱锥的三视图如图12所示，该四棱锥最长棱的棱长为( )图12A ．1 B. C. D ．2237．C [解析] 根据三视图可得，此四棱锥是底面是正方形，有一条侧棱和底面垂直的四棱锥，如图所示，所以最长棱的棱长为PC ＝＝，故选C.12＋12＋1239．G2[2015·福建卷] ( )图13A ．8＋2B ．11＋2 22C ．14＋2D ．1529．B [解析] 由三视图可知，该几何体是底面为直角梯形的直四棱柱，其表面积S ＝(1＋1＋2＋)×2＋×(1＋2)×1×2＝11＋2 .212210．G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率＝)( )新工件的体积原工件的体积图13A.B.89π827πC. D.24（2－1）3π8（2－1）3π10．A [解析] 由三视图知，原工件是底面半径为1，母线长为3的圆锥．设新正方体工件的棱长为x ，借助轴截面，由三角形相似可得，＝，得x ＝x 32－121－22x 1，故V 正＝x 3＝，又V 圆锥＝π×12×＝，故利用率为＝，选223162271332－1222π316227223π89πA.5．G2[2015·陕西卷]12所示，则该几何体的表面积为( )图12A ．3πB ．4πC ．2π＋4D ．3π＋45．D [解析] 该几何体是底面半径为1、高为2的圆柱被其轴截面截开的半个圆柱，其表面积为×2π×1×2＋2××π×12＋2×2＝3π＋4.121214．G2，G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中，∠BAC ＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M ，N ，P 分别是棱AB ，BC ，B 1C 1的中点，则三棱锥P A 1MN 的体积是________．14.　[解析] 由题意知，三棱柱的底面是直角边长为1的等腰直角三角形，棱柱的高124为1且该棱柱为直三棱柱，其底面积为，三棱锥A 1PMN 的底面积是××1，高为，故12121212三棱锥P A 1MN 的体积为××＝.13121412410．G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位：m)，则该几何体的体积为________m 3.图1310.π　[解析] 根据三视图可知，该几何体是圆柱与两个圆锥的组合体，其体积V ＝π×8312×2＋2××π×12×1＝π(m 3)．13832．G2[2015·浙江卷] 某几何体的三视图如图11所示(单位：cm)，则该几何体的体积是( )图11A ．8 cm 3B ．12 cm 3C. cm 3D. cm 33234032．C [解析] 该几何体为一个正方体和一个四棱锥的组合体，故所求体积为23＋×2×132×2＝.323G3 平面的基本性质、空间两条直线6．G3[2015·广东卷] 若直线l 1和l 2是异面直线，l 1在平面α内，l 2在平面β内，l 是平面α与平面β的交线，则下列命题正确的是( )A ．l 与l 1，l 2都不相交B ．l 与l 1，l 2都相交C ．l 至多与l 1，l 2中的一条相交D ．l 至少与l 1，l 2中的一条相交6．D [解析] 若直线l 1和l 2是异面直线，l 1在平面α内，l 2在平面β内，l 是平面α与平面β的交线，则l 至少与l 1，l 2中的一条相交，故选D.5．A2、G3[2015·湖北卷] l 1，l 2表示空间中的两条直线，若p ：l 1，l 2是异面直线；q ：l 1，l 2不相交，则( )A ．p 是q 的充分条件，但不是q 的必要条件B ．p 是q 的必要条件，但不是q 的充分条件C ．p 是q 的充分必要条件D．p既不是q的充分条件，也不是q的必要条件5．A　[解析] 由l1，l2是异面直线，可得l1，l2不相交，所以p⇒q；由l1，l2不相交，可得l1，l2是异面直线或l1∥l2，所以q⇒/ p．所以p是q的充分条件，但不是q的必要条件．故选A.G4 空间中的平行关系18．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.(1)证明：BC∥平面PDA；(2)证明：BC⊥PD；(3)求点C到平面PDA的距离．图1318．G1，G4，G5[2015·北京卷] 如图15，在三棱锥VABC中，平面VAB⊥平面ABC，2△VAB为等边三角形，AC⊥BC且AC＝BC＝，O，M分别为AB，VA的中点．(1)求证：VB∥平面MOC；(2)求证：平面MOC⊥平面VAB；(3)求三棱锥VABC的体积．图1518．解：(1)证明：因为O，M分别为AB，VA的中点，所以OM∥VB.又因为VB⊄平面MOC，OM⊂平面MOC，所以VB∥平面MOC.(2)证明：因为AC＝BC，O为AB的中点，所以OC⊥AB.又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC⊂平面ABC，所以OC⊥平面VAB.又因为OC⊂平面MOC，所以平面MOC⊥平面VAB.2(3)在等腰直角三角形ACB中，AC＝BC＝，所以AB＝2，OC＝1.所以等边三角形VAB的面积S△VAB＝.3又因为OC⊥平面VAB，所以三棱锥CVAB的体积等于OC ·S △VAB ＝.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等，所以三棱锥V ABC 的体积为.3318．G4、G5[2015·山东卷] 如图13，三棱台DEF ABC 中，AB ＝2DE ，G ，H 分别为AC ，BC 的中点．(1)求证：BD ∥平面FGH ；(2)若CF ⊥BC ，AB ⊥BC ，求证：平面BCD ⊥平面EGH .18．证明：(1)证法一：如图，连接DG ，CD ，设CD ∩GF ＝M ，连接MH .在三棱台DEF ABC 中，AB ＝2DE ，G 为AC 的中点，可得DF ∥GC ，DF ＝GC ，所以四边形DFCG 为平行四边形，则M 为CD 的中点．又H 为BC 的中点，所以HM ∥BD .又HM ⊂平面FGH ，BD ⊄平面FGH ，所以BD ∥平面FGH .证法二：在三棱台DEF ABC 中，由BC ＝2EF ，H 为BC 的中点，可得BH ∥EF ，BH ＝EF ，所以四边形HBEF 为平行四边形，可得BE ∥HF .在△ABC 中，G 为AC 的中点，H 为BC 的中点，所以GH ∥AB .又GH ∩HF ＝H ，AB ∩BE ＝B ，所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ，所以BD ∥平面FGH .(2)如图，连接HE ，GE .因为G ，H 分别为AC ，BC 的中点，所以GH ∥AB .由AB ⊥BC ，得GH ⊥BC ，又H 为BC 的中点，所以EF ∥HC ，EF ＝HC ，因此四边形EFCH 是平行四边形，所以CF ∥HE .又CF⊥BC，所以HE⊥BC.又HE，GH⊂平面EGH，HE∩GH＝H，所以BC⊥平面EGH.又BC⊂平面BCD，所以平面BCD⊥平面EGH.18．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；(3)证明：直线DF图1218．解：(1)点F，G，H的位置如图所示．(2)平面BEG∥平面ACH.证明如下：因为ABCDEFGH为正方体，所以BC∥FG，BC＝FG，又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，于是BCHE为平行四边形，所以BE∥CH.又CH⊂平面ACH，BE⊄平面ACH，所以BE∥平面ACH.同理BG∥平面ACH.又BE∩BG＝B，所以平面BEG∥平面ACH.(3)证明：连接FH.因为ABCDEFGH为正方体，所以DH⊥平面EFGH.因为EG⊂平面EFGH，所以DH⊥EG，又EG⊥FH，EG∩FH＝O，所以EG⊥平面BFHD.又DF⊂平面BFHD，所以DF⊥EG.同理DF⊥BG.又EG∩BG＝G，所以DF⊥平面BEG.17．G4、G5、G11[2015·天津卷] 如图14，已知AA1⊥平面ABC，BB1∥AA1，AB＝AC＝3，BC ＝2，AA 1＝，BB 1＝2，点E 和F 分别为BC 和A 1C 中点．577(1)求证：EF ∥平面A 1B 1BA ；(2)求证：平面AEA 1⊥平面BCB 1；(3)求直线A 1B 1与平面BCB 1所成角的大小．17．解：(1)证明：如图所示，连接A 1B .在△A 1BC 中，因为E 和F 分别是BC 和A 1C 的中点，所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明：因为AB ＝AC ，E 为BC BC .因为AA 1⊥平面ABC ，BB 1∥AA 1，所以BB 1⊥平面ABC ，从而BB 1⊥AE .又因为BC ∩BB 1＝B ，所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1，所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ，连接A 1M ，A 1N ，NE .因为N 和E 分别为B 1C 和BC的中点，所以NE ∥B 1B ，NE ＝B 1B ，故NE ∥A 1A ，且NE ＝A 1A ，所以A 1N ∥AE ，且A 1N ＝12AE .又因为AE ⊥平面BCB 1，所以A 1N ⊥平面BCB 1，从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角．在△ABC 中，可得AE ＝2，所以A 1N ＝AE ＝2.因为BM ∥AA 1，BM ＝AA 1，所以A 1M ∥AB ，A 1M ＝AB, 又由AB ⊥BB 1，得A 1M ⊥BB 1.在Rt △A 1MB 1中，可得A 1B 1＝＝4.B 1M 2＋A 1M 2在Rt △A 1NB 1中，sin ∠A 1B 1N ＝＝，因此∠A 1B 1N ＝30°，A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4．G4，G5[2015·浙江卷] 设α，β是两个不同的平面，l ，m 是两条不同的直线，且l ⊂α，m ⊂β( )A ．若l ⊥β，则α⊥βB ．若α⊥β，则l ⊥mC ．若l ∥β，则α∥βD ．若α∥β，则l ∥m4．A [解析] 由两平面垂直的判定定理知，A 正确；对于B ，直线l ，m 相交、平行、异面都有可能，故不正确；对于C ，要求α内两条相交直线都平行于β，才能推出α∥β，故不正确；对于D ，l ，m 平行和异面都有可能，故不正确．16．G4、G5[2015·江苏卷] 如图12，在直三棱柱ABC A 1B 1C 1中，已知AC ⊥BC ，BC ＝CC 1，设AB 1的中点为D ，B 1C ∩BC 1＝E .求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.图1216．证明：(1)由题意知，E为B1C的中点，又D为AB1的中点，因此DE∥AC.又因为DE⊄平面AA1C1C，AC⊂平面AA1C1C，所以DE∥平面AA1C1C.(2)因为三棱柱ABCA1B1C1是直三棱柱，所以CC1⊥平面ABC.因为AC⊂平面ABC，所以AC⊥CC1.又因为AC⊥BC，CC1⊂平面BCC1B1，BC⊂平面BCC1B1，BC∩CC1＝C，所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1，所以BC1⊥AC.因为BC＝CC1，所以矩形BCC1B1是正方形，因此BC1⊥B1C.因为AC，B1C⊂平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC，所以BC1⊥AB1.G5 空间中的垂直关系18．G4，G5，G11[2015·广东卷] 如图13，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.(1)证明：BC∥平面PDA；(2)证明：BC⊥PD；(3)求点C到平面PDA的距离．图1320．G5、G12[2015·湖北卷] 《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图14所示的阳马P ABCD 中，侧棱PD ⊥底面ABCD ，且PD ＝CD ，点E 是PC 的中点，连接DE ，BD ，BE .(1)证明：DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑，若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由．(2)记阳马P ABCD 的体积为V 1，四面体EBCD 的体积为V 2，求的值．V 1V2图1420．解：(1)证明：因为PD ⊥底面ABCD ，所以PD ⊥BC .由底面ABCD 为长方形，有BC ⊥CD ，而PD ∩CD ＝D ，所以BC ⊥平面PCD .又DE ⊂平面PCD ，所以BC ⊥DE .又因为PD ＝CD ，点E 是PC 的中点，所以DE ⊥PC .而PC ∩BC ＝C ，所以DE ⊥平面PBC .由BC ⊥平面PCD ，DE ⊥平面PBC ，可知四面体EBCD 的四个面都是直角三角形，即四面体EBCD 是一个鳖臑，其四个面的直角分别是∠BCD ，∠BCE ，∠DEC ，∠DEB .(2)由已知，PD 是阳马P ABCD 的高，所以V 1＝S 长方形ABCD ·PD ＝BC ·CD ·PD ；1313由(1)知，DE 是鳖臑D BCE 的高，BC ⊥CE ，所以V 2＝S △BCE ·DE ＝BC ·CE ·DE .1316在Rt △PDC 中，因为PD ＝CD ，点E 是PC 的中点，所以DE ＝CE ＝CD .22于是＝＝＝4.V 1V 213BC ·CD ·PD 16BC ·CE ·DE 2CD ·PD CE ·DE18．G5[2015·全国卷Ⅰ] 如图15，四边形ABCD 为菱形，G 为AC 与BD 的交点，BE ⊥平面ABCD .(1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC, 三棱锥E ACD 的体积为，求该三棱锥的侧面积．63图1518．解：(1)证明：因为四边形ABCD 为菱形，所以AC ⊥BD .因为BE ⊥平面ABCD ，所以AC ⊥BE ，故AC ⊥平面BED .又AC ⊂平面AEC ，所以平面AEC ⊥平面BED .(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝x ，GB ＝GD ＝.32x2因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝x .32由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝x .22由已知得，三棱锥E ACD 的体积V E ACD ＝×AC ·GD ·BE ＝x 3＝，131262463故x ＝2.从而可得AE ＝EC ＝ED ＝，6所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为.5故三棱锥E ACD 的侧面积为3＋2.518．G1，G4，G5[2015·北京卷] 如图15，在三棱锥V ABC 中，平面VAB ⊥平面ABC ，△VAB 为等边三角形，AC ⊥BC 且AC ＝BC ＝，O ，M 分别为AB ，VA 的中点．2(1)求证：VB ∥平面MOC ；(2)求证：平面MOC ⊥平面VAB ；(3)求三棱锥V ABC 的体积．图1518．解：(1)证明：因为O ，M 分别为AB ，VA 的中点，所以OM ∥VB .又因为VB ⊄平面MOC ，OM ⊂平面MOC ，所以VB ∥平面MOC .(2)证明：因为AC ＝BC ，O 为AB 的中点，所以OC ⊥AB .又因为平面VAB ⊥平面ABC ，平面VAB ∩平面ABC ＝AB ，且OC ⊂平面ABC ，所以OC ⊥平面VAB .又因为OC ⊂平面MOC ，所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中，AC ＝BC ＝，2所以AB ＝2，OC ＝1.所以等边三角形VAB 的面积S △VAB ＝.3又因为OC ⊥平面VAB ，所以三棱锥C VAB 的体积等于OC ·S △VAB ＝.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等，所以三棱锥V ABC 的体积为.3320．G5、G12[2015·福建卷] 如图15，AB 是圆O 的直径，点C 是圆O 上异于A ，B 的点，PO 垂直于圆O 所在的平面，且PO ＝OB ＝1.(1)若D 为线段AC 的中点，求证：AC ⊥平面PDO ；(2)求三棱锥P ABC 体积的最大值；(3)若BC ＝，点E 在线段PB 上，求CE ＋OE 的最小值．2图1520．解：方法一：(1)证明：在△AOC 中，因为OA ＝OC ，D 为AC 的中点，所以AC ⊥DO .又PO 垂直于圆O 所在的平面，所以PO ⊥AC .因为DO ∩PO ＝O ，DO ⊂平面PDO ，PO ⊂平面PDO ，所以AC ⊥平面PDO .(2)因为点C 在圆O 上，所以当CO ⊥AB 时，C 到AB 的距离最大，且最大值为1.又AB ＝2，所以△ABC 面积的最大值为×2×1＝1.12又因为三棱锥P ABC 的高PO ＝1，故三棱锥P ABC 体积的最大值为×1×1＝.1313(3)在△POB 中，PO ＝OB ＝1，∠POB ＝90°，所以PB ＝＝.12＋122同理PC ＝，所以PB ＝PC ＝BC .2在三棱锥P ABC 中，将侧面BCP 绕PB 旋转至平面BC ′P, 使之与平面ABP 共面，如图所示．当O ，E ，C ′共线时，CE ＋OE 取得最小值．又因为OP ＝OB ，C ′P ＝C ′B ，所以OC ′垂直平分PB ，即E 为PB 中点．从而OC ′＝OE ＋EC ′＝＋＝，22622＋62亦即CE ＋OE 的最小值为.2＋62方法二：(1)(2)同方法一．(3)在△POB 中，PO ＝OB ＝1，∠POB ＝90°，所以∠OPB ＝45°，PB ＝＝.12＋122同理PC ＝.2所以PB ＝PC ＝BC ，所以∠CPB ＝60°.在三棱锥P ABC 中，将侧面BCP 绕PB 旋转至平面BC ′P ，使之与平面ABP 共面，如图所示．当O ，E ，C ′共线时，CE ＋OE 取得最小值．所以在△OC ′P 中，由余弦定理得，OC ′2＝1＋2－2×1××cos(45°＋60°)＝1＋2－2 ××－×＝2＋.22221222323从而OC ′＝＝.2＋32＋62所以CE ＋OE 的最小值为＋.226218．G1、G5[2015·湖南卷] 如图14，直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形，E ，F 分别是BC ，CC 1的中点．(1)证明：平面AEF ⊥平面B 1BCC 1；(2)若直线A 1C 与平面A 1ABB 1所成的角为45°，求三棱锥F AEC 的体积．18．解：(1)证明：如图，因为三棱柱ABC A 1B 1C 1是直三棱柱，所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点，所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ，所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ，连接A 1D 因为△ABC 是正三角形，所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱，所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1，于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角．由题设，∠CA 1D ＝45°，所以A 1D ＝CD ＝AB ＝.323在Rt △AA 1D 中，AA 1＝＝＝，所以FC ＝AA 1＝.A 1D 2－AD 23－121222故三棱锥F AEC 的体积V ＝S △AEC ·FC ＝××＝.1313322261218．G4、G5[2015·山东卷] 如图13，三棱台DEF ABC 中，AB ＝2DE ，G ，H 分别为AC ，BC 的中点．(1)求证：BD ∥平面FGH ；(2)若CF ⊥BC ，AB ⊥BC ，求证：平面BCD ⊥平面EGH .18．证明：(1)证法一：如图，连接DG ，CD ，设CD ∩GF ＝M ，连接MH .在三棱台DEF ABC 中，AB ＝2DE ，G 为AC 的中点，可得DF ∥GC ，DF ＝GC ，所以四边形DFCG 为平行四边形，则M 为CD 的中点．又H 为BC 的中点，所以HM ∥BD .又HM ⊂平面FGH ，BD ⊄平面FGH ，所以BD ∥平面FGH .证法二：在三棱台DEF ABC 中，由BC ＝2EF ，H 为BC 的中点，可得BH ∥EF ，BH ＝EF ，所以四边形HBEF 为平行四边形，可得BE ∥HF .在△ABC 中，G 为AC 的中点，H 为BC 的中点，所以GH ∥AB .又GH ∩HF ＝H ，AB ∩BE ＝B ，所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ，所以BD ∥平面FGH .(2)如图，连接HE ，GE .因为G ，H 分别为AC ，BC 的中点，所以GH ∥AB .由AB ⊥BC ，得GH ⊥BC ，又H 为BC 的中点，所以EF ∥HC ，EF ＝HC ，因此四边形EFCH 是平行四边形，所以CF ∥HE .又CF ⊥BC ，所以HE ⊥BC .又HE ，GH ⊂平面EGH ，HE ∩GH ＝H ，所以BC ⊥平面EGH .又BC ⊂平面BCD ，所以平面BCD ⊥平面EGH .18．G5[2015·陕西卷] 如图15(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝，AB ＝π2BC ＝AD ＝a ，E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A 1BE12的位置，得到四棱锥A 1 BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1 BCDE 的体积为36，求a 的值．2图1518．解：(1)证明：在图(1)中，因为AB ＝BC ＝AD ＝a ，E 是AD 的中点，12∠BAD ＝，所以BE ⊥AC ，π2即在图(2)中，BE ⊥A 1O ，BE ⊥OC ，从而BE ⊥平面A 1OC .又CD ∥BE ，所以CD ⊥平面A 1OC .(2)由已知，平面A 1BE ⊥平面BCDE ，且平面A 1BE ∩平面BCDE ＝BE ，又由(1)知，A 1O ⊥BE ，所以A 1O ⊥平面BCDE ，即A 1O 是四棱锥A 1 BCDE 的高．由图(1)知，A 1O ＝AB ＝a ，平行四边形BCDE 的面积S ＝BC ·AB ＝a 2.2222从而四棱锥A 1 BCDE 的体积V ＝×S ×A 1O ＝×a 2×a ＝a 3.13132226由a 3＝36，得a ＝6.26218．G1，G4，G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示．(1)请将字母F ，G ，H 标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG 与平面ACH 的位置关系，并证明你的结论；(3)证明：直线DF图1218．解：(1)点F ，G ，H 的位置如图所示．(2)平面BEG ∥平面ACH .证明如下：因为ABCD EFGH 为正方体，所以BC ∥FG ，BC ＝FG ，又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH ，于是BCHE 为平行四边形，所以BE ∥CH .又CH ⊂平面ACH ，BE ⊄平面ACH ，所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG ＝B ，所以平面BEG ∥平面ACH .(3)证明：连接FH .因为ABCD EFGH 为正方体，所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ，所以DH ⊥EG ，又EG ⊥FH ，EG ∩FH ＝O ，所以EG ⊥平面BFHD .又DF ⊂平面BFHD ，所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG ＝G ，所以DF ⊥平面BEG .17．G4、G5、G11[2015·天津卷] 如图14，已知AA 1⊥平面ABC ，BB 1∥AA 1，AB ＝AC ＝3，BC ＝2，AA 1＝，BB 1＝2，点E 和F 分别为BC 和A 1C 中点．577(1)求证：EF ∥平面A 1B 1BA ；(2)求证：平面AEA 1⊥平面BCB 1；(3)求直线A 1B 1与平面BCB 1所成角的大小．17．解：(1)证明：如图所示，连接A 1B .在△A 1BC 中，因为E 和F 分别是BC 和A 1C 的中点，所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明：因为AB ＝AC ，E 为BC BC .因为AA 1⊥平面ABC ，BB 1∥AA 1，所以BB 1⊥平面ABC ，从而BB 1⊥AE .又因为BC ∩BB 1＝B ，所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1，所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ，连接A 1M ，A 1N ，NE .因为N 和E 分别为B 1C 和BC的中点，所以NE ∥B 1B ，NE ＝B 1B ，故NE ∥A 1A ，且NE ＝A 1A ，所以A 1N ∥AE ，且A 1N ＝12AE .又因为AE ⊥平面BCB 1，所以A 1N ⊥平面BCB 1，从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角．在△ABC 中，可得AE ＝2，所以A 1N ＝AE ＝2.因为BM ∥AA 1，BM ＝AA 1，所以A 1M ∥AB ，A 1M ＝AB, 又由AB ⊥BB 1，得A 1M ⊥BB 1.在Rt △A 1MB 1中，可得A 1B 1＝＝4.B 1M 2＋A 1M 2在Rt △A 1NB 1中，sin ∠A 1B 1N ＝＝，因此∠A 1B 1N ＝30°，A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4．G4，G5[2015·浙江卷] 设α，β是两个不同的平面，l ，m 是两条不同的直线，且l ⊂α，m ⊂β( )A ．若l ⊥β，则α⊥βB ．若α⊥β，则l ⊥mC ．若l ∥β，则α∥βD ．若α∥β，则l ∥m4．A [解析] 由两平面垂直的判定定理知，A 正确；对于B ，直线l ，m 相交、平行、异面都有可能，故不正确；对于C ，要求α内两条相交直线都平行于β，才能推出α∥β，故不正确；对于D ，l ，m 平行和异面都有可能，故不正确．18．G5，G11[2015·浙江卷] 如图14，在三棱柱ABC A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝2，A 1A ＝4，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．(1)证明：A 1D ⊥平面A 1BC ；(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值．图1418．解：(1)证明：设E 为BC 的中点，连接DE .由题意得A 1E ⊥平面ABC ，所以A 1E ⊥AE .因为AB ＝AC ，所以AE ⊥BC .故AE ⊥平面A 1BC .由D ，E 分别为B 1C 1，BC 的中点，得DE ∥B 1B 且DE ＝B 1B ，从而DE ∥A 1A 且DE ＝A 1A ，所以四边形AA 1DE 为平行四边形．于是A 1D ∥AE .又因为AE ⊥平面A 1BC ，所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ，垂足为F ，连接BF .因为A 1E ⊥平面ABC ，所以BC ⊥A 1E .因为BC ⊥AE ，所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ，所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角．由AB ＝AC ＝2，∠CAB ＝90°，得EA ＝EB ＝.2由A 1E ⊥平面ABC ，得A 1A ＝A 1B ＝4，A 1E ＝.14由DE ＝BB 1＝4，DA 1＝EA ＝，∠DA 1E ＝90°，得A 1F ＝.272所以sin ∠A 1BF ＝＝.A 1F A 1B 7820．G5、G7[2015·重庆卷] 如图14，三棱锥P ABC 中，平面PAC ⊥平面ABC ，∠ABC ＝，点D ，E 在线段AC 上，且AD ＝DE ＝EC ＝2，PD ＝PC ＝4，点F 在线段AB 上，且π2EF ∥BC .(1)证明：AB ⊥平面PFE ；(2)若四棱锥P DFBC 的体积为7，求线段BC 的长．图1420．解：(1)证明：由DE ＝EC ，PD ＝PC 知，E 为等腰三角形PDC 中DC 边的中点，故PE ⊥AC .又平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，PE ⊂平面PAC ，PE ⊥AC ，所以PE ⊥平面ABC ，从而PE ⊥AB .因为∠ABC ＝，EF ∥BC ，故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ，EF 都垂直，所以AB ⊥平面PFE .(2)设BC ＝x ，则在直角三角形ABC 中，AB ＝＝，AC 2－BC 236－x 2从而S △ABC ＝AB ·BC ＝x .121236－x 2由EF ∥BC 知，＝＝，△AFE ∽△ABC ，故＝2＝，即S △AFE ＝S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD ＝AE ，得S △AFD ＝S △AFE ＝×S △ABC ＝S △ABC ＝x ，12121249291936－x 2从而四边形DFBC 的面积为S 四边形DFBC ＝S △ABC －S △AFD ＝x －x ＝x1236－x 21936－x 2718.36－x 2由(1)知，PE ⊥平面ABC ，所以PE 为四棱锥P DFBC 的高．在直角三角形PEC 中，PE ＝＝＝2.PC 2－EC 242－223所以V 四棱锥P DFBC ＝·S 四边形DFBC ·PE ＝×x ·2＝7，131371836－x 23故得x 4－36x 2＋243＝0，解得x 2＝9或x 2＝27，由于x >0，可得x ＝3或x ＝3.3所以BC ＝3或BC ＝3.3G6 多面体与球G7 棱柱与棱锥10．G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示，现将该工件通过切削，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为(材料利用率＝)( )新工件的体积原工件的体积图13A.B.89π827πC.D.24（2－1）3π8（2－1）3π10．A [解析] 由三视图知，原工件是底面半径为1，母线长为3的圆锥．设新正方体工件的棱长为x ，借助轴截面，由三角形相似可得，＝，得x ＝x 32－121－22x1，故V 正＝x 3＝，又V 圆锥＝π×12×＝，故利用率为＝，选223162271332－1222π316227223π89πA.14．G2，G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中，∠BAC ＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边的长为1的等腰直角三角形，设点M ，N ，P 分别是棱AB ，BC ，B 1C 1的中点，则三棱锥P A 1MN 的体积是________．14.　[解析] 由题意知，三棱柱的底面是直角边长为1的等腰直角三角形，棱柱的高124为1且该棱柱为直三棱柱，其底面积为，三棱锥A 1PMN 的底面积是××1，高为，故12121212三棱锥P A1MN 的体积为××＝.1312141245．G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示，则该几何体的体积为( )图12A.＋2πB.1313π6C. D.7π35π25．B [解析] 由三视图知，该几何体为一个圆柱与一个半圆锥的组合体，其中圆柱的底面半径为1、高为2，半圆锥的底面半径为1、高为1，所以该几何体的体积V ＝××π×131212×1＋π×12×2＝.13π620．G5、G7[2015·重庆卷] 如图14，三棱锥P ABC 中，平面PAC ⊥平面ABC ，∠ABC ＝，点D ，E 在线段AC 上，且AD ＝DE ＝EC ＝2，PD ＝PC ＝4，点F 在线段AB 上，且π2EF ∥BC .(1)证明：AB ⊥平面PFE ；(2)若四棱锥P DFBC 的体积为7，求线段BC 的长．图1420．解：(1)证明：由DE ＝EC ，PD ＝PC 知，E 为等腰三角形PDC 中DC 边的中点，故PE ⊥AC .又平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，PE ⊂平面PAC ，PE ⊥AC ，所以PE ⊥平面ABC ，从而PE ⊥AB .因为∠ABC ＝，EF ∥BC ，故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ，EF 都垂直，所以AB ⊥平面PFE .(2)设BC ＝x ，则在直角三角形ABC 中，AB ＝＝，AC 2－BC 236－x 2从而S △ABC ＝AB ·BC ＝x .121236－x 2由EF ∥BC 知，＝＝，△AFE ∽△ABC ，故＝2＝，即S △AFE ＝S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD ＝AE ，得S △AFD ＝S △AFE ＝×S △ABC ＝S △ABC ＝x ，12121249291936－x 2从而四边形DFBC 的面积为S 四边形DFBC ＝S △ABC －S △AFD ＝x －x ＝x1236－x 21936－x 2718.36－x 2由(1)知，PE ⊥平面ABC ，所以PE 为四棱锥P DFBC 的高．在直角三角形PEC 中，PE ＝＝＝2.PC 2－EC 242－223所以V 四棱锥P DFBC ＝·S 四边形DFBC ·PE ＝×x ·2＝7，131371836－x 23故得x 4－36x 2＋243＝0，解得x 2＝9或x 2＝27，由于x >0，可得x ＝3或x ＝3.3所以BC ＝3或BC ＝3.39．G7[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________．9.　[解析] 设新的底面半径为r ，则π×52×4＋π×22×8＝πr 2×4＋πr 2×8 ，71313即πr 2＝π＋32π，解得r ＝.28310037G8 多面体与球5．G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示，则该几何体的体积为( )图12A.＋2πB.1313π6C.D.7π35π25．B [解析] 由三视图知，该几何体为一个圆柱与一个半圆锥的组合体，其中圆柱的底面半径为1、高为2，半圆锥的底面半径为1、高为1，所以该几何体的体积V ＝××π×131212×1＋π×12×2＝.13π610．G8[2015·全国卷Ⅱ] 已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π10．C [解析] 因为V 三棱锥O ABC ＝V 三棱锥C OAB ，所以三棱锥O ABC 体积的最大值即三棱锥C OAB 体积的最大值，所以当C 到平面OAB 的距离最大时，即CO ⊥平面OAB 时，体积最大，设球的半径为r ，则V 三棱锥O ABC ＝V 三棱锥C OAB ＝r 3＝36，所以r ＝6，则球O16的表面积S ＝4πr 2＝144π.图12A.＋2πB.1313π6C.D.7π35π2G9　空间向量及运算G10 空间向量解决线面位置关系G11 空间角与距离的求法17．G4、G5、G11[2015·天津卷] 如图14，已知AA 1⊥平面ABC ，BB 1∥AA 1，AB ＝AC ＝3，BC ＝2，AA 1＝，BB 1＝2，点E 和F 分别为BC 和A 1C 中点．577(1)求证：EF ∥平面A 1B 1BA ；(2)求证：平面AEA 1⊥平面BCB 1；(3)求直线A 1B 1与平面BCB 117．解：(1)证明：如图所示，连接A 1B .在△A 1BC 中，因为E 和F 分别是BC 和A 1C 的中点，所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明：因为AB ＝AC ，E 为BC BC .因为AA 1⊥平面ABC ，BB 1∥AA 1，所以BB 1⊥平面ABC ，从而BB 1⊥AE .又因为BC ∩BB 1＝B ，所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1，所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ，连接A 1M ，A 1N ，NE .因为N 和E 分别为B 1C 和BC的中点，所以NE ∥B 1B ，NE ＝B 1B ，故NE ∥A 1A ，且NE ＝A 1A ，所以A 1N ∥AE ，且A 1N ＝12AE .又因为AE ⊥平面BCB 1，所以A 1N ⊥平面BCB 1，从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角．在△ABC 中，可得AE ＝2，所以A 1N ＝AE ＝2.因为BM ∥AA 1，BM ＝AA 1，所以A 1M ∥AB ，A 1M ＝AB, 又由AB ⊥BB 1，得A 1M ⊥BB 1.在Rt △A 1MB 1中，可得A 1B 1＝＝4.B 1M 2＋A 1M 2在Rt △A 1NB 1中，sin ∠A 1B 1N ＝＝，因此∠A 1B 1N ＝30°，A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.18．G5，G11[2015·浙江卷] 如图14，在三棱柱ABC A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝2，A 1A ＝4，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．(1)证明：A 1D ⊥平面A 1BC ；(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值．图1418．解：(1)证明：设E 为BC 的中点，连接DE .由题意得A 1E ⊥平面ABC ，所以A 1E ⊥AE .因为AB ＝AC ，所以AE ⊥BC .故AE ⊥平面A 1BC .由D ，E 分别为B 1C 1，BC 的中点，得DE ∥B 1B 且DE ＝B 1B ，从而DE ∥A 1A 且DE ＝A 1A ，所以四边形AA 1DE 为平行四边形．于是A 1D ∥AE .又因为AE ⊥平面A 1BC ，所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ，垂足为F ，连接BF .因为A 1E ⊥平面ABC ，所以BC ⊥A 1E .因为BC ⊥AE ，所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ，所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角．由AB ＝AC ＝2，∠CAB ＝90°，得EA ＝EB ＝.2由A 1E ⊥平面ABC ，得A 1A ＝A 1B ＝4，A 1E ＝.14由DE ＝BB 1＝4，DA 1＝EA ＝，∠DA 1E ＝90°，得A 1F ＝.272所以sin ∠A 1BF ＝＝.A 1F A 1B 7818．G4，G5，G11[2015·广东卷] 如图13，三角形PDC 所在的平面与长方形ABCD 所在的平面垂直，PD ＝PC ＝4，AB ＝6，BC ＝3.(1)证明：BC ∥平面PDA ；(2)证明：BC ⊥PD ；(3)求点C 到平面PDA 的距离．图13图1422．G11、G12[2015·江苏卷] 如图16，在四棱锥P ABCD 中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，∠ABC ＝∠BAD ＝，PA ＝AD ＝2，AB ＝BC ＝1.π2(1)求平面PAB 与平面PCD 所成二面角的余弦值；(2)点Q 是线段BP 上的动点，当直线CQ 与DP 所成的角最小时，求线段BQ 的长．图1622．解：以{，，}为正交基底建立如图所示的空间直角坐标系A xyz ，则各点的AB → AD → AP →坐标为B (1，0，0)，C (1，1，0)，D (0，2，0)，P (0，0，2)．(1)因为AD ⊥平面PAB ，所以是平面PAB 的一个法向量，＝(0，2，0)．AD → AD →因为＝(1，1，－2)，＝(0，2，－2)，PC → PD →设平面PCD 的一个法向量为m ＝(x ，y ，z )，所以m ·＝0，m ·＝0，PC → PD →即令y ＝1，解得z ＝1，x ＝1，{x ＋y －2z ＝0，2y －2z ＝0.)所以m ＝(1，1，1)是平面PCD 的一个法向量．。

2007年高考真题试卷山东卷数学文科参考答案

2007年普通高等学校招生全国统一考试（山东文卷）答案一、选择题 1．B 2．C 3．D 4．A 5．C 6．B 7．C 8．A 9．B10．A11．B12．D二、填空题 13．1200714．1 15．5m -≤ 16．22(2)(2)2x y -+-=三、解答题 17．解：（1）sin tan 3737cos CC C=∴=，又22sin cos 1C C +=解得1cos 8C =±．tan 0C >，C ∴是锐角．1cos 8C ∴=．（2）52CB CA =，5cos 2ab C ∴=， 20ab ∴=．又9a b +=22281a ab b ∴++=． 2241a b ∴+=．2222cos 36c a b ab C ∴=+-=．6c ∴=．18．解：（1）由已知得1231327:(3)(4)3.2a a a a a a ++=⎧⎪⎨+++=⎪⎩，解得22a =．设数列{}n a 的公比为q ，由22a =，可得1322a a q q==，．又37S =，可知2227q q++=，即22520q q -+=，解得12122q q ==，．由题意得12q q >∴=，． 11a ∴=．故数列{}n a 的通项为12n n a -=．（2）由于31ln 12n n b a n +==，，，，由（1）得3312n n a +=3ln 23ln 2n n b n ∴==又13ln 2n n n b b +-={}n b ∴是等差数列．12n n T b b b ∴=+++1()2(3ln 23ln 2)23(1)ln 2.2n n b b n n n +=+=+=故3(1)ln 22n n n T +=． 19．解：设公司在甲电视台和乙电视台做广告的时间分别为x 分钟和y 分钟，总收益为z 元，由题意得3005002009000000.x y x y x y +⎧⎪+⎨⎪⎩≤，≤，≥，≥目标函数为30002000z x y =+．二元一次不等式组等价于3005290000.x y x y x y +⎧⎪+⎨⎪⎩≤，≤，≥，≥作出二元一次不等式组所表示的平面区域，即可行域．如图：100 200 300100200 300 400500yxlM作直线:300020000l x y +=，即320x y +=．平移直线l ，从图中可知，当直线l 过M 点时，目标函数取得最大值．联立30052900.x y x y +=⎧⎨+=⎩，解得100200x y ==，．∴点M 的坐标为(100200)，．max 30002000700000z x y ∴=+=（元）答：该公司在甲电视台做100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最大收益是70万元．20．（1）证明：在直四棱柱1111ABCD A BC D -中，连结1C D ，1DC DD =，∴四边形11DCC D 是正方形． 11DC DC ∴⊥．又AD DC ⊥，11AD DD DC DD D =⊥，⊥，AD ∴⊥平面11DCC D ，1D C ⊂平面11DCC D ，1AD DC ∴⊥．1AD DC ⊂，平面1ADC ，且AD DC D =⊥，1D C ∴⊥平面1ADC ，又1AC ⊂平面1ADC ，1DC AC ∴1⊥．（2）连结1AD ，连结AE ，设11AD A D M =，BCDA1A1D1C1BB CD A1A1D1C1BMEBD AE N =，连结MN ，平面1AD E平面1A BD MN =，要使1D E ∥平面1A BD ，须使1MN D E ∥，又M 是1AD 的中点．N ∴是AE 的中点．又易知ABN EDN △≌△， AB DE ∴=．即E 是DC 的中点．综上所述，当E 是DC 的中点时，可使1D E ∥平面1A BD ．21．证明：因为2()ln 0f x ax b x ab =+≠，，所以()f x 的定义域为(0)+∞，． ()f x '222b ax b ax x x+=+=．当0ab >时，如果00()0()a b f x f x '>>>，，，在(0)+∞，上单调递增；如果00()0()a b f x f x '<<<，，，在(0)+∞，上单调递减．所以当0ab >，函数()f x 没有极值点．当0ab <时，222()b b a x x a a f x x⎛⎫⎛⎫+--- ⎪⎪⎝⎭⎝⎭'=令()0f x '=，将1(0)2b x a =--∉+∞，（舍去），2(0)2bx a=-+∞，，当00a b ><，时，()()f x f x '，随x 的变化情况如下表：x02b a ⎛⎫- ⎪ ⎪⎝⎭， 2ba- 2ba ⎛⎫-+∞ ⎪ ⎪⎝⎭，()f x ' -0 +()f x极小值从上表可看出，函数()f x 有且只有一个极小值点，极小值为1ln 222b b b f a a ⎛⎫⎡⎤⎛⎫-=--- ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎝⎭．当00a b <>，时，()()f x f x '，随x 的变化情况如下表：x02b a ⎛⎫- ⎪ ⎪⎝⎭， 2ba- 2b a ⎛⎫-+∞ ⎪ ⎪⎝⎭， ()f x ' -0 +()f x极大值从上表可看出，函数()f x 有且只有一个极大值点，极大值为1ln 222b b b f a a ⎛⎫⎡⎤⎛⎫-=--- ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎝⎭．综上所述，当0ab >时，函数()f x 没有极值点；当0ab <时，若00a b ><，时，函数()f x 有且只有一个极小值点，极小值为1ln 22b b a ⎡⎤⎛⎫--- ⎪⎢⎥⎝⎭⎣⎦．若00a b <>，时，函数()f x 有且只有一个极大值点，极大值为1ln 22b b a ⎡⎤⎛⎫--- ⎪⎢⎥⎝⎭⎣⎦． 22．解：（1）由题意设椭圆的标准方程为22221(0)x y a b a b+=>>，由已知得：31a c a c +=-=，，222213a cb ac ==∴=-=，，∴椭圆的标准方程为22143x y +=．（2）设1122()()A x y B x y ，，，．联立22 1.43y kx m x y =+⎧⎪⎨+=⎪⎩，得 222(34)84(3)0k x mkx m +++-=，则22222212221226416(34)(3)03408344(3).34m k k m k m mk x x k m x x k ⎧⎪∆=-+->+->⎪⎪+=-⎨+⎪⎪-=⎪+⎩，即，，又22221212121223(4)()()()34m k y y kx m kx m k x x mk x x m k -=++=+++=+．因为以AB 为直径的圆过椭圆的右顶点(20)D ，，1AD BD k k ∴=-，即1212122y y x x =---．1212122()40y y x x x x ∴+-++=．2222223(4)4(3)1540343434m k m mk k k k --∴+++=+++． 2271640m mk k ∴++=．解得：12227k m k m =-=-，，且均满足22340k m +->．当12m k =-时，l 的方程(2)y k x =-，直线过点(20)，，与已知矛盾；当227k m =-时，l 的方程为27y k x ⎛⎫=- ⎪⎝⎭，直线过定点207⎛⎫⎪⎝⎭，．所以，直线l 过定点，定点坐标为207⎛⎫ ⎪⎝⎭，．。

2007年高考文科数学试题及参考答案(山东卷)

2007年普通高等学校招生全国统一考试（山东卷）文科数学第Ⅰ卷（共60分）一、选择题：本大题共12小题，每小题5分，共50分，在每小题给出的四个选项中，选择一个符合题目要求的选项．1．复数43i1+2i+的实部是（） A ．2- B ．2C ．3D ．4【答案】:B 【分析】：将原式(43)(12)25(12)(12)i i i i i +-=-+-，所以复数的实部为2。

2．已知集合11{11}|242x M N x x +⎧⎫=-=<<∈⎨⎬⎩⎭Z ，，，，则M N = （） A ．{11}-，B ．{0}C ．{1}-D ．{10}-，【答案】:C 【分析】：求{}1124,1,02x N xx Z +⎧⎫=<<∈=-⎨⎬⎩⎭。

3．下列几何体各自的三视图中，有且仅有两个视图相同的是（）A ．①② B．①③ C ．①④ D．②④【答案】D 【分析】：正方体的三视图都相同，而三棱台的三视图各不相同，正确答案为D 。

4．要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象（） A ．向右平移π6个单位 B ．向右平移π3个单位 C ．向左平移π3个单位D ．向左平移π6个单位【答案】A 【分析】：本题看似简单，必须注意到余弦函数是偶函数。

注意题中给出的函数不同名，而cos cos y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪33⎝⎭⎝⎭sin[()]sin()2x x πππ=--=+36，故应选A 。

①正方形②圆锥 ③三棱台 ④正四棱锥5．已知向量(1)(1)n n ==-，，，a b ，若2-a b 与b 垂直，则=a （） A ．1BC ．2D ．4【答案】:C 【分析】：2(3,)n -a b =，由2-a b 与b 垂直可得：2(3,)(1,)30n n n n ⋅-=-+=⇒= 2=a 。

6．给出下列三个等式：()()()()()()f xy f x f y f x y f x f y =++=，，()()()1()()f x f y f x y f x f y ++=-．下列函数中不满足其中任何一个等式的是（）A ．()3xf x =B ．()sin f x x =C ．2()log f x x =D ．()tan f x x =【答案】:B 【分析】：依据指、对数函数的性质可以发现A 满足()()()f x y f x f y +=，C 满足()()()f xy f x f y =+，而D 满足()()()1()()f x f y f x y f x f y ++=-，B 不满足其中任何一个等式.7．命题“对任意的3210x x x ∈-+R ，≤”的否定是（） A ．不存在3210x R x x ∈-+，≤ B ．存在3210x R x x ∈-+，≤ C ．存在3210x R x x ∈-+>，D ．对任意的3210x R x x ∈-+>，【答案】C 【分析】注意两点：（18．某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：每一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；……第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒的学生人数占全班人数的百分比为x ，成绩大于等于 15秒且小于17秒的学生人数为y ，则从频率分布直方图中可以分析出x 和y 分别为（）A ．0.935，B ．0.945，C ．0.135，D ．0.145，【答案】 A 【分析】：从频率分布直方图上可以看出1(0.060.04)0.9x =-+=，50(0.360.34)35y =⨯+=.秒9．设O 是坐标原点，F 是抛物线22(0)y px p =>的焦点，A 是抛物线上的一点，FA 与x 轴正向的夹角为60，则OA 为（） A ．214pBCpD ．1336p 【答案】B 【分析】：（利用圆锥曲线的第二定义）过A 作AD x ⊥轴于D ，令FD m =，则2FA m =，2p m m +=，m p =。

2007年高考文科数学试题及参考答案(山东卷)

10本科第四学期口语试题Topic group 1 Friendship1.Do you have many friends? How important are they to you?你有很多朋友吗?他们对你有多重要?2.What kind of people do you want to make friends with? Why?你想和什么样的人做朋友吗?为什么?3.How do you think “ A friend in need is a friend indeed”?你怎么认为“患难之交”?4.How do you make friends?你如何处朋友的?5.How can we keep friendship alive?我们在生活中怎样才能保持友谊?6.How valuable is friendship in a person’s life?人生中友谊是多么宝贵?7.“A friend without faults will never be found.” What’s your understanding?“没有缺点的朋友是永远找不到的。

“你有什么看法?8.“A life without a friend is a life without a sun.” Can we live without a friend?“人生在世无朋友,犹如生活无太阳。

“我们生活中可以没有朋友吗?Topic group 2 Cultural differences1.What do cultural differences mean? Can you give some examples?文化差异是什么意思?你能举些例子吗?2.How do people’s cultural backgrounds influence their way of thinking?人们的文化背景如何影响他们的思维方式的?3.What problems may be caused by our failure to recognize cultural differences?什么问题可能是使我们认识的文化有差异呢?4.How can failure to recognize cultural differences hinder communication?怎么可以不承认文化差异阻碍沟通吗?5.How can we deal with cultural differences?我们如何处理文化差异?6.What should we do before visiting other countries to avoid misunderstanding?以后我们访问其他国家如何避免（由于文化差异带来的）误解？我们应该做些什么?ment on the proverb “Do in Rome as the Romans do.”评论这个谚语“入乡随俗”。

(7年真题推荐)山东省2007-高考数学真题分类汇编立体几何

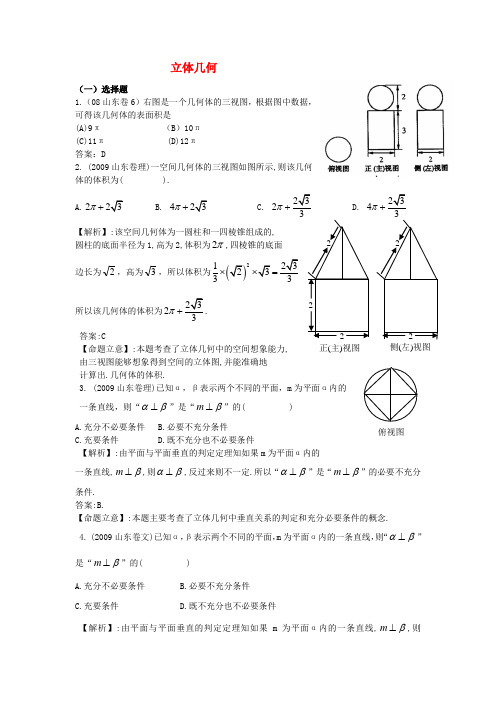
立体几何（一）选择题1.（08山东卷6）右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是(A)9π （B ）10π (C)11π (D)12π 答案：D2. (2009山东卷理)一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 23π+D. 4π+ 【解析】:该空间几何体为一圆柱和一四棱锥组成的, 圆柱的底面半径为1,高为2,体积为2π,四棱锥的底面边长为2，高为3，所以体积为2133⨯=所以该几何体的体积为23π+. 答案:C 【命题立意】:本题考查了立体几何中的空间想象能力,由三视图能够想象得到空间的立体图,并能准确地计算出.几何体的体积.3. (2009山东卷理)已知α，β表示两个不同的平面，m 为平面α内的一条直线，则“αβ⊥”是“m β⊥”的( ) A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】:由平面与平面垂直的判定定理知如果m 为平面α内的一条直线,m β⊥,则αβ⊥,反过来则不一定.所以“αβ⊥”是“m β⊥”的必要不充分条件. 答案:B.【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念. 4. (2009山东卷文)已知α，β表示两个不同的平面，m 为平面α内的一条直线，则“αβ⊥”是“m β⊥”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】:由平面与平面垂直的判定定理知如果m 为平面α内的一条直线,m β⊥,则侧(左)视图正(主)视图俯视图αβ⊥,反过来则不一定.所以“αβ⊥”是“m β⊥”的必要不充分条件.答案:B.【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念. 5、（2010山东数）在空间，下列命题正确的是 A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行【答案】D【解析】由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以得出答案。

2007-2015年高考文科数学山东卷

高考文科数学2007-2015年试题三角函数2007年 17．（本小题满分12分）在ABC △中，角A B C ，，的对边分别为tan a b c C =，，，（1）求cos C ；（2）若52CB CA =，且9a b +=，求c ．2008年(17)（本小题满分12分）已知函数())cos()(0,0)f x x x ωϕωϕϕπω=+-+<<>为偶函数，且函数y =f (x )图象的两相邻对称轴间的距离为.2π (Ⅰ)求()8f π的值; (Ⅱ)将函数y =f (x )的图象向右平移6π个单位后，得到函数y=g(x)的图象，求g (x )的单调递减区间.2009年17.(本小题满分12分)设函数f(x)=2)0(sin sin cos 2cos sin 2πϕϕϕ<<-+x x x 在π=x 处取最小值.(1) 求ϕ的值;(2) 在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C.2010年（17）（本小题满分12分）已知函数2()sin()cos cos(0)f x x x x πωωωω=-+＞的最小正周期为π．（Ⅰ）求ω的值．（Ⅱ）将函数()y f x =的图像上各点的横坐标缩短到原来的21，纵坐标不变，得到函数()y g x =的图像，求函数()g x 在区间0,16π⎡⎤⎢⎥⎣⎦上的最小值。

2011年 17．（本小题满分12分）在∆ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ．已知cos A-2cos C 2c-a=cos B b．（I ）求sin sin CA的值；（II ）若cosB=14，5b ABC 的周长为，求的长.2012年(17)(本小题满分12分)在△ABC 中，内角,,A B C 所对的边分别为,,a b c ，已知sin (tan tan )tan tan B A C A C +=. (Ⅰ)求证：,,a b c 成等比数列；(Ⅱ)若1,2a c ==，求△ABC 的面积S .2013年(18)(本小题满分12分)设函数2()sin cos (0)f x x x x ωωωω=->，且()y f x =的图象的一个对称中心到最近的对称轴的距离为，(Ⅰ)求ω的值(Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值2014年(17) （本小题满分12分）ABC ∆中，角A ，B ，C 所对的边分别为,,a b c . 已知3,cos 2a A B A π===+. （Ｉ）求b 的值；（II ）求ABC ∆的面积.2015年 16．（本小题满分12分）ABC ∆中，角C B,A,所对的边分别为c b a ,,，已知33cos =B ， 32,96)sin(==+ac B A ，求A sin 和c 的值.高考文科数学2007-2015年试题立体几何2007年 20．（本小题满分12分）如图，在直四棱柱1111ABCD A B C D -中，已知122DC DD AD AB ===，AD DC AB DC ⊥，∥．（1）求证：11DC AC ⊥；（2）设E 是DC 上一点，试确定E 的位置，使1D E ∥平面1A BD ，并说明理由．2008年（19）（本小题满分12分）如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，AB ∥DC ,△P AD 是等边三角形，已知BD ＝2AD =8, AB =2DC=（Ⅰ）设M 是PC 上的一点，证明：平面MBD ⊥平面P AD ; （Ⅱ）求四棱锥P -ABCD 的体积. 2009年18.（本小题满分12分）如图，在直四棱柱ABCD-A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB//CD ，AB=4, BC=CD=2, AA 1=2, E 、E 1分别是棱AD 、AA 1的中点（Ⅰ）设F 是棱AB 的中点,证明：直线EE 1//平面FCC 1；（Ⅱ）证明:平面D 1AC ⊥平面BB 1C 1C.BCDA1A1D1C1BEAB CFE 1A 1B 1C 1D 1D2010年（20）（本小题满分12分）在如图所示的几何体中，四边形ABCD 是正方形，BCD A MA 平面⊥,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点，且2MA PD AD ==．（Ⅰ）求证：平面PDC EFG 平面⊥; （Ⅱ）求三棱锥的体积之比与四棱锥ABCD P MAB P --．2011年 19．（本小题满分12分）如图，在四棱台1111ABCD A B C D -中，1DD ⊥平面ABCD ，底面ABCD 是平行四边形，AB=2AD ，11AD=A B ，BAD=∠60°（Ⅰ）证明：1AA BD ⊥；（Ⅱ）证明：11CC A BD ∥平面．2012年(19) (本小题满分12分)如图，几何体E ABCD -是四棱锥，△ABD 为正三角形，,CB CD EC BD =⊥.(Ⅰ)求证：BE DE =；(Ⅱ)若∠120BCD =︒，M 为线段AE 的中点，求证：DM ∥平面BEC .2013年(19)(本小题满分12分)如图，四棱锥P ABCD -中，,AB AC AB PA ⊥⊥,,2AB CD AB CD =∥,,,,,E F G M N 分别为,,,,PB AB BC PD PC 的中点(Ⅰ)求证：CE PAD ∥平面 (Ⅱ)求证：EFG EMN ⊥平面平面2014年(18)（本小题满分12分）如图，四棱锥P ABCD -中，1,,,,2AP PCD AD BC AB BC AD E F ⊥==平面∥分别为线段,AD PC 的中点.（Ｉ）求证：AP BEF ∥平面；（II ）求证：BE PAC ⊥平面.2015年 17．（本小题满分12分）如图，三棱台ABC -DEF 中，2,,AB DE G H =分别为BC AC ,的中点，（I ）求证：//BD 平面FGH ；（II ）若BC AB BC CF ⊥⊥,，求证：平面⊥BCD 平面FGH .高考文科数学2007-2015年试题概率2007年19．（本小题满分12分）本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司事来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？2008年（18）（本小题满分12分）现有8名奥运会志愿者，其中志愿者A1、A2、A3通晓日语，B1、B2、B3通晓俄语，C1、C2通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组.（Ⅰ）求A1被选中的概率;（Ⅱ）求B1和C1不全被选中的概率.2009年19. （本小题满分12分）一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.（1）求z的值（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;（3）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6,8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.2010年（19）（本小题满分12分）一个袋中装有四个形状大小完全相同的球，球的编号分别为1,2,3,4，（Ⅰ）从袋中随机取出两个球，求取出的球的编号之和不大于4的概率；（Ⅱ）先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求2n m ＜的概率。

2007-2015山东卷高考数学文科专题真题-立体几何’

(2007—2015)9年山东高考数学分类汇总(文)

2007年高考“立体几何”题--(文科)高考数学试题全解

2007年高考“立体几何”题

数学高考真题-2015年山东卷文科

2015年高考试题汇编数学文-立体几何

2007年高考数学试题汇编——立体几何(三)

2015年山东省高考数学试卷(文科)答案与解析

2015年高考数学（文科）真题分类汇编G单元立体几何

2007年高考真题试卷山东卷数学文科参考答案

2007年高考文科数学试题及参考答案(山东卷)

2007年高考文科数学试题及参考答案(山东卷)

(7年真题推荐)山东省2007-高考数学 真题分类汇编 立体几何

2007-2015年高考文科数学山东卷

(7年真题推荐)山东省2007-高考数学真题分类汇编立体几何