汽车半主动悬架的自适应LQG控制

合集下载

车辆主动悬架LQG控制器的设计与仿真分析16

112 路面模型的建立
的方法是让白噪声通过一成形滤波器[ 1 ] , 所以前、后车轮受到的路面激励为 α x 9 = - 2Π f 0 x 9 + 2Π α x 10 = - 2Π f 0 x 10 + 2Π
G 0 v 0w G 0 v 0w
1
在分析悬架系统的动态特性时, 路面模型的建立是一个重要部分。这里, 生成随机路面不平度轮廓
Abstract A 1 2 ca r m odel and a road inp u t m odel w ere estab lished ba sed on the op t im a l con t ro l theo ry w h ich w a s u sed to design a LQ G con t ro ller of au tom ob ile act ive su sp en sion. A system sim u la t ion m odel ba sed on M a t lab Sim u link environm en t w a s bu ilt and u sed fo r sim u la t ion. Fou r p erfo rm 2 ance indexes, body accelera t ion, p itch ang le accelera t ion, su sp en sion dynam ic t ravel and t ire dyn 2 am ic deflect ion, w ere com p a red. T he sim u la t ion resu lt s dem on st ra ted tha t the act ive su sp en sion w ith a LQ G con t ro ller cou ld im p rove au tom ob ile rid ing com fo rt p erfo rm ance eno rm ou sly. Key words V eh icle, A ct ive su sp en sion, LQ G con t ro ller, Sim u la t ion

基于层次分析法的半主动悬架LQG控制器的设计

Internal Combustion Engine & Parts
· 63 ·
基于层次分析法的半主动悬架 LQG 控制器的设计
林爱桢
（重庆交通大学机电与车辆工程学院，重庆 400074）
摘要院采用滤波白噪声生成路面时域模型袁建立了 5 自由度半主动悬架模型袁并应用最优控制理论设计了车辆半主动悬架的 LQG 控制器袁采用层次分析法确定各性能指标的加权系数袁在 MATLAB/simulink 环境下建立半主动悬架进行仿真遥仿真结果表明袁通过对相关的系数进行加权化处理能够较好的改善车辆悬架的振动特性袁有利于提高车辆的乘坐舒适性遥
（4）
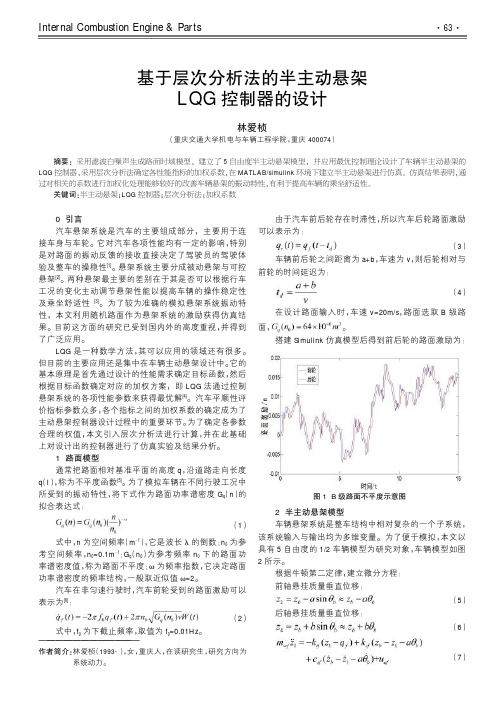
在设计路面输入时，车速 v=20m/s，路面选取 B 级路
面，
。
搭建 Simulink 仿真模型后得到前后轮的路面激励为：
图 1 B 级路面不平度示意图
2 半主动悬架模型车辆悬架系统是整车结构中相对复杂的一个子系统，该系统输入与输出均为多维变量。为了便于模拟，本文以具有 5 自由度的 1/2 车辆模型为研究对象，车辆模型如图 2 所示。根据牛顿第二定律，建立微分方程：前轴悬挂质量垂直位移：
关键词院半主动悬架曰LQG 控制器曰层次分析法曰加权系数
0 引言汽车悬架系统是汽车的主要组成部分，主要用于连接车身与车轮。它对汽车各项性能均有一定的影响，特别是对路面的振动反馈的接收直接决定了驾驶员的驾驶体验及整车的操稳性[1]。悬架系统主要分成被动悬架与可控悬架[2]。两种悬架最主要的差别在于其是否可以根据行车工况的变化主动调节悬架性能以提高车辆的操作稳定性及乘坐舒适性 [3]。为了较为准确的模拟悬架系统振动特性，本文利用随机路面作为悬架系统的激励获得仿真结果。目前这方面的研究已受到国内外的高度重视，并得到了广泛应用。 LQG 是一种数学方法，其可以应用的领域还有很多。但目前的主要应用还是集中在车辆主动悬架设计中。它的基本原理是首先通过设计的性能需求确定目标函数，然后根据目标函数确定对应的加权方案，即 LQG 法通过控制悬架系统的各项性能参数来获得最优解[4]。汽车平顺性评价指标参数众多，各个指标之间的加权系数的确定成为了主动悬架控制器设计过程中的重要环节。为了确定各参数合理的权值，本文引入层次分析法进行计算，并在此基础上对设计出的控制器进行了仿真实验及结果分析。 1 路面模型通常把路面相对基准平面的高度 q，沿道路走向长度 q（I），称为不平度函数[5]。为了模拟车辆在不同行驶工况中所受到的振动特性，将下式作为路面功率谱密度 G（q n）的拟合表达式：

基于遗传算法的汽车主动悬架LQG控制器的设计

㊀第２５卷㊀第５期厦门理工学院学报Ｖｏｌ．２５㊀Ｎｏ．５㊀㊀２０１７年１０月ＪｏｕｒｎａｌｏｆＸｉａｍｅｎＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙＯｃｔ．２０１７㊀㊀［收稿日期］２０１７－０８－０５㊀㊀㊀㊀［修回日期］２０１７－１０－２０［基金项目］福建警察学院青年课题资助项目（ＱＮ１６０６）［作者简介］陈丽静（１９８９－），女，讲师，硕士，研究方向为汽车悬架优化设计分析，Ｅ⁃ｍａｉｌ：ｆｊｃｈｅｎｌｉｊｉｎｇ＠１６３ｃｏｍ㊂基于遗传算法的汽车主动悬架ＬＱＧ控制器的设计陈丽静（福建警察学院治安系，福建福州３５０００７）［摘㊀要］采用合适种群规模遗传算法，寻求在一定范围内满足车身垂向加速度㊁轮胎垂向变形量㊁悬架动挠度均方根值相对于被动悬架都降低的最优加权系数，设计了基于遗传算法的汽车主动悬架线性ＬＱＧ控制器㊂Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ仿真实验表明：采用合适种群规模遗传算法选取最优加权系数的用时数只需常规编程的１１７％；采用最优加权系数的ＬＱＧ控制器的汽车主动悬架，可以在不影响汽车操纵稳定性和悬架行程的前提下，很好地提高汽车的行驶平顺性㊂［关键词］汽车主动悬架；ＬＱＧ控制器；遗传算法；加权系数［中图分类号］Ｕ４６３３３㊀［文献标志码］Ａ㊀［文章编号］１６７３－４４３２（２０１７）０５－００１２－０５车辆悬架系统在很大程度上决定着整车的行驶平顺性㊁操纵稳定性与通过性，对减振效果等多项使用性能都有着很大影响［１］㊂主动悬架能够根据实际路面的激励作用实时地对控制力进行调节，从而减小地面对汽车的冲击，起到减震和缓冲的作用［２］㊂赵文娟等［３］通过研究表明具有ＬＱＧ控制器的主动悬架对汽车行驶平顺性改善有良好的效果㊂大部分学者对ＬＱＧ控制器进行设计研究时，往往借助经验确定加权系数，该方法虽然可以降低车身垂向加速度，但同时会增大轮胎变形量，影响汽车操纵稳定性㊂本文通过遗传算法和编程方法寻求在一定范围内满足车身垂向加速度㊁轮胎垂向变形量㊁悬架动挠度均方根值相对于被动悬架都降低的最优加权系数，设计基于遗传算法的汽车主动悬架ＬＱＧ控制器，并借助Ｍａｔｌａｂ进行车辆１／４悬架模型控制仿真，验证了主动悬架ＬＱＧ控制器的准确性㊂１㊀１／４主动悬架模型Z 2m 2Z 1Z 0C 1C 2m 1K 1K 2F图11/4悬架模型Fig.11/4suspension model２自由度悬架模型较为简单，且能较好地反映车身的垂向振动情况，而车身垂向振动又能很好地阐述汽车的行驶平顺性，因此采用１／４悬架模型，如图１所示㊂根据牛顿第二定律，可知主动悬架的动力学方程为ｍ２Ｚ㊆２＝－Ｋ２（Ｚ２－Ｚ１）－Ｃ２Ｚ㊃２－Ｚ㊃１）＋Ｆ，ｍ１Ｚ㊆１＝Ｋ２（Ｚ２－Ｚ１）＋Ｃ２（Ｚ㊃２－Ｚ㊃１）－Ｆ－Ｋ１（Ｚ１－Ｚ０）－Ｃ１（Ｚ㊃１－Ｚ㊃０）㊂{（１）式（１）中：ｍ１为非簧载质量；ｍ２为簧载质量；Ｋ１为轮胎垂向刚度；Ｋ２为等效弹簧刚度；Ｃ１为轮胎等效阻尼系数；Ｃ２为减振器等效阻尼系数；Ｚ０为路面垂向位移；Ｚ１为轮胎垂向位移；Ｚ２为车身垂向位移㊂在对汽车进行振动分析时，路面不平度表达式常采用路面功率谱密度，路面输入采用白噪声模型［４］，即：̇ｑ（ｔ）＝－２πｎ００ｕｑ（ｔ）＋２πｎ０Ｇｑ（ｎ０）ｕＷ（ｔ）㊂（２）式（２）中：ｎ００为下截止空间频率，ｎ００＝０．０１１ｍ－１；ｑ（ｔ）为路面随机高程㊀第５期陈丽静：基于遗传算法的汽车主动悬架ＬＱＧ控制器的设计位移；Ｇｑ（ｎ０）为路面不平度系数；Ｗ（ｔ）为均值为零的高斯白噪声㊂２㊀悬架ＬＱＧ控制器设计２１㊀ＬＱＧ控制器模型的建立结合式（１），选取状态变量Ｘ＝［Ｚ２Ｚ㊃２Ｚ１Ｚ㊃１］，控制输入Ｕ＝Ｆ，干扰变量Ｗ＝［Ｚ０Ｚ㊃０］，将模型整理成包含干扰量的矩阵形式：Ｘ㊃＝ＡＸ＋Ｂ１Ｕ＋Ｂ２Ｗ㊂（３）因此Ａ＝０１００－Ｋ２ｍ２－Ｃ２ｍ２Ｋ２ｍ２Ｃ２ｍ２０００１Ｋ２ｍ１Ｃ２ｍ１－（Ｋ１＋Ｋ２)ｍ１－（Ｃ１＋Ｃ２)ｍ１éëêêêêêêêùûúúúúúúú，Ｂ１＝０１ｍ２０－１ｍ１[]Ｔ，Ｂ２＝０００Ｋ１ｍ１０００Ｃ１ｍ１éëêêêêùûúúúúＴ㊂㊀㊀ＬＱＧ控制器就是寻求控制向量Ｕ，使得目标函数ＪＡ达到极小，从而实现最优控制㊂性能指标ＪＡ为车身垂直加速度㊁轮胎动变形以及悬架动挠度的加权平方和在时域Ｔ内的积分值［３］，即：ＪＡ＝ｌｉｍ１ＴʏＴ０｛ρ１Ｚ㊆２２＋ρ２（Ｚ１－Ｚ０）２＋ρ３（Ｚ２－Ｚ１）２｝ｄｔ，（４）式（４）中：ρ１为车身垂向加速度加权系数；ρ２为轮胎变形量加权系数；ρ３为悬架动挠度加权系数㊂将式（４）整理成标准的二次型为ＪＡ＝ｌｉｍ１ＴʏＴ０（ＸＴＱＸ＋ＵＴＲＵ＋２ＸＴＮＵ＋２ＸＴＨＷ＋ＷＴＴＷ）ｄｔ㊂（５）因此Ｑ＝ρ１Ａ（２，：）ＴＡ（２，：）＋ρ２ａＴ１１ａ１１＋ρ３ａＴ２２ａ２２，Ｒ＝ρ１（１ｍ２）２，Ｎ＝ρ１ｍ２Ａ（２，：）Ｔ㊂其中Ａ（２，：）表示由矩阵Ａ第二行组成的１ˑ４矩阵，ａ１１＝［０，０，１，０］，ａ２２＝［１，０，－１，０］㊂为选取合适的主动悬架ＬＱＧ控制器，采用ｌｑｒ函数进行求取，可以简单迅速并可借助Ｍａｔｌａｂ实现仿真获得较好的性能指标，Ｍａｔｌａｂ中的ｌｑｒ函数如式（６）所示㊂［Ｋ，Ｓ，Ｅ］＝ｌｑｒ（Ａ，Ｂ１，Ｑ，Ｒ，Ｎ）㊂（６）㊀㊀因此，控制输入Ｕ可以转化为与状态变量Ｘ相关的表达式，即Ｕ＝－ＫＸ，可将式（３）转为Ｘ㊃＝（Ａ－Ｂ１Ｋ）Ｘ＋Ｂ２Ｗ㊂２２㊀加权系数的选取在主动悬架ＬＱＧ控制器设计中，加权系数的选取表明了设计者对悬架性能的倾向㊂将加权系数㊃３１㊃厦门理工学院学报２０１７年作为设计变量ｘ＝（ρ１，ρ２，ρ３）Ｔ，将有控制主动悬架汽车的车身垂向加速度㊁悬架动挠度㊁轮胎垂向变形量均方根与无控制的被动悬架汽车的比值之和作为目标函数，即ｆ（ｘ）＝ＲＭＳ（Ｚ㊆２ｚｄ）ＲＭＳ（Ｚ㊆２ｂｄ）＋ＲＭＳ（（Ｚ１－Ｚ０）ｚｄ）ＲＭＳ（（Ｚ１－Ｚ０）ｂｄ）＋ＲＭＳ（（Ｚ２－Ｚ１）ｚｄ）ＲＭＳ（（Ｚ２－Ｚ１）ｂｄ）㊂（７）式（７）中：ＲＭＳ（Ｚ㊆２ｚｄ），ＲＭＳ（Ｚ㊆２ｂｄ）分别为主㊁被动悬架的车身垂向加速度均方根值；ＲＭＳ（（Ｚ１－Ｚ０）ｚｄ），ＲＭＳ（（Ｚ１－Ｚ０）ｂｄ）分别为主㊁被动悬架轮胎垂向变形量的均方根值；ＲＭＳ（（Ｚ２－Ｚ１）ｚｄ），ＲＭＳ（（Ｚ２－Ｚ１）ｂｄ）分别为主㊁被动悬架动挠度均方根值㊂为了保证汽车更好的行驶平顺性㊁操纵稳定性，还需保证主动悬架的车身垂向加速度㊁轮胎垂向变形量和悬架动挠度均方根值均小于被动悬架㊂２２１㊀常规编程方法参考文献［５］，经过多次仿真，在ρ１ɪ［０，１］，ρ２ɪ［１０００，１５００００］，ρ３ɪ［１００，１００００］经过编程可求得满足车身垂向加速度㊁轮胎垂向变形量㊁悬架动挠度均方根值相对于被动悬架都降低情况下的ｆ（ｘ）最小值，加权系数选取流程图如图２所示㊂输入初始值P 1，P 2，P 3ρ1=P 1，ρ2=P 2，ρ3=P 3求出f （x ）P =f （ρ1，ρ2，ρ3）P =j ，ρ1=P 1ρ2=P 2，ρ3=P 3P 1<1P 2<150000P 3<100000P 3=100否否是是是是否否P 3=P 3+100输出ρ1，ρ2，ρ3P 1=P 1+0.1P 2=1000P 2=P 2+1000求出j j =f （P 1，P 2，P 3）P >j车身垂向加速度、轮胎垂向变形量、悬架动挠度都小于被动悬架图2加权系数选取流程图Fig.2Flowchart of weighing parameter selection２２２㊀遗传算法编程方法借助Ｍａｔｌａｂ自带的ｇａ函数可以快速寻找到最佳的自变量，其语法格式如式８所示㊂［ｘ，ｆｖａｌ］＝ｇａ（＠ｆｉｔｎｅｓｓｆｕｎ，ｎｖａｒｓ，ｏｐｔｉｏｎｓ）㊂（８）式（８）中：ｘ为经遗传进化后自变量最佳染色体返回值；ｆｖａｌ为最佳染色体适应值；ｆｉｔｎｅｓｓｆｕｎ为适应度句柄函数；ｎｖａｒｓ为自变量个数㊂３㊀模拟仿真某辆轿车的悬架具体参数为：ｍ１＝５５ｋｇ，ｍ２＝３３７ｋｇ，Ｋ１＝２４５０００Ｎ／ｍ，Ｋ２＝１６０００Ｎ／ｍ，Ｃ１＝㊃４１㊃㊀第５期陈丽静：基于遗传算法的汽车主动悬架ＬＱＧ控制器的设计３０１２Ｎ㊃ｓ／ｍ，Ｃ２＝１３８５．４Ｎ㊃ｓ／ｍ㊂采用Ｍａｔｌａｂ模拟该车以ｕ＝１２ｍ／ｓ在Ｃ级路面行驶３０ｓ，仿真模型如图３所示㊂图3主被动悬架仿真模型Fig.3Model of active and passive suspension simulationx ′=Ax +Bu y =Cx +Du主动悬架z 2zz 2zz 2jzz 21zz 10z 2jz 21z 10x ′=Ax +Bu y =Cx +Du被动悬架z 01[t,x ]d 11s d 2From workspaceGainIntegrator gain1To workspace12To workspaceTo workspace1To workspace2To workspace3To workspace4To workspace5To workspace6To workspace7+-在其他条件不变的前提下，遗传算法根据种群规模的不同仿真用时有所不同，基本成正比关系，具体如表１所示㊂表１㊀不同种群个体数目仿真对比Ｔａｂｌｅ１㊀Ｓｉｍｕｌａｔｉｏｎｉｎｄｉｆｆｅｒｅｎｔｐｏｐｕｌａｔｉｏｎｎｕｍｂｅｒｓｃｏｍｐａｒｅｄｓ种群规模ρ１ρ２／１０５ρ３／１０４仿真用时／ｓＲＭＳ（Ｚ㊆２ｚｄ）／ｍ㊃ｓ－２ＲＭＳ（（Ｚ１－Ｚ０）ｚｄ）／ｍｍＲＭＳ（（Ｚ２－Ｚ１）ｚｄ）／ｍｍｆ（ｘ）２００．５１４２０．７３２８０．７７６６４２００．５１１４６．９２．１２．４８２０５００．４５０６０．６４２００．６５８３１０４３０．５１１３６．９２．１２．４８１５１０００．５９８３０．８５１４０．８７０６２１４６０．５１０９６．９２．１２．４８１３１５００．４０９００．５８１７０．６０１４３３７１０．５１０７６．９２．１２．４８１２２０００．５４５６０．７７４００．８２１０４７１４０．５０９７６．９２．１２．４８１２从表１可以看出，随种群个体数目的增加，主动悬架的车身垂向加速度均方根值有微小下降，但相差甚微，轮胎垂向变形量㊁悬架动挠度均方根值基本没有差别㊂常规算法需花约１０ｈ仿真，当ρ１＝０．５，ρ２＝０．７１ˑ１０５，ρ３＝０．７５ˑ１０４时车身垂向加速度㊁轮胎垂向变形量和悬架动挠度都小于被动悬架，且目标函数ｆ（ｘ）最小；为更快产生响应，发挥主动悬架作用，现对采用种群规模为２０的遗传算法与采用常规算法产生的加权系数ＬＱＧ主动悬架进行对比，如表２所示㊂表２㊀主被动悬架对比Ｔａｂｌｅ２㊀Ａｃｔｉｖｅａｎｄｐａｓｓｉｖｅｓｕｓｐｅｎｓｉｏｎｃｏｍｐａｒｅｄ性能指标主动悬架遗传算法常规算法被动悬架车身垂向加速度均方根值／ｍ㊃ｓ－２０．５１１４０．５１０１０．７９５７悬架动挠度均方根值／ｍｍ６．９６．９８．２轮胎垂向变形量均方根值／ｍｍ２．１２．１２．１ｆ（ｘ）２．４８２０２．４８１３仿真用时／ｓ４２０３６０００由表２可以看出，采用遗传算法计算的加权系数虽然与常规计算的加权系数有些微差距，但是经计算后的车身垂向加速度均方根值㊁悬架动扰度均方根值㊁轮胎垂向变形量均方根值基本一致；相较于被动悬架，都有较大的改善，主动悬架的车身垂向加速度较于被动悬架下降了３５％以上㊂对主被动悬架的车身垂向加速度如果直接采用加速度对比图的话，会因数据量较大，难以区分，㊃５１㊃厦门理工学院学报２０１７年频率/Hz51525351020300.070.060.050.040.030.020.010车身垂向加速度功率谱密度/（m ·s -2）2·H z -1被动悬架主动悬架（遗传算法）被动悬架（常规算法）图4车身垂向加速度功率谱密度对比图Fig.4Comparison of vertical acceleration power spectral density因此采用功率谱密度图进行分析㊂在对悬架进行在随机路面上的振动仿真过程中，路面空间频率只需能够覆盖车辆主要部件的固有频率即可，一般取值范围为０．０１１２．８３ｍ－１㊂因此当汽车以１２ｍ／ｓ的速度在Ｃ级路面行驶时，其等效的时间频率范围为０１３２３３９６Ｈｚ㊂被动悬架与主动悬架模型车身垂向加速度功率谱密度对比图如图４所示㊂从图４可以看出，主动悬架车身垂向加速度功率谱密度都小于被动悬架，采用遗传算法和常规算法计算加权系数的主动悬架车身垂向加速度功率谱密度基本一致㊂４㊀结论１）在相对于被动悬架的车身垂向加速度和悬架动扰度以及轮胎垂向变形量均方根值的改善程度基本一致的前提下，采用合适种群规模遗传算法可以快速计算出主动悬架ＬＱＧ的加权系数，计算时间约为常规算法的１１７％；２）采用最优加权系数的ＬＱＧ控制器的汽车主动悬架，可以在不影响汽车操纵稳定性和悬架行程的前提下，很好地提高汽车的行驶平顺性㊂［参考文献］［１］唐传茵，马岩，赵广耀，等．基于模糊控制策略的车辆主动悬架研究［Ｊ］．动力学与控制学报，２０１５，１３（３）：２１０⁃２１４．［２］张春友，张志山，赵宏丽．汽车主动悬架动态特性分析与平顺性分析［Ｊ］．中国农机化学报，２０１５，３６（２）：１７６⁃１７９．［３］赵文娟，赵丹平，瞿育文．基于Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ的主动悬架仿真研究［Ｊ］．现代制造技术与装备，２０１５（４）：１０⁃１３．［４］陈杰平，陈无畏，祝辉，等．基于Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ的随机路面建模与不平度仿真［Ｊ］．农业机械学报，２０１０，４１（３）：１１⁃１５．［５］陈双，宗长富．车辆主动悬架的遗传粒子群ＬＱＧ控制方法［Ｊ］．汽车工程，２０１５，３７（２）：１８９⁃１９３．ＤｅｓｉｇｎｏｆａｎＡｃｔｉｖｅＳｕｓｐｅｎｓｉｏｎＬＱＧＣｏｎｔｒｏｌｌｅｒＢａｓｅｄｏｎＧｅｎｅｔｉｃＡｌｇｏｒｉｔｈｍＣＨＥＮＬｉｊｉｎｇＤｅｐａｒｔｍｅｎｔｏｆＰｕｂｌｉｃＳｅｃｕｒｉｔｙＦｕｊｉａｎＰｏｌｉｃｅＣｏｌｌｅｇｅＦｕｚｈｏｕ３５０００７ＣｈｉｎａＡｂｓｔｒａｃｔＡｎａｃｔｉｖｅｓｕｓｐｅｎｓｉｏｎＬＱＧｃｏｎｔｒｏｌｌｅｒｗａｓｄｅｓｉｇｎｅｄｂａｓｅｄｏｎｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｗｉｔｈａｐｐｒｏｐｒｉａｔｅｐｏｐｕｌａｔｉｏｎｓｉｚｅｂｙｏｐｔｉｍａｌｗｅｉｇｈｉｎｇｐａｒａｍｅｔｅｒｓｗｈｉｃｈｈａｄｗｉｔｈｉｎａｃｅｒｔａｉｎｒａｎｇｅｒｅｄｕｃｅｄｖｅｒｔｉｃａｌａｃｃｅｌｅｒａｔｉｏｎａｎｄｖｅｒｔｉｃａｌｔｉｒｅｄｅｆｏｒｍａｔｉｏｎａｎｄｔｈｅｒｏｏｔｍｅａｎｓｑｕａｒｅｏｆｓｕｓｐｅｎｓｉｏｎｄｅｆｌｅｃｔｉｏｎｔｏｔｈｅｐａｓｓｉｖｅｓｕｓｐｅｎｓｉｏｎ．ＲｅｓｕｌｔｓｏｆＭａｔｌａｂ／Ｓｉｍｕｌｉｎｋｓｉｍｕｌａｔｉｏｎｅｘｐｅｒｉｍｅｎｔｓｈｏｗｔｈａｔｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｗｉｔｈａｐｐｒｏｐｒｉａｔｅｐｏｐｕｌａｔｉｏｎｓｉｚｅｓｐｅｎｄｓｏｎｌｙａｂｏｕｔ１．１７％ｏｆｔｈｅｔｉｍｅｂｙｃｏｎｖｅｎｔｉｏｎａｌｐｒｏｇｒａｍｍｉｎｇｉｎｓｅｌｅｃｔｉｎｇｏｐｔｉｍａｌｗｅｉｇｈｔｉｎｇｐａｒａｍｅｔｅｒｓａｎｄａｃｔｉｖｅｓｕｓｐｅｎｓｉｏｎｗｉｔｈＬＱＧｃｏｎｔｒｏｌｌｅｒｗｉｔｈｏｐｔｉｍａｌｗｅｉｇｈｔｉｎｇｐａｒａｍｅｔｅｒｓｃａｎｉｍｐｒｏｖｅｔｈｅｒｉｄｅｃｏｍｆｏｒｔｏｆｔｈｅｖｅｈｉｃｌｅｗｉｔｈｏｕｔａｆｆｅｃｔｉｎｇｔｈｅｓｔａｂｉｌｉｔｙｏｆｔｈｅｖｅｈｉｃｌｅａｎｄｓｕｓｐｅｎｓｉｏｎｄｅｆｌｅｃｔｉｏｎ．ＫｅｙｗｏｒｄｓａｃｔｉｖｅｓｕｓｐｅｎｓｉｏｎＬＱＧｃｏｎｔｒｏｌｌｅｒｇｅｎｅｔｉｃａｌｇｏｒｉｔｈｍｗｅｉｇｈｉｎｇｐａｒａｍｅｔｅｒ（责任编辑㊀李㊀宁）㊃６１㊃。

基于AHP的车辆主动悬架LQG控制器设计

振第３２卷第２期
动
与
冲
பைடு நூலகம்击
ＪＯＵＲＮＡＬＯＦＶＩＢＲＡＴＩＯＮＡＮＤＳＨＯＣＫ
基于ＡＨＰ的车辆主动悬架ＬＱＧ控制器设计
罗鑫源，杨世文
（中北大学机电工程学院，太原０３００５１）
摘要：基于层次分析法（ＡＨＰ）设计了一种能够降低车身加速度（ＢＡ）、悬架动行程（ＳＷＳ）和轮胎动位移（ＤＴＤ）
ａｎｄｄｙｎａｍｉｃｔｙｒｅｄｉｓｐｌａｃｅｍｅｎｔ（ＤＴＤ）．Ａ２－ＤＯＦｄｙｎａｍｉｃｍｏｄｅｌｏｆａ１／４ｖｅｈｉｃｌｅｐａｓｓｉｖｅａｎｄａｃｔｉｖｅｓｕｓｐｅｎｓｉｏｎｗａｓｉｆｒｓｔｌｙ
ＬＵＯＸｉｎ — ｙｕａｎ，ＹＡＮＧＳｈｉ — ｗｅｎ
（ＣｏｌｌｅｇｅｏｆＭｅｃｈａｔｒｏｎｉｃＥｎｇｉｎｅｅｒｉｎｇ，ＮｏＡｈＵｎｉｖｅｒｓｉｔｙｏｆＣｈｉｎａ，Ｔａｉｙｕａｎ０３００５１，Ｃｈｉｎａ）
的车辆主动悬架线性最优（ＬＱＧ）控制器。首先建立了２自由度１／４车辆主被动悬架动力学模型；然后采用ＡＨＰ确定了
悬架各性能评价指标的加权系数并利用最优控制理论设计了车辆主动悬架控制器；最后在Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ环境下进行

LQG控制方法

1.主动悬架控制模型的建立车辆悬架系统是一个多输入多输出的系统。

它具有整车、1／2车辆和1／4车辆模型。

根据本文研究的性质和为了研究的方便，以车辆1／4模型作为研究对象(图1)，它是一个二自由度的线性系统。

根据图1所示，主动悬架系统的运动方程为式中：M b为1／4车身质量；M w为车轮质量；U为控制器产生的作用力；K t为轮胎刚度；x0为路面的扰动输入；x1为车轮垂直位移量；x。

2为车身垂直加速度。

其状态方程与输出方程可写成如下形式：取状态变量X=(x2-x1，x。

2，x0—x1，x。

1)T作为状态变量，把系统运动方程写为矩阵形式：选取Y=[x。

2，x2-x1，x0—x1，k t(x0—x1)]T为输出变量。

这样主要考虑研究车辆平顺性时比较方便，故选取车身垂直加速度x。

2、悬架的动扰度x2-x1、车轮的跳动量x0—x1和车轮动载荷k t(x0—x1)为输出变量。

故得输出矩阵根据现代控制理论，对系统方程寻求控制U使二次型目标函数取最小值的问题就是二次型最优控制问题。

在悬架的设计中，必须综合考虑轮胎的接地性、车身的加速度及悬架的动挠度。

线性二次型最优控制可以借助加权系数，对各种性能指标进行综合考虑，取，为LQG控制器的性能指标。

在此三项的平方和中，以车身加速度x。

2为基准，系数取1，q1，q2的值是相对x。

2来说的，分别是轮胎动位移和悬架动挠度的加权系数。

根据最优控制理论，式(5)写成标准二次型的形式式中：Q为状态变量的加权矩阵，R为控制变量的加权矩阵。

其中这里，q l和q2为加权系数。

矩阵Q的大小与轮胎动位移加权系数q1和悬架动挠度加权系数q2有关，q l和q2取不同的值就意味着对不同的分量加不同的加权系数。

当某个分量要特别约束时，我们就可以增大此分量的权系数，若此分量对所要研究的问题影响无足轻重时，则可以设它的加权系数为零。

因此，正确选取加权矩阵的值是十分重要的，不同的加权系数对系统的特性具有不同的影响。

车辆主动悬架LQG控制器的设计与仿真分析(1)

W
BN5"FC5
W
W
W
W
W
W
W
W A#c@W W
eW
W
W
W
W
W
W
W
W A#c@Wg
h i W !"F4 W AL"IJ W A!"FC@ W W W W a
]6 W !"F4 W 8"IJ W W W A!"FC5 W W
l dW W W W W W W W #c jWkW
_6
eW W W W W W W W
/ 主动悬架系统和控制系统的建立
/0/ 悬架系统的建立车辆悬架系统是一个多输入多输出系统-为了
研究的方便以及更好地与车辆行驶的情况相吻合本文以具有 #自由度的 $,!车辆模型为研究对象车辆模型如图 $所示=
前轴悬挂质量垂向位移
‘w12‘3]!7:45‘3]4
小)即可以取 @&,@(3@F,@K3@L,@M)在性能指标中以 ABC!和 ABCE为基准)即取 @&3@(均为 &.由最优控制理论)
把式 GLJR GQJ写成标准二次型形式 )即整理成
> 4,
89:
;< =
& ;
;
GTUVTD WUXWD (TUYWJO+
"
得
^ @FD@K " IZ@FD[@K "
W
W fa
l #c jWkWg
输出矩阵为 m6n[7o^X取矩阵 n为 !Wp !W的单的方法是让白噪声通过一成形滤波器h!iX所以前S后

汽车底盘悬挂系统的主动与半主动控制

汽车底盘悬挂系统的主动与半主动控制汽车底盘悬挂系统是汽车重要的组成部分，负责支撑和缓解车身震动，保证车辆稳定性和乘坐舒适性。

随着科技的不断进步，汽车底盘悬挂系统的控制方式也在不断创新，主动和半主动控制成为了现代汽车悬挂系统的重要发展方向。

主动悬挂系统是指通过传感器实时监测路面情况和车辆动态，通过悬挂系统的控制单元主动调节悬挂刚度、减震力度等参数，以优化车辆的悬挂性能。

主动悬挂系统可以根据不同路况和行驶状态主动作出调整，提高车辆的操控性和舒适性。

采用主动悬挂系统的车辆可以更好地适应复杂路况，减少车身的侧倾和颠簸感，提升行驶平稳性。

主动悬挂系统的工作原理是利用电液控制技术，实现悬挂系统的快速响应和精准控制，从而提升车辆悬挂性能。

半主动悬挂系统是介于传统被动悬挂系统和主动悬挂系统之间的一种系统。

半主动悬挂系统同样可以根据路况和行驶状态调节悬挂参数，但是其调节范围和速度相对主动悬挂系统较小，无法实现完全主动的悬挂调节。

半主动悬挂系统采用电磁阻尼器、气压悬挂等技术，通过主动改变阻尼力和气压来调节悬挂刚度和减震效果，提高车辆悬挂性能。

半主动悬挂系统的优点在于成本较低、结构简单，对悬挂系统的改造和升级相对容易，因此在许多中高端车型中得到了广泛应用。

综上所述，主动和半主动悬挂系统在汽车底盘悬挂领域具有重要的应用前景。

随着汽车科技的不断发展，悬挂系统的控制技术将会越来越智能化和高效化，为驾驶员提供更加舒适和安全的驾驶体验，推动汽车行业向着智能化和高端化方向发展。

汽车底盘悬挂系统的主动与半主动控制必将成为未来汽车发展的一个重要趋势。

基于lqg方法的汽车主动悬架控制力的研究

基于lqg方法的汽车主动悬架控制力的研究
作为一种主动悬架系统，机动车悬架自适应控制系统有效改善了机动车悬架参数和行
驶性能。

利用LQG控制技术优化机动车主动悬架控制力，有助于更加精确调节和稳定悬架
系统，能够更好地满足行车要求。

LQG控制是一种综合了线性和非线性技术、采用最优分析方法设计的控制技术。

这里，LQG控制方法以线性系统为基础，通过构建合适的观测器和控制器，加以随机调节控制非
线性悬架系统，进而精确控制悬架所改变的震振。

在实际研究中，首先确定出机动车悬架系统的线性等效模型，构建LQG控制器，将系
统的状态变量投影到观测器状态空间，给出观测器状态的估计，同时建立相应的误差函数，设计出在系统最优响应的情况下出现最小均方根值的LQG控制器，保证控制器的稳定性。

最后，综合采用MATLAB平台实现只考虑汽车行程参数的悬架车控制，研究其加速状
态和减速状态下悬架系总力关系，并且结合实际应用检验耦合LQG控制器控制力的性能，
最终达到了汽车良好的悬架行驶参数和性能。

半主动悬架的自适应滑模控制算法研究

半主动悬架的自适应滑模控制算法研究摘要：本研究聚焦于半主动悬架的自适应滑模控制算法，旨在通过深入的理论分析和实验验证，提升车辆行驶的平顺性和稳定性。

半主动悬架作为一种先进的汽车悬架系统，能够通过传感器感知路面状况和车身姿态，实时调节阻尼参数，从而优化车辆性能。

而自适应滑模控制算法的应用，则能进一步提升半主动悬架的性能表现。

我们提出了一种基于改进的理想天棚系统的自适应滑模变结构控制算法。

该算法的核心在于在实际被控系统和参考模型之间的误差动力学系统中产生渐进稳定的滑模运动。

通过李雅普诺夫稳定性原理，我们证明了所设计的滑模控制算法的稳定性。

以某重型车辆为例进行的MATLAB 仿真结果显示，与传统被动悬架和最优控制相比，自适应滑模控制器能够显著改善车辆的平顺性，并对模型参数的不确定性和外界扰动展现出良好的适应性和鲁棒性。

滑模控制算法也存在抖振问题，这也是未来研究需要重点关注的方向。

为了解决这一问题，我们探讨了各种削弱抖振的方案，并在实验验证中观察到滑模控制的抖振现象相对较小，这表明所设计的滑模控制器能够很好地改善悬架性能，达到预期效果。

我们还研究了轮胎阻尼对悬架系统性能的影响，提出了一种考虑轮胎非线性阻尼的四分之一车模型。

通过在不同路面条件下的仿真分析，我们深入探讨了滑模控制和天棚控制在不同车速和路面频率下的性能表现。

本研究为半主动悬架的自适应滑模控制算法提供了深入的理论和实验支持，为进一步提升汽车行驶性能提供了新的思路和方法。

滑模控制的抖振问题仍需进一步研究和完善，以适应更复杂的道路和驾驶条件。

Abstract：This study focuses on the adaptive sliding mode control algorithm of semi-active suspension, aiming to improve the smoothness and stability of vehicle driving throughin-depth theoretical analysis and experimental verification. As an advanced automotive suspension system, semi-active suspension can perceive road conditions and body posture through sensors, adjust damping parameters in real time, and optimize vehicle performance. The application of adaptive sliding mode control algorithm can further improve the performance of semi-active suspension. We propose an adaptive sliding mode variable structure control algorithm based on an improved ideal ceiling system. The core of this algorithm lies in generating asymptotically stable sliding mode motion in the error dynamics system between the actual controlled system and the reference model. We have demonstrated the stability of thedesigned sliding mode control algorithm through the Lyapunov stability principle. The MATLAB simulation results using a heavy vehicle as an example show that compared with traditional passive suspension and optimal control, the adaptive sliding mode controller can significantly improve the smoothness of the vehicle, and demonstrate good adaptability and robustness to the uncertainty of model parameters and external disturbances. The sliding mode control algorithm also has the problem of chattering, which is also a focus of future research. To address this issue, we have explored various solutions to reduce chattering and observed in experimental verification that the chattering phenomenon of sliding mode control is relatively small. This indicates that the designed sliding mode controller can effectively improve suspension performance and achieve the expected results. We also studied the effect of tire damping on suspension system performance and proposed a quarter car model that considers tire nonlinear damping. Through simulation analysis under different road conditions, we delved into the performance of sliding mode control and canopy controlunder different vehicle speeds and road frequencies. This study provides in-depth theoretical and experimental support for the adaptive sliding mode control algorithm of semi-active suspension, and provides new ideas and methods for further improving the driving performance of automobiles. The chattering problem of sliding mode control still needs further research and improvement to adapt to more complex road and driving conditions.一、概述随着汽车工业的不断发展，对车辆行驶平顺性和稳定性的要求也在日益提高。

车辆悬架系统LQG控制器仿真

现代控制理论与工程小设计：车辆悬架系统LQG控制器仿真工程背景悬架是车辆的重要组成之一，用于传递车体和车轮之间的力和力矩，起缓冲和减震作用。

悬架按工作原理可分为被动悬架、主动悬架和半主动悬架。

国外在50年代提出主动悬架概念，为改善车辆悬架性能提供了一条新的途径。

目前，国外一些发达国家已经在某些车型上应用了主动悬架，国内也对主动悬架系统进行了控制算法的优化设计、理论分析及实验研究。

主动悬架具有外部能源输入，能够根据车辆的行驶状态和路面状况作出主动的响应。

从理论上讲，对主动悬架的设计可转换为对控制方法的设计。

在众多的控制方法中，具有二次型性能指标的最优一．建模过程见附页参考资料，结果为：X YFWBUAXX dtd=++=控制器性能指标：⎰+=∞→TTT T dt RU U QX X TJ 0)(1lim二．仿真过程及结果参数选取为：根据所选择参数，带入模型中，进行编程：1.确定系统状态空间表达式及性能指标表达式clear;A=[0 1 0 0 0 0 0 0 0 0 ;0 0 0 0 -39.62 0 -29.23 0 0 0;0 0 0 1 0 0 0 0 0 0 ;0 0 0 0 18.84 0 -19.99 0 0 0;0 1 0 -0.968 0 -1 0 0 0 0;-5207.55 0 5040.9 0 5984.90 0 0 0 5207.55 0;0 1 0 1.39 0 0 0 -1 0 0 ;-5655.74 0 -7872.79 0 0 0 6278.69 0 0 5655.74;0 0 0 0 0 0 0 0 -0.06 0;0 0 0 0 0 0 0 0 0 -0.06];B=[0 0.002 0 -0.0009 0 -0.037 0 0 0 0;0 0.002 0 0.001 0 0 0 -0.041 0 0 ]';Q=[200 0 42.4 0 -100 0 -100 0 -100 -100;0 0 0 0 0 0 0 0 0 0;42.4 0 109.1 0 96.8 0 -139.2 0 96.8 -139.2;0 0 0 0 0 0 0 0 0 0;-100 0 96.8 0 100826.24 0 1197.69 0 100 0;0 0 0 0 0 0 0 0 0 0;-100 0 -139.2 0 1197.69 0 102092.1 0 0 100;0 0 0 0 0 0 0 0 0 0;-100 0 96.8 0 100 0 0 0 100 0;-100 0 -139.2 0 0 0 100 0 0 100];R=[0.0000083 0.00000433;0.00000433 0.00001267 ];2.用lqr命令求取最优反馈矩阵KK=lqr(A,B,Q,R);3.用lqe命令求取卡尔曼滤波器反馈矩阵KcQ0=[1 0;0 1];R0=[0.1 0 0 0 0 0 0 0 0 0;0 0.1 0 0 0 0 0 0 0 0;0 0 0.1 0 0 0 0 0 0 0;0 0 0 0.1 0 0 0 0 0 0;0 0 0 0 0.1 0 0 0 0 0;0 0 0 0 0 0.1 0 0 0 0;0 0 0 0 0 0 0.1 0 0 0;0 0 0 0 0 0 0 0.1 0 0;0 0 0 0 0 0 0 0 0.1 0;0 0 0 0 0 0 0 0 0 0.1];C=[1 0 0 0 0 0 0 0 0 0;0 1 0 0 0 0 0 0 0 0;0 0 1 0 0 0 0 0 0 0;0 0 0 1 0 0 0 0 0 0;0 0 0 0 1 0 0 0 0 0;0 0 0 0 0 1 0 0 0 0;0 0 0 0 0 0 1 0 0 0;0 0 0 0 0 0 0 1 0 0;0 0 0 0 0 0 0 0 1 0;0 0 0 0 0 0 0 0 0 1];F=[0 0 0 0 0 0 0 0 22.51 0;0 0 0 0 0 0 0 0 0 22.51]'; KC=lqe(A,F,C,Q0,R0);计算结果为：矩阵K:矩阵Kc:进行SIMULINK仿真：被动悬架仿真模型（无控制）：主动悬架仿真模型：车轮路面的输入情况：随机噪声前轮：后轮：编程把输出的10维向量分离，并对比被动悬架与主动悬架的输出结果：a1=simout.signals.values(:,1);a2=simout.signals.values(:,2);a3=simout.signals.values(:,3);a4=simout.signals.values(:,4);a5=simout.signals.values(:,5);a6=simout.signals.values(:,6);a7=simout.signals.values(:,7);a8=simout.signals.values(:,8);a9=simout.signals.values(:,9);a10=simout.signals.values(:,10);b1=simout1.signals.values(:,1);b2=simout1.signals.values(:,2);b3=simout1.signals.values(:,3);b4=simout1.signals.values(:,4);b5=simout1.signals.values(:,5);b6=simout1.signals.values(:,6);b7=simout1.signals.values(:,7);b8=simout1.signals.values(:,8);b9=simout1.signals.values(:,9);b10=simout1.signals.values(:,10);figure(1),hold onplot(a1','');plot(b1',':r');hold offfigure(2),hold onplot(a2','');plot(b2',':r');hold offfigure(3),hold onplot(a3','');plot(b3',':r');hold offfigure(4),hold onplot(a4','');plot(b4',':r');hold offfigure(5),hold onplot(a5','');plot(b5',':r');hold offfigure(6),hold onplot(a6','');plot(b6',':r');hold offfigure(7),hold onplot(a7','');plot(b7',':r');hold offfigure(8),hold onplot(a8','');plot(b8',':r');hold offfigure(9),hold onplot(a9','');plot(b9',':r');hold offfigure(10),hold onplot(a10','');plot(b10',':r');hold off虚线为被动悬架，实现为主动悬架车身垂直位移：车身加速度仰俯角仰俯角加速度前悬架动速度后悬架动速度前轮路面输入后轮路面输入三．结论通过对LQG控制器的仿真研究，表明具有LQG控制器的主动悬架可以有效地降低车身垂直加速度、悬架动绕度和轮胎动位移。

车辆半主动悬架最优控制方法研究

车辆半主动悬架最优控制方法研究一、引言车辆悬架系统对车辆行驶性能和乘坐舒适性有着重要影响，悬架系统的控制方法研究是提高车辆安全性能和行驶舒适性的关键之一。

车辆悬架系统的控制方式可分为主动、半主动和被动三种，其中半主动悬架系统因为具有较好的安全性能和经济性，近年来受到了研究者的广泛关注。

本文旨在研究车辆半主动悬架最优控制方法，提高车辆行驶性能和乘坐舒适性。

二、车辆半主动悬架系统车辆悬架系统主要由减震器、弹簧和悬架支撑等组成。

在半主动悬架系统中，增加了一些控制器和执行器，通过调整减震器和弹簧的刚度和阻尼来控制车辆悬架系统的状态。

半主动悬架系统根据控制方式可分为阻尼可调和弹簧可调两种。

阻尼可调悬架最早应用于赛车领域，通过控制阻尼来减小车身振动，提高行驶稳定性。

弹簧可调悬架则利用可变刚度弹簧来调整悬架系统阻尼和刚度，实现悬架系统的控制。

半主动悬架系统的控制方式有当前反馈、预测控制和模型参考控制等，其中预测控制是一种现在较为流行的控制方法。

三、车辆半主动悬架最优控制方法半主动悬架系统最优控制方法的目标是最大限度地提高车辆行驶性能和乘坐舒适性。

提高行驶性能需要控制车辆的悬架系统调整，提高车辆的悬架系统的阻尼和刚度，减小车身的姿态变化，提高悬架系统对路面的适应能力。

提高乘坐舒适性需要减小车辆悬架系统的振动，提高乘坐的平稳性和舒适性。

最优控制方法包括控制器设计和优化问题两个方面。

控制器的设计可以采用反馈线性二次型控制器，并采用Kalman滤波器估计状态变量。

为了确保悬架系统的最优性能，需要根据不同车辆和不同路面情况进行优化设计。

优化问题中，应该考虑到车辆行驶的安全性能和乘坐舒适性。

可以采用多目标优化方法，将行驶安全性能和乘坐舒适性综合考虑，在保证安全性能的前提下，最大程度地提高乘坐舒适性。

四、实验结果与分析将半主动悬架最优控制方法应用于某种车辆上，通过实验验证了该方法的有效性。

在不同路面条件下，实验结果表明，半主动悬架系统最优控制方法能够显著提高车辆行驶性能和乘坐舒适性。

汽车底盘悬挂系统的主动与半主动控制方法

汽车底盘悬挂系统的主动与半主动控制方法汽车底盘悬挂系统是整个汽车的重要组成部分，它直接影响着行车的舒适性、稳定性和安全性。

随着科技的不断进步，底盘悬挂系统的控制方式也得到了不断的优化和创新，其中主动与半主动控制方法成为当前研究的热点。

本文将重点介绍汽车底盘悬挂系统的主动与半主动控制方法。

一、主动控制方法主动悬挂系统是指可以主动调节悬挂刚度、高度和阻尼等参数的系统。

主动控制方法通过悬挂系统自身的传感器获取道路情况和车辆状态，再通过电子控制单元（ECU）对悬挂系统进行实时调节，从而保证车辆在不同道路和行驶状态下的稳定性和舒适性。

主动控制方法的优点在于可以根据实际情况主动作出调整，保持车辆在最佳状态下行驶。

例如，当车辆行驶在颠簸路面时，主动悬挂系统会加大阻尼力和提高悬挂高度，从而减小车身的颠簸感；当车辆高速行驶时，主动悬挂系统会降低悬挂高度和减小阻尼力，提高车辆的稳定性。

二、半主动控制方法半主动悬挂系统是指在主动悬挂系统的基础上进行改进，可以根据预设的控制算法主动调节悬挂参数。

与主动悬挂系统相比，半主动悬挂系统需要更少的电子控制单元和传感器，成本较低，但调节效果也相对有限。

半主动控制方法通过预设的控制算法对悬挂系统进行调节，例如将车辆的行驶状态、车速和转向角度等信息输入到控制算法中，再根据算法输出的结果对悬挂系统进行调节。

虽然半主动控制方法的调节精度不如主动控制方法准确，但在提升车辆性能和舒适性方面也有一定的作用。

三、主动与半主动控制方法的比较主动悬挂系统和半主动悬挂系统各有其优缺点。

主动悬挂系统可以实现更精确的调节，适应性更强，但成本相对较高；而半主动悬挂系统成本更低，适用性更广，但调节精度有所不足。

在实际应用中，需要根据车辆的具体情况和需求选择适合的悬挂控制方法。

综上所述，汽车底盘悬挂系统的主动与半主动控制方法在提升车辆性能和舒适性方面发挥着重要作用。

随着科技的不断发展和进步，相信底盘悬挂系统的控制方法会越来越完善，为驾驶员提供更加安全、舒适的行车体验。

车辆半主动悬架自适应预测控制

测、动优化、馈校正实现目标函数的最优控制，时对路面变化、型误差均具有自适应能力。滚反同模
仿真研究证实了算法的有效性。
关键词：汽车工程；主动悬架；广义预测控制；动优化；多目标控制半滚中图分类号：Ｕ６．３４３３文献标志码：Ａ文章编号：１０ —０３２１）２０４－５００１９（０１０２２０
Ａｂｓｒｃ：Ｔｈｉｅｃｍｆｒａｄｒａｏｄｎｆｖｈｃｅｃｎｂｂｉｕｌｍｐｏｅｙｕｉｇｔｅｓｍｉａ－ｔａｔｅｒｄｏｏｔｎｏｄｈｌｉｇｏｅｉｌａｅｏｖｏｓｙｉｒｖｄｂｓｎｈｅ－ｃ
ｍｉａｉｎ，ａｄ￣ｅｂｃｏｅｓｔｎｔｐｉｚｈｂｅｔｅｆｎｔｎｉｌｔｎｒｓｌｈｗｔａｈｚｔｏｎｄａｋｃｍｐｎａｉｏｏｔｅｔｅｏｊｃｉｕｃｉ．Ｓｍｕａｉｅｕｔｓｏｈｔｔｅｏｍｉｖｏｏｓ
ｃｕｅｙｔｅｉｌｏｄｖｒａｃａｓｄｂｈｅｖｈｃｅｌａａｉｎｅ，ｖｒａｃｆｓｓｅｓｏｏａｉｎｅｏｕｐｎｉｎｃｍｐｎｎ，ｅｃＴｈｅｅａｉｅｅｉｔｖｏｅｔｔ．ｅｇｎｒｌｚｄｐｒｄｃｉｅ
ｖｒａｃｆｒａｒｅｕａｉｙａｄｖｈｃｅｖｌｃｔ．Ｔｈｐｉｌｃｎｒｌｌｗｓａｐｉｅｔｈｄｌｅｒｒａｉｎｅｏｏｄｉｒｇｌｒｔｎｅｉｌｅｏｉｙｅｏｔｍａｏｔｏａｉｄａｔｖｏｔｅｍｏｅｒｏ

基于层次分析法的主动悬架LQG控制器设计

ｇｕｓｎＬＧ控制算法能够通过给出所需的最优ａｓａ，Ｑ）ｉ
性能指标，定系统状态变量和控制变量的加权矩确
阵，为设计者提供了一定的设计空间。ＬＧ方法应Ｑ用在车辆主动悬架设计中，以由不同的性能需要可
ｅｓｆｒａｔｅａｄｐｓｉｅｓｓｅｓｏｓａｅｂｕｌｎｅｔａ／Ｓｍｕｉｋｅｖｒｎｎｔｉｌｔｎｆｌｗｅ．ＴｈｌｏｃｉｎａｓｖｕｐｎｉｎｒｉｕｄｒＭａｌｂｉｌｎｎｉｏｍｅｔｗｉａｓｍｕａｉｏｌｖｔｈｏｏｄｅ
来提出不同的目标函数，定相应的加权矩阵，确即

ＬＧ方法可以通过综合考虑车辆悬架系统中的各种Ｑ
ＫｅｗｒｓａｔｅｓｓｅｓｎＱＧｏｔｏｌｒＡｙｏｄ：ｃｉｕｐｎｉ；Ｌｖｏｃｎｒｌ；ＨＰ；ｉｌｔｎｅｓｍｕａｉｏ
础也比较完善，中的线性二次型（ｉｅｒｑａｒｔ其１ａｕｄａｃｎｉ
ＨＩＪ舌
ａｃｖｌａｏｄｃｔｓｒｄｔｒｎｄｂｓｇａａｔｉａｃｙｐｏｅｓ（Ｈ）ａｄｔｅｅｓｕａｉｏ — ｎｅｅａｔｎｉｉａｒａｅｅｍｉｅｙｉｎｌｉｈｅｒｈｒｃｓＡＰ，ｎｎｔｉｌｔｎｍｄｕｉｎｏｅｕｎｙｃｒｈｈｍｏ
汽车主动悬架的控制方法是其核心技术之一，国内外专家在控制算法方面做了大量的研究，多许

基于混合蛙跳算法的半主动悬架LQG控制器设计

的【司ｌＪ』堡、｝；１１．』己１订＆变化，Ｅｒ＾适应４＜１．１况ｎ，
网而难以满ｔ‘ｉ驶ｊ程
性操
纵定 · 的嘤求。ｉ动恳架能够根州实际
ｉ况埘．恺进ｆ，此与被动悬架棚较，
＇Ｉ－－卜动悬架行驶过ｉ１，ｊ更好的使用性能 …，加Ｚ．Ｅ｝Ｅ｛ｉｇｆｌ，、制能更加迅速午占确等
关键词：半主动悬架；平顺性；ＬＱＧ控制；混合蛙跳法
１引言
ｌ髓荇１ＩＩ、Ｉｌｊ技术的不断发展，为更
好地提升ｉｉ的发仓手ｌ】Ｓｆ适性，悬系统能也地柬地｛川ｉｉ．；Ｉ１人”ｌｌ＇［ＩＪ瓜｝。于被动悬絮
电峰怂，提山ｒ一种Ｉ，ＱＧ控制法，
【ＩＪ’以｝－ｊ般道路友好性和、 Ⅲ惟；宋龙蜒
幻屯ｌｊｌ｛ｚＩＪｊ系统的不确定，果川ｒＩ适
ＩＱ（；制策略，井发现能够仃效降低 ‘ｉ吁
动，Ｉ抛高ｒ平顺性和操也ｊ ’ 鑫源
架为撼｛：．Ｈｊ，朵川改进的尺棚阻尼方法进行
真实验，验ｒ人１＝｝】ｆＪＩＪ已方法对操纵稳定性的捉． “ 。惯糊圳果ｆ｝ｊ语言的控制
则，４Ｊ１ｊｌ嘤系统数摸型，易ｊ胖解。
ｓＪ１ｔｕａｎｇ捉Ｉｔ５１Ａ适应幞糊滑摸控
馍糊｛圳』较 ☆ ０效。其对复杂系统的

主动悬架LQG最优控制设计

主动悬架LQG最优控制设计吕福麟113085234379摘要：根据汽车行驶性能的要求，建立二自由度的1/4汽车动力学模型，利用最优控制理论对主动悬架的LQG（Linear Quadratic Gaussian）控制器进行设计，运用MATLAB/simulink对模型仿真，对比主动悬架与被动悬架在控制效果上的差别。

仿真结果表明，具有LQG控制器的主动悬架可以明显的提高汽车行驶的操稳性能。

关键词：主动悬架；LQG控制器；MATLAB/simulink；仿真结果ABSTRACT：According to the requirement of the vehicle driving performance,a 2-degree-of-freedoms 1/4 car dynamic model was build.LQG(Linear Quadratic Gaussian) controller for active suspension was designed with the optimal control law,MATLAB/simulink was used to simulation the model,compared the difference of control performance with active suspension and passive suspension.The result of simulation show that it could improve the car driving handling and stability with LQG controller.Key Words:active suspension,LQG controller,MATLAB/simulink,simulation result1前言传统的悬架主要由弹性元件、减震器和导向装置组成，他们的阻尼和刚度已经确定就不便于调节，而且只能在特定的路面激励和特定的车速下才能达到最优控制，灵活性较差。

汽车半主动悬架的模型参考自适应控制

汽车半主动悬架的模型参考自适应控制背景与意义汽车平顺性和行驶安全性始终是矛盾的两个方面。

对汽车悬架的控制就是为了在平顺性和行驶安全性之间寻找一个最优的结合点。

理论上，主动悬架能获得一个优质的隔振系统，实现理想悬架的控制目标。

但主动悬架能耗高，成本高，且控制系统复杂。

半主动悬架结构简单，制造方便，几乎不需要向系统提供附加能量，同时，在控制品质上又能接近于主动悬架，因而有着广阔的应用前景。

模型参考的自适应控制器自适应控制器由可调前置控制器G和状态反馈控制器F 两部分组成（1）最终的设计即为求G'与F' 过程，也就是模型参考自适应控制器的控制律求系统的自适应控制律，还需要求出系统的参考模型的状态方程与对象模型的状态方程车辆动力学参考模型为：通过受力分析可求得动力学方程为：（2）式中:m s，为簧载质量;x sr为簧载质量的位移;z r为非簧载质量的位移;d为路面输人;k s为悬架刚度;k t为轮胎的刚度;f dr为天棚控制阻尼力将滤波白噪声作为路面输人模型式中: 为一个白噪声过程;v为车速;a为与路面类型有关的系数。

其自相关函数为式中: 为路面不平度的方差（3）由（2）、（3）式可求得参考模型的状态方程为：（4）式中：Am 、Bm 、Cm为系统矩阵车辆动力学模型为：通过受力分析可求得动力学方程为：（5）同样可求得系统的状态方程为（6）结合（1）、（4）、（6）式，有广义状态方程要实现对象模型与参考模型间的渐近自适应跟踪，必须分别满足下列状态收敛条件和参数收敛条件（7）要使式(7)的前两个方程有解，必须增加约束条件（8）设F(e，t)=F0,G(e，t)=G0时，参考模型与可调系统达到完全的匹配，即（9）将式(9)代人式(8)，得(12)构造以下LYAPUNOV 函数（10）对式(10)两边求导（11）因Am为稳定矩阵，必有PAm + P=-Q ,Q 为正定矩阵。

式(11)右边第一项是负定的。

车辆半主动悬架自适应 LQG 控制

车辆半主动悬架自适应 LQG 控制
管继富;顾亮;侯朝桢
【期刊名称】《系统仿真学报》
【年(卷),期】2004(16)10
【摘要】线性二次型高斯(LQG)随机最优控制理论和卡尔曼滤波器被应用于车辆悬架控制中。

通过仿真分析得到了车体振动加速度均方根值随着悬架变形的均方根值的增大而减小的结论。

提出了符合一类越野车辆实际需要的半主动悬架自适应控制策略。

形成了对路面变化(包含车速)具有自适应能力的LQG控制系统。

对自适应控制的效果进行了仿真分析。

【总页数】4页(P2340-2343)
【关键词】半主动悬架;LQG控制;卡尔曼滤波器;自适应控制;随机控制
【作者】管继富;顾亮;侯朝桢
【作者单位】北京理工大学自动控制系;北京理工大学噪声与振动控制实验室【正文语种】中文
【中图分类】TB533.2;TP273.4
【相关文献】
1.汽车半主动悬架的自适应LQG控制 [J], 方敏;王峻
2.1/4车辆半主动悬架LQG控制仿真分析 [J], 张志达;李韶华;张兵
3.车辆主动悬架自适应LQG控制策略研究 [J], 闫光辉;关志伟;杜峰;刘臣富
4.基于AHP的车辆半主动悬架LQG控制方法研究 [J], 孙宇菲; 陈双; 姜强
5.车辆磁流变半主动悬架模糊LQG控制策略研究 [J], 李刚;顾瑞恒;徐荣霞;胡国良;欧阳娜;徐明
因版权原因，仅展示原文概要，查看原文内容请购买。

车辆半主动悬架自适应预测控制

j －1
F j （ q － 1 ） y m （ k） =
n －1
g ji Δu（ k + j － i － 1 ） ∑ i =0 +
+
g ji Δu（ k + j － i － 1 ） ∑ i=j
j － 1 ） + F j （ q － 1 ） y m （ k） + E j （ q － 1 ） ε（ k + j）．
用丢番图
图1 Fig． 1 单自由度悬架模型 1DOF suspension model
方程可将 ε（ k + j）分为 2 部分 = Ej （ q － 1 ） + q －j Fj （ q － 1 ）， A（ q － 1 ） Δ
1 A（ q － 1 ） Δ 即
244
兵
1 = E j （ q － 1 ） A（ q － 1 ） Δ + q － j F j （ q － 1 ）．代入（ 9 ）式得
第2 期
车辆半主动悬架自适应预测控制
243
· ·
车辆半主动悬架系统是一种噪声主动型的随机系统。其目标函数包含多个目标变量，这些目标变最优控制量在时域或频域上具有相互冲突的关系，的任务就是要协调这些控制目标，使其到达一种统计意义上的最优。同时，由于路面信息作为系统模型噪声输入，其统计特性是未知的和大范围变化的，要求最优控制还必须对满足统计规律的随机过程路面输入和确定性大干扰路面同时具有良好的调节效由于存在建模误差或系统参数因元件老果。另外，化而发生变化，使得依赖于计算机中模型得到的最优控制效果变差，因此要求最优控制律具有良好的鲁棒性。所以，车辆半主动悬架控制问题实际上是随机系统多目标的鲁棒自适应控制问题。其鲁棒性表现在模型误差慢变干扰情况下，保持系统最优控制性能的能力。其自适应性表现在对路面、车速快最优控制的动态调整能力。变干扰输入情况下，针对上述特点，本文提出采用广义预测控制（ GPC ）对车辆半主动悬架进行控制。算法采用模型预测、滚动优化、反馈校正实现目标函数的最优控制。算法中通过测量值和模型预估值的误差反馈来由于模型预测和反馈校正，使得系统校正模型误差，具有很强的抗干扰能力和克服系统不确定性的能力，保证了系统的鲁棒性。算法中的滚动优化采用了多目标变量泛函形式，采用了有限时域的在线滚保证了系统的自适应性。动式优化策略，