2015-2016学年浙江省温州市第二外国语学校高一上学期期末考试数学试题 word版

合集下载

2015-2016学年度第一学期期末测试(数学)

2015～2016学年度第一学期期末测试七年级数学本卷分值 100分，考试时间120分钟．一、选择题（本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置．．．．．．．上） 1．34-的相反数是A ．43-B ．43C ．34-D ．342．单项式225x y-的系数和次数分别是A ．－2，2B ．2-，3C ．25-，2D ．25-，33．在下面的四幅图案中，通过平移图案（1）得到的是图案4．下列各组中的两项，不是．．同类项的是 A ．22x y 与23x y - B ．3x 与3xC ．232ab c -与32c b aD ．1与－18 5．若关于x 的方程710x a +-=解是1x =-，则a 的值等于A ．8B ．－8C ．6D ．－6 6．从三个不同方向看一个几何体，得到的三视图如图所示，则这个几何体是A ．圆锥B ．圆柱C ．棱锥D ．球7．已知有理数a ，b 在数轴上表示的点如图所示，则下列式子中不正确．．．的是 A ．ab＜0 B ．a －b ＞0 C ．a ＋b ＞0 D ．ab ＜0b 0a（1） A B C D（第6题）（第7题）8．如图，直线a ，b 被直线c 所截，则下列说法中错误．．的是 A ．∠1与∠2是邻补角 B ．∠1与∠3是对顶角C ．∠3与∠4是内错角D ．∠2与∠4是同位角 9．如图，点D 在直线AE 上，量得∠CDE=∠A=∠C ，有以下三个结论：①AB ∥CD ；②AD ∥BC ；③∠B=∠CDA ．则正确的结论是A ．①②③B ．①②C ．①D ．②③ 10．王力骑自行车从A 地到B 地，陈平骑自行车从B 地到A 地，两人都沿同一公路匀速前进，已知两人在上午8时同时出发，到上午10时，两人还相距36 km ，到中午12时，两人又相距36 km ．求A 、B 两地间的路程．可设A 、B 两地间的路程为x km ，则下列所列方程中：①363624x x -+=；②36363622x -+=；③36362x -=⨯； ④3636x -=；其中正确的个数为A ．1个B ．2个C ．3个D ．4个二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置．．．．．．．上） 11．用科学记数法表示9600000为 ▲ ．12．点A 、B 在同一条数轴上，其中点A 表示的数为－1，若点B 与点A 之间距离为3，则点B 表示的数为 ▲ ． 13．已知2a b -的值是2015，则124a b -+的值等于 ▲ ．14．若23(2)0x y -++=，则16xy = ▲ ．15．飞机的无风航速为a 千米／小时，风速为20千米／小时．则飞机逆风飞行4小时的行程是 ▲ 千米．16．某服装店以每件180元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，若盈利记为正，亏损记为负，则该店卖这两件衣服总的盈亏金额是 ▲ 元．17．如图，把小河里的水引到田地A 处就作AB ⊥l ，垂足为B ，沿AB 挖水沟，这条水沟最短的理由是 ▲ ． 18. 如图，将三角板与两组对边分别平行的直尺贴在一起，使三角板的顶点C （AC ⊥BC ）落在直尺的一边上，若∠1=24°，则∠2等于 ▲ 度． 19．如图，平面内有公共端点的6条射线OA 、OB 、OC 、 OD 、OE 、OF ，从射线OA 开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7…，则数字 “2016”应在射线 ▲ 上．20．已知线段AB =12㎝，若M 是AB 的三等分点，N 是AM 的中点，则线段BN 的长度为 ▲ ㎝．三、解答题（本大题共8小题，共60分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文ac1 234 A B C DE（第8题）（第9题）（第17题）（第18题）（第19题）字说明、证明过程或演算步骤） 21．（每小题4分，共16分）计算：（1） (20)(3)(5)(7)-++---+；（2） 111()(12)462+-⨯-；（3） 322(2)(3)(4)2(3)(2)⎡⎤-+-⨯-+--÷-⎣⎦；（4） 471127326631440-+⨯-⨯÷．22．（每小题3分，共6分）（1）如图，点D 是线段AB 的中点，C 是线段AD 的中点，若AB ＝4㎝，求线段CD的长度．（2）如图，货船A 在灯塔O 的北偏东53°35′的方向上，客船B 在灯塔O 的南偏东28°12′的方向上．求∠AOB 的度数．23．（每小题4分，共8分）先化简，再求值：（1）求22113333a abc c a c +--+的值，其中1,2,36abc =-==-；（2）求2211312()()2323x x y x y --+-+的值，其中22,3x y =-=．24．（每小题4分，共8分）解方程：（1）72(33)20x x +-=；（2）121224x x+--=+．25．（本小题6分）如图，AD ∥BC ，∠1=60°，∠B =∠C ，DF 为∠ADC 的平分线．（1）求∠ADC 的度数；（2）试说明DF ∥AB ．解：（1）根据题意完成填空（括号内填写理由）： ∵AD ∥BC （已知）∴∠B =∠1（）又∵∠B =∠C （已知） ∴ =∠1=60°C D （第22题（2）） A O B 西东北南（第22题（1））又∵AD ∥BC （已知）∴∠ADC +∠C =180°（） ∴∠ADC = ．（2）请你完成第2题的解答过程：26．（本小题4分）列方程解应用题：某车间有22名工人，每人每天可以生产1200个螺钉或2000个螺母．1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，应安排生产螺钉和螺母的工人各多少名？ 27．（本小题6分）如图：已知AB ∥CD ，∠ABE 与∠CDE 两个角的角平分线相交于点F ．（1）如图1，若∠E ＝78°，则∠BFD = °；（2）如图2，若∠ABM ＝14∠ABF ，∠CDM ＝14∠CDF ，则∠M 和∠E 之间的数量关系为；（3）如图2，∠ABM ＝1n ∠MBF ，∠CDM ＝1n∠MDF ，设∠M ＝m °，直接用含有n ，m 的代数式表示出∠E ＝ °．28．（本小题6分）如图，在∠AOB 的内部作射线OC ，使∠AOC 与∠AOB 互补．将射线OA ，OC 同时绕点O 分别以每秒12°，每秒8°的速度按逆时针方向旋转，旋转后的射线OA ，OC 分别记为OM ，ON ，设旋转时间为t 秒．已知t ＜30，∠AOB ＝114°．（1）求∠AOC 的度数；（2）在旋转的过程中，当射线OM ，ON 重合时，求 t 的值；（3）在旋转的过程中，当∠COM 与∠BON 互余时，求 t 的值．BE DFACBE DFA CM 图1图2CMNB（第27题）。

高中高一数学上学期第三次月考试卷(含解析)-人教版高一全册数学试题

2015-2016学年某某省某某市航天高中高一（上）第三次月考数学试卷一．选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符是合题目要求的．）1．设集合A={x|x﹣1＞0}，B={x|2x＞0}，则A∩B=（）A．{x|x＞1} B．{x|x＞0} C．{x|x＜﹣1} D．{x|x＜﹣1或x＞1}2．若，且α是第二象限角，则cosα的值等于（）A． B． C．D．3．为了得到函数的图象，只需把函数y=sinx的图象上所有的点（）A．向右平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向左平移个单位长度4．下列四个函数中，既是（0，）上的增函数，又是以π为周期的偶函数的是（）A．y=tanx B．y=|sinx| C．y=cosx D．y=|cosx|5．幂函数y=x m（m∈Z）的图象如图所示，则m的值可以为（）A．1 B．﹣1 C．﹣2 D．26．函数y=ax2+bx+3在（﹣∞，﹣1]上是增函数，在[﹣1，+∞）上是减函数，则（）A．b＞0且a＜0 B．b=2a＜0C．b=2a＞0 D．a，b的符号不确定7．根据表格内的数据，可以断定方程e x﹣x﹣2=0的一个根所在的区间是（）x ﹣1 0 1 2 3e x0.37 1 2.72 7.39 20.08x+2 1 2 3 4 5A．（﹣1，0）B．（0，1）C．（1，2）D．（2，3）8．将下列各式按大小顺序排列，其中正确的是（）A．cos0＜cos＜cos1＜cos30°B．cos0＜cos＜cos30°＜cos1C．cos0＞cos＞cos1＞cos30°D．cos0＞cos＞cos30°＞cos19．若lgx﹣lgy=a，则=（）A．3a B．C．a D．10．若sinα，cosα是关于x的方程4x2+2x+3m=0的两根，则m的值为（）A．B． C．D．11．设函数f（x）=，若方程f（x）=m有三个不同的实数解，则m的取值X围是（）A．m＞0或m＜﹣1 B．m＞﹣1 C．﹣1＜m＜0 D．m＜012．已知a是实数，则函数f（x）=1+asinax的图象不可能是（）A．B．C．D．二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13．已知角α的终边经过点P（﹣4，3），则cosα=．14．已知扇形的周长等于它所在圆的周长的一半，则这个扇形的圆心角是．15．函数，则=．16．当x＞0时，不等式（a2﹣3）x＞（2a）x恒成立，则实数a的取值X围是．三、解答题（本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤.）17．已知（1）求tanα的值；（2）求的值．18．设，（1）在下列直角坐标系中画出f（x）的图象；（2）若f（t）=3，求t值．19．已知x∈[﹣，]，（1）求函数y=cosx的值域；（2）求函数y=﹣3（1﹣cos2x）﹣4cosx+4的值域．20．函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）在x∈（0，7π）内取到一个最大值和一个最小值，且当x=π时，y有最大值3；当x=6π时，y有最小值﹣3．（1）求此函数的解析式；（2）求此函数的单调区间．21．已知二次函数f（x）=x2﹣16x+q+3（1）若函数在区间[﹣1，1]上存在零点，某某数q的取值X围；（2）问：是否存在常数q（0＜q＜10），使得当x∈[q，10]时，f（x）的最小值为﹣51？若存在，求出q的值，若不存在，说明理由．22．已知函数．（1）当a=1时，求函数f（x）在（﹣∞，0）上的值域；（2）若对任意x∈[0，+∞），总有f（x）＜3成立，某某数a的取值X围．2015-2016学年某某省某某市航天高中高一（上）第三次月考数学试卷参考答案与试题解析一．选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符是合题目要求的．）1．设集合A={x|x﹣1＞0}，B={x|2x＞0}，则A∩B=（）A．{x|x＞1} B．{x|x＞0} C．{x|x＜﹣1} D．{x|x＜﹣1或x＞1}【考点】交集及其运算．【专题】计算题；集合思想；定义法；集合．【分析】求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．【解答】解：由A中不等式解得：x＞1，即A={x|x＞1}，由B中不等式变形得：2x＞0，得到B=R，∴A∩B={x|x＞1}，故选：A．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．若，且α是第二象限角，则cosα的值等于（）A． B． C．D．【考点】同角三角函数间的基本关系．【专题】计算题；三角函数的求值．【分析】由sinα的值，以及α的X围，利用同角三角函数间的基本关系求出cosα的值即可．【解答】解：∵sinα=，α是第二象限角，∴cosα=﹣=﹣．故选C【点评】此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．3．为了得到函数的图象，只需把函数y=sinx的图象上所有的点（）A．向右平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向左平移个单位长度【考点】函数y=Asin（ωx+φ）的图象变换．【专题】三角函数的图像与性质．【分析】直接利用函数图象的平移法则逐一核对四个选项得答案．【解答】解：∵由y=sinx到y=sin（x﹣），只是横坐标由x变为x﹣，∴要得到函数y=sin（x﹣）的图象，只需把函数y=sinx的图象上所有的点向右平行移动个单位长度．故选：A．【点评】本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．是基础题．4．下列四个函数中，既是（0，）上的增函数，又是以π为周期的偶函数的是（）A．y=tanx B．y=|sinx| C．y=cosx D．y=|cosx|【考点】正弦函数的图象；余弦函数的图象．【专题】三角函数的图像与性质．【分析】根据函数单调性，周期性和奇偶性分别进行判断即可得到结论．【解答】解：A．函数y=tanx为奇函数，不满足条件．B．函数y=|sinx|满足既是（0，）上的增函数，又是以π为周期的偶函数．C．y=cosx的周期为2π，不满足条件．D．y=|cosx|在（0，）上是减函数，不满足条件．故选：B．【点评】本题主要考查三角函数的图象和性质，要求熟练掌握三角函数的周期性，奇偶性和单调性．5．幂函数y=x m（m∈Z）的图象如图所示，则m的值可以为（）A．1 B．﹣1 C．﹣2 D．2【考点】幂函数的性质．【专题】应用题；函数思想；定义法；函数的性质及应用．【分析】由给出的幂函数的图象，得到幂指数小于0，且幂函数为偶函数，即可判断答案．【解答】解：根据幂函数的图象可知函数在第一象限内单调递减，且为偶函数．则m＜0且为偶数，故选：C．【点评】本题主要考查幂函数的图象和性质，要求熟练掌握幂函数的性质的应用．6．函数y=ax2+bx+3在（﹣∞，﹣1]上是增函数，在[﹣1，+∞）上是减函数，则（）A．b＞0且a＜0 B．b=2a＜0C．b=2a＞0 D．a，b的符号不确定【考点】二次函数的性质．【专题】计算题．【分析】利用对称轴的公式求出对称轴，根据二次函数的单调区间得到，得到选项．【解答】解：∵函数y=ax2+bx+3的对称轴为∵函数y=ax2+bx+3在（﹣∞，﹣1]上是增函数，在[﹣1，+∞）上是减函数∴∴b=2a＜0故选B【点评】解决与二次函数有关的单调性问题，一般要考虑二次函数的开口方向、对称轴．7．根据表格内的数据，可以断定方程e x﹣x﹣2=0的一个根所在的区间是（）x ﹣1 0 1 2 3e x0.37 1 2.72 7.39 20.08x+2 1 2 3 4 5A．（﹣1，0）B．（0，1）C．（1，2）D．（2，3）【考点】二分法求方程的近似解．【专题】计算题；函数的性质及应用．【分析】令f（x）=e x﹣x﹣2，求出选项中的端点函数值，从而由根的存在性定理判断根的位置．【解答】解：由上表可知，令f（x）=e x﹣x﹣2，则f（﹣1）≈0.37+1﹣2＜0，f（0）=1﹣0﹣2=﹣1＜0，f（1）≈2.72﹣1﹣2＜0，f（2）≈7.39﹣2﹣2＞0，f（3）≈20.09﹣3﹣2＞0．故f（1）f（2）＜0，故选：C．【点评】考查了二分法求方程近似解的步骤，属于基础题．8．将下列各式按大小顺序排列，其中正确的是（）A．cos0＜cos＜cos1＜cos30°B．cos0＜cos＜cos30°＜cos1C．cos0＞cos＞cos1＞cos30°D．cos0＞cos＞cos30°＞cos1【考点】余弦函数的单调性．【专题】三角函数的图像与性质．【分析】先将1和化为角度，再根据余弦函数的单调性，判断出四个余弦值的大小关系．【解答】解：∵1≈57.30°，∴≈28.56°，则0＜＜30°＜1，∵y=cosx在（0°，180°）上是减函数，∴cos0＞cos＞cos30°＞cos1，故选D．【点评】本题主要考查余弦函数的单调性，以及弧度与角度之间的转化，属于基础题．9．若lgx﹣lgy=a，则=（）A．3a B．C．a D．【考点】对数的运算性质．【专题】计算题．【分析】直接利用对数的性质化简表达式，然后把lgx﹣lgy2a代入即可．【解答】解： =3（lgx﹣lg2）﹣3（lgy﹣lg2）=3（lgx﹣lgy）=3a故选A．【点评】本题考查对数的运算性质，考查计算能力，是基础题．10．若sinα，cosα是关于x的方程4x2+2x+3m=0的两根，则m的值为（）A．B． C．D．【考点】同角三角函数基本关系的运用．【专题】转化思想；综合法；三角函数的求值．【分析】由条件利用韦达定理求得sinα+cosα=﹣，sinα•cosα=，再利用同角三角函数的基本关系求得sinα•cosα=﹣，从而求得 m的值．【解答】解：∵sinα，cosα是关于x的方程4x2+2x+3m=0的两根，∴sinα+cosα=﹣，sinα•cosα=，再根据1+2sinαcosα=，∴sinα•cosα=﹣，∴m=﹣，故选：D．【点评】本题主要考查韦达定理、同角三角函数的基本关系，属于基础题．11．设函数f（x）=，若方程f（x）=m有三个不同的实数解，则m的取值X围是（）A．m＞0或m＜﹣1 B．m＞﹣1 C．﹣1＜m＜0 D．m＜0【考点】根的存在性及根的个数判断．【专题】函数的性质及应用．【分析】由题意可得函数y=f（x）和直线y=m有3个不同的交点，数形结合可得m的取值X 围．【解答】解：由题意可得函数y=f（x）和直线y=m有3个不同的交点，如图所示：当﹣1＜m＜0时，函数y=f（x）和直线y=m有3个不同的交点，故选C．【点评】本题主要考查方程的根的存在性及个数判断，体现了数形结合的数学思想，属于中档题．12．已知a是实数，则函数f（x）=1+asinax的图象不可能是（）A．B．C．D．【考点】正弦函数的图象．【专题】三角函数的图像与性质．【分析】函数f（x）=1+asinax的图象是一个正弦曲线型的图，其振幅为|a|，周期为，周期与振幅成反比，从这个方向观察四个图象．【解答】解：对于振幅大于1时，三角函数的周期为：，∵|a|＞1，∴T＜2π，而D不符合要求，它的振幅大于1，但周期反而大于了2π．对于选项A，a＜1，T＞2π，满足函数与图象的对应关系，故选D．【点评】由于函数的解析式中只含有一个参数，这个参数影响振幅和周期，故振幅与周期相互制约，这是本题的关键．二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上.）13．已知角α的终边经过点P（﹣4，3），则cosα=．【考点】任意角的三角函数的定义．【专题】计算题．【分析】先求出角α的终边上的点P（﹣4，3）到原点的距离为 r，再利用任意角的三角函数的定义cosα=求出结果．【解答】解：角α的终边上的点P（﹣4，3）到原点的距离为 r=5，由任意角的三角函数的定义得cosα==．故答案为：．【点评】本题考查任意角的三角函数的定义，两点间的距离公式的应用，考查计算能力．14．已知扇形的周长等于它所在圆的周长的一半，则这个扇形的圆心角是（π﹣2）rad ．【考点】弧长公式．【专题】计算题．【分析】由题意，本题中的等量关系是扇形的周长等于弧所在的圆的半周长，可令圆心角为θ，半径为r，弧长为l，建立方程，求得弧长与半径的关系，再求扇形的圆心角．【解答】解：令圆心角为θ，半径为r，弧长为l由题意得2r+l=πr∴l=（π﹣2）r∴θ==π﹣2故答案为：（π﹣2）rad．【点评】本题考查弧长公式，解题的关键是熟练掌握弧长公式，且能利用公式建立方程进行运算，本题考查对公式的准确记忆能力15．函数，则= ﹣．【考点】三角函数的化简求值．【专题】计算题；转化思想；综合法；三角函数的求值．【分析】利用诱导公式先求出f（x）=，再把cos=代入，能求出结果．【解答】解：∵===，∵cos=，∴==．故答案为：﹣．【点评】本题考查三角函数值的求法，是基础题，解题时要认真审题，注意诱导公式的合理运用．16．当x＞0时，不等式（a2﹣3）x＞（2a）x恒成立，则实数a的取值X围是a＞3 ．【考点】函数恒成立问题．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】由题意结合幂函数的单调性列关于a的不等式组得答案．【解答】解：∵x＞0时，不等式（a2﹣3）x＞（2a）x恒成立，∴，解得：a＞3．故答案为：a＞3．【点评】本题考查函数恒成立问题，应用了幂函数的单调性，同时注意指数式的底数大于0且不等于1，是中档题．三、解答题（本大题共6小题，共70分，解答应写出必要的文字说明、证明过程及演算步骤.）17．已知（1）求tanα的值；（2）求的值．【考点】同角三角函数基本关系的运用．【专题】综合题；方程思想；综合法；三角函数的求值．【分析】（1）直接弦化切，即可求tanα的值；（2）法一：求出sinα，cosα，分类讨论求的值．法二：原式分子分母同除以cos2α，弦化切，即可求的值．【解答】解：（1）∵，∴tanα=﹣tanα+1（2）法一：由（1）知：，∴或当，时，原式=当，时，原式=综上：原式=法二：原式分子分母同除以cos2α得：原式==【点评】本题考查同角三角函数关系，考查学生的转化能力，属于中档题．18．设，（1）在下列直角坐标系中画出f（x）的图象；（2）若f（t）=3，求t值．【考点】分段函数的解析式求法及其图象的作法．【专题】计算题；作图题．【分析】由分段函数，按照基本函数作图，第一段一次函数，第二次二次函数，第三次为一次函数，要注意每段的定义域．【解答】解：（1）如图（2）由函数的图象可得：f（t）=3即t2=3且﹣1＜t＜2．∴t=【点评】本题主要考查分段函数的作图和用数形结合解决问题的能力，分段函数知识点容量大且灵活，是高考的热点，在解决中要注意部分与整体的关系．19．已知x∈[﹣，]，（1）求函数y=cosx的值域；（2）求函数y=﹣3（1﹣cos2x）﹣4cosx+4的值域．【考点】余弦函数的图象．【专题】转化思想；综合法；三角函数的图像与性质．【分析】（1）由条件利用余弦函数的定义域和值域，求得函数y=cosx的值域．（2）把函数y的解析式化为y=3（cosx﹣）2﹣，结合cosx∈[﹣，1]，利用二次函数的性质求得y的值域．【解答】解：（1）∵y=cosx在[﹣，0]上为增函数，在[0，]上为减函数，∴当x=0时，y取最大值1；x=时，y取最小值﹣，∴y=cosx的值域为[﹣，1]．（2）原函数化为：y=3cos2x﹣4cosx+1，即y=3（cosx﹣）2﹣，由（1）知，cosx∈[﹣，1]，故y的值域为[﹣，]．【点评】本题主要考查余弦函数的值域，二次函数的性质，属于基础题．20．函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜）在x∈（0，7π）内取到一个最大值和一个最小值，且当x=π时，y有最大值3；当x=6π时，y有最小值﹣3．（1）求此函数的解析式；（2）求此函数的单调区间．【考点】函数y=Asin（ωx+φ）的图象变换；由y=Asin（ωx+φ）的部分图象确定其解析式．【专题】三角函数的图像与性质．【分析】（1）由题意得到A和周期，代入周期公式求ω，在由点（π，3）在此函数图象上结合φ的X围求得φ，则函数解析式可求；（2）直接由复合函数的单调性求函数的单调区间．【解答】解：（1）由题意可知：A=3，，∴T=10π，则，∴y=3sin（φ），∵点（π，3）在此函数图象上，∴，．φ=．∵|φ|＜，∴φ=．∴y=3sin（）；（2）当，即﹣4π+10kπ≤x≤π+10kπ，k∈Z时，函数y=3sin（）单调递增，∴函数的单调增区间为[﹣4π+10kπ，π+10kπ]（k∈Z）；当，即π+10kπ≤x≤6π+10kπ，k∈Z时，函数单调递减，∴函数的单调减区间为[π+10kπ，6π+10kπ]（k∈Z）．【点评】本题考查y=Asin（ωx+φ）型函数图象的求法，考查了复合函数的单调性的求法，复合函数的单调性满足“同增异减”的原则，是中档题．21．已知二次函数f（x）=x2﹣16x+q+3（1）若函数在区间[﹣1，1]上存在零点，某某数q的取值X围；（2）问：是否存在常数q（0＜q＜10），使得当x∈[q，10]时，f（x）的最小值为﹣51？若存在，求出q的值，若不存在，说明理由．【考点】二次函数的性质．【专题】存在型；分类讨论；转化思想；分类法；函数的性质及应用．【分析】（1）若函数在区间[﹣1，1]上存在零点，则，即，解得实数q的取值X围；（2）假定存在满足条件的q值，结合二次函数的图象和性质，对q进行分类讨论，最后综合讨论结果，可得答案．【解答】解：（1）若二次函数f（x）=x2﹣16x+q+3的图象是开口朝上，且以直线x=8为对称轴的抛物线，故函数在区间[﹣1，1]上为减函数，若函数在区间[﹣1，1]上存在零点，则，即，解得：q∈[﹣20，12]；（2）若存在常数q（0＜q＜10），使得当x∈[q，10]时，f（x）的最小值为﹣51，当0＜q≤8时，f（8）=q﹣61=﹣51，解得：q=10（舍去），当8＜q＜10时，f（q）=q2﹣15q+3=﹣51，解得：q=9，或q=6（舍去），综上所述，存在q=9，使得当x∈[q，10]时，f（x）的最小值为﹣51．【点评】本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．22．已知函数．（1）当a=1时，求函数f（x）在（﹣∞，0）上的值域；（2）若对任意x∈[0，+∞），总有f（x）＜3成立，某某数a的取值X围．【考点】函数恒成立问题．【专题】综合题；函数思想；综合法；函数的性质及应用．【分析】（1）法一、把a=1代入函数解析式，由指数函数的单调性求得f（x）在（﹣∞，0）上的值域；法二、令换元，由x的X围求出t的X围，转化为二次函数求值域；（2）由f（x）＜3，即，分离参数a，然后利用换元法求函数的最小值得答案．【解答】解：（1）法一、当a=1时，，由指数函数单调性知f（x）在（﹣∞，0）上为减函数，∴f（x）＞f（0）=3，即f（x）在（﹣∞，1）的值域为（3，+∞）；法二、令，由x∈（﹣∞，0）知：t∈（1，+∞），∴y=g（t）=t2+t+1（t＞1），其对称轴为直线，∴函数g（t）在区间（1，+∞）上为增函数，∴g（t）＞g（1）=3，∴函数f（x）在（﹣∞，1）的值域为（3，+∞）；（2）由题意知，f（x）＜3，即，由于，在[0，+∞）上恒成立．若令2x=t，，则：t≥1且a≤h min（t）．由函数h（t）在[1，+∞）上为增函数，故φmin（t）=φ（1）=1．∴实数a的取值X围是（﹣∞，1]．【点评】本题考查函数恒成立问题，考查了指数函数的单调性，训练了分离变量法，是中档题．。

浙江省温州市第二外国语学校2012-2013学年高一物理下学期期中试题理新人教版必修2 2

浙江省温州市第二外国语学校2012-2013学年高一物理下学期期中试题理新人教版必修2 2温馨提示：1．您现在拿到的试卷满分为100分，共有四大题，21小题，您要在90分钟内完成所有答题；2．本卷重力加速度取g=10m/s2；3．本试卷包括“试卷”和“答题卷”两部分，请务必在“答题卷”上答题，在“试卷”上答题是无效的；4．考试结束后，只需上交“答题卷”，请不要忘记在“答题卷”上填写姓名、班级、学号等相关信息，同时也别忘了要将“试卷”带走并保管好，老师可能还要分析校对的哦！一、单项选择题（本题有10小题，每小题3分，共30分，在每小题所给的四个选项中，只有一个选项最符合题意）1．某质点做曲线运动时，下列说法正确的是A.曲线运动一定是变速运动B.质点受到的合外力必为变力C.速率不变的曲线运动一定没有加速度D.速度的方向与合外力的方向可能在一条直线上2．如图所示，在一张白纸上放置一根直尺，沿直尺的边缘放置一块直角三角板。

将三角板沿刻度尺水平向右匀速运动，同时将一支铅笔从三角板直角边的最下端向上运动，而且向上的速度越来越大，则铅笔在纸上留下的轨迹可能是3．火车轨道在转弯处外轨高于内轨，其高度差由转弯半径与火车速度确定。

若在某转弯处规定行驶的速度为v，则下列说法中正确的是①当以v的速度通过此弯路时，火车重力与轨道面支持力的合力提供向心力②当以v的速度通过此弯路时，火车重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力③当速度大于v时，轮缘挤压外轨④当速度小于v时，轮缘挤压外轨A. ①③B. ①④C. ②③D. ②④4．一轻绳一端固定一质量为m 的小球，以另一端O 点为圆心，使小球在竖直平面内做半径为R 的圆周运动，以下说法正确的是 A.小球过最高点时，绳的弹力可以向上B.C.小球过最高点时最小速度可以为0D.小球过最低点时，绳对球的作用力一定与小球所受重力方向相同5．如图所示，用同样大的力F 拉同一物体，在甲(光滑水平面)、乙(粗糙水平面)、丙(光滑斜面)、丁(粗糙斜面)这四种情景下沿力F 的方向通过同样的距离，比较这四种情况下拉力F 所做的功，则A ．甲中做功最少B ．丁中做功最多C ．做功一样多D ．无法比较6．如图所示，滑雪者由静止开始沿斜坡从A 点下滑，然后在水平面上前进至B 点停下。

浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试物理试题

浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试物理试题（满分100分，考试时间：90分钟）温馨提示：1．您现在拿到的试卷满分为100分，共有四大题，20小题，您要在90分钟内完成所有答题；2．本卷静电力常量229/100.9C m N ⋅⨯=κ；3．本试卷包括“试卷”和“答题卷”两部分，请务必在“答题卷”上答题，在“试卷”上答题是无效的；4．考试结束后，只需上交“答题卷”，请不要忘记在“答题卷”上填写姓名、班级、学号等相关信息，同时也别忘了要将“试卷”带走并保管好，老师可能还要分析校对的哦！一、单项选择题（本题有10小题，每小题3分，共30分，在每小题所给的四个选项中，只有一个选项最符合题意）1、以下哪个是磁感应强度的单位 ( ▲ )A ．特斯拉 B. 韦伯 C. 安培 D. 焦耳 2、关于电场强度，下列说法正确．．的是 ( ▲ ) A ．电场中某点的电场强度与放在该点的试探电荷无关。

B ．由E=F/q 可知，E 与F 成正比，与q 成反比。

C ．将一个点电荷放在电场中的不同点处，若所受的电场力大小相等，则这些点的场强也一定相同。

D ．在电场中某点用检验电荷q 测得电场强度为E ，当撤去q 而放入另一检验电荷-q/2时，该点场强变为-E/2。

3、用如图所示（虚框）是一个欧姆表的外部构造示意图，其正、负插孔内分别插有红、黑表笔，则虚线内的电路图应是图中的（ ▲ ）4、电流表的内阻是Ω=200g R ，满刻度电流值是A I g μ500=，现欲把这电流表改装成量程为1.0V 的电压表，正确．．的方法是（ ▲ ） A. 应串联一个0．1Ω的电阻 B. 应并联一个0．1Ω的电阻 C. 应串联一个1800Ω的电阻 D. 应并联一个1800Ω的电阻 5、下图中的通电导线在磁场中受力分析正确的是 ( ▲ )6、某同学做电学实验，通过改变滑动变阻器电阻大小，观察到电压表和电流表的读数同时变大，则他所连接的电路可能是下图中的（▲）7、条形磁铁竖直放置，闭合圆环水平放置，条形磁铁中心线穿过圆环中心，如图所示，若圆环为弹性环，其形状由Ⅰ扩大到Ⅱ，那么圆环内磁通量的变化情况是 ( ▲ )A．磁通量增大B．磁通量减小C．磁通量不变D．条件不足，无法确定8、以下说法正确的是（▲）A. 磁极之间的作用是通过磁场发生的，通电导体之间的作用是的直接发生B. 磁感应强度的方向就是该处小磁针静止时N极所指的方向C. 只要磁感线是直线，该处的磁场一定是匀强磁场D．磁感线总是从N极出发，终止于S极9、如图所示，直流电跟一个线圈连接成闭合回路，线圈的上方和右侧各有一个可以自由转动的小磁针，由图得出的结论正确的是（▲）A．小磁针的c端为N极，电的a端为正极B．小磁针的c端为N极，电的a端为负极C．小磁针的d端为N极，电的a端为正极D．小磁针的d端为N极，电的a端为负极10、两块大小、形状完全相同的金属平板平行放置，构成以平行板电容器，与它相连接的电路如图所示，接通开关K，电即给电容器充电（▲）A.保持K接通，减小两极板间的距离，则两极板间电场的电场强度减小B.保持K接通，在两极板间插入一块介质，则极板上的电量增大C.断开K，减小两极板间的距离，则两极板间的电场强度减小D.断开K，在两极板间插入一块介质，则两极板间的电势差增大二、不定项选择题（本题有4小题，每小题4分，共16分，在每小题所给的四个选项中，至少有一个是正确的，选对但不全的得2分，有错选或不答的得0分）11、如右图所示，一直流电动机与阻值R＝9 Ω的电阻串联在电上，电电动势E＝30 V，内阻r＝1 Ω，用理想电压表测出电动机两端电压U＝10 V，已知电动机线圈电阻R M＝1 Ω，则下列说法中正确的是 ( ▲)A．通过电动机的电流为10 AB．电动机的输入功率为20 WC．电动机的热功率为4 WD．电动机的输出功率为16 W12、如右图所示电路中，电电动势为E、内阻为r，R0为定值电阻，电容器的电容为C．闭合开关S，增大可变电阻R的阻值，电压表示数的变化量为△U，电流表示数的变化量为△I，则( ▲)A．电压表示数U和电流表示数I的比值不变B．变化过程中△U和△I的比值保持不变C．电阻R0两端电压减小，减小量为△UD．电阻R0两端电压增大，增大量为△U13、关于电动势下列说法正确．．的是 ( ▲)A．电电动势等于电正负极之间的电势差B．用电压表直接测量电两极得到的电压数值，略小于电的电动势大小C．电电动势总等于内、外电路上的电压之和，所以它的数值与外电路的组成有关D．电内部存在有负极指向正极的电场14、R1和R2是材料相同，厚度相同，表面都为正方形的导体，但R1的尺寸比R2大得多，把它们分别连接在如图电路的A、B端，接R1时电压表的读数为U1，接R2时电压表的读数为U2，下列判断正确．．的是（▲）A．R1=R2 B．R1＞R2 C．U1＜U2 D．U1=U2三、填空题（本题有2个小题，每空2分，共18分）15、（1）某同学用游标卡尺测量一圆柱体的长度l，示数如图所示．由图可读出l＝________cm.（2）在测定金属电阻率的实验中，某同学连接电路如图所示．闭合电键后，发现电路有故障(已知电、电表和导线均完好，电电动势为E)：若电流表、电压表示数均为零，该同学利用多用电表检查故障．先将选择开关旋至________挡(填“欧姆×100”“直流电压10 V”或“直流电流2.5 mA”)，再将________(填“红”或“黑”)表笔固定在a接线柱，把另一支表笔依次接b、c、d接线柱.16、有一个小灯泡上标有“4 V、2 W”的字样，现在要用伏安法描绘这个灯泡的I—U 图线．现有下列器材供选用：A．电压表(0～5 V，内阻10 kΩ) B．电压表(0～15 V，内阻20 kΩ)C．电流表(0～3 A，内阻1 Ω) D．电流表(0～0.6 A，内阻0.4 Ω)E．滑动变阻器(10 Ω，2 A) F．滑动变阻器(500 Ω，1 A)G．学生电(直流6 V)、开关、导线若干(1)实验时，选用电路图（填“甲”或者“乙”）完成实验.(2)实验中所用电压表应选________，电流表应选用________，滑动变阻器应选用________，测量得到的小灯泡的电阻与真实的电阻相比（“偏大”或者“偏小”）(用序号字母表示) ．(3)把图中所示的实验器材用实线连接成实物电路图．四、计算题（本题有4小题，共36分，其中17、18每题8分，19、20每题10分，要求画出必要的图形和写出必要的文字说明、方程式、重要的演算步骤，只写出计算结果不给分。

2015-2016学年度第一学期期末考试高一数学试题及参考答案

2015-2016学年度第一学期期末考试高一数学试题一、选择题（该大题共12小题，每小题5分，共计60分） 1.下列图形中，表示⊆M N 的是（ ▲ ）2.120cos ︒= （ ▲ ） A.12-B.12C.32-D.223.下列命题正确的是（ ▲ ）A ．向量AB 与BA 是两平行向量；B ．若,a b 都是单位向量,则a b =；C ．若AB =DC ,则A B CD 、、、四点构成平行四边形； D ．两向量相等的充要条件是它们的始点、终点相同. 4.45154515cos cos sin sin ︒︒-︒︒= （ ▲ ）A.22 B.32C.12D.12-5.如图，在ABC ∆中，D 是AC 的中点，向量AB a =，AC b =，那么向量BD 可表示为（ ▲ ） A.b a 1122- B.a b 12-C.b a 12-D.a b 12-6.函数2212()()=+-+f x x a x 在区间(],4-∞上是递减的，则实数a 的取值范（ ▲ ） A.3≤-a B.3≥-a C.5≤a D.5≥a 7.已知指数函数()xf x a =和函数2()g x ax =+，下列图象正确的是（ ▲ ）A. B. C. D.8.已知平面向量,a b ，8a =||，4||=b ，且,a b 的夹角是150︒，则a 在b 方向上的射影是（ ▲ ）A.4-B.43-C.4D.439.要得到函数2sin 2=y x 的图像，只需将2sin(2)6π=-y x 的图像（ ▲ ）A.向右平移6π个单位 B.向右平移12π个单位 C.向左平移6π个单位D.向左平移12π个单位10.若平面向量(3,4)b =与向量(4,3)a =，则向量,a b 夹角余弦值为（ ▲ ）A.1225 B. 1225- C. 2425- D.2425 11.设()338x f x x =+-,用二分法求方程(),338012xx x +-=∈在内近似解的过程中得()()(),.,.,101501250f f f <><则方程的根落在区间（ ▲ ）A ．(,.)1125B ．(.,.)12515C ．(.,)152D ．不能确定12.若函数tan ,0(2)lg(),0x x f x x x ≥⎧+=⎨-<⎩，则(2)(98)4f f π+⋅-= （ ▲ ）A.12B.12- C.2 D.2-二、填空题（共4小题，每小题5分，共计20分） 13.函数212()log ()=-f x x 的定义域是 ▲ ．14.有一半径为4的扇形，其圆心角是3π弧度，则该扇形的面积是 ▲ ． 15.已知平面向量(4,3)a =-和单位向量b ，且b a ⊥，那么向量b 为 ▲ ． 16.关于函数sin (()42)3f x x ＝＋π，(R)x ∈有下列命题： ①()y f x =是以2π为最小正周期的周期函数；②()y f x =可改写为cos (6)42y x ＝-π； ③()y f x =的图象关于(0)6-，π对称； ④()y f x =的图象关于直线6x =-π对称；其中正确的序号为 ▲ ．M N D.N M C. M N B. MN A. o 2 1 y x2 1 oy x2 1 oyx2 1 oy xD C AB 第5小题三、解答题（共6小题，共计70分） 17.化简或求值：(1)log lg lg 223212732548--⨯++ (2)已知3sin ,054x x =<<π,求cos 2cos()4xx +π. 18.已知全集U R =，集合{}A x x =<<17，集合{}B x a x a 125=+<<+，若满足A B B =，求（1）集合U C A ；（2）实数a 的取值范围．19.若平面向量(1,2)a =，(3,2)b =-， k 为何值时: （1）()(3)ka b a b +⊥-；（2）//()(3)ka b a b +-？20.设函数()2sin(2)(0)f x x =+<<ϕϕπ，()y f x =图象的一个对称中心是(,0)3π.（1）求ϕ；（2）在给定的平面直角坐标系中作出该函数在(0,)2x ∈π的图象；（3）求函数()1()f x x R ≥∈的解集21.已知函数2()3sin 22cos f x x x =+.(1)求函数()f x 的最小正周期和单调递增区间；(2)将()f x 的图象向右平移12π个单位长度，再将周期扩大一倍，得到函数()g x 的图象，求()g x 的解析式．22.已知定义域为R 的函数2()21x x af x -+=+是奇函数（1）求a 值；（2）判断并证明该函数在定义域R 上的单调性；（3）若对任意的t R ∈，不等式22(2)(2)0f t t f t k -+-<恒成立，求实数k 的取值范围.2015-2016学年度第一学期期末考试高一数学试题参考答案一、选择题（该大题共12小题，每小题5分，共计60分）CAACC ADBDD BC二、填空题（共4小题，每小题5分，共计20分） 13. 2{|>x x ,且3}≠x 或者填(2,3)(3,)+∞ ．14.83π. 15.34(,)55和 34(,)55--.16. ② ③ .三、解答题（共6小题，共计70分） 17.（本小题满分8分）解：（1）原式=()lg lg 2193549-⨯-++=()lg 1931009-⨯-+=()19329-⨯-+=1113（2）3sin ,054x x π=<<2cos 1sin xx ∴=-=45227cos 2cos sin cos sin 72552222cos()cos sin 42222x x x x x x x x π-+∴====+-18.（本小题满分10分）解；（1）(,][,)U C A =-∞+∞17（2）A B B =B A ∴⊆（i ）当B φ=时，由a a 251+≤+得a 4≤-（ii ）当B φ≠时，由a a a a 11257125+≥⎧⎪+≤⎨⎪+<+⎩解得a 01≤≤a ∴的取值范围是(,][,]401-∞-.19.（本小题满分12分）解：（1）a b (1,2),(3,2)==- ka b k k (3,22)∴+=-+ a b 3(10,4)-=-()(3)ka b a b +⊥-(k 3)10(2k 2)(4)0∴-⨯++⨯-=解得 k 19=（2）由（1）及//()(3)ka b a b +-得(k 3)(4)(2k 2)100-⨯--+⨯=解得 1k 3=-20.（本小题满分14分）解：（1）(,)π03是函数()y f x = 的图像的对称中心sin()πϕ∴⨯+=2203()k k Z πϕπ∴+=∈23()k k Z πϕπ∴=-∈23(,)πϕπϕ∈∴=03()sin()f x x π∴=+223（2）列表：（3）()f x ≥1即sin()x π+≥2213sin()x π+≥1232解得,k x k k Z πππππ+≤+≤+∈5222636亦即,k x k k Z ππππ-+≤≤+∈124所以，()f x ≥1的解集是[,],k k k Z ππππ-++∈12421.（本小题满分12分）解：（1）依题意，得f x x x =++()3sin 2cos 21x x =++312(sin 2cos 2)122x π=++2sin(2)16将()y f x =的图像向右平移12π个单位长度，得到函数f x x x ππ=-++=+1()2sin[2()]12sin 21126的图像，该函数的周期为π，若将其周期变为π2，则得g x x =+()2sin 1 （2）函数f x ()的最小正周期为T π=，（3）当,k x k k Z πππππ-≤+≤-∈222262时，函数单调递增，解得,k x k k Zππππ-≤≤+∈36∴函数的单调递增区间为 [,],k k k Z ππππ-+∈36. 22.（本小题满分14分）解：（1）由题设，需(),,()xxa f a f x +-==∴=∴=+112001212经验证，()f x 为奇函数，a ∴=1xπ12π3 π712 π56πx π+23 π3π2 ππ32π2π73 ()f x32-23（2）减函数.证明：任意,,,x x R x x x x ∈<∴->1212210由（1）得()()()()()x x x x x x x x f x f x --⨯--=-=++++2112212121121222212121212 ,x x x x x x <∴<<∴-<121212022220，()()x x ++>2112120()()f x f x ∴-<210所以，该函数在定义域R 上是减函数（3）由22(2)(2)0f t t f t k -+-<得f t t f t k -<--22(2)(2)()f x 是奇函数∴f t t f k t -<-22(2)(2)，由（2），()f x 是减函数. ∴原问题转化为t t k t ->-2222，即t t k -->2320对任意t R ∈恒成立.∴k ∆=+<4120，解得k <-13即为所求.。

浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试数学(文)试题

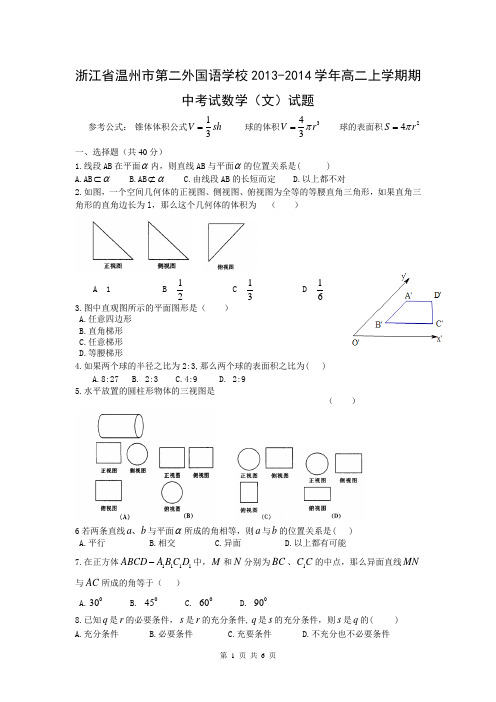
浙江省温州市第二外国语学校2013-2014学年高二上学期期中考试数学（文）试题参考公式：锥体体积公式13V sh = 球的体积343V r π= 球的表面积24S r π= 一、选择题（共40分）1.线段AB 在平面α内，则直线AB 与平面α的位置关系是( ) A.AB α⊂ B.AB α⊄ C.由线段AB 的长短而定 D.以上都不对2.如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为l ，那么这个几何体的体积为（）A 1B21C31 D61 3.图中直观图所示的平面图形是（） A.任意四边形 B.直角梯形 C.任意梯形 D.等腰梯形4.如果两个球的半径之比为2:3,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:9 5.水平放置的圆柱形物体的三视图是（）6若两条直线a b 、与平面α所成的角相等，则a 与b 的位置关系是( ) A.平行 B.相交 C.异面 D.以上都有可能7.在正方体1111ABCD A B C D -中，M 和N 分别为BC 、1C C 的中点，那么异面直线MN 与AC 所成的角等于（）A.030B. 045C. 060D. 0908.已知q 是r 的必要条件，s 是r 的充分条件,q 是s 的充分条件，则s 是q 的( ) A.充分条件 B.必要条件 C.充要条件 D.不充分也不必要条件9.空间四边形ABCD 的两条对角线,AC BD 的长分别为4，5，则平行于两条对角线的截面四边形EFGH 在平移过程中，其周长的取值范围是( ) A.(5,10) B.(8,10) C.(3,6) D(6,9)10.在底面是菱形的四棱锥P ABCD -中，点E 在PD 上，且PE ：ED =2：1,在棱PC 上是存在一点F ,使BF ∥平面AEC ,则PF ：FC 的值为( ) A.1：1 B.2：1 C. 3：1 D. 3：2 二、填空题（共20分）11．若命题“p 且q ”为假，且“非p ”为假，则命题q 的真假为_______． 12.有下列四个命题：①“若0=+y x ，则y x ,互为相反数”的逆命题； ②“全等三角形的面积相等”的否命题；③“若1≤q ，则022=++q x x 有实根”的逆命题；④“等边三角形的三个内角相等”的逆否命题；其中真命题的序号是． 13．正方体1111ABCD A B C D -中，则1C A 与平面ABCD 所成角的正弦值为； 14．正方体1111ABCD A B C D -中，二面角1C AB C --的大小为________．15.角“αβ= ”是“tan tan αβ=”成立的条件. 三解答题16.（8分）某几何体的三视图如图所示，求该几何体的体积. 17.（8分）设有两个命题：（1）关于x 的不等式0422>++ax x 对一切R x ∈恒成立；（2）函数()(52)xf x a =-是增函数，若命题有且只有一个是真命题，求实数a 的取值范围。

高一数学上学期期末考试试卷(含解析)-人教版高一全册数学试题

某某省某某第一中学2015-2016学年高一上学期期末考试数学一、选择题：共10题1．下列说法中,正确的是A.幂函数的图象都经过点(1,1)和点(0,0)B.当a＝0时,函数y＝xα的图象是一条直线C.若幂函数y＝xα的图象关于原点对称,则y＝xα在定义域内y随x的增大而增大D.幂函数y＝xα,当a<0时,在第一象限内函数值随x值的增大而减小【答案】D【解析】本题主要考查幂函数的图象与性质.由幂函数的图象与性质可知，A错误；当x=0时，y=0，故B错误；令a＝-1，则y=x-1，显然C错误；故D正确.2．如图所示,则这个几何体的体积等于A.4B.6C.8D.12【答案】A【解析】由三视图可知所求几何体为四棱锥,如图所示,其中SA⊥平面ABCD,SA=2,AB=2,AD=2,CD=4,且四边形ABCD为直角梯形,∠DAB=90°,∴V=SA×(AB+CD)×AD=×2××(2+4)×2=4,故选A.3．下列关于函数y＝f(x),x∈[a,b]的叙述中,正确的个数为①若x0∈[a,b]且满足f(x0)＝0,则(x0,0)是f(x)的一个零点;②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;③函数f(x)的零点是方程f(x)＝0的根,f(x)＝0的根也一定是函数f(x)的零点;④用二分法求方程的根时,得到的都是根的近似值.A.0B.1C.3D.4【答案】B【解析】本题主要考查方程与根、二分法.由零点的定义知，零点是曲线与x轴交点的横坐标，故①错误；当f(a)=0时，无法用二分法求解，故②错误；显然，③正确；若f(x)=2x-x-1，在区间(-1,1)上的零点，用二分法，可得f(0)=0，显然，④错误.4．如图,在三棱锥S-ABC中,E为棱SC的中点,若AC＝,SA＝SB＝SC＝AB＝BC＝2,则异面直线AC与BE所成的角为A.30°B.45°C.60°D.90°【答案】C【解析】本题主要考查异面直线所成的角.取SA的中点D，连接BD、DE，则,是异面直线AC与BE所成的角或补角，由题意可得BD=BE=，DE=，即三角形BDE是等边三角形，所以5．如图,正方体ABCDA1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF＝,则下列结论中错误的是A.AC⊥BEB.EF∥平面ABCDC.直线AB与平面BEF所成的角为定值D.异面直线AE、BF所成的角为定值【答案】D【解析】本题主要考查线面平行与垂直的判定定理、线面所成的角、异面直线所成的角，考查了空间想象能力.易证AC⊥平面BDD1B1，则AC⊥BE，A正确，不选；易知平面A1B1C1D1∥平面ABCD，则EF∥平面ABCD，B正确，不选；因为平面BEF即是平面BDD1B1，所以直线AB 与平面BEF所成的角为定值，故C正确，不选；故选D.6．若函数且)有两个零点,则实数a的取值X围是A. B. C. D.【答案】B【解析】本题主要考查函数的性质与零点.当时，函数是减函数，最多只有1个零点，不符合题意，故排除A、D；令,易判断函数在区间上分别有一个零点，故排除C，所以B正确.7．已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则A.α∥β且l∥α B.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l【答案】D【解析】本题涉及直线与平面的基本知识,意在考查考生的空间想象能力、分析思考能力,难度中等偏下.由于m,n为异面直线,m⊥平面α,n⊥平面β,则平面α与平面β必相交,但未必垂直,且交线垂直于直线m,n,又直线l满足l⊥m,l⊥n,则交线平行于l ,故选D.8．已知直线(1+k)x+y-k-2＝0过定点P,则点P关于直线x-y-2＝0的对称点的坐标是A.(3,﹣2)B.(2,﹣3)C.(3,﹣1)D.(1,﹣3)【答案】C【解析】本题主要考查直线方程、两条直线的位置关系.将(1+k)x+y-k-2＝0整理为：k(x-1)+x+y-2=0,则x-1=0且x+y-2=0,可得P(1,1),设点P的对称点坐标为(a,b),则，则x=3,y=-1,故答案：C.9．如图,平面⊥平面与两平面所成的角分别为和．过分别作两平面交线的垂线,垂足为,则＝A. B. C. D.【答案】A【解析】本题主要考查线面与面面垂直的判定与性质、直线与平面所成的角，考查了空间想象能力.根据题意，由面面垂直的性质定理可得，,则,则AB=2，则10．经过点P(1,4)的直线在两坐标轴上的截距都是正值,若截距之和最小,则直线的方程为A.x＋2y-6＝0 B.2x＋y-6＝0 C.x-2y＋7＝0 D.x-2y-7＝0【答案】B【解析】本题主要考查直线方程、基本不等式.由直线的斜率为k(k<0)，则y-4=k(x-1),分别令x=0、y=0求出直线在两坐标轴上的截距为：4-k，1-,则4-k+1-,当且仅当-k=-，即k=-2时，等号成立，则直线的方程为2x＋y-6＝0二、填空题：共5题11．已知直线: x+(1+m)y+m-2=0与直线:mx＋2y＋8＝0平行,则经过点A(3,2)且与直线垂直的直线方程为________．【答案】2x-y-4＝0【解析】本题主要考查直线方程、两条直线的位置关系.因为直线: x+(1+m)y+m-2=0与直线:mx＋2y＋8＝0平行,所以(m+1)m-2=0,且8-(m-2),则m=1，直线: x+2y-1=0,根据题意，设所求直线方程为2x-y+t＝0，将点A(3,2)代入可得t=-4，即：2x-y-4＝012．用斜二测画法得到的四边形ABCD是下底角为45°的等腰梯形,其下底长为5,一腰长为,则原四边形的面积是________.【答案】8【解析】本题主要考查平面直观图.根据题意，直观图中，梯形的下底长为5，一腰长为,则易求上底为3，高为1，面积为,所以原四边形的面积是13．已知三棱锥A-BCD的所有棱长都为,则该三棱锥的外接球的表面积为________．【答案】3π【解析】本题主要考查空间几何体的表面积与体积，考查了空间想象能力.将正方体截去四个角可得到一个正四面体，由题意，可将该三棱锥补成一个棱长为1的正方体，所以该三棱锥的外接球的直径即为正方体的对角线，所以2r=，则该三棱锥的外接球的表面积为S=14．已知关于x的方程有两根,其中一根在区间内,另一根在区间内,则m的取值X围是________．【答案】【解析】本题主要考查二次函数的性质与二元一次方程的根.设,由题意可知：，求解可得15．甲、乙、丙、丁四个物体同时以某一点出发向同一个方向运动，其路程关于时间的函数关系式分别为，，，，有以下结论：①当时，甲走在最前面；②当时，乙走在最前面；③当时，丁走在最前面，当时，丁走在最后面；④丙不可能走在最前面，也不可能走在最后面；⑤如果它们一直运动下去，最终走在最前面的是甲.其中，正确结论的序号为_________(把正确结论的序号都填上，多填或少填均不得分).【答案】③④⑤【解析】①错误.因为，，所以，所以时，乙在甲的前面.②错误.因为，，所以，所以时，甲在乙的前面.③正确.当时，，的图象在图象的上方.④正确.当时，丙在甲乙前面，在丁后面，时，丙在丁前面，在甲、乙后面，时，甲、乙、丙、丁四人并驾齐驱.⑤正确.指数函数增长速度越来越快，x充分大时，的图象必定在，，上方，所以最终走在最前面的是甲.三、解答题：共5题16．如图(1)所示,在直角梯形中,BC AP,AB BC,CD AP,又分别为线段的中点,现将△折起,使平面平面(图(2))．(1)求证:平面平面;(2)求三棱锥的体积．【答案】证明:(1)分别是的中点,∵平面,AB平面.∴平面.同理,平面,∵,EF平面平面∴平面平面.(2)＝.【解析】本题主要考查面面与线面平行与垂直的判定与性质、空间几何体的表面积与体积，考查了空间想象能力与等价转化.(1)根据题意,证明、,再利用线面与面面平行的判定定理即可证明;(2)由题意易知，则结果易得.17．已知两点,直线,求一点使,且点到直线的距离等于2．【答案】设点的坐标为.∵．∴的中点的坐标为．又的斜率．∴的垂直平分线方程为,即．而在直线上．∴．①又已知点到的距离为2．∴点必在于平行且距离为2的直线上,设直线方程为,由两条平行直线之间的距离公式得:∴或．∴点在直线或上．∴或②∴①②得:或．∴点或为所求的点．【解析】本题主要考查直线方程与斜率、两条直线的位置关系、中点坐标公式.设点的坐标为，求出统一线段AB的垂直平分线，即可求出a、b的一个关系式；由题意知，点必在于平行且距离为2的直线上, 设直线方程为,由两条平行直线之间的距离公式得:，求出m的值，又得到a、b的一个关系式，两个关系式联立求解即可.18．(1)已知圆C经过两点,且被直线y=1截得的线段长为.求圆C的方程;(2)已知点P(1,1)和圆过点P的动直线与圆交于A,B两点,求线段AB的中点M的轨迹方程.【答案】(1)设圆方程为.因为点O,Q在圆上,代入:又由已知,联立:解得:由韦达定理知:.所以:.即即:.即:.则.所以所求圆方程为:.(2)设点M (x ,y ), 圆的圆心坐标为C (0,2). 由题意:,又.所以: 化简:所以M 点的轨迹方程为【解析】本题主要考查圆的方程、直线与圆的位置关系、圆的性质、直线的斜率公式、方程思想.(1)设圆方程为，将y =1代入圆的方程，利用韦达定理，求出D 、E 、F 的一个关系式，再由点O 、Q 在圆上，联立求出D 、E 、F 的值，即可得到圆的方程;(2) 设点M (x ,y ), 圆的圆心坐标为C (0,2)，由题意:,又，化简求解即可得到结论.19．如图,在四棱锥P —ABCD 中,PA ⊥底面ABCD , AB ⊥AD , AC ⊥CD ,∠ABC ＝60°,PA ＝AB ＝BC ,E 是PC 的中点．C A PB D E(1)求PB 和平面PAD 所成的角的大小;(2)证明:AE ⊥平面PCD ;(3)求二面角A-PD-C的正弦值．【答案】(1)在四棱锥P—ABCD中,∵PA⊥底面ABCD,AB⊂平面ABCD,∴PA⊥A B.又AB⊥AD,PA∩AD＝A,从而AB⊥平面PAD,∴PB在平面PAD内的射影为PA,从而∠APB为PB和平面PAD所成的角．在Rt△PAB中,AB＝PA,故∠APB＝45°.所以PB和平面PAD所成的角的大小为45°.(2)证明:在四棱锥P—ABCD中,∵PA⊥底面ABCD,CD⊂平面ABCD,∴CD⊥PA.由条件CD⊥AC,PA∩AC＝A∵CD⊥平面PA C.又AE⊂平面PAC,∴AE⊥C D.由PA＝AB＝BC,∠ABC＝60°,可得AC＝PA.∵E是PC的中点,∴AE⊥P C.又PC∩CD＝C,综上得AE⊥平面PCD.(3)过点E作EM⊥PD,垂足为M,连接AM,如图所示．由(2)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则可证得AM⊥PD.因此∠AME是二面角A—PD—C的平面角．由已知,可得∠CAD＝30°.设AC＝a,可得PA＝a,AD＝a,PD＝a,AE＝在Rt△ADP中,∵AM⊥PD,∴AM·PD＝PA·AD,则AM＝＝.在Rt△AEM中,sin∠AME＝＝.所以二面角A—PD—C的正弦值为.【解析】本题主要考查线面垂直的判定定理与性质定理、线面角与二面角，考查了空间想象能力.(1)根据题意，证明AB⊥平面PAD,即可得证∠APB为PB和平面PAD所成的角，则易求结果；(2)由题意，易证CD⊥平面PA C，可得AE⊥C D，由题意易知AC＝PA，又因为E是PC 的中点,所以AE⊥P C，则结论易证；(3) 过点E作EM⊥PD,垂足为M,连接AM,如图所示，由(2)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则可证得AM⊥PD，因此∠AME是二面角A—PD—C的平面角，则结论易求.20．诺贝尔奖的奖金发放方式为:每年一发,把奖金总额平均分成6份,分别奖励给在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出最有益贡献的人,每年发放奖金的总金额是基金在该年度所获利息的一半;另一半利息计入基金总额,以便保证奖金数逐年增加．假设基金平均年利率为r＝6.24%.资料显示:1999年诺贝尔发放后基金总额约为19 800万美元．设f(x)表示第x(x∈N*)年诺贝尔奖发放后的基金总额(1999年记为f(1),2000年记为f(2),…,依次类推)(1)用f(1)表示f(2)与f(3),并根据所求结果归纳出函数f(x)的表达式;(2)试根据f(x)的表达式判断网上一则新闻“2009年度诺贝尔奖各项奖金高达150万美元”是否为真,并说明理由．(参考数据:1.031 29≈1.32)【答案】(1)由题意知:f(2)＝f(1)(1＋6.24%)-f(1)·6.24%＝f(1)×(1＋3.12%),f(3)＝f(2)×(1＋6.24%)-f(2)×6.24%＝f(2)×(1＋3.12%)＝f(1)×(1＋3.12%)2,∴f(x)＝19800(1＋3.12%)x-1(x∈N*)．(2)2008年诺贝尔奖发放后基金总额为f(10)＝19800(1＋3.12%)9＝26136,故2009年度诺贝尔奖各项奖金为·f(10)·6.24%≈136(万美元),与150万美元相比少了约14万美元,是假新闻．【解析】本题主要考查指数函数、函数的解析式与求值,考查了分析问题与解决问题的能力、计算能力.(1)由题意知: f(2)＝f(1)(1＋6.24%)-f(1)·6.24%，f(3)＝f(2)×(1＋6.24%)-f(2)×6.24%，化简，即可归纳出函数f(x)的解析式；(2)根据题意，求出2008年诺贝尔奖发放后基金总额为f(10)，再求出2009年度诺贝尔奖各项奖金为·f(10)·6.24%，即可判断出结论.。

浙江省温州市第二外国语学校学年高一物理下学期知识竞赛试题必修2

浙江省温州市第二外国语学校2012-2013学年高一物理下学期知识竞赛试题新人教版必修2本卷除实验题外重力加速度取g=10m/s 2一、单项项选择题（本题共12小题，每小题3分，共36分。

每小题只有一个答案正确。

） 1．关于摩擦力对物体做功，下述几种论断正确的是 A ．滑动摩擦力对物体一定做负功 B ．静摩擦力对物体一定做负功C ．滑动摩擦力既可对物体做负功，也可以对物体做正功D ．静摩擦力对物体一定不做功2. 使两个完全相同的金属小球(均可视为点电荷)分别带上－3Q 和＋5Q 的电荷后，将它们固定在相距为a 的两点，它们之间库仑力的大小为F 1。

现用绝缘工具使两小球相互接触后，再将它们固定在相距为2a 的两点，它们之间库仑力的大小为F 2。

则F 1与F 2之比为A ．2∶1B ．4∶1C ．16∶1D ．60∶13.如下图所示，正电荷q 在电场中由P 向Q 做加速运动，而且加速度越来越大，由此可以判定，它所在的电场是图中的4．美国的NBA 篮球赛非常精彩，吸引了众多观众.经常有这样的场面：在临终场0.1s 的时候，运动员把球投出且准确命中，获得比赛的胜利。

如果运动员投篮过程中对篮球做功为W ，出手高度为h 1，篮筐距地面高度为h 2，球的质量为m ，空气阻力不计，则篮球进筐时的动能为A ．W +21mgh mgh -B ．W +12mgh mgh -C ．21mgh mgh -－WD ．12mgh mgh -－W5．如图所示，在地面上以速度v 0抛出质量为m 的物体，抛出后物体落到比地面低h 的海平面上．若以地面为零势能面而且不计空气阻力，则①物体到海平面时的势能为mgh②抛出到落至海平面重力对物体做的功为mgh③物体在海平面上的动能为12mv 02＋mgh④物体在海平面上的机械能为12mv 02其中正确的是A ．①②③B ．②③④C ．①③④D ．①②④6.速度为v 的子弹，恰可穿透一固定着的木板，如果子弹速度为2v ，子弹穿透木板的阻力视为不变，则可穿透同样固定的木板A. 1 块B. 2 块C. 3 块D.4 块7.如图所示，一物体以一定的速度沿水平面由A 点滑到B 点，摩擦力做功W 1；若该物体以一定的速度从A′沿两斜面滑到B′，不考虑物体在最高点离开斜面情况，摩擦力做的总功为W 2，已知物体与各接触面的动摩擦因数均相同，则 A ．W 1=W 2 B ．W 1＞W 2C ．W 1＜W 2D ．不能确定W 1、W 2大小关系8.如图，两个质量相同的小球A 、B 分别用线悬在等高的O 1、O 2点。

浙江省温州市第二外国语学校2014-2015学年高二下学期知识竞赛英语试题 Word版含答案

温州二外2014学年第二学期高二学科知识竞赛英语试题（考试时间：100分钟满分：100分命题老师：高杨露审题老师：徐丽若）第I 卷(共80分)第一部分：听力理解（共20小题；每小题1 分，满分20分）第一节听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Who is the man?A. The owner.B. A customer.C. A waiter.2. What can we learn about the woman?A. She is attractive.B. She praised a man.C. She doesn‟t like her work.3. What will the speakers probably do next?A. Have a rest.B. See a doctor.C. Move the bed.4. What does the man suggest the woman do?A. Feed the dog.B. Call Franklin for help.C. Show a toy to Charlie.5. What time do the tickets go on sale?A. At noon.B. At 1:00 p.m.C. At midnight.第二节听下面5段对话或独白。

每段对话或独白后有2至4个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有5秒钟的时间阅读各个小题；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段对话，回答第6、7题。

6. What are the speakers mainly talking about?A. A painting.B. A photograph.C. A basket.7. Where did the man find the thing?A. In an art gallery.B. At a hospital.C. On the street.听第7段对话，回答第8至10题。

2015-2016学年高一上学期第一次月考数学试题_Word版含答案

2015--2016学年度高一第一学期第一次月考数学试题（时间：90分钟，总分100分）一、选择题（共10小题，每小题4分）1、已知集合P={x ∈N | 1≤x ≤10}，Q={x ∈R| x 2+x －6=0}，则P ∩Q=（）A. { 1, 2, 3 }B. { 2, 3}C. { 1, 2 }D. { 2 }2、已知集合U={ 1, 2, 3, 4, 5, 6, 7 }，A={ 2, 4, 5, 7 }，B={ 3, 4, 5 }则（C ∪A ）∪（C ∪B ）=（）A. { 1, 6 }B. { 4, 5}C. { 2, 3, 4, 5, 7 }D. { 1, 2, 3, 6, 7 }3、设集合A={ 1, 2 }，则满足A ∪B = { 1, 2, 3 }的集合B 的个数是（）A. 1B. 3C. 4D. 84、函数f(x)=x 2+mx+1的图象关于直线x=1对称，则（）A. m=－2B. m=2C. m=－1D. m=15、设f(x)是定义在R 上的奇函数，当x ≤0时，f(x)=2x 2－x, 则f(1)等于（）A. －3B. －1C. 1D. 36、在区间（－∞，0）上为增函数的是（）A. y=1B. y=2x1x +- C. 1x 2x y 2---= D. y=1+x 27、若函数y=f(x)的定义域[－2，4]，则函数g(x) = f(x) + f(－x)的定义域是（）A. [－4，4]B. [－2，2]C. [－4，－2]D. [2，4]8、设abc>0，二次函数f(x) = ax 2 + bx + c 的图象可能是（）A. B. C. D.9、函数x2y =的单调减区间为（） A. R B. （－∞, 0）∪（0, +∞）C. （－∞, 0）, （0, +∞）D. （0，+∞）10、已知定义在R 上的奇函数f(x)在（－∞, －1）上是单调减函数，则f(0), f(－3)+f(2)的大小关系是（）A. f(0)<f(－3)+f(2)B. f(0)=f(－3)+f(2)C. f(0)> f(－3) +f(2)D. 不确定二、填空题（本大题共5小题，每小题4分）11、已知集合A={－1, 1, 2, 4}, B={－1, 0, 2}，则A ∩B= 。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛数学试题

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛数学试题一．选择题（本题共10小题，每题4分，共40分）1. 已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是A.,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ B.,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦ C.2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D.,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦ 2．设A 到B 的映射f ：x →y=(x －1)2,若集合{}2,1,0=A ，则集合B 不可能是（▲）A 、{}1,0B 、{}2,1,0C 、{}2,1,0-D 、{}1,1,0-3．已知函数()f x 满足(1)(1)f x f x +=-，且对任意的1212,1()x x x x >≠，有1212()()0f x f x x x ->-，设1(),(2),(3)2a f b f c f =-==，则,,a b c 的大小关系为A.c b a <<B. b a c <<C. b c a <<D.a b c <<4．若A 、B 是锐角△ABC 的两个内角，则点P （cosB ﹣sinA ，sinB ﹣cosA ）在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限5.定义运算⎩⎨⎧>≤=*ba b b a a b a ,,，如121=*，则函数()x x x f -*=22的值域是（）A.RB.+R C.(]1,0 D.[)+∞,1 6．已知()π∈α,0，且51cos sin =α+α，则αtan 的值为（） A ．34± B ．43± C ．34-D ．43-7．我们定义渐近线：已知曲线C ，如果存在有一条直线，当曲线C 上任一点M 沿曲线运动时M 可无限趋近于该直线但永远达不到，那么这条直线称为这条曲线的渐近线；下列函数：①2()23f x x x =+- ②()21xg x =+ ③2()log (1)h x x =- ④21()1x t x x +=-⑤22()x u x x+=，其中有渐近线的个数（）A ．2B ．3C ．4D ．58. 函数y=tanx+sinx ﹣|tanx ﹣sinx|在区间内的图象是（）．．． D ．9.设函数()f x x x=-,对任意[)1,,()()0x f mx mf x ∈+∞+<恒成立,则实数m 的取值范围是（）A ．(1,1)-B ．,0m R m ∈≠C ．(,1)-∞-D ．(,1)-∞-()1,⋃+∞10. 已知函数2()2(4)4,()f x x m x m g x mx =+-+-=，若对于任一实数x ，()f x 与()g x 的值至少有一个为正数，则实数m 的取值范围是A ．[4,4]-B ．(4,4)-C ．(,4)-∞D ．(,4)-∞- 二．填空题（本题共5个小题，每题4分，共20分）11.若11112-=⎪⎭⎫ ⎝⎛+x x f ，则()=x f ________12. 函数的图象为C ，如下结论中正确的是．①图象C 关于直线对称； ②图象C 关于点对称；③函数f （x ）在区间内是增函数； ④由y=3sin2x 的图角向右平移个单位长度可以得到图象C ．13. 若函数(1)()(4)2(1)2x a x f x a x x ⎧>⎪=⎨-+≤⎪⎩对于R 上的任意12x x ≠都有0)()(2121>--x x x f x f ，则实数a 的取值范围是 ▲ ． 14. 已知函数()f x x =，2()252g x x mx m =-+-()m R ∈，对于任意的1[2,2]x ∈-，总存在2[2,2]x ∈-，使得12()()f x g x =成立，则实数m 的最小值 ▲15. 关于x 的不等式1(sin 1)sin 2x x m m +-+≥对[0,]2x π∈恒成立，则实数m 的取值范围是．三．解答题（共4个小题，共40分）16.（8分）已知函数()()34log 2-+-=a x ax x f a 的定义域为R ，求实数a 的取值范围。

浙江省温州市第二外国语学校2013-2014学年高一下学期期初语文考试试题

温州市第二外国语学校第二学期期初考试语文试卷一、基础与运用（共10题，选择题每题2分，共21分）1.下列各项加点字读音完全正确的一项是（）A.炽．热 zhì坍．圮tān 朱拓．tà敕．造chìB.粜．米 tiào 岑．寂céng 监．生jiàn 狙．击jūC.滂．沱 pāng 炮烙． luò笨拙． zhuō亘．古gènD.蹙．缩cù熨．帖yù胡诌． zōu 牲醴．lǐ2.下列各项中没有错别字的一项是（）A.裨益阜盛草窠桌帏一愁莫展B.惊蜇雕琢酣眠料峭目不暇接C.蹒跚斑驳缪种沧海功亏一篑D.孺慕瞋视作揖坐落沸反盈天3.下列各项中加点词语运用最准确的一项是（）A.诗评家所谓“老杜饥寒而悯人饥寒者也”，跟白居易“饱暖而悯人饥寒者也”是不同的，饥寒让杜甫刻骨铭心．．．．，所以他写出的诗句更加深刻感人。

B.中药是在中医学理论指导下用以防治疾病的药物，以植物为最多，也包括动物和矿物，其药效一般比较缓和．．。

C.近日，我认真拜读了您的大作，十分钦佩。

可能是一时疏忽，你的文章中有几处不大通畅的语句，我斗胆加以斧正．．。

D.北京出版社出版的高中语文课本，以金庸的《雪山飞狐》替换了鲁迅的《阿Ｑ正传》。

金庸小说的登堂入室．．．．未必不是时代进步的一个表征。

4．下列各句中，没有语病的一项是( )A．在创建“全国文明城市”的活动中，广州市容不仅变得更加整洁，更加美丽，而且市民也变得更守规范，更讲文明。

B．当今社会上制假、贩假的现象屡禁不止，且愈演愈烈，其根本原因是受巨大的经济利益驱使造成的，应引起我们反省。

C．受全球气候变暖的影响，高山生态环境中的许多植物无法在原生长地生存，正向更高海拔“逃生”，以寻找新的栖息地。

D．新型的“DNA流感疫苗”，疗效好，安全性高，适用性广，价格低廉，满足同时抵御多种禽流感病毒的客观需求的优势。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛语文试题

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛语文试题注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

2．全部答案在答题卡上完成，答在本试题上无效。

一、语言文字运用（共20分，其中选择题每小题2分）1．下列词语中加点字的读音全部正确的一项是（▲）A．符．合（fú）档．案（dàng）迫．击炮（pào）稍纵即．逝（jí）B．饕．餮（tāo）蒙．骗（méng）峭楞．楞（lèng）哄．堂大笑（hōng）C．女红．（gōng）憎．恶 (zēng) 梵．婀玲（fàn）量．体裁衣（liàng）D．载．体（zài）懦．弱（nuò）不更．事（gēng）呱．（guā）呱坠地2．下列各句中，没有错别字的一项是（▲）A．人到中年便时有闲愁，怪不得词人会感叹年华一瞬，容消金镜，壮志消残，我也不免有些感触。

B．我们祖先有个根深蒂固的观念，以为一切生灵，都有返本的倾向：鸟恋旧林，鱼思故渊，胡马依北风，狐死必守丘，树高千丈，叶落归根。

C．受外部环境、自身转型等多重因素影响，上海经济下行压力加大，投资出口低速增长，消费、工业出现放缓迹象，转型综合征已逐渐体现出来。

D．虽然人们总是一相情愿地声称“谣言止于制者”，“真相在于公开透明”，“人民的眼睛是雪亮的”。

但辟谣敌不过谣言，科普敌不过迷信，一直是个严峻的事实。

3．将下列选项中的词语依次填入各句横线处，最恰当的一组是（▲）①某市负责人在接受媒体采访时表示，经济建设要注重环境保护；该市的环境保护仍然严重滞后。

②医院作为特殊的公共，应该讲究语言得体，“欢迎你再来”这一类的语言是不宜随便使用的。

③人们在异国他乡为了生存而不得不放弃自己原有的文明，首先放弃也最难放弃的就是母语。

④谈到决赛对手时，教练说：“这将是一场漂亮的比赛，在决赛中和他们会师是一次独一无二的机会。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛政治试题 Word版含答案

温州市第二外国语学校2013学年第一学期学科知识竞赛高一政治试卷（考试总分：100分考试时间：80分钟命题老师：徐必予审题老师：叶坚秀）考生须知：考生答题前,务必将自己的姓名、学号用黑色字迹的签字笔或钢笔填写在答题纸上。

选择题部分一、选择题Ⅰ（共20小题，每小题2分，共40分。

每小题中只有一个选项是符合题意的。

不选、多选、错选均不得分）1．国家在餐饮行业推行刮奖发票，消费者就餐后索要发票应有中奖可能，若餐馆拒绝开具发票，可向税务机关举报。

关于刮奖发票，正确判断是A.推行刮奖发票的主要目的是促进消费B.对无需报账的就餐者可以不开具发票C.提供刮奖发票可显著增强餐馆竞争力D.索要和提供餐饮发票利于减少税收流失2．2013年，我国综合运用各种手段对国民经济进行调控，实现了预期调控目标。

下列调控目标、调控政策、具体措施三者对应最恰当的是( )A.控物价——稳健的货币政策——严控对高耗能、高污染行业的贷款B.稳增长——积极的财政政策——减轻服务业和小微型企业税收负担C.调结构——积极的财政政策——下调金融机构一年期存贷款基准利率D.惠民生——稳健的货币政策——加大对战略性新兴产业财政支持力度3．近年来，智能手机市场的竞争日趋激烈。

除传统手机制造商外，许多网络公司也纷纷斥资研发智能手机，并将内置其网络产品的智能手机推向市场。

在下列选项中，能够解释“网络公司造手机”原因的是A.生产智能手机的利润率高于其他行业B.网络公司的业务创新速度不断加快C.传统手机制造商生产智能手机能力不足D.网络公司延伸产业链提高综合竞争力4．2012年，某县农民种植的土豆产量增大，但市场没有相应的扩充，农民不得不低价销售，收入不增反降。

图5的①②③④中，能够反映这种“丰产不丰收”经济现象的是A.①B.②C.③D.④5．中国H公司与美国某公司签订服装出口合同，约定服装单价为24美元，一年后交货。

H公司生产一件服装的成本是144人民币元。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛历史试题

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛历史试题考生须知：1.本试卷分选择题和非选择两部分，解答题部分在答题卡上，试卷共6页，答题卡共2页，满分100分，考试时间80分钟。

2.考生答题前,务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。

3.选择题的答案须用2B铅笔将答题纸上对应题目的答案标号涂黑，如要改动,须将原填涂处用橡皮擦净。

非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上相应区域内，作图时可先使用2B铅笔，确定后须用黑色字迹的签字笔或钢笔描黑，答案写在本试题卷上无效。

一、选择题（共40小题，每小题2分，共80分。

每小题中只有一个选项是符合题意的。

不选、多选、错选均不得分）1．中国古代常常通过分割和削弱相权来加强皇权。

下列表述正确的是（）A．西汉通过削弱诸侯王势力分化相权 B．北魏实行三长制分割丞相的行政权C．宋代设立三司使来分割丞相的财权 D．清设军机处消除了皇权与相权矛盾2．据《南台备要》记载：“江浙省……调兵剿捕之际，行省官凡有轻重事物，若是一一咨禀，诚恐缓不及事。

……（如今）凡有调遣军情重事及创动官钱，不须咨禀，……交他每（们）从便区处。

”这段材料可以反映出元代的江浙行省（）A．与中央权力之争难以调和 B．获得了紧急事务处置权C．行政长官不再由朝廷任命 D．权力不再受到中央节制3．黄仁宇在论及西汉的统治政策时写道：“新朝代遇到的第一个大问题是帝国跨地过广，不能全部由中央集体管制，于是采取了一种‘斑马式’的省级组织。

”这里“‘斑马式’的省级组织”是指（）A．郡县制 B．封国制与郡县制并存C．州郡县三级交错管理 D．行省制度4．《汉书·地理志》载：“秦遂并兼四海，以为周制微弱，终为诸侯所丧，故不立尺土之封，分天下为郡县。

”材料中的“周制”是指（）A．郡县制 B．分封制 C．王位世袭制 D．行省制5．下列各组古今地名对应正确的是（）①大都—北京②汴梁—开封③临安—苏州④益州—成都A．①②③ B．①②④ C．①③④ D．②③④6．1938年4月，中国飞行员陈怀民在武汉空战中与日军飞行员高桥宪一同归于尽。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛物理试题

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛物理试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

一、单项选择题（本题共8小题，每小题3分，共24分。

每小题给出的四个选项中，只有一项是符合题目要求的）1. 2012年6月1日，空降兵某部官兵使用新装备从260 m超低空跳伞成功．若跳伞空降兵在离地面224 m高处，由静止开始在竖直方向做自由落体运动．一段时间后，立即打开降落伞，以12.5 m/s2的平均加速度匀减速下降，为了空降兵的安全，要求空降兵落地速度最大不得超过5 m/s(g取10 m/s2)．则A．空降兵展开伞时离地面高度至少为125 m，相当于从2.5 m高处自由落下B．空降兵展开伞时离地面高度至少为125 m，相当于从1.25 m高处自由落下C．空降兵展开伞时离地面高度至少为99 m，相当于从1.25 m高处自由落下D．空降兵展开伞时离地面高度至少为99 m，相当于从2.5 m高处自由落下2. 如图所示，水平木板上有质量m＝1.0 kg的物块，受到随时间t变化的水平拉力F作用，用力传感器测出相应时刻物块所受摩擦力F f的大小．取重力加速度g＝10 m/s2，下列判断正确的是A．5 s内位移为零B．4 s末物块所受合力大小为4.0 NC．物块与木板之间的动摩擦因数为0.4D．6 s～9 s内物块的加速度大小为2.0 m/s23. 如图所示，小球用细绳系住，绳的另一端固定于O点．现用水平力F缓慢推动斜面体，小球在斜面上无摩擦地滑动，细绳始终处于直线状态，当小球升到接近斜面顶端时细绳接近水平，此过程中斜面对小球的支持力F N以及绳对小球的拉力F T的变化情况是A．FN保持不变，F T不断增大B．F N不断增大，F T不断减小C．F N保持不变，F T先增大后减小D．F N不断增大，F T先减小后增大4. 倾角为α、质量为M的斜面体静止在水平桌面上，质量为m的木块静止在斜面体上．下列结论正确的是A．木块受到的摩擦力大小是mgcosαB．木块对斜面体的压力大小是mgsinαC．桌面对斜面体的摩擦力大小是mgsinαcosαD．桌面对斜面体的支持力大小是(M＋m)g5．如图，在固定斜面上的一物块受到一外力F的作用，F平行于斜面向上．若要物块在斜面上保持静止，F的取值应有一定范围，已知其最大值和最小值分别为F1和F2(F2>0)．由此可求出A．物块的质量B．斜面的倾角C．物块与斜面间的最大静摩擦力D．物块对斜面的正压力6．一物块静止在粗糙的水平桌面上．从某时刻开始，物块受到一方向不变的水平拉力作用．假设物块与桌面间的最大静摩擦力等于滑动摩擦力．以a表示物块的加速度大小，F表示水平拉力的大小．能正确描述F与a之间关系的图像是7. 质量为m的消防队员从一平台上竖直跳下，下落3 m后双脚触地，接着他用双腿弯曲的方法缓冲，使自身重心又下降了0.6 m，假设在着地过程中地面对他双脚的平均作用力大小恒定，则消防队员A．着地过程中处于失重状态B．着地过程中地面对他双脚的平均作用力等于6mgC．在空中运动的加速度大于触地后重心下降过程中的加速度D．在空中运动的平均速度小于触地后重心下降过程中的平均速度8．如图所示，有一倾角为θ的斜面体B静置在水平地面上，物体A放在斜面上且与B保持相对静止。

XXX2015-2016学年高一数学上学期期中考试试卷

XXX2015-2016学年高一数学上学期期中考试试卷XXX2015-2016学年高一上学期期中考试数学试卷分为两卷，卷（Ⅰ）100分，卷（Ⅱ）50分，满分共计150分。

考试时间为120分钟。

卷（Ⅰ）一、选择题：本大题共10小题，每小题5分，共50分。

1.如果A＝{x|x>−1}，那么正确的结论是A．A⊆B。

{0}∈A C。

{0}∈C2.函数f（x）＝2−2x，则f（1）＝A。

0 B.−2 C.2/2 D.−2/23.设全集I={x|x∈Z−3<x<3}，A={1，2}，B={−2，−1，2}，则A∪(I∩B)等于A。

{1} B。

{1，2} C。

{2} D。

{0，1，2}4.与函数y＝10lg(x−1)的定义域相同的函数是A。

y＝x−1 B。

y＝x−1 C。

y＝1/(x−1) D。

y＝x−15.若函数f（x）＝3＋3x−x与g（x）＝3−3^(−x)的定义域均为R，则A。

f（x）与g（x）均为偶函数 B。

f（x）为偶函数，g （x）为奇函数C。

f（x）与g（x）均为奇函数 D。

f（x）为奇函数，g （x）为偶函数6.设a=log_3(2)，b=ln2，c=5，则A。

a<b<XXX<c<a C。

c<a<b D。

c<b<a7.设函数y=x和y=1/2，则y的交点为（x，y），则x所在的区间是A.（，1）B.（1，2）C.（2，3）D.（3，4）8.已知函数f（x）是R上的偶函数，当x≥1时f(x)=x−1，则f（x）<0的解集是A.（−1，∞）B.（−∞，1）C.（−1，1）D.（−∞，−1）∪(1，∞)9.某商店同时卖出两套西服，售价均为168元，以成本计算，一套盈利20%，另一套亏损20%，此时商店A.不亏不盈B.盈利37.2元C.盈利14元D.亏损14元10.设函数f（x）在R上是减函数，则A。

f（a）>f（2a）B。

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛地理试题

浙江省温州市第二外国语学校2013-2014学年高一上学期知识竞赛地理试题一、选择题(本大题有40小题，每小题2分，共80分。

每小题只有一个正确答案，不选、多选、错选均不得分。

)1．下列条件与地球上生命存在无关的是A．日地距离适中B．昼夜交替周期C．地球的体积和质量适中D．地球自转方向2．形成风的直接原因是A．太阳辐射B．地面冷热不均C．水平气压梯度力D．地转偏向力3．下列地区地壳最厚的是A．青藏高原B．四川盆地C．台湾岛D．马里亚纳海沟4．影响纬度地带分异规律的主导因素是A．水分B．热量C．光照D．地形5．影响土壤形成最活跃的因素是A．气候B．成土母质C．地形D．生物6．太阳黑子出现在太阳大气的A．色球层B．光球层C．日冕层D．色球层、光球层和日冕层7．在地质历史上，第二次全球性的生物大规模灭绝发生在A．古生代早期B．古生代末期C．中生代早期D．中生代末期当人们把目光还停留在温室效应引起“全球变暖”时，研究人员通过观察、研究，发现自1954年以来，在我国每过10年到达地面的太阳辐射便下降约2%。

目前我国大地的光照比50年前平均减弱了10%。

于是提出与温室效应相伴随的还有“地球变暗”效应。

读右图回答8～9题。

8．与“地球变黑”有关的环节是A．①B．②C．③D．④9．为减缓全球变暖，人类倡导低碳经济和低碳生活，可以使A．①增强B．②增强C．③减弱D．④减弱2012年6月16日18时，神舟九号成功发射并进入近地点高度200公里，远地点高度330公里的预定轨道。

据此完成10—11题。

10．当“神舟九号”发射时，地球绕太阳公转到图4中的A．①B．②C．③D．④11．下图所列太阳光照图中，与当日最吻合的是读右图，判断回答12--15题：12.若图表示“海陆间水循环模式图”, 台风登陆属于其中哪个环节（）A B DN①③④0° 30°60°A.①B.②C.③D.④ 13.若箭头表示东亚夏季风，下列说法正确的是 A ．甲地气压高于乙地 B ．甲表示的是太平洋 C ．①气流表示东南季风 D ．②气流的性质温暖湿润14．若该图为北半球三圈环流的一部分，且甲地纬度比乙地高，则A ．该环流是高纬环流B ．甲是赤道低压C ．甲、乙之间近地面为中纬西风带D ．甲、乙之间近地面为低纬信风带 15．若箭头表示大洋环流，下列说法正确的是A. 此大洋环流在南半球中低纬海区B. 此大洋环流在北半球中高纬海区C. ③洋流对沿岸气候具有降温减湿作用D. ④洋流沿岸为热带沙漠气候 16．下列有关自然资源性质的叙述，正确的是： A ．可再生资源与非可再生资源的分类是绝对的 B ．若可再生资源开发利用不当，其再生周期会延长 C ．森林是可再生资源，不可能发生不可逆转的变化 D ．在任何利用方式下，可再生资源都可以再生2012年6月，因连降暴雨，我国东南某地发生了如图下所示的灾害。

浙江省温州市第二外国语学校2014-2015学年高二下学期期末考试数学(理)试题

温州二外2014学年第二学期高二期末考试数学试卷 2015.6（满分100分，考试时间：120分钟命题人：潘和锴审题人：金蕾选择题部分（共32分）一、选择题：本大题共8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项符合题目要求。

1、已知集合2{20},{12}P x x x Q x x =-≥=<…，则()P Q =R ð （ ▲ ）． A.[0,1) B. (0,2] C. (1,2) D. [1,2]2、已知 ,a b 是实数，则a b > 是 22a b > 的( ▲ ) A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件 D ．既不充分也不必要条件 3、一个空间几何体的三视图如图所示，其体积为（ ▲ ）A ．16B ．32C ．48D ．96 4．已知,m n 是两条不同的直线，,,αβγ为三个不同的平面，则下列命题中错误的是( ▲ )A ．若,m m αβ⊥⊥则 //αβB ．若,m n αα⊥⊥,则//m nC ．若//,//,//αγβγαβ则D ．若,,//αγβγαβ⊥⊥则5. 已知变量y x ,满足约束条件⎪⎩⎪⎨⎧-≥≤+-≥-141y y x y x ，目标函数的y x z 23-=，则该目标函数的最大值为 ( ▲ )A.17B. 16C. 15D. 146 函数()sin()(0)6f x A x πωω=+>的图像与x 轴正半轴交点的横坐标构成一个公差为2π的等差数列，若要得到函数()sin g x A x ω=的图像，只要将()f x 的图像（ ▲ ）个单位.A ．6π向左平移B ．6π向右平移C ．12π向左平移D ．12π向右平移7．已知22(0)()|log |(0)x x f x x x ⎧≤=⎨>⎩，则方程[()]2f f x =的根的个数是（A ．3个B ．4个C ．5个D ．6个8．如图，双曲线C ：22221x y a b-=(a ＞0，b ＞0)的左、右焦点12(0)(0)F c F c -，、，，A 为双曲线C 右支上一点，且c AF 21=，（第3题图）侧视图正视图俯视图1AF 与y 轴交于点B ，若B F 2是12F AF ∠的角平分线，则双曲线C 的离心率是A ．233+ B ．31+ C ．353+ D ． 253+ 非选择题部分（共68分）二、填空题：本大题共7小题，9-12题：每小题4分，13-15题：每小题3分，共25分。

浙江省温州市第二外国语学校2020┄2021学年高一下学期期末考试物理试题含答案

温州市第二外国语学校202１年第二学期期末考试物理试题卷温馨提示:1．本试题卷分选择题和非选择题两部分,满分１0０分,考试时间80分钟。

2．本卷计算中，g均取10m/s2。

选择题部分一、选择题Ⅰ(全体考生必做。

本大题共2２小题,每小题2分,共44分。

每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分)１.以下单位属于国际单位制基本单位的是A．N B．kg C.ｍ／s D.J２．下列物理中均为标量的一组是A．位移路程B．功力C．电场强度磁感应强度 D.势能动能3.在高速公路的旁边我们常看到如图所示的路牌。

这是交通管理部门设置的限速标志，它是指汽车经过这一路段时A.瞬时速度大小应该介于60km/h和１00ｋｍ/h之间第3题图B．平均速度大小应该介于60km/h和100km/h之间C．瞬时速度大小应该大于10０km/ｈD．瞬时速度大小应该小于6０km/h4．下列哪种情况中可将物体看成质点A．研究地球的自转规律时,可把地球看成质点B.研究“嫦娥三号”卫星绕月球飞行的轨迹时，可把“嫦娥三号”卫星看成质点C．研究孙杨在1５00ｍ自由泳比赛中的动作时,可把孙杨看成质点D．科学家在研究超级细菌的结构时,可把超级细菌看成质点５．如图所示,甲、乙两同学掰手腕游戏,甲同学“掰倒”乙同学时,下列说法正确的是Ａ．甲对乙的力大于乙对甲的力B.甲对乙的力小于乙对甲的力C．甲对乙的力和乙对甲的力始终大小相等D．甲对乙的力和乙对甲的力是一对平衡力第5题图第6题图第7题图６．如图是大货车载着六辆小汽车在平直公路上行驶的情景，下列说法正确的是A．小汽车的惯性小于大货车的惯性B.大货车的惯性小于小汽车的惯性Ｃ．小汽车与大货车的惯性大小相同D．无法比较大货车和小汽车的惯性大小7．倾角为α、质量为M的斜面体静止在水平桌面上，质量为m的木块静止在斜面体上。

下列结论正确的是( )Ａ.木块受到的摩擦力大小是ｍgｃoｓαＢ．木块对斜两体的压力大小是mg sinαC．桌面对斜面体的摩擦力大小是ｍg sinαcosαD.桌面对斜面体的支持力大小是（Ｍ+ｍ)ｇ9．物体做匀速圆周运动时,下列物理量中一定发生变化的是A.周期ﻩB．转速 C.向心加速度ﻩ D.动能9.如图是我国著名网球运动员李娜精彩的比赛瞬间，如果网球离开球拍后,沿图中虚线做曲线运动,则图中能正确表示网球在相应点速度方向的是Ａ．v1Ｂ.v2C．ｖ3 D.v4１0．如图所示是一电动陶艺机，陶艺机上的圆盘可绕一通过圆心且垂直盘面的竖直轴转动。