拟牛顿法.
拟牛顿算法

拟牛顿算法
拟牛顿算法是一种求解现代机器学习中复杂优化问题的数值解法,又称为增量式牛顿方法或增量算法。
拟牛顿算法是一种迭代优化算法,它是由美国物理学家Isaac Newton发明的牛顿法的改进版本,并被用于优化复杂的函数。
拟牛顿算法的主要思想是使用一组特定的校正器来更新牛顿法中的参数,从而实现更高效的迭代优化。
拟牛顿算法的基本原理是:拟牛顿算法从一个初始状态开始,通过迭代的方式,不断地更新参数,使目标函数最小化。
首先,使用梯度下降法确定一个起始状态,并计算出目标函数的梯度值,即梯度偏导数。
然后,根据牛顿法构建拟牛顿算法,即在更新参数时,使用牛顿法计算出增量向量,从而实现梯度下降,使目标函数尽可能小。
拟牛顿算法可以用于大多数优化问题,如拟合数据、优化机器学习模型等。
它与牛顿法的速度相比非常快速,大大提高了收敛速度,并具有更好的收敛性能。
另外,拟牛顿算法也可以方便地适用于正则化情况,使优化效率更高。
拟牛顿算法不仅可以用于优化机器学习模型,还可以用于一些复杂的优化问题,如现实世界中的优化问题,例如非线性系统优化、智能机器人的行为优化等。
与牛顿法相比,拟牛顿算法具有空间收敛性更强、更少的迭代次数和更快的收敛速度的优势。
拟牛顿算法的缺点也是显而易见的,它的计算量比传统的牛顿法大,而且它需要一些复杂的算法来更新参数,这也是它不能广泛应用的原因之一。
总而言之,拟牛顿算法是一种求解现代机器学习中复杂优化问题的有效数值解法,它具有高效率和更快的收敛速度的优势。
但是,由于它计算量大,需要较复杂的算法,因此不能广泛应用。
牛顿法拟牛顿法

牛顿法拟牛顿法牛顿法是一种求解非线性方程的方法,其原理是在迭代中使用方程的导数来近似方程的根。
虽然牛顿法非常有效,但它往往需要非常精准的初始猜测才能保证收敛性。
另一种类似于牛顿法的方法是拟牛顿法,它可以通过逐步调整矩阵B来近似牛顿法的矩阵Hessian。
本文将介绍牛顿法和拟牛顿法的原理和应用。
一、牛顿法假设有一个n维非线性方程系统f(x)=0,其中x是一个n维向量。
牛顿法中的每个迭代都是通过以下公式来更新当前估计xk的:xk+1=xk-Hk^(-1)fk其中Hk是f(x)的Hessian矩阵在xk处的值,假设Hk是可逆的。
牛顿法的优点是它快速收敛,并且可以通过适当选择初始估计来实现收敛。
另一个好处是它可以直接用于求解大型系统,因为它只涉及二次导数的计算。
然而,牛顿法的缺点是它需要计算Hessian矩阵,这通常是一个费时且复杂的任务。
另一个问题是当Hessian矩阵的条件数(即最大特征值与最小特征值之比)很大时,牛顿法的收敛可能会变得很慢。
二、拟牛顿法拟牛顿法的思想是利用一个矩阵Bk来代替牛顿法中的Hk矩阵。
Bk是一个正定对称的矩阵,其初值通常为单位矩阵In。
在每个迭代中,Bk被更新为一个近似的Hessian逆矩阵。
最常用的拟牛顿法算法之一是BFGS算法,其更新规则如下:Bk+1=Bk+(yk^Tyk)/(yk^Ts)+(BkSkS^TBk)/(sk^TBksk)其中sk=xk+1-xk,yk=g(xk+1)-g(xk),g表示f的梯度,^T表示矩阵转置。
该公式是基于以下观察得出的:Bk+1应该满足以下性质:Bk+1是正定对称的。
Bk+1应该近似于Hk+1的逆,其应该满足以下方程:Bk+1sk=yk另外,BFGS算法的收敛速度也相对比牛顿法要慢,因为BFGS算法需要逐步修正矩阵Bk,直到其逼近Hessian矩阵的逆。
三、应用牛顿法和拟牛顿法在许多实际问题中应用广泛,特别是在数学、物理、金融和工程领域。
数学优化中的牛顿法和拟牛顿法

数学优化中的牛顿法和拟牛顿法在数学中,优化是一个非常重要的研究领域,其目的是找到使某个函数达到最大或最小值的变量集合。
在实际应用中,很多问题都可以转化为优化问题,如机器学习、经济学、物理学等。
在优化领域中,牛顿法和拟牛顿法是两种常见的方法。
本文将介绍这两种优化方法的基本原理、优缺点以及应用场景。
一、牛顿法牛顿法(Newton's method)是由数学家牛顿发明的非线性优化方法,其思想是利用函数的泰勒级数展开进行逼近。
具体来说,牛顿法先求出目标函数的一阶和二阶导数,然后使用二阶导数来逼近目标函数本身,进而得到近似最优解。
牛顿法的数学公式如下:$$\boldsymbol{x}_{k+1}= \boldsymbol{x}_{k} -{\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)^{-1}}\boldsymbol{\nabla} f(\boldsymbol{x}_k)$$其中,$\boldsymbol{x}_k$ 表示第 $k$ 次迭代的解,$\boldsymbol{\nabla} f(\boldsymbol{x}_k)$ 和$\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)$ 分别表示目标函数在$\boldsymbol{x}_k$ 处的一阶和二阶导数。
牛顿法的优点是收敛速度非常快,通常只需要很少的迭代次数即可达到最优解。
另外,牛顿法适用于连续可微、二阶可导的函数,因此适用范围广。
然而,牛顿法也存在一些缺点,例如无法处理不可导或一阶可导但二阶不可导的函数。
此外,牛顿法需要计算目标函数的二阶导数,因此在大规模问题上计算成本很高。
二、拟牛顿法拟牛顿法(quasi-Newton method)是一类基于牛顿法的优化算法,它通过逼近目标函数的海森矩阵来求解。
拟牛顿法没有计算海森矩阵的显式表达式,而是通过估计海森矩阵的变化来逼近。
最简单和最流行的拟牛顿法是BFGS算法和L-BFGS算法。
牛顿法、拟牛顿法、高斯-牛顿法、共轭梯度法推导总结

牛顿法、拟牛顿法、高斯-牛顿法、共轭梯度
法推导总结
一、牛顿法
牛顿法是一种求解非线性方程的迭代方法。
牛顿法的基本思想是:在当前点附近,用一次泰勒展开式近似原函数,然后求解近似函数的极值点。
牛顿法每次迭代所需要的计算量较大,但其收敛速度较快。
二、拟牛顿法
拟牛顿法是一种求解无约束极值问题的优化算法。
拟牛顿法是将牛顿法中Hessian矩阵用近似Hessian矩阵Bk表示的算法。
拟牛顿法的计算量比牛顿法小,但是收敛速度较牛顿法慢。
三、高斯-牛顿法
高斯-牛顿法是求解非线性最小二乘问题的一种迭代算法。
该算法假设误差服从高斯分布,利用牛顿法求解目标函数的局部极小值,以最小化残差平方和。
高斯-牛顿法在处理非线性最小二乘问题时具有很好的收敛性。
四、共轭梯度法
共轭梯度法是解决对称正定线性方程组的迭代算法。
该算法通过对一个对称正定矩阵进行迭代求解,寻找线性方程组的解。
共轭梯度法的优点是可以使用较少的内存和计算量实现高效的求解。
以上算法都是数值优化中比较常用的算法,它们各自具有不同的优缺点,可根据实际问题的特点来选择合适的算法。
最优化方法-拟Newton法

0
1 4
0.25
2 X1 0.5,
f ( X1) 5.5
1 f ( X1) 2
(4)判 断 || f ( X 1 ) |,|转(5)
(5)第二次迭代采用DFP变尺度法,构造 E 0
1 0
G0 0
1
1 S0 X1 - X 0 - 0.5
min
f
(X
)
x2 1
2
x2 2
2 x1 x2
4x1
已知 X 0 [1,1]T , 0.1
解:(1)第一次迭代,实际上是沿负梯度方向进行一维搜索。
(2)
f
(
X
)
2x1 2
x1
2x2 4x2
4 ,
4
f ( X0) 2
,G0 I
➢ 5、DFP算法的收敛速度是超线性的。
Relax 做个题,轻松一下
例:用DFP变尺度算法求解无约束最优化问题
min
f
(X
)
x2 1
2
x2 2
2 x1 x2
4x1
已知 X 0 [1,1]T , 0.1
参照:拟Newton法的基本格式做题:
例:用DFP变尺度算法求解无约束最优化问题
三、对称秩1算法 2、对称秩1算法的性质
四、DFP算法(Davidon-Flether-P0well)
四、DFP算法
在DFP算法中,校正矩阵的构造公式为:
Ek
S
k
S
T k
S kTYk
拟牛顿法

拟牛顿法牛顿法的收敛速度虽然较快,但要求海森矩阵要可逆,要计算二阶导数和逆矩阵,就加大了就算机计算量。
为了克服牛顿法的缺点,同时保持较快收敛速度的优点,就产生了拟牛顿法。
拟牛顿法是牛顿法的直接推广,通过在试探点附近的二次逼近引进牛顿条件来确定线搜索方向,它主要有DFP 和BFGS 两种形式,拟牛顿法的一般步骤为:(1) 给定初始点(0)x ,初始对称正定矩阵0H ,(0)0()g g x =及精度0ε>; (2) 计算搜索方向()k k k p H g =-;(3) 作直线搜索(1)()()(,)k k k xF x p +=,计算(1)(1)11(),()k k k k f f x g g x ++++==,(1)()1,k k k k k k S x x y g g ++=-=-(4) 判断终止准则是否满足;(5) 令1k k k H H E +=+置1k k =+,转步骤(2);不同的拟牛顿法对应不同的k E ,主要介绍DFP 和BFGS 两种拟牛顿法。
1. DFP 法(1) 算法原理DFP 算法中的校正公式为:1k kk kT T k k k kk k T T kk k S S H y y H H H S y y H y +=+-为了保证k H 的正定性,在下面的算法中迭代一定次数后,重置初始点和迭代矩阵再进行迭代。
(2) 算法步骤1) 给定初始点(0)x ,初始矩阵0n H I =及精度0ε>; 2) 若()(0)f xε∇≤,停止,极小点为(0)x ;否则转步骤3);3) 取()(0)(0)0p H f x =-∇,且令0k =; 4) 用一维搜索法求k t ,使得()()()()0()min ()k k k k k k t f Xt p f X tp α≥+=+,令(1)()()k k k x x tp +=+,转步骤5);5) ()(1)k f xε+∇≤,停止,极小值点为(1)k x +;否则转步骤6);6) 若1k n +=,令(0)()n x x =,转步骤3);否则转步骤7);7) 令()()()()()()()()()()()()()()()()()()(1)()(1)()1(1)()(1)()(1)()(1)()(1)()(1)()Tk k k k k k Tk k k k Tk k k k k kTk k k k kx x x x H H xx f x f x H f xf x f x f x H f x f x H f x f x +++++++++--=+-∇-∇∇-∇∇-∇-∇-∇∇-∇,取()()(1)1k k k p H f x ++=-∇,置1k k =+,转步骤4)。
拟牛顿法

•主页•专栏作家•量化基础理论•软件使用经验•量化软件•资源导航•资料下载•量化论坛搜索搜索用户登录用户名:*密码:*登录•创建新帐号•重设密码首页拟牛顿法及相关讨论星期三, 2009-06-17 00:24 —satchel1979使用导数的最优化算法中,拟牛顿法是目前为止最为行之有效的一种算法,具有收敛速度快、算法稳定性强、编写程序容易等优点。
在现今的大型计算程序中有着广泛的应用。
本文试图介绍拟牛顿法的基础理论和若干进展。
牛顿法(Newton Method)牛顿法的基本思想是在极小点附近通过对目标函数做二阶Taylor展开,进而找到的极小点的估计值[1]。
一维情况下,也即令函数为则其导数满足因此(1)将作为极小点的一个进一步的估计值。
重复上述过程,可以产生一系列的极小点估值集合。
一定条件下,这个极小点序列收敛于的极值点。
将上述讨论扩展到维空间,类似的,对于维函数有其中和分别是目标函数的的一阶和二阶导数,表现为维向量和矩阵,而后者又称为目标函数在处的Hesse矩阵。
设可逆,则可得与方程(1)类似的迭代公式:(2)这就是原始牛顿法的迭代公式。
原始牛顿法虽然具有二次终止性(即用于二次凸函数时,经有限次迭代必达极小点),但是要求初始点需要尽量靠近极小点,否则有可能不收敛。
因此人们又提出了阻尼牛顿法[1]。
这种方法在算法形式上等同于所有流行的优化方法,即确定搜索方向,再沿此方向进行一维搜索,找出该方向上的极小点,然后在该点处重新确定搜索方向,重复上述过程,直至函数梯度小于预设判据。
具体步骤列为算法1。
算法1:(1) 给定初始点,设定收敛判据,.(2) 计算和.(3) 若< ,则停止迭代,否则确定搜索方向.(4) 从出发,沿做一维搜索,令.(5) 设,转步骤(2).在一定程度上,阻尼牛顿法具有更强的稳定性。
拟牛顿法(Quasi-Newton Method)如同上一节指出,牛顿法虽然收敛速度快,但是计算过程中需要计算目标函数的二阶偏导数,难度较大。
10--拟牛顿法

一般约束问题的一阶最优性条件
考虑
min f (x)
x Rn
s.t.
gi (x) 0, hj (x) 0,
起作用约束:
i 1,...,m j 1,...,l
gi
(i
I
)
;
hj ( j 1,...,l)
hj ( j 1,...,l)
定理(Fritz John条件) :
设x S, f (x)在x处可微,
wi 0
例min f (x) (x1 2)2 x22
s.t.
g1(x) x1 x22 0
g2 (x) x1 x2 0
验证下列两点
x (1)
00和x(2)
1 1
是否为K T点。
x(1)不是;x(2)是
例min f (x) (x1 1)2 x2
s.t.
g1(x) x1 x2 2 0 g2 (x) x2 0
Hkq(k ) )( p(k ) Hkq(k ) )T q(k)T ( p(k) Hkq(k) )
注释
• 在一定条件下,收敛且具有二次终止性。 • 无法保证Hk的正定性;即使能,也有可能导致
△Hk无界。
DFP算法
秩为
Hk k u(k) u(k)T kv(k) v(k)T
2
p(k ) H k1q(k )
2
f ( x) f ( x(k1) ) 2 f ( x(k1) )(x x(k1) )
f ( x(k) ) f ( x(k1) ) 2 f ( x(k1) )(x(k) x(k1) ) p(k ) : x(k 1) x(k ) q(k ) : f (x(k 1) ) f (x(k ) ) q(k ) 2 f (x(k 1) ) p(k )
最优化算法(牛顿、拟牛顿、梯度下降)
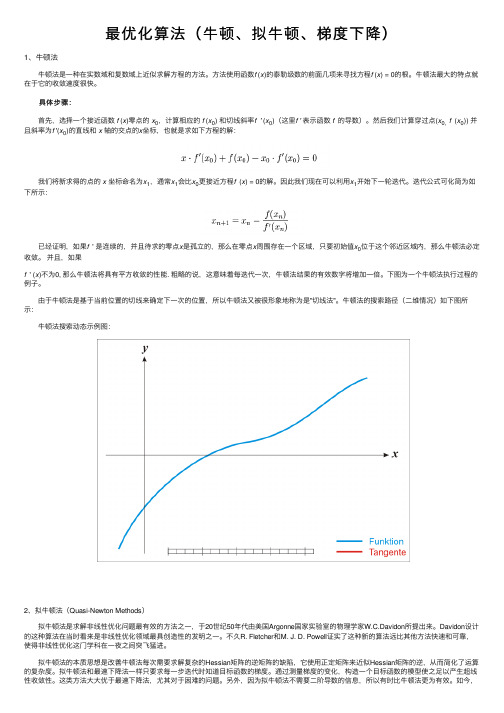
最优化算法(⽜顿、拟⽜顿、梯度下降)1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤: ⾸先,选择⼀个接近函数f (x)零点的x0,计算相应的f (x0) 和切线斜率f ' (x0)(这⾥f ' 表⽰函数f 的导数)。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标,也就是求如下⽅程的解: 我们将新求得的点的x 坐标命名为x1,通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰: 已经证明,如果f ' 是连续的,并且待求的零点x是孤⽴的,那么在零点x周围存在⼀个区域,只要初始值x0位于这个邻近区域内,那么⽜顿法必定收敛。
并且,如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说,这意味着每迭代⼀次,⽜顿法结果的有效数字将增加⼀倍。
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置,所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径(⼆维情况)如下图所⽰: ⽜顿法搜索动态⽰例图:2、拟⽜顿法(Quasi-Newton Methods) 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠,使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使⽤正定矩阵来近似Hessian矩阵的逆,从⽽简化了运算的复杂度。
拟牛顿法公式

拟牛顿法公式拟牛顿法是一种求解非线性方程的迭代算法,它通过逼近问题的局部线性模型来逼近方程的解。
拟牛顿法公式是该算法的核心表达式,用于更新迭代解的数值。
下面将对拟牛顿法公式进行详细介绍。
拟牛顿法公式的一般形式为:x(k+1) = x(k) - [H(k)]^(-1) * g(k)其中,x(k)表示第k次迭代的解向量,x(k+1)表示第k+1次迭代的解向量,g(k)表示第k次迭代的梯度向量,H(k)表示第k次迭代的拟牛顿矩阵。
拟牛顿法的关键是如何选择拟牛顿矩阵H。
常用的拟牛顿法有DFP 方法和BFGS方法。
这两种方法都是基于满足拟牛顿条件的逆Hessian矩阵的递推公式。
DFP方法的递推公式为:H(k+1) = H(k) + (s(k) * s(k)') / (s(k)' * y(k)) - (H(k) * y(k) * y(k)' * H(k)) / (y(k)' * H(k) * y(k))BFGS方法的递推公式为:H(k+1) = H(k) + (1 + (y(k)' * H(k) * y(k)) / (y(k)' * s(k)))* (s(k) * s(k)') / (y(k)' * s(k)) - (H(k) * y(k) * s(k)' - s(k) * y(k)' * H(k)) / (y(k)' * s(k))其中,s(k) = x(k+1) - x(k)表示迭代解的变化量,y(k) = g(k+1) - g(k)表示梯度的变化量。
通过不断迭代,拟牛顿法可以逐步逼近非线性方程的解。
每次迭代,根据拟牛顿法公式更新解向量,直到达到收敛条件为止。
收敛条件可以是解向量的变化量小于某个预设阈值,或者目标函数的梯度小于某个预设阈值。
需要注意的是,拟牛顿法并不一定能够收敛到全局最优解,而是局部最优解。
因此,在实际应用中,我们需要结合问题的特点选择合适的初值和拟牛顿矩阵的初始估计,以提高算法的收敛性和求解精度。
机器学习算法系列(25):最速下降法、牛顿法、拟牛顿法

作为指导。
3.2 DFP算法
DFP算法是以William C.Davidon、Roger Fletcher、Michael J.D.Powell三个人人的名字的首首字⺟母命 名的,它由Davidon于1959年年首首先提出,是最早的拟牛牛顿法。该算法的核心心是:通过迭代的方方
,求λ k,使 f(x ( k ) + λ kp k) = minλ ≥ 0 f(x ( k ) + λp k) 4. 置x ( k + 1 ) = x ( k ) + λ kp k,计算f(x ( k + 1 ) )当 | | f(x ( k + 1 ) ) − f(x ( k ) ) | | < ξ或 | | x ( k = 1 ) − x ( k ) | | < ξ,停止止迭代,令x ∗ = x ( k + 1 ) 5. 否则,置k = k + 1,转到步骤3。 当目目标函数是凸函数时,梯度下降法的解释全局最优解。一一般情况下,其解不不保证是全局最优 解。梯度下降法的收敛速度也未必是很快的。
3.1 拟牛牛顿条件
设经过k + 1次迭代后得到X k + 1,此时将目目标函数f(X)在X k + 1附近作泰勒勒展开,取二二阶近似,得到 1 f( X) ≈ f( X k + 1 ) + ∇ f( X k + 1 ) · ( X − X k + 1 ) + · ( X − X k + 1 ) T · ∇ 2 f( X k + 1 ) · ( X − X k + 1 ) 2 在两边同时作用用一一个梯度算子子 ∇ ,可得 ∇ f( X) ≈ ∇ f ( X k + 1 ) + H k + 1 · ( X − X k + 1 ) 取X = X k并整理理,可得 g k + 1 − g k ≈ H k + 1 · (X k + 1 − X k ) 若引入入记号s k = X k + 1 , y k = g k + 1 − g k则可以改写成
拟牛顿法

•主页•专栏作家•量化基础理论•软件使用经验•量化软件•资源导航•资料下载•量化论坛搜索搜索用户登录用户名:*密码:*登录•创建新帐号•重设密码首页拟牛顿法及相关讨论星期三, 2009-06-17 00:24 —satchel1979使用导数的最优化算法中,拟牛顿法是目前为止最为行之有效的一种算法,具有收敛速度快、算法稳定性强、编写程序容易等优点。
在现今的大型计算程序中有着广泛的应用。
本文试图介绍拟牛顿法的基础理论和若干进展。
牛顿法(Newton Method)牛顿法的基本思想是在极小点附近通过对目标函数做二阶Taylor展开,进而找到的极小点的估计值[1]。
一维情况下,也即令函数为则其导数满足因此(1)将作为极小点的一个进一步的估计值。
重复上述过程,可以产生一系列的极小点估值集合。
一定条件下,这个极小点序列收敛于的极值点。
将上述讨论扩展到维空间,类似的,对于维函数有其中和分别是目标函数的的一阶和二阶导数,表现为维向量和矩阵,而后者又称为目标函数在处的Hesse矩阵。
设可逆,则可得与方程(1)类似的迭代公式:(2)这就是原始牛顿法的迭代公式。
原始牛顿法虽然具有二次终止性(即用于二次凸函数时,经有限次迭代必达极小点),但是要求初始点需要尽量靠近极小点,否则有可能不收敛。
因此人们又提出了阻尼牛顿法[1]。
这种方法在算法形式上等同于所有流行的优化方法,即确定搜索方向,再沿此方向进行一维搜索,找出该方向上的极小点,然后在该点处重新确定搜索方向,重复上述过程,直至函数梯度小于预设判据。
具体步骤列为算法1。
算法1:(1) 给定初始点,设定收敛判据,.(2) 计算和.(3) 若< ,则停止迭代,否则确定搜索方向.(4) 从出发,沿做一维搜索,令.(5) 设,转步骤(2).在一定程度上,阻尼牛顿法具有更强的稳定性。
拟牛顿法(Quasi-Newton Method)如同上一节指出,牛顿法虽然收敛速度快,但是计算过程中需要计算目标函数的二阶偏导数,难度较大。
机器学习算法系列最速下降法牛顿法拟牛顿法

机器学习算法系列最速下降法牛顿法拟牛顿法最速下降法(Gradient Descent)最速下降法是一种常用的优化算法,用于求解无约束的最小化问题。
其原理是通过不断迭代更新参数的方式来逼近最优解。
在最速下降法中,每次迭代的方向是当前位置的负梯度方向,即沿着目标函数下降最快的方向前进。
具体地,对于目标函数f(x),在当前位置x_k处的梯度为g_k=▽f(x_k),则下一次迭代的位置x_{k+1}可以通过以下公式计算:x_{k+1}=x_k-α*g_k其中,α 是一个称为学习率(learning rate)的参数,用于控制每次迭代的步长。
最速下降法的优点是简单易实现,收敛速度较快。
然而,它也有一些缺点。
首先,最速下降法的收敛速度依赖于学习率的选择,过小的学习率会导致收敛速度过慢,而过大的学习率可能会导致跳过最优解。
其次,最速下降法通常会在目标函数呈现弯曲或者高度相关的情况下表现不佳,很难快速收敛到最优解。
牛顿法(Newton's Method)牛顿法是一种通过二阶导数信息来优化的算法,可以更快地收敛到目标函数的最优解。
在牛顿法中,每次迭代的位置x_{k+1}可以通过以下公式计算:x_{k+1}=x_k-(H_k)^{-1}*▽f(x_k)其中,H_k是目标函数f(x)在当前位置x_k处的黑塞矩阵。
黑塞矩阵描述了目标函数的二阶导数信息,可以帮助更准确地估计参数的更新方向。
牛顿法的优点是收敛速度较快,特别是对于目标函数呈现弯曲或者高度相关的情况下,相较于最速下降法可以更快地达到最优解。
然而,牛顿法也有一些缺点。
首先,计算黑塞矩阵的代价较高,尤其是当参数较多时。
其次,黑塞矩阵可能不可逆或者计算代价较大,这时可以通过使用拟牛顿法来避免。
拟牛顿法(Quasi-Newton Method)拟牛顿法是一类基于牛顿法的优化算法,通过估计黑塞矩阵的逆来逼近最优解,从而避免了计算黑塞矩阵的代价较高的问题。
在拟牛顿法中,每次迭代的位置x_{k+1}可以通过以下公式计算:x_{k+1}=x_k-B_k*▽f(x_k)其中,B_k是一个对黑塞矩阵逆的估计。
单目标多变量无约束优化问题的典型优化算法

单目标多变量无约束优化问题在工程和科学领域中广泛存在,求解这类问题需要采用有效的优化算法。
本文将介绍几种典型的优化算法,包括梯度下降法、牛顿法、拟牛顿法、粒子裙算法和遗传算法等,以帮助读者更好地理解和应用这些算法。
一、梯度下降法梯度下降法是一种常用的优化算法,通过不断沿着目标函数的负梯度方向更新参数,以最小化目标函数。
其具体步骤如下:1. 初始化参数向量x和学习率α;2. 计算目标函数的梯度g=∇f(x);3. 更新参数向量:x=x-αg;4. 重复步骤2和步骤3,直到收敛或达到迭代次数。
梯度下降法的优点是简单易用,但也存在收敛速度慢、易陷入局部最优解等缺点。
二、牛顿法牛顿法是一种快速收敛的优化算法,其基本思想是利用目标函数的二阶导数信息加速收敛。
牛顿法的步骤如下:1. 初始化参数向量x;2. 计算目标函数的梯度g=∇f(x)和海森矩阵H=∇²f(x);3. 更新参数向量:x=x-(H^-1)g;4. 重复步骤2和步骤3,直到收敛或达到迭代次数。
牛顿法具有快速收敛的优点,但也存在计算海森矩阵复杂、可能导致矩阵奇异等缺点。
三、拟牛顿法拟牛顿法是对牛顿法的改进,通过估计目标函数的海森矩阵来避免直接计算。
拟牛顿法的步骤如下:1. 初始化参数向量x和拟海森矩阵G;2. 计算目标函数的梯度g=∇f(x);3. 更新参数向量:x=x-Gg;4. 更新拟海森矩阵G;5. 重复步骤2至步骤4,直到收敛或达到迭代次数。
拟牛顿法克服了牛顿法中计算海森矩阵的困难,同时具有较快的收敛速度。
四、粒子裙算法粒子裙算法是一种基于裙体智能的优化算法,模拟了鸟裙觅食的行为。
其基本思想是通过不断更新粒子的位置和速度来搜索最优解。
粒子裙算法的具体步骤如下:1. 初始化粒子的位置和速度;2. 计算目标函数值,并更新个体最优位置和全局最优位置;3. 根据个体最优位置和全局最优位置更新粒子的速度和位置;4. 重复步骤2和步骤3,直到满足停止条件。
例题是唐老师教材_1025_拟牛顿法(DFP算法)

)
Step4: 令 k
k 1,
返回Step2.
注: 第一步迭代与最速下降法相同.
三. 对称秩2算法(DFP校正公式)
设校正矩阵的形式为:
H k H k 1 k uk uk
T
Page 10
k vk vk
T
( II )
其中 k 0, uk = uk 1 , uk 2 , , ukn 0
x
k 1
x k d .
k k
Page 13
Step3: 计算
k 1 x
k 1
x
k 1
k
k 1 f ( x
) f ( x )
k T
H k 1 H k d
k 1
k 1 k 1 k 1 k 1
T k 1
)
H k k 1 k 1 H k
2
0 4 , 10 1
0 8
2 x1 f x , 8 x2
0
2 f x 0
2 2 0 0 f ( x ) , d f ( x ) 8 8
f
T
H1 H 0
1 1
T
T
1 1
H 0 1 1 H 0
T
1 H 0 1 Page 16
T
又
0.26154 1 x x 1.04 x
1
f x
0
0.52308 8.36923
1 0 0
Page 15
f
x 1.47692,
1
0.36923 ,
牛顿法和拟牛顿法

⽜顿法和拟⽜顿法⽜顿法和拟⽜顿法⽜顿法(Newton method)和拟⽜顿法(quasi Newton method)是求解⽆约束最优化问题的常⽤⽅法,收敛速度快。
⽜顿法是迭代算法,每⼀步需要求解海赛矩阵的逆矩阵,计算⽐较复杂。
拟⽜顿法通过正定矩阵近似海赛矩阵的逆矩阵或海赛矩阵,简化了这⼀计算过程。
⽜顿法我们假设点x∗为函数f(x)的根,那么有f(x∗)=0。
现在我们把函数f(x)在点x k处⼀阶泰勒展开有:假设点x k+1为该⽅程的根,则有:可以得到这样我们就得到了⼀个递归⽅程,我们可以通过迭代的⽅式不断的让x趋近于x∗从⽽求得⽅程f(x)的解。
最优化问题对于最优化问题,其极值点处⼀阶导数为0。
因此我们可以在⼀阶导数处利⽤⽜顿法通过迭代的⽅式来求得最优解,即相当于求⼀阶导数对应函数的根。
⾸先,我们对函数在x0点处进⾏⼆阶泰勒展开对x求导可得由于在极值点处,于是从⽽可以得出下⼀个x的位置其迭代形式为对于多维函数,⼆阶导数就变成了⼀个海森矩阵,⼆阶泰勒展开公式如下:图中的便是海森矩阵。
迭代公式就变成了。
我们可以看到,当 H k为正定( H k-1也正定)的时候,可以保证⽜顿法的搜索⽅向是向下搜索的。
拟⽜顿法当特征特别多的时候,求海森矩阵的逆矩阵,运算量是⾮常⼤且慢,考虑⽤⼀个n阶矩阵来替代,这就是拟⽜顿法的基本思路。
通过以上可以得到因此,对于我们所选择的替代矩阵G k,需要满⾜两个条件:1. 拟⽜顿条件,即2. 要保证G k为正定矩阵,这是因为只有正定才能保证搜索⽅向是向下搜索的。
由于每次迭代都需要更新矩阵G k ,下⾯介绍⼀些⽅法。
DFP,这⾥的D K相当于前边提到的G K ,这个迭代公式的关键是每⼀步的校正矩阵ΔD K的构造。
我们采⽤待定法,先将ΔD K待定为下⾯的形式:α和β为待定系数,u和v为待定向量。
uu T和vv T均为对称矩阵,因此可以保证ΔD K也是对称矩阵。
将待定公式代⼊迭代公式,可得:D k+1·y k = s k上述变化是因为是两个数,不妨设为可得将其带⼊s k的表达式,可得不妨直接取代回上⾯α和β的表达式,得:将上两式代回ΔD K的表达式,得这样就可以使⽤迭代公式来进⾏拟⽜顿法的计算了。
拟牛顿法算法步骤

拟牛顿法是一种优化算法,其基本步骤如下:
1. 初始化:选择初始点$x_0$和近似的Hessian矩阵$H_0$(通常选择单位矩阵$I$)。
设定迭代终止条件,包括最大迭代次数和目标函数值收敛阈值。
2. 迭代计算:对于每一次迭代$k$,计算当前点的梯度$g_k=\nabla f(x_k)$。
3. 判断终止条件:检查终止条件,包括梯度范数的大小和目标函数值的收敛性。
如果满足终止条件,则算法结束,返回当前点$x_k$作为近似的最优解。
否则,继续下一步。
以上是拟牛顿法的基本步骤,供您参考,建议咨询专业人士获取更准确的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据Schwartz不等式 (a12 a22 an2 )(b12 b22 bn2 ) (a1b1 anbn )2
故有 ( pT
p)(qTq)(pTq)2 ,从而
( pT
p)(qT q) ( pTq)2 qT q
0
(10.4.21)
p( j)T q( j) jd ( j)T (g j1 g j ) jd ( j)T g j 由于λj>0,gj≠0,Hj
j (H j g j )T
gj
j
g
T j
H
j
g
j
,
正定,从而
p( j)T q( j) 0
(10.4.22)
( yT p( j) )2 p( j)T q( j)
0
(10.4.23)
接下来证明(10.4.20)等式右端两项不能同时为零。 假设第一项为零,则p//q,即p=βq,(β为非零常数)
将
代入上式得到
证明:
思路:归纳法。用k归纳。先证k=1、2时两式成立,再假设 k=m时两式成立,证明k=m+1时也成立。
k
1时,H2 Ap(1)
(H1
p(1) p(1)T p(1) qT (1)
H1q q (1) (1)T H1
q H q (1)T
(1)
1×1
1
) Ap(1)
1×1
Ap(i) A( x(i1) x(i) ) g(i1) g(i) q(i) ,
搜索方向
最速下降法: 共轭梯度法: 牛顿法:
牛顿方向
牛顿方向
是如下问题的解
牛顿法的优缺点
收敛快 --- 二次收敛 程序简单
计算量大 --- 需要二阶导数 要求高 --- 需要二阶导数 需要计算Hesse矩阵,而此矩阵可能非正定, 可能导致搜索方向不是下降方向。
找替代牛顿法的方法
目标: 收敛快 程序简单
f ( x(k ) ) f ( x(k1) ) 2 f ( x(k1) )( x(k ) x(k1) )
p(k ) : x(k1) x(k) q(k ) : f (x(k1) ) f (x(k) )
q(k ) 2 f (x(k1) ) p(k ) p(k ) 2 f (x(k 1) )1 q(k )
(10.4.16)
DFP算法
容易验证,这样定义校正矩阵 Hk,得到的矩阵
Hk1 Hk
p(k) p(k)T p(k )T q(k )
Hk q(k ) q(k )T Hk (10.4.17) q(k)T Hk q(k )
满足拟牛顿条件(10.4.7)。(10.4.17)式称为DFP公式。
DFP方法的计算步骤:
并用(10.4.14)求出在点x(k+1)出发的搜索方向d(k+1)。
以此类推,直至|| f (x(k) ) || ,
是事先给定的允许误差。
DFP算法
Hk k u(k ) u(k )T kv(k ) v(k )T
p(k ) Hk1q(k )
(Hk
k u(k )u(k )T
v v (k ) (k )T k
yT H j y
( yT p( j) )2 p( j)T q ( j)
( yT H jq( j) )2 q ( j)T H j q ( j)
(10.4.18)
11
因为Hj是对称正定阵,故存在对称正定阵Hj1/2,使得
Hj
H
2 j
H
2 j
.
1
1
令
p
H
2 j
y,
q
H
2 j
q(i
)
,
(10.4.19)
则有 yT H j y pT p, yT H jq(j) pT q,
2
1
5 18
4 2
9
4
, 得到
g2
4 9
8
.
9
9
算出
p(1) x(2) x(1) 1d (1)
根据DFP定义的ΔHk,得
10 9
5 9
,
q(1)
g2
g1
40 9
10 9
,
H2
H1
p(1) p(1)T p(1)T q (1)
H1q (1)q (1)T H1 q (1)T H1q (1)
x(1) x(n1)
p(k ) x(k1) x(k ) q(k ) f ( x(k1) ) f ( x(k ) ) H k H k1 H k H k k : k 1
例10.4.1 用DFP方法求解如下问题:
min 2x12 x22 4x1 2
解:
初始点及初始矩阵分别取为:
x( 1 )
DFP算法的正定性及二次终止性
1、正定性 DFP方法构造的矩阵Hk是对称的正定矩阵
搜索方向 d (k) Hkf (x(k) ) 均为下降方向
每次迭代使函数值有所下降
定理10.4.1 若gi≠0(i=1,2,....,n),则DFP方法构造的 矩阵Hi(i=1,2,,.....,n)为对称正定矩阵。
d (k) Hkf (x(k) )
然后沿d(k)方向搜索,求步长 k ,满足
f
(x(k)
k d (k) )
min
0
f
(x(k)
k d (k) )
从而确定出后继点 x(k1) x(k) k d (k)
求出点x(k+1)处的梯度 f (x(k1) ) 以及 p(k) 和q(k) ,再利用
(10.4.13)式计算 Hk+1 ,
(10.4.5) (10.4.6)
p(k ) Hk1q(k )
(10.4.7)
1.秩1校正 2.DFP(Davidon-Fletcher-Powell)算法:
秩2校正
3.BFGS(Broyden-Fletcher-GoldfarbShanno)公式及Broyden族
H1 I; Hk1 Hk Hk
(5)检验是否满足收敛准则,若 f (x(k1)) 时则停止迭代,
得到点 __
x x(k1)
;否则,进行步骤(6)。
(6)若k=n,则令 x(1) x(k1) ,返回步骤(2);否则,进行步骤
(7)。
(7)令 gk1 f (x(k1) ), p(k) x(k1) x(k) , q(k) gk1 gk 。利用 (10.4.17)计算Hk+1,令k=k+1,返回步骤(3)。
同时 不需要二阶导数
找: 像牛顿 又不是牛顿 的家伙!!!
基本思想:
用不包含二阶导数的矩阵近似Hesse矩阵的逆。
拟牛顿条件
d (k) 2 f H( xk(k) )1f ( x(k) )
x x d (k1)
(k)
(k ) (10.4.1)
k
首先分析2 f (x(k) )1与一阶导数的关系:
当i=m+1时,因为Ap(m+1)=q(m+1),代入上式得到
当i<m+1时,有Hm+1Ap(i)=p(i)成立及p(i)TAp(m+1)=0(已证)。在 式(10.4.29)中有 同时,把(10.4.29)中的Ap(i)乘入括号内,则有
2
1
,
H1
1 0
0 1
,
点x=x(x1,x2)T的梯度及在x(1)处的梯度:g
4(x1 1)
2x2
,
4 g1 2 ,
令搜索方向为
d (1)
H1 g1
4 2
从x(1)出发沿d(1)做一维搜索:min 0
f ( x (1) d (1) ),得到λ1=5/18。
令
8
x (2)
x (1)
1d (1)
计 算 步
骤:
重置
x(1) , 0
H1 In , d (1) f ( x(1) ), k 1
Y
f ( x(k) )
x x(k)
N
d (k ) H kf ( x(k ) )
k
arg min 0
f (x(k)
d (k) )
x(k1) x(k ) kd (k )
N
k n?
Y
证明:
思路:归纳法。在DFP方法中H1给定的n阶单位阵,只要假设Hj 是对称正定阵成立,证明Hj也是对称正定阵。
对任意非零量 y Rn ,
yT H j1 y
yT H j y
yT p( j) p( j)T p( j)T q ( j)
yT H j q ( j)q ( j)T H j y q ( j)T H j q ( j)
)q(k )
k u(k )u(k )T q(k ) kv(k )v(k )T q(k ) p(k ) Hkq(k )
令u(k )
p(k );k
1 u(k )T q(k )
;v(k)
Hk q(k ); k
1 v(k )T q(k )
H k
p(k) p(k)T p(k )T q(k )
Hkq(k) q(k)T Hk q(k )T Hkq(k)
先证k=m+1时(10.4.24)成立。
当1=<i<=m时,有 Hm1Ap(i) p(i) ,
由此得出:p(i)T Ap(m1) p(i)T A(m1Hm1gm1) m1gmT 1Hm1Ap(i)
g p T (i)
m1 m1
m1gmT 1id (i).
(10.4.28)
因为有 gmT 1d (i) 0, i m 1,
在 点x ( k 1) 处 进 行 二 阶Tayl or展 开 :
f ( x) f ( x(k1) ) f ( x(k1) )( x x(k1) ) 1 ( x x(k1) )T 2 f ( x(k1) )( x x(k1) )
