几种修正拟牛顿法的比较
牛顿法拟牛顿法

牛顿法拟牛顿法牛顿法是一种求解非线性方程的方法,其原理是在迭代中使用方程的导数来近似方程的根。
虽然牛顿法非常有效,但它往往需要非常精准的初始猜测才能保证收敛性。
另一种类似于牛顿法的方法是拟牛顿法,它可以通过逐步调整矩阵B来近似牛顿法的矩阵Hessian。
本文将介绍牛顿法和拟牛顿法的原理和应用。
一、牛顿法假设有一个n维非线性方程系统f(x)=0,其中x是一个n维向量。
牛顿法中的每个迭代都是通过以下公式来更新当前估计xk的:xk+1=xk-Hk^(-1)fk其中Hk是f(x)的Hessian矩阵在xk处的值,假设Hk是可逆的。
牛顿法的优点是它快速收敛,并且可以通过适当选择初始估计来实现收敛。
另一个好处是它可以直接用于求解大型系统,因为它只涉及二次导数的计算。
然而,牛顿法的缺点是它需要计算Hessian矩阵,这通常是一个费时且复杂的任务。
另一个问题是当Hessian矩阵的条件数(即最大特征值与最小特征值之比)很大时,牛顿法的收敛可能会变得很慢。
二、拟牛顿法拟牛顿法的思想是利用一个矩阵Bk来代替牛顿法中的Hk矩阵。
Bk是一个正定对称的矩阵,其初值通常为单位矩阵In。
在每个迭代中,Bk被更新为一个近似的Hessian逆矩阵。
最常用的拟牛顿法算法之一是BFGS算法,其更新规则如下:Bk+1=Bk+(yk^Tyk)/(yk^Ts)+(BkSkS^TBk)/(sk^TBksk)其中sk=xk+1-xk,yk=g(xk+1)-g(xk),g表示f的梯度,^T表示矩阵转置。
该公式是基于以下观察得出的:Bk+1应该满足以下性质:Bk+1是正定对称的。
Bk+1应该近似于Hk+1的逆,其应该满足以下方程:Bk+1sk=yk另外,BFGS算法的收敛速度也相对比牛顿法要慢,因为BFGS算法需要逐步修正矩阵Bk,直到其逼近Hessian矩阵的逆。
三、应用牛顿法和拟牛顿法在许多实际问题中应用广泛,特别是在数学、物理、金融和工程领域。
利用函数值信息的修正多步拟牛顿法

对于满足拟牛顿方程的 B + , 1最常用的校正公式是 B odn族校正公式 ( r e y 见文献 【 【) 67 . 】】
・ 一 + ,
维普资讯
・
1 ・ 4 4
南京大学学报数学半年刊
27 5 0 年 月 0
其 中
_ ( s
z ) ∑ c丁 ^ 褂1 ( = t)一 , 丁 (z
这 里
() 1 5
㈩j 嚣 ・ = O
,
J ≠t
( 1 6 )
() 1 7
[ 一k] 丽k Y B k s,
( 1 2 )
当 :0时, 就是 经典 的 B GS校 正公 式. F
由以上可以看出, 拟牛顿法是对 ^ X + 做线性插值, 和 k1 然后根据公式 () 2 推导出拟牛顿 方程. 尽管其形式简单, 由于只用了前一个迭代点的信息, 但 在某些情形下, 由公式 (1 得到 1)
收稿 日期: 0 60 -6 修 回日期: 0 61 -3 2 0 -52 ; 2 0- 12 .
E- a l u ii o m i :h a l @h t a l o b o m i. r cn
维普资讯
第1 期
怀丽波: 利用函数值 皇
垒生 生塑鎏
假设 通过迭 代点 线. 即 已经产 生新 的迭 代 点 X + , 义 曲线 X 为一条 过这两 个迭 代点 的直 k1定
=
.
() 2
xr = +7 () ., s 其 中
8k +1 一 Xk
() 3
这 样 ,由 () 3 式得 xo =X ,() k l并且 () kx1 =X+ ,
1 引 言
考虑 无约束 优化 问题
数学优化中的牛顿法和拟牛顿法

数学优化中的牛顿法和拟牛顿法在数学中,优化是一个非常重要的研究领域,其目的是找到使某个函数达到最大或最小值的变量集合。
在实际应用中,很多问题都可以转化为优化问题,如机器学习、经济学、物理学等。
在优化领域中,牛顿法和拟牛顿法是两种常见的方法。
本文将介绍这两种优化方法的基本原理、优缺点以及应用场景。
一、牛顿法牛顿法(Newton's method)是由数学家牛顿发明的非线性优化方法,其思想是利用函数的泰勒级数展开进行逼近。
具体来说,牛顿法先求出目标函数的一阶和二阶导数,然后使用二阶导数来逼近目标函数本身,进而得到近似最优解。
牛顿法的数学公式如下:$$\boldsymbol{x}_{k+1}= \boldsymbol{x}_{k} -{\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)^{-1}}\boldsymbol{\nabla} f(\boldsymbol{x}_k)$$其中,$\boldsymbol{x}_k$ 表示第 $k$ 次迭代的解,$\boldsymbol{\nabla} f(\boldsymbol{x}_k)$ 和$\boldsymbol{\nabla}^2 f(\boldsymbol{x}_k)$ 分别表示目标函数在$\boldsymbol{x}_k$ 处的一阶和二阶导数。
牛顿法的优点是收敛速度非常快,通常只需要很少的迭代次数即可达到最优解。
另外,牛顿法适用于连续可微、二阶可导的函数,因此适用范围广。
然而,牛顿法也存在一些缺点,例如无法处理不可导或一阶可导但二阶不可导的函数。
此外,牛顿法需要计算目标函数的二阶导数,因此在大规模问题上计算成本很高。
二、拟牛顿法拟牛顿法(quasi-Newton method)是一类基于牛顿法的优化算法,它通过逼近目标函数的海森矩阵来求解。
拟牛顿法没有计算海森矩阵的显式表达式,而是通过估计海森矩阵的变化来逼近。
最简单和最流行的拟牛顿法是BFGS算法和L-BFGS算法。
拟牛顿法及其相关解法

本文链接:/miaowei/52925.html最近在看条件随机场中的优化算法。
其中就设计到了无约束化的最优化方法,也就是牛顿法。
在CRF (conditional random field)中,使用的是L-BFGS法。
费了好大的劲把算法的原理及推导算是看明白了,可是到了具体实现上,又碰到问题了,比如在求搜索方向的时候,使用但是程序中如何实现呢?现在转载一篇文章,看过之后,会非常受益。
使用导数的最优化算法中,拟牛顿法是目前为止最为行之有效的一种算法,具有收敛速度快、算法稳定性强、编写程序容易等优点。
在现今的大型计算程序中有着广泛的应用。
本文试图介绍拟牛顿法的基础理论和若干进展。
牛顿法(Newton Method)牛顿法的基本思想是在极小点附近通过对目标函数做二阶Taylor展开,进而找到的极小点的估计值[1]。
一维情况下,也即令函数为则其导数满足因此(1)将作为极小点的一个进一步的估计值。
重复上述过程,可以产生一系列的极小点估值集合。
一定条件下,这个极小点序列收敛于的极值点。
将上述讨论扩展到维空间,类似的,对于维函数有其中和分别是目标函数的的一阶和二阶导数,表现为维向量和矩阵,而后者又称为目标函数在处的Hesse矩阵。
设可逆,则可得与方程(1)类似的迭代公式:(2)这就是原始牛顿法的迭代公式。
原始牛顿法虽然具有二次终止性(即用于二次凸函数时,经有限次迭代必达极小点),但是要求初始点需要尽量靠近极小点,否则有可能不收敛。
因此人们又提出了阻尼牛顿法[1]。
这种方法在算法形式上等同于所有流行的优化方法,即确定搜索方向,再沿此方向进行一维搜索,找出该方向上的极小点,然后在该点处重新确定搜索方向,重复上述过程,直至函数梯度小于预设判据。
具体步骤列为算法1。
算法1:(1) 给定初始点,设定收敛判据,.(2) 计算和.(3) 若 < ,则停止迭代,否则确定搜索方向.(4) 从出发,沿做一维搜索,令.(5) 设,转步骤(2).在一定程度上,阻尼牛顿法具有更强的稳定性。
拟牛顿法

拟牛顿法牛顿法有很好的收敛性,特别是当初始点x0选择在最终解x*附近时,收敛速度叫梯度法更快,但是当初始迭代点远离x*,收敛速度慢且不能保证收敛,当其Hession <0,迭代算法不会像函数值减小的方向前进。
针对newton法的这些弱点,提出了改进方法:拟牛顿方法,包括rank one,DFP和BFGS三种算法。
(1)Rank one选用aster书《An Introduction to Optimization》中实例验证目标函数:f(x1,x2)=x1^2+0.5*x2^2+3,是一个二次型函数。
初始值x0=[1,2]’;,精度1.0e-5控制迭代终止,当norm(G)<=1.0e-5时,迭代终止;取H0=I2,Q=[2,0;0,1];①迭代结果:经过两次迭代之后,迭代停止,得值x=【0,0】’。
②改变初始值为远离x= [0,0]’的值x0=[1000,2]’,和x0=[1000,1000]’,算法经过两步迭代后都收敛到x=【0,0】’。
算法的结果验证了书中结论:不论初始值X0如何选取,稚一算法在n步迭代之内收敛到终解。
稚一算法对于恒定hess矩阵的情况非常好,也就是对二次型问题问题非常有效,但是对于非二次型问题,H(k)可能是非正定的,这样函数不能向下降的方向前进,这就引出下面的稚二算法。
(2)DFP目标函数:f(x1,x2)=2*(x1^2)+x2^2+2*x1*x2+x1-x2;即:f(x1,x2)=1/2*[x1,x2]*[4,2;2,2]* [x1,x2]’-[x1,x2]*[-1,1]’;初始点x0=[0,0]’,取H0=I2,Q=[4,2;2,2]。
H0是一个实对称正定矩阵,第一次迭代后,H1=[0.5,-0.5;-0.5,1.5]是一个非对称正定矩阵,此时就体现出稚二算法的优势,第二次迭代后,满足norm(G)<=1.0e-5条件,迭代终止,的解x=【-1.0,1.5】’。
机器学习算法系列最速下降法牛顿法拟牛顿法

机器学习算法系列最速下降法牛顿法拟牛顿法最速下降法、牛顿法和拟牛顿法都是常用的机器学习优化算法。
它们在求解函数最小化问题中起到关键作用。
1. 最速下降法(Gradient Descent):最速下降法是一种基于函数梯度的迭代优化算法。
其核心思想是沿着负梯度方向以步长α更新参数,直到达到收敛条件。
最速下降法的步骤如下:1)选择初始参数值;2)计算目标函数的梯度;3)沿着负梯度方向更新参数;4)重复步骤2和步骤3,直到达到停止条件。
最速下降法的优点是简单易实现,但它可能会面临局部最小值的问题,收敛速度较慢。
2. 牛顿法(Newton's Method):牛顿法是一种二阶优化算法,利用目标函数的一阶和二阶导数信息来更新参数。
它通过二阶导数矩阵(即Hessian矩阵)来指导方向和步长的选择。
牛顿法的步骤如下:1)选择初始参数值;2)计算目标函数的一阶和二阶导数;3)解线性方程(Hessian矩阵和梯度的乘积);4)更新参数;5)重复步骤2-步骤4,直到达到停止条件。
牛顿法的优点是收敛速度快,但它需要计算二阶导数矩阵,计算量较大,且可能收敛到非全局最小值。
3. 拟牛顿法(Quasi-Newton Methods):拟牛顿法是一种基于牛顿法思想的近似优化算法。
与牛顿法不同,拟牛顿法通过正定矩阵来近似二阶导数矩阵,从而避免了计算复杂的二阶导数矩阵。
拟牛顿法最经典的算法是BFGS算法(Broyden-Fletcher-Goldfarb-Shanno),它通过近似更新逆Hessian矩阵的方式来求解优化问题。
拟牛顿法的步骤如下:1)选择初始参数值和初始逆Hessian矩阵的估计;2)计算目标函数的梯度;3)更新参数;4)更新逆Hessian矩阵的估计;5)重复步骤2-步骤4,直到达到停止条件。
拟牛顿法的优点是避免了计算二阶导数矩阵,计算复杂度相对较低,且具有较好的收敛性质。
总结来说,最速下降法适用于简单的优化问题,牛顿法适用于二次型问题,而拟牛顿法在保持收敛速度的同时减少了计算复杂度。
第四次Newton法与拟Newton法

x k +1 = x k − H k ∇ f ( x k )
2.
考虑更一般的形式: 考虑更一般的形式: x k +1 = x k − t k H k ∇ f ( x k )
x
k +1
= x − t k H k ∇f ( x )
k k
H k ≡ I时 ⇒ 梯度法 最速下降方向 d k = −∇ f ( x k ) 度量为 x = xT I x
3.算法特点
收敛速度快,为二阶收敛。 收敛速度快,为二阶收敛。 初始点要选在初始点附近。 初始点要选在初始点附近。 4.存在缺点及修正 4.存在缺点及修正
(1)
f ( x k +1 ) < f ( x k ) ?
− G k 1的存在性和计算量问题
(2) 初始点的选取困难,甚至无法实施。 ) 初始点的选取困难,甚至无法实施。
k 计算 H k , := k + 1 , 转 step 2.
例如: 例如:请用 DFP算法求解 min f ( x ) =
解:取 H 0 = I , 2 x1 ∇f ( x ) = 8x 2
2 x1
+
2 4x2
1 , 初始点 x = . 1
1
f ( x 0 − t 0 ∇ f ( x 0 )) = min f ( x 0 − t ∇ f ( x 0 )) − t0∇ f ( x
0
= x
0
0 . 73846 )= − 0 . 04616
− 0.26154 s0 = x 1 − x 0 = − 1.04616 − 0.52308 y 0 = ∇ f ( x 1 ) − ∇f ( x 0 ) = g 1 − g 0 = − 8.36923
改进牛顿法

第3节改进牛顿法改进牛顿法改进牛顿法只是在牛顿拉夫法的基础上通过适当近似,对雅可比矩阵进行一定的改动,即改变每次迭代的步长。
由于其收敛判据未变,所有计算结果误差很小。
这里先做两点假设:(1)相邻两节点的电压差很小,因为配电网线路较短,且输送功率不大,这一假设可以成立;(2)没有对地支路(并联电容器组),如果有,则可以看作恒定节点负载,这样,所有对地支路都可以通过初始电压及修正后的电压值转化为节点注入功率。
常规牛顿法中对电压量(状态变量)的修正为:J U S ⋅∆=∆ (7—4)采用极坐标的形式:/HN P JL U U Q θ∆∆⎛⎫⎛⎫⎛⎫⋅= ⎪ ⎪ ⎪∆∆⎝⎭⎝⎭⎝⎭(7—5) 其中:(s i n c o s i j i j i j i j i j i jH U U G B θθ=-- i ≠ j 1(s i n c o s )j nij i j ij ij ij ij j j i H U U G B θθ==≠=-∑i = j (c o s s i n i j i j i j i j i j i jN U U G B θθ=-+i ≠ j21(c o s s i n )2j n ij i j ij ij ij ij i ij j j i N U U G B U G θθ==≠=-+-∑ i = j(c o s s i n i j i j i j i j i j ij J U U G B θθ=+ i ≠ j1(c o s s i n )j n ij i j ij ij ij ij j j i J U U G B θθ==≠=-+∑ i = j(s i n c o s i j i j i j i j i j i j L U U G B θθ=-- i ≠ j 21(s i n c o s )2j n ij i j ij ij ij ij i ij j j i L U U G B U B θθ==≠=--+∑ i = j(7—6)由于相邻节点电压近似相等,且有 1()nij ij ij ii j j iG jB G j jB =≠+=-+=∑对于没有对地支路的系统,雅可比阵可近似写成:1111cos cos cos cos cos cos cos ij i j ij ij j nij i j ij ijj j i ij i j ij ij j nij i j ij ijj j i ij i j ij ij j nij i j ij ijj j i ij i j ij ij j nij ij j ij ijj j i H U U B i j H U U B i j N U U G i j N U U G i j J U U G i j J U U G i j L U U B i j L U U G i θθθθθθθθ==≠==≠==≠==≠≈≠≈-=≈-≠≈=≈≠≈=≈≠≈-=∑∑∑∑j(7—7)从公式(2-7)中可以近似看出,矩阵 N 、H 、L 、J 与节点导纳阵 Y 有相同的特性:对称性、系数性,可改写成如下形式:11Tn B n H L A D A --==11Tn G n J H A D A --=-=(7—8)其中,B D 、G D 为对角阵,对角元素分别为cos i j ij ij U U B θ和sin i j ij ij U U G θ,1111/Tn B G nT n G B n A D D P A A D D U U Q A θ-----⎛⎫∆∆⎛⎫⎛⎫⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪ ⎪ ⎪ ⎪∆∆⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (7—9)如果将节点重新编号,平衡节点号为 0,其余节点号按距离平衡节点之远近分层,重新编号,则1n A - (节点-支路关联矩阵)为一个上三角阵,对角元素为 1,非零非对角元素为-1。
三种牛顿迭代法

三种牛顿迭代法牛顿迭代法是求解方程的一种常用方法。
它是一种迭代法,基本思想是从一个初始点开始,通过函数的局部线性逼近,求得函数的零点。
然后利用新的零点作为下一次迭代的初始点,直到满足预设的精度要求为止。
三种常用的牛顿迭代法包括:常规牛顿迭代法、改进牛顿迭代法和高效牛顿迭代法。
常规牛顿迭代法是最基本的牛顿迭代法,它通过函数的一阶导数和二阶导数来逼近函数的零点。
具体而言,设$f(x)$是要求解的方程,$x_{k}$是当前的估计解,$f^{prime}(x_{k})$是$f(x)$在$x_{k}$处的一阶导数,$f^{prime prime}(x_{k})$是$f(x)$在$x_{k}$处的二阶导数,则常规牛顿迭代法的迭代公式为:$x_{k+1}=x_{k}-frac{f(x_{k})}{f^{prime}(x_{k})}$ 改进牛顿迭代法是针对常规牛顿迭代法的局限性而提出的。
常规牛顿迭代法在求解某些特定的方程时可能会失效,例如当$f^{prime}(x_{k})$接近于零时,迭代公式会出现除零的情况。
改进牛顿迭代法通过加入一个修正因子来避免这种情况的发生。
具体而言,在计算$x_{k+1}$时,改进牛顿迭代法的迭代公式为:$x_{k+1}=x_{k}-frac{f(x_{k})}{f^{prime}(x_{k})+frac{1}{2}f^ {prime prime}(x_{k})(x_{k+1}-x_{k})}$高效牛顿迭代法是一种优化的牛顿迭代法,它通过使用逆Hessian矩阵来加速迭代收敛。
逆Hessian矩阵是函数$f(x)$在$x_{k}$处的Hessian矩阵的逆矩阵,即$H^{-1}(x_{k})=[f^{prime prime}(x_{k})]^{-1}$,其中$[f^{prime prime}(x_{k})]^{-1}$表示$f(x)$在$x_{k}$处的二阶导数矩阵的逆矩阵。
高效牛顿迭代法的迭代公式为:$x_{k+1}=x_{k}-H^{-1}(x_{k})f(x_{k})$总之,牛顿迭代法是一种重要的求解方程的方法,常规牛顿迭代法、改进牛顿迭代法和高效牛顿迭代法是其中的三种常用方法,每种方法都有其适用范围和优缺点。
非线性方程组求解方法的比较与优化

非线性方程组求解方法的比较与优化非线性方程组的求解在科学计算、工程领域以及其他许多实际问题中扮演着重要的角色。
在实际应用中,往往需要高效准确地求解非线性方程组,以获得所需的结果。
本文将对几种常用的非线性方程组求解方法进行比较,并探讨如何进一步优化这些方法,以提高求解效率。
一、牛顿法(Newton's Method)牛顿法是最常用的非线性方程组求解方法之一。
该方法基于泰勒级数展开,通过迭代逼近非线性方程组的解。
具体而言,给定初始猜测值x0,牛顿法通过以下迭代公式进行求解:x^(k+1) = x^k - [J(x^k)]^(-1) * F(x^k)其中,J(x^k)表示方程组F(x)的雅可比矩阵,F(x^k)表示方程组的值向量。
牛顿法通常具有快速收敛的特点,但在某些情况下可能出现发散或收敛速度慢的问题。
二、拟牛顿法(Quasi-Newton Methods)拟牛顿法是对牛顿法的改进和优化。
由于求解雅可比矩阵的逆矩阵相对困难且计算量大,拟牛顿法通过逼近雅可比矩阵的逆矩阵,避免了对逆矩阵的直接求解。
其中,最著名的拟牛顿法是DFP算法和BFGS算法。
DFP算法通过计算Hessian矩阵的逆矩阵的逼近,不断更新该逼近矩阵,以逼近真实的Hessian矩阵的逆矩阵。
BFGS算法同样通过逼近矩阵的更新来求解方程组,但采用了更加复杂的更新策略,相较于DFP算法在某些问题上具有更好的性能。
拟牛顿法通过避免直接计算逆矩阵,一定程度上提高了计算效率,但其迭代过程中的计算相对复杂,因此在实际问题中需要综合考虑。
三、Levenberg-Marquardt算法Levenberg-Marquardt算法是一种解决非线性最小二乘问题的方法,也可用于求解非线性方程组。
该算法基于牛顿法,利用信赖域思想进行调整,以提高求解的稳定性和收敛性。
Levenberg-Marquardt算法通过在牛顿迭代中引入一个参数,将其视为步长的控制因子,从而在迭代过程中实现步长的自适应调整。
牛顿法和拟牛顿法

9 9 0 x x d 1 1 0
1 0 0
因
f x 1 0,
所以迭代终止, 最优点为: x x 0, 0 .
1 T
3. 牛顿法优缺点 优点 (1) 对正定二次函数,迭代一次就可以得到 极小点. (2) 如果 正定且初始点选取合适, 算法
若 f(x k 1 ) ,停止x* xk 1; 否则,令k k 1,转step2
例1. 设 f x 6 x1 x 2 + 2 3 x1 3 x 2 x1 x 2
2
2
求在点 x 1 ( 4, 6)T 处的搜索方向.
分析: 搜索方向
一. 牛顿法
令上式为0:
f(x(k )) f(x(k 1)) 2f(x(k 1))(x(k ) x(k 1)) 0
x
则 H (x (k ))
( k 1)
x
(k )
f(x
2
(k )
) f (x (k ))
1
若Hesse 矩阵正定,即 H (x (k )) 0,
很快收敛.
缺点
(1) 要求函数二阶可微. (2) 收敛性与初始点的选取依赖很大.
(3) 每次都需要计算海森阵 (4) 每次都需要解方程组
方程组有时奇异或病态的, 不是下降方向.
计算量大.
二. 阻尼牛顿法—Newton法改进
1. 基本思想 针对缺点中的(2), 在求新迭代点时,不直 接用公式进行迭代,而是以 sk 作为搜索方 向进行一维搜索,求步长 k ,使
Step3: 沿
sk
k 1 k k x x s ,k k 1, 转Step2. Step4: 令 k
最优化算法(牛顿、拟牛顿、梯度下降)
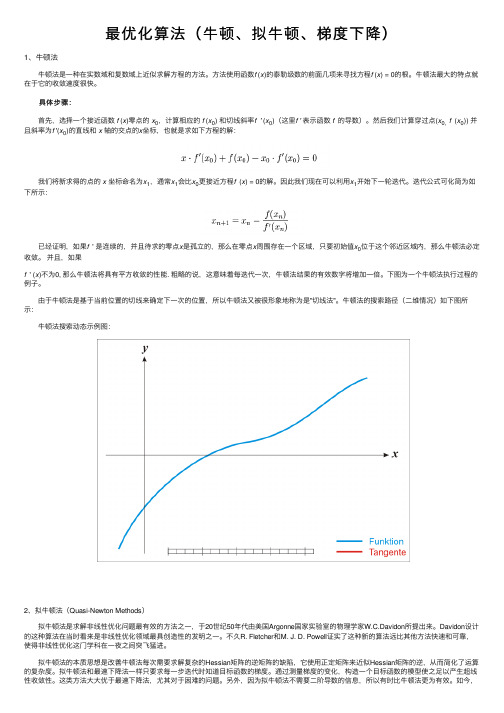
最优化算法(⽜顿、拟⽜顿、梯度下降)1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤: ⾸先,选择⼀个接近函数f (x)零点的x0,计算相应的f (x0) 和切线斜率f ' (x0)(这⾥f ' 表⽰函数f 的导数)。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标,也就是求如下⽅程的解: 我们将新求得的点的x 坐标命名为x1,通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰: 已经证明,如果f ' 是连续的,并且待求的零点x是孤⽴的,那么在零点x周围存在⼀个区域,只要初始值x0位于这个邻近区域内,那么⽜顿法必定收敛。
并且,如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说,这意味着每迭代⼀次,⽜顿法结果的有效数字将增加⼀倍。
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置,所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径(⼆维情况)如下图所⽰: ⽜顿法搜索动态⽰例图:2、拟⽜顿法(Quasi-Newton Methods) 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠,使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使⽤正定矩阵来近似Hessian矩阵的逆,从⽽简化了运算的复杂度。
求解非线性方程组的牛顿法和拟牛顿法

求解非线性方程组的牛顿法和拟牛顿法解决非线性方程组是数学中的一个经典问题,其应用广泛,例如化学、物理、优化和金融等领域。
牛顿法和拟牛顿法是求解非线性方程组的常见方法之一,本文将详细介绍牛顿法和拟牛顿法的原理、优缺点以及实现步骤。
一、牛顿法牛顿法是一种高效的求解非线性方程组的方法,其基本思路是利用一阶泰勒展开式近似于原方程组,并以此构造一个更新方案,通过一步步迭代找到原方程组的解。
以二元非线性方程组为例,假设有方程组:f1(x1, x2) = 0f2(x1, x2) = 0根据泰勒展开式的一阶近似可得:f(x + Δx) ≈ f(x) + Jx Δx其中,Jx为函数f(x)在点x处的Jacobian矩阵,Δx是待求解的更新量,它满足:f(x + Δx) = 0将近似式带入上述方程组中,可得:Jx Δx = - f(x)由此可以推导出牛顿法的迭代式:x(k+1) = x(k) - [Jx(k)]⁻¹f(x(k))其中,k表示迭代次数,x(k)表示第k次迭代的解,[Jx(k)]⁻¹为Jx(k)的逆矩阵。
牛顿法的优点在于它的收敛速度很快,尤其是在初始值接近解时,收敛更加快速。
但是,牛顿法也有很大的局限性,一是它需要求解Jacobian矩阵,在高维情况下计算复杂度很高,二是它的收敛性依赖于初始值,有时候可能会陷入局部最优。
二、拟牛顿法为了克服牛顿法的局限,拟牛顿法被发明出来。
和牛顿法一样,拟牛顿法同样是基于泰勒展开式的近似思想,但是它避免了Jacobian矩阵的计算,从而提高了算法的计算效率。
拟牛顿法的核心是对于迭代过程中的Jacobian矩阵的近似。
常见的近似方法有Damping BFGS(DBFGS)算法、DFP算法和Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法等。
其中,BFGS算法是拟牛顿法的代表,其迭代步骤如下:1. 初始化矩阵B0 = I2. 对于第k次迭代,求出pk = -Bk-1gk,并更新xk+13. 计算sk = xk+1 - xk,yk = gk+1 - gk4. 更新矩阵Bk+1 = Bk + ΔB,其中ΔB = ρskskT - BkykT - ykBkρ = 1/ (ykT sk)其中ΔB称为BFGS修正子,它近似于Jacobian矩阵的逆。
几种迭代修正方法的比较

几种迭代修正方法的比较迭代修正方法是现代算法中应用广泛的一种优化算法,主要用于解决优化问题。
它通过多次迭代计算,不断修正当前解,逐步接近最优解。
在实践中,存在许多不同的迭代修正方法,如梯度下降法、牛顿迭代法、共轭梯度法等。
本文将比较几种常见的迭代修正方法的优缺点,包括梯度下降法、牛顿迭代法和共轭梯度法。
首先,我们来看梯度下降法。
梯度下降法是一种基于偏导数的迭代修正方法,主要用于求解无约束优化问题。
其基本思想是沿着负梯度方向迭代更新解,直到收敛或满足停止准则。
梯度下降法的优点是易于实现和理解,收敛速度较快。
然而,梯度下降法也存在一些问题,如可能陷入局部最优解、需要选择合适的学习率等。
其次,我们来看牛顿迭代法。
牛顿迭代法是一种基于二阶导数的迭代修正方法,主要用于求解非线性优化问题。
其核心思想是利用二阶导数信息来修正当前解,接近真实解。
牛顿迭代法的优点是收敛速度快,可以更快地接近最优解。
然而,牛顿迭代法也存在一些问题,如需要计算和存储二阶导数信息、可能遇到奇点或发散问题等。
最后,我们来看共轭梯度法。
共轭梯度法是一种基于共轭方向的迭代修正方法,主要用于求解对称、正定线性方程组。
其基本思想是在每次迭代中选择一个共轭方向来修正解,直到满足停止准则。
共轭梯度法的优点是收敛速度快,能够在有限次迭代内获得精确解。
然而,共轭梯度法的应用范围受到限制,只适用于求解线性方程组。
综上所述,梯度下降法、牛顿迭代法和共轭梯度法都是常见的迭代修正方法,用于解决优化问题。
梯度下降法易于实现和理解,收敛速度较快,但容易陷入局部最优解;牛顿迭代法收敛速度快,可以更快地接近最优解,但需要计算和存储二阶导数信息;共轭梯度法收敛速度快,能够在有限次迭代内获得精确解,但只适用于求解线性方程组。
综合考虑问题的特点和要求,选择合适的迭代修正方法非常重要。
在实际应用中,通常需要对不同的迭代修正方法进行比较和选择,以获得更好的优化效果。
Newton迭代法浅析

目录第一章:绪论 (2)第二章 Newton迭代原理 (3)2.1 一般迭代思想的设计 (3)2.2 Newton迭代法的原理 (3)2.3小结: (5)第三章 Newton迭代法的收敛性 (6)3.1 Newton迭代法中不收敛的情况 (6)3.2 定理证明 (7)3.3 Newton迭代法的收敛性分析 (10)3.4小结: (12)第四章两种改进的Newton迭代法 (14)4.1 改进初值x的Newton下山法 (14)4.2 一种新的Newton迭代法加速设计 (15)4.3小结: (16)第五章 Newton迭代法的应用 (17)5.1 Newton迭代法的Matlab实现 (17)5.2 数值举例 (17)5.3小结: (20)总论 (21)参考文献 (22)致谢 (23)第一章绪论在自然科学和工程技术中很多问题的解决常常归结为解非线性方程(组)或者线性方程(组)代数方程组,例如电学中的网络问题,船体数学放样中建立三次样条函数问题,用最小而乘求是实验数据的曲线拟合问题,用差分或者有限元方法解常微分方程等。
关于非线性方程(组)的求解,一般有两类解法:直接法和迭代法。
我们知道,只有一次、二次和三次方程有规范的求根公式,而高于三次的方程0)xf是不存在求根公式的。
因此求根变得一异常的困难。
而科学计算却(很好解决了这一问题,其中最基本的算迭代法了,它对于解决非线性方程(组)的根变得异常方面。
就迭代法而言,Newton迭代法可算是其经典之作。
Newton迭代法又称为Newton-Raphson迭代法,它是Newton在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
牛顿迭代法是求非线性方程(组)根的重要方法之一,其迭代格式简单,且在单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。
关于Newton迭代法,许多学者为之做了相当多的研究,并且留下了很多经典的文献([2-6])。
Newton迭代法在解决Banach空间中非线性方程或方程组的应用更为重要,如梯形Newton迭代法。
机器学习算法系列(25):最速下降法、牛顿法、拟牛顿法

作为指导。
3.2 DFP算法
DFP算法是以William C.Davidon、Roger Fletcher、Michael J.D.Powell三个人人的名字的首首字⺟母命 名的,它由Davidon于1959年年首首先提出,是最早的拟牛牛顿法。该算法的核心心是:通过迭代的方方
,求λ k,使 f(x ( k ) + λ kp k) = minλ ≥ 0 f(x ( k ) + λp k) 4. 置x ( k + 1 ) = x ( k ) + λ kp k,计算f(x ( k + 1 ) )当 | | f(x ( k + 1 ) ) − f(x ( k ) ) | | < ξ或 | | x ( k = 1 ) − x ( k ) | | < ξ,停止止迭代,令x ∗ = x ( k + 1 ) 5. 否则,置k = k + 1,转到步骤3。 当目目标函数是凸函数时,梯度下降法的解释全局最优解。一一般情况下,其解不不保证是全局最优 解。梯度下降法的收敛速度也未必是很快的。
3.1 拟牛牛顿条件
设经过k + 1次迭代后得到X k + 1,此时将目目标函数f(X)在X k + 1附近作泰勒勒展开,取二二阶近似,得到 1 f( X) ≈ f( X k + 1 ) + ∇ f( X k + 1 ) · ( X − X k + 1 ) + · ( X − X k + 1 ) T · ∇ 2 f( X k + 1 ) · ( X − X k + 1 ) 2 在两边同时作用用一一个梯度算子子 ∇ ,可得 ∇ f( X) ≈ ∇ f ( X k + 1 ) + H k + 1 · ( X − X k + 1 ) 取X = X k并整理理,可得 g k + 1 − g k ≈ H k + 1 · (X k + 1 − X k ) 若引入入记号s k = X k + 1 , y k = g k + 1 − g k则可以改写成
几种修正拟牛顿法的比较

步 2: 若
,停止迭代; 否则解线性方程组
,得到搜索方向 .
步 3: 由 Armijio 规则确定步长因子 :
(19)
步 4:
.根据下
面的修正 BFGS 校正计算
(20)
其中 由(17),(18)计算.
步 5: 令
,转步 2.
2.2 算法收敛性分析
为了分析 MBFGS 算法的收敛性,我们作如下假设:
式,只需在(5)中将 换成 就可得到(10).虽 然角度不一样,但方式一与方式二的修正策略本质 上是一致的.
(2)两种方式得到的修正拟牛顿条件分别对应 两种形式
实际上两者可统一于形式
,
其中
.
(注: 若 (14) 中 为 非 数 量 矩 阵 时 , 则 取
,作为推广也可取
).
(3)即使满足同一弱拟牛顿条件
,其中
,(17)
.
为了给出文献[6]81-85 广义拟牛顿法的另一种形式,借鉴
上述的修正措施及文献[12]11-15的思想,对 截断如下
(18)
以方式二的形式,给出求解无约束优化问题(1)的
修正 BFGS 拟牛顿算法描述如下(MBFGS 算法):
步 1: 选 取 初 始 点
,初始对称正定矩阵
,参数
.
称为步长.不
同的步长因子 和不同的搜索方向 就构成不同的
方法.为方便,记
求解(1)的数值迭代方法有多种,其中牛顿法
取
,在一定条件下具有局部收敛
性和二阶收敛速率,其困难是目标函数的 Hesse 矩阵
不一定可逆,且曲率计算工作量大;拟牛顿法则
构造对称矩阵 近似 而无需计算二阶导数,在一 定条件下具有超线性收敛速率,是目前所有利用一 阶导数的方法中最有效的一类方法 , [1]82-118 其基本思 想与牛顿法类似,在 附近用目标函数的二阶 Taylor 展开近似
牛顿法与修正牛顿法

▪ 在一般情况下,f ( x ) 不一定是二次函数,因而 x m i n 也不可能是 f ( x ) 的极值点。
x x 但是在 ( k ) 点附近,函数 ( x ) 和 f ( x ) 是近似的,所以可以用 (k 1) 点作为
下一次迭代,即得
x (k 1 ) x (k ) [H (x (K ))] 1 f(x (k )) [ 2 ]
2 f
H(x(0))
x12 2 f
x2x1
2 f
x1x2
2 f
21
1 2
H(x(0))1 1312
1 2
x22
故 s(0) H(x(0))1f(x(0))
1312 1214013128486
(3)极小值
x1x(0)
s (0) (0)
0 8 8 01*66
mifn(x)8
4、优缺点
牛顿法与修正牛顿法
1 、思想来源 2、基本思想 3、迭代步骤
牛顿法和 修正牛顿法
4、优缺点 5、修正牛顿法 6、评价
1、思想来源
▪ 梯度法相邻两次搜索方向总是相互正交,搜索路线 呈锯齿形,使得其在极小点附近,收敛速度越来越 慢。人们试图找到这样一种方向:它直接指向最优 点,使得从任意选定的初始点出发,沿此方向迭代 一次就能达到极小点。
▪ 若不满足,令k=k+1,转第二步继续迭代。
例:
用牛顿法求函数 f(x ) x 1 2 x 2 2 x 1 x 2 1x 1 0 4 x 2 60 的极小值。
解:
(1)取初始点
x (0)
0
0
(2)计算牛顿方向
f(x) 2 2xx12 xx21 14 0xx(0)
1 0 4
机器学习优化算法中梯度下降,牛顿法和拟牛顿法的优缺点详细介绍

机器学习优化算法中梯度下降,牛顿法和拟牛顿法的优缺点详细介绍 1、梯度下降法 梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。
一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。
梯度下降法的优化思想:用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。
最速下降法越接近目标值,步长越小,前进越慢。
缺点: 靠近极小值时收敛速度减慢,求解需要很多次的迭代; 直线搜索时可能会产生一些问题; 可能会“之字形”地下降。
2、牛顿法 牛顿法最大的特点就在于它的收敛速度很快。
优点:二阶收敛,收敛速度快; 缺点: 牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
牛顿法收敛速度为二阶,对于正定二次函数一步迭代即达最优解。
牛顿法是局部收敛的,当初始点选择不当时,往往导致不收敛; 二阶海塞矩阵必须可逆,否则算法进行困难。
关于牛顿法和梯度下降法的效率对比: 从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。
如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。
所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。
(牛顿法目光更加长远,所以少走弯路;相对而言,梯度下降法只考虑了局部的最优,没有全局思想。
) 根据wiki上的解释,从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
3、拟牛顿法 拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定矩阵.
证明 由(17)、(18)、(20)式可知
. 对称正定;若
对称正定,类似文献[3]定理 5.1.3,可证明 也对称
正定;依数学归纳法,引理成立.
引理 2 设 [13]727-739 为对称正定矩阵, 由校正公
式(20)生成.若
,有
(21)
则
,不等式
至少成立 次,其中
.
(22)
为了便于描述,定义指标集
关键词:无约束优化;拟牛顿法;全局收敛性
中图分类号:O242.23
文献标识码:A
文章编号:1674-8891(2011)03-0008-04
Comparison of Some Modified Quasi-Newton Methods
HUANG Hai, LIN Sui-hua
(Department of Mathematics and Computer Science Guangxi Normal University for Nationalities,Guangxi Chongzuo, 532200)
步 2: 若
,停止迭代; 否则解线性方程组
,得到搜索方向 .
步 3: 由 Armijio 规则确定步长因子 :
(19)
步 4:
.根据下
面的修正 BFGS 校正计算
(20)
其中 由(17),(18)计算.
步 5: 令
,转步 2.
2.2 算法收敛性分析
为了分析 MBFGS 算法的收敛性,我们作如下假设:
(2)
其中
为对称矩阵.若 正定,则极小化以上
右式,得到拟牛顿法搜索方向为
(3)
对(2)两边求导可得
,其中
,故
传统的拟牛顿法要求 满足如下标准拟牛顿条件
,
(4)
产生 的不同方法又构成不同的拟牛顿法,其中著
名的标准 BFGS 校正公式为
(5)
标准BFGS方法是传统拟牛顿法中最有效的一个[1]82-118, 然而采用非精确线搜索的标准 BFGS 拟牛顿法对非凸 函数时是不收敛的 , [2]673-701 如何提高实际计算中的运 算效率,如何使得对非凸目标函数保持局部超线性 收敛的同时具有全局收敛性,是人们对拟牛顿算法 研究的两个方向.
Key words:unconstrained optimization, quasi-Newton method, global convergence
0 引言
考虑用数值方法求解如下无约束优化问题
(1)
其中
为二阶连续可微函数,通常利用迭
代算法
,
其中 为第 次迭代点, 为第 次搜索方向,
为步长因子,
摘 要:拟牛顿法是所有利用一阶导数求解无约束优化问题的方法中最有效的一类计算方法,如何提高实际计算中的运算效率,如何
使得对非凸目标函数保持局部超线性收敛的同时具有全局收敛性,是对拟牛顿法进行研究的两个方向.对近年来相关文献的几种修正拟牛
顿法进行分析比较,并提出和分析了一个修正 BFGS 拟牛顿法的收敛性.
1 几种修正拟牛顿法的比较
1.1 拟牛顿条件的修正及相应的校正矩阵 牛顿法成功的关键是利用了 Hesse 矩阵提供的曲
率信息 ,为提 [3]219-222 高拟牛顿算法的运算效率,自然 的想法是使 在某种意义上更好地逼近 Hesse 矩阵
,进而对标准拟牛顿条件及相应的校正矩阵进行 修正以期获得好的效果.
,
两种方式的修正 BFGS 校正并不等价,如
(i) 以下两种修正的 BFGS 校正形式都满足
:
,
其中
,
(16)
,
(ii)取
,但 不恒等 . ,
时 , (16) 中 两
种修正 BFGS 校正形式都满足 ,但 也不
恒等 . 1.2 为全局收敛采取的一些修正措施
对非凸目标函数,满足标准拟牛顿条件的传统 拟牛顿法至今仍没有任何全局收敛性结果,除了要 确保 继承 的正定性外,主要难点是一致有界性
就得到相应于修正的拟牛顿条件(15)的修正 BFGS
公式.
文献[10]15-35 的动机则是基于对非凸函数全局收敛
性的需要.若 为非凸函数,则 不一定正定,由
方程
得到的牛顿法方向 可能不是下降
方向,为克服这一问题,适当修正以 代替 ,其
中
选择为使 正定的正常数,从
而得到修正的牛顿法方向
必是下降方向.
换成
, 得到新的
条件
. (7)
利用以上四个插值条件得到一个三次插值函数,再
让逼近函数(6)在 方向上是该函数的二次 Taylor
展开,得到另一 条件
. (8)
袁亚湘等[5]95-107 还研究了如下一般性的弱拟牛顿
条件
,
(9)
,给出相应于(9)的修正BFGS校正公式为
. (10)
标准拟牛顿条件(4)满足
,有
.
由 一个不等式成立.
由拉格朗日中值定理及
知 , (21) 的 第
,可知
,使
由(17),(18), 及 ,可得
可得(21)的第二个不等式成立.所以引理 2 的条件
满足. 又由引理 1 知, , 从 而 由 (19)
及 知, 为严格下降序列,
引理 3,可得
,再由
. 由引理 2 可知指标集 有无限多个元素,结合上 式及(22)的第二式可得
.
引理 3 设 成立,则
.
证明 由算法步 3 的 Armijio 搜索规则,可知 不满足(19)式,即
(23)
由拉格朗日中值定理及 可知,
使
由算法步 2 知 和(22),可得
(24) ,再由(24),(23),
引理得证. 定理 1 设 ,
成立,
为 MBFGS 算法
生成的序列,则
.
证明 利用反证法.假设定理不成立,即
由(22)的第一式及上式可得
,
这与假设矛盾,定理得证.
3 结束语
拟牛顿法是一类重要的无约束优化计算方法, 其理论分析与算法改进研究已有很多成果.首先分 析比较最近的相关文献,总结出两种拟牛顿条件修 改方式及全局收敛的一些措施,发现这两种方式可 用一种形式统一起来,这种线性或非线性组合的修 正拟牛顿条件还待进一步研究;其次,应用比较的 结果,给出了一个修正的 BFGS 拟牛顿算法,在较弱 的条件下,不需要目标函数的凸性假设,证明了算 法对一般的无约束优化问题具有全局收敛性.
式,只需在(5)中将 换成 就可得到(10).虽 然角度不一样,但方式一与方式二的修正策略本质 上是一致的.
(2)两种方式得到的修正拟牛顿条件分别对应 两种形式
实际上两者可统一于形式
,
其中
.
(注: 若 (14) 中 为 非 数 量 矩 阵 时 , 则 取
,作为推广也可取
).
(3)即使满足同一弱拟牛顿条件
的第 次迭代,得到比文献[8]147-167 更一般的修正拟牛
顿条件
(14)
矩阵 的选择有多种,如可取
.对目标函数
利用
Taylor 公式得到
,
取得,即,利用(14)得,结合 逼近 及
上式得到
对任何满足
, 的向量 ,上式可描述为 ,
取 可得修正拟牛顿条件
(15)
此时
与(7)是一致的, 与 的项
之间有
.将 替换(13)中的 ,
(H1) 在水平集
- 10 -
第 28 卷
黄 海,林穗华 几种修正拟牛顿法的比较
(总第 76 期)
上有界.
(H2) 的导函数 在 上 Lipschitz 连续,
即
使
,
由以上假设可知
,使
,
.不仿假设
,否则稳定点已获得,
算法有限步终止.下面简要证明算法的全局收敛性.
引理 1 MBFGS 算法生成的序列 均为对称正
Abstract: For unconstrained optimization problems, quasi-Newton methods are a class of utilizing, first derivative, the most effective approach. How to improve the computing efficiency of the actual calculation, and how to obtain global convergence and local super linear convergence for non-convex objective function are contents of quasi-Newton research. This paper compares some modified quasi-Newton methods in the recent literature, proposes a modified BFGS quasi-Newton method and analyzes its global convergence.
-9-
2011 年第 3 期
广西民族师范学院学报
6 月 25 日出版
这一思想类推到拟牛顿法,由
,可知
,使 近似 ,从而合理地得
到 满足如下修正拟牛顿条件
进而得到形如(13)的修正 BFGS 校正公式.参数
条件(
,有
)一
般不成立 .为 [1]102-111 了全局收敛性及超线性收敛性的
需要,人们往往提出适当的假设,或采取一些修正
可能是病态的,因此提出用调比因子 使
减少
病态的方案,其做法是由
,用 近似
(亦使 克服病态),得到修正拟牛顿条件
