最优化牛顿法
牛顿法无约束最优化证明

牛顿法无约束最优化证明牛顿法是一种常用的非线性优化方法,它通过逐步逼近最优解来求解无约束最优化问题。
本文将介绍牛顿法的数学原理及其证明过程。
首先,我们考虑一个无约束的最优化问题,即:min f(x)其中,f(x)为目标函数,x为优化变量。
我们的目标是找到一个x,使得f(x)最小。
牛顿法的基本思想是通过求解目标函数的局部二次近似来逐步逼近最优解。
具体来说,我们首先选取一个初始点x0,然后利用目标函数的一、二阶导数信息,计算出目标函数在x0处的局部二次近似:f(x) ≈ f(x0) + f(x0)·(x-x0) + 1/2(x-x0)T·H(x0)·(x-x0) 其中,f(x0)为目标函数在x0处的梯度,H(x0)为目标函数在x0处的黑塞矩阵。
我们将局部二次近似表示为:Q(x) = f(x0) + f(x0)·(x-x0) + 1/2(x-x0)T·H(x0)·(x-x0) 然后,我们将Q(x)的导数置为零,得到如下方程:H(x0)·(x-x0) = -f(x0)接着,我们解出上述方程的解x1,将x1作为新的近似点,重复上述步骤,迭代求解,直到收敛于最优解。
接下来,我们来证明牛顿法的收敛性。
我们假设目标函数f(x)满足如下条件:1. f(x)是二次可微的凸函数。
2. H(x)是正定的。
在这种情况下,我们可以证明牛顿法是线性收敛的。
具体来说,设xk为牛顿法第k次迭代的近似解,x*为最优解,则有:f(xk+1) - f(x*) ≤ C·(f(xk) - f(x*))2其中,C>0是一个常数。
这个式子表明,每次迭代后,算法的误差都会平方级别的减小。
证明过程比较复杂,需要利用函数的泰勒展开式、中值定理等工具。
具体证明过程可以参考相关数学文献。
综上所述,牛顿法是一种有效的无约束最优化方法,其收敛速度较快,但需要满足一定的条件才能保证收敛性。
最优化理论方法——牛顿法
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
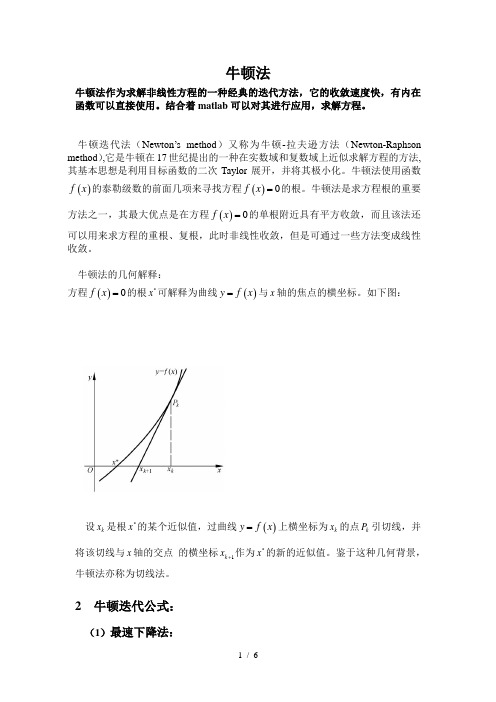
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。
lm算法牛顿法

lm算法牛顿法牛顿法和高斯-牛顿法都是最优化算法,它们通过多轮迭代逐步逼近最优解。
而LM 算法(Levenberg-Marquardt算法)是这两种算法的一种改进,旨在解决高斯-牛顿法在矩阵非正定时可能出现的问题。
以下是对这三种算法的简要介绍:1.牛顿法:牛顿法是一种在实数域和复数域上近似求解方程的方法。
它使用函数f 的泰勒级数的前面几项来寻找方程f(x)=0的根。
牛顿法可以被用来找寻函数的最大值或最小值,这需要将函数的一阶导数设为零并求解,或者将函数的二阶导数设为零并求解以寻找拐点。
牛顿法在求解非线性最优化问题时也非常有效,特别是当问题的局部最优解是全局最优解时。
然而,当问题的维数增加时,计算二阶导数(即Hessian矩阵)可能会变得非常复杂和耗时。
2.高斯-牛顿法:高斯-牛顿法是牛顿法的一个变种,它专门用于求解非线性最小二乘问题。
在每一步迭代中,它使用雅可比矩阵(而不是Hessian矩阵)来逼近函数的Hessian矩阵,从而避免了直接计算二阶导数。
然而,高斯-牛顿法的收敛性依赖于初始值的选取和问题的性质。
如果初始值选取不当或者问题存在多个解,那么高斯-牛顿法可能会收敛到错误的解或者根本不收敛。
3.LM算法:LM算法是结合了梯度下降法和高斯-牛顿法的一种优化算法。
它通过引入一个阻尼因子来调整迭代步长,从而在高斯-牛顿法的基础上增加了算法的稳健性。
当阻尼因子较大时,LM算法更接近于梯度下降法,具有全局收敛性;当阻尼因子较小时,LM算法更接近于高斯-牛顿法,具有快速局部收敛性。
因此,LM算法可以在一定程度上解决高斯-牛顿法在矩阵非正定时出现的问题。
总的来说,这三种算法都是用于求解最优化问题的重要工具,它们各有优缺点并适用于不同类型的问题。
在实际应用中,需要根据问题的性质和需求选择合适的算法进行求解。
最优化问题的算法迭代格式

最优化问题的算法迭代格式最优化问题的算法迭代格式最优化问题是指在一定的条件下,寻找使某个目标函数取得极值(最大值或最小值)的变量取值。
解决最优化问题的方法有很多种,其中较为常见的是迭代法。
本文将介绍几种常用的最优化问题迭代算法及其格式。
一、梯度下降法梯度下降法是一种基于负梯度方向进行搜索的迭代算法,它通过不断地沿着目标函数的负梯度方向进行搜索,逐步接近极值点。
该方法具有收敛速度快、易于实现等优点,在许多应用领域中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和学习率 $\alpha$,梯度下降算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 更新当前点 $x_k$ 为 $x_{k+1}=x_k-\alpha\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则返回第 1 步。
2. 算法特点- 沿着负梯度方向进行搜索,能够快速收敛;- 学习率的选择对算法效果有重要影响;- 可能会陷入局部极小值。
二、共轭梯度法共轭梯度法是一种基于线性方程组求解的迭代算法,它通过不断地搜索与当前搜索方向共轭的新搜索方向,并在该方向上进行一维搜索,逐步接近极值点。
该方法具有收敛速度快、内存占用少等优点,在大规模问题中被广泛使用。
1. 算法描述对于目标函数 $f(x)$,初始点 $x_0$ 和初始搜索方向 $d_0$,共轭梯度算法可以描述为以下步骤:- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$;- 如果满足停止条件,则输出结果;否则进行下一步;- 计算当前搜索方向 $d_k$;- 在当前搜索方向上进行一维搜索,得到最优步长 $\alpha_k$;- 更新当前点为 $x_{k+1}=x_k+\alpha_k d_k$;- 计算新的搜索方向 $d_{k+1}$;- 返回第 2 步。
2. 算法特点- 搜索方向与前面所有搜索方向都正交,能够快速收敛;- 需要存储和计算大量中间变量,内存占用较大;- 可以用于非线性问题的求解。
最优化理论与方法——牛顿法

牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton Newton’’s s method method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
收敛。
牛顿法的几何解释:牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:x-d gk k×Gg sks×GGd 101x x x -(1)令k k G v I k G -=+,其中:,其中:0k v =,如果k G 正定;0,k v >否则。
否则。
(2)计算_k G 的Cholesky 分解,_T k k k k G L D L =。
(3)解_k k G d g =-得k d 。
(4)令1k k k x x d +=+牛顿法的优点是收敛快,缺点一是每步迭代要计算()()'k k f x f x 及,计算量较大且有时()'k fx 计算较困难,二是初始近似值0x 只在根*x附近才能保证收敛,如0x 给的不合适可能不收敛。
牛顿法和牛顿迭代法

⽜顿法和⽜顿迭代法⽜顿法,⼤致的思想是⽤泰勒公式的前⼏项来代替原来的函数,然后对函数进⾏求解和优化。
和稍微有些差别。
⽜顿法⽜顿法⽤来迭代的求解⼀个⽅程的解,原理如下:对于⼀个函数f(x),它的泰勒级数展开式是这样的f(x)=f(x0)+f′(x0)(x−x0)+12f″(x0)(x−x0)2+...+1n!f n(x0)(x−x0)n当使⽤⽜顿法来求⼀个⽅程解的时候,它使⽤泰勒级数前两项来代替这个函数,即⽤ϕ(x)代替f(x),其中:ϕ(x)=f(x0)+f′(x0)(x−x0)令ϕ(x)=0,则x=x0−f(x0) f′(x0)。
所以,⽜顿法的迭代公式是x n+1=x n−f(x n) f′(x n)⽜顿法求解n的平⽅根求解n的平⽅根,其实是求⽅程x2−n=0的解利⽤上⾯的公式可以得到:x i+1=x i−x2i−n2x i=(xi+nx i)/2编程的时候核⼼的代码是:x = (x + n/x)/2应⽤于最优化的⽜顿法应⽤于最优化的⽜顿法是以迭代的⽅式来求解⼀个函数的最优解,常⽤的优化⽅法还有梯度下降法。
取泰勒展开式的⼆次项,即⽤ϕ(x)来代替f(x):ϕ(x)=f(x0)+f′(x0)(x−x0)+12f″(x0)(x−x0)2最优点的选择是ϕ′(x)=0的点,对上式求导ϕ′(x)=f′(x0)+f″(x0)(x−x0)令ϕ′(x)=0,则x=x0−f′(x0) f″(x0)所以,最优化的⽜顿迭代公式是x n+1=x n−f′(x n) f″(x n)⾼维下的⽜顿优化⽅法在⾼维下ϕ(x)=f(x0)+∇f(x0)T(x−x0)+12(x−x0)T∇2f(x0)(x−x0)求∇ϕ(x),并令它等于0,则公式变为了∇f(x0)+∇2f(x0)(x−x0)=0即x=x0−∇2f(x0)−1∇f(x0)所以,迭代公式变为x n+1=x n−∇2f(x n)−1∇f(x n)其中:x n+1,x n都是N*1维的⽮量。
最优化方法牛顿法失效的例子

最优化方法牛顿法失效的例子摘要:一、引言二、牛顿法概述三、牛顿法失效的原因四、牛顿法失效的例子五、总结与建议正文:一、引言牛顿法作为一种最优化方法,以其高效、简洁的特性在众多领域得到了广泛应用。
然而,在实际问题中,我们经常会遇到牛顿法失效的情况。
这种现象的发生往往导致求解过程的失败,从而影响到整个优化问题的解决。
因此,了解牛顿法失效的原因及具体例子,对于优化问题的求解具有重要意义。
二、牛顿法概述牛顿法是一种基于迭代的思想,通过构建目标函数的二阶泰勒展开式,求解最优解的方法。
其迭代公式为:x_{k+1} = x_k - α_k * (f"(x_k) - β_k * f""(x_k))其中,f(x) 为待求解的最优化问题,f"(x) 和f""(x) 分别表示目标函数的一阶导数和二阶导数,α_k 和β_k 为迭代步长。
三、牛顿法失效的原因1.目标函数的性质:牛顿法适用于凸函数和光滑函数的优化问题。
当目标函数存在多个局部最优解或非凸时,牛顿法可能无法收敛,甚至陷入局部最优解。
2.迭代步长的选择:牛顿法的收敛性与迭代步长的选择密切相关。
若步长选取过大或过小,可能导致迭代过程的发散或收敛速度过慢。
3.初始值的选取:牛顿法的收敛性与初始值的选择有关。
不同的初始值可能导致不同的收敛结果,甚至有的初始值会使牛顿法失效。
四、牛顿法失效的例子1.二维平面上的曲线的优化问题:考虑如下二维平面上的曲线优化问题:min_{x,y} f(x,y) = (x-1)^2 + (y-2)^2在二维平面上,该曲线为椭圆。
此时,牛顿法可能无法收敛,因为椭圆内部存在多个局部最优解。
2.非线性方程组的求解:考虑如下非线性方程组:f(x,y) = x^2 + y^2 - 3x - 4y + 5 = 0使用牛顿法求解该方程组时,由于方程组非线性,牛顿法可能失效。
五、总结与建议1.在实际应用中,要充分了解问题的性质,判断是否适用于牛顿法求解。
牛顿迭代法的最优化方法和应用

牛顿迭代法的最优化方法和应用牛顿迭代法是一种优化算法,它基于牛顿法和迭代法的思想,广泛应用于最优化问题的求解中。
在计算机科学、数学和工程等领域,牛顿迭代法被广泛应用于解决各种实际问题,如机器学习、数值分析和物理模拟等。
一、基本原理牛顿迭代法的基本思想是在当前点的邻域内用二次函数近似目标函数,然后在近似函数的极小点处求解最小化问题。
具体而言,假设我们要最小化一个凸函数$f(x)$,我们可以在当前点$x_k$处利用泰勒级数将其近似为:$$f(x_k+p)\approx f(x_k)+\nabla f(x_k)^Tp+\frac12p^T\nabla^2f(x_k)p$$其中,$p$是一个向量,$\nabla f(x_k)$和$\nabla ^2f(x_k)$分别是$f(x_k)$的一阶和二阶导数,也称为梯度和黑塞矩阵。
我们可以令近似函数的一阶导数等于零,即$\nabla f(x_k)+\nabla^2f(x_k)p=0$,然后解出$p$,得到$p=-\nabla ^{-1}f(x_k)\nablaf(x_k)$。
于是我们可以将当前点更新为$x_{k+1}=x_k+p$。
我们可以重复这个过程,直到目标函数收敛到我们所需的精度。
二、应用实例1. 机器学习:牛顿迭代法可以用于训练神经网络和逻辑回归等机器学习模型。
在神经网络中,牛顿迭代法可以帮助我们优化网络的权重和偏置,以提高网络的准确性和鲁棒性。
在逻辑回归中,牛顿迭代法可以帮助我们学习双分类问题的参数和概率分布。
2. 数值分析:牛顿迭代法可以用于求解非线性方程和方程组的根。
例如,我们可以使用牛顿迭代法来解决$sin(x)=0$和$x^2-2=0$这样的方程。
当然,为了保证迭代收敛,我们需要选择一个合适的初始点,并且要确保目标函数是连续和可微的。
3. 物理模拟:牛顿迭代法可以用于求解物理方程组的数值解。
它可以帮助我们模拟地球的运动轨迹、热力学系统的稳态和弹性材料的应力分布等。
最优化方法三分法+黄金分割法+牛顿法

最优化⽅法三分法+黄⾦分割法+⽜顿法最优化_三等分法+黄⾦分割法+⽜顿法⼀、实验⽬的1. 掌握⼀维优化⽅法的集中算法;2. 编写三分法算法3. 编写黄⾦分割法算法4. 编写⽜顿法算法⼆、系统设计三分法1.编程思路:三分法⽤于求解单峰函数的最值。
对于单峰函数,在区间内⽤两个mid将区间分成三份,这样的查找算法称为三分查找,也就是三分法。
在区间[a,b]内部取n=2个内等分点,区间被分为n+1=3等分,区间长度缩短率=1 3 .各分点的坐标为x k=a+b−an+1⋅k (k=1,2) ,然后计算出x1,x2,⋯;y1,y2,⋯;找出y min=min{y k,k=1,2} ,新区间(a,b)⇐(x m−1,x m+1) .coding中,建⽴left,mid1,mid2,right四个变量⽤于计算,⽤新的结果赋值给旧区间即可。
2.算法描述function [left]=gridpoint(left,right,f)epsilon=1e-5; %给定误差范围while((left+epsilon)<right) %检查left,right区间精度margin=(right-left)/3; %将区间三等分,每⼩段长度=marginm1=left+margin; %left-m1-m2-right,三等分需要两个点m2=m1+margin; %m2=left+margin+marginif(f(m1)<=f(m2))right=m2; %离极值点越近,函数值越⼩(也有可能越⼤,视函数⽽定)。
else %当f(m1)>f(m2),m2离极值点更近。
缩⼩区间范围,逼近极值点left=m1; %所以令left=m1.endend %这是matlab的.m⽂件,不⽤写return.黄⾦分割法1.编程思路三分法进化版,区间长度缩短率≈0.618.在区间[a,b]上取两个内试探点,p i,q i要求满⾜下⾯两个条件:1.[a i,q i]与[p i,b i]的长度相同,即b i−p i=q i−a i;2.区间长度的缩短率相同,即b i+1−a i+1=t(b i−a i)]2.算法描述⾃⼰编写的:function [s,func_s,E]=my_golds(func,left,right,delta)tic%输⼊: func:⽬标函数,left,right:初始区间两个端点% delta:⾃变量的容许误差%输出: s,func_s:近似极⼩点和函数极⼩值% E=[ds,dfunc] ds,dfunc分别为s和dfunc的误差限%0.618法的改进形式:每次缩⼩区间时,同时⽐较两内点和两端点处的函数值。
五种最优化方式

五种最优化方式1. 最优化方式概述1.1最优化问题的分类1)无约束和有约束条件;2)确信性和随机性最优问题(变量是不是确信);3)线性优化与非线性优化(目标函数和约束条件是不是线性);4)静态计划和动态计划(解是不是随时刻转变)。
1.2最优化问题的一样形式(有约束条件):式中f(X)称为目标函数(或求它的极小,或求它的极大),si(X)称为不等式约束,hj(X)称为等式约束。
化进程确实是优选X,使目标函数达到最优值。
2.牛顿法2.1简介1)解决的是无约束非线性计划问题;2)是求解函数极值的一种方式;3)是一种函数逼近法。
2.2 原理和步骤3. 最速下降法(梯度法)3.1最速下降法简介1)解决的是无约束非线性计划问题;2)是求解函数极值的一种方式;3)沿函数在该点处目标函数下降最快的方向作为搜索方向;3.2 最速下降法算法原理和步骤4. 模式搜索法(步长加速法)4.1 简介1)解决的是无约束非线性计划问题;2)不需要求目标函数的导数,因此在解决不可导的函数或求导异样麻烦的函数的优化问题时超级有效。
3)模式搜索法每一次迭代都是交替进行轴向移动和模式移动。
轴向移动的目的是探测有利的下降方向,而模式移动的目的那么是沿着有利方向加速移动。
4.2模式搜索法步骤5.评判函数法5.1 简介评判函数法是求解多目标优化问题中的一种要紧方式。
在许多实际问题中,衡量一个方案的好坏标准往往不止一个,多目标最优化的数学描述如下:min (f_1(x),f_2(x),...,f_k(x))s.t. g(x)<=0传统的多目标优化方式本质是将多目标优化中的各分目标函数,经处置或数学变换,转变成一个单目标函数,然后采纳单目标优化技术求解。
经常使用的方式有“线性加权和法”、“极大极小法”、“理想点法”。
选取其中一种线性加权求合法介绍。
5.2 线性加权求合法6. 遗传算法智能优化方式是通过运算机学习和存贮大量的输入-输出模式映射关系,进而达到优化的一种方式,要紧有人工神经网络法,遗传算法和模拟退火法等。
matlab 牛顿法 多维无约束最优化

matlab 牛顿法多维无约束最优化在MATLAB中,你可以使用内置的优化工具箱函数来使用牛顿法进行多维无约束最优化。
具体来说,你可以使用fminunc函数,该函数使用一种基于牛顿法的优化算法。
以下是一个示例:
MATLABfunction [x,fval,exitflag,output] = multidimensional_unconstrained_optimization()
% 定义目标函数
fun = @(x) x(1)^2 + x(2)^2 - 4*cos(x(1)) - 2*cos(x(2));
% 定义初始点
x0 = [0.5,0.5];
% 调用fminunc函数
options = optimoptions('fminunc','Algorithm','quasi-newton');
[x,fval,exitflag,output] = fminunc(fun,x0,options);
end在这个例子中,我们定义了一个目标函数fun,它是一个多维函数,然后我们定义了一个初始点x0。
然后我们调用fminunc函数,并指定我们想要使用的算法为quasi-newton(一种牛顿法)。
最后,我们得到了优化问题的解x,以及目标函数在最优解处的值fval。
注意:这个例子中的目标函数是一个简单的二次函数,其最小值在原点。
因此,对于更复杂的目标函数,你可能需要更精细地调整初始点或选项。
牛顿法和梯度下降

牛顿法和梯度下降牛顿法和梯度下降是最常用的优化算法,在机器学习、深度学习等领域广泛应用。
本文将介绍这两种算法的原理、优缺点以及在实际应用中的使用情况。
一、牛顿法牛顿法是一种求解非线性方程和最优化问题的迭代方法。
其核心思想是利用泰勒展开和牛顿迭代的思想,对函数进行局部近似,并利用近似的函数求得下一步的迭代点,从而达到求解最优解的目的。
1. 算法流程首先,对于一个单峰、连续且可导的函数 f(x),我们可以用二次函数来近似表示:$f(x) \approx Q(x) = f(x_0) + f^\prime(x_0) (x - x_0) + \frac{1}{2} f^{\prime\prime}(x_0)(x -x_0)^2$其中,$x_0$ 是当前点,$f^\prime(x_0)$ 是$x_0$ 处的导数,$f^{\prime\prime}(x_0)$ 是 $x_0$ 处的二阶导数。
通过求解 $Q(x)$ 的极值,我们可以得到牛顿迭代的公式:$x_{n+1} = x_{n} -\frac{f^\prime(x_n)}{f^{\prime\prime}(x_n)}$我们可以通过不断迭代得到最终的极值点。
2. 优缺点优点:(1)收敛速度快。
很多实验表明,与梯度下降法、共轭梯度法相比,牛顿法的收敛速度更快,尤其是在迭代次数不太大的时候。
(2)二次收敛。
牛顿法可以在迭代一次后达到二次收敛的速度,这使得它可以很快地接近最优解。
(3)精度高。
牛顿法可以通过二次近似求导数的方法,可以减少迭代的次数,得到更高精度的结果。
缺点:(1)计算复杂度高。
牛顿法需要计算 Hessian 矩阵和解线性方程组,这使得它的计算复杂度比梯度下降法高。
(2)缺乏稳定性。
在某些情况下,牛顿法可能会出现不收敛、发散等问题。
(3)对于高维数据收敛速度慢。
对于高维度数据,计算 Hessian 矩阵的时间复杂度很高,导致牛顿法收敛速度慢。
3. 应用场景由于牛顿法具有较快的收敛速度和高的精度,因此在许多实际问题中得到广泛的应用,例如图像处理、信号处理等领域,在实现高精度形态估计、图像配准和特征提取等问题上,牛顿法都表现出强大的优势。
求全局最优化的几种确定性算法

求全局最优化的几种确定性算法全局最优化是一个在给定约束条件下寻找函数全局最小或最大值的问题。
确定性算法是指每次运行算法都能得到相同的结果,且结果能确保接近全局最优解。
以下是几种常见的确定性算法:1. 梯度下降法(Gradient Descent)梯度下降法是一种迭代优化算法,通过沿负梯度方向逐步调整参数值,直至找到函数的最小值或最大值。
该算法对于凸函数是有效的,但可能会陷入局部最优解。
可以通过调整学习率和选择不同的初始参数值来改进算法的效果。
2. 牛顿法(Newton's Method)牛顿法利用函数的二阶导数信息来找到函数的最小值或最大值。
它基于泰勒级数展开,通过使用当前点的一阶和二阶导数来逼近函数,然后迭代地更新参数值。
牛顿法通常比梯度下降法更快地收敛到全局最优解,但它可能需要计算和存储较大的二阶导数矩阵。
3. 共轭梯度法(Conjugate Gradient)共轭梯度法是一种迭代法,用于求解线性方程组或优化问题。
它利用问题的海森矩阵或其逼近的特殊性质,在有限次迭代后得到准确解。
共轭梯度法在解决大规模问题时具有可伸缩性,且不需要存储大规模矩阵。
4. BFGS算法(Broyden–Fletcher–Goldfarb–Shanno Algorithm)BFGS算法是一种拟牛顿法,用于解决无约束非线性优化问题。
它通过近似目标函数的海森矩阵的逆矩阵来逼近最优解,从而避免了计算海森矩阵的复杂性。
BFGS算法具有快速的收敛性和较好的全局收敛性。
5. 遗传算法(Genetic Algorithms)遗传算法是一种模拟生物进化过程的优化方法,通过模拟自然界的选择、交叉和变异过程来最优解。
它将问题表示成一个个基因型,通过使用选择、交叉和变异等操作来产生新的个体,并根据适应度函数评估每个个体的好坏。
遗传算法具有全局能力,可以处理非线性、非凸函数以及离散优化问题。
6. 粒子群优化算法(Particle Swarm Optimization)粒子群优化算法是一种模拟鸟群或鱼群行为的优化算法。
最优化算法(牛顿、拟牛顿、梯度下降)
最优化算法(⽜顿、拟⽜顿、梯度下降)1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤: ⾸先,选择⼀个接近函数f (x)零点的x0,计算相应的f (x0) 和切线斜率f ' (x0)(这⾥f ' 表⽰函数f 的导数)。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标,也就是求如下⽅程的解: 我们将新求得的点的x 坐标命名为x1,通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰: 已经证明,如果f ' 是连续的,并且待求的零点x是孤⽴的,那么在零点x周围存在⼀个区域,只要初始值x0位于这个邻近区域内,那么⽜顿法必定收敛。
并且,如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说,这意味着每迭代⼀次,⽜顿法结果的有效数字将增加⼀倍。
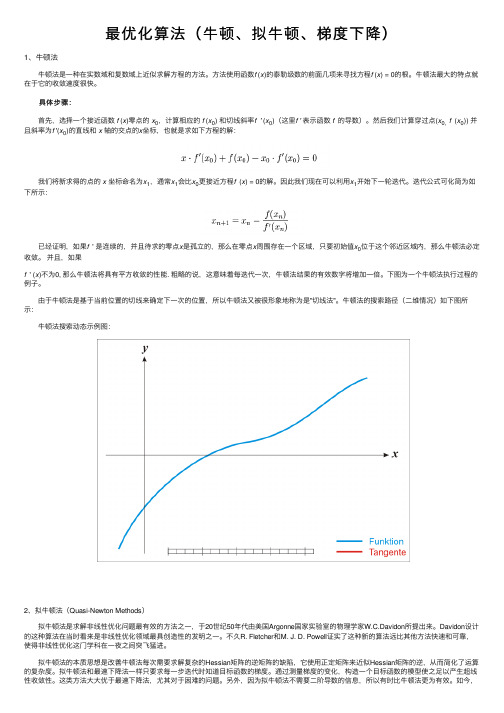
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置,所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径(⼆维情况)如下图所⽰: ⽜顿法搜索动态⽰例图:2、拟⽜顿法(Quasi-Newton Methods) 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠,使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使⽤正定矩阵来近似Hessian矩阵的逆,从⽽简化了运算的复杂度。
最优化牛顿法

最优化牛顿法最优化牛顿法是一种常用的数值计算方法,用于求解无约束优化问题。
它是利用函数的一阶导数和二阶导数信息,通过迭代更新来逼近最优解的方法。
本文将介绍最优化牛顿法的基本原理、步骤和应用。
一、最优化牛顿法的基本原理最优化牛顿法是基于牛顿迭代法发展而来的一种优化算法。
它利用函数的一阶导数和二阶导数信息来逼近最优解。
其基本思想是通过不断迭代来求解函数的最小值或最大值。
最优化牛顿法的步骤主要分为初始化、迭代更新和终止条件三个部分。
1. 初始化:首先需要确定初始值,可以通过人工设定或者其他优化算法得到。
初始值的选取对最优化牛顿法的收敛速度和结果都有一定的影响。
2. 迭代更新:在每一次迭代中,需要计算函数的一阶导数和二阶导数,并更新当前的估计值。
具体而言,首先计算函数的一阶导数和二阶导数,然后利用这些导数信息计算当前的估计值,并更新估计值。
这个过程会不断迭代,直到满足终止条件为止。
3. 终止条件:最优化牛顿法的终止条件可以根据具体问题的要求来确定。
常见的终止条件包括迭代次数达到一定的上限、函数值的变化小于某个阈值等。
三、最优化牛顿法的应用最优化牛顿法在实际问题中有广泛的应用,特别是在机器学习和优化领域。
下面将介绍几个常见的应用案例。
1. 机器学习中的参数优化:在机器学习中,模型的参数优化是一个重要的问题。
最优化牛顿法可以用来求解模型参数的最优值,从而提高模型的性能和准确度。
2. 信号处理中的谱估计:在信号处理中,谱估计是一个关键的问题。
最优化牛顿法可以用来求解谱估计问题,从而提高信号处理的效果。
3. 无线通信中的功率控制:在无线通信中,功率控制是一个重要的问题。
最优化牛顿法可以用来求解功率控制问题,从而提高无线通信系统的性能和覆盖范围。
四、总结最优化牛顿法是一种常用的数值计算方法,用于求解无约束优化问题。
它利用函数的一阶导数和二阶导数信息,通过迭代更新来逼近最优解。
最优化牛顿法的步骤包括初始化、迭代更新和终止条件。
最优化 多目标优化 惩罚函数法 梯度法 牛顿法

2008-12-08 12:30利用梯度法和牛顿法编程求最优解(matlab)f(x)=x1^2+4*x2^2 x0=[2;2] e=0.002利用梯度法和牛顿法编程求最优解方法一.梯度法function y=fun(x1,x2)y=x1^2+4*x2^2; %定义fun.m函数clcsyms x1 x2 d;f=x1^2+4*x2^2;fx1=diff(f,'x1');fx2=diff(f,'x2');x1=2;x2=2;for n=1:100f0=subs(f);f1=subs(fx1);f2=subs(fx2);if (double(sqrt(f1^2+f2^2)) <= 0.002)nvpa(x1)vpa(x2)vpa(f0)break;elseD=fun(x1-d*f1,x2-d*f2);Dd=diff(D,'d');dd=solve(Dd);x1=x1-dd*f1;x2=x2-dd*f2;endend %结果n=10,x1=0.2223e-3,x2=-0.1390e-4,f0=0.5021e-7. 方法二.牛顿法clcsyms x1 x2 ;f=x1^2+4*x2^2;fx1=diff(f,'x1'); fx2=diff(f,'x2');fx1x1=diff(fx1,'x1');fx1x2=diff(fx1,'x2');fx2x1=diff(fx2,'x1');fx2x2= diff(fx2,'x2');x1=2;x2=2;for n=1:100f0=subs(f);f1=subs(fx1);f2=subs(fx2);if (double(sqrt(f1^2+f2^2)) <= 0.002)nx1=vpa(x1,4)x2=vpa(x2,4)f0=vpa(f0,4)break;elseX=[x1 x2]'-inv([fx1x1 fx1x2;fx2x1 fx2x2]) *[f1 f2]';x1=X[1,1];x2=X[2,1];endend %结果 n=2,x1=0,x2=0,f0=0.惩罚函数法(内点法、外点法)求解约束优化问题最优值编程 matlab1 用外点法求下列问题的最优解方法一:外点牛顿法:clcm=zeros(1,50);a=zeros(1,50);b=zeros(1,50);f0=zeros(1,50);%a b为最优点坐标,f0为最优点函数值,f1 f2最优点梯度。
牛顿迭代法的科学计算和工程应用

牛顿迭代法的科学计算和工程应用牛顿迭代法是一种用于求解非线性方程的数值计算方法,该方法以牛顿插值公式为基础,利用导数的概念,通过不断迭代来逼近函数的根。
牛顿迭代法在科学计算和工程应用中具有广泛的应用,例如在求解实际问题中的最优化问题、求解微分方程、图像处理等方面,牛顿迭代法都有着重要的地位。
牛顿迭代法的原理牛顿迭代法通过牛顿插值公式来逼近函数的根。
对于一个函数f(x),在x=a处的一次近似为:f(x)≈f(a)+f'(a)(x-a)其中f'(a)为函数f(x)在x=a处的导数。
若f(x)=0,则有:x=a-(f(a)/f'(a))这便是牛顿迭代法的基本公式。
通过不断迭代即可逼近函数的根。
牛顿迭代法的优缺点牛顿迭代法具有收敛速度快的优点,通常情况下可以迅速地逼近函数的根。
但是在某些情况下,牛顿迭代法的收敛会比较慢,甚至会出现发散的情况。
此外,牛顿迭代法要求函数在根的附近具有一阶导数连续,否则无法适用。
牛顿迭代法的工程应用举例牛顿迭代法可以应用于求解实际问题中的最优化问题、求解微分方程、图像处理等领域。
下面简单介绍几个工程应用举例。
1. 最优化问题最优化问题在工程和科学领域中都有着很广泛的应用。
在求解最优化问题时,需要找到函数的极值点。
利用牛顿迭代法可以快速、准确地找到函数的极值点。
例如,利用牛顿迭代法可以求解f(x)=(1/2)x^2-2x+3的极值点。
首先求取函数的一阶和二阶导数:f'(x)=x-2f''(x)=1然后利用牛顿法进行迭代:x₁=x₀-(f'(x₀))/f''(x₀)=2x₂=2-(f'(2))/(f''(2))=1.5x₃=1.5-(f'(1.5))/(f''(1.5))=1.414可以看出,只需要进行三次迭代就可以求得函数的极值点。
这说明,牛顿迭代法对于求解最优化问题具有很大的优势。
Newton-Raphson算法

Newton-Raphson算法简介⽜顿法⼜叫做⽜顿-拉裴森(Newton-Raphson)⽅法,是⼀维求根⽅法中最著名的⼀种。
其特点是在计算时需要同时计算函数值与其⼀阶导数值,从⼏何上解释,⽜顿法是将当前点处的切线延长,使之与横轴相交,然后把交点处值作为下⼀估值点。
图1从数学上解释,⽜顿法可以从函数的泰勒展开得到。
f(x)的泰勒展开可以表⽰为:f(x+\delta)=f(x)+f’(x)\delta+\frac{f’’(x)}{2}\delta^2+O(\delta^3)对于⾜够⼩的\delta,可以将只保留上式右端关于的⼀阶项,得到:\delta=-\frac{f(x)}{f’(x)}于是得到由到的递推公式:x_{i+1}=x_{i}+\delta=x_i-\frac{f(x_i)}{f’(x_i)}可见⽜顿法是让x沿着f(x)梯度的⽅向下降,类似于最优化⽅法中的梯度下降法。
⽜顿法也可以作为最优化算法,只不过那时需要求函数的⼆阶导数。
⽜顿法相⽐⼆分法、截弦法的优点是收敛速度可以达到⼆阶,在根附近没迭代⼀次,结果的有效数字⼏乎可以翻倍。
当然⽜顿法也可能可能失败,⽐如收敛到⼀个局部极值,其切线⽅向与横轴⽔平,从⽽⽆法计算下⼀个迭代值。
另外,⽜顿法的实现需要⽤户提供⼀个函数⽤于计算函数值f(x)与其⼀阶导数值f'(x),因此⽐较适合函数的导数可以解析求出的情况,如果需要求数值导数,则⽜顿法的收敛速度和精度都会受影响。
我们可以将⽜顿法和⼆分法综合起来形成⼀个混合算法,⼀旦⽜顿法在运⾏过程中出现解跳出给定区间或者猜测值远离实际根导致收敛速度较慢时,就采取⼀步⼆分法。
实现⼀:利⽤预先求出的⼀阶导函数import numpy as npimport matplotlib.pyplot as pltdef f(FV, PMT, r, n):return PMT * (1 + r) * (((1 + r)**n - 1)) / r + FVdef df(FV, PMT, r, n):r_plus_1_power_n = (1 + r)**np1 = N * PMT * r_plus_1_power_n / rp2 = -PMT * (r + 1) * (r_plus_1_power_n - 1) / r / rp3 = PMT * (r_plus_1_power_n - 1) / rreturn p1 + p2 + p3def newtonRaphson2(FV,PMT,n,f,df,xmin,xmax,maxit,shift=0.0001,tol=1.0e-9):'''函数作⽤说明:计算组合收益率FV:⽬标⾦额PMT:每期投资⾦额n:定投期数f:函数值(根据要求的⽅程⾃定义)df:导数值(根据要求的⽅程⾃定义)xmin:根的下限xmax:根的上限maxit:最⼤迭代次数tol:计算精度'''import mathfxmin = f(FV, PMT, xmin, n)if fxmin == 0.0:return xminfxmax = f(FV, PMT, xmax, n)if fxmax == 0.0:return xmaxif fxmin * fxmax > 0.0:print('Root is not bracketed') # 在[xmin, xmax]内函数不变号(没根),或者是变了偶数次号(多个根)return 1if fxmin < 0.0: # 确定搜索⽅向使f(xl)<0xl = xminxh = xmaxelse:xl = xmaxxh = xminx = 0.5 * (xmin + xmax) # 根的预测值if x == 0:x += shiftfx, dfx = f(FV, PMT, x, n), df(FV, PMT, x, n) # 求f(x)和其⼀阶导数dxold = math.fabs(xmax - xmin) # 储存步长dx = dxoldfor ii in range(maxit):# ⽜顿法的解跳出解区间或者收敛速度太慢,则下⼀步改⽤⼆分法if ((x - xh) * dfx - fx) * ((x - xl) * dfx - fx) > 0.0 or (math.fabs(2 * fx) > math.fabs(dxold * dfx)):# ⼆分法dxold = dxdx = 0.5 * (xh - xl)x = xl + dxelse:# ⽜顿法dxold = dxdx = fx / dfxtemp = xx -= dxif temp == x:print("total iterate time:%s " % ii)return xif math.fabs(dx) < tol: # 达到要求精度,返回找到的根print("total iterate time:%s " % ii)return xif x == 0:x += shiftfx, dfx = f(FV, PMT, x, n), df(FV, PMT, x, n) # 否则继续迭代,求f(x)和其⼀阶导数if fx < 0.0: # 使根保持在解区间内xl = xelse:xh = xprint('Maximum number of iterations exceeded')return 1### 测试⽤例:⾸先给定PMT,n,r_analytical,计算FV,然后利⽤PMT,n,FV计算r_numerical,两者应该相等##给定r_analytical计算FVR=0.1r_analytical = R / 12PMT = -4e3N = 30n = N * 12FV = -PMT * (1 + r_analytical) * (((1 + r_analytical)**n - 1)) / r_analytical##给定FV反解r_numericalr_numerical = newtonRaphson2(FV, PMT, n, f, df, -1, 1, 100, tol=1.0e-8)print('\nr_analytical=%s,\nr_numerical=%s\n' % (r_analytical, r_numerical))实现⼆:利⽤TensorFlow提供的⾃动微分计算导函数import numpy as npimport mathimport pandas as pdimport tensorflow as tfimport matplotlib.pyplot as plt##⼀个利⽤tensorflow的⾃动微分功能实现⽜顿法解⽅程的⼩程序class NewtonRaphson:def__init__(self, y, x, session):self.y = yself.x = xself.grad = tf.gradients(y, x)self.sess = sessionsess.run(tf.global_variables_initializer())def _fx(self, x_value):# 尽量避免出现f(x)不能计算的情况,⽐如函数试图计算a/0,log(0)等,如果计算结果为inf则x+0.0001再进⾏计算 temp = self.sess.run(y, feed_dict={x: [x_value]})[0]if np.isinf(temp):return self.sess.run(y, feed_dict={x: [x_value + 0.0001]})[0]else:return tempdef _dfx(self, x_value):return self.sess.run(self.grad, feed_dict={x: [x_value]})[0][0]def solve(self, xmin, xmax, maxiter, tol):fmin = self._fx(xmin)fmax = self._fx(xmax)if fmin == 0:return xminif fmax == 0:return xmaxif fmin * fmax > 0.0:raise ValueError('Root is not brackted!!')if fmin < 0:xl = xminxh = xmaxelse:xl = xmaxxh = xminx = (xmin + xmax) / 2fx, dfx = self._fx(x), self._dfx(x)dxold = math.fabs(xmax - xmin)dx = dxoldfor ii in range(maxiter):if ((x - xh) * dfx - fx) * ((x - xl) * dfx - fx) > 0.0 or (math.fabs(2 * fx) > math.fabs(dxold * dfx)):dxold = dxdx = 0.5 * (xh - xl)x = xl + dxelse:dxold = dxdx = fx / dfxtemp = xx -= dx# newtonif temp == x:print("total iterate time:%s " % ii)return xfx, dfx = self._fx(x), self._dfx(x)if fx < 0.0:xl = xelse:xh = xprint('Maximum number of iterations exceeded')return 1PV = 1e4FV = 3e6N = 20cpi = 0.018RATE = 0.15r = RATE / 12PMT = 10000x = tf.placeholder(shape=[1], dtype=tf.float32)y=r * (FV * (1 + cpi)**(N) - PV * (r + 1)**x) / ((r + 1)**x - 1 - r) - PMT sess = tf.InteractiveSession()solver=NewtonRaphson(y,x,sess)nmin = 2nmax = 300solver.solve(nmin,nmax,100,1e-9)Processing math: 0%。
计算机算力优化牛顿切线法

计算机算力优化牛顿切线法全文共四篇示例,供读者参考第一篇示例:在计算机科学领域中,算力优化是一个极为重要的问题,尤其是对于需要大量运算的算法和模型来说,优化算力可以大大提高计算速度和效率。
牛顿切线法是一种常用的优化方法,通过不断迭代求解函数的零点或极值,以达到最优化的目的。
本文将介绍计算机算力优化牛顿切线法的原理、优势和应用。
一、牛顿切线法原理牛顿切线法,又称牛顿迭代法,是一种用于求解非线性方程的数值算法。
其基本原理是通过不断迭代逼近函数的零点或极值,从而找到最优解。
具体步骤如下:1.选择一个初始点x0,计算函数在该点的导数f'(x0)和函数值f(x0);2.根据函数的导数和函数值,计算出函数的切线方程,即y=f'(x0)*x + (f(x0)-f'(x0)*x0);4.将x1作为新的初始点,重复2、3步,直到满足停止条件,如达到一定的精度要求或达到最大迭代次数。
通过不断迭代求解切线与x轴的交点,可以逼近函数的零点或极值,从而得到最优解。
二、算力优化的意义算力优化在实际应用中有着广泛的意义,特别是在人工智能、机器学习等领域,需要大量的计算资源来训练和优化模型。
通过使用牛顿切线法等优化方法,可以提高计算效率,加快模型训练速度,从而提高算法的性能和精度。
1.快速收敛:牛顿切线法通过不断迭代逼近最优解,收敛速度较快,可以在较少的迭代次数内得到较为精确的解;2.高效节约算力资源:相比于传统的暴力方法,牛顿切线法可以节约大量的算力资源,提高计算效率和速度;3.适用于复杂函数:牛顿切线法适用于各种类型的非线性函数,可以求解包括零点和极值在内的各种目标;4.灵活性强:牛顿切线法可以根据具体问题自定义函数和停止条件,具有较高的灵活性和适用性。
牛顿切线法在计算机算力优化中有着广泛的应用,尤其在求解非线性方程和优化问题时常被使用。
以下是一些典型的应用场景:1.数值求解问题:牛顿切线法可以用于求解非线性方程的零点,如求解方程f(x)=0的根;2.优化问题:牛顿切线法可以用于求解函数的极值,如求解函数的最小值或最大值;3.机器学习:在机器学习领域,牛顿切线法常用于优化模型的参数,如在逻辑回归、神经网络等算法中的参数优化过程中;4.最优化问题:在最优化领域,牛顿切线法可以用于求解最优化问题,如线性规划、非线性规划等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Step 1. 给定初始点x0 ,正定矩阵H0 ,精度 0,k : 0
Step 2. 计算搜索方向d k H kf ( x k );
step 3. 令 x k1 x k tk d k , 其中 tk : f ( x k tk d k ) min f ( x k t d k )。
(sk Hk yk
Hk )T yk
yk
)T
SR1校正:H k1
Hk
(sk
H k yk )(sk H k (sk H k yk )T yk
yk )T
SR1校正具有二次终止性, 即对于二次函数,它不 需要线搜索,
而具有n步终止性质 H n G 1 .
定理
设s0 , s1 ,
,
s
n
线性无关,那么对二次
满足上述方程的解很多 ,我们可以如下确定一 组解:
k uk ukT yk sk kvkvkT yk Hk yk
这样,我们可以取:
uk sk ,
k ukT y k 1,
vk H k y k , k vkT y k 1。
即:
uk sk , vk Hk yk ,
k
1 skT y k
x k1 x k t k H k f ( x k )
xk1 xk tk Hkf ( xk )
H k I时 梯度法 最速下降方向 d k f ( x k ) , 度量为 x xT I x
H k Gk1时 Newton法 Newton方向 d k Gk1f (xk ), 度量为 x xT Gk x
当Gk 0 时,有 f ( xk )T d k f ( xk )T Gk1gk gkT Gk1gk 0 ,
当Gk 0 时,d k是下降方向。
如果对Newton法稍作修正: xk1 xk tkd k tk : f ( x k tk d k ) min f ( x k t d k )
拟Newton条件
Hk
G
1 k
分析:Gk1 需满足的条件,并利用 此条件确定H k 。
记g( x) f ( x), gk f ( x k ) Gk f 2 ( x k ), 则因为
f ( x) f ( x k1 ) f ( x k1 )T ( x x k1 )
1 ( x x k1 )T 2 f ( x K 1 )( x x k1 ) 2
ykT H k ykT skT yk
)
sk skT skT yk
sk
y
T k
H
k
H k yk skT
skT yk
定理:
H0
0
sT k
yk
0, 则BFGS校正可以保证H k
0。
BFGS校正特点
迄今为止最好的拟牛顿 公式,具有DFP校正的各种性质。 此外,当采用不精确搜 索(Wolfe Powell)时,具有总体收 敛性。这个性质对于 DFP还未能证明。 在数值计算中,BFGS也优于DFP,尤其是常能与低精度 线 搜索方法结合使用。
例. 请用BFGS算法求解 min
f (x)
x12
4
x
2 2
,
初始点
x0
11,
选用精确线搜索 .
uv T
)1
A1
A1uv T A1 1 vT A1u
H k1
Hk
(1
ykT H k ykT skT yk
)
sk skT skT yk
sk
y
T k
H
k
Hk
yk skT
skT yk
五、BFGS校正(Broyden Fletcher Goldfard Shanno,1970)
H k1
Hk
(1
5. 存在缺点及修正
(1) f ( x k1 ) f ( x k ) ?
(2) 初始点的选取困难,甚至无法实施。
(3) Gk1的存在性和计算量问题 。
问题一: 如何使得 f ( x k1 ) f ( x k ) ?
在Newton法中,有 x k 1 x k Gk1 gk x k d k
一、Newton 法
1. 问题
min f ( x) xR n
f ( x)是Rn上二次连续可微函数 即f ( x) C 2(Rn )
2. 算法思想
x0 x1 xk xk1
为了由x k产生x k1,用二次函数Q( x)近似f ( x)。
f ( x) Q( x) f ( xk ) f ( xk )T ( x xk )
按照校正公式H k1 H k H k , 计算H k1使得H k1满足 拟Newton条件 或拟Newton方程:H k1 yk sk 。 令 k : k 1,转step 2.
H k 的确定。
三、对称秩一校正( SR1)
如何确定H
?
k
秩1校正法
H k 1
Hk
H k
Hk
uk
v
T k
待定:uk,vk Rn
,
k
1 ykT H k
。 yk
根据上述推导,我们能 够得到H k的DFP的校正公式:
H k 1
Hk
skT sk skT yk
Hk yk ykT Hk ykT Hk yk
DFP校正公式
定理:
H0
0
sT k
yk
0, 则DFP校正可以保证H k
0。
3、DFP算法的步骤;
将变尺度法的第 5步改为:
step 5.
y0
f
( x1 )
f
(x0)
g1
g0
0.52308 。 8.36923
按照DFP的校正公式:
H1
H0
s0T s0 s0T y0
H 0 y0y0T H 0 y0T H 0 y0
1.00380 0.03149
0.03149。 0.12697
搜索方向
d1
H1f
(
x1 )
1.49416 0.09340
由拟牛顿条件
Hk1 yk
(Hk
uk
v
T k
)
yk
sk
uk
v
T k
yk
sk
Hk yk
uk必在sk H k yk上。
假定sk
Hk
yk
( 0 否则,
H
已满足拟牛顿条件)
k
则有
v
T k
要求 H k
yk 0 Hk1 H 对称 H k1 H k
k (
(sk
Hk
yk
)v
T k
sk HvkTk yykk )(sk
1
函数,
SR1校正
方法至多n步终止,即 H n G 1 .
SR1校正特点
1.不需要做线搜索,而具 有二次终止性。
2.具有遗传性质 H i y j s j , j i. 3.不保证 H k 0, 只有(sk H k yk )T yk 0时,才正定。
H k 的确定。
四、DFP算法
1. DFP算法的提出: (1) 1959年Davidon首次提出 (2) 1963年Fletcher和Powell做了改进 (3) 多变量无约束优化问题 的一个重要工作
因为 x0 tf ( x0 ) 1 2t , 1 8t
f ( x0 t0f ( x0 )) min f ( x0 tf ( x0 )) (1 2t )2 4(1 8t )2
解得 t0 0.13 ,
所以 x1 0.73846 。 0.04616
s0
x1
x0
0.26154 , 1.04616
1 ( x xk )T 2 f ( xk )( x xk )
2
f (xk)
gkT
(x
xk )
1(x 2
xk )T Gk ( x
xk )
其中 gk f ( x k )T ,Gk 2 f ( x k )。
令 Q(x) gk Gk (x xk ) 0
若Hesse矩阵Gk正定,即Gk 0,
则有:f ( x k1 ) f ( x k ) 。
问题二: 如何克服缺点(2)和(3)?
二、拟Newton算法 ( 变尺度法 )
1. 先考虑Newton迭代公式: x k1 x k Gk1f ( x k )
在Newton迭代公式中,如果我们 用 正定矩阵H k 替代Gk1,则有:
x k1 x k H k f ( x k ) 2. 考虑更一般的形式:
按照DFP的校正公式:
H k1
Hk
s
T k
sk
s
T k
yk
H
k
y
k
y
T k
H
k
y
T k
H
k
y
k
计算 H k,k : k 1, 转 step 2.
例. 请用DFP算法求解 min
f (x)
x12
4 x22 , 初始点
x0
1. 1
解:取H0 I ,
f
(
x
)
2 8
x1 x2
。
第一步DFP算法与梯度法相同:
2. 如何确定Hk? 秩2校正法
Hk1 Hk Hk Hk k uk ukT kvkvkT
待定:k,k R, uk,vk Rn
根据 拟Newton条件:Hk 1 yk sk,我们有
( Hk k uk ukT kvkvkT ) yk sk
即:k uk ukT yk kvkvkT yk sk Hk yk
称Newton法为变尺度算法。
3. 如何对H k附加某些条件使得: (1)迭代公式具有下降性 质 H k 0
