2019-2020学年人教版八年级上册期末模拟(一)(原卷版)

合集下载

人教版初中数学八年级上册期末测试题(2019-2020学年山东省临沂市河东区

2019-2020学年山东省临沂市河东区八年级（上）期末数学试卷一．选择题（共14小题）1．（3分）下列轴对称图形中，对称轴的数量小于3的是（）A．B．C．D．2．（3分）若分式有意义，则x的取值范围是（）A．x＞1B．x＜1C．x≠1D．x≠03．（3分）下列计算，正确的是（）A．a2•a2＝2a2B．a2+a2＝a4C．（﹣a2）2＝a4D．（a+1）2＝a2+14．（3分）如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于（）A．40°B．45°C．50°D．55°5．（3分）如图，AB平分∠DAC，要用SAS条件确定△ABC≌△ABD，还需要有条件（）A．DB＝CB B．AB＝AB C．AD＝AC D．∠D＝∠C 6．（3分）如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为（）A．30°B．45°C．50°D．75°7．（3分）多项式12ab3c+8a3b的各项公因式是（）A．4ab2B．4abc C．2ab2D．4ab8．（3分）化简的结果是（）A．x﹣2B．C．D．x+29．（3分）若4x2+axy+25y2是一个完全平方式，则a＝（）A．20B．﹣20C．±20D．±1010．（3分）小红同学误将点A的横纵坐标次序颠倒，写成A（a，b），另一学生误将点B的坐标写成关于y轴对称点的坐标，写成B（﹣b，﹣a）；则A，B两点原来的位置关系是（）A．关于x轴对称B．关于y轴对称C．A和B重合D．以上都不对11．（3分）如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是（）A．ab B．（a+b）2C．（a﹣b）2D．a2﹣b212．（3分）某商厦进货员预测一种应季衬衫能够畅销市场，就用10000元购进这种衬衫，面市后果然供不应求，商厦又用22000元购进了第二批这种衬衫，所购数量是第一批购进量的2倍．但单价贵了4元，求这两批衬衫的购进单价，若设第一批衬衫购进单价为x元，则所列方程正确的是（）A．B．C．D．13．（3分）如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）A．∠DAB′＝∠CAB′B．∠ACD＝∠B′CDC．AD＝AE D．AE＝CE14．（3分）如图，已知点A（2，3）和点B（4，1），在x轴或y轴上有一点P，且点P到点A和点B的距离相等，则点P的坐标为（）A．（1，0）或（0，﹣1）B．（﹣1，0）或（0，1）C．（0，3）或（4，0）D．（2，0）或（0，1）二．填空题（共5小题）15．（3分）计算：（）﹣1+（1﹣）0＝．16．（3分）分式的计算结果是．17．（3分）小刚在解分式方程﹣2＝时，处被污染看不清，小明告诉他这里是一个与x无关的常数，且这道题的正确答案是：此方程无解，请你帮小刚猜测一下处的数应是．18．（3分）如图，△ABC中，∠ACB＝90°，∠B＝30°，AC＝4cm，P为BC边的垂直平分线DE上一个动点，则△ACP的周长最小值为cm．19．（3分）如图，点B是线段AC的中点，过点C的射线CE与AC成60°的角，点P为射线CE上一动点，给出以下四个结论：①当AP⊥CE，垂足为P时，∠APB＝30°；②当CP＝AC时，∠APB＝30°；③在射线CE上，使△APC为直角三角形的点P只有1个；④在射线CE上，使△APC为等腰三角形的点P只有1个；其中正确结论的序号是．三．计算题（共3小题）20．计算：（1）a（a+b）﹣b（a﹣b）；（2）（x﹣2y）2﹣（x﹣y）（x+y）﹣2y221．分解因式：（1）9ax2﹣ay2；（2）2x3y+4x2y2+2xy3．22．先化简，再求值：﹣，其中x＝﹣2．三．解答题（共4小题）23．如图．（1）在网格中画出△ABC关于y轴对称的△A1B1C1；（2）写出△ABC关于x轴对称的△A2B2C2的各顶点坐标；（3）在y轴上确定一点P，使P A+PB最短．（只需作图保留作图痕迹）24．在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP ＝CQ．（1）求证：△ABP≌△CAQ；（2）请判断△APQ是什么形状的三角形？试说明你的结论．25．列方程（组）解应用题：为顺利通过国家义务教育均衡发展验收，我市某中学配备了两个多媒体教室，购买了笔记本电脑和台式电脑共120台，购买笔记本电脑用了7.2万元，购买台式电脑用了24万元，已知笔记本电脑单价是台式电脑单价的1.5倍，那么笔记本电脑和台式电脑的单价各是多少？26．如图1，在△ABC中，AE⊥BC于E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系和数量关系，并说明理由；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．①试猜想BD与AC的数量关系，请直接写出结论；②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．2019-2020学年山东省临沂市河东区八年级（上）期末数学试卷参考答案与试题解析一．选择题（共14小题）1．（3分）下列轴对称图形中，对称轴的数量小于3的是（）A．B．C．D．【分析】根据轴对称图形的概念分别确定出各选项图形的对称轴的条数，然后选择即可．【解答】解：A、有4条对称轴，故本选项不符合题意；B、有6条对称轴，故本选项不符合题意；C、有4条对称轴，故本选项不符合题意；D、有2条对称轴，故本选项符合题意．故选：D．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．（3分）若分式有意义，则x的取值范围是（）A．x＞1B．x＜1C．x≠1D．x≠0【分析】分母为零，分式无意义；分母不为零，分式有意义．【解答】解：根据题意得：x﹣1≠0，解得：x≠1．故选：C．【点评】本题考查的知识点为：分式有意义，分母不为0．3．（3分）下列计算，正确的是（）A．a2•a2＝2a2B．a2+a2＝a4C．（﹣a2）2＝a4D．（a+1）2＝a2+1【分析】根据同底数幂相乘判断A，根据合并同类项法则判断B，根据积的乘方与幂的乘方判断C，根据完全平方公式判断D．【解答】解：A、a2•a2＝a4，故此选项错误；B、a2+a2＝2a2，故此选项错误；C、（﹣a2）2＝a4，故此选项正确；D、（a+1）2＝a2+2a+1，故此选项错误；故选：C．【点评】本题主要考查了幂的运算、合并同类项法则及完全平方公式，熟练掌握其法则是解题的关键．4．（3分）如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于（）A．40°B．45°C．50°D．55°【分析】根据三角形外角性质求出∠ACD，根据角平分线定义求出即可．【解答】解：∵∠A＝60°，∠B＝40°，∴∠ACD＝∠A+∠B＝100°，∵CE平分∠ACD，∴∠ECD＝∠ACD＝50°，故选：C．【点评】本题考查了角平分线定义和三角形外角性质，能熟记三角形外角性质的内容是解此题的关键．5．（3分）如图，AB平分∠DAC，要用SAS条件确定△ABC≌△ABD，还需要有条件（）A．DB＝CB B．AB＝AB C．AD＝AC D．∠D＝∠C【分析】根据角平分线得出∠CAB＝∠DAB，隐含条件AB＝AB，根据全等三角形的判定定理判断即可．【解答】解：∵AB平分∠DAC，∴∠CAB＝∠DAB，A、根据DB＝CB，BA＝BA，∠CAB＝∠DAB不能推出两三角形全等，故本选项错误；B、根据BA＝BA，∠CAB＝∠DAB不能推出两三角形全等，故本选项错误；C、∵在△CAB和△DAB中，∴△CAB≌△DAB（SAS），故本选项正确；D、根据BA＝BA，∠CAB＝∠DAB，∠D＝∠C，根据AAS可证△CAB≌△DAB，根据本选项错误；故选：C．【点评】本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．6．（3分）如图，在△ABC中，AB＝AC，∠A＝30°，AB的垂直平分线l交AC于点D，则∠CBD的度数为（）A．30°B．45°C．50°D．75°【分析】根据三角形的内角和定理，求出∠C，再根据线段垂直平分线的性质，推得∠A ＝∠ABD＝30°，由外角的性质求出∠BDC的度数，从而得出∠CBD＝45°．【解答】解：∵AB＝AC，∠A＝30°，∴∠ABC＝∠ACB＝75°，∵AB的垂直平分线交AC于D，∴AD＝BD，∴∠A＝∠ABD＝30°，∴∠BDC＝60°，∴∠CBD＝180°﹣75°﹣60°＝45°．故选：B．【点评】此题主要考查线段的垂直平分线的性质和等腰三角形的性质；利用三角形外角的性质求得求得∠BDC＝60°是解答本题的关键．本题的解法很多，用底角75°﹣30°更简单些．7．（3分）多项式12ab3c+8a3b的各项公因式是（）A．4ab2B．4abc C．2ab2D．4ab【分析】根据公因式定义，对各选项整理然后即可选出有公因式的项．【解答】解：12ab3c+8a3b＝4ab（3b2c+2a2），4ab是公因式，故选：D．【点评】此题考查的是公因式的定义，找公因式的要点是：（1）公因式的系数是多项式各项系数的最大公约数；（2）字母取各项都含有的相同字母；（3）相同字母的指数取次数最低的．在提公因式时千万别忘了“﹣1”．8．（3分）化简的结果是（）A．x﹣2B．C．D．x+2【分析】原式变形后，利用同分母分式的减法法则计算即可得到结果．【解答】解：原式＝﹣＝＝＝x+2．故选：D．【点评】此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．9．（3分）若4x2+axy+25y2是一个完全平方式，则a＝（）A．20B．﹣20C．±20D．±10【分析】根据这里首末两项是2x和5y这两个数的平方，那么中间一项为加上或减去2x 和5y乘积的2倍，即可得出a的值．【解答】解：∵4x2+axy+25y2是一个完全平方式，∴（2x±5y）2＝4x2±20xy+25y2，∴a＝±20，故选：C．【点评】此题主要考查了完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．10．（3分）小红同学误将点A的横纵坐标次序颠倒，写成A（a，b），另一学生误将点B的坐标写成关于y轴对称点的坐标，写成B（﹣b，﹣a）；则A，B两点原来的位置关系是（）A．关于x轴对称B．关于y轴对称C．A和B重合D．以上都不对【分析】根据题意表示出A、B的正确坐标，再根据坐标的关系确定A，B两点原来的位置关系．【解答】解：∵小红同学误将点A的横纵坐标次序颠倒，写成A（a，b），∴A点的正确坐标为（b，a），∵另一学生误将点B的坐标写成关于y轴对称点的坐标，写成B（﹣b，﹣a），∴B点的正确坐标为（b，﹣a），∴A，B两点原来的位置关系是关于x轴对称，故选：A．【点评】此题主要考查了关于x轴、y轴对称的点的坐标，关键是掌握：关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数．关于y轴对称点的坐标特点：横坐标互为相反数，纵坐标不变．11．（3分）如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，则中间空白部分的面积是（）A．ab B．（a+b）2C．（a﹣b）2D．a2﹣b2【分析】先求出正方形的边长，继而得出面积，然后根据空白部分的面积＝正方形的面积﹣矩形的面积即可得出答案．【解答】解：由题意可得，正方形的边长为（a+b），故正方形的面积为（a+b）2，又∵原矩形的面积为4ab，∴中间空的部分的面积＝（a+b）2﹣4ab＝（a﹣b）2．故选：C．【点评】此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的关键，难度一般．12．（3分）某商厦进货员预测一种应季衬衫能够畅销市场，就用10000元购进这种衬衫，面市后果然供不应求，商厦又用22000元购进了第二批这种衬衫，所购数量是第一批购进量的2倍．但单价贵了4元，求这两批衬衫的购进单价，若设第一批衬衫购进单价为x 元，则所列方程正确的是（）A．B．C．D．【分析】设第一批衬衫购进单价为x元，则购进第二批这种衬衫是（x+4）元，根据第二批所购数量是第一批购进数量的2倍，列出方程即可．【解答】解：设第一批衬衫购进单价为x元，则购进第二批这种衬衫是（x+4）元，依题意有：2×＝．故选：A．【点评】本题考查了分式方程的应用，弄清题意并找出题中的数量关系并列出方程是解题的关键．13．（3分）如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（）A．∠DAB′＝∠CAB′B．∠ACD＝∠B′CDC．AD＝AE D．AE＝CE【分析】根据翻折变换的性质可得∠BAC＝∠CAB′，根据两直线平行，内错角相等可得∠BAC＝∠ACD，从而得到∠ACD＝∠CAB′，然后根据等角对等边可得AE＝CE，从而得解．【解答】解：∵矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，∴∠BAC＝∠CAB′，∵AB∥CD，∴∠BAC＝∠ACD，∴∠ACD＝∠CAB′，∴AE＝CE，所以，结论正确的是D选项．故选：D．【点评】本题考查了翻折变换的性质，平行线的性质，矩形的对边互相平行，等角对等边的性质，熟记各性质并准确识图是解题的关键．14．（3分）如图，已知点A（2，3）和点B（4，1），在x轴或y轴上有一点P，且点P到点A和点B的距离相等，则点P的坐标为（）A．（1，0）或（0，﹣1）B．（﹣1，0）或（0，1）C．（0，3）或（4，0）D．（2，0）或（0，1）【分析】利用两点间的距离公式可得结果．【解答】解：设在x轴有一点P（x，0），则有（x﹣2）2+32＝（x﹣4）2+1，解得，x＝1，∴P（1，0）；设在y轴有一点P（0，y），则有22+（y﹣3）2＝42+（y﹣1）2解得，y＝﹣1，∴P（0，﹣1）故选：A．【点评】本题主要考查了两点间的距离公式，熟记公式和坐标轴上点的特点是解答此题的关键．二．填空题（共5小题）15．（3分）计算：（）﹣1+（1﹣）0＝3．【分析】本题涉及负整数指数幂、零指数幂的考点，在计算时，针对每个考点分别计算．【解答】解：原式＝2+1＝3．故答案为：3．【点评】本题考查了整数指数幂、零指数幂的考点，负整数指数幂：a﹣p＝（a≠0，p 为正整数）；零指数幂：a0＝1（a≠0）．16．（3分）分式的计算结果是．【分析】先通分，再把分子相加减即可．【解答】解：原式＝+＝＝．故答案为：．【点评】本题考查的是分式的加减法，在解答此类问题时要注意通分及约分的灵活应用．17．（3分）小刚在解分式方程﹣2＝时，处被污染看不清，小明告诉他这里是一个与x无关的常数，且这道题的正确答案是：此方程无解，请你帮小刚猜测一下处的数应是1．【分析】先设＝y，得出﹣2＝，再去分母x﹣2﹣2（x﹣3）＝y，最后根据此方程无解时x＝3，再代入计算即可．【解答】解：设＝y，则原方程可变形为：﹣2＝，去分母得：x﹣2﹣2（x﹣3）＝y，∵此方程无解，∴x＝3，∴3﹣2﹣2×（3﹣3）＝y，∴y＝1；∴处的数应是1．故答案为：1．【点评】此题考查了分式方程的解，关键是求出分式方程无解时x的值，用到的知识点是解分式方程的步骤，是一道基础题．18．（3分）如图，△ABC中，∠ACB＝90°，∠B＝30°，AC＝4cm，P为BC边的垂直平分线DE上一个动点，则△ACP的周长最小值为12cm．【分析】因为BC的垂直平分线为DE，所以点C和点B关于直线DE对称，所以当点动点P和E重合时则△ACP的周长最小值，再结合题目的已知条件求出AB的长即可．【解答】解：∵P为BC边的垂直平分线DE上一个动点，∴点C和点B关于直线DE对称，∴当点动点P和E重合时则△ACP的周长最小值，∵∠ACB＝90°，∠B＝30°，AC＝4cm，∴AB＝2AC＝8cm，∵AP+CP＝AP+BP＝AB＝8cm，∴△ACP的周长最小值＝AC+AB＝12cm，故答案为：12．【点评】本题考查了轴对称﹣最短路线的问题以及垂直平分线的性质，正确确定P点的位置是解题的关键，确定点P的位置这类题在课本中有原题，因此加强课本题目的训练至关重要．19．（3分）如图，点B是线段AC的中点，过点C的射线CE与AC成60°的角，点P为射线CE上一动点，给出以下四个结论：①当AP⊥CE，垂足为P时，∠APB＝30°；②当CP＝AC时，∠APB＝30°；③在射线CE上，使△APC为直角三角形的点P只有1个；④在射线CE上，使△APC为等腰三角形的点P只有1个；其中正确结论的序号是①②④．【分析】根据等腰三角形的性质，等边三角形的性质，直角三角形的性质判断．【解答】解：∵当AP⊥CE，∠C＝60°，∴∠P AC＝30°，∵B是线段AC的中点，∴AB＝PB，∴∠APB＝∠P AC＝30°，故①正确；当CP＝AC时，∠C＝60°，∴三角形APC为等边三角形，∵B是线段AC的中点，∴∠APB＝∠CPB＝30°，故②正确；在射线CE上，使△APC为直角三角形的点P有2个，一个是∠APC＝90°，另一个是∠P AC＝90°时；故③错误；在射线CE上，使△APC为等腰三角形的点P有1个，使AC＝PC＝AP，故④正确；故答案为①②④．【点评】本题考查了等腰三角形的性质，等边三角形的性质，直角三角形的性质，解题的关键是熟练掌握它们的性质．三．计算题（共3小题）20．计算：（1）a（a+b）﹣b（a﹣b）；（2）（x﹣2y）2﹣（x﹣y）（x+y）﹣2y2【分析】（1）首先计算乘法，然后再合并同类项即可；（2）先算完全平方和乘法，再去括号合并同类项即可．【解答】解：（1）原式＝a2+ab﹣ab+b2＝a2+b2；（2）原式＝x2﹣4xy+4y2﹣（x2﹣y2）﹣2y2，＝x2﹣4xy+4y2﹣x2+y2﹣2y2，＝﹣4xy+3y2．【点评】此题主要考查了整式的混合运算，关键是掌握计算法则和计算顺序．21．分解因式：（1）9ax2﹣ay2；（2）2x3y+4x2y2+2xy3．【分析】根据因式分解点的方法即可求出答案．【解答】解：（1）原式＝a（9x2﹣y2）＝a（3x+y）（3x﹣y）（2）原式＝2xy（x2+2xy+y2）＝2xy（x+y）2【点评】本题考查因式分解，解题的关键是熟练运用因式分解的方法，本题属于基础题型．22．先化简，再求值：﹣，其中x＝﹣2．【分析】根据分式的减法可以化简题目中的式子，然后将x的值代入即可解答本题．【解答】解：﹣＝＝＝，当x＝﹣2时，原式＝．【点评】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．三．解答题（共4小题）23．如图．（1）在网格中画出△ABC关于y轴对称的△A1B1C1；（2）写出△ABC关于x轴对称的△A2B2C2的各顶点坐标；（3）在y轴上确定一点P，使P A+PB最短．（只需作图保留作图痕迹）【分析】（1）分别作出点A、B、C关于y轴对称的点，然后顺次连接即可；（2）根据对称的性质写出△ABC关于x轴对称的△A2B2C2的各顶点坐标；（2）作出点C关于y轴的对称点，然后连接AC1，与y轴的交点即为点P．【解答】解：（1）如图所示：（2）A2（﹣3，﹣2），B2（﹣4，3），C2（﹣1，1）；（3）连结AB1或BA1交y轴于点P，则点P即为所求．【点评】本题考查的是作图﹣轴对称变换，熟知轴对称图形的作法及性质是解答此题的关键．24．在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP ＝CQ．（1）求证：△ABP≌△CAQ；（2）请判断△APQ是什么形状的三角形？试说明你的结论．【分析】（1）根据等边三角形的性质可得AB＝AC，再根据SAS证明△ABP≌△ACQ；（2）根据全等三角形的性质得到AP＝AQ，再证∠P AQ＝60°，从而得出△APQ是等边三角形．【解答】证明：（1）∵△ABC为等边三角形，∴AB＝AC，∠BAC＝60°，在△ABP和△ACQ中，，∴△ABP≌△ACQ（SAS），（2）∵△ABP≌△ACQ，∴∠BAP＝∠CAQ，AP＝AQ，∵∠BAP+∠CAP＝60°，∴∠P AQ＝∠CAQ+∠CAP＝60°，∴△APQ是等边三角形．【点评】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，考查了正三角形的判定，本题中求证△ABP≌△ACQ是解题的关键．25．列方程（组）解应用题：为顺利通过国家义务教育均衡发展验收，我市某中学配备了两个多媒体教室，购买了笔记本电脑和台式电脑共120台，购买笔记本电脑用了7.2万元，购买台式电脑用了24万元，已知笔记本电脑单价是台式电脑单价的1.5倍，那么笔记本电脑和台式电脑的单价各是多少？【分析】设台式电脑的单价是x元，则笔记本电脑的单价为1.5x元，利用购买笔记本电脑和购买台式电脑的台数和列方程+＝120，然后解分式方程即可．【解答】解：设台式电脑的单价是x元，则笔记本电脑的单价为1.5x元，根据题意得+＝120，解得x＝2400，经检验x＝2400是原方程的解，当x＝2400时，1.5x＝3600．答：笔记本电脑和台式电脑的单价分别为3600元和2400元．【点评】本题考查了分式方程的应用：列分式方程解应用题的一般步骤：设、列、解、验、答．26．如图1，在△ABC中，AE⊥BC于E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系和数量关系，并说明理由；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．①试猜想BD与AC的数量关系，请直接写出结论；②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．【分析】（1）延长BD交AC于F，求出∠AEB＝∠AEC＝90°，证出△BED≌△AEC，推出BD＝AC，∠DBE＝∠CAE，根据∠EBD+∠BDE＝90°推出∠ADF+∠CAE＝90°，求出∠AFD＝90°即可；（2）求出∠BED＝∠AEC，证出△BED≌△AEC，推出BD＝AC，∠BDE＝∠ACE，根据∠ACE+∠EOC＝90°求出∠BDE+∠DOF＝90°，求出∠DFO＝90°即可；（3））①如图3中，结论：BD＝AC，只要证明△BED≌△AEC即可；②求出∠BED＝∠AEC，证出△BED≌△AEC，推出∠BDE＝∠ACE，根据三角形内角和定理求出∠DFC即可．【解答】解：（1）BD＝AC，BD⊥AC，理由是：延长BD交AC于F．∵AE⊥BC，∴∠AEB＝∠AEC＝90°，在△BED和△AEC中，，∴△BED≌△AEC，∴BD＝AC，∠DBE＝∠CAE，∵∠BED＝90°，∴∠EBD+∠BDE＝90°，∵∠BDE＝∠ADF，∴∠ADF+∠CAE＝90°，∴∠AFD＝180°﹣90°＝90°，∴BD⊥AC；（2）不发生变化．理由：∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC，∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC；（3）①如图3中，结论：BD＝AC，理由是：∵△ABE和△DEC是等边三角形，∴AE＝BE，DE＝EC，∠EDC＝∠DCE＝60°，∠BEA＝∠DEC＝60°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC，∴BD＝AC．②能．∵△ABE和△DEC是等边三角形，∴AE＝BE，DE＝EC，∠EDC＝∠DCE＝60°，∠BEA＝∠DEC＝60°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC，∴∠BDE＝∠ACE，∴∠DFC＝180°﹣（∠BDE+∠EDC+∠DCF）＝180°﹣（∠ACE+∠EDC+∠DCF）＝180°﹣（60°+60°）＝60°，即BD与AC所成的角的度数为60°．【点评】本题考查了等边三角形性质，等腰直角三角形的性质，全等三角形的性质和判定的应用，主要考查了学生的推理能力．。

2019-2020山西省八年级上册期末英语(人教版)【试卷+答案】

一、情景反应（每小题1分，共5分）本题共5个小题，每小题你将听到一组对话。

请你从每小题所给的A 、B 、C 三幅图片中，选出与你所听到的信息相关联的············一项，并在答题卡上将该项涂黑。

1.ABC2.CABC3.4.FridaySaturdaySundayA B CA B C5.二、对话理解（每小题1分，共5分）本题共5个小题，每小题你将听到一组对话和一个问题。

请你从每小题所给的A 、B 、C 三个选项中，选出一个最佳选项，并在答题卡上将该项涂黑。

6.A.Coffee.B.Tea.k.7.A.Some fruits. B.Some cakes. C.Some flowers.8.A.The biggest screens.B.The cheapest tickets.C.The most comfortable seats.9.A.She is a reporter.B.She is a doctor.C.She is a cook.10.A.He will go to the park.B.He will take the piano lesson.C.He will help with housework.三、语篇理解（每小题1分，共5分）本题你将听到一篇短文。

请你根据短文内容和所提出的5个问题，从每小题所给的A 、B 、C 三个选项中，选出一个最佳选项，并在答题卡上将该项涂黑。

11.How old is Mary?A.11.B.13.C.15.12.What does Mary want to be when she grows up?A.An artist.B.An actress.C.A cook.13.What does David like watching?A.Sports shows.B.Talk shows.C.Cartoons.14.What is David ’s mother making?A.A banana milk shake.B.Russian soup.C.Yunnan Rice Noodles.15.What does David ’s grandpa like doing?A.He likes reading newspapers.B.He likes walking in the garden.C.He likes listening to Beijing Opera.山西省2019-2020学年第一学期八年级期末质量评估试题英语（人教版）注意事项：1.本试卷分听力和笔试两部分。

2019-2020学年新人教版八年级(上)期末数学试卷 (解析版)

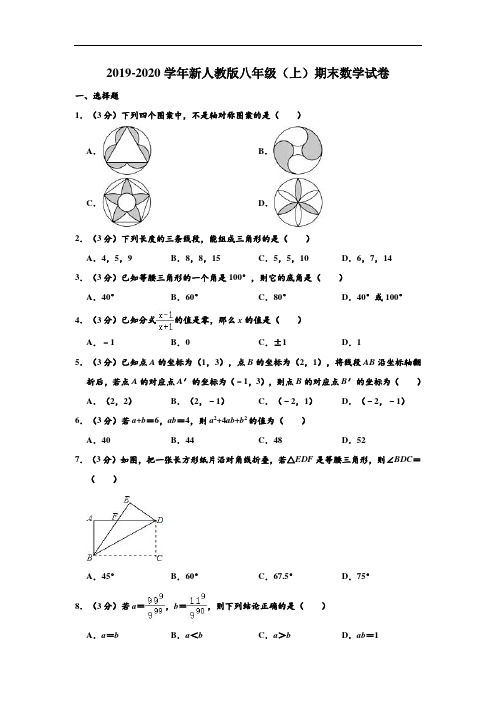
2019-2020学年新人教版八年级（上）期末数学试卷一、选择题1．（3分）下列四个图案中，不是轴对称图案的是（）A．B．C．D．2．（3分）下列长度的三条线段，能组成三角形的是（）A．4，5，9B．8，8，15C．5，5，10D．6，7，143．（3分）已知等腰三角形的一个角是100°，则它的底角是（）A．40°B．60°C．80°D．40°或100°4．（3分）已知分式的值是零，那么x的值是（）A．﹣1B．0C．±1D．15．（3分）已知点A的坐标为（1，3），点B的坐标为（2，1），将线段AB沿坐标轴翻折后，若点A的对应点A′的坐标为（﹣1，3），则点B的对应点B′的坐标为（）A．（2，2）B．（2，﹣1）C．（﹣2，1）D．（﹣2，﹣1）6．（3分）若a+b＝6，ab＝4，则a2+4ab+b2的值为（）A．40B．44C．48D．527．（3分）如图，把一张长方形纸片沿对角线折叠，若△EDF是等腰三角形，则∠BDC＝（）A．45°B．60°C．67.5°D．75°8．（3分）若a＝，b＝，则下列结论正确的是（）A．a＝b B．a＜b C．a＞b D．ab＝19．（3分）在4×4的正方形网格中，以格点为顶点的三角形称为格点三角形，在图中画出与△ABC关于某条直线对称的格点三角形，最多能画（）个．A．5B．6C．7D．810．（3分）若x≠﹣1，则把﹣称为x的“和1负倒数”，如：2的“和1负倒数”为﹣，﹣3的“和1负倒数”为，若x1＝，x2是x1的“和1负倒数”，x3是x2的“和1负倒数”，…依此类推，则x2020的值为（）A．B．﹣C．D．﹣二、填空题（本题有6小题，每小题4分，共24分）11．（4分）计算：（﹣2）0＝．12．（4分）若正多边形的一个外角等于45°，则这个多边形是正边形．13．（4分）如图，在△ABC与△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E在同一条直线上，连接BD，BE，则∠ACE+∠DBC＝°．14．（4分）如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC 的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连结CD．若CD＝AC，∠A＝48°，则∠ACB＝．15．（4分）若x+＝4，则的值是．16．（4分）如图，在△ABC中，∠BAC的平分线AD和边BC的垂直平分线ED相交于点D，过点D作DF垂直于AC交AC的延长线于点F，若AB＝8，AC＝5，则CF＝．三、解答题（本题有8小题，共66分）17．（6分）（1）因式分解：a3﹣4a；（2）解方程：＝．18．（6分）先化简，再求值：（）÷，其中x＝．19．（6分）如图，在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC 交AC于点N，且MN平分∠AMC，若AN＝1．（1）求∠B的度数；（2）求CN的长．20．（6分）在天台县“城乡公交一体化改造项目”中，某工程队承接了6千米地下管廊铺设任务，为了赶在年底前完成，实际每天的工作效率比原计划提高20%，结果提前20天完成了任务．问实际每天铺设管廊多少米．21．（8分）如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E，若AD＝a，DE＝b，（1）如图1，求BE的长，写出求解过程；（用含a，b的式子表示）（2）如图2，点D在△ABC内部时，直接写出BE的长．（用含a，b的式子表示）22．（12分）（1）如图1，在△ABC中，已知OB，OC分别平分∠ABC，∠ACB，BP，CP分别平分∠ABC，∠ACB的外角∠DBC，∠ECB．①若∠A＝50°，则∠O＝，∠P＝；②若∠A＝α，则∠O＝，∠P＝．（用含α的式子表示）（2）如图2，在四边形ABCD中，BP，CP分别平分外角∠EBC，∠FCB，请探究∠P 与∠A，∠D的数量关系，并说明理由；（3）如图3，在六边形ABCDEF中，CP，DP分别平分外角∠GCD，∠HDC，请直接写出∠P与∠A，∠B，∠E，∠F的数量关系．23．（10分）对实数a，b定义运算“*”，，例如，4*3＝42﹣32＝7，3*4＝＝﹣7，．（1）化简：（x+1）*x＝；（2）化简：0*（x2+4x+9）；（3）化简：（3x﹣5）*（x+3）．24．（12分）学习与探究：在等边△ABC中，P是射线AB上的一点．（1）探索实践：如图1，P是边AB的中点，D是线段CP上的一个动点，以CD为边向右侧作等边△CDE，DE与BC交于点M，连结BE．①求证：AD＝BE；②连结BD，当DB+DM最小时，试在图2中确定D的位置，并说明理由；（要求用尺规作图，保留作图痕迹）③在②的条件下，求△CME与△ACM的面积之比．（2）思维拓展：如图3，点P在边AB的延长线上，连接CP，点B关于直线CP的对称点为B'，连结AB'，CB'，AB'交BC于点N，交直线CP于点G，连结BG．请判断∠AGC与∠AGB 的大小关系，并证明你的结论．参考答案一、选择题（本题有10小题，每小题3分，共30分）1．（3分）下列四个图案中，不是轴对称图案的是（）A．B．C．D．解：A、是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项正确；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误．故选：B．2．（3分）下列长度的三条线段，能组成三角形的是（）A．4，5，9B．8，8，15C．5，5，10D．6，7，14解：A、4+5＝9，不能组成三角形，故此选项错误；B、8+8＞16，能组成三角形，故此选项正确；C、5+5＝10，不能组成三角形，故此选项错误；D、6+7＜14，不能组成三角形，故此选项错误；故选：B．3．（3分）已知等腰三角形的一个角是100°，则它的底角是（）A．40°B．60°C．80°D．40°或100°解：∵等腰三角形的一个角为100°，∴100°的角是顶角，底角为（180°﹣100°）＝40°；故选：A．4．（3分）已知分式的值是零，那么x的值是（）A．﹣1B．0C．±1D．1解：由题意可知：x﹣1＝0且x+1≠0，∴x＝1，故选：D．5．（3分）已知点A的坐标为（1，3），点B的坐标为（2，1），将线段AB沿坐标轴翻折后，若点A的对应点A′的坐标为（﹣1，3），则点B的对应点B′的坐标为（）A．（2，2）B．（2，﹣1）C．（﹣2，1）D．（﹣2，﹣1）解：∵将线段AB沿坐标轴翻折后，若点A（1，3）的对应点A′的坐标为（﹣1，3），∴线段AB沿y轴翻折，∴点B关于y轴对称点B'坐标为（﹣2，1）故选：C．6．（3分）若a+b＝6，ab＝4，则a2+4ab+b2的值为（）A．40B．44C．48D．52解：∵a+b＝6，ab＝4，∴原式＝（a+b）2+2ab＝36+8＝44，故选：B．7．（3分）如图，把一张长方形纸片沿对角线折叠，若△EDF是等腰三角形，则∠BDC＝（）A．45°B．60°C．67.5°D．75°解：由翻折可知：△BED≌△BCD，∴∠EBD＝∠CBD，∠E＝∠C＝90°∵△EDF是等腰三角形，∴∠EFD＝∠AFB＝∠ABF＝45°，∴∠CBF＝45°，∴∠CBD＝∠CBE＝22.5°，∴∠BDC＝67.5°，故选：C．8．（3分）若a＝，b＝，则下列结论正确的是（）A．a＝b B．a＜b C．a＞b D．ab＝1解：∵a＝＝＝，b＝，∴a＝b．故选：A．9．（3分）在4×4的正方形网格中，以格点为顶点的三角形称为格点三角形，在图中画出与△ABC关于某条直线对称的格点三角形，最多能画（）个．A．5B．6C．7D．8解：如图，最多能画出7个格点三角形与△ABC成轴对称．故选：C．10．（3分）若x≠﹣1，则把﹣称为x的“和1负倒数”，如：2的“和1负倒数”为﹣，﹣3的“和1负倒数”为，若x1＝，x2是x1的“和1负倒数”，x3是x2的“和1负倒数”，…依此类推，则x2020的值为（）A．B．﹣C．D．﹣解：∵x1＝，∴x2＝﹣＝﹣，x3＝﹣＝﹣，x4＝﹣＝，……∴此数列每3个数为一周期循环，∵2020÷3＝673…1，∴x2020＝x1＝，故选：A．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）计算：（﹣2）0＝1．解：（﹣2）0＝1．故答案为：1．12．（4分）若正多边形的一个外角等于45°，则这个多边形是正8边形．解：外角和是360°，且正多边形的每个外角相等，则多边形的边数是：360÷45＝8，故答案为：8．13．（4分）如图，在△ABC与△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E在同一条直线上，连接BD，BE，则∠ACE+∠DBC＝45°．解：∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，且AB＝AC，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ACE＝∠ABD，∴∠ACE+∠DBC＝∠ABD+∠DBC＝∠ABC＝45°，故答案为：4514．（4分）如图，在△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC 的长为半径作弧，两弧相交于两点M，N；②作直线MN交AB于点D，连结CD．若CD＝AC，∠A＝48°，则∠ACB＝108°．解：∵CD＝AC，∠A＝48°，∴∠ADC＝48°，由作图知MN是BC的垂直平分线，∴DB＝DC，∴∠B＝∠BCD＝∠ADC＝24°，则∠ACB＝180°﹣∠A﹣∠B＝108°，故答案为：108°．15．（4分）若x+＝4，则的值是．解：原式＝＝当x+＝4时，原式＝，故答案为：．16．（4分）如图，在△ABC中，∠BAC的平分线AD和边BC的垂直平分线ED相交于点D，过点D作DF垂直于AC交AC的延长线于点F，若AB＝8，AC＝5，则CF＝．解：如图，连接CD，DB，过点D作DM⊥AB于点M，∵AD平分∠FAB，∴∠FAD＝∠DAM，且AD＝AD，∠AFD＝∠AMD，∴△AFD≌△AMD（AAS）∴AF＝AM，FD＝DM，∵DE垂直平分BC∴CD＝BD，且DF＝DM，∴Rt△CDF≌Rt△BDM（HL）∴BM＝CF∵AB＝AM+BM＝AF+MB＝AC+CF+MB＝AC+2CF∴8＝5+2CF∴CF＝故答案为：三、解答题（本题有8小题，共66分）17．（6分）（1）因式分解：a3﹣4a；（2）解方程：＝．解：（1）原式＝a（a2﹣4）＝a（a+2）（a﹣2）；（2）方程两边同时乘以3（x+1）得：3x＝2，解得：x＝，经检验x＝是分式方程的解．18．（6分）先化简，再求值：（）÷，其中x＝．解：（）÷＝＝＝，当x＝时，原式＝＝﹣1．19．（6分）如图，在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC 交AC于点N，且MN平分∠AMC，若AN＝1．（1）求∠B的度数；（2）求CN的长．解：（1）∵CM平分∠ACB，MN平分∠AMC，∴∠ACM＝∠BCM，∠AMN＝∠CMN，又∵MN∥BC，∴∠AMN＝∠B，∠CMN＝∠BCM，∴∠B＝∠BCM＝∠ACM，∵∠A＝90°，∴∠B＝×90°＝30°；（2）由（1）得，∠AMN＝∠B＝30°，∠MCN＝∠CMN，∠A＝90°，∴MN＝2AN＝2，MN＝CN，∴CN＝2．20．（6分）在天台县“城乡公交一体化改造项目”中，某工程队承接了6千米地下管廊铺设任务，为了赶在年底前完成，实际每天的工作效率比原计划提高20%，结果提前20天完成了任务．问实际每天铺设管廊多少米．解：设原计划每天铺设管廊x米，则实际每天铺设管廊（1+20%）x米，根据题意得：﹣＝20，解得：x＝50，经检验，x＝50是所列方程的解，且符合题意，∴（1+20%）x＝60．答：实际每天铺设管廊60米．21．（8分）如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E，若AD＝a，DE＝b，（1）如图1，求BE的长，写出求解过程；（用含a，b的式子表示）（2）如图2，点D在△ABC内部时，直接写出BE的长a﹣b．（用含a，b的式子表示）解：（1）∵∠ACB＝90°，∴∠ACD+∠BCD＝90°∵AD⊥CE，BE⊥CE，∴∠D＝∠BEC＝90°，∴∠CBE+∠BCD＝90°，∴∠ACD＝∠CBE，且AC＝BC，∠ADC＝∠BEC＝90°∴△ACD≌△CBE（AAS），∴CE＝AD＝a，∵DC＝CE+DE∴BE＝CD＝a+b（2）∵∠ACB＝90°，∴∠ACD+∠BCD＝90°∵AD⊥CE，BE⊥CE，∴∠ADC＝∠BEC＝90°，∴∠CBE+∠BCD＝90°，∴∠ACD＝∠CBE，且AC＝BC，∠ADC＝∠BEC＝90°∴△ACD≌△CBE∴CE＝AD＝a，∵CD＝CE﹣DE∴BE＝CD＝a﹣b，故答案为：a﹣b22．（12分）（1）如图1，在△ABC中，已知OB，OC分别平分∠ABC，∠ACB，BP，CP分别平分∠ABC，∠ACB的外角∠DBC，∠ECB．①若∠A＝50°，则∠O＝115°，∠P＝65°；②若∠A＝α，则∠O＝90°+α，∠P＝90°﹣α．（用含α的式子表示）（2）如图2，在四边形ABCD中，BP，CP分别平分外角∠EBC，∠FCB，请探究∠P 与∠A，∠D的数量关系，并说明理由；（3）如图3，在六边形ABCDEF中，CP，DP分别平分外角∠GCD，∠HDC，请直接写出∠P与∠A，∠B，∠E，∠F的数量关系∠P＝360°﹣（∠A+∠B+∠E+∠F）．解：（1）①解：∠O＝180°﹣∠OBC﹣∠OCB＝180°﹣∠ABC﹣∠ACB＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠A）＝180°﹣（180°﹣50°）＝115°；∠P＝180°﹣∠PBC﹣∠PCB＝180°﹣∠DBC﹣∠ECB＝180°﹣（∠DBC+∠ECB）＝180°﹣（180°﹣∠ABC+180°﹣∠ACB）＝180°﹣[360°﹣（∠ABC+∠ACB）]＝180°﹣[360°﹣（180°﹣∠A）]＝180°﹣[360°﹣（180°﹣50°）]＝65°；故答案为：115°；65°．②解：∠O＝180°﹣∠OBC﹣∠OCB＝180°﹣∠ABC﹣∠ACB＝180°﹣（∠ABC+∠ACB）＝180°﹣（180°﹣∠A）＝180°﹣（180°﹣α）＝90°+α；∠P＝180°﹣∠PBC﹣∠PCB＝180°﹣∠DBC﹣∠ECB＝180°﹣（∠DBC+∠ECB）＝180°﹣（180°﹣∠ABC+180°﹣∠ACB）＝180°﹣[360°﹣（∠ABC+∠ACB）]＝180°﹣[360°﹣（180°﹣∠A）]＝180°﹣[360°﹣（180°﹣α）]＝90°﹣α；故答案为：90°+α；90°﹣α，（2）解：∠P＝180°﹣（∠A+∠D）．理由如下：∠P＝180°﹣（∠PBC+∠PCB）＝180°﹣（∠EBC+∠FCB）＝180°﹣[360°﹣（∠ABC+∠DCB）]＝（∠ABC+∠DCB）＝（360°﹣∠A﹣∠D）＝180°﹣（∠A+∠D）．（3）∠P＝180°﹣（∠GCD+∠HDC）＝180°﹣（180°﹣∠BCD+180°﹣∠CDE）＝（∠BCD+∠CDE）＝[（6﹣2）×180°﹣（∠A+∠B+∠E+∠F）]＝360°﹣（∠A+∠B+∠E+∠F）．故答案为：∠P＝360°﹣（∠A+∠B+∠E+∠F）23．（10分）对实数a，b定义运算“*”，，例如，4*3＝42﹣32＝7，3*4＝＝﹣7，．（1）化简：（x+1）*x＝2x+1；（2）化简：0*（x2+4x+9）；（3）化简：（3x﹣5）*（x+3）．解：（1）因为x+1＞x，所以：（x+1）*x＝（x+1）2﹣x2＝2x+1故答案为：2x+1（2）因为x2+4x+9＝（x+2）2+5＞0，所以：0*（x2+4x+9）＝＝﹣1；（3）当（3x﹣5）≥（x+3），即x≥4时．（3x﹣5）*（x+3）＝（3x﹣5）2﹣（x+3）2＝8x2﹣36x+16；当（3x﹣5）＜（x+3），即x＜4时．（3x﹣5）*（x+3）＝＝＝．24．（12分）学习与探究：在等边△ABC中，P是射线AB上的一点．（1）探索实践：如图1，P是边AB的中点，D是线段CP上的一个动点，以CD为边向右侧作等边△CDE，DE与BC交于点M，连结BE．①求证：AD＝BE；②连结BD，当DB+DM最小时，试在图2中确定D的位置，并说明理由；（要求用尺规作图，保留作图痕迹）③在②的条件下，求△CME与△ACM的面积之比．（2）思维拓展：如图3，点P在边AB的延长线上，连接CP，点B关于直线CP的对称点为B'，连结AB'，CB'，AB'交BC于点N，交直线CP于点G，连结BG．请判断∠AGC与∠AGB 的大小关系，并证明你的结论．【解答】证明：（1）探索实践①在等边△ABC与等边△CDE中AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，∴∠ACD+∠DCM＝∠DCM+∠BCE，∴∠ACD＝∠BCE∴△ACD≌△BCE（SAS）∴AD＝BE（2）②如图，作∠BAC的平分线交CP于D，连结BD，∵P是边等边△ABC中AB边的中点∴CP是AB边上的中线，由“等腰三角形的三线合一”性质知，CP是AB的垂直平分线，CP平分∠ACB，∴DB＝DA，∠PCB＝30°要使DB+DM最小，只要DA+DM最小，即当A，D，M共线时，且AM⊥BC时，AM 最小，此时DB+DM最小③∵∠ACD＝∠CAD＝∠DCM＝∠ECM＝30°，CM⊥AM∴DC＝DA＝DE，DM＝EM＝DE，∴AM＝3ME又∵Rt△CME的边ME上的高与Rt△ACM的边AM上的高均是CM∴S△CME：S△ACM＝1：3（2）思维拓展∠AGC＝∠AGB理由如下：∵点B关于直线CP的对称点为B'，∴BC＝CB'，∠CB'G＝∠CBG，∴AC＝BC＝B'C∴∠CAB'＝∠CB'A，∴∠CAB'＝∠CBG，∴点A，点B，点G，点C四点共圆，∴∠AGC＝∠ABC＝60°，∠AGB＝∠ACB＝60°，∴∠AGC＝∠AGB。

(人教版)四川省成都市双流县太平中学2019-2020学年度第一学期八年级物理期末测试卷(含答案)

八年级上物理期末考试模拟卷一、单项选择题1.根据你对生活中物理量的认识，下列数据中最接近生活实际的是（）A. 人体的密度约为l.0×103kg/m3B. 一名中学生的质量约为5kgC. 中学生的课桌高约为1.5mD. 八年级物理上册课本质量量约200kg2.以下研究方法与研究通过乒乓球跳动的高度反映出振幅的大小的方法相同的是：（）A.研究影响声音响度与振幅的关系时采用控制钢尺长度不变来控制音调B.通过蜡烛火焰的情况来判断声音是否可以传递能量C.研究光时将它分成可见光和不可见光D.研究光的直线传播时引入光线3.在医院、学校和科学研究部门附近，有如图所示禁鸣喇叭的标志．在下列方法中，与这种控制噪声的方法相同的是：（）A. 在摩托车上安装消声器B. 在道路旁设置隔声板C. 工人戴上防噪声耳罩D. 上课时关闭教室的门窗4.下列关于声现象的说法中正确的是（）A. 声音只能在空气中传播B. 正在发出声音的物体一定在振动C. 声音在真空中的传播速度为340m/sD. 超声波的频率很低，所以人耳听不到5.下列对生活中一些现象的解释错误的是（）A.用冰袋给高热病人降温，是因为冰熔化吸热B.用手沾些冷水去拿包子不会太烫，是因为水汽化吸热C.用久了的电灯泡玻璃壁会变黑，是因为灯丝发生了汽化和凝固现象D.舞台上用干冰能制造白雾，是因为干冰升华吸热使水蒸气液化6.下列各图描述了常见的物态变化现象，其中放热的是（）A. 甲、乙B. 丙、丁C. 甲、丙D. 乙、丙7.下列关于图片的说法不正确的是（）A.彩虹是白光经过反射和折射形成的B.夜幕下的光谷，美丽的LED 灯是人造光源C.如图说明光在空气中沿直线传播D.国家大剧院和它的倒影现象属于光的折射8.一只空瓶装满水时的总质量是520g，装满酒精时的总质量是450g,则该空瓶的容积是（）(已知ρ水=1 g/cm3，ρ酒精=0.8 g/cm3)A. 400m3B. 350 cm3C. 250cm3D. 200cm3二．填空题9.质量的国际单位制主单位是，密度的计算公式。

部编本人教版2019---2020学年度八年级历史(上)期末考试卷及答案

密学校班级姓名学号密封线内不得答题部编本人教版2019—2020学年上学期八年级历史（上）期末测试卷及答案（总分：100分时间： 90分钟）一、选择题（每题2分，共60分）1．在谈到道光皇帝（1821—1850年在位）为什么把他的墓修筑得比清代其他帝王墓都要矮小时，历史学家龚书铎说：是因为“在他手上打败仗丢了土地，没有面目见先帝”。

这里所说的“土地”是指（） A ．广州 B ．台湾 C ．香港岛 D ．辽东半岛2．对比是学习中经常运用的方法，请你判断《南京条约》和《马关条约》的相似点是（） ①都有割地条款②都有赔款条款③都规定了帝国主义可以在华设厂④都规定了开放通商口岸 A ．①③④ B ．①②③C ．②③④D ．①②④3．历史大戏《台湾1895》曾在央视一套热播，剧中李雪健饰演的李鸿章在1874年说出“八国联军刚刚火烧了圆明园”的台词，被笑指犯下了低级的历史错误。

这是因为（） A ．李雪健与李鸿章在形象上差异很大 B ．1860年英法联军火烧圆明园 C ．李鸿章没有经历过八国联军侵华战争 D ．圆明园是中日甲午战争后为日军所烧 4．太平天国运动由盛转衰的标志是（） A ．定都天京 B ．太平军北伐 C ．天京事变 D ．天京陷落5．近代以来，腐败的清政府多次被西方列强“惩罚”。

观察漫画《“惩罚”中国》，此次中国被“惩罚”导致了（）A ．中国领土主权开始遭到破坏B ．中国开始被卷进世界资本主义的漩涡C ．中国半殖民地化程度大大加深D ．清政府沦为帝国主义列强统治中国的工具6．洋务派掀起洋务运动的根本目的是（）A．学习西方先进技术B．在中国发展资本主义C．抵制外国经济势力入侵D．维护清朝统治7．下列四部反映晚清历史的影视作品，按历史事件的发生先后顺序排列，正确的是（）①《末代皇帝》②《鸦片战争》③《甲午风云》④《火烧圆明园》A．①②③④B．②④③①C．③④①②D．④①②③8．戊戌变法是一批爱国知识分子为挽救民族危亡而掀起的资产阶级改良运动，下列人物不属于维新变法人士的是（）A．李鸿章B．梁启超C．康有为D．谭嗣同9．他是20世纪中国走在时代前列的第一个伟人，是中国民主革命的伟大先行者。

人教新目标(Go for it)版2019-2020学年八年级上学期英语期末模拟试卷(一)(II )卷

人教新目标(Go for it)版2019-2020学年八年级上学期英语期末模拟试卷（一）（II ）卷一、听下面5个句子，从题中所给的A、B、C三个选项选出最佳答语。

(共5题；共10分)1. （2分）听录音，选择最佳答语（）A . At 8: 00 pm.B . No, I don't.C . Once a week.2. （2分）听录音，选择正确答语A . In a week.B . By plane.C . With my brother.3. （2分）听句子，选出该句的最佳答语（）A . I'm fine.B . I'm reading.C . I'm nineteen.4. （2分）听句子，选择最佳答语（）A . with some students.B . In the morning.C . To the train station.5. （2分）听句子，选出最合适的答语。

A . It's Monday.B . It's April 29C . It's two o'clock二、听下面5段对话，根据对话内容，选择问题的正确答案。

(共5题；共10分)6. （2分）What's the girl's telephone number?A . It's 676—3483.B . It's 676—3843.C . It's 676—8343.7. （2分）Why is the boy so happy?A . Because he got a wonderful gift on his birthday.B . Because he made a good friend.C . Because he got an A in the English test.8. （2分）What club does the girl want to join?A . The sports club.B . The music club.C . The art club.9. （2分）How is the girl's brother?A . TomB . JimC . Jack.10. （2分）What is the weather like in London today?A . SunnyB . SnowyC . Rainy三、听一段对话和一段独白，根据对话和独白内容，选择问题的正确答案 (共2题；共20分)11. （10分）听对话，回答问题（1）What color are the shoes?A . BlackB . BlueC . White（2）What size are the shoes?A . Size 39B . Size 40C . Size 41（3）How much will the mother pay for the shoes and socks?A . 420 yuanB . 400 yuanC . 380 yuan12. （10分）听第一篇短文，回答问题。

2019-2020学年上学期洛阳偃师新前程学校人教版八年级物理上册期末模拟试卷无答案

人教版八年级物理上册期末模拟试卷无答案满分70分时间60分钟一、填空题（每空1分，共14分）1.如图所示是小明同学所拍摄的一幅海边风景照片．由照片所示的情景，可以分析判断出甲船的运动状态是________，乙船的运动状态可能是________．2.小刚上午9点出发骑车前往相距12 km的外婆家，动身前他打电话告诉外婆他到达的时间，他先以15 km/h的正常速度骑了12 min，因在路边书摊买书用了6min，为了不迟到，他随后以18 km/h的速度骑行，最终按时到达外婆家。

则小刚在全程的平均速度为____km/h；小刚在电话里约定的到达时间是____。

3.密度与我们的社会生活联系十分紧密：在新材料的选择上，科学家们一般都选择高强度、________(选填“高”或“低”)密度的合金、玻璃钢等复合材料作为航空器材；在我国北方的楼房中都装有暖气，这种用水作为介质的暖气片，一般都安装在窗户的________(选填“上方”或“下方”)。

4.如图是A、B两种物质的熔化图像，由图像可知________(选填“A”或“B”)物质是晶体，该晶体的熔点是________℃。

5.显微镜的物镜相当于________，由两个凸透镜组成的望远镜的物镜相当于（均选填“照相机”、“投影仪”或“放大镜”），用物镜的放大倍数为10×、目镜的放大倍数为5×的显微镜观察一大小为5度的角，看到角的大小为________ 度。

6.小李同学在百米赛跑时，在前8 s内加速跑完了36 m，接着保持8 m/s的速度跑完全程，则他百米赛跑的成绩是_____s，百米赛跑的平均速度为_____m/s 。

7.在“制作小孔成像观察仪”活动中，需要把制作好的圆筒插入易拉罐中，如图所示，圆筒的______(选填“A”或“B”)端是用半透明薄纸制成的光屏。

用制成的小孔成像观察仪观察静物时，移动圆筒位置，増大光屏与小孔之间距离，则光屏上像将______(选填“变大”“変小或“不变”)。

人教版2019-2020学年八年级上学期期末考试政治试题(I)卷

人教版2019-2020学年八年级上学期期末考试政治试题（I）卷姓名:________ 班级:________ 成绩:________一、判断题 (共10题；共20分)1. （2分） (2017八上·单县月考) 孝敬父母是法律规定子女应尽的义务，不孝敬父母必然要受到法律制裁。

（）2. （2分） (2017七下·桥东期末) 帮助他人要真诚，要考虑对方的实际需要。

3. （2分）礼貌待人是人际交往的最起码的要求。

（）4. （2分） (2017八上·郓城期中) 在与别人交谈时，我们要十分留意倾听他人的发言。

（）5. （2分） (2017八上·桑植期末) 互联网的普及和应用，人们只要通过电话、网络方式参与公共生活就可以了。

（）6. （2分） (2016八上·鄞州期末) 放学路上，几位同学看到一位右腿残疾的同学一瘸一拐地走着，便学着他的样子走路，引来其他同学大笑。

那位同学非常难过。

小华见状，气愤地说：“如果你们是那位同学，你们会有什么感受？”小华同学的做法体现了换位思考，与人为善。

（）7. （2分） (2017九上·苏州期中) 诚信也是一种资源。

（）8. （2分）合作是共享的基础，共享是合作的必然结果。

（）9. （2分） (2017七下·昆山期末) 人没有年龄、体型、职业、家庭差异，所以在人格上也是平等的。

（）10. （2分）思想品德老师要求同学们写一份诚信调查设计方案，小刚同学直接到网上下载了一篇交给老师。

（）二、单项选择题 (共14题；共28分)11. （2分） (2016八上·太原期末) 2015年12月16-18日，第二届世界互联网大会在浙江乌镇举行。

本次大会的主题是（）A . 创造无限机会，打造新时代经济引擎B . 互联互通•共享共治——构建网络空间命运共同体C . 产业融合，互联共享——开拓网络经济新常态，畅想下一个五年D . 共建良好生态环境，朋务美好网络生活12. （2分）(2016·龙江) 2015年9月3日上午，纪念中国人民抗日战争暨世界反法西斯战争胜利周年大会在北京天安门广场隆重举行。

2019-2020学年人教版八年级上册数学期末考试试卷(有答案)-最新精品

云南民族大学附属中学2019-2020学年八年级上学期数学期末考试试卷一、单选题1.已知的三边长分别是6cm、8cm、10cm，则的面积是（）A.B.C.D.【答案】A【考点】三角形的面积，勾股定理的逆定理【解析】【解答】解：∵62+82=102，∴△ABC是直角三角形，∴△ABC的面积为：×6×8=24．故答案为：A．【分析】先利用勾股定理的逆定理判断出△ABC是直角三角形，然后根据直角三角形的面积计算方法即可算出答案。

2.如果，那么（）A.B.C.D.【答案】C【考点】不等式及其性质【解析】【解答】解：A．∵b＞a＞0，∴，∴﹣＞﹣，不符合题意；B．∵b＞a＞0，∴，不符合题意；C．∵b＞a＞0，∴，∴﹣＜﹣，符合题意；D．∵b＞a，∴﹣b＜﹣a，不符合题意．故答案为：C．【分析】由，根据被除数一定除数越大商越小得出，然后根据不等式的性质2，不等式的两边都乘以同一个负数，不等号方向改变，即可判断出A,C的正确与否，由，根据不等式的性质2，不等式的两边都乘以同一个负数，不等号方向改变，即可判断D，综上所述即可得出答案。

3.已知等腰三角形的两边长分别为5cm、2cm，则该等腰三角形的周长是（）A. 7cmB. 9cmC. 12cm或者9cm D. 12cm【答案】D【考点】三角形三边关系，等腰三角形的性质【解析】【解答】解：①5cm为腰，2cm为底，此时周长为12cm；②5cm为底，2cm为腰，则两边和小于第三边无法构成三角形，故舍去．∴其周长是12cm．故选D．【分析】题目给出等腰三角形有两条边长为4cm和2cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．4.面积相等的两个三角形（）A. 必定全等B. 必定不全等 C. 不一定全等 D. 以上答案都不对【答案】C【考点】全等三角形的判定与性质【解析】【解答】因为两个面积相等的三角形，则面积的2倍也相等，也就是底乘高相等；但是一个数可以有许多不同的因数，所以说这两个三角形的对应边、对应高不一定相等；故面积相等的两个三角形不一定全等．故答案为：C．点评：本题考查了全等三角形的判定．解答此题需要熟悉三角形的面积公式．【分析】因为两个面积相等的三角形，则面积的2倍也相等，也就是底乘高相等；但是一个数可以有许多不同的因数，所以说这两个三角形的对应边、对应高不一定相等；故面积相等的两个三角形不一定全等．5.以下现象：荡秋千；呼啦圈；跳绳；转陀螺其中是旋转的有（）A.B.C.D.【答案】D【考点】生活中的旋转现象【解析】【解答】解：①荡秋千是旋转；②呼啦圈运动不是围绕某一点进行运动，不是旋转；③跳绳时绳子在绕人转动，人在上下运动；④转陀螺是旋转．故答案为：D．【分析】在平面内将一个图形绕着某点，按某个方向转动一定的角度，这样的图形变换叫做旋转，根据定义即可一一判断。

2019-2020学年新部编人教版八年级语文上学期期末教学质量检测试题 (含答案)

2019-2020学年八年级语文上学期期末教学质量检测试满分：120分分数_____________注意事项:你拿到的试卷满分为120分(其中卷面书写占5分) 一、语文积累与综合运用。

（33分） 1. 默写古诗文中的名句名篇。

（10分） (1)补写出下列名句中的上句或下句① 烟波江上使人愁。

（崔颢《黄鹤楼》） ②大漠孤烟直，。

（王维《使至塞上》） ③角声满天秋色里，。

（李贺《雁门太守行》） ④ 飞鸟相与还。

（陶渊明《饮酒》） ⑤无可奈何花落去，。

（晏殊《浣溪沙》） ⑥老骥伏枥，。

（曹操《龟虽寿》）（2）默写杜牧的《赤壁》2.阅读下面文字,完成(1)-(4)题（10分）九侯山云雾迷蒙,群峰如苍龙穿行于云海。

峰顶有数十块巨石，叠簇而立，这些巨石z ī（）态万千，情态各异。

有的悄然独立，如 ① 护蛋；有的端庄安祥， ② 蛰伏；有的y ī（）然自得，犹 ③ 卧眠…… （1）给加点字注音，根据拼音写出相应的汉字。

(3分)叠．（）簇 z ī( )态 y ī( )然自得 (2) 文中有错别字的一个词是“ ” 这个词的正确写法是“ ”(2分) （3）选择正确的词语填入短文横线上(3分) ① ② ③A.金蟾B.老牛C.金鸡学校：班级：姓名：考号：…………………………装……………………………订……………………………线……………………………………（4）文中画线的句子运用了修辞。

(2分)3. 运用你积累的课外知识完成（1）-（2）题（4分）（1）《红星照耀中国》又名《》是美国著名记者的不朽名著，是一部文笔优美的纪实性很强的报道性作品。

（2）《昆虫记》的作者是国作家、昆虫学家。

4、为激发同学们阅读经典的兴趣，你所在的班级正在开展“与经典同行，与好书为伴”的综合性学习活动，请你积极参加并完成以下任务。

(9分)(1)请你为这次活动拟写一条宣传标语。

(2分)(2)关于阅读，有很多的名言警句，请你写出一句。

2019-2020学年人教新目标版八年级英语上册期末模拟试卷(含答案)

2019-2020学年八年级上册英语期末模拟试卷满分:120分时间:120分钟听力部分(25分)I.听对话，选择相应的图片。

听一遍。

(5分)( )1. Which sign are they talking about?A.B. C.( )2. What will the girl probably buy for her father?A.B. C.( )3. What does the girl want to be when she grows up?A.B. C.( )4. What was the weather like last Saturday?A.B. C.( )5. What animal doesn’t the man like?A.B.C.II.听对话，选择正确的答案。

听两遍。

(5分) ( )6. Who did the man visit yesterday evening？A.Miss Liu.B. His teacher.C. His grandfather.( )7. What is Nick doing?A. Sleeping.B. Watching TV.C. Cooking.( )8. How was the girls weekend?A.It was great.B. It wasn’t very good.C. We don't know.( )9. What s the boy going to do?A. To do more exerciseB. To get a part time job.C. To get good grades. ( )10. Who is heavier, Tom or Peter?A. TomB. PeterC. My friendⅢ.听下面两段对话，选择正确的答案。

听两遍。

(5分)听第一段对话，回答第11～12小题。

期末考试模拟试卷(1)(原卷版)-2020-2021学年八年级数学下册精讲精练(人教版)

期末考试模拟试卷（1）（满分100分，考试时间120分钟）一、单项选择题（本题8个小题，每题3分，共24分）1.当1＜a＜2时，代数式+|1﹣a|的值是（）A．﹣1 B． 1 C．2a﹣3 D．3﹣2a2.（2019•山东聊城）下列各式不成立的是（）A．﹣＝B．＝2C．＝+＝5 D．＝﹣3．（2020•黑龙江）如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA ＝6，OH＝4，则菱形ABCD的面积为（）A．72 B．24 C．48 D．964．（2020•陕西）如图，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，若BD是△ABC的高，则BD的长为（）A．1013√13B．913√13C．813√13D．713√135．（2020•黑龙江）一组从小到大排列的数据：x ，3，4，4，5（x 为正整数），唯一的众数是4，则该组数据的平均数是（） A ．3.6B ．3.8或3.2C ．3.6或3.4D ．3.6或3.26.（2019广西桂林）如图，四边形ABCD 的顶点坐标分别为(4,0)A -，(2,1)B --，(3,0)C ，(0,3)D ，当过点B 的直线l 将四边形ABCD 分成面积相等的两部分时，直线l 所表示的函数表达式为( )A ．116105y x =+ B ．2133y x =+ C ．1y x =+ D ．5342y x =+ 7．（2020•上海）小明从家步行到学校需走的路程为1800米．图中的折线OAB 反映了小明从家步行到学校所走的路程s （米）与时间t （分钟）的函数关系，根据图象提供的信息，当小明从家出发去学校步行15分钟时，到学校还需步行（）A.150B.250C.350D.4508．（2020•温州）如图，在△ABC 中，∠A ＝40°，AB ＝AC ，点D 在AC 边上，以CB ，CD 为边作▱BCDE ，则∠E 的度数为（）A ．40°B ．50°C ．60°D ．70°二、填空题（本题9个小题，每空3分，共27分）9.（2020•哈尔滨）计算√24+6√16的结果是． 10.若=3﹣x ，则x 的取值范围是．11．Rt △ABC 中，∠ABC=90°，AB=3，BC=4，过点B 的直线把△ABC 分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是_____． 12.(2019•四川绵阳)单项式x -|a -1|y 与2xy 是同类项，则a b =______．13.实数a ，b 在数轴上对应点的位置如图所示，化简||a 的结果是 .14．（2020•湖州）计算：√8+|√2−1|=_______15．（2020•淮安）菱形的两条对角线长分别为6和8，则这个菱形的边长为．16．（2020•甘孜州）如图，在▱ABCD 中，过点C 作CE ⊥AB ，垂足为E ，若∠EAD ＝40°，则∠BCE 的度数为．17．（2020•长沙）长沙地铁3号线、5号线即将试运行，为了解市民每周乘坐地铁出行的次数，某校园小记者随机调查了100名市民，得到如下统计表：次数 7次及以上6 5 4 3 2 1次及以下人数81231241564这次调查中的众数和中位数分别是，．三、解答题（本题6个题，18题6分、19题8分、20题8分、21题8分、22题9分、23题10分，共49分）18.用拆解法化简)23)(25(24335++++19.已知如图，四边形ABCD中，，，，，，求这个四边形的面积．20．阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+=（1+）2．善于思考的小明进行了以下探索：设a+b=（m+n）2（其中a、b、m、n均为整数），则有a+b=m2+2n2+2mn．∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：（1）当a、b、m、n均为正整数时，若a+b=，用含m、n的式子分别表示a、b，得：a= ，b= ；（2）利用所探索的结论，找一组正整数a、b、m、n填空：+2=（+）2；（3）若a+4=，且a、m、n均为正整数，求a的值？21.如图，在□ABCD中，BE平分∠ABC，BC=6，DE=2，求□ABCD的周长．22.小明放学后从学校回家，出发5分钟时，同桌小强发现小明的数学作业卷忘记拿了，立即拿着数学作业卷按照同样的路线去追赶小明．小强出发10分钟时，小明才想起没拿数学作业卷，马上以原速原路返回，在途中与小强相遇．两人离学校的路程y（米）与小强所用时间t（分钟）之间的函数图象如图所示．（1）求函数图象中a的值；（2）求小强的速度；（3）求线段AB的函数解析式，并写出自变量的取值范围．23．（2020•贵阳）2020年2月，贵州省积极响应国家“停课不停学”的号召，推出了“空中黔课”．为了解某中学初三学生每天听空中黔课的时间，随机调查了该校部分初三学生．根据调查结果，绘制出了如图统计图表（不完整），请根据相关信息，解答下列问题：部分初三学生每天听空中黔课时间的人数统计表时间/h 1.5 2 2.5 3 3.5 4人数/人 2 6 6 10 m 4（1）本次共调查的学生人数为，在表格中，m＝；（2）统计的这组数据中，每天听空中黔课时间的中位数是，众数是；（3）请就疫情期间如何学习的问题写出一条你的看法．。

人教版八年级语文上册期末测试卷(含答案) (13)

人教版八年级语文测试题测试题人教版初中语文学易金卷：段考模拟君之2019-2020学年上学期期末原创卷B卷八年级语文·全解全析1．【答案】①霜重鼓寒声不起②国破山河在③而无车马喧④试倩悲风吹泪过扬州⑤天接云涛连晓雾星河欲转千帆舞⑥东风不与周郎便铜雀春深锁二乔⑦兴尽晚回舟误入藕花深处（每空1分）【解析】传统的记忆型默写题，要求学生直接默写出指定的文句，这类题目要求考生日常加强背诵识记，尤其是不仅能背诵，还要能默写。

理解性默写，要求学生能够背诵全文（诗），选择符合语境要求的句子。

“喧”“倩”“藕”是此题中的易错字，作答时要注意字形。

名句的默写，要想得满分，关键在于平时强化记忆，做到“三不”：不漏字、不添字、不写错别字。

2．【答案】（1）昆虫的史诗法布尔（2分）（2）《昆虫记》行文生动活泼，语调轻松诙谐，充满了情趣。

如，在选文中用“骄傲地”来描述会缝纫的蜜蜂，语调轻松诙谐，充满了情趣。

（4分）（3）C（3分）（4）示例：萤火虫；萤火虫很明亮，可以在黑暗里给人照亮。

（3分）【解析】（1）文学常识的考核主要集中在中外的作家、作品、文学现象、文学流派、文体知识等。

重点记忆课本涉及到的和经典阅读中列出的作品。

平时注意积累，理出线索，形成体系。

死记硬背作者名字、书名及书中的重要人物的名字。

此题考查的是有关法布尔《昆虫记》的文学常识。

（2）可从名著的思想价值或艺术价值角度考虑答案。

根据选文的特点，可以通过分析语言来考虑作答思路。

如可分析“很骄傲地用它的腮带走了”“它们打算到邻近的小树林中，把树叶子割成圆形的小片用来包裹它们的收获品”等语句，概括出作品语调轻松诙谐、充满了情趣的特点。

（3）《昆虫记》中说甲虫类受到蝎子毒攻后会坚持长久一点，另外毛虫的幼虫对此似乎免疫。

所给答案中只有千脚虫类似于毛虫。

所以选择C。

（4）本题为开放性试题，只要从《昆虫记》中找出你最喜欢的昆虫，合理解说理由，语句通顺流畅即可。

《昆虫记》中的昆虫有蝉、蟋蟀、螽斯、圣甲虫等。

2019-2020学年人教版八年级上册期末历史试题及答案

人教版八年级上册期末历史试题满分100分，考试时间60分钟。

学校：班级：姓名：一、选择题（共25小题，每小题2分，共50分)在每题所列出的四个选项中，只有一项是最符合题目要求的。

1.右图人民英雄纪念碑上的浮雕展现的是虎门销烟的历史事件，它显示了中国人民抗击外国侵略的坚强意志和决心，领导这一运动的民族英雄是A.关天培B.林则徐C.左宗棠D.邓世昌2．有学者指出：林则徐的虎门销烟和“亚罗号事件”是英国对中国发动两次鸦片战争的导火线，即使没有这些事件，战争也无法避免。

该学者持这一观点的依据是英国A．为了打开鸦片的销售市场B．工业革命后军事力量的强大C．为了打开中国市场 D.为了割占中国领土，争取外交礼仪平等3.2017年是香港回归祖国20周年。

香港的回归不仅洗雪了中国百年国耻，更促进了香港的持续稳定、繁荣。

中国近代史上香港问题的形成开始于A.《南京条约》B.《天津条约》C.《北京条约》D.《辛丑条约》4.某学校初二同学进行历史学科研究性学习时，找到了以下两幅图片，由此可以判断他们研究的内容是A.鸦片战争B.第二次鸦片战争C.甲午中日战争D.八国联军侵华战争5.1902年，北京城某茶馆里有四位老人在聊天。

张老木说：“我给兴中会捐过款。

”李老金说：“公车上书时我签过字。

”王老德说：“我家现住东交民巷。

”赵老刚说：“我在总理衙门当过差。

”他们中有一个人在说谎。

根据所学知识判断，说谎人是A．王老德B．李老金C．张老木D.赵老刚6．鸦片战争后先进的中国人不断探索救国方案，右图是网友归纳的救国方案截图，虽不是很准确，但有些道理。

其中的“康有为说：我变”，是指A．洋务运动B．戊戌变法C．辛亥革命D．新文化运动7．某史学家认为：“民族的反思，是在遭遇极大的困难中产生的，一百多年来，中华民族的第一次反思是在鸦片战争后，渐知诸事不如人，只有学习西方。

第二次则是反思为何学了西方仍然失败。

”其中“第二次反思”开始了A．经济技术方面的探索B．政治制度方面的探索C．思想文化方面的探索 D.军事强国方面的探索8．李鸿章晚年这样评价自己的洋务事业：“我办了一辈子的事，练兵也，海军也，都是纸糊的老虎，……不过勉强涂饰，虚有其表……”这段话说明洋务运动A．以“自强”为口号创办近代军事工业 B．以“求富”为口号创办近代民用企业C.建立新式海陆军D．没有改变落后的封建制度，不能使中国实现富强9.《马关条约》中反映帝国主义列强对华经济侵略由商品输出转变为以资本输出为主的内容是A．割辽东半岛、台湾全岛及所有附属各岛屿、澎湖列岛给日本B．赔偿日本兵费白银2亿两C．开放沙市、重庆、苏州、杭州为商埠D．允许日本在通商口岸开设工厂10.《时局图》是近代爱国者谢缵泰所作，生动形象地揭露了清政府腐败和帝国主义列强对中国的瓜分。

2019-2020学年部编人教版八年级语文第一学期期末测试卷(含答案)

2019-2020学年八年级语文第一学期期末测试卷（满分150分时间120分钟）一、积累（28分）1.对毛泽东主席的这幅书法作品，评价不恰当的选项是（）（3分）A．笔法遒劲有力，结构简省，气势磅礴。

B．运笔自然流畅，线条奔放，纵任狂放。

C．字体大小参差，方正端庄，浑厚大气。

D．用笔收放自如，讲究布局，一气呵成。

2.下面语段中字音、字形全对的选项是（）（3分）船正在放倒桅（）杆准备过桥，船夫们呼唤叫喊，握篙（）盘索。

桥上呼应相接，岸边挥臂助阵，过往行人jù（）集在桥头围观。

而那些赶脚、推车、挑担的人们，却无xiá（）一顾。

A.wéi gāo 聚暇B.weígāo 居暇C.wéi hāo 聚睱D.wéi gāo 居睱3.加点词语使用不正确的选项是（）（3分）A.街上行人摩肩接踵,络绎不绝．．．．,士农工商,男女老少,各行各业,无所不备。

B.丁俊晖在比分落后的情况下，无动于衷．．．．，镇定自若，最终赢得了比赛。

C.这时你会真心佩服昔人所造的两个字“麦浪”，若不是妙手偶得．．．．，便确是经过锤炼的语言的精华。

D.黑恶势力是经济社会健康发展的毒瘤,是人民群众深恶痛疾．．．．的顽症,必须坚决依法予以打击。

4.下列说法不正确的一项是（）（3分）A.孟子是继孔子之后的又一位儒学大师，被尊称为“亚圣”。

B.《列子》是一部很有趣的著作，其中有大量的寓言，比如我们以前学过的《两小儿辩日》《九方皋相马》和《杞人忧天》等。

C.《史记》是我国的第一部纪传体通史，记述了传说中的黄帝到汉武帝共三千余年的史事，包括列传和世家两部分。

D.“风休住，蓬舟吹取三山去！”三山是神话传说中的蓬莱、方丈、瀛洲。

5.默写（8分）（1），；烈士暮年，壮心不已。

（《龟虽寿》）（2）鸢飞戾天者，望峰息心；，。

（《与朱元思书》）（3）《使至塞上》被誉为“独绝千古”的一联是：，。

（4）思乡怀人是古诗中一个常写不衰的主题, 请写出连续的两句：6.名著（8分）（1）《昆虫记》中，“浑身嫩绿，侧面有两条淡白色丝带，身材优美，苗条匀称，两片大翼轻盈如纱”的昆虫是，建筑才能远胜于卢浮宫建筑艺术智慧的昆虫是。

人教版2019-2020学年八年级数学(上)期末复习：全等三角形常考题型复习(解析版)

人教版八年级数学上册期末复习：全等三角形常考基础专题复习一．选择题（共12小题）1．如图，△ABO≌△DCO，∠D＝80°，∠DOC＝70°，则∠B＝（）A．35°B．30°C．25°D．20°2．图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（）A．点A B．点B C．点C D．点D3．如图，已知点B、E、C、F在一条直线上，∠A＝∠D，∠B＝∠DFE，添加以下条件，不能判定△ABC≌△DFE的是（）A．BE＝CF B．AB＝DF C．∠ACB＝∠DEF D．AC＝DE4．如图，已知AB＝AD，那么添加下列一个条件后，仍然不能判定△ABC≌△ADC的是（）A．CB＝CD B．∠B＝∠D＝90°C．∠BAC＝∠DAC D．∠BCA＝∠DCA 5．如图，点B、E、C、F在同一条直线上，AB∥DE，AB＝DE，要用SAS证明△ABC≌△DEF，可以添加的条件是（）A．∠A＝∠D B．AC∥DF C．BE＝CF D．AC＝DF6．如图，已知AB＝AD，那么添加下列一个条件后，能判定△ABC≌△ADC的是（）A．AC＝AC B．∠BAC＝∠DAC C．∠BCA＝∠DCA D．∠B＝∠D7．如图，点B、F、C、E在一条直线上，AB∥ED，AB＝DE，要使△ABC≌△DEF，需要添加下列选项中的一个条件是（）A．BF＝EC B．AC＝DF C．∠B＝∠E D．BF＝FC8．如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB＝6cm，则△DBE的周长是（）A．6 cm B．7 cm C．8 cm D．9 cm9．若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（）的交点．A．角平分线B．高线C．中线D．边的中垂线10．如图，Rt△ABC中，∠C＝90°，∠ABC的平分线BD交AC于D．若CD＝3cm，则点D到AB的距离DE是（）A．5 cm B．4 cm C．3 cm D．2 cm11．如图，直线a、b、c表示三条互相交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A．1处B．2处C．3处D．4处12．如图，OP平分∠MON，P A⊥ON于点A，点Q是射线OM上的一个动点，若P A＝2，则PQ的最小值为（）A．1B．2C．3D．4二．填空题（共8小题）13．如图所示，已知△ABC的面积是36，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，则△ABC的周长是．14．如图，∠C＝90°，∠1＝∠2，若BC＝10，BD＝6，则D到AB的距离为．15．如图，已知∠ABC＝∠DCB，增加下列条件：①AB＝CD；②AC＝DB；③∠A＝∠D；④∠ACB＝∠DBC；能判定△ABC≌△DCB的是．（填序号）16．如图，B、C、E共线，AB⊥BE，DE⊥BE，AC⊥DC，AC＝DC，又AB＝2cm，DE＝1cm，则BE＝．17．已知△ABC≌△DEF，∠A＝30°，∠E＝50°，则∠C＝．18．如图，△ABC≌△ADE，∠EAC＝35°，则∠BAD＝°．19．如图为6个边长相等的正方形的组合图形，则∠1+∠3＝．20．如图，若△ABC≌△ADE，∠EAC＝30°，则∠BAD＝度．三．解答题（共12小题）21．如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC＝PD，且P到OA，OB两条公路的距离相等．22．已知，如图，∠C＝90°，∠B＝30°，AD是△ABC的角平分线．（1）求证：BD＝2CD；（2）若CD＝2，求△ABD的面积．23．如图，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，CD＝3．（1）求DE的长；（2）若AC＝6，BC＝8，求△ADB的面积．24．如图，△ABC中，∠C＝90°，AD是△ABC的角平分线，DE⊥AB于E，AC＝BE．（1）求证：AD＝BD；（2）求∠B的度数．25．如图，在△ABC中，∠C＝90°．（1）作∠BAC的平分线AD，交BC于D；（2）若AB＝10cm，CD＝4cm，求△ABD的面积．26．如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE＝AF．求证：（1）PE＝PF；（2）点P在∠BAC的角平分线上．27．如图，点C、E、B、F在同一直线上，CE＝BF，AC∥DF，AC＝DF，求证：△ABC≌△DEF．28．如图，AB＝AC，AD＝AE，∠1＝∠2，求证：△ABD≌△ACE．29．如图，已知点C，F在线段BE上，AB∥ED，∠ACB＝∠DFE，EC＝BF．求证：△ABC≌△DEF．30．已知：如图，∠A＝∠D＝90°，AC＝BD．求证：OB＝OC．31．如图，△ABC中，AB＝AC，BD⊥AC，CE⊥AB．求证：BD＝CE．32．如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．参考答案与试题解析部分一．选择题（共12小题）1．如图，△ABO≌△DCO，∠D＝80°，∠DOC＝70°，则∠B＝（）A．35°B．30°C．25°D．20°【分析】根据三角形内角和定理求出∠C，根据全等三角形的性质解答即可．【解答】解：∵∠D＝80°，∠DOC＝70°，∴∠C＝180°﹣∠D﹣∠DOC＝30°，∵△ABO≌△DCO，∴∠B＝∠C＝30°，故选：B．2．图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（）A．点A B．点B C．点C D．点D【分析】根据全等三角形的性质和已知图形得出即可．【解答】解：∵△MNP≌△MEQ，∴点Q应是图中的D点，如图，故选：D．3．如图，已知点B、E、C、F在一条直线上，∠A＝∠D，∠B＝∠DFE，添加以下条件，不能判定△ABC≌△DFE的是（）A．BE＝CF B．AB＝DF C．∠ACB＝∠DEF D．AC＝DE【分析】根据全等三角形的判定方法对各选项进行判断．【解答】解：∵∠A＝∠D，∠B＝∠DFE，∴当BE＝CF时，即BC＝EF，△ABC≌△DFE（AAS）；当AB＝DF时，即BC＝EF，△ABC≌△DFE（ASA）；当AC＝DE时，即BC＝EF，△ABC≌△DFE（AAS）．故选：C．4．如图，已知AB＝AD，那么添加下列一个条件后，仍然不能判定△ABC≌△ADC的是（）A．CB＝CD B．∠B＝∠D＝90°C．∠BAC＝∠DAC D．∠BCA＝∠DCA 【分析】要判定△ABC≌△ADC，已知AB＝AD，AC是公共边，具备了两组边对应相等，故添加CB＝CD、∠BAC＝∠DAC、∠B＝∠D＝90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC，而添加∠BCA＝∠DCA后则不能．【解答】解：A、添加CB＝CD，根据SSS，能判定△ABC≌△ADC，故A选项不符合题意；B、添加∠B＝∠D＝90°，根据HL，能判定△ABC≌△ADC，故D选项不符合题意；C、添加∠BAC＝∠DAC，根据SAS，能判定△ABC≌△ADC，故B选项不符合题意；D、添加∠BCA＝∠DCA时，不能判定△ABC≌△ADC，故C选项符合题意；故选：D．5．如图，点B、E、C、F在同一条直线上，AB∥DE，AB＝DE，要用SAS证明△ABC≌△DEF，可以添加的条件是（）A．∠A＝∠D B．AC∥DF C．BE＝CF D．AC＝DF【分析】根据AB∥DE得出∠B＝∠DEF，添加条件BC＝EF，则利用SAS定理证明△ABC ≌△DEF．【解答】解：∵AB∥DE，∴∠B＝∠DEF，可添加条件BC＝EF，理由：∵在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）；故选：C．6．如图，已知AB＝AD，那么添加下列一个条件后，能判定△ABC≌△ADC的是（）A．AC＝AC B．∠BAC＝∠DAC C．∠BCA＝∠DCA D．∠B＝∠D【分析】要判定△ABC≌△ADC，已知AB＝AD，AC是公共边，具备了两组边对应相等，故添加CB＝CD、∠BAC＝∠DAC、∠B＝∠D＝90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC，而添加∠BCA＝∠DCA后则不能．【解答】解：A、添加AC＝AC，根据SS，不能判定△ABC≌△ADC，故本选项错误；B、添加∠BAC＝∠DAC，根据SAS，能判定△ABC≌△ADC，故本选项正确；C、添加∠BCA＝∠DCA时，根据SSA不能判定△ABC≌△ADC，故本选项错误；D、添加∠B＝∠D，根据SSA不能判定△ABC≌△ADC，故本选项错误；故选：B．7．如图，点B、F、C、E在一条直线上，AB∥ED，AB＝DE，要使△ABC≌△DEF，需要添加下列选项中的一个条件是（）A．BF＝EC B．AC＝DF C．∠B＝∠E D．BF＝FC【分析】根据“SAS”可添加BF＝EC使△ABC≌△DEF．【解答】解：∵AB∥ED，AB＝DE，∴∠B＝∠E，∴当BF＝EC时，可得BC＝EF，可利用“SAS”判断△ABC≌△DEF．故选：A．8．如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB＝6cm，则△DBE的周长是（）A．6 cm B．7 cm C．8 cm D．9 cm【分析】根据角平分线上的点到角的两边的距离相等可得DE＝CD，再根据等腰直角三角形的性质求出AC＝BC＝AE，然后求出△DBE的周长＝AB，代入数据即可得解．【解答】解：∵AD平分∠CAB，DE⊥AB，∠C＝90°，∴DE＝CD，又∵AC＝BC，AC＝AE，∴AC＝BC＝AE，∴△DBE的周长＝DE+BD+EB＝CD+BD+EB＝BC+EB＝AE+EB＝AB，∵AB＝6cm，∴△DBE的周长＝6cm．故选：A．9．若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（）的交点．A．角平分线B．高线C．中线D．边的中垂线【分析】由角平分线性质的逆定理：到角的两边的距离相等的点在角的平分线上，则这个点是三角形三条角平分线的交点．【解答】解：∵到角的两边的距离相等的点在角的平分线上，∴这个点是三角形三条角平分线的交点．故选：A．10．如图，Rt△ABC中，∠C＝90°，∠ABC的平分线BD交AC于D．若CD＝3cm，则点D到AB的距离DE是（）A．5 cm B．4 cm C．3 cm D．2 cm【分析】过D作DE⊥AB于E，由已知条件，根据角平分线上的点到角的两边的距离相等解答．【解答】解：过D作DE⊥AB于E，∵BD是∠ABC的平分线，∠C＝90°，DE⊥AB，∴DE＝CD，∵CD＝3cm，∴DE＝3cm．故选：C．11．如图，直线a、b、c表示三条互相交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）A．1处B．2处C．3处D．4处【分析】由三角形内角平分线的交点到三角形三边的距离相等，可得三角形内角平分线的交点满足条件；然后利用角平分线的性质，可证得三角形两条外角平分线的交点到其三边的距离也相等，这样的点有3个，可得可供选择的地址有4个．【解答】解：∵△ABC内角平分线的交点到三角形三边的距离相等，∴△ABC内角平分线的交点满足条件；如图：点P是△ABC两条外角平分线的交点，过点P作PE⊥AB，PD⊥BC，PF⊥AC，∴PE＝PF，PF＝PD，∴PE＝PF＝PD，∴点P到△ABC的三边的距离相等，∴△ABC两条外角平分线的交点到其三边的距离也相等，满足这条件的点有3个；综上，到三条公路的距离相等的点有4个，∴可供选择的地址有4个．故选：D．12．如图，OP平分∠MON，P A⊥ON于点A，点Q是射线OM上的一个动点，若P A＝2，则PQ的最小值为（）A．1B．2C．3D．4【分析】由垂线段最短可知当PQ⊥OM时PQ最小，当PQ⊥OM时，则由角平分线的性质可知P A＝PQ，可求得PQ＝2．【解答】解：∵垂线段最短，∴当PQ⊥OM时，PQ有最小值，又∵OP平分∠MON，P A⊥ON，∴PQ＝P A＝2，故选：B．二．填空题（共8小题）13．如图所示，已知△ABC的面积是36，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，则△ABC的周长是18．【分析】作OE⊥AB于E，OF⊥AC于F，根据角平分线的性质得到OE＝OF＝OD＝4，根据三角形的面积公式计算即可．【解答】解：作OE⊥AB于E，OF⊥AC于F，∵OB、OC分别平分∠ABC和∠ACB，OD⊥BC，OE⊥AB，OF⊥AC，∴OE＝OF＝OD＝4，由题意得，×AB×OE+×CB×OD+×AC×OF＝36，解得，AB+BC+AC＝18，则△ABC的周长是18，故答案为：18．14．如图，∠C＝90°，∠1＝∠2，若BC＝10，BD＝6，则D到AB的距离为4．【分析】由已知条件首先求出线段CD的大小，接着利用角平分线的性质得点D到边AB 的距离等于CD的大小，问题可解．【解答】解：∵BC＝10，BD＝6，∴CD＝4，∵∠C＝90°，∠1＝∠2，∴点D到边AB的距离等于CD＝4，故答案为：4．15．如图，已知∠ABC＝∠DCB，增加下列条件：①AB＝CD；②AC＝DB；③∠A＝∠D；④∠ACB＝∠DBC；能判定△ABC≌△DCB的是①③④．（填序号）【分析】根据全等三角形的判定方法一一判断即可．【解答】解：因为∠ABC＝∠DCB，BC＝CB，①AB＝CD，根据SAS可以判定△ABC≌△DCB．②AC＝DB，无法判断△ABC≌△DCB．③∠A＝∠D，根据AAS可以判定△ABC≌△DCB．④∠ACB＝∠DBC，根据ASA可以判定△ABC≌△DCB．故答案为：①③④．16．如图，B、C、E共线，AB⊥BE，DE⊥BE，AC⊥DC，AC＝DC，又AB＝2cm，DE＝1cm，则BE＝3cm．【分析】易证△ABC≌△CED，可得AB＝CE，BC＝DE，可以求得BE的值．【解答】解：∵AC⊥DC，∴∠ACB+∠ECD＝90°∵AB⊥BE，∴∠ACB+∠A＝90°，∴∠A＝∠ECD，在△ABC和△CED中，，∴△ABC≌△CED（AAS），∴AB＝CE＝2cm，BC＝DE＝1cm，∴BE＝BC+CE＝3cm．故答案为3cm．17．已知△ABC≌△DEF，∠A＝30°，∠E＝50°，则∠C＝100°．【分析】根据全等三角形的性质求出∠B，根据三角形内角和定理计算即可．【解答】解：∵△ABC≌△DEF，∴∠B＝∠E＝50°，∴∠C＝180°﹣∠A﹣∠B＝100°，故答案为：100°．18．如图，△ABC≌△ADE，∠EAC＝35°，则∠BAD＝35°．【分析】根据全等三角形性质得出∠BAC＝∠DAE，求出∠BAD＝∠EAC，代入求出即可．【解答】解：∵△ABC≌△ADE，∴∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∵∠EAC＝35°，∴∠BAD＝35°，故答案为：35．19．如图为6个边长相等的正方形的组合图形，则∠1+∠3＝90°．【分析】首先利用SAS定理判定△ABC≌△DBE，根据全等三角形的性质可得∠3＝∠ACB，再由∠ACB+∠1＝90°，可得∠1+∠3＝90°．【解答】解：∵在△ABC和△DBE中，∴△ABC≌△DBE（SAS），∴∠3＝∠ACB，∵∠ACB+∠1＝90°，∴∠1+∠3＝90°，故答案为：90°．20．如图，若△ABC≌△ADE，∠EAC＝30°，则∠BAD＝30度．【分析】根据△ABC≌△ADE，可得∠CAB＝∠EAD，由于∠EAB是公共角，可得∠EAC ＝∠BAD，即可得解．【解答】解：∵△ABC≌△ADE，∵∠EAB是公共角，∴∠CAB﹣∠EAB＝∠EAD﹣∠EAB，即∠EAC＝∠BAD，已知∠EAC＝30°，∴∠BAD＝30°．故答案填：30．三．解答题（共12小题）21．如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC＝PD，且P到OA，OB两条公路的距离相等．【分析】作∠AOB的角平分线和线段CD的垂直平分线，它们的交点为P点．【解答】解：如图，点P为所作．22．已知，如图，∠C＝90°，∠B＝30°，AD是△ABC的角平分线．（1）求证：BD＝2CD；（2）若CD＝2，求△ABD的面积．【分析】（1）过D作DE⊥AB于E，依据角平分线的性质，即可得到DE＝CD，再根据含30°角的直角三角形的性质，即可得出结论；（2）依据AD＝BD＝2CD＝4，即可得到Rt△ACD中，AC＝＝2，再根据△ABD的面积＝×BD×AC进行计算即可．【解答】解：（1）如图，过D作DE⊥AB于E，∵∠C＝90°，AD是△ABC的角平分线，∴DE＝CD，又∵∠B＝30°，∴Rt△BDE中，DE＝BD，∴BD＝2DE＝2CD；（2）∵∠C＝90°，∠B＝30°，AD是△ABC的角平分线，∴∠BAD＝∠B＝30°，∴AD＝BD＝2CD＝4，∴Rt△ACD中，AC＝＝2，∴△ABD的面积为×BD×AC＝×4×2＝4．23．如图，Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，CD＝3．（1）求DE的长；（2）若AC＝6，BC＝8，求△ADB的面积．【分析】（1）直接根据角平分线的性质可得出结论；（2）先根据勾股定理求出AB的长，再由三角形的面积公式求解即可．【解答】解：（1）∵Rt△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于E，CD＝3，∴DE＝CD＝3；（2）∵Rt△ABC中，∠C＝90°，AC＝6，BC＝8，∴AB＝＝10．∵由（1）知，DE＝3，∴S△ABD＝AB•DE＝×10×3＝1524．如图，△ABC中，∠C＝90°，AD是△ABC的角平分线，DE⊥AB于E，AC＝BE．（1）求证：AD＝BD；（2）求∠B的度数．【分析】（1）根据角平分线的性质得到CD＝DE，根据全等三角形的判定和性质即可得到结论；（2）根据角平分线的定义可得∠CAD＝∠BAD，根据等边对等角可得∠B＝∠BAD，再根据三角形的内角和定理列出方程求解即可．【解答】证：（1）∵DE⊥AB于E，∠C＝90°，AD是△ABC的角平分线，∴CD＝DE，在Rt△ACD与Rt△AED中，∴Rt△ACD≌Rt△AED，∴AC＝AE，∵AC＝BE，∴AE＝BE，∴AD＝BD；（2）∵AD是△ABC的角平分线，∴∠CAD＝∠BAD，∵AD＝BD，∴∠B＝∠BAD，∴∠CAD＝∠BAD＝∠B，∵∠C＝90°，∴∠CAD+∠BAD+∠B＝90°，∴∠B＝30°．25．如图，在△ABC中，∠C＝90°．（1）作∠BAC的平分线AD，交BC于D；（2）若AB＝10cm，CD＝4cm，求△ABD的面积．【分析】（1）根据三角形角平分线的定义，即可得到AD；（2）过D作DE⊥AB于E，根据角平分线的性质得到DE＝CD＝4，由三角形的面积公式即可得到结论．【解答】解：（1）如图所示，AD即为所求；（2）如图，过D作DE⊥AB于E，∵AD平分∠BAC，∴DE＝CD＝4，∴S△ABD＝AB×DE＝×10×4＝20cm2．26．如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE＝AF．求证：（1）PE＝PF；（2）点P在∠BAC的角平分线上．【分析】（1）连接AP，根据HL证明△APF≌△APE，可得到PE＝PF；（2）利用（1）中的全等，可得出∠F AP＝∠EAP，那么点P在∠BAC的平分线上．【解答】证明：（1）如图，连接AP并延长，∵PE⊥AB，PF⊥AC∴∠AEP＝∠AFP＝90°又AE＝AF，AP＝AP，∵在Rt△AFP和Rt△AEP中∴Rt△AEP≌Rt△AFP（HL），∴PE＝PF．（2）∵Rt△AEP≌Rt△AFP，∴∠EAP＝∠F AP，∴AP是∠BAC的角平分线，故点P在∠BAC的角平分线上．27．如图，点C、E、B、F在同一直线上，CE＝BF，AC∥DF，AC＝DF，求证：△ABC≌△DEF．【分析】先由CE＝BF，可得BC＝EF，继而利用SAS可证明结论．【解答】解：∵CE＝BF，∴CE+BE＝BF+BE，即BC＝EF，又∵AC∥DF，∴∠C＝∠F，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．28．如图，AB＝AC，AD＝AE，∠1＝∠2，求证：△ABD≌△ACE．【分析】由∠1＝∠2，可得∠CAE＝∠BAD，进而利用两边夹一角，证明全等．【解答】证明：∵∠1＝∠2，∴∠CAE＝∠BAD，∵AB＝AC，AD＝AE，∴△ABD≌△ACE．29．如图，已知点C，F在线段BE上，AB∥ED，∠ACB＝∠DFE，EC＝BF．求证：△ABC≌△DEF．【分析】利用平行线的性质可得∠ABE＝∠BED，根据等式的性质可得EF＝BC，然后利用ASA判定△ABC≌△DEF即可．【解答】解：∵AB∥ED∴∠ABE＝∠BED，∴EC﹣FC＝BF﹣FC，∴EF＝BC，在△ABC和△DEF中，∴△ABC≌△DFE（SAS）．30．已知：如图，∠A＝∠D＝90°，AC＝BD．求证：OB＝OC．【分析】因为∠A＝∠D＝90°，AC＝BD，BC＝BC，知Rt△BAC≌Rt△CDB（HL），所以∠ACB＝∠DBC，即∠OCB＝∠OBC，所以有OB＝OC．【解答】证明：∵∠A＝∠D＝90°，AC＝BD，BC＝BC，∴Rt△BAC≌Rt△CDB（HL）∴∠ACB＝∠DBC．∴∠OCB＝∠OBC．∴OB＝OC（等角对等边）．31．如图，△ABC中，AB＝AC，BD⊥AC，CE⊥AB．求证：BD＝CE．【分析】欲证BD、CE两边相等，只需证明这两边所在的△ABD与△ACE全等，这两个三角形，有一对直角相等，公共角∠A，AB＝AC，所以两三角形全等．【解答】证明：∵BD⊥AC，CE⊥AB，∴∠ADB＝∠AEC＝90°．在△ABD和△ACE中，，∴△ABD≌△ACE（AAS）．32．如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．【分析】要证角相等，可先证明全等．即证Rt△ABC≌Rt△ADC，进而得出角相等．【解答】证明：∵AB⊥BC，AD⊥DC，∴∠B＝∠D＝90°，∴△ABC与△ACD为直角三角形，在Rt△ABC和Rt△ADC中，∵AB＝AD，AC为公共边，∴Rt△ABC≌Rt△ADC（HL），∴∠1＝∠2．。

2019-2020学年人教版八年级上册期末模拟(一)(原卷版)

2019-2020学年人教版八年级上册期末模拟（一）学校:___________姓名：___________班级：___________考号：___________一、选择题（共12小题，每题4分，共计48分）1．（2018·铁西区期中）小桐把一副直角三角尺按如图所示的方式摆放在一起，其中∠E =90∘，∠C =90∘，∠A =45∘，∠D =30∘，则∠1+∠2等于( )A ．150∘B ．180∘C ．210∘D ．270∘2．（2018·句容市期中）下列各图中a 、b 、c 为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC 全等的是（）A ．甲和乙B ．乙和丙C ．甲和丙D ．只有丙3．（2019·历城区期中）如图，已知BD 是△ABC 的角平分线，ED 是BC 的垂直平分线，∠BAC =90°，AD =3，则CE 的长为（）A ．6B ．5C ．4D ．3√34．（2019·兰陵县期中）如图，等边三角形ABC 中，AD ⊥BC ，垂足为D ，点E 在线段AD 上，∠EBC=45°，则∠ACE 等于（）A．15°B．30°C．45°D．60°5．（2018·资中县期末）已知(x－2015)2＋(x－2017)2＝34，则(x－2016)2的值是( ) A．4B．8C．12D．16 6．（2018·无为县期末）因式分解x2+mx﹣12＝（x+p）（x+q），其中m、p、q都为整数，则这样的m的最大值是（）A．1 B．4 C．11 D．127．（2018·淄博市期中）下列分解因式正确的是（）A．−x2+4x=−x(x+4)B．x2+xy+x=x(x+y)C．x(x−y)+y(y−x)=(x−y)2D．x2−4x+4=(x+2)(x−2) 8．（2019·牡丹区期末）已知a=255，b=344，c=533，d=622 ，那么a，b，c，d大小顺序为（）A．a<b<c<d B．a<b<d<c C．b<a<c<d D．a<d<b<c9．（2018·江西初二期末）已知关于x的分式方程m−2x+1=1的解是负数，则m的取值范围是（）A．m≤3B．m≤3且m≠2C．m＜3D．m＜3且m≠210．（2018·宜春市期末）关于x的分式方程2x+ax+1=1的解为负数，则a的取值范围是() A．a>1B．a<1C．a<1且a≠−2D．a>1且a≠2 11．（2018·潍坊市期末）学校为创建“书香校园”购买了一批图书．已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本．求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（）A．10000x ﹣9000x−5=100B．9000x−5﹣10000x=100C．10000x−5﹣9000x=100D．9000x﹣10000x−5=10012．（2018·故城县期末）已知ab=1，M=11+a+11+b ，N=a 1+a +b1+b ，则M 与N 的关系为 ( ) A ．M>N B ．M=NC ．M<ND ．不能确定二、填空题（共5小题，每小题4分，共计20分）13．（2017·荣成市期中）若x 2+2(m −3)x +16是关于x 的完全平方式，则m =__________． 14．（2018·新蔡县期中）若2x =5，2y =3，则22x+y =_____．15．（2018·新蔡县期中）已知x ，y 满足方程组{x +2y =−3x−2y=5，则x 2−4y 2的值为______． 16．（2019·泉港区期中）化简：2aa 2−4﹣1a−2=_____． 17．（2019·锦江区期末）计算mm 2−1−11−m 2的结果是_____．三、解答题（共4小题，每小题8分，共计32分）18．（2017·海淀区期中）已知a =13m +2015，b =13m +2016，c =13m +2017，求a 2+b 2+c 2−ab −bc −ac 的值．19．（2019·芜湖县期中）文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍，若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.（1）甲乙两种图书的售价分别为每本多少元？（2）书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完.）20．（2018·南通市期末）某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元.(1)第一批饮料进货单价多少元？(2)若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？21．（2018·绿园区期中）观察以下等式：第1个等式：11+02+11×02=1，第2个等式：12+13+12×13=1，第3个等式：13+24+13×24=1，第4个等式：14+35+14×35=1，第5个等式：15+46+15×46=1，……按照以上规律，解决下列问题：（1）写出第6个等式：；（2）写出你猜想的第n个等式：(用含n的等式表示)，并证明.。

人教版2019-2020学年八年级上学期期末数学模拟试卷及答案

人教版2019-2020学年八年级(上)期末数学模拟试卷(二)考试时间:100分钟，满分:120分一、选择题（共10题；共30分）1. ( 3分) 以下各组线段为边，能组成三角形的是（）A. 2，4，6B. 8，6，4C. 2，3，6D. 6，7，142. ( 3分) 下列图案中是中心对称图形但不是轴对称图形的是（）A. B. C. D.3. ( 3分) Rt△ABC中，∠C=90o，∠A为30o，CB长为5cm，则斜边上的中线长是（）A. 15cmB. 10cmC. 5cmD. 2.5cm4. ( 3分) 点P(－2,5)关于x轴对称的点的坐标为（）A. (2,－5)B. (5,－2)C. (－2,－5)D. (2,5)5. ( 3分) 已知一个多边形的内角和是900°，则这个多边形是（）A. 四边形B. 五边形C. 六边形D. 七边形6. ( 3分) 下列运算正确的是（）A. a2•a3=a6B. （a2）3=a5C. 2a2+3a2=5a6D. （a+2b）（a﹣2b）=a2﹣4b27. ( 3分) 计算（x3）5•（﹣3x2y）的结果是（）A. 6x3yB. ﹣3x17yC. ﹣6x3yD. ﹣x3y8. ( 3分) 如图，已知BC=EC，∠BCE=∠ACD，如果只添加一个条件使△ABC≌△DEC，则添加的条件不能为（）A. AB=DEB. ∠B=∠EC. AC=DCD. ∠A=∠D9. ( 3分) 如（x+m）与（x+3）的乘积中不含x的一次项，则m的值为（）A. −3B. 3C. 0D. 110. ( 3分) 如图，点B，C，D，E在同一条直线上，△ABC为等边三角形，AC=CD，AD=DE，若AB=3，AD=m，试用m的代数式表示△ABE的面积( )A. B. m C. m D. 3m二、填空题（共6题；共24分）11. ( 4分) 桥梁上的拉杆，电视塔的底座，都是三角形结构，而活动挂架是四边形结构，这是分别利用三角形和四边形的________．12. ( 4分) 把多项式x3﹣9x分解因式的结果是________．13. ( 4分) 在△ABC中，AB=3，AC=5，则BC边的取值范围是________．14. ( 4分) 当x=________ 时，分式x2−4x的值为0.15. ( 4分) 如图，∠ABD=76°，∠C=38°，BC=30cm，则BD的长为________．16. ( 4分) 如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为________.三、解答题（一）（共3题；共18分）17. ( 6分) （﹣64x4y3）÷（﹣2xy）318. ( 6分) 解方程：36x2−9+3+x3−x=−119. ( 6分) 如图，已知∠DAB＝∠CAE，AB＝AE，AD＝A C．求证：BC＝DE.四、解答题（二）（共3题；共21分）20. ( 7分) 先化简，再求值：6x2－(2x+1)(3x－2)+(x+3)(x－3)，其中x=12.21. ( 7分) 先化简，再求值：xx−1+ x+1x2−1，其中x=2．22. ( 7分) 我校图书馆添置图书，用240元购进一种科普书，同时用200元购进一种文学书．由于科普书单价是文学书单价的1.5倍，因此学校所购买的文学书比科普书多4本．（1）求文学书的单价是多少？（2）学校买了文学书和科普书一共多少本？五、解答题（三）（共3题；共27分）23. ( 9分) △ABC在平面直角坐标系xOy中的位置如图所示.①作△ABC关于点C成中心对称的△A1B1C1.②将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2.③在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）24. ( 9分) 如图，四边形ABCD中，∠A=∠B=90度，E是AB上一点，且AE=BC，∠1=∠2（1）Rt△ADE与Rt△BEC全等吗？请说明理由；（2）证明：AB＝AD＋BC；（3）△CDE是不是直角三角形？请说明理由.25. ( 9分) 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E.（1）当∠BDA=115°时，∠BAD=________°；点D从B向C运动时，∠BDA逐渐变________（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状也在改变，判断当∠BDA等于多少度时，△ADE是等腰三角形.参考答案及试题解析部分一、选择题1.【答案】B【解析】【解答】解：A、∵2+4=6，∴以2、4、6为边不能组成三角形，故本选项不符合题意；B、∵8+6＞4，4+6＞8，8+4＞6，∴以8、6、4为边能组成三角形，故本选项符合题意；C、∵2+3＜6，∴以2、3、6为边不能组成三角形，故本选项不符合题意；D、∵6+7=13＜14，∴以6、7、14为边不能组成三角形，故本选项不符合题意；故答案为：：B．【分析】看看是否符合三角形三边关系定理即可．2.【答案】C【解析】【解答】解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项错误；C、此图形旋转180°后能与原图形重合，此图形是中心对称图形，但不是轴对称图形，故此选项正确；D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项错误．故选：C．【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．3.【答案】C【解析】【分析】依题意知在Rt△ABC中，∠C=90o∠A为30o，则斜边AB=2BC=10.由于直角三角形斜边上的中线等于斜边一半，所以斜边上的中线长为5cm.【点评】本题难度较低，主要考查学生对直角三角形中线定理的掌握。

2019-2020学年人教版八年级上期末测模拟(一)

2019-2020学年人教版八年级上期末测模拟（一）考试时间：120分钟满分：120分姓名：__________ 班级：__________考号：__________题号一二三总分评分第Ⅰ卷客观题一、单选题（共10题；共30分）1. ( 3分) 分式有意义时，x的取值范围是（）A. x≠0B. x≠1C. x≠0或x≠1D. x≠0且x≠12. ( 3分) 下列各式从左边到右边的变形中，是因式分解的是（）A. ax-ay=a（x-y）B. x2-4x+4=x（x-4）+4C. x2-9+8x=（x+3）（x-3）+8xD. （3a-2）（-3a-2）=4-9a23. ( 3分) 如图，在△ABC中，∠C=40 °，按图中虚线将∠C剪去后，∠1+∠2等于（）.A. 140°B. 210°C. 220°D. 320°4. ( 3分) 如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是( )A. 线段CD的中点B. OA与OB的垂直平分线的交点C. OA与CD的垂直平分线的交点D. CD与∠AOB的平分线的交点5. ( 3分) 如图在△ABC中，BC＝8，AB，AC的垂直平分线与BC分别交于E，F两点，则△AEF的周长为( )A. 2B. 4C. 8D. 不能确定6. ( 3分) 下列从左到右的变形中,因式分解正确的是（）A. 2x2-4x+1=2x(x-2)+1B. x2-2x=x(x-2)C. (x+1)(x-1)=x2-1D. x2+2x+4=(x+2)27. ( 3分) 如果把分式中的m和n都扩大2倍，那么分式的值（）A. 不变B. 扩大2倍C. 缩小2倍D. 扩大4倍8. ( 3分) 如图，AC＝BC，AE＝CD，AE⊥CE于点E，BD⊥CD于点D，AE＝7，BD＝2，则DE的长是（）A. 7B. 5C. 3D. 29. ( 3分) 如图所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下四个结论：①△ACD≌△BCE；②AD＝BE；③∠AOB＝60°；④△CPQ是等边三角形．其中正确的是（）A. ①②③④B. ②③④C. ①③④D. ①②③10. ( 3分) 如图，A，B，C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B l C1的面积是（）A. 4B. 5C. 6D. 7第Ⅱ卷主观题二、填空题（共6题；共18分）11. ( 3分) 从一个多边形的一个顶点出发可以引5条对角线，这个多边形的边数是________．12. ( 3分) 已知x m＝8，x n＝2，则x m﹣n＝________．13. ( 3分) 如图，在五边形ABCDE中，∠A+∠E+∠D=330°，∠ABC和∠BCD的平分线交于点O，则∠BOC 的度数为________.14. ( 3分) 计算：（2 ）2002（2 +5）2002＝________．15. ( 3分) 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5的度数为________.16. ( 3分) 一批志愿者组成了一个“爱心团队”，专门到全国各地巡回演出，以募集爱心基金．第一个月他们就募集到资金1万元．随着影响的扩大，第n（n≥2）个月他们募集到的资金都将会比上个月增加20%，则当该月所募集到的资金首次完成突破10万元时，相应的n的值为________．（参考数据：1.25≈2.5，1.26≈3.0，1.27≈3.6）三、解答题（共8题；共72分）17. ( 8分) 解下列分式方程：（1）；（2）18. ( 8分) 如图，在△ABC中，∠A=46°，CE是∠ACB的平分线，B，C，D在同一条直线上，DF∥EC，∠D=42°.求∠B的度数.19. ( 8分) 如图，已知在四边形ABCD中，点E在AD上，∠BAC＝∠D，∠B+∠AEC＝180°，BC＝CE．求证：AC=DC．20. ( 8分) 已知多项式与的乘积中不含有一次项和二次项，求常数的值.21. ( 8分) 给出三个多项式X＝2a2+3ab+b2，Y＝3a2+3ab，Z＝a2+ab，请你任选两个进行加（或减）法运算，再将结果分解因式．22. ( 10分) 如图，在△ABC中，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．（1）求证：∠EFA=90°- ∠B；（2）若∠B=60°，求证：EF=DF．23. ( 10分) 已知（|x|﹣4）x+1=1，求整数x的值.小红与小明交流如下：小红：因为a0=1（a≠0），所以x+1=0且|x|﹣4=0，所以x=﹣1．小明：因为1n=1，所以|x|﹣4=1，所以x=±5你认为小红与小明同学的解答完整吗？若不完整，请求出其他所有的整数x的值．24. ( 12分) 如图①所示,已知A、B为直线L上两点,点C为直线L上方一动点,连接AC、BC,分别以AC、BC为边向ABC外作正方形CADF和正方形CBEG,过点D作DD 1l于点D1,过点E作EE1l于点E1. （1）如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB；（2）在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由；（3）如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)2019-2020学年人教版八年级上期末测模拟（一）考试时间：120分钟满分：120分姓名：__________ 班级：__________考号：__________题号一二三总分评分第Ⅰ卷客观题一、单选题（共10题；共30分）1. ( 3分) 分式有意义时，x的取值范围是（）A. x≠0B. x≠1C. x≠0或x≠1D. x≠0且x≠1【答案】D【考点】分式有意义的条件【解答】由题意得：x(x-1)≠0，则x≠0且x≠1 ,故答案为：D.【分析】要使分式有意义，即是分母不等于0，据此列式求出x的范围即可。

2019-2020学年人教版八年级上册期末模拟(一)(原卷版)

人教版初中数学八年级上册期末测试题(2019-2020学年山东省临沂市河东区

2019-2020山西省八年级上册期末英语(人教版)【试卷+答案】

2019-2020学年新人教版八年级(上)期末数学试卷 (解析版)

(人教版)四川省成都市双流县太平中学2019-2020学年度第一学期八年级物理期末测试卷(含答案)

部编本人教版2019---2020学年度八年级历史(上)期末考试卷及答案

人教新目标(Go for it)版2019-2020学年八年级上学期英语期末模拟试卷(一)(II )卷

2019-2020学年上学期洛阳偃师新前程学校人教版八年级物理上册期末模拟试卷 无答案

人教版2019-2020学年八年级上学期期末考试政治试题(I)卷

2019-2020学年人教版八年级上册数学期末考试试卷(有答案)-最新精品

2019-2020学年新部编人教版八年级语文上学期期末教学质量检测试题 (含答案)

2019-2020学年人教新目标版八年级英语上册期末模拟试卷(含答案)

期末考试模拟试卷(1)(原卷版)-2020-2021学年八年级数学下册精讲精练(人教版)

人教版八年级语文上册期末测试卷(含答案) (13)

2019-2020学年人教版八年级上册期末历史试题及答案

最新人教版八年级上册物理期末考试试卷(附答案)

2019-2020学年部编人教版八年级语文第一学期期末测试卷(含答案)

人教版2019-2020学年八年级数学(上)期末复习：全等三角形常考题型复习(解析版)

2019-2020学年人教版八年级上册期末模拟(一)(原卷版)

人教版2019-2020学年八年级上学期期末数学模拟试卷及答案

2019-2020学年人教版八年级上期末测模拟(一)

2019-2020学年上学期洛阳偃师新前程学校人教版八年级物理上册期末模拟试卷无答案