江苏省射阳县盘湾中学高中数学 1.2流程图复习课教案 苏教版必修3
高中数学 1.2《流程图》教案 苏教版必修3

1.2 流程图教学目标:1.理解流程图的概念;2.能识别和理解简单框图的功能.教学重点:流程图的概念.教学难点:用流程图表示算法.教学过程:一、建构教学1.流程图的概念:流程图是用一些图框和流程线来表示算法程序结构的一种图形程序.它直观、清晰,便于检查和修改.其中,图框表示各种操作的类型,图框中的文字和符号表示操作的内容,流程线表示操作的先后次序.2.规范流程图的表示:①使用标准的框图符号;②框图一般按从上到下、从左到右的方向画,流程线要规范;③除判断框外,大多数框图符号只有一个进入点和一个退出点.④在图形符号内描述的语言要非常简练、清楚.二、数学运用例1 已知1()21x f x =+,写出求(4)(3)(2)(4)f f f f -+-+-++的一个算法,并画出流程图.解 1S 0S ←; 2S 4I ←-;3S 1()21I f I ←+; 4S ()S S f I ←+;5S 1I I ←+;S若46I≤,转3S,否则输出S.例2 高一某班一共有50名学生,设计一个算法,统计班上数学成绩良好(分数大于80且小于90)和优秀(分数大或等于90)的学生人数,并画出流程图.解:算法如下:a←,0n←,01S1b←;S输入成绩r;23S若89S;←+,转5r>,则1a a←+;b b4r>,则1S若80←+;n nS15n≤,转2S,否则,输出a和b;S若506三、要点归纳与方法小结本节课学习了以下内容:1.如何识别简单的流程图所描述的算法.2. 能识别和理解简单框图的功能第(1)课时课题:书法---写字基本知识课型:新授课教学目标:1、初步掌握书写的姿势,了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点:基本笔画的书写。
难点:运笔的技法。
教学过程:一、了解书法的发展史及字体的分类:1、介绍我国书法的发展的历史。
2、介绍基本书体:颜、柳、赵、欧体,分类出示范本,边欣赏边讲解。
江苏省盐城市射阳县第二中学高中数学 1.2 流程图(2)选择结构导学案 苏教版必修3

结束开始流程图(2)选择结构预 习 案课题:流程图(2)(选择结构) 教学目标:1.理解选择结构的执行过程2.学会在流程图中用选择框表示选择结构 3.理解多分支选择结构的流程 重点难点:重点:掌握选择结构的执行过程;用流程图表示选择结构的算法。
难点:选择结构程序执行的过程;用多分支结构描述求解问题的算法。
一.复习导入:1.完成交换变量m,n 的值的流程图.2.上面的流程图的功能是 . 二.数学建构:先根据条件作出判断,再决定执行哪一种操作的结构称为 (或称“ ”)。
如下图中,虚线框内是一个选择结构,它包含一个判断,当条件p 成立(或称为“真”)时执行A ,否则执行B 。
在A 和B 中,有且只能有一个被执行,不可能同时被执行,但A 和B 两个框中可以有一个是空的,即不执行任何操作。
开始输入整数x r=1 输出x 是输出x 是偶结 束YNr=x 除以2的余数探 究 案探究一:1. 下图的算法流程图是为 问题而设计的.(1) (2)2.如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,完成上的流程图. 探究二:1、下面的流程图当输入值分别是2,8,3时,输出的值为NYPA BY P AN开始 输入成绩xYN及格结束开始 输入实数aa ≥0Y N输出输出“不存在” 结束a(1)(2)(3)2、上面是一个算法的流程图,当输入的值为3时,输出的结果为3、完成下面的流程图:.完成下面的解一元二次方程ax2+bx+c=0的流程图.。
苏教版高中数学必修三《流程图(第1课时)》教案

开始输入n计算2)1(+nn的值>2004 使n 的值增加Y 输出n结束N1.2 流程图(第1课时)流程图、顺序结构教学目标:1.了解常用流程图符号(输入输出框,处理框,判断框,起止框,流程线等)的意义2.能用流程图表示顺序结构3.能识别简单的流程图所描述的算法4.在学习用流程图描述算法的过程中,发展有条理地思考与表达的能力,提高逻辑思维能力.教学重点:运用程序框图表达顺序结构和条件结构的算法教学难点:规范程序框图的表示以及条件结构算法的框图教学过程:一、自学导航:二、探究新知探究1:回答下面的问题:(1)1+2+3+…+100=;(2)1+2+3+…+n=;(3)求当1+2+3+…+n>2 004时,满足条件的n的最小正整数。
第(3)个问题的算法:S1 取n等于1;S2 计算2)1(+nn;S3 如果计算的值小于等于2 004,那么让n的值增加1后转到S2重复操作,否则n就是最终所要求的结果。
算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更为直观,我们可以用图形的方式,即流程图来表示算法.新知1:流程图上述问题(3)的算法流程图表示如右:流程图(flow chart)是用一些规定的图形、连线及简单的文字说明来表示算法及程序结构的一种图形程序.它直观、清晰、易懂,便于检查和修改. 流程图中各类图框表示各种操作的类型,具体说明如下表: 程序框 名称 功能起止框表示一个算法的开始和结束输入、输出框 表示一个算法输入和输出的信息处理框赋值、计算判断框判断某一个条件是否成立,成立的在出口处标明“是”或“Y”;不成立时标明“否”或“N”画流程图实际上是将问题的算法用流程图符号表示出来,所以首先要明确需要解决什么问题,采用什么算法解决。
探究2:问题:写出作ABC ∆的外接圆的一个算法,并画出流程图。
【解】算法如下:1S 作AB 的垂直平分线1l ;2S 作BC 的垂直平分线2l ;3S 以1l 与2l 的交点M 为圆心,MA 为半径作圆,圆M 即为ABC ∆的外接圆.用流程图表示出作△ABC 的外接圆的算法:开始 结束作AB 的垂直平分线1l作BC 的垂直平分线2l以1l 与2l 的交点为圆心,MA 为半径作圆思考:上述算法的过程有何特点? 新知2:顺序结构以上过程通过依次执行三个步骤,完成了作外接圆这一问题。
2019-2020年高中数学 流程图(1)教案 苏教版必修3

2019-2020年高中数学流程图(1)教案苏教版必修3教学目标:1.了解流程图的概念,会用通用的图形符号表示算法;2.了解算法的基本逻辑结构:顺序结构、选择结构、循环结构,会画出顺序结构的流程图。
教学重点:重点是流程图的基本概念、基本图形符号;对算法的三个基本逻辑结构中的顺序结构的理解及应用教学难点:难点是能用这些知识画出流程图教学过程一、问题情境:阅读课本第7页,思考:流程图是怎样构成的?如何用流程图描述基本的算法结构?二、建构数学1.流程图:流程图基本概念:(1)流程图的概念:流程图是由一些图框和带箭头的流线组成的,其中图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流线表示操作的先后次序.说明:①一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序(2)构成程序框的图形符号及其作用⑶算法的三种基本逻辑结构:顺序结构、选择结构、循环结构.2.顺序结构依次进行多个处理的结构称为顺序结构.如右图所示,虚线框内是一个顺序结构,其中A和B两个框是依次执行的.顺序结构是一种最简单、最基本的结构. 三、数学应用例1 已知两个单元分别存放了变量x 和变量y 的值,试交换这两个变量的值.例2 半径为r 的圆的面积公式为S= r 2,当r =10时,写出计算圆的面积的算法,画出流程图.四、课堂练习:1.下列所画流程图是已知直角三角形两条直角边a 、b 求斜边的算法,其中正确的是( )2.如图的流程图,其运行结果为 .A .B .C .D .第2题图2019-2020年高中数学流程图教案苏教版必修3教学目标:使学生了解顺序结构的特点,并能解决一些与此有关的问题.教学重点:顺序结构的特性.教学难点:顺序结构的运用.教学过程:Ⅰ.课题导入算法内容是将数学中的算法与计算机技术建立联系,形式化地表示算法.为了有条理地、清晰地表达算法,往往需要将解决问题的过程整理成程序框图.流程图是一种传统的算法表示法,它利用几何图形的框来代表各种不同性质的操作,用流程线来指示算法的执行方向.由于它简单直观,所以应用广泛.问题:右面的“框图”可以表示一个算法吗?按照这一程序操作时,输出的结果是多少?若第一个“输入框”中输入的是77,则输出的结果又是多少?答:这个框图表示的是一个算法,按照这一程序操作时,输出的结果是0;若第一个“输入框”中输入的是77,则输出的结果是5。
江苏省射阳县盘湾中学高中数学 1.3基本算法语句复习课教案 苏教版必修3

江苏省射阳县盘湾中学高中数学 1.3基本算法语句复习课教案 苏教版必修3教学目标:进一步巩固基本算法语句:赋值语句、输入输出语句、条件语句、循环语句的概念,并掌握其结构;会灵活应用基本算法语句编写程序. 教学重点:各种算法语句的表示方法、结构和用法.教学难点:灵活应用各种算法语句编写程序.教学过程:一、学生活动:1、下面给出的赋值语句正确的是( )A 、4← mB 、m ← -mC 、B ←A-3D 、x+y ←02、已知变量a 、b 已被赋值,要交换a 、b 的值,应采用算法为( )A 、a ←b ,b ←aB 、a ←c ,b ←a ,c ←bC 、a ←c ,b ←a ,c ←aD 、c ←a ,a ←b ,b ←c3、为了运行下面的程序之后得到9,键盘输入应是( )A 、-4B 、-2C 、4或-4D 、2或-2(第3题) (第4题)4、根据如图所示的伪代码,可知输出的结果为( )A 、17B 、19C 、21D 、23二、例题讲解:例1(1)用伪代码写出求三个数中最小数的一个算法。
Read x If x<0 then y ← (x+1)(x+1) Else y ← (x-1)(x-1) End if Print y I ←1 While I<8 I ← I+2 S ←2I+3 End While Print S(2)用伪代码写出求a1,a2,…,a100中最小数的一个算法。
小结:例2、判断某年份是否为闰年,要看此年份能否被4整除。
若不能被4整除,则是平年,2月是28天;若能被4整除,但不能被100整除,则该年为闰年,2月是29天;若能被4整除,又能被100整除,还要看能否被400整除,若能则为闰年,否则也为平年。
画出上述算法的流程图,并写出伪代码。
苏教版高中数学必修三教学案:第1章 1.2 流 程 图

第1章 算 法 初 步1.2013年全运会在沈阳举行,运动员A 报名参赛100米短跑并通过预赛、半决赛、决赛最后获得了银牌.问题1:请简要写出该运动员参赛并获银牌的过程. 提示:报名参赛→预赛→半决赛→决赛. 问题2:上述参赛过程有何特征? 提示:参赛过程是明确的.问题3:假若你家住南京,想去沈阳观看A 的决赛,你如何设计你的旅程?提示:首先预约定票,然后选择合适的交通工具到沈阳,按时到场,检票入场,进入比赛场地,观看比赛.2.给出方程组⎩⎪⎨⎪⎧x +y =2, ①x -y =1, ②问题1:利用代入法求解此方程组. 提示:由①得y =2-x ,③把③代入②得x -(2-x )=1, 即x =32.④把④代入③得y =12.得到方程组的解⎩⎪⎨⎪⎧x =32,y =12.问题2:利用消元法求解此方程组. 提示:①+②得x =32.③将③代入①得y =12,得方程组的解⎩⎪⎨⎪⎧x =32,y =12.问题3:从问题1、2可以看出,解决一类问题的方法唯一吗? 提示:不唯一.1.算法的概念对一类问题的机械的、统一的求解方法称为算法. 2.算法的特征(1)算法是指用一系列运算规则能在有限步骤内求解某类问题,其中的每条规则必须是明确定义的、可行的.(2)算法从初始步骤开始,每一个步骤只能有一个确定的后继步骤,从而组成一个步骤序列,序列的终止表示问题得到解答或指出问题没有解答.1.算法的基本思想就是探求解决问题的一般性方法,并将解决问题的步骤用具体化、程序化的语言加以表述.2.算法是机械的,有时要进行大量重复计算,只要按部就班地去做,总能算出结果,通常把算法过程称为“数学机械化”,其最大优点是可以让计算机来完成.3.求解某一个问题的算法不一定只有唯一的一个,可能有不同的算法.[例1] 下列关于算法的说法: ①求解某一类问题的算法是唯一的 ②算法必须在有限步操作后停止③算法的每一步操作必须是明确的,不能存在歧义 ④算法执行后一定能产生确定的结果 其中,不正确的有________.[思路点拨] 利用算法特征对各个表述逐一判断,然后解答.[精解详析] 由算法的不唯一性,知①不正确; 由算法的有穷性,知②正确; 由算法的确定性,知③和④正确. [答案] ① [一点通]1.针对这个类型的问题,正确理解算法的概念及其特点是解决此类问题的关键. 2.注意算法的特征:有限性、确定性、可行性.1.下列语句表达中是算法的有________.①从济南到巴黎可以先乘火车到北京,再坐飞机抵达 ②利用公式S =12ah 计算底为1,高为2的三角形的面积③12x >2x +4 ④求M (1,2)与N (-3,-5)两点连线的方程,可先求MN 的斜率,再利用点斜式方程求得 解析:算法是解决问题的步骤与过程,这个问题并不仅仅限于数学问题.①②④都表达了一种算法.答案:①②④2.计算下列各式中的S 值,能设计算法求解的是________. ①S =1+2+3+…+100 ②S =1+2+3+…+100+… ③S =1+2+3+…+n (n ≥1且n ∈N)解析:算法的设计要求步骤是可行的,并且在有限步之内能完成任务.故①、③可设计算法求解.答案:①③[例2] 已知直线l 1:3x -y +12=0和l 2:3x +2y -6=0,求l 1,l 2,y 轴围成的三角形的面积.写出解决本题的一个算法.[思路点拨] 先求出l 1,l 2的交点坐标,再求l 1,l 2与y 轴的交点的纵坐标,即得到三角形的底;最后求三角形的高,根据面积公式求面积.[精解详析] 第一步 解方程组⎩⎪⎨⎪⎧3x -y +12=0,3x +2y -6=0得l 1,l 2的交点P (-2,6);第二步 在方程3x -y +12=0中令x =0得y =12,从而得到A (0,12);第三步 在方程3x +2y -6=0中令x =0得y =3,得到B (0,3); 第四步 求出△ABP 底边AB 的长|AB |=12-3=9; 第五步 求出△ABP 的底边AB 上的高h =2; 第六步 代入三角形的面积公式计算S =12|AB |·h ;第七步 输出结果. [一点通]设计一个具体问题的算法,通常按以下步骤: (1)认真分析问题,找出解决此题的一般数学方法; (2)借助有关变量或参数对算法加以表述; (3)将解决问题的过程划分为若干步骤; (4)用简练的语言将这个步骤表示出来.3.写出求两底半径分别为1和4,高也为4的圆台的侧面积、表面积及体积的算法.解:算法步骤如下:第一步 取r 1=1,r 2=4,h =4; 第二步 计算l =r 2-r 12+h 2;第三步 计算S 1=πr 21,S 2=πr 22;S 侧=π(r 1+r 2)l ; 第四步 计算S 表=S 1+S 2+S 侧; 第五步 计算V =13(S 1+S 1S 2+S 2)h .4.已知球的表面积为16π,求球的体积.写出解决该问题的两个算法. 解:算法1: 第一步 S =16π; 第二步 计算R =S4π(由于S =4πR 2);第三步 计算V =43πR 3;第四步 输出运算结果V . 算法2:第一步 S =16π; 第二步 计算V =43π(S4π)3;第三步 输出运算结果V .[例3] (12分)某居民区的物业部门每月向居民收取卫生费,计算方法是:3人或3人以下的住房,每月收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费.[精解详析] 设某户有x 人,根据题意,应收取的卫生费y 是x 的分段函数,即y =⎩⎪⎨⎪⎧5, x ≤3,1.2x +1.4,x >3.(4分)算法如下:第一步 输入人数x ;(6分)第二步 如果x ≤3,则y =5, 如果x >3,则y =1.2x +1.4; (10分)第三步 输出应收卫生费y .(12分)[一点通]对于此类算法设计应用问题,应当首先建立过程模型,根据模型,完成算法.注意每步设计时要用简炼的语言表述.5.如下算法: 第一步 输入x 的值;第二步 若x ≥0成立,则y =2x,否则执行第三步; 第三步 y =log 2(-x ); 第四步 输出y 的值.若输出结果y 的值为4,则输入的x 的值为________. 解析:算法执行的功能是给定x ,求分段函数y =⎩⎪⎨⎪⎧2x,x ≥0,log 2-x ,x <0对应的函数值.由y =4知2x=4或log 2(-x )=4. ∴x =2或-16. 答案:2或-166.已知直角三角形的两条直角边分别为a ,b ,设计一个求该三角形周长的算法. 解:算法如下:第一步 计算斜边c =a 2+b 2; 第二步 计算周长l =a +b +c ;第三步 输出l .1.算法的特点:有限性、确定性、逻辑性、不唯一性、普遍性. 2.在具体设计算法时,要明确以下要求:(1)算法设计是一类问题的一般解法的抽象与概括,它要借助一般问题的解决方法,又要包含这类问题的所有可能情形.设计算法时往往要把问题的解法划分为若干个可执行的步骤,有些步骤是重复执行的,但最终却必须在有限个步骤之内完成.(2)借助有关的变量或参数对算法加以表述. (3)要使算法尽量简单,步骤尽量少.课下能力提升(一)一、填空题1.写出解方程2x +3=0的一个算法过程.第一步__________________________________________________________________; 第二步__________________________________________________________________. 答案:第一步 将常数项3移到方程右边得2x =-3; 第二步 在方程两边同时除以2,得x =-32.2.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均分的一个算法为:第一步 令A =89,B =96,C =99; 第二步 计算总分S =________; 第三步 计算平均分M =________; 第四步 输出S 和M .解析:总分S 为三个成绩数之和, 平均数M =A +B +C 3=S3. 答案:A +B +C S33.给出下列算法:第一步 输入x 的值;第二步 当x >4时,计算y =x +2;否则执行下一步; 第三步 计算y =4-x ; 第四步 输出y .当输入x =0时,输出y =__________. 解析:由于x =0>4不成立,故y =4-x =2. 答案:24.已知点P 0(x 0,y 0)和直线l :Ax +By +C =0,求点到直线距离的一个算法有如下几步: ①输入点的坐标x 0,y 0; ②计算z 1=Ax 0+By 0+C ; ③计算z 2=A 2+B 2;④输入直线方程的系数A ,B 和常数C ; ⑤计算d =|z 1|z 2;⑥输出d 的值.其正确的顺序为________. 解析:利用点到直线的距离公式:d =|Ax 0+By 0+C |A 2+B2. 答案:①④②③⑤⑥5.已知数字序列:2,5,7,8,15,32,18,12,52,8.写出从该序列搜索18的一个算法. 第一步 输入实数a .第二步 __________________________________________________________________. 第三步 输出a =18.解析:从序列数字中搜索18,必须依次输入各数字才可以找到. 答案:若a =18,则执行第三步,否则返回第一步 二、解答题6.写出求a ,b ,c 中最小值的算法. 解:算法如下:第一步 比较a ,b 的大小,当a >b 时,令“最小值”为b ;否则,令“最小值”为a ; 第二步 比较第一步中的“最小值”与c 的大小,当“最小值”大于c 时,令“最小值”为c ;否则,“最小值”不变;第三步 “最小值”就是a ,b ,c 中的最小值,输出“最小值”. 7.某铁路部门规定甲、乙两地之间旅客托运行李的费用为c =⎩⎪⎨⎪⎧0.53ω, ω≤50,50×0.53+ω-50×0.85, ω>50.其中ω(单位:kg)为行李的重量,如何设计计算费用c (单位:元)的算法. 解:算法步骤如下:第一步 输入行李的重量ω;第二步 如果ω≤50,那么c =0.53ω;如果ω>50,那么c =50×0.53+(ω-50)×0.85; 第三步 输出运费c .8.下面给出一个问题的算法: 第一步 输入a ;第二步 若a ≥4,则执行第三步,否则执行第四步; 第三步 输出2a -1; 第四步 输出a 2-2a +3.问题:(1)这个算法解决的是什么问题? (2)当输入a 等于多少时,输出的值最小? 解:(1)这个算法解决的问题是求分段函数f (x )=⎩⎪⎨⎪⎧2x -1,x ≥4,x 2-2x +3,x <4的函数值问题.(2)当x ≥4时,f (x )=2x -1≥7,当x <4时,f (x )=x 2-2x +3=(x -1)2+2≥2. ∴当x =1时,f (x )min =2.即当输入a 的值为1时,输出的值最小.。
苏教版高中数学必修三《流程图(第3课时)》教案

1.2 流程图(第3课时)1.2.3 循环结构教学目标:1.了解循环结构的概念,能运用流程图表示循环结构;2.能识别简单的流程图所描述的算法;3.发展学生有条理的思考与表达能力,培养学生的逻辑思维能力.教学重点:运用流程图表示循环结构的算法.教学难点:规范流程图的表示以及循环结构算法的流程图.教学过程:一.问题情境1.情境:北京获得了2008年第29届奥运会的主办权。
你知道在申奥的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?对遴选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票数最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止。
2.问题:怎样用算法结构表述上面的操作过程?二.学生活动学生讨论,教师引导学生进行算法表达,然后画出流程图.解:算法为:1S投票;S统计票数,如果有一个城市得票超过总2票数的一半,那么该城市就获得举办权,转S,否则淘汰得票数最少的城市,转1S;3S宣布主办城市.3上述算法可以用流程图表示为:教师边讲解边画出图.三.建构数学1.循环结构的概念:需要重复执行同一操作的结构称为循环结构.如图:虚线框内是一个循环结构,先执行A 框,再判断给定的条件p 是否为假; 若p 为假,则再执行A ,再判断给定的条件p 是否为假……,如此反复,直到p 为真,该循环过程结束。
2.说明:(1)循环结构主要用在反复做某项工作的问题中;(2)循环结构是通过选择结构来实现。
3.思考:教材第7页图521--所示的算法中,哪些步骤构成了循环结构?四.数学运用1.循环结构举例例1.(教材第13页例4)写出求12345⨯⨯⨯⨯值的一个算法,并画出流程图. 解:算法1:逐一相加(见教材第13页);算法2:1S 1T ←; {使1T =}2S 2I ←; {使2I =}3S T T I ←⨯; {求T I ⨯,乘积结果仍放在变量T 中} 4S 1I I ←+; {使I 的值增加1}5S 如果5I ≤,转3S ,否则输出T 。
高中数学1.2《流程图》第1课时教案(苏教版必修3)
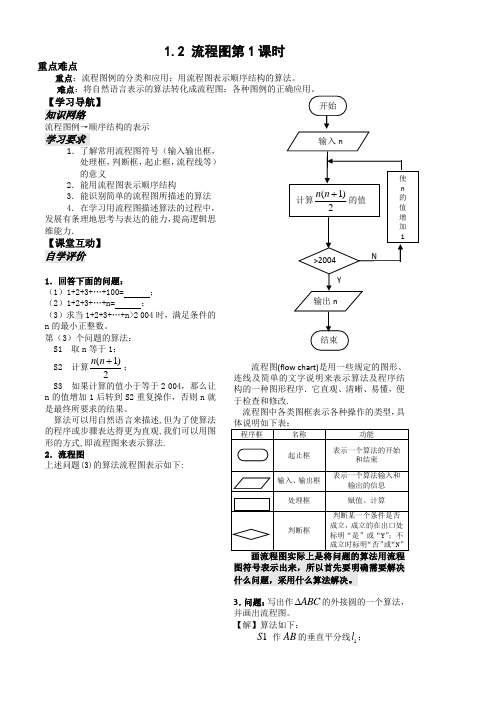
1.2 流程图第1课时重点难点重点:流程图例的分类和应用;用流程图表示顺序结构的算法。
难点:将自然语言表示的算法转化成流程图;各种图例的正确应用。
【学习导航】知识网络流程图例→顺序结构的表示学习要求1.了解常用流程图符号(输入输出框,处理框,判断框,起止框,流程线等)的意义2.能用流程图表示顺序结构3.能识别简单的流程图所描述的算法4.在学习用流程图描述算法的过程中,发展有条理地思考与表达的能力,提高逻辑思维能力.【课堂互动】自学评价1.回答下面的问题:(1)1+2+3+…+100= ;(2)1+2+3+…+n= ;(3)求当1+2+3+…+n>2 004时,满足条件的n的最小正整数。
第(3)个问题的算法:S1 取n等于1;S2 计算2)1(+nn;S3 如果计算的值小于等于2 004,那么让n的值增加1后转到S2重复操作,否则n就是最终所要求的结果。
算法可以用自然语言来描述,但为了使算法的程序或步骤表达得更为直观,我们可以用图形的方式,即流程图来表示算法.2.流程图上述问题(3)的算法流程图表示如下:流程图(flow chart)是用一些规定的图形、连线及简单的文字说明来表示算法及程序结构的一种图形程序.它直观、清晰、易懂,便于检查和修改.流程图中各类图框表示各种操作的类型,具3.问题:写出作ABC∆的外接圆的一个算法,并画出流程图。
【解】算法如下:1S作AB的垂直平分线1l;2S 作BC 的垂直平分线2l ;3S 以1l 与2l 的交点M 为圆心,MA 为半径作圆,圆M 即为ABC ∆的外接圆.用流程图表示出作△ABC 的外接圆的算法:思考:上述算法的过程有何特点?4.顺序结构以上过程通过依次执行三个步骤,完成了作外接圆这一问题。
像这种依次进行多个处理的结构称为顺序结构(sequence structure )。
顺序结构是一种最简单、最基本的结构。
【经典范例】例1 已知两个变量x 和y ,试交换这两个变量的值。
苏教版高中数学必修3-1.2《流程图》参考学案

3、绘制流程图一般步骤是:
(1)分析用自然语言描述的问题的流程,将其分解为若干个比较明确的步骤;
(2)分析每一步是否可以直接表达,或借助于逻辑结构来表达;
(3)分析各步骤之间的关系;
(4)画出流程图表示整个流程.
自学检测:
1.下列框图中,是流程图的是()
A.a→b→c→d→e→fB.a→c→d→f→e→b
C.a→e→b→c→d→fD.b→a→c→d→f→e
4.下面的工艺流程图中,设备采购的下一道工序是()
A.设备安装B.土建设计
C.厂房土建D.工程设计
注明知识要求:A“识记类”
B“理解类”
C“应用类”
D“能力提升类”
A.→→
B.→→
C.→→→
D.
2.如下图是求12+22+32+…+1002的程序框图,则图中的①②分别是()
A.①S=S+i②i=i+1
B.①S=S+i2②i=i+1
C.①i=i+1②S=S+i
D.①i=i+1②S=S+i2
3.进入互联网时代,发电子邮件是必不可少的,一般而言,发电子邮件要分成以下几个步骤:a.打开电子信箱;b.输入发送地址;c.输入主题;d.输入信件内容;e.点击“写邮件”;f.点击“发送邮件”.则正确的是()
课题
流程图
教
学
目
标
知识与技能
1.进一步认识程序框图,了解工序流程图.
2.能绘制简单实际问题的流程图,体会流程图在解决实际问题中的作用.
过程与方法
在使用流程图的过程中,逐步把握好额运用流程图来表述实际问题的方法。
情感态度
与价值观
在使用流程图的过程中,发展学生的理性思考能力和逻辑思维能力
高中数学新苏教版精品教案《苏教版高中数学必修3 1.2 流程图》

流程图教学目标:1了解流程图的概念,了解常用流程图符号〔输入输出框、处理框、判断框、起止框、流程线等〕的意义;2能用程序图表示顺序结构的算法;3开展学生有条理的思考与表达能力,培养学生的逻辑思维能力教学重点:运用流程图表示顺序结构的算法.教学难点:标准流程图的表示.教学过程:一.问题情境1.情境:答复下面的问题:〔1〕;〔2〕;2.问题:,求的最小值,试设计算法.二.学生活动学生讨论,教师引导学生进行表达.解:取;计算;假设,那么输出;否那么,使,转.上述算法可以用框图直观地描述出来:教师边讲解边画出第7页图.这样的框图我们称之为流程图.三.建构数学1.流程图的概念:流程图是用一些规定的图形、指向线及简单的文字说明来表示算法几程序结构的一种图形程序.它直观、清晰,便于检查和修改其中,图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流程线〔指向线〕表示操作的先后次序.2.构成流程图的图形符号及其作用〔课本第7页〕,结合图形讲解.3.标准流程图的表示:①使用标准的框图符号;②框图一般按从上到下、从左到右的方向画,流程线要标准;③除判断框外,大多数框图符号只有一个进入点和一个退出点④在图形符号内描述的语言要非常简练、清楚4.从流程图可以看出,该算法步骤中,有些是按顺序执行,有些需要选择执行,而另外一些需要循环执行.事实上,算法都可以由顺序结构、选择结构、循环结构这三块“积木〞通过组合和嵌套表达出来.5.顺序结构的概念:依次进行多个处理的结构称为顺序结构.四.数学运用1.顺序结构举例例1.写出作的外接圆的一个算法.解:作的垂直平分线;作的垂直平分线;以与的交点为圆心,为半径作圆,圆即为的外接圆.说明:1.以上过程通过依次执行到这三个步骤,完成了作外接圆这一问题,这种依次进行多个处理的结构就是顺序结构.2.上述算法的流程图如下列图1所示,它是一个顺序结构.图1 图2例2.两个单元分别存放了变量和的值,试交换这两个变量值.说明:1.在计算机中,每个变量都分配了一个存储单元,它们都有各自的地址.2.为了表达方便,我们用符号“〞表示“把赋给〞〔见教材第1页〕 解:为了到达交换的目的,需要一个单元存放中间变量.算法是:; 先将的值赋给变量,这时存放变量的单元可作它用; 再将的值赋给,这时存放变量的单元可作它用. 最后将的值赋给,两个变量和的值便完成了交换说明:上述算法的流程图如上图2所示,它是一个顺序结构.例3程图.解:算法如下:;;输出.说明:上述算法的流程图如右图所示,它是一个顺序结构.2.练习:课本第9页练习第1、2题.五.回忆小结1.流程图的概念:流程图是用一些规定的图形、指向线及简单的文字说明来表示算法几程序结构的一种图形程序.它直观、清晰,便于检查和修改2.画流程图的步骤:首先用自然语言描述解决问题的一个算法,再把自然语言转化为流程图;3.顺序结构的概念:依次进行多个处理的结构称为顺序结构.六.课外作业:课本第14页习题第1,3题.。
盘湾中学高中数学 1.2 流程图与顺序结构教案 苏教版必修3(2021年整理)

江苏省射阳县盘湾中学高中数学1.2 流程图与顺序结构教案苏教版必修3 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省射阳县盘湾中学高中数学1.2 流程图与顺序结构教案苏教版必修3)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省射阳县盘湾中学高中数学1.2 流程图与顺序结构教案苏教版必修3的全部内容。
流程图与顺序结构教学目标:了解流程图的概念,了解常用流程图符号(输入输出框、处理框、判断框、起止框、流程线等)的意义;能用程序图表示顺序结构的算法;发展学生有条理的思考与表达能力,培养学生的逻辑思维能力.教学重点:运用流程图表示顺序结构的算法.教学难点:规范流程图的表示.教学过程:一.问题情境1.情境:回答下面的问题:(1)123100++++=;(2)123n++++=;2.问题:已知1232006++++>,求n的最小值,试设计算法.n二.学生活动探究:上述算法可以用框图直观地描述出来:三.建构数学1.流程图的概念:2.构成流程图的图形符号及其作用:3.规范流程图的表示:①使用标准的框图符号;②框图一般按从上到下、从左到右的方向画,流程线要规范;③除判断框外,大多数框图符号只有一个进入点和一个退出点。
④在图形符号内描述的语言要非常简练、清楚.4.顺序结构的概念:四.数学运用例1.写出作ABC∆的外接圆的一个算法.小结:例2.已知两个单元分别存放了变量x 和y 的值,试交换这两个变量值.小结: 例3.半径为r 的圆的面积计算公式为2S r π=,当10r =时,写出计算圆面积的算法,画出流程图.小结:练习:书P9 1、21、确定已知线段AB 的三等分点,试设计一个算法,用流程图表示。
江苏省射阳县盘湾中学高中数学 1.2流程图循环结构教案 苏教版必修3

江苏省射阳县盘湾中学高中数学 1.2流程图-循环结构教案
苏教版必修3
教学目标:了解循环结构的概念,能运用流程图表示循环结构;能识别简单的流程图所描述的算法;发展学生有条理的思考与表达能力,培养学生的逻辑
思维能力.
教学重点:运用流程图表示循环结构的算法.
教学难点:规范流程图的表示以及循环结构算法的流程图.
教学过程:
一.问题情境
1.情境:在学校的长跑测试中,你每跑一圈,会想是否跑完了全程。
如果没有跑完全程,那么又会想离终点还有多远
2.问题:怎样用算法结构表示这个过程?
二.学生活动
探究:
1、算法:
2、流程图:
三.建构数学
1.循环结构的概念:
流程图表示:
2.说明:
3.思考:教材图1-2-9所示的算法中,哪些步骤构成了循环结构?
四.数学运用
⨯⨯⨯⨯值的一个算法,并画出流程图.
例1.写出求12345
思考:你使用了哪一种循环结构?如何用另一种循环结构来描述同样的问题?
⨯⨯⨯⨯⨯值的一个算法,并画出流程图.
变题:写出求1357911
小结:
例2.设计一个计算10个数平均数的算法,并画出流程图.
小结:
例3、下图是某流程图的主要部分,你能看出这部分流程图表示一个什么样的算法吗?
小结:
练习:书P15 练习 1、2
五.回顾小结
知识:思想方法:
六.课外作业:
书P16 4、7。
高中数学 1.2 流程图复习课教案 苏教版必修3-苏教版高中必修3数学教案

流程图
教学目标:能运用流程图表示顺序、选择、循环这三种基本结构;能识别简单的流程图所描述的算法;训练有条理的思考与准确表达自己想法的能力,提
高逻辑思维能力.
教学重点:运用流程图表示顺序、选择、循环这三种基本结构.
教学难点:循环结构算法的流程图.
教学过程:
一、学生活动:
1、下列几个选项中,不是流程图符号的是()
2、虽然算法叙述的形式有很多种类型,但算法表示为流程图,按逻辑结构分类仅有
()种
A、1
B、2
C、3
D、4
3、下图(1)流程图表示的算法是____________________________________
4、下图(2)表示的是解不等式ax+b>0 (a≠0)的算法流程图,则菱形方框中应填的是________________________
5、下图(3)的算法流程图表示的算法结果是______________________________
二、例题讲解:
---(其中例1、已知三角形的面积公式是S△ABC=p(p a)(p b)(p c) 1
p(a b c)
=++),试根据公式画出已知三边a,b,c,求三角形面积的流程
2
图。
(提示:输入三个数后先判断以它们为三边长能否构成三角形)
例2、写出求(共有6个2)的值的一个算法,并画出流程图。
练习:1、火车站对乘客在一定时段内退票要收取一定的费用,收费的办法是:按票价每10元(不足10元按10元计)核收2元,2元以下的票价不退。
试分步写出将票价为x元的车票退掉后,返还的金额y的算法,并画出流程图。
三、回顾反思:
知识:思想方法:
四、作业布置:。
江苏省射阳县盘湾中学高中数学 1.3基本算法语句复习课教案 苏教版必修3

江苏省射阳县盘湾中学高中数学 1.3基本算法语句复习课教案苏教版必修3教学目标:进一步巩固基本算法语句:赋值语句、输入输出语句、条件语句、循环语句的概念,并掌握其结构;会灵活应用基本算法语句编写程序.教学重点:各种算法语句的表示方法、结构和用法.教学难点:灵活应用各种算法语句编写程序.教学过程:一、学生活动:1、下面给出的赋值语句正确的是()A、4← mB、m ← -mC、B←A-3D、x+y←02、已知变量a、b已被赋值,要交换a、b的值,应采用算法为()A、a←b,b←aB、a←c,b←a,c←bC、a←c,b←a,c←aD、c←a,a←b,b←c3、为了运行下面的程序之后得到9,键盘输入应是()A 、-4B 、-2C 、4或-4 D 、2或-2(第3题) (第4题) 4、根据如图所示的伪代码,可知输出的结果为( ) A 、17 B 、19 C 、21D 、23二、例题讲解:例1(1)用伪代码写出求三个数中最小数的一个算法。
(2)用伪代码写出求a 1,a 2,…,a 100中最小数的一个算法。
小结:例2、判断某年份是否为闰年,要看此年份能否被4整除。
若不能被4整除,则是平年,2月是28天;若能被4整除,但不能被100整除,则该年为闰年,2月是29天;若能被4整除,又能被100整除,还要看能否被400整除,若能则为闰年,否则也为平年。
画出上述算法的流程图,并写出伪代码。
Read x If x<0 then y ← (x+1)(x+1) Else y ← (x-1)(x-1) End if Print yI ←1 While I<8 I ← I+2 S ←2I+3 End While Print S。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省射阳县盘湾中学高中数学 1.2流程图复习课教案 苏教
版必修3
教学目标:能运用流程图表示顺序、选择、循环这三种基本结构;能识别简单的流
程图所描述的算法;训练有条理的思考与准确表达自己想法的能力,提高逻辑思维能力.
教学重点:运用流程图表示顺序、选择、循环这三种基本结构.
教学难点:循环结构算法的流程图.
教学过程:
一、学生活动:
1、下列几个
选项
中,不是流程图符号的是( )
2、虽然算法叙述的形式有很多种类型,但算法表示为流程图,按逻辑结构分类仅有( )种
A 、1
B 、2
C 、3
D 、4
3、下图(1)流程图表示的算法是______________________________________
4、下图(2)表示的是解不等式ax+b>0 (a ≠0)的算法流程图,则菱形方框中应填的是________________________
5、下图(3)的算法流程图表示的算法结果是______________________________
二、例题讲解:
例1、已知三角形的面积公式是S△ABC
=(其中
1
p(a b c)
2
=++),试根据公式画出已知三边a,b,c,求三角形面积的流程图。
(提示:输入三个数后先判断以它们为三边长能否构成三角形)
例2、写出求(共有6个2)的值的一个算法,并画出流程图。
练习:1、火车站对乘客在一定时段内退票要收取一定的费用,收费的办法是:按票价每10元(不足10元按10元计)核收2元,2元以下的票价不退。
试分步写出将票价为x元的车票退掉后,返还的金额y的算法,并画出流程图。
三、回顾反思:
知识:思想方法:
四、作业布置:。
