安溪县2013年秋季九年级期末考数学试卷

合集下载

2013年秋学期期末考试九年级数学试卷

2013年秋学期期末考试九年级数学试卷（考试时间：120分钟；满分：150分；考试形式：闭卷）一、选择题（每小题3分，共24分）1.若式子2 x 在实数范围内有意义，则x 的取值范围是（） A.x ≥2 B.x ≤2 C.x>2 D.x<22.若等腰三角形的顶角为80°，则电脑的底角度数为（） A.80° B.50° C.40° D.20°3.一元次方程x 2=5x 的根是（） A.x=5 B.x=0 C.x 1=5,x 2=0 D.x 1=0,x 2=-54.如图，在⊙O 中，∠ABC=50°，则∠AOC 等于（） A.50° B.80° C.90° D.100°5.如图，在△ABC 中，∠C=90°，AB=5，BC=3，则sinA 的值是（） A.43 B.34 C.53 D.546.某镇为了发展教育事业，加强对教育经费的投入，2011年投入3000万元，预计2013年投入5000万元，设教育经费年平均增长率为x,根据题意，下列所列方程正确的是（） A.3000(1+x)2=5000; B.3000x 2=5000C.3000(1+x%)2=5000D.3000(1+x)+3000(1+x)2=50007.下列说法正确的是（） A.“打开电视机，正在播足球赛”是必然事件；B.甲组数据的方差s 2甲=0.24,乙组数据的方差s 2乙=0.03,则乙组数据比甲组数据稳定C.一组数据2，4，5，5，3，6的众数和中位数都是5D.“掷一枚硬币下面朝上的概率是0.5”，表示每抛掷两次就有1次下面朝上8.已知二次函数y=ax 2+bx+c(a ≠0)的图像如图所示，则下列结论正确的是（）A.a>0B.3是方程ax 2+bx+c=0的一个根C.a+b+c=0D.当X<1时，y 随x 增大而减小二、填空题（每小题3分，共30分） 9.计算()23-的结果是________10.我县2014年1月份某周的最低气温（单位:℃）分别是-4，2，3，-1，0，-1，-3.这组数据的极差为________ 11.计算：()()2323-+=_______12.已知⊙O 的半径OA=5cm,弦AB=8cm,P 为弦AB 上一动点，则OP 的最短距离为_____ 13.计算：cos 245°+tan30°·sin60°=_______14.把一张矩形纸片ABCD 按如图方式折叠，使顶点B 和顶点D 重合，折痕为EF ，若BF=6，FC=3，则∠DEF 的度数是________15.在△ABC中，若∠A 、∠B满足,022sin 23cos 2=⎪⎪⎭⎫⎝⎛-+-B A 则∠C=_____ 16.如图，ABCD 是平行四边形，AB 是⊙O 的直径，点D 在⊙O 上，AD=OA=1，则图中阴影部分的面积为________ 17.如图，抛物线29bx x y 2++=与y 轴相交于点A ，与过点A 平行于x 轴的直线相交于点B （点B 在第一象限），抛物线顶点C 在直线OB 上，对称轴与x 轴相交于点D ，平移抛物线，使其经过点A 、D ，则平移后的抛物线解析式为_______________ 18.如图，⊙A 与⊙B 外切于点D ，PC 、PD 、PE 分别是圆的切线，C 、D 、E 是切点，若∠DCE=25°，则∠DPE=______ 三、解答题（本大题共10题，共96分） 19.（8分）（1）计算：()0130cos 2312201312-⎪⎭⎫⎝⎛--+--第17题（2）解方程：x2-4x+1=020.(8分)如图，在正方形ABCD中，E是对角线AC上一点，连接EB、ED.（1）求证：△BEC≌△DEC；（2）延长BE交AD于点F，若∠ADE=35°，求∠AFE的度数。

安溪县2013年秋季八年级(上)期末考数学试卷

安溪县2013年秋季八年级（上）期末考数学试卷（满分：150分；考试时间：120分钟）一、选择题（每题3分，共21分，每小题只有一个正确答案，请把正确答案的代号填在题后的括号内） 1．4的算术平方根是（）． A ．2- B ．2 C ．±2 D ．16 2．计算32()x -的结果是（） A ．5x - B ．5x C ．6x - D ．6x 3．以下列各组数为边长的三角形中，能组成直角三角形的是（） A ．2，4，6 B ．4，6，8 C ．6，8，10 D ．8，10，12 4．若229(3)x mx x ++=-，则m =（） A ．6 B ．6- C ．3 D ．3- 5．如图，AB ＝AC ，若要使△ABE ≌△ACD ，则添加的一个条件不能．．是（） A ．∠B ＝∠C B ．BD ＝CE C ．BE ＝CD D ．∠ADC ＝∠AEB 6．我县有13所高中校和40所初中校，要了解我县中学生视力情况，下列抽样方式最合适的是（）． A ．随机抽取一所中学的所有学生 B ．从高中校和初中校各随机抽取一个年级的学生 C ．从初中校随机抽取1000名学生 D ．从53所中学随机抽取1000名学生 7．原命题为：“若a ＞0，b ＞0，则a b +＞0”，逆命题为：“若a b +＞0，则a ＞0，b ＞0”．下列判定正确的是（） A ．原命题为真命题，逆命题为假命题 B ．原命题与逆命题均为真命题 C ．原命题为假命题，逆命题为真命题 D ．原命题与逆命题均为假命题二、填空题（每题4分，共40分） 8≈ ．（精确到0.01） 9．计算：2(2)x xy x -÷= ． 10．因式分解：2x x +＝． 11．比较大小：（填入“＞”或“＜”号） 12．若等腰三角形的一个底角为70°，则此等腰三角形的顶角为．13．如图是某校初中三个年级学生人数分布扇形统计图，若七年级学生160人，则九年级学生人．14．如图，Rt △AOB ≌Rt △COD ，若∠A ＝36°，则∠D ＝ °．15．如图，在△ABC 中，AB 的垂直平分线交AB 于E ，交BC 于D ．连结AD ，已知AC ＝4cm ，△ADC 的周长为11cm ，则BC 的长为 cm ．＝．17．如图，已知Rt △ABC 是直角边长为l 的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，……依此类推．①第4个等腰直角三角形的面积是；②第n 个（n ＞2）等腰直角三角形的面积是．三、解答题（共89分）18．（9|1．19．（9分）因式分解：2221a a b ++-．20．（9分）先化简，再求值：222(32)3(21)a a a a a ++-+，其中2a =-．21．（9分）已知：如图，∠1＝∠2，∠C ＝∠D ．求证：OC ＝OD ．22．（9分）如图，在△ABC 中，AD ⊥BC 于D ，AB ＝13，AD ＝12，BC ＝14，求BD 、AC 的长．23．（9分）为了了解我县八年级学生的身体素质情况，随机抽取了50名学生进行一分钟跳绳次数测试，将测试情况绘制出部分频数分布表和部分频数分布直方图如下．请根据统计图表完成下列问题：（1）a ＝；（2）将频数分布直方图补充完整；（3）若八年级学生一分钟跳绳次数（x ）的达标要求是：x ≥100．请计算“达标”出现的频率是．24．（9分）已知1a b -=，2213a b +=，求下列各式的值：（1）ab ；（2）2()a b +．25．（12分）如图，在边长为4的等边△ABC 中，BD ＝CE ，AD 与BE 相交于点P ．（1）求证：△ABD ≌△BCE ；（2）求∠APE 的度数；（3）若四边形PDCE 的面积为2，求点P 到AB 的距离．26．（14分）如图，点O是等腰直角三角形ABC内一点，∠CAB＝90°，∠BOC＝120°，将△AOB绕点A按逆时针方向旋转90°得到△ADC，连结OD．（1）求证：△AOD是等腰直角三角形；（2）记∠AOB＝α．①分别用含α的代数式表示∠DOC、∠CDO和∠DCO；②当α为多少度时，△COD是等腰三角形．α四、附加题（每题5分，共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况。

安溪期末考数学试卷初三

一、选择题（每题4分，共40分）1. 已知一元二次方程x²-5x+6=0的两个根分别为x₁和x₂，则x₁+x₂的值为（）A. 5B. 6C. 10D. 112. 下列函数中，在定义域内是单调递减的是（）A. y=x²B. y=x³C. y=2xD. y=√x3. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数为（）A. 45°B. 60°C. 75°D. 90°4. 已知等腰三角形底边长为6，腰长为8，则其面积为（）A. 24B. 32C. 48D. 645. 若一个正方体的对角线长为6，则其体积为（）A. 8B. 12C. 18D. 246. 下列各式中，正确的是（）A. 3x²=9xB. 3x²=9x²C. 3x²=3xD. 3x²=97. 已知一次函数y=kx+b的图象过点（2，3），则k+b的值为（）A. 5B. 4C. 3D. 28. 在△ABC中，∠A=45°，∠B=60°，则sinC的值为（）A. 1/2B. √3/2C. √2/2D. √39. 下列函数中，是奇函数的是（）A. y=x²B. y=x³C. y=2xD. y=√x10. 若一个数列的通项公式为an=2n+1，则该数列的前5项和为（）A. 15B. 20C. 25D. 30二、填空题（每题4分，共40分）11. 若一个一元二次方程的根为x₁=-2，x₂=3，则该方程为______。

12. 已知等腰三角形的底边长为8，腰长为10，则其面积为______。

13. 若一个正方体的对角线长为√3，则其体积为______。

14. 若一个一次函数的图象过点（1，2）和（2，3），则该函数的解析式为______。

15. 在△ABC中，∠A=30°，∠B=75°，则cosC的值为______。

秋季学期九年级数学上册期末质量检测试题及答案

2013年秋季学期九年级数学上册期末质量检测试题及答案2013年下期九年级期末质量检测数学试卷卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页全卷满分120分,考试时间共120分钟。

题号一二三总分1718192021222324得分第Ⅰ卷（选择题共30分）一、选择题：（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一个选项符合题意．1.在函数中，自变量的取值范围是（）.Ax＞1Bx＜1Cx≥1Dx≤12.下列关于x的一元二次方程中，没有实数根的方程是（）.A.x2+4=0B.4x2﹣4x﹣1=0C.x2﹣x﹣3=0D.x2+2x﹣1=03.已知二次根式与是同类二次根式，则的值不可能是（）. A．3B．31C．13.5D．54.把ΔABC沿轴向下平移3个单位得到，如果A(2,4),则的坐标是（）.A.(5,4)B.(-1,4)C.(2,7)D.(2,1)5.在Rt△ABC中，已知：45°＜A＜90°，则下列各式成立的是（）.A．sinA=cosAB．sinA＞cosAC．sinA＞tanAD．sinA＜cosA6.如右图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（）.A.AB∥EFB.AB+DC=2EFC.四边形AEFB和四边形ABCD相似.D.EG=FH7.今年以来，某种食品不断上涨，在9月份的售价为8.1元/kg，11月份的售价为10元/kg。

这种食品平均每月上涨的百分率约等于（）.A.15℅B.11℅C.20℅D.9℅8.下列说法正确的是（）.A.三角形的重心是三角形三边垂直平分线的交点.B.三角形的一条中位线与第三边上的中线互相平分.C.坡面的水平长度与铅垂高度的比是坡比D.相似三角形对应高的比等于相似比的平方.9.如图2，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形与矩形OABC关于点O位似，且矩形的面积等于矩形OABC面积的1/4，那么点B/的坐标是().A．B．C．或D．或10.如图3所示，△ABC∽△DEF其相似比为K,则一次函数的图像与两坐标轴围成的三角形面积是（）A.0.5B.4C.2D.1第Ⅱ卷（非选择题共90分）二、填空题：（本大题共6个小题,每小题3分,共18分）把答案直接填在题中横线上．11.小明掷一枚骰子，投到6点的概率是.12.已知在△ABC中，BC=6cm.如果D、E分别是AB、AC的中点，那么DE=cm.13.，那么＝.14.化简的结果是.15.已知一元二次方程（≠0）的一个根是1，且,则一元二次方程的另一个根是．16.以下结论正确的有.（填番号）（1）在△ACB中，F是BC上一点，如果∠AFC=∠BAC,则(2)在Rt△ABC中∠C=90°，若cosB=，则.(3)计算（）÷的结果是1+.(4)是一元二次方程，则不等式的解集是＞-1.三、解答题：（本大题共8个小题，共72分）解答应写出必要的文字说明、证明过程或演算步骤．17．（本小题满分7分）解方程：18.（本小题满分8分）我县今年初中的实验考试，采用学生抽签的方式决定自己的考试内容，规定：每位考生先在物理学科三个实验题（题签分别用代码B1、B2、B3表示）中抽取一个，再在化学学科三个实验题（题签分别用代码J1、J2、J3表示）中抽取一个进行实验操作考试．如果你在看不到题签的情况下，分别随机地各抽取一个题签．(1)用树状图或列表法表示出所有可能的结果；(2)求你抽到的题签代码的下标（例如“B1”的下表为“1”）均为奇数的概率．19.（本小题满分8分）观察下列分母有理化的计算：，，，…从计算结果中找出规律，并利用这一规律计算：20.（本小题满分8分）．如图，在正方形网格上有△ABC 和△DEF．（1）求证:△ABC∽△DEF；（2）计算这两个三角形的周长比；（3）根据上面的计算结果，你有何猜想？21.（本小题满分9分）2013年10月31日20时02分在台湾花莲县，发生6.7级地震，某地震救援队接到上级命令后立即赶赴震区进行救援。

福建省安溪八中2013-2014学年九年级上期中数学试题

2013年秋季安溪八中初三期初考试数学试卷命题人：温培珠日期;20130901一、选择题：（每小题3分，共30分）1.要使分式1有意义，x 必须满足的条件是（） 2. 某校篮球队五名主力队员的身高分别为174、174、178、176、180（单位：cm ），则这组数据的中位数是（）3. 在平面直角坐标系中，点（2，﹣3）关于x 轴对称的点的坐标是（）4．一次函数y=2x-3的图象不经过（） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限5．如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△AOC ≌△BOC 的是（）A.43∠=∠B. B A ∠=∠C. AO=BOD. AC=BC6.若关于x 的方程221-=--x m x x 有增根，则m 的值是（） A ．0 B.l C ．2 D.37.如果3-a 是二次根式，那么a 应满足（）．A ．0≥aB ．3 aC ．3=aD ．3≥a8．若ab ＜0，则正比例函数y=a x与反比例函数b y x=在同一坐标系中的大致图象可能（）9.方程x 2－2x=0的根是（）．A ．x 1=0，x 2=2B ．x 1=0，x 2=－2C ．x=0D ．x=210.如果23=b a ，那么ba a +等于（） A. 3：2 B. 2：3 C. 3：5 D. 5：3二、填空题：（每小题4分，共40分）11．计算：ca ab ⋅＝ . 12．已知空气的单位体积质量是001239.0克/3厘米，将001239.0用科学记数法表示为．13．数据2，4，5，7的极差是__________．14.如图，若△ABC ≌△DEF ，且∠A=80°，∠B=30°，则∠F= °．15．小青在八年级上学期的物理成绩分别为：平时平均成绩得84分，期中考试得90分，期末考试得87分．如果按照如图所显示的平时、期中、期末成绩的权重，那么小青该学期的总评成绩应该为分16．命题“两直线平行，同旁内角互补”的逆命题是“ ”．17．在直角坐标系中，反比例函数xy 2=的图象在第象限． 18. 当1 x 时，2)1(-x = ．19. 如果x 2－5x+k=0的两根之差的平方是16，则k=________．20．在一次函数12+=x y 中，（1）y 随x 的增大而（填“增大”或“减小”）；（2）点),(11y x A 、),(22y x B 是一次函数12+=x y 图象上不同．．的两点，若))((2121y y x x t --=，则t 0.（用“≤、≥、>、<、=”符号表示）三、解答题：（共80分）21.（12分）计算：（1）310242011---+ ；（2）3113112-- 22．（10分）如图，∠1＝∠2，请添一个．．条件，使△ABC ≌△ADC ，并证明．（1）添加的条件是：．（2）证明：23.（10分）已知如图，一次函数y=kx+b 的图象与反比例函数xm y =的图象相交于A ，B 两点．（1）利用图中条件，求反比例函数和一次函数的解析式；（2）根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围．24．（10分）如图，梯形ABCD 中，AB ∥CD ，AC 平分∠BAD ，CE ∥AD 交AB 于点E ．求证：四边形AECD 是菱形．25.（10分）已知1+-b a 与42++b a 是互为相反数，求2008)(b a -的值．26. (14分)甲加工A 型零件60个所用时间和乙加工B 型零件80个所用时间相同，每天甲、乙两人共加工35个零件，设甲每天加工x 个.（1）直接写出乙每天加工的零件个数（用含x 的代数式表示）；（2）求甲、乙每天各加工多少个；（3）根据市场预测估计，加工A 型零件所获得的利润为m 元/ 件（3≤m ≤5），加工B 型零件所获得的利润每件比A 型少1元。

安溪期末考数学试卷初三

一、选择题（每题4分，共40分）1. 若a > b，则下列不等式中正确的是（）A. a + 1 > b + 1B. a - 1 < b - 1C. a - b > 0D. a + b < b + a2. 下列函数中，自变量x的取值范围是全体实数的是（）A. y = 2x + 3B. y = 1/xC. y = √(x - 1)D. y = x^23. 已知二次函数y = ax^2 + bx + c的图像开口向上，且顶点坐标为(-2, 1)，则a的取值范围是（）A. a > 0B. a < 0C. a ≥ 0D. a ≤ 04. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是（）A. 60°B. 45°C. 75°D. 30°5. 下列关于直角坐标系中点P（2，3）的描述正确的是（）A. 点P在第二象限B. 点P在第三象限C. 点P在第四象限D. 点P在第一象限6. 若等差数列{an}的公差d = 3，且a1 + a5 = 20，则a3的值为（）A. 7B. 8C. 9D. 107. 下列关于一次函数y = kx + b的图像描述正确的是（）A. 当k > 0时，图像经过第一、二、三象限B. 当k < 0时，图像经过第一、二、四象限C. 当b > 0时，图像与y轴的交点在x轴上方D. 当b < 0时，图像与y轴的交点在x轴下方8. 在平面直角坐标系中，点A（3，4）关于原点的对称点B的坐标是（）A.（-3，-4）B.（3，-4）C.（-3，4）D.（4，-3）9. 下列关于不等式组{2x - 1 > 0, x + 3 ≤ 5}的解集描述正确的是（）A. x > 1/2B. x ≤ 2C. 1/2 < x ≤ 2D. x > 210. 下列关于平行四边形ABCD的对角线AC和BD的描述正确的是（）A. AC = BDB. AC ≠ BDC. AC = 2BDD. AC = BD/2二、填空题（每题4分，共20分）11. 已知等差数列{an}的第三项a3 = 9，公差d = 2，则第10项a10 = ________。

2013年下学期九年级期末考试数学试卷及参考答案.doc

2013年下学期九年级期末考试试卷数学（时量：120分钟满分：120分）一、精心选一选，旗开得胜 (每小题3分,满分24分，请将正确答案的序号填写在下表内) 1. 方程x 2=x 的解是 A. x=0 B. x=1 C. x=±1 D. x=1或 x=02．如果一元二次方程212270x x ++=的两个根是12,x x ,那么12x x +的值为A. －6B. －12C. 12D. 27 3. 下列说法中正确的是A ．所有的等腰三角形都相似B ．所有的菱形都相似C ．所有的矩形都相似D ．所有的等腰直角三角形都相似 4．如图1：点O 是等边△ABC 的中心，A ′、B ′、C ′分别是OA ，OB ，OC 的中点，则△ABC 与△A ′B ′C ′是位似三角形，此时，△A ′B ′C ′与△ABC 的位似比、位似中心分别为A ．12, 点A ′ B ．2，点AC ．12，点OD ．2，点O5．在Rt △ABC 中，∠C=90°，当已知∠A 和a 时，求c ，应选择的关系式是A ．c=A a sinB ．c=A acos C ．c=A a tan ⋅ D ．c=Aatan 6. 计算： 0222sin304cos 30tan 45+-的值等于A ．4B ．C ．3D ．27. 学校评选出30名优秀学生，要选5名代表参加全市优秀学生表彰会，已经确定了1名代表，则剩余学生参加全市优秀学生表彰会的概率是 A.61 B.152 C.295 D.294 C图3AB CDE8．如图，若将四根木条钉成的矩形木框变为平行四边形ABCD ，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 ( ) A.30º B. 45º C.600D.900二、耐心填一填，一锤定音 (每小题3分, 满分24分)9. 把方程x 2-2x-3=0变为(x-a)2=b 的形式为_____________________________________ . 10．若(a －b): (a+b)=3:7, 则a :b=_______________11. 在ABC 中,∠C=900，若a=4,b=3，则sinA=____________. 12. 如果两个相似三角形的相似比为2 :3, 那么这两个相似三角形的面积比为_______________________ .13.定理“等腰梯形的对角线相等”的逆定理是 ____________________________________ .14. 如图3，△ABC 中，D,E 分别在AB 、AC 上,且DE 与BC 不平行，请填上一个适当的条件： _____________________________，可得△ADE ∽△ACB.15. 菱形的两条对角线的长分别是6cm 和8cm ，则菱形的周长是__________cm ． 16. 张洁和曾巧两个同学的生日在同一个月的概率是____________ .三、细心想一想，慧眼识金17．解下列方程(8分)（1）2230x x --=；（2）(1)(2)4x x -+=．18.计算:cos450.tan450.tan300-2cos600.sin450(6分)19. 已知关于x的一元二次方程5x2+kx－10=0一个根是－5，求k的值及方程的另一个根.（6分）20．如图4，某同学身高1.6米，由路灯下向前步行4米，发现自己的影子长有2米，问此路灯有多高？（6分）图421．从1,2,3这三个数字中任意取出一个、两个或三个可以构成不同的一位数、两位数或三位数,所有这些数中均无重复数字(如22，311等为有重复数字的数).(1)列举所有可能出现的结果.(2)出现奇数的概率是多少?（6分）四、用心做一做，马到成功 (每小题6分，满分12分)22、如图5，梯形ABCD 中，AD ∥BC,AB=DC,P 为梯形ABCD 外一点，PA 、PD 分别交线段BC 于点E 、F,且PA=PD.（1）写出图中三对你认为全等的三角形（不再添加辅助线）；（2）选择你在（1）中写出的全等三角形中的任意一对进行证明.图523.如图6，BE 是△ABC 中∠ABC 的平分线.DE ∥BC ，若AE ＝3，AD ＝4，AC ＝5,求DE 的长.（6分）图6ABCDE1 2_ _ B五、综合用一用，再接再厉(每小题8分，满分16分)24.在一块长方形镜面玻璃的四周镶上与它的周长相等的边框，制成一面镜子．镜子的长与宽的比是2∶1．已知镜面玻璃的价格是每平方米120元，边框的价格是每米30元，另外制作这面镜子还需加工费45元．如果制作这面镜子共花了195元，求这面镜子的长和宽．25．如图7,直升飞机在资江大桥AB 的上方P 点处，此时飞机离地面的高度PO=450米，且A 、B 、O 三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的跨度AB ．OB A450图7六、探究试一试，超越自我 (第26题12分)25.如图8，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M 、N 分别在边AD 、BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E 、F ．（1）求梯形ABCD 的面积；（2）设AE ＝x,用含x 的代数式表示四边形MEFN 的面积．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．图8C D ABEFNM2013年下学期期末考试九年级数学参考答案一、(每小题3分, 满分24分)二、(每小题3分, 满分24分) 9、(x-1)2=4 10、10：4 11、5412、4 ：9 13.对角线相等的梯形是等腰梯形 14、∠ ADE =∠ C,或∠ AED=∠ B 或AB AE =AC AD , 任选一种情况均可 15.20 16、121三、(第17题8分，第18题6分)17.(1)121,3x x =-= (2) 122,3x x ==-18.1 19.k=23225x =-20、△CDE ∽△ABE , 则 BEDE AB CD =,即4226.1+=AB ，AB=4.8米 21、(1)所有可能出现的结果: 一位数3个:1、2、3; 两位数6个:12、13、21、23、31、32;三位数6个:123、132、213、231、312、321.(2)出现奇数的概率为32四、(每小题6分, 满分16分)22、（1）△ABE ≌△DCF ，△ABP ≌△DCP ，△PBE ≌△PCF ，△PBF ≌△PCE 任写三种情况均可（2）证明过程略 23、先证DE =DB 再求DB =38五、(每小题8分, 满分16分)24、设长方形镜子的宽为x m , 则长为2x m, 则1954563021202=+⨯+⨯x x (4分) 即05682=-+x x 解得5.0),(25.421=-=x x 舍去答略 (4分)25、 30,45PAO PBO ∠=︒∠=︒，tan 30,tan 45PO POOA OB=︒=︒，(4分) 450tan 30OA ∴==︒， 450450tan 45OB ==︒， 1)()AB OA OB m ∴=-= 答略 (4分)六、 (12分)26、（1）分别过D 、C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ．易证四边形DGHC 为矩形，∴GH ＝DC ＝1．又可证△AGD ≌△BHC ． ∴ AG ＝BH ＝3．在Rt △AGD 中，AG ＝3，AD ＝5， ∴ DG ＝4．∴16247)(1=⨯+=ABCD S 梯形． (4分) （2）易证四边形MEFN 为矩形, △MEA ≌△NFB , △MEA ∽△DGA ∴ AE ＝BF ．设AE ＝x ，则EF ＝7－2x ．∴DG ME AG AE =． ME ＝x 34． ∴ x x x x EF ME S MEFN 32838)2(7342+-=-=⋅=矩形． (4分) （3）能．四边形MEFN 为正方形，则ME ＝EF ．由（2）知，AE ＝x ，EF ＝7－2x ，ME ＝x 34．∴ =34x7－2x ．解得1021=x ．∴ EF ＝51427=-x ＜4．（< DG ） ∴251965142=⎪⎭⎫⎝⎛=MEFN S 正方形． (4分)ABE FG H。

2013九年级数学上册期末质量检测试题(有答案)

2013九年级数学上册期末质量检测试题（有答案）洛江区2012—2013学年度初三年上学期期末质量检测数学试题温馨提示：请在答题卡上相应题目的答题区域内作答，否则不得分．一、选择题（单项选择，每小题3分，共21分）在答题卡上相应题目的答题区域内作答.1．下列计算正确的是（）A．B．C．D．2．如图，是∠的边上一点，且点的坐标为（3，4），则sin的值是（）A.B.C.D.无法确定3．一个不透明的袋子中装有2个红球，3个白球，4个黄球，这些球除颜色外没有任何其它区别，现从这个盒子中随机摸出一个球，摸到白球的概率是（）A．B．C．D．4．用配方法解方程，下列配方结果正确的是（）A.；B.；C.；D..5．如果二次根式有意义，那么的取值范围是（）．A．≥5B．≤5C．>5D．6．对于的图象下列叙述正确的是（）A．顶点坐标为（-3，2）B．对称轴为直线=3C．当=3时，有最大值2D．当≥3时随增大而减小7．如图，△ABC中，、分别是、的中点，给出下列结论：①；②；③；④∽．其中正确的结论有（）A．1个B．2个C．3个D．4个二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答.8．化简：；9．一元二次方程的解是．10．计算：sin30°＋tan45°＝．11．某商品经过两次降价，单价由50元降为30元．已知两次降价的百分率相同，求每次降价的百分率．若设每次降价百分率为，则可列方程：.12．已知抛物线的表达式是，那么它的顶点坐标是；13．在中，=90°,若cosA=，=2㎝，则=_________㎝；14．已知,则；15.如图、分别在的边、上，要使△AED∽△ABC，应添加条件是；(只写出一种即可).16．如图，点是的重心，中线＝3㎝，则＝㎝．17．是关于的方程的根，且，则的值是．三、解答题（共89分）在答题卡上相应题目的答题区域内作答.18．(9分)计算：19．(9分)解方程：20．（9分）已知，，求代数式的值．21．(9分)如图，为测楼房BE的高，用测量仪在距楼底部30米的D处，用高1.2米的测角仪测得楼顶B的仰角α为60°.求楼房BE的高度.（精确到0.1米）.22．（9分）如图，已知是原点，、两点的坐标分别为（3，-1）、（2，1）．（1）以点为位似中心，在轴的左侧将放大两倍（即新图与原图的位似比为2），画出图形并写出点、的对应点的坐标；（2）如果内部一点的坐标为，写出的对应点的坐标．23．（9分）为了节约用水，某水厂规定：某单元居民如果一个月的用水量不超过吨，那么这个月该单元居民只交10元水费．如果超过吨，则这个月除了仍要交10元水费外，超过那部分按每吨元交费．（1）该单元居民8月份用水80吨，超过了“规定的吨”，则超过部分应交水费（80-x）元（用含的式子表示）．（2）下表是该单元居民9月、10月的用水情况和交费情况：月份用水量（吨）交费总数（元）9月份852510月份5010根据上表数据，求该吨是多少？24．（9分）甲、乙、丙三位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛．请用树状图法或列表法，求恰好选中甲、乙两位同学打第一场比赛的概率．25．（13分）如图，抛物线与轴相交于点、，且经过点（5，4）．该抛物线顶点为．（1）求的值和该抛物线顶点的坐标．（2）求的面积；（3）若将该抛物线先向左平移4个单位，再向上平移2个单位，求出平移后抛物线的解析式．26．（13分）如图，在中，．点是线段边上的一动点（不含、两端点），连结,作，交线段于点．1．求证：∽；2．设,,请写与之间的函数关系式，并求的最小值。

福建省泉州市安溪县九年级数学上学期期末试题(含解析) 新人教版

福建省泉州市安溪县2015届九年级数学上学期期末试题一、选择题（每题3分，共21分．每题有且只有一个正确答案，请将正确的代号填在题后的括号内．）1．下列计算正确的是( )A．B．C．•D．2．cos60°的值等于( )A．B．C．D．3．如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是( )A．B．C．D．4．已知Rt△ABC中，∠C=90°，∠A=50°，AB=2，则AC=( )A．2sin50° B．2sin40° C．2tan50° D．2tan40°5．某商品经过两次降价，零售价降为原来的，已知两次降价的百分率均为x，则列出方程正确的是( )A．B．C．（1+x）2=2 D．（1﹣x）2=26．二次函数y=x2+2x的图象可能是( )A．B．C．D．7．如图，在正△ABC中，D、E分别在AC、AB上，且，AE=BE，则有( )A．△AED∽△ABC B．△ADB∽△BED C．△BCD∽△ABC D．△AED∽△CBD二、填空题（每小题4分，共40分）8．当x__________时，二次根式有意义．9．若关于x的一元二次方程x2+2x+a=0有实数根，则a的取值范围是__________．10．关于x的方程x2﹣mx﹣2=0有一根是﹣1，则m=__________．11．如图，在△ABC中，DE∥BC，EC=2AE，BD=6，则AD=__________．12．如图，已知△ABC∽△ACP，∠A=70°，∠APC=65°，则∠B=__________．13．随机掷一枚均匀的硬币两次，两次都是正面朝上的概率是__________．14．一个袋中装有10个红球、8个黑球、6个白球，每个球除颜色外完全相同，从袋中任意摸出一个球，那么摸到黑球的概率是__________．15．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则ac__________0．（填“＞”、“=”或“＜”）16．抛物线y=2（x+2）2﹣1的顶点坐标是__________．17．在Rt△ABC中，∠C=90°，AC=BC=4，D是AC中点，则：（1）sin∠DBC=__________；（2）tan∠DBA=__________．三、解答题（共89分）18．计算：．19．解方程：2x（x﹣1）﹣3（x﹣1）=0．20．已知抛物线的顶点坐标为（1，﹣2），且抛物线经过点（2，3），求抛物线的表达式．21．一副直角三角板如图放置，点A在ED上，∠F=∠ACB=90°，∠E=30°，∠B=45°，AC=12，试求BD的长．22．如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADB+∠EDC=120°．（1）求证：△ABD∽△DCE；（2）若BD=3，CE=2，求△ABC的边长．23．一个不透明的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，另外有一个可以自由旋转的圆盘，被分成面积相等的3个扇形区域，分别标有数字1，2，3（如图所示）．（1）从口袋中摸出一个小球，所摸球上的数字大于2的概率为__________；（2）小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于5，那么小龙去；否则小东去．你认为游戏公平吗？请用树状图或列表法说明理由．24．如图，点A、B为6×6的网格中的格点，每个小正方形的边长都为1，其中A点的坐标为（0，4）．（1）请直接写出B点的坐标；（2）若点C为6×6的网格中的格点，且∠ACB=90°，请求出符合条件的点C的坐标．25．（13分）如图，在△ABC中，AB=6cm，BC=12cm，∠B=90°．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q 分别从A、B同时出发，设移动时间为t（s）．（1）当t=2时，求△PBQ的面积；（2）当t为多少时，四边形APQC的面积最小？最小面积是多少？（3）当t为多少时，△PQB与△ABC相似？26．（13分）如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k 经过点A、B．求：（1）点A、B的坐标；（2）抛物线的函数表达式；（3）在抛物线对称轴上是否存在点P，使得以A、B、P为顶点的三角形为等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．2014-2015学年福建省泉州市安溪县九年级（上）期末数学试卷一、选择题（每题3分，共21分．每题有且只有一个正确答案，请将正确的代号填在题后的括号内．）1．下列计算正确的是( )A．B．C．•D．【考点】二次根式的混合运算．【分析】根据二次根式的加减法对A进行判断；根据二次根式的除法法则对B进行判断；根据二次根式的乘法法则对C、D进行判断．【解答】解：A、与﹣不能合并，所以A选项错误；B、原式=，所以B选项错误；C、原式==，所以C选项正确；D、原式=2，所以D选项错误．故选C．【点评】本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．2．cos60°的值等于( )A．B．C．D．【考点】特殊角的三角函数值．【分析】根据特殊角的三角函数值解题即可．【解答】解：cos60°=．故选：A．【点评】本题考查特殊角的三角函数值，准确掌握特殊角的函数值是解题关键．3．如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是( )A．B．C．D．【考点】几何概率．【分析】确定阴影部分的面积在整个转盘中占的比例，根据这个比例即可求出转盘停止转动时指针指向阴影部分的概率．【解答】解：如图：转动转盘被均匀分成6部分，阴影部分占2份，转盘停止转动时指针指向阴影部分的概率是：=；故选：C．【点评】本题考查了几何概率．用到的知识点为：概率=相应的面积与总面积之比．4．已知Rt△ABC中，∠C=90°，∠A=50°，AB=2，则AC=( )A．2sin50° B．2sin40° C．2tan50° D．2tan40°【考点】锐角三角函数的定义．【分析】根据在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，可得答案．【解答】解：由Rt△ABC中，∠C=90°，∠A=50°，得∠B=40°，由sin∠B=，得AC=ABsin∠B=2sin40°，故选：B．【点评】本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．5．某商品经过两次降价，零售价降为原来的，已知两次降价的百分率均为x，则列出方程正确的是( )A．B．C．（1+x）2=2 D．（1﹣x）2=2【考点】由实际问题抽象出一元二次方程．【专题】增长率问题．【分析】可设原价为1，关系式为：原价×（1﹣降低的百分率）2=现售价，把相关数值代入即可．【解答】解：设原价为1，则现售价为，∴可得方程为：1×（1﹣x）2=，故选B．【点评】此题主要考查了增长率的问题，一般公式为原来的量×（1±x）2=后来的量，增长用+，减少用﹣．6．二次函数y=x2+2x的图象可能是( )A．B．C．D．【考点】二次函数的图象．【分析】由二次函数性质知道其对称轴x==﹣1，当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，最后得到答案．【解答】解：∵二次函数y=x2+2x，∴此二次函数图象的开口向上，对称轴是x=﹣1，故选：C．【点评】本题考查了二次函数的性质：二次函数的称轴x=；当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大．7．如图，在正△ABC中，D、E分别在AC、AB上，且，AE=BE，则有( )A．△AED∽△ABC B．△ADB∽△BED C．△BCD∽△ABC D．△AED∽△CBD【考点】相似三角形的判定．【分析】根据等边三角形的性质得出角相等，再由已知条件求出，即两边对应成比例并且夹角相等，因此两个三角形相似．【解答】解：∵△ABC是等边三角形，=，∴AB=BC=AC，∠A=∠C，设AD=x，AC=3x，则BC=3x，CD=2x，∵AE=BE=x，∴，，∴，∴△AED∽△CBD；故选：D．【点评】本题考查了相似三角形的判定方法、等边三角形的性质；熟练掌握相似三角形的判定方法是解决问题的关键．二、填空题（每小题4分，共40分）8．当x x≥﹣1时，二次根式有意义．【考点】二次根式有意义的条件．【分析】二次根式有意义的条件是被开方数是非负数，据此即可求解．【解答】解：根据题意得：x+1≥0解得：x≥﹣1故答案是：x≥﹣1【点评】本题主要考查了二次根式有意义的条件，是一个基础的题目．9．若关于x的一元二次方程x2+2x+a=0有实数根，则a的取值范围是a≤1．【考点】根的判别式．【分析】在与一元二次方程有关的求值问题中，必须满足下列条件：（1）二次项系数不为零；[来源:]（2）在有实数根下必须满足△=b2﹣4ac≥0．【解答】解：因为关于x的一元二次方程有实根，所以△=b2﹣4ac=4﹣4a≥0，解之得a≤1．故答案为a≤1．【点评】本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．10．关于x的方程x2﹣mx﹣2=0有一根是﹣1，则m=1．【考点】一元二次方程的解．【分析】已知了一元二次方程的一个实数根，可将其代入该方程中，即可求出m的值．【解答】解：∵方程x2﹣mx﹣2=0的一根是﹣1，∴（﹣1）2﹣m×（﹣1）﹣2=0，解答：m=1，故答案为：1；【点评】此题主要考查了方程解的定义，所谓方程的解，即能够使方程左右两边相等的未知数的值．11．如图，在△ABC中，DE∥BC，EC=2AE，BD=6，则AD=3．【考点】平行线分线段成比例．【专题】计算题．【分析】根据平行线分线段成比例定理，由DE∥BC得到=，然后把EC=2AE，BD=6代入后利用比例的性质计算即可．【解答】解：∵DE∥BC，∴=，∵EC=2AE，BD=6，∴==，∴AD=3．故答案为3．【点评】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．12．如图，已知△ABC∽△ACP，∠A=70°，∠APC=65°，则∠B=45°．【考点】相似三角形的性质．【分析】根据相似三角形对应角相等可得∠ACB=∠APC=65°，再根据三角形内角和定理即可求解．【解答】解：∵△ABC∽△ACP，∴∠ACB=∠APC=65°，∵∠A=70°，∴∠B=180°﹣∠A﹣∠ACB=180°﹣70°﹣65°=45°．故答案为45°．【点评】本题考查了相似三角形的性质，掌握相似三角形对应角相等是解题的关键．也考查了三角形内角和定理．13．随机掷一枚均匀的硬币两次，两次都是正面朝上的概率是．【考点】列表法与树状图法．【分析】首先可以利用列举法，求得随机掷一枚均匀的硬币两次所出现的所有等可能的结果，然后利用概率公式直接求解即可．【解答】解：∵随机掷一枚均匀的硬币两次，可能出现的情况为：正正，正反，反正，反反，∴两次都是正面朝上的概率是．【点评】此题考查了列举法求概率的知识．解题的关键是注意不重不漏的列举出所有等可能的结果．用到的知识点为：概率=所求情况数与总情况数之比．14．一个袋中装有10个红球、8个黑球、6个白球，每个球除颜色外完全相同，从袋中任意摸出一个球，那么摸到黑球的概率是．【考点】概率公式．【分析】用黑球的个数除以所有球的个数即可求得摸到黑球的概率．【解答】解：∵共有10+8+6=24个球，其中黑球有8个，∴从袋中任意摸出一个球，那么摸到黑球的概率是=，故答案为：．【点评】考查了概率的公式，解题时用到的知识点为：概率=所求情况数与总情况数之比．15．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则ac＞0．（填“＞”、“=”或“＜”）【考点】二次函数图象与系数的关系．【分析】根据开口方向、抛物线与y轴的交点，确定a、c的符号，得到答案．[来源:] 【解答】解：∵抛物线开口向上，∴a＞0，∵抛物线与y轴交于正半轴，∴c＞0，ac＞0．故答案为：＞．【点评】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键．16．抛物线y=2（x+2）2﹣1的顶点坐标是（﹣2，﹣1）．【考点】二次函数的性质．【分析】直接根据二次函数的顶点式可得出结论．【解答】解：∵抛物线的解析式为：y=2（x+2）2﹣1，∴其顶点坐标为（﹣2，﹣1）．故答案为：（﹣2，﹣1）．【点评】本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键．17．在Rt△ABC中，∠C=90°，AC=BC=4，D是AC中点，则：（1）sin∠DBC=；（2）tan∠DBA=．【考点】解直角三角形；勾股定理；等腰直角三角形．【分析】（1）先由D是AC中点，AC=4，得出CD=AC=2，然后在Rt△BCD中，利用勾股定理求出BD==2，再根据三角函数定义即可求出sin∠DBC的值；（2）过点D作DE⊥AB于点E，先由△ABC是等腰直角三角形，得出∠A=∠ABC=45°，AB=4．再证明△ADE是等腰直角三角形，得出DE=AE=AD=，于是BE=AB﹣AE=4﹣=3，然后在Rt△BDE中，根据三角函数定义即可求出tan∠DBA的值．【解答】解：（1）∵D是AC中点，AC=4，∴CD=AD=AC=2，∵在Rt△BCD中，∠C=90°，BC=4，CD=2，∴BD==2，∴sin∠DBC===；（2）过点D作DE⊥AB于点E，∵在Rt△ABC中，∠C=90°，AC=BC=4，∴∠A=∠ABC=45°，AB=4．∵在Rt△ADE中，∠AED=90°，∠A=45°，AD=2，∴DE=AE=AD=，∴BE=AB﹣AE=4﹣=3，在Rt△BDE中，tan∠DBA===．故答案为：；．【点评】本题考查了解直角三角形，等腰直角三角形的判定与性质，勾股定理，锐角三角函数的定义，难度适中．准确作出辅助线构造直角三角形是解决（2）小题的关键．三、解答题（共89分）18．计算：．【考点】二次根式的混合运算．【专题】计算题．【分析】先根据完全平方公式和平方差公式计算得到原式=+3﹣1，然后合并即可．【解答】解：原式=+3﹣1=3﹣3﹣2+2=﹣1．【点评】本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．19．解方程：2x（x﹣1）﹣3（x﹣1）=0．【考点】解一元二次方程-因式分解法．【分析】将（x﹣1）作为公因式，提公因式解答即可．【解答】解：原方程可化为（x﹣1）（2x﹣3）=0，解得x1=1，x2=．【点评】本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．20．已知抛物线的顶点坐标为（1，﹣2），且抛物线经过点（2，3），求抛物线的表达式．【考点】待定系数法求二次函数解析式．【分析】抛物线的顶点式解析式y=a（x﹣h）2+k代入顶点坐标另一点求出a的值即可．[来源:Z&xx&]【解答】解：由抛物线的顶点坐标为（1，﹣2），设抛物线的表达式为y=a（x﹣1）2﹣2，∵抛物线经过点（2，3），∴3=a（2﹣1）2﹣2，解得a=5，∴所求的二次函数的表达式为y=5（x﹣1）2﹣2．【点评】此题考查待定系数法求函数解析式，根据题目中的已知条件，灵活选用二次函数解析式的形式解决问题是解题的关键．21．一副直角三角板如图放置，点A在ED上，∠F=∠ACB=90°，∠E=30°，∠B=45°，AC=12，试求BD的长．【考点】解直角三角形．【分析】先解Rt△ABC，由∠ACB=90°，∠B=45°，得出BC=AC=12．再解Rt△ACD，求出∠ADC=90°﹣∠E=60°，根据三角函数定义得到CD==4，那么BD=BC﹣DC=12﹣4．【解答】解：∵在Rt△ABC中，∠ACB=90°，∠B=45°，∴BC=AC=12．∵在Rt△ACD中，∠ACD=90°，∠ADC=90°﹣∠E=60°，∴CD==4，∴BD=BC﹣DC=12﹣4．【点评】本题考查了解直角三角形，锐角三角函数的定义，求出BC与DC的长是解题的关键．22．如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADB+∠EDC=120°．（1）求证：△ABD∽△DCE；（2）若BD=3，CE=2，求△ABC的边长．【考点】相似三角形的判定与性质．【分析】（1）根据等边三角形性质求出∠B=∠C=60°，根据等式性质求出∠BAD=∠CDE，即可证明△ABD∽△DCE；（2）由（1）知道△ABD∽△DCE，对应边成比例得出，列方程解答即可．【解答】解：（1）∵△ABC为正三角形，∴∠B=∠C=60°，∴∠ADB+∠BAD=120°，∵∠ADB+∠CDE=120°，∴∠BAD=∠CDE，∴△ABD∽△DCE．（2）∵△ABD∽△DCE∴，设正三角形边长为x，则，解得x=9，即△ABC的边长为9．【点评】本题考查了等边三角形性质，相似三角形的性质和判定，主要考查学生运用性质进行推理和计算的能力．能够证明△ABD∽△DCE是解决问题的关键．23．一个不透明的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，另外有一个可以自由旋转的圆盘，被分成面积相等的3个扇形区域，分别标有数字1，2，3（如图所示）．（1）从口袋中摸出一个小球，所摸球上的数字大于2的概率为；（2）小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于5，那么小龙去；否则小东去．你认为游戏公平吗？请用树状图或列表法说明理由．【考点】游戏公平性；概率公式；列表法与树状图法．【分析】（1）因为口袋中有4个小球，大于2的有两个分别是3，4，由此可求出其概率．（2）游戏公平，分别求出题目各自获胜的概率，比较概率是否相等，即可判定游戏是否公平．【解答】解：（1）∵的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，∴从口袋中摸出一个小球，所摸球上的数字大于2的概率为；故答案为：；（2）游戏公平．列举所有等可能的结果12个：1 2 3 41 2 3 4 52 3 4 5 63 4 5 6 7∴所摸球上的数字与圆盘上转出数字之和小于5的概率为P=，∴游戏公平．【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．游戏双方获胜的概率相同，游戏就公平，否则游戏不公平．用到的知识点为：概率=所求情况数与总情况数之比24．如图，点A、B为6×6的网格中的格点，每个小正方形的边长都为1，其中A点的坐标为（0，4）．（1）请直接写出B点的坐标；（2）若点C为6×6的网格中的格点，且∠ACB=90°，请求出符合条件的点C的坐标．【考点】勾股定理；坐标与图形性质；勾股定理的逆定理．【分析】（1）由A点的坐标为（0，4）可建立平面直角坐标系，由此即可求出点B的坐标；（2）由（1）中的平面直角坐标系，当∠ACB=90°，利用勾股定理的逆定理即可求出符合条件的点C的坐标．【解答】解：（1）建立如图所示的平面直角坐标系，则点B（﹣2，0）；（2）如图所示：则C（0，0）或（﹣2，4）或C（1，1）或C（1，3）．【点评】本题考查了勾股定理以及其逆定理的运用，解题的关键是熟记勾股定理以及其逆定理．勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方；勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．25．（13分）如图，在△ABC中，AB=6cm，BC=12cm，∠B=90°．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q 分别从A、B同时出发，设移动时间为t（s）．（1）当t=2时，求△PBQ的面积；（2）当t为多少时，四边形APQC的面积最小？最小面积是多少？（3）当t为多少时，△PQB与△ABC相似？【考点】相似三角形的判定与性质；二次函数的最值．【专题】动点型．【分析】（1）根据直角三角形的面积公式求解即可；（2）四边形APQC的面积=△ABC的面积﹣△PBQ的面积，再根据配方法即可求解；（3）分两种情况讨论，△BPQ∽△BAC，△BPQ∽△CBA，列比例式求解即可．【解答】解：（1）当t=2时，AP=2，BQ=4，PB=4，∴S△PBQ=BP•BQ=8（cm2），（2）∵AP=t，BQ=2t，PB=6﹣t，∴S四边形APQC=AB•BC﹣BP•BQ=36﹣（6﹣t）t=t2﹣6t+36=（t﹣3）2+27，∴当t=3时，S四边形APQC有最小值27cm2．（3）∵△PQB、△ABC是直角三角形∴由即解得t=3，由即解得t=1.2，∴当t=1.2或t=3时，△PQB与△ABC相似．【点评】此题主要考查了二次函数应用和相似三角形的判定，熟悉二次函数的性质和相似三角形的判定是解决问题的关键．26．（13分）如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k 经过点A、B．求：（1）点A、B的坐标；（2）抛物线的函数表达式；（3）在抛物线对称轴上是否存在点P，使得以A、B、P为顶点的三角形为等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．【考点】二次函数综合题．【分析】（1）由y=﹣3x+3得，当x=0时，y=3；当y=0时，x=1，即可确定点A，B的坐标；（2）把点A（1，0）、B（0，3）代入y=a（x﹣2）2+k得：，解得，即可解答；（3）存在，由AO=1，BO=3，得到AB=．设对称x轴交于点D，P（2y），D（2，0），所以DA=1，PD=|y|，PA2=PD2+DA2=y2+1，分三种情况讨论解答：当PA=AB即PA2=AB2=10时；当PB=AB即PB2=AB2=10时；当PA=PB即PA2=PB2时．【解答】解：（1）由y=﹣3x+3得，当x=0时，y=3；当y=0时，x=1∴A（1，0）、B（0，3）．（2）把点A（1，0）、B（0，3）代入y=a（x﹣2）2+k得：解得∴抛物线的函数表达式为y=（x﹣2）2﹣1．（3）∵AO=1，BO=3，∴AB=．设对称x轴交于点D，P（2，y），D（2，0），∴DA=1，PD=|y|，PA2=PD2+DA2=y2+1，当PA=AB即PA2=AB2=10时，∴y2+1=10，解得y=±3∴P（2，±3），但当P（2，﹣3）时，P、A、B在同一条直线上，不合题意舍去．∴P1（2，3），当PB=AB即PB2=AB2=10时，如图，过B作BE⊥对称轴于点E，则E（2，3），EB=2，PE2=（y﹣3）2，∴PB2=PE2+BE2=（y﹣3）2+4=10，解得∴P2（2，3+）、P3（2，3﹣），当PA=PB即PA2=PB2时，y2+1=（y﹣3）2+4解得y=2，∴P4（2，2）．综上所述，所求的点为P1（2，3），P2（2，3+），P3（2，3﹣），P4（2，2）．【点评】本题是二次函数的综合题型，其中涉及到的知识点有二元一次方程组的解法，等腰三角形的性质，勾股定理，二次函数的性质，在（3）中解决问题的关键是采用分类讨论思想解答．。

2013年初中毕业班九校联考质量检测(数学科)

2013年初中毕业班九校联考质量检测(数学科)注意事项: 本试卷共三大题25小题，共4页，满分150分．考试时间120分钟． 1．答卷前，考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考号、姓名；再用2B 铅笔把对应考号的标号涂黑．2．选择题的每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3．填空题和解答题都不要抄题，必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4．考生可以．．使用计算器．必须保持答题卡的整洁，考试结束后，交回答题卡和答卷．第一部分选择题（共30分）一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1、 3-的绝对值是（﹡）．（A ）3（B ）3-（C ）13（D ）13-2、下列图形中既是轴对称图形又是中心对称图形的是（﹡）（A ）（B ）（C ）（D ）3、不等式组 1021x x +≥⎧⎨-≤⎩的解集在数轴上的正确表示为（﹡）4、下列运算中，结果正确的是（﹡）．（A ）844a a a =+ （B ）523a a a =∙ （C ）428a a a =÷ （D ）()63262a a -=- 5、如果1x ，2x 是一元二次方程0262=--x x 的两个实数根，那么21x x +的值是（﹡）．（A ）.－2 （B ） 2 （C ）－6 （D ） 6 6、下列各点中，在反比例函数6y x=图象上的是（﹡）（A ）()23-，（B ）()23-，（C ）()16，（D ）()16-，－1 3 －1 3－1 3－1 3（A ）（B ）（C ）（D ）俯视图左视图正视图7、如图所示，AB CD ∥，∠E ＝27°，∠C ＝52°，则EAB ∠的度数为（ ﹡ ）．（A ） 25° （B ）63° （C ）79° （D ）101°8、将4个红球和若干个白球放入不透明的一个袋子内，摇匀后随机摸出一球，若摸出红球的概率为23，那么白球的个数为（﹡ ）（A ）1个（B ）2个（C ）3个（D ）6个9、已知圆锥的母线长是5cm ，侧面积是15πcm 2，则这个圆锥底面圆的半径是（﹡）．（A ）32cm （B ）3cm （C ）4cm （D ）6cm 10、方程x 2+1 =2x的正根的个数为(﹡)．（A ）3个（B ） 2个（C ）1个（D ）0个第二部分非选择题（共120分）二、耐心填一填（本题有6个小题，每小题3分，共18分）．11、如图是一个立体图形的三视图，则这个立体图形是 ﹡ ．12、如图在⊙O 中，弦AB 长为8，O C ⊥AB 于C 且OC=3，则⊙O 的半径是 ﹡ ． 13、如图，在高为2m ，坡角为30的楼梯上铺地毯，地毯的长度至少应计划 ﹡ （结果保留根号）第11题图第12题图第13题图14、分解因式：224a ab -= ﹡ ．15、已知：⊙1O 与⊙2O 外切，⊙1O 的半径为3，且128O O =，则⊙2O 的半径=R ﹡16、正方形A 1B 1C 1O ，A 2B 2C 2C 1，A 3B 3C 3C 2，…按如图所示的方式放置．点A 1，A 2，A 3，… 和点C 1，C 2，C 3，…分别在直线y kx b =+(k ＞0)和x 轴上，C D A BEyB 2A 2A 3B 3A 1已知点B 1(1，1)，B 2(3，2)，则B n 的坐标是﹡ ．三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分9分）解分式方程：1311+=-x x 18．（本小题满分9分）如图，已知，DCB ABC DC AB ∠=∠=,AC E 为、BD 的交点.① 求证：△ABC ≌△DCB ； ② 若的长求CE cm BE ,5=.19．（本小题满分10分）今年初，我省出台了一系列推进素质教育的新举措，提出了“三个还给”，即把时间还给学生，把健康还给学生，把能力还给学生．同学们利用课外活动时间积极参加体育锻炼，小东和小莉就本班同学“我最喜爱的体育项目”进行了一次调查统计，图1和图2是他们通过收集数据后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：（1）求该班共有多少名学生？（2）补全条形图；（3）在扇形统计图中，求出“乒乓球”部分所对应的圆心角的度数；（4）若全校有1500名学生，请估计“其他”的学生有多少名？20．（本小题满分10分）如图，图形中每一小格正方形的边长为1，已知ABC △（1） AC 的长等于_______．（结果保留根号）（2）将ABC △向右平移2个单位得到A B C '''△，则A 点的对应点A '的坐标是______；（3）画出将ABC △绕点C 按顺时针方向旋转90 后得到∆A 1B 1C 1，并写出A 点对应点A 1的坐标？21. (本小题满分l2分)九年级三班在召开期末总结表彰会前，班主任安排班长李小明去商店买奖品，下面是李小明与售货员的对话：李小明：阿姨，您好！售货员：同学，你好，想买点什么？李小明：我只有100元，请帮我安排买10支钢笔和15本笔记本.售货员：好，每支钢笔比每本笔记本贵2元，退你5元，请清点好，再见. 根据这段对话，你能算出钢笔和笔记本的单价各是多少吗？22. (本小题满分l2分)如图7，PA 、PB 是⊙O 的切线，A 、B 为切点，∠OAB ＝30°．（1）求∠APB 的度数；（2）当OA ＝3时，求AP 的长．23. (本小题满分l2分) 已知函数2y x=和()10y kx k =+≠．（1）若这两个函数的图象都经过点()1a ，，求a 和k 的值；（2）当k 取何值时，这两个函数的图象总有公共点？24. （本小题满分14分）如图，在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2，点P 在线段AD 上移动（点P 与点A 、D 不重合），连接PB 、PC ．（1）当△ABP ∽△PCB 时，请写出图中所有与∠ABP 相等的角，并证明你的结论；（2）求（1）中AP 的长；（3）如果PE 交线段BC 于E 、交DC 的延长线．．．于点Q ，当△ABP ∽△PEB 时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数关系式，并写出x 的取值范围．25．（本小题满分14分）如图1，在平面直角坐标系中，二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点，与y 轴交于C 点，与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），OB ＝OC ，tan∠ACO＝31．（1）求这个二次函数的表达式．（2）经过C 、D 两点的直线，与x 轴交于点E ，在该抛物线上是否存在这样的点F ，使以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请求出点F 的坐标；若不存在，请说明理由．（3）若平行于x 轴的直线与该抛物线交于M 、N 两点，且以MN 为直径的圆与x 轴相切，求该圆半径的长度．（4）如图2，若点G （2，y ）是该抛物线上一点，点P 是直线AG 下方的抛物线上一动点，当点P 运动到什么位置时，△APG 的面积最大？求出此时P 点的坐标和△APG 的最大面积.PBAO图1 图22013年初中毕业班九校联考质量检测参考答案(数学科)一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 A D DB DC CB BC 二、填空题题号 11 12 131415 16答案圆柱体52+232(-2)a a b5()-12-1,2n n三、解答题17．x+1=3(x-1) ----------------------------3’x-3x=-3-1 --------------------- 5’ -2x= -4 ------------------------------6’ x=2 --- ------------------------------7’检验：把2=x 代入0331)1)(1(≠=⨯=+-x x ----------8’∴2=x 是方程的根 ---------9’18. （1）证：在△ABC 与△DCB 中，∵AB DC ABC DCB BC CB=∠∠=⎧⎪⎨⎪⎩＝， ………………………………………3’∴△ABC ≌△DCB ……………………………………………………………………5’（2）解：∵△ABC ≌△DCB ，∴∠ACB =∠DBC ， ………………………………………………………………7’ ∴EC =EB =5cm ．……………………………………………………………………9’ 19. (1)15÷30% = 50 (名)……………2’(2)图略(条形高度不准确扣1分,徒手画图扣1分)………………………6’ (3)16÷50 × 360°=115.2°(直接用32%×360度，没有交代32%的来由扣1分)…………………8’(4)乒乓球占 16÷50=32%∴全校报“其他”项目的有 1500×(1-18%-32%-30%)=300 (名)(直接用20%×1500人，没有交代20%的来由扣1分)…………………10’ 20. (1)10………………………………………………………………3’(2)(1，2)……………………………………………………………6’(3)图3分点1分(3，0)………………………………………………………10’21. 解：设钢笔每支为x 元，笔记本每本y 元，据题意得------------------------1’⎩⎨⎧-=++=510015102y x y x ----------------------------------------6’解方程组得，⎩⎨⎧==35y x -------------------------------------------11’答;钢笔每支5元，笔记本每本3元.----------------------------------12’22.解：（1）方法一：∵在△ABO 中，OA ＝OB ，∠OAB ＝30°∴∠AOB ＝180°－2×30°＝120° ………………………3’ ∵PA 、PB 是⊙O 的切线∴OA ⊥PA ，OB ⊥PB ．即∠OAP ＝∠OBP ＝90°………………………5’ ∴在四边形OAPB 中，∠APB ＝360°－120°－90°－90°＝60°． ………………………6’ 方法二：∵PA 、PB 是⊙O 的切线 ∴PA ＝PB ，OA ⊥PA ...........................3’ ∵∠OAB ＝30°， OA ⊥PA ∴∠BAP ＝90°－30°＝60° (5)’ ∴△ABP 是等边三角形∴∠APB ＝60°． ………………………6’ （2）方法一：如图①，连结OP ………………………7’ ∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ，即∠APO ＝12∠APB ＝30° ………………………9’又∵在Rt △OAP 中，OA ＝3， ∠APO ＝30°∴AP ＝tan 30OA°＝33．………………………12’方法二：如图②，作OD ⊥AB 交AB 于点D ………………………7’ ∵在△OAB 中，OA ＝OB ∴AD ＝12AB …………9’∵在Rt △AOD 中，OA ＝3，∠OAD ＝30° ∴AD ＝OA ·cos30°＝332………………………11’ ∴AP ＝ AB ＝33．………………………12’22. 解：（1）两函数的图象都经过点()1a ，，211a a k ⎧=⎪∴⎨⎪=+⎩，．········· 4’21a k =⎧∴⎨=⎩，． ······························· 6’ （2）将2y x=代入1y kx =+，消去y ，得220kx x +-=． ··········9’0k ≠，∴要使得两函数的图象总有公共点，只要0∆≥即可． 18k ∆=+ ， ·····························10’ 180k ∴+≥，解得18k -≥．18k ∴-≥且0k ≠． ···········12’24. (1) 解：有∠PCB 和∠DPC ．……………………………………………………………2’∵△ABP ∽△PCB ，∴∠ABP =∠PCB ， ∵AD ∥BC ，∴∠DPC =∠PCB ，∴∠DPC =∠ABP ．…………………………………………5’(2) 解：梯形ABCD 中，∵AD ∥BC ，AB ＝DC ，∴∠A =∠D ．∵∠DPC =∠ABP ∴△ABP ∽△DPC ∴=AP DCAB DP．……………8’ PB AO图①PB AOD图②设AP =x ，则DP =5- x ，∴=-225x x．………………………………9’ 解得x 1= 1，x 2= 4，∴AP = 1或 4 ． ………………………………………………10’ (3) 解：∵△ABP ∽△PEB，∴∠ABP =∠PEB∵AD ∥BC ， ∴∠PEB =∠DPQ ∴∠ABP =∠DPQ ．在梯形ABCD 中，∵AB ＝DC ，∴∠D =∠A∴△ABP ∽△DPQ ．……………………………12’ ∴DQAPPD AB =． ∵AP ＝x ，CQ ＝y ，∴PD ＝5-x ，DQ ＝2 + y ． ∴y x x +=-252．∴225212-+-=x x y ．令y >0，即2152022x x -+->．观察图象得1＜x ＜4，又∵x >0，5-x >0，综上所述1＜x ＜4；…………………………………………14’ 25．（本小题满分14分）解：（1）方法一：由已知得：C （0，－3），A （－1，0） …………………………1’将A 、B 、C 三点的坐标代入得⎪⎩⎪⎨⎧-==++=+-30390c c b a c b a …………………………2’解得：⎪⎩⎪⎨⎧-=-==321c b a …………………………3’所以这个二次函数的表达式为：322--=x x y ………………………4’方法二：由已知得：C （0，－3），A （－1，0） …………………………1’ 设该表达式为：)3)(1(-+=x x a y …………………………2’ 将C 点的坐标代入得：1=a …………………………3’ 所以这个二次函数的表达式为：322--=x x y …………………………4’（注：表达式的最终结果用三种形式中的任一种都不扣分）（2）方法一：存在，F 点的坐标为（2，－3） …………………………5’2-2-451Oyx41理由：易得D （1，－4），所以直线CD 的解析式为：3--=x y∴E 点的坐标为（－3，0） …………………………5’ 由A 、C 、E 、F 四点的坐标得：AE ＝CF ＝2，AE ∥CF ∴以A 、C 、E 、F 为顶点的四边形为平行四边形∴存在点F ，坐标为（2，－3） …………………………7’ 方法二：易得D （1，－4），所以直线CD 的解析式为：3--=x y∴E 点的坐标为（－3，0） …………………………5’ ∵以A 、C 、E 、F 为顶点的四边形为平行四边形∴F 点的坐标为（2，－3）或（―2，―3）或（－4，3）代入抛物线的表达式检验，只有（2，－3）符合∴存在点F ，坐标为（2，－3） …………………………7’ （3）如图，①当直线MN 在x 轴上方时，设圆的半径为R （R>0），则N （R+1，R ），代入抛物线的表达式，解得2171+=R…………9’ ②当直线MN 在x 轴下方时，设圆的半径为r （r>0），则N （r+1，－r ），代入抛物线的表达式，解得2171+-=r………10’ ∴圆的半径为2171+或2171+-． ……………11’（4）过点P 作y 轴的平行线与AG 交于点Q ，易得G （2，－3），直线AG 为1--=x y ．……………12’ 设P （x ，322--x x ），则Q （x ，－x －1），PQ 22++-=x x ．3)2(212⨯++-=+=∆∆∆x x S S S GPQ APQ APG …………………………13’ 当21=x 时，△APG 的面积最大此时P 点的坐标为⎪⎭⎫⎝⎛-415,21，827的最大值为APG S ∆． …………………………14’RRrr 11NNMMAB DOxy。

2013-2014学年度第一学期期末考试九年级数学试卷(2021年整理)

2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2013-2014学年度第一学期期末考试九年级数学试卷(word版可编辑修改)的全部内容。

2013~2014学年度第一学期期末抽测九年级数学试题本试卷分卷Ⅰ(1至2页)和卷Ⅱ（3至8页）两部分．全卷满分120分，考试时间90分钟.卷Ⅰ一、选择题(本大题共有8小题,每小题3分，共24分．请将正确选项前的字母代号填写在第3页相应的答题栏内，在卷Ⅰ上答题无效)1．两圆的半径分别为3和4，圆心距为7,则这两圆的位置关系为A ．相交B ．内含C ．内切D ．外切 2．如图,OA 、OB 是⊙O 的两条半径，且OA ⊥OB ，点C 在⊙O 上,则∠ACB 的度数为 A ．45° B ．35° C ．25° D ．20°3．如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ,如果AB ＝20，CD ＝16．那么线段OE 的长为A ．4B ．5C ．6D ．84．如果将抛物线2=y x 向上平移1个单位，那么所得抛物线对应的函数关系式是A ．21=+y xB ．21=-y xC ．2(1)=+y xD ．2(1)=-y x5．菱形具有而矩形不一定具有的性质是A ．对角线相等B ．对角线互相垂直C ．对角线互相平分D ．对角互补6．若圆锥的轴截面为等边三角形，则称此圆锥为正圆锥．正圆锥侧面展开图的圆心角是 A ．90° B ．120°C ．150°D ．180°（第2题）（第3题）7．根据下列表格的对应值：可得方程2530+-=x x 一个解x 的范围是A ．0＜x ＜0。

9数学答案

PE 1 9 10 ED 1 4 5
∴ PD ED PE …… 7 分
2 2 2
∴△PDE 为直角三角形 ∴PD⊥PE， ………… 8 分 ∵点 D 在⊙P 上， ∴直线 l 与⊙P 相切．…… 10 分 27．解：（1）设顾客一次至少购买 x 件，由题意，得
九数学答案第 3 页（共 6 页）
21．解：根据题意得： B 4 AC 0
2
………………………………………… 6 分 ………………………………………… 8 分 ………………………………………… 2 分
(b 2) 2 4(6 b) 0
解得： b1 2 ， b2 10 ………………………………………… 4 分
y (55 50 1.6) x
∴ y 3.4 x 综上，利润 y（元）与出售量 x（件）之间的函数关系式为：
y 0.1x 2 9.4x （10＜x≤60）， y 3.4 x （x＞60）
……………………………… 8 分（3）∵当 10＜x≤60 时，
y 0.1x 2 9.4x
解之得： x1 2 ， x2 9 （舍去） ………………………… 7 分 ∴长为：9cm，宽为：5cm．
九数学答案第 2 页（共 6 页）
∴包装盒的体积为：9× 5× 2=90cm ． ………………………………… 10 分 25．（1）证明：b2－4ac＝m2－4(m－2) ＝m2－4m＋4＋4 ＝(m－2)2＋4 ∵(m－2) ≥0 ∴(m－2)2＋4 ＞0 ∴x2－mx＋m－2＝0 一定有两个不等的实数解．…………………… 2 分 ∴无论 m 为任何实数，该二次函数的图象与 x 轴都有两个交点； …………………… 3 分（2）解：①把 x＝－1，y＝3，代入 y＝x2－mx＋m－2，解得 m＝2 则二次函数的关系式为 y＝x －2x 配方得 y＝（x－1）－1 ∴顶点坐标为（1，－1） ②画图正确；(图略) ③当 y＜0 时 x 的取值范围为 0＜x＜2． 26．解：（1）正确画出△ABC 的外接圆 △ABC 外接圆的圆心为 P（－1，0） ∵A（1，1），B（－3，－1） ∴ AB ∴r …………………… 6 分 …………………… 8 分 …………………… 10 分 …………………… 2 分 …………………… 3 分

安溪县2013年秋季九年级期末考数学试卷

1-0 1安溪县2013年秋季九年级期末考数学试卷一、选择题（单项选择，每小题3分，共21分） 1（）A ．5B ．±5C ．5-D ．3- 2．下列计算正确的是（）A ．=B ．3412=C 3=D ．24±= 3．用配方法解方程2250x x --=时，原方程应变形为（） A ．2(1)6x += B ．2(2)9x += C ．2(1)6x -= D ．2(2)9x -= 4．下列三角形一定相似的是（）A ．两个等边三角形B ．两个直角三角形C ．有一个角为30°的两个等腰三角形D．两个等腰三角形5．在梯形ABCD中，AD ∥BC ，AC 、BD 相交于O ，如果那么下列结论正确的是（）A ．S △COD ＝9S △AODB ．S △ABC ＝9S △ACD C ．S △BOC ＝9S △AOD D ．S △DBC ＝9S △AOD 6．点P （3-，2）关于y 轴对称的点的坐标是（）A. （－3，－2）B. （3-，2）C. （3，－2）D. （3，2）7．实数a 、b）A ．2b -B ．2a -C ．22a b --D ．22a b -+二、填空题（每小题4分，共40分） 8．当x 时，二次根式有意义．9．方程230x x -=的根是．10．计算：(2= ． 11．已知23=b a ，则=-b b a ________． 12．已知：△ABC ∽ △DEF ，且相似比为1:2，则它们的面积比是．13．若点A （－2，3）先向右平移3个单位，再向下平移2个单位后所得的点的坐标是．14．布袋中装有2个红球，3个白球，5个黑球，它们除颜色外均相同，则从袋中任意摸出一个球是白球．．的概率是__________．15．已知梯形上底长为8cm ，下底长为12cm ，则梯形的中位线长为 cm ． 16．某坡面的坡度为3:1，则它的坡角是度．17．如图，已知△ABC 中，AB= 10，BC= 6 ，AC= 8 ，PQ ∥AB ，CPQAA DC B E F P 点在AC 上（与点A 、C 不重合），Q 点在BC 上．①当△PQC 的面积与四边形PABQ 的面积相等时，CP 的长等于． ②当△PQC 的周长与四边形PABQ 的周长相等时，CP 的长等于．三、解答题（共89分）18．（9(+ 19．（9分）用适当的方法解方程：22(3)18x -=．20．（9分）已知a 、b 、c 为△ABC 的三边长，且36a b c ++=，345a b c==，求△ABC 三边的长． 21．（9分）如图，矩形ABCD 中，E 为BC 上一点，DF ⊥AE 于点F ．（1）求证：△ABE ∽△DFA ；（2）若AB=6，AD=12，BE=8，求DF 的长．22．（9分）如图，已知△ABC 的三个顶点坐标为A （0，2-）、B （3，1-）、C （2，1）．（1）在网格图中，画出△ABC 以点B 为位似中心，放大到2倍后的△11A B C ；（2）写出1A 、1C 的坐标．23．（9分）在一个黑色的布口袋里装着白、红、黑三种颜色的小球，它们除了颜色之外没有其它区别，其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀．（1）随机地从袋中摸出1只球，则摸出白球的概率是多少？（2）随机地从袋中摸出1只球，放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果，并求两次都摸出白球的概率．24．（9分）将进货价为40元的商品按50元售出时，能卖出500个，已知这种商品每个涨价1元，其销售量就减少10个.若设这种商品每个涨价x元．（1）用含x的代数式表示：①每个商品的实际利润是元，②实际的销售量是个；（2）为了获得8000元的利润，售价应定为多少？25．（12分）如图，在△ABC中，∠C=90°，BC = 7cm，AC = 24cm，P点在BC上，从B点到C点运动（不包括C 点），点P运动的速度为2cm/s；Q点在AC上，从C点运动到A点（不包括A点），速度为5cm/s.若点P、Q分别从B、C同时运动，设经过了x秒，请解答下面的问题，并写出探索的主要过程：（2）经过多少时间，△PCQ的面积为15cm2；（3）经过多少时间，△PCQ的面积最大，最大面积是多少？EF26．（14分）如图，平面直角坐标系中，直线AB 解析式为：y=33x+3．直线与x 轴、y 轴分别交于A 、B 两点．（1）写出线段OA 、OB 的长度，OA= ，OB= ；（2）若点C 是AB 的中点，过点C 作CD ⊥x 轴于点D ，E 、F 分别为BC 、OD 的中点，求点E 的坐标；（3）在第一象限内是否存在点P ，使得以P 、O 、B 为顶点的三角形与△OBA 相似.若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．A BDE C四、附加题（共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷总分已经达到或超过90分，则本题的得分不计入全卷总分． 1．（5分）计算：=-3233 ．2．（5分）如图，在△ABC 中，BC=2，则中位线DE= ．。

安溪县2013年秋季九年级期末考数学试卷

5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。

我们只说喜欢，就算喜欢也是偷偷摸摸的。

”6.方茴说：“我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。

”7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。

8.这些孩子都很活泼与好动，即便吃饭时也都不太老实，不少人抱着陶碗从自家出来，凑到了一起。

9.石村周围草木丰茂，猛兽众多，可守着大山，村人的食物相对来说却算不上丰盛，只是一些粗麦饼、野果以及孩子们碗中少量的肉食。

1.“噢，居然有土龙肉，给我一块！”2.老人们都笑了，自巨石上起身。

而那些身材健壮如虎的成年人则是一阵笑骂，数落着自己的孩子，拎着骨棒与阔剑也快步向自家中走去。

安溪县2013年秋季九年级期末考数学试卷（考试时间；120分钟；总分：150分）一、选择题（单项选择，每小题3分，共21分） 1（）A ．5B ．±5C ．5-D ．3- 2．下列计算正确的是（）A ．=B ．3412=C 3=D ．24±= 3．用配方法解方程2250x x --=时，原方程应变形为（） A ．2(1)6x += B ．2(2)9x += C ．2(1)6x -= D ．2(2)9x -= 4．下列三角形一定相似的是（）A ．两个等边三角形B ．两个直角三角形C ．有一个角为30°的两个等腰三角形D ．两个等腰三角形5．在梯形ABCD 中，AD ∥BC ，AC 、BD 相交于O ，如果那么下列结论正确的是（）A ．S △COD ＝9S △AODB ．S △ABC ＝9S △ACD C ．S △BOC ＝9S △AOD D ．S △DBC ＝9S △AOD5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。

我们只说喜欢，就算喜欢也是偷偷摸摸的。

安溪县2013年秋季七年级(上)期末考数学试卷

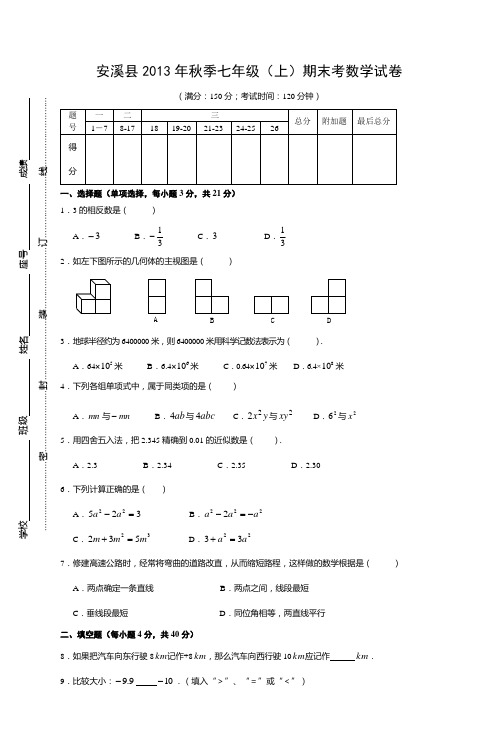
北安溪县2013年秋季七年级（上）期末考数学试卷（满分：150分；考试时间：120分钟）一、选择题（单项选择，每小题3分，共21分） 1．3的相反数是（） A ．3- B ．31-C ．3D ．31 2．如左下图所示的几何体的主视图是（）3．地球半径约为6400000米，则6400000米用科学记数法表示为（）． A ．64×510米 B ．6.4×610米 C ．0.64×710米 D ．6.4×810米 4．下列各组单项式中，属于同类项的是（） A ．mn 与mn -B ．ab 4与abc 4C ．y x 22与2xyD ．26与2x5．用四舍五入法，把2.345精确到0.01的近似数是（）．A ．2.3B ．2.34C ．2.35D ．2.30 6．下列计算正确的是（）A ．32522=-a a B ．2222a a a -=- C ．32532m m m =+ D ．2233a a =+7．修建高速公路时，经常将弯曲的道路改直，从而缩短路程，这样做的数学根据是（） A ．两点确定一条直线 B ．两点之间，线段最短 C ．垂线段最短D ．同位角相等，两直线平行二、填空题（每小题4分，共40分）8．如果把汽车向东行驶8km 记作+8km ，那么汽车向西行驶10km 应记作 km ． 9．比较大小：9.9- 10-．（填入“＞”、“＝”或“＜”） 10．计算：｜3-｜＝．11. 若∠α=75°，则∠α的补角．．等于 °． 12．如图，已知直线a ∥b ，∠1＝35°，则∠2的度数是 °． 13．“比a 的3倍小2的数”用整式表示是．14．把多项式3221x x x +-- 按x 降幂排列：___________________． 15. 如图，160∠=︒，则射线OA 表示北偏西． 16．如图，是一个正方体的表面展开图，原正方体中“新”面的对面上的字是．17．规定一种新运算“*”，规则：abba b a +=*（0≠ab ），如2*1＝232121=⨯+．（1）直接写出计算结果3*)2(-＝；（2）该运算是否满足交换律，为什么？请举例子说明．．三、解答题（共89分）18．（6分）点A 、B 在数轴上的位置如图所示：（1）点A 表示的数是，点B 表示的数是；（2）在原图中分别标出表示＋4的点C 、表示 2.5-的点D ；（3）在上述条件下，B 、C 两点间的距离是，A 、C 两点间的距离是．19．计算下列各题（每小题6分，共24分）（1）()()()4685+-+--- （2）)6(48)4()3(-÷-+⨯- （3）30)312153(⨯+-（4）[]22)2(5511--⨯--20．化简或计算（每小题6分，共12分）祝年快你新乐（1）先去括号，再合并同类项：)21(3)13(2a a -+-．（2）先化简，再求值：)()35(2222n m mn mn n m +--，其中21=m ，1-=n ． 21．（6分）如图，D 是线段AC 的中点，E是线段AB 的中点．已知AD=2.5cm ，BC=2cm ，求线段AB 和EC 的长度．22．（6分）如图，点P 是AOB ∠的边OB 上的一点．（1）过点P 画OB 的垂线，交OA 于点C ；（2）过点P 画OA 的垂线，垂足为H ；（3）线段PH 的长度是点P 到的距离，是点C 到直线OB 的距离．23．（6分）如图，已知：∠DAF=∠F ，∠B=∠D ，试说明AB ∥DC ．下面是解答过程，请你在括号内填写理由．解：∵∠DAF=∠F （已知）∴ AD ∥BF （）· · · · · A D E C BABCD EF∴ ∠D=∠DCF （） ∵∠B=∠D （已知）∴∠B=∠DCF （等量代换）∴AB ∥DC （）24．（6分）检修小组从A 地出发，在东西走向的路上检修线路，如果规定向东为正，向西为负，一天中每次行驶记录如下（单位：千米）；5-，+8，7-，+11，+4，3-，2-．（1）收工时在A 地的哪个方向？距A 地多远？（2）距A 地最远的是哪一次？（3）若每千米耗油0.8升，从出发到收工共耗油多少升？ 25．（11分）观察下列等式：211211-=⨯，3121321-=⨯ ，4131431-=⨯．将以上三个等式两边分别相加得：4341141313121211431321211=-=-+-+-=⨯+⨯+⨯ （1）猜想并写出：)1(1+⋅n n =_______________________；（2）直接写出下列各式的计算结果： ①111112233410061007++++=⨯⨯⨯⨯ _____________________________； ②=+⋅++⨯+⨯+⨯)1(1431321211n n _______________________________；（3）探究并计算：111124466820122014++++⨯⨯⨯⨯ ．26．（12分）（1）如图1，OM 平分∠AOB ，ON 平分∠BOC ．①若∠AOB=90º，∠BOC=30º，求∠MON 的度数； ②若∠AOB=α，∠BOC=β（β为锐角），求∠MON 的度数；（2）如图2，OM 平分∠AOC ，ON 平分∠BOC ．若∠AOB ＝α，∠BOC ＝β，求∠MON 的度数．从结果你能看出∠MON 与∠AOB 有什么关系？A OMBNC 图1图2四、附加题（共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷得分已经达到或超过90分，则本题的得分不计入全卷总分．1．（5分）计算：0(3)⨯-＝．2．（5分）已知∠A＝︒50，则∠A的余角是度．。

安溪初中毕业试卷数学

一、选择题（每题3分，共30分）1. 下列数中，不是有理数的是（）A. 0.6B. √2C. -3/5D. 0.333...2. 已知a、b是实数，且a+b=3，ab=4，则a²+b²的值为（）A. 5B. 13C. 17D. 253. 下列函数中，不是一次函数的是（）A. y=2x+1B. y=3x-5C. y=x²+2x+1D. y=54. 已知等腰三角形底边长为8cm，腰长为10cm，则该三角形的面积为（）A. 40cm²B. 48cm²C. 64cm²D. 80cm²5. 在平面直角坐标系中，点A（2，3）关于y轴的对称点为（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）6. 下列不等式中，正确的是（）A. 2x > 4B. 3x < 6C. 4x ≤ 8D. 5x ≥ 107. 已知二次函数y=ax²+bx+c的图象开口向上，且顶点坐标为（1，-2），则a、b、c的值分别为（）A. a=1，b=2，c=-3B. a=1，b=-2，c=3C. a=-1，b=2，c=3D. a=-1，b=-2，c=-38. 在△ABC中，∠A=45°，∠B=60°，则∠C的度数为（）A. 75°B. 105°C. 120°D. 135°9. 下列命题中，正确的是（）A. 平行四边形的对边相等B. 等腰三角形的底角相等C. 相似三角形的面积比等于边长比D. 直角三角形的斜边最长10. 下列函数中，不是反比例函数的是（）A. y=2/xB. y=3/x+1C. y=4/x²D. y=5/x³二、填空题（每题5分，共25分）11. 若|a|=3，则a=______（写出所有可能的值）。

12. 若x²-5x+6=0，则x=______。