第5章指派问题

合集下载

第5章整数-指派问题

(if i ≠ k ); cij , bij = ckj + a, (if i = k ).
则以b 则以 ij为系数的新指派问题的目标函数为 n n z = ∑i =1 ∑ j =1 bij xij
= ∑i ≠ k ∑ j =1 cij xij + ∑ j =1 (ckj + a ) xkj
n n
= ∑i =1 ∑ j =1 cij xij + a ∑ j =1 xkj = z + a
n n n
利用性质1, 利用性质 ,可使原系数矩阵变换为含有很多0元素的新系数矩阵元素的新系数矩阵, 有很多元素的新系数矩阵,而最优解保持不变,在系数矩阵(b 中持不变,在系数矩阵 ij)中,我们关心位于不同行不同列的0元素元素, 于不同行不同列的元素,以下简称为独立的0元素. 立的元素. 元素利用性质2,若能在系数矩阵(b 中找利用性质 , 若能在系数矩阵 ij)中找个独立的0元素出n个独立的元素;则令解矩阵 ij)中对个独立的元素;则令解矩阵(x 中对应这n个独立的元素的元素取值为1, 个独立的0元素的元素取值为应这个独立的元素的元素取值为 ,其他元素取值为0. 他元素取值为 .将其代入目标函数中得到zb=0,它一定是最小. ,它一定是最小. 这就是以 ij)为系数矩阵的指派问题的这就是以(b 为系数矩阵的指派问题的最优解.也就得到了原问题的最优解. 最优解.也就得到了原问题的最优解.
解按上述第一步,将这系数矩阵进行变换.
min 12 7 9 7 9 7 5 0 2 0 8 9 6 6 6 6 2 3 0 0 7 17 12 14 9 7 → 0 10 5 7 15 14 6 6 10 6 9 8 0 0 4 10 7 10 9 4 0 6 3 6 2 0 2 4 5

指派问题

-2 -4 -9 -7
0 13 11 6 0 10 0 5 7 0 1 4
-4
2 11 4 2
-2
x14 1, x22 1, x31 1, x43 1
其余全为0。
步骤2：用圈0法确定 C1 中的独立0元素。若独立零元素个素有n个，则已得最优解。若独立零元素的个数 < n, 则转
min Z 4x11 8x12 10x54 6x55
5 xij 1 i 1,2, 5 j5 1 s.t. xij 1 j 1,2, 5 i 1 xij 0 或1
B1
B2
B3
B4
B5
C
A1 4 A2 7 A3 6 A4 6 A5 6
入步骤3。
在只有一个0元素的行（或列）加圈，表示此人只能做该事
（或此事只能由该人来做），每圈一个“0”，同时把位于同列（或同行）的其他零元素划去。表示此时已不能再由他
人来做（或此人已不能做其它事）。如此反复，直到矩阵
中所有零元素都被圈去或划去为至。
在遇到所有行和列中，零元素都不止一个时，可任选其中
注：指派问题是一种特殊的LP问题，是一种特殊的运输问题。下用目前认为最简洁的方法—匈牙利法求解 (The Hungarian
Method of Assignment )。
例12：某商业公司计划开办五家新商店。为了尽早建成
营业，商业公司决定由5家建筑公司分别承建。已知建筑
公司 Ai (i 1,2,,5) 对新商店 B j ( j 1,2,,5) 的建造报价（万元）为 cij (i, j 1,2,,5) ，见下矩阵。商业公司应当对5家建筑公司怎样分配建筑任务，才能使总的建筑费用最少？

第五章整数规划

第五章整数规划主要内容：1、分枝定界法； 2、割平面法； 3、0－1型整数规划； 4、指派问题。

重点与难点：分枝定界法和割平面法的原理、求解方法，0－1型规划模型的建立及求解步骤，用匈牙利法求解指派问题的方法和技巧。

要求：理解本章内容，熟练掌握求解整数规划的方法和步骤，能够运用这些方法解决实际问题。

§1 问题的提出要求变量取为整数的线性规划问题，称为整数规则问题（简称IP ）。

如果所有的变量都要求为（非负）整数，称之为纯整数规划或全整数规划；如果仅一部分变量要求为整数，称为混合整数规划。

例1 求解下列整数规划问题211020m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,13522445x x x x x x x x 如果不考虑整数约束，就是一个线性规划问题（称这样的问题为原问题相应的线性规划问题），很容易求得最优解为：96m ax ,0,8.421===z x x 。

用图解法将结果表示于图中画“+”号的点都是可行的整数解，为满足要求，将等值线向原点方向移动，当第一次遇到“+”号点（1,421==x x ）时得最优解为1,421==x x ，最优值为z=90。

由上例可看出，用枚举法是容易想到的，但常常得到最优解比较困难，尤其是遇到变量的取值更多时，就更困难了。

下面介绍几种常用解法。

§2 分枝定界法分枝定界法可用于解纯整数或混合的整数规划问题。

基本思路：设有最大化的整数规划问题A ，与之相应的线性规划问题B ，从解B 开始，若其最优解不符合A 的整数条件，那么B 的最优值必是A 的最优值*z的上界，记为z ；而A 的任意可行解的目标函数值是*z的一个下界z ，采取将B 的可行域分枝的方法，逐步减少z 和增大z ，最终求得*z 。

现举例说明：例2 求解A219040m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,702075679x x x x x x x x 解：先不考虑条件⑤，即解相应的线性规划B （①--④），得最优解=1x 4.81, =2x 1.82,①② ③ ④ ⑤=0z 356（见下图）。

第5章整数线性规划-第1-4节

现设想，如能找到像CD那样的直线去切割域R(图 5-6)，去掉三角形域ACD，那么具有整数坐标的C 点(1，1)就是域R′的一个极点，
如在域R′上求解①～④，而得到的最优解又恰巧在C点就得到原问题的整数解，所以解法的关键就是怎样构造一个这样的“割平面”CD，尽管它可能不是唯一的，也可能不是一步能求到的。下面仍就本例说明：
例 2
求解A
max z=40x1+90x2 9x1+7x2≤56 7x1+20x2≤70 x1，x2≥0 x1，x2整数
① ② ③ (5.2) ④ ⑤
解先不考虑条件⑤，即解相应的线性规划B,①～④ (见图5-2)，得最优解x1=4.81，x2=1.82，z0=356
可见它不符合整数条件⑤。这时z0是问题A的最优目标函数值 z*的上界，记作z0= z 。而在x1=0，x2=0时，显然是问题A的一个整数可行解，这时z=0，是z*的一个下界， z 记作 =0，即0≤z*≤356 z。
第3节割平面解法
在原问题的前两个不等式中增加非负松弛变量x3、x4，使两式变成等式约束： -x1+x2+x3 =1 ⑥ 3x1+x2 +x4=4 ⑦ 不考虑条件⑤，用单纯形表解题，见表5-2。
表5-2
CB 0 0 1 1 cj XB x3 x4 cj-zj x1 x2 cj-zj b 1 4 0 3/4 7/4 -5/2 1 x1 -1 3 1 1 0 0 1 x2 1 1 1 0 1 0 0 x3 1 0 0 -1/4 3/4 -1/2 0 x4 0 1 0 1/4 1/5 -1/2
第二步：比较与剪支
各分支的最优目标函数中若有小于 z 者，则剪掉这支(用打×表示)，即以后不再考虑了。若大于 z ，且不符合整数条件，则重复第一步骤。一直到最后得到z*为止，得最优整数解xj* ，j=1，…，n。用分支定界法可解纯整数线性规划问题和混合整数线性规划问题。它比穷举法优越。因为它仅在一部分可行解的整数解中寻求最优解，计算量比穷举法小。若变量数目很大，其计算工作量也是相当可观的。

第五章匈牙利法与最佳指派问题

7 2 2
4
3
8 3 5 3
11 8
4
4 1 4
情况一出现，即得到了最优解，其相应的解矩阵为：
0 1 0 0 0
0 0 1 0 0
xij
1
0
0
0
0
0 0 0 1 0
0 0 0 0 1
由此得知最优指派方案为甲完成任务B，乙完成任务
C，丙完成任务A，丁完成任务D，戊完成任务E，最少时
间为
min z 7 6 7 6 6 32
而总的最少时间为32天．
当然，由于方法中的第二步4中的情况二的出现，造成指派问题的最优解常常是不唯一的，但不同最优解的最优值总是相同的．
第三节非标准指派问题
前一节的匈牙利法只适用于目标函数为极小、价值系数矩阵为方阵且价值系数矩阵中元素均为非负的情况。当指派问题不满足上述三个条件时，就应先化成标准的指派问题，然后再用匈牙利法求解．
解：
ABC DEF
甲 16 10 12 15 0 0 8 2
甲 16 10 12 15 0 0
8
2
乙 11 12 10 18 0 0 3 2 3
乙
11
12
10
18
0
0
3
2
3
丙 8 17 13 16 0 0 7 3 1
丙
8
17 13 16
0
0
7
3
1
8 10 10 15
本例经过反复的行、列检验后得到如下矩阵：
5 2 2
2
3
10 5 7 5
9
8
4
6 3 6 2
情况三出现，亦即未得到完全分配方案，求解过程按以下步骤继续进行。

运筹学第3版熊伟编著习题答案

表1－23
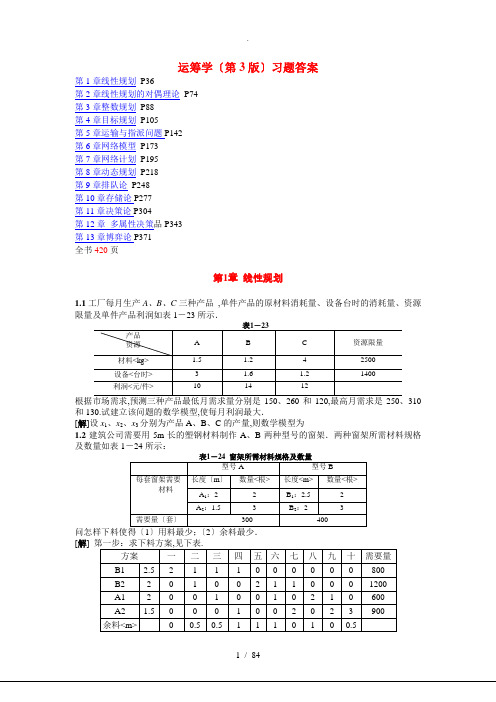
产品
资源
A
B
C
资源限量
材料<kg>
1.5
1.2
4
2500
设备<台时>
3
1.6
1.2
1400
利润<元/件>
10
14
12
根据市场需求,预测三种产品最低月需求量分别是150、260和120,最高月需求是250、310和130.试建立该问题的数学模型,使每月利润最大．
[解]设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
-16
对应的顶点：
基可行解
可行域的顶点
X<1>=〔0,0,6,10,4〕、
X<2>=〔0,2.5,1,0,1.5,〕、
X<3>=〔2,2,0,0,0〕
X<4>=〔2,2,0,0,0〕
〔0,0〕
〔0,2.5〕
<2,2>
〔2,2〕
最优解：X=〔2,2,0,0,0〕；最优值Z＝－16
该题是退化基本可行解,5个基本可行解对应4个极点.
第2章线性规划的对偶理论P74
第3章整数规划P88
第4章目标规划P105
第5章运输与指派问题P142
第6章网络模型P173
第7章网络计划P195
第8章动态规划P218
第9章排队论P248
第10章存储论P277
第11章决策论P304
第12章多属性决策品P343
第13章博弈论P371
全书420页
第
1.1工厂每月生产A、B、C三种产品,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示．

运筹学习题集第五章

判断题判断正误,如果错误请更正第五章运输与指派问题1.运输问题中用位势法求得的检验数不唯一。

2.产地数为3,销地数围的平衡运输中,变量组｛X11,X13,X22,X33,X34｝可作为一组基变量。

3.不平衡运输问题不一定有最优解。

4.m+n-1个变量构成基变量组的充要条件就是它们不包含闭合回路。

5.运输问题中的位势就就是其对偶变量。

6.含有孤立点的变量组不包含有闭回路。

7.不包含任何闭回路的变量组必有孤立点。

8.产地个数为m销地个数为 n的平衡运输问题的对偶问题有m+n个约束。

9.运输问题的检验数就就是对偶问题的松弛变量的值。

10.产地个数为m销地个数为 n的平衡运输问题的系数矩阵为A,则有r(A)〈=m+n-1。

11.用一个常数k加到运价C的某列的所有元素上,则最优解不变。

12.令虚设的产地或销地对应的运价为一任意大于0的常数C(C>0),则最优解不变。

13.若运输问题中的产量或销量为整数则其最优解也一定为整数。

14.运输问题中的单位运价表的每一行都分别乘以一个非0常数,则最优解不变。

15.按最小元素法求得运输问题的初始方案,从任一非基格出发都存在唯一一个闭回路。

16.在指派问题的效率表的某行乘以一个大于零的数最优解不变。

选择题在下列各题中,从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。

第五章运输与指派问题1.下列变量组就是一个闭回路的有A{x21,x11,x12,x32,x33,x23} B{x11,x12,x23,x34,x41,x13} C {x21,x13,x34,x41,x12} D{x12,x32,x33,x23,x21,x11} D{x12,x22,x32,x33,x23,x21}2.具有M个产地N个销地的平衡运输问题模型具有特征A有MN个变量M+N个约束B有M+N个变量MN个约束C 有MN个变量M+N-1个约束D 有M+N-1个基变量MN-M-N+1个非基变量E 系数矩阵的秩等于M+N-13.下列说法正确的有A 运输问题的运价表第r行的每个cij 同时加上一个非0常数k,其最优调运方案不变。

《指派问题》课件

指派问题的扩展研究
多目标指派问题
应用场景：生产调度、资源分配等

解决方法：线性规划、启发式算法等
定义：指派问题在多个目标下的扩展
挑战：如何在多个目标之间找到最优解
动态指派问题
动态指派问题的定义
动态指派问题的应用场景
动态指派问题的求解方法
动态指派问题的优化策略
大规模指派问题
问题定义：大规模指派问题是指在给定一组任务和一组资源，如何将任务分配给资源，使得总成本最小化或总收益最大化。
混合算法
混合算法的概念：将多种算法进行组合，以获得更好的优化效果
混合算法的优点：能够充分利用各种算法的优点，提高优化效果
混合算法的应用：在指派问题中，混合算法可以结合多种算法，如遗传算法、模拟退火算法等，以提高优化效果
混合算法的挑战：如何合理选择和组合各种算法，以获得最佳的优化效果
应用场景：大规模指派问题广泛应用于物流、供应链、生产调度等领域。
研究方法：大规模指派问题的研究方法包括启发式算法、遗传算法、神经网络等。
挑战与展望：大规模指派问题的挑战在于如何设计高效的算法，以及如何解决大规模问题中的优化问题。未来的研究方向包括分布式计算、并行计算等。
禁忌搜索法：在搜索过程中引入禁忌表，避免重复搜索已搜索过的解
元启发式方法
基本概念：元启发式方法，也称为元启发式算法，是一种基于启发式策略的优化方法。
特点：元启发式方法具有自适应性、鲁棒性和易于实现等特点。
应用：元启发式方法在指派问题、路径规划、调度等问题中都有广泛的应用。
实例：遗传算法、模拟退火算法、蚁群算法等都是元启发式方法的典型代表。

运筹学：指派问题

求佳产品公司问题指派问题变形的电子表格模型
Designing School Attendance Zones 设计学生入学区域
米德尔城学区问题指派问题变形的电子表格模型
小结
Session Summary 本讲小结
运输问题考虑（确实的或是比喻的）从出发地运送货物到目的地。每一个出发地都有一个固定的供应量，每一个目的地都有一个固定的需求量
指派问就要处理应当将哪一项任务指派给哪一个被指派者，才能使完成这些任务的总达到最小
把可能会面临的问题描述为一个运输问题或者指派问题或者它们的变形并进行分析
案例
Case Study
案例研究
案例3：富而克消费用品公司
作业: 第五章奇数习题
西北新闻纸公司（See the Course Package）
▪每一个被指派者只完成一项任务 ▪每一项任务只能由一个被指派者来完成
▪每个被指派者和每项任务的组合有一个相关成本 ▪目标是要确定怎样进行指派才能使得总成本最小
Variants of Assignment Problem 指派问题的变形
指派问题的变形: ▪有一些被指派者并不能进行某一些的任务 ▪任务比被指派者多 ▪被指派者比要完成的任务多 ▪每个被指派者可以同时被指派给多于一个的任务 ▪每一项任务都可以由多个被指派者共同完成
下一讲：网络最优化问题
阅读：Text1,Chapter6 和课件及课程网页相关内容

The End of Session 4
The Assignment Problem 指派问题
现实生活之中，我们也经常遇到指派人员做某项工作的情况。指派问题的许多应用都用来帮助管理人员解决如何为一项将要开展进行的工作指派人员的问题。其他的一些应用如为一项任务指派机器、设备或者是工厂

运筹学习题集(第五章)电子版本

运筹学习题集(第五章)判断题判断正误，如果错误请更正第五章运输与指派问题1.运输问题中用位势法求得的检验数不唯一。

2.产地数为3，销地数围的平衡运输中，变量组｛X11，X13，X22，X33，X34｝可作为一组基变量。

3.不平衡运输问题不一定有最优解。

4.m+n-1个变量构成基变量组的充要条件是它们不包含闭合回路。

5.运输问题中的位势就是其对偶变量。

6.含有孤立点的变量组不包含有闭回路。

7.不包含任何闭回路的变量组必有孤立点。

8.产地个数为m销地个数为 n的平衡运输问题的对偶问题有m+n个约束。

9.运输问题的检验数就是对偶问题的松弛变量的值。

10.产地个数为m销地个数为 n的平衡运输问题的系数矩阵为A，则有r(A)〈=m+n-1。

11.用一个常数k加到运价C的某列的所有元素上，则最优解不变。

12.令虚设的产地或销地对应的运价为一任意大于0的常数C（C>0），则最优解不变。

13.若运输问题中的产量或销量为整数则其最优解也一定为整数。

14.运输问题中的单位运价表的每一行都分别乘以一个非0常数，则最优解不变。

15.按最小元素法求得运输问题的初始方案，从任一非基格出发都存在唯一一个闭回路。

16.在指派问题的效率表的某行乘以一个大于零的数最优解不变。

选择题在下列各题中，从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。

第五章运输与指派问题1.下列变量组是一个闭回路的有 A{x21,x11,x12,x32,x33,x23} B{x11,x12,x23,x34,x41,x13} C {x21,x13,x34,x41,x12}D{x12,x32,x33,x23,x21,x11} D{x12,x22,x32,x33,x23,x21}2.具有M个产地N个销地的平衡运输问题模型具有特征 A有MN个变量M+N个约束 B 有M+N个变量MN个约束 C 有MN个变量M+N-1个约束D 有M+N-1个基变量MN-M-N+1个非基变量E 系数矩阵的秩等于M+N-13.下列说法正确的有 A 运输问题的运价表第r行的每个cij 同时加上一个非0常数k，其最优调运方案不变。

运筹学教材习题答案详解

X(2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料650根
显然用料最少的方案最优。
1.4A、B两种产品，都需要经过前后两道工序加工，每一个单位产品A需要前道工序1小时和后道工序2小时，每一个单位产品B需要前道工序2小时和后道工序3小时．可供利用的前道工序有11小时，后道工序有17小时．
3
B1：2.0
3
需要量（套）
200
150
问怎样下料使得（1）用料最少；（2）余料最少．
【解】第一步：求下料方案，见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
《运筹学》
第1章线性规划
第2章线性规划的对偶理论
第3章整数规划
第4章目标规划
第5章运输与指派问题
第6章网络模型
第7章网络计划
第8章动态规划
第9章排队论
第10章存储论
第11章决策论
第12章对策论
习题一
1.1讨论下列问题：

指派问题优秀课件

A由甲或丙完毕，乙和丁效率设为M C由丙或丁完毕, 甲和乙效率设为M E由甲，乙或丁完毕，丙效率设为M 虚设一种人，丙和丁旳最小值作为虚设人旳效率系数，所以应虚设一行为
（34 27 28 23 45）
min 0 0 4 2
列变换
0 13 7 0 60 69
0 5 3 2
0 1 0 0
环节二、试指派(找独立旳0元素)
(记独立0元素个数为m,矩阵阶数为n.当m=n 时,问题到此结束.m<n旳情况下一题讨论)
0 0 0 1
0 6
0 0
13 0 5 1
7 6 3 0
0
9
所以：最优解为0 1
19 18 6 0 13 最终一列减去5 19 18 6 0 8
17 0 1 13 5
17 0 1 13 0
1
19
7
0
22
1 19 7 0 17
0 0 0 0 M
0 0 0 0 M
因为M是一种较大旳数，减去5后来仍为一种较大旳数，所以仍以M表达
找独立旳0元素并试指派
0 4 6 17 7
ABC D E
甲
25
29
31
42
37
乙
39
38
26
20
33
丙 34 27 28 40 32
丁 24 42 30 23 45
要求:
1、E必须完毕，其他一人一项
2、一人完毕两项，其他一人一项
3、A由甲或丙完毕，C由丙或丁完毕。E由甲，乙或丁完毕，丙或丁完毕两项，其他一人一项
• 分析：
0
0
0
此时m=n=4，
0 找到了最优解

运输与指派问题课程设计

运输与指派问题课程设计一、课程目标知识目标：1. 让学生理解运输与指派问题的基本概念，掌握线性规划在实际问题中的应用。

2. 使学生掌握运用线性规划方法解决运输与指派问题的步骤和技巧。

3. 帮助学生了解运输与指派问题在实际生活中的广泛应用。

技能目标：1. 培养学生运用数学模型解决实际问题的能力，提高逻辑思维和数学运算能力。

2. 培养学生运用计算机软件（如Excel、Lingo等）辅助解决运输与指派问题的能力。

情感态度价值观目标：1. 培养学生对数学学科的兴趣和热情，激发学生主动探索问题的积极性。

2. 培养学生的团队协作精神，学会与他人合作解决问题，增强沟通能力。

3. 培养学生具备面对实际问题时，能够运用所学知识进行分析、解决问题的能力，增强学生的社会责任感。

课程性质：本课程属于数学学科，旨在通过解决实际问题，培养学生的数学建模能力和计算机辅助解决问题的能力。

学生特点：学生处于高年级阶段，已具备一定的数学基础和逻辑思维能力，对实际问题有一定的探索欲望。

教学要求：教师需结合学生特点，以实际问题为载体，引导学生运用所学知识解决运输与指派问题，注重培养学生的动手操作能力和团队协作精神。

在教学过程中，将目标分解为具体的学习成果，以便进行教学设计和评估。

二、教学内容1. 运输与指派问题基本概念：介绍运输问题、指派问题的定义及其在实际生活中的应用。

- 教材章节：第五章第三节“线性规划应用——运输与指派问题”2. 线性规划在运输与指派问题中的应用：讲解线性规划模型在解决运输与指派问题中的应用。

- 教材章节：第五章第四节“线性规划在运输与指派问题中的应用”3. 运输与指派问题解决方法：- 北西角法：介绍北西角法的步骤及操作方法。

- 最小成本法：讲解最小成本法的原理及实施过程。

- 教材章节：第五章第五节“运输与指派问题的解决方法”4. 计算机软件辅助解决运输与指派问题：介绍Excel、Lingo等软件在解决运输与指派问题中的应用。

指派问题详解

第一章绪论1、指派问题的背景及意义指派问题又称分配问题，其用途非常广泛，比如某公司指派n个人去做n 件事，各人做不同的一件事，如何安排人员使得总费用最少？若考虑每个职工对工作的效率（如熟练程度等），怎样安排会使总效率达到最大？这些都是一个企业经营管理者必须考虑的问题，所以该问题有重要的应用价值.虽然指派问题可以用0-1规划问题来解，设X(I,J)是0-1变量, 用X(I,J)=1表示第I个人做第J件事, X(I,J)=0表示第I个人不做第J件事. 设非负矩阵C（I，J）表示第I个人做第J件事的费用，则问题可以写成LINGO程序SETS:PERSON/1..N/;WORK/1..N/;WEIGHT(PERSON, WORK): C, X ;ENDSETSDATA:W=…ENDDATAMIN=@ SUM(WEIGHT: C*X);@FOR(PERSON(I): @SUM(WORK(J):X(I,J))=1);@FOR(WORK(J): @SUM(PERSONM(I):X(I,J))=1);@FOR(WEIGHT: @BIN(X));其中2*N个约束条件是线性相关的, 可以去掉任意一个而得到线性无关条件.但是由于有N^2个0-1变量, 当N很大时，用完全枚举法解题几乎是不可能的. 而已有的0-1规划都是用隐枚举法做的，计算量较大. 对于指派问题这种特殊的0-1规划，有一个有效的方法——匈牙利算法，是1955年W. W. Kuhn利用匈牙利数学家D.König的二部图G的最大匹配的大小等于G的最小顶点覆盖的大小的定理提出的一种算法，这种算法是多项式算法，计算量为O(N3).匈牙利算法的基本原理是基于以下两个定理.定理1设C=(C ij)n×n是指派问题的效益矩阵，若将C中的任一行（或任一列）减去该行（或该列）中的最小元素，得到新的效率矩阵C’，则C’对应的新的指派问题与原指派问题有相同的最优解.证明：设X’是最优解, 即@SUM(WEIGHT: C*X’)<= @SUM(WEIGHT: C*X), 则当C中任一行或任一列减去该行或该列的最小数m时,得到的阵C’还是非负矩阵, 且@SUM(WEIGHT: C’*X’)<=@SUM(WEIGHT: C*X)-m=@SUM(WEIGHT: C’*X)定理2效率矩阵C中独立的0元素的最多个数等于覆盖所有0元素的最少直线数. 当独立零元素的个数等于矩阵的阶数时就得到最优解.3、理论基础定义:图G的一个匹配M是图G中不相交的边的集合. 属于匹配M中的边的所有端点称为被该匹配M饱和, 其他的顶点称为M-未饱和的. 如果一个匹配M 饱和了图G的所有顶点，则称该匹配M是一个完全匹配. 可见顶点数是奇数的图没有完全匹配. 一个匹配M称为是极大匹配, 如果它不能再扩张成更大的一个匹配. 一个匹配称为是最大匹配, 如果不存在比它更大的匹配.定义:对于一个匹配M, 图G的一个M-交替路是图G中的边交替地在M中及不在M中的边组成. 从M-未饱和点出发到M-为饱和点结束的M-交替路称为一条M-增广路. 把M-增广路中不是M中的边改成新的匹配M’中的边, 把M-增广路中M中的边不作为M’中的边, 在M-增广路以外的M中的边仍作为M’中的边, 则M’的大小比M大1. 故名M-增广路. 因此最大匹配M不存在M-增广路.定义:若图G和图H有相同的顶点集V, 我们称G和H的对称差,记为G∆H,是一个以V为顶点集的图, 但其边集是G和H的边集的对称差: E(G∆H)=E(G) ∆E(H)=E(G)⋂E(H)-(E(G)⋃E(H))=(E(G)-E(H)) ⋂ (E(H)-E(G))定理: (Berge, 1957) 图G的一个匹配M是最大匹配,当且仅当G中没有M-增广路.证明: 我们只要证明, G中没有M-增广路时, M是最大匹配. 用反证法, 若有一个比M大的匹配M’. 令G的一个子图F, E(F)=M∆M’, 因M和M’都是匹配, F的顶点的最大度数至多是2, 从而F由不相交的路和环组成, 它们的边交替地来自M和M’, 于是F中的环的长度是偶数. 由于M’比M大, F中存在一个连通分支,其中M’中的边数大于M中的边数. 这个分支只能是起始和终止的边都在M’中. 而这就是一条G中的M-增广路. 与假设矛盾. 证毕.定理(Hall, 1935)设G是一个二部图, X和Y是其二分集, 则存在匹配M 饱和X当且仅当对于X中的任意子集S, Y 中与S中的点相邻的点组成的集合N(S)中元素的个数大于等于集合S中元素的个数.证明：必要性是显然的. 对于充分性, 假设 |N(S)|≥|S|, ∀S⊂X, 考虑G的一个最大匹配M, 我们用反证法，若M没有饱和X, 我们来找一个集合S不满足假设即可. 设u∈X是一个M-未饱和顶点, 令S⊂X和T⊂Y分别是从u出发的M-交替路上相应的点.我们来证明M中的一些边是T到S-u上的一个匹配. 因为不存在M-增广路，T中的每个点是M-饱和的. 这意味着T中的点通过M中的边到达S中的一个顶点. 另外, S-u中的每个顶点是从T中的一个顶点通过M中的一条边到达的. 因此M 中的这些边建立了T与S-u的一个双射, 即|T|=|S-u|. 这就证明了M中的这些边是T到S-u上的一个匹配，从而意味着T⊂N(S), 实际上, 我们可证明T=N(S). 这是因为连接S和Y-T中的点y的边是不属于M的, 因为不然的话, 就有一条到达y的M-增广路, 与y∉T矛盾. 故|N(S)|=|T|=|S-u|=|S|-1<|S|, 与假设矛盾.当X与Y的集合的大小相同时的Hall定理称为婚姻问题,是由Frobenius(1917)证明的.推论: k-正则的二部图（X的每一点和Y的每一点相关联的二部图）(k>0)存在完全匹配.证明: 设二分集是X,Y. 分别计算端点在X和端点在Y的边的个数, 得k|X|=k|Y|, 即|X|=|Y|.因此只要证明Hall的条件成立即可. 使X饱和的匹配就是完全匹配. 考虑∀S⊂X, 设连接S与N(S)有m条边, 由G的正则性, m=k|S|. 因这m条边是与N(S)相关联的, m≤k|N(S)|, 即k|S|≤ k|N(S)|, 即|N(S)|≥|S|. 这就是Hall的条件.用求M-增广路的方法来得到最大匹配是很费时的. 我们来给出一个对偶最优化问题.定义:图G的一个顶点覆盖是集合S⊂V(G), 使得G的每条边至少有一个端点在S中. 我们称S中的一个顶点覆盖一些边, 若这个顶点是这些边的公共端点.因为匹配的任意两条边不能被同一个顶点覆盖, 所以顶点覆盖的大小不小于匹配的大小: |S|≥|M|. 所以当|S|=|M| 时就同时得到了最大的匹配和最小的顶点覆盖.定理(König [1931],Egerváry[1931])二部图G的最大匹配的大小等于G的最小顶点覆盖的大小.证明: 设M是G的任一个匹配, 对应的二分集是X,Y. 设U是一个最小的顶点覆盖, 则|U|≥|M|, 我们只要由顶点覆盖U来构造一个大小等于|U|的匹配即完成证明. 令R=U⋃X, T=U⋃Y, 令H, H’分别是由顶点集R⋂(Y-T)及T⋂(X-R)诱导的G的子图. 我们应用Hall的定理来证明H有一个R到Y-T中的完全匹配，H’有一个从T到X-R中的完全匹配. 再因这两个子图是不相交的, 这两个匹配合起来就是G中的一个大小为|U|的匹配.因为R⋂T是G的一个覆盖, Y-T与X-R之间没有边相联接. 假设S⊂R, 考虑在H中S的邻接顶点集N(S), N(S) ⊂Y-T. 如果|N(S)|<|S|, 因为N(S)覆盖了不被T覆盖的与S相关联所有边, 我们可以把N(S) 代替S作为U中的顶点覆盖而得到一个更小的顶点覆盖. U的最小性意味着H中Hall条件成立. 对H'作类似的讨论得到余下的匹配. 证毕.最大匹配的增广路算法输入: 一个二分集为X，Y的二部图G，一个G中的匹配M， X中的M-未饱和顶点的集合U.思路: 从U出发探求M-交替路，令S⊂X，T⊂Y为这些路到达过的顶点集. 标记S中不能再扩张的顶点. 对于每个x∈(S⋂T)-U, 记录在M-增广路上位于x前的点.初始化: S=U,T=∅.叠代: 若S中没有未标记过的顶点, 结束并报告T⋂(X-S)是最小顶点覆盖而M是最大匹配.不然, 选取S中未标记的点x, 考虑每个y∈N(x)且xy∉M, 若y是M-未饱和的, 则得到一个更大的匹配，它是把xy加入原来的匹配M得到的,将x从S中去除. 不然, y是由M中的一条边wy相连接的, w∈X, 把y加入T(也有可能y本来就在T中), 把w加入S. w未标记, 记录w前的点是y. 对所有关联到x的边进行这样的探索后, 标记x. 再次叠代.定理: 增广路算法可以得到一个相同大小的匹配和顶点覆盖.证明: 考虑这个算法终止的情况, 即标记了S中所有的点. 我们要证明R=T⋂(X-S)是大小为|M|的一个顶点覆盖.从U出发的M-交替路只能通过M中的边进入X中的顶点, 所以S-U中的每个顶点通过M与T中的顶点匹配, 并且没有M中的边连接S和Y-T. 一旦一条M-交替路到达x∈S, 可以继续沿着任何未饱和的边进入T, 由于算法是对于x的所有邻域顶点进行探索才终止的,所以从S 到Y-T 没有未饱和边. 从而S 到Y-T 没有边, 证明了R 是一个顶点覆盖.因为算法是找不到M-增广路时终止, T 的每一个顶点是饱和的. 这意味着每个顶点y ∈T 是通过M 匹配与S 中的一个顶点. 由于U ⊂S, X-S 的每个顶点是饱和的, 故M 中与X-S 相关联的边不和T 中的点相连接. 即它们与是饱和T 的边不同的, 这样我们可见M 至少有|T|+|X-S|条边. 因不存在一个比顶点覆盖更大的匹配，所以有|M|=|T|+|X-S|=|R|.设二部图G 的二分集X 和Y 都是n 个元素的点集, 在其边j i y x 上带有非负的权ij w , 对于G 的一个匹配M, M 上各边的权和记作w(M).定义: 一个n ×n 矩阵A 的一个横截(transversal)是A 中的n 个位置, 使得在每行每列中有且只有一个位置（有的文献中把横截化为独立零元素的位置来表示）.定义: 指派问题就是给定一个图G=n n K ,(完全二部图, 即每个X 中的顶点和Y 中的每个顶点有边相连接的二部图)的边的权矩阵A, 求A 的一个横截, 使得这个横截上位置的权和最大. 这是最大带权匹配问题的矩阵形式.定义: 对于图G=n n K ,，设其二分集是X ，Y ，给定G 的边j i y x 的n ×n 权矩阵W={ij w }.考虑G 的子图v u G ,, 设其二分集是U ⊂X ，V ⊂Y, 边集是E(v u G ,)，对于子图v u G ,的带权覆盖u,v 是一组非负实数{i u },{j v },使得ij j i w v u ≥+,)(,v u j i G E y x ∈∀, v u G ,的带权覆盖的费用是∑∑+j i v u 记为C(u,v), 最小带权覆盖问题就是求一个具有最小费用C(u,v)的带权覆盖u,v.引理: 若M ⊂E(v u G ,)是一个带权二部子图v u G ,的最大匹配, 且u, v 是v u G ,的带权覆盖, 则C(u,v)≥w(M). 而且, C(u,v)=w(M)当且仅当ij j i w v u =+，M y x j i ∈∀. 这时M 是v u G ,最大带权匹配, u,v 是v u G ,的最小带权覆盖，定义这时的v u G ,为G 的相等子图（equality subgraph ）.证明: 因为匹配M 中的边是不相交的, 由带权覆盖的定义就得C(u,v)≥w(M). 而且C(u,v)=w(M)当且仅当ij j i w v u =+，M y x j i ∈∀成立. 因一般地有C(u,v)≥w(M).所以当C(u,v)=w(M)时. 意味着没有一个匹配的权比C(u,v)大, 也没有一个覆盖的费用比w(M)小.Kuhn 得到一个指派问题的算法，命名为匈牙利算法, 为的是将荣耀归于匈牙利数学家König 和Egerv áry.指派问题的匈牙利算法(Kuhn[1955], Munkres[1957]):输入G=n n K ,的边的权矩阵A, 及G 的二分集X,Y.初始化: 任取一个可行的带权覆盖，例如)(max ij ji w u =，0=j v ，建立G 的相等子图v u G ,, 其二分集是X, Y ’⊂Y, 求v u G ,的一个最大匹配M. 这个匹配的权和w(M)=C(u,v), M 的带权覆盖是具有最小费用的.叠代: 如M 是G 的一个完全匹配, 停止叠代, 输出最大带权匹配M. 不然, 令U 是X 中的M-未饱和顶点. 令S ⊂X, T ⊂Y 是从U 中顶点出发的M-交替路到达的顶点的集合.令},:min{T Y y S x w v u j i ij j i -∈∈-+=ε.对于所有的S x i ∈, 将i u 减少ε, 对于所有的T y j ∈,将j v 增加ε,形成新的带权覆盖u ’,v ’及对应的新的相等子图v u G '',.如果这个新的相等子图含有M-增广路, 求它的最大匹配M ’, 不然不改变M 再进行叠代.定理: 匈牙利算法能找到一个最大权匹配和一个最小费用覆盖.证明: 算法由一个覆盖开始，算法的每个叠代产生一个覆盖，仅在相等子图有一个完全的匹配为止。

5.5 指派问题

cij 为第 i 个人为完成第 j 项任务时的工时消
3. 指派问题数学模型—标准形式如果一个指派模型满足以下三个条件：
1)目标要求为min
2)效率矩阵(cij)为m阶方阵
3)效率矩阵中所有元素cij≥0,且为常数
则称上面的数学模型为指派问题的标准形.
4. 指派模型的标准形的特点: 含有m×m个决策变量,均为0-1变量 m+m＝2m个约束方程给定一个指派问题时，必须给出效率矩阵（系数矩阵） C=(cij)mxm,且cij0，因此必有最优解。
0 1 0 0
0 0 0 1
指派问题的解矩阵应具有如下特点：（1）解矩阵(xij)中各行各列的元素之和都是1；（2）可行解（最优解）中恰含有４个非零元，即4个1；（3）可行解（最优解）矩阵中的1恰取于不同行不同列。
人工作译成英文译成日文译成德文译成俄文任务
甲 2 15 13 4 1
定理1 如果从指派问题效率矩阵[cij]的每一行元素中分别减去(或加上)一个常数ui(被称为该行的位势)，从每一列分别减去(或加上)一个常数vj(称为该列的位势) 得到一个新的效率矩阵[bij]，若其中bij=cij-ui-vj，则[bij]的最优解的结构等价于[cij]的最优解的结构.
证明：将从[bij]中得到的解代入分配问题模型的目标函数式，有
从只有一个0元素的行（或列）开始，
给这个0元素加圈，记，这表示对这行所代表的人，只有一种任务可指派。然后划去所在的列（或行）的其他0元素，记作Ø。这表示这列所代表的任务已指派完，不必再考虑别人
0
6
13
7 6 3 0
0 9 2 0

5 1
0
给只有一个0元素的列（或行）中的0元素加圈，记，然后划去所在的行（或列）的其他0元素，记作Ø。这表示这行所代表的人已指派完，不必再考虑他做别的任务了。反复进行上述两步，直到所有的0元素都被圈出和划掉为止。