厦门市2020届高中毕业班第一次质量检查理科参考解答
厦门市2020届高三毕业班3月线上质量检查理科综合试题与答案

厦门市2020届高中毕业班线上质量检查(一)理科综合能力测试(本试卷满分300分,考试时间150分)★祝考试顺利★可能用到的相对原子质量:H-I C-12 O-16 Na23 P31 S32 K39 Mn 55 Fe56 Co59第I卷(选择题共126分)一、选择题:(本题共13小题,只有一项符合题目要求,每小题6分,共78分。
)1.下列关于人体细胞有氧呼吸和无氧呼吸相同点的叙述,错误的是A.都是在生物膜上完成反应B.都能生成三磷酸腺苷C.都需要多种酶的催化 D.都能产生丙酮酸和[H]2.下列关于酒精在生物实验中的相关应用,叙述不正确的是A.在使用苏丹in鉴定脂肪的实验中,酒精的作用是洗去实验材料上的浮色B.无水酒精在绿叶中色素的提取和分离实验中既可作为提取液也可作为层析液C.观察根尖分生组织细胞的有丝分裂实验,解离液需要用到体积分数为95%的酒精D.探究酵母菌细胞呼吸方式实验中,酒精可使溶有重铬酸钾的浓硫酸溶液变成灰绿色3.某植株的一条染色体发生缺失突变,获得该缺失染色体的花粉不育,缺失染色体上具有红色显性基因B,正常染色体上具有白色隐性基因b(如图)。
如以该植株为父本,测交后代中约有11%植株表现为红色性状。
下列解释最合理的是A.减数第二次分裂时姐妹染色单体3与4彼此分离B.减数第一次分裂时非姐妹染色单体之间交叉互换C.减数分裂时染色单体1或2上的基因b突变为BD.减数第二次分裂时非姐妹染色单体之间自由组合4.在离体实验条件下,突触后膜受到不同刺激,膜电位变化的情况如图所示,有关说法正确的是A.突触后膜只能是下一个神经元的胞体膜B.突触后膜上的受体与相应递质结合发挥作用后受体即被灭活C.电位2表示突触后膜受到抑制性递质的作用,可能是K+大量外流所致D.电位1表示突触后膜受到兴奋性递质的作用,是Na+大量内流导致的5.核酶是具有催化功能的RNA分子,在特异的结合并切割特定的mRNA后,核酶可以从杂交链上解脱下来,重新结合和切割其他的mRNA分子,下列说法正确的是A.核酶具有热稳定性,故核酶的活性不受温度的影响B.向含有核酶的溶液中滴加双缩脲试剂,可以发生紫色反应C.核酶发挥作用时有氢键的形成,也有磷酸二酯键的断裂D.与不加酶相比,加核酶组mRNA降解较快,由此可以反映酶的高效性6.如图为某动物卵细胞的形成过程示意图,下列相关叙述正确的是A.过程①发生着丝点分裂B.过程②可发生交叉互换C.细胞A是次级卵母细胞D.细胞B中的细胞质基因只能传给后代中的雌性个体7.下列有关垃圾分类说法错误的是A.废弃的聚乙烯塑料属于白色垃圾,不能使溴水退色B.可回收的易拉罐中含金属铝,可通过电解氧化铝制取C.废旧电池中含有镍、镉等重金属离子,不能填埋处理D.含丝、毛的废旧衣物燃烧处理时只生成CO2和H2O8.螺环化合物可用于制造生物检测机器人,下列有关该化合物的说法错误的是A.分子式为C5H8OB.是环氧乙烷的同系物C.一氯代物有2种(不考虑空间异构)D.所有碳原子不处于同一平面9.设NA为阿伏加德罗常数值。
厦门市2020届高三年级市一检 理科综合试题含答案

厦门市2020届高中毕业班第一次质量检查理综(化学)参考答案说明:化学方程式中,化学式写错的不得分;化学式对而未配平或重要条件有误的、气体或沉淀符号未标、化学方程式用“→”标明或用错“=” 与“”的扣一分。
专有名词有错别字不得分。
一、选择题(本题包括7小题,每小题6分,共42分)二、填空题(本题包括5个小题,共58分)(一)必考题(3小题,共43分)26.(14分)(1)ABC (2分)(2)恒压滴液漏斗双氧水(各1分,共2分)(3)在油水分离器中加满乙酸丁酯(2分)(4)降低共沸物的沸点,防止温度过高,过氧乙酸分解(2分)(5)①当最后一滴KMnO4溶液滴入时,溶液由无色变为浅红色,且半分钟内不褪色(2分)②CH3COOOH+2Fe2++2H+= CH3COOH+2Fe3++H2O (2分)③(2分)27.(15分)(1)NaH2PO2 + I2+ H2O =H3PO3 + NaI+ HI(2分)(2)FeS(s)+Pb2+(aq) = PbS(s)+Fe2+(aq) (2分)(3)NaH2PO3 (1分)(4)除铁(将NaH2PO3 变为Na2HPO3)(2分)(5)9.8(2分)(6)①Na+交换膜(2分)②2H2O-4e- = O2↑+4H+(2分)③I-会在阳极放电,沉积在阳极表面,损伤阳极板(2分)28.(14分)(1)-164.4 kJ·mol-1(2分)(2)4×104 L·mol-1(2分)(3)①a (2分)②20.93ev 6.62eV (各1分,共2分)③ACD (2分)(4)①反应1反应2为竞争反应,CH3OH浓度增大,同SO3反应,抑制了SO3和水反应,硫酸浓度减少(a的静电作用力强,甲醇浓度增大,有利于生成a,不利于生成硫酸)(2分)②H2O浓度越大,使得甲醇和SO3的碰撞几率减小,硫酸氢甲酯浓度降低。
(2分)(二)选考题(15分)35. (15分)(1)或(1分)(2)4N A(2分)HCOOH和CO2都为分子晶体,HCOOH分子间形成氢键(2分)(3)N>O>C (1分)(4)Cl,C (1分)(5)前者(2分)(6)①sp2杂化(2分)②(2分)③184/VN A(2分)36. (15分)(1)浓硫酸,浓硝酸;55~60 ℃水浴加热(各1分,共2分)硝基(1分)(2)(2分)(3)、、、、(3分)(4)还原反应(1分)(5)(2分)(6)不能,如互换,先酸化,醇会发生消去反应(或H中的酯基会水解生成羧基,和SOCl2反应生成酰氯)(2分)(7)(2分)。
福建省厦门市2020届高中毕业班第一次质量检查 数学(理科)(含答案)

A. x1 +x2=2
B. e x1 e x2 > 2e
ln x1 C. x1 +x2lnx2 < 0
二、填空题:本大题共 4 小题。,每小题 5 分,共 20 分。
e D. x1x2 > 2
13.己知数列{an}的前 n 项和为 Sn,且 Sn=9-2an,则 a3=
.
(1 x)(2 1 )6
D,O 点为坐标原点.
15 (1)若|AB|= 2 ,求 l 的方程; (2)已知 P 为 AB 的中点,y 轴上是否存在定点 Q,使得 OP PQ =0?若存在,求 Q 的坐标;若不存
在,说明理由. 20.(12 分) 小明和爸爸玩亲子游戏,规则如下:袋中装有 3 个大小相同的球,1 个白球,2 个红球,每次摸出 一个球,记下颜色后放回,若摸出白球,则下一次由原摸球人继续摸球;若摸出红球,则下一次由 对方摸球,规定摸球 m 次,最后一次由谁摸球就算谁获胜,第一次由小明摸球.
冥王星轨道的半长轴长约为 60 亿千米,则冥王星的运行周期约为
A. 150 年 B. 200 年 C.250 年 D. 300 年 6.某程序框图如图所示,该程序运行后输出的 S 的值是
A. -3
1 B. 2
1 C. 3
D.2
7.如图是某圆锥的三视图,其正视图是一个边长为 1 的正三角形,圆锥表面上的点 M、N 在正视
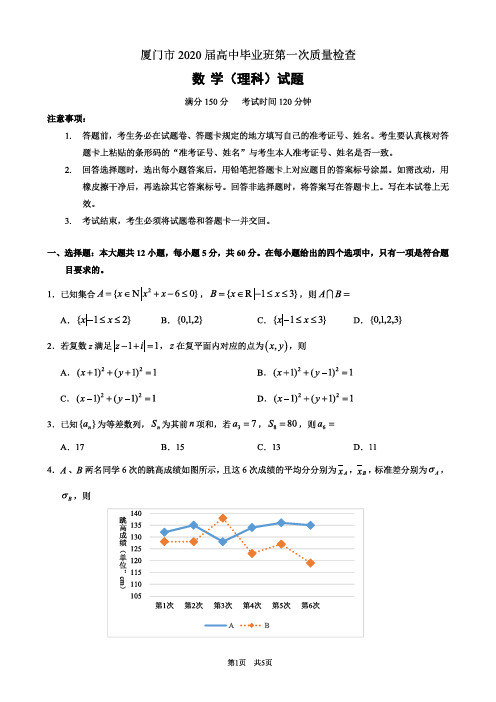
4.A、B 两名同学 6 次的跳高成绩如图所示,且这 6 次成绩的平均分分别为 xA , xB ,标准差分别
为σA,σB,则
A. xA , > xB , σA <σB B. xA , < xB , σA<σB
C. xA , > xB , σA>σB D. xA , < xB , , σA>σB
福建省厦门市2020届高三第一次质检理科综合试题及答案( word版)

厦门市2020届高中毕业班第一次质量检查理科综合能力测试可能用到的相对原子质量:H-I C-12 N-14 O-16第I卷(选择题共126分)一、选择题:(本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项符合题目要求)1.下列关于激素、酶和神经递质的叙述,正确的是A.激素和酶一经靶细胞接受并起作用后就被灭活了B.激素和神经递质都可以作为信息分子调节生命活动C.激素和酶都是蛋白质,能产生酶的细胞一定能产生激素D.酶和神经递质都能降低化学反应活化能,因此具有高效性2.下图是基因型为AABb的某生物体(2N=4)正常细胞分裂示意图(不考虑基因突变),下列叙述错误的是A.该细胞处于有丝分裂后期B.若染色体①有基因A,则④有基因A或aC.该图所示的细胞含有4个染色体组D.该细胞产生的子细胞中有2对同源染色体3.机体缺氧时,缺氧诱导因子( HIF)聚集到细胞核中,激活靶基因特定的DNA片段(HRE),促进促红细胞生成素( EPO)的合成。
EPO是一种糖蛋白质激素,可作用于骨髓造血组织,促进红细胞生成,改善缺氧。
氧含量的增加促进HIF解体,以减少EPO的合成,调节过程如图所示。
下列说法正确的是A.EPO合成场所是细胞核B.缺氧时,EPO在HIF的作用下转变成了血红蛋白C.氧气充足时,HIF被解体以减少EPO的合成,这属于负反馈调节D.EPO作用的靶细胞是红细胞,红细胞数量增加可以改善缺氧情况4. 13三体综合征是一种严重的遗传病,患儿的畸形和临床表现比21三体综合征更严重。
该病在新生儿中的发病率约为1/25000,女性明显多于男性。
下列叙述正确的是A.可根据患儿中女性多于男性推测出该病受X染色体上的显性基因控制B.患儿多出的13号染色体若来自母方,则可判定原因是形成卵细胞时着丝点未分裂C.临床上可以通过基因测序来确定胎儿是否患有该病D.可以取胎儿体细胞在显微镜下检查,通过分析染色体形态、数目来辅助临床诊断5.下图表示某细菌细胞中部分氨基酸的代谢过程。
福建省厦门市2020届高中毕业班第一次质量检查数学(理科)试题及答案
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题,每个试题考 生都必须作答。第 22 题、第 23 题为选考题,考生根据要求作答。
(一)必考题:共 60 分。 17.本题考查正弦定理、余弦定理、三角形的面积公式和三角恒等变换等基础知识;考查运算求解能力、
推理论证能力;考查数形结合思想、函数与方程思想.满分 12 分.
解:(1)依题设及正弦定理可得, sin Acos A + C = sin B sin A ------------------------------------------------ 1 分 2
因为 sin A 0,所以 cos A + C = cos − B = sin B --------------------------------------------------------- 2 分
M
故 ABC 为等腰三角形.
则 c = a , BM
=a
A
C
--------------------------------------------------------------------------------------------------- 8 分
2
在 MBC 中由余弦定理可得, MC2 = BM 2 + BC2 − 2BM BC cos B
解法 2:
设
P(
x0
,
y0
)
,
F1
(−
c,
0)
,
F2
(c,
0)
,依题意得
M
(
2
x0 − 3
c
,
2 y0 3
福建省厦门市高中毕业班第一次质量检查理科综合能力测试题参考答案

福建省厦门市高中毕业班第一次质量检查理科综合能力测试题&参考答案(本试卷满分300分,考试时间150分钟)可用到的相对原子质量:H-l C-12O-16第I卷(选择题共126分)一、选择题:(本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求)1.下列所选的材料对植物细胞发生质壁分离影响最小的是A.细胞是否为活细胞B.细胞是否具有大液泡C.细胞的液泡是否具有颜色D.外界溶液浓度是否大于细胞液浓度2.下列关于酶与ATP的叙述,正确的是A.细胞内的酶和ATP均为多聚体B.酶和ATP的合成过程均需要能量C.酶与ATP均要在细胞器中合成D.生物体内的生化反应均需要酶和ATP 参与3.下列关于同一个体中神经细胞、胰岛B细胞、T细胞的叙述,正确的是A.细胞器的种类和数量都相同B. mRNA的种类和数量都相同C.都能分泌蛋口质作用于靶细胞D.都能参与内环境稳态的维持4.下图为某二倍体生物生殖腺中的细胞分裂示意图,下列叙述正确的是A.在显微镜下可观察到某细胞从一丙一丁连续分裂的过程B.屮细胞分裂结束,形成1个丙细胞和3个丁细胞C.甲、乙、丙、丁细胞中的染色体组数目依次为2、2、1、1D.乙细胞所示阶段发生同源染色体的分离和非同源染色体的自山组合5.日本科学家大隅良典因发现“细胞自噬”机制而获得了2016年诺贝尔生理学或医学奖。
细胞自噬是指当细胞接收到诱导信号后,胞内的一些膜会把周圉的细胞质乔进去形成“自噬体”,随后与溶酶体融合,经消化后,一些可利用的物质被送回细胞质循环利用。
下列推论不合理的是A.细胞“自噬体”对细胞质成分的呑噬具有特异性B.当营养物质不足时,细胞的自噬作用会明显加强C.胚胎发育过程中需要通过自噬作用来处理废弃的细胞器D.自噬机制发生缺陷,会导致细胞内废物和垃圾增多6.下表为築患者血液化验的部分结果:据此分析,其体内最可能发生的是A.会出现抽搐等症状B.神经细胞膜静息电位的绝对值增大C.胰岛素促进葡萄糖运出肝细胞D.肾小管和集合管重吸收水分增加7.化学在生活中应用广泛,下列物质性质与对应用途错误的是A.明矶易水解生成胶体,可用作净水剂B.晶体硅熔点高硬度大,可用作芯片C.氮气化学性质稳定,可用作粮食保护气D.漠化银见光易分解,可用作胶片感光剂8.设N A为阿伏加徳罗常数的值。
福建省厦门市高中毕业班第一次质量检查理科数学试题参考答案

福建省厦门市高中毕业班第一次质量检查理科数学试题&参考答案本试卷分第I卷(选择题)和第II卷(非选择题)两部分.满分150分,考试时间120分钟.第I卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={A]X2-5X-6<0}, B = k-|-L>ot,则等于A. [—1,6]B. (1,6]C. [—1,+s) D・[2,3](其中7为虚数单位),若Z为纯虚数,则实数"等于A. —1B. 0C. 13. 的内角A, B, C的对边分别为a, b, c,若A = 45°, a = >/2, b = y/3 >A. 30°B. 60°C. 30°或150。
D. 60。
或120。
[x>\“占的最小值为4.若实数x, y满足条件< x-2y + 3>0fy > xD. 15 •已知平面a丄平面0, aQ\p=l ,直线m cz a ,直线nu 0 ,且加丄”,有以下四个结论:①若n//l,则m丄p②若加丄0,则加〃③也丄0和“丄a同时成立④加丄0和”丄a中至少有一个成立其中正确的是A.①③B.①④C. (2X3)D. ®@6.已知Rt^ABC,点£>为斜边BC的中点,|而| = 6石,|AC|=6, =则正•丽等于A. -14B. -9C. 9D.147.抛物线y2 = 4x的焦点为F ,点A(3,2), P为抛物线上一点,且P不在直线AF上,则AE4F周长的最小值为A. 4B. 5C. 4+2迈D.5+x/58.某校高三年级有男生220人,学籍编号1, 2,…,220:女生380人,学籍编号221, 222,…,600•为了解学生学习的心理状态,按学籍编号釆用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),然后再从这10位学生中随机抽取3人座谈,则3人中既有男生又有女生的概率是A. -B. —C. —D.-5 10 10 59.二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入= L电=2, J=0.1,则输出“的值为A.2B.3C.4D. 510.已知定义在(0,+00)上连续可导的函数“0满足W)+/(X)= J,且/(1) = 1, 则A. f(x)是增函数B. .f(x)是减函数C. f(x)有最大值1D. /(x)有最小值111 •已知双曲线二-二= 1(“" >0),过X 轴上点P 的直线/与双曲线的右支交于 cr M, N 两点(M 在第一象限),直线MO 交双曲线左支于点0 (O 为坐标原点),连接0N •若ZA/PO = 60。
2020届福建省厦门市高三第一次质量检查(一模)数学试题(理科)(解析版)

厦门市2020届高中毕业班第一次质量检查数学(理科)试题满分150分 考试时间120分钟注意事项:1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致. 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束,考生必须将试题卷和答题卡一并交回.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}260A x N x x =∈+-≤,{}R 13B x x =∈-≤≤,则A B =I ( ) A. {}12x x -≤≤B. {}0,1,2C. {}13x x -≤≤D. {}0,1,2,3 【答案】B【解析】【分析】解不等式化简集合A ,再进行交集运算,即可得答案;【详解】Q {}{}2600,1,2A x N x x =∈+-≤=, ∴{}0,1,2A B ⋂=.故选:B.【点睛】本题考查集合的交运算,考查运算求解能力,求解时注意x ∈N 这一条件的应用.2.若复数z 满足11z i -+=,z 在复平面内对应的点为(),x y ,则( )A. ()()22111x y +++=B. ()()22111x y ++-= C. ()()22111x y -+-=D. ()()22111x y -++= 【答案】D【解析】【分析】设(,)z x yi x y R =+∈,代入11z i -+=中,再利用模的运算,即可得答案; 【详解】设(,)z x yi x y R =+∈,代入11z i -+=得:()()22111x y -++=,故选:D.【点睛】本题考查复数模的运算、复数对应点的轨迹方程,考查函数与方程思想、转化与化归思想,考查运算求解能力,属于基础题. 3.已知{}n a 为等差数列,n S 为其前n 项和,若37a =,880S =,则6a =( )A. 17B. 15C. 13D. 11 【答案】C【解析】【分析】根据37a =,880S =求得1,a d 的值,再代入通项公式,即可得答案; 【详解】Q 37a =,880S =,∴11127,3,872,880,2a d a d a d +=⎧=⎧⎪⇒⎨⎨⨯=⋅+=⎩⎪⎩∴61513a a d =+=,故选:C.【点睛】本题考查等差数列基本量运算,考查函数与方程思想,考查运算求解能力,属于基础题.4.A 、B 两名同学6次的跳高成绩如图所示,且这6次成绩的平均分分别为A x ,B x ,标准差分别为A σ,B σ,则( )A. >A B x x ,A B σσ<B. <A B x x ,A B σσ<C. >A B x x ,A B σσ>D. <A B x x ,A B σσ>【答案】A【解析】【分析】根据图形中的数据,易得A 同学的平均值较高,且数据比较集中,即可得答案;【详解】根据图形中的数据知A 同学只是第3次成绩低于B 同学,可直观看出A 同学的平均成绩较高,故A B x x >;由于B 同学的成绩波动较大,所以A B σσ<;故选:A.【点睛】本题考查统计中的平均数与标准差,考查数据处理能力,属于基础题.5.1618年德国物理学家开普勒在《宇宙谐和论》上提出:绕以太阳为焦点的椭圆轨道运行的所有行星,其各自椭圆轨道半长轴长(单位:米)的立方()3a 与它的公转周期(单位:秒)的平方()2T 之比是一个常量,即32a k T=,24GM k π=(其中k 为开普勒常数,M 为中心天体质量,G 为引力常量).已知地球轨道的半长轴长约为1.5亿千米,地球的运行周期约为1年,距离太阳最远的冥王星轨道的半长轴长约为60亿千米,则冥王星的运行周期约为( )A. 150年B. 200年C. 250年D. 300年【答案】C【解析】【分析】地球轨道的半长轴长和运行周期可求得k 的值,再进一步利用公式计算冥王星的运行周期. 【详解】由题意得:321.51k =, ∴3332222360 1.560(365243600)(365243600) 1.5T T ⨯⨯⨯=⇒=⨯⨯, 365225436000T ⨯⨯≈⨯(秒)∴250T ≈年.故选:C.【点睛】本题考查数学文化,考查函数与方程思想,考查运算求解能力,求解时注意对时间单位的理解,可减少计算量.6.某程序框图如图所示,该程序运行后输出的S 的值是( )A. 3-B. 12-C. 13D. 2【答案】D【解析】【分析】 根据程序框图可知S 是一个周期数列,求出当2020i =时,对应S 的值,即可得答案;【详解】1,3i S ==-,212,42i S -===-, 1123,332i S ===, 434,223i S ===, 5,3i S ==-,L L2020,2i S ==,2021i =,输出2S =,故选:D.【点睛】本题考查程序框图中的循环结构,考查运算求解能力,求解时注意何时终止循环.7.如图是某圆锥的三视图,其正视图是一个边长为1的正三角形,圆锥表面上的点M ,N 在正视图上的对应点分别是A 、B .则在此圆锥的侧面上,从M 到N 的路径中,最短路径的长度为( )A. 1B. 2C. 2D. π 【答案】B【解析】【分析】由三视图可知几何体的直观图为圆锥,则圆锥的侧展图如图所示,再根据三视图中的数据,即可得答案;【详解】由三视图可知几何体的直观图为圆锥, Q 圆锥的底面周长为122ππ⨯=,∴圆锥侧展图的圆心角为π,由三视图可得,点,A B 在侧展图的位置,如图所示,Q 1OA OB ==,OA OB ⊥,∴2AB =.故选:B.【点睛】本题考查三视图还原几何体的直观图、圆锥表面上两点间的最短距离,考查空间想象能力、运算求解能力.8.在直角ABC V 中,90A =︒,6AB =,8AC =,D 是ABC V 的内心,则BD =u u u r( ) A. 2134AB AC -+u u u r u u u r B. 2134AB AC -u u u r u u u r C. 2133AB AC -+u u u r u u u r D. 2133AB AC -u u u r u u u r 【答案】A【解析】【分析】根据图形的特点建立直角坐标系,写出相关点的坐标,再利用平面向量基本定理的坐标运算,即可得答案;【详解】以A 为坐标原点,,AB AC 分别为,x y 轴建立直角坐标系,则(6,0)B ,(0,8)C ,Q 90A =︒,∴10BC =,设内切圆的半径为r ,则11(6810)68222r r ⋅++⋅=⋅⋅⇒=, ∴(2,2)D ,∴(6,0),(0,8),(4,2)AB AC BD ===-u u u r u u u r u u u r , 设BD x AB y AC =+u u u r u u u r u u u r ,∴2,46,328,1,4x x y y ⎧=-⎪-=⎧⎪⇒⎨⎨=⎩⎪=⎪⎩∴2134BD AB AC =-+u u u r u u u r u u u r . 故选:A.【点睛】本题考查平面向量基本定理的坐标运算、三角形的内切圆半径求解,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力.9.关于函数()cos sin f x x x =+有下述四个结论:①()f x 是偶函数;②()f x 在区间0,2π⎛⎫ ⎪⎝⎭上是增函数;③()f x 的最大值为2;④()f x 的周期为2π. 其中所有正确结论的编号是( )A. ①②B. ①④C. ①③④D. ②③④ 【答案】B【解析】【分析】对①,根据偶函数定义可判断;对②,去绝对值并利用导数判断;对③,直接根据同角三角函数的基本关系判断;对④,利用排除法可排除选项.【详解】对①,Q 函数的定义域为R 关于原点对称,且()()f x f x -=,∴()f x 为偶函数,故①正确; 对②,当0,2x π⎛⎫∈ ⎪⎝⎭时,()sin cos f x x x =+,则'()cos sin f x x x =-,Q '()0f x ≥在0,2x π⎛⎫∈ ⎪⎝⎭不恒成立,∴()f x 在区间0,2π⎛⎫ ⎪⎝⎭上是增函数错误,故②错误; 对③,若()f x 的最大值为2,则cos 1,sin 1x x ==,显然不可能同时取到,故③错误;利用排除法,可选排除选项ACD.故选:B.【点睛】本题考查三角函数的图象与性质运用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意排除法的运用.10.已知点()1,2M ,点P 在抛物线28y x =上运动,点Q 在圆()2221x y -+=上运动,则PM PQ +的最小值为( )A. 2B. 3C. 4D. 5【答案】A【解析】【分析】 先根据圆外一点到圆上一点距离的最小值得PM PQ PM PF r +≥+-,再利用抛物线的定义,即可得答案;【详解】如图所示,过P 作准线的垂线交于N , Q 11PM PQ PM PF r PM PF PM PN +≥+-=+-=+-,∴当,,P M N 三点共线时,PM PN +取得最小值3, ∴PM PQ +的最小值为2.故选:A.【点睛】本题考查圆外一点到圆上一点距离的最小值、抛物线的定义,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力、运算求解能力,求解时注意线段之间转换的应用.11.在四面体ABCD 中,2AB CD ==,5AC BD ==7AD BC ==α同时与直线AB 、直线CD 平行,且与四面体的每一个面都相交,由此得到一个多边形截面,则该多边形截面面积的最大值为( ) A. 338 B. 32 C. 538 D. 38【答案】B【解析】【分析】根据题意可得截面为平行四边形,求出异面直线,AB CD 所成的角,再代入三角形的面积公式,利用基本不等式可求得面积的最值.【详解】如图所示,在四面体ABCD 中,截面为EFGH ,由线面平行的性质定理可得//,////AB EF AB HG EF HG ⇒,同理可得://EH FG ;∴四边形EFGH 为平行四边形;当,,,E F G H 分别为边的棱的中点时, Q 2222211(2)2()4AE BC AB AC AE +=+⇒=, Q G 为AD 中点,AE DE =,∴EG AD ⊥, ∴22117144EG AE AG =-=-=, Q 1EF FG ==,∴3EFG π∠=;设CF x =,则5EF x EF x AB AC =⇒=,5(5)5FG x FG x CD AC -=⇒=-, ∴334533(5)555x x S EF FG x x ⎛⎫+-=⋅⋅=⋅-⋅≤⨯= ⎪ ⎪⎝⎭,等号成立当且仅当52x =, ∴多边形截面面积的最大值为3, 故选:B.【点睛】本题考查线面平行性质定理的运用、截面的面积最值、基本不等式的应用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意基本不等式求最值的运用.12.已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()11,A x y ,()22,B x y ,则下列结论错误的是( )A. 122x x +=B. 122x x e e e +>C. 1221ln ln 0x x x x +<D. 122e x x > 【答案】D【解析】【分析】对A ,分别作出函数2y x =-+,x y e =,ln y x =的图象,通过图象观察易得122x x +=成立;利用基本不等式可证B 成立;构造函数()ln x f x x=可证C 成立;构造函数()2ln g x x x =--可得21x e <<再利用函数ln y x x =的单调性,可证得D 不成立;【详解】对A ,如图,作出函数xy e =、ln y x =和y x =的草图,因为A ,B 关于C 对称,且1201x x <<<,因为()1,1C ,所以122x x +=,故A 正确;对B ,由基本不等式,121222x x x x e e e e ++≥=,因为12x x ≠,所以等号不成立,故B 正确;对C ,因为21212012x x x x +⎛⎫<<= ⎪⎝⎭,所以12101x x <<<,记()ln x f x x =, 则()21ln x f x x -'=,故01x <<时,()0f x '>,所以()ln x f x x=在()0,1上单调递增,所以()121f x f x ⎛⎫< ⎪⎝⎭,即1222121lnln ln 1x x x x x x <=-,即1221ln ln 0x x x x +<,故C 正确; 对D ,记()2ln g x x x =--,则()110g =>,132022g e e e ==<,则21x e <<()1222222ln x x x x x x =-=,易知ln y x x =在()1,e 上单调递增,故1222ln e x x x x e e =<=,故D 错误.故选:D .【点睛】本题考查利用导数研究不等式问题,考查函数与方程思想、转化与化归思想、数形结合思想,考查逻辑推理能力、运算求解能力,求解时注意函数构造法的应用.二、填空题:本大题共4小题,每小题5分,共20分.13.已知数列{}n a 的前n 项和为n S ,且92n n S a =-,则3a =________. 【答案】43 【解析】【分析】根据递推关系令1,2,3n n n ===,即可求得3a 的值.【详解】当1n =时,1111923S a a a =-=⇒=,当2n =时,22122922S a a a a =-=+⇒=,当3n =时,3312334923S a a a a a =-=++⇒=, 故答案为:43. 【点睛】本题考查数列递推关系的运用,考查函数与方程思想,考查运算求解能力,属于基础题.14.()6112x x ⎛⎫-+ ⎪⎝⎭的展开式中常数项为________.(用数字作答) 【答案】128-【解析】【分析】 利用二项式定理求出612x ⎛⎫+ ⎪⎝⎭通项公式,再根据r 的取值,即可得答案; 【详解】Q 612x ⎛⎫+ ⎪⎝⎭的展开式的通项公式61612(),0,,6r r r r T C r x -+==L 当0r =和1r =时,可得展开式中常数项为06156622128C C -=-, 故答案为:128-.【点睛】本题考查二项式定理求指定项的系数,考查逻辑推理能力、运算求解能力,求解时注意符号问题. 15.设函数()f x 的定义域为R ,满足()()2f x f x +-=,且当0x >时,()221f x x x =--+.若()234f m -≤,则实数m 的取值范围是________.【答案】[)1,+∞【解析】【分析】由题意得函数()f x 关于(0,1)呈中心对称,由0x >的解析式可得函数在(0,)+∞单调递减,并求出()f x 的解析式,可得(1)4f -=,从而得到关于m 的不等式,即可得答案.【详解】Q ()()2f x f x +-=,∴()f x 关于(0,1)中心对称,当0x <时,设(,)x y 为图象上任意一点,则(,)x y 关于(0,1)对称点为(,2)x y --, ∴222()2()121y x x y x x -=----+⇒=-+,()()2f x f x +-=中,当0x =时,(0)1f =,∴2221,0,()1,0,21,0,x x x f x x x x x ⎧--+>⎪==⎨⎪-+<⎩所以()f x 在R 上单调递减,且(1)4f -=,∴()()23423(1)231f m f m f m -≤⇔-≤-⇔-≥-,解得m 1≥,故答案为:[)1,+∞.【点睛】本题考查函数的性质、利用函数的单调性解不等式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力. 16.已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为1F 、2F ,O 为坐标原点,P 是双曲线上一点,且OP =,点M 满足12F M MP =u u u u r u u u r ,20OP MF ⋅=u u u r u u u u r ,则双曲线的离心率为________.【答案】2【解析】【分析】取1PF 另一三等分点N ,则有2//ON MF ,又M 是PN 中点,则有Q 是OP 中点,再由平行四边形的对角线平方和等于四边的平方和,列出关于,a c 的方程,即可得答案;【详解】因为点M 满足12F M MP =u u u u r u u u r ,所以M 是1PF 一个三等分点,取1PF 另一三等分点N ,则有2//ON MF ,又M 是PN 中点,则有Q 是OP 中点,因为220OP MF OP MF FQ OP ⋅=⇒⊥⇒⊥u u u r u u u u r u u u r u u u u r , 所以22PF OF c ==,则12PF a c =+,Q 由平行四边形对角线平方和等于四边的平方和, ∴22221212224PF PF F F PO +=+,∴22222(2)2(2)46a c c c a ++=+⋅,化简得2e =.故答案为:2.【点睛】本题考查双曲线的离心率求解,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意平面几何知识的运用.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22题、第23题为选考题,考生根据要求作答.(一)必考题:共60分.17.ABC V 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cossin 2A C a b A +=. (1)求B ;(2)若6A π=,AB 边上的中线27CM =,求ABC V 的面积.【答案】(1)23B π=(2)43【解析】【分析】 (1)由正弦定理可得sin cossin sin 2A C A B A +=,再利用诱导公式和倍角公式,求得23B π=,即可得答案; (2)利用余弦定理求出4a =,再代入三角形的面积公式,即可得答案;【详解】(1)依题设及正弦定理可得,sin cossin sin 2A C AB A +=, 因为sin 0A >,所以cos cos sin 222A CB B π+-==, 所以sin 2sin cos 222B B B =, 又sin 02B >,所以1cos 22B =, 又022B π<<,所以23B π=,即23B π=. (2)因为23B π=,6A π=, 所以6C A B ππ=--=,故ABC V 为等腰三角形. 则c a =,2a BM =在MBC △中由余弦定理可得,2222cos MC BM BC BM BC B =+-⋅⋅, 即()2222272cos 223a a a a π⎛⎫=+-⋅⋅⋅ ⎪⎝⎭,解得4a =, 所以113sin 4443222ABC S ac B ==⨯⨯⨯=V .【点睛】本题考查正弦定理、余弦定理、三角形的面积公式和三角恒等变换等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想.18.如图,平行四边形ABCD 中,26AD AB ==,E 、F 分别为AD ,BC 的中点.以EF 为折痕把四边形EFCD 折起,使点C 到达点M 的位置,点D 到达点N 的位置,且NF NA =.(1)求证:AF ⊥平面NEB ;(2)若3BE =N BE M --的余弦值.【答案】(1)见解析(2)22. 【解析】【分析】 (1)记AF BE O =I ,连接NO ,证明,,AF BE AF NO ⊥⊥即可证明结论;(2)先证明NO ⊥平面ABFE ,再以直线OE 为x 轴,直线OA 为y 轴,直线ON 为z 轴建立空间直角坐标系,求出平面MBE 的法向量()0,1,1a =r ,平面NBE 的一个法向量()6,0OA =u u u r ,代入向量的夹角公式,即可求得二面角N BE M --的余弦值.【详解】(1)证明:记AF BE O =I ,连接NO ,可知四边形ABFE 是菱形,所以AF BE ⊥,且O 为AF ,BE 的中点,又NF NA =,所以AF NO ⊥,又因为NO BE O =I ,NO ,BE ⊂平面NEB ,所以AF ⊥平面NEB .(2)因为23BE =,所以3EO =,23NF =,所以226FO EF EO =-=, 所以226NO NF FO =-=,所以2229NO EO NE +==,所以NO BE ⊥,又由(1)可知:NO AF ⊥,且AF BE O =I ,AF ,BE ⊂平面ABFE ,所以NO ⊥平面ABFE ,以直线OE 为x 轴,直线OA 为y 轴,直线ON 为z 轴建立空间直角坐标系,则()0,6,0A ,()3,0,0B -,()3,0,0E,()0,6,0F -,()0,0,6N ,Q OM ON NM ON AB =+=+u u u u r u u u r u u u u r u u u r u u u r ()()0,0,63,6,0=+--()3,6,6=--所以()3,6,6M --,所以()0,6,6BM =-u u u u r ,()23,0,0BE =u u u r , 设(),,a x y z =r是平面MBE 的法向量,则 0660000230y z x a BM y z a BE x ⎧⎧-+==⎧⋅=⎪⎪⇒⇒⎨⎨⎨=⋅==⎩⎪⎪⎩⎩u u u u v v u u u v v ,取1y =,得()0,1,1a =r , 又平面NBE 的一个法向量为()0,6,0OA =u u u r , 所以62cos ,226a OA a OA a OA⋅===⨯⋅u u u r r u u u r r u u u r r , 所以二面角N BE M --的余弦值为22.【点睛】本题考查直线与平面垂直、二面角、空间向量等基础知识;考查空间想象能力、运算求解能力、推理论证能力;考查数形结合思想、化归与转化思想等.19.已知椭圆22:12x C y +=,A 为C 的上顶点,过A 的直线l 与C 交于另一点B ,与x 轴交于点D ,O 点为坐标原点.(1)若2AB =,求l 的方程; (2)已知P 为AB 的中点,y 轴上是否存在定点Q ,使得0OP DQ ⋅=u u u r u u u r ?若存在,求Q 的坐标;若不存在,说明理由.【答案】(1):12l y x =±+(2)存在()0,2Q 【解析】【分析】(1)对直线的斜率进行讨论,当斜率不存在时显然不满足,当直线斜率存在时,设出直线方程,代入弦长公式求出斜率的值,即可得答案;(2)利用中点坐标公式求得2221,2121k P k k -⎛⎫⎪++⎝⎭,根据0OP DQ ⋅=u u u r u u u r 求出,DQ 的方程,即可得到定点坐标.【详解】(1)①当直线的斜率不存在时,:0l x =,2AB =,舍去;②当直线的斜率存在时,:1l y kx =+,0k ≠, 联立方程22122y kx x y ⎧=+⎨+=⎩,化简得()222140k x kx ++=, 解得0x =或2421k x k -=+,所以222412,2121k k B k k ⎛⎫-- ⎪++⎝⎭,所以240212k AB k -=-=+,化简得4244150k k +-=,解得232k =或252k =-(舍去),即k =所以:1l y x =+.(2)①:1l y kx =+,由(1)得2221,2121k P k k -⎛⎫⎪++⎝⎭,1,0D k ⎛⎫- ⎪⎝⎭, 所以12OP k k=-,又因为0OP DQ ⋅=u u u r u u u r ,所以OP DQ ⊥,所以2DQ k k =, 所以1:222DQ l y k x kx k ⎛⎫=+=+ ⎪⎝⎭, 即存在定点()0,2Q 满足条件.②:0l x =,则O ,P 重合,()0,2Q 也满足条件综上,存在()0,2Q 满足条件.【点睛】本题考查直线的方程、直线与椭圆的位置关系等知识;考查运算求解能力、推理论证能力等;考查数形结合思想、函数与方程思想、化归与转化思想等.20.小明和爸爸玩亲子游戏,规则如下:袋中装有3个大小相同的球,1个白球,2个红球,每次摸出一个球,记下颜色后放回,若摸出白球,则下一次由原摸球人继续摸球;若摸出红球,则下一次由对方摸球,规定摸球m 次,最后一次由谁摸球就算谁获胜.第一次由小明摸球.(1)求前3次摸球中小明恰好摸2次的概率;(2)设第n 次()n m ≤由小明摸球的概率为n P ,则11P =.(ⅰ)求4P ;(ⅱ)在19m =与20m =之中选其一,小明应选哪个?(只写结果,不必说明理由!)【答案】(1)23(2)(ⅰ)1327(ⅱ)选19次. 【解析】【分析】(1)设事件A ={前3次摸球中小明恰好摸2次球},事件i B ={第i 次由小明摸球},利用相互独立事件的概率计算,即可得答案;(2)(ⅰ)第4次由小明摸球有4种情况,分别计算概率,即可得到4P 的值:(ⅱ)由(ⅰ),猜测192012P P >>,所以选19次. 【详解】(1)设事件A ={前3次摸球中小明恰好摸2次球},事件i B ={第i 次由小明摸球},所以()()()()1231231231231222233333P A P B B B B B B P B B B P B B B =+=+=⨯+⨯=. (2)第4次由小明摸球有以下情况:则4,1111133327P =⨯⨯=, 则4,2122433327P =⨯⨯=, 则4,3221433327P =⨯⨯=, 则4,4212433327P =⨯⨯=, 所以44,14,24,34,41327P P P P P =+++=. (ⅱ)由(ⅰ),猜测192012P P >>,所以选19次. 【点睛】本题考查概率的性质和概率与数列的综合应用等知识;考查数学抽象、逻辑推理、数学建模、数学运算素养;考查统计与概率、或然与必然思想等.21.已知函数()ln 1f x a x x =+-,()31g x x =-. (1)若直线:1l y x =-+与曲线()y f x =相切,求实数a 的值;(2)用{}min ,m n 表示m ,n 中的最小值,设函数()()(){}()min ,0h x f x g x x =>,讨论()h x 零点的个数.【答案】(1)2a =-.(2)当1a ≥-时,()h x 有1个零点;当1a <-时,()h x 有2个零点.【解析】【分析】(1)设切点()00,P x y 利用切点既在曲线上又在切线上,导数的几何意义,可得方程组0011,ln 11,a x a x a ⎧+=-⎪⎪⎨⎪--=⎪⎩消去0x 得ln 10222a a a ⎛⎫---= ⎪⎝⎭(*),利用导数解方程,即可得答案; (2)对x 分三种情况考虑,即01x <<、1x =、1x >,可得01x <<时无零点,1x =时一个零点,1x >时,()0g x >,()h x 的零点即为()f x 的零点,再利用零点存在定理,即可得答案;【详解】(1)依题意,()1a f x x'=+, 则曲线()y f x =在点()00,P x y 处的切线方程为()0001a y y x x x ⎛⎫-=+- ⎪⎝⎭, 又000ln 1y a x x =+-,代入整理得001ln 1a y x a x a x ⎛⎫=++-- ⎪⎝⎭,此直线与:1l y x =-+重合,得0011,ln 11,a x a x a ⎧+=-⎪⎪⎨⎪--=⎪⎩消去0x 得ln 10222a a a ⎛⎫---= ⎪⎝⎭(*), 记()ln 1r x x x x =-+-,则()ln r x x '=-,当01x <<时,()0r x '>,()r x 单调递增;当1x >时,()0r x '<,()r x 单调递减;所以()()10r x r ≤=,当且仅当1x =时取等号.由(*)式可知02a r ⎛⎫-= ⎪⎝⎭,所以12a -=,即2a =-. (2)①当01x <<时,()310g x x =-<,所以()()0h x g x ≤<,无零点,②当1x =时,()()110f g ==,从而()10h =,故1x =为()h x 的一个零点,③当1x >时,()0g x >,则()h x 的零点即为()f x 的零点,令()10a x a f x x x+=+==',得x a =-, (ⅰ)若1a -≤,即1a ≥-时,()0x a f x x +'=>, 从而()f x 在()1,+∞上单调递增,进而()()10f x f >=,又()()10g x g >=,所以()0h x >,此时()h x 在()1,+∞上无零点.(ⅱ)若1a ->,即1a <-时,因为()f x 在()1,a -上单调递减,在(),a -+∞上单调递增,因为()10f =,()()10f a f -<=,故()f x 在()1,a -上无零点.另外,由(1)可知()110r r x ⎛⎫≤=⎪⎝⎭恒成立,即ln 1x x ≤-对0x >恒成立, 则()()()2ln 42ln 2221a a a =-≤--,所以()()()22224ln 44122141210f a a a a a a a a =+-≥⨯--+-=-->,故存在()20,4x a a ∈-,进而存在()0,x a ∈-+∞,使得()00f x =,即()00h x =, 此时()h x 在()1,+∞上存在唯一零点.综上可得,当1a ≥-时,()h x 有1个零点;当1a <-时,()h x 有2个零点.【点睛】本题考查函数的单调性、导数几何意义及其应用、不等式等基础知识;考查推理论证能力、运算求解能力、创新意识等;考查函数与方程思想、化归与转化思想、分类与整合思想等.(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,直线l 的方程为2x =-,曲线C 的方程为22(1)1x y -+=,动点P 到原点O 的距离与到l 的距离相等.以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系.(1)求C 的极坐标方程和P 点轨迹的极坐标方程;(2)若Q 是曲线C 上一点,且4OP OQ =u u u r u u u r ,求||OP .【答案】(1)2cos ρθ=,21cos ρθ=-.(2)4 【解析】 【分析】(1)利用222,cos x y x ρρθ=+=,代入圆的方程2220x y x +-=,即可得到圆的极坐标方程;对点P 在y 轴右侧时,P 在y 轴,y 轴左侧时,三种情况进行讨论,均可得到21cos ρθ=-; (2)因为4OP OQ =u u u r u u u r,所以设点()()12,,,P Q ρθρθ,且124ρρ=,求出cos θ的值,即可得答案; 【详解】(1)由22(1)1x y -+=得,2220x y x +-=.因为222,cos x y x ρρθ=+=,所以2cos ρθ=,即为C 的极坐标方程. 当P 在y 轴右侧时,过点P 作x 轴的垂线,垂足为M ,作y 轴的垂线,垂足为N ,设l 与x 轴的交点为R , 因为点P 到原点距离与到l 距离相等,所以||||||||||OP PN MR OR OM ===+.在RT OPM V 中,||||cos cos OM OP θρθ==,所以2cos ρρθ=+.因为0θ≠,所以21cos ρθ=-. 当P 在y 轴或y 轴左侧时,满足21cos ρθ=-. 综上,P 点轨迹的极坐标方程为21cos ρθ=-. (2)因为4OP OQ =u u u r u u u r ,所以设点()()12,,,P Q ρθρθ,且124ρρ=.又122,2cos 1cos ρρθθ==-,所以28cos 1cos θθ=-, 解得1cos 2θ=,所以2||4112OP ==-. 【点睛】本题考查曲线的极坐标方程等基础知识,考查直线与圆锥曲线的位置关系;考查运算求解能力、推理论证能力;考查数形结合思想、化归与转化思想、分类与整合思想等.[选修4-5:不等式选讲]23.已知函数()f x x a x b x c =+++++.(1)若a ,b ,0c >,()01f =,证明:13ab bc ac ++≤; (2)若1a b ==,对于任意的(,2]x ∈-∞-,()4f x ≥恒成立,求c 的取值范围.【答案】(1)见解析(2)0c ≤或4c ≥【解析】【分析】(1)由已知得()01f a b c =++=,两边平方再利用基本不等式,即可得答案;(2)对于任意的(],2x ∈-∞-,()4f x ≥恒成立,取()24f -≥得到c 的范围,进而验证0c ≤或4c ≥符合题意.【详解】(1)由已知得,()01f a b c a b c =++-=++=,所以()2222222a b c a b c ab bc ac ++=+++++ ()()()22222212222a b b c a c ab bc ac ⎡⎤=++++++++⎣⎦ ()12222222ab bc ac ab bc ac ≥+++++ ()3ab bc ac =++ . 所以13ab bc ac ++≤. (2)当1a b ==时,()21f x x x c =+++,因为对于任意的(],2x ∈-∞-,()4f x ≥恒成立,所以()2224f c -=+-+≥,解得0c ≤或4c ≥,①当0c ≤时,()()2132f x x x c x c =+++=-++在(],2x ∈-∞-为减函数,所以()()min 244f x f c =-=-+≥,即0c ≤,②当4c ≥时,()()2,22132,x c c x f x x x c x c x c ⎧--+-<≤-⎪=+++=⎨-++≤-⎪⎩在(],2x ∈-∞-为减函数, 所以()()min 24f x f c =-=≥,即4c ≥,综上所述,0c ≤或4c ≥.【点睛】本题考查基本不等式、含绝对值不等式等基础知识;考查推理论证能力、运算求解能力等;考查数形结合、转化与化归、函数与方程、分类与整合等数学思想方法.。
福建省厦门市高中毕业班第一次质量检查理科综合能力测试题参考答案

福建省厦门市高中毕业班第一次质量检查理科综合能力测试题&参考答案(本试卷满分300分,考试时间150分钟)可用到的相对原子质量:H -1 C-12 O-16第I卷(选择题共126分)一、选择题:(本题共13小题,每小题6分,在每小题给出的四个选项中,只有一项是符合题目要求)1.下列所选的材料对植物细胞发生质壁分离影响最小的是A.细胞是否为活细胞B.细胞是否具有大液泡C.细胞的液泡是否具有颜色D.外界溶液浓度是否大于细胞液浓度2.下列关于酶与ATP的叙述,正确的是A.细胞内的酶和ATP均为多聚体B.酶和ATP的合成过程均需要能量C.酶与ATP均要在细胞器中合成D.生物体内的生化反应均需要酶和ATP 参与3.下列关于同一个体中神经细胞、胰岛B细胞、T细胞的叙述,正确的是A.细胞器的种类和数量都相同B.mRNA的种类和数量都相同C.都能分泌蛋白质作用于靶细胞D.都能参与内环境稳态的维持4.下图为某二倍体生物生殖腺中的细胞分裂示意图,下列叙述正确的是A.在显微镜下可观察到某细胞从→丙→丁连续分裂的过程B.甲细胞分裂结束,形成1个丙细胞和3个丁细胞C.甲、乙、丙、丁细胞中的染色体组数目依次为2、2、1、1D,乙细胞所示阶段发生同源染色体的分离和非同源染色体的自由组合5.日本科学家大隅良典因发现“细胞自噬”机制而获得了2016年诺贝尔生理学或医学奖。
细胞自噬是指当细胞接收到诱导信号后,胞内的一些膜会把周围的细胞质吞进去形成“自噬体”,随后与溶酶体融合,经消化后,一些可利用的物质被送回细胞质循环利用。
下列推论不合理的是A.细胞“自噬体”对细胞质成分的吞噬具有特异性B.当营养物质不足时,细胞的自噬作用会明显加强C.胚胎发育过程中需要通过自噬作用来处理废弃的细胞器D.自噬机制发生缺陷,会导致细胞内废物和垃圾增多6.下表为椠患者血液化验的部分结果:据此分析,其体内最可能发生的是A.会出现抽搐等症状B.神经细胞膜静息电位的绝对值增大C.胰岛素促进葡萄糖运出肝细胞D.肾小管和集合管重吸收水分增加7.化学在生活中应用广泛,下列物质性质与对应用途错误的是A.明矾易水解生成胶体,可用作净水剂B.晶体硅熔点高硬度大,可用作芯片C.氮气化学性质稳定,可用作粮食保护气D.溴化银见光易分解,可用作胶片感光剂8.设N A为阿伏加徳罗常数的值。
高三下学期第一次质量检查理综物理试题解析版

理科综合能力测试(物理)
第I卷(选择题共48分)
一、选择题:本题共8小题,每小题6分,共48分。在每小题给出的四个选项中,第1-5题只有一项符合题目要求,第6-8题有多项符合要求。全部选对的得6分,选对但不全的得3分,有选错的得0分。
1. 手机给人们的生活带来了很多便利,如以滴滴为代表的出行软件不仅极大地方便了人们的出行,更是缓解了城市交通中出租车的压力。下图为小敏从家打车到某超市的软件界面截图及该次的行程单,则( )
(3)滑块与斜面间的动摩擦因数 =____(用k,g,d,θ表示)
【答案】(1). 2.4 (2). (3).
【解析】
【详解】(1)[1]游标卡尺的读数为
(2)[2]用滑块通过光电门时的平均速度来代替瞬时速度大小,故
(3)[3]根据速度位移公式有
根据牛顿第二定律可得
结合
,
联立解得
10. 二极管具有单向导电性,小明同学在实验室找到了一个旧的二极管,他想通过实验来描绘该二极管正向导电时的伏安特性曲线。
A. 打车软件根据载客行驶 位移大小进行计费
B. 研究汽车在此次行程的运动轨迹时,可以把汽车当做质点
C. 上车时间“16:30”中,“16:30”指的是时间
D. 利用行程单中的数据可以计算出整个行程的平均速度
【答案】B
【解析】
【详解】AD.打车软件根据载客行驶的实际轨迹,即路程来收费的,故根据行程单中的数据可以计算出整个行程的平均速率,不知道位移,所以无法计算平均速度,AD错误;
A. 行星“飞马座5lb”的第一宇宙速度约为地球的11.4倍
B. 行星“飞马座5lb”的第一宇宙速度约为地球的3.4倍
C. 类日恒星的质量与太阳的质量之比约为3:1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在 HON 中: NH = 1 NF = 3 , OH = 1 BM = 1 AN = 3 , NO = 6
2
2
2
所以 cos HON = 6 + 3 − 3 = 2 ------------------------------------------------------------------------------ 11 分 2 6 3 2
2
2
2
所以 sin B = 2sin B cos B ------------------------------------------------------------------------------------------- 3 分
2
22
又 sin B 0 ,所以 cos B = 1 -------------------------------------------------------------------------------------- 4 分
所以二面角 N − BE − M 的余弦值为 2 .------------------------------------------------------------------------12 分 2
19.本题考查直线的方程、直线与椭圆的位置关系等知识;考查运算求解能力、推理论证能力等;考查数
厦门市 2020 届高中毕业班第一次质量检查
数 学(理科)试题参考解答
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题
目要求的。
题号 1
2
3
4
5
6
7
8
9
10
11
12
答案 B
D
C
A
C
D
B
A
B
A
B
D
第 12 题解答提示:
如图,作出函数 y = ex 、 y = ln x 和 y = x 的草图,因为 A, B 关于 C 对称,
2
22
又 0 B ,所以 B = ,即 B = 2 ----------------------------------------------------------------------- 5 分
22
23
3
第2页 共14页
(2)因为 B = 2 , A =
3
6
所以 C = − A − B = ------------------------------------------------------------B---------------------------------- 6 分 6
第3页 共14页
则 A(0, 6,0) , B(− 3,0,0) , E( 3,0,0) ,
F (0, − 6,0) , N (0,0, 6)
OM = ON + NM = ON + AB = (0,0, 6) + (− 3, − 6,0) , = (− 3,− 6, 6)
所以 M (− 3, − 6, 6)
Mz
N
C D
F
B
O
E
x
Ay
所以 BM = (0,− 6, 6) , BE = (2 3,0,0) (亦可不求 M ,由 BM = AN = (0,− 6, 6) )
设 a = (x, y, z) 是平面 MBE 的法向量,则
a
BM
=
0
0
−
6y +
a BE = 0 2 3x = 0
6z
=0
x = 0
② l : y = kx +1, k 0 ,
y = kx + 1
联立方程
x
2
+
2y2
=
2
,化简得 (2k 2
+ 1)x2
+
4kx
=
0
A PLeabharlann 解得 x = 0 或 x =
−4k 2k 2 +
1
,所以
B(
−4k 2k 2 +
1
,
1− 2k 2k 2 +
2
) 1
BD
O
x
-------------------------------------------------------------- 3 分
13. 4 3
14. −128
第 16 题解答提示:
15.1, +)
16. 2
解法 1:
取 PF1 另一三等分点 N ,则有 ON / /MF2 ,又 M 是 PN 中点,则有 Q 是 OP 中点,所以 | PF2 |=| OF2 |= c ,
第1页 共14页
则 | PF1 |= 2a + c ,由平行四边形法则 2 | PF1 |2 +2 | PF2 |2 =| F1F2 |2 +4 | PO |2 ,化简得 e = 2 .
M
故 ABC 为等腰三角形.
则 c = a , BM
=a
A
C
--------------------------------------------------------------------------------------------------- 8 分
2
在 MBC 中由余弦定理可得, MC2 = BM 2 + BC2 − 2BM BC cos B
B1
所以 AB =
1 + k 2 −4k − 0 = 2k2 +1
15 ,化简得 4k4 + 4k2 −15 = 0 2
---------- 4 分
解得 k 2 = 3 或 k 2 = − 5 (舍去),即 k = 6 --------------------------------------------------------------------- 5 分
,
则
f
(
x
)
=
1
− ln x2
x
,故
0
x 1时,
f (x) 0 ,所以
f
(x) =
ln x x
在 (0,1)
上单调递增,所以
ln 1
f
( x1 )
f
1 x2
,即
ln x1 x1
x2 1
=
−
x2
ln
x2
,即
ln x1 x1
+ x2 ln x2
0 ,C 正确.
x2
( ) 记 g ( x) = 2 − x − ln x ,则 g(1) = 1 0 , g
18.本题考查直线与平面垂直、二面角、空间向量等基础知识;考查空间想象能力、运算求解能力、推理
论证能力;考查数形结合思想、化归与转化思想等.满分 12 分.
(1)证明:记 AF BE = O ,连接 NO 可知四边形 ABFE 是菱形,所以 AF ⊥ BE 且 O 为 AF、BE 的中点 又 NF = NA ,所以 AF ⊥ NO
(2)因为 BE = 2 3 ,所以 EO = 3 , NF = 2 3
所以 FO = EF 2 − EO2 = 6
所以 NO = NF 2 − FO2 = 6 所以 NO2 + EO2 = 9 = NE2 ,所以 NO ⊥ BE --------------------------------------------------------------------- 6 分 解法一: 又由(1)可知: NO ⊥ AF ,且 AF BE = O , AF、BE 平面 ABFE 所以 NO ⊥ 平面 ABFE 以直线 OE 为 x 轴,直线 OA 为 y 轴,直线 ON 为 Z 轴建立空间直角坐标系----------------------------- 7 分
即 (2
7)2
=
a 2
2
+ a2
−2
a 2
a cos
2 3
,解得 a
=
4 ------------------------------------------------------10
分
所以 SABC
=
1 2
ac sin
B
=
1 4 4 2
3 =4 2
3 ---------------------------------------------------------------12 分
解:(1)依题设及正弦定理可得, sin Acos A + C = sin B sin A ------------------------------------------------ 1 分 2
因为 sin A 0,所以 cos A + C = cos − B = sin B --------------------------------------------------------- 2 分
且 0 x1 1 x2 ,
因为 C (1,1) ,所以 x1 + x2 =2 ,A 正确;
由基本不等式,ex1 + ex2 2 ex1+x2 =2e ,因为 x1 x2 ,所以等号不成立,
B 正确;
因为 0
x1x2
x1
+ 2
x2
2
= 1,所以 0
x1
1 x2
1 ,记
f
(x)
=
ln x x
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题,每个试题考 生都必须作答。第 22 题、第 23 题为选考题,考生根据要求作答。
