上海市杨浦区2017届高考数学一模(含答案)12月份

合集下载

2017年杨浦一模试卷(18,24,25)

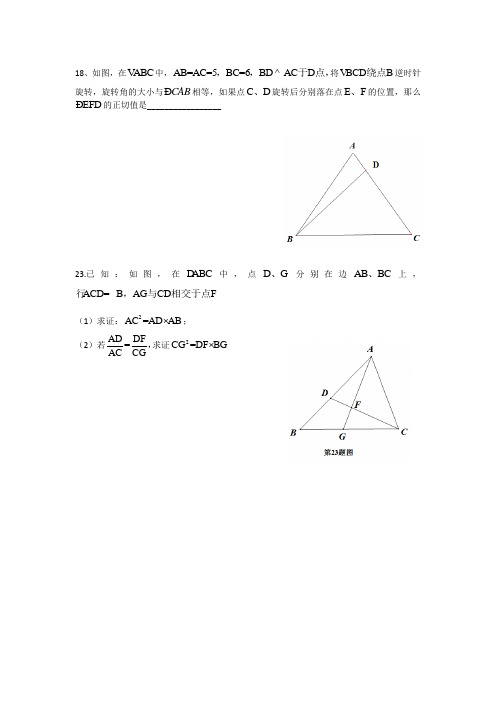
18、如图，在ABC 中，AB=AC=5BC=6BD AC D ^，，于点，将BCD B 绕点逆时针旋转，旋转角的大小与CAB Ð相等，如果点C D 、旋转后分别落在点E F 、的位置，那么EFD Ð的正切值是_________________
23.已知：如图，在ABC D 中，
点D G 、分别在边AB BC 、上，
A C D =
B A G
C
D 行，与相交于点
（1）求证：2AC =AD AB ×；
（2）若AD
DF
=AC CG ，求证2CG =DF BG ×
24、在直角坐标系中，抛物线2443(0)y ax ax a a =-++<的顶点为D ，它的对称轴与x 轴交点为M ；
（1）求D M 、的坐标
（2）如果该抛物线与y 轴的交点为A ，点P 在抛物线上，且AM DP ，AM=2DP ，求a 的值
25、在直角三角形ABC 中，ACB=90AC=BC=2Ð ，，点P 为边BC 上一动点（不与B C
、重合），点P AC AB 关于直线、的对称点分别为M N 、，联结MN 交AB 于点F ，AC E 交边于点；
（1）如图，当点P 为边BC 的中点时，求M Ð的正切值
（2）联结FP ，设,.MPF CP x S y D ==求y 关于x 的函数解析式，并写出定义域
（3）联结AM ，当点P 在边BC 上运动时，AEF ABM D
D 和是否一定相似？若是，请证明，若不是，请求出AEF ABM D
D 和相似时CP 的长；。

2017高考上海各区数学一模(含答案)

上海市宝山区2017届高三一模数学试卷一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 23lim1n n n →∞+=+2. 设全集U R =，集合{1,0,1,2,3}A =-，{|2}B x x =≥，则U AC B =3. 不等式102x x +<+的解集为 4. 椭圆5cos 4sin x y θθ=⎧⎨=⎩（θ为参数）的焦距为5. 设复数z 满足23z z i +=-（i 为虚数单位），则z =6. 若函数cos sin sin cos x xy x x=的最小正周期为a π，则实数a 的值为7. 若点(8,4)在函数()1log a f x x =+图像上，则()f x 的反函数为 8. 已知向量(1,2)a =，(0,3)b =，则b 在a 的方向上的投影为9. 已知一个底面置于水平面上的圆锥，其左视图是边长为6的正三角形，则该圆锥的侧面积为10. 某班级要从5名男生和2名女生中选出3人参加公益活动，则在选出的3人中男、女生均有的概率为（结果用最简分数表示）11. 设常数0a >，若9()a x x+的二项展开式中5x 的系数为144，则a =12. 如果一个数列由有限个连续的正整数组成（数列的项数大于2），且所有项之和为N ，那么称该数列为N 型标准数列，例如，数列2，3，4，5，6为20型标准数列，则2668型标准数列的个数为二. 选择题（本大题共4题，每题5分，共20分）13. 设a R ∈，则“1a =”是“复数(1)(2)(3)a a a i -+++为纯虚数”的（） A. 充分非必要条件 B. 必要非充分条件 C. 充要条件 D. 既非充分又非必要条件14. 某中学的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生120 人，则该样本中的高二学生人数为（）A. 80B. 96C. 108D. 110 15. 设M 、N 为两个随机事件，给出以下命题：（1）若M 、N 为互斥事件，且1()5P M =，1()4P N =，则9()20P M N =；（2）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（3）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（4）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（5）若1()2P M =，1()3P N =，5()6P MN =，则M 、N 为相互独立事件；其中正确命题的个数为（）A. 1B. 2C. 3D. 416. 在平面直角坐标系中，把位于直线y k =与直线y l =（k 、l 均为常数，且k l <）之间的点所组成区域（含直线y k =，直线y l =）称为“k l ⊕型带状区域”，设()f x 为二次函数，三点(2,(2)2)f --+、(0,(0)2)f +、(2,(2)2)f +均位于“04⊕型带状区域”，如果点(,1)t t +位于“13-⊕型带状区域”，那么，函数|()|y f t =的最大值为（） A. 72 B. 3 C. 52D. 2三. 解答题（本大题共5题，共14+14+14+16+18=76分） 17. 如图，已知正三棱柱111ABC A B C -的底面积为934，侧面积为36；（1）求正三棱柱111ABC A B C -的体积；（2）求异面直线1AC 与AB 所成的角的大小；18. 已知椭圆C 的长轴长为26，左焦点的坐标为(2,0)-；（1）求C 的标准方程；（2）设与x 轴不垂直的直线l 过C 的右焦点，并与C 交于A 、B 两点，且||6AB =，试求直线l 的倾斜角；19. 设数列{}n x 的前n 项和为n S ，且430n n x S --=（*n N ∈）；（1）求数列{}n x 的通项公式；（2）若数列{}n y 满足1n n n y y x +-=（*n N ∈），且12y =，求满足不等式559n y >的最小正整数n 的值；20. 设函数()lg()f x x m =+（m R ∈）；（1）当2m =时，解不等式1()1f x >；（2）若(0)1f =，且1()()2x f x λ=+在闭区间[2,3]上有实数解，求实数λ的范围；（3）如果函数()f x 的图像过点(98,2)，且不等式[cos(2)]lg2n f x <对任意n N ∈均成立，求实数x 的取值集合；21. 设集合A 、B 均为实数集R 的子集，记：{|,}A B a b a A b B +=+∈∈；（1）已知{0,1,2}A =，{1,3}B =-，试用列举法表示A B +；（2）设123a =，当*n N ∈，且2n ≥时，曲线2221119x y n n n +=-+-的焦距为n a ，如果 12{,,,}n A a a a =⋅⋅⋅，122{,,}993B =---，设A B +中的所有元素之和为n S ，对于满足3m n k +=，且m n ≠的任意正整数m 、n 、k ，不等式0m n k S S S λ+->恒成立，求实数λ的最大值；（3）若整数集合111A A A ⊆+，则称1A 为“自生集”，若任意一个正整数均为整数集合2A 的某个非空有限子集中所有元素的和，则称2A 为“*N 的基底集”，问：是否存在一个整数集合既是自生集又是*N 的基底集？请说明理由；上海市宝山区2017届高三一模数学试卷一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 23lim1n n n →∞+=+2. 设全集U R =，集合{1,0,1,2,3}A =-，{|2}B x x =≥，则U AC B =3. 不等式102x x +<+的解集为 4. 椭圆5cos 4sin x y θθ=⎧⎨=⎩（θ为参数）的焦距为5. 设复数z 满足23z z i +=-（i 为虚数单位），则z =6. 若函数cos sin sin cos x xy x x=的最小正周期为a π，则实数a 的值为7. 若点(8,4)在函数()1log a f x x =+图像上，则()f x 的反函数为 8. 已知向量(1,2)a =，(0,3)b =，则b 在a 的方向上的投影为9. 已知一个底面置于水平面上的圆锥，其左视图是边长为6的正三角形，则该圆锥的侧面积为10. 某班级要从5名男生和2名女生中选出3人参加公益活动，则在选出的3人中男、女生均有的概率为（结果用最简分数表示）11. 设常数0a >，若9()a x x+的二项展开式中5x 的系数为144，则a =12. 如果一个数列由有限个连续的正整数组成（数列的项数大于2），且所有项之和为N ，那么称该数列为N 型标准数列，例如，数列2，3，4，5，6为20型标准数列，则2668型标准数列的个数为二. 选择题（本大题共4题，每题5分，共20分）13. 设a R ∈，则“1a =”是“复数(1)(2)(3)a a a i -+++为纯虚数”的（） A. 充分非必要条件 B. 必要非充分条件 C. 充要条件 D. 既非充分又非必要条件14. 某中学的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生120 人，则该样本中的高二学生人数为（）A. 80B. 96C. 108D. 110 15. 设M 、N 为两个随机事件，给出以下命题：（1）若M 、N 为互斥事件，且1()5P M =，1()4P N =，则9()20P M N =；（2）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（3）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（4）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（5）若1()2P M =，1()3P N =，5()6P MN =，则M 、N 为相互独立事件；其中正确命题的个数为（）A. 1B. 2C. 3D. 416. 在平面直角坐标系中，把位于直线y k =与直线y l =（k 、l 均为常数，且k l <）之间的点所组成区域（含直线y k =，直线y l =）称为“k l ⊕型带状区域”，设()f x 为二次函数，三点(2,(2)2)f --+、(0,(0)2)f +、(2,(2)2)f +均位于“04⊕型带状区域”，如果点(,1)t t +位于“13-⊕型带状区域”，那么，函数|()|y f t =的最大值为（） A. 72 B. 3 C. 52D. 2三. 解答题（本大题共5题，共14+14+14+16+18=76分） 17. 如图，已知正三棱柱111ABC A B C -的底面积为934，侧面积为36；（1）求正三棱柱111ABC A B C -的体积；（2）求异面直线1AC 与AB 所成的角的大小；18. 已知椭圆C 的长轴长为26，左焦点的坐标为(2,0)-；（1）求C 的标准方程；（2）设与x 轴不垂直的直线l 过C 的右焦点，并与C 交于A 、B 两点，且||6AB =，试求直线l 的倾斜角；19. 设数列{}n x 的前n 项和为n S ，且430n n x S --=（*n N ∈）；（1）求数列{}n x 的通项公式；（2）若数列{}n y 满足1n n n y y x +-=（*n N ∈），且12y =，求满足不等式559n y >的最小正整数n 的值；20. 设函数()lg()f x x m =+（m R ∈）；（1）当2m =时，解不等式1()1f x >；（2）若(0)1f =，且1()()2x f x λ=+在闭区间[2,3]上有实数解，求实数λ的范围；（3）如果函数()f x 的图像过点(98,2)，且不等式[cos(2)]lg2n f x <对任意n N ∈均成立，求实数x 的取值集合；21. 设集合A 、B 均为实数集R 的子集，记：{|,}A B a b a A b B +=+∈∈；（1）已知{0,1,2}A =，{1,3}B =-，试用列举法表示A B +；（2）设123a =，当*n N ∈，且2n ≥时，曲线2221119x y n n n +=-+-的焦距为n a ，如果 12{,,,}n A a a a =⋅⋅⋅，122{,,}993B =---，设A B +中的所有元素之和为n S ，对于满足3m n k +=，且m n ≠的任意正整数m 、n 、k ，不等式0m n k S S S λ+->恒成立，求实数λ的最大值；（3）若整数集合111A A A ⊆+，则称1A 为“自生集”，若任意一个正整数均为整数集合2A 的某个非空有限子集中所有元素的和，则称2A 为“*N 的基底集”，问：是否存在一个整数集合既是自生集又是*N 的基底集？请说明理由；上海市崇明县2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 复数(2)i i +的虚部为 2. 设函数2log ,0()4,0xx x f x x >⎧=⎨≤⎩，则((1))f f -=3. 已知{||1|2,}M x x x R =-≤∈，1{|0,}2xP x x R x -=≥∈+，则M P =4. 抛物线2y x =上一点M 到焦点的距离为1，则点M 的纵坐标为5. 已知无穷数列{}n a 满足112n n a a +=*()n N ∈，且21a =，记n S 为数列{}n a 的前n 项和，则lim n n S →∞=6. 已知,x y R +∈，且21x y +=，则xy 的最大值为7. 已知圆锥的母线10l =，母线与旋转轴的夹角30α︒=，则圆锥的表面积为8. 若21(2)nx x+*()n N ∈的二项展开式中的第9项是常数项，则n =9. 已知,A B 分别是函数()2sin f x x ω=(0)ω>在y 轴右侧图像上的第一个最高点和第一个最低点，且2AOB π∠=，则该函数的最小正周期是10. 将序号分别为1、2、3、4、5的5张参观券全部分给4人，每人至少一张，如果分给同一人的2张参观券连号，那么不同的分法种数是11. 在平面直角坐标系中，横、纵坐标均为整数的点叫做格点，若函数()y f x =的图像恰好经过k 个格点，则称函数()y f x =为k 阶格点函数，已知函数：①2y x =；②2sin y x =；③1xy π=-；④cos()3y x π=+；其中为一阶格点函数的序号为（注：把你认为正确的序号都填上）12. 已知AB 为单位圆O 的一条弦，P 为单位圆O 上的点，若()||f AP AB λλ=-()R λ∈ 的最小值为m ，当点P 在单位圆上运动时，m 的最大值为43，则线段AB 长度为二. 选择题（本大题共4题，每题5分，共20分）13. 下列函数在其定义域内既是奇函数又是增函数的是（）A. tan y x =B. 3xy = C. 13y x = D. lg ||y x =14. 设,a b R ∈，则“21a b ab +>⎧⎨>⎩”是“1a >且1b >”的（）条件A. 充分非必要B. 必要非充分C. 充要D. 既非充分也非必要 15. 如图，已知椭圆C 的中心为原点O ，(25,0)F -为C 的左焦点，P 为C 上一点，满足||||OP OF =且||4PF =，则椭圆C 的方程为（）A.221255x y += B. 2213010x y += C.2213616x y += D. 2214525x y += 16. 实数a 、b 满足0ab >且a b ≠，由a 、b 、2a b+、ab 按一定顺序构成的数列（） A. 可能是等差数列，也可能是等比数列 B. 可能是等差数列，但不可能是等比数列 C. 不可能是等差数列，但可能是等比数列 D. 不可能是等差数列，也不可能是等比数列三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 在正三棱柱111ABC A B C -中，1AB =，12BB =，求：（1）异面直线11B C 与1AC 所成角的大小；（2）四棱锥111A B BCC -的体积；18. 在一个特定时段内，以点E 为中心的7海里以内海域被设为警戒水域，点E 正北55海里处有一个雷达观测站A ，某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45°且与点A 相距402海里的位置B 处，经过40分钟又测得该船已行驶到点A 北偏东45θ︒+ （其中26sin 26θ=，090θ︒︒<<）且与点A 相距1013海里的位置C 处；（1）求该船的行驶速度；（单位：海里/小时）（2）若该船不改变航行方向继续行驶，判断它是否会进入警戒水域，并说明理由；19. 已知点1F 、2F 为双曲线222:1y C x b-=(0)b >的左、右焦点，过2F 作垂直于x 轴的直线，在x 轴上方交双曲线C 于点M ，且1230MF F ︒∠=；（1）求双曲线C 的方程；（2）过双曲线C 上任意一点P 作该双曲线两条渐近线的垂线，垂足分别为1P 、2P ，求12PP PP ⋅的值；20. 设12()2x x a f x b+-+=+，,a b 为实常数；（1）当1a b ==时，证明：()f x 不是奇函数；（2）若()f x 是奇函数，求a 与b 的值；（3）当()f x 是奇函数时，研究是否存在这样的实数集的子集D ，对任何属于D 的x 、c ，都有2()33f x c c <-+成立？若存在，试找出所有这样的D ；若不存在，说明理由；21. 已知数列{}n a 、{}n b 满足2(2)n n n S a b =+，其中n S 是数列{}n a 的前n 项和；（1）若数列{}n a 是首项为23，公比为13-的等比数列，求数列{}n b 的通项公式；（2）若n b n =，23a =，求证：数列{}n a 满足212n n n a a a +++=，并写出{}n a 通项公式；（3）在（2）的条件下，设nn na cb =，求证：数列{}nc 中的任意一项总可以表示成该数列其他两项之积；参考答案一. 填空题1. 22. 2-3. [1,1]-4.34 5. 4 6. 187. 75π 8. 12 9. 833 10. 96 11. ②③ 12. 423二. 选择题13. C 14. B 15. C 16. D三. 解答题 17.（1）5arccos10；（2）33；18.（1）155；（2）357d =<，会进入警戒水域；19.（1）2212y x -=；（2）29；20.（1）(1)(1)f f -≠-；（2）12a b =⎧⎨=⎩，12a b =-⎧⎨=-⎩；（3）当121()22x x f x +-+=+，D R =；当121()22x x f x +--=-，(0,)D =+∞，25(,log ]7D =-∞；21.（1）12n b =；（2）1n a n =+；（3）略；上海市金山区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 若集合2{|20}M x x x =-<，{|||1}N x x =>，则MN =2. 若复数z 满足232z z i +=-，其中i 为虚数单位，则z =3. 如果5sin 13α=-，且α为第四象限角，则tan α的值是 4. 函数cos sin ()sin cos x xf x x x=的最小正周期是5. 函数()2x f x m =+的反函数为1()y f x -=，且1()y f x -=的图像过点(5,2)Q ，那么m =6. 点(1,0)到双曲线2214x y -=的渐近线的距离是 7. 如果实数x 、y 满足2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2x y +的最大值是8. 从5名学生中任选3人分别担任语文、数学、英语课代表，其中学生甲不能担任数学课代表，共有种不同的选法（结果用数值表示） 9. 方程22242340x y tx ty t +--+-=（t 为参数）所表示的圆的圆心轨迹方程是（结果化为普通方程） 10. 若n a 是(2)nx +（*n N ∈，2n ≥，x R ∈）展开式中2x 项的二项式系数，则23111lim()n na a a →∞++⋅⋅⋅+= 11. 设数列{}n a 是集合{|33,stx x s t =+<且,}s t N ∈中所有的数从小到大排列成的数列，即14a =，210a =，312a =，428a =，530a =，636a =，，将数列{}n a 中各项按照上小下大，左小右大的原则排成如图的等腰直角三角形数表，则15a 的值为12. 曲线C 是平面内到直线1:1l x =-和直线2:1l y =的距离之积等于常数2k （0k >）的点的轨迹，下列四个结论：① 曲线C 过点(1,1)-；② 曲线C 关于点(1,1)-成中心对称； ③ 若点P 在曲线C 上，点A 、B 分别在直线1l 、2l 上，则||||PA PB +不小于2k ；④ 设0P 为曲线C 上任意一点，则点0P 关于直线1:1l x =-，点(1,1)-及直线2:1l y =对称的点分别为1P 、2P 、3P ，则四边形0123P PP P 的面积为定值24k ；其中，所有正确结论的序号是41012283036⋅⋅⋅二. 选择题（本大题共4题，每题5分，共20分）13. 给定空间中的直线l 与平面α，则“直线l 与平面α垂直”是“直线l 垂直于平面α上无数条直线”的（）条件A. 充分非必要B. 必要非充分C. 充要D. 既不充分也不必要 14. 已知x 、y R ∈，且0x y >>，则（） A.110x y-> B. 11()()022x y -<C. 22log log 0x y +>D. sin sin 0x y -> 15. 某几何体的三视图如图所示，则它的体积是（）A. 283π-B. 83π- C. 82π- D. 23π16. 已知函数2(43)30()log (1)10a x a x a x f x x x ⎧+-+<=⎨++≥⎩（0a >且1a ≠）在R 上单调递减，且关于x 的方程|()|2f x x =-恰好有两个不相等的实数解，则a 的取值范围是（）A. 2(0,]3B. 23[,]34C. 123[,]{}334D. 123[,){}334三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PA ⊥平面ABCD ，PB 、PD 与平面ABCD 所成的角依次是4π和1arctan 2，2AP =，E 、F 依次是PB 、PC 的中点；（1）求异面直线EC 与PD 所成角的大小；（结果用反三角函数值表示）（2）求三棱锥P AFD -的体积；18. 已知△ABC 中，1AC =，23ABC π∠=，设BAC x ∠=，记()f x AB BC =⋅；（1）求函数()f x 的解析式及定义域；（2）试写出函数()f x 的单调递增区间，并求方程1()6f x =的解；19. 已知椭圆C 以原点为中心，左焦点F 的坐标是(1,0)-，长轴长是短轴长的2倍，直线l 与椭圆C 交于点A 与B ，且A 、B 都在x 轴上方，满足180OFA OFB ︒∠+∠=；（1）求椭圆C 的标准方程；（2）对于动直线l ，是否存在一个定点，无论OFA ∠如何变化，直线l 总经过此定点？若存在，求出该定点的坐标；若不存在，请说明理由；20. 已知函数2()21g x ax ax b =-++(0)a >在区间[2,3]上的最大值为4，最小值为1，记()(||)f x g x =，x R ∈；（1）求实数a 、b 的值；（2）若不等式222()()log 2log 3f x g x k k +≥--对任意x R ∈恒成立，求实数k 的范围；（3）对于定义在[,]p q 上的函数()m x ，设0x p =，n x q =，用任意i x (1,2,,1)i n =⋅⋅⋅- 将[,]p q 划分成n 个小区间，其中11i i i x x x -+<<，若存在一个常数0M >，使得不等式01121|()()||()()||()()|n n m x m x m x m x m x m x M --+-+⋅⋅⋅+-≤恒成立，则称函数()m x为在[,]p q 上的有界变差函数，试证明函数()f x 是在[1,3]上的有界变差函数，并求出M 的最小值；21. 数列{}n b 的前n 项和为n S ，且对任意正整数n ，都有(1)2n n n S +=；（1）试证明数列{}n b 是等差数列，并求其通项公式；（2）如果等比数列{}n a 共有2017项，其首项与公比均为2，在数列{}n a 的每相邻两项i a 与1i a +之间插入i 个(1)i i b -*()i N ∈后，得到一个新数列{}n c ，求数列{}n c 中所有项的和；（3）如果存在*n N ∈，使不等式11820(1)()(1)n n n n n b n b b b λ++++≤+≤+成立，若存在，求实数λ的范围，若不存在，请说明理由；参考答案一. 填空题1. (1,2)2. 12i -3. 512-4. π5. 16. 557. 4 8. 48 9. 20x y -= 10. 2 11. 324 12. ②③④二. 选择题13. A 14. B 15. A 16. C三. 解答题 17.（1）310arccos 10；（2）43；18.（1）2211()sin sin()sin(2)33366f x x x x ππ=+=+-，(0,)3x π∈；（2）递增区间(0,]6π，6x π=；19.（1）2212x y +=；（2）(2,0)-； 20.（1）0b =，1a =；（2）1[,8]2；（3）min 4M =；21.（1）n b n =；（2）201822033134+；（3）不存在；上海市虹口区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 已知集合{1,2,4,6,8}A =，{|2,}B x x k k A ==∈，则A B =2. 已知21zi i=+-，则复数z 的虚部为 3. 设函数()sin cos f x x x =-，且()1f a =，则sin 2a =4. 已知二元一次方程111222a xb yc a x b y c +=⎧⎨+=⎩的增广矩阵是111113-⎛⎫⎪⎝⎭，则此方程组的解是5. 数列{}n a 是首项为1，公差为2的等差数列，n S 是它前n 项和，则2lim n n nSa →∞=6. 已知角A 是ABC ∆的内角，则“1cos 2A =”是“3sin 2A =”的条件（填“充分非必要”、“必要非充分”、“充要条件”、“既非充分又非必要”之一）7. 若双曲线2221y x b-=的一个焦点到其渐近线距离为22，则该双曲线焦距等于8. 若正项等比数列{}n a 满足：354a a +=，则4a 的最大值为 9. 一个底面半径为2的圆柱被与其底面所成角是60°的平面所截，截面是一个椭圆，则该椭圆的焦距等于10. 设函数61()211x x f x x x ⎧≥=⎨--≤-⎩，则当1x ≤-时，则[()]f f x 表达式的展开式中含2x 项的系数是11. 点(20,40)M ，抛物线22y px =（0p >）的焦点为F ，若对于抛物线上的任意点P ，||||PM PF +的最小值为41，则p 的值等于12. 当实数x 、y 满足221x y +=时，|2||32|x y a x y +++--的取值与x 、y 均无关，则实数a 的取值范围是二. 选择题（本大题共4题，每题5分，共20分）13. 在空间，α表示平面，m 、n 表示二条直线，则下列命题中错误的是（） A. 若m ∥α，m 、n 不平行，则n 与α不平行 B. 若m ∥α，m 、n 不垂直，则n 与α不垂直 C. 若m α⊥，m 、n 不平行，则n 与α不垂直 D. 若m α⊥，m 、n 不垂直，则n 与α不平行14. 已知函数()sin(2)3f x x π=+在区间[0,]a （其中0a >）上单调递增，则实数a 的取值范围是（） A. 02a π<≤B. 012a π<≤C. 12a k ππ=+，*k N ∈ D. 2212k a k πππ<≤+，k N ∈15. 如图，在圆C 中，点A 、B 在圆上，则AB AC ⋅的值（）A. 只与圆C 的半径有关B. 既与圆C 的半径有关，又与弦AB 的长度有关C. 只与弦AB 的长度有关D. 是与圆C 的半径和弦AB 的长度均无关的定值16. 定义(){}f x x =（其中{}x 表示不小于x 的最小整数）为“取上整函数”，例如{2.1}3=，{4}4=，以下关于“取上整函数”性质的描述，正确的是（）①(2)2()f x f x =；② 若12()()f x f x =，则121x x -<；③ 任意1x 、2x R ∈，1212()()()f x x f x f x +≤+；④1()()(2)2f x f x f x ++=； A. ①② B. ①③ C. ②③ D. ②④三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 在正三棱锥P ABC -中，已知底面等边三角形的边长为6，侧棱长为4；（1）求证：PA BC ⊥；（2）求此三棱锥的全面积和体积；18. 如图，我海蓝船在D 岛海域例行维权巡航，某时刻航行至A 处，此时测得其北偏东30° 方向与它相距20海里的B 处有一外国船只，且D 岛位于海蓝船正东18海里处；（1）求此时该外国船只与D 岛的距离；（2）观测中发现，此外国船只正以每小时4海里的速度沿正南方航行，为了将该船拦截在离D 岛12海里的E 处（E 在B 的正南方向），不让其进入D 岛12海里内的海域，试确定海蓝船的航向，并求其速度的最小值（角度精确到0.1°，速度精确到0.1海里/小时）；19. 已知二次函数2()4f x ax x c =-+的值域为[0,)+∞；（1）判断此函数的奇偶性，并说明理由；（2）判断此函数在2[,)a+∞的单调性，并用单调性的定义证明你的结论；（3）求出()f x 在[1,)+∞上的最小值()g a ，并求()g a 的值域；20. 椭圆2222:1x y C a b+=（0a b >>）过点(2,0)M ，且右焦点为(1,0)F ，过F 的直线l 与椭圆C 相交于A 、B 两点，设点(4,3)P ，记PA 、PB 的斜率分别为1k 和2k ；（1）求椭圆C 的方程；（2）如果直线l 的斜率等于1-，求出12k k ⋅的值；（3）探讨12k k +是否为定值？如果是，求出该定值，如果不是，求出12k k +的取值范围；21. 已知函数()2|2||1|f x x x =+-+，无穷数列{}n a 的首项1a a =；（1）若()n a f n =（*n N ∈），写出数列{}n a 的通项公式；（2）若1()n n a f a -=（*n N ∈且2n ≥），要使数列{}n a 是等差数列，求首项a 取值范围；（3）如果1()n n a f a -=（*n N ∈且2n ≥），求出数列{}n a 的前n 项和n S ；参考答案一. 填空题1. {2,4,8}2. 13. 04. 21x y =⎧⎨=⎩ 5. 146. 充分非必要7. 68. 29. 43 10. 6011. 22或42 12. [5,)+∞二. 选择题13. A 14. B 15. C 16. C三. 解答题17.（1）略；（2）9793S =+，63V =； 18.（1）291；（2）东偏北41.8︒， 6.4v =海里/小时； 19.（1）非奇非偶函数；（2）单调递增；（3）当02a <<，()0g a =；当2a ≥，4()4g a a a=+-；值域[0,)+∞； 20.（1）22143x y +=；（2）12；（3）2；21.（1）3n a n =+；（2）{3}[1,)a ∈--+∞；（3）当2a ≤-，3(1)(2)(1)(3)2n n n S a n a --=+---+；当21a -<≤-，3(1)(2)(1)(35)2n n n S a n a --=+-++；当1a >-，3(1)2n n n S na -=+；上海市闵行区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 方程lg(34)1x +=的解x = 2. 若关于x 的不等式0x ax b->-（,a b R ∈）的解集为(,1)(4,)-∞+∞，则a b += 3. 已知数列{}n a 的前n 项和为21n n S =-，则此数列的通项公式为4. 函数()1f x x =+的反函数是5. 6(12)x +展开式中3x 项的系数为（用数字作答）6. 如图，已知正方形1111ABCD A BC D -，12AA =，E 为棱1CC 的中点，则三棱锥1D ADE -的体积为 7. 从单词“shadow ”中任意选取4个不同的字母排成一排，则其中含有“a ”的共有种排法（用数字作答）8. 集合{|cos(cos )0,[0,]}x x x ππ=∈= （用列举法表示） 9. 如图，已知半径为1的扇形AOB ，60AOB ∠=︒，P 为弧AB 上的一个动点，则OP AB ⋅取值范围是 10. 已知x 、y 满足曲线方程2212x y+=，则22x y +的取值范围是11. 已知两个不相等的非零向量a 和b ，向量组1234(,,,)x x x x 和1234(,,,)y y y y 均由2个a 和2个b 排列而成，记11223344S x y x y x y x y =⋅+⋅+⋅+⋅，那么S 的所有可能取值中的最小值是（用向量a 、b 表示）12. 已知无穷数列{}n a ，11a =，22a =，对任意*n N ∈，有2n n a a +=，数列{}n b 满足 1n n n b b a +-=（*n N ∈），若数列2{}nnb a 中的任意一项都在该数列中重复出现无数次，则满足要求的1b 的值为二. 选择题（本大题共4题，每题5分，共20分） 13. 若a 、b 为实数，则“1a <”是“11a>”的（）条件 A. 充要 B. 充分不必要 C. 必要不充分 D. 既不充分也不必要 14. 若a 为实数，(2)(2)4ai a i i +-=-（i 是虚数单位），则a =（）A. 1-B. 0C. 1D. 215. 函数2()||f x x a =-在区间[1,1]-上的最大值是a ，那么实数a 的取值范围是（） A. [0,)+∞ B. 1[,1]2 C. 1[,)2+∞ D. [1,)+∞16. 曲线1:sin C y x =，曲线22221:()2C x y r r ++-=（0r >），它们交点的个数（）A. 恒为偶数B. 恒为奇数C. 不超过2017D. 可超过2017三. 解答题（本大题共5题，共14+14+14+16+18=76分） 17. 如图，在Rt AOB ∆中，6OAB π∠=，斜边4AB =，D 是AB 中点，现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥，点C 为圆锥底面圆周上一点，且90BOC ∠=︒，（1）求圆锥的侧面积；（2）求直线CD 与平面BOC 所成的角的大小；（用反三角函数表示）18. 已知(23,1)m =，2(cos ,sin )2An A =，A 、B 、C 是ABC ∆的内角；（1）当2A π=时，求||n 的值；（2）若23C π=，||3AB =，当m n ⋅取最大值时，求A 的大小及边BC 的长；19. 如图所示，沿河有A 、B 两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为0.7()25f m m=⋅（万元），m 表示污水流量，铺设管道的费用（包括管道费）() 3.2g x x =（万元），x 表示输送污水管道的长度（千米）；已知城镇A 和城镇B 的污水流量分别为13m =、25m =，A 、B 两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）（1）若在城镇A 和城镇B 单独建厂，共需多少总费用？（2）考虑联合建厂可能节约总投资，设城镇A 到拟建厂的距离为x 千米，求联合建厂的总费用y 与x 的函数关系式，并求y 的取值范围；20. 如图，椭圆2214y x +=的左、右顶点分别为A 、B ，双曲线Γ以A 、B 为顶点，焦距为25，点P 是Γ上在第一象限内的动点，直线AP 与椭圆相交于另一点Q ，线段AQ 的中点为M ，记直线AP 的斜率为k ，O 为坐标原点；（1）求双曲线Γ的方程；（2）求点M 的纵坐标M y 的取值范围；（3）是否存在定直线l ，使得直线BP 与直线OM 关于直线l 对称？若存在，求直线l 方程，若不存在，请说明理由；21. 在平面直角坐标系上，有一点列01231,,,,,,n n P P P P P P -⋅⋅⋅，设点k P 的坐标(,)k k x y （k N ∈，k n ≤），其中k x 、k y Z ∈，记1k k k x x x -∆=-，1k k k y y y -∆=-，且满足 ||||2k k x y ∆⋅∆=（*k N ∈，k n ≤）；（1）已知点0(0,1)P ，点1P 满足110y x ∆>∆>，求1P 的坐标；（2）已知点0(0,1)P ，1k x ∆=（*k N ∈，k n ≤），且{}k y （k N ∈，k n ≤）是递增数列，点n P 在直线:38l y x =-上，求n ；（3）若点0P 的坐标为(0,0)，2016100y =，求0122016x x x x +++⋅⋅⋅+的最大值；上海市松江区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 设集合2{|}M x x x ==，{|lg 0}N x x =≤，则MN =2. 已知a 、b R ∈，i 是虚数单位，若2a i bi +=-，则2()a bi +=3. 已知函数()1x f x a =-的图像经过(1,1)点，则1(3)f -=4. 不等式|1|0x x ->的解集为5. 已知(sin ,cos )a x x =，(sin ,sin )b x x =，则函数()f x a b =⋅的最小正周期为6. 里约奥运会游泳小组赛采用抽签方法决定运动员比赛的泳道，在由2名中国运动员和6 名外国运动员组成的小组中，2名中国运动员恰好抽在相邻泳道的概率为 7. 按下图所示的程序框图运算：若输入17x =，则输出的x 值是8. 设230123(1)n n n x a a x a x a x a x +=++++⋅⋅⋅+，若2313a a =，则n = 9. 已知圆锥底面半径与球的半径都是1cm ，如果圆锥的体积与球的体积恰好也相等，那么这个圆锥的侧面积是 2cm10. 设(,)P x y 是曲线22:1259x y C +=上的点，1(4,0)F -，2(4,0)F ，则12||||PF PF +的最大值为11. 已知函数243,13()28,3xx x x f x x ⎧-+-≤≤⎪=⎨->⎪⎩，若()()F x f x kx =-在其定义域内有3个零点，则实数k ∈12. 已知数列{}n a 满足11a =，23a =，若1||2n n n a a +-=*()n N ∈，且21{}n a -是递增数列，2{}n a 是递减数列，则212lim n n na a -→∞=二. 选择题（本大题共4题，每题5分，共20分） 13. 已知a 、b R ∈，则“0ab >”是“2b aa b+>”的（） A. 充分非必要条件 B. 必要非充分条件 C. 充要条件 D. 既非充分又非必要条件14. 如图，在棱长为1的正方体1111ABCD A BC D -中，点P 在截面1A DB 上，则线段AP 的最小值为（） A.13 B. 12 C. 33 D. 2215. 若矩阵11122122a a a a ⎛⎫⎪⎝⎭满足：11a 、12a 、21a 、22{0,1}a ∈，且111221220a a a a =，则这样的互不相等的矩阵共有（）A. 2个B. 6个C. 8个D. 10个 16. 解不等式11()022xx -+>时，可构造函数1()()2x f x x =-，由()f x 在x R ∈是减函数及()(1)f x f >，可得1x <，用类似的方法可求得不等式263arcsin arcsin 0x x x x +++> 的解集为（）A. (0,1]B. (1,1)-C. (1,1]-D. (1,0)-三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 如图，在正四棱锥P ABCD -中，PA AB a ==，E 是棱PC 的中点；（1）求证：PC BD ⊥；（2）求直线BE 与PA 所成角的余弦值；18. 已知函数21()21x xa f x ⋅-=+（a 为实数）；（1）根据a 的不同取值，讨论函数()y f x =的奇偶性，并说明理由；（2）若对任意的1x ≥，都有1()3f x ≤≤，求a 的取值范围；19. 松江天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”，兴趣小组同学实施如下方案来测量塔的倾斜度和塔高，如图，记O 点为塔基、P 点为塔尖、点P 在地面上的射影为点H ，在塔身OP 射影所在直线上选点A ，使仰角45HAP ︒∠=，过O 点与OA 成120︒的地面上选B 点，使仰角45HBP ︒∠=（点A 、B 、O 都在同一水平面上），此时测得27OAB ︒∠=，A 与B 之间距离为33.6米，试求：（1）塔高；（即线段PH 的长，精确到0.1米）（2）塔的倾斜度；（即OPH ∠的大小，精确到0.1︒）20. 已知双曲线2222:1x y C a b-=经过点(2,3)，两条渐近线的夹角为60︒，直线l 交双曲线于A 、B 两点；（1）求双曲线C 的方程；（2）若l 过原点，P 为双曲线上异于A 、B 的一点，且直线PA 、PB 的斜率PA k 、PB k 均存在，求证：PA PB k k ⋅为定值；（3）若l 过双曲线的右焦点1F ，是否存在x 轴上的点(,0)M m ，使得直线l 绕点1F 无论怎样转动，都有0MA MB ⋅=成立？若存在，求出M 的坐标；若不存在，请说明理由；21. 如果一个数列从第2项起，每一项与它前一项的差都大于2，则称为“H 型数列”；（1）若数列{}n a 为“H 型数列”，且113a m =-，21a m=，34a =，求实数m 的范围；（2）是否存在首项为1的等差数列{}n a 为“H 型数列”，其前n 项和n S 满足2n S n n <+*()n N ∈？若存在，请求出{}n a 的通项公式；若不存在，请说明理由；（3）已知等比数列{}n a 的每一项均为正整数，且{}n a 为“H 型数列”；若23n n b a =，n c =5(1)2n n a n -+⋅，当数列{}n b 不是“H 型数列”时，试判断数列{}n c 是否为“H 型数列”，并说明理由；参考答案一. 填空题1. {1}2. 34i -3. 24. (0,1)(1,)+∞5. π6.147. 143 8. 11 9. 17π 10. 10 11. 3(0,)312. 12-二. 选择题13. B 14. C 15. D 16. A三. 解答题 17.（1）略；（2）33； 18.（1）1a =-，偶函数；1a =，奇函数；a R ∈且1a ≠±，非奇非偶函数；（2）[2,3]；19.（1）18.9米；（2）6.9°；20.（1）2213y x -=；（2）3；（3）(1,0)-； 21.（1）1(,0)(,)2-∞+∞；（2）不存在；（3）132n n a -=⋅时，{}n c 不是“H 型数列”；14n n a -=时，{}n c 是“H 型数列”；上海市浦东新区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分） 1. 已知U R =，集合{|421}A x x x =-≥+，则U C A =2. 三阶行列式351236724---中元素5-的代数余子式的值为 3. 8(1)2x -的二项展开式中含2x 项的系数是4. 已知一个球的表面积为16π，则它的体积为5. 一个袋子中共有6个球，其中4个红色球，2个蓝色球，这些球的质地和形状一样，从中任意抽取2个球，则所抽的球都是红色球的概率是6. 已知直线:0l x y b -+=被圆22:25C x y +=所截得的弦长为6，则b =7. 若复数(1)(2)ai i +-在复平面上所对应的点在直线y x =上，则实数a =8. 函数()(3sin cos )(3cos sin )f x x x x x =+-的最小正周期为9. 过双曲线222:14x y C a -=的右焦点F 作一条垂直于x 轴的垂线交双曲线C 的两条渐近线于A 、B 两点，O 为坐标原点，则△OAB 的面积的最小值为10. 若关于x 的不等式1|2|02xx m --<在区间[0,1]内恒成立，则实数m 的范围11. 如图，在正方形ABCD 中，2AB =，M 、N 分别是边BC 、CD 上的两个动点，且2MN =，则AM AN ⋅的取值范围是12. 已知定义在*N 上的单调递增函数()y f x =，对于任意的*n N ∈，都有*()f n N ∈，且(())3f f n n =恒成立，则(2017)(1999)f f -=二. 选择题（本大题共4题，每题5分，共20分）13. 将cos 2y x =图像向左平移6π个单位，所得的函数为（） A. cos(2)3y x π=+ B. cos(2)6y x π=+C. cos(2)3y x π=-D. cos(2)6y x π=-14. 已知函数()y f x =的反函数为1()y f x -=，则()y f x =-与1()y f x -=-图像（） A. 关于y 轴对称 B. 关于原点对称 C. 关于直线0x y +=对称 D. 关于直线0x y -=对称 15. 设{}n a 是等差数列，下列命题中正确的是（）A. 若120a a +>，则230a a +>B. 若130a a +<，则120a a +<C. 若120a a <<，则213a a a >D. 若10a <，则2123()()0a a a a --> 16. 元旦将近，调查鲜花市场价格得知：购买2只玫瑰与1只康乃馨所需费用之和大于8元，而购买4只玫瑰与5只康乃馨所需费用之和小于22元；设购买2只玫瑰花所需费用为A 元，购买3只康乃馨所需费用为B 元，则A 、B 的大小关系是（）A. A B >B. A B <C. A B =D. A 、B 的大小关系不确定三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 在长方体1111ABCD A BC D -中（如图），11AD AA ==，2AB =，点E 是棱AB 中点；（1）求异面直线1AD 与EC 所成角的大小；（2）《九章算术》中，将四个面都是直角三角形的四面体成为鳖臑，试问四面体1DCDE 是否为鳖臑？并说明理由；18. 已知△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ；（1）若3B π=，7b =，△ABC 的面积332S =，求a c +的值；（2）若22cos ()C BA BC AB AC c ⋅+⋅=，求角C ；。

杨浦区2017学年度第一学期高三模拟高质量调研

杨浦区2017学年度第一学期高三模拟质量调研英语学科试卷2017. 12 本试卷分为第I卷（第1-11页）和第II卷（第12页）两部分。

全卷共12页。

满分140分。

考试时间120分钟。

考生注意：1．答第I卷前，考生务必将条形码粘贴在答题纸的指定区域内。

2. 第I卷（1-20小题，31---70小题）由机器阅卷，答案必须全部涂写在答题卡上。

考生应将代表正确答案的小方格用铅笔涂黑。

注意试题题号和答题卡编号一一对应，不能错位。

答案需要更改时，必须将原选项用橡皮擦去，重新选择。

答案写在试卷上一律不给分。

第I卷中的第21-30小题，IV. Summary Writing部分和第II卷的试题，其答案用钢笔或水笔写在答题纸的规定区域内，如用铅笔答题，或写在试卷上则无效。

第I卷（共100分）I. Listening ComprehensionSection ADirections: In Section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1. A. In a professor's office. B. In a second-hand book shop.C. In a library.D. In a hospital.2. A. 10 yuan. B. 20 yuan.C. 30 yuan.D. 50 yuan.3. A. House agent and customer. B. Shop assistant and customer.C. Car mechanic and car owner.D. Employer and employee.4. A. The man doesn't believe what the woman says.B. The weather report spoils the man's good mood.C. They will cancel the hiking due to the bad weather.D. The man thinks it unnecessary to give up the adventure.5. A. She always talks bad about her colleagues.B. She has a good reputation among her colleagues.C. She is good at handling complicated relationships.D. She has good relations with her colleagues and boss.6. A. Harmony in a community. B. Safety in the neighborhood.C. Preparation for Christmas.D. Ways to save electricity.7. A. Watching advertisements may help ease eyestrain（眼疲劳）.B. It's a great chance to break the habit of watching TV.C. The advertisements are long enough for her to have a nap.D. Focusing eyes on the screen for a long time is harmful to eyes.8. A. The man decides to go home by rail.B. Most people travel by car during the festival.C. Most people arrive beyond the scheduled time.D. The man will have a sound sleep on the bus.9. A. He is not a bit overweight.B. He likes his fitness instructor.C. She has set too many rules for him.D. She should talk with his personal trainer.10. A. Greeks are not allowed to get married before 18.B. Greek kids are not as independent as American kids.C. American parents don’t pay for children's wedding.D. Greek parents will take care of children until they are 18.Section BDirections: In Section B, you will hear several longer conversation(s) and short passage(s), and you will be asked several questions on each of the conversation(s) and the passage(s). The conversation(s) and passage(s) will be read twice, but the questions will be spoken only once. When you hear a question, read the four possible answers on your paper and decide which one would be the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.11. A. The burn is 20 millimeters across.B. The burn is small but very painful.C. The burn takes away the victim's feeling.D. The burn is small but the skin is damaged.12. A. Use a clean plastic bag to keep warm.B. Bind up the burn with bandage or cloth.C. Treat the burned area with cold running water.D. Flush（冲洗）the burn with ice water for several minutes.13. A. To avoid infection. B. To ease pain.C. To speed recovery.D. To reduce stickiness. Questions 14 through 16 are based on the following passage.14. A. A cell phone. B. A leather wallet.C. A mini camera.D. An alarm clock.15. A. The wallet will sound an alarm.B. It will track the thief with GPS system.C. It will contact the bank to block balance.D. Its owner will receive a picture of the thief.16. A. It's out-dated in this digital age.B. It can text messages automatically.C. It is a multifunctional wallet.D. It is unique in appearance and function.Questions 17 through 20 are based on the following conversation.17. A. The concert is beyond her curfew(宵禁).B. She can’t go out on school night.C. Her mother is not available.D. She doesn’t like the band.18. A. His parents set a strict rule for him.B. His parents don’t care when he is back.C. He is self-disciplined and trustworthy.D. He envies those who have curfews.19. A. Promoting maturity. B. Giving sense of security.C. Improving sense of responsibility.D. Discouraging independence.20. A. It’s a severe punishment. B. It’s for her good.C. It’s a ridiculous practice.D. It’s an exceptional case.II. Grammar and VocabularySection ADirections: After reading the passage below, fill in the blanks to make the passages coherent and grammatically correct. For the blanks with a given word, fill in each blank with the proper form of the given word; for the other blanks, use one word that best fits each blank.It’s interesting when you think about how Japan is a nation (21) ______ appreciates the virtues of silence and good manners, and yet when it comes to eating noodles, Japanese people can be (22) ______ (loud) in the world.According to lifestyle website grapee.jp, slurping (发出"哧溜"声) when eating noodles (23) ______ (encourage) in Japanese culture. It’s believed that taking air into your mouth (24) ______ enhance the flavor of the noodles, and that it helps cool down the noodles. It’s also considered to be a way to show appreciation for the dish. Sometimes, just making the noise alone seems to make the noodles more enjoyable.It wasn’t until a new expression –“noodle harassment（骚扰）”-- came out last year on social media (25) ______ Japanese people started to realize that the slurping noise is making some foreign visitors uncomfortable.(26) ______ a response, Japanese instant noodle maker Nissin introduced a so-called noise-canceling fork last month. The fork, which looks like an electric toothbrush, is connected wirelessly to a smart phone. When the person using the fork starts to slurp, the fork sends asignal to the person’s phone, (27) ______ (make) it play a sound to mask the slurping noise.But is it really necessary? Dining traditions do vary. (28) ______ is considered to be proper table manners in one country is likely to be seen as rude in another. In India, people eat with their hands (29) ______ they think in this way they build a connection with the food. However, people who are used to eating with forks might find it uncomfortable to get their hands (30) ______ (cover) in oil and bits of food. But this eating method is part of Indian's culture, just like Japan's slurping is part of its own.“So, if your are eating noodles, whether that’s ramen, uudon, or soba, please slurp,” wrote reporter Brian Ashcraft on blog Kotaku. “If anyone gets annoyed while you are doing that, pay them no mind because they're missing the point entirely.”Section BDirections: Fill in each blank with a proper word chosen from the box. Each word can only be used once. Note that there is one word more than you need.A. tissueB. treatedC. potentialD. engineeringE. environmentF. limitedG. procedure H. commercial I. promising J. expanding K. internalScientists have developed a new surgical glue that could transform emergency treatments by sealing up critical wounds in the skin or the organs, without the need for staples or sutures（钉合或缝合）.It’s called MeTro. It was developed by researchers from both Harvard Medical School and the University of Sydney, led by Nasim Annabi, an assistant professor of chemical __31__. The glue is made from a modified （改良的）human protein that responds to UV light, allowing the application and drying of the gel-like substance in just a minute.According to the international team of researchers behind the glue,it could quite literally be a lifesaver, sealing up wounds in 60 seconds without stopping the natural __32__ and relaxing of the organ or the skin it’s applied to. Wounds __33__ with MeTro can heal up in half the time compared with stitches or staples, the researchers claim, and if surgeryis required then MeTro can simplify that __34__ too. It's also one of several ways researchers are exploring to engineer our body's own natural substances to help repair it when needed.The __35__ applications are powerful – from treating serious __36__ wounds at emergency sites such as following car accidents and in war zones, as well as improving hospital surgeries.MeTro is simple to apply, can be easily stored, and works closely with natural __37__ to heal a wound. What’s more, it degrades without leaving any kind of poisonous leftovers in the body.For now the trials are __38__ to animal models. But human trials are in the works, and the results to date are incredibly __39__. If the MeTro can be further developed into a __40__ product, it could become an essential part of a first responder’s toolkit.III. Reading ComprehensionSection ADirections:For each blank in the following passage there are four words or phrases marked A, B, C and D. Fill in each blank with the word or phrase that best fits the context.Competition is good for businesses. In the world of navigation（导航） systems, however, competition is also a necessity --- it may not be wise to rely on foreign systems for positioning and tracking services. Now, ___41___ remarkable accuracy and reliability, China’s BeiDou system has made its presence felt.The BeiDou project was set up in 1994. The first BeiDou satellite was not launched until 2000. Now, ___42___, there are already more than 20 BeiDou satellites in orbit (轨道) . They form a ___43___ network that provides positioning, navigation and timing services for China and several other Asian countries.This “home-grown" system is now ___44___ a major upgrade. Earlier this month, two BeiDou-3 satellites, the first of China’s most powerful ___45___of navigation satellites, were launched into space. The launch marks the beginning of the global ___46___ of the BeiDou navigation system. Over the next three years, China plans to send up 30 more BeiDou-3 satellites; The expanded navigation system will ___47___ create a network that is able to support military and civilian applications around the world.Scientists involved in the project said the new system would give civilian users an accuracy of 2.5 meters to five meters, overtaking that of the ___48___ positioning technologies. BeiDou’s chief designer said the new satellites would be able to __49___ which lane a car is using on a motorway and __50___ the swing of a building in high winds. It will also be able to guide fire trucks to the nearest water hydrant (消防栓).The Chinese military, meanwhile, will be able to use coded signals for millimeter（毫米）___51___ .China is only the third country in the world to develop a navigation system on its own, after the United States (GPS) and Russia (GLONASS). Developing BeiDou is a necessity. The system __52___ national security by ending a reliance on foreign systems. Moreover, it enhances China’s international reputation for technological ___53___.For most of us, the benefits of the new satellite system will be felt in a couple of years when more phones are ___54___ with BeiDou chips (芯片). Many smartphones today still use GPS and GLONASS. That’ll soon change with the development of BeiDou. One product manager ___55___ mostsmartphones to be able to receive BeiDou signals. He says: “In three years’time, people may still say ‘I’m using GPS’, but in fact, their phone is tune in to BeiDou. ”41. A. dominating B. boasting C. shifting D. inputting42. A. however B. afterwards C. moreover D. therefore43. A. continental B. local C. domestic D. regional44. A. enduring B. encountering C. undergoing D. processing45. A. generation B. information C. examination D. revolution46. A. extension B. expansion C. interaction D. invasion47. A. objectively B. eventually C. sufficiently D. essentially48. A. existing B. progressing C. upcoming D. everlasting49. A. explore B. investigate C. spot D. remind50. A. detect B. prevent C. protect D. adjust51. A. privacy B. accuracy C. fluency D.currency52. A. convinces B. insures C. highlights D. strengthens53. A. innovation B. consumption C. emission D. exhibition54. A. decorated B. furnished C. equipped D. connected55. A. respects B. instructs C. inspects D. expectsSection BDirections: Read the following three passages. Each passage is followed by several questions or unfinished statements. For each of them there are four choices marked A, B, C and D. Choose the one that fits best according to the information given in the passage you have just read.(A)A Swedish power plant is taking reuse and recycle to the next level by burning unusable clothing instead of coal, Bloomberg reports.Retail giant Hennes & Mauritz, more commonly known as H&M, is helping the utility transition away from coal through its moldy (发霉的) or otherwise unsalable clothing.The multi-fuel power and heating station in Västerås, central Sweden, is planning to be completely fossil-fuel free by 2020. It’s thelargest station of its kind and Sweden claims it’s one of Europe’s cleanest. To kick its coal habit, the station is turning instead to other burnable materials including recycled wood, rubbish and yes, clothes.“Our goal is to use only renewable and recycled fuels,” Jens Neren, head of fuel supplies at the utility company which owns and operates the Västerås plant, told Bloomberg.Johanna Dahl, head of communications for H&M in Sweden, told Bloomberg that the company allows only the burning of clothes which are no longer safe to use.“It is our legal obligation to make sure that clothes that contain mold or do not meet the requirements of our strict restriction on chemicals are destroyed,” she said.The Västerås plant has burned around 15 tons of old H&M clothes so far this year, compared with about 400,000 tons of rubbish, Neren told Bloomberg.Sweden has one of the world’s greener energy generating systems, and has invested in bioenergy, solar power and electric buses. In 2015, the Scandinavian country announced an ambitious aim to become one of the first nations in the world to end its dependence on fossil fuels. According to the Swedish government, the country has already heavily reduced its dependence on oil, which accounted for 75% of the energy supply in 1970, and now makes up a 20% share.56. Which of the following can serve as fuel in the Västerås plant?A. Fashionable coats in H&M chain store.B. Old TV sets deserted as rubbish.C. Wooden furniture in second-hand shop.D. H&M clothes unsuitable for sale.57. The underlined word in the last paragraph “generating” is closestin meaning to ______.A. eliminatingB. adjustingC. producingD. circulating58. What can we learn from the passage?A. The Swedish government discourages the development of bioenergy.B. Clothes only take up a small proportion of the burning material.C. Sweden’s fossil-fuel free plan is almost accomplished by now.D. Sweden has an ambition to be the cleanest country in the world.59. What is the main idea of the passage?A. A Swedish power plant is burning unusable H&M clothes for fuel.B. The Swedish government aims high and is taking effective action.C. H&M is looking for a new way to strengthen its position in fashion.D. Coal and oil are no longer regarded as the primary fuels in Sweden.(B)60. Before an adventure, a trekker should ______.A. tell the park officials his destination and time scheduleB. pack up some jungle fruit juice and pre-cooked mealsC. consult a local guide about the most adventurous routeD. have his fitness level assessed at the tourist center61. Which of the following is NOT suitable for a rainforest trekking?A. Long-sleeved cotton shirts.B. Tight sports shorts.C. Hiking boots.D. A wide brimmed hat.62. If a trekker starts out at dawn, he may ______.A. escape being caught in the rainB. sight scared wildlifeC. enjoy the heat of the tropical sunD. see animals seeking food(C)The largest genetic study of mosquitoes has found their ability to resist insecticides is evolving rapidly and spreading across Africa, putting millions of people at higher risk of contracting malaria（疟疾）.British scientists who led the work said mosquitoes' growing resistance to control tools such as insecticide-treated bed nets and insecticide spraying, which have helped cut malaria cases since 2000, now threatens “to disturb malaria control” in Africa.“Our study highlights the severe challenges facing public efforts to control mosquitoes and to manage and limit insecticide resistance,” said Martin Donnelly of the Liverpool School of Tropical Medicine, who worked on the study with a team from Britain’s Wellcome Trust Sanger Institute.Latest World Health Organization (WHO) data show that 216 million people were infected last year with the malaria parasite(寄生虫), which is transmitted by blood-sucking Anopheles mosquitoes.The disease killed 445,000 people in 2016, and the majority of them were children in sub-Saharan Africa.To understand how mosquitoes are evolving, the researchers sequenced the DNA of 765 wild Anopheles mosquitoes taken from 15 locations across eight African countries. Their work, published in the journal Nature on Wednesday, created the largest data resource on natural genetic variation for any species of insect.Analyzing the data, the scientists found that the Anopheles gambiae mosquitoes（冈比亚疟蚊）were extremely genetically diverse （多样化的）compared with most other animal species. This high genetic diversity enables rapid evolution, they said, and helps to explain how mosquitoes develop insecticide resistance so quickly.The data also showed the rapid evolution of insecticide resistance appeared to be due to many previously unknown genetic variants（变体）within certain genes. The scientists said these genetic variants for insecticide resistance were not only emerging independently in different parts of Africa, but were also being spread across the continent by mosquito migration.Michael Chew, an expert at Britain’s Wellcome Trust global health charity which helped fund the research, said the finds underlined the importance of pushing scientific research ahead to control malaria.Global efforts to control malaria through effective vaccine, insecticides and the best drug combinations require urgent, united action by scientists, drug companies, governments and the WHO.63. Which of the following is scientists’ headache?A. The number of mosquitoes in Africa is growing rapidly.B. Some genetic variants of mosquitoes are still unknown.C. The existing insecticides aren’t as effective as they used to be.D. Millions of African people have resistance to medicines for malaria.64. Malaria cases can be cut by ______.A. threatening drug companiesB. spraying insecticidesC. limiting blood donationD. transmitting data65. What CANNOT be concluded from the passage?A. Children are more likely to be bit by mosquitoes.B. Many previously unknown variants are found in the study.C. The mosquito migration contributes to the spread of variants.D. Anopheles mosquitoes have great genetic diversity.66. Which is FALSE about the genetic study of mosquitoes?A. It created the largest data on natural genetic variation for any insect species.B. It found the possible causes for the rapid evolution of insecticide resistance.C. It discovered where the genetic variants emerged and how they were spread.D. It highlighted the public efforts and appealed to limit the use of insecticides.Section CDirections: Read the following passage. Fill in each blank with a proper sentence given in the box. Each sentence can be used only once. Note that there are two more sentences than you need.Imagine you're standing in line to buy an afterschool snack at a store. You step up to the counter and the cashier scans your food. Next, you have to pay. But instead of scanning a QR code with your smartphone, you just hold out your hand so the cashier can scan your fingerprint. Or, a camera scans your face, your eyes or even your ear.__________67__________ As technology companies move away from traditional password, biometric（生物识别） security, which includes fingerprint, face and voice ID, is becoming increasingly popular.In 2013, Apple introduced the iPhone 5s, one of the first smartphones with a fingerprint scanner. Since then, using one’s fingerprint to unlock a phone and make mobile payments has become commonplace, bringing convenience to our lives. And since last year, Samsung has featured eye-scanning technology in its top smartphones, while Apple’s new iPhone X can even scan a user’s face.__________68__________ “Biometrics, ideally, are good,”John Michener, a biometric expert, told tech website Inverse. “In practice, not so much.”When introducing the new iPhone’s Face ID feature at Apple’s Keynote Event in September, Phil Schiller, Apple’s senior vice president, said, “__________69__________”But it’s already been done. In a video posted on community website Reddit on Nov 3, two brothers showed how they were each able to unlock the same iPhone X using their own face, Quartz reported. And they aren’t even twins.“We may expect too much from biometrics,” Anil Jain, a computer science professor at Michigan State University, told CBS news. “No security systems are perfect.”Earlier this year, Jain found a way to trick biometric security. Using a printed copy of a thumbprint, she was able to unlock a dead person's smartphone for police.“It’s good to see biometrics being used more,” Jain told CBS News, “because it adds another factor for security. __________70__________”IV. Summary WritingDirections: Read the following passage. Summarize the main idea and the main point(s) of the passage in no more than 60 words. Use your own words as far as possible.It’s a common sight to see food delivery workers riding electric bikes through big cities in China. Most of them seem to be in a hurry, as they run red lights to deliver their meals in time. However, such reckless （鲁莽的）behavior often causes serious problems.In the first half of this year, food delivery drivers had 76 traffic accidents in Shanghai alone, according to the Shanghai Public Security Bureau. This means that on average, there is a food delivery worker that gets hurt or even dies on the road in Shanghai every 2.5 days.Other cities also share similar problems. In Nanjing, three people died and 2,473 were injured in road accidents related to food delivery workers in the same period, according to the Ministry of Public Security.The rise of reckless behavior among food delivery workers is closely related to the growing demand for their service, reported People’s Daily. About 150 million people in China use food delivery services, according to China Radio International (CRI). Such a big market has led to a large demand for food delivery workers, with some companies offering high salaries to attract new workers.However, food delivery workers are often under high pressure from their employers. They face company fines of 20 yuan for delivering food late and upwards of 200 yuan for receiving complaints, reported CRI. Moreover, the more orders they take, the more commission（佣金）they can earn, leading to some workers checking their mobile phones for new orders while they're riding their bikes.While most companies have measures requiring delivery workers to follow traffic rules, “there remains a problem of whether these requirements and rules for delivery workers are truly entering their ears, brains and hearts,” Wang Liang, deputy head of the Traffic Police Security Bureau, told news website The Paper.To solve the problem, some cities have taken action. Shanghai has asked companies to train their workers on traffic rules and safety. Now in Shenzhen, if a delivery worker gets caught breaking traffic rules more than twice, he or she will be banned from driving food delivery vehicles for a whole year.第II卷（共40分）I. TranslationDirections: Translate the following sentences into English, using the words given in the brackets.1.这个比赛旨在鼓励年轻人继承中国文化的传统。

2017年上海市杨浦区高考数学一模试卷带解析【精品】

第1页（共17页）页）2017年上海市杨浦区高考数学一模试卷一、填空题（本大题满分54分）共12小题，1-6题每题4分，7-12题每题5分 1．（4分）若“a ＞b ”，则“a 3＞b 3”是命题（填：真、假） 2．（4分）已知A ＝（﹣∞，0]，B ＝（a ，+∞），若A ∪B ＝R ，则a 的取值范围是．3．（4分）z +2＝9+4i （i 为虚数单位），则|z |＝．4．（4分）若△ABC 中，a +b ＝4，∠C ＝30°，则△ABC 面积的最大值是．5．（4分）若函数f （x ）＝log 2的反函数的图象经过点（﹣2，3），则a ＝． 6．（4分）过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60°，则该截面的面积是．7．（5分）抛掷一枚均匀的骰子（刻有1，2，3，4，5，6）三次，得到的数字依次记作a ，b ，c ，则a +bi （i 为虚数单位）是方程x 2﹣2x +c ＝0的根的概率是．8．（5分）设常数a ＞0，（x +）9展开式中x 6的系数为4，则（a +a 2+…+a n）＝．9．（5分）已知直线l 经过点且方向向量为（2，﹣1），则原点O 到直线l 的距离为．10．（5分）若双曲线的一条渐近线为x +2y ＝0，且双曲线与抛物线y ＝x 2的准线仅有一个公共点，则此双曲线的标准方程为．11．（5分）平面直角坐标系中，给出点A （1，0），B （4，0），若直线x +my ﹣1＝0存在点P ，使得|P A |＝2|PB |，则实数m 的取值范围是． 12．（5分）函数y ＝f （x ）是最小正周期为4的偶函数，且在x ∈[﹣2，0]时，f （x ）＝2x +1，若存在x 1，x 2，…x n 满足0≤x 1＜x 2＜…＜x n ，且|f （x 1）﹣f （x 2）|+|f （x 2）﹣f （x 1）|+…+|f （xn ﹣1﹣f （x n ））|＝2016，则n +x n的最小值为．二、选择题（本大题共4题，满分20分）13．（5分）若与﹣都是非零向量，则“•＝•”是“⊥（﹣）”的（）A ．充分但非必要条件B ．必要但非充分条件C ．充要条件D ．既非充分也非必要条件14．（5分）行列式中，元素7的代数余子式的值为（） A ．﹣15B ．﹣3C ．3D ．1215．（5分）一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，另两名员工数据不清楚，那么8位员工月工资的中位数不可能是（） A ．5800 B ．6000C ．6200D ．640016．（5分）若直线+＝1通过点P （cos θ，sin θ），则下列不等式正确的是（） A ．a 2+b 2≤1 B ．a 2+b 2≥1C ．+≤1D ．+≥1三、解答题（满分76分）共5题17．（14分）某柱体实心铜制零件的截面边长是长度为55毫米线段AB 和88毫米的线段AC 以及圆心为P ，半径为PB 的一段圆弧BC 构成，其中∠BAC ＝60°．（1）求半径PB 的长度；（2）现知该零件的厚度为3毫米，毫米，试求该零件的重量试求该零件的重量试求该零件的重量（每（每1个立方厘米铜重8.9克，按四舍五入精确到0.1克）．V 柱＝S 底•h ．18．（14分）如图所示，l 1，l 2是互相垂直的异面直线，MN 是它们的公垂线段，点A ，B 在直线l 1上，且位于M 点的两侧，C 在l 2上，AM ＝BM ＝NM ＝CN （1）求证：异面直线AC 与BN 垂直；（2）若四面体ABCN 的体积V ABCN ＝9，求异面直线l 1，l 2之间的距离．19．（14分）如图所示，椭圆C：+y2＝1，左右焦点分别记作F1，F2，过F1，F2分别作直线l1，l2交椭圆AB，CD，且l1∥l2．（1）当直线l 1的斜率k1与直线BC的斜率k2都存在时，求证：k1•k2为定值；（2）求四边形ABCD面积的最大值．20．（14分）数列{a n}，定义{△a n}为数列{a n}的一阶差分数列，其中△a n＝a n+1﹣a n（n∈N*）（1）若a n＝n2﹣n，试判断{△a n}是否是等差数列，并说明理由；（2）若a1＝1，△a n﹣a n＝2n，求数列{a n}的通项公式；（3）对（b）中的数列{a n}，是否存在等差数列{b n}，使得b1C+b2C+…+b n C ＝a n，对一切n∈N*都成立，若存在，求出数列{b n}的通项公式，若不存在，请说明理由．21．（20分）对于函数f（x）（x∈D），若存在正常数T，使得对任意的x∈D，都有f（x+T）≥f（x）成立，我们称函数f（x）为“T同比不减函数”．（1）求证：对任意正常数T，f（x）＝x2都不是“T同比不减函数”；（2）若函数f（x）＝kx+sin x是“同比不减函数”，求k的取值范围；（3）是否存在正常数T，使得函数f（x）＝x+|x﹣1|﹣|x+1|为“T同比不减函数”；若存在，求T的取值范围；若不存在，请说明理由．2017年上海市杨浦区高考数学一模试卷参考答案与试题解析一、填空题（本大题满分54分）共12小题，1-6题每题4分，7-12题每题5分 1．（4分）若“a＞b”，则“a3＞b3”是真命题（填：真、假）【解答】解：函数f（x）＝x3在R是单调增函数，∴当a＞b，一定有a3＞b3，故是真命题答案为：真．2．（4分）已知A＝（﹣∞，0]，B＝（a，+∞），若A∪B＝R，则a的取值范围是 a≤0．．【解答】解：若A∪B＝R，A＝（﹣∞，0]，B＝（a，+∞），必有a≤0；故答案为：a≤0．3．（4分）z+2＝9+4i（i为虚数单位），则|z|＝ 5 ．【解答】解：设z＝x+yi（x，y∈R），∵z+2＝9+4i，∴x+yi+2（x﹣yi）＝9+4i，化为：3x﹣yi＝9+4i，∴3x＝9，﹣y＝4，解得x＝3，y＝﹣4．∴|z|＝＝5．故答案为：5．4．（4分）若△ABC中，a+b＝4，∠C＝30°，则△ABC面积的最大值是 1 ．【解答】解：在△ABC中，∵C＝30°，a+b＝4，∴△ABC的面积S＝ab•sin C＝ab•sin30°＝ab≤×（）2＝×4＝1，当且仅当a＝b＝2时取等号，故答案为：1．5．（4分）若函数f（x）＝log2的反函数的图象经过点（﹣2，3），则a＝ 2 ．【解答】解：∵函数f（x）＝log2的反函数的图象经过点（﹣2，3），∴函数f（x）＝log2的图象经过点（3，﹣2），∴﹣2＝log2，∴a＝2，故答案为2．6．（4分）过半径为2的球O表面上一点A作球O的截面，若OA与该截面所成的角是60°，则该截面的面积是 π ．【解答】解：设截面的圆心为Q，由题意得：∠OAQ＝60°，QA＝1，∴S＝π•12＝π．答案：π．7．（5分）抛掷一枚均匀的骰子（刻有1，2，3，4，5，6）三次，得到的数字依次记作a，b，c，则a+bi（i为虚数单位）是方程x2﹣2x+c＝0的根的概率是．【解答】解：抛掷一枚均匀的骰子（刻有1，2，3，4，5，6）三次，得到的数字依次记作a，b，c，基本事件总数n＝6×6×6＝216，∵a+bi（i为虚数单位）是方程x2﹣2x+c＝0的根，∴（a+bi）2﹣2（a+bi）+c＝0，即，∴a＝1，c＝b2+1，∴a+bi（i为虚数单位）是方程x2﹣2x+c＝0的根包含的基本事件为：（1，1，2），（1，2，5），∴a+bi（i为虚数单位）是方程x2﹣2x+c＝0的根的概率是p＝．故答案为：．8．（5分）设常数a＞0，（x+）9展开式中x6的系数为4，则（a+a2+…+a n）＝．【解答】解：∵常数a＞0，（x+）9展开式中x6的系数为4，∴＝，当时，r ＝2，∴＝4，解得a ＝，∴a +a 2+…+a n ＝＝＝（1﹣），∴（a +a 2+…+a n ）＝＝．故答案为：．9．（5分）已知直线l 经过点且方向向量为（2，﹣1），则原点O 到直线l 的距离为 1 ．【解答】解：直线的方向向量为（2，﹣1），所以直线的斜率为：﹣，直线方程为：x +2y +＝0，由点到直线的距离可知：＝1；故答案为：1．10．（5分）若双曲线的一条渐近线为x +2y ＝0，且双曲线与抛物线y ＝x 2的准线仅有一个公共点，则此双曲线的标准方程为．【解答】解：抛物线y ＝x 2的准线：y ＝﹣，双曲线与抛物线y ＝x 2的准线仅有一个公共点，可得双曲线实半轴长为a ＝，焦点在y 轴上．双曲线的一条渐近线为x +2y ＝0，∴＝，可得b ＝，则此双曲线的标准方程为：．故答案为：．11．（5分）平面直角坐标系中，给出点A （1，0），B （4，0），若直线x +my ﹣1＝0存在点P ，使得|P A |＝2|PB |，则实数m 的取值范围是 m ≥或m ≤﹣．【解答】解：设P （1﹣my ，y ）， ∵|P A |＝2|PB |， ∴|P A |2＝4|PB |2，∴（1﹣my ﹣1）2+y 2＝4（1﹣my ﹣4）2+y 2，化简得（m 2+1）y 2+8my +12＝0则△＝64m 2﹣48m 2﹣48≥0，解得m ≥或m ≤﹣，即实数m 的取值范围是m ≥或m ≤﹣．故答案为：m ≥或m ≤﹣．12．（5分）函数y ＝f （x ）是最小正周期为4的偶函数，且在x ∈[﹣2，0]时，f （x ）＝2x +1，若存在x 1，x 2，…x n 满足0≤x 1＜x 2＜…＜x n ，且|f （x 1）﹣f （x 2）|+|f （x 2）﹣f （x 1）|+…+|f （x n ﹣1﹣f （x n ））|＝2016，则n +x n 的最小值为 1513 ．【解答】解：∵函数y ＝f （x ）是最小正周期为4的偶函数，且在x ∈[﹣2，0]时，f （x ）＝2x +1，∴函数的值域为[﹣3，1]，对任意x i ，x j （i ，j ＝1，2，3，…，m ），都有|f （x i ）﹣f （x j ）|≤f （x ）max ﹣f （x ）min ＝4，要使n +x n 取得最小值，尽可能多让x i （i ＝1，2，3，…，m ）取得最高点，且f （0）＝1，f （2）＝﹣3，∵0≤x 1＜x 2＜…＜x m ，|f （x 1）﹣f （x 2）|+|f （x 2）﹣f （x 3）|+…+|f （x n ﹣1）﹣f （x n ）|＝2016， ∴n 的最小值为，相应的x n 最小值为1008，则n +x n 的最小值为1513．故答案为：1513．二、选择题（本大题共4题，满分20分）13．（5分）若与﹣都是非零向量，则“•＝•”是“⊥（﹣）”的（）A ．充分但非必要条件B ．必要但非充分条件C ．充要条件D ．既非充分也非必要条件【解答】解：“•＝•”⇔“•﹣•＝0”⇔“•（﹣）＝0”⇔“⊥（﹣）”，故“•＝•”是“⊥（﹣）”的充要条件，故选：C ． 14．（5分）行列式中，元素7的代数余子式的值为（） A ．﹣15B ．﹣3C ．3D ．12【解答】解：∵行列式，∴元素7的代数余子式为： D 13＝（﹣1）4＝2×6﹣5×3＝﹣3．故选：B ．15．（5分）一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，另两名员工数据不清楚，那么8位员工月工资的中位数不可能是（） A ．5800B ．6000C ．6200D ．6400【解答】解：∵一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，∴当另外两名员工的工资都小于5300时，中位数为＝5400，当另外两名员工的工资都大于6500时，中位数为＝6300，∴8位员工月工资的中位数的取值区间为[5400，6300]， ∴8位员工月工资的中位数不可能是6400．故选：D ．16．（5分）若直线+＝1通过点P （cos θ，sin θ），则下列不等式正确的是（）A ．a 2+b 2≤1 B ．a 2+b 2≥1 C ．+≤1D ．+≥1【解答】解：直线+＝1通过点P （cos θ，sin θ）， ∴b cos θ+a sin θ＝ab ， ∴sin （θ+φ）＝ab ，其中tan φ＝， ∴≥ab ，∴a 2+b 2≥a 2b 2， ∴+≥1，故选：D ．三、解答题（满分76分）共5题 17．（14分）某柱体实心铜制零件的截面边长是长度为55毫米线段AB 和88毫米的线段AC 以及圆心为P ，半径为PB 的一段圆弧BC 构成，其中∠BAC ＝60°．（1）求半径PB 的长度；（2）现知该零件的厚度为3毫米，毫米，试求该零件的重量试求该零件的重量试求该零件的重量（每（每1个立方厘米铜重8.9克，按四舍五入精确到0.1克）．V 柱＝S 底•h ．【解答】解：（1）∵AB ＝55，AC ＝88，BP ＝R ，∠BAC ＝60°．AP ＝88﹣R ， ∴在△ABP 中，由余弦定理可得：BP 2＝AB 2+AP 2﹣2AB •AP •cos ∠BAC ，可得：R 2＝552+（88﹣R ）2﹣2×55×（88﹣R ）×cos60°， ∴解得：R ＝49mm ．（2）在△ABP 中，AP ＝88﹣49＝39mm ，AB ＝55，BP ＝49， cos ∠BP A ＝＝≈0.2347， ∴sin ∠BP A ≈0.972． ∴∠BP A ＝arcsin0.972．V柱＝S底•h＝（S△ABP+S扇形BPC）•h＝（+）•3该零件的重量＝（+）•3÷1000×8.9≈82.7．18．（14分）如图所示，l1，l2是互相垂直的异面直线，MN是它们的公垂线段，点A，B在直线l1上，且位于M点的两侧，C在l2上，AM＝BM＝NM＝CN （1）求证：异面直线AC与BN垂直；（2）若四面体ABCN的体积V ABCN＝9，求异面直线l1，l2之间的距离．【解答】解：（1）证明：由已知l2⊥MN，l2⊥l1，MN∩l1＝M，可得l2⊥平面ABN．由已知MN⊥l1，AM＝MB＝MN，可知AN＝NB且AN⊥NB．又AN为AC在平面ABN内的射影．∴AC⊥NB（2）∵AM＝BM＝NM＝CN，MN是它们的公垂线段，就是异面直线l1，l2之间的距离，由中垂线的性质可得AN＝BN，四面体ABCN的体积V ABCN＝9，可得：V ABCN＝9＝＝MN3，∴MN＝3．异面直线l1，l2之间的距离为3．19．（14分）如图所示，椭圆C：+y2＝1，左右焦点分别记作F1，F2，过F1，F2分别作直线l1，l2交椭圆AB，CD，且l1∥l2．（1）当直线l 1的斜率k1与直线BC的斜率k2都存在时，求证：k1•k2为定值；（2）求四边形ABCD面积的最大值．【解答】（1）证明：由椭圆C：+y2＝1，得a2＝4，b2＝1，∴．设k1＝k，则AB所在直线方程为y＝kx+，CD所在直线方程为y＝kx﹣，联立，得（1+4k2）x2+8k2x+12k2﹣4＝0．解得，不妨取，则同理求得，．则＝＝，则k1•k2＝；（2）解：由（1）知，，|AB|＝＝＝．AB、CD的距离d＝，∴＝．令1+4k2＝t（t≥1），则，∴当t＝3时，S max＝4．20．（14分）数列{a n}，定义{△a n}为数列{a n}的一阶差分数列，其中△a n＝a n+1﹣a n（n∈N*）（1）若a n＝n2﹣n，试判断{△a n}是否是等差数列，并说明理由；（2）若a1＝1，△a n﹣a n＝2n，求数列{a n}的通项公式；（3）对（b）中的数列{a n}，是否存在等差数列{b n}，使得b1C+b2C+…+b n C ＝a n，对一切n∈N*都成立，若存在，求出数列{b n}的通项公式，若不存在，请说明理由．【解答】解：（1）若a n＝n2﹣n，试判断{△a n}是等差数列，理由如下：∵a n＝n2﹣n，∴△a n＝a n+1﹣a n＝（n+1）2﹣（n+1）﹣（n2﹣n）＝2n，∵△a n+1﹣△a n＝2，且△a1＝4，∴{△a n}是首项为4，公差为2的等差数列；（2）∵△a n﹣a n＝2n．△a n＝a n+1﹣a n，∴a n+1﹣2a n＝2n，∴﹣＝，（6分）∴数列{}构成以为首项，为公差的等差数列，即＝⇒a n＝n•2n﹣1；（3）b1∁n1+b2∁n2+…+b n∁n n＝a n，即b1∁n1+b2∁n2+…+b n∁n n＝n•2n﹣1，∵1∁n1+2∁n2+3∁n3+…+n∁n n＝n（C n﹣10+C n﹣11+C n﹣12+…+C n﹣1n﹣1）＝n•2n﹣1，∴存在等差数列{b n}，b n＝n，使得b1∁n1+b2∁n2+…+b n∁n n＝a n对一切自然n∈N都成立．21．（20分）对于函数f（x）（x∈D），若存在正常数T，使得对任意的x∈D，都有f（x+T）≥f（x）成立，我们称函数f（x）为“T同比不减函数”．（1）求证：对任意正常数T，f（x）＝x2都不是“T同比不减函数”；（2）若函数f（x）＝kx+sin x是“同比不减函数”，求k的取值范围；（3）是否存在正常数T，使得函数f（x）＝x+|x﹣1|﹣|x+1|为“T同比不减函数”；若存在，求T的取值范围；若不存在，请说明理由．【解答】解：（1）∵f（x）＝x2，∴f（x+T）﹣f（x）＝（x+T）2﹣x2＝2xT+T2＝T（2x+T），由于2x+T与0的小无法比较，∴f（x+T）≥f（x）不一定成立，∴对任意正常数T，f（x）＝x2都不是“T同比不减函数，（2）∵函数f（x）＝kx+sin x是“同比不减函数，∴f（x+）﹣f（x）＝k（x+）+sin（x+）﹣kx﹣sin x＝+cos x﹣sin x＝﹣sin（x﹣）≥0恒成立，∴k≥sin（x﹣），∵﹣1≤sin（x﹣）≤1，∴k≥，（3）f（x）＝x+|x﹣1|﹣|x+1|图象如图所示，由图象可知，只要把图象向左至少平移4个单位，即对任意的x∈D，都有f（x+T）≥f（x）成立，∴T≥4．赠送—高中数学知识点【2.1.1】指数与指数幂的运算（1）根式的概念）根式的概念①如果,,,1nx a a R x R n =ÎÎ>，且n N +Î，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n 次方根用符号n a 表示；当n 是偶数时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号n a -表示；表示；00的n 次方根是0；负数a 没有n 次方根．次方根．②式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ³．③根式的性质：()nna a =；当n 为奇数时，nna a =；当n 为偶数时，(0)|| (0)nn a a a a a a ³ì==í-<î．（2）分数指数幂的概念）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,m nmna a a m n N +=>Î且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：11()()(0,,,mmmn nnaa m n N a a-+==>Î且1)n >．0的负分数指数幂没有意义．的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．底数取倒数，指数取相反数．（3）分数指数幂的运算性质）分数指数幂的运算性质①(0,,)r s r s a a a a r s R +×=>Î ②()(0,,)r s rs a a a r s R =>Î ③()(0,0,)r r rab a b a b r R =>>Î【2.1.2】指数函数及其性质（4）指数函数）指数函数函数名称函数名称指数函数指数函数定义定义函数(0xy a a =>且1)a ¹叫做指数函数叫做指数函数图象图象1a >01a <<定义域定义域 R值域值域 (0,)+¥过定点过定点图象过定点(0,1)，即当0x =时，1y =．奇偶性奇偶性非奇非偶非奇非偶单调性单调性在R 上是增函数上是增函数在R 上是减函数上是减函数函数值的函数值的变化情况变化情况1(0)1(0)1(0)xx x a x a x a x >>==<< 1(0)1(0)1(0)xx x a x a x a x <>==>< a 变化对变化对图象的影响象的影响在第一象限内，a 越大图象越高；在第二象限内，a 越大图象越低．越大图象越低．xa y =xy(0,1)O1y =xa y =xy (0,1)O 1y =〖2.2〗对数函数【2.2.1】对数与对数运算（1）对数的定义）对数的定义①若(0,1)xa N a a =>¹且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．叫做真数．②负数和零没有对数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =Û=>¹>．（2）几个重要的对数恒等式）几个重要的对数恒等式log 10a =，log 1a a =，log b aa b =．（3）常用对数与自然对数）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．（4）对数的运算性质）对数的运算性质如果0,1,0,0a a M N >¹>>，那么，那么①加法：log log log ()a a aM N MN += ②减法：log log log a a a M M N N-= ③数乘：log log ()n a a n M M n R =Î ④log a Na N =⑤log log (0,)bn a a n M M b n R b=¹Î ⑥换底公式：log log (0,1)log b ab N N b b a=>¹且【2.2.2】对数函数及其性质（5）对数函数）对数函数函数函数名称名称对数函数对数函数定义定义函数log (0a yx a =>且1)a ¹叫做对数函数叫做对数函数图象图象1a > 01a <<xyO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=定义域定义域(0,)+¥值域值域R过定点过定点图象过定点(1,0)，即当1x=时，0y=．奇偶性奇偶性非奇非偶非奇非偶单调性单调性在(0,)+¥上是增函数上是增函数在(0,)+¥上是减函数上是减函数函数值的函数值的变化情况变化情况log0(1)log0(1)log0(01)aaax xx xx x>>==<<<log0(1)log0(1)log0(01)aaax xx xx x<>==><<a变化对变化对图象的影响象的影响在第一象限内，a越大图象越靠低；在第四象限内，a越大图象越靠高．越大图象越靠高．。

2017年高考数学上海卷-答案

上海市2017年普通高等学校招生全国统一考试数学答案解析一、填空题1.【答案】{3,4}解析：利用交集定义直接求解。

【考点】交集的求法。

2.【答案】3m =解析：36654P =⨯⨯，故3m =.【考点】实数值的求法。

3.【答案】(,0)-∞【解析】由11x x -＞得：11110x x x ->⇒⇒＜0＜。

【考点】解分式不等式4.【答案】9π【解析】代解：球的体积为36π，设球的半径为R ，可得34π36π3R =，可得3R =，该球主视图为半径为3的圆，可得面积为2π9πR =．故答案为：9π．【考点】球的体积公式，以及主视图的形状和面积求法。

5.【解析】设i(,)z a b a b =+∈R ，代入23z =-，由复数相等的条件列式求得a ，b 的值得答案．【考点】复数代数形式的乘除运算。

6.【答案】11【解析】根据题意，由双曲线的方程可得a 的值，结合双曲线的定义可得12||||||6PF PF -=，解可得2||PF 的值，即可得答案．【考点】双曲线的几何性质。

7.【答案】(4,3,2)-【解析】解：如图，以长方体ABCD ﹣A 1B 1C 1D 1的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系，∵1DB 的坐标为(4,3,2)，∴(4,0,0)A ，1(0,3,2)C ，∴1(4,3,2)AC =-.故答案为：(4,3,2)-．【考点】空间向量的坐标的求法。

8.【答案】89【解析】由奇函数的定义，当0x ＞时，0x -＜，代入已知解析式，即可得到所求0x ＞的解析式，再由互为反函数的两函数的自变量和函数值相反，即可得到所求值.【考点】函数的奇偶性和运用。

9.【答案】13【解析】从四个函数中任选2个，基本事件总数246n C ==，再利用列举法求出事件A ：“所选2个函数的图象有且只有一个公共点”包含的基本事件的个数，由此能求出事件A ：“所选2个函数的图象有且只有一个公共点”的概率.【考点】概率的求法。

上海市各区2017届高三一模数学试卷

3．已知 M x
1 x P x ≥ 0, x R ， x 1 ≤ 2, x R ，则 M ∩P 等于 x 2
．
．
4．抛物线 y x 2 上一点 M 到焦点的距离为 1，则点 M 的纵坐标为 5．已知无穷数列 {an } 满足 an 1
18.（本题满分 14 分）本题共有 2 个小题，第(1)小题满分 6 分，第(2)小题满分 8 分. 在一个特定时段内，以点 D 为中心的 7 海里以内海域被设为警戒水域．点 D 正北 55 海里处有一个雷达观测站 A．某时刻测得一艘匀速直线行驶的船只位于点 A 北偏东 45 且与点 A 相距 40 2 海里的位置 B 处，经过 40 分钟又测得该船已行驶到点 A 北偏东 45 （其
你认为正确论断的序号都填上）
（注：把
12．已知 AB 为单位圆 O 的一条弦，P 为单位圆 O 上的点．若 f ( ) AP AB ( R) 的
最小值为 m ，当点 P 在单位圆上运动时， m 的最大值为为．
4 ，则线段 AB 的长度 3
二、选择题（本大题共有 4 题，满分 20 分）
x 1 0 的解集为 x2 x 5cos 4. 椭圆（为参数）的焦距为 y 4sin
3. 不等式 5. 设复数 z 满足 z 2 z 3 i （ i 为虚数单位），则 z 6. 若函数 y
cos x sin x
sin x cos x
n
求实数 x 的取值集合；
21. 设集合 A 、 B 均为实数集 R 的子集，记： A B {a b | a A, b B} ；（1）已知 A {0,1, 2} ， B {1,3} ，试用列举法表示 A B ；

2017届上海市十二校高三12月联考理科数学试卷及答案精品

2017学年第一学期十二校联考高三数学（理）考试试卷一、填空题（本大题满分56分，每题4分）1．已知全集U {}5,4,3,2,1=，A {}3,1=，B {}4,3,2=，那么=⋃)(B C A U __． 2．函数)12arcsin(-=x y 的定义域为．3．若数列{}n a 满足：111,2()n n a a a n N *+==∈，则前6项的和6S = .（用数字作答）4. 计算：2(1)(13)lim(2)(1)n n n n n n →∞+-=-++________．5．集合{}12-<<=x x A ，{}0<-=a x x B ，若B A ⊆，则实数a 的取值范围是．6. 设()887872x a x a x -=++…10a x a +，则87a a ++…0a +＝．7. 已知函数)(x f 有反函数)(1x f -，且[),,0,24)(1+∞∈-=+x x f x x 则=-)0(1f ．8. 已知袋中有大小相同的红球和白球若干个，其中红、白球个数的比为4:3．假设从袋中任取2个球，取到的都是红球的概率为413．那么袋中的红球有 __个． 9. 已知函数32tansin )(x xx x f ++=，)1,1(-∈x ，则满足不等式0)12()1(<-+-a f a f 的实数a 的取值范围是．10. 已知x 是7,6,5,,3,2,1x 这7个数据的中位数，且y x -,,2,12这四个数据的平均数为1，则xy 1-的最小值为．11．设ω>0，若函数)(x f = sin 2x ω cos 2x ω 在区间[－3π，4π]上单调递增，则ω的范围是_____________．12. 设正项数列}{n a 的前n 项和是n S ,若}{n a 和}{n S 都是等差数列,且公差相等,则1a =_______________.13．函数)(x f y =的图像与直线b x a x ==,及x 轴所围成图形的面积称为函数)(x f 在[]b a ,上的面积，已知函数nx y sin =在⎥⎦⎤⎢⎣⎡n π,0上的面积为)(2*∈N n n ，则函数1)3sin(+-=πx y 在⎥⎦⎤⎢⎣⎡34,3ππ上的面积为．14．（理）函数)(x f 的定义域为A ，若A x x ∈21,且)()(21x f x f =时总有21x x =，则称)(x f 为单函数，例如，函数)(12)(R x x x f ∈+=是单函数．下列命题： ①函数)()(2R x x x f ∈=是单函数；②指数函数)(2)(R x x f x ∈=是单函数；③若)(x f 为单函数，A x x ∈21,且21x x ≠，则)()(21x f x f ≠； ④在定义域上具有单调性的函数一定是单函数；⑤若)(x f 为单函数，则函数)(x f 在定义域上具有单调性。

2017年上海市杨浦区高考数学一模试卷

2017年上海市杨浦区高考数学一模试卷一、填空题（本大题满分54分）共12小题，1-6题每题4分，7-12题每题5分1. 若“”，则“”是________命题（填：真、假）【答案】真【考点】命题的真假判断与应用不等式的概念与应用【解析】利用函数在是单调增函数判定．【解答】解：函数在是单调增函数，∴当，一定有，故是真命题答案为：真．2. 已知,，若，则的取值范围是________．【答案】．【考点】并集及其运算【解析】利用集合的性质直接求解，解题时要注意的是是成立的【解答】解：若，,，必有；故答案为：．3. （为虚数单位），则________．【答案】【考点】复数的模【解析】设，代入，化为：，利用复数相等即可得出．【解答】解：设，∵，∴，化为：，∴，，解得，．∴．故答案为：．4. 若中，，，则面积的最大值是________．【答案】【考点】正弦定理【解析】由条件可得的面积，再利用正弦函数的值域、基本不等式求得的最大值．【解答】解：在中，∵，，∴的面积，当且仅当时取等号，故答案为：．5. 若函数的反函数的图象经过点，则________．【答案】【考点】反函数【解析】由函数的反函数的图象经过点，得函数的图象经过点，代入计算可得结论．【解答】解：∵函数的反函数的图象经过点，∴函数的图象经过点，∴，∴，故答案为．6. 过半径为的球表面上一点作球的截面，若与该截面所成的角是，则该截面的面积是________．【答案】【考点】直线与平面所成的角球的性质【解析】充分利用球的半径、球心与截面圆心的连线、在截面圆上的射影构成的直角三角形解决即可．【解答】设截面的圆心为，由题意得：，，∴．7. 抛掷一枚均匀的骰子（刻有，，，，，）三次，得到的数字依次记作，，，则（为虚数单位）是方程的根的概率是________．【答案】【考点】古典概型及其概率计算公式【解析】基本事件总数，由（为虚数单位）是方程的根，得，，由此能求出（为虚数单位）是方程的根的概率．【解答】解：抛掷一枚均匀的骰子（刻有，，，，，）三次，得到的数字依次记作，，，基本事件总数，∵（为虚数单位）是方程的根，∴，即，∴，，∴（为虚数单位）是方程的根包含的基本事件为：，，∴（为虚数单位）是方程的根的概率是．故答案为：．8. 设常数，展开式中的系数为，则________．【答案】【考点】二项式定理的应用【解析】由，根据的系数为，求出，从而，解得，由此能求出的值．【解答】解：∵常数，展开式中的系数为，∴，当时，，∴，解得，∴，∴．故答案为：．9. 已知直线经过点且方向向量为，则原点到直线的距离为________．【答案】【考点】点到直线的距离公式【解析】通过方向向量求出直线的斜率，利用点斜式写出直线方程，通过点到直线的距离求解即可．【解答】解：直线的方向向量为，所以直线的斜率为：，直线方程为：，由点到直线的距离可知：；故答案为：．10. 若双曲线的一条渐近线为，且双曲线与抛物线的准线仅有一个公共点，则此双曲线的标准方程为________．【答案】【考点】直线与抛物线的位置关系抛物线的求解直线与双曲线的位置关系【解析】求出抛物线的准线方程，得到双曲线的实半轴的长，利用双曲线的渐近线方程，求解即可．【解答】解：抛物线的准线：，双曲线与抛物线的准线仅有一个公共点，可得双曲线实半轴长为，焦点在轴上．双曲线的一条渐近线为，∴，可得，则此双曲线的标准方程为：．故答案为：．11. 平面直角坐标系中，给出点，，若直线存在点，使得，则实数的取值范围是________．【答案】或【考点】两点间的距离公式【解析】根据题意，设出点，代入，化简得，由，求出实数的取值范围．【解答】解：设，∵，∴，∴，化简得，则，解得或，即实数的取值范围是或．故答案为：或．12. 已知偶函数满足，且在时，，若存在，，…满足，且（，则最小值为________．【答案】【考点】函数的最值及其几何意义【解析】由函数是最小正周期为的偶函数可知函数的值域为，对任意，,…,，都有，要使取得最小值，尽可能多让,…,取得最高点，然后可得的最小值．【解答】解：∵偶函数满足，∴函数是周期为4的偶函数，且当时，，∴函数的值域为，对任意，,…,，都有，若，注意到在上是单调递减函数，，，则，∴不妨设当时，，要使取得最小值，则尽可能多让,…,取得最高点与最低点，且，，，∵，且，=2018，根据，且，相应的最小值为．故答案为：．二、选择题（本大题共4题，满分20分）若与都是非零向量，则“”是“”的（）A.充分但非必要条件B.必要但非充分条件C.充要条件D.既非充分也非必要条件【答案】C【考点】平面向量数量积的运算必要条件、充分条件与充要条件的判断【解析】根据向量数量积运算和向量垂直的充要条件，可得答案．【解答】解：“”“”“”“”，故“”是“”的充要条件，故选：行列式中，元素的代数余子式的值为（）A. B. C. D.【答案】B【考点】二阶行列式的定义【解析】利用代数余子式的定义和性质求解．【解答】解：∵行列式，∴元素的代数余子式为：．故选：．一个公司有名员工，其中名员工的月工资分别为，，，，，，另两名员工数据不清楚，那么位员工月工资的中位数不可能是（）A. B. C. D.【答案】D【考点】众数、中位数、平均数【解析】由已知能求出位员工月工资的中位数的取值区间为，由此能求出结果．【解答】∵一个公司有名员工，其中名员工的月工资分别为，，，，，，∴当另外两名员工的工资都小于时，中位数为，当另外两名员工的工资都大于时，中位数为，∴位员工月工资的中位数的取值区间为，∴位员工月工资的中位数不可能是若直线通过点，则下列不等式正确的是（）A. B.C. D.【答案】D【考点】不等式比较两数大小【解析】先把点代入得到，即可得到，得到，问题得以判断【解答】解：直线通过点，∴，∴，其中，∴，∴，∴，故选：三、解答题（满分76分）共5题某柱体实心铜制零件的截面边长是长度为毫米线段和毫米的线段以及圆心为，半径为的一段圆弧构成，其中．（1）求半径的长度；（2）现知该零件的厚度为毫米，试求该零件的重量（每个立方厘米铜重克，按四舍五入精确到克）．柱底．【答案】解：（1）∵，，，．，∴在中，由余弦定理可得：，可得：，∴解得：．（2）在中，，，，，∴．∴．柱底扇形该零件的重量．【考点】弧长公式【解析】（1）在中，由余弦定理建立方程，即可求半径的长度；（2）求出柱底，即可求该零件的重．量【解答】解：（1）∵，，，．，∴在中，由余弦定理可得：，可得：，∴解得：．（2）在中，，，，，∴．∴．柱底扇形该零件的重量．如图所示，，是互相垂直的异面直线，是它们的公垂线段，点，在直线上，且位于点的两侧，在上，（1）求证：异面直线与垂直；（2）若四面体的体积，求异面直线，之间的距离．【答案】解：（1）证明：由已知，，，可得平面．由已知，，可知且．又为在平面内的射影．∴（2）∵，是它们的公垂线段，就是异面直线，之间的距离，由中垂线的性质可得，四面体的体积，可得：，∴．异面直线，之间的距离为．【考点】点、线、面间的距离计算【解析】（1）欲证，可先证面，根据线面垂直的判定定理只需证，即可；（2）判断异面直线的距离，利用体积公式求解即可．【解答】解：（1）证明：由已知，，，可得平面．由已知，，可知且．又为在平面内的射影．∴（2）∵，是它们的公垂线段，就是异面直线，之间的距离，由中垂线的性质可得，四面体的体积，可得：，∴．异面直线，之间的距离为．如图所示，椭圆，左右焦点分别记作，，过，分别作直线，交椭圆，，且．（1）当直线的斜率与直线的斜率都存在时，求证：为定值；（2）求四边形面积的最大值．【答案】（1）证明：由椭圆，得，，∴．设，则所在直线方程为，所在直线方程为，联立，得．解得，不妨取，则同理求得，．则，则；（2）解：由（1）知，，．、的距离，∴．四边形令，则，∴当时，．【考点】直线与椭圆的位置关系【解析】（1）由椭圆方程求出焦点坐标，得到直线、的方程，与椭圆方程联立求得、的坐标，求出所在直线斜率得答案；（2）由（1）结合弦长公式求得，再由两平行线间的距离公式求出边、的距离，代入平行四边形面积公式，利用换元法求得最值．【解答】（1）证明：由椭圆，得，，∴．设，则所在直线方程为，所在直线方程为，联立，得．解得，不妨取，则同理求得，．则，则；（2）解：由（1）知，，．、的距离，∴．四边形令，则，∴当时，．数列，定义为数列的一阶差分数列，其中（1）若，试判断是否是等差数列，并说明理由；（2）若，，求数列的通项公式；（3）对中的数列，是否存在等差数列，使得，对一切都成立，若存在，求出数列的通项公式，若不存在，请说明理由．【答案】解：（1）若，试判断是等差数列，理由如下：∵，∴，∵，且，∴是首项为，公差为的等差数列；（2）∵．，∴，∴，∴数列构成以为首项，为公差的等差数列，即；（3），即，∵，∴存在等差数列，，使得对一切自然都成立．【考点】数列的求和数列递推式【解析】（1）根据数列的通项公式，结合新定义，可判定是首项为，公差为的等差数列；（2）由入手能够求出数列的通项公式；（3）结合组合数的性质：进行求解．【解答】解：（1）若，试判断是等差数列，理由如下：∵，∴，∵，且，∴是首项为，公差为的等差数列；（2）∵．，∴，∴，∴数列构成以为首项，为公差的等差数列，即；（3），即，∵，∴存在等差数列，，使得对一切自然都成立．对于函数，若存在正常数，使得对任意的，都有成立，我们称函数为“同比不减函数”．（1）求证：对任意正常数，都不是“同比不减函数”；（2）若函数是“同比不减函数”，求的取值范围；（3）是否存在正常数，使得函数为“同比不减函数”；若存在，求的取值范围；若不存在，请说明理由．【答案】解：（1）∵，∴，由于与的小无法比较，∴不一定成立，∴对任意正常数，都不是“同比不减函数，（2）∵函数是“同比不减函数，∴恒成立，∴，∵，∴，（3）图象如图所示，由图象可知，只要把图象向左至少平移个单位，即对任意的，都有成立，∴．【考点】函数与方程的综合运用【解析】（1）根据同比不减函数的定义即可证明，（2）根据同比不减函数的定义，分离参数得到，根据三角形函数的性质即可求出的范围，（3）画出函数的图象，根据图象的平移即可求出的范围．【解答】解：（1）∵，∴，由于与的小无法比较，∴不一定成立，∴对任意正常数，都不是“同比不减函数，（2）∵函数是“同比不减函数，∴恒成立，∴，∵，∴，（3）图象如图所示，由图象可知，只要把图象向左至少平移个单位，即对任意的，都有成立，∴．。

2017年上海高三数学一模中档题

7. 抛掷一枚均匀的骰子（刻有1、2、3、4、5、6）三次，得到的数字依次记作a 、b 、c ，则a bi +（i 为虚数单位）是方程220x x c -+=的根的概率是8. 设常数0a >，9(x+展开式中6x 的系数为4，则2lim()n n a a a →∞++⋅⋅⋅+=9. 已知直线l 经过点(且方向向量为(2,1)-，则原点O 到直线l 的距离为10. 若双曲线的一条渐近线为20x y +=，且双曲线与抛物线2y x =的准线仅有一个公共点，则此双曲线的标准方程为11.平面直角坐标系中，给出点(1,0)A 、(4,0)B ，若直线10x my +-=上存在点P ，使得 ||2||PA PB =，则实数m 的取值范围是15. 一个公司有8名员工，其中6位员工的月工资分别为5200、5300、5500、6100、6500、 6600，另两位员工数据不清楚，那么8位员工月工资的中位数不可能是（）A. 5800B. 6000C. 6200D. 64007. 若函数22,0(),0x x f x x m x ⎧≤⎪=⎨-+>⎪⎩的值域为(,1]-∞，则实数m 的取值范围是 8. 如图，在△ABC 中，若3AB AC ==，1cos 2BAC ∠=，2DC BD =uuu r uu u r ，则AD BC ⋅=uuu r uu u r9. 定义在R 上的偶函数()y f x =，当0x ≥时，2()lg(33)f x x x =-+，则()f x 在R 上的零点个数为个10. 将6辆不同的小汽车和2辆不同的卡车驶入如图所示的10个车位中的某8个内，其中2辆卡车必须停在A 与B 的位置，那么不同的停车位置安排共有种（结果用数值表示）11. 已知数列{}n a 是首项为1，公差为2m 的等差数列，前n 项和为n S ，设2n n n S b n =⋅ *()n N ∈，若数列{}n b 是递减数列，则实数m 的取值范围是18. 已知函数23sin ()cos 1x x f x x -=；（1）当[0,]2x π∈时，求()f x 的值域；（2）已知△ABC 的内角,,A B C 的对边分别为,,a b c ，若()32Af =4a =，5b c +=，求△ABC 的面积；上海市长宁、嘉定区2017届高三一模数学试卷8. 若数列{}n a 23n n =+（*n N ∈），则 1221lim ()231n n a a a n n →∞++⋅⋅⋅+=+ 9. 如图，在ABC ∆中，45B ∠=︒，D 是BC 边上的一点，5AD =，7AC =，3DC =，则AB 的长为10. 有以下命题：① 若函数()f x 既是奇函数又是偶函数，则()f x 的值域为{0}；② 若函数()f x 是偶函数，则(||)()f x f x =；③ 若函数()f x 在其定义域内不是单调函数，则()f x 不存在反函数；④ 若函数()f x 存在反函数1()f x -，且1()f x -与()f x 不完全相同，则()f x 与1()f x -图像的公共点必在直线y x =上；其中真命题的序号是（写出所有真命题的序号）17. 如图，已知AB ⊥平面BCD ，BC CD ⊥，AD 与平面BCD 所成的角为30°，且2AB BC ==；（1）求三棱锥A BCD -的体积；（2）设M 为BD 的中点，求异面直线AD 与CM所成角的大小（结果用反三角函数值表示）；8. 已知圆222:220C x y kx y k ++++=（k R ∈）和定点(1,1)P -，若过P 可以作两条直线与圆C 相切，则k 的取值范围是9. 如图，在直三棱柱111ABC A B C -中，90ABC ∠=︒， 1AB BC ==，若1A C 与平面11B BCC 所成的角为6π，则三棱锥1A ABC -的体积为 10. 掷两颗骰子得两个数，若两数的差为d ，则{2,1,0,1,2}d ∈--出现的概率的最大值为（结果用最简分数表示）15. 设l αβ--是直二面角，直线a 在平面α内，直线b 在平面β内，且a 、b 与l 均不垂直，则（）A. a 与b 可能垂直，但不可能平行B. a 与b 可能垂直，也可能平行C. a 与b 不可能垂直，但可能平行D. a 与b 不可能垂直，也不可能平行18. 已知椭圆2222:1x y a bΓ+=（0a b >>）的左、右两个焦点分别为1F 、2F ，P 是椭圆上位于第一象限内的点，PQ x ⊥轴，垂足为Q ，且12||6F F =，12PF F ∠=12PF F ∆的面积为（1）求椭圆Γ的方程；（2）若M 是椭圆上的动点，求||MQ 的最大值，并求出||MQ 取得最大值时M 的坐标；8. 若21(2)n x x +*()n N ∈的二项展开式中的第9项是常数项，则n = 9. 已知,A B 分别是函数()2sin f x x ω=(0)ω>在y 轴右侧图像上的第一个最高点和第一个最低点，且2AOB π∠=，则该函数的最小正周期是10. 将序号分别为1、2、3、4、5的5张参观券全部分给4人，每人至少一张，如果分给同一人的2张参观券连号，那么不同的分法种数是15. 如图，已知椭圆C 的中心为原点O ，(F -为C 的左焦点，P 为C 上一点，满足||||OP OF =且||4PF =，则椭圆C 的方程为（）A. 221255x y +=B. 2213010x y += C. 2213616x y += D. 2214525x y += 18. 在一个特定时段内，以点E 为中心的7海里以内海域被设为警戒水域，点E 正北55海里处有一个雷达观测站A ，某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45°且与点A 相距B 处，经过40分钟又测得该船已行驶到点A 北偏东45θ︒+（其中sin 26θ=，090θ︒︒<<）且与点A 相距海里的位置C 处；（1）求该船的行驶速度；（单位：海里/小时）（2）若该船不改变航行方向继续行驶，判断它是否会进入警戒水域，并说明理由；9. 已知一个底面置于水平面上的圆锥，其左视图是边长为6的正三角形，则该圆锥的侧面积为10. 某班级要从5名男生和2名女生中选出3人参加公益活动，则在选出的3人中男、女生均有的概率为（结果用最简分数表示）11. 设常数0a >，若9()a x x +的二项展开式中5x 的系数为144，则a =15. 设M 、N 为两个随机事件，给出以下命题：（1）若M 、N 为互斥事件，且1()5P M =，1()4P N =，则9()20P M N =U ；（2）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（3）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（4）若1()2P M =，1()3P N =，1()6P MN =，则M 、N 为相互独立事件；（5）若1()2P M =，1()3P N =，5()6P MN =，则M 、N 为相互独立事件；其中正确命题的个数为（）A. 1B. 2C. 3D. 417. 如图，已知正三棱柱111ABC A B C -的底面积为4，侧面积为36；（1）求正三棱柱111ABC A B C -的体积；（2）求异面直线1A C 与AB 所成的角的大小；上海市松江区2017届高三一模数学试卷8. 设230123(1)n n n x a a x a x a x a x +=++++⋅⋅⋅+，若2313a a =，则n = 9. 已知圆锥底面半径与球的半径都是1cm ，如果圆锥的体积与球的体积恰好也相等，那么这个圆锥的侧面积是 2cm10. 设(,)P x y是曲线1C =上的点，1(4,0)F -，2(4,0)F ，则12||||PF PF + 的最大值为15. 若矩阵11122122a a a a ⎛⎫ ⎪⎝⎭满足：11a 、12a 、21a 、22{0,1}a ∈，且111221220a a a a =，则这样的互不相等的矩阵共有（） A. 2个 B. 6个 C. 8个 D. 10个18. 已知函数21()21x x a f x ⋅-=+（a 为实数）；（1）根据a 的不同取值，讨论函数()y f x =的奇偶性，并说明理由；（2）若对任意的1x ≥，都有1()3f x ≤≤，求a 的取值范围；8. 如图，一个空间几何体的主视图、左视图、俯视图均为全等的等腰直角三角形，如果直角三角形的直角边长都为1，那么这个几何体的表面积为9. 已知互异复数0mn ≠，集合22{,}{,}m n m n =，则 m n +=10. 已知等比数列{}n a 的公比为q ，前n 项和为n S ，对任意的*n N ∈，0n S >恒成立，则公比q 的取值范围是15. 已知函数22sin ,0()cos(),0x x x f x x x x α⎧+≥⎪=⎨-++<⎪⎩([0,2))απ∈是奇函数，则α=（） A. 0 B. 2π C. π D. 32π 18. 已知函数22()log (2)x x f x a a =+-(0)a >，且(1)2f =；（1）求a 和()f x 的单调区间；（2）(1)()2f x f x +->；8. 已知数列{}n a 的通项公式为2n a n bn =+，若数列{}n a 是单调递增数列，则实数b 的取值范围是9. 将边长为10的正三角形ABC ，按“斜二测”画法在水平放置的平面上画出为△A B C '''，则△A B C '''中最短边的边长为（精确到0.01）10. 已知点A 是圆22:4O x y +=上的一个定点，点B 是圆O 上的一个动点，若满足 ||||AO BO AO BO +=-uuu r uu u r uuu r uu u r ，则AO AB ⋅=uuu r uu u r14. 已知空间两条直线m 、n ，两个平面α、β，给出下面四个命题：①m ∥n ，m n αα⊥⇒⊥；②α∥β，m α，n β⇒m ∥n ；③m ∥n ，m ∥αn ⇒∥α；④α∥β，m ∥n ，m α⊥n β⇒⊥；其中正确的序号是（）A. ①④B. ②③C. ①②④D. ①③④17. 如图所示，三棱柱111ABC A B C -的侧面11ABB A 是圆柱的轴截面，C 是圆柱底面圆周上不与A 、B 重合的一个点；（1）若圆柱的轴截面是正方形，当点C 是弧AB 的中点时，求异面直线1A C 与AB 的所成角的大小（结果用反三角函数值表示）；（2）当点C 是弧AB 的中点时，求四棱锥111A BCC B -与圆柱的体积比；上海市浦东新区2017届高三一模数学试卷9. 过双曲线222:14x y C a -=的右焦点F 作一条垂直于x 轴的垂线交双曲线C 的两条渐近线于A 、B 两点，O 为坐标原点，则△OAB 的面积的最小值为10. 若关于x 的不等式1|2|02x x m --<在区间[0,1]内恒成立，则实数m 的范围14. 已知函数()y f x =的反函数为1()y f x -=，则()y f x =-与1()y f x -=-图像（） A. 关于y 轴对称 B. 关于原点对称C. 关于直线0x y +=对称D. 关于直线0x y -=对称15. 设{}n a 是等差数列，下列命题中正确的是（）A. 若120a a +>，则230a a +>B. 若130a a +<，则120a a +<C. 若120a a <<，则2a >D. 若10a <，则2123()()0a a a a --> 18. 已知△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ；（1）若3B π=，b =，△ABC 的面积2S =，求a c +的值；（2）若22cos ()C BA BC AB AC c ⋅+⋅=u u r u u u r u u u r u u u r ，求角C ；上海市闵行区2017届高三一模数学试卷7. 从单词“shadow ”中任意选取4个不同的字母排成一排，则其中含有“a ”的共有种排法（用数字作答）8. 集合{|cos(cos )0,[0,]}x x x ππ=∈= （用列举法表示）9. 如图，已知半径为1的扇形AOB ，60AOB ∠=︒，P为弧»AB 上的一个动点，则OP AB ⋅uu u r uu u r 取值范围是10. 已知x 、y 满足曲线方程2212x y +=，则22x y +的取值范围是17. 如图，在Rt AOB ∆中，6OAB π∠=，斜边4AB =，D 是AB 中点，现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥，点C 为圆锥底面圆周上一点，且90BOC ∠=︒，（1）求圆锥的侧面积；（2）求直线CD 与平面BOC 所成的角的大小；（用反三角函数表示）上海市虹口区2017届高三一模数学试卷8. 若正项等比数列{}n a 满足：354a a +=，则4a 的最大值为9. 一个底面半径为2的圆柱被与其底面所成角是60°的平面所截，截面是一个椭圆，则该椭圆的焦距等于10. 设函数61()211x x f x x x ⎧≥=⎨--≤-⎩，则当1x ≤-时，则[()]f f x 表达式的展开式中含2x 项的系数是13. 在空间，α表示平面，m 、n 表示二条直线，则下列命题中错误的是（）A. 若m ∥α，m 、n 不平行，则n 与α不平行B. 若m ∥α，m 、n 不垂直，则n 与α不垂直C. 若m α⊥，m 、n 不平行，则n 与α不垂直D. 若m α⊥，m 、n 不垂直，则n 与α不平行15. 如图，在圆C 中，点A 、B 在圆上，则AB AC ⋅u u u r u u u r 的值（）A. 只与圆C 的半径有关B. 既与圆C 的半径有关，又与弦AB 的长度有关C. 只与弦AB 的长度有关D. 是与圆C 的半径和弦AB 的长度均无关的定值18. 如图，我海蓝船在D 岛海域例行维权巡航，某时刻航行至A 处，此时测得其北偏东30° 方向与它相距20海里的B 处有一外国船只，且D 岛位于海蓝船正东18海里处；（1）求此时该外国船只与D 岛的距离；（2）观测中发现，此外国船只正以每小时4海里的速度沿正南方航行，为了将该船拦截在离D 岛12海里的E 处（E 在B 的正南方向），不让其进入D 岛12海里内的海域，试确定海蓝船的航向，并求其速度的最小值（角度精确到0.1°，速度精确到0.1海里/小时）；7. 根据相关规定，机动车驾驶人血液中的酒精含量大于（等于）20毫克/100毫克的行为属于饮酒驾驶，假设饮酒后，血液中的酒精含量为0p 毫克/100毫克，经过x 个小时，酒精含量降为p 毫克/100毫克，且满足关系式0rx p p e =⋅（r 为常数）若某人饮酒后血液中的酒精含量为89毫克/100毫克，2小时后，测得其血液中酒精含量降为61毫克/100毫克，则此人饮酒后需经过小时方可驾车8. 已知奇函数()f x 是定义在R 上的增函数，数列{}n x 是一个公差为2的等差数列，满足 78()()0f x f x +=，则2017x 的值为9. 直角三角形ABC 中，3AB =，4AC =，5BC =，点M 是三角形ABC 外接圆上任意一点，则AB AM ⋅u u u r u u u u r 的最大值为13. 某班班会准备从含甲、乙的6名学生中选取4人发言，要求甲、乙两人至少有一人参加，那么不同的发言顺序有（）A. 336种B. 320种C. 192种D. 144种17. 设双曲线22:123x y C -=，1F 、2F 为其左右两个焦点；（1）设O 为坐标原点，M 为双曲线C 右支上任意一点，求1OM F M ⋅uuu r uuu u r 的取值范围；（2）若动点P 与双曲线C 的两个焦点1F 、2F 的距离之和为定值，且12cos F PF ∠的最小值为19-，求动点P 的轨迹方程；7. 如果实数x 、y 满足2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2x y +的最大值是8. 从5名学生中任选3人分别担任语文、数学、英语课代表，其中学生甲不能担任数学课代表，共有种不同的选法（结果用数值表示）9. 方程22242340x y tx ty t +--+-=（t 为参数）所表示的圆的圆心轨迹方程是（结果化为普通方程）10. 若n a 是(2)n x +（*n N ∈，2n ≥，x R ∈）展开式中2x 项的二项式系数，则23111lim()n na a a →∞++⋅⋅⋅+=15. 某几何体的三视图如图所示，则它的体积是（）A. 283π-B. 83π- C. 82π- D. 23π17. 如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PA ⊥平面ABCD ，PB 、PD 与平面ABCD 所成的角依次是4π和1arctan 2，2AP =，E 、F 依次是PB 、PC 的中点；（1）求异面直线EC 与PD 所成角的大小；（结果用反三角函数值表示）（2）求三棱锥P AFD -的体积；。

上海市浦东新区2017届高三12月教学质量检测(一模)数学

高三数学试卷一、填空题（本大题共有12题，满分54分）只要求直接填写结果，1-6题每个空格填对得4分，7-12题每个空格填对得5分，否则一律得零分．1.已知U R =，集合{}|421A x x x =-≥+，则U C A =____________．2.三阶行列式351236724---中元素-5的代数余子式的值为____________． 3. 812x ⎛⎫- ⎪⎝⎭的二项展开式中含2x 项的系数是____________．4.已知一个球的表面积为16π，则它的体积为____________．5．一个袋子中共有6个球，其中4个红色球，2个蓝色球．这些球的质地和形状一样，从中任意抽取2个球，则所抽的球都是红色球的概率是____________．6．已知直线:0l x y b -+=被圆22:25C x y +=所截得的弦长为6，则b =____________． 7．若复数()()12ai i +-在复平面上所对应的点在直线y x =上，则实数a =____________． 8．函数())cos sin f x x xx x =+-的最小正周期为____________．9．过双曲线222:14x y C a -=的右焦点F 作一条垂直于x 轴的垂线交双曲线C 的两条渐近线于两点A B 、，O 为坐标原点，则OAB ∆的面积的最小值为____________． 10．若关于x 的不等式1202xxm --<在区间[]0,1内恒成立，则实数m 的取值范围为____________．11．如图，在正方形ABCD 中，2,,AB M N =分别是边,BC CD 上的两个动点，且MN =则AM AN 的取值范围是____________．12．已知定义在*N 上的单调递增函数()y f x =，对于任意的*n N ∈，都有()*f n N ∈，且()()3f f n n =恒成立，则()()20171999f f -=____________．二、选择题（本大题共有4题，满分20分）每小题都给出四个选项中，其中有且只有一个选项是正确的，选对得5分，否则一律得零分．13.将cos 2y x =图像向左平移6π个单位，所得的函数为（）． A ．cos 23y x π⎛⎫=+⎪⎝⎭B ．cos 26y x π⎛⎫=+⎪⎝⎭C ．cos 23y x π⎛⎫=-⎪⎝⎭D ．cos 26y x π⎛⎫=-⎪⎝⎭14.已知函数()y f x =的反函数为()1y f x -=，则函数()y f x =-与()1y f x -=-的图像（）．A ．关于y 轴对称B ．关于原点对称C ．关于直线0x y +=对称D ．关于直线0x y -=对称 15.设{}n a 是等差数列，下列命题中正确的是（）．A ．若120a a +>，则230a a +>B ．若130a a +<，则120a a +<C ．若120a a <<，则2a >．若10a <，则()()21230a a a a -->16.元旦将近，调查鲜花市场价格得知：购买2只玫瑰与1只康乃馨所需费用之和大于8元，而购买4只玫瑰与5只康乃馨所需费用额小于22元；设购买2只玫瑰花所需费用为A 元，购买3只康乃馨所需费用为B 元，则A B 、的大小关系是（）．A ．AB > B ． A B <C ．A B =D ．A B 、的大小关系不确定三、解答题（本大题共5小题，共76分.解答应写出文字说明、证明过程或演算步骤.） 17.（本小题满分14分，第1小题满分6分，第2小题满分8分）在长方体1111ABCD A BC D -中（如图）, 11,2AD AA AB ===，点E 是棱AB 的中点. （1）求异面直线1AD 与EC 所成角的大小；（2）《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑.试问四面体1DCDE 是否为鳖臑？并说明理由.18.（本小题满分14分，第1小题满分7分，第2小题满分7分）已知ABC ∆的内角,,A B C 的对边分别为,,a b c .（1）若,3B b ABC π==∆的面积2S =，求a c +值；（2）若()22cos C BA BC AB AC c +=，求角C .19.（本小题满分14分，第1小题满分6分，第2 小题满分8分）已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为12F F 、，过2F 的一条直线交椭圆于P Q 、两点，若12PF F ∆的周长为4+.（1）求椭圆C 的方程；（2）若12F P F Q PQ +=，求直线PQ 的方程.20.（本小题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分）设数列{}n a 满足221241,2n n n n a a n n b a n n +=+-+=+-；（1）若12a =，求证：数列{}n b 为等比数列；（2）在（1）的条件下，对于正整数()22q r q r <<、、，若25q r b b b 、、这三项经适当排序后能构成等差数列，求符合条件的数组(),q r ；（3）若11,c ,n n n n a b n d M ==+=是n d 的前n 项和，求不超过2016M 的最大整数.21.（本小题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分）已知定义在R 上的函数()x ϕ的图像是一条连续不断的曲线，且在任意区间上()x ϕ都不是常值函数.设011i i n a t t t t t b -=<<<<<<=，其中分点121n t t t -、、、将区间[],a b 任意划分成()*n n N ∈个小区间[]1,i i t t -，记{}()()()()()()01121,,n n M a b n t t t t t t ϕϕϕϕϕϕ-=-+-++-，称为()x ϕ关于区间[],a b 的n 阶划分“落差总和”.当{},,M a b n 取得最大值且n 取得最小值0n 时，称()x ϕ存在“最佳划分”{}0,,M a b n . （1）已知()x x ϕ=，求{}1,2,2M -的最大值0M ；（2）已知()()a b ϕϕ<，求证：()x ϕ在[],a b 上存在“最佳划分”{},,1M a b 的充要条件是()x ϕ在[],a b 上单调递增.（3）若()x ϕ是偶函数且存在“最佳划分”{}0,,M a a n -，求证：0n 是偶数，且00110i i n t t t t t -+++++=.参考答案一、填空题1. ()1+∞，2. 343. 74.323π 5. 25 6. ± 7. 3 8. π 9. 8 10.32⎛⎫⎪⎝⎭，211. 4⎡⎣12. 54 二、选择题13. A 14. D 15. C 16. A 三、解答题17.解：（1）作//AE CE '交CD 于E '，因为11AD AA DE '===，所以1AE D E ''==1AD E '∆为正三角形，异面直线1AD 与EC 所成角为60°……………………………6分（2）E 是棱AB 上的中点，则ADE CBE ∆∆、均为等腰直角三角形，而显然11DD E DDC ∆∆、均为直角三角形，故四面体1DCDE 四个面均为直角三角形，．．．．．．． 14分 18．解：（1）∵1,sin 322ABC B S ac B π∆===，∴6ac =……………………………2分由余弦定理得2222cos a c b ac B +-=……………………………………4分 ∴()225,5a c a c +=+=……………………………………….7分（2）∵()()22c o s c o s B b c c o s A 2c o s c o s c o s C a c C aB b A c +=⇒+= (10)分又∵cos cos a B b A c +=……………………………12分 ∴12cos 1,cos 2C C ==， ∵()0,C π∈，∴3C π=……………………………………14分19.解：（1）由条件可知：224a c +=+，:a b =，∵222a b c =+，解得：2,2a b c ===，……………………………4分所以椭圆C 的方程为22184x y +=…………………………6分（2）设直线2PF 的方程为：()()11222,,,,x ty P x y Q x y =+；因为1212F P F Q FO OP F O OQ OP OQ +=+++=+，所以OP OQ PQ +=，所以OP OQ ⊥，所以12120x x y y +=…………………………9分()222212440842x y t y ty x ty ⎧+=⎪⇒++-=⎨⎪=+⎩， 12122244,22t y y y y t t --+==++……………………………11分 ()()2412121212121x x y y t y y t y y ++=+++解得：21,22t t ==±………………………………………13分所以直线PQ0y ±-=…………………………………14分20.解：（1）由21241n n a a n n +=+-+，∴()()()22112122n n a n n a n n +++-+=+-，即12n n b b +=，又11110b a =-=≠，∴数列{}n b 是以1 为首项，2为公比的等比数列；………………4分（2）由（1）知()1*22,5,,n n q r b n N b b b -=∈这三项经适当排序后能构成等差数列； ①若225q r b b b ⨯=+，则211110222q r ---⨯=+，∴122225q r +---=，左边为偶数，右边为奇数，∴等式不成立；…………………………………8分 ③若225r q b b b =+，同理也不成立；综合①②③得，()(),3,5q r =；…………………………………10分（3）由211111210a b =⇒=+-⨯=，∴0n b =，…………………………………12分 ∴0n c n n =+=；………………………………13分由()()()()2222222222211111111111n n n n n n n d c c n n n n +++++=++=++=++ ()()()()2222211111111111n n n n n d n n n n n n n n ++++⎛⎫=⇒==+=+- ⎪+++⎝⎭+；∴2016122016111111223M d d d ⎡⎤⎡⎤⎛⎫⎛⎫=+++=+-++-+⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦111112016120172016201720172017⎡⎤⎛⎫++-=+-=- ⎪⎢⎥⎝⎭⎣⎦. ∴不超过2016M 的最大整数为2016…………………………………16分21.解：（1）()()()()010023M ϕϕϕϕ=--+-=………………………4分（2）若()x ϕ在[],a b 上单调递增，则{}()()()(){}11,,,,1ni i i M a b n t t b a M a b ϕϕϕϕ-==-=-=⎡⎤⎣⎦∑，故()x ϕ在[],a b 上存在“最佳划分”{},,1M a b …………………………6分若()x ϕ在[],a b 上存在“最佳划分”{},,1M a b ，倘若()x ϕ在[],a b 上不单调递增，则存在[]()()121212,,,,x x a b x x x x ϕϕ∈<>.由()()()()()()()()1122a b a x x x x b ϕϕϕϕϕϕϕϕ-≤-+-+-…………………………（*）等号当且仅当()()()()()()11220,0,0a x x x x b ϕϕϕϕϕϕ-≥->-≥时取得，此时()()()()()()()()()()11220a b a x x x x b a b ϕϕϕϕϕϕϕϕϕϕ-=-+-+-=-<，与题设矛盾，舍去，故（*）式中等号不成立，即：增加分点12,x x 后，“落差总和”会增加，故{},,M a b n 取最大值时n 的最小值大于1，与条件矛盾.所以()x ϕ在[],a b 上单调递增……………………………………………10分（3）由（2）的证明过程可知，在任间区间[],a b 上，若()x ϕ存在最佳划分{},,1a b ，则当()()a b ϕϕ=时，()x ϕ为常值函数（舍）；当()()a b ϕϕ<时，()x ϕ单调递增；当()()a b ϕϕ>时，()x ϕ单调递减…………………………………12分若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则此时在每个小区间[]()10,1,2,,i i t t i n -=上均为最佳划分{}1,,1i i M t t -.否则，添加分点后可使()x ϕ在[],a b 上的“落差总和”增大，从而{}0,,M a b n 不是“落差总和”的最大值，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾，故()x ϕ在每个小区间[]()10,1,2,,n i i t t i -=上都是单调 (14)分若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则()x ϕ在相邻的两个区间[][]11,,i i i i t t t t -+、上具有不同的单调性，否则，()()()()()()11111i i i i i t t t t t t ϕϕϕϕϕϕ-+-+-=-+-，减少分点i t ，“落差总和”的值不变，而n 的值减少1，故n 的最小值不是0n ，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾………………………16分()x ϕ存在“最佳划分”{}0,,M a a n -，故()x ϕ在每个小区间[]()10,1,2,,n i i t t i -=上都单调，而()x ϕ是偶函数，故()x ϕ在y 轴两侧的单调区间对称，共有偶数个单调区间，且当000,1,,2n i j n i ⎛⎫+== ⎪⎝⎭时，0i j t t +=，从而有00120n t t t t ++++=……………………………18分。

2017年上海杨浦区高考一模数学

2017年上海市杨浦区高考一模数学一、填空题(本大题满分54分)共12小题，1-6题每题4分，7-12题每题5分1.若“a＞b”，则“a 3＞b 3”是____命题(填：真、假)解析：函数f(x)=x 3在R 是单调增函数，∴当a ＞b ，一定有a 3＞b 3，故是真命题. 答案：真.2.已知A=(﹣∞，0]，B=(a ，+∞)，若A ∪B=R ，则a 的取值范围是____. 解析：若A ∪B=R ，A=(﹣∞，0]，B=(a ，+∞)，必有a ≤0. 答案：a ≤0.3.z+2z =9+4i(i 为虚数单位)，则|z|=____.解析：设z=x+yi(x ，y ∈R)，∵z+2z =9+4i ，∴x+yi+2(x ﹣yi)=9+4i ，化为：3x ﹣yi=9+4i ， ∴3x=9，﹣y=4，解得x=3，y=﹣4. ∴223(4)5z =+-=.答案：5.4.若△ABC 中，a+b=4，∠C=30°，则△ABC 面积的最大值是____. 解析：在△ABC 中，∵C=30°，a+b=4， ∴△ABC 的面积211111sin sin 30412244)4(2S ab C ab b ab a =⋅=⋅︒==+≤⨯⨯=，当且仅当a=b=2时取等号.答案：1.5.若函数()2g 1lo x f x ax -+=的反函数的图象经过点(﹣2，3)，则a=____. 解析：∵函数()2g 1lo x f x ax -+=的反函数的图象经过点(﹣2，3)，∴函数()2g 1lo x f x ax -+=的图象经过点(3，﹣2)，∴232log 31a-=-+，∴a=2. 答案：2.6.过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60°，则该截面的面积是____.解析：设截面的圆心为Q ，由题意得：∠OAQ=60°，QA=1，∴S=π·12=π. 答案：π.7.抛掷一枚均匀的骰子(刻有1，2，3，4，5，6)三次，得到的数字依次记作a ，b ，c ，则a+bi(i 为虚数单位)是方程x 2﹣2x+c=0的根的概率是____.解析：抛掷一枚均匀的骰子(刻有1，2，3，4，5，6)三次，得到的数字依次记作a ，b ，c ，基本事件总数n=6×6×6=216，∵a+bi(i 为虚数单位)是方程x 2﹣2x+c=0的根，∴(a+bi)2﹣2(a+bi)+c=0，即222022a b c a ab b⎧-+-=⎨=⎩，∴a=1，c=b 2+1， ∴a+bi(i 为虚数单位)是方程x 2﹣2x+c=0的根包含的基本事件为： (1，1，2)，(1，2，5)，∴a+bi(i 为虚数单位)是方程x 2﹣2x+c=0的根的概率是21216108p ==. 答案：1108.8.设常数a ＞0，9(x 展开式中x 6的系数为4，则()2lim n n a a a →∞++⋯+=____.解析：∵常数a ＞0，9(x +展开式中x 6的系数为4， ∴183922199r r r rrrr r T C x a xa C x---+==，当18362r-=时，r=2， ∴2294a C =，解得13a =，∴2211(1)1111133(1)13332313n n n na a a -+++==⋯-+-++= ， ∴()2111lim lim[(1)]232nn n n a a a →∞→∞++-==⋯+. 答案：12.9.已知直线l 经过点(且方向向量为(2，﹣1)，则原点O 到直线l 的距离为____. 解析：直线的方向向量为(2，﹣1)，所以直线的斜率为：﹣12，直线方程为：， 1=；答案：1.10.若双曲线的一条渐近线为x+2y=0，且双曲线与抛物线y=x 2的准线仅有一个公共点，则此双曲线的标准方程为____. 解析：抛物线y=x 2的准线：14y =-，双曲线与抛物线y=x 2的准线仅有一个公共点，可得双曲线实半轴长为14a =，焦点在y 轴上. 双曲线的一条渐近线为x+2y=0，∴12a b =，可得12b =，则此双曲线的标准方程为：22111164y x -=. 答案：22111164y x -=.11.平面直角坐标系中，给出点A(1，0)，B(4，0)，若直线x+my ﹣1=0存在点P ，使得|PA|=2|PB|，则实数m 的取值范围是____. 解析：设P(1﹣my ，y)， ∵|PA|=2|PB|，∴|PA|2=4|PB|2，∴(1﹣my ﹣1)2+y 2=4(1﹣my ﹣4)2+y 2，化简得(m 2+1)y 2+8my+12=0则△=64m 2﹣48m 2﹣48≥0，解得mm即实数m 的取值范围是mm答案：mm12.函数y=f(x)是最小正周期为4的偶函数，且在x ∈[﹣2，0]时，f(x)=2x+1，若存在x 1，x 2，…x n 满足0≤x 1＜x 2＜…＜x n ，且|f(x 1)﹣f(x 2)|+|f(x 2)﹣f(x 1)|+…+|f(x n ﹣1﹣f(x n ))|=2016，则n+x n 的最小值为____.解析：∵函数y=f(x)是最小正周期为4的偶函数，且在x ∈[﹣2，0]时，f(x)=2x+1， ∴函数的值域为[﹣3，1]，对任意x i ，x j (i ，j=1，2，3，…，m)，都有|f(x i )﹣f(x j )|≤f(x)max ﹣f(x)min =4，要使n+x n 取得最小值，尽可能多让x i (i=1，2，3，…，m)取得最高点，且f(0)=1，f(2)=﹣3，∵0≤x 1＜x 2＜…＜x m ，|f(x 1)﹣f(x 2)|+|f(x 2)﹣f(x 3)|+…+|f(x n ﹣1)﹣f(x n )|=2016， ∴n 的最小值为201615054+=，相应的x n 最小值为1008，则n+x n 的最小值为1513. 答案：1513.二、选择题(本大题共4题，满分20分) 13.若a 与b c - 都是非零向量，则“a b a c ⋅=⋅ ”是“()a b c ⊥-”的()A.充分但非必要条件B.必要但非充分条件C.充要条件D.既非充分也非必要条件解析：“a b a c ⋅=⋅ ”⇔“0a b a c ⋅-⋅= ”⇔“()0a b c ⋅-= ”⇔“()a b c ⊥-”，故“a b a c ⋅=⋅ ”是“()a b c ⊥-”的充要条件.答案：C14.行列式147258369中，元素7的代数余子式的值为() A.﹣15 B.﹣3 C.3 D.12解析：∵行列式147258369， ∴元素7的代数余子式为： D 13=(﹣1)42536=2×6﹣5×3=﹣3.答案：B.15.一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，另两名员工数据不清楚，那么8位员工月工资的中位数不可能是() A.5800 B.6000 C.6200 D.6400解析：∵一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，∴当另外两名员工的工资都小于5300时，中位数为5300550054002+=，当另外两名员工的工资都大于6500时，中位数为6100650063002+=， ∴8位员工月工资的中位数的取值区间为[5400，6300]， ∴8位员工月工资的中位数不可能是6400. 答案：D. 16.若直线1x ya b+=通过点P(cos θ，sin θ)，则下列不等式正确的是() A.a 2+b 2≤1 B.a 2+b 2≥1C.22111a b +≤ D.22111a b+≥ 解析：直线1x ya b+=通过点P(cos θ，sin θ)，∴bcos θ+asin θ=ab ，)ab θφ+=，其中tan b aφ=，ab ≥， ∴a +b ≥a b ，∴22111a b+≥，答案：D三、解答题(满分76分)共5题17.某柱体实心铜制零件的截面边长是长度为55毫米线段AB 和88毫米的线段AC 以及圆心为P ，半径为PB 的一段圆弧BC 构成，其中∠BAC=60°. (1)求半径PB 的长度；(2)现知该零件的厚度为3毫米，试求该零件的重量(每1个立方厘米铜重8.9克，按四舍五入精确到0.1克).V 柱=S 底·h.解析：(1)在△ABP 中，由余弦定理建立方程，即可求半径PB 的长度； (2)求出V 柱=S 底·h ，即可求该零件的重量.答案：(1)∵AB=55，AC=88，BP=R ，∠BAC=60°.AP=88﹣R ，∴在△ABP 中，由余弦定理可得：BP 2=AB 2+AP 2﹣2AB ·AP ·cos ∠BAC ，可得：R 2=552+(88﹣R)2﹣2×55×(88﹣R)×cos60°， ∴解得：R=49mm.(2)在△ABP 中，AP=88﹣49=39mm ，AB=55，BP=49，222394955897cos 0.2347239493822BPA +-∠==≈⨯⨯，∴sin ∠BPA ≈0.972.∴∠BPA=arcsin0.972.V 柱=S 底·h=(S △ABP +S 扇形BPC ) ·h=21(arcsin 0.972)49(5539)322360π⋅⨯⨯⨯+⋅该零件的重量=213(arcsin 0.972)49(5539)32360π⋅⨯⨯⨯+⋅÷1000×8.9≈82.7.18.如图所示，l 1，l 2是互相垂直的异面直线，MN 是它们的公垂线段，点A ，B 在直线l 1上，且位于M 点的两侧，C 在l 2上，AM=BM=NM=CN (1)求证：异面直线AC 与BN 垂直；(2)若四面体ABCN 的体积V ABCN =9，求异面直线l 1，l 2之间的距离.解析：(1)欲证AC ⊥NB ，可先证BN ⊥面ACN ，根据线面垂直的判定定理只需证AN ⊥BN ，CN ⊥BN 即可；(2)判断异面直线的距离，利用体积公式求解即可.答案：(1)证明：由已知l 2⊥MN ，l 2⊥l 1，MN ∩l 1=M ，可得l 2⊥平面ABN.由已知MN ⊥l 1，AM=MB=MN ，可知AN=NB 且AN ⊥NB.又AN 为AC 在平面ABN 内的射影. ∴AC ⊥NB(2)∵AM=BM=NM=CN ，MN 是它们的公垂线段，就是异面直线l 1，l 2之间的距离，由中垂线的性质可得AN=BN ，四面体ABCN 的体积V ABCN =9，可得：31119323ABCN V AB MN CN MN ==⨯⨯⨯=， ∴MN=3.异面直线l 1，l 2之间的距离为3.19.如图所示，椭圆C ：2241x y +=，左右焦点分别记作F 1，F 2，过F 1，F 2分别作直线l 1，l 2交椭圆AB ，CD ，且l 1∥l 2.(1)当直线l 1的斜率k 1与直线BC 的斜率k 2都存在时，求证：k 1·k 2为定值； (2)求四边形ABCD 面积的最大值.解析：(1)由椭圆方程求出焦点坐标，得到直线AB 、CD 的方程，与椭圆方程联立求得A 、D 的坐标，求出AD 所在直线斜率得答案；(2)由(1)结合弦长公式求得|AB|，再由两平行线间的距离公式求出边AB 、CD 的距离，代入平行四边形面积公式，利用换元法求得最值.答案：(1)证明：由椭圆C ：2241x y +=，得a 2=4，b 2=1，∴c =设k 1=k ，则AB 所在直线方程为，CD 所在直线方程为y=kx，联立2241y kx y x ⎧=+⎪⎨+=⎪⎩，得(1+4k 2)x 22x+12k 2﹣4=0.解得2214x k -±=+不妨取221＝B x --，则2214＝B y k -+ 同理求得2214C x k -=+2214＝C y k-+.则214k k ==-，则12·()44k k k k =⋅-=-；(2)解：由(1)知，＝A B x x +，2212414＝A B k x x k -+()224114k AB k +===+. AB 、CD的距离d =，(224114四边形＝ABCD k S k +=+令1+4k 2=t(t ≥1)，则2311118316816＝S t t ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝+⎭-+，∴当t=3时，S max =4.20.数列{a n }，定义{△a n }为数列{a n }的一阶差分数列，其中△a n =a n+1﹣a n (n ∈N *)(1)若a n =n 2﹣n ，试判断{△a n }是否是等差数列，并说明理由；(2)若a 1=1，△a n ﹣a n =2n，求数列{a n }的通项公式；(3)对(b)中的数列{a n }，是否存在等差数列{b n }，使得1212nn n n n n bC b C b C a ++⋯+=，对一切n ∈N *都成立，若存在，求出数列{b n }的通项公式，若不存在，请说明理由.解析：(1)根据数列{a n }的通项公式a n =n 2﹣n ，结合新定义，可判定{△a n }是首项为4，公差为2的等差数列；(2)由△a n ﹣a n =2n入手能够求出数列{a n }的通项公式；(3)结合组合数的性质：1C n 1+2C n 2+3C n 3+…+nC n n =n(C n ﹣10+C n ﹣11+C n ﹣12+…+C n ﹣1n ﹣1)=n·2n ﹣1进行求解.答案：(1)若a n =n 2﹣n ，试判断{△a n }是等差数列，理由如下：∵a n =n 2﹣n ，∴△a n =a n+1﹣a n =(n+1)2﹣(n+1)﹣(n 2﹣n)=2n ， ∵△a n+1﹣△a n =2，且△a 1=4，∴{△a n }是首项为4，公差为2的等差数列；(2)∵△a n ﹣a n =2n.△a n =a n+1﹣a n ，∴a n+1﹣2a n =2n，∴111222n n n n a a ++-=， ∴数列2n na ⎧⎫⎨⎬⎩⎭构成以12为首项，12为公差的等差数列，即1222﹣n n n n a n a n =⇒=⋅； (3)b 1C n 1+b 2C n 2+…+b n C n n=a n ，即b 1C n 1+b 2C n 2+…+b n C n n=n·2n ﹣1， ∵1C n 1+2C n 2+3C n 3+…+nC n n =n(C n ﹣10+C n ﹣11+C n ﹣12+…+C n ﹣1n ﹣1)=n ·2n ﹣1，∴存在等差数列{b n }，b n =n ，使得b 1C n 1+b 2C n 2+…+b n C n n=a n 对一切自然n ∈N 都成立.21.对于函数f(x)(x ∈D)，若存在正常数T ，使得对任意的x ∈D ，都有f(x+T)≥f(x)成立，我们称函数f(x)为“T 同比不减函数”.(1)求证：对任意正常数T ，f(x)=x 2都不是“T 同比不减函数”； (2)若函数f(x)=kx+sinx 是“2π同比不减函数”，求k 的取值范围； (3)是否存在正常数T ，使得函数f(x)=x+|x ﹣1|﹣|x+1|为“T 同比不减函数”；若存在，求T 的取值范围；若不存在，请说明理由.解析：(1)根据T 同比不减函数的定义即可证明，(2)根据T 同比不减函数的定义，分离参数得到)4﹣k x ππ≥，根据三角形函数的性质即可求出k 的范围，(3)画出函数f(x)的图象，根据图象的平移即可求出T 的范围.答案：(1)∵f(x)=x 2，∴f(x+T)﹣f(x)=(x+T)2﹣x 2=2xT+T 2=T(2x+T)，由于2x+T 与0的小无法比较， ∴f(x+T)≥f(x)不一定成立，∴对任意正常数T ，f(x)=x 2都不是“T 同比不减函数，(2)∵函数f(x)=kx+sinx 是“2π同比不减函数， ∴sin sin 222（）（）（）（）f x f x k x x kx x πππ+-=+++--=cos sin 0224（）k k x x x πππ+-=-≥恒成立，∴4（）k x ππ≥-， ∵﹣1≤sin(x ﹣4π)≤1，∴k ≥(3)f(x)=x+|x ﹣1|﹣|x+1|图象如图所示，由图象可知，只要把图象向左至少平移4个单位，即对任意的x ∈D ，都有f(x+T)≥f(x)成立， ∴T ≥4.。

上海市杨浦区高考数学一模试卷解析版

高考数学一模试卷一、选择题（本大题共4小题，共12.0分）1.已知a，b为非零实数，且a＞b，则下列不等式成立的是（）A. a2＞b2B.C. |a|＞|b|D. 2a＞2b2.要得到函数y=2sin（2x+）的图象，只要将y=2sin2x的图象（）A. 向左平移个单位B. 向右平移个单位C. 向左平移个单位D. 向右平移个单位3.设z1，z2为复数，则下列命题中一定成立的是（）A. 如果z1-z2＞0，那么z1＞z2B. 如果|z1|=|z2|，那么z1=±z2C. 如果，那么|z1|＞|z2|D. 如果z12+z22=0，那么z1=z2=04.对于全集R的子集A，定义函数为A的特征函数．设A，B为全集R的子集，下列结论中错误的是（）A. 若A⊆B，f A（x）≤f B（x）B. f（x）=1-f A（x）C. f A∩B（x）=f A（x）•f B（x）D. f A∪B（x）=f A（x）+f B（x）二、填空题（本大题共12小题，共36.0分）5.函数y=x，的定义域为______ ．6.关于x，y的方程组的增广矩阵为______．7.己知函数f（x）的反函数f-1（x）=log2x，则f（-1）=______．8.设a∈R，a2-a-2+（a+1）i为纯虚数（i为虚数单位），则a=______．9.己知圆锥的底面半径为lcm，侧面积为2πcm2，则母线与底面所成角的大小为______．10.己知（ax+1）7的二项展开式中x3的系数为280，则实数a=______．11.椭圆的焦点为F1，F2，P为椭圆上一点，若|PF1|=5，则cos∠F1PF2=______．12.己知数列{a n}的通项公式为，S n是数列{a n}的前n项和，则S n=______．13.在直角坐标平面xOy中，A（-2，0），B（0，1），动点P在圆C：x2+y2=2上，则的取值范围为______．14.己知六个函数：①；②y=cos x；③；④y=arcsin x；⑤；⑥y=x+1，从中任选三个函数，则其中既有奇函数又有偶函数的选法共有______种15.己知函数，若关于x的方程[f（x）]2+mf（x）+2m+3=0有三个不相等的实数解，则实数m的取值范围为______．16.向量集合，对于任意，∈S，以及任意λ∈（0，1），都有λ+（1-λ）∈S，则称S为“C类集”，现有四个命题：①若S为“C类集”，则集合也是“C类集”；②若S，T都是“C类集”，则集合也是“C类集”；③若A1，A2都是“C类集”，则A1∪A2也是“C类集”；④若A1，A2都是“C类集”，且交集非空，则A1∩A2也是“C类集”．其中正确的命题有______（填所有正确命题的序号）．三、解答题（本大题共5小题，共60.0分）17.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，AB=PA=1，，E，F分别为棱PD，PA的中点．（1）求证：B、C、E、F四点共面；（2）求异面直线PB与AE所成的角．18.己知函数f（x）=2x+，其中a为实常数．（1）若f（0）=7，解关于x的方程f（x）=5；（2）判断函数f（x）的奇偶性，并说明理由．19.东西向的铁路上有两个道口A、B，铁路两侧的公路分布如图，C位于A的南偏西15°，且位于B的南偏东15°方向，D位于A的正北方向，AC=AD=2km，C处一辆救护车欲通过道口前往D处的医院送病人，发现北偏东45°方向的E处（火车头位置）有一列火车自东向西驶来，若火车通过每个道口都需要1分钟，救护车和火车的速度均为60km/h．（1）判断救护车通过道口A是否会受火车影响，并说明理由；（2）为了尽快将病人送到医院，救护车应选择A、B中的哪个道口？通过计算说明．20.如图，在平面直角坐标系xOy中，已知抛物线C：y2=4x的焦点为F，点A是第一象限内抛物线C上的一点，点D的坐标为（t，0）（t＞0）．（1）若，求点A的坐标；（2）若△AFD为等腰直角三角形，且∠FAD=90°，求点D的坐标；（3）弦AB经过点D，过弦AB上一点P作直线x=-t的垂线，垂足为点Q，求证：“直线QA与抛物线相切”的一个充要条件是“P为弦AB的中点”．21.己知无穷数列{a n}的前n项和为S n，若对于任意的正整数n，均有S2n-1≥0，S2n≤0，则称数列{a n}具有性质P．（1）判断首项为1，公比为-2的无穷等比数列{a n}是否具有性质P，并说明理由；（2）己知无穷数列{a n}具有性质P，且任意相邻四项之和都相等，求证：S4=0；（3）己知b n=2n-1（n∈N*），数列{c n}是等差数列，a n=，若无穷数列{a n}具有性质P，求c2019的取值范围．答案和解析1.【答案】D【解析】解：A选项不正确，当a=1，b=-2时，不等式就不成立；B选项不正确，因为a=1，b=-2时，不等式就不成立；C选项不正确，因为a=1，b=-2时，不等式就不成立；D选项正确，因为y=2x是一个增函数，故当a＞b时一定有2a＞2b，故选D．由不等式的相关性质，对四个选项逐一判断，由于a，b为非零实数，故可利用特例进行讨论得出正确选项本题考查不等关系与不等式，解题的关键是熟练掌握不等式的有关性质，且能根据这些性质灵活选用方法进行判断，如本题采用特值法排除三个选项，用单调性判断正确选项．2.【答案】A【解析】解：将y=2sin2x的图象向左平移个单位，可得函数y=2sin（2x+）的图象，故选：A．由题意利用函数y=A sin（ωx+φ）的图象变换规律，得出结论．本题主要考查函数y=A sin（ωx+φ）的图象变换规律，属于基础题．3.【答案】C【解析】解：对于A，反例z1=3+i，z2=1+i，满足，z1-z2＞0，当时z1＞z2不正确，所以A不正确；对于B，反例z1=1+i，z2=1-i，满足|z1|=|z2|，但是z1=±z2不正确；对于C，，那么|z1|＞|z2|，正确；对于D，反例z1=1+i，z2=1-i，满足z12+z22=0，不满足z1=z2=0，所以D不正确；故选：C．通过反例判断A的正误；复数的模与复数的关系判断B、C的正误；反例判断D的正误即可．本题考查命题的真假的判断，复数的模以及复数的性质的判断，是基本知识的考查，基础题．4.【答案】D【解析】解：A：∵A⊆B，可得x∈A则x∈B，∵，，而C R A中可能有B的元素，但C R B中不可能有A的元素，∴f A（x）≤f B（x），故A正确；B：因为f（x）=，综合f A（x）的表达式，可得f=1-f A（x），故B正确；C：f A∩B（x）====f A（x）•f B （x），故C正确；D：f A∪B（x）=≠f A（x）+f B（x），故D错误；故选：D．根据题中特征函数的定义，利用几何的交集、并集、补集运算法则，对A、B、C、D各项中的运算加以验证，进而求解；考查接受新知识，理解运用新知识的能力，交集、并集、补集运算法则，属于中档题；5.【答案】（0，+∞）【解析】解：∵y=x=，使函数有意义只要满足x＞0即可，故函数y=x的定义域为：（0，+∞）；故答案为：（0，+∞）先将函数解析式化为根式，进而可得要使函数有意义只要满足x＞0即可．本题考查的知识点是幂函数的定义域，熟练掌握幂函数的图象和性质是解答的关键．6.【答案】【解析】解：由增广矩阵的定义可知，关于x，y的方程组的增广矩阵为，故答案为：由增广矩阵的定义可求解；考查增广矩阵的概念，属于基础题；7.【答案】【解析】解：把y=-1代入反函数f-1（x）=log2x=-1，故x=，故答案为：．根据函数与反函数点关于y=x对称，代入求出．题考查了反函数的求法，属于基础题．8.【答案】2【解析】解：∵a2-a-2+（a+1）i为纯虚数，∴，解得a=2．故答案为：2．直接由实部为0且虚部不为0列式求解a值．本题考查复数的基本概念，是基础题．9.【答案】【解析】解：由圆锥侧面积公式S=πrl=π•1•l=2π，解得l=2，设母线与底面所成角为θ，则cosθ==，∴θ=，故答案为：．由圆锥侧面积公式S=πrl=π•1•l=2π，解得l=2，进而可求出母线与底面所成角的余弦值，进而求解；考查圆锥侧面积公式，三角函数的应用，属于基础题；10.【答案】2【解析】解：二项式展开的通项公式得，令r=4，得x3的系数，，a=2，故答案为：2．先求得二项式展开式的通项公式，再令x的幂指数等于3，求得r的值，即可求得含x3项的系数．本题主要考查二项式定理的应用，二项式展开式的通项公式，二项式系数的性质，属基础题．11.【答案】【解析】解：椭圆的焦点为F1，F2，P为椭圆上一点，若|PF1|=5，可得|PF2|=6-5=1，|F2F1|=2c=2，由余弦定理可得：cosθ===．故答案为：．利用椭圆的定义，结合余弦定理转化求解即可．本题考查椭圆的简单性质的应用，是基本知识的考查，中档题．12.【答案】【解析】解：由，知数列{a n}自第三项起是以为首项，以为公比的等比数列，则S n=（a1+a2+a3+…+a n）=a1+a2+（a3+a4+…+a n）=1+2+=．故答案为：．由题意可得数列{a n}自第三项起是以为首项，以为公比的等比数列，再由无穷递缩等比数列的极限求解．本题考查数列极限的求法，熟记无穷递缩等比数列的极限为是关键，是基础题．13.【答案】【解析】解：令（θ∈[0，2π]），且A（-2，0），B（0，1），∴====，其中tanφ=-2，∴的取值范围为．故答案为：．根据题意，可令，从而可求出，，然后进行数量积的坐标运算，并根据两角和的正弦公式得出，从而可得出的取值范围．本题考查了圆的参数方程，利用坐标解决向量问题的方法，根据点的坐标可求向量的坐标，向量数量积的坐标运算，考查了计算能力，属于基础题．14.【答案】12【解析】解：根据题意，六个函数：①，②y=cos x，③，④y=arcsin x，⑤，⑥y=x+1中，奇函数有④y=arcsin x和⑤，共2个，偶函数有：①和②y=cos x，共2个，非奇非偶函数有：④y=arcsin x和⑥y=x+1，共2个，从6个函数中任选3个，若有1个奇函数和2个偶函数，有1×2=2种选法，若有2个奇函数和1个偶函数，有1×2=2种选法，若有1个奇函数、1个偶函数和1个非奇非偶函数，有2×2×2=8种选法，则既有奇函数又有偶函数的选法共有2+2+8=12种；故答案为：12．根据题意，分析6个函数的奇偶性，进而分3种情况讨论选出函数中既有奇函数又有偶函数的选法数目，由加法原理计算可得答案．本题考查排列、组合的应用，涉及函数奇偶性的判定，属于基础题．15.【答案】（-，-]【解析】解：画出函数的图象，如图所示，令y=f（x），则y2+my+2m+3=0有2个不相等的实数解，其范围分别为（0，1）和[1，+∞），则解得＜m≤-故答案为：（-，-]．分析f（x）的图象，可知关于f（x）的二次方程有2根，范围分别为（0，1）和（1，+∞），在按二次方程根的分布处理．考查含有绝对值函数的图象，复合函数根的个数问题的处理，属于拔高题；16.【答案】①②④【解析】解：①若S为“C类集”，则对于任意，∈S，以及任意λ∈（0，1），都有λ+（1-λ）∈S，集合，可得对于任意μ，μ∈M，以及任意λ∈（0，1），都有λμ+（1-λ）μ∈M，故①正确；②若S是“C类集”，则对于任意，∈S，以及任意λ∈（0，1），都有λ+（1-λ）∈S，T是“C类集”，则对于任意，∈T，以及任意λ∈（0，1），都有λ+（1-λ）∈T，可得对于任意+∈M，+∈M，以及任意λ∈（0，1），都有λ（+）+（1-λ）（+）∈M，故②正确；③若A1“C类集”，可得对于任意，∈A1，以及任意λ∈（0，1），都有λ+（1-λ）∈A1，A2是“C类集”，对于任意，∈A2，以及任意λ∈（0，1），都有λ+（1-λ）∈A2，设M=A1∪A2，M为A1，A2中的元素的合并而得，且不重复，不符合“C类集”的定义，故③错误；④若A1“C类集”，可得对于任意，∈A1，以及任意λ∈（0，1），都有λ+（1-λ）∈A1，A2是“C类集”，对于任意，∈A2，以及任意λ∈（0，1），都有λ+（1-λ）∈A2，设M=A1∩A2，M为A1，A2中的元素的公共部分而得，且不为空集，符合“C类集”的定义，故④正确．故答案为：①②④．由新定义“C类集”，结合不等式的性质和集合的运算性质，即可判断结论．本题考查集合的新定义的理解和运用，考查定义法解题，以及推理能力，属于基础题．17.【答案】解：（1）在△PAD中，由E、F为PD，PA中点得，EF为中位线，即EF∥AD，又∵底面为矩形，AD∥BC，∴EF∥BC，∴由平行线确定唯一平面得E、F、B、C在同一平面上．（2）如图，以A为原点，AB为x轴，AD为y轴，AP为z轴建立空间直角坐标系，依题意得：A（0，0，0），B（1，0，0），P（0，0，1），E（0，，），=（1，0，-1），=（0，，），cosθ===，∴异面直线PB与AE夹角为：arccos．【解析】（1）要证B、C、E、F四点共面，只需证明EF∥BC，进而求解；（2）以A为原点，AB为x轴，AD为y轴，AP为z轴建立空间直角坐标系，进而求解；考查空间内的点共面的证明，异面直线夹角的求法，空间直角坐标系的应用，属于中档题；18.【答案】解：（1）由题意f（0）=1+a=7，∴a=6，f（x）=，由=5可得2x=2或2x=3，∴x=1或x=log23，（2）函数定义域R，①当f（x）为奇函数时，f（-x）=-f（x），∴=-（2x+），∴（1+a）（）=0，∴a=-1；②当f（x）为偶函数时，f（-x）=f（x），∴=（2x+），∴（1-a）（）=0，∴a=1；③当a≠±1时，函数f（x）为非奇非偶函数．【解析】（1）由题意f（0）=7，代入即可求解，（2）要判断函数的奇偶性，只有检验f（-x）与f（x）的关系即可．本题主要考查了指数方程的求解及函数的奇偶性的判断，体现了分类讨论思想的应用》19.【答案】解：（1）依据题意：在△ACE中，正弦定理：=，即，解得：AE=，∴救护车到达A处需要时间：==2min，火车到达A处需要时间：=1.41min，火车影响A道口时间为[，]，2∈[，]，∴救护车经过A会受影响．（2）若选择A道口：一共需要花费时间为：t A=+1+×60=（3+）=4.41min若选择B道口：∵BE＞BC，通过B道口不受火车影响；一共花费时间为：t B=，由余弦定理求AB长：AB2=BC2+AC2-2BC•AC cos∠ACB，即AB=-，∴BD==，t B==×60min=4.25min＜t A，∴选择B过道．【解析】（1）利用正弦定理求出AE，进而求出火车到达A处的时间，进而求解；（2）分别求出选择A道口，B道口的时间，进而求解．考查利用三角函数解决实际问题的能力，分类讨论的思想，属于中档题．20.【答案】解：（1）抛物线C：y2=4x的焦点为F，点A是第一象限内抛物线C上的一点，可设A（m，n），即n2=4m，m＞0，n＞0，又，可得m2+n2=5，解得m=1，n=2，即A（1，2）；（2）设A（x，y），由F（1，0），D（t，0），∠FAD=90°⇒•=（1-x，-y）•（t-x，-y）=（1-x）（t-x）+y2=0，①由△AFD为等腰三角形，可得A在x轴上的投影为FD的中点，即有x=，且y2=4x，代入①解得t=5±4，由t＞0，可得D（5+4，0）；（3）先证由“P为弦AB的中点”可得“直线QA与抛物线相切”．设直线AB的方程为x=ay+t，联立抛物线方程y2=4x，可得y2-4ay-4t=0，设A（x1，y1），B（x2，y2），可得y1+y2=4a，AB的中点P（t+2a2，2a），Q（-t，2a），直线QA的斜率为k=，又x1=ay1+t，可得k=，又y2=4x两边对x求导，可得2yy′=4，即y′=，则在A处的切线的斜率为，由-==0，可得QA为抛物线的切线；再证由“直线QA与抛物线相切”可得“P为弦AB的中点”．设Q（-t，s），即P的纵坐标为s，可得切线QA的方程为y-s=（x+t），联立抛物线方程y2=4x可得-y++s=0，由△=1-4••（+s）=0，整理可得y12-2sy1-4t=0，②由y1为y2-4ay-4t=0的根，可得y12-4ay1-4t=0，③由②③为同一方程，可得2s=4a，即s=2a=，可得P为AB的中点，综上可得“直线QA与抛物线相切”的一个充要条件是“P为弦AB的中点”．【解析】（1）设A（m，n），即n2=4m，m＞0，n＞0，再由两点的距离公式，计算可得所求坐标；（2）设A（x，y），由F（1，0），D（t，0），由等腰直角三角形的定义，结合向量垂直的条件和中点坐标公式，解方程可得D的坐标；（3）先证由“P为弦AB的中点”可得“直线QA与抛物线相切”，设出AB的方程，联立抛物线方程，运用韦达定理和中点坐标公式，以及导数求得A处的切线的斜率，作差可得证明；再证由“直线QA与抛物线相切”可得“P为弦AB的中点”．设Q（-t，s），即P的纵坐标为s，可得切线QA的方程为y-s=（x+t），联立抛物线方程，运用直线和抛物线相切的条件可得判别式为0，整理，结合方程重合，即可得证．本题考查抛物线的方程和性质，考查直线方程和抛物线的方程联立，运用韦达定理和中点坐标公式，以及直线和抛物线相切的条件，考查化简运算能力和推理能力，属于难题．21.【答案】解：（1）a n=a1q n-1=（-2）n-1，S2n-1==（1+22n-1）＞0，S2n==（1-22n）＜0，则数列{a n}具有性质P；（2）证明：由题意可得{a n}具有周期性，a n=a n+4，则S4n=nS4，由{a n}具有性质P，可得S4n≤0，S4n+1≥0，运用反证法，若S4＜0，则S4n+1=nS4+a4n+1=nS4+a1，令n=[-]+1，则S4n+1＜0，（当n=-+1时，S4n+1=0，则当n=[-]+1，则S4n+1＜0），与S4n+1≥0矛盾，可得S4≥0，又S4n≤0，具有S4=0成立；（3）由题意b n=2n-1，可设{c n}的前n项和为T n=An2+Bn，{b n}的前n项和为R n=n2，无穷数列{a n}具有性质P，可得S2n-1≥0，S2n≤0，其中S2n-1含有n项奇数项，n-1项偶数项，有S2n-1=（a1+a3+…+a2n-1）+（a2+a4+…+a2n-2）=（b1+b2+…+b n）+（c1+c2+…+c n-1）=n2+A （n-1）2+B（n-1），其中S2n含有n项奇数项，n项偶数项，有S2n=（a1+a3+…+a2n-1）+（a2+a4+…+a2n）=（b1+b2+…+b n）+（c1+c2+…+c n）=n2+An2+Bn，由性质P可得对任意n∈N*成立，则A，B满足，即，可得c2019=T2019-T2018=B-4037∈[-4039，-4037]．【解析】（1）由等比数列的求和公式和不等式的性质，结合性质P，即可判断；（2）由题意可得a n=a n+4，则S4n=nS4，由性质P和反证法，即可得证；（3）可设{c n}的前n项和为T n=An2+Bn，{b n}的前n项和为R n=n2，运用性质P和数列的分组求和，解不等式可得A，B的范围，进而得到所求范围．本题考查等差数列和等比数列的通项公式和求和公式的运用，考查反证法和分类讨论思想的运用，以及化简运算能力和推理能力，属于中档题．。

2017年上海高三数学一模基础题

一. 填空题1. 若“a b >”，则“33a b >”是命题（填：真、假）2. 已知(,0]A =-∞，(,)B a =+∞，若A B R =U ，则a 的取值范围是3. 294z z i +=+（i 为虚数单位），则||z =4. 若△ABC 中，4a b +=，30C ︒∠=，则△ABC 面积的最大值是5. 若函数2()log 1x a f x x -=+的反函数的图像过点(2,3)-，则a = 6. 若半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60︒，则该截面的面积是二. 选择题13. 若a r 与b c -r r 都是非零向量，则“a b a c ⋅=⋅r r r r ”是“()a b c ⊥-r r r ”的（）条件A. 充分不必要B. 必要不充分C. 充分必要D. 既不充分也不必要14. 行列式147258369中，元素7的代数余子式的值为（）A. 15-B. 3-C. 3D. 12一. 填空题 1. 25lim 1n n n →∞-=+ 2. 已知抛物线C 的顶点在平面直角坐标系原点，焦点在x 轴上，若C 经过点(1,3)M ，则其焦点到准线的距离为3. 若线性方程组的增广矩阵为0201a b ⎛⎫⎪⎝⎭，解为21x y =⎧⎨=⎩，则a b +=4. 若复数z 满足：i z i ⋅=（i 是虚数单位），则||z = 5. 在622()x x +的二项展开式中第四项的系数是（结果用数值表示）6. 在长方体1111ABCD A B C D -中，若1AB BC ==，1AA ，则异面直线1BD 与1CC 所成角的大小为二. 选择题13. “4x k ππ=+()k Z ∈”是“tan 1x =”的（）条件A. 充分不必要B. 必要不充分C. 充分必要D. 既不充分也不必要14. 若1（i 是虚数单位）是关于x 的方程20x bx c ++=的一个复数根，则（）A. 2b =，3c =B. 2b =，1c =-C. 2b =-，1c =-D. 2b =-，3c =三. 解答题17. 已知PA ⊥平面ABC ，AC AB ⊥，2AP BC ==，30CBA ︒∠=，D 是AB 的中点；（1）求PD 与平面PAC 所成角的大小；（结果用反三角函数值表示）（2）求△PDB 绕直线PA 旋转一周所构成的旋转体的体积；（结果保留π）上海市长宁、嘉定区2017届高三一模数学试卷一. 填空题1. 设集合{||2|1,}A x x x R =-<∈，集合B Z =，则A B =I2. 函数sin()3y x πω=-（0ω>）的最小正周期是π，则ω=3. 设i 为虚数单位，在复平面上，复数23(2)i -对应的点到原点的距离为 4. 若函数2()log (1)f x x a =++的反函数的图像经过点(4,1)，则实数a =5. 已知(3)n a b +展开式中，各项系数的和与各项二项式系数的和之比为64，则n =6. 甲、乙两人从5门不同的选修课中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有种；7. 若圆锥的侧面展开图是半径为2cm ，圆心角为270°的扇形，则这个圆锥的体积为 3cm二. 选择题13. “2x <”是“24x <”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分也非必要条件14. 若无穷等差数列{}n a 的首项10a <，公差0d >，{}n a 的前n 项和为n S ，则以下结论中一定正确的是（）A. n S 单调递增B. n S 单调递减C. n S 有最小值D. n S 有最大值三. 解答题18. 在ABC ∆中，a 、b 、c 分别是角A 、B 、C 的对边，且28sin2cos 272B C A +-=；（1）求角A 的大小；（2）若a =3b c +=，求b 和c 的值；一. 填空题1. 若集合2{|,}A x y x y R ==∈，{|sin ,}B y y x x R ==∈，则A B =I2. 若22ππα-<<，3sin 5α=，则cot 2α= 3. 函数2()1log f x x =+（1x ≥）的反函数1()f x -=4. 若550125(1)x a a x a x a x +=+++⋅⋅⋅+，则125a a a ++⋅⋅⋅+=5. 设k R ∈，2212y x k k -=-表示焦点在y 轴上的双曲线，则半焦距的取值范围是 6. 设m R ∈，若23()(1)1f x m x mx =+++是偶函数，则()f x 的单调递增区间是7. 方程22log (95)2log (32)x x -=+-的解x = 二. 选择题13. 若0a b <<，则下列不等关系中，不能成立的是（）A. 11a b> B. 11a b a >- C. 1133a b < D. 22a b > 14. 设无穷等比数列{}n a 的首项为1a ，公比为q ，前n 项和为n S ，则“11a q +=”是 “lim 1n n S →∞=”成立的（）条件 A. 充分非必要 B. 必要非充分 C. 充要 D. 既非充分也非必要三. 解答题17. 已知a R ∈，函数1()||f x a x =+；（1）当1a =时，解不等式()2f x x ≤；（2）若关于x 的方程()20f x x -=在区间[2,1]--上有解，求实数a 的取值范围；一. 填空题1. 复数(2)i i +的虚部为2. 设函数2log ,0()4,0x x x f x x >⎧=⎨≤⎩，则((1))f f -= 3. 已知{||1|2,}M x x x R =-≤∈，1{|0,}2x P x x R x -=≥∈+，则M P =I 4. 抛物线2y x =上一点M 到焦点的距离为1，则点M 的纵坐标为5. 已知无穷数列{}n a 满足112n n a a +=*()n N ∈，且21a =，记n S 为数列{}n a 的前n 项和，则lim n n S →∞= 6. 已知,x y R +∈，且21x y +=，则xy 的最大值为7. 已知圆锥的母线10l =，母线与旋转轴的夹角30α︒=，则圆锥的表面积为二. 选择题13. 下列函数在其定义域内既是奇函数又是增函数的是（）A. tan y x =B. 3x y =C. 13y x =D. lg ||y x =14. 设,a b R ∈，则“21a b ab +>⎧⎨>⎩”是“1a >且1b >”的（）条件A. 充分非必要B. 必要非充分C. 充要D. 既非充分也非必要三. 解答题17. 在正三棱柱111ABC A B C -中，1AB =，12BB =，求：（1）异面直线11B C 与1A C 所成角的大小；（2）四棱锥111A B BCC -的体积；一. 填空题 1. 23lim 1n n n →∞+=+ 2. 设全集U R =，集合{1,0,1,2,3}A =-，{|2}B x x =≥，则U A C B =I3. 不等式102x x +<+的解集为 4. 椭圆5cos 4sin x y θθ=⎧⎨=⎩（θ为参数）的焦距为 5. 设复数z 满足23z z i +=-（i 为虚数单位），则z =6. 若函数cos sin sin cos x xy x x =的最小正周期为a π，则实数a 的值为7. 若点(8,4)在函数()1log a f x x =+图像上，则()f x 的反函数为8. 已知向量(1,2)a =r ，(0,3)b =r ，则b r 在a r 的方向上的投影为二. 选择题13. 设a R ∈，则“1a =”是“复数(1)(2)(3)a a a i -+++为纯虚数”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14. 某中学的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生120 人，则该样本中的高二学生人数为（）A. 80B. 96C. 108D. 110三. 解答题18. 已知椭圆C 的长轴长为(2,0)-；（1）求C 的标准方程；（2）设与x 轴不垂直的直线l 过C 的右焦点，并与C 交于A 、B 两点，且||AB =试求直线l 的倾斜角；一. 填空题1. 设集合2{|}M x x x ==，{|lg 0}N x x =≤，则M N =I2. 已知a 、b R ∈，i 是虚数单位，若2a i bi +=-，则2()a bi +=3. 已知函数()1x f x a =-的图像经过(1,1)点，则1(3)f-=4. 不等式|1|0x x ->的解集为5. 已知(sin ,cos )a x x =r ，(sin ,sin )b x x =r ，则函数()f x a b =⋅r r 的最小正周期为6. 里约奥运会游泳小组赛采用抽签方法决定运动员比赛的泳道，在由2名中国运动员和6 名外国运动员组成的小组中，2名中国运动员恰好抽在相邻泳道的概率为二. 选择题13. 已知a 、b R ∈，则“0ab >”是“2b a a b+>”的（） A. 充分非必要条件 B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14. 如图，在棱长为1的正方体1111ABCD A B C D -中，点P 在截面1A DB 上，则线段AP 的最小值为（）A.13 B. 12C. D. 2三. 解答题17. 如图，在正四棱锥P ABCD -中，PA AB a ==，E 是棱PC 的中点；（1）求证：PC BD ⊥；（2）求直线BE 与PA 所成角的余弦值；一. 填空题1. 已知集合{2,1}A =--，{1,2,3}B =-，则A B =I2. 已知复数z 满足(1)2z i -=，其中i 是虚数单位，则z =3. 方程lg(3)lg 1x x -+=的解x =4. 已知()log a f x x =(0,1)a a >≠，且1(1)2f --=，则1()f x -=5. 若对任意正实数x ，不等式21x a ≤+恒成立，则实数a 的最小值为6. 若抛物线22y px =的焦点与椭圆2215x y +=的右焦点重合，则p = 7. 中位数为1010的一组数构成等差数列，其末项为2015，则该数列的首项为二. 选择题13. 对于常数m 、n ，“0mn <”是“方程221mx ny +=表示的曲线是双曲线”的（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14. 若方程()20f x -=在(,0)-∞内有解，则()y f x =的图像可能是（）A. B. C. D.三. 解答题 17. 已知圆锥母线长为5，底面圆半径长为4，点M 是母线PA 的中点，AB 是底面圆的直径，点C 是弧AB 的中点；（1）求三棱锥P ACO -的体积；（2）求异面直线MC 与PO 所成的角；一. 填空题1. 已知复数2z i =+（i 为虚数单位），则2z =2. 已知集合1{|216}2x A x =≤<，22{|log (9)}B x y x ==-，则A B =I 3. 在二项式62()x x +的展开式中，常数项是4. 等轴双曲线222x y a -=与抛物线216y x =的准线交于A 、B 两点，且||AB = 则该双曲线的实轴长等于5. 若由矩阵2222a x a a y a +⎛⎫⎛⎫⎛⎫=⎪⎪ ⎪⎝⎭⎝⎭⎝⎭表示x 、y 的二元一次方程组无解，则实数a = 7. 若圆锥侧面积为20π，且母线与底面所成角为4arccos 5，则该圆锥的体积为二. 选择题13. 已知()sin3f x x π=，{1,2,3,4,5,6,7,8}A =，现从集合A 中任取两个不同元素s 、t ，则使得()()0f s f t ⋅=的可能情况为（） A. 12种 B. 13种 C. 14种 D. 15种三. 解答题18. 已知函数22()cos ()4f x x x π=+-（x R ∈）；（1）求函数()f x 在区间[0,]2π上的最大值；（2）在ABC ∆中，若A B <，且1()()2f A f B ==，求BC AB 的值；上海市浦东新区2017届高三一模数学试卷一. 填空题1. 已知U R =，集合{|421}A x x x =-≥+，则U C A =2. 三阶行列式351236724---中元素5-的代数余子式的值为 3. 8(1)2x -的二项展开式中含2x 项的系数是4. 已知一个球的表面积为16π，则它的体积为5. 一个袋子中共有6个球，其中4个红色球，2个蓝色球，这些球的质地和形状一样，从中任意抽取2个球，则所抽的球都是红色球的概率是6. 已知直线:0l x y b -+=被圆22:25C x y +=所截得的弦长为6，则b =7. 若复数(1)(2)ai i +-在复平面上所对应的点在直线y x =上，则实数a =8.函数()cos sin )f x x x x x =+-的最小正周期为二. 选择题 13. 将cos 2y x =图像向左平移6π个单位，所得的函数为（） A. cos(2)3y x π=+ B. cos(2)6y x π=+ C. cos(2)3y x π=- D. cos(2)6y x π=- 三. 解答题17. 在长方体1111ABCD A B C D -中（如图），11AD AA ==，2AB =，点E 是棱AB 中点；（1）求异面直线1AD 与EC 所成角的大小；（2）《九章算术》中，将四个面都是直角三角形的四面体成为鳖臑，试问四面体1D CDE 是否为鳖臑？并说明理由；上海市闵行区2017届高三一模数学试卷一. 填空题1. 方程lg(34)1x +=的解x =2. 若关于x 的不等式0x a x b->-（,a b R ∈）的解集为(,1)(4,)-∞+∞U ，则a b += 3. 已知数列{}n a 的前n 项和为21n n S =-，则此数列的通项公式为4. 函数()1f x =的反函数是 5. 6(12)x +展开式中3x 项的系数为（用数字作答）6. 如图，已知正方形1111ABCD A B C D -，12AA =，E 为棱1CC 的中点，则三棱锥1D ADE -的体积为二. 选择题13. 若a 、b 为实数，则“1a <”是“11a>”的（）条件 A. 充要 B. 充分不必要 C. 必要不充分 D. 既不充分也不必要14. 若a 为实数，(2)(2)4ai a i i +-=-（i 是虚数单位），则a =（）A. 1-B. 0C. 1D. 2三. 解答题18. 已知m =u r ，2(cos ,sin )2A n A =r ，A 、B 、C 是ABC ∆的内角；（1）当2A π=时，求||n r 的值；（2）若23C π=，||3AB =，当m n ⋅u u r r 取最大值时，求A 的大小及边BC 的长；上海市虹口区2017届高三一模数学试卷一. 填空题1. 已知集合{1,2,4,6,8}A =，{|2,}B x x k k A ==∈，则A B =I2. 已知21z i i=+-，则复数z 的虚部为 3. 设函数()sin cos f x x x =-，且()1f a =，则sin 2a =4. 已知二元一次方程111222a xb yc a x b y c +=⎧⎨+=⎩的增广矩阵是111113-⎛⎫ ⎪⎝⎭，则此方程组的解是 5. 数列{}n a 是首项为1，公差为2的等差数列，n S 是它前n 项和，则2lim nn n S a →∞= 6. 已知角A 是ABC ∆的内角，则“1cos 2A =”是“sin A =”的条件（填“充分非必要”、“必要非充分”、“充要条件”、“既非充分又非必要”之一）7. 若双曲线2221y x b -=的一个焦点到其渐近线距离为，则该双曲线焦距等于二. 选择题14. 已知函数()sin(2)3f x x π=+在区间[0,]a （其中0a >）上单调递增，则实数a 的取值范围是（）A. 02a π<≤ B. 012a π<≤ C. 12a k ππ=+，*k N ∈ D. 2212k a k πππ<≤+，k N ∈三. 解答题 17. 在正三棱锥P ABC -中，已知底面等边三角形的边长为6，侧棱长为4；（1）求证：PA BC ⊥；（2）求此三棱锥的全面积和体积；一. 填空题1. “0x <”是“x a <”的充分非必要条件，则a 的取值范围是2. 函数2()13sin ()4f x x π=-+的最小正周期为3. 若复数z 为纯虚数，且满足(2)i z a i -=+（i 为虚数单位），则实数a 的值为4. 二项式251()x x +的展开式中，x 的系数为5. 用半径1米的半圆形薄铁皮制作圆锥型无盖容器，其容积为立方米6. 已知α为锐角，且3cos()45πα+=，则sin α= 二. 选择题11. 若空间三条直线a 、b 、c 满足a b ⊥，b c ⊥，则直线a 与c （）A. 一定平行B. 一定相交C. 一定是异面直线D. 平行、相交、是异面直线都有可能 12. 在无穷等比数列{}n a 中，121lim()2n n a a a →∞++⋅⋅⋅+=，则1a 的取值范围是（） A. 1(0,)2 B. 1(,1)2 C. (0,1) D. 11(0,)(,1)22U 三. 解答题16. 已知正四棱柱1111ABCD A B C D -，AB a =，12AA a =，E 、F 分别是棱AD 、CD 的中点；（1）求异面直线1BC 与EF 所成角的大小；（2）求四面体1CA EF 的体积；一. 填空题1. 若集合2{|20}M x x x =-<，{|||1}N x x =>，则M N =I2. 若复数z 满足232z z i +=-，其中i 为虚数单位，则z =3. 如果5sin 13α=-，且α为第四象限角，则tan α的值是 4. 函数cos sin ()sin cos x xf x x x=的最小正周期是 5. 函数()2x f x m =+的反函数为1()y f x -=，且1()y f x -=的图像过点(5,2)Q ，那么m =6. 点(1,0)到双曲线2214x y -=的渐近线的距离是二. 选择题13. 给定空间中的直线l 与平面α，则“直线l 与平面α垂直”是“直线l 垂直于平面α上无数条直线”的（）条件A. 充分非必要B. 必要非充分C. 充要D. 既不充分也不必要14. 已知x 、y R ∈，且0x y >>，则（）A. 110x y ->B. 11()()022x y -< C. 22log log 0x y +> D. sin sin 0x y ->三. 解答题18. 已知△ABC 中，1AC =，23ABC π∠=，设BAC x ∠=，记()f x AB BC =⋅u u u r u u u r ；（1）求函数()f x 的解析式及定义域；（2）试写出函数()f x 的单调递增区间，并求方程1()6f x =的解；。

杨浦区2017届高三一模数学卷答案及官方评分标准

8
2
MN 就是异面直线 l1
l2 之间的距离
10
设 d = AM = BM = NM = CN
1 1 1 所以 VABCN = ( (2d ⋅ d ) ⋅ d = d 3 = 9 3 2 3
所以 d = 3 ，即异面直线 l1
12
l2 之间的距离为 3
14
19
本题满证明：根据对
14
本题共有 2 个小题，第 1 小题满
x = −1 时，因为 f (−1 + T ) ≥ f (−1) = 1 = f (3) 成立，所以 −1 + T ≥ 3 ，所以 T ≥ 4 13 而另一方面，若 T ≥ 4 ， x ∈ (−∞, − 1] 时， f ( x + T ) − f ( x) = x + T + | x + T − 1| − | x + T + 1| −( x + 2) = T + | x + T − 1| − | x + T + 1| −2 因为 | x + T − 1| − | x + T + 1| ≥ − | ( x + T − 1) − ( x + T + 1) |= −2 所以 f ( x + T ) − f ( x) ≥ T − 2 − 2 ≥ 0 ，所以有 f ( x + T ) ≥ f ( x) 成立 15 x ∈ [−1, + ∞ ) 时， f ( x + T ) − f ( x) = x + T − 2 − ( x + | x − 1| − | x + 1|) = T − 2− | x − 1| + | x + 1| 因为 | x + 1| − | x − 1| ≥ − | ( x + 1) − ( x − 1) |= −2 所以 f ( x + T ) − f ( x) ≥ T − 2 − 2 ≥ 0 即 f ( x + T ) ≥ f ( x ) 成立 17 综，恒有有 f ( x + T ) ≥ f ( x ) 成立所以 T 的取值范围是 [4, + ∞) 18

2017年上海市高考数学试卷-含答案详解

绝密★启用前2017年普通高等学校招生全国统一考试（上海卷）数学副标题考试范围：xxx ；考试时间：100分钟；命题人：xxx注意事项:1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在试卷上无效。

3.考试结束后，本试卷和答题卡一并交回。

第I 卷（选择题）一、单选题（本大题共4小题，共20.0分。

在每小题列出的选项中，选出符合题目的一项）1. 关于x 、y 的二元一次方程组{x +5y =02x +3y =4的系数行列式D 为( )A. ∣∣∣0543∣∣∣B. ∣∣∣1024∣∣∣C. ∣∣∣1523∣∣∣D. ∣∣∣6054∣∣∣2. 在数列{a n }中，a n =(−12)n ，n ∈N ∗，则lim n→∞a n ( ) A. 等于−12B. 等于0C. 等于12D. 不存在3. 已知a 、b 、c 为实常数，数列{x n }的通项x n =an 2+bn +c ，n ∈N ∗，则“存在k ∈N ∗，使得x 100+k 、x 200+k 、x 300+k 成等差数列”的一个必要条件是( )A. a ≥0B. b ≤0C. c =0D. a −2b +c =04. 在平面直角坐标系xOy 中，已知椭圆C 1：x 236+y 24=1和C 2：x 2+y 29=1，P 为C 1上的动点，Q 为C 2上的动点，w 是OP ⃗⃗⃗⃗⃗ ⋅OQ ⃗⃗⃗⃗⃗⃗ 的最大值．记Ω={(P,Q)|P 在C 1上，Q 在C 2上，且OP ⃗⃗⃗⃗⃗ ⋅OQ⃗⃗⃗⃗⃗⃗ =w}，则Ω中元素个数为( ) A. 2个 B. 4个 C. 8个D. 无穷个第II 卷（非选择题）二、填空题（本大题共12小题，共54.0分）……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※……○…………内…………○…………装…………○…………订…………○…………线…………○…………5. 已知集合A ={1,2,3,4}，集合B ={3,4,5}，则A ∩B = ．6. 若排列数P 6m=6×5×4，则m = ______ ． 7. 不等式x−1x>1的解集为．8. 已知球的体积为36π，则该球主视图的面积等于______ ． 9. 已知复数z 满足z +3z =0，则|z|= ． 10. 设双曲线x 29−y 2b2=1(b >0)的焦点为F 1、F 2，P 为该双曲线上的一点，若|PF 1|=5，则|PF 2|= ．11. 如图，以长方体ABCD −A 1B 1C 1D 1的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系，若DB 1⃗⃗⃗⃗⃗⃗⃗⃗ 的坐标为(4,3,2)，则AC 1⃗⃗⃗⃗⃗⃗⃗ 的坐标是12. 定义在(0,+∞)上的函数y =f(x)的反函数为y =f −1(x)，若g(x)={3x −1,x ≤0f(x),x >0为奇函数，则f −1(x)=2的解为． 13. 已知四个函数：①y =−x ，②y =−1x ，③y =x 3，④y =x 12，从中任选2个，则事件“所选2个函数的图象有且仅有一个公共点”的概率为．14. 已知数列{a n }和{b n }，其中a n =n 2，n ∈N ∗，{b n }的项是互不相等的正整数，若对于任意n ∈N ∗，{b n }的第a n 项等于{a n }的第b n 项，则lg(b 1b 4b 9b 16)lg(b 1b 2b 3b 4)= ．15. 设α1，α2∈R ，且12+sinα1+12+sin2α2=2，则|10π−α1−α2|的最小值等于． 16. 如图，用35个单位正方形拼成一个矩形，点P 1、P 2、P 3、P 4以及四个标记为“▲”的点在正方形的顶点处，设集合Ω={P 1,P 2,P 3,P 4}，点P ∈Ω，过P 作直线l P ，使得不在l P 上的“▲”的点分布在l P 的两侧．用D 1(l P )和D 2(l P )分别表示l P 一侧和另一侧的“▲”的点到l P 的距离之和．若过P 的直线l P 中有且只有一条满足D 1(l P )=……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………D 2(l P )，则Ω中所有这样的P 为______ ．三、解答题（本大题共5小题，共76.0分。

2017年上海市浦东区高考数学一模试卷(含答案)(推荐文档)

上海市浦东新区2017届高三一模数学试卷2016.12一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分）1. 已知U R =，集合{|421}A x x x =-≥+，则U C A =2. 三阶行列式351236724---中元素5-的代数余子式的值为 3. 8(1)2x -的二项展开式中含2x 项的系数是4. 已知一个球的表面积为16π，则它的体积为5. 一个袋子中共有6个球，其中4个红色球，2个蓝色球，这些球的质地和形状一样，从中任意抽取2个球，则所抽的球都是红色球的概率是6. 已知直线:0l x y b -+=被圆22:25C x y +=所截得的弦长为6，则b =7. 若复数(1)(2)ai i +-在复平面上所对应的点在直线y x =上，则实数a =8.函数()cos sin )f x x x x x =+-的最小正周期为 9. 过双曲线222:14x y C a -=的右焦点F 作一条垂直于x 轴的垂线交双曲线C 的两条渐近线于A 、B 两点，O 为坐标原点，则△OAB 的面积的最小值为10. 若关于x 的不等式1|2|02x x m --<在区间[0,1]内恒成立，则实数m 的范围11. 如图，在正方形ABCD 中，2AB =，M 、N 分别是边BC 、CD上的两个动点，且MN =AM AN ⋅u u u u r u u u r的取值范围是12. 已知定义在*N 上的单调递增函数()y f x =，对于任意的*n N ∈，都有*()f n N ∈，且 (())3f f n n =恒成立，则(2017)(1999)f f -=二. 选择题（本大题共4题，每题5分，共20分）13. 将cos 2y x =图像向左平移6π个单位，所得的函数为（） A. cos(2)3y x π=+ B. cos(2)6y x π=+ C. cos(2)3y x π=- D. cos(2)6y x π=-14. 已知函数()y f x =的反函数为1()y f x -=，则()y f x =-与1()y f x -=-图像（）A. 关于y 轴对称B. 关于原点对称C. 关于直线0x y +=对称D. 关于直线0x y -=对称15. 设{}n a 是等差数列，下列命题中正确的是（）A. 若120a a +>，则230a a +>B. 若130a a +<，则120a a +<C. 若120a a <<，则2a >D. 若10a <，则2123()()0a a a a -->16. 元旦将近，调查鲜花市场价格得知：购买2只玫瑰与1只康乃馨所需费用之和大于8元，而购买4只玫瑰与5只康乃馨所需费用之和小于22元；设购买2只玫瑰花所需费用为A 元，购买3只康乃馨所需费用为B 元，则A 、B 的大小关系是（）A. A B >B. A B <C. A B =D. A 、B 的大小关系不确定三. 解答题（本大题共5题，共14+14+14+16+18=76分）17. 在长方体1111ABCD A B C D -中（如图），11AD AA ==，2AB =，点E 是棱AB 中点；（1）求异面直线1AD 与EC 所成角的大小；（2）《九章算术》中，将四个面都是直角三角形的四面体成为鳖臑，试问四面体1D CDE 是否为鳖臑？并说明理由；18. 已知△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ；（1）若3B π=，b =ABC 的面积2S =，求a c +的值；（2）若22cos ()C BA BC AB AC c ⋅+⋅=u u u r u u u r u u u r u u u r ，求角C ；19. 已知椭圆2222:1x y C a b+=(0)a b >>的左、右焦点分别为1F 、2F ，过2F 的一条直线交椭圆于P 、Q 两点，若△12PF F的周长为4+；（1）求椭圆C 的方程；（2）若12||||F P F Q PQ +=u u u r u u u u r u u u r ，求直线PQ 的方程；20. 设数列{}n a 满足21241n n a a n n +=+-+，22n n b a n n =+-；（1）若12a =，求证：数列{}n b 为等比数列；（2）在（1）的条件下，对于正整数2、q 、r (2)q r <<，若25b 、q b 、r b 这三项经适当排序后能构成等差数列，求符合条件的数组(,)q r ；（3）若11a =，n n c b n =+，n d =n M 是n d 的前n 项和，求不超过2016M 的最大整数；21. 已知定义在R 上的函数()x ϕ的图像是一条连续不断的曲线，且在任意区间上()x ϕ都不是常值函数，设011i i n a t t t t t b -=<<⋅⋅⋅<<<⋅⋅⋅<=，其中分点1t 、2t 、⋅⋅⋅、1n t -将区间[,]a b 划分为n *()n N ∈个小区间1[,]i i t t -，记0112{,,}|()()||()()|M a b n t t t t ϕϕϕϕ=-+- 1|()()|n n t t ϕϕ-+⋅⋅⋅+-，称为()x ϕ关于区间[,]a b 的n 阶划分的“落差总和”；当{,,}M a b n 取得最大值且n 取得最小值0n 时，称()x ϕ存在“最佳划分”0{,,}M a b n ；（1）已知()||x x ϕ=，求{1,2,2}M -的最大值0M ；（2）已知()()a b ϕϕ<，求证：()x ϕ在[,]a b 上存在“最佳划分”{,,1}M a b 的充要条件是()x ϕ在[,]a b 上单调递增；（3）若()x ϕ是偶函数且存在“最佳划分”0{,,}M a a n -，求证：0n 是偶数，且 00110i i n t t t t t -++⋅⋅⋅+++⋅⋅⋅+=；参考答案一. 填空题1. {|1}x x >2. 34-3. 74. 323π5. 256. ±7. 3 8. π 9. 8 10. 3(,2)2 11. [4,8- 12. 54二. 选择题13. A 14. D 15. C 16. A三. 解答题17.（1）3π；（2）是； 18.（1）5a c +=；（2）3π；19.（1）22184x y +=；（2）2)y x =-； 20.（1）12n n b -=；（2）(3,5)；（3）2016；21.（1）03M =；（2）略；（3）略；。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上海市杨浦区2017届高三一模数学试卷
2016.12
一. 填空题（本大题共12题，1-6每题4分，7-12每题5分，共54分）
1. 若“a b >”，则“33a b >”是命题（填：真、假）
2. 已知(,0]A =-∞，(,)B a =+∞，若A B R = ，则a 的取值范围是
3. 294z z i +=+（i 为虚数单位），则||z =
4. 若△ABC 中，4a b +=，30C ︒
∠=，则△ABC 面积的最大值是 5. 若函数2
()log 1
x a f x x -=+的反函数的图像过点(2,3)-，则a = 6. 若半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60︒，则该截面的面积是
7. 抛掷一枚均匀的骰子（刻有1、2、3、4、5、6）三次，得到的数字依次记作a 、b 、c ，则a bi +（i 为虚数单位）是方程220x x c -+=的根的概率是
8. 设常数0a >，9(x
+展开式中6x 的系数为4，则2lim()n n a a a →∞++⋅⋅⋅+=
9. 已知直线l 经过点(且方向向量为(2,1)-，则原点O 到直线l 的距离为
10. 若双曲线的一条渐近线为20x y +=，且双曲线与抛物线2y x =的准线仅有一个公共点，则此双曲线的标准方程为
11.平面直角坐标系中，给出点(1,0)A 、(4,0)B ，若直线10x my +-=上存在点P ，使得 ||2||PA PB =，则实数m 的取值范围是
12. 函数()y f x =是最小正周期为4的偶函数，且在[2,0]x ∈-时，()21f x x =+，若存在1x 、2x 、⋅⋅⋅、n x 满足120n x x x ≤<<⋅⋅⋅<，且1223|()()||()()|f x f x f x f x -+-+⋅⋅⋅ 1|()()|2016n n f x f x -+-=，则n n x +最小值为；
二. 选择题（本大题共4题，每题5分，共20分）
13. 若a 与b c - 都是非零向量，则“a b a c ⋅=⋅ ”是“()a b c ⊥- ”的（）条件
A. 充分不必要
B. 必要不充分
C. 充分必要
D. 既不充分也不必要
14. 行列式147
258369
中，元素7的代数余子式的值为（）
A. 15-
B. 3-
C. 3
D. 12
15. 一个公司有8名员工，其中6位员工的月工资分别为5200、5300、5500、6100、6500、 6600，另两位员工数据不清楚，那么8位员工月工资的中位数不可能是（）
A. 5800
B. 6000
C. 6200
D. 6400
16. 若直线1x y a b
+=通过点(cos ,sin )P θθ，则下列不等式正确的是（） A. 221a b +≤ B. 221a b +≥ C. 22111a b +≤ D. 22111a b
+≥
三. 解答题（本大题共5题，共14+14+14+16+18=76分）
17. 如图，某柱体实心铜制零件的截面边界是长度为55毫米线段AB 和88毫米的线段AC 以及圆心为P ，半径为PB 的一段圆弧BC 构成，其中60BAC ︒
∠=；
（1）求半径PB 的长度；
（2）现知该零件的厚度为3毫米，试求该零件的重量（每1个立方厘米铜重8.9克，按四舍五入精确到0.1克）；（V s h =⋅柱底）
18. 如图所示，1l 、2l 是互相垂直的异面直线，MN 是它们的公垂线段，点A 、B 在1l 上，且位于M 点的两侧，C 在2l 上，AM BM NM CN ===；
（1）求证：异面直线AC 与BN 垂直；
（2）若四面体ABCN 的体积9ABCN V =，求异面直线1l 、2l 之间的距离；
19. 如图所示，椭圆2
2:14
x C y +=，左右焦点分别记作1F 、2F ，过1F 、2F 分别作直线 1l 、2l 交椭圆于AB 、CD ，且1l ∥2l ；
（1）当直线1l 的斜率1k 与直线BC 的斜率2k 都存在时，求证：12k k ⋅为定值；
（2）求四边形ABCD 面积的最大值；
20. 数列{}n a ，定义{}n a ∆为数列{}n a 的一阶差分数列，其中1n n n a a a +∆=-，*
n N ∈；
（1）若2n a n n =-，试判断{}n a ∆是否是等差数列，并说明理由；
（2）若11a =，2n n n a a ∆-=，求数列{}n a 的通项公式；
（3）对（2）中的数列{}n a ，是否存在等差数列{}n b ，使得1212n n n n n n bC b C b C a ++⋅⋅⋅+= 对一切*
n N ∈都成立，若存在，求出数列{}n b 的通项公式；若不存在，请说明理由；
21. 对于函数()f x ()x D ∈，若存在正常数T ，使得对任意x D ∈，都有()()f x T f x +≥ 成立，我们称函数()f x 为“T 同比不减函数”；
（1）求证：对任意正常数T ，2()f x x =都不是“T 同比不减函数”；
（2）若函数()sin f x kx x =+是“2
π同比不减函数”，求k 的取值范围；（3）是否存在正常数T ，使得函数()|1||1|f x x x x =+--+为“T 同比不减函数”，若存在，求T 的取值范围，若不存在，请说明理由；
参考答案
一. 填空题
1. 真
2. 0a ≤
3. 5
4. 1
5. π
6. 2
7. 1
108 8. 1
2 9. 1 10. 221641y x -=
11. (,)-∞+∞ 12. 1513
二. 选择题
13. C 14. B 15. D 16. D
三. 解答题
17.（1）49；（2）82.7克；
18.（1）略；（2）3；
19.（1）1
4-；（2）4；
20.（1）2n a n ∆=；（2）12n n a n -=⋅；（3）n b n =；
21.（1）略；（2）k π≥；（3）4T ≥；。