四川省宜宾市2015届高三第一次诊断考试数学理试题
四川省绵阳市高中2015届高三第一次诊断性考试数学理试题 扫描版

绵阳市高2015级第一次诊断性考试数学(理工类)参考解答及评分标准一、选择题:本大题共10小题,每小题5分,共50分.DBDAC BACDAax+对x∈R恒成立,显然a≥0,b≤1+x e-ax.10题提示:由1+x e≥b若a=0,则ab=0.若a >0,则ab ≤a 1+x e -a 2x .设函数=)(x f x a ae x 21-+,求导求出f (x )的最小值为a a a a f ln 2)1(ln 22-=-.设)0(ln 2)(22>-=a a a a a g ,求导可以求出g(a )的最大值为32321)(e e g =, 即ab 的最大值是321e ,此时232321e b e a ==,.二、填空题:本大题共5小题,每小题5分,共25分.11.53-12.-1 13.40 14.3021 15.①③④15题提示:①容易证明正确.②不正确.反例:x x f =)(在区间[0,6]上.③正确.由定义:21020m m mx x --=--得1)1(10020+=⇒-=-x m m x x , 又0x )11(,-∈所以实数m 的取值范围是)20(,∈m .④正确.理由如下:由题知ab ab x --=ln ln ln 0.要证明abx 1ln 0<,即证明: b a a b ab a b a b ab a b a b -=-<⇔<--ln 1ln ln ,令1>=t ab ,原式等价于01ln 21ln 2<+-⇔-<t t t t t t .令)1(1ln 2)(>+-=t t t t t h ,则0)1(12112)(22222<--=-+-=--='tt t t t t t t h , 所以0)1(1ln 2)(=<+-=h tt t t h 得证.三、解答题:本大题共6小题,共75分.16.解:(Ⅰ)=)(x f 2m·n -11cos 2cos sin 22-+⋅=x x x ωωω=)42sin(22cos 2sin πωωω+=+x x x . ……………………………6分由题意知:π=T ,即πωπ=22,解得1=ω.…………………………………7分 (Ⅱ) 由(Ⅰ)知)42sin(2)(π+=x x f ,∵6π≤x ≤4π,得127π≤42π+x ≤43π, 又函数y =sin x 在[127π,43π]上是减函数,∴ )34sin(2127sin 2)(max πππ+==x f …………………………………10分3sin 4cos 23cos 4sin 2ππππ+==213+.…………………………………………………………12分17.解:(Ⅰ) 由题知⎩⎨⎧≥->-,,0102t t 解得21<≤t ,即)21[,=D .……………………3分(Ⅱ) g (x )=x 2+2mx -m 2=222)(m m x -+,此二次函数对称轴为m x -=.……4分 ① 若m -≥2,即m ≤-2时, g (x )在)21[,上单调递减,不存在最小值;②若21<-<m ,即12-<<-m 时, g (x )在)1[m -,上单调递减,]2(,m -上递增,此时22)()(2min ≠-=-=m m g x g ,此时m 值不存在;③m -≤1即m ≥-1时, g (x )在)21[,上单调递增,此时221)1()(2min =-+==m m g x g ,解得m =1. …………………………11分 综上:1=m . …………………………………………………………………12分 18.解:(Ⅰ) 51cos 5=∠=ABC AB ,,2BC =, 由余弦定理:ABC BC BA BC BA AC ∠⋅⋅-+=cos 2222=52+22-2×5×2×51=25,∴ 5=AC . ……………………………………………………………………3分又(0,)π∠∈ABC ,所以562cos 1sin 2=∠-=∠ABC ABC , 由正弦定理:ABC ACACB AB ∠=∠sin sin ,得562sin sin =∠⨯=∠AC ABC AB ACB .………………………………………6分 (Ⅱ) 以BC BA ,为邻边作如图所示的平行四边形ABCE ,如图, 则51cos cos -=∠-=∠ABC BCE ,BE =2BD =7,CE =AB =5,在△BCE 中,由余弦定理:BCE CE CB CE CB BE ∠⋅⋅-+=cos 2222.即)51(5225492-⨯⨯⨯-+=CB CB ,解得:4=CB . ………………………………………………………………10分 在△ABC 中,335145245cos 222222=⨯⨯⨯-+=∠⋅⋅-+=ABC BC BA BC BA AC , 即33=AC .…………………………………………………………………12分 19.解:(Ⅰ) 由832539a a a S ⋅==,,得:⎪⎩⎪⎨⎧+⋅+=+=⨯+,,)7()2()4(9223311211d a d a d a d a 解得:121==d a ,.∴ 1+=n a n ,n n n n S n 2322)12(2+=++=. …………………………………5分(Ⅱ) 由题知=n c )12(2λ-+n n . 若使}{n c 为单调递减数列,则B CDA E=-+n n c c 1)22(21λ-++n n -)12(2λ-+n n =0)1224(2<-+-+λn n n 对一切n ∈N *恒成立, …………………8分即: max )1224(01224+-+>⇔<-+-+n n n n λλ,又1224+-+n n =322232)1)(2(22++=++=++nn n n n n n n ,……………………10分 当1=n 或2时, max )1224(+-+n n =31. ∴31>λ.………………………………………………………………………12分20.(Ⅰ)证明: 由1)(--=ax e x f x ,得a e x f x -=')(.…………………………1分由)(x f '>0,即a e x ->0,解得x >ln a ,同理由)(x f '<0解得x <ln a , ∴ )(x f 在(-∞,ln a )上是减函数,在(ln a ,+∞)上是增函数, 于是)(x f 在a x ln =取得最小值.又∵ 函数)(x f 恰有一个零点,则0)(ln )(min ==a f x f , ………………… 4分 即01ln ln =--a a e a .………………………………………………………… 5分 化简得:1ln 1ln 01ln -=-==--a a a a a a a a a 于是,即,,∴ 1-=a a e a . ………………………………………………………………… 6分 (Ⅱ)解:由(Ⅰ)知,)(x f 在a x ln =取得最小值)(ln a f ,由题意得)(ln a f ≥0,即1ln --a a a ≥0,……………………………………8分 令1ln )(--=a a a a h ,则a a h ln )(-=', 由0)(>'a h 可得0<a <1,由0)(<'a h 可得a >1.∴ )(a h 在(0,1)上单调递增,在(1,+∞)上单调递减,即0)1()(max ==h a h , ∴ 当0<a <1或a >1时,h (a )<0,∴ 要使得)(x f ≥0对任意x ∈R 恒成立,.1=a∴a 的取值集合为{1} ……………………………13分2015高考英语签约提分,保证最低涨10-40分,不达目标全额退费,详情QQ2835745855,其它各科试题及答案登陆QQ757722345或关注微信公众号qisuen21.解:(Ⅰ)由x e n x m x f +=ln )(得xxe xmx nx m x f ln )(--='(0>x ).由已知得0)1(=-='e nm f ,解得m =n . 又ee nf 2)1(==,即n =2,∴ m =n =2.……………………………………………………………………3分(Ⅱ) 由 (Ⅰ)得)ln 1(2)(x x x xex f x --=',令=)(x p x x x ln 1--,)0(∞+∈,x ,当x ∈(0,1)时,0)(>x p ;当x ∈(1,+∞)时,0)(<x p ,又0>x e ,所以当x ∈(0,1)时,0)(>'x f ; 当x ∈(1,+∞)时,0)(<'x f , ∴ )(x f 的单调增区间是(0,1),)(x f 的单调减区间是(1,+∞).……8分(Ⅲ) 证明:由已知有)ln 1()1ln()(x x x xx x g --+=,)0(∞+∈,x , 于是对任意0>x ,21)(-+<e x g 等价于)1()1ln(ln 12-++<--e x xx x x ,由(Ⅱ)知=)(x p x x x ln 1--,)0(∞+∈,x ,∴ )ln (ln 2ln )(2---=--='e x x x p ,)0(∞+∈,x . 易得当)0(2-∈e x ,时,0)(>'x p ,即)(x p 单调递增;当)(2∞+∈-,e x 时,0)(<'x p ,即)(x p 单调递减. 所以)(x p 的最大值为221)(--+=e e p ,故x x x ln 1--≤21-+e .设)1ln()(x x x q +-=,则01)(>+='x xx q , 因此,当)0(∞+∈,x 时,)(x q 单调递增,0)0()(=>q x q .故当)0(∞+∈,x 时,0)1ln()(>+-=x x x q ,即1)1ln(>+x x.∴ x x x ln 1--≤21-+e <)1()1ln(2-++e x x.∴ 对任意0>x ,21)(-+<e x g . ……………………………………………14分。
【数学】四川省宜宾一中2015届高三第二次诊断性测试(理)

俯视图侧(左)视图正(主)视图四川省宜宾一中2015届高三第二次诊断性测试(理)第Ⅰ卷(选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑.一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合2{|1}M y y x ==+,{|1}N x y x ==+,则MN =(A ){(01)},(B )[1)+∞, (C ){(01)(12)},,, (D )}1|{>y y 2.在复平面内,复数2iz i=+对应的点所在的象限是 (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 3.抛物线x y 42=的焦点到双曲线222=-y x 的渐近线的距离是(A )22(B )2 (C )21 (D )24.某三棱锥的三视图如图所示,该三棱锥的体积是 (A )643 (B )32 (C )16 (D )3235.下列说法中正确的是 (A )命题“若0>>b a ,则ba 11<”的逆命题是真命题(B )命题:p x R ∀∈,012>+-x x ,则0:p x R ⌝∃∈,01020<+-x x (C )“11>>b a ,”是“1>ab ”成立的充分条件 (D )“b a >”是“22b a >”成立的充分不必要条件 6.函数()x xx f ln 1+=的图象大致为7.设R m ∈,过定点A 的动直线01=-+y mx 与过定点B 的 动直线02=++-m my x 交于点),(y x P ,则||||+的 最大值为(A )2 (B )12+ (C )22 (D )22+8.右图是用计算机随机模拟的方法估计概率的程序框图,P 表示估计结果,则输出P 的近似值为(A )41 (B )21(C )43 (D )87 9.已知抛物线2:2(0)C y px p =>,O 为坐标原点,过点(20)M p ,作直线l 交抛物线于A B 、两点.有如下命题: ①222||||||OA OB AB += ②||4AB p ≥③2min ()4OAB S p ∆= ④OAB ∆周长的最小值为p 则上述命题正确的是(A )①② (B )①②③ (C )②③④ (D )①②③④10.若方程02)1(4=--+-m mx x 各个实根1x ,2x ,…,k x (*4,k k N ≤∈)所对应的点)12,(-i i x x ,2,1(=i ,…,)k 均在直线x y =的同侧,则实数m 的取值范围是 (A ))71(,- (B ))1()7(∞+---∞,, (C ))17(,- (D ))7()1(∞+-∞,, 第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5个小题,每小题5分,共25分.11.在正项等比数列{n a }中,若491=⋅a a ,则+++322212l o g l o g l o g a a a …=+92log a .12.在52)1)(1(x x x +++的展开式中,3x 的系数为 .13.在ABC ∆中, 角A 、B 、C 所对的边分别是a ,b ,c , 若B c A b sin 3sin =,3=a ,2cos 3B =,则b 的值为 . 14.某学校高一、高二、高三三个年级学生人数分别为2000人,1500人,1000人,用分层抽样的方法,从该校三个年级的学生中抽取9人,现将这9人分配到甲、乙两个工厂参观,要求每个工厂每个年级至少去一人,则共有 种不同的分配方案(用数字作答).15.如果)(x f y =的定义域为R ,对于定义域内的任意x ,存在实数a 使得)()(x f a x f -=+成立,则称此函数具有“)(a P 性质”. 给出下列命题:①函数x ysin =具有“)(a P 性质”;②若奇函数)(x f y =具有“)2(P 性质”,且1)1(=f ,则(2015)1f =;③若函数)(x f y =具有“(4)P 性质”, 图象关于点(10),成中心对称,且在(1,0)-上单调递减,则)(x f y =在(2,1)--上单调递减,在(1,2)上单调递增;④若不恒为零的函数)(x f y =同时具有“)0(P 性质”和 “(3)P 性质”,且函数)(x g y =对R x x ∈∀21,,都有1212|()()||()()|f x f x g x g x -≥-成立,则函数)(x g y =是周期函数. 其中正确的是(写出所有正确命题的编号).三、解答题:本大题共6个小题,共75分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)根据十八大的精神,全国在逐步推进教育教学制度改革,各高校自主招生在高考录取中所占的比例正在逐渐加大.对此,某高校在今年的自主招生考试中制定了如下的规则:笔试阶段,考生从6道备选试题中一次性抽取3道题,并独立完成所抽取的3道题,至少正确完成其中2道试题则可以进入面试.已知考生甲正确完成每道题的概率为23,且每道题正确完成与否互不影响;考生乙能正确完成6道试题中的4道题,另外2道题不能完成.(I)求考生甲至少正确完成2道题的概率; (II)求考生乙能通过笔试进入面试的概率;(III)记所抽取的三道题中考生乙能正确完成的题数为ξ,求ξ的分布列和数学期望.x17.(本小题满分12分)如图,在平面直角坐标系xOy 中,角α以x 负半轴为始边,其终边与单位圆交于点P ,过点P 作x 轴的垂线与射线)0(3≥=x x y 交于点Q ,其中().22ππα∈-,(I)若;,求POQ ∠=cos 31sin α(II)求OPQ ∆面积的最大值.18.(本小题满分12分)如图,在四棱锥E ABCD -中,ABD ∆是正三角形,BCD ∆是等腰三角形,120BCD ∠=︒,EC DE ⊥.(I)求证:BE DE =;(II) 若32=AB ,AE =EBD ⊥平面ABCD ,直线AE 与平面ABD 所成的角为o45.(i)试判断在线段AE 是否存在点M ,使得//DM 平面BEC ,并说明理由; (ii)求二面角B AE D --的余弦值.19.(本小题满分12分)已知公差为d 的等差数列{}n a 满足:*12n n a a n n N ++=∈,.(I)求首项1a 和公差d ,并求数列{}n a 的通项公式; (II)令()111n n n n nb a a ++=-⋅,*n N ∈,求数列{}n b 的前n 项和n S .20.(本小题满分13分)已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(10)F ,,且点3(1)2-,在椭圆上,过点(40)P ,且不垂直于x 轴直线l 与椭圆C 相交于A 、B 两点.(I)求椭圆C 的方程; (II)求OA OB ⋅的取值范围;(III)若点B 关于x 轴的对称点是E ,证明:直线AE 过定点.21.(本小题满分14分)ln()()()x a bf x a b R a b x++=∈已知函数、,、为常数,且()y f x =在1x =处切线方程为 1.yx =-(I)a b 求,的值;(II)()()x g x f e =设函数, (i)()g x 求的单调区间; (ii)223()112()()2()0().xxf x h x k x h x x x k x e e e+'==><+设,,求证:当时,参考答案。
2015年高考四川理科数学试题及答案解析

2015年普通高等学校招生全国统一考试(四川卷)数学(理科)第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)【2015年四川,理1】设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则A B =( )(A ){}1|3x x -<< (B){}|11x x -<< (C ){}|12x x << (D){}|23x x << 【答案】A【解析】∵{|12}A x x =-<<,{|13}B x x =<<,{|13}A B x x ∴=-<<,故选A . (2)【2015年四川,理2】设i 是虚数单位,则复数32i i-=( )(A)i - (B )3i - (C )i (D)3i 【答案】C【解析】3222ii i i 2i i i i-=--=-+=,故选C .(3)【2015年四川,理3】执行如图所示的程序框图,输出S 的值是( )(A )3 (3 (C )12- (D )12【答案】D【解析】易得当1,2,3,4k =时时执行的是否,当5k =时就执行是的步骤,所以51sin 62S π==,故选D .(4)【2015年四川,理4】下列函数中,最小正周期为π且图象关于原点对称的函数是( )(A )cos(2)2y x π=+ (B )sin(2)2y x π=+ (C)sin 2cos2y x x =+ (D )sin cos y x x =+【答案】A 【解析】显然对于A ,cos(2)sin 22y x x π=+=-,为关于原点对称,且最小正周期是π,符合题意,故选A .(5)【2015年四川,理5】过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B两点,则||AB =( ) (43(B )23 (C)6 (D )43【答案】D【解析】由题意可知双曲线的渐近线方程为3y x =,且右焦点(2,0),则直线2x =与两条渐近线的交点分别为A 3),B (2,23)-,∴||43AB =D .(6)【2015年四川,理6】用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C)96个 (D )72个 【答案】B【解析】这里大于40000的数可以分两类:①当5在万位时,个位可以排0、2、4三个数中的一个,十位百位和千位没有限制∴有133472C A =种;②当4在万位时,个位可以排0、2两个数中的一个,十位百位和千位没有限制,∴有132448C A =种, 综上所述:总共有72+48=120种,故选B .(7)【2015年四川,理7】设四边形ABCD 为平行四边形,6AB =,4AD =.若点M ,N 满足3BM MC =,2DN NC =,则AM NM ⋅=( )(A )20 (B)15 (C )9 (D)6【答案】C【解析】这里可以采用最快速的方法,把平行四边形矩形化,因此,过B 建立直角坐标系,可得到()0,6A ,()3,0M ,()4,2N ,∴()3,6AM =-,()1,2NM =--,∴3129AM NM ⋅=-+=,故选C .(8)【2015年四川,理8】设a ,b 都是不等于1的正数,则“331a b >>"是“log 3log 3a b <”的( )(A )充要条件 (B )充分不必要条件 (C)必要不充分条件 (D)既不充分也不必要条件 【答案】B【解析】由已知条件333a b >>可得1a b >>.当1a b >>时,33log log 0a b >>.∴3311log log a b<,即log 3log 3a b <.∴“333a b >>"是“log 3log 3a b <”的充分条件.然而取1133a b =<<=则log 30log 3a b <<,满足log 3log 3a b <,却不满足1a b >>.∴“333a b >>"是“log 3log 3a b <”的不必要条件.综上“333a b >>”是“log 3log 3a b <”的充分不必要条件,故选B .(9)【2015年四川,理9】如果函数()()()()212810,02f x m x n x m n =-+-+≥≥在区间1,22⎡⎤⎢⎥⎣⎦单调递减,则mn的最大值为( )(A)16 (B )18 (C )25 (D )812【答案】B【解析】()()'28f x m x n =-+-,由于()f x 单调递减得:∴()0f x '≤,∴()280m x n -+-≤在1,22⎡⎤⎢⎥⎣⎦上恒成立.设()()28g x m x n =-+-,则一次函数()g x 在1,22⎡⎤⎢⎥⎣⎦上为非正数.∴只须在两个端点处102f ⎛⎫'≤ ⎪⎝⎭和()20f '≤即可.即()()128022280m n m n ⎧-+-≤⎪⎨⎪-+-≤⎩①②,由②得:()1122m n ≤-.∴()211121218222n n mn n n +-⎛⎫≤-≤= ⎪⎝⎭.mn 当且仅当3,6m n ==时取到最大值18.经验证,3,6m n ==满足条件①和②,故选B .(10)【2015年四川,理10】设直线l 与抛物线24y x =相交于A ,B 两点,与圆()()22250x y r r -+=> 相切于点M ,且M 为线段AB 的中点. 若这样的直线l 恰有4条,则r 的取值范围是( )(A )()1,3 (B )()1,4 (C )()2,3 (D )()2,4 【答案】D【解析】设()11,A x y ,()22,B x y ,()5cos ,sin M r r θθ+,则21122244y x y x ⎧=⎪⎨=⎪⎩,()()()1212124y y y y x x +-=-,当直线l 有两条.当直线l 的斜率存在时,可得:()()1212121222sin 4sin AB y y r y y x x k x x r θθ--=-⇒==-, 又∵sin 0sin 5cos 5cos MC r k r θθθθ-==+-,∴1cos sin AB MC k k θθ=-=-, ∴2cos 22sin sin cos r r θθθθ=-⇒=-> 由于M 在抛物线的内部,∴()()()2sin 45cos 204cos 204212r r r θθθ<+=+=+⨯-=,∴sin r θ<2sin 164r r r r θ==<<⇒<,因此,24r <<,故选D .第II 卷(共100分)二、填空题:本大题共5小题,每小题5分(11)【2015年四川,理11】在()521x -的展开式中,含2x 的项的系数是 . 【答案】—40【解析】由题意可知2x 的系数为:22352(1)40C ⨯⨯-=-.(12)【2015年四川,理12】°°sin15sin 75+的值是 .【解析】()sin15sin 75sin15cos15154560︒+︒=︒+︒=︒+︒︒==. (13)【2015年四川,理13】某食品的保鲜时间y (单位:小时)与储藏温度x (单位:°C )满足函数关系kx b y e +=( 2.718e =为自然对数的底数,k ,b 为常数).若该食品在°0C 的保鲜时间是192小时,在°23C 的保鲜时间是48小时,则该食品在°33C 的保鲜时间是________小时. 【答案】24【解析】0+192k b e ⨯= ①,2248k b e ⨯+= ②,∴221142k k e e ==⇒=②①,∴当33x =时,33k b e x += ③,∴()3331248192k k xe e x ====⇒=③①.(14)【2015年四川,理14】如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面相互垂直,动点M 在线段PQ上,E ,F 分别为AB ,BC 中点,设异面直线EM 与AF 所成的角为θ,则cos θ的最大值为 .【答案】25【解析】以AB 为x 轴,AD 为y 轴,AQ 为z 轴建立空间直角坐标系,并设正方形边长为2,则()0,0,0A ,()2,1,0F ,()1,0,0E ,()0,,2M m ,∴()2,1,0AF =,()1,,2EM m =-∴cos 5AF EM AF EMθ⋅==⋅令[]()0,2)f m m =∈()f m '=[]0,2m ∈,()0f m '∴<max 2()(0)5f m f ∴==,从而max2cos 5θ=. (15)【2015年四川,理15】已知函数()2x f x =,()2g x x ax =+(其中a R ∈).对于不相等的实数1x ,2x ,设()()1212f x f x m x x -=-,()()1212g x g x n x x -=-,现有如下命题:(1) 对于任意不相等的实数1x ,2x ,都有0m >; (2) 对于任意a 的及任意不相等的实数1x ,2x ,都有0n >; (3) 对于任意的a ,存在不相等的实数1x ,2x ,使得m n =; (4) 对于任意的a ,存在不相等的实数1x ,2x ,使得m n =-.其中的真命题有_______(写出所有真命题的序号). 【答案】(1) (4)【解析】(1)设1x ,2x ,∵函数2xy =是增函数,∴1222x x >,120x x ->,则1212()()f x f x m x x -=-=12x 1222x x x -->0,所以正确;(2)设12x x >,则120x x ->,∴()()22121122121212g x gx x ax x ax n x x a x x x x -+--===++-- 不妨我们设121,2,3x x a =-=-=-,则60n =-<,矛盾,所以(2)错.A(3)∵m n =,由(1)(2)可得:()()()()12121212f x f xg x g x m n x x x x --===--,化简得到,()()()()1212f x f x g x g x -=-,也即()()()()1122f x g x f x g x -=-,令()()()22x h x f x g x x ax =-=--,即对于任意的a 函数()h x 在定义域范围内存在有两个不相等的实数根1x ,2x .则()2'2ln 2x h x x a =--,2()2ln 2x h x x a '=--,显然当a →-∞时,()'0h x >恒成立,即()h x 单调递增,最多与x 轴有一个交点,不满足题意,所以错误.(4)同理可得()()()()1122f x g x g x f x +=+,设()()()22x h x f x g x x ax =+=++,即对于任意的a 函数()h x 在定义域范围内存在有两个不相等的实数根1x ,2x ,从而()h x 不是恒为单调函数.()'2ln 22x h x x a =++,()()2''2ln 220x h x =+>恒成立,∴()'h x 单调递增,又∵x →-∞时,()'0h -∞<,x →+∞时,()'0h +∞>.所以()h x 为先减后增的函数,满足要求,所以正确.三、解答题:本大题共6题,共75分. (16)【2015年四川,理16】(本小题满分12分)设数列{}n a 的前n 项和12n n S a a =-,且1a ,21a +,3a 成等差数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)记数列1{}n a 的前n 项和n T ,求得使1|1|1000n T -<成立的n 的最小值.解:(Ⅰ)当2n ≥时有,11112(2)n n n n n a S S a a a a --=-=---,则12n n a a -=(2)n ≥,12n n aa 2n ,∴数列{}n a 是以1a 为首项,2为公比的等比数列.又由题意得21322a a a +=+,1112224a a a ∴⋅+=+,∴12a =,∴2n n a =*()n N ∈(Ⅱ)由题意得112n n a =,∴111[1()]11221()12212n nn n i i T =-===--∑,则2111-=()22n nT -=(),又1091111,210242512==,即11110241000512<<111000n T ∴-<成立时,n 的最小值为10n =. (17)【2015年四川,理17】(本小题满分12分)某市A ,B 两所中学的学生组队参加辩论赛,A 中学推荐3名男生,2名女生,B 中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队. (Ⅰ)求A 中学至少有1名学生入选代表队的概率;(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X 表示参赛的男生人数,求X 得分布列和数学期望.解:(Ⅰ)设事件A 表示“A 中学至少有1名学生入选代表队”,可以采用反面求解:33343366199()11100100C C P A C C =-⋅=-=(Ⅱ)由题意,知1,2,3X =,3133461(1)5C C P X C ===;2233463(2)5C C P X C ===;1333461(3)5C C P X C === 因此期望为:131()1232555E X =⋅+⋅+⋅=.(18)【2015年四川,理18】(本小题满分12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC 的中点为M ,GH 的中点为N .(Ⅰ)请将字母标记在正方体相应的顶点处(不需说明理由);(Ⅱ)证明:直线//MN 平面BDH ;(Ⅲ)求二面角A EG M --的余弦值. 解:(Ⅰ)如下图所示:(Ⅱ)如答图所示,连接BD ,AC 相交于点O ,连接MO∵M 、O 分别为线段BC 、BD 的中点,∴////MO CD GH 且1122MO CD GH NH ===∴四边形QMNH 为平行四边形,∴//OH MN ,又∵OH ⊂平面BDH ,∴//MN 平面BDH (Ⅲ)连接EG ,过点M 作MP AC ⊥于点P ,过点P 作PQ EG ⊥于点Q ,连接MQ ,由三垂线定理可得EG MQ ⊥,∴PQM ∠为二面角A EG M --的平面角,设正方体棱长为4a ,则4PQ BC a ==, ∴2MC a =,∵45MCP ∠=︒,MP =,所以tan MP PQM PQ ∠===,所以cos PQM ∠=,所以cos cos A EG M MLK <-->=∠=(19)【2015年四川,理19】(本小题满分12分)如图,,,,A B C D 为平面四边形ABCD 的四个内角.(Ⅰ)证明:1cos tan 2sin A AA-=;(Ⅱ)若180o A C +=,6AB =,3BC =,4CD =,5AD =,求tan tan tan tan 2222A B C D+++.解:(Ⅰ)证明:2sin 2sin 1cos 22tan 2sin cos 2sin cos 222A A A A A A A A-===⋅. (Ⅱ)∵180o A C +=,∴()()cos cos 180cos ,sin sin 180sin C A A C A A =︒-=-=︒-=,∴1cos 1cos 1cos 1cos 2tantan 22sin sin sin sin sin A C A C A A A C A A A---++=+=+=,∵180o A C +=,∴180o B D += 同理可得2tan tan 22sin B D B +=,∴11tan tan tan tan 22222sin sin A B C D A B ⎛⎫+++=+ ⎪⎝⎭连接BD ,设BD x =,在ABD ∆和CBD ∆中分别利用余弦定理及180o A C +=可得:cos cos A C =-, 即22222265342234x x +-+-=-⋅⋅,解得22477x =,从而得3cos 7A =,sin A =同理可得,1cos 19B =, sin B =∴11tan tan tan tan 2()2222sin sin A B C D A B +++=+==. (20)【2015年四川,理20】(本小题满分13分)如图,椭圆2222:1x y E a b+=,过点(0,1)P 的动直线l 与椭圆相交于,A B 两点.当直线l 平行于x 轴时,直线l 被椭圆E 截得的线段长为 (Ⅰ)球椭圆E 的方程;(Ⅱ)在平面直角坐标系xoy 中,是否存在与点P 不同的定点Q ,使得QA PAQB PB=恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.CAECA EEACE解:(Ⅰ)由题知椭圆过点()2,1.因此可得:2222222211c e a a b a b c⎧==⎪⎪⎪+=⎨⎪⎪⎪=+⎩,解得:2a =,2b c ==.∴椭圆E 的方程为:22142x y +=.(Ⅱ)假设存在满足题意的定点Q .当直线l 平行于x 轴时,则1QA PA QBPB==,,A B 两点关于y 轴对称,∴Q 点在y 轴上.不妨设()0,Q a ,当直线l 垂直于x 轴时,()()0,2,0,2A B -, 212212QA PA a QBPBa --===++,解得2a =或1a =(舍去,否则Q 点就是P 点),∴P 点的坐标为()0,2.下面我们证明对于一般的直线:1l y kx =+,()0,2Q 也满足题意. ∵QA PA QBPB=,∴由角平分线定理可知,y 轴为AQB ∠的角平分线.所以QA QB k k =-.设()11,A x y ,()22,B x y ,则111y kx =+,221y kx =+,联立:22124y kx x y =+⎧⎨+=⎩,消去y 可得,()2212420k x kx ++-=, 由韦达定理可得,122412k x x k +=-+,122212x x k -=+, ∴11111211QA y kx k k x x x --===-,22222211QB y kx k k x x x --===-,两式相加得,121212112+2220QA QB x xk k k k k k x x x x ⎛⎫++=-=-=-= ⎪⎝⎭,即QA QB k k =-,从而,假设成立,即存在与点P 不同的定点Q ,使得QA PAQB PB=恒成立. (21)【2015年四川,理21】(本题满分14分)已知函数()()222ln 22f x x a x x ax a a =-++--+,其中0a >.(Ⅰ)设()g x 是()f x 的导函数,讨论()g x 的单调性;(Ⅱ)证明:存在()0,1a ∈,使得()0f x ≥在区间()1,+∞内恒成立,且()0f x =在区间()1,+∞内有唯一解.解:(Ⅰ)∵()()222ln 22f x x a x x ax a a =-++--+,∴求导可得,()2'2ln 222af x x x a x=---+-,即()()22ln 2220,0ag x x x a a x x==---+->>∴()()()222222'20,0x x a a g x a x x x x -+-=++=>>, 对于多项式2x x a -+,(1)当140a ∆=-≤,即14a ≥时,20x x a -+≥恒成立.此时,()'0g x ≥恒成立,所以()g x 恒单调递增.(2)当104a <<时,一元二次方程20x x a -+=有两个实数根,设为12,x x . 那么求根可得:111410,22a x --⎛⎫=∈ ⎪⎝⎭,21141,122a x +-⎛⎫=∈ ⎪⎝⎭①令()'0g x >,即()200x x a x -+<>,解得:10x x <<,2x x >.所以()g x 在()10,x ,()2,x +∞,时单调递增.②令()'0g x <,即()200x x a x -+<>,解得:12x x x <<,所以()g x 在()12,x x ,时单调递减. 综上所述:当14a ≥时,()g x 在()0,+∞上单调递增. 当104a <<时,()g x在)+∞上单调递减.(Ⅱ)∵()0,1a ∈,∴由(Ⅰ)可知()()'f x g x =在()1,+∞内单调递增.又1x +→时,()()1lim ''1222240x f x f a a a +→==--+-=-<, 当x →+∞时,显然()()lim ''0x f x f →+∞=+∞>.而()'f x 在()1,+∞是单调递增的,因此在()1,+∞内必定存在唯一的0x 使得()00002'2ln 2220af x x x a x =---+-= …………….. ① ∴当01x x <<时,()'0f x <,当0x x >时,()'0f x >,∴()f x 在0(1,)x 上单调递减,在0(,)x +∞上单调递增,∴()()0min f x f x =. 由已知条件()0f x =在区间()1,+∞内有唯一解,∴必有()()0min 0f x f x ==. 即()()22000002ln 220f x x a x x ax a a =-++--+= ………………………. ② 由①式得到000ln 2a x x a x =+-+带入②式化简得:()()2232000025220a x x a x x +---=,即()()200220xx a x a -+-=,注意这里的a 比较容易解出,因此我们可以用0x 表示a ,解得:2x a =,2002a x x =- (1)当01(,1)22x a =∈时,带入①式可得,22ln 230a a --=………………….. ③即讨③是否有解.令()22ln 23h a a a =--,()()212'20a h a a a-=-=< ∴()h a 在1,12⎛⎫ ⎪⎝⎭上单调递减.又∵()11302h a h ⎛⎫<=-< ⎪⎝⎭,∴③式无解.(2)当2002a x x =-时,∵01a <<,∴012x <<,把2002a x x =-带入①式可得, 20022ln 60x x --= ………………..④即讨论④是否有解.又设2000()22ln 6h x x x =--,()()2000002212'4x h x x x x -=-=,∵()01,2x ∈, ∴()0'0h x >恒成立,∴0()h x 在()1,2上单调递增.∴()(1)4h x h >=-,()()222ln 20h x h <=->. ∴()h x 与x 轴有交点,从而20022ln 60x x --=在()1,2上有解. 从而命题得证!。
【解析】四川省成都市2015届高中毕业班第一次诊断性检测数学理试题

四川省成都市2015届高中毕业班第一次诊断性检测数学试题(理科)【试卷综述】本试卷是高三理科试卷,以基础知识和基本技能为载体,以能力测试为主导,在注重考查学科核心知识的同时,突出考查考纲要求的基本能力,重视学生科学素养的考查.知识考查注重基础、注重常规、注重主干知识,兼顾覆盖面.试题重点考查:集合、不等式、向量、三视图、导数、简单的线性规划、直线与圆、数列、充要条件等;考查学生解决实际问题的综合能力,是份较好的试卷。
【题文】一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.设全集{|0}=≥U x x ,集合{1}=P ,则U P =ð (A )[0,1)(1,)+∞ (B )(,1)-∞(C )(,1)(1,)-∞+∞ (D )(1,)+∞【知识点】集合的补集 A1【答案】【解析】A 解析:因为{|0}=≥U x x ,{1}=P ,所以U P =ð[0,1)(1,)+∞,故选A.【思路点拨】由补集运算直接计算可得.【题文】2.若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是(A ) (B ) (C ) (D ) 【知识点】三视图 G2 【答案】【解析】C 解析:由题意可得,A 是正方体,B 是三棱柱,C 是半个圆柱,D 是圆柱,C 不能满足正视图和侧视图是两个全等的正方形,故选C. 【思路点拨】由三视图的基本概念即可判断.【题文】3.已知复数z 43i =--(i 是虚数单位),则下列说法正确的是(A )复数z 的虚部为3i - (B )复数z 的虚部为3(C )复数z 的共轭复数为z 43i =+ (D )复数z 的模为5 【知识点】复数运算 L4 【答案】【解析】D 解析:由复数概念可知虚部为-3,其共轭为43i -+,故选D. 【思路点拨】由复数概念直接可得.【题文】4.函数31,0()1(),03x x x f x x ⎧+<⎪=⎨≥⎪⎩的图象大致为(A ) (B ) (C ) (D ) 【知识点】函数的图像 B6 B8【答案】【解析】A 解析:当0x <时,将3y x =的图像向上平移一个单位即可;当0x ≥时,取1()3xy =的图像即可,故选A.【思路点拨】由基本函数3y x =和1()3xy =的图像即可求得分段函数的图像.【题文】5.已知命题p :“若22≥+x a b ,则2≥x ab ”,则下列说法正确的是( ) (A )命题p 的逆命题是“若22<+x a b ,则2<x ab ” (B )命题p 的逆命题是“若2<x ab ,则22<+x a b ” (C )命题p 的否命题是“若22<+x a b ,则2<x ab ” (D )命题p 的否命题是“若22x a b ≥+,则2<x ab ”【知识点】四种命题 A2 【答案】【解析】C 解析:“若p 则q ”的逆命题是“若q 则p ”,否命题是“若p ⌝则q ⌝”,故选C. 【思路点拨】将原命题的条件和结论互换位置即可得到逆命题,分别写出条件和结论的否定为否命题. 【题文】6.若关于x 的方程240+-=x ax 在区间[2,4]上有实数根,则实数a 的取值范围是( ) (A )(3,)-+∞ (B )[3,0]- (C )(0,)+∞ (D )[0,3] 【知识点】二次函数 B5【答案】【解析】B 解析:因为240+-=x ax 在区间[2,4]上有实数根,令2(x)4f x ax =+-所以(2)(4)0f f ≤ ,即()21240a x +≤,30a ∴-≤≤ ,故选B.【思路点拨】二次函数在给定区间上根的分布问题,只需找准条件即可,不能丢解.【题文】7.已知F 是椭圆22221+=x y a b(0>>a b )的左焦点,A 为右顶点,P 是椭圆上一点,⊥PF x轴.若14=PF AF ,则该椭圆的离心率是( ) (A )14 (B )34 (C )12(D【知识点】椭圆的几何性质 H5【答案】【解析】B 解析:Rt PFA 中,222|PF ||FA ||PA |+=,||c FA a =+,2|PF |b a=, 又14=PF AF ,21(c)4b a a =+,得22430c ac a +-=,34c a ∴=,故选B.【思路点拨】Rt PFA 中, ||c FA a =+,2|PF |b a=,且14=PF AF ,得22430c ac a +-=,可求离心率.【题文】8.已知m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,则下列叙述正确的是(A )若//αβ,则//m n (B )若//m n ,则//αβ (C )若n α⊥,则m β⊥ (D )若m β⊥,则αβ⊥ 【知识点】线线关系,线面关系 G4 G5【答案】【解析】D 解析:A 中m ,n 可能异面;B 中α,β可能相交;C 中可能m β⊂或//m β,故选D.【思路点拨】熟悉空间中线线,线面关系的判断,逐一排除即可. 【题文】9.若552sin =α,1010)sin(=-αβ,且],4[ππα∈,]23,[ππβ∈,则αβ+的值是 (A )74π (B )94π (C )54π或74π (D )54π或94π【知识点】两角和与差的正弦、余弦 C7【答案】【解析】A 解析:()2αββαα+=-+,552sin =α,],4[ππα∈cos 2α∴=[,]42ππα∈,又1010)sin(=-αβ,[,]42ππα∈,]23,[ππβ∈,cos()βα∴-=sin()sin[()2]αββαα+=-+sin()cos 2cos()sin 2βααβαα=-+-((=+=, 又5[,2]4παβπ+∈,所以74παβ+=,故选A. 【思路点拨】利用角的变换()2αββαα+=-+,得sin()sin[()2]αββαα+=-+ sin()cos 2cos()sin 2βααβαα=-+-即可求解.【题文】10.如图,已知正方体1111ABCD A B C D -棱长为4,点H 在棱1AA 上,且11HA =.在侧面11BCC B 内作边长为1的正方形1EFGC ,P 是侧面11BCC B 内一动点,且点P 到平面11CDD C 距离等于线段PF 的长.则当点P 运动时, 2HP 最小值是( )(A )21 (B )22 (C )23 (D )25 【知识点】点、线、面间的距离计算 G11【答案】【解析】B 解析:点P 到平面11CDD C 距离就是点P 到直线1CC 的距离,所以点P 到点F 的距离等于点P 到直线1CC 的距离,因此点P 的轨迹是以F 为焦点,以1CC 为准线的抛物线,在面11A ABB 中作1HK BB ⊥于K ,连接KP ,在Rt HKP 中,222|HK ||PK ||HP |+=,而|HK |4=,要想2|HP |最小,只要|K |P 最小即可,由题意易求得min 2|K |6P =,所以2|HP |最小值为22,故选B.【思路点拨】注意到点P 到点F 的距离等于点P 到直线1CC 的距离,即点P 的轨迹是以F 为焦点,以1CC 为准线的抛物线,在Rt HKP 中,222|HK ||PK ||HP |+=,而|HK |4=,要想2|HP |最小,只要|K |P 最小即可.【题文】二、填空题:本大题共5小题,每小题5分,共25分.【题文】11.若非零向量a ,b 满足a b a b +=-,则a ,b 的夹角的大小为__________. 【知识点】向量的夹角 F3 【答案】【解析】090解析:a b a b +=-22||||a b a b ∴+=-,即0a b =,所以a b ⊥,a ,b 的夹角为090,故答案为090.【思路点拨】由a b a b +=-可得0a b =,所以夹角为090.【题文】12.二项式261()x x-的展开式中含3x 的项的系数是__________.(用数字作答) 【知识点】二项式定理 J3【答案】【解析】-20解析:2r6r6r 361661()()(1)r r r r T C x C x x---+=-=-,求展开式中含3x 的项的系数,此时3633r r -=∴=,因此系数为6r 366(1)120r C C --=-⨯=-,故答案为-20.【思路点拨】利用通项2r6r6r 361661()()(1)r r r r T C x C x x---+=-=-,可求r,即可求出系数.【题文】13.在∆ABC 中,内角,,A B C 的对边分别为,,a b c ,若2=c a ,4=b ,1cos 4=B ,则∆ABC 的面积=S __________.【知识点】余弦定理,正弦定理 C8【答案】2222cos b a c ac B =+-,得222116444a a a =+-⨯,2,4a c ∴==.面积11sin 2422S ac B ==⨯⨯=【思路点拨】【思路点拨】由余弦定理2222cos b a c ac B =+-可求24a =,再利用1sin 2S ac B =即可. 【题文】14.已知定义在R 上的奇函数()f x ,当0x ≥时,3()log (1)=+f x x .若关于x 的不等式2[(2)](22)f x a a f ax x ++≤+的解集为A ,函数()f x 在[8,8]-上的值域为B ,若“x A ∈”是“x B ∈”的充分不必要条件,则实数a 的取值范围是__________. 【知识点】充分、必要条件 A2【答案】【解析】[2,0]-解析:因为0x ≥时,奇函数3()log (1)=+f x x ,所以函数()f x 在R 上为增函数,2[(2)](22)f x a a f ax x ++≤+,2(2)22x a a ax x ∴++≤+,即()222(2)0x a x a a -+++≤,2a x a ∴≤≤+,{|2}A x a x a =≤≤+,{|22}B x x =-≤≤,因为“x A ∈”是“x B ∈”的充分不必要条件,所以A B ⊄,即22022a a a ≥-⎧∴-≤≤⎨+≤⎩,故答案为[2,0]-. 【思路点拨】因为“x A ∈”是“x B ∈”的充分不必要条件,所以A B ⊄,然后根据题意分别求出集合,A B 即可.【题文】15.已知曲线C :22y x a =+在点n P (n (0,a n >∈N )处的切线n l 的斜率为n k ,直线n l 交x 轴,y 轴分别于点(,0)n n A x ,(0,)n n B y ,且00=x y .给出以下结论: ①1a =;②当*n ∈N 时,n y 的最小值为54;③当*n ∈N 时,n k <;④当*n ∈N 时,记数列{}n k 的前n 项和为n S ,则1)n S . 其中,正确的结论有 (写出所有正确结论的序号) 【知识点】命题的真假判断A2【答案】【解析】①③④解析:因为曲线C :22y x a =+,所以()2'2'2y yy ==,即1'y k y === ,n k =,点n P ()n (0,a n >∈N )处的切线n l 为)y x n =-,,n n x n a y ∴=--= ,①00|x ||y |=,0,|||1n a a ∴=-=∴= ,正确;②1122n y ===12=112≥⨯=,所以n y 的最小值为1,错误;③012n <≤,∴> <亦即n k <,正确;④n k ==121n n n ++=+,22(2n 1)<+,<,<=,因为n k =,所以122(21321)n n S k k k n n =+++<-+-+++- 1), 故正确.【思路点拨】依题意,分别求出n k =, ,n n x n a y =--=,依次进行判断即可. 【题文】三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.【题文】16.(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球. (Ⅰ)求恰有一个黑球的概率; (Ⅱ)记取出红球的个数为随机变量X ,求X 的分布列和数学期望()E X . 【知识点】古典概型,分布列 K2 K6 【答案】【解析】(Ⅰ)15(Ⅱ)X 的分布列为:X 的数学期望1310121555=⨯+⨯+⨯=EX (Ⅰ)记“恰有一个黑球”为事件A ,则21243641()205⋅===C C P A C .……………………………………………………4分 (Ⅱ)X 的可能取值为0,1,2,则343641(0)205====C P X C ………………………………………………………2分122436123(1)205⋅====C C P X C …………………………………………………2分 1(2)()5===P X P A ……………………………………………………2分 ∴X 的分布列为∴X 的数学期望1310121555=⨯+⨯+⨯=EX .………………………………2分【思路点拨】)X 的可能取值为0,1,2,再分别求出(0)P X =,(1)P X =,(2)P X =即可.【题文】17.(本小题满分12分)如图,ABC ∆为正三角形,EC ⊥平面ABC ,//DB EC ,F 为EA 的中点,2EC AC ==,1BD =. (Ⅰ)求证:DF //平面ABC ;(Ⅱ)求平面DEA 与平面ABC 所成的锐二面角的余弦值.【知识点】线面平行,空间向量解决线面位置关系 G4 G10 【答案】【解析】 (Ⅰ)证明:作AC 的中点O ,连结BO .在∆AEC 中,//=FO 12EC ,又据题意知,//=BD 12EC . ∴//=FO BD ,∴四边形FOBD 为平行四边形. ∴//DF OB ,又⊄DF 平面ABC ,⊂OB 平面ABC .∴//DF 平面ABC .……………………………………4分 (Ⅱ)∵//FO EC ,∴⊥FO 平面ABC .在正∆ABC 中,⊥BO AC ,∴,,OA OB OF 三线两两垂直. 分别以,,OA OB OF 为,,z x y 轴,建系如图.则(1,0,0)A ,(1,0,2)-E,D . ∴(2,0,2)=-AE,(1=-AD . 设平面ADE 的一个法向量为1(,,z)=x y n ,则110⎧⋅=⎪⎨⋅=⎪⎩AE AD n n,即2200-+=⎧⎪⎨-++=⎪⎩x z x z ,令1=x ,则1,0==z y .∴平面ADE 的一个法向量为1(1,0,1)=n . 又平面ABC 的一个法向量为2(0,0,1)=n .∴121212,2⋅>===cos <n n n n n n . ∴平面DEA 与平面ABC.…………………………8分 【思路点拨】(Ⅰ)求证线面平行,可以利用线线平行,本题很容易找出//DF OB ; (Ⅱ)分别求平面DEA 与平面ABC 的法向量1(1,0,1)=n 2(0,0,1)=n ,∴121212,2⋅>===cos <n n n n n n ,即可求出余弦值. 【题文】18.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且22n n S a =-;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T .【知识点】等差数列,等比数列【答案】【解析】(Ⅰ)2n n a =,21n b n =-(Ⅱ)1(23)24+=-+n n T n (Ⅰ)∵22n n S a =- ①当2≥n 时,1122--=-n n S a ②①-②得,122-=-n n n a a a ,即12-=n n a a (2≥n ). 又当1≥n 时,1122=-S a ,得12=a .∴数列{}n a 是以2为首项,公比为2的等比数列,∴数列{}n a 的通项公式为1222-=⋅=n n n a .…………………………………4分 又由题意知,11b =,12n n b b +=+,即12+-=n n b b ∴数列{}n b 是首项为1,公差为2的等差数列,∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n .………………………2分 (Ⅱ)(Ⅱ)由(Ⅰ)知,(21)2=-n n c n …………………………………………1分 ∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅n n n T n n ③231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅n n n n T n n n ④由③-④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅n n n n T n ……………1分23112(12222)(21)2-+-=++++--⋅n n n n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n ……………………………………………1分 ∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n ∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n …………………………………3分【思路点拨】(Ⅰ)由条件直接求解即可;(Ⅱ)数列(21)2=-nn c n ,为差比数列,利用错位相减法直接求解. 【题文】19.(本小题满分12分)某大型企业一天中不同时刻的用电量y (单位:万千瓦时)关于时间t (024t ≤≤,单位:小时)的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象.(Ⅰ)根据图象,求A ,ω,ϕ,B 的值;(Ⅱ)若某日的供电量()g t (万千瓦时)与时间t (小时)近似满足函数关系式205.1)(+-=t t g (012t ≤≤).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1). 参考数据:【知识点】函数模型及其应用B10 【答案】【解析】(Ⅰ)1,22A B == ,12T =,6πω=(Ⅱ)11.625时(Ⅰ)由图知12T =,6πω=.………………………………………………1分2125.15.22m i n m a x =-=-=y y A ,225.15.22min max =+=+=y y B .……………2分 ∴0.5sin()26y x πϕ=++.又函数0.5sin()26y x πϕ=++过点(0,2.5).代入,得22k πϕπ=+,又0ϕπ<<,∴2πϕ=.…………………………………2分综上,21=A ,6πω=,2πϕ=,21=B . ………………………………………1分即2)26sin(21)(++=ππt t f . (Ⅱ)令)()()(t g t f t h -=,设0)(0=t h ,则0t 为该企业的停产时间. 由0)11()11()11(<-=g f h ,0)12()12()12(>-=g f h ,则)12,11(0∈t . 又0)5.11()5.11()5.11(<-=g f h ,则)12,5.11(0∈t .又0)75.11()75.11()75.11(>-=g f h ,则)75.11,5.11(0∈t .又0)625.11()625.11()625.11(<-=g f h ,则)75.11,625.11(0∈t .又0)6875.11()6875.11()6875.11(>-=g f h ,则)6875.11,625.11(0∈t .…4分……………………………………………1分∴应该在11.625时停产.……………………………………………………………1分(也可直接由0)625.11()625.11()625.11(<-=g f h ,0)6875.11()6875.11()6875.11(>-=g f h ,得出)6875.11,625.11(0∈t ;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产).【思路点拨】(Ⅰ)由三角函数图像可直接求)1,22A B == ,12T =,6πω=,代点(0,2.5)可求2πϕ=;(Ⅱ)理解二分法定义即可求解本题.【题文】20.(本小题满分13分) 已知椭圆Γ:12222=+byx (0>>b a )的右焦点为)0,22(,且椭圆Γ上一点M 到其两焦点12,F F的距离之和为(Ⅰ)求椭圆Γ的标准方程;(Ⅱ)设直线:(l y x m m =+∈R)与椭圆Γ交于不同两点A ,B ,且AB =0(,2)P x 满足=PA PB,求0x 的值.【知识点】直线与椭圆H8【答案】【解析】(Ⅰ)141222=+yx (Ⅱ)0x 的值为3-或1- (Ⅰ)由已知2=a =a ,又=c∴2224=-=b a c . ∴椭圆Γ的方程为141222=+y x .…………………………………………………4分 (Ⅱ)由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分 ∵直线l 与椭圆Γ交于不同两点A 、B ,∴△0)123(163622>--=m m ,得216<m .设),(11y x A ,),(22y x B ,则1x ,2x 是方程①的两根,则2321m x x -=+, 2123124-⋅=m x x .∴12=-==AB x又由AB =231294-+=m ,解之2m =±.……………………………3分 据题意知,点P 为线段AB 的中垂线与直线2=y 的交点.设AB 的中点为),(00y x E ,则432210m x x x -=+=,400m m x y =+=, ①当2m =时,31(,)22E - ∴此时,线段AB 的中垂线方程为13()22y x -=-+,即1y x =--. 令2=y ,得03x =-.…………………………………………………………………2分②当2m =-时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x +=--,即1y x =-+. 令2=y ,得01x =-.………………………………………………………………2分综上所述,0x 的值为3-或1-.【思路点拨】联立直线与椭圆,可得2m =±,因为=PA PB ,所以点P 为线段AB 的中垂线与直线2=y 的交点,分情况讨论即可求0x .【题文】21.(本小题满分14分)已知函数2()ln mx f x x =-,2()emx mx g x m =-,其中m ∈R 且0m ≠.e 2.71828=为自然对数的底数.(Ⅰ)当0m <时,求函数()f x 的单调区间和极小值; (Ⅱ)当0m >时,若函数()g x 存在,,a b c 三个零点,且a b c <<,试证明:10e a b c -<<<<<;(Ⅲ)是否存在负数m ,对1(1,)x ∀∈+∞,2(,0)x ∀∈-∞,都有12()()f x g x >成立?若存在,求出m 的取值范围;若不存在,请说明理由.【知识点】函数综合B14【答案】【解析】(Ⅰ)()2f x me =-极小值(Ⅱ)略(Ⅲ)(,(21)∈-∞-+m e e 解:(Ⅰ)2222)(ln )ln 21()(ln ln 2)(ln 1ln 2)(x x mx x x x x m x x x x x m x f -⋅=-=⋅--='(0>x 且1≠x ).∴由0)(>'x f ,得21e x >;由0)(<'x f ,得210e x <<,且1≠x .…………………1分∴函数)(x f的单调递减区间是(0,1),(1,单调递增区间是),(+∞e .……………2分 ∴me e f x f 2)()(-==极小值.……………………………………………………………1分 (Ⅱ)222(2)(),(0)mx mx mx mx mxe mx e m mx mx g x m e e--'=-=>. ∴()g x 在(,0)-∞上单调递增,2(0,)m 上单调递减,2(,)m +∞上单调递增. ∵函数()g x 存在三个零点. ∴20(0)02402()00>⎧>⎧⎪⎪⎪⇒⇒<<⎨⎨<⎪⎪-<⎩⎪⎩m g m e g m m m e . ∴02<<me …………………………………………………………………………………3分由(1)(1)0-=-=-<m m g m me m e . ∴22()(1)0=-=-<em em me e g e m m e e.……………………………………………………1分 综上可知,()0,(0)0,(1)0<>-<g e g g ,结合函数()g x 单调性及a b c <<可得:(1,0),(0,),(,)a b e c e ∈-∈∈+∞.即10a b e c -<<<<<,得证.…………………………………………………………1分(III )由题意,只需min max ()()>f x g x ∵2(12ln )()(ln )-'=mx x f x x 由0<m ,∴函数()f x 在12(1,)e 上单调递减,在12(,)e +∞上单调递增. ∴12min ()()2==-f x f e me .………………………………………………………………2分 ∵(2)()-'=mx mx mx g x e由0<m ,∴函数()g x 在2(,)m -∞上单调递增,2(,0)m 上单调递减. ∴max 224()()==-g x g m m e m.…………………………………………………………2分 ∴242->-me m e m ,不等式两边同乘以负数m ,得22242-<-m e m e.∴224(21)e m e+>,即224(21)m e e >+.由0<m ,解得(21)m e e <-+. 综上所述,存在这样的负数(,)(21)∈-∞-+m e e 满足题意.……………………………1分 【思路点拨】(Ⅰ)2(12ln )()(ln )mx x f x x ⋅-'=,由0)(>'x f 和0)(<'x f ,求得其单调区间,进而可求极值 ;(Ⅱ)(2)(),(0)mx mx mx g x m e -'=>,∴()g x 在(,0)-∞上单调递增,2(0,)m 上单调递减,2(,)m +∞上单调递增,得()0,(0)0,(1)0<>-<g e g g ,结合函数()g x 单调性及a b c <<可得10a b e c -<<<<<.(III )由题意,只需min max ()()>f x g x ,12min ()()2==-f x f e me ,max 224()()==-g x g m m e m,求解即可.。
2015年四川省宜宾市高考数学一诊试卷(理科)
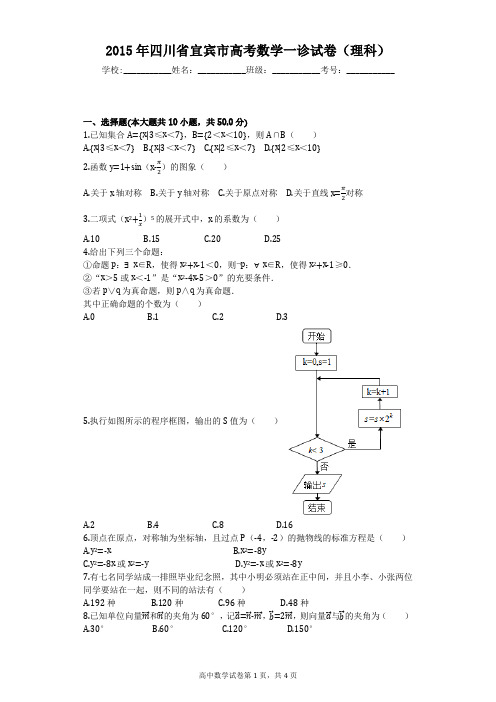
2015年四川省宜宾市高考数学一诊试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.已知集合A={x|3≤x<7},B={2<x<10},则A∩B()A.{x|3≤x<7}B.{x|3<x<7}C.{x|2≤x<7}D.{x|2≤x<10}2.函数y=1+sin(x-)的图象()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线x=对称3.二项式(x2+)5的展开式中,x的系数为()A.10B.15C.20D.254.给出下列三个命题:①命题p:∃x∈R,使得x2+x-1<0,则¬p:∀x∈R,使得x2+x-1≥0.②“x>5或x<-1”是“x2-4x-5>0”的充要条件.③若p∨q为真命题,则p∧q为真命题.其中正确命题的个数为()A.0B.1C.2D.35.执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.166.顶点在原点,对称轴为坐标轴,且过点P(-4,-2)的抛物线的标准方程是()A.y2=-xB.x2=-8yC.y2=-8x或x2=-yD.y2=-x或x2=-8y7.有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起,则不同的站法有()A.192种B.120种C.96种D.48种8.已知单位向量和的夹角为60°,记=-,=2,则向量与的夹角为()A.30°B.60°C.120°D.150°9.双曲线>,>的左右焦点为F1,F2,P是双曲线上一点,满足|PF2|=|F1F2|,直线PF1与圆x2+y2=a2相切,则双曲线的离心率为()A. B. C. D.10.设函数f(x)=,,>,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2a2t2+at,则正实数a的最小值是()A.2B.C.D.二、填空题(本大题共5小题,共25.0分)11.已知i是虚数单位,则= ______ .12.函数f(x)=x2+lnx的图象在点A(1,1)处的切线方程为______ .13.在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足bsin A=acos B,则角B 的大小为______ .14.在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1的中心,点Q在线段PD上运动,则异面直线BQ与A1D1所成角θ最大时,cosθ= ______ .15.对于函数f(x)=∞,有下列4个命题:①任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立;②f(x)=2kf(x+2k)(k∈N*),对于一切x∈[0,+∞)恒成立;③函数y=f(x)-ln(x-1)有3个零点;④对任意x>0,不等式f(x)≤恒成立.则其中所有真命题的序号是______ .三、解答题(本大题共6小题,共75.0分)16.已知函数f(x)=cos2ωx+2sinωxcosωx-sin2ωx(ω>0),且周期为π.(Ⅰ)求ω的值;(Ⅱ)当x∈[0,]时,求f(x)最大值及取得最大值时x的值.17.在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上,某种茶饮料一天的销售量与该天的日平均气温(单位:℃)有关,若日平均气温不超过15℃,则日销售量为100瓶;若日平均气温超过15℃但不超过20℃,则日销售量为150瓶;若日平均气温超过20℃,则日销售量为200瓶.据宜宾市气象部门预测,该地区在运动会期间每一天日平均气温不超过15℃,超过15℃但不超过20℃,超过20℃这三种情况发生的概率分别为P1,P2,P3,又知P1,P2为方程5x2-3x+a=0的两根,且P2=P3.(Ⅰ)求P1,P2,P3的值;(Ⅱ)记ξ表示该茶饮料在运动会期间任意两天的销售量总和(单位:瓶),求ξ的分布列及数学期望.18.如图,一简单几何体ABCDE的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(Ⅰ)证明:GH∥平面ACD;(Ⅱ)若AC=BC=BE=2,求二面角O-CE-B的余弦值.19.已知数列{a n}的前n项和为S n,向量=(S n,1),=(2n-1,),满足条件=λ,λ∈R且λ≠0.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设函数f(x)=()x,数列{b n}满足条件b1=2,f(b n+1)=,(n∈N+)(i)求数列{b n}的通项公式;(ii)设c n=,求数列{c n}的前n项和T n.20.已知点P,Q的坐标分别为(-2,0),(2,0),直线PM,QM相交于点M,且它们的斜率之积是-.(Ⅰ)求点M的轨迹方程;(Ⅱ)过点O作两条互相垂直的射线,与点M的轨迹交于A、B两点.试判断点O到直线AB的距离是否为定值.若是请求出这个定值,若不是请说明理由.21.已知函数f(x)=x4+ax3+bx2+c,其图象在y轴上的截距为-5,在区间[0,1]上单调递增,在[1,2]上单调递减,又当x=0,x=2时取得极小值.(Ⅰ)求函数f(x)的解析式;(Ⅱ)能否找到垂直于x轴的直线,使函数f(x)的图象关于此直线对称,并证明你的结论;(Ⅲ)设使关于x的方程f(x)=λ2x2-5恰有三个不同实根的实数λ的取值范围为集合A,且两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+2≤|x1-x2|对任意t∈[-3,3],λ∈A恒成立?若存在,求m的取值范围;若不存在,请说明理由.。
四川省绵阳市2015届高三数学第一次诊断试题 理

四川省绵阳市2015届高三数学第一次诊断试题 理本试卷分第I 卷〔选择题〕和第II 卷〔非选择题〕。
第I 卷1至2页,第II 卷2至4页.共4页。
总分为150分。
考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试完毕后,将答题卡交回。
第1卷〔选择题,共50分〕 须知事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
第I 卷共10小题。
一、选择题:本大题共10小题,每一小题5分,共50分.在每一小题给出的四个选项中,只有一个是符合题目要求的.集合A={x ∈Z|x2-1≤0},B={x|x2-x-2=0},如此A ∩B= (A)(B) {2}(C) {0}(D) {-1}2.如下说法中正确的答案是(A)命题“)0(∞+∈∀,x ,12>x 〞的否认是“)0(0∞+∉∃,x ,02x ≤1〞 (B)命题“)0(∞+∈∀,x ,12>x 〞的否认是“)0(0∞+∈∃,x ,02x ≤1〞 (C)命题“假设b a >,如此22b a >〞的逆否命题是“假设22b a <,如此b a <〞 (D)命题“假设b a >,如此22b a >〞的逆否命题是“假设2a ≥2b ,如此a ≥b 〞3.设各项均不为0的数列{an}满足n n a a 21=+(n≥1),Sn 是其前n 项和,假设5422a a a =,如此S4=(A) 42(B)28 (C) 233+(D) 266+4.如图,正六边形ABCDEF 的边长为1,如此DB AD ⋅= (A) -3 (B)3-(C) 3(D) 3ABDE F5.53)4cos(=-x π,那么sin 2x = (A) 2518 (B)2524±(C)257-(D)2576.x ,y 满足⎪⎩⎪⎨⎧≤--≥-+≥+-,,,0330101y x y x y x 如此2x-y 的最大值为(A) 1 (B) 2(C) 3 (D) 4 ://www 7.x ∈[π-,π],如此“x ∈]22[ππ,-〞是“sin(sinx)<cos(cosx)成立〞的 (A) 充要条件(B) 必要不充分条件(C) 充分不必要条件(D) 既不充分也不必要条件8.)(x f 是定义在非零实数集上的函数,)(x f '为其导函数,且0>x 时,0)()(<-'x f x f x ,记5log )5(log 2.0)2.0(2)2(22222.02.0f c f b f a ===,,,如此(A)c b a <<(B)c a b << (C)b a c <<(D)a b c <<9.函数⎪⎩⎪⎨⎧>≠><-=0)10(log 01)2sin()(x a a x x x x f a ,,且,,π的图象上关于y 轴对称的点至少有3对,如此实数a 的取值范围是(A))330(,(B) )155(,(C) )133(, (D))550(, 10.∈b a ,R ,且1+x e ≥b ax +对x ∈R 恒成立,如此ab 的最大值是(A)321e (B)322e (C) 323e (D)3e第II 卷〔非选择题 共100分〕 须知事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指的答题区域内作答。
四川省成都市2015届高中毕业班第一次诊断性检测数学(理)试题含答案

成都市2015届高中毕业班第一次诊断性检测数学试题(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{|0}=≥U x x,集合{1}=P,则UP=ð(A)[0,1)(1,)+∞(B)(,1)-∞(C)(,1)(1,)-∞+∞(D)(1,)+∞2.若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是(A)(B)(C)(D)3.已知复数z43i=--(i是虚数单位),则下列说法正确的是(A)复数z的虚部为3i-(B)复数z的虚部为3(C)复数z的共轭复数为z43i=+(D)复数z的模为54.函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为(A)(B)(C)(D)5.已知命题p:“若22≥+x a b,则2≥x ab”,则下列说法正确的是(A)命题p的逆命题是“若22<+x a b,则2<x ab”(B)命题p的逆命题是“若2<x ab,则22<+x a b”G FEHPACBDA 1B 1C 1D 1(C )命题p 的否命题是“若22<+x a b ,则2<x ab ” (D )命题p 的否命题是“若22x a b ≥+,则2<x ab ”6.若关于x 的方程240+-=x ax 在区间[2,4]上有实数根,则实数a 的取值范围是 (A )(3,)-+∞ (B )[3,0]- (C )(0,)+∞ (D )[0,3]7.已知F 是椭圆22221+=x y a b(0>>a b )的左焦点,A 为右顶点,P 是椭圆上一点,⊥PF x 轴.若14=PF AF ,则该椭圆的离心率是 (A )14(B )34 (C )12(D )28.已知m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,则下列叙述正确的是(A )若//αβ,则//m n (B )若//m n ,则//αβ (C )若n α⊥,则m β⊥ (D )若m β⊥,则αβ⊥9.若552sin =α,1010)sin(=-αβ,且],4[ππα∈,]23,[ππβ∈,则αβ+的值是 (A )74π (B )94π (C )54π或74π (D )54π或94π 10.如图,已知正方体1111ABCD A B C D -棱长为4,点H 在棱1AA 上,且11HA =.在侧面11BCC B 内作边长为1的正方形1EFGC ,P 是侧面11BCC B 内一动点,且点P 到平面11CDD C 距离等于线段PF 的长.则当点P 运动时, 2HP 的最小值是 (A )21(B )22 (C )23 (D )25二、填空题:本大题共5小题,每小题5分,共25分.11.若非零向量a ,b 满足a b a b +=-,则a ,b 的夹角的大小为__________. 12.二项式261()x x-的展开式中含3x 的项的系数是__________.(用数字作答) 13.在∆ABC 中,内角,,A B C 的对边分别为,,a b c ,若2=c a ,4=b ,1cos 4=B ,则∆ABC 的面积=S __________.14.已知定义在R 上的奇函数()f x ,当0x ≥时,3()log (1)=+f x x .若关于x 的不等式2[(2)](22)f x a a f ax x ++≤+的解集为A ,函数()f x 在[8,8]-上的值域为B ,若“x A ∈”是“x B ∈”的充分不必要条件,则实数a 的取值范围是__________.15.已知曲线C :22y x a =+在点n P (n (0,a n >∈N )处的切线n l 的斜率为n k ,直线n l 交x 轴,y 轴分别于点(,0)n n A x ,(0,)n n B y ,且00=x y .给出以下结论: ①1a =;②当*n ∈N 时,n y 的最小值为54; ③当*n ∈N 时,n k <; ④当*n ∈N 时,记数列{}n k 的前n 项和为n S ,则1)n S .其中,正确的结论有 (写出所有正确结论的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球. (Ⅰ)求恰有一个黑球的概率;(Ⅱ)记取出红球的个数为随机变量X ,求X 的分布列和数学期望()E X .17.(本小题满分12分)如图,ABC ∆为正三角形,EC ⊥平面ABC ,//DB EC ,F 为EA 的中点,2EC AC ==,1BD =.(Ⅰ)求证:DF //平面ABC ;(Ⅱ)求平面DEA 与平面ABC 所成的锐二面角的余弦值. 18.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且22n n S a =-;数列{}n b 满足11b =,12n n b b +=+.*n ∈N .(Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)记n n n c a b =,*n ∈N .求数列{}n c 的前n 项和n T . 19.(本小题满分12分)某大型企业一天中不同时刻的用电量y (单位:万千瓦时)关于时间t (024t ≤≤,单位:小时)的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<,下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象. (Ⅰ)根据图象,求A ,ω,ϕ,B 的值; (Ⅱ)若某日的供电量()g t (万千瓦时)与时间t (小时)近似满足函数关系式205.1)(+-=t t g (012t ≤≤).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1). 参考数据:20.(本小题满分13分)已知椭圆Γ:12222=+by a x (0>>b a )的右焦点为)0,22(,且椭圆Γ上一点M 到其两焦点12,F F 的距离之和为(Ⅰ)求椭圆Γ的标准方程; (Ⅱ)设直线:(l y x m m =+∈R)与椭圆Γ交于不同两点A ,B ,且AB =若点0(,2)P x 满足=PA PB ,求0x 的值. 21.(本小题满分14分)已知函数2()ln mx f x x =-,2()emx mx g x m =-,其中m ∈R 且0m ≠.e 2.71828=为自然对数的底数.(Ⅰ)当0m <时,求函数()f x 的单调区间和极小值;(Ⅱ)当0m >时,若函数()g x 存在,,a b c 三个零点,且a b c <<,试证明:10e a b c -<<<<<;(Ⅲ)是否存在负数m ,对1(1,)x ∀∈+∞,2(,0)x ∀∈-∞,都有12()()f x g x >成立?若存在,求出m 的取值范围;若不存在,请说明理由.数学(理科)参考答案及评分意见第Ⅰ卷(选择题,共50分)一、选择题:(本大题共10个小题,每小题5分,共50分)1.A ; 2.C ; 3.D ;4.A ;5.C ;6.B ;7.B ;8.D ;9.A ;10.B .第Ⅱ卷(非选择题,共100分)二、填空题:(本大题共5个小题,每小题5分,共25分)11.90︒ 12.20- 1314.[2,0]- 15.①③④ 三、解答题:(本大题共6个小题,共75分) 16.(本小题满分12分) 解:(Ⅰ)记“恰有一个黑球”为事件A ,则21243641()205⋅===C C P A C .……………………………………………………………4分 (Ⅱ)X 的可能取值为0,1,2,则343641(0)205====C P X C ……………………………………………………………2分122436123(1)205⋅====C C P X C ………………………………………………………2分 1(2)()5===P X P A ………………………………………………………………2分 ∴X 的分布列为∴X 的数学期望1310121555=⨯+⨯+⨯=EX .…………………………………2分 17.(本小题满分12分)(Ⅰ)证明:作AC 的中点O ,连结BO .在∆AEC 中,//=FO 12EC ,又据题意知,//=BD 12EC .∴//=FO BD ,∴四边形FOBD 为平行四边形. ∴//DF OB ,又⊄DF 平面ABC ,⊂OB 平面ABC .∴//DF 平面ABC .……………………………………4分(Ⅱ)∵//FO EC ,∴⊥FO 平面ABC .在正∆ABC 中,⊥BO AC ,∴,,OA OB OF 三线两两垂直. 分别以,,OA OB OF 为,,z x y 轴,建系如图. 则(1,0,0)A ,(1,0,2)-E,D . ∴(2,0,2)=-AE,(1=-AD . 设平面ADE 的一个法向量为1(,,z)=x y n ,则110⎧⋅=⎪⎨⋅=⎪⎩AE AD n n,即2200-+=⎧⎪⎨-++=⎪⎩x z x z ,令1=x ,则1,0==z y .∴平面ADE 的一个法向量为1(1,0,1)=n . 又平面ABC 的一个法向量为2(0,0,1)=n .∴121212,2⋅>===cos <n n n n n n . ∴平面DEA 与平面ABC8分 18.(本小题满分12分) 解:(Ⅰ)∵22n n S a =- ①当2≥n 时,1122--=-n n S a ②①-②得,122-=-n n n a a a ,即12-=n n a a (2≥n ). 又当1≥n 时,1122=-S a ,得12=a .∴数列{}n a 是以2为首项,公比为2的等比数列,∴数列{}n a 的通项公式为1222-=⋅=n n n a .………………………………………4分 又由题意知,11b =,12n n b b +=+,即12+-=n n b b ∴数列{}n b 是首项为1,公差为2的等差数列,∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n .……………………………2分(Ⅱ)(Ⅱ)由(Ⅰ)知,(21)2=-n n c n ………………………………………………1分 ∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅n n n T n n ③231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅n n n n T n n n ④由③-④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅n n n n T n …………………1分23112(12222)(21)2-+-=++++--⋅n n n n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n …………………………………………………1分 ∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n ∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n ………………………………………3分 19.(本小题满分12分) 解:(Ⅰ)由图知12T =,6πω=.………………………………………………………1分2125.15.22m i n m a x =-=-=y y A ,225.15.22min max =+=+=y y B .……………2分 ∴0.5sin()26y x πϕ=++.又函数0.5sin()26y x πϕ=++过点(0,2.5).代入,得22k πϕπ=+,又0ϕπ<<,∴2πϕ=.…………………………………2分综上,21=A ,6πω=,2πϕ=,21=B . ………………………………………1分即2)26sin(21)(++=ππt t f . (Ⅱ)令)()()(t g t f t h -=,设0)(0=t h ,则0t 为该企业的停产时间. 由0)11()11()11(<-=g f h ,0)12()12()12(>-=g f h ,则)12,11(0∈t . 又0)5.11()5.11()5.11(<-=g f h ,则)12,5.11(0∈t .又0)75.11()75.11()75.11(>-=g f h ,则)75.11,5.11(0∈t . 又0)625.11()625.11()625.11(<-=g f h ,则)75.11,625.11(0∈t .又0)6875.11()6875.11()6875.11(>-=g f h ,则)6875.11,625.11(0∈t .…4分……………………………………………1分 ∴应该在11.625时停产.……………………………………………………………1分 (也可直接由)625.11()625.11()625.11(<-=g f h ,0)6875.11()6875.11()6875.11(>-=g f h ,得出)6875.11,625.11(0∈t ;答案在11.625—11.6875之间都是正确的;若换算成时间应为11点37分到11点41分停产) 20.(本小题满分13分)(Ⅰ)由已知2=a=a,又=c ∴2224=-=b a c .∴椭圆Γ的方程为141222=+y x .…………………………………………………4分 (Ⅱ)由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分∵直线l 与椭圆Γ交于不同两点A 、B ,∴△0)123(163622>--=m m , 得216<m .设),(11y x A ,),(22y x B ,则1x ,2x 是方程①的两根,则2321mx x -=+, 2123124-⋅=m x x .∴12=-=AB x又由AB =231294-+=m ,解之2m =±.……………………………3分 据题意知,点P 为线段AB 的中垂线与直线2=y 的交点.设AB 的中点为),(00y x E ,则432210m x x x -=+=,400mm x y =+=, ①当2m =时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x -=-+,即1y x =--. 令2=y ,得03x =-.…………………………………………………………………2分 ②当2m =-时,31(,)22E -∴此时,线段AB 的中垂线方程为13()22y x +=--,即1y x =-+. 令2=y ,得01x =-.………………………………………………………………2分 综上所述,0x 的值为3-或1-. 21.(本小题满分14分)解:(Ⅰ)2222)(ln )ln 21()(ln ln 2)(ln 1ln 2)(x x mx x x x x m x x x x x mx f -⋅=-=⋅--='(0>x 且1≠x ).∴由0)(>'x f ,得21e x >;由0)(<'xf ,得210e x <<,且1≠x .……………………1分 ∴函数)(x f的单调递减区间是(0,1),(1,单调递增区间是),(+∞e .………………2分 ∴me e f x f 2)()(-==极小值.………………………………………………………………1分(Ⅱ)222(2)(),(0)mx mx mx mxmxe mx e m mx mx g x m e e--'=-=>. ∴()g x 在(,0)-∞上单调递增,2(0,)m上单调递减,2(,)m +∞上单调递增.∵函数()g x 存在三个零点.∴20(0)02402()00>⎧>⎧⎪⎪⎪⇒⇒<<⎨⎨<⎪⎪-<⎩⎪⎩m g m e g m m m e . ∴02<<me …………………………………………………………………………………3分 由(1)(1)0-=-=-<mmg m me m e .∴22()(1)0=-=-<em em me e g e m m e e.……………………………………………………1分综上可知,()0,(0)0,(1)0<>-<g e g g ,结合函数()g x 单调性及a b c <<可得:(1,0),(0,),(,)a b e c e ∈-∈∈+∞.即10a b e c -<<<<<,得证.…………………………………………………………1分 (III )由题意,只需min max ()()>f x g x ∵2(12ln )()(ln )-'=mx x f x x 由0<m ,∴函数()f x 在12(1,)e 上单调递减,在12(,)e +∞上单调递增.∴12min ()()2==-f x f e me .………………………………………………………………2分 ∵(2)()-'=mxmx mx g x e由0<m ,∴函数()g x 在2(,)m -∞上单调递增,2(,0)m上单调递减. ∴max 224()()==-g x g m m e m .……………………………………………………………2分 ∴242->-me m e m ,不等式两边同乘以负数m ,得22242-<-m e m e.∴224(21)e m e+>,即224(21)m e e >+.由0<m ,解得m <.综上所述,存在这样的负数(,)(21)∈-∞-+m e e 满足题意.……………………………1分。
【数学】2014-2015年四川省宜宾市高三(上)期中数学试卷与答案(理科)

2014-2015学年四川省宜宾市高三(上)期中数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1.(5分)tan(﹣210°)=()A.B.﹣C.D.﹣2.(5分)若a>b>0,c>d>0,则一定有()A.>B.<C.>D.<3.(5分)计算的结果为()A.B.2lg7 C.0 D.14.(5分)已知角α的终边经过点P(﹣5,12),则cosα=()A.B.﹣C.D.﹣5.(5分)等比数列的前n项,前2n项,前3n项的和分别为a,b,c,则()A.b+a=c B.b2=ac C.a2+b2=a(b+c)D.(a+b)﹣c=b26.(5分)要得到y=cos2x的图象只需将y=cos(﹣2x+)的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位7.(5分)已知x,y满足约束条件,则z=3x+5y的最大值为()A.0 B.5 C.3 D.178.(5分)利用校园内围墙一角和篱笆围成一个面积为128m2的直角梯形花园,已知两围墙所成角为135°(如图),则所用篱笆总长度的最小值为()A.16m B.32m C.64m D.16m9.(5分)已知△ABC中,设角A,B,C所对的边分别为a,b,c,G为△ABC的重心,且a+b+c=,则△ABC为()A.等腰直角三角形 B.直角三角形C.等腰三角形D.等边三角形10.(5分)已知函数:①f(x)=3lnx;②f(x)=3e cosx;③f(x)=3e x;④f(x)=3cosx.其中对于f(x)定义域内的任意一个自变量x1都存在唯一一个自变量x2,使=3成立的函数是()A.③B.②③C.①②④D.④二、填空题:本大题共5小题,每小题5分,共25分.11.(5分)已知||=12,||=9,•=﹣54,则与的夹角为.12.(5分)在等差数列{a n}中,a2+a7=20,则数列{a n}的前8项之和S8=.13.(5分)已知函数f(x)=的定义域为R,则实数k的取值范围为.14.(5分)已知长度分别为1、2、3、4、6的5根小棒,只可拼接不可折断,将这5根小棒拼接成一个三角形,当这个三角形的面积最大时,则最大角的余弦值为.15.(5分)已知函数f(x)=,设函数g(x)=f2(x)+f(x)+t,则关于g(x)的零点,下列说法正确的是.(请填上你认为正确答案的序号)①t=时,g(x)有一个零点②﹣2<t<时,g(x)有两个零点③t=﹣2时,g(x)有三个零点④t<﹣2时,g(x)有四个零点.三、解答题:本大题共6小题,共75分.解答须写出文字说明,证明过程或演算步骤.16.(12分)在等比数列{a n}中,a5﹣a1=15,a4为a2与6的等差中项,求数列{a n}的公比及通项公式.17.(12分)已知函数f(x)=sin(2x+)+cos(2x﹣),(x∈R)(Ⅰ)求f(x)的单调增区间;(Ⅱ)若f(﹣)=,α∈(,π),求tan(α﹣)的值.18.(12分)已知点O(0,0),A(1,2),B(4,5),C(1,﹣2),=+λ.(1)当λ=2时,求的坐标;(2)若⊥,且向量=(2+t,),其中t∈(0,+∞),求•的最大值.19.(12分)在△ABC,角A、B、C所对的边分别为a,b,c,满足=(Ⅰ)求角C;(Ⅱ)若c=,且△ABC的面积为,求a+b的值.20.(13分)已知数列{a n}满足a1=1,且点A(a n,a n+1)(n∈N*)在直线y=x+2上,数列{b n}的前n项和为S n,且S n=2b n﹣2(n∈N*)(Ⅰ)求数列{a n}及{b n}的通项公式;(Ⅱ)设c n=b n sin2﹣a n cos2(n∈N*),求数列{c n}的前2n项和T2n.21.(14分)已知f(x)=lnx,g(x)=(a是常数),F(x)=f(x)﹣g(x)(Ⅰ)当a<0时,求函数F(x)的单调区间;(Ⅱ)若F(x)在[1,e]上的最小值为,求a的值;(Ⅲ)是否存在实数m,使得函数y=g()+m﹣1(a≠0)的图象与函数y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围;若不存在,请说明理由.2014-2015学年四川省宜宾市高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的1.(5分)tan(﹣210°)=()A.B.﹣C.D.﹣【解答】解:tan(﹣210°)=﹣tan210°=﹣tan(180°+30°)=﹣tan30°=﹣,故选:D.2.(5分)若a>b>0,c>d>0,则一定有()A.>B.<C.>D.<【解答】解:∵c>d>0,∴,又a>b>0,∴.故选:C.3.(5分)计算的结果为()A.B.2lg7 C.0 D.1【解答】解:原式=+lg5+1=+1=.故选:A.4.(5分)已知角α的终边经过点P(﹣5,12),则cosα=()A.B.﹣C.D.﹣【解答】解:r==13,则cosα==﹣,故选:B.5.(5分)等比数列的前n项,前2n项,前3n项的和分别为a,b,c,则()A.b+a=c B.b2=ac C.a2+b2=a(b+c)D.(a+b)﹣c=b2【解答】解:由等比数列的性质可知,等比数列的第一个n项和,第二个n项和,第三个n项和仍然构成等比数列,则有:a,b﹣a,c﹣b构成等比数列,∴(b﹣a)2=a(c﹣b),即b2﹣2ab+a2=ac﹣ab,∴a2+b2=a(b+c).故选:C.6.(5分)要得到y=cos2x的图象只需将y=cos(﹣2x+)的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【解答】解:将y=cos(﹣2x+)=cos(2x﹣)的图象向左平移个单位,可得y=cos[2(x+)+]=cos2x的图象,故选:B.7.(5分)已知x,y满足约束条件,则z=3x+5y的最大值为()A.0 B.5 C.3 D.17【解答】解:作出不等式组对应的平面区域如图:由z=3x+5y得y=﹣x+,平移直线y=﹣x+,由图象可知当直线y=﹣x+经过点A时,直线y=﹣x+的截距最大,此时z最大,由,解得,即A(),此时z=2×+5×=17,故选:D.8.(5分)利用校园内围墙一角和篱笆围成一个面积为128m2的直角梯形花园,已知两围墙所成角为135°(如图),则所用篱笆总长度的最小值为()A.16m B.32m C.64m D.16m【解答】解:如图,设BD=x,设篱笆长度为y,则CD=y﹣x,AB=y﹣2x,梯形的面积为=128,整理得y=,当=x等号成立,所以篱笆总长度最小为16m.故选:A.9.(5分)已知△ABC中,设角A,B,C所对的边分别为a,b,c,G为△ABC的重心,且a+b+c=,则△ABC为()A.等腰直角三角形 B.直角三角形C.等腰三角形D.等边三角形【解答】解:∵G为△ABC的重心,∴,又a+b+c=,∴=,∴a﹣1=b﹣1=c﹣1=0,解得a=b=c=1,∴△ABC是等边三角形.故选:D.10.(5分)已知函数:①f(x)=3lnx;②f(x)=3e cosx;③f(x)=3e x;④f(x)=3cosx.其中对于f(x)定义域内的任意一个自变量x1都存在唯一一个自变量x2,使=3成立的函数是()A.③B.②③C.①②④D.④【解答】解:在①f(x)=3lnx中,∵f(1)=0,∴不存在自变量x 2,使=3成立,故①不成立;在②f(x)=3e cosx中,∵函数不是单调函数,∴对于定义域内的任意一个自变量x 1,使=3成立的自变量x2不唯一,故②不成立;在③f(x)=3e x中,函数是单调函数,且函数值不为0,故定义域内的任意一个自变量x 1都存在唯一一个自变量x2,使=3成立,故③成立;在④f(x)=3cosx中,∵f()=0,∴不存在自变量x 2,使=3成立,故④不成立.故选:A.二、填空题:本大题共5小题,每小题5分,共25分.11.(5分)已知||=12,||=9,•=﹣54,则与的夹角为.【解答】解:由||=12,||=9,•=﹣54,可得=12×9cos<,>=﹣54,即cos<,>=﹣,由0≤<,>≤π,则有与的夹角为.故答案为:.12.(5分)在等差数列{a n}中,a2+a7=20,则数列{a n}的前8项之和S8=80.【解答】解:由等差数列的性质可得a1+a8=a2+a7=20,∴数列{a n}的前8项之和S8==80故答案为:8013.(5分)已知函数f(x)=的定义域为R,则实数k的取值范围为[0,4).【解答】解:∵函数f(x)=的定义域为R,∴等价为kx2+kx+1>0恒成立,若k=0,则不等式等价为1>0,成立,若k≠0,要使不等式恒成立,则满足,即,解得0<k<4,综上0≤k<4,故答案为:[0,4)14.(5分)已知长度分别为1、2、3、4、6的5根小棒,只可拼接不可折断,将这5根小棒拼接成一个三角形,当这个三角形的面积最大时,则最大角的余弦值为.【解答】解:最大三角形的边长应为6,5,5,∴由余弦定理可得:最大角的余弦值==.故答案为:.15.(5分)已知函数f(x)=,设函数g(x)=f2(x)+f(x)+t,则关于g(x)的零点,下列说法正确的是①②③.(请填上你认为正确答案的序号)①t=时,g(x)有一个零点②﹣2<t<时,g(x)有两个零点③t=﹣2时,g(x)有三个零点④t<﹣2时,g(x)有四个零点.【解答】解:作出函数f(x)的图象,如右.对于①,t=时,g(x)=f2(x)+f(x)+,令g(x)=0,则f(x)=﹣,由图象可得y=﹣和y=f(x)只有一个交点,则零点个数为1,故①对;对于②,﹣2<t<时,由f2(x)+f(x)+t=0,判别式△=1﹣4t,可得0<<3,解得f(x)=,即有﹣<f(x)<1,或﹣2<f(x)<﹣,由图象可得有两个交点,则有2个零点,故②对;对于③,t=﹣2时,g(x)=0,解得f(x)=﹣2或1,由图象可得x1=0,x2=﹣3,x3=﹣,则有3个零点,故③对;对于④,t<﹣2时,由f2(x)+f(x)+t=0,判别式△=1﹣4t,可得>3,解得f(x)=,则有f(x)>1或f(x)<﹣2,则由图象可得有两个交点,则有2个零点,故④错.故答案为:①②③.三、解答题:本大题共6小题,共75分.解答须写出文字说明,证明过程或演算步骤.16.(12分)在等比数列{a n}中,a5﹣a1=15,a4为a2与6的等差中项,求数列{a n}的公比及通项公式.【解答】解:设等比数列{a n}的公比为q,∵a5﹣a1=15,a4为a2与6的等差中项,∴a1q4﹣a1=15,①,a1q3=a1q+6,②由①②得=,解得a=或q=2,当q=时,a1=﹣16,a n=﹣25﹣n;当q=2时,a1=1,a n=2n﹣117.(12分)已知函数f(x)=sin(2x+)+cos(2x﹣),(x∈R)(Ⅰ)求f(x)的单调增区间;(Ⅱ)若f(﹣)=,α∈(,π),求tan(α﹣)的值.【解答】解:(I)f(x)=sin(2x+)+cos(2x﹣)=+==,令:,(k∈Z).解得:,(k∈Z).所以:函数的单调递增区间为:[](k∈Z);(II)根据f(x)=,所以:,解得:2sin,,由于,所以:.tanα=﹣,tan2α==﹣,所以:=.18.(12分)已知点O(0,0),A(1,2),B(4,5),C(1,﹣2),=+λ.(1)当λ=2时,求的坐标;(2)若⊥,且向量=(2+t,),其中t∈(0,+∞),求•的最大值.【解答】解:(1)由已知=(1,2),=(3,3),λ=2,则=+2=(1,2)+2(3,3)=(7,8).所以=(7,8);(2)若⊥,,=+λ=(1+3λ,2+3λ).所以1+3λ﹣2(2+3λ)=0,即λ=﹣1,所以=(﹣2,﹣1),向量=(2+t,),其中t∈(0,+∞),所以•=﹣4﹣2t﹣=﹣4﹣2(t+)≤﹣4﹣4=﹣8,当且仅当t==1时等号成立;19.(12分)在△ABC,角A、B、C所对的边分别为a,b,c,满足=(Ⅰ)求角C;(Ⅱ)若c=,且△ABC的面积为,求a+b的值.【解答】解:(Ⅰ)由正弦定理=即为=,即b(a﹣b)=(a+c)(a﹣c),即有a2+b2﹣c2=ab,由余弦定理可得cosC===,由于C为三角形的内角,则C=;(Ⅱ)c2=a2+b2﹣2abcos60°=a2+b2﹣ab,即有a2+b2﹣ab=7,即(a+b)2﹣3ab=7,S△ABC=absin60°=,即ab=6,则(a+b)2=7+3ab=7+18=25,则有a+b=5.20.(13分)已知数列{a n}满足a1=1,且点A(a n,a n+1)(n∈N*)在直线y=x+2上,数列{b n}的前n项和为S n,且S n=2b n﹣2(n∈N*)(Ⅰ)求数列{a n}及{b n}的通项公式;(Ⅱ)设c n=b n sin2﹣a n cos2(n∈N*),求数列{c n}的前2n项和T2n.【解答】解:(Ⅰ)数列{a n}满足a1=1,且点A(a n,a n+1)(n∈N*)在直线y=x+2上,∴a n=a n+2,…(1分)+1∴{a n}是等差数列,公差为2,首项a1=1,∴a n=2n﹣1.…(3分)又当n=1时,S1=b1=2b1﹣2,解得b1=2,…(4分)当n≥2时,b n=S n﹣S n﹣1=2b n﹣2b n﹣1,…(5分)∴b n=2b n﹣1,n≥2,∴{b n}是等比数列,公比为2,首项b1=2,∴,…(6分)(Ⅱ)∵c n=b n sin2﹣a n cos2(n∈N*),∴,…(9分)T2n=(b1+b3+…+b2n﹣1)﹣(a2+a4+…+a2n)…(11分)=(2+23+…+22n﹣1)﹣[3+7+…+(4n﹣1)]=﹣2n2﹣n.…(13分)21.(14分)已知f(x)=lnx,g(x)=(a是常数),F(x)=f(x)﹣g(x)(Ⅰ)当a<0时,求函数F(x)的单调区间;(Ⅱ)若F(x)在[1,e]上的最小值为,求a的值;(Ⅲ)是否存在实数m,使得函数y=g()+m﹣1(a≠0)的图象与函数y=f(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围;若不存在,请说明理由.【解答】解:(I)F(x)=lnx﹣,其定义域为(0,+∞),…(1分)又F′(x)=,…(2分)∵a<0,x∈(﹣a,+∞),F′(x)>0,x∈(0,﹣a),F′(x)<0…(3分)故F(x)的增区间是(﹣a,+∞),减区间是(0,﹣a),…(4分)(Ⅱ)由题可知,F′(x)=,①若a≥﹣1,则x+a≥0,f(x)在[1,e]上为增函数,[F(x)]min=f(1)=﹣a=,∴a=﹣(舍去);…(5分)②若a ≤﹣e ,则x +a ≤0,f (x )在[1,e ]上为减函数, [F (x )]min =f (e )=1﹣=,∴a=﹣,(舍去);…(6分)③若﹣e <a <﹣1,1<x <﹣a ,F′(x )<0,函数在(1,﹣a )上为减函数,﹣a <x <e ,F′(x )>0,函数在(1,﹣a )上为增函数, [F (x )]min =f (﹣a )=ln (﹣a )+1=,∴a=﹣,综上所述,a=﹣.…(8分)(Ⅲ)y=g ()+m ﹣1=x 2+m ﹣的图象与函数y=f (1+x 2)=ln (1+x 2)的图象恰有四个不同的交点,即x 2+m ﹣=ln (1+x 2)有四个不同的根,亦即m=ln (1+x 2)﹣x 2﹣有四个不同的根;令G (x )=ln (1+x 2)﹣x 2﹣, 则G'(x )=当x 变化时,G'(x ),G (x )的变化情况如下表,由表格知,G (x )的极小值G (0)=﹣,G (x )的极大值G (1)=G (﹣1)=ln2>0.∴m ∈(,ln2),y=G (x )与y=m 恰有四个不同的交点, 即当m ∈(,ln2)时,函数y=g ()+m ﹣1的图象与函数y=f (1+x 2)的图象恰有四个不同的交点.…(14分)赠送—高中数学知识点二次函数(1)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔xy1x 2x 0>a O∙ab x 2-=0)(>k f k x y1x 2x O∙ab x 2-=k<a 0)(<k f②x 1≤x 2<k ⇔xy1x 2x 0>a O∙ab x 2-=k 0)(>k f xy1x 2x O∙ab x 2-=k<a 0)(<k f③x 1<k <x 2 ⇔ af (k )<0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1<x 1≤x 2<k 2 ⇔⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔ f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2<k fxy1x 2x O∙<a 1k∙2k 0)(1>k f 0)(2<k f⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ②02b x a->,则()M f p = x>O-=f(p) f (q)()2b f a-x>O-=f (p)f (q)()2b f a-x(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,则()M f q =①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =.x>O -=f(p) f(q) ()2b f a-0x x<O-=f (p) f (q) ()2bf a-x<O-=f (p)f(q)()2b f a-x<O-=f (p)f(q)()2bf a-0xx<O-=f (p)f (q)()2b f a-x<O-=f (p)f (q)()2b f a-0x。
宜宾市2015届一诊考试数学理试题含答案

- 1 - 宜宾2014高三一诊理科数学1.已知集合102,73x x B x x A ,则BA (A) 73x x (B) 73x x (C) 72x x (D) 102x x 2.函数)2sin(1x y 的图象(A) 关于x 轴对称(B) 关于y 轴对称(C) 关于原点对称(D)关于直线2x 对称3.二项式52)1x x (的展开式中,x 的系数为(A) 10 (B) 15 (C) 20 (D) 254.给出下列三个命题:①命题p :x R ,使得012x x ,则p :x R ,使得012x x ②”或“15x x 是“2450x x ”的充要条件. ③若p q 为真命题,则p q 为真命题. 其中正确..命题的个数为(A) 0(B) 1(C) 2(D) 35.执行如图所示的程序框图,输出的S 值是(A) 2 (B) 4 (C) 8 (D) 166.顶点在原点,对称轴为坐标轴,且过点)24(,P 的抛物线的标准方程是(A) x y 2(B) yx 82(C) x y 82或y x 2(D) x y 2或yx 827.有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起,则不同的站法有(A) 192种 (B) 120种 (C) 96种 (D) 48种8.已知单位向量m 和n 的夹角为60,记a =n -m , 2b =m , 则向量a 与b 的夹角为(A)30 (B)60 (C) 120 (D) 1509.双曲线)0,012222b a b y a x (的左右焦点为21F F ,,P 是双曲线右支上一点,满足条件是k=0,S=1开始k<3? S=S .2k k=k+1输出S结束否。
四川省宜宾市高三上学期第一次诊断考试数学(理)试题参考答案

高2013级高三第一次诊断性测试数学(理工农医类)答案说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则. 二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分. 一、选择题二、填空题11.1212.32(原创有错,建议全部给分)13.()(],01,3-∞U 14.15.①③④ 三、解答题16.解:(Ⅰ)由题已知:cos A A ⋅=+=Q m n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅2分2sin()6A π∴+=sin()62A π+=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅4分 由A 为锐角得:63A ππ+=,6A π=.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分(Ⅱ)由(Ⅰ)知12sin A =,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅7分2()cos22sin 12sin 2sin f x x x x x =+=-+=213222(sin )x --+.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅9分x ∈R Q ,[]sin 11x ∴∈-,,因此,当12sin A =时,()f x 有最大值23,当sin 1x =-时,()f x 有最小值3-,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅11分 故所求函数()f x 的值域是23[3]-,.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分17.解:(Ⅰ)所有可能的申请方式有43种,恰有3人申请A 类助学金的申请方式有81234=⋅C C 种,所以,所求概率为818384==P ;⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5分 方法二:()8183231313344=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=C P ;(Ⅱ)ξ的所有可能取值为1、2、3.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅6分()27131413===C P ξ()()27143242234222423=+==A C C C C P ξ ()943343324===A C P ξ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅9分综上知:ξ的分布列为所以:.2765943271422711=⨯+⨯+⨯=ξE ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅12分 18.解:(Ⅰ)在图2中,过P 作//PQ BC 交A B '于Q .………………………………1分Q 3CP PA '=,14PQ A P BC A C '∴==' 4,1BC PQ =∴=Q ,…………………2分 //,1DE BC DE =Q //DE PQ ∴,得,//DEQP DP EQ ∴Y ………………………………………………………………4分DP ⊄Q 平面,A BE EQ '⊂平面A BE '//DP ∴平面A BE '.………………………………………………………………5分(Ⅱ)在图2中,过A '作A F BE '⊥于F .Q 平面A BE '⊥平面BCDE ,∴A F '⊥平面BCDE ……………………………6分90BA E '∠=︒Q ,33A B A E ''==,30A EB '∴∠=︒,33322A F EF '==, 过F 作FG DE ⊥交DE 延长线于G ,则39344FG EG ==,…………………7分 如图,建立空间直角坐标系D xyz -则9333(,,)442EA '=u u u r ,933(,,0)(1,0,0)44EF DE ==u u u r u u u r ,………8分 设平面A BE '的法向量(,,)n x y z =r,则933304293304x y z x y ⎧++=⎪⎪⎨⎪+=⎪⎩,可取(1,3,0)n =-r ………………………………………9分 设平面A DE '的法向量111(,,)m x y z =u r,则1111933304420x y z x ⎧++=⎪⎨⎪=⎩,可取(0,2,3)m =-u r …………………………………10分 2321cos ,71343m n -∴<>==-+⋅+u r r ……………………………………11分 Q 二面角B A E D '--为钝角∴二面角B A E D '--的余弦的大小为7-………………………………………12分 注:(Ⅰ)向量法参照给分;(Ⅱ)传统法:过D 作DH BE ⊥交BE 延长线于H ,再过H 作HN A E '⊥交A E '延长线于N …参照给分.19.解:(1)∵3482++=n n n a a S∴3481121++=---n n n a a S (2≥n )∴1122144)(8-----+=-n n n n n n a a a a S S ∴)(41122--+=-n n n n a a a a ∵0>n a ∴41=--n n a a (2≥n )∴数列{n a }是以4为公差的等差数列………3分 又∵3481211++=a a S ∴034121=+-a a 而31<a ∴11=a ………5分 ∴34-=n a n (n *∈N )………6分 (2)12-=n n n b ………7分122102121)1(......213212211--⨯+⨯-++⨯+⨯+⨯=n n n n n T n n n n n T 2121)1(......2122112121⨯+⨯-++⨯+⨯=- , 两式相减得n n n n n n T 2222121......21212121210+-=⨯-++++=-, 1224-+-=∴n n n T ………9分 1224)1(--<-∴n n λ若n 为偶数,则3 ,2241<∴-<∴-λλn ………10分若n 为奇数,则2,2,2241->∴<-∴-<-∴-λλλn ………11分32<<-∴λ………12分20.(Ⅰ)∵224230+--+=x y x y ∴()()22212-+-=x y .………1分设圆C 的圆心为C (,)a b ,又因为圆C 与圆D 关于直线4250+-=x y 对称, 即圆心D (2,1)与(,)a b 关于直线4250+-=x y 对称.∴()121221425022-⎧⋅-=-⎪⎪-⎨++⎪⋅+⋅-=⎪⎩b a a b ………3分∴00=⎧⎨=⎩a b .所以圆C 的方程为222+=x y .………4分(Ⅱ)①因为点(2,0)P ,(0,2)M,所以=PM ………5分 设点Q 到PM 的距离为h ,圆心C 到PM 的距离为d ,所以12∆=⋅=QPM S PM h . ∆QPM 面积的最大值即需要h 取的最大值,此时点Q 与圆心C 的连线与PM 垂直,故有最大值=+==h d r4∆=QPM S ,………7分此时点Q 坐标为点()1,1--.………8分 ②直线AB 与直线PM 垂直,理由如下:………9分因为过点Q ()1,1--作两条相异直线分别与圆C 相交于A 、B 两点,直线QA 、QB 的倾斜角互补,所以直线QA 、QB 斜率都存在.设直线QA 的斜率为k ,则直线QB 斜率为-k ,所以直线QA 的方程:1(1)+=+y k x 221(1)2+=+⎧⎨+=⎩y k x x y ()()222121210⇒++-+--=k x k k x k k ………10分 又因为点Q ()1,1--在圆C 上,故有2221(1)1--⋅-=+A k k x k ,所以22211-++=+A k k x k ,同理22211--+=+B k k x k ,………11分(1)1(1)1()21--+--++-+-====---B A B A B A AB B A B A B Ay y k x k x k x x kk x x x x x x ,………12分又20102-==--PM k ,所以有1⋅=-PM AB k k , 故直线AB 与直线PM 垂直.………13分21.解:(Ⅰ)由2()ln ()f x x x ax x a =+-∈R 可知0x >,有:()ln 12f x x a x '=++-∵函数()f x 在区间[)e,+∞上为减函数,∴当[)e,x ∈+∞时()0f x '≤,即ln 120x a x ++-≤在区间[)e,+∞上恒成立,……2分 ∴2ln 1a x x ≤--在[)e,x ∈+∞上恒成立. 令()2ln 1g x x x =--,121()2x g x x x -'=-=,当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时,()0,()g x g x '≥单增;1(0,2x ⎤∈⎥⎦时,()0,()g x g x '≤单减.∴[)e,x ∈+∞时,min ()(e)2e 2g x g ==- ∴2e 2a ≤-.……………5分(Ⅱ)若对任意(1,)x ∈+∞,2()(1)f x x k a x k >-++--恒成立, 即(1)ln k x x x x -<+恒成立. 法一:∵(1,)x ∈+∞,∴10x ->. 则问题转化为ln 1x x xk x +<-对任意(1,)x ∈+∞恒成立,……………7分设函数ln ()1x x xh x x +=-,则2ln 2()(1)x x h x x --'=-,再设()ln 2m x x x =--,则1()1m x x'=-. ∵(1,)x ∈+∞,∴()0m x '>,则()ln 2m x x x =--在(1,)x ∈+∞上为增函数, ∵(3)1ln30m =-<,(4)2ln 40m =->, ∴0(3,4)x ∃∈,使000()ln 20m x x x =--=.∴当0(1,)x x ∈时,()0,()0m x h x <<;当0(,)x x ∈+∞时,()0,()0m x h x >>……10分∴ln ()1x x xh x x +=-在0(1,)x x ∈上递减,在0(,)x x ∈+∞上递增.∴()h x 的最小值为00000ln ()1x x x h x x +=-.∵000()ln 20m x x x =--=,∴00ln()11x x +=-,代入函数00000ln ()1x x x h x x +=-得00()h x x =,∵0(3,4)x ∈,且()k h x <,对任意(1,)x ∈+∞恒成立, ∴min 0()k h x x <=,∴3k ≤, ∴k 的值为1,2,3.……………14分法二(同比例给分):令()()()1ln (1)=-+--=--+⎡⎤⎣⎦g x f x k a x k x x k x k (1)>x ∴()ln 1(1)ln 2'=+--=+-g x x k x k当20-≥k 时,即2≤k 时,()0'>g x ,()g x 在(1,2)上单调递增, ∴()(1)10>=>g x g 恒成立,而k *∈N ∴1=k 或2=k .当20-<k 时,即2>k 时,2()0e -'=⇒=k g x x ,∴()g x 在2(1,e)-k 上单调递减,在2(e ,)-+∞k 上单调递增,∴2222min ()(e )e (2)(1)e e0---->=---+=->k k k k g x g k k k k 恒成立, ∴2>e-k k ,而k *∈N ,∴3=k .综上可得,1=k 或2=k 或3=k 时成立.。
2015秋期宜宾市高三半期考试参考答案

2015秋期宜宾市高三半期考试参考答案第I 卷二、选择题答案:(48分,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
)14.C 15.C 16.B 17.A 18.B 19.AD 20.AD 21.BC三、实验题:22.(5分) (1) 2224t mrn π (2) hmgr (3) g 24π 23.(10分)(1) m <<M (2) T x x 243+ ; 23216549)()(Tx x x x x x ++-++ (3) )()(54x x g M m ++; []22432658)()()(T x x x x M m +-++ 四、计算题:(32分)24. (12分)解:(1)设汽车滑行距离为x ,由牛顿运动定律有:F =ma ① (2分) 根据运动规律有:v 12=2ax ② (2分) 由①②并代入数据解得 x =50m (1分)(2) 设最大速度为v 2,从发现危险到车停止,汽车将经过匀速运动与匀减速运动,其中匀速运动的位移为x 1 x 1=v 2t 0 ③ (2分) 匀减速运动的位移为x 2 v 22=2ax 2 ④ (2分) 根据题设条件 s 0=x 1+x 2 ⑤ (1分) 由①③④⑤并代入数据解得最大速度v 2=18m/s (2分)25.(20分)解:(1)A 物体从P 点到返回P 点的过程,由动能定理有201010210)(25.0)(mv x x mg x x mg -=+-+- ① (3分) A 物体从P 点到O '的过程)(25.021)(102010x x mg mv x x mg E p +-++= ② (3分) 由①②并代入数据解得 E p =25J (2分)(2) A 物体在与B 物体分离时有 0.25mg +mg =ma ③ (1分) 对于AB 整体有 (k +1)mg +0.25(k +1)mg +F =(k +1)ma ④ (1分)由③④并代入数据解得 F =0 即二者在弹簧原长时分离刚好分离时,对系统有:2E p =(1+k )mgx 1+0.25(1+k )mgx 1 ⑤ (3分)解得 k =9 (1分)A 物体从分离时到刚好能到达P 点的过程中,设刚好分离时的速度为v ,有:20210)25.0(kmv x kmg kmg -=+- ⑥ (2分) 系统从O '到恰好分离的过程有:p E mv k x mg k mgx k 2)1(21))1(25.0)1(211=+++++ ⑦ (2分) 由⑥⑦并代入数据解得解得 k =1 (1分)故91≤≤k (1分)33.(15分)(1)ABD (5分选对1个得2分,选对2个得4分,选对3个得5分;每选错1个扣3分,最低得分为0分)(2)(10分)解:根据题意有 λ)43(n x B += (n =0,1,2,3,…..) (4分) 得:nx B 434+=λ 代入数据可解得n 43280+=λ (2分) 又由m m 8020〈〈λ有: (1分)m m 11280;4021==λλ (3分)。
四川省宜宾市高三数学第一次诊断性考试试题 理

2014年秋期普通高中三年级第一次诊断测试数 学(理工农医类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至4页.考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效.满分150分,考试时间120分钟. 考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题,共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 一、选择题:本大题共10个小题,每小题5分,共50分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}102,73<<=<≤=x x B x x A ,则=B A(A) {}73<≤x x (B) {}73<<x x (C) {}72<≤x x (D) {}102<≤x x 2.函数)2sin(1π-+=x y 的图象(A) 关于x 轴对称 (B) 关于y 轴对称 (C) 关于原点对称 (D)关于直线2π=x 对称3.二项式52)1xx +(的展开式中,x 的系数为 (A) 10 (B) 15 (C) 20 (D) 25 4.给出下列三个命题:①命题p :x R ∃∈,使得012<-+x x , 则p ⌝:x R ∀∈,使得012≥-+x x② ”或“15-<>x x 是“2450x x -->”的充要条件.③若p q ∨为真命题,则p q ∧为真命题.其中正确..命题的个数为 (A) 0 (B) 1 (C) 2 (D) 35.执行如图所示的程序框图,输出的S 值是(A) 2 (B) 4(C) 8(D) 166.顶点在原点,对称轴为坐标轴,且过点)24(--,P 的抛物线的标准方程是 (A) x y -=2 (B) y x 82-=(C) x y 82-=或y x -=2(D) x y -=2或y x 82-=7.有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起, 则不同的站法有 (A) 192种(B) 120种(C) 96种 (D) 48种8.已知单位向量m 和n 的夹角为60,记a =n -m , 2b =m , 则向量a 与b 的夹角为 (A)30(B) 60 (C) 120 (D)1509.双曲线)0,012222>>=-b a by a x (的左右焦点为21F F ,,P 是双曲线右支上一点,满足条件212F F PF =,直线1PF 与圆222a y x =+相切,则双曲线的离心率为(A)45(B)3 (C)332 (D)3510.设函数⎩⎨⎧>≤=0,log 0,2)(2x x x x f x ,若对任意给定的),1(+∞∈t ,都存在唯一的R x ∈,满足at t a x f f +=222))((,则正实数...a 的最小值是(A) 2 (B)12 (C) 14 第Ⅱ卷(非选择题,共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.试题卷上作答无效. 二、填空题:本大题共5小题,每小题5分,共25分. 11.已知i 是虚数单位,则21i i=+▲.12.函数x x x f ln )(2+=的图像在点)1,1(A 处的切线方程为▲.13.在ABC ∆中,内角C B A ,,所对的边分别为,,a b c ,且满足B a A b cos sin =,则角B 的大小为▲.14.在正方体1111D C B A ABCD -中,点P 是上底面1111D C B A 的中心,点Q 在线段PD 上运动,则异面直线BQ 与11D A 所成角θ最大时,=θcos ▲.15.对于函数[]sin ,0,2()1(2),(2,)2x x f x f x x π⎧∈⎪=⎨-∈+∞⎪⎩,有下列4个结论:①任取[)120,x x ∈+∞、,都有12()()2f x f x -≤恒成立; ②()2(2)f x kf x k =+*()k ∈N ,对于一切[)0,x ∈+∞恒成立; ③函数()ln(1)y f x x =--有3个零点; ④对任意0x >,不等式2()f x x≤恒成立. 则其中所有正确结论的序号是▲.三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.不能答试卷上,请答在答题卡相应的方框内. 16.(本题满分12分)已知函数)0(sin cos sin 2cos )(22>-+=ωωωωωx x x x x f ,且周期为π. (I )求ω的值;(II )当x ∈[20π,]时,求)(x f 的最大值及取得最大值时x 的值.17.(本题满分12分)在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上,某种茶饮料一天的销售量与该天的日平均气温(单位:℃)有关,若日平均气温不超过15 ℃,则日销售量为100瓶;若日平均气温超过15℃但不超过20 ℃,则日销售量为150 瓶;若日平均气温超过20 ℃,则日销售量为200瓶.据宜宾市气象部门预测,该地区在运动会期间每一天日平均气温不超过15 ℃,超过15 ℃但不超过20 ℃,超过20 ℃这三种情况发生的概率分别为P 1,P 2,P 3,又知P 1,P 2为方程5x 2-3x +a =0的两根,且P 2=P 3. (I )求P 1,P 2,P 3的值;(II )记ξ表示该茶饮料在运动会期间任意两天的销售量总和(单位:瓶),求ξ的分布列及数学期望.18.(本题满分12分)如图,一简单几何体ABCDE 的一个面ABC 内接于圆O, G 、H 分别是AE 、BC 的中点,AB 是圆O 的直径,四边形DCBE 为平行四边形,且DC ⊥平面ABC. (I )证明:GH //平面ACD ;(II )若AC=BC=BE =2,求二面角O-CE-B 的余弦值.19. (本题满分12分)已知数列{}n a 的前n 项和为n S ,向量)1,n S (=a ,)21,12-=n(b ,满足条件b a λ=,R ∈λ且0≠λ.(I )求数列{}n a 的通项公式;(II )设函数xx f )21()(=,数列{}n b 满足条件21=b ,)(,)3(1)(1*+∈--=N n b f b f n n(i) 求数列{}n b 的通项公式;(ii)设nnn a b c =,求数列{}n c 的前n 和n T .20. (本题满分13分)已知点Q P ,的坐标分别为(2,0)-,(2,0),直线QM PM ,相交于点M ,且它们的斜率之积是14-(I )求点M 的轨迹方程;(II )过点O 作两条互相垂直的射线,与点M 的轨迹交于,A B 两点.试判断点O 到直线AB的距离是否为定值.若是请求出这个定值,若不是请说明理由.21. (本题满分14分)已知函数c bx ax x x f +++=234)(,在y 轴上的截距为5-,在区间[]10,上单调递增,在[]21,上单调递减,又当2,0==x x 时取得极小值. (I )求函数)(x f 的解析式;(II )能否找到函数)(x f 垂直于x 轴的对称轴,并证明你的结论;(Ⅲ)设使关于x 的方程5)(22-=x x f λ恰有三个不同实根的实数λ的取值范围为集合A ,且两个非零实根为12,x x ,试问:是否存在实数m ,使得不等式2122x x tm m -≤++对任意[]A t ∈-∈λ,3,3恒成立?若存在,求m 的取值范围;若不存在,请说明理由.高中2012级一诊测试数学(理工类)试题参考答案及评分意见说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分.二、填空题(每小题5分,共25分)11. 1+i 12. 3x-y-2=0 13. 4π14.615. ①③④三、解答题(共75分)16.解:(1)∵)2sin 222cos 22(22sin 2cos )(x x x x x f ωωωω+=+=.....(2分) =)42sin(2πω+x ..................................................................(4分) ∵π=T 且ω>, 故1,22==ωπωπ则......................................................................(6分) (2):由(1)知)42sin(2)(π+=x x f∵20π≤≤x∴45424πππ≤+≤x ................................................................................(7分) ∴1)42sin(22≤+≤-πx . ∴2)42sin(21≤+≤-πx .......................................................................................(9分) ∴当242ππ=+x 时,即8π=x ,y取得最大值为2............................................(12分)17.解:(I )由已知得1231223135P P P P P P P++=⎧⎪⎪+=⎨⎪=⎪⎩,解得:123122,, (4555)P P P ===(分) (II)ξ的可能取值为200,250,300,350,400...........................5(分)11(200),55124(250)2,552512228(300)2,555525228(350)2,5525224(400) (105525)P P P P P ξξξξξ==⨯==⨯⨯===⨯⨯+⨯===⨯⨯===⨯=(分)随机变量ξ的分布列为所求的数学期望为14884200250300350400320() (122525252525)E ξ=⨯+⨯+⨯+⨯+⨯=瓶(分)18.解: (1)证明:连结GO,OH ∵GO//AD,OH//AC...................................................................................................................(2分) ∴GO//平面ACD,OH//平面ACD,又GO 交HO 于O...............................................................(.4分) ∴平面GOH//平面ACD..........................................................................................................(5分) ∴GH//平面ACD.....................................................................................................................(6分)(2)法一:以CB 为x 轴,CB 为y 轴,CD 为z 轴,建立如图所示的直角坐标系 则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)平面BCE 的法向量)0,1,0(=,设平面OCE 的法向量),,(000z y x =.......................(8分))0,1,1(),2,0,2(==CO CE∴⎪⎩⎪⎨⎧=⋅=⋅00则⎩⎨⎧=+=+00220000y x z x ,故⎩⎨⎧-=-=0000x y x z令)1,1,1(,10-=-=n x ..........................................................................................................(10分)∵二面角O-CE-B 是锐二面角,记为θ,则33311,cos cos =⨯==⋅><=θ................................................................(12分)法二:过H 作HM ⊥CE 于M ,连结OM∵DC ⊥平面ABC ∴平面BCDE ⊥平面ABC 又∵AB 是圆O 的直径 ∴AC ⊥BC,而AC//OH ∴OH ⊥BC ∴OH ⊥平面BCE..........................................................................................(8分)∴OH ⊥CE ,又HM ⊥CE 于M ∴CE ⊥平面OHM ∴CE ⊥OM ∴OMH ∠是二面角O-CE-B 的平面角...................................................(10分) 由,~CBE Rt CMH Rt ∆∆且CE=22. ∴2212=⇒=HM CE CH BE HM∴22=HM 又OH=121=AC在2622122=⎪⎪⎭⎫ ⎝⎛+=∆OH OHM Rt 中,. .................................................................(11分)∴332622cos ===∠OH HM OMH ......................................................................................(12分) 19.(Ⅰ)因为a=λb 所以22,12211-=-=+n n n n S S . 当2≥n 时,n n n n n n S S a 2)22()22(11=---=-=+- ...........................................(2分)当1=n 时,2221111=-==+S a ,满足上式所以n n a 2= ..................................................................(4分) (Ⅱ)(ⅰ))3(1)(,)21()(1n n xb f b f x f --==+ 11(b )(3)n n f f b +=--n n b b --=∴+3)21(1)21(1nn b b +=∴+321211∴ 31+=+n n b b3-1=+n n b b ,又2)1(1=-=f b ∴{}n b 是以2为首项3为公差的等差数列∴13-=n b n ................................................................(8分)(ⅱ) n n n n n a b c 213-==n n n n n T 2132432825221321-+-+⋅⋅⋅+++=-143221324328252221+-+-+⋅⋅⋅+++=n n n n n T-1432213-23232323121+-+⋅⋅⋅++++=n n n n T 1121321-1)21-1413121+---⋅+=n n n n T (11213)21-123121+---+=n n n n T (n n n n T 213)21-1321--+=-(nn n n T 21323-321--+=-nn n T 253-5+= ................................................................(12分)20.(Ⅰ)解:,)M x y (,由题可得1.224y y x x =-+- ..............................(4分)2214x y +=所以点M的轨迹方程为2214x y +=2)x ≠±( . .............................(6分 ) (Ⅱ)点O 到直线AB 的距离为定值 ,设),(),,(2211y x B y x A ,① 当直线AB 的斜率不存在时,则AOB ∆为等腰直角三角形,不妨设直线OA :x y =将x y =代入1422=+y x ,解得552±=x 所以点O 到直线AB 的距离为552=d ; ............................(8分) ② 当直线AB 的斜率存在时,设直线AB 的方程为m kx y +=与2212)4x y x +=≠±(联立消去y 得222(14)8440k x kmx m +++-=122814km x x k +=-+,21224414m x x k-=+ ............................(9分) 因为OB OA ⊥,所以02121=+y y x x ,1212()()0x x kx m kx m +++= 即0)()1(221212=++++m x x km x x k 所以2222222448(1)01414m k m k m k k -+-+=++,整理得2254(1)m k =+,........................(12分 )所以点O 到直线AB 的距离d ==综上可知点O 到直线AB 的距离为定值552........................(13分 ) 21.解:(Ⅰ)易知5c =- ……………………(1分)又32()432f x x ax bx '=++由(1)0f '=,得32 4.................................a b +=-①……………………(2分)令()0f x '=,得2(432)0x x ax b ++=由(2)0f '=,得380.................................a b ++=②……………………(3分)由①②得4,4b a ==- 432()445f x x x x ∴=-+- ……………………(4分)(Ⅱ)若()f x 关于直线x t =对称(显然0t ≠), 则取点(0,5)A -关于直线对称的点(2,5)A t '-必在()f x 上,即(2)5f t =-,得22(21)0t t t -+= ……………………(6分) 又0t≠1t ∴= ……………………(7分)验证,满足(1)(1)f x f x -=+ ……………………(9分)(也可直接证明()()f t x f t x -=+,计算较繁琐;)(Ⅲ)由(1)知,432224455xx x x λ-+-=-, 即4322244xx x x λ-+= 又0x =为其一根,得224(4)0x x λ-+-=22164(4)40λλ∴∆=--=>且21240x x λ=-≠故{|022}A R λλλλ=∈≠≠≠-且且 ……………………(10分) 又1221244x x x x λ+=⎧⎨=-⎩,得222121212()()44x x x x x x λ-=+-=, 12||2||x x λ∴-=,故,2||0A λλ∀∈>且2||4λ≠ , ……………………(11分) 2[3,3],,22||t A m tm λλ∴∀∈-∈++≤对使恒成立’即只需[3,3],t ∀∈-220m tm ++≤恒成立 ……………………(12分) 设2()2,[3,3]g t mt m t =++∈-(3)012(3)021g m g m ≤≤≤⎧⎧∴⇒⇒⎨⎨-≤-≤≤-⎩⎩无解即不存在满足题意的实数m. ……………………(14分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省宜宾市2015届高三第一次诊断考试数学理试题一、选择题:本大题共10个小题,每小题5分,共50分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}102,73<<=<≤=x x B x x A ,则=B A(A) {}73<≤x x (B) {}73<<x x (C) {}72<≤x x (D) {}102<≤x x 2.函数)2sin(1π-+=x y 的图象(A) 关于x 轴对称 (B) 关于y 轴对称 (C) 关于原点对称 (D)关于直线2π=x 对称3.二项式52)1xx +(的展开式中,x 的系数为 (A) 10 (B) 15 (C) 20 (D) 254.给出下列三个命题:①命题p :x R ∃∈,使得012<-+x x , 则p ⌝:x R ∀∈,使得012≥-+x x② ”或“15-<>x x 是“2450x x -->”的充要条件. ③若p q ∨为真命题,则p q ∧为真命题.其中正确..命题的个数为 (A) 0 (B) 1 (C) 2 (D) 35.执行如图所示的程序框图,输出的S 值是 (A) 2 (B) 4(C) 8(D) 166.顶点在原点,对称轴为坐标轴,且过点)24(--,P 的抛物线的标准方程是 (A) x y -=2(B) y x 82-=(C) x y 82-=或y x -=2(D) x y -=2或y x 82-=7.有七名同学站成一排照毕业纪念照,其中小明必须站在正中间,并且小李、小张两位同学要站在一起, 则不同的站法有 (A) 192种(B) 120种(C) 96种 (D) 48种8.已知单位向量m 和n 的夹角为60,记a =n -m , 2b =m , 则向量a 与b 的夹角为 (A) 30(B) 60 (C) 120 (D) 1509.双曲线)0,012222>>=-b a by a x (的左右焦点为21F F ,,P 是双曲线右支上一点,满足条件212F F PF =,直线1PF 与圆222a y x =+相切,则双曲线的离心率为(A)45(B)3 (C)332 (D)3510.设函数⎩⎨⎧>≤=0,log 0,2)(2x x x x f x ,若对任意给定的),1(+∞∈t ,都存在唯一的R x ∈,满足at t a x f f +=222))((,则正实数...a 的最小值是(A) 2 (B)12 (C) 14(D)第Ⅱ卷(非选择题,共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.试题卷上作答无效. 二、填空题:本大题共5小题,每小题5分,共25分. 11.已知i 是虚数单位,则21i i=+▲.12.函数x x x f ln )(2+=的图像在点)1,1(A 处的切线方程为▲.13.在ABC ∆中,内角C B A ,,所对的边分别为,,a b c ,且满足B a A b cos sin =,则角B 的大小为▲.14.在正方体1111D C B A ABCD -中,点P 是上底面1111D C B A 的中心,点Q 在线段PD 上运动,则异面直线BQ 与11D A 所成角θ最大时,=θcos ▲.15.对于函数[]sin ,0,2()1(2),(2,)2x x f x f x x π⎧∈⎪=⎨-∈+∞⎪⎩,有下列4个结论:①任取[)120,x x ∈+∞、,都有12()()2f x f x -≤恒成立; ②()2(2)f x kf x k =+*()k ∈N ,对于一切[)0,x ∈+∞恒成立;③函数()ln(1)y f x x =--有3个零点; ④对任意0x >,不等式2()f x x≤恒成立. 则其中所有正确结论的序号是▲.三、解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.不能答试卷上,请答在答题卡相应的方框内. 16.(本题满分12分)已知函数)0(sin cos sin 2cos )(22>-+=ωωωωωx x x x x f ,且周期为π. (I )求ω的值;(II )当x ∈[20π,]时,求)(x f 的最大值及取得最大值时x 的值.17.(本题满分12分)在2014年11月4日宜宾市举办的四川省第十四届少数民族传统体育运动会的餐饮点上,某种茶饮料一天的销售量与该天的日平均气温(单位:℃)有关,若日平均气温不超过15 ℃,则日销售量为100瓶;若日平均气温超过15℃但不超过20 ℃,则日销售量为150 瓶;若日平均气温超过20 ℃,则日销售量为200瓶.据宜宾市气象部门预测,该地区在运动会期间每一天日平均气温不超过15 ℃,超过15 ℃但不超过20 ℃,超过20 ℃这三种情况发生的概率分别为P 1,P 2,P 3,又知P 1,P 2为方程5x 2-3x +a =0的两根,且P 2=P 3. (I )求P 1,P 2,P 3的值;(II )记ξ表示该茶饮料在运动会期间任意两天的销售量总和(单位:瓶),求ξ的分布列及数学期望.18.(本题满分12分)如图,一简单几何体ABCDE 的一个面ABC 内接于圆O, G 、H 分别是AE 、BC 的中点,AB 是圆O 的直径,四边形DCBE 为平行四边形,且DC ⊥平面ABC.(I )证明:GH //平面ACD ;(II )若AC=BC=BE =2,求二面角O-CE-B 的余弦值.19. (本题满分12分)已知数列{}n a 的前n 项和为n S ,向量)1,n S (=a ,)21,12-=n (b ,满足条件b a λ=,R ∈λ且0≠λ.(I )求数列{}n a 的通项公式;(II )设函数x x f )21()(=,数列{}n b 满足条件21=b ,)(,)3(1)(1*+∈--=N n b f b f n n(i) 求数列{}n b 的通项公式;(ii)设nnn a b c =,求数列{}n c 的前n 和n T .20. (本题满分13分)已知点Q P ,的坐标分别为(2,0)-,(2,0),直线QM PM ,相交于点M ,且它们的斜率之积是14-(I )求点M 的轨迹方程;(II )过点O 作两条互相垂直的射线,与点M 的轨迹交于,A B 两点.试判断点O 到直线AB的距离是否为定值.若是请求出这个定值,若不是请说明理由.21. (本题满分14分)已知函数c bx ax x x f +++=234)(,在y 轴上的截距为5-,在区间[]10,上单调递增,在[]21,上单调递减,又当2,0==x x 时取得极小值. (I )求函数)(x f 的解析式;(II )能否找到函数)(x f 垂直于x 轴的对称轴,并证明你的结论;(Ⅲ)设使关于x 的方程5)(22-=x x f λ恰有三个不同实根的实数λ的取值范围为集合A ,且两个非零实根为12,x x ,试问:是否存在实数m ,使得不等式2122x x tm m -≤++对任意[]A t ∈-∈λ,3,3恒成立?若存在,求m 的取值范围;若不存在,请说明理由.高中2012级一诊测试数学(理工类)试题参考答案及评分意见说明:一、本解答给出了一种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分.二、填空题(每小题5分,共25分)11. 1+i 12. 3x-y-2=0 13. 4π14. 15. ①③④三、解答题(共75分)16.解:(1)∵)2sin 222cos 22(22sin 2cos )(x x x x x f ωωωω+=+=.....(2分) =)42sin(2πω+x ..................................................................(4分)∵π=T 且0ω>, 故1,22==ωπωπ则......................................................................(6分)(2):由(1)知)42sin(2)(π+=x x f∵20π≤≤x ∴45424πππ≤+≤x ................................................................................(7分) ∴1)42sin(22≤+≤-πx . ∴2)42sin(21≤+≤-πx .......................................................................................(9分)∴当242ππ=+x 时,即8π=x ,y 取得最大值为2............................................(12分)17.解:(I )由已知得1231223135P P P P P P P++=⎧⎪⎪+=⎨⎪=⎪⎩,解得:123122,, (4555)P P P ===(分) (II )ξ的可能取值为200,250,300,350,400...........................5(分)11(200),55124(250)2,552512228(300)2,555525228(350)2,5525224(400) (105525)P P P P P ξξξξξ==⨯==⨯⨯===⨯⨯+⨯===⨯⨯===⨯=(分)随机变量ξ的分布列为所求的数学期望为14884200250300350400320() (122525252525)E ξ=⨯+⨯+⨯+⨯+⨯=瓶(分)18.解: (1)证明:连结GO,OH∵GO//AD,OH//AC ...................................................................................................................(2分)∴GO//平面ACD,OH//平面ACD,又GO 交HO 于O ...............................................................(.4分) ∴平面GOH//平面ACD..........................................................................................................(5分) ∴GH//平面ACD.....................................................................................................................(6分) (2)法一:以CB 为x 轴,CB 为y 轴,CD 为z 轴,建立如图所示的直角坐标系 则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)平面BCE 的法向量)0,1,0(=m ,设平面OCE 的法向量),,(000z y x n =.......................(8分))0,1,1(),2,0,2(==CO CE∴⎪⎩⎪⎨⎧=⋅=⋅00CO n CE n 则⎩⎨⎧=+=+00220000y x z x ,故⎩⎨⎧-=-=0000x y x z令)1,1,1(,10-=-=n x ..........................................................................................................(10分)∵二面角O-CE-B 是锐二面角,记为θ,则33311cos cos =⨯<=m θ................................................................(12分)法二:过H 作HM ⊥CE 于M ,连结OM∵DC ⊥平面ABC ∴平面BCDE ⊥平面ABC 又∵AB 是圆O 的直径 ∴AC ⊥BC,而AC//OH∴OH ⊥BC ∴OH ⊥平面BCE ..........................................................................................(8分) ∴OH ⊥CE ,又HM ⊥CE 于M ∴CE ⊥平面OHM∴CE ⊥OM ∴OMH ∠是二面角O-CE-B 的平面角...................................................(10分) 由,~CBE Rt CMH Rt ∆∆且CE=22. ∴2212=⇒=HM CE CH BE HM ∴22=HM 又OH=121=AC 在2622122=⎪⎪⎭⎫ ⎝⎛+=∆OH OHM Rt 中,. .................................................................(11分)∴332622cos ===∠OH HM OMH ......................................................................................(12分)19.(Ⅰ)因为a=λb 所以22,12211-=-=+n n n n S S .当2≥n 时,n n n n n n S S a 2)22()22(11=---=-=+- ...........................................(2分)当1=n 时,2221111=-==+S a ,满足上式所以n n a 2= ..................................................................(4分)(Ⅱ)(ⅰ))3(1)(,)21()(1n n x b f b f x f --==+ 11(b )(3)n n f f b +=--n n b b --=∴+3)21(1)21(1nn b b +=∴+321211∴ 31+=+n n b b3-1=+n n b b ,又2)1(1=-=f b ∴{}n b 是以2为首项3为公差的等差数列∴13-=n b n ................................................................(8分)(ⅱ) n n n n n a b c 213-==n n n n n T 2132432825221321-+-+⋅⋅⋅+++=-143221324328252221+-+-+⋅⋅⋅+++=n nn n n T-得1432213-23232323121+-+⋅⋅⋅++++=n n n n T1121321-1)21-1413121+---⋅+=n n n n T (11213)21-123121+---+=n n n n T (n n n n T 213)21-1321--+=-(n n n n T 21323-321--+=-nn n T 253-5+= ................................................................(12分)20.(Ⅰ)解:,)Mx y (,由题可得1.224y y x x =-+- ..............................(4分) 2214x y +=所以点M 的轨迹方程为2214x y +=2)x ≠±( . .............................(6分 ) (Ⅱ)点O 到直线AB 的距离为定值 ,设),(),,(2211y x B y x A ,① 当直线AB 的斜率不存在时,则AOB ∆为等腰直角三角形,不妨设直线OA :x y =将x y =代入1422=+y x ,解得552±=x所以点O 到直线AB 的距离为552=d ; ............................(8分)② 当直线AB 的斜率存在时,设直线AB 的方程为m kx y +=与2212)4x y x +=≠±(联立消去y 得222(14)8440k x kmx m +++-=122814km x x k +=-+,21224414m x x k -=+ ............................(9分) 因为OB OA ⊥,所以02121=+y y x x ,1212()()0x x kx m kx m +++= 即0)()1(221212=++++m x x km x x k所以2222222448(1)01414m k m k m k k-+-+=++,整理得2254(1)m k =+,........................(12分 )所以点O 到直线AB 的距离d ==综上可知点O 到直线AB 的距离为定值552........................(13分 )21.解:(Ⅰ)易知5c =- ……………………(1分)又32()432f x x ax bx '=++由(1)0f '=,得32 4.................................a b +=-①……………………(2分) 令()0f x '=,得2(432)0x x ax b ++=由(2)0f '=,得380.................................a b ++=②……………………(3分)由①②得4,4b a ==- 432()445f x x x x ∴=-+- ……………………(4分)(Ⅱ)若()f x 关于直线x t =对称(显然0t ≠),则取点(0,5)A -关于直线对称的点(2,5)A t '-必在()f x 上,即(2)5f t =-,得22(21)0t t t -+= ……………………(6分) 又0t≠1t ∴= ……………………(7分)验证,满足(1)(1)f x f x -=+ ……………………(9分)(也可直接证明()()f t x f t x -=+,计算较繁琐;) (Ⅲ)由(1)知,432224455x x x x λ-+-=-,即4322244x x x x λ-+=又0x=为其一根,得224(4)0x x λ-+-=22164(4)40λλ∴∆=--=>且21240x x λ=-≠故{|022}A R λλλλ=∈≠≠≠-且且 ……………………(10分)又1221244x x x x λ+=⎧⎨=-⎩,得222121212()()44x x x x x x λ-=+-=,12||2||x x λ∴-=,故,2||0A λλ∀∈>且2||4λ≠ , ……………………(11分) 2[3,3],,22||t A m tm λλ∴∀∈-∈++≤对使恒成立’即只需[3,3],t ∀∈-220m tm ++≤恒成立 ……………………(12分)设2()2,[3,3]g t mt m t =++∈-(3)012(3)021g m g m ≤≤≤⎧⎧∴⇒⇒⎨⎨-≤-≤≤-⎩⎩无解 即不存在满足题意的实数m. ……………………(14分)。
