2020届高考数学二轮复习系列之疯狂专练:3 框图(文)
2020届高考数学二轮复习疯狂专练3框图文

框图疯狂专练3一、选择题1.执行如图所示的程序框图,输出的结果是()11383123..DA. B.Ck值为()2.执行如图所示的程序框图,输出的5764 D .A. B. C.?i4?t,则输出的.执行如图所示的程序框图,若输入的()31613107.D .C .B .A.4.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,aa?1418b()若输入的,,分别为,则输出的14420.D C.A.. B,把这些数据经过)(单位:台5.某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图中记录了每天的销售量?S()如图所示的程序框图处理后,输出的2031962829 D. B.. C.A25s?,则判断框中可填入的条件是()6.执行如图所示的程序框图,若输出的5?5?i?i4?ii?4??? C .DA.B ..31N??3x,则输出.如图所示的程序框图的算法思路源于世界数学名题“问题”.执行该程序框图,若7?i()的.9876. B.D C.A.yxx值相等,则的可能值的个数为()8.给出一个如图所示的程序框图,若要使输入的值与输出的3412个个 DA..个 B.个 C..我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:“今有出门望见九堤,堤有九木,木有九9枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?”现在我们用如图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是()6?n?nSS?10000??10000??5? A..B .D C.t1?a?a?12?a3??a4a?()的值为,,若输入的执行如图所示的程序框图,10.,,则输出的,41320.1051412..B .D C.A111?...??处应填(2)11.如图给出的是计算的值的一个程序框图,则图中判断框内(1)处和执行框中的10042的语句是()2n??in?2?50n??i??i??i100nn?1100nn?250n,, D C.A.,.. B,3S 12.若执行如图所示的程序框图,输出的值为,则判断框中应填入的条件是()9?k8?k?7?k???k6?.D .A .C .B二、填空题_______13.阅读下面的程序框图,运行相应的程序,输出的结果为.S等于. 14.某程序框图如图所示,则输出的结果S的值是________.执行如图所示的程序框图,那么输出. 15S的值为..执行如图所示的程序框图,输出16.与解析案答一、选择题B1.【答案】【解析】执行程序框图,23?2a?1?第一次循环:满足判断条件,;211?2a?3?第二次循环:满足判断条件,;11a? B不满足判断条件,此时输出.,故选B.【答案】2 【解析】执行程序框图,2k?a?2;第一次循环:,3k?a?4;第二次循环:,4k?a?8第三次循环:;,5k?16k?5a?,第四次循环:.,此时满足判断条件,终止循环,输出D .【答案】30?i?1St?4输入,,,【解析】i?1S?0?1??1i?4S?4;不是质数,,,i?4S??1?4??5i?7S?4;,不是质数,,i?7S??5?7?2i?10S?4;,,是质数,i?10S?2?10??8i?13S?4;,不是质数,,i?13S??8?13?5i?16S?4i?16.是质数,,退出循环,故输出的,,故选D.4.【答案】Ba?14b?1818?14?4b,,,则【解析】变为a14?4?10a?b,变为,则由于a10?4?ba?6,,则由于变为a6?4?a?b2,变为,则由于4?2?2b?ab,由于,则变为a?b?2a?2.,则输出由5.【答案】B【解析】由程序框图可知,该程序框图输出的是销售量的平均值,20?22?26?33?33?34?35?29?S,故选B结合茎叶图可知,输出的.7.6.【答案】Ci?1s?100?5?95i?2;,,【解析】执行程序框图,s?95?10?85i?3;,s?85?15?70i?4;,s?70?20?50i?5;,s?50?25?25i?6s?25.,,退出循环.此时输出的结合选项知选C.7.【答案】Cn?10i?2;,【解析】第一步:n?5i?3;,第二步:n?16i?4;,第三步:n?8i?5;,第四步:n?4i?6;,第五步:n?2i?7;,第六步:n?1i?8i?8,故选,C.第七步:,结束循环,输出的8.【答案】C【解析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:??2,xx?2?y?2x?3,2?x?5的值,该程序的作用是计算并输出分段函数??1?,x?5x?y x值相等,值与输出的又∵输入的x?2x?0x?12xx?,当或,解得时,2?x?5x?2x?3x?3,,解得当时,1?x x??1x?5(舍去)时,当,解得,xx3个,故选C值共有.故满足条件的9.【答案】BS?9?9?9?9?9?59049.【解析】根据题意,利用程序框图求禽的数目,输出结果应为5S?10000?n?5?n?6?”.故选”或“B.循环共执行了”或“次,所以判断框中应填入的条件是“10.【答案】Di?1t?1,初始值,【解析】t?2?1?2?0i?2;,第一次循环,得t?0?3?3i?3;,第二次循环,得.4??5i?t?2?31;,第三次循环,得5??14i?2?5?4t,第四次循环,得,14?t.不满足循环条件,退出循环,输出的,故选DC 【答案】11.111?...??50共【解析】因为个数,10042i5050?i次,所以变量所以算法框图应运行,应满足n2??nn满足.因为是求偶数的和,所以应使变量C【答案】12.根据程序框图,运行结果如下:【解析】3logS?3?k,第一次循环:;24log3?S?log4?k,第二次循环:;325log4?log3?logS?5?k,;第三次循环:4236?log4?log5S?log3?log6k?;,第四次循环:54237?log?log63log?log4?log5S?7k?,第五次循环:;624353??log8?log7?log84S?log3?log?log5?log68?k,,第六次循环:25426738?3k?S故如果输出,那么只能进行六次循环,故判断框内应填入的条件是.二、填空题1y?1?x2z?,.13【解析】;,y?2z?31?x;,,y?3z?52?x;,,y?5z?83x?;,,y?8z?135?x;,,y13?8?x21?z.,,8x57 14.【答案】2k?57???????S4k3S11k4S26k5S,;;,,,【解析】;,57S?.退出循环,输出2.【答案】152015Sk??2,,运行框图,输入【解析】.11?S??2016k?2018??k2015?1;,,满足条件2?111??S2017k?2018??2016?1k,;,满足条件211?1?S?212018?k?2018S?2kk?2017?1?2018,满足条件.,,不成立,输出?121009【答案】16.π1?00?1?sin?S?201833?i?,;,【解析】执行程序框图,2π331??0?0S??1?3?sin20185?i?5;,,2π55?1??5?sin3?0??S?0?132018??77i;…;,,22017π?0?130S??1???3??2017?2017?sin2018i?20192019?,,,2S?0?1?3?5?7?2015?2017输出?(?2015?2017)?(0?1)?(?3?5)?(?7?9)??1?2?2??2?1?504?2?1009.。
2020届高考数学大二轮刷题首选卷文数文档:第一部分+考点五+程序框图+Word版含解析

考点五程序框图一、选择题1.(2019·全国卷Ⅰ)如图是求12+12+12的程序框图,图中空白框中应填入() A.A=12+AB.A=2+1AC.A=11+2AD.A=1+12A答案A解析对于选项A,A=12+A.当k=1时,A=12+12,当k=2时,A=12+12+12,故A正确;经验证选项B,C,D均不符合题意.故选A.2.(2019·湖北八校第二次联考)如图程序中,输入x=ln 2,y=log32,z=12,则输出的结果为()A.x B.y C.z D.无法确定答案A解析图中程序的功能是输出x,y,z的最大值,因为ln 3>1,所以y=log32=ln 2ln 3<ln 2=x,x=ln 2>ln e=12=z,所以输出x.3.(2019·全国卷Ⅲ)执行如图所示的程序框图,如果输入的为0.01,则输出s的值等于()A.2-124B.2-125C.2-126D.2-127答案C解析=0.01,x=1,s=0,s=0+1=1,x=12,x<不成立;s=1+12,x=14,x<不成立;s=1+12+14,x=18,x<不成立;s=1+12+14+18,x=116,x<不成立;s=1+12+14+18+116,x=132,x<不成立;s=1+12+14+18+116+132,x=164,x<不成立;s=1+12+14+18+116+132+164,x=1128,x<成立,此时输出s=2-126.故选C.4.(2019·山东临沂三模)秦九韶,中国古代数学家,对中国数学乃至世界数学的发展做出了杰出贡献.他所创立的秦几韶算法,直到今天,仍是多项式求值比较先进的算法.用秦九韶算法将f(x)=2019x2018+2018x2017+2017x2016+…+2x+1化为f(x)=(…((2019x+2018)x+2017)x+…+2)x+1再进行运算,计算f(x0)的值时,设计了如图所示的程序框图,则在◇和▭中可分别填入()A.n≥2和S=Sx0+n B.n≥2和S=Sx0+n-1C.n≥1和S=Sx0+n D.n≥1和S=Sx0+n-1答案C解析由题意可知,当n=1时程序循环过程应该继续进行,n=0时程序跳出循环,故判断框中应填入n≥1,由秦九韶算法的递推关系可知矩形框中应填入的递推关系式为S=Sx0+n,故选C.5.(2019·河南八市重点高中联考)相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.“三分损益”包含“三分损一”和“三分益一”,用现代数学的方法解释如下,“三分损一”是在原来的长度减去一分,即变为原来的三分之二;“三分益一”是在原来的长度增加一分,即变为原来的三分之四,如图的程序是与“三分损益”结合的计算过程,若输入的x 的值为1,输出的x的值为()A.6481 B.3227 C.89 D.1627答案B解析由题意,执行循环结构的程序框图,可得第1次循环:x=23,i=2,不满足判断条件;第2次循环:x=89,i=3,不满足判断条件;第3次循环:x=3227,i=4,满足判断条件,输出结果3227,故选B.6.(2019·辽宁丹东质量测试(一))计算机在数据处理时使用的是二进制,例如十进制数1,2,3,4的二进制数分别表示为1,10,11,100,二进制数…dcba化为十进制数的公式为…dcba=a·20+b·21+c·22+d·23+…,例如二进制数11等于十进制数1·20+1·21=3,又如二进制数101等于十进制数1·20+0·21+1·22=5,如图是某同学设计的将二进制数11111化为十进制数的程序框图,则判断框内应填入的条件是()A.i>4 B.i≤4 C.i>5 D.i≤5答案B解析在将二进制数11111化为十进制数的程序中循环次数由循环变量i决定,∵11111共有5位,因此要循环4次才能完成整个转换过程,∴退出循环的条件根据程序框图和答案选项,应设为i≤4,故选B.7.(2019·黑龙江哈尔滨三中二模)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是()A.i<20,S=S-1i,i=2iB.i≤20,S=S-1i,i=2iC .i <20,S =S 2,i =i +1D .i ≤20,S =S 2,i =i +1答案 D解析 根据题意可知,截取1天后S =12,所以满足S =S 2,不满足S =S -1i ,故排除A ,B ;由框图可知,计算截取20天后的剩余时,有S =S 2,且i =21,所以循环条件应该是i ≤20.故选D.8.(2019·湖北重点中学高三起点考试)美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a ,n ,ξ的值分别为8,2,0.5,每次运算都精确到小数点后两位,则输出的结果为( )A .2.81B .2.82C .2.83D .2.84答案 D解析 输入a =8,n =2,ξ=0.5,m =82=4,n =4+22=3,|4-3|=1>0.5;m=83≈2.67,n ≈2.67+32≈2.84,|2.67-2.84|=0.17<0.5,输出的结果为2.84.二、填空题9.执行如图所示的程序框图,若输出的结果为12,则输入的实数x的值是________.答案2解析因为输出的结果为12,所以有⎩⎪⎨⎪⎧log2x=12,x>1或⎩⎪⎨⎪⎧x-1=12,x≤1.解得x= 2.所以输入的实数x的值为 2.10.(2019·辽宁沈阳育才学校八模)我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举.这个伟大创举与古希腊的算法——“辗转相除法”实质一样.如图的程序框图即源于“辗转相除法”,当输入a =288,b=123时,输出的a=________.答案3解析解法一:按照程序框图运行程序,输入:a=288,b=123,则r=42,a=123,b=42,不满足r=0,循环;则r=39,a=42,b=39,不满足r=0,循环;则r=3,a=39,b=3,不满足r=0,循环;则r=0,a=3,b=0,满足r=0,输出a=3.解法二:程序框图的功能为“辗转相除法”求解两个正整数的最大公约数,因为288与123的最大公约数为3,所以a=3.11.(2019·安徽A10联盟最后一卷)《九章算术》中有如下问题:“今有牛、羊、马食人苗,苗主责之粟五斗,羊主曰:‘我羊食半马.’马主曰:‘我马食半牛.’今欲衰偿之,问各出几何?”翻译为:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说“我马吃的禾苗只有牛的一半”打算按此比率偿还,问:牛、马、羊的主人各应赔偿多少粟?已知1斗=10升,针对这一问题,设计程序框图如图所示,若输出k的值为2,则m=________.答案50 7解析运行该程序,第一次循环,S=50-m,k=1;第二次循环,S=50-3m,k=2;第三次循环,S=50-7m,此时要输出k的值,则50-7m=0,解得m=50 7.12.(2019·湖北七校联盟期末)设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=746,则I(a)=467,D(a)=764),阅读如图所示的程序框图,运行相应的程序,若输入的a为123,则输出的b为________.答案495解析由程序框图,知第一次循环a=123,b=321-123=198;第二次循环a=198,b=981-189=792;第三次循环a=792,b=972-279=693;第四次循环a=693,b=963-369=594;第五次循环a=594,b=954-459=495;第六次循环a=495,b=954-459=495,满足条件a=b,跳出循环体,输出495.一、选择题1.(2019·湖南衡阳三模)著名的“3n+1猜想”是对任何一个正整数进行规定的变换,最终都会变成 1.如图的程序框图示意了“3n+1”猜想,则输出的n为()A.5 B.6 C.7 D.8答案B解析a=10是偶数,a=5,n=1,a>1,a=5是奇数,a=16,n=2,a>1,a=16是偶数,a=8,n=3,a>1,a=8是偶数,a=4,n=4,a>1,a=4是偶数,a=2,n=5,a>1,a=2是偶数,a=1,n=6,a≤1成立,输出n=6,故选B.2.(2019·福建高三检测)程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为()A.120 B.84 C.56 D.28答案B解析i=0,n=0,S=0;i=1,n=1,S=1,i≥7,否;i=2,n=3,S=1+3,i≥7,否;i=3,n=6,S=1+3+6,i≥7,否;i=4,n=10,S=1+3+6+10,i≥7,否;…i=7,n=28,S=1+3+6+10+15+21+28,i≥7,是;输出S=84.3.(2019·湖南长沙高三统考)若正整数N除以正整数m后的余数为r,则记为N=r(mod m),例如10=2(mod 4).如图所示程序框图的算法源于我国古代数学名著《孙子算经》中的“中国剩余定理”,则执行该程序框图输出的i等于()A.3 B.9 C.27 D.81答案C解析第一次执行循环体,得i=3,N=14,此时14=2(mod 3),但14≠1(mod 7).第二次执行循环体,得i=9,N=23,此时23=2(mod 3),但23≠1(mod 7).第三次执行循环体,得i=27,N=50,此时50=2(mod 3),且50=1(mod 7),退出循环,所以输出i的值为27,故选C.4.(2019·江西九校重点中学协作体第一次联考)《九章算术》是中国古代数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之.”翻译成现代语言如下:第一步,任意给定两个正整数,判断它们是否都是偶数,若是,用2约简;若不是,执行第二步;第二步,以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作,直到所得的数相等,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.现给出更相减损术的程序图如图所示,如果输入的a=114,b=30,则输出的n为()A.3 B.6 C.7 D.8答案C解析∵a=114,b=30,满足a,b都是偶数,则a=a2=57,b=b2=15,k=2;不满足a,b都是偶数,且不满足a=b,满足a>b,则a=57-15=42,n=1,不满足a=b,满足a>b,则a=42-15=27,n=2,不满足a=b,满足a>b,则a=27-15=12,n=3,不满足a=b,不满足a>b,则c=12,a=15,b=12,则a=15-12=3,n=4,不满足a=b,不满足a>b,则c=3,a=12,b=3,则a=12-3=9,n=5,不满足a=b,满足a>b,则a=9-3=6,n=6,不满足a=b,满足a>b,则a=6-3=3,n=7,满足a=b,结束循环,输出n=7,故选C.5.(2019·江西新八校第二次联考)如图所示的程序框图所实现的功能是()A.输入a的值,计算(a-1)×32021+1B.输入a的值,计算(a-1)×32020+1C.输入a的值,计算(a-1)×32019+1D.输入a的值,计算(a-1)×32018+1答案B解析由程序框图,可知a1=a,a n+1=3a n-2,由i的初值为1,末值为2019,可知,此递推公式共执行了2019+1=2020次,又由a n+1=3a n-2,得a n+1-1=3(a n-1),得a n-1=(a-1)×3n-1,即a n=(a-1)×3n-1+1,故a2021=(a-1)×32021-1+1=(a-1)×32020+1,故选B.6.(2019·四川泸州第二次质量诊断)某班共有50名学生,其数学学业水平考试成绩记作a i(i=1,2,3,…,50),若成绩不低于60分为合格,则如图所示的程序框图的功能是()A.求该班学生数学学业水平考试的不合格人数B.求该班学生数学学业水平考试的不合格率C.求该班学生数学学业水平考试的合格人数D.求该班学生数学学业水平考试的合格率答案D解析执行程序框图,可知输入50个学生成绩a i,k表示该班学生数学成绩为该班学生数学学业水平考试的合格合格的人数,程序结束时i=51,输出的ki-1率,故选D.7.如果每对兔子(一雄一雌)每月能生殖一对小兔子(也是一雄一雌,下同),且每对小兔子刚出生的前两个月没有生育能力,但从出生后的第三个月开始便能每月生一对小兔子.假定这些兔子都不发生死亡现象,现有一对刚出生的兔子,那么从这对兔子刚出生开始,到第十个月会有多少对兔子呢?同学A据此建立了一个数列模型,设F(0)=0,第n个月兔子的对数为F(n),由此得到F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*).如图是同学B根据同学A的数列模型设计的程序框图,求该数列的前10项和,则在空白框内分别填入的语句是()A.P=M;n≤9? B.N=P;n≤9?C.P=M;n≤10? D.N=P;n≤10?答案B解析F(1)=1,F(2)=1,F(3)=2,F(4)=3,F(5)=5,F(6)=8,F(7)=13,F(8)=21,F(9)=34,F(10)=55,输出的S=F(0)+F(1)+F(2)+…+F(10).由程序框图可知,当n=2时,S=0+1,P=0+1=1,S=1+1,M=1,N=1;当n =3时,S=0+1+1+2,则处理框内应填入“N=P”,排除A,C;又最终输出S 时,n=10,所以判断框内应填入“n≤9?”,故选B.8.(2019·河北邯郸一模)我国古代数学名著《九章算术》里有一道关于买田的问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶田各几何?”其意思为:“今有好田1亩价值300钱;坏田7亩价值500钱.今合买好、坏田1顷,价值10000钱.问好、坏田各有多少亩?”已知1顷为100亩,现有下列四个程序框图,其中S 的单位为钱,则输出的x ,y 分别为此题中好、坏田的亩数的是( )答案 B解析 由题意得,田的价值S =300x +5007y ,可排除C ,亩数x +y =100.由⎩⎨⎧ 300x +5007y =10000,x +y =100,解得⎩⎪⎨⎪⎧x =12.5,y =87.5,若初始变量x =0.5,则累加变量x =x +3满足题意,故选B. 二、填空题9.(2019·湘赣十四校第一次联考)执行如图所示的程序框图,则输出n 的值为________.答案23解析当n=7时,可知n=2×7+1=15,又i=1+1=2<3,循环;当n=15时,可知n=15-4=11,又i=2+1=3,循环;当n=11时,可知n=2×11+1=23,又i=3+1=4>3,输出n,则n=23.10.(2019·广西南宁第一次适应性考试)元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示.若将“没了壶中酒”改为“剩余原壶中13的酒量”,即输出值是输入值的13,则输入的x=________.答案21 23解析 i =1时,x =2x -1;i =2时,x =2(2x -1)-1=4x -3;i =3时,x =2(4x-3)-1=8x -7;i =4时,退出循环.此时,8x -7=13x ,解得x =2123.11.公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值 3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n 值为________.(参考数据:3≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)答案 24解析 由程序框图,n ,S 值依次为:n =6,S ≈2.598;n =12,S =3;n =24,S ≈3.1056,此时满足S ≥3.10,输出n =24.12.(2019·山东德州一模)在《九章算术》中记载着一道关于“持金出关”的题目,大意是:“在古代出关要交税.一天,某人拿钱若干出关,第1关交所拿钱数的12,第2关交所剩钱数的13,第3关交所剩钱数的14,…”.现以这则故事中蕴含的数学思想,设计如图所示的程序框图,则运行此程序,输出n 的值为________.答案6解析n=1,a=72,S=0,S<60,是;S=0+11×2×72=36,n=2,S<60,是;S=36+12×3×72=48,n=3,S<60,是;S=48+13×4×72=54,n=4,S<60,是;S=54+14×5×72=57.6,n=5,S<60,是;S=57.6+15×6×72=60,n=6,S<60,否;输出n=6.。
2020届高考数学二轮复习疯狂专练3框图(文)

疯狂专练3 框图1.执行如图所示的程序框图,输出的结果是()A.3B.11C.38D.123 2.执行如图所示的程序框图,输出的k值为()A.4B.5C.6D.7 3.执行如图所示的程序框图,若输入的4t=,则输出的i=()A.7B.10C.13D.16一、选择题4.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图, 若输入的a ,b 分别为14,18,则输出的a =()A .0B .2C .4D .145.某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图中记录了每天的销售量(单位:台),把这些数据经过如图所示的程序框图处理后,输出的S =()A .28B .29C .196D .2036.执行如图所示的程序框图,若输出的25s =,则判断框中可填入的条件是()A .4?i ≤B .4?i ≥C .5?i ≤D .5?i ≥7.如图所示的程序框图的算法思路源于世界数学名题“31x +问题”.执行该程序框图,若3N =,则输出的i =()A .6B .7C .8D .98.给出一个如图所示的程序框图,若要使输入的x 值与输出的y 值相等,则x 的可能值的个数为()A .1个B .2个C .3个D .4个9.我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:“今有出门望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?”现在我们用如图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是()A .10000?S >B .10000?S <C .5?n ≥D .6?n ≤10.执行如图所示的程序框图,若输入的04a =,11a =-,23a =,32a =-,41a =,则输出的t 的值为()A .5B .10C .12D .1411.如图给出的是计算111 (24100)+++的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()A .100i >,1n n =+B .100i >,2n n =+C .50i >,2n n =+D .50i ≤,2n n =+12.若执行如图所示的程序框图,输出S 的值为3,则判断框中应填入的条件是()A .6?k <B .7?k <C .8?k <D .9?k <13.阅读下面的程序框图,运行相应的程序,输出的结果为_______.14.某程序框图如图所示,则输出的结果S等于.15.执行如图所示的程序框图,那么输出S的值是________.16.执行如图所示的程序框图,输出S的值为.二、填空题1.【答案】B【解析】执行程序框图,第一次循环:满足判断条件,2123a =+=; 第二次循环:满足判断条件,23211a =+=; 不满足判断条件,此时输出11a =,故选B . 2.【答案】B【解析】执行程序框图, 第一次循环:2a =,2k =; 第二次循环:4a =,3k =; 第三次循环:8a =,4k =;第四次循环:16a =,5k =,此时满足判断条件,终止循环,输出5k =. 3.【答案】D【解析】输入4t =,1i =,0S =,1i =不是质数,011S =-=-,4i =,4S <;4i =不是质数,145S =--=-,7i =,4S <; 7i =是质数,572S =-+=,10i =,4S <; 10i =不是质数,2108S =-=-,13i =,4S <;13i =是质数,8135S =-+=,16i =,4S >,退出循环,故输出的16i =.故选D . 4.【答案】B【解析】14a =,18b =,则b 变为18144-=, 由于a b >,则a 变为14410-=, 由于a b >,则a 变为1046-=, 由于a b >,则a 变为642-=, 由于a b <,则b 变为422-=, 由2a b ==,则输出2a =. 5.【答案】B【解析】由程序框图可知,该程序框图输出的是销售量的平均值, 结合茎叶图可知,输出的20222633333435297S ++++++==,故选B .6.【答案】C答 案 与解析一、选择题【解析】执行程序框图,1i =,100595s =-=,2i =;951085s =-=,3i =;851570s =-=,4i =; 702050s =-=,5i =;502525s =-=,6i =,退出循环.此时输出的25s =.结合选项知选C . 7.【答案】C【解析】第一步:10n =,2i =; 第二步:5n =,3i =; 第三步:16n =,4i =; 第四步:8n =,5i =; 第五步:4n =,6i =; 第六步:2n =,7i =;第七步:1n =,8i =,结束循环,输出的8i =,故选C . 8.【答案】C【解析】分析程序中各变量、各语句的作用, 再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数2,223,251,5x x y x x x x⎧⎪≤⎪=-<≤⎨⎪⎪>⎩的值,又∵输入的x 值与输出的y 值相等, 当2x ≤时,2x x =,解得0x =或1x =, 当25x <≤时,23x x =-,解得3x =, 当5x >时,1x x=,解得1x =±(舍去), 故满足条件的x 值共有3个,故选C . 9.【答案】B【解析】根据题意,利用程序框图求禽的数目,输出结果应为9999959049S =⨯⨯⨯⨯=.循环共执行了5次,所以判断框中应填入的条件是“10000?S <”或“5n ≤?”或“6?n <”.故选B . 10.【答案】D【解析】初始值1i =,1t =,第一次循环,得2120t =⨯-=,2i =; 第二次循环,得033t =+=,3i =; 第三次循环,得2315t =⨯-=,4i =; 第四次循环,得25414t =⨯+=,5i =,不满足循环条件,退出循环,输出的14t =,故选D . 11.【答案】C 【解析】因为111 (24100)+++共50个数, 所以算法框图应运行50次,所以变量i 应满足50i >, 因为是求偶数的和,所以应使变量n 满足2n n =+. 12.【答案】C【解析】根据程序框图,运行结果如下: 第一次循环:2log 3S =,3k =; 第二次循环:23log 3log 4S =⋅,4k =; 第三次循环:234log 3log 4log 5S =⋅⋅,5k =; 第四次循环:2345log 3log 4log 5log 6S =⋅⋅⋅,6k =; 第五次循环:23456log 3log 4log 5log 6log 7S =⋅⋅⋅⋅,7k =;第六次循环:2345672log 3log 4log 5log 6log 7log 8log 83S =⋅⋅⋅⋅⋅==,8k =, 故如果输出3S =,那么只能进行六次循环,故判断框内应填入的条件是8k <.13.【解析】1x =,1y =,2z =;1x =,2y =,3z =; 2x =,3y =,5z =; 3x =,5y =,8z =; 5x =,8y =,13z =; 8x =,21z =,138y x =. 14.【答案】57【解析】2k =,4S =;3k =,11S =;4k =,26S =;5k =,57S =, 退出循环,输出57S =. 15.【答案】2【解析】运行框图,输入2S =,2015k =, 满足条件2018k <,1112S ==--,201512016k =+=; 二、填空题满足条件2018k <,11112S ==+,201612017k =+=; 满足条件2018k <,12112S ==-,201712018k =+=,2018k <不成立,输出2S =.16.【答案】1009【解析】执行程序框图,π01sin012S =+⋅=+,3i =,32018≤; 3π013sin0132S =++⋅=+-,5i =,52018≤; 5π0135sin01352S =+-+⋅=+-+,7i =,72018≤;…; 2017π0132017sin01320172S =+-++⋅=+-++,2019i =,20192018>,输出0135720152017S =+-+--+(01)(35)(79)(20152017)=++-++-+++-+1222150421009=++++=+⨯=.。
2018届高考数学(文)二轮复习系列之疯狂专练4 框图 Word版含解析
1.[2017·静海县一中]已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x 值为( )A .2或2-B .1-或2-C .1或2-D .2或1-【答案】C【解析】当0x ≥时,210x -=,即1x =;当0x <时,220x x +=,即2x =-,所以输入的x 的值为1或2-.2.[2017·鞍山质检]执行下图程序框图,如果输入的x ,t 均为2,则输出的S =( )A .7B .6C .5D .4【答案】A一、选择题(5分/题)【解析】若2x t ==,则第一次循环,12≤成立,则122,235,21M S k =⨯==+==;第二次循环,22≤成立,则222,257,32M S k =⨯==+==,此时32≤不成立,输出7S =,故选A .3.[2017·湖师附中]执行如图所示的程序框图,则输出的i 值为( )A .3B .4C .5D .6【答案】B【解析】第一次循环,1,1m i ==时,112,2m i =+==;第二次循环,1,3m i ==;第三次循环,0,4m i ==,结束循环,输出4i =,选B .4.[2017·长郡中学]执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( )A .8?n ≤B .8?n >C .7?n ≤D .7?n >【答案】D【解析】开始,033S =+=,5a =,判断,应执行否,112n =+=;358S =+=,7a =,判断,应执行否,213n =+=; 8715S =+=,9a =,判断,应执行否,314n =+=; 15924S =+=,11a =,判断,应执行否,415n =+=; 241135S =+=,13a =,判断,应执行否,516n =+=; 351348S =+=,15a =,判断,应执行否,617n =+=; 481563S =+=,17a =,判断,应执行否,718n =+=;631780S =+=,19a =,判断,此时应输出,所以判断框内应填7n >,故选择D .5.[2017·长安区一中]下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为1A 、2A 、⋅⋅⋅⋅⋅⋅、16A ,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )A .6B .10C .91D .92【答案】B【解析】由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10.故选B .6.[2017·吉大附中]已知函数()2f x x x =+,执行如图所示的程序框图,输出的k 值是( )A .4B .5C .6D .7【答案】C【解析】模拟程序运行,可得:0S =,0k =, 不满足条件56S >,1k =,12S =; 不满足条件56S >,2k =,1126S =+; 不满足条件56S >,3k =,1112612S =++; 不满足条件56S >,4k =,1111261220S =+++; 不满足条件56S >,5k =,1111126122030S =++++; 不满足条件56S >,6k =,111111626122030427S =+++++=; 满足条件56S >,退出循环,输出k 的值为6. 本题选择C 选项.7.[2017·重庆一中]执行如图所示的程序框图,输出S 的值为( )A .0B .1-C .12-D .32-【答案】A【解析】开始10==n S ,;10cos 32S π=+=,3=n ,否;11cos 22S =+π=-,5=n ,否;111cos 02322S 5π=-+=-+=,7=n ,是;输出0,故选A . 8.[2017·正定中学]下图是函数()y f x =求值的程序框图,若输出函数()y f x =的值域为[]48,,则输入函数()y f x =的定义域不可能...为( ) 2xy -=A .[]32--,B .[){}322--,C .[]32-,D .[]{}322--,【答案】C【解析】由题意得,当[]02x ∈,时,只有()24f =;当[]02x ∉,时,由428x-≤≤可得32x --≤≤,故所给函数的定义域可以为[]{}322--,或[){}322--,或[]32--,.本题选择C 选项.9.[2017·钦州模拟]执行如图所示的程序框图(*N ∈N ),那么输出的p 是( )A .33N N A ++ B .22N N A ++C .11N N A ++D .NN A【答案】C【解析】第一次执行循环体,111k p A ==,,满足继续循环的条件,2k =; 第二次执行循环体,222k p A ==,,满足继续循环的条件,3k =;第三次执行循环体,333k p A ==,,满足继续循环的条件,4k =;⋯第N 次执行循环体,NN k N p A ==,,满足继续循环的条件,1k N =+; 第1N +次执行循环体,111N N k N p A ++=+=,,不满足继续循环的条件,故输出的p 值为11N N A ++,故选:C .10.[2017·西安铁一中]执行如图所示的程序框图,输出的结果为( )A .3B .4C .5D .6【答案】B【解析】由程序框图可知1220110133b b k a a⎛⎫===⨯==< ⎪⎝⎭,,,;2228312213394b k k b a a a ⎛⎫=+====⨯==< ⎪⎝⎭,,,;332827133143932b k k b a a a ⎛⎫=+====⨯==< ⎪⎝⎭,,,;482649144193818b k k b a a a ⎛⎫=+====⨯==> ⎪⎝⎭,,,;输出 4k =.故本题答案选B .11.[2017·广安期末]若如图所示的流程图输出的S 是30,则在判断框中M 表示的“条件”应该是( )A .3n ≥B .4n ≥C .5n ≥D .6n ≥【答案】B【解析】由程序框图知:第一次运行12n S ==,;第二次运行22226n S ==+=,;第三次运行23322214n S ==++=,;第四次运行2344222230n S ==+++=,,因为输出30S =,所以条件应是4n ≥,故选B .12.[2017·内丘中学]我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )【答案】B【解析】程序运行过程中,各变量值如下表所示:第1次循环:1142s i =-=,, 第2次循环:111824s i =--=,,第3次循环:111116248s i =---=,,⋯依此类推,第7次循环:11111256248128s i =-----=,, 此时不满足条件,退出循环,其中判断框内①应填入的条件是:128?i …,执行框②应填入:1s s i=-,③应填入:2i i =.本题选择B 选项.二、填空题(5分/题)13.[2017·怀仁县一中]如图是某算法的程序框图,若任意输入1192⎡⎤⎢⎥⎣⎦,中的实数x ,则输出的x 大于49的概率为__________.【答案】2437【解析】由循环结构流程图知输出()22211187x x ---=-⎡⎤⎣⎦,又87497x x ->⇒>,因此所求概率为19724137192-=-. 14.[2017·莆田六中]下面的程序框图中,若输入40n =,则输出的结果为__________.【答案】121【解析】40n =,40S =,32,72n S ==,0?n =否,24,96n S ==,0?n =否,16,112n S ==,0?n =否,8,120n S ==,0?n =否,0,120n S ==,0?n =是,121S =,输出121S =.15.[2017·山西八校]如图所示,输出的x 的值为__________.【答案】17【解析】从题设中提供的算法流程图中运算程序可以看出: 当51221a b ==,时,a b <,则170b b a a b =-=<,,则17051119b b a a b =-=-=<,,则1195168b b a a b =-=-=<,,则685117b b a a b =-=-=>,,则511734a a b =-=>,,则34171717a a b a b x b =-=-====,,,这时运算程序结束,应填答案:17. 16.[2017·德州二模]执行如图所示的程序框图,则输出的结果是__________.【答案】8 【解析】2222223412log log log ......log log 34522n S n n +=++++=++,当22log 22n =-+时,6n =,当7n =时,当2S <-,此时18n n =+=,故填:8.。
参考-数学高考(文)二轮复习系列之疯狂专练4框图-含解析

数学高考(文)二轮复习系列之疯狂专练4框图-含解析A .或B .或C .或D .或22-1-2-12-21-【答案】C【解析】当时,,即;当时,,即,所以输入的的值为或.0x≥210x -=1x =0x <220x x +=2x =-x 12- 2.[2017·鞍山质检]执行下图程序框图,如果输入的,均为,则输出的( )x 2S = A .7 B .6 C .5 D .4【答案】A【解析】若,则第一次循环,成立,则;第二次循环,成立,则,此时不成立,输出,故选A .2x t ==12≤122,235,21M S k =⨯==+==3.[2017·湖师附中]执行如图所示的程序框图,则输出的值为( ) A .3 B .4 C .5 D .6【答案】B参考-数学框图【解析】第一次循环,时,;第二次循环,;第三次循环,,结束循环,输出,选B .1,1mi ==112,2m i =+==1,3m i ==0,4m i ==4i = 4.[2017·长郡中学]执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( ) A . B . C .D .8?n ≤8?n >7?n ≤7?n >【答案】D【解析】开始,,,判断,应执行否,;033S =+=5a =112n =+= 358S =+=,,判断,应执行否,;7a =213n =+= 8715S =+=,,判断,应执行否,;9a =314n =+= 15924S =+=,,判断,应执行否,;11a =415n =+= 241135S =+=,,判断,应执行否,;13a =516n =+= 351348S =+=,,判断,应执行否,;15a =617n =+= 481563S =+=,,判断,应执行否,;17a =718n =+=631780S =+=,,判断,此时应输出,所以判断框内应填,19a =7n >故选择D .5.[2017·××区一中]下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为、、、,如图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )1A 2A ⋅⋅⋅⋅⋅⋅16AA .6B .10C .91D .92【答案】B【解析】由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10.故选B .6.[2017·吉大附中]已知函数,执行如图所示的程序框图,输出的值是( )()2f x x x =+kA .4B .5C .6D .7【答案】C【解析】模拟程序运行,可得:,,0S =0k =不满足条件,,;56S >1k =12S = 不满足条件,,;56S >2k =1126S =+ 不满足条件,,;56S >3k =1112612S =++ 不满足条件,,;56S >4k =1111261220S =+++ 不满足条件,,;56S >5k =1111126122030S =++++不满足条件,,;56S >6k =111111626122030427S =+++++=满足条件,退出循环,输出的值为6.56S >k本题选择C 选项.7.[2017·重庆一中]执行如图所示的程序框图,输出的值为( )SA .0B .C .D .1-12-32-【答案】A【解析】开始;,,否;,,否;,,是;输出0,故选A.10==n S ,10cos 32S π=+=3=n 11c o s 22S =+π=-5=n 111c o s 02322S 5π=-+=-+=7=n8.[2017·正定中学]下图是函数求值的程序框图,若输出函数的值域为,则输入函数的定义域不可能为( )()y f x =()y f x =[]48,()y f x =A .B .C .D .[]32--,[){}322--,[]32-,[]{}322--,【答案】C【解析】由题意得,当时,只有;当时,由可得,故所给函数的定义域可以为或或.本题选择C选项.[]02x∈,()24f =[]02x ∉,428x -≤≤32x --≤≤[]{}322--,[){}322--,[]32--,9.[2017·钦州模拟]执行如图所示的程序框图(),那么输出的是( )*N∈N pA .B .C .D .33N N A ++22N N A ++11N N A ++N N A【答案】C【解析】第一次执行循环体,,满足继续循环的条件,;111k p A ==,2k =第二次执行循环体,,满足继续循环的条件,;222k p A ==,3k = 第三次执行循环体,,满足继续循环的条件,;333k p A ==,4k = 第次执行循环体,,满足继续循环的条件,;N N N k Np A ==,1k N =+ 第次执行循环体,,不满足继续循环的条件,1N +111N N kN pA ++=+=, 故输出的值为,故选:C .p 11N N A ++ 10.[2017·西安铁一中]执行如图所示的程序框图,输出的结果为( ) A .3 B .4 C .5 D .6【答案】B【解析】由程序框图可知;1220110133b b k a a ⎛⎫===⨯==< ⎪⎝⎭,,, 2228312213394b k k ba a a ⎛⎫=+====⨯==< ⎪⎝⎭,,,; 332827133143932b k k ba a a ⎛⎫=+====⨯==< ⎪⎝⎭,,,; 482649144193818b k k ba a a ⎛⎫=+====⨯==> ⎪⎝⎭,,,; 输出.故本题答案选B . 4k =11.[2017·广安期末]若如图所示的流程图输出的是30,则在判断框中表示的“条件”应该是( )S MA .B .C .D .3n ≥4n ≥5n ≥6n ≥【答案】B【解析】由程序框图知:第一次运行;第二次运行;第三次运行;第四次运行,因为输出,所以条件应是,故选B.12n S ==,22226n S ==+=,23322214n S ==++=,2344222230n S ==+++=,30S =4n ≥12.[2017·内丘中学]我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完,现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )【答案】B【解析】程序运行过程中,各变量值如下表所示:第1次循环:,1142s i =-=, 第2次循环:,111824s i =--=, 第3次循环:,111116248s i =---=,依此类推,第7次循环:,11111256248128s i =-----=,此时不满足条件,退出循环,其中判断框内①应填入的条件是:,执行框②应填入:,③应填入:.本题选择B 选项.128?i…1s s i =-2i i = 13.[2017·××一中]如图是某算法的程序框图,若任意输入中的实数,则输出的大于49的概率为__________.1192⎡⎤⎢⎥⎣⎦,x x【答案】2437【解析】由循环结构流程图知输出,又,因此所求概率为.()22211187x x ---=-⎡⎤⎣⎦87497x x ->⇒>14.[2017·莆田六中]下面的程序框图中,若输入,则输出的结果为__________. 【答案】121【解析】,,,否,,否,,否,,否,,是,,输出.32,72nS ==0?n =24,96n S ==0?n =16,112n S ==0?n =8,120n S ==0?n =0,120n S ==0?n =121S =121S =15.[2017·山西八校]如图所示,输出的的值为__________.x【答案】17【解析】从题设中提供的算法流程图中运算程序可以看出: 当时,,则,则,51221a b ==,a b <170b b a a b =-=<,17051119b b a a b =-=-=<,则,则,则,1195168b b a a b =-=-=<,685117b b a a b =-=-=>,511734a a b =-=>,则,这时运算程序结束,应填答案:.34171717aa b a b x b =-=-====,,17 16.[2017·德州二模]执行如图所示的程序框图,则输出的结果是__________. 【答案】8【解析】,当时,,当时,当,此时,故填:8.2222223412l o g l o g l o g ......l o g l o g 34522n S n n +=++++=++22log 22n =-+6n =7n =2S <-18n n =+=。
2020届高考数学二轮复习疯狂专练21模拟训练一文

疯狂专练21 模拟训练一一、选择题?x?1???203?A?x?x?2x?AB2B?x?是(),则,.若集合1 ??x?1??x?x?1}3}1x?{x?3{xx??3?或 B或A..3}x?1?{x?3x{x?3??1?x?3}.C.或Dsin43?sin107?+cos223?sin197??() 2.1133?? C.DA.. B.222221ba?m3?4??2m?(),则.设,且 3ab2312366 AD.B.. C.a?a?a?24{?a?18a}S{a}a?a9等于()4.等差数列项和,则数列中,,的前9369n4n1745546381.. B.D A.C x?y?2??222)??((x?2)y9??3y2x的最大值为() 5.已知,则??x?0?34 C.25B.D.34A.5ac2ABCC△ABC△bBA sinaA,,且.6,,的内角已知,的面积为,所对的边分别为,a22?c?b cosA?()则1232. B.D CA..3564BE?ADDE BCABC△DCBD?4()边上一点,若是中,是的中点,则7.在,92142941AB?AB?AC?AC?ABAB?ACACD.B.CA..55510510555ABCDCA24的.已知某圆柱的底面周长为8,高为,矩形是该圆柱的轴截面,则在此圆柱侧面上,从到路径中,最短路径的长度为().1751361 C..A. B .D3)?f(x?)f(x x则满足.设函数的取值范围是()的9?1x??logx,2?3[0,3](1,3],1]??([0,1] x1??1x3?,B.D C.A..234(1))fx)(1,?f(x)yf(axf(x)?x?(a?2)x?处的切线方程10.设函数为偶函数,则曲线.若在点为()0?5??08x?y8?02x?y?0x?y?5x2?y B.C..DA.2x1,0)(?2NC1y??MA1的右顶点为,过交于的直线与两点,.已知椭圆11且斜率为,4则()?AM?AN123302 D.. B.C .A551??x?2x2x?acos(fx)?sin??,??a的取值范围是().若函数在单调递增,则12 21,1][?(?1,1) B A..(??,?1]1)(??,?[1,??)(1,??). C.D二、填空题10分钟的概率 13.某人午觉醒来,发现表停了,他打开收音机,想听电台整点报时,则他等待时间不多于为_______.22kll4)??y1x(?2)A(0,等直线分成两段弧,将圆过点14.的直线当劣弧所对的圆心角最小时,的斜率._______于22yx x?3y?1?0A,B0)?b??C:?1(aABM,中点为15.已知直线交于与椭圆两点,且线段22ab CO?135OM的离心率为_______(,则椭圆为坐标原点)的倾斜角为.若直线π?f(x)??)??0?m)(??(fx)?mcos(x BA C?0为,点,,的部分图像如图所示,,已知函数16.2π12A(,0),的图像与坐标轴的交点,且,,DBCD?2)D(,?π629m?.则与解析案答一、选择题C.【答案】1????3x?B?x1?1?x?A?x?3根据题意【解析】,,3}??1x1??3?x{x或所以.,故答案选CB【答案】2.3?cos17?+cos43?sin17?43?sin?.【解析】原式2A 3.【答案】ba?43m?a?logm b?logm,【解析】,,得由3421?2log3?log4,,则mm ab212??2m?3624?2log3?log2?log36,,所以,所以,即因为mmm ab m?0m?6,答案选A,故.又4.【答案】Ca?a?2aa?a?2a,【解析】由等差数列的性质可得,631497a?a?a?2418a?a?a?,,又∵9367143a?24a?a?148a3?18a6?a?,,∴,解得,∴,6646449(a?a)9?1464?S??63}{a9.的前项和∴数列9n22B【答案】.5222,2)(A?2)?(xy(?2)?的距离,如图,表示可行域内的点到点【解析】.1)?B(3,2,2)(?A34??9z?25到可行域中点画出可行域可知,点.距离最大,则max C【答案】6.12AasinbcsinAS??2bca?2,所以【解析】由三角形面积公式可得,ABC△22222222234abc?aa8ba?ca??(b?c)??2???cosA?又.244abc2bc2A.【答案】7 【解析】根据向量的运算法则,可得4414AC?)?ABAB?(AC?AB?AD?AB?BD?ABBC?,5555291AC??ABABAD?BE??.所以,故选A5102C【答案】8.524,则在此圆柱侧面上,宽为【解析】圆柱的侧面展开图如图,圆柱的侧面展开图是矩形,且矩形的长为ACCA22.从的最短路径为线段到,13??AC?125B【答案】9.x?13?31?10?xx?当时,,解得;【解析】3logx?2?3x?1x?1?当,解得.时,33x?0?x 综上,.的取值范围是,故答案选BD【答案】10.2432?a?2?0a x?x2?xf()x?)'(x?4x4f,因为函数【解析】,是偶函数,所以,解得,所以)x(f?3(1)f?f(1)8?,,所以.0?y?5(1,f(1))8x?y?f(x)1)??y?38(x,所以曲线,即在点处的切线方程为.故选DD【答案】11.2?x21?y??1,0)(?1x?y?1,且斜率为,与椭圆方程联立【解析】根据题意,过的直线方程4??1??xy?3820x?8x?5(0,1)N),?M(?,解得,,消元整理得55318(2,0)A2,1)???(,?),ANAM?(,所以,又5533183??1?(?))(AM?AN???(?2)从而.555A【答案】12.?????0?x)f(x)f(????,????,单2?3?sinx?xsin?2?2sinx?axf)(x?cos2?a根据题意,,【解析】调递增,∴∵在上恒成立.在???21,1])(x?0[f[x?tsin??1,1]?????,02tg()??t?at??3令在上恒成立转化为在上恒成立,,则g(?1)?0??1?a?1,故答案选A,解得.只要满足?g(1)?0?二、填空题1【答案】13.6分钟,【解析】该人等待时间可能性有60 分钟,则他等待整点时间不多于10分钟时间的可能性有10101??P10.分钟的概率为则他等待时间不多于6062【答案】14.22222(x?1)?y?42)(?(01)?2)?A(0,43?的内部.在圆可知,点由【解析】.C(1,0)C,要使劣弧所对的圆心角最小,,则圆心为设圆的圆心为12??k?CAl?.,所以则k2CA6 15.【答案】3A(x,y),B(x,y),M(x,y),【解析】设021*********yyxxyxA,B2112??1??1??1,在椭圆上,∴∵点,222222ababab22yyy?by?yyy?b021???2211???两式相减整理得,,∴22axx?xxxx?ax?2102211221b11b2b?????tan135??,∴即,∴,??k?k6cbC的离心率为.∴椭圆?1??e?22aa323.【答案】ABOM222a3a33a2216122(0,?3)C,0)?2)CD?(πDDB(π,B,可得,点坐标为【解析】由及点坐标为2932πππ2???2π)??2(π?(A,0)T.,,∴∵T663ππ?)x(f)?cos(2??0,0)A(,,可得把点代入66πππ??ππkk?????,∴,326ππ????又,∴,62π3m?2f(0)?=?3?mcos∴,解得.6。
2020届高考数学(文)课标版二轮复习训练习题:中档提升练 第四练

第四练一、选择题1.(2019课标全国Ⅲ,11,5分)记不等式组表示的平面区域为D.命题p:∃(x,y){x +y ≥6,2x ‒y ≥0∈D,2x+y ≥9;命题q:∀(x,y)∈D,2x+y ≤12.下面给出了四个命题①p ∨q ②¬p ∨q ③p ∧¬q ④¬p ∧¬q 这四个命题中,所有真命题的编号是( ) A.①③B.①② C.②③ D.③④答案 A 由不等式组画出平面区域D,如图中阴影部分所示,在图中画出直线2x+y=9,可知命题p 正确,作出直线2x+y=12,2x+y ≤12表示直线及其下方区域,易知命题q 错误.∴¬p 为假,¬q 为真,∴p ∨q 为真,¬p ∨q 为假,p ∧¬q 为真,¬p ∧¬q 为假.故真命题的编号为①③,故选A.2.定义在R 上的函数f(x)满足f(x+1)=f(x-1),且f(x)=其中a ∈R,若f(-5){x +a ,‒1≤x <0,|2‒x |,0≤x <1,=f(4.5),则a=( )A.0.5B.1.5C.2.5D.3.5答案 C 由f(x+1)=f(x-1),得f(x)是周期为2的函数,又f(-5)=f(4.5),所以f(-1)=f(0.5),即-1+a=1.5,所以a=2.5,故选C.3.已知直线l 过点(-2,0)且倾斜角为α,若l 与圆(x-3)2+y 2=20相切,则sin=( )(3π2‒2α)A. B.-C. D.-35354545答案 A 由题意可设直线l 的方程为y=(x+2)tan α,因为l 与圆(x-3)2+y 2=20相切,所以=,所以tan 2α=4,因此sin=-cos 2α=-=-=-=.故选A.|5tanα|1+tan 2α20(3π2‒2α)cos 2α‒sin 2αcos 2α+sin 2α1‒tan 2α1+tan 2α1‒41+4354.已知双曲线-=1(a>0,b>0)的左焦点为F,离心率为,若经过F 和P(0,4)两点的直线平行x 2a 2y 2b 22于双曲线的一条渐近线,则双曲线的方程为( )A.x 2-y 2=1B.-=1x 22y 22C.-=1D.-=1x 24y 24x 28y 28答案 D 由题意得双曲线的左焦点为F(-c,0).由离心率e==,得c=a,c 2=2a 2=a 2+b 2,即c a 22a=b,所以双曲线的渐近线方程为y=±x,则经过F 和P(0,4)两点的直线的斜率k==1,得c=4,所4c 以a=b=2,所以双曲线的方程为-=1,故选D.2x 28y 28二、填空题5.已知点A(2,1),O 是坐标原点,点P(x,y)的坐标满足设z=·,则z 的最{2x ‒y ≤0,x ‒2y +3≥0,y ≥0,OP OA 大值是 . 答案 4解析 解法一:由题意,作出可行域,如图中阴影部分所示,z=·=2x+y,作出直线2x+y=0OP OA 并平移,可知当直线过点C 时,z 取得最大值.由得即C(1,2),则z 的最大{2x ‒y =0,x ‒2y +3=0,{x =1,y =2,值是4.解法二:由题意,作出可行域,如图中阴影部分所示,可知可行域是三角形封闭区域.z=·=2x+y,易知目标函数z=2x+y 的最大值在顶点处取得,求出三个顶点的坐标分别为OP OA (0,0),(1,2),(-3,0),分别将(0,0),(1,2),(-3,0)代入z=2x+y,对应z 的值为0,4,-6,故z 的最大值是4.6.在△ABC 中,A,B,C 所对的边分别为a,b,c,已知a 2+b 2-c 2=ab,且acsin B=2sin C,则△33ABC 的面积为 . 答案 32解析 因为a 2+b 2-c 2=ab,所以由余弦定理得cos C===,又0<C<π,所以C=.3a 2+b 2‒c 22ab 3ab 2ab 32π6因为acsin B=2sin C,所以结合正弦定理可得abc=2c,所以ab=2.故S △ABC =absin C=33312×2sin =.123π632三、解答题7.如图,平行四边形ABCD 中,BC=2AB=4,∠ABC=60°,PA ⊥平面ABCD,PA=2,E 为BC 的中点,F 为PE 的中点.(1)求证:AF ⊥平面PED;(2)求点C 到平面PED 的距离.解析 (1)证明:如图,连接AE,在平行四边形ABCD 中,BC=2AB=4,∠ABC=60°,E 为BC 的中点,∴AE=2,ED=2,3∴AE 2+ED 2=AD 2,∴AE ⊥ED.∵PA ⊥平面ABCD,ED ⊂平面ABCD,∴PA ⊥ED,又PA ∩AE=A,PA,AE ⊂平面PAE,∴ED ⊥平面PAE,又AF ⊂平面PAE,∴ED ⊥AF.∵PA=AE=2,F 为PE 的中点,∴AF ⊥PE.又PE ∩ED=E,PE,ED ⊂平面PED,∴AF ⊥平面PED.(2)设点C 到平面PED 的距离为d.由ED ⊥平面PAE,PE ⊂平面PAE,得DE ⊥PE.在Rt △PED 中,PE=2,ED=2,∴S △PED =2.236在△ECD 中,EC=CD=2,∠ECD=120°,∴S △ECD =×2×2×sin 120°=.123连接PC,由V C-PED =V P-ECD 得,S △PED ·d=S △ECD ·PA,1313∴d===,S △ECD ·PAS △PED3×22622故点C 到平面PED 的距离为.228.随着移动互联网的发展,与餐饮美食相关的手机软件层出不穷.现从某市使用A 款订餐软件和使用B 款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.使用A 款订餐软件的100个商家的“平均送达时间”的频率分布直方图使用B 款订餐软件的100个商家的“平均送达时间”的频率分布直方图(1)已知抽取的100个使用A 款订餐软件的商家中,甲商家的“平均送达时间”为18分钟,现从使用A 款订餐软件且“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;(2)试估计该市使用A 款订餐软件的商家的“平均送达时间”的众数及平均数(同一组中的数据用该组区间的中点值代表);(3)如果以“平均送达时间”的平均数作为决策依据,从A 和B 两款订餐软件中选择一款订餐,你会选择哪一款?解析 (1)使用A 款订餐软件且“平均送达时间”不超过20分钟的商家共有100×0.006×10=6(个),分别记为甲,a,b,c,d,e,从中随机抽取3个商家的所有情况为{甲,a,b},{甲,a,c},{甲,a,d},{甲,a,e},{甲,b,c},{甲,b,d},{甲,b,e},{甲,c,d},{甲,c,e},{甲,d,e},{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,d,e},{b,c,d},{b,c,e},{b,d,e},{c,d,e},共20种.甲商家被抽到的情况为{甲,a,b},{甲,a,c},{甲,a,d},{甲,a,e},{甲,b,c},{甲,b,d},{甲,b,e},{甲,c,d},{甲,c,e},{甲,d,e},共10种.记事件A 为甲商家被抽到,则P(A)==.102012(2)依题意可得,使用A 款订餐软件的商家的“平均送达时间”的众数为55,平均数为15×0.006×10+25×0.034×10+35×0.012×10+45×0.004×10+55×0.040×10+65×0.004×10=40.(3)使用B 款订餐软件的商家的“平均送达时间”的平均数为15×0.004×10+25×0.020×10+35×0.056×10+45×0.014×10+55×0.004×10+65×0.002×10=35<40.所以选择B 款订餐软件.。
2020届高考数学(文)课标版二轮复习训练习题:中档提升练 第七练
第七练一、选择题 1.执行如图所示的程序框图,则输出的n 的值为( )A.63B.47C.23D.7答案 C 执行程序框图,得n=7,i=1;n=15,i=2;n=11,i=3;n=23,i=4,此时满足i>3,结束循环,输出n=23,故选C.2.在不等式组所表示的平面区域内随机取一点P,则点P 到直线l:x=-1的距离{x ‒y ≥0,x +y ‒2≤0,y +1≥0小于或等于1的概率为( )A. B.1214C. D.18116答案 C 画出不等式组,所表示的平面区域如图中阴影部分所示,作出直线{x ‒y ≥0,x +y ‒2≤0y +1≥0l:x=-1.易得A(-1,-1),B(3,-1),C(1,1),则阴影部分的面积为×4×2=4.易知满足条件的点P 恰好落在△12OAM 内(含该三角形的边界),且△OAM 的面积为×1×1=,∴点P 到直线l:x=-1的距离小于1212或等于1的概率为=.故选C.124183.在△ABC 中,内角A,B,C 的对边分别为a,b,c.p:B+C=2A,且b+c=2a;q:△ABC 是正三角形.则p 是q 的( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件答案 A 对于p,在△ABC 中,B+C=2A,所以π-A=2A,即A=,又b+c=2a,所以由正弦定理得π3sin B+sin C=2sin A=,所以sin B+sin =,整理得sin=,所以3(2π3‒B)33(B +π6)3sin=1,因为B ∈,所以B=,所以C=,即△ABC是正三角形.所以p 是q 的充要条(B +π6)(0,2π3)π3π3件,故选A.4.已知F 1,F 2为椭圆C:+=1(a>b>0)的左,右焦点,过原点O 且倾斜角为30°的直线l 与椭圆x 2a 2y 2b 2C 的一个交点为A,若AF 1⊥AF 2,则=2,则椭圆C 的方程为( )S △AF 1F2A.+=1 B.+=1x 26y 22x 28y 24C.+=1D.+=1x 28y 22x 220y 216答案 A 因为点A 在椭圆上,所以|AF 1|+|AF 2|=2a,对其平方,得|AF 1|2+|AF 2|2+2|AF 1||AF 2|=4a 2,又AF 1⊥AF 2,所以|AF 1|2+|AF 2|2=4c 2,则2|AF 1||AF 2|=4a 2-4c 2=4b 2,即|AF 1||AF 2|=2b 2,所以=|AF 1||AF 2|=b 2=2.又△AF 1F 2是直角三角形,∠F 1AF 2=90°,且O 为F 1F 2的中点,所以S △AF1F 212|OA|=|F 1F 2|=c,由已知不妨设A 在第一象限,则∠AOF 2=30°,所以A,则12(32c ,12c )=|F 1F 2|·c=c 2=2,c 2=4,故a 2=b 2+c 2=6,所以椭圆C的方程为+=1,故选A.S △AF1F 2121212x 26y 22二、填空题5.在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2AA 1,则异面直线A 1B 与B 1C 所成角的余弦值为 .答案 15解析 如图,连接A 1D,BD,因为A 1D ∥B 1C,所以∠BA 1D 或其补角即A 1B 与B 1C 所成的角.设A 1A=1,则AB=BC=2,在△A 1BD 中,A 1B=A 1D=,BD=2,所以cos ∠BA 1D=52==.A 1D 2+A 1B 2‒BD 22A 1D ·A 1B 5+5‒82×5156.设S n 是数列{a n }的前n 项和,若a n +S n =2n ,=2a n+2-a n+1,则++…+= .2b n1b 112b 21100b 100答案 100101解析 因为a n +S n =2n ①,所以a n+1+S n+1=2n+1②,②-①得2a n+1-a n =2n ,所以2a n+2-a n+1=2n+1,又=2a n+2-a n+1=2n+1,所以b n =n+1,==-,则++…+=1-+-+…+-=1-2b n1nb n 1n (n +1)1n 1n +11b 112b 21100b 10012121311001101=.1101100101三、解答题7.已知函数f(x)=x 3+ax-2ln x.(1)当a=-1时,求函数f(x)的单调区间;(2)若f(x)≥0在定义域内恒成立,求实数a 的取值范围.解析 (1)当a=-1时, f(x)=x 3-x-2ln x(x>0), f '(x)=3x 2-1-==.2x 3x 3‒x ‒2x (x ‒1)(3x 2+3x +2)x ∵3x 2+3x+2>0恒成立,∴当x ∈(1,+∞)时, f '(x)>0,f(x)单调递增;当x ∈(0,1)时, f '(x)<0, f(x)单调递减.故f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).(2)∵f(x)=x 3+ax-2ln x ≥0在(0,+∞)上恒成立,∴当x ∈(0,+∞)时,=x 2+a-≥0恒成立.令g(x)=x 2+a-,f (x )x 2lnxx 2lnxx g'(x)=2x-2×=2×,(lnx )'·x ‒lnx ·x 'x 2x 3+lnx ‒1x 2令h(x)=x 3+ln x-1,则h(x)在(0,+∞)上单调递增,且h(1)=0,∴当x ∈(0,1)时,h(x)<0,g'(x)<0,即g(x)单调递减;当x ∈(1,+∞)时,h(x)>0,g'(x)>0,即g(x)单调递增.∴g(x)min =g(1)=1+a ≥0,a ≥-1,故实数a 的取值范围是[-1,+∞).8.[选修4-4]在平面直角坐标系xOy 中,曲线C 1的参数方程为(φ为参数),以{x =2+2cosφ,y =2sinφ原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=4sin θ.(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程;(2)已知曲线C 3是过原点且倾斜角为α的直线,点A 是曲线C 3与曲线C 1的交点,点B 是曲线C 3与曲线C 2的交点,点A,B 均异于原点O,|AB|=4,求α的值.2[选修4-5]已知f(x)=|ax-2|-|x+2|.(1)当a=2时,解不等式f(x)≤1;(2)若关于x 的不等式-4≤f(x)≤4对x ∈R 恒成立,求实数a 的值.解析 [选修4-4](1)由消去参数φ,得C 1的普通方程为(x-2)2+y 2=4.∵ρ=4sin θ,∴ρ2=4ρsin θ,{x =2+2cosφ,y =2sinφ∴曲线C 2的直角坐标方程为x 2+(y-2)2=4.(2)由(1)得曲线C 1:(x-2)2+y 2=4,其极坐标方程为ρ=4cos θ,由题意设A(ρ1,α),B(ρ2,α),则|AB|=|ρ1-ρ2|=4|sin α-cos α|=4=4,∴sin =±1,∴α-=+kπ(k ∈Z),2|sin (α‒π4)|2(α‒π4)π4π2∵0<α<π,∴a=.3π4[选修4-5](1)当a=2时, f(x)≤1即|2x-2|-|x+2|≤1.当x ≥1时,(2x-2)-(x+2)≤1,∴1≤x ≤5;当x ≤-2时,-(2x-2)+(x+2)≤1,x ≥3,∴无解;当-2<x<1时,-(2x-2)-(x+2)≤1,x ≥-,∴-≤x<1.1313综上可知,不等式f(x)≤1的解集为.{x |‒13≤x ≤5}(2)∵-4≤f(x)≤4对x ∈R 恒成立,则||x+2|-|ax-2||≤4恒成立,而||x+2|-|ax-2||≤|(1+a)x|,或||x+2|-|ax-2||≤|(1-a)x+4|,∴只需|(1+a)x|≤4恒成立或|(1-a)x+4|≤4恒成立,∴a=-1或a=1.。
2020高考理科数学二轮提分广西等课标3卷专用课件:第三部分 三、解答题的解法

即 an+1(λ-1)=λan.
由 a1≠0,λ≠0 得 an≠0,
所以������������+1
������������
=
���������-���1.
因此{an}是首项为11-������,公比为���������-���1的等比数列,
于是
1
an=1-������
������ ������-1
求和常用方法有:公式法、错位相减法、裂项相消法、倒序相加 法、分组求和法.
-8-
一二三四五六
对点训练2(2019陕西西安第三次质检,17)设数列{an}的前n项和
为Sn,已知Sn=2an-1.
(1)求数列{an}的通项公式;
(2)若
bn=(������
������
+1
������������ +1 -1)(������������
5
5
(ⅱ) ∑ ���������2��� =55, ∑ ������������yi=18.8, 1.7≈1.3;
������=1
������=1
(ⅲ)若随机变量Z服从正态分布N(μ,σ2),则P(μ-σ<Z<μ+σ)≈0.682
7,P(μ-2σ<Z<μ+2σ)≈0.954 5,P(μ-3σ<Z<μ+3σ)≈0.997 3.
=
b^ t+���^���,其中���^���
=
∑ ������������ ������������-������������ ������
������=1
������
∑ ������
������=1
2 ������
2019-2020年高考数学二轮复习第一篇求准提速基础小题不失分第17练程序框图练习文

2019-2020年高考数学二轮复习第一篇求准提速基础小题不失分第17练程序框图练习文[明考情]程序框图是每年必考题,一般以选择题形式呈现,中低档难度;近几年有和其他知识或传统文化相结合的题目出现.[知考向]1.程序框图的输出.2.程序框图的填充.3.程序框图的综合应用.考点一程序框图的输出方法技巧程序框图中循环结构是高考考查的重点,确定循环结构的输出结果要注意以下几点:(1)明确循环次数和循环条件,把握循环变量的变化情况.(2)模拟运行循环变量取初始值和最后几个值时输出结果的变化.1.阅读如图所示的程序框图,若运行相应的程序,则输出的S的值是( )A.39B.21C.81D.102答案 D解析第一次循环,S=3,n=2;第二次循环,S=3+2×32=21,n=3;第三次循环,S=21+3×33=102,n=4;第四次循环,不满足条件,输出S=102.2.执行如图所示的程序框图,则输出的结果为( )A.49B.511C.712D.613 答案 B解析 根据题意,本程序框图为求和运算. 第1次循环:S =0+11×3=13,k =3; 第2次循环:S =13+13×5=615=25,k =5;第3次循环:S =25+15×7=37,k =7;第4次循环:S =37+17×9=49,k =9;第5次循环:S =49+19×11=511,k =11;此时,k >10,输出S =511.3.如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a 等于( )A.0B.2C.4D.14答案 B解析 第一次执行,输入a =14,b =18,因为a <b ,所以b =18-14=4;第二次执行,因为a =14,b =4,a >b ,所以a =14-4=10;第三次执行,因为a =10,b =4,a >b ,所以a =10-4=6;第四次执行,因为a =6,b =4,a >b ,所以a =6-4=2;第五次执行,因为a =2,b =4,a <b ,所以b =4-2=2,此时a =b =2.4.执行如图所示的程序框图,如果输入的t ∈[-1,3],则输出的s 的取值范围为______.答案 [-3,4]解析 本程序的条件结果对应的表达式为s =⎩⎪⎨⎪⎧3t ,t <1,4t -t 2,t ≥1,则当t ∈[-1,1)时,s =3t ∈[-3,3);当t ∈[1,3]时,s =4t -t 2=-(t -2)2+4∈[3,4]. 综上,s ∈[-3,4].5.《孙子算经》中有道算数题:“今有百鹿入城,家取一鹿不尽,又三家共一鹿适尽,问城中家几何?”,意思是有100头鹿,每户分1头还有剩余;再每3户共分一头,正好分完,问共有多少户人家?设计框图如下,则输出i 的值是( )A.74B.75C.76D.77 答案 B解析 程序在执行过程中,i =1,i =2,…,i =75,满足100-i -i3=0,输出i =75,故选B.考点二 程序框图的填充方法技巧 (1)条件结构的程序框图可结合分段函数的思想根据输出结果确定填充内容. (2)循环结构的程序框图可先假设i >n 或i <n ,模拟运行,直到运行结果和题目要求一致. 6.如图所示的程序框图能判断任意输入的数x 的奇偶性,其中判断框内的条件是( )A.m =0?B.m =1?C.x =0?D.x =1? 答案 B解析 由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0.由图可知应该填m =1?.7.执行如图所示的程序框图,若输出的结果S =720,则判断框内应填的是( )A.i ≤7?B.i >7?C.i ≤9?D.i >9? 答案 B解析 第一次循环:i =10满足条件,S =1×10=10,i =9. 第二次循环:i =9满足条件,S =10×9=90,i =8. 第三次循环:i =8满足条件,S =90×8=720,i =7.此时不满足条件,输出的S =720.故i =8,9,10满足条件,i =7不满足条件,所以判断框内应填“i >7?”. 8.执行如图所示的程序框图,若输出的结果为137,则判断框中应填入的条件是( )A.k >5?B.k >6?C.k >7?D.k >8?答案 B解析 第一次运行S =1+11×2,k =2;第二次运行S =1+11×2+12×3,k =3;…;第n 次运行S =1+11×2+12×3+…+1n (n +1)=137,k =n +1,此时结束循环,得n =6,故判断框中应该填入“k >6?”.9.执行如图所示的程序框图,如果输入三个实数a ,b ,c ,要求输出这三个数中最大的数,那么在空白的判断框中应填入( )A.c >x ?B.x >c ?C.c >b ?D.b >c ?答案 A解析由于要取a,b,c中的最大数,输出的x应当是a,b,c中的最大者,所以应填比较x与c大小的语句,结合各选项知选A.10.执行如图所示的程序框图,如果输出s=3,那么判断框内应填入的条件是( )A.k≤6?B.k≤7?C.k≤8?D.k≤9?答案 B解析k=2,s=1,s=1×log23=log23;k=3,s=log23·log34=log24;k=4,s=log24·log45=log25;k=5,s=log25·log56=log26;k=6,s=log26·log67=log27;k=7,s=log27·log78=log28=3.停止,说明判断框内应填k≤7?.考点三程序框图的综合应用方法技巧程序框图往往借助其他数学问题实现,常与函数求值、数列求和、统计量计算、不等式求解相结合,解决这类问题的关键是准确理解程序框图的实际意义,把握算法运行的规律.11.根据如图所示程序框图,对大于2的整数N,输出的数列的通项公式是( )A.a n =2nB.a n =2(n -1)C.a n =2nD.a n =2n -1答案 C解析 因为N >2,所以可取N =3,则a 1=2×1=2,S =a 1=2,i =1+1=2; 判断2>3是否满足?否,返回运算,a 2=2S =4,S =a 2=4,i =3; 判断3>3是否满足?否,返回运算,a 3=2S =8. 因此a 1=2,a 2=4,a 3=8,只有C 选项符合.12.如图所示是用模拟方法估计圆周率π值的程序框图,P 表示估计结果,则图中空白框内应填入( )A.P =N 1 000B.P =4N 1 000C.P =M 1 000D.P =4M1 000答案 D解析∵x i,y i为0~1之间的随机数,构成以1为边长的正方形面,当x2i+y2i≤1时,点(x i,y i)均落在以原点为圆心,以1为半径且在第一象限的14圆内,当x2i+y2i>1时对应点落在阴影部分中(如图所示).∴NM=1-π4π4,Nπ=4M-Mπ,π(M+N)=4M,π=4M1 000.13.(xx·原创押题预测卷)如图所示,若程序框图输出的所有实数对(x,y)所对应的点都在函数f(x)=ax+bx+c的图象上,则实数a,b,c的值依次为( )A.1,2,-2B.2,-3,2C.52,3,-92D.-1,32,12答案 C解析由程序框图可知,输出的实数对(x,y)依次为(1,1),(2,2),(3,4),若这些点都在函数f(x)=ax+bx+c的图象上,则⎩⎪⎨⎪⎧a+b+c=1,2a+b2+c=2,3a+b3+c=4,解得a=52,b=3,c=-92.14.执行如图所示的程序框图,若输入x=10,则输出y的值为________.答案-54解析 当x =10时,y =12×10-1=4,此时|y -x |=6>1,不符合条件;当x =4时,y =12×4-1=1,此时|y -x |=3>1,不符合条件;当x =1时,y =12×1-1=-12,此时|y -x |=32>1,不符合条件;当x =-12时,y =12×⎝ ⎛⎭⎪⎫-12-1=-54,此时|y -x |=34<1,符合条件,所以输出y 的值为-54.15.(xx·原创押题预测卷)执行如图所示的程序框图,则输出的结果S 的值为________.答案 -1解析 因为函数y =cosn π2的最小正周期是T =2ππ2=4,且从程序框图所提供的算法程序可知:n =1,S =0;n =2,S =-1;n =3,S =-1;n =4,S =0;n =5,S =0;n =6,S =-1,…,故n =2 014,S =-1;n =2 015,S =-1;n =2 016,跳出循环.1.(xx·广州一模)阅读如图的程序框图.若输入n =5,则输出k 的值为( )A.2B.3C.4D.5 答案 B解析 经过第一次循环得到的结果为k =0,n =16, 经过第二次循环得到的结果为k =1,n =49, 经过第三次循环得到的结果为k =2,n =148,经过第四次循环得到的结果为k =3,n =445,满足判断框中的条件,执行“是”输出的k 为3.2.执行如图所示的程序框图,若输出k 的值为8,则判断框内可填入的条件是( )A.s ≤34?B.s ≤56?C.s ≤1112?D.s ≤2524?答案 C解析 由s =0,k =0满足条件,则k =2,s =12,满足条件;k =4,s =12+14=34,满足条件;k =6,s =34+16=1112,满足条件;k =8,s =1112+18=2524,不满足条件,输出k =8,所以应填“s ≤1112?”.3.(xx·原创押题预测卷)运行如图所示的程序框图,若输出的结果为1 0082 017,则判断框内不可以填( )A.k >2 016?B.k ≥2 016?C.k ≥2 017?D.k >2 017? 答案 D解析 执行程序框图可知,该程序是计算1k (k +2)=12⎝ ⎛⎭⎪⎫1k -1k +2各项的和,即s =12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1-13+⎝ ⎛⎭⎪⎫13-15+⎝ ⎛⎭⎪⎫15-17+…+⎝ ⎛⎭⎪⎫1k -1k +2=k +12(k +2),当k =2 015时,s =1 0082 017,则判断框内不可以填k ≥2 017?故选D.解题秘籍 (1)程序运行的输出结果可以模拟运行的过程,列出了一步运行后变量的取值. (2)循环结构要把握循环中止的条件,注意赋值的先后顺序不同对变量取值的影响.1.(xx·甘肃一模)关于如图两个程序框图,说法正确的是( )A.(1)和(2)都是顺序结构B.(1)和(2)都是条件分支结构C.(1)是当型循环结构,(2)是直到型循环结构D.(1)是直到型循环结构,(2)是当型循环结构 答案 C解析 观察图(1),它是先判断后循环,故是当型循环的程序框图;观察图(2),它是先循环后判断,故是直到型循环的程序框图.2.执行如图所示的程序框图,如果输入的t∈[0,5],则输出的S的取值范围为( )A.[-4,10)B.[-5,2]C.[-4,3]D.[-2,5]答案 A解析当t∈[0,2)时,5t∈[0,10);当t∈[2,5]时,t2-4t∈[-4,5],所以S∈[-4,10).故选A.3.若如图所示框图所给的程序运行结果为S=35,那么判断框中应填入的关于k的条件是( )A.k=7?B.k≤6?C.k<6?D.k>6?答案 D解析要实现所求算法,框图中最后一次执行循环体时k的值应为6,结合满足条件时执行循环体知当k=6>6时就会终止循环,所以判断框内的条件,可为k>6?.4.(xx·全国Ⅰ)执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )A.y=2xB.y=3xC.y=4xD.y=5x答案 C解析 执行题中的程序框图知, 第一次进入循环体:x =0+1-12=0,y =1×1=1,x 2+y 2<36; 第二次执行循环体:n =1+1=2,x =0+2-12=12,y =2×1=2,x 2+y 2<36;第三次执行循环体:n =2+1=3,x =12+3-12=32,y =3×2=6,x 2+y 2>36,满足x 2+y 2≥36,故退出循环,输出x =32,y =6,满足y =4x ,故选C.5.执行如图所示的程序框图,则输出的A 等于( )A.2 047B.2 049C.1 023D.1 025 答案 A解析 本题计算的是递推数列,a 0=1,a n +1=2a n +1(n =0,1,2,…)的第11项,{a n +1}是首项为2、公比为2的等比数列,故a 10+1=211,故a 10=2 047,故选A.6.执行如图所示的程序框图,若要使输入的x 值与输出的y 值相等,则这样的x 值的个数是( )A.1B.2C.3D.4 答案 D解析 该程序的功能是计算并输出分段函数y =⎩⎪⎨⎪⎧x 3,x ≤1,3x -3,1<x ≤3,1x ,x >3的函数值,当x ≤1时,由x 3=x ,解得x =-1或x =0或x =1,这三个x 值均满足条件;当1<x ≤3时,由3x -3=x ,解得x =32,满足条件;当x >3时,由1x=x ,解得x =-1或x =1,这两个x 值均不满足条件.综上所述,满足条件的x 值的个数是4,故选D.7.(xx·乌鲁木齐模拟)某程序框图如图所示,若输出的S =26,则判断框内应填( )A.k >3?B.k >4?C.k >5?D.k >6? 答案 A解析 第一次循环:k =2,S =4; 第二次循环:k =3,S =11; 第三次循环:k =4,S =26;若输出S =26,则应该退出循环,故判断框内可填k >3?.8.某市乘坐出租车的收费办法如下:不超过4千米的里程收费12元;超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费);当车程超过4千米时,另收燃油附加费1元.相应系统收费的程序框图如图所示,其中x (单位:千米)为行驶里程,y (单位:元)为所收费用,用[x ]表示不大于x 的最大整数,则图中①处应填( )A.y =2⎣⎢⎡⎦⎥⎤x -12+4B.y =2⎣⎢⎡⎦⎥⎤x -12+5C.y =2⎣⎢⎡⎦⎥⎤x +12+4 D.y =2⎣⎢⎡⎦⎥⎤x +12+5 答案 D解析 由题意,得当x >4时,所收费用y =12+⎣⎢⎡⎦⎥⎤x -4+12×2+1=2⎣⎢⎡⎦⎥⎤x +12+5,故选D. 9.(xx·天津)阅读下面的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为( )A.0B.1C.2D.3 答案 C解析 第一次循环执行条件语句,此时N =24,24能被3整除,则N =24÷3=8. ∵8≤3不成立,∴进入第二次循环执行条件语句,此时N =8,8不能被3整除,则N =8-1=7. ∵7≤3不成立,∴进入第三次循环执行条件语句,此时N =7,7不能被3整除,则N =7-1=6. ∵6≤3不成立,∴进入第四次循环执行条件语句,此时N =6,6能被3整除,则N =6÷3=2. ∵2≤3成立,∴此时输出N =2.故选C.10.(xx·全国Ⅲ)执行如图所示的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A.5B.4C.3D.2 答案 D解析 假设N =2,程序执行过程如下:t =1,M =100,S =0,1≤2,S =0+100=100,M =-10010=-10,t =2,2≤2,S =100-10=90,M =--1010=1,t =3,3>2,输出S =90<91.符合题意. ∴N =2成立.显然2是最小值. 故选D.11.(xx·山东)执行两次如图所示的程序框图,若第一次输入的x 的值为7,第二次输入的x 的值为9,则第一次、第二次输出的a 的值分别为( )A.0,0B.1,1C.0,1D.1,0答案 D解析当x=7时,∵b=2,∴b2=4<7=x.又7不能被2整除,∴b=2+1=3.此时b2=9>7=x,∴退出循环,a=1,∴输出a=1.当x=9时,∵b=2,∴b2=4<9=x.又9不能被2整除,∴b=2+1=3.此时b2=9=x,又9能被3整除,∴退出循环,a=0.∴输出a=0.故选D.12.(xx·全国Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在◇和▭两个空白框中,可以分别填入( )A.A>1 000?和n=n+1B.A>1 000?和n=n+2C.A≤1 000?和n=n+1D.A≤1 000?和n=n+2答案 D解析因为题目要求的是“满足3n-2n>1 000的最小偶数n”,所以n的叠加值为2,所以▭内填入“n=n+2”.由程序框图知,当◇内的条件不满足时,输出n,所以◇内填入“A≤1 000?”.故选D.。
2020届高考数学二轮复习疯狂专练3框图(理)
疯狂专练3 框图1.执行如图所示的程序框图,则S的值为()A.16B.32C.64D.1282.如图所示的程序框图的算法思路源于世界数学名题“31x+问题”,执行该程序框图,若3N=,则输出的i=()A.6B.7C.8D.93.执行如图所示的程序框图,若输出结果为15,则判断框中应填入的条件M为()A.16k≥B.8k<C.16k<D.8k≥4.运行如图所示程序框图,若输入的1[,3]2t∈-,则输出s的取值范围为()一、选择题A .[1B .1[,8]2C .[1D .[0,8]5.中国南宋数学家秦九韶(公元12081268:)在《数书九章》中给出了求n 次多项式1110n n n n a x a x a x a --++++L 在x t =处的值的简捷算法,例如多项式323210a x a x a x a +++可改写为3210(())a x a x a x a +++后,再进行求值.如图是实现该算法的一个程序框图,该程序框图可计算的多项式为()A .432234x x x x ++++B .4322345x x x x ++++C .54322345x x x x x +++++D .543223456x x x x x +++++6.元代数学家朱世杰的数学名著《算术启蒙》是中国古代数学的通论,其中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若32a =,12b =,则输出的n 等于()A .3B .4C .5D .67.阅读如图的程序框图,如果输出5k =,那么空白的判断框中应填入的条件是()A .24S <-B .25S <-C .26S <-D .25S >-8.运行如图所示的程序框图,则输出的结果S 为()A .1-B .0C .12D .32-9.执行如图所示的程序框图,若输入的04a =,11a =-,23a =,32a =-,41a =,则输出的t 的值为()A .5B .10C .12D .1410.如图给出的是计算11124100+++L 的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()A .100i >,1n n =+B .100i >,2n n =+C .50i >,2n n =+D .50i ≤,2n n =+11.执行如图所示的程序框图,输出的S 值是()A .B .0C D 12.执行如图所示的程序框图,当输出的2S =时,则输入的S 的值为()A .2-B .1-C .12-D .1213.如图所示的茎叶图为某班54名学生的政治考试成绩,程序框图中输入的1a ,2a ,…,54a 为茎叶图中的学生成绩,则输出的S 和n 的值分别是.14.执行如图所示的程序框图,输出的s 值为.二、填空题15.执行如图所示的程序框图,输出S的值为.=在16.运行如图所示的程序框图,设输出的数据构成集合A,从集合A中任取一个元素α,则函数y xα(0,)+∞上是增函数的概率为.1.【答案】D【解析】模拟程序的运行,可得1i =,1S =, 执行循环体,2S =,2i =,满足条件4i ≤, 执行循环体,8S =,4i =,满足条件4i ≤,执行循环体,128S =,8i =,此时,不满足条件4i ≤,退出循环,输出S 的值为128. 2.【答案】C【解析】第一步:10n =,2i =;第二步:5n =,3i =; 第三步:16n =,4i =;第四步:8n =,5u =; 第五步:4n =,6i =;第六步:2n =,7i =; 第七步:1n =,8i =,结束循环,输出的8i =. 3.【答案】A【解析】根据题中所给的程序框图,可以确定该题要求的是1248S =++++L , 对应的正好是以1为首项,以2为公比的等比数列,该数列的前4项和正好是15. 4.【答案】C【解析】由程序框图可知,该程序表示分段函数222π12cos π,1221(),132t t t t t s t -⎧-≤<⎪⎪=⎨⎪≤≤⎪⎩,当112t -≤<时,解析式化为π2sin(π)16s t =++,ππ7ππ[,)636t +∈-,[1s ∈,当13t ≤≤时,2321t t -≤-≤,1[,8]2s ∈, 综上所述,s 的取值范围是[1. 5.【答案】C【解析】依次运行程序可得,①1i =,1P x =+,满足条件,继续运行.②2i =,2(1)22P x x x x =++=++,满足条件,继续运行.③3i =,232(2)323P x x x x x x =+++=+++,满足条件,继续运行.④4i =,32432(23)4234P x x x x x x x x =++++=++++,满足条件,继续运行. ⑤5i =,4325432(234)52345P x x x x x x x x x x =+++++=+++++,不满足条件,答 案 与解析一、选择题停止运行,输出54322345x x x x x +++++. 6.【答案】B【解析】记执行第n 次循环时,a 的值为n a ,则有332()2nn a =⨯,记执行第n 次循环时,b 的值为n b ,则有122nn b =⨯,令332()1222n n⨯≤⨯,则有33()48n≤,故4n ≥. 7.【答案】A【解析】第一次执行循环体后,1S =,1k =,不满足输出的条件,2k =,第二次执行循环体后,0S =,2k =,不满足输出的条件, 3k =,第三次执行循环体后,3S =-,3k =,不满足输出的条件, 4k =,第四次执行循环体后,10S =-,4k =,不满足输出的条件, 5k =,第五次执行循环体后,25S =-,5k =,满足输出的条件.8.【答案】B【解析】由程序框图知,1n =,12S =;2n =,0S =;3n =,1S =-;4n =,32S =-;5n =,1S =-;6n =,0S =;7n =,12S =;8n =,0S =;9n =,1S =-, 故S 的值以6为周期循环,而20163366=⨯,所以0S =. 9.【答案】D【解析】初始值1i =,1t =,第一次循环,得2120t =⨯-=,2i =;第二次循环,得033t =+=,3i =; 第三次循环,得2315t =⨯-=,4i =;第四次循环得25414t =⨯+=,5i =,不满足循环条件,退出循环,输出的14t =. 10.【答案】C 【解析】因为12,14,…,1100共50个数,所以算法框图应运行50次,所以变量i 应满足50i >, 因为是求偶数的和,所以应使变量n 满足2n n =+. 11.【答案】D【解析】当1n =,0S =时,πsin3S ==2n =;22018n =<,执行第一次循环可得2πsin 3S =+=3n =;32018n =<,执行第二次循环可得sin πS ==,4n =;42018n =<,执行第三次循环可得4πsin3S ==,5n =;52018n =<,执行第四次循环可得5πsin 03S =+=,6n =; 62018n =<,执行第五次循环可得6πsin03S ==,7n =; 72018n =<,执行第六次循环可得2S =; …,归纳可知,其周期为6,所以20182S S ==S =12.【答案】B【解析】若输入2S =-,则执行循环得13S =,2k =;32S =,3k =;2S =-,4k =;13S =,5k =;32S =,6k =;2S =-,7k =;13S =,8k =;32S =,9k =,结束循环,输出32S =,与题意输出的2S =矛盾; 若输入1S =-,则执行循环得12S =,2k =;2S =,3k =;1S =-,4k =; 12S =,5k =;2S =,6k =;1S =-,7k =;12S =,8k =;2S =,9k =, 结束循环,输出2S =,符合题意; 若输入12S =-,则执行循环得23S =,2k =;3S =,3k =;12S =-,4k =; 23S =,5k =;3S =,6k =;12S =-,7k =;23S =,8k =;3S =,9k =, 结束循环,输出3S =,与题意输出的2S =矛盾; 若输入12S =,则执行循环得2S =,2k =;1S =-,3k =;12S =,4k =; 2S =,5k =;1S =-,6k =;12S =,7k =;2S =,8k =;1S =-,9k =, 结束循环,输出1S =-,与题意输出的2S =矛盾.二、填空题13.【答案】86,13【解析】S 为大于等于80分的学生的平均成绩,计算得86S =,n 表示60分以下的学生人数, 由茎叶图可知13n =. 14.【答案】12-【解析】运行程序如下12018≤,3s =-,2n =,22018≤,12s =-;3n =,32018≤,13s =; 4n =,42018≤,2s =;5n =,所以s 的周期为4,因为2018除以4的余数为2,所以输出12s =-. 15.【答案】1009【解析】执行程序框图,π01sin012S =+⋅=+,3i =,32018≤; 3π013sin0132S =++⋅=+-,5i =,52018≤; 5π0135sin01352S =+-+⋅=+-+,7i =,72018≤; …,2017π0132017sin01320172S =+-++⋅=+-++L L ,2019i =,20192018>, 输出0135720152017S =+-+--+L(01)(35)(79)(20152017)=++-++-+++-+L1222150421009=++++=+⨯=L .16.【答案】23【解析】执行如图所示的程序框图,可知,第一次循环,满足1i <,2(2)22(2)8y =--⨯-=,输出8y =,此时1i =-; 第二次循环,满足1i <,2(1)2(1)3y =--⨯-=,输出3y =,此时0i =;第三次循环,满足1i <,20200y =-⨯=,输出0y =,此时1i =,此时终止循环,所以输出的集合{8,3,0}A =,所以从集合A 中任取一个元素α,则函数y x α=在(0,)+∞上是增函数的概率为23P =.11。
2020届高考数学(文)二轮考点专训卷:(5)解三角形

考点专训卷(5)解三角形1、在ABC △中,45,60c B C ==︒=︒,则b =( )A.B. C. D.2、已知△ABC 中,a =b =60B =︒,那么角A 等于( ) A.135︒B.90︒C.45︒D.30︒3、在ABC △中,角,,A B C 所对的边分别为,,a b c ,222a b c =-,则角B 的大小是( ) A.45°B.60°C.90°D.135°4、在锐角ABC △中,角,,A B C 所对的边分别为,,a b c ,若22sin A =2a =,2ABC S △则b 的值为( ) A 3B 32C .2D .235、在ABC △中,角,,A B C 的对边分别为,,a b c ,若2cos cos a c Cb B=-,4b =,则ABC △的面积的最大值为( ) A.43 B.3 C.3336、在ABC △中,,,a b c 分别为内角,,A B C 的对边,且2223323sin a b c bc A =+-,则C 的值为( ) A .π3B .π6C .π4D .2π37、ABC △的内角,,A B C 的对边分别为,,a b c 若,,a b c 成等比数列,且2c a =,则cos C =( ) A .14-B .2C .14D 28、在ABC △中,三内角,,A B C 的对边分别为,,a b c ,且222b c a +=,2bc =,则角C 的大小是( )A.π6或2π3 B.π3 C.2π3D.π6 9、在 ABC △中,角,,A B C 的对边分别是,,a b c 若 cos cos 2c a B b A -=,则cos cos cos a A b Ba B-的最小值为( )10、设ABC △的内角,,A B C 所对的边分别为,,a b c ,若cos cos a A b B =,则ABC △是( )A.等腰直角三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形11、在ABC △中,若2cos sin sin B A C =,则ABC △的形状一定是( ) A. 等腰直角三角形B. 等腰三角形C. 直角三角形D. 等边三角形12、如图,为了测量山坡上灯塔CD 的高度,某人从高为=40h 的楼AB 的底部A 处和楼顶B 处分别测得仰角为=60β,=30α,若山坡高为=35a ,则灯塔高度是( )A.15B.25C.40D.6013、北京2008年第29届奥运会开幕式上举行升旗仪式,在坡度15︒的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60︒和30︒,第一排和最后一排的距离为10650秒,升旗手匀速升旗的速度为( )A.35(米/秒) B.5(米/秒)C.(米/秒)D.15(米/秒)14、在20米高的楼顶测得对面一塔吊顶部的仰角为60o ,塔基的俯角为45o ,那么这塔吊的高度是( )A.20(1)3+B. C. D.20(115、ABC ∆的内角,,A B C 的对边分别为,,,a b c 已知s i n c o s b Aa B +=,则B =__________.16、若ABC △222),a c b +-且C 为钝角,则c a的取值范围是__________.17、设ABC △中的内角A B C ,,所对的边分别为a b c ,,,且2π3,3a b c C +===,则ABC △的面积为________18、在ABC △中,,A B C 所对的边分别为,,a b c 已知2222a b c ab +-=,且sin 3sin ac B C =,则ABC △的面积为______.19、在锐角ABC △中,角,,A B C 所对的边为,,a b c ,若cos cos (cos 3)0A B C C +-=.且1b =,则a c +的取值范围为_____.20、ABC ∆中,角,,A B C 的对边分别为,,a b c ,若(2)cos cos b c A a C -=,则cos A =__________.21、在ABC △中,角,,A B C 的对边分别为,,a b c ,且满足(2)cos cos a c B b C -=, 1.求角B 的大小; 2.若7,4b a c =+=,求ABC △的面积。
【人教版】备考2020高考数学二轮复习 选择填空狂练三 框图 文

3 框图1.[2018·唐山一摸]已知程序框图如右图所示则该程序框图的功能是( )A .求1111357+++的值B .求111113579++++的值C .求1111357-++的值D .求111113579-+++的值2.[2018·东师附中]执行如图所示的程序框图,如果输入的[]2,2x ∈-,则输出的y 值的取值范围是( )A .52y ≤-或0y ≥B .223y -≤≤C .2y ≤-或203y ≤≤ D .2y ≤-或23y ≥3.[2018·宝安区调研]定义某种运算:S m n ⊗=⊗的运算原理如右边的流程图所示,则6547⊗-⊗=( )一、选择题A.3 B.1 C.4 D.0 4.[2018·南昌测试]某程序框图如图所示,若输出3S=,则判断框中M为()A.14?k>k≤D.15?k<B.14?k≤C.15?5.[2018·南昌联考]执行如图所示的程序框图,输出的值为()A.14 B.15 C.24 D.30 6.[2018·拉萨中学]执行如图所示的程序框图,输出的k值为()A .4B .5C .6D .77.[2018·南昌二模]执行如图所示的程序框图,输出S 的值为( )A .15B .16C .24D .258.[2018·南昌检测]根据某校10位高一同学的身高(单位:cm )画出的茎叶图(图1),其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,设计一个程序框图(图2),用()1210i A i =L ,,,表示第个同学的身高,计算这些同学身高的方差,则程序框图①中要补充的语句是( )A .iB B A =+B .2i B B A =+C .()2i B B A A =+-D .22i B B A =+9.[2018·南昌检测]执行如图所示的程序框图,则输出的结果为( )A .1-B .0C .1D .210.[2018·哈尔滨六中]《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的S 的值为350,则判断框中可填( )A .6?i >B .7?i >C .8?i >D .9?i >11.[2018·山东模拟]下面程序框图是为了求出满足321000n n ->的最小偶数n ,,那么在◇和□两个空白框中,可以分别填入( )A .1000A >和1n n =+B .1000A >和2n n =+C .1000A ≤和1n n =+D .1000A ≤和2n n =+12.[2018·银川一中]我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )A .7i <,1S S i=-,2i i =B .7i ≤,1S S i=-,2i i =C .7i <,2SS =,1i i =+ D .7i ≤,2SS =,1i i =+13.[2018·南昌检测]某程序框图如图所示, 则输出的结果是__________.14.[2018·中原名校]如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a ,b ,i 的值分别为8,6,1,输出a 和i 的值,若正数x ,y 满足251x y+=,则ax iy +的最小值为__________.二、填空题15.[2018·宁德质检]我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人,他在《张丘建算经》中给出一个解不定方程的百鸡问题,问题如下:鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一.百钱买百鸡,问鸡翁母雏各几何?用代数方法表述为:设鸡翁、鸡母、鸡雏的数量分别为x ,y ,z ,则鸡翁、鸡母、鸡雏的数量即为方程组531003100z x y x y z ⎧++=⎪⎨⎪++=⎩的解.其解题过程可用框图表示如下图所示,则框图中正整数m 的值为 ______.16.[2018·湖北模拟]如图所示的茎叶图为高三某班54名学生的政治考试成绩,程序框图中输入的1a ,2a ,L ,54a 为茎叶图中的学生成绩,则输出的S 和n 的值分别是__________.1.【答案】C【解析】由题意,执行如图所示的程序框图可知:开始1a=,1n=,0S=;第一次循环:1S=,1a=-,3n=;第二次循环:113S=-,1a=,5n=;第三次循环:11135S=-+,1a=-,7n=;第四次循环:1111357S=-++,1a=,9n=;此时终止循环,输出结果,所以该程序框图是计算输出1111357S=-++的值,故选C.2.【答案】C【解析】由题意知,该程序的功能是求函数()021120xxxf xx xx⎧≤≤⎪⎪+=⎨⎪+-≤<⎪⎩,,的值域.①当02x≤≤时,()1111xf xx x==-++在区间[]0,2上单调递增,∴()()()02f f x f≤≤,即()23f x≤≤;②当20x-≤<时,()112f x x xx x⎛⎫=+=--+≤=-⎪-⎝⎭,当且仅当1xx-=-,即1x=-时等号成立.综上输出的y值的取值范围是2y≤-或23y≤≤.故选C.3.【答案】A【解析】由流程图得()6565124⊗=⨯-=,()4774121⊗=⨯-=,∴654724213⊗-⊗=-=,故选A.4.【答案】B【解析】由框图程序可知S=+L,=1S+L∴13S==,解得15n=,即当15n=时程序退出,故选B.5.【答案】C【解析】结合流程图可知流程图运行过程如下:首先初始化数据:0S=,1i=,第一次循环,满足5i<,执行12i i=+=,此时不满足i为奇数,执行1222iS S S-=+=+=;第二次循环,满足5i<,执行13i i=+=,此时满足i为奇数,执行2157S S i S=+-=+=;第三次循环,满足5i<,执行14i i=+=,此时不满足i为奇数,执行12815iS S S-=+=+=;答案与解析一、选择题第四次循环,满足5i <,执行15i i =+=,此时满足i 为奇数,执行21924S S i S =+-=+=; 第五次循环,不满足5i <,跳出循环,输出S 的值为24. 故选C . 6.【答案】B【解析】模拟程序的运行,可得:1a =,1k =,不满足条件10a >,执行循环体,2a =,2k =;不满足条件10a >,执行循环体,4a =,3k =; 不满足条件10a >,执行循环体,8a =,4k =;不满足条件10a >,执行循环体,16a =,5k =; 满足条件10a >,退出循环体,输出k 的值为5,故选B . 7.【答案】B【解析】进入循环,当1i =时,15<,i 为奇数,1S =;当2i =时,25<,i 为偶数,123S =+=; 当3i =时,35<,i 为奇数,358S =+=;当4i =时,45<,i 为偶数,8816S =+=; 当5i =时,55≥,结束循环,输出16S =.故选B . 8.【答案】B 【解析】由()()()()222222212121222n n n x x x x x x x x x x x x x nx s nn-+-+⋅⋅⋅+-++⋅⋅⋅+-++⋅⋅⋅++==22222222212122n n x x x nx nx x x x x n n++⋅⋅⋅+-+++⋅⋅⋅+==-,循环退出时11i =,知221A x i ⎛⎫= ⎪-⎝⎭.∴2221210B A A A =++⋅⋅⋅+,故程序框图①中要补充的语句是2i B B A =+.故选B . 9.【答案】D【解析】由循环结构的计算原理,依次代入求得如下:1S =,1i =, ①2S =,2i =;②2S =,3i =;③1S =,4i =; ④1S =,5i =;⑤2S =,6i =;⑥2S =,7i =;⑦1S =,8i =;⑧1S =,9i =;⑨2S =,10i =;∴输出2S =.故选D . 10.【答案】B【解析】模拟程序的运行,可得0S =,1i =;执行循环体,290S =,2i =; 不满足判断框内的条件,执行循环体,300S =,3i =; 不满足判断框内的条件,执行循环体,310S =,4i =; 不满足判断框内的条件,执行循环体,320S =,5i =; 不满足判断框内的条件,执行循环体,330S =,6i =; 不满足判断框内的条件,执行循环体,340S =,7i =;不满足判断框内的条件,执行循环体,350S =,8i =;由题意,此时,应该满足判断框内的条件,退出循环,输出S 的值为350. 可得判断框中的条件为7?i >.故选B . 11.【答案】D【解析】本题考查程序框图问题.∵要求1000A >时输出,且框图中在“否”时输出,∴“◇”内不能输入“1000A >”, 又要求n 为偶数,且n 的初始值为0,∴“□”中n 依次加2可保证其为偶数, ∴D 选项满足要求,故选D . 12.【答案】D【解析】算法为循环结构,循环7次,每次对长度折半计算,也就是2S S =,因此②填2S S =, 又①填判断语句,需填7i ≤,③填1i i =+.故选D .13.【答案】3+【解析】由题意得0tan 0tan tan tan tan 21312643S ππππ=+++++=-+. 14.【答案】49【解析】输入a ,b ,i 的值分别为8,6,1;第一次循环,2i =,2a =;第二次循环,3i =,4b =;第三次循环,4i =,2b =;第四次循环,5i =,b a =; 退出循环,输出2a =,5i =,()2510102542549y xax iy x y x y x y ⎛⎫+=++=+++≥ ⎪⎝⎭, 当x y =时,等号成立,即ax iy +的最小值为49,故答案为49. 15.【答案】4【解析】由531003100z x y x y z ⎧++=⎪⎨⎪++=⎩得7254y x =-,故x 必为4的倍数, 当4x t =时,257y t =-,由2570y t =->得t 的最大值为3, 故判断框应填入的是4t <?,即4m =,故答案为4. 16.【答案】86,13【解析】S 为大于等于80分的学生的平均成绩,计算得86S =;n 表示60分以下的学生人数,由茎叶图可知13n =.二、填空题。
【2020】最新高考数学(理)二轮复习系列之疯狂专练8 三视图推荐下载

A .B .C .D .【答案】B【解析】由题设中提供的正视图可推知:该几何体有一个侧面是垂直于底面的,且右侧面是垂直于底面,而B 选项中俯视图则表明该几何体的左侧面是垂直于底面的,与正视图不符,所以B 是错误的,应选B .9.[20xx·梅州一模]某几何体的三视图如图所示,则这个几何体的体积为( )A .B .C .D .42032638【答案】B【解析】由三视图可得到几何体的直观图如图所示,该几何体是由一个四棱锥和一个三棱锥组成,四棱锥的底面面积为,高为,所以体积是;三棱锥的底面积为,高为,故体积是,所以该几何体的体积为,故选B .A CDEF -F ABC -A CDEF -441164433V =⨯⨯=F ABC -224320310.[20xx ·临析期中]某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .B .2C .D .3【答案】D2AB CD ==5BC AD SB ===O SC 1ABO 1O SBC 1BO x =11SO BO x==22(2)1x x -+=54x =254111616R OB ==+=24144S R π=π=13.[20xx·枣庄期末]如图,网格纸上每个小正方形的边长为,若粗线画出的是某几何体的三视图,则此几何体的体积为__________.【答案】10【解析】由三视图知,该几何体是底面为直角边分别为5和4、高为3的三棱锥,所以该几何体的体积.14.[20xx ·汕头期末]一个几何体的三视图如图所示,正视图和侧视图是两个全等的三角形,俯视图是个圆,则该几何体的体积等于__________.【答案】【解析】由三视图知该几何体为底面半径为3、高为4的个圆锥,所以所求体积.15.[20xx·虹口二模]三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于__________.【答案】【解析】由题可知,正三棱锥的侧棱长为,主视图的高也是正三棱锥的高,则,主视图的面积为.16.[20xx·黄陵中学]如图为某几何体的三视图,则其体积为__________.【答案】【解析】几何体为一个四棱锥与一个半圆柱的组合体,其中四棱锥的高为1、底面为棱长为2的正方形;半圆柱的高为2,底面为半径为1的半圆,所以体积为.。
2020版高考数学二轮复习专题三数列高考热点追踪(三)学案文苏教版(2021-2022学年)

高考热点追踪(三)交汇性试题,向来是高考试题中最为亮丽的风景线,这类问题着重考查观察发现,类比转化以及运用数学知识分析和解决数学问题的能力.下面举例说明数列的交汇性运用,请同学们赏析.一、数列与几何图形交汇(2019·南通模拟)如图是一个面积为1的三角形,现进行如下操作.第一次操作:分别连结这个三角形三边的中点,构成4个三角形,挖去中间一个三角形(如图①中阴影部分所示),并在挖去的三角形上贴上数字标签“1";第二次操作:连结剩余的三个三角形三边的中点,再挖去各自中间的三角形 (如图②中阴影部分所示),同时在挖去的3个三角形上都贴上数字标签“2”;第三次操作: 连结剩余的各三角形三边的中点,再挖去各自中间的三角形,同时在挖去的三角形上都贴上数字标签“3";……,如此下去.记第n次操作后剩余图形的总面积为a n.(1)求a1、a2;(2)欲使剩余图形的总面积不足原三角形面积的错误!未定义书签。
,问至少经过多少次操作?(3)求第n次操作后,挖去的所有三角形上所贴标签上的数字和S n.【解】 (1)a1=错误!,a2=错误!未定义书签。
.(2)因为{a n}是以错误!未定义书签。
为首项,以错误!未定义书签。
为公比的等比数列,所以an=错误!未定义书签。
错误!.由错误!错误!未定义书签。
<错误!,得3n<4n-1.因为31>40,32>41,33>42,34〉43,35<44,所以当n=5时,错误!未定义书签。
错误!〈错误!.ﻬ所以至少经过5次操作,可使剩余图形的总面积不足原三角形面积的错误!未定义书签。
.(3)设第n次操作挖去b n个三角形,则{b n}是以1为首项,3为公比的等比数列,即b n=3n-1.所以所有三角形上所贴标签上的数字的和S n=1×1+2×3+…+n×3n-1,则3S n=1×3+2×32+…+n×3n,两式相减,得-2Sn=(1+3+32+…+3n-1)-n×3n=错误!未定义书签。
浙江专版2020年高考数学二轮专题复习保分大题规范专练四(20201124122828)

保分大题规范专练(四)1.函数f(x) =2sin( G.Y+/)( G>0, 0< 0<丁)的部分图象如图所示,M为最髙点,该图象与y轴交于点尸(0, a与X轴交于点B, G且△•蚊的面积为几・(1)求函数f&)的解析式;⑵若彳°一+)=^^,求cos 2 O的值.解:⑴因为Ssr=*X2X A證=刃,2 H所以最小一正周期T=2 H = ‘ Q = l,(I)由/(0) =2sin e=型,得sin 0=乎,因为0< 所以0=亍所以f3=2sin(*+-jj・(2)由彳a— )=2sin a得sin a =誓,所以cos 2.=l-2sin:a=z.2•如图,四边形個刃是圆台0Q的轴截面,AB=2CD=\.点“在底而圆周上,且ZAO)f=^r, DM LAC.(1)求圆台血的体积:(2)求二而角月DM 0的平而角的余弦值.解:法一:(1)由已知可得01/丄平面月血又AC丄DM从而有ACLD0.由平面几何性质可得ACLCB.设00,=h,在Rt △遊中,AC+BC=Aff.即(9+尸)+ (1+牙)=16, ••丄=羽,lw]台oa 的体积K=| n h(£ + +£) = —.(2)过点0在内作0EA.DM,作如丄平而加也垂足分别为E、连接胡易得EHLDM.故乙OEH 就是二面角於DM 0的平而角.在△QQ/中,0E=©易得D 、f=A )f=2筋AD=2, Sz 产寸i ・ 由V 检備0 /"=卩險俊0亦,则二面角月DM 0的余弦值为芈.法二:(1)由题意可得0久0如 血两两互相垂直,以0为原点,分别以直线。
也OB. oa 、)7 X, y, z 轴建立空间直角坐标系(图略),设 0Q=/?(QO ),则 D (0, -1, h ). M2, 0, 0), J (0, -2, 0), C (0, b A ),A DM = (2, b -A), AC = (0, 3, A),DM A. AC. :.~DM • ~AC=3-/f=0. 解得h 卡,鬪台 OOi 的体积 K=| n 力Crj + iYn+iD =?£(2)由(1)知加=(2,2,0), 莎=(2,1, —萌),而=(2,0,0), 设平^ADM,平而〃H 的法向量分别为U= (-V1,Jit zj,卩=(上,必,7),取 u=£, 一萌,1),卩=(0, © 1),u ■ “ \i77 *又二面角川DM 0为锐角,则二面角月DM 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.【答案】C
【解析】根据程序框图,运行结果如下:
第一次循环: , ;
第二次循环: , ;
第三次循环: , ;
第四次循环: , ;
第五次循环: , ;
第六次循环: , ,
故如果输出 ,那么只能进行六次循环,故判断框内应填入的条件是 .
13.【解析】 , , ;
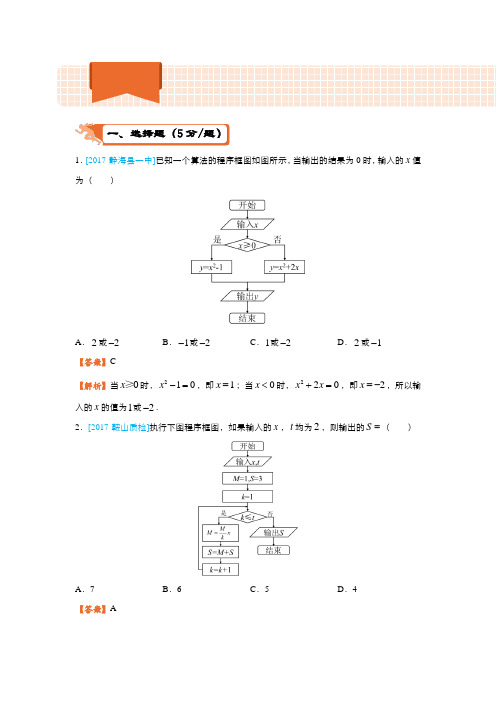
若输入的 , 分别为 , ,则输出的 ()
A. B. C. D.
5.某品牌洗衣机专柜在国庆期间举行促销活动,茎叶图中记录了每天的销售量(单位:台),把这些数据经过如图所示的程序框图处理后,输出的 ()
A. B. C. D.
6.执行如图所示的程序框图,若输出的 ,则判断框中可填入的条件是()
A. B. C. D.
7.如图所示的程序框图的算法思路源于世界数学名题“ 问题”.执行该程序框图,若 ,则输出的 ()
A. B. C. D.
8.给出一个如图所示的程序框图,若要使输入的 值与输出的 值相等,则 的可能值的个数为()
A. 个B. 个C. 个D. 个
9.我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:“今有出门望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?”现在我们用如图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是()
, , ;…;
, , ,
输出
.
结合茎叶图可知,输出的 ,故选B.
6.【答案】C
【解析】执行程序框图, , , ;
, ;
, ;
, ;
, ,退出循环.此时输出的 .
结合选项知选C.
7.【答案】C
【解析】第一步: , ;
第二步: , ;
第三步: , ;
第四步: , ;
第五步: , ;
第六步: , ;
第七步: , ,结束循环,输出的 ,故选C.
A. B. C. D.
13.阅读下面的程序框图,运行相应的程序,输出的结果为_______.
14.某程序框图如图所示,则输出的结果 等于.
15.执行如图所示的程序框图,那么输出 的值是________.
16.执行如图所示的程序框图,输出 的值为.
1.【答案】B
【解析】执行程序框图,
第一次循环:满足判断条件, ;
8.【答案】C
【解析】分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:
该程序的作用是计算并输出分段函数 的值,
又∵输入的 值与输出的 值相等,
当 时, ,解得 或 ,
当 时, ,解得 ,
当 时, ,解得 (舍去),
故满足条件的 值共有 个,故选C.
9.【答案】B
【解析】根据题意,利用程序框图求禽的数目,输出结果应为 .
1.执行如图所示的程序框图,输出的结果是()
A. B. C. D.
2.执行如图所示的程序框图,输出的 值为()
A. B. C. D.
3.执行如图所示的程序框图,若输入的 ,则输出的 ()
A. B. C. D.
4.下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,
第二次循环:满足判断条件, ;
不满足判断条件,此时输出 ,故选B.
2.【答案】B
【解析】执行程序框图,
第一次循环: , ;
第二次循环: , ;
第三次循环: , ;
第四次循环: , ,此时满足判断条件,终止循环,输出 .Байду номын сангаас
3.【答案】D
【解析】输入 , , ,
不是质数, , , ;
不是质数, , , ;
是质数, , , ;
不是质数, , , ;
是质数, , , ,退出循环,故输出的 .
故选D.
4.【答案】B
【解析】 , ,则 变为 ,
由于 ,则 变为 ,
由于 ,则 变为 ,
由于 ,则 变为 ,
由于 ,则 变为 ,
由 ,则输出 .
5.【答案】B
【解析】由程序框图可知,该程序框图输出的是销售量的平均值,
循环共执行了 次,所以判断框中应填入的条件是“ ”或“ ”或“ ”.故选B.
10.【答案】D
【解析】初始值 , ,
第一次循环,得 , ;
第二次循环,得 , ;
第三次循环,得 , ;
第四次循环,得 , ,
不满足循环条件,退出循环,输出的 ,故选D.
11.【答案】C
【解析】因为 共 个数,
所以算法框图应运行 次,所以变量 应满足 ,
A. B. C. D.
10.执行如图所示的程序框图,若输入的 , , , , ,则输出的 的值为()
A. B. C. D.
11.如图给出的是计算 的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()
A. , B. , C. , D. ,
12.若执行如图所示的程序框图,输出 的值为 ,则判断框中应填入的条件是()
, , ;
, , ;
, , ;
, , ;
, , .
14.【答案】
【解析】 , ; , ; , ; , ,
退出循环,输出 .
15.【答案】
【解析】运行框图,输入 , ,
满足条件 , , ;
满足条件 , , ;
满足条件 , , , 不成立,输出 .
16.【答案】
【解析】执行程序框图, , , ;
, , ;
