九年高考(2010-2018高考)理科数学真题分类训练 专题六 数列 第十六讲 等比数列(附详解)
十年真题(2010-2019)高考数学(文)分类汇编专题07 数列(新课标Ⅰ卷)(原卷版)

专题07数列历年考题细目表历年高考真题汇编1.【2015年新课标1文科07】已知{a n}是公差为1的等差数列,S n为{a n}的前n项和,若S8=4S4,则a10=()A.B.C.10 D.122.【2013年新课标1文科06】设首项为1,公比为的等比数列{a n}的前n项和为S n,则()A.S n=2a n﹣1 B.S n=3a n﹣2 C.S n=4﹣3a n D.S n=3﹣2a n3.【2012年新课标1文科12】数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为()A.3690 B.3660 C.1845 D.18304.【2019年新课标1文科14】记S n为等比数列{a n}的前n项和.若a1=1,S3,则S4=.5.【2015年新课标1文科13】在数列{a n}中,a1=2,a n+1=2a n,S n为{a n}的前n项和,若S n=126,则n =.6.【2012年新课标1文科14】等比数列{a n}的前n项和为S n,若S3+3S2=0,则公比q=.7.【2019年新课标1文科18】记S n为等差数列{a n}的前n项和.已知S9=﹣a5.(1)若a3=4,求{a n}的通项公式;(2)若a1>0,求使得S n≥a n的n的取值范围.8.【2018年新课标1文科17】已知数列{a n}满足a1=1,na n+1=2(n+1)a n,设b n.(1)求b1,b2,b3;(2)判断数列{b n}是否为等比数列,并说明理由;(3)求{a n}的通项公式.9.【2017年新课标1文科17】记S n为等比数列{a n}的前n项和.已知S2=2,S3=﹣6.(1)求{a n}的通项公式;(2)求S n,并判断S n+1,S n,S n+2是否成等差数列.10.【2016年新课标1文科17】已知{a n}是公差为3的等差数列,数列{b n}满足b1=1,b2,a n b n+1+b n+1=nb n.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{b n}的前n项和.11.【2014年新课标1文科17】已知{a n}是递增的等差数列,a2,a4是方程2﹣5+6=0的根.(1)求{a n }的通项公式; (2)求数列{}的前n 项和.12.【2013年新课标1文科17】已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5=﹣5. (Ⅰ)求{a n }的通项公式; (Ⅱ)求数列{}的前n 项和.13.【2011年新课标1文科17】已知等比数列{a n }中,a 1,公比q .(Ⅰ)S n 为{a n }的前n 项和,证明:S n(Ⅱ)设b n =log 3a 1+log 3a 2+…+log 3a n ,求数列{b n }的通项公式. 14.【2010年新课标1文科17】设等差数列{a n }满足a 3=5,a 10=﹣9. (Ⅰ)求{a n }的通项公式;(Ⅱ)求{a n }的前n 项和S n 及使得S n 最大的序号n 的值. 考题分析与复习建议本专题考查的知识点为:数列的概念与简单表示法,等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为:等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.预测明年本考点题目会比较稳定,备考方向以知识点等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项为重点较佳.最新高考模拟试题1.等差数列{}n a ,等比数列{}n b ,满足111a b ==,53a b =,则9a 能取到的最小整数是( ) A .1-B .0C .2D .32.中国古代数学名著《九章算术》中有这样一个问題今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰“我羊食半马、“马主曰“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说“我羊所吃的禾苗只有马的一半,”马主人说“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟? A .253B .503C .507D .10073.我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入33⨯的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数21,2,3,,n L 填入n n ⨯个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ,如图三阶幻方的315N =,那么 9N 的值为( )A .41B .45C .369D .3214.设数列{}n a 的前n 项和为n S ,且11a = 2(1)()n n S a n n N n *=+-∈,则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是( ) A .290B .920C .511D .10115.意大利数学家列昂那多·斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,L L ,即()()()()()121,12F F F n F n F n ===-+-()3,n n N*≥∈,此数列在现代物理“准晶体结构”、化学等都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{}n a ,则数列{}n a 的前2019项的和为( ) A .672B .673C .1346D .20196.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若261033a a a ⋅⋅=16117b b b π++=,则21039tan1b b a a +-⋅的值是( )A .1B.2C.2-D.7.已知数列{}n a 满足2*123111()23n a a a a n n n N n ++++=+∈L ,设数列{}n b 满足:121n n n n b a a ++=,数列{}n b 的前n 项和为n T,若*()1n n N T n nλ<∈+恒成立,则实数λ的取值范围为( ) A .1[,)4+∞B .1(,)4+∞C .3[,)8+∞D .3(,)8+∞8.已知函数()y f x =的定义域为R ,当0x <时()1f x >,且对任意的实数,x y R ∈,等式()()()f x f y f x y =+成立,若数列{}n a 满足()()1111n n f a f n N a *+⎛⎫=∈ ⎪+⎝⎭,且()10a f =,则下列结论成立的是( ) A .()()20162018f a f a > B .()()20172020f a f a > C .()()20182019f a f a > D .()()20162019f a f a >9.在数列{}n a 中,1111,,(*)2019(1)n n a a a n N n n +==+∈+,则2019a 的值为______. 10.已知正项等比数列{}n a 满足5432a a a +=,若存在两项m a ,n a,使得1a =,则91m n+的最小值为__________. 11.已知数列{}n a 满足对*,m n N ∀∈,都有m n m n a a a ++=成立,72a π=,函数()f x =2sin 24cos2xx +,记()n n y f a =,则数列{}n y 的前13项和为______.12.已知数列{}n a 的前n 项和为n S ,满足22()n n S a n n N *=+∈,则n a =_____.13.等差数列{}n a 中,410a =且3a ,6a ,10a 成等比数列,数列{}n a 前20项的和20S =____ 14.已知正项等比数列{}n a 的前n 项和为n S .若9362S S S =+,则631S S +取得最小值时,9S 的值为_______.15.设数列{}n a 的前n 项和为n S ,且满足11222n n a a a n -++⋯+=,则5S =____.16.已知数列{}n a 满足112(1)0,4n n n a na a ++-==,则数列(1)(2)na n n ⎧⎫⎨⎬++⎩⎭的前n 项和为___________.17.定义:从数列{}n a 中抽取(,3)m m N m ∈≥项按其在{}n a 中的次序排列形成一个新数列{}n b ,则称{}n b 为{}n a 的子数列;若{}n b 成等差(或等比),则称{}n b 为{}n a 的等差(或等比)子数列. (1)记数列{}n a 的前n 项和为n S ,已知21n n S =-. ①求数列{}n a 的通项公式;②数列{}n a 是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由. (2)已知数列{}n a 的通项公式为()n a n a a Q +=+∈,证明:{}n a 存在等比子数列. 18.在等差数列{}n a 中,已知公差2d =,2a 是1a 与4a 的等比中项 (1)求数列{}n a 的通项公式; (2)若数列{}n b 满足3122331313131n n n b b b ba =++++++++L ,求数列{}nb 的通项公式; (3)令()*4n nn a b c n N =∈,数列{}n c 的前n 项和为n T . 19.已知等差数列{}n a 满足32421,7a a a =-=,等比数列{}n b 满足()35242b b b b +=+,且()2*22n n b b n =∈N .(1)求数列{}n a ,{}n b 的通项公式;(2)记数列{}n a 的前n 项和为n S ,若数列{}n c 满足()*1212n n nc c c S n b b b ++⋯+=∈N ,求{}n c 的前n 项和为n T .20.等差数列{}n a 前n 项和为n S ,且432S =,13221S =. (1)求{}n a 的通项公式n a ;(2)数列{}n b 满足()*1n n n b b a n N+-=∈且13b =,求1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T . 21.设{}n a 是单调递增的等比数列,n S 为数列{}n a 的前n 项和.已知313S =,且13a +,23a ,35a +构成等差数列. (1)求n a 及n S ;(2)是否存在常数λ.使得数列{}n S λ+是等比数列?若存在,求λ的值;若不存在,请说明理由. 22.对于无穷数列{}n a ,{}n b ,若{}{}1212max ,,,min ,,,k k k b a a a a a a =-L L ,1,2,3,k =L ,则称{}n b 是{}n a 的“收缩数列”.其中{}12max ,,,k a a a L ,{}12min ,,,k a a a L 分别表示12,,,k a a a L 中的最大数和最小数.已知{}n a 为无穷数列,其前n 项和为n S ,数列{}n b 是{}n a 的“收缩数列”. (1)若21n a n =+,求{}n b 的前n 项和; (2)证明:{}n b 的“收缩数列”仍是{}n b ;(3)若121(1)(1)(1,2,3,)22n n n n n n S S S a b n +-+++=+=L L 且11a =,22a =,求所有满足该条件的{}n a .。
2010-2019高考真题分类训练理数专题六 数列 第十八讲 数列的综合应用答案

专题六 数列 第十八讲 数列的综合应用答案部分 2019年1.解析:对于B ,令2104x λ-+=,得12λ=, 取112a =,所以211,,1022n a a ==<L , 所以当14b =时,1010a <,故B 错误;对于C ,令220x λ--=,得2λ=或1λ=-, 取12a =,所以22,,210n a a ==<L , 所以当2b =-时,1010a <,故C 错误; 对于D ,令240x λ--=,得12λ±=,取1a =2a =,…,10n a =<, 所以当4b =-时,1010a <,故D 错误;对于A ,221122a a =+…,223113224a a ⎛⎫=++ ⎪⎝⎭…,242431911714216216a a a ⎛⎫=++++=> ⎪⎝⎭…,10n n a a +->,{}n a 递增,当4n …时,11132122n n n n a a a a +=+>+=,所以5465109323232a a a a a a ⎧>⎪⎪⎪>⎪⎨⎪⎪⎪>⎪⎩M,所以610432a a ⎛⎫> ⎪⎝⎭,所以107291064a >>故A 正确.故选A . 2.解析:(1)设数列{}n a 的公差为d ,由题意得11124,333a d a d a d +=+=+,解得10,2a d ==.从而*22,n a n n =-∈N .由12,,n n n n n n S b S b S b +++++成等比数列得()()()212n n n n n n S b S b S b +++=++.解得()2121n n n n b S S S d++=-. 所以2*,n b n n n =+∈N .(2)*n c n ===∈N . 我们用数学归纳法证明.①当n =1时,c 1=0<2,不等式成立;②假设()*n k k =∈N时不等式成立,即12h c c c +++<L . 那么,当1n k =+时,121k k c c c c +++++<<L<==即当1n k =+时不等式也成立.根据(1)和(2),不等式12n c c c +++<L 对任意*n ∈N 成立.3.解析(1)设等比数列{a n }的公比为q ,所以a 1≠0,q ≠0.由245321440a a a a a a =⎧⎨-+=⎩,得244112111440a q a q a q a q a ⎧=⎨-+=⎩,解得112a q =⎧⎨=⎩. 因此数列{}n a 为“M—数列”.(2)①因为1122n n n S b b +=-,所以0n b ≠. 由1111,b S b ==,得212211b =-,则22b =. 由1122n n n S b b +=-,得112()n n n n n b b S b b ++=-, 当2n ≥时,由1n n n b S S -=-,得()()111122n n n nn n n n n b b b b b b b b b +-+-=---,整理得112n n n b b b +-+=.所以数列{b n }是首项和公差均为1的等差数列. 因此,数列{b n }的通项公式为b n =n ()*n ∈N .②由①知,b k =k ,*k ∈N .因为数列{c n }为“M–数列”,设公比为q ,所以c 1=1,q >0.因为c k ≤b k ≤c k +1,所以1k kq k q -≤≤,其中k =1,2,3,…,m .当k =1时,有q ≥1; 当k =2,3,…,m 时,有ln ln ln 1k kq k k ≤≤-. 设f (x )=ln (1)x x x >,则21ln ()xf 'x x -=. 令()0f 'x =,得x =e.列表如下:x (1,e)e (e ,+∞) ()f 'x+0 –f (x )极大值因为ln 2ln8ln 9ln 32663=<=,所以max ln 3()(3)3f k f ==.取q =k =1,2,3,4,5时,ln ln kq k…,即k k q ≤, 经检验知1k q k -≤也成立.因此所求m 的最大值不小于5.若m ≥6,分别取k =3,6,得3≤q 3,且q 5≤6,从而q 15≥243,且q 15≤216, 所以q 不存在.因此所求m 的最大值小于6. 综上,所求m 的最大值为5.3.解析:(I )1,3,5,6.(答案不唯一).(II )设长度为q 末项为0n a 的一个递增子列为110,...,,q r r n a a a -.由p q <,10p q r r n a a a -≤<.因为{}n a 的长度为p 的递增子列末项的最小值为0m a .又12,,...,p r r r a a a 是{}n a 的长度为p 的递增子列,所以0,p m r a a ≤所以00m n a a <.(III )由题设知,所有正奇数都是{}n a 中的项.先证明:若2m 是{}n a 中的项,则2m 必排在2m -1之前(m 为正整数).假设2m 排在2m -1之后,设121,,...,,21m p p p a a a m --是数列{}n a 的长度为m 末项为2m -1的递增子列,则121,,...,,2 1.2m p p p a a a m m --是数列{}n a 的长度为m+1末项为2m 的递增子列,与已知矛盾.再证明:所有正偶数都是{}n a 中的项.假设存在正偶数不是{}n a 中的项,设不在{}n a 中的最小正偶数为2m.因为2k 排在2k -1之前() 1,2,1k m =⋯- ,所以2k 和2k -1不可能在{}n a 的同一个子列中. 又{}n a 中不超过 21m +的数为1,2,….., 21m -, 21m +, 所以{}n a 的长度为 1m +末项为 21m +的递增子列个数至多为12222112 2m m -⨯⨯⨯⋅⋅⋅⨯⨯⨯=<,与已知矛盾.最后证明 2m 排在 23m -之后( 2m ≥为整数).假设存在 2m ( 2m ≥),使得 2m 排在 23m -之前,则{}n a 的长度为 1m +末项为 21m +的递增子列个数小于 2m ,与已知矛盾.综上,数列{}n a 只可能为2,1,4,3,,23,2,21,m m m ⋅⋅⋅--⋅⋅⋅. 经验证,数列2,1,4,3,,23,2,21,m m m ⋅⋅⋅--⋅⋅⋅符合条件,所以1,1.n n n a n n +⎧=⎨-⎩为奇数为偶数.2010-2018年1.A 【解析】对数列进行分组如图k321∙∙∙,222121,2k 22,21,20,20,20,20则该数列前k 组的项数和为(1)1232k k k ++++⋅⋅⋅+= 由题意可知100N >,即(1)1002k k +>,解得14k ≥,n ∈*N 即N 出现在第13组之后.又第k 组的和为122112kk -=-- 前k 组的和为1(12)(122)k +++⋅⋅⋅+++⋅⋅⋅+12(21)(21)(21)k =-+-+⋅⋅⋅+- 12(222)k k =++⋅⋅⋅+-122k k +=--,设满足条件的的N 在第1k +(k ∈*N ,13k ≥)组,且第N 项为第1k +的第m ()m ∈*N 个数,第1k +组的前m 项和为211222m -+++⋅⋅⋅+21m =-,要使该数列的前N 项和为2的整数幂, 即21m -与2k --互为相反数, 即212mk -=+, 所以23mk =-,由14k ≥,所以2314m-≥,则5m ≥,此时52329k =-= 对应满足的最小条件为29(291)54402N +=+=,故选A . 2.C 【解析】由题意可得10a =,81a =,2a ,3a ,…,7a 中有3个0、3个1,且满足对任意k ≤8,都有1a ,2a ,…,k a 中0的个数不少于1的个数,利用列举法可得不同的“规范01数列”有00001111,00010111, 00011011, 00011101,00100111, 00101011,00101101,00110011,00110101,01000111,01001011,01001101,01010011,01010101,共14个.3.A 【解析】对命题p :12,,,n a a a L 成等比数列,则公比)3(1≥=-n a a q n n且0≠n a ; 对命题q ,①当0=n a 时,22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L 成立;②当0≠n a 时,根据柯西不等式,等式22222221212312231()()()n n n n a a a a a a a a a a a a --++++++=+++L L L 成立,则nn a a a a a a 13221-=⋅⋅⋅==,所以12,,,n a a a L 成等比数列, 所以p 是q 的充分条件,但不是q 的必要条件.4.A 【解析】2a ,4a ,8a 成等比数列,∴2428a a a =⋅,即2111(6)(2)(14)a a a +=++,解得12a =,所以(1)n S n n =+.5.B 【解析】∵21)(x x f =在[0,1]上单调递增,可得1110()()0f a f a ->,1211()()0f a f a ->,…,199198()()0f a f a ->,∴111101211199198|()()||()()||()()|I f a f a f a f a f a f a =-+-+⋅⋅⋅+-1110121119919819910()()+()()()()=()()f a f a f a f a f a f a f a f a --+⋅⋅⋅+--=299-0=199() ∵),(2)(22x x x f -=在490]99[,上单调递增,在50[,1]99单调递减 ∴2120()()0f a f a ->,…,249248()()0f a f a ->,250249()()0f a f a -=,251250()()0f a f a -<,…,299298()()0f a f a -<∴221202221299298|()()||()()||()()|I f a f a f a f a f a f a =-+-+⋅⋅⋅+- =24920299250()()[()()]f a f a f a f a ---=250202992()()()f a f a f a --=505098004(1)199999801⨯⨯-=< ∵|2sin |31)(3x x f π=在24[0,]99,5074[,]9999上单调递增,在2549[,]9999,75[,1]99上单调递减,可得33253493742492()2()2(=(2sin sin )39999I f a f a f a ππ=-+-)252(2sin sin )(1312123444ππ>-=-=> 因此312I I I <<.6.27【解析】所有的正奇数和2n (*n ∈N )按照从小到大的顺序排列构成{}n a ,在数列{}n a中,52前面有16个正奇数,即5212a =,6382a =.当1n =时,1211224S a =<=,不符合题意;当2n =时,2331236S a =<=,不符合题意;当3n =时,3461248S a =<=,不符合题意;当4n =时,45101260S a =<=,不符合题意;……;当26n =时,52621(141)2(12)212S ⨯+⨯-=+-= 441 +62= 503<2712516a =,不符合题意;当27n =时,52722(143)2(12)212S ⨯+⨯-=+-=484 +62=546>2812a =540,符合题意.故使得112n n S a +>成立的n 的最小值为27.7.5【解析】设数列的首项为1a ,则12015210102020a +=⨯=,所以15a =,故该数列的首项为5.8.12【解析】将82a =代入111n n a a +=-,可求得712a =;再将712a =代入111n na a +=-,可求得61a =-;再将61a =-代入111n na a +=-得52a =;由此可知数列{}n a 是一个周期数列,且周期为3,所以1712a a ==. 9.64【解析】由11a =且125,,a a a 成等比数列,得2111(4)()a a d a d +=+,解得2d =,故81878642S a d ⨯=+=. 102a t =,则23112t q t q t q ++≤≤≤≤≤≤,由于1t ≥,所以max{q t ≥,故q.11.4【解析】由题意得1122(4)()(1)(14)()3322(4)()(1)(14)()33k k k k k k k k k k k k -+⎧+>--+⎪⎪⎨⎪+>+++⎪⎩,得22(1)1010k k ⎧-<⎨>⎩,因此*k N ∈,所以4k =.12.【解析】(1)由条件知:(1)n a n d =-,12n n b -=.因为1||n n a b b -≤对n =1,2,3,4均成立, 即1|(1)2|1n n d ---≤对n =1,2,3,4均成立,即1≤1,1≤d ≤3,3≤2d ≤5,7≤3d ≤9,得7532d ≤≤. 因此,d 的取值范围为75[,]32.(2)由条件知:1(1)n a b n d =+-,11n n b b q -=.若存在d ,使得1||n n a b b -≤(n =2,3,···,m +1)成立,即1111|(1)|n b n d b q b -+--≤(n =2,3,···,m +1),即当2,3,,1n m =+L 时,d 满足1111211n n q q b d b n n ---≤≤--.因为q ∈,则112n m q q -<≤≤,从而11201n q b n --≤-,1101n q b n ->-,对2,3,,1n m =+L 均成立. 因此,取d =0时,1||n n a b b -≤对2,3,,1n m =+L 均成立.下面讨论数列12{}1n q n ---的最大值和数列1{}1n q n --的最小值(2,3,,1n m =+L ). ①当2n m ≤≤时,111 2222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---, 当112mq <≤时,有2n m q q ≤≤,从而1() 20n n n n q q q ---+>.因此,当21n m ≤≤+时,数列12{}1n q n ---单调递增,故数列12{}1n q n ---的最大值为2m q m-. ②设()()21x f x x =-,当0x >时,ln 21(0(n )l 22)x f x x '=--<, 所以()f x 单调递减,从而()(0)1f x f <=.当2n m ≤≤时,111112111()()()nn n q q n n f q n n n n --=≤-=<-, 因此,当21n m ≤≤+时,数列1{}1n q n --单调递减,故数列1{}1n q n --的最小值为mq m. 因此,d 的取值范围为11(2)[,]m mb q b q m m-.13.【解析】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q .由已知2312b b +=,得21()12b q q +=,而12b =,所以260q q +-=. 又因为0q >,解得2q =.所以,2nn b =.由3412b a a =-,可得138d a -= ①. 由114=11S b ,可得1516a d += ②,联立①②,解得11a =,3d =,由此可得32n a n =-.所以,数列{}n a 的通项公式为32n a n =-,数列{}n b 的通项公式为2nn b =.(Ⅱ)设数列221{}n n a b -的前n 项和为n T ,由262n a n =-,12124n n b --=⨯,有221(31)4nn n a b n -=-⨯, 故23245484(31)4nn T n =⨯+⨯+⨯++-⨯L ,23414245484(34)4(31)4n n n T n n +=⨯+⨯+⨯++-⨯+-⨯L ,上述两式相减,得231324343434(31)4n n n T n +-=⨯+⨯+⨯++⨯--⨯L1112(14)4(31)414(32)48.n n n n n ++⨯-=---⨯-=--⨯- 得1328433n n n T +-=⨯+. 所以,数列221{}n n a b -的前n 项和为1328433n n +-⨯+. 14.【解析】(Ⅰ)用数学归纳法证明:0n x >当1n =时,110x => 假设n k =时,0k x >,那么1n k =+时,若10k x +≤,则110ln(1)0k k k x x x ++<=++≤,矛盾,故10k x +>. 因此0n x >()n ∈*N所以111ln(1)n n n n x x x x +++=++>因此10n n x x +<<()n ∈*N(Ⅱ)由111ln(1)n n n n x x x x +++=++>得2111111422(2)ln(1)n n n n n n n n x x x x x x x x ++++++-+=-+++ 记函数2()2(2)ln(1)(0)f x x x x x x =-+++≥函数()f x 在[0,)+∞上单调递增,所以()(0)f x f ≥=0, 因此2111112(2)ln(1)()0n n n n n x x x x f x +++++-+++=≥ 故112(N )2n n n n x x x x n *++-∈≤ (Ⅲ)因为11111ln(1)2n n n n n n x x x x x x +++++=+++=≤所以112n n x -≥得 由1122n n n n x x x x ++-≥得 111112()022n n x x +-->≥ 所以12111111112()2()2222n n n n x x x -----⋅⋅⋅-=≥≥≥ 故212n n x -≤综上,1211(N )22n n n x n *--∈≤≤ .15.【解析】(Ⅰ)由已知,1211,1,n n n n S qS S qS +++=+=+两式相减得到21,1n n a qa n ++=?.又由211S qS =+得到21a qa =,故1n n a qa +=对所有1n ³都成立. 所以,数列{}n a 是首项为1,公比为q 的等比数列. 从而1=n n a q -.由2322+2a a a ,,成等比数列,可得322=32a a +,即22=32,q q +, 则(21)(2)0q+q -=, 由已知,0q >,故 =2q . 所以1*2()n n a n -=?N . (Ⅱ)由(Ⅰ)可知,1n n a q -=.所以双曲线2221ny x a -=的离心率n e =由53q =解得43q =. 因为2(1)2(1)1+k k q q -->1*k q k -?N (). 于是11211+1n n n q e e e q q q --++鬃?>+鬃?=-,故1231433n nn e e e --++鬃?>. 16.【解析】(Ⅰ)由题意有,1110451002a d a d +=⎧⎨=⎩ ,即1129202a d a d +=⎧⎨=⎩.解得112a d =⎧⎨=⎩ 或1929a d =⎧⎪⎨=⎪⎩,故1212n n n a n b -=-⎧⎪⎨=⎪⎩或11(279)929()9n n n a n b -⎧=+⎪⎪⎨⎪=⋅⎪⎩. (Ⅱ)由1d >,知21n a n =-,12n n b -=,故1212n n n c --=,于是 2341357921122222n n n T --=++++++L , ① 2345113579212222222n n n T -=++++++L . ② ①-②可得221111212323222222n n n n n n T --+=++++-=-L ,故n T 12362n n -+=-. 17.【解析】(Ⅰ)2()()212,nn n F x f x x x x =-=+++-L 则(1)10,n F n =->1211111112()1220,12222212n nn n F +⎛⎫- ⎪⎛⎫⎛⎫⎝⎭=+++-=-=-< ⎪ ⎪⎝⎭⎝⎭-L 所以()n F x 在1,12⎛⎫⎪⎝⎭内至少存在一个零点n x . 又1()120n n F x x nx-'=++>L ,故在1,12⎛⎫⎪⎝⎭内单调递增,所以()n F x 在1(,1)2内有且仅有一个零点n x .因为n x 是()n F x 的零点,所以()=0n n F x ,即11201n n nx x +--=-,故111=+22n n n x x +.(Ⅱ)解法一:由题设,()()11().2nnn x g x ++=设()()211()()()1,0.2nnn n n x h x f x g x x x x x ++=-=+++->L当1x =时, ()()n n f x g x = 当1x ≠时, ()111()12.2n n n n x h x x nx--+'=++-L若01x <<,()11111()22n n n n n n h x xx nx x ----+'>++-L()()11110.22n n n n n n x x --++=-=若1x >,()11111()22n n n n n n h x x x nx x ----+'<++-L()()11110.22n n n n n n x x --++=-=所以()h x 在(0,1)上递增,在(1,)+∞上递减, 所以()(1)0h x h <=,即()()n n f x g x <.综上所述,当1x =时, ()()n n f x g x =;当1x ≠时()()n n f x g x <. 解法二 由题设,()()211()1,(),0.2nn n n n x f x x x x g x x ++=+++=>L当1x =时, ()()n n f x g x =;当1x ≠时, 用数学归纳法可以证明()()n n f x g x <. 当2n =时, 2221()()(1)0,2f xg x x -=--<所以22()()f x g x <成立. 假设(2)n k k =≥时,不等式成立,即()()k k f x g x <. 那么,当+1n k =时,()()111k+1k 11()()()2kk k k k k x f x f x x g x x x+++++=+<+=+()12112k k x k x k +++++=.又()()11k+121111()22k k k k x k x k kx k x g x ++++++-++-=令()1()11(x 0)k k k h x kx k x +=-++>, 则()()11()(k 1)11(x 1)kk k k h x k x k k xk k x --'=+-+=+-.所以当01x <<,()0kh x '<,()k h x 在(0,1)上递减; 当1x >,()0kh x '>,()k h x 在(1,)+∞上递增. 所以()(1)0k k h x h >=,从而()1k+1211()2k k x k x k g x +++++>.故11()()k k f x g x ++<.即+1n k =,不等式也成立. 所以,对于一切2n ≥的整数,都有()()n n f x g x <.解法三:由已知,记等差数列为{}k a ,等比数列为{}k b ,1,2,...,1k n =+.则111a b ==,11nn n a b x ++==,所以()11+1(2n)n k x a k k n-=-⋅≤≤,1(2),k k b x k n -=≤≤ 令()()111(x)1,0(2).n k k k k k x m a b x x k n n---=-=+->≤≤当1x =时, =k k a b ,所以()()n n f x g x =. 当1x ≠时, ()()12211()(k 1)11n k k n k k k m x nx x k x x n----+-'=--=--, 而2k n ≤≤,所以10k ->,11n k -+≥. 若01x <<, 11n k x -+<,()0k m x '<,当1x >,11n k x-+>,()0km x '>, 从而()k m x 在(0,1)上递减,()k m x 在(1,)+∞上递增.所以()(1)0k k m x m >=, 所以当01(2),k k x x a b k n >≠>≤≤且时,又11a b =,11n n a b ++=,故()()n n f x g x < 综上所述,当1x =时, ()()n n f x g x =;当1x ≠时()()n n f x g x <18.【解析】(Ⅰ)由21=0=22()n n n a a a n N λμ++-=∈,,有.若存在某个0,n N +∈使得0,no a =则由上述递推公式易得10,no a -=重复上述过程可得10a =,此与13a =矛盾,所以对任意,0n n N a +∈≠.从而12(),n n a a n N ++=∈即{}n a 是一个公比2q =的等比数列.故11132n n n a a q --==⋅.(Ⅱ)由01,1k λμ==-,数列{}n a 的递推关系式变为211010n n n n a a a a k +++-=, 变形为2101()().n n n a a a n N k +++=∈由上式及130a =>, 归纳可得12130n n a a a a +=>>⋅⋅⋅>>>⋅⋅⋅>.因为22220010001111111n nn n n n n a a k k a a k k a a a k k +-+===-?+++, 所以对01,2,,n k =⋅⋅⋅求和得01010121()()k k k a a a a a a ++=+-+⋅⋅⋅+-010000102011111 =()111k a k k k k a k a k a -⋅+⋅++⋅⋅⋅++++0000011111>2+( )231313131k k k k k k ⋅++⋅⋅⋅+=+++++1444442444443. 另一方面,由上已证的不等式知001212k k a a a a +>>⋅⋅⋅>>>,得00110000102011111()111k k a a k k k k a k a k a +=-⋅+⋅++⋅⋅⋅++++0000011111<2+()221212121k k k k k k ⋅++⋅⋅⋅+=+++++1444442444443. 综上,0100112+23121k a k k +<<+++.19.【解析】(Ⅰ),64,2,,2141211d a S d a S a S d +=+===4122421,,S S S S S S =∴成等比Θ解得12,11-=∴=n a a n (Ⅱ))121121()1(4)1(111++--=-=-+-n n a a n b n n n n n ,当n 为偶数时11111(1)()()33557n T =+-+++-L L1111()()23212121n n n n ++-+---+ 1221211+=+-=∴n nn T n 11111(1)()()33557n n T =+-+++--L L 当为奇数时, 1111()()23212121n n n n +++---+12221211++=++=∴n n n T n ⎪⎪⎩⎪⎪⎨⎧+++=∴为奇数为偶数n n n n n nT n ,1222,122. 20.【解析】(Ⅰ)由题意,()()*∈=N n a a a nb n 221Λ,326b b-=,知3238b b a -==,又由12a =,得公比2q =(2q =-舍去),所以数列{}n a 的通项公式为2()n n a n N *=∈,所以()()1121232n n n n n a a a a ++==L ,故数列{}n b 的通项公式为,()1()n b n n n N *=+∈; (Ⅱ)(i )由(Ⅰ)知,11111()21n n n n c n N a b n n *⎛⎫=-=--∈ ⎪+⎝⎭, 所以11()12n n S n N n *=-∈+; (ii )因为12340,0,0,0c c c c =>>>; 当5n ≥时,()()11112n nn n c n n +⎡⎤=-⎢⎥+⎣⎦,而()()()()()11112120222n n n n n n n n n ++++++--=>, 得()()51551122n n n ++≤<, 所以当5n ≥时,0n c <,综上对任意n N *∈恒有4n S S ≥,故4k =.21.【解析】(I )因为{}n a 是递增数列,所以11n n n n n a a a a p ++-=-=.而11a =,因此又123,2,3a a a 成等差数列,所以21343a a a =+,因而230p p -=, 解得1,03p p == 当0p =时,1n n a a +=,这与{}n a 是递增数列矛盾。
理科数学2010-2018高考真题分类专题六 数列 第十六讲 等比数列答案

专题六 数列第十六讲 等比数列答案部分1.D 【解析】从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于第一个单音的频率为f ,由等比数列的概念可知,这十三个单音的频率构成一个首项为f ,公比为{}n a ,则第八个单音频率为818a f -=⋅=,故选D .2.B 【解析】解法一 因为ln 1x x -≤(0x >),所以1234123ln()a a a a a a a +++=++1231a a a ++-≤,所以41a -≤,又11a >,所以等比数列的公比0q <.若1q -≤,则212341(1)(10a a a a a q q +++=++)≤, 而12311a a a a ++>≥,所以123ln()0a a a ++>, 与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<,所以13a a >,24a a <,故选B .解法二 因为1xe x +≥,1234123ln()a a a a a a a +++=++,所以123412312341a a a a ea a a a a a a +++=++++++≥,则41a -≤,又11a >,所以等比数列的公比0q <.若1q -≤,则212341(1)(10a a a a a q q +++=++)≤, 而12311a a a a ++>≥,所以123ln()0a a a ++> 与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<,所以13a a >,24a a <,故选B .3.B 【解析】设塔顶共有灯1a 盏,根据题意各层等数构成以1a 为首项,2为公比的等比数列,∴77171(12)(21)38112a S a -==-=-,解得13a =.选B . 4.B 【解析】由于241(1)21a qq ,13a ,所以4260q q ,所以22q(23q舍去),所以36a ,512a ,724a ,所以35742a a a .5.D 【解析】由等比数列的性质得,23960a a a ⋅=≠,因此269,,a a a 一定成等比数列.6.C 【解析】设等比数列{}n a 的公比为q ,∵32110S a a =+,∴1232110a a a a a ++=+,即319a a =,∴29q =,由59a =,即419a q =,∴119a =. 7.B 【解析】取特殊值可排除A 、C 、D ,由均值不等式可得2221313222a a a a a +⋅=.8.B 【解析】由116n n n a a +=,得11216n n n a a +++=,两式相除得1121161616n n n n n n a a a a ++++==,∴216q =,∵116n n n a a +=,可知公比q 为正数,∴4q =.9.C 【解析】设{n a }的公比为q ,则由等比数列的性质知,231412a a a a a ⋅=⋅=,即42a =.由4a 与27a 的等差中项为54知,475224a a +=⨯, 7415(2)24a a ∴=⨯-14=.∴37418a q a ==,即12q =.3411128a a q a ==⨯=,116a ∴=,55116(1)231112S -==-. 10.A 【解析】通过2580a a +=,设公比为q ,将该式转化为08322=+q a a ,解得q =-2,所以5522113211114S q S q -+===---. 11.D 【解析】取等比数列1,2,4,令1n =得1,3,7X Y Z ===代入验算,只有选项D 满足.12.C 【解析】2341010123451m a a a a a a q q q q q a q ==⋅⋅⋅==,因此有11m =.13.B 【解析】两式相减得, 3433a a a =-,44334,4a a a q a =∴==.14.C 【解析】显然q ≠1,所以3639(1)1=1211q q q q q q --⇒+⇒=--,所以1{}na 是首项为1,公比为12的等比数列, 前5项和5511()31211612T -==-. 15.8-【解析】设{}n a 的首项为1a ,公比为q ,所以1121113a a q a a q +=-⎧⎨-=-⎩, 解得112a q =⎧⎨=-⎩ ,则3418a a q ==-.16.32【解析】设{}n a 的公比为q ,由题意1q ≠,由636331191S q q S q-==+=-,所以2q =,由313(1)714a q S q -==-,得114a =,所以77581122324a a q ==⨯==. 17.1【解析】设{}n a 的公差为d ,{}nb 的公比为q ,由题意3138d q -+=-=,所以3d =,2q =-,所以22131(2)a b -+==--. 18.64【解析】设{}n a 的公比为q ,由1310a a +=,245a a +=得118,2a q ==, 则24a =,32a =,41a =,512a =,所以12123464n a a a a a a a ⋅⋅⋅=.19.1 121 【解析】由于1221421a a a a +=⎧⎨=+⎩,解得11a =,由1121n n n n a S S S ++=-=+,所以1113()22n n S S ++=+,所以1{}2n S +是以32为首项,3为公比的等比数列, 所以113322n n S -+=⨯,所以5121S =.20.21n【解析】由题意,14231498a a a a a a +=⎧⎨⋅=⋅=⎩,解得141,8a a ==或148,1a a ==,而数列{}n a 是递增的等比数列,所以141,8a a ==,即3418a q a ==,所以2q =,因而数列{}n a 的前n 项和1(1)1221112n nn n a q S q --===---.21.5【解析】由等比数列的性质可知215243a a a a a ==,于是,由154a a =得32a =,故1234532a a a a a =,则2122232425log +log +log +log +log =a a a a a2123452log ()log 325a a a a a ==.22.50【解析】因{}n a 是等比数列,∴1201011912a a a a a a ==,由512911102e a a a a =+得∴5120a a e =,∴1220ln ln ln a a a +++=101220120ln()ln()a a a a a ⋅⋅⋅==50.23.4【解析】 设等比数列}{n a 的公比为q ,0q >.则8642a a a =+,即为424442a q a q a =+,解得22q =(负值舍去),又21a =,所以4624a a q =.24.15【解析】12341,2,4,8a a a a ==-==-,∴ 1234||||a a a a +++=15. 25.12,22n +-【解析】由35a a +=()24q a a +得2q =;()()3241a a a q q +=+=20,得12a =;∴()12122212n n n S +-==--.26.12【解析】设正项等比数列}{n a 首项为1a ,公比为q ,则:⎪⎩⎪⎨⎧=+=3)1(215141q q a q a ,得:1a =132,q =2,62nn a -=.记521212-=+++=n n n a a a T , 2)1(212nn n n a a a -==∏ .n n T ∏>,则2)1(52212n n n ->-,化简得:5211212212+->-n n n,当5211212+->n n n 时,12212113≈+=n . 当n =12时,1212∏>T ,当n =13时,1313∏<T ,故max 12n =.27.11【解析】由2120n n n a a a +++-=,可得220n n n a q a q a +-=,由11a =可知0,1n a q ≠≠,求得公比2q =-,可得5S =11.28.2【解析】222112()5,2(1)5,2(1)5,22n n n n n a a a a q a q q q q q +++=∴+=∴+===解得或 因为数列为递增数列,且10,1,2a q q >>∴=所以.29.32【解析】依题意可得,2112111443311111(1)32232201(1)23220321a q a q a q a q a q q a q a q a q a q a q q ⎧-=+⎪⎧-++-=-⎪⎪⇒⎨⎨--++-=⎪⎪⎩=+⎪-⎩两式相减可得423111122330a q a q a q a q --+=,即42322330q q q q --+=,解得1q =±(舍)或0q =或32q =。
理科数学2010-2019高考真题分类训练16专题六 数列 第十六讲 等比数列—附解析答案

{an}的首项、公首项为
3 2
的等比数列{an} 的前
n
项和为
Sn (n
N*)
,
且
2S2 , S3, 4S4 成
等差数列.
(Ⅰ) 求数列{an} 的通项公式;
(Ⅱ)
证明
Sn
1 Sn
13 (n N*) . 6
39.(2011 新课标)已知等比数列{an}的各项均为正数,且 2a1 3a2 1, a32 9a2a6 .
y
P4 P3
P2
P1 O x1 x2 x3
x x4
33.(2016 年全国 III 高考)已知数列{an}的前 n 项和 Sn 1 an ,其中 0 .
(Ⅰ)证明 {an } 是等比数列,并求其通项公式;
(Ⅱ)若
S5
31 32
,求
.
34.(2014 新课标)已知数列an 满足 a1 =1, an1 3an 1.
(Ⅱ )若数列{an}唯一,求 a 的值. 41.(2011 安徽)在数 1 和 100 之间插入 n 个实数,使得这 n 2 个数构成递增的等比数列,
将这 n 2 个数的乘积记作Tn ,再令 an lgTn, n≥1.
(Ⅰ)求数列 {an } 的通项公式;
(Ⅱ)设 bn tan an tan an1, 求数列{bn}的前 n 项和 Sn .
( )
a1 1− q4
1−q
a1q4 = 3a1q
2
= 15 + 4a1
,解得
aq1
=1 =2
.
所以 a3
= 22
= 4 .故选 C.
3.解析:(1)由题设得 4(an+1
+
2010年全国统一高考数学试卷(理科)(新课标)及解析

2010年全国统一高考数学试卷(理科)(新课标)一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知集合A={x∈R||x|≤2}},,则A∩B=()A.(0,2)B.[0,2]C.{0,2}D.{0,1,2}2.(5分)已知复数,是z的共轭复数,则=()A.B.C.1 D.23.(5分)曲线y=在点(﹣1,﹣1)处的切线方程为()A.y=2x+1 B.y=2x﹣1 C.y=﹣2x﹣3 D.y=﹣2x﹣24.(5分)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P 0(,﹣),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A.B.C.D.5.(5分)已知命题p1:函数y=2x﹣2﹣x在R为增函数,p2:函数y=2x+2﹣x在R为减函数,则在命题q:p1∨p2,q2:p1∧p2,q3:(¬p1)∨1p2和q4:p1∧(¬p2)中,真命题是()A.q1,q3 B.q2,q3 C.q1,q4 D.q2,q46.(5分)某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X 的数学期望为()A.100 B.200 C.300 D.4007.(5分)如果执行右面的框图,输入N=5,则输出的数等于()A.B.C.D.8.(5分)设偶函数f(x)满足f(x)=2x﹣4(x≥0),则{x|f(x﹣2)>0}=()A.{x|x<﹣2或x>4}B.{x|x<0或x>4} C.{x|x<0或x>6} D.{x|x<﹣2或x>2}9.(5分)若,α是第三象限的角,则=()A.B.C.2 D.﹣210.(5分)设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为()A.πa2B. C.D.5πa211.(5分)已知函数,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A.(1,10)B.(5,6)C.(10,12)D.(20,24)12.(5分)已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为()A. B. C. D.二、填空题(共4小题,每小题5分,满分20分)13.(5分)设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…x N和y1,y2,…y N,由此得到N个点(x i,y i)(i=1,2,…,N),再数出其中满足y i≤f(x i)(i=1,2,…,N)的点数N 1,那么由随机模拟方案可得积分的近似值为.14.(5分)正视图为一个三角形的几何体可以是(写出三种)15.(5分)过点A(4,1)的圆C与直线x﹣y=1相切于点B(2,1),则圆C的方程为.16.(5分)在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为,则∠BAC=.三、解答题(共8小题,满分90分)17.(12分)设数列满足a1=2,a n+1﹣a n=3•22n﹣1(1)求数列{a n}的通项公式;(2)令b n=na n,求数列{b n}的前n项和S n.18.(12分)如图,已知四棱锥P﹣ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点(1)证明:PE⊥BC(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.19.(12分)为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如表:(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.附:20.(12分)设F1,F2分别是椭圆的左、右焦点,过F1斜率为1的直线ℓ与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.(1)求E的离心率;(2)设点P(0,﹣1)满足|PA|=|PB|,求E的方程.21.(12分)设函数f(x)=e x﹣1﹣x﹣ax2.(1)若a=0,求f(x)的单调区间;(2)若当x≥0时f(x)≥0,求a的取值范围.22.(10分)如图:已知圆上的弧,过C点的圆的切线与BA的延长线交于E点,证明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE•CD.23.(10分)已知直线C1(t为参数),C2(θ为参数),(Ⅰ)当α=时,求C1与C2的交点坐标;(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.24.(10分)设函数f(x)=|2x﹣4|+1.(Ⅰ)画出函数y=f(x)的图象:(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.2010年全国统一高考数学试卷(理科)(新课标)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2010•宁夏)已知集合A={x∈R||x|≤2}},,则A∩B=()A.(0,2)B.[0,2]C.{0,2}D.{0,1,2}【分析】先化简集合A和B,注意集合B中的元素是整数,再根据两个集合的交集的意义求解.【解答】解:A={x∈R||x|≤2,}={x∈R|﹣2≤x≤2},故A∩B={0,1,2}.应选D.2.(5分)(2010•宁夏)已知复数,是z的共轭复数,则=()A.B.C.1 D.2【分析】因为,所以先求|z|再求的值.【解答】解:由可得.另解:故选A.3.(5分)(2010•宁夏)曲线y=在点(﹣1,﹣1)处的切线方程为()A.y=2x+1 B.y=2x﹣1 C.y=﹣2x﹣3 D.y=﹣2x﹣2【分析】欲求在点(﹣1,﹣1)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=﹣1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.【解答】解:∵y=,∴y′=,所以k=y′|x=﹣1=2,得切线的斜率为2,所以k=2;所以曲线y=f(x)在点(﹣1,﹣1)处的切线方程为:y+1=2×(x+1),即y=2x+1.故选A.4.(5分)(2010•新课标)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P 0(,﹣),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A.B.C.D.【分析】本题的求解可以利用排除法,根据某具体时刻点P的位置到到x轴距离来确定答案.【解答】解:通过分析可知当t=0时,点P到x轴距离d为,于是可以排除答案A,D,再根据当时,可知点P在x轴上此时点P到x轴距离d为0,排除答案B,故应选C.5.(5分)(2010•宁夏)已知命题p1:函数y=2x﹣2﹣x在R为增函数,p2:函数y=2x+2﹣x在R为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是()A.q1,q3 B.q2,q3 C.q1,q4 D.q2,q4【分析】先判断命题p1是真命题,P2是假命题,故p1∨p2为真命题,(﹣p2)为真命题,p1∧(﹣p2)为真命题.【解答】解:易知p1是真命题,而对p2:y′=2x ln2﹣ln2=ln2(),当x∈[0,+∞)时,,又ln2>0,所以y′≥0,函数单调递增;同理得当x∈(﹣∞,0)时,函数单调递减,故p2是假命题.由此可知,q1真,q2假,q3假,q4真.故选C.6.(5分)(2010•宁夏)某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为()A.100 B.200 C.300 D.400【分析】首先分析题目已知某种种子每粒发芽的概率都为0.9,现播种了1000粒,即不发芽率为0.1,故没有发芽的种子数ξ服从二项分布,即ξ~B(1000,0.1).又没发芽的补种2个,故补种的种子数记为X=2ξ,根据二项分布的期望公式即可求出结果.【解答】解:由题意可知播种了1000粒,没有发芽的种子数ξ服从二项分布,即ξ~B(1000,0.1).而每粒需再补种2粒,补种的种子数记为X故X=2ξ,则EX=2Eξ=2×1000×0.1=200.故选B.7.(5分)(2010•新课标)如果执行右面的框图,输入N=5,则输出的数等于()A.B.C.D.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=的值.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=的值.∵S==1﹣=故选D.8.(5分)(2010•新课标)设偶函数f(x)满足f(x)=2x﹣4(x≥0),则{x|f(x﹣2)>0}=()A.{x|x<﹣2或x>4}B.{x|x<0或x>4} C.{x|x<0或x>6}D.{x|x<﹣2或x>2}【分析】由偶函数f(x)满足f(x)=2x﹣4(x≥0),可得f(x)=f (|x|)=2|x|﹣4,根据偶函数的性质将函数转化为绝对值函数,再求解不等式,可得答案.【解答】解:由偶函数f(x)满足f(x)=2x﹣4(x≥0),可得f(x)=f(|x|)=2|x|﹣4,则f(x﹣2)=f(|x﹣2|)=2|x﹣2|﹣4,要使f(|x﹣2|)>0,只需2|x ﹣2|﹣4>0,|x﹣2|>2解得x>4,或x<0.应选:B.9.(5分)(2010•宁夏)若,α是第三象限的角,则=()A.B.C.2 D.﹣2【分析】将欲求式中的正切化成正余弦,还要注意条件中的角α与待求式中角的差别,注意消除它们之间的不同.【解答】解:由,α是第三象限的角,∴可得,则,应选A.10.(5分)(2010•宁夏)设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为()A.πa2B. C.D.5πa2【分析】由题意可知上下底面中心连线的中点就是球心,求出球的半径,即可求出球的表面积.【解答】解:根据题意条件可知三棱柱是棱长都为a的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为,球的表面积为,故选B.11.(5分)(2010•新课标)已知函数,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A.(1,10)B.(5,6)C.(10,12)D.(20,24)【分析】画出函数的图象,根据f(a)=f(b)=f(c),不妨a<b<c,求出abc的范围即可.【解答】解:作出函数f(x)的图象如图,不妨设a<b<c,则ab=1,则abc=c∈(10,12).故选C.12.(5分)(2010•宁夏)已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为()A. B. C. D.【分析】已知条件易得直线l的斜率为1,设双曲线方程,及A,B 点坐标代入方程联立相减得x1+x2=﹣24,根据=,可求得a 和b的关系,再根据c=3,求得a和b,进而可得答案.【解答】解:由已知条件易得直线l的斜率为k=k PN=1,设双曲线方程为,A(x1,y1),B(x2,y2),则有,两式相减并结合x1+x2=﹣24,y1+y2=﹣30得=,从而==1即4b2=5a2,又a2+b2=9,解得a2=4,b2=5,故选B.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(2010•宁夏)设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…x N和y1,y2,…y N,由此得到N个点(x i,y i)(i=1,2,…,N),再数出其中满足y i≤f(x i)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分的近似值为.【分析】要求∫f(x)dx的近似值,利用几何概型求概率,结合点数比即可得.【解答】解:由题意可知得,故积分的近似值为.故答案为:.14.(5分)(2010•宁夏)正视图为一个三角形的几何体可以是三棱锥、三棱柱、圆锥(其他正确答案同样给分)(写出三种)【分析】三棱锥一个侧面的在正视图为一条线段的情形;圆锥;四棱锥有两个侧面在正视图为线段的情形,即可回答本题.【解答】解:正视图为一个三角形的几何体可以是三棱锥、三棱柱(放倒的情形)、圆锥、四棱锥等等.故答案为:三棱锥、圆锥、三棱柱.15.(5分)(2010•宁夏)过点A(4,1)的圆C与直线x﹣y=1相切于点B(2,1),则圆C的方程为(x﹣3)2+y2=2.【分析】设圆的标准方程,再用过点A(4,1),过B,两点坐标适合方程,圆和直线相切,圆心到直线的距离等于半径,求得圆的方程.【解答】解:设圆的方程为(x﹣a)2+(y﹣b)2=r2,则,解得,故所求圆的方程为(x﹣3)2+y2=2.故答案为:(x﹣3)2+y2=2.16.(5分)(2010•宁夏)在△ABC中,D为边BC上一点,BD=DC,∠ADB=120°,AD=2,若△ADC的面积为,则∠BAC=60°.【分析】先根据三角形的面积公式利用△ADC的面积求得DC,进而根据三角形ABC的面积求得BD和BC,进而根据余弦定理求得AB.最后在三角形ABC中利用余弦定理求得cos∠BAC,求得∠BAC的值.【解答】解:由△ADC的面积为可得解得,则.AB2=AD2+BD2﹣2AD•BD•cos120°=,,则=.故∠BAC=60°.三、解答题(共8小题,满分90分)17.(12分)(2010•宁夏)设数列满足a1=2,a n+1﹣a n=3•22n﹣1(1)求数列{a n}的通项公式;(2)令b n=na n,求数列{b n}的前n项和S n.【分析】(Ⅰ)由题意得a n+1=[(a n+1﹣a n)+(a n﹣a n﹣1)+…+(a2﹣a1)]+a1=3(22n﹣1+22n﹣3+…+2)+2=22(n+1)﹣1.由此可知数列{a n}的通项公式为a n=22n﹣1.(Ⅱ)由b n=na n=n•22n﹣1知S n=1•2+2•23+3•25++n•22n﹣1,由此入手可知答案.【解答】解:(Ⅰ)由已知,当n≥1时,a n+1=[(a n+1﹣a n)+(a n﹣a n)+…+(a2﹣a1)]+a1﹣1=3(22n﹣1+22n﹣3+…+2)+2=3×+2=22(n+1)﹣1.而a1=2,所以数列{a n}的通项公式为a n=22n﹣1.(Ⅱ)由b n=na n=n•22n﹣1知S n=1•2+2•23+3•25+…+n•22n﹣1①从而22S n=1•23+2•25+…+n•22n+1②①﹣②得(1﹣22)•S n=2+23+25+…+22n﹣1﹣n•22n+1.即.18.(12分)(2010•宁夏)如图,已知四棱锥P﹣ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点(1)证明:PE⊥BC(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.【分析】以H为原点,HA,HB,HP分别为x,y,z轴,线段HA的长为单位长,建立空间直角坐标系.(1)表示,,计算,就证明PE⊥BC.(2)∠APB=∠ADB=60°,求出C,P的坐标,再求平面PEH的法向量,求向量,然后求与面PEH的法向量的数量积,可求直线PA与平面PEH所成角的正弦值.【解答】解:以H为原点,HA,HB,HP分别为x,y,z轴,线段HA 的长为单位长,建立空间直角坐标系如图,则A(1,0,0),B(0,1,0)(Ⅰ)设C(m,0,0),P(0,0,n)(m<0,n>0)则.可得.因为所以PE⊥BC.(Ⅱ)由已知条件可得m=,n=1,故C(﹣),设=(x,y,z)为平面PEH的法向量则即因此可以取,由,可得所以直线PA与平面PEH所成角的正弦值为.19.(12分)(2010•新课标)为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如表:(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.附:【分析】(1)由列联表可知调查的500位老年人中有40+30=70位需要志愿者提供帮助,两个数据求比值得到该地区老年人中需要帮助的老年人的比例的估算值.(2)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,看出有多大把握说该地区的老年人是否需要帮助与性别有关.(3)从样本数据老年人中需要帮助的比例有明显差异,调查时,可以先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.【解答】解:(1)∵调查的500位老年人中有40+30=70位需要志愿者提供帮助,∴该地区老年人中需要帮助的老年人的比例的估算值为.(2)根据列联表所给的数据,代入随机变量的观测值公式,.∵9.967>6.635,∴有99%的把握认为该地区的老年人是否需要帮助与性别有关.(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.20.(12分)(2010•宁夏)设F1,F2分别是椭圆的左、右焦点,过F1斜率为1的直线ℓ与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.(1)求E的离心率;(2)设点P(0,﹣1)满足|PA|=|PB|,求E的方程.【分析】(I)根据椭圆的定义可知|AF2|+|BF2|+|AB|=4a,进而根据|AF2|,|AB|,|BF2|成等差数表示出|AB|,进而可知直线l的方程,设A(x1,y1),B(x2,y2),代入直线和椭圆方程,联立消去y,根据韦达定理表示出x1+x2和x1x2进而根据,求得a和b的关系,进而求得a和c的关系,离心率可得.(II)设AB的中点为N(x0,y0),根据(1)则可分别表示出x0和y0,根据|PA|=|PB|,推知直线PN的斜率,根据求得c,进而求得a和b,椭圆的方程可得.【解答】解:(I)由椭圆定义知|AF2|+|BF2|+|AB|=4a,又2|AB|=|AF2|+|BF2|,得,l的方程为y=x+c,其中.设A(x1,y1),B(x2,y2),则A、B两点坐标满足方程组化简的(a2+b2)x2+2a2cx+a2(c2﹣b2)=0则因为直线AB斜率为1,|AB|=|x 1﹣x2|=,得,故a2=2b2所以E的离心率(II)设AB的中点为N(x0,y0),由(I)知,.由|PA|=|PB|,得k PN=﹣1,即得c=3,从而故椭圆E的方程为.21.(12分)(2010•宁夏)设函数f(x)=e x﹣1﹣x﹣ax2.(1)若a=0,求f(x)的单调区间;(2)若当x≥0时f(x)≥0,求a的取值范围.【分析】(1)先对函数f(x)求导,导函数大于0时原函数单调递增,导函数小于0时原函数单调递减.(2)根据e x≥1+x可得不等式f′(x)≥x﹣2ax=(1﹣2a)x,从而可知当1﹣2a≥0,即时,f′(x)≥0判断出函数f(x)的单调性,得到答案.【解答】解:(1)a=0时,f(x)=e x﹣1﹣x,f′(x)=e x﹣1.当x∈(﹣∞,0)时,f'(x)<0;当x∈(0,+∞)时,f'(x)>0.故f(x)在(﹣∞,0)单调减少,在(0,+∞)单调增加(II)f′(x)=e x﹣1﹣2ax由(I)知e x≥1+x,当且仅当x=0时等号成立.故f′(x)≥x﹣2ax=(1﹣2a)x,从而当1﹣2a≥0,即时,f′(x)≥0(x≥0),而f(0)=0,于是当x≥0时,f(x)≥0.由e x>1+x(x≠0)可得e﹣x>1﹣x(x≠0).从而当时,f′(x)<e x﹣1+2a(e﹣x﹣1)=e﹣x(e x﹣1)(e x﹣2a),故当x∈(0,ln2a)时,f'(x)<0,而f(0)=0,于是当x∈(0,ln2a)时,f(x)<0.综合得a的取值范围为.22.(10分)(2010•新课标)如图:已知圆上的弧,过C点的圆的切线与BA的延长线交于E点,证明:(Ⅰ)∠ACE=∠BCD.(Ⅱ)BC2=BE•CD.【分析】(I)先根据题中条件:“”,得∠BCD=∠ABC.再根据EC 是圆的切线,得到∠ACE=∠ABC,从而即可得出结论.(II)欲证BC2=BE x CD.即证.故只须证明△BDC~△ECB即可.【解答】解:(Ⅰ)因为,所以∠BCD=∠ABC.又因为EC与圆相切于点C,故∠ACE=∠ABC所以∠ACE=∠BCD.(5分)(Ⅱ)因为∠ECB=∠CDB,∠EBC=∠BCD,所以△BDC~△ECB,故.即BC2=BE×CD.(10分)23.(10分)(2010•新课标)已知直线C1(t为参数),C2(θ为参数),(Ⅰ)当α=时,求C1与C2的交点坐标;(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.【分析】(I)先消去参数将曲线C1与C2的参数方程化成普通方程,再联立方程组求出交点坐标即可,(II)设P(x,y),利用中点坐标公式得P点轨迹的参数方程,消去参数即得普通方程,由普通方程即可看出其是什么类型的曲线.【解答】解:(Ⅰ)当α=时,C1的普通方程为,C2的普通方程为x2+y2=1.联立方程组,解得C1与C2的交点为(1,0).(Ⅱ)C1的普通方程为xsinα﹣ycosα﹣sinα=0①.则OA的方程为xcosα+ysinα=0②,联立①②可得x=sin2α,y=﹣cosαsinα;A点坐标为(sin2α,﹣cosαsinα),故当α变化时,P点轨迹的参数方程为:,P点轨迹的普通方程.故P点轨迹是圆心为,半径为的圆.24.(10分)(2010•新课标)设函数f(x)=|2x﹣4|+1.(Ⅰ)画出函数y=f(x)的图象:(Ⅱ)若不等式f(x)≤ax的解集非空,求a的取值范围.【分析】(I)先讨论x的范围,将函数f(x)写成分段函数,然后根据分段函数分段画出函数的图象即可;(II)根据函数y=f(x)与函数y=ax的图象可知先寻找满足f(x)≤ax的零界情况,从而求出a的范围.【解答】解:(Ⅰ)由于f(x)=,函数y=f(x)的图象如图所示.(Ⅱ)由函数y=f(x)与函数y=ax的图象可知,极小值在点(2,1)当且仅当a<﹣2或a≥时,函数y=f(x)与函数y=ax的图象有交点.故不等式f(x)≤ax的解集非空时,a的取值范围为(﹣∞,﹣2)∪[,+∞).。
历年高考理科数列真题汇编含答案解析

高考数列选择题部分(2016全国I )(3)已知等差数列{}n a 前9项的和为27,10=8a ,则100=a(A )100 (B )99 (C )98 (D )97(2016上海)已知无穷等比数列{}n a 的公比为q ,前n 项和为n S ,且S S n n =∞→lim .下列条件中,使得()*∈<N n S S n 2恒成立的是( )(A )7.06.0,01<<>q a (B )6.07.0,01-<<-<q a(C )8.07.0,01<<>q a (D )7.08.0,01-<<-<q a(2016四川)5. 【题设】某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30)( A )2018年 (B )2019年 (C )2020年 (D )2021年 (2016天津)(5)设{a n }是首项为正数的等比数列,公比为q ,则“q <0”是“对任意的正整数n ,a 2n −1+a 2n <0”的( )(A )充要条件 (B )充分而不必要条件 (C )必要而不充分条件 (D )既不充分也不必要条件(2016浙江)6. 如图,点列{A n },{B n }分别在某锐角的两边上,且1122,,n n n n n n A A A A A A n ++++=≠∈*N ,1122,,n n n n n n B B B B B B n ++++=≠∈*N ,(P Q P Q ≠表示点与不重合). 若1n n n n n n n d A B S A B B +=,为△的面积,则A .{}n S 是等差数列B .2{}n S 是等差数列C .{}n d 是等差数列D .2{}n d 是等差数列1.【2015高考重庆,理2】在等差数列{}n a 中,若2a =4,4a =2,则6a = ( )A 、-1B 、0C 、1D 、62.【2015高考福建,理8】若,a b 是函数()()20,0f x x px q p q =-+>> 的两个不同的零点,且,,2a b - 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q + 的值等于( ) A .6 B .7 C .8 D .93.【2015高考北京,理6】设{}n a 是等差数列. 下列结论中正确的是( )A .若120a a +>,则230a a +>B .若130a a +<,则120a a +<C .若120a a <<,则213a a a >D .若10a <,则()()21230a a a a -->4.【2015高考浙江,理3】已知{}n a 是等差数列,公差d 不为零,前n 项和是n S ,若3a ,4a ,8a 成等比数列,则( )A.140,0a d dS >>B. 140,0a d dS <<C. 140,0a d dS ><D.140,0a d dS <>1.【2014年重庆卷(理02)】对任意等比数列{}n a ,下列说法一定正确的是( )139.,,A a a a 成等比数列 236.,,B a a a 成等比数列 248.,,C a a a 成等比数列 369.,,D a a a 成等比数列2.【2014年全国大纲卷(10)】等比数列{}n a 中,452,5a a ==,则数列{lg }n a 的前8项和等于( )A .6B .5C .4D .35.【2014年福建卷(理03)】等差数列{a n }的前n 项和为S n ,若a 1=2,S 3=12,则a 6等于( )A .8B .10C .12D .14高考数列填空题部分(2016全国I )(15)设等比数列{}n a 满足a 1+a 3=10,a 2+a 4=5,则a 1a 2 …a n 的最大值为 .(2016上海)无穷数列{}n a 由k 个不同的数组成,n S 为{}n a 的前n 项和.若对任意*∈N n ,{}3,2∈n S ,则k 的最大值为________.(2016北京)12.已知{}n a 为等差数列,n S 为其前n 项和,若16a =,350a a +=,则6=S _______..(2016江苏)8. 已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是 ▲ .(2016浙江)13.设数列{a n }的前n 项和为S n .若S 2=4,a n +1=2S n +1,n ∈N *,则a 1= ,S 5= .5.【2015高考安徽,理14】已知数列{}n a 是递增的等比数列,14239,8a a a a +==,则数列{}n a 的前n 项和等于 .6.【2015高考新课标2,理16】设n S 是数列{}n a 的前n 项和,且11a =-,11n n n a S S ++=,则n S =________.7.【2015高考广东,理10】在等差数列{}n a 中,若2576543=++++a a a a a ,则82a a += .8.【2015高考陕西,理13】中位数1010的一组数构成等差数列,其末项为2015,则该数列的首项为 .9.【2015江苏高考,11】数列}{n a 满足11=a ,且11+=-+n a a n n (*N n ∈),则数列}1{na 的前10项和为3.【2014年广东卷(理13)】若等比数列{}n a 的各项均为正数,且512911102e a a a a =+,则1220ln ln ln a a a +++= 。
十年真题(2010-近年)高考数学真题分类汇编专题07数列理(含解析)(最新整理)

故选:C.
4.【2017 年新课标 1 理科 12】几位大学生响应国家的创业号召,开发了一款应用软件.为
激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码"的活动.这款软件的激活
码为下面数学问题的答案:已知数列 1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中
第一项是 20,接下来的两项是 20,21,再接下来的三项是 20,21,22,依此类推.求满足如下条件
9a5.
∴a100=a5+95d=98, 故选:C.
6.【2013 年新课标 1 理科 07】设等差数列{an}的前 n 项和为 Sn,若 Sm﹣1=﹣2,Sm=0,Sm+1=
3,则 m=(
)
A.3
B.4
C.5
D.6
【解答】解:am=Sm﹣Sm﹣1=2,am+1=Sm+1﹣Sm=3,
所以公差 d=am+1﹣am=1,
故选:D.
9.【2019 年新课标 1 理科 14】记 Sn 为等比数列{an}的前 n 项和.若 a1 ,a42=a6,则 S5 =. 【解答】解:在等比数列中,由 a42=a6,得 q6a12=q5a1>0, 即 q>0,q=3,
则 S5
,
故答案为:
10.【2018 年新课标 1 理科 14】记 Sn 为数列{an}的前 n 项和.若 Sn=2an+1,则 S6
m(a1+am)=0, (m+1)(a1+am+1)=3,
可得 a1=﹣am,﹣2am+am+1+am+1
0,
解得 m=5.
故选:C.
7.【2013 年新课标 1 理科 12】设△AnBn∁ n 的三边长分别为 an,bn,cn,△AnBn∁ n 的面积为 Sn,
2010-2018全国卷分类汇编(函数解答题)

2010-2018新课标全国卷分类汇编(函数解答题)(2018课标全国Ⅰ 21)(12分)已知函数()1ln f x x a x x=-+. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,证明:()()12122f x f x a x x -<--.解:(1)由已知,得2'2211()1(0)a x ax f x x x x x-+=--+=-> 令2()1(0)g x x ax x =-+>,24a ∆=-① 当0∆≤,即22a -≤≤时,()0g x ≥,则'()0f x ≤⇒函数()f x 在(0,)+∞上单调递增.② 当0∆>,即22a a <->或时,令1x =,2x =(i )当2a <-时,则120x x <<∴当0x >时,()0g x >,则'()0f x <⇒函数()f x 在(0,)+∞上单调递增. (ii )当2a >时,则210x x >>∴当120x x x x <<>或时,()0g x >,则'()0f x <,()f x 单调递减;当12x x x <<时,()0g x <,则'()0f x >,()f x 单调递增.综上所述,当2a ≤时,函数()f x 在(0,)+∞上单调递增;当2a >时,函数()f x在(0,2a,()2a +∞上单调递减,在(22a a +上单调递增.(2)法一:由(1)知,()f x 存在两个极值点当且仅当2a >()f x 的两个极值点1x ,2x 满足210x ax -+=∴121x x =,不妨设120x x <<,则21x >11221212121211ln (ln )()()x a x x a x f x f x x x x x x x -+--+-=-- 121212ln ln 11x x a x x x x -=--+- 1221222ln ln 2ln 22x x x aa x x x x --=-+=-+-- ∴1222122()()122ln 0f x f x a x x x x x -<-⇔-+<-令1()2ln (1)g x x x x x=-+>由(1)知,()g x 在(1,)+∞上单调递减()(1)0g x g ∴<=,即22212ln x x x -+<0∴原命题得证,即1212()()2f x f x a x x -<--.法二:由(1)知,()f x 存在两个极值点当且仅当2a >()f x 的两个极值点1x ,2x 满足210x ax -+=∴121x x =,不妨设120x x <<,则21x >11221212121211ln (ln )()()x a x x a x f x f x x x x x x x -+--+-=-- 121212ln ln 11x x a x x x x -=--+- 1212ln ln 2x x ax x -=-+-∴12221121()()2ln 0f x f x xa x x x x x -<-⇔-+<-令21(1)x t t x =>,则2111221x t x x x x x ⎧⎧==⎪⎪⇒⎨⎨⎪⎪==⎩⎩令()ln 1)g t t t =>则2'1()0t tt g t t -==< ()g t ∴在(1,)+∞上单调递减,则()(1)0g t g <=.∴原命题得证,即1212()()2f x f x a x x -<--.(2018课标全国Ⅱ理21)(12分)已知函数2()e x f x ax =-.(1)若1a =,证明:当0x ≥时,()1f x ≥; (2)若()f x 在(0,)+∞只有一个零点,求a .21.解:(1)当1a =时,()1f x ≥等价于2(1)e 10x x -+-≤.设函数2()(1)e 1x g x x -=+-,则22()(21)e (1)e x x g'x x x x --=--+=--. 当1x ≠时,()0g'x <,所以()g x 在(0,)+∞单调递减.而(0)0g =,故当0x ≥时,()0g x ≤,即()1f x ≥. (2)设函数2()1e x h x ax -=-.()f x 在(0,)+∞只有一个零点当且仅当()h x 在(0,)+∞只有一个零点. (i )当0a ≤时,()0h x >,()h x 没有零点;(ii )当0a >时,()(2)e x h'x ax x -=-.当(0,2)x ∈时,()0h'x <;当(2,)x ∈+∞时,()0h'x >.所以()h x 在(0,2)单调递减,在(2,)+∞单调递增.故24(2)1eah =-是()h x 在[0,)+∞的最小值. ①若(2)0h >,即2e4a <,()h x 在(0,)+∞没有零点;②若(2)0h =,即2e4a =,()h x 在(0,)+∞只有一个零点;③若(2)0h <,即2e4a >,由于(0)1h =,所以()h x 在(0,2)有一个零点,由(1)知,当0x >时,2e x x >,所以33342241616161(4)11110e (e )(2)a a a a a h a a a=-=->-=->. 故()h x 在(2,4)a 有一个零点,因此()h x 在(0,)+∞有两个零点.综上,()f x 在(0,)+∞只有一个零点时,2e4a =.(2018课标全国Ⅲ理21)(12分)已知函数()()()22ln 12f x x ax x x =+++-.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >时,()0f x >; (2)若0x =是()f x 的极大值点,求a .解:(1)当0a =时,()(2)ln(1)2f x x x x =++-,()ln(1)1xf x x x'=+-+. 设函数()()ln(1)1x g x f x x x '==+-+,则2()(1)x g x x '=+. 当10x -<<时,()0g x '<;当0x >时,()0g x '>.故当1x >-时,()(0)0g x g ≥=,且仅当0x =时,()0g x =,从而()0f x '≥,且仅当0x =时,()0f x '=.所以()f x 在(1,)-+∞单调递增.又(0)0f =,故当10x -<<时,()0f x <;当0x >时,()0f x >. (2)(i )若0a ≥,由(1)知,当0x >时,()(2)ln(1)20(0)f x x x x f ≥++->=,这与0x =是()f x 的极大值点矛盾.(ii )若0a <,设函数22()2()ln(1)22f x xh x x x ax x ax ==+-++++.由于当||min{x <时,220x ax ++>,故()h x 与()f x 符号相同.又(0)(0)0h f ==,故0=是()f x 的极大值点当且仅当0x =是()h x 的极大值点.2222222212(2)2(12)(461)()1(2)(1)(2)x ax x ax x a x ax a h x x x ax x ax x ++-++++'=-=++++++.如果610a +>,则当6104a x a +<<-,且||m in{1,x <时,()0h x '>,故0x =不是()h x 的极大值点.如果610a +<,则224610a x ax a +++=存在根10x <,故当1(,0)x x ∈,且||min{x <时,()0h x '<,所以0x =不是()h x 的极大值点. 如果610a +=,则322(24)()(1)(612)x x h x x x x -'=+--.则当(1,0)x ∈-时,()0h x '>;当(0,1)x ∈时,()0h x '<.所以0x =是()h x 的极大值点,从而0x =是()f x 的极大值点综上,16a =-.(2017课标全国Ⅰ21)(12分)已知函数()()2e 2e x xf x a a x =+--.(1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围.【解析】(1)由于()()2e 2e x xf x a a x =+--故()()()()22e 2e 1e 12e 1x x x xf x a a a '=+--=-+①当0a ≤时,e 10x a -<,2e 10x +>.从而()0f x '<恒成立. ()f x 在R 上单调递减②当0a >时,令()0f x '=,从而e 10x a -=,得ln x a =-.当0a >时,()f x 在(,ln )a -∞-上单调递减,在(ln ,)a -+∞上单调递增(2)由(1)知,当0a ≤时,()f x 在R 上单调减,故()f x 在R 上至多一个零点,不满足条件. 当0a >时,()min 1ln 1ln f f a a a=-=-+. 令()11ln g a a a =-+. 令()()11ln 0g a a a a =-+>,则()211'0g a a a=+>.从而()g a 在()0+∞,上单调增,而()10g =.故当01a <<时,()0g a <.当1a =时()0g a =.当1a >时()0g a >若1a >,则()min 11ln 0f a g a a=-+=>,故()0f x >恒成立,从而()f x 无零点,不满足条件. 若1a =,则min 11ln 0f a a=-+=,故()0f x =仅有一个实根ln 0x a =-=,不满足条件.若01a <<,则m i n 11l n 0f a a =-+<,注意到ln 0a ->.()22110e e ea a f -=++->. 故()f x 在()1ln a --,上有一个实根,而又31ln 1ln ln a a a ⎛⎫->=- ⎪⎝⎭.且33ln 1ln 133ln(1)e e 2ln 1a a f a a a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫-=⋅+--- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭()3333132ln 11ln 10a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫=-⋅-+---=---> ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 故()f x 在3ln ln 1a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,上有一个实根. 又()f x 在()ln a -∞-,上单调减,在()ln a -+∞,单调增,故()f x 在R 上至多两个实根.又()f x 在()1ln a --,及3ln ln 1a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,上均至少有一个实数根,故()f x 在R 上恰有两个实根.综上,01a <<.(2017课标全国Ⅱ理21)(12分)已知函数2()ln f ax a x x x x =--,且()0f x ≥. (1)求a ;(2)证明:()f x 存在唯一的极大值点0x ,且220e ()2f x --<<. 【答案】(1)1a =;(2)证明见解析.(2)由(1)知 ()2ln f x x x x x =--,()22ln f 'x x x =--.设()22ln h x x x =--,则1()2'x h x=-.当1(0,)2x ∈ 时,()0h'x < ;当1(,)2x ∈+∞ 时,()0h'x >, 所以()h x 在1(0,)2上单调递减,在1(,)2+∞上单调递增.又()2e0h ->,1()02h <,()10h =,所以()h x 在1(0,)2有唯一零点0x ,在1[,)2+∞有唯一零点1,且当()00,x x ∈时,()0h x >;当()0,1x x ∈时,()0h x <,当()1,x ∈+∞时,()0h x >. 因为()()f 'x h x =,所以0x x =是()f x 的唯一极大值点. 由0()0f 'x =得()00ln 21x x =-,故()()0001f x x x =-. 由()00,1x ∈得()014f x <. 因为0x x =是()f x 在(0,1)的最大值点, 由()1e 0,1-∈,1(e )0f '-≠得120()(e )e f x f -->=.所以()220e2f x --<<.【考点】利用导数研究函数的单调性、利用导数研究函数的极值【名师点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出.导数专题在高考中的命题方向及命题角度:从高考来看,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系;(2)利用导数求函数的单调区间,判断单调性;已知单调性求参数;(3)利用导数求函数的最值(极值),解决生活中的优化问题;(4)考查数形结合思想的应用.(2017课标全国Ⅲ理21)(12分)已知函数()1ln f x x a x =--.(1)若()0f x ≥,求a 的值;(2)设m 为整数,且对于任意正整数n ,2111(1)(1)(1)222nm ++鬃?<,求m 的最小值.【解析】⑴ ()1ln f x x a x =--,0x >则()1a x af x x x-'=-=,且(1)0f = 当0a ≤时,()0f x '>,()f x 在()0+∞,上单调增,所以01x <<时,()0f x <,不满足题意; 当0a >时,当0x a <<时,()0f x '<,则()f x 在(0,)a 上单调递减; 当x a >时,()0f x '>,则()f x 在(,)a +∞上单调递增.①若1a <,()f x 在(,1)a 上单调递增∴当(,1)x a ∈时()(1)0f x f <=矛盾 ②若1a >,()f x 在(1,)a 上单调递减∴当(1,)x a ∈时()(1)0f x f <=矛盾 ③若1a =,()f x 在(0,1)上单调递减,在(1,)+∞上单调递增∴()(1)0f x f =≥满足题意综上所述1a =.⑵ 当1a =时()1ln 0f x x x =--≥即ln 1x x -≤则有ln(1)x x +≤当且仅当0x =时等号成立∴11ln(1)22k k +<,*k ∈N一方面:221111111ln(1)ln(1)...ln(1) (112222222)n n n ++++++<+++=-<,即2111(1)(1)...(1)e 222n +++<.另一方面:223111111135(1)(1)...(1)(1)(1)(1)222222264n +++>+++=>当3n ≥时,2111(1)(1)...(1)(2,e)222n +++∈∵*m ∈N ,2111(1)(1)...(1)222n m +++<,∴m 的最小值为3.(2016课标全国Ⅰ,理21)(本小题满分12分) 已知函数2)1()2()(-+-=x a e x x f x 有两个零点. (Ⅰ)求a 的取值范围;(Ⅱ)设21,x x 是)(x f 的两个零点,证明:221<+x x .【解析】:⑴ 由已知得:()()()()()'12112x x f x x e a x x e a =-+-=-+① 若0a =,那么()()0202x f x x e x =⇔-=⇔=,()f x 只有唯一的零点2x =,不合题意;② 若0a >,那么20x x e a e +>>,所以当1x >时,()'0f x >,()f x 单调递增;当1x <时,()'0f x <,()f x 单调递减; 即:由于()20f a =>,()10f e =-<,则()()210f f <, 根据零点存在性定理,()f x 在()1,2上有且仅有一个零点. 而当1x <时,x e e <,210x -<-<,故()()()()()()()222212111x f x x e a x e x a x a x e x e =-+->-+-=-+--则()0f x =的两根11t =,21t =, 12t t <,因为0a >,故当1x t <或2x t >时,()()2110a x e x e -+-->因此,当1x <且1x t <时,()0f x >又()10f e =-<,根据零点存在性定理,()f x 在(),1-∞有且只有一个零点. 此时,()f x 在R 上有且只有两个零点,满足题意.③ 若02ea -<<,则()ln 2ln 1a e -<=,当()ln 2x a <-时,()1ln 210x a -<--<,()ln 2220a x e a e a -+<+=,即()()()'120x f x x e a =-+>,()f x 单调递增; 当()ln 21a x -<<时,10x -<,()ln 2220a x e a ea -+>+=,即()()()'120x f xx ea =-+<,()f x 单调递减; 当1x >时,10x ->,()ln 2220a x e a e a -+>+=,即()'0f x >,()f x 单调递增.即:()()()(){}22ln 22ln 22ln 21ln 2210f a a a a a a a -=---+--=--+<⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦故当1x ≤时,()f x 在()ln 2x a =-处取到最大值()l n 2f a -⎡⎤⎣⎦,那么()()l n 20fx f a -<⎡⎤⎣⎦≤恒成立,即()0f x =无解 而当1x >时,()f x 单调递增,至多一个零点 此时()f x 在R 上至多一个零点,不合题意.④ 若2ea =-,那么()ln 21a -=当()1ln 2x a <=-时,10x -<,()ln 2220a x e a e a -+<+=,即()'0f x >,()f x 单调递增当()1ln 2x a >=-时,10x ->,()ln 2220a x e a e a -+>+=,即()'0f x >,()f x 单调递增又()f x 在1x =处有意义,故()f x 在R 上单调递增,此时至多一个零点,不合题意.⑤ 若2ea <-,则()ln 21a ->当1x <时,10x -<,()ln 212220a x e a e a e a -+<+<+=,即()'0f x >,()f x 单调递增当()1ln 2x a <<-时,10x ->,()ln 2220a x e a ea -+<+=,即()'0f x <,()f x 单调递减当()ln 2x a >-时,()1ln 210x a ->-->,()ln 2220a x e a ea -+>+=,即()'0f x >,()f x 单调递增即:0<恒成立,即()0f x =无解当()ln 2x a >-时,()f x 单调递增,至多一个零点,此时()f x 在R 上至多一个零点,不合题意.综上所述,当且仅当0a >时符合题意,即a 的取值范围为()0,+∞. ⑵ 由已知得:()()120f x f x ==,不难发现11x ≠,21x ≠,故可整理得:()()()()121222122211x x x e x e a x x ---==--,()()()221xx e g x x -=-,则()()12g x g x = ()()()2321'1x x g x e x -+=-,当1x <时,()'0g x <,()g x 单调递减;当1x >时,()'0g x >,()g x 单调递增.设0m >,构造代数式: ()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设()2111m m h m e m -=++,0m >,则()()2222'01m m h m e m =>+,故()h m 单调递增,有()()00h m h >=.因此,对于任意的0m >,()()11g m g m +>-.由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上,不妨设12x x <,则必有121x x <<令110m x =->,则有()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦而121x ->,21x >,()g x 在()1,+∞上单调递增,因此:()()121222g x g x x x ->⇔-> 整理得:122x x +<.(2016课标全国Ⅱ,理21)(本小题满分12分)(Ⅰ)讨论函数xx 2f (x)x 2-=+e 的单调性,并证明当0x >时,(2)20xx e x -++>;(Ⅱ)证明:当[0,1)a ∈时,函数2x =(0)x e ax ag x x-->()有最小值.设()g x 的最小值为()h a ,求函数()h a 的值域. 【解析】试题分析:(Ⅰ)先求定义域,用导数法求函数的单调性,当时,证明结论;(Ⅱ)用导数法求函数的最值,在构造新函数,又用导数法求解.试题解析:(Ⅰ)的定义域为.且仅当时,,所以在单调递增,因此当时,所以(II )由(I )知,单调递增,对任意因此,存在唯一使得即,当时,单调递减; 当时,单调递增.因此在处取得最小值,最小值为于是,由单调递增所以,由得因为单调递增,对任意存在唯一的使得所以的值域是综上,当时,有,的值域是考点: 函数的单调性、极值与最值.(2016课标全国Ⅲ,理21)(本小题满分12分)设函数()cos 2(1)(cos 1)f x a x a x =+-+,其中0a >,记|()|f x 错误!未找到引用源。
[2014-2018]北京高考数学真题分类汇编 专题六 数列
![[2014-2018]北京高考数学真题分类汇编 专题六 数列](https://img.taocdn.com/s3/m/1cfe49725a8102d276a22fdc.png)
专题六 数列1.(2018.9)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为 . 2.(2017.10)若等差数列{a n }和等比数列{b n }满足a 1=b 1=﹣1,a 4=b 4=8,则a 2b 2= .3.(2017.20)设{a n }和{b n }是两个等差数列,记c n =max {b 1﹣a 1n ,b 2﹣a 2n ,…,b n ﹣a n n }(n =1,2,3,…),其中max {x 1,x 2,…,x s }表示x 1,x 2,…,x s 这s 个数中最大的数. (1)若a n =n ,b n =2n ﹣1,求c 1,c 2,c 3的值,并证明{c n }是等差数列; (2)证明:或者对任意正数M ,存在正整数m ,当n ≥m 时,c n n>M ;或者存在正整数m ,使得c m ,c m +1,c m +2,…是等差数列.4.(2016.12)已知{a n }为等差数列,S n 为其前n 项和.若a 1=6,a 3+a 5=0,则S 6= .5.(2016.20)设数列A :a 1,a 2,…,a N (N ≥2).如果对小于n (2≤n ≤N )的每个正整数k 都有a k <a n ,则称n 是数列A 的一个“G 时刻”,记G (A )是数列A 的所有“G 时刻”组成的集合.(Ⅰ)对数列A :﹣2,2,﹣1,1,3,写出G (A )的所有元素; (Ⅱ)证明:若数列A 中存在a n 使得a n >a 1,则G (A )≠∅;(Ⅲ)证明:若数列A 满足a n ﹣a n ﹣1≤1(n =2,3,…,N ),则G (A )的元素个数不小于a N ﹣a 1.6. (2015.6)设{a n }是等差数列,下列结论中正确的是( ) A .若a 1+a 2>0,则a 2+a 3>0 B .若a 1+a 3<0,则a 1+a 2<0C .若0<a 1<a 2,则a 2>√a 1a 3D .若a 1<0,则(a 2﹣a 1)(a 2﹣a 3)>07.(2015.20)已知数列{a n }满足:a 1∈N *,a 1≤36,且a n +1={2a n ,a n ≤182a n −36,a n >18(n =1,2,…),记集合M ={a n |n ∈N *}.(Ⅰ)若a 1=6,写出集合M 的所有元素;(Ⅱ)如集合M 存在一个元素是3的倍数,证明:M 的所有元素都是3的倍数; (Ⅲ)求集合M 的元素个数的最大值.8. (2014.5)设{a n }是公比为q 的等比数列,则“q >1”是“{a n }为递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.(2014.12)若等差数列{a n }满足a 7+a 8+a 9>0,a 7+a 10<0,则当n = 时,{a n }的前n 项和最大.专题六 数列 答案部分1.解:∵{a n }是等差数列,且a 1=3,a 2+a 5=36, ∴{a 1=3a 1+d +a 1+4d =36, 解得a 1=3,d =6,∴a n =a 1+(n ﹣1)d =3+(n ﹣1)×6=6n ﹣3. ∴{a n }的通项公式为a n =6n ﹣3. 故答案为:a n =6n ﹣3.2. 解:等差数列{a n }和等比数列{b n }满足a 1=b 1=﹣1,a 4=b 4=8, 设等差数列的公差为d ,等比数列的公比为q . 可得:8=﹣1+3d ,d =3,a 2=2; 8=﹣q 3,解得q =﹣2,∴b 2=2. 可得a 2b 2=1.故答案为:1.3. 解:(1)a 1=1,a 2=2,a 3=3,b 1=1,b 2=3,b 3=5, 当n =1时,c 1=max {b 1﹣a 1}=max {0}=0,当n =2时,c 2=max {b 1﹣2a 1,b 2﹣2a 2}=max {﹣1,﹣1}=﹣1,当n =3时,c 3=max {b 1﹣3a 1,b 2﹣3a 2,b 3﹣3a 3}=max {﹣2,﹣3,﹣4}=﹣2,下面证明:对∀n∈N*,且n≥2,都有c n=b1﹣na1,当n∈N*,且2≤k≤n时,则(b k﹣na k)﹣(b1﹣na1),=[(2k﹣1)﹣nk]﹣1+n,=(2k﹣2)﹣n(k﹣1),=(k﹣1)(2﹣n),由k﹣1>0,且2﹣n≤0,则(b k﹣na k)﹣(b1﹣na1)≤0,则b1﹣na1≥b k﹣na k,因此,对∀n∈N*,且n≥2,c n=b1﹣na1=1﹣n,c n+1﹣c n=﹣1,∴c2﹣c1=﹣1,∴c n+1﹣c n=﹣1对∀n∈N*均成立,∴数列{c n}是等差数列;(2)证明:设数列{a n}和{b n}的公差分别为d1,d2,下面考虑的c n取值,由b1﹣a1n,b2﹣a2n,…,b n﹣a n n,考虑其中任意b i﹣a i n,(i∈N*,且1≤i≤n),则b i﹣a i n=[b1+(i﹣1)d1]﹣[a1+(i﹣1)d2]×n,=(b1﹣a1n)+(i﹣1)(d2﹣d1×n),下面分d1=0,d1>0,d1<0三种情况进行讨论,①若d1=0,则b i﹣a i n═(b1﹣a1n)+(i﹣1)d2,当若d2≤0,则(b i﹣a i n)﹣(b1﹣a1n)=(i﹣1)d2≤0,则对于给定的正整数n而言,c n=b1﹣a1n,此时c n+1﹣c n=﹣a1,∴数列{c n}是等差数列;当d2>0,(b i﹣a i n)﹣(b n﹣a n n)=(i﹣n)d2>0,则对于给定的正整数n而言,c n=b n﹣a n n=b n﹣a1n,此时c n+1﹣c n=d2﹣a1,∴数列{c n}是等差数列;此时取m=1,则c1,c2,…,是等差数列,命题成立;②若d1>0,则此时﹣d1n+d2为一个关于n的一次项系数为负数的一次函数,故必存在m∈N*,使得n≥m时,﹣d1n+d2<0,则当n≥m时,(b i﹣a i n)﹣(b1﹣a1n)=(i﹣1)(﹣d1n+d2)≤0,(i∈N*,1≤i≤n),因此当n ≥m 时,c n =b 1﹣a 1n ,此时c n +1﹣c n =﹣a 1,故数列{c n }从第m 项开始为等差数列,命题成立; ③若d 1<0,此时﹣d 1n +d 2为一个关于n 的一次项系数为正数的一次函数, 故必存在s ∈N *,使得n ≥s 时,﹣d 1n +d 2>0,则当n ≥s 时,(b i ﹣a i n )﹣(b n ﹣a n n )=(i ﹣1)(﹣d 1n +d 2)≤0,(i ∈N *,1≤i ≤n ), 因此,当n ≥s 时,c n =b n ﹣a n n , 此时=b n −a n n n =−a n +bn n, =﹣d 2n +(d 1﹣a 1+d 2)+b 1−d 2n, 令﹣d 1=A >0,d 1﹣a 1+d 2=B ,b 1﹣d 2=C , 下面证明:c n n=An +B +Cn 对任意正整数M ,存在正整数m ,使得n ≥m ,c n n>M ,若C ≥0,取m =[|M−B|A+1],[x ]表示不大于x 的最大整数,当n ≥m 时,c n n≥An +B ≥Am +B =A [|M−B|A+1]+B >A •M−B A+B =M ,此时命题成立; 若C <0,取m =[|M−C−B|A]+1,当n ≥m 时,c n n≥An +B +Cn ≥Am +B +C >A •|M−C−B|A+B +C ≥M ﹣C ﹣B +B +C =M ,此时命题成立,因此对任意正数M ,存在正整数m ,使得当n ≥m 时,c n n>M ;综合以上三种情况,命题得证.4. 解:∵{a n }为等差数列,S n 为其前n 项和. a 1=6,a 3+a 5=0, ∴a 1+2d +a 1+4d =0, ∴12+6d =0, 解得d =﹣2,∴S 6=6a 1+6×52d =36﹣30=6. 故答案为:6.5. 解:(Ⅰ)根据题干可得,a 1=﹣2,a 2=2,a 3=﹣1,a 4=1,a 5=3,a 1<a 2满足条件,2满足条件,a 2>a 3不满足条件,3不满足条件,a 2>a 4不满足条件,4不满足条件,a 1,a 2,a 3,a 4,均小于a 5,因此5满足条件,因此G (A )={2,5}.(Ⅱ)因为存在a n >a 1,设数列A 中第一个大于a 1的项为a k ,则a k >a 1≥a i ,其中2≤i ≤k ﹣1,所以k ∈G (A ),G (A )≠∅;(Ⅲ)设A 数列的所有“G 时刻”为i 1<i 2<…<i k ,对于第一个“G 时刻”i 1,有a i 1>a 1≥a i (i =2,3,…,i 1﹣1),则 a i 1−a 1≤a i 1−a i 1−1≤1.对于第二个“G 时刻”i 1,有a i 2>a i 1≥a i (i =2,3,…,i 1﹣1),则 a i 2−a i 1≤a i 2−a i 2−1≤1.类似的a i 3−a i 2≤1,…,a i k −a i k−1≤1.于是,k ≥(a i k −a i k−1)+(a i k−1−a i k−2)+…+(a i 2−a i 1)+(a i 1−a 1)=a i k −a 1. 对于a N ,若N ∈G (A ),则a i k =a N .若N ∉G (A ),则a N ≤a i k ,否则由(2)知a i k ,a i k+1,…,a N ,中存在“G 时刻”与只有k 个“G 时刻”矛盾. 从而k ≥a i k −a 1≥a N ﹣a 1.6. 解:若a 1+a 2>0,则2a 1+d >0,a 2+a 3=2a 1+3d >2d ,d >0时,结论成立,即A 不正确; 若a 1+a 3<0,则a 1+a 2=2a 1+d <0,a 2+a 3=2a 1+3d <2d ,d <0时,结论成立,即B 不正确; {a n }是等差数列,0<a 1<a 2,2a 2=a 1+a 3>2√a 1a 3,∴a 2>√a 1a 3,即C 正确; 若a 1<0,则(a 2﹣a 1)(a 2﹣a 3)=﹣d 2≤0,即D 不正确. 故选:C .7. 解:(Ⅰ)若a 1=6,由于a n +1={2a n ,a n ≤182a n −36,a n >18(n =1,2,…),M ={a n |n ∈N *}.故集合M 的所有元素为6,12,24;(Ⅱ)因为集合M 存在一个元素是3的倍数,所以不妨设a k 是3的倍数,由a n +1={2a n ,a n ≤182a n −36,a n >18(n =1,2,…),可归纳证明对任意n ≥k ,a n 是3的倍数. 如果k =1,M 的所有元素都是3的倍数;如果k >1,因为a k =2a k ﹣1,或a k =2a k ﹣1﹣36,所以2a k ﹣1是3的倍数;于是a k ﹣1是3的倍数;类似可得,a k ﹣2,…,a 1都是3的倍数; 从而对任意n ≥1,a n 是3的倍数;综上,若集合M 存在一个元素是3的倍数,则集合M 的所有元素都是3的倍数 (Ⅲ)对a 1≤36,a n ={2a n−1,a n ≤182a n−1−36,a n >18(n =1,2,…),可归纳证明对任意n ≥k ,a n <36(n =2,3,…)因为a 1是正整数,a 2={2a 1,a 1≤182a 1−36,a 1>18,所以a 2是2的倍数.从而当n ≥2时,a n 是2的倍数.如果a 1是3的倍数,由(Ⅱ)知,对所有正整数n ,a n 是3的倍数. 因此当n ≥3时,a n ∈{12,24,36},这时M 的元素个数不超过5. 如果a 1不是3的倍数,由(Ⅱ)知,对所有正整数n ,a n 不是3的倍数. 因此当n ≥3时,a n ∈{4,8,16,20,28,32},这时M 的元素个数不超过8. 当a 1=1时,M ={1,2,4,8,16,20,28,32},有8个元素. 综上可知,集合M 的元素个数的最大值为8.5.解:等比数列﹣1,﹣2,﹣4,…,满足公比q =2>1,但{a n }不是递增数列,充分性不成立.若a n =﹣1⋅(12)n−1为递增数列,但q =12>1不成立,即必要性不成立, 故“q >1”是“{a n }为递增数列”的既不充分也不必要条件, 故选:D .6. 解:由等差数列的性质可得a 7+a 8+a 9=3a 8>0, ∴a 8>0,又a 7+a 10=a 8+a 9<0,∴a 9<0,∴等差数列{a n}的前8项为正数,从第9项开始为负数,∴等差数列{a n}的前8项和最大,故答案为:8.。
【理科数学2010-2018高考真题分类】专题六数列第十六讲等比数列答案

≤ a1 a2 a3 1 ,所以 a4 ≤ 1 ,又 a1 1 ,所以等比数列的公比 q 0 . 若 q ≤ 1,则 a1 a2 a3 a4 a1 (1 q)(1 q 2)≤ 0 ,
而 a1 a2 a3 ≥ a1 1 ,所以 ln( a1 a2 a3 ) 0 ,
与 ln( a1 a2 a3) a1 a2 a3 a4 ≤ 0 矛盾,
一线名师凭借教学实践科学分类,高质量的解析,你能感受到名家不一样的解题思路
列,∴ S7
a1 (1 27) 12
(27 1)a1
381 ,解得 a1
3 .选 B .
4. B 【解析】由于
2
4
a1(1+ q + q ) = 21 , a1 = 3 ,所以
q4 + q2 -
6 = 0 ,所以
q2
=2
( q 2 = - 3 舍去 ),所以 a3 = 6 , a5 = 12 , a7 = 24 ,所以 a3 + a5 + a7 = 42 .
1 ,由 S6 S3
1 q6 1 q3
1 q3
9 ,所以 q
2,
由 S3
a1 (1 q3 ) 1q
7 ,得 a1
4
1
,所以
4
a8
a1 q7
1 27 4
25
32 .
17. 1【解析】设 an 的公差为 d , bn 的公比为 q ,由题意 1 3d q3 8 ,
所以 d 3, q
2 ,所以 a2 b2
所以 1 q
0 ,所以 a1 a3
2
a1(1 q )
0 , a2 a4
2
a1q(1 q )
十年真题(2010_2019)高考数学真题分类汇编专题07数列(文)(含解析)
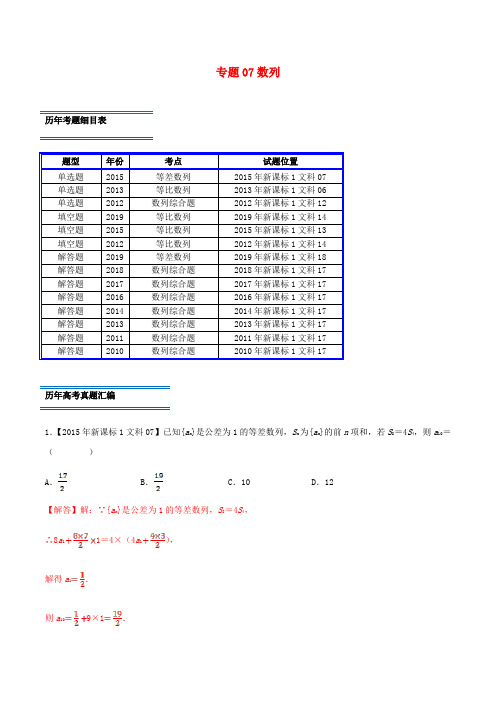
专题07数列历年考题细目表题型年份考点试题位置单选题2015 等差数列2015年新课标1文科07单选题2013 等比数列2013年新课标1文科06单选题2012 数列综合题2012年新课标1文科12填空题2019 等比数列2019年新课标1文科14填空题2015 等比数列2015年新课标1文科13填空题2012 等比数列2012年新课标1文科14解答题2019 等差数列2019年新课标1文科18解答题2018 数列综合题2018年新课标1文科17解答题2017 数列综合题2017年新课标1文科17解答题2016 数列综合题2016年新课标1文科17解答题2014 数列综合题2014年新课标1文科17解答题2013 数列综合题2013年新课标1文科17解答题2011 数列综合题2011年新课标1文科17解答题2010 数列综合题2010年新课标1文科17历年高考真题汇编1.【2015年新课标1文科07】已知{a n}是公差为1的等差数列,S n为{a n}的前n项和,若S8=4S4,则a10=()A.B.C.10 D.12【解答】解:∵{a n}是公差为1的等差数列,S8=4S4,∴8a11=4×(4a1),解得a1.则a109×1.故选:B.2.【2013年新课标1文科06】设首项为1,公比为的等比数列{a n}的前n项和为S n,则()A.S n=2a n﹣1 B.S n=3a n﹣2 C.S n=4﹣3a n D.S n=3﹣2a n【解答】解:由题意可得a n=1,∴S n33﹣23﹣2a n,故选:D.3.【2012年新课标1文科12】数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,则{a n}的前60项和为()A.3690 B.3660 C.1845 D.1830【解答】解:由于数列{a n}满足a n+1+(﹣1)n a n=2n﹣1,故有a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97.从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a11+a9=2,a12+a10=40,a15+a13=2,a16+a14=56,…从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.{a n}的前60项和为 15×2+(15×8)=1830,故选:D.4.【2019年新课标1文科14】记S n为等比数列{a n}的前n项和.若a1=1,S3,则S4=.【解答】解:∵等比数列{a n}的前n项和,a1=1,S3,∴q≠1,,整理可得,,解可得,q,则S4.故答案为:【2015年新课标1文科13】在数列{a n}中,a1=2,a n+1=2a n,S n为{a n}的前n项和,若S n=126,则n=.5.【解答】解:∵a n+1=2a n,∴,∵a1=2,∴数列{a n}是a1=2为首项,以2为公比的等比数列,∴S n2n+1﹣2=126,∴2n+1=128,∴n+1=7,∴n=6.故答案为:66.【2012年新课标1文科14】等比数列{a n}的前n项和为S n,若S3+3S2=0,则公比q=.【解答】解:由题意可得,q≠1∵S3+3S2=0∴∴q3+3q2﹣4=0∴(q﹣1)(q+2)2=0∵q≠1∴q=﹣2故答案为:﹣27.【2019年新课标1文科18】记S n为等差数列{a n}的前n项和.已知S9=﹣a5.(1)若a3=4,求{a n}的通项公式;(2)若a1>0,求使得S n≥a n的n的取值范围.【解答】解:(1)根据题意,等差数列{a n}中,设其公差为d,若S9=﹣a5,则S99a5=﹣a5,变形可得a5=0,即a1+4d=0,若a3=4,则d2,则a n=a3+(n﹣3)d=﹣2n+10,(2)若S n≥a n,则na1d≥a1+(n﹣1)d,当n=1时,不等式成立,当n≥2时,有d﹣a1,变形可得(n﹣2)d≥﹣a1,又由S9=﹣a5,即S99a5=﹣a5,则有a5=0,即a1+4d=0,则有(n﹣2)a1,又由a1>0,则有n≤10,则有2≤n≤10,综合可得:n的取值范围是{n|1≤n≤10,n∈N}.8.【2018年新课标1文科17】已知数列{a n}满足a1=1,na n+1=2(n+1)a n,设b n.(1)求b1,b2,b3;(2)判断数列{b n}是否为等比数列,并说明理由;(3)求{a n}的通项公式.【解答】解:(1)数列{a n}满足a1=1,na n+1=2(n+1)a n,则:(常数),由于,故:,数列{b n}是以b1为首项,2为公比的等比数列.整理得:,所以:b1=1,b2=2,b3=4.(2)数列{b n}是为等比数列,由于(常数);(3)由(1)得:,根据,所以:.9.【2017年新课标1文科17】记S n为等比数列{a n}的前n项和.已知S2=2,S3=﹣6.(1)求{a n}的通项公式;(2)求S n,并判断S n+1,S n,S n+2是否成等差数列.【解答】解:(1)设等比数列{a n}首项为a1,公比为q,则a3=S3﹣S2=﹣6﹣2=﹣8,则a1,a2,由a1+a2=2,2,整理得:q2+4q+4=0,解得:q=﹣2,则a1=﹣2,a n=(﹣2)(﹣2)n﹣1=(﹣2)n,∴{a n}的通项公式a n=(﹣2)n;(2)由(1)可知:S n [2+(﹣2)n+1],则S n+1[2+(﹣2)n+2],S n+2[2+(﹣2)n+3],由S n+1+S n+2[2+(﹣2)n+2][2+(﹣2)n+3],[4+(﹣2)×(﹣2)n+1+(﹣2)2×(﹣2)n+1],[4+2(﹣2)n+1]=2×[(2+(﹣2)n+1)],=2S n,即S n+1+S n+2=2S n,∴S n+1,S n,S n+2成等差数列.10.【2016年新课标1文科17】已知{a n}是公差为3的等差数列,数列{b n}满足b1=1,b2,a n b n+1+b n+1=nb n.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{b n}的前n项和.【解答】解:(Ⅰ)∵a n b n+1+b n+1=nb n.当n=1时,a1b2+b2=b1.∵b1=1,b2,∴a1=2,又∵{a n}是公差为3的等差数列,∴a n=3n﹣1,(Ⅱ)由(I)知:(3n﹣1)b n+1+b n+1=nb n.即3b n+1=b n.即数列{b n}是以1为首项,以为公比的等比数列,∴{b n}的前n项和S n(1﹣3﹣n).11.【2014年新课标1文科17】已知{a n}是递增的等差数列,a2,a4是方程x2﹣5x+6=0的根.(1)求{a n}的通项公式;(2)求数列{}的前n项和.【解答】解:(1)方程x2﹣5x+6=0的根为2,3.又{a n}是递增的等差数列,故a2=2,a4=3,可得2d=1,d,故a n=2+(n﹣2)n+1,(2)设数列{}的前n项和为S n,S n,①S n,②①﹣②得S n,解得S n2.12.【2013年新课标1文科17】已知等差数列{a n}的前n项和S n满足S3=0,S5=﹣5.(Ⅰ)求{a n}的通项公式;(Ⅱ)求数列{}的前n项和.【解答】解:(Ⅰ)设数列{a n}的首项为a1,公差为d,则.由已知可得,即,解得a1=1,d=﹣1,故{a n}的通项公式为a n=a1+(n﹣1)d=1+(n﹣1)•(﹣1)=2﹣n;(Ⅱ)由(Ⅰ)知.从而数列{}的前n项和S n.13.【2011年新课标1文科17】已知等比数列{a n}中,a1,公比q.(Ⅰ)S n为{a n}的前n项和,证明:S n(Ⅱ)设b n=log3a1+log3a2+…+log3a n,求数列{b n}的通项公式.【解答】证明:(I)∵数列{a n}为等比数列,a1,q∴a n,S n又∵S n∴S n(II)∵a n∴b n=log3a1+log3a2+…+log3a n=﹣log33+(﹣2log33)+…+(﹣n log33)=﹣(1+2+…+n)∴数列{b n}的通项公式为:b n14.【2010年新课标1文科17】设等差数列{a n}满足a3=5,a10=﹣9.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{a n}的前n项和S n及使得S n最大的序号n的值.【解答】解:(1)由a n=a1+(n﹣1)d及a3=5,a10=﹣9得a1+9d=﹣9,a1+2d=5解得d=﹣2,a1=9,数列{a n}的通项公式为a n=11﹣2n(2)由(1)知S n =na 1d =10n ﹣n 2.因为S n =﹣(n ﹣5)2+25. 所以n =5时,S n 取得最大值.考题分析与复习建议本专题考查的知识点为:数列的概念与简单表示法,等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为:等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.预测明年本考点题目会比较稳定,备考方向以知识点等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项为重点较佳.最新高考模拟试题1.等差数列{}n a ,等比数列{}n b ,满足111a b ==,53a b =,则9a 能取到的最小整数是( ) A .1- B .0C .2D .3【答案】B 【解析】等差数列{}n a 的公差设为d ,等比数列{}n b 的公比设为q ,0q ≠,由111a b ==,53a b =,可得214d q +=,则,可得9a 能取到的最小整数是0. 故选:B .2.中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?A .253B .503C .507D .1007【答案】D 【解析】因为5斗=50升,设羊、马、牛的主人应偿还的量分别为123,,a a a , 由题意可知其构成了公比为2的等比数列,且350S =则,解得1507a =, 所以马主人要偿还的量为:,故选D.3.我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入33⨯的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数21,2,3,,n L 填入n n ⨯个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ,如图三阶幻方的315N =,那么 9N 的值为( )A .41B .45C .369D .321【答案】C 【解析】根据题意可知,幻方对角线上的数成等差数列,,,,….故.故选:C4.设数列{}n a 的前n 项和为n S ,且11a =,则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是( ) A .290 B .920C .511D .1011【答案】C 【解析】 由得,当2n ≥时,,整理得,所以{}n a 是公差为4的等差数列,又11a =, 所以,从而,所以,数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和.故选C .5.意大利数学家列昂那多·斐波那契以兔子繁殖为例,引入“兔子数列”:,即,此数列在现代物理“准晶体结构”、化学等都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{}n a ,则数列{}n a 的前2019项的和为( ) A .672 B .673C .1346D .2019【答案】C由数列各项除以2的余数, 可得{}n a 为,所以{}n a 是周期为3的周期数列, 一个周期中三项和为1102++=, 因为,所以数列{}n a 的前2019项的和为,故选C.6.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若,,则的值是( )A .1 B.22C .22-D .3-【答案】D 【解析】{}n a Q 是等比数列 63a ∴= {}n b Q 是等差数列673b π∴=本题正确选项:D 7.已知数列{}n a 满足,设数列{}n b 满足:121n n n n b a a ++=,数列{}n b 的前n 项和为nT,若恒成立,则实数λ的取值范围为( )A .1[,)4+∞B .1(,)4+∞C .3[,)8+∞D .3(,)8+∞【解析】 解:数列{}n a 满足,①当2n ≥时,,②①﹣②得:12n a n n=, 故:22n a n =,数列{}n b 满足:,则:,由于恒成立,故:,整理得:244n n λ+>+,因为在*n N ∈上单调递减,故当1n =时,所以38λ>. 故选:D .8.已知函数()y f x =的定义域为R ,当0x <时()1f x >,且对任意的实数,x y R ∈,等式成立,若数列{}n a 满足,且()10a f =,则下列结论成立的是( ) A . B . C .D .【答案】A 【解析】 由,令0x =,1y =-,则0x <Q 时,()1f x > ()11f ∴-> ()01f ∴= 11a ∴=当0x >时,令y x =-,则,即又()1f x -> ∴当0x >时,令21x x >,则21>0-x x,即()f x ∴在R 上单调递减又令1n =,212a =-;令2n =,32a =-;令3n =,41a = ∴数列{}n a 是以3为周期的周期数列,,,,()f x Q 在R 上单调递减,,,本题正确选项:A9.在数列{}n a中,,则2019a的值为______.【答案】1【解析】因为所以,...,,各式相加,可得,,所以,20191a=,故答案为1.10.已知正项等比数列{}n a满足,若存在两项m a,n a,使得,则91m n+的最小值为__________.【答案】2【解析】Q 正项等比数列{}na满足,,整理,得210+2q q -=,又0q >,解得,12q =, Q 存在两项m a ,n a 使得18m n a a a =g ,,整理,得8m n +=,∴,则91m n+的最小值为2. 当且仅当9m n n m=取等号,但此时m ,*n N ∉.又8m n +=, 所以只有当6m =,2n =时,取得最小值是2. 故答案为:211.已知数列{}n a 满足对,都有成立,72a π=,函数()f x =,记()n n y f a =,则数列{}n y 的前13项和为______. 【答案】26 【解析】 解:对,都有成立,可令1m =即有,为常数,可得数列{}n a 为等差数列, 函数,由,可得()f x 的图象关于点,22π⎛⎫⎪⎝⎭对称,Q,∴,∴可得数列{}n y 的前13项和为.故答案为:26.12.已知数列{}n a 的前n 项和为n S ,满足,则n a =_____.【答案】122n +- 【解析】由题意,数列{}n a 满足,则,两式相减可得,即整理得,即,即,当1n =时,1122S a =+,即1122a a =+,解得12a =-, 所以数列{}2n a -表示首项为124a -=-,公比为2的等比数列, 所以,所以122n n a +=-.13.等差数列{}n a 中,410a =且3a ,6a ,10a 成等比数列,数列{}n a 前20项的和20S =____ 【答案】200或330 【解析】设数列{}n a 的公差为d ,则, ,由3610,,a a a 成等比数列,得23106a a a =,即,整理得,解得0d =或1d =,当0d =时,;当1d =时,,于是,故答案为200或330.14.已知正项等比数列{}n a 的前n 项和为n S .若,则631S S +取得最小值时,9S 的值为_______. 【答案】733【解析】 由,得:q≠1,所以,化简得:,即,即,得32q =,化简得631S S +==,当11311a q q a -=-,即113q a -=时,631S S +取得最小值, 所以=733故答案为:73315.设数列{}n a 的前n 项和为n S ,且满足,则5S =____.【答案】3116【解析】 解:,可得1n =时,11a = ,2n ≥时,,又,两式相减可得121n n a -=,即112n n a -⎛⎫= ⎪⎝⎭,上式对1n =也成立,可得数列{}n a 是首项为1,公比为12的等比数列, 可得.故答案为:3116.16.已知数列{}n a 满足,则数列的前n 项和为___________.【答案】2222n n +-+【解析】 由,得,所以数列n a n ⎧⎫⎨⎬⎩⎭是以1141a a ==为首项,2为公比的等比数列,于是,所以12n n a n +=⋅,因为,所以的前n 项和2222n n +=-+. 17.定义:从数列{}n a 中抽取项按其在{}n a 中的次序排列形成一个新数列{}n b ,则称{}n b 为{}n a 的子数列;若{}n b 成等差(或等比),则称{}n b 为{}n a 的等差(或等比)子数列. (1)记数列{}n a 的前n 项和为n S ,已知21n n S =-. ①求数列{}n a 的通项公式;②数列{}n a 是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由. (2)已知数列{}n a 的通项公式为,证明:{}n a 存在等比子数列.【答案】(1)①12n n a -=;②见解析;(2)见证明【解析】解:(1)①因为21n n S =-,所以当1n =时,,当2n ≥时,,所以.综上可知:12n n a -=.②假设从数列{}n a 中抽3项成等差,则,即,化简得:.因为k l m <<,所以0l k ->,0m k ->,且l k -,m k -都是整数, 所以22l k -⨯为偶数,12m k -+为奇数,所以不成立.因此,数列{}n a 不存在三项等差子数列. 若从数列{}n a 中抽项,其前三项必成等差数列,不成立.综上可知,数列{}n a 不存在等差子数列.(2)假设数列{}n a 中存在3项0n a +,0n a k ++,成等比.设0n a b +=,则b Q +∈,故可设qb p=(p 与q 是互质的正整数). 则需满足,即需满足,则需满足.取k q =,则2l k pq =+.此时,.故此时成立.因此数列{}n a 中存在3项0n a +,0n a k ++,成等比,所以数列{}n a 存在等比子数列.18.在等差数列{}n a 中,已知公差2d =,2a 是1a 与4a 的等比中项 (1)求数列{}n a 的通项公式; (2)若数列{}n b 满足,求数列{}n b 的通项公式;(3)令,数列{}n c 的前n 项和为n T .【答案】(1)2n a n =;(2);(3).【解析】(1)因为2a 是1a 与4a 的等比中项,所以,∴数列{}n a 的通项公式为2n a n =. (2)∵①∴②②-①得:,,故。
2010-2018高考真题理科数学分类汇编解析版第16讲 等比数列

专题六 数列第十六讲 等比数列一、选择题1.(2018北京) “十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于f ,则第八个单音的频率为A B C . D .2.(2018浙江)已知1a ,2a ,3a ,4a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则A .13a a <,24a a <B .13a a >,24a a <C .13a a <,24a a >D .13a a >,24a a >3.(2017新课标Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯A .1盏B .3盏C .5盏D .9盏4.(2015新课标Ⅱ)等比数列{}n a 满足13a =,13521a a a ++=,则357a a a ++=A .21B .42C .63D .845.(2014重庆)对任意等比数列{}n a ,下列说法一定正确的是A .139,,a a a 成等比数列B .236,,a a a 成等比数列C .248,,a a a 成等比数列D .269,,a a a 成等比数列6.(2013新课标Ⅱ)等比数列{}n a 的前n 项和为n S ,已知32110S a a =+,59a =,则1a =A .13B .13-C .19D .19- 7.(2012北京) 已知{}n a 为等比数列.下面结论中正确的是A .1322a a a +…B .2221322a a a +…C .若13a a =,则12a a =D .若31a a >,则42a a >8.(2011辽宁)若等比数列{}n a 满足116n n n a a +=,则公比为A .2B .4C .8D .169.(2010广东)已知数列{}n a 为等比数列,n S 是是它的前n 项和,若2312a a a ⋅=,且4a 与27a 的等差中项为54,则5S = A .35 B .33 C .3l D .2910.(2010浙江)设n s 为等比数列{}n a 的前n 项和,2580a a +=则52S S = A .-11 B .-8 C .5 D .11 11.(2010安徽)设{}n a 是任意等比数列,它的前n 项和,前2n 项和与前3n 项和分别为,,X Y Z ,则下列等式中恒成立的是A .2X Z Y +=B .()()Y Y X Z Z X -=-C .2Y XZ =D .()()Y Y X X Z X -=-12.(2010北京)在等比数列{}n a 中,11a =,公比1q ≠.若12345m a a a a a a =,则m =A .9B .10C .11D .1213.(2010辽宁)设n S 为等比数列{}n a 的前n 项和,已知3432S a =-,2332S a =-,则公比q =A .3B .4C .5D .614.(2010天津)已知{}n a 是首项为1的等比数列,n s 是{}n a 的前n 项和,且369s s =,则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为 A .158或5 B .3116或5 C .3116 D .158二、填空题15.(2017新课标Ⅲ)设等比数列{}n a 满足121a a +=-,133a a -=-,则4a = _______.16.(2017江苏)等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知374S =,6634S =,则8a = .17.(2017北京)若等差数列{}n a 和等比数列{}n b 满足111a b ==-,448a b ==, 则22a b =_____. 18.(2016年全国I )设等比数列{}n a 满足1310a a +=,245a a +=,则12n a a a ⋅⋅⋅的最大值为 .19.(2016年浙江)设数列{}n a 的前n 项和为n S .若24S =,121n n a S +=+,*n N ∈,则 1a = ,5S = .20.(2015安徽)已知数列{}n a 是递增的等比数列,14329,8a a a a +==,则数列{}n a 的前n 项和等于 .21.(2014广东)等比数列{}n a 的各项均为正数,且154a a =,则2122232425log +log +log +log +log =a a a a a ________.22.(2014广东)若等比数列{}n a 的各项均为正数,且512911102e a a a a =+,则1220ln ln ln a a a +++= .23.(2014江苏)在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是 .24.(2013广东)设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= .25.(2013北京)若等比数列{}n a 满足24a a +=20,35a a +=40,则公比q = ;前n项和n S = .26.(2013江苏)在正项等比数列{}n a 中,215=a ,376=+a a .则满足 n n a a a a a a a a ......321321>++++的最大正整数n 的值为 .27.(2012江西)等比数列{}n a 的前n 项和为n S ,公比不为1。
2010-2019高考真题分类训练理数专题六 数列 第十八讲 数列的综合应用

专题六 数列 第十八讲 数列的综合应用2019年1.(2019浙江10)设a ,b ∈R ,数列{a n }中a n =a ,a n +1=a n 2+b ,n *∈N ,则 A .当b =12时,a 10>10 B .当b =14时,a 10>10C .当b =-2时,a 10>10D .当b =-4时,a 10>102.(2019浙江20)设等差数列{}n a 的前n 项和为n S ,34a =,43a S =,数列{}n b 满足:对每个12,,,n n n n n n n S b S b S b *++∈+++N 成等比数列.(1)求数列{},{}n n a b 的通项公式; (2)记,n c n *=∈N证明:12+.n c c c n *++<∈N L 3.(2019江苏20)定义首项为1且公比为正数的等比数列为“M -数列”.(1)已知等比数列{a n }*()n ∈N 满足:245324,440a a a a a a =-+=,求证:数列{a n }为“M -数列”;(2)已知数列{b n }*()n ∈N 满足:111221,n n n b S b b +==-,其中S n 为数列{b n }的前n 项和. ①求数列{b n }的通项公式;②设m 为正整数,若存在“M -数列”{c n }*()n ∈N ,对任意正整数k ,当k ≤m 时,都有1k k k c b c +剟成立,求m 的最大值.4.(2019北京理20)已知数列{}n a ,从中选取第 1i 项、第2i 项、…、第m i 项()12m i i i <<⋯<,若12mi i i a a a <<<L ,则称新数列12mi i i a a a ⋅⋅⋅L 为{}n a 的长度为m 的递增子列。
规定:数列{}n a 的任意一项都是{}n a 的长度为1的递增子列。
(Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;(Ⅱ)已知数列{}n a 的长度为P 的递增子列的末项的最小值为o m a ,长度为q 的递增子列的末项的最小值为on a ,若p <q ,求证:o o m n a a <;(Ⅲ)设无穷数列{}n a 的各项均为正整数,且任意两项均不相等,若{}n a 的长度为s 的递增子列末项的最小值为2s -1,且长度为s 末项为2s -1的递增子列恰有12s -个(s =1,2,…),求数列{}n a 的通项公式.2010-2018年一、选择题1.(2017新课标Ⅰ)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16 ,…,其中第一项是02,接下来的两项是02,12,再接下来的三项是02,12,22,依此类推.求满足如下条件的最小整数N :100N >且该数列的前N 项和为2的整数幂.那么该款软件的激活码是A .440B .330C .220D .1102.(2016年全国Ⅲ)定义“规范01数列”{}n a 如下:{}n a 共有2m 项,其中m 项为0,m 项为1,且对任意2k m ≤,12,,,k a a a L 中0的个数不少于1的个数.若m =4,则不同的“规范01数列”共有 (A )18个(B )16个(C )14个(D )12个3.(2015湖北)设12,,,n a a a ∈R L ,3n ≥.若p :12,,,n a a a L 成等比数列;q :222121()n a a a -+++⨯L 22222312231()()n n n a a a a a a a a a -+++=+++L L ,则A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D .p 既不是q 的充分条件,也不是q 的必要条件4.(2014新课标2)等差数列{}n a 的公差为2,若2a ,4a ,8a 成等比数列,则{}n a 的前n项和n S =A .()1n n +B .()1n n -C .()12n n + D .()12n n -5.(2014浙江)设函数21)(x x f =,),(2)(22x x x f -=|2sin |31)(3x x f π=,99i ia =, 0,1,2,,99i =⋅⋅⋅,记10|()()|k k k I f a f a =-+21|()()|k k f a f a -+⋅⋅⋅+ 9998|()()|k k f a f a -,.3,2,1=k 则A .321I I I <<B . 312I I I <<C . 231I I I <<D . 123I I I << 二、填空题6.(2018江苏)已知集合*{|21,}A x x n n ==-∈N ,*{|2,}n B x x n ==∈N .将A B U 的所有元素从小到大依次排列构成一个数列{}n a .记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为 .7.(2015陕西)中位数为1 010的一组数构成等差数列,其末项为2 015,则该数列的首项为 .8.(2014新课标2)数列{}n a 满足111n na a +=-,2a =2,则1a =_________. 9.(2013重庆)已知{}n a 是等差数列,11a =,公差0d ≠,n S 为其前n 项和,若125,,a a a 成等比数列,则8_____S =.10.(2011江苏)设7211a a a ≤≤≤≤Λ,其中7531,,,a a a a 成公比为q 的等比数列,642,,a a a 成公差为1的等差数列,则q 的最小值是________.11.(2011浙江)若数列2(4)()3n n n ⎧⎫+⎨⎬⎩⎭中的最大项是第k 项,则k =_______________. 三、解答题12.(2018江苏)设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列.(1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,(1a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+L 均成立,并求d 的取值范围(用1,,b m q 表示).13.(2017天津)已知{}n a 为等差数列,前n 项和为()n S n *∈N ,{}n b 是首项为2的等比数列,且公比大于0,2312b b +=,3412b a a =-,11411S b =. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)求数列221{}n n a b -的前n 项和()n *∈N .14.(2017浙江)已知数列{}n x 满足:11x =,11ln(1)n n n x x x ++=++()n ∈*N .证明:当n ∈*N 时 (Ⅰ)10n n x x +<<; (Ⅱ)1122n n n n x x x x ++-≤; (Ⅲ)121122n n n x --≤≤.15.(2016年四川高考)已知数列{n a }的首项为1,n S 为数列{n a }的前n 项和,11n n S qS +=+ ,其中q >0,*n N ∈ .(I )若2322,,2a a a + 成等差数列,求n a 的通项公式;(Ⅱ)设双曲线2221ny x a -=的离心率为n e ,且253e =,证明:121433n n n n e e e --++⋅⋅⋅+>.16.(2015湖北)设等差数列{}n a 的公差为d ,前n 项和为n S ,等比数列{}n b 的公比为q .已知11b a =,22b =,q d =,10100S =. (Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)当1d >时,记nn na cb =,求数列{}n c 的前n 项和n T . 17.(2015陕西)设()n f x 是等比数列1,x ,2x ,⋅⋅⋅,n x 的各项和,其中0x >,n ∈N ,2n ≥.(Ⅰ)证明:函数()()2n n F x f x =-在1(,1)2内有且仅有一个零点(记为n x ),且11122n n n x x +=+; (Ⅱ)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为()n g x ,比较()n f x 与()n g x 的大小,并加以证明.18.(2015重庆)在数列{}n a 中,13a =,2110n n n n a a a a λμ++++=()n N +∈.(Ⅰ)若0,2λμ==-,求数列{}n a 的通项公式; (Ⅱ)若0001(,2)k N k k λ+=∈≥,1μ=-,证明:010011223121k a k k ++<<+++.19.(2014山东)已知等差数列}{n a 的公差为2,前n 项和为n S ,且1S ,2S ,4S 成等比数列.(Ⅰ)求数列}{n a 的通项公式; (Ⅱ)令n b =,4)1(11+--n n n a a n求数列}{n b 的前n 项和n T . 20.(2014浙江)已知数列{}n a 和{}n b 满足()()*∈=N n a a a nb n 221Λ.若{}na 为等比数列,且.6,2231b b a +== (Ⅰ)求n a 与n b ; (Ⅱ)设()*∈-=N n b a c nn n 11.记数列{}n c 的前n 项和为n S . (ⅰ)求n S ;(ⅱ)求正整数k ,使得对任意*∈N n ,均有n k S S ≥. 21.(2014湖南)已知数列{n a }满足*111,||,.n n n a a a p n N +=-=∈(Ⅰ)若{n a }是递增数列,且12,3,23a a a 成等差数列,求p 的值; (Ⅱ)若12p =,且{21n a -}是递增数列,{2n a }是递减数列,求数列{n a }的通项公式. 22.(2014四川)设等差数列{}n a 的公差为d ,点(,)n n a b 在函数()2xf x =的图象上(*n N ∈).(Ⅰ)若12a =-,点87(,4)a b 在函数()f x 的图象上,求数列{}n a 的前n 项和n S ; (Ⅱ)若11a =,函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-,求数列{}nna b 的前n 项和n T . 23.(2014江苏)设数列}{n a 的前n 项和为n S .若对任意正整数n ,总存在正整数m ,使得m n a S =,则称}{n a 是“H 数列”. (Ⅰ)若数列}{n a 的前n 项和n n S 2=(∈n N *),证明: }{n a 是“H 数列”;(Ⅱ)设}{n a 是等差数列,其首项11=a ,公差0<d .若}{n a 是“H 数列”,求d 的值;(Ⅲ)证明:对任意的等差数列}{n a ,总存在两个“H 数列”}{n b 和}{n c ,使得n n n c b a +=(∈n N *)成立.24.(2013安徽)设数列{}n a 满足12a =,248a a +=,且对任意*n N ∈,函数1212()()cos -sin n n n n n f x a a a x a x a x ++++=-++⋅⋅,满足'()02f π=(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若122nn n a b a =+(),求数列{}n b 的前n 项和n S . 25.(2013广东)设各项均为正数的数列{}n a 的前n 项和为n S ,满足21441n n S a n +=--,*n N ∈,且2514,,a a a 构成等比数列.(Ⅰ)证明:2a =(Ⅱ)求数列{}n a 的通项公式; (Ⅲ)证明:对一切正整数n ,有1223111112n n a a a a a a ++++<L . 26.(2013湖北)已知n S 是等比数列{}n a 的前n 项和,4S ,2S ,3S 成等差数列,且23418a a a ++=-.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)是否存在正整数n ,使得2013n S ≥?若存在,求出符合条件的所有n 的集合;若不存在,说明理由.27.(2013江苏)设{}n a 是首项为a ,公差为d 的等差数列()0d ≠,n S 是其前n 项和.记2nn nS b n c=+,N n *∈,其中c 为实数.(Ⅰ) 若0c =,且1b ,2b ,4b 成等比数列,证明:()2N nk k S n S k,n *=∈;(Ⅱ) 若{}n b 是等差数列,证明:0c =.28. (2012山东)已知等差数列{}n a 的前5项和为105,且1052a a =.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意*m ∈N ,将数列{}n a 中不大于27m 的项的个数记为m b .求数列{}m b 的前m项和m S .29.(2012湖南)某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d 万元,并将剩余资金全部投入下一年生产.设第n 年年底企业上缴资金后的剩余资金为n a 万元. (Ⅰ)用d 表示12,a a ,并写出1n a +与n a 的关系式;(Ⅱ)若公司希望经过m (m ≥3)年使企业的剩余资金为4000万元,试确定企业每年上缴资金d 的值(用m 表示).30.(2012浙江)已知数列{}n a 的前n 项和为n S ,且n S =22n n +,n ∈N ﹡,数列{}n b 满足24log 3n n a b =+,*n N ∈. (Ⅰ)求,n n a b ;(Ⅱ)求数列{}n n a b ⋅的前n 项和n T .31.(2012山东)在等差数列{}n a 中,84543=++a a a ,973a =(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意的*N m ∈,将数列{}n a 中落入区间()29,9m m 内的项的个数为m b ,求数列{}m b 的前m 项和m S .32.(2012江苏)已知各项均为正数的两个数列{}n a 和{}n b满足:1n a n *+=∈N .(Ⅰ)设11n n nb b n a *+=+∈N ,,求证:数列2n n b a ⎧⎫⎛⎫⎪⎪⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是等差数列;(Ⅱ)设1nn nb b n a *+=∈N ,,且{}n a 是等比数列,求1a 和1b 的值. 33.(2011天津)已知数列{}{}n n a b 与满足11(2)1nn n n n b a b a +++=-+,1*13(1),,22n n b n N a -+-=∈=且.(Ⅰ)求23,a a 的值;(Ⅱ)设*2121,n n n c a a n N +-=-∈,证明{}n c 是等比数列;(Ⅲ)设n S 为{}n a 的前n 项和,证明*21212122121().3n n n n S S S S n n N a a a a --++++≤-∈L 34.(2011天津)已知数列{}n a 与{}n b 满足:1123(1)0,2nn n n n n n b a a b a b ++++-++==,*n ∈N ,且122,4a a ==.(Ⅰ)求345,,a a a 的值;(Ⅱ)设*2121,n n n c a a n N -+=+∈,证明:{}n c 是等比数列;(Ⅲ)设*242,,k k S a a a k N =++⋅⋅⋅+∈证明:4*17()6nk k kS n N a =<∈∑. 35.(2010新课标)设数列{}n a 满足21112,32n n n a a a -+=-=g(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令n n b na =,求数列的前n 项和n S .36.(2010湖南)给出下面的数表序列:124 4 8表1 表2 表3 ∙∙∙1 1 3 1 3 5其中表n (n =1,2,3 L )有n 行,第1行的n 个数是1,3,5,L 2n -1,从第2行起,每行中的每个数都等于它肩上的两数之和.(Ⅰ)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n (n ≥3)(不要求证明);(Ⅱ)每个数列中最后一行都只有一个数,它们构成数列1,4,12L ,记此数列为{}n b 求和:32412231n n n bb b b bb b b b ++++L *()n N ∈ .。
理科数学2010-2019高考真题分类训练专题六 数列 第十六讲 等比数列答案

27.11【解析】由 an+2 + an+1 − 2an = 0 ,可得 anq2 + anq − 2an = 0 ,
由 a1 = 1可知 an 0, q 1,求得公比 q = −2 ,可得 S5 =11.
28.2【解析】
2(an
+
an+2
)
=
5an+1 , 2an
(1 +
q2
)
=
5an q, 2(1 +
关注微信公众号:数学研讨 获取更多数学资源
专题六 数列
第十六讲 等比数列
答案部分
2019 年
1.解析:在等比数列中,由
a42
=
a6
,得
a12q6
=
a1q5>0
.又
a1
=
1 3
,所以解得 q
=
3.
( ) ( ) 则
S5
=
a1
1− q5 1− q
1 1− 35 =3
1−3
= 121 . 3
2.解析 设等比数列{an} 的公比为 q(q 0) ,则由前 4 项和为 15,且 a5 = 3a3 + 4a1 ,有
n
=
a1a2 an
=
( n −1) n
2 2 . Tn
n
,则
2
n− 25
1
( n −1) n
22
,
化简得: 2n
−1
1 n2 −11n+5
2 2 2 ,当 n
1
n2
− 11 n
+
5 时, n
2010年-2018年新课标全国卷历年数列真题(解析版)

一、全国卷数列真题1.(2018年文科一卷)已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=. (1)求123b b b ,,; (2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式. 解:(1)由条件可得a n +1=2(1)n n a n+. 将n =1代入得,a 2=4a 1,而a 1=1,所以,a 2=4. 将n =2代入得,a 3=3a 2,所以,a 3=12. 从而b 1=1,b 2=2,b 3=4.(2){b n }是首项为1,公比为2的等比数列. 由条件可得121n na a n n+=+,即b n +1=2b n ,又b 1=1,所以{b n }是首项为1,公比为2的等比数列. (3)由(2)可得12n n a n-=,所以a n =n ·2n -1.2.(2018年理科二卷)记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.解:(1)设{}n a 的公差为d ,由题意得13315a d +=-. 由17a =-得d =2.所以{}n a 的通项公式为29n a n =-.(2)由(1)得228(4)16n S n n n =-=--. 所以当n =4时,n S 取得最小值,最小值为−16.3.(2018年理科三卷)等比数列{}n a 中,15314a a a ==,. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m . 解:(1)设{}n a 的公比为q ,由题设得1n n a q-=.由已知得424q q =,解得0q =(舍去),2q =-或2q =. 故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m-=-,此方程没有正整数解. 若12n n a -=,则21nn S =-.由63m S =得264m=,解得6m =.综上,6m =.4.(2017年文科一卷)记S n 为等比数列{}n a 的前n 项和,已知S 2=2,S 3=-6. (1)求{}n a 的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列。
九年高考(2010-2018高考)理科数学真题分类训练 专题四 三角函数与解三角形 第十二讲 解三角形(附详解)

专题四 三角函数与解三角形第十二讲 解三角形一、选择题1.(2018全国卷Ⅱ)在△ABC 中,cos 25=C ,1=BC ,5=AC ,则=ABA .BCD .2.(2018全国卷Ⅲ)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,若ABC ∆的面积为2224a b c +-,则C = A .2π B .3π C .4π D .6π 3.(2017山东)在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c .若ABC ∆为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是A .2a b =B .2b a =C .2A B =D .2B A =4.(2016年天津)在ABC ∆中,若AB BC =3,120C ∠= ,则AC =A .1B .2C .3D .45.(2016年全国III )在ABC △中,π4B =,BC 边上的高等于13BC ,则cos A =A B C .- D .-6.(2014新课标Ⅱ)钝角三角形ABC 的面积是12,1AB =,BC =AC =A .5BC .2D .17.(2014重庆)已知ABC ∆的内角A ,B ,C 满足sin 2sin()A A B C +-+=sin()C A B --12+,面积S 满足12S ≤≤,记a ,b ,c 分别为A ,B ,C 所对的边,则下列不等式一定成立的是A .8)(>+c b bcB .()ab a b +>C .126≤≤abcD .1224abc ≤≤8.(2014江西)在ABC ∆中,a ,b ,c 分别为内角A ,B ,C 所对的边长,若22()6c a b =-+,3C π=,则ABC ∆的面积是A .3B .239C .233 D .33 9.(2014四川)如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75,30,此时气球的高是60cm ,则河流的宽度BC 等于A.1)m B.1)mC .1)mD .1)m10.(2013新课标Ⅰ)已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos A + cos 20A =,7a =,6c =,则b =A .10B .9C .8D .511.(2013辽宁)在ABC ∆,内角,,A B C 所对的边长分别为,,a b c .若sin cos a B C +1sin cos 2c B A b =,且a b >,则B ∠= A .6π B .3π C .23π D.56π 12.(2013天津)在△ABC 中,,3,4ABBC ABC π∠===则sin BAC ∠= ABCD 13. (2013陕西)设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=,则△ABC 的形状为A .锐角三角形B .直角三角形C .钝角三角形D .不确定14.(2012广东)在ABC ∆中,若60,45,AB BC ︒︒∠=∠==AC =A .B. CD 15.(2011辽宁)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,2sin cos cos a A B b A +=,则=abA .B .C D16.(2011天津)如图,在△ABC 中,D 是边AC 上的点,且,2AB AD AB ==,2BC BD =,则sin C 的值为CA B C D16.(2010湖南)在ABC ∆中,角,,A B C 所对的边长分别为,,a b c .若120C ∠=,c =,则A .a b >B .a b <C .a b =D .a 与b 的大小关系不能确定二、填空题 18.(2018江苏)在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 .19.(2018浙江)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .若a =2b =,60A =,则sin B =___________,c =___________.20.(2017浙江)已知ABC ∆,4AB AC ==,2BC =. 点D 为AB 延长线上一点,2BD =,连结CD ,则BDC ∆的面积是___________,cos BDC ∠=__________.21.(2017浙江)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度。
(2010-2019)高考数学真题分类汇编专题07数列理(含解析)
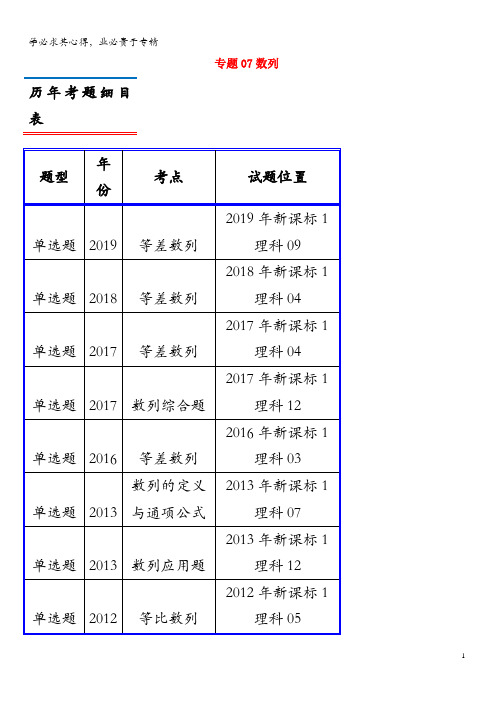
专题07数列历年考题细目表历年高考真题汇编1.【2019年新课标1理科09】记S n为等差数列{a n}的前n项和.已知S4=0,a5=5,则()A.a n=2n﹣5 B.a n=3n﹣10 C.S n=2n2﹣8n D.S n n2﹣2n【解答】解:设等差数列{a n}的公差为d,由S4=0,a5=5,得,∴,∴a n=2n﹣5,,故选:A.2.【2018年新课标1理科04】记S n为等差数列{a n}的前n项和.若3S3=S2+S4,a1=2,则a5=()A.﹣12 B.﹣10 C.10 D.12【解答】解:∵S n为等差数列{a n}的前n项和,3S3=S2+S4,a1=2,∴a1+a1+d+4a1d,把a1=2,代入得d=﹣3∴a5=2+4×(﹣3)=﹣10.故选:B.3.【2017年新课标1理科04】记S n为等差数列{a n}的前n项和.若a4+a5=24,S6=48,则{a n}的公差为()A.1 B.2 C.4 D.8【解答】解:∵S n为等差数列{a n}的前n项和,a4+a5=24,S6=48,∴,解得a1=﹣2,d=4,∴{a n}的公差为4.故选:C.4.【2017年新课标1理科12】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )A.440 B.330 C.220 D.110【解答】解:设该数列为{a n},设b n2n+1﹣1,(n∈N+),则a i,由题意可设数列{a n}的前N项和为S N,数列{b n}的前n项和为T n,则T n=21﹣1+22﹣1+…+2n+1﹣1=2n+1﹣n﹣2,可知当N为时(n∈N+),数列{a n}的前N项和为数列{b n}的前n项和,即为2n+1﹣n﹣2,容易得到N>100时,n≥14,A项,由435,440=435+5,可知S440=T29+b5=230﹣29﹣2+25﹣1=230,故A项符合题意.B项,仿上可知325,可知S330=T25+b5=226﹣25﹣2+25﹣1=226+4,显然不为2的整数幂,故B项不符合题意.C项,仿上可知210,可知S220=T20+b10=221﹣20﹣2+210﹣1=221+210﹣23,显然不为2的整数幂,故C项不符合题意.D项,仿上可知105,可知S110=T14+b5=215﹣14﹣2+25﹣1=215+15,显然不为2的整数幂,故D项不符合题意.故选A.方法二:由题意可知:,,,,根据等比数列前n项和公式,求得每项和分别为:21﹣1,22﹣1,23﹣1,…,2n﹣1,每项含有的项数为:1,2,3,…,n,总共的项数为N=1+2+3+…+n,所有项数的和为S n:21﹣1+22﹣1+23﹣1+…+2n﹣1=(21+22+23+…+2n)﹣n n=2n+1﹣2﹣n,由题意可知:2n+1为2的整数幂.只需将﹣2﹣n消去即可,则①1+2+(﹣2﹣n)=0,解得:n=1,总共有2=3,不满足N >100,②1+2+4+(﹣2﹣n)=0,解得:n=5,总共有3=18,不满足N>100,③1+2+4+8+(﹣2﹣n)=0,解得:n=13,总共有4=95,不满足N>100,④1+2+4+8+16+(﹣2﹣n)=0,解得:n=29,总共有5=440,满足N>100,∴该款软件的激活码440.故选:A.5.【2016年新课标1理科03】已知等差数列{a n}前9项的和为27,a10=8,则a100=( )A.100 B.99 C.98 D.97【解答】解:∵等差数列{a n}前9项的和为27,S99a5.∴9a5=27,a5=3,又∵a10=8,∴d=1,∴a100=a5+95d=98,故选:C.6.【2013年新课标1理科07】设等差数列{a n}的前n项和为S n,若S m﹣1=﹣2,S m=0,S m+1=3,则m=()A.3 B.4 C.5 D.6【解答】解:a m=S m﹣S m﹣1=2,a m+1=S m+1﹣S m=3,所以公差d=a m+1﹣a m=1,S m0,m﹣1>0,m>1,因此m不能为0,得a1=﹣2,所以a m=﹣2+(m﹣1)•1=2,解得m=5,另解:等差数列{a n}的前n项和为S n,即有数列{}成等差数列,则,,成等差数列,可得2•,即有0,解得m=5.又一解:由等差数列的求和公式可得(m﹣1)(a1+a m﹣1)=﹣2,m(a1+a m)=0,(m+1)(a1+a m+1)=3,可得a1=﹣a m,﹣2a m+a m+1+a m+10,解得m=5.故选:C.7.【2013年新课标1理科12】设△A n B n∁n的三边长分别为a n,b n,c n,△A n B n∁n的面积为S n,n=1,2,3…若b1>c1,b1+c1=2a1,a n+1=a n,,,则()A.{S n}为递减数列B.{S n}为递增数列C.{S2n﹣1}为递增数列,{S2n}为递减数列D.{S2n﹣1}为递减数列,{S2n}为递增数列【解答】解:b1=2a1﹣c1且b1>c1,∴2a1﹣c1>c1,∴a1>c1,∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1>0,∴b1>a1>c1,又b1﹣c1<a1,∴2a1﹣c1﹣c1<a1,∴2c1>a1,∴,由题意,a n,∴b n+1+c n+1﹣2a n(b n+c n﹣2a n),∵b1+c1=2a1,∴b1+c1﹣2a1=0,∴b n+c n﹣2a n=0,∴b n+c n=2a n=2a1,∴b n+c n=2a1,由此可知顶点A n在以B n、c n为焦点的椭圆上,又由题意,b n+1﹣c n+1,∴a1﹣b n,∴b n+1﹣a1,∴b n﹣a1,∴,c n=2a1﹣b n,∴[][][]单调递增(可证当n=1时0)故选:B.8.【2012年新课标1理科05】已知{a n}为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=()A.7 B.5 C.﹣5 D.﹣7【解答】解:∵a4+a7=2,由等比数列的性质可得,a5a6=a4a7=﹣8∴a4=4,a7=﹣2或a4=﹣2,a7=4当a4=4,a7=﹣2时,,∴a1=﹣8,a10=1,∴a1+a10=﹣7当a4=﹣2,a7=4时,q3=﹣2,则a10=﹣8,a1=1∴a1+a10=﹣7综上可得,a1+a10=﹣7故选:D.9.【2019年新课标1理科14】记S n为等比数列{a n}的前n项和.若a1,a42=a6,则S5=.【解答】解:在等比数列中,由a42=a6,得q6a12=q5a1>0,即q>0,q=3,则S5,故答案为:10.【2018年新课标1理科14】记S n为数列{a n}的前n项和.若S n =2a n+1,则S6=.【解答】解:S n为数列{a n}的前n项和,S n=2a n+1,①当n=1时,a1=2a1+1,解得a1=﹣1,当n≥2时,S n﹣1=2a n﹣1+1,②,由①﹣②可得a n=2a n﹣2a n﹣1,∴a n=2a n﹣1,∴{a n}是以﹣1为首项,以2为公比的等比数列,∴S663,故答案为:﹣6311.【2016年新课标1理科15】设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为64 .【解答】解:等比数列{a n}满足a1+a3=10,a2+a4=5,可得q(a1+a3)=5,解得q.a1+q2a1=10,解得a1=8.则a1a2…a n=a1n•q1+2+3+…+(n﹣1)=8n•,当n=3或4时,表达式取得最大值:26=64.故答案为:64.12.【2013年新课标1理科14】若数列{a n}的前n项和为S n a n,则数列{a n}的通项公式是a n=.【解答】解:当n=1时,a1=S1,解得a1=1当n≥2时,a n=S n﹣S n﹣1=()﹣(),整理可得,即2,故数列{a n}从第二项开始是以﹣2为首项,﹣2为公比的等比数列,故当n≥2时,a n=(﹣2)n﹣1,经验证当n=1时,上式也适合,故答案为:(﹣2)n﹣113.【2012年新课标1理科16】数列{a n}满足a n+1+(﹣1)n a n=2n ﹣1,则{a n}的前60项和为.【解答】解:∵a n+1+(﹣1)n a n=2n﹣1,故有a2﹣a1=1,a3+a2=3,a4﹣a3=5,a5+a4=7,a6﹣a5=9,a7+a6=11,…a50﹣a49=97.从而可得a3+a1=2,a4+a2=8,a7+a5=2,a8+a6=24,a9+a11=2,a12+a10=40,a13+a11=2,a16+a14=56,…从第一项开始,依次取2个相邻奇数项的和都等于2,从第二项开始,依次取2个相邻偶数项的和构成以8为首项,以16为公差的等差数列.{a n}的前60项和为15×2+(15×8)=183014.【2015年新课标1理科17】S n为数列{a n}的前n项和,已知a n >0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n,求数列{b n}的前n项和.【解答】解:(I)由a n2+2a n=4S n+3,可知a n+12+2a n+1=4S n+1+3两式相减得a n+12﹣a n2+2(a n+1﹣a n)=4a n+1,即2(a n+1+a n)=a n+12﹣a n2=(a n+1+a n)(a n+1﹣a n),∵a n>0,∴a n+1﹣a n=2,∵a12+2a1=4a1+3,∴a1=﹣1(舍)或a1=3,则{a n}是首项为3,公差d=2的等差数列,∴{a n}的通项公式a n=3+2(n﹣1)=2n+1:(Ⅱ)∵a n=2n+1,∴b n(),∴数列{b n}的前n项和T n()().15.【2014年新课标1理科17】已知数列{a n}的前n项和为S n,a1=1,a n≠0,a n a n+1=λS n﹣1,其中λ为常数.(Ⅰ)证明:a n+2﹣a n=λ(Ⅱ)是否存在λ,使得{a n}为等差数列?并说明理由.【解答】(Ⅰ)证明:∵a n a n+1=λS n﹣1,a n+1a n+2=λS n+1﹣1,∴a n+1(a n+2﹣a n)=λa n+1∵a n+1≠0,∴a n+2﹣a n=λ.(Ⅱ)解:假设存在λ,使得{a n}为等差数列,设公差为d.则λ=a n+2﹣a n=(a n+2﹣a n+1)+(a n+1﹣a n)=2d,∴.∴,,∴λS n=1,根据{a n}为等差数列的充要条件是,解得λ=4.此时可得,a n=2n﹣1.因此存在λ=4,使得{a n}为等差数列.也可以先考虑前3项成等差数列,得出λ,再进一步验证即可.16.【2011年新课标1理科17】等比数列{a n}的各项均为正数,且2a1+3a2=1,a32=9a2a6,(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=log3a1+log3a2+…+log3a n,求数列{}的前n项和.【解答】解:(Ⅰ)设数列{a n}的公比为q,由a32=9a2a6得a32=9a42,所以q2.由条件可知各项均为正数,故q.由2a1+3a2=1得2a1+3a1q=1,所以a1.故数列{a n}的通项式为a n.(Ⅱ)b n(1+2+…+n),故2()则2[(1)+()+…+()],所以数列{}的前n项和为.17.【2010年新课标1理科17】设数列满足a1=2,a n+1﹣a n=3•22n﹣1 (1)求数列{a n}的通项公式;(2)令b n=na n,求数列{b n}的前n项和S n.【解答】解:(Ⅰ)由已知,当n≥1时,a n+1=[(a n+1﹣a n)+(a n ﹣a n﹣1)+…+(a2﹣a1)]+a1=3(22n﹣1+22n﹣3+…+2)+2=32=22(n+1)﹣1.而a1=2,所以数列{a n}的通项公式为a n=22n﹣1.(Ⅱ)由b n=na n=n•22n﹣1知S n=1•2+2•23+3•25+…+n•22n﹣1①从而22S n=1•23+2•25+…+n•22n+1②①﹣②得(1﹣22)•S n=2+23+25+…+22n﹣1﹣n•22n+1.即.考题分析与复习建议本专题考查的知识点为:数列的概念与简单表示法,等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.历年考题主要以选择填空或解答题题型出现。
2010-2018年高考文科数学试题分类汇编之专题六 数列

专题六 数列第十五讲 等差数列一、选择题1.(2017浙江)已知等差数列{}n a 的公差为d ,前n 项和为n S ,则“0d >”是“465+2S S S >”的A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D .既不充分也不必要条件 2.(2015新课标2)设n S 是数列}{n a 的前n 项和,若3531=++a a a ,则=5SA .5B .7C .9D .13.(2015新课标1)已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和,若844S S =,则10a = A .172 B .192C .10D .12 4.(2014辽宁)设等差数列{}n a 的公差为d ,若数列1{2}n a a为递减数列,则A .0d <B .0d >C .10a d <D .10a d >5.(2014福建)等差数列{}n a 的前n 项和n S ,若132,12a S ==,则6a =A .8B .10C .12D .14 6.(2014重庆)在等差数列{}n a 中,1352,10a a a =+=,则7a =A .5B .8C .10D .147.(2013新课标1)设等差数列{}n a 的前n 项和为n S ,1m S -=-2,m S =0,1m S +=3,则m =A .3B .4C .5D .68.(2013辽宁)下面是关于公差0d >的等差数列{}n a 的四个命题:{}1:n p a 数列是递增数列;{}2:n p na 数列是递增数列; 3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列;{}4:3n p a nd +数列是递增数列; 其中的真命题为A .12,p pB .34,p pC .23,p pD .14,p p 9.(2012福建)等差数列{}n a 中,1510a a +=,47a =,则数列{}n a 的公差为A .1B .2C .3D .410.(2012辽宁)在等差数列{}n a 中,已知48+=16a a ,则该数列前11项和11=S A .58 B .88 C .143 D .17611.(2011江西)设{}n a 为等差数列,公差2d =-,n s 为其前n 项和,若1011S S =,则1a =A .18B .20C .22D .2412.(2011安徽)若数列}{n a 的通项公式是1210(1)(32),n n a n a a a =--+++=则A .15B .12C .-12D .-1513.(2011天津)已知{}n a 为等差数列,其公差为-2,且7a 是3a 与9a 的等比中项,n S 为{}n a 的前n 项和,*n N ∈,则10S 的值为A .-110B .-90C .90D .11014.(2010安徽)设数列{}n a 的前n 项和2n S n =,则8a 的值为A .15B .16C .49D .64 二、填空题15.(2015陕西)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为_____.16.(2014北京)若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =____时,{}n a 的前n 项和最大.17.(2014江西)在等差数列{}n a 中,71=a ,公差为d ,前n 项和为n S ,当且仅当8=n 时n S 取最大值,则d 的取值范围_________.18.(2013新课标2)等差数列{}n a 的前n 项和为n S ,已知100S =,1525S =,则n nS 的最小值为____.19.(2013广东)在等差数列{}n a 中,已知3810a a +=,则573a a +=_____. 20.(2012北京)已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a = ;n S = .21.(2012江西)设数列{},{}n n a b 都是等差数列,若117a b +=,3321a b +=,则55a b +=____.22.(2012广东)已知递增的等差数列{}n a 满足11a =,2324a a =-,则n a =____.23.(2011广东)等差数列{}n a 前9项的和等于前4项的和.若11a =,40k a a +=,则k =_________.三、解答题24.(2018全国卷Ⅱ)记n S 为等差数列{}n a 的前n 项和,已知17=-a ,315=-S .(1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.25.(2018北京)设{}n a 是等差数列,且123ln 2,5ln 2a a a =+=.(1)求{}n a 的通项公式; (2)求12e e e n a aa+++.26.(2017天津)已知{}n a 为等差数列,前n 项和为*()n S n ∈N ,{}n b 是首项为2的等比数列,且公比大于0,2312b b +=,3412b a a =-,11411S b =. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)求数列2{}n n a b 的前n 项和*()n ∈N . 27.(2017江苏)对于给定的正整数k ,若数列{}n a 满足11112n k n k n n n k n k n a a a a a a ka --+-++-+++⋅⋅⋅+++⋅⋅⋅++=对任意正整数n ()n k >总成立,则称数列{}n a 是“()P k 数列”. (1)证明:等差数列{}n a 是“(3)P 数列”;(2)若数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”,证明:{}n a 是等差数列. 28.(2016年北京)已知{}n a 是等差数列,{}n b 是等差数列,且23b =,39b =,11a b =,144a b =.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设n n n c a b =+,求数列{}n c 的前n 项和.29.(2016年山东)已知数列{}n a 的前n 项和238n S n n =+,{}n b 是等差数列,且1n n n a b b +=+.(I )求数列{}n b 的通项公式;(II )令1(1)(2)n n n nn a c b ++=+.求数列{}n c 的前n 项和n T .30.(2015福建)等差数列{}n a 中,24a =,4715a a +=.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设22n a n b n -=+,求12310b b b b +++⋅⋅⋅+的值.31.(2015山东)已知数列}{n a 是首项为正数的等差数列,数列11{}n n a a +⋅的前n 项和为12+n n. (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设(1)2n an n b a =+⋅,求数列}{n b 的前n 项和n T . 32.(2015北京)已知等差数列{}n a 满足1210a a +=,432a a -=.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设等比数列{}n b 满足23b a =,37b a =.问:6b 与数列{}n a 的第几项相等? 33.(2014新课标1)已知{}n a 是递增的等差数列,2a ,4a 是方程2560x x -+=的根.(Ⅰ)求{}n a 的通项公式; (Ⅱ)求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和. 34.(2014新课标1)已知数列{n a }的前n 项和为n S ,1a =1,0n a ≠,11n n n a a S λ+=-,其中λ为常数.(Ⅰ)证明:2n n a a λ+-=;(Ⅱ)是否存在λ,使得{n a }为等差数列?并说明理由.35.(2014浙江)已知等差数列{}n a 的公差0d >,设{}n a 的前n 项和为n S ,11a =,2336S S ⋅=(Ⅰ)求d 及n S ;(Ⅱ)求,m k (*,m k N ∈)的值,使得1265m m m m k a a a a +++++++=.36.(2013新课标1)已知等差数列{}n a 的前n 项和n S 满足30S =,55S =-.(Ⅰ)求{}n a 的通项公式; (Ⅱ)求数列21211{}n n a a -+的前n 项和.37.(2013福建)已知等差数列{}n a 的公差1d =,前n 项和为n S .(Ⅰ)若131,,a a 成等比数列,求1a ; (Ⅱ)若519S a a >,求1a 的取值范围.38.(2013新课标2)已知等差数列{}n a 的公差不为零,125a =,且11113,,a a a 成等比数列.(Ⅰ)求{}n a 的通项公式; (Ⅱ)求14732+n a a a a -++⋅⋅⋅+.39.(2013山东)设等差数列{}n a 的前n 项和为n S ,且424S S =,221n n a a =+(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设数列{}n b 的前n 项和n T ,且12n n na T λ++=(λ为常数),令2n nc b =(*n ∈N ).求数列{}n c 的前n 项和n R .40.(2011福建)已知等差数列{}n a 中,1a =1,33a =-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n a 的前k 项和35k S =-,求k 的值.41.(2010浙江)设1a ,d 为实数,首项为1a ,公差为d 的等差数列{}n a 的前n 项和为n S ,满足56S S +15=0.(Ⅰ)若5S =5,求6S 及1a ; (Ⅱ)求d 的取值范围.专题六 数列第十五讲 等差数列答案部分1.C 【解析】∵655465()()S S S S a a d ---=-=,当0d >,可得465+2S S S >;当465+2S S S >,可得0d >.所以“0d >”是“465+2S S S >” 充分必要条件, 选C .2.A 【解析】13533331a a a a a ++==⇒=,()15535552a a S a +===.故选A . 3.B 【解析】设等差数列{}n a 的首项为1a ,公差为d ,由题设知1d =,844S S =,所以118284(46)a a +=+,解得112a =,所以10119922a =+=. 4.C 【解析】∵数列1{2}n a a为递减数列,111111[(1)]()n a a a a n d a dn a a d =+-=+-,等式右边为关于n 的一次函数,∴10a d <.5.C 【解析】 设等差数列{}n a 的公差为d ,则3133S a d =+,所以12323d =⨯+,解得2d =,所以612a =.6.B 【解析】由等差数列的性质得1735a a a a +=+,因为12a =,3510a a +=,所以78a =,选B .7.C 【解析】有题意知m S =1()2m m a a +=0,∴1a =-m a =-(m S -1m S -)=-2, 1m a += 1m S +-m S =3,∴公差d =1m a +-m a =1,∴3=1m a +=-2m +,∴m =5,故选C .8.D 【解析】设1(1)n a a n d dn m =+-=+,所以1p 正确;如果312n a n =-则满足已知,但2312n na n n =-并非递增所以2p 错;如果若1n a n =+,则满足已知,但11n a n n=+,是递减数列,所以3p 错;34n a nd dn m +=+,所以是递增数列,4p 正确.9.B 【解析】由题意有153210a a a +==,35a =,又∵47a =,∴432a a -=,∴2d =. 10.B 【解析】4866+=2=16=8a a a a ∴,而()11111611+==11=882a a S a ,故选B. 11.B 【解析】由1011S S =,得1111100a S S =-=,111(111)0(10)(2)20a a d =+-=+-⨯-=.12.A 【解析】10121014710(1)(3102)a a a ++⋅⋅⋅+=-+-++⋅⋅⋅+-⋅⨯-910(14)(710)[(1)(392)(1)(3102)]15=-++-++⋅⋅⋅+-⋅⨯-+-⋅⨯-=.13.D 【解析】因为7a 是3a 与9a 的等比中项,所以2739a a a =,又数列{}n a 的公差为-2,所以2111(12)(4)(16)a a a -=--,解得120a =,故20(1)(2)222n a n n =+-⨯-=-,所以1101010()5(202)1102a a S +==⨯+=.14.A 【解析】887644915a S S =-=-=.15.5【解析】设该数列的首项为1a ,由等差数列的性质知1201510102a +=, 所以1202020155a =-=.16.8【解析】∵数列{}n a 是等差数列,且789830a a a a ++=>,80a >.又710890a a a a +=+<,∴90a <.当n =8时,其前n 项和最大.17.7(1,)8--【解析】由题意可知,当且仅当8=n 时n S 取最大值,可得8900d a a <⎧⎪>⎨⎪<⎩,解得718d -<<-. 18.-49【解析】设{}n a 的首项为1a ,公差d ,由100S =,1525S =,得112903215a d a d +=⎧⎨+=⎩,解得123,3a d =-=,∴()321103n nS n n =-,设()()321103f n n n =-,()220,3f n n n '=- 当2003n <<时()0f n '<,当203n >,()0f n '>,由*n N ∈,当6n =时,()()31661036483f =-⨯=-当7n =时,()()3217107493f n =-⨯=-∴7n =时,n nS 取得最小值49-. 19.20【解析】 依题意12910a d +=,所以()57111334641820a a a d a d a d +=+++=+=. 或:()57383220a a a a +=+=20.1,(1)4n n +【解析】设公差为d ,则1122a d a d +=+,把112a =代入得12d =, ∴21a =,n S =1(1)4n n +21.35【解析】(解法一)因为数列{},{}n n a b 都是等差数列,所以数列{}n n a b +也是等差数列.故由等差中项的性质,得()()()5511332a b a b a b +++=+, 即()557221a b ++=⨯,解得5535a b +=. (解法二)设数列{},{}n n a b 的公差分别为12,d d ,因为331112(2)(2)a b a d b d +=+++1112()2()a b d d =+++1272()21d d =++= 所以127d d +=.所以553312()2()35a b a b d d +=+++=.22.21n a n =-【解析】221321,412(1)4a a a d d ==-⇔+=+-221n d a n ⇔=⇔=-.23.10【解析】设{}n a 的公差为d ,由94S S =及11a =,得9843914122d d ⨯⨯⨯+=⨯+,所以16d =-.又40k a a +=,所以11[1(1)()][1(41)()]066k +-⨯-++-⨯-=,即10k =.24.【解析】(1)设{}n a 的公差为d ,由题意得13315a d +=-.由17a =-得2=d .所以{}n a 的通项公式为29n a n =-.(2)由(1)得228(4)16n S n n n =-=--.所以当4=n 时,n S 取得最小值,最小值为−16. 25.【解析】(1)设等差数列{}n a 的公差为d ,∵235ln 2a a +=, ∴1235ln 2a d +=, 又1ln 2a =,∴ln 2d =. ∴1(1)ln 2n a a n d n =+-=. (2)由(1)知ln 2n a n =, ∵ln 2ln 2ee e =2nna n n ==,∴{e }n a是以2为首项,2为公比的等比数列. ∴212ln 2ln 2ln 2e e e e e e nn a aa+++=+++2=222n +++1=22n +-.∴12e e e n a aa+++1=22n +-.26.【解析】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q .由已知2312b b +=,得21()12b q q +=,而12b =,所以260q q +-=. 又因为0q >,解得2q =.所以,2nn b =.由3412b a a =-,可得138d a -=①.由11411S b =,可得1516a d +=②, 联立①②,解得11,3a d ==,由此可得32n a n =-.所以,{}n a 的通项公式为32n a n =-,{}n b 的通项公式为2nn b =.(Ⅱ)解:设数列2{}n n a b 的前n 项和为n T ,由262n a n =-,有2342102162(62)2n n T n =⨯+⨯+⨯++-⨯,2341242102162(68)2(62)2n n n T n n +=⨯+⨯+⨯++-⨯+-⨯,上述两式相减,得23142626262(62)2n n n T n +-=⨯+⨯+⨯++⨯--⨯1212(12)4(62)2(34)21612n n n n n ++⨯-=---⨯=----.得2(34)216n n T n +=-+.所以,数列2{}n n a b 的前n 项和为2(34)216n n +-+.27.【解析】证明:(1)因为{}n a 是等差数列,设其公差为d ,则1(1)n a a n d =+-,从而,当n 4≥时,n k n k a a a -++=+11(1)(1)n k d a n k d --+++-122(1)2n a n d a =+-=,1,2,3,k =所以n n n n n n n a a a a a a a ---+++++=321123+++6, 因此等差数列{}n a 是“(3)P 数列”.(2)数列{}n a 既是“(2)P 数列”,又是“(3)P 数列”,因此, 当3n ≥时,n n n n n a a a a a --+++++=21124,①当4n ≥时,n n n n n n n a a a a a a a ---++++++++=3211236.② 由①知,n n n a a a ---+=-32141()n n a a ++,③n n n a a a ++++=-23141()n n a a -+,④将③④代入②,得n n n a a a -++=112,其中4n ≥, 所以345,,,a a a 是等差数列,设其公差为d'.在①中,取4n =,则235644a a a a a +++=,所以23a a d'=-, 在①中,取3n =,则124534a a a a a +++=,所以122a a d'=-, 所以数列{}n a 是等差数列.28.【解析】(I )等比数列{}n b 的公比32933b q b ===,所以211b b q==,4327b b q ==. 设等差数列{}n a 的公差为d .因为111a b ==,14427a b ==,所以11327d +=,即2d =. 所以21n a n =-(1n =,2,3,⋅⋅⋅). (II )由(I )知,21n a n =-,13n n b -=.因此1213n n n n c a b n -=+=-+.从而数列{}n c 的前n 项和()11321133n n S n -=++⋅⋅⋅+-+++⋅⋅⋅+()12113213n n n +--=+-2312n n -=+.29.【解析】(Ⅰ)由题意当2≥n 时,561+=-=-n S S a n n n ,当1=n 时,1111==S a ;所以56+=n a n ;设数列的公差为d , 由⎩⎨⎧+=+=322211b b a b b a ,即⎩⎨⎧+=+=d b db 321721111,解之得3,41==d b ,所以13+=n b n .(Ⅱ)由(Ⅰ)知112)1(3)33()66(=-⋅+=++=n nn n n n n c ,又n n c c c c T +⋅⋅⋅+++=321, 即23413[223242(1)2]n n T n +=⨯+⨯+⨯+⋅⋅⋅++,所以]2)1(242322[322543+++⋅⋅⋅+⨯+⨯+⨯=n n n T ,以上两式两边相减得234123[22222(1)2]n n n T n ++-=⨯+++⋅⋅⋅+-+224(21)3[4(1)2]3221n n n n n ++-=+-+=-⋅-.所以223+⋅=n n n T .30.【解析】(Ⅰ)设等差数列{}n a 的公差为d .由已知得()()11143615a d a d a d +=⎧⎪⎨+++=⎪⎩,解得131a d =⎧⎨=⎩.所以()112n a a n d n =+-=+.(Ⅱ)由(Ⅰ)可得2nn b n =+,所以231012310(21)(22)(23)(210)b b b b ++++=+=+=++++…………2310(2222)=+++++......(1+2+3+ (10)102(12)(110)10122-+⨯=+-11(22)55=-+112532101=+=. 31.【解析】(Ⅰ)设数列{}n a 的公差为d ,令1n =,得12113a a =,所以123a a =. 令2n =,得12231125a a a a +=,所以2315a a =. 解得11,2a d ==,所以21n a n =-.(Ⅱ)由(Ⅰ)知24224,n n n b n n -=⋅=⋅所以121424......4,n n T n =⋅+⋅++⋅ 所以23141424......(1)44,n n n T n n +=⋅+⋅++-⋅+⋅ 两式相减,得121344......44n n n T n +-=+++-⋅114(14)13444,1433n n n n n ++--=-⋅=⨯--所以113144(31)44.999n n n n n T ++-+-⋅=⨯+= 32.【解析】(Ⅰ)设等差数列{}n a 的公差为d .因为432a a -=,所以2d =.又因为1210a a +=,所以1210a d +=,故14a =. 所以42(1)22(1,2,)n a n n n =+-=+=.(Ⅱ)设等比数列{}n b 的公比为q .因为238b a ==,3716b a ==,所以2q =,14b =.所以61642128b -=⨯=.由128=22n +得63n =.所以6b 与数列{}n a 的第63项相等.33.【解析】(Ⅰ)方程2560x x -+=的两根为2,3,由题意得242, 3.a a ==设数列{}n a 的公差为d ,则422,a a d -=故1,2d =从而13,2a = 所以{}n a 的通项公式为112n a n =+. (Ⅱ)设2n n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,由(I )知12,22n nn a n ++=则 2313412...,2222n n n n n S +++=++++ 341213412 (22222)n n n n n S ++++=++++ 两式相减得31213112(...)24222n n n n S +++=+++-123112(1).4422n n n -++=+-- 所以1422n n n S ++=-.34.【解析】(Ⅰ)由题设,11211, 1.n n n n n n a a S a a S λλ++++=-=-两式相减得121().n n n a a a a λ+++-= 由于10n a +≠,所以 2.n n a a λ+-=(Ⅱ)由题设,11a =,1211a a S λ=-,可得2 1.a λ=- 由(Ⅰ)知,3 1.a λ=+ 令2132a a a =+,解得 4.λ= 故24n n a a +-=,由此可得{}21n a -是首项为1,公差为4的等差数列,2143n a n -=-; {}2n a 是首项为3,公差为4的等差数列,241n a n =-.所以21n a n =-,12n n a a --=.因此存在4λ=,使得数列{}n a 为等差数列. 35.【解析】(Ⅰ)由题意,36)33)(2(11=++d a d a ,将11=a 代入上式得2=d 或5-=d ,因为0>d ,所以2=d ,从而12-=n a n ,2n S n =(*∈N n ).(Ⅱ)由(Ⅰ)知,)1)(12(1+-+=+⋅⋅⋅++++k k m a a a k n n n , 所以65)1)(12(=+-+k k m ,由*∈N ,k m 知,1)1)(12(>+-+k k m , 所以⎩⎨⎧=+=-+511312k k m ,所以⎩⎨⎧==45k m .36.【解析】(Ⅰ)设{}n a 的公差为d ,则n S =1(1)2n n na d -+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题六 数列第十六讲 等比数列一、选择题1.(2018北京) “十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于f ,则第八个单音的频率为A B C . D .2.(2018浙江)已知1a ,2a ,3a ,4a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则A .13a a <,24a a <B .13a a >,24a a <C .13a a <,24a a >D .13a a >,24a a >3.(2017新课标Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯A .1盏B .3盏C .5盏D .9盏4.(2015新课标Ⅱ)等比数列{}n a 满足13a =,13521a a a ++=,则357a a a ++=A .21B .42C .63D .845.(2014重庆)对任意等比数列{}n a ,下列说法一定正确的是A .139,,a a a 成等比数列B .236,,a a a 成等比数列C .248,,a a a 成等比数列D .269,,a a a 成等比数列6.(2013新课标Ⅱ)等比数列{}n a 的前n 项和为n S ,已知32110S a a =+,59a =,则1a =A .13B .13-C .19D .19- 7.(2012北京) 已知{}n a 为等比数列.下面结论中正确的是A .1322a a a +…B .2221322a a a +…C .若13a a =,则12a a =D .若31a a >,则42a a >8.(2011辽宁)若等比数列{}n a 满足116n n n a a +=,则公比为A .2B .4C .8D .169.(2010广东)已知数列{}n a 为等比数列,n S 是是它的前n 项和,若2312a a a ⋅=,且4a 与27a 的等差中项为54,则5S = A .35 B .33 C .3l D .2910.(2010浙江)设n s 为等比数列{}n a 的前n 项和,2580a a +=则52S S = A .-11 B .-8 C .5 D .11 11.(2010安徽)设{}n a 是任意等比数列,它的前n 项和,前2n 项和与前3n 项和分别为,,X Y Z ,则下列等式中恒成立的是A .2X Z Y +=B .()()Y Y X Z Z X -=-C .2Y XZ =D .()()Y Y X X Z X -=-12.(2010北京)在等比数列{}n a 中,11a =,公比1q ≠.若12345m a a a a a a =,则m =A .9B .10C .11D .1213.(2010辽宁)设n S 为等比数列{}n a 的前n 项和,已知3432S a =-,2332S a =-,则公比q =A .3B .4C .5D .614.(2010天津)已知{}n a 是首项为1的等比数列,n s 是{}n a 的前n 项和,且369s s =,则数列1n a ⎧⎫⎨⎬⎩⎭的前5项和为 A .158或5 B .3116或5 C .3116 D .158二、填空题15.(2017新课标Ⅲ)设等比数列{}n a 满足121a a +=-,133a a -=-,则4a = _______.16.(2017江苏)等比数列{}n a 的各项均为实数,其前n 项的和为n S ,已知374S =,6634S =,则8a = .17.(2017北京)若等差数列{}n a 和等比数列{}n b 满足111a b ==-,448a b ==, 则22a b =_____. 18.(2016年全国I )设等比数列{}n a 满足1310a a +=,245a a +=,则12n a a a ⋅⋅⋅的最大值为 .19.(2016年浙江)设数列{}n a 的前n 项和为n S .若24S =,121n n a S +=+,*n N ∈,则 1a = ,5S = .20.(2015安徽)已知数列{}n a 是递增的等比数列,14329,8a a a a +==,则数列{}n a 的前n 项和等于 .21.(2014广东)等比数列{}n a 的各项均为正数,且154a a =,则2122232425log +log +log +log +log =a a a a a ________.22.(2014广东)若等比数列{}n a 的各项均为正数,且512911102e a a a a =+,则1220ln ln ln a a a +++= .23.(2014江苏)在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是 .24.(2013广东)设数列{}n a 是首项为1,公比为2-的等比数列,则1234||||a a a a +++= .25.(2013北京)若等比数列{}n a 满足24a a +=20,35a a +=40,则公比q = ;前n项和n S = .26.(2013江苏)在正项等比数列{}n a 中,215=a ,376=+a a .则满足 n n a a a a a a a a ......321321>++++的最大正整数n 的值为 .27.(2012江西)等比数列{}n a 的前n 项和为n S ,公比不为1。
若11a =,且对任意的n N +∈都有2120n n n a a a +++-=,则5S =_________________.28.(2012辽宁)已知等比数列}{n a 为递增数列,若01>a ,且125)(2++=+n n n a a a ,则数列{}n a 的公比=q .29.(2012浙江)设公比为(0)q q >的等比数列{}n a 的前n 项和为n S .若2232S a =+,4432S a =+,则q = .30.(2011北京)在等比数列{}n a 中,112a =,44a =-,则公比q =_____ _________; 12...n a a a +++=____________.三、解答题31.(2018全国卷Ⅲ)等比数列{}n a 中,11a =,534a a =.(1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .32.(2017山东)已知{}n x 是各项均为正数的等比数列,且123x x +=,322x x -=.(Ⅰ)求数列{}n x 的通项公式;(Ⅱ)如图,在平面直角坐标系xOy 中,依次连接点11(,1)P x ,22(,2)Px ,…,11(,1)n n P x n +++得到折线1P 2P …1n P +,求由该折线与直线0y =,1x x =,1n x x +=所围成的区域的面积n T .33.(2016年全国III 高考)已知数列{}n a 的前n 项和1n n S a λ=+,其中0λ≠.(Ⅰ)证明{}n a 是等比数列,并求其通项公式; (Ⅱ)若53132S =,求λ. 34.(2014新课标)已知数列{}n a 满足1a =1,131n n a a +=+. (Ⅰ)证明{}12n a +是等比数列,并求{}n a 的通项公式; (Ⅱ)证明:1231112n a a a ++<…+. 35.(2014福建)在等比数列{}n a 中,253,81a a ==. (Ⅰ)求n a ;(Ⅱ)设3log n n b a =,求数列{}n b 的前n 项和n S .36.(2014江西)已知数列{}n a 的前n 项和*∈-=N n n n S n ,232. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)证明:对任意1>n ,都有*∈N m ,使得m n a a a ,,1成等比数列.37.(2013四川) 在等比数列{}n a 中,212a a -=,且22a 为13a 和3a 的等差中项,求数列{}n a 的首项、公比及前n 项和。
38. (2013天津)已知首项为32的等比数列{}n a 的前n 项和为(*)n S n ∈N , 且234,2,4S S S -成等差数列.(Ⅰ) 求数列{}n a 的通项公式;(Ⅱ) 证明13*)61(n n S n S +≤∈N . 39.(2011新课标)已知等比数列{}n a 的各项均为正数,且212326231,9a a a a a +==.(Ⅰ)求数列{}n a 的通项公式.(Ⅱ )设31323log log log n n b a a a =+++ ,求数列1{}nb 的前n 项和.40.(2011江西)已知两个等比数列{},{}n n a b ,满足(),,a a a b a 111=>0-=1,b a b a 2233-=2-=3.(Ⅰ)若a =1,求数列{}n a 的通项公式;(Ⅱ )若数列{}n a 唯一,求a 的值.41.(2011安徽)在数1和100之间插入n 个实数,使得这2n +个数构成递增的等比数列,将这2n +个数的乘积记作n T ,再令,lg n n a T =1n ≥.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设1tan tan ,n n n b a a += 求数列{}n b 的前n 项和n S .专题六 数列第十六讲 等比数列答案部分1.D 【解析】从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于第一个单音的频率为f ,由等比数列的概念可知,这十三个单音的频率构成一个首项为f ,公比为{}n a ,则第八个单音频率为818a f -=⋅=,故选D .2.B 【解析】解法一 因为ln 1x x -≤(0x >),所以1234123ln()a a a a a a a +++=++ 1231a a a ++-≤,所以41a -≤,又11a >,所以等比数列的公比0q <. 若1q -≤,则212341(1)(10a a a a a q q +++=++)≤,而12311a a a a ++>≥,所以123ln()0a a a ++>,与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<, 所以13a a >,24a a <,故选B .解法二 因为1x e x +≥,1234123ln()a a a a a a a +++=++,所以123412312341a a a a e a a a a a a a +++=++++++≥,则41a -≤,又11a >,所以等比数列的公比0q <.若1q -≤,则212341(1)(10a a a a a q q +++=++)≤,而12311a a a a ++>≥,所以123ln()0a a a ++>与1231234ln()0a a a a a a a ++=+++≤矛盾,所以10q -<<,所以2131(1)0a a a q -=->,2241(1)0a a a q q -=-<, 所以13a a >,24a a <,故选B .3.B 【解析】设塔顶共有灯1a 盏,根据题意各层等数构成以1a 为首项,2为公比的等比数列,∴77171(12)(21)38112a S a -==-=-,解得13a =.选B . 4.B 【解析】由于241(1)21a q q ++=,13a =,所以4260q q +-=,所以22q =(23q =-舍去),所以36a =,512a =,724a =,所以35742a a a ++=.5.D 【解析】由等比数列的性质得,23960a a a ⋅=≠,因此269,,a a a 一定成等比数列.6.C 【解析】设等比数列{}n a 的公比为q ,∵32110S a a =+,∴1232110a a a a a ++=+,即319a a =,∴29q =,由59a =,即419a q =,∴119a =. 7.B 【解析】取特殊值可排除A 、C 、D ,由均值不等式可得2221313222a a a a a +⋅=…. 8.B 【解析】由116n n n a a +=,得11216n n n a a +++=,两式相除得1121161616n n n n n n a a a a ++++==, ∴216q =,∵116n n n a a +=,可知公比q 为正数,∴4q =.9.C 【解析】设{n a }的公比为q ,则由等比数列的性质知,231412a a a a a ⋅=⋅=,即42a =.由4a 与27a 的等差中项为54知,475224a a +=⨯, 7415(2)24a a ∴=⨯-14=.∴37418a q a ==,即12q =.3411128a a q a ==⨯=, 116a ∴=,55116(1)231112S -==-. 10.A 【解析】通过2580a a +=,设公比为q ,将该式转化为08322=+q a a ,解得q =-2,所以5522113211114S q S q -+===---. 11.D 【解析】取等比数列1,2,4,令1n =得1,3,7X Y Z ===代入验算,只有选项D 满足.12.C 【解析】2341010123451m a a a a a a q q q q q a q ==⋅⋅⋅==,因此有11m =.13.B 【解析】两式相减得, 3433a a a =-,44334,4a a a q a =∴==.14.C 【解析】显然q ≠1,所以3639(1)1=1211q q q q q q--⇒+⇒=--,所以1{}n a 是首项为1,公比为12的等比数列, 前5项和5511()31211612T -==-. 15.8-【解析】设{}n a 的首项为1a ,公比为q ,所以1121113a a q a a q +=-⎧⎨-=-⎩, 解得112a q =⎧⎨=-⎩ ,则3418a a q ==-. 16.32【解析】设{}n a 的公比为q ,由题意1q ≠,由636331191S q q S q-==+=-,所以2q =,由313(1)714a q S q -==-,得114a =,所以77581122324a a q ==⨯==. 17.1【解析】设{}n a 的公差为d ,{}nb 的公比为q ,由题意3138d q -+=-=,所以3d =,2q =-,所以22131(2)a b -+==--. 18.64【解析】设{}n a 的公比为q ,由1310a a +=,245a a +=得118,2a q ==, 则24a =,32a =,41a =,512a =,所以12123464n a a a a a a a ⋅⋅⋅=…. 19.1 121 【解析】由于1221421a a a a +=⎧⎨=+⎩,解得11a =,由1121n n n n a S S S ++=-=+, 所以1113()22n n S S ++=+,所以1{}2n S +是以32为首项,3为公比的等比数列, 所以113322n n S -+=⨯,所以5121S =. 20.21n -【解析】由题意,14231498a a a a a a +=⎧⎨⋅=⋅=⎩,解得141,8a a ==或148,1a a ==,而数列{}n a 是递增的等比数列,所以141,8a a ==,即3418a q a ==,所以2q =,因而数列{}n a 的前n 项和1(1)1221112n nn n a q S q --===---.21.5【解析】由等比数列的性质可知215243a a a a a ==,于是,由154a a =得32a =,故1234532a a a a a =,则2122232425log +log +log +log +log =a a a a a 2123452log ()log 325a a a a a ==.22.50【解析】因{}n a 是等比数列,∴1201011912a a a a a a ==,由512911102e a a a a =+得 ∴5120a a e =,∴1220ln ln ln a a a +++= 101220120ln()ln()a a a a a ⋅⋅⋅==50. 23.4【解析】 设等比数列}{n a 的公比为q ,0q >.则8642a a a =+,即为424442a q a q a =+,解得22q =(负值舍去),又21a =,所以4624a a q =. 24.15【解析】12341,2,4,8a a a a ==-==-,∴ 1234||||a a a a +++=15.25.12,22n +-【解析】由35a a +=()24q a a +得2q =;()()3241a a a q q +=+=20, 得12a =;∴()12122212n n n S +-==--.26.12【解析】设正项等比数列}{n a 首项为1a ,公比为q ,则:⎪⎩⎪⎨⎧=+=3)1(215141q q a q a ,得:1a =132,q =2,62n n a -=.记521212-=+++=n n n a a a T , 2)1(212nn n n a a a -==∏ .n n T ∏>,则2)1(52212n n n ->-, 化简得:5211212212+->-n n n ,当5211212+->n n n 时,12212113≈+=n . 当n =12时,1212∏>T ,当n =13时,1313∏<T ,故max 12n =. 27.11【解析】由2120n n n a a a +++-=,可得220n n n a q a q a +-=,由11a =可知0,1n a q ≠≠,求得公比2q =-,可得5S =11. 28.2【解析】222112()5,2(1)5,2(1)5,22n n n n n a a a a q a q q q q q +++=∴+=∴+===解得或 因为数列为递增数列,且10,1,2a q q >>∴=所以.29.32【解析】依题意可得,2112111443311111(1)32232201(1)23220321a q a q a q a q a q q a q a q a q a q a q q ⎧-=+⎪⎧-++-=-⎪⎪⇒⎨⎨--++-=⎪⎪⎩=+⎪-⎩两式相减可得423111122330a q a q a q a q --+=,即42322330q q q q --+=,解得1q =±(舍)或0q =或32q =。
